Sparsity prior for electrical impedance tomography with partial data

Abstract

This paper focuses on prior information for improved sparsity reconstruction in electrical impedance tomography with partial data, i.e. Cauchy data measured on subsets of the boundary. Sparsity is enforced using an ${\ell }_1$ norm of the basis coefficients as the penalty term in a Tikhonov functional, and prior information is incorporated by applying a spatially distributed regularization parameter. The resulting optimization problem allows great flexibility with respect to the choice of measurement subsets of the boundary and incorporation of prior knowledge. In fact, the measurement subsets can be chosen completely arbitrary. The problem is solved using a generalized conditional gradient method applying soft thresholding. Numerical examples with noisy simulated data show that the addition of prior information in the proposed algorithm gives vastly improved reconstructions, even for the partial data problem. Moreover, numerical examples show that a reliable reconstruction for the partial data problem can only be found close to the measurement subsets. The method is in addition compared to a total variation approach.

Keywords:

• electrical impedance tomography
• inverse boundary value problem
• ill-posed problem
• partial data
• sparsity

AMS Subject Classifications:

• 65N20
• 65N21

1. Introduction

The inverse problem in electrical impedance tomography (EIT) consists of reconstructing an electrical conductivity distribution in the interior of an object from electrostatic boundary measurements on the surface of the object. EIT is an emerging technology with applications in medical imaging,[1] geophysics [2] and industrial tomography.[3] The underlying mathematical problem is known as the Calderón problem in recognition of Calderón’s seminal paper.[4]

Consider a bounded domain $\mathrm{\Omega }\subset {\mathbb{R}}^n,n\ge 2,$ with smooth boundary $\mathit{\partial }\mathrm{\Omega }$. In order to consider partial boundary measurements, we introduce the subsets ${\mathrm{\Gamma }}^N,{\mathrm{\Gamma }}^D\subseteq \mathit{\partial }\mathrm{\Omega }$ for the Neumann and Dirichlet data, respectively. Let $\mathit{\sigma }\in L^{\infty }(\mathrm{\Omega })$ with $0<c\le \mathit{\sigma }$ a.e. denote the real-valued conductivity distribution in $\mathrm{\Omega }$. Applying a boundary current flux $g$ (Neumann condition) through ${\mathrm{\Gamma }}^N\subseteq \mathit{\partial }\mathrm{\Omega }$ gives rise to the interior electric potential $u$ characterized as the solution to(1.1) $$\begin{array}{c}\hfill \mathrm{\nabla }·(\mathit{\sigma }\mathrm{\nabla }u)=0\text{in}\mathrm{\Omega },\mathit{\sigma }\frac{\mathit{\partial }u}{\mathit{\partial }\mathit{\nu }}=g\text{on}\mathit{\partial }\mathrm{\Omega },{\int }_{{\mathrm{\Gamma }}^D}{u|}_{\mathit{\partial }\mathrm{\Omega }}\mathrm{d}s=0,\end{array}$$(1.1)

where $\mathit{\nu }$ is an outward unit normal to $\mathit{\partial }\mathrm{\Omega }$. The latter condition in (1.1(1.1) $$\begin{array}{c}\hfill \mathrm{\nabla }·(\mathit{\sigma }\mathrm{\nabla }u)=0\text{in}\mathrm{\Omega },\mathit{\sigma }\frac{\mathit{\partial }u}{\mathit{\partial }\mathit{\nu }}=g\text{on}\mathit{\partial }\mathrm{\Omega },{\int }_{{\mathrm{\Gamma }}^D}{u|}_{\mathit{\partial }\mathrm{\Omega }}\mathrm{d}s=0,\end{array}$$(1.1) ) is a grounding of the total electric potential along the subset ${\mathrm{\Gamma }}^D\subseteq \mathit{\partial }\mathrm{\Omega }$. To be precise, we define the spaces$$\begin{array}{cc}\hfill L_{\diamond }^2(\mathit{\partial }\mathrm{\Omega })& \equiv \left\{g\in L^2(\mathit{\partial }\mathrm{\Omega })\mid {\int }_{\mathit{\partial }\mathrm{\Omega }}g\mathrm{d}s=0\right\},\hfill \\ \hfill H_{\diamond }^{-1/2}(\mathit{\partial }\mathrm{\Omega })& \equiv \{g\in H^{-1/2}(\mathit{\partial }\mathrm{\Omega })\mid g,1=0\},\hfill \end{array}$$

consisting of boundary functions with mean zero, and the spaces$$\begin{array}{cc}\hfill H_{{\mathrm{\Gamma }}^D}^1(\mathrm{\Omega })& \equiv \{u\in H^1(\mathrm{\Omega })\mid u{|}_{\mathit{\partial }\mathrm{\Omega }}\in H_{{\mathrm{\Gamma }}^D}^{1/2}(\mathit{\partial }\mathrm{\Omega })\},\hfill \\ \hfill H_{{\mathrm{\Gamma }}^D}^{1/2}(\mathit{\partial }\mathrm{\Omega })& \equiv \left\{f\in H^{1/2}(\mathit{\partial }\mathrm{\Omega })\mid {\int }_{{\mathrm{\Gamma }}^D}f\mathrm{d}s=0\right\},\hfill \end{array}$$

consisting of functions with mean zero on ${\mathrm{\Gamma }}^D$ designed to encompass the partial boundary data. Since $\mathit{\sigma }$ is real valued, it is sufficient to consider the above spaces as real vector spaces, for the use of real-valued Cauchy data in the measurements. Using standard elliptic theory, it follows that (1.1(1.1) $$\begin{array}{c}\hfill \mathrm{\nabla }·(\mathit{\sigma }\mathrm{\nabla }u)=0\text{in}\mathrm{\Omega },\mathit{\sigma }\frac{\mathit{\partial }u}{\mathit{\partial }\mathit{\nu }}=g\text{on}\mathit{\partial }\mathrm{\Omega },{\int }_{{\mathrm{\Gamma }}^D}{u|}_{\mathit{\partial }\mathrm{\Omega }}\mathrm{d}s=0,\end{array}$$(1.1) ) has a unique solution $u\in H_{{\mathrm{\Gamma }}^D}^1(\mathrm{\Omega })$ for any $g\in H_{\diamond }^{-1/2}(\mathit{\partial }\mathrm{\Omega })$. This defines the Neumann-to-Dirichlet map (ND-map) $R_{\mathit{\sigma }}$ as an operator from $H_{\diamond }^{-1/2}(\mathit{\partial }\mathrm{\Omega })$ into $H_{{\mathrm{\Gamma }}^D}^{1/2}(\mathit{\partial }\mathrm{\Omega })$ by ${g\mapsto u|}_{\mathit{\partial }\mathrm{\Omega }}$, and the partial ND-map as $g\mapsto (R_{\mathit{\sigma }}g){|}_{{\mathrm{\Gamma }}^D}$.

The data for the classical Calderón problem is the full operator $R_{\mathit{\sigma }}$ with ${\mathrm{\Gamma }}^D={\mathrm{\Gamma }}^N=\mathit{\partial }\mathrm{\Omega }$. The problem is well studied and there are numerous publications addressing different aspects of its solution; we mention only a few: the uniqueness and reconstruction problem was solved in [5–10] using the so-called complex geometrical optics (CGO) solutions; for a recent survey see [11]. Stability estimates of log type were obtained in [12, 13] and shown to be optimal in [14]. Thus any computational algorithm must rely on regularization. Such computational regularization algorithms following the CGO approach were designed, implemented and analysed in [15–19].

Recently, the partial data Calderón problem have been studied intensively. In 3D uniqueness has been proved under certain conditions on ${\mathrm{\Gamma }}^D$ and ${\mathrm{\Gamma }}^N$,[20–24] and in 2D the general problem with localized data i.e. ${\mathrm{\Gamma }}^D={\mathrm{\Gamma }}^N=\mathrm{\Gamma }$ for some, possibly small, subset $\mathrm{\Gamma }\subseteq \mathit{\partial }\mathrm{\Omega }$ has been shown to possess uniqueness.[25] Also stability estimates of log–log type have been obtained for the partial data problem [26]; this suggests that the partial data problem is even more ill-posed and hence requires more regularization than the full data problem. Recently, a computational algorithm for the partial data problem in 2D was suggested and investigated in [27].

The boundary condition in (1.1(1.1) $$\begin{array}{c}\hfill \mathrm{\nabla }·(\mathit{\sigma }\mathrm{\nabla }u)=0\text{in}\mathrm{\Omega },\mathit{\sigma }\frac{\mathit{\partial }u}{\mathit{\partial }\mathit{\nu }}=g\text{on}\mathit{\partial }\mathrm{\Omega },{\int }_{{\mathrm{\Gamma }}^D}{u|}_{\mathit{\partial }\mathrm{\Omega }}\mathrm{d}s=0,\end{array}$$(1.1) ) is the continuum model which is related to the above-mentioned uniqueness results, and actual electrode measurements can be seen as an approximation to this model, see for instance [28]. Another more realistic model is the Complete Electrode Model (CEM) introduced in [29]. The approach to the reconstruction problem in EIT considered here can be formulated with CEM as well, see [30, 31].

A general approach to linear inverse problems with sparsity regularization was given in [32], and in [33, 34] the method was adapted to non-linear problems using a so-called generalized conditional gradient method. In [30, 35, 36], the method was applied to the reconstruction problem in EIT with full boundary data. A study was made in [31] with 3D sparse reconstruction with current injection and voltage measurements on disjoint sets of electrodes on a planar EIT device, where it was possible to reconstruct a 2D position of an inclusion close to the measured boundary. In this paper, we seek a general approach with regards to the measurement boundaries ${\mathrm{\Gamma }}^D$ and ${\mathrm{\Gamma }}^N$, and the use of prior information to improve the reconstruction further away from the measured boundary. In the numerical examples in Section 4 we consider the case of local data, with Cauchy data on the same part of the boundary. For other approaches to EIT using optimization methods, we refer to [37].

In this paper, we will focus on the partial data problem for which we develop a reconstruction algorithm based on a least squares formulation with sparsity regularization. The results are twofold: first we extend the full data algorithm of [36] to the case of partial data, second we show how prior information about the spatial location of the perturbation in the conductivity can be used in the design of a spatially varying regularization parameter. We will restrict the treatment to 2D, however everything extends to 3D with some minor assumptions on the regularity of the Neumann data.[38]

The data considered here consist of a finite number of Cauchy data, corresponding to the number of applied current patterns, taken on the subsets ${\mathrm{\Gamma }}^D$ and ${\mathrm{\Gamma }}^N$, i.e.(1.2) $$\begin{array}{c}\hfill {\{(f_k,g_k)\mid g_k\in H_{\diamond }^{-1/2}(\mathit{\partial }\mathrm{\Omega }),\ast supp(g_k)\subseteq {\mathrm{\Gamma }}^N,f_k=R_{\mathit{\sigma }}{g}_k{|}_{{\mathrm{\Gamma }}^D}\}}_{k=1}^K,K\in \mathbb{N}.\end{array}$$(1.2)

We assume that the true conductivity is given as $\mathit{\sigma }={\mathit{\sigma }}_0+\mathit{\delta }\mathit{\sigma }$, where ${\mathit{\sigma }}_0$ is a known background conductivity. Define the closed and convex subset(1.3) $$\begin{array}{c}\hfill {\mathcal{A}}_0\equiv \{\mathit{\delta }\mathit{\gamma }\in H_0^1(\mathrm{\Omega })\mid c\le {\mathit{\sigma }}_0+\mathit{\delta }\mathit{\gamma }\le c^{-1}\text{a.e. in}\mathrm{\Omega }\}\end{array}$$(1.3)

for some $c\in (0,1)$, and ${\mathit{\sigma }}_0\in H^1(\mathrm{\Omega })$ where $c\le {\mathit{\sigma }}_0\le c^{-1}$. Similarly define$$\mathcal{A}\equiv \{\mathit{\delta }\mathit{\gamma }+{\mathit{\sigma }}_0\mid \mathit{\delta }\mathit{\gamma }\in {\mathcal{A}}_0\}=\{\mathit{\gamma }\in H^1(\mathrm{\Omega })\mid c\le \mathit{\gamma }\le c^{-1}{\text{a.e. in}\mathrm{\Omega },\mathit{\gamma }|}_{\mathit{\partial }\mathrm{\Omega }}={\mathit{\sigma }}_0{|}_{\mathit{\partial }\mathrm{\Omega }}\}.$$

The inverse problem is then to approximate $\mathit{\delta }\mathit{\sigma }\in {\mathcal{A}}_0$ given the data (1.2(1.2) $$\begin{array}{c}\hfill {\{(f_k,g_k)\mid g_k\in H_{\diamond }^{-1/2}(\mathit{\partial }\mathrm{\Omega }),\ast supp(g_k)\subseteq {\mathrm{\Gamma }}^N,f_k=R_{\mathit{\sigma }}{g}_k{|}_{{\mathrm{\Gamma }}^D}\}}_{k=1}^K,K\in \mathbb{N}.\end{array}$$(1.2) ).

Let ${\{{\mathit{\psi }}_j\}}_{j=1}^{\infty }$ denote a chosen orthonormal basis for $H_0^1(\mathrm{\Omega })$. For sparsity regularization, we approximate $\mathit{\delta }\mathit{\sigma }$ by $\ast {argmin}_{\mathit{\delta }\mathit{\gamma }\in {\mathcal{A}}_0}\mathrm{\Psi }(\mathit{\delta }\mathit{\gamma })$ using the following Tikhonov functional [36](1.4) $$\begin{array}{c}\hfill \mathrm{\Psi }(\mathit{\delta }\mathit{\gamma })\equiv \sum _{k=1}^K{J}_k(\mathit{\delta }\mathit{\gamma })+P(\mathit{\delta }\mathit{\gamma }),\mathit{\delta }\mathit{\gamma }\in {\mathcal{A}}_0,\end{array}$$(1.4)

with$$J_k(\mathit{\delta }\mathit{\gamma })\equiv \frac{1}{2}{R_{{\mathit{\sigma }}_0+\mathit{\delta }\mathit{\gamma }}{g}_k-f_k}_{L^2({\mathrm{\Gamma }}^D)}^2,P(\mathit{\delta }\mathit{\gamma })\equiv \sum _{j=1}^{\infty }{\mathit{\alpha }}_j{c}_j,$$

for $c_j\equiv {\mathit{\delta }\mathit{\gamma },{\mathit{\psi }}_j}_{H^1(\mathrm{\Omega })}$. The regularization parameter ${\mathit{\alpha }}_j>0$ for the sparsity-promoting ${\ell }_1$ penalty term $P$ is distributed such that each basis coefficient can be regularized differently; we will return to this in Section 3. It should be noted how easy and natural the use of partial data is introduced in this way, simply by only minimizing the discrepancy on ${\mathrm{\Gamma }}^D$ on which the Dirichlet data are known and ignoring the rest of the boundary.

This paper is organized as follows: in Section 2 we derive the Fréchet derivative of $J_k$ and reformulate the optimization problem using the generalized conditional gradient method as a sequence of linearized optimization problems. In Section 3, we explain the idea of the spatially dependent regularization parameter designed for the use of prior information. Then, in Section 4 we show the feasibility of the algorithm by several numerical examples, and finally we conclude in Section 5.

2. Sparse reconstruction

In this section, the sparse reconstruction of $\mathit{\delta }\mathit{\sigma }$ based on the optimization problem (1.4(1.4) $$\begin{array}{c}\hfill \mathrm{\Psi }(\mathit{\delta }\mathit{\gamma })\equiv \sum _{k=1}^K{J}_k(\mathit{\delta }\mathit{\gamma })+P(\mathit{\delta }\mathit{\gamma }),\mathit{\delta }\mathit{\gamma }\in {\mathcal{A}}_0,\end{array}$$(1.4) ) is investigated for a bounded domain $\mathrm{\Omega }\subset {\mathbb{R}}^2$ with smooth boundary $\mathit{\partial }\mathrm{\Omega }$. The penalty term emphasizes that $\mathit{\delta }\mathit{\sigma }$ should only be expanded by few basis functions in a given orthonormal basis, and the level of sparsity is controlled by the regularization parameter. Using a distributed regularization parameter, it is possible to further apply prior information about which basis functions that should be included in the expansion of $\mathit{\delta }\mathit{\sigma }$. The partial data problem comes into play in the discrepancy term, in which we only fit the data on part of the boundary. Ultimately, this leads to the algorithm given in Algorithm 1 at the end of this section.

Denote by $F_g(\mathit{\sigma })$ the unique solution to (1.1(1.1) $$\begin{array}{c}\hfill \mathrm{\nabla }·(\mathit{\sigma }\mathrm{\nabla }u)=0\text{in}\mathrm{\Omega },\mathit{\sigma }\frac{\mathit{\partial }u}{\mathit{\partial }\mathit{\nu }}=g\text{on}\mathit{\partial }\mathrm{\Omega },{\int }_{{\mathrm{\Gamma }}^D}{u|}_{\mathit{\partial }\mathrm{\Omega }}\mathrm{d}s=0,\end{array}$$(1.1) ) and let ${\mathcal{F}}_g(\mathit{\sigma })$ be its trace (note that $R_{\mathit{\sigma }}g={\mathcal{F}}_g(\mathit{\sigma })$). Let $\mathit{\gamma }\in \mathcal{A}$, $g\in L^p(\mathit{\partial }\mathrm{\Omega })\cap H_{\diamond }^{-1/2}(\mathit{\partial }\mathrm{\Omega })$ for $p>1$, then following the proofs of Theorem 2.2 and Corollary 2.1 in [35] whilst applying the partial boundary ${\mathrm{\Gamma }}^D$ we have(2.1) $$\begin{array}{c}\hfill \underset{\begin{array}{c}{\mathit{\eta }}_{H^1(\mathrm{\Omega })}\to 0\\ \mathit{\gamma }+\mathit{\eta }\in \mathcal{A}\end{array}}{lim}\frac{{{\mathcal{F}}_g(\mathit{\gamma }+\mathit{\eta })-{\mathcal{F}}_g(\mathit{\gamma })-{({\mathcal{F}}_g)}_{\mathit{\gamma }}^{\prime }\mathit{\eta }}_{H_{{\mathrm{\Gamma }}^D}^{1/2}(\mathit{\partial }\mathrm{\Omega })}}{{\mathit{\eta }}_{H^1(\mathrm{\Omega })}}=0.\end{array}$$(2.1)

Here ${({\mathcal{F}}_g)}_{\mathit{\gamma }}^{\prime }$ is the linear map that maps $\mathit{\eta }$ to ${w|}_{\mathit{\partial }\mathrm{\Omega }}$, where $w$ is the unique solution to(2.2) $$\begin{array}{c}\hfill -\mathrm{\nabla }·(\mathit{\gamma }\mathrm{\nabla }w)=\mathrm{\nabla }·(\mathit{\eta }\mathrm{\nabla }{F}_g(\mathit{\gamma }))\text{in}\mathrm{\Omega },\mathit{\sigma }\frac{\mathit{\partial }w}{\mathit{\partial }\mathit{\nu }}=0\text{on}\mathit{\partial }\mathrm{\Omega },{\int }_{{\mathrm{\Gamma }}^D}{w|}_{\mathit{\partial }\mathrm{\Omega }}\mathrm{d}s=0.\end{array}$$(2.2)

It is noted that ${({\mathcal{F}}_g)}_{\mathit{\gamma }}^{\prime }$ resembles a Fréchet derivative of ${\mathcal{F}}_g$ evaluated at $\mathit{\gamma }$ due to (2.1(2.1) $$\begin{array}{c}\hfill \underset{\begin{array}{c}{\mathit{\eta }}_{H^1(\mathrm{\Omega })}\to 0\\ \mathit{\gamma }+\mathit{\eta }\in \mathcal{A}\end{array}}{lim}\frac{{{\mathcal{F}}_g(\mathit{\gamma }+\mathit{\eta })-{\mathcal{F}}_g(\mathit{\gamma })-{({\mathcal{F}}_g)}_{\mathit{\gamma }}^{\prime }\mathit{\eta }}_{H_{{\mathrm{\Gamma }}^D}^{1/2}(\mathit{\partial }\mathrm{\Omega })}}{{\mathit{\eta }}_{H^1(\mathrm{\Omega })}}=0.\end{array}$$(2.1) ), however $\mathcal{A}$ is not a linear vector space, thus the requirement $\mathit{\gamma },\mathit{\gamma }+\mathit{\eta }\in \mathcal{A}$.

The first step in minimizing $\mathrm{\Psi }$ using a gradient descent-type iterative algorithm is to determine a derivative to the discrepancy terms $J_k$.

Lemma 2.1

Let $\mathit{\gamma }={\mathit{\sigma }}_0+\mathit{\delta }\mathit{\gamma }$ for $\mathit{\delta }\mathit{\gamma }\in {\mathcal{A}}_0$, and ${\mathit{\chi }}_{{\mathrm{\Gamma }}^D}$ be a characteristic function on ${\mathrm{\Gamma }}^D$. Then(2.3) $$\begin{array}{c}\hfill E_k\equiv -\mathrm{\nabla }{F}_{g_k}(\mathit{\gamma })·\mathrm{\nabla }{F}_{{\mathit{\chi }}_{{\mathrm{\Gamma }}^D}(R_{\mathit{\gamma }}{g}_k-f_k)}(\mathit{\gamma })\in L^r(\mathrm{\Omega })\subset H^{-1}(\mathrm{\Omega })\end{array}$$(2.3)

for some $r>1$, and the Fréchet derivative ${(J_k)}_{\mathit{\delta }\mathit{\gamma }}^{\prime }$ of $J_k$ on $H_0^1(\mathrm{\Omega })$ evaluated at $\mathit{\delta }\mathit{\gamma }$ is given by(2.4) $$\begin{array}{c}\hfill {(J_k)}_{\mathit{\delta }\mathit{\gamma }}^{\prime }\mathit{\eta }={\int }_{\mathrm{\Omega }}{E}_k\mathit{\eta }\mathrm{d}x,\mathit{\delta }\mathit{\gamma }+\mathit{\eta }\in {\mathcal{A}}_0.\end{array}$$(2.4)

Proof

For the proof, the index $k$ is suppressed. First it is proved that $E\in L^r(\mathrm{\Omega })$ for some $r>1$, which is shown by estimates on $F_g(\mathit{\gamma })$ and $F_h(\mathit{\gamma })$ where $h\equiv {\mathit{\chi }}_{{\mathrm{\Gamma }}^D}(R_{\mathit{\gamma }}g-f)$. Note that $R_{\mathit{\gamma }}g\in H_{{\mathrm{\Gamma }}^D}^{1/2}(\mathit{\partial }\mathrm{\Omega })$ and $f\in L_{\diamond }^2({\mathrm{\Gamma }}^D)$, i.e. $h\in L_{\diamond }^2(\mathit{\partial }\mathrm{\Omega })\subset L^2(\mathit{\partial }\mathrm{\Omega })\cap H_{\diamond }^{-1/2}(\mathit{\partial }\mathrm{\Omega })$. Now using [35, Theorem 3.1], there exists $Q>2$ such that(2.5) $$\begin{array}{c}\hfill {F_h(\mathit{\gamma })}_{W^{1,q}(\mathrm{\Omega })}\le C{h}_{L^2(\mathit{\partial }\mathrm{\Omega })},\end{array}$$(2.5)

where $q\in (2,Q)\cap [2,4]$. Since $F_g(\mathit{\gamma })\in H_{{\mathrm{\Gamma }}^D}^1(\mathrm{\Omega })$ then $\mathrm{\nabla }{F}_g(\mathit{\gamma })\in L^2(\mathrm{\Omega })$. It has already been established in (2.5(2.5) $$\begin{array}{c}\hfill {F_h(\mathit{\gamma })}_{W^{1,q}(\mathrm{\Omega })}\le C{h}_{L^2(\mathit{\partial }\mathrm{\Omega })},\end{array}$$(2.5) ) that $F_h(\mathit{\gamma })\in W^{1,q}(\mathrm{\Omega })$ for $q\in (2,min\{Q,4\})$, so $\mathrm{\nabla }{F}_h(\mathit{\gamma })\in L^q(\mathrm{\Omega })$. By Hölder’s generalized inequality$$E=-\mathrm{\nabla }{F}_g(\mathit{\gamma })·\mathrm{\nabla }{F}_h(\mathit{\gamma })\in L^r(\mathrm{\Omega }),\frac{1}{r}=\frac{1}{2}+\frac{1}{q},$$

and as $q>2$ then $r>1$. Let $r^{\prime }$ be the conjugate exponent to $r$, then $r^{\prime }\in [1,\infty )$, i.e. the Sobolev imbedding theorem [39] implies that $H^1(\mathrm{\Omega })\hookrightarrow L^{r^{\prime }}(\mathrm{\Omega })$ as $\mathrm{\Omega }\subset {\mathbb{R}}^2$. Thus $E\in {(L^{r^{\prime }}(\mathrm{\Omega }))}^{\prime }\subset {(H^1(\mathrm{\Omega }))}^{\prime }\subset {(H_0^1(\mathrm{\Omega }))}^{\prime }=H^{-1}(\mathrm{\Omega })$.

Now it will be shown that $J_{\mathit{\delta }\mathit{\gamma }}^{\prime }$ can be identified with $E$. $J_{\mathit{\delta }\mathit{\gamma }}^{\prime }\mathit{\eta }$ is by the chain rule (utilizing that $R_{\mathit{\gamma }}g={\mathcal{F}}_g(\mathit{\gamma })$) given as(2.6) $$\begin{array}{c}\hfill J_{\mathit{\delta }\mathit{\gamma }}^{\prime }\mathit{\eta }={\int }_{\mathit{\partial }\mathrm{\Omega }}{\mathit{\chi }}_{{\mathrm{\Gamma }}^D}(R_{\mathit{\gamma }}g-f){({\mathcal{F}}_g)}_{\mathit{\gamma }}^{\prime }\mathit{\eta }\mathrm{d}s,\end{array}$$(2.6)

where ${\mathit{\chi }}_{{\mathrm{\Gamma }}^D}$ is enforcing that the integral is over ${\mathrm{\Gamma }}^D$. The weak formulations of (1.1(1.1) $$\begin{array}{c}\hfill \mathrm{\nabla }·(\mathit{\sigma }\mathrm{\nabla }u)=0\text{in}\mathrm{\Omega },\mathit{\sigma }\frac{\mathit{\partial }u}{\mathit{\partial }\mathit{\nu }}=g\text{on}\mathit{\partial }\mathrm{\Omega },{\int }_{{\mathrm{\Gamma }}^D}{u|}_{\mathit{\partial }\mathrm{\Omega }}\mathrm{d}s=0,\end{array}$$(1.1) ), with Neumann data ${\mathit{\chi }}_{{\mathrm{\Gamma }}^D}(R_{\mathit{\gamma }}g-f)$, and (2.2(2.2) $$\begin{array}{c}\hfill -\mathrm{\nabla }·(\mathit{\gamma }\mathrm{\nabla }w)=\mathrm{\nabla }·(\mathit{\eta }\mathrm{\nabla }{F}_g(\mathit{\gamma }))\text{in}\mathrm{\Omega },\mathit{\sigma }\frac{\mathit{\partial }w}{\mathit{\partial }\mathit{\nu }}=0\text{on}\mathit{\partial }\mathrm{\Omega },{\int }_{{\mathrm{\Gamma }}^D}{w|}_{\mathit{\partial }\mathrm{\Omega }}\mathrm{d}s=0.\end{array}$$(2.2) ) are(2.7) $$\begin{array}{cc}\hfill {\int }_{\mathrm{\Omega }}\mathit{\gamma }\mathrm{\nabla }{F}_{{\mathit{\chi }}_{{\mathrm{\Gamma }}^D}(R_{\mathit{\gamma }}g-f)}(\mathit{\gamma })·\mathrm{\nabla }v\mathrm{d}x& ={\int }_{\mathit{\partial }\mathrm{\Omega }}{\mathit{\chi }}_{{\mathrm{\Gamma }}^D}(R_{\mathit{\gamma }}g-f){v|}_{\mathit{\partial }\mathrm{\Omega }}\mathrm{d}s,\forall v\in H^1(\mathrm{\Omega }),\hfill \end{array}$$(2.7) (2.8) $$\begin{array}{cc}\hfill {\int }_{\mathrm{\Omega }}\mathit{\gamma }\mathrm{\nabla }w·\mathrm{\nabla }v\mathrm{d}x& =-{\int }_{\mathrm{\Omega }}\mathit{\eta }\mathrm{\nabla }{F}_g(\mathit{\gamma })·\mathrm{\nabla }v\mathrm{d}x,\forall v\in H^1(\mathrm{\Omega }).\hfill \end{array}$$(2.8)

Now by letting $v\equiv w$ in (2.7(2.7) $$\begin{array}{cc}\hfill {\int }_{\mathrm{\Omega }}\mathit{\gamma }\mathrm{\nabla }{F}_{{\mathit{\chi }}_{{\mathrm{\Gamma }}^D}(R_{\mathit{\gamma }}g-f)}(\mathit{\gamma })·\mathrm{\nabla }v\mathrm{d}x& ={\int }_{\mathit{\partial }\mathrm{\Omega }}{\mathit{\chi }}_{{\mathrm{\Gamma }}^D}(R_{\mathit{\gamma }}g-f){v|}_{\mathit{\partial }\mathrm{\Omega }}\mathrm{d}s,\forall v\in H^1(\mathrm{\Omega }),\hfill \end{array}$$(2.7) ) and $v\equiv F_{{\mathit{\chi }}_{{\mathrm{\Gamma }}^D}(R_{\mathit{\gamma }}g-f)}(\mathit{\gamma })$ in (2.8(2.8) $$\begin{array}{cc}\hfill {\int }_{\mathrm{\Omega }}\mathit{\gamma }\mathrm{\nabla }w·\mathrm{\nabla }v\mathrm{d}x& =-{\int }_{\mathrm{\Omega }}\mathit{\eta }\mathrm{\nabla }{F}_g(\mathit{\gamma })·\mathrm{\nabla }v\mathrm{d}x,\forall v\in H^1(\mathrm{\Omega }).\hfill \end{array}$$(2.8) ), we obtain using the definition ${w|}_{\mathit{\partial }\mathrm{\Omega }}={({\mathcal{F}}_g)}_{\mathit{\gamma }}^{\prime }\mathit{\eta }$ that$$\begin{array}{cc}\hfill J_{\mathit{\delta }\mathit{\gamma }}^{\prime }\mathit{\eta }& ={\int }_{\mathit{\partial }\mathrm{\Omega }}{\mathit{\chi }}_{{\mathrm{\Gamma }}^D}(R_{\mathit{\gamma }}g-f){({\mathcal{F}}_g)}_{\mathit{\gamma }}^{\prime }\mathit{\eta }\mathrm{d}s={\int }_{\mathrm{\Omega }}\mathit{\gamma }\mathrm{\nabla }{F}_{{\mathit{\chi }}_{{\mathrm{\Gamma }}^D}(R_{\mathit{\gamma }}g-f)}(\mathit{\gamma })·\mathrm{\nabla }w\mathrm{d}x\hfill \\ \hfill & =-{\int }_{\mathrm{\Omega }}\mathit{\eta }\mathrm{\nabla }{F}_g(\mathit{\gamma })·\mathrm{\nabla }{F}_{{\mathit{\chi }}_{{\mathrm{\Gamma }}^D}(R_{\mathit{\gamma }}g-f)}(\mathit{\gamma })\mathrm{d}x={\int }_{\mathrm{\Omega }}E\mathit{\eta }\mathrm{d}x.\hfill \end{array}$$$\square$

Remark 2.2

It should be noted that ${(J_k)}_{\mathit{\delta }\mathit{\gamma }}^{\prime }$ is related to the Fréchet derivative $R_{\mathit{\gamma }}^{\prime }$ of $\mathit{\gamma }\mapsto R_{\mathit{\gamma }}$ evaluated at $\mathit{\gamma }$, by ${(J_k)}_{\mathit{\delta }\mathit{\gamma }}^{\prime }\mathit{\eta }={\int }_{{\mathrm{\Gamma }}^D}(R_{\mathit{\gamma }}{g}_k-f_k)R_{\mathit{\gamma }}^{\prime }[\mathit{\eta }]g_k\mathrm{d}s$.

Define$$J_{\mathit{\delta }\mathit{\gamma }}^{\prime }\equiv \sum _{k=1}^K{(J_k)}_{\mathit{\delta }\mathit{\gamma }}^{\prime }=-\sum _{k=1}^K\mathrm{\nabla }{F}_{g_k}(\mathit{\gamma })·\mathrm{\nabla }{F}_{{\mathit{\chi }}_{{\mathrm{\Gamma }}^D}(R_{\mathit{\gamma }}{g}_k-f_k)}(\mathit{\gamma }).$$

For a gradient-type descent method, we seek to find a direction $\mathit{\eta }$ for which the discrepancy decreases. As $J_{\mathit{\delta }\mathit{\gamma }}^{\prime }\in H^{-1}(\mathrm{\Omega })$ it is known from Riesz’ representation theorem that there exists a unique function in $H_0^1(\mathrm{\Omega })$, denoted by $G(\mathit{\delta }\mathit{\gamma })$, such that(2.9) $$\begin{array}{c}\hfill J_{\mathit{\delta }\mathit{\gamma }}^{\prime }\mathit{\eta }={G(\mathit{\delta }\mathit{\gamma }),\mathit{\eta }}_{H^1(\mathrm{\Omega })},\mathit{\eta }\in H_0^1(\mathrm{\Omega }).\end{array}$$(2.9)

Now $\mathit{\eta }\equiv -G(\mathit{\delta }\mathit{\gamma })$ points in the direction of steepest descend among the viable directions. Furthermore, since ${G(\mathit{\delta }\mathit{\gamma })|}_{\mathit{\partial }\mathrm{\Omega }}=0$ the boundary condition ${\mathit{\delta }\mathit{\sigma }|}_{\mathit{\partial }\mathrm{\Omega }}=0$ will automatically be fulfilled for the approximation. In [40], $G(\mathit{\delta }\mathit{\gamma })$ is called a Sobolev gradient, and it is the unique solution to$$(-\mathrm{\Delta }+1)v=J_{\mathit{\delta }\mathit{\gamma }}^{\prime }\text{in}\mathrm{\Omega },v=0\text{on}\mathit{\partial }\mathrm{\Omega },$$

for which (2.9(2.9) $$\begin{array}{c}\hfill J_{\mathit{\delta }\mathit{\gamma }}^{\prime }\mathit{\eta }={G(\mathit{\delta }\mathit{\gamma }),\mathit{\eta }}_{H^1(\mathrm{\Omega })},\mathit{\eta }\in H_0^1(\mathrm{\Omega }).\end{array}$$(2.9) ) is the weak formulation.

In each iteration step, we need to determine a step size $s_i$ for an algorithm resembling a steepest descent $\mathit{\delta }{\mathit{\gamma }}_{i+1}=\mathit{\delta }{\mathit{\gamma }}_i-s_{i}G(\mathit{\delta }{\mathit{\gamma }}_i)$. Here a Barzilai–Borwein step size rule [36, 41, 42] will be applied, for which we determine $s_i$ such that $\frac{1}{s_i}(\mathit{\delta }{\mathit{\gamma }}_i-\mathit{\delta }{\mathit{\gamma }}_{i-1})=\frac{1}{s_i}({\mathit{\gamma }}_i-{\mathit{\gamma }}_{i-1})\simeq G(\mathit{\delta }{\mathit{\gamma }}_i)-G(\mathit{\delta }{\mathit{\gamma }}_{i-1})$ in the least squares sense(2.10) $$\begin{array}{c}\hfill s_i\equiv \ast {argmin}_s{s^{-1}\left(\mathit{\delta }{\mathit{\gamma }}_i-\mathit{\delta }{\mathit{\gamma }}_{i-1}\right)-\left(G(\mathit{\delta }{\mathit{\gamma }}_i)-G(\mathit{\delta }{\mathit{\gamma }}_{i-1})\right)}_{H^1(\mathrm{\Omega })}^2.\end{array}$$(2.10)

Assuming that ${\mathit{\delta }{\mathit{\gamma }}_i-\mathit{\delta }{\mathit{\gamma }}_{i-1},G(\mathit{\delta }{\mathit{\gamma }}_i)-G(\mathit{\delta }{\mathit{\gamma }}_{i-1})}_{H^1(\mathrm{\Omega })}\ne 0$ yields(2.11) $$\begin{array}{c}\hfill s_i=\frac{{\mathit{\delta }{\mathit{\gamma }}_i-\mathit{\delta }{\mathit{\gamma }}_{i-1}}_{H^1(\mathrm{\Omega })}^2}{{\mathit{\delta }{\mathit{\gamma }}_i-\mathit{\delta }{\mathit{\gamma }}_{i-1},G(\mathit{\delta }{\mathit{\gamma }}_i)-G(\mathit{\delta }{\mathit{\gamma }}_{i-1})}_{H^1(\mathrm{\Omega })}}.\end{array}$$(2.11)

A maximum step size $s_{max}$ is enforced to avoid the situations where ${\mathit{\delta }{\mathit{\gamma }}_i-\mathit{\delta }{\mathit{\gamma }}_{i-1},G(\mathit{\delta }{\mathit{\gamma }}_i)-G(\mathit{\delta }{\mathit{\gamma }}_{i-1})}_{H^1(\mathrm{\Omega })}\simeq 0$.

With inspiration from [42], $s_i$ will be initialized by (2.11(2.11) $$\begin{array}{c}\hfill s_i=\frac{{\mathit{\delta }{\mathit{\gamma }}_i-\mathit{\delta }{\mathit{\gamma }}_{i-1}}_{H^1(\mathrm{\Omega })}^2}{{\mathit{\delta }{\mathit{\gamma }}_i-\mathit{\delta }{\mathit{\gamma }}_{i-1},G(\mathit{\delta }{\mathit{\gamma }}_i)-G(\mathit{\delta }{\mathit{\gamma }}_{i-1})}_{H^1(\mathrm{\Omega })}}.\end{array}$$(2.11) ), after which it is thresholded to lie in $[s_{min},s_{max}]$, for positive constants $s_{min}$ and $s_{max}$. It is noted in [42] that Barzilai–Borwein step rules lead to faster convergence if we do not restrict $\mathrm{\Psi }$ to decrease in every iteration. Allowing an occasional increase in $\mathrm{\Psi }$ can be used to avoid places where the method has to take many small steps to ensure the decrease of $\mathrm{\Psi }$. Therefore, one makes sure that the following so called weak monotonicity is satisfied, which compares $\mathrm{\Psi }(\mathit{\delta }{\mathit{\gamma }}_{i+1})$ with the most recent $M$ steps. Let $\mathit{\tau }\in (0,1)$ and $M\in \mathbb{N}$, then $s_i$ is said to satisfy the weak monotonicity with respect to $M$ and $\mathit{\tau }$ if the following is satisfied [42](2.12) $$\begin{array}{c}\hfill \mathrm{\Psi }(\mathit{\delta }{\mathit{\gamma }}_{i+1})\le \underset{i-M+1\le j\le i}{max}\mathrm{\Psi }(\mathit{\delta }{\mathit{\gamma }}_j)-\frac{\mathit{\tau }}{2s_i}{\mathit{\delta }{\mathit{\gamma }}_{i+1}-\mathit{\delta }{\mathit{\gamma }}_i}_{H^1(\mathrm{\Omega })}^2.\end{array}$$(2.12)

If (2.12(2.12) $$\begin{array}{c}\hfill \mathrm{\Psi }(\mathit{\delta }{\mathit{\gamma }}_{i+1})\le \underset{i-M+1\le j\le i}{max}\mathrm{\Psi }(\mathit{\delta }{\mathit{\gamma }}_j)-\frac{\mathit{\tau }}{2s_i}{\mathit{\delta }{\mathit{\gamma }}_{i+1}-\mathit{\delta }{\mathit{\gamma }}_i}_{H^1(\mathrm{\Omega })}^2.\end{array}$$(2.12) ) is not satisfied, the step size $s_i$ is reduced until this is the case. To solve the non-linear minimization problem for (1.4(1.4) $$\begin{array}{c}\hfill \mathrm{\Psi }(\mathit{\delta }\mathit{\gamma })\equiv \sum _{k=1}^K{J}_k(\mathit{\delta }\mathit{\gamma })+P(\mathit{\delta }\mathit{\gamma }),\mathit{\delta }\mathit{\gamma }\in {\mathcal{A}}_0,\end{array}$$(1.4) ), we iteratively solve the following linearized problem(2.13) $$\begin{array}{cc}\hfill {\mathit{\zeta }}_{i+1}& \equiv \ast {argmin}_{\mathit{\delta }\mathit{\gamma }\in H_0^1(\mathrm{\Omega })}\left[\frac{1}{2}{\mathit{\delta }\mathit{\gamma }-(\mathit{\delta }{\mathit{\gamma }}_i-s_{i}G(\mathit{\delta }{\mathit{\gamma }}_i))}_{H^1(\mathrm{\Omega })}^2+s_i\sum _{j=1}^{\infty }{\mathit{\alpha }}_j{c}_j\right],\hfill \\ \hfill \mathit{\delta }{\mathit{\gamma }}_{i+1}& \equiv {\mathcal{P}}_{{\mathcal{A}}_0}({\mathit{\zeta }}_{i+1}).\hfill \end{array}$$(2.13)

Here ${\{{\mathit{\psi }}_j\}}_{j=1}^{\infty }$ is an orthonormal basis for $H_0^1(\mathrm{\Omega })$ in the $H^1$-metric, and ${\mathcal{P}}_{{\mathcal{A}}_0}$ is the projection of $H_0^1(\mathrm{\Omega })$ onto ${\mathcal{A}}_0$ to ensure that (1.1(1.1) $$\begin{array}{c}\hfill \mathrm{\nabla }·(\mathit{\sigma }\mathrm{\nabla }u)=0\text{in}\mathrm{\Omega },\mathit{\sigma }\frac{\mathit{\partial }u}{\mathit{\partial }\mathit{\nu }}=g\text{on}\mathit{\partial }\mathrm{\Omega },{\int }_{{\mathrm{\Gamma }}^D}{u|}_{\mathit{\partial }\mathrm{\Omega }}\mathrm{d}s=0,\end{array}$$(1.1) ) is solvable (note that $H_0^1(\mathrm{\Omega })$ does not imbed into $L^{\infty }(\mathrm{\Omega })$, i.e. ${\mathit{\zeta }}_{i+1}$ may be unbounded). By use of the map ${\mathcal{S}}_{\mathit{\beta }}:\mathbb{R}\to \mathbb{R}$ defined below, known as the soft shrinkage/thresholding map with threshold $\mathit{\beta }>0$,(2.14) $$\begin{array}{c}\hfill {\mathcal{S}}_{\mathit{\beta }}(x)\equiv \mathrm{s}gn(x)max\{x-\mathit{\beta },0\},x\in \mathbb{R},\end{array}$$(2.14)

the solution to (2.13(2.13) $$\begin{array}{cc}\hfill {\mathit{\zeta }}_{i+1}& \equiv \ast {argmin}_{\mathit{\delta }\mathit{\gamma }\in H_0^1(\mathrm{\Omega })}\left[\frac{1}{2}{\mathit{\delta }\mathit{\gamma }-(\mathit{\delta }{\mathit{\gamma }}_i-s_{i}G(\mathit{\delta }{\mathit{\gamma }}_i))}_{H^1(\mathrm{\Omega })}^2+s_i\sum _{j=1}^{\infty }{\mathit{\alpha }}_j{c}_j\right],\hfill \\ \hfill \mathit{\delta }{\mathit{\gamma }}_{i+1}& \equiv {\mathcal{P}}_{{\mathcal{A}}_0}({\mathit{\zeta }}_{i+1}).\hfill \end{array}$$(2.13) ) is easy to find directly (see also [32, Section 1.5]):(2.15) $$\begin{array}{c}\hfill {\mathit{\zeta }}_{i+1}=\sum _{j=1}^{\infty }{\mathcal{S}}_{s_i{\mathit{\alpha }}_j}(d_j){\mathit{\psi }}_j,\end{array}$$(2.15)

where $d_j\equiv {\mathit{\delta }{\mathit{\gamma }}_i-s_{i}G(\mathit{\delta }{\mathit{\gamma }}_i),{\mathit{\psi }}_j}_{H^1(\mathrm{\Omega })}$ are the basis coefficients for $\mathit{\delta }{\mathit{\gamma }}_i-s_{i}G(\mathit{\delta }{\mathit{\gamma }}_i)$.

Remark 2.3

The soft threshold in (2.15(2.15) $$\begin{array}{c}\hfill {\mathit{\zeta }}_{i+1}=\sum _{j=1}^{\infty }{\mathcal{S}}_{s_i{\mathit{\alpha }}_j}(d_j){\mathit{\psi }}_j,\end{array}$$(2.15) ) assumes that the coefficients ${\{d_j\}}_{j=1}^{\infty }$ are real valued, as in this case with real-valued conductivity $\mathit{\sigma }$ and Cauchy-data. For complex-valued admittivity $\mathit{\sigma }$, appropriate use of complex conjugation is required for the derivative in Lemma 2.1, and a minimizer for (2.13(2.13) $$\begin{array}{cc}\hfill {\mathit{\zeta }}_{i+1}& \equiv \ast {argmin}_{\mathit{\delta }\mathit{\gamma }\in H_0^1(\mathrm{\Omega })}\left[\frac{1}{2}{\mathit{\delta }\mathit{\gamma }-(\mathit{\delta }{\mathit{\gamma }}_i-s_{i}G(\mathit{\delta }{\mathit{\gamma }}_i))}_{H^1(\mathrm{\Omega })}^2+s_i\sum _{j=1}^{\infty }{\mathit{\alpha }}_j{c}_j\right],\hfill \\ \hfill \mathit{\delta }{\mathit{\gamma }}_{i+1}& \equiv {\mathcal{P}}_{{\mathcal{A}}_0}({\mathit{\zeta }}_{i+1}).\hfill \end{array}$$(2.13) ) can be found in [42].

The projection ${\mathcal{P}}_{{\mathcal{A}}_0}:H_0^1(\mathrm{\Omega })\to {\mathcal{A}}_0$ is defined as(2.16) $$\begin{array}{c}\hfill {\mathcal{P}}_{{\mathcal{A}}_0}(v)\equiv T_c({\mathit{\sigma }}_0+v)-{\mathit{\sigma }}_0,v\in H_0^1(\mathrm{\Omega }),\end{array}$$(2.16)

where $T_c$ is the following truncation that depends on the constant $c\in (0,1)$ in (1.3(1.3) $$\begin{array}{c}\hfill {\mathcal{A}}_0\equiv \{\mathit{\delta }\mathit{\gamma }\in H_0^1(\mathrm{\Omega })\mid c\le {\mathit{\sigma }}_0+\mathit{\delta }\mathit{\gamma }\le c^{-1}\text{a.e. in}\mathrm{\Omega }\}\end{array}$$(1.3) )$$\begin{array}{c}\hfill T_c(v)\equiv \left\{\begin{array}{cc}c\hfill & \text{where}v<c\text{a.e.},\hfill \\ c^{-1}\hfill & \text{where}v>c^{-1}\text{a.e.},\hfill \\ v\hfill & \text{else.}\hfill \end{array}\right.\end{array}$$

Since ${\mathit{\sigma }}_0\in H^1(\mathrm{\Omega })$ and $c\le {\mathit{\sigma }}_0\le c^{-1}$, it follows directly from [43, Lemma 1.2] that $T_c$ and ${\mathcal{P}}_{{\mathcal{A}}_0}$ are well defined, and it is easy to see that ${\mathcal{P}}_{{\mathcal{A}}_0}$ is a projection.

Remark 2.4

In the numerical examples in Section 4, the value of $c$ is chosen small enough that the truncation in ${\mathcal{P}}_{{\mathcal{A}}_0}$ does not occur during the iterations. If tight bounds on $\mathit{\sigma }$ are known a priori, the truncation may lead to improved rate of convergence and gives reconstructions in the correct dynamic range.

It should also be noted that $0\in {\mathcal{A}}_0$ since $c\le {\mathit{\sigma }}_0\le c^{-1}$, thus we may choose $\mathit{\delta }{\mathit{\gamma }}_0\equiv 0$ as the initial guess in the algorithm. The algorithm is summarized in Algorithm 1. In this paper, the stopping criterion is when the step size $s_i$ gets below a threshold $s_{}\text{stop}$.

Remark 2.5

Note that ${\sum }_j{\mathit{\delta }{\mathit{\gamma }}_i-s_{i}G(\mathit{\delta }{\mathit{\gamma }}_i),{\mathit{\psi }}_j}_{H^1(\mathrm{\Omega })}{\mathit{\psi }}_j$ corresponds to only having the discrepancy term in (2.13(2.13) $$\begin{array}{cc}\hfill {\mathit{\zeta }}_{i+1}& \equiv \ast {argmin}_{\mathit{\delta }\mathit{\gamma }\in H_0^1(\mathrm{\Omega })}\left[\frac{1}{2}{\mathit{\delta }\mathit{\gamma }-(\mathit{\delta }{\mathit{\gamma }}_i-s_{i}G(\mathit{\delta }{\mathit{\gamma }}_i))}_{H^1(\mathrm{\Omega })}^2+s_i\sum _{j=1}^{\infty }{\mathit{\alpha }}_j{c}_j\right],\hfill \\ \hfill \mathit{\delta }{\mathit{\gamma }}_{i+1}& \equiv {\mathcal{P}}_{{\mathcal{A}}_0}({\mathit{\zeta }}_{i+1}).\hfill \end{array}$$(2.13) ), while the penalty term $s_i{\sum }_{j=1}^{\infty }{\mathit{\alpha }}_j{\mathit{\delta }\mathit{\gamma },{\mathit{\psi }}_j}_{H^1(\mathrm{\Omega })}$ leads to the soft thresholding in (2.15(2.15) $$\begin{array}{c}\hfill {\mathit{\zeta }}_{i+1}=\sum _{j=1}^{\infty }{\mathcal{S}}_{s_i{\mathit{\alpha }}_j}(d_j){\mathit{\psi }}_j,\end{array}$$(2.15) ).

Remark 2.6

The functional $\mathrm{\Psi }$ in (1.4(1.4) $$\begin{array}{c}\hfill \mathrm{\Psi }(\mathit{\delta }\mathit{\gamma })\equiv \sum _{k=1}^K{J}_k(\mathit{\delta }\mathit{\gamma })+P(\mathit{\delta }\mathit{\gamma }),\mathit{\delta }\mathit{\gamma }\in {\mathcal{A}}_0,\end{array}$$(1.4) ) is non-convex. Thus, the best we can hope is to find a local minimum. The quality of the reconstruction depends on the initial guess, and as we expect the reconstruction to be sparse, then $\mathit{\delta }{\mathit{\gamma }}_0\equiv 0$ is a reasonable initial guess.

Remark 2.7

The main computational cost lies in computing $J_{\mathit{\delta }{\mathit{\gamma }}_i}^{\prime }$, which involves solving $2K$ well-posed PDE’s (note that $F_{g_k}({\mathit{\gamma }}_i)$ can be reused from the evaluation of $\mathrm{\Psi }$), where $K$ is the number of current patterns used in the measurements. It should be noted that each of the $2K$ problems consists of solving the same problem, but with different boundary conditions, which leads to only having to assemble and factorize the finite element method (FEM) matrix once per iteration.

3. Prior information

Prior information is typically introduced in the penalty term $P$ for Tikhonov-like functionals, and here the regularization parameter determines how much this prior information is enforced. In the case of sparsity regularization, this implies knowledge of how sparse we expect the solution is in general. Instead of applying the same prior information for each basis function, a distributed parameter is applied. Let$${\mathit{\alpha }}_j\equiv \mathit{\alpha }{\mathit{\mu }}_j,$$

where $\mathit{\alpha }$ is the usual regularization parameter, corresponding to the case where no prior information is considered about specific basis functions. The ${\mathit{\mu }}_j\in (0,1]$ will be used to weight the penalty depending on whether a specific basis function should be included in the expansion of $\mathit{\delta }\mathit{\sigma }$. The ${\mathit{\mu }}_j$ are chosen as$${\mathit{\mu }}_j=\left\{\begin{array}{cc}1,\hfill & \text{no prior on}{c}_j,\hfill \\ \sim 0,\hfill & \text{prior that}{c}_j\ne 0,\hfill \end{array}\right.$$

i.e. if we know that a coefficient in the expansion of $\mathit{\delta }\mathit{\sigma }$ should be non-zero, we can choose to penalize that coefficient less. Using a basis with localized support, the sparsity assumption translates to an assumption on the support of the inclusion.

3.1. Applying the FEM basis

In order to improve the sparsity solution for finding small inclusions, it seems appropriate to include prior information about the support of the inclusions. There are different methods available for obtaining such information assuming piecewise constant conductivity [44, 45] or real-analytic conductivity.[46] An example of the reconstruction of $\ast supp\mathit{\delta }\mathit{\sigma }$ is shown in Figure 1, where it is observed that numerically it is possible to reconstruct a reasonable convex approximation to the support. Thus, it is possible to acquire estimates of $\ast supp\mathit{\delta }\mathit{\sigma }$for free, in the sense that it is gained directly from the data without further assumptions on the location.

Figure 1. (a) Phantom with kite-shaped piecewise constant inclusion $\mathit{\delta }\mathit{\sigma }$. (b) Reconstruction of $\ast supp\mathit{\delta }\mathit{\sigma }$ using monotonicity relations from the approach in [45] by use of simulated noiseless data.

Another approach is to consider other reconstruction methods such as total variation (TV) regularization that tends to give good approximations to the support, but has issues with reconstructing the contrast if the amplitude of $\mathit{\delta }\mathit{\sigma }$ is large as seen in Section 4.3. The idea is to be able to apply such information in the sparsity algorithm in order to get good contrast in the reconstruction while maintaining the correct support, even for the partial data problem.

Suppose that as a basis we consider a FEM basis ${\{{\mathit{\psi }}_j\}}_{j=1}^N$ for the subspace $V_h\subseteq H_0^1(\mathrm{\Omega })$ of piecewise affine elements. This basis comprises basis functions that are piecewise affine with degrees of freedom at the mesh nodes, i.e. ${\mathit{\psi }}_j(x_k)={\mathit{\delta }}_{j,k}$ at mesh node $x_k$ in the applied mesh. Let $\mathit{\delta }\mathit{\sigma }\in V_h$, then $\mathit{\delta }\mathit{\sigma }(x)={\sum }_j\mathit{\delta }\mathit{\sigma }(x_j){\mathit{\psi }}_j(x)$, i.e. for each node there is a basis function for which the coefficient contains local information about the expanded function; this is convenient when applying prior information about the support of an inclusion. Note that the FEM basis functions are not mutually orthogonal, since basis functions corresponding to neighbouring nodes are non-negative and have overlapping support. However, for any non-neighbouring pair of nodes the corresponding basis functions are orthogonal.

When applying the FEM basis for mesh nodes ${\{x_j\}}_{j=1}^N$, the corresponding functional is$$\mathrm{\Psi }(\mathit{\delta }\mathit{\gamma })=\frac{1}{2}\sum _{k=1}^K{R_{{\mathit{\sigma }}_0+\mathit{\delta }\mathit{\gamma }}{g}_k-f_k}_{L^2({\mathrm{\Gamma }}^D)}^2+\sum _{j=1}^N{\mathit{\alpha }}_j\mathit{\delta }\mathit{\gamma }(x_j).$$

It is evident that the penalty corresponds to determining inclusions with small support, and prior information on the sparsity corresponds to prior information on the support of $\mathit{\delta }\mathit{\sigma }$. We cannot directly utilize (2.15(2.15) $$\begin{array}{c}\hfill {\mathit{\zeta }}_{i+1}=\sum _{j=1}^{\infty }{\mathcal{S}}_{s_i{\mathit{\alpha }}_j}(d_j){\mathit{\psi }}_j,\end{array}$$(2.15) ) due to the FEM basis not being an orthonormal basis for $H_0^1(\mathrm{\Omega })$, and instead we suggest the following iteration step:(3.1) $$\begin{array}{cc}\hfill {\mathit{\zeta }}_{i+1}(x_j)& ={\mathcal{S}}_{s_i{\mathit{\alpha }}_j/{{\mathit{\psi }}_j}_{L^1(\mathrm{\Omega })}}(\mathit{\delta }{\mathit{\gamma }}_i(x_j)-s_{i}G(\mathit{\delta }{\mathit{\gamma }}_i)(x_j)),j=1,2,\cdots ,N,\hfill \\ \hfill \mathit{\delta }{\mathit{\gamma }}_{i+1}& ={\mathcal{P}}_{{\mathcal{A}}_0}({\mathit{\zeta }}_{i+1}).\hfill \end{array}$$(3.1)

Note that the regularization parameter will depend quite heavily on the discretization of the mesh, i.e. for the same domain a good regularization parameter $\mathit{\alpha }$ will be much larger on a coarse mesh than on a fine mesh. This is quite inconvenient, and instead we can weight the regularization parameter according to the mesh cells, by having ${\mathit{\alpha }}_j\equiv \mathit{\alpha }{\mathit{\beta }}_j{\mathit{\mu }}_j$. This leads to a discretization of a weighted $L^1$-norm penalty term:$$\mathit{\alpha }{\int }_{\mathrm{\Omega }}{f}_{\mathit{\mu }}\mathit{\delta }\mathit{\gamma }\mathrm{d}x\simeq \mathit{\alpha }\sum _{j=1}^N{\mathit{\beta }}_j{\mathit{\mu }}_j\mathit{\delta }\mathit{\gamma }(x_j),$$

where $f_{\mathit{\mu }}:\mathrm{\Omega }\to (0,1]$ is continuous and $f_{\mathit{\mu }}(x_j)={\mathit{\mu }}_j$. For a triangulated mesh, the weights ${\mathit{\beta }}_j$ consists of the node area computed in 2D as 1/3 of the area of $\ast supp{\mathit{\psi }}_j$. This corresponds to splitting each cell’s area evenly amongst the nodes, and it will not lead to instability on a regular mesh. This will make the choice of $\mathit{\alpha }$ almost independent of the mesh, and is used in the numerical examples in the following section.

Remark 3.1

The corresponding algorithm with the FEM basis is the same as Algorithm 1, except that the update is applied via (3.1(3.1) $$\begin{array}{cc}\hfill {\mathit{\zeta }}_{i+1}(x_j)& ={\mathcal{S}}_{s_i{\mathit{\alpha }}_j/{{\mathit{\psi }}_j}_{L^1(\mathrm{\Omega })}}(\mathit{\delta }{\mathit{\gamma }}_i(x_j)-s_{i}G(\mathit{\delta }{\mathit{\gamma }}_i)(x_j)),j=1,2,\cdots ,N,\hfill \\ \hfill \mathit{\delta }{\mathit{\gamma }}_{i+1}& ={\mathcal{P}}_{{\mathcal{A}}_0}({\mathit{\zeta }}_{i+1}).\hfill \end{array}$$(3.1) ) instead of (2.13(2.13) $$\begin{array}{cc}\hfill {\mathit{\zeta }}_{i+1}& \equiv \ast {argmin}_{\mathit{\delta }\mathit{\gamma }\in H_0^1(\mathrm{\Omega })}\left[\frac{1}{2}{\mathit{\delta }\mathit{\gamma }-(\mathit{\delta }{\mathit{\gamma }}_i-s_{i}G(\mathit{\delta }{\mathit{\gamma }}_i))}_{H^1(\mathrm{\Omega })}^2+s_i\sum _{j=1}^{\infty }{\mathit{\alpha }}_j{c}_j\right],\hfill \\ \hfill \mathit{\delta }{\mathit{\gamma }}_{i+1}& \equiv {\mathcal{P}}_{{\mathcal{A}}_0}({\mathit{\zeta }}_{i+1}).\hfill \end{array}$$(2.13) ).

4. Numerical examples

In this section we illustrate, through several examples, the numerical algorithm implemented using the finite element library FEniCS.[47] We consider the full data case ${\mathrm{\Gamma }}^D={\mathrm{\Gamma }}^N=\mathit{\partial }\mathrm{\Omega }$ first without prior information and then with prior information, and afterwards we do the same for the partial data case. Finally, a brief comparison is made with another sparsity promoting method based on TV.

For the following examples $\mathrm{\Omega }$ is the unit disk in ${\mathbb{R}}^2$ (however, the algorithm can be applied to any bounded domain with smooth boundary). The regularization parameter $\mathit{\alpha }$ is chosen manually by trial and error. The other parameters are ${\mathit{\sigma }}_0\equiv 1$, $M=5$, $\mathit{\tau }={10}^{-5}$, $s_{min}=1$, $s_{max}=1000$, and the stopping criteria are when the step size is below $s_{\text{stop}}={10}^{-3}$. We take $K=10$ with the applied Neumann data of the form $g_n^c(\mathit{\theta })\equiv cos(n\mathit{\theta })$ and $g_n^s(\mathit{\theta })\equiv sin(n\mathit{\theta })$ for $n=1,\cdots ,5$ and $\mathit{\theta }$ being the angular variable. Such trigonometric current patterns are realistic approximations to electrode measurements, see for instance [28]. For the partial data, an interval $\mathrm{\Gamma }={\mathrm{\Gamma }}^N={\mathrm{\Gamma }}^D=\{\mathit{\theta }\in ({\mathit{\theta }}_1,{\mathit{\theta }}_2)\}$ is considered, and $g_n^c$ and $g_n^s$ are scaled and translated such that they have $n$ periods in the interval.

When applying prior information, the coefficients ${\mathit{\mu }}_j$ are chosen as ${10}^{-2}$ where the support of $\mathit{\delta }\mathit{\sigma }$ is assumed, and $1$ elsewhere. It should be noted that in order to get fast transitions for sharp edges when prior information is applied, a local mesh refinement is used during the iterations to refine the mesh where $\mathrm{\nabla }\mathit{\delta }{\mathit{\gamma }}_i$ is large.

For the simulated Dirichlet data, the forward problem is computed on a very fine mesh, and afterwards interpolated onto a different much coarser mesh (with roughly 2800 triangle elements) in order to avoid inverse crimes. White Gaussian noise has been added to the Dirichlet data ${\{f_k\}}_{k=1}^K$ on the discrete nodes on the boundary of the mesh. The standard deviation of the noise is chosen as $\mathit{ϵ}{max}_k{max}_{x_j\in {\mathrm{\Gamma }}^D}{f}_k(x_j)$ as in [36], where the noise level is fixed as $\mathit{ϵ}={10}^{-2}$ (corresponding to 1% noise) unless otherwise stated.

Figure 2. Numerical phantoms. (a) Circular piecewise constant inclusion. (b) Kite-shaped piecewise constant inclusion. (c) Multiple $C^2$ inclusions.

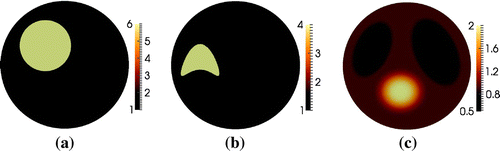
Figure 2 shows the numerical phantoms: where one is a simple circular inclusion, another is the non-convex kite-shaped phantom. Finally, we also shortly investigate the case of multiple smoother inclusions.

4.1. Full boundary data

For ${\mathrm{\Gamma }}^D={\mathrm{\Gamma }}^N=\mathit{\partial }\mathrm{\Omega }$, it is possible to get quite good reconstructions of both shape and contrast for the convex inclusions as seen in Figure 3, and for the case with multiple inclusions there is a reasonable separation of the inclusions.

Figure 3. Full data sparse reconstruction of the phantoms in Figure 2 without prior information on the support of inclusions.

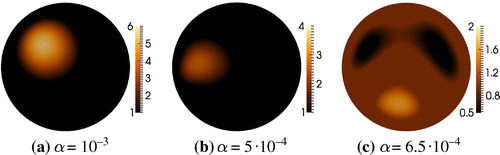
For the kite-shaped phantom, we only get what seems like a convex approximation of the shape. It is seen in [36] that the algorithm is able to reconstruct some types of non-convex inclusions such as the hole in a ring-shaped phantom, however those inclusions are much larger which makes it easier to distinguish from similar convex inclusions.

We note that the method is very noise robust. Figure 4 demonstrates that even unreasonably large amounts of noise lead to only small deformations in the shape of the reconstructed inclusion.

Figure 4. Left: Dirichlet data corresponding to $g=cos(\mathit{\theta })$ for the phantom in Figure 2(a), with 10% and 50% noise level. Middle: full data reconstruction for 10% noise level. Right: full data reconstruction for 50% noise level.

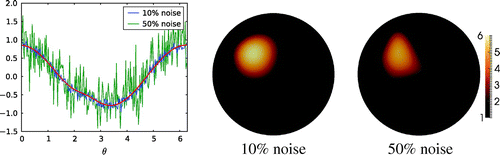
Figure 5. Full data sparse reconstruction of the phantom in Figure 2(a) varying the assumed support given by a dilation $\mathit{\delta }r$. The colour bar is truncated at $[1,6]$. For $\mathit{\delta }r<0$, the contrast in the reconstruction is higher than in the phantom.

In order to investigate the use of prior information, we consider the phantom in Figure 2(a), and let $B(r)$ denote a ball centred at the correct inclusion and with radius $r$. Now we can investigate reconstructions with prior information assuming that the support of the inclusion is $\overline{B((1+\mathit{\delta }r)r^{\ast })}$ for $r^{\ast }$ being the correct radius of the inclusion. Figure 5 shows that underestimating the support of the inclusion $\mathit{\delta }r<0$ is heavily enforced, and the contrast is vastly overestimated in the reconstruction as shown in Figure 6 (note that this cannot be seen in Figure 5 as the color scale for the phantom is applied).

Figure 6. Behaviour of full data sparsity reconstruction based on the phantom in Figure 2(a) by varying $\mathit{\delta }r$ characterizing the assumed support. The correct support of the inclusion is a ball $\overline{B(r^{\ast })}$ while the assumed support is $\overline{B((1+\mathit{\delta }r)r^{\ast })}$. ${\mathit{\sigma }}_B$ is the average of reconstruction $\mathit{\sigma }$ over $B(r^{\ast })$ and ${\mathit{\sigma }}_{B^C}$ is the average on the complement of $B(r^{\ast })$. ${\mathit{\sigma }}_{\text{max}}$ is the maximum of $\mathit{\sigma }$ on the mesh nodes.

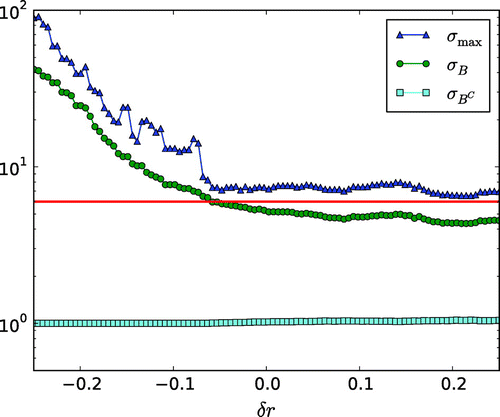
Interestingly, when overestimating the support, the contrast and support of the reconstructed inclusion does not suffer particularly. Intuitively, this corresponds to increasing $\mathit{\delta }r$ such that the assumed support of $\mathit{\delta }\mathit{\sigma }$ contains the entire domain $\mathrm{\Omega }$, which corresponds to the case with no prior information. Denote by ${\mathit{\sigma }}_B\equiv {B(r^{\ast })}^{-1}{\int }_{B(r^{\ast })}\mathit{\sigma }\mathrm{d}x$ the average of the reconstruction $\mathit{\sigma }$ on $\overline{B(r^{\ast })}$, the correct support of the inclusion, and by ${\mathit{\sigma }}_{B^C}$ the average of $\mathit{\sigma }$ on the complement to $B(r^{\ast })$. Denote by ${\mathit{\sigma }}_{max}\equiv {max}_j\mathit{\sigma }(x_j)$ the maximum of $\mathit{\sigma }$ on the mesh nodes. Then Figure 6 gives a good indication of the aforementioned intuition, where around $\mathit{\delta }r=0$ both ${\mathit{\sigma }}_B$ and ${\mathit{\sigma }}_{max}$ level off around the correct contrast of the inclusion (the red line) and stays there for $\mathit{\delta }r>0$. It should be noted that even a 25% overestimation of the support leads to a better contrast in the reconstruction than if no prior information was applied, as seen in Figure 5.

Having an overestimation of the support for $\mathit{\delta }\mathit{\sigma }$ also seems to be a reasonable assumption. Definitely there is the case of no prior information which means that $\ast supp\mathit{\delta }\mathit{\sigma }$ is assumed to be $\mathrm{\Omega }$. If the estimation comes from another method such as TV regularization, then the support is typically slightly overestimated while the contrast suffers.[48] Thus, we can use the overestimated support to get a good localization and contrast reconstruction simultaneously.

Figure 7 shows how the reconstruction of the kite-shaped phantom can be vastly improved. Note that not only is $\ast supp\mathit{\delta }\mathit{\sigma }$ better approximated, but the contrast is also highly improved. It is not surprising that we can achieve an almost perfect reconstruction if $\ast supp\mathit{\delta }\mathit{\sigma }$ is exactly known, however it is a good benchmark to compare the cases for the overestimated support as it shows how well the method can possibly do.

4.2. Partial boundary data

For the partial data problem we choose $\mathrm{\Gamma }={\mathrm{\Gamma }}^D={\mathrm{\Gamma }}^N=\{\mathit{\theta }\in ({\mathit{\theta }}_1,{\mathit{\theta }}_2)\}$ for $0\le {\mathit{\theta }}_1<{\mathit{\theta }}_2\le 2\mathit{\pi }$.

In Figure 8 we observe that with data on the top half of the unit circle, it is actually possible to get very good contrast and also reasonable localization of the two large inclusions. There is still a clear separation of the inclusions, while the small inclusion is not reconstructed at all. With data on the bottom half, the small inclusion is reconstructed almost as well as with full boundary data, but the larger inclusions are only vaguely visible. This is the kind of behaviour that is expected from partial data EIT, and in practice it implies that we can only expect reasonable reconstruction close to where the measurements are taken.

In the rightmost reconstruction in Figure 8, there is a small artefact to the left in a region where a reliable reconstruction is expected. This may be due to the partial data problem being very noise sensitive and the low number of current patterns ($K=10$).

Figure 7. Full data sparse reconstruction of the phantom in Figure 2(b). The applied prior information for the overestimated support is a 10% dilation of the correct shape.

Figure 8. Sparse reconstruction of the phantom in Figure 2(c). Left: $\mathrm{\Gamma }=\mathit{\partial }\mathrm{\Omega }$. Middle: $({\mathit{\theta }}_1,{\mathit{\theta }}_2)=(0,\mathit{\pi })$. Right: $({\mathit{\theta }}_1,{\mathit{\theta }}_2)=(\mathit{\pi },2\mathit{\pi })$.

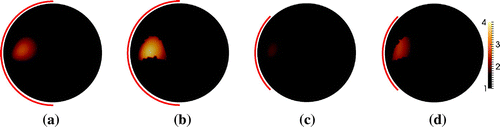
Figure 9. Sparse reconstruction of the phantom with a ball inclusion in Figure 2(a). (a) 50% boundary data, no prior. (b): 50% boundary data with 5% overestimated support. (c): 25% boundary data, no prior. (d): 25% boundary data with 5% overestimated support.

Figure 10. Sparse reconstruction of the phantom with a kite-shaped inclusion in Figure 2(b). (a) 50% boundary data, no prior. (b) 50% boundary data with 10% overestimated support. (c) 25% boundary data, no prior. (d) 25% boundary data with 10% overestimated support.

In Figures 9 and 10 panels (a) and (c) it is observed that as the length of $\mathrm{\Gamma }$ becomes smaller, the reconstructed shape of the inclusion is rapidly deformed. By including prior information about the support of $\mathit{\delta }\mathit{\sigma }$, it is possible to rectify the deformation of the shape, and get reconstructions with almost the correct shape but with a slightly worse reconstructed contrast compared to full boundary data reconstructions. This is observed for the ball- and kite-shaped inclusions in Figures 9 and 10, respectively.

4.3. Comparison with TV regularization

Another sparsity promoting method is TV regularization, which promotes a sparse gradient in the solution. This can be achieved by minimizing the functional(4.1) $$\begin{array}{c}\hfill {\mathrm{\Psi }}_{\text{TV}}(\mathit{\delta }\mathit{\gamma })\equiv \sum _{k=1}^K{J}_k(\mathit{\delta }\mathit{\gamma })+P_{\text{TV}}(\mathit{\delta }\mathit{\gamma }),\mathit{\delta }\mathit{\gamma }\in {\mathcal{A}}_0,\end{array}$$(4.1)

where the discrepancy terms $J_k$ remain the same as in (1.4(1.4) $$\begin{array}{c}\hfill \mathrm{\Psi }(\mathit{\delta }\mathit{\gamma })\equiv \sum _{k=1}^K{J}_k(\mathit{\delta }\mathit{\gamma })+P(\mathit{\delta }\mathit{\gamma }),\mathit{\delta }\mathit{\gamma }\in {\mathcal{A}}_0,\end{array}$$(1.4) ), but the penalty term is now given by(4.2) $$\begin{array}{c}\hfill P_{\text{TV}}(\mathit{\delta }\mathit{\gamma })\equiv \mathit{\alpha }{\int }_{\mathrm{\Omega }}\sqrt{{\mathrm{\nabla }\mathit{\delta }\mathit{\gamma }}^2+b}\mathrm{d}x.\end{array}$$(4.2)

Here $b>0$ is a constant that implies that $P_{\text{TV}}$ is differentiable, but chosen small such that $P_{\text{TV}}$ approximates $\mathit{\alpha }{\int }_{\mathrm{\Omega }}\mathrm{\nabla }\mathit{\delta }\mathit{\gamma }\mathrm{d}x$. The computational cost for determining the derivative of ${\mathrm{\Psi }}_{\text{TV}}$ is the same as for the sparsity regularization in (1.4(1.4) $$\begin{array}{c}\hfill \mathrm{\Psi }(\mathit{\delta }\mathit{\gamma })\equiv \sum _{k=1}^K{J}_k(\mathit{\delta }\mathit{\gamma })+P(\mathit{\delta }\mathit{\gamma }),\mathit{\delta }\mathit{\gamma }\in {\mathcal{A}}_0,\end{array}$$(1.4) ), as it is dominated by the same $2K$ PDE’s (see Remark 2.7). Minimizing the functional (4.1(4.1) $$\begin{array}{c}\hfill {\mathrm{\Psi }}_{\text{TV}}(\mathit{\delta }\mathit{\gamma })\equiv \sum _{k=1}^K{J}_k(\mathit{\delta }\mathit{\gamma })+P_{\text{TV}}(\mathit{\delta }\mathit{\gamma }),\mathit{\delta }\mathit{\gamma }\in {\mathcal{A}}_0,\end{array}$$(4.1) ) is implemented numerically using a plain steepest descend method.

For the numerical examples, the piecewise constant phantoms in Figure 2 panels (a) and (b) are used, with the same noise level as in the previous sections. The value $b={10}^{-5}$ is used for the penalty term in all the examples.

It should be noted that the colour scale in the following examples is not the same scale as for the phantoms, unlike the previous reconstructions. This is because the TV reconstructions have a significantly lower contrast, in particular for the partial data reconstructions, and would be visually difficult to distinguish from the background conductivity in the correct colour scale.

Figure 11. TV reconstruction of the phantom with a ball inclusion in Figure 2(a). (a) Full boundary data. (b) 50% boundary data. (c) 25% boundary data.

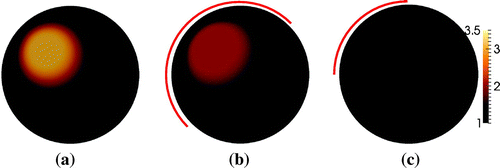
Figure 12. TV reconstruction of the phantom with a kite-shaped inclusion in Figure 2(b). (a) Full boundary data. (b) 50% boundary data. (c) 25% boundary data.

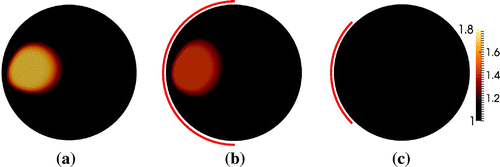
As seen from Figures 11 and 12, the support of the inclusion is slightly overestimated in the case of full boundary data, and for the partial data cases the support is slightly larger than the counterparts in Figures 9 and 10. It is also noticed that the TV reconstructions have a much lower contrast than the ${\ell }_1$ sparsity reconstructions, and the contrast for the TV reconstructions is severely reduced when partial data are used. It is also observed that the same type of shape deformation occurs for both methods in case of partial data.

A typical feature of the TV regularization is piecewise constant reconstructions; however, the reconstructions seen here have constant contrast levels with a smooth transition between them. This is partly due to the slight smoothing of the penalty term with the parameter $b>0$ to make it differentiable, but mostly because the discrepancy terms are not convex which may lead to local minima. The same kind of smooth transitions is also observed in TV-based methods for EIT in [48].

5. Conclusions

We have extended the algorithm developed in [36], for sparse reconstruction in electrical impedance tomography, to the case of partial data. Furthermore, we have shown how a distributed regularization parameter can be applied to utilize spatial prior information. This lead to numerical results showing improved reconstructions for the support of the inclusions and the contrast simultaneously. The use of the distributed regularization parameter enables sharper edges in the reconstruction and vastly reduces the deformation of the inclusions in the partial data problem, even when the prior is overestimated.

The optimization problem is non-convex and the suggested algorithm is therefore only expected to find a local minimum. Initializing with the background conductivity in the numerical examples yields acceptable reconstructions for both full boundary data and partial boundary data.

The algorithm can be generalized for 3D reconstruction, under further assumptions on the boundary conditions ${\{g_k\}}_{k=1}^K$ and the amplitude of the perturbation $\mathit{\delta }\mathit{\sigma }$. This will be considered in a forthcoming paper [38].

Additional information

Funding

This research is supported by the European Research Council [advanced grant number 291405 HD-Tomo].

Notes

No potential conflict of interest was reported by the authors.