Shape optimization of a breakwater

Abstract

In this paper, we optimize the shape of a breakwater which protects a harbour basin from incoming waves. More specifically, our objective is reducing the harbour resonance due to long-range ocean waves. We consider the complex-valued Helmholtz equation as our model state equation and minimize the average wave height in the harbour basin with the shape of the breakwater as optimization variable. The geometry is described by the level set method, i.e. the domain is given as the subzero level set of a function. In contrast to many publications we use the volume expression of the shape derivative, which lends itself naturally to a level set update via a transport equation. The model problem features intrinsic geometric constraints which we treat in the form of forbidden regions. We guarantee feasibility of the iterates by projecting the gradient onto a suitable admissible set.

Keywords:

• Shape optimization
• level set method
• Helmholtz equation
• harbor resonance
• geometric constraints

AMS Subject Classifications:

• 49Q10
• 35J05
• 74J20

1. Introduction

Since the introduction of the level set method to shape optimization at the turn of the century it has developed into one of the most powerful techniques in this area. Some early works are [1–5]. Many publications deal with structural optimization, usually the Ersatz material approach in the hold-all domain $D$ is used to compute the mechanical properties of the structure and the domain $\mathrm{\Omega }$ is never explicitly resolved. But there are also approaches where the domain is exactly meshed, consult for instance.[6–12] The literature is extensive, we refer to the review paper [13] for an overview of level set-based methods in structural topology and shape optimization. The survey [14] presents the level set method in combination with inverse problems and optimal design. For a more comprehensive exposition of the broad field of shape optimization we mention the monographs.[15–23]

In this paper, our objective is to reduce the resonance of a harbour due to long range ocean waves. In practice many publications (e.g. [24–28]) employ the mild slope equation to model wave effects in coastal areas. It was first derived by Berkhoff [29] and can be written as(1) $$\begin{array}{c}\hfill \mathrm{\nabla }·C{C}_g\mathrm{\nabla }\mathit{\phi }+k^{2}C{C}_g\mathit{\phi }=0,\end{array}$$(1)

where $\mathit{\phi }$ is the horizontal variation in velocity potential, $k$ is the wave number, $\mathit{\omega }$ is the wave frequency, $C=\mathit{\omega }/k$ is the wave celerity, $C_g=\frac{C}{2}\left(1+\frac{2kh}{sinh2kh}\right)$ is the group velocity and $h$ is the water depth. Usually it is enriched with additional effects such as partial absorption boundaries, bottom friction, entrance loss, etc. However, the aim of this paper is to introduce the necessary steps for solving the associated shape optimization problem with the level set method and not a realistic modelling of harbour resonance. For this reason, we assume as simplification that the water depth is constant throughout, which leads to the well-known Helmholtz equation(2) $$\begin{array}{c}\hfill \mathrm{\Delta }\mathit{\phi }+k^2\mathit{\phi }=0.\end{array}$$(2)

Note that the potential $\mathit{\phi }$ in this case is complex valued. To the best of our knowledge such a shape optimization problem was only briefly considered in the thesis [30]. The author used the real-valued Helmholtz equation as state equation, an explicit discrete geometry description via the finite element mesh and computed the shape derivative by differentiating with respect to nodal coordinates.

We will consider the complex-valued Helmholtz equation as our model state equation and want to minimize the average wave height in the harbour basin with the shape of the breakwater as optimization variable. The geometry will be described by the level set method,[31–34] i.e. the domain $\mathrm{\Omega }$ is given as the subzero level set of a function $\mathrm{\Phi }:D\to \mathbb{R}$, where $D\subset {\mathbb{R}}^2$ is the hold-all domain. In the numerical realization the level set function is given on a regular grid and we approximate $\mathit{\partial }\mathrm{\Omega }$ with one or more polygonal curves. In each iteration, we construct a triangulation of $D$ which resolves the interface and use it to compute the state, adjoint state and gradient of the cost functional. The model state equation is given on an exterior domain. Since we want to use finite elements we follow the presentation in [35] and reformulate the problem on a bounded domain. In contrast to many publications, we use the volume expression of the shape derivative, which lends itself naturally to a level set update via a transport equation. It requires less regular finite element functions and in our experience the volume expression is numerically more stable than the Hadamard form. This assessment is shared in the recent papers [36,37]. In [37], the volume expression of the shape derivative and the level set method are also used.

The model problem naturally involves geometric constraints in the form of forbidden regions. We strictly enforce those constraints by projecting the gradient onto a suitable admissible set. From a theoretic point of view the scalar product used for the projection should be at least as smooth as the scalar product used to determine the gradient. In the numerical experiments we will study different choices of gradient and projection and see that sometimes a less regular projection leads to better results.

2. Description of the physical model

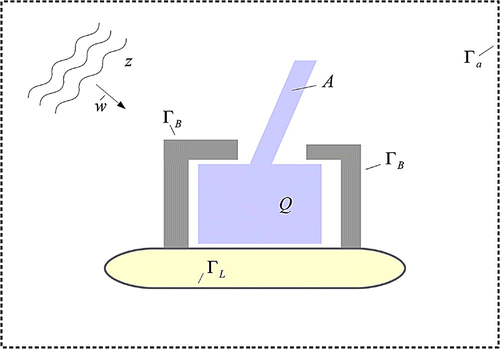
We study the situation depicted in Figure 1. We have an isle bounded by the contour ${\mathrm{\Gamma }}_L$, some breakwaters given by ${\mathrm{\Gamma }}_B$ and a surrounding ocean denoted by ${\mathrm{\Omega }}^{+}$. We want to compute the scattered wave $u$ induced by an incoming planar monochromatic wave $z(x)=exp(ik{w}^{T}x)$ with incident direction $w\in {\mathbb{R}}^2$ and wave number $k>0$. The total surface perturbation is given by $y=u+z$. We study the model(3) $$\begin{array}{c}\hfill \begin{array}{ccc}\hfill \mathrm{\Delta }y+k^{2}y& =0\hfill & \text{in}{\mathrm{\Omega }}^{+}\hfill \\ \hfill ay+{\mathit{\partial }}_{n}y& =0\hfill & \text{on}{\mathrm{\Gamma }}_I:={\mathrm{\Gamma }}_B\cup {\mathrm{\Gamma }}_L.\hfill \end{array}\end{array}$$(3)

Here $a:{\mathbb{R}}^2\to \mathbb{C}$ describes the absorption coefficient at the boundary. The boundaries ${\mathrm{\Gamma }}_L,{\mathrm{\Gamma }}_B$ are assumed to be Lipschitz. Let us discuss appropriate boundary conditions. It is a standard assumption that the scattered wave satisfies the Sommerfeld radiation condition$$\begin{array}{c}\hfill iku-{\mathit{\partial }}_{R}u=o(R^{-\frac{1}{2}}),\text{for}R\to \infty .\end{array}$$

Figure 1. The domain $\mathrm{\Omega }$.

If we want to study this problem in a weak form on the unbounded domain ${\mathrm{\Omega }}^{+}$ we would need to introduce different weighted Sobolev spaces for the test and ansatz functions and include the Sommerfeld radiation condition in the ansatz space. See [38, Chapter 4] and [35, Section 2.3] for more details. This approach leads, however, to various difficulties in the numerical realization if a finite element discretization is employed. While it would be possible to handle the Helmholtz equation on an exterior domain with the boundary element method, an extension to the more realistic mild slope equation would be very challenging. For this reason we focus on the finite element approach.

An alternative is to decompose the domain ${\mathrm{\Omega }}^{+}$ disjointly into a bounded domain $\mathrm{\Omega }$ and an unbounded domain ${\mathrm{\Omega }}_a$ by introducing an artificial smooth boundary ${\mathrm{\Gamma }}_a$, such that ${\mathrm{\Omega }}^{+}=\mathrm{\Omega }\cup {\mathrm{\Gamma }}_a\cup {\mathrm{\Omega }}_a$. The problem (3(3) $$\begin{array}{c}\hfill \begin{array}{ccc}\hfill \mathrm{\Delta }y+k^{2}y& =0\hfill & \text{in}{\mathrm{\Omega }}^{+}\hfill \\ \hfill ay+{\mathit{\partial }}_{n}y& =0\hfill & \text{on}{\mathrm{\Gamma }}_I:={\mathrm{\Gamma }}_B\cup {\mathrm{\Gamma }}_L.\hfill \end{array}\end{array}$$(3) ) is then equivalent to the following coupled problem (cf. [39])(4) $$\begin{array}{c}\hfill \begin{array}{ccc}\hfill \mathrm{\Delta }{y}_{-}+k^2{y}_{-}& =0\hfill & \text{in}\mathrm{\Omega }\hfill \\ \hfill a{y}_{-}+{\mathit{\partial }}_n{y}_{-}& =0\hfill & \text{on}{\mathrm{\Gamma }}_I\hfill \\ \hfill y_{-}& =y_{+}\hfill & \text{on}{\mathrm{\Gamma }}_a\hfill \\ \hfill {\mathit{\partial }}_n{y}_{-}& ={\mathit{\partial }}_n{y}_{+}\hfill & \text{on}{\mathrm{\Gamma }}_a\hfill \\ \hfill \mathrm{\Delta }{y}_{+}+k^2{y}_{+}& =0\hfill & \text{in}{\mathrm{\Omega }}_a\hfill \\ \hfill ik{u}_{+}-{\mathit{\partial }}_R{u}_{+}& =o(R^{-\frac{1}{2}})\hfill & \text{for}R\to \infty .\hfill \end{array}\end{array}$$(4)

For a given $u_{-}$ on ${\mathrm{\Gamma }}_a$ one can solve the unbounded Dirichlet problem (recall $u=y-z$)$$\begin{array}{ccc}\hfill \mathrm{\Delta }{u}_{+}+k^2{u}_{+}& =0\hfill & \text{in}{\mathrm{\Omega }}_a\hfill \\ \hfill u_{+}& =u_{-}\hfill & \text{on}{\mathrm{\Gamma }}_a\hfill \\ \hfill ik{u}_{+}-{\mathit{\partial }}_R{u}_{+}& =o(R^{-\frac{1}{2}})\hfill & \text{for}R\to \infty ,\hfill \end{array}$$

compare [38]. If we have the solution $u_{+}$ we can easily compute ${\mathit{\partial }}_n{u}_{+}={\mathit{\partial }}_n{u}_{-}\text{on}{\mathrm{\Gamma }}_a$. We denote the mapping $u_{-}\mapsto {\mathit{\partial }}_n{u}_{-}$ by $G_e$ and observe that $G_e\in \mathcal{L}(H^{\frac{1}{2}}({\mathrm{\Gamma }}_a),H^{-\frac{1}{2}}({\mathrm{\Gamma }}_a))$. This operator is called the Dirichlet-to-Neumann operator. There exists an integral and a series representation of the non-local operator $G_e$, the integral variant is also called the Steklov–Poincaré operator. The Neumann condition ${\mathit{\partial }}_n{y}_{-}={\mathit{\partial }}_n{y}_{+}\text{on}{\mathrm{\Gamma }}_a$ can be reformulated by$${\mathit{\partial }}_n{y}_{-}={\mathit{\partial }}_n{u}_{-}+{\mathit{\partial }}_{n}z=G_e{u}_{-}+{\mathit{\partial }}_{n}z=G_e{y}_{-}-G_{e}z+{\mathit{\partial }}_{n}z.$$

We replace $G_e$ by some yet unspecified $G\in \mathcal{L}(H^{\frac{1}{2}}({\mathrm{\Gamma }}_a),H^{-\frac{1}{2}}({\mathrm{\Gamma }}_a))$, which might be some approximation of the exact solution operator $G_e$. Hence we arrive at the bounded problem(5) $$\begin{array}{c}\hfill \begin{array}{ccc}\hfill \mathrm{\Delta }y+k^{2}y& =0\hfill & \text{in}\mathrm{\Omega }\hfill \\ \hfill ay+{\mathit{\partial }}_{n}y& =0\hfill & \text{on}{\mathrm{\Gamma }}_I\hfill \\ \hfill \mathit{\partial }y& =Gy-Gz+{\mathit{\partial }}_{n}z\hfill & \text{on}{\mathrm{\Gamma }}_a,\hfill \end{array}\end{array}$$(5)

which is equivalent to (3(3) $$\begin{array}{c}\hfill \begin{array}{ccc}\hfill \mathrm{\Delta }y+k^{2}y& =0\hfill & \text{in}{\mathrm{\Omega }}^{+}\hfill \\ \hfill ay+{\mathit{\partial }}_{n}y& =0\hfill & \text{on}{\mathrm{\Gamma }}_I:={\mathrm{\Gamma }}_B\cup {\mathrm{\Gamma }}_L.\hfill \end{array}\end{array}$$(3) ) for the choice $G=G_e$.

Let us fix some conventions and notation at this point. We define the usual bilinear $L^2$-scalar product for real-valued functions on some set $B\subset {\mathbb{R}}^n$ as ${(·,·)}_{L^2(B)}$ and the corresponding sesquilinear form as ${(f,g)}_{L_{\mathbb{C}}^2(B)}:={(f,\overline{g})}_{L^2(B)}$ for some complex valued functions $f,g$. Furthermore we introduce the real-valued scalar product$${(f,g)}_{L_{\mathbb{R}}^2(B)}:=\text{Re}{(f,g)}_{L_{\mathbb{C}}^2(B)}.$$

The norm $||·{||}_{L_{\mathbb{R}}^2(B)}$ induced by this scalar product coincides with the norm induced by the sesquilinear form. Hence the elements of the space$$L_{\mathbb{R}}^2{(B):=\{f:A\mapsto \mathbb{C}|||f||}_{L_{\mathbb{R}}^2(B)}<\infty \}$$

coincide with the elements of $\{f:B\mapsto \mathbb{C}|||f|{|}_{L_{\mathbb{C}}^2(B)}<\infty \}$, but since we use the ${(·,·)}_{L_{\mathbb{R}}^2(B)}$ scalar product we have a different Hilbert space structure. Other Hilbert spaces will be treated analogously (e.g. $H_{\mathbb{R}}^1(B)$).

Let us get back to the model problem. We make the following simplifying assumption:

Assumption 2.1

We choose $G$ as the 0th-order approximation of $G_e$$$\begin{array}{c}\hfill {⟨Gy,\mathit{\phi }⟩}_{H_{\mathbb{R}}^{-\frac{1}{2}}({\mathrm{\Gamma }}_a),H_{\mathbb{R}}^{\frac{1}{2}}({\mathrm{\Gamma }}_a)}={(iky,\mathit{\phi })}_{L_{\mathbb{R}}^2({\mathrm{\Gamma }}_a)},\end{array}$$

cf. [35, Section 3.]. Furthermore the absorption coefficient is set to $a\equiv 0$ (i.e. perfect reflection).

Remark 2.2

(1)

The choice of $G$ is a rather crude simplification, but in this paper our focus is more on methodology and not so much on realistic modelling. The low-order approximation of $G_e$ introduces artificial reflections at ${\mathrm{\Gamma }}_a$, but since this makes the shape optimization problem presumably harder to solve we accept that for the moment. For more evolved methods of treating the artificial boundary ${\mathrm{\Gamma }}_a$ and the operator $G_e$ we refer to [35, Chapter 3].

(2)

Setting the absorption coefficient to zero implies that there is no damping effect by absorption of energy at the reflecting boundary. We note again that this presumably makes the optimization problem harder to solve since small design changes might have large non-local effects due to wave interference. Furthermore, while breakwaters are efficient in reducing the wave amplitude for waves with short wave periods (like wind waves), this does not hold for long wave periods. Harbour oscillations and resonance due to long waves has been widely studied in coastal engineering literature, see for example [40] and the references therein.

The weak formulation of (5(5) $$\begin{array}{c}\hfill \begin{array}{ccc}\hfill \mathrm{\Delta }y+k^{2}y& =0\hfill & \text{in}\mathrm{\Omega }\hfill \\ \hfill ay+{\mathit{\partial }}_{n}y& =0\hfill & \text{on}{\mathrm{\Gamma }}_I\hfill \\ \hfill \mathit{\partial }y& =Gy-Gz+{\mathit{\partial }}_{n}z\hfill & \text{on}{\mathrm{\Gamma }}_a,\hfill \end{array}\end{array}$$(5) ), with $G$ and $a$ chosen to satisfy Assumption 2.1, reads(6) $$\begin{array}{c}\hfill \left\{\begin{array}{c}\text{Find}y\in H_{\mathbb{R}}^1(\mathrm{\Omega }):\hfill \\ b(y,\mathit{\phi })=f(\mathit{\phi }),\forall \mathit{\phi }\in H_{\mathbb{R}}^1(\mathrm{\Omega }),\hfill \end{array}\right.\end{array}$$(6)

where we define(7) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill b(y,\mathit{\phi })& :={(\mathrm{\nabla }y,\mathrm{\nabla }\mathit{\phi })}_{L_{\mathbb{R}}^2(\mathrm{\Omega })}-k^2{(y,\mathit{\phi })}_{L_{\mathbb{R}}^2(\mathrm{\Omega })}-{(iky,\mathit{\phi })}_{L_{\mathbb{R}}^2({\mathrm{\Gamma }}_a)},\hfill \\ \hfill f(\mathit{\phi })& :={({\mathit{\partial }}_{n}z-ikz,\mathit{\phi })}_{L_{\mathbb{R}}^2({\mathrm{\Gamma }}_a)}.\hfill \end{array}\end{array}$$(7)

Results concerning the existence of a unique solution of (6(6) $$\begin{array}{c}\hfill \left\{\begin{array}{c}\text{Find}y\in H_{\mathbb{R}}^1(\mathrm{\Omega }):\hfill \\ b(y,\mathit{\phi })=f(\mathit{\phi }),\forall \mathit{\phi }\in H_{\mathbb{R}}^1(\mathrm{\Omega }),\hfill \end{array}\right.\end{array}$$(6) ) and its regularity are well known:

Theorem 2.3

Let $\mathrm{\Omega }$ be a Lipschitz domain. Then there exists a unique solution $y\in H_{\mathbb{R}}^1(\mathrm{\Omega })$ of (6(6) $$\begin{array}{c}\hfill \left\{\begin{array}{c}\text{Find}y\in H_{\mathbb{R}}^1(\mathrm{\Omega }):\hfill \\ b(y,\mathit{\phi })=f(\mathit{\phi }),\forall \mathit{\phi }\in H_{\mathbb{R}}^1(\mathrm{\Omega }),\hfill \end{array}\right.\end{array}$$(6) ) for any right-hand side $f\in H_{\mathbb{R}}^1{(\mathrm{\Omega })}^{\ast }$ and we have ${||y||}_{H_{\mathbb{R}}^1(\mathrm{\Omega })}\le {c||f||}_{H_{\mathbb{R}}^1{(\mathrm{\Omega })}^{\ast }}$ for some $c>0$.

Proof

We have the Gelfand-triple $H_{\mathbb{R}}^1(\mathrm{\Omega })\hookrightarrow L_{\mathbb{R}}^2(\mathrm{\Omega })\hookrightarrow H_{\mathbb{R}}^1{(\mathrm{\Omega })}^{\ast }$. Further $b(·,·)$ is $H_{\mathbb{R}}^1(\mathrm{\Omega })$-coercive. Hence the Fredholm alternative holds: Either there exists a unique solution of (6(6) $$\begin{array}{c}\hfill \left\{\begin{array}{c}\text{Find}y\in H_{\mathbb{R}}^1(\mathrm{\Omega }):\hfill \\ b(y,\mathit{\phi })=f(\mathit{\phi }),\forall \mathit{\phi }\in H_{\mathbb{R}}^1(\mathrm{\Omega }),\hfill \end{array}\right.\end{array}$$(6) ) for any $f\in H_{\mathbb{R}}^1(\mathrm{\Omega })$ or there exists a non-trivial solution $y_0\ne 0$ of the homogenous problem$$\begin{array}{c}\hfill b(y,\mathit{\phi })=0,\forall \mathit{\phi }\in H_{\mathbb{R}}^1(\mathrm{\Omega }).\end{array}$$

For our choice of $G$ the solution of the homogenous problem is unique [35, Theorem 3.2]. $\square$

Theorem 2.4

Let $\mathrm{\Omega }$ be a $C^2$-domain. The solution $y\in H_{\mathbb{R}}^1(\mathrm{\Omega })$ of (6(6) $$\begin{array}{c}\hfill \left\{\begin{array}{c}\text{Find}y\in H_{\mathbb{R}}^1(\mathrm{\Omega }):\hfill \\ b(y,\mathit{\phi })=f(\mathit{\phi }),\forall \mathit{\phi }\in H_{\mathbb{R}}^1(\mathrm{\Omega }),\hfill \end{array}\right.\end{array}$$(6) ) has the additional regularity $y\in H_{\mathbb{R}}^2(\mathrm{\Omega })$.

Proof

Follows from standard regularity results for elliptic equations cf. [41, Theorem 9.1.20]. $\square$

3. Shape optimization problem

As announced in the introduction our objective is to minimize the average wave height in the harbour basin $Q$ (compare Figure 1). Given a solution $y$ of (6(6) $$\begin{array}{c}\hfill \left\{\begin{array}{c}\text{Find}y\in H_{\mathbb{R}}^1(\mathrm{\Omega }):\hfill \\ b(y,\mathit{\phi })=f(\mathit{\phi }),\forall \mathit{\phi }\in H_{\mathbb{R}}^1(\mathrm{\Omega }),\hfill \end{array}\right.\end{array}$$(6) ) we define the cost functional as$$J(y)=\frac{1}{2}{||y||}_{L_{\mathbb{R}}^2(Q)}^2.$$

Obviously enclosing the whole harbour basin by a breakwater is not a feasible solution, so we have to introduce an harbour approach $A$ and demand that $Q\cup A$ is always part of the ocean. Furthermore, we do not want to remove parts of the island (the inhabitants might complain). As usual in shape optimization we restrict our considerations to a holdall domain $D\subset {\mathbb{R}}^2$ which contains all relevant shapes. In our setting it is natural to choose $D$ such that $\mathit{\partial }D={\mathrm{\Gamma }}_a$. Hence, we define the admissible set of domains to be(8) $$\begin{array}{c}\hfill {\mathcal{O}}_{ad}:=\{\mathrm{\Omega }\subset D|(Q\cup A)\subset \mathrm{\Omega },\mathrm{\Omega }\cap L=\mathrm{\varnothing }\},\end{array}$$(8)

where $\mathrm{\Omega }\in {\mathcal{O}}_{ad}$ represents the ocean. Of course one could impose additional constraints, e.g. a volume constraint on the set of admissible domains. We can now formulate the abstract shape optimization problem$$\begin{array}{c}\hfill \text{minimize}J(y)\text{such that}\mathrm{\Omega }\in {\mathcal{O}}_{ad},\text{and}y\text{solves}\text{(6) on}\mathrm{\Omega }.\end{array}$$

In this paper, we will not concern ourselves with the question of existence of a solution of the shape optimization problem. For a detailed discussion of techniques and conditions which guarantee the existence and uniqueness of solutions to shape optimization problems, we refer to [18,19]. In order to find a solution (if it exists) we develop a framework for a gradient descent method. For this we follow the usual optimal control approach of introducing a design-to-state mapping $\mathrm{\Omega }\mapsto y(\mathrm{\Omega })$ and computing the derivative of the reduced objective $j(\mathrm{\Omega }):=J(y(\mathrm{\Omega }))$. In the next section, we outline the theory of computing shape derivatives and apply it to our problem setting.

4. Shape sensitivity analysis

Following the presentation in [18,42] we introduce a bounded hold-all Lipschitz domain $D\subset {\mathbb{R}}^n$, $D\ne \mathrm{\varnothing }$, which contains all relevant geometrical objects, and study vector fields $V:\overline{D}\to {\mathbb{R}}^d$, satisfying the conditions(9) $$\begin{array}{c}\hfill V\text{is globally Lipschitz continuous in}\overline{D},\text{and supp}(V)\subset D.\end{array}$$(9)

Note that in [18,42] a more general setting is considered, but this suffices for our purposes. If the velocity field $V$ satisfies condition (9(9) $$\begin{array}{c}\hfill V\text{is globally Lipschitz continuous in}\overline{D},\text{and supp}(V)\subset D.\end{array}$$(9) ) we associate it with the flow map$$T_V:[0,\mathit{\tau }]\times \overline{D}\to {\mathbb{R}}^n\text{which satisfies}{\mathit{\partial }}_t{T}_V(t,x)=V(x).$$

We abbreviate $T_V(t):=T_V(t,·)$. The flow map transforms a set $\mathrm{\Omega }\subset \overline{D}$ into a new domain$$T_V(t)(\mathrm{\Omega })=\{T_V(t,x)|\forall x\in \mathrm{\Omega }\},$$

which is also contained in $\overline{D}$. Furthermore, we introduce the spaces of $k$-times differentiable functions ${\mathbb{R}}^n\to {\mathbb{R}}^n$ with compact support in $D$, i.e.$$\begin{array}{c}\hfill C_c^k(D,{\mathbb{R}}^n):=\{V\in C^k(D,{\mathbb{R}}^n)|\text{supp}V{\subset }_{c}D\}.\end{array}$$

If $V$ satisfies (9(9) $$\begin{array}{c}\hfill V\text{is globally Lipschitz continuous in}\overline{D},\text{and supp}(V)\subset D.\end{array}$$(9) ) the transformation $T_V(t)$ is bi-Lipschitz for all $\mathit{\tau }>0$ and $t\in [0,\mathit{\tau }]$, cf. [18, Theorem 4.2.1]. If $V\in C_c^k(D,{\mathbb{R}}^n)$ then $T_V(t)$ is a $C^k$-diffeomorphism.

Recall the classical notions of the Eulerian semiderivative and shape differentiability:

Definition 4.1

[42, Definitions 3.1 and 3.2] Let $\mathcal{O}\subset \mathcal{P}(D)$ be an appropriate set of shape variables contained in the hold-all domain $D\subset {\mathbb{R}}^n$.

(1)

The Eulerian semiderivative of a shape functional $j:\mathcal{O}\to \mathbb{R}$ at $\mathrm{\Omega }\in \mathcal{O}$ in a direction $V$ satisfying (9(9) $$\begin{array}{c}\hfill V\text{is globally Lipschitz continuous in}\overline{D},\text{and supp}(V)\subset D.\end{array}$$(9) ) is given by$$dj(\mathrm{\Omega };V):=\underset{t\searrow 0}{lim}\frac{j(T_V(t)(\mathrm{\Omega }))-j(\mathrm{\Omega })}{t},$$ if the limit exists and is finite.

(2)

The shape functional $j:\mathcal{O}\to \mathbb{R}$ is said to be shape differentiable at $\mathrm{\Omega }\in \mathcal{O}$, if the Eulerian semiderivative exists for all $V\in C_c^{\infty }(D,{\mathbb{R}}^n)$ and the map$$dj(\mathrm{\Omega };·):C_c^{\infty }(D,{\mathbb{R}}^n)\to \mathbb{R},V\mapsto dj(\mathrm{\Omega };V),$$ is linear and continuous.

Remark 4.2

(1)	The Hadamard-Zolesio structure theorem (cf. [42, Theorem 3.2]) shows that the support of the vector distribution $dj(\mathrm{\Omega };·)\in C_c^{\infty }{(D,{\mathbb{R}}^n)}^{\ast }$ is contained in $\mathit{\partial }\mathrm{\Omega }\cap D$.
(2)	The proofs of most formulas for the computation of shape derivatives rely on the representation of the shape functional $j$ in terms of the transformation $T_V(t)$. If $j$ depends on the integral over a $n$-dimensional subset of $T_V(t)(\mathrm{\Omega })$ and a shape-depended state $y$ the directional derivative has a natural representation as a volume integral. If the boundary $\mathit{\partial }\mathrm{\Omega }$ is smooth enough this can be related via the Gauß divergence theorem to a boundary representation in accordance with the structure predicted by the Hadamard-Zolesio theorem.
(3)	If the boundary $\mathit{\partial }\mathrm{\Omega }$ of $\mathrm{\Omega }\subset \text{int}D$ is compact then $dj(\mathrm{\Omega };·)$ is continuous for the $C_c^k(D,{\mathbb{R}}^n)$-topology for some $k\ge 0$, and $dj(\mathrm{\Omega };·)\in H^{-s}(D,{\mathbb{R}}^n)$ for some $s\ge 0$ (cf. [18, Remark 9.3.1]).
(4)	The derivative $dj(\mathrm{\Omega };·)\in C_c^{\infty }{(D,{\mathbb{R}}^n)}^{\ast }$ is often called the shape gradient. We think that the terms derivative and gradient should be clearly separated. Whereas, the derivative is an element of the dual space of some vector space, in our terminology the gradient is the Riesz representative of the derivative with respect to some scalar product. So if $dj(\mathrm{\Omega };·)\in H^{\ast }$ for some Hilbert space $H$ the gradient $\mathrm{\nabla }j(\mathrm{\Omega })$ with respect to the $H$-scalar-product is given by$${(\mathrm{\nabla }j(\mathrm{\Omega }),V)}_H=dj(\mathrm{\Omega };V),\forall V\in H.$$

Let us demonstrate how the shape derivative of $j(\mathrm{\Omega })=J(y(\mathrm{\Omega }))$ in a direction $V$ satisfying (9(9) $$\begin{array}{c}\hfill V\text{is globally Lipschitz continuous in}\overline{D},\text{and supp}(V)\subset D.\end{array}$$(9) ) can be calculated. This is not trivial since the states $y(T_V(t)(\mathrm{\Omega }))\in H_{\mathbb{R}}^1(T_V(t)(\mathrm{\Omega }))$ depend on the varying domains and are defined in function spaces which also depend on $t$. The standard approach to this problem is to introduce a function space parameterization. It is based on the equivalence$$\begin{array}{c}\hfill g\in H_{\mathbb{R}}^1(T_V(t)(\mathrm{\Omega }))\iff g\circ T_V(t)\in H_{\mathbb{R}}^1(\mathrm{\Omega })\end{array}$$

which goes back to [43, Section 2.3.1]. Hence we can transform the state equation given on $T_V(t)(\mathrm{\Omega })$ onto the current domain $\mathrm{\Omega }$. This operation is also called pull back.

We introduce the notation$$\begin{array}{cc}\hfill D{T}_V(t)& :=\text{Jacobian matrix of}{T}_V(t),\hfill \\ \hfill A(t)& :=det(D{T}_V(t))D{T}_V{(t)}^{-1}D{T}_V{(t)}^{-T},\hfill \end{array}$$

and note that $det(D{T}_V(t))=|det(D{T}_V(t))|\text{for}t\ge 0$ small. Furthermore $V=0$ on ${\mathrm{\Gamma }}_a$ by (9(9) $$\begin{array}{c}\hfill V\text{is globally Lipschitz continuous in}\overline{D},\text{and supp}(V)\subset D.\end{array}$$(9) ) and hence $T_V(t)({\mathrm{\Gamma }}_a)={\mathrm{\Gamma }}_a$ for all $t\ge 0$. Consider now the solution $y_t$ of the state Equation (6(6) $$\begin{array}{c}\hfill \left\{\begin{array}{c}\text{Find}y\in H_{\mathbb{R}}^1(\mathrm{\Omega }):\hfill \\ b(y,\mathit{\phi })=f(\mathit{\phi }),\forall \mathit{\phi }\in H_{\mathbb{R}}^1(\mathrm{\Omega }),\hfill \end{array}\right.\end{array}$$(6) ) on the varying domains $T_V(t)(\mathrm{\Omega })$ for $t\in [0,\mathit{\tau }]$. We transform the left-hand side$$\begin{array}{cc}\hfill b_t(y_t,{\mathit{\phi }}_t)& :={(\mathrm{\nabla }{y}_t,\mathrm{\nabla }{\mathit{\phi }}_t)}_{L_{\mathbb{R}}^2(T_V(t)(\mathrm{\Omega }))}-k^2{(y_t,{\mathit{\phi }}_t)}_{L_{\mathbb{R}}^2(T_V(t)(\mathrm{\Omega }))}-{(ik{y}_t,{\mathit{\phi }}_t)}_{L_{\mathbb{R}}^2(T_V(t)({\mathrm{\Gamma }}_a))}\hfill \end{array}$$

onto the reference domain via $y^t=y_t\circ T_V(t)$, ${\mathit{\phi }}^t={\mathit{\phi }}_t\circ T_V(t)$, and$$\begin{array}{cc}\hfill b(t,y^t,{\mathit{\phi }}^t)& :={(A(t)\mathrm{\nabla }{y}^t,\mathrm{\nabla }{\mathit{\phi }}^t)}_{L_{\mathbb{R}}^2(\mathrm{\Omega })}-k^2{(det(D{T}_V(t))y^t,{\mathit{\phi }}^t)}_{L_{\mathbb{R}}^2(\mathrm{\Omega })}-{(ik{y}^t,{\mathit{\phi }}^t)}_{L_{\mathbb{R}}^2({\mathrm{\Gamma }}_a)}.\hfill \end{array}$$

The boundary conditions are defined on the fixed boundary ${\mathrm{\Gamma }}_a$ and do not change through the transformation$$f(t,{\mathit{\phi }}^t)={\left(\frac{\mathit{\partial }z}{\mathit{\partial }n}-ikz,{\mathit{\phi }}^t\right)}_{L_{\mathbb{R}}^2({\mathrm{\Gamma }}_a)}={\left(\frac{\mathit{\partial }z}{\mathit{\partial }n}-ikz,{\mathit{\phi }}_0\right)}_{L_{\mathbb{R}}^2({\mathrm{\Gamma }}_a)}=f({\mathit{\phi }}_0).$$

Hence, the state $y^t:=y_t\circ T_V(t)\in H_{\mathbb{R}}^1(\mathrm{\Omega })$ solves the transformed state equation(10) $$\begin{array}{c}\hfill b(t,y^t,\mathit{\phi })=f(t,\mathit{\phi }),\forall \mathit{\phi }\in H_{\mathbb{R}}^1(\mathrm{\Omega }).\end{array}$$(10)

We also need to transform the objective. Due to (8(8) $$\begin{array}{c}\hfill {\mathcal{O}}_{ad}:=\{\mathrm{\Omega }\subset D|(Q\cup A)\subset \mathrm{\Omega },\mathrm{\Omega }\cap L=\mathrm{\varnothing }\},\end{array}$$(8) ) we consider only velocity fields satisfying $V=0$ on $Q$. Introducing $\tilde{j}:[0,\mathit{\tau }]\to \mathbb{R}$ with $\tilde{j}(t):=\frac{1}{2}||y^t{||}_{L_{\mathbb{R}}^2(Q)}^2$ it holds$$\tilde{j}(t)=\frac{1}{2}||y^t{||}_{L_{\mathbb{R}}^2(Q)}^2=J(y_t)=j(T_V(t)(\mathrm{\Omega })).$$

Due to [18, Theorem 9.3.4] the shape derivative of $j$ at $\mathrm{\Omega }$ can be obtained as$$\begin{array}{c}\hfill dj(\mathrm{\Omega };V)={\tilde{j}}^{\prime }(0).\end{array}$$

Remark 4.3

Calculating the derivative of $\tilde{j}$ amounts to calculating the material derivative ${\dot{y}}^t:={lim}_{t\searrow 0}(y^t-y^0)/t$. An alternative approach would be the local shape derivative of $y_t$, but in our opinion the material derivative approach is more general and canonical. As usual in PDE-constrained optimization if one is interested in the whole derivative $j^{\prime }(\mathrm{\Omega })$ the direct approach of calculating directional derivatives is infeasible. Instead it is advantageous to employ the adjoint approach. We demonstrate this now briefly.

Introducing the Lagrange functional$$\mathcal{L}:[0,\mathit{\tau }]\times H_{\mathbb{R}}^1(\mathrm{\Omega })\times H_{\mathbb{R}}^1(\mathrm{\Omega })\to \mathbb{R}:\mathcal{L}(t,y,p)=J(y)+b(t,y,p)-f(p),$$

we note that for a solution $y^t\in H_{\mathbb{R}}^1(\mathrm{\Omega })$ of the state equation it holds$$\tilde{j}(t)=\mathcal{L}(t,y^t,p),\forall p\in H_{\mathbb{R}}^1(\mathrm{\Omega }).$$

Furthermore, if $p^t\in H_{\mathbb{R}}^1(\mathrm{\Omega })$ solves the adjoint equation(11) $$\begin{array}{c}\hfill {⟨{\mathit{\partial }}_y\mathcal{L}(t,y^t,p^t),\mathit{\psi }⟩}_{H_{\mathbb{R}}^1{(\mathrm{\Omega })}^{\ast },H_{\mathbb{R}}^1(\mathrm{\Omega })}={(y^t,\mathit{\psi })}_{L_{\mathbb{R}}^2(Q)}+b(t,\mathit{\psi },p^t)=0,\forall \mathit{\psi }\in H_{\mathbb{R}}^1(\mathrm{\Omega }),\end{array}$$(11)

then$$\begin{array}{cc}\hfill dj(\mathrm{\Omega };V)={\tilde{j}}^{\prime }(0)=& {\mathit{\partial }}_t\mathcal{L}(0,y^0,p^0)={\mathit{\partial }}_{t}b(0,y^0,p^0)\hfill \end{array}$$

Note that ${\mathit{\partial }}_{t}det(D{T}_V(0))=\text{div}(V)$ and$${\mathit{\partial }}_{t}A(0)=\text{div}(V)\mathcal{I}-DV-D{V}^T,$$

where $\mathcal{I}$ denotes the identity matrix in ${\mathbb{R}}^2$, cf. [18, Section 9.4.1]. Hence we obtain the following volume representation of the shape derivative(12) $$\begin{array}{c}\hfill dj(\mathrm{\Omega };V)={(A^{\prime }(0)\mathrm{\nabla }{y}^0,\mathrm{\nabla }{p}^0)}_{L_{\mathbb{R}}^2(\mathrm{\Omega })}-k^2{(\text{div}(V)y^0,p^0)}_{L_{\mathbb{R}}^2(\mathrm{\Omega })}.\end{array}$$(12)

It is easy to check that $dj(\mathrm{\Omega };·)\in W^{1,\infty }{(D,{\mathbb{R}}^2)}^{\ast }$ and hence $dj(\mathrm{\Omega };·)\in H^s{(D,{\mathbb{R}}^2)}^{\ast }$ for $s>2$. Note that we can choose a bounded, open Lipschitz holdall domain $D\subset {\mathbb{R}}^2$. In this case, $W^{1,\infty }(D,{\mathbb{R}}^2)=C^{0,1}(D,{\mathbb{R}}^2)$ algebraically and topologically.

5. Geometric constraints

In this section we describe how to incorporate geometric constraints in the shape optimization problem. Geometric constraints appear frequently in applications. In our breakwater optimization example we have the following: the harbour basin $Q$ and the harbour approach $A$ should always be water regions, i.e. be a part of $\mathrm{\Omega }$. On the other hand the island $L$ should never be a part of $\mathrm{\Omega }$.

A very natural idea for solving the constrained optimization problem(13) $$\begin{array}{c}\hfill \text{minimize}j(\mathrm{\Omega })\text{such that}\mathrm{\Omega }\in {\mathcal{O}}_{ad},\end{array}$$(13)

is to use appropriate projections. The projected descent method is the prototypical example of an algorithm which always stays feasible with regard to the constraints. The idea is to take a step in an appropriately chosen descent direction and afterwards to project onto the admissible set. The method is classical in the context of optimization in Hilbert spaces (cf. [44, Section 2.2.2] and has recently also been generalized to the Banach space context (cf. [45]). Unfortunately an extension to the shape optimization framework is not straightforward. While one can define a metric on the group of images of a domain ([18, Chapter 3]) the practical realization of such the associated projection is a challenging topic. We leave this option open and note that it would be a very interesting topic for further research. There are also other approaches to define metrics on families of sets, some of them even feature associated projections which are easy to implement. However, for these metrics there is no intrinsic notion of an appropriate general tangent space available. Hence, the computation of derivatives which are compatible with these metrics can only be done in specific situations, but not in a canonical way.

We propose to use an alternative approach. We project the descent direction onto a suitable set of velocity fields which keep the deformed domain in the admissible set. The easiest way to ensure this is to define$$\begin{array}{c}\hfill {\mathcal{V}}_{feas}:=\{V\in C^{0,1}(\overline{D},{\mathbb{R}}^2){|V|}_{\mathcal{F}}=0,\mathcal{F}=Q\cup A\cup L\cup \mathit{\partial }D\}.\end{array}$$

Obviously if $\mathrm{\Omega }\in {\mathcal{O}}_{ad}$ and $V\in {\mathcal{V}}_{feas}$, then $T_V(t)(\mathrm{\Omega })\in {\mathcal{O}}_{ad}$ for all $t>0$. There is some freedom in defining the descent direction and the associated projection. Note that, in general, these two quantities should be derived with respect to the same scalar product. Otherwise one cannot guarantee that the projected direction is a descent direction. There are already easy examples in finite dimension showing that the projected Newton direction is not necessarily a descent direction. Hence we consider

Assumption 5.1

$\mathcal{H}\hookrightarrow C^{0,1}(\overline{D},{\mathbb{R}}^2)$ is a Hilbert space and ${(·,·)}_a:\mathcal{H}\times \mathcal{H}\to \mathbb{R}$ is a symmetric, continuous, and coercive bilinear form with associated norm $||·{||}_a$.

Remark 5.2

(1)	We work here with an imbedded Hilbert space instead of the Banach space $C^{0,1}(D,{\mathbb{R}}^d)$. It might be interesting to see whether one can transfer the results of [45] also to our setting.
(2)	One can easily generalize the fixed bilinear form ${(·,·)}_a$ to a variable one and retain convergence of the corresponding algorithm under suitable uniformness requirements, cf. e.g. [45]. Thus it is possible to consider second-order information in the bilinear form.

Definition 5.3

Let Assumption 5.1 be satisfied and denote ${\mathcal{V}}_{ad}:={\mathcal{V}}_{feas}\cap \mathcal{H}$. Define the projection with respect to ${(·,·)}_a$$$\begin{array}{c}\hfill P_a:\mathcal{H}\to {\mathcal{V}}_{ad}:P_a(V)\in {\mathcal{V}}_{ad},\text{and}(V-P_{a}V,W)=0\forall W\in {\mathcal{V}}_{ad},\end{array}$$

and for ${\mathrm{\Omega }}^k\in {\mathcal{O}}_{ad}$ the direction$$\begin{array}{c}\hfill V_k\in \mathcal{H}:{(V_k,W)}_a=dj({\mathrm{\Omega }}^k;W)\forall W\in \mathcal{H}.\end{array}$$

Remark 5.4

We will in the following refer to $V_k$ as gradient, since it is the Riesz representative of $dj({\mathrm{\Omega }}^k;·)$ with respect to ${(·,·)}_a$. In particular $-V_k$ is the direction of steepest descent w.r.t. $||·{||}_a$. Note again, that with a suitable choice of the bilinear form one could also obtain a Newton-type direction, or some other gradient related direction.

Since ${\mathcal{V}}_{ad}$ is a linear subspace the projection can be implemented efficiently. In fact, instead of first computing the gradient $V_k$ and then projecting it we can directly compute the gradient with respect to the subspace and obtain the same velocity field.

Lemma 5.5

Let Assumption 5.1 be satisfied. The element $U_k\in {\mathcal{V}}_{ad}$ satisfies(14) $$\begin{array}{c}\hfill {(U_k,W)}_a=dj({\mathrm{\Omega }}^k;W)\forall W\in {\mathcal{V}}_{ad}\end{array}$$(14)

if and only if there holds $U_k=P_a(V_k)$.

Proof

By definition of the gradient it holds for all $W\in \mathcal{H}$$$\begin{array}{c}\hfill {(V_k-U_k,W)}_a={(V_k,W)}_a-{(U_k,W)}_a=dj({\mathrm{\Omega }}^k;W)-{(U_k,W)}_a.\end{array}$$

Considering $W\in {\mathcal{V}}_{ad}$ shows the equivalence of the statements. $\square$

We have the following result concerning the optimality of the current iterate ${\mathrm{\Omega }}^k$.

Lemma 5.6

Let Assumption 5.1 be satisfied.

(1)	If $P_a(V_k)=0$, then it holds $dj({\mathrm{\Omega }}^k;W)=0$ for all $W\in {\mathcal{V}}_{ad}$.
(2)	If $P_a(V_k)\ne 0$, then $P_a(-V_k)$ is a descent direction, i.e.$$\begin{array}{c}\hfill dj({\mathrm{\Omega }}^k;P_a(-V_k))=-||P_a(V_k){||}_a^2<0.\end{array}$$

Proof

This follows directly from the definitions, respectively, from the above equivalence. $\square$

Remark 5.7

Note that Lemma 5.6 does not guarantee us, that ${\mathrm{\Omega }}^k$ is a local solution of (13(13) $$\begin{array}{c}\hfill \text{minimize}j(\mathrm{\Omega })\text{such that}\mathrm{\Omega }\in {\mathcal{O}}_{ad},\end{array}$$(13) ) if $P_a(V_k)=0$. We can only expect to obtain a local solution of the restricted problem$$\begin{array}{c}\hfill \text{minimize}j(\mathrm{\Omega })\text{such that}\mathrm{\Omega }\in \{T_V(t)({\mathrm{\Omega }}_0)|V\in {\mathcal{V}}_{ad},t\ge 0\}.\end{array}$$

In that sense we are only computing a suboptimal solution of the original problem.

6. Level set method

The level set method was introduced in [31] and is widely used to describe propagating fronts, moving interfaces, image segmentation, morphing bodies and many similar applications. We refer to the monographs [32,34] for a detailed presentation of this rich topic. The core idea is to describe some $\mathrm{\Omega }\subset {\mathbb{R}}^n$ as the subzero level set$$\mathrm{\Omega }:=\{x\in {\mathbb{R}}^n|\mathrm{\Phi }(x)<0\}$$

of some continuous function $\mathrm{\Phi }:{\mathbb{R}}^n\to \mathbb{R}$. Denote $\mathrm{\Gamma }=\{x\in {\mathbb{R}}^n|\mathrm{\Phi }(x)=0\}$ and assume $\mathrm{\Gamma }=\mathit{\partial }\mathrm{\Omega }$. For $\mathrm{\Phi }\in C^k({\mathbb{R}}^n,\mathbb{R})$, $k\ge 1$, $\mathrm{\Gamma }\ne \mathrm{\varnothing }$ and assuming $\mathrm{\nabla }\mathrm{\Phi }(x)\ne 0\forall x\in \mathrm{\Gamma }$, it holds that $\mathrm{\Gamma }$ is a $C^k$-submanifold of dimension $(n-1)$ in ${\mathbb{R}}^n$.

Let $V$ satisfy (9(9) $$\begin{array}{c}\hfill V\text{is globally Lipschitz continuous in}\overline{D},\text{and supp}(V)\subset D.\end{array}$$(9) ). A family of domains $T_V(t)(\mathrm{\Omega })$ can be encoded via a family of level set functions. Setting$$\begin{array}{c}\hfill \mathrm{\Phi }:[0,\mathit{\tau }]\times {\mathbb{R}}^n:\mathrm{\Phi }(t,x)={\mathrm{\Phi }}_0(T_V{(t)}^{-1}(x)),\end{array}$$

where ${\mathrm{\Phi }}_0$ is a level set function of $\mathrm{\Omega }$, it holds $T_V(t)(\mathrm{\Omega })=\{x\in {\mathbb{R}}^n|\mathrm{\Phi }(t,x)<0\}$. Indeed it is a classical result that a solution of the transport equation(15) $$\begin{array}{c}\hfill {\mathit{\partial }}_t\mathrm{\Psi }+\mathrm{\nabla }{\mathrm{\Psi }}^{T}V=0\text{with initial condition}\mathrm{\Psi }(0,x)={\mathrm{\Phi }}_0(x),\end{array}$$(15)

where $\mathrm{\nabla }{\mathrm{\Psi }}^{T}V$ is meant in the weak sense, satisfies for a.e. $x\in {\mathbb{R}}^n$ and all $t\in [0,\mathit{\tau }]$$$\begin{array}{c}\hfill \mathrm{\Psi }(t,x)={\mathrm{\Phi }}_0(T_V{(t)}^{-1}(x),\end{array}$$

cf. [46, Proposition 3.3]. Note that this result is due to the regularity of $V$. In general the transport equation may lead to shocks, discontinuous solutions and special solution concepts are required. We point out in particular the concept of viscosity solutions, cf. e.g. [33,47].

Summarizing if the velocity field along which we want to transform the current domain ${\mathrm{\Omega }}^k$ is given by the projected negative gradient $P_a(-V_k)$ we can use (15(15) $$\begin{array}{c}\hfill {\mathit{\partial }}_t\mathrm{\Psi }+\mathrm{\nabla }{\mathrm{\Psi }}^{T}V=0\text{with initial condition}\mathrm{\Psi }(0,x)={\mathrm{\Phi }}_0(x),\end{array}$$(15) ) to obtain a representation of the next iterate level set function and thus of ${\mathrm{\Omega }}^{k+1}$.

7. Optimization and discretization aspects

Let us briefly sketch Algorithm 7.1 before going into details. Starting with a level-set function $\mathrm{\Phi }$ given on a regular grid we extract a discretization of the domain $\mathrm{\Omega }$ and the interface ${\mathrm{\Gamma }}_I={\mathrm{\Gamma }}_B\cup {\mathrm{\Gamma }}_L$. We solve the state and adjoint equations on the discretized domain using piecewise linear finite elements. Now we can compute the shape derivative of the reduced objective and obtain a projected gradient representation from (14(14) $$\begin{array}{c}\hfill {(U_k,W)}_a=dj({\mathrm{\Omega }}^k;W)\forall W\in {\mathcal{V}}_{ad}\end{array}$$(14) ). Finally the level set function is evolved according to (15(15) $$\begin{array}{c}\hfill {\mathit{\partial }}_t\mathrm{\Psi }+\mathrm{\nabla }{\mathrm{\Psi }}^{T}V=0\text{with initial condition}\mathrm{\Psi }(0,x)={\mathrm{\Phi }}_0(x),\end{array}$$(15) ) along the negative projected gradient for some time span $\mathrm{\Delta }t$ which we choose such that it satisfies the Armijo condition.

We approximate the interface ${\mathrm{\Gamma }}_I$, given by the zero level-set of $\mathrm{\Phi }$, by one or multiple polygonal curves. Between each pair of neighbouring points on the regular grid at which the level set function has different signs there is an intersection point of the zero level set with the edges of the grid. We approximate this intersection point using an affine model for $\mathrm{\Phi }$ along the edge. Connecting all these intersection points, we obtain the polygonal approximation ${\mathrm{\Gamma }}_{I,h}$ to ${\mathrm{\Gamma }}_I$ and thus the current domain ${\mathrm{\Omega }}_h$.

In the next step, the domains ${\mathrm{\Omega }}_h$ and $D$ are discretized with triangular meshes which resolve the polygonal boundary ${\mathrm{\Gamma }}_{I,h}$. Furthermore, the mesh representing ${\mathrm{\Omega }}_h$ consists of a subset of the triangles of the mesh for $D$. Cells of the rectangular grid for which all four vertices have the same sign of $\mathrm{\Phi }$ are split along their diagonal into two triangles, and cells which are intersected by ${\mathrm{\Gamma }}_{I,h}$ are split depending on how they are intersected. In order to avoid triangles that are too degenerate and cause numerical difficulties, we enforce a certain minimum ratio between edges of all mesh triangles.

The mesh on ${\mathrm{\Omega }}_h$ is used to solve the state and adjoint equations, and the mesh on $D$ is used to solve (14(14) $$\begin{array}{c}\hfill {(U_k,W)}_a=dj({\mathrm{\Omega }}^k;W)\forall W\in {\mathcal{V}}_{ad}\end{array}$$(14) ) for the projected gradient. Our mesh construction ensures that each point of the original regular grid is also a vertex of the triangle mesh, so that we can extract $P_a(-V_k)$ on each grid point to solve (15(15) $$\begin{array}{c}\hfill {\mathit{\partial }}_t\mathrm{\Psi }+\mathrm{\nabla }{\mathrm{\Psi }}^{T}V=0\text{with initial condition}\mathrm{\Psi }(0,x)={\mathrm{\Phi }}_0(x),\end{array}$$(15) ).

Let us briefly comment on the discretization of the state and adjoint equation. We use the usual machinery of piecewise linear continuous finite elements to discretize the scalar products ${(f,g)}_{L^2({\mathrm{\Omega }}_h)},{(\mathrm{\nabla }f,\mathrm{\nabla }g)}_{L^2({\mathrm{\Omega }}_h)},\text{and}{(f,g)}_{L^2({\mathrm{\Gamma }}_a)}$ for some real valued functions $f,g$. Recall the notation from Section 2. Splitting every complex valued function $f$ into $f=f_1+i{f}_2$, with $f_i:{\mathrm{\Omega }}_h\to \mathbb{R}$, we find$${(f,g)}_{L_{\mathbb{R}}^2({\mathrm{\Omega }}_h)}=\text{Re}{(f_1+i{f}_2,g_1+i{g}_2)}_{L_{\mathbb{C}}^2({\mathrm{\Omega }}_h)}={(f_1,g_1)}_{L^2({\mathrm{\Omega }}_h)}+{(f_2,g_2)}_{L^2({\mathrm{\Omega }}_h)}.$$

Analogously it holds that$${(\mathrm{\nabla }f,\mathrm{\nabla }g)}_{L_{\mathbb{R}}^2({\mathrm{\Omega }}_h)}={(\mathrm{\nabla }{f}_1,\mathrm{\nabla }{g}_1)}_{L^2({\mathrm{\Omega }}_h)}+{(\mathrm{\nabla }{f}_2,\mathrm{\nabla }{g}_2)}_{L^2({\mathrm{\Omega }}_h)},$$

and(16) $$\begin{array}{c}\hfill {(if,g)}_{L_{\mathbb{R}}^2({\mathrm{\Gamma }}_a)}={(f_1,g_2)}_{L^2({\mathrm{\Gamma }}_a)}-{(f_2,g_1)}_{L^2({\mathrm{\Gamma }}_a)}.\end{array}$$(16)

Note that $z(x)=exp(ik{w}^{T}x)$ which implies ${\mathit{\partial }}_{n}z-ikz=ik(w^{T}n-1)z$. Hence we only need to implement the boundary expression (16(16) $$\begin{array}{c}\hfill {(if,g)}_{L_{\mathbb{R}}^2({\mathrm{\Gamma }}_a)}={(f_1,g_2)}_{L^2({\mathrm{\Gamma }}_a)}-{(f_2,g_1)}_{L^2({\mathrm{\Gamma }}_a)}.\end{array}$$(16) ). Combining these formulas with the usual mass and stiffness matrices we can easily assemble the system matrix and right-hand side of the state equation (10(10) $$\begin{array}{c}\hfill b(t,y^t,\mathit{\phi })=f(t,\mathit{\phi }),\forall \mathit{\phi }\in H_{\mathbb{R}}^1(\mathrm{\Omega }).\end{array}$$(10) ) and adjoint equation (11(11) $$\begin{array}{c}\hfill {⟨{\mathit{\partial }}_y\mathcal{L}(t,y^t,p^t),\mathit{\psi }⟩}_{H_{\mathbb{R}}^1{(\mathrm{\Omega })}^{\ast },H_{\mathbb{R}}^1(\mathrm{\Omega })}={(y^t,\mathit{\psi })}_{L_{\mathbb{R}}^2(Q)}+b(t,\mathit{\psi },p^t)=0,\forall \mathit{\psi }\in H_{\mathbb{R}}^1(\mathrm{\Omega }),\end{array}$$(11) ).

Note that, in order to guarantee the minimum regularity of $C^{0,1}(D,{\mathbb{R}}^2)$ for the velocity field, we would need to compute the gradient in $H^s(D,{\mathbb{R}}^2)$ with $s>2$. In our numerical experiments we neglect to do so. For ease of implementation we only use piecewise linear continuous finite elements to discretize the ansatz and test spaces of (14(14) $$\begin{array}{c}\hfill {(U_k,W)}_a=dj({\mathrm{\Omega }}^k;W)\forall W\in {\mathcal{V}}_{ad}\end{array}$$(14) ). We employ the triangulation of D as described above. We experiment with different choices of the scalar product used to compute the gradient and the projection, cf. Section 8. The derivative of the reduced objective in the direction $V$ is given by$$dj(0;V)={(A^{\prime }(0)\mathrm{\nabla }y,\mathrm{\nabla }p)}_{L_{\mathbb{R}}^2({\mathrm{\Omega }}_h)}-k^2{(\text{div}(V)y,p)}_{L_{\mathbb{R}}^2({\mathrm{\Omega }}_h)}.$$

Using simple matrix manipulations we can rewrite this expression such that the discretized version $d{j}_h(0)$ of the derivative can be evaluated by a simple vector multiplication $d{j}_h{(0)}^{T}V$.

Once we have computed the projected gradient, we need to update our geometry. For this we solve(17) $$\begin{array}{c}\hfill {\mathit{\partial }}_t\mathrm{\Psi }(t)+U^T\mathrm{\nabla }\mathrm{\Psi }(t)=0\forall t\in (0,\mathrm{\Delta }t),\mathrm{\Psi }(0)=\mathrm{\Phi },\end{array}$$(17)

with $U=P_a(-V_k)$ and use $\mathrm{\Psi }(\mathrm{\Delta }t)$ as the new level set function in the next iteration. The time span $\mathrm{\Delta }t$ is determined by the Armijo rule, i.e.(18) $$\begin{array}{c}\hfill \tilde{j}(\mathrm{\Delta }t)\le \tilde{j}(0)+\mathrm{\Delta }t\mathit{\gamma }{\tilde{j}}^{\prime }(0).\end{array}$$(18)

As was suggested in [37], we employ the Local Lax-Friedrichs flux (cf. [48]) and an explicit Euler time stepping scheme to evolve $\mathrm{\Psi }$. In our setting this leads to the level set function updates(19) $$\begin{array}{c}\hfill {\mathrm{\Psi }}_{ij}^{l+1}={\mathrm{\Psi }}_{ij}^l-\mathit{\delta }t{H}^{LLF}.\end{array}$$(19)

Here ${\mathrm{\Psi }}_{ij}^l$ is the value of the level set function in the node $(x_i,y_j)$ of the regular grid at the $l$th time step,$$H^{LLF}=\frac{p^{-}+p^{+}}{2}{U}_1+\frac{q^{-}+q^{+}}{2}{U}_2-\frac{1}{2}(p^{+}-p^{-})|U_1|-\frac{1}{2}(q^{+}-q^{-})|U_2|,$$

and$$\begin{array}{cc}\hfill p^{-}=\frac{{\mathrm{\Psi }}_{ij}^l-{\mathrm{\Psi }}_{i-1,j}^l}{\mathrm{\Delta }x},& p^{+}=\frac{{\mathrm{\Psi }}_{i+1,j}^l-{\mathrm{\Psi }}_{ij}^l}{\mathrm{\Delta }x},\hfill \\ \hfill q^{-}=\frac{{\mathrm{\Psi }}_{ij}^l-{\mathrm{\Psi }}_{i,j-1}^l}{\mathrm{\Delta }y},& q^{+}=\frac{{\mathrm{\Psi }}_{i,j+1}^l-{\mathrm{\Psi }}_{ij}^l}{\mathrm{\Delta }y}.\hfill \end{array}$$

The time step size $\mathit{\delta }t$ is chosen to satisfy the Courant-Friedrichs-Lewy condition which guarantees the stability of the time stepping scheme. If many time steps are necessary it is common to reinitialize the level set function every few steps for numerical stability. We use the signed distance function of the current domain (as defined by ${\mathrm{\Psi }}^l$) which we obtain via a fast marching algorithm.[49] In our numerical experiments the reinitialization was only rarely necessary.

8. Numerical experiments

We implemented the proposed projected gradient method in GNU Octave.[50] The routines for generating the geometry from the level set function and assembling the finite element mesh are using the Octave package level-set.[51] It also provides a method to compute the signed distance function using a fast marching algorithm.

In our numerical experiments the harbour basin $Q$ corresponds to the box $|x|\le 0.4,$ and $-0.3\le y\le 0.0$. The harbour approach is given by $|x|\le 0.1,0\le y$ and the isle by $|x|\le 0.55,-0.6\le y\le -0.4$. We present the results for two different initial layouts of the breakwater ${\mathrm{\Gamma }}_B$, cf. Figure 2. The computational effort is reduced by imposing that everything outside the box $-1\le x,y\le 1$ is ocean. We study an incoming wave with wave number $k=7$ and compare the effects of different scalar products for the computation of the projected gradient. We present results for the choices ${(·,·)}_a={(·,·)}_{H^1(D)}$ and an approximation of the bi-Laplacian scalar product, i.e.$${(·,·)}_a\approx {(·,·)}_{L^2(D)}+{(\mathrm{\Delta }·,\mathrm{\Delta }·)}_{L^2(D)}.$$

Furthermore, we experiment with an $H^1$ gradient which is projected with respect to the $L^2$ scalar product. Note that in this case we are not guaranteed to have a descent direction, cf. Section 5. However, this choice also has some advantages and, with a slight modification, performs sometimes better than the other two variants.

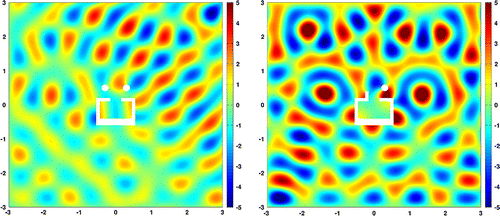
For the first experiment the regular grid consists of $501\times 501$ points and the incident wave direction is $w={(\sqrt{0.5},-\sqrt{0.5})}^T$. The initial geometry can be seen on the left side of Figure 2. Note the wave resonance in the harbour basin. In order to be able to compare the results, the $L^2$ norm of the projected gradient is used as performance criterion in all examples. Note that optimization and discretization do not commute in our approach. Furthermore, we are only using a first-order method, hence convergence towards a critical point of the discrete problem cannot be expected in a reasonable number of steps. We stop the algorithm either if the $L^2$ norm of the gradient is below 1.0e-5 or after 3000 iterations. In general, the performance of the different methods reflects the smoothness of the different gradients. Whereas the bi-Laplacian and $H^1$ gradients smoothly transform the initial geometry, the $L^2$ projected gradient leads to more drastic shape and topology changes at the beginning of the optimization. This is not only due to the decreased regularity. The $L^2$ projected gradient is not pulled down to zero in the vicinity of the forbidden region, thus allowing the breakwater to touch the forbidden region and to move away again in later iterations. If we introduce a rescaling of the gradient if it is larger than a given threshold the $L^2$ projected gradient method is well behaved and actually often leads to better results than its smoother counterparts. This might be explained by a greater flexibility of the gradient which allows more local changes.

A note regarding topology changes: although the algorithm allows topology changes we do not compute a topological derivative. Hence, the sensitivity with regard to topology changes is not represented in the geometry update. This can lead to very small step sizes or even a stalling of the algorithm if this update leads to topology changes which increase the objective value. This observation motivates the use of non-monotone line search methods and is subject of current research.

Figure 2. Wave pattern for initial geometry of the first (left) and second experiment (right).

Figure 3. Experiment 1: Convergence of the $H^1$ projected gradient method (left) and the bi-Laplacian gradient method (right).

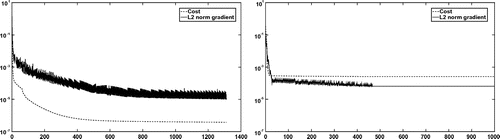
Figure 4. Experiment 1: Wave pattern for the optimized geometry using the $H^1$ projected gradient (left) and the bi-Laplacian gradient (right).

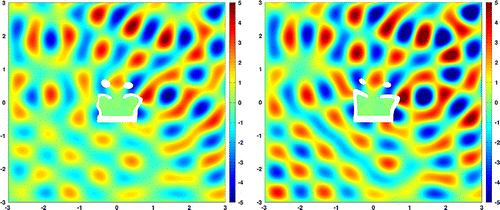
Figure 5. Experiment 1: Wave pattern for the optimized geometry using the $L^2$ projected gradient without rescaling (left) and with rescaling (right).

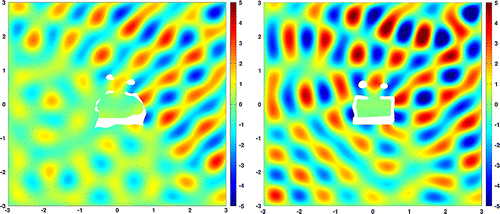
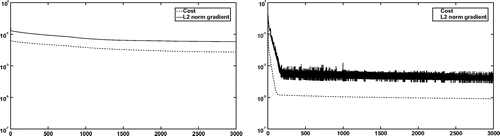
Figure 6. Experiment 1: Convergence of the $L^2$ projected gradient method without rescaling (left) and with rescaling (right).

The $H^1$ gradient method reaches in iteration 1312 an $L^2$ norm of the gradient below 1.0e-5 and is terminated. The objective value of 3.8e-7 is very close to the lower bound of 0. The bi-Laplacian gradient method gets stuck after 467 iterations. Whereas the $L^2$ norm of the gradient 6.5e-5 is already pretty small the objective 2.6e-4 is several orders of magnitude higher than the result of the $H^1$ gradient method. If we take a look at the convergence plots in Figure 3 we see that in the beginning the bi-Laplacian gradient method reduces the $L^2$ norm of the gradient much faster than the $H^1$ gradient method. Comparing the final geometries in Figure 4 shows that the lower regularity of the $H^1$ gradient allows for more flexible changes which lead to a better objective value. The same behaviour could be observed in other tests as well. The bi-Laplacian gradient method reduces the $L^2$ norm of the gradient quickly in few iterations, but then gets stuck. If we project the $H^1$ gradient with respect to the $L^2$ scalar product (effectively simply cutting it off in the forbidden regions) we observe a heavily deformed breakwater with topology changes, cf. Figure 5. But the convergence plot, cf. Figure 6, shows that the descent is very slow, after the first iterations only very small step sizes are chosen. In iteration 3000 the objective value is 7.4e-3 and the $L^2$ norm of the gradient is 3.3e-2. If the mentioned rescaling of large gradients is introduced a much better performance can be observed. After 3000 iterations the objective value is 8.3e-6 and the $L^2$ norm of the gradient is 2.5e-4.

Figure 7. Experiment 2: Wave pattern for the final geometry using the $H^1$ projected gradient (left) and the bi-Laplacian gradient (right).

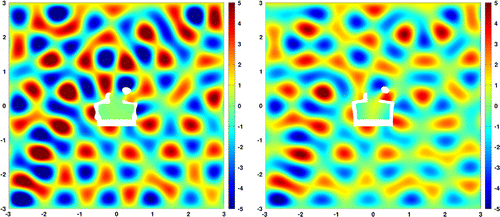
Figure 8. Experiment 2: Convergence of the $L^2$ projected gradient method without rescaling (left) and with rescaling (right).

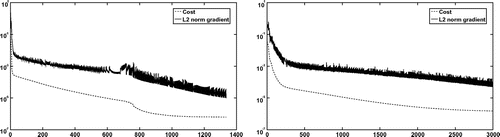
Figure 9. Experiment 2: Wave pattern for the optimized geometry using the $L^2$ projected gradient without rescaling (left) and with rescaling (right).

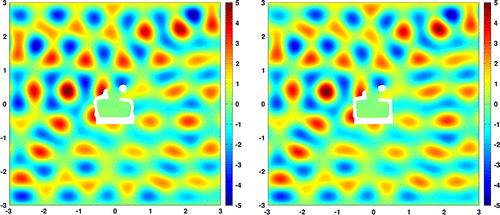
In the second experiment the regular grid consists of $601\times 601$ points and the incident wave direction is $w={(0,-1)}^T$. The initial geometry can be seen on the right side of Figure 2. After a good start the $H^1$ projected gradient method is slowly decreasing the objective and after 3000 iterations achieves an objective value of 1.7e-5 and the $L^2$ norm of the gradient is 4.7e-4. The bi-Laplacian gradient method gets stuck already after seven iterations. The final geometries are shown in Figure 7. In this example, the $L^2$ projected gradient performs the best. After 3000 iterations the rescaled method achieves an objective value of 1.5e-6 and the $L^2$ norm of the gradient is 8.4e-5. And without rescaling of the gradient it is even better. After choosing small step sizes in the first iterations the algorithm terminates in iteration 1337 with an $L^2$ norm of the gradient below 1.0e-5 and an objective value of 6.3e-7. The convergence plots are shown in Figure 8 and the optimized geometries in Figure 9.

In most of our experiments the volume of the breakwater did not vary much during the optimization. Still it might be interesting to add a volume constraint which might be realized by e.g. an Augmented Lagrange method.

9. Possible extensions and future research

This paper is just a first step towards a very interesting (real) application of shape optimization and should be considered a proof of concept. Various simplifications were made in the derivation of the physical model and need to be reconsidered in a more realistic setting. However, we think that these do not lead to fundamental new difficulties, only the derivation of the shape derivative and the actual implementation will require more effort. Furthermore, the model problem is easily extended to a situation where several different incident waves are considered. From the optimization point of view also various extensions are possible. As already mentioned the possibility of topology changes, which are not represented in the shape derivative, makes non-monotone line search methods a promising alternative. Moreover it would be interesting to consider, at least partially, second-order information in the scalar product ${(·,·)}_a$ or employ other speed-up strategies like non-linear conjugate gradients or approximate Newton-type methods. Finally, as mentioned in Section 5, other strategies for handling the geometric constraints are possible. Some of these topics are already subject of current research.

Acknowledgements

We wish to thank Prof. Wolfgang Ring (University of Graz) for valuable discussions and a careful proofreading of this article. Furthermore, we thank the anonymous referees for their feedback which helped us clarify the presentation.

Additional information

Funding

We gratefully acknowledge support from the International Research Training Group IGDK1754, funded by the German Science Foundation (DFG) and the Austrian Science Fund (FWF). The computations were carried out on a Linux cluster that was partially funded by the grant DFG INST 95/919-1 FUGG.

Notes

No potential conflict of interest was reported by the authors.