A Radon-type transform arising in photoacoustic tomography with circular detectors: spherical geometry

Abstract

In this paper, we propose a detector geometry for photoacoustic tomography that offers the practical advantage that it could be implemented with a single circular detector. The Radon-type transform that arises can be decomposed into the spherical Radon transform and the Funk–Minkowski transform. An inversion formula and a range description are obtained by combining existing inversion formulas and range descriptions for the spherical Radon transform and the Funk–Minkowski transform. Numerical simulations are performed to demonstrate our proposed algorithm.

Keywords:

• Radon transform
• tomography
• photoacoustic
• thermoacoustic
• integrating detectors

AMS Subject Classifications:

• 44A12
• 65R10
• 92C55
• 35L05

1. Introduction

Hybrid biomedical imaging modalities have been an active area of research lately, combining different physical signals in order to utilize their advantages to enhance images. Photoacoustic tomography (PAT), which incorporates ultrasound and optical or radio-frequency electromagnetic waves, is one of the most successful examples of such a combination. Whilst pure ultrasound imaging typically leads to high-resolution images, the contrast between cancerous and healthy tissue is rather low. On the other hand, optical or radio-frequency electromagnetic imaging can provide a significant contrast; however, it has low resolution. The photoacoustic effect, discovered by Bell [1], allows one to take advantage of the strengths of the pure optical and ultrasound imaging, and it forms the basis of PAT.

In PAT, an object of interest is irradiated by pulsed non-ionizing electromagnetic energy. Due to the photoacoustic effect, an acoustic wave dependent on the electromagnetic absorption properties of the object is generated.[2,3] This wave is then measured by ultrasound detectors placed outside the object. The internal photoacoustic sources are reconstructed from the measurements to produce a three-dimensional image (tomogram). Irradiated cancerous tissues, in particular, are displayed with high contrast. This is due to the fact that such tissues absorb several times more electromagnetic energy than healthy ones, and electromagnetic deposition is proportional to the strength of the generated acoustic wave. Since the initially generated acoustic wave contains diagnostic information, one of the classical mathematical problems of PAT is the recovery of this initial acoustic pressure field from ultrasound measurements made outside the object.

The initial approach for detecting ultrasound signals in PAT has been to use small piezoelectric transducers. As these transducers mimic point-like measurements, reconstruction algorithms produce images with a spatial resolution limited by the size of the transducers. Another drawback of such detectors is the difficulty in manufacturing small transducers with high sensitivity. To overcome these deficiencies, various other types of acoustic detectors have been introduced, e.g. linear, planar, cylindrical and circular detectors.[4–9] These detectors are modelled as measuring the integrals of the pressure over the shape of the detector.

Some works [9–11,13] have considered PAT with circular integrating detectors on cylindrical geometry: a stack of parallel circular detectors whose centres lie on a cylinder. It was shown that the data from PAT with circular detectors is the solution of a certain initial value problem, and this fact was used to reduce the problem of recovery of the initial pressure to that of inversion of the circular Radon transform in [9,12,13]. The cases where the centres of the circular detectors are located on a plane or a sphere have been discussed in [10]. In [12], Zangerl and Scherzer studied PAT with circular integrating detectors in a spherical geometry. The authors proposed circular detectors of various sizes with centres moving on a fixed plane.

Here, we also consider a spherical geometry and circular detectors; however, the set-up is different, as only detectors with the same radius are required and the centres of all circular detectors are fixed at the origin, see Figure 1. The data could therefore be gathered by repeating the experiment with a single detector that is rotated about the origin. Also, our approach is to define a Radon-type transform arising in this version of PAT, and we show that this transform can be decomposed into the spherical Radon transform and the Minkowski–Funk transform, both of which are well studied.

This paper is organized as follows. Section 2 is devoted to the construction of a Radon-type transform arising in PAT with circular integrating detectors. In Section 3, we show that the Radon-type transform is the composition of the Minkowski–Funk transform and the spherical Radon transform with centres on a sphere, and we present the inversion formula using this fact. In Section 4, we describe the range of this Radon-type transform, and we give necessary and sufficient conditions for a function to arise as data measured by the circular detectors in the spherical geometry. Section 5 is concerned with numerical implementation. Section 6 contains some final remarks. The appendices provide proofs of some technical statements.

2. PAT with circular integrating detectors

In PAT, the acoustic pressure $p(\overrightarrow{x},t)$ satisfies the following initial value problem:(1) $$\begin{array}{c}\hfill \begin{array}{ccc}& {\mathit{\partial }}_t^{2}p(\overrightarrow{x},t)={\mathrm{\Delta }}_{\overrightarrow{x}}p(\overrightarrow{x},t)\hfill & (\overrightarrow{x},t)\in {\mathbb{R}}^3\times (0,\infty ),\hfill \\ \hfill & p(\overrightarrow{x},0)=f(\overrightarrow{x})\hfill & \overrightarrow{x}=(x_1,x_2,x_3)\in {\mathbb{R}}^3,\hfill \\ \hfill & {\mathit{\partial }}_{t}p(\overrightarrow{x},0)=0\hfill & \overrightarrow{x}\in {\mathbb{R}}^3.\hfill \end{array}\end{array}$$(1)

Here, we assume that the sound speed is equal to $1$ everywhere, including the interior of the object. The goal of PAT is to recover the initial pressure $f$ from measurements of $p$ outside the support of $f$.

Throughout this article, it is assumed that the initial pressure field $f$ is smooth and supported in $B(0,r_{det})$ - the ball in ${\mathbb{R}}^3$ with radius $r_{det}$ centred at the origin. We also assume that the acoustic signals are measured by a set of circular detectors centred at the origin with radius $r_{det}$ - that is, the detector circles are great circles on the sphere $\mathit{\partial }B(0,r_{det})$ (see Figure 1).

Figure 1. The great circle on the sphere $\mathit{\partial }B(0,r_{det})$ of radius $r_{det}$ in the plane perpendicular to $\widehat{\mathit{\theta }}$.

The data $P(\widehat{\mathit{\theta }},t)$, for $(\widehat{\mathit{\theta }},t)\in S^2\times (0,\infty )$ measured by the circular detector lying in the plane perpendicular to $\widehat{\mathit{\theta }}$ (see Figure 1) can be expressed as$$P(\widehat{\mathit{\theta }},t)=\frac{1}{2\mathit{\pi }}{\int }_{\widehat{\mathit{\theta }}·\widehat{\mathit{\alpha }}=0}p(r_{det}\widehat{\mathit{\alpha }},t)dS(\widehat{\mathit{\alpha }}),$$

where $dS$ is the measure on the unit circle $S^1$.

Everywhere in the text we will use the hat notation to indicate a unit vector in two or three dimensions, and $dS$ to denote the measure either on the circle or on the sphere. The dimension will be clear from the context.

Using Kirchhoff’s formula for the solution of  (1(1) $$\begin{array}{c}\hfill \begin{array}{ccc}& {\mathit{\partial }}_t^{2}p(\overrightarrow{x},t)={\mathrm{\Delta }}_{\overrightarrow{x}}p(\overrightarrow{x},t)\hfill & (\overrightarrow{x},t)\in {\mathbb{R}}^3\times (0,\infty ),\hfill \\ \hfill & p(\overrightarrow{x},0)=f(\overrightarrow{x})\hfill & \overrightarrow{x}=(x_1,x_2,x_3)\in {\mathbb{R}}^3,\hfill \\ \hfill & {\mathit{\partial }}_{t}p(\overrightarrow{x},0)=0\hfill & \overrightarrow{x}\in {\mathbb{R}}^3.\hfill \end{array}\end{array}$$(1) ) (e.g. [14]):$$p(\overrightarrow{x},t)={\mathit{\partial }}_t\left(\frac{1}{4\mathit{\pi }t}{\int }_{\mathit{\partial }B(\overrightarrow{x},t)}f(\widehat{\mathit{\beta }})dS(\widehat{\mathit{\beta }})\right),$$

we can represent the measurements $P(\widehat{\mathit{\theta }},t)$ as follows:(2) $$\begin{array}{c}\hfill \begin{array}{cc}P(\widehat{\mathit{\theta }},t)\hfill & {\displaystyle =\frac{1}{2\mathit{\pi }}{\int }_{\widehat{\mathit{\theta }}·\widehat{\mathit{\alpha }}=0}{\mathit{\partial }}_t\left(\frac{1}{4\mathit{\pi }t}{\int }_{\mathit{\partial }B(r_{det}\widehat{\mathit{\alpha }},t)}f(\widehat{\mathit{\beta }})dS(\widehat{\mathit{\beta }})\right)dS(\widehat{\mathit{\alpha }})}\hfill \\ \hfill & {\displaystyle =\frac{1}{8{\mathit{\pi }}^2}{\mathit{\partial }}_t\left(t{\int }_{\widehat{\mathit{\theta }}·\widehat{\mathit{\alpha }}=0}{\int }_{S^2}f(r_{det}\widehat{\mathit{\alpha }}+t\widehat{\mathit{\beta }})dS(\widehat{\mathit{\beta }})dS(\widehat{\mathit{\alpha }})\right),}\hfill \end{array}\end{array}$$(2)

where $S^2$ is the unit sphere in ${\mathbb{R}}^3$. Let us define the new Radon-type transform$${\displaystyle {\mathcal{R}}_{P}f(\widehat{\mathit{\theta }},t)={\int }_{\widehat{\mathit{\theta }}·\widehat{\mathit{\alpha }}=0}{\int }_{S^2}f(r_{det}\widehat{\mathit{\alpha }}+t\widehat{\mathit{\beta }})dS(\widehat{\mathit{\beta }})dS(\widehat{\mathit{\alpha }}).}$$

Then, (2(2) $$\begin{array}{c}\hfill \begin{array}{cc}P(\widehat{\mathit{\theta }},t)\hfill & {\displaystyle =\frac{1}{2\mathit{\pi }}{\int }_{\widehat{\mathit{\theta }}·\widehat{\mathit{\alpha }}=0}{\mathit{\partial }}_t\left(\frac{1}{4\mathit{\pi }t}{\int }_{\mathit{\partial }B(r_{det}\widehat{\mathit{\alpha }},t)}f(\widehat{\mathit{\beta }})dS(\widehat{\mathit{\beta }})\right)dS(\widehat{\mathit{\alpha }})}\hfill \\ \hfill & {\displaystyle =\frac{1}{8{\mathit{\pi }}^2}{\mathit{\partial }}_t\left(t{\int }_{\widehat{\mathit{\theta }}·\widehat{\mathit{\alpha }}=0}{\int }_{S^2}f(r_{det}\widehat{\mathit{\alpha }}+t\widehat{\mathit{\beta }})dS(\widehat{\mathit{\beta }})dS(\widehat{\mathit{\alpha }})\right),}\hfill \end{array}\end{array}$$(2) ) reads as(3) $$\begin{array}{c}\hfill P(\widehat{\mathit{\theta }},t)=\frac{1}{8{\mathit{\pi }}^2}{\mathit{\partial }}_t\left(t{\mathcal{R}}_{P}f(\widehat{\mathit{\theta }},t)\right).\end{array}$$(3)

In what follows, ${\mathcal{R}}_P$ is seen to be the composition of the spherical Radon transform with centres on $\mathit{\partial }B(0,r_{det})$ and the Minkowski–Funk transform.

This observation will allow us to recover $f$ from the measurements $P$ as well as to describe necessary and sufficient conditions for a given function to arise as data measured by the circular integrating detectors.

3. Reconstruction

The following definitions will be used in the rest of this paper.

Definition 1:

The Minkowski–Funk transform $F$ maps a locally integrable function $\mathit{\varphi }$ defined on $S^2\times [0,\infty )$ such that $\mathit{\varphi }(\widehat{\mathit{\alpha }},t)=\mathit{\varphi }(-\widehat{\mathit{\alpha }},t)$ into$$F\mathit{\varphi }(\widehat{\mathit{\theta }},t)={\int }_{\widehat{\mathit{\theta }}·\widehat{\mathit{\alpha }}=0}\mathit{\varphi }(\widehat{\mathit{\alpha }},t)dS(\widehat{\mathit{\alpha }}),\text{for}(\widehat{\mathit{\theta }},t)\in S^2\times [0,\infty ).$$

Definition 2:

The spherical Radon transform $R_S$ maps a locally integrable function $f$ on ${\mathbb{R}}^3$ into$$R_{S}f(\widehat{\mathit{\alpha }},t)={\int }_{S^2}f(r_{det}\widehat{\mathit{\alpha }}+t\widehat{\mathit{\beta }})dS(\widehat{\mathit{\beta }}),\text{for}(\widehat{\mathit{\alpha }},t)\in S^2\times [0,\infty ).$$

Now it is easily seen that the following representation of ${\mathcal{R}}_{P}f$ holds.

Theorem 3:

For any $f\in C^{\infty }({\mathbb{R}}^3)$ compactly supported in $B(0,r_{det})$, we have ${\mathcal{R}}_{P}f(\widehat{\mathit{\theta }},t)=F(R_{S}f)(\widehat{\mathit{\theta }},t)$.

If $f$ is odd, i.e. $f(\overrightarrow{x})=-f(-\overrightarrow{x})$, then ${\mathcal{R}}_{P}f$ is equal to zero because $\mathit{\varphi }=R_{S}f$ is odd in $\widehat{\mathit{\alpha }}$ and $F\mathit{\varphi }$ is zero when $\mathit{\varphi }$ is odd. For purposes of imaging, we consider functions that are compactly supported in the upper hemisphere of $B(0,r_{det})$ and extend them to even functions with support in $B(0,r_{det})$. Thus, from now on, we will assume that $f$ is even.

In order to reconstruct the initial pressure $f$, we will employ known inversion formulas for the Minkowski–Funk and the spherical Radon transforms. A number of inversion formulas for these transforms have been derived, e.g. some of those for the spherical Radon transform can be found in [15–19] and those for the Minkowski–Funk transform are studied in [20–24].

We choose the inversion formula for the spherical Radon transform given in [15,16] and present the relation between the Minkowski–Funk transform and the regular Radon transform in the following theorem:

Theorem 4:

Let $\mathit{\varphi }$ be a continuous and even function on $S^2$, i.e. $\mathit{\varphi }(\widehat{\mathit{\theta }})=\mathit{\varphi }(-\widehat{\mathit{\theta }})$. If$$F\mathit{\varphi }(\widehat{\mathit{\theta }})={\int }_{\widehat{\mathit{\theta }}·\widehat{\mathit{\alpha }}=0}\mathit{\varphi }(\widehat{\mathit{\alpha }})dS(\widehat{\mathit{\alpha }}),\text{for}\widehat{\mathit{\theta }}\in S^2,$$

then, if $\widehat{\mathit{\theta }}\ne (0,0,1)$ and $\widehat{\mathit{\theta }}\ne (0,0,-1)$, the following relation holds,$$\begin{array}{c}\hfill F\mathit{\varphi }(\widehat{\mathit{\theta }})=\frac{1}{|{\mathit{\theta }}^{\prime }|}R\mathrm{\Phi }\left(\frac{{\mathit{\theta }}^{\prime }}{|{\mathit{\theta }}^{\prime }|},-\frac{{\mathit{\theta }}_3}{|{\mathit{\theta }}^{\prime }|}\right),\end{array}$$

where $\widehat{\mathit{\theta }}=({\mathit{\theta }}^{\prime },{\mathit{\theta }}_3)=({\mathit{\theta }}_1,{\mathit{\theta }}_2,{\mathit{\theta }}_3)\in S^2,\widehat{\mathit{\alpha }}=({\mathit{\alpha }}^{\prime },{\mathit{\alpha }}_3)\in S^2$, $\mathrm{\Phi }({\mathit{\alpha }}^{\prime }/{\mathit{\alpha }}_3)=2\mathit{\varphi }(\widehat{\mathit{\alpha }}){\mathit{\alpha }}_3^2$, and$$R[\mathrm{\Phi }(x_1,x_2)](\widehat{\mathit{\omega }},s)={\int }_{\mathbb{R}}\mathrm{\Phi }(s\widehat{\mathit{\omega }}+\mathit{\nu }{\widehat{\mathit{\omega }}}^{\perp })d\mathit{\nu },\text{for}(\widehat{\mathit{\omega }},s)\in S^1\times \mathbb{R}.$$

The proof of this Theorem is provided in the Appendix. Our main result is given in the theorem below.

Theorem 5:

Let $f\in C^{\infty }({\mathbb{R}}^3)$ be an even function with compact support in $B(0,r_{det})$. Then, if $G(\widehat{\mathit{\omega }},s,t)={(1+s^2)}^{-\frac{1}{2}}{\mathcal{R}}_{p}f\left(\widehat{\mathit{\omega }}/\sqrt{1+s^2},-s/\sqrt{1+s^2},t\right)$, the following relation holds:(4) $$\begin{array}{c}\hfill f(\overrightarrow{x})=-\frac{r_{det}}{64{\mathit{\pi }}^4}{\int }_{S^2}\left({\int }_{S^1}p.v.{\int }_{\mathbb{R}}\frac{{\mathit{\partial }}_s{\mathit{\partial }}_{t}t{\mathit{\partial }}_{t}tG(\widehat{\mathit{\omega }},s,t){|}_{t=|r_{det}\widehat{\mathit{\alpha }}-\overrightarrow{x}|}}{{\mathit{\alpha }}_3\widehat{\mathit{\omega }}·{\mathit{\alpha }}^{\prime }-s{\mathit{\alpha }}_3^2}\frac{dsdS(\widehat{\mathit{\omega }})}{|r_{det}\widehat{\mathit{\alpha }}-\overrightarrow{x}|}\right)dS(\widehat{\mathit{\alpha }}).\end{array}$$(4)

Proof:

Let $\mathit{\varphi }(\widehat{\mathit{\theta }},t)$ be a smooth function. From Theorem 4, we have(5) $$\begin{array}{c}\hfill F\mathit{\varphi }(\widehat{\mathit{\theta }},t)=\frac{1}{|{\mathit{\theta }}^{\prime }|}R[\mathrm{\Phi }(x_1,x_2,t)]\left(\frac{{\mathit{\theta }}^{\prime }}{|{\mathit{\theta }}^{\prime }|},-\frac{{\mathit{\theta }}_3}{|{\mathit{\theta }}^{\prime }|},t\right),\end{array}$$(5)

where $\widehat{\mathit{\theta }}=({\mathit{\theta }}^{\prime },{\mathit{\theta }}_3)$, $\widehat{\mathit{\alpha }}=({\mathit{\alpha }}^{\prime },{\mathit{\alpha }}_3)\in S^2$, $\mathrm{\Phi }({\mathit{\alpha }}^{\prime }/{\mathit{\alpha }}_3,t)=2\mathit{\varphi }(\widehat{\mathit{\alpha }},t){\mathit{\alpha }}_3^2$ and $R$ is the 2D Radon transform of $\mathrm{\Phi }$ with respect to the first two variables. That is,$$R[\mathrm{\Phi }(x_1,x_2,t)](\widehat{\mathit{\omega }},s,t)={\int }_{\mathbb{R}}\mathrm{\Phi }(s\widehat{\mathit{\omega }}+\mathit{\nu }{\widehat{\mathit{\omega }}}^{\perp },t)d\mathit{\nu },\text{for}(\widehat{\mathit{\omega }},s)\in S^1\times \mathbb{R}.$$

After changing variables $\widehat{\mathit{\theta }}\to (\widehat{\mathit{\omega }},-s)/\sqrt{1+s^2}$ in (5(5) $$\begin{array}{c}\hfill F\mathit{\varphi }(\widehat{\mathit{\theta }},t)=\frac{1}{|{\mathit{\theta }}^{\prime }|}R[\mathrm{\Phi }(x_1,x_2,t)]\left(\frac{{\mathit{\theta }}^{\prime }}{|{\mathit{\theta }}^{\prime }|},-\frac{{\mathit{\theta }}_3}{|{\mathit{\theta }}^{\prime }|},t\right),\end{array}$$(5) ) we obtain the relation(6) $$\begin{array}{c}\hfill R[\mathrm{\Phi }(x_1,x_2,t)](\widehat{\mathit{\omega }},s,t)=\frac{1}{\sqrt{1+s^2}}F\mathit{\varphi }\left(\frac{\widehat{\mathit{\omega }}}{\sqrt{1+s^2}},\frac{-s}{\sqrt{1+s^2}},t\right).\end{array}$$(6)

In order to recover $\mathrm{\Phi }$, we use the filtered backprojection formula for the inversion of the 2D Radon transform [25, Theorem 12.6].(7) $$\begin{array}{cc}\hfill \mathrm{\Phi }(x_1,x_2,t)& =\frac{1}{4\mathit{\pi }}(R^{\#}H{\mathit{\partial }}_{s}R\mathrm{\Phi })(x_1,x_2,t)\hfill \\ \hfill & =\frac{1}{4{\mathit{\pi }}^2}\underset{S^1}{\int }{\left.\left(p.v.{\int }_{\mathbb{R}}\frac{{\mathit{\partial }}_{s^{\prime }}(R\mathrm{\Phi })(\widehat{\mathit{\omega }},s^{\prime },t)}{s-s^{\prime }}d{s}^{\prime }\right)\right|}_{s=\overrightarrow{x}·\widehat{\mathit{\omega }}}dS(\widehat{\mathit{\omega }}),\hfill \end{array}$$(7)

where ${\displaystyle R^{\#}u(x_1,x_2):={\int }_{S^1}u(\widehat{\mathit{\omega }},(x_1,x_2)·\widehat{\mathit{\omega }})dS(\widehat{\mathit{\omega }})}$ is the backprojection operator and ${\displaystyle Hu(s):=p.v.\frac{1}{\mathit{\pi }}{\int }_{\mathbb{R}}\frac{u(s^{\prime })}{s-s^{\prime }}d{s}^{\prime }}$ is the Hilbert transform.

Applying (7(7) $$\begin{array}{cc}\hfill \mathrm{\Phi }(x_1,x_2,t)& =\frac{1}{4\mathit{\pi }}(R^{\#}H{\mathit{\partial }}_{s}R\mathrm{\Phi })(x_1,x_2,t)\hfill \\ \hfill & =\frac{1}{4{\mathit{\pi }}^2}\underset{S^1}{\int }{\left.\left(p.v.{\int }_{\mathbb{R}}\frac{{\mathit{\partial }}_{s^{\prime }}(R\mathrm{\Phi })(\widehat{\mathit{\omega }},s^{\prime },t)}{s-s^{\prime }}d{s}^{\prime }\right)\right|}_{s=\overrightarrow{x}·\widehat{\mathit{\omega }}}dS(\widehat{\mathit{\omega }}),\hfill \end{array}$$(7) )–(6(6) $$\begin{array}{c}\hfill R[\mathrm{\Phi }(x_1,x_2,t)](\widehat{\mathit{\omega }},s,t)=\frac{1}{\sqrt{1+s^2}}F\mathit{\varphi }\left(\frac{\widehat{\mathit{\omega }}}{\sqrt{1+s^2}},\frac{-s}{\sqrt{1+s^2}},t\right).\end{array}$$(6) ) leads to(8) $$\begin{array}{cc}\hfill \mathit{\varphi }(\widehat{\mathit{\alpha }},t)& =2^{-1}{\mathit{\alpha }}_3^{-2}\mathrm{\Phi }({\mathit{\alpha }}^{\prime }/{\mathit{\alpha }}_3,t)\hfill \\ \hfill & =\frac{1}{8\mathit{\pi }{\mathit{\alpha }}_3^2}{R}^{\#}\left(H{\mathit{\partial }}_s\left[\frac{1}{\sqrt{1+s^2}}F\mathit{\varphi }\left(\frac{\widehat{\mathit{\omega }}}{\sqrt{1+s^2}},\frac{-s}{\sqrt{1+s^2}},t\right)\right]\right)\left(\frac{{\mathit{\alpha }}^{\prime }}{{\mathit{\alpha }}_3},t\right).\hfill \end{array}$$(8)

Now let $\mathit{\varphi }(\widehat{\mathit{\alpha }},t)=(R_{S}f)(\widehat{\mathit{\alpha }},t)$. Theorem 3 implies that $F\mathit{\varphi }={\mathcal{R}}_{P}f$. Hence, we obtain the following expression for the spherical Radon transform of $f$:(9) $$\begin{array}{cc}\hfill R_{S}f(\widehat{\mathit{\alpha }},t)& =\frac{1}{8\mathit{\pi }{\mathit{\alpha }}_3^2}{R}^{\#}\left(H{\mathit{\partial }}_s\left[\frac{1}{\sqrt{1+s^2}}({\mathcal{R}}_{P}f)\left(\frac{\widehat{\mathit{\omega }}}{\sqrt{1+s^2}},\frac{-s}{\sqrt{1+s^2}},t\right)\right]\right)\left(\frac{{\mathit{\alpha }}^{\prime }}{{\mathit{\alpha }}_3},t\right)\hfill \\ \hfill & =\frac{1}{8\mathit{\pi }{\mathit{\alpha }}_3^2}{R}^{\#}H{\mathit{\partial }}_s\left[G(\widehat{\mathit{\omega }},s,t)\right]\left(\frac{{\mathit{\alpha }}^{\prime }}{{\mathit{\alpha }}_3},t\right).\hfill \end{array}$$(9)

In order to recover $f$, we apply the inversion formula for $R_S$ given in [16]:(10) $$\begin{array}{c}\hfill f(\overrightarrow{x})=-\frac{r_{det}}{8{\mathit{\pi }}^2}{\int }_{S^2}{\left.\frac{{\mathit{\partial }}_{t}t{\mathit{\partial }}_{t}t{R}_{S}f(\widehat{\mathit{\alpha }},t)}{t}\right|}_{t=|r_{det}\widehat{\mathit{\alpha }}-\overrightarrow{x}|}dS(\widehat{\mathit{\alpha }}).\end{array}$$(10)

Combining two Equations (9(9) $$\begin{array}{cc}\hfill R_{S}f(\widehat{\mathit{\alpha }},t)& =\frac{1}{8\mathit{\pi }{\mathit{\alpha }}_3^2}{R}^{\#}\left(H{\mathit{\partial }}_s\left[\frac{1}{\sqrt{1+s^2}}({\mathcal{R}}_{P}f)\left(\frac{\widehat{\mathit{\omega }}}{\sqrt{1+s^2}},\frac{-s}{\sqrt{1+s^2}},t\right)\right]\right)\left(\frac{{\mathit{\alpha }}^{\prime }}{{\mathit{\alpha }}_3},t\right)\hfill \\ \hfill & =\frac{1}{8\mathit{\pi }{\mathit{\alpha }}_3^2}{R}^{\#}H{\mathit{\partial }}_s\left[G(\widehat{\mathit{\omega }},s,t)\right]\left(\frac{{\mathit{\alpha }}^{\prime }}{{\mathit{\alpha }}_3},t\right).\hfill \end{array}$$(9) ) and (10(10) $$\begin{array}{c}\hfill f(\overrightarrow{x})=-\frac{r_{det}}{8{\mathit{\pi }}^2}{\int }_{S^2}{\left.\frac{{\mathit{\partial }}_{t}t{\mathit{\partial }}_{t}t{R}_{S}f(\widehat{\mathit{\alpha }},t)}{t}\right|}_{t=|r_{det}\widehat{\mathit{\alpha }}-\overrightarrow{x}|}dS(\widehat{\mathit{\alpha }}).\end{array}$$(10) ) gives us$$\begin{array}{c}\hfill f(\overrightarrow{x})=-\frac{r_{det}}{64{\mathit{\pi }}^3}\underset{S^2}{\int }\frac{1}{{\mathit{\alpha }}_3^2}{R}^{\#}\left[H{\mathit{\partial }}_s{\mathit{\partial }}_{t}t{\mathit{\partial }}_{t}tG(\widehat{\mathit{\omega }},s,t)\right]\left(\frac{{\mathit{\alpha }}^{\prime }}{{\mathit{\alpha }}_3},t\right){|}_{t=|r_{det}\widehat{\mathit{\alpha }}-\overrightarrow{x}|}\frac{dS(\widehat{\mathit{\alpha }})}{|r_{det}\widehat{\mathit{\alpha }}-\overrightarrow{x}|},\end{array}$$

which is equivalent to (4(4) $$\begin{array}{c}\hfill f(\overrightarrow{x})=-\frac{r_{det}}{64{\mathit{\pi }}^4}{\int }_{S^2}\left({\int }_{S^1}p.v.{\int }_{\mathbb{R}}\frac{{\mathit{\partial }}_s{\mathit{\partial }}_{t}t{\mathit{\partial }}_{t}tG(\widehat{\mathit{\omega }},s,t){|}_{t=|r_{det}\widehat{\mathit{\alpha }}-\overrightarrow{x}|}}{{\mathit{\alpha }}_3\widehat{\mathit{\omega }}·{\mathit{\alpha }}^{\prime }-s{\mathit{\alpha }}_3^2}\frac{dsdS(\widehat{\mathit{\omega }})}{|r_{det}\widehat{\mathit{\alpha }}-\overrightarrow{x}|}\right)dS(\widehat{\mathit{\alpha }}).\end{array}$$(4) ). $\square$

Corollary 6:

Let $f\in C^{\infty }({\mathbb{R}}^3)$ be an even function with compact support in $B(0,r_{det})$. Then, if $g(\widehat{\mathit{\omega }},s,t)={(1+s^2)}^{-\frac{1}{2}}P\left(\widehat{\mathit{\omega }}/\sqrt{1+s^2},-s/\sqrt{1+s^2},t\right)$, the following relation holds$$f(\overrightarrow{x})=-\frac{r_{det}}{8{\mathit{\pi }}^2}{\int }_{S^2}\left({\int }_{S^1}p.v.{\int }_{\mathbb{R}}\frac{{\mathit{\partial }}_s{\mathit{\partial }}_{t}tg(\widehat{\mathit{\omega }},s,t){|}_{t=|r_{det}\widehat{\mathit{\alpha }}-\overrightarrow{x}|}}{{\mathit{\alpha }}_3\widehat{\mathit{\omega }}·{\mathit{\alpha }}^{\prime }-s{\mathit{\alpha }}_3^2}\frac{\mathrm{d}s\mathrm{d}S(\widehat{\mathit{\omega }})}{|r_{det}\widehat{\mathit{\alpha }}-\overrightarrow{x}|}\right)dS(\widehat{\mathit{\alpha }}).$$

Indeed, since $P(\widehat{\mathit{\theta }},t)={(8{\mathit{\pi }}^2)}^{-1}{\mathit{\partial }}_{t}t{\mathcal{R}}_{P}f(\widehat{\mathit{\theta }},t)$ (see (3(3) $$\begin{array}{c}\hfill P(\widehat{\mathit{\theta }},t)=\frac{1}{8{\mathit{\pi }}^2}{\mathit{\partial }}_t\left(t{\mathcal{R}}_{P}f(\widehat{\mathit{\theta }},t)\right).\end{array}$$(3) )) we can write$$\begin{array}{c}\hfill g(\widehat{\mathit{\omega }},s,t)=\frac{1}{\sqrt{1+s^2}}P\left(\frac{\widehat{\mathit{\omega }}}{\sqrt{1+s^2}},\frac{-s}{\sqrt{1+s^2}},t\right)=\frac{{\mathit{\partial }}_{t}tG(\widehat{\mathit{\omega }},s,t)}{8{\mathit{\pi }}^2\sqrt{1+s^2}},\end{array}$$

where $G(\widehat{\mathit{\omega }},s,t)$ is the function defined in the preceding theorem. Then the result follows immediately from Theorem 5.

4. Range description

In this section, we describe the range of ${\mathcal{R}}_P$ and necessary and sufficient conditions for a function $P$ to arise as data measured by the circular detectors.

As mentioned before, the Minkowski–Funk transform and the spherical Radon transform are well studied, so their range descriptions have already been discussed (see [26–30]). In [29,30], it was proved that the Minkowski–Funk transform is a (continuous) bijection from $C_e^{\infty }(S^{n-1})$ to itself, where $C_e^{\infty }(S^{n-1})=\{\mathit{\varphi }\in C^{\infty }(S^{n-1}):\mathit{\varphi }(\widehat{\mathit{\theta }})=\mathit{\varphi }(-\widehat{\mathit{\theta }})\}$. Agranovsky et al. [26] provided four different types of complete range descriptions for the spherical mean transform. In particular, one of the range descriptions states that necessary and sufficient conditions for the function $g\in C_c^{\infty }(S^2\times [0,2r_{det}])$ to be representable as $g=R_{S}f$ for some $f\in C_c^{\infty }(B(0,r_{det}))$, is that for any integers $m,l$, the $(m,l)$th order spherical harmonic term ${({\mathbf{H}}_{\frac{n}{2}-1}g)}_{m,l}(\mathit{\lambda })$ of ${\mathbf{H}}_{\frac{n}{2}-1}g(\widehat{\mathit{\theta }},\mathit{\lambda })$ vanishes at non-zeros of the Bessel function $J_{m+n/2-1}(\mathit{\lambda })$, where$${\mathbf{H}}_{\frac{n}{2}-1}g(\widehat{\mathit{\theta }},\mathit{\lambda })={\int }_0^{\infty }g(\widehat{\mathit{\theta }},t)j_{\frac{n}{2}-1}(\mathit{\lambda }t)t^{n-1}\mathrm{d}t.$$

Here $j_n(t)$ is the spherical Bessel function:$$j_n(t)=\frac{2^n\mathrm{\Gamma }(n+1)J_n(t)}{t^n},$$

where $J_n(t)$ is the Bessel function of the first kind of order $n$ and $\mathrm{\Gamma }(t)$ is the Gamma function.

Combining these two range descriptions, we have the following range description for ${\mathcal{R}}_P$:

Theorem 7:

Let $g\in C_c^{\infty }(S^2\times [0,2r_{det}])$. The following conditions are necessary and sufficient for the function $g$ to be representable as $g={\mathcal{R}}_{P}f$ for some $f\in C_c^{\infty }(B(0,r_{det}))$:

• $g$ is even in $\widehat{\mathit{\theta }}\in S^2$, i.e. $g(\widehat{\mathit{\theta }},t)=g(-\widehat{\mathit{\theta }},t)$.

• For any positive integer $n$, let$${\mathbf{H}}_{\frac{n}{2}-1}g(\widehat{\mathit{\theta }},\mathit{\lambda })={\int }_0^{\infty }g(\widehat{\mathit{\theta }},t)j_{\frac{n}{2}-1}(\mathit{\lambda }t)t^{n-1}\mathrm{d}t.$$ Then for any integers $m,l$, the $(m,l)$th order spherical harmonic term ${({\mathbf{H}}_{\frac{n}{2}-1}g)}_{m,l}(\mathit{\lambda })$ of ${\mathbf{H}}_{\frac{n}{2}-1}g(\widehat{\mathit{\theta }},\mathit{\lambda })$ vanishes at non-zeros of the Bessel function $J_{m+n/2-1}(\mathit{\lambda })$.

Proof:

It is enough to show that the $(m,l)$th order spherical harmonic term ${({\mathbf{H}}_{\frac{n}{2}-1}g)}_{m,l}(\mathit{\lambda })$ of ${\mathbf{H}}_{\frac{n}{2}-1}g(\widehat{\mathit{\theta }},\mathit{\lambda })$ vanishes at non-zeros of the Bessel function $J_{m+n/2-1}(\mathit{\lambda })$ if and only if the $(m,l)$th order spherical harmonic term ${({\mathbf{H}}_{\frac{n}{2}-1}[F^{-1}g])}_{m,l}(\mathit{\lambda })$ of ${\mathbf{H}}_{\frac{n}{2}-1}[F^{-1}g](\widehat{\mathit{\theta }},\mathit{\lambda })$ vanishes at non-zeros of the Bessel function $J_{m+n/2-1}(\mathit{\lambda })$, where $F^{-1}$ is the inversion of the Minkowski–Funk transform.

In [22,24], the inversion formula for the Funk–Minkowski transform is presented as follows:$$\mathit{\varphi }(\widehat{\mathit{\alpha }})=\frac{1}{4{\mathit{\pi }}^2}{\left.\left\{\frac{\mathrm{d}}{\mathrm{d}u}{\int }_0^u{\int }_{S^2}F\mathit{\varphi }(\widehat{\mathit{\theta }})\mathit{\delta }(\widehat{\mathit{\theta }}·\widehat{\mathit{\alpha }}-\sqrt{1-v^2})\frac{\mathrm{d}S(\widehat{\mathit{\theta }})\mathrm{d}v}{{(u^2-v^2)}^{1/2}}\right\}\right|}_{u=1},$$

where $\mathit{\delta }$ is the Dirac delta function. Therefore, $F^{-1}g(\widehat{\mathit{\alpha }},t)$ can be represented as$$\frac{1}{4{\mathit{\pi }}^2}{\left.\left\{\frac{\mathrm{d}}{\mathrm{d}u}{\int }_0^u{\int }_{S^2}g(\widehat{\mathit{\theta }},t)\mathit{\delta }(\widehat{\mathit{\theta }}·\widehat{\mathit{\alpha }}-\sqrt{1-v^2})\frac{\mathrm{d}S(\widehat{\mathit{\theta }})\mathrm{d}v}{{(u^2-v^2)}^{1/2}}\right\}\right|}_{u=1}.$$

Consider the $(m,l)$th order spherical harmonic term ${({\mathbf{H}}_{\frac{n}{2}-1}[F^{-1}g])}_{m,l}(\mathit{\lambda })$:(11) $$\begin{array}{cc}& {({\mathbf{H}}_{\frac{n}{2}-1}[F^{-1}g])}_{m,l}(\mathit{\lambda })={\int }_{S^2}{\mathbf{H}}_{\frac{n}{2}-1}[F^{-1}g](\widehat{\mathit{\alpha }},\mathit{\lambda })Y_l^m(\widehat{\mathit{\alpha }})dS(\widehat{\mathit{\alpha }})\hfill \\ \hfill & =\frac{1}{4{\mathit{\pi }}^2}{\int }_{S^2}{\left.\left\{\frac{\mathrm{d}}{\mathrm{d}u}{\int }_0^u{\int }_{S^2}{\mathbf{H}}_{\frac{n}{2}-1}g(\widehat{\mathit{\theta }},\mathit{\lambda })\mathit{\delta }(\widehat{\mathit{\theta }}·\widehat{\mathit{\alpha }}-\sqrt{1-v^2})\frac{\mathrm{d}S(\widehat{\mathit{\theta }})\mathrm{d}v}{{(u^2-v^2)}^{1/2}}\right\}\right|}_{u=1}{Y}_l^m(\widehat{\mathit{\alpha }})dS(\widehat{\mathit{\alpha }})\hfill \\ \hfill & =\frac{1}{4{\mathit{\pi }}^2}{\left.\left\{\frac{\mathrm{d}}{\mathrm{d}u}{\int }_0^u{\int }_{S^2}{\mathbf{H}}_{\frac{n}{2}-1}g(\widehat{\mathit{\theta }},\mathit{\lambda }){\int }_{S^2}\mathit{\delta }(\widehat{\mathit{\theta }}·\widehat{\mathit{\alpha }}-\sqrt{1-v^2})Y_l^m(\widehat{\mathit{\alpha }})dS(\widehat{\mathit{\alpha }})\frac{\mathrm{d}S(\widehat{\mathit{\theta }})\mathrm{d}v}{{(u^2-v^2)}^{1/2}}\right\}\right|}_{u=1},\hfill \end{array}$$(11)

where in the last line, we used the Fubini–Tonelli Theorem.

To compute the inner integral with respect to $\widehat{\mathit{\alpha }}$ of (11(11) $$\begin{array}{cc}& {({\mathbf{H}}_{\frac{n}{2}-1}[F^{-1}g])}_{m,l}(\mathit{\lambda })={\int }_{S^2}{\mathbf{H}}_{\frac{n}{2}-1}[F^{-1}g](\widehat{\mathit{\alpha }},\mathit{\lambda })Y_l^m(\widehat{\mathit{\alpha }})dS(\widehat{\mathit{\alpha }})\hfill \\ \hfill & =\frac{1}{4{\mathit{\pi }}^2}{\int }_{S^2}{\left.\left\{\frac{\mathrm{d}}{\mathrm{d}u}{\int }_0^u{\int }_{S^2}{\mathbf{H}}_{\frac{n}{2}-1}g(\widehat{\mathit{\theta }},\mathit{\lambda })\mathit{\delta }(\widehat{\mathit{\theta }}·\widehat{\mathit{\alpha }}-\sqrt{1-v^2})\frac{\mathrm{d}S(\widehat{\mathit{\theta }})\mathrm{d}v}{{(u^2-v^2)}^{1/2}}\right\}\right|}_{u=1}{Y}_l^m(\widehat{\mathit{\alpha }})dS(\widehat{\mathit{\alpha }})\hfill \\ \hfill & =\frac{1}{4{\mathit{\pi }}^2}{\left.\left\{\frac{\mathrm{d}}{\mathrm{d}u}{\int }_0^u{\int }_{S^2}{\mathbf{H}}_{\frac{n}{2}-1}g(\widehat{\mathit{\theta }},\mathit{\lambda }){\int }_{S^2}\mathit{\delta }(\widehat{\mathit{\theta }}·\widehat{\mathit{\alpha }}-\sqrt{1-v^2})Y_l^m(\widehat{\mathit{\alpha }})dS(\widehat{\mathit{\alpha }})\frac{\mathrm{d}S(\widehat{\mathit{\theta }})\mathrm{d}v}{{(u^2-v^2)}^{1/2}}\right\}\right|}_{u=1},\hfill \end{array}$$(11) ), we need the Funk–Hecke theorem [31–33]: if ${\int }_{-1}^1|h(t)|\mathrm{d}t<\infty$,$$\begin{array}{cc}& {\int }_{S^{n-1}}h(\widehat{\mathit{\theta }}·\widehat{\mathit{\omega }})Y_l^m(\widehat{\mathit{\omega }})dS(\widehat{\mathit{\omega }})=c(n,m)Y_l^m(\widehat{\mathit{\theta }}),\hfill \\ \hfill & c(n,m)=|S^{n-2}|{\int }_{-1}^{1}h(t)C_m^{(n-2)/2}(t){(1-t^2)}^{(n-3)/2}\mathrm{d}t.\hfill \end{array}$$

Here $C_m^{\mathit{\nu }}(t),\mathit{\nu }>-1/2$ is the Gegenbauer polynomial of degree $m$ and $C_m^{\frac{1}{2}}(t)=P_m(t)$ is the Legendre polynomial of degree $m$. Applying the Funk–Hecke theorem to the inner integral of (11(11) $$\begin{array}{cc}& {({\mathbf{H}}_{\frac{n}{2}-1}[F^{-1}g])}_{m,l}(\mathit{\lambda })={\int }_{S^2}{\mathbf{H}}_{\frac{n}{2}-1}[F^{-1}g](\widehat{\mathit{\alpha }},\mathit{\lambda })Y_l^m(\widehat{\mathit{\alpha }})dS(\widehat{\mathit{\alpha }})\hfill \\ \hfill & =\frac{1}{4{\mathit{\pi }}^2}{\int }_{S^2}{\left.\left\{\frac{\mathrm{d}}{\mathrm{d}u}{\int }_0^u{\int }_{S^2}{\mathbf{H}}_{\frac{n}{2}-1}g(\widehat{\mathit{\theta }},\mathit{\lambda })\mathit{\delta }(\widehat{\mathit{\theta }}·\widehat{\mathit{\alpha }}-\sqrt{1-v^2})\frac{\mathrm{d}S(\widehat{\mathit{\theta }})\mathrm{d}v}{{(u^2-v^2)}^{1/2}}\right\}\right|}_{u=1}{Y}_l^m(\widehat{\mathit{\alpha }})dS(\widehat{\mathit{\alpha }})\hfill \\ \hfill & =\frac{1}{4{\mathit{\pi }}^2}{\left.\left\{\frac{\mathrm{d}}{\mathrm{d}u}{\int }_0^u{\int }_{S^2}{\mathbf{H}}_{\frac{n}{2}-1}g(\widehat{\mathit{\theta }},\mathit{\lambda }){\int }_{S^2}\mathit{\delta }(\widehat{\mathit{\theta }}·\widehat{\mathit{\alpha }}-\sqrt{1-v^2})Y_l^m(\widehat{\mathit{\alpha }})dS(\widehat{\mathit{\alpha }})\frac{\mathrm{d}S(\widehat{\mathit{\theta }})\mathrm{d}v}{{(u^2-v^2)}^{1/2}}\right\}\right|}_{u=1},\hfill \end{array}$$(11) ), the $(m,l)$th order spherical harmonic term ${({\mathbf{H}}_{\frac{n}{2}-1}[F^{-1}g])}_{m,l}(\mathit{\lambda })$ is equal to$$\begin{array}{c}\hfill \frac{1}{2\mathit{\pi }}{\left.\left\{\frac{\mathrm{d}}{\mathrm{d}u}{\int }_0^u{\int }_{S^2}{\mathbf{H}}_{\frac{n}{2}-1}g(\widehat{\mathit{\theta }},\mathit{\lambda })Y_l^m(\widehat{\mathit{\theta }})dS(\widehat{\mathit{\theta }})\frac{P_m(\sqrt{1-v^2})}{{(u^2-v^2)}^{1/2}}\mathrm{d}v\right\}\right|}_{u=1}.\end{array}$$

Thus, we have(12) $$\begin{array}{c}\hfill {({\mathbf{H}}_{\frac{n}{2}-1}[F^{-1}g])}_{m,l}(\mathit{\lambda })=\frac{{({\mathbf{H}}_{\frac{n}{2}-1}g)}_{m,l}(\mathit{\lambda })}{2\mathit{\pi }}{\left.\left\{\frac{\mathrm{d}}{\mathrm{d}u}{\int }_0^u\frac{P_m(\sqrt{1-v^2})}{{(u^2-v^2)}^{1/2}}\mathrm{d}v\right\}\right|}_{u=1}.\end{array}$$(12)

Since for any integer $m$, there exists a positive number $\mathit{ϵ}$ such that $P_m(\sqrt{1-v^2}){(u^2-v^2)}^{-1/2}$ is not equal to zero on the interval $[1-\mathit{ϵ},1]$, ${\int }_0^u{P}_m(\sqrt{1-v^2}){(u^2-v^2)}^{-1/2}\mathrm{d}v$ is not constant on $[1-\mathit{ϵ},1]$. Therefore, from (12(12) $$\begin{array}{c}\hfill {({\mathbf{H}}_{\frac{n}{2}-1}[F^{-1}g])}_{m,l}(\mathit{\lambda })=\frac{{({\mathbf{H}}_{\frac{n}{2}-1}g)}_{m,l}(\mathit{\lambda })}{2\mathit{\pi }}{\left.\left\{\frac{\mathrm{d}}{\mathrm{d}u}{\int }_0^u\frac{P_m(\sqrt{1-v^2})}{{(u^2-v^2)}^{1/2}}\mathrm{d}v\right\}\right|}_{u=1}.\end{array}$$(12) ), we have ${({\mathbf{H}}_{\frac{n}{2}-1}g)}_{m,l}(\mathit{\lambda })=0$ if and only if ${({\mathbf{H}}_{\frac{n}{2}-1}[F^{-1}g])}_{m,l}(\mathit{\lambda })=0$. $\square$

Since $P(\widehat{\mathit{\theta }},t)={(8{\mathit{\pi }}^2)}^{-1}{\mathit{\partial }}_{t}t{\mathcal{R}}_{P}f(\widehat{\mathit{\theta }},t)$, we have the following necessary and sufficient conditions for a function $P$ to be data measured by the circular detector from the initial pressure field.

Theorem 8:

Let $P\in C_c^{\infty }(S^2\times [0,2r_{det}])$. The following conditions are necessary and sufficient for the function $P$ to be data measured by the circular detectors from the initial pressure field $f\in C_c^{\infty }(B(0,r_{det}))$:

• $P$ is even in $\widehat{\mathit{\theta }}\in S^2$, i.e. $P(\widehat{\mathit{\theta }},t)=P(-\widehat{\mathit{\theta }},t)$.

• The integral of $P$ with respect to $t$ from $0$ to $2r_{det}$ is equal to zero.

• For any positive integer $n$, let$${\mathbf{H}}_{\frac{n}{2}-1}P(\widehat{\mathit{\theta }},\mathit{\lambda })={\int }_0^{\infty }{\int }_0^{t}P(\widehat{\mathit{\theta }},\mathit{\tau })j_{\frac{n}{2}-1}(\mathit{\lambda }t)t^{n-2}\mathrm{d}\mathit{\tau }\mathrm{d}t.$$ Then for any integers $m,l$, the $(m,l)$th order spherical harmonic term ${({\mathbf{H}}_{\frac{n}{2}-1}P)}_{m,l}(\mathit{\lambda })$ of ${\mathbf{H}}_{\frac{n}{2}-1}P(\widehat{\mathit{\theta }},\mathit{\lambda })$ vanishes at non-zeros of the Bessel function $J_{m+n/2-1}(\mathit{\lambda })$.

Proof:

Let us define a function $g$ on $S^2\times [0,2r_{det}]$ by$$g(\widehat{\mathit{\theta }},t)=\frac{1}{t}{\int }_0^{t}P(\widehat{\mathit{\theta }},\mathit{\tau })\mathrm{d}\mathit{\tau }.$$

Then $g$ is infinitely differentiable with respect to $t$ away from zero, $g(\widehat{\mathit{\theta }},0)=0$ is equivalent to $P(\widehat{\mathit{\theta }},0)=0$ by L’Hôpital’s rule, and $g(\widehat{\mathit{\theta }},2r_{det})=0$ is equivalent to$${\int }_0^{2r_{det}}P(\widehat{\mathit{\theta }},\mathit{\tau })\mathrm{d}\mathit{\tau }=0.$$

It is sufficient to show that $g$ is infinitely differentiable and continuous at 0. This will be accomplished in the following two lemmas, which are proved in Appendix 1.

Lemma 9:

Let $\mathit{\varphi }\in C^{\infty }([0,\mathit{ϵ}])$ for some $\mathit{ϵ}>0$ satisfy $\mathit{\varphi }(0)=0$, and let $n$ be a positive integer. For any positive integer $k\le n$, we have$${\int }_0^t\mathit{\varphi }(\mathit{\tau }){\mathit{\partial }}_t^k\left(\frac{{(t-\mathit{\tau })}^{n+1}}{t}\right)\mathrm{d}\mathit{\tau }\to 0\text{as}t\to 0.$$

Lemma 9 is used to prove:

Lemma 10:

Let $\mathit{\varphi }\in C^{\infty }([0,\mathit{ϵ}])$ satisfy $\mathit{\varphi }(0)=0$, and let $h(t)={\int }_0^t\mathit{\varphi }(\mathit{\tau })\mathrm{d}\mathit{\tau }/t$. Then $h\in C^{\infty }([0,\mathit{ϵ}])$ and $h(0)=0$.

Theorem 7 now immediately follows by applying Lemma 10 to $g(\widehat{\mathit{\theta }},t)$ considered as a function of $t$ for fixed $\widehat{\mathit{\theta }}$. $\square$

5. Numerical experiments

In this section, we show the results of numerical experiments reconstructing the initial pressure field $f$ from the data $P(\widehat{\mathit{\theta }},t)=\frac{1}{8{\mathit{\pi }}^2}{\mathit{\partial }}_t\left(t{\mathcal{R}}_{P}f(\widehat{\mathit{\theta }},t)\right)$. We set $r_{det}=1$ and assume that $P(\widehat{\mathit{\theta }},t)$ is given on a rectangular grid in the polar and azimuthal angles and a uniform grid in $t\in [0,2]$.

We follow the method of reconstruction provided by Theorem 5, namely,

(1)	Given the data $P(·,t)$, invert the Funk–Minkowski transform for each fixed $t$ to get the values of $p(\widehat{\mathit{\theta }},t)$ on $S^2\times [0,2]$
(2)	Invert the wave operator to compute $f(\overrightarrow{x})$

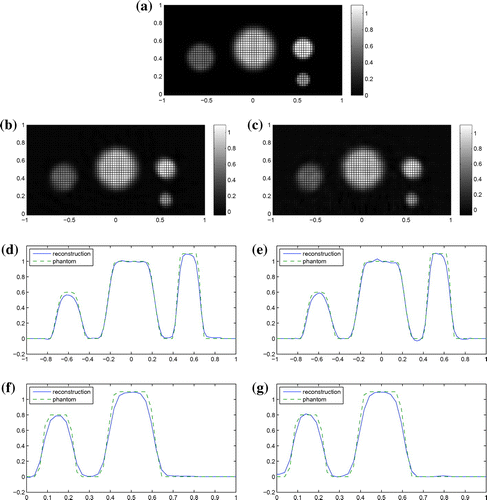
Figure 2. Reconstructions of a sharp phantom with centres $(0,-0.6,0.4)$, $(0,0,0.5)$, $(0,0.55,0.5)$, and $(0,0.55,0.15)$, radii 0.2, 0.3, 0.15, and 0.1 and values 0.6, 1, 1.1, and 0.8, respectively. (a) Cross section of the phantom in the $x_2{x}_3$-plane, (b) Cross section of the reconstruction in the $x_2{x}_3$-plane, (c) Slice of the reconstruction and phantom along the $x_3$-axis and (d) Slice of the reconstruction and phantom along the line $x_1=0,x_3=0.5$.

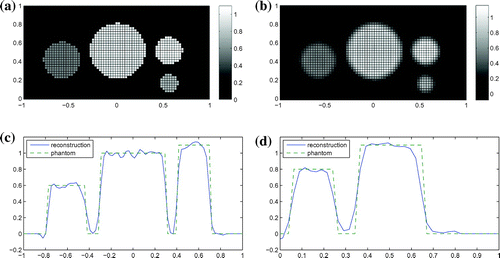
Figure 3. Reconstructions of a smooth phantom with centres $(0,-0.6,0.4)$, $(0,0,0.5)$, $(0,0.55,0.5)$ and $(0,0.55,0.15)$, outer radii 0.2, 0.3, 0.15 and 0.1, inner radii 0.1, 0.15, 0.075 and 0.05 and central values 0.6, 1, 1.1 and 0.8, respectively. (a) Cross section of the phantom in the $x_2{x}_3$-plane, (b) Cross section of the reconstruction in the $x_2{x}_3$-plane from exact data, (c) Cross section of the reconstruction in the $x_2{x}_3$-plane from data with 20% uniform random noise, (d) Slice of the reconstruction and phantom along the $x_3$-axis from exact data, (e) Slice of the reconstruction and phantom along the $x_3$-axis from data with 20% uniform random noise, (f) Slice of the reconstruction and phantom along the line $x_1=0,x_3=0.5$ from exact data, (g) Slice of the reconstruction and phantom along the line $x_1=0,x_3=0.5$ from data with 20% uniform random noise.

Our phantoms are taken to be either sum of multiples of characteristic functions of balls(13) $$\begin{array}{c}\hfill {\mathit{\chi }}_0(\overrightarrow{x})=c\left\{\begin{array}{cc}1\hfill & \text{if}|\overrightarrow{x}-\overrightarrow{x_0}|<r\hfill \\ 0\hfill & \text{if}|\overrightarrow{x}-\overrightarrow{x_0}|\ge r\hfill \end{array}\right.\end{array}$$(13)

or the sum of $C^1$-functions of the form(14) $$\begin{array}{c}\hfill {\mathit{\chi }}_1(\overrightarrow{x})=c\mathit{\phi }\left(|\overrightarrow{x}-\overrightarrow{x_0}{|}^2\right),\end{array}$$(14)

where $\mathit{\phi }$ is defined by$$\begin{array}{c}\hfill \mathit{\phi }\left(s^2\right)=\left\{\begin{array}{cc}1\hfill & \text{if}|s|\le r\hfill \\ {\displaystyle 1-3{\left(\frac{s-r}{R-r}\right)}^2+2{\left(\frac{s-r}{R-r}\right)}^3}\hfill & \text{if}r<|s|<R\hfill \\ 0\hfill & \text{if}|s|\ge R\hfill \end{array}\right.\end{array}$$

and $0<r<R$. Our algorithm reconstructs the even part of the phantom, so we consider only phantoms supported in the upper half of the unit ball.

The acoustic pressure generated by ${\mathit{\chi }}_0$ is$$\begin{array}{c}\hfill p(\overrightarrow{x},t)=\left\{\begin{array}{cc}{\displaystyle c\frac{|\overrightarrow{x}-\overrightarrow{x_0}|-t}{2|\overrightarrow{x}-\overrightarrow{x_0}|}}\hfill & \text{if}|\overrightarrow{x}-\overrightarrow{x_0}|-t<r\hfill \\ 0\hfill & \text{if}|\overrightarrow{x}-\overrightarrow{x_0}|-t\ge r\hfill \end{array}\right.\end{array}$$

and the acoustic pressure generated by ${\mathit{\chi }}_1$ is given by$$\begin{array}{c}\hfill p(\overrightarrow{x},t)=c\frac{|\overrightarrow{x}-\overrightarrow{x_0}|-t}{2|\overrightarrow{x}-\overrightarrow{x_0}|}\mathit{\phi }\left((|\overrightarrow{x}-\overrightarrow{x_0}|-t{)}^2\right)\end{array}$$(see [34, Theorem 5.2]). In order to compute the data $P(\widehat{\mathit{\theta }},t)$ measured by our detectors, we use a quadrature on each detector circle at each grid point in $t$, with the trapezoid rule and 100 points.

The Funk–Minkowski transform is inverted at each time step using the inverse two-dimensional Radon transform as prescribed by Theorem 4. A direct inversion of $F$ using Theorem 4 would involve dividing by ${\mathit{\alpha }}_3^2$, which could cause instability near the ${\mathit{\alpha }}_1{\mathit{\alpha }}_2$-plane. To avoid this, one possible remedy is to cyclically permute ${\mathit{\theta }}_1$, ${\mathit{\theta }}_2$, and ${\mathit{\theta }}_3$ in (5(5) $$\begin{array}{c}\hfill F\mathit{\varphi }(\widehat{\mathit{\theta }},t)=\frac{1}{|{\mathit{\theta }}^{\prime }|}R[\mathrm{\Phi }(x_1,x_2,t)]\left(\frac{{\mathit{\theta }}^{\prime }}{|{\mathit{\theta }}^{\prime }|},-\frac{{\mathit{\theta }}_3}{|{\mathit{\theta }}^{\prime }|},t\right),\end{array}$$(5) ) and sum the results to obtain$$\begin{array}{c}\hfill 2p(\widehat{\mathit{\alpha }},t)({\mathit{\alpha }}_1^2+{\mathit{\alpha }}_2^2+{\mathit{\alpha }}_3^2)=2p(\widehat{\mathit{\alpha }},t).\end{array}$$

In fact, we can further reduce the contribution from points near the ${\mathit{\alpha }}_i=0$ plane (where ${\mathit{\alpha }}_i$ is the coordinate in the denominator of (5(5) $$\begin{array}{c}\hfill F\mathit{\varphi }(\widehat{\mathit{\theta }},t)=\frac{1}{|{\mathit{\theta }}^{\prime }|}R[\mathrm{\Phi }(x_1,x_2,t)]\left(\frac{{\mathit{\theta }}^{\prime }}{|{\mathit{\theta }}^{\prime }|},-\frac{{\mathit{\theta }}_3}{|{\mathit{\theta }}^{\prime }|},t\right),\end{array}$$(5) ) after a cyclic permutation of ${\mathit{\theta }}_1$, ${\mathit{\theta }}_2$, and ${\mathit{\theta }}_3$). To achieve this we multiply the result of (5(5) $$\begin{array}{c}\hfill F\mathit{\varphi }(\widehat{\mathit{\theta }},t)=\frac{1}{|{\mathit{\theta }}^{\prime }|}R[\mathrm{\Phi }(x_1,x_2,t)]\left(\frac{{\mathit{\theta }}^{\prime }}{|{\mathit{\theta }}^{\prime }|},-\frac{{\mathit{\theta }}_3}{|{\mathit{\theta }}^{\prime }|},t\right),\end{array}$$(5) ) by ${\mathit{\alpha }}_i^k$ and sum the results:$$\begin{array}{c}\hfill 2p(\widehat{\mathit{\alpha }},t)({\mathit{\alpha }}_1^{k+2}+{\mathit{\alpha }}_2^{k+2}+{\mathit{\alpha }}_3^{k+2}).\end{array}$$

The function $p(\widehat{\mathit{\alpha }},t)$ is then easily obtained by dividing by $2({\mathit{\alpha }}_1^{k+2}+{\mathit{\alpha }}_2^{k+2}+{\mathit{\alpha }}_3^{k+2})$. In our reconstructions, we use $k=2$ in this formula.

In our experiments, the function $p(\widehat{\mathit{\theta }},t)$ is reconstructed on a spherical grid of 50 polar angles and 200 azimuthal angles, for a grid of 50 values of $t$ on the interval [0,2]. The polar angles range from $[\mathit{\pi }/25,\mathit{\pi }/2]$.

We start our polar grid slightly away from 0 because when we invert the Funk–Minkowski transform using Theorem 4, small values of the polar angle correspond to $s$ values near infinity, and having to account for large values of $s$ makes implementation of the inverse Radon transform difficult. It is also not necessary to take polar angles past $\mathit{\pi }/2$ because we are reconstructing the even part of $f$. Our final reconstructions are calculated on an $80\times 80\times 80$ grid in $\overrightarrow{x}$.

Figure 2 shows the reconstruction of a phantom comprising four sharp balls of the form (13(13) $$\begin{array}{c}\hfill {\mathit{\chi }}_0(\overrightarrow{x})=c\left\{\begin{array}{cc}1\hfill & \text{if}|\overrightarrow{x}-\overrightarrow{x_0}|<r\hfill \\ 0\hfill & \text{if}|\overrightarrow{x}-\overrightarrow{x_0}|\ge r\hfill \end{array}\right.\end{array}$$(13) ) from exact data. A reconstruction of a smooth phantom comprising four functions of the form (14(14) $$\begin{array}{c}\hfill {\mathit{\chi }}_1(\overrightarrow{x})=c\mathit{\phi }\left(|\overrightarrow{x}-\overrightarrow{x_0}{|}^2\right),\end{array}$$(14) ) from exact and noisy data is shown in Figure 3.

6. Conclusion

We studied a Radon-type transform arising in PAT with circular detectors and showed that it can be decomposed into the Funk–Minkowski transform and the spherical Radon transform. An inversion formula and range conditions were provided. In addition, numerical experiments demonstrated the feasibility of the reconstruction formula and showed good reconstructions from noisy data.

Acknowledgements

The authors are grateful to the anonymous referees for the useful suggestions which helped to improve the paper.

Additional information

Funding

S. Moon was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of science, ICT and future planning [grant number 2015R1C1A1A02037662].

Notes

No potential conflict of interest was reported by the authors.

Appendix 1

Proofs of Theorem 4 and Lemmas 9 and 10

Theorem 4:

Let $\mathit{\varphi }$ be a continuous and even function on $S^2$, i.e. $\mathit{\varphi }(\widehat{\mathit{\theta }})=\mathit{\varphi }(-\widehat{\mathit{\theta }})$. If$$F\mathit{\varphi }(\widehat{\mathit{\theta }})={\int }_{\widehat{\mathit{\theta }}·\widehat{\mathit{\alpha }}=0}\mathit{\varphi }(\widehat{\mathit{\alpha }})dS(\widehat{\mathit{\alpha }}),\text{for}\widehat{\mathit{\theta }}\in S^2,$$

then, if $\widehat{\mathit{\theta }}\ne (0,0,1)$ and $\widehat{\mathit{\theta }}\ne (0,0,-1)$, the following relation holds,(A1) $$\begin{array}{c}\hfill F\mathit{\varphi }(\widehat{\mathit{\theta }})=\frac{1}{|{\mathit{\theta }}^{\prime }|}R\mathrm{\Phi }\left(\frac{{\mathit{\theta }}^{\prime }}{|{\mathit{\theta }}^{\prime }|},-\frac{{\mathit{\theta }}_3}{|{\mathit{\theta }}^{\prime }|}\right),\end{array}$$(A1)

where $\widehat{\mathit{\theta }}=({\mathit{\theta }}^{\prime },{\mathit{\theta }}_3)=({\mathit{\theta }}_1,{\mathit{\theta }}_2,{\mathit{\theta }}_3)\in S^2,\widehat{\mathit{\alpha }}=({\mathit{\alpha }}^{\prime },{\mathit{\alpha }}_3)\in S^2$, $\mathrm{\Phi }({\mathit{\alpha }}^{\prime }/{\mathit{\alpha }}_3)=2\mathit{\varphi }(\widehat{\mathit{\alpha }}){\mathit{\alpha }}_3^2$, and$$R[\mathrm{\Phi }(x_1,x_2)](\widehat{\mathit{\omega }},s)={\int }_{\mathbb{R}}\mathrm{\Phi }(s\widehat{\mathit{\omega }}+\mathit{\nu }{\widehat{\mathit{\omega }}}^{\perp })d\mathit{\nu },\text{for}(\widehat{\mathit{\omega }},s)\in S^1\times \mathbb{R}.$$

The map $\widehat{\mathit{\alpha }}\mapsto ({\mathit{\alpha }}^{\prime }/{\mathit{\alpha }}_3,1)$ takes a point $\widehat{\mathit{\alpha }}$ on the upper hemisphere to the plane $x_3=1$ along the line connecting the origin to $\widehat{\mathit{\alpha }}$. This transformation maps half-great circles to lines in the plane, which gives a geometrical explanation for the theorem.

Proof:

By definition, $F\mathit{\varphi }$ can be written as$$F\mathit{\varphi }(\widehat{\mathit{\theta }})={\int }_0^{2\mathit{\pi }}\mathit{\varphi }(\widehat{u}cost+\widehat{v}sint)\mathrm{d}t,$$

where$$\widehat{u}=(u_1,u_2,u_3)=\frac{1}{|{\mathit{\theta }}^{\prime }|}(-{\mathit{\theta }}_2,{\mathit{\theta }}_1,0)\in S^2\text{and}\widehat{v}=(v_1,v_1,v_3)=\frac{1}{|{\mathit{\theta }}^{\prime }|}({\mathit{\theta }}_1{\mathit{\theta }}_3,{\mathit{\theta }}_2{\mathit{\theta }}_3,-|{\mathit{\theta }}^{\prime }{|}^2)\in S^2.$$

Note that $\widehat{u},\widehat{v}$ and $\widehat{\mathit{\theta }}$ are orthonormal, so that $\widehat{u}cost+\widehat{v}sint,$ for $t\in [0,2\mathit{\pi }]$ is a parametrization of the great circle orthogonal to $\widehat{\mathit{\theta }}$.

By the evenness of $\mathit{\varphi }$ and the definition of $\mathrm{\Phi }$, we have$$\begin{array}{cc}\hfill F\mathit{\varphi }(\widehat{\mathit{\theta }})& ={\int }_0^{\mathit{\pi }}\mathrm{\Phi }\left(\frac{u^{\prime }cost+v^{\prime }sint}{v_{3}sint}\right)\frac{\mathrm{d}t}{v_3^2{sin}^{2}t}={\int }_0^{\mathit{\pi }}\mathrm{\Phi }\left(\frac{u^{\prime }}{v_3}cott+\frac{v^{\prime }}{v_3}\right)\frac{\mathrm{d}t}{v_3^2{sin}^{2}t}\hfill \\ \hfill & ={\int }_{\mathbb{R}}\mathrm{\Phi }\left(\frac{u^{\prime }}{v_3}t+\frac{v^{\prime }}{v_3}\right)v_3^{-2}\mathrm{d}t,\hfill \end{array}$$

where in the last line, we changed the variables $cott\to t$. Here $u^{\prime }=(u_1,u_2)$ and $v^{\prime }=(v_1,v_2)$. Thus $F\mathit{\varphi }(\widehat{\mathit{\theta }})$ is the integral of $\mathrm{\Phi }$ over the line with direction $u^{\prime }/v_3$ and passing through $v^{\prime }/v_3$. We can represent $F\mathit{\varphi }$ as$$\begin{array}{cc}\hfill F\mathit{\varphi }(\widehat{\mathit{\theta }})& ={\int }_{\mathbb{R}}\mathrm{\Phi }\left(u^{\prime }\frac{t}{v_3}+\frac{v^{\prime }}{|v^{\prime }|}\frac{|v^{\prime }|}{v_3}\right)v_3^{-2}\mathrm{d}t={\int }_{\mathbb{R}}\mathrm{\Phi }\left(u^{\prime }t+\frac{v^{\prime }}{|v^{\prime }|}\frac{|v^{\prime }|}{v_3}\right){|v_3|}^{-1}\mathrm{d}t\hfill \\ \hfill & =|v_3{|}^{-1}R\mathrm{\Phi }\left(\frac{v^{\prime }}{|v^{\prime }|},\frac{|v^{\prime }|}{v_3}\right),\hfill \end{array}$$

where in the second line, we changed the variables $t/v_3\to t$. The following identities complete our proof:$$\frac{v^{\prime }}{|v^{\prime }|}=\frac{{\mathit{\theta }}^{\prime }}{|{\mathit{\theta }}^{\prime }|},\frac{|v^{\prime }|}{v_3}=-\frac{{\mathit{\theta }}_3}{|{\mathit{\theta }}^{\prime }|},\text{and}{|v_3|}^{-1}=\frac{1}{|{\mathit{\theta }}^{\prime }|}.$$$\square$

Lemma 9:

Let $\mathit{\varphi }\in C^{\infty }([0,\mathit{ϵ}])$ for some $\mathit{ϵ}>0$ satisfy $\mathit{\varphi }(0)=0$, and let $n$ be a positive integer. For any positive integer $k\le n$, we have$${\int }_0^t\mathit{\varphi }(\mathit{\tau }){\mathit{\partial }}_t^k\left(\frac{{(t-\mathit{\tau })}^{n+1}}{t}\right)\mathrm{d}\mathit{\tau }\to 0\text{as}t\to 0.$$

Proof:

It is enough to show that for any positive integer $m$,(A2) $$\begin{array}{c}\hfill {\int }_0^t\mathit{\varphi }(\mathit{\tau })\frac{{(t-\mathit{\tau })}^{m^{\prime }}}{t^m}\mathrm{d}\mathit{\tau }\to 0\text{as}t\to 0,\text{for any}{m}^{\prime }\ge m\end{array}$$(A2)

since$${\mathit{\partial }}_t^k\left(\frac{{(t-\mathit{\tau })}^{n+1}}{t}\right)=\sum _{j=0}^k{c}_{k,j}{(t-\mathit{\tau })}^{n+1-j}{t}^{-k+j-1},$$

where $c_{k,j}$ are some constants depending on $k$ and $j$. To show (A2(A2) $$\begin{array}{c}\hfill {\int }_0^t\mathit{\varphi }(\mathit{\tau })\frac{{(t-\mathit{\tau })}^{m^{\prime }}}{t^m}\mathrm{d}\mathit{\tau }\to 0\text{as}t\to 0,\text{for any}{m}^{\prime }\ge m\end{array}$$(A2) ), it is enough that for any positive integer $m$,(A3) $$\begin{array}{c}\hfill {\int }_0^t\mathit{\varphi }(\mathit{\tau })\frac{{\mathit{\tau }}^{m^{\prime }}}{t^m}\mathrm{d}\mathit{\tau }\to 0\text{as}t\to 0,\text{for any}{m}^{\prime }\ge m\end{array}$$(A3)

since$${(t-\mathit{\tau })}^{m^{\prime }}=\sum _{j=0}^{m^{\prime }}{}_{m^{\prime }}{C}_j{t}^j{\mathit{\tau }}^{m^{\prime }-j},$$

where ${}_{m^{\prime }}{C}_j$ is the number of $j$-combination from a given set of $m^{\prime }$ elements.

Applying L’Hôpital’s rule to (A3(A3) $$\begin{array}{c}\hfill {\int }_0^t\mathit{\varphi }(\mathit{\tau })\frac{{\mathit{\tau }}^{m^{\prime }}}{t^m}\mathrm{d}\mathit{\tau }\to 0\text{as}t\to 0,\text{for any}{m}^{\prime }\ge m\end{array}$$(A3) ), we have$$\frac{\mathit{\varphi }(t)t^{m^{\prime }}}{m{t}^{m-1}}=\mathit{\varphi }(t)t^{m^{\prime }-m+1}\to 0\text{as}t\to 0.$$$\square$

Lemma 10:

Let $\mathit{\varphi }\in C^{\infty }([0,\mathit{ϵ}])$ satisfy $\mathit{\varphi }(0)=0$, and let $h(t)={\int }_0^t\mathit{\varphi }(\mathit{\tau })\mathrm{d}\mathit{\tau }/t$. Then $h\in C^{\infty }([0,\mathit{ϵ}])$ and $h(0)=0$.

Proof:

The smoothness of $h$ is obvious except at $t=0$. In order to prove smoothness at $t=0$, we will use mathematical induction. First of all, $h(0)$ is equal to $\mathit{\varphi }(0)$, which is equal to zero, by L’Hôpital’s rule. Suppose $h^{(n-1)}(0)={\mathit{\varphi }}^{(n-1)}(0)/n$ and $h^{(n-1)}(t)$ is continuous at 0. Consider the Taylor expansion of ${\int }_0^t\mathit{\varphi }(\mathit{\tau })\mathrm{d}\mathit{\tau }$ at $t=0$. Then for any $n$, we have$$\begin{array}{cc}\hfill {\int }_0^t\mathit{\varphi }(\mathit{\tau })\mathrm{d}\mathit{\tau }=& t\mathit{\varphi }(0)+\frac{t^2}{2!}{\mathit{\varphi }}^{\prime }(0)+\frac{t^3}{3!}{\mathit{\varphi }}^{(2)}(0)+\cdots \hfill \\ \hfill & +\frac{t^n}{n!}{\mathit{\varphi }}^{(n-1)}(0)+\frac{t^{(n+1)}}{(n+1)!}{\mathit{\varphi }}^{(n)}(0)+{\int }_0^t\frac{{\mathit{\varphi }}^{(n+1)}(\mathit{\tau })}{(n+1)!}{(t-\mathit{\tau })}^{n+1}\mathrm{d}\mathit{\tau },\hfill \end{array}$$

where ${\mathit{\varphi }}^{(n)}(0)$ is the $n$th derivative of $\mathit{\varphi }$ evaluated at $t=0$. Hence, we have$$\begin{array}{cc}\hfill h(t)=& \frac{1}{t}{\int }_0^t\mathit{\varphi }(\mathit{\tau })\mathrm{d}\mathit{\tau }\hfill \\ \hfill =& \mathit{\varphi }(0)+\frac{t}{2!}{\mathit{\varphi }}^{\prime }(0)+\cdots +\frac{t^n}{(n+1)!}{\mathit{\varphi }}^{(n)}(0)+\frac{1}{t}{\int }_0^t\frac{{\mathit{\varphi }}^{(n+1)}(\mathit{\tau })}{(n+1)!}{(t-\mathit{\tau })}^{n+1}\mathrm{d}\mathit{\tau }.\hfill \end{array}$$

For any $k\le n$, the $k$th derivative of the last term (or the reminder term) is(A4) $$\begin{array}{cc}\hfill {\mathit{\partial }}_t^k{\int }_0^t\frac{{\mathit{\varphi }}^{(n+1)}(\mathit{\tau })}{(n+1)!}\frac{{(t-\mathit{\tau })}^{n+1}}{t}\mathrm{d}\mathit{\tau }& ={\mathit{\partial }}_t^{k-1}{\int }_0^t\frac{{\mathit{\varphi }}^{(n+1)}(\mathit{\tau })}{(n+1)!}{\mathit{\partial }}_t\left(\frac{{(t-\mathit{\tau })}^{n+1}}{t}\right)\mathrm{d}\mathit{\tau }\hfill \\ \hfill & ⋮\hfill \\ \hfill & ={\int }_0^t\frac{{\mathit{\varphi }}^{(n+1)}(\mathit{\tau })}{(n+1)!}{\mathit{\partial }}_t^k\left(\frac{{(t-\mathit{\tau })}^{n+1}}{t}\right)\mathrm{d}\mathit{\tau },\hfill \end{array}$$(A4)

since ${\mathit{\partial }}_t^{k^{\prime }}({(t-\mathit{\tau })}^{n+1}/t)={(t-\mathit{\tau })}^{n+1-k^{\prime }}[(n+1)!/(n-k^{\prime })!t^{-1}+\cdots +{(-1)}^{k^{\prime }}{k}^{\prime }!{(t-\mathit{\tau })}^{k^{\prime }}{t}^{-k^{\prime }-1}]$ for $k^{\prime }\le n$.

Hence, for $t$ near 0, we have$$h^{(n-1)}(t)=\frac{1}{n}{\mathit{\varphi }}^{(n-1)}(0)+\frac{t}{n+1}{\mathit{\varphi }}^{(n)}(0)+{\int }_0^t\frac{{\mathit{\varphi }}^{(n+1)}(\mathit{\tau })}{(n+1)!}{\mathit{\partial }}_t^{n-1}\left(\frac{{(t-\mathit{\tau })}^{n+1}}{t}\right)\mathrm{d}\mathit{\tau }$$

and$$h^{(n)}(t)=\frac{1}{n+1}{\mathit{\varphi }}^{(n)}(0)+{\int }_0^t\frac{{\mathit{\varphi }}^{(n+1)}(\mathit{\tau })}{(n+1)!}{\mathit{\partial }}_t^n\left(\frac{{(t-\mathit{\tau })}^{n+1}}{t}\right)\mathrm{d}\mathit{\tau }.$$

By Lemma 9, we have$$h^{(n)}(t)\to \frac{1}{n+1}{\mathit{\varphi }}^{(n)}(0)\text{as}t\to 0.$$

Hence we have$$\begin{array}{cc}\hfill h^{(n)}(0)& {\displaystyle =\underset{t\to 0}{lim}\frac{1}{t}\left(\frac{t}{n+1}{\mathit{\varphi }}^{(n)}(0)+{\int }_0^t\frac{{\mathit{\varphi }}^{(n+1)}(\mathit{\tau })}{(n+1)!}{\mathit{\partial }}_t^{n-1}\left(\frac{{(t-\mathit{\tau })}^{n+1}}{t}\right)\mathrm{d}\mathit{\tau }\right)}\hfill \\ \hfill & {\displaystyle =\frac{{\mathit{\varphi }}^{(n)}(0)}{n+1}+\underset{t\to 0}{lim}{\int }_0^t\frac{{\mathit{\varphi }}^{(n+1)}(\mathit{\tau })}{(n+1)!}{\mathit{\partial }}_t^n\left(\frac{{(t-\mathit{\tau })}^{n+1}}{t}\right)\mathrm{d}\mathit{\tau }=\frac{{\mathit{\varphi }}^{(n)}(0)}{n+1},}\hfill \end{array}$$

where in the second line, we used L’Hôpital’s rule, (A4(A4) $$\begin{array}{cc}\hfill {\mathit{\partial }}_t^k{\int }_0^t\frac{{\mathit{\varphi }}^{(n+1)}(\mathit{\tau })}{(n+1)!}\frac{{(t-\mathit{\tau })}^{n+1}}{t}\mathrm{d}\mathit{\tau }& ={\mathit{\partial }}_t^{k-1}{\int }_0^t\frac{{\mathit{\varphi }}^{(n+1)}(\mathit{\tau })}{(n+1)!}{\mathit{\partial }}_t\left(\frac{{(t-\mathit{\tau })}^{n+1}}{t}\right)\mathrm{d}\mathit{\tau }\hfill \\ \hfill & ⋮\hfill \\ \hfill & ={\int }_0^t\frac{{\mathit{\varphi }}^{(n+1)}(\mathit{\tau })}{(n+1)!}{\mathit{\partial }}_t^k\left(\frac{{(t-\mathit{\tau })}^{n+1}}{t}\right)\mathrm{d}\mathit{\tau },\hfill \end{array}$$(A4) ), and Lemma 9. This means that $h$ is $n$th differentiable at 0 and $h^{(n)}(t)$ is continuous at 0. $\square$