Determination of a time-dependent convolution kernel in a non-linear hyperbolic equation

Abstract

A non-linear wave equation with an unknown time-convolution kernel is considered. The missing kernel is recovered from an additional (space) integral measurement. The global in time existence, uniqueness as well as the regularity of a solution is addressed. A new numerical algorithm based on Rothe’s method is designed and error estimates are derived.

Keywords:

• Wave equation
• convolution kernel
• reconstruction
• error estimate
• time discretization

AMS Subject Classifications:

• 65M32
• 65M20

1. Introduction

We consider a bounded domain $\mathrm{\Omega }\subset {\mathbb{R}}^N,N\ge 1$ with sufficiently smooth boundary $\mathrm{\Gamma }$. The symbol $\mathit{\nu }$ stands for the outer normal vector associated with $\mathrm{\Gamma }$. In this paper, we are interested in determining of an unknown couple $(u,K)$ obeying the following non-linear hyperbolic problem of second order(1) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\displaystyle {\mathit{\partial }}_{tt}u(\mathit{x},t)-\mathrm{\Delta }u(\mathit{x},t)+(K\ast u(\mathit{x}))(t)=f(\mathit{x},t,u(\mathit{x},t),{\mathit{\partial }}_{t}u(\mathit{x},t)),}\hfill & {\displaystyle \text{in}\mathrm{\Omega }\times (0,T),}\hfill \\ {\displaystyle -\mathrm{\nabla }u(\mathit{x},t)·\mathit{\nu }=g(\mathit{x},t),}\hfill & {\displaystyle \text{on}\mathrm{\Gamma }\times (0,T),}\hfill \\ {\displaystyle {\mathit{\partial }}_{t}u(\mathbf{x},0)=v_0(\mathbf{x}),}\hfill & {\displaystyle \text{in}\mathrm{\Omega },}\hfill \\ {\displaystyle u(\mathbf{x},0)=u_0(\mathbf{x}),}\hfill & {\displaystyle \text{in}\mathrm{\Omega },}\hfill \end{array}\right.\end{array}$$(1)

where $T>0$ and $f,g,u_0,v_0$ are given real functions. By $K\ast u$ we denote the usual convolution in time, namely $(K\ast u(\mathit{x}))(t)={\int }_0^{t}K(t-s)u(\mathit{x},s)\text{d}s$ . The missing time-convolution kernel $K=K(t)$ will be recovered from the following integral-type measurement(2) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}u(\mathbf{x},t)\text{d}\mathit{x}=m(t),t\in [0,T].\end{array}$$(2)

The integral-type over-determination in inverse problems (IPs) combined with evolutionary partial differential equations (PDEs) has been studied in several papers, e.g. [1–3] and the references therein.

A well-known example of (a homogeneous version of) the general wave equation is the telegraph equation. It describes the voltage $u(x,t)$ inside a piece of telegraph/transmission wire, whose electrical properties per unit length are: resistance $R$, inductance $L$, capacitance $C$ and conductance of leakage current $G$:$$\begin{array}{c}\hfill u_{tt}+\mathit{\gamma }{u}_t+ku-a^2{u}_{xx}=0.\end{array}$$

where $a^2=\frac{1}{LC},\mathit{\gamma }=\frac{G}{C}+\frac{R}{L}$, and $k=\frac{GR}{CL}.$ When considering transport for long distances, the memory effects can be modelled by a additional convolution term.

Identification of missing memory kernels in evolutionary PDEs represents an interesting topic in IPs. Intensive study of such problems was implemented in 1990’s cf. [4–16]. The paper [12] deals with a linear hyperbolic equation without a damping term. Here, the time convolution operator is applied to the Laplacian of solution. The missing data are recovered from a point measurement. There is no constructive algorithm for finding a solution for this IP. The manuscript [11] studies identification of convolution kernels in abstract linear hyperbolic integro-differential problems. The author shows local in time solvability of this IP. No constructive algorithm for recovery of missing convolution kernel is present. The study performed in [14] is devoted to a one-dimensional linear hyperbolic integro-differential problem. The author uses finite differences for numerical scheme with dependent time and space mesh-steps. The error estimates are derived under high regularity of solution. Bukhgeĭm and Dyatlov [4] presents a nice study of properties of Dirichlet-to-Neumann maps for memory reconstruction for linear settings. The paper [16] studies IPs for identifying memory kernels in linear heat conduction and viscoelasticity by the method of least squares with Tikhonov regularization. In [8] a global in time existence and uniqueness result for an IP arising in the theory of heat conduction for materials with memory has been studied. The Ref. [6] derives some local and global in time existence results for the recovery of memory kernels, but there is no description of constructive algorithms how to find a solution. The papers [9,10] deals with the identification of missing memory kernel in a parabolic problem.

The ultimate highlight of this paper is to design a constructive algorithm for finding the solution and to recover the unknown kernel in non-linear hyperbolic problems. This is not achieved by minimization of a cost functional (which is typical for IPs [17–19]), but on the time discretization based on method of lines.[20,21] This technique was already applied for parabolic settings in [9]. First, we start with derivation of a suitable variational formulation. Section 2 is devoted to a time discretization, where (based on backward Euler scheme) the continuous problem is approximated by a sequence of steady state settings at each point of a time partitioning. Section 3 deals with existence and uniqueness of a solution. Stability analysis of approximates is performed in appropriate function spaces and convergence (based on compactness argument) is established in Theorem 3.1. Uniqueness is addressed in Theorem 3.2. Theorem 3.3 shows the error estimates for time discretization.

Denote by $\left(·,·\right)$ the standard inner product of $L^2(\mathrm{\Omega })$ and $∥·∥$ its induced norm. When working at the boundary $\mathrm{\Gamma }$ we use a similar notation, namely ${\left(·,·\right)}_{\mathrm{\Gamma }}$, $L^2(\mathrm{\Gamma })$ and ${∥·∥}_{\mathrm{\Gamma }}$. By $C\left([0,T],X\right)$ we denote the set of abstract functions $w:[0,T]\to X$ equipped with the usual norm ${max}_{t\in [0,T]}{∥·∥}_X$ and $L^p\left((0,T),X\right)$ is furnished with the norm ${\displaystyle {\left({\int }_0^T{∥·∥}_X^p\text{d}t\right)}^{\frac{1}{p}}}$ with $p>1$, cf. [22]. The symbol $X^{\ast }$ stands for the dual space to $X$. The symbols $C,\mathit{\epsilon }$ and $C_{\mathit{\epsilon }}$ will denote generic positive constants (they may change from line to line) depending only on a priori known quantities, where $\mathit{\epsilon }$ is small and $C_{\mathit{\epsilon }}=C\left({\mathit{\epsilon }}^{-1}\right)$ is large. Further, we set$$\mathit{V}=\left\{\mathit{\phi }\in H^1(\mathrm{\Omega });∥\mathrm{\Delta }\mathit{\phi }∥<\infty \right\}.$$

Denoting the primitive function of $K$ by ${\displaystyle {\mathrm{\Phi }}_K(t):={\int }_0^{t}K(s)\text{d}s}$ we may rewrite the convolution kernel by integration by parts formula in an another way as follows$$\begin{array}{c}\hfill (K\ast u)(t)={\mathrm{\Phi }}_K(t)u_0+\left({\mathrm{\Phi }}_K\ast {\mathit{\partial }}_{t}u\right)(t).\end{array}$$

Hence the governing PDE takes the form(3) $$\begin{array}{c}\hfill {\displaystyle {\mathit{\partial }}_{tt}u(\mathit{x},t)-\mathrm{\Delta }u(\mathit{x},t)+{\mathrm{\Phi }}_K(t)u_0(\mathit{x})+({\mathrm{\Phi }}_K\ast {\mathit{\partial }}_{t}u(\mathit{x}))(t)=f(\mathit{x},t,u(\mathit{x},t),{\mathit{\partial }}_{t}u(\mathit{x},t))}\end{array}$$(3)

in $\mathrm{\Omega }\times (0,T)$. We take a test function $\mathit{\phi }\in H^1(\mathrm{\Omega })$, and derive after integration over $\mathrm{\Omega }$ and making use of the Green’s first identity(P) $$\begin{array}{c}\hfill \left({\mathit{\partial }}_{tt}u,\mathit{\phi }\right)+\left(\mathrm{\nabla }u,\mathrm{\nabla }\mathit{\phi }\right)+{\left(g,\mathit{\phi }\right)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_K\left(u_0,\mathit{\phi }\right)+\left({\mathrm{\Phi }}_K\ast {\mathit{\partial }}_{t}u,\mathit{\phi }\right)=\left(f(u,{\mathit{\partial }}_{t}u),\mathit{\phi }\right).\end{array}$$(P)

Setting $\mathit{\phi }=1$ in (P(P) $$\begin{array}{c}\hfill \left({\mathit{\partial }}_{tt}u,\mathit{\phi }\right)+\left(\mathrm{\nabla }u,\mathrm{\nabla }\mathit{\phi }\right)+{\left(g,\mathit{\phi }\right)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_K\left(u_0,\mathit{\phi }\right)+\left({\mathrm{\Phi }}_K\ast {\mathit{\partial }}_{t}u,\mathit{\phi }\right)=\left(f(u,{\mathit{\partial }}_{t}u),\mathit{\phi }\right).\end{array}$$(P) ) we obtain together with the measurement $(u(t),1)=m(t)$ that(MP) $$\begin{array}{c}\hfill m^{″}+{(g,1)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_{K}m(0)+{\mathrm{\Phi }}_K\ast m^{\prime }=\left(f(u,{\mathit{\partial }}_{t}u),1\right).\end{array}$$(MP)

The relations (P(P) $$\begin{array}{c}\hfill \left({\mathit{\partial }}_{tt}u,\mathit{\phi }\right)+\left(\mathrm{\nabla }u,\mathrm{\nabla }\mathit{\phi }\right)+{\left(g,\mathit{\phi }\right)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_K\left(u_0,\mathit{\phi }\right)+\left({\mathrm{\Phi }}_K\ast {\mathit{\partial }}_{t}u,\mathit{\phi }\right)=\left(f(u,{\mathit{\partial }}_{t}u),\mathit{\phi }\right).\end{array}$$(P) ) and (MP(MP) $$\begin{array}{c}\hfill m^{″}+{(g,1)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_{K}m(0)+{\mathrm{\Phi }}_K\ast m^{\prime }=\left(f(u,{\mathit{\partial }}_{t}u),1\right).\end{array}$$(MP) ) represent the variational formulation of (1(1) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\displaystyle {\mathit{\partial }}_{tt}u(\mathit{x},t)-\mathrm{\Delta }u(\mathit{x},t)+(K\ast u(\mathit{x}))(t)=f(\mathit{x},t,u(\mathit{x},t),{\mathit{\partial }}_{t}u(\mathit{x},t)),}\hfill & {\displaystyle \text{in}\mathrm{\Omega }\times (0,T),}\hfill \\ {\displaystyle -\mathrm{\nabla }u(\mathit{x},t)·\mathit{\nu }=g(\mathit{x},t),}\hfill & {\displaystyle \text{on}\mathrm{\Gamma }\times (0,T),}\hfill \\ {\displaystyle {\mathit{\partial }}_{t}u(\mathbf{x},0)=v_0(\mathbf{x}),}\hfill & {\displaystyle \text{in}\mathrm{\Omega },}\hfill \\ {\displaystyle u(\mathbf{x},0)=u_0(\mathbf{x}),}\hfill & {\displaystyle \text{in}\mathrm{\Omega },}\hfill \end{array}\right.\end{array}$$(1) ) and (2(2) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}u(\mathbf{x},t)\text{d}\mathit{x}=m(t),t\in [0,T].\end{array}$$(2) ).

2. Time discretization

Rothe’s method [20,21] represents a constructive method suitable for solving evolution problems. Using a simple discretization in time, a time-dependent problem is approximated by a sequence of elliptic problems which have to be solved successively with increasing time step. This standard technique is in our case complicated by the unknown convolution kernel $K$. There exists a simple way to overcome this difficulty.

For ease of explanation we consider an equidistant time partitioning of the time frame $[0,T]$ with a step $\mathit{\tau }=T/n,$ for any $n\in \mathbb{N}$. We use the notation $t_i=i\mathit{\tau }$ and for any function $z$ we write$$\begin{array}{c}\hfill z_i=z(t_i),\mathit{\delta }{z}_i=\frac{z_i-z_{i-1}}{\mathit{\tau }},{\mathit{\delta }}^2{z}_i=\mathit{\delta }(\mathit{\delta }{z}_i).\end{array}$$

Further, we set ${\mathrm{\Phi }}_i:={({\mathrm{\Phi }}_K)}_i$ to omit double indices. We will consider a decoupled system with unknowns $(u_i,{\mathrm{\Phi }}_i)$ for $i=1,\dots ,n$. At time $t_i$ we infer from (3(3) $$\begin{array}{c}\hfill {\displaystyle {\mathit{\partial }}_{tt}u(\mathit{x},t)-\mathrm{\Delta }u(\mathit{x},t)+{\mathrm{\Phi }}_K(t)u_0(\mathit{x})+({\mathrm{\Phi }}_K\ast {\mathit{\partial }}_{t}u(\mathit{x}))(t)=f(\mathit{x},t,u(\mathit{x},t),{\mathit{\partial }}_{t}u(\mathit{x},t))}\end{array}$$(3) ) the backward Euler scheme(4) $$\begin{array}{c}\hfill {\mathit{\delta }}^2{u}_i-\mathrm{\Delta }{u}_i+{\mathrm{\Phi }}_i{u}_0+\sum _{k=1}^i{\mathrm{\Phi }}_k\mathit{\delta }{u}_{i-k}\mathit{\tau }=f_{i-1},\end{array}$$(4)

where $f_i=f(u_i,\mathit{\delta }{u}_i)$. Like (P(P) $$\begin{array}{c}\hfill \left({\mathit{\partial }}_{tt}u,\mathit{\phi }\right)+\left(\mathrm{\nabla }u,\mathrm{\nabla }\mathit{\phi }\right)+{\left(g,\mathit{\phi }\right)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_K\left(u_0,\mathit{\phi }\right)+\left({\mathrm{\Phi }}_K\ast {\mathit{\partial }}_{t}u,\mathit{\phi }\right)=\left(f(u,{\mathit{\partial }}_{t}u),\mathit{\phi }\right).\end{array}$$(P) ) and (MP(MP) $$\begin{array}{c}\hfill m^{″}+{(g,1)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_{K}m(0)+{\mathrm{\Phi }}_K\ast m^{\prime }=\left(f(u,{\mathit{\partial }}_{t}u),1\right).\end{array}$$(MP) ) one obtains for $\mathit{\phi }\in H^1(\mathrm{\Omega })$ that(DPi) $$\begin{array}{c}\hfill \left({\mathit{\delta }}^2{u}_i,\mathit{\phi }\right)+\left(\mathrm{\nabla }{u}_i,\mathrm{\nabla }\mathit{\phi }\right)+{\left(g_i,\mathit{\phi }\right)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_i\left(u_0,\mathit{\phi }\right)+\left(\sum _{k=1}^i{\mathrm{\Phi }}_k\mathit{\delta }{u}_{i-k}\mathit{\tau },\mathit{\phi }\right)=\left(f_{i-1},\mathit{\phi }\right)\end{array}$$(DPi)

along with $\mathit{\delta }{u}_0:=v_0$ and(DMPi) $$\begin{array}{c}\hfill m_i^{″}+{(g_i,1)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_i{m}_0+\sum _{k=1}^i{\mathrm{\Phi }}_k{m}_{i-k}^{\prime }\mathit{\tau }=(f_{i-1},1).\end{array}$$(DMPi)

Note that for a given $i\in \{1,\dots ,n\}$ we solve first (DMP$i$(DMPi) $$\begin{array}{c}\hfill m_i^{″}+{(g_i,1)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_i{m}_0+\sum _{k=1}^i{\mathrm{\Phi }}_k{m}_{i-k}^{\prime }\mathit{\tau }=(f_{i-1},1).\end{array}$$(DMPi) ) and then (DP$i$(DPi) $$\begin{array}{c}\hfill \left({\mathit{\delta }}^2{u}_i,\mathit{\phi }\right)+\left(\mathrm{\nabla }{u}_i,\mathrm{\nabla }\mathit{\phi }\right)+{\left(g_i,\mathit{\phi }\right)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_i\left(u_0,\mathit{\phi }\right)+\left(\sum _{k=1}^i{\mathrm{\Phi }}_k\mathit{\delta }{u}_{i-k}\mathit{\tau },\mathit{\phi }\right)=\left(f_{i-1},\mathit{\phi }\right)\end{array}$$(DPi) ). Further, we increase $i$ to $i+1$.

Lemma 2.1:

Let $f:{\mathbb{R}}^{N+3}\to \mathbb{R}$ be bounded, i.e. $|f|\le C$. Moreover assume that $m\in C^2([0,T])$, $m(0)\ne 0$, $g\in C\left([0,T],L^2(\mathrm{\Gamma })\right)$, $u_0,v_0\in L^2(\mathrm{\Omega })$. Then there exist $C>0$ and ${\mathit{\tau }}_0>0$ such that for any $\mathit{\tau }<{\mathit{\tau }}_0$ and each $i\in \{1,\dots ,n\}$ we have

(i)

there exist ${\mathrm{\Phi }}_i\in \mathbb{R}$ and $u_i\in \mathit{V}$ obeying (DMP$i$(DMPi) $$\begin{array}{c}\hfill m_i^{″}+{(g_i,1)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_i{m}_0+\sum _{k=1}^i{\mathrm{\Phi }}_k{m}_{i-k}^{\prime }\mathit{\tau }=(f_{i-1},1).\end{array}$$(DMPi) ) and (DP$i$(DPi) $$\begin{array}{c}\hfill \left({\mathit{\delta }}^2{u}_i,\mathit{\phi }\right)+\left(\mathrm{\nabla }{u}_i,\mathrm{\nabla }\mathit{\phi }\right)+{\left(g_i,\mathit{\phi }\right)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_i\left(u_0,\mathit{\phi }\right)+\left(\sum _{k=1}^i{\mathrm{\Phi }}_k\mathit{\delta }{u}_{i-k}\mathit{\tau },\mathit{\phi }\right)=\left(f_{i-1},\mathit{\phi }\right)\end{array}$$(DPi) )

(ii)

${\displaystyle \underset{1\le i\le n}{max}|{\mathrm{\Phi }}_i|\le C}$.

Proof:

(i) Set ${\displaystyle {\mathit{\tau }}_0=min\left\{1,\frac{\left|m_0\right|}{2\left|m_0^{\prime }\right|}\right\}}$. Then for any $\mathit{\tau }<{\mathit{\tau }}_0$ we may write by triangle inequality that$$0<\left|m_0\right|-\left|m_0^{\prime }\right|{\mathit{\tau }}_0\le \left|m_0\right|-\left|m_0^{\prime }\right|\mathit{\tau }\le \left|m_0+m_0^{\prime }\mathit{\tau }\right|.$$

We apply the following recursive deduction for $i=1,\dots ,n$.

(1)

Let $u_{i-1},\mathit{\delta }{u}_{i-1}\in L^2(\mathrm{\Omega })$ and ${\mathrm{\Phi }}_1,\dots ,{\mathrm{\Phi }}_{i-1}$ be given. Then (DMP$i$(DMPi) $$\begin{array}{c}\hfill m_i^{″}+{(g_i,1)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_i{m}_0+\sum _{k=1}^i{\mathrm{\Phi }}_k{m}_{i-k}^{\prime }\mathit{\tau }=(f_{i-1},1).\end{array}$$(DMPi) ) implies the existence of ${\mathrm{\Phi }}_i\in \mathbb{R}$ such that(5) $$\begin{array}{c}\hfill {\mathrm{\Phi }}_i\left[m_0+m_0^{\prime }\mathit{\tau }\right]=\left(f_{i-1},1\right)-m_i^{″}-{\left(g_i,1\right)}_{\mathrm{\Gamma }}-\sum _{k=1}^{i-1}{\mathrm{\Phi }}_k{m}_{i-k}^{\prime }\mathit{\tau }.\end{array}$$(5)

(2)

The existence and uniqueness of $u_i\in H^1(\mathrm{\Omega })$ follows from (DP$i$(DPi) $$\begin{array}{c}\hfill \left({\mathit{\delta }}^2{u}_i,\mathit{\phi }\right)+\left(\mathrm{\nabla }{u}_i,\mathrm{\nabla }\mathit{\phi }\right)+{\left(g_i,\mathit{\phi }\right)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_i\left(u_0,\mathit{\phi }\right)+\left(\sum _{k=1}^i{\mathrm{\Phi }}_k\mathit{\delta }{u}_{i-k}\mathit{\tau },\mathit{\phi }\right)=\left(f_{i-1},\mathit{\phi }\right)\end{array}$$(DPi) ) by the Lax-Milgram lemma.

Inspecting the relation (DP$i$(DPi) $$\begin{array}{c}\hfill \left({\mathit{\delta }}^2{u}_i,\mathit{\phi }\right)+\left(\mathrm{\nabla }{u}_i,\mathrm{\nabla }\mathit{\phi }\right)+{\left(g_i,\mathit{\phi }\right)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_i\left(u_0,\mathit{\phi }\right)+\left(\sum _{k=1}^i{\mathrm{\Phi }}_k\mathit{\delta }{u}_{i-k}\mathit{\tau },\mathit{\phi }\right)=\left(f_{i-1},\mathit{\phi }\right)\end{array}$$(DPi) ) we may write for any $\mathit{\phi }\in H^1(\mathrm{\Omega })$ that$$-\left(\mathrm{\Delta }{u}_i,\mathit{\phi }\right)=\left(\mathrm{\nabla }{u}_i,\mathrm{\nabla }\mathit{\phi }\right)+{\left(g_i,\mathit{\phi }\right)}_{\mathrm{\Gamma }}=\left(f_{i-1},\mathit{\phi }\right)-\left({\mathit{\delta }}^2{u}_i,\mathit{\phi }\right)-{\mathrm{\Phi }}_i\left(u_0,\mathit{\phi }\right)-\left(\sum _{k=1}^i{\mathrm{\Phi }}_k\mathit{\delta }{u}_{i-k}\mathit{\tau },\mathit{\phi }\right).$$ The term $-\mathrm{\Delta }{u}_i$ has to be understood in the sense of duality, as a functional on $H^1(\mathrm{\Omega })$. The right-hand side can be estimated by $C_i(\mathit{\tau })∥\mathit{\phi }∥$. Thus there exists an extension of $-\mathrm{\Delta }{u}_i$ to $L^2(\mathrm{\Omega })$ according to Hahn-Banach theorem, cf. [23, p.173]. This extension will have the same norm as the functional on $H^1(\mathrm{\Omega })$ and$$-\mathrm{\Delta }{u}_i=f_{i-1}-{\mathit{\delta }}^2{u}_i-{\mathrm{\Phi }}_i{u}_0-\sum _{k=1}^i{\mathrm{\Phi }}_k\mathit{\delta }{u}_{i-k}\mathit{\tau }\in L^2(\mathrm{\Omega }).$$(ii) The relation (5(5) $$\begin{array}{c}\hfill {\mathrm{\Phi }}_i\left[m_0+m_0^{\prime }\mathit{\tau }\right]=\left(f_{i-1},1\right)-m_i^{″}-{\left(g_i,1\right)}_{\mathrm{\Gamma }}-\sum _{k=1}^{i-1}{\mathrm{\Phi }}_k{m}_{i-k}^{\prime }\mathit{\tau }.\end{array}$$(5) ) yields$$\left|{\mathrm{\Phi }}_i\right|\le C\left(1+\sum _{k=1}^{i-1}\left|{\mathrm{\Phi }}_k\right|\mathit{\tau }\right),$$

which is valid for any $i=1,\dots ,n$. An application of the discrete Grönwall lemma [24] gives the uniform bound of $\left|{\mathrm{\Phi }}_i\right|$. $\square$

Lemma 2.2:

Let the conditions of Lemma 2.1 be satisfied. Moreover assume that $u_0\in H^1(\mathrm{\Omega })$. Then there exists $C>0$ such that for any $\mathit{\tau }<{\mathit{\tau }}_0$$$\begin{array}{c}\hfill \underset{1\le j\le n}{max}{∥\mathit{\delta }{u}_j∥}^2+\underset{1\le j\le n}{max}{∥\mathrm{\nabla }{u}_i∥}^2+\sum _{i=1}^n{∥\mathit{\delta }{u}_i-\mathit{\delta }{u}_{i-1}∥}^2+\sum _{i=1}^n{∥\mathrm{\nabla }{u}_i-\mathrm{\nabla }{u}_{i-1}∥}^2\le C.\end{array}$$

Proof:

If we set $\mathit{\phi }=\mathit{\delta }{u}_i\mathit{\tau }$ in (DP$i$(DPi) $$\begin{array}{c}\hfill \left({\mathit{\delta }}^2{u}_i,\mathit{\phi }\right)+\left(\mathrm{\nabla }{u}_i,\mathrm{\nabla }\mathit{\phi }\right)+{\left(g_i,\mathit{\phi }\right)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_i\left(u_0,\mathit{\phi }\right)+\left(\sum _{k=1}^i{\mathrm{\Phi }}_k\mathit{\delta }{u}_{i-k}\mathit{\tau },\mathit{\phi }\right)=\left(f_{i-1},\mathit{\phi }\right)\end{array}$$(DPi) ) and sum up for $i=1,\dots ,j$ we obtain$$\begin{array}{cc}& {\displaystyle \sum _{i=1}^j\left({\mathit{\delta }}^2{u}_i,\mathit{\delta }{u}_i\right)\mathit{\tau }+\sum _{i=1}^j\left(\mathrm{\nabla }{u}_i,\mathrm{\nabla }\mathit{\delta }{u}_i\right)\mathit{\tau }+\sum _{i=1}^j{\left(g_i,\mathit{\delta }{u}_i\right)}_{\mathrm{\Gamma }}\mathit{\tau }+\sum _{i=1}^j{\mathrm{\Phi }}_i\left(u_0,\mathit{\delta }{u}_i\right)\mathit{\tau }}\hfill \end{array}$$(6) $$\begin{array}{cc}& {\displaystyle +\sum _{i=1}^j\left(\sum _{k=1}^i{\mathrm{\Phi }}_k\mathit{\delta }{u}_{i-k}\mathit{\tau },\mathit{\delta }{u}_i\right)\mathit{\tau }=\sum _{i=1}^j\left(f_{i-1},\mathit{\delta }{u}_i\right)\mathit{\tau }.}\hfill \end{array}$$(6)

Let $\{a_i\}$ be any sequence of real numbers, then the following obvious identity holds true$$\sum _{i=1}^j{a}_i(a_i-a_{i-1})=\frac{1}{2}\left[a_j^2-a_0^2+\sum _{i=1}^j{(a_i-a_{i-1})}^2\right].$$

Thus$$\begin{array}{c}\hfill \sum _{i=1}^j\left({\mathit{\delta }}^2{u}_i,\mathit{\delta }{u}_i\right)\mathit{\tau }=\sum _{i=1}^j(\mathit{\delta }{u}_i-\mathit{\delta }{u}_{i-1},\mathit{\delta }{u}_i)=\frac{1}{2}\left({∥\mathit{\delta }{u}_j∥}^2-{∥v_0∥}^2+\sum _{i=1}^j{∥\mathit{\delta }{u}_i-\mathit{\delta }{u}_{i-1}∥}^2\right)\end{array}$$

and$$\begin{array}{c}\hfill \sum _{i=1}^j\left(\mathrm{\nabla }\mathit{\delta }{u}_i,\mathrm{\nabla }{u}_i\right)\mathit{\tau }=\sum _{i=1}^j(\mathrm{\nabla }{u}_i-\mathrm{\nabla }{u}_{i-1},\mathrm{\nabla }{u}_i)=\frac{1}{2}\left({∥\mathrm{\nabla }{u}_j∥}^2-{∥\mathrm{\nabla }{u}_0∥}^2+\sum _{i=1}^j{∥\mathrm{\nabla }{u}_i-\mathrm{\nabla }{u}_{i-1}∥}^2\right).\end{array}$$ For any real sequences ${\{z_i\}}_{i=1}^{\infty }$ and ${\{w_i\}}_{i=1}^{\infty }$ the following (summation by parts) identity takes place(7) $$\begin{array}{c}\hfill \sum _{i=1}^j{z}_i(w_i-w_{i-1})=z_j{w}_j-z_0{w}_0-\sum _{i=1}^j(z_i-z_{i-1})w_{i-1}.\end{array}$$(7)

For the third term of (6(6) $$\begin{array}{cc}& {\displaystyle +\sum _{i=1}^j\left(\sum _{k=1}^i{\mathrm{\Phi }}_k\mathit{\delta }{u}_{i-k}\mathit{\tau },\mathit{\delta }{u}_i\right)\mathit{\tau }=\sum _{i=1}^j\left(f_{i-1},\mathit{\delta }{u}_i\right)\mathit{\tau }.}\hfill \end{array}$$(6) ) we get by (7(7) $$\begin{array}{c}\hfill \sum _{i=1}^j{z}_i(w_i-w_{i-1})=z_j{w}_j-z_0{w}_0-\sum _{i=1}^j(z_i-z_{i-1})w_{i-1}.\end{array}$$(7) )$$\begin{array}{cc}\hfill {\displaystyle \left|\sum _{i=1}^j{(g_i,\mathit{\delta }{u}_i)}_{\mathrm{\Gamma }}\mathit{\tau }\right|}& {\displaystyle =\left|{\left(g_j,u_j\right)}_{\mathrm{\Gamma }}-{\left(g_0,u_0\right)}_{\mathrm{\Gamma }}-\sum _{i=1}^j{\left(\mathit{\delta }{g}_i,u_{i-1}\right)}_{\mathrm{\Gamma }}\mathit{\tau }\right|}\hfill \\ \hfill & {\displaystyle \le {∥g_j∥}_{\mathrm{\Gamma }}{∥u_j∥}_{\mathrm{\Gamma }}+{∥g_0∥}_{\mathrm{\Gamma }}{∥u_0∥}_{\mathrm{\Gamma }}+\sum _{i=1}^j{∥\mathit{\delta }{g}_i∥}_{\mathrm{\Gamma }}{∥u_{i-1}∥}_{\mathrm{\Gamma }}\mathit{\tau }}\hfill \\ \hfill & {\displaystyle \le \mathit{\epsilon }{∥u_j∥}_{\mathrm{\Gamma }}^2+C_{\mathit{\epsilon }}+C_{\mathit{\epsilon }}\sum _{i=1}^j{∥u_{i-1}∥}_{\mathrm{\Gamma }}^2\mathit{\tau }}\hfill \\ \hfill & {\displaystyle \le \mathit{\epsilon }{∥u_j∥}_{H^1(\mathrm{\Omega })}^2+C_{\mathit{\epsilon }}+C_{\mathit{\epsilon }}\sum _{i=1}^j{∥u_{i-1}∥}_{H^1(\mathrm{\Omega })}^2\mathit{\tau }}\hfill \\ \hfill & {\displaystyle \le \mathit{\epsilon }{∥\mathrm{\nabla }{u}_j∥}^2+C_{\mathit{\epsilon }}\left(1+\sum _{i=1}^j{∥\mathrm{\nabla }{u}_i∥}^2\mathit{\tau }+\sum _{i=1}^j{∥\mathit{\delta }{u}_i∥}^2\mathit{\tau }\right).}\hfill \end{array}$$

by Cauchy’s inequality, the trace theorem and Young’s inequality. The fourth guy in (6(6) $$\begin{array}{cc}& {\displaystyle +\sum _{i=1}^j\left(\sum _{k=1}^i{\mathrm{\Phi }}_k\mathit{\delta }{u}_{i-k}\mathit{\tau },\mathit{\delta }{u}_i\right)\mathit{\tau }=\sum _{i=1}^j\left(f_{i-1},\mathit{\delta }{u}_i\right)\mathit{\tau }.}\hfill \end{array}$$(6) ) is easily bounded by$$\begin{array}{c}\hfill \left|\sum _{i=1}^j{\mathrm{\Phi }}_i(u_0,\mathit{\delta }{u}_i)\mathit{\tau }\right|\le C\left(1+\sum _{i=1}^j{∥\mathit{\delta }{u}_i∥}^2\mathit{\tau }\right),\end{array}$$

as ${\mathrm{\Phi }}_i$ is bounded, see Lemma 2.1. The last term in the left-hand side of (6(6) $$\begin{array}{cc}& {\displaystyle +\sum _{i=1}^j\left(\sum _{k=1}^i{\mathrm{\Phi }}_k\mathit{\delta }{u}_{i-k}\mathit{\tau },\mathit{\delta }{u}_i\right)\mathit{\tau }=\sum _{i=1}^j\left(f_{i-1},\mathit{\delta }{u}_i\right)\mathit{\tau }.}\hfill \end{array}$$(6) ) is$$\left|\sum _{i=1}^j\sum _{k=1}^i({\mathrm{\Phi }}_k\mathit{\delta }{u}_{i-k},\mathit{\delta }{u}_i){\mathit{\tau }}^2\right|\le C\sum _{i=1}^j\sum _{k=1}^i∥\mathit{\delta }{u}_{i-k}∥∥\mathit{\delta }{u}_i)∥{\mathit{\tau }}^2\le C\left(1+\sum _{i=1}^j{∥\mathit{\delta }{u}_i∥}^2\mathit{\tau }\right)$$

again as ${\mathrm{\Phi }}_i$ is bounded, see Lemma 2.1. The right-hand side of (6(6) $$\begin{array}{cc}& {\displaystyle +\sum _{i=1}^j\left(\sum _{k=1}^i{\mathrm{\Phi }}_k\mathit{\delta }{u}_{i-k}\mathit{\tau },\mathit{\delta }{u}_i\right)\mathit{\tau }=\sum _{i=1}^j\left(f_{i-1},\mathit{\delta }{u}_i\right)\mathit{\tau }.}\hfill \end{array}$$(6) ) can be estimated as follows$$\begin{array}{c}\hfill \left|\sum _{i=1}^j(f_{i-1},\mathit{\delta }{u}_i)\mathit{\tau }\right|\le \sum _{i=1}^j∥f_{i-1}∥∥\mathit{\delta }{u}_i∥\mathit{\tau }\le C\left(1+\sum _{i=1}^j{∥\mathit{\delta }{u}_i∥}^2\mathit{\tau }\right).\end{array}$$

Collecting the estimates together and fixing a sufficiently small $\mathit{\epsilon }>0$ we obtain$$\begin{array}{cc}& {\displaystyle {∥\mathit{\delta }{u}_j∥}^2+{∥\mathrm{\nabla }{u}_j∥}^2+\sum _{i=1}^k{∥\mathit{\delta }{u}_i-\mathit{\delta }{u}_{i-1}∥}^2+\sum _{i=1}^k{∥\mathrm{\nabla }{u}_i-\mathrm{\nabla }{u}_{i-1}∥}^2}\hfill \\ \hfill & {\displaystyle \le C\left(1+\sum _{i=1}^j{∥\mathrm{\nabla }{u}_i∥}^2\mathit{\tau }+\sum _{i=1}^j{∥\mathit{\delta }{u}_i∥}^2\mathit{\tau }\right).}\hfill \end{array}$$

Applying the discrete Grönwall lemma we conclude the proof. $\square$

Lemma 2.3:

Let $f:{\mathbb{R}}^{N+3}\to \mathbb{R}$ be bounded, i.e. $|f|\le C$, and globally Lipschitz continuous. Suppose that (MP(MP) $$\begin{array}{c}\hfill m^{″}+{(g,1)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_{K}m(0)+{\mathrm{\Phi }}_K\ast m^{\prime }=\left(f(u,{\mathit{\partial }}_{t}u),1\right).\end{array}$$(MP) ) is valid at the time $t=0$ (compatibility condition). Moreover assume that $m\in C^3([0,T])$, $m(0)\ne 0$, ${\mathit{\partial }}_{tt}g\in L^2\left((0,T),L^2(\mathrm{\Gamma })\right)$, $v_0\in H^1(\mathrm{\Omega })$ and $u_0\in \mathit{V}$. Then there exists $C>0$ such that

(i)	${\displaystyle \underset{1\le j\le n}{max}{∥\mathrm{\nabla }\mathit{\delta }{u}_j∥}^2+\underset{1\le j\le n}{max}{∥\mathrm{\Delta }{u}_j∥}^2+\sum _{i=1}^n{∥\mathrm{\nabla }\mathit{\delta }{u}_i-\mathrm{\nabla }\mathit{\delta }{u}_{i-1}∥}^2+\sum _{i=1}^n{∥\mathrm{\Delta }{u}_i-\mathrm{\Delta }{u}_{i-1}∥}^2\le C}$
(ii)	${\displaystyle \underset{1\le j\le n}{max}∥{\mathit{\delta }}^2{u}_j∥\le C}$
(iii)	${\displaystyle \underset{1\le j\le n}{max}\left|K_j\right|=\underset{1\le j\le n}{max}\left|\mathit{\delta }{\mathrm{\Phi }}_j\right|\le C}$.

Proof:

(i) Multiplying (4(4) $$\begin{array}{c}\hfill {\mathit{\delta }}^2{u}_i-\mathrm{\Delta }{u}_i+{\mathrm{\Phi }}_i{u}_0+\sum _{k=1}^i{\mathrm{\Phi }}_k\mathit{\delta }{u}_{i-k}\mathit{\tau }=f_{i-1},\end{array}$$(4) ) by $-\mathrm{\Delta }\mathit{\delta }{u}_i\mathit{\tau }$ and summing up for $i=1,\dots ,j$ we get$$\begin{array}{cc}& {\displaystyle \sum _{i=1}^j\left({\mathit{\delta }}^2{u}_i,-\mathrm{\Delta }\mathit{\delta }{u}_i\right)\mathit{\tau }+\sum _{i=1}^j\left(\mathrm{\Delta }{u}_i,\mathrm{\Delta }\mathit{\delta }{u}_i\right)\mathit{\tau }+\sum _{i=1}^j\left({\mathrm{\Phi }}_i{u}_0,-\mathrm{\Delta }\mathit{\delta }{u}_i\right)\mathit{\tau }}\hfill \\ \hfill & {\displaystyle +\sum _{i=1}^j\left(\sum _{k=1}^i{\mathrm{\Phi }}_k\mathit{\delta }{u}_{i-k}\mathit{\tau },-\mathrm{\Delta }\mathit{\delta }{u}_i\right)\mathit{\tau }=\sum _{i=1}^j\left(f_{i-1},-\mathrm{\Delta }\mathit{\delta }{u}_i\right)\mathit{\tau }.}\hfill \end{array}$$

We apply the Green’s theorem to find out$$\begin{array}{cc}& {\displaystyle \sum _{i=1}^j\left(\mathrm{\nabla }{\mathit{\delta }}^2{u}_i,\mathrm{\nabla }\mathit{\delta }{u}_i\right)\mathit{\tau }+\sum _{i=1}^j\left(\mathrm{\Delta }{u}_i,\mathrm{\Delta }\mathit{\delta }{u}_i\right)\mathit{\tau }+\sum _{i=1}^j{\mathrm{\Phi }}_i\left(\mathrm{\nabla }{u}_0,\mathrm{\nabla }\mathit{\delta }{u}_i\right)\mathit{\tau }+\sum _{i=1}^j\left(\sum _{k=1}^i{\mathrm{\Phi }}_k\mathrm{\nabla }\mathit{\delta }{u}_{i-k}\mathit{\tau },\mathrm{\nabla }\mathit{\delta }{u}_i\right)\mathit{\tau }}\hfill \\ \hfill & {\displaystyle =\sum _{i=1}^j\left(\mathrm{\nabla }{f}_{i-1},\mathrm{\nabla }\mathit{\delta }{u}_i\right)\mathit{\tau }-\sum _{i=1}^j{\left({\mathit{\delta }}^2{u}_i,\mathit{\delta }{g}_i\right)}_{\mathrm{\Gamma }}\mathit{\tau }-\sum _{i=1}^j{\mathrm{\Phi }}_i{\left(u_0,\mathit{\delta }{g}_i\right)}_{\mathrm{\Gamma }}\mathit{\tau }-\sum _{i=1}^j{\left(\sum _{k=1}^i{\mathrm{\Phi }}_k\mathit{\delta }{u}_{i-k}\mathit{\tau },\mathit{\delta }{g}_i\right)}_{\mathrm{\Gamma }}\mathit{\tau }}\hfill \\ \hfill & {\displaystyle +\sum _{i=1}^j{\left(f_{i-1},\mathit{\delta }{g}_i\right)}_{\mathrm{\Gamma }}\mathit{\tau }.}\hfill \end{array}$$ It holds$$\sum _{i=1}^j\left(\mathrm{\nabla }{\mathit{\delta }}^2{u}_i,\mathrm{\nabla }\mathit{\delta }{u}_i\right)\mathit{\tau }=\frac{1}{2}\left({∥\mathrm{\nabla }\mathit{\delta }{u}_j∥}^2-{∥\mathrm{\nabla }\mathit{\delta }{u}_0∥}^2+\sum _{i=1}^j{∥\mathrm{\nabla }\mathit{\delta }{u}_i-\mathrm{\nabla }\mathit{\delta }{u}_{i-1}∥}^2\right)$$

and$$\sum _{i=1}^j\left(\mathrm{\Delta }{u}_i,\mathrm{\Delta }\mathit{\delta }{u}_i\right)\mathit{\tau }=\frac{1}{2}\left({∥\mathrm{\Delta }{u}_j∥}^2-{∥\mathrm{\Delta }{u}_0∥}^2+\sum _{i=1}^j{∥\mathrm{\Delta }{u}_i-\mathrm{\Delta }{u}_{i-1}∥}^2\right).$$

Employing the Cauchy and Young inequalities we easily see that$$\begin{array}{cc}\hfill \left|\sum _{i=1}^j{\mathrm{\Phi }}_i\left(\mathrm{\nabla }{u}_0,\mathrm{\nabla }\mathit{\delta }{u}_i\right)\mathit{\tau }\right|& \le \sum _{i=1}^j\left|{\mathrm{\Phi }}_i\right|∥\mathrm{\nabla }{u}_0∥∥\mathrm{\nabla }\mathit{\delta }{u}_i∥\mathit{\tau }\le C\left(1+\sum _{i=1}^j{∥\mathrm{\nabla }\mathit{\delta }{u}_i∥}^2\mathit{\tau }\right),\hfill \\ \hfill \left|\sum _{i=1}^j\left(\sum _{k=1}^i{\mathrm{\Phi }}_k\mathrm{\nabla }\mathit{\delta }{u}_{i-k}\mathit{\tau },\mathrm{\nabla }\mathit{\delta }{u}_i\right)\mathit{\tau }\right|& \le \sum _{i=1}^j\sum _{k=1}^i\left|{\mathrm{\Phi }}_k\right|∥\mathrm{\nabla }\mathit{\delta }{u}_{i-k}∥∥\mathrm{\nabla }\mathit{\delta }{u}_i∥{\mathit{\tau }}^2\le C\left(1+\sum _{i=1}^j{∥\mathrm{\nabla }\mathit{\delta }{u}_i∥}^2\mathit{\tau }\right),\hfill \\ \hfill {\displaystyle \left|\sum _{i=1}^j\left(\mathrm{\nabla }{f}_{i-1},\mathrm{\nabla }\mathit{\delta }{u}_i\right)\mathit{\tau }\right|}& {\displaystyle \le \sum _{i=1}^j∥\mathrm{\nabla }{f}_{i-1}∥∥\mathrm{\nabla }\mathit{\delta }{u}_i∥\mathit{\tau }}\hfill \\ \hfill & {\displaystyle \le C\sum _{i=1}^j\left(∥\mathrm{\nabla }{u}_{i-1}∥+∥\mathrm{\nabla }\mathit{\delta }{u}_{i-1}∥\right)∥\mathrm{\nabla }\mathit{\delta }{u}_i∥\mathit{\tau }}\hfill \\ \hfill & {\displaystyle \le C\left(1+\sum _{i=1}^j{∥\mathrm{\nabla }\mathit{\delta }{u}_i∥}^2\mathit{\tau }\right),}\hfill \\ \hfill \left|\sum _{i=1}^j{\mathrm{\Phi }}_i{\left(u_0,\mathit{\delta }{g}_i\right)}_{\mathrm{\Gamma }}\mathit{\tau }\right|& \le \sum _{i=1}^j\left|{\mathrm{\Phi }}_i\right|{∥u_0∥}_{\mathrm{\Gamma }}{∥\mathit{\delta }{g}_i∥}_{\mathrm{\Gamma }}\mathit{\tau }\le C,\hfill \\ \hfill \left|\sum _{i=1}^j{\left(f_{i-1},\mathit{\delta }{g}_i\right)}_{\mathrm{\Gamma }}\mathit{\tau }\right|& \le \sum _{i=1}^j{∥f_{i-1}∥}_{\mathrm{\Gamma }}{∥\mathit{\delta }{g}_i∥}_{\mathrm{\Gamma }}\mathit{\tau }\le C,\hfill \\ \hfill {\displaystyle \left|\sum _{i=1}^j{\left(\sum _{k=1}^i{\mathrm{\Phi }}_k\mathit{\delta }{u}_{i-k}\mathit{\tau },\mathit{\delta }{g}_i\right)}_{\mathrm{\Gamma }}\mathit{\tau }\right|}& {\displaystyle \le \sum _{i=1}^j\sum _{k=1}^i\left|{\mathrm{\Phi }}_k\right|{∥\mathit{\delta }{u}_{i-k}∥}_{\mathrm{\Gamma }}{∥\mathit{\delta }{g}_i∥}_{\mathrm{\Gamma }}{\mathit{\tau }}^2}\hfill \\ \hfill & {\displaystyle \le C\left(1+\sum _{i=1}^j{∥\mathit{\delta }{u}_i∥}_{\mathrm{\Gamma }}^2\mathit{\tau }\right)}\hfill \\ \hfill & {\displaystyle \le C\left(1+\sum _{i=1}^j{∥\mathrm{\nabla }\mathit{\delta }{u}_i∥}^2\mathit{\tau }\right).}\hfill \end{array}$$ We recall the Nečas inequality [25](8) $$\begin{array}{c}\hfill {∥z∥}_{\mathrm{\Gamma }}^2\le \mathit{\epsilon }{∥\mathrm{\nabla }z∥}^2+C_{\mathit{\epsilon }}{∥z∥}^2,\forall z\in H^1(\mathrm{\Omega }),0<\mathit{\epsilon }<{\mathit{\epsilon }}_0.\end{array}$$(8)

Summation by parts formula, Cauchy and Young inequalities, trace theorem together with (8(8) $$\begin{array}{c}\hfill {∥z∥}_{\mathrm{\Gamma }}^2\le \mathit{\epsilon }{∥\mathrm{\nabla }z∥}^2+C_{\mathit{\epsilon }}{∥z∥}^2,\forall z\in H^1(\mathrm{\Omega }),0<\mathit{\epsilon }<{\mathit{\epsilon }}_0.\end{array}$$(8) ) allow us to deduce that$$\begin{array}{cc}\hfill {\displaystyle \left|\sum _{i=1}^j{\left({\mathit{\delta }}^2{u}_i,\mathit{\delta }{g}_i\right)}_{\mathrm{\Gamma }}\mathit{\tau }\right|}& {\displaystyle =\left|{\left(\mathit{\delta }{u}_j,\mathit{\delta }{g}_j\right)}_{\mathrm{\Gamma }}-{\left(\mathit{\delta }{u}_0,\mathit{\delta }{g}_0\right)}_{\mathrm{\Gamma }}-\sum _{i=1}^j{\left(\mathit{\delta }{u}_{i-1},{\mathit{\delta }}^2{g}_i\right)}_{\mathrm{\Gamma }}\mathit{\tau }\right|}\hfill \\ \hfill & {\displaystyle \le {∥\mathit{\delta }{u}_j∥}_{\mathrm{\Gamma }}{∥\mathit{\delta }{g}_j∥}_{\mathrm{\Gamma }}+{∥\mathit{\delta }{u}_0∥}_{\mathrm{\Gamma }}{∥\mathit{\delta }{g}_0∥}_{\mathrm{\Gamma }}+\sum _{i=1}^j{∥\mathit{\delta }{u}_{i-1}∥}_{\mathrm{\Gamma }}{∥{\mathit{\delta }}^2{g}_i∥}_{\mathrm{\Gamma }}\mathit{\tau }}\hfill \\ \hfill & {\displaystyle \le C\left({∥\mathit{\delta }{u}_j∥}_{\mathrm{\Gamma }}^2+1+\sum _{i=1}^j{∥\mathit{\delta }{u}_{i-1}∥}_{\mathrm{\Gamma }}^2\mathit{\tau }\right)}\hfill \\ \hfill & {\displaystyle \le \mathit{\epsilon }{∥\mathrm{\nabla }\mathit{\delta }{u}_j∥}_{\mathrm{\Gamma }}^2+C_{\mathit{\epsilon }}\left(1+\sum _{i=1}^j{∥\mathrm{\nabla }\mathit{\delta }{u}_i∥}^2\mathit{\tau }\right).}\hfill \end{array}$$

Summarizing all estimates and fixing a suitable small $\mathit{\epsilon }>0$ we arrive at$${∥\mathrm{\nabla }\mathit{\delta }{u}_j∥}^2+{∥\mathrm{\Delta }{u}_j∥}^2+\sum _{i=1}^j{∥\mathrm{\nabla }\mathit{\delta }{u}_i-\mathrm{\nabla }\mathit{\delta }{u}_{i-1}∥}^2+\sum _{i=1}^j{∥\mathrm{\Delta }{u}_i-\mathrm{\Delta }{u}_{i-1}∥}^2\le C\left(1+\sum _{i=1}^j{∥\mathrm{\nabla }\mathit{\delta }{u}_i∥}^2\mathit{\tau }\right).$$ Employing Grönwall’s lemma we conclude the proof.

(ii) The assertion follows from (i) and (4(4) $$\begin{array}{c}\hfill {\mathit{\delta }}^2{u}_i-\mathrm{\Delta }{u}_i+{\mathrm{\Phi }}_i{u}_0+\sum _{k=1}^i{\mathrm{\Phi }}_k\mathit{\delta }{u}_{i-k}\mathit{\tau }=f_{i-1},\end{array}$$(4) ) as follows$$∥{\mathit{\delta }}^2{u}_i∥\le ∥\mathrm{\Delta }{u}_i∥+\left|{\mathrm{\Phi }}_i\right|∥u_0∥+\sum _{k=1}^i\left|{\mathrm{\Phi }}_k\right|∥\mathit{\delta }{u}_{i-k}∥\mathit{\tau }+∥f_{i-1}∥\le C.$$(iii) Subtract (MP(MP) $$\begin{array}{c}\hfill m^{″}+{(g,1)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_{K}m(0)+{\mathrm{\Phi }}_K\ast m^{\prime }=\left(f(u,{\mathit{\partial }}_{t}u),1\right).\end{array}$$(MP) ) at the time $t=0$ from (DMP$i$(DMPi) $$\begin{array}{c}\hfill m_i^{″}+{(g_i,1)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_i{m}_0+\sum _{k=1}^i{\mathrm{\Phi }}_k{m}_{i-k}^{\prime }\mathit{\tau }=(f_{i-1},1).\end{array}$$(DMPi) ) for $i=1$ to observe(9) $$\begin{array}{c}\hfill \mathit{\delta }{m}_1^{″}+{\left(\mathit{\delta }{g}_1,1\right)}_{\mathrm{\Gamma }}+K_1{m}_0+{\mathrm{\Phi }}_1{m}_0^{\prime }\mathit{\tau }=0⟹\left|K_1\right|\le C.\end{array}$$(9)

Applying the $\mathit{\delta }$-operator to (DMP$i$(DMPi) $$\begin{array}{c}\hfill m_i^{″}+{(g_i,1)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_i{m}_0+\sum _{k=1}^i{\mathrm{\Phi }}_k{m}_{i-k}^{\prime }\mathit{\tau }=(f_{i-1},1).\end{array}$$(DMPi) ) we get for $i\ge 2$(10) $$\begin{array}{c}\hfill \mathit{\delta }{m}_i^{″}+{\left(\mathit{\delta }{g}_i,1\right)}_{\mathrm{\Gamma }}+K_i{m}_0+{\mathrm{\Phi }}_i{m}_0^{\prime }+\sum _{k=1}^i{\mathrm{\Phi }}_k{m}_{i-k}^{\prime }\mathit{\tau }=\left(\mathit{\delta }{f}_{i-1},1\right)\end{array}$$(10)

Taking into account Lemmas 2.1, 2.2 and Lipschitz continuity of $f$ we easily see that$$\begin{array}{cc}\hfill {\displaystyle \left|K_{i}m(0)\right|}& {\displaystyle \le \left|\left(\mathit{\delta }{f}_{i-1},1\right)\right|+\left|\mathit{\delta }{m}_i^{″}\right|+\left|{\left(\mathit{\delta }{g}_i,1\right)}_{\mathrm{\Gamma }}\right|+\left|{\mathrm{\Phi }}_i{m}_0^{\prime }\right|+\left|\sum _{k=1}^i{\mathrm{\Phi }}_k{m}_{i-k}^{\prime }\mathit{\tau }\right|}\hfill \\ \hfill & {\displaystyle \le C\left(1+∥\mathit{\delta }{u}_{i-1}∥+∥{\mathit{\delta }}^2{u}_{i-1}∥\right)}\hfill \\ \hfill & {\displaystyle \le C.}\hfill \end{array}$$$\square$

3. Existence of a solution, uniqueness and error estimates

Now, let us introduce the following piecewise linear functions in time$$u_n:[0,T]\to L^2(\mathrm{\Omega }):t\mapsto \left\{\begin{array}{cc}{u}_0\hfill & t=0\hfill \\ u_{i-1}+(t-t_{i-1})\mathit{\delta }{u}_i\hfill & t\in (t_{i-1},t_i]\hfill \end{array}\right.,1\le i\le n,$$$$v_n:[0,T]\to L^2(\mathrm{\Omega }):t\mapsto \left\{\begin{array}{cc}{v}_0\hfill & t=0\hfill \\ \mathit{\delta }{u}_{i-1}+(t-t_{i-1}){\mathit{\delta }}^2{u}_i\hfill & t\in (t_{i-1},t_i]\hfill \end{array}\right.,1\le i\le n,$$

and step functions$${\overline{u}}_n:[0,T]\to L^2(\mathrm{\Omega }):t\mapsto \left\{\begin{array}{cc}{u}_0\hfill & t=0\hfill \\ u_i\hfill & t\in (t_{i-1},t_i]\hfill \end{array}\right.,1\le i\le n,$$$${\overline{v}}_n:[0,T]\to L^2(\mathrm{\Omega }):t\mapsto \left\{\begin{array}{cc}{v}_0\hfill & t=0\hfill \\ \mathit{\delta }{u}_i\hfill & t\in (t_{i-1},t_i]\hfill \end{array}\right.,1\le i\le n.$$

Similarly we define ${\mathrm{\Phi }}_n$, ${\overline{\mathrm{\Phi }}}_n$, ${\overline{g}}_n$, ${\overline{m}}_n$, ${\overline{m^{\prime }}}_n$ and ${\overline{m^{″}}}_n$. These prolongations are also called Rothe’s (piecewise linear and continuous, or piecewise constant) functions. Now, we can rewrite (DP$i$(DPi) $$\begin{array}{c}\hfill \left({\mathit{\delta }}^2{u}_i,\mathit{\phi }\right)+\left(\mathrm{\nabla }{u}_i,\mathrm{\nabla }\mathit{\phi }\right)+{\left(g_i,\mathit{\phi }\right)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_i\left(u_0,\mathit{\phi }\right)+\left(\sum _{k=1}^i{\mathrm{\Phi }}_k\mathit{\delta }{u}_{i-k}\mathit{\tau },\mathit{\phi }\right)=\left(f_{i-1},\mathit{\phi }\right)\end{array}$$(DPi) ) and (DMP$i$(DMPi) $$\begin{array}{c}\hfill m_i^{″}+{(g_i,1)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_i{m}_0+\sum _{k=1}^i{\mathrm{\Phi }}_k{m}_{i-k}^{\prime }\mathit{\tau }=(f_{i-1},1).\end{array}$$(DMPi) ) on the whole time frame as¹$$\begin{array}{cc}& {\displaystyle \left({\mathit{\partial }}_t{v}_n,\mathit{\phi }\right)+\left(\mathrm{\nabla }{\overline{u}}_n,\mathrm{\nabla }\mathit{\phi }\right)+{\left({\overline{g}}_n,\mathit{\phi }\right)}_{\mathrm{\Gamma }}+{\overline{\mathrm{\Phi }}}_n\left(u_0,\mathit{\phi }\right)+\left(\sum _{k=1}^{{\lfloor t\rfloor }_{\mathit{\tau }}}{\overline{\mathrm{\Phi }}}_n(t_k){\overline{v}}_n(t-t_k)\mathit{\tau },\mathit{\phi }\right)}\hfill \end{array}$$(DP) $$\begin{array}{cc}& {\displaystyle =\left(f({\overline{u}}_n(t-\mathit{\tau }),{\overline{v}}_n(t-\mathit{\tau })),\mathit{\phi }\right).}\hfill \end{array}$$(DP)

and(DMP) $$\begin{array}{c}\hfill {\overline{m^{″}}}_n+{({\overline{g}}_n,1)}_{\mathrm{\Gamma }}+{\overline{\mathrm{\Phi }}}_n{m}_0+\sum _{k=1}^{{\lfloor t\rfloor }_{\mathit{\tau }}}{\overline{\mathrm{\Phi }}}_n(t_k){\overline{m^{\prime }}}_n(t-t_k)\mathit{\tau }=\left(f({\overline{u}}_n(t-\mathit{\tau }),{\overline{v}}_n(t-\mathit{\tau })),1\right).\end{array}$$(DMP)

Now, we are in a position to prove the existence of a weak solution to (P(P) $$\begin{array}{c}\hfill \left({\mathit{\partial }}_{tt}u,\mathit{\phi }\right)+\left(\mathrm{\nabla }u,\mathrm{\nabla }\mathit{\phi }\right)+{\left(g,\mathit{\phi }\right)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_K\left(u_0,\mathit{\phi }\right)+\left({\mathrm{\Phi }}_K\ast {\mathit{\partial }}_{t}u,\mathit{\phi }\right)=\left(f(u,{\mathit{\partial }}_{t}u),\mathit{\phi }\right).\end{array}$$(P) ) and (MP(MP) $$\begin{array}{c}\hfill m^{″}+{(g,1)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_{K}m(0)+{\mathrm{\Phi }}_K\ast m^{\prime }=\left(f(u,{\mathit{\partial }}_{t}u),1\right).\end{array}$$(MP) ).

Theorem 3.1:

Suppose the conditions of Lemma 2.3 are fulfilled. Then there exists a solution $(u,K)$ to (P(P) $$\begin{array}{c}\hfill \left({\mathit{\partial }}_{tt}u,\mathit{\phi }\right)+\left(\mathrm{\nabla }u,\mathrm{\nabla }\mathit{\phi }\right)+{\left(g,\mathit{\phi }\right)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_K\left(u_0,\mathit{\phi }\right)+\left({\mathrm{\Phi }}_K\ast {\mathit{\partial }}_{t}u,\mathit{\phi }\right)=\left(f(u,{\mathit{\partial }}_{t}u),\mathit{\phi }\right).\end{array}$$(P) ) and (MP(MP) $$\begin{array}{c}\hfill m^{″}+{(g,1)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_{K}m(0)+{\mathrm{\Phi }}_K\ast m^{\prime }=\left(f(u,{\mathit{\partial }}_{t}u),1\right).\end{array}$$(MP) ), where $u\in C\left([0,T],L^2(\mathrm{\Omega })\right)\cap L^{\infty }\left((0,T),\mathit{V}\right)$ with ${\mathit{\partial }}_{t}u\in C\left([0,T],L^2(\mathrm{\Omega })\right)\cap L^{\infty }\left((0,T),H^1(\mathrm{\Omega })\right)$, $u_{tt}\in L^{\infty }\left((0,T),L^2(\mathrm{\Omega })\right)$ and ${\mathrm{\Phi }}_K\in C^{(}[0,T])$ with $K\in L^{\infty }(0,T)$.

Proof:

The functions ${\mathrm{\Phi }}_n$ and ${\mathit{\partial }}_t{\mathrm{\Phi }}_n$ are uniformly bounded in $[0,T]$. By Arzelà Ascoli theorem we get for a subsequence of ${\mathrm{\Phi }}_n$ (which we denote by the same symbol again to skip double indices) that ${\mathrm{\Phi }}_n\to \mathrm{\Phi }$ in $C([0,T])$ and$$\left|\mathrm{\Phi }(t)-\mathrm{\Phi }(t^{\prime })\right|=\underset{n\to \infty }{lim}\left|{\mathrm{\Phi }}_n(t)-{\mathrm{\Phi }}_n(t^{\prime })\right|=\underset{n\to \infty }{lim}\left|{\int }_{t^{\prime }}^t{\mathit{\partial }}_t{\mathrm{\Phi }}_n\right|\le \underset{n\to \infty }{lim}{\int }_{t^{\prime }}^t\left|{\mathit{\partial }}_t{\mathrm{\Phi }}_n\right|\le C\left|t-t^{\prime }\right|.$$ Hence, $K={\mathit{\partial }}_t\mathrm{\Phi }$ is a.e. in $[0,T]$ bounded. Moreover we have(11) $$\begin{array}{c}\hfill \left|{\mathrm{\Phi }}_n(t)-{\overline{\mathrm{\Phi }}}_n(t)\right|\le C\mathit{\tau }.\end{array}$$(11)

A priori estimates say that ${\displaystyle {∥{\overline{u}}_n∥}_{\mathit{V}}+∥{\mathit{\partial }}_t{u}_n∥\le C}$. Due to the compact embedding $\mathit{V}⋐L^2(\mathrm{\Omega })$ we may invoke [20, Lemma 1.3.13] to claim the existence of $u\in C\left([0,T],L^2(\mathrm{\Omega })\right)\cap L^{\infty }\left((0,T),\mathit{V}\right)$ with $u_t\in L^{\infty }\left((0,T),L^2(\mathrm{\Omega })\right)$ and a subsequence of $u_n$ (denoted by the same symbol again) such that$$\begin{array}{cc}\hfill u_n\to u,& \text{in}C\left([0,T],L^2(\mathrm{\Omega })\right)\hfill \\ \hfill u_n(t)\rightharpoonup u(t),& \text{in}\mathit{V},\forall t\in [0,T]\hfill \\ \hfill {\overline{u}}_n(t)\rightharpoonup u(t),& \text{in}\mathit{V},\forall t\in [0,T]\hfill \\ \hfill {\mathit{\partial }}_t{u}_n\rightharpoonup {\mathit{\partial }}_{t}u,& \text{in}{L}^2\left((0,T),L^2(\mathrm{\Omega })\right).\hfill \end{array}$$

The limit function $u:[0,T]\to L^2(\mathrm{\Omega })$ is moreover Lipschitz continuous, which follows from$$∥u_n(t)-u_n(t^{\prime })∥=∥{\int }_t^{t^{\prime }}{\mathit{\partial }}_t{u}_n∥\le C\left|t-t^{\prime }\right|$$

when passing to the limit for $n\to \infty$. Similarly we have(12) $$\begin{array}{c}\hfill ∥u_n(t)-{\overline{u}}_n(t)∥+∥{\overline{u}}_n(t)-{\overline{u}}_n(t-\mathit{\tau })∥\le C\mathit{\tau }.\end{array}$$(12)

The stability result ${\displaystyle {∥{\overline{v}}_n∥}_{H^1(\mathrm{\Omega })}+∥{\mathit{\partial }}_t{v}_n∥\le C}$ and the compact embedding $H^1(\mathrm{\Omega })⋐L^2(\mathrm{\Omega })$ give (by [20, Lemma 1.3.13]) the existence of $v\in C\left([0,T],L^2(\mathrm{\Omega })\right)\cap L^{\infty }\left((0,T),H^1(\mathrm{\Omega })\right)$ with $v_t\in L^{\infty }\left((0,T),L^2(\mathrm{\Omega })\right)$ and a subsequence of $v_n$ (denoted by the same symbol again) such that$$\begin{array}{cc}\hfill v_n\to v,& \text{in}C\left([0,T],L^2(\mathrm{\Omega })\right)\hfill \\ \hfill v_n(t)\rightharpoonup v(t),& \text{in}{H}^1(\mathrm{\Omega }),\forall t\in [0,T]\hfill \\ \hfill {\overline{v}}_n(t)\rightharpoonup v(t),& \text{in}{H}^1(\mathrm{\Omega }),\forall t\in [0,T]\hfill \\ \hfill {\mathit{\partial }}_t{v}_n\rightharpoonup {\mathit{\partial }}_{t}v,& \text{in}{L}^2\left((0,T),L^2(\mathrm{\Omega })\right).\hfill \end{array}$$

The limit function $v:[0,T]\to L^2(\mathrm{\Omega })$ is again Lipschitz continuous, which follows from$$∥v_n(t)-v_n(t^{\prime })∥=∥{\int }_t^{t^{\prime }}{\mathit{\partial }}_t{v}_n∥\le C\left|t-t^{\prime }\right|$$

when passing to the limit for $n\to \infty$. Analogously, we get(13) $$\begin{array}{c}\hfill ∥v_n(t)-{\overline{v}}_n(t)∥+∥{\overline{v}}_n(t)-{\overline{v}}_n(t-\mathit{\tau })∥\le C\mathit{\tau }.\end{array}$$(13)

Moreover, taking into account ${\displaystyle u_n(t)-u_0={\int }_0^t{\mathit{\partial }}_t{u}_n={\int }_0^t{\overline{v}}_n}$, letting $n$ go to infinity and differentiating the result with respect to the time variable we see that $v={\mathit{\partial }}_{t}u$.

Finally, the regularity of $g$, $m$ together with the convergences above allow us to pass to the limit for $n\to \infty$ in (DP(DP) $$\begin{array}{cc}& {\displaystyle =\left(f({\overline{u}}_n(t-\mathit{\tau }),{\overline{v}}_n(t-\mathit{\tau })),\mathit{\phi }\right).}\hfill \end{array}$$(DP) ) and (DMP(DMP) $$\begin{array}{c}\hfill {\overline{m^{″}}}_n+{({\overline{g}}_n,1)}_{\mathrm{\Gamma }}+{\overline{\mathrm{\Phi }}}_n{m}_0+\sum _{k=1}^{{\lfloor t\rfloor }_{\mathit{\tau }}}{\overline{\mathrm{\Phi }}}_n(t_k){\overline{m^{\prime }}}_n(t-t_k)\mathit{\tau }=\left(f({\overline{u}}_n(t-\mathit{\tau }),{\overline{v}}_n(t-\mathit{\tau })),1\right).\end{array}$$(DMP) ) to arrive at (P(P) $$\begin{array}{c}\hfill \left({\mathit{\partial }}_{tt}u,\mathit{\phi }\right)+\left(\mathrm{\nabla }u,\mathrm{\nabla }\mathit{\phi }\right)+{\left(g,\mathit{\phi }\right)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_K\left(u_0,\mathit{\phi }\right)+\left({\mathrm{\Phi }}_K\ast {\mathit{\partial }}_{t}u,\mathit{\phi }\right)=\left(f(u,{\mathit{\partial }}_{t}u),\mathit{\phi }\right).\end{array}$$(P) ) and (MP(MP) $$\begin{array}{c}\hfill m^{″}+{(g,1)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_{K}m(0)+{\mathrm{\Phi }}_K\ast m^{\prime }=\left(f(u,{\mathit{\partial }}_{t}u),1\right).\end{array}$$(MP) ). Thus the couple $(u,\mathrm{\Phi })$ is a solution to (P(P) $$\begin{array}{c}\hfill \left({\mathit{\partial }}_{tt}u,\mathit{\phi }\right)+\left(\mathrm{\nabla }u,\mathrm{\nabla }\mathit{\phi }\right)+{\left(g,\mathit{\phi }\right)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_K\left(u_0,\mathit{\phi }\right)+\left({\mathrm{\Phi }}_K\ast {\mathit{\partial }}_{t}u,\mathit{\phi }\right)=\left(f(u,{\mathit{\partial }}_{t}u),\mathit{\phi }\right).\end{array}$$(P) ) and (MP(MP) $$\begin{array}{c}\hfill m^{″}+{(g,1)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_{K}m(0)+{\mathrm{\Phi }}_K\ast m^{\prime }=\left(f(u,{\mathit{\partial }}_{t}u),1\right).\end{array}$$(MP) ). $\square$

Now, we are in a position to state unicity of solution. Suppose $(u_1,K_1)$ and $(u_2,K_2)$ solve (P(P) $$\begin{array}{c}\hfill \left({\mathit{\partial }}_{tt}u,\mathit{\phi }\right)+\left(\mathrm{\nabla }u,\mathrm{\nabla }\mathit{\phi }\right)+{\left(g,\mathit{\phi }\right)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_K\left(u_0,\mathit{\phi }\right)+\left({\mathrm{\Phi }}_K\ast {\mathit{\partial }}_{t}u,\mathit{\phi }\right)=\left(f(u,{\mathit{\partial }}_{t}u),\mathit{\phi }\right).\end{array}$$(P) )–(MP(MP) $$\begin{array}{c}\hfill m^{″}+{(g,1)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_{K}m(0)+{\mathrm{\Phi }}_K\ast m^{\prime }=\left(f(u,{\mathit{\partial }}_{t}u),1\right).\end{array}$$(MP) ). We set $K:=K_1-K_2$ and $u:=u_1-u_2$. Then by subtracting the corresponding variational formulations from each other we obtain

Theorem 3.2:

Let $f:{\mathbb{R}}^{N+3}\to \mathbb{R}$ be bounded, i.e. $|f|\le C$, and globally Lipschitz continuous. Moreover assume that $m\in C^2([0,T])$, $m(0)\ne 0$, ${\mathit{\partial }}_{t}g\in L^2\left((0,T),L^2(\mathrm{\Gamma })\right)$, $v_0\in L^2(\mathrm{\Omega })$ and $u_0\in H^1(\mathrm{\Omega })$. Then the problem (P(P) $$\begin{array}{c}\hfill \left({\mathit{\partial }}_{tt}u,\mathit{\phi }\right)+\left(\mathrm{\nabla }u,\mathrm{\nabla }\mathit{\phi }\right)+{\left(g,\mathit{\phi }\right)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_K\left(u_0,\mathit{\phi }\right)+\left({\mathrm{\Phi }}_K\ast {\mathit{\partial }}_{t}u,\mathit{\phi }\right)=\left(f(u,{\mathit{\partial }}_{t}u),\mathit{\phi }\right).\end{array}$$(P) )–(MP(MP) $$\begin{array}{c}\hfill m^{″}+{(g,1)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_{K}m(0)+{\mathrm{\Phi }}_K\ast m^{\prime }=\left(f(u,{\mathit{\partial }}_{t}u),1\right).\end{array}$$(MP) ) has at most one solution satisfying $u\in C\left([0,T],L^2(\mathrm{\Omega })\right)\cap L^{\infty }\left((0,T),\mathit{V}\right)$ with ${\mathit{\partial }}_{t}u\in C\left([0,T],L^2(\mathrm{\Omega })\right)\cap L^{\infty }\left((0,T),H^1(\mathrm{\Omega })\right)$, $u_{tt}\in L^{\infty }\left((0,T),L^2(\mathrm{\Omega })\right)$ and ${\mathrm{\Phi }}_K\in C^{(}[0,T])$ with $K\in L^{\infty }(0,T)$.

Proof:

The Lipschitz continuity of $f$ and (14b) imply$$\left|{\mathrm{\Phi }}_K(t)\right|\le C\left(∥u(t)∥+∥{\mathit{\partial }}_{t}u(t)∥+{\int }_0^t\left|{\mathrm{\Phi }}_K(s)\right|\text{d}s\right),$$

which by Grönwall’s lemma gives$$\begin{array}{cc}\hfill {\displaystyle \left|{\mathrm{\Phi }}_K(t)\right|}& {\displaystyle \le C\left(∥u(t)∥+∥{\mathit{\partial }}_{t}u(t)∥+{\int }_0^t\left[∥u(s)∥+∥{\mathit{\partial }}_{t}u(s)∥\right]\text{d}s\right)}\hfill \end{array}$$(15) $$\begin{array}{cc}& {\displaystyle \le C\left(∥{\mathit{\partial }}_{t}u(t)∥+{\int }_0^t∥{\mathit{\partial }}_{t}u(s)∥\text{d}s\right)}\hfill \end{array}$$(15)

We put $\mathit{\phi }={\mathit{\partial }}_{t}u$ in (14a) and integrate in time$$\begin{array}{cc}& {\displaystyle \frac{1}{2}{∥{\mathit{\partial }}_{t}u(t)∥}^2+\frac{1}{2}{∥\mathrm{\nabla }u(t)∥}^2+{\int }_0^t{\mathrm{\Phi }}_K\left(u_0,{\mathit{\partial }}_{t}u\right)+{\int }_0^t\left({\mathrm{\Phi }}_K\ast {\mathit{\partial }}_t{u}_2,{\mathit{\partial }}_{t}u\right)+{\int }_0^t\left({\mathrm{\Phi }}_{K_1}\ast {\mathit{\partial }}_{t}u,{\mathit{\partial }}_{t}u\right)}\hfill \\ \hfill & {\displaystyle ={\int }_0^t\left(f(u_1,{\mathit{\partial }}_t{u}_1)-f(u_2,{\mathit{\partial }}_t{u}_2),{\mathit{\partial }}_{t}u\right).}\hfill \end{array}$$ Using Cauchy’s inequality, we obtain successively the bounds$$\begin{array}{cc}\hfill {\displaystyle \left|{\int }_0^t\left(f(u_1,{\mathit{\partial }}_t{u}_1)-f(u_2,{\mathit{\partial }}_t{u}_2),{\mathit{\partial }}_{t}u\right)\right|}& {\displaystyle \le {\int }_0^t∥f(u_1,{\mathit{\partial }}_t{u}_1)-f(u_2,{\mathit{\partial }}_t{u}_2)∥∥{\mathit{\partial }}_{t}u∥}\hfill \\ \hfill & {\displaystyle \le {\int }_0^t\left(∥u∥+∥{\mathit{\partial }}_{t}u∥\right)∥{\mathit{\partial }}_{t}u∥}\hfill \\ \hfill & {\displaystyle \le C{\int }_0^t\left({∥u∥}^2+{∥{\mathit{\partial }}_{t}u∥}^2\right)}\hfill \\ \hfill & {\displaystyle \le C{\int }_0^t{∥{\mathit{\partial }}_{t}u∥}^2}\hfill \end{array}$$

as $f$ is Lipschitz,$$\begin{array}{cc}\hfill {\displaystyle \left|{\int }_0^t\left({\mathrm{\Phi }}_{K_1}\ast {\mathit{\partial }}_{t}u,{\mathit{\partial }}_{t}u\right)\right|}& {\displaystyle \le {\int }_0^t∥{\mathrm{\Phi }}_{K_1}\ast {\mathit{\partial }}_{t}u∥∥{\mathit{\partial }}_{t}u∥}\hfill \\ \hfill & {\displaystyle \le C{\int }_0^t\left({∥{\mathrm{\Phi }}_{K_1}\ast {\mathit{\partial }}_{t}u∥}^2+{∥{\mathit{\partial }}_{t}u∥}^2\right)}\hfill \\ \hfill & {\displaystyle \le C{\int }_0^t{∥{\mathit{\partial }}_{t}u∥}^2}\hfill \end{array}$$

using $\left|{\mathrm{\Phi }}_{K_1}(t)\right|\le C$. Taking into account $∥{\mathit{\partial }}_t{u}_2(t)∥\le C$ and (15(15) $$\begin{array}{cc}& {\displaystyle \le C\left(∥{\mathit{\partial }}_{t}u(t)∥+{\int }_0^t∥{\mathit{\partial }}_{t}u(s)∥\text{d}s\right)}\hfill \end{array}$$(15) )$$\begin{array}{cc}\hfill {\displaystyle \left|{\int }_0^t\left({\mathrm{\Phi }}_K\ast {\mathit{\partial }}_t{u}_2,{\mathit{\partial }}_{t}u\right)\right|}& {\displaystyle \le {\int }_0^t∥{\mathrm{\Phi }}_K\ast {\mathit{\partial }}_t{u}_2∥∥{\mathit{\partial }}_{t}u∥}\hfill \\ \hfill & {\displaystyle \le C{\int }_0^t\left({∥{\mathrm{\Phi }}_K\ast {\mathit{\partial }}_t{u}_2∥}^2+{∥{\mathit{\partial }}_{t}u∥}^2\right)}\hfill \\ \hfill & {\displaystyle \le C{\int }_0^t\left({\left|{\mathrm{\Phi }}_K\right|}^2+{∥{\mathit{\partial }}_{t}u∥}^2\right)}\hfill \\ \hfill & {\displaystyle \le C{\int }_0^t{∥{\mathit{\partial }}_{t}u∥}^2.}\hfill \end{array}$$

Finally, we deduce that by (15(15) $$\begin{array}{cc}& {\displaystyle \le C\left(∥{\mathit{\partial }}_{t}u(t)∥+{\int }_0^t∥{\mathit{\partial }}_{t}u(s)∥\text{d}s\right)}\hfill \end{array}$$(15) )$$\begin{array}{c}\hfill {\displaystyle \left|{\int }_0^t{\mathrm{\Phi }}_K\left(u_0,{\mathit{\partial }}_{t}u\right)\right|\le C{\int }_0^t\left|{\mathrm{\Phi }}_K\right|∥{\mathit{\partial }}_{t}u∥\le C{\int }_0^t\left({\left|{\mathrm{\Phi }}_K\right|}^2+{∥{\mathit{\partial }}_{t}u∥}^2\right)\le C{\int }_0^t{∥{\mathit{\partial }}_{t}u∥}^2.}\end{array}$$

Grouping all estimates together we see that$${∥{\mathit{\partial }}_{t}u(t)∥}^2+{∥\mathrm{\nabla }u(t)∥}^2\le C{\int }_0^t{∥{\mathit{\partial }}_{t}u∥}^2\forall t\in [0,T].$$

Grönwall’s lemma implies that $u(t)=0$ and from (15(15) $$\begin{array}{cc}& {\displaystyle \le C\left(∥{\mathit{\partial }}_{t}u(t)∥+{\int }_0^t∥{\mathit{\partial }}_{t}u(s)∥\text{d}s\right)}\hfill \end{array}$$(15) ) we conclude ${\mathrm{\Phi }}_K(t)=0$. By differentiation we have $K(t)=0$. $\square$

The convergences of Rothe’s functions towards the weak solution (P(P) $$\begin{array}{c}\hfill \left({\mathit{\partial }}_{tt}u,\mathit{\phi }\right)+\left(\mathrm{\nabla }u,\mathrm{\nabla }\mathit{\phi }\right)+{\left(g,\mathit{\phi }\right)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_K\left(u_0,\mathit{\phi }\right)+\left({\mathrm{\Phi }}_K\ast {\mathit{\partial }}_{t}u,\mathit{\phi }\right)=\left(f(u,{\mathit{\partial }}_{t}u),\mathit{\phi }\right).\end{array}$$(P) )–(MP(MP) $$\begin{array}{c}\hfill m^{″}+{(g,1)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_{K}m(0)+{\mathrm{\Phi }}_K\ast m^{\prime }=\left(f(u,{\mathit{\partial }}_{t}u),1\right).\end{array}$$(MP) ) (as stated in the proof of Theorem 3.1) have been shown for a subsequence. Note, that taking into account Theorem 3.2 we see that the whole Rothe’s functions converge against the solution. Error estimates are addressed in the next theorem.

Theorem 3.3:

Suppose the conditions of Lemma 2.3 are fulfilled. Then$$\underset{t\in [0,T]}{max}{\left|{\mathrm{\Phi }}_K(t)-{\mathrm{\Phi }}_n(t)\right|}^2+\underset{t\in [0,T]}{max}{∥{\mathit{\partial }}_{t}u(t)-v_n(t)∥}^2+\underset{t\in [0,T]}{max}{∥u(t)-u_n(t)∥}_{H^1(\mathrm{\Omega })}^2\le C\mathit{\tau }.$$

Proof:

Subtract (MP(MP) $$\begin{array}{c}\hfill m^{″}+{(g,1)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_{K}m(0)+{\mathrm{\Phi }}_K\ast m^{\prime }=\left(f(u,{\mathit{\partial }}_{t}u),1\right).\end{array}$$(MP) ) from (DMP(DMP) $$\begin{array}{c}\hfill {\overline{m^{″}}}_n+{({\overline{g}}_n,1)}_{\mathrm{\Gamma }}+{\overline{\mathrm{\Phi }}}_n{m}_0+\sum _{k=1}^{{\lfloor t\rfloor }_{\mathit{\tau }}}{\overline{\mathrm{\Phi }}}_n(t_k){\overline{m^{\prime }}}_n(t-t_k)\mathit{\tau }=\left(f({\overline{u}}_n(t-\mathit{\tau }),{\overline{v}}_n(t-\mathit{\tau })),1\right).\end{array}$$(DMP) ) to get$$\begin{array}{cc}\hfill {\displaystyle \left({\mathrm{\Phi }}_n-{\mathrm{\Phi }}_K\right)m_0}& {\displaystyle =\left({\mathrm{\Phi }}_K-{\mathrm{\Phi }}_n\right)\ast m^{\prime }+{\mathrm{\Phi }}_n\ast m^{\prime }-\sum _{k=1}^{{\lfloor t\rfloor }_{\mathit{\tau }}}{\overline{\mathrm{\Phi }}}_n(t_k){\overline{m^{\prime }}}_n(t-t_k)\mathit{\tau }}\hfill \\ \hfill & {\displaystyle +\left(f({\overline{u}}_n(t-\mathit{\tau }),{\overline{v}}_n(t-\mathit{\tau }))-f(u(t),{\mathit{\partial }}_{t}u(t)),1\right)}\hfill \end{array}$$(16) $$\begin{array}{cc}& {\displaystyle +m^{″}-{\overline{m^{″}}}_n-{({\overline{g}}_n-g,1)}_{\mathrm{\Gamma }}-\left({\overline{\mathrm{\Phi }}}_n-{\mathrm{\Phi }}_n\right)m_0.}\hfill \end{array}$$(16)

Clearly$$\begin{array}{c}\hfill \left|m^{″}-{\overline{m^{″}}}_n\right|+\left|{({\overline{g}}_n-g,1)}_{\mathrm{\Gamma }}\right|=\mathcal{O}\left(\mathit{\tau }\right)\end{array}$$

by the mean value theorem, $m\in C^3([0,T])$ and ${\mathit{\partial }}_{tt}g\in L^2\left((0,T),L^2(\mathrm{\Gamma })\right)$. Triangle inequality, (12(12) $$\begin{array}{c}\hfill ∥u_n(t)-{\overline{u}}_n(t)∥+∥{\overline{u}}_n(t)-{\overline{u}}_n(t-\mathit{\tau })∥\le C\mathit{\tau }.\end{array}$$(12) ), (13(13) $$\begin{array}{c}\hfill ∥v_n(t)-{\overline{v}}_n(t)∥+∥{\overline{v}}_n(t)-{\overline{v}}_n(t-\mathit{\tau })∥\le C\mathit{\tau }.\end{array}$$(13) ), Lipschitz continuity of $f$ imply$$\begin{array}{c}\hfill {\displaystyle \left|\left(f({\overline{u}}_n(t-\mathit{\tau }),{\overline{v}}_n(t-\mathit{\tau }))-f(u(t),{\mathit{\partial }}_{t}u(t)),1\right)\right|\le C\left(∥u_n(t)-u(t)∥+∥v_n(t)-{\mathit{\partial }}_{t}u(t)∥\right)+\mathcal{O}\left(\mathit{\tau }\right).}\end{array}$$ Using $m\in C^3([0,T])$ and (11(11) $$\begin{array}{c}\hfill \left|{\mathrm{\Phi }}_n(t)-{\overline{\mathrm{\Phi }}}_n(t)\right|\le C\mathit{\tau }.\end{array}$$(11) ) we easily get$$\left|{\mathrm{\Phi }}_n\ast m^{\prime }-\sum _{k=1}^{{\lfloor t\rfloor }_{\mathit{\tau }}}{\overline{\mathrm{\Phi }}}_n(t_k){\overline{m^{\prime }}}_n(t-t_k)\mathit{\tau }\right|+\left|\left({\overline{\mathrm{\Phi }}}_n-{\mathrm{\Phi }}_n\right)m_0\right|=\mathcal{O}\left(\mathit{\tau }\right).$$

This together with (16(16) $$\begin{array}{cc}& {\displaystyle +m^{″}-{\overline{m^{″}}}_n-{({\overline{g}}_n-g,1)}_{\mathrm{\Gamma }}-\left({\overline{\mathrm{\Phi }}}_n-{\mathrm{\Phi }}_n\right)m_0.}\hfill \end{array}$$(16) ) and (13(13) $$\begin{array}{c}\hfill ∥v_n(t)-{\overline{v}}_n(t)∥+∥{\overline{v}}_n(t)-{\overline{v}}_n(t-\mathit{\tau })∥\le C\mathit{\tau }.\end{array}$$(13) ) say$$\left|{\mathrm{\Phi }}_n(t)-{\mathrm{\Phi }}_K(t)\right|\le C\left(\mathit{\tau }+∥u_n(t)-u(t)∥+∥v_n(t)-{\mathit{\partial }}_{t}u(t)∥+{\int }_0^t\left|{\mathrm{\Phi }}_n(s)-{\mathrm{\Phi }}_K(s)\right|\text{d}s\right).$$ Hence, by Grönwall’s argument we obtain$$\begin{array}{cc}\hfill {\displaystyle \left|{\mathrm{\Phi }}_n(t)-{\mathrm{\Phi }}_K(t)\right|}& {\displaystyle \le C\left(\mathit{\tau }+∥u_n(t)-u(t)∥+∥v_n(t)-{\mathit{\partial }}_{t}u(t)∥\right)}\hfill \end{array}$$(17) $$\begin{array}{cc}& {\displaystyle +C{\int }_0^t\left(∥u_n(t)-u(t)∥+∥v_n-{\mathit{\partial }}_{t}u∥\right)\text{d}s.}\hfill \end{array}$$(17)

Now, subtract (DP(DP) $$\begin{array}{cc}& {\displaystyle =\left(f({\overline{u}}_n(t-\mathit{\tau }),{\overline{v}}_n(t-\mathit{\tau })),\mathit{\phi }\right).}\hfill \end{array}$$(DP) ) from (P(P) $$\begin{array}{c}\hfill \left({\mathit{\partial }}_{tt}u,\mathit{\phi }\right)+\left(\mathrm{\nabla }u,\mathrm{\nabla }\mathit{\phi }\right)+{\left(g,\mathit{\phi }\right)}_{\mathrm{\Gamma }}+{\mathrm{\Phi }}_K\left(u_0,\mathit{\phi }\right)+\left({\mathrm{\Phi }}_K\ast {\mathit{\partial }}_{t}u,\mathit{\phi }\right)=\left(f(u,{\mathit{\partial }}_{t}u),\mathit{\phi }\right).\end{array}$$(P) ) to get$$\begin{array}{cc}& {\displaystyle \left({\mathit{\partial }}_{tt}u-{\mathit{\partial }}_t{v}_n,\mathit{\phi }\right)+\left(\mathrm{\nabla }u-\mathrm{\nabla }{\overline{u}}_n,\mathrm{\nabla }\mathit{\phi }\right)+{\left(g-{\overline{g}}_n,\mathit{\phi }\right)}_{\mathrm{\Gamma }}}\hfill \\ \hfill & {\displaystyle +\left({\mathrm{\Phi }}_K-{\overline{\mathrm{\Phi }}}_n\right)\left(u_0,\mathit{\phi }\right)+\left({\mathrm{\Phi }}_K\ast {\mathit{\partial }}_{t}u-\sum _{k=1}^{{\lfloor t\rfloor }_{\mathit{\tau }}}{\overline{\mathrm{\Phi }}}_n(t_k){\overline{v}}_n(t-t_k)\mathit{\tau },\mathit{\phi }\right)}\hfill \\ \hfill & {\displaystyle =\left(f(u,{\mathit{\partial }}_{t}u)-f({\overline{u}}_n(t-\mathit{\tau }),{\overline{v}}_n(t-\mathit{\tau })),\mathit{\phi }\right).}\hfill \end{array}$$

Based on the triangle inequality, (11(11) $$\begin{array}{c}\hfill \left|{\mathrm{\Phi }}_n(t)-{\overline{\mathrm{\Phi }}}_n(t)\right|\le C\mathit{\tau }.\end{array}$$(11) )–(13(13) $$\begin{array}{c}\hfill ∥v_n(t)-{\overline{v}}_n(t)∥+∥{\overline{v}}_n(t)-{\overline{v}}_n(t-\mathit{\tau })∥\le C\mathit{\tau }.\end{array}$$(13) ) and$$\begin{array}{c}\hfill {∥u_n(t)-{\overline{u}}_n(t)∥}_{H^1(\mathrm{\Omega })}+{∥{\overline{u}}_n(t)-{\overline{u}}_n(t-\mathit{\tau })∥}_{H^1(\mathrm{\Omega })}\le C\mathit{\tau }\end{array}$$

we are allowed to write$$\begin{array}{cc}& {\displaystyle \left({\mathit{\partial }}_{tt}u-{\mathit{\partial }}_t{v}_n,\mathit{\phi }\right)+\left(\mathrm{\nabla }u-\mathrm{\nabla }{u}_n,\mathrm{\nabla }\mathit{\phi }\right)+\left({\mathrm{\Phi }}_K-{\mathrm{\Phi }}_n\right)\left(u_0,\mathit{\phi }\right)+\left(\left({\mathrm{\Phi }}_K-{\mathrm{\Phi }}_n\right)\ast {\mathit{\partial }}_{t}u,\mathit{\phi }\right)}\hfill \end{array}$$(18) $$\begin{array}{cc}& {\displaystyle +\left({\mathrm{\Phi }}_n\ast \left({\mathit{\partial }}_{t}u-v_n\right),\mathit{\phi }\right)=\left(f(u,{\mathit{\partial }}_{t}u)-f(u_n,v_n),\mathit{\phi }\right)+\mathcal{O}\left(\mathit{\tau }\right){∥\mathit{\phi }∥}_{H^1(\mathrm{\Omega })}.}\hfill \end{array}$$(18)

Now, we set $\mathit{\phi }={\mathit{\partial }}_t(u-u_n)$ and integrate in time$$\begin{array}{cc}& {\displaystyle {\int }_0^t\left({\mathit{\partial }}_{tt}u-{\mathit{\partial }}_t{v}_n,{\mathit{\partial }}_t(u-u_n)\right)+\frac{1}{2}{∥\mathrm{\nabla }u(t)-\mathrm{\nabla }{u}_n(t)∥}^2+{\int }_0^t\left({\mathrm{\Phi }}_K-{\mathrm{\Phi }}_n\right)\left(u_0,{\mathit{\partial }}_t(u-u_n)\right)}\hfill \\ \hfill & {\displaystyle +{\int }_0^t\left(\left({\mathrm{\Phi }}_K-{\mathrm{\Phi }}_n\right)\ast {\mathit{\partial }}_{t}u,{\mathit{\partial }}_t(u-u_n)\right)+{\int }_0^t\left({\mathrm{\Phi }}_n\ast \left({\mathit{\partial }}_{t}u-v_n\right),{\mathit{\partial }}_t(u-u_n)\right)}\hfill \end{array}$$(19) $$\begin{array}{cc}& {\displaystyle ={\int }_0^t\left(f(u,{\mathit{\partial }}_{t}u)-f(u_n,v_n),{\mathit{\partial }}_t(u-u_n)\right)+\mathcal{O}\left(\mathit{\tau }\right){\int }_0^t{∥{\mathit{\partial }}_t(u-u_n)∥}_{H^1(\mathrm{\Omega })}.}\hfill \end{array}$$(19)

The following estimate is the classical bottleneck for hyperbolic problems, i.e. the $\mathcal{O}\left(\mathit{\tau }\right)$ bound$$\begin{array}{cc}\hfill {\displaystyle {\int }_0^t\left({\mathit{\partial }}_{tt}u-{\mathit{\partial }}_t{v}_n,{\mathit{\partial }}_t(u-u_n)\right)}& {\displaystyle ={\int }_0^t\left({\mathit{\partial }}_{tt}u-{\mathit{\partial }}_t{v}_n,{\mathit{\partial }}_{t}u-v_n\right)+{\int }_0^t\left({\mathit{\partial }}_{tt}u-{\mathit{\partial }}_t{v}_n,v_n-{\mathit{\partial }}_t{u}_n\right)}\hfill \\ \hfill & {\displaystyle \ge \frac{1}{2}{∥{\mathit{\partial }}_{t}u(t)-v_n(t)∥}^2-C\mathit{\tau }.}\hfill \end{array}$$

A simple deduction yields$$\begin{array}{cc}\hfill {\displaystyle \left|{\int }_0^t\left({\mathrm{\Phi }}_K-{\mathrm{\Phi }}_n\right)\left(u_0,{\mathit{\partial }}_t(u-u_n)\right)\right|}& {\displaystyle \le {\int }_0^t\left|{\mathrm{\Phi }}_K-{\mathrm{\Phi }}_n\right|∥u_0∥∥{\mathit{\partial }}_t(u-u_n)∥}\hfill \\ \hfill & {\displaystyle \le C\left({\int }_0^t{\left|{\mathrm{\Phi }}_K-{\mathrm{\Phi }}_n\right|}^2+{\int }_0^t{∥{\mathit{\partial }}_t(u-u_n)∥}^2\right)}\hfill \\ \hfill & {\displaystyle \stackrel{(13)}{\le }C\left({\mathit{\tau }}^2+{\int }_0^t{\left|{\mathrm{\Phi }}_K-{\mathrm{\Phi }}_n\right|}^2+{\int }_0^t{∥{\mathit{\partial }}_{t}u-v_n)∥}^2\right)}\hfill \\ \hfill & {\displaystyle \stackrel{(17)}{\le }C\left({\mathit{\tau }}^2+{\int }_0^t{∥u-u_n)∥}^2+{\int }_0^t{∥{\mathit{\partial }}_{t}u-v_n)∥}^2\right)}\hfill \\ \hfill & {\displaystyle \stackrel{(13)}{\le }C\left({\mathit{\tau }}^2+{\int }_0^t{∥{\mathit{\partial }}_{t}u-v_n)∥}^2\right).}\hfill \end{array}$$

Similarly we deduce$$\begin{array}{c}\hfill \left|{\int }_0^t\left(\left({\mathrm{\Phi }}_K-{\mathrm{\Phi }}_n\right)\ast {\mathit{\partial }}_{t}u,{\mathit{\partial }}_t(u-u_n)\right)\right|\le C\left({\mathit{\tau }}^2+{\int }_0^t{∥{\mathit{\partial }}_{t}u-v_n)∥}^2\right)\end{array}$$

as $∥{\mathit{\partial }}_{t}u∥\le C$. Further$$\begin{array}{cc}\hfill {\displaystyle \left|{\int }_0^t\left({\mathrm{\Phi }}_n\ast \left({\mathit{\partial }}_{t}u-v_n\right),{\mathit{\partial }}_t(u-u_n)\right)\right|}& {\displaystyle \le C{\int }_0^t∥{\mathrm{\Phi }}_n\ast \left({\mathit{\partial }}_{t}u-v_n\right)∥∥{\mathit{\partial }}_t(u-u_n)∥}\hfill \\ \hfill & {\displaystyle \le C\left({\int }_0^t{∥{\mathrm{\Phi }}_n\ast \left({\mathit{\partial }}_{t}u-v_n\right)∥}^2+{\int }_0^t{∥{\mathit{\partial }}_t(u-u_n)∥}^2\right)}\hfill \\ \hfill & {\displaystyle \stackrel{(13)}{\le }C\left({\mathit{\tau }}^2+{\int }_0^t{∥{\mathrm{\Phi }}_n\ast \left({\mathit{\partial }}_{t}u-v_n\right)∥}^2+{\int }_0^t{∥{\mathit{\partial }}_{t}u-v_n)∥}^2\right)}\hfill \\ \hfill & {\displaystyle \le C\left({\mathit{\tau }}^2+{\int }_0^t{∥{\mathit{\partial }}_{t}u-v_n)∥}^2\right)}\hfill \end{array}$$ as $|{\mathrm{\Phi }}_n(t)|\le C$. Using the Lipschitz continuity of $f$ we derive in a standard way$$\begin{array}{cc}\hfill {\displaystyle \left|{\int }_0^t\left(f(u,{\mathit{\partial }}_{t}u)-f(u_n,v_n),{\mathit{\partial }}_t(u-u_n)\right)\right|}& {\displaystyle \le {\int }_0^t∥f(u,{\mathit{\partial }}_{t}u)-f(u_n,v_n)∥∥{\mathit{\partial }}_t(u-u_n)∥}\hfill \\ \hfill & {\displaystyle \le C{\int }_0^t\left(∥u-u_n∥+∥{\mathit{\partial }}_t{u}_n-v_n∥\right)∥{\mathit{\partial }}_t(u-u_n)∥}\hfill \\ \hfill & {\displaystyle \stackrel{(13)}{\le }C{\int }_0^t\left(∥u-u_n∥+∥{\mathit{\partial }}_t{u}_n-v_n∥\right)\left(\mathit{\tau }+∥{\mathit{\partial }}_{t}u-v_n)∥\right)}\hfill \\ \hfill & {\displaystyle \le C\left({\mathit{\tau }}^2+{\int }_0^t{∥{\mathit{\partial }}_t{u}_n-v_n∥}^2\right).}\hfill \end{array}$$ Summarizing all estimates we arrive at$${∥{\mathit{\partial }}_{t}u(t)-v_n(t)∥}^2+{∥\mathrm{\nabla }u(t)-\mathrm{\nabla }{u}_n(t)∥}^2\le C\left(\mathit{\tau }+{\int }_0^t{∥{\mathit{\partial }}_t{u}_n-v_n∥}^2\right)$$

which holds true in $[0,T]$. By Grönwall’s argument we conclude$$\underset{t\in [0,T]}{max}{∥{\mathit{\partial }}_{t}u(t)-v_n(t)∥}^2+\underset{t\in [0,T]}{max}{∥\mathrm{\nabla }u(t)-\mathrm{\nabla }{u}_n(t)∥}^2\le C\mathit{\tau }.$$

Clearly$$∥u(t)-u_n(t)∥\le {\int }_0^t∥{\mathit{\partial }}_{t}u-{\mathit{\partial }}_t{u}_n∥\le {\int }_0^t\left(∥{\mathit{\partial }}_{t}u-v_n∥+∥v_n-{\mathit{\partial }}_t{u}_n∥\right)\stackrel{(12)}{\le }C\sqrt{\mathit{\tau }}$$

and by (17(17) $$\begin{array}{cc}& {\displaystyle +C{\int }_0^t\left(∥u_n(t)-u(t)∥+∥v_n-{\mathit{\partial }}_{t}u∥\right)\text{d}s.}\hfill \end{array}$$(17) ) we conclude$$\left|{\mathrm{\Phi }}_K(t)-{\mathrm{\Phi }}_n(t)\right|\le C\sqrt{\mathit{\tau }}.$$$\square$

4. Numerical experiment

In this section, we support theoretical results from previous sections on a concrete example, testing convergence of the computational scheme and error estimates from Theorem 3.3. Let’s take $x\in \mathbb{R},x\in [0,\mathit{\pi }]$ and $T=\mathit{\pi }/2$. Further we set$$\begin{array}{cc}\hfill g(x,t)& =(1+2t-t^2)cosx,\hfill \\ \hfill u_0(x)& =sinx,\hfill \\ \hfill v_0(x)& =2sinx,\hfill \\ \hfill f(x,t,u(x,t),{\mathit{\partial }}_{t}u(x,t))& =({\text{e}}^t+2t-2)sinx,\hfill \\ \hfill m(t)& =2+4t-t^2.\hfill \end{array}$$

Figure 1. Convergence rate on logarithmic scale.

Figure 2. Absolute error $|K_i-K(t_i)|$ for different $\mathit{\tau }$.

One can easily check that the exact solution to (1(1) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\displaystyle {\mathit{\partial }}_{tt}u(\mathit{x},t)-\mathrm{\Delta }u(\mathit{x},t)+(K\ast u(\mathit{x}))(t)=f(\mathit{x},t,u(\mathit{x},t),{\mathit{\partial }}_{t}u(\mathit{x},t)),}\hfill & {\displaystyle \text{in}\mathrm{\Omega }\times (0,T),}\hfill \\ {\displaystyle -\mathrm{\nabla }u(\mathit{x},t)·\mathit{\nu }=g(\mathit{x},t),}\hfill & {\displaystyle \text{on}\mathrm{\Gamma }\times (0,T),}\hfill \\ {\displaystyle {\mathit{\partial }}_{t}u(\mathbf{x},0)=v_0(\mathbf{x}),}\hfill & {\displaystyle \text{in}\mathrm{\Omega },}\hfill \\ {\displaystyle u(\mathbf{x},0)=u_0(\mathbf{x}),}\hfill & {\displaystyle \text{in}\mathrm{\Omega },}\hfill \end{array}\right.\end{array}$$(1) ) and (2(2) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}u(\mathbf{x},t)\text{d}\mathit{x}=m(t),t\in [0,T].\end{array}$$(2) ) is $u(x,t)=(1+2t-t^2)sinx$ and $K={\text{e}}^t$. We divide the space interval in 200 equidistant subintervals. We choose the time step as $\mathit{\tau }=2^j\mathit{\pi }/100$, where $j=0,-1,-2,-3$. We denote the left-hand side of inequality from Theorem 3.3 as $E$:$$E=\underset{t\in [0,T]}{max}{\left|{\mathrm{\Phi }}_K(t)-{\mathrm{\Phi }}_n(t)\right|}^2+\underset{t\in [0,T]}{max}{∥{\mathit{\partial }}_{t}u(t)-v_n(t)∥}^2+\underset{t\in [0,T]}{max}{∥u(t)-u_n(t)∥}_{H^1(\mathrm{\Omega })}^2.$$

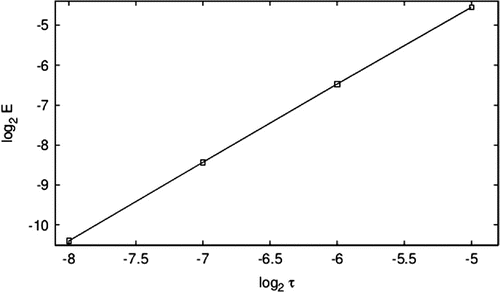
The errors for mentioned $\mathit{\tau }$ are depicted in Figure 1, where the errors ${log}_{2}E$ are plotted as a function of ${log}_2\mathit{\tau }$. The linear regression line through all the data points is given by ${log}_{2}E=1.9502{log}_2\mathit{\tau }+5.2155$, which indicates the convergence rate $\mathcal{O}\left(\mathit{\tau }\right)$. 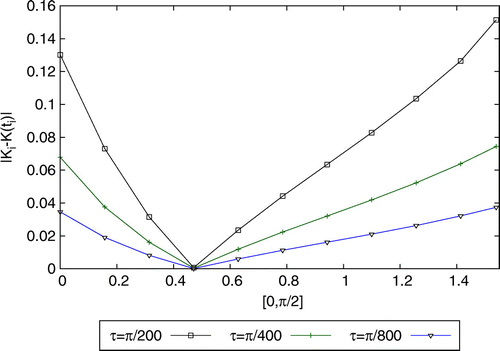This error estimate is better that the theoretical result $\mathcal{O}\left(\sqrt{\mathit{\tau }}\right)$ from Theorem 3.3. The absolute error for $K$,i.e. $|K_i-K(t_i)|$, is shown for $\mathit{\tau }=2^j\mathit{\pi }/50,j=-1,-2,-3$ in Figure 2.

5. Conclusion

A semilinear hyperbolic integro-differential problem of second order with an unknown convolution kernel is considered. The well-posedness of a weak solution for the IBVP is proved. The missing integral kernel is recovered from an additional space-integral measurement. A numerical algorithm based on Rothe’s method is established, convergence of approximations towards the exact solution is demonstrated and the error estimates are derived. The IP was reformulated to a direct system of two equations. Please note that the suggested algorithm involves time derivatives of measurements, thus the IP is moderately ill-posed. There arises a natural question how to deal with noisy data? In such a case we suggest to regularize the measurements first and then to apply the suggested scheme.

Additional information

Funding

The research was supported by the IAP P7/02-project of the Belgian Science Policy.

Notes

No potential conflict of interest was reported by the authors.

1 ${\lfloor t\rfloor }_{\mathit{\tau }}=i$ when $t\in (t_{i-1},t_i]$.