A coupled complex boundary method for the Cauchy problem

Abstract

Considered in this paper is a Cauchy problem governed by an elliptic partial differential equation. In the Cauchy problem, one wants to recover the unknown Neumann and Dirichlet data on a part of the boundary from the measured Neumann and Dirichlet data, usually contaminated with noise, on the remaining part of the boundary. The Cauchy problem is an inverse problem with severe ill-posedness. In this paper, a coupled complex boundary method (CCBM), originally proposed in [Cheng XL, Gong RF, Han W, et al. A novel coupled complex boundary method for solving inverse source problems. Inverse Prob. 2014;30:055002], is applied to solve the Cauchy problem stably. With the CCBM, all the data, including the known and unknown ones on the boundary are used in a complex Robin boundary on the whole boundary. As a result, the Cauchy problem is transferred into a complex Robin boundary problem of finding the unknown data such that the imaginary part of the solution equals zero in the domain. Then the Tikhonov regularization is applied to the resulting new formulation. Some theoretical analysis is performed on the CCBM-based Tikhonov regularization framework. Moreover, through the adjoint technique, a simple solver is proposed to compute the regularized solution. The finite-element method is used for the discretization. Numerical results are given to show the feasibility and effectiveness of the proposed method.

Keywords:

• Cauchy problems
• ill-posedness
• Tikhonov regularization
• convergence analysis
• adjoint problem

AMS Subject Classifications:

• 65F22
• 65N12

1. Introduction

In this paper, we consider the Cauchy problem of recovering the unknown Neumann and Dirichlet data on a part of the boundary from the knowledge of the Cauchy data on the rest of the boundary. This kind of identification problem, also known as data completion [1] has attracted a large amount of attention from mathematicians, physicists and engineers because of its wide applications in physics and engineering such as thermostatics [2] linear elasticity [3] plasma physics [4] mechanical engineering [5] electrocardiography [6] and corrosion non-destructive evaluation,[7] etc.

Let $\mathrm{\Omega }\subset {\mathbb{R}}^d$ ($d=2,3$: space dimension) be an open bounded set with Lipschitz boundary $\mathrm{\Gamma }:=\mathit{\partial }\mathrm{\Omega }$, which is split into two measurable subsets: $\mathrm{\Gamma }={\mathrm{\Gamma }}_m\bigcup {\mathrm{\Gamma }}_u$ with ${\mathrm{\Gamma }}_m\bigcap {\mathrm{\Gamma }}_u=\mathrm{\varnothing }$. In applications, ${\mathrm{\Gamma }}_m$ and ${\mathrm{\Gamma }}_u$ are known as the accessible and inaccessible parts of the boundary for the object of interest, respectively. Denote by n the unit outward normal to $\mathrm{\Gamma }$. We consider the following Cauchy problem governed by the steady-state heat equation.

Problem 1.1:

Given $\mathit{\kappa },f$ in $\mathrm{\Omega }$, and Cauchy data $(\mathrm{\Phi },T)$ on ${\mathrm{\Gamma }}_m$, find $(\mathit{\varphi },t)$ on ${\mathrm{\Gamma }}_u$ such that the following relations hold:(1) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}-\text{div}(\mathit{\kappa }\mathrm{\nabla }u)=f\hfill & \text{in}\mathrm{\Omega },\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }u}{\mathit{\partial }n}=\mathrm{\Phi },u=T\hfill & \text{on}{\mathrm{\Gamma }}_m,\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }u}{\mathit{\partial }n}=\mathit{\varphi },u=t\hfill & \text{on}{\mathrm{\Gamma }}_u.\hfill \end{array}\right.\end{array}$$(1)

The Cauchy problem governed by Helmholtz-type equations are studied in [8–15]. We refer to [16–18] and references therein for analysis of the Cauchy problem governed by other equations and for systemic discussions about the Cauchy problems.

It is well known that Problem 1.1 is ill-posed [19]. Hadamard [20] presented an example to illustrate the ill-posedness of the Cauchy problem for the Laplace equation ($\mathit{\kappa }=1$). A rigorous proof of the ill-posedness was given in [21] for a general domain. Moreover, after reformulating the Cauchy problem as a variational equation, Ben Belgacem showed in [19] that the Cauchy problem is exponentially ill-posed for both smooth and non-smooth domains. Lavrent’ev demonstrated in [22] that the solution of the Cauchy problem for the Laplace equation is stable given a supplementary condition. Payne [23] generalized the work of [22] and deduced a pointwise bound for the problem in n-dimensions. Some Carleman estimates of the Cauchy problem for the Laplace equation were established in [24,25]. We also refer to [26] for an overview on the stability of the Cauchy problem for general elliptic equations under rather weak assumptions on the problem domain.

Due to the severe ill-posedness of the Cauchy problem, a regularization strategy is needed to obtain a stable approximate solution, especially when the measured data $(\mathit{\varphi },T)$ are polluted inevitably by the random noise. In the literature, the Tikhonov regularization [2,27–29] and quasi-reversibility method [25,30–32] are two of the most frequently used approaches for this purpose. Other methods include iterative regularization [33–37] Lavrentiev regularization [38–40] truncation regularization method [41–43] discretization method [44,45] moment problem method [46–49] and perturbation regularization method [43,50,51]. The Cauchy problem for a 3D elliptic equation solved on real data obtained from the physical experiments can be found in [52,53]. Among these methods, a commonly used technique is to convert Problem 1.1 to the following minimization problem with a Kohn–Vogelius-type functional $J_{KV}$ [1,54]:(2) $$\begin{array}{c}\hfill (\mathit{\varphi },t)=arg\underset{\mathit{\eta },s}{min}{J}_{KV}(\mathit{\eta },s)\end{array}$$(2)

with$$\begin{array}{c}\hfill J_{KV}(\mathit{\eta },s)={\int }_{\mathrm{\Omega }}\mathit{\kappa }{|\mathrm{\nabla }{u}_1-\mathrm{\nabla }{u}_2|}^2\mathrm{d}x,\end{array}$$

where $u_1,u_2\in V:=H^1(\mathrm{\Omega })$ are the weak solutions of the following mixed boundary value problems (BVPs):(3) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}-\text{div}(\mathit{\kappa }\mathrm{\nabla }{u}_1)=f\hfill & \text{in}\mathrm{\Omega },\hfill \\ u_1=T\hfill & \text{on}{\mathrm{\Gamma }}_m,\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }{u}_1}{\mathit{\partial }n}=\mathit{\eta }\hfill & \text{on}{\mathrm{\Gamma }}_u,\hfill \end{array}\right.\end{array}$$(3)

and(4) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}-\text{div}(\mathit{\kappa }\mathrm{\nabla }{u}_2)=f\hfill & \text{in}\mathrm{\Omega },\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }{u}_2}{\mathit{\partial }n}=\mathrm{\Phi }\hfill & \text{on}{\mathrm{\Gamma }}_m,\hfill \\ u_2=s\hfill & \text{on}{\mathrm{\Gamma }}_u,\hfill \end{array}\right.\end{array}$$(4)

respectively. Unlike conventional objective functionals (see [44,55,56] for example), the Kohn–Vogelius functional transfers the data needed to fit ${\mathrm{\Gamma }}_m$ into the ones in $\mathrm{\Omega }$, and is generally expected to lead to more robust optimization procedures [57]. A Tikhonov regularization framework is obtained if a regularization term is added to $J_{KV}$ of the problem (2(2) $$\begin{array}{c}\hfill (\mathit{\varphi },t)=arg\underset{\mathit{\eta },s}{min}{J}_{KV}(\mathit{\eta },s)\end{array}$$(2) ).

Recently, Cheng et al. [58] proposed a coupled complex boundary method (CCBM) for an inverse source problem, where a complex Robin boundary condition is used to treat simultaneously both Dirichlet and Neumann conditions. As is shown in [58], the CCBM makes inverse source problems more robust and more efficient in computations. In this paper, a CCBM-based Tikhonov regularization framework is proposed for solving Problem 1.1. With our method, similar to problem (2(2) $$\begin{array}{c}\hfill (\mathit{\varphi },t)=arg\underset{\mathit{\eta },s}{min}{J}_{KV}(\mathit{\eta },s)\end{array}$$(2) ), the data needed to fit is transferred from ${\mathrm{\Gamma }}_m$ to $\mathrm{\Omega }$, and the missing data $(\mathit{\varphi },t)$ on ${\mathrm{\Gamma }}_u$ and the state u in $\mathrm{\Omega }$ can be reconstructed simultaneously. All boundary conditions, including known and unknown ones, are used as parts of a Robin boundary condition on the whole boundary $\mathrm{\Gamma }$. Thus no Dirichlet BVP needs to be solved and this makes the numerical solution of the forward problem easier. Moreover, in the methods where (3(3) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}-\text{div}(\mathit{\kappa }\mathrm{\nabla }{u}_1)=f\hfill & \text{in}\mathrm{\Omega },\hfill \\ u_1=T\hfill & \text{on}{\mathrm{\Gamma }}_m,\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }{u}_1}{\mathit{\partial }n}=\mathit{\eta }\hfill & \text{on}{\mathrm{\Gamma }}_u,\hfill \end{array}\right.\end{array}$$(3) )–(4(4) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}-\text{div}(\mathit{\kappa }\mathrm{\nabla }{u}_2)=f\hfill & \text{in}\mathrm{\Omega },\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }{u}_2}{\mathit{\partial }n}=\mathrm{\Phi }\hfill & \text{on}{\mathrm{\Gamma }}_m,\hfill \\ u_2=s\hfill & \text{on}{\mathrm{\Gamma }}_u,\hfill \end{array}\right.\end{array}$$(4) ) are used, the Dirichlet data T and t need to have the regularity $T\in H^{1/2}({\mathrm{\Gamma }}_m)$ or $t\in H^{1/2}({\mathrm{\Gamma }}_u)$ for $u_1,u_2\in V$. In applications, T is polluted by random noise and it is not appropriate to assume $T\in H^{1/2}({\mathrm{\Gamma }}_m)$. In our method, we only need $T\in Q_{{\mathrm{\Gamma }}_m}:=L^2({\mathrm{\Gamma }}_m)$ and $t\in Q_{{\mathrm{\Gamma }}_u}:=L^2({\mathrm{\Gamma }}_u)$. This avoids the use of the fractional-order Sobolev functions. With the help of adjoint equation, the solution of the regularized reconstruction framework can be computed through a system of BVPs; thus, no iteration is needed and the computation is effective.

We introduce some notation. For a set G (e.g. $\mathrm{\Omega }$, $\mathrm{\Gamma }$, ${\mathrm{\Gamma }}_m$ or ${\mathrm{\Gamma }}_u$), we denote by $W^{m,s}(G)$ the standard Sobolev space with the norm ${\Vert ·\Vert }_{m,s,G}$. Let $W^{0,s}(G):=L^s(G)$. In particular, $H^m(G)$ represents $W^{m,2}(G)$ with the corresponding inner product ${(·,·)}_{m,G}$ and norm ${\Vert ·\Vert }_{m,G}$. Let ${\mathbf{H}}^m(G)$ be the complex version of $H^m(G)$ with the inner product ${((·,·))}_{m,G}$ and norm $|||·{|||}_{m,G}$ defined as follows: $\forall u,v\in {\mathbf{H}}^m(G)$, ${((u,v))}_{m,G}={(u,\overline{v})}_{m,G}$, ${|||v|||}_{m,G}^2={((v,v))}_{m,G}$. In addition to the symbols V, $Q_{{\mathrm{\Gamma }}_m}$, $Q_{{\mathrm{\Gamma }}_u}$, denote $\mathbf{V}={\mathbf{H}}^1(\mathrm{\Omega })$, $Q=L^2(\mathrm{\Omega })$, $\mathbf{Q}={\mathbf{L}}^2(\mathrm{\Omega })$, $Q_{\mathrm{\Gamma }}=L^2(\mathrm{\Gamma })$, and ${\mathbf{Q}}_{\mathrm{\Gamma }}={\mathbf{L}}^2(\mathrm{\Gamma })$. In the following, c denotes a constant which may have a different value at a different place.

The structure of the paper is as follows. Applying CCBM, we present in Section 2 a reformulation of Problem 1.1. In Section 3, we apply the Tikhonov regularization to the resulting formulation. The well-posedness result of the new regularization framework and a limiting behaviour of the regularized solution when both the noise level and the regularization parameters go to zero are also stated in Section 3. With an adjoint equation, a simple solver of the regularized optimization problem and its finite-element discretization are given in Section 4. Several numerical examples are presented in Section 5 to demonstrate the feasibility and efficiency of the proposed method. Finally, concluding remarks are given in Section 6.

2. A reformulation of the Cauchy problem

Let $f\in Q$ and $\mathrm{\Gamma }$ be Lipschitz continuous so that the unit outward normal vector on the boundary is defined a.e. Assume $\mathit{\kappa }\in L^{\infty }(\mathrm{\Omega })$, $\mathit{\kappa }\ge {\mathit{\kappa }}_0$ a.e. in $\mathrm{\Omega }$ for some positive constant ${\mathit{\kappa }}_0$.

Consider a complex BVP:(5) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}-\text{div}(\mathit{\kappa }\mathrm{\nabla }u)=f\hfill & \text{in}\mathrm{\Omega },\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }u}{\mathit{\partial }n}+iu=\mathrm{\Phi }+iT\hfill & \text{on}{\mathrm{\Gamma }}_m,\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }u}{\mathit{\partial }n}+iu=\mathit{\varphi }+it\hfill & \text{on}{\mathrm{\Gamma }}_u,\hfill \end{array}\right.\end{array}$$(5)

where $i=\sqrt{-1}$ is the imaginary unit. Obviously, if $(u,\mathit{\varphi },t)$ satisfy (1(1) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}-\text{div}(\mathit{\kappa }\mathrm{\nabla }u)=f\hfill & \text{in}\mathrm{\Omega },\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }u}{\mathit{\partial }n}=\mathrm{\Phi },u=T\hfill & \text{on}{\mathrm{\Gamma }}_m,\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }u}{\mathit{\partial }n}=\mathit{\varphi },u=t\hfill & \text{on}{\mathrm{\Gamma }}_u.\hfill \end{array}\right.\end{array}$$(1) ), then (5(5) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}-\text{div}(\mathit{\kappa }\mathrm{\nabla }u)=f\hfill & \text{in}\mathrm{\Omega },\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }u}{\mathit{\partial }n}+iu=\mathrm{\Phi }+iT\hfill & \text{on}{\mathrm{\Gamma }}_m,\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }u}{\mathit{\partial }n}+iu=\mathit{\varphi }+it\hfill & \text{on}{\mathrm{\Gamma }}_u,\hfill \end{array}\right.\end{array}$$(5) ) holds. Conversely, let $(u,\mathit{\varphi },t)$ satisfy (5(5) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}-\text{div}(\mathit{\kappa }\mathrm{\nabla }u)=f\hfill & \text{in}\mathrm{\Omega },\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }u}{\mathit{\partial }n}+iu=\mathrm{\Phi }+iT\hfill & \text{on}{\mathrm{\Gamma }}_m,\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }u}{\mathit{\partial }n}+iu=\mathit{\varphi }+it\hfill & \text{on}{\mathrm{\Gamma }}_u,\hfill \end{array}\right.\end{array}$$(5) ), with $u=u_1+i{u}_2$, $u_1,u_2$ being the real and imaginary parts of u. Then the real-valued functions $u_1,u_2$ satisfy(6) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}-\text{div}(\mathit{\kappa }\mathrm{\nabla }{u}_1)=f\hfill & \text{in}\mathrm{\Omega },\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }{u}_1}{\mathit{\partial }n}-u_2=\mathrm{\Phi }\hfill & \text{on}{\mathrm{\Gamma }}_m,\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }{u}_1}{\mathit{\partial }n}-u_2=\mathit{\varphi }\hfill & \text{on}{\mathrm{\Gamma }}_u,\hfill \end{array}\right.\end{array}$$(6)

and(7) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}-\text{div}(\mathit{\kappa }\mathrm{\nabla }{u}_2)=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }{u}_2}{\mathit{\partial }n}+u_1=T\hfill & \text{on}{\mathrm{\Gamma }}_m,\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }{u}_2}{\mathit{\partial }n}+u_1=t\hfill & \text{on}{\mathrm{\Gamma }}_u,\hfill \end{array}\right.\end{array}$$(7)

respectively. If $u_2=0\text{in}\mathrm{\Omega }$, then $u_2=0$ and $\frac{\mathit{\partial }{u}_2}{\mathit{\partial }n}=0$ on $\mathrm{\Gamma }$. Consequently, from BVPs (6(6) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}-\text{div}(\mathit{\kappa }\mathrm{\nabla }{u}_1)=f\hfill & \text{in}\mathrm{\Omega },\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }{u}_1}{\mathit{\partial }n}-u_2=\mathrm{\Phi }\hfill & \text{on}{\mathrm{\Gamma }}_m,\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }{u}_1}{\mathit{\partial }n}-u_2=\mathit{\varphi }\hfill & \text{on}{\mathrm{\Gamma }}_u,\hfill \end{array}\right.\end{array}$$(6) )–(7(7) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}-\text{div}(\mathit{\kappa }\mathrm{\nabla }{u}_2)=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }{u}_2}{\mathit{\partial }n}+u_1=T\hfill & \text{on}{\mathrm{\Gamma }}_m,\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }{u}_2}{\mathit{\partial }n}+u_1=t\hfill & \text{on}{\mathrm{\Gamma }}_u,\hfill \end{array}\right.\end{array}$$(7) ), we know that $(u_1,\mathit{\varphi },t)$ satisfy (1(1) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}-\text{div}(\mathit{\kappa }\mathrm{\nabla }u)=f\hfill & \text{in}\mathrm{\Omega },\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }u}{\mathit{\partial }n}=\mathrm{\Phi },u=T\hfill & \text{on}{\mathrm{\Gamma }}_m,\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }u}{\mathit{\partial }n}=\mathit{\varphi },u=t\hfill & \text{on}{\mathrm{\Gamma }}_u.\hfill \end{array}\right.\end{array}$$(1) ).

Based on the above discussion, we can reformulate Problem 1.1 as follows.

Problem 2.1:

Given $\mathit{\kappa },f$ in $\mathrm{\Omega }$, $(\mathrm{\Phi },T)$ on ${\mathrm{\Gamma }}_m$, find $(\mathit{\varphi },t)$ on ${\mathrm{\Gamma }}_u$ such that$$\begin{array}{c}\hfill u_2=0\text{in}\mathrm{\Omega },\end{array}$$

where $u_2$ is the imaginary part of the solution $u=u_1+i{u}_2$ of the BVP (5(5) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}-\text{div}(\mathit{\kappa }\mathrm{\nabla }u)=f\hfill & \text{in}\mathrm{\Omega },\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }u}{\mathit{\partial }n}+iu=\mathrm{\Phi }+iT\hfill & \text{on}{\mathrm{\Gamma }}_m,\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }u}{\mathit{\partial }n}+iu=\mathit{\varphi }+it\hfill & \text{on}{\mathrm{\Gamma }}_u,\hfill \end{array}\right.\end{array}$$(5) ).

Remark 1:

Note that $T\in H^{1/2}({\mathrm{\Gamma }}_m)$ is required for the equivalence of Problems 1.1 and 2.1. In the case where these regularity assumptions are not satisfied, the reformulation above provides a way of an approximate resolution of Problem 1.1. With the new reformulation, the data needed to fit are transferred from the boundary ${\mathrm{\Gamma }}_m$ to the interior $\mathrm{\Omega }$. Moreover, compared with the existing work, all the data on the boundary here are used in a unified way of a Robin boundary condition.

Define(8) $$\begin{array}{cc}\hfill a(u,v)& ={\int }_{\mathrm{\Omega }}\mathit{\kappa }\mathrm{\nabla }u·\mathrm{\nabla }\overline{v}\mathrm{d}x+i{\int }_{\mathrm{\Gamma }}u\overline{v}\mathrm{d}s\forall u,v\in \mathbf{V},\hfill \end{array}$$(8) (9) $$\begin{array}{cc}\hfill F(\mathit{\varphi },t;v)& ={\int }_{\mathrm{\Omega }}f\overline{v}\mathrm{d}x+{\int }_{{\mathrm{\Gamma }}_m}(\mathrm{\Phi }+iT)\overline{v}\mathrm{d}s+{\int }_{{\mathrm{\Gamma }}_u}(\mathit{\varphi }+it)\overline{v}\mathrm{d}s\forall v\in \mathbf{V}.\hfill \end{array}$$(9)

Then the weak form of the BVP (5(5) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}-\text{div}(\mathit{\kappa }\mathrm{\nabla }u)=f\hfill & \text{in}\mathrm{\Omega },\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }u}{\mathit{\partial }n}+iu=\mathrm{\Phi }+iT\hfill & \text{on}{\mathrm{\Gamma }}_m,\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }u}{\mathit{\partial }n}+iu=\mathit{\varphi }+it\hfill & \text{on}{\mathrm{\Gamma }}_u,\hfill \end{array}\right.\end{array}$$(5) ) is(10) $$\begin{array}{c}\hfill u\in \mathbf{V},a(u,v)=F(\mathit{\varphi },t;v)\forall v\in \mathbf{V}.\end{array}$$(10)

In this work, Tikhonov regularization will be applied to Problem 2.1 to recover the missing Neumann and Dirichlet data $(\mathit{\varphi },t)$ on the inaccessible boundary ${\mathrm{\Gamma }}_u$. We first show a well-posedness result about the forward BVP (5(5) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}-\text{div}(\mathit{\kappa }\mathrm{\nabla }u)=f\hfill & \text{in}\mathrm{\Omega },\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }u}{\mathit{\partial }n}+iu=\mathrm{\Phi }+iT\hfill & \text{on}{\mathrm{\Gamma }}_m,\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }u}{\mathit{\partial }n}+iu=\mathit{\varphi }+it\hfill & \text{on}{\mathrm{\Gamma }}_u,\hfill \end{array}\right.\end{array}$$(5) ) in the following.

Proposition 2.2:

Given $f\in Q$, $(\mathrm{\Phi },T)\in Q_{{\mathrm{\Gamma }}_m}\times Q_{{\mathrm{\Gamma }}_m}$, $(\mathit{\varphi },t)\in Q_{{\mathrm{\Gamma }}_u}\times Q_{{\mathrm{\Gamma }}_u}$, the problem (10(10) $$\begin{array}{c}\hfill u\in \mathbf{V},a(u,v)=F(\mathit{\varphi },t;v)\forall v\in \mathbf{V}.\end{array}$$(10) ) admits a unique solution $u\in \mathbf{V}$ which depends continuously on all data. Moreover,(11) $$\begin{array}{c}\hfill {|||u|||}_{1,\mathrm{\Omega }}\le {c(\Vert f\Vert }_{0,\mathrm{\Omega }}+{\Vert \mathrm{\Phi }\Vert }_{0,{\mathrm{\Gamma }}_m}+{\Vert T\Vert }_{0,{\mathrm{\Gamma }}_m}+{\Vert \mathit{\varphi }\Vert }_{0,{\mathrm{\Gamma }}_u}+{\Vert t\Vert }_{0,{\mathrm{\Gamma }}_u}).\end{array}$$(11)

Proof:

For any $u,v\in \mathbf{V}$, by applying the Cauchy–Schwarz inequality and the trace inequality, we have the continuity of $a(·,·)$ and $F(\mathit{\varphi },t;·)$:(12) $$\begin{array}{cc}\hfill |a(u,v)|& \le {c|||u|||}_{1,\mathrm{\Omega }}{|||v|||}_{1,\mathrm{\Omega }},\hfill \end{array}$$(12) (13) $$\begin{array}{cc}\hfill |F(\mathit{\varphi },t;v)|& \le {c(\Vert f\Vert }_{0,\mathrm{\Omega }}+{\Vert \mathrm{\Phi }\Vert }_{0,{\mathrm{\Gamma }}_m}+{\Vert T\Vert }_{0,{\mathrm{\Gamma }}_m}+{\Vert \mathit{\varphi }\Vert }_{0,{\mathrm{\Gamma }}_u}+{\Vert t\Vert }_{0,{\mathrm{\Gamma }}_u}{)|||v|||}_{1,\mathrm{\Omega }}.\hfill \end{array}$$(13)

Moreover, it is not difficult to conclude that(14) $$\begin{array}{c}\hfill |a(v,v)|\ge c_0{|||v|||}_{1,\mathrm{\Omega }}^2\forall v\in \mathbf{V}.\end{array}$$(14)

Therefore, applying the complex version of Lax–Milgram Lemma [59, p.368–369], we conclude that the problem (10(10) $$\begin{array}{c}\hfill u\in \mathbf{V},a(u,v)=F(\mathit{\varphi },t;v)\forall v\in \mathbf{V}.\end{array}$$(10) ) admits a unique solution $u\in \mathbf{V}$.

The bound (18(18) $$\begin{array}{c}\hfill |||u^{\mathit{\delta }}{|||}_{1,\mathrm{\Omega }}\le {c(\Vert f\Vert }_{0,\mathrm{\Omega }}+\Vert {\mathrm{\Phi }}^{\mathit{\delta }}{\Vert }_{0,{\mathrm{\Gamma }}_m}+\Vert T^{\mathit{\delta }}{\Vert }_{0,{\mathrm{\Gamma }}_m}+{\Vert \mathit{\varphi }\Vert }_{0,{\mathrm{\Gamma }}_u}+{\Vert t\Vert }_{0,{\mathrm{\Gamma }}_u}).\end{array}$$(18) ) follows directly from (10(10) $$\begin{array}{c}\hfill u\in \mathbf{V},a(u,v)=F(\mathit{\varphi },t;v)\forall v\in \mathbf{V}.\end{array}$$(10) ), (13(13) $$\begin{array}{cc}\hfill |F(\mathit{\varphi },t;v)|& \le {c(\Vert f\Vert }_{0,\mathrm{\Omega }}+{\Vert \mathrm{\Phi }\Vert }_{0,{\mathrm{\Gamma }}_m}+{\Vert T\Vert }_{0,{\mathrm{\Gamma }}_m}+{\Vert \mathit{\varphi }\Vert }_{0,{\mathrm{\Gamma }}_u}+{\Vert t\Vert }_{0,{\mathrm{\Gamma }}_u}{)|||v|||}_{1,\mathrm{\Omega }}.\hfill \end{array}$$(13) ) and (14(14) $$\begin{array}{c}\hfill |a(v,v)|\ge c_0{|||v|||}_{1,\mathrm{\Omega }}^2\forall v\in \mathbf{V}.\end{array}$$(14) ). $\square$

3. Tikhonov regularization and theoretical analysis

In this section, based on the reformulation, Problem 2.1, we propose a Tikhonov regularization framework for the Cauchy problem with the noisy Cauchy data. Let the Cauchy data $(\mathrm{\Phi },T)$ contain random noise with a known level $\mathit{\delta }$, denoted as $({\mathrm{\Phi }}^{\mathit{\delta }},T^{\mathit{\delta }})$. Then the forward BVP (5(5) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}-\text{div}(\mathit{\kappa }\mathrm{\nabla }u)=f\hfill & \text{in}\mathrm{\Omega },\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }u}{\mathit{\partial }n}+iu=\mathrm{\Phi }+iT\hfill & \text{on}{\mathrm{\Gamma }}_m,\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }u}{\mathit{\partial }n}+iu=\mathit{\varphi }+it\hfill & \text{on}{\mathrm{\Gamma }}_u,\hfill \end{array}\right.\end{array}$$(5) ) is modified to(15) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}-\text{div}(\mathit{\kappa }\mathrm{\nabla }{u}^{\mathit{\delta }})=f\hfill & \text{in}\mathrm{\Omega },\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }{u}^{\mathit{\delta }}}{\mathit{\partial }n}+iu={\mathrm{\Phi }}^{\mathit{\delta }}+i{T}^{\mathit{\delta }}\hfill & \text{on}{\mathrm{\Gamma }}_m,\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }{u}^{\mathit{\delta }}}{\mathit{\partial }n}+iu=\mathit{\varphi }+it\hfill & \text{on}{\mathrm{\Gamma }}_u,\hfill \end{array}\right.\end{array}$$(15)

with$$\begin{array}{c}\hfill \Vert {\mathrm{\Phi }}^{\mathit{\delta }}{-\mathrm{\Phi }\Vert }_{0,{\mathrm{\Gamma }}_m}\le \mathit{\delta },{\Vert T^{\mathit{\delta }}-T\Vert }_{0,{\mathrm{\Gamma }}_m}\le \mathit{\delta }.\end{array}$$

Similarly, define(16) $$\begin{array}{c}\hfill F^{\mathit{\delta }}(\mathit{\varphi },t;v)={\int }_{\mathrm{\Omega }}f\overline{v}\mathrm{d}x+{\int }_{{\mathrm{\Gamma }}_m}({\mathrm{\Phi }}^{\mathit{\delta }}+i{T}^{\mathit{\delta }})\overline{v}\mathrm{d}s+{\int }_{{\mathrm{\Gamma }}_u}(\mathit{\varphi }+it)\overline{v}\mathrm{d}s\forall v\in \mathbf{V}.\end{array}$$(16)

The weak form of the BVP (15(15) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}-\text{div}(\mathit{\kappa }\mathrm{\nabla }{u}^{\mathit{\delta }})=f\hfill & \text{in}\mathrm{\Omega },\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }{u}^{\mathit{\delta }}}{\mathit{\partial }n}+iu={\mathrm{\Phi }}^{\mathit{\delta }}+i{T}^{\mathit{\delta }}\hfill & \text{on}{\mathrm{\Gamma }}_m,\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }{u}^{\mathit{\delta }}}{\mathit{\partial }n}+iu=\mathit{\varphi }+it\hfill & \text{on}{\mathrm{\Gamma }}_u,\hfill \end{array}\right.\end{array}$$(15) ) is(17) $$\begin{array}{c}\hfill u^{\mathit{\delta }}\in \mathbf{V},a(u^{\mathit{\delta }},v)=F^{\mathit{\delta }}(\mathit{\varphi },t;v)\forall v\in \mathbf{V}.\end{array}$$(17)

Like Proposition 2.2, we have the well-posedness results on the problem (17(17) $$\begin{array}{c}\hfill u^{\mathit{\delta }}\in \mathbf{V},a(u^{\mathit{\delta }},v)=F^{\mathit{\delta }}(\mathit{\varphi },t;v)\forall v\in \mathbf{V}.\end{array}$$(17) ).

Proposition 3.1:

Given $f\in Q$, $({\mathrm{\Phi }}^{\mathit{\delta }},T^{\mathit{\delta }})\in Q_{{\mathrm{\Gamma }}_m}\times Q_{{\mathrm{\Gamma }}_m}$, $(\mathit{\varphi },t)\in Q_{{\mathrm{\Gamma }}_u}\times Q_{{\mathrm{\Gamma }}_u}$, the problem (17(17) $$\begin{array}{c}\hfill u^{\mathit{\delta }}\in \mathbf{V},a(u^{\mathit{\delta }},v)=F^{\mathit{\delta }}(\mathit{\varphi },t;v)\forall v\in \mathbf{V}.\end{array}$$(17) ) admits a unique solution $u^{\mathit{\delta }}\in \mathbf{V}$ which depends continuously on all data. Moreover, we have(18) $$\begin{array}{c}\hfill |||u^{\mathit{\delta }}{|||}_{1,\mathrm{\Omega }}\le {c(\Vert f\Vert }_{0,\mathrm{\Omega }}+\Vert {\mathrm{\Phi }}^{\mathit{\delta }}{\Vert }_{0,{\mathrm{\Gamma }}_m}+\Vert T^{\mathit{\delta }}{\Vert }_{0,{\mathrm{\Gamma }}_m}+{\Vert \mathit{\varphi }\Vert }_{0,{\mathrm{\Gamma }}_u}+{\Vert t\Vert }_{0,{\mathrm{\Gamma }}_u}).\end{array}$$(18)

Denote by $u,u^{\mathit{\delta }}\in \mathbf{V}$ the solutions of the problems (10(10) $$\begin{array}{c}\hfill u\in \mathbf{V},a(u,v)=F(\mathit{\varphi },t;v)\forall v\in \mathbf{V}.\end{array}$$(10) ) and (17(17) $$\begin{array}{c}\hfill u^{\mathit{\delta }}\in \mathbf{V},a(u^{\mathit{\delta }},v)=F^{\mathit{\delta }}(\mathit{\varphi },t;v)\forall v\in \mathbf{V}.\end{array}$$(17) ). Then it is easy to get(19) $$\begin{array}{c}\hfill |||u^{\mathit{\delta }}-{u|||}_{1,\mathrm{\Omega }}\le c\mathit{\delta }.\end{array}$$(19)

For any $(\mathit{\varphi },t)\in Q_{{\mathrm{\Gamma }}_u}\times Q_{{\mathrm{\Gamma }}_u}$, write $u^{\mathit{\delta }}(\mathit{\varphi },t)=u_1^{\mathit{\delta }}(\mathit{\varphi },t)+i{u}_2^{\mathit{\delta }}(\mathit{\varphi },t)\in \mathbf{V}$ for the solution of (17(17) $$\begin{array}{c}\hfill u^{\mathit{\delta }}\in \mathbf{V},a(u^{\mathit{\delta }},v)=F^{\mathit{\delta }}(\mathit{\varphi },t;v)\forall v\in \mathbf{V}.\end{array}$$(17) ). Define an objective functional(20) $$\begin{array}{c}\hfill J_{\mathit{\epsilon }}^{\mathit{\delta }}(\mathit{\varphi },t)=\frac{1}{2}\Vert u_2^{\mathit{\delta }}{(\mathit{\varphi },t)\Vert }_{0,\mathrm{\Omega }}^2+\frac{\mathit{\epsilon }}{2}{\Vert \mathit{\varphi }\Vert }_{0,{\mathrm{\Gamma }}_u}^2+\frac{\mathit{\epsilon }}{2}{\Vert t\Vert }_{0,{\mathrm{\Gamma }}_u}^2,\end{array}$$(20)

and introduce the following Tikhonov regularization framework for Problem 2.1.

Problem 3.2:

Find $({\mathit{\varphi }}_{\mathit{\epsilon }}^{\mathit{\delta }},t_{\mathit{\epsilon }}^{\mathit{\delta }})\in Q_{{\mathrm{\Gamma }}_u}\times Q_{{\mathrm{\Gamma }}_u}$ such that$$J_{\mathit{\epsilon }}^{\mathit{\delta }}({\mathit{\varphi }}_{\mathit{\epsilon }}^{\mathit{\delta }},t_{\mathit{\epsilon }}^{\mathit{\delta }})=\underset{(\mathit{\eta },s)\in Q_{{\mathrm{\Gamma }}_u}\times Q_{{\mathrm{\Gamma }}_u}}{inf}{J}_{\mathit{\epsilon }}^{\mathit{\delta }}(\mathit{\eta },s).$$

Remark 2:

Alternatively, we may consider a different but related Tikhonov regularization framework by replacing $J_{\mathit{\epsilon }}^{\mathit{\delta }}$ in (20(20) $$\begin{array}{c}\hfill J_{\mathit{\epsilon }}^{\mathit{\delta }}(\mathit{\varphi },t)=\frac{1}{2}\Vert u_2^{\mathit{\delta }}{(\mathit{\varphi },t)\Vert }_{0,\mathrm{\Omega }}^2+\frac{\mathit{\epsilon }}{2}{\Vert \mathit{\varphi }\Vert }_{0,{\mathrm{\Gamma }}_u}^2+\frac{\mathit{\epsilon }}{2}{\Vert t\Vert }_{0,{\mathrm{\Gamma }}_u}^2,\end{array}$$(20) ) with the objective functional$$\begin{array}{c}\hfill {\tilde{J}}_{\mathit{\epsilon }}^{\mathit{\delta }}(\mathit{\varphi },t)=\frac{1}{2}\Vert u_2^{\mathit{\delta }}{(\mathit{\varphi },t)\Vert }_{1,\mathrm{\Omega }}^2+\frac{\mathit{\epsilon }}{2}{\Vert \mathit{\varphi }\Vert }_{0,{\mathrm{\Gamma }}_u}^2+\frac{\mathit{\epsilon }}{2}{\Vert t\Vert }_{0,{\mathrm{\Gamma }}_u}^2.\end{array}$$

We can verify that for any $(\mathit{\varphi },t),(\mathit{\eta },s)\in Q_{{\mathrm{\Gamma }}_u}\times Q_{{\mathrm{\Gamma }}_u}$,$$\begin{array}{cc}\hfill {(J_{\mathit{\epsilon }}^{\mathit{\delta }})}^{\prime }(\mathit{\varphi },t)(\mathit{\eta },s)& ={(u_2^{\mathit{\delta }}(\mathit{\varphi },t),u_2^{\mathit{\delta }}(\mathit{\eta },s)-u_2^{\mathit{\delta }}(0,0))}_{0,\mathrm{\Omega }}+\mathit{\epsilon }{(\mathit{\varphi },\mathit{\eta })}_{0,{\mathrm{\Gamma }}_u}+\mathit{\epsilon }{(t,s)}_{0,{\mathrm{\Gamma }}_u},\hfill \\ \hfill {(J_{\mathit{\epsilon }}^{\mathit{\delta }})}^{″}(\mathit{\varphi },t){(\mathit{\eta },s)}^2& =\Vert u_2^{\mathit{\delta }}(\mathit{\eta },s)-u_2^{\mathit{\delta }}{(0,0)\Vert }_{0,\mathrm{\Omega }}^2+{\mathit{\epsilon }\Vert \mathit{\eta }\Vert }_{0,{\mathrm{\Gamma }}_u}^2+\mathit{\epsilon }{\Vert s\Vert }_{0,{\mathrm{\Gamma }}_u}^2.\hfill \end{array}$$

Hence, for $\mathit{\epsilon }>0$, $J_{\mathit{\epsilon }}^{\mathit{\delta }}(·)$ is strictly convex.

About Problem 3.2, we first give the following well-posedness result and the first-order optimization condition.

Proposition 3.3:

For any $\mathit{\epsilon }>0$, Problem 3.2 has a unique solution $({\mathit{\varphi }}_{\mathit{\epsilon }}^{\mathit{\delta }},t_{\mathit{\epsilon }}^{\mathit{\delta }})\in Q_{{\mathrm{\Gamma }}_u}\times Q_{{\mathrm{\Gamma }}_u}$ which depends continuously on all data. Moreover, $({\mathit{\varphi }}_{\mathit{\epsilon }}^{\mathit{\delta }},t_{\mathit{\epsilon }}^{\mathit{\delta }})$ is characterized by(21) $$\begin{array}{c}\hfill {\mathit{\varphi }}_{\mathit{\epsilon }}^{\mathit{\delta }}=-\frac{1}{\mathit{\epsilon }}{w}_2^{\mathit{\delta }}{{|}_{{\mathrm{\Gamma }}_u},t_{\mathit{\epsilon }}^{\mathit{\delta }}=-\frac{1}{\mathit{\epsilon }}{w}_1^{\mathit{\delta }}|}_{{\mathrm{\Gamma }}_u},\end{array}$$(21)

where $w_1^{\mathit{\delta }}=w_1^{\mathit{\delta }}({\mathit{\varphi }}_{\mathit{\epsilon }}^{\mathit{\delta }},t_{\mathit{\epsilon }}^{\mathit{\delta }})$ and $w_2^{\mathit{\delta }}=w_2^{\mathit{\delta }}({\mathit{\varphi }}_{\mathit{\epsilon }}^{\mathit{\delta }},t_{\mathit{\epsilon }}^{\mathit{\delta }})$ are the real and imaginary parts of the weak solution $w^{\mathit{\delta }}$ of the adjoint BVP:(22) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}-\mathrm{div}(\mathit{\kappa }\mathrm{\nabla }{w}^{\mathit{\delta }})=u_2^{\mathit{\delta }}\hfill & \text{in}\mathrm{\Omega },\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }{w}^{\mathit{\delta }}}{\mathit{\partial }n}+iw=0\hfill & \text{on}\mathrm{\Gamma },\hfill \end{array}\right.\end{array}$$(22)

and $u_2^{\mathit{\delta }}=u_2^{\mathit{\delta }}({\mathit{\varphi }}_{\mathit{\epsilon }}^{\mathit{\delta }},t_{\mathit{\epsilon }}^{\mathit{\delta }})$ is the imaginary part of the solution of the problem (17(17) $$\begin{array}{c}\hfill u^{\mathit{\delta }}\in \mathbf{V},a(u^{\mathit{\delta }},v)=F^{\mathit{\delta }}(\mathit{\varphi },t;v)\forall v\in \mathbf{V}.\end{array}$$(17) ), with $(\mathit{\varphi },t)$ being replaced by $({\mathit{\varphi }}_{\mathit{\epsilon }}^{\mathit{\delta }},t_{\mathit{\epsilon }}^{\mathit{\delta }})$.

Proof:

For $\mathit{\epsilon }>0$, $J_{\mathit{\epsilon }}^{\mathit{\delta }}$ is strictly convex over $Q_{{\mathrm{\Gamma }}_u}\times Q_{{\mathrm{\Gamma }}_u}$. Thus, the well-posedness of Problem 3.2 follows from a standard result on convex minimization problems.[60,61] Moreover, the solution $({\mathit{\varphi }}_{\mathit{\epsilon }}^{\mathit{\delta }},t_{\mathit{\epsilon }}^{\mathit{\delta }})$ is characterized by(23) $$\begin{array}{c}\hfill {(J_{\mathit{\epsilon }}^{\mathit{\delta }})}^{\prime }({\mathit{\varphi }}_{\mathit{\epsilon }}^{\mathit{\delta }},t_{\mathit{\epsilon }}^{\mathit{\delta }})(\mathit{\eta },s)=0\forall (\mathit{\eta },s)\in Q_{{\mathrm{\Gamma }}_u}\times Q_{{\mathrm{\Gamma }}_u}.\end{array}$$(23)

With arguments similar to those in the proofs of [58, Proposition 3.1], we have$$\begin{array}{c}\hfill {(u_2^{\mathit{\delta }}({\mathit{\varphi }}_{\mathit{\epsilon }}^{\mathit{\delta }},t_{\mathit{\epsilon }}^{\mathit{\delta }}),u_2^{\mathit{\delta }}(\mathit{\eta },s)-u_2^{\mathit{\delta }}(0,0))}_{0,\mathrm{\Omega }}={(w_1^{\mathit{\delta }},s)}_{0,{\mathrm{\Gamma }}_u}+{(w_2^{\mathit{\delta }},\mathit{\eta })}_{0,{\mathrm{\Gamma }}_u}.\end{array}$$

Therefore,(24) $$\begin{array}{c}\hfill {(J_{\mathit{\epsilon }}^{\mathit{\delta }})}^{\prime }({\mathit{\varphi }}_{\mathit{\epsilon }}^{\mathit{\delta }},t_{\mathit{\epsilon }}^{\mathit{\delta }})(\mathit{\eta },s)={(w_1^{\mathit{\delta }}+\mathit{\epsilon }{t}_{\mathit{\epsilon }}^{\mathit{\delta }},s)}_{0,{\mathrm{\Gamma }}_u}+{(w_2^{\mathit{\delta }}+\mathit{\epsilon }{\mathit{\varphi }}_{\mathit{\epsilon }}^{\mathit{\delta }},\mathit{\eta })}_{0,{\mathrm{\Gamma }}_u}.\end{array}$$(24)

Substitute (24(24) $$\begin{array}{c}\hfill {(J_{\mathit{\epsilon }}^{\mathit{\delta }})}^{\prime }({\mathit{\varphi }}_{\mathit{\epsilon }}^{\mathit{\delta }},t_{\mathit{\epsilon }}^{\mathit{\delta }})(\mathit{\eta },s)={(w_1^{\mathit{\delta }}+\mathit{\epsilon }{t}_{\mathit{\epsilon }}^{\mathit{\delta }},s)}_{0,{\mathrm{\Gamma }}_u}+{(w_2^{\mathit{\delta }}+\mathit{\epsilon }{\mathit{\varphi }}_{\mathit{\epsilon }}^{\mathit{\delta }},\mathit{\eta })}_{0,{\mathrm{\Gamma }}_u}.\end{array}$$(24) ) into (23(23) $$\begin{array}{c}\hfill {(J_{\mathit{\epsilon }}^{\mathit{\delta }})}^{\prime }({\mathit{\varphi }}_{\mathit{\epsilon }}^{\mathit{\delta }},t_{\mathit{\epsilon }}^{\mathit{\delta }})(\mathit{\eta },s)=0\forall (\mathit{\eta },s)\in Q_{{\mathrm{\Gamma }}_u}\times Q_{{\mathrm{\Gamma }}_u}.\end{array}$$(23) ) and take $\mathit{\eta }=w_2^{\mathit{\delta }}{{|}_{{\mathrm{\Gamma }}_u}+\mathit{\epsilon }{\mathit{\varphi }}_{\mathit{\epsilon }}^{\mathit{\delta }},s=w_1^{\mathit{\delta }}|}_{{\mathrm{\Gamma }}_u}+\mathit{\epsilon }{t}_{\mathit{\epsilon }}^{\mathit{\delta }}$ to get (21(21) $$\begin{array}{c}\hfill {\mathit{\varphi }}_{\mathit{\epsilon }}^{\mathit{\delta }}=-\frac{1}{\mathit{\epsilon }}{w}_2^{\mathit{\delta }}{{|}_{{\mathrm{\Gamma }}_u},t_{\mathit{\epsilon }}^{\mathit{\delta }}=-\frac{1}{\mathit{\epsilon }}{w}_1^{\mathit{\delta }}|}_{{\mathrm{\Gamma }}_u},\end{array}$$(21) ). $\square$

Next we explore a limiting behaviour of $({\mathit{\varphi }}_{\mathit{\epsilon }}^{\mathit{\delta }},t_{\mathit{\epsilon }}^{\mathit{\delta }})$ as $\mathit{\delta },\mathit{\epsilon }\to 0$. For this purpose, assume the exact Cauchy data $(\mathrm{\Phi },T)$ are compatible. Then according to [62], Problem 1.1 admits a solution $({\mathit{\varphi }}^{\ast },t^{\ast })\in H^{-1/2}({\mathrm{\Gamma }}_u)\times H^{1/2}({\mathrm{\Gamma }}_u)$. Moreover, from [59], the solution is unique. For a sequence of noise levels ${\{{\mathit{\delta }}_n\}}_{n\ge 1}$ which converges to 0 in $\mathbb{R}$ as $n\to \infty$, let ${\mathit{\epsilon }}_n=\mathit{\epsilon }({\mathit{\delta }}_n)$ be chosen satisfying ${\mathit{\epsilon }}_n\to 0$ and ${\mathit{\delta }}_n^2/{\mathit{\epsilon }}_n\to 0$, as $n\to \infty$. Denote by $({\mathit{\varphi }}_{{\mathit{\epsilon }}_n}^{{\mathit{\delta }}_n},t_{{\mathit{\epsilon }}_n}^{{\mathit{\delta }}_n})\in Q_{{\mathrm{\Gamma }}_u}\times Q_{{\mathrm{\Gamma }}_u}$ the solution of Problem 3.2 with $({\mathrm{\Phi }}^{\mathit{\delta }},T^{\mathit{\delta }})$ and $\mathit{\epsilon }$ replaced by $({\mathrm{\Phi }}^{{\mathit{\delta }}_n},T^{{\mathit{\delta }}_n})$ and ${\mathit{\epsilon }}_n$ respectively, and assume additionally that ${\mathit{\varphi }}^{\ast }$ belongs to $Q_{{\mathrm{\Gamma }}_u}$. Then the following result holds:

Proposition 3.4:

The solution sequence ${\{({\mathit{\varphi }}_{{\mathit{\epsilon }}_n}^{{\mathit{\delta }}_n},t_{{\mathit{\epsilon }}_n}^{{\mathit{\delta }}_n})\}}_{n=1}^{\infty }$ converges to $({\mathit{\varphi }}^{\ast },t^{\ast })$ in $Q_{{\mathrm{\Gamma }}_u}\times Q_{{\mathrm{\Gamma }}_u}$ as $n\to \infty$.

Proof:

For simplicity in exposition, set ${\mathrm{\Phi }}^n={\mathrm{\Phi }}^{{\mathit{\delta }}_n}$, $T^n=T^{{\mathit{\delta }}_n}$, ${\mathit{\varphi }}^n={\mathit{\varphi }}_{{\mathit{\epsilon }}_n}^{{\mathit{\delta }}_n}$ and $t^n=t_{{\mathit{\epsilon }}_n}^{{\mathit{\delta }}_n}$. Moreover, denote by $u^n=u_1^n+i{u}_2^n=u^{{\mathit{\delta }}_n}({\mathit{\varphi }}^n,t^n)\in \mathbf{V}$ for the solution of (17(17) $$\begin{array}{c}\hfill u^{\mathit{\delta }}\in \mathbf{V},a(u^{\mathit{\delta }},v)=F^{\mathit{\delta }}(\mathit{\varphi },t;v)\forall v\in \mathbf{V}.\end{array}$$(17) ). Recall that $({\mathit{\varphi }}^{\ast },t^{\ast })$ is the unique solution of Problem 1.1. Then, it is also the unique solution of Problem 1.1 due to the equivalence of the two problems, and thus $u_2({\mathit{\varphi }}^{\ast },t^{\ast })=0$ in $\mathrm{\Omega }$, where $u_2({\mathit{\varphi }}^{\ast },t^{\ast })$ is the imaginary part of the solution of the problem (10(10) $$\begin{array}{c}\hfill u\in \mathbf{V},a(u,v)=F(\mathit{\varphi },t;v)\forall v\in \mathbf{V}.\end{array}$$(10) ) with $(\mathit{\varphi },t)$ replaced by $({\mathit{\varphi }}^{\ast },t^{\ast })$. Therefore, from the definition of $({\mathit{\varphi }}^n,t^n)$ and using (19(19) $$\begin{array}{c}\hfill |||u^{\mathit{\delta }}-{u|||}_{1,\mathrm{\Omega }}\le c\mathit{\delta }.\end{array}$$(19) ), we have(25) $$\begin{array}{cc}\hfill J_{{\mathit{\epsilon }}_n}^{{\mathit{\delta }}_n}({\mathit{\varphi }}^n,t^n)\le J_{{\mathit{\epsilon }}_n}^{{\mathit{\delta }}_n}({\mathit{\varphi }}^{\ast },t^{\ast })& =\frac{1}{2}\Vert u_2^{{\mathit{\delta }}_n}({\mathit{\varphi }}^{\ast },t^{\ast }){\Vert }_{0,\mathrm{\Omega }}^2+\frac{{\mathit{\epsilon }}_n}{2}\Vert {\mathit{\varphi }}^{\ast }{\Vert }_{0,{\mathrm{\Gamma }}_u}^2+\frac{{\mathit{\epsilon }}_n}{2}{\Vert t^{\ast }\Vert }_{0,{\mathrm{\Gamma }}_u}^2\hfill \\ \hfill & =\frac{1}{2}\Vert u_2^{{\mathit{\delta }}_n}({\mathit{\varphi }}^{\ast },t^{\ast })-u_2({\mathit{\varphi }}^{\ast },t^{\ast }){\Vert }_{0,\mathrm{\Omega }}^2+\frac{{\mathit{\epsilon }}_n}{2}\Vert {\mathit{\varphi }}^{\ast }{\Vert }_{0,{\mathrm{\Gamma }}_u}^2+\frac{{\mathit{\epsilon }}_n}{2}{\Vert t^{\ast }\Vert }_{0,{\mathrm{\Gamma }}_u}^2\hfill \\ \hfill & \le c{\mathit{\delta }}_n^2+\frac{{\mathit{\epsilon }}_n}{2}\Vert {\mathit{\varphi }}^{\ast }{\Vert }_{0,{\mathrm{\Gamma }}_u}^2+\frac{{\mathit{\epsilon }}_n}{2}{\Vert t^{\ast }\Vert }_{0,{\mathrm{\Gamma }}_u}^2,\hfill \end{array}$$(25)

implying(26) $$\begin{array}{c}\hfill \Vert {\mathit{\varphi }}^n{\Vert }_{0,{\mathrm{\Gamma }}_u}^2+\Vert t^n{\Vert }_{0,{\mathrm{\Gamma }}_u}^2\le c\frac{{\mathit{\delta }}_n^2}{{\mathit{\epsilon }}_n}+\Vert {\mathit{\varphi }}^{\ast }{\Vert }_{0,{\mathrm{\Gamma }}_u}^2+{\Vert t^{\ast }\Vert }_{0,{\mathrm{\Gamma }}_u}^2.\end{array}$$(26)

Moreover, from (18(18) $$\begin{array}{c}\hfill |||u^{\mathit{\delta }}{|||}_{1,\mathrm{\Omega }}\le {c(\Vert f\Vert }_{0,\mathrm{\Omega }}+\Vert {\mathrm{\Phi }}^{\mathit{\delta }}{\Vert }_{0,{\mathrm{\Gamma }}_m}+\Vert T^{\mathit{\delta }}{\Vert }_{0,{\mathrm{\Gamma }}_m}+{\Vert \mathit{\varphi }\Vert }_{0,{\mathrm{\Gamma }}_u}+{\Vert t\Vert }_{0,{\mathrm{\Gamma }}_u}).\end{array}$$(18) ), there holds(27) $$\begin{array}{cc}\hfill |||u^n{|||}_{1,\mathrm{\Omega }}& \le c(\Vert f{\Vert }_{0,\mathrm{\Omega }}+\Vert {\mathrm{\Phi }}^n{\Vert }_{0,{\mathrm{\Gamma }}_m}+\Vert T^n{\Vert }_{0,{\mathrm{\Gamma }}_m}+\Vert {\mathit{\varphi }}^n{\Vert }_{0,{\mathrm{\Gamma }}_u}+\Vert t^n{\Vert }_{0,{\mathrm{\Gamma }}_u})\hfill \\ \hfill & \le c(\Vert f{\Vert }_{0,\mathrm{\Omega }}+2{\mathit{\delta }}_n+\Vert \mathrm{\Phi }{\Vert }_{0,{\mathrm{\Gamma }}_m}+\Vert T{\Vert }_{0,{\mathrm{\Gamma }}_m}+\Vert {\mathit{\varphi }}^n{\Vert }_{0,{\mathrm{\Gamma }}_u}+\Vert t^n{\Vert }_{0,{\mathrm{\Gamma }}_u}).\hfill \end{array}$$(27)

Therefore, combining (26(26) $$\begin{array}{c}\hfill \Vert {\mathit{\varphi }}^n{\Vert }_{0,{\mathrm{\Gamma }}_u}^2+\Vert t^n{\Vert }_{0,{\mathrm{\Gamma }}_u}^2\le c\frac{{\mathit{\delta }}_n^2}{{\mathit{\epsilon }}_n}+\Vert {\mathit{\varphi }}^{\ast }{\Vert }_{0,{\mathrm{\Gamma }}_u}^2+{\Vert t^{\ast }\Vert }_{0,{\mathrm{\Gamma }}_u}^2.\end{array}$$(26) ) and (27(27) $$\begin{array}{cc}\hfill |||u^n{|||}_{1,\mathrm{\Omega }}& \le c(\Vert f{\Vert }_{0,\mathrm{\Omega }}+\Vert {\mathrm{\Phi }}^n{\Vert }_{0,{\mathrm{\Gamma }}_m}+\Vert T^n{\Vert }_{0,{\mathrm{\Gamma }}_m}+\Vert {\mathit{\varphi }}^n{\Vert }_{0,{\mathrm{\Gamma }}_u}+\Vert t^n{\Vert }_{0,{\mathrm{\Gamma }}_u})\hfill \\ \hfill & \le c(\Vert f{\Vert }_{0,\mathrm{\Omega }}+2{\mathit{\delta }}_n+\Vert \mathrm{\Phi }{\Vert }_{0,{\mathrm{\Gamma }}_m}+\Vert T{\Vert }_{0,{\mathrm{\Gamma }}_m}+\Vert {\mathit{\varphi }}^n{\Vert }_{0,{\mathrm{\Gamma }}_u}+\Vert t^n{\Vert }_{0,{\mathrm{\Gamma }}_u}).\hfill \end{array}$$(27) ), for n large enough, $\{({\mathit{\varphi }}^n,t^n,u^n)\}$ is uniformly bounded with respect to n in $Q_{{\mathrm{\Gamma }}_u}\times Q_{{\mathrm{\Gamma }}_u}\times \mathbf{V}$, and there is a subsequence $\{n^{\prime }\}$ of the sequence $\{n\}$, and some elements $({\mathit{\varphi }}^{\infty },t^{\infty })\in Q_{{\mathrm{\Gamma }}_u}\times Q_{{\mathrm{\Gamma }}_u}$, $u^{\infty }\in \mathbf{V}$ such that as $n^{\prime }\to \infty$,(28) $$\begin{array}{cc}& ({\mathit{\varphi }}^{n^{\prime }},t^{n^{\prime }})\rightharpoonup ({\mathit{\varphi }}^{\infty },t^{\infty })\text{in}{Q}_{{\mathrm{\Gamma }}_u}\times Q_{{\mathrm{\Gamma }}_u},\hfill \\ \hfill & u^{n^{\prime }}\rightharpoonup u^{\infty }\text{in}\mathbf{V},u^{n^{\prime }}\to u^{\infty }\text{in}\mathbf{Q},u^{n^{\prime }}\to u^{\infty }\text{in}{\mathbf{Q}}_{\mathrm{\Gamma }}.\hfill \end{array}$$(28)

It is not difficult to verify that $u^{\infty }=u({\mathit{\varphi }}^{\infty },t^{\infty })$. In fact, from the definition of $u^{n^{\prime }}$, we have(29) $$\begin{array}{c}\hfill a(u^{n^{\prime }},v)=F^{{\mathit{\delta }}_{n^{\prime }}}({\mathit{\varphi }}^{n^{\prime }},t^{n^{\prime }};v)\forall v\in \mathbf{V}.\end{array}$$(29)

Let $n^{\prime }\to \infty$ in (29(29) $$\begin{array}{c}\hfill a(u^{n^{\prime }},v)=F^{{\mathit{\delta }}_{n^{\prime }}}({\mathit{\varphi }}^{n^{\prime }},t^{n^{\prime }};v)\forall v\in \mathbf{V}.\end{array}$$(29) ), and use convergence relations (28(28) $$\begin{array}{cc}& ({\mathit{\varphi }}^{n^{\prime }},t^{n^{\prime }})\rightharpoonup ({\mathit{\varphi }}^{\infty },t^{\infty })\text{in}{Q}_{{\mathrm{\Gamma }}_u}\times Q_{{\mathrm{\Gamma }}_u},\hfill \\ \hfill & u^{n^{\prime }}\rightharpoonup u^{\infty }\text{in}\mathbf{V},u^{n^{\prime }}\to u^{\infty }\text{in}\mathbf{Q},u^{n^{\prime }}\to u^{\infty }\text{in}{\mathbf{Q}}_{\mathrm{\Gamma }}.\hfill \end{array}$$(28) ) to get(30) $$\begin{array}{c}\hfill a(u^{\infty },v)=F({\mathit{\varphi }}^{\infty },t^{\infty };v)\forall v\in \mathbf{V},\end{array}$$(30)

i.e. $u^{\infty }=u({\mathit{\varphi }}^{\infty },t^{\infty })$. Moreover, as $n^{\prime }\to \infty$,(31) $$\begin{array}{c}\hfill J_{{\mathit{\epsilon }}_{n^{\prime }}}^{{\mathit{\delta }}_{n^{\prime }}}({\mathit{\varphi }}^{n^{\prime }},t^{n^{\prime }})=\frac{1}{2}\Vert u_2^{n^{\prime }}{\Vert }_{0,\mathrm{\Omega }}^2+\frac{{\mathit{\epsilon }}_{n^{\prime }}}{2}\Vert {\mathit{\varphi }}^{n^{\prime }}{\Vert }_{0,{\mathrm{\Gamma }}_u}^2+\frac{{\mathit{\epsilon }}_{n^{\prime }}}{2}\Vert t^{n^{\prime }}{\Vert }_{0,{\mathrm{\Gamma }}_u}^2\to \frac{1}{2}{\Vert u_2^{\infty }\Vert }_{0,\mathrm{\Omega }}^2,\end{array}$$(31)

where we use the uniform boundedness of $({\mathit{\varphi }}^{n^{\prime }},t^{n^{\prime }})$ and the fact that ${\mathit{\epsilon }}_{n^{\prime }}\to 0$ as $n^{\prime }\to \infty$.

From (25(25) $$\begin{array}{cc}\hfill J_{{\mathit{\epsilon }}_n}^{{\mathit{\delta }}_n}({\mathit{\varphi }}^n,t^n)\le J_{{\mathit{\epsilon }}_n}^{{\mathit{\delta }}_n}({\mathit{\varphi }}^{\ast },t^{\ast })& =\frac{1}{2}\Vert u_2^{{\mathit{\delta }}_n}({\mathit{\varphi }}^{\ast },t^{\ast }){\Vert }_{0,\mathrm{\Omega }}^2+\frac{{\mathit{\epsilon }}_n}{2}\Vert {\mathit{\varphi }}^{\ast }{\Vert }_{0,{\mathrm{\Gamma }}_u}^2+\frac{{\mathit{\epsilon }}_n}{2}{\Vert t^{\ast }\Vert }_{0,{\mathrm{\Gamma }}_u}^2\hfill \\ \hfill & =\frac{1}{2}\Vert u_2^{{\mathit{\delta }}_n}({\mathit{\varphi }}^{\ast },t^{\ast })-u_2({\mathit{\varphi }}^{\ast },t^{\ast }){\Vert }_{0,\mathrm{\Omega }}^2+\frac{{\mathit{\epsilon }}_n}{2}\Vert {\mathit{\varphi }}^{\ast }{\Vert }_{0,{\mathrm{\Gamma }}_u}^2+\frac{{\mathit{\epsilon }}_n}{2}{\Vert t^{\ast }\Vert }_{0,{\mathrm{\Gamma }}_u}^2\hfill \\ \hfill & \le c{\mathit{\delta }}_n^2+\frac{{\mathit{\epsilon }}_n}{2}\Vert {\mathit{\varphi }}^{\ast }{\Vert }_{0,{\mathrm{\Gamma }}_u}^2+\frac{{\mathit{\epsilon }}_n}{2}{\Vert t^{\ast }\Vert }_{0,{\mathrm{\Gamma }}_u}^2,\hfill \end{array}$$(25) ), there holds(32) $$\begin{array}{c}\hfill 0\le J_{{\mathit{\epsilon }}_{n^{\prime }}}^{{\mathit{\delta }}_{n^{\prime }}}({\mathit{\varphi }}^{n^{\prime }},t^{n^{\prime }})\le J_{{\mathit{\epsilon }}_{n^{\prime }}}^{{\mathit{\delta }}_{n^{\prime }}}({\mathit{\varphi }}^{\ast },t^{\ast })\le c{\mathit{\delta }}_{n^{\prime }}^2+\frac{{\mathit{\epsilon }}_{n^{\prime }}}{2}\Vert {\mathit{\varphi }}^{\ast }{\Vert }_{0,{\mathrm{\Gamma }}_u}^2+\frac{{\mathit{\epsilon }}_{n^{\prime }}}{2}{\Vert t^{\ast }\Vert }_{0,{\mathrm{\Gamma }}_u}^2\to 0\text{as}{n}^{\prime }\to \infty .\end{array}$$(32)

Combine (31(31) $$\begin{array}{c}\hfill J_{{\mathit{\epsilon }}_{n^{\prime }}}^{{\mathit{\delta }}_{n^{\prime }}}({\mathit{\varphi }}^{n^{\prime }},t^{n^{\prime }})=\frac{1}{2}\Vert u_2^{n^{\prime }}{\Vert }_{0,\mathrm{\Omega }}^2+\frac{{\mathit{\epsilon }}_{n^{\prime }}}{2}\Vert {\mathit{\varphi }}^{n^{\prime }}{\Vert }_{0,{\mathrm{\Gamma }}_u}^2+\frac{{\mathit{\epsilon }}_{n^{\prime }}}{2}\Vert t^{n^{\prime }}{\Vert }_{0,{\mathrm{\Gamma }}_u}^2\to \frac{1}{2}{\Vert u_2^{\infty }\Vert }_{0,\mathrm{\Omega }}^2,\end{array}$$(31) ) and (32(32) $$\begin{array}{c}\hfill 0\le J_{{\mathit{\epsilon }}_{n^{\prime }}}^{{\mathit{\delta }}_{n^{\prime }}}({\mathit{\varphi }}^{n^{\prime }},t^{n^{\prime }})\le J_{{\mathit{\epsilon }}_{n^{\prime }}}^{{\mathit{\delta }}_{n^{\prime }}}({\mathit{\varphi }}^{\ast },t^{\ast })\le c{\mathit{\delta }}_{n^{\prime }}^2+\frac{{\mathit{\epsilon }}_{n^{\prime }}}{2}\Vert {\mathit{\varphi }}^{\ast }{\Vert }_{0,{\mathrm{\Gamma }}_u}^2+\frac{{\mathit{\epsilon }}_{n^{\prime }}}{2}{\Vert t^{\ast }\Vert }_{0,{\mathrm{\Gamma }}_u}^2\to 0\text{as}{n}^{\prime }\to \infty .\end{array}$$(32) ) to get$$\begin{array}{c}\hfill u_2^{\infty }=0\text{in}\mathrm{\Omega },\end{array}$$

which shows that $({\mathit{\varphi }}^{\infty },t^{\infty })\in Q_{{\mathrm{\Gamma }}_u}\times Q_{{\mathrm{\Gamma }}_u}$ is a solution of Problem 2.1. Since $({\mathit{\varphi }}^{\ast },t^{\ast })$ is the unique solution of Problem 2.1, we conclude that $({\mathit{\varphi }}^{\infty },t^{\infty })=({\mathit{\varphi }}^{\ast },t^{\ast })$. Thus the limit does not depend on the subsequence selected, and then the entire solution sequence $({\mathit{\varphi }}^n,t^n)\rightharpoonup ({\mathit{\varphi }}^{\ast },t^{\ast })$ in $Q_{{\mathrm{\Gamma }}_u}\times Q_{{\mathrm{\Gamma }}_u}$ as $n\to \infty$.

Finally, using (26(26) $$\begin{array}{c}\hfill \Vert {\mathit{\varphi }}^n{\Vert }_{0,{\mathrm{\Gamma }}_u}^2+\Vert t^n{\Vert }_{0,{\mathrm{\Gamma }}_u}^2\le c\frac{{\mathit{\delta }}_n^2}{{\mathit{\epsilon }}_n}+\Vert {\mathit{\varphi }}^{\ast }{\Vert }_{0,{\mathrm{\Gamma }}_u}^2+{\Vert t^{\ast }\Vert }_{0,{\mathrm{\Gamma }}_u}^2.\end{array}$$(26) ) and the weak convergence, we have$$\begin{array}{cc}& \Vert {\mathit{\varphi }}^n-{\mathit{\varphi }}^{\ast }{\Vert }_{0,{\mathrm{\Gamma }}_u}^2+{\Vert t^n-t^{\ast }\Vert }_{0,{\mathrm{\Gamma }}_u}^2\hfill \\ \hfill & =\Vert {\mathit{\varphi }}^n{\Vert }_{0,{\mathrm{\Gamma }}_u}^2+\Vert t^n{\Vert }_{0,{\mathrm{\Gamma }}_u}^2+\Vert {\mathit{\varphi }}^{\ast }{\Vert }_{0,{\mathrm{\Gamma }}_u}^2+{\Vert t^{\ast }\Vert }_{0,{\mathrm{\Gamma }}_u}^2-2{({\mathit{\varphi }}^n,{\mathit{\varphi }}^{\ast })}_{0,{\mathrm{\Gamma }}_u}-2{(t^n,t^{\ast })}_{0,{\mathrm{\Gamma }}_u}\hfill \\ \hfill & \le c\frac{{\mathit{\delta }}_n^2}{{\mathit{\epsilon }}_n}+2\Vert {\mathit{\varphi }}^{\ast }{\Vert }_{0,{\mathrm{\Gamma }}_u}^2+2{\Vert t^{\ast }\Vert }_{0,{\mathrm{\Gamma }}_u}^2-2{({\mathit{\varphi }}^n,{\mathit{\varphi }}^{\ast })}_{0,{\mathrm{\Gamma }}_u}-2{(t^n,t^{\ast })}_{0,{\mathrm{\Gamma }}_u}\to 0\hfill \end{array}$$

as $n\to \infty$. This shows the strong convergence. $\square$

Note that if ${\mathit{\varphi }}^{\ast }\in H^{-1/2}({\mathrm{\Gamma }}_u)$ rather than ${\mathit{\varphi }}^{\ast }\in Q_{{\mathrm{\Gamma }}_u}$, we can prove that $({\mathit{\varphi }}_{{\mathit{\epsilon }}_n}^{{\mathit{\delta }}_n},t_{{\mathit{\epsilon }}_n}^{{\mathit{\delta }}_n})\to ({\mathit{\varphi }}^{\ast },t^{\ast })$ in $H^{-1/2}({\mathrm{\Gamma }}_u)\times Q_{{\mathrm{\Gamma }}_u}$ as $n\to \infty$, with arguments similar to those above, with a slight modification.

4. An algorithm for the regularized optimal problem

As $Q_{{\mathrm{\Gamma }}_u}$, ${\mathbf{Q}}_{{\mathrm{\Gamma }}_u}$ are linear spaces, we obtain linear system for the solution of the optimization Problem 3.2. Indeed, by Proposition 3.3, substitute (21(21) $$\begin{array}{c}\hfill {\mathit{\varphi }}_{\mathit{\epsilon }}^{\mathit{\delta }}=-\frac{1}{\mathit{\epsilon }}{w}_2^{\mathit{\delta }}{{|}_{{\mathrm{\Gamma }}_u},t_{\mathit{\epsilon }}^{\mathit{\delta }}=-\frac{1}{\mathit{\epsilon }}{w}_1^{\mathit{\delta }}|}_{{\mathrm{\Gamma }}_u},\end{array}$$(21) ) back into (17(17) $$\begin{array}{c}\hfill u^{\mathit{\delta }}\in \mathbf{V},a(u^{\mathit{\delta }},v)=F^{\mathit{\delta }}(\mathit{\varphi },t;v)\forall v\in \mathbf{V}.\end{array}$$(17) ) to give(33) $$\begin{array}{c}\hfill a(u^{\mathit{\delta }},v)+\frac{1}{\mathit{\epsilon }}{(w_2^{\mathit{\delta }},\overline{v})}_{0,{\mathrm{\Gamma }}_u}+i\frac{1}{\mathit{\epsilon }}{(w_1^{\mathit{\delta }},\overline{v})}_{0,{\mathrm{\Gamma }}_u}={(f,\overline{v})}_{0,\mathrm{\Omega }}+{({\mathrm{\Phi }}^{\mathit{\delta }}+i{T}^{\mathit{\delta }},\overline{v})}_{0,{\mathrm{\Gamma }}_m}\forall v\in \mathbf{V}.\end{array}$$(33)

The weak form of (22(22) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}-\mathrm{div}(\mathit{\kappa }\mathrm{\nabla }{w}^{\mathit{\delta }})=u_2^{\mathit{\delta }}\hfill & \text{in}\mathrm{\Omega },\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }{w}^{\mathit{\delta }}}{\mathit{\partial }n}+iw=0\hfill & \text{on}\mathrm{\Gamma },\hfill \end{array}\right.\end{array}$$(22) ) reads:(34) $$\begin{array}{c}\hfill w^{\mathit{\delta }}\in \mathbf{V},a(w^{\mathit{\delta }},v)={(u_2^{\mathit{\delta }},\overline{v})}_{0,\mathrm{\Omega }}\forall v\in \mathbf{V}.\end{array}$$(34)

Then by combining (21(21) $$\begin{array}{c}\hfill {\mathit{\varphi }}_{\mathit{\epsilon }}^{\mathit{\delta }}=-\frac{1}{\mathit{\epsilon }}{w}_2^{\mathit{\delta }}{{|}_{{\mathrm{\Gamma }}_u},t_{\mathit{\epsilon }}^{\mathit{\delta }}=-\frac{1}{\mathit{\epsilon }}{w}_1^{\mathit{\delta }}|}_{{\mathrm{\Gamma }}_u},\end{array}$$(21) ), (33(33) $$\begin{array}{c}\hfill a(u^{\mathit{\delta }},v)+\frac{1}{\mathit{\epsilon }}{(w_2^{\mathit{\delta }},\overline{v})}_{0,{\mathrm{\Gamma }}_u}+i\frac{1}{\mathit{\epsilon }}{(w_1^{\mathit{\delta }},\overline{v})}_{0,{\mathrm{\Gamma }}_u}={(f,\overline{v})}_{0,\mathrm{\Omega }}+{({\mathrm{\Phi }}^{\mathit{\delta }}+i{T}^{\mathit{\delta }},\overline{v})}_{0,{\mathrm{\Gamma }}_m}\forall v\in \mathbf{V}.\end{array}$$(33) ) and (34(34) $$\begin{array}{c}\hfill w^{\mathit{\delta }}\in \mathbf{V},a(w^{\mathit{\delta }},v)={(u_2^{\mathit{\delta }},\overline{v})}_{0,\mathrm{\Omega }}\forall v\in \mathbf{V}.\end{array}$$(34) ), we give the following solver of Problem 3.2:

(1)

Solve(35) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{(\mathit{\kappa }\mathrm{\nabla }{u}_1,\mathrm{\nabla }v)}_{0,\mathrm{\Omega }}-{(u_2,v)}_{0,\mathrm{\Gamma }}+\frac{1}{\mathit{\epsilon }}{(w_2,v)}_{0,{\mathrm{\Gamma }}_u}\hfill & ={(f,v)}_{0,\mathrm{\Omega }}+{({\mathrm{\Phi }}^{\mathit{\delta }},v)}_{0,{\mathrm{\Gamma }}_m}\forall v\in V,\hfill \\ {(\mathit{\kappa }\mathrm{\nabla }{u}_2,\mathrm{\nabla }v)}_{0,\mathrm{\Omega }}+{(u_1,v)}_{0,\mathrm{\Gamma }}+\frac{1}{\mathit{\epsilon }}{(w_1,v)}_{0,{\mathrm{\Gamma }}_u}\hfill & ={(T^{\mathit{\delta }},v)}_{0,{\mathrm{\Gamma }}_m}\forall v\in V,\hfill \\ -{(u_2,v)}_{0,\mathrm{\Omega }}+{(\mathit{\kappa }\mathrm{\nabla }{w}_1,\mathrm{\nabla }v)}_{0,\mathrm{\Omega }}-{(w_2,v)}_{0,\mathrm{\Gamma }}\hfill & =0\forall v\in V,\hfill \\ {(\mathit{\kappa }\mathrm{\nabla }{w}_2,\mathrm{\nabla }v)}_{0,\mathrm{\Omega }}+{(w_1,v)}_{0,\mathrm{\Gamma }}\hfill & =0\forall v\in V.\hfill \end{array}\right.\end{array}$$(35)

(2)

Compute(36) $$\begin{array}{c}\hfill {\mathit{\varphi }}_{\mathit{\epsilon }}^{\mathit{\delta }}=-\frac{1}{\mathit{\epsilon }}{w}_2{{|}_{{\mathrm{\Gamma }}_u},t_{\mathit{\epsilon }}^{\mathit{\delta }}=-\frac{1}{\mathit{\epsilon }}{w}_1|}_{{\mathrm{\Gamma }}_u}.\end{array}$$(36)

For real reconstruction, (35(35) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{(\mathit{\kappa }\mathrm{\nabla }{u}_1,\mathrm{\nabla }v)}_{0,\mathrm{\Omega }}-{(u_2,v)}_{0,\mathrm{\Gamma }}+\frac{1}{\mathit{\epsilon }}{(w_2,v)}_{0,{\mathrm{\Gamma }}_u}\hfill & ={(f,v)}_{0,\mathrm{\Omega }}+{({\mathrm{\Phi }}^{\mathit{\delta }},v)}_{0,{\mathrm{\Gamma }}_m}\forall v\in V,\hfill \\ {(\mathit{\kappa }\mathrm{\nabla }{u}_2,\mathrm{\nabla }v)}_{0,\mathrm{\Omega }}+{(u_1,v)}_{0,\mathrm{\Gamma }}+\frac{1}{\mathit{\epsilon }}{(w_1,v)}_{0,{\mathrm{\Gamma }}_u}\hfill & ={(T^{\mathit{\delta }},v)}_{0,{\mathrm{\Gamma }}_m}\forall v\in V,\hfill \\ -{(u_2,v)}_{0,\mathrm{\Omega }}+{(\mathit{\kappa }\mathrm{\nabla }{w}_1,\mathrm{\nabla }v)}_{0,\mathrm{\Omega }}-{(w_2,v)}_{0,\mathrm{\Gamma }}\hfill & =0\forall v\in V,\hfill \\ {(\mathit{\kappa }\mathrm{\nabla }{w}_2,\mathrm{\nabla }v)}_{0,\mathrm{\Omega }}+{(w_1,v)}_{0,\mathrm{\Gamma }}\hfill & =0\forall v\in V.\hfill \end{array}\right.\end{array}$$(35) ) and (36(36) $$\begin{array}{c}\hfill {\mathit{\varphi }}_{\mathit{\epsilon }}^{\mathit{\delta }}=-\frac{1}{\mathit{\epsilon }}{w}_2{{|}_{{\mathrm{\Gamma }}_u},t_{\mathit{\epsilon }}^{\mathit{\delta }}=-\frac{1}{\mathit{\epsilon }}{w}_1|}_{{\mathrm{\Gamma }}_u}.\end{array}$$(36) ) need to be solved numerically. Standard conforming linear finite-element methods are applied to solve (35(35) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{(\mathit{\kappa }\mathrm{\nabla }{u}_1,\mathrm{\nabla }v)}_{0,\mathrm{\Omega }}-{(u_2,v)}_{0,\mathrm{\Gamma }}+\frac{1}{\mathit{\epsilon }}{(w_2,v)}_{0,{\mathrm{\Gamma }}_u}\hfill & ={(f,v)}_{0,\mathrm{\Omega }}+{({\mathrm{\Phi }}^{\mathit{\delta }},v)}_{0,{\mathrm{\Gamma }}_m}\forall v\in V,\hfill \\ {(\mathit{\kappa }\mathrm{\nabla }{u}_2,\mathrm{\nabla }v)}_{0,\mathrm{\Omega }}+{(u_1,v)}_{0,\mathrm{\Gamma }}+\frac{1}{\mathit{\epsilon }}{(w_1,v)}_{0,{\mathrm{\Gamma }}_u}\hfill & ={(T^{\mathit{\delta }},v)}_{0,{\mathrm{\Gamma }}_m}\forall v\in V,\hfill \\ -{(u_2,v)}_{0,\mathrm{\Omega }}+{(\mathit{\kappa }\mathrm{\nabla }{w}_1,\mathrm{\nabla }v)}_{0,\mathrm{\Omega }}-{(w_2,v)}_{0,\mathrm{\Gamma }}\hfill & =0\forall v\in V,\hfill \\ {(\mathit{\kappa }\mathrm{\nabla }{w}_2,\mathrm{\nabla }v)}_{0,\mathrm{\Omega }}+{(w_1,v)}_{0,\mathrm{\Gamma }}\hfill & =0\forall v\in V.\hfill \end{array}\right.\end{array}$$(35) ). Specifically, let ${\{{\mathcal{T}}_h\}}_h$ be a regular family of finite-element partitions of $\overline{\mathrm{\Omega }}$, and define the linear finite-element space$$V^h=\{v\in C(\overline{\mathrm{\Omega }})\mid v\text{is linear in}T\forall T\in {\mathcal{T}}_h\}.$$

Then a finite-element discretization of (35(35) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{(\mathit{\kappa }\mathrm{\nabla }{u}_1,\mathrm{\nabla }v)}_{0,\mathrm{\Omega }}-{(u_2,v)}_{0,\mathrm{\Gamma }}+\frac{1}{\mathit{\epsilon }}{(w_2,v)}_{0,{\mathrm{\Gamma }}_u}\hfill & ={(f,v)}_{0,\mathrm{\Omega }}+{({\mathrm{\Phi }}^{\mathit{\delta }},v)}_{0,{\mathrm{\Gamma }}_m}\forall v\in V,\hfill \\ {(\mathit{\kappa }\mathrm{\nabla }{u}_2,\mathrm{\nabla }v)}_{0,\mathrm{\Omega }}+{(u_1,v)}_{0,\mathrm{\Gamma }}+\frac{1}{\mathit{\epsilon }}{(w_1,v)}_{0,{\mathrm{\Gamma }}_u}\hfill & ={(T^{\mathit{\delta }},v)}_{0,{\mathrm{\Gamma }}_m}\forall v\in V,\hfill \\ -{(u_2,v)}_{0,\mathrm{\Omega }}+{(\mathit{\kappa }\mathrm{\nabla }{w}_1,\mathrm{\nabla }v)}_{0,\mathrm{\Omega }}-{(w_2,v)}_{0,\mathrm{\Gamma }}\hfill & =0\forall v\in V,\hfill \\ {(\mathit{\kappa }\mathrm{\nabla }{w}_2,\mathrm{\nabla }v)}_{0,\mathrm{\Omega }}+{(w_1,v)}_{0,\mathrm{\Gamma }}\hfill & =0\forall v\in V.\hfill \end{array}\right.\end{array}$$(35) ) and (36(36) $$\begin{array}{c}\hfill {\mathit{\varphi }}_{\mathit{\epsilon }}^{\mathit{\delta }}=-\frac{1}{\mathit{\epsilon }}{w}_2{{|}_{{\mathrm{\Gamma }}_u},t_{\mathit{\epsilon }}^{\mathit{\delta }}=-\frac{1}{\mathit{\epsilon }}{w}_1|}_{{\mathrm{\Gamma }}_u}.\end{array}$$(36) ) reads:

(1)

Solve(37) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{(\mathit{\kappa }\mathrm{\nabla }{u}_1^h,\mathrm{\nabla }{v}^h)}_{0,\mathrm{\Omega }}-{(u_2^h,v^h)}_{0,\mathrm{\Gamma }}+\frac{1}{\mathit{\epsilon }}{(w_2^h,v)}_{0,{\mathrm{\Gamma }}_u}\hfill & ={(f,v^h)}_{0,\mathrm{\Omega }}+{({\mathrm{\Phi }}^{\mathit{\delta }},v^h)}_{0,{\mathrm{\Gamma }}_m}\forall v^h\in V^h,\hfill \\ {(\mathit{\kappa }\mathrm{\nabla }{u}_2^h,\mathrm{\nabla }{v}^h)}_{0,\mathrm{\Omega }}+{(u_1^h,v^h)}_{0,\mathrm{\Gamma }}+\frac{1}{\mathit{\epsilon }}{(w_1^h,v^h)}_{0,{\mathrm{\Gamma }}_u}\hfill & ={(T^{\mathit{\delta }},v^h)}_{0,{\mathrm{\Gamma }}_m}\forall v^h\in V^h,\hfill \\ -{(u_2^h,v^h)}_{0,\mathrm{\Omega }}+{(\mathit{\kappa }\mathrm{\nabla }{w}_1^h,\mathrm{\nabla }{v}^h)}_{0,\mathrm{\Omega }}-{(w_2^h,v^h)}_{0,\mathrm{\Gamma }}\hfill & =0\forall v^h\in V^h,\hfill \\ {(\mathit{\kappa }\mathrm{\nabla }{w}_2^h,\mathrm{\nabla }{v}^h)}_{0,\mathrm{\Omega }}+{(w_1^h,v^h)}_{0,\mathrm{\Gamma }}\hfill & =0\forall v^h\in V^h.\hfill \end{array}\right.\end{array}$$(37)

(2)

Compute(38) $$\begin{array}{c}\hfill {\mathit{\varphi }}_{\mathit{\epsilon }}^h=-\frac{1}{\mathit{\epsilon }}{w}_2^h{{|}_{{\mathrm{\Gamma }}_u},t_{\mathit{\epsilon }}^h=-\frac{1}{\mathit{\epsilon }}{w}_1^h|}_{{\mathrm{\Gamma }}_u}.\end{array}$$(38)

Set ${\mathbf{V}}^h=V^h\oplus i{V}^h$, and define$$Q_{{\mathrm{\Gamma }}_u}^h=\{g^h\in Q_{{\mathrm{\Gamma }}_u}\mid \exists v^h\in V^h\text{s.t.}{g}^h=v^h{|}_{{\mathrm{\Gamma }}_u}\}.$$

Then it is easy to verify that$$({\mathit{\varphi }}_{\mathit{\epsilon }}^h,t_{\mathit{\epsilon }}^h)=arg\underset{({\mathit{\eta }}^h,s^h)\in Q_{{\mathrm{\Gamma }}_u}^h\times Q_{{\mathrm{\Gamma }}_u}^h}{min}{J}_{\mathit{\epsilon }}^h({\mathit{\eta }}^h,s^h)$$

with$$J_{\mathit{\epsilon }}^h(\mathit{\varphi },t)=\frac{1}{2}\Vert u_2^h{(\mathit{\varphi },t)\Vert }_{0,\mathrm{\Omega }}^2+\frac{\mathit{\epsilon }}{2}{\Vert \mathit{\varphi }\Vert }_{0,{\mathrm{\Gamma }}_u}^2+\frac{\mathit{\epsilon }}{2}{\Vert t\Vert }_{0,{\mathrm{\Gamma }}_u}^2,$$

where $u_2^h(\mathit{\varphi },t)$ is the imaginary part of the solution $u^h\in {\mathbf{V}}^h$ of$$a(u^h,v^h)=F^{\mathit{\delta }}(\mathit{\varphi },t;v^h)\forall v^h\in {\mathbf{V}}^h.$$

For fixed $\mathit{\delta },\mathit{\epsilon }>0$, we can prove $({\mathit{\varphi }}_{\mathit{\epsilon }}^h,t_{\mathit{\epsilon }}^h)\to ({\mathit{\varphi }}_{\mathit{\epsilon }}^{\mathit{\delta }},t_{\mathit{\epsilon }}^{\mathit{\delta }})$ in $Q_{{\mathrm{\Gamma }}_u}\times Q_{{\mathrm{\Gamma }}_u}$ as $h\to 0$. We omit the detailed argument of this convergence result here.

5. Numerical results

In this section, we present some numerical results to illustrate the feasibility and effectiveness of the CCBM-based Tikhonov regularization for solving the Cauchy problem. Denote by $({\mathit{\varphi }}^{\ast },t^{\ast })$ the true Neumann and Dirichlet data we want to recover on ${\mathrm{\Gamma }}_u$, and by $({\mathit{\varphi }}_{\mathit{\epsilon }}^h,t_{\mathit{\epsilon }}^h)$ the approximation of $({\mathit{\varphi }}^{\ast },t^{\ast })$ computed from (37(37) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{(\mathit{\kappa }\mathrm{\nabla }{u}_1^h,\mathrm{\nabla }{v}^h)}_{0,\mathrm{\Omega }}-{(u_2^h,v^h)}_{0,\mathrm{\Gamma }}+\frac{1}{\mathit{\epsilon }}{(w_2^h,v)}_{0,{\mathrm{\Gamma }}_u}\hfill & ={(f,v^h)}_{0,\mathrm{\Omega }}+{({\mathrm{\Phi }}^{\mathit{\delta }},v^h)}_{0,{\mathrm{\Gamma }}_m}\forall v^h\in V^h,\hfill \\ {(\mathit{\kappa }\mathrm{\nabla }{u}_2^h,\mathrm{\nabla }{v}^h)}_{0,\mathrm{\Omega }}+{(u_1^h,v^h)}_{0,\mathrm{\Gamma }}+\frac{1}{\mathit{\epsilon }}{(w_1^h,v^h)}_{0,{\mathrm{\Gamma }}_u}\hfill & ={(T^{\mathit{\delta }},v^h)}_{0,{\mathrm{\Gamma }}_m}\forall v^h\in V^h,\hfill \\ -{(u_2^h,v^h)}_{0,\mathrm{\Omega }}+{(\mathit{\kappa }\mathrm{\nabla }{w}_1^h,\mathrm{\nabla }{v}^h)}_{0,\mathrm{\Omega }}-{(w_2^h,v^h)}_{0,\mathrm{\Gamma }}\hfill & =0\forall v^h\in V^h,\hfill \\ {(\mathit{\kappa }\mathrm{\nabla }{w}_2^h,\mathrm{\nabla }{v}^h)}_{0,\mathrm{\Omega }}+{(w_1^h,v^h)}_{0,\mathrm{\Gamma }}\hfill & =0\forall v^h\in V^h.\hfill \end{array}\right.\end{array}$$(37) ) and (38(38) $$\begin{array}{c}\hfill {\mathit{\varphi }}_{\mathit{\epsilon }}^h=-\frac{1}{\mathit{\epsilon }}{w}_2^h{{|}_{{\mathrm{\Gamma }}_u},t_{\mathit{\epsilon }}^h=-\frac{1}{\mathit{\epsilon }}{w}_1^h|}_{{\mathrm{\Gamma }}_u}.\end{array}$$(38) ). Note that (37(37) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{(\mathit{\kappa }\mathrm{\nabla }{u}_1^h,\mathrm{\nabla }{v}^h)}_{0,\mathrm{\Omega }}-{(u_2^h,v^h)}_{0,\mathrm{\Gamma }}+\frac{1}{\mathit{\epsilon }}{(w_2^h,v)}_{0,{\mathrm{\Gamma }}_u}\hfill & ={(f,v^h)}_{0,\mathrm{\Omega }}+{({\mathrm{\Phi }}^{\mathit{\delta }},v^h)}_{0,{\mathrm{\Gamma }}_m}\forall v^h\in V^h,\hfill \\ {(\mathit{\kappa }\mathrm{\nabla }{u}_2^h,\mathrm{\nabla }{v}^h)}_{0,\mathrm{\Omega }}+{(u_1^h,v^h)}_{0,\mathrm{\Gamma }}+\frac{1}{\mathit{\epsilon }}{(w_1^h,v^h)}_{0,{\mathrm{\Gamma }}_u}\hfill & ={(T^{\mathit{\delta }},v^h)}_{0,{\mathrm{\Gamma }}_m}\forall v^h\in V^h,\hfill \\ -{(u_2^h,v^h)}_{0,\mathrm{\Omega }}+{(\mathit{\kappa }\mathrm{\nabla }{w}_1^h,\mathrm{\nabla }{v}^h)}_{0,\mathrm{\Omega }}-{(w_2^h,v^h)}_{0,\mathrm{\Gamma }}\hfill & =0\forall v^h\in V^h,\hfill \\ {(\mathit{\kappa }\mathrm{\nabla }{w}_2^h,\mathrm{\nabla }{v}^h)}_{0,\mathrm{\Omega }}+{(w_1^h,v^h)}_{0,\mathrm{\Gamma }}\hfill & =0\forall v^h\in V^h.\hfill \end{array}\right.\end{array}$$(37) ) reduces to a linear system $Ax=b$, which can be solved by the biconjugate gradient method. To better assess the solution accuracy, we define the $L^2$-norm relative errors in the solutions ${\mathit{\varphi }}_{\mathit{\epsilon }}^h$ and $t_{\mathit{\epsilon }}^h$, and the one in the corresponding state $u_1^h$ in (37(37) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{(\mathit{\kappa }\mathrm{\nabla }{u}_1^h,\mathrm{\nabla }{v}^h)}_{0,\mathrm{\Omega }}-{(u_2^h,v^h)}_{0,\mathrm{\Gamma }}+\frac{1}{\mathit{\epsilon }}{(w_2^h,v)}_{0,{\mathrm{\Gamma }}_u}\hfill & ={(f,v^h)}_{0,\mathrm{\Omega }}+{({\mathrm{\Phi }}^{\mathit{\delta }},v^h)}_{0,{\mathrm{\Gamma }}_m}\forall v^h\in V^h,\hfill \\ {(\mathit{\kappa }\mathrm{\nabla }{u}_2^h,\mathrm{\nabla }{v}^h)}_{0,\mathrm{\Omega }}+{(u_1^h,v^h)}_{0,\mathrm{\Gamma }}+\frac{1}{\mathit{\epsilon }}{(w_1^h,v^h)}_{0,{\mathrm{\Gamma }}_u}\hfill & ={(T^{\mathit{\delta }},v^h)}_{0,{\mathrm{\Gamma }}_m}\forall v^h\in V^h,\hfill \\ -{(u_2^h,v^h)}_{0,\mathrm{\Omega }}+{(\mathit{\kappa }\mathrm{\nabla }{w}_1^h,\mathrm{\nabla }{v}^h)}_{0,\mathrm{\Omega }}-{(w_2^h,v^h)}_{0,\mathrm{\Gamma }}\hfill & =0\forall v^h\in V^h,\hfill \\ {(\mathit{\kappa }\mathrm{\nabla }{w}_2^h,\mathrm{\nabla }{v}^h)}_{0,\mathrm{\Omega }}+{(w_1^h,v^h)}_{0,\mathrm{\Gamma }}\hfill & =0\forall v^h\in V^h.\hfill \end{array}\right.\end{array}$$(37) ) as follows:$$\begin{array}{c}\hfill {\text{Err}}_{\mathit{\varphi }}=\frac{\Vert {\mathit{\varphi }}_{\mathit{\epsilon }}^h-{\mathit{\varphi }}^{\ast }{\Vert }_{0,{\mathrm{\Gamma }}_u}}{\Vert {\mathit{\varphi }}^{\ast }{\Vert }_{0,{\mathrm{\Gamma }}_u}},{\text{Err}}_t=\frac{\Vert t_{\mathit{\epsilon }}^h-t^{\ast }{\Vert }_{0,{\mathrm{\Gamma }}_u}}{\Vert t^{\ast }{\Vert }_{0,{\mathrm{\Gamma }}_u}},{\text{Err}}_u=\frac{\Vert u_1^h-u^{\ast }{\Vert }_{0,{\mathrm{\Gamma }}_u}}{\Vert u^{\ast }{\Vert }_{0,{\mathrm{\Gamma }}_u}},\end{array}$$

where $u^{\ast }$, corresponding to $({\mathit{\varphi }}^{\ast },t^{\ast })$, is the true state in (1(1) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}-\text{div}(\mathit{\kappa }\mathrm{\nabla }u)=f\hfill & \text{in}\mathrm{\Omega },\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }u}{\mathit{\partial }n}=\mathrm{\Phi },u=T\hfill & \text{on}{\mathrm{\Gamma }}_m,\hfill \\ \mathit{\kappa }\frac{\mathit{\partial }u}{\mathit{\partial }n}=\mathit{\varphi },u=t\hfill & \text{on}{\mathrm{\Gamma }}_u.\hfill \end{array}\right.\end{array}$$(1) ).

For comparison of the present work with the existing ones, we consider the examples from [1]. Specifically, in the following experiments, let $\mathrm{\Omega }\subset {\mathbb{R}}^2$ be a ring with inner radius $r_1=0.6$ and external radius $r_2=1$. Assume the Cauchy data $(\mathrm{\Phi },T)$ on the external circle ${\mathrm{\Gamma }}_m$ is computed from a true state $u^{\ast }$ given in advance. Then we recover the data $({\mathit{\varphi }}^{\ast },t^{\ast })$ on the inner circle ${\mathrm{\Gamma }}_u$ from the Cauchy data $(\mathrm{\Phi },T)$. All experiments are implemented on a mesh with 1416 nodes, 2592 elements and mesh size $h=0.07145$. To be concise, we omit all figures about the solution $u_1^h$ in $\mathrm{\Omega }$ except noting that in all experiments below, the accuracy in $u_1^h$ is better than that in ${\mathit{\varphi }}_{\mathit{\epsilon }}^h$ and $t_{\mathit{\epsilon }}^h$.

Example 1:

We first consider an analytic example. Specifically, set $\mathit{\kappa }\equiv 1$ and $f(x,y)=0$ in $\mathrm{\Omega }$, and let $u^{\ast }(x,y)=e^{x}cos(y)$. Then $T(x,y)=e^{x}cos(y)$, $\mathrm{\Phi }(x,y)=e^x(xcos(y)-ysin(y))$, ${\mathit{\varphi }}^{\ast }(x,y)=\frac{5}{3}{e}^x(ysin(y)-xcos(y))$ and $t^{\ast }(x,y)=e^{x}cos(y)$.

For $\mathit{\epsilon }={10}^{-6}$, (37(37) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{(\mathit{\kappa }\mathrm{\nabla }{u}_1^h,\mathrm{\nabla }{v}^h)}_{0,\mathrm{\Omega }}-{(u_2^h,v^h)}_{0,\mathrm{\Gamma }}+\frac{1}{\mathit{\epsilon }}{(w_2^h,v)}_{0,{\mathrm{\Gamma }}_u}\hfill & ={(f,v^h)}_{0,\mathrm{\Omega }}+{({\mathrm{\Phi }}^{\mathit{\delta }},v^h)}_{0,{\mathrm{\Gamma }}_m}\forall v^h\in V^h,\hfill \\ {(\mathit{\kappa }\mathrm{\nabla }{u}_2^h,\mathrm{\nabla }{v}^h)}_{0,\mathrm{\Omega }}+{(u_1^h,v^h)}_{0,\mathrm{\Gamma }}+\frac{1}{\mathit{\epsilon }}{(w_1^h,v^h)}_{0,{\mathrm{\Gamma }}_u}\hfill & ={(T^{\mathit{\delta }},v^h)}_{0,{\mathrm{\Gamma }}_m}\forall v^h\in V^h,\hfill \\ -{(u_2^h,v^h)}_{0,\mathrm{\Omega }}+{(\mathit{\kappa }\mathrm{\nabla }{w}_1^h,\mathrm{\nabla }{v}^h)}_{0,\mathrm{\Omega }}-{(w_2^h,v^h)}_{0,\mathrm{\Gamma }}\hfill & =0\forall v^h\in V^h,\hfill \\ {(\mathit{\kappa }\mathrm{\nabla }{w}_2^h,\mathrm{\nabla }{v}^h)}_{0,\mathrm{\Omega }}+{(w_1^h,v^h)}_{0,\mathrm{\Gamma }}\hfill & =0\forall v^h\in V^h.\hfill \end{array}\right.\end{array}$$(37) ) and (38(38) $$\begin{array}{c}\hfill {\mathit{\varphi }}_{\mathit{\epsilon }}^h=-\frac{1}{\mathit{\epsilon }}{w}_2^h{{|}_{{\mathrm{\Gamma }}_u},t_{\mathit{\epsilon }}^h=-\frac{1}{\mathit{\epsilon }}{w}_1^h|}_{{\mathrm{\Gamma }}_u}.\end{array}$$(38) ) are applied to compute approximate solutions $({\mathit{\varphi }}_{\mathit{\epsilon }}^h,t_{\mathit{\epsilon }}^h)$ of $({\mathit{\varphi }}^{\ast },t^{\ast })$ from the Cauchy data $(\mathrm{\Phi },T)$. 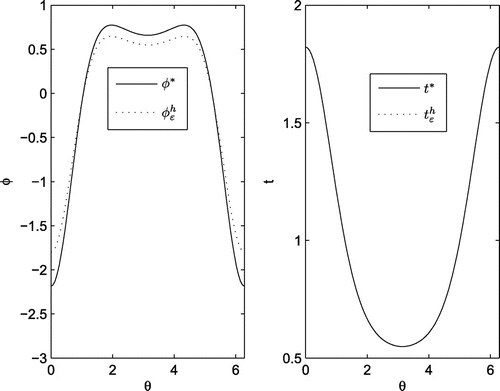We plot $({\mathit{\varphi }}_{\mathit{\epsilon }}^h,t_{\mathit{\epsilon }}^h)$ in Figure 1. Observe that the results are quite satisfactory.

To verify the stability of the reconstruction model explored here, a uniformly distributed noise with a noise level $\mathit{\delta }=0.05,0.10$ and 0.20, respectively, is added to $(\mathrm{\Phi },T)$ of Test 1 to get $({\mathrm{\Phi }}^{\mathit{\delta }},T^{\mathit{\delta }})$:$$\begin{array}{c}\hfill {\mathrm{\Phi }}^{\mathit{\delta }}(x)=[1+\mathit{\delta }·(2\text{rand}(x)-1)]\mathrm{\Phi }(x),x\in {\mathrm{\Gamma }}_m,\\ \hfill T^{\mathit{\delta }}(x)=[1+\mathit{\delta }·(2\text{rand}(x)-1)]T(x),x\in {\mathrm{\Gamma }}_m,\end{array}$$

where rand(x) returns a pseudo-random value drawn from a uniform distribution on [0, 1]. The experiments are repeated on the same mesh for $\mathit{\epsilon }={10}^{-4}$. The errors in the solutions are listed in Table 1. We conclude from Table 1 that Problem 3.2 is stable.

Figure 1. Reconstructed ${\mathit{\varphi }}_{\mathit{\epsilon }}^h$ and $t_{\mathit{\epsilon }}^h$ from $(\mathrm{\Phi },T)$ (Example 1).

Table 1. The dependence of the errors on $\mathit{\delta }$ (Example 1).

$\mathit{\delta }$	0	$5\%$	$10\%$	$20\%$
Err${}_{\mathit{\varphi }}$	9.1482e$-$3	9.2774e$-$2	8.5991e$-$2	9.9572e$-$2
Err${}_t$	1.7730e$-$3	7.4745e$-$2	7.7622e$-$2	8.7462e$-$2
Err${}_u$	6.1776e$-$4	2.8125e$-$2	3.3620e$-$2	4.8458e$-$2

Example 2:

In the second example, let $f(x,y)=0$,$$\mathit{\kappa }=\left[\begin{array}{cc}1\hfill & 0\hfill \\ 0\hfill & \mathit{ϵ}\hfill \end{array}\right],$$

and $u^{\ast }(x,y)={\text{e}}^{\sqrt{\mathit{ϵ}}x}cos(y)$. Then$$\begin{array}{c}\hfill \mathrm{\Phi }(x,y)={\text{e}}^{\sqrt{\mathit{ϵ}}x}(\sqrt{\mathit{ϵ}}xcos(y)-\mathit{ϵ}ysin(y)),T(x,y)={\text{e}}^{\sqrt{\mathit{ϵ}}x}cos(y)\text{on}{\mathrm{\Gamma }}_m,\\ \hfill {\mathit{\varphi }}^{\ast }(x,y)=\frac{5}{3}{\text{e}}^{\sqrt{\mathit{ϵ}}x}(\mathit{ϵ}ysin(y)-\sqrt{\mathit{ϵ}}xcos(y)),t^{\ast }(x,y)={\text{e}}^{\sqrt{\mathit{ϵ}}x}cos(y)\text{on}{\mathrm{\Gamma }}_u.\end{array}$$

This model arises in applications of orthotropic materials.

 

Figure 2. Reconstructed ${\mathit{\varphi }}_{\mathit{\epsilon }}^h$ from $(\mathrm{\Phi },T)$ for different $\mathit{ϵ}$ (Example 2).

Figure 3. Reconstructed $t_{\mathit{\epsilon }}^h$ from $(\mathrm{\Phi },T)$ for different $\mathit{ϵ}$ (Example 2).

Relations (37(37) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{(\mathit{\kappa }\mathrm{\nabla }{u}_1^h,\mathrm{\nabla }{v}^h)}_{0,\mathrm{\Omega }}-{(u_2^h,v^h)}_{0,\mathrm{\Gamma }}+\frac{1}{\mathit{\epsilon }}{(w_2^h,v)}_{0,{\mathrm{\Gamma }}_u}\hfill & ={(f,v^h)}_{0,\mathrm{\Omega }}+{({\mathrm{\Phi }}^{\mathit{\delta }},v^h)}_{0,{\mathrm{\Gamma }}_m}\forall v^h\in V^h,\hfill \\ {(\mathit{\kappa }\mathrm{\nabla }{u}_2^h,\mathrm{\nabla }{v}^h)}_{0,\mathrm{\Omega }}+{(u_1^h,v^h)}_{0,\mathrm{\Gamma }}+\frac{1}{\mathit{\epsilon }}{(w_1^h,v^h)}_{0,{\mathrm{\Gamma }}_u}\hfill & ={(T^{\mathit{\delta }},v^h)}_{0,{\mathrm{\Gamma }}_m}\forall v^h\in V^h,\hfill \\ -{(u_2^h,v^h)}_{0,\mathrm{\Omega }}+{(\mathit{\kappa }\mathrm{\nabla }{w}_1^h,\mathrm{\nabla }{v}^h)}_{0,\mathrm{\Omega }}-{(w_2^h,v^h)}_{0,\mathrm{\Gamma }}\hfill & =0\forall v^h\in V^h,\hfill \\ {(\mathit{\kappa }\mathrm{\nabla }{w}_2^h,\mathrm{\nabla }{v}^h)}_{0,\mathrm{\Omega }}+{(w_1^h,v^h)}_{0,\mathrm{\Gamma }}\hfill & =0\forall v^h\in V^h.\hfill \end{array}\right.\end{array}$$(37) ) and (38(38) $$\begin{array}{c}\hfill {\mathit{\varphi }}_{\mathit{\epsilon }}^h=-\frac{1}{\mathit{\epsilon }}{w}_2^h{{|}_{{\mathrm{\Gamma }}_u},t_{\mathit{\epsilon }}^h=-\frac{1}{\mathit{\epsilon }}{w}_1^h|}_{{\mathrm{\Gamma }}_u}.\end{array}$$(38) ) are applied again to obtain approximations of $({\mathit{\varphi }}^{\ast },t^{\ast })$ from $(\mathrm{\Phi },T)$. 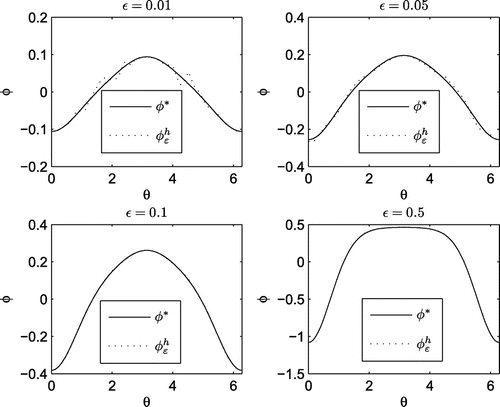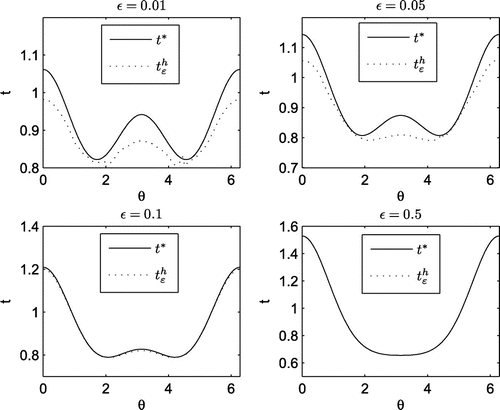We show in Figures 2 and 3 the Neumann data ${\mathit{\varphi }}_{\mathit{\epsilon }}^h$ and Dirichlet data ${\mathit{\varphi }}_t^h$ with $\mathit{ϵ}=0.01$, 0.05, 0.1 and 0.5. The regularization parameters for the four reconstructions are ${10}^{-4}$, ${10}^{-4}$, ${10}^{-5}$ and ${10}^{-6}$, respectively. We can see from Figures 2 and 3 the results are satisfactory even for small parameter $\mathit{ϵ}$. 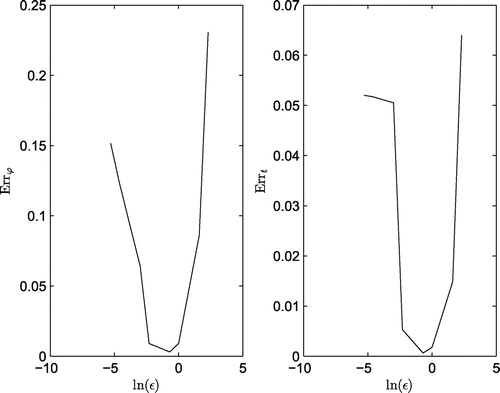The solution accuracy improves when $\mathit{ϵ}$ gets closer to 1. For clarity, the dependence of the errors in ${\mathit{\varphi }}_{\mathit{\epsilon }}^h$ and ${\mathit{\varphi }}_t^h$ on $\mathit{ϵ}\in [0.005,10]$ is plotted in Figure 4.

Figure 4. The dependence of the errors in solutions on $\mathit{ϵ}$ (Example 2).

Fixing $\mathit{ϵ}=0.1$, a uniformly distributed noise with $\mathit{\delta }=0.05,0.10$ and 0.20, respectively, is added to $(\mathrm{\Phi },T)$ to get noisy Cauchy data $({\mathrm{\Phi }}^{\mathit{\delta }},T^{\mathit{\delta }})$. The experiments are repeated with $\mathit{\epsilon }={10}^{-4}$, and the errors in the solutions are reported in Table 2. Table 2 shows again that Problem 3.2 is stable. During our experiments, we found that when $\mathit{ϵ}$ is near 1, the results are rather stable even for big $\mathit{\delta }$ like 0.2; when $\mathit{ϵ}$ is far away from 1, the results are still stable for not too big $\mathit{\delta }$ like $\mathit{\delta }\le 0.05$.

Table 2. The dependence of the errors on $\mathit{\delta }$ (Example 2).

$\mathit{\delta }$	0	$5\%$	$10\%$	$20\%$
Err${}_{\mathit{\varphi }}$	9.0739e$-$3	1.5405e$-$1	2.8359e$-$1	5.4733e$-$1
Err${}_t$	5.2960e$-$3	5.4152e$-$2	6.0903e$-$2	7.8367e$-$2
Err${}_u$	2.3831e$-$3	2.6601e$-$2	3.2882e$-$2	4.8345e$-$2

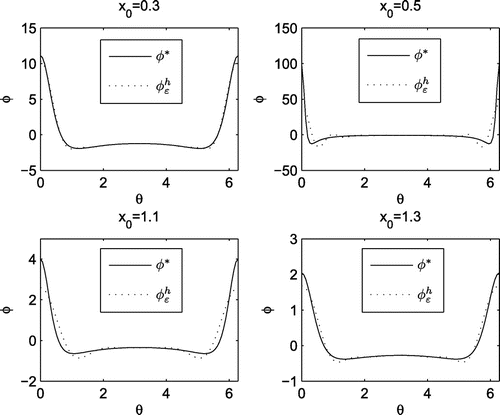
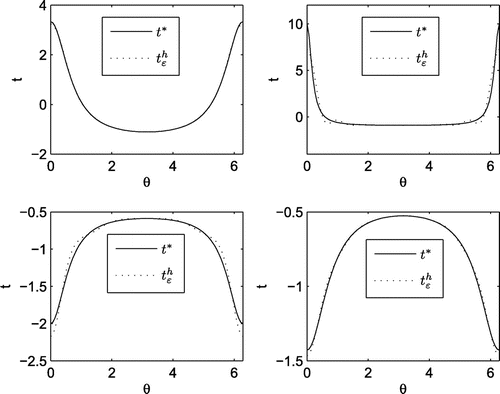
Example 3:

In the last example, we intend to recover the singular data on ${\mathrm{\Gamma }}_u$. Specifically, let a point source $P_0$ be placed at $(x_0,y_0)$ which is near the unaccessible or accessible boundary and assume $u^{\ast }(z)=$Re$(1/(z-z_0))$, with $z_0=x_0+i{y}_0$, $z=x+iy$, $(x,y)\in \mathrm{\Omega }$. Then$$\begin{array}{c}\hfill \mathrm{\Phi }(z)=\text{Re}(-z/{(z-z_0)}^2),T(z)=\text{Re}(1/(z-z_0))\text{on}{\mathrm{\Gamma }}_m,\\ \hfill {\mathit{\varphi }}^{\ast }(z)=\frac{5}{3}\text{Re}(z/{(z-z_0)}^2),t^{\ast }(z)=\text{Re}(1/(z-z_0))\text{on}{\mathrm{\Gamma }}_u.\end{array}$$

For simplicity of statements, let $y_0=0$. For $x_0=0.3$, 0.5, 1.1 and 1.3, (37(37) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{(\mathit{\kappa }\mathrm{\nabla }{u}_1^h,\mathrm{\nabla }{v}^h)}_{0,\mathrm{\Omega }}-{(u_2^h,v^h)}_{0,\mathrm{\Gamma }}+\frac{1}{\mathit{\epsilon }}{(w_2^h,v)}_{0,{\mathrm{\Gamma }}_u}\hfill & ={(f,v^h)}_{0,\mathrm{\Omega }}+{({\mathrm{\Phi }}^{\mathit{\delta }},v^h)}_{0,{\mathrm{\Gamma }}_m}\forall v^h\in V^h,\hfill \\ {(\mathit{\kappa }\mathrm{\nabla }{u}_2^h,\mathrm{\nabla }{v}^h)}_{0,\mathrm{\Omega }}+{(u_1^h,v^h)}_{0,\mathrm{\Gamma }}+\frac{1}{\mathit{\epsilon }}{(w_1^h,v^h)}_{0,{\mathrm{\Gamma }}_u}\hfill & ={(T^{\mathit{\delta }},v^h)}_{0,{\mathrm{\Gamma }}_m}\forall v^h\in V^h,\hfill \\ -{(u_2^h,v^h)}_{0,\mathrm{\Omega }}+{(\mathit{\kappa }\mathrm{\nabla }{w}_1^h,\mathrm{\nabla }{v}^h)}_{0,\mathrm{\Omega }}-{(w_2^h,v^h)}_{0,\mathrm{\Gamma }}\hfill & =0\forall v^h\in V^h,\hfill \\ {(\mathit{\kappa }\mathrm{\nabla }{w}_2^h,\mathrm{\nabla }{v}^h)}_{0,\mathrm{\Omega }}+{(w_1^h,v^h)}_{0,\mathrm{\Gamma }}\hfill & =0\forall v^h\in V^h.\hfill \end{array}\right.\end{array}$$(37) ) and (38(38) $$\begin{array}{c}\hfill {\mathit{\varphi }}_{\mathit{\epsilon }}^h=-\frac{1}{\mathit{\epsilon }}{w}_2^h{{|}_{{\mathrm{\Gamma }}_u},t_{\mathit{\epsilon }}^h=-\frac{1}{\mathit{\epsilon }}{w}_1^h|}_{{\mathrm{\Gamma }}_u}.\end{array}$$(38) ) are used to recover $({\mathit{\varphi }}_{\mathit{\epsilon }}^h,t_{\mathit{\epsilon }}^h)$ from $(\mathrm{\Phi },T)$. The regularization parameters corresponding to four $x_0$ are ${10}^{-7}$, ${10}^{-8}$, ${10}^{-5}$ and ${10}^{-6}$ respectively. 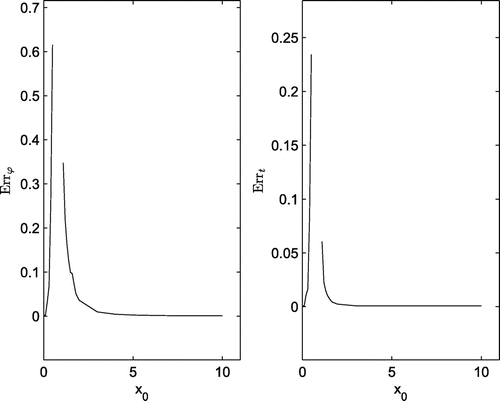We show in Figures 5 and 6 the Neumann data ${\mathit{\varphi }}_{\mathit{\epsilon }}^h$ and the Dirichlet data ${\mathit{\varphi }}_t^h$ respectively. The results are still reasonable when the data on the boundary are singular, and the solution accuracy improves when the singularity reduces. For clarity, the dependence of the relative errors in $({\mathit{\varphi }}_{\mathit{\epsilon }}^h,t_{\mathit{\epsilon }}^h)$ on the value of $x_0\in [0,0.5]\cup [1.1,10]$ is shown in Figure 7, which shows that the results get better as the source moves away from $\mathrm{\Omega }$.

Figure 5. Reconstructed ${\mathit{\varphi }}_{\mathit{\epsilon }}^h$ from $(\mathrm{\Phi },T)$ for different positions of point sources (Example 3).

Figure 6. Reconstructed $t_{\mathit{\epsilon }}^h$ from $(\mathrm{\Phi },T)$ for different positions of point sources (Example 3).

Figure 7. The dependence of the errors on $x_0$ (Example 3).

To verify the stability, we fix $x_0=1.3$ and add uniformly distributed noise with $\mathit{\delta }=0.05$, 0.10 and 0.20 to $\mathrm{\Phi }$ and T, The experiments are performed repeatedly. The regularization parameters corresponding to the four different $\mathit{\delta }$ are ${10}^{-6}$, ${10}^{-5}$, ${10}^{-5}$ and ${10}^{-4}$, respectively. The errors in the solutions are listed in Table 3. Again, the results are stable. Moreover, like the behaviour of the parameter $\mathit{ϵ}$ in Example 2, the position $(x_0,y_0)$ of the point source $P_0$ affect the stability of the solutions. Specifically, the results are rather stable even for big $\mathit{\delta }$ when $P_0$ is far way from the boundary $\mathrm{\Gamma }$ of $\mathrm{\Omega }$; when $P_0$ is near to $\mathrm{\Gamma }$, the results are still stable for not too big $\mathit{\delta }$, $\mathit{\delta }\le 0.05$ for instance.

Table 3. The dependence of the errors on $\mathit{\delta }$ (Example 3).

$\mathit{\delta }$	0	$5\%$	$10\%$	$20\%$
Err${}_{\mathit{\varphi }}$	1.6575e$-$1	2.3465e$-$1	2.7432e$-$1	3.3648e$-$1
Err${}_t$	1.5189e$-$2	3.0876e$-$2	3.3795e$-$2	1.0920e$-$1
Err${}_u$	5.1688e$-$3	1.1388e$-$2	1.5667e$-$2	3.6711e$-$2

We note that in all experiments above, because the true solution $({\mathit{\varphi }}^{\ast },t^{\ast })$ is known, all optimal regularization parameters are chosen approximately by sweeping them from ${10}^{-1},{10}^{-2},{10}^{-3},\dots$. When $({\mathit{\varphi }}^{\ast },t^{\ast })$ is not available, many methods such as discrepancy principle (DP), L-curve rule, quasi-optimality, monotone error rule, generalized cross-validation (GCV), etc., can be used for proper selection of $\mathit{\epsilon }$. For example, using the Morozov DP, Example 1 is tested again and we get similar convergence results. We refer to [63,64] for some further comments on these methods for the choice of the regularization parameters.

6. Conclusions

A CCBM-based Tikhonov regularization framework is presented for solving the Cauchy problem on a general domain. With the proposed method, the data needed to fit the boundary is transferred to the inner of the domain, and the missing data on the unaccessible boundary as well as the corresponding solution in the inner can be reconstructed simultaneously. Since all boundary conditions are used as parts of a Robin boundary condition, no Dirichlet BVP needs to be solved. This makes the resolution of the forward problem easier. Particularly, this allows us to recover both $\mathit{\varphi }$ and t in $Q_{{\mathrm{\Gamma }}_u}$. Moreover, through a complex adjoint equation, a simple solver is given to derive the solution of the regularized optimal problem. Thus no iteration is needed and the resolution is fast. In conclusion, as shown by the theories and numerical experiments, the method explored in this paper is feasible, effective and stable, for both smooth and non-smooth solutions. We comment that the method discussed in this paper can be applied directly to the Cauchy problem governed by other types of partial differential equations.

Acknowledgements

We thank the three anonymous referees for their careful review of our manuscript and for their constructive comments.

Additional information

Funding

The work of the first author was supported partly by the Key Project of the Major Research Plan of NSFC [grant number 91130004]; the Natural Science Foundation of China [grant number 11571311]. The work of the second author was supported partly by the Natural Science Foundation of China [grant number 11401304]; the Natural Science Foundation of Jiangsu Province [grant number BK20130780]; the Fundamental Research Funds for the Central Universities [grant number NS2014078]. The work of the third author was partly supported by Simons Foundation [grant number 207052], [grant number 228187]; the National Science Foundation [grant number DMS-1521684].

Notes

No potential conflict of interest was reported by the authors.