Numerical solution of a Cauchy problem for Laplace equation in 3-dimensional domains by integral equations

Abstract

A numerical method based on integral equations is proposed and investigated for the Cauchy problem for the Laplace equation in 3-dimensional smooth bounded doubly connected domains. To numerically reconstruct a harmonic function from knowledge of the function and its normal derivative on the outer of two closed boundary surfaces, the harmonic function is represented as a single-layer potential. Matching this representation against the given data, a system of boundary integral equations is obtained to be solved for two unknown densities. This system is rewritten over the unit sphere under the assumption that each of the two boundary surfaces can be mapped smoothly and one-to-one to the unit sphere. For the discretization of this system, Weinert’s method (PhD, Göttingen, 1990) is employed, which generates a Galerkin type procedure for the numerical solution, and the densities in the system of integral equations are expressed in terms of spherical harmonics. Tikhonov regularization is incorporated, and numerical results are included showing the efficiency of the proposed procedure.

Keywords:

• Laplace equation
• Cauchy problem
• double connected 3D domain
• single- and double-layer potentials
• integral equation of the first kind
• Tikhonov regularization
• discrete projection method

1. Introduction

The Cauchy problem for the Laplace equation is one of the classical inverse ill-posed problems, [1] having the typical challenging feature of an inverse problem, that is instability with respect to noise in the input data. It also shares another common feature of inverse problems namely a wide range of important applications, for example, in cardiology, corrosion detection, electrostatics, geophysics, leak identification, non-destructive testing and plasma physics, for references see [2] where also references to some methods for Cauchy problems are given.

It would lead us completely astray to attempt to give an overview of methods and results for the Cauchy problem (for some methods and references see, [3–5]). Instead, we turn to the main focus of this work namely a continuation of the work by the authors on developing a single-layer approach for Cauchy problems.

It is well known that layer-approaches leading to first-kind Fredholm integral equations have been successful for well-posed boundary value problems. Starting with the work [2] and building on results from [6], a string of works has been produced showing that a single-layer approach can also be applied to ill-posed Cauchy problems, and is in fact a simple and straightforward but yet mathematically rigorous approach. This single-layer approach has been implemented and tested in various planar domains, both doubly and simply connected, as well as unbounded. Moreover, the method is not restricted to the Laplace equation but can also be applied for the similar problem in elasticity and stationary fluid flow.

Recently, see [7], some 3-dimensional axisymmetric solution domains have been incorporated as well; using the symmetry the integral equations are reduced to the planar case. In the present work, and this will count as the main aim and result, the single-layer approach will be extended and implemented for general smooth bounded doubly connected domains.

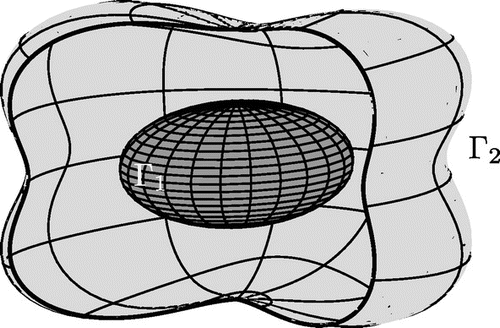
We formulate more precisely the problem to be studied. Let $D_2\subset {\mathrm{I}\mathrm{R}}^3$ be a bounded simply connected domain with boundary surface ${\mathrm{\Gamma }}_2$, and let $D_1\subset D_2$ be a simply connected domain having a boundary surface ${\mathrm{\Gamma }}_1$ lying in $D_2$. The solution domain is $D=D_2\backslash {\overline{D}}_1$, see Figure for an example of the configuration (only a part of the surface ${\mathrm{\Gamma }}_2$ is shown to see the interior surface ${\mathrm{\Gamma }}_1$); $\mathit{\nu }$ is the outward unit normal to the boundary of D.

Let $u\in C^2(D)\cap C^1(\overline{D})$ be a harmonic function, that is a solution to the Laplace equation(1.1) $$\begin{array}{c}\hfill \mathrm{\Delta }u=0\text{in}D\end{array}$$(1.1)

and suppose additionally that u satisfies the boundary conditions(1.2) $$\begin{array}{c}\hfill u=f\text{on}{\mathrm{\Gamma }}_2\text{and}\frac{\mathit{\partial }u}{\mathit{\partial }\mathit{\nu }}=g\text{on}{\mathrm{\Gamma }}_2.\end{array}$$(1.2)

The linear inverse problem we study is: find the harmonic function u in the domain D, in particular, reconstruct the Cauchy data u and ${\displaystyle \frac{\mathit{\partial }u}{\mathit{\partial }\mathit{\nu }}}$ on the interior surface ${\mathrm{\Gamma }}_1$.

We assume that data are compatible and given such that there exists a solution (it is possible to weaken the smoothness of the data, see [8]). Note that uniqueness of the solution is well known, [9,10] and moreover, it is also well known that the Cauchy problem () and () is ill-posed, and measurement errors can destroy the reconstructions unless regularizing methods are employed.

Figure 1. A solution domain D with boundary part ${\mathrm{\Gamma }}_1$ contained within the outer boundary surface ${\mathrm{\Gamma }}_2$.

We represent the solution to () and () as a single-layer potential with unknown densities. Matching the given Cauchy data, a system of boundary integral equations is derived from which the densities over the two boundary surfaces can be obtained. To build a numerical solver for this system, we shall assume that each boundary surface can be mapped (via a parameterization) smoothly and one-to-one to the unit sphere. Boundary integral techniques that make use of parameterizations have successfully been used for various planar boundary value problems, see for example, [11–13]. An analogous approach for 3-dimensional boundary surfaces is Weinert’s method [14]. This method has drawn some recent interest, see [15–19]. We shall be timely and incorporate the method [14].

More precisely, the system of boundary integral equations to be derived for the Cauchy problem will then be rewritten over the unit sphere. For the discretization, a Galerkin projection method is employed involving approximation of the densities in terms of spherical harmonic polynomials. Tikhonov regularization is incorporated for the solution of the corresponding finite dimensional discrete system.

A limitation of our approach is the assumption that the given boundary surfaces can each be mapped onto the unit sphere. However, there is a sufficiently large class of domains relevant for applications that can be mapped in this way to the unit sphere. Moreover, for more general boundary surfaces, one can approximate these with surfaces of the requested kind, or even only construct the map numerically.

We note that an alternative strategy for the Cauchy problem also only needing information on the boundary is to employ the boundary element method (BEM). The main difference compared with the present approach is that the BEM requires approximation of the boundary surfaces, whilst no such discretization is needed here due to the assumption that the boundary surfaces can be mapped to the unit sphere. References to works on inverse problems and the BEM are included in those mentioned in the second paragraph. Note though, that there are in general few numerical works for Cauchy problems in full 3-dimensional domains.

For the outline of this work, in Section , we present the single-layer approach for the Cauchy problem leading to a system of integral equations. It is shown in the setting of square integrable functions that this system has a unique solution for a dense set of data, see Theorem . In Section , this system is rewritten over the unit sphere. In Section , discretization of the system is explained, and explicit formulas for the formation of the coefficients in the corresponding finite dimensional linear system are given. In Section , these formulas are further investigated leading to computationally efficient ways of generating the required coefficients in the linear approximation. Numerical results for some Cauchy problems are given in Section .

2. Reduction to boundary integral equations

The solution to the Cauchy problem () and () is sought in the form of a sum of single-layer potentials over the two boundary surfaces,(2.1) $$\begin{array}{c}\hfill u(x)=\underset{{\mathrm{\Gamma }}_1}{\int }{\mathit{\varphi }}_1(y)\mathrm{\Phi }(x,y)\mathrm{d}s(y)+\underset{{\mathrm{\Gamma }}_2}{\int }{\mathit{\varphi }}_2(y)\mathrm{\Phi }(x,y)\mathrm{d}s(y),x\in D,\end{array}$$(2.1)

where ${\mathit{\varphi }}_1\in C({\mathrm{\Gamma }}_1)$ and ${\mathit{\varphi }}_2\in C({\mathrm{\Gamma }}_2)$ are unknown densities, and $\mathrm{\Phi }(x,y)=\frac{1}{4\mathit{\pi }}\frac{1}{|x-y|}$ is the fundamental solution of the Laplace equation in ${\mathrm{I}\mathrm{R}}^3$.

We shall make use of the following boundary integral operators(2.2) $$\begin{array}{c}\hfill \left(S_{\ell j}\mathit{\mu }\right)(x)=\underset{{\mathrm{\Gamma }}_j}{\int }\mathit{\mu }(y)\mathrm{\Phi }(x,y)\mathrm{d}s(y),x\in {\mathrm{\Gamma }}_{\ell }\end{array}$$(2.2)

and(2.3) $$\begin{array}{c}\hfill \left(K_{\ell j}\mathit{\mu }\right)(x)=\underset{{\mathrm{\Gamma }}_j}{\int }\mathit{\mu }(y)\frac{\mathit{\partial }\mathrm{\Phi }(x,y)}{\mathit{\partial }\mathit{\nu }(x)}\mathrm{d}s(y),x\in {\mathrm{\Gamma }}_{\ell }\end{array}$$(2.3)

with $\ell ,j=1,2$.

Using jump properties of these operators, it follows that an element of the form () satisfies () and () provided that the densities are solutions of the following system(2.4) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle S_{21}{\mathit{\varphi }}_1+S_{22}{\mathit{\varphi }}_2=f\text{on}{\mathrm{\Gamma }}_2,}\hfill \\ {\displaystyle K_{21}{\mathit{\varphi }}_1+\left(\frac{1}{2}I+K_{22}\right){\mathit{\varphi }}_2=g\text{on}{\mathrm{\Gamma }}_2.}\hfill \end{array}\right.\end{array}$$(2.4)

Given that one can find a solution to this system in the form of a pair of densities, using these densities in the representation (), we have a solution to the Cauchy problem () and ().

To investigate solutions to (), we shall make use of an operator $A:L^2({\mathrm{\Gamma }}_1)\times L^2({\mathrm{\Gamma }}_2)\to L^2({\mathrm{\Gamma }}_2)\times L^2({\mathrm{\Gamma }}_2)$, defined by(2.5) $$\begin{array}{c}\hfill A=\left(\begin{array}{cc}{S}_{21}& S_{22}\\ K_{21}& {\displaystyle \frac{1}{2}}I+K_{22}\end{array}\right).\end{array}$$(2.5)

Since the system () corresponds to the ill-posed Cauchy problem () and (), this system will also be ill-posed and thus we cannot invoke Fredholm theory in the hope of showing well-posedness. Instead, we recall the steps in [6, Theorem 4.1] and extend it to the 3-dimensional setting.

Theorem 1.1 The operator A defined in () is injective and has dense range.

Proof We start by showing injectivity. Assume that $A\mathit{\varphi }=0$, where $\mathit{\varphi }=({\mathit{\varphi }}_1,{\mathit{\varphi }}_2)\in L^2({\mathrm{\Gamma }}_1)\times L^2({\mathrm{\Gamma }}_2)$. The element u given by () is a solution to the Laplace equation outside the boundary surfaces and, according to [20, Theorem 6.12] and the note thereafter, is in $H^{3/2}(D)$ and the restriction of this solution and its normal derivative to ${\mathrm{\Gamma }}_2$ are well defined in $L^2({\mathrm{\Gamma }}_2)$. Hence, u has zero Cauchy data on the outer boundary surface ${\mathrm{\Gamma }}_2$ and satisfies the Laplace equation in D. Thus, from the uniqueness of a solution to the Cauchy problem (for an overview on uniqueness and strong unique continuation properties of elliptic equations see [21,22]) we conclude that $u=0$ in $\overline{D}$. The element u is also a solution to the Laplace equation in the exterior of ${\mathrm{\Gamma }}_2$ with zero boundary data. Since the exterior Dirichlet problem is uniquely solvable in ${\mathrm{I}\mathrm{R}}^3$ (in for example the class of solutions with $u(x)=O(|x{|}^{-1}),|x|\to \infty$ in ${\mathrm{I}\mathrm{R}}^3$ ), we conclude that u is zero also in the exterior of ${\mathrm{\Gamma }}_2$. Jump relations of the derivative of the single-layer potential across ${\mathrm{\Gamma }}_2$ immediately gives ${\mathit{\varphi }}_2=0$. Since $u=0$ also on the interior surface ${\mathrm{\Gamma }}_1$, using that the single-layer operator on ${\mathrm{\Gamma }}_1$ has an inverse, see Corollary [20, Corollary 8.11], gives ${\mathit{\varphi }}_1=0$. Hence, the operator A is injective.

For the denseness, we show that the adjoint operator is injective. Let $\mathit{\zeta }=(\mathit{\phi },\mathit{\psi })$ be an element of $L^2({\mathrm{\Gamma }}_2)\times L^2({\mathrm{\Gamma }}_2)$. One can check that(2.6) $$\begin{array}{c}\hfill {(A\mathit{\varphi },\mathit{\zeta })}_{L^2({\mathrm{\Gamma }}_2)\times L^2({\mathrm{\Gamma }}_2)}={(\mathit{\varphi },A^{\ast }\mathit{\zeta })}_{L^2({\mathrm{\Gamma }}_1)\times L^2({\mathrm{\Gamma }}_2)},\end{array}$$(2.6)

with(2.7) $$\begin{array}{c}\hfill A^{\ast }=\left(\begin{array}{cc}{S}_{12}& W_{12}\\ S_{22}& \frac{1}{2}I+W_{22}\end{array}\right),\end{array}$$(2.7)

where(2.8) $$\begin{array}{c}\hfill (W_{\ell j}\mathit{\psi })(x)={\int }_{{\mathrm{\Gamma }}_j}\frac{\mathit{\partial }\mathrm{\Phi }(x,y)}{\mathit{\partial }\mathit{\nu }(y)}\mathit{\psi }(y)\mathrm{d}s(y),x\in {\mathrm{\Gamma }}_{\ell },\end{array}$$(2.8) $\ell ,j=1,2$, is of classical double-layer type.

Assume that $A^{\ast }\mathit{\zeta }=0$. This translates into(2.9) $$\begin{array}{c}\hfill S_{12}\mathit{\phi }+W_{12}\mathit{\psi }=0\text{on}{\mathrm{\Gamma }}_1\end{array}$$(2.9)

and(2.10) $$\begin{array}{c}\hfill S_{22}\mathit{\phi }+\frac{1}{2}\mathit{\psi }+W_{22}\mathit{\psi }=0\text{on}{\mathrm{\Gamma }}_2.\end{array}$$(2.10)

Define the function(2.11) $$\begin{array}{c}\hfill v(x)={\int }_{{\mathrm{\Gamma }}_2}\mathrm{\Phi }(x,y)\mathit{\phi }(y)\mathrm{d}s(y)+{\int }_{{\mathrm{\Gamma }}_2}\frac{\mathit{\partial }\mathrm{\Phi }(x,y)}{\mathit{\partial }\mathit{\nu }(y)}\mathit{\psi }(y)\mathrm{d}s(y).\end{array}$$(2.11)

This element v is a solution to the Laplace equation in D, and according to () this solution has zero Dirichlet condition on the boundary ${\mathrm{\Gamma }}_1$. In fact, () is a solution to the Laplace equation also in the interior of ${\mathrm{\Gamma }}_1$, hence, due to the zero boundary condition on ${\mathrm{\Gamma }}_1$, it follows that $v=0$ throughout the interior of ${\mathrm{\Gamma }}_1$. Since v is smooth across ${\mathrm{\Gamma }}_1,v=0$ also in between ${\mathrm{\Gamma }}_2$ and ${\mathrm{\Gamma }}_1$ by analytic continuation. Furthermore, v is a solution to the Laplace equation in the exterior of ${\mathrm{\Gamma }}_2$ with behaviour at infinity of the form which guarantees uniqueness of a solution. Equation () means that v is zero on ${\mathrm{\Gamma }}_2$ when approached from the exterior. This, together with uniqueness of a solution to the exterior problem, implies that v is zero in the exterior of ${\mathrm{\Gamma }}_2$.

We have then shown that v is zero both in the exterior and interior of ${\mathrm{\Gamma }}_2$. Using jump properties for the function v and its derivative across ${\mathrm{\Gamma }}_2$, we find that $\mathit{\phi }=\mathit{\psi }=0$. Hence, $A^{\ast }$ is injective and thus A has dense range. $\square$

It is possible to consider other spaces as well for the operator A in (). The $L^2$ setting is attractive from a practical point of view, since data are typically contaminated with noise destroying any smoothness assumption on the data. The uniqueness for the Cauchy problem needed in the proof also fits well into an $L^2$ setting since the element () has, for square integrable densities, traces in $H^1(\mathrm{\Gamma })$ and $L^2(\mathrm{\Gamma })$ for the function values and normal derivative, respectively. However, it is possible to consider the natural trace spaces $H^{1/2}({\mathrm{\Gamma }}_2)$ and $H^{-1/2}({\mathrm{\Gamma }}_2)$ for the Cauchy data and generate uniqueness, see [22]. One can thus show the above result about injectivity and denseness for the operator A with densities in $H^{-1/2}({\mathrm{\Gamma }}_j),j=1,2$ and A then maps into the natural trace spaces on ${\mathrm{\Gamma }}_2$; such an analysis is carried out in [23] for the Helmholtz equation. As was noted there, for noisy data a smoothing operator is in general then required to make the given data belong to the required spaces.

In terms of solving the Cauchy problem () and (), we are in particular interested to reconstruct from the given Cauchy data the solution and its normal derivative on the interior boundary surface ${\mathrm{\Gamma }}_1$. With our approach, it is easy to formally write down expressions for these elements since we can invoke jump properties of layer potentials when taking the restriction of the solution () to ${\mathrm{\Gamma }}_1$; we find that(2.12) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle u=S_{11}{\mathit{\varphi }}_1+S_{12}{\mathit{\varphi }}_2\text{on}{\mathrm{\Gamma }}_1,}\hfill \\ {\displaystyle \frac{\mathit{\partial }u}{\mathit{\partial }\mathit{\nu }}=\left(-\frac{1}{2}I+K_{11}\right){\mathit{\varphi }}_1+K_{12}{\mathit{\varphi }}_2\text{on}{\mathrm{\Gamma }}_1.}\hfill \end{array}\right.\end{array}$$(2.12)

3. Rewriting the system () over the unit sphere

In order to find the requested Cauchy data, we first have to solve (), and we shall therefore start by rewriting this equation over the unit sphere.

The basic assumption of the present work is that the surfaces ${\mathrm{\Gamma }}_1$ and ${\mathrm{\Gamma }}_2$ can each be smoothly and bijectively mapped onto the unit sphere ${\mathbb{S}}^2$. Thus, there exist one-to-one mappings(3.1) $$\begin{array}{c}\hfill q_1:{\mathbb{S}}^2\to {\mathrm{\Gamma }}_1\text{and}{q}_2:{\mathbb{S}}^2\to {\mathrm{\Gamma }}_2\end{array}$$(3.1)

having smoothly varying Jacobians $J_{q_1}$ and $J_{q_2}$, respectively. Employing these mappings, we can rewrite the integral equations () over the unit sphere to bring them into the form(3.2) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle {\tilde{S}}_{21}{\mathit{\psi }}_1+{\tilde{S}}_{22}{\mathit{\psi }}_2=\tilde{f}\text{on}{\mathbb{S}}^2,}\hfill \\ {\displaystyle {\tilde{K}}_{21}{\mathit{\psi }}_1+\left(\frac{1}{2}I+{\tilde{K}}_{22}\right){\mathit{\psi }}_2=\tilde{g}\text{on}{\mathbb{S}}^2,}\hfill \end{array}\right.\end{array}$$(3.2)

where the densities are given by(3.3) $$\begin{array}{c}\hfill {\mathit{\psi }}_{\ell }(\widehat{x})={\mathit{\varphi }}_{\ell }(q_{\ell }(\widehat{x})),\ell =1,2,\end{array}$$(3.3)

and the data(3.4) $$\begin{array}{c}\hfill \tilde{f}(\widehat{x})=f(q_2(\widehat{x})),\tilde{g}(\widehat{x})=g(q_2(\widehat{x}))\end{array}$$(3.4)

for $\widehat{x}\in {\mathbb{S}}^2$. The integral operators are parameterizations over the unit sphere of () and () and take the form(3.5) $$\begin{array}{c}\hfill \left({\tilde{S}}_{\ell j}\mathit{\sigma }\right)(\widehat{x})=\underset{{\mathbb{S}}^2}{\int }\mathit{\sigma }(\widehat{y})L_{\ell j}(\widehat{x},\widehat{y})\mathrm{d}s(\widehat{y}),\widehat{x}\in {\mathbb{S}}^2\end{array}$$(3.5)

and(3.6) $$\begin{array}{c}\hfill \left({\tilde{K}}_{\ell j}\mathit{\sigma }\right)(\widehat{x})=\underset{{\mathbb{S}}^2}{\int }\mathit{\sigma }(\widehat{y})M_{\ell j}(\widehat{x},\widehat{y})\mathrm{d}s(\widehat{y}),\widehat{x}\in {\mathbb{S}}^2.\end{array}$$(3.6)

The kernels are$$L_{\ell j}(\widehat{x},\widehat{y})=\left\{\begin{array}{cc}\mathrm{\Phi }(q_{\ell }(\widehat{x}),q_j(\widehat{y}))J_{q_j}(\widehat{y}),\hfill & \ell \ne j,\hfill \\ {\displaystyle [0.2cm]\frac{R_{\ell }(\widehat{x},\widehat{y})}{|\widehat{x}-\widehat{y}|},}\hfill & \ell =j,\hfill \end{array}\right.$$

and$$M_{\ell j}(\widehat{x},\widehat{y})=\left\{\begin{array}{cc}{\displaystyle -\frac{〈q_{\ell }(\widehat{x})-q_j(\widehat{y}),\mathit{\nu }(q_{\ell }(\widehat{x}))〉}{4\mathit{\pi }{\left|q_{\ell }(\widehat{x})-q_j(\widehat{y})\right|}^3}{J}_{q_j}(\widehat{y}),}\hfill & \ell \ne j,\hfill \\ {\displaystyle \frac{{\tilde{R}}_{\ell }(\widehat{x},\widehat{y})}{|\widehat{x}-\widehat{y}|},}\hfill & \ell =j,\hfill \end{array}\right.$$

where$$R_{\ell }(\widehat{x},\widehat{y})=J_{q_{\ell }}(\widehat{y})\left\{\begin{array}{cc}{\displaystyle \frac{1}{4\mathit{\pi }}\frac{|\widehat{x}-\widehat{y}|}{|q_{\ell }(\widehat{x})-q_{\ell }(\widehat{y})|},}\hfill & \widehat{x}\ne \widehat{y},\hfill \\ {\displaystyle \frac{1}{4\mathit{\pi }}\frac{1}{J_{q_{\ell }}(\widehat{x})},}\hfill & \widehat{x}=\widehat{y},\hfill \end{array}\right.$$

and$${\tilde{R}}_{\ell }(\widehat{x},\widehat{y})=-R_{\ell }(\widehat{x},\widehat{y})\left\{\begin{array}{cc}{\displaystyle \frac{\left(q_{\ell }(\widehat{x})-q_{\ell }(\widehat{y}),\mathit{\nu }(q_{\ell }(\widehat{x}))\right)}{{\left|q_{\ell }(\widehat{x})-q_{\ell }(\widehat{y})\right|}^2},}\hfill & \widehat{x}\ne \widehat{y},\hfill \\ {\displaystyle -\frac{2\sum _{j=1}^3{q}_{\ell j}{}^{\prime }(\widehat{x}){\mathit{\nu }}_j(\widehat{x})-\sum _{j=1}^3{q}_{\ell j}{}^{″}(\widehat{x}){\mathit{\nu }}_j(\widehat{x})}{2J_{q_{\ell }}^2(\widehat{x})},}\hfill & \widehat{x}=\widehat{y}.\hfill \end{array}\right.$$

Here, we used that$${\displaystyle \underset{\widehat{y}\to \widehat{x}}{lim}\frac{|\widehat{x}-\widehat{y}|}{|q_{\ell }(\widehat{x})-q_{\ell }(\widehat{y})|}=\frac{1}{J_{q_{\ell }}(\widehat{x})}.}$$

Points on the unit sphere are expressed in the standard spherical coordinates,(3.7) $$\begin{array}{c}\hfill \widehat{x}=p(\mathit{\theta },\mathit{\phi })=(sin\mathit{\theta }cos\mathit{\phi },sin\mathit{\theta }sin\mathit{\phi },cos\mathit{\theta }),\text{with}\mathit{\theta }\in [0,\mathit{\pi }],\mathit{\phi }\in [0,2\mathit{\pi }].\end{array}$$(3.7)

The integral operators ${\tilde{S}}_{\ell \ell }$ and ${\tilde{K}}_{\ell \ell }$, $\ell =1,2$, are weakly singular. As is known for such singularities, for approximation and numerical implementation, it is advantageous to make the singularities explicit. Thus, we move these such that each appear at the north pole $\widehat{n}=(0,0,1)$ of the unit sphere. To achieve this, we make use of the orthogonal transformations (used in [14,17,24]) defined for $\mathit{\alpha }\in \mathrm{I}\mathrm{R}$ by$$\begin{array}{ccc}{D}_F(\mathit{\alpha })=\left(\begin{array}{ccc}cos\mathit{\alpha }& -sin\mathit{\alpha }& 0\\ sin\mathit{\alpha }& cos\mathit{\alpha }& 0\\ 0& 0& 1\end{array}\right)& \text{and}& D_T(\mathit{\alpha })=\left(\begin{array}{ccc}cos\mathit{\alpha }& 0& -sin\mathit{\alpha }\\ 0& 1& 0\\ sin\mathit{\alpha }& 0& cos\mathit{\alpha }\end{array}\right).\end{array}$$

Then the linear orthogonal transformation(3.8) $$\begin{array}{c}\hfill T_{\widehat{x}}=D_F(\mathit{\phi })D_T(\mathit{\theta })D_F(-\mathit{\phi })\end{array}$$(3.8)

has the property that $T_{\widehat{x}}\widehat{x}=\widehat{n}$ for every $\widehat{x}\in {\mathbb{S}}^2$. Moreover, $|\widehat{x}-\widehat{y}|=|T_{\widehat{x}}^{-1}(\widehat{n}-\widehat{\mathit{\eta }})|=|\widehat{n}-\widehat{\mathit{\eta }}|$, and $\widehat{\mathit{\eta }}=T_{\widehat{x}}\widehat{y}$.

Invoking this transformation in the operators ${\tilde{S}}_{\ell \ell }$ and ${\tilde{K}}_{\ell \ell }$, $\ell =1,2$, defined in () and (), these operators are transformed into(3.9) $$\begin{array}{c}\hfill ({\tilde{S}}_{\ell \ell }\mathit{\sigma })(\widehat{x})=\underset{{\mathbb{S}}^2}{\int }\mathit{\sigma }(T_{\widehat{x}}^{-1}\widehat{\mathit{\eta }})\frac{R_{\ell }(\widehat{x},T_{\widehat{x}}^{-1}\widehat{\mathit{\eta }})}{|\widehat{n}-\widehat{\mathit{\eta }}|}\mathrm{d}s(\widehat{\mathit{\eta }}),\widehat{x}\in {\mathbb{S}}^2\end{array}$$(3.9)

and(3.10) $$\begin{array}{c}\hfill ({\tilde{K}}_{\ell \ell }\mathit{\sigma })(\widehat{x})=\underset{{\mathbb{S}}^2}{\int }\mathit{\sigma }(T_{\widehat{x}}^{-1}\widehat{\mathit{\eta }})\frac{{\tilde{R}}_{\ell }(\widehat{x},T_{\widehat{x}}^{-1}\widehat{\mathit{\eta }})}{|\widehat{n}-\widehat{\mathit{\eta }}|}\mathrm{d}s(\widehat{\mathit{\eta }}),\widehat{x}\in {\mathbb{S}}^2\end{array}$$(3.10)

for $\ell =1,2$.

The representation () for the Cauchy data on the interior surface ${\mathrm{\Gamma }}_1$ can also be rewritten over the unit sphere, and we obtain(3.11) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle u={\tilde{S}}_{11}{\mathit{\psi }}_1+{\tilde{S}}_{12}{\mathit{\psi }}_2\text{on}{\mathbb{S}}^2,}\hfill \\ {\displaystyle \frac{\mathit{\partial }u}{\mathit{\partial }\mathit{\nu }}=\left(-\frac{1}{2}I+{\tilde{K}}_{11}\right){\mathit{\psi }}_1+{\tilde{K}}_{12}{\mathit{\psi }}_2\text{on}{\mathbb{S}}^2,}\hfill \end{array}\right.\end{array}$$(3.11)

with the operators defined above and densities given by ().

4. Discretization and Tikhonov regularization

We discretize the equations () to obtain a linear system, and then discuss how to solve it in a stable way.

The following quadrature is used for integrals over the unit sphere having continuous integrands(4.1) $$\begin{array}{c}\hfill {\int }_{{\mathbb{S}}^2}f(\widehat{y})\mathrm{d}s(\widehat{y})\approx \sum _{{\mathit{\rho }}^{\prime }=0}^{2n^{\prime }+1}\sum _{s^{\prime }=1}^{n^{\prime }+1}{\tilde{\mathit{\mu }}}_{{\mathit{\rho }}^{\prime }}{\tilde{a}}_{s^{\prime }}f({\widehat{y}}_{s^{\prime }{\mathit{\rho }}^{\prime }}),\end{array}$$(4.1)

where ${\widehat{y}}_{s^{\prime }{\mathit{\rho }}^{\prime }}=p({\tilde{\mathit{\theta }}}_{s^{\prime }},{\tilde{\mathit{\phi }}}_{{\mathit{\rho }}^{\prime }})$, ${\tilde{\mathit{\phi }}}_{{\mathit{\rho }}^{\prime }}={\mathit{\rho }}^{\prime }\mathit{\pi }/(n^{\prime }+1)$, ${\tilde{\mathit{\theta }}}_{s^{\prime }}=arccos{z}_{s^{\prime }}$ with $z_{s^{\prime }}$ being the zeros of the Legendre polynomials $P_{n^{\prime }+1}$, ${\tilde{a}}_{s^{\prime }}=2(1-z_{s^{\prime }}^2)/{((n^{\prime }+1)P_{n^{\prime }}(z_{s^{\prime }}))}^2$ and ${\tilde{\mathit{\mu }}}_{{\mathit{\rho }}^{\prime }}=\mathit{\pi }/(n^{\prime }+1)$.

For the case of a weak singularity in the integrand, we employ the quadrature rule(4.2) $$\begin{array}{c}\hfill {\int }_{{\mathbb{S}}^2}\frac{f(\widehat{y})}{|\widehat{n}-\widehat{y}|}\mathrm{d}s(\widehat{y})\approx \sum _{{\mathit{\rho }}^{\prime }=0}^{2n^{\prime }+1}\sum _{s^{\prime }=1}^{n^{\prime }+1}{\tilde{\mathit{\mu }}}_{{\mathit{\rho }}^{\prime }}{\tilde{b}}_{s^{\prime }}f({\widehat{y}}_{s^{\prime }{\mathit{\rho }}^{\prime }})\end{array}$$(4.2)

with weights$${\tilde{b}}_{s^{\prime }}={\tilde{a}}_{s^{\prime }}\sum _{i=0}^{n^{\prime }}{P}_i(z_{s^{\prime }}).$$

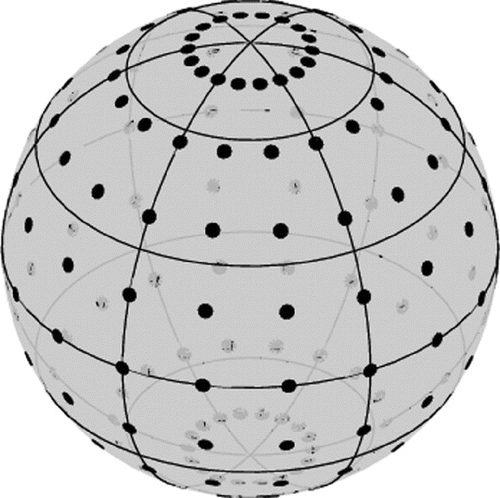
Both quadratures are obtained by approximation of the regular part of the integrand via spherical harmonics and then using exact integration. According to results in [14,17], these quadrature rules have super-algebraic convergence order. In Figure is an example of the distribution of these quadrature points on the unit sphere for $n{}^{\prime }=8$ (there are no quadrature points on the north or south pole).

Figure 2. The quadrature points ${\widehat{y}}_{s^{\prime }{p}^{\prime }}$ ($·$) with $n{}^{\prime }=8$.

Returning to the ill-posed system of integral equations (), it will be discretized using a projection Galerkin method. This means that we search for the numerical solution of this system in the form(4.3) $$\begin{array}{c}\hfill {\mathit{\psi }}_{\ell }(\widehat{x})\approx {\tilde{\mathit{\psi }}}_{\ell }(\widehat{x})=\sum _{k=0}^n\sum _{m=-k}^k{\mathit{\psi }}_{k,m}^{\ell }{Y}_{k,m}^R(\widehat{x}),\text{for}\widehat{x}\in {\mathbb{S}}^2,\ell =1,2,\end{array}$$(4.3)

where ${\mathit{\psi }}_{k,m}^{\ell }$ are unknown coefficients. Here, the real-valued spherical harmonics are(4.4) $$\begin{array}{c}\hfill Y_{k,m}^R=\left\{\begin{array}{cc}\text{Im}{Y}_{k,|m|},\hfill & 0<m\le k,\hfill \\ \text{Re}{Y}_{k,|m|},\hfill & -k\le m\le 0,\hfill \end{array}\right.\end{array}$$(4.4)

with $Y_{k,m}(\mathit{\theta },\mathit{\phi })=c_k^m{P}_k^{|m|}(cos\mathit{\theta })e^{im\mathit{\phi }}$ the classical (complex-valued) spherical harmonic functions, $P_k^m$ the Legendre functions and(4.5) $$\begin{array}{c}\hfill {\displaystyle c_k^m={(-1)}^{\frac{|m|-m}{2}}\sqrt{\frac{2k+1}{4\mathit{\pi }}\frac{(k-|m|)!}{(k+|m|)!}},m=-k,\dots ,k,k=0,1,\dots ,.}\end{array}$$(4.5)

Let(4.6) $$\begin{array}{c}\hfill (v,w)=\sum _{\mathit{\rho }=0}^{2n+1}\sum _{s=1}^{n+1}{\mathit{\mu }}_{\mathit{\rho }}{a}_{s}v({\widehat{y}}_{s\mathit{\rho }})w({\widehat{y}}_{s\mathit{\rho }}),\end{array}$$(4.6)

which is a discrete inner product on the space of spherical polynomials of degree n (this can be seen since it is obtained from the quadrature rule () which is exact for spherical polynomials of degree 2n). The coefficients $a_s$ and ${\mathit{\mu }}_p$ are generated as in (), but they depend here on a possibly different integer $n\in \mathrm{I}\mathrm{N}$.

We first discretize () by assuming that the densities are given by (), and then employing the quadrature rules () and (). To identify the coefficients in the approximation of the densities, we use discrete projection, that is taking the discrete inner product () of each equation in the discretized system with an element $Y_{k,m}^R$.

This strategy leads to the linear system(4.7) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \sum _{k=0}^n\sum _{m=-k}^k\left({\mathit{\psi }}_{k,m}^1{A}_{kk{}^{\prime }mm{}^{\prime }}^{21}+{\mathit{\psi }}_{k,m}^2{A}_{kk{}^{\prime }mm{}^{\prime }}^{22}\right)=\sum _{\mathit{\rho }=0}^{2n+1}\sum _{s=1}^{n+1}{\mathit{\mu }}_{\mathit{\rho }}{a}_s\tilde{f}({\widehat{x}}_{s\mathit{\rho }})Y_{k{}^{\prime },m{}^{\prime }}^R({\widehat{x}}_{s\mathit{\rho }})}\hfill \\ {\displaystyle \sum _{k=0}^n\sum _{m=-k}^k\left({\mathit{\psi }}_{k,m}^1{\tilde{A}}_{kk{}^{\prime }mm{}^{\prime }}^{21}+{\mathit{\psi }}_{k,m}^2{\tilde{A}}_{kk{}^{\prime }mm{}^{\prime }}^{22}\right)=\sum _{\mathit{\rho }=0}^{2n+1}\sum _{s=1}^{n+1}{\mathit{\mu }}_{\mathit{\rho }}{a}_s\tilde{g}({\widehat{x}}_{s\mathit{\rho }})Y_{k{}^{\prime },m{}^{\prime }}^R({\widehat{x}}_{s\mathit{\rho }})}\hfill \end{array}\right.,\end{array}$$(4.7) $k{}^{\prime }=0,\dots ,n,m=-k{}^{\prime },\dots ,k{}^{\prime }$ (note that $k{}^{\prime }$ and $m{}^{\prime }$ depend on the integer n and not $n{}^{\prime }$), with coefficients(4.8) $$\begin{array}{c}\hfill \begin{array}{cc}{\displaystyle A_{kk{}^{\prime }mm{}^{\prime }}^{2j}}\hfill & {\displaystyle =\sum _{\mathit{\rho }=0}^{2n+1}\sum _{s=1}^{n+1}\sum _{\mathit{\rho }{}^{\prime }=0}^{2n{}^{\prime }+1}\sum _{s{}^{\prime }=1}^{n{}^{\prime }+1}{\tilde{\mathit{\mu }}}_{\mathit{\rho }{}^{\prime }}{\mathit{\mu }}_{\mathit{\rho }}{a}_s{Y}_{k{}^{\prime },m{}^{\prime }}^R({\widehat{x}}_{s\mathit{\rho }})\left\{\begin{array}{cc}{\displaystyle {\tilde{a}}_{s{}^{\prime }}{L}_{2j}({\widehat{x}}_{s\mathit{\rho }},{\widehat{y}}_{s{}^{\prime }\mathit{\rho }{}^{\prime }})Y_{k,m}^R({\widehat{y}}_{s{}^{\prime }\mathit{\rho }{}^{\prime }}),}\hfill & j=1\hfill \\ {\displaystyle {\tilde{b}}_{s{}^{\prime }}{R}_2({\widehat{x}}_{s\mathit{\rho }},{\widehat{y}}_{s\mathit{\rho }}^{s{}^{\prime }\mathit{\rho }{}^{\prime }})Y_{k,m}^R({\widehat{y}}_{s\mathit{\rho }}^{s{}^{\prime }\mathit{\rho }{}^{\prime }}),}\hfill & j=2\hfill \end{array}\right.}\hfill \end{array}\end{array}$$(4.8)

and(4.9) $$\begin{array}{c}\hfill \begin{array}{cc}{\tilde{A}}_{kk{}^{\prime }mm{}^{\prime }}^{2j}\hfill & {\displaystyle =\sum _{\mathit{\rho }=0}^{2n+1}\sum _{s=1}^{n+1}\sum _{\mathit{\rho }{}^{\prime }=0}^{2n{}^{\prime }+1}\sum _{s{}^{\prime }=1}^{n{}^{\prime }+1}{\tilde{\mathit{\mu }}}_{\mathit{\rho }{}^{\prime }}{\mathit{\mu }}_{\mathit{\rho }}{a}_s{Y}_{k{}^{\prime },m{}^{\prime }}^R({\widehat{x}}_{s\mathit{\rho }})}\hfill \\ \hfill & \times \left(\left\{\begin{array}{cc}{\tilde{a}}_{s{}^{\prime }}{M}_{2j}({\widehat{x}}_{s\mathit{\rho }},{\widehat{y}}_{s{}^{\prime }\mathit{\rho }{}^{\prime }})Y_{k,m}^R({\widehat{y}}_{s{}^{\prime }\mathit{\rho }{}^{\prime }}),\hfill & j=1\hfill \\ {\tilde{b}}_{s{}^{\prime }}{\tilde{R}}_2({\widehat{x}}_{s\mathit{\rho }},{\widehat{y}}_{s\mathit{\rho }}^{s{}^{\prime }\mathit{\rho }{}^{\prime }})Y_{k,m}^R({\widehat{y}}_{s\mathit{\rho }}^{s{}^{\prime }\mathit{\rho }{}^{\prime }}),\hfill & j=2\hfill \end{array}\right.\right.\hfill \\ \hfill & +\left.\left\{\begin{array}{cc}0,\hfill & j=1\hfill \\ {\displaystyle \frac{1}{2}{Y}_{k,m}^R({\widehat{x}}_{s\mathit{\rho }}),}\hfill & j=2\hfill \end{array}\right.\right),\hfill \end{array}\end{array}$$(4.9) $j=1,2$. In order to see that these coefficients come from the above strategy, note that the inner two sums with primed indices correspond to discretization of a boundary integral operator using either () or () depending on whether it is singular or not and the outer two sums are discrete projection with the element $Y_{k{}^{\prime },m{}^{\prime }}^R$ using (). In the above expression,(4.10) $$\begin{array}{c}\hfill {\widehat{y}}_{sp}^{s{}^{\prime }\mathit{\rho }{}^{\prime }}=T_{{\widehat{x}}_{s\mathit{\rho }}}^{-1}{\widehat{y}}_{s{}^{\prime }\mathit{\rho }{}^{\prime }},\end{array}$$(4.10)

with ${\widehat{y}}_{s{}^{\prime }\mathit{\rho }{}^{\prime }}$ being points on the unit sphere generated by () with angles $s{}^{\prime }$ and $\mathit{\rho }{}^{\prime }$ generated as described after () and the transformation $T_{{\widehat{x}}_{s\mathit{\rho }}}$ is as stated in () with $\widehat{x}={\widehat{x}}_{s\mathit{\rho }}$ (the angles s and $\mathit{\rho }$ are generated as $s{}^{\prime }$ and $\mathit{\rho }{}^{\prime }$ but with the integer $n{}^{\prime }$ replaced by n).

We use the convention that primed indices for coefficients and for points on the unit sphere correspond to discretizations of the layer-integrals () and () using the quadratures () and () with the approximation () of the densities, whilst the corresponding unprimed coefficients and points correspond to discretization of the $L^2$ inner product that is application of (). In the numerical examples, we choose the same integer n for the quadrature points in the discretization of the layer-integrals as for the discrete inner product, but for clarity here we use the prime and unprimed notation; in principal different integers can be chosen.

Solving the linear system (), we get an approximation to the densities in () via the expression (). We point out that in solving this linear system, standard Tikhonov regularization is applied with a regularization parameter $\mathit{\lambda }>0$. There are many different ways of choosing this regularizing parameter; in the numerical section the heuristic L-curve rule [25] will be employed.

Using also quadrature in () we can find an approximation to the solution u of the Cauchy problem () and (), and it is of the form(4.11) $$\begin{array}{c}\hfill u(x)\approx u_n(x)=\sum _{\ell =1}^2\sum _{{\mathit{\rho }}^{\prime }=0}^{2n^{\prime }+1}\sum _{s^{\prime }=1}^{n^{\prime }+1}{\tilde{\mathit{\mu }}}_{{\mathit{\rho }}^{\prime }}{\tilde{a}}_{s^{\prime }}{\tilde{\mathit{\psi }}}_{\ell }({\widehat{y}}_{s^{\prime }{\mathit{\rho }}^{\prime }})\mathrm{\Phi }(x,{\widehat{y}}_{s^{\prime }{\mathit{\rho }}^{\prime }})J_{q_{\ell }}({\widehat{y}}_{s^{\prime }{\mathit{\rho }}^{\prime }}),x\in D.\end{array}$$(4.11)

As mentioned earlier, of particular interest is the function values and normal derivative of the solution of the Cauchy problem on the interior surface ${\mathrm{\Gamma }}_1$. Invoking the obtained approximation () of the densities in the expression () together with quadrature, the sought values on ${\mathrm{\Gamma }}_1$ are found to be(4.12) $$\begin{array}{c}\hfill u_n(\widehat{x})=\sum _{s{}^{\prime }=1}^{n{}^{\prime }+1}\sum _{\mathit{\rho }{}^{\prime }=0}^{2n{}^{\prime }+1}\left({\tilde{b}}_{s{}^{\prime }}{\tilde{\mathit{\mu }}}_{\mathit{\rho }{}^{\prime }}{\tilde{\mathit{\psi }}}_1(T_{\widehat{x}}^{-1}{\widehat{y}}_{s{}^{\prime }\mathit{\rho }{}^{\prime }})R_1(\widehat{x},T_{\widehat{x}}^{-1}{\widehat{y}}_{s{}^{\prime }\mathit{\rho }{}^{\prime }})+{\tilde{a}}_{s{}^{\prime }}{\tilde{\mathit{\mu }}}_{\mathit{\rho }{}^{\prime }}{\tilde{\mathit{\psi }}}_2({\widehat{y}}_{s{}^{\prime }\mathit{\rho }{}^{\prime }})L_{12}(\widehat{x},{\widehat{y}}_{s{}^{\prime }\mathit{\rho }{}^{\prime }})\right)\end{array}$$(4.12)

and(4.13) $$\begin{array}{cc}\hfill \frac{\mathit{\partial }{u}_n}{\mathit{\partial }\mathit{\nu }}(\widehat{x})=& \sum _{s{}^{\prime }=1}^{n{}^{\prime }+1}\sum _{\mathit{\rho }{}^{\prime }=0}^{2n{}^{\prime }+1}\left({\tilde{b}}_{s{}^{\prime }}{\tilde{\mathit{\mu }}}_{\mathit{\rho }{}^{\prime }}{\tilde{\mathit{\psi }}}_1(T_{\widehat{x}}^{-1}{\widehat{y}}_{s{}^{\prime }\mathit{\rho }{}^{\prime }}){\tilde{R}}_1(\widehat{x},T_{\widehat{x}}^{-1}{\widehat{y}}_{s{}^{\prime }\mathit{\rho }{}^{\prime }})+{\tilde{a}}_{s{}^{\prime }}{\tilde{\mathit{\mu }}}_{\mathit{\rho }{}^{\prime }}{\tilde{\mathit{\psi }}}_2({\widehat{y}}_{s{}^{\prime }\mathit{\rho }{}^{\prime }})M_{12}(\widehat{x},{\widehat{y}}_{s{}^{\prime }\mathit{\rho }{}^{\prime }})\right)\hfill \\ \hfill & -\frac{1}{2}{\tilde{\mathit{\psi }}}_1(\widehat{x}),\hfill \end{array}$$(4.13)

where $\widehat{x}\in {\mathbb{S}}^2$.

5. Implementation

For the effective implementation of the proposed algorithm for generating a solution to the Cauchy problem () and (), it is important to have a clear and efficient way of computing the coefficients $A_{kk{}^{\prime }mm{}^{\prime }}^{2j}$ and ${\tilde{A}}_{kk{}^{\prime }mm{}^{\prime }}^{2j}$ in the linear system ().

Starting with the real-valued spherical harmonics (), using the definition () of the spherical harmonics, we have the expression$$Y_{k,m}^R(\mathit{\theta },\mathit{\phi })=c_k^m{P}_k^{|m|}(cos\mathit{\theta })\left\{\begin{array}{cc}cos(|m|\mathit{\phi }),\hfill & m<0\hfill \\ 1,\hfill & m=0\hfill \\ sin(|m|\mathit{\phi }),\hfill & m>0\hfill \end{array}\right..$$

We need to evaluate these real-valued spherical harmonics at the points (). This can be achieved using expressions for rotated spherical harmonics, given in [17, pp. 224–225], to get$$\begin{array}{cc}\hfill Y_{k,m}^R({\widehat{y}}_{s\mathit{\rho }}^{s{}^{\prime }\mathit{\rho }{}^{\prime }})& =\sum _{|\tilde{m}|\le k}{Y}_{k,\tilde{m}}({\widehat{y}}_{s{}^{\prime }\mathit{\rho }{}^{\prime }})e^{-i\tilde{m}{\mathit{\phi }}_{\mathit{\rho }}}\hfill \\ \hfill & \times \left\{\begin{array}{cc}\frac{1}{2i}\left(F_{sk\tilde{m}|m|}{e}^{i|m|{\mathit{\phi }}_{\mathit{\rho }}}-{(-1)}^{|m|}{F}_{sk\tilde{m}-|m|}{e}^{-i|m|{\mathit{\phi }}_{\mathit{\rho }}}\right),\hfill & m>0\hfill \\ F_{sk\tilde{m}|m|},\hfill & m=0\hfill \\ \frac{1}{2}\left(F_{sk\tilde{m}|m|}{e}^{i|m|{\mathit{\phi }}_{\mathit{\rho }}}+{(-1)}^{|m|}{F}_{sk\tilde{m}-|m|}{e}^{-i|m|{\mathit{\phi }}_{\mathit{\rho }}}\right),\hfill & m<0\hfill \end{array}\right.,\hfill \end{array}$$

where$${\displaystyle F_{sk\tilde{m}m}=e^{i(m-\tilde{m})\frac{\mathit{\pi }}{2}}\sum _{|l|\le k}{d}_{\tilde{m}l}^{(k)}\left(\frac{\mathit{\pi }}{2}\right)d_{ml}^{(k)}\left(\frac{\mathit{\pi }}{2}\right)e^{il{\mathit{\theta }}_s}}$$

and$${\displaystyle d_{ml}^{(k)}\left(\frac{\mathit{\pi }}{2}\right)=2^m\sqrt{\frac{(k+m)!(k-m)!}{(k+l)!(k-l)!}}{P}_{k+m}^{(l-m,-l-m)}(0).}$$

Here, $P_n^{(\mathit{\alpha },\mathit{\beta })}$ are the normalized Jacobi polynomials$$P_n^{(\mathit{\alpha },\mathit{\beta })}(0)=2^{-n}\sum _{t=0}^n{(-1)}^t\left(\begin{array}{c}n+a\hfill \\ n-t\hfill \end{array}\right)\left(\begin{array}{c}n+b\hfill \\ t\hfill \end{array}\right),a\ge 0,b\ge 0.$$

When $l-m,-l-m$ are negative, we can calculate the elements ${\displaystyle d_{ml}^{(k)}\left(\frac{\mathit{\pi }}{2}\right)}$ using the symmetry relation$$d_{ml}^{(k)}(\mathit{\phi })={(-1)}^{m-l}{d}_{lm}^{(k)}(\mathit{\phi })=d_{-l-m}^{(k)}(\mathit{\phi })=d_{ml}^{(k)}(-\mathit{\phi }).$$

The formula () for calculating the coefficients $A_{kk{}^{\prime }mm{}^{\prime }}^{2j}$, with the above expressions it can be written as$$\begin{array}{cc}{A}_{kk{}^{\prime }mm{}^{\prime }}^{2j}\hfill & {\displaystyle =\sum _{s=1}^{n+1}{a}_s{c}_{k{}^{\prime }}^{m{}^{\prime }}{P}_{k{}^{\prime }}^{|m{}^{\prime }|}(cos{\mathit{\theta }}_s)\sum _{\mathit{\rho }=0}^{2n+1}{\mathit{\mu }}_{\mathit{\rho }}\left\{\begin{array}{cc}cos(|m{}^{\prime }|{\mathit{\phi }}_{\mathit{\rho }}),\hfill & m{}^{\prime }<0\hfill \\ 1,\hfill & m{}^{\prime }=0\hfill \\ sin(|m{}^{\prime }|{\mathit{\phi }}_{\mathit{\rho }}),\hfill & m{}^{\prime }>0\hfill \end{array}\right.}\hfill \\ \hfill & {\displaystyle \times \sum _{\mathit{\rho }{}^{\prime }=0}^{2n{}^{\prime }+1}{\tilde{\mathit{\mu }}}_{\mathit{\rho }{}^{\prime }}\sum _{s{}^{\prime }=1}^{n{}^{\prime }+1}\left\{\begin{array}{cc}{\tilde{a}}_{s{}^{\prime }}{L}_{21}({\widehat{x}}_{s\mathit{\rho }},{\widehat{y}}_{s{}^{\prime }\mathit{\rho }{}^{\prime }}),\hfill & j=1\hfill \\ {\tilde{b}}_{s{}^{\prime }}{R}_2({\widehat{x}}_{s\mathit{\rho }},{\widehat{y}}_{s\mathit{\rho }}^{s{}^{\prime }\mathit{\rho }{}^{\prime }}),\hfill & j=2\hfill \end{array}\right.}\hfill \\ \hfill & \times \left\{\begin{array}{cc}{\displaystyle \sum _{\tilde{m}\le k}{c}_k^{\tilde{m}}{P}_k^{\tilde{m}}(cos\widetilde{{\mathit{\theta }}_{s{}^{\prime }}})e^{i\tilde{m}(\widetilde{{\mathit{\phi }}_{\mathit{\rho }{}^{\prime }}}-{\mathit{\phi }}_{\mathit{\rho }})}},\hfill & \ell =j\hfill \\ c_k^m{P}_k^{|m|}(cos\widetilde{{\mathit{\theta }}_{s{}^{\prime }}})\left\{\begin{array}{cc}cos(|m|\widetilde{{\mathit{\phi }}_{\mathit{\rho }{}^{\prime }}}),\hfill & m<0\hfill \\ 1,\hfill & m=0\hfill \\ sin(|m|\widetilde{{\mathit{\phi }}_{\mathit{\rho }{}^{\prime }}}),\hfill & m>0\hfill \end{array}\right.,\hfill & \ell \ne j\hfill \end{array}\right.\hfill \\ \hfill & \times \left\{\begin{array}{cc}\left\{\begin{array}{cc}{\displaystyle \frac{1}{2i}\left(F_{sk\tilde{m}|m|}{e}^{i|m|{\mathit{\phi }}_{\mathit{\rho }}}-{(-1)}^{|m|}{F}_{sk\tilde{m}-|m|}{e}^{-i|m|{\mathit{\phi }}_{\mathit{\rho }}}\right),}\hfill & m>0\hfill \\ {\displaystyle F_{sk\tilde{m}|m|},}\hfill & m=0\hfill \\ {\displaystyle \frac{1}{2}\left(F_{sk\tilde{m}|m|}{e}^{i|m|{\mathit{\phi }}_{\mathit{\rho }}}+{(-1)}^{|m|}{F}_{sk\tilde{m}-|m|}{e}^{-i|m|{\mathit{\phi }}_{\mathit{\rho }}}\right),}\hfill & m<0\hfill \end{array}\right.,\hfill & j=2\hfill \\ 1,\hfill & j=1\hfill \end{array}\right.\hfill \end{array}.$$

Although this expression follows logically from previously derived formulas it looks a bit long and involved. However, it can be written more economically as$${\displaystyle A_{kk{}^{\prime }mm{}^{\prime }}^{2j}=\sum _{s=1}^{n+1}{a}_s{G}_{k{}^{\prime }m{}^{\prime }s}{B}_{kmm{}^{\prime }s}^{2j},}$$

where$$\begin{array}{cc}\hfill {\displaystyle G_{kms}}& =c_k^m{P}_k^{|m|}(cos{\mathit{\theta }}_s),\hfill \\ \hfill {\displaystyle B_{kmm{}^{\prime }s}^{2j}}& {\displaystyle =\sum _{\mathit{\rho }=0}^{2n+1}{\mathit{\mu }}_{\mathit{\rho }}{H}_{m{}^{\prime }\mathit{\rho }}{C}_{kms\mathit{\rho }}^{2j},}\hfill \\ \hfill {\displaystyle H_{m\mathit{\rho }}}& =\left\{\begin{array}{cc}cos(|m|{\mathit{\phi }}_{\mathit{\rho }}),\hfill & m<0\hfill \\ 1,\hfill & m=0\hfill \\ sin(|m|{\mathit{\phi }}_{\mathit{\rho }}),\hfill & m>0\hfill \end{array},\right.\hfill \\ \hfill C_{kms\mathit{\rho }}^{2j}& =\left\{\begin{array}{c}{\displaystyle \sum _{|\tilde{m}|\le k}{e}^{-i\tilde{m}{\mathit{\phi }}_{\mathit{\rho }}}{D}_{ksp\tilde{m}}^{2j}}\hfill \\ \times \left\{\begin{array}{cc}{\displaystyle \frac{1}{2i}\left(F_{sk\tilde{m}|m|}{e}^{i|m|{\mathit{\phi }}_{\mathit{\rho }}}-{(-1)}^{|m|}{F}_{sk\tilde{m}-|m|}{e}^{-i|m|{\mathit{\phi }}_{\mathit{\rho }}}\right),}\hfill & m>0\hfill \\ {\displaystyle F_{sk\tilde{m}|m|},}\hfill & m=0\hfill \\ {\displaystyle \frac{1}{2}\left(F_{sk\tilde{m}|m|}{e}^{i|m|{\mathit{\phi }}_{\mathit{\rho }}}+{(-1)}^{|m|}{F}_{sk\tilde{m}-|m|}{e}^{-i|m|{\mathit{\phi }}_{\mathit{\rho }}}\right),}\hfill & m<0\hfill \end{array}\right.,\hfill & j=2\hfill \\ {\displaystyle D_{ks\mathit{\rho }m}^{2j},}\hfill & j=1\hfill \end{array}\right.,\hfill \\ \hfill {\displaystyle D_{ks\mathit{\rho }\tilde{m}}^{2j}}& =\sum _{s{}^{\prime }=1}^{n{}^{\prime }+1}{G}_{k\tilde{m}s{}^{\prime }}{E}_{s\mathit{\rho }\tilde{m}s{}^{\prime }}^{2j}\left\{\begin{array}{cc}{\tilde{a}}_{s{}^{\prime }},\hfill & j=1\hfill \\ {\tilde{b}}_{s{}^{\prime }},\hfill & j=2\hfill \end{array}\right.,\hfill \end{array}$$

and$${\displaystyle E_{s\mathit{\rho }\tilde{m}s{}^{\prime }}^{2j}=\sum _{\mathit{\rho }{}^{\prime }=0}^{2n{}^{\prime }+1}\widetilde{{\mathit{\mu }}_{\mathit{\rho }{}^{\prime }}}\left\{\begin{array}{cc}{e}^{i\tilde{m}\widetilde{{\mathit{\phi }}_{\mathit{\rho }{}^{\prime }}}}{R}_2({\widehat{x}}_{s\mathit{\rho }},{\widehat{y}}_{s\mathit{\rho }}^{s{}^{\prime }\mathit{\rho }{}^{\prime }}),\hfill & j=2\hfill \\ H_{\tilde{m}\mathit{\rho }{}^{\prime }}{L}_{21}({\widehat{x}}_{s\mathit{\rho }},{\widehat{y}}_{s{}^{\prime }\mathit{\rho }{}^{\prime }}),\hfill & j=1\hfill \end{array}\right..}$$

The calculation of the coefficients ${\tilde{A}}_{kk{}^{\prime }mm{}^{\prime }}^{2j}$ given by the formula () can be handled in the similar way.

6. Numerical examples

In this section, we illustrate the robustness of the proposed integral equation-based method for the reconstruction of the harmonic function satisfying the Cauchy problem () and (), for both exact and noisy data. In the case of noisy data, random pointwise errors are added to the function values f with the percentage given in terms of the $L^2$-norm.

We recall that the integer n is the degree of the spherical harmonic polynomials approximating the densities via (), $n^{\prime }$ is the number of points chosen in the quadrature (cubature) rules () and (); the numbers n and $n^{\prime }$ enter into the approximation via (). We give results when $n=n^{\prime }$. Given an integer n, the number of discretization points on each surface is $2{(n+1)}^2$, see Figure for an example with $n=8$. Further improvements can possibly be made by other choices of $n^{\prime }$.

Figure 3. The solution domain in Examples and .

Figure 4. L-curves ($n=12$) in Example .

Figure 5. The exact and numerical approximation ($n=12$) of function values on the boundary surface ${\mathrm{\Gamma }}_1$ with 3 % noise for Example .

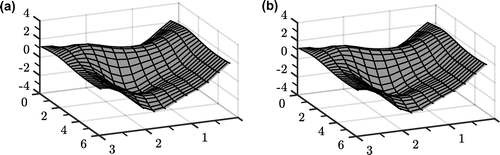
Figure 6. The exact and numerical approximation ($n=12$) of the normal derivative on the boundary surface ${\mathrm{\Gamma }}_1$ with 3 % noise for Example .

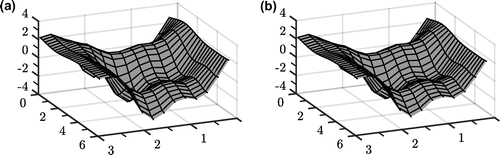
Table 1. Errors in the case of exact data in Example .

$n=n{}^{\prime }$	$\mathit{\lambda }$	$\Vert u-u_n{\Vert }_{L^2({\mathrm{\Gamma }}_1)}$	${∥\frac{\mathit{\partial }u}{\mathit{\partial }\mathit{\nu }}-\frac{\mathit{\partial }{u}_n}{\mathit{\partial }\mathit{\nu }}∥}_{L^2({\mathrm{\Gamma }}_1)}$
4	${10}^{-5}$	1.72E$-02$	8.88E$-02$
6	${10}^{-7}$	8.86E$-04$	6.45E$-03$
8	${10}^{-7}$	5.26E$-05$	3.85E$-04$
10	${10}^{-9}$	2.12E$-06$	2.45E$-05$
12	${10}^{-10}$	1.21E$-07$	1.58E$-06$

Table 2. Errors in the case of data with 3 % noise in Example .

$n=n{}^{\prime }$	$\mathit{\lambda }$	$\Vert u-u_n{\Vert }_{L^2({\mathrm{\Gamma }}_1)}$	${∥\frac{\mathit{\partial }u}{\mathit{\partial }\mathit{\nu }}-\frac{\mathit{\partial }{u}_n}{\mathit{\partial }\mathit{\nu }}∥}_{L^2({\mathrm{\Gamma }}_1)}$
4	${10}^{-3}$	5.17E$-01$	9.38E$-01$
6	${10}^{-2}$	2.35E$-01$	6.51E$-01$
8	${10}^{-2}$	2.30E$-01$	4.41E$-01$
10	${10}^{-2}$	1.72E$-01$	6.76E$-01$
12	$8·{10}^{-3}$	1.61E$-001$	6.48E$-01$

Example 1 Let the solution domain D be the region bounded by the two surfaces$${\mathrm{\Gamma }}_1=\left\{\mathit{\xi }(\mathit{\theta },\mathit{\phi })=3(sin\mathit{\theta }cos\mathit{\phi },sin\mathit{\theta }sin\mathit{\phi },cos\mathit{\theta }),0\le \mathit{\theta }\le \mathit{\pi },0\le \mathit{\phi }\le 2\mathit{\pi }\right\}$$

and$${\mathrm{\Gamma }}_2=\left\{\mathit{\xi }(\mathit{\theta },\mathit{\phi })=r(\mathit{\theta },\mathit{\phi })(sin\mathit{\theta }cos\mathit{\phi },sin\mathit{\theta }sin\mathit{\phi },cos\mathit{\theta }),0\le \mathit{\theta }\le \mathit{\pi },0\le \mathit{\phi }\le 2\mathit{\pi }\right\}$$

with the radial function ${\displaystyle r(\mathit{\theta },\mathit{\phi })=0.5\left(0.6+\sqrt{4.25+2cos3\mathit{\theta }}\right)}$; an acorn inside a sphere, see Figure (a). Both these surfaces satisfy by construction the assumption of the existence of a smooth one-to-one map to the unit sphere. In fact, to see this more clearly, we can write$$q_1(\mathit{\theta },\mathit{\phi })=3p(\mathit{\theta },\mathit{\phi })$$

and$$q_2(\mathit{\theta },\mathit{\phi })=\left(0.5\left(0.6+\sqrt{4.25+2cos3\mathit{\theta }}\right)\right)p(\mathit{\theta },\mathit{\phi }),$$

with $p(\mathit{\theta },\mathit{\phi })$ as in (); these are then the requested mappings in ().

We choose as the exact solution of the Laplace equation the function$$u_{ex}(x)=x_3^2-x_1^2+x_2,$$

and this then generates the following Cauchy data$$f(x)=u_{ex}(x),x\in {\mathrm{\Gamma }}_2\text{and}g(x)=\frac{\mathit{\partial }{u}_{ex}}{\mathit{\partial }\mathit{\nu }}(x),x\in {\mathrm{\Gamma }}_2.$$

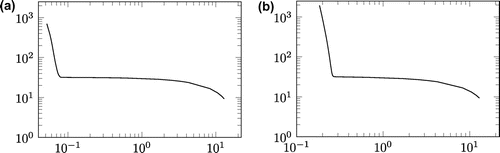
The results of the reconstruction of the corresponding Cauchy data on the interior surface ${\mathrm{\Gamma }}_1$ are given in the Tables and for exact and 3 % noisy data, respectively. The value of the regularization parameter in the Tikhonov regularization is chosen by the L-curve rule [25]. This involves a log–log plot of the norm of the regularized solution against the residual norm as a function of the Tikhonov regularization parameter. The regularizing parameter value is chosen near the corner of the curve; the L-curves for exact and noisy data are given in Figure (all figures for the numerical examples are generated with $n=12$). Reconstructions in the case of noisy data for the function values and normal derivative on ${\mathrm{\Gamma }}_1$ are given in Figures and , respectively. It is always complicated to present and inspect 3-dimensional figures and it is easy to be deceived. However, the graphical reconstructions reflect well the above-stated error levels.

Accurate approximations are obtained with the order of accuracy comparable with the input noise. Also the normal derivative can be stably retrieved. In the noisy case, the accuracy is improving with the number n up to a threshold, where the system becomes too ill-conditioned. It seems like noise levels above 5 % make results deteriorate albeit in a somewhat stable and predictable manner.

The proposed method is straightforward to implement and mathematically sound being based on classical layer operators. Thus, no real surprise is to be expected by varying the domain or data. Of course, more complicated domains or rapidly varying data, will force more quadrature points to be used, which in turn makes the problem more ill-conditioned and the results obtained less accurate. To convince the reader that the proposed method is applicable for a range of domains and data, and to show that the results obtained in this example are by no means optimized to be best possible, we give approximations for one more example.

Figure 7. L-curves ($n=12$) in Example .

Figure 8. The exact and numerical approximation ($n=12$) of function values on the boundary surface ${\mathrm{\Gamma }}_1$ with 3 % noise for Example .

Figure 9. The exact and numerical approximation ($n=12$) of the normal derivative on the boundary surface ${\mathrm{\Gamma }}_1$ with 3 % noise for Example .

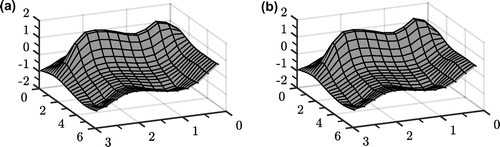
Table 3. Errors in the case of exact data in Example .

$n=n{}^{\prime }$	$\mathit{\lambda }$	$\Vert u-u_n{\Vert }_{L^2({\mathrm{\Gamma }}_1)}$	${∥\frac{\mathit{\partial }u}{\mathit{\partial }\mathit{\nu }}-\frac{\mathit{\partial }{u}_n}{\mathit{\partial }\mathit{\nu }}∥}_{L^2({\mathrm{\Gamma }}_1)}$
4	${10}^{-3}$	9.29E$-02$	4.21E$-01$
6	${10}^{-3}$	2.12E$-02$	8.44E$-02$
8	${10}^{-4}$	5.39E$-03$	3.61E$-02$
10	${10}^{-4}$	3.47E$-03$	2.60E$-02$
12	${10}^{-5}$	1.31E$-03$	1.23E$-02$

Table 4. Errors in the case of data with 3 % noise in Example .

$n=n{}^{\prime }$	$\mathit{\lambda }$	$\Vert u-u_n{\Vert }_{L^2({\mathrm{\Gamma }}_1)}$	${∥\frac{\mathit{\partial }u}{\mathit{\partial }\mathit{\nu }}-\frac{\mathit{\partial }{u}_n}{\mathit{\partial }\mathit{\nu }}∥}_{L^2({\mathrm{\Gamma }}_1)}$
4	${10}^{-3}$	7.94E$-02$	3.86E$-01$
6	${10}^{-3}$	2.87E$-02$	1.28E$-01$
8	${10}^{-3}$	1.31E$-02$	9.79E$-02$
10	${10}^{-3}$	2.48E$-02$	7.56E$-02$
12	${10}^{-3}$	2.08E$-02$	9.19E$-02$

Example 2 The domain is the region bounded by the surfaces$${\mathrm{\Gamma }}_1=\left\{{\mathit{\xi }}_1(\mathit{\theta },\mathit{\phi })=r_1(\mathit{\theta },\mathit{\phi })(sin\mathit{\theta }cos\mathit{\phi },sin\mathit{\theta }sin\mathit{\phi },cos\mathit{\theta }),0\le \mathit{\theta }\le \mathit{\pi },0\le \mathit{\phi }\le 2\mathit{\pi }\right\},$$

with the radial function ${\displaystyle r_1(\mathit{\theta },\mathit{\phi })=\sqrt{0.8+0.2(cos(2\mathit{\phi })-1)(cos(4\mathit{\theta })-1)}}$, and$${\mathrm{\Gamma }}_2=\left\{{\mathit{\xi }}_2(\mathit{\theta },\mathit{\phi })=r_2(\mathit{\theta },\mathit{\phi })(sin\mathit{\theta }cos\mathit{\phi },2sin\mathit{\theta }sin\mathit{\phi },cos\mathit{\theta }),0\le \mathit{\theta }\le \mathit{\pi },0\le \mathit{\phi }\le 2\mathit{\pi }\right\},$$${\displaystyle r_2(\mathit{\theta },\mathit{\phi })=\frac{1}{(2\sqrt{1+\sqrt{2}})}\sqrt{cos(2\mathit{\theta })+\sqrt{2-{sin}^2(2\mathit{\theta })}}.}$

These surfaces satisfy by construction the assumption of the existence of a smooth one-to-one map to the unit sphere. To see this more clearly, simply write the above mappings as$$\begin{array}{c}\hfill q_1(\mathit{\theta },\mathit{\phi })=\sqrt{0.8+0.2(cos(2\mathit{\phi })-1)(cos(4\mathit{\theta })-1)}p(\mathit{\theta },\mathit{\phi }),\\ \hfill q_2(\mathit{\theta },\mathit{\phi })=\frac{1}{(2\sqrt{1+\sqrt{2}})}\sqrt{cos(2\mathit{\theta })+\sqrt{2-{sin}^2(2\mathit{\theta })}}p(\mathit{\theta },\mathit{\phi }),\end{array}$$

with $p(\mathit{\theta },\mathit{\phi })$ as in (); these are then the requested mappings in ().

We choose the exact solution in the form$$u_{ex}(x)=cos{x}_1{e}^{x_2}+x_3$$

and the Cauchy data are then generated as$$f(x)=u_{ex}(x),x\in {\mathrm{\Gamma }}_2\text{and}g(x)=\frac{\mathit{\partial }{u}_{ex}}{\mathit{\partial }\mathit{\nu }}(x),x\in {\mathrm{\Gamma }}_2.$$

The errors for the reconstruction on the interior surface ${\mathrm{\Gamma }}_1$ are given in Tables and for exact and 3 % noisy data, respectively.

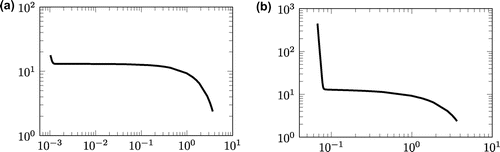
The value of the Tikhonov regularization parameter is chosen by the L-curve rule; the L-curves are given in Figure . Reconstructions in the case of noisy data for the function values and normal derivative are given in Figures and , respectively.

As mentioned at the end of Example , the results are comparable with the first example as expected, showing that the proposed method is applicable for a range of domains and data.

Notes

No potential conflict of interest was reported by the authors.