Determination of all planar sloshing containers found analytically using the inverse solution method

Abstract

A study is conducted to determine all possible prescriptions of frequency $\mathit{\omega }$ with fluid depth H for sloshing in planar geometries using the inverse method of solution for potential functions of separable form. Known solutions for the rectangular well, the ${90}^{\circ }$ wedge, a hyperbolic basin and the isochronous container are recovered. In addition, three new families of containers, here denoted C1, C2 and C3, parameterized by streamfunction separation constant B are found. Containers C1 exist for $1\le B\le \infty$ correspond to a family of hyperbolic cotangent variations of frequency with depth. Containers C2 exist for $0\le B\le \infty$ correspond to a family of hyperbolic tangent variations of frequency with depth. Containers C3 exist for $0\le B\le 1$ correspond to a family of cotangent variations of frequency with depth. There is an affinity between the C1 and C2 families in that their limiting container profiles, found as $B\to \infty$, take the shape of identical isochronous containers. Also there is an affinity between the C1 and C3 families in that their $B=1$ shapes asymptotically tend to a 90${}^{\circ }$ wedge at low depth. Plots of the shapes of the containers and their frequency variations are given.

Keywords:

• Sloshing
• inverse method
• new containers
• classic containers
• first-mode

AMS Subject Classifications:

• 34Bxx

1. Introduction

Sloshing in containers of various geometries have practical application and are of mathematical interest. Early treatises on the subject may be found in Lamb [1], Moiseev [2], Moiseev and Petrov [3] and recent monographs are given by Ibrahim [4] and Faltinsen and Timokha [5].

In this study, we determine all possible variations of frequency with liquid depth that gives rise to planar container shapes using the inverse method of solution. The inverse method for solution of a partial differential equation relaxes some of the boundary conditions, but requires that the solution possess certain other properties. As noted by Troesch [6], the procedure may be characterized by the statement that ‘instead of finding a solution to a given problem, a physically reasonable problem is found for a given solution.’ L. Euler seems to have been the first to apply this method by searching for solutions of the potential function in polynomial form; see Nemenyi [7] and Euler [8]. The inverse method was also used by Sen [9] who, inter alia, found the frequency variation for standing waves in a number of three-dimensional containers including a hyperbolic paraboloid and a rectangular parallelepiped basin of arbitrary length and width. See also the work of Storchi [10].

Troesch [6] applied the inverse method to axisymmetric containers by assuming the velocity potential(1.1) $$\begin{array}{c}\hfill \mathit{\varphi }(r,\mathit{\theta },z)=\mathit{\psi }(r,z)cosm\mathit{\theta }\end{array}$$(1.1)

and choosing polynomial forms for $\mathit{\psi }(r,z)$ to compute streamlines, thus obtaining possible container shapes. It should be noted that neither Troesch [6] nor Sen [9] made an $\stackrel{`}{\text{a}}$priori assumption on the variation of frequency with liquid depth – that variation was obtained during the course of solution. Many interesting container shapes were found, including conical and hyperboloid containers with oscillations about m nodal diameters or a nodal circle. In these cases, there was some algebraic variation of frequency with depth. More elaborate choices of the polynomials require computation of the container shape by integration of ordinary differential equations in parametric form. In this manner, a very interesting axisymmetric geometry with nonmonotonic variation of height with radius was found for oscillations about a nodal circle.

In a follow on study, Troesch and Weidman [11] searched for isochronous container shapes. Isochronous containers are those for which a frequency of a given mode of oscillation is invariant with liquid depth. Troesch and Weidman [11] found planar geometries for the first four isochronous modes, the first of which is given analytically as(1.2) $$\begin{array}{c}\hfill z(x)=-\frac{1}{\mathit{\lambda }}log(cos\mathit{\lambda }x)\end{array}$$(1.2)

where $\mathit{\lambda }={\mathit{\omega }}^2/g$. The remaining three isochronous planar containers were computed numerically using a Rayleigh–Ritz technique. The isochronous nature of these containers was verified in the experiments conducted by Weidman and Mamrol [12]. An extension of this work to include the effect of surface tension was reported by Weidman [13]. Troesch and Weidman [11] also found axisymmetric isochronous containers for oscillations having $m\ge 1$ nodal diameters on the free surface.

Aghabeigi [14] notes that the study by Troesch [6] and the solutions reported in Troesch and Weidman [11] and appear to be the ‘only attempts at determination of a container shape assuming desired dynamic characteristics and no further study has been conducted for designing the shape of liquid carriers/storages for arbitrary relationship between fluid depth and fundamental sloshing frequency.’ Aghabeigi [14] then proceeds to implement a Schwarz–Christoffel mapping to develop a numerical algorithm for determining container shapes for three models of how the fundamental sloshing frequency varies with liquid depth.

In the present investigation, we employ the inverse solution method to determine all possible prescriptions of frequency $\mathit{\omega }$ with fluid level H that leads to planar geometries for fluid sloshing for potential functions of separable form. To place this study in perspective, we note that, to the author’s knowledge, the only planar configurations for which the sloshing frequencies are known analytically are the rectangular tank, the 90${}^{\circ }$ wedge, the hyperbolic basin, and the isochronous container. For a rectangular tank of width L, the first sloshing mode is given by Lamb [1] (Section 257)(1.3) $$\begin{array}{c}\hfill \frac{{\mathit{\omega }}^2}{g}=\frac{\mathit{\pi }}{L}tanh\left(\frac{\mathit{\pi }H}{L}\right).\end{array}$$(1.3)

The first sloshing mode in a ${90}^{\circ }$ wedge found by Lamb [1] (Section 258) is given as(1.4) $$\begin{array}{c}\hfill \frac{{\mathit{\omega }}^2}{g}=\frac{1}{H}\end{array}$$(1.4)

for which the free surface is flat. For asymptotic container width L, the isochronous container (1.2(1.2) $$\begin{array}{c}\hfill z(x)=-\frac{1}{\mathit{\lambda }}log(cos\mathit{\lambda }x)\end{array}$$(1.2) ) has frequency corresponding to the deep water limit of the rectangular tank (1.3(1.3) $$\begin{array}{c}\hfill \frac{{\mathit{\omega }}^2}{g}=\frac{\mathit{\pi }}{L}tanh\left(\frac{\mathit{\pi }H}{L}\right).\end{array}$$(1.3) ), viz.(1.5) $$\begin{array}{c}\hfill \frac{{\mathit{\omega }}^2}{g}=\frac{\mathit{\pi }}{L}.\end{array}$$(1.5)

The final planar container, only recently discovered by Roberts [15], takes the form of a hyperbola with first mode sloshing frequency given by(1.6) $$\begin{array}{c}\hfill \frac{{\mathit{\omega }}^2}{g}=\frac{1}{H+z_0}\end{array}$$(1.6)

where $z_0$ is chosen to place the bottom of the hyperbola at $z=0$. It is interesting to note that this simple solution is not found in Lamb [1] nor in the monographs by Ibrahim [4] and Faltinsen and Timokha [5].

The presentation is as follows. The general theory given in Section 2 is solved for particular cases in Sections 3 and 4. A comparison of new container shapes and frequency distributions with corresponding results for classical geometries is given in Section 5. A discussion of results and concluding remarks are given in Section 6.

2. Mathematical formulation

Cartesian coordinates (x, z) with corresponding velocities (u, w) are employed. The potential function $\mathbf{u}=\mathbf{\nabla }\mathrm{\Phi }$ for linear oscillations at frequency $\mathit{\omega }$ of an inviscid, incompressible, irrotational fluid in container V with free surface S is of the form(2.1a) $$\begin{array}{c}\hfill \mathrm{\Phi }(x,z,t)=\mathit{\varphi }(x,z)cos\mathit{\omega }t.\end{array}$$(2.1a)

In what follows, we use the notation and formulation of Faltinsen and Timokha [5, Section 2.4.2]. The function $\mathit{\varphi }(x,z)$ satisfies Laplace’s equation(2.1b) $$\begin{array}{c}\hfill {\mathrm{\nabla }}^2\mathit{\varphi }=0(\text{inside container V})\end{array}$$(2.1b)

to be solved with kinematic free surface condition(2.1c) $$\begin{array}{c}\hfill {\mathit{\eta }}_t={\mathrm{\Phi }}_z(\text{on the free surface S})\end{array}$$(2.1c)

as well as the combined kinematic and dynamic free surface condition(2.1d) $$\begin{array}{c}\hfill {\mathrm{\Phi }}_{tt}+g{\mathrm{\Phi }}_z=0(\text{on the free surface S})\end{array}$$(2.1d)

and the impermeability condition(2.1e) $$\begin{array}{c}\hfill \mathbf{n}·\mathbf{\nabla }\mathit{\varphi }=0(\text{on the container wall})\end{array}$$(2.1e) where $\mathbf{n}$ is the outer unit normal and g is gravity.

Inserting (2.1a(2.1a) $$\begin{array}{c}\hfill \mathrm{\Phi }(x,z,t)=\mathit{\varphi }(x,z)cos\mathit{\omega }t.\end{array}$$(2.1a) ) into (2.1d(2.1d) $$\begin{array}{c}\hfill {\mathrm{\Phi }}_{tt}+g{\mathrm{\Phi }}_z=0(\text{on the free surface S})\end{array}$$(2.1d) ) gives(2.2) $$\begin{array}{c}\hfill {\mathit{\varphi }}_z=\frac{{\mathit{\omega }}^2}{g}\mathit{\varphi }\end{array}$$(2.2)

on the free surface and we seek all possible solutions for which the frequency varies with liquid depth, i.e. $\mathit{\omega }=\mathit{\omega }(z)$. Inserting this into (2.2(2.2) $$\begin{array}{c}\hfill {\mathit{\varphi }}_z=\frac{{\mathit{\omega }}^2}{g}\mathit{\varphi }\end{array}$$(2.2) ) and integrating gives the separable form(2.3a) $$\begin{array}{c}\hfill \mathit{\varphi }(x,z)=F(x)G(z)\end{array}$$(2.3a)

where(2.3b) $$\begin{array}{c}\hfill G(z)=\text{exp}\left(\frac{1}{g}\int {\mathit{\omega }}^2(z)\mathrm{d}z\right).\end{array}$$(2.3b) Inserting (2.3a(2.3a) $$\begin{array}{c}\hfill \mathit{\varphi }(x,z)=F(x)G(z)\end{array}$$(2.3a) ) into Laplace’s Equation (2.1b(2.1b) $$\begin{array}{c}\hfill {\mathrm{\nabla }}^2\mathit{\varphi }=0(\text{inside container V})\end{array}$$(2.1b) ) then furnishes two possible cases.

For Case 1, we have(2.4a) $$\begin{array}{cc}\hfill F(x)& =\{sinkx,coskx\},G_{zz}-k^{2}G=0\hfill \end{array}$$(2.4a)

and inserting (2.3b(2.3b) $$\begin{array}{c}\hfill G(z)=\text{exp}\left(\frac{1}{g}\int {\mathit{\omega }}^2(z)\mathrm{d}z\right).\end{array}$$(2.3b) ) into the above ODE for G(z) gives the Ricatti equation for $Q(z)={\mathit{\omega }}^2(z)$ as(2.4b) $$\begin{array}{c}\hfill \frac{\mathrm{d}Q}{\mathrm{d}z}+\frac{Q^2}{g}=k^{2}g.\end{array}$$(2.4b)

For Case 2, one finds(2.5a) $$\begin{array}{c}\hfill F(x)=\{sinhkx,coshkx\},G_{zz}+k^{2}G=0\end{array}$$(2.5a)

and inserting (2.3b(2.3b) $$\begin{array}{c}\hfill G(z)=\text{exp}\left(\frac{1}{g}\int {\mathit{\omega }}^2(z)\mathrm{d}z\right).\end{array}$$(2.3b) ) into this ODE for G(z) gives(2.5b) $$\begin{array}{c}\hfill \frac{\mathrm{d}Q}{\mathrm{d}z}+\frac{Q^2}{g}=-k^{2}g.\end{array}$$(2.5b)

The goal is to solve the above Ricatti equations for all possible $\mathit{\omega }(z)$ and determine the corresponding container geometries. Cases 1 and 2 are separately considered in Sections 3 and 4, respectively. Before proceeding, we consider the limiting case $k=0$.

2.1. The case $k=0$

When $k=0$, Equations (2.4b(2.4b) $$\begin{array}{c}\hfill \frac{\mathrm{d}Q}{\mathrm{d}z}+\frac{Q^2}{g}=k^{2}g.\end{array}$$(2.4b) ) and (2.5b(2.5b) $$\begin{array}{c}\hfill \frac{\mathrm{d}Q}{\mathrm{d}z}+\frac{Q^2}{g}=-k^{2}g.\end{array}$$(2.5b) ) for Q(z) are identical and separable. The solution is readily found as(2.6) $$\begin{array}{c}\hfill Q(z)=\frac{g}{z+z_0}\end{array}$$(2.6)

where $z_0$ is a constant of integration. For this Q(z), one finds $G(z)=z+z_0$ from Equation (2.3b(2.3b) $$\begin{array}{c}\hfill G(z)=\text{exp}\left(\frac{1}{g}\int {\mathit{\omega }}^2(z)\mathrm{d}z\right).\end{array}$$(2.3b) ). The corresponding solutions for F(x) are $\{1,x\}$. Thus, one option for the potential function is $\mathit{\varphi }(x,z)=z+z_0$ with corresponding streamfunction $\mathit{\psi }(x,z)=-x+B$ which does not give a container shape for any constant B. The other option is $\mathit{\varphi }(x,z)=x(z+z_0)$ with corresponding streamfunction $\mathit{\psi }(x,z)=({(z+z_0)}^2-x^2)/2-B/2$. Setting this to zero gives the hyperbolic container(2.7) $$\begin{array}{c}\hfill z=\sqrt{x^2+B}-z_0,z_0=\sqrt{B}\end{array}$$(2.7)

in which $z_0$ is chosen to position the bottom of the container at $z=0$. We have taken only the positive square root to give an equation valid for the upper branch of the pair of hyperbolae which asymptote to the parallel lines $z=\pm x-z_0$. For liquid levels $z=H$, the frequency-depth relation leading to the family of hyperbolic containers obtained from Equation (2.6(2.6) $$\begin{array}{c}\hfill Q(z)=\frac{g}{z+z_0}\end{array}$$(2.6) ) is(2.8) $$\begin{array}{c}\hfill \frac{{\mathit{\omega }}^2}{g}=\frac{1}{H+z_0}\text{(hyperbolic containers)}.\end{array}$$(2.8)

This constitutes our first solution for a prescribed variation of sloshing frequency as a function of liquid depth, found in a manner different from that of Roberts [15]. The corresponding free surface waveform obtained from time integration of the kinematic free surface condition (2.1c(2.1c) $$\begin{array}{c}\hfill {\mathit{\eta }}_t={\mathrm{\Phi }}_z(\text{on the free surface S})\end{array}$$(2.1c) ) is(2.9) $$\begin{array}{c}\hfill \mathit{\eta }(x,t)={\mathit{\eta }}_{0}xcos\mathit{\omega }t\end{array}$$(2.9)

showing that the solution corresponds to the first sloshing mode and the free surface is flat. Note that on taking $B=0$, one recovers the solution for first-mode sloshing in a 90${}^{\circ }$ wedge found by Lamb [1].

3. Case 1 solutions

A solution of (2.4b(2.4b) $$\begin{array}{c}\hfill \frac{\mathrm{d}Q}{\mathrm{d}z}+\frac{Q^2}{g}=k^{2}g.\end{array}$$(2.4b) ) is given by $Q_1=kg$ so, we follow the usual procedure for Ricatti equations and set $Q(z)=Q_1+u(z)$ to obtain(3.1) $$\begin{array}{c}\hfill \frac{\mathrm{d}u}{\mathrm{d}z}+2ku+\frac{1}{g}{u}^2=0\end{array}$$(3.1)

which is recognized as a Bernoulli equation. Upon setting $u(z)=1/v(z)$, we find the linear equation(3.2) $$\begin{array}{c}\hfill \frac{\mathrm{d}v}{\mathrm{d}z}-2kv=\frac{1}{g}\end{array}$$(3.2)

which has general solution(3.3) $$\begin{array}{c}\hfill v(z)=A{e}^{2kz}-\frac{1}{2kg}\end{array}$$(3.3)

where A is a constant. Working back, one finds the solution for Q(z) as(3.4) $$\begin{array}{c}\hfill Q(z)=kg\left(\frac{D{e}^{2kz}+1}{D{e}^{2kz}-1}\right)\end{array}$$(3.4)

for arbitrary constant D. At this point, there are three options which are separately considered below.

3.1. Option 1

The limit $D\to \infty$ gives $Q(z)=Q_1=kg$. Inserting this into (2.3b(2.3b) $$\begin{array}{c}\hfill G(z)=\text{exp}\left(\frac{1}{g}\int {\mathit{\omega }}^2(z)\mathrm{d}z\right).\end{array}$$(2.3b) ) gives $G(z)=e^{k(z+z_0)}$. A possible potential function is then $\mathit{\varphi }(x,z)=sinkx{e}^{k(z+z_0)}$ which has corresponding streamfunction(3.5) $$\begin{array}{c}\hfill \mathit{\psi }(x,z)=coskx{e}^{k(z+z_0)}-B\end{array}$$(3.5)

and setting this to zero gives the container shape(3.6) $$\begin{array}{c}\hfill z(x)=-\frac{1}{k}ln(coskx).\end{array}$$(3.6)

This is seen to be the isochronous container given by Equation (1.1(1.1) $$\begin{array}{c}\hfill \mathit{\varphi }(r,\mathit{\theta },z)=\mathit{\psi }(r,z)cosm\mathit{\theta }\end{array}$$(1.1) ). Taking $k=\mathit{\pi }/L$ so the asymptotic width of the container is L, the isochronous frequency is(3.7) $$\begin{array}{c}\hfill \frac{{\mathit{\omega }}^2}{g}=\frac{\mathit{\pi }}{L}\text{(isochronous container)}\end{array}$$(3.7)

in agreement with Equation (1.5(1.5) $$\begin{array}{c}\hfill \frac{{\mathit{\omega }}^2}{g}=\frac{\mathit{\pi }}{L}.\end{array}$$(1.5) ). This constitutes our second solution for a prescribed variation of sloshing frequency as a function of liquid depth. The corresponding free surface waveform obtained from the kinematic free surface condition (2.1c(2.1c) $$\begin{array}{c}\hfill {\mathit{\eta }}_t={\mathrm{\Phi }}_z(\text{on the free surface S})\end{array}$$(2.1c) ) is(3.8) $$\begin{array}{c}\hfill \mathit{\eta }(x,t)={\mathit{\eta }}_{0}sinkxsin\mathit{\omega }t\end{array}$$(3.8)

showing that the solution corresponds to the first sloshing mode. Here, ${\mathit{\eta }}_0$ is the amplitude of the oscillation, assumed to be small for linear theory to apply. Taking $\mathit{\varphi }(x,z)=coskx{e}^{k(z+z_0)}$ gives the same container shape (3.6(3.6) $$\begin{array}{c}\hfill z(x)=-\frac{1}{k}ln(coskx).\end{array}$$(3.6) ), but horizontally shifted in x, as may be seen from the relation $coskx=sin(kx+\mathit{\pi }/2)$.

3.2. Option 2

On choosing $D=e^{2k{z}_0}$ in Equation (3.4(3.4) $$\begin{array}{c}\hfill Q(z)=kg\left(\frac{D{e}^{2kz}+1}{D{e}^{2kz}-1}\right)\end{array}$$(3.4) ), using ${\mathit{\omega }}^2(z)=Q(z)$, one finds(3.9) $$\begin{array}{c}\hfill {\mathit{\omega }}^2(z)=kgcothk(z+z_0)\end{array}$$(3.9)

and inserting this into Equation (2.3b(2.3b) $$\begin{array}{c}\hfill G(z)=\text{exp}\left(\frac{1}{g}\int {\mathit{\omega }}^2(z)\mathrm{d}z\right).\end{array}$$(2.3b) ) gives $G(z)=sinhk(z+z_0)$. Associated with this, G(z) are the trigonometric solutions for F(x) in (2.4a(2.4a) $$\begin{array}{cc}\hfill F(x)& =\{sinkx,coskx\},G_{zz}-k^{2}G=0\hfill \end{array}$$(2.4a) ) giving two variants for Option 2.

For the first variant, we take(3.10a) $$\begin{array}{c}\hfill \mathit{\varphi }(x,z)=sinkxsinhk(z+z_0)\end{array}$$(3.10a)

from which one finds the corresponding streamfunction(3.10b) $$\begin{array}{c}\hfill \mathit{\psi }(x,z)=coskxcoshk(z+z_0)-B\end{array}$$(3.10b) for arbitrary constant B. Setting the streamfunction to zero gives(3.11) $$\begin{array}{c}\hfill z=\frac{1}{k}{cosh}^{-1}(Bseckx)-z_0,z_0=\frac{1}{k}{cosh}^{-1}B\end{array}$$(3.11)

which will be referred to as the C1 family of containers. Since $z_0$ is chosen so that the bottom of the container lies at $z=0$, the liquid level in the container is H in which case the prescribed frequency distribution (3.9(3.9) $$\begin{array}{c}\hfill {\mathit{\omega }}^2(z)=kgcothk(z+z_0)\end{array}$$(3.9) ) is(3.12) $$\begin{array}{c}\hfill \frac{{\mathit{\omega }}^2}{g}=kcothk(H+z_0)(C1\text{family of containers)}.\end{array}$$(3.12)

The free surface waveform found from (2.1c(2.1c) $$\begin{array}{c}\hfill {\mathit{\eta }}_t={\mathrm{\Phi }}_z(\text{on the free surface S})\end{array}$$(2.1c) ) is(3.13) $$\begin{array}{c}\hfill \mathit{\eta }(x,t)={\mathit{\eta }}_{0}sinkxsin\mathit{\omega }t\end{array}$$(3.13)

so the family of C1 containers are for the first sloshing mode.

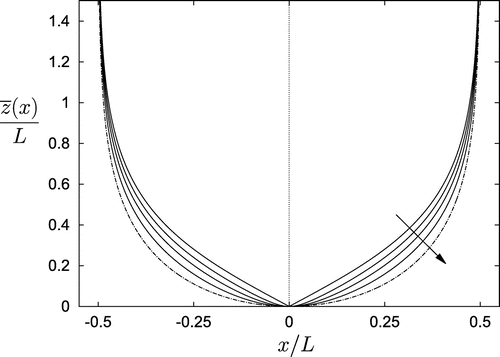
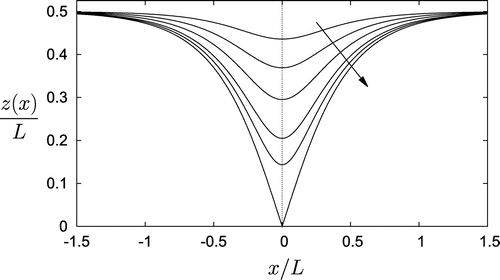
Real solutions for container shapes (3.11(3.11) $$\begin{array}{c}\hfill z=\frac{1}{k}{cosh}^{-1}(Bseckx)-z_0,z_0=\frac{1}{k}{cosh}^{-1}B\end{array}$$(3.11) ) exist only for $1\le B\le \infty$. Taking $k=\mathit{\pi }/L$, C1 container shapes $\overline{z}(x)=z(x)-z_0$ are plotted in Figure 1 for $B=\{1.0,1.01,1.05,1.2,\infty \}$. The arrow shows the direction of increasing B. The container for $B=1$ starts out as a ${90}^{\circ }$ wedge and evolves to vertical walls with separation distance L as $z\to \infty$. All other container shapes in this family have zero slope at the bottom and tend monotonically to the asymptotic width L as $z\to \infty$.

Figure 1. C1 container shapes plotted for $B=\{1.0,1.01,1.05,1.2,\infty \}$ taking $k=\mathit{\pi }/L$. The arrow shows the direction of increasing B. The container for $B=1$ starts out as a ${90}^{\circ }$ wedge and evolves to vertical walls with separation distance L as $\overline{z}\to \infty$. The $B=\infty$ isochronous shape given by Equation (3.7(3.7) $$\begin{array}{c}\hfill \frac{{\mathit{\omega }}^2}{g}=\frac{\mathit{\pi }}{L}\text{(isochronous container)}\end{array}$$(3.7) ) shown as the dash-dot-dash curve.

Using the identity(3.14) $$\begin{array}{c}\hfill {cosh}^{-1}\mathit{\alpha }=ln\left(\mathit{\alpha }+\sqrt{{\mathit{\alpha }}^2-1}\right),\end{array}$$(3.14)

the limiting C1 container shape found as $B\to \infty$ is readily found to be that of an isochronous container(3.15) $$\begin{array}{c}\hfill \overline{z}(x)=\frac{1}{k}ln(seckx)(B\to \infty )\end{array}$$(3.15)

here written in a slightly different from that given in Equation (1.2(1.2) $$\begin{array}{c}\hfill z(x)=-\frac{1}{\mathit{\lambda }}log(cos\mathit{\lambda }x)\end{array}$$(1.2) ).

Analysis of Equation (3.12(3.12) $$\begin{array}{c}\hfill \frac{{\mathit{\omega }}^2}{g}=kcothk(H+z_0)(C1\text{family of containers)}.\end{array}$$(3.12) ) for the $B=1$ container in the shallow-water limit gives(3.16a) $$\begin{array}{c}\hfill \frac{{\mathit{\omega }}^2}{g}\sim \frac{1}{H}(H\to 0)\end{array}$$(3.16a)

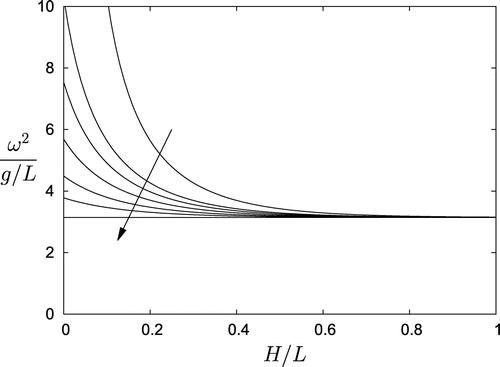
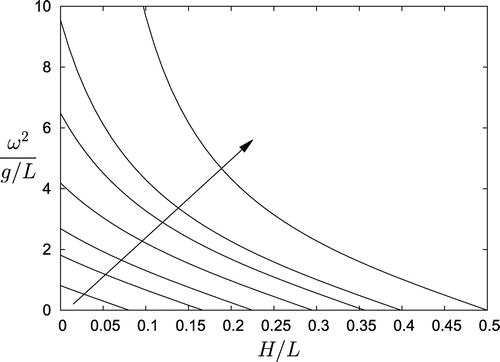
and for deep water, one finds(3.16b) $$\begin{array}{c}\hfill \frac{{\mathit{\omega }}^2}{g}\sim k(H\to \infty ).\end{array}$$(3.16b) The former result is in agreement with Equation (1.4(1.4) $$\begin{array}{c}\hfill \frac{{\mathit{\omega }}^2}{g}=\frac{1}{H}\end{array}$$(1.4) ) for a ${90}^{\circ }$ wedge, while the latter represents the deep water limit for a rectangular box. Sample C1 container frequencies for $k=\mathit{\pi }/L$ are plotted in Figure 2 for $B=\{1.0,1.05,1.1,1.2,1.4,1.8,\infty \}$. The arrow shows the direction of increasing B and the limiting isochronous container is depicted as the dash-dot-dash curve.

Figure 2. C1 container frequencies plotted at $B=\{1.0,1.05,1.1,1.2,1.4,1.8,\infty \}$ for $k=\mathit{\pi }/L$. The arrow shows the direction of increasing B. The limiting frequency for $B=\infty$ is the isochronous frequency for a container with asymptotic width L given by Equation (1.5(1.5) $$\begin{array}{c}\hfill \frac{{\mathit{\omega }}^2}{g}=\frac{\mathit{\pi }}{L}.\end{array}$$(1.5) ).

We note that the second variant $\mathit{\varphi }(x,z)=coskxsinhk(z+z_0)$ gives this same C1 family of containers, but horizontally shifted in x.

3.3. Option 3

For the choice $D=-e^{2k{z}_0}$ in Equation (3.4(3.4) $$\begin{array}{c}\hfill Q(z)=kg\left(\frac{D{e}^{2kz}+1}{D{e}^{2kz}-1}\right)\end{array}$$(3.4) ), using ${\mathit{\omega }}^2(z)=Q(z)$, one finds(3.17) $$\begin{array}{c}\hfill {\mathit{\omega }}^2(z)=kgtanhk(z+z_0).\end{array}$$(3.17)

Inserting this into Equation (2.3b(2.3b) $$\begin{array}{c}\hfill G(z)=\text{exp}\left(\frac{1}{g}\int {\mathit{\omega }}^2(z)\mathrm{d}z\right).\end{array}$$(2.3b) ) gives $G(z)=coshk(z+z_0)$. Still associated with this solution are the trigonometric functions for F(x) in (2.4a(2.4a) $$\begin{array}{cc}\hfill F(x)& =\{sinkx,coskx\},G_{zz}-k^{2}G=0\hfill \end{array}$$(2.4a) ) giving two variants to Option 3.

For the first variant, we take(3.18a) $$\begin{array}{c}\hfill \mathit{\varphi }(x,z)=sinkxcoshk(z+z_0)\end{array}$$(3.18a)

which has corresponding streamfunction(3.18b) $$\begin{array}{c}\hfill \mathit{\psi }(x,z)=coskxsinhk(z+z_0)-B.\end{array}$$(3.18b) Setting the streamfunction to zero furnishes the container shapes(3.19) $$\begin{array}{c}\hfill z=\frac{1}{k}{sinh}^{-1}(Bseckx)-z_0,z_0=\frac{1}{k}{sinh}^{-1}B\end{array}$$(3.19)

which will be referred to as the C2 family of containers. Since the bottom lies at $z=0$, the liquid level is at $z=H$, and the prescribed frequency distribution (3.18) is(3.20) $$\begin{array}{c}\hfill \frac{{\mathit{\omega }}^2}{g}=ktanhk(H+z_0)(C2\text{family of containers)}.\end{array}$$(3.20)

The free surface waveform found from (2.1c(2.1c) $$\begin{array}{c}\hfill {\mathit{\eta }}_t={\mathrm{\Phi }}_z(\text{on the free surface S})\end{array}$$(2.1c) ) is given as (3.13(3.13) $$\begin{array}{c}\hfill \mathit{\eta }(x,t)={\mathit{\eta }}_{0}sinkxsin\mathit{\omega }t\end{array}$$(3.13) ) showing that the C2 family of containers correspond to first mode sloshing.

Real solutions for container shapes (3.19(3.19) $$\begin{array}{c}\hfill z=\frac{1}{k}{sinh}^{-1}(Bseckx)-z_0,z_0=\frac{1}{k}{sinh}^{-1}B\end{array}$$(3.19) ) exist only for $0\le B\le \infty$. Taking $k=\mathit{\pi }/L$, C2 container shapes $\overline{z}(x)=z(x)-z_0$ are plotted in Figure 3 for $B=\{0.001,0.02,0.1,0.2,0.8,4.0,\infty \}$ in which the arrow shows the direction of increasing B. At low depth the containers have zero slope and curve upwards to achieve vertical walls with separation distance L as $z\to \infty$. At $B=0$, the container takes the form of a rectangular box of width L.

Figure 3. C2 container shapes plotted for $B=\{0.001,0.02,0.1,0.2,0.8,4.0,\infty \}$ taking $k=\mathit{\pi }/L$. The arrow shows the direction of increasing B. As $B\to 0$, the container takes the shape of a rectangular tank of width L. The $B=\infty$ isochronous shape given by Equation (3.21(3.21) $$\begin{array}{c}\hfill {sinh}^{-1}\mathit{\alpha }=ln\left(\mathit{\alpha }+\sqrt{{\mathit{\alpha }}^2+1}\right)\end{array}$$(3.21) ) is shown as the dash-dot-dash curve.

Using the identity(3.21) $$\begin{array}{c}\hfill {sinh}^{-1}\mathit{\alpha }=ln\left(\mathit{\alpha }+\sqrt{{\mathit{\alpha }}^2+1}\right)\end{array}$$(3.21) , the limiting C3 container shape is readily found to be that of an isochronous container(3.22) $$\begin{array}{c}\hfill z(x)=\frac{1}{k}ln(seckx)(B\to \infty )\end{array}$$(3.22)

identical to the limiting profile found for the C2 family of containers.

At near zero liquid depth, Equation (3.20(3.20) $$\begin{array}{c}\hfill \frac{{\mathit{\omega }}^2}{g}=ktanhk(H+z_0)(C2\text{family of containers)}.\end{array}$$(3.20) ) shows that the oscillation frequency for $k\ne 0$ begins at the finite value(3.23a) $$\begin{array}{c}\hfill \frac{{\mathit{\omega }}^2}{g}=ktanhk{z}_0\end{array}$$(3.23a)

and increases monotonically to the deep water limit(3.23b) $$\begin{array}{c}\hfill \frac{{\mathit{\omega }}^2}{g}\to k(H\to \infty ).\end{array}$$(3.23b)

With $B=0$ for which $z_0=0$, Equation (3.20(3.20) $$\begin{array}{c}\hfill \frac{{\mathit{\omega }}^2}{g}=ktanhk(H+z_0)(C2\text{family of containers)}.\end{array}$$(3.20) ) shows that one recovers the first mode frequency distribution for a rectangular tank of width L given by Equation (1.3(1.3) $$\begin{array}{c}\hfill \frac{{\mathit{\omega }}^2}{g}=\frac{\mathit{\pi }}{L}tanh\left(\frac{\mathit{\pi }H}{L}\right).\end{array}$$(1.3) ). Therefore, the frequency distributions for this family of containers are exactly those for a rectangular tank, but depth-shifted according to Equation (3.20(3.20) $$\begin{array}{c}\hfill \frac{{\mathit{\omega }}^2}{g}=ktanhk(H+z_0)(C2\text{family of containers)}.\end{array}$$(3.20) ). The frequency distributions for the C2 family with $k=\mathit{\pi }/L$ are displayed in Figure 4 at the selected values $B=\{0.0,0.2,0.4,0.6,0.9,1.5,\infty \}$ and again the arrow shows the direction of increasing B.

Figure 4. C2 container frequencies plotted for $k=\mathit{\pi }/L$ at the selected values $B=\{0.0,0.20,0.40,0.60,0.90,1.5,\infty \}$. The arrow shows the direction of increasing B.

As with Option 2, the second variant $\mathit{\varphi }(x,z)=coskxcoshk(z+z_0)$ for this option gives this same C2 family of containers, but horizontally shifted in x.

4. Case 2 solutions

Following the same methodology for solving Ricatti equations, one finds the solution of (2.5b(2.5b) $$\begin{array}{c}\hfill \frac{\mathrm{d}Q}{\mathrm{d}z}+\frac{Q^2}{g}=-k^{2}g.\end{array}$$(2.5b) ) is given by(4.1) $$\begin{array}{c}\hfill Q(z)=ikg\left(\frac{D{e}^{2ikz}-1}{D{e}^{2ikz}+1}\right)\end{array}$$(4.1)

for arbitrary constant D. The case $D=0$ renders $Q=-ikg$ imaginary and is thus to be discounted. Likewise, the choice $D=e^{2ik{z}_0}$ gives(4.2) $$\begin{array}{c}\hfill Q(z)={\mathit{\omega }}^2(z)=-kgtank(z+z_0)\end{array}$$(4.2)

so $\mathit{\omega }(z)$ is imaginary and is therefore discounted. This leaves only the single option presented below.

4.1. Option 1

Choosing $D=-e^{2ik{z}_0}$ in Equation (4.1(4.1) $$\begin{array}{c}\hfill Q(z)=ikg\left(\frac{D{e}^{2ikz}-1}{D{e}^{2ikz}+1}\right)\end{array}$$(4.1) ) gives(4.3) $$\begin{array}{c}\hfill {\mathit{\omega }}^2(z)=kgcotk(z+z_0).\end{array}$$(4.3)

Inserting this into Equation (2.3b(2.3b) $$\begin{array}{c}\hfill G(z)=\text{exp}\left(\frac{1}{g}\int {\mathit{\omega }}^2(z)\mathrm{d}z\right).\end{array}$$(2.3b) ) gives $G(z)=sink(z+z_0)$. Associated with this solution are the hyperbolic functions for F(x) in (2.5a(2.5a) $$\begin{array}{c}\hfill F(x)=\{sinhkx,coshkx\},G_{zz}+k^{2}G=0\end{array}$$(2.5a) ) giving two variants.

For the first variant, we take(4.4a) $$\begin{array}{c}\hfill \mathit{\varphi }(x,z)=sinhkxsink(z+z_0)\end{array}$$(4.4a)

the corresponding streamfunction for which is(4.4b) $$\begin{array}{c}\hfill \mathit{\psi }(x,z)=-coshkxcosk(z+z_0)+B\end{array}$$(4.4b) for arbitrary constant B. Setting the streamfunction to zero gives(4.5) $$\begin{array}{c}\hfill z=\frac{1}{k}{cos}^{-1}(B\text{sech}kx)-z_0,z_0=\frac{1}{k}{cos}^{-1}B\end{array}$$(4.5)

which will be referred to as the C3 family of containers. Since $z_0$ is chosen so that the bottom of the container lies at $z=0$, the liquid level in the container is H in which case the prescribed frequency distribution (4.3(4.3) $$\begin{array}{c}\hfill {\mathit{\omega }}^2(z)=kgcotk(z+z_0).\end{array}$$(4.3) ) is(4.6) $$\begin{array}{c}\hfill \frac{{\mathit{\omega }}^2}{g}=kcotk(H+z_0)(C3\text{family of containers)}.\end{array}$$(4.6)

The free surface waveform found from (2.1c(2.1c) $$\begin{array}{c}\hfill {\mathit{\eta }}_t={\mathrm{\Phi }}_z(\text{on the free surface S})\end{array}$$(2.1c) ) is(4.7) $$\begin{array}{c}\hfill \mathit{\eta }(x,t)={\mathit{\eta }}_{0}sinhkxsin\mathit{\omega }t\end{array}$$(4.7)

showing the family of C3 containers are for the first sloshing mode and that the waveform is hyperbolic as opposed to trigonometric.

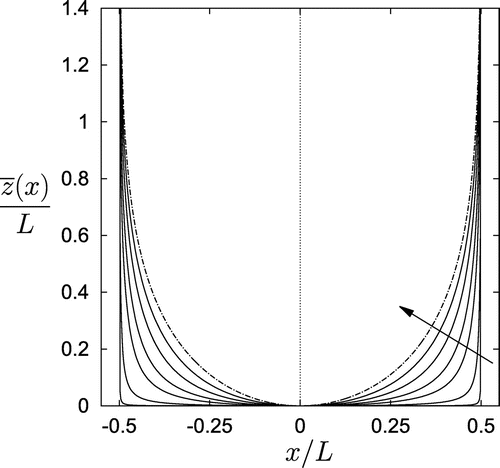
Figure 5. C3 container shapes plotted for $k=\mathit{\pi }/L$ at the selected values $B=\{0.2,0.4,0.6,0.8,0.9,1.0\}$. The arrow shows the direction of increasing B. The container for $B=1$ starts out as a ${90}^{\circ }$ wedge and splays out to attain horizontal walls at $z/L=\frac{1}{2}$ as $x\to \pm \infty$.

Real solutions for the container shapes (4.5(4.5) $$\begin{array}{c}\hfill z=\frac{1}{k}{cos}^{-1}(B\text{sech}kx)-z_0,z_0=\frac{1}{k}{cos}^{-1}B\end{array}$$(4.5) ) exist only for $0\le B\le 1$. Figure 5 displays C3 container shapes z(x) for $B=\{0.2,0.4,0.6,0.8,0.9,1.0\}$ in which the arrow shows the direction of increasing B. We have taken $z_0=0$ for ease in viewing results. It is to be noted that this family of containers have finite height ranging from $z/L=\frac{1}{2}$ at $B=1$ to zero height at $B=0$.

The container for $B=1$ starts out as a ${90}^{\circ }$ wedge and then splays out to form horizontal surfaces $z=1$ as $x\to \pm \infty$. All other containers in this family have zero slope at the bottom, but also splay outwards to attain horizontal surfaces as $x\to \pm \infty$. For $B=0$, there is no liquid-bearing container, only a horizontal surface.

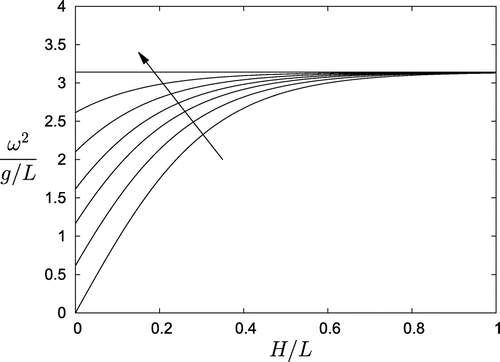
The shallow water limit of Equation (4.6(4.6) $$\begin{array}{c}\hfill \frac{{\mathit{\omega }}^2}{g}=kcotk(H+z_0)(C3\text{family of containers)}.\end{array}$$(4.6) ) for the $B=1$ container with $k=\mathit{\pi }/L$ gives(4.8a) $$\begin{array}{c}\hfill \frac{{\mathit{\omega }}^2}{g}\sim \frac{1}{H}(H\to 0)\end{array}$$(4.8a)

and at the maximum depth, one finds(4.8b) $$\begin{array}{c}\hfill \frac{{\mathit{\omega }}^2}{g}\to 0\left(H/L\to \frac{1}{2}\right).\end{array}$$(4.8b) The former in is agreement with Equation (1.4(1.4) $$\begin{array}{c}\hfill \frac{{\mathit{\omega }}^2}{g}=\frac{1}{H}\end{array}$$(1.4) ) for a ${90}^{\circ }$ wedge, whilst the latter shows that the oscillation frequency tends to zero as both sides of the vessel tends to a horizontal surface. Indeed, this latter result applies to all fully filled C3 containers. Figure 6 displays C3 container frequencies for $k=\mathit{\pi }/L$ and $B=\{0.25,0.50,0.65,0.80,0.90,0.95,1.0\}$ with the arrow in the direction of increasing B.

Figure 6. C3 container frequencies plotted for $k=\mathit{\pi }/L$ at the selected values $B=\{0.25,0.50,0.65,0.80,0.90,0.95,1.0\}$. The arrow shows the direction of increasing B.

For the second variant, we take(4.9a) $$\begin{array}{c}\hfill \mathit{\varphi }(x,z)=coshkxsink(z+z_0)\end{array}$$(4.9a)

and find the corresponding streamfunction(4.9b) $$\begin{array}{c}\hfill \mathit{\psi }(x,z)=-sinhkxcosk(z+z_0)+B\end{array}$$(4.9b) for arbitrary constant B. Setting the streamfunction to zero gives(4.10) $$\begin{array}{c}\hfill z=\frac{1}{k}{cos}^{-1}(B\text{csch}kx)-z_0.\end{array}$$(4.10)

Computations show that no containers of this form exist for any value of the arbitrary constant B.

5. Comparison with classical geometries

A comparison of the frequency variation with liquid depth for the three new containers with those for a rectangular box, a ${90}^{\circ }$ wedge, and the isochronous container are shown in Figure 7. The frequency curves for the new containers are marked C1, C2 and C3 in the figure. Note that containers C1 and C3 asymptote to the wedge frequency given by the dashed line as $H\to 0$. Also we see that containers C1 and C2, as well as the box container shown as the dark solid line and the isochronous container shown by the dash-dot-dash line, all asymptote to the deep water box frequency $\mathit{\pi }/L$ as $H\to \infty$.

Figure 7. Comparison of container frequencies with classic results plotted for $B=1$ and $k=\mathit{\pi }/L$. Rectangular box (thick solid line), wedge (dashed line), isochronous container (dash-dot-dash line) and containers C1, C2, C3 as indicated.

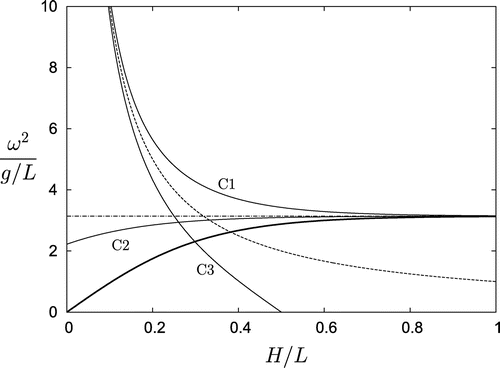
Figure 8. Comparison of container shapes $\overline{z}(x)$ with classic results plotted for $B=1$ and $k=\mathit{\pi }/L$. Rectangular box (solid line), wedge (dashed line), isochronous container (dash-dot-dash line), and containers C1, C2, C3 as indicated.

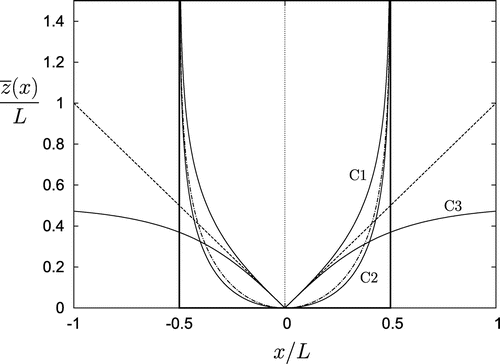
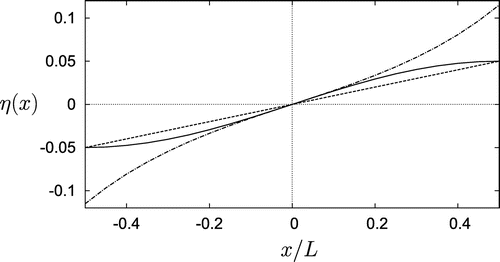
Figure 9. Comparison of free surface waveforms with classic results plotted for $B=1$ and ${\mathit{\eta }}_0=0.05$. The solid line for $sinkx$ is that for a rectangular box, the isochronous container, and containers C1 and C2. The dash-dot-dash line is the profile $sinhkx$ for container C3. The dashed line is the flat free surface for sloshing in the ${90}^{\circ }$ wedge which also applies for the C1 and C3 containers at very low depth.

The shapes of the containers are compared in Figure 8 using the same notations: dark solid lines for the box geometry, dash-dot-dash line for the isochronous container, dashed line for the ${90}^{\circ }$ wedge, and labels C1, C2 and C3 for the new geometries.

The three distinct waveforms that appear are: (i) ${\mathit{\eta }}_{0}sinkx$, (ii) ${\mathit{\eta }}_{0}sinhkx$, and (iii) ${\mathit{\eta }}_{0}x$. In each case the fluid oscillates about the centre nodal line. The sine waveform (i) is found for containers C1, C2, the rectangular box, and the isochronous container. The hyperbolic sine waveform (ii) is found only for container C3 and the linear waveform (iii) applies to the ${90}^{\circ }$ wedge geometry and to oscillations at very low depth in the C1 and C3 containers. These free-surface waveforms are compared in Figure 9 for the small amplitude ${\mathit{\eta }}_0=0.05$.

6. Discussion and conclusion

A formulation for sloshing in planar containers has been devised to determine all possible variations of frequency with fluid depth which lead to viable container geometries. Summarising the possibilities, we have

$1{\mathit{\omega }}^2={\displaystyle \frac{g}{H}}$ (90${}^{\circ }$ wedge)

$2{\mathit{\omega }}^2={\displaystyle \frac{g}{H+z_0}}$ (hyperbolic containers)

$3{\mathit{\omega }}^2=g{\displaystyle \frac{\mathit{\pi }}{L}}$ (isochronous container)

$4{\mathit{\omega }}^2=g{\displaystyle \frac{\mathit{\pi }}{L}}cothk(H+z_0)$-pagination               (C1 family of containers)

$5{\mathit{\omega }}^2=g{\displaystyle \frac{\mathit{\pi }}{L}}tanhk(H+z_0)$-pagination               (C2 family of containers)

$6{\mathit{\omega }}^2=g{\displaystyle \frac{\mathit{\pi }}{L}}cotk(H+z_0)$-pagination                 (C3 family of containers)

where $z_0$ is chosen so that the bottom of the container lies as $z=0$, H is the fluid depth, and L is the asymptotic width of containers associated with $3-$6.

All containers found here are for the fundamental mode of sloshing about a single nodal line. Container shapes for even modes and all higher odd modes are not obtained by the inverse solution method.

The new families of first sloshing mode containers denoted as C1, C2 and C3 are parameterized by streamfunction separation constant B. Containers C1 exist for $1\le B\le \infty$, containers C2 exist for $0\le B\le \infty$, and containers C3 exist for $0\le B\le 1$. It is worth remembering that for $z_0=0$ the C1 container corresponds to first mode sloshing in a rectangular tank.

At $B=1$ containers C1 and C3 have the shape of a ${90}^{\circ }$ wedge at low depths but the former tends to vertical walls as $z\to \infty$, whilst the latter tends to horizontal walls as $x\to \pm \infty$. Container C2 assumes the shape of a rectangular box at $B=0$.

There is an affinity between the C1 and C2 families in that their $B\to \infty$ limiting shapes are first-mode isochronous containers. Thus, the C1 family of shapes vary from the $B=1$ shape (evolving from a ${90}^{\circ }$ wedge at low depth to vertical walls at large depth) to the $B=\infty$ isochronous container. The C3 family of shapes varies from the $B=0$ rectangular box geometry to the $B=\infty$ isochronous container. There is an affinity between the C1 and C3 families in that their $B=1$ shapes asymptotically tend to a ${90}^{\circ }$ wedge at low depth.

The frequencies of the C1 and C3 families tend to the ${90}^{\circ }$ wedge frequency at low depths. At large depths the frequencies of the C1 and C2 families tend to the rectangular box frequency which is essentially isochronous for depths $H/L>1$. Frequencies for the C3 container only exist in the range $0\le H/L<\frac{1}{2}$, since at the upper limit $H/L=\frac{1}{2}$, the frequency is zero and no sloshing takes place. While the C1 and C2 families of containers are of infinite height, all containers in the C3 family are of finite height.

The fundamental mode free-surface waveforms for containers C1 and C3 are the $sinkx$ form for a rectangular box. The hyperbolic C2 free-surface waveform $sinhkx$ seems to be unique. Lamb [1] (Section 258) gives the waveforms for higher sloshing modes in a ${90}^{\circ }$ wedge as linear combinations of $\{sinkx,sinhkx\}$ for the odd modes and as linear combinations of $\{coskx,coshkx\}$ for the even modes, but the shapes $sinhkx$ and $coshkx$ never appear in isolation, certainly not for the fundamental mode where the free surface waveform is flat.

This study shows that the inverse solution method for permissible frequency variations applies only to potential functions of separable form. Thus, the container shapes found using polynomial forms of the potential function cannot be found using the inverse method.

In closing, it is noted that the inverse method of solution used here might be applied to find new container geometries for sloshing in axisymmetric containers. This provides the basis of future work.

Notes

No potential conflict of interest was reported by the author.