A three-dimensional image reconstruction algorithm for electrical impedance tomography using planar electrode arrays

Abstract

We present a three-dimensional non-iterative reconstruction algorithm developed for conductivity imaging with real data collected on a planar rectangular array of electrodes. Such an electrode configuration as well as the proposed imaging technique is intended to be used for breast cancer detection. The algorithm is based on linearizing the conductivity about a constant value and allows real-time reconstructions. The performance of the algorithm was tested on numerically simulated data and we successfully detected small inclusions with conductivities three or four times the background lying beneath the data collection surface. The results were fairly stable with respect to the noise level in the data and displayed very good spatial resolution in the plane of electrodes.

Keywords:

• Electrical Impedance Tomography (EIT)
• planar electrode arrays
• breast cancer detection
• image reconstruction
• inverse problem
• ill-posed problem
• linearization

AMS Subject Classifications:

• 31B10
• 45Q05
• 47A52
• 65F20
• 65F22

1. Introduction

Electrical Impedance Tomography (EIT) is a technology used to image the distribution of electrical properties such as conductivity and/or permittivity within an object using measurements of electric currents and voltages on its surface. Since different materials display different electrical properties, EIT can be used as a method of industrial, geophysical and medical imaging (see, for example, [1] and the references therein). The application of EIT considered in this paper is breast cancer imaging.

Breast cancer is routinely investigated by palpation, X-ray mammography or ultrasound imaging with sensitivity rates of up to 90%. The diagnoses, however, yield rather unspecific results. Only one in five biopsies of suspicious lesions leads to a malignant histological diagnosis,[2] causing unnecessary distress for the patient and significant delays in establishing a diagnosis. Research is therefore aimed at developing alternative imaging techniques to diagnose malignant breast tumours more accurately and possibly earlier. Since in vivo studies have discovered a difference of three times or more in the specific electrical conductivity and permittivity between healthy and cancerous tissue,[3–5] imaging the electrical properties of breast tissues could improve the specificity of mammograms. The advantages (portability, low cost, little or zero patient discomfort, no known patient risk and no known side effects) of an impedance imaging system over traditional X-ray mammography could make this technology a welcome addition to the tools available in the fight against breast cancer. Although much research has been devoted to both the theoretical and the practical developments of Electrical Impedance Mammography,[6–19] to date, the technique has not reached clinical acceptance because of its sensitivity to measurement errors, high computational demands and practical issues: errors in electrode positions or boundary shape, high and uncontrollable contact impedance of the skin (variations of 20% or more).

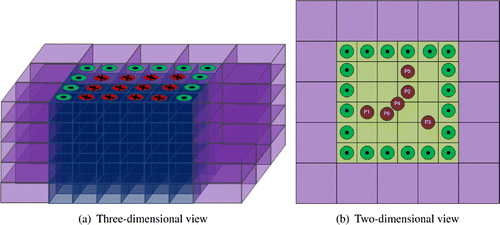
Several EIT mammographic sensors have been developed recently at the University of Mainz in collaboration with Oxford Brookes University. In contrast to most previous EIT instruments designed for breast cancer detection,[9] but similar to devices studied by [6,7,16,18,20,21], these mammographic sensors are planar. Detailed descriptions of earlier prototypes can be found in [22,23]. The latest design consists of a planar sensing head with 36 disk electrodes of equal size arranged in a rectangular array of 20 outer (active) electrodes where the external currents are injected, and 16 inner (passive) electrodes where the induced voltages are measured, see Figure 1. To avoid any problems due to the unknown contact impedance, the voltages are not measured at the active electrodes, but at the passive electrodes, very high impedance voltage measurements are taken, and the problem of the unknown contact impedance does not arise. These voltage measurements are relative to the systems ground. Moreover, the device has a fixed geometry and the positions of the electrodes are exactly known.

Almost all previous EIT devices [6,7,9,16,18,20,21] use the same electrodes for current injection and voltage measurement. The excitation current is injected (extracted) at one pair of electrodes at a time and the resulting voltage is measured at all or some of the remaining electrodes. The novelty of our EIT devices, and hence of the image reconstruction methods proposed consists precisely in the distinct use of active and passive electrodes. The active electrodes are used only for current injection while the passive electrodes only for voltage measurements.

Figure 1. Layout of the rectangular electrode array of the latest prototype developed at the University of Mainz in collaboration with Oxford Brookes University:

are the active electrodes used for current injection, and

are the passive electrodes used for potential measurements.

In two-dimensions, two different non-iterative algorithms for imaging the conductivity at the surface using the tomographs designed at the University of Mainz were described in [22,23]. In both cases numerical reconstructions had very good spatial resolution, and the algorithms were robust with respect to errors in the data. A three-dimensional iterative reconstruction method that enforced sparsity and used an adapted complete electrode model was also applied to these devices in [24]. Although it produced good images, this iterative procedure proved to be quite demanding computationally and sensitive to the choice of the regularization parameter.

The purpose of the current paper is to respond to these issues i.e. the two-dimensional nature of the first two algorithms and the numerical sensitivity of the sparsity algorithm, by developing a simple, direct and rapid three-dimensional reconstruction algorithm to image the region beneath the rectangular electrode array. The proposed inversion technique is intended to be used in the future for conductivity imaging using real data collected by the specific EIT device described above. The reconstruction method is similar to an approach described in [20] and is based on linearizing the conductivity distribution about a constant approximation in order to reduce the computational demands.

The structure of the paper is as follows. In Section 2, we present the mathematical formulation of the inverse problem and of the method proposed to image the conductivity. Section 3 is dedicated to the numerical implementation of the reconstruction algorithm. The performance of the algorithm is illustrated by showing a number of reconstructions from simulated data in Section 4.

2. Mathematical formulation

Since the EIT sensor is much smaller than the human body to which it is applied, and given the rapid decay of the induced potentials as we move away from the top surface (see Equation (3(3) $$\begin{array}{c}\hfill \left|u\left(\mathbf{x}\right)\right|=\mathcal{O}\left(1/\Vert \mathbf{x}\Vert \right)\text{as}\Vert \mathbf{x}\Vert \to \infty ,\end{array}$$(3) )), the mathematical analysis of breast cancer detection can be considered to be the inverse conductivity problem of EIT on an unbounded domain, specifically the lower half space. Let $\mathrm{\Omega }=\{(x,y,z):z<0\}\subset {\mathbb{R}}^3$ be a conductive object with boundary $\mathrm{\Gamma }=\{(x,y,z):z=0\}$ and $Q\subset L^{\infty }(\mathrm{\Omega })$ be a set of uniformly strictly positive parameters. Suppose that $\mathit{\sigma }\in Q$ is an isotropic scalar electrical conductivity distribution and that there are no current sources inside $\mathrm{\Omega }$. A set of L electrodes is placed on $\mathrm{\Gamma }$ in a rectangular array. Let ${\{e_l\}}_{l=1}^M$ be the set of passive electrodes (voltage measurement) and ${\{e_l\}}_{l=M+1}^L$ be the active electrodes (current injection). If low-frequency currents are applied to the active electrodes, the electric potential u satisfies the generalized Laplace equation(1) $$\begin{array}{c}\hfill \mathrm{\nabla }·\left(\mathit{\sigma }(x,y,z)\mathrm{\nabla }u(x,y,z)\right)=0\text{in}\mathrm{\Omega },\end{array}$$(1)

subject to the boundary condition(2) $$\begin{array}{c}\hfill \mathit{\sigma }(x,y,0)\frac{\mathit{\partial }u}{\mathit{\partial }z}(x,y,0)=j(x,y)\text{on}\mathrm{\Gamma },\end{array}$$(2)

where j is the induced current density distribution.

In this paper, we restrict our analysis to currents $j\in {\mathcal{L}}_{\diamond }^2(\mathrm{\Gamma })$ with bounded support and to weak solutions $u\in \mathcal{H}$ of Equation (1(1) $$\begin{array}{c}\hfill \mathrm{\nabla }·\left(\mathit{\sigma }(x,y,z)\mathrm{\nabla }u(x,y,z)\right)=0\text{in}\mathrm{\Omega },\end{array}$$(1) ) in the lower half-space $\mathrm{\Omega }$ for which the following point-wise estimates hold uniformly with respect to the direction of $\mathbf{x}=(x,y,z)$:(3) $$\begin{array}{c}\hfill \left|u\left(\mathbf{x}\right)\right|=\mathcal{O}\left(1/\Vert \mathbf{x}\Vert \right)\text{as}\Vert \mathbf{x}\Vert \to \infty ,\end{array}$$(3)

and(4) $$\begin{array}{c}\hfill \left|\frac{\mathit{\partial }u}{\mathit{\partial }\mathit{\zeta }}\left(\mathbf{x}\right)\right|=\mathcal{O}\left(1/\left(\Vert \mathbf{x}\Vert \right)\right)\text{as}\Vert \mathbf{x}\Vert \to \infty \text{for}\mathit{\zeta }=x,y,z.\end{array}$$(4)

Here, ${\mathcal{L}}_{\diamond }^2(\mathrm{\Gamma })$ denotes the space of $L^2$-functions with vanishing integral mean on $\mathrm{\Gamma }$ and $\mathcal{H}=H^{1,\mathit{\alpha }}(\mathrm{\Omega })$ is a completion of suitable $C^{\infty }$-functions with respect to the norm ${\Vert ·\Vert }_{1,\mathit{\alpha }}$ parametrized by the weight function ${\mathit{\rho }}_{\mathit{\alpha }}\left(x,y,z\right)={\left(1+\Vert \mathbf{x}\Vert \right)}^{\mathit{\alpha }}$ with $\mathit{\alpha }>1$. Further details on the definition of the weighted Sobolev spaces $H^{1,\mathit{\alpha }}(\mathrm{\Omega })$ and on the derivation of these asymptotic estimates can be found in [25].

The weak formulation for the boundary value problem (1(1) $$\begin{array}{c}\hfill \mathrm{\nabla }·\left(\mathit{\sigma }(x,y,z)\mathrm{\nabla }u(x,y,z)\right)=0\text{in}\mathrm{\Omega },\end{array}$$(1) )–(2(2) $$\begin{array}{c}\hfill \mathit{\sigma }(x,y,0)\frac{\mathit{\partial }u}{\mathit{\partial }z}(x,y,0)=j(x,y)\text{on}\mathrm{\Gamma },\end{array}$$(2) ) and its properties are well known. However, we will use the same formulation as in [25], i.e. a function $u\in \mathcal{H}$ is called a weak solution of this Neumann boundary problem if(5) $$\begin{array}{c}\hfill T\left(\mathit{\sigma },u,v\right)=L_j(v),\text{for any}v\in \mathcal{H},\end{array}$$(5)

where the trilinear form $T:L^{\infty }(\mathrm{\Omega })\times \mathcal{H}\times \mathcal{H}\to \mathbb{R}$ and the linear form $L_j:\mathcal{H}\to \mathbb{R}$ are defined by(6) $$\begin{array}{cc}\hfill T\left(\mathit{\sigma },u,v\right)& ={\int }_{\mathrm{\Omega }}\mathit{\sigma }\mathrm{\nabla }u·\mathrm{\nabla }v\mathrm{d}V,\hfill \end{array}$$(6) (7) $$\begin{array}{cc}\hfill L_j(v)& ={\int }_{\mathrm{\Gamma }}jv\mathrm{d}S.\hfill \end{array}$$(7)

Hence, the solution of the Neumann boundary value problem (1(1) $$\begin{array}{c}\hfill \mathrm{\nabla }·\left(\mathit{\sigma }(x,y,z)\mathrm{\nabla }u(x,y,z)\right)=0\text{in}\mathrm{\Omega },\end{array}$$(1) )–(2(2) $$\begin{array}{c}\hfill \mathit{\sigma }(x,y,0)\frac{\mathit{\partial }u}{\mathit{\partial }z}(x,y,0)=j(x,y)\text{on}\mathrm{\Gamma },\end{array}$$(2) ) is given by $u=T_{\mathit{\sigma }}^{-1}{L}_j$, where $T_{\mathit{\sigma }}^{-1}\in L({\mathcal{H}}^{\ast },\mathcal{H})$, the inverse of $T(\mathit{\sigma },·,·)$, exists and is bounded and continuous.[26,27]

Since in our application the voltages are not measured at the active electrodes, the ave-gap electrode model [12] can be used. We, therefore, assume that the current density is uniformly distributed over each active electrode and that it is zero outside of the support of all active electrodes. Hence, we approximate j in Equation (2(2) $$\begin{array}{c}\hfill \mathit{\sigma }(x,y,0)\frac{\mathit{\partial }u}{\mathit{\partial }z}(x,y,0)=j(x,y)\text{on}\mathrm{\Gamma },\end{array}$$(2) ) by(8) $$\begin{array}{c}\hfill j(x,y)=\left\{\begin{array}{cc}{I}_l/A_l,& (x,y)\text{on}{e}_l,l=M+1,\dots ,L\\ 0,& \text{otherwise},\end{array}\right.\end{array}$$(8)

where $I_l$ is the current sent to the lth active electrode $e_l$ and $A_l$ is the area of $e_l$.

In our experimental set-up, a basis of current patterns $\{{\mathbf{I}}^1,\dots ,{\mathbf{I}}^{L-M-1}\}$ is applied to the set of $L-M$ active electrodes ${\{e_l\}}_{l=M+1}^L$. For each current pattern ${\mathbf{I}}^k=\left(I_{M+1}^k,\dots ,I_L^k\right)$, $k=1,\dots ,L-M-1$, the resulting potentials ${\mathbf{U}}^k=\left(U_1^k,\dots ,U_M^k\right)$ are measured at the set of M passive electrodes ${\{e_l\}}_{l=1}^M$. The ave-gap model predicts the voltage measured on each electrode as the average of the solution $u^k$ to (1(1) $$\begin{array}{c}\hfill \mathrm{\nabla }·\left(\mathit{\sigma }(x,y,z)\mathrm{\nabla }u(x,y,z)\right)=0\text{in}\mathrm{\Omega },\end{array}$$(1) ), (2(2) $$\begin{array}{c}\hfill \mathit{\sigma }(x,y,0)\frac{\mathit{\partial }u}{\mathit{\partial }z}(x,y,0)=j(x,y)\text{on}\mathrm{\Gamma },\end{array}$$(2) ) and (8(8) $$\begin{array}{c}\hfill j(x,y)=\left\{\begin{array}{cc}{I}_l/A_l,& (x,y)\text{on}{e}_l,l=M+1,\dots ,L\\ 0,& \text{otherwise},\end{array}\right.\end{array}$$(8) ) with $j=j^k$ over the surface of the electrode:(9) $$\begin{array}{c}\hfill U_l^k=\frac{1}{A_l}{\int }_{e_l}{u}^k(x,y,0)\mathrm{d}S,l=1,\dots ,M.\end{array}$$(9)

The inverse problem is to estimate the conductivity $\mathit{\sigma }(x,y,z)$ from all $L-M-1$ linearly independent sets of surface measurements.

The reconstruction algorithm presented in this paper is based on the assumption that the spatially varying conductivity is a small perturbation from a constant and known background conductivity ${\mathit{\sigma }}_0$, i.e.(10) $$\begin{array}{c}\hfill \mathit{\sigma }(x,y,z)={\mathit{\sigma }}_0+\mathit{\delta }\mathit{\sigma }(x,y,z),\end{array}$$(10)

where $\mathit{\sigma }={\mathit{\sigma }}_0$ near $\mathrm{\Gamma }$. Let us also express the corresponding potential u in terms of $u_0$, the solution of (1(1) $$\begin{array}{c}\hfill \mathrm{\nabla }·\left(\mathit{\sigma }(x,y,z)\mathrm{\nabla }u(x,y,z)\right)=0\text{in}\mathrm{\Omega },\end{array}$$(1) ), (2(2) $$\begin{array}{c}\hfill \mathit{\sigma }(x,y,0)\frac{\mathit{\partial }u}{\mathit{\partial }z}(x,y,0)=j(x,y)\text{on}\mathrm{\Gamma },\end{array}$$(2) ) and (8(8) $$\begin{array}{c}\hfill j(x,y)=\left\{\begin{array}{cc}{I}_l/A_l,& (x,y)\text{on}{e}_l,l=M+1,\dots ,L\\ 0,& \text{otherwise},\end{array}\right.\end{array}$$(8) ) for $\mathit{\sigma }={\mathit{\sigma }}_0$, as(11) $$\begin{array}{c}\hfill u(x,y,z)=u_0(x,y,z)+\mathit{\delta }u(x,y,z).\end{array}$$(11)

It is shown in [26,27] that both the parameter-to-solution map(12) $$\begin{array}{c}\hfill A_{\mathit{\sigma }}:Q\to \mathcal{H},\mathit{\sigma }\mapsto T_{\mathit{\sigma }}^{-1}{L}_j.\end{array}$$(12)

and the complete parameter-to-solution map (i.e. forward operator for a single measurement with current density j)(13) $$\begin{array}{c}\hfill A_j:Q\to {\mathcal{L}}_{\diamond }^{2,\mathit{\alpha }}(\mathrm{\Gamma }),\mathit{\sigma }\mapsto \mathit{\gamma }\circ T_{\mathit{\sigma }}^{-1}{L}_j,\end{array}$$(13)

are analytic on each uniformly strictly positive open set Q. It therefore follows that $\mathit{\delta }u=\mathcal{O}\left(\mathit{\delta }\mathit{\sigma }\right)$ in $\overline{\mathrm{\Omega }}$. Here, $\mathit{\gamma }:\mathcal{H}\to {\mathcal{L}}_{\diamond }^{2,\mathit{\alpha }}(\mathrm{\Gamma })$ is the trace operator and ${\mathcal{L}}_{\diamond }^{2,\mathit{\alpha }}$ is the weighted ${\mathcal{L}}_{\diamond }^2$-space with respect to ${\mathit{\rho }}_{\mathit{\alpha }}$.

Our method now follows the approach of Calderón [28]. Inserting Equations (10(10) $$\begin{array}{c}\hfill \mathit{\sigma }(x,y,z)={\mathit{\sigma }}_0+\mathit{\delta }\mathit{\sigma }(x,y,z),\end{array}$$(10) ) and (11(11) $$\begin{array}{c}\hfill u(x,y,z)=u_0(x,y,z)+\mathit{\delta }u(x,y,z).\end{array}$$(11) ) into (1(1) $$\begin{array}{c}\hfill \mathrm{\nabla }·\left(\mathit{\sigma }(x,y,z)\mathrm{\nabla }u(x,y,z)\right)=0\text{in}\mathrm{\Omega },\end{array}$$(1) ) and simplifying leads to the following linearized equation(14) $$\begin{array}{c}\hfill \mathrm{\nabla }·{\mathit{\sigma }}_0\mathrm{\nabla }\mathit{\delta }u+\mathrm{\nabla }·\mathit{\delta }\mathit{\sigma }\mathrm{\nabla }{u}_0=\mathcal{O}\left(\mathit{\delta }\mathit{\sigma }\right).\end{array}$$(14)

We choose a test function $v_0\in \mathcal{H}$ that is the solution of the following boundary value problem:(15) $$\begin{array}{cc}\hfill \mathrm{\nabla }·\left({\mathit{\sigma }}_0\mathrm{\nabla }{v}_0(x,y,z)\right)& =0,\text{in}\mathrm{\Omega },\hfill \end{array}$$(15) (16) $$\begin{array}{cc}\hfill {\mathit{\sigma }}_0\frac{\mathit{\partial }{v}_0}{\mathit{\partial }z}(x,y,0)& =\tilde{j}(x,y)=\left\{\begin{array}{cc}{\tilde{I}}_l/A_l,(x,y)\text{on}\hfill & e_l,l=1,\dots ,M\hfill \\ 0,\hfill & \text{otherwise},\hfill \end{array}\right.,\hfill \end{array}$$(16)

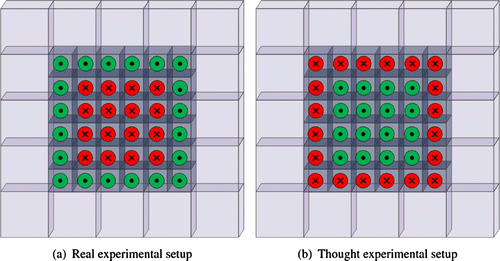
where ${\tilde{I}}_l$ is a simulated current applied at the lth passive electrode. More explicitly, $u_0$ is the (weak) potential created in $\mathrm{\Omega }$ if it consisted of a material of constant conductivity ${\mathit{\sigma }}_0$, while $v_0$ is the induced (weak) potential when currents are applied to this object of uniform conductivity distribution but reversing the roles of the active and passive electrodes. An illustration of the thought experimental set-up corresponding to the homogeneous forward problem (15(15) $$\begin{array}{cc}\hfill \mathrm{\nabla }·\left({\mathit{\sigma }}_0\mathrm{\nabla }{v}_0(x,y,z)\right)& =0,\text{in}\mathrm{\Omega },\hfill \end{array}$$(15) )–(16(16) $$\begin{array}{cc}\hfill {\mathit{\sigma }}_0\frac{\mathit{\partial }{v}_0}{\mathit{\partial }z}(x,y,0)& =\tilde{j}(x,y)=\left\{\begin{array}{cc}{\tilde{I}}_l/A_l,(x,y)\text{on}\hfill & e_l,l=1,\dots ,M\hfill \\ 0,\hfill & \text{otherwise},\hfill \end{array}\right.,\hfill \end{array}$$(16) ) is presented in Figure 1. There are $M-1$ linearly independent simulated current patterns $\{{\tilde{\mathbf{I}}}^1,\dots ,{\tilde{\mathbf{I}}}^{M-1}\}$, where ${\tilde{\mathbf{I}}}^i=\left(I_1^i,\dots ,I_M^i\right)$, that can be applied to the M passive electrodes.

We now multiply the expression in Equation (14(14) $$\begin{array}{c}\hfill \mathrm{\nabla }·{\mathit{\sigma }}_0\mathrm{\nabla }\mathit{\delta }u+\mathrm{\nabla }·\mathit{\delta }\mathit{\sigma }\mathrm{\nabla }{u}_0=\mathcal{O}\left(\mathit{\delta }\mathit{\sigma }\right).\end{array}$$(14) ) by this test function $v_0$ and integrate over $\mathrm{\Omega }$. Applying Gauss’s divergence theorem [29] and taking into account the asymptotic behaviour of weak solutions of (1(1) $$\begin{array}{c}\hfill \mathrm{\nabla }·\left(\mathit{\sigma }(x,y,z)\mathrm{\nabla }u(x,y,z)\right)=0\text{in}\mathrm{\Omega },\end{array}$$(1) ) and (15(15) $$\begin{array}{cc}\hfill \mathrm{\nabla }·\left({\mathit{\sigma }}_0\mathrm{\nabla }{v}_0(x,y,z)\right)& =0,\text{in}\mathrm{\Omega },\hfill \end{array}$$(15) ) given by Equations (3(3) $$\begin{array}{c}\hfill \left|u\left(\mathbf{x}\right)\right|=\mathcal{O}\left(1/\Vert \mathbf{x}\Vert \right)\text{as}\Vert \mathbf{x}\Vert \to \infty ,\end{array}$$(3) )–(4(4) $$\begin{array}{c}\hfill \left|\frac{\mathit{\partial }u}{\mathit{\partial }\mathit{\zeta }}\left(\mathbf{x}\right)\right|=\mathcal{O}\left(1/\left(\Vert \mathbf{x}\Vert \right)\right)\text{as}\Vert \mathbf{x}\Vert \to \infty \text{for}\mathit{\zeta }=x,y,z.\end{array}$$(4) ) yields(17) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Gamma }}\mathbf{n}·v_0\left({\mathit{\sigma }}_0\mathrm{\nabla }\mathit{\delta }u+\mathit{\delta }\mathit{\sigma }\mathrm{\nabla }{u}_0\right)\mathrm{d}S={\int }_{\mathrm{\Omega }}\left({\mathit{\sigma }}_0\mathrm{\nabla }{v}_0·\mathrm{\nabla }\mathit{\delta }u+\mathit{\delta }\mathit{\sigma }\mathrm{\nabla }{v}_0·\mathrm{\nabla }{u}_0\right)\mathrm{d}V+\mathcal{O}(\mathit{\delta }\mathit{\sigma }),\end{array}$$(17)

where $\mathbf{n}$ is the outward normal unit vector.

Furthermore, multiplying Equation (15(15) $$\begin{array}{cc}\hfill \mathrm{\nabla }·\left({\mathit{\sigma }}_0\mathrm{\nabla }{v}_0(x,y,z)\right)& =0,\text{in}\mathrm{\Omega },\hfill \end{array}$$(15) ) by $\mathit{\delta }u\in \mathcal{H}$ and repeating the same steps as above, we obtain(18) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Gamma }}\mathbf{n}·\left({\mathit{\sigma }}_0\mathit{\delta }{u}_0\mathrm{\nabla }{v}_0\right)\mathrm{d}S={\int }_{\mathrm{\Omega }}{\mathit{\sigma }}_0\mathrm{\nabla }\mathit{\delta }u·\mathrm{\nabla }{v}_0\mathrm{d}V.\end{array}$$(18)

Inserting this result in Equation (17(17) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Gamma }}\mathbf{n}·v_0\left({\mathit{\sigma }}_0\mathrm{\nabla }\mathit{\delta }u+\mathit{\delta }\mathit{\sigma }\mathrm{\nabla }{u}_0\right)\mathrm{d}S={\int }_{\mathrm{\Omega }}\left({\mathit{\sigma }}_0\mathrm{\nabla }{v}_0·\mathrm{\nabla }\mathit{\delta }u+\mathit{\delta }\mathit{\sigma }\mathrm{\nabla }{v}_0·\mathrm{\nabla }{u}_0\right)\mathrm{d}V+\mathcal{O}(\mathit{\delta }\mathit{\sigma }),\end{array}$$(17) ) gives(19) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Gamma }}\mathbf{n}·v_0\left({\mathit{\sigma }}_0\mathrm{\nabla }\mathit{\delta }u+\mathit{\delta }\mathit{\sigma }\mathrm{\nabla }{u}_0\right)\mathrm{d}S={\int }_{\mathrm{\Gamma }}\mathbf{n}·\left({\mathit{\sigma }}_0\mathit{\delta }u\mathrm{\nabla }{v}_0\right)\mathrm{d}S+{\int }_{\mathrm{\Omega }}\mathit{\delta }\mathit{\sigma }\mathrm{\nabla }{v}_0·\mathrm{\nabla }{u}_0\mathrm{d}V+\mathcal{O}(\mathit{\delta }\mathit{\sigma }).\end{array}$$(19)

Since both u and $u_0$ satisfy the same Neumann boundary condition (2(2) $$\begin{array}{c}\hfill \mathit{\sigma }(x,y,0)\frac{\mathit{\partial }u}{\mathit{\partial }z}(x,y,0)=j(x,y)\text{on}\mathrm{\Gamma },\end{array}$$(2) ), it follows that $\mathbf{n}·{\left.\left({\mathit{\sigma }}_0\mathrm{\nabla }\mathit{\delta }u+\mathit{\delta }\mathit{\sigma }\mathrm{\nabla }{u}_0\right)\right|}_{\mathrm{\Gamma }}+\mathcal{O}(\mathit{\delta }\mathit{\sigma })=0$ and Equation (19(19) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Gamma }}\mathbf{n}·v_0\left({\mathit{\sigma }}_0\mathrm{\nabla }\mathit{\delta }u+\mathit{\delta }\mathit{\sigma }\mathrm{\nabla }{u}_0\right)\mathrm{d}S={\int }_{\mathrm{\Gamma }}\mathbf{n}·\left({\mathit{\sigma }}_0\mathit{\delta }u\mathrm{\nabla }{v}_0\right)\mathrm{d}S+{\int }_{\mathrm{\Omega }}\mathit{\delta }\mathit{\sigma }\mathrm{\nabla }{v}_0·\mathrm{\nabla }{u}_0\mathrm{d}V+\mathcal{O}(\mathit{\delta }\mathit{\sigma }).\end{array}$$(19) ) becomes(20) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Gamma }}\mathbf{n}·\left({\mathit{\sigma }}_0\mathit{\delta }u\mathrm{\nabla }{v}_0\right)\mathrm{d}S=-{\int }_{\mathrm{\Omega }}\mathit{\delta }\mathit{\sigma }\mathrm{\nabla }{v}_0·\mathrm{\nabla }{u}_0\mathrm{d}V+\mathcal{O}(\mathit{\delta }\mathit{\sigma }).\end{array}$$(20)

Within this setting, for fixed Neumann data $\mathbf{n}·{\left.{\mathit{\sigma }}_0\mathrm{\nabla }{u}_0\right|}_{\mathrm{\Gamma }}=j$, Equation (20(20) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Gamma }}\mathbf{n}·\left({\mathit{\sigma }}_0\mathit{\delta }u\mathrm{\nabla }{v}_0\right)\mathrm{d}S=-{\int }_{\mathrm{\Omega }}\mathit{\delta }\mathit{\sigma }\mathrm{\nabla }{v}_0·\mathrm{\nabla }{u}_0\mathrm{d}V+\mathcal{O}(\mathit{\delta }\mathit{\sigma }).\end{array}$$(20) ) expresses in weak form the change in the Neumann-to-Dirichlet map which occurs due to a change in ${\mathit{\sigma }}_0$ for some test function $v_0\in \mathcal{H}$ that is the solution of Equation (15(15) $$\begin{array}{cc}\hfill \mathrm{\nabla }·\left({\mathit{\sigma }}_0\mathrm{\nabla }{v}_0(x,y,z)\right)& =0,\text{in}\mathrm{\Omega },\hfill \end{array}$$(15) ) with Neumann trace $\mathbf{n}·{\left.{\mathit{\sigma }}_0\mathrm{\nabla }{v}_0\right|}_{\mathrm{\Gamma }}=\tilde{j}\in {\mathcal{L}}_{\diamond }^2(\mathrm{\Gamma })$.

Equation (20(20) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Gamma }}\mathbf{n}·\left({\mathit{\sigma }}_0\mathit{\delta }u\mathrm{\nabla }{v}_0\right)\mathrm{d}S=-{\int }_{\mathrm{\Omega }}\mathit{\delta }\mathit{\sigma }\mathrm{\nabla }{v}_0·\mathrm{\nabla }{u}_0\mathrm{d}V+\mathcal{O}(\mathit{\delta }\mathit{\sigma }).\end{array}$$(20) ) is true for any $u^k$ and $u_0^k$, (weak) solutions of Equation (1(1) $$\begin{array}{c}\hfill \mathrm{\nabla }·\left(\mathit{\sigma }(x,y,z)\mathrm{\nabla }u(x,y,z)\right)=0\text{in}\mathrm{\Omega },\end{array}$$(1) ) for a given current pattern $j^k$ applied to the active electrodes, and for any $v_0^i$, (weak) solution of Equation (15(15) $$\begin{array}{cc}\hfill \mathrm{\nabla }·\left({\mathit{\sigma }}_0\mathrm{\nabla }{v}_0(x,y,z)\right)& =0,\text{in}\mathrm{\Omega },\hfill \end{array}$$(15) ) subject to a current density ${\tilde{j}}^i$ corresponding to the ith simulated current pattern ${\tilde{\mathbf{I}}}^i$ applied at the passive electrodes and given by Equation (16(16) $$\begin{array}{cc}\hfill {\mathit{\sigma }}_0\frac{\mathit{\partial }{v}_0}{\mathit{\partial }z}(x,y,0)& =\tilde{j}(x,y)=\left\{\begin{array}{cc}{\tilde{I}}_l/A_l,(x,y)\text{on}\hfill & e_l,l=1,\dots ,M\hfill \\ 0,\hfill & \text{otherwise},\hfill \end{array}\right.,\hfill \end{array}$$(16) ). Thus, the linearized problem (20(20) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Gamma }}\mathbf{n}·\left({\mathit{\sigma }}_0\mathit{\delta }u\mathrm{\nabla }{v}_0\right)\mathrm{d}S=-{\int }_{\mathrm{\Omega }}\mathit{\delta }\mathit{\sigma }\mathrm{\nabla }{v}_0·\mathrm{\nabla }{u}_0\mathrm{d}V+\mathcal{O}(\mathit{\delta }\mathit{\sigma }).\end{array}$$(20) ) can be approximated by the following system of equations(21) $$\begin{array}{ccc}\hfill \sum _{l=1}^M{\int }_{e_l}\left(u_0^k-u^k\right){\tilde{j}}^i\mathrm{d}S& \approx \hfill & \hfill {\int }_{\mathrm{\Omega }}\mathit{\delta }\mathit{\sigma }\mathrm{\nabla }{v}_0^i·\mathrm{\nabla }{u}_0^k\mathrm{d}V,\\ \hfill & k=1,\dots ,L-M-1\text{and}i=1,\dots ,M-1.\hfill \end{array}$$(21)

Using the ave-gap model for the electrodes, the inverse problem becomes that of finding the perturbation $\mathit{\delta }\mathit{\sigma }$ satisfying the following system of equations(22) $$\begin{array}{cc}\hfill \sum _{l=1}^M\left(U_{0,l}^k-U_l^k\right){\tilde{I}}_l^i& ={\int }_{\mathrm{\Omega }}\mathit{\delta }\mathit{\sigma }\mathrm{\nabla }{v}_0^i·\mathrm{\nabla }{u}_0^k\mathrm{d}V,\hfill \\ \hfill & k=1,\dots ,L-M-1\text{and}i=1,\dots ,M-1,\hfill \end{array}$$(22)

where(23) $$\begin{array}{c}\hfill U_{0,l}^k=\frac{1}{A_l}{\int }_{e_l}{u}_0^k(x,y,0)\mathrm{d}S.\end{array}$$(23)

The left-hand side of (22(22) $$\begin{array}{cc}\hfill \sum _{l=1}^M\left(U_{0,l}^k-U_l^k\right){\tilde{I}}_l^i& ={\int }_{\mathrm{\Omega }}\mathit{\delta }\mathit{\sigma }\mathrm{\nabla }{v}_0^i·\mathrm{\nabla }{u}_0^k\mathrm{d}V,\hfill \\ \hfill & k=1,\dots ,L-M-1\text{and}i=1,\dots ,M-1,\hfill \end{array}$$(22) ) contains only measured and simulated quantities, $U_l^k$ and $U_{0,l}^k$, respectively, and will be denoted by B(i, k), i.e.(24) $$\begin{array}{c}\hfill B(i,k)=\sum _{l=1}^M\left(U_{0,l}^k-U_l^k\right){\tilde{I}}_l^i.\end{array}$$(24)

A further simplification that can be introduced to aid the image reconstruction process comes from the fact that our objective is to identify a small object(tumour) of uniform conductivity lying within a region (breast tissue) of uniform, but different and known, conductivity. We may therefore assume that the conductivity is piecewise constant. In this case the half-space can be approximated by voxels, ${\{V_n\}}_{n=1}^{\infty }$, and thus$$\mathit{\delta }\mathit{\sigma }(x,y,z)=\sum _{n=1}^{\infty }\mathit{\delta }{\mathit{\sigma }}_n{\mathit{\chi }}_n(x,y,z),$$

where ${\mathit{\chi }}_n$ is the characteristic function over the nth voxel, i.e.$${\mathit{\chi }}_n(x,y,z)=\left\{\begin{array}{cc}1,& (x,y,z)\in V_n,\\ 0,& \text{otherwise},\end{array}\right.$$

However, in practice, we only have a finite number of measurements and, hence, we can reconstruct the conductivities of a finite number N of voxels, where $N\le (L-M-1)\times (M-1)$. In this case, Equation (22(22) $$\begin{array}{cc}\hfill \sum _{l=1}^M\left(U_{0,l}^k-U_l^k\right){\tilde{I}}_l^i& ={\int }_{\mathrm{\Omega }}\mathit{\delta }\mathit{\sigma }\mathrm{\nabla }{v}_0^i·\mathrm{\nabla }{u}_0^k\mathrm{d}V,\hfill \\ \hfill & k=1,\dots ,L-M-1\text{and}i=1,\dots ,M-1,\hfill \end{array}$$(22) ) reduces to an over-determined linear system of equations(25) $$\begin{array}{c}\hfill B(i,k)=\sum _{n=1}^{N}A(i,k,n)\mathit{\delta }{\mathit{\sigma }}_n,k=1,\dots ,L-M-1\text{and}i=1,\dots ,M,\end{array}$$(25)

where(26) $$\begin{array}{c}\hfill A(i,k,n)={\int }_{V_n}\mathrm{\nabla }{v}_0^i·\mathrm{\nabla }{u}_0^k\mathrm{d}V.\end{array}$$(26)

Note that the matrix $\mathbf{A}$ is independent of the measured voltage data and it can be computed in advance and stored for use with other reconstructions in the same geometry.

Since, the linearized system of Equations (25(25) $$\begin{array}{c}\hfill B(i,k)=\sum _{n=1}^{N}A(i,k,n)\mathit{\delta }{\mathit{\sigma }}_n,k=1,\dots ,L-M-1\text{and}i=1,\dots ,M,\end{array}$$(25) ) inherits ill-posedness from the original non-linear inverse conductivity problem, the matrix $\mathbf{A}$ is ill-conditioned and regularization is required. The system of Equations (25(25) $$\begin{array}{c}\hfill B(i,k)=\sum _{n=1}^{N}A(i,k,n)\mathit{\delta }{\mathit{\sigma }}_n,k=1,\dots ,L-M-1\text{and}i=1,\dots ,M,\end{array}$$(25) ) is therefore solved by means of generalized inverse and truncated singular value decomposition was used as the regularization scheme.[30] In this way, very small singular values (i.e. smaller than a certain threshold $\mathit{ϵ}$) will be neglected and will not enter in the reconstruction.

3. Numerical implementation

3.1. Electrode and voxel configuration

As described earlier, our planar array of electrodes is rectangular and consists of $L\left(=36\right)$ circular electrodes of radius $r_l\left(=3.5\text{mm}\right)$, $l=1,\dots ,L$, which are equally spaced. The distance between the centres of two adjacent electrodes is $d\left(=12\text{mm}\right)$. There are $M\left(=16\right)$ passive (inner) electrodes and $L-M\left(=20\right)$ active (outer) electrodes. The terms outer and inner are relative to the positions of the electrodes in the array. As seen in Figure 1, all the electrodes located on the boundary of the rectangular array are active, while the remaining ones are passive. At this point, it is important to note that this electrode configuration not only provides a simpler geometry than the hexagonal pattern of the earlier prototypes in [22,23], but for some electrical impedance imaging problems in geophysics, archaeology, medical diagnosis and industrial plant control, an appropriate electrode geometry may be that of a rectangular array of electrodes placed on a surface plane. For example, rectangular electrode configurations have been employed before for medical applications such as: breast cancer detection,[6,7,20,31] respiratory monitoring, functional imaging of the digestive system and peripheral venography,[32] or for engineering and environmental studies (e.g. [33] and the references therein).

For the numerical implementation of our algorithm, we use a layered voxel configuration similar to the one introduced in [20] and it is depicted in Figure 2. There are 52 inner voxels in each layer:

• 36 small inner voxels aligned immediately under the electrodes of dimensions $12\text{mm}\times 12\text{mm}\times 2\text{mm}$, and

• 16 outer large voxels arranged around the boundary of the electrode array of dimensions $24\text{mm}\times 24\text{mm}\times 2\text{mm}$ (i.e. the same height, $2\text{mm}$, but four times the volume of a small voxel).

Although our interest is to image the conductivity in the region under the electrode array, the voxel configuration has to model, nevertheless, an unbounded domain. The reason for introducing the outer large voxels is to achieve this in a practical manner. As mentioned in Section 2, the total number of voxels should satisfy $N\le (L-M-1)\times (M-1)=285$. Hence, since there are 52 voxels per layer, we cannot consider more than 5 layers of voxels (i.e. $N=5\times 52=260\le 285$). Note that the number of voxels per layer is determined by the geometry of the electrode array, while the total number of layers is constrained by the number of active and passive electrodes, i.e. the total number ($=285$) of possible combinations of measured and simulated currents. The height of each voxel layer, however, is not fixed and it can be adjusted to allow conductivity reconstructions up to the required depths. Most of breast tumours are located near the skin surface.[34] The results of a clinical study of single-breast lesions located at least 0.5 cm from the skin surface and pectoralis margin and at least 2.0cm from the nipple showed that the mean distance from the skin surface to the lesion was 0.9 cm (range, $0.5-1.7$ cm).[35] Therefore, in this approach we chose a voxel configuration which allows reconstructions up to a depth of 1 cm ($=5$ layers$\times$2 mm).

Figure 2. Voxel configuration: are the active electrodes, are the passive electrodes, and $P1-P5$ denote the positions in the xy-plane where inclusions were placed in our numerical simulations.

3.2. Computation of matrix $\mathbf{A}$

Before we discuss the construction of matrix $\mathbf{A}$ in (26(26) $$\begin{array}{c}\hfill A(i,k,n)={\int }_{V_n}\mathrm{\nabla }{v}_0^i·\mathrm{\nabla }{u}_0^k\mathrm{d}V.\end{array}$$(26) ), we need to address the problem of computing the potentials $u_0$ and $v_0$ for a homogeneous medium.

Let $P=(x,y,z)$ be an interior point in $\mathrm{\Omega }$, $Q_0=(x^{\prime },y^{\prime },0)$ be a point on the boundary $\mathrm{\Gamma }$ and $Q_l=(x_l,y_l,0)$ be the centre of lth electrode. For a constant conductivity distribution ${\mathit{\sigma }}_0$, the solutions of the two theoretical forward problems, defined by (1(1) $$\begin{array}{c}\hfill \mathrm{\nabla }·\left(\mathit{\sigma }(x,y,z)\mathrm{\nabla }u(x,y,z)\right)=0\text{in}\mathrm{\Omega },\end{array}$$(1) ), (2(2) $$\begin{array}{c}\hfill \mathit{\sigma }(x,y,0)\frac{\mathit{\partial }u}{\mathit{\partial }z}(x,y,0)=j(x,y)\text{on}\mathrm{\Gamma },\end{array}$$(2) ) and (8(8) $$\begin{array}{c}\hfill j(x,y)=\left\{\begin{array}{cc}{I}_l/A_l,& (x,y)\text{on}{e}_l,l=M+1,\dots ,L\\ 0,& \text{otherwise},\end{array}\right.\end{array}$$(8) ) with $j=j^i$ and (15(15) $$\begin{array}{cc}\hfill \mathrm{\nabla }·\left({\mathit{\sigma }}_0\mathrm{\nabla }{v}_0(x,y,z)\right)& =0,\text{in}\mathrm{\Omega },\hfill \end{array}$$(15) )–(16(16) $$\begin{array}{cc}\hfill {\mathit{\sigma }}_0\frac{\mathit{\partial }{v}_0}{\mathit{\partial }z}(x,y,0)& =\tilde{j}(x,y)=\left\{\begin{array}{cc}{\tilde{I}}_l/A_l,(x,y)\text{on}\hfill & e_l,l=1,\dots ,M\hfill \\ 0,\hfill & \text{otherwise},\hfill \end{array}\right.,\hfill \end{array}$$(16) ) with $\tilde{j}={\tilde{j}}^k$, are straightforward [29]:(27) $$\begin{array}{cc}\hfill u_0^k(x,y,z)& =\frac{1}{2\mathit{\pi }{\mathit{\sigma }}_0}{\int }_{\mathrm{\Gamma }}\frac{1}{r_{P{Q}_0}}{j}^k(x^{\prime },y^{\prime })\mathrm{d}{x}^{\prime }\mathrm{d}{y}^{\prime }\hfill \\ \hfill & =\frac{1}{2\mathit{\pi }{\mathit{\sigma }}_0}\sum _{l^{\prime }=M+1}^L\frac{I_{l^{\prime }}^k}{A_{l^{\prime }}}{\int }_{e_{l^{\prime }}}\frac{1}{r_{P{Q}_0}}\mathrm{d}{x}^{\prime }\mathrm{d}{y}^{\prime },k=1,\dots ,L-M-1,\hfill \end{array}$$(27)

and, respectively,(28) $$\begin{array}{cc}\hfill v_0^i(x,y,z)& =\frac{1}{2\mathit{\pi }{\mathit{\sigma }}_0}{\int }_{\mathrm{\Gamma }}\frac{1}{r_{P{Q}_0}}{\tilde{j}}^i(x^{\prime },y^{\prime })\mathrm{d}{x}^{\prime }\mathrm{d}{y}^{\prime }\hfill \\ \hfill & =\frac{1}{2\mathit{\pi }{\mathit{\sigma }}_0}\sum _{l=1}^M\frac{{\tilde{I}}_l^i}{A_l}{\int }_{e_l}\frac{1}{r_{P{Q}_0}}\mathrm{d}{x}^{\prime }\mathrm{d}{y}^{\prime },i=1,\dots ,M-1,\hfill \end{array}$$(28)

where $r_{P{Q}_0}=|P-Q_0|=\sqrt{{(x-x^{\prime })}^2+{(y-y^{\prime })}^2+z^2}$.

In order to compute the entries of the matrix $\mathbf{A}$, we have to discretize the volume integral in (26(26) $$\begin{array}{c}\hfill A(i,k,n)={\int }_{V_n}\mathrm{\nabla }{v}_0^i·\mathrm{\nabla }{u}_0^k\mathrm{d}V.\end{array}$$(26) ). To this end, we follow the same approach as in [20] and we divide each of the voxels into m subvoxels $V_n^j$ ($j=m=1$ for the inner voxels and $j=1,\dots ,m=4$ for the outer ones). Thus, there will be 100 subvoxels of equal volume per layer. The volume of the jth subvoxel of the nth voxel $V_n^j$ is, therefore, $Vo{l}_n^j=12\times 12\times 2=288{\text{mm}}^3$. Using this discretization, and the expressions for $u_0^k$ and $v_0^i$ given by Equations (27(27) $$\begin{array}{cc}\hfill u_0^k(x,y,z)& =\frac{1}{2\mathit{\pi }{\mathit{\sigma }}_0}{\int }_{\mathrm{\Gamma }}\frac{1}{r_{P{Q}_0}}{j}^k(x^{\prime },y^{\prime })\mathrm{d}{x}^{\prime }\mathrm{d}{y}^{\prime }\hfill \\ \hfill & =\frac{1}{2\mathit{\pi }{\mathit{\sigma }}_0}\sum _{l^{\prime }=M+1}^L\frac{I_{l^{\prime }}^k}{A_{l^{\prime }}}{\int }_{e_{l^{\prime }}}\frac{1}{r_{P{Q}_0}}\mathrm{d}{x}^{\prime }\mathrm{d}{y}^{\prime },k=1,\dots ,L-M-1,\hfill \end{array}$$(27) ) and (28(28) $$\begin{array}{cc}\hfill v_0^i(x,y,z)& =\frac{1}{2\mathit{\pi }{\mathit{\sigma }}_0}{\int }_{\mathrm{\Gamma }}\frac{1}{r_{P{Q}_0}}{\tilde{j}}^i(x^{\prime },y^{\prime })\mathrm{d}{x}^{\prime }\mathrm{d}{y}^{\prime }\hfill \\ \hfill & =\frac{1}{2\mathit{\pi }{\mathit{\sigma }}_0}\sum _{l=1}^M\frac{{\tilde{I}}_l^i}{A_l}{\int }_{e_l}\frac{1}{r_{P{Q}_0}}\mathrm{d}{x}^{\prime }\mathrm{d}{y}^{\prime },i=1,\dots ,M-1,\hfill \end{array}$$(28) ), we obtain the following expression for the entries of the matrix $\mathbf{A}$ by evaluating the integral (26(26) $$\begin{array}{c}\hfill A(i,k,n)={\int }_{V_n}\mathrm{\nabla }{v}_0^i·\mathrm{\nabla }{u}_0^k\mathrm{d}V.\end{array}$$(26) ) at the points $P_n^j$, the centres of subvoxels $V_n^j$:(29) $$\begin{array}{cc}\hfill A(i,k,n)=& \sum _{j=1}^m\frac{Vo{l}_n^j}{{(2\mathit{\pi }{\mathit{\sigma }}_0)}^2}\sum _{l=1}^M\sum _{l^{\prime }=M+1}^L\frac{{\tilde{I}}_l^i{I}_{l^{\prime }}^k}{A_l{A}_{l^{\prime }}}\times \hfill \\ \hfill & {\left[{\mathrm{\nabla }}_P{\int }_{e_l}\frac{1}{r_{P{Q}_0}}\mathrm{d}{x}^{\prime }\mathrm{d}{y}^{\prime }\right]}_{P=P_n^j}·{\left[{\mathrm{\nabla }}_P{\int }_{e_{l^{\prime }}}\frac{1}{r_{P{Q}_0}}\mathrm{d}{x}^{\prime }\mathrm{d}{y}^{\prime }\right]}_{P=P_n^j}.\hfill \end{array}$$(29)

In order to evaluate these entries, we have to calculate(30) $$\begin{array}{c}\hfill {\mathrm{\nabla }}_P{\int }_{e_l}\frac{1}{r_{P{Q}_0}}\mathrm{d}{x}^{\prime }\mathrm{d}{y}^{\prime }={\mathrm{\nabla }}_P{\int }_{e_l}\frac{1}{\left|(P-Q_l)-(Q_0-Q_l)\right|}\mathrm{d}{x}^{\prime }\mathrm{d}{y}^{\prime },\text{for}l=1,\dots ,L.\end{array}$$(30)

These quantities were computed analytically by converting the integrals to cylindrical coordinates as follows. Let $(r,\mathit{\theta },z)$ and $(s,\mathit{\vartheta },0)$ be the cylindrical coordinates of $\tilde{P}=P-Q_l$ and ${\tilde{Q}}_0=Q_0-Q_l$, respectively. Specifically, $\tilde{Q}=(\tilde{x},\tilde{y},0)$, where $\tilde{x}=x^{\prime }-x_l=scos(\mathit{\vartheta })$ and $\tilde{y}=y^{\prime }-y_l=ssin(\mathit{\vartheta })$. Then, $r_{P{Q}_0}$ can be expressed in cylindrical coordinates as(31) $$\begin{array}{c}\hfill r_{P{Q}_0}=|\tilde{P}-\tilde{Q}|=\sqrt{r^2+s^2-2rscos(\mathit{\vartheta }-\mathit{\theta })+z^2}.\end{array}$$(31)

It is clear from symmetry that the following integral is independent of the polar angle $\mathit{\theta }$, i.e.(32) $$\begin{array}{cc}\hfill {\int }_{e_l}\frac{1}{r_{P{Q}_0}}\mathrm{d}{x}^{\prime }\mathrm{d}{y}^{\prime }& ={\int }_0^{r_l}{\int }_0^{2\mathit{\pi }}\frac{1}{\sqrt{r^2+s^2-2rscos(\mathit{\vartheta }-\mathit{\theta })+z^2}}s\mathrm{d}s\mathrm{d}\mathit{\vartheta }\hfill \\ \hfill & ={\int }_0^{r_l}{\int }_0^{2\mathit{\pi }}\frac{1}{\sqrt{r^2+s^2-2rscos\mathit{\vartheta }+z^2}}s\mathrm{d}s\mathrm{d}\mathit{\vartheta }.\hfill \end{array}$$(32)

Hence,(33) $$\begin{array}{c}\hfill {\mathrm{\nabla }}_P{\int }_{e_l}\frac{1}{r_{P{Q}_0}}\mathrm{d}{x}^{\prime }\mathrm{d}{y}^{\prime }=\left({\mathbf{e}}_r\frac{\mathit{\partial }}{\mathit{\partial }r}+{\mathbf{e}}_z\frac{\mathit{\partial }}{\mathit{\partial }z}\right){\int }_0^{r_l}{\int }_0^{2\mathit{\pi }}\frac{1}{r_{P{Q}_0}}s\mathrm{d}s\mathrm{d}\mathit{\vartheta },\end{array}$$(33)

with(34) $$\begin{array}{c}\hfill \frac{\mathit{\partial }}{\mathit{\partial }r}{\int }_0^{r_l}{\int }_0^{2\mathit{\pi }}\frac{1}{r_{P{Q}_0}}s\mathrm{d}s\mathrm{d}\mathit{\vartheta }=2\sqrt{\frac{r_l}{r\mathit{\kappa }}}\left[2E\left(\mathit{\kappa }\right)-(2-\mathit{\kappa })K\left(\mathit{\kappa }\right)\right],\end{array}$$(34)

and(35) $$\begin{array}{cc}\hfill \frac{\mathit{\partial }}{\mathit{\partial }z}{\int }_0^{r_l}{\int }_0^{2\mathit{\pi }}\frac{1}{r_{P{Q}_0}}s\mathrm{d}s\mathrm{d}\mathit{\vartheta }& =\frac{1}{2}\sqrt{\frac{\mathit{\kappa }}{r{r}_l}}\left[4zK\left(\mathit{\kappa }\right)-2i\times \left((r-r_l-iz)\mathrm{\Pi }\left(\left.\frac{2r_l}{r+r_l-iz}\right|\mathit{\kappa }\right)\right.\right.\hfill \\ \hfill & +\left.\left.(-r+r_l-iz)\mathrm{\Pi }\left(\left.\frac{2r_l}{r+r_l+iz}\right|\mathit{\kappa }\right)\right)\right],\hfill \end{array}$$(35)

where $\mathit{\kappa }=\frac{4r{r}_l}{{(r+r_l)}^2+z^2}$, and $K(\mathit{\kappa })$, $E(\mathit{\kappa })$ and $\mathrm{\Pi }(n|\mathit{\kappa })$ are the complete elliptic integrals of first, second and third kind, respectively. Further details about these special functions can be found in [36]. Both the r-component and the z-component of the gradient given by Equations (34(34) $$\begin{array}{c}\hfill \frac{\mathit{\partial }}{\mathit{\partial }r}{\int }_0^{r_l}{\int }_0^{2\mathit{\pi }}\frac{1}{r_{P{Q}_0}}s\mathrm{d}s\mathrm{d}\mathit{\vartheta }=2\sqrt{\frac{r_l}{r\mathit{\kappa }}}\left[2E\left(\mathit{\kappa }\right)-(2-\mathit{\kappa })K\left(\mathit{\kappa }\right)\right],\end{array}$$(34) ) and (35(35) $$\begin{array}{cc}\hfill \frac{\mathit{\partial }}{\mathit{\partial }z}{\int }_0^{r_l}{\int }_0^{2\mathit{\pi }}\frac{1}{r_{P{Q}_0}}s\mathrm{d}s\mathrm{d}\mathit{\vartheta }& =\frac{1}{2}\sqrt{\frac{\mathit{\kappa }}{r{r}_l}}\left[4zK\left(\mathit{\kappa }\right)-2i\times \left((r-r_l-iz)\mathrm{\Pi }\left(\left.\frac{2r_l}{r+r_l-iz}\right|\mathit{\kappa }\right)\right.\right.\hfill \\ \hfill & +\left.\left.(-r+r_l-iz)\mathrm{\Pi }\left(\left.\frac{2r_l}{r+r_l+iz}\right|\mathit{\kappa }\right)\right)\right],\hfill \end{array}$$(35) ), respectively, are real valued functions. However, due to numerical inaccuracies in the computer algorithms used to evaluate these functions, there are always some residual imaginary parts in the order of the machine precision. To overcome this issue, only their real parts are considered in further computations.

Note that although in our implementation we preferred to use the above closed form expressions, all these integrals could also be evaluated to great accuracy by using a numerical quadrature method such as boundary elements (see, for example, [37]). This would be more consistent with the numerical experiments where the forward model is a bounded domain but at the cost of increased computation time.

3.3. Construction of matrix $\mathbf{B}$

For the construction of matrix $\mathbf{B}$ given by Equation (24(24) $$\begin{array}{c}\hfill B(i,k)=\sum _{l=1}^M\left(U_{0,l}^k-U_l^k\right){\tilde{I}}_l^i.\end{array}$$(24) ), we need the measured and simulated voltages, $U_l^k$ and $U_{0,l}^k$, respectively.

In practice, the voltages $U_l^k$ are known experimental data. However, as no real data is yet available, in this paper we simulate the measured voltages numerically as explained in Section 4.

In order to find the values of the simulated voltages $U_{0,l}^k$ given by Equation (23(23) $$\begin{array}{c}\hfill U_{0,l}^k=\frac{1}{A_l}{\int }_{e_l}{u}_0^k(x,y,0)\mathrm{d}S.\end{array}$$(23) ), we need to compute first $u_0^k\left(x,y\right)=u_0^k\left(x,y,z=0\right)$ by evaluating the expression in Equation (27(27) $$\begin{array}{cc}\hfill u_0^k(x,y,z)& =\frac{1}{2\mathit{\pi }{\mathit{\sigma }}_0}{\int }_{\mathrm{\Gamma }}\frac{1}{r_{P{Q}_0}}{j}^k(x^{\prime },y^{\prime })\mathrm{d}{x}^{\prime }\mathrm{d}{y}^{\prime }\hfill \\ \hfill & =\frac{1}{2\mathit{\pi }{\mathit{\sigma }}_0}\sum _{l^{\prime }=M+1}^L\frac{I_{l^{\prime }}^k}{A_{l^{\prime }}}{\int }_{e_{l^{\prime }}}\frac{1}{r_{P{Q}_0}}\mathrm{d}{x}^{\prime }\mathrm{d}{y}^{\prime },k=1,\dots ,L-M-1,\hfill \end{array}$$(27) ) at $z=0$. To this end, we use the same change of variables as in section 3.2 and Equation (32(32) $$\begin{array}{cc}\hfill {\int }_{e_l}\frac{1}{r_{P{Q}_0}}\mathrm{d}{x}^{\prime }\mathrm{d}{y}^{\prime }& ={\int }_0^{r_l}{\int }_0^{2\mathit{\pi }}\frac{1}{\sqrt{r^2+s^2-2rscos(\mathit{\vartheta }-\mathit{\theta })+z^2}}s\mathrm{d}s\mathrm{d}\mathit{\vartheta }\hfill \\ \hfill & ={\int }_0^{r_l}{\int }_0^{2\mathit{\pi }}\frac{1}{\sqrt{r^2+s^2-2rscos\mathit{\vartheta }+z^2}}s\mathrm{d}s\mathrm{d}\mathit{\vartheta }.\hfill \end{array}$$(32) ). Note that due to the symmetry considerations of the integral (32(32) $$\begin{array}{cc}\hfill {\int }_{e_l}\frac{1}{r_{P{Q}_0}}\mathrm{d}{x}^{\prime }\mathrm{d}{y}^{\prime }& ={\int }_0^{r_l}{\int }_0^{2\mathit{\pi }}\frac{1}{\sqrt{r^2+s^2-2rscos(\mathit{\vartheta }-\mathit{\theta })+z^2}}s\mathrm{d}s\mathrm{d}\mathit{\vartheta }\hfill \\ \hfill & ={\int }_0^{r_l}{\int }_0^{2\mathit{\pi }}\frac{1}{\sqrt{r^2+s^2-2rscos\mathit{\vartheta }+z^2}}s\mathrm{d}s\mathrm{d}\mathit{\vartheta }.\hfill \end{array}$$(32) ), the solution $u_0^k$ is also independent of the polar angle $\mathit{\theta }$. Hence, $u_0^k\left(r,\mathit{\theta },z=0\right)=u_0^k\left(r\right)$, and we obtain(36) $$\begin{array}{c}\hfill u_0^k\left(r\right)=\frac{1}{2\mathit{\pi }{\mathit{\sigma }}_0}\sum _{l^{\prime }=M+1}^L\frac{I_{l^{\prime }}^k}{A_{l^{\prime }}}{\int }_0^{r_{l^{\prime }}}{\int }_0^{2\mathit{\pi }}\frac{1}{\sqrt{r^2+s^2-2rscos\mathit{\vartheta }}}s\mathrm{d}s\mathrm{d}\mathit{\vartheta },k=1,\dots ,L-M-1.\end{array}$$(36)

The integral in Equation (36(36) $$\begin{array}{c}\hfill u_0^k\left(r\right)=\frac{1}{2\mathit{\pi }{\mathit{\sigma }}_0}\sum _{l^{\prime }=M+1}^L\frac{I_{l^{\prime }}^k}{A_{l^{\prime }}}{\int }_0^{r_{l^{\prime }}}{\int }_0^{2\mathit{\pi }}\frac{1}{\sqrt{r^2+s^2-2rscos\mathit{\vartheta }}}s\mathrm{d}s\mathrm{d}\mathit{\vartheta },k=1,\dots ,L-M-1.\end{array}$$(36) ) can be computed analytically, i.e.(37) $$\begin{array}{c}\hfill {\int }_0^{r_{l^{\prime }}}{\int }_0^{2\mathit{\pi }}\frac{1}{\sqrt{r^2+s^2-2rscos\mathit{\vartheta }}}s\mathrm{d}s\mathrm{d}\mathit{\vartheta }\\ \hfill =2\left(r+r_{l^{\prime }}\right)E\left(\frac{4r{r}_{l^{\prime }}}{{\left(r+r_{l^{\prime }}\right)}^2}\right)-2\left(r-r_{l^{\prime }}\right)K\left(\frac{4r{r}_{l^{\prime }}}{{\left(r+r_{l^{\prime }}\right)}^2}\right).\end{array}$$(37)

Once the currents applied at the active electrodes $I_{l^{\prime }}^k$ are known from measurements, $u_0^k$ can be estimated in a straightforward way using Equations (36(36) $$\begin{array}{c}\hfill u_0^k\left(r\right)=\frac{1}{2\mathit{\pi }{\mathit{\sigma }}_0}\sum _{l^{\prime }=M+1}^L\frac{I_{l^{\prime }}^k}{A_{l^{\prime }}}{\int }_0^{r_{l^{\prime }}}{\int }_0^{2\mathit{\pi }}\frac{1}{\sqrt{r^2+s^2-2rscos\mathit{\vartheta }}}s\mathrm{d}s\mathrm{d}\mathit{\vartheta },k=1,\dots ,L-M-1.\end{array}$$(36) )–(37(37) $$\begin{array}{c}\hfill {\int }_0^{r_{l^{\prime }}}{\int }_0^{2\mathit{\pi }}\frac{1}{\sqrt{r^2+s^2-2rscos\mathit{\vartheta }}}s\mathrm{d}s\mathrm{d}\mathit{\vartheta }\\ \hfill =2\left(r+r_{l^{\prime }}\right)E\left(\frac{4r{r}_{l^{\prime }}}{{\left(r+r_{l^{\prime }}\right)}^2}\right)-2\left(r-r_{l^{\prime }}\right)K\left(\frac{4r{r}_{l^{\prime }}}{{\left(r+r_{l^{\prime }}\right)}^2}\right).\end{array}$$(37) ) at different points on the surfaces of passive electrodes $e_l$, $l=1,\dots ,M$, and then obtain $U_{0,l}^k$ by evaluating numerically the integral in Equation (23(23) $$\begin{array}{c}\hfill U_{0,l}^k=\frac{1}{A_l}{\int }_{e_l}{u}_0^k(x,y,0)\mathrm{d}S.\end{array}$$(23) ).

The simulated currents ${\tilde{\mathbf{I}}}^i=\left({\tilde{I}}_1^i,\dots ,{\tilde{I}}_{16}^i\right)$, $i=1,\dots ,M-1=15$, are assumed to be standard linearly independent trigonometric current patterns, i.e.(38) $$\begin{array}{c}\hfill {\tilde{I}}_l^i=\left\{\begin{array}{cc}cos\left(i(l-1)\frac{2\mathit{\pi }}{M}\right),& i=1,\dots ,\lfloor \frac{M}{2}\rfloor ,\\ sin\left(\left(i-\lfloor \frac{M}{2}\rfloor \right)(l-1)\frac{2\mathit{\pi }}{M}\right),& i=\lfloor \frac{M}{2}\rfloor ,\dots ,M-1,\end{array}\right.\end{array}$$(38)

and $l=1,\cdots ,M$.

4. Numerical examples

In this section, we present some reconstructions obtained by applying the above reconstruction algorithm to simulated data. The set-up of our numerical tests mimicked closely the laboratory experiments presented in [23,24]. We considered a rectangular tank of length $L\left(=15\text{cm}\right)$, width $W\left(=15\text{cm}\right)$ and height $H\left(=7.5\text{cm}\right)$ which contained an isotropic medium of conductivity approximately equal to that of healthy breast tissue, ${\mathit{\sigma }}_0=200$ mS/m. The rectangular array of electrodes was placed at the centre of the top of the tank (i.e. $z=0$ cm). The dimensions of the tank were much larger than those of the electrode array (7.2 cm$\times$7.2 cm) and of the voxel configuration (12 cm$\times$12 cm$\times$1 cm) used for conductivity reconstructions, thus approximating an infinite half space.

Figure 3. Conductivity reconstructions for a cylindrical object of radius $R_{25}$ of conductivity 800 mS/m placed at position P1 and $z=-2$ mm. The thick continuous line in (e) marks the position and the height of the inclusion along the z-axis.

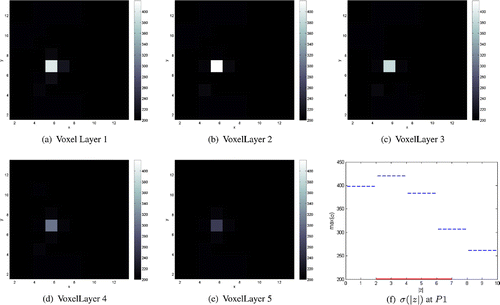
Figure 4. Conductivity reconstructions for a cylindrical object of radius $R_{25}$ of conductivity 800 mS/m placed at position P1 and $z=-3$ mm. The thick continuous line in (e) marks the position and the height of the inclusion along the z-axis.

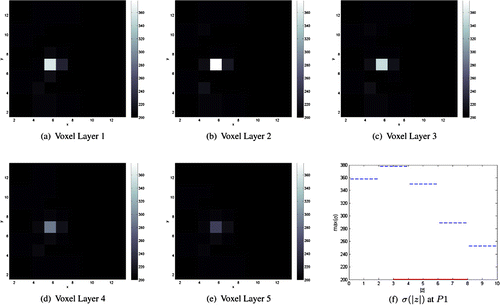
Figure 5. Conductivity reconstructions for a cylindrical object of radius $R_{25}$ of conductivity 800 mS/m placed at position P1 and $z=-6$ mm. The thick continuous line in (e) marks the position and the height of the inclusion along the z-axis.

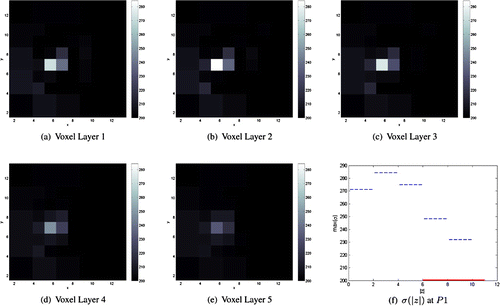
Figure 6. Conductivity reconstructions for a cylindrical object of radius $R_{35}$ of conductivity 800 mS/m placed at position P2 and $z=-3$ mm. The thick continuous line in (e) marks the position and the height of the inclusion along the z-axis.

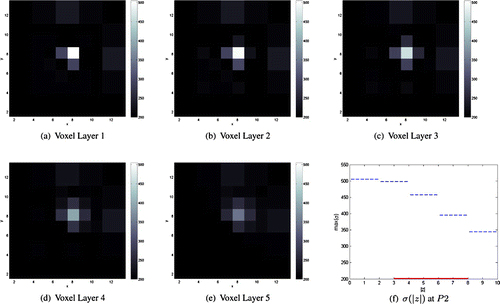
Figure 7. Conductivity reconstructions for a cylindrical object of radius $R_{25}$ of conductivity 800 mS/m placed at position P2 and $z=-3$ mm. The thick continuous line in (e) marks the position and the height of the inclusion along the z-axis.

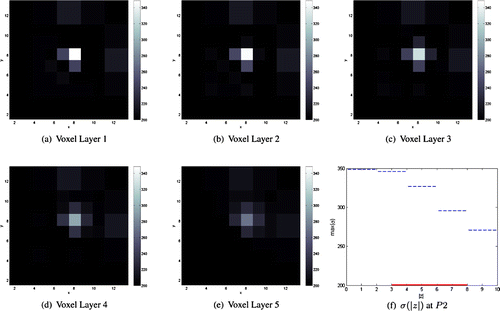
Figure 8. Conductivity reconstructions for a cylindrical object of radius $R_{15}$ of conductivity 800mS/m placed at position P2 and $z=-3$ mm. The thick continuous line in (e) marks the position and the height of the inclusion along the z-axis.

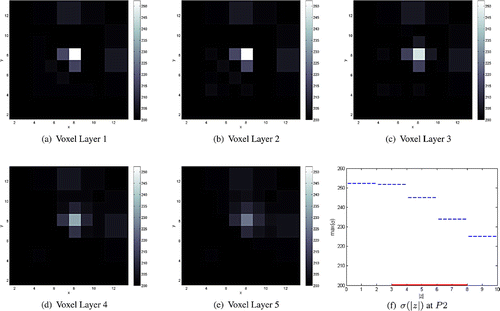
Figure 9. Conductivity reconstructions for a cylindrical object of radius $R_{25}$ of conductivity 800 mS/m placed at position P3 and $z=-3$ mm.

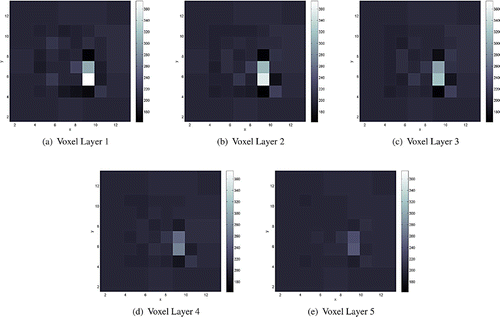
Figure 10. Conductivity reconstructions for a cylindrical object of radius $R_{25}$ of conductivity 800 mS/m placed at position P4 and $z=-3$ mm.

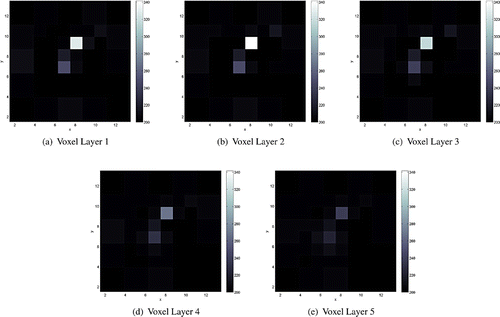
Figure 11. Conductivity reconstructions for a cylindrical object of radius $R_{35}$ of conductivity 800 mS/m placed at position P1 and $z=-4$ mm in the presence of a resistive medium (50 mS/m) in Voxel Layer 1. The thick continuous line in (e) marks the position and the height of the inclusion along the z-axis.

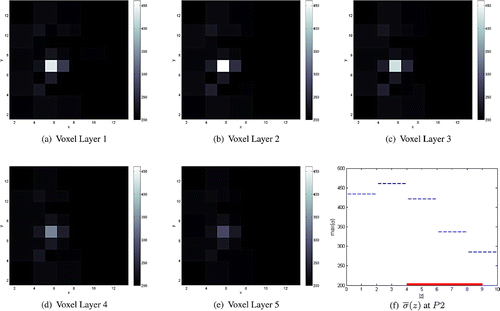
Figure 12. Conductivity reconstructions for two cylindrical objects of radii $R_{25}$ and $R_{15}$ of conductivities 800 mS/m placed at positions P5 and P6, respectively, and $z=-3$ mm.

Figure 13. Conductivity reconstructions for two cylindrical objects, one of radius $R_{25}$ and of conductivity 600 mS/m, and the other of radius $R_{15}$ and of conductivity 800 mS/m, placed at positions P5 and P6, respectively, and $z=-3$ mm.

Cylindrical inclusions of radii $R_{15}=1.5$ mm, $R_{25}=2.5$ mm and/or $R_{35}=3.5$ mm, heights $h=5$ mm and conductivities $\mathit{\sigma }=800$ mS/m or 600mS/m were then placed on below positions $P1-P5$ in the xy-plane (see Figure 2) and at different depths z. Note that the largest cylindrical object $R_{35}$ has the same radius as the electrodes, while the other two, $R_{25}$ and $R_{15}$, have much smaller radii. P1, P2 and P5 in Figure 2 are positions directly below a passive electrode, while P4 and P5 are positions between the passive electrodes.

To simulate the measured values of the potential on the boundary, we first had to solve the direct problem (1(1) $$\begin{array}{c}\hfill \mathrm{\nabla }·\left(\mathit{\sigma }(x,y,z)\mathrm{\nabla }u(x,y,z)\right)=0\text{in}\mathrm{\Omega },\end{array}$$(1) )–(8(8) $$\begin{array}{c}\hfill j(x,y)=\left\{\begin{array}{cc}{I}_l/A_l,& (x,y)\text{on}{e}_l,l=M+1,\dots ,L\\ 0,& \text{otherwise},\end{array}\right.\end{array}$$(8) ). In order to avoid inverse crimes and to test the robustness of our inversion techniques, we used EIDORS [38] as a forward solver. EIDORS is a finite element software package which has no connection with the reconstruction method under consideration. Current patterns similar to those defined in Equation (38(38) $$\begin{array}{c}\hfill {\tilde{I}}_l^i=\left\{\begin{array}{cc}cos\left(i(l-1)\frac{2\mathit{\pi }}{M}\right),& i=1,\dots ,\lfloor \frac{M}{2}\rfloor ,\\ sin\left(\left(i-\lfloor \frac{M}{2}\rfloor \right)(l-1)\frac{2\mathit{\pi }}{M}\right),& i=\lfloor \frac{M}{2}\rfloor ,\dots ,M-1,\end{array}\right.\end{array}$$(38) ) were applied at the active electrodes, ${\mathbf{I}}^k=\left(I_{17}^k,\dots ,I_{36}^k\right)$, $k=1,\dots ,L-M-1=19$. The direct problem was solved for each of the 19 different current patterns and we obtain the values of the corresponding voltages at the passive electrodes ${\mathbf{U}}^k=\left(U_1^k,\dots ,U_{16}^k\right)$, $k=1,\dots ,19$, by interpolating the numerical solution at points on the surface of the electrodes and evaluating numerically the integral in Equation (9(9) $$\begin{array}{c}\hfill U_l^k=\frac{1}{A_l}{\int }_{e_l}{u}^k(x,y,0)\mathrm{d}S,l=1,\dots ,M.\end{array}$$(9) ). This was the data used by our reconstruction algorithm. The conductivities of all $N=260$ voxels were obtained by inverting the over-determined linear system of Equations (25(25) $$\begin{array}{c}\hfill B(i,k)=\sum _{n=1}^{N}A(i,k,n)\mathit{\delta }{\mathit{\sigma }}_n,k=1,\dots ,L-M-1\text{and}i=1,\dots ,M,\end{array}$$(25) ). In the numerical examples considered, singular values smaller than $\mathit{ϵ}={10}^{-5}$ were cut off (i.e. 35 singular values were used in the reconstructions).

In EIT a noise level of $1\%$ is reasonable in many circumstances, but in some medical applications greater accuracy can be achieved.[39] However, since our reconstruction method is quite stable with respect to the noise level in the data, in all the numerical examples discussed below, we present reconstruction results for data with $2\%$ additive Gaussian random errors. Note that in all figures presented below the colour ranges are the same for each subplot. Moreover, the homogeneity properties of the proposed algorithm are good as, although not displayed here, we were able to reconstruct a uniform distribution of conductivity of 200 mS/m using simulated data for the tank with no inclusions.

In Figures 3–5, we present the conductivity reconstructions for the medium size cylindrical object of radius $R_{25}$ and conductivity 800mS/m (i.e. four times higher than the background conductivity) placed below position P1 (i.e. below an electrode and next to an active electrode) and at depths $z=-2$, $-3$ and $-6$mm, respectively, from the array of electrodes. The position of the inclusion in the xy-plane was successfully recovered in all three cases but the reconstructed conductivity values were smaller than the actual conductivity values. This difficulty in recovering the amplitude of high contrast conductivities is a common feature of EIT linearization methods, see for example [20,22,40]. We also found that estimating the depth of the inhomogeneity was more ill-posed than reconstructing its position in the xy-plane. For an inclusion placed at this position, the values of the reconstructed conductivities at position P1 were larger in the upper voxel layers with a maximum value attained in the second layer irrespective of the depths of the inclusions. However, the deeper the object, the smaller the values of the reconstructed conductivity. This suggests that some information about the depth location of the inclusions is present in the data, but as seen from Figures 3 and 4 there is limited information about objects’ heights as it seems as if the inclusion extends over all five voxel layers. This conclusion is in agreement with our findings in [24].

To test the spatial resolution of our algorithm, we placed cylindrical inclusions of conductivity 800 mS/m and of different radii $R_{35}$, $R_{25}$ and $R_{15}$ at position P2 (i.e. below an electrode, but further away from the active electrodes) and depth $z=-3$ mm. The numerical results can be found in Figures 6–8, respectively. Similar to the previous numerical experiments, the position of the inclusion in the plane of electrodes was well characterized. The values of the reconstructed conductivities at position P2 were also smaller than the true ones, but overall larger in the upper voxel layers with a maximum value attained in the first layer in this case. Moreover, as expected, the smaller the size of the inhomogeneity, the smaller were the values of the reconstructed conductivity. Note that, by using the electrode array and the experimental set-up under consideration as well as the proposed three-dimensional reconstruction algorithm, we managed to detect inhomogeneities which are much smaller in size (i.e. a cylinder of radius $R_{15}$ and height 5 mm whose conductivity is only four times higher than the background) and up to larger depths than in [20,23,24].

When a cylindrical inhomogeneity of radius $R_{25}$ and of conductivity 800 mS/m was placed on a position between two electrodes, P3, or in the middle of four neighbouring electrodes, P4, then the conductivity of all two or four adjacent voxels was much larger than that of the background, see Figures 9 and 10.

Next we demonstrate that the detection of a small conductive inhomogeneity is not affected by the presence of a more resistive tissue layer (i.e. the skin) at the surface. To this end, we included a 2 mm thick resistive layer of conductivity 50 mS/m layer directly under the surface. A cylindrical object of radius $R_{35}$ was positioned at P1 and $z=-4$ mm. As seen from the numerical reconstructions presented in Figure 11, the presence of the object is visible and its position in the xy-plane is well characterized.

The final simulations included in the paper consist of reconstructions of two conductive objects of radii $R_{25}$ and $R_{15}$ placed at positions P5 and P6, respectively, and at the same depth ($z=-3$ mm). Firstly, in Figure 12 we present the results obtained when the two inclusions have the same conductivity (800 mS/m). In this case, the presence of the smaller cylindrical object ($R_{15}$) is slightly shielded by the larger object ($R_{25}$). Then, in Figure 13 we show the reconstructions of objects of different conductivities (600 mS/m and 800 mS/m, respectively) when the presence of the smaller object is more pronounced.

5. Conclusion

In this article, we have presented a three-dimensional non-iterative reconstruction method developed for conductivity imaging in breast cancer detection using real data from a planar EIT device developed at the University of Mainz in collaboration with Oxford Brookes University. The head of the sensor contains both active electrodes, where standard trigonometric current patterns are applied, and passive electrodes, where the induced voltages are measured, arranged in a rectangular array. A finite region beneath the surface was discretized into voxels of different sizes depending on their position relative to the electrode array and their conductivities were determined from the data measured on the electrode array. The reconstruction algorithm is based on linearizing the conductivity about a constant value. It is simple, direct and fast, and it allows reconstructions in real-time.

The performance of the algorithm was tested on numerically simulated data. Small inclusions of various conductivities placed at several depths were detected and their positions in the plane of the electrode array were successfully recovered. Although the depth resolution is rather poor, the reconstructions have good spatial resolution in the xy-plane and are quite stable with respect to the noise level in the data. The most relevant feature is the fact that it can detect smaller objects up to larger depths than the other two-dimensional non-iterative approaches developed for similar planar EIT devices in [23,24]. In future, we plan to obtain reconstructions from real data and try to improve the depth resolution of the algorithm by possibly imposing a priori and/or a posteriori sparsity constraints on the reconstructed conductivity values in each voxel.

Acknowledgements

The authors would like to express their gratitude to Professor Khaled Hayatleh for a number of useful conversations concerning this work.

Notes

No potential conflict of interest was reported by the authors.