A global domain/boundary integral equation method for the inverse wave source and backward wave problems

Abstract

A g-analytic function theory, the Cauchy–Riemann equations of g-analytic function and the g-conformal invariant for the wave equation are derived in this paper. As a consequence, there exist two global spectral relations for the wave equation. By suitably choosing two different types of Trefftz test functions in the derived Green’s second identity, we can recover unknown wave source function very well using the global domain/boundary integral equation method (BIEM), which is robust against large noise up to $20\%$. Then, we develop a numerical algorithm based on the BIEM, which is effective for the backward wave problem, as well as for the long-term solution of the wave equation. Numerical examples are used to demonstrate the efficiency and accuracy of these methods.

Keywords:

• Backward wave problem
• inverse wave source problem
• g-analytic function theory
• Green’s second identity
• global domain/boundary integral equation method

AMS Subject Classifications:

• 65M32

1. Introduction

The wave motions appear in many engineering problems, for example, the stress wave in solids, the wave propagation in fluids, the scattering problems of electromagnetic waves, the sound wave propagation in media and the phase transformation kinetics.[1,2] There are many available methods for solving the wave equations of direct problems.[3–8]

Sometimes, we may encounter the problem that the wave source function F(x, t) in the wave equation is unknown. To resolve such an inverse wave source problem using the control results of distributed systems has been developed by Yamamoto [9,10], Bruckner and Yamamoto [11], and Yamamoto and Zhang [12]. They used some observability estimates and controllability results, and used the multiplier method and the Hilbert uniqueness method to deduce the uniqueness of solution and the reconstruction process. For the wave equation, this method successfully leads to the reconstruction of point sources in a one-dimensional domain by boundary observations. In higher dimensional domains, the reciprocity gap functional technique leads to the reconstruction of smooth unknown sources using boundary observations.[13,14] Komornik and Yamamoto [15] have determined the positions of point sources in a one-dimensional wave equation, and later the estimation results are extended to multi-dimension in [16]. Most researchers are concerned with the determination of point sources. We will develop a novel and powerful method for the recovery of space-time varying wave source in a one-dimensional wave equation using two extra measurements of displacement and velocity at a final time.

Then, for the Dirichlet problem of the wave equation:(1) $$\begin{array}{cc}\hfill \frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{t}^2}& =c^2\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2},(x,t)\in \mathrm{\Omega }:=\{0<x<\ell ,0<t\le t_f\},\hfill \end{array}$$(1) (2) $$\begin{array}{cc}\hfill u(0,t)& =u_0(t),u(\ell ,t)=u_{\ell }(t),0\le t\le t_f,\hfill \end{array}$$(2) (3) $$\begin{array}{cc}\hfill u(x,0)& =f(x),u(x,t_f)=h(x),0\le x\le \ell ,\hfill \end{array}$$(3)

which is also known as the backward wave problem (BWP), we will recover the initial velocity:(4) $$\begin{array}{c}\hfill u_t(x,0)=g(x).\end{array}$$(4)

The BWP is a boundary value problem in space-time domain for the wave equation, which looks like the interior problem of Laplace equation. However, the properties of these two problems are drastically different.[17] From the aspect of wave control, this inverse wave problem is solving the problem that given what initial condition of $u_t(x,0)$, the wave at a time $t_f$ will vibrate under the desired quantity h(x). The BWP as pointed out by Ames and Straugham [18] has important applications in geophysics and optimal control theory.

The BWP is an ill-posed problem, which has been studied by Bourgin and Duffin [19], John [20], Fox and Pucci [21], Dunninger and Zachmanoglou [22], Abdul-Latif and Diaz [23], Papi Frosali [24], Levine and Vessella [25], Vakhania [26], and Kabanikhin and Bektemesov [27]. Sobolev [28] has studied the ill-posed property of the corresponding first-order hyperbolic system under imposed boundary conditions. Bourgin and Duffin [19] and Abdul-Latif and Diaz [23] have proved that the BWP has a unique solution only when $c{t}_f/\ell$=irrational. But when $c{t}_f/\ell$=rational, the uniqueness is not satisfied. Liu [29] has proposed a second-kind Fredholm integral regularization method to solve the BWP.

In this paper, we are going to develop a novel boundary integral equation method (BIEM) to solve both the BWP and the wave source recovery problem. This method has been firstly developed by Liu [30] to solve the Cauchy problem and the source recovery problem of the Poisson equation, and then Liu [31] and Liu and Chang [32] extended this method to recover unknown space and time-dependent heat source. The advantages of BIEM are easy to be numerically implemented, stable and accurate for solving the inverse problems. Although there are many numerical methods which can be used to recover the initial velocity from the terminal data observation for the one-dimensional wave equation, the present method is a promising one to cover the related inverse problems of one-dimensional wave equation.

The remaining portion of this paper is arranged as follows. In Section 2, we introduce a g-number in the Minkowski space as a frame to study the wave equation, where the Minkowskian polar coordinates of the wave equation are introduced. In Section 3, we develop a new g-analytic function theory for the g-function, and the Cauchy–Riemann equations of g-analytic function and the g-conformal invariant are introduced for the wave equation. The Green’s second identity and two global spectral relations are proved in Section 4. Then, a numerical algorithm of the BIEM based on the derived global relation is developed in Section 5 for the Dirichlet problem of the wave equation, whose numerical examples are given in Section 6. For the inverse wave source problem, by imposing the extra measurements of displacement and velocity at a final time, we recover the unknown wave source function in Section 7 using a global domain/BIEM. For a long-term solution of the wave equation, we introduce another BIEM and numerical examples are given in Section 8. Finally, some conclusions are addressed in Section 9.

2. The Minkowski space ${\mathbb{M}}^{1,1}$

2.1. Mathematical preliminaries of g-function

Liu [33] has introduced the g number $w=x+gy$, where 1 and g are bases of a Jordan algebraic system which obey the following binary product rule:

Using $g^2:=g·g=1$ in the series expansion of $e^{g\mathit{\theta }}$,$$e^{g\mathit{\theta }}=1+g\mathit{\theta }+\frac{1}{2}{g}^2{\mathit{\theta }}^2+\cdots ,$$

it is easy to deduce(5) $$\begin{array}{c}\hfill e^{g\mathit{\theta }}=cosh\mathit{\theta }+gsinh\mathit{\theta }.\end{array}$$(5)

As pointed out by Liu [34] the g-number bears certain similarity with the complex number, and it forms a Jordan algebra, which is a special case of the double numbers introduced by Yaglom [35]. The applications of the Jordan algebra can refer [36,37]. As the definition for the complex function, a function with $w=x+gy$ as an independent variable is called the g-function.

2.2. The wave equation in the Minkowski space ${\mathbb{M}}^{1,1}$

Through a suitable transformation of the t coordinate in Equation (1(1) $$\begin{array}{cc}\hfill \frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{t}^2}& =c^2\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2},(x,t)\in \mathrm{\Omega }:=\{0<x<\ell ,0<t\le t_f\},\hfill \end{array}$$(1) ), it is always that ${(ct)}^2>x^2$ for all $(x,t)\in \mathrm{\Omega }$ with |x| bounded. In our problem, the spatial domain is fixed with $\ell >0$ a finite value, and the time is always going ahead. We take t to be a new time coordinate with $t=\mathit{\tau }+t_0$, where $\mathit{\tau }>0$ is the original time and $t_0=\ell /c$. Then, we have $ct=c\mathit{\tau }+c{t}_0>\ell$, and on the other hand $0<x<\ell$, such that we have ${(ct)}^2-x^2>0$ in the problem domain $\mathrm{\Omega }$.

Let(6) $$\begin{array}{cc}\hfill y& :=ct,\hfill \end{array}$$(6) (7) $$\begin{array}{cc}\hfill (r,\mathit{\theta })& :=\left(\sqrt{y^2-x^2},ln\sqrt{\frac{y+x}{y-x}}\right),\hfill \end{array}$$(7) (8) $$\begin{array}{cc}\hfill x& :=rsinh\mathit{\theta },y:=rcosh\mathit{\theta }.\hfill \end{array}$$(8)

We must emphasize that $y^2-x^2>0$ in the domain $\mathrm{\Omega }$ and then the definitions (8(8) $$\begin{array}{cc}\hfill x& :=rsinh\mathit{\theta },y:=rcosh\mathit{\theta }.\hfill \end{array}$$(8) ) and (9(9) $$\begin{array}{c}\hfill w=y+gx=r{e}^{g\mathit{\theta }}.\end{array}$$(9) ) make sense. So a time-like point can be expressed as(9) $$\begin{array}{c}\hfill w=y+gx=r{e}^{g\mathit{\theta }}.\end{array}$$(9)

The pair $(r,\mathit{\theta })$ is named the Minkowskian polar coordinates. According to Equation (7(7) $$\begin{array}{cc}\hfill (r,\mathit{\theta })& :=\left(\sqrt{y^2-x^2},ln\sqrt{\frac{y+x}{y-x}}\right),\hfill \end{array}$$(7) ), Equation (1(1) $$\begin{array}{cc}\hfill \frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{t}^2}& =c^2\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2},(x,t)\in \mathrm{\Omega }:=\{0<x<\ell ,0<t\le t_f\},\hfill \end{array}$$(1) ) can be written as(10) $$\begin{array}{c}\hfill \frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{y}^2}-\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}=0.\end{array}$$(10)

The above form is the wave equation in the Minkowski space ${\mathbb{M}}^{1,1}$.

3. The g-analytic function and Cauchy–Riemann equations

The g-analytic function theory for the wave equation was first developed by Liu [17]. For the g number $w=y+gx$, we can view it as a point in the Minkowski space ${\mathbb{M}}^{1,1}$, and $w^{\prime }=y^{\prime }+g{x}^{\prime }=e^{g\mathit{\theta }}(y+gx)$ can be deemed as a rotation of w in ${\mathbb{M}}^{1,1}$:(11) $$\begin{array}{c}\hfill \left[\begin{array}{c}{y}^{\prime }\\ x^{\prime }\end{array}\right]=\left[\begin{array}{cc}cosh\mathit{\theta }& sinh\mathit{\theta }\\ sinh\mathit{\theta }& cosh\mathit{\theta }\end{array}\right]\left[\begin{array}{c}y\\ x\end{array}\right].\end{array}$$(11)

Before the proof of Theorem 1, we need the following Lemma.

Lemma 1:

A matrix$$\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]$$

represents a multiplication by a g-number if and only if $a=d$ and $b=c$. The g-number in the multiplication is $a+gc=d+gb$.

Proof:

Let us consider the multiplication by the g-number $a+gc$. It sends $y+gx$ to $(a+gc)(y+gx)=ay+cx+g(ax+cy)$, which is the same as$$\left[\begin{array}{cc}a& c\\ c& a\end{array}\right]\left[\begin{array}{c}y\\ x\end{array}\right].$$

In converse, we have$$\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]\left[\begin{array}{c}y\\ x\end{array}\right]=w(y+gx)$$

for a g-number $w=\mathit{\alpha }+g\mathit{\beta }$. Then, we obtain$$\begin{array}{cc}& ay+bx=\mathit{\alpha }y+\mathit{\beta }x,\hfill \\ \hfill & cy+\mathrm{d}x=\mathit{\alpha }x+\mathit{\beta }y\hfill \end{array}$$

for all (x, y). They imply $a=\mathit{\alpha }=d$ and $b=\mathit{\beta }=c$, and so the proof is finished. $\square$

For simple notation, we let ${\mathbb{M}}^{+}$ be the future cone in ${\mathbb{M}}^{1,1}$ with $(x,y)\in {\mathbb{M}}^{1,1}$ a time-like vector, $y^2-x^2>0$ and $y>0$. The following results also hold for the space-like vector $(x,y)\in {\mathbb{M}}^{1,1}$, $x^2-y^2>0$.

Theorem 1:

Let $f:=u+gv:\mathcal{D}\subset {\mathbb{M}}^{+}\mapsto {\mathbb{M}}^{+}$ be a given g-function, with $\mathcal{D}$ an open set in the future cone. Then, $f^{\prime }(w_0)$ exists if and only if f is a differentiable function in the sense of real variable and, at $(x_0,y_0)=w_0$, u and v satisfy the Cauchy–Riemann equations:(12) $$\begin{array}{c}\hfill \frac{\mathit{\partial }u(x,y)}{\mathit{\partial }x}=\frac{\mathit{\partial }v(x,y)}{\mathit{\partial }y},\frac{\mathit{\partial }u(x,y)}{\mathit{\partial }y}=\frac{\mathit{\partial }v(x,y)}{\mathit{\partial }x}.\end{array}$$(12)

Thus, if $\mathit{\partial }u/\mathit{\partial }x$, $\mathit{\partial }u/\mathit{\partial }y$, $\mathit{\partial }v/\mathit{\partial }x$ and $\mathit{\partial }v/\mathit{\partial }y$ exist, then f is analytic on $\mathcal{D}$. If $f^{\prime }(w_0)$ does exist, then(13) $$\begin{array}{c}\hfill f^{\prime }(w_0)=\frac{\mathit{\partial }u(x,y)}{\mathit{\partial }x}+g\frac{\mathit{\partial }v(x,y)}{\mathit{\partial }x}=\frac{\mathit{\partial }v(x,y)}{\mathit{\partial }y}+g\frac{\mathit{\partial }u(x,y)}{\mathit{\partial }y}.\end{array}$$(13)

Proof:

A separate and more direct proof is given in [17]. From the definition of $f^{\prime }$, the statement that $f^{\prime }(w_0)$ exists is equivalent to the statement that for any $\mathit{\epsilon }>0$, there is a $\mathit{\delta }>0$ such that $|w-w_0|<\mathit{\delta }$ implies(14) $$\begin{array}{c}\hfill |f(w)-f(w_0)-f^{\prime }(w_0)(w-w_0)|<\mathit{\epsilon }|w-w_0|.\end{array}$$(14)

We recall that $Df(x_0,y_0)$ is the unique matrix with the property that for any $\mathit{\epsilon }>0$, there is a $\mathit{\delta }>0$, such that using $w=(x,y)$ and $w_0=(x_0,y_0)$, $|w-w_0|<\mathit{\delta }$ implies that(15) $$\begin{array}{c}\hfill |f(w)-f(w_0)-Df(w_0)(w-w_0)|<\mathit{\epsilon }|w-w_0|.\end{array}$$(15)

If we compare Equation (16(16) $$\begin{array}{c}\hfill Df(w_0)=\left[\begin{array}{cc}{u}_x& u_y\\ v_x& v_y\end{array}\right]\end{array}$$(16) ) with Equation (15(15) $$\begin{array}{c}\hfill |f(w)-f(w_0)-Df(w_0)(w-w_0)|<\mathit{\epsilon }|w-w_0|.\end{array}$$(15) ), and recall that the multiplication by a g-number is a linear map, we conclude that f is differentiable, and that the matrix $Df(w_0)$ exactly represents the multiplication by the g-number $f^{\prime }(w_0)$. Thus, applying Lemma 1 to the following matrix:(16) $$\begin{array}{c}\hfill Df(w_0)=\left[\begin{array}{cc}{u}_x& u_y\\ v_x& v_y\end{array}\right]\end{array}$$(16)

with $a=u_x$, $b=u_y$, $c=v_x$ and $d=v_y$, we have $a=d$ and $b=c$, which are the Cauchy–Riemann equations (13(13) $$\begin{array}{c}\hfill f^{\prime }(w_0)=\frac{\mathit{\partial }u(x,y)}{\mathit{\partial }x}+g\frac{\mathit{\partial }v(x,y)}{\mathit{\partial }x}=\frac{\mathit{\partial }v(x,y)}{\mathit{\partial }y}+g\frac{\mathit{\partial }u(x,y)}{\mathit{\partial }y}.\end{array}$$(13) ). Conversely, if the Cauchy–Riemann Equations (13(13) $$\begin{array}{c}\hfill f^{\prime }(w_0)=\frac{\mathit{\partial }u(x,y)}{\mathit{\partial }x}+g\frac{\mathit{\partial }v(x,y)}{\mathit{\partial }x}=\frac{\mathit{\partial }v(x,y)}{\mathit{\partial }y}+g\frac{\mathit{\partial }u(x,y)}{\mathit{\partial }y}.\end{array}$$(13) ) hold, $Df(w_0)$ represents the multiplication by a g-number as stated in Lemma 1, and then as above the definition of differentiability in the sense of real variables reduces to that for the derivative of g-variable function. The formula for $f^{\prime }(w_0)$ follows from the last statement in Lemma 1. $\square$

The analytic function is well developed in the complex theory. In order to distinct the present analytic function with that in the complex theory, we call it the g-analytic function with its real and g parts satisfying the Cauchy–Riemann Equations (13(13) $$\begin{array}{c}\hfill f^{\prime }(w_0)=\frac{\mathit{\partial }u(x,y)}{\mathit{\partial }x}+g\frac{\mathit{\partial }v(x,y)}{\mathit{\partial }x}=\frac{\mathit{\partial }v(x,y)}{\mathit{\partial }y}+g\frac{\mathit{\partial }u(x,y)}{\mathit{\partial }y}.\end{array}$$(13) ). Next, we prove that

Theorem 2:

Let $f:\mathcal{D}\subset {\mathbb{M}}^{+}\mapsto {\mathbb{M}}^{+}$ be a g-analytic function, with $f(w)=u(x,y)+gv(x,y)$. Then, u and v satisfy the wave Equation (11(11) $$\begin{array}{c}\hfill \left[\begin{array}{c}{y}^{\prime }\\ x^{\prime }\end{array}\right]=\left[\begin{array}{cc}cosh\mathit{\theta }& sinh\mathit{\theta }\\ sinh\mathit{\theta }& cosh\mathit{\theta }\end{array}\right]\left[\begin{array}{c}y\\ x\end{array}\right].\end{array}$$(11) ):(17) $$\begin{array}{cc}\hfill \frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{y}^2}-\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}& =0,\hfill \end{array}$$(17) (18) $$\begin{array}{cc}\hfill \frac{{\mathit{\partial }}^{2}v}{\mathit{\partial }{y}^2}-\frac{{\mathit{\partial }}^{2}v}{\mathit{\partial }{x}^2}& =0.\hfill \end{array}$$(18)

Proof:

From Equation (13(13) $$\begin{array}{c}\hfill f^{\prime }(w_0)=\frac{\mathit{\partial }u(x,y)}{\mathit{\partial }x}+g\frac{\mathit{\partial }v(x,y)}{\mathit{\partial }x}=\frac{\mathit{\partial }v(x,y)}{\mathit{\partial }y}+g\frac{\mathit{\partial }u(x,y)}{\mathit{\partial }y}.\end{array}$$(13) ), it follows that$$\begin{array}{cc}\hfill \frac{{\mathit{\partial }}^{2}u(x,y)}{\mathit{\partial }{y}^2}& =\frac{{\mathit{\partial }}^{2}v(x,y)}{\mathit{\partial }x\mathit{\partial }y},\hfill \\ \hfill \frac{{\mathit{\partial }}^{2}u(x,y)}{\mathit{\partial }{x}^2}& =\frac{{\mathit{\partial }}^{2}v(x,y)}{\mathit{\partial }y\mathit{\partial }x}.\hfill \end{array}$$

Subtracting the above two equations, we obtain Equation (18(18) $$\begin{array}{cc}\hfill \frac{{\mathit{\partial }}^{2}v}{\mathit{\partial }{y}^2}-\frac{{\mathit{\partial }}^{2}v}{\mathit{\partial }{x}^2}& =0.\hfill \end{array}$$(18) ). On the other hand, Equation (13(13) $$\begin{array}{c}\hfill f^{\prime }(w_0)=\frac{\mathit{\partial }u(x,y)}{\mathit{\partial }x}+g\frac{\mathit{\partial }v(x,y)}{\mathit{\partial }x}=\frac{\mathit{\partial }v(x,y)}{\mathit{\partial }y}+g\frac{\mathit{\partial }u(x,y)}{\mathit{\partial }y}.\end{array}$$(13) ) renders$$\begin{array}{cc}\hfill \frac{{\mathit{\partial }}^{2}v(x,y)}{\mathit{\partial }{y}^2}& =\frac{{\mathit{\partial }}^{2}u(x,y)}{\mathit{\partial }x\mathit{\partial }y},\hfill \\ \hfill \frac{{\mathit{\partial }}^{2}v(x,y)}{\mathit{\partial }{x}^2}& =\frac{{\mathit{\partial }}^{2}u(x,y)}{\mathit{\partial }y\mathit{\partial }x}.\hfill \end{array}$$

A similar procedure leads to Equation (19(19) $$\begin{array}{c}\hfill \frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{\mathit{\eta }}^2}-\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{\mathit{\xi }}^2}=0,\end{array}$$(19) ). $\square$

Theorem 3:

Let $f:\mathcal{D}\subset {\mathbb{M}}^{+}\mapsto {\mathbb{M}}^{+}$ be a g-analytic function, with $\mathit{\xi }+g\mathit{\eta }=f(w)=\mathit{\xi }(x,y)+g\mathit{\eta }(x,y)$ being a g-conformal mapping from (x, y) to $(\mathit{\xi },\mathit{\eta })$. Then, the wave Equation (11(11) $$\begin{array}{c}\hfill \left[\begin{array}{c}{y}^{\prime }\\ x^{\prime }\end{array}\right]=\left[\begin{array}{cc}cosh\mathit{\theta }& sinh\mathit{\theta }\\ sinh\mathit{\theta }& cosh\mathit{\theta }\end{array}\right]\left[\begin{array}{c}y\\ x\end{array}\right].\end{array}$$(11) ) is invariant under the g-conformal mapping, i.e.(19) $$\begin{array}{c}\hfill \frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{\mathit{\eta }}^2}-\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{\mathit{\xi }}^2}=0,\end{array}$$(19)

Proof:

Let the new variables $(\mathit{\xi },\mathit{\eta })$ be(20) $$\begin{array}{c}\hfill \mathit{\xi }=\mathit{\xi }(x,y),\mathit{\eta }=\mathit{\eta }(x,y).\end{array}$$(20)

Assume that $\mathit{\xi }$ and $\mathit{\eta }$ are twice continuously differentiable and that the Jacobian matrix is non-singular in the considered domain:(21) $$\begin{array}{c}\hfill J={\mathit{\xi }}_x{\mathit{\eta }}_y-{\mathit{\eta }}_x{\mathit{\xi }}_y\ne 0.\end{array}$$(21)

Because $\mathit{\xi }+g\mathit{\eta }$ is a g-analytic function, by Theorem 1, $(\mathit{\xi },\mathit{\eta })$ satisfy the Cauchy–Riemann equations:(22) $$\begin{array}{c}\hfill {\mathit{\xi }}_x(x,y)={\mathit{\eta }}_y(x,y),{\mathit{\xi }}_y(x,y)={\mathit{\eta }}_x(x,y),\end{array}$$(22)

and, by Theorem 2, the wave equations:(23) $$\begin{array}{c}\hfill {\mathit{\xi }}_{yy}-{\mathit{\xi }}_{xx}=0,{\mathit{\eta }}_{yy}-{\mathit{\eta }}_{xx}=0.\end{array}$$(23)

Through some elementary operations, we can derive(24) $$\begin{array}{cc}\hfill u_{xx}& =u_{\mathit{\xi }\mathit{\xi }}{\mathit{\xi }}_x^2+2u_{\mathit{\xi }\mathit{\eta }}{\mathit{\xi }}_x{\mathit{\eta }}_x+u_{\mathit{\eta }\mathit{\eta }}{\mathit{\eta }}_x^2+u_{\mathit{\xi }}{\mathit{\xi }}_{xx}+u_{\mathit{\eta }}{\mathit{\eta }}_{xx},\hfill \end{array}$$(24) (25) $$\begin{array}{cc}\hfill u_{yy}& =u_{\mathit{\xi }\mathit{\xi }}{\mathit{\xi }}_y^2+2u_{\mathit{\xi }\mathit{\eta }}{\mathit{\xi }}_y{\mathit{\eta }}_y+u_{\mathit{\eta }\mathit{\eta }}{\mathit{\eta }}_y^2+u_{\mathit{\xi }}{\mathit{\xi }}_{yy}+u_{\mathit{\eta }}{\mathit{\eta }}_{yy}.\hfill \end{array}$$(25)

Inserting them into Equation (11(11) $$\begin{array}{c}\hfill \left[\begin{array}{c}{y}^{\prime }\\ x^{\prime }\end{array}\right]=\left[\begin{array}{cc}cosh\mathit{\theta }& sinh\mathit{\theta }\\ sinh\mathit{\theta }& cosh\mathit{\theta }\end{array}\right]\left[\begin{array}{c}y\\ x\end{array}\right].\end{array}$$(11) ), we have(26) $$\begin{array}{cc}\hfill u_{yy}-u_{xx}& =u_{\mathit{\xi }\mathit{\xi }}({\mathit{\xi }}_y^2-{\mathit{\xi }}_x^2)+2u_{\mathit{\xi }\mathit{\eta }}({\mathit{\xi }}_y{\mathit{\eta }}_y-{\mathit{\xi }}_x{\mathit{\eta }}_x)\hfill \\ \hfill & +u_{\mathit{\eta }\mathit{\eta }}({\mathit{\eta }}_y^2-{\mathit{\eta }}_x^2)+u_{\mathit{\xi }}({\mathit{\xi }}_{yy}-{\mathit{\xi }}_{xx})+u_{\mathit{\eta }}({\mathit{\eta }}_{yy}-{\mathit{\eta }}_{xx})=0,\hfill \end{array}$$(26)

which, using Equations (23(23) $$\begin{array}{c}\hfill {\mathit{\xi }}_{yy}-{\mathit{\xi }}_{xx}=0,{\mathit{\eta }}_{yy}-{\mathit{\eta }}_{xx}=0.\end{array}$$(23) ) and (24(24) $$\begin{array}{cc}\hfill u_{xx}& =u_{\mathit{\xi }\mathit{\xi }}{\mathit{\xi }}_x^2+2u_{\mathit{\xi }\mathit{\eta }}{\mathit{\xi }}_x{\mathit{\eta }}_x+u_{\mathit{\eta }\mathit{\eta }}{\mathit{\eta }}_x^2+u_{\mathit{\xi }}{\mathit{\xi }}_{xx}+u_{\mathit{\eta }}{\mathit{\eta }}_{xx},\hfill \end{array}$$(24) ) reduces to(27) $$\begin{array}{c}\hfill u_{yy}-u_{xx}=(u_{\mathit{\eta }\mathit{\eta }}-u_{\mathit{\xi }\mathit{\xi }})({\mathit{\xi }}_x^2-{\mathit{\xi }}_y^2)=0.\end{array}$$(27)

From Equations (22(22) $$\begin{array}{c}\hfill {\mathit{\xi }}_x(x,y)={\mathit{\eta }}_y(x,y),{\mathit{\xi }}_y(x,y)={\mathit{\eta }}_x(x,y),\end{array}$$(22) ) and (23(23) $$\begin{array}{c}\hfill {\mathit{\xi }}_{yy}-{\mathit{\xi }}_{xx}=0,{\mathit{\eta }}_{yy}-{\mathit{\eta }}_{xx}=0.\end{array}$$(23) ) it follows that(28) $$\begin{array}{c}\hfill J={\mathit{\xi }}_x{\mathit{\eta }}_y-{\mathit{\eta }}_x{\mathit{\xi }}_y={\mathit{\xi }}_x^2-{\mathit{\xi }}_y^2\ne 0.\end{array}$$(28)

Then, in view of Equations (28(28) $$\begin{array}{c}\hfill J={\mathit{\xi }}_x{\mathit{\eta }}_y-{\mathit{\eta }}_x{\mathit{\xi }}_y={\mathit{\xi }}_x^2-{\mathit{\xi }}_y^2\ne 0.\end{array}$$(28) ) and (29(29) $$\begin{array}{c}\hfill \square u(x,y)=u_{yy}-u_{xx}.\end{array}$$(29) ), we end the proof of this theorem. $\square$

Theorem 3 is similar to that for the Laplace equation, which under a conformal mapping performed by an analytic function is invariant. Due to this similarity, we have called the mapping from (x, y) to $(\mathit{\xi },\mathit{\eta })$ performed by a g-analytic function a g-conformal mapping.

4. Green’s second identity

We will demonstrate the Green’s second identity for the Dirichlet wave problem (1(1) $$\begin{array}{cc}\hfill \frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{t}^2}& =c^2\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2},(x,t)\in \mathrm{\Omega }:=\{0<x<\ell ,0<t\le t_f\},\hfill \end{array}$$(1) )–(4(4) $$\begin{array}{c}\hfill u_t(x,0)=g(x).\end{array}$$(4) ). The Cauchy integral formula is very important for the Laplace equation, which renders a famous Poisson integral formula, where u is fully determined by the boundary values of u on the circle. But for the boundary value problem of the wave equation, i.e. BWP, we cannot derive a similar formula.[17]

Before embarking the derivation of Green’s second identity for the wave equation, we introduce the wave operator:(29) $$\begin{array}{c}\hfill \square u(x,y)=u_{yy}-u_{xx}.\end{array}$$(29)

Lemma 2:

(Green’s Theorem in the plane)Let $\mathrm{\Omega }$ be a bounded region in the plane (x, y) with a counter-clockwise contour $\mathrm{\Gamma }$ consists of finitely many smooth curves. Let $F_1(x,y)$ and $F_2(x,y)$ be functions that are differentiable in $\mathrm{\Omega }$ and continuous on $\overline{\mathrm{\Omega }}$. Then,(30) $$\begin{array}{c}\hfill \int {\int }_{\mathrm{\Omega }}\left[\frac{\mathit{\partial }{F}_2}{\mathit{\partial }x}-\frac{\mathit{\partial }{F}_1}{\mathit{\partial }y}\right]\mathrm{d}x\mathrm{d}y={\oint }_{\mathrm{\Gamma }}(F_1\mathrm{d}x+F_2\mathrm{d}y).\end{array}$$(30)

Using Lemma 2, we can prove the Green’s second identity for the wave operator.

Theorem 4:

(Green’s second identity)Let $\mathrm{\Omega }$ be a bounded region in the plane (x, y) with a counter-clockwise contour $\mathrm{\Gamma }$ consists of finitely many smooth curves. Let u(x, y) and v(x, y) be functions that are differentiable in $\mathrm{\Omega }$ and continuous on $\overline{\mathrm{\Omega }}$. Then,(31) $$\begin{array}{c}\hfill \int {\int }_{\mathrm{\Omega }}(u\square v-v\square u)\mathrm{d}\mathit{\sigma }={\oint }_{\mathrm{\Gamma }}(u{v}_{\mathrm{T}}-v{u}_{\mathrm{T}})\mathrm{d}s,\end{array}$$(31)

where $\mathrm{d}\mathit{\sigma }=\mathrm{d}y\mathrm{d}x=-\mathrm{d}x\mathrm{d}y$ is an area element in the plane and the subscript $\mathrm{T}$ denotes the directional derivative with respect to the tangent $\mathbf{T}=(\mathrm{d}y/\mathrm{d}s,\mathrm{d}x/\mathrm{d}s)$.

Proof:

Let(32) $$\begin{array}{c}\hfill F_1=u{v}_y-v{u}_y,F_2=u{v}_x-v{u}_x,\end{array}$$(32)

which being inserted into the left-hand side of Equation (31(31) $$\begin{array}{c}\hfill \int {\int }_{\mathrm{\Omega }}(u\square v-v\square u)\mathrm{d}\mathit{\sigma }={\oint }_{\mathrm{\Gamma }}(u{v}_{\mathrm{T}}-v{u}_{\mathrm{T}})\mathrm{d}s,\end{array}$$(31) ) and according to the definition (30(30) $$\begin{array}{c}\hfill \int {\int }_{\mathrm{\Omega }}\left[\frac{\mathit{\partial }{F}_2}{\mathit{\partial }x}-\frac{\mathit{\partial }{F}_1}{\mathit{\partial }y}\right]\mathrm{d}x\mathrm{d}y={\oint }_{\mathrm{\Gamma }}(F_1\mathrm{d}x+F_2\mathrm{d}y).\end{array}$$(30) ), leads to(33) $$\begin{array}{c}\hfill \int {\int }_{\mathrm{\Omega }}\left[\frac{\mathit{\partial }{F}_2}{\mathit{\partial }x}-\frac{\mathit{\partial }{F}_1}{\mathit{\partial }y}\right]\mathrm{d}x\mathrm{d}y=\int {\int }_{\mathrm{\Omega }}(u\square v-v\square u)\mathrm{d}y\mathrm{d}x.\end{array}$$(33)

From Equation (33(33) $$\begin{array}{c}\hfill \int {\int }_{\mathrm{\Omega }}\left[\frac{\mathit{\partial }{F}_2}{\mathit{\partial }x}-\frac{\mathit{\partial }{F}_1}{\mathit{\partial }y}\right]\mathrm{d}x\mathrm{d}y=\int {\int }_{\mathrm{\Omega }}(u\square v-v\square u)\mathrm{d}y\mathrm{d}x.\end{array}$$(33) ), it follows that(34) $$\begin{array}{cc}\hfill F_1\mathrm{d}x+F_2\mathrm{d}y& =(u{v}_y-v{u}_y)\mathrm{d}x+(u{v}_x-v{u}_x)\mathrm{d}y\hfill \\ \hfill & =u(v_y\mathrm{d}x+v_x\mathrm{d}y)-v(u_y\mathrm{d}x+u_x\mathrm{d}y)=(u\mathrm{\nabla }v·\mathbf{T}-v\mathrm{\nabla }u·\mathbf{T})\mathrm{d}s,\hfill \end{array}$$(34)

where $\mathbf{T}=(\mathrm{d}y/\mathrm{d}s,\mathrm{d}x/\mathrm{d}s)$. Inserting it into the right-hand side of Equation (31(31) $$\begin{array}{c}\hfill \int {\int }_{\mathrm{\Omega }}(u\square v-v\square u)\mathrm{d}\mathit{\sigma }={\oint }_{\mathrm{\Gamma }}(u{v}_{\mathrm{T}}-v{u}_{\mathrm{T}})\mathrm{d}s,\end{array}$$(31) ) and equating to Equation (34(34) $$\begin{array}{cc}\hfill F_1\mathrm{d}x+F_2\mathrm{d}y& =(u{v}_y-v{u}_y)\mathrm{d}x+(u{v}_x-v{u}_x)\mathrm{d}y\hfill \\ \hfill & =u(v_y\mathrm{d}x+v_x\mathrm{d}y)-v(u_y\mathrm{d}x+u_x\mathrm{d}y)=(u\mathrm{\nabla }v·\mathbf{T}-v\mathrm{\nabla }u·\mathbf{T})\mathrm{d}s,\hfill \end{array}$$(34) ), the proof is finished. $\square$

We note that $\mathrm{d}\mathit{\sigma }=\mathrm{d}y\mathrm{d}x=-\mathrm{d}x\mathrm{d}y$ and $\mathbf{T}=(\mathrm{d}y/\mathrm{d}s,\mathrm{d}x/\mathrm{d}s)$ in Theorem 4, which are different from that with $\mathrm{d}x\mathrm{d}y$ and $\mathrm{d}\mathbf{r}/\mathrm{d}s=(\mathrm{d}x/\mathrm{d}s,\mathrm{d}y/\mathrm{d}s)$ as the area element and the tangential direction used in the Green’s second identity for the Laplace equation. Here, we interchange (x, y) to (y, x).

The above approach of Green’s second identity in a finite space-time domain is different from that in [38], of which the latter is for the purpose of the construction of a Green function in the infinite space domain. On the other hand, in the canonical coordinates system for the application of Green theorem to construct the Riemann function, one can refer [39,40].

We use the following examples to demonstrate the Green’s second identity for the wave equation.

Example 1:

Let$$u=x^2+y^2+xy,v=xy,$$

with $\square u=\square v=0$. The closed curve is given by $\mathrm{\Gamma }={\mathrm{\Gamma }}_1\cup {\mathrm{\Gamma }}_2\cup {\mathrm{\Gamma }}_3\cup {\mathrm{\Gamma }}_4$$=\{0\le x\le a,y=0\}\cup \{x=a,0\le y\le b\}\cup \{0\le x\le a,y=b\}\cup \{x=0,0\le y\le b\}$. Inserting them into the following integral, we have$$\begin{array}{ccc}& {\oint }_{\mathrm{\Gamma }}(u{v}_y-v{u}_y)\mathrm{d}x+(u{v}_x-v{u}_x)\mathrm{d}y\hfill & \hfill ={\int }_0^a{x}^3\mathrm{d}x+{\int }_0^b(y^3-a^{2}y)\mathrm{d}y\\ \hfill & -{\int }_0^a(x^3-b^{2}x)\mathrm{d}x-{\int }_0^b{y}^3\mathrm{d}y\hfill \\ \hfill & =\frac{a^4}{4}+\frac{b^4}{4}-\frac{a^2{b}^2}{2}+\frac{a^2{b}^2}{2}-\frac{a^4}{4}-\frac{b^4}{4}=0.\hfill \\ \hfill \end{array}$$

This shows the identity in Equation (32(32) $$\begin{array}{c}\hfill F_1=u{v}_y-v{u}_y,F_2=u{v}_x-v{u}_x,\end{array}$$(32) ).

Example 2:

In contrast, for$$u=x^2+y^2+xy,v=x{y}^2,$$

with $\square u=0$ and $\square v=2x\ne 0$, and $a=b=1$ in $\mathrm{\Gamma }$ of Example 1, one has$${\oint }_{\mathrm{\Gamma }}(u{v}_y-v{u}_y)\mathrm{d}x+(u{v}_x-v{u}_x)\mathrm{d}y=-\frac{7}{6}\ne 0.$$

On the other hand, one has$$\begin{array}{cc}\hfill \int {\int }_{\mathrm{\Omega }}(u\square v-v\square u)\mathrm{d}y\mathrm{d}x& =-\int {\int }_{\mathrm{\Omega }}(u\square v-v\square u)\mathrm{d}x\mathrm{d}y\hfill \\ \hfill & =-{\int }_0^1{\int }_0^{1}2(x^3+x^{2}y+x{y}^2)\mathrm{d}x\mathrm{d}y=-\frac{7}{6},\hfill \end{array}$$

which justifies the result of Equation (32(32) $$\begin{array}{c}\hfill F_1=u{v}_y-v{u}_y,F_2=u{v}_x-v{u}_x,\end{array}$$(32) ) in Theorem 4, because both the values on the left-hand side and right-hand side are equal to $-7/6$.

We have the following important results.

Theorem 5:

(Global relation) For the Dirichlet wave problem in Equations (1(1) $$\begin{array}{cc}\hfill \frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{t}^2}& =c^2\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2},(x,t)\in \mathrm{\Omega }:=\{0<x<\ell ,0<t\le t_f\},\hfill \end{array}$$(1) )–(4(4) $$\begin{array}{c}\hfill u_t(x,0)=g(x).\end{array}$$(4) ), the initial velocity g(x) satisfies the following global relation:(35) $$\begin{array}{cc}\hfill {\oint }_{\mathrm{\Gamma }}(u{v}_{\mathrm{T}}-v{u}_{\mathrm{T}})\mathrm{d}s& ={\int }_0^{\ell }[f(x)v_t(x,0)-v(x,0)g(x)]\mathrm{d}x\hfill \\ \hfill & +{\int }_0^{t_f}[u_{\ell }(t)v_x(\ell ,t)-v(\ell ,t)u_x(\ell ,t)]\mathrm{d}t\hfill \\ \hfill & -{\int }_0^{\ell }[h(x)v_t(x,t_f)-v(x,t_f)u_t(x,t_f)]\mathrm{d}x\hfill \\ \hfill & -{\int }_0^{t_f}[u_0(t)v_x(0,t)-v(0,t)u_x(0,t)]\mathrm{d}t=0,\hfill \end{array}$$(35)

for any function v with $\square v=0$.

Proof:

Inserting $\square u=0$ and $\square v=0$ into Equation (32(32) $$\begin{array}{c}\hfill F_1=u{v}_y-v{u}_y,F_2=u{v}_x-v{u}_x,\end{array}$$(32) ), integrating along the contour $\mathrm{\Gamma }={\mathrm{\Gamma }}_1\cup {\mathrm{\Gamma }}_2\cup {\mathrm{\Gamma }}_3\cup {\mathrm{\Gamma }}_4$$=\{0\le x\le \ell ,y=0\}\cup \{x=\ell ,0\le y\le t_f\}\cup \{0\le x\le \ell ,y=t_f\}\cup \{x=0,0\le y\le t_f\}$, and inserting the corresponding conditions in Equations (2(2) $$\begin{array}{cc}\hfill u(0,t)& =u_0(t),u(\ell ,t)=u_{\ell }(t),0\le t\le t_f,\hfill \end{array}$$(2) )–(4(4) $$\begin{array}{c}\hfill u_t(x,0)=g(x).\end{array}$$(4) ), we can prove this theorem. $\square$

We can decompose the wave Equation (11(11) $$\begin{array}{c}\hfill \left[\begin{array}{c}{y}^{\prime }\\ x^{\prime }\end{array}\right]=\left[\begin{array}{cc}cosh\mathit{\theta }& sinh\mathit{\theta }\\ sinh\mathit{\theta }& cosh\mathit{\theta }\end{array}\right]\left[\begin{array}{c}y\\ x\end{array}\right].\end{array}$$(11) ) into(36) $$\begin{array}{c}\hfill \left(\frac{\mathit{\partial }}{\mathit{\partial }y}+g\frac{\mathit{\partial }}{\mathit{\partial }x}\right)\left(\frac{\mathit{\partial }}{\mathit{\partial }y}-g\frac{\mathit{\partial }}{\mathit{\partial }x}\right)u=0,\end{array}$$(36)

and hence derive a neater form:(37) $$\begin{array}{c}\hfill \frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }w\mathit{\partial }\overline{w}}=0,\end{array}$$(37)

where $w=y+gx$ and $\overline{w}=y-gx$.

Theorem 6:

(Global spectral relation)Let $\mathrm{\Omega }$ be a bounded region in the plane (x, y) with a counter-clockwise contour $\mathrm{\Gamma }$ consists of finitely many smooth curves. Let $v(x,y)=e^{-g\mathit{\lambda }w}$ be a solution of Equation (38(38) $$\begin{array}{c}\hfill {\oint }_{\mathrm{\Gamma }}{e}^{-g\mathit{\lambda }w}\left(\frac{\mathit{\partial }u}{\mathit{\partial }\mathrm{T}}+\mathit{\lambda }u\frac{\mathrm{d}w}{\mathrm{d}s}\right)\mathrm{d}s=0,\end{array}$$(38) ), and then for any solution u of the wave equation, we have the following global spectral relation:(38) $$\begin{array}{c}\hfill {\oint }_{\mathrm{\Gamma }}{e}^{-g\mathit{\lambda }w}\left(\frac{\mathit{\partial }u}{\mathit{\partial }\mathrm{T}}+\mathit{\lambda }u\frac{\mathrm{d}w}{\mathrm{d}s}\right)\mathrm{d}s=0,\end{array}$$(38)

where $w=y+gx$ and $\mathit{\lambda }$ is a given g-value spectrum.

Proof:

First, it is easy to check that(39) $$\begin{array}{c}\hfill v=e^{-g\mathit{\lambda }w}\end{array}$$(39)

is a solution of Equation (38(38) $$\begin{array}{c}\hfill {\oint }_{\mathrm{\Gamma }}{e}^{-g\mathit{\lambda }w}\left(\frac{\mathit{\partial }u}{\mathit{\partial }\mathrm{T}}+\mathit{\lambda }u\frac{\mathrm{d}w}{\mathrm{d}s}\right)\mathrm{d}s=0,\end{array}$$(38) ). Then, by letting$$w=y+gx,\overline{w}=y-gx,$$

we have$$\begin{array}{cc}\hfill x& =\frac{g}{2}(w-\overline{w}),\hfill \\ \hfill y& =\frac{1}{2}(w+\overline{w}),\hfill \\ \hfill \frac{\mathit{\partial }v}{\mathit{\partial }y}& =\frac{\mathit{\partial }v}{\mathit{\partial }w}+\frac{\mathit{\partial }v}{\mathit{\partial }\overline{w}},\hfill \\ \hfill \frac{\mathit{\partial }v}{\mathit{\partial }x}& =g\frac{\mathit{\partial }v}{\mathit{\partial }w}-g\frac{\mathit{\partial }v}{\mathit{\partial }\overline{w}}.\hfill \end{array}$$

Then, through some operations, we can derive(40) $$\begin{array}{c}\hfill \frac{\mathit{\partial }v}{\mathit{\partial }\mathrm{T}}\mathrm{d}s=\frac{\mathit{\partial }v}{\mathit{\partial }x}\mathrm{d}y+\frac{\mathit{\partial }v}{\mathit{\partial }y}\mathrm{d}x=-\mathit{\lambda }{e}^{-g\mathit{\lambda }w}\mathrm{d}w.\end{array}$$(40)

Inserting $\square v=0$, $\square u=0$ and the above equation into Equation (32(32) $$\begin{array}{c}\hfill F_1=u{v}_y-v{u}_y,F_2=u{v}_x-v{u}_x,\end{array}$$(32) ), we can obtain(41) $$\begin{array}{c}\hfill {\oint }_{\mathrm{\Gamma }}(-u\mathit{\lambda }{e}^{-g\mathit{\lambda }w}\mathrm{d}w-v{u}_{\mathrm{T}}\mathrm{d}s)=0.\end{array}$$(41)

By inserting Equation (40(40) $$\begin{array}{c}\hfill \frac{\mathit{\partial }v}{\mathit{\partial }\mathrm{T}}\mathrm{d}s=\frac{\mathit{\partial }v}{\mathit{\partial }x}\mathrm{d}y+\frac{\mathit{\partial }v}{\mathit{\partial }y}\mathrm{d}x=-\mathit{\lambda }{e}^{-g\mathit{\lambda }w}\mathrm{d}w.\end{array}$$(40) ) for v and removing the common term $e^{-g\mathit{\lambda }w}$ outside the brace, we can derive Equation (39(39) $$\begin{array}{c}\hfill v=e^{-g\mathit{\lambda }w}\end{array}$$(39) ). This ends the proof. $\square$

A simpler one is obtained from Equation (38(38) $$\begin{array}{c}\hfill {\oint }_{\mathrm{\Gamma }}{e}^{-g\mathit{\lambda }w}\left(\frac{\mathit{\partial }u}{\mathit{\partial }\mathrm{T}}+\mathit{\lambda }u\frac{\mathrm{d}w}{\mathrm{d}s}\right)\mathrm{d}s=0,\end{array}$$(38) ):(42) $$\begin{array}{c}\hfill \frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }w\mathit{\partial }\overline{w}}=0\iff \frac{\mathit{\partial }}{\mathit{\partial }\overline{w}}\left(e^{-g\mathit{\lambda }w}\frac{\mathit{\partial }u}{\mathit{\partial }w}\right)=0.\end{array}$$(42)

Integrating it with respect to $\mathrm{d}\overline{w}\mathrm{d}w$ inside a domain $\mathrm{\Omega }$, and then changing the domain integral into an integral along a closed contour, we have(43) $$\begin{array}{c}\hfill {\oint }_{\mathrm{\Gamma }}\left(e^{-g\mathit{\lambda }w}\frac{\mathit{\partial }u}{\mathit{\partial }w}\right)\mathrm{d}w=0.\end{array}$$(43)

The above two equalities in Equations (39(39) $$\begin{array}{c}\hfill v=e^{-g\mathit{\lambda }w}\end{array}$$(39) ) and (44(44) $$\begin{array}{c}\hfill v(x,t)=sin\frac{k\mathit{\pi }x}{\ell }sin\frac{k\mathit{\pi }(t-t_f)}{\ell },\end{array}$$(44) ) with respect to any spectral value $\mathit{\lambda }$ provide the global spectral relations, which are similar to that for the Laplace equation discussed by Fokas and his co-workers [41–43].

5. The numerical algorithm of BIEM

In Theorem 5, we can choose a simple test function v(x, t), such that Equation (36(36) $$\begin{array}{c}\hfill \left(\frac{\mathit{\partial }}{\mathit{\partial }y}+g\frac{\mathit{\partial }}{\mathit{\partial }x}\right)\left(\frac{\mathit{\partial }}{\mathit{\partial }y}-g\frac{\mathit{\partial }}{\mathit{\partial }x}\right)u=0,\end{array}$$(36) ) can be easily used to solve g(x). For this purpose, we can take(44) $$\begin{array}{c}\hfill v(x,t)=sin\frac{k\mathit{\pi }x}{\ell }sin\frac{k\mathit{\pi }(t-t_f)}{\ell },\end{array}$$(44)

which is a solution of the wave equation for each $k\in \mathbb{N}$. Because v(x, t) automatically satisfies the wave equation, it is a Trefftz test function. Inserting(45) $$\begin{array}{cc}\hfill v(0,t)& =0,v(\ell ,t)=0,v(x,t_f)=0,v(x,0)=-sin\frac{k\mathit{\pi }{t}_f}{\ell }sin\frac{k\mathit{\pi }x}{\ell },\hfill \\ \hfill v_t(x,0)& =\frac{k\mathit{\pi }}{\ell }cos\frac{k\mathit{\pi }{t}_f}{\ell }sin\frac{k\mathit{\pi }x}{\ell },v_t(x,t_f)=\frac{k\mathit{\pi }}{\ell }sin\frac{k\mathit{\pi }x}{\ell },\hfill \\ \hfill v_x(0,t)& =\frac{k\mathit{\pi }}{\ell }sin\frac{k\mathit{\pi }(t-t_f)}{\ell },v_x(\ell ,t)=\frac{k\mathit{\pi }}{\ell }cos(k\mathit{\pi })sin\frac{k\mathit{\pi }(t-t_f)}{\ell }\hfill \end{array}$$(45)

into Equation (36(36) $$\begin{array}{c}\hfill \left(\frac{\mathit{\partial }}{\mathit{\partial }y}+g\frac{\mathit{\partial }}{\mathit{\partial }x}\right)\left(\frac{\mathit{\partial }}{\mathit{\partial }y}-g\frac{\mathit{\partial }}{\mathit{\partial }x}\right)u=0,\end{array}$$(36) ), we can derive(46) $$\begin{array}{ccc}& {\int }_0^{\ell }sin\frac{k\mathit{\pi }{t}_f}{\ell }sin\frac{k\mathit{\pi }x}{\ell }g(x)\mathrm{d}x\hfill & \hfill ={\int }_0^{\ell }\frac{k\mathit{\pi }}{\ell }sin\frac{k\mathit{\pi }x}{\ell }\left[h(x)-f(x)cos\frac{k\mathit{\pi }{t}_f}{\ell }\right]\mathrm{d}x\\ \hfill & +{\int }_0^{t_f}\frac{k\mathit{\pi }}{\ell }sin\frac{k\mathit{\pi }(t-t_f)}{\ell }\hfill \\ \hfill & \times [u_0(t)-u_{\ell }(t)cos(k\mathit{\pi })]\mathrm{d}t=:C_k,\hfill \end{array}$$(46)

where $C_k$ is a different constant for different k.

Hence, we can obtain(47) $$\begin{array}{c}\hfill {\int }_0^{\ell }sin\frac{k\mathit{\pi }x}{\ell }g(x)\mathrm{d}x=e_k,\end{array}$$(47)

where $e_k=C_k/sin(k\mathit{\pi }{t}_f/\ell )$ and $sin(k\mathit{\pi }{t}_f/\ell )\ne 0$ because $t_f/\ell$ is an irrational number. Let(48) $$\begin{array}{c}\hfill g(x)=a_0+\sum _{j=1}^m{a}_{j}cos(jx)+b_{j}sin(jx).\end{array}$$(48)

Inserting it into Equation (48(48) $$\begin{array}{c}\hfill g(x)=a_0+\sum _{j=1}^m{a}_{j}cos(jx)+b_{j}sin(jx).\end{array}$$(48) ), we can derive a linear system:(49) $$\begin{array}{c}\hfill \mathbf{A}\mathbf{c}=\mathbf{e},\end{array}$$(49)

where(50) $$\begin{array}{cc}\hfill \mathbf{e}& :={[e_1\dots e_n]}^{\text{T}},\hfill \\ \hfill \mathbf{c}& :={[a_1\dots a_m{b}_1\dots b_m{a}_0]}^{\text{T}},\hfill \\ \hfill A_{k,j}& =\frac{1-cos(k\mathit{\pi }+j\ell )}{2\left(\frac{k\mathit{\pi }}{\ell }+j\right)}+\frac{1-cos(k\mathit{\pi }-j\ell )}{2\left(\frac{k\mathit{\pi }}{\ell }-j\right)},j=1,\dots ,m,\hfill \\ \hfill A_{k,m+j}& =\frac{sin(k\mathit{\pi }-j\ell )}{2\left(\frac{k\mathit{\pi }}{\ell }-j\right)}-\frac{sin(k\mathit{\pi }+j\ell )}{2\left(\frac{k\mathit{\pi }}{\ell }+j\right)},j=1,\dots ,m,\hfill \\ \hfill A_{k,n}& =\frac{\ell }{k\mathit{\pi }}[1-cos(k\mathit{\pi })],\hfill \end{array}$$(50)

in which $A_{k,j}$ is the kj-component of $\mathbf{A}$.

Instead of Equation (50(50) $$\begin{array}{cc}\hfill \mathbf{e}& :={[e_1\dots e_n]}^{\text{T}},\hfill \\ \hfill \mathbf{c}& :={[a_1\dots a_m{b}_1\dots b_m{a}_0]}^{\text{T}},\hfill \\ \hfill A_{k,j}& =\frac{1-cos(k\mathit{\pi }+j\ell )}{2\left(\frac{k\mathit{\pi }}{\ell }+j\right)}+\frac{1-cos(k\mathit{\pi }-j\ell )}{2\left(\frac{k\mathit{\pi }}{\ell }-j\right)},j=1,\dots ,m,\hfill \\ \hfill A_{k,m+j}& =\frac{sin(k\mathit{\pi }-j\ell )}{2\left(\frac{k\mathit{\pi }}{\ell }-j\right)}-\frac{sin(k\mathit{\pi }+j\ell )}{2\left(\frac{k\mathit{\pi }}{\ell }+j\right)},j=1,\dots ,m,\hfill \\ \hfill A_{k,n}& =\frac{\ell }{k\mathit{\pi }}[1-cos(k\mathit{\pi })],\hfill \end{array}$$(50) ), we can solve a normal linear system:(51) $$\begin{array}{c}\hfill \mathbf{D}\mathbf{c}={\mathbf{b}}_1,\end{array}$$(51)

where(52) $$\begin{array}{c}\hfill {\mathbf{b}}_1:={\mathbf{A}}^{\text{T}}\mathbf{e},\mathbf{D}:={\mathbf{A}}^{\text{T}}\mathbf{A}>\mathbf{0}.\end{array}$$(52)

The algorithm of conjugate gradient method (CGM) for solving Equation (52(52) $$\begin{array}{c}\hfill {\mathbf{b}}_1:={\mathbf{A}}^{\text{T}}\mathbf{e},\mathbf{D}:={\mathbf{A}}^{\text{T}}\mathbf{A}>\mathbf{0}.\end{array}$$(52) ) is summarized as follows.

(i)

Give an initial ${\mathbf{c}}_0$ and then compute ${\mathbf{r}}_0=\mathbf{D}{\mathbf{c}}_0-{\mathbf{b}}_1$ and set ${\mathbf{p}}_0={\mathbf{r}}_0$.

(ii)

For $k=0,1,2,\dots$, we repeat the following iterations:(53) $$\begin{array}{cc}\hfill {\mathit{\eta }}_k& =\frac{\Vert {\mathbf{r}}_k{\Vert }^2}{{\mathbf{p}}_k^{\text{T}}\mathbf{D}{\mathbf{p}}_k},\hfill \\ \hfill {\mathbf{c}}_{k+1}& ={\mathbf{c}}_k-{\mathit{\eta }}_k{\mathbf{p}}_k,\hfill \\ \hfill {\mathbf{r}}_{k+1}& =\mathbf{D}{\mathbf{c}}_{k+1}-{\mathbf{b}}_1,\hfill \\ \hfill {\mathit{\alpha }}_{k+1}& =\frac{\Vert {\mathbf{r}}_{k+1}{\Vert }^2}{\Vert {\mathbf{r}}_k{\Vert }^2},\hfill \\ \hfill {\mathbf{p}}_{k+1}& ={\mathit{\alpha }}_{k+1}{\mathbf{p}}_k+{\mathbf{r}}_{k+1}.\hfill \end{array}$$(53) If ${\mathbf{c}}_{k+1}$ converges according to a given stopping criterion $\Vert {\mathbf{r}}_{k+1}\Vert <\mathit{\epsilon }$, then stop; otherwise, go to step (ii).

6. Numerical examples of Dirichlet problems

Now, we are ready to apply the novel BIEM to the BWP, which is a problem that with $u_t(x,0)=g(x)$ in Equation (4(4) $$\begin{array}{c}\hfill u_t(x,0)=g(x).\end{array}$$(4) ) missing, we attempt to recover g(x) using the data of $u(x,t_f)$. When the input measured data are contaminated by a random noise, we are concerned with the stability of BIEM, which is investigated by adding a different level of random noise on the final time data:(54) $$\begin{array}{c}\hfill \widehat{u}(x_i,t_f)=u(x_i,t_f)+sR(i),\end{array}$$(54)

where $u(x_i,t_f)$ are the exact data, R(i) are random numbers in $[-1,1]$, and s is the level of noise. Then, the noisy data $\widehat{u}(x_i,t_f)$ are used in the numerical solution.

We use the following examples to show the efficiency of the present method to solve the Dirichlet problem of the wave equation.

Example 3:

Let(55) $$\begin{array}{c}\hfill u(x,t)=sinxsint\end{array}$$(55)

be an exact solution of the wave equation.

We take $\ell =2\mathit{\pi }$, $t_f=2$ and $m=10$. We start from the initial guess ${\mathbf{c}}_0=\mathbf{0}$, and although under a stringent convergence criterion with $\mathit{\epsilon }={10}^{-10}$, the CGM is convergence with two steps as shown in Figure 1(a). Upon comparing the recovered initial velocity with the exact one $g(x)=sinx$, the maximum error is amazingly in the order of $6.08\times {10}^{-14}$ as shown in Figure 1(b) under $s=0$. Really, the present method is not sensitive to the initial guess of ${\mathbf{c}}_0$; for example, if we take ${\mathbf{c}}_0=0.1\mathbf{1}$ where $\mathbf{1}$ is a vector with all components being 1, the CGM is convergence with six steps, and with the maximum error being $5.08\times {10}^{-14}$. It can be seen that the BIEM as shown here is very powerful.

Figure 1. For the recovery of initial velocity in Example 3 without noise, (a) the convergence rate, and (b) the numerical error.

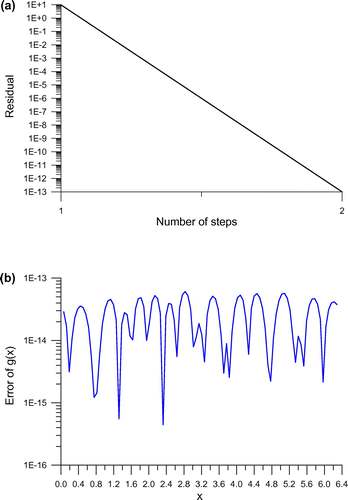
Figure 2. For the recovery of initial velocity in Example 3 under a large noise, (a) the convergence rate, and (b) the numerical error.

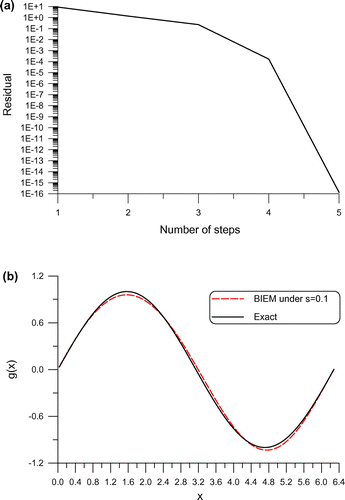
We raise the noise to $s=0.1$, and take $m=2$. Although under a stringent convergence criterion with $\mathit{\epsilon }={10}^{-10}$, the CGM is convergence with five steps as shown in Figure 2(a) by starting from the initial guess ${\mathbf{c}}_0=\mathbf{0}$. Upon comparing the recovered initial velocity with the exact one $g(x)=sinx$, the maximum error is $5.33\times {10}^{-2}$ as shown in Figure 2(b). It can be seen that the BIEM is quite robust against large noise up to $s=10\%$.

Example 4:

Let(56) $$\begin{array}{c}\hfill u(x,t)=2x^4+12x^2{t}^2+2t^4+x^3+3x^{2}t+3x{t}^2+t^3,0<x<\mathit{\pi },0<t\le 2\end{array}$$(56)

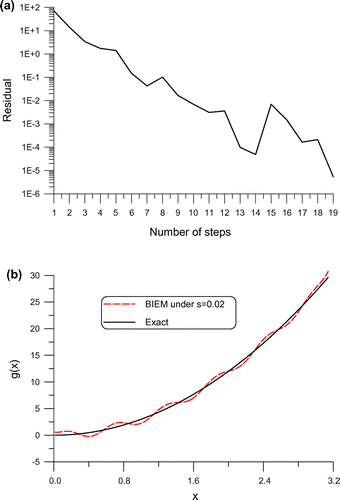
be an exact solution of the wave equation. We use the BIEM with $m=10$ to solve the solution, which is convergence with 19 steps, starting from the initial guess ${\mathbf{c}}_0=\mathbf{0}$. In Figure 3, we can see that the solution obtained by the BIEM is close to the exact initial velocity, whose maximum error is 1.13, where a noise with intensity 0.02 is added on the final time data.

Figure 3. For the recovery of initial velocity in Example 4 under a large noise, (a) the convergence rate, and (b) the numerical error.

Example 5:

Let us consider a much difficult case with(57) $$\begin{array}{c}\hfill u(x,t)=exp[-{(x-t)}^2]+exp[-{(x+t)}^2],0<x<\mathit{\pi },0.1<t\le 8.1.\end{array}$$(57)

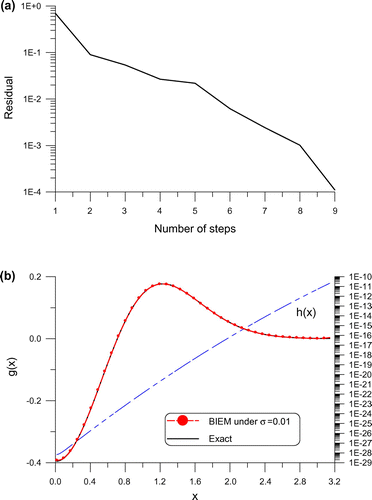
We use the BIEM with $m=8$ to solve the solution, which is convergence with nine steps as shown in Figure 4(a), by starting from the initial guess ${\mathbf{c}}_0=\mathbf{0}$. In Figure 4(b), we can see that the solution obtained by the BIEM is very close to the exact initial velocity, whose maximum error is $3.67\times {10}^{-3}$, where a noise with relative intensity 0.01 is added on the final time data whose value is very small as shown in Figure 4(b) by the dashed-dotted line marked by h(x).

Figure 4. For the recovery of initial velocity in Example 5 under a very small final time data, (a) the convergence rate, and (b) the numerical error.

7. Inverse wave source problem

In this section, we will use the Green’s second identity and two types of Trefftz test functions to construct the linear equations to solve the following inverse wave source problem:(58) $$\begin{array}{cc}\hfill u_{tt}-u_{xx}& =F(x,t),0<x<\ell ,0<t<t_f,\hfill \\ \hfill u(x,0)& =f_1(x),0\le x\le \ell ,\hfill \\ \hfill u_t(x,0)& =g_1(x),0\le x\le \ell ,\hfill \\ \hfill u(\ell ,t)& =f_2(t),0\le t\le t_f,\hfill \\ \hfill u(0,t)& =f_4(t),0\le t\le t_f,\hfill \end{array}$$(58)

where $f_1(x)$, $g_1(x)$, $f_2(t)$ and $f_4(t)$ are given functions. In the inverse wave source problem, we suppose that the following data are overspecified:(59) $$\begin{array}{cc}\hfill u(x,t_f)& =f_3(x),0\le x\le \ell ,\hfill \\ \hfill u_t(x,t_f)& =g_3(x),0\le x\le \ell ,\hfill \end{array}$$(59)

and determine the unknown source function F(x, t) in Equation (59(59) $$\begin{array}{cc}\hfill u(x,t_f)& =f_3(x),0\le x\le \ell ,\hfill \\ \hfill u_t(x,t_f)& =g_3(x),0\le x\le \ell ,\hfill \end{array}$$(59) ).

Theorem 4 indicates that we can choose two simple Trefftz test functions v(x, t) and w(x, t), such that Equation (32(32) $$\begin{array}{c}\hfill F_1=u{v}_y-v{u}_y,F_2=u{v}_x-v{u}_x,\end{array}$$(32) ) can be easily used to solve F(x, t). For this purpose, we can take(60) $$\begin{array}{c}\hfill v(x,t)=sin\frac{k\mathit{\pi }x}{\ell }cos\left(\frac{k\mathit{\pi }t}{\ell }\right),w(x,t)=sin\frac{k\mathit{\pi }x}{\ell }sin\left(\frac{k\mathit{\pi }t}{\ell }\right),\end{array}$$(60)

which are solution of the wave equation for each $k\in \mathbb{N}$; hence, they are called the Trefftz test functions. Inserting Equations (59(59) $$\begin{array}{cc}\hfill u(x,t_f)& =f_3(x),0\le x\le \ell ,\hfill \\ \hfill u_t(x,t_f)& =g_3(x),0\le x\le \ell ,\hfill \end{array}$$(59) )–(61(61) $$\begin{array}{ccc}& {\int }_0^{t_f}{\int }_0^{\ell }v(x,t)F(x,t)\mathrm{d}x\mathrm{d}t\hfill & \hfill ={\int }_0^{\ell }[f_1(x)v_t(x,0)-g_1(x)v(x,0)]\mathrm{d}x\\ \hfill & -{\int }_0^{\ell }[f_3(x)v_t(x,t_f)-g_3(x)v(x,t_f)]\mathrm{d}x\hfill \\ \hfill & +{\int }_0^{t_f}[f_2(t)v_x(\ell ,t)-f_4(t)v_x(0,t)]\mathrm{d}t,\hfill \\ \hfill & {\int }_0^{t_f}{\int }_0^{\ell }w(x,t)F(x,t)\mathrm{d}x\mathrm{d}t\hfill & \hfill ={\int }_0^{\ell }[f_1(x)w_t(x,0)-g_1(x)w(x,0)]\mathrm{d}x\\ \hfill & -{\int }_0^{\ell }[f_3(x)w_t(x,t_f)-g_3(x)w(x,t_f)]\mathrm{d}x\hfill \\ \hfill & +{\int }_0^{t_f}[f_2(t)w_x(\ell ,t)-f_4(t)w_x(0,t)]\mathrm{d}t.\hfill \end{array}$$(61) ) into Equation (32(32) $$\begin{array}{c}\hfill F_1=u{v}_y-v{u}_y,F_2=u{v}_x-v{u}_x,\end{array}$$(32) ), we can derive(61) $$\begin{array}{ccc}& {\int }_0^{t_f}{\int }_0^{\ell }v(x,t)F(x,t)\mathrm{d}x\mathrm{d}t\hfill & \hfill ={\int }_0^{\ell }[f_1(x)v_t(x,0)-g_1(x)v(x,0)]\mathrm{d}x\\ \hfill & -{\int }_0^{\ell }[f_3(x)v_t(x,t_f)-g_3(x)v(x,t_f)]\mathrm{d}x\hfill \\ \hfill & +{\int }_0^{t_f}[f_2(t)v_x(\ell ,t)-f_4(t)v_x(0,t)]\mathrm{d}t,\hfill \\ \hfill & {\int }_0^{t_f}{\int }_0^{\ell }w(x,t)F(x,t)\mathrm{d}x\mathrm{d}t\hfill & \hfill ={\int }_0^{\ell }[f_1(x)w_t(x,0)-g_1(x)w(x,0)]\mathrm{d}x\\ \hfill & -{\int }_0^{\ell }[f_3(x)w_t(x,t_f)-g_3(x)w(x,t_f)]\mathrm{d}x\hfill \\ \hfill & +{\int }_0^{t_f}[f_2(t)w_x(\ell ,t)-f_4(t)w_x(0,t)]\mathrm{d}t.\hfill \end{array}$$(61)

Let(62) $$\begin{array}{c}\hfill F(x,t)=\sum _{i=1}^m\sum _{j=1}^i{c}_{ij}{x}^{i-j}{t}^{j-1},\end{array}$$(62)

where the coefficients $c_{ij}$ with number of $m(m+1)/2$ are to be determined. Inserting it into Equations (62(62) $$\begin{array}{c}\hfill F(x,t)=\sum _{i=1}^m\sum _{j=1}^i{c}_{ij}{x}^{i-j}{t}^{j-1},\end{array}$$(62) ) and (62(62) $$\begin{array}{c}\hfill F(x,t)=\sum _{i=1}^m\sum _{j=1}^i{c}_{ij}{x}^{i-j}{t}^{j-1},\end{array}$$(62) ) and letting $k=1,\dots ,m_0$, we can derive a linear system:(63) $$\begin{array}{c}\hfill \mathbf{A}\mathbf{c}=\mathbf{e}\end{array}$$(63)

to solve the expansion coefficients, where the dimension of $\mathbf{A}$ is $2m_0\times m(m+1)/2$.

Example 6:

We consider(64) $$\begin{array}{c}\hfill u(x,t)=exp(x+2t),F(x,t)=3exp(x+2t),0<x<1,0<t<1.5.\end{array}$$(64)

The noise with intensity s is imposed on all measured data.

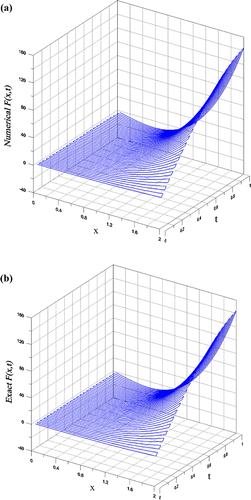
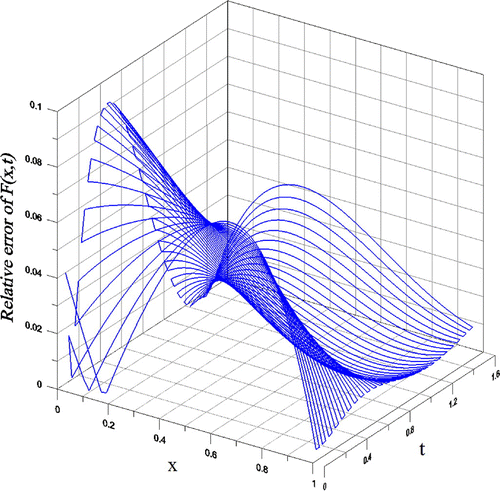
We take $m=6$, $m_0=10$ and a noise with $s=0.2$. Under $\mathit{\epsilon }={10}^{-5}$, the BIEM is convergence with 18 steps starting from the initial guess ${\mathbf{c}}_0=\mathbf{0}$. The maximum error 3.93 in the recovery of F(x, t) is small upon comparing with the maximum value 164 of the source function. In Figure 5, the absolute relative error is plotted, whose maximum value is 0.093.

Figure 5. For the recovery of wave source in Example 6 under a large noise 0.2, showing the relative error in the recovery of F(x, t).

Example 7:

Then, we consider(65) $$\begin{array}{c}\hfill u(x,t)=sin(\mathit{\pi }x)sin(\mathit{\pi }t)+4x^3{t}^3,F(x,y)=24x^{3}t-24x{t}^3,0<x<2,0<t<1.\end{array}$$(65)

We take $m=5$, $m_0=20$ and a large noise with $s=0.2$. Under $\mathit{\epsilon }={10}^{-5}$, the BIEM is convergence with 26 steps starting from the initial guess ${\mathbf{c}}_0=\mathbf{0}$. The maximum error is 1.12, which is acceptable upon comparing with the maximum value 144 of the source function. In Figure 6, we compare the numerically recovered F(x, t) with the exact wave source, which are close.

Figure 6. For the recovery of wave source in Example 7 under a large noise 0.2, comparing (a) numerical and (b) exact F(x, t).

8. A BIEM for long-term wave solutions

Although there are many methods to solve the wave equations,[1] the development of highly accurate and stable wave solvers is still an important issue in the computational physics. For the direct problem of the wave equation:(66) $$\begin{array}{cc}\hfill \frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{t}^2}& =\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2},(x,t)\in \mathrm{\Omega }:=\{0<x<\ell ,0<t\le t_f\},\hfill \end{array}$$(66) (67) $$\begin{array}{cc}\hfill u(0,t)& =u_0(t),u(\ell ,t)=u_{\ell }(t),0\le t\le t_f,\hfill \end{array}$$(67) (68) $$\begin{array}{cc}\hfill u(x,0)& =f(x),u_t(x,0)=g(x),0\le x\le \ell ,\hfill \end{array}$$(68)

the conventional time marching numerical algorithm is ineffective for a long-term solution. Now, we test the BIEM to the direct problems through numerical examples by developing the BIEM to solve them.

We can take(69) $$\begin{array}{c}\hfill v(x,t)=sin\frac{k\mathit{\pi }x}{\ell }\left[(1-R)cos\frac{k\mathit{\pi }(t-t_f)}{\ell }+Rsin\frac{k\mathit{\pi }(t-t_f)}{\ell }\right],\end{array}$$(69)

which is a solution of the wave equation, and $k\in \mathbb{N}$ is a positive integer. For the computation of $F(x):=u(x,t_f)$, we can take $R=1$, and for the computation of $G(x):=u_t(x,t_f)$, we can take $R=0$. Using(70) $$\begin{array}{cc}\hfill v(0,t)& =0,v(\ell ,t)=0,\hfill \\ \hfill v(x,t_f)& =(1-R)sin\frac{k\mathit{\pi }x}{\ell },v_t(x,t_f)=\frac{k\mathit{\pi }R}{\ell }sin\frac{k\mathit{\pi }x}{\ell },\hfill \end{array}$$(70)

and Equation (32(32) $$\begin{array}{c}\hfill F_1=u{v}_y-v{u}_y,F_2=u{v}_x-v{u}_x,\end{array}$$(32) ), we can derive(71) $$\begin{array}{cc}& {\int }_0^{\ell }sin\frac{k\mathit{\pi }x}{\ell }\left(\frac{k\mathit{\pi }R}{\ell }F(x)-(1-R)G(x)\right)\mathrm{d}x\hfill \\ \hfill & ={\int }_0^{\ell }[v_t(x,0)f(x)-v(x,0)g(x)]\mathrm{d}x\hfill \\ \hfill & +{\int }_0^{t_f}[v_x(\ell ,t)u_{\ell }(t)-v_x(0,t)u_0(t)]\mathrm{d}t=:e_k,\hfill \end{array}$$(71)

where $u(x,t_f)=F(x)$ and $u_t(x,t_f)=G(x)$ are displacement and velocity at a time $t_f$ we want to find, and $e_k$ is a different constant for different k. For simple notations, we take(72) $$\begin{array}{cc}\hfill v(x,0)& =sin\frac{k\mathit{\pi }x}{\ell }\left[(1-R)cos\frac{k\mathit{\pi }{t}_f}{\ell }-Rsin\frac{k\mathit{\pi }{t}_f}{\ell }\right],\hfill \\ \hfill v_t(x,0)& =\frac{k\mathit{\pi }}{\ell }sin\frac{k\mathit{\pi }x}{\ell }\left[Rcos\frac{k\mathit{\pi }{t}_f}{\ell }+(1-R)sin\frac{k\mathit{\pi }{t}_f}{\ell }\right],\hfill \\ \hfill v_x(0,t)& =\frac{k\mathit{\pi }}{\ell }\left[(1-R)cos\frac{k\mathit{\pi }(t-t_f)}{\ell }+Rsin\frac{k\mathit{\pi }(t-t_f)}{\ell }\right],\hfill \\ \hfill v_x(\ell ,t)& =\frac{k\mathit{\pi }}{\ell }cos(k\mathit{\pi })\left[(1-R)cos\frac{k\mathit{\pi }(t-t_f)}{\ell }+Rsin\frac{k\mathit{\pi }(t-t_f)}{\ell }\right].\hfill \end{array}$$(72)

Figure 7. Comparing the long-term solutions of wave equation of Example 8 using the GPS, MGPS and BIEM.

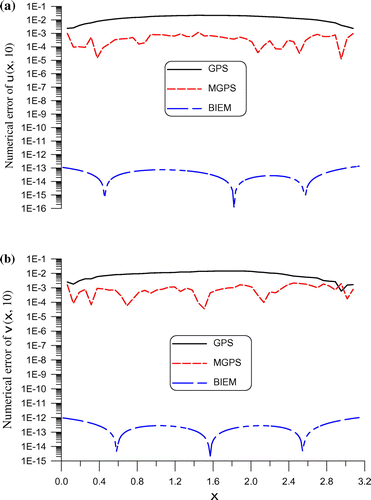
Figure 8. Although under a large time $t=5000$, the BIEM provides very accurate solutions of displacement and velocity.

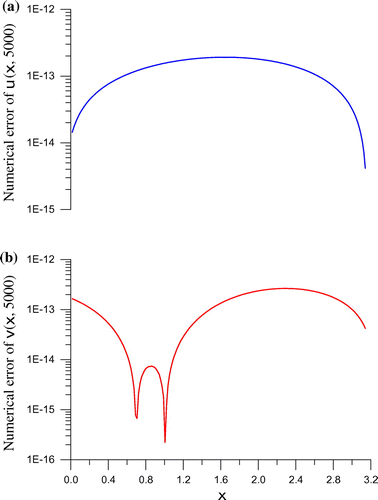
Figure 9. Comparing the long-term solutions of wave equation of Example 9 using the BIEM and exact ones.

Equation (73(73) $$\begin{array}{c}\hfill F(x)=a_0+\sum _{j=1}^m{a}_{j}cos(jx)+b_{j}sin(jx),G(x)=c_0+\sum _{j=1}^m{c}_{j}cos(jx)+d_{j}sin(jx).\end{array}$$(73) ) is a boundary integral equation which can be used to solve F(x) or G(x) from other given boundary conditions. Let(73) $$\begin{array}{c}\hfill F(x)=a_0+\sum _{j=1}^m{a}_{j}cos(jx)+b_{j}sin(jx),G(x)=c_0+\sum _{j=1}^m{c}_{j}cos(jx)+d_{j}sin(jx).\end{array}$$(73)

Inserting them into Equation (73(73) $$\begin{array}{c}\hfill F(x)=a_0+\sum _{j=1}^m{a}_{j}cos(jx)+b_{j}sin(jx),G(x)=c_0+\sum _{j=1}^m{c}_{j}cos(jx)+d_{j}sin(jx).\end{array}$$(73) ), we can derive a linear system to determine the coefficients $a_0,a_j,b_j,j=1\dots m$, when we take $R=1$, and the coefficients $c_0,c_j,d_j,j=1\dots m$, when we take $R=0$.

Remark 1:

A key point in the development of a simple BIEM to solve u(x, t) is the selection of a simple Trefftz test function v(x, t). For different type problems, v(x, t) is different, for example, v(x, t) in Equation (71(71) $$\begin{array}{cc}& {\int }_0^{\ell }sin\frac{k\mathit{\pi }x}{\ell }\left(\frac{k\mathit{\pi }R}{\ell }F(x)-(1-R)G(x)\right)\mathrm{d}x\hfill \\ \hfill & ={\int }_0^{\ell }[v_t(x,0)f(x)-v(x,0)g(x)]\mathrm{d}x\hfill \\ \hfill & +{\int }_0^{t_f}[v_x(\ell ,t)u_{\ell }(t)-v_x(0,t)u_0(t)]\mathrm{d}t=:e_k,\hfill \end{array}$$(71) ) is different from that in Equations (45(45) $$\begin{array}{cc}\hfill v(0,t)& =0,v(\ell ,t)=0,v(x,t_f)=0,v(x,0)=-sin\frac{k\mathit{\pi }{t}_f}{\ell }sin\frac{k\mathit{\pi }x}{\ell },\hfill \\ \hfill v_t(x,0)& =\frac{k\mathit{\pi }}{\ell }cos\frac{k\mathit{\pi }{t}_f}{\ell }sin\frac{k\mathit{\pi }x}{\ell },v_t(x,t_f)=\frac{k\mathit{\pi }}{\ell }sin\frac{k\mathit{\pi }x}{\ell },\hfill \\ \hfill v_x(0,t)& =\frac{k\mathit{\pi }}{\ell }sin\frac{k\mathit{\pi }(t-t_f)}{\ell },v_x(\ell ,t)=\frac{k\mathit{\pi }}{\ell }cos(k\mathit{\pi })sin\frac{k\mathit{\pi }(t-t_f)}{\ell }\hfill \end{array}$$(45) ) and (61(61) $$\begin{array}{ccc}& {\int }_0^{t_f}{\int }_0^{\ell }v(x,t)F(x,t)\mathrm{d}x\mathrm{d}t\hfill & \hfill ={\int }_0^{\ell }[f_1(x)v_t(x,0)-g_1(x)v(x,0)]\mathrm{d}x\\ \hfill & -{\int }_0^{\ell }[f_3(x)v_t(x,t_f)-g_3(x)v(x,t_f)]\mathrm{d}x\hfill \\ \hfill & +{\int }_0^{t_f}[f_2(t)v_x(\ell ,t)-f_4(t)v_x(0,t)]\mathrm{d}t,\hfill \\ \hfill & {\int }_0^{t_f}{\int }_0^{\ell }w(x,t)F(x,t)\mathrm{d}x\mathrm{d}t\hfill & \hfill ={\int }_0^{\ell }[f_1(x)w_t(x,0)-g_1(x)w(x,0)]\mathrm{d}x\\ \hfill & -{\int }_0^{\ell }[f_3(x)w_t(x,t_f)-g_3(x)w(x,t_f)]\mathrm{d}x\hfill \\ \hfill & +{\int }_0^{t_f}[f_2(t)w_x(\ell ,t)-f_4(t)w_x(0,t)]\mathrm{d}t.\hfill \end{array}$$(61) ). Some principles are given as follows. (a) v(x, t) is a solution of the wave equation known as the Trefftz function. (b) On the boundary, including the boundary of time, where the data of u (or the derivative of u) are not given, the derivative of v (or v) must be zero on that boundary. Mathematically speaking, v(x, t) satisfies the adjoint boundary conditions. (c) On the boundary where we want to find the data of u (or the derivative of u), the derivative of v (or v) must be nonzero on that boundary. For each boundary, the above (b) and (c) are alternative. v(x, t) can be constructed for general boundary functions $u_0(t)$ and $u_{\ell }(t)$, and general initial functions f(x) and g(x).

Example 8:

Let(74) $$\begin{array}{c}\hfill u(x,t)=sinxcost,0<x<\mathit{\pi },0<t\le t_f\end{array}$$(74)

be an exact solution of the wave equation.

Multiplying Equation (68(68) $$\begin{array}{cc}\hfill u(x,0)& =f(x),u_t(x,0)=g(x),0\le x\le \ell ,\hfill \end{array}$$(68) ) by $2u_t$ and integrating it, we can obtain(75) $$\begin{array}{cc}\hfill 2{\int }_0^{\ell }{u}_t{u}_{tt}\mathrm{d}x-2{\int }_0^{\ell }{u}_t{u}_{xx}\mathrm{d}x& =0,\hfill \\ \hfill \frac{\mathrm{d}}{\mathrm{d}t}{\int }_0^{\ell }{u}_t^2\mathrm{d}x+\frac{\mathrm{d}}{\mathrm{d}t}{\int }_0^{\ell }{u}_x^2\mathrm{d}x-2u_x{u}_t{|}_0^{\ell }& =0.\hfill \end{array}$$(75)

If the wave equation is subjected to the self-adjoint boundary conditions, then we have(76) $$\begin{array}{c}\hfill \frac{\mathrm{d}}{\mathrm{d}t}{\int }_0^{\ell }(u_t^2+u_x^2)\mathrm{d}x=0,\end{array}$$(76)

which means that the energy is a constant value:(77) $$\begin{array}{c}\hfill {\int }_0^{\ell }(u_t^2+u_x^2)\mathrm{d}x=\text{Constant}.\end{array}$$(77)

Inserting $\ell =\mathit{\pi }$ and Equation (76(76) $$\begin{array}{c}\hfill \frac{\mathrm{d}}{\mathrm{d}t}{\int }_0^{\ell }(u_t^2+u_x^2)\mathrm{d}x=0,\end{array}$$(76) ) into the above, we find that the constant energy is $\mathit{\pi }/2$.

For the purpose of comparison, we use the differential quadrature (DQ) to discretize $u_{xx}$ in Equation (1(1) $$\begin{array}{cc}\hfill \frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{t}^2}& =c^2\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2},(x,t)\in \mathrm{\Omega }:=\{0<x<\ell ,0<t\le t_f\},\hfill \end{array}$$(1) ) and then we apply the group-preserving scheme (GPS) [44] and modified group-preserving scheme (MGPS) [45] to integrate the resultant ODEs. The MGPS adjusts the integrating factor, such that the energy listed in the above is conserved. With $\mathrm{\Delta }x=\mathit{\pi }/50$ and a small $\mathrm{\Delta }t=0.005$, the scalar factor used in DQ is taken to be $R_0=4.5$. The numerical errors of u(x, t) and $v(x,t):=u_t(x,t)$ are obtained by comparing with the exact ones at $t_f=10$ as shown in Figure 7. Under $t_f=10$, $m=2$, we solve this problem by the BIEM, which is convergence with four steps under $\mathit{\epsilon }={10}^{-10}$, by starting from the initial guess ${\mathbf{c}}_0=\mathbf{0}$. It can be seen that the accuracy of the BIEM is much better than that obtained by the GPS and MGPS as shown in Figure 7. In the BIEM the maximum errors of u(x, t) and $v(x,t):=u_t(x,t)$ are, $1.41\times {10}^{-13}$ and $9.83\times {10}^{-8}$, respectively.

Although we raise the value of time to $t=5000$, the numerical errors of displacement and velocity as shown in Figure 8 are still very small, with the maximum errors being $1.92\times {10}^{-13}$ and $2.65\times {10}^{-13}$, respectively.

Example 9:

We revisit Example 4 again; however, we consider a direct problem with exact solution given by(78) $$\begin{array}{c}\hfill u(x,t)=2x^4+12x^2{t}^2+2t^4+x^3+3x^{2}t+3x{t}^2+t^3,0<x<\mathit{\pi },0<t\le 10.\end{array}$$(78)

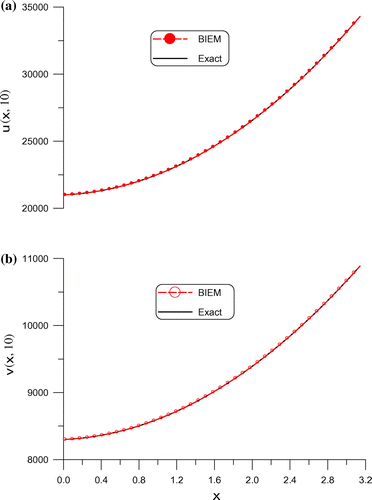
We use the BIEM with $m=15$ to solve the solution at $t_f=10$, which is convergence with 381 steps under $\mathit{\epsilon }={10}^{-10}$, by starting from the initial guess ${\mathbf{c}}_0=\mathbf{0}$. In Figure 9, we can see that the solutions obtained by the BIEM are close to the exact displacement and velocity, whose maximum errors are, 0.0317 and 0.0325, respectively. Upon knowing the values of displacement and velocity are large up to 35,000 and 11,000, the results obtained by the BIEM are very accurate.

9. Conclusions

We have developed a new g-analytic function theory for the wave equation in the Minkowski space ${\mathbb{M}}^{1,1}$. The real and g parts of a g-analytic function satisfy the Cauchy–Riemann equations and both are solutions of the wave equation. According to the g-analytic function theory, we can derive two global spectral relations for the wave equation. The Green’s second identity has been derived for the Dirichlet problem of the wave equation, and we have developed numerical algorithm based on the BIEM to solve this ill-posed problem with high accuracy and stability against a large noise. The unknown wave source function F(x, t) has been recovered with high accuracy using the global domain/BIEM, which is robust against a large noise up to $20\%$. We found that the derived global relation can be used to develop a boundary type integral method for the long-term solution of the wave equation. It is interesting that we can find any solution at a large time span, e.g. $t=5000$, very accurately, with the error in the order of ${10}^{-13}$. This performance is very hard to be achieved by the conventional time-marching algorithm.

Additional information

Funding

The project NSC-102-2221-E-002-125-MY3 from the Ministry of Science and Technology of Taiwan granted to the author is highly appreciated.

Notes

No potential conflict of interest was reported by the author.