Deterministic versus stochastic level-set regularization in nonlinear phase contrast tomography

Abstract

A new nonlinear level-set regularization method to reconstruct the complex refractive index distribution with in-line phase contrast tomography measurements is presented under the assumption that the index is piecewise constant. The nonlinear iterative approach is based on the Fréchet derivative of the intensity recorded at a single propagation distance and for several projection angles. The algorithm is successfully applied to a multi-material object for several noise levels. Better reconstruction results are achieved with a stochastic perturbation of the level-set function. This evolution corresponds to a stochastic evolution of the shape of the reconstructed regions. The reconstruction errors can be further decreased with topological derivatives. The different algorithms are tested on various multi-material objects.

Keywords:

• Inverse problems
• phase constrast tomography
• X-ray imaging

AMS Subject Classifications:

• 65J22
• 65J20
• 65K10

1. Introduction

X-ray microtomography is a widely used imaging technique in medical imaging.[1,2] Yet, X-ray in-line phase contrast tomography is now a much more sensitive technique for soft tissues within dense materials. This imaging technique is based on a coupling of tomography and phase retrieval. The first uses of this technique can be found in [2,3]. It allows to reconstruct the complex refractive index.[4,5] For coherent X-rays obtained with synchrotrons, the Fresnel intensity is recorded for one or several propagation distances and for several projection angles after interaction of the X-rays with the object. The intensity recorded is related to the phase shift in the sample by the Fresnel diffraction theory and this nonlinear relationship leads to a nonlinear inverse ill-posed problem that must be regularized to obtain stable solutions for the complex refractive index.[6–8]

In order to reconstruct the refractive index, several types of priors can be included like the smoothness of the index. For objects with several homogeneous materials, it is often assumed that the ratio of the imaginary to the real part of the complex refractive index is piecewise constant.[4,9–11] If the attenuation image can be measured, a scaled version of this attenuation map can be taken into account to insert a prior knowledge of the phase in the regularization functional.[4] Most approaches in the literature are linear inversion methods.[10,12–16] Yet, the coupling of phase retrieval with tomography sets an ill-posed nonlinear inverse problem. The simultaneous nonlinear reconstruction of the real and of the imaginary part of the refractive index from noisy intensity measurements for different projection angles in in-line phase tomography has been theoretically investigated recently with the classical Tikhonov regularization on a simple geometry with homogeneous materials.[17,18] The reconstruction results obtained are rather poor for initial maps of the real and imaginary parts of the refraction index far from the ground truth to be recovered and for noisy measurements. The Sobolev prior is not the best prior for objects made up of several homogeneous materials.

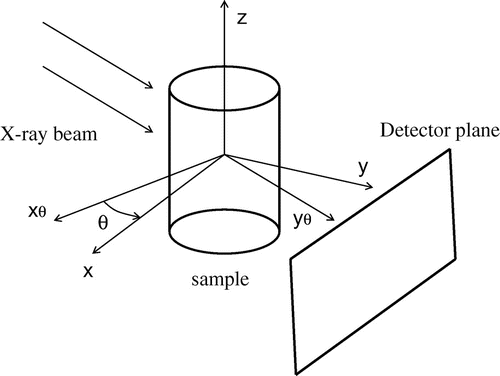
Figure 1. Experimental set-up in propagation-based phase contrast tomography with a single propagation-distance showing the X-ray beam, the rotated coordinate system $(x_{\mathit{\theta }},y_{\mathit{\theta }},z)$ for a rotation angle $\mathit{\theta }$, the sample and the detector.

The main contribution of this paper with respect to the work about deterministic Tikhonov regularization presented in [17] is threefold. First, we regularize the phase contrast tomography problem with a new scheme based on the level-set formalism. For volumes with several homogeneous materials, it can be assumed that the imaginary and real parts of the index are piecewise constant. This type of assumption has already been used for the linear treatment of the phase retrieval problem.[4,9,11] In order to improve the reconstruction, we investigate in this work a new inversion scheme based on a level-set regularization that takes into account such an a priori information. The level-set regularization was investigated for the phase contrast problem in [19] which consists to recover the phase from the Fresnel diffraction patterns. We extend here this type of regularization method for the phase contrast tomography problem where the Fresnel operator is coupled with the Radon operator. The inverse problem is formulated as a shape optimization problem since the discrete values that can be taken by the real and imaginary parts of the index are assumed to be known. On the contrary, the distribution of the materials inside the volume, the absorption and the phase which are obtained as line integrals of the real and imaginary parts of the index for different projection angles are unknown. The only measured quantity is the Fresnel diffraction pattern obtained by a convolution with the Fresnel propagator with the transmittance function. We also show that this regularization method is useful not only for binary values of the refractive index but also in the multi-level case. Yet, the nonlinear phase contrast tomography problem is non-convex and the reconstructed solution obtained with the deterministic level-set regularization is a local minimum. A second aim of this work was to investigate stochastic perturbations of the boundaries performed with tools similar to the ones used for binary tomography in [20] to improve the reconstruction and escape the critical point of the cost functional obtained with the deterministic method. This type of perturbation corresponds to a random change of the shape of the regions. The third point studied in this paper is the efficiency of topological derivatives included in the optimization scheme to improve further the reconstruction and to detect the regions that cannot be detected with shape changes.

This article is structured as follows: we first summarize the direct problem of the image formation based on a coupling of tomography and Fresnel diffraction. Then we detail the level-set regularization method. In the next section, we present the stochastic level-set approach and the topological derivatives. The numerical results obtained on several noisy simulated data with multi-material object are presented and discussed in the next section before the conclusion.

2. The direct operator in in-line phase contrast tomography

2.1. The direct operator in phase retrieval

In this section, we summarize the properties of the direct operator in in-line phase contrast tomography.[17] The real and imaginary parts of the complex refractive index to reconstruct from the Fresnel intensity measurements, denoted as $\mathit{\delta }$ and $\mathit{\beta }$ are defined on a 3D bounded domain ($\mathrm{\Sigma }$) with spatial coordinates (x, y, z). We denote $(x_{\mathit{\theta }},y_{\mathit{\theta }},z)$ to be the rotated spatial coordinate system for an angle $\mathit{\theta }$ around the z axis. The two coordinate systems are displayed on Figure 1 which shows the experimental set-up used for the propagation-based imaging technique. We consider a monochromatic, coherent, parallel X-ray beam propagating in the $y_{\mathit{\theta }}$ direction with the wavelength $\mathit{\lambda }$. The physical properties of an object interacting with an X-ray beam are determined by its complex refractive index written [21,22]:(1) $$\begin{array}{c}\hfill n(x,y,z)=1-\mathit{\delta }(x,y,z)+i\mathit{\beta }(x,y,z)\end{array}$$(1)

where $\mathit{\delta }$ is the refractive index decrement and $\mathit{\beta }$ is the absorption index. For a fixed projection angle $\mathit{\theta }$, thin objects and straight line propagation of the beam along the $y_{\mathit{\theta }}$ direction, this interaction can be described by a transmittance function $T_{\mathit{\theta }}$ of the coordinates $X_{\mathit{\theta }}=(x_{\mathit{\theta }},z)$:(2) $$\begin{array}{c}\hfill T_{\mathit{\theta }}(X_{\mathit{\theta }})=exp\left[-B_{\mathit{\theta }}(X_{\mathit{\theta }})+i{\mathit{\phi }}_{\mathit{\theta }}(X_{\mathit{\theta }})\right]=a_{\mathit{\theta }}(X_{\mathit{\theta }})exp\left[i{\mathit{\phi }}_{\mathit{\theta }}(X_{\mathit{\theta }})\right]\end{array}$$(2)

where $a_{\mathit{\theta }}(X_{\mathit{\theta }})$ is the absorption and ${\mathit{\phi }}_{\mathit{\theta }}(X)$ the phase shift induced by the object for the projection angle $\mathit{\theta }$.[4] The phase and the negative logarithm of the absorption, $B_{\mathit{\theta }}(X)=-\text{log}(a_{\mathit{\theta }}(X))$, are the line integrals of the absorption index and refraction index, respectively:(3) $$\begin{array}{c}\hfill B_{\mathit{\theta }}(X_{\mathit{\theta }})=\frac{2\mathit{\pi }}{\mathit{\lambda }}\int \mathit{\beta }(y_{\mathit{\theta }},X_{\mathit{\theta }})\mathrm{d}{y}_{\mathit{\theta }}\end{array}$$(3)

and(4) $$\begin{array}{c}\hfill {\mathit{\phi }}_{\mathit{\theta }}(X_{\mathit{\theta }})=\frac{2\mathit{\pi }}{\mathit{\lambda }}\int \left(1-\mathit{\delta }(y_{\mathit{\theta }},X_{\mathit{\theta }})\right)\mathrm{d}{y}_{\mathit{\theta }}\end{array}$$(4)

As explained in the next section, these quantities can be rewritten with the Radon operator. In the framework of the Fresnel diffraction theory, the intensity detected at a distance D after the sample is given by the squared modulus of the two-dimensional convolution between the transmittance $T_{\mathit{\theta }}$ and the Fresnel propagator $P_D$ for a distance D downstream of the object [4]:(5) $$\begin{array}{c}\hfill I_{D,\mathit{\theta }}(X_{\mathit{\theta }})={|T_{\mathit{\theta }}(X_{\mathit{\theta }})\ast P_D(X_{\mathit{\theta }})|}^2\end{array}$$(5)

where the Fresnel propagator is written:(6) $$\begin{array}{c}\hfill P_D(X_{\mathit{\theta }})=\frac{1}{i\mathit{\lambda }D}\exp (i\frac{\mathit{\pi }}{\mathit{\lambda }D}|X_{\mathit{\theta }}{|}^2).\end{array}$$(6)

2.2. The coupling with the Radon projector

The direct intensity $I_D$ operator can thus be considered as a nonlinear function of $\mathit{\delta }$ and $\mathit{\beta }$ and it can be rewritten with the Radon projector. We first summarize some properties of this projection operator. Let $\mathrm{\Omega }\subset {\mathbb{R}}^2$ be a bounded open domain with coordinates (r, s), the mathematical model for 2D-tomography is the Radon transform R which maps a function $f\in L^1(\mathrm{\Omega })$ to its line integrals. Let $L(\mathit{\theta },x_{\mathit{\theta }})$ be the line defined by $L(\mathit{\theta },x_{\mathit{\theta }})=\{y_{\mathit{\theta }}{\overline{\mathit{\theta }}}^{\ast }+x_{\mathit{\theta }}\overline{\mathit{\theta }}:\mathit{\tau }\in \mathbb{R}\}$, with $\overline{\mathit{\theta }}=(cos(\mathit{\theta }),sin(\mathit{\theta }))$ and ${\overline{\mathit{\theta }}}^{\ast }=(-sin(\mathit{\theta }),cos(\mathit{\theta }))$, Ran(R) the range of the Radon transform and $Z=[0,\mathit{\pi }]\times Ran(R)$, the Radon transform for $f\in L^1(\mathrm{\Omega })$ is the function $Rf(\mathit{\theta },x_{\mathit{\theta }})$ defined on Z by:(7) $$\begin{array}{c}\hfill Rf(\mathit{\theta },x_{\mathit{\theta }})=R_{\mathit{\theta }}f(x_{\mathit{\theta }})={\int }_{t\in L(\mathit{\theta },x_{\mathit{\theta }})\cap \mathrm{\Omega }}f(t)\mathrm{d}t\end{array}$$(7)

For parallel beam projection, with a beam parallel to the $X=(x,y)$ plane and $f\in L^1(\mathrm{\Sigma })$(8) $$\begin{array}{c}\hfill Rf(\mathit{\theta },x_{\mathit{\theta }},z)=R_{\mathit{\theta }}f(x_{\mathit{\theta }})={\int }_{t\in L(\mathit{\theta },x_{\mathit{\theta }},z)\cap \mathrm{\Sigma }}f(t)\mathrm{d}t\end{array}$$(8)

where $L(\mathit{\theta },x_{\mathit{\theta }},z)$ is the $L(\mathit{\theta },x_{\mathit{\theta }})$ line for the coordinate z.

Ignoring constant terms, the phase and the absorption can be rewritten with the Radon projection operator:(9) $$\begin{array}{c}\hfill B_{\mathit{\theta }}(X_{\mathit{\theta }})=\frac{2\mathit{\pi }}{\mathit{\lambda }}R[\mathit{\beta }](\mathit{\theta },X_{\mathit{\theta }})=\frac{2\mathit{\pi }}{\mathit{\lambda }}{R}_{\mathit{\theta }}[\mathit{\beta }](X_{\mathit{\theta }})\end{array}$$(9)

and(10) $$\begin{array}{c}\hfill {\mathit{\phi }}_{\mathit{\theta }}(X_{\mathit{\theta }})=\frac{2\mathit{\pi }}{\mathit{\lambda }}R[\mathit{\delta }](\mathit{\theta },X_{\mathit{\theta }})=\frac{2\mathit{\pi }}{\mathit{\lambda }}{R}_{\mathit{\theta }}[\mathit{\delta }](X_{\mathit{\theta }})\end{array}$$(10)

Let M the multiplication operator of two functions u and v defined for $x\in \mathrm{\Omega }$ by $M(u,v)(x)=u(x)v(x)$, $F_D$ the convolution with the kernel $P_D$ (Equation (6(6) $$\begin{array}{c}\hfill P_D(X_{\mathit{\theta }})=\frac{1}{i\mathit{\lambda }D}\exp (i\frac{\mathit{\pi }}{\mathit{\lambda }D}|X_{\mathit{\theta }}{|}^2).\end{array}$$(6) )) and $\mathit{\psi }$ defined by $\mathit{\psi }(B,\mathit{\varphi })=exp(-B)exp(i\mathit{\varphi })$. With the above-defined operators, the nonlinear intensity operator $I_D[\mathit{\delta },\mathit{\beta }](\mathit{\theta },X_{\mathit{\theta }}):L^2(\mathrm{\Sigma })\times L^2(\mathrm{\Sigma })\to L^2([0,\mathit{\pi }]\times {\mathbb{R}}^2)$ admits the following decomposition with $I_D[\mathit{\delta },\mathit{\beta }](\mathit{\theta },X_{\mathit{\theta }})=I_{D,\mathit{\theta }}[\mathit{\delta },\mathit{\beta }](X_{\mathit{\theta }})$ [17]:(11) $$\begin{array}{c}\hfill I_{D,\mathit{\theta }}(X_{\mathit{\theta }})=M(F_D\circ \mathit{\psi },\overline{F_D\circ \mathit{\psi }})(\frac{2\mathit{\pi }}{\mathit{\lambda }}{R}_{\mathit{\theta }}[\mathit{\delta }](X_{\mathit{\theta }}),\frac{2\mathit{\pi }}{\mathit{\lambda }}{R}_{\mathit{\theta }}[\mathit{\beta }](X_{\mathit{\theta }}))\end{array}$$(11)

This decomposition shows that the Fresnel intensity is the composition of Radon operators, convolution and of the square of the modulus of the Fresnel amplitude. It is useful to calculate the Fréchet derivative of the intensity.

3. Level-set regularization of in-line phase contrast tomography

3.1. The level-set approach

Level-set methods have been designed to reconstruct solutions of inverse problems with non-smooth and piecewise constant solutions.[23,24] For simplicity, we assume that $\mathit{\delta }$ and $\mathit{\beta }$ are piecewise constants and that they can take two values ${\mathit{\delta }}_1$, ${\mathit{\delta }}_2$ and ${\mathit{\beta }}_1$, ${\mathit{\beta }}_2$ on disjoint measureable subsets ${\mathrm{\Sigma }}_1$, ${\mathrm{\Sigma }}_2$ such that $\mathrm{\Sigma }={\mathrm{\Sigma }}_1\cup {\mathrm{\Sigma }}_2$. In order to represent the unknown functions $\mathit{\delta }$ and $\mathit{\beta }$, we have used a level-set function of the first-order Sobolev space $\mathit{\eta }\in H_1(\mathrm{\Sigma })$:(12) $$\begin{array}{cc}\hfill \mathit{\beta }& ={\mathit{\beta }}_1+H(\mathit{\eta })({\mathit{\beta }}_2-{\mathit{\beta }}_1)\hfill \end{array}$$(12) (13) $$\begin{array}{cc}\hfill \mathit{\delta }& ={\mathit{\delta }}_1+H(\mathit{\eta })({\mathit{\delta }}_2-{\mathit{\delta }}_1)\hfill \end{array}$$(13) H is the Heaviside distribution, $H(\mathit{\eta })=1$ if $\mathit{\eta }>0$ and 0 otherwise. With this representation, the boundary (B) between the two regions ${\mathrm{\Sigma }}_1$ and ${\mathrm{\Sigma }}_2$ is the zero level-set of the function $\mathit{\eta }$:(14) $$\begin{array}{c}\hfill B=\{\overrightarrow{r}\in \mathrm{\Sigma }|\mathit{\eta }(\overrightarrow{r},t)=0\}\end{array}$$(14)

The $\mathit{\eta }$ function is such that it takes positive values inside the connected components and negative values outside.

The following smooth approximation of the Heaviside function H has been used:(15) $$\begin{array}{c}\hfill H_{\mathit{ϵ}}(\mathit{\eta })=\frac{1+2\mathit{ϵ}}{2}\left(\text{erf}(\mathit{\eta }/\mathit{ϵ})+1\right)-\mathit{ϵ}\end{array}$$(15)

where the parameter $\mathit{ϵ}$ controls the scale at which the discontinuity is approximated and erf is the error function.

By the nonlinear transformation, the inverse problem consists in determining the level-set function $\mathit{\eta }$. The values ${\mathit{\delta }}_1$, ${\mathit{\delta }}_2$, ${\mathit{\beta }}_1$, ${\mathit{\beta }}_2$ are known, is formulated as a shape optimization problem. In order to obtain stable solutions, we have considered a variational approach and a regularization functional which can be written:(16) $$\begin{array}{c}\hfill F[\mathit{\eta }]=\Vert I_{D,\mathit{\theta }}[\mathit{\eta }]-I_{{\mathit{\delta }}_n}{\Vert }_2^2+J[\mathit{\eta }]\end{array}$$(16)

where $I_{{\mathit{\delta }}_n}$ are the noisy intensity data and J a regularization term. In this work, we have considered a first-order Sobolev space $H_1$ regularization of the level-set function:(17) $$\begin{array}{c}\hfill J(\mathit{\eta })={\mathit{\alpha }}_1{\Vert \mathit{\eta }\Vert }_{H_1}^2={\mathit{\alpha }}_1\left({\Vert \mathit{\eta }\Vert }_{L_2}^2+{\Vert |\mathrm{\nabla }\mathit{\eta }|\Vert }_{L_2}^2\right)\end{array}$$(17)

The parameter ${\mathit{\alpha }}_1$ determines the relative weights of the data term and of the regularization term included in the regularization functional. Since H is discontinuous, the minimizers of the regularization functional have to be approximated by the minimizers of smoothed regularization functional with $H_{\mathit{ϵ}}$. With this relaxation, the standard nonlinear Tikhonov regularization theory between Hilbert spaces can be applied.[23–25]

It should be noted that the former method can be generalized to inverse problems involving more than two levels for the functions $\mathit{\delta }$ and $\mathit{\beta }$. In order to represent the unknown functions $\mathit{\delta }$ and $\mathit{\beta }$, it is then necessary to use several level-set functions. For three levels, ${\mathit{\beta }}_1$, ${\mathit{\beta }}_2$ and ${\mathit{\beta }}_3$, the imaginary part of the refractive index can be written:(18) $$\begin{array}{c}\hfill \mathit{\beta }={\mathit{\beta }}_{2}H({\mathit{\eta }}_2)H({\mathit{\eta }}_1)+{\mathit{\beta }}_{3}H({\mathit{\eta }}_2)\left(1-H({\mathit{\eta }}_1)\right)+{\mathit{\beta }}_1\left(1-H({\mathit{\eta }}_1)\right)\left(1-H({\mathit{\eta }}_2)\right)\end{array}$$(18)

where ${\mathit{\eta }}_1$ and ${\mathit{\eta }}_2$ are the level-set functions that belong to the first-order Sobolev space $H_1(\mathrm{\Omega })$. A similar equation holds for the real part $\mathit{\delta }$ of the refractive index. With respect to ${\mathit{\eta }}_1$ and ${\mathit{\eta }}_2$, the reconstruction problem becomes nonlinear. Similarly to the level-set method for the binary case, the minimizers of the regularization function should be replaced by the ones of a smoothed approximate regularization functional with the smoothed approximation $H_{\mathit{ϵ}}$. The regularization functional to be minimized can then be written as:(19) $$\begin{array}{c}\hfill F({\mathit{\eta }}_1,{\mathit{\eta }}_2)=\frac{\Vert I_{D,\mathit{\theta }}[{\mathit{\eta }}_1,{\mathit{\eta }}_2]-I_{{\mathit{\delta }}_n}{\Vert }_2^2}{2}+J({\mathit{\eta }}_1)+J({\mathit{\eta }}_2)\end{array}$$(19)

where J is a regularization term for the level-set functions. In this work, we have considered a Total Variation-$H_1$ regularization functional for each level-set function. The smoothed regularizatoin functional to be minimized is given by:(20) $$\begin{array}{c}\hfill F_{\mathit{ϵ}}({\mathit{\eta }}_1,{\mathit{\eta }}_2)=\frac{\Vert I_{D,\mathit{\theta }}[{\mathit{\eta }}_1,{\mathit{\eta }}_2]-I_{{\mathit{\delta }}_n}{\Vert }_2^2}{2}+{\mathit{\alpha }}_1\Vert {\mathit{\eta }}_1{\Vert }_{H_1}^2+{\mathit{\alpha }}_2{\Vert {\mathit{\eta }}_2\Vert }_{H_1}^2\end{array}$$(20)

3.2. Implementation of the nonlinear regularization approach

The use of the classical Filtered Back Projection algorithm for the tomographic reconstruction step coupled with phase retrieval methods gives very poor results and it is necessary to use iterative methods to minimize the regularization functional of Equation (16(16) $$\begin{array}{c}\hfill F[\mathit{\eta }]=\Vert I_{D,\mathit{\theta }}[\mathit{\eta }]-I_{{\mathit{\delta }}_n}{\Vert }_2^2+J[\mathit{\eta }]\end{array}$$(16) ). In the field of discrete algebraic reconstruction techniques for tomography, several schemes have been studied which are some variants of the Landweber methods.[26–28] Based on these different methods, we can consider various iterative schemes coupling tomographic reconstruction methods and the adjoint of the Fresnel transform. In this work, one projection angle $\mathit{\theta }$ is selected for the Radon operator at each iteration as in the Simultaneous Algebraic Reconstruction Technique.[26–28] This choice of a single projection angle to apply the first-order optimality conditons (Eqaution (20(20) $$\begin{array}{c}\hfill F_{\mathit{ϵ}}({\mathit{\eta }}_1,{\mathit{\eta }}_2)=\frac{\Vert I_{D,\mathit{\theta }}[{\mathit{\eta }}_1,{\mathit{\eta }}_2]-I_{{\mathit{\delta }}_n}{\Vert }_2^2}{2}+{\mathit{\alpha }}_1\Vert {\mathit{\eta }}_1{\Vert }_{H_1}^2+{\mathit{\alpha }}_2{\Vert {\mathit{\eta }}_2\Vert }_{H_1}^2\end{array}$$(20) )–(22(22) $$\begin{array}{c}\hfill \left([I_{D,\mathit{\theta }}^{\prime \ast }[{\mathit{\eta }}^k]I_{D,\mathit{\theta }}^{\prime }[{\mathit{\eta }}^k]\right)\mathit{\delta }\mathit{\eta }+{\mathit{\alpha }}_1(I-\mathrm{\Delta })\mathit{\delta }\mathit{\eta }=-F^{\prime }[{\mathit{\eta }}^k]\end{array}$$(22) )) below corresponds to a Kaczmarz-type method where at each iteration the solution is projected orthogonally on the hyperplan corresponding to the measurement.[29] We also use the Gauss–Newton method and the Fréchet derivative of the intensity to minimize the regularization functional.

Figure 2. Ground truth $\mathit{\beta }$ and $\mathit{\delta }$ maps for the object ($O_2$).

3.2.1. Bilevel approach

The minimizers of the regularization are found numerically with first-order optimality conditions for the smoothed functional. These conditions are given by $F^{\prime }[\mathit{\eta }]=0$, where $F^{\prime }[\mathit{\eta }]$ is the variation of the regularization functional with respect to $\mathit{\eta }$:(21) $$\begin{array}{c}\hfill F^{\prime }[\mathit{\eta }]=I_{D,\mathit{\theta }}^{\prime \ast }[\mathit{\eta }]\left[I_{D,\mathit{\theta }}[\mathit{\eta }]-I_{{\mathit{\delta }}_n}\right]+{\mathit{\alpha }}_1(I-\mathrm{\Delta })[\mathit{\eta }]\end{array}$$(21)

where $I_D^{\prime \ast }$ denotes the adjoint of the Fréchet derivative of the intensity operator with respect to $L_2$ spaces. I represents identity and $\mathrm{\Delta }$ the Laplacian operator. The solutions of the optimality are obtained with a Gauss–Newton method. The update is given by ${\mathit{\eta }}_{k+1}={\mathit{\eta }}_k+\mathit{\delta }\mathit{\eta }$ and $\mathit{\delta }\mathit{\eta }$ is obtained with the linear system:(22) $$\begin{array}{c}\hfill \left([I_{D,\mathit{\theta }}^{\prime \ast }[{\mathit{\eta }}^k]I_{D,\mathit{\theta }}^{\prime }[{\mathit{\eta }}^k]\right)\mathit{\delta }\mathit{\eta }+{\mathit{\alpha }}_1(I-\mathrm{\Delta })\mathit{\delta }\mathit{\eta }=-F^{\prime }[{\mathit{\eta }}^k]\end{array}$$(22)

3.2.2. Multi-level approach

The minimizers of the Tikhonov functionals are found with first-order optimality conditions for the two level-set functions of the smoothed functionals:(23) $$\begin{array}{c}\hfill \frac{\mathit{\partial }{F}_{\mathit{ϵ}}}{\mathit{\partial }{\mathit{\eta }}_1}=G_1({\mathit{\eta }}_1,{\mathit{\eta }}_2)=0\end{array}$$(23)

with(24) $$\begin{array}{c}\hfill G_1({\mathit{\eta }}_1,{\mathit{\eta }}_2)={\left(\frac{\mathit{\partial }{I}_{D,\mathit{\theta }}}{\mathit{\partial }{\mathit{\eta }}_1}\right)}^{\ast }[{\mathit{\eta }}_1,{\mathit{\eta }}_2]\left[I_{D,\mathit{\theta }}[{\mathit{\eta }}_1,{\mathit{\eta }}_2]-I_{{\mathit{\delta }}_n}\right]+{\mathit{\alpha }}_1(I-\mathrm{\Delta })[{\mathit{\eta }}_1]\end{array}$$(24)

where $\frac{\mathit{\partial }{I}_{D,\mathit{\theta }}}{\mathit{\partial }{\mathit{\eta }}_1}$ is the Fréchet derivative of $I_{D,\mathit{\theta }}$ with respect to ${\mathit{\eta }}_1$. The same type of formula holds for ${\mathit{\eta }}_2$. These optimality conditions are solved with Gauss–Newton method. A critical point of the regularization functional can be obtained with an alternate minimization with respect to the level-set functions ${\mathit{\eta }}_1$ and ${\mathit{\eta }}_2$.[24,30]

3.3. The Fréchet derivative of the Fresnel intensity operator and its adjoint

3.3.1. Bilevel case

An explicit formula can be derived for the Fréchet derivative of the intensity $I_D[\mathit{\delta },\mathit{\beta }]$ and its adjoint. Let $T_k=\exp (-B[{\mathit{\beta }}_k]-i\mathit{\phi }[{\mathit{\delta }}_k])$, $U_k=[\overline{T_k}\ast \overline{P_D}]$, $\mathrm{\Delta }\mathit{\beta }={\mathit{\beta }}_2-{\mathit{\beta }}_1$,$\mathrm{\Delta }\mathit{\delta }={\mathit{\delta }}_2-{\mathit{\delta }}_1$, the Fréchet derivative of the operator $I_D[{\mathit{\eta }}_k]$ at the point ${\mathit{\eta }}_k$ is the operator $I_D^{\prime }[{\mathit{\eta }}_k]:$$L^2(\mathrm{\Sigma })$$\to$$L^2([0,\mathit{\pi }]\times {\mathbb{R}}^2)$ defined by:(25) $$\begin{array}{c}\hfill I_{D,\mathit{\theta }}^{\prime }[{\mathit{\eta }}_k](\mathit{ϵ})=2Real\{[((-R_{\mathit{\theta }}{H}_{\mathit{ϵ}}^{\prime }[{\mathit{\eta }}_k](\mathrm{\Delta }\mathit{\beta }+i\mathrm{\Delta }\mathit{\delta })\mathit{ϵ}{T}_k)\ast P_D]U_k\}\end{array}$$(25)

where $H_{\mathit{ϵ}}^{\prime }$ is the derivative of the smoothed Heaviside function.

The $L_2$ Hilbert space adjoint $I_D^{\prime }{[{\mathit{\eta }}_k]}^{\ast }:L^2([0,\mathit{\pi }]\times {\mathbb{R}}^2)\to L^2(\mathrm{\Sigma })$ is thus defined by $I_{D,\mathit{\theta }}^{\prime }{[{\mathit{\eta }}_k]}^{\ast }(u)=2Real(v_1+v_2)$ with:(26) $$\begin{array}{c}\hfill v_1=({\mathit{\beta }}_2-{\mathit{\beta }}_1)H_{\mathit{ϵ}}^{\prime }[{\mathit{\eta }}_k]R_{\mathit{\theta }}^{\ast }\{[-u(T_k\ast P_D)\ast \overline{P_D}]\overline{T_k}\}\end{array}$$(26)

and(27) $$\begin{array}{c}\hfill v_2=({\mathit{\delta }}_2-{\mathit{\delta }}_1)H_{\mathit{ϵ}}^{\prime }[{\mathit{\eta }}_k]R_{\mathit{\theta }}^{\ast }\{[(u(T_k\ast P_D)\ast \overline{P_D}]i\overline{T_k}\}\end{array}$$(27)

This formula can be derived from the results in [17] for the Tikhonov regularization.

3.3.2. Multi-level regularization

For the multi-level case, Equation (25(25) $$\begin{array}{c}\hfill I_{D,\mathit{\theta }}^{\prime }[{\mathit{\eta }}_k](\mathit{ϵ})=2Real\{[((-R_{\mathit{\theta }}{H}_{\mathit{ϵ}}^{\prime }[{\mathit{\eta }}_k](\mathrm{\Delta }\mathit{\beta }+i\mathrm{\Delta }\mathit{\delta })\mathit{ϵ}{T}_k)\ast P_D]U_k\}\end{array}$$(25) ) is replaced by:(28) $$\begin{array}{c}\hfill \frac{I_{D,\mathit{\theta }}}{\mathit{\partial }{\mathit{\eta }}_1}\left[{\mathit{\eta }}_1^k,{\mathit{\eta }}_2^k\right](\mathit{ϵ})=2Real\left\{\left[\left(-R_{\mathit{\theta }}{H}_{\mathit{ϵ}}^{\prime }[{\mathit{\eta }}_1^k]\left(\frac{\mathit{\partial }\mathit{\beta }}{\mathit{\partial }{\mathit{\eta }}_1}\left({\mathit{\eta }}_1^k\right)+i\frac{\mathit{\partial }\mathit{\delta }}{\mathit{\partial }{\mathit{\eta }}_1}\left({\mathit{\eta }}_1^k\right)\right)\mathit{ϵ}{T}_k\right)\ast P_D\right]U_k\right\}\end{array}$$(28)

and a similar equation holds for the variation with respect to ${\mathit{\eta }}_2$, $\frac{I_{D,\mathit{\theta }}}{\mathit{\partial }{\mathit{\eta }}_2}[{\mathit{\eta }}_1^k,{\mathit{\eta }}_2^k]$. The derivative of the imaginary part of the index $\mathit{\beta }$ with respect to ${\mathit{\eta }}_1$ and ${\mathit{\eta }}_2$ is given by:(29) $$\begin{array}{c}\hfill \frac{\mathit{\partial }\mathit{\beta }}{\mathit{\partial }{\mathit{\eta }}_1}({\mathit{\eta }}_1,{\mathit{\eta }}_2)=({\mathit{\beta }}_2-{\mathit{\beta }}_3)H^{\prime }({\mathit{\eta }}_1)-{\mathit{\beta }}_1{H}^{\prime }({\mathit{\eta }}_1)\left(1-H({\mathit{\eta }}_2)\right)\end{array}$$(29) (30) $$\begin{array}{c}\hfill \frac{\mathit{\partial }\mathit{\beta }}{\mathit{\partial }{\mathit{\eta }}_2}({\mathit{\eta }}_1,{\mathit{\eta }}_2)={\mathit{\beta }}_2{H}^{\prime }({\mathit{\eta }}_2)H({\mathit{\eta }}_1)+{\mathit{\beta }}_3{H}^{\prime }({\mathit{\eta }}_2)\left(1-H({\mathit{\eta }}_1)\right)-{\mathit{\beta }}_1\left(1-H({\mathit{\eta }}_1)\right)H^{\prime }({\mathit{\eta }}_2)\end{array}$$(30)

Similar formula can be obtained for the derivative of $\mathit{\delta }$ with respect ${\mathit{\eta }}_1$ and ${\mathit{\eta }}_2$.

The Hilbert space adjoint in Equation (24(24) $$\begin{array}{c}\hfill G_1({\mathit{\eta }}_1,{\mathit{\eta }}_2)={\left(\frac{\mathit{\partial }{I}_{D,\mathit{\theta }}}{\mathit{\partial }{\mathit{\eta }}_1}\right)}^{\ast }[{\mathit{\eta }}_1,{\mathit{\eta }}_2]\left[I_{D,\mathit{\theta }}[{\mathit{\eta }}_1,{\mathit{\eta }}_2]-I_{{\mathit{\delta }}_n}\right]+{\mathit{\alpha }}_1(I-\mathrm{\Delta })[{\mathit{\eta }}_1]\end{array}$$(24) ) is given by: $u\to \frac{\mathit{\partial }{I}_D}{\mathit{\partial }{\mathit{\eta }}_1}{[{\mathit{\eta }}_1^k,{\mathit{\eta }}_2^k]}^{\ast }(u)=2Real(v_1+v_2)$ with $v_1$ and $v_2$ given by:(31) $$\begin{array}{c}\hfill v_1=\frac{\mathit{\partial }\mathit{\beta }}{\mathit{\partial }{\mathit{\eta }}_1}\left({\mathit{\eta }}_1^k,{\mathit{\eta }}_2^k\right)H_{\mathit{ϵ}}^{\prime }\left[{\mathit{\eta }}_1^k\right]R_{\mathit{\theta }}^{\ast }\{[-u(T_k\ast P_D)\ast \overline{P_D}]\overline{T_k}\}\end{array}$$(31)

and(32) $$\begin{array}{c}\hfill v_2=\frac{\mathit{\partial }\mathit{\delta }}{\mathit{\partial }{\mathit{\eta }}_1}\left({\mathit{\eta }}_1^k,{\mathit{\eta }}_2^k\right)H_{\mathit{ϵ}}^{\prime }\left[{\mathit{\eta }}_1^k\right]R_{\mathit{\theta }}^{\ast }\{[u(T_k\ast P_D)\ast \overline{P_D}]i\overline{T_k}\}\end{array}$$(32)

The adjoint $u\to \frac{\mathit{\partial }{I}_D}{\mathit{\partial }{\mathit{\eta }}_2}{[{\mathit{\eta }}_1^k,{\mathit{\eta }}_2^k]}^{\ast }(u)$ can be obtained in the same way.

4. Stochastic level-set methods and topological derivative

The deterministic optimization presented above is often stopped in local minima.[31] The level-set regularization is used to include the piecewise constant hypothesis about the refractive index and it is very useful to handle shape changes. Yet, the optimization problem is not convex and it may be stuck at non-optimal shapes with missing components. We propose to improve the optimization scheme with stochastic level-set evolution and topological derivatives.

4.1. Stochastic level-set evolution

The aim of this section is to present a new stochastic evolution of the boundary curve to improve the reconstruction based on a new stochastic level-set method. Level-set methods have been much studied for image processing tasks [32] but the stochastic level-set approach has been proposed only for segmentation [33] or binary tomography.[31]

Let $(\mathrm{\Omega },\mathcal{F},P)$ be a probability space, in order to obtain the global minimum of a function $g:{\mathbb{R}}^m\to \mathbb{R}$, a random trajectory X(t) governed by a diffusion process of the type $dX(t)=-\mathrm{\nabla }g(X(t))\mathrm{d}t+\mathit{\rho }(t)\mathrm{d}W(t)$ is often used [34–37], where $W=(W_1(t),\dots ,W_m(t))$ is the standard m-dimensional Brownian motion and $\mathit{\rho }(t)$ the noise strength. It has been shown that if g is twice continuously differentiable and if the Radon–Nikodym derivative of the distribution of the process X(t) with respect to the probability measure P is square integrable, the transition probability of the random process X(t) converges weakly to a probability measure which has its support on the set of global minimizers of g [34–37], for annealing schedule given by $\mathit{\rho }(t)=\frac{c}{\sqrt{\log (t)}}$, where c is a constant positive scalar.

Figure 3. Ground truth $\mathit{\delta }$ maps for the object ($O_3$).

We apply the same formalism to the level-set function. The evolution of the boundary curve is independent of the level-set function used for its representation with the Stratanovich integral formalism [33]. We thus propose to improve the reconstruction image obtained with the deterministic level-set evolution with the following stochastic partial differential equation for the level-set function $\mathit{\eta }$, given for $\overrightarrow{r}\in \mathrm{\Sigma }$ by:(33) $$\begin{array}{c}\hfill \mathrm{d}\mathit{\eta }(\overrightarrow{r},t)=\mathit{\delta }\mathit{\eta }(\overrightarrow{r},t)+\mathit{\rho }(t)|\mathrm{\nabla }\mathit{\eta }(\overrightarrow{r},t)|o\mathrm{d}W(t)\end{array}$$(33)

where o denotes the Stratanovitch convention [38] and $\mathit{\delta }\mathit{\eta }$ is the deterministic change calculated with the Gauss–Newton method of Equation (20(20) $$\begin{array}{c}\hfill F_{\mathit{ϵ}}({\mathit{\eta }}_1,{\mathit{\eta }}_2)=\frac{\Vert I_{D,\mathit{\theta }}[{\mathit{\eta }}_1,{\mathit{\eta }}_2]-I_{{\mathit{\delta }}_n}{\Vert }_2^2}{2}+{\mathit{\alpha }}_1\Vert {\mathit{\eta }}_1{\Vert }_{H_1}^2+{\mathit{\alpha }}_2{\Vert {\mathit{\eta }}_2\Vert }_{H_1}^2\end{array}$$(20) ) as explained in Section 3.2. We obtain the following Itô stochastic differential equation with the definition of the Stratanovich integral [33,38]:(34) $$\begin{array}{cc}\hfill \mathrm{d}\mathit{\eta }(\overrightarrow{r},t)& =\mathit{\delta }\mathit{\eta }+\mathit{\rho }(t)|\mathrm{\nabla }\mathit{\eta }(\overrightarrow{r},t)|\mathrm{d}W(t)+\frac{1}{2}\mathit{\rho }(t)(▵\mathit{\eta }(\overrightarrow{r},t)\hfill \\ \hfill & -|\mathrm{\nabla }\mathit{\eta }(\overrightarrow{r},t)|\mathrm{div}\left(\frac{\mathrm{\nabla }\mathit{\eta }(\overrightarrow{r},t)}{|\mathrm{\nabla }\mathit{\eta }(\overrightarrow{r},t)|}\right)\hfill \end{array}$$(34)

In this study, the deterministic level-set and stochastic level-set schemes are applied successively on random time intervals with an intermittent diffusion [36]. The main idea is to alternate the deterministic and stochastic steps with periodic reinitialization of the level-set function $\mathit{\eta }$. For the stochastic evolution, the time interval lengths and the diffusion strengths $\mathit{\rho }$ are chosen at random with a uniform distribution in the range $[0,T_{\max }]$ and $[0,{\mathit{\rho }}_{\max }]$ where ${\mathit{\rho }}_{max}$ is the scale for the diffusion strength and $T_{\max }$ is the scale for the diffusion time.

The alternated minimization algorithm is summarized in Algorithm 1:

In this algorithm, the parameters ${\mathit{\rho }}_{\max }$ and $T_{\max }$ are chosen to obtain the larger decrease in the data term. The initialization of the level-set functions with the signed distance function is widely used in the literature.

4.2. Topological derivative

The derivative in Equations (19(19) $$\begin{array}{c}\hfill F({\mathit{\eta }}_1,{\mathit{\eta }}_2)=\frac{\Vert I_{D,\mathit{\theta }}[{\mathit{\eta }}_1,{\mathit{\eta }}_2]-I_{{\mathit{\delta }}_n}{\Vert }_2^2}{2}+J({\mathit{\eta }}_1)+J({\mathit{\eta }}_2)\end{array}$$(19) ) and (20(20) $$\begin{array}{c}\hfill F_{\mathit{ϵ}}({\mathit{\eta }}_1,{\mathit{\eta }}_2)=\frac{\Vert I_{D,\mathit{\theta }}[{\mathit{\eta }}_1,{\mathit{\eta }}_2]-I_{{\mathit{\delta }}_n}{\Vert }_2^2}{2}+{\mathit{\alpha }}_1\Vert {\mathit{\eta }}_1{\Vert }_{H_1}^2+{\mathit{\alpha }}_2{\Vert {\mathit{\eta }}_2\Vert }_{H_1}^2\end{array}$$(20) ) describes the sensitivity of the regularization functional with respect to deterministic changes of shape of the boundary between the regions of constant values for the real and imaginary parts of the index. The Equations (24(24) $$\begin{array}{c}\hfill G_1({\mathit{\eta }}_1,{\mathit{\eta }}_2)={\left(\frac{\mathit{\partial }{I}_{D,\mathit{\theta }}}{\mathit{\partial }{\mathit{\eta }}_1}\right)}^{\ast }[{\mathit{\eta }}_1,{\mathit{\eta }}_2]\left[I_{D,\mathit{\theta }}[{\mathit{\eta }}_1,{\mathit{\eta }}_2]-I_{{\mathit{\delta }}_n}\right]+{\mathit{\alpha }}_1(I-\mathrm{\Delta })[{\mathit{\eta }}_1]\end{array}$$(24) ) and (25(25) $$\begin{array}{c}\hfill I_{D,\mathit{\theta }}^{\prime }[{\mathit{\eta }}_k](\mathit{ϵ})=2Real\{[((-R_{\mathit{\theta }}{H}_{\mathit{ϵ}}^{\prime }[{\mathit{\eta }}_k](\mathrm{\Delta }\mathit{\beta }+i\mathrm{\Delta }\mathit{\delta })\mathit{ϵ}{T}_k)\ast P_D]U_k\}\end{array}$$(25) ) correspond to stochastic perturbations of the geometry. Yet, in some cases the shape derivative does not lead a sufficient decrease in the cost functional and does not yield the optimal shape. The evolution of the geometry is stuck in local minima when some regions are not reconstructed. The topology optimization is also an important issue. Topology changes like splitting and merging of domains can be obtained with the level-set approach.[39] The level-set method is designed to describe the propagation of interfaces but with classical methods it is not possible to introduce new components of the shape at positions far from the boundary. Thus, it has been suggested to incorporate in some way topological derivatives into level-set methods. These derivatives are based on a variation of the cost functional with respect to small holes at certain positions.

A first algorithm introducing new components by propagating the level-set function across the zero-plane at some points has been investigated in [40]. This method is based on a modified first-order Hamilton–Jacobi equation for the level-set function including a source term dependent on the topological derivative:(35) $$\begin{array}{c}\hfill \frac{\mathit{\partial }\mathit{\eta }}{\mathit{\partial }t}+F|\mathit{\eta }|+\mathit{\omega }G=0\end{array}$$(35)

F is the speed of the zero level-set function $\mathit{\eta }$, $\mathit{\omega }$ is a positive real parameter controlling the influence of the source term G. The level-set function is moved towards zero if a topology change is favourable. A simple choice is $G(x,t)=-sgn(\mathit{\eta }(x,t))g(x,t)$ where g(x,t) is the gradient of the objective function.[40]

Figure 4. Ground truth $\mathit{\delta }$ maps for the object ($O_3$).

To escape local minima, new components can also be created in the level-set framework away for the current interface following the methodology presented in [41]. This approach was followed since it gives better numerical results. The objective function decreases faster and the nucleation of new regions is easier than with the former method. The idea is that the improvement due to the insertion of new components in the $\mathit{\delta }$ and $\mathit{\beta }$ maps corresponding to topology changes is related to the magnitude of the gradient of the data term of the objective functional, $I_D^{\prime \ast }[\mathit{\eta }][I_D[\mathit{\eta }]-I_{{\mathit{\delta }}_n}]$. If the norm of the gradient is large at some locations, a change in the values of $\mathit{\delta }$ and $\mathit{\beta }$ has a large effect on the cost functional. The numerical implementation of the calculation of the topological derivative can be summarized by the following algorithm. The different optimal parameters are determined by trial and error.

The new components nucleated may be suppressed by the geometric motion. The topological derivative is also included in an intermittent way with the optimization algorithm summarized in Algorithm 3.

The adjustable parameters $\mathit{\alpha }$ and ${\mathit{\sigma }}_g$ have been chosen to obtain the best decrease in the data term.

5. Numerical results and discussion

In the following, we compare the deterministic level-set algorithm with the modified algorithms with the stochastic evolution and topological derivatives. The algorithms are tested on different objects with several homogeneous materials. The synthetic results presented here allow us to validate the effectiveness of the stochastic perturbation and topology optimization approaches.

5.1. Simulation details

The deterministic and intermittent stochastic level-set algorithms and the deterministic algorithm with a topological derivative have been compared on two multi-material objects made up of two homogeneous materials. The multi-level regularization approach has been tested on a simple phantom made up of three homogeneous materials.

The first simulated test object ($O_1$) consists of an Al cylinder of 20 $\mathrm{\mu }m$ in diameter and 110 $\mathrm{\mu }m$ in height embedded in PMMA (object $O_1$). The second simulated object ($O_2$) consists of an Al cylinder of 20 $\mathrm{\mu }m$ in diameter and 110 $\mathrm{\mu }m$ in height embedded in PMMA and of an Al cylinder of 4 $\mathrm{\mu }m$ in diameter and 110 $\mathit{\mu }m$ in height. Some horizontal sections of the $\mathit{\beta }$ and $\mathit{\delta }$ maps of the simulated object $(O_1)$ and $(O_2)$ are displayed in Figures 2 and 3, respectively. A section of the $\mathit{\delta }$ map of the third phantom $(O_3)$ is shown in Figure 3. It consists of two ellipsoids of PMMA and Al surrounded by an oil ellipsoid. In the following, we denote ${\mathit{\delta }}^{\ast }$ and ${\mathit{\beta }}^{\ast }$ the real and imaginary parts of the complex refractive index to be retrieved.

Let $\mathit{\mu }=\frac{4\mathit{\pi }\mathit{\beta }}{\mathit{\lambda }}$, the $\mathit{\delta }$ and $\mathit{\mu }$ values used for PMMA, Al and oil for 24 keV X-rays are summarized in Table 1. The $\mathit{\beta }$ and $\mathit{\delta }$ values were discretized on a regular grid with a pixel size of 1.5 $\mathrm{\mu }$m. The cylinder is included in a rectangular volume of size $N_1\times N_1\times N_2$ pixels with $N_1=74$ and $N_2=109$ used for the simulations. The simulation box size is $120\times 120\times 50$ for the object $(0_3)$. The reconstructions results are not modified by an increase in the discretization level. The number of projection angles $N_{\mathit{\theta }}$ used for the simulation are $N_{\mathit{\theta }}$=75, 125 and 180. A single sample-to-detector distance D=100 mm is considered. Similar reconstructions results have been obtained for distances D in the range 50–200 mm. The discrete approximation of the Radon transform is the projection operator implemented in the Mablab Toolbox. The intensity data were corrupted with additive Gaussian white noise. This noise distribution corresponds to the noise measured experimentally. The signal to noise ratio was measured with the peak-to-peak signal to noise ratio (PPSNR) defined as:(36) $$\begin{array}{c}\hfill \mathrm{PPSNR}=20{\text{log}}_{10}\left(\frac{f_{\max }}{n_{\max }}\right)\end{array}$$(36)

where $f_{\max }$ is the maximum signal amplitude, $n_{\max }$ the maximum noise amplitude. To obtain a good accuracy, the $\mathit{ϵ}$ parameter of the smooth approximation of the Heaviside function (Equation (15(15) $$\begin{array}{c}\hfill H_{\mathit{ϵ}}(\mathit{\eta })=\frac{1+2\mathit{ϵ}}{2}\left(\text{erf}(\mathit{\eta }/\mathit{ϵ})+1\right)-\mathit{ϵ}\end{array}$$(15) )) was fixed to $\mathit{ϵ}=0.03$ for the simulated objects $(O_1)$ and $(O_2)$. For the object $(O_3)$, better numerical results have been obtained with a smaller value $\mathit{ϵ}=0.01$. For the multi-level algorithm, better reconstruction results are obtained if the level-set function is reinitialized every 100 iterations after thresholding with a distance function.

Figure 5. Horizontal section of the initial $\mathit{\beta }$ and $\mathit{\delta }$ maps for the object ($0_2$).

Figure 6. Horizontal section of the final error map for $\mathit{\beta }$ and $\mathit{\delta }$ for a PPSNR of 48 dB.

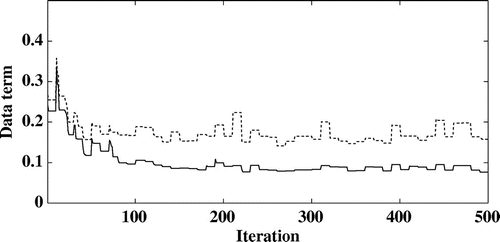
Figure 7. Evolution of the data term with the iterations for the noise levels 48 dB (plain line) and 30 dB (dotted line).

In the following, we present some simulations results obtained with deterministic level-set, stochastic level-set regularization and topological derivatives. In order to evaluate the efficiency of the reconstruction the data term $\frac{\Vert I_{D,\mathit{\theta }}[{\mathit{\eta }}_k]-I_{{\mathit{\delta }}_n}\Vert }{\Vert I_{{\mathit{\delta }}_n}\Vert }$ and the relative mean square errors (RMSE) using the $L_2(\mathrm{\Sigma })$ norm, $\Vert {\mathit{\delta }}^{\ast }{-\mathit{\delta }\Vert }_2/{\Vert {\mathit{\delta }}^{\ast }\Vert }_2$ and $\Vert {\mathit{\beta }}^{\ast }{-\mathit{\beta }\Vert }_2/{\Vert {\mathit{\beta }}^{\ast }\Vert }_2$ have been studied. Let $D_k=\frac{\Vert I_{D,\mathit{\theta }}[{\mathit{\eta }}_k]-I_{{\mathit{\delta }}_n}\Vert }{\Vert I_{{\mathit{\delta }}_n}\Vert }$ the value of the data term for the projection angle $\mathit{\theta }$ and the value ${\mathit{\eta }}_k$. The iterations are stopped when the average value of the variation of the data term $D_{k+1}-D_k$ evaluated on 10 iterations is below 0.05.

Table 1. Values of the $\mathit{\delta }$ and $\mathit{\mu }$ values for the materials in the object, at 24 keV X-rays from url http://henke.lbl.gov/optical$\_$constants.

Material	$\mathit{\delta }({10}^{-7})$	$\mathit{\mu }(m^{-1})$
PMMA	4.628	41.2
Al	9.396	502.6
Oil	3.60	25.66

5.2. Numerical results for deterministic level-set method

5.2.1. Bilevel algorithm

When the noise level is high or when the relative error between the initial guess for the $\mathit{\delta }$ and $\mathit{\beta }$ maps and the ground truth maps measured with the $L_2$ norm is higher than $50\%$, the Tikhonov regularization does not lead to good reconstruction results. This reconstruction error can be separated into two components, an error on the value of $\mathit{\delta }$ and $\mathit{\beta }$ and an error on the shape of the reconstructed regions. For piecewise constant $\mathit{\delta }$ and $\mathit{\beta }$ maps, the reconstruction results can be improved with the level-set regularization because some a priori information on the possible values of $\mathit{\delta }$ and $\mathit{\beta }$ is included. Some simulations have been performed to reconstruct the object $(O_1)$ with an initial diameter of the central Al cylinder equal to 40 $\mathrm{\mu }m$, twice the diameter of the cylinder to be reconstructed and noise levels of 30 and 48 dB. This initial guess with such a wrong diameter is motivated by the fact that, with the Tikhonov regularization method, after segmentation and projection of the reconstructed index map on the values corresponding to the different materials, a very poor approximation of the shape of the different regions is obtained. With these starting maps for the refractive index, the inverse problem is an easier shape optimization problem in which only the possible discrete values of the real and imaginary parts of the refractive index are known but not the shape of the regions where the refractive index takes constant values.

Figure 8. Evolution of the RMSE on $\mathit{\delta }$ with the iterations for the noise levels 30 dB (dotted line) and 48 dB (plain line).

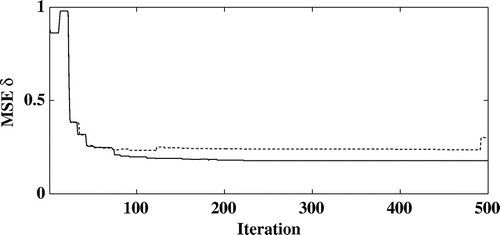
Figure 9. Evolution of the RMSE on $\mathit{\beta }$ with the iterations for the noise levels 30 dB (dotted line) and 48 dB (plain line).

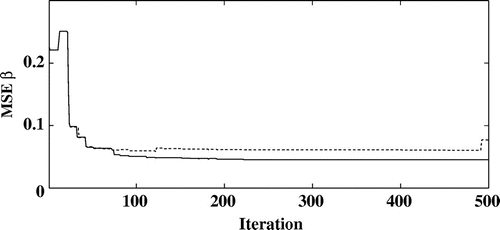
Figure 10. Evolution of the RMSE on $\mathit{\beta }$ with the iterations for the noise level 48 dB (dotted line) and $N_{\mathit{\theta }}$=180 (blue line), $N_{\mathit{\theta }}$=125 (black line) and $N_{\mathit{\theta }}$=75 (dotted line) projection angles for the reconstruction with the stochastic level-set algorithm.

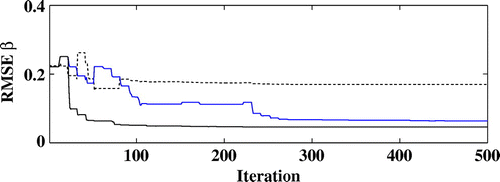
Figure 11. Evolution of the RMSE on $\mathit{\beta }$ with the iterations for the noise level 48 dB (dotted line) and $N_{\mathit{\theta }}$=180 (blue line), $N_{\mathit{\theta }}$=125 (black line) and $N_{\mathit{\theta }}$=75 (dotted line) projection angles for the reconstruction with the stochastic level-set algorithm.

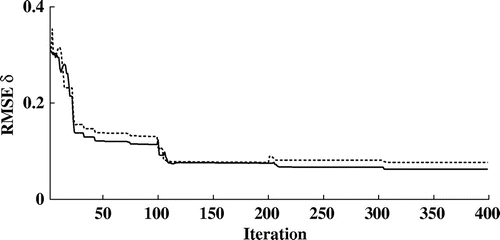
Figure 12. Evolution of the data term without topological derivative for the noise level 24 dB (black line) and with the topological derivative for the PPSNR 18 dB (blue line) and 24 dB (dotted line).

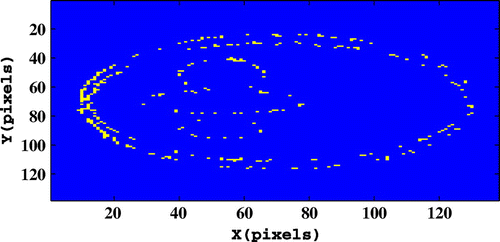
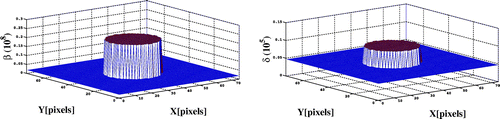
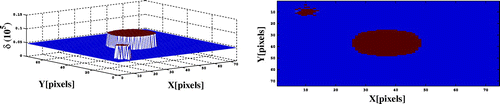
Figure 4 displays the horizontal section of the initial $\mathit{\beta }$ and $\mathit{\delta }$ maps. Figure 5 presents some horizontal sections of the errors for the real and imaginary parts of the reconstructed index map for a PPSNR of 48 dB after 500 iterations. These figures show that the reconstruction errors have been significantly reduced. Some errors are still present on the boundaries between the two materials. Similar results are obtained for the other sections and the noise level of 30 dB with reconstruction errors at the interface between the different regions.

The evolution of the data term $\Vert I_{D,\mathit{\theta }}[\mathit{\eta }]-I_{{\mathit{\delta }}_n}\Vert /\Vert I_{{\mathit{\delta }}_n}\Vert$ with the iterations is displayed in Figure 6 for the two noise levels investigated. In order to have a more quantitative information about the convergence of the method, the evolution of the relative mean square errors (RMSE) $\Vert {\mathit{\delta }}^{\ast }{-\mathit{\delta }\Vert }_2/{\Vert {\mathit{\delta }}^{\ast }\Vert }_2$ and $\Vert {\mathit{\beta }}^{\ast }{-\mathit{\beta }\Vert }_2/{\Vert {\mathit{\beta }}^{\ast }\Vert }_2$, are displayed as a function of the number of iterations for a PPSNR of 30 dB and 48 dB on Figures 7 and 8. The relative mean square errors on the two components $\mathit{\beta }$ and $\mathit{\delta }$ of the refractive index are much decreased.

The projection angle $\mathit{\theta }$ in Equations (21(21) $$\begin{array}{c}\hfill F^{\prime }[\mathit{\eta }]=I_{D,\mathit{\theta }}^{\prime \ast }[\mathit{\eta }]\left[I_{D,\mathit{\theta }}[\mathit{\eta }]-I_{{\mathit{\delta }}_n}\right]+{\mathit{\alpha }}_1(I-\mathrm{\Delta })[\mathit{\eta }]\end{array}$$(21) )–(23(23) $$\begin{array}{c}\hfill \frac{\mathit{\partial }{F}_{\mathit{ϵ}}}{\mathit{\partial }{\mathit{\eta }}_1}=G_1({\mathit{\eta }}_1,{\mathit{\eta }}_2)=0\end{array}$$(23) ) is changed randomly during the optimization scheme and some fluctuations of the reconstruction errors may be observed after several hundreds of iterations (see Figures 7 and 8, noise level 30 dB) but no clear decrease in the data term is obtained and the iterations are stopped. The uncertainty on the RMSE can be estimated to $5\%$.

For comparison, the lowest RMSE for $\mathit{\beta }$ and $\mathit{\delta }$ obtained with the Tikhonov regularization for the same intial guess with an optimal choice of the regularization parameter are summarized in Table 2 for $N_{\mathit{\theta }}=180$. From this table, we see that the level-set regularization outperforms the Tikhonov regularization for the in-line phase tomography problem for simulated objects with homogeneous materials.

For a number of projection angles higher than 180, the reconstruction results stagnates. When the number of projection angles $N_{\mathit{\theta }}$ is decreased, the reconstruction errors are higher as shown on Figure 9 for the imaginary parts of the refractive index.

Table 2. RMSE for $\mathit{\beta }$ and $\mathit{\delta }$ for the level-set (LS) and Tikhonov regularization approaches.

	RMSE $\mathit{\beta }$, LS	RMSE $\mathit{\delta }$,LS	RMSE $\mathit{\beta }$, Tikhonov	RMSE $\mathit{\delta }$, Tikhonov
PPSNR=30 dB	0.06	0.25	0.14	0.35
PPSNR=48 dB	0.05	0.17	0.1	0.25

5.2.2. Multi-level algorithm

Some simulations have been performed to reconstruct the object $(O_3)$ with the multi-level approach. In the initial configuration, the Al and oil ellipsoids axis values are 120 $\%$ higher and the Al ellipsoid axis values 30$\%$ lower than in the ground truth. The simulations have been performed with 180 projections and for noise levels of 30 and 48 dB.

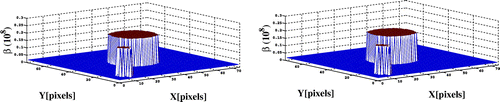
Figure 13. Horizontal section of the difference image between the ground truth and the reconstructed $\mathit{\beta }$ maps with the stochastic and the deterministic level-set algorithms for the noise level 24 dB.

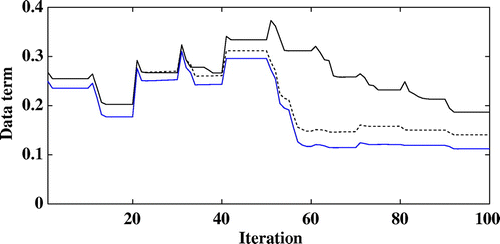
Figure 14. Evolution of the data term for the deterministic level-set algorithm for 24 dB (black line), for the intermittent stochastic level-set algorithm for 24 dB (blue line) and for the intermittent stochastic level-set algorithm for 18 dB (dotted line).

Figure 15. Evolution of the RMSE for $\mathit{\beta }$ and $\mathit{\delta }$ for the deterministic level-set algorithm for 24 dB (black line), for the intermittent stochastic level-set algorithm for 24 dB (blue line) and for the intermittent stochastic level-set algorithm for 18 dB (dotted line).

The evolution of the relative mean square errors (RMSE) $\Vert {\mathit{\delta }}^{\ast }{-\mathit{\delta }\Vert }_2/{\Vert {\mathit{\delta }}^{\ast }\Vert }_2$ is displayed as a function of the number of iterations for a PPSNR of 30 dB and 48 dB on Figure 11 for 180 projections. The decrease in the relative mean square errors on the component $\mathit{\beta }$ is very similar.

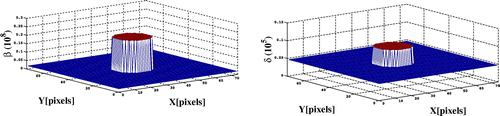
Horizontal sections of the error map for the real part of the index $\mathit{\delta }$ are displayed in Figure 12 for the noise level 48 dB. The reconstructions errors are located on the boundaries of the different regions similarly to what was obtained for the bilevel case. The reconstruction errors have been decreased and the multi-level approach is efficient to reconstruct simple shapes with several discrete values for the real and imaginary parts of the refractive index.

5.3. Deterministic level-set versus stochastic level-set algorithm

For higher noise levels and initializations maps with very different shape from the ground truth, the level-set regularization algorithm may be stuck in local optima. In these cases, the stochastic level-set algorithm may be useful to decrease further the cost functional. In order to perform a comparison of the deterministic and stochastic level-set algorithm, a first reconstruction is performed on the simulated object ($O_1$). The initial guess is a large cylinder with a diameter twice the diameter of the object ($0_1$). Then Algorithm 1 is applied to this initial reconstruction for PPSNR of 24 and 18 dB. Following Algorithm 1, the numbers of stochatic iterations are chosen randomly with a uniform distribution in [1,50] and the noise strength in the range $[1,{10}^{-3}]$. For the simulation of Equation (34(34) $$\begin{array}{cc}\hfill \mathrm{d}\mathit{\eta }(\overrightarrow{r},t)& =\mathit{\delta }\mathit{\eta }+\mathit{\rho }(t)|\mathrm{\nabla }\mathit{\eta }(\overrightarrow{r},t)|\mathrm{d}W(t)+\frac{1}{2}\mathit{\rho }(t)(▵\mathit{\eta }(\overrightarrow{r},t)\hfill \\ \hfill & -|\mathrm{\nabla }\mathit{\eta }(\overrightarrow{r},t)|\mathrm{div}\left(\frac{\mathrm{\nabla }\mathit{\eta }(\overrightarrow{r},t)}{|\mathrm{\nabla }\mathit{\eta }(\overrightarrow{r},t)|}\right)\hfill \end{array}$$(34) ), we use an explicit scheme with finite differences, the WENO scheme [42] with $\mathrm{\Delta }x=0.1$ and $\mathrm{\Delta }t=0.01$. An iterated deterministic minimization is performed for comparison with periodic reinitialization of the level-set function and projection angles chosen at random.

The evolutions of the data term, $\Vert I_{D,\mathit{\theta }}[\mathit{\eta }]-I_{{\mathit{\delta }}_n}\Vert /\Vert I_{{\mathit{\delta }}_n}\Vert$ are displayed on Figure 13 for the deterministic and intermittent stochastic algorithms starting from the initial reconstruction for the noise levels 18 and 24 dB. The deterministic algorithm is not efficient to achieve lower reconstruction errors. On the contrary, the reconstruction errors for $\mathit{\beta }$ and $\mathit{\delta }$ are much reduced with the intermittent stochastic diffusion. The data term may display different behaviours depending on the random projection angles $\mathit{\theta }$ (Equations (20(20) $$\begin{array}{c}\hfill F_{\mathit{ϵ}}({\mathit{\eta }}_1,{\mathit{\eta }}_2)=\frac{\Vert I_{D,\mathit{\theta }}[{\mathit{\eta }}_1,{\mathit{\eta }}_2]-I_{{\mathit{\delta }}_n}{\Vert }_2^2}{2}+{\mathit{\alpha }}_1\Vert {\mathit{\eta }}_1{\Vert }_{H_1}^2+{\mathit{\alpha }}_2{\Vert {\mathit{\eta }}_2\Vert }_{H_1}^2\end{array}$$(20) )–(22(22) $$\begin{array}{c}\hfill \left([I_{D,\mathit{\theta }}^{\prime \ast }[{\mathit{\eta }}^k]I_{D,\mathit{\theta }}^{\prime }[{\mathit{\eta }}^k]\right)\mathit{\delta }\mathit{\eta }+{\mathit{\alpha }}_1(I-\mathrm{\Delta })\mathit{\delta }\mathit{\eta }=-F^{\prime }[{\mathit{\eta }}^k]\end{array}$$(22) )) for similar noise levels. Yet, after hundred iterations, only small fluctuations are observed on the real and imaginary parts of the refractive index, $\mathit{\beta }$ and $\mathit{\delta }$, and the uncertainty on the RMSE given in the Tables in this work is below $5\%$ for a given noise level.

In order to show the efficiency of the method, the evolution of the normalized mean square error, $\Vert {\mathit{\delta }}^{\ast }{-\mathit{\delta }\Vert }_2/{\Vert {\mathit{\delta }}^{\ast }\Vert }_2$ and $\Vert {\mathit{\beta }}^{\ast }{-\mathit{\beta }\Vert }_2/{\Vert {\mathit{\beta }}^{\ast }\Vert }_2$, are displayed as a function of the number of iterations for the deterministic and stochastic algorithms on Figure 14. The iterated deterministic minimization cannot escape the local minimum corresponding to the initial reconstructed $\mathit{\delta }$ and $\mathit{\beta }$ volumes. A larger decrease is obtained with the stochastic scheme. Table 3 presents the reconstuction quality results for different noise levels and the different algorithms. The results corresponds to an average over three trials.

Table 3. RMSE for $\mathit{\beta }$ and $\mathit{\delta }$ for deterministic level-set and stochastic level-set.

	RMSE $\mathit{\beta }$, LS	RMSE $\mathit{\delta }$,LS	RMSE $\mathit{\beta }$, stochastic LS	RMSE $\mathit{\delta }$, stochastic LS
PPSNR=18 dB	0.28	0.85	0.15	0.55
PPSNR=24 dB	0.22	0.80	0.06	0.26

Figure 16. Horizontal section of the difference image between the ground truth and the reconstructed $\mathit{\beta }$ maps with the stochastic and the deterministic level-set algorithms for the noise level 24 dB.

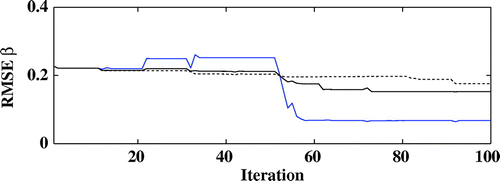
Figure 17. Evolution of the RMSE on $\mathit{\beta }$ with the iterations for the noise level 48 dB (dotted line) and $N_{\mathit{\theta }}$=180 (blue line), $N_{\mathit{\theta }}$=125 (black line) and $N_{\mathit{\theta }}$=75 (dotted line) projection angles for the reconstruction with the stochastic level-set algorithm.

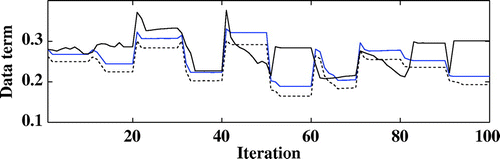
Figure 15 displays some horizontal sections of the difference image between the ground truth image and the reconstructed real index map obtained for the minimum of the discrepancy term for 24 dB with the stochastic or the deterministic methods. These figures show that the reconstruction errors have been significantly reduced. The visual comparison leads to the same conclusion for the imaginary part of the refractive index. Figure 16 displays the increase in the reconstruction errors for lower numbers of projections angles $N_{\mathit{\theta }}$ for the stochastic level-set algorithm. The increase in the number of projection angles does not improve the results.

Figure 18. Evolution of the data term without topological derivative for the noise level 24 dB (black line) and with the topological derivative for the PPSNR 18 dB (blue line) and 24 dB (dotted line).

Figure 19. Horizontal section of the reconstructed $\mathit{\beta }$ maps for the intermittent stochastic/deterministic algorithm with and without topological derivative for the noise level 24 dB.

Figure 20. Horizontal section of the reconstructed $\mathit{\delta }$ maps with the topological derivative for the noise level 24 dB and upper view of this section.

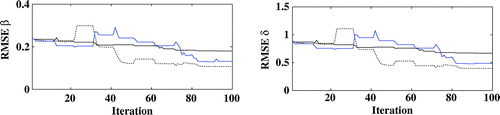
5.4. Effect of topological derivative on intermittent deterministic/stochastic level-set

In this section, we present a comparison of the mixed intermittent deterministic/stochastic level-set algorithms with and without topological derivative. The tests are performed on the object ($O_2$) with two cylinders. The intial $\mathit{\beta }$ and $\mathit{\delta }$ maps are the ones made up of large cylinders with the diameter 40 $\mathrm{\mu }m$ and the noise levels investigated corresponds to PPSNR of 24 and 18 dB. The small cylinder is missing in the initialization maps. The evolution of the data term and of the RMSE for $\mathit{\beta }$ and $\mathit{\delta }$ are displayed on Figures 14 and 15 for the stochastic level-set algorithm with and without the topological derivative. The iterations are stopped after a significant decrease in the data term. Some sections of the reconstructed $\mathit{\beta }$ with and without topological derivatives are displayed for the two cases investigated in Figure 16 for the noise level 24 dB. 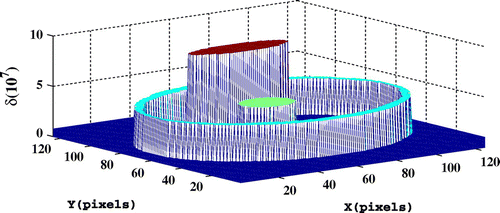The $\mathit{\delta }$ maps have similar features. Figure 17 displays the reconstructed $\mathit{\delta }$ map with an upper view. The missing cylinder is well-reconstructed with the topological derivative. On the contrary, it is missing in the mixed deterministic/stochastic level-set approach without the topological derivative. The reconstructions are much improved with the topological derivative and smaller error values are achieved.

5.5. Conclusion

In this work, we have investigated the nonlinear inverse problem associated to the reconstruction of the real and imaginary parts of the refractive index in phase contrast tomography. The a priori information that the real and imaginary parts $\mathit{\delta }$ and $\mathit{\beta }$ are piecewise constant is introduced and the regularization is performed on the level-set functions representing the real and imaginary components of the index. Our iterative scheme is based on the use of the adjoint of the Fréchet derivative of the intensity operator. The proposed regularization methods is tested on a several simple phantoms with two or three levels for the real and imaginary parts of the refractive index. The reconstruction errors are much decreased. Yet, this original approach stagnates and is not able to decrease the error for higher noise levels and for a first guess index map far from the ground truth. The reconstruction results are still improved with a stochastic perturbations of the shape of the reconstructed region with a stochastic level-set evolution and by taking into account the topological derivatives of the data term. The applicability of the method to real data will be investigated more precisely in future works.

Notes

No potential conflict of interest was reported by the author.