An adjoint method in inverse problems of chromatography

Abstract

How to determine adsorption isotherms is an issue of significant importance in chromatography. A modern technique of obtaining adsorption isotherms is to solve an inverse problem so that the simulated batch separation coincides with actual experimental results. In this work, as well as the natural least-square approach, we consider a Kohn–Vogelius type formulation for the reconstruction of adsorption isotherms in chromatography, which converts the original boundary fitting problem into a domain fitting problem. Moreover, using the first momentum regularizing strategy, a new regularization algorithm for both the Equilibrium-Dispersive model and the Transport-Dispersive model is developed. The mass transfer resistance coefficients in the Transport-Dispersive model are also estimated by the proposed inverse method. The computation of the gradients of objective functions for both of the two models is derived by the adjoint method. Finally, numerical simulations for both a synthetic problem and a real-world problem are given to show the robustness of the proposed algorithm.

Keywords:

• Chromatography
• adsorption isotherm
• inverse problem
• regularization
• convection–diffusion equation
• adjoint method

AMS Subject Classifications:

• 35R25
• 35R30
• 65M32
• 65M08
• 65K15

1. Introduction

Preparative chromatography is a powerful separation method to get pure compounds from more or less complex gas/liquid mixtures. Computer simulations can be used to optimize preparative chromatography, while the competitive adsorption isotherms are usually required. Roughly speaking, adsorption isotherms describe the dependence of the amount of adsorbed substance on the partial pressure of the solution concentration at a constant temperature. They are used to calculate the specific surface area of materials, mean size of deposited particles, as well as pore size or particle size distribution.

Experimental adsorption isotherms are the most common way to describe the adsorption phenomena.[1,2] Methods for getting the adsorption data for the adsorption isotherms are based on measuring the amount of gas/liquid removed from the gas/liquid phase during adsorption, and on various ways of determining the amount of adsorbed substance/adsorbate on the surface of the adsorbing substance/adsorbent: for instance, the volumetric method, the gravimetric method, etc.

Adsorption isotherms are often classified according to their shape.[3] There are six main types of adsorption isotherms. The most common ones are Type-I (Langmuir or similar) that are microporous solids with a relatively small proportion of the outer surface. Type-II refers to polymolecular adsorption in non-porous or macroporous adsorbents. Type-III is characteristic of non-porous sorbents with low energy adsorbent-adsorbate interaction. Types-IV and V are similar to types-II and III, but refer to porous adsorbents, while Type-VI isotherm is characteristic of non-porous adsorbents with a homogeneous surface.

However, the above classification only provides a qualitative representation of the adsorption isotherm. There are several methods of mathematically representing adsorption isotherms $q^{\ast }$, with different models used to describe the adsorption process.[4,5] At low surface coverage by the adsorbate, the adsorption isotherm equation for a uniform surface is given by Henry’s equation: $q^{\ast }(C)=aC$, where a is a constant and C denotes the concentration. At medium coverage, Freundlich’s empirical equation can be applied: $q^{\ast }(C)=a{C}^n$, where a and n are constants. A rigorous adsorption isotherm theory was proposed by Langmuir for the model of monolayer adsorption on a uniform surface, in which the attraction between adsorbate molecules and their mobility along the surface can be ignored. Langmuir’s isotherm equation has the form: $q^{\ast }(C)=aC/(1+bC)$, where a and b are constants.

In the multicomponent preparative case, we will have a non-linear adsorption isotherm, for each component, that is a function of all component concentrations because of competition for access to the adsorption sites. The simplest competitive non-linear adsorption isotherm is the competitive Langmuir one, where for component i in a n-component system we have that,(1) $$\begin{array}{c}\hfill q_i^{\ast }=q_i^{\ast }(C;\mathit{\xi })=\frac{a_i{C}^{(i)}}{1+{\sum }_{j=1}^n{b}_j{C}^{(j)}},i=1,\dots ,n.\end{array}$$(1)

Here $\mathit{\xi }=(a_1,\dots ,a_n,b_1,\dots ,b_n)$ denotes as a collection of all parameters, and $C^{(i)}$ is the concentration of ith component.

Recently, so-called model free methods have been developed for the estimation of complicated adsorption isotherms in liquid chromatography. These types of methods estimate the adsorption isotherm $q^{\ast }(C)$ [6] or its derivative $d{q}^{\ast }/dC$ [7] using monotone piecewise interpolation. In these methods, one divides the range of C into a finite number of segments and interpolates between the segments boundary points using basis function $\mathit{\varphi }(C)$ such that continuity, up to a certain order, is preserved across the boundaries, where $\mathit{\xi }$ denotes as a collection of all parameters. To be more precise, consider the case with a single component. Denote by ${{\{}_{k}C\}}_{k=1}^m$ a collection of m values of concentration C. Set $q^{\ast }(C;\mathit{\xi })={\sum }_{k=1}^m{q}^{\ast }{(}_{k}C){\mathit{\varphi }}_k(C)$, where $\{{\mathit{\varphi }}_k\}$ are basis functions and $\mathit{\xi }=(q^{\ast }{(}_{1}C),\dots ,q^{\ast }{(}_{m}C))$ is a vector of coefficients.

Inverse methods are a more practical alternative that have been developed in recent years.[8,9] These methods only require a few injections of different sample concentrations, so solute consumption and time requirements are very modest. The adsorption isotherm parameters $\mathit{\xi }$ cannot be obtained directly from the experimental elution data, in contrast to the traditional methods such as the frontal analysis method, which is usually carried out in a series of programmed concentration steps, each step resulting in a so-called breakthrough front giving one point on the adsorption isotherm curve.[10] Instead, the parameters are estimated numerically by solving an inverse problem in partial differential equations (PDEs). In this study, as well as the natural least-square approach, we propose a Kohn–Vogelius type formulation for reconstructing adsorption isotherms in chromatography. By the Kohn–Vogelius formulation, data to be fitted is transferred from boundary into the whole domain.[11] Therefore, this method is more efficient than the least-squares approach for the numerical reconstruction.[12] Furthermore, applying the first momentum regularization, we have developed a new regularizing algorithm to reconstruct the adsorption isotherm.

The remainder of the paper is structured as follows. Section 2 states the model we are dealing with, and introduces the original least-square problem and the corresponding Kohn–Vogelius type formulation of the problem. Applying the gradient descent method, in Section 3, we obtain a novel algorithm of reconstructing adsorption isotherms in chromatography. Methods of computing exact gradients of objective functions for both the Equilibrium-Dispersive model and the Transport-Dispersive model are also developed in the same section. Moreover, a method of estimating the mass transfer resistance in the Transport-Dispersive model is proposed in Section 3. In Section 4, some implementation issues with the proposed numerical algorithms are discussed. Various numerical examples with both the synthetic data and real data are presented in Section 5 to demonstrate the robustness of the proposed method. Finally, concluding remarks are given in Section 6.

2. Mathematical models

2.1. Models

There are various mathematical models for chromatographic processes.[5,13–15] The most commonly used model to describe the travel of multicomponents is the following time-dependent convection–diffusion system with the Danckwert’s boundary condition(2) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }C}{\mathit{\partial }t}+F\frac{\mathit{\partial }q}{\mathit{\partial }t}+u\frac{\mathit{\partial }C}{\mathit{\partial }x}=D_a\frac{{\mathit{\partial }}^{2}C}{\mathit{\partial }{x}^2},\hfill & x\in \mathcal{X}\equiv (0,L),t\in \mathcal{T}\equiv (0,T],\hfill \\ C(x,0)=g(x),\hfill & x\in \mathcal{X},t=0,\hfill \\ uC(0,t)-D_a\frac{\mathit{\partial }C(0,t)}{\mathit{\partial }x}=uh(t),\hfill & x=0,t\in \mathcal{T},\hfill \\ D_a\frac{\mathit{\partial }C(L,t)}{\mathit{\partial }x}=0,\hfill & x=L,t\in \mathcal{T}.\hfill \end{array}\right.\end{array}$$(2)

where C and q are concentrations in mobile and stationary phase, respectively; u is mobile phase velocity and F is stationary/mobile phase ratio, and $D_a$ is the diffusion parameter. Note that all of u, F and $D_a$ are given constants in this work. L is the length of chromatographic column, and T is an appropriate time point slightly larger than the dead time of chromatographic time $T_0=L/u$. In this work, we set $T=1.5T_0$. x is distance and t is time. Further, g is the initial condition and h is the boundary condition, which describes the injection profile of the problem. For the problem with n components, C, q, g and h are vector functions of size $n\times 1$.

Define $L^2(\mathcal{Y})$ ($\mathcal{Y}=\mathcal{X},\mathcal{T}$ or $\mathcal{X}\times \mathcal{T}$) as the space of square Lebesgue integrable functions, equipped with the standard norm, i.e. ${\Vert ·\Vert }_{L^2(\mathcal{Y})}^2={\int }_{\mathcal{Y}}{[·]}^2\mathrm{d}y$.[16] Denote $L^2{(\mathcal{Y})}^n=L^2(\mathcal{Y})\times ···\times L^2(\mathcal{Y})$ and ${\Vert C\Vert }_{L^2{(\mathcal{Y})}^n}^2={\sum }_{i=1}^n{\Vert C^{(i)}\Vert }_{L^2(\mathcal{Y})}^2$, where $C=(C^{(1)},\dots ,C^{(n)})$. Suppose that $g\in L^2{(\mathcal{X})}^n$, $h\in L^2{(\mathcal{T})}^n$ and C, $q\in W_2^{2,1}{(\mathcal{X}\times \mathcal{T})}^n$ (a Sobolev space with norm ${\Vert C\Vert }_{W_2^{2,1}{(\mathcal{X}\times \mathcal{T})}^n}^2={\sum }_{0\le r+2s\le 2}{\Vert {\mathit{\partial }}_t^s{\mathit{\partial }}_x^{r}C\Vert }_{L^2{(\mathcal{X}\times \mathcal{T})}^n}^2$ [17,18]).

If there is no diffusion, i.e. $D_a=0$, we have the hyperbolic model, which is mostly of theoretical interest.[8] In this study, we focus on the case when $D_a\ne 0$.

• If $q=q^{\ast }(C)$ we have the Equilibrium-Dispersive model. In this model, the mass transfer resistance for adsorption/desorption is assumed to be small, though not negligible (fast kinetics).

• If(3) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }q}{\mathit{\partial }t}=k_f(q^{\ast }(C)-q),\hfill & t\in \mathcal{T},\hfill \\ q=q^{\ast }(C),\hfill & t=0,\hfill \end{array}\right.\end{array}$$(3) we obtain the Transport-Dispersive model, which is commonly used when the mass transfer resistance for adsorption/desorption cannot be assumed to be small (slow kinetics). Here, vector $k_f={(k_f^{(1)},\dots ,k_f^{(n)})}^T$ represents the mass transfer resistance for species. The superscript T represents the transpose of a matrix.

Remark 2.1:

$k_{f}C$ reads as $k_f\ast C={(k_f^{(1)}{C}^{(1)},\dots ,k_f^{(n)}{C}^{(n)})}^T$. Nevertheless, for simplicity, we will ignore the operator ‘$\ast$’ after $k_f$ from now on.

Before discussing the inverse problem based on Equation (2(2) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }C}{\mathit{\partial }t}+F\frac{\mathit{\partial }q}{\mathit{\partial }t}+u\frac{\mathit{\partial }C}{\mathit{\partial }x}=D_a\frac{{\mathit{\partial }}^{2}C}{\mathit{\partial }{x}^2},\hfill & x\in \mathcal{X}\equiv (0,L),t\in \mathcal{T}\equiv (0,T],\hfill \\ C(x,0)=g(x),\hfill & x\in \mathcal{X},t=0,\hfill \\ uC(0,t)-D_a\frac{\mathit{\partial }C(0,t)}{\mathit{\partial }x}=uh(t),\hfill & x=0,t\in \mathcal{T},\hfill \\ D_a\frac{\mathit{\partial }C(L,t)}{\mathit{\partial }x}=0,\hfill & x=L,t\in \mathcal{T}.\hfill \end{array}\right.\end{array}$$(2) ), let us make the following assumption on the forward problem.

(A)

The non-linear PDE (2(2) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }C}{\mathit{\partial }t}+F\frac{\mathit{\partial }q}{\mathit{\partial }t}+u\frac{\mathit{\partial }C}{\mathit{\partial }x}=D_a\frac{{\mathit{\partial }}^{2}C}{\mathit{\partial }{x}^2},\hfill & x\in \mathcal{X}\equiv (0,L),t\in \mathcal{T}\equiv (0,T],\hfill \\ C(x,0)=g(x),\hfill & x\in \mathcal{X},t=0,\hfill \\ uC(0,t)-D_a\frac{\mathit{\partial }C(0,t)}{\mathit{\partial }x}=uh(t),\hfill & x=0,t\in \mathcal{T},\hfill \\ D_a\frac{\mathit{\partial }C(L,t)}{\mathit{\partial }x}=0,\hfill & x=L,t\in \mathcal{T}.\hfill \end{array}\right.\end{array}$$(2) ) for both the Equilibrium-Dispersive model and the Transport-Dispersive model has an unique stable solution in $W_2^{2,1}{(\mathcal{X}\times \mathcal{T})}^n$.

Indeed, the well posedness of the forward problem (2(2) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }C}{\mathit{\partial }t}+F\frac{\mathit{\partial }q}{\mathit{\partial }t}+u\frac{\mathit{\partial }C}{\mathit{\partial }x}=D_a\frac{{\mathit{\partial }}^{2}C}{\mathit{\partial }{x}^2},\hfill & x\in \mathcal{X}\equiv (0,L),t\in \mathcal{T}\equiv (0,T],\hfill \\ C(x,0)=g(x),\hfill & x\in \mathcal{X},t=0,\hfill \\ uC(0,t)-D_a\frac{\mathit{\partial }C(0,t)}{\mathit{\partial }x}=uh(t),\hfill & x=0,t\in \mathcal{T},\hfill \\ D_a\frac{\mathit{\partial }C(L,t)}{\mathit{\partial }x}=0,\hfill & x=L,t\in \mathcal{T}.\hfill \end{array}\right.\end{array}$$(2) ) can be obtained by the general theory of quasilinear parabolic equations under some appropriate assumptions, see [17,18] for details.

2.2. The identification problem

The purpose of this work is to find parameter $\mathit{\xi }$ such that the solution of (2(2) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }C}{\mathit{\partial }t}+F\frac{\mathit{\partial }q}{\mathit{\partial }t}+u\frac{\mathit{\partial }C}{\mathit{\partial }x}=D_a\frac{{\mathit{\partial }}^{2}C}{\mathit{\partial }{x}^2},\hfill & x\in \mathcal{X}\equiv (0,L),t\in \mathcal{T}\equiv (0,T],\hfill \\ C(x,0)=g(x),\hfill & x\in \mathcal{X},t=0,\hfill \\ uC(0,t)-D_a\frac{\mathit{\partial }C(0,t)}{\mathit{\partial }x}=uh(t),\hfill & x=0,t\in \mathcal{T},\hfill \\ D_a\frac{\mathit{\partial }C(L,t)}{\mathit{\partial }x}=0,\hfill & x=L,t\in \mathcal{T}.\hfill \end{array}\right.\end{array}$$(2) ) satisfies$$\begin{array}{c}\hfill C(L,t;\mathit{\xi })=C_{obs}(t),t\in \mathcal{T},\end{array}$$

where $C_{obs}(t)=(C_{obs}^{(1)}(t),\dots ,C_{obs}^{(n)}(t))$ denotes the observation data measured at the outlet. The output least-squares approach for this identifying process is used most commonly as the optimization problem in $L^2{(\mathcal{T})}^n$:(4) $$\begin{array}{c}\hfill \underset{\mathit{\xi }}{min}{J}_{BF}(C;\mathit{\xi }):=\underset{\mathit{\xi }}{min}\frac{1}{2}{∥C(L,t;\mathit{\xi })-C_{obs}(t)∥}_{L^2{(\mathcal{T})}^n}^2,\end{array}$$(4)

where $C(x,t;\mathit{\xi })$ solves PDE (2(2) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }C}{\mathit{\partial }t}+F\frac{\mathit{\partial }q}{\mathit{\partial }t}+u\frac{\mathit{\partial }C}{\mathit{\partial }x}=D_a\frac{{\mathit{\partial }}^{2}C}{\mathit{\partial }{x}^2},\hfill & x\in \mathcal{X}\equiv (0,L),t\in \mathcal{T}\equiv (0,T],\hfill \\ C(x,0)=g(x),\hfill & x\in \mathcal{X},t=0,\hfill \\ uC(0,t)-D_a\frac{\mathit{\partial }C(0,t)}{\mathit{\partial }x}=uh(t),\hfill & x=0,t\in \mathcal{T},\hfill \\ D_a\frac{\mathit{\partial }C(L,t)}{\mathit{\partial }x}=0,\hfill & x=L,t\in \mathcal{T}.\hfill \end{array}\right.\end{array}$$(2) ). It is not difficult to show that the functional $J_{BF}(C;\mathit{\xi })$ does not take into account the position of the profiles, which implies the ill posedness of the formulation of problem. Indeed, $J_{BF}(C;\mathit{\xi })$ remains constant if one moves $C(L,t;\mathit{\xi })$ along the t-axis when $supp(C(L,·;\mathit{\xi })\cap C_{obs}(·))=\mathrm{\varnothing }$.[8] It is well known that to obtain a stable approximate solution for an ill-posed problem, regularization procedure should be employed. Within the framework of the Tikhonov regularization algorithm, the problem (4(4) $$\begin{array}{c}\hfill \underset{\mathit{\xi }}{min}{J}_{BF}(C;\mathit{\xi }):=\underset{\mathit{\xi }}{min}\frac{1}{2}{∥C(L,t;\mathit{\xi })-C_{obs}(t)∥}_{L^2{(\mathcal{T})}^n}^2,\end{array}$$(4) ) is substituted by(5) $$\begin{array}{c}\hfill \underset{\mathit{\xi }}{min}{\mathcal{J}}_{BF,\mathit{\alpha }}(\mathit{\xi })=\underset{\mathit{\xi }}{min}{J}_{BF}(C;\mathit{\xi })+\mathit{\alpha }\mathrm{\Omega }(C;\mathit{\xi }),\end{array}$$(5)

where $\mathit{\alpha }>0$ is the regularization parameter and the second term in the cost represents a regularization term, which guarantees the continuity of the mappings from the observation $C_{obs}\in L^2{(\mathcal{T})}^n$ to a solution for appropriate choice of $\mathrm{\Omega }(·)$ and $\mathit{\alpha }$. In this work, we apply the first momentum regularizing strategy, introduced in [8]. Define the first moment $\mathit{\mu }$ of a function C(t) by(6) $$\begin{array}{c}\hfill \mathit{\mu }(C(t))={\int }_{\mathcal{T}}tC(t)\mathrm{d}t.\end{array}$$(6)

Then, if C happens to be a concentration profile, the two moments $\mathit{\mu }(C_1)$ and $\mathit{\mu }(C_2)$ are related to the retention times of the two components.[4] Hence, the regularization term for our problem is defined as(7) $$\begin{array}{c}\hfill {\mathrm{\Omega }}_{BF}=\frac{1}{2}{\Vert \mathit{\mu }(C(L,t;\mathit{\xi })-C_{obs}(t))\Vert }_2^2,\end{array}$$(7)

where ${\Vert ·\Vert }_2$ is the standard norm in ${\mathbf{R}}^n$.

In [19,20], a Kohn–Vogelius type functional is used for the data fitting in solving the inverse source problem. For our problem, the Kohn–Vogelius type formulation becomes(8) $$\begin{array}{c}\hfill \underset{\mathit{\xi }\in \mathrm{\Theta }}{min}{\mathcal{J}}_{KV,\mathit{\alpha }}(\mathit{\xi })\equiv \underset{\mathit{\xi }\in \mathrm{\Theta }}{min}{J}_{KV}(\mathit{\xi })+\mathit{\alpha }{\mathrm{\Omega }}_{KV}(\mathit{\xi }),\end{array}$$(8)

where $\mathrm{\Theta }$ is a convex closed set in ${\mathbf{R}}^m$, which contains the a priori information of the parameter (m is the dimensionality of the parameter space) and$$\begin{array}{c}\hfill \begin{array}{c}{J}_{KV}(\mathit{\xi })=\frac{1}{2}{∥C_1(x,t;\mathit{\xi })-C_2(x,t;\mathit{\xi })∥}_{L^2{(\mathcal{X}\times \mathcal{T})}^n}^2,\hfill \\ {\mathrm{\Omega }}_{KV}(\mathit{\xi })=\frac{1}{2}{\Vert \mathit{\mu }(C_1(x,t;\mathit{\xi })-C_2(x,t;\mathit{\xi }))\Vert }_2^2,\mathit{\mu }(\bullet )={\int }_{\mathcal{X}\times \mathcal{T}}x·t·\bullet \mathrm{d}x\mathrm{d}t.\hfill \end{array}\end{array}$$$C_1(x,t;\mathit{\xi })$ is the solution of (1(1) $$\begin{array}{c}\hfill q_i^{\ast }=q_i^{\ast }(C;\mathit{\xi })=\frac{a_i{C}^{(i)}}{1+{\sum }_{j=1}^n{b}_j{C}^{(j)}},i=1,\dots ,n.\end{array}$$(1) )–(2(2) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }C}{\mathit{\partial }t}+F\frac{\mathit{\partial }q}{\mathit{\partial }t}+u\frac{\mathit{\partial }C}{\mathit{\partial }x}=D_a\frac{{\mathit{\partial }}^{2}C}{\mathit{\partial }{x}^2},\hfill & x\in \mathcal{X}\equiv (0,L),t\in \mathcal{T}\equiv (0,T],\hfill \\ C(x,0)=g(x),\hfill & x\in \mathcal{X},t=0,\hfill \\ uC(0,t)-D_a\frac{\mathit{\partial }C(0,t)}{\mathit{\partial }x}=uh(t),\hfill & x=0,t\in \mathcal{T},\hfill \\ D_a\frac{\mathit{\partial }C(L,t)}{\mathit{\partial }x}=0,\hfill & x=L,t\in \mathcal{T}.\hfill \end{array}\right.\end{array}$$(2) ) (or (1(1) $$\begin{array}{c}\hfill q_i^{\ast }=q_i^{\ast }(C;\mathit{\xi })=\frac{a_i{C}^{(i)}}{1+{\sum }_{j=1}^n{b}_j{C}^{(j)}},i=1,\dots ,n.\end{array}$$(1) )–(3(3) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }q}{\mathit{\partial }t}=k_f(q^{\ast }(C)-q),\hfill & t\in \mathcal{T},\hfill \\ q=q^{\ast }(C),\hfill & t=0,\hfill \end{array}\right.\end{array}$$(3) ) for the Transport-Dispersive model) with $C(x,t;\mathit{\xi })$ replaced by $C_1(x,t;\mathit{\xi })$ and $C_2(x,t;\mathit{\xi })$ is the solution to(9) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }{C}_2}{\mathit{\partial }t}+F\frac{\mathit{\partial }q(C_2)}{\mathit{\partial }t}+u\frac{\mathit{\partial }{C}_2}{\mathit{\partial }x}=D_a\frac{{\mathit{\partial }}^2{C}_2}{\mathit{\partial }{x}^2},\hfill & (x,t)\in \mathcal{X}\times \mathcal{T},\hfill \\ C_2(x,0)=g(x),\hfill & t=0,x\in \mathcal{X},\hfill \\ u{C}_2(0,t)-D_a\frac{\mathit{\partial }{C}_2(0,t)}{\mathit{\partial }x}=uh(t),\hfill & x=0,t\in \mathcal{T},\hfill \\ C_2(L,t)=C_{obs}(t),\hfill & x=L,t\in \mathcal{T}.\hfill \end{array}\right.\end{array}$$(9)

with additional information (1(1) $$\begin{array}{c}\hfill q_i^{\ast }=q_i^{\ast }(C;\mathit{\xi })=\frac{a_i{C}^{(i)}}{1+{\sum }_{j=1}^n{b}_j{C}^{(j)}},i=1,\dots ,n.\end{array}$$(1) ) ((1(1) $$\begin{array}{c}\hfill q_i^{\ast }=q_i^{\ast }(C;\mathit{\xi })=\frac{a_i{C}^{(i)}}{1+{\sum }_{j=1}^n{b}_j{C}^{(j)}},i=1,\dots ,n.\end{array}$$(1) ) and (3(3) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }q}{\mathit{\partial }t}=k_f(q^{\ast }(C)-q),\hfill & t\in \mathcal{T},\hfill \\ q=q^{\ast }(C),\hfill & t=0,\hfill \end{array}\right.\end{array}$$(3) ) for the Transport-Dispersive model).

Remark 2.2:

For simplicity, the smooth function $C_{obs}(t)$ is constructed by the linear interpolation of discrete observation data $\{C_{obs}(t_j)\}$. This is necessary since, in general, the time grids of numerical solution of PDE (2(2) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }C}{\mathit{\partial }t}+F\frac{\mathit{\partial }q}{\mathit{\partial }t}+u\frac{\mathit{\partial }C}{\mathit{\partial }x}=D_a\frac{{\mathit{\partial }}^{2}C}{\mathit{\partial }{x}^2},\hfill & x\in \mathcal{X}\equiv (0,L),t\in \mathcal{T}\equiv (0,T],\hfill \\ C(x,0)=g(x),\hfill & x\in \mathcal{X},t=0,\hfill \\ uC(0,t)-D_a\frac{\mathit{\partial }C(0,t)}{\mathit{\partial }x}=uh(t),\hfill & x=0,t\in \mathcal{T},\hfill \\ D_a\frac{\mathit{\partial }C(L,t)}{\mathit{\partial }x}=0,\hfill & x=L,t\in \mathcal{T}.\hfill \end{array}\right.\end{array}$$(2) ) do not fit the time grids of the observation data. Obviously, one can apply spline technique to obtain a better smooth function $C_{obs}(t)$.

Remark 2.3:

The objective function $J_{BF}(\mathit{\xi })$ has been used widely [9,21] for identification problems in chromatography. To the best of our knowledge, the Kohn–Vogelius type formulation of the problem has not been tried for the inverse chromatography problem. In general, compared to least-squares boundary fitting function, the Kohn–Vogelius type function is expected to lead to more robust optimization procedures.[12]

3. The solution method

3.1. The algorithm

To solve the inverse problem requires advanced optimization algorithms. It should be noted that in most cases a global optimization algorithm is needed, otherwise the algorithm might get stuck in local minima. However, local optimization algorithms can be used to refine the solution found by the global optimization algorithm. One branch of local optimization algorithms that have been tried previously is non-gradient algorithms,[22] but the drawback is slow convergence. Another approach is to use a gradient-based algorithm such as the steepest descent method and the conjugate gradient method. In this work, we use a gradient descent method combined with a Barzilai–Borwein step [23]: see Algorithm 1 for details.

3.2. Methods of calculating the Jacobian of objective functions

The estimation of the Jacobian by numeric or complex step differentiation is not accurate and the gradient-based algorithm converges slowly or not at all. For the hyperbolic model, i.e. $D_a=0$, in [24], the authors converted adsorption isotherms into a part of the flux of the system by variable change and obtained the exact computation of the Jacobian of objective function ${\mathcal{J}}_{BF,\mathit{\alpha }}(\mathit{\xi })$. However, the variable change is complicated and the neglected diffusion will cause a significant error. Hence, in this work, without variable change and neglecting diffusion, we try to derive the exact Jacobian of the objective functions mentioned in Section 2.

3.2.1. Equilibrium-dispersive model

We first study the Jacobian of the objective function in the Equilibrium-Dispersive model.

Proposition 3.1:

The Jacobian of the objective function ${\mathcal{J}}_{BF,\mathit{\alpha }}(\mathit{\xi })$ for the Equilibrium-Dispersive model is$$\begin{array}{c}\hfill {\mathcal{J}}_{BF,\mathit{\alpha }}^{\prime }(\mathit{\xi })=-F·{\int }_{\mathcal{X}\times \mathcal{T}}\mathrm{d}x\mathrm{d}t\frac{\mathit{\partial }{\left[\frac{\mathit{\partial }q(C;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}\right]}^T}{\mathit{\partial }t}p,\\ \hfill \end{array}$$

where C is the solution of (2(2) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }C}{\mathit{\partial }t}+F\frac{\mathit{\partial }q}{\mathit{\partial }t}+u\frac{\mathit{\partial }C}{\mathit{\partial }x}=D_a\frac{{\mathit{\partial }}^{2}C}{\mathit{\partial }{x}^2},\hfill & x\in \mathcal{X}\equiv (0,L),t\in \mathcal{T}\equiv (0,T],\hfill \\ C(x,0)=g(x),\hfill & x\in \mathcal{X},t=0,\hfill \\ uC(0,t)-D_a\frac{\mathit{\partial }C(0,t)}{\mathit{\partial }x}=uh(t),\hfill & x=0,t\in \mathcal{T},\hfill \\ D_a\frac{\mathit{\partial }C(L,t)}{\mathit{\partial }x}=0,\hfill & x=L,t\in \mathcal{T}.\hfill \end{array}\right.\end{array}$$(2) ) and p is the solution to the following adjoint problem(10) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }p}{\mathit{\partial }t}+F{\left[\frac{\mathit{\partial }q(C;\mathit{\xi })}{\mathit{\partial }C}\right]}^T\frac{\mathit{\partial }p}{\mathit{\partial }t}+u\frac{\mathit{\partial }p}{\mathit{\partial }x}+D_a\frac{{\mathit{\partial }}^{2}p}{\mathit{\partial }{x}^2}=0,\hfill & (x,t)\in \mathcal{X}\times \mathcal{T},\hfill \\ p(x,T)=0,\hfill & t=T,x\in \mathcal{X},\hfill \\ up(L,t)+D_a\frac{\mathit{\partial }p(L,t)}{\mathit{\partial }x}=\frac{\mathit{\partial }{\mathcal{J}}_{BF,\mathit{\alpha }}}{\mathit{\partial }C},\hfill & x=L,t\in \mathcal{T},\hfill \\ D_a\frac{\mathit{\partial }p(0,t)}{\mathit{\partial }x}=0,\hfill & x=0,t\in \mathcal{T},\hfill \end{array}\right.\end{array}$$(10)

where $\mathit{\partial }{\mathcal{J}}_{BF,\mathit{\alpha }}/\mathit{\partial }C=(C(L,t;\mathit{\xi })-C_{obs}(t))+\mathit{\alpha }t\mathit{\mu }(C(L,t;\mathit{\xi })-C_{obs}(t))$.

Proof:

Let us consider the weak form of (2(2) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }C}{\mathit{\partial }t}+F\frac{\mathit{\partial }q}{\mathit{\partial }t}+u\frac{\mathit{\partial }C}{\mathit{\partial }x}=D_a\frac{{\mathit{\partial }}^{2}C}{\mathit{\partial }{x}^2},\hfill & x\in \mathcal{X}\equiv (0,L),t\in \mathcal{T}\equiv (0,T],\hfill \\ C(x,0)=g(x),\hfill & x\in \mathcal{X},t=0,\hfill \\ uC(0,t)-D_a\frac{\mathit{\partial }C(0,t)}{\mathit{\partial }x}=uh(t),\hfill & x=0,t\in \mathcal{T},\hfill \\ D_a\frac{\mathit{\partial }C(L,t)}{\mathit{\partial }x}=0,\hfill & x=L,t\in \mathcal{T}.\hfill \end{array}\right.\end{array}$$(2) )(11) $$\begin{array}{c}\hfill \begin{array}{c}{\int }_{\mathcal{X}}\mathrm{d}x{\left[(C+Fq(C;\mathit{\xi }))·\mathit{\varphi }\right]}_{t=T}-{\int }_{\mathcal{X}}\mathrm{d}x{\left[(g(x)+Fq(C;\mathit{\xi }))·\mathit{\varphi }\right]}_{t=0}\hfill \\ -{\int }_{\mathcal{X}\times \mathcal{T}}(C+Fq(C;\mathit{\xi }))·\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }t}\mathrm{d}x\mathrm{d}t+{\int }_{\mathcal{T}}\mathrm{d}t{\left[uC·\mathit{\varphi }\right]}_{x=L}-{\int }_{\mathcal{T}}\mathrm{d}t{\left[uh(t)·\mathit{\varphi }\right]}_{x=0}\hfill \\ -{\int }_{\mathcal{X}\times \mathcal{T}}uC·\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }x}\mathrm{d}x\mathrm{d}t+D_a{\int }_{\mathcal{X}\times \mathcal{T}}\frac{\mathit{\partial }C}{\mathit{\partial }x}·\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }x}\mathrm{d}x\mathrm{d}t=0,\mathit{\varphi }\in D{(\mathcal{X}\times \mathcal{T})}^n\hfill \end{array}\end{array}$$(11)

where the test function space $D(\mathcal{X}\times \mathcal{T})$ is a subspace of $C^{\infty }(\mathcal{X}\times \mathcal{T})$, whose elements (functions) have a compact support.[16] $D{(\mathcal{X}\times \mathcal{T})}^n=D(\mathcal{X}\times \mathcal{T})\times ···\times D(\mathcal{X}\times \mathcal{T})$.

Using integration by parts, the last term of (11(11) $$\begin{array}{c}\hfill \begin{array}{c}{\int }_{\mathcal{X}}\mathrm{d}x{\left[(C+Fq(C;\mathit{\xi }))·\mathit{\varphi }\right]}_{t=T}-{\int }_{\mathcal{X}}\mathrm{d}x{\left[(g(x)+Fq(C;\mathit{\xi }))·\mathit{\varphi }\right]}_{t=0}\hfill \\ -{\int }_{\mathcal{X}\times \mathcal{T}}(C+Fq(C;\mathit{\xi }))·\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }t}\mathrm{d}x\mathrm{d}t+{\int }_{\mathcal{T}}\mathrm{d}t{\left[uC·\mathit{\varphi }\right]}_{x=L}-{\int }_{\mathcal{T}}\mathrm{d}t{\left[uh(t)·\mathit{\varphi }\right]}_{x=0}\hfill \\ -{\int }_{\mathcal{X}\times \mathcal{T}}uC·\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }x}\mathrm{d}x\mathrm{d}t+D_a{\int }_{\mathcal{X}\times \mathcal{T}}\frac{\mathit{\partial }C}{\mathit{\partial }x}·\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }x}\mathrm{d}x\mathrm{d}t=0,\mathit{\varphi }\in D{(\mathcal{X}\times \mathcal{T})}^n\hfill \end{array}\end{array}$$(11) ) can be expressed as$$\begin{array}{cc}& D_a{\int }_{\mathcal{X}\times \mathcal{T}}\frac{\mathit{\partial }C}{\mathit{\partial }x}·\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }x}\mathrm{d}x\mathrm{d}t\hfill \\ \hfill & ={\int }_{\mathcal{T}}\mathrm{d}t{\left[D_{a}C·\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }x}\right]}_{x=L}-{\int }_{\mathcal{T}}\mathrm{d}t{\left[D_{a}C·\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }x}\right]}_{x=0}-{\int }_{\mathcal{X}\times \mathcal{T}}{D}_{a}C·\frac{{\mathit{\partial }}^2\mathit{\varphi }}{\mathit{\partial }{x}^2}\mathrm{d}x\mathrm{d}t.\hfill \end{array}$$

Assume that the derivative of C with respect to $\mathit{\xi }$ in the direction $\mathit{\delta }\mathit{\xi }$ is M, i.e. $M:={\mathrm{\nabla }}_{\mathit{\delta }\mathit{\xi }}C(x,t;\mathit{\xi })$. Then from (11(11) $$\begin{array}{c}\hfill \begin{array}{c}{\int }_{\mathcal{X}}\mathrm{d}x{\left[(C+Fq(C;\mathit{\xi }))·\mathit{\varphi }\right]}_{t=T}-{\int }_{\mathcal{X}}\mathrm{d}x{\left[(g(x)+Fq(C;\mathit{\xi }))·\mathit{\varphi }\right]}_{t=0}\hfill \\ -{\int }_{\mathcal{X}\times \mathcal{T}}(C+Fq(C;\mathit{\xi }))·\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }t}\mathrm{d}x\mathrm{d}t+{\int }_{\mathcal{T}}\mathrm{d}t{\left[uC·\mathit{\varphi }\right]}_{x=L}-{\int }_{\mathcal{T}}\mathrm{d}t{\left[uh(t)·\mathit{\varphi }\right]}_{x=0}\hfill \\ -{\int }_{\mathcal{X}\times \mathcal{T}}uC·\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }x}\mathrm{d}x\mathrm{d}t+D_a{\int }_{\mathcal{X}\times \mathcal{T}}\frac{\mathit{\partial }C}{\mathit{\partial }x}·\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }x}\mathrm{d}x\mathrm{d}t=0,\mathit{\varphi }\in D{(\mathcal{X}\times \mathcal{T})}^n\hfill \end{array}\end{array}$$(11) ), we obtain that M will satisfy$$\begin{array}{c}\hfill \begin{array}{c}{\int }_{\mathcal{X}}\mathrm{d}x{\left[(M+F\frac{\mathit{\partial }q}{\mathit{\partial }C}M+F\frac{\mathit{\partial }q}{\mathit{\partial }\mathit{\xi }}\mathit{\delta }\mathit{\xi })·\mathit{\varphi }\right]}_{t=T}-{\int }_{\mathcal{X}}\mathrm{d}x{\left[F\frac{\mathit{\partial }q}{\mathit{\partial }\mathit{\xi }}\mathit{\delta }\mathit{\xi }·\mathit{\varphi }\right]}_{t=0}\hfill \\ -{\int }_{\mathcal{X}\times \mathcal{T}}(M+F\frac{\mathit{\partial }q}{\mathit{\partial }C}M+F\frac{\mathit{\partial }q}{\mathit{\partial }\mathit{\xi }}\mathit{\delta }\mathit{\xi })·\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }t}\mathrm{d}x\mathrm{d}t+{\int }_{\mathcal{T}}\mathrm{d}t{\left[uM·\mathit{\varphi }+D_{a}M·\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }x}\right]}_{x=L}\hfill \\ -{\int }_{\mathcal{T}}\mathrm{d}t{\left[D_{a}M·\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }x}\right]}_{x=0}-{\int }_{\mathcal{X}\times \mathcal{T}}(uM·\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }x}+D_{a}M·\frac{{\mathit{\partial }}^2\mathit{\varphi }}{\mathit{\partial }{x}^2})\mathrm{d}x\mathrm{d}t=0,\hfill \end{array}\end{array}$$

i.e.(12) $$\begin{array}{c}\hfill \begin{array}{cc}& {\int }_{\mathcal{T}}\mathrm{d}t{\left[M·(u\mathit{\varphi }+D_a\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }x})\right]}_{x=L}\hfill \\ \hfill & =-{\int }_{\mathcal{X}}\mathrm{d}x{\left[M·(\mathit{\varphi }+F{[\frac{\mathit{\partial }q}{\mathit{\partial }C}]}^T\mathit{\varphi })+F{[\frac{\mathit{\partial }q}{\mathit{\partial }\mathit{\xi }}]}^T\mathit{\varphi }·\mathit{\delta }\mathit{\xi }\right]}_{t=T}+{\int }_{\mathcal{X}}\mathrm{d}x{\left[F{[\frac{\mathit{\partial }q}{\mathit{\partial }\mathit{\xi }}]}^T\mathit{\varphi }·\mathit{\delta }\mathit{\xi }\right]}_{t=0}\hfill \\ \hfill & +{\int }_{\mathcal{X}\times \mathcal{T}}M·(\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }t}+F{[\frac{\mathit{\partial }q}{\mathit{\partial }C}]}^T\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }t}+u\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }x}+D_a\frac{{\mathit{\partial }}^2\mathit{\varphi }}{\mathit{\partial }{x}^2})\mathrm{d}x\mathrm{d}t\hfill \\ \hfill & +{\int }_{\mathcal{X}\times \mathcal{T}}F{[\frac{\mathit{\partial }q}{\mathit{\partial }\mathit{\xi }}]}^T\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }t}·\mathit{\delta }\mathit{\xi }\mathrm{d}x\mathrm{d}t+{\int }_{\mathcal{T}}\mathrm{d}t{\left[D_{a}M·\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }x}\right]}_{x=0}.\hfill \end{array}\end{array}$$(12)

Note that the derivative of ${\mathcal{J}}_{BF,\mathit{\alpha }}(\mathit{\xi })$ with respect to $\mathit{\xi }$ in the direction $\mathit{\delta }\mathit{\xi }$ is$$\begin{array}{c}\hfill {\mathcal{J}}_{BF,\mathit{\alpha }}^{\prime }(\mathit{\xi })[\mathit{\delta }\mathit{\xi }]={\int }_{\mathcal{T}}\mathrm{d}t{\left[(C^{\prime }(\mathit{\xi })[\mathit{\delta }\mathit{\xi }])·\frac{\mathit{\partial }{\mathcal{J}}_{BF,\mathit{\alpha }}}{\mathit{\partial }C}\right]}_{x=L}={\int }_{\mathcal{T}}\mathrm{d}t{\left[M·\frac{\mathit{\partial }{\mathcal{J}}_{BF,\mathit{\alpha }}}{\mathit{\partial }C}\right]}_{x=L}.\end{array}$$

If we replace $\mathit{\varphi }$ by p in Equation (12(12) $$\begin{array}{c}\hfill \begin{array}{cc}& {\int }_{\mathcal{T}}\mathrm{d}t{\left[M·(u\mathit{\varphi }+D_a\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }x})\right]}_{x=L}\hfill \\ \hfill & =-{\int }_{\mathcal{X}}\mathrm{d}x{\left[M·(\mathit{\varphi }+F{[\frac{\mathit{\partial }q}{\mathit{\partial }C}]}^T\mathit{\varphi })+F{[\frac{\mathit{\partial }q}{\mathit{\partial }\mathit{\xi }}]}^T\mathit{\varphi }·\mathit{\delta }\mathit{\xi }\right]}_{t=T}+{\int }_{\mathcal{X}}\mathrm{d}x{\left[F{[\frac{\mathit{\partial }q}{\mathit{\partial }\mathit{\xi }}]}^T\mathit{\varphi }·\mathit{\delta }\mathit{\xi }\right]}_{t=0}\hfill \\ \hfill & +{\int }_{\mathcal{X}\times \mathcal{T}}M·(\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }t}+F{[\frac{\mathit{\partial }q}{\mathit{\partial }C}]}^T\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }t}+u\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }x}+D_a\frac{{\mathit{\partial }}^2\mathit{\varphi }}{\mathit{\partial }{x}^2})\mathrm{d}x\mathrm{d}t\hfill \\ \hfill & +{\int }_{\mathcal{X}\times \mathcal{T}}F{[\frac{\mathit{\partial }q}{\mathit{\partial }\mathit{\xi }}]}^T\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }t}·\mathit{\delta }\mathit{\xi }\mathrm{d}x\mathrm{d}t+{\int }_{\mathcal{T}}\mathrm{d}t{\left[D_{a}M·\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }x}\right]}_{x=0}.\hfill \end{array}\end{array}$$(12) ) (it is allowed since $p\in W_2^{2,1}{(\mathcal{X}\times \mathcal{T})}^n\subset D{(\mathcal{X}\times \mathcal{T})}^n$), i.e. when $\mathit{\varphi }$ is a solution to Equation (10(10) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }p}{\mathit{\partial }t}+F{\left[\frac{\mathit{\partial }q(C;\mathit{\xi })}{\mathit{\partial }C}\right]}^T\frac{\mathit{\partial }p}{\mathit{\partial }t}+u\frac{\mathit{\partial }p}{\mathit{\partial }x}+D_a\frac{{\mathit{\partial }}^{2}p}{\mathit{\partial }{x}^2}=0,\hfill & (x,t)\in \mathcal{X}\times \mathcal{T},\hfill \\ p(x,T)=0,\hfill & t=T,x\in \mathcal{X},\hfill \\ up(L,t)+D_a\frac{\mathit{\partial }p(L,t)}{\mathit{\partial }x}=\frac{\mathit{\partial }{\mathcal{J}}_{BF,\mathit{\alpha }}}{\mathit{\partial }C},\hfill & x=L,t\in \mathcal{T},\hfill \\ D_a\frac{\mathit{\partial }p(0,t)}{\mathit{\partial }x}=0,\hfill & x=0,t\in \mathcal{T},\hfill \end{array}\right.\end{array}$$(10) ), by relation (12(12) $$\begin{array}{c}\hfill \begin{array}{cc}& {\int }_{\mathcal{T}}\mathrm{d}t{\left[M·(u\mathit{\varphi }+D_a\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }x})\right]}_{x=L}\hfill \\ \hfill & =-{\int }_{\mathcal{X}}\mathrm{d}x{\left[M·(\mathit{\varphi }+F{[\frac{\mathit{\partial }q}{\mathit{\partial }C}]}^T\mathit{\varphi })+F{[\frac{\mathit{\partial }q}{\mathit{\partial }\mathit{\xi }}]}^T\mathit{\varphi }·\mathit{\delta }\mathit{\xi }\right]}_{t=T}+{\int }_{\mathcal{X}}\mathrm{d}x{\left[F{[\frac{\mathit{\partial }q}{\mathit{\partial }\mathit{\xi }}]}^T\mathit{\varphi }·\mathit{\delta }\mathit{\xi }\right]}_{t=0}\hfill \\ \hfill & +{\int }_{\mathcal{X}\times \mathcal{T}}M·(\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }t}+F{[\frac{\mathit{\partial }q}{\mathit{\partial }C}]}^T\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }t}+u\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }x}+D_a\frac{{\mathit{\partial }}^2\mathit{\varphi }}{\mathit{\partial }{x}^2})\mathrm{d}x\mathrm{d}t\hfill \\ \hfill & +{\int }_{\mathcal{X}\times \mathcal{T}}F{[\frac{\mathit{\partial }q}{\mathit{\partial }\mathit{\xi }}]}^T\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }t}·\mathit{\delta }\mathit{\xi }\mathrm{d}x\mathrm{d}t+{\int }_{\mathcal{T}}\mathrm{d}t{\left[D_{a}M·\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }x}\right]}_{x=0}.\hfill \end{array}\end{array}$$(12) ) and boundary condition $up+D_a\frac{\mathit{\partial }p}{\mathit{\partial }x}=\frac{\mathit{\partial }{\mathcal{J}}_{BF,\mathit{\alpha }}}{\mathit{\partial }C}$ we deduce$$\begin{array}{c}\hfill \begin{array}{cc}{\mathcal{J}}_{BF,\mathit{\alpha }}^{\prime }(\mathit{\xi })[\mathit{\delta }\mathit{\xi }]\hfill & ={\int }_{\mathcal{T}}\mathrm{d}t{\left[M·\frac{\mathit{\partial }{\mathcal{J}}_{BF,\mathit{\alpha }}}{\mathit{\partial }C}\right]}_{x=L}={\int }_{\mathcal{T}}\mathrm{d}t{\left[M·(up+D_a\frac{\mathit{\partial }p}{\mathit{\partial }x})\right]}_{x=L}\hfill \\ \hfill & =-{\int }_{\mathcal{X}}\mathrm{d}x{\left[F{[\frac{\mathit{\partial }q}{\mathit{\partial }\mathit{\xi }}]}^{T}p·\mathit{\delta }\mathit{\xi }\right]}_{t=T}+{\int }_{\mathcal{T}}\mathrm{d}t{\left[F{[\frac{\mathit{\partial }q}{\mathit{\partial }\mathit{\xi }}]}^{T}p·\mathit{\delta }\mathit{\xi }\right]}_{t=0}\hfill \\ \hfill & +{\int }_{\mathcal{X}\times \mathcal{T}}F{[\frac{\mathit{\partial }q}{\mathit{\partial }\mathit{\xi }}]}^T\frac{\mathit{\partial }p}{\mathit{\partial }t}·\mathit{\delta }\mathit{\xi }\mathrm{d}x\mathrm{d}t,\hfill \end{array}\end{array}$$

which implies$$\begin{array}{c}\hfill \begin{array}{cc}{\mathcal{J}}_{BF,\mathit{\alpha }}^{\prime }(\mathit{\xi })\hfill & =-{\int }_{\mathcal{X}}\mathrm{d}x{\left[F{[\frac{\mathit{\partial }q}{\mathit{\partial }\mathit{\xi }}]}^{T}p\right]}_{t=T}+{\int }_{\mathcal{T}}\mathrm{d}t{\left[F{[\frac{\mathit{\partial }q}{\mathit{\partial }\mathit{\xi }}]}^{T}p\right]}_{t=0}\hfill \\ \hfill & +{\int }_{\mathcal{X}\times \mathcal{T}}F{[\frac{\mathit{\partial }q}{\mathit{\partial }\mathit{\xi }}]}^T\frac{\mathit{\partial }p}{\mathit{\partial }t}\mathrm{d}x\mathrm{d}t\hfill \\ \hfill & =-F·{\int }_{\mathcal{X}\times \mathcal{T}}\mathrm{d}x\mathrm{d}t\frac{\mathit{\partial }{\left[\frac{\mathit{\partial }q(C;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}\right]}^T}{\mathit{\partial }t}p(\text{integration by parts}).\hfill \end{array}\end{array}$$

This yields the required result.

At the end of the proof, let us discuss the computation of $\frac{\mathit{\partial }{\mathcal{J}}_{BF,\mathit{\alpha }}}{\mathit{\partial }C}$. Actually, using the inner products ${⟨·,·⟩}_{L^2{(\mathcal{T})}^n}$ and ${⟨·,·⟩}_2$ in $L^2{(\mathcal{T})}^n$ and ${\mathbf{R}}^2$, respectively, we have$$\begin{array}{c}\hfill \begin{array}{cc}{\mathcal{J}}_{BF,\mathit{\alpha }}=\hfill & \frac{1}{2}{⟨C(L,t;\mathit{\xi })-C_{obs}(t),C(L,t;\mathit{\xi })-C_{obs}(t)⟩}_{L^2{(\mathcal{T})}^n}\hfill \\ \hfill & +\frac{\mathit{\alpha }}{2}{⟨\mathit{\mu }(C(L,t;\mathit{\xi })-C_{obs}(t)),\mathit{\mu }(C(L,t;\mathit{\xi })-C_{obs}(t))⟩}_2.\hfill \end{array}\end{array}$$

By definition of the first moment functional $\mathit{\mu }$ in (6(6) $$\begin{array}{c}\hfill \mathit{\mu }(C(t))={\int }_{\mathcal{T}}tC(t)\mathrm{d}t.\end{array}$$(6) ), the derivative of ${\mathcal{J}}_{BF,\mathit{\alpha }}$ with respect to C in the direction $\mathit{\delta }C$ can be calculated as$$\begin{array}{c}\hfill \begin{array}{cc}\frac{\mathit{\partial }{\mathcal{J}}_{BF,\mathit{\alpha }}}{\mathit{\partial }C}[\mathit{\delta }C]\hfill & ={⟨\mathit{\delta }C(L,t;\mathit{\xi }),C(L,t;\mathit{\xi })-C_{obs}(t)⟩}_{L^2{(\mathcal{T})}^n}\hfill \\ \hfill & +\mathit{\alpha }{⟨{\int }_{\mathcal{T}}t·\mathit{\delta }C(L,t;\mathit{\xi })\mathrm{d}t,\mathit{\mu }(C(L,t;\mathit{\xi })-C_{obs}(t))⟩}_2\hfill \\ \hfill & ={⟨\mathit{\delta }C(L,t;\mathit{\xi }),C(L,t;\mathit{\xi })-C_{obs}(t)⟩}_{L^2{(\mathcal{T})}^n}\hfill \\ \hfill & +\mathit{\alpha }{\sum }_{i=1}^n\left\{{\int }_{\mathcal{T}}t·\mathit{\delta }{C}^{(i)}(L,t;\mathit{\xi })\mathrm{d}t\right\}·\left\{{\int }_{\mathcal{T}}t·(C^{(i)}(L,t;\mathit{\xi })-C_{obs}^{(i)}(t))\mathrm{d}t\right\}\hfill \\ \hfill & ={⟨\mathit{\delta }C(L,t;\mathit{\xi }),C(L,t;\mathit{\xi })-C_{obs}(t)⟩}_{L^2{(\mathcal{T})}^n}\hfill \\ \hfill & +\mathit{\alpha }{\sum }_{i=1}^n{\int }_{\mathcal{T}}\left\{\mathit{\delta }{C}^{(i)}(L,t;\mathit{\xi })·t·\left[{\int }_{\mathcal{T}}t·(C^{(i)}(L,t;\mathit{\xi })-C_{obs}^{(i)}(t))\mathrm{d}t\right]\right\}\mathrm{d}t\hfill \\ \hfill & ={⟨\mathit{\delta }C,C(L,t;\mathit{\xi })-C_{obs}(t)⟩}_{L^2{(\mathcal{T})}^n}+\mathit{\alpha }{⟨\mathit{\delta }C,t\mathit{\mu }(C(L,t;\mathit{\xi })-C_{obs}(t))⟩}_{L^2{(\mathcal{T})}^n}.\hfill \end{array}\end{array}$$

This implies that $\frac{\mathit{\partial }{\mathcal{J}}_{BF,\mathit{\alpha }}}{\mathit{\partial }C}=C(L,t;\mathit{\xi })-C_{obs}(t)+\mathit{\alpha }t\mathit{\mu }(C(L,t;\mathit{\xi })-C_{obs}(t))$. $\square$

Remark 3.2:

The existence of the derivative of C with respect to $\mathit{\xi }$ can be derived from assumption (A) immediately. Furthermore, the existence of ${\mathcal{J}}_{BF,\mathit{\alpha }}^{\prime }$ can be obtained if the adjoint Equation (10(10) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }p}{\mathit{\partial }t}+F{\left[\frac{\mathit{\partial }q(C;\mathit{\xi })}{\mathit{\partial }C}\right]}^T\frac{\mathit{\partial }p}{\mathit{\partial }t}+u\frac{\mathit{\partial }p}{\mathit{\partial }x}+D_a\frac{{\mathit{\partial }}^{2}p}{\mathit{\partial }{x}^2}=0,\hfill & (x,t)\in \mathcal{X}\times \mathcal{T},\hfill \\ p(x,T)=0,\hfill & t=T,x\in \mathcal{X},\hfill \\ up(L,t)+D_a\frac{\mathit{\partial }p(L,t)}{\mathit{\partial }x}=\frac{\mathit{\partial }{\mathcal{J}}_{BF,\mathit{\alpha }}}{\mathit{\partial }C},\hfill & x=L,t\in \mathcal{T},\hfill \\ D_a\frac{\mathit{\partial }p(0,t)}{\mathit{\partial }x}=0,\hfill & x=0,t\in \mathcal{T},\hfill \end{array}\right.\end{array}$$(10) ) has a solution.

Similarly, it is not difficult to obtain the Jacobian of the Kohn–Vogelius type objective function for the Equilibrium-Dispersive model, i.e. the following proposition holds.

Proposition 3.3:

The Jacobian of ${\mathcal{J}}_{KV,\mathit{\alpha }}(\mathit{\xi })$ for the Equilibrium-Dispersive model is$$\begin{array}{c}\hfill {\mathcal{J}}_{KV,\mathit{\alpha }}^{\prime }(\mathit{\xi })=F·{\int }_{\mathcal{X}\times \mathcal{T}}\mathrm{d}x\mathrm{d}t\left\{\frac{\mathit{\partial }{\left[\frac{\mathit{\partial }q(C_1;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}\right]}^T}{\mathit{\partial }t}·p_1+\frac{\mathit{\partial }{\left[\frac{\mathit{\partial }q(C_2;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}\right]}^T}{\mathit{\partial }t}·p_2\right\},\end{array}$$

where $C_1$ is the solution to Equation (2(2) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }C}{\mathit{\partial }t}+F\frac{\mathit{\partial }q}{\mathit{\partial }t}+u\frac{\mathit{\partial }C}{\mathit{\partial }x}=D_a\frac{{\mathit{\partial }}^{2}C}{\mathit{\partial }{x}^2},\hfill & x\in \mathcal{X}\equiv (0,L),t\in \mathcal{T}\equiv (0,T],\hfill \\ C(x,0)=g(x),\hfill & x\in \mathcal{X},t=0,\hfill \\ uC(0,t)-D_a\frac{\mathit{\partial }C(0,t)}{\mathit{\partial }x}=uh(t),\hfill & x=0,t\in \mathcal{T},\hfill \\ D_a\frac{\mathit{\partial }C(L,t)}{\mathit{\partial }x}=0,\hfill & x=L,t\in \mathcal{T}.\hfill \end{array}\right.\end{array}$$(2) ) with C replaced with $C_1$, $C_2$ is the solution to (9(9) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }{C}_2}{\mathit{\partial }t}+F\frac{\mathit{\partial }q(C_2)}{\mathit{\partial }t}+u\frac{\mathit{\partial }{C}_2}{\mathit{\partial }x}=D_a\frac{{\mathit{\partial }}^2{C}_2}{\mathit{\partial }{x}^2},\hfill & (x,t)\in \mathcal{X}\times \mathcal{T},\hfill \\ C_2(x,0)=g(x),\hfill & t=0,x\in \mathcal{X},\hfill \\ u{C}_2(0,t)-D_a\frac{\mathit{\partial }{C}_2(0,t)}{\mathit{\partial }x}=uh(t),\hfill & x=0,t\in \mathcal{T},\hfill \\ C_2(L,t)=C_{obs}(t),\hfill & x=L,t\in \mathcal{T}.\hfill \end{array}\right.\end{array}$$(9) ), and $p_1$ satisfies$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }{p}_1}{\mathit{\partial }t}+F{\left[\frac{\mathit{\partial }q(C_1;\mathit{\xi })}{\mathit{\partial }{C}_1}\right]}^T\frac{\mathit{\partial }{p}_1}{\mathit{\partial }t}+u\frac{\mathit{\partial }{p}_1}{\mathit{\partial }x}+D_a\frac{{\mathit{\partial }}^2{p}_1}{\mathit{\partial }{x}^2}=\frac{\mathit{\partial }{\mathcal{J}}_{KV,\mathit{\alpha }}}{\mathit{\partial }{C}_1},\hfill & (x,t)\in \mathcal{X}\times \mathcal{T},\hfill \\ p_1(x,T)=0,\hfill & t=T,x\in \mathcal{X},\hfill \\ u{p}_1(L,t)+D_a\frac{\mathit{\partial }{p}_1(L,t)}{\mathit{\partial }x}=0,\hfill & x=L,t\in \mathcal{T},\hfill \\ D_a\frac{\mathit{\partial }{p}_1(0,t)}{\mathit{\partial }x}=0,\hfill & x=0,t\in \mathcal{T},\hfill \end{array}\right.\end{array}$$

while $p_2$ satisfies$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }{p}_2}{\mathit{\partial }t}+F{\left[\frac{\mathit{\partial }q(C_2;\mathit{\xi })}{\mathit{\partial }{C}_2}\right]}^T\frac{\mathit{\partial }{p}_2}{\mathit{\partial }t}+u\frac{\mathit{\partial }{p}_2}{\mathit{\partial }x}+D_a\frac{{\mathit{\partial }}^2{p}_2}{\mathit{\partial }{x}^2}=\frac{\mathit{\partial }{\mathcal{J}}_{KV,\mathit{\alpha }}}{\mathit{\partial }{C}_2},\hfill & (x,t)\in \mathcal{X}\times \mathcal{T},\hfill \\ p_2(x,T)=0,\hfill & t=T,x\in \mathcal{X},\hfill \\ p_2(L,t)=0,\hfill & x=L,t\in \mathcal{T},\hfill \\ D_a\frac{\mathit{\partial }{p}_2(0,t)}{\mathit{\partial }x}=0,\hfill & x=0,t\in \mathcal{T},\hfill \end{array}\right.\end{array}$$

where$$\begin{array}{c}\hfill \frac{\mathit{\partial }{\mathcal{J}}_{KV,\mathit{\alpha }}}{\mathit{\partial }{C}_1}=-\frac{\mathit{\partial }{\mathcal{J}}_{KV,\mathit{\alpha }}}{\mathit{\partial }{C}_2}=C_1(x,t;\mathit{\xi })-C_2(x,t;\mathit{\xi })+\mathit{\alpha }·x·t·\mathit{\mu }(C_1(x,t;\mathit{\xi })-C_2(x,t;\mathit{\xi })).\end{array}$$

3.2.2. Transport-Dispersive model

Now, consider the Transport-Dispersive model. Using the technique shown in Section 3.2.1, it is possible to obtain Jacobians of objective functions ${\mathcal{J}}_{i,\mathit{\alpha }}$ for the Transport-Dispersive model. For simplicity, we only discuss the Jacobian of the Kohn–Vogelius function.

Proposition 3.4:

The Jacobian of ${\mathcal{J}}_{KV,\mathit{\alpha }}(\mathit{\xi })$ for the Transport-Dispersive model is$$\begin{array}{c}\hfill {\mathcal{J}}_{KV,\mathit{\alpha }}^{\prime }(\mathit{\xi })=F·{\int }_{\mathcal{X}\times \mathcal{T}}\mathrm{d}x\mathrm{d}t\left\{\frac{\mathit{\partial }\left({\frac{\mathit{\partial }q(C_1;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T\right)}{\mathit{\partial }t}{p}_1+\frac{\mathit{\partial }\left({\frac{\mathit{\partial }q(C_2;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T\right)}{\mathit{\partial }t}{p}_2\right\},\end{array}$$

where $C_1$ is the solution of (2(2) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }C}{\mathit{\partial }t}+F\frac{\mathit{\partial }q}{\mathit{\partial }t}+u\frac{\mathit{\partial }C}{\mathit{\partial }x}=D_a\frac{{\mathit{\partial }}^{2}C}{\mathit{\partial }{x}^2},\hfill & x\in \mathcal{X}\equiv (0,L),t\in \mathcal{T}\equiv (0,T],\hfill \\ C(x,0)=g(x),\hfill & x\in \mathcal{X},t=0,\hfill \\ uC(0,t)-D_a\frac{\mathit{\partial }C(0,t)}{\mathit{\partial }x}=uh(t),\hfill & x=0,t\in \mathcal{T},\hfill \\ D_a\frac{\mathit{\partial }C(L,t)}{\mathit{\partial }x}=0,\hfill & x=L,t\in \mathcal{T}.\hfill \end{array}\right.\end{array}$$(2) ), (3(3) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }q}{\mathit{\partial }t}=k_f(q^{\ast }(C)-q),\hfill & t\in \mathcal{T},\hfill \\ q=q^{\ast }(C),\hfill & t=0,\hfill \end{array}\right.\end{array}$$(3) ) with C replaced with $C_1$, $C_2$ is the solution of (9(9) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }{C}_2}{\mathit{\partial }t}+F\frac{\mathit{\partial }q(C_2)}{\mathit{\partial }t}+u\frac{\mathit{\partial }{C}_2}{\mathit{\partial }x}=D_a\frac{{\mathit{\partial }}^2{C}_2}{\mathit{\partial }{x}^2},\hfill & (x,t)\in \mathcal{X}\times \mathcal{T},\hfill \\ C_2(x,0)=g(x),\hfill & t=0,x\in \mathcal{X},\hfill \\ u{C}_2(0,t)-D_a\frac{\mathit{\partial }{C}_2(0,t)}{\mathit{\partial }x}=uh(t),\hfill & x=0,t\in \mathcal{T},\hfill \\ C_2(L,t)=C_{obs}(t),\hfill & x=L,t\in \mathcal{T}.\hfill \end{array}\right.\end{array}$$(9) ) and Equation (3(3) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }q}{\mathit{\partial }t}=k_f(q^{\ast }(C)-q),\hfill & t\in \mathcal{T},\hfill \\ q=q^{\ast }(C),\hfill & t=0,\hfill \end{array}\right.\end{array}$$(3) ) with C replaced with $C_2$, $p_1$ satisfies(13) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }{p}_1}{\mathit{\partial }t}+F{\frac{\mathit{\partial }q(C_1;\mathit{\xi })}{\mathit{\partial }{C}_1}}^T\frac{\mathit{\partial }{p}_1}{\mathit{\partial }t}+u\frac{\mathit{\partial }{p}_1}{\mathit{\partial }x}+D_a\frac{{\mathit{\partial }}^2{p}_1}{\mathit{\partial }{x}^2}=\frac{\mathit{\partial }{\mathcal{J}}_{KV,\mathit{\alpha }}}{\mathit{\partial }{C}_1},\hfill & (x,t)\in \mathcal{X}\times \mathcal{T},\hfill \\ p_1(x,T)=0,\hfill & t=T,x\in \mathcal{X},\hfill \\ u{p}_1(L,t)+D_a\frac{\mathit{\partial }{p}_1(L,t)}{\mathit{\partial }x}=0,\hfill & x=L,t\in \mathcal{T},\hfill \\ D_a\frac{\mathit{\partial }{p}_1(0,t)}{\mathit{\partial }x}=0,\hfill & x=0,t\in \mathcal{T}\hfill \end{array}\right.\end{array}$$(13)

and $p_2$ satisfies(14) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }{p}_2}{\mathit{\partial }t}+F{\frac{\mathit{\partial }q(C_2;\mathit{\xi })}{\mathit{\partial }{C}_2}}^T\frac{\mathit{\partial }{p}_2}{\mathit{\partial }t}+u\frac{\mathit{\partial }{p}_2}{\mathit{\partial }x}+D_a\frac{{\mathit{\partial }}^2{p}_2}{\mathit{\partial }{x}^2}=\frac{\mathit{\partial }{\mathcal{J}}_{KV,\mathit{\alpha }}}{\mathit{\partial }{C}_2},\hfill & (x,t)\in \mathcal{X}\times \mathcal{T},\hfill \\ p_2(x,T)=0,\hfill & t=T,x\in \mathcal{X},\hfill \\ p_2(L,t)=0,\hfill & x=L,t\in \mathcal{T},\hfill \\ D_a\frac{\mathit{\partial }{p}_2(0,t)}{\mathit{\partial }x}=0,\hfill & x=0,t\in \mathcal{T},\hfill \end{array}\right.\end{array}$$(14)

where$$\begin{array}{c}\hfill \frac{\mathit{\partial }{\mathcal{J}}_{KV,\mathit{\alpha }}}{\mathit{\partial }{C}_1}=-\frac{\mathit{\partial }{\mathcal{J}}_{KV,\mathit{\alpha }}}{\mathit{\partial }{C}_2}=C_1(x,t;\mathit{\xi })-C_2(x,t;\mathit{\xi })+\mathit{\alpha }x·t·[\mathit{\mu }(C_1(x,t;\mathit{\xi })-C_2(x,t;\mathit{\xi }))],\end{array}$$$M_{C_1}=\frac{\mathit{\partial }q(C_1;\mathit{\xi })}{\mathit{\partial }{C}_1}$ satisfies$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }{M}_{C_1}}{\mathit{\partial }t}=k_f(\frac{\mathit{\partial }{q}^{\ast }(C_1;\mathit{\xi })}{\mathit{\partial }{C}_1}-M_{C_1}),\hfill & t\in \mathcal{T},\hfill \\ M_{C_1}=0,\hfill & t=0,\hfill \end{array}\right.\end{array}$$

and $M_{C_2}=\frac{\mathit{\partial }q(C_2;\mathit{\xi })}{\mathit{\partial }{C}_2}$ satisfies$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }{M}_{C_2}}{\mathit{\partial }t}=k_f(\frac{\mathit{\partial }{q}^{\ast }(C_2;\mathit{\xi })}{\mathit{\partial }{C}_2}-M_{C_2}),\hfill & t\in \mathcal{T},\hfill \\ M_{C_2}=0,\hfill & t=0.\hfill \end{array}\right.\end{array}$$

However, if the unknown parameter $\mathit{\xi }$ contains too many elements, i.e. $m\gg 1$, it is difficult to calculate $\frac{\mathit{\partial }q(C_1;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}$ and $\frac{\mathit{\partial }q(C_2;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}$ for the Transport-Dispersive model, which implies a large computation cost. Therefore, we will use the following strategy to find the Jacobian.

Proposition 3.5:

The Jacobian of objective function ${\mathcal{J}}_{KV,\mathit{\alpha }}(\mathit{\xi })$ for the Transport-Dispersive model is$$\begin{array}{c}\hfill {\mathcal{J}}_{KV,\mathit{\alpha }}^{\prime }(\mathit{\xi })=-F{\int }_{\mathcal{X}\times \mathcal{T}}{k}_f\frac{\mathit{\partial }\left({\frac{\mathit{\partial }q\ast (C_1;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T\right)}{\mathit{\partial }t}{\overline{p}}_1\mathrm{d}x\mathrm{d}t-F{\int }_{\mathcal{X}\times \mathcal{T}}{k}_f\frac{\mathit{\partial }\left({\frac{\mathit{\partial }q\ast (C_2;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T\right)}{\mathit{\partial }t}{\overline{p}}_2\mathrm{d}x\mathrm{d}t,\end{array}$$

where ${\overline{p}}_1$, ${\overline{p}}_2$ are the solution of adjoint equations(15) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }{\overline{p}}_1}{\mathit{\partial }t}-k_f{\overline{p}}_1=p_1,\hfill & (x,t)\in \mathcal{X}\times \mathcal{T},\hfill \\ {\overline{p}}_1=0,\hfill & t=T,x\in \mathcal{X},\hfill \end{array}\right.\end{array}$$(15)

and(16) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }{\overline{p}}_2}{\mathit{\partial }t}-k_f{\overline{p}}_2=p_2,\hfill & (x,t)\in \mathcal{X}\times \mathcal{T},\hfill \\ {\overline{p}}_2=0,\hfill & t=T,x\in \mathcal{X},\hfill \end{array}\right.\end{array}$$(16)

respectively. Here $p_1$ and $p_2$ are defined in Proposition 3.4.

Proof:

By Proposition 3.4, we obtain(17) $$\begin{array}{c}\hfill \begin{array}{cc}{\mathcal{J}}_{KV,\mathit{\alpha }}^{\prime }(\mathit{\xi })\hfill & ={\int }_{\mathcal{X}\times \mathcal{T}}F\frac{\mathit{\partial }\left({\frac{\mathit{\partial }q(C_1;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T\right)}{\mathit{\partial }t}{p}_1\mathrm{d}x\mathrm{d}t+{\int }_{\mathcal{X}\times \mathcal{T}}F\frac{\mathit{\partial }\left({\frac{\mathit{\partial }q(C_2;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T\right)}{\mathit{\partial }t}{p}_2\mathrm{d}x\mathrm{d}t\hfill \\ \hfill & =F{\int }_{\mathcal{X}\times \mathcal{T}}{k}_f\left({\frac{\mathit{\partial }{q}^{\ast }(C_1;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T-M_{\mathit{\xi }1}\right)p_1\mathrm{d}x\mathrm{d}t\hfill \\ \hfill & +F{\int }_{\mathcal{X}\times \mathcal{T}}{k}_f\left({\frac{\mathit{\partial }{q}^{\ast }(C_2;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T-M_{\mathit{\xi }2}\right)p_2\mathrm{d}x\mathrm{d}t,\hfill \end{array}\end{array}$$(17)

where $M_{\mathit{\xi }1}={\frac{\mathit{\partial }q(C_1;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T$, $M_{\mathit{\xi }2}={\frac{\mathit{\partial }q(C_2;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T$ satisfy(18) $$\begin{array}{c}\hfill \begin{array}{cc}& {\int }_{\mathcal{X}}\mathrm{d}x{[M_{\mathit{\xi }1}\tilde{p}]}_{t=T}-{\int }_{\mathcal{X}}\mathrm{d}x{\left[{\frac{\mathit{\partial }{q}^{\ast }(C_1;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T\tilde{p}\right]}_{t=0}-{\int }_{\mathcal{X}\times \mathcal{T}}{M}_{\mathit{\xi }1}\frac{\mathit{\partial }\tilde{p}}{\mathit{\partial }t}\mathrm{d}x\mathrm{d}t\hfill \\ \hfill & ={\int }_{\mathcal{X}\times \mathcal{T}}{k}_f{\frac{\mathit{\partial }{q}^{\ast }(C_1;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T\tilde{p}\mathrm{d}x\mathrm{d}t-{\int }_{\mathcal{X}\times \mathcal{T}}{k}_f{M}_{\mathit{\xi }1}\tilde{p}\mathrm{d}x\mathrm{d}t,\tilde{p}\in D{(\mathcal{X}\times \mathcal{T})}^n\hfill \end{array}\end{array}$$(18)

and(19) $$\begin{array}{c}\hfill \begin{array}{cc}& {\int }_{\mathcal{X}}\mathrm{d}x{[M_{\mathit{\xi }2}\tilde{p}]}_{t=T}-{\int }_{\mathcal{X}}\mathrm{d}x{\left[{\frac{\mathit{\partial }{q}^{\ast }(C_2;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T\tilde{p}\right]}_{t=0}-{\int }_{\mathcal{X}\times \mathcal{T}}{M}_{\mathit{\xi }2}\frac{\mathit{\partial }\tilde{p}}{\mathit{\partial }t}\mathrm{d}x\mathrm{d}t\hfill \\ \hfill & ={\int }_{\mathcal{X}\times \mathcal{T}}{k}_f{\frac{\mathit{\partial }{q}^{\ast }(C_2;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T\tilde{p}\mathrm{d}x\mathrm{d}t-{\int }_{\mathcal{X}\times \mathcal{T}}{k}_f{M}_{\mathit{\xi }2}\tilde{p}\mathrm{d}x\mathrm{d}t,\tilde{p}\in D{(\mathcal{X}\times \mathcal{T})}^n\hfill \end{array}\end{array}$$(19)

respectively. Rewrite (18(18) $$\begin{array}{c}\hfill \begin{array}{cc}& {\int }_{\mathcal{X}}\mathrm{d}x{[M_{\mathit{\xi }1}\tilde{p}]}_{t=T}-{\int }_{\mathcal{X}}\mathrm{d}x{\left[{\frac{\mathit{\partial }{q}^{\ast }(C_1;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T\tilde{p}\right]}_{t=0}-{\int }_{\mathcal{X}\times \mathcal{T}}{M}_{\mathit{\xi }1}\frac{\mathit{\partial }\tilde{p}}{\mathit{\partial }t}\mathrm{d}x\mathrm{d}t\hfill \\ \hfill & ={\int }_{\mathcal{X}\times \mathcal{T}}{k}_f{\frac{\mathit{\partial }{q}^{\ast }(C_1;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T\tilde{p}\mathrm{d}x\mathrm{d}t-{\int }_{\mathcal{X}\times \mathcal{T}}{k}_f{M}_{\mathit{\xi }1}\tilde{p}\mathrm{d}x\mathrm{d}t,\tilde{p}\in D{(\mathcal{X}\times \mathcal{T})}^n\hfill \end{array}\end{array}$$(18) ) and (19(19) $$\begin{array}{c}\hfill \begin{array}{cc}& {\int }_{\mathcal{X}}\mathrm{d}x{[M_{\mathit{\xi }2}\tilde{p}]}_{t=T}-{\int }_{\mathcal{X}}\mathrm{d}x{\left[{\frac{\mathit{\partial }{q}^{\ast }(C_2;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T\tilde{p}\right]}_{t=0}-{\int }_{\mathcal{X}\times \mathcal{T}}{M}_{\mathit{\xi }2}\frac{\mathit{\partial }\tilde{p}}{\mathit{\partial }t}\mathrm{d}x\mathrm{d}t\hfill \\ \hfill & ={\int }_{\mathcal{X}\times \mathcal{T}}{k}_f{\frac{\mathit{\partial }{q}^{\ast }(C_2;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T\tilde{p}\mathrm{d}x\mathrm{d}t-{\int }_{\mathcal{X}\times \mathcal{T}}{k}_f{M}_{\mathit{\xi }2}\tilde{p}\mathrm{d}x\mathrm{d}t,\tilde{p}\in D{(\mathcal{X}\times \mathcal{T})}^n\hfill \end{array}\end{array}$$(19) ) into$$\begin{array}{c}\hfill \begin{array}{cc}& {\int }_{\mathcal{X}\times \mathcal{T}}{M}_{\mathit{\xi }1}\left(\frac{\mathit{\partial }\tilde{p}}{\mathit{\partial }t}-k_f\tilde{p}\right)\mathrm{d}x\mathrm{d}t\hfill \\ \hfill & ={\int }_{\mathcal{X}}\mathrm{d}x{[M_{\mathit{\xi }1}\tilde{p}]}_{t=T}-{\int }_{\mathcal{X}}\mathrm{d}x{\left[{\frac{\mathit{\partial }{q}^{\ast }(C_1;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T\tilde{p}\right]}_{t=0}-{\int }_{\mathcal{X}\times \mathcal{T}}{k}_f{\frac{\mathit{\partial }{q}^{\ast }(C_1;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T\tilde{p}\mathrm{d}x\mathrm{d}t,\hfill \\ \hfill & {\int }_{\mathcal{X}\times \mathcal{T}}{M}_{\mathit{\xi }2}\left(\frac{\mathit{\partial }\tilde{p}}{\mathit{\partial }t}-k_f\tilde{p}\right)\mathrm{d}x\mathrm{d}t\hfill \\ \hfill & ={\int }_{\mathcal{X}}\mathrm{d}x{[M_{\mathit{\xi }2}\tilde{p}]}_{t=T}-{\int }_{\mathcal{X}}\mathrm{d}x{\left[{\frac{\mathit{\partial }{q}^{\ast }(C_2;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T\tilde{p}\right]}_{t=0}-{\int }_{\mathcal{X}\times \mathcal{T}}{k}_f{\frac{\mathit{\partial }{q}^{\ast }(C_2;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T\tilde{p}\mathrm{d}x\mathrm{d}t\hfill \end{array}\end{array}$$

and substitute the test function $\tilde{p}$ by ${\overline{p}}_1$ and ${\overline{p}}_2$, respectively. Since ${\overline{p}}_1$ is the solution to (15(15) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }{\overline{p}}_1}{\mathit{\partial }t}-k_f{\overline{p}}_1=p_1,\hfill & (x,t)\in \mathcal{X}\times \mathcal{T},\hfill \\ {\overline{p}}_1=0,\hfill & t=T,x\in \mathcal{X},\hfill \end{array}\right.\end{array}$$(15) ) (${\overline{p}}_2$ is the solution to (16(16) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }{\overline{p}}_2}{\mathit{\partial }t}-k_f{\overline{p}}_2=p_2,\hfill & (x,t)\in \mathcal{X}\times \mathcal{T},\hfill \\ {\overline{p}}_2=0,\hfill & t=T,x\in \mathcal{X},\hfill \end{array}\right.\end{array}$$(16) )), we deduce that(20) $$\begin{array}{c}\hfill {\int }_{\mathcal{X}\times \mathcal{T}}{M}_{\mathit{\xi }1}{p}_1\mathrm{d}x\mathrm{d}t=-{\int }_{\mathcal{X}}\mathrm{d}x{\left[{\frac{\mathit{\partial }{q}^{\ast }(C_1;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T{\overline{p}}_1\right]}_{t=0}-{\int }_{\mathcal{X}\times \mathcal{T}}{k}_f{\frac{\mathit{\partial }{q}^{\ast }(C_1;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T{\overline{p}}_1\mathrm{d}x\mathrm{d}t,\end{array}$$(20)

and(21) $$\begin{array}{c}\hfill {\int }_{\mathcal{X}\times \mathcal{T}}{M}_{\mathit{\xi }2}{p}_2\mathrm{d}x\mathrm{d}t=-{\int }_{\mathcal{X}}\mathrm{d}x{\left[{\frac{\mathit{\partial }{q}^{\ast }(C_2;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T{\overline{p}}_2\right]}_{t=0}-{\int }_{\mathcal{X}\times \mathcal{T}}{k}_f{\frac{\mathit{\partial }{q}^{\ast }(C_2;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T{\overline{p}}_2\mathrm{d}x\mathrm{d}t.\end{array}$$(21)

Combine (17(17) $$\begin{array}{c}\hfill \begin{array}{cc}{\mathcal{J}}_{KV,\mathit{\alpha }}^{\prime }(\mathit{\xi })\hfill & ={\int }_{\mathcal{X}\times \mathcal{T}}F\frac{\mathit{\partial }\left({\frac{\mathit{\partial }q(C_1;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T\right)}{\mathit{\partial }t}{p}_1\mathrm{d}x\mathrm{d}t+{\int }_{\mathcal{X}\times \mathcal{T}}F\frac{\mathit{\partial }\left({\frac{\mathit{\partial }q(C_2;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T\right)}{\mathit{\partial }t}{p}_2\mathrm{d}x\mathrm{d}t\hfill \\ \hfill & =F{\int }_{\mathcal{X}\times \mathcal{T}}{k}_f\left({\frac{\mathit{\partial }{q}^{\ast }(C_1;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T-M_{\mathit{\xi }1}\right)p_1\mathrm{d}x\mathrm{d}t\hfill \\ \hfill & +F{\int }_{\mathcal{X}\times \mathcal{T}}{k}_f\left({\frac{\mathit{\partial }{q}^{\ast }(C_2;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T-M_{\mathit{\xi }2}\right)p_2\mathrm{d}x\mathrm{d}t,\hfill \end{array}\end{array}$$(17) ), (20(20) $$\begin{array}{c}\hfill {\int }_{\mathcal{X}\times \mathcal{T}}{M}_{\mathit{\xi }1}{p}_1\mathrm{d}x\mathrm{d}t=-{\int }_{\mathcal{X}}\mathrm{d}x{\left[{\frac{\mathit{\partial }{q}^{\ast }(C_1;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T{\overline{p}}_1\right]}_{t=0}-{\int }_{\mathcal{X}\times \mathcal{T}}{k}_f{\frac{\mathit{\partial }{q}^{\ast }(C_1;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T{\overline{p}}_1\mathrm{d}x\mathrm{d}t,\end{array}$$(20) ) and (21(21) $$\begin{array}{c}\hfill {\int }_{\mathcal{X}\times \mathcal{T}}{M}_{\mathit{\xi }2}{p}_2\mathrm{d}x\mathrm{d}t=-{\int }_{\mathcal{X}}\mathrm{d}x{\left[{\frac{\mathit{\partial }{q}^{\ast }(C_2;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T{\overline{p}}_2\right]}_{t=0}-{\int }_{\mathcal{X}\times \mathcal{T}}{k}_f{\frac{\mathit{\partial }{q}^{\ast }(C_2;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T{\overline{p}}_2\mathrm{d}x\mathrm{d}t.\end{array}$$(21) ), we obtain$$\begin{array}{cc}& {\mathcal{J}}_{KV,\mathit{\alpha }}^{\prime }(\mathit{\xi })\hfill \\ \hfill & =F\{{\int }_{\mathcal{X}\times \mathcal{T}}{k}_f{\frac{\mathit{\partial }{q}^{\ast }(C_1;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T{p}_1\mathrm{d}x\mathrm{d}t\hfill \\ \hfill & +{\int }_{\mathcal{X}}\mathrm{d}x{\left[k_f{\frac{\mathit{\partial }{q}^{\ast }(C_1;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T{\overline{p}}_1\right]}_{t=0}+{\int }_{\mathcal{X}\times \mathcal{T}}{k}_f^2{\frac{\mathit{\partial }{q}^{\ast }(C_1;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T{\overline{p}}_1\mathrm{d}x\mathrm{d}t\hfill \\ \hfill & +{\int }_{\mathcal{X}\times \mathcal{T}}{k}_f{\frac{\mathit{\partial }{q}^{\ast }(C_2;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T{p}_2\mathrm{d}x\mathrm{d}t+{\int }_{\mathcal{X}}\mathrm{d}x{\left[k_f{\frac{\mathit{\partial }{q}^{\ast }(C_1;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T{\overline{p}}_2\right]}_{t=0}\hfill \\ \hfill & +{\int }_{\mathcal{X}\times \mathcal{T}}{k}_f^2{\frac{\mathit{\partial }{q}^{\ast }(C_2;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T{\overline{p}}_2\mathrm{d}x\mathrm{d}t\}\hfill \\ \hfill & =F\{{\int }_{\mathcal{X}}\mathrm{d}x{\left[k_f{\frac{\mathit{\partial }{q}^{\ast }(C_1;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T{\overline{p}}_1\right]}_{t=0}+{\int }_{\mathcal{X}\times \mathcal{T}}{k}_f{\frac{\mathit{\partial }{q}^{\ast }(C_1;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T\frac{\mathit{\partial }{\overline{p}}_1}{\mathit{\partial }t}\mathrm{d}x\mathrm{d}t\hfill \\ \hfill & +{\int }_{\mathcal{X}}\mathrm{d}x{\left[k_f{\frac{\mathit{\partial }{q}^{\ast }(C_2;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T{\overline{p}}_2\right]}_{t=0}\hfill \\ \hfill & +{\int }_{\mathcal{X}\times \mathcal{T}}{k}_f{\frac{\mathit{\partial }{q}^{\ast }(C_2;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T\frac{\mathit{\partial }{\overline{p}}_2}{\mathit{\partial }t})\mathrm{d}x\mathrm{d}t\}\hfill \\ \hfill & =-F\left\{{\int }_{\mathcal{X}\times \mathcal{T}}{k}_f\frac{\mathit{\partial }({\frac{q^{\ast }(C_1;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T)}{\mathit{\partial }t}{\overline{p}}_1\mathrm{d}x\mathrm{d}t+{\int }_{\mathcal{X}\times \mathcal{T}}{k}_f\frac{\mathit{\partial }({\frac{q^{\ast }(C_2;\mathit{\xi })}{\mathit{\partial }\mathit{\xi }}}^T)}{\mathit{\partial }t}{\overline{p}}_2\mathrm{d}x\mathrm{d}t\right\},\hfill \end{array}$$ which yields the desired result. $\square$

For the Transport-Dispersive model, the mass transfer resistance coefficients $k_f$ should be estimated. In chemistry, different techniques can be used to experimentally determine mass transfer coefficients, such as frontal analysis, pulse on a plateau method, nuclear magnetic resonance, uptake curve measurement and the Wicke–Kallenbach method – see review articles [25,26] for details. In this work, instead of the experimental approaches, we will estimate the mass transfer coefficient $k_f$ by the inverse method. To be more precise, denote $\mathit{\zeta }=\{\mathit{\xi },k_f\}$. Suppose that $k_f\in {\mathrm{\Theta }}_{k_f}$, where ${\mathrm{\Theta }}_{k_f}$ is a convex closed set in ${\mathbf{R}}^n$. Obviously, ${\mathrm{\Theta }}_{TD}=\left\{\mathit{\zeta }=\{\mathit{\xi },k_f\}:\mathit{\xi }\in \mathrm{\Theta },k_f\in {\mathrm{\Theta }}_{k_f}\right\}$ is also a convex closed set in ${\mathbf{R}}^{m+n}$. Then, the reconstructing process for parameter $\mathit{\zeta }$ can be described in the following algorithm

Note that ${\mathcal{J}}_{i,\mathit{\alpha }}^{\prime }({\mathit{\xi }}^l;k_f^l)$ in step 3 of Algorithm 2 means the derivative of function ${\mathcal{J}}_{i,\mathit{\alpha }}$ with respect to vector ${\mathit{\xi }}^l$ with the fixed mass transfer resistance $k_f=k_f^l$. The derivative of functional ${\mathcal{J}}_{i,\mathit{\alpha }}$ with respect to vector $k_f$ with the fixed $\mathit{\xi }$ can be calculated analogously. Here, we only show the result for the Kohn–Vogelius type objective functional.

Proposition 3.6:

The Jacobian of objective function ${\mathcal{J}}_{KV,\mathit{\alpha }}$ with respect to $k_f$ with the fixed adsorption isotherm parameter $\mathit{\xi }$ is$$\begin{array}{cc}\hfill {\mathcal{J}}_{KV,\mathit{\alpha }}^{\prime }(k_f;\mathit{\xi })& =F{\int }_{\mathcal{X}\times \mathcal{T}}(q^{\ast }(C_1;\mathit{\zeta })-q(C_1;\mathit{\zeta }))(p_1+k_f{\overline{p}}_1)\hfill \\ \hfill & +(q^{\ast }(C_2;\mathit{\zeta })-q(C_2;\mathit{\zeta }))(p_2+k_f{\overline{p}}_2)\mathrm{d}x\mathrm{d}t,\hfill \end{array}$$

where ${\overline{p}}_1$, ${\overline{p}}_2$ are the solution of adjoint equations(22) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }{\overline{p}}_1}{\mathit{\partial }t}-k_f{\overline{p}}_1=p_1,\hfill & (x,t)\in \mathcal{X}\times \mathcal{T},\hfill \\ {\overline{p}}_1=0,\hfill & t=T,x\in \mathcal{X},\hfill \end{array}\right.\end{array}$$(22)

and(23) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }{\overline{p}}_2}{\mathit{\partial }t}-k_f{\overline{p}}_2=p_2,\hfill & (x,t)\in \mathcal{X}\times \mathcal{T},\hfill \\ {\overline{p}}_2=0,\hfill & t=T,x\in \mathcal{X},\hfill \end{array}\right.\end{array}$$(23)

respectively. Here $q(C_1;\mathit{\zeta })$, $q(C_2;\mathit{\zeta })$, $p_1$ and $p_2$ are defined in Proposition 3.4.

Proof:

By Proposition 3.4, we have(24) $$\begin{array}{c}\hfill \begin{array}{cc}{\mathcal{J}}_{KV,\mathit{\alpha }}^{\prime }(k_f;\mathit{\xi })\hfill & ={\int }_{\mathcal{X}\times \mathcal{T}}F\frac{\mathit{\partial }({\frac{\mathit{\partial }q(C_1;\mathit{\zeta })}{\mathit{\partial }{k}_f}}^T)}{\mathit{\partial }t}{p}_1\mathrm{d}x\mathrm{d}t+{\int }_{\mathcal{X}\times \mathcal{T}}F\frac{\mathit{\partial }({\frac{\mathit{\partial }q(C_2;\mathit{\zeta })}{\mathit{\partial }{k}_f}}^T)}{\mathit{\partial }t}{p}_2\mathrm{d}x\mathrm{d}t\hfill \\ \hfill & =F{\int }_{\mathcal{X}\times \mathcal{T}}(q^{\ast }(C_1;\mathit{\zeta })-q(C_1;\mathit{\zeta })-k_f{M}_{k_{f}1})p_1\mathrm{d}x\mathrm{d}t\hfill \\ \hfill & +F{\int }_{\mathcal{X}\times \mathcal{T}}(q^{\ast }(C_2;\mathit{\zeta })-q(C_2;\mathit{\zeta })-k_f{M}_{k_{f}2})p_2\mathrm{d}x\mathrm{d}t.\hfill \end{array}\end{array}$$(24)

Here $M_{k_{f}1}={\frac{\mathit{\partial }q(C_1;\mathit{\zeta })}{\mathit{\partial }{k}_f}}^T$ and $M_{k_{f}2}={\frac{\mathit{\partial }q(C_2;\mathit{\zeta })}{\mathit{\partial }{k}_f}}^T$ satisfy(25) $$\begin{array}{c}\hfill \begin{array}{cc}& {\int }_{\mathcal{X}}\mathrm{d}x{[M_{k_{f}1}\tilde{p}]}_{t=T}-{\int }_{\mathcal{X}\times \mathcal{T}}{M}_{k_{f}1}\frac{\mathit{\partial }\tilde{p}}{\mathit{\partial }t}\mathrm{d}x\mathrm{d}t\hfill \\ \hfill & ={\int }_{\mathcal{X}\times \mathcal{T}}(q^{\ast }(C_1;\mathit{\zeta })-q(C_1;\mathit{\zeta })-k_f{M}_{k_{f}1})\tilde{p}\mathrm{d}x\mathrm{d}t,\tilde{p}\in D{(\mathcal{X}\times \mathcal{T})}^n\hfill \end{array}\end{array}$$(25)

and(26) $$\begin{array}{c}\hfill \begin{array}{cc}& {\int }_{\mathcal{X}}\mathrm{d}x{[M_{k_{f}2}\tilde{p}]}_{t=T}-{\int }_{\mathcal{X}\times \mathcal{T}}{M}_{k_{f}2}\frac{\mathit{\partial }\tilde{p}}{\mathit{\partial }t}\mathrm{d}x\mathrm{d}t\hfill \\ \hfill & ={\int }_{\mathcal{X}\times \mathcal{T}}(q^{\ast }(C_2;\mathit{\zeta })-q(C_2;\mathit{\zeta })-k_f{M}_{k_{f}2})\tilde{p}\mathrm{d}x\mathrm{d}t,\tilde{p}\in D{(\mathcal{X}\times \mathcal{T})}^n\hfill \end{array}\end{array}$$(26)

respectively. Rewrite (25(25) $$\begin{array}{c}\hfill \begin{array}{cc}& {\int }_{\mathcal{X}}\mathrm{d}x{[M_{k_{f}1}\tilde{p}]}_{t=T}-{\int }_{\mathcal{X}\times \mathcal{T}}{M}_{k_{f}1}\frac{\mathit{\partial }\tilde{p}}{\mathit{\partial }t}\mathrm{d}x\mathrm{d}t\hfill \\ \hfill & ={\int }_{\mathcal{X}\times \mathcal{T}}(q^{\ast }(C_1;\mathit{\zeta })-q(C_1;\mathit{\zeta })-k_f{M}_{k_{f}1})\tilde{p}\mathrm{d}x\mathrm{d}t,\tilde{p}\in D{(\mathcal{X}\times \mathcal{T})}^n\hfill \end{array}\end{array}$$(25) ) and (26(26) $$\begin{array}{c}\hfill \begin{array}{cc}& {\int }_{\mathcal{X}}\mathrm{d}x{[M_{k_{f}2}\tilde{p}]}_{t=T}-{\int }_{\mathcal{X}\times \mathcal{T}}{M}_{k_{f}2}\frac{\mathit{\partial }\tilde{p}}{\mathit{\partial }t}\mathrm{d}x\mathrm{d}t\hfill \\ \hfill & ={\int }_{\mathcal{X}\times \mathcal{T}}(q^{\ast }(C_2;\mathit{\zeta })-q(C_2;\mathit{\zeta })-k_f{M}_{k_{f}2})\tilde{p}\mathrm{d}x\mathrm{d}t,\tilde{p}\in D{(\mathcal{X}\times \mathcal{T})}^n\hfill \end{array}\end{array}$$(26) ) into$$\begin{array}{c}\hfill \begin{array}{cc}& {\int }_{\mathcal{X}\times \mathcal{T}}{M}_{k_{f}1}(\frac{\mathit{\partial }\tilde{p}}{\mathit{\partial }t}-k_f\tilde{p})\mathrm{d}x\mathrm{d}t\hfill \\ \hfill & ={\int }_{\mathcal{X}}\mathrm{d}x{[M_{\mathit{\zeta }1}\tilde{p}]}_{t=T}-{\int }_{\mathcal{X}\times \mathcal{T}}(q^{\ast }(C_1;\mathit{\zeta })-q(C_1;\mathit{\zeta }))\tilde{p}\mathrm{d}x\mathrm{d}t,\hfill \\ \hfill & {\int }_{\mathcal{X}\times \mathcal{T}}{M}_{k_{f}2}(\frac{\mathit{\partial }\tilde{p}}{\mathit{\partial }t}-k_f\tilde{p})\mathrm{d}x\mathrm{d}t\hfill \\ \hfill & ={\int }_{\mathcal{X}}\mathrm{d}x{[M_{\mathit{\zeta }2}\tilde{p}]}_{t=T}-{\int }_{\mathcal{X}\times \mathcal{T}}(q^{\ast }(C_2;\mathit{\zeta })-q(C_2;\mathit{\zeta }))\tilde{p}\mathrm{d}x\mathrm{d}t\hfill \end{array}\end{array}$$

and let $\tilde{p}={\overline{p}}_1$ and $\tilde{p}={\overline{p}}_2$, where ${\overline{p}}_1$ and ${\overline{p}}_2$ are solutions to (22(22) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }{\overline{p}}_1}{\mathit{\partial }t}-k_f{\overline{p}}_1=p_1,\hfill & (x,t)\in \mathcal{X}\times \mathcal{T},\hfill \\ {\overline{p}}_1=0,\hfill & t=T,x\in \mathcal{X},\hfill \end{array}\right.\end{array}$$(22) ) and (23(23) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }{\overline{p}}_2}{\mathit{\partial }t}-k_f{\overline{p}}_2=p_2,\hfill & (x,t)\in \mathcal{X}\times \mathcal{T},\hfill \\ {\overline{p}}_2=0,\hfill & t=T,x\in \mathcal{X},\hfill \end{array}\right.\end{array}$$(23) ), respectively, we deduce that(27) $$\begin{array}{c}\hfill {\int }_{\mathcal{X}\times \mathcal{T}}{M}_{k_{f}1}{p}_1\mathrm{d}x\mathrm{d}t=-{\int }_{\mathcal{X}\times \mathcal{T}}(q^{\ast }(C_1;\mathit{\zeta })-q(C_1;\mathit{\zeta })){\overline{p}}_2,\end{array}$$(27)

and(28) $$\begin{array}{c}\hfill {\int }_{\mathcal{X}\times \mathcal{T}}{M}_{k_{f}2}{p}_2\mathrm{d}x\mathrm{d}t=-{\int }_{\mathcal{X}\times \mathcal{T}}(q^{\ast }(C_2;\mathit{\zeta })-q(C_2;\mathit{\zeta })){\overline{p}}_2.\end{array}$$(28)

Combine (24(24) $$\begin{array}{c}\hfill \begin{array}{cc}{\mathcal{J}}_{KV,\mathit{\alpha }}^{\prime }(k_f;\mathit{\xi })\hfill & ={\int }_{\mathcal{X}\times \mathcal{T}}F\frac{\mathit{\partial }({\frac{\mathit{\partial }q(C_1;\mathit{\zeta })}{\mathit{\partial }{k}_f}}^T)}{\mathit{\partial }t}{p}_1\mathrm{d}x\mathrm{d}t+{\int }_{\mathcal{X}\times \mathcal{T}}F\frac{\mathit{\partial }({\frac{\mathit{\partial }q(C_2;\mathit{\zeta })}{\mathit{\partial }{k}_f}}^T)}{\mathit{\partial }t}{p}_2\mathrm{d}x\mathrm{d}t\hfill \\ \hfill & =F{\int }_{\mathcal{X}\times \mathcal{T}}(q^{\ast }(C_1;\mathit{\zeta })-q(C_1;\mathit{\zeta })-k_f{M}_{k_{f}1})p_1\mathrm{d}x\mathrm{d}t\hfill \\ \hfill & +F{\int }_{\mathcal{X}\times \mathcal{T}}(q^{\ast }(C_2;\mathit{\zeta })-q(C_2;\mathit{\zeta })-k_f{M}_{k_{f}2})p_2\mathrm{d}x\mathrm{d}t.\hfill \end{array}\end{array}$$(24) ), (27(27) $$\begin{array}{c}\hfill {\int }_{\mathcal{X}\times \mathcal{T}}{M}_{k_{f}1}{p}_1\mathrm{d}x\mathrm{d}t=-{\int }_{\mathcal{X}\times \mathcal{T}}(q^{\ast }(C_1;\mathit{\zeta })-q(C_1;\mathit{\zeta })){\overline{p}}_2,\end{array}$$(27) ) and (28(28) $$\begin{array}{c}\hfill {\int }_{\mathcal{X}\times \mathcal{T}}{M}_{k_{f}2}{p}_2\mathrm{d}x\mathrm{d}t=-{\int }_{\mathcal{X}\times \mathcal{T}}(q^{\ast }(C_2;\mathit{\zeta })-q(C_2;\mathit{\zeta })){\overline{p}}_2.\end{array}$$(28) ), we obtain$$\begin{array}{c}\hfill \begin{array}{cc}{\mathcal{J}}_{KV,\mathit{\alpha }}^{\prime }(k_f;\mathit{\xi })\hfill & =F{\int }_{\mathcal{X}\times \mathcal{T}}(q^{\ast }(C_1;\mathit{\zeta })-q(C_1;\mathit{\zeta }))p_1+k_f(q^{\ast }(C_1;\mathit{\zeta })-q(C_1;\mathit{\zeta })){\overline{p}}_1\mathrm{d}x\mathrm{d}t\hfill \\ \hfill & +F{\int }_{\mathcal{X}\times \mathcal{T}}(q^{\ast }(C_2;\mathit{\zeta })-q(C_2;\mathit{\zeta }))p_2+k_f(q^{\ast }(C_2;\mathit{\zeta })-q(C_2;\mathit{\zeta })){\overline{p}}_2\mathrm{d}x\mathrm{d}t\hfill \\ \hfill & =F{\int }_{\mathcal{X}\times \mathcal{T}}\left(q^{\ast }(C_1;\mathit{\zeta })-q(C_1;\mathit{\zeta })\right)(p_1+k_f{\overline{p}}_1)\hfill \\ \hfill & +\left(q^{\ast }(C_2;\mathit{\zeta })-q(C_2;\mathit{\zeta })\right)(p_2+k_f{\overline{p}}_2)\mathrm{d}x\mathrm{d}t,\hfill \end{array}\end{array}$$

which is the required result in the proposition. $\square$

4. Implementation issues

In this section, we briefly discuss some numerical issues that arise in the implementation of the developed approaches – see Algorithms 1(1) $$\begin{array}{c}\hfill q_i^{\ast }=q_i^{\ast }(C;\mathit{\xi })=\frac{a_i{C}^{(i)}}{1+{\sum }_{j=1}^n{b}_j{C}^{(j)}},i=1,\dots ,n.\end{array}$$(1) and 2(2) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }C}{\mathit{\partial }t}+F\frac{\mathit{\partial }q}{\mathit{\partial }t}+u\frac{\mathit{\partial }C}{\mathit{\partial }x}=D_a\frac{{\mathit{\partial }}^{2}C}{\mathit{\partial }{x}^2},\hfill & x\in \mathcal{X}\equiv (0,L),t\in \mathcal{T}\equiv (0,T],\hfill \\ C(x,0)=g(x),\hfill & x\in \mathcal{X},t=0,\hfill \\ uC(0,t)-D_a\frac{\mathit{\partial }C(0,t)}{\mathit{\partial }x}=uh(t),\hfill & x=0,t\in \mathcal{T},\hfill \\ D_a\frac{\mathit{\partial }C(L,t)}{\mathit{\partial }x}=0,\hfill & x=L,t\in \mathcal{T}.\hfill \end{array}\right.\end{array}$$(2) .

4.1. Regularization parameter selection methods

There exist various regularization parameter selection methods such as a priori methods [27] or a posteriori methods.[28] However, all of them need the error information since a regularizing algorithm without using error level exists only for the well-posed problems. Therefore, there is no systematic rule for $\mathit{\alpha }$ since the error level is not available for the real problem. Note that introducing a small amount of the momentum criterion $\mathrm{\Omega }$ improves the convergence towards the minimum, because there is a better control on the position of the peaks. On the other hand, if $\mathit{\alpha }$ is too large, the position of the shocks becomes predominant, and the shape of the peaks cannot be improved. By performing a number of computer simulations, we recommend the following two regularization parameter selection strategies:

(S1)	Chose $\mathit{\alpha }$ such that(29) $$\begin{array}{c}\hfill \mathit{\alpha }=\mathit{ϵ}{\mathcal{J}}_i({\mathit{\xi }}_0)/{\mathrm{\Omega }}_i({\mathit{\xi }}_0),i=BF\text{or}KV.\end{array}$$(29)
(S2)	At the step k of iteration, chose ${\mathit{\alpha }}_k$ such that(30) $$\begin{array}{c}\hfill {\mathit{\alpha }}_k=\mathit{ϵ}{\mathcal{J}}_i({\mathit{\xi }}_k)/{\mathrm{\Omega }}_i({\mathit{\xi }}_k),i=BF\text{or}KV.\end{array}$$(30)

Here ${\mathit{\xi }}_0$ is an initial guess of the parameter, ${\mathit{\xi }}_k$ is the estimated parameter at the step k and the constant $\mathit{ϵ}$ is a given threshold. For the computations in this paper, we chose $\mathit{ϵ}=0.001$.

Remark 4.1:

By demonstrating several artificial noised data, we found that the results of strategy (S2) are similar as the results of strategy (S1). Hence, in the simulation, we only display the results from strategy (S1).

4.2. Solution of the forward problem

The chromatography model (2(2) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }C}{\mathit{\partial }t}+F\frac{\mathit{\partial }q}{\mathit{\partial }t}+u\frac{\mathit{\partial }C}{\mathit{\partial }x}=D_a\frac{{\mathit{\partial }}^{2}C}{\mathit{\partial }{x}^2},\hfill & x\in \mathcal{X}\equiv (0,L),t\in \mathcal{T}\equiv (0,T],\hfill \\ C(x,0)=g(x),\hfill & x\in \mathcal{X},t=0,\hfill \\ uC(0,t)-D_a\frac{\mathit{\partial }C(0,t)}{\mathit{\partial }x}=uh(t),\hfill & x=0,t\in \mathcal{T},\hfill \\ D_a\frac{\mathit{\partial }C(L,t)}{\mathit{\partial }x}=0,\hfill & x=L,t\in \mathcal{T}.\hfill \end{array}\right.\end{array}$$(2) ) is a non-linear convection–diffusion PDE with dominated convection terms. A complication is that discontinuities in the solutions can develop even for smooth initial data, which is known as self-sharpening, and can easily cause numerical instability. We use a high resolution koren flux-limiting finite volume scheme,[15] which can suppress numerical oscillation and capture sharp discontinuity of chromatographic fronts on coarse grids.

For the numerical simulation of the Equilibrium-Dispersive model, we will have one first-order ODE for each discretization point in space for each component, i.e. if the number of discretization points (cells) is $n_x$ and the number of components is $n_c$, we will have a system with $n_x{n}_c$ ODE’s of the form, $\mathrm{d}{C}_i/\mathrm{d}t=f_i(t,C)$. In the simulation, we use the Runge–Kutta method and to evaluate $f_i$ one needs to solve a full linear system where the coefficient matrix is the Jacobian $\frac{\mathit{\partial }C}{\mathit{\partial }q}$ with size $n_c^2$. I.e. we must solve $n_x$ number of $n_c^2$ full linear system systems in each time step. This can be done by assembling all $n_x$ number of $n_c^2$ full linear system in a block-diagonal matrix.

Similarly, for the Transport-Dispersive model we have to solve a system with $2n_x{n}_c$ ODEs of the form, $\mathrm{d}{C}_i/\mathrm{d}t=f_{i,0}(t,C,q)$, $\mathrm{d}{q}_i/\mathrm{d}t=f_{i,1}(t,C,q)$, which is a sparse linear system (but not a block-diagonal matrix). MATLAB uses an Unsymmetric MultiFrontal method [29] to LU-factorize the sparse linear system that arises in the Transport-Dispersive model [5] of chromatography. In this work, we apply column approximate minimum degree permutation technique [30] to permute the columns of the coefficient matrix. The LU-factorization of the column permuted coefficient matrix is almost 4.5 times faster than LU-factorization of the original coefficient matrix. It should be noted that the column/row permutation needs to be calculated only once in the Finite-Volume code and can then be applied to all sparse coefficient matrices that arise. For a test case, the portion of the time spent in the code doing LU-factorization was reduced from $\sim 25\%$ to $\sim 7.5\%$ with column permutation, and the total runtime was reduced by $\sim 22\%$.

4.3. Solution of the adjoint problem

Consider the adjoint problem (10(10) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }p}{\mathit{\partial }t}+F{\left[\frac{\mathit{\partial }q(C;\mathit{\xi })}{\mathit{\partial }C}\right]}^T\frac{\mathit{\partial }p}{\mathit{\partial }t}+u\frac{\mathit{\partial }p}{\mathit{\partial }x}+D_a\frac{{\mathit{\partial }}^{2}p}{\mathit{\partial }{x}^2}=0,\hfill & (x,t)\in \mathcal{X}\times \mathcal{T},\hfill \\ p(x,T)=0,\hfill & t=T,x\in \mathcal{X},\hfill \\ up(L,t)+D_a\frac{\mathit{\partial }p(L,t)}{\mathit{\partial }x}=\frac{\mathit{\partial }{\mathcal{J}}_{BF,\mathit{\alpha }}}{\mathit{\partial }C},\hfill & x=L,t\in \mathcal{T},\hfill \\ D_a\frac{\mathit{\partial }p(0,t)}{\mathit{\partial }x}=0,\hfill & x=0,t\in \mathcal{T},\hfill \end{array}\right.\end{array}$$(10) ) with boundary fitting method (5(5) $$\begin{array}{c}\hfill \underset{\mathit{\xi }}{min}{\mathcal{J}}_{BF,\mathit{\alpha }}(\mathit{\xi })=\underset{\mathit{\xi }}{min}{J}_{BF}(C;\mathit{\xi })+\mathit{\alpha }\mathrm{\Omega }(C;\mathit{\xi }),\end{array}$$(5) ). In order to distinguish the original problem (2(2) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }C}{\mathit{\partial }t}+F\frac{\mathit{\partial }q}{\mathit{\partial }t}+u\frac{\mathit{\partial }C}{\mathit{\partial }x}=D_a\frac{{\mathit{\partial }}^{2}C}{\mathit{\partial }{x}^2},\hfill & x\in \mathcal{X}\equiv (0,L),t\in \mathcal{T}\equiv (0,T],\hfill \\ C(x,0)=g(x),\hfill & x\in \mathcal{X},t=0,\hfill \\ uC(0,t)-D_a\frac{\mathit{\partial }C(0,t)}{\mathit{\partial }x}=uh(t),\hfill & x=0,t\in \mathcal{T},\hfill \\ D_a\frac{\mathit{\partial }C(L,t)}{\mathit{\partial }x}=0,\hfill & x=L,t\in \mathcal{T}.\hfill \end{array}\right.\end{array}$$(2) ) and its adjoint problem (10(10) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }p}{\mathit{\partial }t}+F{\left[\frac{\mathit{\partial }q(C;\mathit{\xi })}{\mathit{\partial }C}\right]}^T\frac{\mathit{\partial }p}{\mathit{\partial }t}+u\frac{\mathit{\partial }p}{\mathit{\partial }x}+D_a\frac{{\mathit{\partial }}^{2}p}{\mathit{\partial }{x}^2}=0,\hfill & (x,t)\in \mathcal{X}\times \mathcal{T},\hfill \\ p(x,T)=0,\hfill & t=T,x\in \mathcal{X},\hfill \\ up(L,t)+D_a\frac{\mathit{\partial }p(L,t)}{\mathit{\partial }x}=\frac{\mathit{\partial }{\mathcal{J}}_{BF,\mathit{\alpha }}}{\mathit{\partial }C},\hfill & x=L,t\in \mathcal{T},\hfill \\ D_a\frac{\mathit{\partial }p(0,t)}{\mathit{\partial }x}=0,\hfill & x=0,t\in \mathcal{T},\hfill \end{array}\right.\end{array}$$(10) ) more clearly, we perform a change of variables $\overline{p}(x,t)=p(x,T-t)$, $\overline{q}(x,t)=q(x,T-t)$ and $\overline{h}(t)=h(T-t)$, where $h=C(L,t;\mathit{\xi })-C_{obs}(t)+\mathit{\alpha }t\mathit{\mu }\left(C(L,t;\mathit{\xi })-C_{obs}(t)\right)$. Then, $\overline{p}$ satisfies(31) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }\overline{p}}{\mathit{\partial }t}+F{\frac{\mathit{\partial }\overline{q}}{\mathit{\partial }C}}^T\frac{\mathit{\partial }\overline{p}}{\mathit{\partial }t}-u\frac{\mathit{\partial }\overline{p}}{\mathit{\partial }x}=D_a\frac{{\mathit{\partial }}^2\overline{p}}{\mathit{\partial }{x}^2},\hfill & (x,t)\in \mathcal{X}\times \mathcal{T},\hfill \\ \overline{p}(x,0)=0,\hfill & t=0,x\in \mathcal{X},\hfill \\ u\overline{p}(L,t)+D_a\frac{\mathit{\partial }\overline{p}(L,t)}{\mathit{\partial }x}=\overline{h},\hfill & x=L,t\in \mathcal{T},\hfill \\ D_a\frac{\mathit{\partial }\overline{p}(0,t)}{\mathit{\partial }x}=0,\hfill & x=0,t\in \mathcal{T}.\hfill \end{array}\right.\end{array}$$(31)

As one can see in (31(31) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }\overline{p}}{\mathit{\partial }t}+F{\frac{\mathit{\partial }\overline{q}}{\mathit{\partial }C}}^T\frac{\mathit{\partial }\overline{p}}{\mathit{\partial }t}-u\frac{\mathit{\partial }\overline{p}}{\mathit{\partial }x}=D_a\frac{{\mathit{\partial }}^2\overline{p}}{\mathit{\partial }{x}^2},\hfill & (x,t)\in \mathcal{X}\times \mathcal{T},\hfill \\ \overline{p}(x,0)=0,\hfill & t=0,x\in \mathcal{X},\hfill \\ u\overline{p}(L,t)+D_a\frac{\mathit{\partial }\overline{p}(L,t)}{\mathit{\partial }x}=\overline{h},\hfill & x=L,t\in \mathcal{T},\hfill \\ D_a\frac{\mathit{\partial }\overline{p}(0,t)}{\mathit{\partial }x}=0,\hfill & x=0,t\in \mathcal{T}.\hfill \end{array}\right.\end{array}$$(31) ), the main difference between Equations (2(2) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }C}{\mathit{\partial }t}+F\frac{\mathit{\partial }q}{\mathit{\partial }t}+u\frac{\mathit{\partial }C}{\mathit{\partial }x}=D_a\frac{{\mathit{\partial }}^{2}C}{\mathit{\partial }{x}^2},\hfill & x\in \mathcal{X}\equiv (0,L),t\in \mathcal{T}\equiv (0,T],\hfill \\ C(x,0)=g(x),\hfill & x\in \mathcal{X},t=0,\hfill \\ uC(0,t)-D_a\frac{\mathit{\partial }C(0,t)}{\mathit{\partial }x}=uh(t),\hfill & x=0,t\in \mathcal{T},\hfill \\ D_a\frac{\mathit{\partial }C(L,t)}{\mathit{\partial }x}=0,\hfill & x=L,t\in \mathcal{T}.\hfill \end{array}\right.\end{array}$$(2) ) and (31(31) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }\overline{p}}{\mathit{\partial }t}+F{\frac{\mathit{\partial }\overline{q}}{\mathit{\partial }C}}^T\frac{\mathit{\partial }\overline{p}}{\mathit{\partial }t}-u\frac{\mathit{\partial }\overline{p}}{\mathit{\partial }x}=D_a\frac{{\mathit{\partial }}^2\overline{p}}{\mathit{\partial }{x}^2},\hfill & (x,t)\in \mathcal{X}\times \mathcal{T},\hfill \\ \overline{p}(x,0)=0,\hfill & t=0,x\in \mathcal{X},\hfill \\ u\overline{p}(L,t)+D_a\frac{\mathit{\partial }\overline{p}(L,t)}{\mathit{\partial }x}=\overline{h},\hfill & x=L,t\in \mathcal{T},\hfill \\ D_a\frac{\mathit{\partial }\overline{p}(0,t)}{\mathit{\partial }x}=0,\hfill & x=0,t\in \mathcal{T}.\hfill \end{array}\right.\end{array}$$(31) ) is the change of sign in the flux term. Hence, we have to use a different upwind scheme to solve them. A simple method is the forward difference method when approximating $\mathit{\partial }\overline{p}/\mathit{\partial }x$, which just provides first order accurate. In order to improve the accurate, we apply similar koren flux-limiting finite-volume scheme as in [31].

4.4. Constrains and starting guess

Now, we consider some constraints and initial starting point (vector) on the adsorption isotherm parameters to improve the speed and quality of the proposed optimization algorithm.

4.4.1. The competitive Langmuir adsorption isotherm

Bound constraints will be used in all tests, i.e. $\mathrm{\Theta }=\{\mathit{\xi }\in {\mathbf{R}}^m:{\underline{\mathit{\xi }}}_i\le {\mathit{\xi }}_i\le {\overline{\mathit{\xi }}}_i,i=1,\dots ,m\}$. Furthermore, in analytical chromatography, the adsorption isotherm is assumed as a linear function, i.e. $q_i={\overline{a}}_i{C}_i$. Therefore, a reasonable initial guess is $a_{0,i}={\overline{a}}_i,b_{0,i}=0$. Further from [9], ${\overline{a}}_i$ can be approximated by(32) $$\begin{array}{c}\hfill {\overline{a}}_i=\left(u{t}_{R,i}/L-1\right)/F,\end{array}$$(32)

where $t_{R,i}$ is elution time of the ith component.

4.4.2. Approximate adsorption isotherm using piecewise polynomial

For simplicity, for this model, we only consider the case with a single component. For the adsorption isotherm, we have the following monotone constraints$$\begin{array}{c}\hfill q{(}_{k}C)\le q{(}_{k+1}C)\text{for}{}_{k}C\le {}_{k+1}C,\end{array}$$

where ${}_{k}C$ is the value of C at a point.

A simple initial guess is $q{(}_{k}C)=\overline{a}·{}_{k}C$, where $\overline{a}$ can be calculated by (32(32) $$\begin{array}{c}\hfill {\overline{a}}_i=\left(u{t}_{R,i}/L-1\right)/F,\end{array}$$(32) ). For different types of adsorption isotherms, we can specify different bound constraints to reduce the computational time.[6] For example, if the adsorption isotherm is concave downward, the bound for each recovered parameters can be expressed as$$\begin{array}{c}\hfill \overline{a}·{}_{k}C\le q{(}_{k}C)\le \overline{q},\end{array}$$

where $\overline{q}=\overline{a}·{}_k\overline{C}$ and ${}_k\overline{C}$ is the upper bound of ${}_{k}C$.

4.5. The choice of interpolation points and interpolation functions

For a large number of interpolation points, the optimization will take a long time. According to the properties of the adsorption isotherm, we could use an uneven distribution of the interpolation points; that is, more interpolation points should be placed at the important part of adsorption isotherm.

It is important to choose suitable interpolation functions to approximate the adsorption isotherm. In [6], the authors applied linear interpolation, which needs numerous interpolation points to approximate non-linear adsorption isotherm. In this work, we apply Stineman interpolation combined with linear basis functions, developed in [7], which greatly reduces the interpolation points, and has continuous derivatives, whereas linear interpolation has discontinuous ones.

5. Simulations

In this section, we do some numerical experiments to validate the accuracy and effectiveness of the proposed approach. Note that, before performing our algorithm (Algorithms 1(1) $$\begin{array}{c}\hfill q_i^{\ast }=q_i^{\ast }(C;\mathit{\xi })=\frac{a_i{C}^{(i)}}{1+{\sum }_{j=1}^n{b}_j{C}^{(j)}},i=1,\dots ,n.\end{array}$$(1) and 2(2) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }C}{\mathit{\partial }t}+F\frac{\mathit{\partial }q}{\mathit{\partial }t}+u\frac{\mathit{\partial }C}{\mathit{\partial }x}=D_a\frac{{\mathit{\partial }}^{2}C}{\mathit{\partial }{x}^2},\hfill & x\in \mathcal{X}\equiv (0,L),t\in \mathcal{T}\equiv (0,T],\hfill \\ C(x,0)=g(x),\hfill & x\in \mathcal{X},t=0,\hfill \\ uC(0,t)-D_a\frac{\mathit{\partial }C(0,t)}{\mathit{\partial }x}=uh(t),\hfill & x=0,t\in \mathcal{T},\hfill \\ D_a\frac{\mathit{\partial }C(L,t)}{\mathit{\partial }x}=0,\hfill & x=L,t\in \mathcal{T}.\hfill \end{array}\right.\end{array}$$(2) ) one can apply any global optimization algorithm based on gradient or combine global optimization of free gradient and a local optimization algorithm based on gradient. In the following simulations, assume that we have already got a ‘good’ initial guess by a global optimization algorithm such as genetic algorithm,[32] and we improve this initial guess by the constrained non-linear local optimization algorithm fmincon, which is implemented in the MATLAB Optimization Toolbox, Version 7.9.0. Note that in the initial guess for fmincon, it is not necessary to be very close to the exact parameter.

5.1. Computer simulation

Our first group of examples deals with synthetic data in order to demonstrate the robustness of the developed approach. The simulations consist of three steps. First, a simulated concentration in mobile phase at the outlet $\overline{C}(L,t;\overline{\mathit{\xi }})$ is generated by computer according to PDE (2(2) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }C}{\mathit{\partial }t}+F\frac{\mathit{\partial }q}{\mathit{\partial }t}+u\frac{\mathit{\partial }C}{\mathit{\partial }x}=D_a\frac{{\mathit{\partial }}^{2}C}{\mathit{\partial }{x}^2},\hfill & x\in \mathcal{X}\equiv (0,L),t\in \mathcal{T}\equiv (0,T],\hfill \\ C(x,0)=g(x),\hfill & x\in \mathcal{X},t=0,\hfill \\ uC(0,t)-D_a\frac{\mathit{\partial }C(0,t)}{\mathit{\partial }x}=uh(t),\hfill & x=0,t\in \mathcal{T},\hfill \\ D_a\frac{\mathit{\partial }C(L,t)}{\mathit{\partial }x}=0,\hfill & x=L,t\in \mathcal{T}.\hfill \end{array}\right.\end{array}$$(2) ) for a given parameter $\mathit{\xi }=\overline{\mathit{\xi }}$. The collected exact data at time grid ${\left\{t_j\right\}}_{j=1}^{N_t}$ at the outlet are denoted by ${\left\{\overline{C}(L,t_j;\overline{\mathit{\xi }})\right\}}_{j=1}^{N_t}$. Denote $\overline{C}={[{\overline{C}}_j^i]}_{n\times N_t}$ as the data matrix. We then define the artificial measured data by adding independent and identically distributed (i.i.d.) Gaussian random variables ${\{{\mathit{\vartheta }}_j^i\}}_{i,j=1}^{n,N_t}$, i.e. ${[C_{\mathit{\delta }}]}_j^i={\overline{C}}_j^i·(1+\mathit{\delta }{\mathit{\vartheta }}_j^i)$, where $\mathit{\delta }$ is the error level. At the last step of the simulation, the observation data $C_{\mathit{\delta }}$ are processed through our algorithm, and the retrieved parameter is compared with the input one.

The parameters of the concentration elution profiles for simulation are: $L=10\text{cm}$, $F=0.6667$, $u=0.1061\text{cm/s}$, number of theoretical plates is $N_x=2000$, $D_a=Lu/2N_x$, $g(x)\equiv {[0,0]}^T\text{M}$, $h(t)=H(10-t)·{[50,50]}^T\text{M}$, where $H(·)$ denotes the Heaviside step function.

Figure 1. Estimated adsorption isotherms by synthetic data with different error levels $\mathit{\delta }$ of and their corresponding relative errors $\mathrm{\Delta }$. (a) $\mathit{\delta }=0$ and $\mathrm{\Delta }=0.0154$. (b) $\mathit{\delta }=1\%$ and $\mathrm{\Delta }=0.0404$. (c) $\mathit{\delta }=5\%$ and $\mathrm{\Delta }=0.0520$. (d) $\mathit{\delta }=10\%$ and $\mathrm{\Delta }=0.0790$.

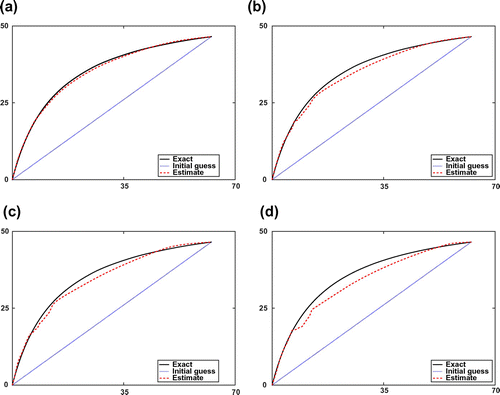
5.1.1. Estimating the adsorption isotherm using piecewise interpolation for the case with a single component.

In this example, a simulated concentration in mobile phase at the outlet $\overline{C}(L,t;\overline{\mathit{\xi }})$ is generated by computer according to PDE (2(2) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\frac{\mathit{\partial }C}{\mathit{\partial }t}+F\frac{\mathit{\partial }q}{\mathit{\partial }t}+u\frac{\mathit{\partial }C}{\mathit{\partial }x}=D_a\frac{{\mathit{\partial }}^{2}C}{\mathit{\partial }{x}^2},\hfill & x\in \mathcal{X}\equiv (0,L),t\in \mathcal{T}\equiv (0,T],\hfill \\ C(x,0)=g(x),\hfill & x\in \mathcal{X},t=0,\hfill \\ uC(0,t)-D_a\frac{\mathit{\partial }C(0,t)}{\mathit{\partial }x}=uh(t),\hfill & x=0,t\in \mathcal{T},\hfill \\ D_a\frac{\mathit{\partial }C(L,t)}{\mathit{\partial }x}=0,\hfill & x=L,t\in \mathcal{T}.\hfill \end{array}\right.\end{array}$$(2) ) for a given model ${\overline{q}}^{\ast }(C)=4·C/\left(1+0.2C\right)$. Similarly, denote vector $\overline{C}={\{{\overline{C}}_j\}}_{j=1}^{N_t}$ as the exact data and then generate a noised data $C_{\mathit{\delta }}$ by adding i.i.d. Gaussian random variables. The reconstructed adsorption isotherms ${\widehat{q}}^{\ast }(C)$ by noisy data $C_{\mathit{\delta }}$ with different error levels $\mathit{\delta }$ and their corresponding relative errors $\mathrm{\Delta }=\Vert {\widehat{q}}^{\ast }(C)-{\overline{q}}^{\ast }{\Vert }_{L^2(\mathcal{X}\times \mathcal{T})}/{\Vert {\widehat{q}}^{\ast }(C)\Vert }_{L^2(\mathcal{X}\times \mathcal{T})}$ are displayed in Figure 1. Note that only the Equilibrium-Dispersive model is used in this simulation.

5.1.2. The competitive Langmuir adsorption isotherm for the binary case, $n=2$

In the second group of simulations, the Langmuir adsorption isotherm model with parameters $\mathit{\xi }=[a_1,a_2,b_1,b_2]=[2,4,0.1,0.2]$ is used. Boundary constraints are $0\le a_i,b_i\le 10$, $i=1,2$. In our simulations, the least-squares boundary fitting method, i.e. problem ${min}_{\mathit{\xi }}{J}_{BF,\mathit{\alpha }}$, needs stronger boundary constraints: $0\le a_{1,2}\le 5,0\le b_{1,2}\le 1$.

Table 1. Estimated adsorption isotherms and computational costs (the number objective function evaluation (NOFE)) of the boundary fitting method (BF) and the Kohn–Vogelius method (KV) with different error levels for both the Equilibrium-Dispersive (ED) model and the Transport-Dispersive (TD) model with the given mass transfer resistance $k_f={[95,135]}^T$.

		Exact parameters	$a_1=2$	$a_2=4$	$b_1=0.1$	$b_2=0.2$
		Initial guesses	$a_1=1$	$a_2=1$	$b_1=1$	$b_2=1$
Method	Model	Error level $\mathit{\delta }$	$a_1$	$a_2$	$b_1$	$b_2$	NOFE
BF	ED	Exact data	2.7620	4.9963	0.0896	0.3472	75
KV	ED	Exact data	2.0082	3.9898	0.0995	0.1988	76
BF	ED	$\mathit{\delta }=1\%$	3.0839	4.9961	0.0704	0.3978	75
KV	ED	$\mathit{\delta }=1\%$	2.0328	4.0250	0.1008	0.1999	105
BF	ED	$\mathit{\delta }=5\%$	3.3173	4.9911	0.0213	0.4662	66
KV	ED	$\mathit{\delta }=5\%$	1.9354	3.9432	0.0951	0.1959	114
BF	ED	$\mathit{\delta }=10\%$	3.4073	4.9936	0.0272	0.4704	85
KV	ED	$\mathit{\delta }=10\%$	1.8629	3.7265	0.0942	0.1765	104
BF	TD	Exact data	1.8381	3.6223	0.1144	0.2065	79
KV	TD	Exact data	1.9745	3.9047	0.1011	0.2017	80
BF	TD	$\mathit{\delta }=1\%$	1.6980	4.5962	0.0658	0.1959	76
KV	TD	$\mathit{\delta }=1\%$	2.1897	4.0484	0.1145	0.1606	132
BF	TD	$\mathit{\delta }=5\%$	1.3459	3.4064	0.1650	0.3968	88
KV	TD	$\mathit{\delta }=5\%$	2.3259	5.0769	0.0786	0.1811	168
BF	TD	$\mathit{\delta }=10\%$	2.9460	6.7001	0.1957	0.4217	121
KV	TD	$\mathit{\delta }=10\%$	0.9633	3.6654	0.0748	0.1407	138

Table 2. Estimated adsorption isotherm parameters and mass transfer resistance by the boundary fitting method (BF) and the Kohn–Vogelius method (KV) with different error levels in the Transport-Dispersive (TD) model.

			$a_1$	$a_2$	$b_1$	$b_2$	$k_f^{(1)}$	$k_f^{(2)}$
		Exact	2	4	0.1	0.2	95	195
		Initial	1	1	1	1	100	100
Method	Model	Error level	$a_1$	$a_2$	$b_1$	$b_2$	$k_f^{(1)}$	$k_f^{(2)}$	NOFE
BF	TD	Exact	2.3897	4.2487	0.0760	0.1801	89.5	198.7	108
KV	TD	Exact	2.0298	4.0564	0.1014	0.2013	94.8	195.4	131
BF	TD	$\mathit{\delta }=1\%$	2.2764	3.5694	0.1123	0.2361	82.7	181.3	137
KV	TD	$\mathit{\delta }=1\%$	1.9517	4.0574	0.1033	0.2020	89.8	200.0	178
BF	TD	$\mathit{\delta }=5\%$	1.6137	3.3100	0.0958	0.1576	93.1	171.4	204
KV	TD	$\mathit{\delta }=5\%$	2.2069	4.2908	0.0970	0.2059	90.7	180.7	219
BF	TD	$\mathit{\delta }=10\%$	2.9420	5.8474	0.1345	0.3480	68.3	163.9	190
KV	TD	$\mathit{\delta }=10\%$	1.6851	4.7107	0.0771	0.1572	71.8	169.1	232

The numerical results with different error levels for both the Equilibrium-Dispersive model and the Transport-Dispersive model with the given mass transfer resistance $k_f={[95,135]}^T$ are displayed in Table 1. The results for the Transport-Dispersive model with unknown mass transfer resistance are given in Table 2. The constraints for the mass transfer are $\{k_f:50\le k_f^{(1)},k_f^{(2)}\le 200\}$.

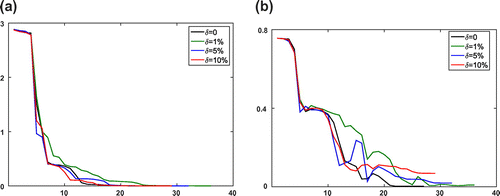
Moreover, in Figures 2 and 3, we depict the objective function $J_{i,\mathit{\alpha }}$ and relative error $\Vert {\mathit{\xi }}^l{-\overline{\mathit{\xi }}\Vert }_2/{\Vert {\mathit{\xi }}^l\Vert }_2$ of the recovered parameters in the Equilibrium-Dispersive model at every iteration for both the boundary fitting method and the Kohn–Vogelius type method, respectively. As seen from the numerical results, although the computation cost of optimization processes Kohn–Vogelius type functional is larger than least-square boundary fitting functional, the relative error of recovered parameters by the Kohn–Vogelius type method is convergence, and smaller than the result from the boundary fitting method. The results with the Transport-Dispersive model are shown in Figures 4 and 5.

Figure 2. Numerical results of the boundary fitting method for the Equilibrium-Dispersive model with different error levels $\mathit{\delta }$ at every iteration step l. (a) The value of objective function ${\mathcal{J}}_{BF,\mathit{\alpha }}$ and (b) the relative error $\Vert {\mathit{\xi }}^l{-\overline{\mathit{\xi }}\Vert }_2/{\Vert {\mathit{\xi }}^l\Vert }_2$ of recovered parameters.

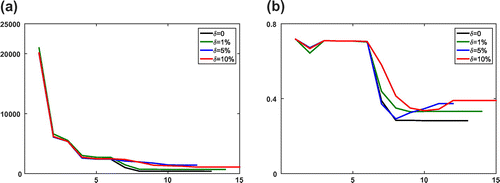
Figure 3. Numerical results of KV method for the Equilibrium-Dispersive model with different error levels $\mathit{\delta }$ at every iteration step l. (a) The value of objective function ${\mathcal{J}}_{KV,\mathit{\alpha }}$ and (b) the relative error $\Vert {\mathit{\xi }}^l{-\overline{\mathit{\xi }}\Vert }_2/{\Vert {\mathit{\xi }}^l\Vert }_2$ of recovered parameters.

Figure 4. The relative error of estimated adsorption isotherm parameters for the Transport-Dispersive model with different error levels $\mathit{\delta }$ at every iteration step l. (a) The boundary fitting method and (b) the Kohn–Vogelius method.

Figure 5. The relative errors of estimated adsorption isotherms and mass transfer resistance for the Transport-Dispersive model with different error levels $\mathit{\delta }$ at every iteration step l. (a) The relative errors of estimated adsorption isotherms $\Vert {\mathit{\xi }}^l{-\overline{\mathit{\xi }}\Vert }_2/{\Vert {\mathit{\xi }}^l\Vert }_2$ and (b) The relative errors of estimated mass transfer $\Vert k_f^l-k_f{\Vert }_2/{\Vert k_f^l\Vert }_2$.

5.2. Real data application

In the above subsection, the algorithm was used on test data to verify that the solution converged correctly. In practice, one never knows which model and model parameters are ‘correct’. The practitioner is satisfied when the observed model agreement is ‘good enough’, and the estimated parameters are consistent in the sense that they can be used to make accurate predictions even when the initial and boundary conditions are varied. To exemplify this, the algorithm was tested on actual experimental data.

Unfortunately, having separate response data ${\{C_{obs}^{(i)}(t)\}}_{i=1,2}$ for the individual components in a binary competitive experiment is extremely rare. It either requires special detectors or so-called fractioning, i.e. collecting a large number of samples at the outlet of the column and analyzing each one of these samples to get the concentration/response of the individual components at the collection time, an extremely time-consuming procedure. In this real data simulation, we have done the single component measurements for two components, i.e. we have just one component present in the injected sample. From these single components experiments, we can estimate the competitive adsorption isotherm surface. Then we can check how well the simulations using this competitive adsorption isotherm surface match experimental binary elution profiles.

Propranolol and alprenolol, two pharmaceutical substances were found to separate well on a Kromasil C18 column (Eka Chemicals, Bohus, Sweden) at 25 ${}^{\circ }$C using a mobile phase composed of 28:72 (v/v) acetonitrile: aqueous phosphate buffer (pH 2.54, ion strength 0.1). Other experimental details can be found in our previous work in [9]. Ten binary (propranolol and alprenolol) elution profiles with $g(x)\equiv {[0,0]}^T\text{mM}$ and h(t) equal to [0.75, 0]mM, [0, 0.75]mM, [5, 0]mM, [0, 5]mM, [10, 0]mM, [0, 10]mM, [15, 0]mM, [0, 15]mM, [30, 0]mM, [0, 30]mM were recorded, respectively. Other parameters were as follows: $L=15$ cm (inner diameter, 0.46 cm), $F=0.78$, $u=0.125$ cm/s, $N_x=9000$ and injection volume $=50\mathrm{\mu }l$. The elution profiles were recorded using an Agilent 1100 Chemstation LC instrument (Agilent, Palo Alto, CA, USA) with a UV detector. The calibration curves were linear ($R^2\ge 0.9996$ up to 0.2 M) for both substances at all mobile-phase compositions. Therefore, in this work, we assume that the response curve is just the concentration at the outlet.

Figure 6. The reconstructed adsorption isotherms by KV method for the Equilibrium-Dispersive model.

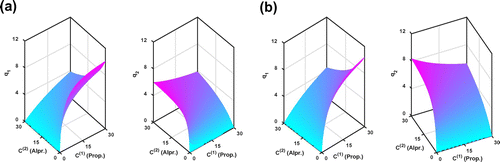
Figure 7. The reconstructed adsorption isotherms by KV method for the Transport-Dispersive model. (a) Fixed mass transfer resistance $k_f^{(1)}=95$ and $k_f^{(2)}=195$. (b) Estimating mass transfer resistance by inverse algorithm with the constraints $20\le k_f^{(i)}\le 400$, $i=1,2$.

In this real-world problem, only a poor fit could be obtained using the Langmuir adsorption isotherms, relation (1(1) $$\begin{array}{c}\hfill q_i^{\ast }=q_i^{\ast }(C;\mathit{\xi })=\frac{a_i{C}^{(i)}}{1+{\sum }_{j=1}^n{b}_j{C}^{(j)}},i=1,\dots ,n.\end{array}$$(1) ), with only four parameters, whereas excellent results were obtained using the following bi-Langmuir adsorption isotherms with four more parameters$$\begin{array}{c}\hfill q_i^{\ast }(C;\mathit{\xi })=\frac{a_{I,i}{C}^{(i)}}{1+b_{I,1}{C}^{(1)}+b_{I,2}{C}^{(2)}}+\frac{a_{II,i}{C}^{(i)}}{1+b_{II,1}{C}^{(1)}+b_{II,2}{C}^{(2)}},i=1,2.\end{array}$$

Moreover, in this real data application, before performing our adjoint method, we apply the genetic algorithm to obtain an appropriate starting point ${\mathit{\xi }}_0$. The termination conditions of our genetic algorithm in this work is the following (a) the number of generations reached equals 200 and (b) the computation time is less than 6 h.

The reconstructed adsorption isotherms by our regularized Kohn–Vogelius approach for both the Equilibrium-Dispersive model and the Transport-Dispersive model are displayed in Figures 6 and 7, respectively. As we can see, the reconstructed adsorption isotherms for the Equilibrium-Dispersive model ${\widehat{\mathit{\xi }}}_{ED}$ and the Transport-Dispersive model with the estimated mass transfer resistance ${\widehat{\mathit{\xi }}}_{TDE}$ are almost the same $\Vert {\widehat{\mathit{\xi }}}_{ED}-{\widehat{\mathit{\xi }}}_{TDE}{\Vert }_2/$$\Vert {\widehat{\mathit{\xi }}}_{ED}{\Vert }_2=0.0020$. Hence, in the later analysis, we only take the results of the Equilibrium-Dispersive model, for example.

The estimated adsorption isotherm parameters by a fixed model (ED, TD or TDE) $\widehat{\mathit{\xi }}$ with different injection profiles h(t) are similar up to $5\%$, i.e. $\Vert {\widehat{\mathit{\xi }}}_i-{\widehat{\mathit{\xi }}}_j{\Vert }_2/{\Vert {\widehat{\mathit{\xi }}}_i\Vert }_2\le 5\%$, where ${\widehat{\mathit{\xi }}}_i$ (or ${\widehat{\mathit{\xi }}}_j$) is the estimated adsorption isotherm parameter with the injection profile $h^{(i)}(t)$ (or $h^{(j)}(t)$). In practice, as in the Figure 6, we use the average of estimated adsorption isotherm parameters with different injection profiles as the final estimated parameter.

Figure 8. A comparison between the experimental elution profile (solid line) and the simulated total elution profile (dashed line) corresponds to the estimated parameter $\widehat{\mathit{\xi }}$ in the Equilibrium-Dispersive model. (a) Injection profile $h(t)=[0.75,0]\mathrm{mM}$. (b) Injection profile $h(t)=[0,15]\mathrm{mM}$.

To verify our result, the comparison between how the experimental elution profile (solid line) and the simulated elution profile (dashed line) correspond to the estimated parameter $\widehat{\mathit{\xi }}$ in the Equilibrium-Dispersive model is displayed in the in Figure 8 (we only display the results with the injection elution profiles $[0.75,0]\mathrm{mM}$ and $[0,15]\mathrm{mM}$).

Though we do not know the exact adsorption isotherm model for the real problem, we can verify our result by checking the following physical property of adsorption isotherms(33) $$\begin{array}{c}\hfill \frac{\mathit{\partial }{q}_i}{\mathit{\partial }{C}_i}\ge 0,\frac{\mathit{\partial }{q}_i}{\mathit{\partial }{C}_j}\le 0,i=1,\dots ,n,j\ne i.\end{array}$$(33)

For our result (Figure 6) one can check that $\mathit{\partial }{q}_1/\mathit{\partial }{C}_1\ge 0$, $\mathit{\partial }{q}_2/\mathit{\partial }{C}_2\ge 0$ and $\mathit{\partial }{q}_1/\mathit{\partial }{C}_2\le 0$, $\mathit{\partial }{q}_2/\mathit{\partial }{C}_1\le 0$, which also verified the reliability of reconstructed adsorption isotherms.

Finally, we apply the estimated adsorption isotherms to the ‘real’ binary data with injections $h(t)=[0.375,0.375]\mathrm{mM}$, $[0.75,0.75]\mathrm{mM}$, $[5,5]\mathrm{mM}$, $[10,10]\mathrm{mM}$, $[15,15]\mathrm{mM}$, $[5,15]\mathrm{mM}$, $[15,5]\mathrm{mM}$ and $[30,30]\mathrm{mM}$, respectively. The simulated total elution profile with injection $h(t)=[0.75,0.75]\mathrm{mM}$ and the evolution of objective function ${\mathcal{J}}_{BV,\mathit{\alpha }}$, which can be considered as the residual error of the model, are displayed in Figure 9.

Figure 9. (a) A comparison between the experimental elution profile (solid line) with injection $h(t)=[0.75,0.75]mM$ and the simulated total elution profile (dashed line) corresponds to the estimated parameter $\widehat{\mathit{\xi }}$. (b) The value of objective function ${\mathcal{J}}_{BV,\mathit{\alpha }}$ in the logarithmic scale at every iteration step l.

6. Conclusions

The numerical experiments performed above on both synthetic and experimental data indicate that the developed regularized Kohn–Vogelius method is an efficient approach for reconstructing adsorption isotherms in chromatography. The advantages of the proposed methods are several. Firstly, we use the original convection–diffusion equation while traditional methods only deal with the hyperbolic model. The second improvement concern from exist methods in the literature: we introduce two PDEs, so that the original boundary fitting is transferred to domain fitting. From a practical point of view, this is meaningful since the effects of noise in the forward boundary condition and noise in the measurement on solution accuracy are different. The final improvement is how the Jacobian of the regularizing cost function was calculated: using a variational technique, we obtained an exact formula of the Jacobian, achieving a substantial improvement in accuracy and reduction in execution time. Though the above improvements were applied to a specific parameter identification problem, they are sufficiently general to be applicable to many other problems.

Acknowledgements

We express our gratitude to the anonymous reviewers whose valuable comments and suggestions lead to an improvement of the manuscript.

Additional information

Funding

This work was supported by (i) the Swedish Knowledge Foundation for the KK HÖG 2014 project ‘SOMI: Studies of Molecular Interactions for Quality Assurance, Bio-Specific Measurement & Reliable Supercritical Purification’ [grant number 20140179], by (ii) the ÅForsk Foundation in the project ‘Improved Purification Procedures to Satisfy Modern Drug Quality Assurance and Environ-mental Criteria’ [grant number 15/497] and by (iii) the Swedish Research Council (VR) in the project ‘Fundamental Studies on Molecular Interactions aimed at Preparative Separations and Biospecific Measurements’ [grant number 2015-04627]. G. Lin and X. Cheng gratefully acknowledge the financial support from STINT [grant number IB2015-5989] and NSCF [grant number 11571311].

Notes

No potential conflict of interest was reported by the authors.