Iterative computational identification of a space-wise dependent source in parabolic equation

Abstract

Coefficient inverse problems related to identifying the right-hand side of an equation with use of additional information is of interest among inverse problems for partial differential equations. When considering non-stationary problems, tasks of recovering the dependence of the right-hand side on time and spatial variables can be treated as independent. These tasks relate to a class of linear inverse problems, which sufficiently simplifies their study. This work is devoted to finding the dependence of right-hand side of multidimensional parabolic equation on spatial variables using additional observations of the solution at the final point of time – the final overdetermination. More general problems are associated with some integral observation of the solution in time – the integral overdetermination. The first method of numerical solution of inverse problems is based on iterative solution of boundary value problem for time derivative with non-local acceleration. The second method is based on the known approach with iterative refinement of desired dependence of the right-hand side on spatial variables. Capabilities of proposed methods are illustrated by numerical examples for a two-dimensional problem of identifying the right-hand side of a parabolic equation. The standard finite-element approximation in space is used, whilst the time discretization is based on fully implicit two-level schemes.

Keywords:

• Inverse problem
• identification of the coefficient
• parabolic partial differential equation
• finite element method
• two-level difference scheme

AMS Subject Classifications:

• 65M06
• 65M32
• 80A23

1. Introduction

Coefficient inverse problems related to identifying coefficient and/or the right-hand side of an equation with use of some additional information is of interest among inverse problems for partial differential equations.[1,2] When considering non-stationary problems, tasks of recovering the dependence of the right-hand side on time or spatial variables can be usually treated as independent. These tasks relate to a class of linear inverse problems, which sufficiently simplifies their study.[3,4] Only in some cases we have linear inverse problems – identification of the right-hand side of equation, Other coefficient inverse problems are non-linear, that significantly complicate their study.

The problem of identifying the dependence of the right-hand side on spatial variables is one of the most important problems. Additional conditions are often formulated using the solution at the final moment of time – final overdetermination. In a more general case the overdetermination condition is stated as some time integral average – integral overdetermination. The existence and uniqueness of the solution to such an inverse problem and well-posedness of this problem in various functional classes are examined, for example, in the works.[5–9]

In the numerical solution of inverse problem the main focus is on the development of stable computational algorithms that take into account the peculiar properties of inverse problems.[10,11] Inverse problems for partial differential equations can be formulated as optimal control problems.[12,13] Computational algorithms are based on using gradient iterative methods for the corresponding residual functional.[14–16] The implementation of such approaches relates to the solution of initial-boundary problems for the original parabolic equation and its conjugate.

For the required right-hand side of a parabolic equation, which does not depend on time, an inverse problem with final overdetermination can be formulated as a boundary problem for evolution equation of the second order. In this case, we can use standard computational algorithms for the solution of stationary boundary value problems. Such direct computational algorithms based on finite-difference approximation are described in the book [11] (Section 6.4). In the work [17] the identification problem is numerically solved on the basis of transition to an evolutionary problem for the derivative of the solution with respect to time, peculiarity of which is the non-local boundary condition.

In this work, we construct special iterative methods for approximate solution of identification problem of a space-wise dependence of the source in a parabolic equation. They fully take into account inverse problem features, which relate to their evolutionary character. These methods are based on the numerical solution of the standard Cauchy problems at each iteration. The first method is based on the iterative refinement of initial condition for time derivative of the solution. The second method relates to the iterative refinement of the dependence of the right-hand side on the spatial variables. Such approach have been used before.[8,18,19]

The paper is organized as follows. Statements of direct and inverse problems for second-order parabolic equation are given in Section 2. We consider identification problem of the right-hand side of two-dimensional parabolic equation, which does not depend on time. The additional information about the solution of the equation is given at the final moment of time. The finite-element approximation in space is used. The method of approximate solution of inverse problem based on the iterative solution of evolutionary problem for time derivative of the solution with non-local boundary conditions is considered in Section 3. The computational algorithms of iterative identification of the right-hand side of the parabolic equation is discussed in Section 4. In Section 5, we describe the algorithms for solving inverse problems with integral overdetermination. More general inverse problems, which relate to known dependence of the right-hand side on time, are considered in Section 6. Results of computational experiment for model boundary value problem are represented in Section 7. Results of the work are summed up in Section 8.

2. Problem formulation

For simplicity, we restrict ourselves to a 2D problem. Generalization to the 3D case is straightforward. Let $\mathit{x}=(x_1,x_2)$ and $\mathrm{\Omega }$ be a bounded polygon. The direct problem is formulated as follows. We search $u(\mathit{x},t)$, $0\le t\le T,T>0$ such that it is the solution of the parabolic equation of second order:(1) $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }t}-\mathrm{div}(k(\mathit{x})\mathrm{grad}u)+c(\mathit{x})u=f(\mathit{x}),\mathit{x}\in \mathrm{\Omega },0<t\le T,\end{array}$$(1)

with coefficients $0<k_1\le k(\mathit{x})\le k_2$, $c(\mathit{x})\ge c_0>0$. The boundary conditions are also specified:(2) $$\begin{array}{c}\hfill k(\mathit{x})\frac{\mathit{\partial }u}{\mathit{\partial }n}+\mathit{\mu }(\mathit{x})u=0,\mathit{x}\in \mathit{\partial }\mathrm{\Omega },0<t\le T,\end{array}$$(2)

where $\mathit{\mu }(\mathit{x})\ge 0,\mathit{x}\in \mathit{\partial }\mathrm{\Omega }$ and n is the normal to $\mathrm{\Omega }$. The initial condition is(3) $$\begin{array}{c}\hfill u(\mathit{x},0)=u_0(\mathit{x}),\mathit{x}\in \mathrm{\Omega }.\end{array}$$(3)

The formulation (1(1) $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }t}-\mathrm{div}(k(\mathit{x})\mathrm{grad}u)+c(\mathit{x})u=f(\mathit{x}),\mathit{x}\in \mathrm{\Omega },0<t\le T,\end{array}$$(1) )–(3(3) $$\begin{array}{c}\hfill u(\mathit{x},0)=u_0(\mathit{x}),\mathit{x}\in \mathrm{\Omega }.\end{array}$$(3) ) presents the direct problem, where the right-hand side, coefficients of the equation as well as the boundary and initial conditions are specified.

Let us consider the inverse problem, where in Equation (1(1) $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }t}-\mathrm{div}(k(\mathit{x})\mathrm{grad}u)+c(\mathit{x})u=f(\mathit{x}),\mathit{x}\in \mathrm{\Omega },0<t\le T,\end{array}$$(1) ), the right-hand side $f(\mathit{x})$ is unknown. An additional condition is often formulated as(4) $$\begin{array}{c}\hfill u(\mathit{x},T)=u_T(\mathit{x}),\mathit{x}\in \mathrm{\Omega }.\end{array}$$(4)

In this case, we speak about the final overdetermination.

We assume that the above inverse problem of finding a pair of $(u(\mathit{x},t),f(\mathit{x}))$ from Equations (1(1) $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }t}-\mathrm{div}(k(\mathit{x})\mathrm{grad}u)+c(\mathit{x})u=f(\mathit{x}),\mathit{x}\in \mathrm{\Omega },0<t\le T,\end{array}$$(1) )–(3(3) $$\begin{array}{c}\hfill u(\mathit{x},0)=u_0(\mathit{x}),\mathit{x}\in \mathrm{\Omega }.\end{array}$$(3) ) and additional conditions (4(4) $$\begin{array}{c}\hfill u(\mathit{x},T)=u_T(\mathit{x}),\mathit{x}\in \mathrm{\Omega }.\end{array}$$(4) ) is uniquely solvable. The corresponding conditions for existence and uniqueness of the solution are available in the above-mentioned works in Section 1.

In the Hilbert space $H=L_2(\mathrm{\Omega })$, we define the scalar product and norm in the standard way:$$(u,v)={\int }_{\mathrm{\Omega }}u(\mathit{x})v(\mathit{x})\mathrm{d}\mathit{x},\Vert u\Vert ={(u,u)}^{1/2}.$$

To solve numerically the problem (1(1) $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }t}-\mathrm{div}(k(\mathit{x})\mathrm{grad}u)+c(\mathit{x})u=f(\mathit{x}),\mathit{x}\in \mathrm{\Omega },0<t\le T,\end{array}$$(1) )–(3(3) $$\begin{array}{c}\hfill u(\mathit{x},0)=u_0(\mathit{x}),\mathit{x}\in \mathrm{\Omega }.\end{array}$$(3) ), we employ finite-element approximations in space.[20,21] We define the bilinear form$$a(u,v)={\int }_{\mathrm{\Omega }}\left(k\mathrm{grad}u\mathrm{grad}v+cuv\right)\mathrm{d}\mathit{x}+{\int }_{\mathit{\partial }\mathrm{\Omega }}\mathit{\mu }uv\mathrm{d}\mathit{x}.$$

We have$$a(u,u)\ge {\mathit{\delta }\Vert u\Vert }^2,\mathit{\delta }>0.$$

Define a subspace of finite elements $V^h\subset H^1(\mathrm{\Omega })$. Let ${\mathit{x}}_i,i=1,2,\dots ,M_h$ be triangulation points for the domain $\mathrm{\Omega }$. For example, when using Lagrange finite elements of the first-order (piece-wise linear approximation) we can define pyramid function ${\mathit{\chi }}_i(\mathit{x})\subset V^h,i=1,2,\dots ,M_h$, where$${\mathit{\chi }}_i({\mathit{x}}_j)=\left\{\begin{array}{cc}1,\hfill & \mathrm{i}fi=j,\hfill \\ 0,\hfill & \mathrm{i}fi\ne j.\hfill \end{array}\right.$$

For $v\in V^h$, we have$$v(\mathit{x})=\sum _{i=i}^{M_h}{v}_i{\mathit{\chi }}_i(\mathit{x}),$$

where $v_i=v({\mathit{x}}_i),i=1,2,\dots ,M_h$.

We define the discrete elliptic operator A as$$(Ay,v)=a(y,v),\forall y,v\in V^h.$$

The operator A acts on a finite-dimensional space $V^h$ and(5) $$\begin{array}{c}\hfill A=A^{\ast }\ge \mathit{\delta }I,\mathit{\delta }>0,\end{array}$$(5)

where I is the identity operator in $V^h$.

For the problem (1(1) $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }t}-\mathrm{div}(k(\mathit{x})\mathrm{grad}u)+c(\mathit{x})u=f(\mathit{x}),\mathit{x}\in \mathrm{\Omega },0<t\le T,\end{array}$$(1) )–(3(3) $$\begin{array}{c}\hfill u(\mathit{x},0)=u_0(\mathit{x}),\mathit{x}\in \mathrm{\Omega }.\end{array}$$(3) ), we put into the correspondence the operator equation for $w(t)\in V^h$:(6) $$\begin{array}{cc}& \frac{\mathrm{d}w}{\mathrm{d}t}+Aw=\mathit{\phi },0<t\le T,\hfill \end{array}$$(6) (7) $$\begin{array}{cc}& w(0)=\mathit{\varphi },\hfill \end{array}$$(7)

where $\mathit{\phi }=Pf$, $\mathit{\varphi }=P{u}_0$ with P denoting $L_2$-projection onto $V^h$. When considering the inverse problem taking into account (4(4) $$\begin{array}{c}\hfill u(\mathit{x},T)=u_T(\mathit{x}),\mathit{x}\in \mathrm{\Omega }.\end{array}$$(4) ) assume(8) $$\begin{array}{c}\hfill w(T)=\mathit{\psi },\end{array}$$(8)

where $\mathit{\psi }=P{u}_T$.

3. Iterative solution of time derivative problem

For the numerical solution of the inverse problem (6(6) $$\begin{array}{cc}& \frac{\mathrm{d}w}{\mathrm{d}t}+Aw=\mathit{\phi },0<t\le T,\hfill \end{array}$$(6) )–(8(8) $$\begin{array}{c}\hfill w(T)=\mathit{\psi },\end{array}$$(8) ) with finding $(w(t),\mathit{\phi })$ the simplest approach is to eliminate variable $\mathit{\phi }$.[11,17] Differentiating Equation (6(6) $$\begin{array}{cc}& \frac{\mathrm{d}w}{\mathrm{d}t}+Aw=\mathit{\phi },0<t\le T,\hfill \end{array}$$(6) ) on time, we obtain(9) $$\begin{array}{c}\hfill \frac{{\mathrm{d}}^{2}w}{\mathrm{d}{t}^2}+A\frac{\mathrm{d}w}{\mathrm{d}t}=0,0<t\le T.\end{array}$$(9)

Further, we consider the boundary value problem (7(7) $$\begin{array}{cc}& w(0)=\mathit{\varphi },\hfill \end{array}$$(7) )–(9(9) $$\begin{array}{c}\hfill \frac{{\mathrm{d}}^{2}w}{\mathrm{d}{t}^2}+A\frac{\mathrm{d}w}{\mathrm{d}t}=0,0<t\le T.\end{array}$$(9) ). The correctness of such problem, the computational algorithm and examples of the numerical solution are presented in [11]. The weakness of such approach is caused by the computational complexity of the numerical solution of the boundary problem (7(7) $$\begin{array}{cc}& w(0)=\mathit{\varphi },\hfill \end{array}$$(7) )–(9(9) $$\begin{array}{c}\hfill \frac{{\mathrm{d}}^{2}w}{\mathrm{d}{t}^2}+A\frac{\mathrm{d}w}{\mathrm{d}t}=0,0<t\le T.\end{array}$$(9) ). We practically lose the evolutionary character of original problem and must store data in each time step.

The second approach (see, for example, [17]) is based on considering the time derivative. Let $v={\displaystyle \frac{\mathrm{d}w}{\mathrm{d}t}}$, then Equation (9(9) $$\begin{array}{c}\hfill \frac{{\mathrm{d}}^{2}w}{\mathrm{d}{t}^2}+A\frac{\mathrm{d}w}{\mathrm{d}t}=0,0<t\le T.\end{array}$$(9) ) can be written as(10) $$\begin{array}{c}\hfill \frac{\mathrm{d}v}{\mathrm{d}t}+Av=0,0<t\le T.\end{array}$$(10)

For (10(10) $$\begin{array}{c}\hfill \frac{\mathrm{d}v}{\mathrm{d}t}+Av=0,0<t\le T.\end{array}$$(10) ) we formulate non-local boundary conditions. From (6(6) $$\begin{array}{cc}& \frac{\mathrm{d}w}{\mathrm{d}t}+Aw=\mathit{\phi },0<t\le T,\hfill \end{array}$$(6) ) we have$$\begin{array}{cc}\hfill v(0)& +Aw(0)=\mathit{\phi },\hfill \\ \hfill v(T)& +Aw(T)=\mathit{\phi }.\hfill \end{array}$$

Taking into account (7(7) $$\begin{array}{cc}& w(0)=\mathit{\varphi },\hfill \end{array}$$(7) ), (8(8) $$\begin{array}{c}\hfill w(T)=\mathit{\psi },\end{array}$$(8) ) yields(11) $$\begin{array}{c}\hfill v(T)-v(0)=\mathit{\chi },\mathit{\chi }=A(\mathit{\varphi }-\mathit{\psi }).\end{array}$$(11)

The issues of well-posedness and solvability of non-local problems for parabolic equations are discussed in many papers. We highlight the works [22,23] as the first studies (in our mind) in this direction of investigations

For numerical solution of the problem (10(10) $$\begin{array}{c}\hfill \frac{\mathrm{d}v}{\mathrm{d}t}+Av=0,0<t\le T.\end{array}$$(10) ), (11(11) $$\begin{array}{c}\hfill v(T)-v(0)=\mathit{\chi },\mathit{\chi }=A(\mathit{\varphi }-\mathit{\psi }).\end{array}$$(11) ) we use the simplest iterative refinement of the initial condition for Equation (10(10) $$\begin{array}{c}\hfill \frac{\mathrm{d}v}{\mathrm{d}t}+Av=0,0<t\le T.\end{array}$$(10) ). The iterative process is organized as follows. The new approximation $k+1$ is found by solving the Cauchy problem:(12) $$\begin{array}{cc}& v^{k+1}(0)=v^k(T)-\mathit{\chi },\hfill \end{array}$$(12) (13) $$\begin{array}{cc}& \frac{\mathrm{d}{v}^{k+1}}{\mathrm{d}t}+A{v}^{k+1}=0,0<t\le T,k=0,1,\dots ,\hfill \end{array}$$(13)

with some given $v^0(0)$. The desired right-hand side of Equation (6(6) $$\begin{array}{cc}& \frac{\mathrm{d}w}{\mathrm{d}t}+Aw=\mathit{\phi },0<t\le T,\hfill \end{array}$$(6) ) is determined using $v^{k+1}(0)$, for example, from the equality(14) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=A\mathit{\varphi }+v^{k+1}(0).\end{array}$$(14)

When studying the convergence of the iterative process (12(12) $$\begin{array}{cc}& v^{k+1}(0)=v^k(T)-\mathit{\chi },\hfill \end{array}$$(12) ), (13(13) $$\begin{array}{cc}& \frac{\mathrm{d}{v}^{k+1}}{\mathrm{d}t}+A{v}^{k+1}=0,0<t\le T,k=0,1,\dots ,\hfill \end{array}$$(13) ) we consider the problem for error $z^{k+1}(t)=v^{k+1}(t)-v(t)$:(15) $$\begin{array}{cc}& z^{k+1}(0)=z^k(T),\hfill \end{array}$$(15) (16) $$\begin{array}{cc}& \frac{\mathrm{d}{z}^{k+1}}{\mathrm{d}t}+A{z}^{k+1}=0,0<t\le T,k=0,1,\dots ,\hfill \end{array}$$(16)

with given $z^0(0)$. Multiplying Equation (16(16) $$\begin{array}{cc}& \frac{\mathrm{d}{z}^{k+1}}{\mathrm{d}t}+A{z}^{k+1}=0,0<t\le T,k=0,1,\dots ,\hfill \end{array}$$(16) ) for $z^k$ in $V^h$ by $z^k$, we obtain$$\left(\frac{\mathrm{d}{z}^k}{\mathrm{d}t},z^k\right)+(A{z}^k,z^k)=0.$$

Taking into account (5(5) $$\begin{array}{c}\hfill A=A^{\ast }\ge \mathit{\delta }I,\mathit{\delta }>0,\end{array}$$(5) ) and$$\left(\frac{\mathrm{d}{z}^k}{\mathrm{d}t},z^k\right)=\frac{1}{2}\frac{\mathrm{d}}{\mathrm{d}t}{\Vert z^k\Vert }^2,$$

yields$$\frac{\mathrm{d}}{\mathrm{d}t}\Vert z^k{\Vert }^2+2\mathit{\delta }{\Vert z^k\Vert }^2\le 0.$$

Thus,(17) $$\begin{array}{c}\hfill \Vert z^k(t)\Vert \le exp(-\mathit{\delta }t)\Vert z^k(0)\Vert .\end{array}$$(17)

From (15(15) $$\begin{array}{cc}& z^{k+1}(0)=z^k(T),\hfill \end{array}$$(15) ) taking into account (17(17) $$\begin{array}{c}\hfill \Vert z^k(t)\Vert \le exp(-\mathit{\delta }t)\Vert z^k(0)\Vert .\end{array}$$(17) ) we have$$\Vert z^{k+1}(0)\Vert =\Vert z^k(T)\Vert \le exp(-\mathit{\delta }T)\Vert z^k(0)\Vert .$$

This gives the desired estimate(18) $$\begin{array}{c}\hfill \Vert v^{k+1}(0)-v(0)\Vert \le \mathit{\varrho }\Vert v^k(0)-v(0)\Vert ,\mathit{\varrho }=exp(-\mathit{\delta }T),\end{array}$$(18)

for the convergence of the iterative process (12(12) $$\begin{array}{cc}& v^{k+1}(0)=v^k(T)-\mathit{\chi },\hfill \end{array}$$(12) )–(14(14) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=A\mathit{\varphi }+v^{k+1}(0).\end{array}$$(14) ) with linear speed $\mathit{\varrho }<1$. For the right-hand side with (14(14) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=A\mathit{\varphi }+v^{k+1}(0).\end{array}$$(14) ) we have$$\Vert {\mathit{\phi }}^{k+1}-\mathit{\phi }\Vert \le \mathit{\varrho }\Vert v^k(0)-v(0)\Vert .$$

For computational implementation of proposed algorithm the time approximation deserves special attention. Let us define a uniform for simplicity grid in time$$t_n=n\mathit{\tau },n=0,1,\dots ,N,\mathit{\tau }N=T$$

and denote $y_n=y(t_n),t_n=n\mathit{\tau }$. We consider two-level schemes an so, there is no problem to make a transition to non-uniform temporal grids.

For the numerical solution of the problem (10(10) $$\begin{array}{c}\hfill \frac{\mathrm{d}v}{\mathrm{d}t}+Av=0,0<t\le T.\end{array}$$(10) ), (11(11) $$\begin{array}{c}\hfill v(T)-v(0)=\mathit{\chi },\mathit{\chi }=A(\mathit{\varphi }-\mathit{\psi }).\end{array}$$(11) ) we used fully implicit two-level scheme [24,25](19) $$\begin{array}{cc}\hfill \frac{v_{n+1}-v_n}{\mathit{\tau }}+A{v}_{n+1}& =0,n=0,1,\dots ,N-1,\hfill \end{array}$$(19) (20) $$\begin{array}{cc}\hfill v_N-v_0& =\mathit{\chi }.\hfill \end{array}$$(20)

The grid problem (19(19) $$\begin{array}{cc}\hfill \frac{v_{n+1}-v_n}{\mathit{\tau }}+A{v}_{n+1}& =0,n=0,1,\dots ,N-1,\hfill \end{array}$$(19) ), (20(20) $$\begin{array}{cc}\hfill v_N-v_0& =\mathit{\chi }.\hfill \end{array}$$(20) ) is solved using the following iterative process:(21) $$\begin{array}{cc}\hfill v_0^{k+1}& =v_N^k-\mathit{\chi },\hfill \end{array}$$(21) (22) $$\begin{array}{cc}\hfill \frac{v_{n+1}^{k+1}-v_n^{k+1}}{\mathit{\tau }}+A{v}_{n+1}^{k+1}& =0,n=0,1,\dots ,N-1,k=0,1,\dots ,\hfill \end{array}$$(22)

and(23) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=A\mathit{\varphi }+v_0^{k+1}.\end{array}$$(23)

The study of the iterative process (21(21) $$\begin{array}{cc}\hfill v_0^{k+1}& =v_N^k-\mathit{\chi },\hfill \end{array}$$(21) )–(23(23) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=A\mathit{\varphi }+v_0^{k+1}.\end{array}$$(23) ) is conducted using the same approach as for the iterative process (12(12) $$\begin{array}{cc}& v^{k+1}(0)=v^k(T)-\mathit{\chi },\hfill \end{array}$$(12) )–(14(14) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=A\mathit{\varphi }+v^{k+1}(0).\end{array}$$(14) ). Let now $z_{n+1}^{k+1}=v_{n+1}^{k+1}-v_{n+1}$, then(24) $$\begin{array}{cc}\hfill z_0^{k+1}& =z_N^k,\hfill \end{array}$$(24) (25) $$\begin{array}{cc}\hfill \frac{z_{n+1}^{k+1}-z_n^{k+1}}{\mathit{\tau }}+A{z}_{n+1}^{k+1}& =0,n=0,1,\dots ,N-1,k=0,1,\dots .\hfill \end{array}$$(25)

The key moment of our consideration consists in finding an estimate as (17(17) $$\begin{array}{c}\hfill \Vert z^k(t)\Vert \le exp(-\mathit{\delta }t)\Vert z^k(0)\Vert .\end{array}$$(17) ).

We multiply Equation (25(25) $$\begin{array}{cc}\hfill \frac{z_{n+1}^{k+1}-z_n^{k+1}}{\mathit{\tau }}+A{z}_{n+1}^{k+1}& =0,n=0,1,\dots ,N-1,k=0,1,\dots .\hfill \end{array}$$(25) ) for $z_{n+1}^k$ in $V^h$ by $\mathit{\tau }{z}_{n+1}^k$ and obtain$$\Vert z_{n+1}^k{\Vert }^2+\mathit{\tau }\left(A{z}_{n+1}^k,z_{n+1}^k\right)=\left(z_n^k,z_{n+1}^k\right).$$

Taking into account (5(5) $$\begin{array}{c}\hfill A=A^{\ast }\ge \mathit{\delta }I,\mathit{\delta }>0,\end{array}$$(5) ) and$$\left(z_n^k,z_{n+1}^k\right)\le \Vert z_n^k\Vert \Vert z_{n+1}^k\Vert$$

we have ($\Vert z_n^k\Vert \ne 0$)$$(1+\mathit{\tau }\mathit{\delta })\Vert z_{n+1}^k\Vert \le \Vert z_n^k\Vert ,n=0,1,\dots ,N-1.$$

Thus,(26) $$\begin{array}{c}\hfill \Vert z_n^k{\Vert \le (1+\mathit{\tau }\mathit{\delta })}^{-n}\Vert z_0^k\Vert ,n=1,2,\dots ,N.\end{array}$$(26)

Using (24(24) $$\begin{array}{cc}\hfill z_0^{k+1}& =z_N^k,\hfill \end{array}$$(24) ), a priori estimate (26(26) $$\begin{array}{c}\hfill \Vert z_n^k{\Vert \le (1+\mathit{\tau }\mathit{\delta })}^{-n}\Vert z_0^k\Vert ,n=1,2,\dots ,N.\end{array}$$(26) ) allows us to obtain$$\Vert z_0^{k+1}\Vert =\Vert z_N^k{\Vert \le (1+\mathit{\tau }\mathit{\delta })}^{-N}\Vert z_0^k\Vert .$$

Thereby(27) $$\begin{array}{c}\hfill \Vert v_0^{k+1}-v_0\Vert \le \overline{\mathit{\varrho }}\Vert v_0^k-v_0{\Vert ,\overline{\mathit{\varrho }}=(1+\mathit{\tau }\mathit{\delta })}^{-N},\end{array}$$(27)

which provides the convergence of the iterative process (21(21) $$\begin{array}{cc}\hfill v_0^{k+1}& =v_N^k-\mathit{\chi },\hfill \end{array}$$(21) ), (22(22) $$\begin{array}{cc}\hfill \frac{v_{n+1}^{k+1}-v_n^{k+1}}{\mathit{\tau }}+A{v}_{n+1}^{k+1}& =0,n=0,1,\dots ,N-1,k=0,1,\dots ,\hfill \end{array}$$(22) ) ($\overline{\mathit{\varrho }}<1$). The convergence of the right-hand side with (23(23) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=A\mathit{\varphi }+v_0^{k+1}.\end{array}$$(23) ) is ensured by the estimate(28) $$\begin{array}{c}\hfill \Vert {\mathit{\phi }}^{k+1}-\mathit{\phi }\Vert \le \overline{\mathit{\varrho }}\Vert v_0^k-v_0\Vert .\end{array}$$(28)

This allows us to formulate the following main assertion.

Theorem 3.1:

The iterative process (21(21) $$\begin{array}{cc}\hfill v_0^{k+1}& =v_N^k-\mathit{\chi },\hfill \end{array}$$(21) )–(23(23) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=A\mathit{\varphi }+v_0^{k+1}.\end{array}$$(23) ) for the numerical solution of the problem (6(6) $$\begin{array}{cc}& \frac{\mathrm{d}w}{\mathrm{d}t}+Aw=\mathit{\phi },0<t\le T,\hfill \end{array}$$(6) )–(8(8) $$\begin{array}{c}\hfill w(T)=\mathit{\psi },\end{array}$$(8) ) converges linearly with speed $\overline{\mathit{\varrho }}<1$ and the estimates (27(27) $$\begin{array}{c}\hfill \Vert v_0^{k+1}-v_0\Vert \le \overline{\mathit{\varrho }}\Vert v_0^k-v_0{\Vert ,\overline{\mathit{\varrho }}=(1+\mathit{\tau }\mathit{\delta })}^{-N},\end{array}$$(27) ), (28(28) $$\begin{array}{c}\hfill \Vert {\mathit{\phi }}^{k+1}-\mathit{\phi }\Vert \le \overline{\mathit{\varrho }}\Vert v_0^k-v_0\Vert .\end{array}$$(28) ) are valid.

The outline of the iterative process (21(21) $$\begin{array}{cc}\hfill v_0^{k+1}& =v_N^k-\mathit{\chi },\hfill \end{array}$$(21) )–(23(23) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=A\mathit{\varphi }+v_0^{k+1}.\end{array}$$(23) ) is as follows:

(1)	The initial condition is determined using (21(21) $$\begin{array}{cc}\hfill v_0^{k+1}& =v_N^k-\mathit{\chi },\hfill \end{array}$$(21) ). When $k=0$, we assume, for example, $v_0^0=-\mathit{\chi }$;
(2)	With this initial condition we solve the grid Cauchy problem (22(22) $$\begin{array}{cc}\hfill \frac{v_{n+1}^{k+1}-v_n^{k+1}}{\mathit{\tau }}+A{v}_{n+1}^{k+1}& =0,n=0,1,\dots ,N-1,k=0,1,\dots ,\hfill \end{array}$$(22) ). After that we refine the initial condition again.

Thus, the computational implementation is based on solving the standard Cauchy problem for parabolic equation at each iteration.

4. Iterative process for identifying the right-hand side

When studying the correctness of the inverse problem (1(1) $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }t}-\mathrm{div}(k(\mathit{x})\mathrm{grad}u)+c(\mathit{x})u=f(\mathit{x}),\mathit{x}\in \mathrm{\Omega },0<t\le T,\end{array}$$(1) )–(4(4) $$\begin{array}{c}\hfill u(\mathit{x},T)=u_T(\mathit{x}),\mathit{x}\in \mathrm{\Omega }.\end{array}$$(4) ) the constructive method of iterative refinement of the right-hand side is often used (see, for example, [8,18,19]). We consider the possibility of using this approach for the approximate solution of the problem (6(6) $$\begin{array}{cc}& \frac{\mathrm{d}w}{\mathrm{d}t}+Aw=\mathit{\phi },0<t\le T,\hfill \end{array}$$(6) )–(8(8) $$\begin{array}{c}\hfill w(T)=\mathit{\psi },\end{array}$$(8) ).

In the new iterative step the right-hand side is determined using (6(6) $$\begin{array}{cc}& \frac{\mathrm{d}w}{\mathrm{d}t}+Aw=\mathit{\phi },0<t\le T,\hfill \end{array}$$(6) ) for $t=T$, taking into account (8(8) $$\begin{array}{c}\hfill w(T)=\mathit{\psi },\end{array}$$(8) ):(29) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=\frac{\mathrm{d}{w}^k}{\mathrm{d}t}(T)+A\mathit{\psi },k=0,1,\dots ,\end{array}$$(29)

with some given initial assumption ${\mathit{\phi }}^0$. Then, the Cauchy problem is solved:(30) $$\begin{array}{cc}\hfill \frac{\mathrm{d}{w}^{k+1}}{\mathrm{d}t}+A{w}^{k+1}& ={\mathit{\phi }}^{k+1},0<t\le T,\hfill \end{array}$$(30) (31) $$\begin{array}{cc}\hfill w^{k+1}(0)& =\mathit{\varphi }.\hfill \end{array}$$(31)

To estimate the convergence we introduce$${\mathit{\eta }}^{k+1}={\mathit{\phi }}^{k+1}-\mathit{\phi },z^{k+1}(t)=w^{k+1}(t)-w(t),0\le t\le T,k=0,1,\dots .$$

Then, from (29(29) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=\frac{\mathrm{d}{w}^k}{\mathrm{d}t}(T)+A\mathit{\psi },k=0,1,\dots ,\end{array}$$(29) )–(31(31) $$\begin{array}{cc}\hfill w^{k+1}(0)& =\mathit{\varphi }.\hfill \end{array}$$(31) ) we obtain(32) $$\begin{array}{cc}& {\mathit{\eta }}^{k+1}=\frac{\mathrm{d}{z}^k}{\mathrm{d}t}(T),k=0,1,\dots ,\hfill \end{array}$$(32) (33) $$\begin{array}{cc}& \frac{\mathrm{d}{z}^{k+1}}{\mathrm{d}t}+A{z}^{k+1}={\mathit{\eta }}^{k+1},0<t\le T,\hfill \end{array}$$(33) (34) $$\begin{array}{cc}& z^{k+1}(0)=0.\hfill \end{array}$$(34)

We differentiate Equation (33(33) $$\begin{array}{cc}& \frac{\mathrm{d}{z}^{k+1}}{\mathrm{d}t}+A{z}^{k+1}={\mathit{\eta }}^{k+1},0<t\le T,\hfill \end{array}$$(33) ) with respect to time and rewrite it for ${\displaystyle v^k=\frac{\mathrm{d}{z}^k}{\mathrm{d}t}}$ in the form(35) $$\begin{array}{c}\hfill \frac{\mathrm{d}{v}^k}{\mathrm{d}t}+A{v}^k=0,0<t\le T,\end{array}$$(35)

The initial condition for (35(35) $$\begin{array}{c}\hfill \frac{\mathrm{d}{v}^k}{\mathrm{d}t}+A{v}^k=0,0<t\le T,\end{array}$$(35) ) we obtain from (33(33) $$\begin{array}{cc}& \frac{\mathrm{d}{z}^{k+1}}{\mathrm{d}t}+A{z}^{k+1}={\mathit{\eta }}^{k+1},0<t\le T,\hfill \end{array}$$(33) ) with $t=0$, using (34(34) $$\begin{array}{cc}& z^{k+1}(0)=0.\hfill \end{array}$$(34) ):(36) $$\begin{array}{c}\hfill v^k(0)={\mathit{\eta }}^k.\end{array}$$(36)

Similar to (17(17) $$\begin{array}{c}\hfill \Vert z^k(t)\Vert \le exp(-\mathit{\delta }t)\Vert z^k(0)\Vert .\end{array}$$(17) ) we have the estimate(37) $$\begin{array}{c}\hfill \Vert v^k(t)\Vert \le exp(-\mathit{\delta }t)\Vert {\mathit{\eta }}^k\Vert \end{array}$$(37)

for the solution of the problem (35(35) $$\begin{array}{c}\hfill \frac{\mathrm{d}{v}^k}{\mathrm{d}t}+A{v}^k=0,0<t\le T,\end{array}$$(35) ), (36(36) $$\begin{array}{c}\hfill v^k(0)={\mathit{\eta }}^k.\end{array}$$(36) ). In view of (37(37) $$\begin{array}{c}\hfill \Vert v^k(t)\Vert \le exp(-\mathit{\delta }t)\Vert {\mathit{\eta }}^k\Vert \end{array}$$(37) ) from (32(32) $$\begin{array}{cc}& {\mathit{\eta }}^{k+1}=\frac{\mathrm{d}{z}^k}{\mathrm{d}t}(T),k=0,1,\dots ,\hfill \end{array}$$(32) ) we have the estimate$$\Vert {\mathit{\eta }}^{k+1}\Vert =\Vert v^k(T)\Vert \le exp(-\mathit{\delta }T)\Vert {\mathit{\eta }}^k\Vert ,k=0,1,\dots$$

for the convergence of desired right-hand side.

The time discretization is again formulated based on implicit approximation. Formally, we define the solution of the problem (33(33) $$\begin{array}{cc}& \frac{\mathrm{d}{z}^{k+1}}{\mathrm{d}t}+A{z}^{k+1}={\mathit{\eta }}^{k+1},0<t\le T,\hfill \end{array}$$(33) ), (34(34) $$\begin{array}{cc}& z^{k+1}(0)=0.\hfill \end{array}$$(34) ) on expanded grid:$$t_n=n\mathit{\tau },n=-1,0,\dots ,N,\mathit{\tau }N=T.$$

From (6(6) $$\begin{array}{cc}& \frac{\mathrm{d}w}{\mathrm{d}t}+Aw=\mathit{\phi },0<t\le T,\hfill \end{array}$$(6) )–(8(8) $$\begin{array}{c}\hfill w(T)=\mathit{\psi },\end{array}$$(8) ) we come to the problem(38) $$\begin{array}{cc}& \frac{w_{n+1}-w_n}{\mathit{\tau }}+A{w}_{n+1}=\mathit{\phi },n=-1,0,\dots ,N-1\hfill \end{array}$$(38) (39) $$\begin{array}{cc}& w_0=\mathit{\varphi },\hfill \end{array}$$(39) (40) $$\begin{array}{cc}& w_N=\mathit{\psi }.\hfill \end{array}$$(40)

For the numerical solution of the problem (38(38) $$\begin{array}{cc}& \frac{w_{n+1}-w_n}{\mathit{\tau }}+A{w}_{n+1}=\mathit{\phi },n=-1,0,\dots ,N-1\hfill \end{array}$$(38) )–(40(40) $$\begin{array}{cc}& w_N=\mathit{\psi }.\hfill \end{array}$$(40) ) the grid analogue of the iterative process (29(29) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=\frac{\mathrm{d}{w}^k}{\mathrm{d}t}(T)+A\mathit{\psi },k=0,1,\dots ,\end{array}$$(29) )–(31(31) $$\begin{array}{cc}\hfill w^{k+1}(0)& =\mathit{\varphi }.\hfill \end{array}$$(31) ) is applied. Now, we compare the relationship(41) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=\frac{w_N^k-w_{N-1}^k}{\mathit{\tau }}+A\mathit{\psi },k=0,1,\dots ,\end{array}$$(41)

with (29(29) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=\frac{\mathrm{d}{w}^k}{\mathrm{d}t}(T)+A\mathit{\psi },k=0,1,\dots ,\end{array}$$(29) ). To approximate Equation (30(30) $$\begin{array}{cc}\hfill \frac{\mathrm{d}{w}^{k+1}}{\mathrm{d}t}+A{w}^{k+1}& ={\mathit{\phi }}^{k+1},0<t\le T,\hfill \end{array}$$(30) ) the implicit difference scheme is used(42) $$\begin{array}{c}\hfill \frac{w_{n+1}^{k+1}-w_n^{k+1}}{\mathit{\tau }}+A{w}_{n+1}^{k+1}={\mathit{\phi }}^{k+1},n=-1,0,\dots ,N-1,\end{array}$$(42)

under condition (see (31(31) $$\begin{array}{cc}\hfill w^{k+1}(0)& =\mathit{\varphi }.\hfill \end{array}$$(31) ))(43) $$\begin{array}{c}\hfill w_0^{k+1}=\mathit{\varphi }.\end{array}$$(43)

Theorem 4.1:

The iterative process (41(41) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=\frac{w_N^k-w_{N-1}^k}{\mathit{\tau }}+A\mathit{\psi },k=0,1,\dots ,\end{array}$$(41) )–(43(43) $$\begin{array}{c}\hfill w_0^{k+1}=\mathit{\varphi }.\end{array}$$(43) ) for the numerical solution of the problem (38(38) $$\begin{array}{cc}& \frac{w_{n+1}-w_n}{\mathit{\tau }}+A{w}_{n+1}=\mathit{\phi },n=-1,0,\dots ,N-1\hfill \end{array}$$(38) )–(40(40) $$\begin{array}{cc}& w_N=\mathit{\psi }.\hfill \end{array}$$(40) ) converges linearly with speed$$\overline{\mathit{\varrho }}={(1+\mathit{\tau }\mathit{\delta })}^{-N},$$

and the estimate(44) $$\begin{array}{c}\hfill \Vert {\mathit{\phi }}^{k+1}-\mathit{\phi }\Vert \le \overline{\mathit{\varrho }}\Vert {\mathit{\phi }}^k-\mathit{\phi }\Vert .\end{array}$$(44)

is valid.

We define$${\mathit{\eta }}^{k+1}={\mathit{\phi }}^{k+1}-\mathit{\phi },z_{n+1}^{k+1}=w_{n+1}^{k+1}-w_{n+1},n=-1,0,\dots ,N-1,k=0,1,\dots .$$

From (41(41) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=\frac{w_N^k-w_{N-1}^k}{\mathit{\tau }}+A\mathit{\psi },k=0,1,\dots ,\end{array}$$(41) )–(43(43) $$\begin{array}{c}\hfill w_0^{k+1}=\mathit{\varphi }.\end{array}$$(43) ) we obtain(45) $$\begin{array}{cc}& {\mathit{\eta }}^{k+1}=\frac{z_N^k-z_{N-1}^k}{\mathit{\tau }},k=0,1,\dots ,\hfill \end{array}$$(45) (46) $$\begin{array}{cc}& \frac{z_{n+1}^{k+1}-z_n^{k+1}}{\mathit{\tau }}+A{z}_{n+1}^{k+1}={\mathit{\eta }}^{k+1},n=-1,0,\dots ,N-1,\hfill \end{array}$$(46) (47) $$\begin{array}{cc}& z_0^{k+1}=0.\hfill \end{array}$$(47)

Let’s assume$$v_{n+1}^k=\frac{z_{n+1}^k-z_n^k}{\mathit{\tau }},n=-1,0,\dots ,N-1.$$

From (46(46) $$\begin{array}{cc}& \frac{z_{n+1}^{k+1}-z_n^{k+1}}{\mathit{\tau }}+A{z}_{n+1}^{k+1}={\mathit{\eta }}^{k+1},n=-1,0,\dots ,N-1,\hfill \end{array}$$(46) ) we get(48) $$\begin{array}{c}\hfill \frac{v_{n+1}^k-v_n^k}{\mathit{\tau }}+A{v}_{n+1}^k=0,n=0,1,\dots ,N-1.\end{array}$$(48)

From Equation (46(46) $$\begin{array}{cc}& \frac{z_{n+1}^{k+1}-z_n^{k+1}}{\mathit{\tau }}+A{z}_{n+1}^{k+1}={\mathit{\eta }}^{k+1},n=-1,0,\dots ,N-1,\hfill \end{array}$$(46) ) when $n=0$ using the condition (47(47) $$\begin{array}{cc}& z_0^{k+1}=0.\hfill \end{array}$$(47) ) we have(49) $$\begin{array}{c}\hfill v_0^k={\mathit{\eta }}^k.\end{array}$$(49)

Similar to (26(26) $$\begin{array}{c}\hfill \Vert z_n^k{\Vert \le (1+\mathit{\tau }\mathit{\delta })}^{-n}\Vert z_0^k\Vert ,n=1,2,\dots ,N.\end{array}$$(26) ) for the solution of the problem (48(48) $$\begin{array}{c}\hfill \frac{v_{n+1}^k-v_n^k}{\mathit{\tau }}+A{v}_{n+1}^k=0,n=0,1,\dots ,N-1.\end{array}$$(48) ), (49(49) $$\begin{array}{c}\hfill v_0^k={\mathit{\eta }}^k.\end{array}$$(49) ) we prove the a priori estimate(50) $$\begin{array}{c}\hfill \Vert v_n^k{\Vert \le (1+\mathit{\tau }\mathit{\delta })}^{-n}\Vert {\mathit{\eta }}^k\Vert ,n=1,2,\dots ,N.\end{array}$$(50)

From (45(45) $$\begin{array}{cc}& {\mathit{\eta }}^{k+1}=\frac{z_N^k-z_{N-1}^k}{\mathit{\tau }},k=0,1,\dots ,\hfill \end{array}$$(45) ) and (50(50) $$\begin{array}{c}\hfill \Vert v_n^k{\Vert \le (1+\mathit{\tau }\mathit{\delta })}^{-n}\Vert {\mathit{\eta }}^k\Vert ,n=1,2,\dots ,N.\end{array}$$(50) ) taking into account introduced notation yields$$\Vert {\mathit{\eta }}^{k+1}\Vert =\Vert v_N^k{\Vert \le (1+\mathit{\tau }\mathit{\delta })}^{-N}\Vert {\mathit{\eta }}^k\Vert ,k=0,1,\dots .$$

Thus, we have established the estimate (44(44) $$\begin{array}{c}\hfill \Vert {\mathit{\phi }}^{k+1}-\mathit{\phi }\Vert \le \overline{\mathit{\varrho }}\Vert {\mathit{\phi }}^k-\mathit{\phi }\Vert .\end{array}$$(44) ).

5. Integral overdetermination

When considering inverse problem of identifying the right-hand side of parabolic equation, the integral overdetermination is often used instead of the final overdetermination. In this case, in place of Equation (4(4) $$\begin{array}{c}\hfill u(\mathit{x},T)=u_T(\mathit{x}),\mathit{x}\in \mathrm{\Omega }.\end{array}$$(4) ) the following condition is involved(51) $$\begin{array}{c}\hfill {\int }_0^T\mathit{\omega }(t)u(\mathit{x},t)\mathrm{d}t=u_T(\mathit{x}),\mathit{x}\in \mathrm{\Omega },\end{array}$$(51)

where $\mathit{\omega }(t)$ is a given function and$$\mathit{\omega }(t)\ge 0,{\int }_0^T\mathit{\omega }(t)\mathrm{d}t=1.$$

For the numerical solution of the inverse problem (1(1) $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }t}-\mathrm{div}(k(\mathit{x})\mathrm{grad}u)+c(\mathit{x})u=f(\mathit{x}),\mathit{x}\in \mathrm{\Omega },0<t\le T,\end{array}$$(1) )–(3(3) $$\begin{array}{c}\hfill u(\mathit{x},0)=u_0(\mathit{x}),\mathit{x}\in \mathrm{\Omega }.\end{array}$$(3) ), (51(51) $$\begin{array}{c}\hfill {\int }_0^T\mathit{\omega }(t)u(\mathit{x},t)\mathrm{d}t=u_T(\mathit{x}),\mathit{x}\in \mathrm{\Omega },\end{array}$$(51) ) the iterative process considered above can be used. Here, we note capabilities of iterative refinement of the desired right-hand side.[8,18]

After finite-element approximation in space we come to Equation (6(6) $$\begin{array}{cc}& \frac{\mathrm{d}w}{\mathrm{d}t}+Aw=\mathit{\phi },0<t\le T,\hfill \end{array}$$(6) ), which is supplemented with the initial condition (7(7) $$\begin{array}{cc}& w(0)=\mathit{\varphi },\hfill \end{array}$$(7) ). Taking into account (51(51) $$\begin{array}{c}\hfill {\int }_0^T\mathit{\omega }(t)u(\mathit{x},t)\mathrm{d}t=u_T(\mathit{x}),\mathit{x}\in \mathrm{\Omega },\end{array}$$(51) ), we have(52) $$\begin{array}{c}\hfill {\int }_0^T\mathit{\omega }(t)w(t)\mathrm{d}t=\mathit{\psi }.\end{array}$$(52)

instead of (8(8) $$\begin{array}{c}\hfill w(T)=\mathit{\psi },\end{array}$$(8) ). Integrating Equation (6(6) $$\begin{array}{cc}& \frac{\mathrm{d}w}{\mathrm{d}t}+Aw=\mathit{\phi },0<t\le T,\hfill \end{array}$$(6) ) with weight $\mathit{\omega }(t)$ over t from 0 to T and taking into account (52(52) $$\begin{array}{c}\hfill {\int }_0^T\mathit{\omega }(t)w(t)\mathrm{d}t=\mathit{\psi }.\end{array}$$(52) ), we obtain(53) $$\begin{array}{c}\hfill {\int }_0^T\mathit{\omega }(t)\frac{\mathrm{d}w}{\mathrm{d}t}(t)\mathrm{d}t+A\mathit{\psi }=\mathit{\phi }.\end{array}$$(53)

The iterative refinement of the right-hand side is based on the relation (53(53) $$\begin{array}{c}\hfill {\int }_0^T\mathit{\omega }(t)\frac{\mathrm{d}w}{\mathrm{d}t}(t)\mathrm{d}t+A\mathit{\psi }=\mathit{\phi }.\end{array}$$(53) ) (see (29(29) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=\frac{\mathrm{d}{w}^k}{\mathrm{d}t}(T)+A\mathit{\psi },k=0,1,\dots ,\end{array}$$(29) )):(54) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}={\int }_0^T\mathit{\omega }(t)\frac{\mathrm{d}{w}^k}{\mathrm{d}t}(t)\mathrm{d}t+A\mathit{\psi },k=0,1,\dots .\end{array}$$(54)

With new approximation for the right-hand side the Cauchy problem (30(30) $$\begin{array}{cc}\hfill \frac{\mathrm{d}{w}^{k+1}}{\mathrm{d}t}+A{w}^{k+1}& ={\mathit{\phi }}^{k+1},0<t\le T,\hfill \end{array}$$(30) ), (51(51) $$\begin{array}{c}\hfill {\int }_0^T\mathit{\omega }(t)u(\mathit{x},t)\mathrm{d}t=u_T(\mathit{x}),\mathit{x}\in \mathrm{\Omega },\end{array}$$(51) ) is solved. The study of the convergence of the iterative process is performed similarly to the study of the convergence of the process (29(29) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=\frac{\mathrm{d}{w}^k}{\mathrm{d}t}(T)+A\mathit{\psi },k=0,1,\dots ,\end{array}$$(29) ), (51(51) $$\begin{array}{c}\hfill {\int }_0^T\mathit{\omega }(t)u(\mathit{x},t)\mathrm{d}t=u_T(\mathit{x}),\mathit{x}\in \mathrm{\Omega },\end{array}$$(51) ).

In view of early introduced notation we have(55) $$\begin{array}{c}\hfill {\mathit{\eta }}^{k+1}={\int }_0^T\mathit{\omega }(t)\frac{\mathrm{d}{z}^k}{\mathrm{d}t}(t)\mathrm{d}t,k=0,1,\dots ,\end{array}$$(55)

and for $z^{k+1}$ we have the problem (33(33) $$\begin{array}{cc}& \frac{\mathrm{d}{z}^{k+1}}{\mathrm{d}t}+A{z}^{k+1}={\mathit{\eta }}^{k+1},0<t\le T,\hfill \end{array}$$(33) ), (34(34) $$\begin{array}{cc}& z^{k+1}(0)=0.\hfill \end{array}$$(34) ). For ${\displaystyle v^k=\frac{\mathrm{d}{z}^k}{\mathrm{d}t}}$ we have the problem (35(35) $$\begin{array}{c}\hfill \frac{\mathrm{d}{v}^k}{\mathrm{d}t}+A{v}^k=0,0<t\le T,\end{array}$$(35) ), (36(36) $$\begin{array}{c}\hfill v^k(0)={\mathit{\eta }}^k.\end{array}$$(36) ) and the estimate (37(37) $$\begin{array}{c}\hfill \Vert v^k(t)\Vert \le exp(-\mathit{\delta }t)\Vert {\mathit{\eta }}^k\Vert \end{array}$$(37) ) exists. Taking into account this from (5(5) $$\begin{array}{c}\hfill A=A^{\ast }\ge \mathit{\delta }I,\mathit{\delta }>0,\end{array}$$(5) ) we obtain$$\begin{array}{cc}\hfill \Vert {\mathit{\eta }}^{k+1}\Vert & =∥{\int }_0^T\mathit{\omega }(t)v^k(t)\mathrm{d}t∥={\int }_0^T\mathit{\omega }(t)\Vert v^k(t)\Vert \mathrm{d}t\hfill \\ \hfill & \le {\int }_0^T\mathit{\omega }(t)exp(-\mathit{\delta }t)\mathrm{d}t\Vert {\mathit{\eta }}^k\Vert ,k=0,1,\dots .\hfill \end{array}$$

Thus,(56) $$\begin{array}{c}\hfill \Vert {\mathit{\phi }}^{k+1}-\mathit{\phi }\Vert \le \mathit{\varrho }\Vert {\mathit{\phi }}^k-\mathit{\phi }\Vert ,k=0,1,\dots ,\end{array}$$(56)

where$$\mathit{\varrho }={\int }_0^T\mathit{\omega }(t)exp(-\mathit{\delta }t)\mathrm{d}t.$$

For usual assumptions about continuity of the weight function $\mathit{\omega }(t)$ we have $\mathit{\varrho }<1$. In the limit case $\mathit{\omega }(t)=\mathit{\delta }(t-T)$, where $\mathit{\delta }(t)$ is the $\mathit{\delta }$-function, from (52(52) $$\begin{array}{c}\hfill {\int }_0^T\mathit{\omega }(t)w(t)\mathrm{d}t=\mathit{\psi }.\end{array}$$(52) ) we obtain the condition of final overdetermination (8(8) $$\begin{array}{c}\hfill w(T)=\mathit{\psi },\end{array}$$(8) ). Other limit case, when $\mathit{\omega }(t)=\mathit{\delta }(t)$, is not interesting, since two condition at $t=0$ are set and, as expected, the iterative process does not converge ($\mathit{\varrho }=1$).

Theorem 5.1:

The iterative process (30(30) $$\begin{array}{cc}\hfill \frac{\mathrm{d}{w}^{k+1}}{\mathrm{d}t}+A{w}^{k+1}& ={\mathit{\phi }}^{k+1},0<t\le T,\hfill \end{array}$$(30) ), (31(31) $$\begin{array}{cc}\hfill w^{k+1}(0)& =\mathit{\varphi }.\hfill \end{array}$$(31) ), (55(55) $$\begin{array}{c}\hfill {\mathit{\eta }}^{k+1}={\int }_0^T\mathit{\omega }(t)\frac{\mathrm{d}{z}^k}{\mathrm{d}t}(t)\mathrm{d}t,k=0,1,\dots ,\end{array}$$(55) ) for the numerical solution of the problem (6(6) $$\begin{array}{cc}& \frac{\mathrm{d}w}{\mathrm{d}t}+Aw=\mathit{\phi },0<t\le T,\hfill \end{array}$$(6) ), (7(7) $$\begin{array}{cc}& w(0)=\mathit{\varphi },\hfill \end{array}$$(7) ), (52(52) $$\begin{array}{c}\hfill {\int }_0^T\mathit{\omega }(t)w(t)\mathrm{d}t=\mathit{\psi }.\end{array}$$(52) ) for (5(5) $$\begin{array}{c}\hfill A=A^{\ast }\ge \mathit{\delta }I,\mathit{\delta }>0,\end{array}$$(5) ) converges linearly with the speed $\mathit{\varrho }$, while the estimate (56(56) $$\begin{array}{c}\hfill \Vert {\mathit{\phi }}^{k+1}-\mathit{\phi }\Vert \le \mathit{\varrho }\Vert {\mathit{\phi }}^k-\mathit{\phi }\Vert ,k=0,1,\dots ,\end{array}$$(56) ) holds.

Applying an approach similar to the one in Section 3, the iterative process is studied when implicit time discretization is used.

6. More general problems

We have investigated iterative methods for the numerical solution of the inverse problem (1(1) $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }t}-\mathrm{div}(k(\mathit{x})\mathrm{grad}u)+c(\mathit{x})u=f(\mathit{x}),\mathit{x}\in \mathrm{\Omega },0<t\le T,\end{array}$$(1) )–(4(4) $$\begin{array}{c}\hfill u(\mathit{x},T)=u_T(\mathit{x}),\mathit{x}\in \mathrm{\Omega }.\end{array}$$(4) ), when the right-hand side in (1(1) $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }t}-\mathrm{div}(k(\mathit{x})\mathrm{grad}u)+c(\mathit{x})u=f(\mathit{x}),\mathit{x}\in \mathrm{\Omega },0<t\le T,\end{array}$$(1) ) does not depend on time. In more general case, instead of (1(1) $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }t}-\mathrm{div}(k(\mathit{x})\mathrm{grad}u)+c(\mathit{x})u=f(\mathit{x}),\mathit{x}\in \mathrm{\Omega },0<t\le T,\end{array}$$(1) ), we can consider the following equation:(57) $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }t}-\mathrm{div}(k(\mathit{x})\mathrm{grad}u)+c(\mathit{x})u=\mathit{\beta }(t)f(\mathit{x}),\mathit{x}\in \mathrm{\Omega },0<t\le T,\end{array}$$(57)

where $\mathit{\beta }(t)$ is some given function. The inverse problem of finding the pair $(u(\mathit{x},t),f(\mathit{x}))$ from (2(2) $$\begin{array}{c}\hfill k(\mathit{x})\frac{\mathit{\partial }u}{\mathit{\partial }n}+\mathit{\mu }(\mathit{x})u=0,\mathit{x}\in \mathit{\partial }\mathrm{\Omega },0<t\le T,\end{array}$$(2) )–(4(4) $$\begin{array}{c}\hfill u(\mathit{x},T)=u_T(\mathit{x}),\mathit{x}\in \mathrm{\Omega }.\end{array}$$(4) ), (57(57) $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }t}-\mathrm{div}(k(\mathit{x})\mathrm{grad}u)+c(\mathit{x})u=\mathit{\beta }(t)f(\mathit{x}),\mathit{x}\in \mathrm{\Omega },0<t\le T,\end{array}$$(57) ) is stated. We assume that(58) $$\begin{array}{c}\hfill \mathit{\beta }(t)>0,\frac{\mathrm{d}\mathit{\beta }}{\mathrm{d}t}\ge 0,0\le t\le T,\mathit{\beta }(T)=1.\end{array}$$(58)

After approximation in space we arrive at the equation(59) $$\begin{array}{c}\hfill \frac{\mathrm{d}w}{\mathrm{d}t}+Aw=\mathit{\beta }(t)\mathit{\phi },0<t\le T,\end{array}$$(59)

for $w(t)\in V^h$, which is supplemented by (7(7) $$\begin{array}{cc}& w(0)=\mathit{\varphi },\hfill \end{array}$$(7) ), (8(8) $$\begin{array}{c}\hfill w(T)=\mathit{\psi },\end{array}$$(8) ). Taking into account condition (8(8) $$\begin{array}{c}\hfill w(T)=\mathit{\psi },\end{array}$$(8) ) and normalization $\mathit{\beta }(T)=1$ Equation (59(59) $$\begin{array}{c}\hfill \frac{\mathrm{d}w}{\mathrm{d}t}+Aw=\mathit{\beta }(t)\mathit{\phi },0<t\le T,\end{array}$$(59) ) for $t=T$ gives(60) $$\begin{array}{c}\hfill \mathit{\phi }=\frac{\mathrm{d}w}{\mathrm{d}t}(T)+A\mathit{\psi }.\end{array}$$(60)

Iterative refinement of the right-hand side is performed using (60(60) $$\begin{array}{c}\hfill \mathit{\phi }=\frac{\mathrm{d}w}{\mathrm{d}t}(T)+A\mathit{\psi }.\end{array}$$(60) ) and has the form (29(29) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=\frac{\mathrm{d}{w}^k}{\mathrm{d}t}(T)+A\mathit{\psi },k=0,1,\dots ,\end{array}$$(29) ). When right-hand side is known at the new iteration we solve equation(61) $$\begin{array}{c}\hfill \frac{\mathrm{d}{w}^{k+1}}{\mathrm{d}t}+A{w}^{k+1}=\mathit{\beta }(t){\mathit{\phi }}^{k+1},0<t\le T,\end{array}$$(61)

with the initial condition (31(31) $$\begin{array}{cc}\hfill w^{k+1}(0)& =\mathit{\varphi }.\hfill \end{array}$$(31) ). For errors ${\mathit{\eta }}^{k+1}$ and $z^{k+1}(t)$ we obtain the relation (29(29) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=\frac{\mathrm{d}{w}^k}{\mathrm{d}t}(T)+A\mathit{\psi },k=0,1,\dots ,\end{array}$$(29) ), and equation(62) $$\begin{array}{c}\hfill \frac{\mathrm{d}{z}^{k+1}}{\mathrm{d}t}+A{z}^{k+1}=\mathit{\beta }(t){\mathit{\eta }}^{k+1},0<t\le T,\end{array}$$(62)

with a uniform initial condition (34(34) $$\begin{array}{cc}& z^{k+1}(0)=0.\hfill \end{array}$$(34) ).

As before, when considering the convergence of the iterative process (29(29) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=\frac{\mathrm{d}{w}^k}{\mathrm{d}t}(T)+A\mathit{\psi },k=0,1,\dots ,\end{array}$$(29) )–(31(31) $$\begin{array}{cc}\hfill w^{k+1}(0)& =\mathit{\varphi }.\hfill \end{array}$$(31) ), we study the problem for ${\displaystyle v^k=\frac{\mathrm{d}{z}^k}{\mathrm{d}t}}$. From (62(62) $$\begin{array}{c}\hfill \frac{\mathrm{d}{z}^{k+1}}{\mathrm{d}t}+A{z}^{k+1}=\mathit{\beta }(t){\mathit{\eta }}^{k+1},0<t\le T,\end{array}$$(62) ) we have(63) $$\begin{array}{c}\hfill \frac{\mathrm{d}{v}^k}{\mathrm{d}t}+A{v}^k=\frac{\mathrm{d}\mathit{\beta }}{\mathrm{d}t}(t){\mathit{\eta }}^{k+1},0<t\le T.\end{array}$$(63)

From Equation (62(62) $$\begin{array}{c}\hfill \frac{\mathrm{d}{z}^{k+1}}{\mathrm{d}t}+A{z}^{k+1}=\mathit{\beta }(t){\mathit{\eta }}^{k+1},0<t\le T,\end{array}$$(62) ) for $t=0$ taking into account (34(34) $$\begin{array}{cc}& z^{k+1}(0)=0.\hfill \end{array}$$(34) ) the initial condition for Equation (63(63) $$\begin{array}{c}\hfill \frac{\mathrm{d}{v}^k}{\mathrm{d}t}+A{v}^k=\frac{\mathrm{d}\mathit{\beta }}{\mathrm{d}t}(t){\mathit{\eta }}^{k+1},0<t\le T.\end{array}$$(63) ) is obtained:(64) $$\begin{array}{c}\hfill v^k(0)=\mathit{\beta }(0){\mathit{\eta }}^k.\end{array}$$(64)

We multiply Equation (63(63) $$\begin{array}{c}\hfill \frac{\mathrm{d}{v}^k}{\mathrm{d}t}+A{v}^k=\frac{\mathrm{d}\mathit{\beta }}{\mathrm{d}t}(t){\mathit{\eta }}^{k+1},0<t\le T.\end{array}$$(63) ) by $V^h$ on $v^k$, which leads to$$\left(\frac{\mathrm{d}{v}^k}{\mathrm{d}t},v^k\right)+(A{v}^k,v^k)=\frac{\mathrm{d}\mathit{\beta }}{\mathrm{d}t}(t)({\mathit{\eta }}^k,v^k).$$

Taking into account that the derivative of the function $\mathit{\beta }(t)$ is non-negative and inequality$$({\mathit{\eta }}^k,v^k)\le \Vert {\mathit{\eta }}^k\Vert \Vert v^k\Vert ,$$

we obtain$$\frac{\mathrm{d}}{\mathrm{d}t}\Vert v^k\Vert +\mathit{\delta }\Vert v^k\Vert \le \frac{\mathrm{d}\mathit{\beta }}{\mathrm{d}t}(t)\Vert {\mathit{\eta }}^k\Vert .$$

This implies$$\frac{\mathrm{d}}{\mathrm{d}t}(exp(\mathit{\delta }t)\Vert v^k\Vert )\le exp(\mathit{\delta }t)\frac{\mathrm{d}\mathit{\beta }}{\mathrm{d}t}(t)\Vert {\mathit{\eta }}^k\Vert .$$

Integration by t from 0 to T yields$$exp(\mathit{\delta }T)\Vert v^k(T)\Vert -\Vert v^k(0)\Vert \le {\int }_0^{T}exp(\mathit{\delta }t)\frac{\mathrm{d}\mathit{\beta }}{\mathrm{d}t}(t)\mathrm{d}t\Vert {\mathit{\eta }}^k\Vert .$$

Given the initial condition (64(64) $$\begin{array}{c}\hfill v^k(0)=\mathit{\beta }(0){\mathit{\eta }}^k.\end{array}$$(64) ) and$${\int }_0^{T}exp(\mathit{\delta }(t-T))\frac{\mathrm{d}\mathit{\beta }}{\mathrm{d}t}(t)\mathrm{d}t\le {\int }_0^T\frac{\mathrm{d}\mathit{\beta }}{\mathrm{d}t}(t)\mathrm{d}t=1-\mathit{\beta }(0),$$

we have(65) $$\begin{array}{c}\hfill \Vert z^k(T)\Vert \le \mathit{\varrho }\Vert z^k(0)\Vert ,\end{array}$$(65)

where(66) $$\begin{array}{c}\hfill \mathit{\varrho }=1-\mathit{\beta }(0)(1-exp(-\mathit{\delta }T)).\end{array}$$(66)

From (29(29) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=\frac{\mathrm{d}{w}^k}{\mathrm{d}t}(T)+A\mathit{\psi },k=0,1,\dots ,\end{array}$$(29) ) and (65(65) $$\begin{array}{c}\hfill \Vert z^k(T)\Vert \le \mathit{\varrho }\Vert z^k(0)\Vert ,\end{array}$$(65) ) we obtain the estimate (65(65) $$\begin{array}{c}\hfill \Vert z^k(T)\Vert \le \mathit{\varrho }\Vert z^k(0)\Vert ,\end{array}$$(65) ), where $\mathit{\varrho }<1$ is determined according to (66(66) $$\begin{array}{c}\hfill \mathit{\varrho }=1-\mathit{\beta }(0)(1-exp(-\mathit{\delta }T)).\end{array}$$(66) ). The result of consideration is the following statement.

Theorem 6.1:

The iterative process (29(29) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=\frac{\mathrm{d}{w}^k}{\mathrm{d}t}(T)+A\mathit{\psi },k=0,1,\dots ,\end{array}$$(29) ), (30(30) $$\begin{array}{cc}\hfill \frac{\mathrm{d}{w}^{k+1}}{\mathrm{d}t}+A{w}^{k+1}& ={\mathit{\phi }}^{k+1},0<t\le T,\hfill \end{array}$$(30) ), (61(61) $$\begin{array}{c}\hfill \frac{\mathrm{d}{w}^{k+1}}{\mathrm{d}t}+A{w}^{k+1}=\mathit{\beta }(t){\mathit{\phi }}^{k+1},0<t\le T,\end{array}$$(61) ) for the numerical solution of the problem (7(7) $$\begin{array}{cc}& w(0)=\mathit{\varphi },\hfill \end{array}$$(7) ), (8(8) $$\begin{array}{c}\hfill w(T)=\mathit{\psi },\end{array}$$(8) ), (59(59) $$\begin{array}{c}\hfill \frac{\mathrm{d}w}{\mathrm{d}t}+Aw=\mathit{\beta }(t)\mathit{\phi },0<t\le T,\end{array}$$(59) ) for (5(5) $$\begin{array}{c}\hfill A=A^{\ast }\ge \mathit{\delta }I,\mathit{\delta }>0,\end{array}$$(5) ) converges linearly at a rate of $\mathit{\varrho }$, which is determined according to (66(66) $$\begin{array}{c}\hfill \mathit{\varrho }=1-\mathit{\beta }(0)(1-exp(-\mathit{\delta }T)).\end{array}$$(66) ), while the estimate (65(65) $$\begin{array}{c}\hfill \Vert z^k(T)\Vert \le \mathit{\varrho }\Vert z^k(0)\Vert ,\end{array}$$(65) ) holds.

7. Numerical experiments

We illustrate the performance of iterative solution of inverse problems of identification of the right-hand side of parabolic equations by results of the numerical solution of a test problem. We consider the model problem(67) $$\begin{array}{cc}& \frac{\mathit{\partial }u}{\mathit{\partial }t}-\mathrm{div}\mathrm{grad}u+cu=f(\mathit{x}),\mathit{x}\in \mathrm{\Omega },0<t\le T,\hfill \end{array}$$(67) (68) $$\begin{array}{cc}& \frac{\mathit{\partial }u}{\mathit{\partial }n}=0,\mathit{x}\in \mathit{\partial }\mathrm{\Omega },f0<t\le T,\hfill \end{array}$$(68) (69) $$\begin{array}{cc}& u(\mathit{x},0)=0,\mathit{x}\in \mathrm{\Omega }.\hfill \end{array}$$(69)

The forward problem is solved in the unit square$$\mathrm{\Omega }=\{\mathit{x}=(x_1,x_2)|0<x_1<1,0<x_2<1\}$$

with given right-hand side $f(\mathit{x})$ and the solution at the final time is found(70) $$\begin{array}{c}\hfill u_T(\mathit{x})=u(\mathit{x},T).\end{array}$$(70)

After that, the inverse problem is solved when $u_T(\mathit{x})$ is known, but we need to find $f(\mathit{x})$. The right-hand side is taken as(71) $$\begin{array}{c}\hfill f(\mathit{x})=\frac{1}{1+exp(\mathit{\gamma }(x_1-x_2))}.\end{array}$$(71)

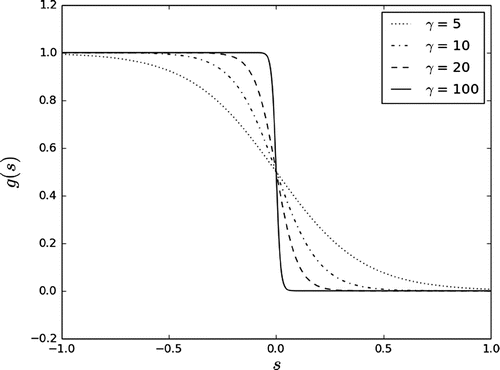
For $\mathit{\gamma }\to \infty$, the right-hand side becomes discontinuous (Figure 1).

Figure 1. Function $g(s)={(1+exp(\mathit{\gamma }s))}^{-1}$ at different values $\mathit{\gamma }$.

For the base case we set $c=10$, $T=0.1$, $\mathit{\gamma }=10$. When solving the forward problem (67(67) $$\begin{array}{cc}& \frac{\mathit{\partial }u}{\mathit{\partial }t}-\mathrm{div}\mathrm{grad}u+cu=f(\mathit{x}),\mathit{x}\in \mathrm{\Omega },0<t\le T,\hfill \end{array}$$(67) )–(69(69) $$\begin{array}{cc}& u(\mathit{x},0)=0,\mathit{x}\in \mathrm{\Omega }.\hfill \end{array}$$(69) ) with $f(\mathit{x})$ given by (71(71) $$\begin{array}{c}\hfill f(\mathit{x})=\frac{1}{1+exp(\mathit{\gamma }(x_1-x_2))}.\end{array}$$(71) ) we use the Crank-Nicolson scheme for time discretization, the time step is $\mathit{\tau }={10}^{-4}$. The uniform mesh with the division into 50 intervals in each direction is used, the Lagrangian finite elements of the second degree are applied. The solution $u(\mathit{x},T)$ at the final time is shown in Figure 2. This is used as input data for the inverse problem. In our analysis we focus on the iterative solution of the problem of identification after the finite element approximation in space. Because of this, we do not discuss the dependence of the accuracy of the approximate solution on the approximation in the space, which is more appropriate in another study. We perform the evaluation of the effect of computational errors on the basis of calculations on different time grids, when using the input data derived from the solution of the forward problem on more detailed time grid and with more accurate approximations in time.

Figure 2. The solution of the forward problem $u_T(\mathit{x})=u(\mathit{x},T)$ (the horizontal axis is $x_1$, the vertical axis is $x_2$).

The inverse problem is solved using fully implicit scheme (see (22(22) $$\begin{array}{cc}\hfill \frac{v_{n+1}^{k+1}-v_n^{k+1}}{\mathit{\tau }}+A{v}_{n+1}^{k+1}& =0,n=0,1,\dots ,N-1,k=0,1,\dots ,\hfill \end{array}$$(22) ) and (30(30) $$\begin{array}{cc}\hfill \frac{\mathrm{d}{w}^{k+1}}{\mathrm{d}t}+A{w}^{k+1}& ={\mathit{\phi }}^{k+1},0<t\le T,\hfill \end{array}$$(30) )). The errors of the approximate solution at iteration k are evaluated as follows:$${\mathit{\epsilon }}_{\infty }(k)=\underset{\mathit{x}\in \mathrm{\Omega }}{max}|{\mathit{\phi }}^k(\mathit{x})-f(\mathit{x})|,{\mathit{\epsilon }}_2(k)=\Vert {\mathit{\phi }}^k(\mathit{x})-f(\mathit{x})\Vert .$$

In conducting test predictions, the main issue is to evaluate an actual convergence rate for the iterative processes under the consideration. We need to recognize clearly how quickly the accuracy of an approximate solution is stabilized with increasing the iteration number. The obtained error itself depends on a time step, namely, the smaller time step, the higher accuracy of the approximate solution. 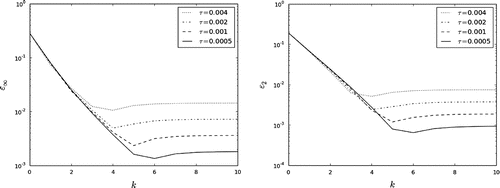Influence of time step of the iterative process (21(21) $$\begin{array}{cc}\hfill v_0^{k+1}& =v_N^k-\mathit{\chi },\hfill \end{array}$$(21) )–(23(23) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=A\mathit{\varphi }+v_0^{k+1}.\end{array}$$(23) ) on accuracy is illustrated in Figure 3. We see the rapid convergence of the iterative process and the improvement of the accuracy of the approximate solution by reducing the time step. Similar results for the iterative process (41(41) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=\frac{w_N^k-w_{N-1}^k}{\mathit{\tau }}+A\mathit{\psi },k=0,1,\dots ,\end{array}$$(41) )–(43(43) $$\begin{array}{c}\hfill w_0^{k+1}=\mathit{\varphi }.\end{array}$$(43) ) are shown in Figure 4. The initial approximation is taken in the form$$v^0(0)=A\mathit{\psi },{\mathit{\phi }}^0=A\mathit{\psi }.$$

To increase accuracy of computations, we need to use finer grids in time that result in increasing computational costs. The computational cost trade-off between the time interval and error can be obtained only in practical computations of applied problems.

Figure 3. The iterative process (21(21) $$\begin{array}{cc}\hfill v_0^{k+1}& =v_N^k-\mathit{\chi },\hfill \end{array}$$(21) )–(23(23) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=A\mathit{\varphi }+v_0^{k+1}.\end{array}$$(23) ).

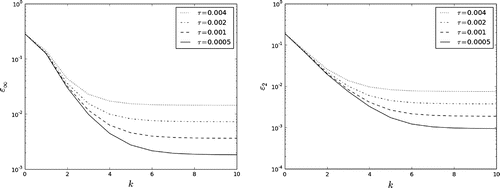
Figure 4. The iterative process (41(41) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=\frac{w_N^k-w_{N-1}^k}{\mathit{\tau }}+A\mathit{\psi },k=0,1,\dots ,\end{array}$$(41) )–(43(43) $$\begin{array}{c}\hfill w_0^{k+1}=\mathit{\varphi }.\end{array}$$(43) ).

The rate of convergence of iterative processes (21(21) $$\begin{array}{cc}\hfill v_0^{k+1}& =v_N^k-\mathit{\chi },\hfill \end{array}$$(21) )–(23(23) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=A\mathit{\varphi }+v_0^{k+1}.\end{array}$$(23) ) and (41(41) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=\frac{w_N^k-w_{N-1}^k}{\mathit{\tau }}+A\mathit{\psi },k=0,1,\dots ,\end{array}$$(41) )–(43(43) $$\begin{array}{c}\hfill w_0^{k+1}=\mathit{\varphi }.\end{array}$$(43) ) depends essentially on the observation interval, see (28(28) $$\begin{array}{c}\hfill \Vert {\mathit{\phi }}^{k+1}-\mathit{\phi }\Vert \le \overline{\mathit{\varrho }}\Vert v_0^k-v_0\Vert .\end{array}$$(28) ) and (44(44) $$\begin{array}{c}\hfill \Vert {\mathit{\phi }}^{k+1}-\mathit{\phi }\Vert \le \overline{\mathit{\varrho }}\Vert {\mathit{\phi }}^k-\mathit{\phi }\Vert .\end{array}$$(44) ). The relevant numerical results are presented in Figures 5 and 6. These computations are carried out for $\mathit{\tau }={10}^{-3}$.

Figure 5. The dependence on T: the iterative process (21(21) $$\begin{array}{cc}\hfill v_0^{k+1}& =v_N^k-\mathit{\chi },\hfill \end{array}$$(21) )–(23(23) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=A\mathit{\varphi }+v_0^{k+1}.\end{array}$$(23) ).

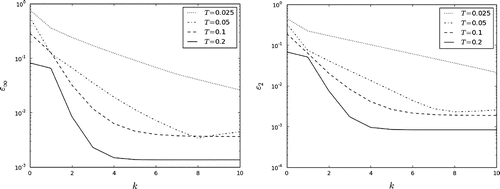
Figure 6. The dependence on T: the iterative process (41(41) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=\frac{w_N^k-w_{N-1}^k}{\mathit{\tau }}+A\mathit{\psi },k=0,1,\dots ,\end{array}$$(41) )–(43(43) $$\begin{array}{c}\hfill w_0^{k+1}=\mathit{\varphi }.\end{array}$$(43) ).

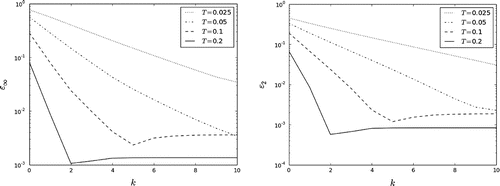
There is a similar dependence of the rate of convergence of the iterative processes (21(21) $$\begin{array}{cc}\hfill v_0^{k+1}& =v_N^k-\mathit{\chi },\hfill \end{array}$$(21) )–(23(23) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=A\mathit{\varphi }+v_0^{k+1}.\end{array}$$(23) ) and (41(41) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=\frac{w_N^k-w_{N-1}^k}{\mathit{\tau }}+A\mathit{\psi },k=0,1,\dots ,\end{array}$$(41) )–(43(43) $$\begin{array}{c}\hfill w_0^{k+1}=\mathit{\varphi }.\end{array}$$(43) ) on the value of $\mathit{\delta }$. For our test problem (67(67) $$\begin{array}{cc}& \frac{\mathit{\partial }u}{\mathit{\partial }t}-\mathrm{div}\mathrm{grad}u+cu=f(\mathit{x}),\mathit{x}\in \mathrm{\Omega },0<t\le T,\hfill \end{array}$$(67) )–(69(69) $$\begin{array}{cc}& u(\mathit{x},0)=0,\mathit{x}\in \mathrm{\Omega }.\hfill \end{array}$$(69) ) we have $\mathit{\delta }=c$. 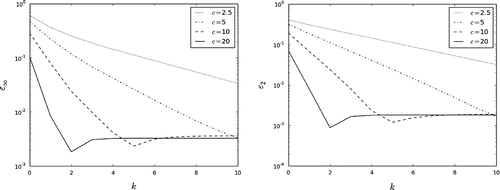The convergence for different values of c is illustrated in Figures 7 and 8. These computations are carried out for $\mathit{\tau }={10}^{-3}$ when $T=0.1$. For some values of problem parameters (e.g. small time intervals T in Figures 5 and 6 or small values of the coefficient c in Figures 7 and 8), ten iterations do not guarantee the convergence of iterative processes in our predictions.

Figure 7. The dependence on c: the iterative process (21(21) $$\begin{array}{cc}\hfill v_0^{k+1}& =v_N^k-\mathit{\chi },\hfill \end{array}$$(21) )–(23(23) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=A\mathit{\varphi }+v_0^{k+1}.\end{array}$$(23) ).

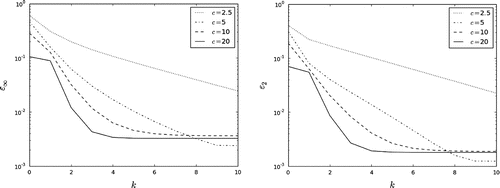
Figure 8. The dependence on c: the iterative process (41(41) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=\frac{w_N^k-w_{N-1}^k}{\mathit{\tau }}+A\mathit{\psi },k=0,1,\dots ,\end{array}$$(41) )–(43(43) $$\begin{array}{c}\hfill w_0^{k+1}=\mathit{\varphi }.\end{array}$$(43) ).

The accuracy of the approximate solution, the rate of convergence of the iterative processes (21(21) $$\begin{array}{cc}\hfill v_0^{k+1}& =v_N^k-\mathit{\chi },\hfill \end{array}$$(21) )–(23(23) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=A\mathit{\varphi }+v_0^{k+1}.\end{array}$$(23) ) and (41(41) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=\frac{w_N^k-w_{N-1}^k}{\mathit{\tau }}+A\mathit{\psi },k=0,1,\dots ,\end{array}$$(41) )–(43(43) $$\begin{array}{c}\hfill w_0^{k+1}=\mathit{\varphi }.\end{array}$$(43) ) weakly depends on the right-hand side. This is particularly evidenced by the data presented in Tables 1 and 2.

Table 1. The dependence of ${\mathit{\epsilon }}_{\infty }$ on $\mathit{\gamma }$: the iterative process (21(21) $$\begin{array}{cc}\hfill v_0^{k+1}& =v_N^k-\mathit{\chi },\hfill \end{array}$$(21) )–(23(23) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=A\mathit{\varphi }+v_0^{k+1}.\end{array}$$(23) ).

k	$\mathit{\gamma }=5$	$\mathit{\gamma }=10$	$\mathit{\gamma }=20$	$\mathit{\gamma }=100$
0	0.2698616	0.2859782	0.2915919	0.2935690
1	0.1147344	0.1266791	0.1307726	0.1321993
2	0.0300993	0.0320972	0.0327864	0.0330277
3	0.0111847	0.0117121	0.0118796	0.0119350
4	0.0059519	0.0062735	0.0063679	0.0063972
5	0.0042635	0.0045563	0.0046405	0.0046662

Table 2. The dependence of ${\mathit{\epsilon }}_2$ on $\mathit{\gamma }$: the iterative process (21(21) $$\begin{array}{cc}\hfill v_0^{k+1}& =v_N^k-\mathit{\chi },\hfill \end{array}$$(21) )–(23(23) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=A\mathit{\varphi }+v_0^{k+1}.\end{array}$$(23) ).

k	$\mathit{\gamma }=5$	$\mathit{\gamma }=10$	$\mathit{\gamma }=20$	$\mathit{\gamma }=100$
0	0.1889483	0.1910198	0.1918367	0.1921380
1	0.0596180	0.0633147	0.0647253	0.0652396
2	0.0200653	0.0203738	0.0204951	0.0205398
3	0.0082159	0.0082824	0.0083087	0.0083185
4	0.0040403	0.0041006	0.0041245	0.0041333
5	0.0025596	0.0026414	0.0026734	0.0026853

Below are the main points of solving the problem of source identification, where input data (4(4) $$\begin{array}{c}\hfill u(\mathit{x},T)=u_T(\mathit{x}),\mathit{x}\in \mathrm{\Omega }.\end{array}$$(4) ) is given with an error. For the inverse problem (67(67) $$\begin{array}{cc}& \frac{\mathit{\partial }u}{\mathit{\partial }t}-\mathrm{div}\mathrm{grad}u+cu=f(\mathit{x}),\mathit{x}\in \mathrm{\Omega },0<t\le T,\hfill \end{array}$$(67) )–(70(70) $$\begin{array}{c}\hfill u_T(\mathit{x})=u(\mathit{x},T).\end{array}$$(70) ), we assume that we have noisy data for the solution at the final time-moment. Instead of the exact function $u(\mathit{x},T)$, we have(72) $$\begin{array}{c}\hfill u^{\mathit{\epsilon }}(\mathit{x},T)=u(\mathit{x},T)+\mathit{\epsilon }(\mathit{\sigma }(\mathit{x})-0.5),\end{array}$$(72)

where $\mathit{\sigma }(\mathit{x})$ is a random function uniformly distributed over the interval [0, 1].

The value of $\mathit{\epsilon }$ specifies the perturbation amplitude. For the basic variant with $c=10,\mathit{\gamma }=10,T=0.1$, the perturbation in the form (72(72) $$\begin{array}{c}\hfill u^{\mathit{\epsilon }}(\mathit{x},T)=u(\mathit{x},T)+\mathit{\epsilon }(\mathit{\sigma }(\mathit{x})-0.5),\end{array}$$(72) ) is introduced at each node of the computational grid. An example of a noisy solution at the final time-moment that is obtained for the error level corresponding to $\mathit{\epsilon }=5·{10}^{-3}$ is shown in Figure 9 (the exact data are presented in Figure 2).

Figure 9. Input noisy data $u^{\mathit{\delta }}(\mathit{x},T)$ for $\mathit{\delta }=5·{10}^{-3}$.

Figure 10. Smoothed data for $\mathit{\delta }=5·{10}^{-3}$.

Figure 11. The exact solution of the inverse problem.

Figure 12. Solution of the inverse problem for $\mathit{\delta }=5·{10}^{-3}$.

Figure 13. Solution of the inverse problem for $\mathit{\delta }=5·{10}^{-4}$.

It is necessary to perform a preliminary processing of input data. In our case, this is due to the fact that this overdetermination data should have necessary smoothness. The iterative method (12(12) $$\begin{array}{cc}& v^{k+1}(0)=v^k(T)-\mathit{\chi },\hfill \end{array}$$(12) ), (13(13) $$\begin{array}{cc}& \frac{\mathrm{d}{v}^{k+1}}{\mathrm{d}t}+A{v}^{k+1}=0,0<t\le T,k=0,1,\dots ,\hfill \end{array}$$(13) ) for solving the non-local problem (10(10) $$\begin{array}{c}\hfill \frac{\mathrm{d}v}{\mathrm{d}t}+Av=0,0<t\le T.\end{array}$$(10) ), (11(11) $$\begin{array}{c}\hfill v(T)-v(0)=\mathit{\chi },\mathit{\chi }=A(\mathit{\varphi }-\mathit{\psi }).\end{array}$$(11) ) is associated with the evaluation of $A\mathit{\psi }$ (see (11(11) $$\begin{array}{c}\hfill v(T)-v(0)=\mathit{\chi },\mathit{\chi }=A(\mathit{\varphi }-\mathit{\psi }).\end{array}$$(11) )). When using the iterative method (29(29) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=\frac{\mathrm{d}{w}^k}{\mathrm{d}t}(T)+A\mathit{\psi },k=0,1,\dots ,\end{array}$$(29) )–(31(31) $$\begin{array}{cc}\hfill w^{k+1}(0)& =\mathit{\varphi }.\hfill \end{array}$$(31) ), calculations are also based on the evaluation of $A\mathit{\psi }$ (see the right-hand side of (29(29) $$\begin{array}{c}\hfill {\mathit{\phi }}^{k+1}=\frac{\mathrm{d}{w}^k}{\mathrm{d}t}(T)+A\mathit{\psi },k=0,1,\dots ,\end{array}$$(29) )). Thus, we can expect that the desired approximation of the right-hand side will be smooth if $A\mathit{\psi }$ is smooth.

We solve the inverse problem with$$\mathit{\psi }(\mathit{x})\approx u^{\mathit{\epsilon }}(\mathit{x},T),$$

where $\mathit{\psi }(\mathit{x})$ is obtained by smoothing $u^{\mathit{\epsilon }}(\mathit{x},T)$. Taking into account the need to work with $A\mathit{\psi }$, we choose the smoothing functional [26] in the form(73) $$\begin{array}{c}\hfill J_{\mathit{\alpha }}(\mathit{\psi })=\Vert \mathit{\psi }-u^{\mathit{\epsilon }}{(·,T)\Vert }^2+\mathit{\alpha }{\Vert A\mathit{\psi }\Vert }^2,\end{array}$$(73)

where $\mathit{\alpha }>0$ is a parameter of smoothing (regularization). The value of $\mathit{\alpha }$ is selected using the discrepancy principle$$\Vert \mathit{\psi }-u^{\mathit{\epsilon }}\Vert =\mathit{\epsilon }.$$

The minimization problem (73(73) $$\begin{array}{c}\hfill J_{\mathit{\alpha }}(\mathit{\psi })=\Vert \mathit{\psi }-u^{\mathit{\epsilon }}{(·,T)\Vert }^2+\mathit{\alpha }{\Vert A\mathit{\psi }\Vert }^2,\end{array}$$(73) ) is equivalent to solving the problem$$\mathit{\alpha }{A}^2\mathit{\psi }+\mathit{\psi }=u^{\mathit{\epsilon }}.$$

Thus, it is necessary to solve the corresponding boundary value problem for the fourth-order elliptic equation. Computational implementation is based on the use of mixed finite element methods,[27] where the fourth-order equation is written as a system of two second-order equations:$$\mathit{\alpha }A\mathit{\xi }+\mathit{\psi }=u^{\mathit{\epsilon }},A\mathit{\psi }=\mathit{\xi }.$$

For $\mathit{\epsilon }=5·{10}^{-3}$, in the example under the consideration (see Figure 9), the regularization parameter is about $\mathit{\alpha }\approx 0.00080$. The smoothed input data is shown in Figure 10. The exact solution of the inverse problem (the function $f(\mathit{x})$ with $\mathit{\gamma }=10$) is depicted in Figure 11. The numerical solution of the inverse problem with noisy data is presented in Figure 12.

Reducing the error amplitude allows to obtain an approximate solution of the inverse problem with higher accuracy. For $\mathit{\epsilon }=5·{10}^{-4}$, the regularization parameter $\mathit{\alpha }\approx 4.5·{10}^{-5}$. The accuracy of the reconstruction of the right-hand side for this case is shown in Figure 13.

8. Conclusions

 

(1)	The problem of identifying the source of a parabolic equation of the second order, which depends only on the space variables, is considered in the work. Additional information about the solution is set at the final time. To approximate in space we use the standard Lagrange finite elements for the triangulation of the computational domain.
(2)	The original inverse problem is formulated as a problem with a non-local condition for an evolution equation of the first order. For the approximate solutions of non-classical boundary value problem we propose the iterative process of refinement of the initial condition. We have investigated the rate of convergence of the iterative process with respect to the permanent positive definiteness of operator of the problem and interval time.
(3)	We constructed the numerical algorithm based on the well-known approach with iterative refinement of the right-hand side. This algorithm has previously been used to prove the unique solvability of the inverse problem. We have investigated the rate of convergence of the iterative process for an operator differential equation of first order (semi-discrete approximation). Similar results are obtained when using a fully implicit approximations of time (fully discrete approximation).
(4)	We have also considered the inverse problem of identification of the right side of the heat equation when the measured data is given in the form of a weighted average over time. The convergence of the iterative process with the refinement of the required right-hand side and the rate of convergence has been given.
(5)	We have also studied the more general problem with multiplicative right-hand side, when one multiplier determines the known dependence of the right-hand side on the time, and the second defines the unknown dependence on the spatial variables. The estimates of the rate of convergence of the iterative process with refinement of the right-hand side with respect to parameters of the problem have been obtained.
(6)	The capabilities of considered computational algorithms of identification of the right-hand side have been illustrated by the results of a numerical solution of the model inverse problem for the two-dimensional parabolic equation in the unit square. Within the quasi-real computational experiment the additional data for the inverse problem is found using the results of the numerical solution of the forward problem. The calculated data shows a high rate of convergence of the discussed iterative processes of Picard type which do not contain any adjusting parameters. To find the approximate solution of the inverse problem it is sufficient to perform 5–6 iterations, where the standard boundary value problem for a parabolic equation is solved.
(7)	Numerical results are presented for the model inverse problem, where data of overdetermination (the solution at the final time) is given with error. This data is smoothed and a smoothing parameter is selected in correspondence with an error level of input data. It was shown that for the problem of identification of the right-hand side, the accuracy of the approximate solution increases with decreasing the error in the input data.

Acknowledgements

Author would like to thank Prof. Daniel Lesnic and the three reviewers for their insightful comments and suggestions on this manuscript.

Additional information

Funding

This research was supported by RFBR [project 14-01-00785].

Notes

No potential conflict of interest was reported by the author.