An inverse problem for a family of time fractional diffusion equations

Abstract

We consider a diffusion equation involving fractional derivative in time of order $\mathit{\beta }$ ($0<\mathit{\beta }<1$) with a nonlocal boundary condition involving a parameter $\mathit{\alpha }>0$. A bi-orthogonal system of functions constructed from two Riesz basis of $L^2(0,1)$ is used to prove the existence and uniqueness of classical solution of the direct problem. The inverse problem of determination of the temperature distribution and the unknown source term is considered. The inverse problem is proved to be well-posed in the sense of Hadamard whenever an overdetermination condition of the final temperature is given.

Keywords:

• Fractional derivative
• nonlocal boundary conditions
• bi-orthogonal system of functions
• Mittag-Leffler function

AMS Subject Classifications:

• 80A23
• 65N21
• 26A33
• 45J05
• 34K37
• 42A16

1. Introduction

We are concerned with the following fractional differential equation(1.1) $$\begin{array}{c}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}u(x,t)=\mathit{\rho }{u}_{xx}(x,t)+F(x,t),(x,t)\in \mathrm{\Pi },\end{array}$$(1.1)

with the initial condition(1.2) $$\begin{array}{c}\hfill u(x,0)=\mathit{\varphi }(x),0<x<1,\end{array}$$(1.2)

and nonlocal family of boundary conditions(1.3) $$\begin{array}{c}\hfill u_x(0,t)=u_x(1,t)+\mathit{\alpha }u(1,t),u(0,t)=0,t\in (0,T],\mathit{\alpha }>0,\end{array}$$(1.3)

where $\mathrm{\Pi }:=\{(x,t):0<x<1,t\in (0,T]\}$, ${}^C{D}_{0_{+}}^{\mathit{\beta }}$ stands for the left sided Caputo fractional derivative of order $0<\mathit{\beta }<1$, $\mathit{\rho }$ is a positive constant and F(x, t) is the source term. The fractional derivative in (1.1(1.1) $$\begin{array}{c}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}u(x,t)=\mathit{\rho }{u}_{xx}(x,t)+F(x,t),(x,t)\in \mathrm{\Pi },\end{array}$$(1.1) ) appears when we deal with the anomalous diffusion. For $\mathit{\alpha }=0$ the boundary conditions in (1.3(1.3) $$\begin{array}{c}\hfill u_x(0,t)=u_x(1,t)+\mathit{\alpha }u(1,t),u(0,t)=0,t\in (0,T],\mathit{\alpha }>0,\end{array}$$(1.3) ) become the well-known Samarskii–Ionkin boundary conditions which arise from particle diffusion in turbulent plasma and in heat propagation where the law of variation of total quantity of the heat is given.[1] For applications of more general nonlocal boundary conditions see [2,3] and the monograph.[4]

The determination of a function u(x, t) which satisfies the initial boundary value problem (IBVP) (1.1(1.1) $$\begin{array}{c}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}u(x,t)=\mathit{\rho }{u}_{xx}(x,t)+F(x,t),(x,t)\in \mathrm{\Pi },\end{array}$$(1.1) )–(1.3(1.3) $$\begin{array}{c}\hfill u_x(0,t)=u_x(1,t)+\mathit{\alpha }u(1,t),u(0,t)=0,t\in (0,T],\mathit{\alpha }>0,\end{array}$$(1.3) ) such that $u(.,t)\in C^2[0,1]$ and ${}^C{D}_{0_{+}}^{\mathit{\beta }}u(x,.)\in C[0,T]$, whenever the source term F(x, t) and the initial data $\mathit{\varphi }(x)$ are given, is called strong or classical solution of the IBVP (1.1(1.1) $$\begin{array}{c}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}u(x,t)=\mathit{\rho }{u}_{xx}(x,t)+F(x,t),(x,t)\in \mathrm{\Pi },\end{array}$$(1.1) )–(1.3(1.3) $$\begin{array}{c}\hfill u_x(0,t)=u_x(1,t)+\mathit{\alpha }u(1,t),u(0,t)=0,t\in (0,T],\mathit{\alpha }>0,\end{array}$$(1.3) ). This problem is usually known as the direct problem. We prove, under certain assumptions (see Theorem 3.1 of Section 3) that there exist a unique classical solution of the direct problem.

We also consider the inverse source problem (ISP) for the IBVP (1.1(1.1) $$\begin{array}{c}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}u(x,t)=\mathit{\rho }{u}_{xx}(x,t)+F(x,t),(x,t)\in \mathrm{\Pi },\end{array}$$(1.1) )–(1.3(1.3) $$\begin{array}{c}\hfill u_x(0,t)=u_x(1,t)+\mathit{\alpha }u(1,t),u(0,t)=0,t\in (0,T],\mathit{\alpha }>0,\end{array}$$(1.3) ), the source term F(x, t) is supposed to be space dependent only, i.e. for the ISP, we have $F(x,t):=f(x)$. Let us define the solution of the ISP in a formal way; the determination of a pair of functions $\{u(x,t),f(x)\}$ for the problem (1.1(1.1) $$\begin{array}{c}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}u(x,t)=\mathit{\rho }{u}_{xx}(x,t)+F(x,t),(x,t)\in \mathrm{\Pi },\end{array}$$(1.1) )–(1.3(1.3) $$\begin{array}{c}\hfill u_x(0,t)=u_x(1,t)+\mathit{\alpha }u(1,t),u(0,t)=0,t\in (0,T],\mathit{\alpha }>0,\end{array}$$(1.3) ) such that $u(.,t)\in C^2[0,1]$, ${}^C{D}_{0_{+}}^{\mathit{\beta }}u(x,.)\in C[0,T]$ and $f\in C[0,1],$ is said to be a solution of the ISP. This ISP is ill-posed in the sense of Hadamard. In order to determine the source term uniquely we need an extra condition, usually known as overdetermination condition. In this paper, we have the final temperature distribution at time $t=T<\infty$ as overdetermination condition, i.e.(1.4) $$\begin{array}{c}\hfill u(x,T)=\mathit{\psi }(x).\end{array}$$(1.4)

We intend to solve the direct as well as ISP by using the Fourier’s method, frequently known as separation of variables. The spectral problem for the corresponding homogeneous equation of the IBVP (1.1(1.1) $$\begin{array}{c}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}u(x,t)=\mathit{\rho }{u}_{xx}(x,t)+F(x,t),(x,t)\in \mathrm{\Pi },\end{array}$$(1.1) )–(1.3(1.3) $$\begin{array}{c}\hfill u_x(0,t)=u_x(1,t)+\mathit{\alpha }u(1,t),u(0,t)=0,t\in (0,T],\mathit{\alpha }>0,\end{array}$$(1.3) ) is(1.5) $$\begin{array}{cc}\hfill X^{{}^{″}}& =-\mathit{\lambda }X,\hfill \end{array}$$(1.5) (1.6) $$\begin{array}{cc}\hfill X(0)=0,& X^{{}^{\prime }}(0)=X^{{}^{\prime }}(1)+\mathit{\alpha }X(1),\hfill \end{array}$$(1.6)

where $\mathit{\lambda }=\mathit{\mu }/\mathit{\rho },$ and $\mathit{\mu }$ is the spectral parameter.

The spectral problem (1.5(1.5) $$\begin{array}{cc}\hfill X^{{}^{″}}& =-\mathit{\lambda }X,\hfill \end{array}$$(1.5) )–(1.6(1.6) $$\begin{array}{cc}\hfill X(0)=0,& X^{{}^{\prime }}(0)=X^{{}^{\prime }}(1)+\mathit{\alpha }X(1),\hfill \end{array}$$(1.6) ) is non-self-adjoint and the set of eigenfunctions is proved to be a complete set in $L^2[0,1]$ see [5]. The set of eigenfunctions of the spectral problem is not orthogonal (see Section 2.1). For spectral expansion, completeness of the eigenfunctions of non-self-adjoint differential operators, the reader is referred to the following articles [6,7] and reference therein. In order to apply the separation of variables technique for the solution of the direct and the inverse source problem for IBVP (1.1(1.1) $$\begin{array}{c}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}u(x,t)=\mathit{\rho }{u}_{xx}(x,t)+F(x,t),(x,t)\in \mathrm{\Pi },\end{array}$$(1.1) )–(1.3(1.3) $$\begin{array}{c}\hfill u_x(0,t)=u_x(1,t)+\mathit{\alpha }u(1,t),u(0,t)=0,t\in (0,T],\mathit{\alpha }>0,\end{array}$$(1.3) ), we shall use a bi-orthogonal system of functions which was constructed by Mokin [5]. The construction of a bi-orthogonal system of functions (see Section 2.1) is based on the set of eigenfunctions of the spectral problem (1.5(1.5) $$\begin{array}{cc}\hfill X^{{}^{″}}& =-\mathit{\lambda }X,\hfill \end{array}$$(1.5) )–(1.6(1.6) $$\begin{array}{cc}\hfill X(0)=0,& X^{{}^{\prime }}(0)=X^{{}^{\prime }}(1)+\mathit{\alpha }X(1),\hfill \end{array}$$(1.6) ) and its adjoint (conjugate) problem given by(1.7) $$\begin{array}{cc}\hfill Y^{{}^{″}}& =-\mathit{\lambda }Y,\hfill \end{array}$$(1.7) (1.8) $$\begin{array}{cc}\hfill Y(0)=Y(1),& Y^{{}^{\prime }}(1)+\mathit{\alpha }Y(1)=0.\hfill \end{array}$$(1.8)

In this paper, we prove (see Section 3), the direct problem for the IBVP (1.1(1.1) $$\begin{array}{c}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}u(x,t)=\mathit{\rho }{u}_{xx}(x,t)+F(x,t),(x,t)\in \mathrm{\Pi },\end{array}$$(1.1) )–(1.3(1.3) $$\begin{array}{c}\hfill u_x(0,t)=u_x(1,t)+\mathit{\alpha }u(1,t),u(0,t)=0,t\in (0,T],\mathit{\alpha }>0,\end{array}$$(1.3) ) is well-posed in the sense of Hadamard, when the initial data satisfy certain smoothness conditions. The direct problem for the homogeneous equation, that is, $F(x,t)=0$ in (1.1(1.1) $$\begin{array}{c}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}u(x,t)=\mathit{\rho }{u}_{xx}(x,t)+F(x,t),(x,t)\in \mathrm{\Pi },\end{array}$$(1.1) ), when $\mathit{\beta }=1$, was considered in [5]. Our results for the direct problem are the generalization of the results proved in [5], indeed, we recover the results of [5] from our results. For the ISP of the IBVP (1.1(1.1) $$\begin{array}{c}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}u(x,t)=\mathit{\rho }{u}_{xx}(x,t)+F(x,t),(x,t)\in \mathrm{\Pi },\end{array}$$(1.1) )–(1.4(1.4) $$\begin{array}{c}\hfill u(x,T)=\mathit{\psi }(x).\end{array}$$(1.4) ), we present the results of existence, uniqueness and stability of the solution on the given data, that is, ISP is proved to be well-posed.

Let us dwell on the literature concerning the time fractional diffusion equation and its related inverse problems. The fractional order integrals and derivatives are being used in the reaction-diffusion equations [8,9] to explain the well-known phenomena of anomalous diffusion observed in the experiments.[8,10,11] There are several other techniques available to explain the anomalies in the diffusion and transport phenomena such as Continuous Time Random Walks (CTRW) (see [12] and references therein), multicomponent diffusion,[13] stochastic process, Brownian motions.[14,15] The relation between the fractional order operators and CTRW was established in [16], which explains the consideration of the fractional operators in reaction-diffusion equations.[17]

The literature on the inverse problems related to fractional differential equations is not as rich when compared to its counterpart, that is, the inverse problems of integer order differential equations. For $\mathit{\alpha }=0$ the ISP was considered in [18] and the authors proved existence and uniqueness results of the inverse source problem. An inverse problem of determination of potential term in a Sturm–Liouville problem is considered by Jin and Rundell [19], they proposed a numerical algorithm for the solution. Li et al. [20] considered the determination of diffusion coefficient as well as the order of time fractional derivative for a diffusion equation. They proposed a regularization technique and suppose the uniqueness of the unknown terms. Lukashchuk [21] considered the simultaneous determination of order of fractional derivative and diffusion coefficient for a one-dimensional diffusion equation. Let us mention that order of fractional derivative plays a vital role in explaining the anomalous diffusion see the topical review article.[22] A uniqueness result and a reconstruction algorithm are proposed in [23] for the determination of nonlinear source term using maximum principle technique for the fractional differential equation. An inverse problem of determination of non linear boundary conditions for a time fractional differential equation was considered in [24]. Kirane et al. [25] investigated an ISP with nonlocal boundary conditions in two-dimensional space, the problem is proved to be well-posed in the sense of Hadamard. The direct and inverse problems involving Hadamard fractional derivative in abstract Cauchy problem were considered in [26]. In [27] the direct and inverse source problems for a space–time fractional diffusion equation are analysed, the inverse problem is proved to be well-posed. A numerical algorithm based on the optimization of an error functional for the ISP for space–time fractional diffusion equation is proposed in [28]. For a nonlinear time fractional diffusion equation an inverse coefficient problem was considered in [29] while direct and inverse problems for fractional elastoplasticity model were discussed in [30]. For a space–time fractional diffusion equation inverse problems of recovering order of fractional time and space derivatives are considered in [31,32]. A topical review on inverse problems related to fractional diffusion equations is provided in [33]. The inverse problems related to several diffusion equations involving time and space fractional derivatives have been reported (for more details see [33]).

The rest of the paper is organized as follows: in the next section we present some preliminaries and basic results for the sake of the readers. Our main results are presented in Section 3 and Section 4. Existence, uniqueness and stability results for the direct problem are proved in Section 3, while the ISP is proved to be well-posed in the sense of Hadamard in Section 4. In Section 5, we provide some examples and in the last section the paper has been concluded.

2. Preliminaries and some basic results

In this section, we recall some definitions, notations from fractional calculus (see [34,35]) and some basic results for the convenience of the readers.

For a locally integrable function $g:{\mathbb{R}}^{+}\to \mathbb{R}$, the left sided Riemann–Liouville fractional integral of order $0<\mathit{\beta }<1$ is defined by(2.1) $$\begin{array}{c}\hfill J_{0_{+}}^{\mathit{\beta }}g(t):=\frac{1}{\mathrm{\Gamma }(\mathit{\beta })}\underset{0}{\overset{t}{\int }}\frac{g(\mathit{\tau })}{{(t-\mathit{\tau })}^{1-\mathit{\beta }}}\mathrm{d}\mathit{\tau },\end{array}$$(2.1)

where $\mathrm{\Gamma }$ is the Euler Gamma function.

The left sided Riemann–Liouville fractional derivative of order $0<\mathit{\beta }<1$, if it exists, is given by(2.2) $$\begin{array}{c}\hfill D_{0_{+}}^{\mathit{\beta }}g(t):=\frac{\mathrm{d}}{\mathrm{d}t}{J}_{0_{+}}^{1-\mathit{\beta }}g(t)=\frac{1}{\mathrm{\Gamma }(1-\mathit{\beta })}\underset{0}{\overset{t}{\int }}\frac{g(\mathit{\tau })}{{(t-\mathit{\tau })}^{\mathit{\beta }}}\mathrm{d}\mathit{\tau }.\end{array}$$(2.2)

In particular, $D_{0_{+}}^{0}g(t)=g(t)$ and when $\mathit{\beta }\to 1$, $D_{0_{+}}^{\mathit{\beta }}g(t)\to g^{\prime }(t)$. The Riemann–Liouville fractional derivative of a constant is not equal to zero.

The left sided Caputo fractional derivative of order $0<\mathit{\beta }<1$ is(2.3) $$\begin{array}{c}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}g(t):=J_{0_{+}}^{1-\mathit{\beta }}{g}^{\prime }(t)=\frac{1}{\mathrm{\Gamma }(1-\mathit{\beta })}\underset{0}{\overset{t}{\int }}\frac{g^{\prime }(\mathit{\tau })}{{(t-\mathit{\tau })}^{\mathit{\beta }}}\mathrm{d}\mathit{\tau }.\end{array}$$(2.3)

For an absolutely continuous function, the relation between Riemann–Liouville fractional derivative and Caputo fractional derivative is given by the following relation$$D_{0_{+}}^{\mathit{\beta }}(g(t)-g(0)){=}^C{D}_{0_{+}}^{\mathit{\beta }}g(t).$$

In [36], it is proved that the violation of the well-known Leibnitz rule for two differentiable functions is a characteristic of fractional derivatives. For $0<\mathit{\beta }<1$, we have$$J_{0_{+}}^{\mathit{\beta }}{D}_{0_{+}}^{\mathit{\beta }}(g(t)-g(0))=J_{0_{+}}^{\mathit{\beta }}{}^C{D}_{0_{+}}^{\mathit{\beta }}g(t)=g(t)-g(0).$$

The Laplace transforms of the Riemann–Liouville integral and the Riemann–Liouville derivative of order $0<\mathit{\beta }<1$ are(2.4) $$\begin{array}{c}\hfill \mathcal{L}\{J_{0_{+}}^{\mathit{\beta }}g(t)\}=\frac{\mathcal{L}\{g(t)\}}{s^{\mathit{\beta }}},\mathcal{L}\{D_{0_{+}}^{\mathit{\beta }}g(t)\}=\mathcal{L}\{g(t)\}{s}^{\mathit{\beta }}-J_{0_{+}}^{1-\mathit{\beta }}g(0),\end{array}$$(2.4)

respectively, where $\mathcal{L}\{g(t)\}$ is the Laplace transform of the function g(t). The Laplace transform of the Caputo fractional derivative of order $0<\mathit{\beta }<1$ is(2.5) $$\begin{array}{c}\hfill \mathcal{L}{\{}^C{D}_{0_{+}}^{\mathit{\beta }}g(t)\}=\mathcal{L}\{g(t)\}{s}^{\mathit{\beta }}-g(0)s^{\mathit{\beta }-1}.\end{array}$$(2.5)

The Mittag-Leffler function with two parameters $E_{\mathit{\xi },\mathit{\eta }}(z)$, is defined by$$\begin{array}{c}\hfill E_{\mathit{\xi },\mathit{\eta }}(z)=\sum _{k=0}^{+\infty }\frac{z^k}{\mathrm{\Gamma }(\mathit{\xi }k+\mathit{\eta })},(z\in \mathbb{C};Re(\mathit{\eta })>0,Re(\mathit{\xi })>0),\end{array}$$

for $\mathit{\eta }=1$, we have $E_{\mathit{\xi },1}={\sum }_{k=0}^{+\infty }\frac{z^k}{\mathrm{\Gamma }(\mathit{\xi }k+1)}.$ In particular, $E_{1,1}(z)=e^z$.

Let $e_{\mathit{\xi }}(t,\mathit{\mu }):=E_{\mathit{\xi }}(-\mathit{\mu }{t}^{\mathit{\xi }})$ and $e_{\mathit{\xi },\mathit{\eta }}(t,\mathit{\mu }):=t^{\mathit{\eta }-1}{E}_{\mathit{\xi },\mathit{\eta }}(-\mathit{\mu }{t}^{\mathit{\xi }})$, where $\mathit{\mu }$ is a positive real number. The Mittag-Leffler functions $e_{\mathit{\xi }}(t;\mathit{\mu })$ and $e_{\mathit{\xi },\mathit{\eta }}(t;\mathit{\mu })$ for $\mathit{\mu }>0$ and $0<\mathit{\xi }⩽1$, $0<\mathit{\xi }⩽\mathit{\eta }⩽1,$ respectively, are completely monotone functions, i.e.$${(-1)}^n(\frac{{\mathrm{d}}^n}{\mathrm{d}{t}^n})[e_{\mathit{\xi }}(t,\mathit{\mu })]⩾0\text{and}{(-1)}^n(\frac{{\mathrm{d}}^n}{\mathrm{d}{t}^n})[e_{\mathit{\xi },\mathit{\eta }}(t,\mathit{\mu })]⩾0,n\in \mathbb{N}\cup \{0\}.$$

The Mittag-Leffler type functions $e_{\mathit{\xi }}(t,\mathit{\mu }),e_{\mathit{\xi },\mathit{\eta }}(t;\mathit{\mu })$ for $0<\mathit{\xi }⩽1$, $0<\mathit{\xi }⩽\mathit{\eta }⩽1$ respectively, are positive decreasing functions (see [37, Lemma 2, p.3 ]), furthermore the following estimate is available (see [38])(2.6) $$\begin{array}{c}\hfill e_{\mathit{\xi }}(t;\mathit{\mu })\simeq e^{-\mathit{\mu }{t}^{\mathit{\xi }}/\mathrm{\Gamma }(\mathit{\xi }+1)},\text{for}t<<1.\end{array}$$(2.6)

Using Theorem (1.6) in [39], we can have the following estimates(2.7) $$\begin{array}{cc}\hfill \mathit{\lambda }{t}^{\mathit{\xi }}|E_{\mathit{\xi },\mathit{\eta }}(-\mathit{\lambda }{t}^{\mathit{\xi }})|& ⩽M,0<\mathit{\xi }<2,Re(\mathit{\eta })>0,t⩾0,\mathit{\lambda }⩾0,\hfill \end{array}$$(2.7) (2.8) $$\begin{array}{cc}\hfill |\mathit{\lambda }{t}^{\mathit{\xi }-1}{E}_{\mathit{\xi },\mathit{\xi }}(-\mathit{\lambda }{t}^{\mathit{\xi }})|& ⩽\frac{N}{t}\frac{t^{\mathit{\xi }}\mathit{\lambda }}{1+{\mathit{\lambda }}^{\mathit{\xi }}}⩽\frac{N}{t}⩽C,t\in (\mathit{ϵ},T],\hfill \end{array}$$(2.8)

where $\mathit{ϵ}>0,M,N$ and C are some constants.

2.1. Construction of the bi-orthogonal system

The eigenvalues of the boundary value problem (BVP) (1.5(1.5) $$\begin{array}{cc}\hfill X^{{}^{″}}& =-\mathit{\lambda }X,\hfill \end{array}$$(1.5) )–(1.6(1.6) $$\begin{array}{cc}\hfill X(0)=0,& X^{{}^{\prime }}(0)=X^{{}^{\prime }}(1)+\mathit{\alpha }X(1),\hfill \end{array}$$(1.6) ) are$${\mathit{\lambda }}_0={(2y_0)}^2,{\mathit{\lambda }}_k^{(1)}={(2k\mathit{\pi })}^2,{\mathit{\lambda }}_k^{(2)}={(2y_k)}^2,k\in \mathbb{N},$$

where $y_k$ is the solution of the equation $tan(y)=\mathit{\alpha }/2y$ and satisfies the following$$\mathit{\pi }k<y_k<\mathit{\pi }k+\mathit{\pi }/2.$$

The eigenfunctions corresponding to ${\mathit{\lambda }}_0,{\mathit{\lambda }}_k^{(1)}$ and ${\mathit{\lambda }}_k^{(2)}$ are given by(2.9) $$\begin{array}{c}\hfill u_0=sin(2y_{0}x),u_k^{(1)}=sin(2\mathit{\pi }kx),u_k^{(2)}=sin(2y_{k}x),k\in \mathbb{N}.\end{array}$$(2.9)

The eigenvalues of both the spectral problem (1.5(1.5) $$\begin{array}{cc}\hfill X^{{}^{″}}& =-\mathit{\lambda }X,\hfill \end{array}$$(1.5) )–(1.6(1.6) $$\begin{array}{cc}\hfill X(0)=0,& X^{{}^{\prime }}(0)=X^{{}^{\prime }}(1)+\mathit{\alpha }X(1),\hfill \end{array}$$(1.6) ) and adjoint (conjugate) problem (1.7(1.7) $$\begin{array}{cc}\hfill Y^{{}^{″}}& =-\mathit{\lambda }Y,\hfill \end{array}$$(1.7) )–(1.8(1.8) $$\begin{array}{cc}\hfill Y(0)=Y(1),& Y^{{}^{\prime }}(1)+\mathit{\alpha }Y(1)=0.\hfill \end{array}$$(1.8) ) are same. The eigenfunctions of the BVP (1.7(1.7) $$\begin{array}{cc}\hfill Y^{{}^{″}}& =-\mathit{\lambda }Y,\hfill \end{array}$$(1.7) )–(1.8(1.8) $$\begin{array}{cc}\hfill Y(0)=Y(1),& Y^{{}^{\prime }}(1)+\mathit{\alpha }Y(1)=0.\hfill \end{array}$$(1.8) ) are(2.10) $$\begin{array}{cc}\hfill v_0& =C_{0}cos(y_0(1-2x)),\text{for}{\mathit{\lambda }}_0,v_k^{(1)}=C_k^{(1)}cos(2\mathit{\pi }kx+{\mathit{\psi }}_k),\text{for}{\mathit{\lambda }}_k^{(1)},\hfill \\ \hfill v_k^{(2)}& =C_k^{(2)}cos(y_k(1-2x)),\text{for}{\mathit{\lambda }}_k^{(2)},k\in \mathbb{N},\hfill \end{array}$$(2.10)

where$$\begin{array}{cc}\hfill {\mathit{\psi }}_k& =arctan(\frac{\mathit{\alpha }}{2k\mathit{\pi }}),C_0=[0.5sin(y_0)(1+sinc(2y_0)){]}^{-1},\hfill \\ \hfill C_k^{(1)}& =-[0.5sin({\mathit{\psi }}_k){]}^{-1},C_k^{(2)}=[0.5sin(y_k)(1+sinc(2y_k)){]}^{-1},\hfill \end{array}$$

and $sinc(a):=sin(a)/a$.

Notice that the sets $\{u_0,u_k^{(1)},u_k^{(2)}\}$ and $\{v_0,v_k^{(1)},v_k^{(2)}\}$ are not orthogonal, for example$$\begin{array}{cc}\hfill {\int }_0^1{u}_k^{(1)}(x)u_k^{(2)}(x)\mathrm{d}x& =\frac{\mathit{\pi }ksin(2y_k)}{2(y_k^2-{\mathit{\pi }}^2{k}^2)},\hfill \\ \hfill {\int }_0^1{v}_k^{(1)}(x)v_k^{(2)}(x)\mathrm{d}x& =\frac{C_k^{(1)}{C}_k^{(2)}{y}_{k}cos({\mathit{\psi }}_k)sin(y_k)}{y_k^2-{\mathit{\pi }}^2{k}^2}.\hfill \end{array}$$

At this stage let us recall the following Lemma from [5]:

Lemma 2.1:

The set of eigenfunctions of the spectral problem (1.5(1.5) $$\begin{array}{cc}\hfill X^{{}^{″}}& =-\mathit{\lambda }X,\hfill \end{array}$$(1.5) )–(1.6(1.6) $$\begin{array}{cc}\hfill X(0)=0,& X^{{}^{\prime }}(0)=X^{{}^{\prime }}(1)+\mathit{\alpha }X(1),\hfill \end{array}$$(1.6) ) and its adjoint (conjugate) problem (1.7(1.7) $$\begin{array}{cc}\hfill Y^{{}^{″}}& =-\mathit{\lambda }Y,\hfill \end{array}$$(1.7) )–(1.8(1.8) $$\begin{array}{cc}\hfill Y(0)=Y(1),& Y^{{}^{\prime }}(1)+\mathit{\alpha }Y(1)=0.\hfill \end{array}$$(1.8) ) given by (2.9(2.9) $$\begin{array}{c}\hfill u_0=sin(2y_{0}x),u_k^{(1)}=sin(2\mathit{\pi }kx),u_k^{(2)}=sin(2y_{k}x),k\in \mathbb{N}.\end{array}$$(2.9) ) and (2.10(2.10) $$\begin{array}{cc}\hfill v_0& =C_{0}cos(y_0(1-2x)),\text{for}{\mathit{\lambda }}_0,v_k^{(1)}=C_k^{(1)}cos(2\mathit{\pi }kx+{\mathit{\psi }}_k),\text{for}{\mathit{\lambda }}_k^{(1)},\hfill \\ \hfill v_k^{(2)}& =C_k^{(2)}cos(y_k(1-2x)),\text{for}{\mathit{\lambda }}_k^{(2)},k\in \mathbb{N},\hfill \end{array}$$(2.10) ), respectively, are complete sets in the space $L^2[0,1]$ for any $\mathit{\alpha }>0$.

By virtue of the eigenfunctions of the spectral problem (1.5(1.5) $$\begin{array}{cc}\hfill X^{{}^{″}}& =-\mathit{\lambda }X,\hfill \end{array}$$(1.5) )–(1.6(1.6) $$\begin{array}{cc}\hfill X(0)=0,& X^{{}^{\prime }}(0)=X^{{}^{\prime }}(1)+\mathit{\alpha }X(1),\hfill \end{array}$$(1.6) ) and its corresponding conjugate problem (1.7(1.7) $$\begin{array}{cc}\hfill Y^{{}^{″}}& =-\mathit{\lambda }Y,\hfill \end{array}$$(1.7) )–(1.8(1.8) $$\begin{array}{cc}\hfill Y(0)=Y(1),& Y^{{}^{\prime }}(1)+\mathit{\alpha }Y(1)=0.\hfill \end{array}$$(1.8) ), the following sets were constructed in [5](2.11) $$\begin{array}{c}\hfill W_{\mathit{\alpha }}=\{w_k:k\in \mathbb{N}\cup \{0\}\},R_{\mathit{\alpha }}=\{r_k:k\in \mathbb{N}\cup \{0\}\},\end{array}$$(2.11)

where$$\begin{array}{cc}\hfill w_0(x)& :=u_0(x)/2y_0,w_{(2k-1)}(x):=(u_k^{(2)}(x)-u_k^{(1)}(x))/2{\mathit{\delta }}_k,w_{2k}(x):=u_k^{(1)}(x),\hfill \\ \hfill r_0(x)& :=2y_0{v}_0(x),r_{(2k-1)}(x):=2{\mathit{\delta }}_k{v}_k^{(2)}(x),r_{2k}(x):=v_k^{(2)}(x)+v_k^{(1)}(x),\hfill \end{array}$$

and ${\mathit{\delta }}_k=y_k-\mathit{\pi }k,$ furthermore, we have the following estimate$$0<{\mathit{\delta }}_k<\frac{\mathit{\alpha }}{2\mathit{\pi }k},k\in \mathbb{N},$$

see [40, p.60].

For the sets $W_{\mathit{\alpha }}$ and $R_{\mathit{\alpha }}$, we have the following Lemma:

Lemma 2.2:

[see [5]]The sets $W_{\mathit{\alpha }}$ and $R_{\mathit{\alpha }}$ given by (2.11(2.11) $$\begin{array}{c}\hfill W_{\mathit{\alpha }}=\{w_k:k\in \mathbb{N}\cup \{0\}\},R_{\mathit{\alpha }}=\{r_k:k\in \mathbb{N}\cup \{0\}\},\end{array}$$(2.11) ), form Riesz basis in the space $L^2[0,1]$ for any $\mathit{\alpha }>0$.

From the sets $W_{\mathit{\alpha }}$ and $R_{\mathit{\alpha }}$, we can construct a bi-orthogonal system of functions under the following one to one correspondence$$\begin{array}{cc}\hfill \{\underset{\downarrow }{\underbrace{w_0}},& \underset{\downarrow }{\underbrace{w_{2k-1}}},\underset{\downarrow }{\underbrace{w_{2k}}}\},\hfill \\ \hfill \{r_0,& r_{2k-1},r_{2k}\},\hfill \end{array}$$

that is$${\int }_0^1{w}_k(x)r_m(x)\mathrm{d}x=\left\{\begin{array}{cc}1,\hfill & k=m,\hfill \\ 0,\hfill & k\ne m.\hfill \end{array}\right.$$

3. The direct problem

In this section, we are going to present the existence, uniqueness and stability results for the direct problem.

The IBVP (1.1(1.1) $$\begin{array}{c}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}u(x,t)=\mathit{\rho }{u}_{xx}(x,t)+F(x,t),(x,t)\in \mathrm{\Pi },\end{array}$$(1.1) )–(1.3(1.3) $$\begin{array}{c}\hfill u_x(0,t)=u_x(1,t)+\mathit{\alpha }u(1,t),u(0,t)=0,t\in (0,T],\mathit{\alpha }>0,\end{array}$$(1.3) ) is linear, so we can write the solution in the following form$$u(x,t)=s(x,t)+v(x,t),$$

where s(x, t) is the solution of the following homogenous problem(3.1) $$\begin{array}{cc}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}s(x,t)& =\mathit{\rho }{s}_{xx}(x,t),(x,t)\in \mathrm{\Pi },\hfill \end{array}$$(3.1) (3.2) $$\begin{array}{cc}\hfill s(x,0)& =\mathit{\varphi }(x),0<x<1,\hfill \end{array}$$(3.2) (3.3) $$\begin{array}{cc}\hfill s(0,t)& =0,s_x(0,t)=s_x(1,t)+\mathit{\alpha }s(1,t),t>0,\mathit{\alpha }>0,\hfill \end{array}$$(3.3)

and v(x, t) is the solution of the following non-homogenous problem(3.4) $$\begin{array}{cc}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}v(x,t)& =\mathit{\rho }{v}_{xx}(x,t)+F(x,t),(x,t)\in \mathrm{\Pi },\hfill \end{array}$$(3.4) (3.5) $$\begin{array}{cc}\hfill v(x,0)& =0,0<x<1,\hfill \end{array}$$(3.5) (3.6) $$\begin{array}{cc}\hfill v(0,t)& =0,v_x(0,t)=v_x(1,t)+\mathit{\alpha }v(1,t),t>0,\mathit{\alpha }>0.\hfill \end{array}$$(3.6)

Theorem 3.1:

[Classical solution of the direct problem]If $\mathit{\varphi }\in C^2[0,1]$ satisfying the consistency relation with boundary conditions (1.3(1.3) $$\begin{array}{c}\hfill u_x(0,t)=u_x(1,t)+\mathit{\alpha }u(1,t),u(0,t)=0,t\in (0,T],\mathit{\alpha }>0,\end{array}$$(1.3) ), that is, $\mathit{\varphi }(0)=0$ and ${\mathit{\varphi }}^{{}^{\prime }}(0)={\mathit{\varphi }}^{{}^{\prime }}(1)+\mathit{\alpha }\mathit{\varphi }(1)$. Then, there exists a unique classical solution of the IBVP (3.1(3.1) $$\begin{array}{cc}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}s(x,t)& =\mathit{\rho }{s}_{xx}(x,t),(x,t)\in \mathrm{\Pi },\hfill \end{array}$$(3.1) )–(3.3(3.3) $$\begin{array}{cc}\hfill s(0,t)& =0,s_x(0,t)=s_x(1,t)+\mathit{\alpha }s(1,t),t>0,\mathit{\alpha }>0,\hfill \end{array}$$(3.3) ) given by$$\begin{array}{cc}\hfill s(x,t)& ={\mathit{\varphi }}_0{e}_{\mathit{\beta }}(t;{\mathit{\lambda }}_0)\frac{sin(2y_{0}x)}{2y_0}+\sum _{k=1}^{+\infty }[{\mathit{\varphi }}_{2k-1}{e}_{\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(2)})\frac{sin(2y_{k}x)-sin(2k\mathit{\pi }x)}{2{\mathit{\delta }}_k}\hfill \\ \hfill & +\frac{{\mathit{\varphi }}_{2k-1}}{2{\mathit{\delta }}_k}\{e_{\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(2)})-e_{\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(1)})\}sin(2k\mathit{\pi }x)+{\mathit{\varphi }}_{2k}{e}_{\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(1)})sin(2k\mathit{\pi }x)],\hfill \end{array}$$

where(3.7) $$\begin{array}{c}\hfill {\mathit{\varphi }}_0={\int }_0^1\mathit{\varphi }(x)r_0(x)\mathrm{d}x,{\mathit{\varphi }}_{2k-1}={\int }_0^1\mathit{\varphi }(x)r_{2k-1}(x)\mathrm{d}x,{\mathit{\varphi }}_{2k}={\int }_0^1\mathit{\varphi }(x)r_{2k}(x)\mathrm{d}x.\end{array}$$(3.7)

In order to find the solution of the IBVP (3.1(3.1) $$\begin{array}{cc}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}s(x,t)& =\mathit{\rho }{s}_{xx}(x,t),(x,t)\in \mathrm{\Pi },\hfill \end{array}$$(3.1) )–(3.3(3.3) $$\begin{array}{cc}\hfill s(0,t)& =0,s_x(0,t)=s_x(1,t)+\mathit{\alpha }s(1,t),t>0,\mathit{\alpha }>0,\hfill \end{array}$$(3.3) ). We will expand s(x, t) by using the bi-orthogonal system,(3.8) $$\begin{array}{c}\hfill s(x,t)=T_0(t)w_0(x)+\sum _{k=1}^{+\infty }[T_{2k-1}(t)w_{2k-1}(x)+T_{2k}(t)w_{2k}(x)],\end{array}$$(3.8)

where $T_0(t),T_{2k-1}(t)$ and $T_{2k}(t)$ are unknowns to be determined. By using orthogonality condition of the bi-orthogonal system and (3.1(3.1) $$\begin{array}{cc}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}s(x,t)& =\mathit{\rho }{s}_{xx}(x,t),(x,t)\in \mathrm{\Pi },\hfill \end{array}$$(3.1) ), the following system of coupled linear fractional differential equations is obtained(3.9) $$\begin{array}{cc}\hfill {}^C{D}_{0+}^{\mathit{\beta }}{T}_0(t)& =-{\mathit{\lambda }}_0{T}_0(t),\hfill \end{array}$$(3.9) (3.10) $$\begin{array}{cc}\hfill {}^C{D}_{0+}^{\mathit{\beta }}{T}_{2k-1}(t)& =-{\mathit{\lambda }}_k^{(2)}{T}_{2k-1}(t),\hfill \end{array}$$(3.10) (3.11) $$\begin{array}{cc}\hfill {}^C{D}_{0+}^{\mathit{\beta }}{T}_{2k}(t)& =-{\mathit{\lambda }}_k^{(1)}{T}_{2k}(t)+\frac{{\mathit{\lambda }}_k^{(1)}-{\mathit{\lambda }}_k^{(2)}}{2{\mathit{\delta }}_k}{T}_{2k-1}(t).\hfill \end{array}$$(3.11)

By taking Laplace transform on both sides of (3.9(3.9) $$\begin{array}{cc}\hfill {}^C{D}_{0+}^{\mathit{\beta }}{T}_0(t)& =-{\mathit{\lambda }}_0{T}_0(t),\hfill \end{array}$$(3.9) ) (using (2.5(2.5) $$\begin{array}{c}\hfill \mathcal{L}{\{}^C{D}_{0_{+}}^{\mathit{\beta }}g(t)\}=\mathcal{L}\{g(t)\}{s}^{\mathit{\beta }}-g(0)s^{\mathit{\beta }-1}.\end{array}$$(2.5) )), we get$$\mathcal{L}\{T_0(t)\}=\frac{T_0(0)}{s^{\mathit{\beta }}+{\mathit{\lambda }}_0}{s}^{\mathit{\beta }-1}.$$

Applying the inverse Laplace transform on both sides, the solution of (3.9(3.9) $$\begin{array}{cc}\hfill {}^C{D}_{0+}^{\mathit{\beta }}{T}_0(t)& =-{\mathit{\lambda }}_0{T}_0(t),\hfill \end{array}$$(3.9) ) is $T_0(t)=T_0(0)e_{\mathit{\beta }}(t;{\mathit{\lambda }}_0)$. Similarly, the solution of (3.10(3.10) $$\begin{array}{cc}\hfill {}^C{D}_{0+}^{\mathit{\beta }}{T}_{2k-1}(t)& =-{\mathit{\lambda }}_k^{(2)}{T}_{2k-1}(t),\hfill \end{array}$$(3.10) ) and (3.11(3.11) $$\begin{array}{cc}\hfill {}^C{D}_{0+}^{\mathit{\beta }}{T}_{2k}(t)& =-{\mathit{\lambda }}_k^{(1)}{T}_{2k}(t)+\frac{{\mathit{\lambda }}_k^{(1)}-{\mathit{\lambda }}_k^{(2)}}{2{\mathit{\delta }}_k}{T}_{2k-1}(t).\hfill \end{array}$$(3.11) ) are$$\begin{array}{cc}\hfill T_{2k-1}(t)& =T_{2k-1}(0)e_{\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(2)}),\hfill \\ \hfill T_{2k}(t)& =(e_{\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(2)})-e_{\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(1)}))\frac{T_{2k-1}(0)}{2{\mathit{\delta }}_k}+T_{2k}(0)e_{\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(1)}),\hfill \end{array}$$

where $T_0(0),T_{2k-1}(0)$ and $T_{2k}(0)$ are to be determined. By using the initial condition (3.2(3.2) $$\begin{array}{cc}\hfill s(x,0)& =\mathit{\varphi }(x),0<x<1,\hfill \end{array}$$(3.2) ), we have $T_0(0)={\mathit{\varphi }}_0,T_{2k-1}(0)={\mathit{\varphi }}_{2k-1},T_{2k}(0)={\mathit{\varphi }}_{2k},$ where ${\mathit{\varphi }}_0,{\mathit{\varphi }}_{2k-1},$${\mathit{\varphi }}_{2k}$ are the coefficients of the series expansion of initial data $\mathit{\varphi }(x)$ when expanded using the bi-orthogonal system and are given by (3.7(3.7) $$\begin{array}{c}\hfill {\mathit{\varphi }}_0={\int }_0^1\mathit{\varphi }(x)r_0(x)\mathrm{d}x,{\mathit{\varphi }}_{2k-1}={\int }_0^1\mathit{\varphi }(x)r_{2k-1}(x)\mathrm{d}x,{\mathit{\varphi }}_{2k}={\int }_0^1\mathit{\varphi }(x)r_{2k}(x)\mathrm{d}x.\end{array}$$(3.7) ).

From the expressions of ${\mathit{\varphi }}_0,{\mathit{\varphi }}_{2k-1}$ and ${\mathit{\varphi }}_{2k}$ given by (3.7(3.7) $$\begin{array}{c}\hfill {\mathit{\varphi }}_0={\int }_0^1\mathit{\varphi }(x)r_0(x)\mathrm{d}x,{\mathit{\varphi }}_{2k-1}={\int }_0^1\mathit{\varphi }(x)r_{2k-1}(x)\mathrm{d}x,{\mathit{\varphi }}_{2k}={\int }_0^1\mathit{\varphi }(x)r_{2k}(x)\mathrm{d}x.\end{array}$$(3.7) ) and integration by parts gives us$$\begin{array}{cc}\hfill {\mathit{\varphi }}_0& =-\frac{1}{{\mathit{\lambda }}_0}⟨{\mathit{\varphi }}^{{}^{″}}(x),r_0(x)⟩,{\mathit{\varphi }}_{2k-1}=-\frac{1}{{\mathit{\lambda }}_k^{(2)}}⟨{\mathit{\varphi }}^{{}^{″}}(x),r_{2k-1}(x)⟩,\hfill \\ \hfill {\mathit{\varphi }}_{2k}& =-\frac{1}{{\mathit{\lambda }}_k^{(1)}}⟨{\mathit{\varphi }}^{{}^{″}}(x),r_{2k}(x)⟩+\frac{{\mathit{\lambda }}_k^{(2)}-{\mathit{\lambda }}_k^{(1)}}{2{\mathit{\delta }}_k{\mathit{\lambda }}_k^{(1)}{\mathit{\lambda }}_k^{(2)}}⟨{\mathit{\varphi }}^{{}^{″}}(x),r_{2k-1}(x)⟩.\hfill \end{array}$$

Using Cauchy–Schwarz inequality, we have$$\begin{array}{ccc}\hfill |{\mathit{\varphi }}_{2k-1}|& ⩽\hfill & \hfill \frac{1}{{\mathit{\lambda }}_k^{(2)}}\Vert {\mathit{\varphi }}^{{}^{″}}(x)\Vert \Vert r_{2k-1}(x)\Vert ,\\ \hfill |{\mathit{\varphi }}_{2k}|& ⩽\hfill & \hfill \frac{1}{{\mathit{\lambda }}_k^{(1)}}\Vert {\mathit{\varphi }}^{{}^{″}}(x)\Vert \Vert r_{2k}(x)\Vert +|\frac{1}{2{\mathit{\delta }}_k}\frac{{\mathit{\lambda }}_k^{(2)}-{\mathit{\lambda }}_k^{(1)}}{{\mathit{\lambda }}_k^{(1)}{\mathit{\lambda }}_k^{(2)}}|\Vert {\mathit{\varphi }}^{{}^{″}}(x)\Vert \Vert r_{2k-1}(x)\Vert .\end{array}$$

By virtue of the relations$$\frac{1}{{\mathit{\lambda }}_k^{(2)}}⩽\frac{1}{k^2},\frac{1}{{\mathit{\lambda }}_k^{(1)}}⩽\frac{1}{k^2},\frac{{\mathit{\lambda }}_k^{(2)}-{\mathit{\lambda }}_k^{(1)}}{2{\mathit{\delta }}_k{\mathit{\lambda }}_k^{(1)}{\mathit{\lambda }}_k^{(2)}}⩽\frac{3}{8{\mathit{\pi }}^3{k}^3},$$

we have the estimate(3.12) $$\begin{array}{c}\hfill |{\mathit{\varphi }}_k|⩽\frac{D}{k^2}\Vert {\mathit{\varphi }}^{{}^{″}}(x)\Vert ,k\in \mathbb{N},\end{array}$$(3.12)

where D is a constant independent of k.

Existence of the solution of IBVP (3.1(3.1) $$\begin{array}{cc}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}s(x,t)& =\mathit{\rho }{s}_{xx}(x,t),(x,t)\in \mathrm{\Pi },\hfill \end{array}$$(3.1) )–(3.3(3.3) $$\begin{array}{cc}\hfill s(0,t)& =0,s_x(0,t)=s_x(1,t)+\mathit{\alpha }s(1,t),t>0,\mathit{\alpha }>0,\hfill \end{array}$$(3.3) ): The formal solution of the IBVP (3.1(3.1) $$\begin{array}{cc}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}s(x,t)& =\mathit{\rho }{s}_{xx}(x,t),(x,t)\in \mathrm{\Pi },\hfill \end{array}$$(3.1) )–() is given by the series (3.8(3.8) $$\begin{array}{c}\hfill s(x,t)=T_0(t)w_0(x)+\sum _{k=1}^{+\infty }[T_{2k-1}(t)w_{2k-1}(x)+T_{2k}(t)w_{2k}(x)],\end{array}$$(3.8) ), we need to show that the series representations of $s(x,t),s_{xx}(x,t)$ and ${}^C{D}_{0_{+}}^{\mathit{\beta }}s(x,t)$ are uniformly convergent in $\overline{\mathrm{\Pi }}$.

Setting$$\begin{array}{cc}\hfill {\mathcal{S}}_0(x,t)& :={\mathit{\varphi }}_0{e}_{\mathit{\beta }}(t;{\mathit{\lambda }}_0)\frac{sin(2y_{0}x)}{2y_0},\hfill \\ \hfill {\mathcal{S}}_{2k-1}(x,t)& :={\mathit{\varphi }}_{2k-1}{e}_{\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(2)})(\frac{sin(2y_{k}x)-sin(2\mathit{\pi }kx)}{2{\mathit{\delta }}_k}),\hfill \\ \hfill {\mathcal{S}}_{2k}(x,t)& :=\frac{{\mathit{\varphi }}_{2k-1}}{2{\mathit{\delta }}_k}\{e_{\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(2)})-e_{\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(1)})\}sin(2\mathit{\pi }kx)+{\mathit{\varphi }}_{2k}{e}_{\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(1)})sin(2\mathit{\pi }kx),\hfill \end{array}$$

then, the solution of the IBVP (3.1(3.1) $$\begin{array}{cc}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}s(x,t)& =\mathit{\rho }{s}_{xx}(x,t),(x,t)\in \mathrm{\Pi },\hfill \end{array}$$(3.1) )–(3.3(3.3) $$\begin{array}{cc}\hfill s(0,t)& =0,s_x(0,t)=s_x(1,t)+\mathit{\alpha }s(1,t),t>0,\mathit{\alpha }>0,\hfill \end{array}$$(3.3) ) given by (3.8(3.8) $$\begin{array}{c}\hfill s(x,t)=T_0(t)w_0(x)+\sum _{k=1}^{+\infty }[T_{2k-1}(t)w_{2k-1}(x)+T_{2k}(t)w_{2k}(x)],\end{array}$$(3.8) ) becomes(3.13) $$\begin{array}{c}\hfill s(x,t)={\mathcal{S}}_0(x,t)+\sum _{k=1}^{+\infty }[{\mathcal{S}}_{2k}(x,t)+{\mathcal{S}}_{2k-1}(x,t)].\end{array}$$(3.13)

We will show that for any $\mathit{ϵ}>0$, the series given in (3.13(3.13) $$\begin{array}{c}\hfill s(x,t)={\mathcal{S}}_0(x,t)+\sum _{k=1}^{+\infty }[{\mathcal{S}}_{2k}(x,t)+{\mathcal{S}}_{2k-1}(x,t)].\end{array}$$(3.13) ), its second-order space derivative, and the series corresponding to ${}^C{D}_{0_{+}}^{\mathit{\beta }}s(x,t)$ are uniformly convergent in ${\mathrm{\Pi }}_{\mathit{ϵ}}:=(0,1)\times [\mathit{ϵ},T],$ for $T>0$.

Before we present existence of the solution for IBVP (3.1(3.1) $$\begin{array}{cc}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}s(x,t)& =\mathit{\rho }{s}_{xx}(x,t),(x,t)\in \mathrm{\Pi },\hfill \end{array}$$(3.1) )–(3.3(3.3) $$\begin{array}{cc}\hfill s(0,t)& =0,s_x(0,t)=s_x(1,t)+\mathit{\alpha }s(1,t),t>0,\mathit{\alpha }>0,\hfill \end{array}$$(3.3) ), we recall the following Lemma from [5].

Lemma 3.1:

The functions $h_k(t)={(2{\mathit{\delta }}_k)}^{-1}[e^{-{\mathit{\lambda }}_k^{(1)}t}-e^{-{\mathit{\lambda }}_k^{(2)}t}]$ for fixed $\mathit{\alpha }\ne 0$, $k\in \mathbb{N}$, satisfy the inequalities$$0⩽h_k(t)<\frac{E}{k}⩽E,t>0,0⩽h_k(t)<C_{y}k{e}^{-k^2\mathit{ϵ}},t⩾\mathit{ϵ},$$

with a constant E and $C_y$ depending only on the choice of $\mathit{\alpha }$.

Using (3.12(3.12) $$\begin{array}{c}\hfill |{\mathit{\varphi }}_k|⩽\frac{D}{k^2}\Vert {\mathit{\varphi }}^{{}^{″}}(x)\Vert ,k\in \mathbb{N},\end{array}$$(3.12) ) and Lemma 3.1, we have the following estimates(3.14) $$\begin{array}{ccc}\hfill |{\mathcal{S}}_{2k-1}|& ⩽\hfill & \hfill \frac{D\Vert {\mathit{\varphi }}^{{}^{″}}(x)\Vert }{{(2k-1)}^2}{e}_{\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(2)}),\end{array}$$(3.14) (3.15) $$\begin{array}{ccc}\hfill |{\mathcal{S}}_{2k}|& ⩽\hfill & \hfill D\Vert {\mathit{\varphi }}^{{}^{″}}(x)\Vert [\frac{E}{{(2k-1)}^2}+\frac{e_{\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(1)})}{{(2k)}^2}].\end{array}$$(3.15)

From the expression of ${\mathcal{S}}_0(x,t)$, using (2.6(2.6) $$\begin{array}{c}\hfill e_{\mathit{\xi }}(t;\mathit{\mu })\simeq e^{-\mathit{\mu }{t}^{\mathit{\xi }}/\mathrm{\Gamma }(\mathit{\xi }+1)},\text{for}t<<1.\end{array}$$(2.6) ) and $|{\mathit{\varphi }}_0|⩽\mathcal{M},$ for some constant $\mathcal{M}$, we have(3.16) $$\begin{array}{c}\hfill |{\mathcal{S}}_0|⩽\mathcal{M}{e}^{-{\mathit{\lambda }}_0{\mathit{ϵ}}^{\mathit{\beta }}/\mathrm{\Gamma }(\mathit{\beta }+1)}.\end{array}$$(3.16)

Due to completely monotonicitic nature of the Mittag-Leffler type functions and the estimate (2.6(2.6) $$\begin{array}{c}\hfill e_{\mathit{\xi }}(t;\mathit{\mu })\simeq e^{-\mathit{\mu }{t}^{\mathit{\xi }}/\mathrm{\Gamma }(\mathit{\xi }+1)},\text{for}t<<1.\end{array}$$(2.6) ), the inequalities (3.14(3.14) $$\begin{array}{ccc}\hfill |{\mathcal{S}}_{2k-1}|& ⩽\hfill & \hfill \frac{D\Vert {\mathit{\varphi }}^{{}^{″}}(x)\Vert }{{(2k-1)}^2}{e}_{\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(2)}),\end{array}$$(3.14) )–(3.15(3.15) $$\begin{array}{ccc}\hfill |{\mathcal{S}}_{2k}|& ⩽\hfill & \hfill D\Vert {\mathit{\varphi }}^{{}^{″}}(x)\Vert [\frac{E}{{(2k-1)}^2}+\frac{e_{\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(1)})}{{(2k)}^2}].\end{array}$$(3.15) ) become(3.17) $$\begin{array}{ccc}\hfill |{\mathcal{S}}_{2k-1}|& ⩽\hfill & \hfill \frac{D\Vert {\mathit{\varphi }}^{{}^{″}}(x)\Vert }{{(2k-1)}^2}{e}^{-{\mathit{\lambda }}_k^{(2)}{\mathit{ϵ}}^{\mathit{\beta }}/\mathrm{\Gamma }(\mathit{\beta }+1)},\end{array}$$(3.17) (3.18) $$\begin{array}{ccc}\hfill |{\mathcal{S}}_{2k}|& ⩽\hfill & \hfill D\Vert {\mathit{\varphi }}^{{}^{″}}(x)\Vert [\frac{E}{{(2k-1)}^2}+\frac{e^{-{\mathit{\lambda }}_k^{(1)}{\mathit{ϵ}}^{\mathit{\beta }}/\mathrm{\Gamma }(\mathit{\beta }+1)}}{{(2k)}^2}].\end{array}$$(3.18)

By virtue of estimates (3.16(3.16) $$\begin{array}{c}\hfill |{\mathcal{S}}_0|⩽\mathcal{M}{e}^{-{\mathit{\lambda }}_0{\mathit{ϵ}}^{\mathit{\beta }}/\mathrm{\Gamma }(\mathit{\beta }+1)}.\end{array}$$(3.16) )–(3.18(3.18) $$\begin{array}{ccc}\hfill |{\mathcal{S}}_{2k}|& ⩽\hfill & \hfill D\Vert {\mathit{\varphi }}^{{}^{″}}(x)\Vert [\frac{E}{{(2k-1)}^2}+\frac{e^{-{\mathit{\lambda }}_k^{(1)}{\mathit{ϵ}}^{\mathit{\beta }}/\mathrm{\Gamma }(\mathit{\beta }+1)}}{{(2k)}^2}].\end{array}$$(3.18) ), the series in (3.13(3.13) $$\begin{array}{c}\hfill s(x,t)={\mathcal{S}}_0(x,t)+\sum _{k=1}^{+\infty }[{\mathcal{S}}_{2k}(x,t)+{\mathcal{S}}_{2k-1}(x,t)].\end{array}$$(3.13) ) are bounded above by the convergent series and by the Weirstrass M-test these series are uniformly convergent. Consequently, the function s(x, t) given by (3.13(3.13) $$\begin{array}{c}\hfill s(x,t)={\mathcal{S}}_0(x,t)+\sum _{k=1}^{+\infty }[{\mathcal{S}}_{2k}(x,t)+{\mathcal{S}}_{2k-1}(x,t)].\end{array}$$(3.13) ) represents a continuous function.

Similarly, we can have the following estimates(3.19) $$\begin{array}{ccc}\hfill |\frac{{\mathit{\partial }}^2{\mathcal{S}}_0}{\mathit{\partial }{x}^2}|& ⩽\hfill & \hfill \mathit{\pi }\mathcal{M}{e}^{-{\mathit{\lambda }}_0{\mathit{ϵ}}^{\mathit{\beta }}/\mathrm{\Gamma }(\mathit{\beta }+1)},\end{array}$$(3.19) (3.20) $$\begin{array}{ccc}\hfill |\frac{{\mathit{\partial }}^2{\mathcal{S}}_{2k-1}}{\mathit{\partial }{x}^2}|& ⩽\hfill & \hfill \frac{D\mathit{\alpha }\Vert {\mathit{\varphi }}^{{}^{″}}(x)\Vert }{k\mathit{\pi }{(2k-1)}^2}{e}^{-{\mathit{\lambda }}_k^{(2)}{\mathit{ϵ}}^{\mathit{\beta }}/\mathrm{\Gamma }(\mathit{\beta }+1)},\end{array}$$(3.20) (3.21) $$\begin{array}{ccc}\hfill |\frac{{\mathit{\partial }}^2{\mathcal{S}}_{2k}}{\mathit{\partial }{x}^2}|& ⩽\hfill & \hfill D\Vert {\mathit{\varphi }}^{{}^{″}}{(x)\Vert (2\mathit{\pi }k)}^2[\frac{C_{y}k{e}^{-k^2\mathit{ϵ}}}{{(2k-1)}^2}+\frac{e^{-{\mathit{\lambda }}_k^{(2)}{\mathit{ϵ}}^{\mathit{\beta }}/\mathrm{\Gamma }(\mathit{\beta }+1)}}{{(2k)}^2}].\end{array}$$(3.21)

The series expression of $s_{xx}(x,t)$ from (3.13(3.13) $$\begin{array}{c}\hfill s(x,t)={\mathcal{S}}_0(x,t)+\sum _{k=1}^{+\infty }[{\mathcal{S}}_{2k}(x,t)+{\mathcal{S}}_{2k-1}(x,t)].\end{array}$$(3.13) ) is uniformly convergent due to the estimates (3.19(3.19) $$\begin{array}{ccc}\hfill |\frac{{\mathit{\partial }}^2{\mathcal{S}}_0}{\mathit{\partial }{x}^2}|& ⩽\hfill & \hfill \mathit{\pi }\mathcal{M}{e}^{-{\mathit{\lambda }}_0{\mathit{ϵ}}^{\mathit{\beta }}/\mathrm{\Gamma }(\mathit{\beta }+1)},\end{array}$$(3.19) )–(3.21(3.21) $$\begin{array}{ccc}\hfill |\frac{{\mathit{\partial }}^2{\mathcal{S}}_{2k}}{\mathit{\partial }{x}^2}|& ⩽\hfill & \hfill D\Vert {\mathit{\varphi }}^{{}^{″}}{(x)\Vert (2\mathit{\pi }k)}^2[\frac{C_{y}k{e}^{-k^2\mathit{ϵ}}}{{(2k-1)}^2}+\frac{e^{-{\mathit{\lambda }}_k^{(2)}{\mathit{ϵ}}^{\mathit{\beta }}/\mathrm{\Gamma }(\mathit{\beta }+1)}}{{(2k)}^2}].\end{array}$$(3.21) ) and the Weirstrass M-test.

It remains to show that the series corresponding to ${}^C{D}_0^{\mathit{\beta }}s(x,t)$ is also uniformly convergent in $[\mathit{ϵ},T]$. For this we use the following (see [35, p.278, Lemma 15.2 ]):

Let $f_i$ be a sequence of functions defined on $(0,x_1]$ for each $i\in \mathbb{N}$, such that the following two conditions are satisfied:

(1)	for a given $\mathit{\beta }>0$ the fractional derivative ${}^C{D}_{0_{+}}^{\mathit{\beta }}{f}_i(t)$ exists for all $i\in \mathbb{N},$$t\in (0,x_1]$;
(2)	both series ${\sum }_{i=1}^{\infty }{f}_i(t)$ and ${\sum }_{i=1}^{\infty }{}^C{D}_{0_{+}}^{\mathit{\beta }}{f}_i(t)$ are uniformly convergent on the interval $[\mathit{ϵ},x_1]$ for any $\mathit{ϵ}>0$.

Then, ${\sum }_{i=1}^{\infty }{f}_i(t)$ is $\mathit{\beta }$ differentiable, where ${\sum }_{i=1}^{\infty }{f}_i(t)$ is the series of functions and it must satisfy ${}^C{D}_{0_{+}}^{\mathit{\beta }}{\sum }_{i=1}^{\infty }{f}_i(t)={\sum }_{i=1}^{\infty }{}^C{D}_{0_{+}}^{\mathit{\beta }}{f}_i(t)$.

We need to show that ${}^C{D}_{0_{+}}^{\mathit{\beta }}s(x,t)$ is uniformly convergent in $[\mathit{ϵ},T]$. From the series (3.13(3.13) $$\begin{array}{c}\hfill s(x,t)={\mathcal{S}}_0(x,t)+\sum _{k=1}^{+\infty }[{\mathcal{S}}_{2k}(x,t)+{\mathcal{S}}_{2k-1}(x,t)].\end{array}$$(3.13) ) and using ${}^C{D}_{0_{+}}^{\mathit{\beta }}{e}_{\mathit{\beta }}(t;\mathit{\mu })=-\mathit{\mu }{e}_{\mathit{\beta }}(t;\mathit{\mu })$, we have$$\begin{array}{cc}\hfill {}^C{D}_{0+}^{\mathit{\beta }}{\mathcal{S}}_0(x,t)& =-{\mathit{\lambda }}_0{\mathcal{S}}_0(x,t),\hfill \\ \hfill {}^C{D}_{0+}^{\mathit{\beta }}{\mathcal{S}}_{2k-1}(x,t)& =-{\mathit{\lambda }}_k^{(2)}{\mathcal{S}}_{2k-1}(x,t),\hfill \\ \hfill {}^C{D}_{0+}^{\mathit{\beta }}{\mathcal{S}}_{2k}(x,t)& =-{\mathit{\lambda }}_k^{(1)}{\mathcal{S}}_{2k}(x,t)+\frac{{\mathit{\lambda }}_k^{(1)}-{\mathit{\lambda }}_k^{(2)}}{2{\mathit{\delta }}_k}{w}_{2k}(x)T_{2k-1}(t).\hfill \end{array}$$

Using properties of the Mittag-Leffler type functions, the following estimates of fractional derivatives are obtained$$\begin{array}{ccc}\hfill {|}^C{D}_{0+}^{\mathit{\beta }}{\mathcal{S}}_0(x,t)|& ⩽\hfill & \hfill {\mathit{\pi }}^2\Vert {\mathit{\varphi }}_0\Vert e^{-{\mathit{\lambda }}_0{\mathit{ϵ}}^{\mathit{\beta }}/\mathrm{\Gamma }(\mathit{\beta }+1)},\\ \hfill {|}^C{D}_{0+}^{\mathit{\beta }}{\mathcal{S}}_{2k-1}(x,t)|& ⩽\hfill & \hfill 4D{\mathit{\pi }}^2\Vert {\mathit{\varphi }}^{{}^{″}}(x)\Vert e^{-{\mathit{\lambda }}_k^{(2)}{\mathit{ϵ}}^{\mathit{\beta }}/\mathrm{\Gamma }(\mathit{\beta }+1)},k>1,\\ \hfill {|}^C{D}_{0+}^{\mathit{\beta }}{\mathcal{S}}_{2k}(x,t)|& ⩽\hfill & \hfill D\Vert {\mathit{\varphi }}^{{}^{″}}{(x)\Vert (2\mathit{\pi }k)}^2[\frac{C_{y}k{e}^{-k^2\mathit{ϵ}}}{{(2k-1)}^2}+\frac{e^{-{\mathit{\lambda }}_k^{(2)}{\mathit{ϵ}}^{\mathit{\beta }}/\mathrm{\Gamma }(\mathit{\beta }+1)}}{{(2k)}^2}]\\ \hfill & +\frac{16kD\Vert {\mathit{\varphi }}^{{}^{″}}(x)\Vert }{{(2k-1)}^2}{e}^{-{\mathit{\lambda }}_k^{(2)}{\mathit{ϵ}}^{\mathit{\beta }}/\mathrm{\Gamma }(\mathit{\beta }+1)}.\hfill \end{array}$$

The series ${\sum }_{k=1}^{\infty }{}^C{D}_0^{\mathit{\beta }}s(x,t)$ is bounded above by the following convergent series$$\begin{array}{cc}& {\mathit{\pi }}^2\Vert {\mathit{\varphi }}_0\Vert e^{-{\mathit{\lambda }}_0{\mathit{ϵ}}^{\mathit{\beta }}/\mathrm{\Gamma }(\mathit{\beta }+1)}+\sum _{k=1}^{\infty }[5{\mathit{\pi }}^2+\frac{16k}{{(2k-1)}^2}]D\Vert {\mathit{\varphi }}^{{}^{″}}(x)\Vert e^{-{\mathit{\lambda }}_k^{(2)}{\mathit{ϵ}}^{\mathit{\beta }}/\mathrm{\Gamma }(\mathit{\beta }+1)}\hfill \\ \hfill & +\frac{C_{y}k{e}^{-k^2\mathit{ϵ}}}{{(2k-1)}^2}D\Vert {\mathit{\varphi }}^{{}^{″}}(x)\Vert {(2\mathit{\pi }k)}^2.\hfill \end{array}$$

Hence, ${\sum }_{k=1}^{\infty }{}^C{D}_0^{\mathit{\beta }}s(x,t)$ is uniformly convergent.

Uniqueness of the solution of IBVP (3.1(3.1) $$\begin{array}{cc}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}s(x,t)& =\mathit{\rho }{s}_{xx}(x,t),(x,t)\in \mathrm{\Pi },\hfill \end{array}$$(3.1) )–(3.3(3.3) $$\begin{array}{cc}\hfill s(0,t)& =0,s_x(0,t)=s_x(1,t)+\mathit{\alpha }s(1,t),t>0,\mathit{\alpha }>0,\hfill \end{array}$$(3.3) ): Let $\overline{s}(x,t)=s_1(x,t)-s_2(x,t)$, where $s_1(x,t)$ and $s_2(x,t)$ be two solutions of the IBVP (3.1(3.1) $$\begin{array}{cc}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}s(x,t)& =\mathit{\rho }{s}_{xx}(x,t),(x,t)\in \mathrm{\Pi },\hfill \end{array}$$(3.1) )–(3.3(3.3) $$\begin{array}{cc}\hfill s(0,t)& =0,s_x(0,t)=s_x(1,t)+\mathit{\alpha }s(1,t),t>0,\mathit{\alpha }>0,\hfill \end{array}$$(3.3) ). The functions $\overline{u}(x,t)$ satisfy the following system(3.22) $$\begin{array}{cc}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}\overline{s}(x,t)& =\mathit{\rho }{\overline{s}}_{xx}(x,t),(x,t)\in \mathrm{\Pi },\hfill \\ \hfill \overline{s}(x,0)& =0,0<x<1,\hfill \\ \hfill \overline{s}(0,t)& =0,{\overline{s}}_x(0,t)={\overline{s}}_x(1,t)+\mathit{\alpha }\overline{s}(1,t),t>0,\mathit{\alpha }>0,\hfill \end{array}$$(3.22)

Expanding $\overline{s}(x,t)$ in the basis $W_{\mathit{\alpha }}$, the following system of fractional differential equations is obtained$$\begin{array}{cc}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}{\overline{T}}_0(t)& =-{\mathit{\lambda }}_0{\overline{T}}_0(t),\hfill \\ \hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}{\overline{T}}_{2k-1}(t)& =-{\mathit{\lambda }}_k^{(2)}{\overline{T}}_{2k-1}(t),\hfill \\ \hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}{\overline{T}}_{2k}(t)& =-{\mathit{\lambda }}_k^{(1)}{\overline{T}}_{2k}(t)+(\frac{{\mathit{\lambda }}_k^{(1)}-{\mathit{\lambda }}_k^{(2)}}{2{\mathit{\delta }}_k}){\overline{T}}_{2k-1}(t).\hfill \end{array}$$

In view of the initial condition (3.22(3.22) $$\begin{array}{cc}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}\overline{s}(x,t)& =\mathit{\rho }{\overline{s}}_{xx}(x,t),(x,t)\in \mathrm{\Pi },\hfill \\ \hfill \overline{s}(x,0)& =0,0<x<1,\hfill \\ \hfill \overline{s}(0,t)& =0,{\overline{s}}_x(0,t)={\overline{s}}_x(1,t)+\mathit{\alpha }\overline{s}(1,t),t>0,\mathit{\alpha }>0,\hfill \end{array}$$(3.22) ), we have$${\overline{T}}_0(0)=0,{\overline{T}}_{2k-1}(0)=0,{\overline{T}}_{2k}(0)=0,$$

Consequently, $\overline{s}(x,t)=0.$

3.1. Stability of the solution of the direct problem

Setting ${\mathcal{M}}_{\mathit{ϵ}}=max\{e^{-{\mathit{\lambda }}_0{\mathit{ϵ}}^{\mathit{\beta }}/\mathrm{\Gamma }(\mathit{\beta }+1)},e^{-{\mathit{\lambda }}_k^{(1)}{\mathit{ϵ}}^{\mathit{\beta }}/\mathrm{\Gamma }(\mathit{\beta }+1)},e^{-{\mathit{\lambda }}_k^{(2)}{\mathit{ϵ}}^{\mathit{\beta }}/\mathrm{\Gamma }(\mathit{\beta }+1)},E\},$ where E is a constant introduced in Lemma 3.1, we have the following stability result.

Theorem 3.2:

The solution of the IBVP (3.1(3.1) $$\begin{array}{cc}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}s(x,t)& =\mathit{\rho }{s}_{xx}(x,t),(x,t)\in \mathrm{\Pi },\hfill \end{array}$$(3.1) )–(3.3(3.3) $$\begin{array}{cc}\hfill s(0,t)& =0,s_x(0,t)=s_x(1,t)+\mathit{\alpha }s(1,t),t>0,\mathit{\alpha }>0,\hfill \end{array}$$(3.3) ) given by (3.13(3.13) $$\begin{array}{c}\hfill s(x,t)={\mathcal{S}}_0(x,t)+\sum _{k=1}^{+\infty }[{\mathcal{S}}_{2k}(x,t)+{\mathcal{S}}_{2k-1}(x,t)].\end{array}$$(3.13) ), under the assumptions of Theorem 3.1 depends continuously on the initial data.

Let s(x, t) and $\tilde{s}(x,t)$ be the solutions of the IBVP (3.1(3.1) $$\begin{array}{cc}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}s(x,t)& =\mathit{\rho }{s}_{xx}(x,t),(x,t)\in \mathrm{\Pi },\hfill \end{array}$$(3.1) )–(3.3(3.3) $$\begin{array}{cc}\hfill s(0,t)& =0,s_x(0,t)=s_x(1,t)+\mathit{\alpha }s(1,t),t>0,\mathit{\alpha }>0,\hfill \end{array}$$(3.3) ) corresponding to the inital data $\mathit{\varphi }$ and $\tilde{\mathit{\varphi }}$, respectively.

Consider$$\begin{array}{ccc}\hfill |s(x,t)-\tilde{s}(x,t)|& ⩽\hfill & \hfill |e_{\mathit{\beta }}(t;{\mathit{\lambda }}_0)({\mathit{\varphi }}_0-\widetilde{{\mathit{\varphi }}_0})|+\sum _{k=1}^{\infty }[|e_{\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(2)})({\mathit{\varphi }}_{2k-1}-{\tilde{\mathit{\varphi }}}_{2k-1})|\\ \hfill & +|\frac{e_{\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(2)})-e_{\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(1)})}{2{\mathit{\delta }}_k}({\mathit{\varphi }}_{2k-1}-{\tilde{\mathit{\varphi }}}_{2k-1})|\hfill \\ \hfill & +|e_{\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(1)})({\mathit{\varphi }}_{2k}-{\tilde{\mathit{\varphi }}}_{2k})|].\hfill \end{array}$$

By using (2.6(2.6) $$\begin{array}{c}\hfill e_{\mathit{\xi }}(t;\mathit{\mu })\simeq e^{-\mathit{\mu }{t}^{\mathit{\xi }}/\mathrm{\Gamma }(\mathit{\xi }+1)},\text{for}t<<1.\end{array}$$(2.6) ) and Lemma 3.1, we have$$\begin{array}{ccc}\hfill |s(x,t)-\tilde{s}(x,t)|& ⩽\hfill & \hfill |e^{-{\mathit{\lambda }}_0{\mathit{ϵ}}^{\mathit{\beta }}/\mathrm{\Gamma }(\mathit{\beta }+1)}({\mathit{\varphi }}_0-\widetilde{{\mathit{\varphi }}_0})|+\sum _{k=1}^{\infty }|e^{-{\mathit{\lambda }}_k^{(2)}{\mathit{ϵ}}^{\mathit{\beta }}/\mathrm{\Gamma }(\mathit{\beta }+1)}({\mathit{\varphi }}_{2k-1}-{\tilde{\mathit{\varphi }}}_{2k-1})|\\ \hfill & +\sum _{k=1}^{\infty }E|({\mathit{\varphi }}_{2k-1}-{\tilde{\mathit{\varphi }}}_{2k-1})|+\sum _{k=1}^{\infty }|e^{-{\mathit{\lambda }}_k^{(1)}{\mathit{ϵ}}^{\mathit{\beta }}/\mathrm{\Gamma }(\mathit{\beta }+1)}({\mathit{\varphi }}_{2k}-{\tilde{\mathit{\varphi }}}_{2k})|,\hfill \\ \hfill & ⩽\hfill & \hfill {\mathcal{M}}_{\mathit{ϵ}}|{\mathit{\varphi }}_0-{\tilde{\mathit{\varphi }}}_0|+{\mathcal{M}}_{\mathit{ϵ}}\sum _{k=1}^{\infty }|{\mathit{\varphi }}_k-{\tilde{\mathit{\varphi }}}_k|,\\ \hfill & ⩽\hfill & \hfill {\mathcal{M}}_{\mathit{ϵ}}|{\mathit{\varphi }}_0-{\tilde{\mathit{\varphi }}}_0|+\sum _{k=1}^{\infty }{\mathcal{M}}_{\mathit{ϵ}}\frac{D}{k^2}\Vert {\mathit{\varphi }}^{{}^{″}}(x)-{\tilde{\mathit{\varphi }}}^{{}^{″}}(x)\Vert ,\\ \hfill & ⩽\hfill & \hfill \mathcal{N}\Vert \mathit{\varphi }(x)-\tilde{\mathit{\varphi }}(x)\Vert ,\end{array}$$

where $\mathcal{N}$ is a constant independent of k.$$\Vert s(x,t)-\tilde{s}(x,t)\Vert ⩽\mathcal{N}\Vert \mathit{\varphi }(x)-\tilde{\mathit{\varphi }}(x)\Vert .$$

Remark:

For $\mathit{\beta }=1$ the solution of IBVP (3.1(3.1) $$\begin{array}{cc}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}s(x,t)& =\mathit{\rho }{s}_{xx}(x,t),(x,t)\in \mathrm{\Pi },\hfill \end{array}$$(3.1) )–(3.3(3.3) $$\begin{array}{cc}\hfill s(0,t)& =0,s_x(0,t)=s_x(1,t)+\mathit{\alpha }s(1,t),t>0,\mathit{\alpha }>0,\hfill \end{array}$$(3.3) ) given by (3.13(3.13) $$\begin{array}{c}\hfill s(x,t)={\mathcal{S}}_0(x,t)+\sum _{k=1}^{+\infty }[{\mathcal{S}}_{2k}(x,t)+{\mathcal{S}}_{2k-1}(x,t)].\end{array}$$(3.13) ) becomes$$\begin{array}{c}\hfill s(x,t)={\mathit{\varphi }}_0{e}^{-{\mathit{\lambda }}_{0}t}{w}_0(x)+\sum _{k=1}^{\infty }[{\mathit{\varphi }}_{2k-1}{e}^{-{\mathit{\lambda }}_k^{(2)}t}{w}_{2k-1}(x)+({\mathit{\varphi }}_{2k}{e}^{-{\mathit{\lambda }}_k^{(1)}t}-{\mathit{\varphi }}_{2k-1}{(2{\mathit{\delta }}_k)}^{-1}\\ \hfill \{e^{-{\mathit{\lambda }}_k^{(1)}t}-e^{-{\mathit{\lambda }}_k^{(2)}t}\})w_{2k}(x)],\end{array}$$

which was obtained in [5].

The solution of the problem (3.4(3.4) $$\begin{array}{cc}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}v(x,t)& =\mathit{\rho }{v}_{xx}(x,t)+F(x,t),(x,t)\in \mathrm{\Pi },\hfill \end{array}$$(3.4) )–(3.6(3.6) $$\begin{array}{cc}\hfill v(0,t)& =0,v_x(0,t)=v_x(1,t)+\mathit{\alpha }v(1,t),t>0,\mathit{\alpha }>0.\hfill \end{array}$$(3.6) ) can be obtained by using generalized Duhamel’s principle [41,42] and is given by$$v(x,t)={\int }_0^t{u}^v(x,t,\mathit{\tau })\mathrm{d}\mathit{\tau },$$

where $u^v(x,t,\mathit{\tau })$ is the solution of the following system(3.23) $$\begin{array}{cc}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}{u}^v(x,t,\mathit{\tau })& =u_{xx}^v(x,t,\mathit{\tau }),(x,t)\in \mathrm{\Pi },0<\mathit{\tau }⩽t\hfill \end{array}$$(3.23) (3.24) $$\begin{array}{cc}\hfill u^v(x,t,\mathit{\tau }){|}_{t=\mathit{\tau }}& =D_{0_{+}}^{1-\mathit{\beta }}F(x,\mathit{\tau }),0<\mathit{\tau }⩽t\hfill \end{array}$$(3.24) (3.25) $$\begin{array}{cc}\hfill u^v(0,t,\mathit{\tau })=0,u_x^v(0,t,\mathit{\tau })& =u_x^v(1,t,\mathit{\tau })+\mathit{\alpha }{u}^v(1,t,\mathit{\tau }),t>0,\mathit{\alpha }>0,0<\mathit{\tau }⩽t.\hfill \\ \hfill \end{array}$$(3.25)

Following the same strategy, we can obtain the solution of IBVP (3.23(3.23) $$\begin{array}{cc}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}{u}^v(x,t,\mathit{\tau })& =u_{xx}^v(x,t,\mathit{\tau }),(x,t)\in \mathrm{\Pi },0<\mathit{\tau }⩽t\hfill \end{array}$$(3.23) )–(3.25(3.25) $$\begin{array}{cc}\hfill u^v(0,t,\mathit{\tau })=0,u_x^v(0,t,\mathit{\tau })& =u_x^v(1,t,\mathit{\tau })+\mathit{\alpha }{u}^v(1,t,\mathit{\tau }),t>0,\mathit{\alpha }>0,0<\mathit{\tau }⩽t.\hfill \\ \hfill \end{array}$$(3.25) ) which is given by$$\begin{array}{cc}\hfill u^v(x,t,\mathit{\tau })& =e_{\mathit{\beta }}(t;{\mathit{\lambda }}_0)w_0(x)D_{0_{+}}^{1-\mathit{\beta }}{f}_0(\mathit{\tau })+\sum _{k=1}^{+\infty }[e_{\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(2)})w_{2k-1}(x)D_{0_{+}}^{1-\mathit{\beta }}{f}_{2k-1}(\mathit{\tau })\hfill \\ \hfill & +\{(\frac{e_{\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(2)})-e_{\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(1)})}{2{\mathit{\delta }}_k})D_{0_{+}}^{1-\mathit{\beta }}{f}_{2k-1}(\mathit{\tau })+D_{0_{+}}^{1-\mathit{\beta }}{f}_{2k}(\mathit{\tau })e_{\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(1)})\}{w}_{2k}(x)],\hfill \end{array}$$

The second problem is the ISP in which apart from u(x, t), space -dependent source term $F(x,t)=f(x)$ is to be determined.

4. Solution of the inverse problem

In this section, first we shall prove the existence and uniqueness of the ISP. In order to find u(x, t) and f(x), we expand both functions using bi-orthogonal system(4.1) $$\begin{array}{cc}\hfill u(x,t)& =w_0(x)T_0^u(t)+\sum _{k=1}^{+\infty }(w_{2k-1}(x)T_{2k-1}^u(t)+w_{2k}(x)T_{2k}^u(t)),\hfill \end{array}$$(4.1) (4.2) $$\begin{array}{cc}\hfill f(x)& =w_0(x)f_0+\sum _{k=1}^{+\infty }(w_{2k-1}(x)f_{2k-1}+w_{2k}(x)f_{2k}),\hfill \end{array}$$(4.2)

where $T_0^u(t),T_{2k-1}^u(t),T_{2k}^u(t),f_0,f_{2k-1}$ and $f_{2k}$ satisfy the following system of coupled fractional differential equations(4.3) $$\begin{array}{cc}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}{T}_0^u(t)& =-{\mathit{\lambda }}_0{T}_0^u(t)+f_0,\hfill \end{array}$$(4.3) (4.4) $$\begin{array}{cc}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}{T}_{2k-1}^u(t)& =-{\mathit{\lambda }}_k^{(2)}{T}_{2k-1}^u(t)+f_{2k-1},\hfill \end{array}$$(4.4) (4.5) $$\begin{array}{cc}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}{T}_{2k}^u(t)& =-{\mathit{\lambda }}_k^{(1)}{T}_{2k}^u(t)+(\frac{{\mathit{\lambda }}_k^{(1)}-{\mathit{\lambda }}_k^{(2)}}{2{\mathit{\delta }}_k})T_{2k-1}^u(t)+f_{2k}.\hfill \end{array}$$(4.5)

The solutions of (4.3(4.3) $$\begin{array}{cc}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}{T}_0^u(t)& =-{\mathit{\lambda }}_0{T}_0^u(t)+f_0,\hfill \end{array}$$(4.3) )–(4.5(4.5) $$\begin{array}{cc}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}{T}_{2k}^u(t)& =-{\mathit{\lambda }}_k^{(1)}{T}_{2k}^u(t)+(\frac{{\mathit{\lambda }}_k^{(1)}-{\mathit{\lambda }}_k^{(2)}}{2{\mathit{\delta }}_k})T_{2k-1}^u(t)+f_{2k}.\hfill \end{array}$$(4.5) ), using Laplace transform and initial condition (1.2(1.2) $$\begin{array}{c}\hfill u(x,0)=\mathit{\varphi }(x),0<x<1,\end{array}$$(1.2) ), are given by(4.6) $$\begin{array}{cc}\hfill T_0^u(t)& ={\mathit{\varphi }}_0{e}_{\mathit{\beta }}(t;{\mathit{\lambda }}_0)+f_0{e}_{\mathit{\beta },\mathit{\beta }+1}(t;{\mathit{\lambda }}_0),\hfill \end{array}$$(4.6) (4.7) $$\begin{array}{cc}\hfill T_{2k-1}^u(t)& ={\mathit{\varphi }}_{2k-1}{e}_{\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(2)})+f_{2k-1}{e}_{\mathit{\beta },\mathit{\beta }+1}(t;{\mathit{\lambda }}_k^{(2)}),\hfill \end{array}$$(4.7) (4.8) $$\begin{array}{cc}\hfill T_{2k}^u(t)& ={\mathit{\varphi }}_{2k}{e}_{\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(1)})+f_{2k}{e}_{\mathit{\beta },\mathit{\beta }+1}(t;{\mathit{\lambda }}_k^{(1)})+\frac{{\mathit{\lambda }}_k^{(1)}-{\mathit{\lambda }}_k^{(2)}}{2{\mathit{\delta }}_k}({\mathit{\varphi }}_{2k-1}{e}_{\mathit{\beta },\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(1)})\hfill \\ \hfill & \ast e_{\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(2)})+f_{2k-1}{e}_{\mathit{\beta },\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(1)})\ast e_{\mathit{\beta },\mathit{\beta }+1}(t;{\mathit{\lambda }}_k^{(2)})),\hfill \end{array}$$(4.8)

where $\ast$ is the convolution operator.

Due to the overdetermination condition, that is, (1.4(1.4) $$\begin{array}{c}\hfill u(x,T)=\mathit{\psi }(x).\end{array}$$(1.4) ), we have(4.9) $$\begin{array}{cc}\hfill f_0& =\frac{{\mathit{\psi }}_0-{\mathit{\varphi }}_0{e}_{\mathit{\beta }}(T;{\mathit{\lambda }}_0)}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_0)},f_{2k-1}=\frac{{\mathit{\psi }}_{2k-1}-{\mathit{\varphi }}_{2k-1}{e}_{\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(2)})}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(2)})},\hfill \end{array}$$(4.9) (4.10) $$\begin{array}{cc}\hfill f_{2k}& =\frac{{\mathit{\psi }}_{2k}-{\mathit{\varphi }}_{2k}{e}_{\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(1)})}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(1)})}-\frac{{\mathit{\lambda }}_k^{(1)}-{\mathit{\lambda }}_k^{(2)}}{2{\mathit{\delta }}_k{e}_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_0)}({\mathit{\varphi }}_{2k-1}{e}_{\mathit{\beta },\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(1)})\ast e_{\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(2)}))\hfill \\ \hfill & -\frac{{\mathit{\lambda }}_k^{(1)}-{\mathit{\lambda }}_k^{(2)}}{2{\mathit{\delta }}_k{e}_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_0)}(\frac{{\mathit{\psi }}_{2k-1}-{\mathit{\varphi }}_{2k-1}{e}_{\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(2)})}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(2)})})\hfill \\ \hfill & e_{\mathit{\beta },\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(1)})\ast e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(2)}).\hfill \end{array}$$(4.10)

We have the following theorem:

Theorem 4.1:

If $\mathit{\varphi },\mathit{\psi }\in C^2[0,1]$ be such that $\mathit{\varphi }(0)=0,{\mathit{\varphi }}^{{}^{\prime }}(0)={\mathit{\varphi }}^{{}^{\prime }}(1)+\mathit{\alpha }\mathit{\varphi }(1),\mathit{\psi }(0)=0,{\mathit{\psi }}^{{}^{\prime }}(0)={\mathit{\psi }}^{{}^{\prime }}(1)+\mathit{\alpha }\mathit{\psi }(1),$ then, there exists a unique solution of the inverse problem.

First, we are going to show that the solution of ISP given by the series (4.1(4.1) $$\begin{array}{cc}\hfill u(x,t)& =w_0(x)T_0^u(t)+\sum _{k=1}^{+\infty }(w_{2k-1}(x)T_{2k-1}^u(t)+w_{2k}(x)T_{2k}^u(t)),\hfill \end{array}$$(4.1) ) and (4.2(4.2) $$\begin{array}{cc}\hfill f(x)& =w_0(x)f_0+\sum _{k=1}^{+\infty }(w_{2k-1}(x)f_{2k-1}+w_{2k}(x)f_{2k}),\hfill \end{array}$$(4.2) ) is unique. Let $\{u_1(x,t),f_1(x)\}$ and $\{u_2(x,t),f_2(x)\}$ be two solutions of the inverse problem, define $\overline{u}(x,t)=u_1(x,t)-u_2(x,t),\overline{f}(x)=f_1(x)-f_2(x).$ The functions $\overline{u}(x,t)$ and $\overline{f}(x)$ satisfy the following system(4.11) $$\begin{array}{cc}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}\overline{u}(x,t)& ={\overline{u}}_{xx}+\overline{f}(x),(x,t)\in \mathrm{\Pi },\hfill \\ \hfill \overline{u}(x,0)& =0,\overline{u}(x,T)=0,0⩽x⩽1,\hfill \\ \hfill {\overline{u}}_x(0,t)& ={\overline{u}}_x(1,t)+\mathit{\alpha }\overline{u}(1,t),\overline{u}(0,t)=0,t\in (0,T],\mathit{\alpha }>0.\hfill \end{array}$$(4.11)

Expanding $\overline{u}(x,t)$ and $\overline{f}(x)$ in the basis $W_{\mathit{\alpha }}$, we obtain the following system of fractional differential equations$$\begin{array}{cc}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}{\overline{T}}_0^u(t)& =-{\mathit{\lambda }}_0{\overline{T}}_0^u(t)+{\overline{f}}_0,\hfill \\ \hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}{\overline{T}}_{2k-1}^u(t)& =-{\mathit{\lambda }}_k^2{\overline{T}}_{2k-1}^u(t)+{\overline{f}}_{2k-1},\hfill \\ \hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}{\overline{T}}_{2k}^u(t)& =-{\mathit{\lambda }}_k^{(1)}{\overline{T}}_{2k}^u(t)+(\frac{{\mathit{\lambda }}_k^{(1)}-{\mathit{\lambda }}_k^{(2)}}{2{\mathit{\delta }}_k}){\overline{T}}_{2k-1}^u(t)+{\overline{f}}_{2k}.\hfill \end{array}$$

In view of the initial condition and the final temperature condition (4.11(4.11) $$\begin{array}{cc}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}\overline{u}(x,t)& ={\overline{u}}_{xx}+\overline{f}(x),(x,t)\in \mathrm{\Pi },\hfill \\ \hfill \overline{u}(x,0)& =0,\overline{u}(x,T)=0,0⩽x⩽1,\hfill \\ \hfill {\overline{u}}_x(0,t)& ={\overline{u}}_x(1,t)+\mathit{\alpha }\overline{u}(1,t),\overline{u}(0,t)=0,t\in (0,T],\mathit{\alpha }>0.\hfill \end{array}$$(4.11) ), we have$${\overline{T}}_0^u(0)=0={\overline{T}}_0^u(T),{\overline{T}}_{2k-1}^u(0)=0={\overline{T}}_{2k-1}^u(T),{\overline{T}}_{2k}^u(0)=0={\overline{T}}_{2k}^u(T),$$

and$${\overline{f}}_0=0,{\overline{f}}_{2k-1}=0,{\overline{f}}_{2k}=0,\Rightarrow \overline{f}(x)=0.$$

Consequently, $\overline{u}(x,t)=0.$

Existence of the solution of the inverse problem: We will show that the series corresponding to $u(x,t),u_{xx}(x,t),$${}^C{D}_{0_{+}}^{\mathit{\beta }}u(x,t)$, and f(x) are uniformly convergent. Under the assumptions of Theorem 4.1 and integration by parts, we have(4.12) $$\begin{array}{cc}\hfill {\mathit{\psi }}_0& =-\frac{1}{{\mathit{\lambda }}_0}⟨{\mathit{\psi }}_{xx}(x),r_0(x)⟩,{\mathit{\psi }}_{2k-1}=-\frac{1}{{\mathit{\lambda }}_k^{(2)}}⟨{\mathit{\psi }}_{xx}(x),r_{2k-1}(x)⟩,\hfill \end{array}$$(4.12) (4.13) $$\begin{array}{cc}\hfill {\mathit{\psi }}_{2k}& =-\frac{1}{{\mathit{\lambda }}_k^{(1)}}⟨{\mathit{\psi }}_{xx}(x),r_{2k}(x)⟩+\frac{1}{2{\mathit{\delta }}_k}\frac{{\mathit{\lambda }}_k^{(2)}-{\mathit{\lambda }}_k^{(1)}}{{\mathit{\lambda }}_k^{(1)}{\mathit{\lambda }}_k^{(2)}}⟨{\mathit{\psi }}_{xx}(x),r_{2k-1}(x)⟩,\hfill \end{array}$$(4.13)

where ${\mathit{\psi }}_0,{\mathit{\psi }}_{2k},{\mathit{\psi }}_{2k-1}$ are the coefficients of $\mathit{\psi }(x)$, when expanded using bi-orthogonal system of functions. Let us mention that we have obtained similar expressions for $\mathit{\varphi }(x)$ in (3.12(3.12) $$\begin{array}{c}\hfill |{\mathit{\varphi }}_k|⩽\frac{D}{k^2}\Vert {\mathit{\varphi }}^{{}^{″}}(x)\Vert ,k\in \mathbb{N},\end{array}$$(3.12) ). From here onwards $c_i$, $i=0,1,\dots ,17$, represent constants independent of k unless mentioned otherwise.

The expressions of $f_0,f_{2k-1}$, $f_{2k}$ from (4.9(4.9) $$\begin{array}{cc}\hfill f_0& =\frac{{\mathit{\psi }}_0-{\mathit{\varphi }}_0{e}_{\mathit{\beta }}(T;{\mathit{\lambda }}_0)}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_0)},f_{2k-1}=\frac{{\mathit{\psi }}_{2k-1}-{\mathit{\varphi }}_{2k-1}{e}_{\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(2)})}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(2)})},\hfill \end{array}$$(4.9) )–(4.10(4.10) $$\begin{array}{cc}\hfill f_{2k}& =\frac{{\mathit{\psi }}_{2k}-{\mathit{\varphi }}_{2k}{e}_{\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(1)})}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(1)})}-\frac{{\mathit{\lambda }}_k^{(1)}-{\mathit{\lambda }}_k^{(2)}}{2{\mathit{\delta }}_k{e}_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_0)}({\mathit{\varphi }}_{2k-1}{e}_{\mathit{\beta },\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(1)})\ast e_{\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(2)}))\hfill \\ \hfill & -\frac{{\mathit{\lambda }}_k^{(1)}-{\mathit{\lambda }}_k^{(2)}}{2{\mathit{\delta }}_k{e}_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_0)}(\frac{{\mathit{\psi }}_{2k-1}-{\mathit{\varphi }}_{2k-1}{e}_{\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(2)})}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(2)})})\hfill \\ \hfill & e_{\mathit{\beta },\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(1)})\ast e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(2)}).\hfill \end{array}$$(4.10) ), and using properties of Mittag-Leffler type functions (2.6(2.6) $$\begin{array}{c}\hfill e_{\mathit{\xi }}(t;\mathit{\mu })\simeq e^{-\mathit{\mu }{t}^{\mathit{\xi }}/\mathrm{\Gamma }(\mathit{\xi }+1)},\text{for}t<<1.\end{array}$$(2.6) )–(2.8(2.8) $$\begin{array}{cc}\hfill |\mathit{\lambda }{t}^{\mathit{\xi }-1}{E}_{\mathit{\xi },\mathit{\xi }}(-\mathit{\lambda }{t}^{\mathit{\xi }})|& ⩽\frac{N}{t}\frac{t^{\mathit{\xi }}\mathit{\lambda }}{1+{\mathit{\lambda }}^{\mathit{\xi }}}⩽\frac{N}{t}⩽C,t\in (\mathit{ϵ},T],\hfill \end{array}$$(2.8) ), the following estimates are obtained(4.14) $$\begin{array}{ccc}\hfill |f_0|& ⩽\hfill & \hfill c_0,\end{array}$$(4.14) (4.15) $$\begin{array}{ccc}\hfill |f_{2k-1}|& ⩽\hfill & \hfill \frac{c_1}{k^2}(1+e^{-\frac{{\mathit{\lambda }}_k^{(2)}{T}^{\mathit{\beta }}}{\mathrm{\Gamma }(\mathit{\beta }+1)}}),\end{array}$$(4.15) (4.16) $$\begin{array}{ccc}\hfill |f_{2k}|& ⩽\hfill & \hfill \frac{c_2}{k^2}(1+e^{-\frac{{\mathit{\lambda }}_k^{(1)}{T}^{\mathit{\beta }}}{\mathrm{\Gamma }(\mathit{\beta }+1)}})+T\frac{c_3}{k^3}(1+e^{-\frac{{\mathit{\lambda }}_k^{(2)}{T}^{\mathit{\beta }}}{\mathrm{\Gamma }(\mathit{\beta }+1)}}).\end{array}$$(4.16)

The following relations are used to get the estimates (4.15(4.15) $$\begin{array}{ccc}\hfill |f_{2k-1}|& ⩽\hfill & \hfill \frac{c_1}{k^2}(1+e^{-\frac{{\mathit{\lambda }}_k^{(2)}{T}^{\mathit{\beta }}}{\mathrm{\Gamma }(\mathit{\beta }+1)}}),\end{array}$$(4.15) ) and (4.16(4.16) $$\begin{array}{ccc}\hfill |f_{2k}|& ⩽\hfill & \hfill \frac{c_2}{k^2}(1+e^{-\frac{{\mathit{\lambda }}_k^{(1)}{T}^{\mathit{\beta }}}{\mathrm{\Gamma }(\mathit{\beta }+1)}})+T\frac{c_3}{k^3}(1+e^{-\frac{{\mathit{\lambda }}_k^{(2)}{T}^{\mathit{\beta }}}{\mathrm{\Gamma }(\mathit{\beta }+1)}}).\end{array}$$(4.16) )$$\frac{1}{{\mathit{\lambda }}_k^{(2)}}⩽\frac{1}{k^2},\frac{1}{{\mathit{\lambda }}_k^{(1)}}⩽\frac{1}{k^2},\frac{{\mathit{\lambda }}_k^{(2)}-{\mathit{\lambda }}_k^{(1)}}{2{\mathit{\delta }}_k}⩽16k,\frac{{\mathit{\lambda }}_k^{(2)}-{\mathit{\lambda }}_k^{(1)}}{{\mathit{\lambda }}_k^{(1)}{\mathit{\lambda }}_k^{(2)}}⩽\frac{4}{k^4}.$$

Setting$$u_0(x,t)=w_0(x)T_0^u(t),u_{2k-1}(x,t)=w_{2k-1}(x)T_{2k-1}^u(t),u_{2k}(x,t)=w_{2k}(x)T_{2k}^u(t),$$

where $T_0^u(t),T_{2k-1}^u(t)$ and $T_{2k}^u(t)$ are given by (4.6(4.6) $$\begin{array}{cc}\hfill T_0^u(t)& ={\mathit{\varphi }}_0{e}_{\mathit{\beta }}(t;{\mathit{\lambda }}_0)+f_0{e}_{\mathit{\beta },\mathit{\beta }+1}(t;{\mathit{\lambda }}_0),\hfill \end{array}$$(4.6) )–(4.8(4.8) $$\begin{array}{cc}\hfill T_{2k}^u(t)& ={\mathit{\varphi }}_{2k}{e}_{\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(1)})+f_{2k}{e}_{\mathit{\beta },\mathit{\beta }+1}(t;{\mathit{\lambda }}_k^{(1)})+\frac{{\mathit{\lambda }}_k^{(1)}-{\mathit{\lambda }}_k^{(2)}}{2{\mathit{\delta }}_k}({\mathit{\varphi }}_{2k-1}{e}_{\mathit{\beta },\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(1)})\hfill \\ \hfill & \ast e_{\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(2)})+f_{2k-1}{e}_{\mathit{\beta },\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(1)})\ast e_{\mathit{\beta },\mathit{\beta }+1}(t;{\mathit{\lambda }}_k^{(2)})),\hfill \end{array}$$(4.8) ), then (4.1(4.1) $$\begin{array}{cc}\hfill u(x,t)& =w_0(x)T_0^u(t)+\sum _{k=1}^{+\infty }(w_{2k-1}(x)T_{2k-1}^u(t)+w_{2k}(x)T_{2k}^u(t)),\hfill \end{array}$$(4.1) ) becomes(4.17) $$\begin{array}{c}\hfill u(x,t)=u_0(x,t)+\sum _{k=1}^{\infty }{u}_{2k-1}(x,t)+\sum _{k=1}^{\infty }{u}_{2k}(x,t).\end{array}$$(4.17)

By virtue of (2.6(2.6) $$\begin{array}{c}\hfill e_{\mathit{\xi }}(t;\mathit{\mu })\simeq e^{-\mathit{\mu }{t}^{\mathit{\xi }}/\mathrm{\Gamma }(\mathit{\xi }+1)},\text{for}t<<1.\end{array}$$(2.6) )–(2.8(2.8) $$\begin{array}{cc}\hfill |\mathit{\lambda }{t}^{\mathit{\xi }-1}{E}_{\mathit{\xi },\mathit{\xi }}(-\mathit{\lambda }{t}^{\mathit{\xi }})|& ⩽\frac{N}{t}\frac{t^{\mathit{\xi }}\mathit{\lambda }}{1+{\mathit{\lambda }}^{\mathit{\xi }}}⩽\frac{N}{t}⩽C,t\in (\mathit{ϵ},T],\hfill \end{array}$$(2.8) ) and the estimates of $f_0,f_{2k-1},f_{2k},$ from (4.14(4.14) $$\begin{array}{ccc}\hfill |f_0|& ⩽\hfill & \hfill c_0,\end{array}$$(4.14) )–(4.16(4.16) $$\begin{array}{ccc}\hfill |f_{2k}|& ⩽\hfill & \hfill \frac{c_2}{k^2}(1+e^{-\frac{{\mathit{\lambda }}_k^{(1)}{T}^{\mathit{\beta }}}{\mathrm{\Gamma }(\mathit{\beta }+1)}})+T\frac{c_3}{k^3}(1+e^{-\frac{{\mathit{\lambda }}_k^{(2)}{T}^{\mathit{\beta }}}{\mathrm{\Gamma }(\mathit{\beta }+1)}}).\end{array}$$(4.16) ), we have(4.18) $$\begin{array}{ccc}\hfill |u_0(x,t)|& ⩽\hfill & \hfill \mathcal{M}{e}^{-\frac{{\mathit{\lambda }}_0{\mathit{ϵ}}^{\mathit{\beta }}}{\mathrm{\Gamma }(\mathit{\beta }+1)}}+c_0{e}_{\mathit{\beta },\mathit{\beta }+1}(t;{\mathit{\lambda }}_0),\end{array}$$(4.18) (4.19) $$\begin{array}{ccc}\hfill |u_{2k-1}(x,t)|& ⩽\hfill & \hfill \frac{c_4}{k^2}(1+e^{-\frac{{\mathit{\lambda }}_k^{(2)}\mathit{ϵ}{}^{\mathit{\beta }}}{\mathrm{\Gamma }(\mathit{\beta }+1)}}),\end{array}$$(4.19) (4.20) $$\begin{array}{ccc}\hfill |u_{2k}(x,t)|& ⩽\hfill & \hfill \frac{c_5}{k^2}{e}^{-\frac{{\mathit{\lambda }}_k^{(1)}\mathit{ϵ}{}^{\mathit{\beta }}}{\mathrm{\Gamma }(\mathit{\beta }+1)}}+\frac{c_6}{k^2}(1+e^{-\frac{{\mathit{\lambda }}_k^{(2)}{T}^{\mathit{\beta }}}{\mathrm{\Gamma }(\mathit{\beta }+1)}}).\end{array}$$(4.20)

Due to the estimates (4.18(4.18) $$\begin{array}{ccc}\hfill |u_0(x,t)|& ⩽\hfill & \hfill \mathcal{M}{e}^{-\frac{{\mathit{\lambda }}_0{\mathit{ϵ}}^{\mathit{\beta }}}{\mathrm{\Gamma }(\mathit{\beta }+1)}}+c_0{e}_{\mathit{\beta },\mathit{\beta }+1}(t;{\mathit{\lambda }}_0),\end{array}$$(4.18) )–(4.20(4.20) $$\begin{array}{ccc}\hfill |u_{2k}(x,t)|& ⩽\hfill & \hfill \frac{c_5}{k^2}{e}^{-\frac{{\mathit{\lambda }}_k^{(1)}\mathit{ϵ}{}^{\mathit{\beta }}}{\mathrm{\Gamma }(\mathit{\beta }+1)}}+\frac{c_6}{k^2}(1+e^{-\frac{{\mathit{\lambda }}_k^{(2)}{T}^{\mathit{\beta }}}{\mathrm{\Gamma }(\mathit{\beta }+1)}}).\end{array}$$(4.20) ), the series in (4.17(4.17) $$\begin{array}{c}\hfill u(x,t)=u_0(x,t)+\sum _{k=1}^{\infty }{u}_{2k-1}(x,t)+\sum _{k=1}^{\infty }{u}_{2k}(x,t).\end{array}$$(4.17) ) are bounded above by uniformly convergent numerical series. Hence, by Weierstrass M-test, the series in (4.17(4.17) $$\begin{array}{c}\hfill u(x,t)=u_0(x,t)+\sum _{k=1}^{\infty }{u}_{2k-1}(x,t)+\sum _{k=1}^{\infty }{u}_{2k}(x,t).\end{array}$$(4.17) ) are uniformly convergent.

The series corresponding to $u_{xx}(x,t)$ is uniformly convergent due to the following estimates$$\begin{array}{ccc}\hfill |\frac{{\mathit{\partial }}^2{u}_{2k-1}}{\mathit{\partial }{x}^2}|& ⩽\hfill & \hfill c_7{e}^{-\frac{{\mathit{\lambda }}_k^{(2)}\mathit{ϵ}{}^{\mathit{\beta }}}{\mathrm{\Gamma }(\mathit{\beta }+1)}}(1+\frac{1}{k^2})+\frac{c_8}{k^2},\\ \hfill |\frac{{\mathit{\partial }}^2{u}_{2k}}{\mathit{\partial }{x}^2}|& ⩽\hfill & \hfill c_9{e}^{-\frac{{\mathit{\lambda }}_k^{(1)}\mathit{ϵ}{}^{\mathit{\beta }}}{\mathrm{\Gamma }(\mathit{\beta }+1)}}+c_{10}{e}^{-\frac{{\mathit{\lambda }}_k^{(2)}\mathit{ϵ}{}^{\mathit{\beta }}}{\mathrm{\Gamma }(\mathit{\beta }+1)}}+\frac{c_{11}}{k^2}.\end{array}$$

It remains to show that the series corresponding to ${}^C{D}_{0_{+}}^{\mathit{\beta }}{u}_{(}x,t)$ is uniformly convergent on ${\mathrm{\Pi }}_{\mathit{ϵ}}:=[\mathit{ϵ},T]\times (0,1)$. By virtue of (2.6(2.6) $$\begin{array}{c}\hfill e_{\mathit{\xi }}(t;\mathit{\mu })\simeq e^{-\mathit{\mu }{t}^{\mathit{\xi }}/\mathrm{\Gamma }(\mathit{\xi }+1)},\text{for}t<<1.\end{array}$$(2.6) )–(2.8(2.8) $$\begin{array}{cc}\hfill |\mathit{\lambda }{t}^{\mathit{\xi }-1}{E}_{\mathit{\xi },\mathit{\xi }}(-\mathit{\lambda }{t}^{\mathit{\xi }})|& ⩽\frac{N}{t}\frac{t^{\mathit{\xi }}\mathit{\lambda }}{1+{\mathit{\lambda }}^{\mathit{\xi }}}⩽\frac{N}{t}⩽C,t\in (\mathit{ϵ},T],\hfill \end{array}$$(2.8) ), and (4.15(4.15) $$\begin{array}{ccc}\hfill |f_{2k-1}|& ⩽\hfill & \hfill \frac{c_1}{k^2}(1+e^{-\frac{{\mathit{\lambda }}_k^{(2)}{T}^{\mathit{\beta }}}{\mathrm{\Gamma }(\mathit{\beta }+1)}}),\end{array}$$(4.15) )–(4.16(4.16) $$\begin{array}{ccc}\hfill |f_{2k}|& ⩽\hfill & \hfill \frac{c_2}{k^2}(1+e^{-\frac{{\mathit{\lambda }}_k^{(1)}{T}^{\mathit{\beta }}}{\mathrm{\Gamma }(\mathit{\beta }+1)}})+T\frac{c_3}{k^3}(1+e^{-\frac{{\mathit{\lambda }}_k^{(2)}{T}^{\mathit{\beta }}}{\mathrm{\Gamma }(\mathit{\beta }+1)}}).\end{array}$$(4.16) ), we have the following estimates(4.21) $$\begin{array}{ccc}\hfill {|}^C{D}_{0_{+}}^{\mathit{\beta }}{u}_0(x,t)|& ⩽\hfill & \hfill {\mathit{\pi }}^2[\Vert {\mathit{\varphi }}_0\Vert e^{-\frac{{\mathit{\lambda }}_0{\mathit{ϵ}}^{\mathit{\beta }}}{\mathrm{\Gamma }(\mathit{\beta }+1)}}+\frac{c_{12}}{k^2}]+c_0,\end{array}$$(4.21) (4.22) $$\begin{array}{ccc}\hfill {|}^C{D}_{0_{+}}^{\mathit{\beta }}{u}_{2k-1}(x,t)|& ⩽\hfill & \hfill c_{13}{e}^{-\frac{{\mathit{\lambda }}_k^{(2)}{\mathit{ϵ}}^{\mathit{\beta }}}{\mathrm{\Gamma }(\mathit{\beta }+1)}}+\frac{c_{14}}{k^2}(1+e^{-\frac{{\mathit{\lambda }}_k^{(2)}{T}^{\mathit{\beta }}}{\mathrm{\Gamma }(\mathit{\beta }+1)}}),\end{array}$$(4.22) (4.23) $$\begin{array}{ccc}\hfill {|}^C{D}_{0_{+}}^{\mathit{\beta }}{u}_{2k}(x,t)|& ⩽\hfill & \hfill c_{15}{e}^{\frac{-{\mathit{\lambda }}_k^{(1)}{\mathit{ϵ}}^{\mathit{\beta }}}{\mathrm{\Gamma }(\mathit{\beta }+1)}}+c_{16}{e}^{\frac{-{\mathit{\lambda }}_k^{(2)}{\mathit{ϵ}}^{\mathit{\beta }}}{\mathrm{\Gamma }(\mathit{\beta }+1)}}+\frac{c_{17}}{k^2}.\end{array}$$(4.23)

Due to the estimates (4.21(4.21) $$\begin{array}{ccc}\hfill {|}^C{D}_{0_{+}}^{\mathit{\beta }}{u}_0(x,t)|& ⩽\hfill & \hfill {\mathit{\pi }}^2[\Vert {\mathit{\varphi }}_0\Vert e^{-\frac{{\mathit{\lambda }}_0{\mathit{ϵ}}^{\mathit{\beta }}}{\mathrm{\Gamma }(\mathit{\beta }+1)}}+\frac{c_{12}}{k^2}]+c_0,\end{array}$$(4.21) )–(4.23(4.23) $$\begin{array}{ccc}\hfill {|}^C{D}_{0_{+}}^{\mathit{\beta }}{u}_{2k}(x,t)|& ⩽\hfill & \hfill c_{15}{e}^{\frac{-{\mathit{\lambda }}_k^{(1)}{\mathit{ϵ}}^{\mathit{\beta }}}{\mathrm{\Gamma }(\mathit{\beta }+1)}}+c_{16}{e}^{\frac{-{\mathit{\lambda }}_k^{(2)}{\mathit{ϵ}}^{\mathit{\beta }}}{\mathrm{\Gamma }(\mathit{\beta }+1)}}+\frac{c_{17}}{k^2}.\end{array}$$(4.23) ) the series corresponding to the fractional derivative ${}^C{D}_{0_{+}}^{\mathit{\beta }}u(x,t)$ is uniformly convergent.

4.1. Stability of the solution of the inverse problem

In this subsection $a_i$’s, $i=1,2,\dots ,12$, $b_0,b_1,b_2$ are constants independent of k. Let us give some useful estimates, by properties of Mittag-Leffler function we can have(4.24) $$\begin{array}{c}\hfill \left.\begin{array}{cc}\frac{e_{\mathit{\beta },\mathit{\beta }+1}(t;{\mathit{\lambda }}_k^{(i)})}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(i)})}⩽\frac{a_i}{k^2},e_{\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(j)})\frac{e_{\mathit{\beta },\mathit{\beta }+1}(t;{\mathit{\lambda }}_k^{(j)})}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(j)})}⩽\frac{b_j}{k^4}& i,j=0,1,2,3\\ {\int }_0^t{e}_{\mathit{\beta },\mathit{\beta }}(\mathit{\tau };{\mathit{\lambda }}_k^{(1)})e_{\mathit{\beta },\mathit{\beta }+1}(t-\mathit{\tau };{\mathit{\lambda }}_k^{(2)})\mathrm{d}\mathit{\tau }⩽\frac{MC}{k^4}T.\end{array}\right\}\end{array}$$(4.24)

By virtue of (4.24(4.24) $$\begin{array}{c}\hfill \left.\begin{array}{cc}\frac{e_{\mathit{\beta },\mathit{\beta }+1}(t;{\mathit{\lambda }}_k^{(i)})}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(i)})}⩽\frac{a_i}{k^2},e_{\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(j)})\frac{e_{\mathit{\beta },\mathit{\beta }+1}(t;{\mathit{\lambda }}_k^{(j)})}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(j)})}⩽\frac{b_j}{k^4}& i,j=0,1,2,3\\ {\int }_0^t{e}_{\mathit{\beta },\mathit{\beta }}(\mathit{\tau };{\mathit{\lambda }}_k^{(1)})e_{\mathit{\beta },\mathit{\beta }+1}(t-\mathit{\tau };{\mathit{\lambda }}_k^{(2)})\mathrm{d}\mathit{\tau }⩽\frac{MC}{k^4}T.\end{array}\right\}\end{array}$$(4.24) ) we have the following estimates(4.25) $$\begin{array}{c}\hfill \left.\begin{array}{ccc}\hfill \frac{{\mathit{\lambda }}_k^{(2)}-{\mathit{\lambda }}_k^{(1)}}{2{\mathit{\delta }}_k}({\int }_0^t{e}_{\mathit{\beta },\mathit{\beta }}(\mathit{\tau };{\mathit{\lambda }}_k^{(1)})e_{\mathit{\beta },\mathit{\beta }+1}(t-\mathit{\tau };{\mathit{\lambda }}_k^{(2)})\mathrm{d}\mathit{\tau })\frac{e_{\mathit{\beta },\mathit{\beta }+1}(t;{\mathit{\lambda }}_k^{(1)})}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(1)})}& ⩽\hfill & \hfill \frac{a_3}{k^5},\\ \hfill \frac{{\mathit{\lambda }}_k^{(2)}-{\mathit{\lambda }}_k^{(1)}}{2{\mathit{\delta }}_k}(\frac{{\int }_0^t{e}_{\mathit{\beta },\mathit{\beta }}(\mathit{\tau };{\mathit{\lambda }}_k^{(1)})e_{\mathit{\beta },\mathit{\beta }+1}(t-\mathit{\tau };{\mathit{\lambda }}_k^{(2)})\mathrm{d}\mathit{\tau }}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(2)})})& ⩽\hfill & \hfill \frac{a_4}{k^3},\\ \hfill \frac{{\mathit{\lambda }}_k^{(2)}-{\mathit{\lambda }}_k^{(1)}}{2{\mathit{\delta }}_k}(\frac{{\int }_0^t{e}_{\mathit{\beta },\mathit{\beta }}(\mathit{\tau };{\mathit{\lambda }}_k^{(1)})e_{\mathit{\beta },\mathit{\beta }+1}(t-\mathit{\tau };{\mathit{\lambda }}_k^{(2)})\mathrm{d}\mathit{\tau }}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(2)})})e_{\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(1)})& ⩽\hfill & \hfill \frac{a_5}{k^5},\\ \hfill \frac{{\mathit{\lambda }}_k^{(2)}-{\mathit{\lambda }}_k^{(1)}}{2{\mathit{\delta }}_k}({\int }_0^t{e}_{\mathit{\beta },\mathit{\beta }}(\mathit{\tau };{\mathit{\lambda }}_k^{(1)})e_{\mathit{\beta }}(t-\mathit{\tau };{\mathit{\lambda }}_k^{(2)})\mathrm{d}\mathit{\tau })& ⩽\hfill & \hfill \frac{a_6}{k^2}.\end{array}\right\}\end{array}$$(4.25)

Theorem 4.2:

For any $\mathit{\varphi }$ and $\mathit{\psi }$ satisfying the assumptions of Theorem 4.1, the solution of the inverse problem depends continuously on the given data.

Let $\{f(x),u(x,t)\}$ and $\{\tilde{f}(x),\tilde{u}(x,t)\}$ be the two solution sets of the inverse problem corresponding to the data $\{\mathit{\varphi }(x),\mathit{\psi }(x)\}$ and $\{\tilde{\mathit{\varphi }}(x),\tilde{\mathit{\psi }}(x)\}$, respectively. From (4.17(4.17) $$\begin{array}{c}\hfill u(x,t)=u_0(x,t)+\sum _{k=1}^{\infty }{u}_{2k-1}(x,t)+\sum _{k=1}^{\infty }{u}_{2k}(x,t).\end{array}$$(4.17) ), we have$$\begin{array}{ccc}\hfill |u(x,t)-\tilde{u}(x,t)|& ⩽\hfill & \hfill |u_0(x,t)-{\tilde{u}}_0(x,t)|\\ \hfill & +\sum _{k=1}^{\infty }(|u_{2k-1}(x,t)-{\tilde{u}}_{2k-1}(x,t)|+|u_{2k}(x,t)-{\tilde{u}}_{2k}(x,t)|).\hfill \end{array}$$

We need to find the estimates of $|u_0(x,t)-{\tilde{u}}_0(x,t)|,|u_{2k-1}(x,t)-{\tilde{u}}_{2k-1}(x,t)|,|u_{2k}(x,t)-{\tilde{u}}_{2k}(x,t)|$. By using (4.24(4.24) $$\begin{array}{c}\hfill \left.\begin{array}{cc}\frac{e_{\mathit{\beta },\mathit{\beta }+1}(t;{\mathit{\lambda }}_k^{(i)})}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(i)})}⩽\frac{a_i}{k^2},e_{\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(j)})\frac{e_{\mathit{\beta },\mathit{\beta }+1}(t;{\mathit{\lambda }}_k^{(j)})}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(j)})}⩽\frac{b_j}{k^4}& i,j=0,1,2,3\\ {\int }_0^t{e}_{\mathit{\beta },\mathit{\beta }}(\mathit{\tau };{\mathit{\lambda }}_k^{(1)})e_{\mathit{\beta },\mathit{\beta }+1}(t-\mathit{\tau };{\mathit{\lambda }}_k^{(2)})\mathrm{d}\mathit{\tau }⩽\frac{MC}{k^4}T.\end{array}\right\}\end{array}$$(4.24) )–(4.25(4.25) $$\begin{array}{c}\hfill \left.\begin{array}{ccc}\hfill \frac{{\mathit{\lambda }}_k^{(2)}-{\mathit{\lambda }}_k^{(1)}}{2{\mathit{\delta }}_k}({\int }_0^t{e}_{\mathit{\beta },\mathit{\beta }}(\mathit{\tau };{\mathit{\lambda }}_k^{(1)})e_{\mathit{\beta },\mathit{\beta }+1}(t-\mathit{\tau };{\mathit{\lambda }}_k^{(2)})\mathrm{d}\mathit{\tau })\frac{e_{\mathit{\beta },\mathit{\beta }+1}(t;{\mathit{\lambda }}_k^{(1)})}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(1)})}& ⩽\hfill & \hfill \frac{a_3}{k^5},\\ \hfill \frac{{\mathit{\lambda }}_k^{(2)}-{\mathit{\lambda }}_k^{(1)}}{2{\mathit{\delta }}_k}(\frac{{\int }_0^t{e}_{\mathit{\beta },\mathit{\beta }}(\mathit{\tau };{\mathit{\lambda }}_k^{(1)})e_{\mathit{\beta },\mathit{\beta }+1}(t-\mathit{\tau };{\mathit{\lambda }}_k^{(2)})\mathrm{d}\mathit{\tau }}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(2)})})& ⩽\hfill & \hfill \frac{a_4}{k^3},\\ \hfill \frac{{\mathit{\lambda }}_k^{(2)}-{\mathit{\lambda }}_k^{(1)}}{2{\mathit{\delta }}_k}(\frac{{\int }_0^t{e}_{\mathit{\beta },\mathit{\beta }}(\mathit{\tau };{\mathit{\lambda }}_k^{(1)})e_{\mathit{\beta },\mathit{\beta }+1}(t-\mathit{\tau };{\mathit{\lambda }}_k^{(2)})\mathrm{d}\mathit{\tau }}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(2)})})e_{\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(1)})& ⩽\hfill & \hfill \frac{a_5}{k^5},\\ \hfill \frac{{\mathit{\lambda }}_k^{(2)}-{\mathit{\lambda }}_k^{(1)}}{2{\mathit{\delta }}_k}({\int }_0^t{e}_{\mathit{\beta },\mathit{\beta }}(\mathit{\tau };{\mathit{\lambda }}_k^{(1)})e_{\mathit{\beta }}(t-\mathit{\tau };{\mathit{\lambda }}_k^{(2)})\mathrm{d}\mathit{\tau })& ⩽\hfill & \hfill \frac{a_6}{k^2}.\end{array}\right\}\end{array}$$(4.25) ), we have(4.26) $$\begin{array}{cc}\hfill |u_0-{\tilde{u}}_0|& ⩽|\{e^{-{\mathit{\lambda }}_0{t}^{\mathit{\beta }}/\mathrm{\Gamma }(\mathit{\beta }+1)})+\frac{b_0}{k^4}\}({\mathit{\varphi }}_0-{\tilde{\mathit{\varphi }}}_0)|,\hfill \end{array}$$(4.26) (4.27) $$\begin{array}{cc}\hfill |u_{2k-1}-{\tilde{u}}_{2k-1}|& ⩽|\{e^{-{\mathit{\lambda }}_k^{(2)}{t}^{\mathit{\beta }}/\mathrm{\Gamma }(\mathit{\beta }+1)})+\frac{b_2}{k^4}\}({\mathit{\varphi }}_{2k-1}-{\tilde{\mathit{\varphi }}}_{2k-1})|+\frac{a_2}{k^2}|{\mathit{\psi }}_{2k-1}-{\tilde{\mathit{\psi }}}_{2k-1}|,\hfill \end{array}$$(4.27) (4.28) $$\begin{array}{cc}\hfill |u_{2k}-{\tilde{u}}_{2k}|& ⩽\{e^{-{\mathit{\lambda }}_k^{(1)}{t}^{\mathit{\beta }}/\mathrm{\Gamma }(\mathit{\beta }+1)}+\frac{b_1}{k^4}\}|{\mathit{\varphi }}_{2k}-{\tilde{\mathit{\varphi }}}_{2k}|\hfill \\ \hfill & \times (\frac{a_3}{k^5}+\frac{a_7{a}_3}{k^5}+\frac{a_6}{k^2}+\frac{a_5}{k^5})|{\mathit{\varphi }}_{2k-1}-\widetilde{{\mathit{\varphi }}_{2k-1}}|\hfill \\ \hfill & +\frac{a_1}{k^2}|{\mathit{\psi }}_{2k}-\widetilde{{\mathit{\psi }}_{2k}}|+|\frac{a_3{a}_8}{k^5}+\frac{a_4}{k^3}||{\mathit{\psi }}_{2k-1}-\widetilde{{\mathit{\psi }}_{2k-1}}|.\hfill \end{array}$$(4.28)

By virtue of (4.26(4.26) $$\begin{array}{cc}\hfill |u_0-{\tilde{u}}_0|& ⩽|\{e^{-{\mathit{\lambda }}_0{t}^{\mathit{\beta }}/\mathrm{\Gamma }(\mathit{\beta }+1)})+\frac{b_0}{k^4}\}({\mathit{\varphi }}_0-{\tilde{\mathit{\varphi }}}_0)|,\hfill \end{array}$$(4.26) )–(4.28(4.28) $$\begin{array}{cc}\hfill |u_{2k}-{\tilde{u}}_{2k}|& ⩽\{e^{-{\mathit{\lambda }}_k^{(1)}{t}^{\mathit{\beta }}/\mathrm{\Gamma }(\mathit{\beta }+1)}+\frac{b_1}{k^4}\}|{\mathit{\varphi }}_{2k}-{\tilde{\mathit{\varphi }}}_{2k}|\hfill \\ \hfill & \times (\frac{a_3}{k^5}+\frac{a_7{a}_3}{k^5}+\frac{a_6}{k^2}+\frac{a_5}{k^5})|{\mathit{\varphi }}_{2k-1}-\widetilde{{\mathit{\varphi }}_{2k-1}}|\hfill \\ \hfill & +\frac{a_1}{k^2}|{\mathit{\psi }}_{2k}-\widetilde{{\mathit{\psi }}_{2k}}|+|\frac{a_3{a}_8}{k^5}+\frac{a_4}{k^3}||{\mathit{\psi }}_{2k-1}-\widetilde{{\mathit{\psi }}_{2k-1}}|.\hfill \end{array}$$(4.28) ) the following estimates are obtained$$\begin{array}{ccc}\hfill |u_0-{\tilde{u}}_0|& ⩽\hfill & \hfill \frac{a_9}{k^2}|{\mathit{\varphi }}_0-{\tilde{\mathit{\varphi }}}_0|,\\ \hfill |u_{2k-1}-{\tilde{u}}_{2k-1}|& ⩽\hfill & \hfill \frac{a_9}{k^2}[|{\mathit{\varphi }}_{2k-1}-{\tilde{\mathit{\varphi }}}_{2k-1}|+|{\mathit{\psi }}_{2k-1}-{\tilde{\mathit{\psi }}}_{2k-1}|],\\ \hfill |u_{2k}-{\tilde{u}}_{2k}|& ⩽\hfill & \hfill \frac{a_9}{k^2}[|{\mathit{\varphi }}_{2k}-{\tilde{\mathit{\varphi }}}_{2k}|+|{\mathit{\varphi }}_{2k-1}-{\tilde{\mathit{\varphi }}}_{2k-1}|+|{\mathit{\psi }}_{2k}-{\tilde{\mathit{\psi }}}_{2k}|+|{\mathit{\psi }}_{2k-1}-{\tilde{\mathit{\psi }}}_{2k-1}|],\end{array}$$

where$$\begin{array}{cc}\hfill a_9=max\{& a_1,a_3,a_4,a_5,a_6,a_3{a}_7,a_4{a}_8,b_1,b_2,\hfill \\ \hfill & k^4{e}^{-{\mathit{\lambda }}_0{t}^{\mathit{\beta }}/\mathrm{\Gamma }(\mathit{\beta }+1)},k^4{e}^{-{\mathit{\lambda }}_k^{(1)}{t}^{\mathit{\beta }}/\mathrm{\Gamma }(\mathit{\beta }+1)},k^4{e}^{-{\mathit{\lambda }}_k^{(2)}{t}^{\mathit{\beta }}/\mathrm{\Gamma }(\mathit{\beta }+1)}\}.\hfill \end{array}$$

Thus, we have$$\begin{array}{c}\hfill |u(x,t)-\tilde{u}(x,t)|⩽a_{10}(|{\mathit{\varphi }}_0-{\tilde{\mathit{\varphi }}}_0|+|{\mathit{\psi }}_0-{\tilde{\mathit{\psi }}}_0|)+\sum _{k=1}^{\infty }[\frac{a_9}{k^2}(2|{\mathit{\varphi }}_{2k-1}-{\tilde{\mathit{\varphi }}}_{2k-1}|\\ \hfill +2|{\mathit{\psi }}_{2k-1}-{\tilde{\mathit{\psi }}}_{2k-1}|+|{\mathit{\varphi }}_{2k}-{\tilde{\mathit{\varphi }}}_{2k}|+|{\mathit{\psi }}_{2k}-{\tilde{\mathit{\psi }}}_{2k}|)].\end{array}$$

Due to the estimate (3.12(3.12) $$\begin{array}{c}\hfill |{\mathit{\varphi }}_k|⩽\frac{D}{k^2}\Vert {\mathit{\varphi }}^{{}^{″}}(x)\Vert ,k\in \mathbb{N},\end{array}$$(3.12) ), we obtained$$\begin{array}{cc}\hfill |u(x,t)-\tilde{u}(x,t)|⩽& a_{10}(|{\mathit{\varphi }}_0-{\tilde{\mathit{\varphi }}}_0|+|{\mathit{\psi }}_0-{\tilde{\mathit{\psi }}}_0|)\hfill \\ \hfill & +\sum _{k=1}^{\infty }[a_{11}\frac{D}{k^4}(|{\mathit{\varphi }}^{{}^{″}}(x)-{\tilde{\mathit{\varphi }}}^{{}^{″}}(x)|+|{\mathit{\psi }}^{{}^{″}}(x)-{\tilde{\mathit{\psi }}}^{{}^{″}}(x)|)].\hfill \end{array}$$

Consequently,$$\Vert u(x,t)-\tilde{u}(x,t)\Vert ⩽a_{12}[\Vert \mathit{\varphi }(x)-\tilde{\mathit{\varphi }}(x)\Vert +\Vert \mathit{\psi }(x)-\tilde{\mathit{\psi }}(x)\Vert ].$$

Similarly, we can have the expression for the source term f(x).

5. Examples for ISP

In this section, we provide some examples of the ISP, recall that we are looking for $\{u(x,t),F(x,t)=f(x)\}$ for (1.1(1.1) $$\begin{array}{c}\hfill {}^C{D}_{0_{+}}^{\mathit{\beta }}u(x,t)=\mathit{\rho }{u}_{xx}(x,t)+F(x,t),(x,t)\in \mathrm{\Pi },\end{array}$$(1.1) )–(1.3(1.3) $$\begin{array}{c}\hfill u_x(0,t)=u_x(1,t)+\mathit{\alpha }u(1,t),u(0,t)=0,t\in (0,T],\mathit{\alpha }>0,\end{array}$$(1.3) ), whenever overdetermination condition (1.4(1.4) $$\begin{array}{c}\hfill u(x,T)=\mathit{\psi }(x).\end{array}$$(1.4) ) is given.

Example 1:

For the following given initial and final temperature distributions$$\mathit{\varphi }(x)=sin(2\mathit{\pi }x),\mathit{\psi }(x)=T(x^2-x)cos(\mathit{\pi }x).$$

In this example the parameter in the nonlocal boundary condition is $\mathit{\alpha }=3$ and the fractional order derivative $\mathit{\beta }$ is arbitrary.

The coefficients of the series expansion of $\mathit{\varphi }(x)$ given by (3.7(3.7) $$\begin{array}{c}\hfill {\mathit{\varphi }}_0={\int }_0^1\mathit{\varphi }(x)r_0(x)\mathrm{d}x,{\mathit{\varphi }}_{2k-1}={\int }_0^1\mathit{\varphi }(x)r_{2k-1}(x)\mathrm{d}x,{\mathit{\varphi }}_{2k}={\int }_0^1\mathit{\varphi }(x)r_{2k}(x)\mathrm{d}x.\end{array}$$(3.7) ), when expanded using the bi-orthogonal system of functions (2.11(2.11) $$\begin{array}{c}\hfill W_{\mathit{\alpha }}=\{w_k:k\in \mathbb{N}\cup \{0\}\},R_{\mathit{\alpha }}=\{r_k:k\in \mathbb{N}\cup \{0\}\},\end{array}$$(2.11) ) are$${\mathit{\varphi }}_0=0,{\mathit{\varphi }}_{2k-1}=0,k\in \mathbb{N},{\mathit{\varphi }}_{2k}=\left\{\begin{array}{c}1,k=1\hfill \\ 0,k=2,3,\dots .\hfill \end{array}\right.$$

Similarly, for $\mathit{\psi }(x)$, we have$${\mathit{\psi }}_0=0,{\mathit{\psi }}_{2k-1}=0,{\mathit{\psi }}_{2k}=-\frac{16T(4k^3+3k)}{{\mathit{\pi }}^3{(4k^2-1)}^3},k\in \mathbb{N}.$$

Then using (4.9(4.9) $$\begin{array}{cc}\hfill f_0& =\frac{{\mathit{\psi }}_0-{\mathit{\varphi }}_0{e}_{\mathit{\beta }}(T;{\mathit{\lambda }}_0)}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_0)},f_{2k-1}=\frac{{\mathit{\psi }}_{2k-1}-{\mathit{\varphi }}_{2k-1}{e}_{\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(2)})}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(2)})},\hfill \end{array}$$(4.9) )–(4.10(4.10) $$\begin{array}{cc}\hfill f_{2k}& =\frac{{\mathit{\psi }}_{2k}-{\mathit{\varphi }}_{2k}{e}_{\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(1)})}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(1)})}-\frac{{\mathit{\lambda }}_k^{(1)}-{\mathit{\lambda }}_k^{(2)}}{2{\mathit{\delta }}_k{e}_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_0)}({\mathit{\varphi }}_{2k-1}{e}_{\mathit{\beta },\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(1)})\ast e_{\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(2)}))\hfill \\ \hfill & -\frac{{\mathit{\lambda }}_k^{(1)}-{\mathit{\lambda }}_k^{(2)}}{2{\mathit{\delta }}_k{e}_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_0)}(\frac{{\mathit{\psi }}_{2k-1}-{\mathit{\varphi }}_{2k-1}{e}_{\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(2)})}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(2)})})\hfill \\ \hfill & e_{\mathit{\beta },\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(1)})\ast e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(2)}).\hfill \end{array}$$(4.10) ), we obtained$$f_0=0,f_{2k-1}=0,f_{2k}=\left\{\begin{array}{c}\frac{{\mathit{\psi }}_2-{\mathit{\varphi }}_2{e}_{\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(1)})}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(1)})},k=1\hfill \\ -\frac{{\mathit{\psi }}_{2k}}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(1)})},k=2,3,\dots ,\hfill \end{array}\right.$$

and by virtue of (4.6(4.6) $$\begin{array}{cc}\hfill T_0^u(t)& ={\mathit{\varphi }}_0{e}_{\mathit{\beta }}(t;{\mathit{\lambda }}_0)+f_0{e}_{\mathit{\beta },\mathit{\beta }+1}(t;{\mathit{\lambda }}_0),\hfill \end{array}$$(4.6) )–(4.8(4.8) $$\begin{array}{cc}\hfill T_{2k}^u(t)& ={\mathit{\varphi }}_{2k}{e}_{\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(1)})+f_{2k}{e}_{\mathit{\beta },\mathit{\beta }+1}(t;{\mathit{\lambda }}_k^{(1)})+\frac{{\mathit{\lambda }}_k^{(1)}-{\mathit{\lambda }}_k^{(2)}}{2{\mathit{\delta }}_k}({\mathit{\varphi }}_{2k-1}{e}_{\mathit{\beta },\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(1)})\hfill \\ \hfill & \ast e_{\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(2)})+f_{2k-1}{e}_{\mathit{\beta },\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(1)})\ast e_{\mathit{\beta },\mathit{\beta }+1}(t;{\mathit{\lambda }}_k^{(2)})),\hfill \end{array}$$(4.8) ), we have$$T_0^u=0,T_{2k-1}^u=0,T_{2k}^u=\left\{\begin{array}{c}{e}_{\mathit{\beta }}(t;{\mathit{\lambda }}_1^{(1)})f_2{e}_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_1^{(1)}),k=1\hfill \\ f_{2k}{e}_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(1)}),k=2,3,\dots .\hfill \end{array}\right.$$

Consequently, the solution of the ISP is given by(5.1) $$\begin{array}{cc}\hfill f(x)& =-\frac{sin(2\mathit{\pi }x)}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(1)})}(\frac{80T}{27{\mathit{\pi }}^3}+e_{\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(1)}))\hfill \\ \hfill & +\sum _{k=2}^{\infty }(-\frac{sin(2\mathit{\pi }kx)}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(1)})}\frac{16T(4k^3+k)}{{\mathit{\pi }}^3{(4k^2-1)}^3})\hfill \\ \hfill u(x,t)& =[(\frac{-80T}{27{\mathit{\pi }}^3}-e_{\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(1)}))\frac{e_{\mathit{\beta },\mathit{\beta }+1}(t;{\mathit{\lambda }}_1^{(1)})}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_1^{(1)})}+e_{\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(1)})]sin(2\mathit{\pi }x)\hfill \\ \hfill & +\sum _{k=2}^{\infty }(-\frac{16T(4k^3+k)}{{\mathit{\pi }}^3{(4k^2-1)}^3}\frac{e_{\mathit{\beta },\mathit{\beta }+1}(t;{\mathit{\lambda }}_k^{(1)})}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(1)})}sin(2\mathit{\pi }kx)).\hfill \end{array}$$(5.1)

Example 2:

For the second example, we consider $\mathit{\alpha }=2$, $\mathit{\beta }$ is arbitrary. The initial and final temperatures are$$\mathit{\varphi }(x)=x^2-2x,\mathit{\psi }(x)=0.$$

We have$$\begin{array}{cc}\hfill {\mathit{\varphi }}_0& =-1.7159,{\mathit{\varphi }}_{2k-1}=\frac{4{\mathit{\delta }}_k}{(sin{y}_k)(2y_k+sin(2y_k))y_k^2}(y_{k}cos{y}_k-y_k^{2}sin{y}_k-sin{y}_k),\hfill \\ \hfill {\mathit{\varphi }}_{2k}& =\frac{\mathit{\pi }k-cot{\mathit{\psi }}_k}{{\mathit{\pi }}^2{k}^2}+\frac{2y_{k}cot{y}_k-2-2y_k^2}{y_k^2(2y_k+sin2y_k)},k\in \mathbb{N},\hfill \\ \hfill {\mathit{\psi }}_0& =0,{\mathit{\psi }}_{2k-1}=0{\mathit{\psi }}_{2k}=0,k\in \mathbb{N},\hfill \end{array}$$

then by using (4.9(4.9) $$\begin{array}{cc}\hfill f_0& =\frac{{\mathit{\psi }}_0-{\mathit{\varphi }}_0{e}_{\mathit{\beta }}(T;{\mathit{\lambda }}_0)}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_0)},f_{2k-1}=\frac{{\mathit{\psi }}_{2k-1}-{\mathit{\varphi }}_{2k-1}{e}_{\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(2)})}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(2)})},\hfill \end{array}$$(4.9) )–(4.10(4.10) $$\begin{array}{cc}\hfill f_{2k}& =\frac{{\mathit{\psi }}_{2k}-{\mathit{\varphi }}_{2k}{e}_{\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(1)})}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(1)})}-\frac{{\mathit{\lambda }}_k^{(1)}-{\mathit{\lambda }}_k^{(2)}}{2{\mathit{\delta }}_k{e}_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_0)}({\mathit{\varphi }}_{2k-1}{e}_{\mathit{\beta },\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(1)})\ast e_{\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(2)}))\hfill \\ \hfill & -\frac{{\mathit{\lambda }}_k^{(1)}-{\mathit{\lambda }}_k^{(2)}}{2{\mathit{\delta }}_k{e}_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_0)}(\frac{{\mathit{\psi }}_{2k-1}-{\mathit{\varphi }}_{2k-1}{e}_{\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(2)})}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(2)})})\hfill \\ \hfill & e_{\mathit{\beta },\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(1)})\ast e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(2)}).\hfill \end{array}$$(4.10) ) and (4.6(4.6) $$\begin{array}{cc}\hfill T_0^u(t)& ={\mathit{\varphi }}_0{e}_{\mathit{\beta }}(t;{\mathit{\lambda }}_0)+f_0{e}_{\mathit{\beta },\mathit{\beta }+1}(t;{\mathit{\lambda }}_0),\hfill \end{array}$$(4.6) )–(4.8(4.8) $$\begin{array}{cc}\hfill T_{2k}^u(t)& ={\mathit{\varphi }}_{2k}{e}_{\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(1)})+f_{2k}{e}_{\mathit{\beta },\mathit{\beta }+1}(t;{\mathit{\lambda }}_k^{(1)})+\frac{{\mathit{\lambda }}_k^{(1)}-{\mathit{\lambda }}_k^{(2)}}{2{\mathit{\delta }}_k}({\mathit{\varphi }}_{2k-1}{e}_{\mathit{\beta },\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(1)})\hfill \\ \hfill & \ast e_{\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(2)})+f_{2k-1}{e}_{\mathit{\beta },\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(1)})\ast e_{\mathit{\beta },\mathit{\beta }+1}(t;{\mathit{\lambda }}_k^{(2)})),\hfill \end{array}$$(4.8) ) we can obtain expressions for u(x, t) and f(x).

Figure 1. (a) Plot of noisy data $\tilde{\mathit{\psi }}(x)$ and the plot of $\mathit{\psi }(x)$. (b) For $\mathit{\alpha }=3$, $\mathit{\beta }=0.25$, plot of $\tilde{f}(x)$$(-)$ and plot of f(x) $(·-·-)$.

Figure 2. (a) For $\mathit{\alpha }=3$, $\mathit{\beta }=0.5$, plot of $\tilde{f}(x)$$(-)$ and plot of f(x) $(·-·-)$ (b) For $\mathit{\alpha }=3$, $\mathit{\beta }=0.75$, plot of $\tilde{f}(x)$$(-)$ and plot of f(x) $(·-·-)$.

5.1. Numerical examples with noisy data

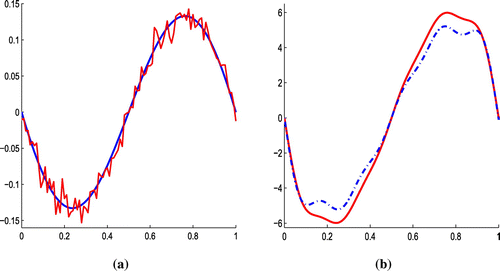
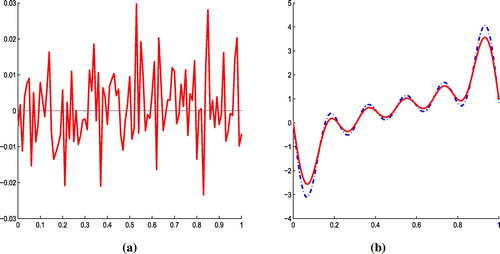
This subsection is devoted to providing the numerical examples with noisy data. The noisy data (perturbed data) were used to reconstruct the inverse source, i.e. f(x). The final temperature distribution, that is, $\mathit{\psi }(x)$, has been perturbed by using the ‘random’ command of MATLAB and the resulting noisy (perturbed) data are represented by $\tilde{\mathit{\psi }}(x)$. The solution f(x) corresponds to the data $\mathit{\psi }(x)$ and $\tilde{f}(x)$ corresponds to the noisy data $\tilde{\mathit{\psi }}(x)$. In all figures the solid lines represent the output with noisy data and the plots with dot followed by dash, i.e. ($.-$) represent the plot without noise. All the simulations are carried out using MTALAB 7.9.0 on a machine intel core i3 with 8 GB RAM.

Figure 3. (a) Plot of noisy data $\tilde{\mathit{\psi }}(x)$ and the plot $\mathit{\psi }(x)=0$. (b) For $\mathit{\alpha }=2$ and $\mathit{\beta }=0.25$, plot of $\tilde{f}(x)$$(-)$ and plot of f(x) $(·-·-)$.

Figure 4. (a) For $\mathit{\alpha }=2$ and $\mathit{\beta }=0.5$, plot of $\tilde{f}(x)$$(-)$ and plot of f(x) $(·-·-)$ (b) For $\mathit{\alpha }=2$ and $\mathit{\beta }=0.75$, plot of $\tilde{f}(x)$$(-)$ and plot of f(x) $(·-·-)$.

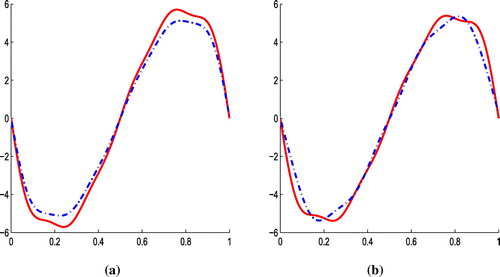
Figures 1 and 2 show the numerical simulations of Example 1, Figure 1(a) shows the plot of $\mathit{\psi }(x)$ and noisy data $\tilde{\mathit{\psi }}(x)$. The function f(x) is calculated from the expression (5.1(5.1) $$\begin{array}{cc}\hfill f(x)& =-\frac{sin(2\mathit{\pi }x)}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(1)})}(\frac{80T}{27{\mathit{\pi }}^3}+e_{\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(1)}))\hfill \\ \hfill & +\sum _{k=2}^{\infty }(-\frac{sin(2\mathit{\pi }kx)}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(1)})}\frac{16T(4k^3+k)}{{\mathit{\pi }}^3{(4k^2-1)}^3})\hfill \\ \hfill u(x,t)& =[(\frac{-80T}{27{\mathit{\pi }}^3}-e_{\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(1)}))\frac{e_{\mathit{\beta },\mathit{\beta }+1}(t;{\mathit{\lambda }}_1^{(1)})}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_1^{(1)})}+e_{\mathit{\beta }}(t;{\mathit{\lambda }}_k^{(1)})]sin(2\mathit{\pi }x)\hfill \\ \hfill & +\sum _{k=2}^{\infty }(-\frac{16T(4k^3+k)}{{\mathit{\pi }}^3{(4k^2-1)}^3}\frac{e_{\mathit{\beta },\mathit{\beta }+1}(t;{\mathit{\lambda }}_k^{(1)})}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(1)})}sin(2\mathit{\pi }kx)).\hfill \end{array}$$(5.1) ), whereas $\tilde{f}(x)$ is evaluated using the noisy data and by taking $T=1$. The plots of the source term for $\mathit{\alpha }=3$, $\mathit{\beta }=0.25$, are given in Figure 1(b), whereas plots for $\mathit{\alpha }=3,\mathit{\beta }=0.5$ and $\mathit{\alpha }=3,\mathit{\beta }=0.75$ are given in Figure 2(a) and (b), respectively.

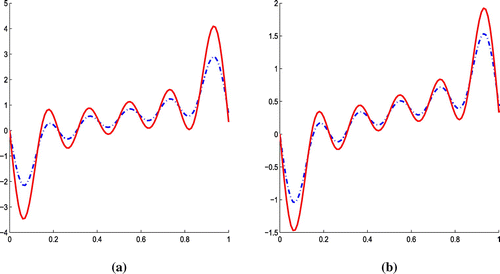
Figures 3 and 4 show the numerical simulations of Example 2, as for the previous example Figure 3(a) shows the plot of $\mathit{\psi }(x)=0$ and noisy data $\tilde{\mathit{\psi }}(x)$, which in this example is the noise only. The function f(x) is calculated from the expression (4.9(4.9) $$\begin{array}{cc}\hfill f_0& =\frac{{\mathit{\psi }}_0-{\mathit{\varphi }}_0{e}_{\mathit{\beta }}(T;{\mathit{\lambda }}_0)}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_0)},f_{2k-1}=\frac{{\mathit{\psi }}_{2k-1}-{\mathit{\varphi }}_{2k-1}{e}_{\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(2)})}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(2)})},\hfill \end{array}$$(4.9) )–(4.10(4.10) $$\begin{array}{cc}\hfill f_{2k}& =\frac{{\mathit{\psi }}_{2k}-{\mathit{\varphi }}_{2k}{e}_{\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(1)})}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(1)})}-\frac{{\mathit{\lambda }}_k^{(1)}-{\mathit{\lambda }}_k^{(2)}}{2{\mathit{\delta }}_k{e}_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_0)}({\mathit{\varphi }}_{2k-1}{e}_{\mathit{\beta },\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(1)})\ast e_{\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(2)}))\hfill \\ \hfill & -\frac{{\mathit{\lambda }}_k^{(1)}-{\mathit{\lambda }}_k^{(2)}}{2{\mathit{\delta }}_k{e}_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_0)}(\frac{{\mathit{\psi }}_{2k-1}-{\mathit{\varphi }}_{2k-1}{e}_{\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(2)})}{e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(2)})})\hfill \\ \hfill & e_{\mathit{\beta },\mathit{\beta }}(T;{\mathit{\lambda }}_k^{(1)})\ast e_{\mathit{\beta },\mathit{\beta }+1}(T;{\mathit{\lambda }}_k^{(2)}).\hfill \end{array}$$(4.10) ), whereas $\tilde{f}(x)$ is evaluated using the noisy data and by taking $T=1$. The plots of the source term for $\mathit{\alpha }=2$, $\mathit{\beta }=0.25$ are given in Figure 3(b), whereas plots for $\mathit{\alpha }=2,\mathit{\beta }=0.5$ and $\mathit{\alpha }=2,\mathit{\beta }=0.75$ are given in Figure 4(a) and (b), respectively.

6. Conclusions and perspectives

The direct and ISPs for a time fractional diffusion equation with nonlocal boundary condition involving a parameter have been investigated. First, the well-posedness in the sense of Hadamard of the classical solution for the direct problem is proved. The results of [5] can be obtained from the results presented in this paper by taking order of fractional time derivative equal to 1, i.e. $\mathit{\beta }=1$. Moreover, from the final temperature data, the determination of a space-dependent source term along with solution has been studied. The results about the unique solvability and stability of the ISP are presented. Numerical examples with perturbed data are provided for the ISP.

In [43] an inverse problem for a so-called generalized time fractional diffusion was considered. The fractional derivative used in [43] is a generalization of the well-known Riemann–Liouville and Caputo fractional derivatives. Indeed, the generalized fractional derivative interpolates the Riemann–Liouville and Caputo fractional derivatives. The results presented in this paper can be extended by considering the generalized fractional derivative. The inverse problem involving fractional derivative in both time and space variables will be considered in the future.

Acknowledgements

The authors are thankful to the referees for their suggestions and comments which improved quality of the paper.

Notes

No potential conflict of interest was reported by the authors.