 ?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.
?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.Abstract
In this paper, we consider an inverse problem for the time-fractional diffusion equation with inhomogeneous source to determine an initial data from the observation data provided at a later time. In general, this problem is ill-posed, therefore we construct a regularizing solution using the quasi-boundary value method. We also proposed both parameter choice rule methods, the a-priori and the a-posteriori methods, to estimate the convergence rate of the regularized methods. In addition, the proposed regularized methods have been verified by numerical experiments, and a comparison of the convergence rate between the a-priori and the a-posteriori choice rule methods is also given.
1. Introduction
The aim of this paper is to design the methods to recover the initial data from a final value problem for an inhomogeneous time-fractional diffusion equation. Diffusive transport is one of the most important transport mechanisms found in nature. At a microscopic level, the diffusion is the result of the random motion of individual particles, and the use of the Laplacian operator to model this motion relies on the key assumption that this random motion is a stochastic Gaussian process. However, a growing number of studies on diffusive phenomena have shown the prevalence of anomalous diffusion, in which the mean square variance grows faster (in the case of superdiffusion) or slower (in the case of subdiffusion) than in a Gaussian diffusion process. Nowadays, anomalous diffusion becomes ’normal’ in spatially disordered systems, porous media, fractal media,[Citation1–Citation14] turbulent fluids and plasmas [Citation15,Citation16], biological media with traps, binding sites or macro-molecular crowding,[Citation17,Citation18] stock price movements.[Citation19,Citation20] As we know, the study on the inverse problems for fractional-order systems are still not well-covered. Since the fractional derivative is nonlocal, the backward problems for such models become much more difficult due to the following two reasons: The first reason, the backward problems for diffusion processes are ill posed, corresponding to the irreversibility of time; the second reason, the strong smoothing effect of the forward diffusion process makes it very difficult to reconstruct the possible discontinuities arising in the initial status.
In this work, we consider the problem of recovering the distribution u(x, 0) from a final value problem for the following inhomogeneous time-fractional diffusion equation:(1.1)
(1.1)
where is a bounded domain in
with sufficient smooth boundary
, and
is a given number; the source function
and the final data
are given. Here
is the fractional order of
referred to the Caputo fractional derivative with respect to t of the order
defined by
and denotes the standard Gamma function. The operator A is a symmetric uniformly elliptic operator. Note that if the fractional order
tends to unity, the fractional derivative
becomes the first-order derivative
, and thus problem (Equation1.1
(1.1)
(1.1) ) reproduces the standard parabolic equation. The objective of this study is to obtain the initial status of a physical field from its measurement data at the present time. Therefore, our backward problem (Equation1.1
(1.1)
(1.1) ) is to find the approximate solution u(x, t) for
corresponding to (g, F) from the noisy data
such that
(1.2)
(1.2)
for some known error level .
As it is well known, that the problem (Equation1.1(1.1)
(1.1) ) is ill-posed, i.e. the solutions do not always exist, and in the case of existence, the solutions do not depend continuously on the given data. In fact, from small noise of physical measurement data, the corresponding solutions may have the large errors. It makes difficult to a numerical calculation. Hence, a regularization method is required.
When , the problem (Equation1.1
(1.1)
(1.1) ) is a classical problem and has been particularly active in the past 30 years using many regularization methods, for example, see [Citation8] and the references therein. However, there are not many studies on the fractional backward problem (Equation1.1
(1.1)
(1.1) ) for
. For the homogeneous case of backward problem, i.e.
in (Equation1.1
(1.1)
(1.1) ), there are very few works. For example, Sakamoto and Yamamoto [Citation6] have proved that there exists a unique weak solution for this backward problem; Liu et al. [Citation21] used a quasi-reversibility method to solve the homogeneous backward problem in one-dimensional case for special coefficients; and very recently, it has been considered by some other authors, such as [Citation10–Citation12,Citation22–Citation24].
Up-to-date, to the best of our knowledge, we could not find any result on backward problem for inhomogeneous time-fractional diffusion equation. Motivated by this reason, in this paper, we mainly propose a priori and an a posteriori regularization parameter choice rule using the quasi boundary value method. The quasi boundary value method, also called non-local boundary value problem method, is a regularization technique by replacing the final condition by a new approximate condition in such a way that the new problem is well-posed. In comparison with previous studies [Citation3,Citation11,Citation21,Citation22] on solving a time-fractional backward diffusion problem, our method shows an improvement in dealing with the time-fractional inverse diffusion problems with inhomogeneous source.
The manuscript is organized as follows. In Section 2, we introduce some well-known results on a forward problem. The conditional stability are described in Section 3. In Section 4, we propose a quasi-boundary value (QBV) method and provide two convergence estimates under an a priori assumption for the exact solution, and two regularization parameter choice rules. Eventually, two numerical examples are verified in Section 5.
2. The forward time-fractional diffusion problem
In order to solve the backward problem, we first recall in this section some well-known results from the forward problem for inhomogeneous time-fractional diffusion. The forward problem reads as: Given and F, find u satisfying
(2.1)
(2.1)
Here, A is a symmetric uniformly elliptic operator defined by
where the coefficient functions (for
) and
satisfy
Here, is a positive constant independent of x and
.
Since A is a linear densely defined self-adjoint and positive definite elliptic operator on the connected bounded domain with zero Dirichlet boundary condition, the eigenvalues of A satisfy
with as
; see [Citation25]. The corresponding eigenfunctions are denoted, respectively, by
. Thus the eigenpair
,
, satisfies
The functions are normalized so that
is an orthonormal basis of
.
Defining
where is the inner product in
, then
is a Hilbert space equipped with norm
The exact solution u of (Equation2.1(2.1)
(2.1) ) can be represented by its Fourier series as follows (see [Citation26])
(2.2)
(2.2)
where the Mittag–Leffler function which plays an important role in time-fractional PDEs and is defined, for
and
, by
And
An existence and uniqueness result for the forward problem (Equation2.1(2.1)
(2.1) ) has been obtained in Sakamoto and Yamamoto [Citation6]. Numerical methods for this problem have been studied; see for example Jin et al. [Citation27], McLean [Citation28], Mustapha and McLean [Citation29]. We finish this section by recalling some asymptotic results for the Mittag–Leffler function which can be found in [Citation21] or in [Citation2, Chapter 1]. More general results can be found in [Citation2].
Lemma 2.1:
Let Then there exists positive constants
,
,
, and
such that for all
there hold
Lemma 2.2:
Assume that . Then the Mittag–Leffler function have the asymptotic
In next section, we consider a backward problem for inhomogeneous time fractional diffusion equation by using regularization methods.
3. The backward time-fractional diffusion problem
3.1. The existence and regularity of solutions
Before proceeding to derive the existence and regularity of the solution of the problem (Equation1.1(1.1)
(1.1) ), we introduce a useful lemma.
Lemma 3.1:
| (a) | Let | ||||
| (b) | Suppose further that | ||||
Part (a): First, we note that for there holds
(3.2)
(3.2)
Moreover, it follows from [Citation6, Lemma 3.2] that which together with
implies
On the other hand, [Citation6, Lemma 3.3] gives so that
for all
. Hence
(3.3)
(3.3)
Combining (Equation3.2(3.2)
(3.2) ) and (Equation3.3
(3.3)
(3.3) ) yields
It is known that for
, where C is a positive constant independent of n; see e.g. Courant and Hilbert [Citation30]. Hence for
by letting
we prove (Equation3.1
(3.1)
(3.1) ). Similarly, we have
If and
(implying
), then by letting
we complete the proof Part (a).
Part (b): For , we have
and the boundedness of follows as that of
.
The following theorem gives the necessary and sufficient conditions for the existence of the solution of (Equation1.1(1.1)
(1.1) ).
Theorem 3.2:
Assume that and
.
| (a) | If the problem (Equation1.1 | ||||
| (b) | The problem (Equation1.1 | ||||
| (c) | If g, F satisfies | ||||
Part (a): Suppose Problem (Equation1.1(1.1)
(1.1) ) has a unique solution u. Then u is the solution of the forward problem (Equation2.1
(2.1)
(2.1) ) with
It follows from (Equation2.2
(2.2)
(2.2) ) that
which implies (Equation3.4(3.4)
(3.4) ). Solving (Equation3.4
(3.4)
(3.4) ) for
we obtain
(3.7)
(3.7)
Therefore(3.8)
(3.8)
Lemma 2.1 gives
Using the inequality and Lemma 3.1 we deduce
Thus (Equation3.5(3.5)
(3.5) ) is followed.
Part (b): Now assume that (Equation1.1(1.1)
(1.1) ) has a unique solution. Then (Equation3.7
(3.7)
(3.7) ) gives
Conversely, if (Equation3.6(3.6)
(3.6) ) holds, then if
is defined by
(3.9)
(3.9)
then clearly . Now, we consider the problem of finding u satisfying the forward time-fractional diffusion problem
Since and
, the above problem has a unique solution u given by (Equation2.2
(2.2)
(2.2) ). Combining (Equation2.2
(2.2)
(2.2) ) and (Equation3.9
(3.9)
(3.9) ), we obtain
so that u is a solution of the backward problem (Equation1.1
(1.1)
(1.1) ).
Part (c): Finally, we prove that if g and F satisfy and
then the condition (Equation3.6
(3.6)
(3.6) ) holds. In fact, we have
(3.10)
(3.10)
Using the inequality (see Lemma 2.1) we obtain
(3.11)
(3.11)
and(3.12)
(3.12)
where in the last step we used Lemma 3.1(b). Combining (Equation3.10(3.10)
(3.10) )–(Equation3.12
(3.12)
(3.12) ), we complete the proof of Part (c).
Theorem 3.3:
Assume that (Equation1.1(1.1)
(1.1) ) has a solution u which satisfies
for some
. Let M be a positive constant which satisfies
(3.13)
(3.13)
Then we have(3.14)
(3.14)
where
where is the constant given by Lemma 3.1.
It follows from (Equation3.8(3.8)
(3.8) ) that
(3.15)
(3.15)
where
The term can be estimated by using Lemma 2.1 and (Equation3.7
(3.7)
(3.7) ) as follows
(3.16)
(3.16)
The term can be easily estimated by using Lemma 3.1
(3.17)
(3.17)
Combining (Equation3.15(3.15)
(3.15) )–(Equation3.17
(3.17)
(3.17) ), we complete the proof of the Theorem.
4. QBV regularization method and error estimate
In this section, we shall regularize the problem (Equation1.1(1.1)
(1.1) ) with pertubed given data
and
satisfying (Equation1.2
(1.2)
(1.2) ). The regularized problem reads as: Find
satisfying
(4.1)
(4.1)
where is a regularizing parameter. The basic idea of the above regularization, which was initially developed for parabolic final value problems,[Citation31,Citation32] is to add an appropriate ‘corrector’,
, into the final value condition. This regularization is called the QBV method which is applied for some other ill-posed problem, for example [Citation4,Citation9,Citation33,Citation35].
The condition gives
(4.2)
(4.2)
Therefore, (Equation4.1(4.1)
(4.1) ) can be rewritten as
(4.3)
(4.3)
where(4.4)
(4.4)
4.1. The existence, uniqueness of a solution of the problem (Equation4.1 (4.1)
(4.1)  (4.1) )
(4.1) )
In the next theorem, we shall study the existence, uniqueness and stability of (weak) solution of the problem (Equation4.1(4.1)
(4.1) ).
Theorem 4.1:
The problem (Equation4.1(4.1)
(4.1) ) has uniquely a solution
-pagination satisfying
(4.5)
(4.5)
Moreover, the solution depends continuously on .
According the results of the forward problem, it is easy to show that the solution of Problem (Equation4.3(4.3)
(4.3) ) satisfies (Equation4.5
(4.5)
(4.5) ). We omit it here. In the following section, we will provide two convergence estimates for
by using an a priori and posteriori choice rules for the regularization parameter. To do so, we introduce the function
as follows:
(4.6)
(4.6)
We show the smoothness of the regularization . Indeed, using the inequality
and Lemma 3.1, part a, we get for all
(4.7)
(4.7)
This implies that .
4.2. Convergence estimate under an a priori regularization parameter choice rule
In the following, even though we will choose depending on
, we still clearly show the dependence of the solution of (4.1) on
, namely we will still denote the solution by
, because the different choices of
give rise to different error estimates. We first introduce the following elementary lemma.
Lemma 4.2:
Let be positive constant. Let G be a function defined by
(4.8)
(4.8)
where is defined in Lemma 2.1. Then
(4.9)
(4.9)
where(4.10)
(4.10)
| (1) | If | ||||
| (2) | If | ||||
Hence,(4.13)
(4.13)
We are now ready to prove the main result with a priori choices of the regularization parameter .
Theorem 4.3:
Let us choose the regularizing parameter satisfying
(4.14)
(4.14) (1) Assuming that (Equation1.1
(1.1)
(1.1) ) has a solution u satisfying
. Then for
, the following estimate holds
(4.15)
(4.15) (2) Suppose the a priori condition (Equation3.13
(3.13)
(3.13) ) holds for some
and
. Then we have
(4.16)
(4.16)
Here and
are recalled from Lemmas 3.1 and 2.1, respectively
Remark 4.4:
| (1) | Let us choose | ||||
| (2) | (a) If | ||||
By the triangle inequality, we know(4.18)
(4.18) Proof Part 1: For
, we first give an estimate for the first term. In fact, from (Equation4.5
(4.5)
(4.5) ), (Equation4.6
(4.6)
(4.6) ), and using the inequality
, we obtain
(4.19)
(4.19)
where we used that Next, we continue to estimate the second term as follows:
(4.20)
(4.20) Combining (Equation4.17
(4.17)
(4.17) ) and (Equation4.18
(4.18)
(4.18) ), we obtain (Equation4.14
(4.14)
(4.14) ).
Proof Part 2:
Now, we return to the proof of Part 2. We have the following estimate:(4.21)
(4.21)
On other hand, using the inequality and Lemma 4.1, we have
(4.22)
(4.22)
Combining (Equation4.17(4.17)
(4.17) ), (Equation4.19
(4.19)
(4.19) ), (Equation4.20
(4.20)
(4.20) ), we obtain
(4.23)
(4.23)
The proof is completed.
4.3. Convergence estimate under an a posteriori regularization parameter choice rule
First, we recall as in (Equation4.5
(4.5)
(4.5) ) as follows
(4.24)
(4.24)
Denoting(4.25)
(4.25)
In this section, we introduce the convergence estimate for by using an a posteriori choice rule for the regularization parameter.
To find u(x, 0), we just need to solve the following integral equation(4.26)
(4.26)
where the kernel is(4.27)
(4.27)
Next, we know that is an orthogonal basic in
and (Equation4.24
(4.24)
(4.24) ), we know that the singular values
for the linear self-adjoint compact operator K are
(4.28)
(4.28)
and corresponding eigenvectors is .
Motivated by the remarks at the end of Section 4.4 in [Citation3], we apply a modified discrepancy principle in the following form(4.29)
(4.29)
where is a constant. According to the following lemma, there exists a unique solution for (Equation4.27
(4.27)
(4.27) ) if
.
Lemma 4.5:
Set . If
then the following results are obtained:
| (a) |
| ||||
| (b) |
| ||||
| (c) |
| ||||
| (d) |
| ||||
The proofs of (a), (b), (c) and (d) are straightforward results by the expression of(4.30)
(4.30)
Theorem 4.6:
Suppose that the a priori condition ,
and assumption (Equation4.28
(4.28)
(4.28) ) holds. Let
such that
with B defined in Lemma 4.3. The regularization parameter
is chosen by the modified discrepancy principle (Equation4.27
(4.27)
(4.27) ). Then we obtain:
(1) If , we have a convergence estimate
(4.31)
(4.31)
whereby(4.32)
(4.32) (2) If
, we have a convergence estimate
(4.33)
(4.33)
whereby(4.34)
(4.34)
Before proving Theorem 4.3, we introduce the following Lemma.
Lemma 4.7:
For constants , we have:
(4.35)
(4.35)
where and
Proof:
| (1) | If | ||||
| (2) | If | ||||
From (Equation4.27(4.27)
(4.27) ), we obtain
(4.39)
(4.39)
Using the inequality , we get
(4.40)
(4.40)
Since , we have the following estimate
(4.41)
(4.41)
Therefore(4.42)
(4.42)
Now we begin to prove Theorem 4.3.
Proof part 1: , by the triangle inequality, we have
(4.43)
(4.43) Step 1: We first estimate the first term on the right-hand side of (Equation4.36
(4.36)
(4.36) ),
(4.44)
(4.44) Step 2: Continuing to estimate the second term on the right-hand side of (Equation4.36
(4.36)
(4.36) ),
. From (Equation4.22
(4.22)
(4.22) ) and (Equation4.23
(4.23)
(4.23) ), and the a priori bounded condition of u(x, 0), we have:
(4.45)
(4.45)
Using the Hölder’s inequality, we obtain(4.46)
(4.46)
where(4.47)
(4.47)
(4.48)
(4.48)
The first term is estimated as follows
(4.49)
(4.49)
The second term can be estimated
(4.50)
(4.50)
Combining (Equation4.42(4.42)
(4.42) ) and (Equation4.43
(4.43)
(4.43) ) into (Equation4.39
(4.39)
(4.39) ), we obtain:
(4.51)
(4.51)
where we used (Equation4.35(4.35)
(4.35) ).
Proof part 2: For , The proof in this case is similar to above proof in part 1.
First, we have(4.52)
(4.52)
Using the Hölder inequality, we obtain that(4.53)
(4.53)
where and
are defined in (Equation4.40
(4.40)
(4.40) ) and (Equation4.41
(4.41)
(4.41) ). Now we need to estimate
. Since
, there exists a positive number a such that
. This leads to
(4.54)
(4.54)
Combining (Equation4.42(4.42)
(4.42) ), (Equation4.46
(4.46)
(4.46) ), (Equation4.47
(4.47)
(4.47) ) gives
(4.55)
(4.55)
Using the inequality and noting (Equation4.35(4.35)
(4.35) ) for
, we conclude that
(4.56)
(4.56)
5. Numerical experiments
To verify our proposal methods, we carry out numerical experiments for above regularization methods. Two different numerical examples corresponding to , and
and 0.6 are described in this section. In order to illustrated the sensitivity of the computational accuracy to the noise of the measurement data, we use the random function to generate the noisy data. The perturbation was defined as
rand(size()), where rand(size()) is a random number, and
plays as an amplitude of the errors. For computing the Mittag-Leffler function, we applied an algorithm in [Citation3].
In this example, we consider a two-dimensional case of Problem (1.1) as follows:(5.1)
(5.1)
whereby: (5.2)
(5.2)
By choosing , and from (Equation3.7
(3.7)
(3.7) ) and (Equation4.22
(4.22)
(4.22) ) we can deduce the exact and its regularized solutions as follows:
(5.3)
(5.3)
The whole numerical procedure is proceeded in the following steps:
Step 1. Choosing I,J and L to generate spatial and temporal discretizations as follows:(5.4)
(5.4)
Of course, the higher value of I, J and L will provide more stable and accurate numerical calculation, however in the following examples are satisfied.
Step 2. We choose couple as observed data-set including the noise in such a way that:
(5.5)
(5.5) Step 3. We put
and
, constructing two matrices contained all discrete values of
and u(., ., 0) denoted by
and
, respectively.
(5.6)
(5.6) Step 4. The error estimation is followed by
Relative error estimation:(5.7)
(5.7)
Absolute error estimation:(5.8)
(5.8)
For the a priori choice rule method we choose , then from the exact solution we have
with
in the case of
; and with
in the case of
. For the a posteriori parameter choice rule method, we choose
based on
, with
at
, and
at
, respectively.
Table 1. Error estimation between the exact and its regularized solutions for both, the a priori and the a posteriori parameter choice rule methods in Example 2 with .
Table 2. Error estimation between the exact and its regularized solutions for both, the a priori and the a posteriori parameter choice rule methods in Example 2 with .
Figure 1. A comparison between the exact and its regularized solutions for the a priori parameter choice rule in Example with .
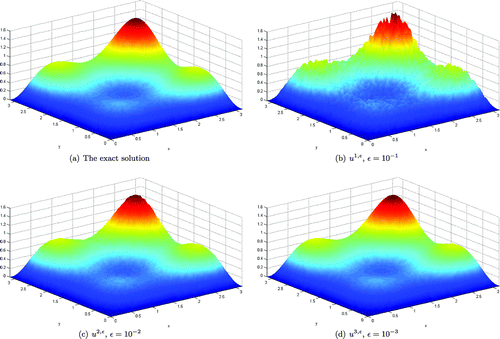
Figure 2. A comparison between the exact and its regularized solutions for the a posteriori parameter choice rule in Example with .

Figure 3. A comparison between the exact and its regularized solutions for the a priori parameter choice rule in Example with .
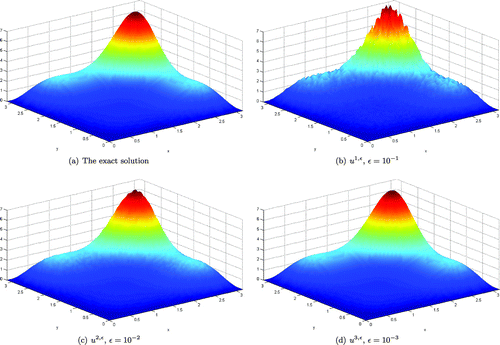
Figure 4. A comparison between the exact and its regularized solutions for the a posteriori parameter choice rule in Example with .
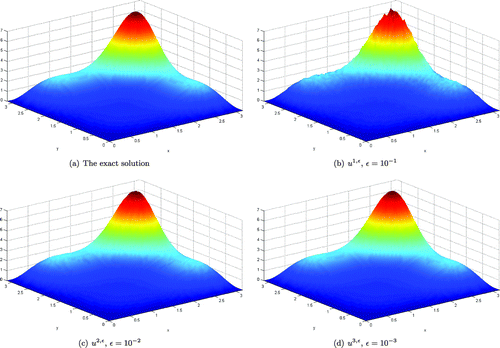
Figures and show a comparison between the exact and its regularized solutions for both parameter choice rule methods, the a priori and the a posteriori, with . Figures and show a comparison between the exact and its regularized solutions for both parameter choice rule methods, the a priori and the a posteriori, with
. Tables and show the relative and absolute error estimates between the exact and its regularized solutions for both, the a priori and the a posteriori parameter choice rule methods with
and
, respectively. It shows in the Figures – that when
in comparison with the posteriori parameter choice rule method, the numerical solution of the priori parameter choice rule method is more oscillated around the exact solution. However once
tends to zero, both methods have been converged to the exact solution very well. The numerical results obtained from
and
show the same tendency. At the beginning of the calculation, when the error estimation between the exact and its regularized solutions is still large (about
), the solutions obtained from the a priori parameter choice rule are oscillated around the exact solution more than the results obtained the a posteriori parameter choice rule. As shown in Tables and , in general the a posteriori choice rule method is converged to the exact solution faster than the a priori parameter choice rule method by about one order of
.
6. Conclusion
In this paper, we investigate the backward problem for the time-fractional diffusion equation with inhomogeneous source. We applied the QBV method to regularize the problem. In the theoretical results, we obtain the error estimate for both proposed methods, the a priori and the a posteriori parameter choice rule methods, based on the priori stability condition. From numerical results, we try to test with very complicated source term functions, it shows that our proposed regularization methods are converged very well to the exact solutions. Furthermore, it also shows that the posteriori choice rule method is converged to the exact solution better than the priori choice rule method. Since the time-fractional diffusion is more focused on the subdiffusion phenomena, which are characterized by a heavy-tailed waiting time distribution in diverging temporal moments and a non-Markovian dynamics, in the future work, we plan to study on a backward problem for space-time fractional diffusion problems, which can deal with both subdiffusive and superdiffusive problems appeared in a wide range of practical problems in surface and subsurface hydrology, biology and epidemiology. Furthermore, in the problem (Equation1.1(1.1)
(1.1) ) we still have not taken in account the convection term, if the diffusion process is also driven by a hydrodynamic problem, it absolutely needs to add this term into the problem (Equation1.1
(1.1)
(1.1) ), the backward problem would be more challenging, and it is on demand in a future work as well.
Acknowledgements
The authors would like to thank the anonymous referees for their valuable suggestions and comments leading to the improvement of our manuscript.
Additional information
Funding
Notes
No potential conflict of interest was reported by the authors.
References
- Pachepsky Y, Timlin D, Rawis W. Generalized Richards equation to simulate water transport in unsaturated soils. J Hydrol. 2003;272:3–13.
- Podlubny I. Fractional differential equations. San Diego: Academic Press; 1999.
- Podlubny I, Kacenak M. Mittag-leffler function. The MATLAB routine, 2006. Available from: http://www.mathworks.com/matlabcentral/fileexchange.
- Pham Hoang Q, Dang Duc T, Le Minh T, et al. A modified quasi-boundary value method for regularizing of a backward problem with time-dependent coefficient. Inverse Probl Sci Eng. 2011;19:409–423.
- Roman EH, Alemany AP. Continuous-time random walks and the fractional diffusion equation. J Phys A. 1994;27:3407–3410.
- Sakamoto K, Yamamoto M. Initial value/boundary value problems for fractional diffusion-wave equations and applications to some inverse problems. J Math Anal Appl. 2011;382:426–447.
- Samko GS, Kilbas AA, Marichev IO. Fractional integrals and derivatives: theory and applications. New York (NY): Gordon and Breach; 1993.
- Duc Dang T, Huy Nguyen T. Regularization and error estimates for nonhomogeneous backward heat problems. Electron. J Differ Equ. 2006;2006:1–10.
- Dang Duc T, Pham Hoang Q, Nguyen Huy T. A quasi-boundary value method for regularizing nonlinear ill-posed problems. Electron J Differ Equ. 2009;109:16.
- Wang GJ, Zhou YB, Ting W. A posteriori regularization parameter choice rule for the quasi-boundary value method for the backward time-fractional diffusion problem. Appl Math Lett. 2013;26:741–747.
- Wei T, Wang GJ. A modified quasi-boundary value method for the backward time-fractional diffusion problem. ESAIM Math Model Numer Anal. 2014;48:603–621.
- Wei T, Wang GJ. A modified quasi-boundary value method for an inverse source problem of the time-fractional diffusion equation. Appl Numer Math. 2014;78:95–111.
- Yang M, Liu JJ. Solving a final value fractional diffusion problem by boundary condition regularization. Appl Numer Math. 2013;66:45–58.
- Yu B, Jiang X, Wang C. Numerical algorithms to estimate relaxation parameters and Caputo fractional derivative for a fractional thermal wave model in spherical composite medium. Appl. Math. Comput.. 2016;274:106–118.
- Berkowitz B, Cortis A, Dentz M, et al. Modelling non-Fickian transport in geological formations as a continuous time random walk. Rev Geophys. 2006;44:RG2003.
- Deng ZQ, Singh VP. A fractional dispersion model for overland solute transport. Water Resour Res. 2006;42:W03416.
- Huang G, Huang Q, Zhan H. Evidence of one-dimensional scale-dependent fractional advection-dispersion. J Contam Hydrol. 2006;85:53–71.
- Kim S, Kavvas ML. Generalized Ficks law and fractional ADE for pollution transport in a river: detailed derivation. J Hydrol Eng. 2006;11:80–83.
- Del Castillo Negrete D, Carreras BA, Lynch VE. Fractional diffusion in plasma turbulence. Phys Plasmas. 2004;11:3854–3864.
- Del Castillo Negrete D, Carreras BA, Lynch VE. Nondiffusive transport in plasma turbulence: a fractional diffusion approach. Phys Rev Lett. 2005;94:065003.
- Liu JJ, Yamamoto M. A backward problem for the time-fractional diffusion equation. Appl Anal. 2010;89:1769–1788.
- Ren C, Xu X, Lu S. Regularization by projection for a backward problem of the time-fractional diffusion equation. J Inverse Ill-Posed Probl. 2014;22:121–139.
- Cheng J, Nakagawa J, Yamamoto M, Yamazaki T. Uniqueness in an inverse problem one-dimensional fractional diffusion equation. J Inverse Probl. 2009;25, Article ID: 115002 (16p).
- Liu F, Zhuang P, Turner I, et al. A new fractional finite volume method for solving the fractional diffusion equation. Appl Math Model. 2014;38:3871–3878.
- Evans LC. Partial differential equations. Providence: American Mathematical Society; 1998.
- Gorenflo R, Mainardi F. Fractional calculus: integral and differential equations of fractional order. In: Carpinteri A, Mainardi F, editors. Fractals and fractional calculus in continuum mechanics. New York (NY): Springer-Verlag; 1997. p. 223–276.
- Jin B, Lazarov R, Zhou Z. Error estimates for a semidiscrete finite element method for fractional order parabolic equations. SIAM J Numer Anal. 2013;51:445–466.
- McLean W. Regularity of solutions to a time-fractional diffusion equation. ANZIAM J. 2010;52:123–138.
- Mustapha K, McLean W. Superconvergence of a discontinuous Galerkin method for fractional diffusion and wave equations. SIAM J Numer Anal. 2013;51:491–515.
- Courant R, Hilbert D. Methods of mathematical physics. New York (NY): Interscience; 1953.
- Clark GW, Oppenheimer SF. Quasireversibility methods for non-well posed problems. Elect J Differ Equ. 1994;301:1–9.
- Denche M, Bessila K. A modified quasi-boundary value method for ill-posed problems. J Math Anal Appl. 2005;301:419–426.
- Xiaoli F, Wantao N, Zhi Q. A quasi-boundary-value method for a Cauchy problem of an elliptic equation in multiple dimensions. Inverse Probl Sci Eng. 2014;22:1045–1061.
- Zhang HW. Modified quasi-boundary value method for a Cauchy problem of semi-linear elliptic equation. Int J Comput Math. 2012;89:1689–1703.
- Xiao-Li F, Lars E, Chu Li F. A quasi-boundary-value method for the Cauchy problem for elliptic equations with nonhomogeneous Neumann data. J Inverse Ill-Posed Probl. 2010;18:617–645.
