Simultaneous inversion for the diffusion and source coefficients in the multi-term TFDE

Abstract

This article deals with an inverse problem of determining the space-dependent diffusion coefficient and the source coefficient simultaneously in the multi-term time fractional diffusion equation (TFDE in short) using measurements at one inner point. From a view point of optimality, solving the inverse problem is transformed to minimize an error functional with the help of the solution operator from the unknown to the additional observation. The solution operator is nonlinear but it is of Lipschitz continuity by which existence of a minimum to the error functional is obtained using Sobolev embedding theorems. The homotopy regularization algorithm is introduced to solve the simultaneous inversion problem based on the minimization problem, and numerical examples are presented. The inversion solutions give good approximations to the exact solutions demonstrating that the homotopy regularization algorithm is efficient for the simultaneous inversion problem arising in the multi-term TFDE.

Keywords:

• Multi-term time fractional diffusion
• simultaneous inversion problem
• minimization problem
• Lipschitz continuity
• numerical inversion

AMS Subject Classifications:

• 35R11
• 35R30
• 65M06

1. Introduction

The fractional diffusion equations have played an important role in modelling of the anomalous diffusion phenomena and in the theory of the complex systems (see e.g. [1–6], and references therein) during the last few decades. The so-called time fractional diffusion equation arises when replacing the first-order time derivative by a fractional derivative of order $\mathit{\alpha }$ with $0<\mathit{\alpha }<1$. On the attempting to describe some real processes with the equations of the fractional derivative, several researches confronted with the situation that the time fractional derivative from the corresponding model equations did not remain constant and changed, say, in the interval from 0 to 1, from 1 to 2 or even from 0 to 2. To manage these phenomena, several approaches were suggested. One of them introduces the fractional derivatives of the variable order, i.e. the derivatives with the order that can change with the time or/and depending on the spatial coordinates (see e.g. [7,8]), and the other way is to employ the multi-term time fractional diffusion equations. Let $\mathrm{\Omega }=(0,l)$ where $l>0$, and denote ${\mathrm{\Omega }}_T=\mathrm{\Omega }\times (0,T]$ for $T>0$, the 1D multi-term time fractional diffusion equation with space-dependent diffusion coefficient is given as(1.1) $$\begin{array}{cc}\hfill \frac{{\mathit{\partial }}^{\mathit{\alpha }}u}{\mathit{\partial }{t}^{\mathit{\alpha }}}+\sum _{j=1}^m{r}_j\frac{{\mathit{\partial }}^{{\mathit{\alpha }}_j}u}{\mathit{\partial }{t}^{{\mathit{\alpha }}_j}}=\frac{\mathit{\partial }}{\mathit{\partial }x}\left(D(x)\frac{\mathit{\partial }u}{\mathit{\partial }x}\right)+s(x,t),& (x,t)\in {\mathrm{\Omega }}_T,\hfill \end{array}$$(1.1)

where $u=u(x,t)$ denotes the state variable at space point x and time t, $D(x)>0$ is the space-dependent diffusion coefficient, s(x, t) is a source term, and $\mathit{\alpha }$ denotes the principal fractional order, and ${\mathit{\alpha }}_1,{\mathit{\alpha }}_2,\dots ,{\mathit{\alpha }}_m$ are the multi-term fractional orders of the derivatives, which satisfy the condition of order:(1.2) $$\begin{array}{c}\hfill 0<{\mathit{\alpha }}_m<{\mathit{\alpha }}_{m-1}<\cdots <{\mathit{\alpha }}_1<\mathit{\alpha }<1,\end{array}$$(1.2)

and $r_1,r_2,\dots ,r_m$ are positive constants, and all of the above time-fractional derivatives are defined in the meaning of Caputo from the left-hand side, which for example for $\mathit{\alpha }\in (0,1)$ the fractional derivative of a function $h=h(t)$ at $t\in (0,T]$ is given as(1.3) $$\begin{array}{c}\hfill \frac{{\mathit{\partial }}^{\mathit{\alpha }}h}{\mathit{\partial }{t}^{\mathit{\alpha }}}=\frac{1}{\mathrm{\Gamma }(1-\mathit{\alpha })}{\int }_0^t\frac{h^{\prime }(s)}{{(t-s)}^{\mathit{\alpha }}}\mathrm{d}s,\end{array}$$(1.3)

where $\mathrm{\Gamma }(·)$ is the usual Gamma function. See, e.g. Podlubny [9] and Kilbas et al. [10] for the definition and properties of the Caputo’s derivative.

From the past few years, there are quite a few researches on the forward problem of multi-term time fractional diffusion equations like Equation (1.1(1.1) $$\begin{array}{cc}\hfill \frac{{\mathit{\partial }}^{\mathit{\alpha }}u}{\mathit{\partial }{t}^{\mathit{\alpha }}}+\sum _{j=1}^m{r}_j\frac{{\mathit{\partial }}^{{\mathit{\alpha }}_j}u}{\mathit{\partial }{t}^{{\mathit{\alpha }}_j}}=\frac{\mathit{\partial }}{\mathit{\partial }x}\left(D(x)\frac{\mathit{\partial }u}{\mathit{\partial }x}\right)+s(x,t),& (x,t)\in {\mathrm{\Omega }}_T,\hfill \end{array}$$(1.1) ), for instance, see [11,12] for the maximum principles, see [13–15] for the uniqueness and existence results, see [16–19] for the analytic solutions, and see [20,21] for numerical solutions of finite difference method, and recently see [22] for the finite element solution, etc.

However, for real problems, the part of the boundary, or the initial data, or the diffusion coefficient, or the source term cannot be obtained directly and we have to determine them by some additional measurements, which yields to inverse problems arising in the fractional diffusion models. There are still some researches on inverse problems in the single-term time fractional diffusion equation, see, e.g. Murio [23], Liu and Yamamoto [24], Sakamoto and Yamamoto [25], Tuan [26], Jin [27], Yamamoto [28], Luchko et al. [29], Miller and Yamamoto [30] and Wei et al. [31]. Recently, see Jin et al. [32] for a tutorial review on inverse problems for anomalous diffusion processes, and see Liu et al. [33] for the research on recovering a time-dependent boundary source using nonlocal measurement data, and see Zhang [34] for an inverse problem of determining a time-dependent diffusion coefficient in the time fractional diffusion equation using monotonicity of the input–output operator and fixed point method, and see Wei et al. [35] for the research on uniqueness and stability for determining the time-dependent source term also in the one-term time fractional diffusion equation.

To our knowledge, there are few literatures concerned with simultaneous inversion problems, especially for the inverse problems in the multi-term time fractional differential equations. Cheng et al. [36] proved the uniqueness result for a simultaneous inverse problem of identifying the diffusion coefficient and the fractional order in the one-term TFDE, which is the first work on simultaneous inverse problems for fractional diffusion equations, and Li et al. [37] considered with the same inverse problem but with more general conditions and numerical inversions. Li and Yamamoto [38] studied an inverse problem of identifying the multiple fractional orders in the multi-term TFDE, and they gave uniqueness of the solution to the inverse problem using Laplace transform and analytical method, and Li et al. [39] considered the similar model and they proved the uniqueness of determining the fractional orders, the number of the fractional terms and the spatially varying coefficient simultaneously. On the other hand, Rodrigues, Orlande and Dulikravich [40] ever considered a simultaneous inversion problem but in the integer-order diffusion equation by the conjugate gradient method, Zhang et al. [41] considered a simultaneous inversion problem for the space-dependent diffusion coefficient and the source coefficient in the one-term TFDE, and they gave quite a few numerical inversions using the homotopy regularization algorithm, and recently Jia et al. [42] studied a simultaneous inversion problem of determining the diffusion coefficient and the source term in 1D space fractional advection diffusion equation by the optimal perturbation regularization algorithm.

In this paper, by setting $s(x,t)=f(x)\mathit{\beta }(t)$ in Equation (1.1(1.1) $$\begin{array}{cc}\hfill \frac{{\mathit{\partial }}^{\mathit{\alpha }}u}{\mathit{\partial }{t}^{\mathit{\alpha }}}+\sum _{j=1}^m{r}_j\frac{{\mathit{\partial }}^{{\mathit{\alpha }}_j}u}{\mathit{\partial }{t}^{{\mathit{\alpha }}_j}}=\frac{\mathit{\partial }}{\mathit{\partial }x}\left(D(x)\frac{\mathit{\partial }u}{\mathit{\partial }x}\right)+s(x,t),& (x,t)\in {\mathrm{\Omega }}_T,\hfill \end{array}$$(1.1) ), where the time-decay factor $\mathit{\beta }(t)$ is known, we also deal with the simultaneous inversion problem of determining the space-dependent diffusion coefficient D(x) and the space-dependent source magnitude f(x) but for the multi-term TFDE. It is noticeable that the simultaneous inversion problem here for identifying the space-dependent diffusion coefficient and the source function becomes severely ill-posed as compared with the previous problems since the model is difficult to simulate and the two unknowns are both variable. From a view point of optimality, solving the inverse problem is transformed to minimize an error functional based on the solution operator. Since the solution operator from the unknowns to the additional observations is nonlinear, it is not convex for the error functional, however, we can prove its the Lipschitz continuity by which existence of a minimum to the error functional is obtained using Sobolev embedding theorems. Furthermore, the homotopy regularization algorithm is introduced based on the error functional, and numerical inversions with random noisy data are performed. It is noted that the inversion algorithm can also be employed to determine the space-dependent diffusion coefficient and time-dependent decay factor simultaneously in the case that the spacewise-dependent source magnitude is known.

The rest of the paper is organized as follows. In Section 2, the forward problem for the multi-term TFDE is discussed, and the Lipschitz continuity of the solution operator is proved, and a finite difference scheme to the forward problem is given. In Section 3, the simultaneous inversion problem of determining the diffusion coefficient and the source magnitude by the additional data at one inner point is set forth, and existence of an minimum to the error functional is obtained by the Sobolev embedding theorems. In Section 4, the homotopy regularization algorithm is introduced based on the minimization problem, and numerical inversions are presented, and conclusions are given in Section 5.

2. The forward problem

By $\overline{\mathrm{\Omega }}$ we denote the closure of the space domain $\mathrm{\Omega }$. Consider the initial boundary value problem composed by Equation (1.1(1.1) $$\begin{array}{cc}\hfill \frac{{\mathit{\partial }}^{\mathit{\alpha }}u}{\mathit{\partial }{t}^{\mathit{\alpha }}}+\sum _{j=1}^m{r}_j\frac{{\mathit{\partial }}^{{\mathit{\alpha }}_j}u}{\mathit{\partial }{t}^{{\mathit{\alpha }}_j}}=\frac{\mathit{\partial }}{\mathit{\partial }x}\left(D(x)\frac{\mathit{\partial }u}{\mathit{\partial }x}\right)+s(x,t),& (x,t)\in {\mathrm{\Omega }}_T,\hfill \end{array}$$(1.1) ) with the initial condition(2.1) $$\begin{array}{c}\hfill \begin{array}{cc}u(x,0)=g(x),\hfill & x\in \overline{\mathrm{\Omega }};\hfill \end{array}\end{array}$$(2.1)

and the homogeneous Neumann boundary condition(2.2) $$\begin{array}{c}\hfill \begin{array}{cc}{u}_x(0,t)=u_x(l,t)=0,\hfill & 0<t\le T.\hfill \end{array}\end{array}$$(2.2)

For convenience, we give some general settings and notations used in this paper.

Let $L^2(\mathrm{\Omega })$ be a usual $L^2$-space with the inner product $(·,·)$ and the norm ${\Vert ·\Vert }_{L^2(\mathrm{\Omega })}=\sqrt{(·,·)}$, and $H^k(\mathrm{\Omega })$ and $C^k(\overline{\mathrm{\Omega }})$ ($k\in \{\mathbf{0}\}\cup \mathbf{N}$) denote the Sobolev spaces (see, e.g. Adams [43]). For $1\le p<\infty$ and a Banach space X, we say that an abstract function $u\in L^p(0,T;X)$ provided$${\Vert u\Vert }_{L^p(0,T;X)}:={\left({\int }_0^T{\Vert u(·,t)\Vert }_X^p\mathrm{d}t\right)}^{1/p}<\infty .$$

For example:$$L^2(0,T;L^2(\mathrm{\Omega }))=\{u(x,t):{\left({\int }_0^T{\Vert u(x,t)\Vert }_{L^2(\mathrm{\Omega })}^2\mathrm{d}t\right)}^{1/2}<\infty \},$$

and$$L^2(0,T;H^1(\mathrm{\Omega }))=\{u(x,t):{\left({\int }_0^T{\Vert u(x,t)\Vert }_{H^1(\mathrm{\Omega })}^2\mathrm{d}t\right)}^{1/2}<\infty \}.$$

2.1. Lipschitz continuity of the solution operator

An inverse problem is always related with a forward problem, and property of the solution to the forward problem is essential to the research of the corresponding inverse problem. On regularity of the solution to the forward problem of TFDEs, we refer to [13,25] for the case of Dirichelet boundary conditions and refer to [35] for the case of Neumann boundary condition in the one-term TFDE. Here for the forward problem (1.1(1.1) $$\begin{array}{cc}\hfill \frac{{\mathit{\partial }}^{\mathit{\alpha }}u}{\mathit{\partial }{t}^{\mathit{\alpha }}}+\sum _{j=1}^m{r}_j\frac{{\mathit{\partial }}^{{\mathit{\alpha }}_j}u}{\mathit{\partial }{t}^{{\mathit{\alpha }}_j}}=\frac{\mathit{\partial }}{\mathit{\partial }x}\left(D(x)\frac{\mathit{\partial }u}{\mathit{\partial }x}\right)+s(x,t),& (x,t)\in {\mathrm{\Omega }}_T,\hfill \end{array}$$(1.1) ), (2.1(2.1) $$\begin{array}{c}\hfill \begin{array}{cc}u(x,0)=g(x),\hfill & x\in \overline{\mathrm{\Omega }};\hfill \end{array}\end{array}$$(2.1) )–(2.2(2.2) $$\begin{array}{c}\hfill \begin{array}{cc}{u}_x(0,t)=u_x(l,t)=0,\hfill & 0<t\le T.\hfill \end{array}\end{array}$$(2.2) ), we give the following lemma to show well-posedness of the solution.

Lemma 2.1:

Under the assumptions in Section 1 for Equation (1.1(1.1) $$\begin{array}{cc}\hfill \frac{{\mathit{\partial }}^{\mathit{\alpha }}u}{\mathit{\partial }{t}^{\mathit{\alpha }}}+\sum _{j=1}^m{r}_j\frac{{\mathit{\partial }}^{{\mathit{\alpha }}_j}u}{\mathit{\partial }{t}^{{\mathit{\alpha }}_j}}=\frac{\mathit{\partial }}{\mathit{\partial }x}\left(D(x)\frac{\mathit{\partial }u}{\mathit{\partial }x}\right)+s(x,t),& (x,t)\in {\mathrm{\Omega }}_T,\hfill \end{array}$$(1.1) ), also assume that the initial function $g(x)=0$ and the source term $s(x,t)\in L^2(0,T;L^2(\mathrm{\Omega }))$. Then there is a unique solution $u=u(x,t)\in L^2(0,T,H^2(\mathrm{\Omega }))$ to the forward problem (1.1(1.1) $$\begin{array}{cc}\hfill \frac{{\mathit{\partial }}^{\mathit{\alpha }}u}{\mathit{\partial }{t}^{\mathit{\alpha }}}+\sum _{j=1}^m{r}_j\frac{{\mathit{\partial }}^{{\mathit{\alpha }}_j}u}{\mathit{\partial }{t}^{{\mathit{\alpha }}_j}}=\frac{\mathit{\partial }}{\mathit{\partial }x}\left(D(x)\frac{\mathit{\partial }u}{\mathit{\partial }x}\right)+s(x,t),& (x,t)\in {\mathrm{\Omega }}_T,\hfill \end{array}$$(1.1) ), (2.1(2.1) $$\begin{array}{c}\hfill \begin{array}{cc}u(x,0)=g(x),\hfill & x\in \overline{\mathrm{\Omega }};\hfill \end{array}\end{array}$$(2.1) ) and (2.2(2.2) $$\begin{array}{c}\hfill \begin{array}{cc}{u}_x(0,t)=u_x(l,t)=0,\hfill & 0<t\le T.\hfill \end{array}\end{array}$$(2.2) ), and there exists a constant $M_1>0$ depending on ${\mathrm{\Omega }}_T,\mathit{\alpha },{\mathit{\alpha }}_j,r_j(j=1,2,\dots ,m)$ such that(2.3) $$\begin{array}{c}\hfill \begin{array}{c}{∥u(x,t)∥}_{L^2(0,T;H^2(\mathrm{\Omega }))}\le M_1{∥s(x,t)∥}_{L^2(0,T;L^2(\mathrm{\Omega }))}.\hfill \end{array}\end{array}$$(2.3)

Noting the properties of the multinomial Mittag–Leffler function, the proof can be completed with a similar method as used in [13,35].

Furthermore, let $s(x,t)=\mathit{\beta }(t)f(x)$, and denote $u=u(D,f)(x,t)$ as the solution to the forward problem (1.1(1.1) $$\begin{array}{cc}\hfill \frac{{\mathit{\partial }}^{\mathit{\alpha }}u}{\mathit{\partial }{t}^{\mathit{\alpha }}}+\sum _{j=1}^m{r}_j\frac{{\mathit{\partial }}^{{\mathit{\alpha }}_j}u}{\mathit{\partial }{t}^{{\mathit{\alpha }}_j}}=\frac{\mathit{\partial }}{\mathit{\partial }x}\left(D(x)\frac{\mathit{\partial }u}{\mathit{\partial }x}\right)+s(x,t),& (x,t)\in {\mathrm{\Omega }}_T,\hfill \end{array}$$(1.1) ), (2.1(2.1) $$\begin{array}{c}\hfill \begin{array}{cc}u(x,0)=g(x),\hfill & x\in \overline{\mathrm{\Omega }};\hfill \end{array}\end{array}$$(2.1) ) and (2.2(2.2) $$\begin{array}{c}\hfill \begin{array}{cc}{u}_x(0,t)=u_x(l,t)=0,\hfill & 0<t\le T.\hfill \end{array}\end{array}$$(2.2) ) for given $\mathit{\beta }(t)>0$ and suitable D(x) and f(x). It is obvious that the solution operator $(D,f)\to u(D,f)$ is nonlinear, however, the Lipschitz continuity of the solution operator can be proved by which existence of a minimum to the minimization problem of the error functional is obtained.

Theorem 2.2:

Under the assumptions in Lemma 2.1, and assume that the source term $s(x,t)=f(x)\mathit{\beta }(t)$ where $\mathit{\beta }(t)\in L^2(0,T)$ is given and satisfies ${∥\mathit{\beta }(t)∥}_{L^2(0,T)}\le E$, and $u_i=u(D_i,f_i)(x,t)$$(i=1,2)$ are the two solutions to the forward problem corresponding to the diffusion coefficients $D_i=D_i(x)\in C^1(\overline{\mathrm{\Omega }})$, $D_i>0$ on $\overline{\mathrm{\Omega }}$$(i=1,2)$ and the source functions $f_i=f_i(x)\in L^2(\mathrm{\Omega })$$(i=1,2)$. Then it follows that(2.4) $$\begin{array}{c}\hfill \begin{array}{c}{∥u_1-u_2∥}_{L^2(0,T;H^2(\mathrm{\Omega }))}\le M\left({∥D_1-D_2∥}_{C^1(\overline{\mathrm{\Omega }})}+{∥f_1-f_2∥}_{L^2(\mathrm{\Omega })}\right),\hfill \end{array}\end{array}$$(2.4)

where $M>0$ is a constant depending only on ${\mathrm{\Omega }}_T,E,\mathit{\alpha }$, and ${\mathit{\alpha }}_j,r_j(j=1,2,\dots ,m)$.

Let $U=u_1-u_2$, and U satisfies the equation(2.5) $$\begin{array}{c}\hfill \frac{{\mathit{\partial }}^{\mathit{\alpha }}U}{\mathit{\partial }{t}^{\mathit{\alpha }}}+\sum _{j=1}^m{r}_j\frac{{\mathit{\partial }}^{{\mathit{\alpha }}_j}U}{\mathit{\partial }{t}^{{\mathit{\alpha }}_j}}=\frac{\mathit{\partial }}{\mathit{\partial }x}\left(D_2(x)\frac{\mathit{\partial }U}{\mathit{\partial }x}\right)+\tilde{s}(x,t),\end{array}$$(2.5)

where$$\tilde{s}(x,t)=\frac{\mathit{\partial }}{\mathit{\partial }x}\left((D_1-D_2)\frac{\mathit{\partial }{u}_1}{\mathit{\partial }x}\right)+\mathit{\beta }(t)(f_1-f_2).$$

Denote $p(x)=D_1(x)-D_2(x)$, and rewrite $\tilde{s}(x,t)$ as(2.6) $$\begin{array}{c}\hfill \tilde{s}(x,t)=p(x)\frac{{\mathit{\partial }}^2{u}_1}{\mathit{\partial }{x}^2}+\frac{\mathit{\partial }p}{\mathit{\partial }x}\frac{\mathit{\partial }{u}_1}{\mathit{\partial }x}+\mathit{\beta }(t)(f_1-f_2).\end{array}$$(2.6)

Noting that $u_1\in L^2(0,T,H^2(\mathrm{\Omega }))$, there hold $\frac{{\mathit{\partial }}^2{u}_1}{\mathit{\partial }{x}^2}\in L^2(0,T;L^2(\mathrm{\Omega }))$ and $\frac{\mathit{\partial }{u}_1}{\mathit{\partial }x}\in L^2(0,T;H^1(\mathrm{\Omega }))$, and there exists a constant $M_2>0$ independent of choices of $D_1,D_2$ and $f_1,f_2$ such that(2.7) $$\begin{array}{c}\hfill \Vert \frac{\mathit{\partial }{u}_1}{\mathit{\partial }x}{\Vert }_{L^2(0,T;H^1(\mathrm{\Omega }))},{\Vert \frac{{\mathit{\partial }}^2{u}_1}{\mathit{\partial }{x}^2}\Vert }_{L^2(0,T;L^2(\mathrm{\Omega }))}\le M_2.\end{array}$$(2.7)

Meantime there hold $p(x)\in L^2(\mathrm{\Omega })$ and $\frac{\mathit{\partial }p}{\mathit{\partial }x}\in L^2(\mathrm{\Omega })$ due to $p(x)\in C^1(\overline{\mathrm{\Omega }})$. Thus we have $\tilde{s}(x,t)\in L^2(0,T;L^2(\mathrm{\Omega }))$, and there holds by Lemma 2.1(2.8) $$\begin{array}{c}\hfill {\Vert U\Vert }_{L^2(0,T;H^2(\mathrm{\Omega }))}\le M_1{\Vert \tilde{s}\Vert }_{L^2(0,T;L^2(\mathrm{\Omega }))}.\end{array}$$(2.8)

Hence orth, we get(2.9) $$\begin{array}{c}\hfill \begin{array}{cc}& {∥p\frac{{\mathit{\partial }}^2{u}_1}{\mathit{\partial }{x}^2}+\frac{\mathit{\partial }p}{\mathit{\partial }x}\frac{\mathit{\partial }{u}_1}{\mathit{\partial }x}∥}_{L^2(0,T;L^2(\mathrm{\Omega }))}^2\hfill \\ \hfill & ={\int }_0^T{\int }_{\mathrm{\Omega }}{(p\frac{{\mathit{\partial }}^2{u}_1}{\mathit{\partial }{x}^2}+\frac{\mathit{\partial }p}{\mathit{\partial }x}\frac{\mathit{\partial }{u}_1}{\mathit{\partial }x})}^2\mathrm{d}x\mathrm{d}t\hfill \\ \hfill & \le 2\left[{\int }_0^T{\int }_{\mathrm{\Omega }}{(p\frac{{\mathit{\partial }}^2{u}_1}{\mathit{\partial }{x}^2})}^2\mathrm{d}x\mathrm{d}t+{\int }_0^T{\int }_{\mathrm{\Omega }}{(\frac{\mathit{\partial }p}{\mathit{\partial }x}\frac{\mathit{\partial }{u}_1}{\mathit{\partial }x})}^2\mathrm{d}x\mathrm{d}t\right]\hfill \\ \hfill & \le 2M_2^2{(\Vert p\Vert }_{C(\overline{\mathrm{\Omega }})}^2+{\Vert p\Vert }_{C^1(\overline{\mathrm{\Omega }})}^2)\hfill \\ \hfill & \le 4M_2^2{\Vert p\Vert }_{C^1(\overline{\mathrm{\Omega }})}^2.\hfill \end{array}\end{array}$$(2.9)

Together with (2.8(2.8) $$\begin{array}{c}\hfill {\Vert U\Vert }_{L^2(0,T;H^2(\mathrm{\Omega }))}\le M_1{\Vert \tilde{s}\Vert }_{L^2(0,T;L^2(\mathrm{\Omega }))}.\end{array}$$(2.8) ) and (2.6(2.6) $$\begin{array}{c}\hfill \tilde{s}(x,t)=p(x)\frac{{\mathit{\partial }}^2{u}_1}{\mathit{\partial }{x}^2}+\frac{\mathit{\partial }p}{\mathit{\partial }x}\frac{\mathit{\partial }{u}_1}{\mathit{\partial }x}+\mathit{\beta }(t)(f_1-f_2).\end{array}$$(2.6) ) we have(2.10) $$\begin{array}{c}\hfill \begin{array}{cc}& {∥U∥}_{L^2(0,T;H^2(\mathrm{\Omega }))}^2\le M_1^2{\Vert \tilde{s}\Vert }_{L^2(0,T;L^2(\mathrm{\Omega }))}^2\hfill \\ \hfill & =M_1^2{∥p\frac{{\mathit{\partial }}^2{u}_1}{\mathit{\partial }{x}^2}+\frac{\mathit{\partial }p}{\mathit{\partial }x}\frac{\mathit{\partial }{u}_1}{\mathit{\partial }x}+\mathit{\beta }(t)(f_1-f_2)∥}_{L^2(0,T;L^2(\mathrm{\Omega }))}^2\hfill \\ \hfill & \le 2M_1^2\left({∥p\frac{{\mathit{\partial }}^2{u}_1}{\mathit{\partial }{x}^2}+\frac{\mathit{\partial }p}{\mathit{\partial }x}\frac{\mathit{\partial }{u}_1}{\mathit{\partial }x}∥}_{L^2(0,T;L^2(\mathrm{\Omega }))}^2+{\Vert \mathit{\beta }\Vert }_{L^2(0,T)}^2{\Vert f_1-f_2\Vert }_{L^2(\mathrm{\Omega })}^2\right)\hfill \\ \hfill & \le 8M_1^2{M}_2^2{\Vert p\Vert }_{C^1(\overline{\mathrm{\Omega }})}^2+2M_1^2{E}^2{\Vert f_1-f_2\Vert }_{L^2(\mathrm{\Omega })}^2\hfill \\ \hfill & \le max\{8M_1^2{M}_2^2,2M_1^2{E}^2\}\left({\Vert p\Vert }_{C^1(\overline{\mathrm{\Omega }})}^2+{\Vert f_1-f_2\Vert }_{L^2(\mathrm{\Omega })}^2\right),\hfill \end{array}\end{array}$$(2.10)

which can end the proof of this theorem.

If the time-dependent decay factor $\mathit{\beta }=\mathit{\beta }(t)$ is unknown and the source magnitude $f=f(x)$ is given, we can get the following assertion with the same method as used in the above.

Corollary 2.3:

Under the assumptions in Lemma 2.1, and assume that the source term $s(x,t)=f(x)\mathit{\beta }(t)$ where $f(x)\in L^2(\mathrm{\Omega })$ is given and satisfies ${∥f(x)∥}_{L^2(\mathrm{\Omega })}\le E$, and $u_i=u(D_i,{\mathit{\beta }}_i)(x,t)$$(i=1,2)$ are the two solutions to the forward problem corresponding to the diffusion coefficients $D_i=D_i(x)\in C^1(\overline{\mathrm{\Omega }})$, $D_i>0$ on $\overline{\mathrm{\Omega }}$$(i=1,2)$ and the time-dependent decay factor ${\mathit{\beta }}_i={\mathit{\beta }}_i(t)\in L^2(0,T)$$(i=1,2)$. Then it follows that(2.11) $$\begin{array}{c}\hfill \begin{array}{c}{∥u_1-u_2∥}_{L^2(0,T;H^2(\mathrm{\Omega }))}\le M\left({∥D_1-D_2∥}_{C^1(\overline{\mathrm{\Omega }})}+{∥{\mathit{\beta }}_1-{\mathit{\beta }}_2∥}_{L^2(0,T)}\right),\hfill \end{array}\end{array}$$(2.11)

where $M>0$ is a constant depending only on ${\mathrm{\Omega }}_T,E,\mathit{\alpha }$, and ${\mathit{\alpha }}_j,r_j(j=1,2,\dots ,m)$.

2.2. The difference scheme to the forward problem

In this subsection, an implicit finite difference scheme is set forth to solve the forward problem (1.1(1.1) $$\begin{array}{cc}\hfill \frac{{\mathit{\partial }}^{\mathit{\alpha }}u}{\mathit{\partial }{t}^{\mathit{\alpha }}}+\sum _{j=1}^m{r}_j\frac{{\mathit{\partial }}^{{\mathit{\alpha }}_j}u}{\mathit{\partial }{t}^{{\mathit{\alpha }}_j}}=\frac{\mathit{\partial }}{\mathit{\partial }x}\left(D(x)\frac{\mathit{\partial }u}{\mathit{\partial }x}\right)+s(x,t),& (x,t)\in {\mathrm{\Omega }}_T,\hfill \end{array}$$(1.1) ), (2.1(2.1) $$\begin{array}{c}\hfill \begin{array}{cc}u(x,0)=g(x),\hfill & x\in \overline{\mathrm{\Omega }};\hfill \end{array}\end{array}$$(2.1) )–(2.2(2.2) $$\begin{array}{c}\hfill \begin{array}{cc}{u}_x(0,t)=u_x(l,t)=0,\hfill & 0<t\le T.\hfill \end{array}\end{array}$$(2.2) ) numerically. Although the similar difference scheme has been discussed in the previous works, see e.g. [20,21], we still give it here for completeness.

Firstly, discretizing the space domain by $x_i=ih(i=0,1,\dots ,M)$ and the time domain by $t_n=n\mathit{\tau }(n=0,1,\dots ,N)$, and the fractional derivatives by the difference discretization, we have(2.12) $$\begin{array}{c}\hfill \frac{{\mathit{\partial }}^{\mathit{\alpha }}u}{\mathit{\partial }{t}^{\mathit{\alpha }}}(x_{i,}{t}_{n+1})=\frac{{\mathit{\tau }}^{-\mathit{\alpha }}}{\mathrm{\Gamma }(2-\mathit{\alpha })}\sum _{k=0}^n[u(x_i,t_{n+1-k})-u(x_i,t_{n-k})][{(k+1)}^{1-\mathit{\alpha }}-k^{1-\mathit{\alpha }})]+\mathrm{O}(\mathit{\tau }),\end{array}$$(2.12)

and(2.13) $$\begin{array}{c}\hfill \frac{{\mathit{\partial }}^{{\mathit{\alpha }}_j}u}{\mathit{\partial }{t}^{{\mathit{\alpha }}_j}}(x_{i,}{t}_{n+1})=\frac{{\mathit{\tau }}^{-{\mathit{\alpha }}_j}}{\mathrm{\Gamma }(2-{\mathit{\alpha }}_j)}\sum _{k=0}^n[u(x_i,t_{n+1-k})-u(x_i,t_{n-k})][{(k+1)}^{1-{\mathit{\alpha }}_j}-k^{1-{\mathit{\alpha }}_j})]+\mathrm{O}(\mathit{\tau }),\end{array}$$(2.13)

where $h=l/M$ is the space mesh step and $\mathit{\tau }=T/N$ is the time mesh step.

Next, we discretize the derivative $\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}$ in Equation (1.1(1.1) $$\begin{array}{cc}\hfill \frac{{\mathit{\partial }}^{\mathit{\alpha }}u}{\mathit{\partial }{t}^{\mathit{\alpha }}}+\sum _{j=1}^m{r}_j\frac{{\mathit{\partial }}^{{\mathit{\alpha }}_j}u}{\mathit{\partial }{t}^{{\mathit{\alpha }}_j}}=\frac{\mathit{\partial }}{\mathit{\partial }x}\left(D(x)\frac{\mathit{\partial }u}{\mathit{\partial }x}\right)+s(x,t),& (x,t)\in {\mathrm{\Omega }}_T,\hfill \end{array}$$(1.1) ) by the general two-order centre difference scheme, which is given as(2.14) $$\begin{array}{c}\hfill \frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}(x_i,t_{n+1})=\frac{u(x_{i+1},t_{n+1})-2u(x_i,t_{n+1})+u(x_{i-1},t_{n+1})}{h^2}+\mathrm{O}(h^2).\end{array}$$(2.14)

Denoting $u_i^n\approx u(x_i,t_n)$, $s_i^n\approx s(x_i,t_n)$, $D_i\approx D(x_i)$, $g_i\approx g(x_i)$, and substituting (2.12(2.12) $$\begin{array}{c}\hfill \frac{{\mathit{\partial }}^{\mathit{\alpha }}u}{\mathit{\partial }{t}^{\mathit{\alpha }}}(x_{i,}{t}_{n+1})=\frac{{\mathit{\tau }}^{-\mathit{\alpha }}}{\mathrm{\Gamma }(2-\mathit{\alpha })}\sum _{k=0}^n[u(x_i,t_{n+1-k})-u(x_i,t_{n-k})][{(k+1)}^{1-\mathit{\alpha }}-k^{1-\mathit{\alpha }})]+\mathrm{O}(\mathit{\tau }),\end{array}$$(2.12) )–(2.14(2.14) $$\begin{array}{c}\hfill \frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}(x_i,t_{n+1})=\frac{u(x_{i+1},t_{n+1})-2u(x_i,t_{n+1})+u(x_{i-1},t_{n+1})}{h^2}+\mathrm{O}(h^2).\end{array}$$(2.14) ) into Equation (1.1(1.1) $$\begin{array}{cc}\hfill \frac{{\mathit{\partial }}^{\mathit{\alpha }}u}{\mathit{\partial }{t}^{\mathit{\alpha }}}+\sum _{j=1}^m{r}_j\frac{{\mathit{\partial }}^{{\mathit{\alpha }}_j}u}{\mathit{\partial }{t}^{{\mathit{\alpha }}_j}}=\frac{\mathit{\partial }}{\mathit{\partial }x}\left(D(x)\frac{\mathit{\partial }u}{\mathit{\partial }x}\right)+s(x,t),& (x,t)\in {\mathrm{\Omega }}_T,\hfill \end{array}$$(1.1) ), and multiplying by ${\mathit{\tau }}^{\mathit{\alpha }}\mathrm{\Gamma }(2-\mathit{\alpha })$, we get(2.15) $$\begin{array}{c}\hfill \begin{array}{cc}& (u_i^{n+1}-u_i^n)\left[1+\sum _{j=1}^m{r}_j{\mathit{\tau }}^{\mathit{\alpha }-{\mathit{\alpha }}_j}\frac{\mathrm{\Gamma }(2-\mathit{\alpha })}{\mathrm{\Gamma }(2-{\mathit{\alpha }}_j)}\right]\hfill \\ \hfill & +\sum _{k=1}^n(u_i^{n+1-k}-u_i^{n-k})\hfill \\ \hfill & \times \left\{\left[{(k+1)}^{1-\mathit{\alpha }}-k^{1-\mathit{\alpha }}\right]+\sum _{j=1}^m{r}_j\left[{(k+1)}^{1-{\mathit{\alpha }}_j}-k^{1-{\mathit{\alpha }}_j}\right]{\mathit{\tau }}^{\mathit{\alpha }-{\mathit{\alpha }}_j}\frac{\mathrm{\Gamma }(2-\mathit{\alpha })}{\mathrm{\Gamma }(2-{\mathit{\alpha }}_j)}\right\}\hfill \\ \hfill & =\frac{D_i{\mathit{\tau }}^{\mathit{\alpha }}\mathrm{\Gamma }(2-\mathit{\alpha })}{h^2}\left(u_{i-1}^{n+1}-2u_i^{n+1}+u_{i+1}^{n+1}\right)+\frac{(D_i-D_{i-1}){\mathit{\tau }}^{\mathit{\alpha }}\mathrm{\Gamma }(2-\mathit{\alpha })}{h^2}\left(u_i^{n+1}-u_{i-1}^{n+1}\right)\hfill \\ \hfill & +{\mathit{\tau }}^{\mathit{\alpha }}\mathrm{\Gamma }(2-\mathit{\alpha })s_i^{n+1},\hfill \end{array}\end{array}$$(2.15)

for $i=1,2,\dots ,M-1$.

Denote$$v=1+\sum _{j=1}^m{r}_j\frac{{\mathit{\tau }}^{\mathit{\alpha }-{\mathit{\alpha }}_j}\mathrm{\Gamma }(2-\mathit{\alpha })}{\mathrm{\Gamma }(2-{\mathit{\alpha }}_j)},$$

and(2.16) $$\begin{array}{c}\hfill d_k=\frac{[{(k+1)}^{1-\mathit{\alpha }}-k^{1-\mathit{\alpha }}]+{\sum }_{j=1}^m{r}_j{\mathit{\tau }}^{\mathit{\alpha }-{\mathit{\alpha }}_j}[{(k+1)}^{1-{\mathit{\alpha }}_j}-k^{1-{\mathit{\alpha }}_j}]\mathrm{\Gamma }(2-\mathit{\alpha })/\mathrm{\Gamma }(2-{\mathit{\alpha }}_j)}{v},\end{array}$$(2.16)

for $k=0,1,\dots ,n$, and(2.17) $$\begin{array}{c}\hfill p_i=\frac{D_i{\mathit{\tau }}^{\mathit{\alpha }}\mathrm{\Gamma }(2-\mathit{\alpha })}{v{h}^2},q_i=\frac{(D_i-D_{i-1}){\mathit{\tau }}^{\mathit{\alpha }}\mathrm{\Gamma }(2-\mathit{\alpha })}{v{h}^2},\end{array}$$(2.17)

for $i=0,1,\dots ,M$. Thus we have by ignoring the remainder terms$$\begin{array}{c}(q_i-p_i)u_{i-1}^{n+1}+(1+2p_i-q_i)u_i^{n+1}-p_i{u}_{i+1}^{n+1}=\sum _{k=1}^n{u}_i^{n-k}(d_{k-1}-d_k)+\frac{{\mathit{\tau }}^{\mathit{\alpha }}\mathrm{\Gamma }(2-\mathit{\alpha })}{v}{s}_i^{n+1},\hfill \end{array}$$

and the initial boundary value conditions are discretized as$$\begin{array}{ccc}{u}_i^0=g_i;\hfill & u_0^n=u_1^n,\hfill & u_{M-1}^n=u_M^n.\hfill \end{array}$$

For $n=1,2,\dots ,N$, let$$U^n={(u_1^n,u_2^n,\dots ,u_{M-1}^n)}^T,S^n={(s_1^n,s_2^n,\dots ,s_{M-1}^n)}^T,g={(g_1,g_2,\dots ,g_{M-1})}^T;$$

and$$c_k=\left\{\begin{array}{cc}1-d_k,\hfill & k=1,\hfill \\ d_{k-1}-d_k,\hfill & k=2,\dots ,n;\hfill \end{array}\right.$$

and $B={(b_{ij})}_{(M-1)\times (M-1)}$, where $b_{ij}$, $i,j=1,\dots ,M-1$, are defined by(2.18) $$\begin{array}{c}\hfill b_{1j}:=\left\{\begin{array}{cc}1+p_1,\hfill & j=1,\hfill \\ -p_1,\hfill & j=2,\hfill \\ 0,\hfill & j=3,\dots ,M-1,\hfill \end{array}\right.\end{array}$$(2.18)

and(2.19) $$\begin{array}{c}\hfill b_{M-1j}:=\left\{\begin{array}{cc}0,\hfill & j=1,\dots ,M-3,\hfill \\ q_{M-1}-p_{M-1},\hfill & j=M-2,\hfill \\ 1+p_{M-1}-q_{M-1},\hfill & j=M-1,\hfill \end{array}\right.\end{array}$$(2.19)

and(2.20) $$\begin{array}{c}\hfill b_{ij}:=\left\{\begin{array}{cc}0,\hfill & j<i-1,\hfill \\ q_i-p_i,\hfill & j=i-1,\hfill \\ 1+2p_i-q_i,\hfill & j=i,\hfill \\ -p_i,\hfill & j=i+1,\hfill \\ 0,\hfill & j>i+1,\hfill \end{array}\right.\end{array}$$(2.20)

for $i=2,\dots ,M-2$, $j=1,2,\dots ,M-1$. Then we get the implicit finite difference scheme in matrix form(2.21) $$\begin{array}{c}\hfill \left\{\begin{array}{c}B{U}^1=U^0+\frac{{\mathit{\tau }}^{\mathit{\alpha }}\mathrm{\Gamma }(2-\mathit{\alpha })}{v}{S}^1,U^0=g;\hfill \\ B{U}^{n+1}=c_1{U}^n+c_2{U}^{n-1}+\cdots +c_n{U}^1+d_n{U}^0+\frac{{\mathit{\tau }}^{\mathit{\alpha }}\mathrm{\Gamma }(2-\mathit{\alpha })}{v}{S}^{n+1}.\hfill \end{array}\right.\end{array}$$(2.21)

Lemma 2.4:

The coefficient matrix B defined by (2.18(2.18) $$\begin{array}{c}\hfill b_{1j}:=\left\{\begin{array}{cc}1+p_1,\hfill & j=1,\hfill \\ -p_1,\hfill & j=2,\hfill \\ 0,\hfill & j=3,\dots ,M-1,\hfill \end{array}\right.\end{array}$$(2.18) )–(2.20(2.20) $$\begin{array}{c}\hfill b_{ij}:=\left\{\begin{array}{cc}0,\hfill & j<i-1,\hfill \\ q_i-p_i,\hfill & j=i-1,\hfill \\ 1+2p_i-q_i,\hfill & j=i,\hfill \\ -p_i,\hfill & j=i+1,\hfill \\ 0,\hfill & j>i+1,\hfill \end{array}\right.\end{array}$$(2.20) ) is strictly diagonally dominant, and the difference scheme (2.21(2.21) $$\begin{array}{c}\hfill \left\{\begin{array}{c}B{U}^1=U^0+\frac{{\mathit{\tau }}^{\mathit{\alpha }}\mathrm{\Gamma }(2-\mathit{\alpha })}{v}{S}^1,U^0=g;\hfill \\ B{U}^{n+1}=c_1{U}^n+c_2{U}^{n-1}+\cdots +c_n{U}^1+d_n{U}^0+\frac{{\mathit{\tau }}^{\mathit{\alpha }}\mathrm{\Gamma }(2-\mathit{\alpha })}{v}{S}^{n+1}.\hfill \end{array}\right.\end{array}$$(2.21) ) has only one solution.

Noting that $p_i=\frac{D_i{\mathit{\tau }}^{\mathit{\alpha }}\mathrm{\Gamma }(2-\mathit{\alpha })}{v{h}^2}>0$ and $p_i-q_i=\frac{D_{i-1}{\mathit{\tau }}^{\mathit{\alpha }}\mathrm{\Gamma }(2-\mathit{\alpha })}{v{h}^2}>0$ for $i=1,\dots ,M-1$, there are(2.22) $$\begin{array}{c}\hfill \sum _{j=1,j\ne i}^{M-1}|b_{1j}|=p_1<1+p_1=b_{11},\end{array}$$(2.22)

and(2.23) $$\begin{array}{c}\hfill \sum _{j=1,j\ne i}^{M-1}|b_{M-1j}|=p_{M-1}-q_{M-1}<1+p_{M-1}-q_{M-1}=b_{M-1M-1}.\end{array}$$(2.23)

Similarly, for $i=2,\dots ,M-2$ we have(2.24) $$\begin{array}{c}\hfill \sum _{j=1,j\ne i}^{M-1}|b_{ij}|=p_i-q_i+p_i=2p_i-q_i<1+2p_i-q_i=b_{ii}.\end{array}$$(2.24)

Combining (2.22(2.22) $$\begin{array}{c}\hfill \sum _{j=1,j\ne i}^{M-1}|b_{1j}|=p_1<1+p_1=b_{11},\end{array}$$(2.22) ), (2.23(2.23) $$\begin{array}{c}\hfill \sum _{j=1,j\ne i}^{M-1}|b_{M-1j}|=p_{M-1}-q_{M-1}<1+p_{M-1}-q_{M-1}=b_{M-1M-1}.\end{array}$$(2.23) ) with (2.24(2.24) $$\begin{array}{c}\hfill \sum _{j=1,j\ne i}^{M-1}|b_{ij}|=p_i-q_i+p_i=2p_i-q_i<1+2p_i-q_i=b_{ii}.\end{array}$$(2.24) ) there holds(2.25) $$\begin{array}{c}\hfill \sum _{j=1,j\ne i}^{M-1}|b_{ij}|<b_{ii},i=1,2,\dots ,M-1,\end{array}$$(2.25)

which implies that the matrix B is strictly diagonally dominant, and the difference scheme (2.21(2.21) $$\begin{array}{c}\hfill \left\{\begin{array}{c}B{U}^1=U^0+\frac{{\mathit{\tau }}^{\mathit{\alpha }}\mathrm{\Gamma }(2-\mathit{\alpha })}{v}{S}^1,U^0=g;\hfill \\ B{U}^{n+1}=c_1{U}^n+c_2{U}^{n-1}+\cdots +c_n{U}^1+d_n{U}^0+\frac{{\mathit{\tau }}^{\mathit{\alpha }}\mathrm{\Gamma }(2-\mathit{\alpha })}{v}{S}^{n+1}.\hfill \end{array}\right.\end{array}$$(2.21) ) has unique solution.

Furthermore, we can prove the implicit difference scheme (2.21(2.21) $$\begin{array}{c}\hfill \left\{\begin{array}{c}B{U}^1=U^0+\frac{{\mathit{\tau }}^{\mathit{\alpha }}\mathrm{\Gamma }(2-\mathit{\alpha })}{v}{S}^1,U^0=g;\hfill \\ B{U}^{n+1}=c_1{U}^n+c_2{U}^{n-1}+\cdots +c_n{U}^1+d_n{U}^0+\frac{{\mathit{\tau }}^{\mathit{\alpha }}\mathrm{\Gamma }(2-\mathit{\alpha })}{v}{S}^{n+1}.\hfill \end{array}\right.\end{array}$$(2.21) ) is of unconditional stability and convergence with a similar method as used in [20,21,44].

Lemma 2.5:

The difference scheme (2.21(2.21) $$\begin{array}{c}\hfill \left\{\begin{array}{c}B{U}^1=U^0+\frac{{\mathit{\tau }}^{\mathit{\alpha }}\mathrm{\Gamma }(2-\mathit{\alpha })}{v}{S}^1,U^0=g;\hfill \\ B{U}^{n+1}=c_1{U}^n+c_2{U}^{n-1}+\cdots +c_n{U}^1+d_n{U}^0+\frac{{\mathit{\tau }}^{\mathit{\alpha }}\mathrm{\Gamma }(2-\mathit{\alpha })}{v}{S}^{n+1}.\hfill \end{array}\right.\end{array}$$(2.21) ) is unconditional stable and convergent to the exact solution of the forward problem for any finite time $T<\infty$.

By Lemma 2.4 there hold${\sum }_{j=1,j\ne i}^{M-1}{b}_{ij}<0$ and ${\sum }_{j=1,j\ne i}^{M-1}|b_{ij}|=b_{ii}-1$ for $i=1,2,\dots ,M-1$. With a completely similar method as used in [20], there holds(2.26) $$\begin{array}{c}\hfill 1\le \mathit{\rho }(B)\le {2\Vert b\Vert }_{\infty }-1,\end{array}$$(2.26)

where $\mathit{\rho }(B)$ is the spectral radius of the coefficient matrix B, and ${\Vert b\Vert }_{\infty }={max}_{1\le i\le M-1}\{b_{ii}\}$. Thus the unconditional stability and convergence of the finite difference scheme (2.21(2.21) $$\begin{array}{c}\hfill \left\{\begin{array}{c}B{U}^1=U^0+\frac{{\mathit{\tau }}^{\mathit{\alpha }}\mathrm{\Gamma }(2-\mathit{\alpha })}{v}{S}^1,U^0=g;\hfill \\ B{U}^{n+1}=c_1{U}^n+c_2{U}^{n-1}+\cdots +c_n{U}^1+d_n{U}^0+\frac{{\mathit{\tau }}^{\mathit{\alpha }}\mathrm{\Gamma }(2-\mathit{\alpha })}{v}{S}^{n+1}.\hfill \end{array}\right.\end{array}$$(2.21) ) can be proved based on the estimation (2.26(2.26) $$\begin{array}{c}\hfill 1\le \mathit{\rho }(B)\le {2\Vert b\Vert }_{\infty }-1,\end{array}$$(2.26) ).

In the follows we discuss a simultaneous inversion problem and its numerical inversion based on the difference solution given by (2.21(2.21) $$\begin{array}{c}\hfill \left\{\begin{array}{c}B{U}^1=U^0+\frac{{\mathit{\tau }}^{\mathit{\alpha }}\mathrm{\Gamma }(2-\mathit{\alpha })}{v}{S}^1,U^0=g;\hfill \\ B{U}^{n+1}=c_1{U}^n+c_2{U}^{n-1}+\cdots +c_n{U}^1+d_n{U}^0+\frac{{\mathit{\tau }}^{\mathit{\alpha }}\mathrm{\Gamma }(2-\mathit{\alpha })}{v}{S}^{n+1}.\hfill \end{array}\right.\end{array}$$(2.21) ).

3. The inverse problem and inversion algorithm

3.1. The inverse problem

As stated in Section 2.1, we assume that the source term is separable in variable, i.e. there is $s(x,t)=f(x)\mathit{\beta }(t)$, where $\mathit{\beta }(t)$ is known which denotes the time-dependent decay factor in the transport process, and f(x) is the space-dependent source magnitude which is unknown. Moreover, the diffusion coefficient D(x) is also unknown. Thus, a simultaneous inversion problem is encountered with if some additional measurements on the solution can be obtained. Let $x_0\in \mathrm{\Omega }$ be the measured point, and the additional measurement at $x_0$ be given as(3.1) $$\begin{array}{c}\hfill \begin{array}{cc}u(x_0,t)=\mathit{\theta }(t),\hfill & t\in (0,T].\hfill \end{array}\end{array}$$(3.1)

The simultaneous inversion problem is formulated that is to determine the diffusion coefficient D(x) and the source term f(x) based on the forward problem together with the overposed condition (3.1(3.1) $$\begin{array}{c}\hfill \begin{array}{cc}u(x_0,t)=\mathit{\theta }(t),\hfill & t\in (0,T].\hfill \end{array}\end{array}$$(3.1) ).

We denote $S=H^2(\mathrm{\Omega })\times H^1(\mathrm{\Omega })$ as the admissible space for the unknowns D(x) and f(x), and define(3.2) $$\begin{array}{c}\hfill S_E={\{(D(x),f(x))\in S:\Vert D\Vert }_{H^2(\mathrm{\Omega })}+{\Vert f\Vert }_{H^1(\mathrm{\Omega })}\le E;D(x)>0,x\in \overline{\mathrm{\Omega }}\}\end{array}$$(3.2)

as the admissible set for the pairs of solutions of the inverse problem, where E is any positive constant.

From the view point of optimality, solving an inverse problem can be transformed to minimizing an error functional between the output and the additional measurement. Also denote u(D, f)(x, t) as the unique solution to the forward problem corresponding to any given input $(D(x),f(x))\in S_E$, we get the input–output solution’s operator $(D,f)\to u(D,f)(x,t)$. Then an operator from the unknowns $(D,f)\in S_E$ to the overposed measurements, which is called the observation operator, can be defined by(3.3) $$\begin{array}{c}\hfill G:S_E\to L^2(0,T),G(D,f)(t):=u(D,f)(x_0,t)=\mathit{\theta }(t),\end{array}$$(3.3)

and the simultaneous inversion problem is transformed to solve the operator equation (3.3(3.3) $$\begin{array}{c}\hfill G:S_E\to L^2(0,T),G(D,f)(t):=u(D,f)(x_0,t)=\mathit{\theta }(t),\end{array}$$(3.3) ). For solving the inverse problem, we define an error functional based on the input–output mapping by(3.4) $$\begin{array}{c}\hfill J(D,f)={\Vert G(D,f)(t)-\mathit{\theta }(t)\Vert }_{L^2(0,T)}^2={\int }_0^T{[u(D,f)(x_0,t)-\mathit{\theta }(t)]}^2\mathrm{d}t,\end{array}$$(3.4)

and solving the simultaneous inversion problem is transformed to the minimization problem(3.5) $$\begin{array}{c}\hfill \underset{(D,f)\in S_E}{min}J(D,f).\end{array}$$(3.5)

For the above minimization problem, we set$$V_E=\{(D(x),f(x))\in C^1(\overline{\mathrm{\Omega }})\times L^2{(\mathrm{\Omega }):\Vert D\Vert }_{C^1(\overline{\mathrm{\Omega }})}+{\Vert f\Vert }_{L^2(\mathrm{\Omega })}\le E;D>0on\overline{\mathrm{\Omega }}\},$$

and the existence of a minimum to the minimization problem (3.5(3.5) $$\begin{array}{c}\hfill \underset{(D,f)\in S_E}{min}J(D,f).\end{array}$$(3.5) ) can be obtained by Theorem 2.2 and Sobolev embedding theorems. Firstly, we have by Theorem 2.2

Corollary 3.1:

The operator $G:V_E\to L^2(0,T)$ is Lipschitz continuous, and there exists a constant $\tilde{M}>0$ such that(3.6) $$\begin{array}{c}\hfill \Vert G(D_1,f_1)-G(D_2,f_2){\Vert }_{L^2(0,T)}\le \tilde{M}\left(\Vert D_1-D_2{\Vert }_{C^1(\overline{\mathrm{\Omega }})}+{\Vert f_1-f_2\Vert }_{L^2(\mathrm{\Omega })}\right),\end{array}$$(3.6)

for all $(D_1,f_1),(D_2,f_2)\in V_E$.

Next by utilizing the Sobolev embedding theorems (see [43] for instance), there holds

Theorem 3.2:

For the minimization problem (3.5(3.5) $$\begin{array}{c}\hfill \underset{(D,f)\in S_E}{min}J(D,f).\end{array}$$(3.5) ), there exists $(D^{\ast },{\mathit{\beta }}^{\ast })\in S_E$ such that(3.7) $$\begin{array}{c}\hfill J(D^{\ast },f^{\ast })\le J(D,f)\end{array}$$(3.7)

for all $(D,f)\in S_E$.

Suppose that there exist a series $\{(D_n,f_n)\}\subset S_E$ such that(3.8) $$\begin{array}{c}\hfill J(D_n,f_n)⟶\underset{(D,f)\in S_E}{inf}J(D,f),\text{as}n\to \infty .\end{array}$$(3.8)

Since $\Vert (D_n,f_n){\Vert }_{S_E}\le E$, $n=1,2,\dots$, there exists subseries, also denoted as $(D_n,f_n)$, which is weakly convergent in S. That is, there is $(D^{\ast },f^{\ast })\in S_E$ such that(3.9) $$\begin{array}{c}\hfill (D_n,f_n)\rightharpoonup (D^{\ast },f^{\ast }),\text{as}n\to \infty .\end{array}$$(3.9)

On the other hand, the embedding relations $H^2(\mathrm{\Omega })\hookrightarrow C^1(\overline{\mathrm{\Omega }})$ and $H^1(\mathrm{\Omega })\hookrightarrow L^2(\mathrm{\Omega })$ are compact for the bounded domain $\mathrm{\Omega }$ in 1D case, then the embedding $S_E\hookrightarrow V_E$ is compact by which the strong convergence is valid(3.10) $$\begin{array}{c}\hfill (D_n,f_n)\to (D^{\ast },f^{\ast })\text{in}{V}_E\text{as}n\to \infty .\end{array}$$(3.10)

Together with the continuity of the functional J on D and f, there holds(3.11) $$\begin{array}{c}\hfill J(D_n,f_n)⟶J(D^{\ast },f^{\ast })\text{as}n\to \infty ,\end{array}$$(3.11)

which implies that(3.12) $$\begin{array}{c}\hfill J(D^{\ast },f^{\ast })=\underset{(D,f)\in S_E}{inf}J(D,f).\end{array}$$(3.12)

The proof is over.

3.2. The inversion algorithm

Suppose that $D(x)\in C^1(\overline{\mathrm{\Omega }})$ and $f(x)\in L^2(\mathrm{\Omega })$ both have Fourier expansions(3.13) $$\begin{array}{c}\hfill D(x)=\sum _{s=1}^{\infty }{a}_s{\mathit{\phi }}_s(x),\end{array}$$(3.13)

and(3.14) $$\begin{array}{c}\hfill f(x)=\sum _{k=1}^{\infty }{b}_k{\mathit{\varphi }}_k(x),\end{array}$$(3.14)

where $a_s$ ($s=1,2,\dots ,$) and $b_k$ ($k=1,2,\dots ,$) are the expansion coefficients of D(x) and f(x), and $\{{\mathit{\phi }}_s(x),s=1,2,\dots ,\}$ and $\{{\mathit{\varphi }}_k(x),k=1,2,\dots ,\}$ are sets of basis functions in $C^1(\mathrm{\Omega })$ and $L^2(\mathrm{\Omega })$, respectively. In numerical approximations, by setting$${\mathrm{\Psi }}^S=\text{span}\{{\mathit{\phi }}_1,{\mathit{\phi }}_2,\dots ,{\mathit{\phi }}_S\},$$

and$${\mathrm{\Phi }}^K=\text{span}\{{\mathit{\varphi }}_1,{\mathit{\varphi }}_2,\dots ,{\mathit{\varphi }}_K\},$$

we have(3.15) $$\begin{array}{c}\hfill D(x)\approx D^S(x)=\sum _{s=1}^S{a}_s{\mathit{\phi }}_s(x),\end{array}$$(3.15)

and(3.16) $$\begin{array}{c}\hfill f(x)\approx f^K(x)=\sum _{k=1}^K{b}_k{\mathit{\varphi }}_k(x),\end{array}$$(3.16)

respectively, where $D^S(x)$ is the S-dimensional approximate solution to D(x) in ${\mathrm{\Psi }}^S$, and $f^K(x)$ is the K-dimensional approximate solution to f(x) in ${\mathrm{\Phi }}^K$, and $S\ge 1$ and $K\ge 1$ are dimensions of the approximate spaces, respectively. On concrete computations, it is convenient to set a S-dimensional vector $\mathbf{a}=(a_1,a_2,\dots ,a_S)\in {\mathbf{R}}^S$ corresponding to $D^S(x)$, and a K-dimensional vector $\mathbf{b}=(b_1,b_2,\dots ,b_K)\in {\mathbf{R}}^K$ corresponding to $f^K(x)$, respectively. Therefore, to get an approximate solution $(D^S(x),f^K(x))\in {\mathrm{\Psi }}^S\times {\mathrm{\Phi }}^K$ is equivalent to finding a vector $(\mathbf{a},\mathbf{b})\in {\mathbf{R}}^S\times {\mathbf{R}}^K$, in which meaning we can say that $(D^S(x),f^K(x)):=(\mathbf{a},\mathbf{b})$ if there is no possibility of confusion. In what follows, we set $\overline{}\}a=(\mathbf{a},\mathbf{b})=(a_1,a_2,\dots ,a_S,b_1,b_2,\dots ,b_K)$, and its norm is denoted by(3.17) $$\begin{array}{c}\hfill ∥\overline{}\}a∥=\sqrt{{a_1}^2+a_2^2+\cdots +a_S^2+{b_1}^2+b_2^2+\cdots +b_K^2}.\end{array}$$(3.17)

For any given $\overline{}\}a\in {\mathbf{R}}^S\times {\mathbf{R}}^K$, denote $u(x,t;\overline{}\}a)=u(D^S,f^K)(x,t)$ as the unique solution to the forward problem. Combining with the additional information (3.1(3.1) $$\begin{array}{c}\hfill \begin{array}{cc}u(x_0,t)=\mathit{\theta }(t),\hfill & t\in (0,T].\hfill \end{array}\end{array}$$(3.1) ), solving the inverse problem is equivalent to a minimization problem(3.18) $$\begin{array}{c}\hfill \underset{\overline{}\}a\in {\mathbf{R}}^S\times {\mathbf{R}}^K}{min}{∥u(x_0,t;\overline{}\}a)-\mathit{\theta }(t)∥}_{L^2(0,T)}^2,\end{array}$$(3.18)

where ${∥u(x_0,t;\overline{}\}a)-\mathit{\theta }(t)∥}_{L^2(0,T)}^2={\int }_0^T{[u(x_0,t;\overline{}\}a)-\mathit{\theta }(t)]}^2\mathrm{d}t$.

By Theorem 3.2, there at least exists one minimum to the minimization problem (3.18(3.18) $$\begin{array}{c}\hfill \underset{\overline{}\}a\in {\mathbf{R}}^S\times {\mathbf{R}}^K}{min}{∥u(x_0,t;\overline{}\}a)-\mathit{\theta }(t)∥}_{L^2(0,T)}^2,\end{array}$$(3.18) ). Following the stabilizing method as used in [41], we utilize the homotopy regularization algorithm to solve (3.18(3.18) $$\begin{array}{c}\hfill \underset{\overline{}\}a\in {\mathbf{R}}^S\times {\mathbf{R}}^K}{min}{∥u(x_0,t;\overline{}\}a)-\mathit{\theta }(t)∥}_{L^2(0,T)}^2,\end{array}$$(3.18) ). Hence orth, it is turned out to solve the following minimization problem instead of (3.18(3.18) $$\begin{array}{c}\hfill \underset{\overline{}\}a\in {\mathbf{R}}^S\times {\mathbf{R}}^K}{min}{∥u(x_0,t;\overline{}\}a)-\mathit{\theta }(t)∥}_{L^2(0,T)}^2,\end{array}$$(3.18) )(3.19) $$\begin{array}{c}\hfill \underset{\overline{}\}a\in {\mathbf{R}}^S\times {\mathbf{R}}^K}{min}\{(1-\mathit{\mu }){∥u(x_0,t;\overline{}\}a)-\mathit{\theta }(t)∥}_{L^2(0,T)}^2+\mathit{\mu }{∥\overline{}\}a∥}^2\},\end{array}$$(3.19)

where $\mathit{\mu }\in (0,1)$ is the homotopy parameter. We refer to [41] for the detailed procedures of the homotopy regularization algorithm, however, we give a sketch for solving the nonlinear minimization problem (3.19(3.19) $$\begin{array}{c}\hfill \underset{\overline{}\}a\in {\mathbf{R}}^S\times {\mathbf{R}}^K}{min}\{(1-\mathit{\mu }){∥u(x_0,t;\overline{}\}a)-\mathit{\theta }(t)∥}_{L^2(0,T)}^2+\mathit{\mu }{∥\overline{}\}a∥}^2\},\end{array}$$(3.19) ) for completeness of the paper.

By denoting $\mathit{\gamma }=\frac{\mathit{\mu }}{1-\mathit{\mu }}$, (3.19(3.19) $$\begin{array}{c}\hfill \underset{\overline{}\}a\in {\mathbf{R}}^S\times {\mathbf{R}}^K}{min}\{(1-\mathit{\mu }){∥u(x_0,t;\overline{}\}a)-\mathit{\theta }(t)∥}_{L^2(0,T)}^2+\mathit{\mu }{∥\overline{}\}a∥}^2\},\end{array}$$(3.19) ) is transformed to(3.20) $$\begin{array}{c}\hfill \underset{\overline{}\}a\in {\mathbf{R}}^S\times {\mathbf{R}}^K}{min}\{{∥u(x_0,t;\overline{}\}a)-\mathit{\theta }(t)∥}_{L^2(0,T)}^2+\mathit{\gamma }{∥\overline{}\}a∥}^2\},\end{array}$$(3.20)

where $\mathit{\gamma }>0$ is regarded as the regularization parameter, which leads to the optimal perturbation regularization algorithm as studied in the previous works, see e.g. [37,42]. In fact, by linerization and numerical differentiation approximations, solving (3.20(3.20) $$\begin{array}{c}\hfill \underset{\overline{}\}a\in {\mathbf{R}}^S\times {\mathbf{R}}^K}{min}\{{∥u(x_0,t;\overline{}\}a)-\mathit{\theta }(t)∥}_{L^2(0,T)}^2+\mathit{\gamma }{∥\overline{}\}a∥}^2\},\end{array}$$(3.20) ) is transformed to solve a normal equation combining with an iteration process:(3.21) $$\begin{array}{c}\hfill \left\{\begin{array}{c}(\mathit{\gamma }I+{\mathbf{G}}^T\mathbf{G})\mathit{\delta }{\overline{\mathbf{a}}}_n={\mathbf{G}}^T(\mathit{\eta }-\mathit{\xi }),\hfill \\ {\overline{\mathbf{a}}}_n+\mathit{\delta }{\overline{\mathbf{a}}}_n\to {\overline{\mathbf{a}}}_{n+1},n=0,1,\dots ,\hfill \end{array}\right.\end{array}$$(3.21)

where $\mathit{\delta }{\overline{\mathbf{a}}}_n$ is a perturbation vector for any given ${\overline{\mathbf{a}}}_n\in {\mathbf{R}}^{S+K}$, n denotes the iterative number and ${\overline{\mathbf{a}}}_0$ is the initial iteration, and(3.22) $$\begin{array}{c}\hfill \mathbf{G}={(g_{qi})}_{Q\ast (S+K)},g_{qi}=\frac{u(x_0,t_q;{\overline{\mathbf{a}}}_n+\mathit{\tau }{\mathbf{e}}_i)-u(x_0,t_q;{\overline{\mathbf{a}}}_n)}{\mathit{\tau }},\end{array}$$(3.22)

here $\mathit{\tau }$ is the numerical differential step, and ${\mathbf{e}}_i$ ($i=1,2,\dots ,S+K$) is the unit basis vector in ${\mathbf{R}}^{S+K}$, and(3.23) $$\begin{array}{c}\hfill \mathit{\xi }={(u(x_0,t_1;{\overline{\mathbf{a}}}_n),u(x_0,t_2;{\overline{\mathbf{a}}}_n),\dots ,u(x_0,t_Q;{\overline{\mathbf{a}}}_n))}^T;\mathit{\eta }={(\mathit{\theta }(t_1),\mathit{\theta }(t_2),\dots ,\mathit{\theta }(t_Q))}^T.\end{array}$$(3.23)

The algorithm can be terminated as long as an optimal perturbation satisfying the condition: $\Vert \mathit{\delta }{\overline{\mathbf{a}}}_n{\Vert }_2\le \text{eps}$, here $\text{eps}$ is the given convergent precision. Noting that $\mathit{\gamma }=\frac{\mathit{\mu }}{1-\mathit{\mu }}$, we have by (3.21(3.21) $$\begin{array}{c}\hfill \left\{\begin{array}{c}(\mathit{\gamma }I+{\mathbf{G}}^T\mathbf{G})\mathit{\delta }{\overline{\mathbf{a}}}_n={\mathbf{G}}^T(\mathit{\eta }-\mathit{\xi }),\hfill \\ {\overline{\mathbf{a}}}_n+\mathit{\delta }{\overline{\mathbf{a}}}_n\to {\overline{\mathbf{a}}}_{n+1},n=0,1,\dots ,\hfill \end{array}\right.\end{array}$$(3.21) )(3.24) $$\begin{array}{c}\hfill \left\{\begin{array}{c}(\mathit{\mu }I+(1-\mathit{\mu }){\mathbf{G}}^T\mathbf{G})\mathit{\delta }{\overline{\mathbf{a}}}_n=(1-\mathit{\mu }){\mathbf{G}}^T(\mathit{\eta }-\mathit{\xi }),\hfill \\ {\overline{\mathbf{a}}}_n+\mathit{\delta }{\overline{\mathbf{a}}}_n\to {\overline{\mathbf{a}}}_{n+1},\hfill \end{array}\right.\end{array}$$(3.24)

where $\mathit{\mu }\in (0,1)$ is just the homotopy parameter which taking values from near 1 decreasingly approximating to 0. Like done in [41] we employee the homotopy parameter given as(3.25) $$\begin{array}{c}\hfill \mathit{\mu }=\mathit{\mu }(n)=\frac{1}{1+exp(\mathit{\rho }(n-n_0))},\end{array}$$(3.25)

where n is the number of iterations, $n_0$ is the pre-estimated number, and $\mathit{\rho }>0$ is the adjust parameter. In the follows, we utilize the above inversion algorithm to perform numerical inversions for the simultaneous inverse problem.

4. Numerical inversion

In all of the computations in this section, we take $T=1$, and $M=100$, $N=100$ in the difference scheme (2.21(2.21) $$\begin{array}{c}\hfill \left\{\begin{array}{c}B{U}^1=U^0+\frac{{\mathit{\tau }}^{\mathit{\alpha }}\mathrm{\Gamma }(2-\mathit{\alpha })}{v}{S}^1,U^0=g;\hfill \\ B{U}^{n+1}=c_1{U}^n+c_2{U}^{n-1}+\cdots +c_n{U}^1+d_n{U}^0+\frac{{\mathit{\tau }}^{\mathit{\alpha }}\mathrm{\Gamma }(2-\mathit{\alpha })}{v}{S}^{n+1}.\hfill \end{array}\right.\end{array}$$(2.21) ) for solving the forward problem, and we choose $n_0=5$ as the preestimated number, $\mathit{\rho }=0.8$ as the adjust parameter, and ${10}^{-5}$ as the convergent precision, and we set initial iteration be zero, and numerical differential step be $1e-2$ in the implementation of the inversion algorithm if there is no specification. Moreover, we deal with the two-term TFDE given as(4.1) $$\begin{array}{c}\hfill \frac{{\mathit{\partial }}^{\mathit{\alpha }}u}{\mathit{\partial }{t}^{\mathit{\alpha }}}+\frac{{\mathit{\partial }}^{{\mathit{\alpha }}_1}u}{\mathit{\partial }{t}^{{\mathit{\alpha }}_1}}=\frac{\mathit{\partial }}{\mathit{\partial }x}\left(D(x)\frac{\mathit{\partial }u}{\mathit{\partial }x}\right)+\mathit{\beta }(t)f(x),(x,t)\in (0,1)\times (0,T).\end{array}$$(4.1)

4.1. Ex. 1 – Inversion with accurate data

Let the exact diffusion coefficient be(4.2) $$\begin{array}{c}\hfill D(x)=exp(x),0\le x\le 1,\end{array}$$(4.2)

and the exact source magnitude function be(4.3) $$\begin{array}{c}\hfill f(x)=cos(x),0\le x\le 1,\end{array}$$(4.3)

and let the initial function be $g(x)=10{\times }^2{(1-x)}^2$, and the time-dependent decay factor be $\mathit{\beta }(t)=exp(-t)$. Using the above data we can obtain the solution of the forward problem and get the additional data at one inner point of $x=x_0\in (0,1)$, and further we utilize the homotopy regularization algorithm to reconstruct the diffusion coefficient and the source function in suitable approximate spaces. We here choose polynomial spaces as the approximate spaces for D(x) and f(x), and then the exact solution to the simultaneous inversion problem is represented by(4.4) $$\begin{array}{c}\hfill (D,f)=\left(1,1,\frac{1}{2!},\frac{1}{3!},\dots ,1,0,-\frac{1}{2!},0,\frac{1}{4!},\dots \right),\end{array}$$(4.4)

due to the expansion properties of the exponential and the trigonometric functions.

Without loss of generality, we choose the fractional orders $\mathit{\alpha }=0.8$ and ${\mathit{\alpha }}_1=0.3$, and the coefficient $r_1=0.5$, and give the additional data at the central point of $x_0=0.5$ to perform the inversion. Since we perform the inversions in the approximate spaces ${\mathrm{\Psi }}^S=\text{span}\{1,x,\dots ,x^{S-1}\}$ and ${\mathrm{\Phi }}^K=\text{span}\{1,x,\dots ,x^{K-1}\}$, the dimensions S and K have important influences on the inversion algorithm especially for nonlinear unknowns. The inversion results with different dimensions are listed in Table 1, where Err1, Err2 and Err3 denote the relative errors in the inversion solutions defined by$$\text{Err1}=\frac{{∥D-D^{\text{inv}}∥}_2}{{∥D∥}_2},$$

and$$\text{Err2}=\frac{{∥f-f^{}\text{inv}∥}_2}{{∥f∥}_2},$$

and$$\text{Err3}=\frac{{∥D-D^{\text{inv}}∥}_2+{∥f-f^{\text{inv}}∥}_2}{{∥D∥}_2+{∥f∥}_2},$$

respectively, where $D^{\text{inv}}$ is the inversion diffusion coefficient and $f^{\text{inv}}$ is the inversion source function, and the norms $\Vert D-D^{\text{inv}}{\Vert }_2$ and ${\Vert D\Vert }_2$ are defined as$$\Vert D-D^{\text{inv}}{\Vert }_2={\left(\sum _{i=0}^M{[D(x_i)-D^{\text{inv}}(x_i)]}^2\right)}^{1/2},$$

and$${\Vert D\Vert }_2={\left(\sum _{i=0}^M{[D(x_i)]}^2\right)}^{1/2},$$

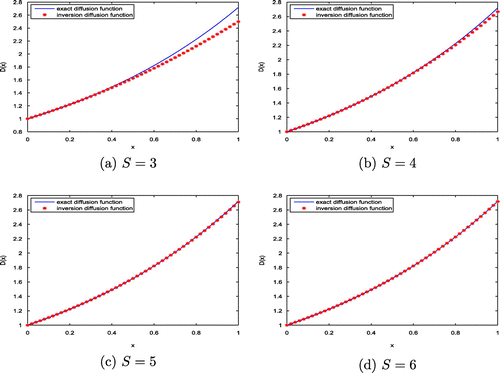
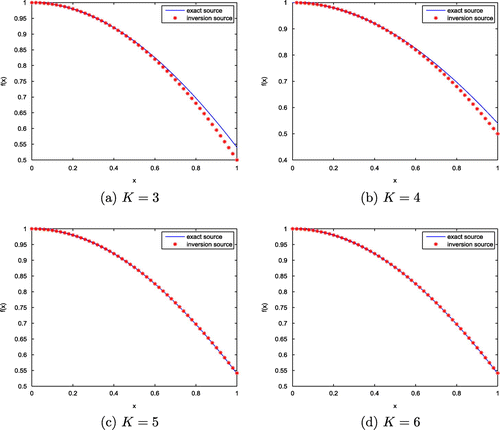
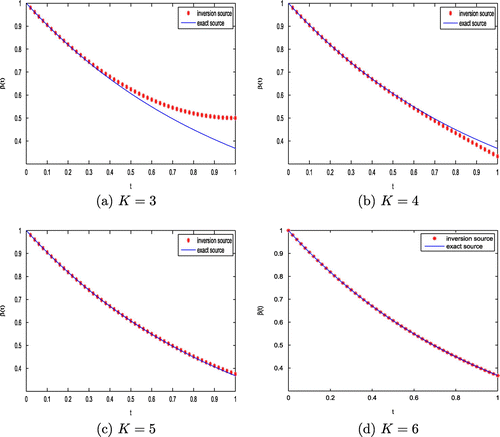
and the same for $\Vert f-f^{\text{inv}}{\Vert }_2$ and ${\Vert f\Vert }_2$, respectively. Moreover, for $S=K=3,4,5,6$, the exact and the inversion diffusion coefficients are plotted in Figure 1(a)–(d), and the exact and the inversion source functions are plotted in Figure 2(a)–(d), respectively.

Table 1. The inversion results with dimensions of the approximate spaces in Ex. 1.

$S=K$	Err1	Err2	Err3
3	4.5123e$-$2	1.6129e$-$2	4.1932e$-$2
4	9.5738e$-$3	1.6130e$-$2	1.1244e$-$2
5	1.6879e$-$3	4.5730e$-$4	1.5592e$-$3
6	2.5371e$-$4	4.5730e$-$4	3.0631e$-$4

Figure 1. The exact and inversion diffusion coefficients with different dimensions in Ex. 1.

Figure 2. The exact and inversion source functions with different dimensions in Ex. 1.

Figure 3. The exact and the average inversion solutions with noisy data in Ex. 2.

Figure 4. The exact and inversion diffusion coefficients in ${\mathrm{\Psi }}^3$ in Remark 1.

From Table 1, Figures 1 and 2, it can be seen that the relative errors in the solutions become small when the dimensions S and K go to large, and the inversion solutions give good approximations to the exact solutions when $S=K\ge 5$, which shows that the inversion algorithm is convergent in the meaning of finite-dimensional approximation.

4.2. Ex. 2 – Inversion with noisy data

In this section, we perform the inversion in the case of using noisy data to testify numerical stability of the algorithm. Suppose that the additional information is polluted with noise which is described by(4.5) $$\begin{array}{c}\hfill {\mathit{\theta }}^{\mathit{\epsilon }}(t)=\mathit{\theta }(t)(1+\mathit{\epsilon }\mathit{\xi }),0\le t\le 1,\end{array}$$(4.5)

where $\mathit{\epsilon }>0$ denotes the noise level and $\mathit{\xi }$ is a random number ranged in $[-1,1]$.

Let the initial function be $g(x)=10x^2{(1-x)}^2$ and the time-dependent decay factor be $\mathit{\beta }(t)=2-t^2$, and the exact diffusion coefficient be $D(x)=1+x-x^2$, and the exact source magnitude function be $f(x)=1+x$. In the approximate spaces ${\mathrm{\Psi }}^4=\text{span}\{1,x,x^2,x^3\}$ and ${\mathrm{\Phi }}^3=\text{span}\{1,x,x^2\}$, the exact solution for the inversion problem here is given by(4.6) $$\begin{array}{c}\hfill \overline{}\}a=(1,1,-1,0,1,1,0).\end{array}$$(4.6)

We take the same inversion parameters as used in Ex. 1 but perform the algorithm with random noisy data. Noting the randomness of the data, we carry out the algorithm with continuous 10-time inversions for each given noise level and take an average of the inversions. It is noted that the inversion could become very difficult when coping with large noises. One approach which can overcome the ill-posedness is to utilize more additional measurements. We choose the observations $\{u(0.4,t)\}$ and $\{u(0.6,t)\}$ as the additional data instead of $\{u(0.5,t)\}$ in the following computations. The average inversion results are listed in Table 2, where $\mathit{\epsilon }$ is the noise level, $\overline{}\}{a}_{\text{avr}}^{\text{inv}}$ is the average inversion solution of the ten-time inversions, and $\overline{\text{Err}}$ denotes the average relative error in the solutions defined by(4.7) $$\begin{array}{c}\hfill \overline{\text{Err}}=\frac{{∥D-D_{\text{avr}}^{\text{inv}}∥}_2+{∥f-f_{\text{avr}}^{\text{inv}}∥}_2}{{∥D∥}_2+{∥f∥}_2},\end{array}$$(4.7)

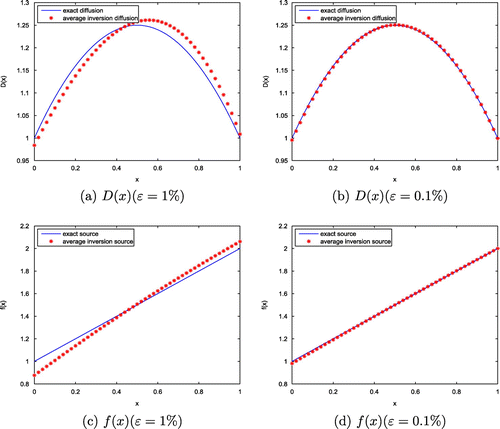
where $D_{\text{avr}}^{\text{inv}}$ is the average inversion diffusion coefficient in ${\mathrm{\Psi }}^4$ and $f_{\text{avr}}^{\text{inv}}$ is the average inversion source function in ${\mathrm{\Phi }}^3$. Moreover, for $\mathit{\epsilon }=1\%,0.1\%$, the exact and the average inversion diffusion coefficients are plotted in Figure 3(a), (b), and the exact and the average inversion source functions are plotted in Figure 3(c), (d), respectively.

Table 2. The average inversion results with noisy data in Ex. 2.

$\mathit{\epsilon }$	$\overline{}\}{a}_{\text{avr}}^{\text{inv}}$	$\overline{\text{Err}}$
$1\%$	(0.9876, 0.8521, $-$0.4275, $-$0.4006, 0.9019, 1.2236, $-$0.0378)	2.9983e$-$2
$0.1\%$	(0.9955, 1.0051, $-$0.9752, $-$0.0266, 0.9783, 1.0713, $-$0.0535)	4.1443e$-$3
$0.01\%$	(0.9995, 1.0007, $-$0.9978, $-$0.0025, 0.9977, 1.0076, $-$0.0059)	4.3607e$-$4
$0.001\%$	(1.0000, 1.0001, $-$0.9998, $-$0.0003, 0.9998, 1.0008, $-$0.0006)	4.3829e$-$5

Figure 5. The exact and inversion time-decay factors in ${\mathrm{\Phi }}^K$ in Remark 1.

From Table 2 and Figure 3, it can be observed that the inversion algorithm is of numerical stability against the noise in the additional data. It is also noted that the inversion becomes difficult if the noise is larger than $1\%$ showing that the simultaneous inversion problem is of severe ill-posedness.

Remark 1:

If the source magnitude $f=f(x)$ is known, and the time-dependent decay factor $\mathit{\beta }=\mathit{\beta }(t)$ and the space-dependent diffusion coefficient $D=D(x)$ are unknown, we can obtain similar results as stated in the above. For example for Equation (4.1(4.1) $$\begin{array}{c}\hfill \frac{{\mathit{\partial }}^{\mathit{\alpha }}u}{\mathit{\partial }{t}^{\mathit{\alpha }}}+\frac{{\mathit{\partial }}^{{\mathit{\alpha }}_1}u}{\mathit{\partial }{t}^{{\mathit{\alpha }}_1}}=\frac{\mathit{\partial }}{\mathit{\partial }x}\left(D(x)\frac{\mathit{\partial }u}{\mathit{\partial }x}\right)+\mathit{\beta }(t)f(x),(x,t)\in (0,1)\times (0,T).\end{array}$$(4.1) ), let the exact time-dependent decay factor be $\mathit{\beta }(t)=exp(-t)$, and the exact space-dependent diffusion coefficient be $D(x)=1+2x$. In addition, choosing the fractional orders $\mathit{\alpha }=0.8$ and ${\mathit{\alpha }}_1=0.3$, and the source magnitude $f(x)=1+x^2$, and we are to reconstruct the time-decay factor $\mathit{\beta }(t)$ and the spatially diffusion coefficient D(x) simultaneously also utilizing the additional measurements at the inner point of $x_0=0.5$. Noting the form of the unknowns, we perform the inversion in the approximate space ${\mathrm{\Psi }}^3\times {\mathrm{\Phi }}^K$ where $K\ge 3$. 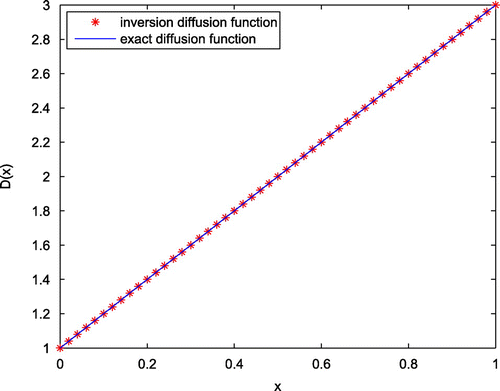The exact and the inversion solutions are plotted in Figures 4 and 5, respectively.

From Figure 5, it can be seen that the relative errors in the solutions become small when the dimension K goes to large, and the inversion solutions give good approximations to the exact source when $K\ge 5$, which shows again that the inversion algorithm is convergent in the meaning of finite-dimensional approximation as observed in Ex. 1.

5. Conclusions

The simultaneous inversion problem of determining the space-dependent diffusion coefficient and the source term in the multi-term TFDE is investigated using measurements at the inner point. We prove the Lipschitz continuity of the solution operator, and then we get the existence of the minimum to the error functional between the additional measurements and the input–output data which gives the basis and possible approaches to solving the inverse problems.

Generally speaking, simultaneous inversion problems of determining multiple types of coefficients in a PDE are more difficult than that of determining a single type of coefficient, especially on the theoretical analysis. However, numerical inversions for such kinds of inverse problems can be performed by suitable inversion algorithms. The numerical results show that the homotopy regularization algorithm is efficient for the simultaneous inversion problem in this paper, and the inversion can also be realized successfully even for the determination of the space-dependent diffusion coefficient and the time-dependent decay factor utilizing the time-series measurements. We will focus our attention on conditional well-posedness analysis for the simultaneous inversion problems in the near future.

Additional information

Funding

The authors thank the anonymous referees and the editor for their valuable and suggestive comments. This work is supported by the National Natural Science Foundation of China [grant number 11371231], [grant number 11071148].

Notes

No potential conflict of interest was reported by the authors.