A meshless method for solving 1D time-dependent heat source problem

Abstract

A novel meshless numerical procedure based on the method of fundamental solutions (MFS) and the heat polynomials is proposed for recovering a time-dependent heat source and the boundary data simultaneously in an inverse heat conduction problem (IHCP). We will transform the problem into a homogeneous IHCP and initial value problems for the first-order ordinary differential equation. An improved method of MFS is used to solve the IHCP and a finite difference method is applied for solving the initial value problems. The advantage of applying the proposed meshless numerical scheme is producing the shape functions which provide the important delta function property to ensure that the essential conditions are fulfilled. Numerical experiments for some examples are provided to show the effectiveness of the proposed algorithm.

Keywords:

• Inverse heat conduction problem
• heat source
• boundary data
• heat polynomial
• method of fundamental solutions
• shape functions
• finite difference method
• Theta method
• fundamental solutions
• ordinary differential equation

AMS Subject Classifications:

• 35R30
• 35K05

1. Introduction

In this paper, we consider the inverse problem of determination a time-dependent heat source and boundary data, simultaneously, in the following parabolic problem:(1) $$\begin{array}{cc}\hfill U_t(x,t)& =c^2{U}_{xx}(x,t)+f(t);0<x<1,0<t<T,\hfill \end{array}$$(1) (2) $$\begin{array}{cc}\hfill U(x,0)& ={\mathit{\varphi }}_0(x);0\le x\le 1,\hfill \end{array}$$(2) (3) $$\begin{array}{cc}\hfill U(0,t)& =g_0(t);0\le t\le T,\hfill \end{array}$$(3) (4) $$\begin{array}{cc}\hfill U(1,t)& =g_1(t);0\le t\le T,\hfill \end{array}$$(4)

where T is final time, c is a constant and the functions ${\mathit{\varphi }}_0$ and $g_1$ are known and continuous in their domains, while the heat source function f(t), the boundary temperature $g_0$ and the heat flux $U_x(0,t)=h(t)$ are unknowns to be determined from the following additional data:(5) $$\begin{array}{cc}\hfill U(x^{\ast },t)& =k(t);0<x^{\ast }<1,0\le t\le T,\hfill \end{array}$$(5) (6) $$\begin{array}{cc}\hfill U(x,T)& ={\mathit{\varphi }}_T(x);0\le x\le 1.\hfill \end{array}$$(6)

The mathematical model (1)–(6) arises in various physical and engineering setting, in particular, in hydrology, material sciences, heat transfer and transport problems. A typical example is groundwater pollutant source estimation in cities with large populations. In this application, it is crucial to accurately identify which companies are responsible for the contamination [1].

In the context of heat conduction and diffusion, where U represents temperature and concentration, the unknown f(t) is interpreted as a heat and material source, respectively, and in a chemical or a biochemical application, f(t) may be interpreted as a reaction term [2]. Although the result in this paper applies to each of these interpretations, the unknown function f(t) will be referred to as a heat source term.

1.1. A brief review of methods existing in the literature

The inverse problem of determining an unknown heat source function in the heat conduction equation has been considered in many theoretical papers, notably [3–7]. The authors of [3], proved the existence and uniqueness of an inverse source problem where the heat source is the product of a space function and a time function. The uniqueness solution of the inverse space-wise dependent heat source problem was considered in [8–11]. Also, this problem is investigated numerically by several authors. Authors of [12,13] used the method of fundamental solutions (MFS) to solve this problem. The boundary element method (BEM) [14], iterative regularization methods [15–17] and finite difference technique [18] are proposed to treated this problem. In [19], an iterative algorithm based on the landweber regularization framework, is proposed to obtain the numerical solution of the problem. In [20], the heat source is a function of both space and time but is separable and the space-dependent source term is recovered with He’s variational iteration method. However, many researchers sought the source as a function of time only [21]. In [22], this problem was studied with the finite difference method. Numerical solution is also considered by use of the MFS in [23]. Authors of [14] applied BEM to treat this problem. In [1] authors used the method of simplified Tikhonov regularization (TR) for dealing with the inverse time-dependent heat source problem. Author of [24] solved the problem with He’s variational iteration method. In [25,26], the author identified the heat source as time dependent only, by the Lie-group shooting method (LGSM). A BEM combined with the TR of various orders is developed in order to obtain a stable solution in [27]. The method of central difference for the inverse time-dependent heat source problem is proposed in [28]. Authors of [29] considered the problem of identifying an unknown heat source depending simultaneously on both space and time variables. First the problem is transformed into an optimization problem and the uniqueness of minimum element is proved rigorously. Then, a variational formulation for solving the optimization problem is given. A conjugate gradient method and a finite difference method are used to solve the variational problem. Author of [30] used the MFS and radial basis functions (RBFs) to solve the problem when source is a function of space and time. First for the approximation of time derivative in the governing equation, the finite difference method is used. Then, the problem is solved by the solution of non-homogeneous equation at each time step. The RBF is used for interpolation of right-hand side of the governing equation and obtaining a particular solution. In [31], the identification of sources in steady-state heat conduction problem was considered without restriction for the form of heat sources, but some information about temperature in some inner point in considered region was used. Author employed the MFS to recover heat source in this problem. Besides, a sequential method in [32], a linear least-squares error method in [33], the Green element method [34], the Lie-group differential algebraic equations method [35], a iterative method [36], a mollification regularization method [37] and the conjugate gradient method [38] are applied to the numerical solution of inverse heat source problems.

1.2. An introduction about MFS

The MFS is a meshless/meshfree boundary collocation method which is applicable to boundary value problems for which a fundamental solution of the operator in the governing equation is known. In spite of this restriction, it has, in recent years, become very popular primarily because of the ease with which it can be implemented, in particular for problems in complex geometries [39]. This meshless method requires neither domain discretization as in the FEM and FDM, nor boundary discretization as in the BEM, thus it improves the computational efficiency and can be easily extended to solve high-order and high-dimensional differential equations [13].

Kupradze and Aleksidze [40] first proposed the concept of the MFS, and then Mathon and Johnston [41] used the MFS to numerically solve the elliptic boundary value problems. Bogomolny [42] established the preliminary mathematical framework for the MFS and fixed the positions of the source distribution.

Since then, there have appeared numerous reports on MFS for computation, see the reviews of the MFS in Fairweather and Karageorghis [43], Golberg and Chen [44], and a systemic introduction on the MFS in Chen et al. [45]. The MFS has been applied to Cauchy and Stokes problems in [46,47], the biharmonic equation in [43,48] and even to a non-linear Poisson problem [49]. Some important properties of the MFS were addressed by Schaback [50]. Recently, the MFS has been successfully applied to solve the inverse problems associated with the heat equation [51], linear elasticity [52,53], steady-state heat conduction in functionally graded materials [54], Helmholtz-type equations [55–57] and source reconstruction in steady-state heat conduction problems [58]. The steady Stokes flow problems were also solved using the steady Stokeslets [59]. Golberg [60] and Golberg et al. [61] further extended the MFS to find a particular solution for the inhomogeneous term of the Poisson equation, using the method of particular solutions. Young et al. [62] solved the time-dependent diffusion equation by the diffusion fundamental solution without temporal finite difference discretization. A new meshless singular boundary method, based on the notion of the BEM and the MFS, is introduced for solving three-dimensional inverse heat conduction problems (IHCPs) and large-scale three-dimensional potential problems in [63,64], respectively.

In this paper, a modified MFS (MMFS) is proposed for solving the IHCP (1)–(6). The method is based on the use of the fundamental solutions of heat equation and heat polynomials. The major advantage of MMFS is that the shape functions created possess the Kronecker delta function property.

The rest of the paper is as follows: In Section 2, the mathematical formulation of the problem is presented. Section 3 is devoted to the numerical procedure, a modified MFS method. In Section 4, Implementation of the proposed method is given. Error analysis is reported in Section 5. Several numerical examples are presented in Section 6. Conclusion is finally discussed in Section 7.

2. Mathematical formulation

In order to use the MMFS to solve the problem (1)–(6), the first goal is finding a new transformation which reduces the problem (1)–(6) to a PDE containing only one unknown function.

Let us define the following suitable transformation:(7) $$\begin{array}{cc}\hfill W(x,t)& =U_{xx}(x,t).\hfill \end{array}$$(7)

According to (7), the problem (1)–(6) is changed to the following problem:(8) $$\begin{array}{cc}\hfill W_t(x,t)& =c^2{W}_{xx}(x,t);0<x<1,0<t<T,\hfill \end{array}$$(8) (9) $$\begin{array}{cc}\hfill W(x,0)& ={\mathit{\varphi }}_0^{″}(x);0\le x\le 1,\hfill \end{array}$$(9) (10) $$\begin{array}{cc}\hfill W(0,t)& =U_{xx}(0,t)=\frac{1}{c^2}(U_t(0,t)-f(t))=\frac{1}{c^2}(g_0^{\prime }(t)-f(t));0\le t\le T,\hfill \end{array}$$(10) (11) $$\begin{array}{cc}\hfill W(1,t)& =U_{xx}(1,t)=\frac{1}{c^2}(U_t(1,t)-f(t))=\frac{1}{c^2}(g_1^{\prime }(t)-f(t));0\le t\le T,\hfill \end{array}$$(11) (12) $$\begin{array}{cc}\hfill W(x^{\ast },t)& =U_{xx}(x^{\ast },t)=\frac{1}{c^2}(U_t(x^{\ast },t)-f(t))=\frac{1}{c^2}(k^{\prime }(t)-f(t));0\le t\le T,\hfill \end{array}$$(12) (13) $$\begin{array}{cc}\hfill W(x,T)& ={\mathit{\varphi }}_T^{″}(x);0\le x\le 1.\hfill \end{array}$$(13)

Eliminating the unknown function f(t) in (11) and (12), we know the W satisfies the following equation:(14) $$\begin{array}{c}\hfill W(1,t)-W(x^{\ast },t)=\frac{1}{c^2}(g_1^{\prime }(t)-k^{\prime }(t));0\le t\le T.\end{array}$$(14)

Then, we can propose a computational method for recovering the heat source and the boundary data by solving three problems.

Problem 1:

At first, we use a modified MFS to solve the following IHCP:(15) $$\begin{array}{cc}\hfill W_t(x,t)& =c^2{W}_{xx}(x,t);0<x<1,0<t<T,\hfill \end{array}$$(15) (16) $$\begin{array}{cc}\hfill W(x,0)& ={\mathit{\varphi }}_0^{″}(x);0\le x\le 1,\hfill \end{array}$$(16) (17) $$\begin{array}{cc}\hfill W(1,t)-W(x^{\ast },t)& =\frac{1}{c^2}(g_1^{\prime }(t)-k^{\prime }(t));0\le t\le T,\hfill \end{array}$$(17) (18) $$\begin{array}{cc}\hfill W(x,T)& ={\mathit{\varphi }}_T^{″}(x);0\le x\le 1.\hfill \end{array}$$(18)

By solving the inverse problem (15)–(18), we obtain the approximate values of $W(1,t),W(0,t)$ and $W_x(0,t)$. Then, we can determine the heat source using Equation (11(11) $$\begin{array}{cc}\hfill W(1,t)& =U_{xx}(1,t)=\frac{1}{c^2}(U_t(1,t)-f(t))=\frac{1}{c^2}(g_1^{\prime }(t)-f(t));0\le t\le T,\hfill \end{array}$$(11) ) as follows:(19) $$\begin{array}{c}\hfill f(t)=g_1^{\prime }(t)-c^{2}W(1,t).\end{array}$$(19)

Problem 2:

From (2) and (10), we know that the boundary data $g_0$ can be recovered by solving the following problem for ordinary partial equation:(20) $$\begin{array}{cc}\hfill g_0^{\prime }(t)& =c^{2}W(0,t)+f(t);0<t<T,\hfill \end{array}$$(20) (21) $$\begin{array}{cc}\hfill g_0(0)& ={\mathit{\varphi }}_0(0).\hfill \end{array}$$(21)

Problem 3:

Now from (7) and (1), we obtain $W_x(x,t)=\frac{d}{dx}{U}_{xx}(x,t)=\frac{1}{c^2}\frac{d}{dt}{U}_x(x,t)$. Then by considering $x=0$ and from (2), the boundary data h(t) can be determined by solving the following ordinary problem:(22) $$\begin{array}{cc}\hfill h^{\prime }(t)& =c^2{W}_x(0,t);0<t<T,\hfill \end{array}$$(22) (23) $$\begin{array}{cc}\hfill h(0)& ={\mathit{\varphi }}_0^{\prime }(0).\hfill \end{array}$$(23)

For the well-posed problems 2 and 3, we solve them in the next section by a finite difference method.

The solution of the inverse problem (15)–(19) is unstable. To show that we construct an example.

Let $T=1$, $c=1$ and $g_1(t)=\frac{e^{1+t}}{n^2}+\frac{cos(n^{2}t)}{n^{2-\mathit{ϵ}}}.$ The solution of the problem (15)–(19) when$$\begin{array}{cc}\hfill {\mathit{\varphi }}_0^{″}(x)& =\frac{e^x}{n^2},g_1^{\prime }(t)-k^{\prime }(t)=\frac{(e^1-e^{x^{\ast }})e^t}{n^2},{\mathit{\varphi }}_T^{″}(x)=\frac{e^{x+1}}{n^2},\hfill \end{array}$$

is given by $w(x,t)=\frac{e^{x+t}}{n^2}.$ Therefore, we have$$sup\{|{\mathit{\varphi }}_0^{″}(x)|+|g_1^{\prime }(t)-k^{\prime }(t)|+|{\mathit{\varphi }}_T^{″}(x)|\}=O\left(\frac{3e^2}{n^2}\right)\to 0,n\to \infty ,$$

but$$sup\{|f(t)|\}=sup\{|g_1^{\prime }(t)-W(1,t)|\}=n^{\mathit{ϵ}}\to \infty ,n\to \infty .$$

This indicates that although the data $(|{\mathit{\varphi }}_0^{″}(x)|+|g_1^{\prime }(t)-k^{\prime }(t)|+|{\mathit{\varphi }}_T^{″}(x)|)$ tends to zero, the solution f is unbounded. In other words, the inverse time-dependent heat source problem (1)–(6) is ill-posed.

3. Methodology

3.1. Heat Polynomials

We consider a solution w of heat equation(24) $$\begin{array}{c}\hfill w_t(x,t)=\mathit{\alpha }{w}_{xx}(x,t),\end{array}$$(24)

in the form [65], Chapter 1, p.16–18]:(25) $$\begin{array}{c}\hfill w(x,t)=\mathit{\eta }(x)\mathit{\kappa }(t).\end{array}$$(25)

Upon substituting (25) into (24) and dividing through by $\mathit{\alpha }\mathit{\eta }\mathit{\kappa }$, it follows that:$$\frac{{\mathit{\kappa }}^{\prime }(t)}{\mathit{\alpha }\mathit{\kappa }(t)}=\frac{{\mathit{\eta }}^{″}(x)}{\mathit{\eta }(x)}={\mathit{\gamma }}^2,$$

where $\mathit{\gamma }$ is a complex constant. Solving the resulting ordinary differential equations$$\left\{\begin{array}{c}{\mathit{\kappa }}^{\prime }(t)={\mathit{\gamma }}^2\mathit{\alpha }\mathit{\kappa }(t),\hfill \\ {\mathit{\eta }}^{″}(x)={\mathit{\gamma }}^2\mathit{\eta }(x),\hfill \end{array}\right.$$

we obtain:(26) $$\begin{array}{c}\hfill w(x,t)=e^{\mathit{\gamma }x+{\mathit{\gamma }}^2\mathit{\alpha }t}.\end{array}$$(26)

By expanding Equation (26(26) $$\begin{array}{c}\hfill w(x,t)=e^{\mathit{\gamma }x+{\mathit{\gamma }}^2\mathit{\alpha }t}.\end{array}$$(26) ) into a Taylor’s series with respect to $\mathit{\gamma }$, we obtain:(27) $$\begin{array}{c}\hfill w(x,t)=\sum _{n=0}^{\infty }{p}_n(x,t)\frac{{\mathit{\gamma }}^n}{n!},\end{array}$$(27)

where $p_n$ are the heat polynomials which hold in Equation (24(24) $$\begin{array}{c}\hfill w_t(x,t)=\mathit{\alpha }{w}_{xx}(x,t),\end{array}$$(24) ).

An explicit formula for $p_n(x,t)$ can be obtained from Cauchy’s multiplying two power series together, since$$e^{\mathit{\gamma }x+{\mathit{\gamma }}^2\mathit{\alpha }t}=e^{\mathit{\gamma }x}{e}^{{\mathit{\gamma }}^2\mathit{\alpha }t}.$$

Setting$$e^{\mathit{\gamma }x}=\sum _{n=0}^{\infty }{a}_n{\mathit{\gamma }}^n,e^{{\mathit{\gamma }}^2\mathit{\alpha }t}=\sum _{n=0}^{\infty }{b}_n{\mathit{\gamma }}^n,$$

where$$a_n=\frac{x^n}{n!},n=0,1,2,\dots ,$$

and$$\begin{array}{cc}\hfill b_n& =\left\{\begin{array}{c}\frac{{\mathit{\alpha }}^d{t}^d}{d!};n=2d,\hfill \\ 0;n=2d+1,d=0,1,\dots ,\hfill \end{array}\right.\hfill \end{array}$$

it follows that:(28) $$\begin{array}{c}\hfill e^{\mathit{\gamma }x+{\mathit{\gamma }}^2\mathit{\alpha }t}=\sum _{n=0}^{\infty }{\mathit{\varsigma }}_n{\mathit{\gamma }}^n,\end{array}$$(28)

where(29) $$\begin{array}{c}\hfill {\mathit{\varsigma }}_n=\sum _{j=0}^n{b}_j{a}_{n-j}=\sum _{d=0}^{[\frac{n}{2}]}\frac{{\mathit{\alpha }}^d{t}^d}{d!}\frac{x^{n-2d}}{(n-2d)!}.\end{array}$$(29)

Here, $[\frac{n}{2}]$ denotes the largest integer less than or equal to $\frac{n}{2}$. From Equations (26(26) $$\begin{array}{c}\hfill w(x,t)=e^{\mathit{\gamma }x+{\mathit{\gamma }}^2\mathit{\alpha }t}.\end{array}$$(26) )–(29(29) $$\begin{array}{c}\hfill {\mathit{\varsigma }}_n=\sum _{j=0}^n{b}_j{a}_{n-j}=\sum _{d=0}^{[\frac{n}{2}]}\frac{{\mathit{\alpha }}^d{t}^d}{d!}\frac{x^{n-2d}}{(n-2d)!}.\end{array}$$(29) ), it is clear that:(30) $$\begin{array}{c}\hfill p_n(x,t)=n!\sum _{d=0}^{[\frac{n}{2}]}\frac{{\mathit{\alpha }}^d{t}^d}{d!}\frac{x^{n-2d}}{(n-2d)!}.\end{array}$$(30)

3.2. A modified MFS

Choose source points $\mathbf{y}=(y_i,{\mathit{\tau }}_i),i=1,2,\dots ,n$, then we can express an approximate solution given by a linear combination of the fundamental solutions of heat equation and the heat polynomials as follows:(31) $$\begin{array}{c}\hfill v(\mathbf{x})=\sum _{i=1}^n{\mathit{\lambda }}_i{\mathit{\psi }}_i(\mathbf{x})+\sum _{j=1}^m{\mathit{\xi }}_j{p}_j(\mathbf{x}),\end{array}$$(31)

where $\mathbf{x}=(x,t),$${\mathit{\psi }}_i(\mathbf{x})=\mathit{\psi }(x-y_i,t-{\mathit{\tau }}_i),\mathit{\psi }(x,t)$ is the time shift function given by $\mathit{\psi }(x,t)=F(x,t+T_0)$, $F(x,t)=\frac{1}{\sqrt{4c^2\mathit{\pi }t}}{e}^{-\frac{x^2}{4c^{2}t}}H(t)$, F is the fundamental solution of heat equation, H is the Heaviside function and $T_0>T$ is a constant. Also, $p_j$ is the heat polynomial and ${\mathit{\lambda }}_i$ and ${\mathit{\xi }}_j$ are unknowns.

To determination the coefficients $({\mathit{\lambda }}_1,\dots ,{\mathit{\lambda }}_n)$ and $({\mathit{\xi }}_1,\dots ,{\mathit{\xi }}_m)$, the collocation method is used. However, in addition to the n equations resulting from collocating (31) at the n points ${\mathbf{x}}_l=(x_l,t_l),l=1,2,\dots ,n$ as follows:(32) $$\begin{array}{c}\hfill v_l=v({\mathbf{x}}_l)=\sum _{i=1}^n{\mathit{\lambda }}_i{\mathit{\psi }}_i({\mathbf{x}}_l)+\sum _{j=1}^m{\mathit{\xi }}_j{p}_j({\mathbf{x}}_l),\end{array}$$(32)

extra m equations are required. This is insured by the following m conditions,(33) $$\begin{array}{c}\hfill \sum _{i=1}^n{\mathit{\lambda }}_i{p}_j({\mathbf{x}}_i)=0;j=1,2,\dots ,m.\end{array}$$(33)

The representation Equations (32(32) $$\begin{array}{c}\hfill v_l=v({\mathbf{x}}_l)=\sum _{i=1}^n{\mathit{\lambda }}_i{\mathit{\psi }}_i({\mathbf{x}}_l)+\sum _{j=1}^m{\mathit{\xi }}_j{p}_j({\mathbf{x}}_l),\end{array}$$(32) ) and (33(33) $$\begin{array}{c}\hfill \sum _{i=1}^n{\mathit{\lambda }}_i{p}_j({\mathbf{x}}_i)=0;j=1,2,\dots ,m.\end{array}$$(33) ) constitute a $(n+m)\times (n+m)$ system of linear algebraic equations which can be expressed in matrix form as follows:(34) $$\begin{array}{c}\hfill \left(\begin{array}{c}\mathbf{V}\\ \mathbf{0}\end{array}\right)=\left(\begin{array}{cc}{\mathbf{\Psi }}_0& {\mathbf{P}}_m\\ {\mathbf{P}}_m^{tr}& \mathbf{0}\end{array}\right)\left(\begin{array}{c}\mathbf{\Lambda }\\ \mathbf{\Xi }\end{array}\right).\end{array}$$(34)

or(35) $$\begin{array}{c}\hfill \left(\begin{array}{c}\mathbf{V}\\ \mathbf{0}\end{array}\right)=\mathbf{G}\left(\begin{array}{c}\mathbf{\Lambda }\\ \mathbf{\Xi }\end{array}\right),\end{array}$$(35)

where$$\begin{array}{c}\hfill {\mathbf{\Psi }}_0=\left(\begin{array}{cccc}{\mathit{\psi }}_1({\mathbf{x}}_1)& {\mathit{\psi }}_2({\mathbf{x}}_1)& \cdots & {\mathit{\psi }}_n({\mathbf{x}}_1)\\ {\mathit{\psi }}_1({\mathbf{x}}_2)& {\mathit{\psi }}_2({\mathbf{x}}_2)& \cdots & {\mathit{\psi }}_n({\mathbf{x}}_2)\\ ⋮& ⋮& \ddots & ⋮\\ {\mathit{\psi }}_1({\mathbf{x}}_n)& {\mathit{\psi }}_2({\mathbf{x}}_n)& \cdots & {\mathit{\psi }}_n({\mathbf{x}}_n)\end{array}\right),{\mathbf{P}}_m=\left(\begin{array}{cccc}{p}_1({\mathbf{x}}_1)& p_2({\mathbf{x}}_1)& \cdots & p_m({\mathbf{x}}_1)\\ p_1({\mathbf{x}}_2)& p_2({\mathbf{x}}_2)& \cdots & p_m({\mathbf{x}}_2)\\ ⋮& ⋮& \ddots & ⋮\\ p_1({\mathbf{x}}_n)& p_2({\mathbf{x}}_n)& \cdots & p_m({\mathbf{x}}_n)\end{array}\right)\end{array}$$$$\mathbf{\Lambda }={({\mathit{\lambda }}_1,{\mathit{\lambda }}_2,\dots ,{\mathit{\lambda }}_n)}^{tr},\mathbf{\Xi }={({\mathit{\xi }}_1,{\mathit{\xi }}_2,\dots ,{\mathit{\xi }}_m)}^{tr}.$$

If the inverse of matrix ${\mathbf{\Psi }}_0$ exists, a unique solution is obtained as:(36) $$\begin{array}{c}\hfill \left(\begin{array}{c}\mathbf{\Lambda }\\ \mathbf{\Xi }\end{array}\right)={\mathbf{G}}^{-1}\left(\begin{array}{c}\mathbf{V}\\ \mathbf{0}\end{array}\right).\end{array}$$(36)

Accordingly, Equation (31(31) $$\begin{array}{c}\hfill v(\mathbf{x})=\sum _{i=1}^n{\mathit{\lambda }}_i{\mathit{\psi }}_i(\mathbf{x})+\sum _{j=1}^m{\mathit{\xi }}_j{p}_j(\mathbf{x}),\end{array}$$(31) ) can be rewritten as(37) $$\begin{array}{c}\hfill \tilde{v}(\mathbf{x})={\mathbf{\Psi }}^{tr}(\mathbf{x})\mathbf{\Lambda }+{\mathbf{P}}^{tr}(\mathbf{x})\mathbf{\Xi }=\left(\begin{array}{cc}{\mathbf{\Psi }}^{tr}(\mathbf{x})& {\mathbf{P}}^{tr}(\mathbf{x})\end{array}\right)\left(\begin{array}{c}\mathbf{\Lambda }\\ \mathbf{\Xi }\end{array}\right),\end{array}$$(37) $${\mathbf{\Psi }}^{tr}(\mathbf{x})=({\mathit{\psi }}_1(\mathbf{x}),{\mathit{\psi }}_2(\mathbf{x}),\dots ,{\mathit{\psi }}_n(\mathbf{x})),{\mathbf{P}}^{tr}(\mathbf{x})=(p_1(\mathbf{x}),p_2(\mathbf{x}),\dots ,p_m(\mathbf{x})),$$

or(38) $$\begin{array}{c}\hfill \tilde{v}(\mathbf{x})=\left(\begin{array}{cc}{\mathbf{\Psi }}^{tr}(\mathbf{x})& {\mathbf{P}}^{tr}(\mathbf{x})\end{array}\right){\mathbf{G}}^{-1}\left(\begin{array}{c}\mathbf{V}\\ \mathbf{0}\end{array}\right)=\mathbf{\Theta }(\mathbf{x})\mathbf{V},\end{array}$$(38)

where the matrix of shape functions $\mathbf{\Theta }(\mathbf{x})$ is defined by(39) $$\begin{array}{c}\hfill \mathbf{\Theta }(\mathbf{x})=\left(\begin{array}{cccccc}{\mathit{\vartheta }}_1(\mathbf{x}),& {\mathit{\vartheta }}_2(\mathbf{x}),& \cdots ,& {\mathit{\vartheta }}_k(\mathbf{x}),& \cdots ,& {\mathit{\vartheta }}_{n+m}(\mathbf{x})\end{array}\right),\end{array}$$(39)

in which$${\mathit{\vartheta }}_k(\mathbf{x})=\sum _{i=1}^n{\mathit{\psi }}_i(\mathbf{x}){\mathbf{G}}_{i,k}^{-1}+\sum _{j=1}^m{p}_j(\mathbf{x}){\mathbf{G}}_{n+j,k}^{-1},$$

and ${\mathbf{G}}_{i,k}^{-1}$ is the (i, k)th element of matrix ${\mathbf{G}}^{-1}$. The shape function $\mathbf{\Theta }(\mathbf{x})$, obtained through the above process, possesses the following properties:

(1)	Linear independence Shape functions are linearly independent in the desired domain. The shape function $\mathbf{\Theta }(\mathbf{x})$ possesses the delta function property, i.e.$${\mathit{\vartheta }}_i({\mathbf{x}}_j)={\mathit{\delta }}_{ij}=\left\{\begin{array}{cc}1& i=j,\\ 0& i\ne j\end{array}\right.$$
(2)	Partitions of unity$$\sum _{i=1}^{n+m}{\mathit{\vartheta }}_i(\mathbf{x})=1.$$
(3)	Linear reproducibility$$\sum _{i=1}^{n+m}{\mathit{\vartheta }}_i(\mathbf{x}){\mathbf{x}}_i=\mathbf{x}.$$
(4)	${\mathit{\vartheta }}_i(\mathbf{x})$ has simple derivatives$${\mathbf{\Theta }}^{(l)}(\mathbf{x})=({\mathit{\vartheta }}_1^{(l)}(\mathbf{x}),{\mathit{\vartheta }}_2^{(l)}(\mathbf{x}),\dots ,{\mathit{\vartheta }}_{n+m}^{(l)}(\mathbf{x})).$$
(5)	The shape function $\mathbf{\Theta }(\mathbf{x})$ satisfies the heat Equation (15(15) $$\begin{array}{cc}\hfill W_t(x,t)& =c^2{W}_{xx}(x,t);0<x<1,0<t<T,\hfill \end{array}$$(15) ), i.e. $\frac{\mathit{\partial }{\mathit{\vartheta }}_i}{\mathit{\partial }t}=c^2\frac{{\mathit{\partial }}^2{\mathit{\vartheta }}_i}{\mathit{\partial }{x}^2};i=1,2,\dots ,n+m.$

4. Implementation of the proposed method

To apply the proposed method to the solution of problem (15)–(18), let $\mathrm{\Omega }=\{(x_r,t_r),r=1,\dots ,s_1+s_2+s_3\}$ be a set of scattered nodes such that $\mathrm{\Omega }={\mathrm{\Omega }}_1\cup {\mathrm{\Omega }}_2\cup {\mathrm{\Omega }}_3$, where(40) $$\begin{array}{cc}\hfill {\mathrm{\Omega }}_1& =\{(x_r,t_r),0\le x_r\le 1,t_r=0,r=1,\dots ,s_1\},\hfill \end{array}$$(40) (41) $$\begin{array}{cc}\hfill {\mathrm{\Omega }}_2& =\{(x_r,t_r),x_r=1,0\le t_r\le 1,r=s_1+1,\dots ,s_1+s_2\},\hfill \end{array}$$(41) (42) $$\begin{array}{cc}\hfill {\mathrm{\Omega }}_3& =\{(x_r,t_r),0\le x_r\le 1,t_r=T,r=s_1+s_2+1,\dots ,s_1+s_2+s_3\}.\hfill \end{array}$$(42)

We assume that an approximation to the solution of the problem (15)–(18) can be expressed as follows:(43) $$\begin{array}{c}\hfill \widehat{W}(x,t)=\sum _{i=1}^{n+m}{w}_i{\mathit{\vartheta }}_i(x,t)=\mathbf{\Theta }{\mathbf{w}}^{tr},\end{array}$$(43)

where $\mathbf{\Theta }=({\mathit{\vartheta }}_1,{\mathit{\vartheta }}_2,\dots ,{\mathit{\vartheta }}_{n+m})$ are the shape functions (39) and $\mathbf{w}=(w_1,w_2,\dots ,w_{n+m})$ are unknowns which remain to be determined.

For this choice of basis functions $\mathbf{\Theta }$; the approximate solution $\widehat{W}$ already satisfies the heat Equation (15(15) $$\begin{array}{cc}\hfill W_t(x,t)& =c^2{W}_{xx}(x,t);0<x<1,0<t<T,\hfill \end{array}$$(15) ). The resultant linear system of equations for the unknown coefficients $w_i$ can then be obtained from the following simple collocation.

Collocating Equation (43(43) $$\begin{array}{c}\hfill \widehat{W}(x,t)=\sum _{i=1}^{n+m}{w}_i{\mathit{\vartheta }}_i(x,t)=\mathbf{\Theta }{\mathbf{w}}^{tr},\end{array}$$(43) ) into (40(40) $$\begin{array}{cc}\hfill {\mathrm{\Omega }}_1& =\{(x_r,t_r),0\le x_r\le 1,t_r=0,r=1,\dots ,s_1\},\hfill \end{array}$$(40) )–(42(42) $$\begin{array}{cc}\hfill {\mathrm{\Omega }}_3& =\{(x_r,t_r),0\le x_r\le 1,t_r=T,r=s_1+s_2+1,\dots ,s_1+s_2+s_3\}.\hfill \end{array}$$(42) ), we obtain$$\begin{array}{cc}\hfill \widehat{W}(x_r,t_r)& =\sum _{i=1}^{n+m}{w}_i{\mathit{\vartheta }}_i(x_r,t_r)=\left\{\begin{array}{cc}{\mathit{\varphi }}_0^{″}(x_r);\hfill & r=1,2,\dots ,s_1,\hfill \\ {\mathit{\varphi }}_T^{″}(x_r);\hfill & r=s_1+s_2+1,\dots ,s_1+s_2+s_3,\hfill \end{array}\right.\hfill \\ \hfill \widehat{W}(x_r,t_r)-\widehat{W}(x^{\ast },t_r)& =\sum _{i=1}^{n+m}{w}_i\{{\mathit{\vartheta }}_i(x_r,t_r)-{\mathit{\vartheta }}_i(x^{\ast },t_r)\}\hfill \\ \hfill & =\frac{1}{c^2}(g_1^{\prime }(t_r)-k^{\prime }(t_r));r=s_1+1,\dots ,s_1+s_2.\hfill \end{array}$$

So we have the following linear system of equations:(44) $$\begin{array}{c}\hfill \mathbf{Aw}=\mathbf{g},\end{array}$$(44)

where$$\mathbf{A}={\left(\begin{array}{c}{\mathit{\vartheta }}_i(x_e,t_e)\\ {\mathit{\vartheta }}_i(x_d,t_d)-{\mathit{\vartheta }}_i(x^{\ast },t_d)\\ {\mathit{\vartheta }}_i(x_z,t_z)\end{array}\right)}_{(s_1+s_2+s_3)\times (n+m)},$$$$\mathbf{g}={\left({\mathit{\varphi }}_0^{″}(x_e),\frac{1}{c^2}(g_1^{\prime }(t_d)-k^{\prime }(t_d)),{\mathit{\varphi }}_T^{″}(x_z)\right)}_{(s_1+s_2+s_3)\times 1},$$$$\mathbf{w}={(w_1,w_2,\dots ,w_{n+m})}_{1\times (n+m)}.$$

where $e=1,2,\dots ,s_1$, $d=s_1+1,\dots ,s_1+s_2$, $z=s_1+s_2+1,\dots ,s_1+s_2+s_3$ and $i=1,2,\dots ,n+m$.

4.1. Regularization

As a direct consequence of the fact that the inverse problem (1)–(4), is highly ill-posed, the discretization matrix $\mathbf{A}$ is severely ill-conditioned. Hence, a direct approach for solving the resulting system of linear algebraic Equation (44(44) $$\begin{array}{c}\hfill \mathbf{Aw}=\mathbf{g},\end{array}$$(44) ), such as the least-square method, would produce highly oscillatory and unbounded solutions, i.e. unstable solutions. The accurate and stable solution of the system of linear algebraic Equation (44(44) $$\begin{array}{c}\hfill \mathbf{Aw}=\mathbf{g},\end{array}$$(44) ) is very important for obtaining physically meaningful numerical results [66]. Regularization methods are among the most popular and successful methods for solving stably and accurately ill-conditioned matrix equations [67]. Here, we apply the standard TR technique [66]. It consists of solving the optimization problem:(45) $$\begin{array}{c}\hfill \underset{\mathbf{w}}{min}\{\Vert \mathbf{A}\mathbf{w}-\mathbf{g}{\Vert }^2+{\mathit{\epsilon }}^2\Vert \mathbf{w}{\Vert }^2\},\end{array}$$(45)

where $\Vert .\Vert$ denotes the usual Euclidean norm and $\mathit{\epsilon }$ is called the regularization parameter. Formally, for a given value of the regularization parameter, $\mathit{\epsilon }$, Tikhonov regularized solution $\mathbf{w}$ of the problem (44) is obtained by solving the normal equation:$$({\mathbf{A}}^{tr}\mathbf{A}+{\mathit{\epsilon }}^{2}I)\mathbf{w}={\mathbf{A}}^{tr}\mathbf{g},$$

namely:$$\mathbf{w}={({\mathbf{A}}^{tr}\mathbf{A}+{\mathit{\epsilon }}^{2}I)}^{-1}{\mathbf{A}}^{tr}\mathbf{g}.$$

The choice of a suitable value of the regularization parameter $\mathit{\epsilon }$ is crucial for the accuracy of the final numerical solution and is still under intensive research [68].

One parameter choice criterion extensively studied is the discrepancy principle [69], however, it requires a reliable estimation of the amount of noise in the data. Heuristical approaches are preferable in the case when no a priori information about the noise is available. For the TR method, several heuristical approaches have been proposed, including the L-curve criterion [70], cross-validation (CV) and generalized cross validation (GCV) [71]. In this paper, we use the GCV to choose the regularization parameter. In GCV the regularization parameter $\mathit{\epsilon }$ chosen to minimize the GCV function:$$G(\mathit{\epsilon })=\frac{{\Vert \mathbf{Aw}-\mathbf{g}\Vert }^2}{{(trace(I-{\mathbf{AA}}^I))}^2};\mathit{\epsilon }>0,$$

where$${\mathbf{A}}^I={({\mathbf{A}}^{tr}\mathbf{A}+{\mathit{\epsilon }}^{2}I)}^{-1}{\mathbf{A}}^{tr}.$$

Denote the solution of Equation (45(45) $$\begin{array}{c}\hfill \underset{\mathbf{w}}{min}\{\Vert \mathbf{A}\mathbf{w}-\mathbf{g}{\Vert }^2+{\mathit{\epsilon }}^2\Vert \mathbf{w}{\Vert }^2\},\end{array}$$(45) ) by $\stackrel{~}{}\}w$. Then, the approximate solution for inverse problem (15)–(18) is(46) $$\begin{array}{c}\hfill \tilde{W}(x,t)=\sum _{i=1}^{n+m}\widetilde{w_i}{\mathit{\vartheta }}_i(x,t),\end{array}$$(46)

and the approximate heat source is(47) $$\begin{array}{c}\hfill \tilde{f}(t)=g_1^{\prime }(t)-c^2\sum _{i=1}^{n+m}\widetilde{w_i}{\mathit{\vartheta }}_i(1,t).\end{array}$$(47)

From (46), we obtain $\tilde{W}(0,t)$ and ${\tilde{W}}_x(0,t)$. Then, the approximate boundary data ${\tilde{g}}_0(t)$ can be obtained by solving the following problem:(48) $$\begin{array}{cc}\hfill g_0^{\prime }(t)& =c^2\sum _{i=1}^{n+m}\widetilde{w_i}{\mathit{\vartheta }}_i(0,t)+\tilde{f}(t);0<t<T,\hfill \end{array}$$(48) (49) $$\begin{array}{cc}\hfill g_0(0)& ={\mathit{\varphi }}_0(0).\hfill \end{array}$$(49)

In order to solve the problem (48) and (49) numerically, we use the following formula (theta-method [72]) for Equation (48(48) $$\begin{array}{cc}\hfill g_0^{\prime }(t)& =c^2\sum _{i=1}^{n+m}\widetilde{w_i}{\mathit{\vartheta }}_i(0,t)+\tilde{f}(t);0<t<T,\hfill \end{array}$$(48) ) which is in the form$$\begin{array}{cc}\hfill {\tilde{g}}_{0_{ȷ+1}}& ={\tilde{g}}_{0_{ȷ}}+\mathrm{\Delta }t\left[\mathit{\theta }\left(c^2\sum _{i=1}^{n+m}\widetilde{w_i}{\mathit{\vartheta }}_i(0,t_{ȷ})+\widetilde{f_{ȷ}}\right)+(1-\mathit{\theta })\left(c^2\sum _{i=1}^{n+m}\widetilde{w_i}{\mathit{\vartheta }}_i(0,t_{ȷ+1})+{\tilde{f}}_{ȷ+1}\right)\right];\hfill \\ \hfill & ȷ=0,1,\dots ,M,\hfill \end{array}$$

where $t=ȷ\mathrm{\Delta }t,M\mathrm{\Delta }t=T$ and ${\tilde{g}}_{0_0}={\mathit{\varphi }}_0(0).$ The approximate values of boundary data $\tilde{h}(t)$ can be obtained by solving the following problem:(50) $$\begin{array}{cc}\hfill {\tilde{h}}^{\prime }(t)& =c^2\sum _{i=1}^{n+m}{\tilde{w}}_i\frac{\mathit{\partial }{\mathit{\vartheta }}_i}{\mathit{\partial }x}(0,t);0<t<T,\hfill \end{array}$$(50) (51) $$\begin{array}{cc}\hfill \tilde{h}(0)& ={\mathit{\varphi }}_0^{\prime }(0).\hfill \end{array}$$(51)

Using theta-method for Equation (50(50) $$\begin{array}{cc}\hfill {\tilde{h}}^{\prime }(t)& =c^2\sum _{i=1}^{n+m}{\tilde{w}}_i\frac{\mathit{\partial }{\mathit{\vartheta }}_i}{\mathit{\partial }x}(0,t);0<t<T,\hfill \end{array}$$(50) ), we have$$\begin{array}{cc}\hfill {\tilde{h}}_{ȷ+1}& ={\tilde{h}}_{ȷ}+\mathrm{\Delta }t\left[\mathit{\theta }\left(c^2\sum _{i=1}^{n+m}\widetilde{w_i}\frac{\mathit{\partial }{\mathit{\vartheta }}_i}{\mathit{\partial }x}(0,t_{ȷ})\right)+(1-\mathit{\theta })\left(c^2\sum _{i=1}^{n+m}\widetilde{w_i}\frac{\mathit{\partial }{\mathit{\vartheta }}_i}{\mathit{\partial }x}(0,t_{ȷ+1})\right)\right];\hfill \\ \hfill & ȷ=0,1,\dots ,M,\hfill \end{array}$$

where $t=ȷ\mathrm{\Delta }t,M\mathrm{\Delta }t=T$ and ${\tilde{h}}_0={\mathit{\varphi }}_0^{\prime }(0).$

The theta-method is of order two for $\mathit{\theta }=\frac{1}{2}$ and otherwise of order one.

Theorem 1:

The theta-method is convergent for every $\mathit{\theta }\in [0,1].$

Proof See [72].

5. Error analysis

Suppose that $H=L^2([0,1]\times [0,T])$ and $\{{\mathit{\vartheta }}_1(\mathbf{x}),{\mathit{\vartheta }}_2(\mathbf{x}),\dots ,{\mathit{\vartheta }}_N(\mathbf{x})\}\subset H$, where $N=n+m$, $\mathbf{x}=(x,t)$, the shape function ${\mathit{\vartheta }}_i(\mathbf{x}),i=1,2,\dots ,N$ are given by (39) and $Y=span\{{\mathit{\vartheta }}_1(\mathbf{x}),{\mathit{\vartheta }}_2(\mathbf{x}),\dots ,{\mathit{\vartheta }}_N(\mathbf{x})\}$ and u be an arbitrary element in H. Since Y is a finite dimensional vector space, u has the unique best approximation out of Y such as $P_{N}u$; that is [73]:$$\forall y\in Y,\Vert u-P_{N}u{\Vert }_2\le \Vert u-y{\Vert }_2.$$

Since $P_{N}u\in Y$, there exists the unique coefficients $w_0,w_1,\dots ,w_M$ such that$$P_{N}u=\sum _{i=1}^N{w}_i{\mathit{\vartheta }}_i(\mathbf{x}).$$

Figure 1. Graph of $g_{1_{no}}^{\prime }$ and ${\mathit{\varphi }}_{0_{no}}^{″}$ with various values of polynomials $(m_1)$ and scattered points $(n_1)$ for Example 1.

Figure 2. Graph of $g_{1_{no}}^{\prime }$ and $k_{no}^{\prime }$ and absolute errors $|g_{1_{Exact}}^{\prime }-g_{1_{{no}_{Numeric}}}^{\prime }|$ and $|k_{Exact}^{\prime }-k_{{no}_{Numeric}}^{\prime }|$ for Example 1.

Figure 3. Graph of $g_{1_{no}}^{\prime }$ and $k_{no}^{\prime }$ and absolute errors $|g_{1_{Exact}}^{\prime }-g_{1_{{no}_{Numeric}}}^{\prime }|$ and $|k_{Exact}^{\prime }-k_{{no}_{Numeric}}^{\prime }|$ for Example 2.

Figure 4. Graph of ${\mathit{\varphi }}_{0_{no}}^{″}$ and ${\mathit{\varphi }}_{T_{no}}^{″}$ and absolute errors $|{\mathit{\varphi }}_{0_{Exact}}^{″}-{\mathit{\varphi }}_{0_{{no}_{Numeric}}}^{″}|$ and $|{\mathit{\varphi }}_{T_{Exact}}^{″}-{\mathit{\varphi }}_{T_{{no}_{Numeric}}}^{″}|$ for Example 1.

Figure 5. Graph of ${\mathit{\varphi }}_{0_{no}}^{″}$ and ${\mathit{\varphi }}_{T_{no}}^{″}$ and absolute errors $|{\mathit{\varphi }}_{0_{Exact}}^{″}-{\mathit{\varphi }}_{0_{{no}_{Numeric}}}^{″}|$ and $|{\mathit{\varphi }}_{T_{Exact}}^{″}-{\mathit{\varphi }}_{T_{{no}_{Numeric}}}^{″}|$ for Example 2.

Figure 6. Graph of f(t) and absolute error $|f_{{}_{Exact}}-f_{{}_{Numeric}}|$ with noiseless and noisy data when $n_1=n_2=n_3=4,s_1=s_2=s_3=5,m=10$ and $T_0=1.2$ for Example 1.

Figure 7. Graph of $g_0(t)$ and absolute error $|g_{0_{Exact}}-g_{0_{Numeric}}|$ with noiseless and noisy data when $n_1=n_2=n_3=4,s_1=s_2=s_3=5,m=10$ and $T_0=1.2$ for Example 1.

Figure 8. Graph of h(t) and absolute error $|h_{Exact}-h_{Numeric}|$ with noiseless and noisy data when $n_1=n_2=n_3=4,s_1=s_2=s_3=5,m=10$ and $T_0=1.2$ for Example 1.

Figure 9. Graph of $RMS(f),RMS(g_0),RMS(h)$ and RES(f),  RES(h) with noiseless data when $n_1=n_2=n_3=4,s_1=s_2=s_3=5,m=10$ and various values of $T_0$ for Example 1.

Figure 10. Graph of f(t) with noiseless and noisy data when $n_1=n_2=n_3=4,s_1=s_2=s_3=5,m=10$ and $T_0=1.5$ for Example 2.

Figure 11. Graph of $g_0(t)$ with noiseless and noisy data when $n_1=n_2=n_3=4,s_1=s_2=s_3=5,m=10$ and $T_0=1.5$ for Example 2.

Figure 12. Graph of h(t) with noiseless and noisy data when $n_1=n_2=n_3=4,s_1=s_2=s_3=5,m=10$ and $T_0=1.5$ for Example 2.

Figure 13. Graph of $RMS(f),RMS(g_0)RMS(h)$ and RES(f),  RES(h) with noiseless data when $n_1=n_2=n_3=4,s_1=s_2=s_3=5,m=10$ and various values of $T_0$ for Example 2.

Theorem 2:

Let $(H,\Vert .{\Vert }_2)$ be a Hilbert space and Y be a closed subspace of H such that $dimY<\infty$ and $\{{\mathit{\vartheta }}_1,{\mathit{\vartheta }}_2,\dots ,{\mathit{\vartheta }}_N\}$ is any basis for Y. Let u be an arbitrary element in H and $P_{N}u$ be the unique best approximation to u out of Y then [73]:$$\Vert u-P_{N}u{\Vert }_2={\left(\frac{Q(u,{\mathit{\vartheta }}_1,{\mathit{\vartheta }}_2,\dots ,{\mathit{\vartheta }}_N)}{Q({\mathit{\vartheta }}_1,{\mathit{\vartheta }}_2,\dots ,{\mathit{\vartheta }}_N)}\right)}^{\frac{1}{2}}$$

where$$Q({\mathit{\vartheta }}_1,{\mathit{\vartheta }}_2,\dots ,{\mathit{\vartheta }}_N)=\left(\begin{array}{cccc}⟨{\mathit{\vartheta }}_1,{\mathit{\vartheta }}_1⟩& ⟨{\mathit{\vartheta }}_1,{\mathit{\vartheta }}_2⟩& \cdots & ⟨{\mathit{\vartheta }}_1,{\mathit{\vartheta }}_N⟩\\ ⟨{\mathit{\vartheta }}_2,{\mathit{\vartheta }}_1⟩& ⟨{\mathit{\vartheta }}_2,{\mathit{\vartheta }}_2⟩& \cdots & ⟨{\mathit{\vartheta }}_2,{\mathit{\vartheta }}_N⟩\\ ⋮& ⋮& \ddots & ⋮\\ ⟨{\mathit{\vartheta }}_N,{\mathit{\vartheta }}_1⟩& ⟨{\mathit{\vartheta }}_N,{\mathit{\vartheta }}_2⟩& \cdots & ⟨{\mathit{\vartheta }}_N,{\mathit{\vartheta }}_N⟩\end{array}\right).$$

Note that the inner product in space H is defined as follows:$$⟨u(\mathbf{x}),y(\mathbf{x})⟩={\int }_0^T{\int }_0^{1}u(x,t)\overline{y(x,t)}\mathrm{d}x\mathrm{d}t,$$

and the norm is as follows:$${\Vert u(\mathbf{x})\Vert }_2={\left({\int }_0^T{\int }_0^1{|u(x,t)|}^2\mathrm{d}x\mathrm{d}t\right)}^{\frac{1}{2}}.$$

Define$$\begin{array}{cc}\hfill P_{N}W& =\sum _{i=1}^{n+m}{w}_i{\mathit{\vartheta }}_i(x,t)=\sum _{i=1}^{n+m}{w}_i\left(\sum _{l=1}^n{\mathit{\psi }}_l(\mathbf{x}){\mathbf{G}}_{l,i}^{-1}+\sum _{j=1}^m{p}_j(\mathbf{x}){\mathbf{G}}_{n+j,i}^{-1}\right)\hfill \\ \hfill & =\sum _{i=1}^{n+m}\sum _{l=1}^n{w}_i{\mathit{\psi }}_l(\mathbf{x}){\mathbf{G}}_{l,i}^{-1}+\sum _{i=1}^{n+m}\sum _{j=1}^m{w}_i{p}_j(\mathbf{x}){\mathbf{G}}_{n+j,i}^{-1}\hfill \\ \hfill & =\sum _{i=1}^{(n+m)}\sum _{j=1}^{(n+m)}{w}_i{\mathit{\zeta }}_{ji}(x,t)=\sum _{s=0}^{{(n+m)}^2-1}{\mathit{\mu }}_s{b}_s(x,t),\hfill \end{array}$$

where$$[b_0,b_1,\dots ,b_{{(n+m)}^2-1}]=[{\mathit{\zeta }}_{11},{\mathit{\zeta }}_{21},\dots ,{\mathit{\zeta }}_{(n+m)1},{\mathit{\zeta }}_{12},{\mathit{\zeta }}_{22},\dots ,{\mathit{\zeta }}_{(n+m)2},\dots ,{\mathit{\zeta }}_{1(n+m)},\dots ,{\mathit{\zeta }}_{{(n+m)}^2}],$$$$[{\mathit{\mu }}_0,{\mathit{\mu }}_1,\dots ,{\mathit{\mu }}_{{(n+m)}^2-1}]=[\stackrel{n+m}{\overbrace{w_1,w_1,\dots ,w_1}},\stackrel{n+m}{\overbrace{w_2,w_2,\dots ,w_2}},\dots ,\stackrel{n+m}{\overbrace{w_{n+m},w_{n+m},\dots ,w_{n+m}}}],$$

and$${\mathit{\zeta }}_{ji}=\left\{\begin{array}{c}{\mathit{\psi }}_j(\mathbf{x}){\mathbf{G}}_{j,i}^{-1};j=1,2,\dots ,n,\hfill \\ \hfill \\ p_{j-n}(\mathbf{x}){\mathbf{G}}_{j,i}^{-1};j=n+1,n+2,\dots ,n+m.\hfill \end{array}\right.$$

In the following we obtain bounds for the error of best approximation for heat source f(x) in terms of Sobolev norms. This norm for a function $W_0(x)$ is defined in the interval (a, b) for $\mathit{\nu }\ge 0$ by$$\Vert W_0{\Vert }_{H^{\mathit{\nu }}}(a,b)={\left(\sum _{k=0}^{\mathit{\nu }}{\int }_a^b{|W_0^{(k)}(x)|}^2\mathrm{d}x\right)}^{\frac{1}{2}}={\left(\sum _{k=0}^{\mathit{\nu }}{\Vert W_0^{(k)}\Vert }_{L^2(a,b)}^2\right)}^{\frac{1}{2}},$$

where $W_0^{(k)}$ denotes the kth derivative of $W_0$. The symbol $|W_0{|}_{H^{\mathit{\nu };N}(0,1)}$ which is introduced in [74] is defined by$$|W_0{|}_{H^{\mathit{\nu };N}(0,1)}={\left(\sum _{k=min(\mathit{\nu },N+1)}^{\mathit{\nu }}{\Vert W_0^{(k)}\Vert }_{L^2(0,1)}^2\right)}^{\frac{1}{2}}.$$

Table 1. The values of RMS(f), RES(f),  $RMS(g_0)$, $RES(g_0)$, RMS(h) and RES(h) with different choose of n and m when $s_1=s_2=s_3=6$ and $\mathit{\sigma }=1\%$ for Example 1.

$n_1$	4	5	6	7	10
$n_2$	4	5	6	7	10
$n_3$	4	5	6	7	10
m	0	0	0	0	0
RMS(f)	0.9346294	0.8176032	5.8213482	2.8554492	0.7765079
RES(f)	0.2664936	0.2331256	1.6598583	0.8141828	0.2214080
$RMS(g_0)$	0.2306375	0.2201657	2.7895291	1.0043515	0.2635528
$RES(g_0)$	Inf	Inf	Inf	Inf	Inf
RMS(h)	0.6876904	0.6363895	4.6353827	2.0763144	0.5000441
RES(h)	1.0377705	0.9603541	6.9951010	3.1332970	0.7545999
m	5	5	5	5	5
RMS(f)	$1.1708181\times {10}^{-4}$	0.0020049	1.2009122	0.8593210	0.5491819
RES(f)	$3.3383883\times {10}^{-5}$	$5.7165785\times {10}^{-4}$	0.3424197	0.2450208	0.1565899
$RMS(g_0)$	$5.7108347\times {10}^{-5}$	$5.1326584\times {10}^{-4}$	0.2980472	0.2751808	0.3038408
$RES(g_0)$	Inf	Inf	Inf	Inf	Inf
RMS(h)	$1.3195569\times {10}^{-4}$	0.0014865	0.9101555	0.4405244	0.2311222
RES(h)	$1.9912992\times {10}^{-4}$	0.0022432	1.3734852	0.6647807	0.3487788
m	10	10	10	10	10
RMS(f)	$7.7663001\times {10}^{-4}$	$3.6622293\times {10}^{-4}$	1.1895994	1.2881577	0.7591267
RES(f)	$2.2144282\times {10}^{-4}$	$1.0442224\times {10}^{-4}$	0.3391940	0.3672962	0.2164520
$RMS(g_0)$	$1.9886186\times {10}^{-4}$	$1.0914386\times {10}^{-4}$	0.2959987	0.5151874	0.1970341
$RES(g_0)$	Inf	Inf	Inf	Inf	Inf
RMS(h)	$5.3880119\times {10}^{-4}$	$2.4684676\times {10}^{-4}$	0.9011449	0.9751129	0.2777104
RES(h)	$8.1308687\times {10}^{-4}$	$3.7250822\times {10}^{-4}$	1.3598877	1.4715103	0.4190836

Table 2. The values of RMS(f), RES(f),  $RMS(g_0)$, $RES(g_0)$, RMS(h) and RES(h) with different choose of $s_1,s_2,s_3$ when $n_1=n_2=n_3=4,m=10$ and $\mathit{\sigma }=1\%$ for Example 1.

$s_1$	4	5	8	10	12	15
$s_2$	4	5	8	10	12	15
$s_3$	4	5	8	10	12	15
RMS(f)	2.3748682	$4.6850674\times {10}^{-4}$	$8.6736970\times {10}^{-4}$	$8.9234946\times {10}^{-4}$	$9.5057167\times {10}^{-4}$	$8.5945433\times {10}^{-4}$
RES(f)	0.6771532	$1.3358673\times {10}^{-4}$	$2.4731571\times {10}^{-4}$	$2.5443826\times {10}^{-4}$	$2.5375868\times {10}^{-4}$	$2.4505876\times {10}^{-4}$
$RMS(g_0)$	0.3374261	$1.1987426\times {10}^{-4}$	$2.2341940\times {10}^{-4}$	$2.3043220\times {10}^{-4}$	$2.3035733\times {10}^{-4}$	$2.2339808\times {10}^{-4}$
$RES(g_0)$	Inf	Inf	Inf	Inf	Inf	Inf
RMS(h)	1.4943393	$3.0130733\times {10}^{-4}$	$6.1014690\times {10}^{-4}$	$6.2990701\times {10}^{-4}$	$6.2858599\times {10}^{-4}$	$6.0600135\times {10}^{-4}$
RES(h)	2.2550576	$4.5469284\times {10}^{-4}$	$9.2075230\times {10}^{-4}$	$9.5057167\times {10}^{-4}$	$9.4857818\times {10}^{-4}$	$9.1449637\times {10}^{-4}$

Table 3. The values of RMS(f) and RES(f) for various values of $T_0$, $\mathit{\sigma }=5\%,m=10$, $n_1=n_2=n_3=4$ and $s_1=s_2=s_3=6$ for Example 1.

$T_0$	1.1	1.5	2.1	10	20
RMS(f)	$9.7665878\times {10}^{-4}$	$5.8738177\times {10}^{-4}$	$9.5202576\times {10}^{-4}$	0.0012657	0.0017081
RES(f)	$2.7847762\times {10}^{-4}$	$1.6748191\times {10}^{-4}$	$2.7145393\times {10}^{-4}$	$3.6088924\times {10}^{-4}$	$4.8702289\times {10}^{-4}$
RMS(f)[23]	0.3322	0.6894	0.2308	0.1774	0.1074
RES(f)[23]	0.0954	0.1979	0.0663	0.0510	0.0308

To state our main results, the following Theorem will be required.

Theorem 3:

Suppose that $W_0\in H^{\mathit{\nu }}(0,1)$ with $\mathit{\nu }\ge 0$. If $P_N{W}_0={\sum }_{s=0}^N{\mathit{\mu }}_s{b}_s(t)$ is the best approximation of $W_0$ then(52) $$\begin{array}{c}\hfill \Vert W_0-P_N{W}_0{\Vert }_{L^2(0,1)}\le c{N}^{-\mathit{\nu }}{|W_0|}_{H^{\mathit{\nu };N}(0,1)},\end{array}$$(52)

and for $1\le r\le \mathit{\nu },$(53) $$\begin{array}{c}\hfill \Vert W_0-P_N{W}_0{\Vert }_{H^r(0,1)}\le c{N}^{2r-\frac{1}{2}-\mathit{\nu }}{|W_0|}_{H^{\mathit{\nu };N}(0,1)},\end{array}$$(53)

where c depends on $\mathit{\nu }.$

Proof Mashayekhi et al. [75] Let $W_0\in H^{\mathit{\nu }}(0,1)$ with $\mathit{\nu }\ge 0$ and ${\sum }_{\mathit{\gamma }=0}^N{\acute{c}}_{\mathit{\gamma }}{L}_{\mathit{\gamma }}$ be the best approximation of $W_0,$ which is constructed using shifted Legendre polynomials $L_{\mathit{\gamma }},\mathit{\gamma }=0,\dots ,N$ in the interval [0, 1]. Then [74](54) $$\begin{array}{c}\hfill {∥W_0-\sum _{\mathit{\gamma }=0}^N{\acute{c}}_{\mathit{\gamma }}{L}_{\mathit{\gamma }}∥}_{L^2(0,1)}\le c{N}^{-\mathit{\nu }}{|W_0|}_{H^{\mathit{\nu };N}(0,1)},\end{array}$$(54)

and for $1\le r\le \mathit{\nu },$(55) $$\begin{array}{c}\hfill {∥W_0-\sum _{\mathit{\gamma }=0}^N{\acute{c}}_{\mathit{\gamma }}{L}_{\mathit{\gamma }}∥}_{H^r(0,1)}\le c{N}^{2r-\frac{1}{2}-\mathit{\nu }}{|W_0|}_{H^{\mathit{\nu };N}(0,1)}.\end{array}$$(55)

Since the best approximation is unique [73], we have(56) $$\begin{array}{cc}\hfill {∥W_0-\sum _{\mathit{\gamma }=0}^N{\acute{c}}_{\mathit{\gamma }}{L}_{\mathit{\gamma }}∥}_{L^2(0,1)}& =\Vert W_0-P_N{W}_0{\Vert }_{L^2(0,1)},{∥W_0-\sum _{\mathit{\gamma }=0}^N{\acute{c}}_{\mathit{\gamma }}{L}_{\mathit{\gamma }}∥}_{H^r(0,1)}\hfill \\ \hfill & =\Vert W_0-P_N{W}_0{\Vert }_{H^r(0,1)},\hfill \end{array}$$(56)

and using Equations (54(54) $$\begin{array}{c}\hfill {∥W_0-\sum _{\mathit{\gamma }=0}^N{\acute{c}}_{\mathit{\gamma }}{L}_{\mathit{\gamma }}∥}_{L^2(0,1)}\le c{N}^{-\mathit{\nu }}{|W_0|}_{H^{\mathit{\nu };N}(0,1)},\end{array}$$(54) )–(56(56) $$\begin{array}{cc}\hfill {∥W_0-\sum _{\mathit{\gamma }=0}^N{\acute{c}}_{\mathit{\gamma }}{L}_{\mathit{\gamma }}∥}_{L^2(0,1)}& =\Vert W_0-P_N{W}_0{\Vert }_{L^2(0,1)},{∥W_0-\sum _{\mathit{\gamma }=0}^N{\acute{c}}_{\mathit{\gamma }}{L}_{\mathit{\gamma }}∥}_{H^r(0,1)}\hfill \\ \hfill & =\Vert W_0-P_N{W}_0{\Vert }_{H^r(0,1)},\hfill \end{array}$$(56) ) we can obtain Equations (52(52) $$\begin{array}{c}\hfill \Vert W_0-P_N{W}_0{\Vert }_{L^2(0,1)}\le c{N}^{-\mathit{\nu }}{|W_0|}_{H^{\mathit{\nu };N}(0,1)},\end{array}$$(52) ) and (53(53) $$\begin{array}{c}\hfill \Vert W_0-P_N{W}_0{\Vert }_{H^r(0,1)}\le c{N}^{2r-\frac{1}{2}-\mathit{\nu }}{|W_0|}_{H^{\mathit{\nu };N}(0,1)},\end{array}$$(53) ).

 

Table 4. The values of RES(f) for various values of $\mathit{\sigma }$ and $x^{\ast }$ when $n_1=n_2=n_3=4,s_1=s_2=s_3=6,m=10$ and $T_0=2.1$ for Example 1.

$x^{\ast }$	MMFS	MMFS	MMFS	MFS [23]	MFS [23]	MFS [23]
	$\mathit{\sigma }=10\%$	$\mathit{\sigma }=1\%$	$\mathit{\sigma }=0.1\%$	$\mathit{\sigma }=10\%$	$\mathit{\sigma }=1\%$	$0.1\%$
0.1	0.0877574	$5.6502939\times {10}^{-4}$	$3.9930249\times {10}^{-4}$	1.3852	0.1445	$1.631\times {10}^{-2}$
0.2	0.0535205	$1.5203652\times {10}^{-5}$	$1.1297643\times {10}^{-5}$	0.8343	0.0869	$8.821\times {10}^{-3}$
0.3	0.0069395	$2.4644146\times {10}^{-4}$	$7.4674617\times {10}^{-6}$	0.6340	0.0645	$6.560\times {10}^{-3}$
0.4	0.0015191	$2.5093960\times {10}^{-4}$	$5.7029333\times {10}^{-6}$	0.5540	0.0542	$5.966\times {10}^{-3}$
0.5	0.0030382	$2.2111907\times {10}^{-4}$	$7.4674617\times {10}^{-6}$	0.5256	0.0507	$5.850\times {10}^{-3}$
0.6	0.0068312	$5.6227131\times {10}^{-5}$	$6.6374241\times {10}^{-6}$	0.5455	0.0539	$6.123\times {10}^{-3}$
0.7	0.0016227	$4.3797139\times {10}^{-5}$	$6.4720234\times {10}^{-6}$	0.6029	0.0648	$7.123\times {10}^{-3}$
0.8	$8.3356403\times {10}^{-4}$	$4.0891921\times {10}^{-4}$	$5.3830217\times {10}^{-6}$	0.9311	0.0933	$1.003\times {10}^{-2}$
0.9	0.0010245	$3.9911678\times {10}^{-4}$	$3.5354251\times {10}^{-6}$	1.8509	0.1870	$1.947\times {10}^{-2}$

Table 5. The values of RMS(f), RES(f),  $RMS(g_0)$, $RES(g_0)$, RMS(h) and RES(h) with different choose of n and m when $\mathit{\sigma }=1\%$ and $s_1=s_2=s_3=6$ for Example 2.

$n_1$	4	5	6	7	10
$n_2$	4	5	6	7	10
$n_3$	4	5	6	7	10
m	0	0	0	0	0
RMS(f)	0.5653877	0.5236957	1.4769239	0.4444294	0.0122931
RES(f)	0.1243311	0.1151629	0.3247817	0.0977319	0.0027033
$RMS(g_0)$	0.1454090	0.1373134	0.2101423	0.2589738	0.0120869
$RES(g_0)$	0.1304997	0.1232342	0.1885958	0.2324204	0.0108476
RMS(h)	0.4290696	0.4016710	0.8378655	0.4415788	0.0176552
RES(h)	Inf	Inf	Inf	Inf	Inf
m	5	5	5	5	5
RMS(f)	0.0013772	0.0065025	0.9937791	0.0916205	0.0169339
RES(f)	$3.0284532\times {10}^{-5}$	0.0014299	0.2185362	0.0201477	0.0037238
$RMS(g_0)$	0.0056976	0.0054787	0.2153635	0.0423792	0.0048539
$RES(g_0)$	0.0051134	0.0049170	0.1932816	0.0380339	0.0043562
RMS(h)	$5.3510792\times {10}^{-4}$	0.0048394	0.7070144	0.0462939	0.0055545
RES(h)	Inf	Inf	Inf	Inf	Inf
m	10	10	10	10	10
RMS(f)	0.0012349	0.0013419	0.8455426	0.2068440	0.0041247
RES(f)	$2.7156682\times {10}^{-4}$	$2.9509986\times {10}^{-4}$	0.1859383	0.0454859	$9.0703566\times {10}^{-4}$
$RMS(g_0)$	0.0057432	0.0056993	0.2217135	0.0787748	0.0071372
$RES(g_0)$	0.0051543	0.0051149	0.1989805	0.0706977	0.0064054
RMS(h)	$3.3999927\times {10}^{-5}$	$4.8030741\times {10}^{-4}$	0.6530542	0.1691280	0.0050551
RES(h)	Inf	Inf	Inf	Inf	Inf

Table 6. The values of RMS(f), RES(f),  $RMS(g_0)$, $RES(g_0)$, RMS(h) and RES(h) with different choose of $s_1,s_2,s_3$ when $\mathit{\sigma }=1\%,m=10$ and $n_1=n_2=n_3=4$ for Example 2.

$s_1$	4	5	8	10	12	15
$s_2$	4	5	8	10	12	15
$s_3$	4	5	8	10	12	15
RMS(f)	1.1994413	0.0011669	0.0065513	0.0058406	0.0021611	0.0066031
RES(f)	0.2637621	$2.5661022\times {10}^{-4}$	0.0014407	0.0012844	$4.7523476\times {10}^{-4}$	0.0014521
$RMS(g_0)$	0.2502911	0.0056858	0.0053042	0.0052823	0.0054196	0.0062030
$RES(g_0)$	0.2246280	0.0051028	0.0047604	0.0047407	0.0048639	0.0055670
RMS(h)	0.8555651	$4.7487152\times {10}^{-5}$	0.0049015	0.0043500	0.0013703	0.0050395
RES(h)	Inf	Inf	Inf	Inf	Inf	Inf

Table 7. The values of RES(f) for various values of $\mathit{\sigma }$ and $x^{\ast }$ when $n_1=n_2=n_3=4,s_1=s_2=s_3=5,m=10$ and $T_0=1.5$ for Example 2.

$x^{\ast }$	$\mathit{\sigma }=10\%$	$\mathit{\sigma }=1\%$	$\mathit{\sigma }=0.1\%$	$\mathit{\sigma }=0.01\%$
0.1	0.0053800	$3.0558216\times {10}^{-4}$	$2.5224462\times {10}^{-4}$	$2.5183178\times {10}^{-4}$
0.2	$3.5759946\times {10}^{-4}$	$2.5873937\times {10}^{-4}$	$2.5187456\times {10}^{-4}$	$2.5183224\times {10}^{-4}$
0.3	0.0059561	$2.5704555\times {10}^{-4}$	$2.5189546\times {10}^{-4}$	$2.5183227\times {10}^{-4}$
0.4	0.0034747	$2.5668941\times {10}^{-4}$	$2.5189138\times {10}^{-4}$	$2.5183227\times {10}^{-4}$
0.5	$7.9545926\times {10}^{-4}$	$2.5661022\times {10}^{-4}$	$2.5188664\times {10}^{-4}$	$2.5183227\times {10}^{-4}$
0.6	$9.4023044\times {10}^{-4}$	$2.5668996\times {10}^{-4}$	$2.5188448\times {10}^{-4}$	$2.5183224\times {10}^{-4}$
0.7	0.0013511	$2.5682483\times {10}^{-4}$	$2.5188469\times {10}^{-4}$	$2.5183227\times {10}^{-4}$
0.8	0.0011087	$2.5699136\times {10}^{-4}$	$2.5188451\times {10}^{-4}$	$2.5183227\times {10}^{-4}$
0.9	$4.9337547\times {10}^{-4}$	$2.5718092\times {10}^{-4}$	$2.5188690\times {10}^{-4}$	$2.5183221\times {10}^{-4}$

In the following Theorems, we obtain error for the approximation functions $f(t),g_0(t)$ and h(t) in Equations (19(19) $$\begin{array}{c}\hfill f(t)=g_1^{\prime }(t)-c^{2}W(1,t).\end{array}$$(19) )–(23(23) $$\begin{array}{cc}\hfill h(0)& ={\mathit{\varphi }}_0^{\prime }(0).\hfill \end{array}$$(23) ).

Theorem 4:

Suppose that $f(t)-g_1^{\prime }(t)\in H^{\mathit{\nu }}(0,1)$ with $\mathit{\nu }\ge 0$ and $P_N{W}_1={\sum }_{s=0}^{{(n+m)}^2-1}{\mathit{\mu }}_s{b}_s(1,t)$ be the best approximation of W(1, t) then$$\Vert f(t)-g_1^{\prime }(t)+c^2{W(1,t)\Vert }_{L^2(0,1)}\le a{({(n+m)}^2-1)}^{-\mathit{\nu }}{|f-g_1^{\prime }|}_{H^{\mathit{\nu };N}(0,1)},$$

and for $1\le r\le \mathit{\nu }$,$$\Vert f(t)-g_1^{\prime }(t)+c^2{W(1,t)\Vert }_{H^r(0,1)}\le a{({(n+m)}^2-1)}^{2r-\frac{1}{2}-\mathit{\nu }}{|f-g_1^{\prime }|}_{H^{\mathit{\nu };N}(0,1)},$$

where a depends on $\mathit{\nu }$.

Proof Consider $P_N{W}_1={\sum }_{s=0}^{{(n+m)}^2-1}{\mathit{\mu }}_s{b}_s(1,t)$ be the best approximation of W(1, t) then ${\tilde{P}}_N{W}_1={\sum }_{s=0}^{{(n+m)}^2-1}(-c^2{\mathit{\mu }}_s)b_s(1,t)={\sum }_{s=0}^{{(n+m)}^2-1}{\tilde{\mathit{\mu }}}_s{b}_s(1,t)$ where ${\tilde{\mathit{\mu }}}_s=-c^2{\mathit{\mu }}_s$, is the best approximation of $-c^{2}W(1,t)$. Now by using Equations (19(19) $$\begin{array}{c}\hfill f(t)=g_1^{\prime }(t)-c^{2}W(1,t).\end{array}$$(19) ) and (52(52) $$\begin{array}{c}\hfill \Vert W_0-P_N{W}_0{\Vert }_{L^2(0,1)}\le c{N}^{-\mathit{\nu }}{|W_0|}_{H^{\mathit{\nu };N}(0,1)},\end{array}$$(52) ) we have:$$\Vert f(t)-g_1^{\prime }(t)-{\tilde{P}}_N{W}_1{\Vert }_{L^2(0,1)}\le a{({(n+m)}^2-1)}^{-\mathit{\nu }}{|f(t)-g_1^{\prime }(t)|}_{H^{\mathit{\nu };N}(0,1)},$$

and for $1\le r\le \mathit{\nu }$, using Equations (19(19) $$\begin{array}{c}\hfill f(t)=g_1^{\prime }(t)-c^{2}W(1,t).\end{array}$$(19) ) and (53(53) $$\begin{array}{c}\hfill \Vert W_0-P_N{W}_0{\Vert }_{H^r(0,1)}\le c{N}^{2r-\frac{1}{2}-\mathit{\nu }}{|W_0|}_{H^{\mathit{\nu };N}(0,1)},\end{array}$$(53) ) we obtain:$$\Vert f(t)-g_1^{\prime }(t)-{\tilde{P}}_N{W}_1{\Vert }_{H^r(0,1)}\le a{({(n+m)}^2-1)}^{2r-\frac{1}{2}-\mathit{\nu }}{|f(t)-g_1^{\prime }(t)|}_{H^{\mathit{\nu };N}(0,1)}.$$

Theorem 5:

Suppose that $g_0(t)-{\mathit{\varphi }}_0(0)-g_1(t)+g_1(0)\in H^{\mathit{\nu }}(0,1)$ with $\mathit{\nu }\ge 0$ and ${\int }_0^t{b}_s(x,\mathit{\tau })\mathrm{d}\mathit{\tau }=B_s(x,t)$ and ${\tilde{P}}_N{W}_0={\sum }_{s=0}^{{(n+m)}^2-1}{\tilde{\mathit{\mu }}}_s{B}_s(0,t)$ and ${\tilde{P}}_N{W}_1={\sum }_{s=0}^{{(n+m)}^2-1}{\tilde{\mathit{\mu }}}_s{B}_s(1,t)$, where $\widetilde{{\mathit{\mu }}_s}=c^2{\mathit{\mu }}_s$, be the best approximations of $c^2{\int }_0^{t}W(0,\mathit{\tau })$ and $c^2{\int }_0^{t}W(1,\mathit{\tau })$, respectively. Then$$\begin{array}{cc}& \Vert g_0(t)-{\mathit{\varphi }}_0(0)-g_1(t)+g_1(0)-{\tilde{P}}_N{W}_0+{\tilde{P}}_N{W}_1{\Vert }_{L^2(0,1)}\hfill \\ \hfill & \le a{({(n+m)}^2-1)}^{-\mathit{\nu }}{|g_0(t)-{\mathit{\varphi }}_0(0)-g_1(t)+g_1(0)|}_{H^{\mathit{\nu };N}(0,1)},\hfill \end{array}$$

and for $1\le r\le \mathit{\nu }$,$$\begin{array}{cc}& \Vert g_0(t)-{\mathit{\varphi }}_0(0)-g_1(t)+g_1(0)-{\tilde{P}}_N{W}_0+{\tilde{P}}_N{W}_1{\Vert }_{H^r(0,1)}\hfill \\ \hfill & \le a{({(n+m)}^2-1)}^{2r-\frac{1}{2}-\mathit{\nu }}{|g_0(t)-{\mathit{\varphi }}_0(0)-g_1(t)+g_1(0)|}_{H^{\mathit{\nu };N}(0,1)},\hfill \end{array}$$

where a depends on $\mathit{\nu }$.

Proof From Equations (19(19) $$\begin{array}{c}\hfill f(t)=g_1^{\prime }(t)-c^{2}W(1,t).\end{array}$$(19) )–(21(21) $$\begin{array}{cc}\hfill g_0(0)& ={\mathit{\varphi }}_0(0).\hfill \end{array}$$(21) ) and by integrating of (20) we get:(57) $$\begin{array}{c}\hfill g_0(t)={\mathit{\varphi }}_0(0)+g_1(t)-g_1(0)+c^2{\int }_0^{t}W(0,\mathit{\tau })\mathrm{d}\mathit{\tau }-c^2{\int }_0^{t}W(1,\mathit{\tau })\mathrm{d}\mathit{\tau }.\end{array}$$(57)

Suppose that ${\tilde{P}}_N{W}_0={\sum }_{s=0}^{{(n+m)}^2-1}{\tilde{\mathit{\mu }}}_s{B}_s(0,t)$ and ${\tilde{P}}_N{W}_1={\sum }_{s=0}^{{(n+m)}^2-1}{\tilde{\mathit{\mu }}}_s{B}_s(1,t)$ be the best approximations of $c^2{\int }_0^{t}W(0,\mathit{\tau })\mathrm{d}\mathit{\tau }$ and $c^2{\int }_0^{t}W(1,\mathit{\tau })\mathrm{d}\mathit{\tau }$, respectively, therefore(58) $$\begin{array}{cc}& g_0(t)-{\mathit{\varphi }}_0(0)-g_1(t)+g_1(0)-{\tilde{P}}_N{W}_0+{\tilde{P}}_N{W}_1=g_0(t)-{\mathit{\varphi }}_0(0)-g_1(t)+g_1(0)\hfill \\ \hfill & -\sum _{s=0}^{{(n+m)}^2-1}{\tilde{\mathit{\mu }}}_s(B_s(0,t)-B_s(1,t))=g_0(t)-{\mathit{\varphi }}_0(0)-g_1(t)+g_1(0)-\sum _{s=0}^{{(n+m)}^2-1}{\tilde{\mathit{\mu }}}_s\tilde{B}(t),\hfill \end{array}$$(58)

where $\tilde{B}(t)=B_s(0,t)-B_s(1,t)$. Then using Equations (52(52) $$\begin{array}{c}\hfill \Vert W_0-P_N{W}_0{\Vert }_{L^2(0,1)}\le c{N}^{-\mathit{\nu }}{|W_0|}_{H^{\mathit{\nu };N}(0,1)},\end{array}$$(52) ) and (58(58) $$\begin{array}{cc}& g_0(t)-{\mathit{\varphi }}_0(0)-g_1(t)+g_1(0)-{\tilde{P}}_N{W}_0+{\tilde{P}}_N{W}_1=g_0(t)-{\mathit{\varphi }}_0(0)-g_1(t)+g_1(0)\hfill \\ \hfill & -\sum _{s=0}^{{(n+m)}^2-1}{\tilde{\mathit{\mu }}}_s(B_s(0,t)-B_s(1,t))=g_0(t)-{\mathit{\varphi }}_0(0)-g_1(t)+g_1(0)-\sum _{s=0}^{{(n+m)}^2-1}{\tilde{\mathit{\mu }}}_s\tilde{B}(t),\hfill \end{array}$$(58) ), we have:$$\begin{array}{cc}& \Vert g_0(t)-{\mathit{\varphi }}_0(0)-g_1(t)+g_1(0)-{\tilde{P}}_N{W}_0+{\tilde{P}}_N{W}_1{\Vert }_{L^2(0,1)}\hfill \\ \hfill & \le a{({(n+m)}^2-1)}^{-\mathit{\nu }}{|g_0(t)-{\mathit{\varphi }}_0(0)-g_1(t)+g_1(0)|}_{H^{\mathit{\nu };N}(0,1)},\hfill \end{array}$$

and for $1\le r\le \mathit{\nu }$, using Equations (53(53) $$\begin{array}{c}\hfill \Vert W_0-P_N{W}_0{\Vert }_{H^r(0,1)}\le c{N}^{2r-\frac{1}{2}-\mathit{\nu }}{|W_0|}_{H^{\mathit{\nu };N}(0,1)},\end{array}$$(53) ) and (58(58) $$\begin{array}{cc}& g_0(t)-{\mathit{\varphi }}_0(0)-g_1(t)+g_1(0)-{\tilde{P}}_N{W}_0+{\tilde{P}}_N{W}_1=g_0(t)-{\mathit{\varphi }}_0(0)-g_1(t)+g_1(0)\hfill \\ \hfill & -\sum _{s=0}^{{(n+m)}^2-1}{\tilde{\mathit{\mu }}}_s(B_s(0,t)-B_s(1,t))=g_0(t)-{\mathit{\varphi }}_0(0)-g_1(t)+g_1(0)-\sum _{s=0}^{{(n+m)}^2-1}{\tilde{\mathit{\mu }}}_s\tilde{B}(t),\hfill \end{array}$$(58) ), we obtain:$$\begin{array}{cc}& \Vert g_0(t)-{\mathit{\varphi }}_0(0)-g_1(t)+g_1(0)-{\tilde{P}}_N{W}_0+{\tilde{P}}_N{W}_1{\Vert }_{H^r(0,1)}\hfill \\ \hfill & \le a{({(n+m)}^2-1)}^{2r-\frac{1}{2}-\mathit{\nu }}{|g_0(t)-{\mathit{\varphi }}_0(0)-g_1(t)+g_1(0)|}_{H^{\mathit{\nu };N}(0,1)}.\hfill \end{array}$$

Theorem 6:

Suppose that $h(t)-{\mathit{\varphi }}_0^{\prime }(0)\in H^{\mathit{\nu }}(0,1)$ with $\mathit{\nu }\ge 0$ and ${\tilde{P}}_N{W}_0={\sum }_{s=0}^{{(n+m)}^2-1}{\tilde{\mathit{\mu }}}_s{R}_s(0,t)$, where $\widetilde{{\mathit{\mu }}_s}=c^2{\mathit{\mu }}_s$ and $R_s(0,t)={\int }_0^t\frac{\mathit{\partial }}{\mathit{\partial }x}{b}_s(0,\mathit{\tau })\mathrm{d}\mathit{\tau }$, be the best approximation of $c^2{\int }_0^t{W}_x(0,\mathit{\tau })\mathrm{d}\mathit{\tau }$ then$$\Vert h(t)-{\mathit{\varphi }}_0^{\prime }(0)-{\tilde{P}}_N{W}_0{\Vert }_{L^2(0,1)}\le a{({(n+m)}^2-1)}^{-\mathit{\nu }}{|h(t)-{\mathit{\varphi }}_0^{\prime }(0)|}_{H^{\mathit{\nu };N}(0,1)},$$

and for $1\le r\le \mathit{\nu }$,$$\Vert h(t)-{\mathit{\varphi }}_0^{\prime }(0)-{\tilde{P}}_N{W}_0{\Vert }_{H^r(0,1)}\le a{({(n+m)}^2-1)}^{2r-\frac{1}{2}-\mathit{\nu }}{|h(t)-{\mathit{\varphi }}_0^{\prime }(0)|}_{H^{\mathit{\nu };N}(0,1)},$$

where a depends on $\mathit{\nu }$.

Proof From Equations (22(22) $$\begin{array}{cc}\hfill h^{\prime }(t)& =c^2{W}_x(0,t);0<t<T,\hfill \end{array}$$(22) )–(23(23) $$\begin{array}{cc}\hfill h(0)& ={\mathit{\varphi }}_0^{\prime }(0).\hfill \end{array}$$(23) ) and by integrating of (22) we get:(59) $$\begin{array}{c}\hfill h(t)-{\mathit{\varphi }}_0^{\prime }(0)=c^2{\int }_0^t{W}_x(0,\mathit{\tau })\mathrm{d}\mathit{\tau }.\end{array}$$(59)

Suppose ${\tilde{P}}_N{W}_0={\sum }_{s=0}^{{(n+m)}^2-1}{\tilde{\mathit{\mu }}}_s{R}_s(0,t)$ be the best approximation of $c^2{\int }_0^t{W}_x(0,\mathit{\tau })\mathrm{d}\mathit{\tau }$ then using Equations (52(52) $$\begin{array}{c}\hfill \Vert W_0-P_N{W}_0{\Vert }_{L^2(0,1)}\le c{N}^{-\mathit{\nu }}{|W_0|}_{H^{\mathit{\nu };N}(0,1)},\end{array}$$(52) ) and (59(59) $$\begin{array}{c}\hfill h(t)-{\mathit{\varphi }}_0^{\prime }(0)=c^2{\int }_0^t{W}_x(0,\mathit{\tau })\mathrm{d}\mathit{\tau }.\end{array}$$(59) ) we have:$$\Vert h(t)-{\mathit{\varphi }}_0^{\prime }(0)-{\tilde{P}}_N{W}_0{\Vert }_{L^2(0,1)}\le a{({(n+m)}^2-1)}^{-\mathit{\nu }}{|h(t)-{\mathit{\varphi }}_0^{\prime }(0)|}_{H^{\mathit{\nu };N}(0,1)}.$$

Also for $1\le r\le \mathit{\nu }$, by using Equations (53(53) $$\begin{array}{c}\hfill \Vert W_0-P_N{W}_0{\Vert }_{H^r(0,1)}\le c{N}^{2r-\frac{1}{2}-\mathit{\nu }}{|W_0|}_{H^{\mathit{\nu };N}(0,1)},\end{array}$$(53) ) and (59(59) $$\begin{array}{c}\hfill h(t)-{\mathit{\varphi }}_0^{\prime }(0)=c^2{\int }_0^t{W}_x(0,\mathit{\tau })\mathrm{d}\mathit{\tau }.\end{array}$$(59) ), we obtain:$$\Vert h(t)-{\mathit{\varphi }}_0^{\prime }(0)-{\tilde{P}}_N{W}_0{\Vert }_{H^r(0,1)}\le a{({(n+m)}^2-1)}^{2r-\frac{1}{2}-\mathit{\nu }}{|h(t)-{\mathit{\varphi }}_0^{\prime }(0)|}_{H^{\mathit{\nu };N}(0,1)}.$$

6. Numerical examples

The inverse problems investigated in this study have been solved using a uniform distribution of the source and collocation points as $\mathbf{y}={\mathbf{x}}_l=\{(x_i,0)=(\frac{i-1}{n_1-1},0),i=1,\dots ,n_1\}\cup \{(0,t_j)=(0,\frac{j}{n_2}),j=1,\dots ,n_2\}\cup \{(1,t_k)=(1,\frac{k}{n_3}),k=1,\dots ,n_3\}$ where $n=n_1+n_2+n_3$. As always with inverse and improperly posed problems, behaviour of the numerical solution in the process of noise is an important part of the stability testing process [76]. Thus, we consider some of the supplemented boundary conditions contaminated with errors. For more clarifications, in the numerical calculations we apply the noisy data$$\begin{array}{cc}\hfill {\mathit{\varphi }}_{0_{no}}(x_e)& ={\mathit{\varphi }}_0(x_e)+\mathit{\sigma }.rand(1),\hfill \\ \hfill g_{1_{no}}(t_d)& =g_1(t_d)+\mathit{\sigma }.rand(1),\hfill \\ \hfill k_{no}(t_d)& =k(t_d)+\mathit{\sigma }.rand(1),\hfill \\ \hfill {\mathit{\varphi }}_{T_{no}}(x_z)& ={\mathit{\varphi }}_T(x_z)+\mathit{\sigma }.rand(1),\hfill \end{array}$$

where ${\mathit{\varphi }}_0(x_e),g_1(t_d),k(t_d)$ and ${\mathit{\varphi }}_T(x_z)$ are the exact data and rand(1) is a random number between (0, 1) and the magnitude $\mathit{\sigma }$ indicates the noise level of measurement data.

To obtain the stable numerical derivatives ${\mathit{\varphi }}_{0_{no}}^{″}(x_e),g_{1_{no}}^{\prime }(t_d),k_{no}^{\prime }(t_d)$ and ${\mathit{\varphi }}_{T_{no}}^{″}(x_z),$ we use the regularized RBF methods in [77,78] to compute them and then the corresponding noisy right-hand side is denoted by ${\mathbf{g}}_{no}.$ According to Theorem 2.2 in [78], we consider ${\mathit{\varphi }}_{0_{no}}(x),g_{1_{no}}(t),k_{no}(t)$ and ${\mathit{\varphi }}_{T_{no}}(x)$, separately, to be a linear combination of the Gaussians function $\mathit{\phi }(\mathit{\chi })=e^{-c_1{|\mathit{\chi }|}^2}$ and polynomials $\{1,\mathit{\chi },{\mathit{\chi }}^2,\dots ,{\mathit{\chi }}^{m_1}\}.$ In two following examples, we take $c_1=0.1$. 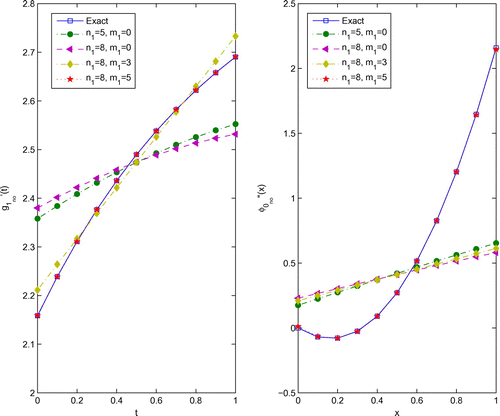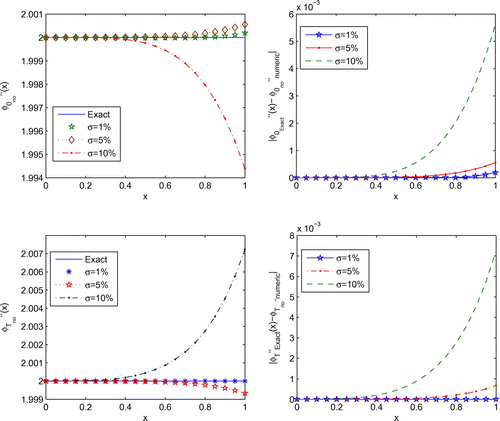Figure 1 presents the values of $g_{1_{no}}^{\prime }$ and ${\mathit{\varphi }}_{0_{no}}^{″}$ with various values of polynomials $(m_1)$ and scattered points $(n_1)$ for Example 1. From this figure the numerical results with increasing $m_1$ and $n_1$ have become better. In Figures 2 and 3 the values of $g_{1_{no}}^{\prime }$ and $k_{no}^{\prime }$ and absolute errors $|g_{1_{Exact}}^{\prime }-g_{1_{{no}_{Numeric}}}^{\prime }|$ and $|k_{Exact}^{\prime }-k_{{no}_{Numeric}}^{\prime }|$ for various values of $\mathit{\sigma }$ are given. Also, the values of ${\mathit{\varphi }}_{0_{no}}^{″}$ and ${\mathit{\varphi }}_{T_{no}}^{″}$ and absolute errors $|{\mathit{\varphi }}_{0_{Exact}}^{″}-{\mathit{\varphi }}_{0_{{no}_{Numeric}}}^{″}|$ and $|{\mathit{\varphi }}_{T_{Exact}}^{″}-{\mathit{\varphi }}_{T_{{no}_{Numeric}}}^{″}|$ are shown in Figures 4 and 5. We take $m_1=10$ and $n_1=12$ in Figures 2–5. It can be seen from these figures that the stable numerical derivatives ${\mathit{\varphi }}_{0_{no}}^{″}(x_e),g_{1_{no}}^{\prime }(t_d),k_{no}^{\prime }(t_d)$ and ${\mathit{\varphi }}_{T_{no}}^{″}(x_z),$ are obtained.

In all following examples we set the scattered nods as $x_e=\frac{e-1}{s_1-1},t_d=\frac{d-s_1}{s_2}$ and $x_z=\frac{z-s_1-s_2}{s_3}$, where $e=1,2,\dots ,s_1$, $d=s_1+1,\dots ,s_1+s_2$, $z=s_1+s_2+1,\dots ,s_1+s_2+s_3.$

To test the accuracy of the approximate solution, we use the root mean square error (RMS) and the relative root mean square error (RES) defined as follows:$$RMS(f)=\sqrt{\frac{1}{n_k}\sum _{i=1}^{n_k}{(f_i^{Exa.}-f_i^{Num.})}^2},$$$$RES(f)=\frac{\sqrt{\sum _{i=1}^{n_k}{(f_i^{Exa.}-f_i^{Num.})}^2}}{\sqrt{\sum _{i=1}^{n_k}{f_i^{Exa.}}^2}},$$

where $n_k$ is total number of testing points in the domain $[0,1]\times [0,T],$$f_i^{Exa.}$ and $f_i^{Num.}$ are the exact and approximate values at this point, respectively.

Example 1:

Consider the problem (1)–(6) with $x^{\ast }=0.5$ and with the following initial, boundary and overspecified conditions [23]:$$\begin{array}{cc}\hfill {\mathit{\varphi }}_0(x)& =sin(x)+0.250x^4,{\mathit{\varphi }}_T(x)=0.3678795sin(x)+3x^2+0.250x^4,\hfill \\ \hfill g_1(t)& =0.8414710e^{-t}+3t+0.250,k(t)=0.47942554e^{-t}+0.7500t+0.0156250.\hfill \end{array}$$

The exact solution of this problem is:$$\begin{array}{cc}\hfill U(x,t)& =e^{-t}sin(x)+3t{x}^2+0.250x^4,f(t)=-6t,\hfill \\ \hfill g_0(t)& =0,h(t)=e^{-t}.\hfill \end{array}$$

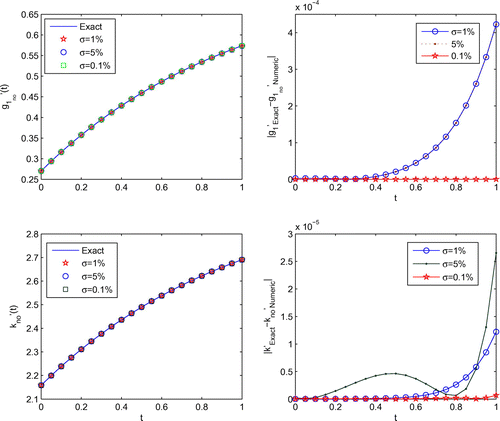
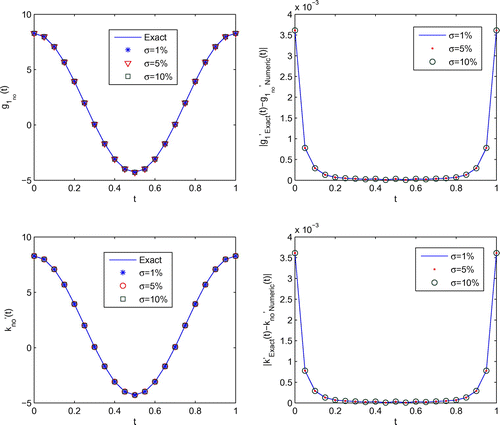
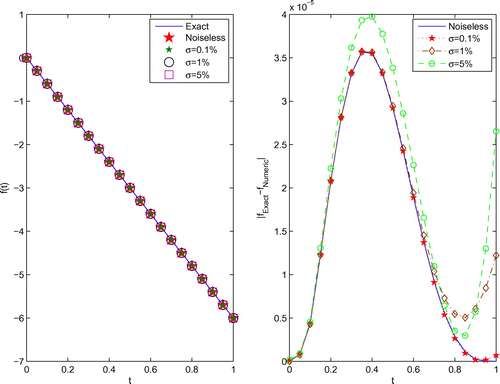
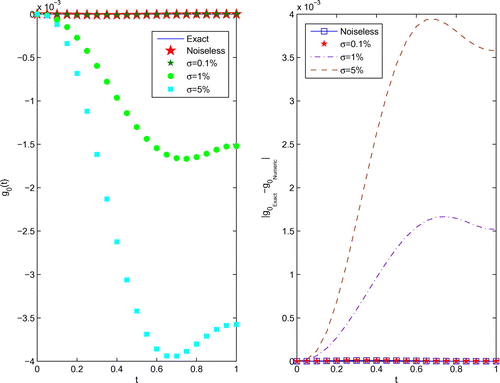
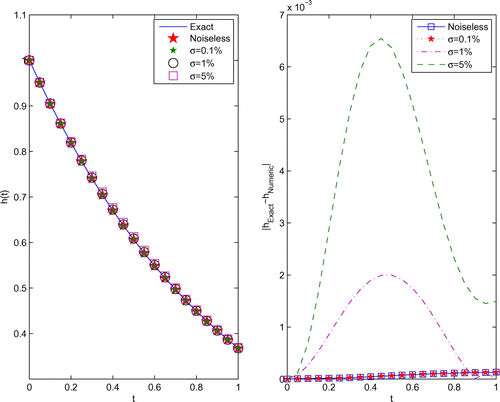
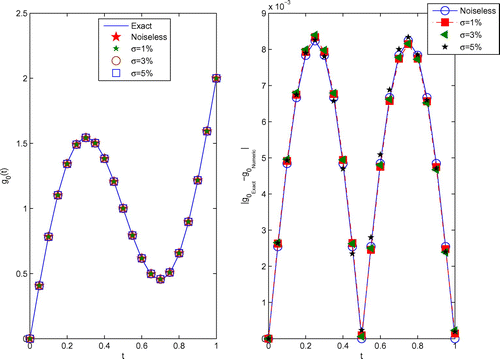
The numerical results for the heat source with various relative noise levels $\mathit{\sigma }=0.1,1,5\%$ are illustrated in Figure 6, and the corresponding boundary temperature and boundary heat flux are presented in Figures 7 and 8, respectively. Compared Figure 6 with Figure 2 in [23], the results by our method are more accurate.

The error distribution for the numerical heat source, boundary temperature and boundary heat flux obtained for using various amounts of noise added into the data, are also presented in Figures 6–8. It can be seen from these Figures that the numerical results retrieved for the heat source, boundary temperature and boundary heat flux represent good approximations for their analytical values. Furthermore, the numerical heat source, boundary temperature and boundary heat flux converge towards their corresponding exact solutions as the amount of noise decreases.

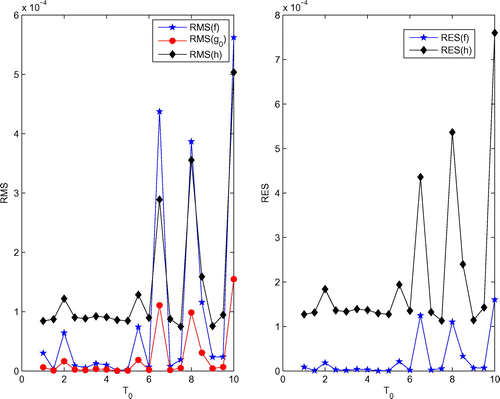
To show the influence of the parameters $T_0$, we compute the RMS and RES for the heat source, boundary temperature and boundary heat flux with various $T_0\in [1.01,10]$ for noiseless data, $s_1=s_2=s_3=5$ and $n_1=n_2=n_3=4$, and the numerical results are shown in Figure 9. It can be seen from this figure that the accuracy of the numerical results is relatively independent of the parameter $T_0$ if $T_0<6$. The insensitivity of the solutions to $T_0$ over fairly large ranges of the parameters is a favourable feature of MMFS because there is no need to search for optimal values of parameters.

To see the effectiveness of the collocation points and the source points, we present the RMS and RES for the heat source, boundary temperature and boundary heat flux with varying the numbers of collocation and source points for a fixed noise level $\mathit{\sigma }=1\%$ in Tables 1 and 2. It can be seen from Table 1 that the numerical errors for the heat source, boundary temperature and boundary heat flux mainly depend on the number $n_1,n_2$ and $n_3$ for a fixed $s_1=s_2=s_3=6$. In Table 2, setting $n_1=n_2=n_3=4$ and varying $s_1,s_2,s_3$, we note that the numerical errors for the heat source, boundary temperature and boundary heat flux are almost constants.

Also in Table 1, we give the RMS and RES for the heat source, boundary temperature and boundary heat flux to show the advantage of adding the heat polynomials in Equation (31(31) $$\begin{array}{c}\hfill v(\mathbf{x})=\sum _{i=1}^n{\mathit{\lambda }}_i{\mathit{\psi }}_i(\mathbf{x})+\sum _{j=1}^m{\mathit{\xi }}_j{p}_j(\mathbf{x}),\end{array}$$(31) ) by choosing the various values of m. From this table, we see that the new method combined with the heat polynomials is more accurate than the pure MFS and adding some heat polynomials make the results more precise.

Next, we analyse the accuracy of the numerical method proposed with respect to the parameter $x^{\ast }$. To do that, we set $T_0=2.1$ for Example 1. Table 4 illustrate the errors RES(f) with various relative noise levels $\mathit{\sigma }=10,1,0.1\%$. From this Table we will see that the numerical errors almost keep a stable level.

To compare our method with MFS [23], the error of RMS and RES for the heat source with $\mathit{\sigma }=5\%$ and various values of $T_0$ are tabulated in Table 3. Also, the error of RES for the heat source with various relative noise level are illustrated in Table 4. It can be observed from Tables 3 and 4 that the numerical errors calculated from our method are more less than MFS [23].

Example 2:

Let us consider the problem (1)–(6) with $x^{\ast }=0.5$ and with the following initial, boundary and overspecified conditions [23]:$$\begin{array}{cc}\hfill {\mathit{\varphi }}_0(x)& =x^2,{\mathit{\varphi }}_T(x)=x^2+2,\hfill \\ \hfill g_1(t)& =1+2t+sin(2\mathit{\pi }t),k(t)=0.25+2t+sin(2\mathit{\pi }t).\hfill \end{array}$$

The exact solution of this problem is:$$\begin{array}{cc}\hfill U(x,t)& =x^2+2t+sin(2\mathit{\pi }t),f(t)=2\mathit{\pi }cos(2\mathit{\pi }t),\hfill \\ \hfill g_0(t)& =2t+sin(2\mathit{\pi }t),h(t)=0.\hfill \end{array}$$

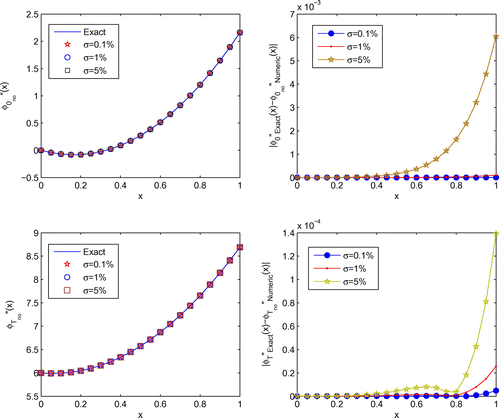
The exact and numerical results for the heat source, boundary temperature, boundary heat flux and their corresponding error distributions obtained with $\mathit{\sigma }=1,3,5\%$ noises added into the data are shown in Figures 10–12, respectively, It can be seen from these Figures that the numerical results are in good agreement with their corresponding exact solutions. Comparing with the results presented in Figure 9 of [23], we conclude that our MMFS approximation are more accurate and stable than that the results in [23].

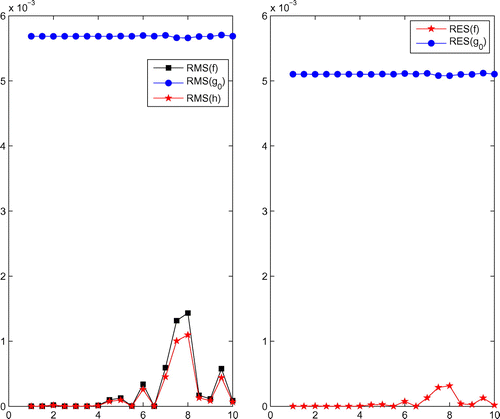
The RMS and RES for the heat source, boundary temperature and boundary heat flux for different values of $T_0\in [1.01,10]$, $s_1=s_2=s_3=5$ and $n_1=n_2=n_3=4$ with noiseless data are reported in Figure 13. It can be observed from this figure that the MMFS approximation provide stable numerical results for $T_0<6.5$.

The values of $RMS(f),RES(f),RMS(g_0),RES(g_0),RMS(h)$ and RES(h) for various values of source and collocation points are presented in Tables 5 and 6. From these Tables, the MMFS depend on the number n for $s_1=s_2=s_3=6$ and almost constants with increasing $s_1,s_2,s_3$ for a fixed $n_1=n_2=n_3=4$.

Also, in Table 5 some results for choosing various values of the heat polynomials in Equation (31(31) $$\begin{array}{c}\hfill v(\mathbf{x})=\sum _{i=1}^n{\mathit{\lambda }}_i{\mathit{\psi }}_i(\mathbf{x})+\sum _{j=1}^m{\mathit{\xi }}_j{p}_j(\mathbf{x}),\end{array}$$(31) ) are shown. From this table it can be seen that our method with some heat polynomials are more accurate than pure MFS.

To verify the relationship between the accuracy of solution and $x^{\ast }$, we compute the RES(f) with various $x^{\ast }$, $\mathit{\sigma }=10,1,0.1,0.01\%$ and $T_0=1.5$, and the numerical results are shown in Table 7. We can see that the numerical errors keep a stable level. Furthermore, the values of RES(f) decrease as the level of noise $\mathit{\sigma }$ added into the input data decrease.

7. Conclusion

In this paper, a meshless method has been developed for obtaining a stable numerical solution to the inverse heat conduction problem. The new approach does not require any domain discretization or any boundary discretization as in FDM and FEM and also is a free integration method. Comparing with the pure MFS in Section 6, we conclude that the proposed method are more accurate.

It should be mentioned that the method used in our paper may be generalized to higher dimensional problems. For instance, we may consider the inverse problem in two or three dimension. A similar approach can be used to the solution of an IHCP in an anisotropic medium [79] and to the solution a time-dependent two-dimensional Cauchy heat conduction problem [80]. One may consider this method to the solution one or two-phase Stefan problem [76]. Also, the main idea behind the new approach can be investigated to solve the partial differential equations studied in [12–15,77].

Although we have only considered Dirichlet boundary condition, there are also solvability theorems for the problem of finding a source for the parabolic heat equation with general boundary conditions [3]. The proposed method can be used for the determination of a single variable source for the heat conduction equation in another inverse formulation, with an integral over determination condition specifying the energy variation of the heat-conducting system [3,14].

Future work will be concerned with the numerical determination of a source $Q(x,t)=f(x)$ or $Q(x,t)=g(t)$ in the following reaction–diffusion–convection equation:(60) $$\begin{array}{c}\hfill u_t=\mathrm{\nabla }.(K\mathrm{\nabla }u)+(\overrightarrow{v}.\mathrm{\nabla })u+\mathit{\sigma }v+Q(x,t),\end{array}$$(60)

where K, v and $\mathit{\sigma }$ are constants. Other possible future work may also concern the numerical determination of a source of the type $Q(x,t)=f(x)+g(t)$ or $Q(x,t)=f(x)g(t).$

Acknowledgements

Authors are very grateful to reviewer for carefully reading the paper and for his/her comments and suggestions which have improved the paper.

Notes

No potential conflict of interest was reported by the authors.