Integral formulas for supersonic reconstruction of the acoustic field

Abstract

The supersonic acoustic intensity is a technique utilized to locate radiating sound regions on a complex vibrating structure. This technology is based on the accurate identification of the supersonic components (or stability regions) of the acoustic field. The identification of these supersonic components is well understood for separable geometries, but unfortunately, there are few results for arbitrarily shaped objects. This work proposes a methodology that efficiently identifies the supersonic components from acoustic pressure measurements. The methodology is based on the spectral decomposition of the power operator that yields a non-negative intensity expression. We will demonstrate using numerical data that the resultant non-negative intensity matches the supersonic intensity.

Keywords:

• Acoustics
• radiation
• supersonic intensity
• source identification

AMS Subject Classifications:

• 45A05
• 35J05

1. Introduction

1.1. Overview

In the structural acoustic study of a complex vibrating object, it is commonly assumed that the radiated sound mainly contains supersonic and subsonic components. The supersonic components are composed of non-evanescent waves that travel unchanged from the near-field into the far-field, and the subsonic components are composed of evanescent waves that decay exponentially but produce high resolution intensity images at the surface of the structure. The later components have little contribution to the far-field radiation because of their evanescent nature. The resultant intensity image from the supersonic components on the surface of the structure is generally only positive, representing outgoing power flow from the surface. Since negative intensity regions of a vibrator are removed, sources of radiation are readily located on the surface of the vibrator. For that reason, a detailed study of the acoustic radiation will mainly focus on the use of supersonic components and the resultant intensity from these components is known as supersonic intensity. The use of the supersonic intensity images allows the correct identification of radiation regions and quantification of the strength of these regions.

Supersonic intensity was introduced in 1995 (see [1]). This technique was the result of the study of radiation from submerged cylindrical shells and the need to locate the radiating regions on the surface of these shells. The theory was formulated for planar surfaces in [2] using the well-known k-space results from the Fourier Transform (FT). In the k-space, the supersonic components are located inside the circle of radius k and the subsonic components outside. The k-space filter limits the resolution of the intensity image to half wavelength of a given frequency. The k-space that results from the FT has been successfully translated to separable surfaces of the wave equation (planes, cylinders and spheres) but cannot be translated directly into arbitrarily shaped surfaces. For arbitrarily shaped surfaces the acoustic field is represented by the numerical discretization of surface integrals and we can expect that the singular value decomposition (SVD), as the FT, will provide an insight about the filtering of the subsonic components. Indeed, it was experimentally shown in [3] that the SVD share some characteristics with the k-space of planar surfaces. Despite the importance of this result, in practice it is highly difficult to develop an efficient numerical methodology that uses this separation methodology. We can find some interesting attempts of this filter methodology in the works of Magalhâes [4], Tenenbaum [5] and Correa [6]. A slight different approach using non-negative functions to approximate the intensity have been proposed [7,8].

Recently we proposed an efficient numerical methodology for the calculation of the supersonic intensity over arbitrarily shaped geometries [9]. This methodology is based on the spectral properties of the power operator and a rule designed to locate the supersonic radiation modes. Although proven to be effective, the rule used to identify supersonic modes was ad-hoc and still requires more theoretical justification. In this work we extend the results in [9] by providing some explicit integral formulations for the power operator and an expression to the supersonic intensity.

1.2. Integral representations of radiating waves

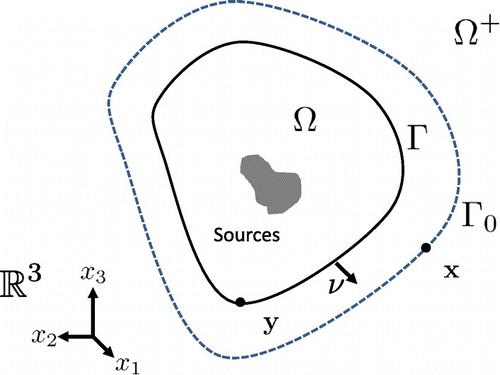
Assume that $\mathrm{\Omega }$ represents a complex vibrating structure, $\mathrm{\Gamma }$ its corresponding boundary and ${\mathrm{\Omega }}^{+}:={\mathbb{R}}^3\backslash \overline{\mathrm{\Omega }}$ is connected. Let ${\mathrm{\Omega }}_0$ be a bounded domain that contains $\overline{\mathrm{\Omega }}$ and let ${\mathrm{\Gamma }}_0$ be its corresponding boundary (see Figure 1). For a steady-state acoustic wave p with time dependence $e^{-i\mathit{\omega }t}$, where $\mathit{\omega }$ is the angular frequency, its radiating behaviour in an homogeneous medium is modelled by the Helmholtz equation(1) $$\begin{array}{cc}\hfill \mathrm{\Delta }p+k^{2}p& =0,in{\mathrm{\Omega }}^{+},\hfill \\ \hfill \underset{r\to \infty }{lim}r\left({\mathit{\partial }}_{r}p-ikp\right)& =0,r=|\mathbf{x}|,\widehat{\mathbf{x}}=\mathbf{x}/r,\hfill \end{array}$$(1)

where $\mathbf{x}=(x_1,x_2,x_3)$, $k=\mathit{\omega }/c$ is the wave number and c is the speed of sound in the medium. The radiating wave in (1(1) $$\begin{array}{cc}\hfill \mathrm{\Delta }p+k^{2}p& =0,in{\mathrm{\Omega }}^{+},\hfill \\ \hfill \underset{r\to \infty }{lim}r\left({\mathit{\partial }}_{r}p-ikp\right)& =0,r=|\mathbf{x}|,\widehat{\mathbf{x}}=\mathbf{x}/r,\hfill \end{array}$$(1) ) follows the far-field behaviour(2) $$\begin{array}{c}\hfill p(\mathbf{x})=\frac{e^{ikr}}{r}\left\{p_{\infty }(\widehat{\mathbf{x}})+O\left(\frac{1}{r}\right)\right\},r\to \infty ,\end{array}$$(2)

where $p_{\infty }$ is known as the far-field pattern of p.

Figure 1. Setup for exterior radiation problem.

For the radiation problems the Direct formulation represents the acoustic wave using the Helmholtz–Kirchhoff integral equation(3) $$\begin{array}{c}\hfill p(\mathbf{x})=\left(Kp\right)(\mathbf{x})-\left(S{\mathit{\partial }}_{\mathit{\nu }}p\right)(\mathbf{x}),\mathbf{x}\in {\mathrm{\Omega }}^{+},\end{array}$$(3)

where we follow the notation of [10], for the single and double layer operators S and K(4) $$\begin{array}{cc}\hfill \left(S\mathit{\phi }\right)(\mathbf{x})& :={\int }_{\mathrm{\Gamma }}\mathrm{\Phi }(\mathbf{x},\mathbf{y})\mathit{\phi }(\mathbf{y})\mathrm{d}S(\mathbf{y}),\hfill \\ \hfill \left(K\mathit{\phi }\right)(\mathbf{x})& :={\int }_{\mathrm{\Gamma }}\frac{\mathit{\partial }\mathrm{\Phi }(\mathbf{x},\mathbf{y})}{\mathit{\partial }\mathit{\nu }(\mathbf{y})}\mathit{\phi }(\mathbf{y})\mathrm{d}S(\mathbf{y}),\hfill \end{array}$$(4)

where(5) $$\begin{array}{c}\hfill \mathrm{\Phi }(\mathbf{x},\mathbf{y})=\frac{exp\left(ik|\mathbf{x}-\mathbf{y}|\right)}{4\mathit{\pi }|\mathbf{x}-\mathbf{y}|},\end{array}$$(5)

is the free space radiating fundamental solution to the Helmholtz equation. In (4(4) $$\begin{array}{cc}\hfill \left(S\mathit{\phi }\right)(\mathbf{x})& :={\int }_{\mathrm{\Gamma }}\mathrm{\Phi }(\mathbf{x},\mathbf{y})\mathit{\phi }(\mathbf{y})\mathrm{d}S(\mathbf{y}),\hfill \\ \hfill \left(K\mathit{\phi }\right)(\mathbf{x})& :={\int }_{\mathrm{\Gamma }}\frac{\mathit{\partial }\mathrm{\Phi }(\mathbf{x},\mathbf{y})}{\mathit{\partial }\mathit{\nu }(\mathbf{y})}\mathit{\phi }(\mathbf{y})\mathrm{d}S(\mathbf{y}),\hfill \end{array}$$(4) ), $\mathit{\nu }$ is the outward unit normal and the jump relations [10] when $\mathbf{x}\in \mathrm{\Gamma }$ yield(6) $$\begin{array}{cc}\hfill {\left(K^{\prime }\mathit{\phi }\right)}^{+}(\mathbf{x})& :={\int }_{\mathrm{\Gamma }}\frac{\mathit{\partial }\mathrm{\Phi }(\mathbf{x},\mathbf{y})}{\mathit{\partial }\mathit{\nu }(\mathbf{x})}\mathit{\phi }(\mathbf{y})\mathrm{d}S(\mathbf{y})-\frac{1}{2}\mathit{\phi }(\mathbf{x}).\hfill \end{array}$$(6)

The indirect formulations are based on representations to the solution of (1(1) $$\begin{array}{cc}\hfill \mathrm{\Delta }p+k^{2}p& =0,in{\mathrm{\Omega }}^{+},\hfill \\ \hfill \underset{r\to \infty }{lim}r\left({\mathit{\partial }}_{r}p-ikp\right)& =0,r=|\mathbf{x}|,\widehat{\mathbf{x}}=\mathbf{x}/r,\hfill \end{array}$$(1) ) like the single layer representation of p (see [11–13])(7) $$\begin{array}{c}\hfill p(\mathbf{x})=\left(S\mathit{\phi }\right)(\mathbf{x}),\mathbf{x}\in {\mathrm{\Omega }}^{+},\end{array}$$(7)

where $\mathit{\phi }$ is known as the source density.

1.3. Radiation theory

The classical structural acoustic theory (see [14,15]) assumes that the radiating sound pressure p results from the interaction between the structure vibration $V_n$ and the normal derivative of the acoustic pressure ${\mathit{\partial }}_{\mathit{\nu }}p$. This interaction is modelled by Euler’s equation(8) $$\begin{array}{c}\hfill V_n(\mathbf{x})=\frac{1}{i\mathit{\rho }\mathit{\omega }}{\mathit{\partial }}_{\mathit{\nu }}p(\mathbf{x}),\mathbf{x}\in \mathrm{\Gamma }.\end{array}$$(8)

where $\mathit{\rho }$ is the medium density. The acoustic pressure p is given in $N{m}^{-2}$ units and the normal velocity $V_n$ in $\text{m}{\text{s}}^{-1}$ units. Using (8(8) $$\begin{array}{c}\hfill V_n(\mathbf{x})=\frac{1}{i\mathit{\rho }\mathit{\omega }}{\mathit{\partial }}_{\mathit{\nu }}p(\mathbf{x}),\mathbf{x}\in \mathrm{\Gamma }.\end{array}$$(8) ), the total power that radiates from the surface $\mathrm{\Gamma }$, for the wave p, is given by(9) $$\begin{array}{c}\hfill \mathrm{\Pi }(\mathrm{\Gamma },p):=\frac{1}{2}Re{\int }_{\mathrm{\Gamma }}p(\mathbf{x})\overline{V_n(\mathbf{x})}\mathrm{d}S(\mathbf{x}).\end{array}$$(9)

By this definition we can understand the normal intensity as$$I(\mathbf{x}):=\frac{1}{2}Re\left\{p(\mathbf{x})\overline{V_n(\mathbf{x})}\right\},\mathbf{x}\in \mathrm{\Gamma },$$

as a power density quantification over the surface of the vibrating structure $\mathrm{\Gamma }$. The resultant units of power are $W$ and the intensity have $W{m}^{-2}$ units.

For the inverse problem of wave continuation [16] or Near-field Acoustical Holography (NAH) [17] there are acoustic sensors located over the surface ${\mathrm{\Gamma }}_0$ which (ideally) is close and conformal to the vibrating structure $\mathrm{\Gamma }$. For this inverse problem we want to reconstruct the complete acoustic field (pressure, velocity and intensity) at the surface $\mathrm{\Gamma }$ from the measurements at ${\mathrm{\Gamma }}_0$. The single layer representation of p, reduces NAH to the solution of the surface integral equation in (7(7) $$\begin{array}{c}\hfill p(\mathbf{x})=\left(S\mathit{\phi }\right)(\mathbf{x}),\mathbf{x}\in {\mathrm{\Omega }}^{+},\end{array}$$(7) ) for $\mathbf{x}\in {\mathrm{\Gamma }}_0$. Then the reconstructions of p and $V_n$ at $\mathrm{\Gamma }$ will be given by(10) $$\begin{array}{c}\hfill p(\mathbf{x})=\left(S\mathit{\phi }\right)(\mathbf{x}),V_n(\mathbf{x})=\frac{1}{i\mathit{\rho }\mathit{\omega }}{\left(K^{\prime }\mathit{\phi }\right)}^{+}(\mathbf{x}).\end{array}$$(10)

For the single layer representation (7(7) $$\begin{array}{c}\hfill p(\mathbf{x})=\left(S\mathit{\phi }\right)(\mathbf{x}),\mathbf{x}\in {\mathrm{\Omega }}^{+},\end{array}$$(7) ) of the acoustic wave p, the radiated power is given by(11) $$\begin{array}{c}\hfill {\mathrm{\Pi }}_k(\mathrm{\Gamma },\mathit{\phi })={\int }_{\mathrm{\Gamma }}\mathit{\phi }(\mathbf{x})\overline{\left(\left(P\mathit{\phi }\right)(\mathbf{x})\right)}\mathrm{d}S(\mathbf{x}),\end{array}$$(11)

where P is known as the power operator. From this representation, we have the explicit expression for the normal intensity(12) $$\begin{array}{c}\hfill I(\mathbf{x}):=\mathit{\phi }(\mathbf{x})\overline{\left(\left(P\mathit{\phi }\right)(\mathbf{x})\right)}.\end{array}$$(12)

The normal intensity shows the distribution of the acoustic energy at the radiating surface. A positive value of the intensity means energy leaving the surface $\mathrm{\Gamma }$ (in direction of the normal), while negative values means energy entering the structure (in opposite direction of the normal).

The NAH technique have been develop to reconstruct high resolution images (resolution higher than half the frequency wave-length), but for certain applications these images are not advantageous. In applications like early sound control (specially over realistic radiating structures), we need to identify radiation regions or regions were the sound radiate into the far-field. The identification of these region can be challenging since we encounter complex combinations of negative and positive intensity values (as seen in Figure 4). If we move away from the structure, the intensity values ‘short circuits’ and we only encounter positive values that correspond to the radiation region (see [14]). The normal intensity in the form of (12(12) $$\begin{array}{c}\hfill I(\mathbf{x}):=\mathit{\phi }(\mathbf{x})\overline{\left(\left(P\mathit{\phi }\right)(\mathbf{x})\right)}.\end{array}$$(12) ) can contain both positive and negative values, but as mentioned above it will be more advantageous to find a non-negative expression to the normal intensity that could potentially reveal the radiation regions. The main result of our work that results from Sections 2 and 3 will be the expression for the ‘supersonic’ intensity(13) $$\begin{array}{c}\hfill I^s(\mathbf{x}):={|\left(P^s\mathit{\phi }\right)(\mathbf{x})|}^2,\end{array}$$(13)

for an operator $P^s$. Notice that this expression for the supersonic intensity yields a non-negative intensity, and this expression will match the same power as in (11(11) $$\begin{array}{c}\hfill {\mathrm{\Pi }}_k(\mathrm{\Gamma },\mathit{\phi })={\int }_{\mathrm{\Gamma }}\mathit{\phi }(\mathbf{x})\overline{\left(\left(P\mathit{\phi }\right)(\mathbf{x})\right)}\mathrm{d}S(\mathbf{x}),\end{array}$$(11) ).

2. Power operator representations

2.1. Mathematical preliminaries

A Lipschitz surface $\mathrm{\Gamma }$, means that $\mathrm{\Gamma }$ is locally the graph of a Lipschitz function. A surface $\mathrm{\Gamma }$ is $C^{r,1}$ if is a locally graph of functions where the rth derivative is Lipschitz. We will assume that $\mathrm{\Gamma }:=\mathit{\partial }\mathrm{\Omega }$ is Lipschitz and $\mathrm{\Omega }$ with connected ${\mathrm{\Omega }}^{+}$. Recall that $H^{(s)}(\mathrm{\Omega })$ denotes the Sobolev space of functions on $\mathrm{\Omega }$ whose partial derivatives up to order s are square integrable and ${\Vert .\Vert }_{(s)}$ denotes the standard norm in this space. Similarly $H_{loc}^{(s)}({\mathrm{\Omega }}^{+})$ denotes the space of functions are $H^{(s)}(B\backslash \overline{\mathrm{\Omega }})$ for every ball B that contains $\overline{\mathrm{\Omega }}$. We let ${\Vert .\Vert }_2={\Vert .\Vert }_{(0)}$ be the norm in the space $L_2(\mathrm{\Omega })$.

Finally we define the inner product between trace functions $f\in H^{(s-1/2)}(\mathrm{\Gamma })$ and $g\in H^{(s+1/2)}(\mathrm{\Gamma })$$${〈f,g〉}_{\mathrm{\Gamma }}:={\int }_{\mathrm{\Gamma }}\overline{f(\mathbf{x})}g(\mathbf{x})\mathrm{d}S(\mathbf{x})$$

with $s\in (-1/2,1/2)$.

We will use the following useful results that can be found in the acoustic literature. Assume that $p\in H_{loc}^{(1)}({\mathrm{\Omega }}^{+})$ is a solution to the Helmholtz Equation (1(1) $$\begin{array}{cc}\hfill \mathrm{\Delta }p+k^{2}p& =0,in{\mathrm{\Omega }}^{+},\hfill \\ \hfill \underset{r\to \infty }{lim}r\left({\mathit{\partial }}_{r}p-ikp\right)& =0,r=|\mathbf{x}|,\widehat{\mathbf{x}}=\mathbf{x}/r,\hfill \end{array}$$(1) ) with $k>0$ and Sommerfeld radiation conditions (1(1) $$\begin{array}{cc}\hfill \mathrm{\Delta }p+k^{2}p& =0,in{\mathrm{\Omega }}^{+},\hfill \\ \hfill \underset{r\to \infty }{lim}r\left({\mathit{\partial }}_{r}p-ikp\right)& =0,r=|\mathbf{x}|,\widehat{\mathbf{x}}=\mathbf{x}/r,\hfill \end{array}$$(1) ). For the following lemmas let ${\mathrm{\Omega }}_0$ be a bounded domain with Lipchitz boundary. Assume that ${\mathrm{\Omega }}_0$ contains $\overline{\mathrm{\Omega }}$. We denote as $B_r$ the ball with center in the origin and radius $r>0$. Similarly ${\mathrm{\Gamma }}_r$ is the boundary of $B_r$.

Lemma 2.1:

We define as the conservation of power the following property(14) $$\begin{array}{c}\hfill {\mathrm{\Pi }}_k(\mathrm{\Gamma },p)={\mathrm{\Pi }}_k(\mathit{\partial }{\mathrm{\Omega }}_0,p).\end{array}$$(14)

ProofFor the proof we refer to [18].

Lemma 2.2:

We have the following trace estimates(15) $$\begin{array}{cc}\hfill 2k\mathit{\rho }\mathit{\omega }{\mathrm{\Pi }}_k(\mathrm{\Gamma },p)& \le \left\{\Vert {\mathit{\partial }}_{\mathit{\nu }}{p\Vert }_{(0)}^2(\mathit{\partial }{\mathrm{\Omega }}_0)+k^2{\Vert p\Vert }_{(0)}^2(\mathit{\partial }{\mathrm{\Omega }}_0)\right\},\hfill \\ \hfill 2k\mathit{\rho }\mathit{\omega }{\mathrm{\Pi }}_k(\mathrm{\Gamma },p)& =\underset{r\to \infty }{lim}\left\{\Vert {\mathit{\partial }}_{\mathit{\nu }}{p\Vert }_{(0)}^2({\mathrm{\Gamma }}_r)+k^2{\Vert p\Vert }_{(0)}^2({\mathrm{\Gamma }}_r)\right\}.\hfill \end{array}$$(15)

ProofAssume that $\mathit{\nu }$ is the outward normal of $\mathit{\partial }{\mathrm{\Omega }}_0$, then the normal velocity assumes the relation (8(8) $$\begin{array}{c}\hfill V_n(\mathbf{x})=\frac{1}{i\mathit{\rho }\mathit{\omega }}{\mathit{\partial }}_{\mathit{\nu }}p(\mathbf{x}),\mathbf{x}\in \mathrm{\Gamma }.\end{array}$$(8) ). For $\mathbf{x}\in \mathit{\partial }{\mathrm{\Omega }}_0$ its trivial to obtain the relation$$2i\mathit{\rho }\mathit{\omega }\text{Re}\left\{p(\mathbf{x})\overline{V_n(\mathbf{x})}\right\}=p(\mathbf{x})\overline{{\mathit{\partial }}_{\mathit{\nu }}p(\mathbf{x})}-\overline{p(\mathbf{x})}{\mathit{\partial }}_{\mathit{\nu }}p(\mathbf{x})$$

then$$\frac{1}{\mathit{\rho }\mathit{\omega }}|{\mathit{\partial }}_{\mathit{\nu }}{p(\mathbf{x})-ikp(\mathbf{x})|}^2=\frac{1}{\mathit{\rho }\mathit{\omega }}|{\mathit{\partial }}_{\mathit{\nu }}{p(\mathbf{x})|}^2+\frac{k^2}{\mathit{\rho }\mathit{\omega }}{|p(\mathbf{x})|}^2-k\text{Re}\left\{p(\mathbf{x})\overline{V_n(\mathbf{x})}\right\}.$$

Then integration over $\mathit{\partial }{\mathrm{\Omega }}_0$, the Sommerfeld radiation condition and the conservation of power yields the results in (15(15) $$\begin{array}{cc}\hfill 2k\mathit{\rho }\mathit{\omega }{\mathrm{\Pi }}_k(\mathrm{\Gamma },p)& \le \left\{\Vert {\mathit{\partial }}_{\mathit{\nu }}{p\Vert }_{(0)}^2(\mathit{\partial }{\mathrm{\Omega }}_0)+k^2{\Vert p\Vert }_{(0)}^2(\mathit{\partial }{\mathrm{\Omega }}_0)\right\},\hfill \\ \hfill 2k\mathit{\rho }\mathit{\omega }{\mathrm{\Pi }}_k(\mathrm{\Gamma },p)& =\underset{r\to \infty }{lim}\left\{\Vert {\mathit{\partial }}_{\mathit{\nu }}{p\Vert }_{(0)}^2({\mathrm{\Gamma }}_r)+k^2{\Vert p\Vert }_{(0)}^2({\mathrm{\Gamma }}_r)\right\}.\hfill \end{array}$$(15) ).

For the following result we will utilize the spherical harmonics, which are defined as(16) $$\begin{array}{c}\hfill Y_n^m(\widehat{\mathbf{x}}):=\sqrt{\frac{2n+1}{4\mathit{\pi }}\frac{(n-m)!}{(n+m)!}}{P}_n^m(cos\mathit{\theta })exp(im\mathit{\varphi }),\end{array}$$(16)

for $n=0,1,2,\dots$ and $m=0,\pm 1,\pm 2,\dots \pm n$, where $\widehat{\mathbf{x}}=(cos\mathit{\varphi }sin\mathit{\theta },sin\mathit{\varphi }sin\mathit{\theta },cos\mathit{\theta })$ and $P_n^m$ is the associated Legendre function. It is well-known that the spherical harmonics form an orthonormal basis at the surface of the unit sphere ${\mathbb{S}}^2$, moreover at ${\mathrm{\Gamma }}_r$$${〈Y_n^m,Y_{n^{\prime }}^{m^{\prime }}〉}_{\mathit{\partial }{B}_r}=r^2{\mathit{\delta }}_n^{n^{\prime }}{\mathit{\delta }}_m^{m^{\prime }},$$

where $\mathit{\delta }$ is the Kronecker delta function. The radiating solution p can be represented in $R^3\backslash B$ (see [19]) as(17) $$\begin{array}{c}\hfill p(\mathbf{x})=\sum _{n=0}^{\infty }\sum _{m=-n}^n{A}_n^m{h}_n(k|\mathbf{x}|)Y_n^m(\widehat{\mathbf{x}}),\end{array}$$(17)

where $h_n$ is the spherical Hankel function of the first kind. This representation yields the explicit expression for the power (see [14, Chapter 6])(18) $$\begin{array}{c}\hfill {\mathrm{\Pi }}_k({\mathrm{\Gamma }}_r,p)=\frac{1}{2}\text{Re}{〈\frac{1}{i\mathit{\rho }\mathit{\omega }}{\mathit{\partial }}_{r}p,p〉}_{{\mathrm{\Gamma }}_r}=\frac{1}{2\mathit{\rho }\mathit{\omega }k}\sum _{n=0}^{\infty }\sum _{m=-n}^n{|A_n^m|}^2.\end{array}$$(18)

Lemma 2.3:

The relation between the power and the far-field is given by(19) $$\begin{array}{c}\hfill {\mathrm{\Pi }}_k(\mathrm{\Gamma },p)=\underset{r\to \infty }{lim}\frac{1}{2\mathit{\rho }c}{\Vert p\Vert }_2^2({\mathrm{\Gamma }}_r)=\frac{1}{2\mathit{\rho }c}{\Vert p_{\infty }\Vert }_2^2({\mathbb{S}}^2).\end{array}$$(19)

ProofIntegrating over a ball $B_r$ that contains $\mathrm{\Omega }$, and using conservation of power Lemma 2.1 we get that ${\mathrm{\Pi }}_k(\mathrm{\Gamma },p)={\mathrm{\Pi }}_k({\mathrm{\Gamma }}_r,p)$. The asymptotic behaviour of the spherical Hankel functions$$\begin{array}{cc}\hfill h_n(t)& ={(-i)}^{n+1}\frac{1}{t}{e}^{it}\left\{1+O\left(\frac{1}{t}\right)\right\},t\to \infty \hfill \\ \hfill h_n^{\prime }(t)& ={(-i)}^n\frac{1}{t}{e}^{it}\left\{1+O\left(\frac{1}{t}\right)\right\},\hfill \end{array}$$

joined with the spherical representation (17(17) $$\begin{array}{c}\hfill p(\mathbf{x})=\sum _{n=0}^{\infty }\sum _{m=-n}^n{A}_n^m{h}_n(k|\mathbf{x}|)Y_n^m(\widehat{\mathbf{x}}),\end{array}$$(17) ) we obtain directly the behaviour for the normal velocity(20) $$\begin{array}{c}\hfill \underset{r\to \infty }{lim}\Vert {\mathit{\partial }}_{\mathit{\nu }}{p\Vert }_{(0)}^2({\mathrm{\Gamma }}_r)=k^2\underset{r\to \infty }{lim}{\Vert p\Vert }_{(0)}^2({\mathrm{\Gamma }}_r).\end{array}$$(20)

The results in (19(19) $$\begin{array}{c}\hfill {\mathrm{\Pi }}_k(\mathrm{\Gamma },p)=\underset{r\to \infty }{lim}\frac{1}{2\mathit{\rho }c}{\Vert p\Vert }_2^2({\mathrm{\Gamma }}_r)=\frac{1}{2\mathit{\rho }c}{\Vert p_{\infty }\Vert }_2^2({\mathbb{S}}^2).\end{array}$$(19) ) follows from using the previous result in Lemma 2.2.

Lemma 2.4:

The acoustical power ${\mathrm{\Pi }}_k(\mathrm{\Gamma },p)$ is positive, moreover if ${\mathrm{\Pi }}_k(\mathrm{\Gamma },p)=0$ then $p=0$ in ${\mathrm{\Omega }}^{+}$.

ProofThis result from the representation (18(18) $$\begin{array}{c}\hfill {\mathrm{\Pi }}_k({\mathrm{\Gamma }}_r,p)=\frac{1}{2}\text{Re}{〈\frac{1}{i\mathit{\rho }\mathit{\omega }}{\mathit{\partial }}_{r}p,p〉}_{{\mathrm{\Gamma }}_r}=\frac{1}{2\mathit{\rho }\mathit{\omega }k}\sum _{n=0}^{\infty }\sum _{m=-n}^n{|A_n^m|}^2.\end{array}$$(18) ) and Rellich’s lemma (see [19]).

Lemma 2.5:

For $-1/2<s<1/2$, we have the following mapping properties(21) $$\begin{array}{cc}\hfill S:=H^{(s-1/2)}(\mathrm{\Gamma })\to H^{(s+1/2)}(\mathrm{\Gamma }),& K^{\prime }:=H^{(s-1/2)}(\mathrm{\Gamma })\to H^{(s-1/2)}(\mathrm{\Gamma }),\hfill \\ \hfill K:=H^{(s+1/2)}(\mathrm{\Gamma })\to H^{(s+1/2)}(\mathrm{\Gamma }),\end{array}$$(21)

If $\mathrm{\Gamma }$ is of class $C^{r+1,1}$ for an integer $r\ge 0$, then (21(21) $$\begin{array}{cc}\hfill S:=H^{(s-1/2)}(\mathrm{\Gamma })\to H^{(s+1/2)}(\mathrm{\Gamma }),& K^{\prime }:=H^{(s-1/2)}(\mathrm{\Gamma })\to H^{(s-1/2)}(\mathrm{\Gamma }),\hfill \\ \hfill K:=H^{(s+1/2)}(\mathrm{\Gamma })\to H^{(s+1/2)}(\mathrm{\Gamma }),\end{array}$$(21) ) and (22(22) $$\begin{array}{c}\hfill P=\frac{1}{4i\mathit{\rho }\mathit{\omega }}\left(S^{\ast }{K}^{\prime }-{\left(K^{\prime }\right)}^{\ast }S\right).\end{array}$$(22) ) hold for $-r-1\le s\le r+1$.

ProofThis result follows directly from [20, Theorem 7.1,7.2].

Notice that S is a self-adjoint operator, while $K^{\ast }=K^{\prime }$. This will be used in the following result:

Theorem 2.6:

For $-1/2<s<1/2$, the single layer representation (7(7) $$\begin{array}{c}\hfill p(\mathbf{x})=\left(S\mathit{\phi }\right)(\mathbf{x}),\mathbf{x}\in {\mathrm{\Omega }}^{+},\end{array}$$(7) ) with $\mathit{\phi }\in H^{(s-1/2)}(\mathrm{\Gamma })$ yields the power operator $P:H^{(s-1/2)}(\mathrm{\Gamma })\to H^{(s+1/2)}(\mathrm{\Gamma })$ in (11(11) $$\begin{array}{c}\hfill {\mathrm{\Pi }}_k(\mathrm{\Gamma },\mathit{\phi })={\int }_{\mathrm{\Gamma }}\mathit{\phi }(\mathbf{x})\overline{\left(\left(P\mathit{\phi }\right)(\mathbf{x})\right)}\mathrm{d}S(\mathbf{x}),\end{array}$$(11) ), with the representation(22) $$\begin{array}{c}\hfill P=\frac{1}{4i\mathit{\rho }\mathit{\omega }}\left(S^{\ast }{K}^{\prime }-{\left(K^{\prime }\right)}^{\ast }S\right).\end{array}$$(22)

ProofNotice the operator relations for $\mathit{\phi }\in H^{(s-1/2)}(\mathrm{\Gamma })$$$\begin{array}{c}\hfill 2\text{Re}{〈\frac{1}{i\mathit{\rho }\mathit{\omega }}{K}^{\prime }\mathit{\phi },S\mathit{\phi }〉}_{\mathrm{\Gamma }}={〈\mathit{\phi },{\left(\frac{1}{i\mathit{\rho }\mathit{\omega }}{K}^{\prime }\right)}^{\ast }S\mathit{\phi }〉}_{\mathrm{\Gamma }}+{〈\mathit{\phi },\frac{1}{i\mathit{\rho }\mathit{\omega }}{S}^{\ast }{K}^{\prime }\mathit{\phi }〉}_{\mathrm{\Gamma }}\end{array}$$

From Lemma 2.5 we obtain that the operators ${(K^{\prime })}^{\ast }S$ and $S^{\ast }{K}^{\prime }$ map $H^{(s-1/2)}(\mathrm{\Gamma })$ to $H^{(s+1/2)}(\mathrm{\Gamma })$, then (22(22) $$\begin{array}{c}\hfill P=\frac{1}{4i\mathit{\rho }\mathit{\omega }}\left(S^{\ast }{K}^{\prime }-{\left(K^{\prime }\right)}^{\ast }S\right).\end{array}$$(22) ) follows.

Lemma 2.7:

For $\mathit{\phi }\in H^{(-1/2)}(\mathrm{\Gamma })$ the single layer representation (7(7) $$\begin{array}{c}\hfill p(\mathbf{x})=\left(S\mathit{\phi }\right)(\mathbf{x}),\mathbf{x}\in {\mathrm{\Omega }}^{+},\end{array}$$(7) ) yields(23) $$\begin{array}{cc}\hfill \frac{1}{2}\text{Re}{〈\frac{1}{i\mathit{\rho }\mathit{\omega }}{K}^{\prime }\mathit{\phi },S\mathit{\phi }〉}_{\mathit{\partial }{\mathrm{\Omega }}_0}& ={〈\mathit{\phi },P\mathit{\phi }〉}_{\mathrm{\Gamma }},\hfill \end{array}$$(23)

where the power operator is defined as the integral operator$$\left(P\mathit{\phi }\right)(\mathbf{x})={\int }_{\mathit{\partial }{\mathrm{\Omega }}_0}{\mathrm{{\rm Y}}}_s(\mathbf{x},\mathbf{y})\mathit{\phi }(\mathbf{y})\mathrm{d}S(\mathbf{y}),$$

where(24) $$\begin{array}{cc}\hfill \mathrm{{\rm Y}}(\mathbf{x},\mathbf{y})& ={\int }_{\mathit{\partial }{\mathrm{\Omega }}_0}\frac{1}{4}\left\{\frac{1}{i\mathit{\rho }\mathit{\omega }}\frac{\mathit{\partial }\mathrm{\Phi }(\mathbf{z},\mathbf{x})}{\mathit{\partial }\mathit{\nu }(\mathbf{z})}\overline{\mathrm{\Phi }(\mathbf{z},\mathbf{y})}+\overline{\frac{1}{i\mathit{\rho }\mathit{\omega }}\frac{\mathit{\partial }\mathrm{\Phi }(\mathbf{z},\mathbf{y})}{\mathit{\partial }\mathit{\nu }(\mathbf{z})}}\mathrm{\Phi }(\mathbf{z},\mathbf{x})\right\}\mathrm{d}S(\mathbf{z}),\hfill \end{array}$$(24)

ProofUsing the single layer representation (7(7) $$\begin{array}{c}\hfill p(\mathbf{x})=\left(S\mathit{\phi }\right)(\mathbf{x}),\mathbf{x}\in {\mathrm{\Omega }}^{+},\end{array}$$(7) ), we can change the order of integration to obtain the relation$$\begin{array}{cc}\hfill {〈\frac{1}{i\mathit{\rho }\mathit{\omega }}{K}^{\prime }\mathit{\phi },S\mathit{\phi }〉}_{\mathit{\partial }{\mathrm{\Omega }}_0}& ={\int }_{\mathit{\partial }{\mathrm{\Omega }}_0}\overline{\frac{1}{i\mathit{\rho }\mathit{\omega }}\left(K^{\prime }\mathit{\phi }\right)(\mathbf{x})}\left(S\mathit{\phi }\right)(\mathbf{x})\mathrm{d}S(\mathbf{x})\hfill \\ \hfill & ={\int }_{\mathit{\partial }{\mathrm{\Omega }}_0}{\int }_{\mathrm{\Gamma }}{\int }_{\mathrm{\Gamma }}\left\{\overline{\frac{1}{i\mathit{\rho }\mathit{\omega }}\frac{\mathit{\partial }\mathrm{\Phi }(\mathbf{x},\mathbf{y})}{\mathit{\partial }\mathit{\nu }(\mathbf{x})}}\overline{\mathit{\phi }(\mathbf{y})}\mathrm{\Phi }(\mathbf{x},\mathbf{z})\mathit{\phi }(\mathbf{z})\right\}\mathrm{d}S(\mathbf{z})\mathrm{d}S(\mathbf{y})\mathrm{d}S(\mathbf{x})\hfill \\ \hfill & ={\int }_{\mathrm{\Gamma }}\mathit{\phi }(\mathbf{z}){\int }_{\mathrm{\Gamma }}\overline{\mathit{\phi }(\mathbf{y})}{\int }_{\mathit{\partial }{\mathrm{\Omega }}_0}\left\{\overline{\frac{1}{i\mathit{\rho }\mathit{\omega }}\frac{\mathit{\partial }\mathrm{\Phi }(\mathbf{x},\mathbf{y})}{\mathit{\partial }\mathit{\nu }(\mathbf{x})}}\mathrm{\Phi }(\mathbf{x},\mathbf{z})\right\}\mathrm{d}S(\mathbf{x})\mathrm{d}S(\mathbf{y})\mathrm{d}S(\mathbf{z})\hfill \\ \hfill & ={\int }_{\mathrm{\Gamma }}\mathit{\phi }(\mathbf{z}){\int }_{\mathrm{\Gamma }}\overline{\mathit{\phi }(\mathbf{y}){\int }_{\mathit{\partial }{\mathrm{\Omega }}_0}\left\{\frac{1}{i\mathit{\rho }\mathit{\omega }}\frac{\mathit{\partial }\mathrm{\Phi }(\mathbf{x},\mathbf{y})}{\mathit{\partial }\mathit{\nu }(\mathbf{x})}\overline{\mathrm{\Phi }(\mathbf{x},\mathbf{z})}\right\}\mathrm{d}S(\mathbf{x})\mathrm{d}S(\mathbf{y})}\mathrm{d}S(\mathbf{z}).\hfill \end{array}$$

Changing variables and the order of integration, we obtain (24(24) $$\begin{array}{cc}\hfill \mathrm{{\rm Y}}(\mathbf{x},\mathbf{y})& ={\int }_{\mathit{\partial }{\mathrm{\Omega }}_0}\frac{1}{4}\left\{\frac{1}{i\mathit{\rho }\mathit{\omega }}\frac{\mathit{\partial }\mathrm{\Phi }(\mathbf{z},\mathbf{x})}{\mathit{\partial }\mathit{\nu }(\mathbf{z})}\overline{\mathrm{\Phi }(\mathbf{z},\mathbf{y})}+\overline{\frac{1}{i\mathit{\rho }\mathit{\omega }}\frac{\mathit{\partial }\mathrm{\Phi }(\mathbf{z},\mathbf{y})}{\mathit{\partial }\mathit{\nu }(\mathbf{z})}}\mathrm{\Phi }(\mathbf{z},\mathbf{x})\right\}\mathrm{d}S(\mathbf{z}),\hfill \end{array}$$(24) ).

2.2. Representation formulas on an infinite medium

For the following theorem we use the result given in Chapter 7 of [21](25) $$\begin{array}{c}\hfill j_0\left(k|\mathbf{x}-\mathbf{y}|\right)=4\mathit{\pi }\sum _{n=0}^{\infty }\sum _{m=-n}^n{j}_n(k|\mathbf{x}|)j_n(k|\mathbf{y}|)\overline{Y_n^m(\widehat{\mathbf{x}})}{Y}_n^m(\widehat{\mathbf{y}}),\end{array}$$(25)

where $j_0(t)=sin(t)/t$ is the spherical bessel function.

Theorem 2.8:

The single source representation (7(7) $$\begin{array}{c}\hfill p(\mathbf{x})=\left(S\mathit{\phi }\right)(\mathbf{x}),\mathbf{x}\in {\mathrm{\Omega }}^{+},\end{array}$$(7) ) for a density $\mathit{\phi }\in H^{(-1/2)}(\mathrm{\Gamma })$ yields the integral representation of the power operator in (11(11) $$\begin{array}{c}\hfill {\mathrm{\Pi }}_k(\mathrm{\Gamma },\mathit{\phi })={\int }_{\mathrm{\Gamma }}\mathit{\phi }(\mathbf{x})\overline{\left(\left(P\mathit{\phi }\right)(\mathbf{x})\right)}\mathrm{d}S(\mathbf{x}),\end{array}$$(11) )(26) $$\begin{array}{c}\hfill \left(P\mathit{\phi }\right)(\mathbf{x}):=\left(\frac{1}{8\mathit{\pi }\mathit{\rho }c}\right){\int }_{\mathrm{\Gamma }}\mathit{\phi }(\mathbf{y})j_0\left(k|\mathbf{x}-\mathbf{y}|\right)\mathrm{d}S(\mathbf{y}).\end{array}$$(26)

ProofAssume that $B_r$ is a ball with radius $r>0$ such that $\overline{\mathrm{\Omega }}\subset B_r$ then Lemmas 2.1 and 2.7 yield that$${\mathrm{\Pi }}_k\left(\mathrm{\Gamma },\mathit{\phi }\right)={\mathrm{\Pi }}_k\left({\mathrm{\Gamma }}_r,\mathit{\phi }\right)=\frac{1}{2}\text{Re}{〈\frac{1}{i\mathit{\rho }\mathit{\omega }}K\mathit{\phi },S\mathit{\phi }〉}_{{\mathrm{\Gamma }}_r}={〈\mathit{\phi },P\mathit{\phi }〉}_{{\mathrm{\Gamma }}_r}.$$

Assume that $|\mathbf{z}|=r$, then notice that $|\mathbf{z}|>|\mathbf{x}|$ and $|\mathbf{z}|>|\mathbf{y}|$ then we have the representation$$\begin{array}{cc}\hfill \frac{\mathit{\partial }\mathrm{\Phi }(\mathbf{z},\mathbf{x})}{\mathit{\partial }\mathit{\nu }(\mathbf{z})}& =i{k}^2\sum _{n=0}^{\infty }\sum _{m=-n}^n{j}_n(k|\mathbf{x}|)\overline{Y_n^m(\widehat{\mathbf{x}})}{h}_n^{\prime }(k|\mathbf{z}|)Y_n^m(\widehat{\mathbf{z}}),\hfill \\ \hfill \mathrm{\Phi }(\mathbf{z},\mathbf{y})& =ik\sum _{n=0}^{\infty }\sum _{m=-n}^n{j}_n(k|\mathbf{y}|)\overline{Y_n^m(\widehat{\mathbf{y}})}{h}_n(k|\mathbf{z}|)Y_n^m(\widehat{\mathbf{z}}).\hfill \end{array}$$

We use these decomposition over the integral representation of ${\mathrm{{\rm Y}}}_s(\mathbf{x},\mathbf{y})$ in (24(24) $$\begin{array}{cc}\hfill \mathrm{{\rm Y}}(\mathbf{x},\mathbf{y})& ={\int }_{\mathit{\partial }{\mathrm{\Omega }}_0}\frac{1}{4}\left\{\frac{1}{i\mathit{\rho }\mathit{\omega }}\frac{\mathit{\partial }\mathrm{\Phi }(\mathbf{z},\mathbf{x})}{\mathit{\partial }\mathit{\nu }(\mathbf{z})}\overline{\mathrm{\Phi }(\mathbf{z},\mathbf{y})}+\overline{\frac{1}{i\mathit{\rho }\mathit{\omega }}\frac{\mathit{\partial }\mathrm{\Phi }(\mathbf{z},\mathbf{y})}{\mathit{\partial }\mathit{\nu }(\mathbf{z})}}\mathrm{\Phi }(\mathbf{z},\mathbf{x})\right\}\mathrm{d}S(\mathbf{z}),\hfill \end{array}$$(24) ) to obtain$$\begin{array}{cc}& {\int }_{{\mathrm{\Gamma }}_r}\left\{\frac{1}{i\mathit{\rho }\mathit{\omega }}\frac{\mathit{\partial }\mathrm{\Phi }(\mathbf{z},\mathbf{x})}{\mathit{\partial }\mathit{\nu }(\mathbf{z})}\overline{\mathrm{\Phi }(\mathbf{z},\mathbf{y})}\right\}\mathrm{d}S(\mathbf{z})\hfill \\ \hfill & =-i\left(\frac{r^2{k}^3}{\mathit{\rho }\mathit{\omega }}\right)\sum _{n=0}^{\infty }\sum _{m=-n}^n{j}_n(k|\mathbf{x}|)j_n(k|\mathbf{y}|)\overline{Y_n^m(\widehat{\mathbf{x}})}{Y}_n^m(\widehat{\mathbf{y}})h_n^{\prime }(k|\mathbf{z}|)\overline{h_n(k|\mathbf{z}|)},\hfill \end{array}$$

and$$\begin{array}{cc}& {\int }_{{\mathrm{\Gamma }}_r}\left\{\overline{\frac{1}{i\mathit{\rho }\mathit{\omega }}\frac{\mathit{\partial }\mathrm{\Phi }(\mathbf{z},\mathbf{y})}{\mathit{\partial }\mathit{\nu }(\mathbf{z})}}\mathrm{\Phi }(\mathbf{z},\mathbf{x})\right\}\mathrm{d}S(\mathbf{z})\hfill \\ \hfill & =i\left(\frac{r^2{k}^3}{\mathit{\rho }\mathit{\omega }}\right)\sum _{n=0}^{\infty }\sum _{m=-n}^n{j}_n(k|\mathbf{x}|)j_n(k|\mathbf{y}|)\overline{Y_n^m(\widehat{\mathbf{x}})}{Y}_n^m(\widehat{\mathbf{y}})\overline{h_n^{\prime }(k|\mathbf{z}|)}{h}_n(k|\mathbf{z}|).\hfill \end{array}$$

Since from Lemma 1.2, $\overline{h_n^{\prime }(t)}{h}_n(t)=\frac{1}{t^2}\left(-i+O\left(\frac{1}{t}\right)\right)$ and r can be arbitrarily large, we let $r\to \infty$ then$$\begin{array}{cc}\hfill {\mathrm{{\rm Y}}}_s(\mathbf{x},\mathbf{y})& =i\left(\frac{r^2{k}^3}{4\mathit{\rho }\mathit{\omega }}\right)\sum _{n=0}^{\infty }\sum _{m=-n}^n{j}_n(k|\mathbf{x}|)j_n(k|\mathbf{y}|)\overline{Y_n^m(\widehat{\mathbf{x}})}{Y}_n^m(\widehat{\mathbf{y}})\left\{\overline{h_n^{\prime }(kr)}{h}_n(kr)-h_n^{\prime }(kr)\overline{h_n(kr)}\right\}\hfill \\ \hfill & =\left(\frac{k}{2\mathit{\rho }\mathit{\omega }}\right)\sum _{n=0}^{\infty }\sum _{m=-n}^n{j}_n(k|\mathbf{x}|)j_n(k|\mathbf{y}|)\overline{Y_n^m(\widehat{\mathbf{x}})}{Y}_n^m(\widehat{\mathbf{y}}).\hfill \end{array}$$

Finally we use (25(25) $$\begin{array}{c}\hfill j_0\left(k|\mathbf{x}-\mathbf{y}|\right)=4\mathit{\pi }\sum _{n=0}^{\infty }\sum _{m=-n}^n{j}_n(k|\mathbf{x}|)j_n(k|\mathbf{y}|)\overline{Y_n^m(\widehat{\mathbf{x}})}{Y}_n^m(\widehat{\mathbf{y}}),\end{array}$$(25) ) to obtain (26(26) $$\begin{array}{c}\hfill \left(P\mathit{\phi }\right)(\mathbf{x}):=\left(\frac{1}{8\mathit{\pi }\mathit{\rho }c}\right){\int }_{\mathrm{\Gamma }}\mathit{\phi }(\mathbf{y})j_0\left(k|\mathbf{x}-\mathbf{y}|\right)\mathrm{d}S(\mathbf{y}).\end{array}$$(26) ).

Corollary 2.9:

Assume that $\mathrm{\Gamma }$ is of class $C^{1,1}$, then the power operator $P:L_2(\mathrm{\Gamma })\to L_2(\mathrm{\Gamma })$ from the single layer representation (7(7) $$\begin{array}{c}\hfill p(\mathbf{x})=\left(S\mathit{\phi }\right)(\mathbf{x}),\mathbf{x}\in {\mathrm{\Omega }}^{+},\end{array}$$(7) ) is a compact positive definite operator. If k is not a Dirichlet eigenvalue of $\mathrm{\Omega }$ then P is strictly positive.

ProofFrom Theorem 2.6 we obtain that $P:L_2(\mathrm{\Gamma })\to H^{(1/2)}(\mathrm{\Gamma })\subset L_2(\mathrm{\Gamma })$. By compact embedding theorems then we obtain the compactness of P. Lemma 2.4 yields that the power operator is positive definite and when k is not a Dirichlet eigenvalue, the uniqueness of the single layer representation guarantees that the operator is strictly positive definite.

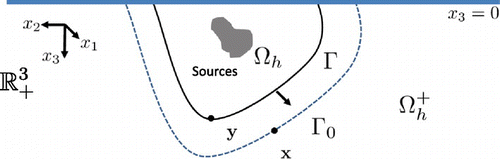
2.3. Representation formulas on a half-space medium

In the previous subsection we focus our analysis of the power operator in an infinite medium. For many acoustical applications it will be a substantial simplification to assume predefined interface conditions over a medium. Let consider the information of the problem be given over $R_{+}^3$ and $\mathrm{\Omega }\cap R_{+}^3\ne \mathrm{\varnothing }$ then we denote ${\mathrm{\Omega }}_h=R_{+}^3\cap \mathrm{\Omega }$, ${\mathrm{\Omega }}_h^{+}=R_{+}^3\backslash {\mathrm{\Omega }}_h$ and ${\mathrm{\Gamma }}_h=\mathit{\partial }{\mathrm{\Omega }}_h$ (see Figure 2).

Figure 2. Half space radiation problem.

The boundary layer operators (4(4) $$\begin{array}{cc}\hfill \left(S\mathit{\phi }\right)(\mathbf{x})& :={\int }_{\mathrm{\Gamma }}\mathrm{\Phi }(\mathbf{x},\mathbf{y})\mathit{\phi }(\mathbf{y})\mathrm{d}S(\mathbf{y}),\hfill \\ \hfill \left(K\mathit{\phi }\right)(\mathbf{x})& :={\int }_{\mathrm{\Gamma }}\frac{\mathit{\partial }\mathrm{\Phi }(\mathbf{x},\mathbf{y})}{\mathit{\partial }\mathit{\nu }(\mathbf{y})}\mathit{\phi }(\mathbf{y})\mathrm{d}S(\mathbf{y}),\hfill \end{array}$$(4) ) and (6(6) $$\begin{array}{cc}\hfill {\left(K^{\prime }\mathit{\phi }\right)}^{+}(\mathbf{x})& :={\int }_{\mathrm{\Gamma }}\frac{\mathit{\partial }\mathrm{\Phi }(\mathbf{x},\mathbf{y})}{\mathit{\partial }\mathit{\nu }(\mathbf{x})}\mathit{\phi }(\mathbf{y})\mathrm{d}S(\mathbf{y})-\frac{1}{2}\mathit{\phi }(\mathbf{x}).\hfill \end{array}$$(6) ) over ${\mathrm{\Omega }}_h^{+}$ are defined by replacing the fundamental solution $\mathrm{\Phi }$ by(27) $$\begin{array}{c}\hfill {\mathrm{\Phi }}_h(\mathbf{x},\mathbf{y})=\frac{exp\left(ik|\mathbf{x}-\mathbf{y}|\right)}{4\mathit{\pi }|\mathbf{x}-\mathbf{y}|}+h\frac{exp\left(ik|\mathbf{x}-{\mathbf{y}}^{\prime }|\right)}{4\mathit{\pi }|\mathbf{x}-{\mathbf{y}}^{\prime }|},{\mathbf{y}}^{\prime }=(y_1,y_2,-y_3).\end{array}$$(27)

The function ${\mathrm{\Phi }}_h$ is the fundamental solution to the half-space Helmholtz equation with $h=-1$ for sound-soft interface or $h=1$ sound-hard interface. The sound soft condition is generally used for underwater problems where we assume that the pressure field is 0 at the air-water interface. Similarly the sound hard condition is used when we assume that the object is laying over a wall or hard object where the normal velocity is 0 at the interface.

For $B_r$, a ball of radius $r>0$, denote $B_{r,h}=B_r\cap R_{+}^3$.

Lemma 2.10:

We have the following relations(28) $$\begin{array}{cc}\hfill Y_n^m(\widehat{\mathbf{x}})+Y_n^m({\widehat{\mathbf{x}}}^{\prime })& =\left\{\begin{array}{cc}2Y_n^m(\widehat{\mathbf{x}}),& n+m=even\\ 0& else\end{array}\right.\hfill \end{array}$$(28) (29) $$\begin{array}{cc}\hfill Y_n^m(\widehat{\mathbf{x}})-Y_n^m({\widehat{\mathbf{x}}}^{\prime })& =\left\{\begin{array}{cc}2Y_n^m(\widehat{\mathbf{x}}),& n+m=odd\\ 0& else\end{array}\right.\hfill \end{array}$$(29) (30) $$\begin{array}{cc}\hfill {〈Y_n^m,Y_{n^{\prime }}^{m^{\prime }}〉}_{\mathit{\partial }{B}_{r,h}}& =\frac{1}{2}{r}^2{\mathit{\delta }}_n^{n^{\prime }}{\mathit{\delta }}_m^{m^{\prime }},\left\{\begin{array}{c}either{n}^{\prime }+m^{\prime }isoddandn+misodd\\ or{n}^{\prime }+m^{\prime }isevenandn+miseven\end{array}\right.\hfill \\ \hfill \end{array}$$(30)

ProofFrom [22, Section 12.5] we get that $P_n^m(-t)={(-1)}^{n+m}{P}_n^m(t)$ then (28(28) $$\begin{array}{cc}\hfill Y_n^m(\widehat{\mathbf{x}})+Y_n^m({\widehat{\mathbf{x}}}^{\prime })& =\left\{\begin{array}{cc}2Y_n^m(\widehat{\mathbf{x}}),& n+m=even\\ 0& else\end{array}\right.\hfill \end{array}$$(28) ) and (29(29) $$\begin{array}{cc}\hfill Y_n^m(\widehat{\mathbf{x}})-Y_n^m({\widehat{\mathbf{x}}}^{\prime })& =\left\{\begin{array}{cc}2Y_n^m(\widehat{\mathbf{x}}),& n+m=odd\\ 0& else\end{array}\right.\hfill \end{array}$$(29) ) follows from the definition of the spherical harmonics. Similarly$$\begin{array}{cc}\hfill {\int }_{-1}^1{P}_n^m(t)P_{n^{\prime }}^m(t)\mathrm{d}t& ={\int }_0^1{P}_n^m(t)P_{n^{\prime }}^m(t)\mathrm{d}t+{\int }_{-1}^0{P}_n^m(t)P_{n^{\prime }}^m(t)\mathrm{d}t\hfill \\ \hfill & ={\int }_0^1{P}_n^m(t)P_{n^{\prime }}^m(t)\mathrm{d}t+{\int }_0^1{P}_n^m(-t)P_{n^{\prime }}^m(-t)\mathrm{d}t\hfill \\ \hfill & =2{\int }_0^1{P}_n^m(t)P_{n^{\prime }}^m(t)\mathrm{d}t\left\{\begin{array}{c}either{n}^{\prime }+misoddandn+misodd\\ or{n}^{\prime }+misevenandn+miseven\end{array}\right.\hfill \end{array}$$

then (30(30) $$\begin{array}{cc}\hfill {〈Y_n^m,Y_{n^{\prime }}^{m^{\prime }}〉}_{\mathit{\partial }{B}_{r,h}}& =\frac{1}{2}{r}^2{\mathit{\delta }}_n^{n^{\prime }}{\mathit{\delta }}_m^{m^{\prime }},\left\{\begin{array}{c}either{n}^{\prime }+m^{\prime }isoddandn+misodd\\ or{n}^{\prime }+m^{\prime }isevenandn+miseven\end{array}\right.\hfill \\ \hfill \end{array}$$(30) ) follows.

Theorem 2.11:

The single source representation (7(7) $$\begin{array}{c}\hfill p(\mathbf{x})=\left(S\mathit{\phi }\right)(\mathbf{x}),\mathbf{x}\in {\mathrm{\Omega }}^{+},\end{array}$$(7) ) for the half-space ${\mathrm{\Omega }}_h^{+}$ for a density $\mathit{\phi }\in H^{(-1/2)}({\mathrm{\Gamma }}_h)$ yields the integral representation of the power operator in (11(11) $$\begin{array}{c}\hfill {\mathrm{\Pi }}_k(\mathrm{\Gamma },\mathit{\phi })={\int }_{\mathrm{\Gamma }}\mathit{\phi }(\mathbf{x})\overline{\left(\left(P\mathit{\phi }\right)(\mathbf{x})\right)}\mathrm{d}S(\mathbf{x}),\end{array}$$(11) )(31) $$\begin{array}{c}\hfill \left(P^h\mathit{\phi }\right)(\mathbf{x}):=\left(\frac{1}{8\mathit{\pi }\mathit{\rho }c}\right){\int }_{{\mathrm{\Gamma }}_h}\mathit{\phi }(\mathbf{y})\left\{j_0\left(k|\mathbf{x}-\mathbf{y}|\right)+h{j}_0\left(k|\mathbf{x}-{\mathbf{y}}^{\prime }|\right)\right\}\mathrm{d}S(\mathbf{y})\end{array}$$(31)

ProofWe proceed as Theorem 2.8, where$$\begin{array}{c}\hfill {\mathrm{{\rm Y}}}_s^h(\mathbf{x},\mathbf{y})=\frac{1}{4}{\int }_{\mathit{\partial }{\mathrm{\Omega }}_{0,h}}\left\{\overline{\frac{1}{i\mathit{\rho }\mathit{\omega }}\frac{\mathit{\partial }{\mathrm{\Phi }}_h(\mathbf{z},\mathbf{x})}{\mathit{\partial }\mathit{\nu }(\mathbf{z})}}{\mathrm{\Phi }}_h(\mathbf{z},\mathbf{y})+\frac{1}{i\mathit{\rho }\mathit{\omega }}\frac{\mathit{\partial }{\mathrm{\Phi }}_h(\mathbf{z},\mathbf{x})}{\mathit{\partial }\mathit{\nu }(\mathbf{z})}\overline{{\mathrm{\Phi }}_h(\mathbf{z},\mathbf{y})}\right\}\mathrm{d}S(\mathbf{z})\end{array}$$

for any domain ${\mathrm{\Omega }}_{0,h}\in R_{+}^3$ that contains ${\mathrm{\Omega }}_h$ and have connected ${\mathrm{\Omega }}_{0,h}^{+}$. Assume that ${\mathrm{\Omega }}_0$ is a ball $B_r$ for some $r>0$. Since $B_r$ contains ${\mathrm{\Omega }}_h$ then $r=|\mathbf{z}|>|\mathbf{x}|$ and $r=|\mathbf{z}|>|\mathbf{y}|$ then we have the spherical harmonic representation representations$$\begin{array}{cc}\hfill {\mathrm{\Phi }}_h(\mathbf{z},\mathbf{y})& =ik\sum _{n=0}^{\infty }\sum _{m=-n}^n{j}_n(k|\mathbf{y}|)\left\{\overline{Y_n^m(\widehat{\mathbf{y}})}+h\overline{Y_n^m({\widehat{\mathbf{y}}}^{\prime })}\right\}{h}_n(k|\mathbf{z}|)Y_n^m(\widehat{\mathbf{z}})\hfill \\ \hfill \frac{\mathit{\partial }{\mathrm{\Phi }}_h(\mathbf{z},\mathbf{x})}{\mathit{\partial }\mathit{\nu }(\mathbf{z})}& =i{k}^2\sum _{n=0}^{\infty }\sum _{m=-n}^n{j}_n(k|\mathbf{x}|)\left\{\overline{Y_n^m(\widehat{\mathbf{x}})}+h\overline{Y_n^m({\widehat{\mathbf{x}}}^{\prime })}\right\}{h}_n^{\prime }(k|\mathbf{z}|)Y_n^m(\widehat{\mathbf{z}})\hfill \end{array}$$

This yields the representation$$\begin{array}{cc}\hfill {\mathrm{{\rm Y}}}_s^h(\mathbf{x},\mathbf{y})& =\frac{k}{8\mathit{\rho }\mathit{\omega }}\sum _{n=0}^{\infty }{j}_n(k|\mathbf{x}|)j_n(k|\mathbf{y}|)\hfill \\ \hfill & \times \sum _{m=-n}^n\left\{\overline{Y_n^m(\widehat{\mathbf{x}})}+h\overline{Y_n^m({\widehat{\mathbf{x}}}^{\prime })}\right\}\left\{Y_n^m(\widehat{\mathbf{y}})+h{Y}_n^m({\widehat{\mathbf{y}}}^{\prime })\right\}+O\left(\frac{1}{r}\right).\hfill \end{array}$$

and the fact that $r>0$ can be arbitrarily large, we conclude formula (31(31) $$\begin{array}{c}\hfill \left(P^h\mathit{\phi }\right)(\mathbf{x}):=\left(\frac{1}{8\mathit{\pi }\mathit{\rho }c}\right){\int }_{{\mathrm{\Gamma }}_h}\mathit{\phi }(\mathbf{y})\left\{j_0\left(k|\mathbf{x}-\mathbf{y}|\right)+h{j}_0\left(k|\mathbf{x}-{\mathbf{y}}^{\prime }|\right)\right\}\mathrm{d}S(\mathbf{y})\end{array}$$(31) ).

3. Numerical methodology

3.1. Spectral decomposition

In this section we will use the spectral decomposition of the power operator P to construct an explicit formula for the supersonic intensity. Assume that k is not a Dirichlet eigenvalue then by Corollary 2.9 we get that P is an strictly positive definite operator. By the Hilbert–Schmidt theorem there exist a complete ortho-normal basis ${\left\{{\mathit{\phi }}_n\right\}}_{n=1}^{\infty }$ in $L_2(\mathrm{\Gamma })$, such that(32) $$\begin{array}{c}\hfill {〈{\mathit{\phi }}_n,P{\mathit{\phi }}_n〉}_{\mathrm{\Gamma }}={\mathit{\lambda }}_n,\end{array}$$(32)

and ${\mathit{\lambda }}_n\to 0$ as $n\to \infty$. Moreover, for any $\mathit{\phi }\in L_2(\mathrm{\Gamma })$ we have the decomposition(33) $$\begin{array}{c}\hfill \mathit{\phi }(\mathbf{x})=\sum _{n=1}^{\infty }{〈\mathit{\phi },{\mathit{\phi }}_n〉}_{\mathrm{\Gamma }}{\mathit{\phi }}_n(\mathbf{x})\end{array}$$(33)

where the series is absolutely convergent, i.e.$$\sum _{n=1}^{\infty }{\left|{〈\mathit{\phi },{\mathit{\phi }}_n〉}_{\mathrm{\Gamma }}\right|}^2<\infty .$$

These functions are known as the power modes [9]. From this result we get that

Theorem 3.1:

Given a function $\mathit{\phi }\in L_2(\mathrm{\Gamma })$ then the total radiated power from the single source representation (7(7) $$\begin{array}{c}\hfill p(\mathbf{x})=\left(S\mathit{\phi }\right)(\mathbf{x}),\mathbf{x}\in {\mathrm{\Omega }}^{+},\end{array}$$(7) ) is given by(34) $$\begin{array}{c}\hfill {\mathrm{\Pi }}_k(\mathrm{\Gamma },\mathit{\phi })=\sum _{n=1}^{\infty }{\mathit{\lambda }}_n{\left|{〈{\mathit{\phi }}_n,\mathit{\phi }〉}_{\mathrm{\Gamma }}\right|}^2,\end{array}$$(34)

and there is an expression for the intensity $I(\mathbf{x})=|{\mathit{\varphi }}_s{(\mathbf{x})|}^2$ where(35) $$\begin{array}{c}\hfill {\mathit{\varphi }}_s(\mathbf{x})=\sum _{n=1}^{\infty }\sqrt{{\mathit{\lambda }}_n}{\mathit{\phi }}_n(\mathbf{x}){〈{\mathit{\phi }}_n,\mathit{\phi }〉}_{\mathrm{\Gamma }}.\end{array}$$(35)

ProofIs trivial to obtain (34(34) $$\begin{array}{c}\hfill {\mathrm{\Pi }}_k(\mathrm{\Gamma },\mathit{\phi })=\sum _{n=1}^{\infty }{\mathit{\lambda }}_n{\left|{〈{\mathit{\phi }}_n,\mathit{\phi }〉}_{\mathrm{\Gamma }}\right|}^2,\end{array}$$(34) ) using (33(33) $$\begin{array}{c}\hfill \mathit{\phi }(\mathbf{x})=\sum _{n=1}^{\infty }{〈\mathit{\phi },{\mathit{\phi }}_n〉}_{\mathrm{\Gamma }}{\mathit{\phi }}_n(\mathbf{x})\end{array}$$(33) ). Notice that$${\int }_{\mathrm{\Gamma }}{\mathit{\varphi }}_s(\mathbf{x})\overline{{\mathit{\varphi }}_s(\mathbf{x})}\mathrm{d}S(\mathbf{x})=\sum _{n=1}^{\infty }{\mathit{\lambda }}_n{\left|{〈{\mathit{\phi }}_n,\mathit{\phi }〉}_{\mathrm{\Gamma }}\right|}^2{\int }_{\mathrm{\Gamma }}{|{\mathit{\phi }}_n(\mathbf{x})|}^2\mathrm{d}S(\mathbf{x})={\mathrm{\Pi }}_k(\mathrm{\Gamma },\mathit{\phi })$$

which yields (35(35) $$\begin{array}{c}\hfill {\mathit{\varphi }}_s(\mathbf{x})=\sum _{n=1}^{\infty }\sqrt{{\mathit{\lambda }}_n}{\mathit{\phi }}_n(\mathbf{x}){〈{\mathit{\phi }}_n,\mathit{\phi }〉}_{\mathrm{\Gamma }}.\end{array}$$(35) ).

The following corollary follows directly from Theorem 3.1.

Corollary 3.2:

Given a function $\mathit{\phi }\in L_2(\mathrm{\Gamma })$ there exists a non-negative expression for the intensity (13(13) $$\begin{array}{c}\hfill I^s(\mathbf{x}):={|\left(P^s\mathit{\phi }\right)(\mathbf{x})|}^2,\end{array}$$(13) ) from the single source representation (7(7) $$\begin{array}{c}\hfill p(\mathbf{x})=\left(S\mathit{\phi }\right)(\mathbf{x}),\mathbf{x}\in {\mathrm{\Omega }}^{+},\end{array}$$(7) ) where$$\left(P^s\mathit{\phi }\right)(\mathbf{x})=\sum _{n=1}^{\infty }\sqrt{{\mathit{\lambda }}_n}{〈\mathit{\phi },{\mathit{\phi }}_n〉}_{\mathrm{\Gamma }}\mathit{\phi }(\mathbf{x}).$$

3.2. Boundary element methods

The numerical methodology will require the numerical discretization of the different surface integral equations introduced in the previous sections. We choose the Boundary Element Methods (BEM) to produce these discretization, since it is the classical accurate numerical methodology in the area of acoustics (see [12,23,24]).

Assume that the pressure measurements are given by ${\mathbf{p}}_m\in {\mathbb{C}}^{m\times 1}$ over m points over the measurement surface ${\mathrm{\Gamma }}_0$ and define as ${\mathbf{p}}^v,{\mathbf{v}}^v\in {\mathbb{C}}^{n\times 1}$ the pressure and normal velocity over n points in the vibrating surface $\mathrm{\Gamma }$. Similarly we define $\mathit{\phi }\in {\mathbb{C}}^{n\times 1}$ the density $\mathit{\phi }$ in (7(7) $$\begin{array}{c}\hfill p(\mathbf{x})=\left(S\mathit{\phi }\right)(\mathbf{x}),\mathbf{x}\in {\mathrm{\Omega }}^{+},\end{array}$$(7) ), (10(10) $$\begin{array}{c}\hfill p(\mathbf{x})=\left(S\mathit{\phi }\right)(\mathbf{x}),V_n(\mathbf{x})=\frac{1}{i\mathit{\rho }\mathit{\omega }}{\left(K^{\prime }\mathit{\phi }\right)}^{+}(\mathbf{x}).\end{array}$$(10) ) over $\mathrm{\Gamma }$. Moreover $\mathrm{\Gamma }$ is decomposed into triangular elements with three nodes. In this paper (as recommended in [23]), iso-parametric linear functions are selected for interpolating the integral quantity $\mathit{\phi }$. Denote as $\mathbf{S}\in {\mathbb{C}}^{m\times n}$ the BEM discretization of the operator S in (4(4) $$\begin{array}{cc}\hfill \left(S\mathit{\phi }\right)(\mathbf{x})& :={\int }_{\mathrm{\Gamma }}\mathrm{\Phi }(\mathbf{x},\mathbf{y})\mathit{\phi }(\mathbf{y})\mathrm{d}S(\mathbf{y}),\hfill \\ \hfill \left(K\mathit{\phi }\right)(\mathbf{x})& :={\int }_{\mathrm{\Gamma }}\frac{\mathit{\partial }\mathrm{\Phi }(\mathbf{x},\mathbf{y})}{\mathit{\partial }\mathit{\nu }(\mathbf{y})}\mathit{\phi }(\mathbf{y})\mathrm{d}S(\mathbf{y}),\hfill \end{array}$$(4) ) for $x\in {\mathrm{\Gamma }}_0$. Similarly ${\mathbf{S}}^v,{\mathbf{K}}^v\in {\mathbb{C}}^{n\times n}$ are, respectively, the singular operators $S,{(K^{\prime })}^{+}$ in (10(10) $$\begin{array}{c}\hfill p(\mathbf{x})=\left(S\mathit{\phi }\right)(\mathbf{x}),V_n(\mathbf{x})=\frac{1}{i\mathit{\rho }\mathit{\omega }}{\left(K^{\prime }\mathit{\phi }\right)}^{+}(\mathbf{x}).\end{array}$$(10) ). In addition define as $\mathbf{P}\in {\mathbb{C}}^{n\times n}$ the discretization of the power operator P in (26(26) $$\begin{array}{c}\hfill \left(P\mathit{\phi }\right)(\mathbf{x}):=\left(\frac{1}{8\mathit{\pi }\mathit{\rho }c}\right){\int }_{\mathrm{\Gamma }}\mathit{\phi }(\mathbf{y})j_0\left(k|\mathbf{x}-\mathbf{y}|\right)\mathrm{d}S(\mathbf{y}).\end{array}$$(26) ).

The numerical application of the NAH technique is reduced to the solution of the matrix equation(36) $$\begin{array}{c}\hfill \mathbf{S}\mathit{\phi }={\mathbf{p}}_m.\end{array}$$(36)

The reconstructed pressure ${\mathbf{p}}^v$ and velocity ${\mathbf{v}}^v$ in $\mathrm{\Gamma }$ is given by the relations (7(7) $$\begin{array}{c}\hfill p(\mathbf{x})=\left(S\mathit{\phi }\right)(\mathbf{x}),\mathbf{x}\in {\mathrm{\Omega }}^{+},\end{array}$$(7) ) or(37) $$\begin{array}{cc}\hfill {\mathbf{p}}^v& ={\mathbf{S}}^v\mathit{\phi },\hfill \\ \hfill {\mathbf{v}}^v& ={\mathbf{K}}^v\mathit{\phi },\hfill \end{array}$$(37)

and ${\mathbf{I}}^v$ the corresponding normal intensity. An evenly distribution of points on the vibrating surface $\mathrm{\Gamma }$ can be used to produce a triangular surface element decomposition. Basic BEM calculations over the resultant surface element decomposition produces integration weights $w_i$ (see [25]), $i=1,\dots ,N$ such that$$\sum _i^n{w}_i=Area(\mathrm{\Gamma }),w_i>0.$$

The power is approximated directly from(38) $$\begin{array}{c}\hfill {\mathrm{\Pi }}_k((\mathrm{\Gamma },\mathit{\phi })\approx \frac{1}{2}\text{Re}\left\{{\left({\mathbf{W}}^{1/2}{\mathbf{v}}^v\right)}^{\ast }\left({\mathbf{W}}^{1/2}{\mathbf{p}}^v\right)\right\},\end{array}$$(38)

where $\mathbf{W}=diag(w_1,\dots ,w_n)$.

Since $\mathbf{P}$ is the discretization of a compact positive definite operator we will have the corresponding numerical eigenvalue decomposition(39) $$\begin{array}{c}\hfill \mathbf{P}=\sum _{i=1}^n{\mathit{\lambda }}_i{\mathbf{u}}_i{\mathbf{u}}_i^{\ast },\end{array}$$(39)

where ${\mathbf{u}}_i$, $i=1,\dots ,n$ is a set of orthonormal vectors. The numerical identification of the supersonic field from pressure measurements in ${\mathrm{\Gamma }}_0$ is reduced to the solution of(40) $$\begin{array}{c}\hfill \mathbf{S}{\mathit{\phi }}_n={\mathbf{p}}_m,{\mathit{\phi }}_n\in span\left\{{\mathbf{u}}_1,\dots ,{\mathbf{u}}_n\right\}.\end{array}$$(40)

The resultant solution of (40(40) $$\begin{array}{c}\hfill \mathbf{S}{\mathit{\phi }}_n={\mathbf{p}}_m,{\mathit{\phi }}_n\in span\left\{{\mathbf{u}}_1,\dots ,{\mathbf{u}}_n\right\}.\end{array}$$(40) ) is given by$${\mathit{\phi }}_n=\sum _{i=1}^n{C}_i{\mathbf{u}}_i,$$

then as (35(35) $$\begin{array}{c}\hfill {\mathit{\varphi }}_s(\mathbf{x})=\sum _{n=1}^{\infty }\sqrt{{\mathit{\lambda }}_n}{\mathit{\phi }}_n(\mathbf{x}){〈{\mathit{\phi }}_n,\mathit{\phi }〉}_{\mathrm{\Gamma }}.\end{array}$$(35) ) we represent the supersonic density and corresponding supersonic intensity as(41) $$\begin{array}{c}\hfill {\mathit{\phi }}^s=\sum _{i=1}^n\sqrt{{\mathit{\lambda }}_i}{C}_i{\mathbf{u}}_i,{\mathbf{I}}^s={|{\mathit{\phi }}^s|}^2.\end{array}$$(41)

Figure 3. Surface element decomposition for the numerical experiments. (a) Spherical surface, (b) cylinder with spherical end-caps, (c) cylindrical box and (d) half-space cylinder with spherical end-caps.

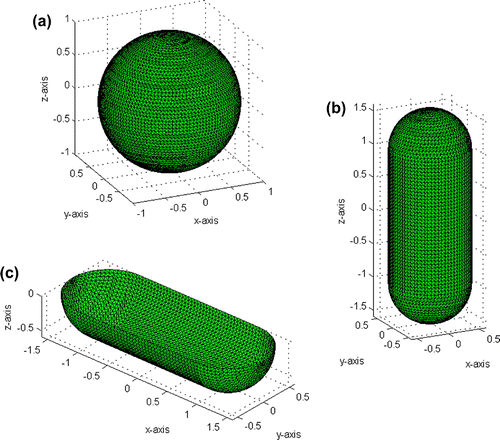
For the following numerical experiments we will choose to validate the proposed supersonic intensity methodology using smooth surfaces (that correspond to star-shaped domains) with different geometrical properties (see Figure 3). In all numerical experiments, the measured pressure at a point $\mathbf{x}\in {\mathrm{\Gamma }}_0$ is generated by the sum of the 10 monopoles distributed over a surface inside $\mathrm{\Omega }$. The analytical formula used to compute the field for each monopole is given by (6(6) $$\begin{array}{cc}\hfill {\left(K^{\prime }\mathit{\phi }\right)}^{+}(\mathbf{x})& :={\int }_{\mathrm{\Gamma }}\frac{\mathit{\partial }\mathrm{\Phi }(\mathbf{x},\mathbf{y})}{\mathit{\partial }\mathit{\nu }(\mathbf{x})}\mathit{\phi }(\mathbf{y})\mathrm{d}S(\mathbf{y})-\frac{1}{2}\mathit{\phi }(\mathbf{x}).\hfill \end{array}$$(6) ) or (27(27) $$\begin{array}{c}\hfill {\mathrm{\Phi }}_h(\mathbf{x},\mathbf{y})=\frac{exp\left(ik|\mathbf{x}-\mathbf{y}|\right)}{4\mathit{\pi }|\mathbf{x}-\mathbf{y}|}+h\frac{exp\left(ik|\mathbf{x}-{\mathbf{y}}^{\prime }|\right)}{4\mathit{\pi }|\mathbf{x}-{\mathbf{y}}^{\prime }|},{\mathbf{y}}^{\prime }=(y_1,y_2,-y_3).\end{array}$$(27) ) for half-space conditions. The column vector ${\mathbf{p}}_m$ contains the exact generated pressure $\mathbf{p}$ in ${\mathrm{\Gamma }}_0$ added by the vector $\mathbf{e}$ with Gaussian entries and 40 dB signal-to-noise ratio (SNR) to simulate measurement errors, i.e.$${\mathbf{p}}_m=\mathbf{p}+\mathbf{e},20ln\left(\frac{\Vert {\mathbf{p}}_m{-\mathbf{p}\Vert }_2}{{\Vert \mathbf{p}\Vert }_2}\right)=-40.$$

3.3. Spherical geometry

Here, $\mathrm{\Gamma }$ and ${\mathrm{\Gamma }}_0$ are spherical surfaces. The surfaces of $\mathrm{\Gamma }$ and ${\mathrm{\Gamma }}_0$ have, respectively, a radius of 1 and 1.05 m. The spherical surfaces are decomposed into 4990 points over 9976 triangles as shown in Figure 3(a). At $\mathrm{\Gamma }$ the maximum diameter between edges of the triangles is 5 cm and in ${\mathrm{\Gamma }}_0$ we keep an identical point distribution. Let the fluid sound speed be the speed of sound in air, $c=343$$\text{m}{\text{s}}^{-1}$ and density $\mathit{\rho }=1.21$$Kg{m}^{-3}$. 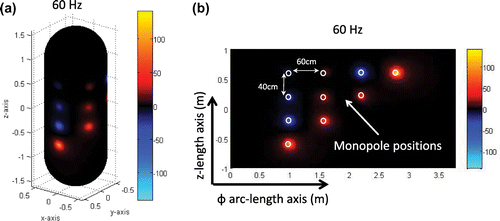The 10 monopoles, used to generate the data, are distributed over a sphere of radius 0.9 m with $(\mathit{\theta },\mathit{\varphi })$ locations shown in Figure 4(a). Between the monopoles, the minimal arc-length distance over the $\mathit{\varphi }$ directions is 60 cm and over the $\mathit{\theta }$ direction is 40 cm.

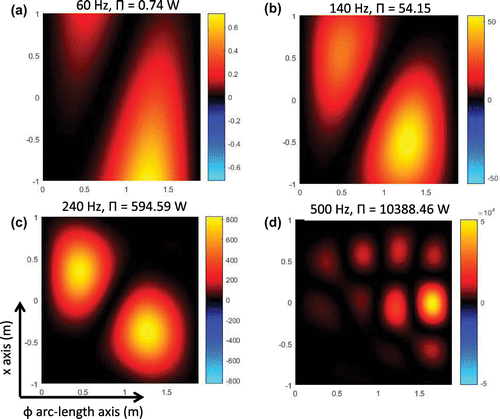
Over a spherical surface there is an explicit representation of the supersonic intensity based on spherical harmonic representation (see [9]). In Figure 5 we show the spherical supersonic intensity reconstruction and resultant power $\mathrm{\Pi }$. Notice that the supersonic intensity can be understood in terms of the half wavelength resolution $\mathit{\lambda }/2$. For 60 Hz, Figure 5(a) shows that the supersonic intensity resolution is 3.14 m. Similarly for 140Hz, Figure 5(b) shows that the supersonic resolution is 1.04 m. In Figure 5(c) the reconstruction for 240 Hz will have a resolution of 0.52 m. Finally Figure 5(d) shows the supersonic reconstruction for 500 Hz with a resolution of 31.4 cm which is smaller than the $\mathit{\varphi }$ arc-length separation between monopoles. In this case the supersonic intensity shows the separation $\mathit{\varphi }$ between the monopoles. Finally notice how close is the resultant power from the supersonic intensity as the exact power, even when the power from the supersonic intensity is a smoother version of the exact power.

The proposed numerical supersonic decomposition is based on the spectral decomposition of the power matrix $\mathbf{P}$ in (39(39) $$\begin{array}{c}\hfill \mathbf{P}=\sum _{i=1}^n{\mathit{\lambda }}_i{\mathbf{u}}_i{\mathbf{u}}_i^{\ast },\end{array}$$(39) ). The resultant basis is utilized to solve (40(40) $$\begin{array}{c}\hfill \mathbf{S}{\mathit{\phi }}_n={\mathbf{p}}_m,{\mathit{\phi }}_n\in span\left\{{\mathbf{u}}_1,\dots ,{\mathbf{u}}_n\right\}.\end{array}$$(40) ) for the coefficients $C_i$ and finally we obtain the non-negative intensity in $\mathrm{\Gamma }$ from (41(41) $$\begin{array}{c}\hfill {\mathit{\phi }}^s=\sum _{i=1}^n\sqrt{{\mathit{\lambda }}_i}{C}_i{\mathbf{u}}_i,{\mathbf{I}}^s={|{\mathit{\phi }}^s|}^2.\end{array}$$(41) ). This non-negative intensity is shown in Figure 6, and we observe that this intensity spatially matches the spherical supersonic intensity results in Figure 5. Moreover in Table 1 we show the power $\mathrm{\Pi }(\mathrm{\Gamma },\mathit{\phi })$ calculated from the exact numerically generated intensity ${\mathbf{I}}^v$ as in (38(38) $$\begin{array}{c}\hfill {\mathrm{\Pi }}_k((\mathrm{\Gamma },\mathit{\phi })\approx \frac{1}{2}\text{Re}\left\{{\left({\mathbf{W}}^{1/2}{\mathbf{v}}^v\right)}^{\ast }\left({\mathbf{W}}^{1/2}{\mathbf{p}}^v\right)\right\},\end{array}$$(38) ) and the power $\mathrm{\Pi }(\mathrm{\Gamma },{\mathit{\phi }}^{(s)})$ that results from the proposed non-negative intensity ${\mathbf{I}}^s$. The error in Table 1 shows that the power from the proposed non-negative intensity matches the exact power.

Figure 4. View of the exact intensity over the spherical plane $\mathit{\theta }$, $\mathit{\varphi }$. (a) Intensity at 60 Hz, (b) 140 Hz, (c) 240 Hz, and (d) 500 Hz.

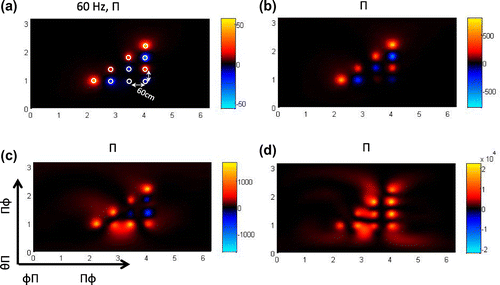
Figure 5. View of the spherical supersonic intensity over the spherical plane $\mathit{\theta }$, $\mathit{\varphi }$. (a) Intensity at 60 Hz, (b) 140 Hz, (c) 240 Hz, and (d) 500 Hz.

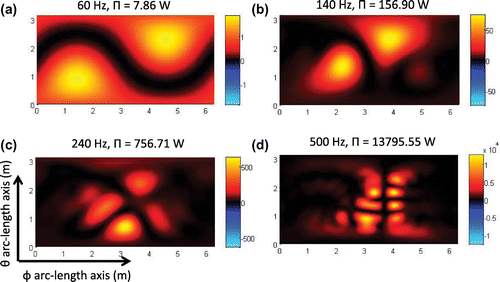
Figure 6. View of the calculated non-negative intensity using the power operator over the spherical plane $\mathit{\theta }$, $\mathit{\varphi }$. (a) Intensity at 60 Hz, (b) 140 Hz, (c) 240 Hz and (d) 500 Hz.

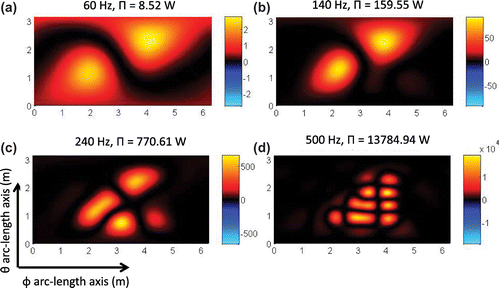
Table 1. Results from proposed supersonic intensity calculation over sphere.

freq (Hz)	$\mathrm{\Pi }(\mathrm{\Gamma },\mathit{\phi })$ (W)	$\mathrm{\Pi }(\mathrm{\Gamma },{\mathit{\phi }}^{(s)})$ (W)	% Relative error
60	8.52493	8.52005	0.05725
100	54.00441	54.02904	0.04559
140	159.21217	159.54925	0.21172
200	442.50394	444.42274	0.43362
240	768.11477	770.60661	0.32441
400	5425.05307	5520.77097	1.76437
500	13,837.04431	14,155.09496	2.29854
600	26,777.86938	27,657.30870	3.28420

3.4. Cylindrical geometry

Here, $\mathrm{\Gamma }$ and ${\mathrm{\Gamma }}_0$ are cylindrical surfaces with endcaps (see Figure 3(b)). $\mathrm{\Gamma }$ have a radius of 0.5 m and a length of 1 m. The corresponding end-caps are closed by half spheres of radius 0.5 m. The surface $\mathrm{\Gamma }$ is decomposed into 2462 points over 4920 triangles as shown in Figure 3(b). At $\mathrm{\Gamma }$ the maximum diameter between edges of the triangles is 5 cm. The cylindrical measurement surface ${\mathrm{\Gamma }}_0$ have a radius of 0.55 m and the length is 1 m. The corresponding spherical end-caps have radius of 0.55 m. There are 2782 points distributed over ${\mathrm{\Gamma }}_0$.

Figure 7. 3D View of exact intensity and the corresponding 2D view at 60 Hz.

Figure 8. View of the calculated non-negative intensity using the power operator over the cylindrical surface. (a) Intensity at 60 Hz, (b) 140 Hz, (c) 240 Hz, and (d) 500 Hz.

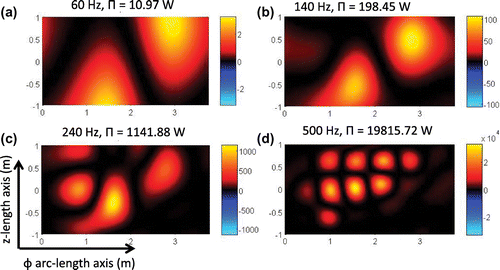
We utilize the proposed non-negative intensity technique as in the previous subsection and we plot the resultant intensity images in Figures 7 and 8. Notice that Figure 7(a) shows the 2D planar image display of the three-dimensional surface $\mathrm{\Gamma }$ image. Figure 7(b) shows the exact intensity ${\mathbf{I}}^v$ generated from 10 monopoles and the corresponding surface position of the monopoles. These monopoles are separated by 60 cm over the arc-length and 40 cm over the z axis. Figure 8 shows the resultant supersonic intensity ${\mathbf{I}}^s$ over four frequencies: 60, 140, 240 and 500 Hz. Notice, as in the case of the spherical geometry, that the resolution of the proposed non-negative intensity image increases with frequency. The image in Figure 8(d) shows that the supersonic reconstruction for 500 Hz have a resolution of 31.4 cm which is smaller than the minimal arc-length separation for the arc-length separation of 60 cm. We expect higher frequencies to be able to separate all monopoles effectively. As in the previous subsection we include Table 2 that compares the resultant power from non-negative intensity and the exact power. This table shows that the power from the non-negative intensity is close to the exact power.

Figure 9. 3D View of exact intensity and the corresponding 2D view at 500 Hz.

Table 2. Results from proposed non-negative intensity calculation over cylinder with spherical end-caps.

Freq (Hz)	$\mathrm{\Pi }(\mathrm{\Gamma },\mathit{\phi })$ (W)	$\mathrm{\Pi }\left(\mathrm{\Gamma },{\mathit{\phi }}^{(s)}\right)$ (W)	% Relative error
60	10.84644	10.96979	1.13721
100	68.11358	68.19500	0.11953
140	201.52913	198.44621	1.52976
200	607.55509	612.58618	0.82809
240	1176.43025	1141.88138	2.93675
400	9942.59951	10,504.16598	5.64808
500	19,218.04750	19,815.71634	3.10994
600	23,986.62309	25,144.01334	4.82515

Table 3. Results from proposed supersonic intensity calculation over half-space cylinder.

freq (Hz)	$\mathrm{\Pi }(\mathrm{\Gamma },\mathit{\phi })$ (W)	$\mathrm{\Pi }\left(\mathrm{\Gamma },{\mathit{\phi }}^{(s)}\right)$ (W)	% Relative error
60	0.58364	0.74105	26.97096
100	9.06277	10.69753	18.03816
140	52.75487	54.14611	2.63718
200	284.66673	287.14063	0.86905
240	586.91535	594.58866	1.30740
400	2806.62606	2862.62272	1.99516
500	10,092.91937	10,388.46125	2.92821
600	28,504.57161	29,537.48015	3.62366

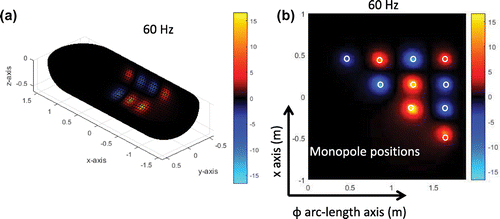
3.5. Half-cylinder

Here, ${\mathrm{\Gamma }}_h$ and ${\mathrm{\Gamma }}_{h,0}$ are half-cylindrical surfaces with spherical endcaps. The cylinders in ${\mathrm{\Gamma }}_h$ and ${\mathrm{\Gamma }}_{h,0}$ have, respectively, a radius of 1 m and 1.05 m and the length over x-axis is 2 m, where we consider only $x_3<0$. $\mathrm{\Gamma }$ is decomposed into 4990 points over 9780 triangles and ${\mathrm{\Gamma }}_0$ into 5392 points. At ${\mathrm{\Gamma }}_h$ the maximum diameter between edges of the triangles is 5cm. We utilize the proposed technique with the half-space power operator given in formula (31(31) $$\begin{array}{c}\hfill \left(P^h\mathit{\phi }\right)(\mathbf{x}):=\left(\frac{1}{8\mathit{\pi }\mathit{\rho }c}\right){\int }_{{\mathrm{\Gamma }}_h}\mathit{\phi }(\mathbf{y})\left\{j_0\left(k|\mathbf{x}-\mathbf{y}|\right)+h{j}_0\left(k|\mathbf{x}-{\mathbf{y}}^{\prime }|\right)\right\}\mathrm{d}S(\mathbf{y})\end{array}$$(31) ) and we plot the resultant intensity images in Figures 9 and 10. Figure 9(a) shows the 2D image display over the three-dimensional surface $\mathrm{\Gamma }$ and in Figure 9(b) we show the exact intensity ${\mathbf{I}}^v$ generated from 10 monopoles and the corresponding surface position of the monopoles. These monopoles have a minimum separation of 60 cm over the z axis and 40 cm separation over polar arc-length. Figure 10 shows the resultant non-negative intensity. Notice, as demonstrated in the previous experiments, that the resolution of the non-negative intensity image increases with frequency. As in the previous subsection we include Table 3 that shows the resultant power from non-negative intensity and the exact power. This table shows that the resultant power from the non-negative intensity is close to the exact power.

Figure 10. View of the calculated non-negative intensity using the power operator over the half cylindrical plane. (a) Intensity at 60 Hz, (b) 140 Hz, (c) 240 Hz, and (d) 500 Hz.

4. Conclusion

Sections 2 and 3 extended the theory proposed in [9]. We have shown explicit formulas of the kernel that corresponds to the power operator. These formulas are applied to discretize the power operator and obtain the eigenvalue decomposition that is used to approximate the non-negative intensity. The successful results for numerically generated data demonstrate that the proposed non-negative intensity approximates the supersonic intensity. Moreover, this non-negative intensity can be used to locate the radiation regions for arbitrary surfaces. There are promising results in Section 2 that can impact the numerical efficiency of the proposed numerical methodologies. Since the power operator is compact, the eigenvalues decay quickly to zero, and efficient Lanczos iterations can avoid the expensive calculation of the full eigenvalue decompositions for large matrix problems that result from complex vibrating structures.

Although it has not been the aim of this paper, there are still questions about the computation of the supersonic intensity for lower frequencies in which the acoustic half-wavelength is larger than the vibrator surface. When structural discontinuities are considerably smaller than the half-wavelength, bipolar intensity fields can occur and the constructed supersonic surface intensity is generally unable to locate the hot spots that radiate to the far-field. It has been proposed in previous papers [8,26] to include some subsonic information. Finally, it is also possible to utilize methodologies with index functions like [27,28], which have proven to resolve sources that are smaller than the acoustic wavelength.

Additional information

Funding

This work was supported by the Office of Naval Research.

Notes

No potential conflict of interest was reported by the author.

Appendix 1

Bessel function estimates

For the following lemma we will use the notation $(2n-1)!!=(2n-1)·(2n-3)··3·1$.

Lemma 1.1:

For $n>0$ we have the relation(A1) $$\begin{array}{cc}\hfill h_n(t)& =-i(2n-1)!!exp(it)\left(\frac{1}{t^{n+1}}+R_n(t)\right),\hfill \\ \hfill h_n^{\prime }(t)& =-i(2n-1)!!exp(it)\left(-\frac{(n+1)}{t^{n+2}}+D_n(t)\right),\hfill \end{array}$$(A1)

with the recurrence relations(A2) $$\begin{array}{cc}\hfill R_{n+1}(t)& =\frac{1}{x}{R}_n(t)-\frac{1}{(2n+1)(2n-1)}\left(R_{n-1}(t)+\frac{1}{t^n}\right),\hfill \end{array}$$(A2) (A3) $$\begin{array}{cc}\hfill D_n(t)& =-\frac{(n+1)}{x}{R}_n(t)+\frac{1}{(2n-1)}\left(R_{n-1}(t)+\frac{1}{t^n}\right),\hfill \\ \hfill R_0(t)& =0,R_1(t)=-\frac{i}{t}\hfill \end{array}$$(A3)

ProofSince $h_0(t)=-iexp(it)/t$ and $h_1(t)=-exp(it)(i+t)/t^2$ is simple to get the formulas for $R_0$ and $R_1$. Using the recurrence [22, Chapter 11.7]$$h_{n+1}(t)=\frac{2n+1}{t}{h}_n(t)-h_{n-1}(t).$$

we get the relations in (A1(A1) $$\begin{array}{cc}\hfill h_n(t)& =-i(2n-1)!!exp(it)\left(\frac{1}{t^{n+1}}+R_n(t)\right),\hfill \\ \hfill h_n^{\prime }(t)& =-i(2n-1)!!exp(it)\left(-\frac{(n+1)}{t^{n+2}}+D_n(t)\right),\hfill \end{array}$$(A1) ), (A2(A2) $$\begin{array}{cc}\hfill R_{n+1}(t)& =\frac{1}{x}{R}_n(t)-\frac{1}{(2n+1)(2n-1)}\left(R_{n-1}(t)+\frac{1}{t^n}\right),\hfill \end{array}$$(A2) ) for $R_n$. Similarly we can use the relation$$h_n^{\prime }(t)=h_{n-1}(t)-\frac{n+1}{t}{h}_n(t)$$

to obtain the relation for $D_n$ in (A1(A1) $$\begin{array}{cc}\hfill h_n(t)& =-i(2n-1)!!exp(it)\left(\frac{1}{t^{n+1}}+R_n(t)\right),\hfill \\ \hfill h_n^{\prime }(t)& =-i(2n-1)!!exp(it)\left(-\frac{(n+1)}{t^{n+2}}+D_n(t)\right),\hfill \end{array}$$(A1) ), (A3(A3) $$\begin{array}{cc}\hfill D_n(t)& =-\frac{(n+1)}{x}{R}_n(t)+\frac{1}{(2n-1)}\left(R_{n-1}(t)+\frac{1}{t^n}\right),\hfill \\ \hfill R_0(t)& =0,R_1(t)=-\frac{i}{t}\hfill \end{array}$$(A3) ).

Lemma 1.2:

For $n>1$ the remainders have the following behaviour(A4) $$\begin{array}{cc}\hfill R_n(t)& =\frac{1}{t}\left\{\frac{{(-i)}^n}{(2n-1)!!}+O\left(\frac{1}{t}\right)\right\},\hfill \end{array}$$(A4) (A5) $$\begin{array}{cc}\hfill D_n(t)& =\frac{1}{t}\left\{\frac{{(-i)}^{n-1}}{(2n-1)!!}+O\left(\frac{1}{t}\right)\right\},\hfill \end{array}$$(A5) (A6) $$\begin{array}{cc}\hfill R_n(t)\overline{D_n(t)}& =\frac{1}{t^2}\left\{-\frac{i}{{((2n-1)!!)}^2}+O\left(\frac{1}{t}\right)\right\},\hfill \end{array}$$(A6)

ProofThe formulas (A4(A4) $$\begin{array}{cc}\hfill R_n(t)& =\frac{1}{t}\left\{\frac{{(-i)}^n}{(2n-1)!!}+O\left(\frac{1}{t}\right)\right\},\hfill \end{array}$$(A4) ), (A5(A5) $$\begin{array}{cc}\hfill D_n(t)& =\frac{1}{t}\left\{\frac{{(-i)}^{n-1}}{(2n-1)!!}+O\left(\frac{1}{t}\right)\right\},\hfill \end{array}$$(A5) ) follows using induction with the remainder recurrence relations in (A2(A2) $$\begin{array}{cc}\hfill R_{n+1}(t)& =\frac{1}{x}{R}_n(t)-\frac{1}{(2n+1)(2n-1)}\left(R_{n-1}(t)+\frac{1}{t^n}\right),\hfill \end{array}$$(A2) ), (A3(A3) $$\begin{array}{cc}\hfill D_n(t)& =-\frac{(n+1)}{x}{R}_n(t)+\frac{1}{(2n-1)}\left(R_{n-1}(t)+\frac{1}{t^n}\right),\hfill \\ \hfill R_0(t)& =0,R_1(t)=-\frac{i}{t}\hfill \end{array}$$(A3) ), respectively. Then using formula (A4(A4) $$\begin{array}{cc}\hfill R_n(t)& =\frac{1}{t}\left\{\frac{{(-i)}^n}{(2n-1)!!}+O\left(\frac{1}{t}\right)\right\},\hfill \end{array}$$(A4) ) in the relation$$R_n(t)\overline{D_n(t)}=-\frac{(n+1)}{t}{|R_n(t)|}^2+\frac{1}{(2n-1)}\left(R_n(t)\overline{R_{n-1}(t)}+\frac{R_n(t)}{t^n}\right)$$

yields (A6(A6) $$\begin{array}{cc}\hfill R_n(t)\overline{D_n(t)}& =\frac{1}{t^2}\left\{-\frac{i}{{((2n-1)!!)}^2}+O\left(\frac{1}{t}\right)\right\},\hfill \end{array}$$(A6) ).