A golden section search method for the identification of skin subsurface abnormalities

Abstract

The metabolic heat generation rate directly quantifies either the presence or the absence of tumour and the degree of inflammations in the biological tissue. This work presents an inverse method aimed at estimating the rate of metabolic heat generation using the dynamic temperature response from the skin obtained under an imposed heat flux by solving the transient non-Fourier thermal wave bioheat equation using the finite difference method. The golden section search method (GSSM)-based inverse method has been applied to solve an inverse problem minimizing the Euclidean norm of the known and guessed temperature distributions. The effect of random noise has been studied and a reasonably accurate identification of healthy and unhealthy metabolic heat generation rates has been characterized. The present work offers a novel inverse technique based on GSSM algorithm to predict the pertinent heat generation rate from the transient temperature distribution that can be obtained using spatially offset Raman spectroscopy, microwave thermography and other potential techniques.

Keywords:

• Inverse problems
• GSSM algorithm
• subsurface temperature
• bioheat transfer
• metabolic heat generation rate

Subject Classification:

• 80A23

1. Introduction

Cancers and tumours are some of the commonly observed phenomena in the contemporary scenario. These disorders involve very high rate of metabolic heat generation and low blood perfusion rates as compared to normal tissues [1,2]. Not only this, high rates of metabolic heat generation also occur in tissues sustaining inflammations [3]. Generally, the temperature at the surface and the subsurface of the skin depends on the metabolic activity, the perfusion rate of blood and the temperature of the surroundings. Microwave thermography [4] and offset Raman spectroscopy [5] are some of the latest and potential methods to determine the subsurface skin temperature. The radiative heat from the body [6], Monte Carlo method [7], telemetry thermistors and thermal camera [8] can be also used to gauge the skin surface temperature. Recent advancements in laser and microwave technologies have resulted in considerable progress in thermal treatment of skin cancer and burns.

In the past, many studies have revealed a wide range of research on heat transfer within the biological tissues [9–11]. The mathematical modelling of biological tissues is broadly categorized into two groups such as the parabolic model based on the Fourier’s law of heat conduction and the hyperbolic model based on the non-Fourier’s law of heat conduction [12]. The non-Fourier hyperbolic heat conduction model is further categorized into two types involving single phase lag and dual phase lag phenomena [13]. However, it is experimentally found that, the wave-type phenomenon of heat conduction exists in certain situations where the Fourier’s model mismatches with the actual situation [14]. One of such situations is the biological tissue for which the thermal relaxation time is lengthy which consequently results in the non-Fourier law of heat conduction and the hyperbolic model becomes valid. The modification of Fourier’s law was revealed by Cattaneo [15] and Vernotte [16] as an extension of the Fourier’s equation. There are several methods on non-Fourier bioheat transfer problems reported in the past. For instance, Zhou et al. [17] studied a heat conduction problem to assess the thermal damage in tissues due to laser heating and it was concluded that the prediction is unreliable without considering the non-Fourier effect. The hyperbolic bioheat transfer problem under focused and collimated laser irradiation was solved with the aid of the MacCormack’s scheme by Jaunich et al. [18]. Xu et al. [19] developed a thermal-neural technique to study the role of non-Fourier effect in the transduction process of skin thermal pain. Liu et al. [20] considered a non-Fourier multi-layer model for skin using Taylor series expansion to study the temperature distribution with time and space. Ahmadikia et al. [21] and Fazlali and Ahmadikia [22] used the Laplace transformation method to solve various parabolic and hyperbolic bioheat transfer problems. Analytical solutions for Fourier and non-Fourier bioheat analysis of skin under general transient heating was investigated by Lin [23]. Kumar et al. [24] used a hybrid method based on the Legendre wavelet basis function to solve non-Fourier bioheat transfer equation numerically. Hyperbolic thermal wave and dual phase lag bioheat equations are solved analytically under constant and oscillatory surface heat flux by Forghani et al. [25]. Recently, Lin and Li [26] provided analytical solutions for non-Fourier bioheat transfer problem subjected to a pulsed laser using the mode superposition method.

It is found from the literature survey that, most of the available literatures on bioheat transfer serve to evaluate the response of the biological tissue under a given set of known and imposed conditions. For example, the appraisal of temperature field at the skin surface and subsurface for a given heat flux is one of such examples. Such kind of approach belongs to the group of well-posed direct (forward) problems where a defined procedure exist [27]. However, the situation becomes different and somewhat difficult when an observed phenomenon is only available, but the exact reason of such consequence remains unidentified. The problem is then referred as an inverse problem [28,29] which is invariably ill-posed and the accuracy of its solution depends on the presence of noise (measurement error) [30]. Nevertheless, some inverse problems aimed at solving bioheat transfer problems are observed in the available literatures. For example, Majchrzak and Mochnacki [31] inversely solved the Pennes bioheat transfer (PBT) equation using the boundary element method. Partridge and Wrobel [32] used the skin surface temperature to estimate the location and size of the skin tumour. For the analysis, they used the dual reciprocity method in conjunction with the genetic algorithm. However, their analysis was also restricted to the Fourier model of bioheat equation. The rate of blood perfusion, thermal conductivity and volumetric heat capacity were estimated by Yue et al. [33] for a Fourier heat conduction-based bioheat transfer problem. They used a real-coded genetic algorithm for the analysis. Using nonlinear least squares method, Trucu et al. [34] performed inverse coefficient identification analysis for a parabaolic heat conduction-based bioheat equation to conclude that additional measurements are necessary for obtaining a unique solution. Trucu et al. [35] further predicted the time-dependent perfusion coefficient in a one-dimensional bio-heat conduction equation using Tikhonov’s regularization method for the inverse analysis. They have also predicted the time and space-dependent perfusion coefficient for the same problem [36]. However, these studies did not consider the hyperbolic thermal wave bioheat model. Das et al. [37] determined the size and the location of tumour in a biological tissue in a Fourier heat conduction-based PBT problem with the aid of genetic algorithm. With the aid of boundary element method in conjunction with the finite difference method (FDM)-assisted Tikhonov regularization, Hazanee and Lesnic [38] retrieve the time-dependent blood perfusion coefficient in a PBT problem. The estimation of size and locations of a tumour in a three-dimensional breast was done by Das and Mishra [39], but the study neglected the non-Fourier effect of heat conduction.

It becomes apparent from the literature survey that many studies estimated diverse biological parameters, which are difficult to be directly measured using inverse method (a powerful tool for predicting parameters). However, the above analyses were restricted to the parabolic nature of Pennes bioheat model. But, the hyperbolic heat conduction-based thermal wave model is not yet considered for the inverse analysis. However, for bioheat transfer analysis, it is more accurate to use the hyperbolic condition because of large thermal relaxation time of the biological tissues [40]. Furthermore, due to the existence of first-order time derivative, the PBT equation should not be used to characterize the temperature oscillation phenomenon in biological tissues [41]. It is well known that as compared to a normal biological human tissue possessing the rate of metabolic heat generation of 368 W/m³ [42], the metabolic heat generation rate in a malignant and inflammation-sustained tissue increases approximately to 29,000 W/m³ and higher [43]. Evidently, the respective thermal signatures at the skin surface and tissue medium due to the discrepancy of metabolic heat generation rates will also differ.

2. Mathematical models and formulation

A one-dimensional transient bioheat transfer analysis for the skin tissue as shown in Figure 1 is undertaken in the present work. The skin surface is subjected to a constant heat flux condition, whereas, the other boundary (i.e. within the tissue) is considered insulated. The transient temperature of the tissue is investigated by solving a forward problem using the FDM. At first, comparisons of the forward analysis are demonstrated to demonstrate the variation between the Fourier’s law of heat conduction-based PBT and the non-Fourier thermal wave bioheat transfer (TWBT) models. Thereafter, the non-Fourier heat conduction-based hyperbolic TWBT model is inversely solved to identify the metabolic heat generation rate to quantify the abnormalities within a biological tissue using the thermal signature of the tissue. The inverse problem is solved with the aid of the golden section search method (GSSM) in conjunction with the FDM. The relevant PBT equation for modelling thermal distribution in the biological tissues can be written as [9],(1) $${\mathit{\rho }}_t{c}_t\frac{\mathit{\partial }T}{\mathit{\partial }t}+{\mathit{\rho }}_b{\mathit{\varpi }}_b{c}_b\left(T-T_a\right)=k\frac{{\mathit{\partial }}^{2}T}{\mathit{\partial }{x}^2}+q_m+q_{\text{ext}},$$(1)

Figure 1. Schematic diagram of the problem.

where ρ _t is the density of skin tissue, c _t is the specific heat of the skin tissue, T is the local temperature of the skin tissue, ρ _b represents the blood density, ${\mathit{\varpi }}_b$ pertains to the blood perfusion rate, c _b is the specific heat of the blood, T _a is the uniform blood temperature and k is the skin thermal conductivity. Additionally, q _m is the rate of metabolic heat generation within the skin tissue and q _ext is the heat generated due to other heating sources.

In order to determine the temperature distribution of the PBT equation, Equation (1(1) $${\mathit{\rho }}_t{c}_t\frac{\mathit{\partial }T}{\mathit{\partial }t}+{\mathit{\rho }}_b{\mathit{\varpi }}_b{c}_b\left(T-T_a\right)=k\frac{{\mathit{\partial }}^{2}T}{\mathit{\partial }{x}^2}+q_m+q_{\text{ext}},$$(1) ), one initial and boundary conditions are required as Equation (1(1) $${\mathit{\rho }}_t{c}_t\frac{\mathit{\partial }T}{\mathit{\partial }t}+{\mathit{\rho }}_b{\mathit{\varpi }}_b{c}_b\left(T-T_a\right)=k\frac{{\mathit{\partial }}^{2}T}{\mathit{\partial }{x}^2}+q_m+q_{\text{ext}},$$(1) ) is the second-order equation in space derivative and first order in the time derivative. The pertinent initial and boundary conditions for PBT model are represented below,(2) $$\text{Initial}\text{conditions}:T\left(x,0\right)=T_a,0\le x\le L;{\left.\frac{\mathit{\partial }T}{\mathit{\partial }t}\right|}_{t=0}=0,0\le x\le L,$$(2) (3) $$\text{Boundary}\text{conditions}:{\left.-k\frac{\mathit{\partial }T}{\mathit{\partial }x}\right|}_{x=0}=q_0;{\left.\frac{\mathit{\partial }T}{\mathit{\partial }x}\right|}_{x=L}=0,$$(3)

where L is the length of the finite tissue domain and q ₀ is the imposed heat flux at the skin surface.

It may be easily noted that the PBT equation revealed in Equation (1(1) $${\mathit{\rho }}_t{c}_t\frac{\mathit{\partial }T}{\mathit{\partial }t}+{\mathit{\rho }}_b{\mathit{\varpi }}_b{c}_b\left(T-T_a\right)=k\frac{{\mathit{\partial }}^{2}T}{\mathit{\partial }{x}^2}+q_m+q_{\text{ext}},$$(1) ) is a parabolic partial differential equation governed by the Fourier’s law of heat conduction. In the Fourier’s law of heat conduction, it is assumed that the propagation speed of thermal distribution is infinite. However, as pointed out earlier that, for heat transfer analysis in biological tissues, it is more appropriate to consider the non-Fourier hyperbolic heat conduction due to large thermal relaxation time of biological tissues [40]. Therefore, with this consideration, Equation (1(1) $${\mathit{\rho }}_t{c}_t\frac{\mathit{\partial }T}{\mathit{\partial }t}+{\mathit{\rho }}_b{\mathit{\varpi }}_b{c}_b\left(T-T_a\right)=k\frac{{\mathit{\partial }}^{2}T}{\mathit{\partial }{x}^2}+q_m+q_{\text{ext}},$$(1) ) modifies into TWBT equation as below [21],(4) $${\mathit{\tau }}_q{\mathit{\rho }}_t{c}_t\frac{{\mathit{\partial }}^{2}T}{\mathit{\partial }{t}^2}+\left({\mathit{\rho }}_t{c}_t+{\mathit{\tau }}_q{\mathit{\rho }}_b{\mathit{\varpi }}_b{c}_b\right)\frac{\mathit{\partial }T}{\mathit{\partial }t}+{\mathit{\rho }}_b{\mathit{\varpi }}_b{c}_b\left(T-T_a\right)=k\frac{{\mathit{\partial }}^{2}T}{\mathit{\partial }{x}^2}+\left(q_m+q_{\text{ext}}+{\mathit{\tau }}_q\frac{\mathit{\partial }{q}_m}{\mathit{\partial }t}+{\mathit{\tau }}_q\frac{\mathit{\partial }{q}_{\text{ext}}}{\mathit{\partial }t}\right),$$(4)

where τ _q = α /C ² is the thermal relaxation time, α is the thermal diffusivity and C is the speed of the thermal wave. Since Equation (4(4) $${\mathit{\tau }}_q{\mathit{\rho }}_t{c}_t\frac{{\mathit{\partial }}^{2}T}{\mathit{\partial }{t}^2}+\left({\mathit{\rho }}_t{c}_t+{\mathit{\tau }}_q{\mathit{\rho }}_b{\mathit{\varpi }}_b{c}_b\right)\frac{\mathit{\partial }T}{\mathit{\partial }t}+{\mathit{\rho }}_b{\mathit{\varpi }}_b{c}_b\left(T-T_a\right)=k\frac{{\mathit{\partial }}^{2}T}{\mathit{\partial }{x}^2}+\left(q_m+q_{\text{ext}}+{\mathit{\tau }}_q\frac{\mathit{\partial }{q}_m}{\mathit{\partial }t}+{\mathit{\tau }}_q\frac{\mathit{\partial }{q}_{\text{ext}}}{\mathit{\partial }t}\right),$$(4) ) involves two second-order derivatives in space and time, thus, in the present work, the following initial and boundary conditions (as shown in Figure 1) are considered,(5) $$\text{Initial}\text{conditions}:T\left(x,0\right)=T_a,0\le x\le L;{\left.\frac{\mathit{\partial }T}{\mathit{\partial }t}\right|}_{t=0}=0,0\le x\le L,$$(5) (6) $$\text{Boundary}\text{conditions}:{\left.-k\frac{\mathit{\partial }T}{\mathit{\partial }x}\right|}_{x=0}=q_0;{\left.\frac{\mathit{\partial }T}{\mathit{\partial }x}\right|}_{x=L}=0.$$(6)

Next, the governing energy equation, Equation (4(4) $${\mathit{\tau }}_q{\mathit{\rho }}_t{c}_t\frac{{\mathit{\partial }}^{2}T}{\mathit{\partial }{t}^2}+\left({\mathit{\rho }}_t{c}_t+{\mathit{\tau }}_q{\mathit{\rho }}_b{\mathit{\varpi }}_b{c}_b\right)\frac{\mathit{\partial }T}{\mathit{\partial }t}+{\mathit{\rho }}_b{\mathit{\varpi }}_b{c}_b\left(T-T_a\right)=k\frac{{\mathit{\partial }}^{2}T}{\mathit{\partial }{x}^2}+\left(q_m+q_{\text{ext}}+{\mathit{\tau }}_q\frac{\mathit{\partial }{q}_m}{\mathit{\partial }t}+{\mathit{\tau }}_q\frac{\mathit{\partial }{q}_{\text{ext}}}{\mathit{\partial }t}\right),$$(4) ) is non-dimensionalized with the aid of the following dimensionless variables,(7) $$\mathrm{\Lambda }=\frac{w_b{c}_b}{{\mathit{\rho }}_t{c}_t}{\mathit{\tau }}_q;\mathit{\theta }=\frac{T-T_a}{q_0}\sqrt{k{w}_b{c}_b};\mathit{\eta }=\frac{w_b{c}_b}{{\mathit{\rho }}_t{c}_t}t;\mathit{\xi }=\sqrt{\frac{w_b{c}_b}{k}}x;\mathit{\psi }=\frac{q_m\sqrt{k}}{q_0\sqrt{w_b{c}_b}},$$(7)

where w _b = ρ _b ${\mathit{\varpi }}_b$. Thus the dimensionless form of the governing non-Fourier TWBT equation, Equation (4(4) $${\mathit{\tau }}_q{\mathit{\rho }}_t{c}_t\frac{{\mathit{\partial }}^{2}T}{\mathit{\partial }{t}^2}+\left({\mathit{\rho }}_t{c}_t+{\mathit{\tau }}_q{\mathit{\rho }}_b{\mathit{\varpi }}_b{c}_b\right)\frac{\mathit{\partial }T}{\mathit{\partial }t}+{\mathit{\rho }}_b{\mathit{\varpi }}_b{c}_b\left(T-T_a\right)=k\frac{{\mathit{\partial }}^{2}T}{\mathit{\partial }{x}^2}+\left(q_m+q_{\text{ext}}+{\mathit{\tau }}_q\frac{\mathit{\partial }{q}_m}{\mathit{\partial }t}+{\mathit{\tau }}_q\frac{\mathit{\partial }{q}_{\text{ext}}}{\mathit{\partial }t}\right),$$(4) ) can be written in the following manner,(8) $$\mathrm{\Lambda }\frac{{\mathit{\partial }}^2\mathit{\theta }}{\mathit{\partial }{\mathit{\eta }}^2}+\left(1+\mathrm{\Lambda }\right)\frac{\mathit{\partial }\mathit{\theta }}{\mathit{\partial }\mathit{\eta }}+\mathit{\theta }=\frac{{\mathit{\partial }}^2\mathit{\theta }}{\mathit{\partial }{\mathit{\xi }}^2}+\mathit{\psi }.$$(8)

The corresponding dimensionless initial and boundary conditions can be derived from Equations (5(5) $$\text{Initial}\text{conditions}:T\left(x,0\right)=T_a,0\le x\le L;{\left.\frac{\mathit{\partial }T}{\mathit{\partial }t}\right|}_{t=0}=0,0\le x\le L,$$(5) ) and (6(6) $$\text{Boundary}\text{conditions}:{\left.-k\frac{\mathit{\partial }T}{\mathit{\partial }x}\right|}_{x=0}=q_0;{\left.\frac{\mathit{\partial }T}{\mathit{\partial }x}\right|}_{x=L}=0.$$(6) ) as,(9) $$\text{Initial}\text{conditions}:\mathit{\theta }\left(\mathit{\xi },0\right)=0;{\left.\frac{\mathit{\partial }\mathit{\theta }}{\mathit{\partial }\mathit{\eta }}\right|}_{\mathit{\eta }=0}=0,$$(9) (10) $$\text{Boundary}\text{conditions}:{\left.\frac{\mathit{\partial }\mathit{\theta }}{\mathit{\partial }\mathit{\xi }}\right|}_{\mathit{\xi }=0}=-1;{\left.\frac{\mathit{\partial }\mathit{\theta }}{\mathit{\partial }\mathit{\xi }}\right|}_{\mathit{\xi }=\sqrt{\frac{w_b{c}_b}{k}}L}=0.$$(10)

It can be observed that the TWBT indicated by Equation (8(8) $$\mathrm{\Lambda }\frac{{\mathit{\partial }}^2\mathit{\theta }}{\mathit{\partial }{\mathit{\eta }}^2}+\left(1+\mathrm{\Lambda }\right)\frac{\mathit{\partial }\mathit{\theta }}{\mathit{\partial }\mathit{\eta }}+\mathit{\theta }=\frac{{\mathit{\partial }}^2\mathit{\theta }}{\mathit{\partial }{\mathit{\xi }}^2}+\mathit{\psi }.$$(8) ) is a hyperbolic partial differential equation. Next, the energy equations, Equations (1(1) $${\mathit{\rho }}_t{c}_t\frac{\mathit{\partial }T}{\mathit{\partial }t}+{\mathit{\rho }}_b{\mathit{\varpi }}_b{c}_b\left(T-T_a\right)=k\frac{{\mathit{\partial }}^{2}T}{\mathit{\partial }{x}^2}+q_m+q_{\text{ext}},$$(1) ) and (8(8) $$\mathrm{\Lambda }\frac{{\mathit{\partial }}^2\mathit{\theta }}{\mathit{\partial }{\mathit{\eta }}^2}+\left(1+\mathrm{\Lambda }\right)\frac{\mathit{\partial }\mathit{\theta }}{\mathit{\partial }\mathit{\eta }}+\mathit{\theta }=\frac{{\mathit{\partial }}^2\mathit{\theta }}{\mathit{\partial }{\mathit{\xi }}^2}+\mathit{\psi }.$$(8) ) subject to the initial conditions, Equations (2(2) $$\text{Initial}\text{conditions}:T\left(x,0\right)=T_a,0\le x\le L;{\left.\frac{\mathit{\partial }T}{\mathit{\partial }t}\right|}_{t=0}=0,0\le x\le L,$$(2) , 9(9) $$\text{Initial}\text{conditions}:\mathit{\theta }\left(\mathit{\xi },0\right)=0;{\left.\frac{\mathit{\partial }\mathit{\theta }}{\mathit{\partial }\mathit{\eta }}\right|}_{\mathit{\eta }=0}=0,$$(9) ) and boundary conditions, Equations (3(3) $$\text{Boundary}\text{conditions}:{\left.-k\frac{\mathit{\partial }T}{\mathit{\partial }x}\right|}_{x=0}=q_0;{\left.\frac{\mathit{\partial }T}{\mathit{\partial }x}\right|}_{x=L}=0,$$(3) ) and (10(10) $$\text{Boundary}\text{conditions}:{\left.\frac{\mathit{\partial }\mathit{\theta }}{\mathit{\partial }\mathit{\xi }}\right|}_{\mathit{\xi }=0}=-1;{\left.\frac{\mathit{\partial }\mathit{\theta }}{\mathit{\partial }\mathit{\xi }}\right|}_{\mathit{\xi }=\sqrt{\frac{w_b{c}_b}{k}}L}=0.$$(10) ) are solved to determine the thermal distribution in the living tissues against the PBT and the TWBT models. In the next section, the solution procedure is explained.

3. Forward analysis

The present section has been dedicated for evaluating the thermal distribution in the living tissues. At first, the TWBT (hyperbolic) equation, Equation (8(8) $$\mathrm{\Lambda }\frac{{\mathit{\partial }}^2\mathit{\theta }}{\mathit{\partial }{\mathit{\eta }}^2}+\left(1+\mathrm{\Lambda }\right)\frac{\mathit{\partial }\mathit{\theta }}{\mathit{\partial }\mathit{\eta }}+\mathit{\theta }=\frac{{\mathit{\partial }}^2\mathit{\theta }}{\mathit{\partial }{\mathit{\xi }}^2}+\mathit{\psi }.$$(8) ), subject to the conditions (9(9) $$\text{Initial}\text{conditions}:\mathit{\theta }\left(\mathit{\xi },0\right)=0;{\left.\frac{\mathit{\partial }\mathit{\theta }}{\mathit{\partial }\mathit{\eta }}\right|}_{\mathit{\eta }=0}=0,$$(9) ) and (10(10) $$\text{Boundary}\text{conditions}:{\left.\frac{\mathit{\partial }\mathit{\theta }}{\mathit{\partial }\mathit{\xi }}\right|}_{\mathit{\xi }=0}=-1;{\left.\frac{\mathit{\partial }\mathit{\theta }}{\mathit{\partial }\mathit{\xi }}\right|}_{\mathit{\xi }=\sqrt{\frac{w_b{c}_b}{k}}L}=0.$$(10) ) has been solved. Thereafter, using a similar approach, the solution of the PBT (parabolic) has been obtained. The governing equation subject to the given conditions (initial and boundary conditions) has been solved by using the FDM by considering τ _q = 16 s, c _t = 3600 J/(kg K), c _b = 3770 J/(kg K), ρ _t = 1190 kg/m³, ρ _b = 1060 kg/m³, ${\mathit{\varpi }}_b$ = 4.7169 × 10⁻⁴ s⁻¹, k = 0.235 W/(m.K) and T _a = 37 °C [42]. The difference equations have been obtained by discretizing the governing equation (Equation 8(8) $$\mathrm{\Lambda }\frac{{\mathit{\partial }}^2\mathit{\theta }}{\mathit{\partial }{\mathit{\eta }}^2}+\left(1+\mathrm{\Lambda }\right)\frac{\mathit{\partial }\mathit{\theta }}{\mathit{\partial }\mathit{\eta }}+\mathit{\theta }=\frac{{\mathit{\partial }}^2\mathit{\theta }}{\mathit{\partial }{\mathit{\xi }}^2}+\mathit{\psi }.$$(8) ) as well as the initial conditions (Equation 9(9) $$\text{Initial}\text{conditions}:\mathit{\theta }\left(\mathit{\xi },0\right)=0;{\left.\frac{\mathit{\partial }\mathit{\theta }}{\mathit{\partial }\mathit{\eta }}\right|}_{\mathit{\eta }=0}=0,$$(9) ) and boundary conditions (Equation 10(10) $$\text{Boundary}\text{conditions}:{\left.\frac{\mathit{\partial }\mathit{\theta }}{\mathit{\partial }\mathit{\xi }}\right|}_{\mathit{\xi }=0}=-1;{\left.\frac{\mathit{\partial }\mathit{\theta }}{\mathit{\partial }\mathit{\xi }}\right|}_{\mathit{\xi }=\sqrt{\frac{w_b{c}_b}{k}}L}=0.$$(10) ) using the following central difference formulae:(11a) $${\left(\frac{{\mathit{\partial }}^2\mathit{\theta }}{\mathit{\partial }{\mathit{\xi }}^2}\right)}_{ij}=\frac{{\mathit{\theta }}_{i+1,j}-2{\mathit{\theta }}_{i,j}+{\mathit{\theta }}_{i-1,j}}{{\left(\mathrm{\Delta }\mathit{\xi }\right)}^2}+O\left(\mathrm{\Delta }{\mathit{\xi }}^2\right),$$(11a) (11b) $${\left(\frac{\mathit{\partial }\mathit{\theta }}{\mathit{\partial }\mathit{\eta }}\right)}_{ij}=\frac{{\mathit{\theta }}_{i,j+1}-{\mathit{\theta }}_{i,j-1}}{2\mathrm{\Delta }\mathit{\eta }}+O\left(\mathrm{\Delta }\mathit{\eta }\right),$$(11b) (11c) $${\left(\frac{{\mathit{\partial }}^2\mathit{\theta }}{\mathit{\partial }{\mathit{\eta }}^2}\right)}_{ij}=\frac{{\mathit{\theta }}_{i,j+1}-2{\mathit{\theta }}_{i,j-1}+{\mathit{\theta }}_{i,j-1}}{{\left(\mathrm{\Delta }\mathit{\eta }\right)}^2}+O\left(\mathrm{\Delta }{\mathit{\eta }}^2\right),$$(11c)

where i is the grid-index in the space coordinate (i.e. ξ direction) with ${\mathit{\xi }}_i=i\times \mathrm{\Delta }\mathit{\xi };i=0,1,2,\dots ..,N_1$ and Δξ is the increment along the ξ-direction. Similarly, j is the grid-index in time coordinate (i.e. η direction) with ${\mathit{\eta }}_j=j\times \mathrm{\Delta }\mathit{\eta };j=1,2,\dots ,N_2$ where Δη is the increment along that η direction. After using the above-described scheme, a system of linear equations has been generated in which the coefficient matrix is written in the form of a tri-diagonal matrix. In order to determine the final result, the tri-diagonal matrix system has been solved by applying the Thomas algorithm, and the final results are obtained after satisfying the desired accuracy. In the present work, the order of accuracy has been considered as $O\left({10}^{-5}\right)$ to minimize the discretization error. Although an implicit scheme is used in the forward analysis, still we have taken care of the numerical stability of the forward method by satisfying the CFL (Courant–Friedrichs–Lewy) condition [44]. For the present problem, the CFL condition for the PBT equation is considered as $\frac{\mathrm{\Delta }\mathit{\eta }}{{\left(\mathrm{\Delta }\mathit{\xi }\right)}^2}\le \frac{1}{2},$ whereas, for TWBT, the CFL condition is taken as, $\frac{1}{\mathrm{\Lambda }}{\left(\frac{\mathrm{\Delta }\mathit{\eta }}{\mathrm{\Delta }\mathit{\xi }}\right)}^2\le 1.0.$ Since the FDM is very well known, the details of this method are omitted here. The details about FDM can be found out in several books on numerical analysis (for example, [44]).

4. Inverse analysis

Here, the approximate solution of the second-order hyperbolic partial differential equation (Equation (8(8) $$\mathrm{\Lambda }\frac{{\mathit{\partial }}^2\mathit{\theta }}{\mathit{\partial }{\mathit{\eta }}^2}+\left(1+\mathrm{\Lambda }\right)\frac{\mathit{\partial }\mathit{\theta }}{\mathit{\partial }\mathit{\eta }}+\mathit{\theta }=\frac{{\mathit{\partial }}^2\mathit{\theta }}{\mathit{\partial }{\mathit{\xi }}^2}+\mathit{\psi }.$$(8) )) subject to the initial and boundary conditions, Equations (9(9) $$\text{Initial}\text{conditions}:\mathit{\theta }\left(\mathit{\xi },0\right)=0;{\left.\frac{\mathit{\partial }\mathit{\theta }}{\mathit{\partial }\mathit{\eta }}\right|}_{\mathit{\eta }=0}=0,$$(9) ) and (10(10) $$\text{Boundary}\text{conditions}:{\left.\frac{\mathit{\partial }\mathit{\theta }}{\mathit{\partial }\mathit{\xi }}\right|}_{\mathit{\xi }=0}=-1;{\left.\frac{\mathit{\partial }\mathit{\theta }}{\mathit{\partial }\mathit{\xi }}\right|}_{\mathit{\xi }=\sqrt{\frac{w_b{c}_b}{k}}L}=0.$$(10) ) is evaluated using the forward method (i.e. the FDM) described above for the case of TWBT equation. Moreover, for solving PBT, the same procedure followed for solving TWBT is used. In this case too, we have considered the same accuracy, i.e. $O\left({10}^{-5}\right)$ and checked the numerical stability condition.

In the direct analysis, the general interest is to assess the local temperature distribution, where the pertinent thermo-physical parameters are already known in advance. Conversely, the situation becomes somewhat difficult and characteristically ill-posed, when a particular set of observed temperature data over a given period of time and the dimensions of the biological material are available. Environmental conditions can be also assumed invariable during the period of analysis. However, for the identification of the healthiness of the tissue, the rate of metabolic heat generation occurring inside the tissue is a challenging assignment. For such instances, the inverse retrieval method finds use to detect the related rate of metabolic heat generation, q _m from the existing information about the transient temperature field, T. This temperature data can be either uncontaminated $\left(\tilde{T}\right)$ or contaminated $\left(\tilde{T}+e_g^h\right)$ due to the occurrence of random measurement noise ($e_g^h$). It is worth to mention here that the occurrence of uncontaminated data is a theoretical phenomenon which is only possible through computational solution of the governing heat equation. However, in reality, the temperature data is invariably affected by the presence of random errors. Consequently, to effectually estimate the metabolic rate of heat generation, the inverse problem is converted into an equivalent optimization problem where the succeeding objective function is minimized,(12) $$F=\sum _{h=0}^N{\left[{\tilde{T}}_g^h-T_g^h\left(q_m\right)\right]}^2:\text{for}{e}_g^h=0$$(12) $$F=\sum _{h=0}^N{\left[\left({\tilde{T}}_g^h+e_g^h\right)-T_g^h\left(q_m\right)\right]}^2:\text{for}{e}_g^h\ne 0,$$

where the index g denotes the space location (g = 0.5 for the current work) and h denotes the number of time durations, N over which the temperature data is acquired. In the above Equation (12(12) $$F=\sum _{h=0}^N{\left[{\tilde{T}}_g^h-T_g^h\left(q_m\right)\right]}^2:\text{for}{e}_g^h=0$$(12) ), N is considered as 50. Additionally, $T_g^h\left(q_m\right)$ is a function of unknown parameter, (i.e. metabolic rate of heat generation, q _m ), whereas, either ${\tilde{T}}_g^h$ or ${\tilde{T}}_g^h+e_g^h$ is a fixed set of data that remains unchanged during every iteration. Since, q _m is progressively refined by the optimization solver (GSSM), consequently, $T_g^h\left(q_m\right)$ is also updated in the iterative process executed by the GSSM algorithm. For the present work, ${\tilde{T}}_g^h$ is obtained by solving a forward problem using the FDM by considering a known value for the metabolic heat generation, q _m . To demonstrate the retrieval methodology using the GSSM, next, in the inverse problem, the metabolic heat generation, q _m is considered unknown. It is also worth to emphasize here that in case of contaminated temperature data (${\tilde{T}}_g^h+e_g^h$), the GSSM algorithm basically minimizes the least squares error between the given noisy data (${\tilde{T}}_g^h+e_g^h$) and the temperature iteratively computed ($T_g^h\left(q_m\right)$) starting with some guessed values of the metabolic heat generation rate (q _m ). For minimizing Equation (12(12) $$F=\sum _{h=0}^N{\left[{\tilde{T}}_g^h-T_g^h\left(q_m\right)\right]}^2:\text{for}{e}_g^h=0$$(12) ), in the current work, the GSSM is applied as discussed in the next fragment of this paper.

GSSM is a line search optimization method to find either the minimum or the maximum of unimodal functions by narrowing the search range in an iterative process. The algorithm develops its name because of the point that, this method keeps the function values at distinct positions whose distances constitute the golden ratio, 1.618. In the present GSSM algorithm, the reciprocal of the golden ratio, γ, is computed as [45,46],(13) $$\mathit{\gamma }=0.618=\frac{\left(\sqrt{5}-1\right)}{2}.$$(13)

The parameter, γ perpetually meet the below-mentioned criterion [45–47],(14) $$\mathit{\gamma }=\frac{1}{1+\mathit{\gamma }}.$$(14)

For unknown parameter prediction problems, the GSSM is observed to be computationally proficient due to its efficacy to treat unimodal objective functions [47]. For the present problem, the guessed temperature distribution, $T_g^h$ is computed and iteratively updated using the FDM and the GSSM methodologies, respectively. The GSSM generates guessed value of the unknown parameter, q _m with the aid of two initially guessed vertices such as V _a and V _b . These vertices are subsequently refined over a number of iterations by minimizing the error function, F of Equation (12(12) $$F=\sum _{h=0}^N{\left[{\tilde{T}}_g^h-T_g^h\left(q_m\right)\right]}^2:\text{for}{e}_g^h=0$$(12) ). In the GSSM algorithm, at first, for two guessed values of the unknown quantity (q _m in the present work) satisfying a given bound, two extra values of the required parameter are created at a spacing, r from the lower to the upper ranges. Therefore, considering a preliminary section of the search uncertainty, say, U = (V _b − V _a ), two additional values, say, V _y and V _z representing the metabolic heat generation rate, q _m are evaluated in the following manner [45–47],(15) $$\begin{array}{cc}{V}_y\hfill & =V_a+\left(1-\mathit{\gamma }\right)\left(V_b-V_a\right),\hfill \\ V_z\hfill & =V_b-\left(1-\mathit{\gamma }\right)\left(V_b-V_a\right).\hfill \end{array}$$(15)

Thereafter, the respective values of the objective functions, such as, F _y and F _z for the newly generated vertices involving V _y and V _z are evaluated. This is followed by the selection of the new region of search uncertainty governed by the following rule,(16a) $$\text{If},F_y>F_z,U=(V_b{V}_y)$$(16a) (16b) $$\text{Else (i}\text{.e)}{F}_y<F_z,U=(V_z-V_a)$$(16b)

Based on the applicable region of uncertainty, say when Equation (16a(16a) $$\text{If},F_y>F_z,U=(V_b{V}_y)$$(16a) ) is valid, the vertex $V_y^k$ modifies to the vertex $V_a^{k+1}$, and $V_b^k$ remains unaltered as $V_b^{k+1}$ for the next iteration, where indices k and k + 1, respectively, represent the successive iteration levels [45]. However, when Equation (16b(16b) $$\text{Else (i}\text{.e)}{F}_y<F_z,U=(V_z-V_a)$$(16b) ) is effective, then, the point, $V_z^k$ is exchanged with $V_b^{k+1}$, but, $V_a^k$ remains unaffected as $V_a^{k+1}$. The related reduction ratio, χ is then computed from the following expression [45–47],(17a) $$\mathit{\chi }=\frac{\left(V_b-V_a\right)}{\left(V_b-V_y\right)}=\frac{1}{\mathit{\gamma }};F_y>F_z,$$(17a) (17b) $$\mathit{\chi }=\frac{\left(V_b-V_a\right)}{\left(V_z-V_a\right)}=\frac{1}{\mathit{\gamma }};F_y<F_z.$$(17b)

The steps indicated in Equations (15–17) are iteratively repeated until the region of uncertainty, U approached zero. In other words, the two vertices, V _a and V _b become nearly equal and do not undergo significant variation after a finite number of iterations, which is found to be reasonably sufficient after 40 iterations. A flowchart of the GSSM [47] for the inverse retrieval of the metabolic heat generation rate, q _m with the aid of temperature data has been shown in Figure 2. In the succeeding section, results and discussion are presented.

Figure 2. Flowchart of GSSM [47].

5. Results and discussion

The derived results (using the present forward method, i.e. the FDM) for both parabolic PBT and hyperbolic TWBT models are validated with the analytical results of Ahmadikia et al. [21]. It is worthy to mention here that Ahmadikia et al. [21] have used the Laplace transformation method to solve the PBT as well as the TWBT equations. The comparisons of the two methods are depicted in Figure 3 for various thermo-physical parameters indicated in the caption. In this figure, the solid line represents the temperature distribution for the PBT model (parabolic model), whereas, the dash-dot line represents the temperature distribution for the TWBT model (hyperbolic model). From Figure 3, it can be noticed that the present forward results are in good agreement with the results obtained by Ahmadikia et al. [21].

Figure 3. Comparison of the temperature distribution obtained in the present work with that of the result obtained by Ahmadikia et al. [21]; ${\mathit{\tau }}_q=16\text{s,}{c}_b=3770\text{J}{\text{kg}}^{-1}{\text{K}}^{-1},T_a=37{}^{\circ }\text{C,}$ $c_t=3600\text{J}{\text{kg}}^{-1}{\text{K}}^{-1},{\mathit{\rho }}_t=1190\text{kg}{\text{m}}^{-3},w_b=0.5\text{kg}{\text{m}}^{-3}{\text{s}}^{-1},x=0.50\text{cm},q_m=368.1\text{W}{\text{m}}^{-3},$ $q_0=5000\text{W}{\text{m}}^{-2},\text{and}k=0.235\text{W}{\text{m}}^{-1}{\text{K}}^{-1}$.

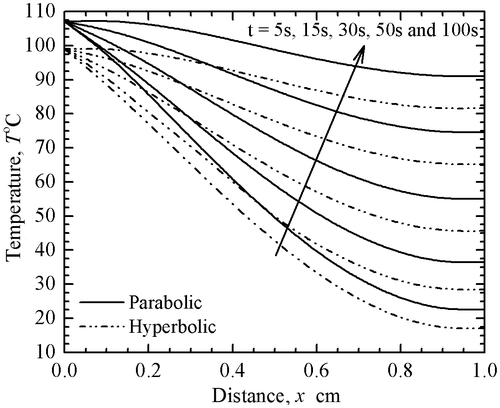
In order to appreciate the difference in local temperature distribution over diverse intervals of time, a study has been done in Figure 4. It can be observed from this figure that the temperature distributions for parabolic and hyperbolic models are different at the studied time levels. For the reason that the hyperbolic conduction for bioheat transfer problems is more accurate (mentioned earlier also), the subsequent analysis in this work has been done for the hyperbolic TWBT model.

Figure 4. Local temperature distribution for parabolic and hyperbolic models; ${\mathit{\tau }}_q=16\text{s,}{c}_b=3770\text{J}{\text{kg}}^{-1}{\text{K}}^{-1},T_a=37{}^{\circ }\text{C,}{c}_t=3600\text{J}{\text{kg}}^{-1}{\text{K}}^{-1},{\mathit{\rho }}_t=1190\text{kg}{\text{m}}^{-3},w_b=0.5\text{kg}{\text{m}}^{-3}{\text{s}}^{-1},$ $q_m=368.1\text{W}{\text{m}}^{-3},q_0=5000\text{W}{\text{m}}^{-2}$ and $k=0.235\text{W}{\text{m}}^{-1}{\text{K}}^{-1}$.

Next, an inverse analysis has been carried out to estimate the unknown metabolic heat generation rate, q _m satisfying a given transient thermal distribution, which is obtained in the present work from the forward analysis (i.e. the FDM). The estimation of the rate of metabolic heat generation, q _m enables to quantify the occurrence of tumour or internal damage to the biological tissue due to burn sustained. Other thermo-physical parameters and environmental conditions provided in Table 1 [42] are considered fixed during the inverse analysis. For any location of the tissue, the analysis has been performed by assuming the transient temperature distribution corresponding to various thermo-physical quantities indicated in Table 1. The inverse analysis has been done for two different cases of metabolic heat generation rates, q _m as indicated in Figure 5. It is inferred from Figure 5 that when q _m increases, the local temperature distribution within the tissue also increases due to more heating source.

Table 1. Parameters considered fixed in the inverse analysis.

Parameters	Values
Thermal relaxation time, τ q	16 s
Specific heat of tissue, c t	3600 J/(kg K)
Specific heat of blood, c b	3770 J/(kg K)
Density of tissue, ρ t	1190 kg/m^3
Density of blood, ρ b	1060 kg/m^3
Perfusion rate of blood, ${\mathit{\varpi }}_b$	4.7169 × 10^−4 s^−1
Thermal conductivity of skin tissue, k	0.235 W/(m K)
Arterial blood temperature, T a	37 °C

Figure 5. Temperature distribution for hyperbolic model at different metabolic heat generation rates; ${\mathit{\tau }}_q=16\text{s,}{c}_b=3770\text{J}{\text{kg}}^{-1}{\text{K}}^{-1},T_a={37}^{\circ }\text{C,}{c}_t=3600\text{J}{\text{kg}}^{-1}{\text{K}}^{-1},q_0=5000\text{W}{\text{m}}^{-2}$ $k=0.235\text{W}{\text{m}}^{-1}{\text{K}}^{-1},{\mathit{\rho }}_t=1190\text{kg}{\text{m}}^{-3},\text{and}{w}_b=0.5\text{kg}{\text{m}}^{-3}{\text{s}}^{-1}$.

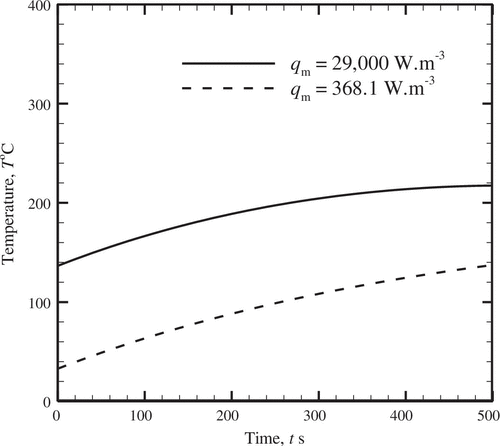
Table 2 compares the exact and the inversely estimated values of the heat generation rate, q _m when the observed temperature distribution, T involves no noise, i.e. $e_g^h$ = 0. There are two broad cases in Table 2. The first case (Sl. Nos. 1–5) involves a normal biological tissue with the metabolic heat generation rate, $q_m=368.1\text{W}{\text{m}}^{-3}$, whereas the second case (Sl. Nos. 6–10) involves a tumour-affected or injured tissue involving high value of the rate of heat generation with q _m = 29 × 10³ W m⁻³. Considering the temperature profile, the study has been done for different initial guesses of the GSSM algorithm, and it is found that an excellent estimation of the unknown quantity is accomplished when the observed transient temperature response involves no noise in the data.

Table 2. Comparison of the exact and the estimated values with the temperature distribution involving no measurement error; $e_g^h=0$.

Sl. No.	Exact value, q m	Range [V a , V b ]	Estimated value, vertex, V a	Estimated value, vertex, V b
1	368.1 W/m^3	[100 W/m^3, 10^5 W/m^3]	368.0981	368.0986
2		[200 W/m^3, 2 × 10^5 W/m^3]	368.0979	368.0987
3		[10 W/m^3, 10^6 W/m^3]	368.0957	368.1000
4		[0.1 W/m^3, 10^6 W/m^3]	368.0951	368.0995
5		[300 W/m^3, 10^5 W/m^3]	368.0981	368.0986
6	29 × 10^3 W/m^3	[100 W/m^3, 10^5 W/m^3]	28,999.9980	28,999.9984
7		[200 W/m^3, 2 × 10^5 W/m^3]	28,999.9978	28,999.9987
8		[10 W/m^3, 10^6 W/m^3]	28,999.9978	28,999.9985
9		[0.1 W/m^3, 10^6 W/m^3]	28,999.9979	28,999.9984
10		[300 W/m^3, 10^5 W/m^3]	28,999.9978	28,999.9984

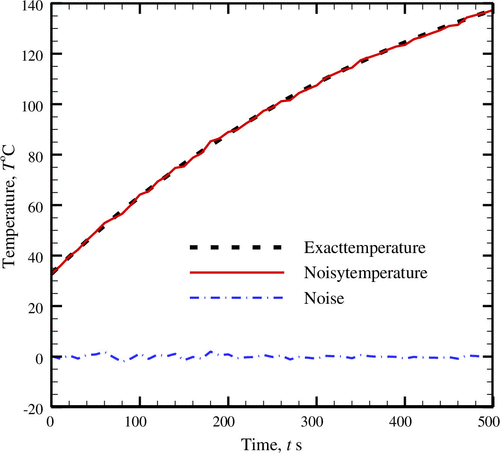
After successfully estimating the unknown parameter (i.e. rate of metabolic heat generation) for the case of pure temperature data, the effect of noisy temperature data has been studied next. Figure 6 presents the variation of the transient temperature for a healthy tissue involving the metabolic heat generation rate, $q_m=368.1\text{W}{\text{m}}^{-3}$. The results are presented for, ${\mathit{\tau }}_q=16\text{s,}{c}_b=3770\text{J}{\text{kg}}^{-1}{\text{K}}^{-1},T_a={37}^{\circ }\text{C,}{c}_t=3600\text{J}{\text{kg}}^{-1}{\text{K}}^{-1},{\mathit{\rho }}_t=1190\text{kg}{\text{m}}^{-3},$ $q_m=368.1\text{W}{\text{m}}^{-3},w_b=0.5\text{kg}{\text{m}}^{-3}{\text{s}}^{-1},\mathit{\xi }=0.4478,q_0=5000\text{W}{\text{m}}^{-2}$ and $k=0.235$ W m^-1 k^-1. In the present work additive white Gaussian noise within ±2.0\has been inducted to the pure temperature data. The consideration of this range is in accordance with the accuracy of recently used temperature sensors as revealed from some of the available studies [48,49].

Figure 6. Comparison of pure and noisy transient temperatures; ${\mathit{\tau }}_q=16\text{s,}{c}_b=3770\text{J}{\text{kg}}^{-1}{\text{K}}^{-1},T_a={37}^{\text{o}}\text{C},c_t=3600\text{J}{\text{kg}}^{-1}{\text{K}}^{-1},{\mathit{\rho }}_t=1190\text{kg}{\text{m}}^{-3},w_b=0.5\text{kg}{\text{m}}^{-3}{\text{s}}^{-1},$ $x=0.50\text{cm},q_m=368.1\text{W}{\text{m}}^{-3},q_0=5000\text{W}{\text{m}}^{-2}$ and $k=0.235\text{W}{\text{m}}^{-1}{\text{K}}^{-1}$.

Table 3 compares the estimated values of the metabolic heat generation rate for healthy and unhealthy tissues, respectively, involving low and high metabolic heat generation rates, q _m . Five runs of the GSSM algorithm involving diverse initial guesses against each case of tissue condition are taken and the respective values of the two vertices after 40 iterations of the optimization algorithm are presented in the table. It is seen from Table 3 that for both conditions of the tissue, the values of the estimated parameter differ to some extent with reference to the actual value.

Table 3. Comparison of the exact and the estimated values with the temperature distribution involving measurement error; $e_g^h\ne 0$.

Sl. No.	Exact value, q m	Range [V a , V b ]	Estimated value, vertex, V a	Estimated value, vertex, V b
1	368.1 W/m^3	[100 W/m^3, 10^5 W/m^3]	337.8895	337.8899
2		[200 W/m^3, 2 × 10^5 W/m^3]	337.8896	337.8904
3		[10 W/m^3, 10^6 W/m^3]	337.8881	337.8925
4		[0.1 W/m^3, 10^6 W/m^3]	337.8873	337.8917
5		[300 W/m^3, 10^5 W/m^3]	337.8894	337.8899
6	29 × 10^3 W/m^3	[100 W/m^3, 10^5 W/m^3]	28,953.0713	28,953.0718
7		[200 W/m^3, 2 × 10^5 W/m^3]	28,953.0713	28,953.0722
8		[10 W/m^3, 10^6 W/m^3]	28,953.0712	28,953.0719
9		[0.1 W/m^3, 10^6 W/m^3]	28,953.0713	28,953.0719
10		[300 W/m^3, 10^5 W/m^3]	28,953.0713	28,953.0720

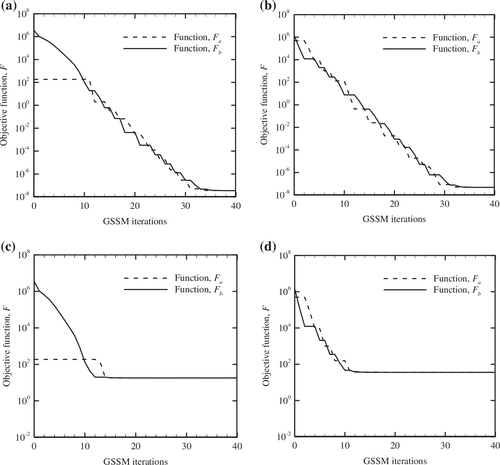
For the studied cases (Sl. No. 1) of Tables 2 and 3, the evolution of the cost function value, F over the iterations of GSSM is studied in Figure 7. From the observed trends (please refer Figure 7(a)–(d)), it is observed that both functions, F _a and F _b progressively reduce and ultimately converge to a unique point. For the temperature data containing no noise, the final objective function, F.

Figure 7. Variation of function values with GSSM iterations, (a) q _m = 368.1 W m⁻³; $e_g^h$ = 0, (b) q _m = 29,000 W m⁻³; $e_g^h$ = 0, (c) q _m = 368.1 W m⁻³; $e_g^h$ ≠ 0, (d) q _m = 29,000 W m⁻³; $e_g^h$ ≠ 0 approaches to O (10⁻⁸) (kindly refer Figure 7(a) and (b)) under both cases of tissue involving low and high heat generation rates. Furthermore, when the measurement of tissue temperature involves noise, the final value of the objective function, F is of higher magnitude, O (10¹) and there is no significant change over a considerable period of the GSSM optimization process (please refer, Figure 7(c) and (d)).

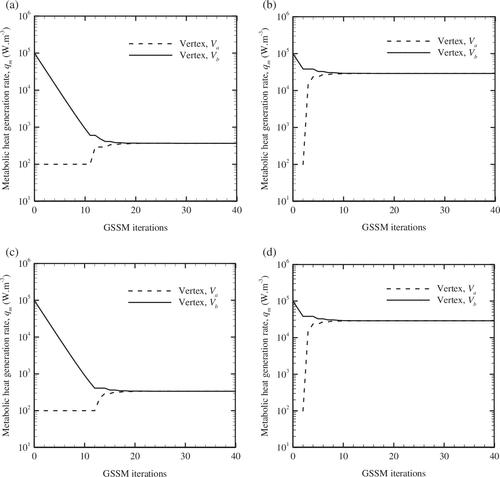
For various instances of Figure 7 conforming to Sl. No. 1 of Tables 2 and 3, the corresponding histories of GSSM vertices, V _a and V _b are compared in Figure 8. In accordance with the previous trends of the cost function, the commonly observed trend in these figures too is the coincidence of the two vertices after a finite number of iterations. Furthermore, it is also observed that when the temperature distribution is less (i.e. when the value of q _m is less), the vertices V _a and V _b meet after about 20 iterations as it can be manifested from Figure 8(a) and (c), irrespective of the contained measurement error, $e_g^h$. However, again regardless of the amount of noise, when the transient temperature distribution is higher (which occur when the value of q _m is more), the two vertices V _a and V _b take relatively lesser number of GSSM iterations to concur (referring Figure 8(b) and (d)). This observation is due to the existence of the actual solution (i.e. q _m in the present work) within a small region of uncertainty corresponding to the former case (Figure 8(a) and (c)). But, when the uncertainty range is large, then the GSSM can trace the actual solution in a relatively easier manner (for instance in Figure 8(b) and (d)).

Figure 8. Variation of vertices with number of GSSM iterations, (a) q _m = 368.1 W m⁻³ and $e_g^h$ = 0, (b) q _m = 29,000 W m⁻³ and $e_g^h$ = 0, (c) q _m = 368.1 W m⁻³ and $e_g^h$ ≠ 0, (d) q _m = 29,000 W m⁻³ and $e_g^h$ ≠ 0.

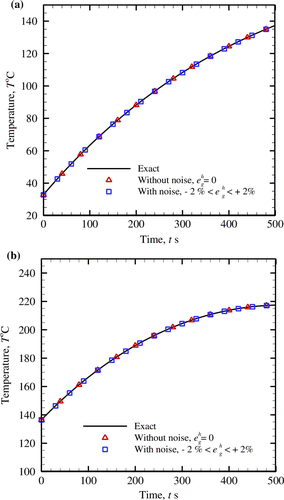
For assessing the suitability of the retrieved rate of metabolic heat generation rate obtained using the GSSM for both pure and noisy temperatures, the comparison of the exact and the reconstructed temperatures has been done in Figure 9. The reconstructed temperature is evaluated using the estimated values of the unknown parameter (i.e. q _m ) for which the objective function and the GSSM vertices are shown in Figures 7 and 8, respectively. A very good agreement between the exact and reconstructed fields can be observed from the comparison.

Figure 9. Evaluation of the exact and the inversely-reconstructed temperature distributions for different cases of metabolic heat generation rates, (a) q _m = 368.1 W m⁻³, (b) q _m = 29,000 W m⁻³.

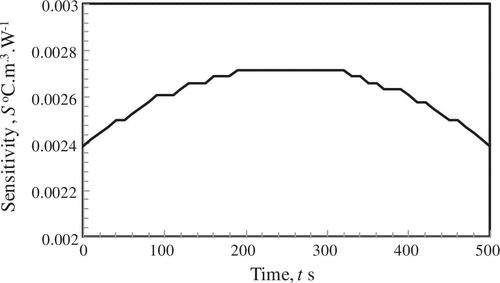
In order to assess the contribution of the metabolic rate of heat generation (q _m ) to the transient thermal field, a comparison of sensitivity coefficient, S is carried out in Figure 10. The sensitivity coefficient, S = $\mathit{\partial }T/\mathit{\partial }{q}_m$ is evaluated by perturbing the metabolic rate of heat generation, q _m = 368.1 W m⁻³ by 1% and noting the change of temperature profiles. It can be seen from Figure 10 that the values of sensitivity coefficient are quite low, O (10⁻³) and it marginally increases from either boundaries of the medium.

Figure 10. Variation of sensitivity coefficient of temperature with heat generation rate.

6. Conclusions

An inverse problem has been studied to predict the metabolic heat generation rate within a one-dimensional biological tissue from the temperature response of the tissue. At first, the FDM has been used to solve the forward problem involving both parabolic Pennes bioheat and hyperbolic thermal bioheat equations. Thereafter, corresponding to a particular transient temperature response of the tissue, an inverse method based on the GSSM has been used to recover the internal metabolic rate of heat generation. The estimations are carried out under the effects of noise in the temperature. It has been found from the study that the inverse quantification of the metabolic heat generation rate done with the aid of GSSM from a temperature field can easily identify the existence of tumour or the damage sustained due to burn.

Nomenclature
C	=	thermal wave speed, (m s−1)
c b	=	specific heat of the blood, (J kg−1 K−1)
c t	=	specific heat of the skin tissue, (J kg−1 K−1)
$e_g^h$	=	random measurement noise
F	=	objective function
k	=	thermal conductivity of skin tissue, (W·m−1·K−1)
L	=	length of the finite domain, (m)
N	=	number of iterations
N 1	=	number of discrete points along ξ
N 2	=	number of discrete points along η
q ext	=	heat generated by other heating sources, ($\text{W}{\text{m}}^{-3}$)
q m	=	metabolic heat generation in skin tissue, ($\text{W}{\text{m}}^{-3}$)
q 0	=	constant heat flux, ($\text{W}{\text{m}}^{-2}$)
S	=	sensitivity coefficient, (C m3 W−1)
T	=	temperature of the skin tissue, (°C)
T a	=	temperature of the arterial blood, (°C)
T	=	time, (s)
x	=	any location along the finite domain of the skin, (m)
V a ,V b ,V y ,V z	=	vertices used in the GSSM

Greek symbols
α	=	thermal diffusivity, (m2 s−1)
γ	=	golden ratio parameter, defined in Equation (13(13) $$\mathit{\gamma }=0.618=\frac{\left(\sqrt{5}-1\right)}{2}.$$(13) )
ξ	=	dimensionless space coordinates (=$\sqrt{\frac{w_b{c}_b}{k}}x$)
η	=	dimensionless time coordinates (=$\frac{w_b{c}_b}{{\mathit{\rho }}_t{c}_t}t$)
Λ	=	dimensionless parameter (=$\frac{w_b{c}_b}{{\mathit{\rho }}_t{c}_t}{\mathit{\tau }}_q$), used in Equation (7(7) $$\mathrm{\Lambda }=\frac{w_b{c}_b}{{\mathit{\rho }}_t{c}_t}{\mathit{\tau }}_q;\mathit{\theta }=\frac{T-T_a}{q_0}\sqrt{k{w}_b{c}_b};\mathit{\eta }=\frac{w_b{c}_b}{{\mathit{\rho }}_t{c}_t}t;\mathit{\xi }=\sqrt{\frac{w_b{c}_b}{k}}x;\mathit{\psi }=\frac{q_m\sqrt{k}}{q_0\sqrt{w_b{c}_b}},$$(7) )
ρ b	=	density of the blood, (kg m−3)
ρ t	=	density of skin tissue, (kg m−3)
θ	=	dimensionless temperature distribution
ψ	=	dimensionless parameter (=$\frac{q_m\sqrt{k}}{q_0\sqrt{w_b{c}_b}}$), used in Equation (7(7) $$\mathrm{\Lambda }=\frac{w_b{c}_b}{{\mathit{\rho }}_t{c}_t}{\mathit{\tau }}_q;\mathit{\theta }=\frac{T-T_a}{q_0}\sqrt{k{w}_b{c}_b};\mathit{\eta }=\frac{w_b{c}_b}{{\mathit{\rho }}_t{c}_t}t;\mathit{\xi }=\sqrt{\frac{w_b{c}_b}{k}}x;\mathit{\psi }=\frac{q_m\sqrt{k}}{q_0\sqrt{w_b{c}_b}},$$(7) )
τ q	=	thermal relaxation time, (s)
${\mathit{\varpi }}_b$	=	blood perfusion rate, (s−1)

Disclosure statement

No potential conflict of interest was reported by the authors.