Application of inverse method to predict the breakthrough curve in fixed-bed adsorption

Abstract

In this paper, at first by means of the differential quadrature element-incremental method as a computationally efficient and accurate numerical tool in conjunction with the Newton-Raphson method, the behaviour of the bicomponent fixed-bed adsorption is studied. The kinetics of the adsorption is formulated based on the linear driving force (LDF) approximation. Then, an inverse algorithm is employed to estimate the overall mass transfer coefficients of the adsorption column by using the measured time histories of the mole fractions of outlet multicomponent. The method allows one to obtain the values of the LDF mass transfer coefficients for the different adsorbents and adsorbates. The conjugate gradient method is adopted for the optimization procedure of the inverse algorithm. The robustness and applicability of the present inverse approach are demonstrated by solving different examples with the exact data of the known kinetics.

Keywords:

• Breakthrough curve
• linear driving force
• inverse algorithm
• differential quadrature element-increment method
• conjugate gradient method

Subject classification code:

• 3504

1. Introduction

For the systems which the separation is based on the adsorption phenomena, the modelling of transport equations strongly depends on the mass transfer resistance between the fluid and the solid particles [1]. Therefore, understanding of the dynamic behaviour, kinetics and equilibria of such systems is essential for the design and optimization of the adsorption process.

Usually, the dynamic behaviour of an adsorption column is described by the approximate methods, in which a parabolic concentration inside the particle is assumed [2]. In the approximate methods, the mass transfer is modelled by a lumped coefficient and a linear driving force (LDF) which is the difference between the fluid or solid phase concentrations. But, when using these methods, the mass transfer coefficient cannot be calculated a priori, and there is no overview of its range and variations with the different adsorbents, adsorbates and concentrations [3]. Consequently, these parameters are estimated by comparing the measured data taken during the breakthrough experiments and those obtained from the simulations. The optimal values of the fitted parameters are determined by minimizing an objective function. But, for the multicomponent systems, this optimization problem is not a simple one and it is difficult to use the regular technique of trial and error. On the other hand, such problems can be solved systematically by using an inverse algorithm. In this technique, the unknown parameters of the system such as the initial conditions, boundary conditions or material properties are estimated by measuring the other parameter (s) of the system at some limited locations [4].

The inverse algorithms have been successfully employed for the different heat transfer problems, see for example Refs. [5–9]. However, despite its relevance in chemical engineering, there are not sufficient published works on the inverse mass transfer problems. To the best of authors’ knowledge, there is still a lack of study on evaluation of the multicomponent breakthrough curve regarding the inverse adsorption analysis. Of course, it should be mentioned that there are some valuable works on the inverse adsorption analysis. For example, Cuco et al. [10] used the epidemic genetic algorithm and the generalized external optimization algorithm for the solution of an inverse mass transfer problem. They estimated adsorption parameters of biomolecules in resin beds. Lage et al. [11] used a simple model with an analytical solution for the breakthrough curves in fixed resin beds. They estimated the mass transfer mechanisms of biomolecules adsorption by inverse problem. Vasconcellos et al. [12] estimated the mass transfer coefficients and the coefficients of the adsorption isotherm using an implicit formulation with the cost function of the squared residues. Folly et al. [13] formulated and solved the inverse problems to determine the physico-chemical parameters in order to characterize adsorption columns which are used in simulated moving beds for biotechnological processes. Jr et al. [14] investigated inverse problem for the gas–liquid interface adsorption isotherm by using a hybrid approach including artificial neural network, Levenberg–Marquardt and simulated annealing methods. Hahn et al. [15] applied an adjoint method to compute model parameter derivatives for a wide range of differentiable liquid chromatography models and provided practical information for the implementation in a generic simulation framework by the example of ion-exchange chromatography. Also, as a first attempt to analyse the inverse kinetic of adsorption, we developed an inverse algorithm to estimate equilibrium adsorption isotherm in a gas storage vessel by using the dynamic transient internal pressure [16]. And next, we estimated the adsorption kinetics inside the spherical particles in a constant molar flow gas adsorber reservoir by measuring the bulk pressure [17].

In this work, an inverse algorithm is employed to estimate the overall mass transfer coefficients in a fixed bed adsorption column (Figure 1). The measured time histories of the mole fractions of the outlet multicomponent are used as the available measured (input) data. The LDF approximation is employed to formulate the kinetics of the adsorption. To validate the approach and demonstrate its computational efficiency, the separation of two adsorbing components with a large amount of carrier gas and through different examples is analysed. For this purpose, the overall mass transfer coefficients are estimated by measuring the mole fractions of the outlet multicomponent time history, which has significant variation during the process of the gas adsorption. Since the inverse problems are mathematically ill-posed [5], the use of an efficient optimization method becomes necessary as a part of the solution procedure. In this study, the iterative regularization method introduced by Alifanov [4], which is composed of the adjoint equation approach together with the conjugate gradient method, is employed. The main advantage of this method is that it does not require the optimal regularization conditions, and also the regularization is fulfilled during the iterative processes [4,5]. In addition, the differential quadrature element-incremental method (DQEIM) as a simple, accurate and computationally efficient numerical method [18] is used to discretize the related governing differential equations in both the spatial and temporal domains. The resulting non-linear system of algebraic equations is solved using Newton-Raphson method. Before performing the inverse analysis, the influences of the different physical parameters on the behaviour of the system under consideration are studied, which can help one to better realize the system reaction. Then, the versatility and robustness of the present inverse approach are demonstrated by showing its accuracy and low CPU time requirement through the different practical examples.

Figure 1. Schematic of the system under consideration.

2. Mathematical modelling

The transient behaviour of the adsorption system can be predicted by solving the governing equations of the fixed-bed column models, which include the global mass balance and the components mass balance of both the adsorber particle and adsorbate. The problem is formulated by considering the following assumptions

(1)	The adsorption has local equilibrium instantaneously,
(2)	The gas phase obeys the ideal gas law,
(3)	The pressure drop along the column is negligible,
(4)	The process is isobaric and isothermal (due to low-concentration of the adsorbing gases).

Usually to validate an inverse algorithm, the solution of the related direct problem with some artificial errors is used as the measured data [19–21]. Hence, in addition to the governing equations of the inverse procedure, the related direct problem should be solved. In this regard, for the problem under consideration, the governing equations of the direct problem are presented in the next section.

2.1. The direct problem

Considering the aforementioned assumptions, the global mass balance over a differential element of the column becomes [22],(1) $$C\frac{\mathit{\partial }\overline{V}}{\mathit{\partial }\overline{z}}+{\mathit{\rho }}_b\sum _{j=1}^2\frac{\mathit{\partial }{\overline{q}}_j}{\mathit{\partial }\overline{t}}=0$$(1)

Based on the kinetic model, the mass balance equations of the adsorbate components in the bulk phase and also the adsorber phase take the following form, respectively [1](2) $$\frac{\mathit{\partial }\left(\overline{V}{\overline{C}}_i\right)}{\mathit{\partial }\overline{z}}-{\mathit{\epsilon }}_b{D}_z\frac{{\mathit{\partial }}^2{\overline{C}}_i}{\mathit{\partial }{\overline{z}}^2}+{\mathit{\epsilon }}_t\frac{\mathit{\partial }{\overline{C}}_i}{\mathit{\partial }\overline{t}}+{\mathit{\rho }}_b\frac{\mathit{\partial }{\overline{q}}_i}{\mathit{\partial }\overline{t}}=0$$(2) (3) $$\frac{\mathit{\partial }{\overline{q}}_i}{\mathit{\partial }\overline{t}}-k_i\left({\overline{q}}_i^{\ast }-{\overline{q}}_i\right)=0$$(3)

where i = 1, 2. Additionally, the following Langmuir model are employed for the equilibrium multicomponent isotherms,(4) $${\overline{q}}_i^{\ast }=q_{m,i}\frac{b_i{\overline{P}}_i}{1+{\sum }_{j=1}^2{b}_j{\overline{P}}_j}$$(4)

The related boundary and initial conditions of Equations (1(1) $$C\frac{\mathit{\partial }\overline{V}}{\mathit{\partial }\overline{z}}+{\mathit{\rho }}_b\sum _{j=1}^2\frac{\mathit{\partial }{\overline{q}}_j}{\mathit{\partial }\overline{t}}=0$$(1) )–(3(3) $$\frac{\mathit{\partial }{\overline{q}}_i}{\mathit{\partial }\overline{t}}-k_i\left({\overline{q}}_i^{\ast }-{\overline{q}}_i\right)=0$$(3) ) are as follows,(5a,b) $$\text{At}\overline{z}=0:\overline{V}=V_0,{\overline{C}}_i=C_{i0}$$(5a,b)

(6a,b) $$\text{At}\overline{z}=L_z:\frac{\mathit{\partial }\overline{V}}{\mathit{\partial }\overline{z}}=0,\frac{\mathit{\partial }{\overline{C}}_i}{\mathit{\partial }\overline{z}}=0$$(6a,b) (7a–c) $$\overline{V}\left|\begin{array}{c}\\ {}_{\overline{t}=0}\hfill \end{array}\right.=V_0,{\overline{C}}_i\left|\begin{array}{c}\\ {}_{\overline{t}=0}\hfill \end{array}\right.=0,{\overline{q}}_i\left|\begin{array}{c}\\ {}_{\overline{t}=0}\hfill \end{array}\right.=0$$(7a–c)

In order to normalize the governing equations, the following dimensionless parameters are introduced,(8a–e) $$z=\frac{\overline{z}}{L_z},t=\frac{V_0\overline{t}}{L_z},V=\frac{\overline{V}}{V_0},Y_i=\frac{{\overline{C}}_i}{C},q_i=\frac{{\overline{q}}_i}{q_{mi}}$$(8a–e)

Therefore, the governing Equations (1(1) $$C\frac{\mathit{\partial }\overline{V}}{\mathit{\partial }\overline{z}}+{\mathit{\rho }}_b\sum _{j=1}^2\frac{\mathit{\partial }{\overline{q}}_j}{\mathit{\partial }\overline{t}}=0$$(1) )–(3(3) $$\frac{\mathit{\partial }{\overline{q}}_i}{\mathit{\partial }\overline{t}}-k_i\left({\overline{q}}_i^{\ast }-{\overline{q}}_i\right)=0$$(3) ) and the related boundary and initial conditions (5)–(7) can be expressed in terms of these dimensionless parameters as, respectively,(9) $$\frac{\mathit{\partial }V}{\mathit{\partial }z}+\sum _{j=1}^2{M}_{aj}\frac{\mathit{\partial }{q}_j}{\mathit{\partial }t}=0$$(9) (10) $$Y_i\frac{\mathit{\partial }V}{\mathit{\partial }z}+V\frac{\mathit{\partial }{Y}_i}{\mathit{\partial }z}-M_b\frac{{\mathit{\partial }}^2{Y}_i}{\mathit{\partial }{z}^2}+{\mathit{\epsilon }}_t\frac{\mathit{\partial }{Y}_i}{\mathit{\partial }t}+M_{ai}\frac{\mathit{\partial }{q}_i}{\mathit{\partial }t}=0$$(10) (11) $$\left(1+\sum _{j=1}^2{M}_{dj}{Y}_j\right)\left(\frac{\mathit{\partial }{q}_i}{\mathit{\partial }t}+M_{ci}{q}_i\right)-M_{ci}{M}_{di}{Y}_i=0$$(11) (12a,b) $$\text{At}z=0:V=1,Y_i=Y_{i0}$$(12a,b) (13a,b) $$\text{At}z=1:\frac{\mathit{\partial }V}{\mathit{\partial }z}=0,\frac{\mathit{\partial }{Y}_i}{\mathit{\partial }z}=0$$(13a,b) (14a-c) $$V\left|\begin{array}{c}\\ {}_{t=0}\hfill \end{array}\right.=1,Y_i\left|\begin{array}{c}\\ {}_{t=0}\hfill \end{array}\right.=0,q_i\left|\begin{array}{c}\\ {}_{t=0}\hfill \end{array}\right.=0$$(14a-c)

where(15a–d) $$M_{ai}=\frac{{\mathit{\rho }}_b{q}_{m,i}}{C},M_b=\frac{{\mathit{\epsilon }}_b{D}_z}{V_o{L}_z},M_{ci}=\frac{k_i{L}_z}{V_o},M_{di}=b_{i}P$$(15a–d)

Since Equations (9(9) $$\frac{\mathit{\partial }V}{\mathit{\partial }z}+\sum _{j=1}^2{M}_{aj}\frac{\mathit{\partial }{q}_j}{\mathit{\partial }t}=0$$(9) )–(11(11) $$\left(1+\sum _{j=1}^2{M}_{dj}{Y}_j\right)\left(\frac{\mathit{\partial }{q}_i}{\mathit{\partial }t}+M_{ci}{q}_i\right)-M_{ci}{M}_{di}{Y}_i=0$$(11) ) are a set of coupled non-linear partial differential equations, it is difficult to solve them analytically. Hence, an approximate method should be implemented. On the other hand, the computational efficiency and accuracy of the differential quadrature method (DQM) has been demonstrated by solving the problems in the different fields of engineering such as structural, mass transfer and fluid mechanics in the recent years [16,18,23–27].

Therefore, in this paper, the extended version of the conventional DQM (i.e. the DQEIM) is employed to discretize the governing equations in both the spatial and temporal domains. According to this method, firstly, the spatial domain is divided into N^e mathematical subdomains (or elements), and the eth mathematical subdomain is discretized into a set of $N_z^e$ grid points along the z-direction. In a similar manner, the temporal domain is divided into N^I increments or temporal subdomains and the Ith temporal subdomain is discretized into a set of $N_t^I$ grid points. Consequently, at a given grid point $\left(z_i,t_j\right)$, the first and second order derivatives of an arbitrary function $g\left(z,t\right)$ are approximated as,(16a–c) $${\left.\frac{\mathit{\partial }g}{\mathit{\partial }z}\right|}_{\left(z_i,t_j\right)}=\sum _{m=1}^{N_z^e}{A}_{im}^{e\left(z\right)}g(z_m,t_j)=\sum _{m=1}^{N_z^e}{A}_{im}^{e\left(z\right)}{g}_{mj},{\left.\frac{{\mathit{\partial }}^{2}g}{\mathit{\partial }{z}^2}\right|}_{\left(z_i,t_j\right)}=\sum _{m=1}^{N_z^e}{B}_{im}^{e\left(z\right)}{g}_{mj},{\left.\frac{\mathit{\partial }g}{\mathit{\partial }t}\right|}_{\left(z_i,t_j\right)}=\sum _{n=1}^{N_t^I}{A}_{jn}^{I\left(t\right)}{g}_{in}$$(16a–c)

where i = 1, 2, …, $N_z^e$, e = 1, 2, …, N^e; and j = 1, 2, …, $N_t^I$, I = 1, 2, …, N^I. Also, $A_{ij}^{e(z)}$ and $B_{ij}^{e(z)}$ are the weighting coefficients of the first and second order derivatives of the eth spatial subdomain with respect to the coordinate variable z; also, $A_{ij}^{I(t)}$ is the weighting coefficient of the first order derivative of the Ith temporal subdomain with respect to time.

After employing the DQ rules to discretize the derivatives appear in the governing equations and the related boundary conditions of subdomains in a temporal increment, these equations are transformed into a system of non-linear algebraic equations. In this study, the Newton–Raphson method is employed to solve the obtained system of non-linear algebraic equations. By repeating this procedure for each temporal increment, the time histories of the field variables at all grid points and are obtained.

2.2. The inverse problem

In the inverse problem, only the overall mass transfer coefficients $\left(k_i\right.$ or its non-dimensional counterpart $\left.M_{ci},i=1,2\right)$ is assumed to be unknown while all the other parameters in the governing equations and the related initial and boundary conditions are assumed to be known. This parameter should be estimated by measuring the mole fraction of the adsorbate components $\left(Y_{i,out},i=1,2\right)$ at the end side of the adsorption column at some selected time t, preferably at the some temporal grid points.

The inverse problem described above may be formulated as an optimization problem which consists of minimizing the following functional,(17) $$J\left(M_{c1},M_{c2}\right)=\underset{0}{\overset{t_f}{\int }}\sum _{i=1}^2{\left[Y_{i,out}\left(t\right)-Y_i^{exp}\left(t\right)\right]}^2\text{d}t$$(17)

where $Y_{i,out}\left(t\right)$ and $Y_i^{exp}\left(t\right)$ are the estimated and measured outlet mole fraction of the ith component in the gas phase at time t, respectively. The estimated mole fractions $\left(Y_{i,out}\left(t\right)\right)$ are determined from the solution of the direct problem described previously by using the estimated values of k_i $\left(\text{or}{M}_{ci}\right)$.

Different schemes such as Levenberg–Marquardt [14] and genetic algorithm [28] can be used to minimize the functional given in Equation (17(17) $$J\left(M_{c1},M_{c2}\right)=\underset{0}{\overset{t_f}{\int }}\sum _{i=1}^2{\left[Y_{i,out}\left(t\right)-Y_i^{exp}\left(t\right)\right]}^2\text{d}t$$(17) ). In this work, the conjugate gradient method, which is a well-known algorithm for its generality and robustness, is employed to do this issue. Based on this iterative algorithm, the searching directions are related to the gradient of the corresponding functional errors and are determined through the adjoint problem, while the optimal step sizes are evaluated from the related sensitivity problems [23,29]. It should be mentioned that both the unknown parameters k₁and k₂ have a similar adjoint problem.

2.3. Sensitivity problems

Since there are two unknown parameters, their sensitivity problems should be formulated separately. For this purpose, perturbing M_c1 to M_c1 + δM_c1 then $V\left(z,t\right)$, $Y_i\left(z,t\right)$ and $q_i\left(z,t\right)$ change to $V\left(z,t\right)+\mathit{\delta }{V}_{M_{c1}}\left(z,t\right)$, $Y_i\left(z,t\right)+\mathit{\delta }{Y}_{i,M_{c1}}\left(z,t\right)$ and $q_i\left(z,t\right)+\mathit{\delta }{q}_{i,M_{c1}}\left(z,t\right)$, respectively. Substituting these new values of the field variables into the direct problem governing equations and the related boundary and initial conditions, and also neglecting the higher order terms, the corresponding sensitivity equations ofM_c1are obtained as(18) $$\frac{\mathit{\partial }\mathit{\delta }{V}_{M_{c1}}}{\mathit{\partial }z}+\sum _{j=1}^2{M}_{aj}\frac{\mathit{\partial }\mathit{\delta }{q}_{j,M_{c1}}}{\mathit{\partial }t}=0$$(18) (19) $$\begin{array}{c}\mathit{\delta }{Y}_{i,M_{c1}}\frac{\mathit{\partial }V}{\mathit{\partial }z}+Y_i\frac{\mathit{\partial }\mathit{\delta }{V}_{M_{c1}}}{\mathit{\partial }z}+\mathit{\delta }{V}_{M_{c1}}\frac{\mathit{\partial }{Y}_i}{\mathit{\partial }z}+V\frac{\mathit{\partial }\mathit{\delta }{Y}_{i,M_{c1}}}{\mathit{\partial }z}\hfill \\ -M_b\frac{{\mathit{\partial }}^2\mathit{\delta }{Y}_{i,M_{c1}}}{\mathit{\partial }{z}^2}+{\mathit{\epsilon }}_t\frac{\mathit{\partial }\mathit{\delta }{Y}_{i,M_{c1}}}{\mathit{\partial }t}+M_{ai}\frac{\mathit{\partial }\mathit{\delta }{q}_{i,M_{c1}}}{\mathit{\partial }t}=0\hfill \end{array}$$(19) (20a) $$\begin{array}{c}\left(\sum _{j=1}^2{M}_{dj}\mathit{\delta }{Y}_{j,M_{c1}}\right)\left(\frac{\mathit{\partial }{q}_1}{\mathit{\partial }t}+M_{c1}{q}_1\right)-M_{d1}\left(Y_1\mathit{\delta }{M}_{c1}+M_{c1}\mathit{\delta }{Y}_{1,M_{c1}}\right)\hfill \\ +\left(1+\sum _{j=1}^2{M}_{dj}\mathit{\delta }{Y}_{j,M_{c1}}\right)\left(\frac{\mathit{\partial }\mathit{\delta }{q}_{1,M_{c1}}}{\mathit{\partial }t}+M_{c1}\mathit{\delta }{q}_{1,M_{c1}}+q_1\mathit{\delta }{M}_{c1}\right)=0\hfill \end{array}$$(20a) (20b) $$\begin{array}{c}\left(\sum _{j=1}^2{M}_{dj}\mathit{\delta }{Y}_{j,M_{c1}}\right)\left(\frac{\mathit{\partial }{q}_2}{\mathit{\partial }t}+M_{c2}{q}_2\right)-M_{d2}{M}_{c2}\mathit{\delta }{Y}_{2,M_{c1}}\hfill \\ +\left(1+\sum _{j=1}^2{M}_{dj}\mathit{\delta }{Y}_{j,M_{c1}}\right)\left(\frac{\mathit{\partial }\mathit{\delta }{q}_{2,M_{c1}}}{\mathit{\partial }t}+M_{c2}\mathit{\delta }{q}_{2,M_{c1}}\right)=0\hfill \end{array}$$(20b) (21a,b) $$\text{At}z=0:\mathit{\delta }{V}_{M_{c1}}=0,\mathit{\delta }{Y}_{i,M_{c1}}=0$$(21a,b) (22a,b) $$\text{At}z=1:\frac{\mathit{\partial }\mathit{\delta }{V}_{M_{c1}}}{\mathit{\partial }z}=0,\frac{\mathit{\partial }\mathit{\delta }{Y}_{i,M_{c1}}}{\mathit{\partial }z}=0$$(22a,b) (23a–c) $$\mathit{\delta }{V}_{M_{c1}}\left|\begin{array}{c}\\ {}_{t=0}\hfill \end{array}\right.=1,\mathit{\delta }{Y}_{i,M_{c1}}\left|\begin{array}{c}\\ {}_{t=0}\hfill \end{array}\right.=0,\mathit{\delta }{q}_{i,M_{c1}}\left|\begin{array}{c}\\ {}_{t=0}\hfill \end{array}\right.=0$$(23a–c)

Similarly, the related sensitivity problem of M_c2can be formulated.

By using the aforementioned solution procedure, these equations are solved to achieve $\mathit{\delta }{V}_{M_{c1}}\left(z,t\right)$, $\mathit{\delta }{V}_{M_{c2}}\left(z,t\right)$, $\mathit{\delta }{Y}_{i,M_{c1}}\left(z,t\right)$, $\mathit{\delta }{Y}_{i,M_{c2}}\left(z,t\right)$, $\mathit{\delta }{q}_{i,M_{c1}}\left(z,t\right)$ and $\mathit{\delta }{q}_{i,M_{c2}}\left(z,t\right)$ which will be used in the inverse problem solution.

2.4. Adjoint problem and gradient equation

The adjoint problem governing equations can be derived by using the Lagrange multiplier approach. Accordingly, the following new functional is defined,(24) $$\begin{array}{cc}\widehat{J}\left(M_{c1},M_{c2}\right)\hfill & =\underset{0}{\overset{t_f}{\int }}\sum _{j=1}^2{\left[Y_{j,out}\left(t\right)-Y_j^{exp}\left(t\right)\right]}^2\text{d}t+\underset{0}{\overset{t_f}{\int }}\underset{0}{\overset{1}{\int }}{\mathit{\lambda }}_V\left(\frac{\mathit{\partial }V}{\mathit{\partial }z}+\sum _{j=1}^2{M}_{aj}\frac{\mathit{\partial }{q}_j}{\mathit{\partial }t}\right)\text{d}z\text{d}t\hfill \\ \hfill & +\sum _{j=1}^2\underset{0}{\overset{t_f}{\int }}\underset{0}{\overset{1}{\int }}{\mathit{\lambda }}_{Y_j}\left(Y_j\frac{\mathit{\partial }V}{\mathit{\partial }z}\right.+V\frac{\mathit{\partial }{Y}_j}{\mathit{\partial }z}\left.-M_b\frac{{\mathit{\partial }}^2{Y}_j}{\mathit{\partial }{z}^2}+{\mathit{\epsilon }}_t\frac{\mathit{\partial }{Y}_j}{\mathit{\partial }t}+M_{aj}\frac{\mathit{\partial }{q}_j}{\mathit{\partial }t}\right)\text{d}z\text{d}t\hfill \\ \hfill & +\sum _{j=1}^2\underset{0}{\overset{t_f}{\int }}\underset{0}{\overset{1}{\int }}{\mathit{\lambda }}_{q_j}\left[\left(1+\sum _{n=1}^2{M}_{dn}{Y}_n\right)\left(\frac{\mathit{\partial }{q}_j}{\mathit{\partial }t}+M_{cj}{q}_j\right)-M_{cj}{M}_{dj}{Y}_j\right]\text{d}z\text{d}t\hfill \end{array}$$(24)

where ${\mathit{\lambda }}_{\mathit{\alpha }}(z,t)\left(\mathit{\alpha }=V,Y_1,Y_2,q_1\text{and}{q}_2\right)$ are the Lagrange multipliers (or adjoint functions). The variation of this new functional with respect to M_c1becomes,(25) $$\begin{array}{cc}\mathit{\delta }{\widehat{J}}_{M_{c1}}\left(M_{c1},M_{c2}\right)\hfill & =\underset{0}{\overset{t_f}{\int }}2\sum _{j=1}^2\left(Y_{j,out}-Y_j^{exp}\right)\mathit{\delta }{Y}_{j,M_{c1}}\text{d}t\hfill \\ \hfill & +\underset{0}{\overset{t_f}{\int }}\underset{0}{\overset{1}{\int }}{\mathit{\lambda }}_V\left(\frac{\mathit{\partial }\mathit{\delta }{V}_{M_{c1}}}{\mathit{\partial }z}+M_{a1}\frac{\mathit{\partial }\mathit{\delta }{q}_{1,M_{c1}}}{\mathit{\partial }t}\right.+M_{a2}\left.\frac{\mathit{\partial }\mathit{\delta }{q}_{2,M_{c1}}}{\mathit{\partial }t}\right)\text{d}z\text{d}t\hfill \\ \hfill & +\sum _{j=1}^2\underset{0}{\overset{t_f}{\int }}\underset{0}{\overset{1}{\int }}{\mathit{\lambda }}_{Y_j}\left(\mathit{\delta }{Y}_{j,M_{c1}}\frac{\mathit{\partial }V}{\mathit{\partial }z}+Y_j\frac{\mathit{\partial }\mathit{\delta }{V}_{M_{c1}}}{\mathit{\partial }z}+\mathit{\delta }{V}_{M_{c1}}\frac{\mathit{\partial }{Y}_j}{\mathit{\partial }z}+V\frac{\mathit{\partial }\mathit{\delta }{Y}_{j,M_{c1}}}{\mathit{\partial }z}\right.-M_b\frac{{\mathit{\partial }}^2\mathit{\delta }{Y}_{j,M_{c1}}}{\mathit{\partial }{z}^2}\left.+{\mathit{\epsilon }}_t\frac{\mathit{\partial }\mathit{\delta }{Y}_{j,M_{c1}}}{\mathit{\partial }t}+M_{aj}\frac{\mathit{\partial }\mathit{\delta }{q}_{j,M_{c1}}}{\mathit{\partial }t}\right)\text{d}z\text{d}t\hfill \\ \hfill & +\underset{0}{\overset{t_f}{\int }}\underset{0}{\overset{1}{\int }}{\mathit{\lambda }}_{q_1}\left[\left(\sum _{j=1}^2{M}_{dj}\mathit{\delta }{Y}_{j,M_{c1}}\right)\left(\frac{\mathit{\partial }{q}_1}{\mathit{\partial }t}+M_{c1}{q}_1\right)\right.-M_{d1}\left(Y_1\mathit{\delta }{M}_{c1}\right.\left.\left.+M_{c1}\mathit{\delta }{Y}_{1,M_{c1}}\right)+\left(1+\sum _{j=1}^2{M}_{dj}\right.\mathit{\delta }{Y}_{j,M_{c1}}\right)\left.\left(\frac{\mathit{\partial }\mathit{\delta }{q}_{1,M_{c1}}}{\mathit{\partial }t}+M_{c1}\mathit{\delta }{q}_{1,M_{c1}}+q_1\mathit{\delta }{M}_{c1}\right)\right]\text{d}z\text{d}t\hfill \\ \hfill & +\underset{0}{\overset{t_f}{\int }}\underset{0}{\overset{1}{\int }}{\mathit{\lambda }}_{q_2}\left[\left(\sum _{j=1}^2{M}_{dj}\mathit{\delta }{Y}_{j,M_{c1}}\right)\left(\frac{\mathit{\partial }{q}_2}{\mathit{\partial }t}+M_{c2}{q}_2\right)\right.-M_{d2}{M}_{c2}\mathit{\delta }{Y}_{2,M_{c1}}\hfill \\ \hfill & +\left(1+\sum _{j=1}^2{M}_{dj}\mathit{\delta }{Y}_{j,M_{c1}}\right)\left.\left(\frac{\mathit{\partial }\mathit{\delta }{q}_{2,M_{c1}}}{\mathit{\partial }t}+M_{c2}\mathit{\delta }{q}_{2,M_{c1}}\right)\right]\text{d}z\text{d}t\hfill \end{array}$$(25)

After performing the integration by parts and implementing the boundary and initial conditions of the sensitivity problems, the governing differential equations and also the related boundary and final conditions of the adjoint problem are obtained as, respectively,(26) $$\frac{\mathit{\partial }{\mathit{\lambda }}_V}{\mathit{\partial }z}+\sum _{j=1}^2{Y}_j\frac{\mathit{\partial }{\mathit{\lambda }}_{Y_j}}{\mathit{\partial }z}=0$$(26) (27a) $$M_{d1}{\mathit{\lambda }}_{q_1}\left[\frac{\mathit{\partial }{q}_1}{\mathit{\partial }t}+M_{c1}\left(q_1-1\right)\right]+M_{d1}{\mathit{\lambda }}_{q_2}\left(\frac{\mathit{\partial }{q}_2}{\mathit{\partial }t}+M_{c2}{q}_2\right)-{\mathit{\epsilon }}_t\frac{\mathit{\partial }{\mathit{\lambda }}_{Y_1}}{\mathit{\partial }t}-V\frac{\mathit{\partial }{\mathit{\lambda }}_{Y_1}}{\mathit{\partial }z}-M_b\frac{{\mathit{\partial }}^2{\mathit{\lambda }}_{Y_1}}{\mathit{\partial }{z}^2}=0$$(27a) (27b) $$M_{d2}{\mathit{\lambda }}_{q_2}\left[\frac{\mathit{\partial }{q}_2}{\mathit{\partial }t}+M_{c2}\left(q_2-1\right)\right]+M_{d2}{\mathit{\lambda }}_{q_1}\left(\frac{\mathit{\partial }{q}_1}{\mathit{\partial }t}+M_{c1}{q}_1\right)-{\mathit{\epsilon }}_t\frac{\mathit{\partial }{\mathit{\lambda }}_{Y_2}}{\mathit{\partial }t}-V\frac{\mathit{\partial }{\mathit{\lambda }}_{Y_2}}{\mathit{\partial }z}-M_b\frac{{\mathit{\partial }}^2{\mathit{\lambda }}_{Y_2}}{\mathit{\partial }{z}^2}=0$$(27b) (28a) $$M_{a1}\left(\frac{\mathit{\partial }{\mathit{\lambda }}_V}{\mathit{\partial }t}+\frac{\mathit{\partial }{\mathit{\lambda }}_{Y_1}}{\mathit{\partial }t}\right)+{\mathit{\lambda }}_{q_1}\left(\sum _{j=1}^2{M}_{dj}\frac{\mathit{\partial }{Y}_j}{\mathit{\partial }t}\right)+\left(1+\sum _{j=1}^2{M}_{dj}{Y}_j\right)\left(\frac{\mathit{\partial }{\mathit{\lambda }}_{q_1}}{\mathit{\partial }t}-M_{c1}{\mathit{\lambda }}_{q_1}\right)=0$$(28a) (28b) $$M_{a2}\left(\frac{\mathit{\partial }{\mathit{\lambda }}_V}{\mathit{\partial }t}+\frac{\mathit{\partial }{\mathit{\lambda }}_{Y_2}}{\mathit{\partial }t}\right)+{\mathit{\lambda }}_{q_2}\left(\sum _{j=1}^2{M}_{dj}\frac{\mathit{\partial }{Y}_j}{\mathit{\partial }t}\right)+\left(1+\sum _{j=1}^2{M}_{dj}{Y}_j\right)\left(\frac{\mathit{\partial }{\mathit{\lambda }}_{q_2}}{\mathit{\partial }t}-M_{c2}{\mathit{\lambda }}_{q_2}\right)=0$$(28b) (29) $$\text{At}z=0:{\mathit{\lambda }}_{Y_i}=0$$(29) (30a,b) $$\text{At}z=1:\left({\mathit{\lambda }}_V+\sum _{j=1}^2{\mathit{\lambda }}_{Y_j}{Y}_j\right)=0,2\left(Y_i-Y_i^{exp}\right)+M_b\frac{\mathit{\partial }{\mathit{\lambda }}_{Y_i}}{\mathit{\partial }z}+V{\mathit{\lambda }}_{Y_i}=0$$(30a,b) (31a-c) $${\mathit{\lambda }}_V\left|\begin{array}{c}\\ {}_{t_f}\hfill \end{array}\right.=0,{\mathit{\lambda }}_{Y_i}\left|\begin{array}{c}\\ {}_{t_f}\hfill \end{array}\right.=0,{\mathit{\lambda }}_{q_i}\left|\begin{array}{c}\\ {}_{t_f}\hfill \end{array}\right.=0$$(31a-c)

The above system of equations is also solved by means of the solution procedure stated in Section 2.1 to obtain the adjoint functions. As will be discussed in the next section, when using the CGM as the optimization tool, the gradients of the functional $\widehat{J}$ with respect to M_c1 and M_c2become necessary for the search directions. In order to evaluate this functional, the variation of $\widehat{J}$ is reduced to the following form by considering Equations (26(26) $$\frac{\mathit{\partial }{\mathit{\lambda }}_V}{\mathit{\partial }z}+\sum _{j=1}^2{Y}_j\frac{\mathit{\partial }{\mathit{\lambda }}_{Y_j}}{\mathit{\partial }z}=0$$(26) )–(31(31a-c) $${\mathit{\lambda }}_V\left|\begin{array}{c}\\ {}_{t_f}\hfill \end{array}\right.=0,{\mathit{\lambda }}_{Y_i}\left|\begin{array}{c}\\ {}_{t_f}\hfill \end{array}\right.=0,{\mathit{\lambda }}_{q_i}\left|\begin{array}{c}\\ {}_{t_f}\hfill \end{array}\right.=0$$(31a-c) ),(32) $$\mathit{\delta }{\widehat{J}}_{M_{c1}}\left(M_{c1},M_{c2}\right)=\underset{0}{\overset{t_f}{\int }}\underset{0}{\overset{1}{\int }}{\mathit{\lambda }}_{q_1}\left[M_{d1}{Y}_1\left(q_1-1\right)+\left(1+M_{d2}{Y}_2\right)q_1\right]\mathit{\delta }{M}_{c1}\text{d}z\text{d}t$$(32)

On the other hand, from Equation (32(32) $$\mathit{\delta }{\widehat{J}}_{M_{c1}}\left(M_{c1},M_{c2}\right)=\underset{0}{\overset{t_f}{\int }}\underset{0}{\overset{1}{\int }}{\mathit{\lambda }}_{q_1}\left[M_{d1}{Y}_1\left(q_1-1\right)+\left(1+M_{d2}{Y}_2\right)q_1\right]\mathit{\delta }{M}_{c1}\text{d}z\text{d}t$$(32) ) one can realize that the variation of the functional $\widehat{J}$ with respect to M_c1 should be as follows, (33) $$\mathit{\delta }{\widehat{J}}_{M_{c1}}=\frac{\mathit{\partial }\widehat{J}}{\mathit{\partial }{M}_{c1}}\mathit{\delta }{M}_{c1}$$(33)

Consequently, the gradient of the functional $\widehat{J}\left(M_{c1},M_{c2}\right)$ with respect to M_c1is obtained as,(34) $$\frac{\mathit{\partial }\widehat{J}}{\mathit{\partial }{M}_{c1}}={\widehat{J^{\prime }}}_{M_{c1}}=\underset{0}{\overset{t_f}{\int }}\underset{0}{\overset{1}{\int }}{\mathit{\lambda }}_{q_1}\left[M_{d1}{Y}_1\left(q_1-1\right)+\left(1+M_{d2}{Y}_2\right)q_1\right]\text{d}z\text{d}t$$(34)

Similarly, the adjoint problem corresponding to M_c2 can be developed. It is worth mentioning that the system of adjoint equations of M_c2 become the same as those of M_c1 [29]. So the adjoint equations must be solved just one time. In addition, the following expression for the gradient of the functional $\widehat{J}\left(M_{c1},M_{c2}\right)$ with respect to M_c2 is obtained,(35) $$\frac{\mathit{\partial }\widehat{J}}{\mathit{\partial }{M}_{c2}}={\widehat{J^{\prime }}}_{M_{c2}}=\underset{0}{\overset{t_f}{\int }}\underset{0}{\overset{1}{\int }}{\mathit{\lambda }}_{q_2}\left[M_{d2}{Y}_2\left(q_2-1\right)+\left(1+M_{d1}{Y}_1\right)q_2\right]\text{d}z\text{d}t$$(35)

2.5. The optimization procedure

According to the CGM to find the optimum values of the unknown parameters $\left(M_{c1},M_{c2}\right)$, an iterative process is started for the estimation of the new values of the unknown parameters by using the information of the previous iterations and the corresponding initial guesses as follows,(36) $$M_{ci}^{n+1}=M_{ci}^n-{\mathit{\beta }}_i^n{d}_i^n\text{for}i=1,2\text{and}n=0,1,2,\dots$$(36)

where ${\mathit{\beta }}_i^n$ is the search step size and its evaluation will be discussed later; $d_i^n$ is the direction of descent (i.e. the search direction) which is obtained according to the following relation,(37a,b) $$d_i^n={\widehat{J^{\prime }}}_{M_{ci}}^n+{\mathit{\gamma }}_i^n{d}_i^{n-1}\text{for}i=1,2;n=1,2,\dots ,\text{and}{d}_i^0=0$$(37a,b)

The parameters ${\mathit{\gamma }}_i^n$(i = 1, 2) are called the conjugate coefficients and depend on the gradient of the functional $\widehat{J}$ at the iterations n and n − 1 as,(38a,b) $${\mathit{\gamma }}_i^n=\frac{{\left({\widehat{J^{\prime }}}_{M_{ci}}^n\right)}^2}{{\left({\widehat{J^{\prime }}}_{M_{ci}}^{n-1}\right)}^2}\text{for}i=1,2;n=1,2,\dots ,\text{and}{\mathit{\gamma }}_i^0=0$$(38a,b)

One can note that by assuming ${\mathit{\gamma }}_i^n=0$ $\left(n=0,1,2,\dots \right)$ in Equation (37), the method reduces to the steepest descent method.

By substituting $M_{ci}^{n+1}$ from Equation (35(35) $$\frac{\mathit{\partial }\widehat{J}}{\mathit{\partial }{M}_{c2}}={\widehat{J^{\prime }}}_{M_{c2}}=\underset{0}{\overset{t_f}{\int }}\underset{0}{\overset{1}{\int }}{\mathit{\lambda }}_{q_2}\left[M_{d2}{Y}_2\left(q_2-1\right)+\left(1+M_{d1}{Y}_1\right)q_2\right]\text{d}z\text{d}t$$(35) ) into Equation (17(17) $$J\left(M_{c1},M_{c2}\right)=\underset{0}{\overset{t_f}{\int }}\sum _{i=1}^2{\left[Y_{i,out}\left(t\right)-Y_i^{exp}\left(t\right)\right]}^2\text{d}t$$(17) ), the functional $J\left(M_{c1}^{n+1},M_{c2}^{n+1}\right)$ is obtained as(39) $$J\left(M_{c1}^{n+1},M_{c2}^{n+1}\right)=\underset{0}{\overset{t_f}{\int }}\sum _{i=1}^2{\left[Y_{i,out}\left(M_{c1}^n-{\mathit{\beta }}_1^n{d}_1^n,M_{c2}^n-{\mathit{\beta }}_2^n{d}_2^n\right)-Y_i^{exp}\right]}^2\text{d}t$$(39)

The integral term in Equation (39(39) $$J\left(M_{c1}^{n+1},M_{c2}^{n+1}\right)=\underset{0}{\overset{t_f}{\int }}\sum _{i=1}^2{\left[Y_{i,out}\left(M_{c1}^n-{\mathit{\beta }}_1^n{d}_1^n,M_{c2}^n-{\mathit{\beta }}_2^n{d}_2^n\right)-Y_i^{exp}\right]}^2\text{d}t$$(39) ) can be easily evaluated by expanding the mole fraction of adsorbate components $Y_{i,out}\left(M_{c1}^n-{\mathit{\beta }}_1^n{d}_1^n,M_{c2}^n-{\mathit{\beta }}_2^n{d}_2^n\right)$ in a Taylor series and neglecting their non-linear terms. Consequently, one obtains,(40) $$J\left(M_{c1}^{n+1},M_{c2}^{n+1}\right)=\underset{0}{\overset{t_f}{\int }}\sum _{i=1}^2{\left[Y_{i,out}\left(M_{c1}^n,M_{c2}^n\right)-{\mathit{\beta }}_1^n\mathit{\delta }{Y}_{i,M_{c1}}-{\mathit{\beta }}_2^n\mathit{\delta }{Y}_{i,M_{c2}}-Y_i^{exp}\right]}^2\text{d}t$$(40)

where $Y_{i,out}\left(i=1,2\right)$ are determined from the solution of the related direct problem by using the estimated values of $M_{ci}^n\left(i=1,2\right)$. Also, by assuming $\mathit{\delta }{M}_{ci}=d_i^n\left(i=1,2\right)$, $\mathit{\delta }{Y}_{i,M_{c1}}$ and $\mathit{\delta }{Y}_{i,M_{c2}}$ are obtained from the solution of the sensitivity problems presented in Section 2.3.

Finally, by minimizing the functional given in Equation (40(40) $$J\left(M_{c1}^{n+1},M_{c2}^{n+1}\right)=\underset{0}{\overset{t_f}{\int }}\sum _{i=1}^2{\left[Y_{i,out}\left(M_{c1}^n,M_{c2}^n\right)-{\mathit{\beta }}_1^n\mathit{\delta }{Y}_{i,M_{c1}}-{\mathit{\beta }}_2^n\mathit{\delta }{Y}_{i,M_{c2}}-Y_i^{exp}\right]}^2\text{d}t$$(40) ) with respect to the search step sizes ${\mathit{\beta }}_i^n\left(i=1,2\right)$, these parameters at iteration n are obtained as(41a,b) $${\mathit{\beta }}_1^n=\frac{\left({\widehat{Y}}_1+{\widehat{Y}}_4\right)\left({\widehat{Y}}_8+{\widehat{Y}}_{10}\right)-\left({\widehat{Y}}_3+{\widehat{Y}}_6\right)\left({\widehat{Y}}_7+{\widehat{Y}}_9\right)}{\left({\widehat{Y}}_2+{\widehat{Y}}_5\right)\left({\widehat{Y}}_8+{\widehat{Y}}_{10}\right)-{\left({\widehat{Y}}_3+{\widehat{Y}}_6\right)}^2},{\mathit{\beta }}_2^n=\frac{\left({\widehat{Y}}_2+{\widehat{Y}}_5\right)\left({\widehat{Y}}_7+{\widehat{Y}}_9\right)-\left({\widehat{Y}}_3+{\widehat{Y}}_6\right)\left({\widehat{Y}}_1+{\widehat{Y}}_4\right)}{\left({\widehat{Y}}_2+{\widehat{Y}}_5\right)\left({\widehat{Y}}_8+{\widehat{Y}}_{10}\right)-{\left({\widehat{Y}}_3+{\widehat{Y}}_6\right)}^2}$$(41a,b)

where,(42a–j) $$\begin{array}{c}{\widehat{Y}}_1=\underset{0}{\overset{t_f}{\int }}\left(Y_1-Y_1^{exp}\right)\mathit{\delta }{Y}_{1,M_{c1}}\text{d}t,{\widehat{Y}}_2=\underset{0}{\overset{t_f}{\int }}\mathit{\delta }{Y}_{1,M_{c1}}^2\text{d}t,{\widehat{Y}}_3=\underset{0}{\overset{t_f}{\int }}\mathit{\delta }{Y}_{1,M_{c1}}\mathit{\delta }{Y}_{1,M_{c2}}\text{d}t,{\widehat{Y}}_4=\underset{0}{\overset{t_f}{\int }}\left(Y_2-Y_2^{exp}\right)\mathit{\delta }{Y}_{2,M_{c1}}\text{d}t\hfill \\ {\widehat{Y}}_5=\underset{0}{\overset{t_f}{\int }}\mathit{\delta }{Y}_{2,M_{c1}}^2\text{d}t,{\widehat{Y}}_6=\underset{0}{\overset{t_f}{\int }}\mathit{\delta }{Y}_{2,M_{c1}}\mathit{\delta }{Y}_{2,M_{c2}}\text{d}t,{\widehat{Y}}_7=\underset{0}{\overset{t_f}{\int }}\left(Y_1-Y_1^{exp}\right)\mathit{\delta }{Y}_{1,M_{c2}}\text{d}t,{\widehat{Y}}_8=\underset{0}{\overset{t_f}{\int }}\mathit{\delta }{Y}_{1,M_{c2}}^2\text{d}t,\hfill \\ {\widehat{Y}}_9=\underset{0}{\overset{t_f}{\int }}\left(Y_2-Y_2^{exp}\right)\mathit{\delta }{Y}_{2,M_{c2}}\text{d}t,{\widehat{Y}}_{10}=\underset{0}{\overset{t_f}{\int }}\mathit{\delta }{Y}_{2,M_{c2}}^2\text{d}t\hfill \end{array}$$(42a–j)

2.6. Stopping criterion

The previously developed iteration processes are repeated until the desirable accuracy is reached, which occurs when the value of the objective functional becomes small, i.e.(43) $$J\left(M_{c1}^{n+1},M_{c2}^{n+1}\right)<\widehat{\mathit{\epsilon }}$$(43)

where $\widehat{\mathit{\epsilon }}$ is a prescribed upper limit of the optimized functional, which depends on the value of measurement errors and will be obtained in the next paragraph. At the first time that the inequality (43) is satisfied, the optimization loop is stopped.

Since the measured mole fraction of adsorbate components may contain some measurement errors, and also in order to improve the accuracy of the inverse approach, the discrepancy principle is chosen as the stopping criterion in this study. Accordingly, the mole fraction residual is approximated as,

(44) $$\sum _{i=1}^2\left[Y_{i,out}\left(t\right)-Y_i^{exp}\left(t\right)\right]\approx {\mathit{\sigma }}_s$$(44)

where σ_s is the standard deviation of the measurement errors, which is assumed to be constant. After substituting Equation (44(44) $$\sum _{i=1}^2\left[Y_{i,out}\left(t\right)-Y_i^{exp}\left(t\right)\right]\approx {\mathit{\sigma }}_s$$(44) ) into Equation (17(17) $$J\left(M_{c1},M_{c2}\right)=\underset{0}{\overset{t_f}{\int }}\sum _{i=1}^2{\left[Y_{i,out}\left(t\right)-Y_i^{exp}\left(t\right)\right]}^2\text{d}t$$(17) ), one gets(45) $$\widehat{\mathit{\epsilon }}={\mathit{\sigma }}_s^2{t}_f$$(45)

It is worth mentioning that the convergence of the CGM is guaranteed [4].

3. Results and discussion

In this section, the accuracy and reliability of the proposed inverse algorithm for predicting the overall mass transfer coefficients by using the measured transient mole fraction of the outlet multicomponent are investigated. It should be mentioned that there is no prior information on the unknown quantities. To validate the approach and display its computational efficiency, different examples with different adsorbate components and for a large amount of carrier gas on zeolite NaX are considered. In these examples, the separation of ${\text{CO}}_2$, ${\text{SO}}_2$ and $\text{NO}$ are analysed. Moreover, the breakthrough curves of ${\text{CO}}_2$ adsorption on ammonia-modified commercial granular activated carbon (OXA-GAC) is estimated.

In this study, a normally distributed uncorrelated error with zero mean and constant standard deviation $\left(\text{i}.\text{e}.{\mathit{\sigma }}_s\right)$ together with the solution of the direct problem is used to simulate the measured data. For example, the simulated measurement data of the field variable Y_i is defined to be

(46) $$Y_i=Y_{i\text{,}exact}+{\mathit{\omega }}_{Y_i}$$(46)

where Y_i,exact is the solution of the direct problem and ${\mathit{\omega }}_{Y_i}$ is the random error corresponding to the field variable Y_i with zero mean and specified standard deviation. The normally distributed uncorrelated disturbance ${\mathit{\omega }}_{Y_i}$ is generated by the function ‘normrnd’ in the MATLAB software.

Before showing the computational efficiency and ability of the present inverse algorithm, in order to better understanding the behaviour of the system under consideration, the effects of the different parameters on its response are investigated. For this purpose, the direct problems of the above-mentioned examples are solved and the corresponding results are displayed. The base parameters of these examples are adopted from the works of Yi et al. [30] and Shafeeyan et al. [31], some of which are given in Table 1 and the others are as follows,$${\mathit{\epsilon }}_b=0.42,{\mathit{\epsilon }}_t=0.74,{\mathit{\rho }}_b=507\left({\text{kg/m}}^{\text{3}}\right),L_z=0.055\left(\text{m}\right),V_0=0.0106\left(\text{m/s}\right),D_z={10}^{-5}\left({\text{m}}^{\text{2}}\text{/s}\right).$$

Table 1. Base parameters of the solved examples (reference conditions: P = 82.425 kPa, T = 323.15 K).

	CO2	SO2	NO
b(Pa^–1)	12.22 × 10^−6	17.61 × 10^−6	48.52 × 10^−6
$q_m\left(\text{mole/kg}\right)$	2.9180	6.4730	0.1581
$k\left({\text{s}}^{-1}\right)$	0.0350	0.0690	0.0702

Based on the performed convergence study, the following values are used for the spatial and temporal domain discretization in the numerical computations: N^e = 7, $N_z^e=7$, N^I = 5 and $N_t^I=11$.

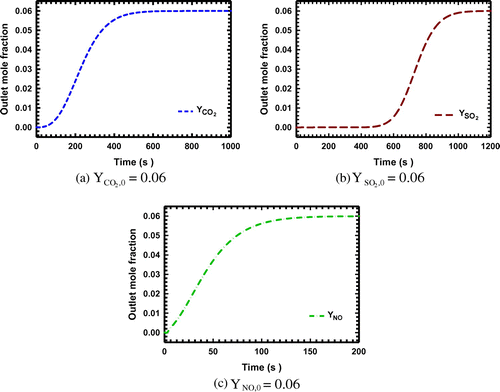
The obtained breakthrough curves for the system with one and two adsorbing components on zeolite NaX are presented in Figures 2–4, respectively. The nature of a solid adsorbent indicates a limitation in the equilibrium adsorption capacity for the solutes, separation from the gas phase into the solid phase under certain temperature and concentration. Therefore, besides the overall mass transfer coefficients, the response of the outlet mole fractions depends on the related adsorbent capacity and input adsorbate concentration. The adsorbent with higher capacity has a longer breakthrough time and the shorter breakthrough time appears for the high input concentration. Figure 2(a) and (b) show this difference for ${\text{CO}}_2$ and ${\text{SO}}_2$, which is due to the fact that the zeolite NaX has higher adsorption capacity for ${\text{SO}}_2$ than ${\text{CO}}_2$. It is notable that a like behaviour is observed in the works of Casas et al. [22], Yi et al. [30], and Marx et al. [32], which validate the solution procedure of the present study. 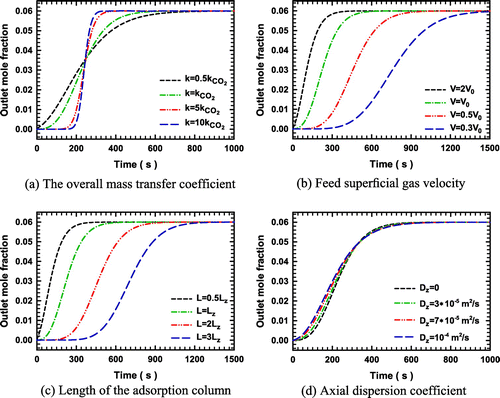The influences of adsorption parameters on the breakthrough curves are studied in Figure 5(a)–(d) for ${\text{CO}}_2$ component on zeolite NaX as a trial example. The effect of the overall mass transfer coefficient on the breakthrough curves is considered in Figure 5(a). It can be seen that as much as the overall mass transfer coefficient increases, the gradient of the breakthrough curve with respect to time increases and the affectivity to it decreases. Hence, at low mass transfer resistance, the kinetics doesn’t have more effect and the LDF approximation in adsorption process approaches to the equilibrium method. Subsequently, the mass transfer zone in the adsorbent bed becomes narrow and also, a breakthrough curve with very sharp profile is obtained. The impact of the superficial gas feed velocity on the breakthrough curve is shown in Figure 5(b). A shift of the breakthrough curves to longer times can be seen at the lower superficial gas feed velocity. A similar behaviour is observed in the work of Pan et al. [33]. This result means that as the space-time of adsorbate in the column increases, the adsorption amount increases. In Figure 5(c) the variation of the breakthrough curves against the adsorption column length is shown. A shift of the breakthrough curves to longer times is observed at the longer adsorption column length. Finally, Figure 5(d) examines the deviation of the breakthrough curves with respect to the axial dispersion coefficient. In this example, it can be seen that the spread of the mass transfer zone due to the axial dispersion coefficient hasn’t significant effect on the breakthrough curve.

Figure 2. (a)–(c): The breakthrough curves for one adsorbing component on zeolite NaX.

Figure 3. (a)–(d): The breakthrough curves for the system with CO₂ and SO₂ as the adsorbing components on zeolite NaX.

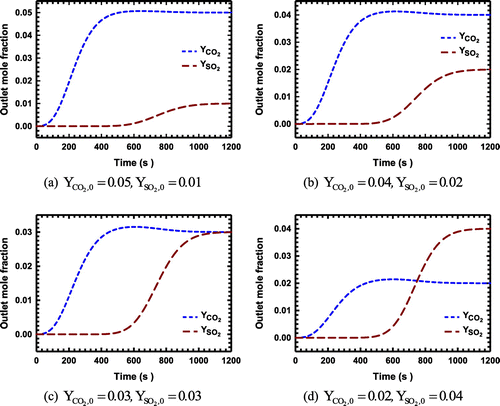
Figure 4. (a)–(d): The breakthrough curves for the system with CO₂ and NO as the adsorbing components on zeolite NaX.

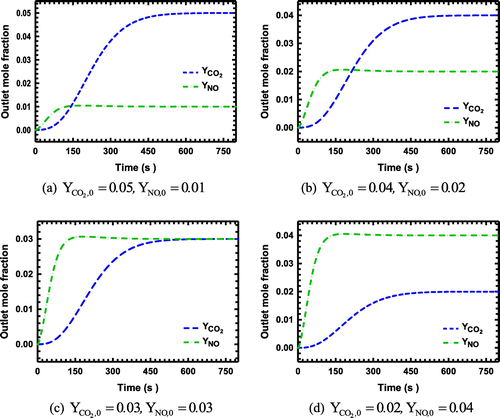
Figure 5. (a)–(d): The influence of adsorption parameters on breakthrough curve for the system with CO₂ as the adsorbing component on zeolite NaX.

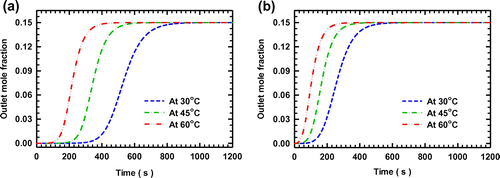
Moreover, the effect of temperature on the breakthrough curves of ${\text{CO}}_2$ adsorption onto OXA-GAC adsorbents are investigated and shown in Figure 6(a) and (b), which is in close agreement with those of the work of Shafeeyan et al. [31].

Figure 6. Effect of temperature on the breakthrough curves of CO₂ adsorption on OXA-GAC (a) at a 50 mL min⁻¹ feed and (b) at a 100 mL min⁻¹ feed flow rate.

At this stage, the results of the inverse algorithm for the different aforementioned examples are presented. In all cases, the per cent of error is determined by using the following equation [23],(47) $$Error\%=100\left|\frac{M_{ci}^{Expected}-M_{ci}^{Estimate}}{M_{ci}^{Expected}}\right|$$(47)

To consider the measurement errors, artificial experimental data generated by using the random noise are added to the data obtained from the direct problem. The comparison of the artificial experimental data and estimated values of the breakthrough curves of the system with CO₂ and SO₂ on as the adsorbing components on zeolite NaX as a trial example is shown in Figure 7. The influences of the measurement errors of the input data (i.e. the mole fractions) on the accuracy of the estimated overall mass transfer coefficients and also the computational efficiency of the present inverse algorithm are presented in Tables 2 and 3 for the examples. In these tables, the corresponding percentage of errors, the CPU times and the number of iterations for the different values of the mole fractions are presented. From the data given in these tables, the high accuracy together with much low computational time efforts of the present approach is quite evident. One can see that in all cases, the estimated unknown parameters are in close agreement with those of the corresponding expected solutions, which validate the present inverse approach.

Figure 7. Comparison of the artificial experimental data and estimated values of the breakthrough curves of the system with CO₂ and SO₂ as the adsorbing components on zeolite NaX.

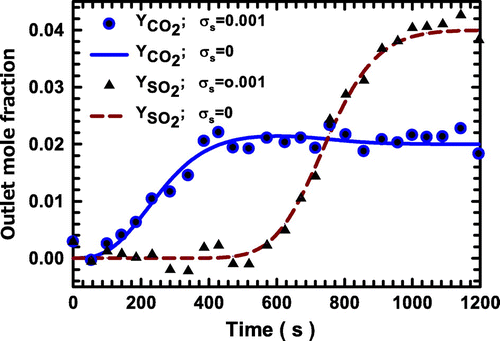
Table 2. The estimated overall mass transfer coefficients, percentage of errors, corresponding CPU times and number of iterations at different mole fractions for the system with CO₂ and SO₂ as the adsorbing components on zeolite NaX.

	$Y_{{\text{CO}}_2,0}$	YSO2,0	$k_{{\text{CO}}_2}^{\text{estimated}}$ (s^−1)	% Error	$k_{{\text{CO}}_2}^{\text{estimated}}$ (s^−1)	% Error	CPU time (s)*
σs = 0	0.06	0	0.0350	$3\times {10}^{-10}$	–	–	50 (9)**
	0.05	0.01	0.0350	$3\times {10}^{-10}$	0.0690	$1.6\times {10}^{-7}$	52 (9)
	0.04	0.02	0.0350	9 × 10^−10	0.0690	$1.6\times {10}^{-7}$	55 (9)
	0.03	0.03	0.0350	$2\times {10}^{-9}$	0.0690	$1.8\times {10}^{-7}$	55 (9)
	0.02	0.04	0.0350	$3\times {10}^{-9}$	0.0690	$2.1\times {10}^{-7}$	56 (9)
	0	0.06	–	–	0.0690	$1.5\times {10}^{-7}$	55 (9)
σs = 5 × 10^−4	0.06	0	0.0347	0.72	–	–	65 (7)
	0.05	0.01	0.0339	3.22	0.0675	2.18	135 (7)
	0.04	0.02	0.0353	0.98	0.0690	0.02	120 (7)
	0.03	0.03	0.0356	1.80	0.0674	2.27	134 (7)
	0.02	0.04	0.0334	2.86	0.0686	0.57	124 (7)
	0	0.06	–	–	0.0697	1.02	67 (7)
σs = 10^−3	0.06	0	0.0358	2.37	–	–	55 (6)
	0.05	0.01	0.0346	1.22	0.0641	7.06	113 (6)
	0.04	0.02	0.0347	0.94	0.0659	4.47	112 (6)
	0.03	0.03	0.0349	0.30	0.0705	2.23	121 (6)
	0.02	0.04	0.0369	5.44	0.0660	0.01	119 (6)
	0	0.06	–	–	0.0696	0.83	57 (6)

* Personal computers with Intel (R), Core(TM)2, Quad CPU Q8400 @ 2.66 GHz, RAM; 4.00 GB

** Number of iteration.

Table 3. The estimated overall mass transfer coefficients, percentage of errors, corresponding CPU times and number of iterations at different mole fractions for the system with CO₂ and NO as the adsorbing components on zeolite NaX.

	$Y_{{\text{CO}}_2,0}$	$Y_{\text{NO,0}}$	$k_{{\text{CO}}_2\left(s^{-1}\right)}^{\text{Estimated}}$	% Error	$k_{\text{NO}\left(s^{-1}\right)}^{\text{Estimated}}$	% Error	CPU time s*
σs = 0	0.05	0.01	0.0350	$1.4\times {10}^{-6}$	0.0702	$4.5\times {10}^{-5}$	46 (8)**
	0.04	0.02	0.0350	$1.3\times {10}^{-6}$	0.0702	$4\times {10}^{-5}$	45 (8)
	0.03	0.03	0.0350	$1.4\times {10}^{-6}$	0.0702	$3.8\times {10}^{-5}$	45 (8)
	0.02	0.04	0.0350	$1.5\times {10}^{-6}$	0.0702	$3.9\times {10}^{-5}$	46 (8)
	0	0.06	–	–	0.0702	$3.2\times {10}^{-5}$	44 (8)
σs = 5 × 10^−4	0.05	0.01	0.0346	1.05	0.0699	0.39	170 (8)
	0.04	0.02	0.0345	1.31	0.0697	0.74	177 (8)
	0.03	0.03	0.0351	0.38	0.0697	0.68	161 (7)
	0.02	0.04	0.0356	1.69	0.0700	0.17	155 (7)
	0	0.06	–	–	0.0696	0.67	69 (7)
σs = 10^−3	0.05	0.01	0.0356	1.88	0.0667	4.93	150 (7)
	0.04	0.02	0.0357	2.19	0.0659	6.11	147 (7)
	0.03	0.03	0.0331	5.54	0.0710	1.18	141 (7)
	0.02	0.04	0.0339	2.76	0.0721	3.17	151 (7)
	0	0.06	–	–	0.0693	1.32	55 (7)

* Personal computers with Intel (R), Core(TM)2, Quad CPU Q8400 @ 2.66 GHz, RAM; 4.00 GB

** Number of iteration.

4. Conclusions

In this work, the DQEIM together with the Newton-Raphson iterative method were employed to solve the non-linear transient governing equations of the bicomponent fixed-bed adsorption based on the LDF. Then, by coupling this method and the conjugate gradient method, a computationally efficient inverse algorithm for the estimation of overall mass transfer coefficients in this system was developed. The measured mole fractions of the outlet multicomponent history in a fixed bed adsorption column were considered as the input data. Using the presented inverse algorithm, different examples of the two adsorbing components with a large amount of carrier gas on zeolite NaX and granular activated carbon were successfully solved as the cases studies. The results showed that the overall mass transfer coefficients of the adsorption column could be estimated with acceptable accuracy and less time and consequently, less computational cost. Through the solving such non-linear problems, the generality and robustness of the present inverse method were revealed and it promotes the application of this inverse method for the other mass transfer problems. Moreover, this algorithm can be used particularly for the characterization of novel synthetic adsorber or the study of the effects of additive materials or other treatments such as microwave swing desorption or temperature swing desorption.

Nomenclature

Table

bi	affinity constant of i compound
C	concentration in the gas phase
${\overline{C}}_i$	concentration of i compound in the gas phase
Dz,i	axial dispersion coefficient of i compound
ki	overall mass transfer coefficient of i compound
Lz	length of the adsorption column
Mci	dimensionless parameter, (Equation (15c))
P	pressure of adsorption column
${\overline{P}}_i$	partial pressure of i compound
qi	dimensionless concentration of i compound in the adsorbed phase
qm,i	maximum concentration of i compound in the adsorbed phase
${\overline{q}}_i$	concentration of i compound in the adsorbed phase
${\overline{q}}_i^{\ast }$	equilibrium concentration of i compound in the adsorbed phase(Equation (4(4) $${\overline{q}}_i^{\ast }=q_{m,i}\frac{b_i{\overline{P}}_i}{1+{\sum }_{j=1}^2{b}_j{\overline{P}}_j}$$(4) ))
ri	radius of the adsorption column
V	dimensionless superficial gas velocity
$\overline{V}$	superficial gas velocity
t	dimensionless time
tf	final time of adsorption
$\overline{t}$	time
T	temperature of column bed
Yi	mole fraction of i compound in the gas phase
Yi,0	inlet mole fraction of i compound in the gas phase
Yi,out	estimated outlet mole fraction of i compound
$Y_i^{exp}$	measured outlet mole fraction of i compound
z	dimensionless coordinate variable
$\overline{z}$	coordinate variable
Greek symbols
ɛb	bed void fraction
ɛt	overall void fraction
$\widehat{\mathit{\epsilon }}$	a prescribed upper limit of the optimized functional J
${\mathit{\lambda }}_{q_i}$	Lagrange multiplier of concentration of i compound in the adsorbed phase
${\mathit{\lambda }}_V$	Lagrange multiplier of velocity
${\mathit{\lambda }}_{Y_i}$	Lagrange multiplier of mole fraction of i compound in the gas phase
ρb	adsorbent apparent density
σs	standard deviation
${\mathit{\omega }}_{Y_i}$	the random error of the field variable Yi

Funding

This work was supported by Persian Gulf University.

Disclosure statement

No potential conflict of interest was reported by the authors.

Acknowledgement

We thank the Persian Gulf University for financial support, for providing various facilities, and for necessary approval.