Direct regularization for system of integral-algebraic equations of index-1

Abstract

It is known that the coupled system consisting of Volterra integral equations of the first and second kind belongs to the class of moderately ill-posed problems. In the present paper, we are interested in numerical solution of Volterra integral-algebraic equations by a direct regularization method, i.e. an approach which does not make use of the adjoint operator as well as any reduction or remodelling of the original problem. A numerical algorithm based on Lavrentiev’s regularization iterated method is constructed that preserves the Volterra structure of the original problem. The convergence analysis of the proposed method is given and its validity and efficiency are also demonstrated through several numerical experiments.

Keywords:

• Ill-posed problem
• Lavrentiev’s iterated method
• regularization parameter
• Volterra integral-algebraic equations
• numerical treatments

AMS Subject Classifications:

• 65R30
• 45Q05
• 35R25

1. Introduction

This article deals with the numerical solution of general system of Volterra integral equations:(1.1) $$\begin{array}{c}\hfill A(t)X(t)=g(t)+{\int }_0^{t}K(t,s)X(s)\mathrm{d}s,t\in \mathrm{\Omega }=[0,T],\end{array}$$(1.1)

where the matrices $A(.),K(.,.)\in {\mathbb{R}}^{d\times d}(d\ge 2)$ and the function $g(.)\in {\mathbb{R}}^d$ are assumed to be continuous on their domains, and the matrix A(t) is singular that is, det $A(t)=0$ and rank $A(t)\ge 1$ on $\mathrm{\Omega }$. Following [1], we will refer to this system of Volterra integral equations as Integral-Algebraic Equations (IAEs), due to the terminology introduced by Gear. Generally, such ill-posed systems consist of a coupled system of Volterra integral equations of the first and second kind which may be arise in many applied problems e.g. in memory kernel identification problems in heat conduction [2], viscoelasticity [3], evolution of a chemical reaction within a small cell [4] and Kirchhoff’s laws.

The Volterra IAEs belong to the class of moderately ill-posed problems, since the ill-posedness is not nearly as serious for Volterra equations as it is for the Fredholm case. However, the first kind Volterra equation which appears in the IAE system is sufficiently unstable as to require regularization techniques in order to compute reasonably accurate solutions. The discretization as well as regularization techniques have a regularizing feature with a regularization parameter which is in a certain manner connected to the level of disturbances of the initial data.

The index notion is a critical issue for the theoretical and numerical analysis of an IAE system, which has been first introduced by Gear [1] and has recently extended by Liang and Brunner [5]. It is closely connected to the concept of $\mathit{\nu }$-smoothing property of a Volterra integral operator which has been defined by Lamm for the case $d=1$ and extended by Brunner for $d\ge 2$. Actually, this is a tool for consideration the ill-posed nature as well as a measure for the degree of ill-posed ness of the first kind Volterra integral equation in the IAE system. Following [6], it is known that for the Volterra IAEs, the degree of instability increases as the degree of $\mathit{\nu }$-smoothing increases.

Although, the analysis of IAEs have received less attention, however, in recent years the numerical solvability of IAEs have been pursued by a few researches. In 2000, Kauthen [7] studied polynomial spline collocation method and the convergence results. Hadizadeh et al. [8] in 2011, presented the Jacobi collocation method including the matrix-vector multiplication representation for IAEs of index-2. A posteriori error estimation is also obtained for the Legendre collocation method by the same authors in [9]. These methods extended to the semi-explicit IAEs of indices 1 and 2 as well as the IAEs with weakly singular kernels by Pishbin [10] in 2013. A multistep method based on Adam’s quadrature rules and extrapolation formulas constructed by Bulatov et al. [11]. More recent studies are due to Liang and Brunner [5,12], who have presented an analysis of piecewise polynomial collocation solutions for general systems of linear IAEs based on the notions of the tractability index and the $\mathit{\nu }$-smoothing property by decoupling the system into the inherent system of regular Volterra integral equations. Actually, most of the numerical methods discussed so far, have been the projection-based approach and according to [12], this approach together with the tractability index are natural ways of analysing the general systems of IAEs. However, owing to some restrictive conditions as well as instability of numerical differentiation, the reduction of the problem to the regular system of Volterra equations may not be always practical from a numerical point of view. Another difficulty is related to high computational complexity of the projection based methods, since the associated projectors onto the nullspaces have to be computed at every integration step, which makes the approach rather expensive. Due to the ill-posed behaviour of the first kind Volterra integral equation in the IAEs, we are seeking for a regularization type method for overcoming the difficulties which may arise in numerical consideration of the problem. Therefore, in the present paper we are interested in certain direct regularization approaches for numerically solving the Volterrs IAEs system i.e. the method which does not make use of an inversion formula or some restrictive conditions for the exact solution and especially which is not based on any reduction procedure for the original problem. Since the most classical regularization methods are based on the inversion of the operator and consequently such methods do not generally preserve the Volterra structure of the original problem, here we pay special attention to applicability of Lavrentiev’s regularization iterated method for the approximate solution of Volterra IAEs system of index-1.

The paper is organized as follows. In Section 2, we give some preliminaries and main results related to general IAE theory and regularization techniques. In Section 3, we describe a direct regularization method based on Lavrentiev’s iterated scheme for IAE system of index-1 and derive an experimental strategy for choosing the optimal value of the regularization parameter. Section 4 deals with the convergence analysis of the method. We end up with some numerical illustrations and report the numerical experiments in Section 5.

2. Preliminaries and IAE theory

In this section, we review some basic facts of IAE theory from [13] and present results on the solvability of an integral-algebraic Equation (1.1(1.1) $$\begin{array}{c}\hfill A(t)X(t)=g(t)+{\int }_0^{t}K(t,s)X(s)\mathrm{d}s,t\in \mathrm{\Omega }=[0,T],\end{array}$$(1.1) ), when the kernel is continuous. Throughout this paper, we assume that all linear operators occurring here map on Hilbert space $L^2(\mathrm{\Omega })$ with the inner product (, ) and norm $\Vert .\Vert$ . We will also give some preliminary results related to positive (monotone) operators which is needed for our convergence analysis of the method presented in Section 4.

The $\mathit{\nu }$-smoothing property is a main concept for describing a measure of the degree of ill-posedness of the first kind Volterra operator, $T:C(\mathrm{\Omega },{\mathbb{R}}^d)\to C(\mathrm{\Omega },{\mathbb{R}}^d)$,$$\begin{array}{c}\hfill (TX)(t):={\int }_0^{t}K(t,s)X(s)\mathrm{d}s,t\in \mathrm{\Omega }.\end{array}$$

This concept defined by Lamm [14] and has been recently extended to the higher case ($d\ge 2$) by Liang and Brunner [5]:

Definition 2.1:

[From [5])]The Volterra integral operator T corresponding to the kernel matrix $K(t,s)=\left[\begin{array}{c}{k}_{pq}(t,s)\\ (p,q=1,2,\dots ,d)\end{array}\right]$, with $d\ge 2,$ said to be $\mathit{\nu }$-smoothing, if there exist integers ${\mathit{\nu }}_{pq}\ge 1$ with $\mathit{\nu }:=ma{x}_{1\le p,q\le d}\}{\mathit{\nu }}_{pq}\{$ such that the following hold:

(a)	$\frac{{\mathit{\partial }}^j{k}_{pq}(t,s)}{\mathit{\partial }{t}^j}{|}_{s=t}=0,t\in \mathrm{\Omega },j=0,1,\dots ,{\mathit{\nu }}_{pq}-2,$
(b)	$\frac{{\mathit{\partial }}^{{\mathit{\nu }}_{pq}-1}{k}_{pq}(t,s)}{\mathit{\partial }{t}^{{\mathit{\nu }}_{pq}-1}}{|}_{s=t}\ne 0,t\in \mathrm{\Omega },$-pagination
(c)	$\frac{{\mathit{\partial }}^{{\mathit{\nu }}_{pq}}{k}_{pq}(t,s)}{\mathit{\partial }{t}^{{\mathit{\nu }}_{pq}}}\in C(D),(D:=\}(t,s):0\le s\le t\le T\{).$

We set ${\mathit{\nu }}_{pq}:=0,$ when $k_{pq}(t,s)\equiv 0$.

A first kind Volterra equation $TX=g$, is called a $\mathit{\nu }$-smoothing problem, if T is a $\mathit{\nu }$-smoothing operator and $g\in C^{\mathit{\nu }}(\mathrm{\Omega }).$

Accordingly, a one-smoothing problem ($\mathit{\nu }=1$) is the least ill-posed, since it requires only one differentiation operation.

In order to review some basic concepts related to IAE theory, let us consider the following semi-explicit linear version of (1.1(1.1) $$\begin{array}{c}\hfill A(t)X(t)=g(t)+{\int }_0^{t}K(t,s)X(s)\mathrm{d}s,t\in \mathrm{\Omega }=[0,T],\end{array}$$(1.1) ):(2.1) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle y(t)=f_1(t)+{\int }_0^t(k_{11}(t,s)y(s)+k_{12}(t,s)z(s))\mathrm{d}s,}\hfill \\ \hfill \\ {\displaystyle 0=f_2(t)+{\int }_0^t(k_{21}(t,s)y(s)+k_{22}(t,s)z(s))\mathrm{d}s.}\hfill \end{array}\right.\end{array}$$(2.1)

The following theorem describes the conditions under which the Equation (2.1(2.1) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle y(t)=f_1(t)+{\int }_0^t(k_{11}(t,s)y(s)+k_{12}(t,s)z(s))\mathrm{d}s,}\hfill \\ \hfill \\ {\displaystyle 0=f_2(t)+{\int }_0^t(k_{21}(t,s)y(s)+k_{22}(t,s)z(s))\mathrm{d}s.}\hfill \end{array}\right.\end{array}$$(2.1) ) possesses a unique continuous solution:

Theorem 2.2:

[From [13])]Let $\mathit{\mu }\ge 0$ and assume that:

(1)	$k_{1l}\in C^{\mathit{\mu }}(D)$ for $l=1,2,$
(2)	$k_{2l}\in C^{\mathit{\mu }+1}(D)$ for $l=1,2$, and $|det(k_{22}(t,t))|\ge k_0>0$,
(3)	$f_1\in C^{\mathit{\mu }}(\mathrm{\Omega })$ and $f_2\in C^{\mathit{\mu }+1}(\mathrm{\Omega })$, with $f_2(0)=0$.

Then the IAE (2.1(2.1) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle y(t)=f_1(t)+{\int }_0^t(k_{11}(t,s)y(s)+k_{12}(t,s)z(s))\mathrm{d}s,}\hfill \\ \hfill \\ {\displaystyle 0=f_2(t)+{\int }_0^t(k_{21}(t,s)y(s)+k_{22}(t,s)z(s))\mathrm{d}s.}\hfill \end{array}\right.\end{array}$$(2.1) ) possesses a unique solution ${(y,z)}^T$ on $\mathrm{\Omega }$, with $y,z\in C^{\mathit{\mu }}(\mathrm{\Omega })$.

The concept of index has been introduced in order to quantify the level of difficulty that is involved in solving a given IAEs. There are several different (but often closely related) definitions of the index for an IAE which reveal the mathematical structure, stability and solvability in the analysis of the IAEs. At first, we recall the definition of differential index of IAEs which is due to Gear [1]:

Definition 2.3:

We say the system (2.1(2.1) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle y(t)=f_1(t)+{\int }_0^t(k_{11}(t,s)y(s)+k_{12}(t,s)z(s))\mathrm{d}s,}\hfill \\ \hfill \\ {\displaystyle 0=f_2(t)+{\int }_0^t(k_{21}(t,s)y(s)+k_{22}(t,s)z(s))\mathrm{d}s.}\hfill \end{array}\right.\end{array}$$(2.1) ) has differential index m, if m is the minimum possible number of differentiating (2.1(2.1) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle y(t)=f_1(t)+{\int }_0^t(k_{11}(t,s)y(s)+k_{12}(t,s)z(s))\mathrm{d}s,}\hfill \\ \hfill \\ {\displaystyle 0=f_2(t)+{\int }_0^t(k_{21}(t,s)y(s)+k_{22}(t,s)z(s))\mathrm{d}s.}\hfill \end{array}\right.\end{array}$$(2.1) ) to obtain a system of second kind Volterra equations.

As shown in [5], the kernel function seriously impacts on the solution as well as the differential index and the tractability index. For this reason, Brunner [13] has defined the tractable index as follows:

Definition 2.4:

[From [13]] The semi-explicit IAE (2.1(2.1) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle y(t)=f_1(t)+{\int }_0^t(k_{11}(t,s)y(s)+k_{12}(t,s)z(s))\mathrm{d}s,}\hfill \\ \hfill \\ {\displaystyle 0=f_2(t)+{\int }_0^t(k_{21}(t,s)y(s)+k_{22}(t,s)z(s))\mathrm{d}s.}\hfill \end{array}\right.\end{array}$$(2.1) ) is said to be index-1 tractable, if the first kind VIE$${\int }_0^t{k}_{22}(t,s)w(s)\mathrm{d}s=g(t),t\in \mathrm{\Omega }=[0,T],$$

is uniquely solvable in $C(\mathrm{\Omega })$ whenever $g\in C^1(\mathrm{\Omega })$ and $g(0)=0$.

Another concept that needs to be introduced is the positivity (monotonicity) of an operator which is discussed in detail in [15] and here we give an explanation of this issue without lengthy and detailed hypothesis:

Definition 2.5:

A bounded self-adjoint linear operator T in Hilbert space is said to be positive (monotone), written $T\ge 0$, if and only if $(Tu,u)\ge 0$, for each u .

As indicated in [15], the positive or monotone operators coincide with sectorial operators, and some references refer them as accretive operators which satisfy $Re(Tu,u)\ge 0$, or equivalently the resolvent set $\mathit{\rho }(-T)$ corresponding to $-T$ contains $(0,\infty ),$ and$${\Vert (T+\mathit{\alpha }I)}^{-1}\Vert \le 1/\mathit{\alpha },\mathit{\alpha }>0,$$

where $\mathit{\alpha }$ is a constant. (cf. [16, Chapter2]).

In the next section, we will present a direct algorithm based on an iterative regularization method for the approximate solution of Volterra system of IAEs of index-1.

3. Regularization for integral-algebraic equations of index-1

Let us consider the linear system of IAEs (1.1(1.1) $$\begin{array}{c}\hfill A(t)X(t)=g(t)+{\int }_0^{t}K(t,s)X(s)\mathrm{d}s,t\in \mathrm{\Omega }=[0,T],\end{array}$$(1.1) ), where $A(t)=\left(\begin{array}{cc}1& 0\\ 0& 0\\ \end{array}\right)$ is a singular matrix, $K(t,s)=\left(\begin{array}{cc}{k}_{11}& k_{12}\\ k_{21}& k_{22}\\ \end{array}\right),$$X(t)=(y(t),z(t){)}^T$ and $g(t)=(f_1(t),f_2(t){)}^T,$ such that the data functions $f_i$ and $k_{ij},i,j=1,2,$ are sufficiently smooth and $f_2(0)=0,$ with $k_{22}$ satisfies $|k_{22}(t,t)|\ge k_0\ge 0,t\in \mathrm{\Omega }.$

It will often be useful to rewrite the Equation (1.1(1.1) $$\begin{array}{c}\hfill A(t)X(t)=g(t)+{\int }_0^{t}K(t,s)X(s)\mathrm{d}s,t\in \mathrm{\Omega }=[0,T],\end{array}$$(1.1) ) in the compact form(3.1) $$\begin{array}{c}\hfill {\mathbf{T}}_{h}X=g,\end{array}$$(3.1)

where the operator ${\mathbf{T}}_h:L^2(\mathrm{\Omega };{\mathbb{R}}^d)\to L^2(\mathrm{\Omega };{\mathbb{R}}^d)$ is defined by$$\begin{array}{c}\hfill {\mathbf{T}}_h=\left(\begin{array}{cc}\mathbf{I}-T_{11}& -T_{12}\\ -T_{21}& -T_{22}\\ \end{array}\right),\end{array}$$

with $d=2$, such that $\mathbf{I}$ is an identity operator and the Volterra integral operators $T_{ij}$ are given by$$\begin{array}{c}\hfill (T_{ij}u)(t):={\int }_0^t{k}_{ij}(t,s)u(s)\mathrm{d}s,t\in \mathrm{\Omega }.\end{array}$$

Due to non-degeneracy of the kernels $k_{ij}$, Equation (1.1(1.1) $$\begin{array}{c}\hfill A(t)X(t)=g(t)+{\int }_0^{t}K(t,s)X(s)\mathrm{d}s,t\in \mathrm{\Omega }=[0,T],\end{array}$$(1.1) ) is ill-posed. Therefore, in the case of perturbed data, we are concerned to $g^{\mathit{\delta }}$ instead of g; where $g^{\mathit{\delta }}$ satisfies $\Vert g-g^{\mathit{\delta }}\Vert \le \mathit{\delta }$ for some $\mathit{\delta }>0$.

For describing our direct approach, we give firstly some results regarding the Lavrentiev’s m-times iterated method which is followed directly from [14]:

For fixed integer $m\ge 1$, and given regularization parameter $\mathit{\alpha }>0$, the Lavrentiev’s m-times iterated method for equation $Au=f$, determines $u_{\mathit{\alpha }}^{\mathit{\delta }}$ via(3.2) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}(A+\mathit{\alpha }I)u_n=\mathit{\alpha }{u}_{n-1}+f^{\mathit{\delta }},\hfill & n=1,2,\dots ,m,\hfill \\ u_{\mathit{\alpha }}^{\mathit{\delta }}:=u_m,\hfill \end{array}\right.\end{array}$$(3.2)

starting from $u_0=0$. For $m=1$, the method reduces to Lavrentiev’s classical method, meanwhile for $m>1$, corrections are applied to further stabilize the problem. (see e.g. [14,17,18] for further details). As, any iterative regularization methods must address several principles e.g. concerning the initial values, the regularization parameter, stopping criterion and convergence properties, we have to show the reasons why the proposed method is a suitable procedure. Note that, typical discretization of the problem leads to a sparse matrix representation which means that the calculation of $u_n$ with an iterated method will be accomplished rather fast. These matrices have very small entries along the diagonals, and thus one way to stabilize such a system would be to augment the values on the diagonal, so adding a term $\mathit{\alpha }u$ (for $\mathit{\alpha }>0$ small) serves to stabilize the numerical process. We refrain from going into more details and refer the reader to [19–21] for further issues.

A perturbed version of system (3.1(3.1) $$\begin{array}{c}\hfill {\mathbf{T}}_{h}X=g,\end{array}$$(3.1) ) may be considered as follows:$$\begin{array}{c}\hfill ({\mathbf{T}}_h+\mathit{\alpha }\mathbf{I})X=g^{\mathit{\delta }},\end{array}$$

which is a (well-posed) second kind Volterra system and has a unique solution depending continuously on data. For numerical implementation of the method, we approximate X(t) in terms of its components $y_{\mathit{\alpha }}^{\mathit{\delta }}$ and $z_{\mathit{\alpha }}^{\mathit{\delta }}$ in the form $y_{\mathit{\alpha }}^{\mathit{\delta }}={\sum }_{j=1}^N{c}_j{\mathit{\psi }}_j,z_{\mathit{\alpha }}^{\mathit{\delta }}={\sum }_{j=1}^N{d}_j{\mathit{\psi }}_j$, where ${\mathit{\psi }}_1,\dots ,{\mathit{\psi }}_N$ are basis functions and $(c_j)$, $(d_j)$ will be determined through the vector $\mathbf{w}$ which is obtained by the following iterative algorithm:$$\begin{array}{c}\hfill \left\{\begin{array}{cc}({\mathbf{T}}_h^N+\mathit{\alpha }\mathrm{\Psi })X_n=\mathit{\alpha }\mathrm{\Psi }{X}_{n-1}+{\mathbf{g}}^N,\hfill & n=1,2,\dots m,\hfill \\ \mathbf{w}:=X_m,\hfill \end{array}\right.\end{array}$$

such that$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathbf{T}}_h^N=(T_h{\mathit{\psi }}_j,{\mathit{\psi }}_i),\hfill \\ {\mathbf{g}}^N=(g,{\mathit{\psi }}_i),\hfill \\ \mathrm{\Psi }=({\mathit{\psi }}_j,{\mathit{\psi }}_i).\hfill \end{array}\right.\end{array}$$

For choosing the parameter $\mathit{\alpha }$, we may start from $X_0=0$ and for fixed m with g replaced by $g^{\mathit{\delta }}$ and $\Vert g-g^{\mathit{\delta }}\Vert <\mathit{\delta }$, for some $\mathit{\delta }>0$, we will use a multi-step process to find the appropriate $\mathit{\alpha }$. To do so, let r be the number of steps so that in each step we have m iteration, and let ${\mathrm{\Delta }}_r^{\mathit{\delta }}$ denotes the defect in each step i.e.$${\mathrm{\Delta }}_r^{\mathit{\delta }}:={\mathbf{T}}_h{X}_r^{\mathit{\delta }}-g^{\mathit{\delta }},$$

where $\mathit{\alpha }=r^{-1}$. Now, for fixed b , we choose some $\mathit{\gamma }>0$, ( here $\mathit{\gamma }=1$, due to a given integer r as a number of steps), and set $r(k)=\mathit{\gamma }k$. The process of computing $X_{r(k)}^{\mathit{\delta }},k=0,1,2,\dots ,$ can be stopped, whilst$$\Vert {\mathrm{\Delta }}_{r(k)}^{\mathit{\delta }}\Vert \le b\mathit{\delta },$$

and then, set $r_{\mathit{\delta }}=r(k_{\mathit{\delta }})$, where $k_{\mathit{\delta }}$ denotes the stopping index.

Under this terminology, for rather small number of iterations m and divisions N , a suitable $\mathit{\alpha }$ is available which gives us an appropriate approximate solution. However, for improving the solution, a good strategy is to proceed the method iteratively with obtained $\mathit{\alpha }$, until the more appropriate solution is attained. This issue will be further discussed experimentally in Section 5 which shows the low computational complexity of the proposed method respect to the other projection based methods.

4. Convergence analysis

Our convergence analysis is mainly based on properties of monotone operators that we have mentioned in Section 2. These operators are one of the most important and particular cases for investigating the application and theoretical analysis of the Lavrentiev’s method. We refrain from going into details and pointed out the analysis of Lavrentiev’s m-times iterated method for Volterra integral equations with monotone operators can be found in [15,22,23] and references therein.

This useful lemma which is due to [24], shows that the usual operator norm holds for general $n\times n$ operator matrices, here $n=2$:

Lemma 4.1:

[From [24])] If A, B, C and D are operators in B(H) which denotes the space of all bounded linear operators on a complex separable Hilbert space H with the usual operator norm $\Vert .\Vert$, which is defined on all of B(H), then$$∥\begin{array}{c}\left[\begin{array}{cc}A& B\\ C& D\\ \end{array}\right]\end{array}∥\le ∥\begin{array}{c}\left[\begin{array}{cc}\Vert A\Vert & \Vert B\Vert \\ \Vert C\Vert & \Vert D\Vert \\ \end{array}\right]\end{array}∥.$$

We are now ready to state the main result on the convergence analysis of the presented method applied to integral-algebraic equations of index-1:

Theorem 4.2:

Consider the operator matrix ${\mathbf{T}}_h$ and let $k_{ij}(t,s)$ be continuous for $t,s\in \mathrm{\Omega }$, where $\mathrm{\Omega }$ be a closed, bounded set in $\mathbb{R}$. Assume that the Integral-Algebraic Equation (3.1(3.1) $$\begin{array}{c}\hfill {\mathbf{T}}_{h}X=g,\end{array}$$(3.1) ) is uniquely solvable for given $f_i\in C^{i-1}(\mathrm{\Omega }),i=1,2$. Let an appropriate regularization parameter $\mathit{\alpha }(\mathit{\delta })$ be chosen such that $\mathit{\alpha }\to 0$ and $\mathit{\delta }/\mathit{\alpha }\to 0$, as $\mathit{\delta }\to 0$. Moreover, the linear and bounded operator ${\mathbf{T}}_h$ is such that(4.1) $$\begin{array}{c}\hfill \Vert {({\mathbf{T}}_h+\mathit{\alpha }\mathbf{I})}^{-1}\Vert \le \frac{1}{\mathit{\alpha }},\mathit{\alpha }>0,\end{array}$$(4.1)

where the norm of $2\times 2$ operator matrix ${\mathbf{T}}_h$ is defined by$$\begin{array}{cc}\hfill \Vert {\mathbf{T}}_h\Vert & =\underset{\Vert U\Vert =1}{sup}\Vert {\mathbf{T}}_{h}U\Vert \hfill \\ \hfill & =\underset{\Vert U\Vert =1}{sup}{\left({\int }_0^1\left(\mid T_{11}{u}_1(t)+T_{12}{u}_2(t){\mid }^2+\mid T_{21}{u}_1(t)+T_{22}{u}_2(t){\mid }^2\right)\mathrm{d}t\right)}^{1/2}.\hfill \end{array}$$

Then, for $X_0=0$, the approximate solution of the proposed method satisfies $\Vert X_{\mathit{\alpha }}-X^{\ast }\Vert \to 0$, where $X^{\ast }\in \overline{R(T)}$ is the exact solution.

Proof The proof is presented in two parts. Let us first consider the case for the exact data.

We replace the Equation (3.1(3.1) $$\begin{array}{c}\hfill {\mathbf{T}}_{h}X=g,\end{array}$$(3.1) ) in Lavrentiev regularization by the linear system of equations $({\mathbf{T}}_h+\mathit{\alpha }\mathbf{I})X=g$, and rewrite the Lavrentiev’s iteration $({\mathbf{T}}_h+\mathit{\alpha }\mathbf{I})X_n=\mathit{\alpha }{X}_{n-1}+g,$ in terms of $X_n$ as$$X_n=\mathit{\alpha }{({\mathbf{T}}_h+\mathit{\alpha }\mathbf{I})}^{-1}{X}_{n-1}+{({\mathbf{T}}_h+\mathit{\alpha }\mathbf{I})}^{-1}g,$$

or$$X=\mathit{\alpha }{({\mathbf{T}}_h+\mathit{\alpha }\mathbf{I})}^{-1}X+{({\mathbf{T}}_h+\mathit{\alpha }\mathbf{I})}^{-1}g.$$

Subtracting $X_n$ from X , obtains(4.2) $$\begin{array}{c}\hfill X-X_n=\mathit{\alpha }{({\mathbf{T}}_h+\mathit{\alpha }\mathbf{I})}^{-1}(X-X_{n-1}).\end{array}$$(4.2)

This is true for any value of n , so we can write(4.3) $$\begin{array}{c}\hfill X-X_{n-1}=\mathit{\alpha }{({\mathbf{T}}_h+\mathit{\alpha }\mathbf{I})}^{-1}(X-X_{n-2}),\end{array}$$(4.3)

substituting (4.3(4.3) $$\begin{array}{c}\hfill X-X_{n-1}=\mathit{\alpha }{({\mathbf{T}}_h+\mathit{\alpha }\mathbf{I})}^{-1}(X-X_{n-2}),\end{array}$$(4.3) ) into (4.2(4.2) $$\begin{array}{c}\hfill X-X_n=\mathit{\alpha }{({\mathbf{T}}_h+\mathit{\alpha }\mathbf{I})}^{-1}(X-X_{n-1}).\end{array}$$(4.2) ), leads to$$X-X_n={(\mathit{\alpha }{({\mathbf{T}}_h+\mathit{\alpha }\mathbf{I})}^{-1})}^2(X-X_{n-2}).$$

Continuing this process n times, the following equation is obtained$$X-X_n={(\mathit{\alpha }{({\mathbf{T}}_h+\mathit{\alpha }\mathbf{I})}^{-1})}^n(X-X_0),$$

this shows that $\}{X}_n\{$ converges to the solution X , if and only if ${(\mathit{\alpha }{({\mathbf{T}}_h+\mathit{\alpha }\mathbf{I})}^{-1})}^n\to 0,$ as $n\to \infty$.

Taking $X_0=0$ as an arbitrary choice of the initial approximation, the sequence $\}{X}_n\{$ can be generated in the following iterative relation$$X_n={\mathbf{T}}_h^{-1}(1-{(\mathit{\alpha }{({\mathbf{T}}_h+\mathit{\alpha }\mathbf{I})}^{-1})}^n)g.$$

Due to the monotonicity property of the operator ${\mathbf{T}}_h$, it follows from the Lemma 4.1 and assumption of the theorem that for all $n\ge 1$,$$\Vert {(\mathit{\alpha }{({\mathbf{T}}_h+\mathit{\alpha }\mathbf{I})}^{-1})}^n\Vert ⩽1,$$

where the norm is the usual operator norm for $2\times 2$ matrix with integral operator entries which has obtained and extended from the corresponding norm in $L^2$. (see e.g. [24], for further details)

From the relation (4.1(4.1) $$\begin{array}{c}\hfill \Vert {({\mathbf{T}}_h+\mathit{\alpha }\mathbf{I})}^{-1}\Vert \le \frac{1}{\mathit{\alpha }},\mathit{\alpha }>0,\end{array}$$(4.1) ), we have ${(\mathit{\alpha }{({\mathbf{T}}_h+\mathit{\alpha }\mathbf{I})}^{-1})}^n\to 0,$ as $n⟶\infty$, or equivalently,$${\mathbf{T}}_h^{-1}\left(1-{\left({\displaystyle \frac{\mathit{\alpha }}{{\mathbf{T}}_h+\mathit{\alpha }\mathbf{I}}}\right)}^n\right)⟶{\mathbf{T}}_h^{-1},\mathrm{as}n⟶\infty ,$$

hence, we conclude $X_n\to X^{\ast }(={\mathbf{T}}_h^{-1}g),$ as $n⟶\infty .$

Eventually in the case of perturbed data, we assume that the free term g is contaminated with noise $\mathit{\delta }$, i.e. we have $({\mathbf{T}}_h+\mathit{\alpha }\mathbf{I})X_n^{\mathit{\delta }}=\mathit{\alpha }{X}_{n-1}^{\mathit{\delta }}+g^{\mathit{\delta }}$, so by setting $X_0=0$, $X_n^{\mathit{\delta }}$ can be obtain by$$X_n^{\mathit{\delta }}={\mathbf{T}}_h^{-1}\left(1-{\left({\displaystyle \frac{\mathit{\alpha }}{{\mathbf{T}}_h+\mathit{\alpha }\mathbf{I}}}\right)}^n\right)g^{\mathit{\delta }}.$$

It can be easily seen that$${\mathbf{T}}_h^{-1}\left(1-{\left({\displaystyle \frac{\mathit{\alpha }}{{\mathbf{T}}_h+\mathit{\alpha }\mathbf{I}}}\right)}^n\right)\le \frac{n}{\mathit{\alpha }}.$$

Assuming $\Vert g-g^{\mathit{\delta }}\Vert <\mathit{\delta }$, we have$$\Vert X_n^{\mathit{\delta }}-X_n\Vert \le \Vert {\mathbf{T}}_h^{-1}\left(1-{\left({\displaystyle \frac{\mathit{\alpha }}{{\mathbf{T}}_h+\mathit{\alpha }\mathbf{I}}}\right)}^n\right)(g-g^{\mathit{\delta }})\Vert \le n\frac{\mathit{\delta }}{\mathit{\alpha }}.$$

Owing to this inequality as well as the consequence of our previous relation ${(\mathit{\alpha }{({\mathbf{T}}_h+\mathit{\alpha }\mathbf{I})}^{-1})}^n\to 0$, we derive the following inequalities$$\begin{array}{cc}\hfill \Vert X_n^{\mathit{\delta }}-X^{\ast }\Vert & \le \Vert X_n-X^{\ast }\Vert +\Vert X_n^{\mathit{\delta }}-X_n\Vert \hfill \\ \hfill & \le \Vert {(\mathit{\alpha }{({\mathbf{T}}_h+\mathit{\alpha }\mathbf{I})}^{-1})}^n{X}^{\ast }\Vert +\Vert T_h^{-1}\left(1-{\left({\displaystyle \frac{\mathit{\alpha }}{{\mathbf{T}}_h+\mathit{\alpha }\mathbf{I}}}\right)}^n\right)(g-g^{\mathit{\delta }})\Vert ,\hfill \end{array}$$

and finally by utilizing an appropriate discrepancy principle (see e.g. [14]), the number of iterations in terms of the error level satisfying $n\mathit{\delta }\to 0,$ as $\mathit{\delta }\to 0$, so the sufficient conditions for convergence of the solution in perturbed case is ensured and $\Vert X_n^{\mathit{\delta }}-X^{\ast }\Vert \to 0$ as $\mathit{\delta }\to 0.$

Remark 4.3:

Following the recent results related to the convergence of Lavrentiev regularization in [25–27], it can be shown that for the monotone bounded linear operators on Hilbert spaces as well as the smoothing property of solution, the rate of convergence $\Vert X_{\mathit{\alpha }}-X^{\ast }\Vert =O({\mathit{\alpha }}^p),as\mathit{\alpha }\to 0$, for some $0<p\le 1$ is attained. We will pay special attention to this issue in the future work.

Remark 4.4:

Note that, if the parameter $\mathit{\alpha }$ varies suitably in the iteration procedure, we may have even more efficient algorithm. Indeed, the monotonicity assumption of the operator ${\mathbf{T}}_h$ is often only theoretical limitations and does not in general mean that the method may not be applicable to a larger class of problems.

Figure 1. Error behaviours of Test Prob. 1 for different values of N .

Figure 2. The effect of $\mathit{\alpha }$ on the number of iteration m for Test Prob. 1 with $N=32$.

Figure 3. Exact and approximate solutions of Test Prob. 1 for $N=8,32$.

Figure 4. Error behaviours of Test Prob. 2 for different values of N .

Figure 5. The effect of $\mathit{\alpha }$ on the number of iteration m for Test Prob. 2 with $N=32$.

Figure 6. Exact and approximate solutions of Test Prob. 2 for $N=8,32$.

Figure 7. Error behaviours of Test Prob. 3 for different values of N .

Figure 8. The effect of $\mathit{\alpha }$ on the number of iteration m for Test Prob. 3 with $N=32$.

Figure 9. Exact and approximate solutions of Test Prob. 3 for $N=8,32$.

5. Numerical experiments and some discussions

Here, we report the results of some numerical tests on one-smoothing problems to illustrate the foregoing convergence analysis and the role of regularization parameter to appropriate approximate solution. The set of experiments illustrates the performance of the proposed regularized iterative method including the parameter choice strategy when applied to some popular test problems taken from [7,12].

The problems have been discretized by a Galerkin type method with piecewise constant functions, with ${\mathit{\psi }}_j={\mathit{\chi }}_{[(j-1)h,jh]},j=1,\dots ,N$, as basis functions and $h=1/N,$ where ${\mathit{\chi }}_M$ denotes the characteristic function corresponding to a set M. Looking at the results, we conclude that the proposed method gives the approximate solution with sufficient accuracy by low computational complexity.

The implementation of the method is demonstrated by solving three test problems of IAEs (1.1(1.1) $$\begin{array}{c}\hfill A(t)X(t)=g(t)+{\int }_0^{t}K(t,s)X(s)\mathrm{d}s,t\in \mathrm{\Omega }=[0,T],\end{array}$$(1.1) ) for the kernels and exact solutions as shown below, and free terms $f_1$ and $f_2$ properly chosen with $A(t)=\left(\begin{array}{cc}1& 0\\ 0& 0\\ \end{array}\right).$

Table

Test Prob.	K(t,s)	Exact solution
2*1	2*$\left(\begin{array}{cc}t+s& t^2+s^2\\ s-t^2& t+s+1\\ \end{array}\right)$	$y(t)=sint$
		$z(t)=cost$
2*2	2*$\left(\begin{array}{cc}{t}^3+s+1& cos3s+1\\ t+s+2& sin3s+2\\ \end{array}\right)$	$y(t)=cost$
		$z(t)=sin3t$
2*3	2*$\left(\begin{array}{cc}1+t-s& e^{t-s}\\ 1& e^{2t-s}\\ \end{array}\right)$	$y(t)=t{e}^{-t}$
		$z(t)=cost$

Tables 1–3 show the numerical results for different values of N, m and $\mathit{\alpha }$. We observe that for small N , an approximate solution with a few iteration m may be obtained, however, normally for improving the accuracy, if N is increased then m should be also increased which caused the high computational complexity of the method. We overcome this difficulty by choosing a suitable $\mathit{\alpha }$. In fact, by increasing N , if we choose an appropriate $\mathit{\alpha }$, we observe that a few number of iteration m is required for getting an appropriate approximate solution. This is one of the key features of the proposed method. The execution time of the method for three types of kernels for different values of N is also reported in Tables 1–3. 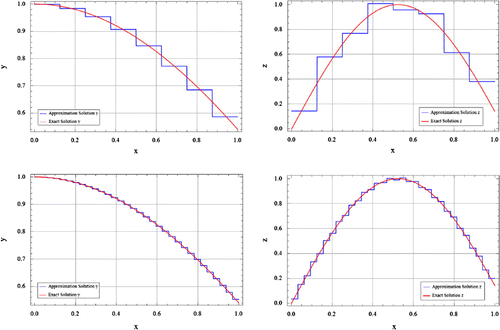All the computations are performed by the Mathematica${}^{\circledR }$ 10 on a standard PC. The numerical results show that the accuracy of ordinary component y is better than to the algebraic component z , which is due to ill-posedness of the first kind equations.

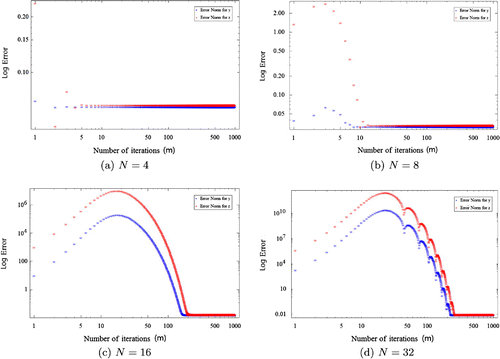
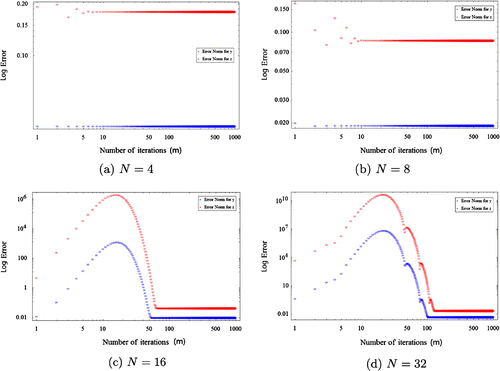
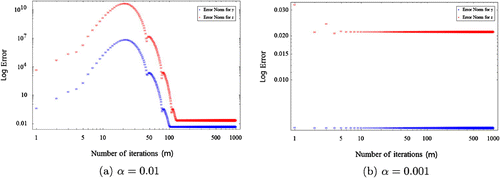
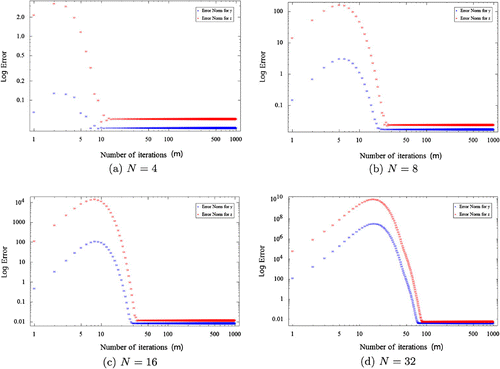
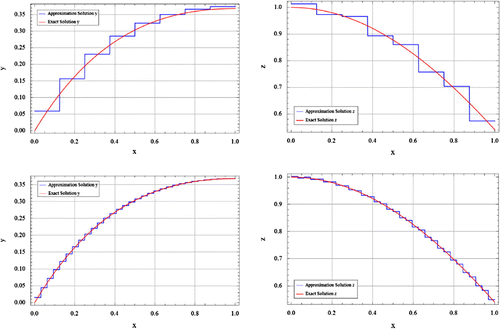
Figures 1, 4, 7 represent the error behaviours of the proposed iterative method for different values of N with suitable $\mathit{\alpha }$. It can be seen that the best possible approximate solutions are attained rapidly for $N=4$ and 8. However, in the case $N=16$ and 32 , more iteration is needed to obtain the same accuracy. 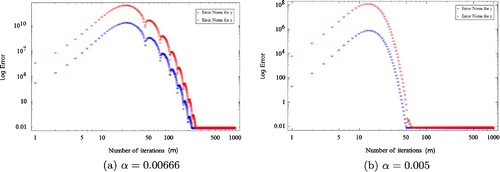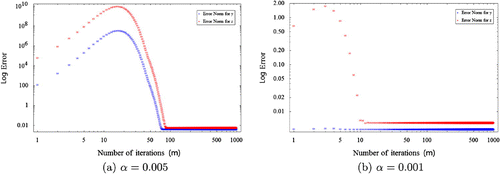Furthermore, our numerical experiments show the effects of varying $\mathit{\alpha }$ on the number of iteration m. Figures 2, 5, 8 demonstrate that as $\mathit{\alpha }$ is decreased, then the number of iteration is also decreased significantly to get an appropriate approximation.

Table 1. Numerical results of Test Prob. 1 for different values of N, m and $\mathit{\alpha }$.

N	$\mathit{\alpha }$	m	$\Vert y_{\mathit{\alpha }}^{\mathit{\delta }}{-\overline{y}\Vert }_2$	$\Vert z_{\mathit{\alpha }}^{\mathit{\delta }}{-\overline{z}\Vert }_2$	Time (s)
2*4	0.05	5	9.21E$-$02	7.56E$-$01	0.15
	0.025	4	6.45E$-$02	5.48E$-$02	0.14
2*8	0.025	30	3.11E$-$02	3.27E$-$02	1.93
	0.01	6	3.11E$-$02	2.88E$-$02	0.40
2*16	0.01	28	1.54E$-$02	1.67E$-$02	3.73
	0.005	12	1.54E$-$02	1.55E$-$02	1.60
3*32	2*0.005	50	1.06E$-$02	6.45E$-$01	15.67
		61	7.69E$-$03	7.97E$-$03	19.48
	0.001	10	7.70E$-$03	7.98E$-$03	3.14

Table 2. Numerical results of Test Prob. 2 for different values of N, m and $\mathit{\alpha }$.

N	$\mathit{\alpha }$	m	$\Vert y_{\mathit{\alpha }}^{\mathit{\delta }}{-\overline{y}\Vert }_2$	$\Vert z_{\mathit{\alpha }}^{\mathit{\delta }}{-\overline{z}\Vert }_2$	Time (s)
2*4	2*0.05	4	3.90E$-$02	1.87E$-$01	0.14
		7	3.90E$-$02	1.79E$-$01	0.26
2*8	2*0.025	2	1.89E$-$02	1.03E$-$01	0.12
		7	1.90E$-$02	8.25E$-$02	0.46
3*16	0.025	65	9.44E$-$03	4.22E$-$02	9.48
	2*0.01	5	9.44E$-$03	2.87E$-$01	0.68
		15	9.44E$-$03	4.26E$-$02	1.93
3*32	2*0.01	108	4.71E$-$03	1.43E$-$01	59.01
		130	4.71E$-$03	2.12E$-$02	88.85
	0.001	6	4.71E$-$03	2.12E$-$02	1.79

Table 3. Numerical results of Test Prob. 3 for different values of N, m and $\mathit{\alpha }$.

N	$\mathit{\alpha }$	m	$\Vert y_{\mathit{\alpha }}^{\mathit{\delta }}{-\overline{y}\Vert }_2$	$\Vert z_{\mathit{\alpha }}^{\mathit{\delta }}{-\overline{z}\Vert }_2$	Time (s)
2*4	2*0.05	6	5.58E$-$02	5.82E$-$01	0.26
		10	3.74E$-$02	4.60E$-$02	0.37
4*8	2*0.025	18	2.65E$-$02	6.96E$-$01	1.42
		30	1.72E$-$02	2.37E$-$02	2.35
	2*0.01	5	1.72E$-$02	1.34E$-$01	0.35
		8	1.72E$-$02	2.28E$-$02	0.54
4*16	2*0.01	27	1.37E$-$02	9.69E$-$01	5.31
		34	8.44E$-$03	1.13E$-$02	6.64
	2*0.005	10	8.68E$-$03	2.59E$-$01	1.85
		14	8.44E$-$03	1.11E$-$02	2.60
4*32	2*0.005	75	4.51E$-$03	3.53E$-$01	28.96
		90	4.20E$-$03	5.73E$-$03	36.18
	2*0.001	5	4.29E$-$03	8.54E$-$01	1.62
		12	4.20E$-$03	5.72E$-$03	3.93

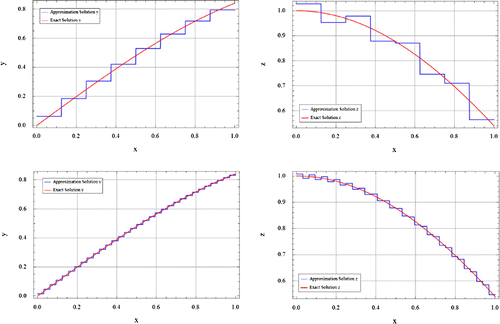
The exact and approximate solutions of the equations for different values of N with appropriate $\mathit{\alpha }$ are represented in Figures 3, 6, 9.

6. Conclusion

Here, we presented a direct approach based on iterative Lavrentiev’s regularization method for obtaining an approximate solution of a system of Volterra integral-algebraic equations of index-1. Numerical experiments reveal the effectiveness of the method and derive an experimental terminology for choosing the optimal values of regularization parameter. A remarkable feature of the proposed method is that one can efficiently control the number of iterations as well as sub divisions by varying the regularization parameter which is valuable in practical applications.

Notes

No potential conflict of interest was reported by the authors.