A non-iterative method for identifying multiple unknown time-dependent sources compactly supported occurring in a 2D parabolic equation

Abstract

We address the non-linear inverse source problem of identifying multiple unknown time-dependent sources spatially supported in some subdomains of a two-dimensional bounded domain subject to an evolution advection–dispersion–reaction equation. Provided to be available within the monitored domain interfaces for recording the state and its flux crossing each suspected zone where a source could occur, we establish an identifiability theorem that yields uniqueness of the unknown elements defining all occurring sources. We develop a non-iterative detection–identification method that goes throughout the monitored domain to detect in each suspected zone whether there exists or not an occurring source. Once a source is detected, the developed method determines lower and upper bounds of the total amount discharged by the occurring source and localizes the geometric centre of its unknown spatial support. Then, given two desired reference geometries for example, squares/discs centred at the already localized geometric centre, the method determines the biggest domain defined by a first reference geometry included in the sought source spatial support as well as the smallest domain defined by a second reference geometry containing this unknown support. In addition, the developed method gives an approximation of the surface area of this latest and identifies its time-dependent intensity function. Some numerical experiments on a variant of the surface water Biological Oxygen Demand pollution model are presented.

Keywords:

• Non-linear inverse source problem
• rough/partial shape identification
• optimization and control
• advection–dispersion–reaction equation

AMS Subject Classifications:

• 65M32
• 65N20
• 65N21

1. Introduction

Inverse source problems aiming to identify unknown compactly supported sources occurring in partial differential equations (PDEs) have attracted a lot of attention over the last few decades. Indeed, this kind of inverse problems have been involved in several areas of science and engineering covering a wide spectrum of applications: Medical applications, for example, electroencephalography (EEG) [1] and photo/optical tomography [2]; Environmental applications, for example, identification of pollution sources in surface water [3–6] and inverse potential gravimetry problem in which one is interested in determining the density inside the earth from gravimetric measurements on its surface [7]; Bioluminescence tomography that consists of determining an internal bioluminescent source distribution generated by luciferase inducted by reporter genes [8]. Besides, results on other geometric inverse problems, for example, detection of an internal moving boundary or of a two-dimensional moving cavity can be found in [9–11]. From the mathematical point of view and as far as shape identification of an unknown spatial support defining a sought source occurring in a PDE is concerned, for elleptic equations both theoretical and computational methods are rather well established [1,8,12,14]. However, for parabolic equations although significant theoretical results are already established, see [15–17], the development of efficient numerical methods for shape identification problems is still in its beginning stages. In the literature, the most known numerical methods are based on iterative algorithms using shape calculus, for instance, see [18–20].

The originality of the present study consists of developing a non-iterative approach for rough/partial shape identification of unknown compact spatial supports defining sought sources occurring in two-dimensional parabolic equations. Indeed, rather than using an iterative process for solving a shape identification problem by reconstructing the boundary of a sought source spatial support, we develop a direct method that starts by localizing the geometric centre of the unknown source spatial support. Thereafter, given two desired reference geometries, for example squares and/or discs centred at the already localized geometric centre, the developed method determines the biggest domain defined by a first reference geometry included in the unknown source spatial support as well as the smallest domain defined by a second reference geometry containing this unknown support and gives an approximation of its surface area. In practice, the method developed in the present study could have double applicabilities: (1) Direct applicability: In several areas of science and engineering, for example, identification of pollution sources in surface water, the knowledge of such properties characterizing the unknown source spatial support i.e. localization of its geometric centre, an approximation of its surface area as well as the smallest and the biggest two domains of given geometries framing this unknown support, could be enough to start treating the occurring source. (2) Indirect applicability: For applications where rather an accurate knowledge of the boundary defining the unknown source spatial support is needed, in the literature the most common numerical tools that enable to meet this need are generally based on iterative algorithms where convergence and accuracy depend sensitively on the used starting domain as an initial iterate. Therefore, the properties characterizing the unknown source spatial support determined by the method developed in the present study could yield a suitable initialization of the iterative algorithms in order to speed up their convergence and improve their accuracy.

The paper is organized as follows: Section 2 is devoted to stating the problem, assumptions and proving some technical results for later use. In Section 3, we establish an identifiability theorem that yields uniqueness of the unknown elements defining all occurring sources. Section 4 is reserved to develop the announced non-iterative detection–identification method that goes throughout the monitored domain to detect the presence of each occurring active source. Once a source is detected, the developed method determines lower and upper bounds of the total amount discharged by the occurring source as well as the earlier mentioned properties defining its unknown spatial support and identifies its loaded time-dependent intensity function. Some numerical experiments on a variant of the surface water Biological Oxygen Demand (BOD) pollution model are presented in Section 5.

2. Problem statement and technical results

Let $T>0$ be a final monitoring time and $\mathrm{\Omega }$ be a bounded and connected open subset of ${\mathbb{R}}^2$ with sufficiently smooth boundary $\mathit{\partial }\mathrm{\Omega }:={\mathrm{\Gamma }}_{in}\cup {\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out}$, where ${\mathrm{\Gamma }}_{in}$ represents the inflow boundary, ${\mathrm{\Gamma }}_{out}$ designates the outflow boundary whereas ${\mathrm{\Gamma }}_L$ regroups the two lateral lower and upper boundaries ${\mathrm{\Gamma }}_L={\mathrm{\Gamma }}_{L_l}\cup {\mathrm{\Gamma }}_{L_u}$. We denote u the state governed by(1) $$\begin{array}{c}\hfill L[u](x,t)=F(x,t)\text{in}\mathrm{\Omega }\times (0,T),\end{array}$$(1)

where F represents the set of all occurring sources/wells and L is the second-order linear parabolic partial differential operator defined as follows:(2) $$\begin{array}{c}\hfill L[u](x,t):={\mathit{\partial }}_{t}u(x,t)-\mathrm{d}iv(D\mathrm{\nabla }u(x,t))+V·\mathrm{\nabla }u(x,t)+Ru(x,t),\end{array}$$(2)

where $V={(V_1,V_2)}^{\top }$ is the mean velocity vector, R is a real number that designates the first-order decay reaction coefficient and D is the following $2\times 2$ symmetric positive definite matrix that represents the mean dispersion tensor:(3) $$\begin{array}{c}\hfill D=\left(\begin{array}{ccc}{D}_1& D_0& \\ D_0& D_2\end{array}\right).\end{array}$$(3)

Besides, for later use we introduce the vector $V^{\perp }={(-V_2,V_1)}^{\top }$ and the two dispersion-current functions $\mathit{\psi }$ and ${\mathit{\psi }}^{\perp }$ defined in an open subset $\mathcal{O}$ of ${\mathbb{R}}^2$ such that $\overline{\mathrm{\Omega }}\subset \mathcal{O}$ by(4) $$\begin{array}{c}\hfill D\mathrm{\nabla }\mathit{\psi }+V=0\text{and}\mathrm{\nabla }{\mathit{\psi }}^{\perp }+V^{\perp }=0.\end{array}$$(4)

Since the matrix D introduced in (3(3) $$\begin{array}{c}\hfill D=\left(\begin{array}{ccc}{D}_1& D_0& \\ D_0& D_2\end{array}\right).\end{array}$$(3) ) is invertible and by setting $\mathit{\psi }(0,0)={\mathit{\psi }}^{\perp }(0,0)=0$ it follows from (4(4) $$\begin{array}{c}\hfill D\mathrm{\nabla }\mathit{\psi }+V=0\text{and}\mathrm{\nabla }{\mathit{\psi }}^{\perp }+V^{\perp }=0.\end{array}$$(4) ) that the two functions $\mathit{\psi }$ and ${\mathit{\psi }}^{\perp }$ are defined for all $x=(x_1,x_2)\in \mathcal{O}$ by(5) $$\begin{array}{c}\hfill \begin{array}{c}\mathit{\psi }(x)=\mathit{\alpha }{x}_1+\mathit{\beta }{x}_2\text{where:}\mathit{\alpha }=\frac{D_0{V}_2-D_2{V}_1}{D_1{D}_2-D_0^2}\text{and}\mathit{\beta }=\frac{D_0{V}_1-D_1{V}_2}{D_1{D}_2-D_0^2}\hfill \\ {\mathit{\psi }}^{\perp }(x)=V_2{x}_1-V_1{x}_2\hfill \end{array}\end{array}$$(5)

Moreover, in view of (4(4) $$\begin{array}{c}\hfill D\mathrm{\nabla }\mathit{\psi }+V=0\text{and}\mathrm{\nabla }{\mathit{\psi }}^{\perp }+V^{\perp }=0.\end{array}$$(4) ), it follows that the following three functions:(6) $$\begin{array}{c}\hfill z(x,t)=e^{Rt}Z(x)\text{for}Z(x)\in \{Z_0,e^{\mathit{\psi }(x)},{\mathit{\psi }}^{\perp }(x)\},\end{array}$$(6)

where $Z_0\ne 0$ is a real number, solve the adjoint equation(7) $$\begin{array}{c}\hfill -{\mathit{\partial }}_{t}z-\mathrm{d}iv(D\mathrm{\nabla }z)-V·\mathrm{\nabla }z+Rz=0\text{in}\mathrm{\Omega }\times (0,T).\end{array}$$(7)

As far as appending boundary and initial conditions to (1(1) $$\begin{array}{c}\hfill L[u](x,t)=F(x,t)\text{in}\mathrm{\Omega }\times (0,T),\end{array}$$(1) )–(2(2) $$\begin{array}{c}\hfill L[u](x,t):={\mathit{\partial }}_{t}u(x,t)-\mathrm{d}iv(D\mathrm{\nabla }u(x,t))+V·\mathrm{\nabla }u(x,t)+Ru(x,t),\end{array}$$(2) ), usually the convective transport dominates the diffusion process and thus, a homogeneous Dirichlet condition on ${\mathrm{\Gamma }}_{in}$ is reasonable. However, on the lateral ${\mathrm{\Gamma }}_L$ and outflow ${\mathrm{\Gamma }}_{out}$ boundaries a Neumann homogeneous condition is more appropriate, see [4,6]. Hence, we use(8) $$\begin{array}{c}\hfill \begin{array}{c}u(·,0)=0\text{in}\mathrm{\Omega }\hfill \\ u=0\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ D\mathrm{\nabla }u·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\times (0,T)\hfill \end{array}\end{array}$$(8)

where $\mathit{\nu }$ is the unit outward vector normal to $\mathit{\partial }\mathrm{\Omega }$. Due to the linearity of the operator L in (2(2) $$\begin{array}{c}\hfill L[u](x,t):={\mathit{\partial }}_{t}u(x,t)-\mathrm{d}iv(D\mathrm{\nabla }u(x,t))+V·\mathrm{\nabla }u(x,t)+Ru(x,t),\end{array}$$(2) ) and from the superposition principle, it follows that using inhomogeneous initial and/or boundary conditions do not affect the results established in this paper.

In the present study, we are interested in the case of multiple time-dependent sources spatially supported in some subdomains of $\mathrm{\Omega }$ occurring in (1(1) $$\begin{array}{c}\hfill L[u](x,t)=F(x,t)\text{in}\mathrm{\Omega }\times (0,T),\end{array}$$(1) )–(2(2) $$\begin{array}{c}\hfill L[u](x,t):={\mathit{\partial }}_{t}u(x,t)-\mathrm{d}iv(D\mathrm{\nabla }u(x,t))+V·\mathrm{\nabla }u(x,t)+Ru(x,t),\end{array}$$(2) ) i.e. F is defined by(9) $$\begin{array}{c}\hfill {\displaystyle F(x,t)=\sum _{n=1}^N{\mathit{\lambda }}_n(t){\mathit{\chi }}_{{\mathit{\omega }}_n}(x)\text{in}\mathrm{\Omega }\times (0,T),}\end{array}$$(9)

where $\mathit{\chi }$ is the characteristic function and for $n=1,\cdots ,N$, the subdomain ${\mathit{\omega }}_n\subset \mathrm{\Omega }$ is a homogeneous open subset of geometric centre (centroid) $G_n=(x_1^{G_n},x_2^{G_n})$ given by(10) $$\begin{array}{c}\hfill {\displaystyle x_1^{G_n}=\frac{1}{\mathcal{A}({\mathit{\omega }}_n)}{\int }_{{\mathit{\omega }}_n}{x}_1\mathrm{d}x\text{and}{x}_2^{G_n}=\frac{1}{\mathcal{A}({\mathit{\omega }}_n)}{\int }_{{\mathit{\omega }}_n}{x}_2\mathrm{d}x,}\end{array}$$(10)

where $\mathcal{A}({\mathit{\omega }}_n)={\int }_{{\mathit{\omega }}_n}\mathrm{d}x$ is the surface area of ${\mathit{\omega }}_n$. Furthermore, ${\mathit{\lambda }}_{n=1,\cdots ,N}$ involved in (9(9) $$\begin{array}{c}\hfill {\displaystyle F(x,t)=\sum _{n=1}^N{\mathit{\lambda }}_n(t){\mathit{\chi }}_{{\mathit{\omega }}_n}(x)\text{in}\mathrm{\Omega }\times (0,T),}\end{array}$$(9) ) designate the time-dependent source intensities that are N functions in $L^2(0,T)$ satisfying:(11) $$\begin{array}{c}\hfill {\int }_0^T{\mathit{\lambda }}_n(t)e^{Rt}\mathrm{d}t\ne 0\text{and}\exists T^0\in (0,T)\text{such that}{\mathit{\lambda }}_n=0\text{in}(T^0,T),\forall n=1,\cdots ,N.\end{array}$$(11)

Then, the direct problem (1(1) $$\begin{array}{c}\hfill L[u](x,t)=F(x,t)\text{in}\mathrm{\Omega }\times (0,T),\end{array}$$(1) )–(2(2) $$\begin{array}{c}\hfill L[u](x,t):={\mathit{\partial }}_{t}u(x,t)-\mathrm{d}iv(D\mathrm{\nabla }u(x,t))+V·\mathrm{\nabla }u(x,t)+Ru(x,t),\end{array}$$(2) ) and (8(8) $$\begin{array}{c}\hfill \begin{array}{c}u(·,0)=0\text{in}\mathrm{\Omega }\hfill \\ u=0\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ D\mathrm{\nabla }u·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\times (0,T)\hfill \end{array}\end{array}$$(8) )–(9(9) $$\begin{array}{c}\hfill {\displaystyle F(x,t)=\sum _{n=1}^N{\mathit{\lambda }}_n(t){\mathit{\chi }}_{{\mathit{\omega }}_n}(x)\text{in}\mathrm{\Omega }\times (0,T),}\end{array}$$(9) ) admits a unique solution u that belongs to the following functional space, see [20,21]:(12) $$\begin{array}{c}\hfill H^{2,1}(\mathrm{\Omega }\times (0,T)):=L^2(0,T;H^2(\mathrm{\Omega }))\cap H^1(0,T;L^2(\mathrm{\Omega })).\end{array}$$(12)

Besides, for later use given $N_{max}\ge N$ let ${\mathrm{\Gamma }}_{i=1,\cdots ,N_{max}}$ be sufficiently smooth interfaces within $\mathrm{\Omega }$ such that by setting ${\mathrm{\Gamma }}_0={\mathrm{\Gamma }}_{in}$, ${\mathrm{\Gamma }}_{N_{max}+1}={\mathrm{\Gamma }}_{out}$ and ${\mathrm{\Omega }}_{i=1,\cdots ,N_{max}+1}$ the subdomains of $\mathrm{\Omega }$ delimited by $\mathit{\partial }{\mathrm{\Omega }}_i={\mathrm{\Gamma }}_{i-1}\cup {\mathrm{\Gamma }}_L^i\cup {\mathrm{\Gamma }}_i$, the following conditions hold true:(13) $$\begin{array}{c}\hfill \begin{array}{c}(C_1){\mathrm{\Gamma }}_i\cap {\mathrm{\Gamma }}_j=\mathrm{\varnothing },\forall i\ne j\in \{0,\cdots ,N_{max}+1\}.\hfill \\ (C_2)|{\mathrm{\Gamma }}_i\cap {\mathrm{\Gamma }}_{L_l}|=|{\mathrm{\Gamma }}_i\cap {\mathrm{\Gamma }}_{L_u}|=1,\forall i=1,\cdots ,N_{max}.\hfill \\ (C_3)\overline{\mathrm{\Omega }}={\cup }_{i=1}^{N_{max}+1}{\overline{\mathrm{\Omega }}}_i\text{where:}{\mathrm{\Omega }}_{N_{max}+1}\subset (\mathrm{\Omega }\backslash {\cup }_{i=1}^N{\overline{\mathit{\omega }}}_n),\hfill \end{array}\end{array}$$(13)

where ${\mathrm{\Gamma }}_L^i$ is the part of the lateral boundary ${\mathrm{\Gamma }}_L$ situated between ${\mathrm{\Gamma }}_{i-1}$ and ${\mathrm{\Gamma }}_i$, and |.| denotes the cardinality of a set. The criteria $(C_{1,2,3})$ in (13(13) $$\begin{array}{c}\hfill \begin{array}{c}(C_1){\mathrm{\Gamma }}_i\cap {\mathrm{\Gamma }}_j=\mathrm{\varnothing },\forall i\ne j\in \{0,\cdots ,N_{max}+1\}.\hfill \\ (C_2)|{\mathrm{\Gamma }}_i\cap {\mathrm{\Gamma }}_{L_l}|=|{\mathrm{\Gamma }}_i\cap {\mathrm{\Gamma }}_{L_u}|=1,\forall i=1,\cdots ,N_{max}.\hfill \\ (C_3)\overline{\mathrm{\Omega }}={\cup }_{i=1}^{N_{max}+1}{\overline{\mathrm{\Omega }}}_i\text{where:}{\mathrm{\Omega }}_{N_{max}+1}\subset (\mathrm{\Omega }\backslash {\cup }_{i=1}^N{\overline{\mathit{\omega }}}_n),\hfill \end{array}\end{array}$$(13) ) are well satisfied if the $N_{max}$ interfaces ${\mathrm{\Gamma }}_{i=1,\cdots ,N_{max}}$ are taken distinct and, for example, ‘parallel’ to the inflow and outflow boundaries ${\mathrm{\Gamma }}_{in}$ and ${\mathrm{\Gamma }}_{out}$ such that all involved sources occur upstream ${\mathrm{\Gamma }}_{N_{max}}$.

In the remainder, we assume the sources involved in (9(9) $$\begin{array}{c}\hfill {\displaystyle F(x,t)=\sum _{n=1}^N{\mathit{\lambda }}_n(t){\mathit{\chi }}_{{\mathit{\omega }}_n}(x)\text{in}\mathrm{\Omega }\times (0,T),}\end{array}$$(9) ) could occur only one by one in the set of all suspected source zones ${\mathrm{\Omega }}_{i=1,\cdots ,N_{max}}\subset \mathrm{\Omega }$ and the interfaces ${\mathrm{\Gamma }}_i=\mathit{\partial }{\mathrm{\Omega }}_i\cap \mathit{\partial }{\mathrm{\Omega }}_{i+1}$ to be available for measuring the state and its flux crossing each interzone. For example, in a monitored portion of a river, pollution is usually the consequence of discharging wastewater by one or several sources among industrials, farmers and city sewers occurring in some zones that can be separated by data recording interfaces. Thus, we assume the source spatial supports ${\overline{\mathit{\omega }}}_{n=1,\cdots ,N}$ defining F in (9(9) $$\begin{array}{c}\hfill {\displaystyle F(x,t)=\sum _{n=1}^N{\mathit{\lambda }}_n(t){\mathit{\chi }}_{{\mathit{\omega }}_n}(x)\text{in}\mathrm{\Omega }\times (0,T),}\end{array}$$(9) ) to be such that(14) $$\begin{array}{cc}& \forall i\in \{1,\cdots ,N_{max}\},\text{there exists}\underline{atmost}\text{one element}n\in \{1,\cdots ,N\}\hfill \\ \hfill & \text{such that}{\mathit{\omega }}_n\subset {\mathrm{\Omega }}_i.\hfill \end{array}$$(14)

In view of (14(14) $$\begin{array}{cc}& \forall i\in \{1,\cdots ,N_{max}\},\text{there exists}\underline{atmost}\text{one element}n\in \{1,\cdots ,N\}\hfill \\ \hfill & \text{such that}{\mathit{\omega }}_n\subset {\mathrm{\Omega }}_i.\hfill \end{array}$$(14) ) and since ${\mathrm{\Omega }}_{i=1,\cdots ,N_{max}}\subset \mathrm{\Omega }$ are such that $\mathit{\partial }{\mathrm{\Omega }}_i={\mathrm{\Gamma }}_{i-1}\cup {\mathrm{\Gamma }}_L^i\cup {\mathrm{\Gamma }}_i$ it follows that the state u solution of the problem (1(1) $$\begin{array}{c}\hfill L[u](x,t)=F(x,t)\text{in}\mathrm{\Omega }\times (0,T),\end{array}$$(1) )–(2(2) $$\begin{array}{c}\hfill L[u](x,t):={\mathit{\partial }}_{t}u(x,t)-\mathrm{d}iv(D\mathrm{\nabla }u(x,t))+V·\mathrm{\nabla }u(x,t)+Ru(x,t),\end{array}$$(2) ) and (8(8) $$\begin{array}{c}\hfill \begin{array}{c}u(·,0)=0\text{in}\mathrm{\Omega }\hfill \\ u=0\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ D\mathrm{\nabla }u·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\times (0,T)\hfill \end{array}\end{array}$$(8) )–(9(9) $$\begin{array}{c}\hfill {\displaystyle F(x,t)=\sum _{n=1}^N{\mathit{\lambda }}_n(t){\mathit{\chi }}_{{\mathit{\omega }}_n}(x)\text{in}\mathrm{\Omega }\times (0,T),}\end{array}$$(9) ) is smooth enough on $\mathit{\partial }\mathrm{\Omega }$ as well as on the interfaces ${\mathrm{\Gamma }}_{i=1,\cdots ,N_{max}}$. That allows to define the observation operator:(15) $$\begin{array}{c}\hfill M[F]:=\left\{D\mathrm{\nabla }u·\mathit{\nu }\text{on}\sum _{in};{\Vert V\Vert }_{2}u\text{on}\sum _L;(u,D\mathrm{\nabla }u·\mathit{\nu })\text{on}\sum _{i=1,\cdots ,N_{max}}\right\},\end{array}$$(15)

where ${\sum }_{in}={\mathrm{\Gamma }}_{in}\times (0,T)$, ${\sum }_i={\mathrm{\Gamma }}_i\times (0,T)$ for $i=1,\cdots ,N_{max}$ and ${\sum }_L={\mathrm{\Gamma }}_L\times (0,T)$. This is the so-called forward problem.

The inverse problem with which we are concerned here is: Assuming (11(11) $$\begin{array}{c}\hfill {\int }_0^T{\mathit{\lambda }}_n(t)e^{Rt}\mathrm{d}t\ne 0\text{and}\exists T^0\in (0,T)\text{such that}{\mathit{\lambda }}_n=0\text{in}(T^0,T),\forall n=1,\cdots ,N.\end{array}$$(11) )–(14(14) $$\begin{array}{cc}& \forall i\in \{1,\cdots ,N_{max}\},\text{there exists}\underline{atmost}\text{one element}n\in \{1,\cdots ,N\}\hfill \\ \hfill & \text{such that}{\mathit{\omega }}_n\subset {\mathrm{\Omega }}_i.\hfill \end{array}$$(14) ) hold true and given the records $d{d}_{in}$ of $D\mathrm{\nabla }u·\mathit{\nu }$ on ${\sum }_{in}$, $d_L$ of u on ${\sum }_L$ and $(d_i,d{d}_i)$ of $(u,D\mathrm{\nabla }u·\mathit{\nu })$ on ${\sum }_{i=1,\cdots ,N_{max}}$, determine the unknown elements: N, ${\mathit{\omega }}_{n=1,\cdots ,N}$ and ${\mathit{\lambda }}_{n=1,\cdots ,N}$ that yield(16) $$\begin{array}{c}\hfill M[F]=\left\{d{d}_{in}\text{on}\sum _{in};{\Vert V\Vert }_2{d}_L\text{on}\sum _L;(d_i,d{d}_i)\text{on}\sum _{i=1,\cdots ,N_{max}}\right\}.\end{array}$$(16)

Remark 2.1:

If along the lateral boundary ${\mathrm{\Gamma }}_L$ the velocity vector V fulfills: $V·\mathit{\nu }=0$ as mass cann’t penetrate a solid interface and $V·\mathit{\tau }=0$ which is the no-slip condition [22], where $\mathit{\tau }$ is a unit vector tangent to ${\mathrm{\Gamma }}_L$ then, ${\Vert V\Vert }_2=0$ on ${\mathrm{\Gamma }}_L$ and thus, the observation operator M[F] in (15(15) $$\begin{array}{c}\hfill M[F]:=\left\{D\mathrm{\nabla }u·\mathit{\nu }\text{on}\sum _{in};{\Vert V\Vert }_{2}u\text{on}\sum _L;(u,D\mathrm{\nabla }u·\mathit{\nu })\text{on}\sum _{i=1,\cdots ,N_{max}}\right\},\end{array}$$(15) ) does not require any measurement related to the state u along ${\sum }_L$.

Lemma 2.2:

Let B be a bounded domain of ${\mathbb{R}}^2$ geometrically centred at the origin $O=(0,0)$. The mapping ${\mathrm{\Psi }}_i$ defined at all $G\in {\mathrm{\Omega }}_i$ for which ${\mathit{\omega }}_G:=G+B\subset {\mathrm{\Omega }}_i$ by(17) $$\begin{array}{c}\hfill {\mathrm{\Psi }}_i(G)=\left(\begin{array}{c}{\displaystyle \frac{1}{\mathcal{A}({\mathit{\omega }}_G)}{\int }_{{\mathit{\omega }}_G}{e}^{\mathit{\psi }(x)}\mathrm{d}x}\\ {\displaystyle \frac{1}{\mathcal{A}({\mathit{\omega }}_G)}{\int }_{{\mathit{\omega }}_G}{\mathit{\psi }}^{\perp }(x)\mathrm{d}x}\end{array}\right)\end{array}$$(17)

is injective, where $\mathit{\psi }$ and ${\mathit{\psi }}^{\perp }$ are the two functions introduced in (5(5) $$\begin{array}{c}\hfill \begin{array}{c}\mathit{\psi }(x)=\mathit{\alpha }{x}_1+\mathit{\beta }{x}_2\text{where:}\mathit{\alpha }=\frac{D_0{V}_2-D_2{V}_1}{D_1{D}_2-D_0^2}\text{and}\mathit{\beta }=\frac{D_0{V}_1-D_1{V}_2}{D_1{D}_2-D_0^2}\hfill \\ {\mathit{\psi }}^{\perp }(x)=V_2{x}_1-V_1{x}_2\hfill \end{array}\end{array}$$(5) ).

ProofLet $G^{(k=1,2)}\in {\mathrm{\Omega }}_i$ be such that ${\mathit{\omega }}_{G^{(k)}}:=G^{(k)}+B\subset {\mathrm{\Omega }}_i$. Since the function $\mathit{\psi }$ in (5(5) $$\begin{array}{c}\hfill \begin{array}{c}\mathit{\psi }(x)=\mathit{\alpha }{x}_1+\mathit{\beta }{x}_2\text{where:}\mathit{\alpha }=\frac{D_0{V}_2-D_2{V}_1}{D_1{D}_2-D_0^2}\text{and}\mathit{\beta }=\frac{D_0{V}_1-D_1{V}_2}{D_1{D}_2-D_0^2}\hfill \\ {\mathit{\psi }}^{\perp }(x)=V_2{x}_1-V_1{x}_2\hfill \end{array}\end{array}$$(5) ) is linear and using the change of variables to go from B to ${\mathit{\omega }}_{G^{(k)}}$, we get(18) $$\begin{array}{c}\hfill {\displaystyle {\int }_{{\mathit{\omega }}_{G^{(k)}}}{e}^{\mathit{\psi }(x)}\mathrm{d}x=e^{\mathit{\psi }(G^{(k)})}{\int }_B{e}^{\mathit{\psi }(x)}\mathrm{d}x}\end{array}$$(18)

As ${\mathit{\omega }}_{G^{(1)}}$ and ${\mathit{\omega }}_{G^{(2)}}$ are defined from shifting the same domain B to be geometrically centred at $G^{(1)}$ and $G^{(2)}$ it follows that $\mathcal{A}({\mathit{\omega }}_{G^{(2)}})=\mathcal{A}({\mathit{\omega }}_{G^{(1)}})$ and thus, from (18(18) $$\begin{array}{c}\hfill {\displaystyle {\int }_{{\mathit{\omega }}_{G^{(k)}}}{e}^{\mathit{\psi }(x)}\mathrm{d}x=e^{\mathit{\psi }(G^{(k)})}{\int }_B{e}^{\mathit{\psi }(x)}\mathrm{d}x}\end{array}$$(18) ) we find(19) $$\begin{array}{cc}& {\displaystyle \frac{1}{\mathcal{A}({\mathit{\omega }}_{G^{(2)}})}{\int }_{{\mathit{\omega }}_{G^{(2)}}}{e}^{\mathit{\psi }(x)}\mathrm{d}x}\hfill \\ \hfill & {\displaystyle =\frac{1}{\mathcal{A}({\mathit{\omega }}_{G^{(1)}})}{\int }_{{\mathit{\omega }}_{G^{(1)}}}{e}^{\mathit{\psi }(x)}\mathrm{d}x\Rightarrow \mathit{\psi }(G^{(2)})=\mathit{\psi }(G^{(1)}).}\hfill \end{array}$$(19)

Besides, from (5(5) $$\begin{array}{c}\hfill \begin{array}{c}\mathit{\psi }(x)=\mathit{\alpha }{x}_1+\mathit{\beta }{x}_2\text{where:}\mathit{\alpha }=\frac{D_0{V}_2-D_2{V}_1}{D_1{D}_2-D_0^2}\text{and}\mathit{\beta }=\frac{D_0{V}_1-D_1{V}_2}{D_1{D}_2-D_0^2}\hfill \\ {\mathit{\psi }}^{\perp }(x)=V_2{x}_1-V_1{x}_2\hfill \end{array}\end{array}$$(5) ) and using the geometric centre $G^{(k)}$ of ${\mathit{\omega }}_{G^{(k)}}$ defined as in (10(10) $$\begin{array}{c}\hfill {\displaystyle x_1^{G_n}=\frac{1}{\mathcal{A}({\mathit{\omega }}_n)}{\int }_{{\mathit{\omega }}_n}{x}_1\mathrm{d}x\text{and}{x}_2^{G_n}=\frac{1}{\mathcal{A}({\mathit{\omega }}_n)}{\int }_{{\mathit{\omega }}_n}{x}_2\mathrm{d}x,}\end{array}$$(10) ) we obtain(20) $$\begin{array}{cc}& {\displaystyle \frac{1}{\mathcal{A}({\mathit{\omega }}_{G^{(k)}})}{\int }_{{\mathit{\omega }}_{G^{(k)}}}{\mathit{\psi }}^{\perp }(x)\mathrm{d}x=\frac{V_2}{\mathcal{A}({\mathit{\omega }}_{G^{(k)}})}{\int }_{{\mathit{\omega }}_{G^{(k)}}}{x}_1\mathrm{d}x-\frac{V_1}{\mathcal{A}({\mathit{\omega }}_{G^{(k)}})}}\hfill \\ \hfill & {\displaystyle {\int }_{{\mathit{\omega }}_{G^{(k)}}}{x}_2\mathrm{d}x={\mathit{\psi }}^{\perp }(G^{(k)}),}\hfill \end{array}$$(20)

which leads to(21) $$\begin{array}{cc}& {\displaystyle \frac{1}{\mathcal{A}({\mathit{\omega }}_{G^{(2)}})}{\int }_{{\mathit{\omega }}_{G^{(2)}}}{\mathit{\psi }}^{\perp }(x)\mathrm{d}x}\hfill \\ \hfill & {\displaystyle =\frac{1}{\mathcal{A}({\mathit{\omega }}_{G^{(1)}})}{\int }_{{\mathit{\omega }}_{G^{(1)}}}{\mathit{\psi }}^{\perp }(x)\mathrm{d}x\Rightarrow {\mathit{\psi }}^{\perp }(G^{(2)})={\mathit{\psi }}^{\perp }(G^{(1)}).}\hfill \end{array}$$(21)

Therefore, in view of the definition of ${\mathrm{\Psi }}_i$ given in (17(17) $$\begin{array}{c}\hfill {\mathrm{\Psi }}_i(G)=\left(\begin{array}{c}{\displaystyle \frac{1}{\mathcal{A}({\mathit{\omega }}_G)}{\int }_{{\mathit{\omega }}_G}{e}^{\mathit{\psi }(x)}\mathrm{d}x}\\ {\displaystyle \frac{1}{\mathcal{A}({\mathit{\omega }}_G)}{\int }_{{\mathit{\omega }}_G}{\mathit{\psi }}^{\perp }(x)\mathrm{d}x}\end{array}\right)\end{array}$$(17) ), from setting ${\mathrm{\Psi }}_i(G^{(2)})={\mathrm{\Psi }}_i(G^{(1)})$ and according to the results in (19(19) $$\begin{array}{cc}& {\displaystyle \frac{1}{\mathcal{A}({\mathit{\omega }}_{G^{(2)}})}{\int }_{{\mathit{\omega }}_{G^{(2)}}}{e}^{\mathit{\psi }(x)}\mathrm{d}x}\hfill \\ \hfill & {\displaystyle =\frac{1}{\mathcal{A}({\mathit{\omega }}_{G^{(1)}})}{\int }_{{\mathit{\omega }}_{G^{(1)}}}{e}^{\mathit{\psi }(x)}\mathrm{d}x\Rightarrow \mathit{\psi }(G^{(2)})=\mathit{\psi }(G^{(1)}).}\hfill \end{array}$$(19) ) and (21(21) $$\begin{array}{cc}& {\displaystyle \frac{1}{\mathcal{A}({\mathit{\omega }}_{G^{(2)}})}{\int }_{{\mathit{\omega }}_{G^{(2)}}}{\mathit{\psi }}^{\perp }(x)\mathrm{d}x}\hfill \\ \hfill & {\displaystyle =\frac{1}{\mathcal{A}({\mathit{\omega }}_{G^{(1)}})}{\int }_{{\mathit{\omega }}_{G^{(1)}}}{\mathit{\psi }}^{\perp }(x)\mathrm{d}x\Rightarrow {\mathit{\psi }}^{\perp }(G^{(2)})={\mathit{\psi }}^{\perp }(G^{(1)}).}\hfill \end{array}$$(21) ) it follows that the two geometric centres $G^{(2)}=(x_1^{G^{(2)}},x_2^{G^{(2)}})$ of ${\mathit{\omega }}_{G^{(2)}}$ and $G^{(1)}=(x_1^{G^{(1)}},x_2^{G^{(1)}})$ of ${\mathit{\omega }}_{G^{(1)}}$ are subject to:(22) $$\begin{array}{c}\hfill \left\{\begin{array}{c}\mathit{\psi }(G^{(2)})=\mathit{\psi }(G^{(1)})\hfill \\ {\mathit{\psi }}^{\perp }(G^{(2)})={\mathit{\psi }}^{\perp }(G^{(1)})\hfill \end{array}\right.\iff \left(\begin{array}{ccc}\mathit{\alpha }& \mathit{\beta }& \\ V_2& -V_1& \\ \end{array}\right)\left(\begin{array}{c}{x}_1^{G^{(2)}}-x_1^{G^{(1)}}\\ x_2^{G^{(2)}}-x_2^{G^{(1)}}\\ \end{array}\right)=\left(\begin{array}{c}0\\ 0\\ \end{array}\right).\end{array}$$(22)

Furthermore, from (4(4) $$\begin{array}{c}\hfill D\mathrm{\nabla }\mathit{\psi }+V=0\text{and}\mathrm{\nabla }{\mathit{\psi }}^{\perp }+V^{\perp }=0.\end{array}$$(4) )–(5(5) $$\begin{array}{c}\hfill \begin{array}{c}\mathit{\psi }(x)=\mathit{\alpha }{x}_1+\mathit{\beta }{x}_2\text{where:}\mathit{\alpha }=\frac{D_0{V}_2-D_2{V}_1}{D_1{D}_2-D_0^2}\text{and}\mathit{\beta }=\frac{D_0{V}_1-D_1{V}_2}{D_1{D}_2-D_0^2}\hfill \\ {\mathit{\psi }}^{\perp }(x)=V_2{x}_1-V_1{x}_2\hfill \end{array}\end{array}$$(5) ) we get: $-(\mathit{\alpha }{V}_1+\mathit{\beta }{V}_2)=V^{\top }{D}^{-1}V>0$ which implies that the $2\times 2$ matrix involved in (22(22) $$\begin{array}{c}\hfill \left\{\begin{array}{c}\mathit{\psi }(G^{(2)})=\mathit{\psi }(G^{(1)})\hfill \\ {\mathit{\psi }}^{\perp }(G^{(2)})={\mathit{\psi }}^{\perp }(G^{(1)})\hfill \end{array}\right.\iff \left(\begin{array}{ccc}\mathit{\alpha }& \mathit{\beta }& \\ V_2& -V_1& \\ \end{array}\right)\left(\begin{array}{c}{x}_1^{G^{(2)}}-x_1^{G^{(1)}}\\ x_2^{G^{(2)}}-x_2^{G^{(1)}}\\ \end{array}\right)=\left(\begin{array}{c}0\\ 0\\ \end{array}\right).\end{array}$$(22) ) is invertible. Thus, the linear system in (22(22) $$\begin{array}{c}\hfill \left\{\begin{array}{c}\mathit{\psi }(G^{(2)})=\mathit{\psi }(G^{(1)})\hfill \\ {\mathit{\psi }}^{\perp }(G^{(2)})={\mathit{\psi }}^{\perp }(G^{(1)})\hfill \end{array}\right.\iff \left(\begin{array}{ccc}\mathit{\alpha }& \mathit{\beta }& \\ V_2& -V_1& \\ \end{array}\right)\left(\begin{array}{c}{x}_1^{G^{(2)}}-x_1^{G^{(1)}}\\ x_2^{G^{(2)}}-x_2^{G^{(1)}}\\ \end{array}\right)=\left(\begin{array}{c}0\\ 0\\ \end{array}\right).\end{array}$$(22) ) admits the unique solution defined by $x_1^{G^{(2)}}=x_1^{G^{(1)}}$ and $x_2^{G^{(2)}}=x_2^{G^{(1)}}$ which means $G^{(2)}=G^{(1)}$.

To establish our identifiability theorem, we prove the following second technical lemma:

Lemma 2.3:

Let $\mathit{\omega }\subset \mathrm{\Omega }$ be an open subset of sufficiently regular boundary. There exists two boundary controls ${\mathit{\zeta }}_{in}\in L^2({\mathrm{\Gamma }}_{in}\times (0,T))$ and ${\mathit{\zeta }}_{out}\in L^2({\mathrm{\Gamma }}_{out}\times (0,T))$ that maintain the solution v of the following system:(23) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathit{\partial }}_{t}v-\mathrm{d}iv(D\mathrm{\nabla }v)-V·\mathrm{\nabla }v+Rv=0\text{in}\mathrm{\Omega }\times (0,T)\hfill \\ v(·,0)=0\text{in}\mathrm{\Omega }\hfill \\ v={\mathit{\zeta }}_{in}\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ (D\mathrm{\nabla }v+vV)·\mathit{\nu }=0\text{on}{\mathrm{\Gamma }}_L\times (0,T)\hfill \\ (D\mathrm{\nabla }v+vV)·\mathit{\nu }={\mathit{\zeta }}_{out}\text{on}{\mathrm{\Gamma }}_{out}\times (0,T)\hfill \end{array}\right.\end{array}$$(23) (24) $$\begin{array}{c}\hfill {\displaystyle \text{such that}{\int }_{\mathit{\omega }}v(x,·)\mathrm{d}x\ne 0\text{a.e. in}(0,T)}\end{array}$$(24)

ProofThe following system:(25) $$\begin{array}{c}\hfill \left\{\begin{array}{c}-{\mathit{\partial }}_t\mathit{\xi }-\mathrm{d}iv(D\mathrm{\nabla }\mathit{\xi })+V·\mathrm{\nabla }\mathit{\xi }+R\mathit{\xi }={\mathit{\chi }}_{\mathit{\omega }}(x)\text{in}\mathrm{\Omega }\times (0,T)\hfill \\ \mathit{\xi }(·,T)=0\text{in}\mathrm{\Omega }\hfill \\ \mathit{\xi }=0\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ D\mathrm{\nabla }\mathit{\xi }·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\times (0,T)\hfill \end{array}\right.\end{array}$$(25)

admits a unique solution $\mathit{\xi }$ that belongs to $H^{2,1}(\mathrm{\Omega }\times (0,T))$, see [20,21]. Then, multiplying the first equation in (25(25) $$\begin{array}{c}\hfill \left\{\begin{array}{c}-{\mathit{\partial }}_t\mathit{\xi }-\mathrm{d}iv(D\mathrm{\nabla }\mathit{\xi })+V·\mathrm{\nabla }\mathit{\xi }+R\mathit{\xi }={\mathit{\chi }}_{\mathit{\omega }}(x)\text{in}\mathrm{\Omega }\times (0,T)\hfill \\ \mathit{\xi }(·,T)=0\text{in}\mathrm{\Omega }\hfill \\ \mathit{\xi }=0\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ D\mathrm{\nabla }\mathit{\xi }·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\times (0,T)\hfill \end{array}\right.\end{array}$$(25) ) by v the solution of the problem (23(23) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathit{\partial }}_{t}v-\mathrm{d}iv(D\mathrm{\nabla }v)-V·\mathrm{\nabla }v+Rv=0\text{in}\mathrm{\Omega }\times (0,T)\hfill \\ v(·,0)=0\text{in}\mathrm{\Omega }\hfill \\ v={\mathit{\zeta }}_{in}\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ (D\mathrm{\nabla }v+vV)·\mathit{\nu }=0\text{on}{\mathrm{\Gamma }}_L\times (0,T)\hfill \\ (D\mathrm{\nabla }v+vV)·\mathit{\nu }={\mathit{\zeta }}_{out}\text{on}{\mathrm{\Gamma }}_{out}\times (0,T)\hfill \end{array}\right.\end{array}$$(23) ) and integrating by parts over $\mathrm{\Omega }$ using Green’s formula gives(26) $$\begin{array}{cc}\hfill {\displaystyle {\int }_{\mathit{\omega }}v(x,t)\mathrm{d}x}& =-\frac{\mathrm{d}}{\mathrm{d}t}{⟨\mathit{\xi }(·,t),v(·,t)⟩}_{L^2(\mathrm{\Omega })}\hfill \\ \hfill & {\displaystyle +{\int }_{{\mathrm{\Gamma }}_{out}}\mathit{\xi }{\mathit{\zeta }}_{out}d\mathrm{\Gamma }-{\int }_{{\mathrm{\Gamma }}_{in}}{\mathit{\zeta }}_{in}D\mathrm{\nabla }\mathit{\xi }·\mathit{\nu }d\mathrm{\Gamma },\forall t\in (0,T).}\hfill \end{array}$$(26)

Suppose that for all ${\mathit{\zeta }}_{in}$ and ${\mathit{\zeta }}_{out}$ there exists $0\le t_0<t_1\le T$ such that ${\int }_{\mathit{\omega }}v(x,·)\mathrm{d}x=0$ in $(t_0,t_1)$. Since according to [23] the time-dependent function ${\int }_{\mathit{\omega }}v(x,·)\mathrm{d}x$ is analytic in (0, T), it follows that ${\int }_{\mathit{\omega }}v(x,·)\mathrm{d}x=0$ in (0, T). Therefore, by integrating (26(26) $$\begin{array}{cc}\hfill {\displaystyle {\int }_{\mathit{\omega }}v(x,t)\mathrm{d}x}& =-\frac{\mathrm{d}}{\mathrm{d}t}{⟨\mathit{\xi }(·,t),v(·,t)⟩}_{L^2(\mathrm{\Omega })}\hfill \\ \hfill & {\displaystyle +{\int }_{{\mathrm{\Gamma }}_{out}}\mathit{\xi }{\mathit{\zeta }}_{out}d\mathrm{\Gamma }-{\int }_{{\mathrm{\Gamma }}_{in}}{\mathit{\zeta }}_{in}D\mathrm{\nabla }\mathit{\xi }·\mathit{\nu }d\mathrm{\Gamma },\forall t\in (0,T).}\hfill \end{array}$$(26) ) we obtain(27) $$\begin{array}{c}\hfill {\displaystyle {\int }_{{\mathrm{\Gamma }}_{out}\times (0,T)}\mathit{\xi }{\mathit{\zeta }}_{out}d\mathrm{\Gamma }\mathrm{d}t-{\int }_{{\mathrm{\Gamma }}_{in}\times (0,T)}{\mathit{\zeta }}_{in}D\mathrm{\nabla }\mathit{\xi }·\mathit{\nu }d\mathrm{\Gamma }\mathrm{d}t=0,\forall {\mathit{\zeta }}_{in},{\mathit{\zeta }}_{out}}\end{array}$$(27)

Consequently, (27(27) $$\begin{array}{c}\hfill {\displaystyle {\int }_{{\mathrm{\Gamma }}_{out}\times (0,T)}\mathit{\xi }{\mathit{\zeta }}_{out}d\mathrm{\Gamma }\mathrm{d}t-{\int }_{{\mathrm{\Gamma }}_{in}\times (0,T)}{\mathit{\zeta }}_{in}D\mathrm{\nabla }\mathit{\xi }·\mathit{\nu }d\mathrm{\Gamma }\mathrm{d}t=0,\forall {\mathit{\zeta }}_{in},{\mathit{\zeta }}_{out}}\end{array}$$(27) ) implies that $\mathit{\xi }=0$ on ${\mathrm{\Gamma }}_{out}\times (0,T)$ and $D\mathrm{\nabla }\mathit{\xi }·\mathit{\nu }=0$ on ${\mathrm{\Gamma }}_{in}\times (0,T)$ which using the unique continuation theorem from [24] leads to $\mathit{\xi }=0$ in $(\mathrm{\Omega }\backslash \overline{\mathit{\omega }})\times (0,T)$. Hence, $\mathit{\xi }(x,t)=\frac{1}{R}(1-e^{-R(T-t)}){\mathit{\chi }}_{\mathit{\omega }}(x)$ in $\mathrm{\Omega }\times (0,T)$. That is absurd since the solution $\mathit{\xi }$ of the problem (25(25) $$\begin{array}{c}\hfill \left\{\begin{array}{c}-{\mathit{\partial }}_t\mathit{\xi }-\mathrm{d}iv(D\mathrm{\nabla }\mathit{\xi })+V·\mathrm{\nabla }\mathit{\xi }+R\mathit{\xi }={\mathit{\chi }}_{\mathit{\omega }}(x)\text{in}\mathrm{\Omega }\times (0,T)\hfill \\ \mathit{\xi }(·,T)=0\text{in}\mathrm{\Omega }\hfill \\ \mathit{\xi }=0\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ D\mathrm{\nabla }\mathit{\xi }·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\times (0,T)\hfill \end{array}\right.\end{array}$$(25) ) belongs to $H^{2,1}(\mathrm{\Omega }\times (0,T))$ and thus, it is continuous in $\mathrm{\Omega }$ for almost all $t\in (0,T)$.

Remark 2.4:

 

(1)

According to (26(26) $$\begin{array}{cc}\hfill {\displaystyle {\int }_{\mathit{\omega }}v(x,t)\mathrm{d}x}& =-\frac{\mathrm{d}}{\mathrm{d}t}{⟨\mathit{\xi }(·,t),v(·,t)⟩}_{L^2(\mathrm{\Omega })}\hfill \\ \hfill & {\displaystyle +{\int }_{{\mathrm{\Gamma }}_{out}}\mathit{\xi }{\mathit{\zeta }}_{out}d\mathrm{\Gamma }-{\int }_{{\mathrm{\Gamma }}_{in}}{\mathit{\zeta }}_{in}D\mathrm{\nabla }\mathit{\xi }·\mathit{\nu }d\mathrm{\Gamma },\forall t\in (0,T).}\hfill \end{array}$$(26) )–(27(27) $$\begin{array}{c}\hfill {\displaystyle {\int }_{{\mathrm{\Gamma }}_{out}\times (0,T)}\mathit{\xi }{\mathit{\zeta }}_{out}d\mathrm{\Gamma }\mathrm{d}t-{\int }_{{\mathrm{\Gamma }}_{in}\times (0,T)}{\mathit{\zeta }}_{in}D\mathrm{\nabla }\mathit{\xi }·\mathit{\nu }d\mathrm{\Gamma }\mathrm{d}t=0,\forall {\mathit{\zeta }}_{in},{\mathit{\zeta }}_{out}}\end{array}$$(27) ), the assertion (24(24) $$\begin{array}{c}\hfill {\displaystyle \text{such that}{\int }_{\mathit{\omega }}v(x,·)\mathrm{d}x\ne 0\text{a.e. in}(0,T)}\end{array}$$(24) ) can be ensured by selecting the boundary controls ${\mathit{\zeta }}_{in}$ and ${\mathit{\zeta }}_{out}$ involved in the problem (23(23) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathit{\partial }}_{t}v-\mathrm{d}iv(D\mathrm{\nabla }v)-V·\mathrm{\nabla }v+Rv=0\text{in}\mathrm{\Omega }\times (0,T)\hfill \\ v(·,0)=0\text{in}\mathrm{\Omega }\hfill \\ v={\mathit{\zeta }}_{in}\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ (D\mathrm{\nabla }v+vV)·\mathit{\nu }=0\text{on}{\mathrm{\Gamma }}_L\times (0,T)\hfill \\ (D\mathrm{\nabla }v+vV)·\mathit{\nu }={\mathit{\zeta }}_{out}\text{on}{\mathrm{\Gamma }}_{out}\times (0,T)\hfill \end{array}\right.\end{array}$$(23) ) as follows: either ${\mathit{\zeta }}_{in}=0$ on ${\mathrm{\Gamma }}_{in}\times (0,T)$ and ${\mathit{\zeta }}_{out}=\mathit{\xi }$ on ${\mathrm{\Gamma }}_{out}\times (0,T)$ or, ${\mathit{\zeta }}_{in}=-D\mathrm{\nabla }\mathit{\xi }·\mathit{\nu }$ on ${\mathrm{\Gamma }}_{in}\times (0,T)$ and ${\mathit{\zeta }}_{out}=0$ on ${\mathrm{\Gamma }}_{out}\times (0,T)$ or, ${\mathit{\zeta }}_{in}=-D\mathrm{\nabla }\mathit{\xi }·\mathit{\nu }$ on ${\mathrm{\Gamma }}_{in}\times (0,T)$ and ${\mathit{\zeta }}_{out}=\mathit{\xi }$ on ${\mathrm{\Gamma }}_{out}\times (0,T)$.

(2)

Since later on we use $\mathit{\omega }={\mathit{\omega }}_n\subset {\mathrm{\Omega }}_i$ where $i\in \{1,\cdots ,N_{max}\}$ it follows that (23(23) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathit{\partial }}_{t}v-\mathrm{d}iv(D\mathrm{\nabla }v)-V·\mathrm{\nabla }v+Rv=0\text{in}\mathrm{\Omega }\times (0,T)\hfill \\ v(·,0)=0\text{in}\mathrm{\Omega }\hfill \\ v={\mathit{\zeta }}_{in}\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ (D\mathrm{\nabla }v+vV)·\mathit{\nu }=0\text{on}{\mathrm{\Gamma }}_L\times (0,T)\hfill \\ (D\mathrm{\nabla }v+vV)·\mathit{\nu }={\mathit{\zeta }}_{out}\text{on}{\mathrm{\Gamma }}_{out}\times (0,T)\hfill \end{array}\right.\end{array}$$(23) )–(25(25) $$\begin{array}{c}\hfill \left\{\begin{array}{c}-{\mathit{\partial }}_t\mathit{\xi }-\mathrm{d}iv(D\mathrm{\nabla }\mathit{\xi })+V·\mathrm{\nabla }\mathit{\xi }+R\mathit{\xi }={\mathit{\chi }}_{\mathit{\omega }}(x)\text{in}\mathrm{\Omega }\times (0,T)\hfill \\ \mathit{\xi }(·,T)=0\text{in}\mathrm{\Omega }\hfill \\ \mathit{\xi }=0\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ D\mathrm{\nabla }\mathit{\xi }·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\times (0,T)\hfill \end{array}\right.\end{array}$$(25) ) can be also considered in ${\mathrm{\Omega }}_i\times (0,T)$ rather than in $\mathrm{\Omega }\times (0,T)$. The last option has the advantage of solving always the two systems (23(23) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathit{\partial }}_{t}v-\mathrm{d}iv(D\mathrm{\nabla }v)-V·\mathrm{\nabla }v+Rv=0\text{in}\mathrm{\Omega }\times (0,T)\hfill \\ v(·,0)=0\text{in}\mathrm{\Omega }\hfill \\ v={\mathit{\zeta }}_{in}\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ (D\mathrm{\nabla }v+vV)·\mathit{\nu }=0\text{on}{\mathrm{\Gamma }}_L\times (0,T)\hfill \\ (D\mathrm{\nabla }v+vV)·\mathit{\nu }={\mathit{\zeta }}_{out}\text{on}{\mathrm{\Gamma }}_{out}\times (0,T)\hfill \end{array}\right.\end{array}$$(23) )–(25(25) $$\begin{array}{c}\hfill \left\{\begin{array}{c}-{\mathit{\partial }}_t\mathit{\xi }-\mathrm{d}iv(D\mathrm{\nabla }\mathit{\xi })+V·\mathrm{\nabla }\mathit{\xi }+R\mathit{\xi }={\mathit{\chi }}_{\mathit{\omega }}(x)\text{in}\mathrm{\Omega }\times (0,T)\hfill \\ \mathit{\xi }(·,T)=0\text{in}\mathrm{\Omega }\hfill \\ \mathit{\xi }=0\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ D\mathrm{\nabla }\mathit{\xi }·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\times (0,T)\hfill \end{array}\right.\end{array}$$(25) ) in a same geometry (discretization) for $\mathit{\omega }\subset {\mathrm{\Omega }}_i$ whatever $i\in \{1,\cdots ,N_{max}\}$. However, as we need also to compute ${\int }_{\mathit{\omega }}v(x,·)\mathrm{d}x$ then, the first option i.e. considering (23(23) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathit{\partial }}_{t}v-\mathrm{d}iv(D\mathrm{\nabla }v)-V·\mathrm{\nabla }v+Rv=0\text{in}\mathrm{\Omega }\times (0,T)\hfill \\ v(·,0)=0\text{in}\mathrm{\Omega }\hfill \\ v={\mathit{\zeta }}_{in}\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ (D\mathrm{\nabla }v+vV)·\mathit{\nu }=0\text{on}{\mathrm{\Gamma }}_L\times (0,T)\hfill \\ (D\mathrm{\nabla }v+vV)·\mathit{\nu }={\mathit{\zeta }}_{out}\text{on}{\mathrm{\Gamma }}_{out}\times (0,T)\hfill \end{array}\right.\end{array}$$(23) )–(25(25) $$\begin{array}{c}\hfill \left\{\begin{array}{c}-{\mathit{\partial }}_t\mathit{\xi }-\mathrm{d}iv(D\mathrm{\nabla }\mathit{\xi })+V·\mathrm{\nabla }\mathit{\xi }+R\mathit{\xi }={\mathit{\chi }}_{\mathit{\omega }}(x)\text{in}\mathrm{\Omega }\times (0,T)\hfill \\ \mathit{\xi }(·,T)=0\text{in}\mathrm{\Omega }\hfill \\ \mathit{\xi }=0\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ D\mathrm{\nabla }\mathit{\xi }·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\times (0,T)\hfill \end{array}\right.\end{array}$$(25) ) in ${\mathrm{\Omega }}_i\times (0,T)$ could be numerically more convenient for using a mesh size small enough to better approximate ${\int }_{\mathit{\omega }}v(x,·)\mathrm{d}x$.

3. Identifiability

In this section, we prove that under some reasonable assumptions the observation operator M[F] introduced in (15(15) $$\begin{array}{c}\hfill M[F]:=\left\{D\mathrm{\nabla }u·\mathit{\nu }\text{on}\sum _{in};{\Vert V\Vert }_{2}u\text{on}\sum _L;(u,D\mathrm{\nabla }u·\mathit{\nu })\text{on}\sum _{i=1,\cdots ,N_{max}}\right\},\end{array}$$(15) ) yields uniqueness of the unknown elements: total number N of all occurring sources, source spatial supports ${\overline{\mathit{\omega }}}_{n=1,\cdots ,N}$ and time-dependent source intensity functions ${\mathit{\lambda }}_{n=1,\cdots ,N}$ defining in (9(9) $$\begin{array}{c}\hfill {\displaystyle F(x,t)=\sum _{n=1}^N{\mathit{\lambda }}_n(t){\mathit{\chi }}_{{\mathit{\omega }}_n}(x)\text{in}\mathrm{\Omega }\times (0,T),}\end{array}$$(9) ) the set F of all sources involved in the problem (1(1) $$\begin{array}{c}\hfill L[u](x,t)=F(x,t)\text{in}\mathrm{\Omega }\times (0,T),\end{array}$$(1) )–(2(2) $$\begin{array}{c}\hfill L[u](x,t):={\mathit{\partial }}_{t}u(x,t)-\mathrm{d}iv(D\mathrm{\nabla }u(x,t))+V·\mathrm{\nabla }u(x,t)+Ru(x,t),\end{array}$$(2) ) and (8(8) $$\begin{array}{c}\hfill \begin{array}{c}u(·,0)=0\text{in}\mathrm{\Omega }\hfill \\ u=0\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ D\mathrm{\nabla }u·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\times (0,T)\hfill \end{array}\end{array}$$(8) ). This result is given by the following theorem:

Theorem 3.1:

Let $F(x,t)={\sum }_{n=1}^N{\mathit{\lambda }}_n(t){\mathit{\chi }}_{{\mathit{\omega }}_n}(x)$ be $N\in {\mathbb{N}}^{\ast }$ sources occurring in the problem (1(1) $$\begin{array}{c}\hfill L[u](x,t)=F(x,t)\text{in}\mathrm{\Omega }\times (0,T),\end{array}$$(1) )–(2(2) $$\begin{array}{c}\hfill L[u](x,t):={\mathit{\partial }}_{t}u(x,t)-\mathrm{d}iv(D\mathrm{\nabla }u(x,t))+V·\mathrm{\nabla }u(x,t)+Ru(x,t),\end{array}$$(2) ) and (8(8) $$\begin{array}{c}\hfill \begin{array}{c}u(·,0)=0\text{in}\mathrm{\Omega }\hfill \\ u=0\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ D\mathrm{\nabla }u·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\times (0,T)\hfill \end{array}\end{array}$$(8) ). Given $N_{max}\ge N$, let ${\mathrm{\Gamma }}_{i=1,\cdots ,N_{max}}$ and ${\mathrm{\Omega }}_{i=1,\cdots ,N_{max}+1}$ be as in (13(13) $$\begin{array}{c}\hfill \begin{array}{c}(C_1){\mathrm{\Gamma }}_i\cap {\mathrm{\Gamma }}_j=\mathrm{\varnothing },\forall i\ne j\in \{0,\cdots ,N_{max}+1\}.\hfill \\ (C_2)|{\mathrm{\Gamma }}_i\cap {\mathrm{\Gamma }}_{L_l}|=|{\mathrm{\Gamma }}_i\cap {\mathrm{\Gamma }}_{L_u}|=1,\forall i=1,\cdots ,N_{max}.\hfill \\ (C_3)\overline{\mathrm{\Omega }}={\cup }_{i=1}^{N_{max}+1}{\overline{\mathrm{\Omega }}}_i\text{where:}{\mathrm{\Omega }}_{N_{max}+1}\subset (\mathrm{\Omega }\backslash {\cup }_{i=1}^N{\overline{\mathit{\omega }}}_n),\hfill \end{array}\end{array}$$(13) ) and M[F] be the observation operator introduced in (15(15) $$\begin{array}{c}\hfill M[F]:=\left\{D\mathrm{\nabla }u·\mathit{\nu }\text{on}\sum _{in};{\Vert V\Vert }_{2}u\text{on}\sum _L;(u,D\mathrm{\nabla }u·\mathit{\nu })\text{on}\sum _{i=1,\cdots ,N_{max}}\right\},\end{array}$$(15) ). Provided Lemmas 2.2 and 2.3 apply, if the functions ${\mathit{\lambda }}_{n=1,\cdots ,N}\in L^2(0,T)$ satisfy (11(11) $$\begin{array}{c}\hfill {\int }_0^T{\mathit{\lambda }}_n(t)e^{Rt}\mathrm{d}t\ne 0\text{and}\exists T^0\in (0,T)\text{such that}{\mathit{\lambda }}_n=0\text{in}(T^0,T),\forall n=1,\cdots ,N.\end{array}$$(11) ) and the spatial supports ${\overline{\mathit{\omega }}}_{n=1,\cdots ,N}$ fulfill (14(14) $$\begin{array}{cc}& \forall i\in \{1,\cdots ,N_{max}\},\text{there exists}\underline{atmost}\text{one element}n\in \{1,\cdots ,N\}\hfill \\ \hfill & \text{such that}{\mathit{\omega }}_n\subset {\mathrm{\Omega }}_i.\hfill \end{array}$$(14) ) then, M[F] yields uniqueness of the elements N, ${\mathit{\omega }}_{n=1,\cdots ,N}$ and ${\mathit{\lambda }}_{n=1,\cdots ,N}$.

ProofLet $u^{(k=1,2)}$ be the solution of the problem (1(1) $$\begin{array}{c}\hfill L[u](x,t)=F(x,t)\text{in}\mathrm{\Omega }\times (0,T),\end{array}$$(1) )–(2(2) $$\begin{array}{c}\hfill L[u](x,t):={\mathit{\partial }}_{t}u(x,t)-\mathrm{d}iv(D\mathrm{\nabla }u(x,t))+V·\mathrm{\nabla }u(x,t)+Ru(x,t),\end{array}$$(2) ) and (8(8) $$\begin{array}{c}\hfill \begin{array}{c}u(·,0)=0\text{in}\mathrm{\Omega }\hfill \\ u=0\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ D\mathrm{\nabla }u·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\times (0,T)\hfill \end{array}\end{array}$$(8) ) involving the set of sources: $F^{(k)}(x,t)={\sum }_{n=1}^{N^{(k)}}{\mathit{\lambda }}_n^{(k)}(t){\mathit{\chi }}_{{\mathit{\omega }}_n^{(k)}}(x)$ where $1\le N^{(k)}\le N_{max}$, ${\mathit{\lambda }}_{n=1,\cdots ,N^{(k)}}^{(k)}\in L^2(0,T)$ satisfy (11(11) $$\begin{array}{c}\hfill {\int }_0^T{\mathit{\lambda }}_n(t)e^{Rt}\mathrm{d}t\ne 0\text{and}\exists T^0\in (0,T)\text{such that}{\mathit{\lambda }}_n=0\text{in}(T^0,T),\forall n=1,\cdots ,N.\end{array}$$(11) ) and ${\mathit{\omega }}_{n=1,\cdots ,N^{(k)}}^{(k)}$ fulfill (14(14) $$\begin{array}{cc}& \forall i\in \{1,\cdots ,N_{max}\},\text{there exists}\underline{atmost}\text{one element}n\in \{1,\cdots ,N\}\hfill \\ \hfill & \text{such that}{\mathit{\omega }}_n\subset {\mathrm{\Omega }}_i.\hfill \end{array}$$(14) ). Furthermore, we denote $M[F^{(k)}]$ the associated observation operator as introduced in (15(15) $$\begin{array}{c}\hfill M[F]:=\left\{D\mathrm{\nabla }u·\mathit{\nu }\text{on}\sum _{in};{\Vert V\Vert }_{2}u\text{on}\sum _L;(u,D\mathrm{\nabla }u·\mathit{\nu })\text{on}\sum _{i=1,\cdots ,N_{max}}\right\},\end{array}$$(15) ). Then, from setting $M[F^{(2)}]=M[F^{(1)}]$ it follows that the variable $w=u^{(2)}-u^{(1)}$ satisfies:(28) $$\begin{array}{c}\hfill D\mathrm{\nabla }w·\mathit{\nu }=0\text{on}\sum _{in},{\Vert V\Vert }_{2}w=0\text{on}\sum _L\text{and}w=D\mathrm{\nabla }w·\mathit{\nu }=0\text{on}\sum _{i=1,\cdots ,N_{max}}.\end{array}$$(28)

Besides, since for $k=1,2$ the source spatial supports ${\overline{\mathit{\omega }}}_{n=1,\cdots ,N^{(k)}}^{(k)}$ satisfy (14(14) $$\begin{array}{cc}& \forall i\in \{1,\cdots ,N_{max}\},\text{there exists}\underline{atmost}\text{one element}n\in \{1,\cdots ,N\}\hfill \\ \hfill & \text{such that}{\mathit{\omega }}_n\subset {\mathrm{\Omega }}_i.\hfill \end{array}$$(14) ) it follows that for all $i\in \{1,\cdots ,N_{max}\}$, in ${\mathrm{\Omega }}_i\subset \mathrm{\Omega }$ holds one of the following three cases: Case 1. There is no source occurring in ${\mathrm{\Omega }}_i$ and thus, $F^{(2)}=F^{(1)}$ in ${\mathrm{\Omega }}_i\times (0,T)$. Case 2. There is a source ${\mathit{\lambda }}_n^{(2)}{\mathit{\chi }}_{{\mathit{\omega }}_n^{(2)}}$ from $F^{(2)}$ and a source ${\mathit{\lambda }}_n^{(1)}{\mathit{\chi }}_{{\mathit{\omega }}_n^{(1)}}$ from $F^{(1)}$ occurring in ${\mathrm{\Omega }}_i$. Case 3. There is an only one source ${\mathit{\lambda }}_n^{(k)}{\mathit{\chi }}_{{\mathit{\omega }}_n^{(k)}}$ where $k\in \{1,2\}$ occurring in ${\mathrm{\Omega }}_i$. We treat Case 2 which leads to conclude also about Case 3. In Case 2 and from (28(28) $$\begin{array}{c}\hfill D\mathrm{\nabla }w·\mathit{\nu }=0\text{on}\sum _{in},{\Vert V\Vert }_{2}w=0\text{on}\sum _L\text{and}w=D\mathrm{\nabla }w·\mathit{\nu }=0\text{on}\sum _{i=1,\cdots ,N_{max}}.\end{array}$$(28) ), w solves(29) $$\begin{array}{c}\hfill \left\{\begin{array}{c}L[w](x,t)={\mathit{\lambda }}_n^{(2)}(t){\mathit{\chi }}_{{\mathit{\omega }}_n^{(2)}}(x)-{\mathit{\lambda }}_n^{(1)}(t){\mathit{\chi }}_{{\mathit{\omega }}_n^{(1)}}(x)\text{in}{\mathrm{\Omega }}_i\times (0,T)\hfill \\ w(·,0)=0\text{in}{\mathrm{\Omega }}_i\hfill \\ w=0\text{on}{\mathrm{\Gamma }}_{i-1}\times (0,T)\hfill \\ D\mathrm{\nabla }w·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L^i\cup {\mathrm{\Gamma }}_i)\times (0,T)\hfill \end{array}\right.\end{array}$$(29)

Moreover, in view of (28(28) $$\begin{array}{c}\hfill D\mathrm{\nabla }w·\mathit{\nu }=0\text{on}\sum _{in},{\Vert V\Vert }_{2}w=0\text{on}\sum _L\text{and}w=D\mathrm{\nabla }w·\mathit{\nu }=0\text{on}\sum _{i=1,\cdots ,N_{max}}.\end{array}$$(28) ) and by applying the unique continuation theorem [24] it follows that $w=0$ in $({\mathrm{\Omega }}_i\backslash ({\overline{\mathit{\omega }}}_n^{(1)}\cup {\overline{\mathit{\omega }}}_n^{(2)}))\times (0,T)$. Therefore, the solution w of (29(29) $$\begin{array}{c}\hfill \left\{\begin{array}{c}L[w](x,t)={\mathit{\lambda }}_n^{(2)}(t){\mathit{\chi }}_{{\mathit{\omega }}_n^{(2)}}(x)-{\mathit{\lambda }}_n^{(1)}(t){\mathit{\chi }}_{{\mathit{\omega }}_n^{(1)}}(x)\text{in}{\mathrm{\Omega }}_i\times (0,T)\hfill \\ w(·,0)=0\text{in}{\mathrm{\Omega }}_i\hfill \\ w=0\text{on}{\mathrm{\Gamma }}_{i-1}\times (0,T)\hfill \\ D\mathrm{\nabla }w·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L^i\cup {\mathrm{\Gamma }}_i)\times (0,T)\hfill \end{array}\right.\end{array}$$(29) ) is either $w=0$ or $w(x,t)={\int }_0^t{\mathit{\lambda }}_n^{(2)}(\mathit{\eta })e^{-R(t-\mathit{\eta })}d\mathit{\eta }{\mathit{\chi }}_{{\mathit{\omega }}_n^{(2)}}(x)-{\int }_0^t{\mathit{\lambda }}_n^{(1)}(\mathit{\eta })e^{-R(t-\mathit{\eta })}d\mathit{\eta }{\mathit{\chi }}_{{\mathit{\omega }}_n^{(1)}}(x)$ in ${\mathrm{\Omega }}_i\times (0,T)$. However, as in (12(12) $$\begin{array}{c}\hfill H^{2,1}(\mathrm{\Omega }\times (0,T)):=L^2(0,T;H^2(\mathrm{\Omega }))\cap H^1(0,T;L^2(\mathrm{\Omega })).\end{array}$$(12) ), since $w\in H^{2,1}(\mathrm{\Omega }\times (0,T))$ then, w is continuous in ${\mathrm{\Omega }}_i$ for a.e. $t\in (0,T)$ and thus, the solution of (29(29) $$\begin{array}{c}\hfill \left\{\begin{array}{c}L[w](x,t)={\mathit{\lambda }}_n^{(2)}(t){\mathit{\chi }}_{{\mathit{\omega }}_n^{(2)}}(x)-{\mathit{\lambda }}_n^{(1)}(t){\mathit{\chi }}_{{\mathit{\omega }}_n^{(1)}}(x)\text{in}{\mathrm{\Omega }}_i\times (0,T)\hfill \\ w(·,0)=0\text{in}{\mathrm{\Omega }}_i\hfill \\ w=0\text{on}{\mathrm{\Gamma }}_{i-1}\times (0,T)\hfill \\ D\mathrm{\nabla }w·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L^i\cup {\mathrm{\Gamma }}_i)\times (0,T)\hfill \end{array}\right.\end{array}$$(29) ) is rather $w=0$ in ${\mathrm{\Omega }}_i\times (0,T)$. That implies ${\mathit{\lambda }}_n^{(2)}={\mathit{\lambda }}_n^{(1)}$ in (0, T) and ${\mathit{\omega }}_n^{(2)}={\mathit{\omega }}_n^{(1)}$ which means that in Case 2, we have also $F^{(2)}=F^{(1)}$ in ${\mathrm{\Omega }}_i\times (0,T)$. In Case 3, the variable w solves a system similar to (29(29) $$\begin{array}{c}\hfill \left\{\begin{array}{c}L[w](x,t)={\mathit{\lambda }}_n^{(2)}(t){\mathit{\chi }}_{{\mathit{\omega }}_n^{(2)}}(x)-{\mathit{\lambda }}_n^{(1)}(t){\mathit{\chi }}_{{\mathit{\omega }}_n^{(1)}}(x)\text{in}{\mathrm{\Omega }}_i\times (0,T)\hfill \\ w(·,0)=0\text{in}{\mathrm{\Omega }}_i\hfill \\ w=0\text{on}{\mathrm{\Gamma }}_{i-1}\times (0,T)\hfill \\ D\mathrm{\nabla }w·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L^i\cup {\mathrm{\Gamma }}_i)\times (0,T)\hfill \end{array}\right.\end{array}$$(29) ) where in the right-hand side of the first equation occurs only ${\mathit{\lambda }}_n^{(k)}{\mathit{\chi }}_{{\mathit{\omega }}_n^{(k)}}$ with $k\in \{1,2\}$. Then, using similar techniques as in Case 2 we obtain $w=0$ in ${\mathrm{\Omega }}_i\times (0,T)$ which implies that ${\mathit{\lambda }}_n^{(k)}{\mathit{\chi }}_{{\mathit{\omega }}_n^{(k)}}=0$ in ${\mathrm{\Omega }}_i\times (0,T)$ and thus, in Case 3 it holds also $F^{(2)}=F^{(1)}$ in ${\mathrm{\Omega }}_i\times (0,T)$. Hence, $F^{(2)}=F^{(1)}$ in ${\mathrm{\Omega }}_i\times (0,T)$ for all $i\in \{1,\cdots ,N_{max}\}$ which means that $F^{(2)}=F^{(1)}$ in $\mathrm{\Omega }\times (0,T)$.

4. Detection-identification method

In view of the identifiability result given by Theorem 3.1 and assuming the unknown elements ${\mathit{\lambda }}_{n=1,\cdots ,N}$ and ${\mathit{\omega }}_{n=1,\cdots ,N}$ defining F in (9(9) $$\begin{array}{c}\hfill {\displaystyle F(x,t)=\sum _{n=1}^N{\mathit{\lambda }}_n(t){\mathit{\chi }}_{{\mathit{\omega }}_n}(x)\text{in}\mathrm{\Omega }\times (0,T),}\end{array}$$(9) ) involved in the problem (1(1) $$\begin{array}{c}\hfill L[u](x,t)=F(x,t)\text{in}\mathrm{\Omega }\times (0,T),\end{array}$$(1) )–(2(2) $$\begin{array}{c}\hfill L[u](x,t):={\mathit{\partial }}_{t}u(x,t)-\mathrm{d}iv(D\mathrm{\nabla }u(x,t))+V·\mathrm{\nabla }u(x,t)+Ru(x,t),\end{array}$$(2) ) and (8(8) $$\begin{array}{c}\hfill \begin{array}{c}u(·,0)=0\text{in}\mathrm{\Omega }\hfill \\ u=0\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ D\mathrm{\nabla }u·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\times (0,T)\hfill \end{array}\end{array}$$(8) ) to be such that (11(11) $$\begin{array}{c}\hfill {\int }_0^T{\mathit{\lambda }}_n(t)e^{Rt}\mathrm{d}t\ne 0\text{and}\exists T^0\in (0,T)\text{such that}{\mathit{\lambda }}_n=0\text{in}(T^0,T),\forall n=1,\cdots ,N.\end{array}$$(11) ) and (14(14) $$\begin{array}{cc}& \forall i\in \{1,\cdots ,N_{max}\},\text{there exists}\underline{atmost}\text{one element}n\in \{1,\cdots ,N\}\hfill \\ \hfill & \text{such that}{\mathit{\omega }}_n\subset {\mathrm{\Omega }}_i.\hfill \end{array}$$(14) ) hold true, we focus on developing from the observation operator M[F] in (15(15) $$\begin{array}{c}\hfill M[F]:=\left\{D\mathrm{\nabla }u·\mathit{\nu }\text{on}\sum _{in};{\Vert V\Vert }_{2}u\text{on}\sum _L;(u,D\mathrm{\nabla }u·\mathit{\nu })\text{on}\sum _{i=1,\cdots ,N_{max}}\right\},\end{array}$$(15) ) a direct detection–identification method that scans throughout the monitored domain $\mathrm{\Omega }$ to detect for $i=1,\cdots ,N_{max}$ whether there exists or not an active source ${\mathit{\lambda }}_n{\mathit{\chi }}_{{\mathit{\omega }}_n}$ occurring in ${\mathrm{\Omega }}_i$, i.e. ${\mathit{\omega }}_n\subset {\mathrm{\Omega }}_i$. Once a source is detected, the developed method localizes the geometric centre $G_n$ of its unknown spatial support ${\overline{\mathit{\omega }}}_n$ and determines lower-upper bounds of the total amount discharged in ${\mathrm{\Omega }}_i$ by the occurring source without having to identify the two unknown elements ${\mathit{\lambda }}_n$ and ${\mathit{\omega }}_n$. Then, given two desired reference geometries, in the sequel we use, for example, squares centred at the already localized geometric centre $G_n$ of ${\mathit{\omega }}_n$, the method determines the biggest domain defined by a first reference geometry included in the unknown source spatial support ${\overline{\mathit{\omega }}}_n$ as well as the smallest domain defined by a second reference geometry containing ${\mathit{\omega }}_n$. It also gives an approximation of its surface area $\mathcal{A}({\mathit{\omega }}_n)$ and identifies its intensity function ${\mathit{\lambda }}_n$ in (0, T).

4.1. Detection of active sources and total discharged amounts

For $i=1,\cdots ,N_{max}$ and according to (14(14) $$\begin{array}{cc}& \forall i\in \{1,\cdots ,N_{max}\},\text{there exists}\underline{atmost}\text{one element}n\in \{1,\cdots ,N\}\hfill \\ \hfill & \text{such that}{\mathit{\omega }}_n\subset {\mathrm{\Omega }}_i.\hfill \end{array}$$(14) ), it follows that if there exists a source ${\mathit{\lambda }}_n{\mathit{\chi }}_{{\mathit{\omega }}_n}$ occurring in ${\mathrm{\Omega }}_i\subset \mathrm{\Omega }$, i.e. ${\mathit{\omega }}_n\subset {\mathrm{\Omega }}_i$ then, by multiplying the main Equations (1(1) $$\begin{array}{c}\hfill L[u](x,t)=F(x,t)\text{in}\mathrm{\Omega }\times (0,T),\end{array}$$(1) )–(2(2) $$\begin{array}{c}\hfill L[u](x,t):={\mathit{\partial }}_{t}u(x,t)-\mathrm{d}iv(D\mathrm{\nabla }u(x,t))+V·\mathrm{\nabla }u(x,t)+Ru(x,t),\end{array}$$(2) ) by $z(x,t)=e^{Rt}Z(x)$ introduced in (6(6) $$\begin{array}{c}\hfill z(x,t)=e^{Rt}Z(x)\text{for}Z(x)\in \{Z_0,e^{\mathit{\psi }(x)},{\mathit{\psi }}^{\perp }(x)\},\end{array}$$(6) ) that solves the adjoint Equation (7(7) $$\begin{array}{c}\hfill -{\mathit{\partial }}_{t}z-\mathrm{d}iv(D\mathrm{\nabla }z)-V·\mathrm{\nabla }z+Rz=0\text{in}\mathrm{\Omega }\times (0,T).\end{array}$$(7) ) and integrating by parts on ${\mathrm{\Omega }}_i\times (0,T)$ using Green’s formula, we obtain(30) $$\begin{array}{cc}\hfill {\overline{\mathit{\lambda }}}_n{\int }_{{\mathit{\omega }}_n}Z(x)\mathrm{d}x& {\displaystyle =e^{RT}{\int }_{{\mathrm{\Omega }}_i}u(x,T)Z(x)\mathrm{d}x}\hfill \\ \hfill & {\displaystyle +{\int }_{\mathit{\partial }{\mathrm{\Omega }}_i\times (0,T)}{e}^{Rt}(u[ZV+D\mathrm{\nabla }Z]-ZD\mathrm{\nabla }u)·\mathit{\nu }\mathrm{d}x\mathrm{d}t,}\hfill \end{array}$$(30)

where ${\overline{\mathit{\lambda }}}_n={\int }_0^T{e}^{Rt}{\mathit{\lambda }}_n(t)\mathrm{d}t$. Since on the lateral boundary ${\sum }_L$ we have $D\mathrm{\nabla }u·\mathit{\nu }=0$ and from substituting in (30(30) $$\begin{array}{cc}\hfill {\overline{\mathit{\lambda }}}_n{\int }_{{\mathit{\omega }}_n}Z(x)\mathrm{d}x& {\displaystyle =e^{RT}{\int }_{{\mathrm{\Omega }}_i}u(x,T)Z(x)\mathrm{d}x}\hfill \\ \hfill & {\displaystyle +{\int }_{\mathit{\partial }{\mathrm{\Omega }}_i\times (0,T)}{e}^{Rt}(u[ZV+D\mathrm{\nabla }Z]-ZD\mathrm{\nabla }u)·\mathit{\nu }\mathrm{d}x\mathrm{d}t,}\hfill \end{array}$$(30) ), Z by $Z=Z_0$, $Z=e^{\mathit{\psi }}$ and $Z={\mathit{\psi }}^{\perp }$ as introduced in (6(6) $$\begin{array}{c}\hfill z(x,t)=e^{Rt}Z(x)\text{for}Z(x)\in \{Z_0,e^{\mathit{\psi }(x)},{\mathit{\psi }}^{\perp }(x)\},\end{array}$$(6) ), it follows that the two unknown elements: spatial support ${\overline{\mathit{\omega }}}_n$ and time-dependent intensity function ${\mathit{\lambda }}_n$ defining an eventual source occurring in ${\mathrm{\Omega }}_i$ satisfy(31) $$\begin{array}{c}\hfill {\overline{\mathit{\lambda }}}_n\mathcal{A}({\mathit{\omega }}_n)=P_1^i,{\overline{\mathit{\lambda }}}_n{\int }_{{\mathit{\omega }}_n}{e}^{\mathit{\psi }(x)}\mathrm{d}x=P_{e^{\mathit{\psi }}}^i\text{and}{\overline{\mathit{\lambda }}}_n{\int }_{{\mathit{\omega }}_n}{\mathit{\psi }}^{\perp }(x)\mathrm{d}x=P_{{\mathit{\psi }}^{\perp }}^i,\end{array}$$(31)

where the coefficients $P_1^i$, $P_{e^{\mathit{\psi }}}^i$ and $P_{{\mathit{\psi }}^{\perp }}^i$ are given by(32) $$\begin{array}{cc}\hfill P_1^i& {\displaystyle =e^{RT}{\int }_{{\mathrm{\Omega }}_i}u(x,T)\mathrm{d}x+{\int }_{({\mathrm{\Gamma }}_{i-1}\cup {\mathrm{\Gamma }}_i)\times (0,T)}{e}^{Rt}(uV-D\mathrm{\nabla }u)·\mathit{\nu }\mathrm{d}x\mathrm{d}t}\hfill \\ \hfill & {\displaystyle +{\int }_{{\mathrm{\Gamma }}_L^i\times (0,T)}{e}^{Rt}uV·\mathit{\nu }\mathrm{d}x\mathrm{d}t,}\hfill \\ \hfill P_{e^{\mathit{\psi }}}^i& {\displaystyle =e^{RT}{\int }_{{\mathrm{\Omega }}_i}{e}^{\mathit{\psi }(x)}u(x,T)\mathrm{d}x-{\int }_{({\mathrm{\Gamma }}_{i-1}\cup {\mathrm{\Gamma }}_i)\times (0,T)}{e}^{\mathit{\psi }+Rt}D\mathrm{\nabla }u·\mathit{\nu }\mathrm{d}x\mathrm{d}t,}\hfill \\ \hfill P_{{\mathit{\psi }}^{\perp }}^i& {\displaystyle =e^{RT}{\int }_{{\mathrm{\Omega }}_i}{\mathit{\psi }}^{\perp }(x)u(x,T)\mathrm{d}x}\hfill \\ \hfill & {\displaystyle +{\int }_{({\mathrm{\Gamma }}_{i-1}\cup {\mathrm{\Gamma }}_i)\times (0,T)}{e}^{Rt}(u[{\mathit{\psi }}^{\perp }V-D{V}^{\perp }]-{\mathit{\psi }}^{\perp }D\mathrm{\nabla }u)·\mathit{\nu }\mathrm{d}x\mathrm{d}t}\hfill \\ \hfill & {\displaystyle +{\int }_{{\mathrm{\Gamma }}_L^i\times (0,T)}{e}^{Rt}u[{\mathit{\psi }}^{\perp }V-D{V}^{\perp }]·\mathit{\nu }\mathrm{d}x\mathrm{d}t.}\hfill \end{array}$$(32)

Moreover, as we will discuss later on in this section, for $i=1,\cdots ,N_{max}$ the coefficients $P_1^i$, $P_{e^{\mathit{\psi }}}^i$ and $P_{{\mathit{\psi }}^{\perp }}^i$ can be completely computed in each ${\mathrm{\Omega }}_i\subset \mathrm{\Omega }$ from the measurements defining the observation operator M[F].

The first two equations in (31(31) $$\begin{array}{c}\hfill {\overline{\mathit{\lambda }}}_n\mathcal{A}({\mathit{\omega }}_n)=P_1^i,{\overline{\mathit{\lambda }}}_n{\int }_{{\mathit{\omega }}_n}{e}^{\mathit{\psi }(x)}\mathrm{d}x=P_{e^{\mathit{\psi }}}^i\text{and}{\overline{\mathit{\lambda }}}_n{\int }_{{\mathit{\omega }}_n}{\mathit{\psi }}^{\perp }(x)\mathrm{d}x=P_{{\mathit{\psi }}^{\perp }}^i,\end{array}$$(31) ) indicate whether there exists or not a source occurring in the suspected section ${\mathrm{\Omega }}_i\subset \mathrm{\Omega }$. Indeed, as from (11(11) $$\begin{array}{c}\hfill {\int }_0^T{\mathit{\lambda }}_n(t)e^{Rt}\mathrm{d}t\ne 0\text{and}\exists T^0\in (0,T)\text{such that}{\mathit{\lambda }}_n=0\text{in}(T^0,T),\forall n=1,\cdots ,N.\end{array}$$(11) ) we have ${\overline{\mathit{\lambda }}}_n\ne 0$ then, for example, using the first equation in (31(31) $$\begin{array}{c}\hfill {\overline{\mathit{\lambda }}}_n\mathcal{A}({\mathit{\omega }}_n)=P_1^i,{\overline{\mathit{\lambda }}}_n{\int }_{{\mathit{\omega }}_n}{e}^{\mathit{\psi }(x)}\mathrm{d}x=P_{e^{\mathit{\psi }}}^i\text{and}{\overline{\mathit{\lambda }}}_n{\int }_{{\mathit{\omega }}_n}{\mathit{\psi }}^{\perp }(x)\mathrm{d}x=P_{{\mathit{\psi }}^{\perp }}^i,\end{array}$$(31) ) it follows that $P_1^i=0$ means $\mathcal{A}({\mathit{\omega }}_n)=0$ and thus, there is no source occurring in ${\mathrm{\Omega }}_i$. However, if $P_1^i\ne 0$ then, there is a source ${\mathit{\lambda }}_n{\mathit{\chi }}_{{\mathit{\omega }}_n}$ occurring in ${\mathrm{\Omega }}_i$, i.e. ${\mathit{\omega }}_n\subset {\mathrm{\Omega }}_i$. Furthermore, if ${\mathit{\lambda }}_n$ keeps a constant sign, for example, ${\mathit{\lambda }}_n\ge 0$-pagination a.e. in (0, T) and the reaction coefficient $R\ge 0$ then, we have: ${\mathit{\lambda }}_n(t)\le {\mathit{\lambda }}_n(t)e^{Rt}\le {\mathit{\lambda }}_n(t)e^{RT}$ in (0, T). Hence, from the first equation in (31(31) $$\begin{array}{c}\hfill {\overline{\mathit{\lambda }}}_n\mathcal{A}({\mathit{\omega }}_n)=P_1^i,{\overline{\mathit{\lambda }}}_n{\int }_{{\mathit{\omega }}_n}{e}^{\mathit{\psi }(x)}\mathrm{d}x=P_{e^{\mathit{\psi }}}^i\text{and}{\overline{\mathit{\lambda }}}_n{\int }_{{\mathit{\omega }}_n}{\mathit{\psi }}^{\perp }(x)\mathrm{d}x=P_{{\mathit{\psi }}^{\perp }}^i,\end{array}$$(31) ) we deduce the following lower and upper bounds of the total amount discharged in ${\mathrm{\Omega }}_i$ by the occurring source ${\mathit{\lambda }}_n{\mathit{\chi }}_{{\mathit{\omega }}_n}$:(33) $$\begin{array}{c}\hfill {\displaystyle e^{-RT}{P}_1^i\le e^{-R{T}^0}{P}_1^i\le \mathcal{A}({\mathit{\omega }}_n){\int }_0^T{\mathit{\lambda }}_n(t)\mathrm{d}t\le P_1^i.}\end{array}$$(33)

The knowledge of the time active limit $T^0$ using [25] improves the lower bound in (33(33) $$\begin{array}{c}\hfill {\displaystyle e^{-RT}{P}_1^i\le e^{-R{T}^0}{P}_1^i\le \mathcal{A}({\mathit{\omega }}_n){\int }_0^T{\mathit{\lambda }}_n(t)\mathrm{d}t\le P_1^i.}\end{array}$$(33) ). Moreover, since the reaction coefficient R is usually small enough it follows that (33(33) $$\begin{array}{c}\hfill {\displaystyle e^{-RT}{P}_1^i\le e^{-R{T}^0}{P}_1^i\le \mathcal{A}({\mathit{\omega }}_n){\int }_0^T{\mathit{\lambda }}_n(t)\mathrm{d}t\le P_1^i.}\end{array}$$(33) ) provides an approximation of the total amount discharged by the unknown source ${\mathit{\lambda }}_n{\mathit{\chi }}_{{\mathit{\omega }}_n}$ occurring in ${\mathrm{\Omega }}_i$ without having to identify the two elements ${\mathit{\lambda }}_n$ and ${\mathit{\omega }}_n$. That leads to know how interesting is the source occurring in ${\mathrm{\Omega }}_i\subset \mathrm{\Omega }$ and thus, to decide whether to go further with the identification or not. In the sequel, we focus on identifying the two unknown elements ${\mathit{\lambda }}_n$ and ${\mathit{\omega }}_n$ defining a detected source ${\mathit{\lambda }}_n{\mathit{\chi }}_{{\mathit{\omega }}_n}$ occurring in ${\mathrm{\Omega }}_i\subset \mathrm{\Omega }$, i.e. ${\mathit{\omega }}_n\subset {\mathrm{\Omega }}_i$ where $i\in \{1,\cdots ,N_{max}\}$. To this end, we prove the following result:

Proposition 4.1:

Let ${\mathit{\lambda }}_n{\mathit{\chi }}_{{\mathit{\omega }}_n}$ be a detected source occurring in ${\mathrm{\Omega }}_i\subset \mathrm{\Omega }$ and B be the bounded domain of ${\mathbb{R}}^2$ geometrically centred at the origin such that ${\mathit{\omega }}_n=G_n+B$. The coefficients $P_1^i$, $P_{e^{\mathit{\psi }}}^i$, $P_{{\mathit{\psi }}^{\perp }}^i$ in (32(32) $$\begin{array}{cc}\hfill P_1^i& {\displaystyle =e^{RT}{\int }_{{\mathrm{\Omega }}_i}u(x,T)\mathrm{d}x+{\int }_{({\mathrm{\Gamma }}_{i-1}\cup {\mathrm{\Gamma }}_i)\times (0,T)}{e}^{Rt}(uV-D\mathrm{\nabla }u)·\mathit{\nu }\mathrm{d}x\mathrm{d}t}\hfill \\ \hfill & {\displaystyle +{\int }_{{\mathrm{\Gamma }}_L^i\times (0,T)}{e}^{Rt}uV·\mathit{\nu }\mathrm{d}x\mathrm{d}t,}\hfill \\ \hfill P_{e^{\mathit{\psi }}}^i& {\displaystyle =e^{RT}{\int }_{{\mathrm{\Omega }}_i}{e}^{\mathit{\psi }(x)}u(x,T)\mathrm{d}x-{\int }_{({\mathrm{\Gamma }}_{i-1}\cup {\mathrm{\Gamma }}_i)\times (0,T)}{e}^{\mathit{\psi }+Rt}D\mathrm{\nabla }u·\mathit{\nu }\mathrm{d}x\mathrm{d}t,}\hfill \\ \hfill P_{{\mathit{\psi }}^{\perp }}^i& {\displaystyle =e^{RT}{\int }_{{\mathrm{\Omega }}_i}{\mathit{\psi }}^{\perp }(x)u(x,T)\mathrm{d}x}\hfill \\ \hfill & {\displaystyle +{\int }_{({\mathrm{\Gamma }}_{i-1}\cup {\mathrm{\Gamma }}_i)\times (0,T)}{e}^{Rt}(u[{\mathit{\psi }}^{\perp }V-D{V}^{\perp }]-{\mathit{\psi }}^{\perp }D\mathrm{\nabla }u)·\mathit{\nu }\mathrm{d}x\mathrm{d}t}\hfill \\ \hfill & {\displaystyle +{\int }_{{\mathrm{\Gamma }}_L^i\times (0,T)}{e}^{Rt}u[{\mathit{\psi }}^{\perp }V-D{V}^{\perp }]·\mathit{\nu }\mathrm{d}x\mathrm{d}t.}\hfill \end{array}$$(32) ) and the function $Q^i$ defined for all $\mathit{\tau }\in (0,T)$ by(34) $$\begin{array}{cc}\hfill Q^i(\mathit{\tau })& {\displaystyle ={\int }_{({\mathrm{\Gamma }}_{i-1}\cup {\mathrm{\Gamma }}_i)\times (0,\mathit{\tau })}(u(x,t)[D\mathrm{\nabla }v(x,\mathit{\tau }-t)+v(x,\mathit{\tau }-t)V]}\hfill \\ \hfill & -v(x,\mathit{\tau }-t)D\mathrm{\nabla }u(x,t))·\mathit{\nu }\mathrm{d}x\mathrm{d}t,\hfill \end{array}$$(34)

where v is the solution of the problem (23(23) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathit{\partial }}_{t}v-\mathrm{d}iv(D\mathrm{\nabla }v)-V·\mathrm{\nabla }v+Rv=0\text{in}\mathrm{\Omega }\times (0,T)\hfill \\ v(·,0)=0\text{in}\mathrm{\Omega }\hfill \\ v={\mathit{\zeta }}_{in}\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ (D\mathrm{\nabla }v+vV)·\mathit{\nu }=0\text{on}{\mathrm{\Gamma }}_L\times (0,T)\hfill \\ (D\mathrm{\nabla }v+vV)·\mathit{\nu }={\mathit{\zeta }}_{out}\text{on}{\mathrm{\Gamma }}_{out}\times (0,T)\hfill \end{array}\right.\end{array}$$(23) )–(24(24) $$\begin{array}{c}\hfill {\displaystyle \text{such that}{\int }_{\mathit{\omega }}v(x,·)\mathrm{d}x\ne 0\text{a.e. in}(0,T)}\end{array}$$(24) ) with $\mathit{\omega }={\mathit{\omega }}_n$, determine uniquely the two unknown elements ${\mathit{\lambda }}_n$ and the geometric centre $G_n$ of ${\mathit{\omega }}_n$ as follows:(35) $$\begin{array}{cc}\hfill {\mathrm{\Psi }}_i(G_n)& =\left(\begin{array}{c}{\displaystyle \frac{P_{e^{\mathit{\psi }}}^i}{P_1^i}}\\ {\displaystyle \frac{P_{{\mathit{\psi }}^{\perp }}^i}{P_1^i}}\end{array}\right)\text{and}\hfill \\ \hfill & {\displaystyle {\int }_0^{\mathit{\tau }}{\mathit{\lambda }}_n(t)({\int }_{{\mathit{\omega }}_n}v(x,\mathit{\tau }-t)\mathrm{d}x)\mathrm{d}t=Q^i(\mathit{\tau }),\forall \mathit{\tau }\in (0,T),}\hfill \end{array}$$(35)

where ${\mathrm{\Psi }}_i$ is the injective function introduced in (17(17) $$\begin{array}{c}\hfill {\mathrm{\Psi }}_i(G)=\left(\begin{array}{c}{\displaystyle \frac{1}{\mathcal{A}({\mathit{\omega }}_G)}{\int }_{{\mathit{\omega }}_G}{e}^{\mathit{\psi }(x)}\mathrm{d}x}\\ {\displaystyle \frac{1}{\mathcal{A}({\mathit{\omega }}_G)}{\int }_{{\mathit{\omega }}_G}{\mathit{\psi }}^{\perp }(x)\mathrm{d}x}\end{array}\right)\end{array}$$(17) ).

ProofLet $i\in \{1,\cdots ,N_{max}\}$ be such that $P_1^i\ne 0$ which implies that there is a source ${\mathit{\lambda }}_n{\mathit{\chi }}_{{\mathit{\omega }}_n}$ occurring in ${\mathrm{\Omega }}_i\subset \mathrm{\Omega }$. Then, by dividing in (31(31) $$\begin{array}{c}\hfill {\overline{\mathit{\lambda }}}_n\mathcal{A}({\mathit{\omega }}_n)=P_1^i,{\overline{\mathit{\lambda }}}_n{\int }_{{\mathit{\omega }}_n}{e}^{\mathit{\psi }(x)}\mathrm{d}x=P_{e^{\mathit{\psi }}}^i\text{and}{\overline{\mathit{\lambda }}}_n{\int }_{{\mathit{\omega }}_n}{\mathit{\psi }}^{\perp }(x)\mathrm{d}x=P_{{\mathit{\psi }}^{\perp }}^i,\end{array}$$(31) ) the last two equations by the first one, it follows from Lemma 2.2 that the geometric centre $G_n$ of the unknown source spatial support ${\overline{\mathit{\omega }}}_n$ yields the unique point of ${\mathrm{\Omega }}_i$ subject to:(36) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \frac{1}{\mathcal{A}({\mathit{\omega }}_n)}{\int }_{{\mathit{\omega }}_n}{e}^{\mathit{\psi }(x)}\mathrm{d}x=\frac{P_{e^{\mathit{\psi }}}^i}{P_1^i}}\hfill \\ {\displaystyle \frac{1}{\mathcal{A}({\mathit{\omega }}_n)}{\int }_{{\mathit{\omega }}_n}{\mathit{\psi }}^{\perp }(x)\mathrm{d}x=\frac{P_{{\mathit{\psi }}^{\perp }}^i}{P_1^i}}\hfill \end{array}\right.\iff {\mathrm{\Psi }}_i(G_n)=\left(\begin{array}{c}{\displaystyle \frac{P_{e^{\mathit{\psi }}}^i}{P_1^i}}\\ {\displaystyle \frac{P_{{\mathit{\psi }}^{\perp }}^i}{P_1^i}}\end{array}\right).\end{array}$$(36)

The uniqueness of the point $G_n\in {\mathrm{\Omega }}_i$ that solves (36(36) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \frac{1}{\mathcal{A}({\mathit{\omega }}_n)}{\int }_{{\mathit{\omega }}_n}{e}^{\mathit{\psi }(x)}\mathrm{d}x=\frac{P_{e^{\mathit{\psi }}}^i}{P_1^i}}\hfill \\ {\displaystyle \frac{1}{\mathcal{A}({\mathit{\omega }}_n)}{\int }_{{\mathit{\omega }}_n}{\mathit{\psi }}^{\perp }(x)\mathrm{d}x=\frac{P_{{\mathit{\psi }}^{\perp }}^i}{P_1^i}}\hfill \end{array}\right.\iff {\mathrm{\Psi }}_i(G_n)=\left(\begin{array}{c}{\displaystyle \frac{P_{e^{\mathit{\psi }}}^i}{P_1^i}}\\ {\displaystyle \frac{P_{{\mathit{\psi }}^{\perp }}^i}{P_1^i}}\end{array}\right).\end{array}$$(36) ) is due to the injectivity of the function ${\mathrm{\Psi }}_i$ introduced in (17(17) $$\begin{array}{c}\hfill {\mathrm{\Psi }}_i(G)=\left(\begin{array}{c}{\displaystyle \frac{1}{\mathcal{A}({\mathit{\omega }}_G)}{\int }_{{\mathit{\omega }}_G}{e}^{\mathit{\psi }(x)}\mathrm{d}x}\\ {\displaystyle \frac{1}{\mathcal{A}({\mathit{\omega }}_G)}{\int }_{{\mathit{\omega }}_G}{\mathit{\psi }}^{\perp }(x)\mathrm{d}x}\end{array}\right)\end{array}$$(17) ). Let ${\mathit{\zeta }}_{in}$ and ${\mathit{\zeta }}_{out}$ be such that the solution v of the system (23(23) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathit{\partial }}_{t}v-\mathrm{d}iv(D\mathrm{\nabla }v)-V·\mathrm{\nabla }v+Rv=0\text{in}\mathrm{\Omega }\times (0,T)\hfill \\ v(·,0)=0\text{in}\mathrm{\Omega }\hfill \\ v={\mathit{\zeta }}_{in}\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ (D\mathrm{\nabla }v+vV)·\mathit{\nu }=0\text{on}{\mathrm{\Gamma }}_L\times (0,T)\hfill \\ (D\mathrm{\nabla }v+vV)·\mathit{\nu }={\mathit{\zeta }}_{out}\text{on}{\mathrm{\Gamma }}_{out}\times (0,T)\hfill \end{array}\right.\end{array}$$(23) ) yields the assertion (24(24) $$\begin{array}{c}\hfill {\displaystyle \text{such that}{\int }_{\mathit{\omega }}v(x,·)\mathrm{d}x\ne 0\text{a.e. in}(0,T)}\end{array}$$(24) ) for $\mathit{\omega }={\mathit{\omega }}_n$, i.e. ${\int }_{{\mathit{\omega }}_n}v(x,·)\mathrm{d}x\ne 0$ a.e. in (0, T). Thus, given $\mathit{\tau }\in (0,T)$ the variable $v_{\mathit{\tau }}(·,t)=v(·,\mathit{\tau }-t)$ solves the following system:(37) $$\begin{array}{c}\hfill \left\{\begin{array}{c}-{\mathit{\partial }}_t{v}_{\mathit{\tau }}-\mathrm{d}iv(D\mathrm{\nabla }{v}_{\mathit{\tau }})-V·\mathrm{\nabla }{v}_{\mathit{\tau }}+R{v}_{\mathit{\tau }}=0\text{in}\mathrm{\Omega }\times (0,\mathit{\tau })\hfill \\ v_{\mathit{\tau }}(·,\mathit{\tau })=0\text{in}\mathrm{\Omega }\hfill \\ v_{\mathit{\tau }}(·,t)={\mathit{\zeta }}_{in}(·,\mathit{\tau }-t)\text{on}{\mathrm{\Gamma }}_{in}\times (0,\mathit{\tau })\hfill \\ (D\mathrm{\nabla }{v}_{\mathit{\tau }}+v_{\mathit{\tau }}(·,t)V)·\mathit{\nu }=0\text{on}{\mathrm{\Gamma }}_L\times (0,\mathit{\tau })\hfill \\ (D\mathrm{\nabla }{v}_{\mathit{\tau }}(·,t)+v_{\mathit{\tau }}(·,t)V)·\mathit{\nu }={\mathit{\zeta }}_{out}(·,\mathit{\tau }-t)\text{on}{\mathrm{\Gamma }}_{out}\times (0,\mathit{\tau })\hfill \end{array}\right.\end{array}$$(37)

Hence, multiplying the Equations (1(1) $$\begin{array}{c}\hfill L[u](x,t)=F(x,t)\text{in}\mathrm{\Omega }\times (0,T),\end{array}$$(1) )–(2(2) $$\begin{array}{c}\hfill L[u](x,t):={\mathit{\partial }}_{t}u(x,t)-\mathrm{d}iv(D\mathrm{\nabla }u(x,t))+V·\mathrm{\nabla }u(x,t)+Ru(x,t),\end{array}$$(2) ) by the variable $v_{\mathit{\tau }}$ and integrating by parts on ${\mathrm{\Omega }}_i\times (0,\mathit{\tau })$ using Green’s formula gives(38) $$\begin{array}{c}\hfill {\displaystyle {\int }_0^{\mathit{\tau }}{\mathit{\lambda }}_n(t)({\int }_{{\mathit{\omega }}_n}v(x,\mathit{\tau }-t)\mathrm{d}x)\mathrm{d}t=Q^i(\mathit{\tau }),\forall \mathit{\tau }\in (0,T),}\end{array}$$(38)

where $Q^i$ is the function introduced in (34(34) $$\begin{array}{cc}\hfill Q^i(\mathit{\tau })& {\displaystyle ={\int }_{({\mathrm{\Gamma }}_{i-1}\cup {\mathrm{\Gamma }}_i)\times (0,\mathit{\tau })}(u(x,t)[D\mathrm{\nabla }v(x,\mathit{\tau }-t)+v(x,\mathit{\tau }-t)V]}\hfill \\ \hfill & -v(x,\mathit{\tau }-t)D\mathrm{\nabla }u(x,t))·\mathit{\nu }\mathrm{d}x\mathrm{d}t,\hfill \end{array}$$(34) ). The uniqueness of ${\mathit{\lambda }}_n\in L^2(0,T)$ that solves (38(38) $$\begin{array}{c}\hfill {\displaystyle {\int }_0^{\mathit{\tau }}{\mathit{\lambda }}_n(t)({\int }_{{\mathit{\omega }}_n}v(x,\mathit{\tau }-t)\mathrm{d}x)\mathrm{d}t=Q^i(\mathit{\tau }),\forall \mathit{\tau }\in (0,T),}\end{array}$$(38) ) is a consequence of Titchmarsh’s theorem on convolution of $L^1$ functions [26] since it holds ${\int }_{{\mathit{\omega }}_n}v(x,·)\mathrm{d}x\ne 0$ a.e. in (0, T).

4.2. Properties characterizing the source spatial support ${\overline{\mathit{\omega }}}_n\subset {\mathrm{\Omega }}_i$

We determine four properties $(P_{1,\cdots ,4})$ characterizing the unknown spatial support ${\overline{\mathit{\omega }}}_n$ defining the detected source ${\mathit{\lambda }}_n{\mathit{\chi }}_{{\mathit{\omega }}_n}$ occurring in ${\mathrm{\Omega }}_i$. We start by determining an approximation of its sought geometric centre $G_n$ that solves the first equation in (35(35) $$\begin{array}{cc}\hfill {\mathrm{\Psi }}_i(G_n)& =\left(\begin{array}{c}{\displaystyle \frac{P_{e^{\mathit{\psi }}}^i}{P_1^i}}\\ {\displaystyle \frac{P_{{\mathit{\psi }}^{\perp }}^i}{P_1^i}}\end{array}\right)\text{and}\hfill \\ \hfill & {\displaystyle {\int }_0^{\mathit{\tau }}{\mathit{\lambda }}_n(t)({\int }_{{\mathit{\omega }}_n}v(x,\mathit{\tau }-t)\mathrm{d}x)\mathrm{d}t=Q^i(\mathit{\tau }),\forall \mathit{\tau }\in (0,T),}\hfill \end{array}$$(35) ). To this end, we apply in ${\mathit{\omega }}_n$ the Taylor formula to the function $e^{\mathit{\psi }(x)}$ at $x_0=G_n$, i.e.(39) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle e^{\mathit{\psi }(x)}=e^{\mathit{\psi }(G_n)}(1+⟨\mathrm{\nabla }\mathit{\psi }(G_n),x-G_n⟩+\frac{1}{2}(⟨\mathrm{\nabla }\mathit{\psi }(G_n),x-G_n⟩{)}^2{e}^{\mathit{\psi }(\mathit{\theta }(x-G_n))})}\hfill \\ {\displaystyle =e^{\mathit{\psi }(G_n)}(1+\mathit{\psi }(x-G_n)+\frac{1}{2}{\mathit{\psi }}^2(x-G_n)e^{\mathit{\psi }(\mathit{\theta }(x-G_n))})}\hfill \\ \approx e^{\mathit{\psi }(G_n)}(1+\mathit{\psi }(x-G_n)),\hfill \end{array}\end{array}$$(39)

where $\mathit{\theta }\in (0,1)$ and $⟨.,.⟩$ denotes the inner product in ${\mathbb{R}}^2$. Furthermore, from (5(5) $$\begin{array}{c}\hfill \begin{array}{c}\mathit{\psi }(x)=\mathit{\alpha }{x}_1+\mathit{\beta }{x}_2\text{where:}\mathit{\alpha }=\frac{D_0{V}_2-D_2{V}_1}{D_1{D}_2-D_0^2}\text{and}\mathit{\beta }=\frac{D_0{V}_1-D_1{V}_2}{D_1{D}_2-D_0^2}\hfill \\ {\mathit{\psi }}^{\perp }(x)=V_2{x}_1-V_1{x}_2\hfill \end{array}\end{array}$$(5) ) and (10(10) $$\begin{array}{c}\hfill {\displaystyle x_1^{G_n}=\frac{1}{\mathcal{A}({\mathit{\omega }}_n)}{\int }_{{\mathit{\omega }}_n}{x}_1\mathrm{d}x\text{and}{x}_2^{G_n}=\frac{1}{\mathcal{A}({\mathit{\omega }}_n)}{\int }_{{\mathit{\omega }}_n}{x}_2\mathrm{d}x,}\end{array}$$(10) ) it follows that ${\int }_{{\mathit{\omega }}_n}\mathit{\psi }(x-G_n)\mathrm{d}x=0$. Thus, by integrating both sides of the approximation in (39(39) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle e^{\mathit{\psi }(x)}=e^{\mathit{\psi }(G_n)}(1+⟨\mathrm{\nabla }\mathit{\psi }(G_n),x-G_n⟩+\frac{1}{2}(⟨\mathrm{\nabla }\mathit{\psi }(G_n),x-G_n⟩{)}^2{e}^{\mathit{\psi }(\mathit{\theta }(x-G_n))})}\hfill \\ {\displaystyle =e^{\mathit{\psi }(G_n)}(1+\mathit{\psi }(x-G_n)+\frac{1}{2}{\mathit{\psi }}^2(x-G_n)e^{\mathit{\psi }(\mathit{\theta }(x-G_n))})}\hfill \\ \approx e^{\mathit{\psi }(G_n)}(1+\mathit{\psi }(x-G_n)),\hfill \end{array}\end{array}$$(39) ) over ${\mathit{\omega }}_n$ we obtain(40) $$\begin{array}{c}\hfill {\displaystyle {\int }_{{\mathit{\omega }}_n}{e}^{\mathit{\psi }(x)}\mathrm{d}x\approx \mathcal{A}({\mathit{\omega }}_n)e^{\mathit{\psi }(G_n)}.}\end{array}$$(40)

Therefore, from using the approximation (40(40) $$\begin{array}{c}\hfill {\displaystyle {\int }_{{\mathit{\omega }}_n}{e}^{\mathit{\psi }(x)}\mathrm{d}x\approx \mathcal{A}({\mathit{\omega }}_n)e^{\mathit{\psi }(G_n)}.}\end{array}$$(40) ) as an equality to replace the left-hand side in the first equation of the system (36(36) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \frac{1}{\mathcal{A}({\mathit{\omega }}_n)}{\int }_{{\mathit{\omega }}_n}{e}^{\mathit{\psi }(x)}\mathrm{d}x=\frac{P_{e^{\mathit{\psi }}}^i}{P_1^i}}\hfill \\ {\displaystyle \frac{1}{\mathcal{A}({\mathit{\omega }}_n)}{\int }_{{\mathit{\omega }}_n}{\mathit{\psi }}^{\perp }(x)\mathrm{d}x=\frac{P_{{\mathit{\psi }}^{\perp }}^i}{P_1^i}}\hfill \end{array}\right.\iff {\mathrm{\Psi }}_i(G_n)=\left(\begin{array}{c}{\displaystyle \frac{P_{e^{\mathit{\psi }}}^i}{P_1^i}}\\ {\displaystyle \frac{P_{{\mathit{\psi }}^{\perp }}^i}{P_1^i}}\end{array}\right).\end{array}$$(36) ) it follows that the sought geometric centre $G_n$ of the unknown source spatial support ${\overline{\mathit{\omega }}}_n\subset {\mathrm{\Omega }}_i$ satisfies(41) $$\begin{array}{c}\hfill \left\{\begin{array}{c}\mathit{\psi }(G_n)=\mathrm{l}n\left({\displaystyle \frac{P_{e^{\mathit{\psi }}}^i}{P_1^i}}\right)\hfill \\ {\displaystyle {\mathit{\psi }}^{\perp }(G_n)=\frac{P_{{\mathit{\psi }}^{\perp }}^i}{P_1^i}}\hfill \end{array}\right.\iff \left(\begin{array}{ccc}\mathit{\alpha }& \mathit{\beta }& \\ V_2& -V_1& \\ \end{array}\right)\left(\begin{array}{c}{x}_1^{G_n}\\ x_2^{G_n}\end{array}\right)=\left(\begin{array}{c}\mathrm{l}n\left({\displaystyle \frac{P_{e^{\mathit{\psi }}}^i}{P_1^i}}\right)\\ {\displaystyle \frac{P_{{\mathit{\psi }}^{\perp }}^i}{P_1^i}}\\ \end{array}\right).\end{array}$$(41)

The second equation of (41(41) $$\begin{array}{c}\hfill \left\{\begin{array}{c}\mathit{\psi }(G_n)=\mathrm{l}n\left({\displaystyle \frac{P_{e^{\mathit{\psi }}}^i}{P_1^i}}\right)\hfill \\ {\displaystyle {\mathit{\psi }}^{\perp }(G_n)=\frac{P_{{\mathit{\psi }}^{\perp }}^i}{P_1^i}}\hfill \end{array}\right.\iff \left(\begin{array}{ccc}\mathit{\alpha }& \mathit{\beta }& \\ V_2& -V_1& \\ \end{array}\right)\left(\begin{array}{c}{x}_1^{G_n}\\ x_2^{G_n}\end{array}\right)=\left(\begin{array}{c}\mathrm{l}n\left({\displaystyle \frac{P_{e^{\mathit{\psi }}}^i}{P_1^i}}\right)\\ {\displaystyle \frac{P_{{\mathit{\psi }}^{\perp }}^i}{P_1^i}}\\ \end{array}\right).\end{array}$$(41) ) is obtained as in (20(20) $$\begin{array}{cc}& {\displaystyle \frac{1}{\mathcal{A}({\mathit{\omega }}_{G^{(k)}})}{\int }_{{\mathit{\omega }}_{G^{(k)}}}{\mathit{\psi }}^{\perp }(x)\mathrm{d}x=\frac{V_2}{\mathcal{A}({\mathit{\omega }}_{G^{(k)}})}{\int }_{{\mathit{\omega }}_{G^{(k)}}}{x}_1\mathrm{d}x-\frac{V_1}{\mathcal{A}({\mathit{\omega }}_{G^{(k)}})}}\hfill \\ \hfill & {\displaystyle {\int }_{{\mathit{\omega }}_{G^{(k)}}}{x}_2\mathrm{d}x={\mathit{\psi }}^{\perp }(G^{(k)}),}\hfill \end{array}$$(20) ). Moreover, the determinant of the $2\times 2$ matrix involved in (41(41) $$\begin{array}{c}\hfill \left\{\begin{array}{c}\mathit{\psi }(G_n)=\mathrm{l}n\left({\displaystyle \frac{P_{e^{\mathit{\psi }}}^i}{P_1^i}}\right)\hfill \\ {\displaystyle {\mathit{\psi }}^{\perp }(G_n)=\frac{P_{{\mathit{\psi }}^{\perp }}^i}{P_1^i}}\hfill \end{array}\right.\iff \left(\begin{array}{ccc}\mathit{\alpha }& \mathit{\beta }& \\ V_2& -V_1& \\ \end{array}\right)\left(\begin{array}{c}{x}_1^{G_n}\\ x_2^{G_n}\end{array}\right)=\left(\begin{array}{c}\mathrm{l}n\left({\displaystyle \frac{P_{e^{\mathit{\psi }}}^i}{P_1^i}}\right)\\ {\displaystyle \frac{P_{{\mathit{\psi }}^{\perp }}^i}{P_1^i}}\\ \end{array}\right).\end{array}$$(41) ) is equal to: $-(\mathit{\alpha }{V}_1+\mathit{\beta }{V}_2)=V^{\top }{D}^{-1}V>0$. Hence, from solving the linear system in (41(41) $$\begin{array}{c}\hfill \left\{\begin{array}{c}\mathit{\psi }(G_n)=\mathrm{l}n\left({\displaystyle \frac{P_{e^{\mathit{\psi }}}^i}{P_1^i}}\right)\hfill \\ {\displaystyle {\mathit{\psi }}^{\perp }(G_n)=\frac{P_{{\mathit{\psi }}^{\perp }}^i}{P_1^i}}\hfill \end{array}\right.\iff \left(\begin{array}{ccc}\mathit{\alpha }& \mathit{\beta }& \\ V_2& -V_1& \\ \end{array}\right)\left(\begin{array}{c}{x}_1^{G_n}\\ x_2^{G_n}\end{array}\right)=\left(\begin{array}{c}\mathrm{l}n\left({\displaystyle \frac{P_{e^{\mathit{\psi }}}^i}{P_1^i}}\right)\\ {\displaystyle \frac{P_{{\mathit{\psi }}^{\perp }}^i}{P_1^i}}\\ \end{array}\right).\end{array}$$(41) ) it follows that the two unknown coordinates defining the geometric centre $G_n=(x_1^{G_n},x_2^{G_n})$ of ${\mathit{\omega }}_n\subset {\mathrm{\Omega }}_i$ are given by(42) $$\begin{array}{c}\hfill (P_1)\left\{\begin{array}{c}{\displaystyle x_1^{G_n}=-\frac{V_1}{V{D}^{-1}V}\mathrm{l}n\left({\displaystyle \frac{P_{e^{\mathit{\psi }}}^i}{P_1^i}}\right)-\frac{\mathit{\beta }}{V{D}^{-1}V}\frac{P_{{\mathit{\psi }}^{\perp }}^i}{P_1^i},}\hfill \\ {\displaystyle x_2^{G_n}=-\frac{V_2}{V{D}^{-1}V}\mathrm{l}n\left({\displaystyle \frac{P_{e^{\mathit{\psi }}}^i}{P_1^i}}\right)+\frac{\mathit{\alpha }}{V{D}^{-1}V}\frac{P_{{\mathit{\psi }}^{\perp }}^i}{P_1^i}.}\hfill \end{array}\right.\end{array}$$(42)

Besides, in the remainder given $\mathit{\eta }>0$ we denote by $S(G_n,\mathit{\eta })$ the square of side length $\mathit{\eta }$ centred at the same geometric centre $G_n$ of ${\mathit{\omega }}_n$ localized in (42(42) $$\begin{array}{c}\hfill (P_1)\left\{\begin{array}{c}{\displaystyle x_1^{G_n}=-\frac{V_1}{V{D}^{-1}V}\mathrm{l}n\left({\displaystyle \frac{P_{e^{\mathit{\psi }}}^i}{P_1^i}}\right)-\frac{\mathit{\beta }}{V{D}^{-1}V}\frac{P_{{\mathit{\psi }}^{\perp }}^i}{P_1^i},}\hfill \\ {\displaystyle x_2^{G_n}=-\frac{V_2}{V{D}^{-1}V}\mathrm{l}n\left({\displaystyle \frac{P_{e^{\mathit{\psi }}}^i}{P_1^i}}\right)+\frac{\mathit{\alpha }}{V{D}^{-1}V}\frac{P_{{\mathit{\psi }}^{\perp }}^i}{P_1^i}.}\hfill \end{array}\right.\end{array}$$(42) ). Let ${\mathit{\eta }}^i$ be the biggest positive real number that yields $S(G_n,{\mathit{\eta }}^i)\subseteq {\mathrm{\Omega }}_i$. Then, multiplying the Equations (1(1) $$\begin{array}{c}\hfill L[u](x,t)=F(x,t)\text{in}\mathrm{\Omega }\times (0,T),\end{array}$$(1) )–(2(2) $$\begin{array}{c}\hfill L[u](x,t):={\mathit{\partial }}_{t}u(x,t)-\mathrm{d}iv(D\mathrm{\nabla }u(x,t))+V·\mathrm{\nabla }u(x,t)+Ru(x,t),\end{array}$$(2) ) by the function $z_{\mathit{\eta }}(x,t)=e^{Rt}{\mathit{\chi }}_{S(G_n,\mathit{\eta })}(x)$ and integrating by parts on ${\mathrm{\Omega }}_i\times (0,T)$ gives(43) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\overline{\mathit{\lambda }}}_n=\frac{g(\mathit{\eta })}{\mathcal{A}({\mathit{\omega }}_n\cap S(G_n,\mathit{\eta }))},\forall \mathit{\eta }\in (0,{\mathit{\eta }}^i],}\hfill \\ {\displaystyle \text{where:}g(\mathit{\eta })=e^{RT}{\int }_{S(G_n,\mathit{\eta })}u(x,T)\mathrm{d}x+{\int }_{\mathit{\partial }S\times (0,T)}{e}^{Rt}(Vu-D\mathrm{\nabla }u)·\mathit{\nu }\mathrm{d}x\mathrm{d}t.}\hfill \end{array}\end{array}$$(43)

In view of (43(43) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\overline{\mathit{\lambda }}}_n=\frac{g(\mathit{\eta })}{\mathcal{A}({\mathit{\omega }}_n\cap S(G_n,\mathit{\eta }))},\forall \mathit{\eta }\in (0,{\mathit{\eta }}^i],}\hfill \\ {\displaystyle \text{where:}g(\mathit{\eta })=e^{RT}{\int }_{S(G_n,\mathit{\eta })}u(x,T)\mathrm{d}x+{\int }_{\mathit{\partial }S\times (0,T)}{e}^{Rt}(Vu-D\mathrm{\nabla }u)·\mathit{\nu }\mathrm{d}x\mathrm{d}t.}\hfill \end{array}\end{array}$$(43) ), we introduce the two functions $g_{incl}$ and $g_{cont}$ defined in $(0,{\mathit{\eta }}^i]$ by(44) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle g_{incl}(\mathit{\eta })=\frac{g(\mathit{\eta })}{\mathcal{A}(S(G_n,\mathit{\eta }))}\text{and}{g}_{cont}(\mathit{\eta })=g(\mathit{\eta }).}\hfill \end{array}\end{array}$$(44)

Thus, (43(43) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\overline{\mathit{\lambda }}}_n=\frac{g(\mathit{\eta })}{\mathcal{A}({\mathit{\omega }}_n\cap S(G_n,\mathit{\eta }))},\forall \mathit{\eta }\in (0,{\mathit{\eta }}^i],}\hfill \\ {\displaystyle \text{where:}g(\mathit{\eta })=e^{RT}{\int }_{S(G_n,\mathit{\eta })}u(x,T)\mathrm{d}x+{\int }_{\mathit{\partial }S\times (0,T)}{e}^{Rt}(Vu-D\mathrm{\nabla }u)·\mathit{\nu }\mathrm{d}x\mathrm{d}t.}\hfill \end{array}\end{array}$$(43) ) and (44(44) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle g_{incl}(\mathit{\eta })=\frac{g(\mathit{\eta })}{\mathcal{A}(S(G_n,\mathit{\eta }))}\text{and}{g}_{cont}(\mathit{\eta })=g(\mathit{\eta }).}\hfill \end{array}\end{array}$$(44) ) lead to determine the following two properties characterizing the unknown source spatial support ${\overline{\mathit{\omega }}}_n\subset {\mathrm{\Omega }}_i$:

$(P_2):$Biggest square centred at $G_n$ and included in ${\mathit{\omega }}_n$: For $\mathit{\eta }=\mathit{\epsilon }>0$ to $\mathit{\eta }={\mathit{\eta }}^i$, all $\mathit{\eta }$ such that $S(G_n,\mathit{\eta })\subseteq {\mathit{\omega }}_n$, (which implies $\mathcal{A}({\mathit{\omega }}_n\cap S(G_n,\mathit{\eta }))=\mathcal{A}(S(G_n,\mathit{\eta }))$), yields, in view of (43(43) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\overline{\mathit{\lambda }}}_n=\frac{g(\mathit{\eta })}{\mathcal{A}({\mathit{\omega }}_n\cap S(G_n,\mathit{\eta }))},\forall \mathit{\eta }\in (0,{\mathit{\eta }}^i],}\hfill \\ {\displaystyle \text{where:}g(\mathit{\eta })=e^{RT}{\int }_{S(G_n,\mathit{\eta })}u(x,T)\mathrm{d}x+{\int }_{\mathit{\partial }S\times (0,T)}{e}^{Rt}(Vu-D\mathrm{\nabla }u)·\mathit{\nu }\mathrm{d}x\mathrm{d}t.}\hfill \end{array}\end{array}$$(43) )–(44(44) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle g_{incl}(\mathit{\eta })=\frac{g(\mathit{\eta })}{\mathcal{A}(S(G_n,\mathit{\eta }))}\text{and}{g}_{cont}(\mathit{\eta })=g(\mathit{\eta }).}\hfill \end{array}\end{array}$$(44) ), $g_{incl}(\mathit{\eta })={\overline{\mathit{\lambda }}}_n$. However, as soon as $\mathit{\eta }$ is such that $S(G_n,\mathit{\eta })⊈{\mathit{\omega }}_n$ it follows from (43(43) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\overline{\mathit{\lambda }}}_n=\frac{g(\mathit{\eta })}{\mathcal{A}({\mathit{\omega }}_n\cap S(G_n,\mathit{\eta }))},\forall \mathit{\eta }\in (0,{\mathit{\eta }}^i],}\hfill \\ {\displaystyle \text{where:}g(\mathit{\eta })=e^{RT}{\int }_{S(G_n,\mathit{\eta })}u(x,T)\mathrm{d}x+{\int }_{\mathit{\partial }S\times (0,T)}{e}^{Rt}(Vu-D\mathrm{\nabla }u)·\mathit{\nu }\mathrm{d}x\mathrm{d}t.}\hfill \end{array}\end{array}$$(43) )–(44(44) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle g_{incl}(\mathit{\eta })=\frac{g(\mathit{\eta })}{\mathcal{A}(S(G_n,\mathit{\eta }))}\text{and}{g}_{cont}(\mathit{\eta })=g(\mathit{\eta }).}\hfill \end{array}\end{array}$$(44) ) that $g_{incl}(\mathit{\eta })={\overline{\mathit{\lambda }}}_n\mathcal{A}({\mathit{\omega }}_n\cap S(G_n,\mathit{\eta }))/\mathcal{A}(S(G_n,\mathit{\eta }))$. Therefore, the element ${\mathit{\eta }}_{in}\in (0,{\mathit{\eta }}^i)$ that yields: $g_{incl}(\mathit{\eta })={\overline{\mathit{\lambda }}}_n$ for all $\mathit{\eta }\in (0,{\mathit{\eta }}_{in}]$ and $|g_{incl}(\mathit{\eta })|<|{\overline{\mathit{\lambda }}}_n|$ for all $\mathit{\eta }\in ({\mathit{\eta }}_{in},{\mathit{\eta }}^i]$ corresponds to the side length of the biggest square $S(G_n,{\mathit{\eta }}_{in})\subseteq {\mathit{\omega }}_n$.

$(P_3):$Smallest square centred at $G_n$ and containing ${\mathit{\omega }}_n$: For $\mathit{\eta }={\mathit{\eta }}^i$ to $\mathit{\eta }=\mathit{\epsilon }>0$, all $\mathit{\eta }$ such that ${\mathit{\omega }}_n\subseteq S(G_n,\mathit{\eta })$, (which implies $\mathcal{A}({\mathit{\omega }}_n\cap S(G_n,\mathit{\eta }))=\mathcal{A}({\mathit{\omega }}_n)$), gives, according to (43(43) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\overline{\mathit{\lambda }}}_n=\frac{g(\mathit{\eta })}{\mathcal{A}({\mathit{\omega }}_n\cap S(G_n,\mathit{\eta }))},\forall \mathit{\eta }\in (0,{\mathit{\eta }}^i],}\hfill \\ {\displaystyle \text{where:}g(\mathit{\eta })=e^{RT}{\int }_{S(G_n,\mathit{\eta })}u(x,T)\mathrm{d}x+{\int }_{\mathit{\partial }S\times (0,T)}{e}^{Rt}(Vu-D\mathrm{\nabla }u)·\mathit{\nu }\mathrm{d}x\mathrm{d}t.}\hfill \end{array}\end{array}$$(43) )–(44(44) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle g_{incl}(\mathit{\eta })=\frac{g(\mathit{\eta })}{\mathcal{A}(S(G_n,\mathit{\eta }))}\text{and}{g}_{cont}(\mathit{\eta })=g(\mathit{\eta }).}\hfill \end{array}\end{array}$$(44) ), $g_{cont}(\mathit{\eta })={\overline{\mathit{\lambda }}}_n\mathcal{A}({\mathit{\omega }}_n)$. However, as soon as $\mathit{\eta }$ is such that ${\mathit{\omega }}_n⊈S(G_n,\mathit{\eta })$ it follows from (43(43) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\overline{\mathit{\lambda }}}_n=\frac{g(\mathit{\eta })}{\mathcal{A}({\mathit{\omega }}_n\cap S(G_n,\mathit{\eta }))},\forall \mathit{\eta }\in (0,{\mathit{\eta }}^i],}\hfill \\ {\displaystyle \text{where:}g(\mathit{\eta })=e^{RT}{\int }_{S(G_n,\mathit{\eta })}u(x,T)\mathrm{d}x+{\int }_{\mathit{\partial }S\times (0,T)}{e}^{Rt}(Vu-D\mathrm{\nabla }u)·\mathit{\nu }\mathrm{d}x\mathrm{d}t.}\hfill \end{array}\end{array}$$(43) )–(44(44) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle g_{incl}(\mathit{\eta })=\frac{g(\mathit{\eta })}{\mathcal{A}(S(G_n,\mathit{\eta }))}\text{and}{g}_{cont}(\mathit{\eta })=g(\mathit{\eta }).}\hfill \end{array}\end{array}$$(44) ) that $g_{cont}(\mathit{\eta })={\overline{\mathit{\lambda }}}_n\mathcal{A}({\mathit{\omega }}_n\cap S(G_n,\mathit{\eta }))$. Hence, the element ${\mathit{\eta }}_{out}\in (0,{\mathit{\eta }}^i)$ that yields: $g_{cont}(\mathit{\eta })={\overline{\mathit{\lambda }}}_n\mathcal{A}({\mathit{\omega }}_n)$ for all $\mathit{\eta }\in [{\mathit{\eta }}_{out},{\mathit{\eta }}^i]$ and $|g_{cont}(\mathit{\eta })|<|{\overline{\mathit{\lambda }}}_n|\mathcal{A}({\mathit{\omega }}_n)$ for all $\mathit{\eta }\in (0,{\mathit{\eta }}_{out})$ corresponds to the side length of the smallest square $S(G_n,{\mathit{\eta }}_{out})\supseteq {\mathit{\omega }}_n$.

To determine the biggest ${\mathit{\eta }}_{in}$ and the smallest ${\mathit{\eta }}_{out}$ that yield $S(G_n,{\mathit{\eta }}_{in})\subseteq {\mathit{\omega }}_n\subseteq S(G_n,{\mathit{\eta }}_{out})$, in practice we proceed as follows: (1) From the function $g_{incl}$, we determine the side length ${\mathit{\eta }}_{in}$ as the biggest element of $(0,{\mathit{\eta }}^i)$ after which $g_{incl}$ is not anymore equal to its initial constant value. (2) From the function $g_{cont}$, we determine the side length ${\mathit{\eta }}_{out}$ as the smallest element of $(0,{\mathit{\eta }}^i)$ from which $g_{cont}$ becomes equal to its final constant value. Afterwards, we deduce ${\overline{\mathit{\lambda }}}_n$ and the surface area $\mathcal{A}({\mathit{\omega }}_n)$ of the unknown spatial support ${\overline{\mathit{\omega }}}_n$ as follows:(45) $$\begin{array}{c}\hfill \begin{array}{c}(P_4):\mathcal{A}({\mathit{\omega }}_n)=g_{cont}(\mathit{\eta })/{\overline{\mathit{\lambda }}}_n\text{for}\mathit{\eta }\in [{\mathit{\eta }}_{out},{\mathit{\eta }}^i],\hfill \\ \text{where}{\overline{\mathit{\lambda }}}_n=g_{incl}(\mathit{\eta })\text{for}\mathit{\eta }\in (0,{\mathit{\eta }}_{in}].\hfill \end{array}\end{array}$$(45)

Remark 4.2:

 

(1)

We used squares centred at the localized geometric centre $G_n$ of the unknown spatial support ${\overline{\mathit{\omega }}}_n\subset {\mathrm{\Omega }}_i$ as two reference geometries i.e. we determined the biggest square included in ${\mathit{\omega }}_n$ and the smallest square containing ${\mathit{\omega }}_n$. If rather other reference geometries are desired then, we redefine (43(43) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\overline{\mathit{\lambda }}}_n=\frac{g(\mathit{\eta })}{\mathcal{A}({\mathit{\omega }}_n\cap S(G_n,\mathit{\eta }))},\forall \mathit{\eta }\in (0,{\mathit{\eta }}^i],}\hfill \\ {\displaystyle \text{where:}g(\mathit{\eta })=e^{RT}{\int }_{S(G_n,\mathit{\eta })}u(x,T)\mathrm{d}x+{\int }_{\mathit{\partial }S\times (0,T)}{e}^{Rt}(Vu-D\mathrm{\nabla }u)·\mathit{\nu }\mathrm{d}x\mathrm{d}t.}\hfill \end{array}\end{array}$$(43) ) from replacing the square $S(G_n,\mathit{\eta })$ by the wished geometries. The behaviour of $g_{incl}$ and $g_{cont}$ with respect to the variation of the surface areas defining the new used domains lead to determine from $g_{incl}$ the biggest domain included in ${\mathit{\omega }}_n$ and from $g_{cont}$ the smallest domain containing ${\mathit{\omega }}_n$.

(2)

Let $0<\ell \le L$ be the width and the length of the monitored domain $\mathrm{\Omega }$. The non-dimensional term: $-\mathit{\psi }(\mathcal{L})=\mathcal{L}{D}^{-1}V$ where $\mathcal{L}=(L,\ell )$, is a Peclet like number that represents the ratio of the contributions to mass transport by convection to those by dispersion [27]. If $\mathcal{L}{D}^{-1}V$ is a relatively small number then, since for all $x\in {\mathit{\omega }}_n\subset {\mathrm{\Omega }}_i\subset \mathrm{\Omega }$ we have $\Vert x-G_n{\Vert }_2<<{\Vert \mathcal{L}\Vert }_2$, it makes sense to neglect the second-order term ${\mathit{\psi }}^2(x-G_n)$ against the first order term $\mathit{\psi }(x-G_n)=-(x-G_n)D^{-1}V$ to obtain the approximation in (39(39) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle e^{\mathit{\psi }(x)}=e^{\mathit{\psi }(G_n)}(1+⟨\mathrm{\nabla }\mathit{\psi }(G_n),x-G_n⟩+\frac{1}{2}(⟨\mathrm{\nabla }\mathit{\psi }(G_n),x-G_n⟩{)}^2{e}^{\mathit{\psi }(\mathit{\theta }(x-G_n))})}\hfill \\ {\displaystyle =e^{\mathit{\psi }(G_n)}(1+\mathit{\psi }(x-G_n)+\frac{1}{2}{\mathit{\psi }}^2(x-G_n)e^{\mathit{\psi }(\mathit{\theta }(x-G_n))})}\hfill \\ \approx e^{\mathit{\psi }(G_n)}(1+\mathit{\psi }(x-G_n)),\hfill \end{array}\end{array}$$(39) ).

Nevertheless, the state u in $\mathrm{\Omega }$ is subject to only knowledge of its value and the value of its flux on the interfaces ${\mathrm{\Gamma }}_{i=1,\cdots ,N_{max}}$. Hence, the determination of the total discharged amount in (33(33) $$\begin{array}{c}\hfill {\displaystyle e^{-RT}{P}_1^i\le e^{-R{T}^0}{P}_1^i\le \mathcal{A}({\mathit{\omega }}_n){\int }_0^T{\mathit{\lambda }}_n(t)\mathrm{d}t\le P_1^i.}\end{array}$$(33) ) and the localization from (42(42) $$\begin{array}{c}\hfill (P_1)\left\{\begin{array}{c}{\displaystyle x_1^{G_n}=-\frac{V_1}{V{D}^{-1}V}\mathrm{l}n\left({\displaystyle \frac{P_{e^{\mathit{\psi }}}^i}{P_1^i}}\right)-\frac{\mathit{\beta }}{V{D}^{-1}V}\frac{P_{{\mathit{\psi }}^{\perp }}^i}{P_1^i},}\hfill \\ {\displaystyle x_2^{G_n}=-\frac{V_2}{V{D}^{-1}V}\mathrm{l}n\left({\displaystyle \frac{P_{e^{\mathit{\psi }}}^i}{P_1^i}}\right)+\frac{\mathit{\alpha }}{V{D}^{-1}V}\frac{P_{{\mathit{\psi }}^{\perp }}^i}{P_1^i}.}\hfill \end{array}\right.\end{array}$$(42) ) of the unknown geometric centre $G_n$ defining the source spatial support ${\overline{\mathit{\omega }}}_n\subset {\mathrm{\Omega }}_i$, as well as the unknown elements in (45(45) $$\begin{array}{c}\hfill \begin{array}{c}(P_4):\mathcal{A}({\mathit{\omega }}_n)=g_{cont}(\mathit{\eta })/{\overline{\mathit{\lambda }}}_n\text{for}\mathit{\eta }\in [{\mathit{\eta }}_{out},{\mathit{\eta }}^i],\hfill \\ \text{where}{\overline{\mathit{\lambda }}}_n=g_{incl}(\mathit{\eta })\text{for}\mathit{\eta }\in (0,{\mathit{\eta }}_{in}].\hfill \end{array}\end{array}$$(45) ) are not so far available due to the not given terms $u(·,T)$ involved in (31(31) $$\begin{array}{c}\hfill {\overline{\mathit{\lambda }}}_n\mathcal{A}({\mathit{\omega }}_n)=P_1^i,{\overline{\mathit{\lambda }}}_n{\int }_{{\mathit{\omega }}_n}{e}^{\mathit{\psi }(x)}\mathrm{d}x=P_{e^{\mathit{\psi }}}^i\text{and}{\overline{\mathit{\lambda }}}_n{\int }_{{\mathit{\omega }}_n}{\mathit{\psi }}^{\perp }(x)\mathrm{d}x=P_{{\mathit{\psi }}^{\perp }}^i,\end{array}$$(31) )–(32(32) $$\begin{array}{cc}\hfill P_1^i& {\displaystyle =e^{RT}{\int }_{{\mathrm{\Omega }}_i}u(x,T)\mathrm{d}x+{\int }_{({\mathrm{\Gamma }}_{i-1}\cup {\mathrm{\Gamma }}_i)\times (0,T)}{e}^{Rt}(uV-D\mathrm{\nabla }u)·\mathit{\nu }\mathrm{d}x\mathrm{d}t}\hfill \\ \hfill & {\displaystyle +{\int }_{{\mathrm{\Gamma }}_L^i\times (0,T)}{e}^{Rt}uV·\mathit{\nu }\mathrm{d}x\mathrm{d}t,}\hfill \\ \hfill P_{e^{\mathit{\psi }}}^i& {\displaystyle =e^{RT}{\int }_{{\mathrm{\Omega }}_i}{e}^{\mathit{\psi }(x)}u(x,T)\mathrm{d}x-{\int }_{({\mathrm{\Gamma }}_{i-1}\cup {\mathrm{\Gamma }}_i)\times (0,T)}{e}^{\mathit{\psi }+Rt}D\mathrm{\nabla }u·\mathit{\nu }\mathrm{d}x\mathrm{d}t,}\hfill \\ \hfill P_{{\mathit{\psi }}^{\perp }}^i& {\displaystyle =e^{RT}{\int }_{{\mathrm{\Omega }}_i}{\mathit{\psi }}^{\perp }(x)u(x,T)\mathrm{d}x}\hfill \\ \hfill & {\displaystyle +{\int }_{({\mathrm{\Gamma }}_{i-1}\cup {\mathrm{\Gamma }}_i)\times (0,T)}{e}^{Rt}(u[{\mathit{\psi }}^{\perp }V-D{V}^{\perp }]-{\mathit{\psi }}^{\perp }D\mathrm{\nabla }u)·\mathit{\nu }\mathrm{d}x\mathrm{d}t}\hfill \\ \hfill & {\displaystyle +{\int }_{{\mathrm{\Gamma }}_L^i\times (0,T)}{e}^{Rt}u[{\mathit{\psi }}^{\perp }V-D{V}^{\perp }]·\mathit{\nu }\mathrm{d}x\mathrm{d}t.}\hfill \end{array}$$(32) ) and $(Vu-D\mathrm{\nabla }u)·\mathit{\nu }$ involved in (43(43) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\overline{\mathit{\lambda }}}_n=\frac{g(\mathit{\eta })}{\mathcal{A}({\mathit{\omega }}_n\cap S(G_n,\mathit{\eta }))},\forall \mathit{\eta }\in (0,{\mathit{\eta }}^i],}\hfill \\ {\displaystyle \text{where:}g(\mathit{\eta })=e^{RT}{\int }_{S(G_n,\mathit{\eta })}u(x,T)\mathrm{d}x+{\int }_{\mathit{\partial }S\times (0,T)}{e}^{Rt}(Vu-D\mathrm{\nabla }u)·\mathit{\nu }\mathrm{d}x\mathrm{d}t.}\hfill \end{array}\end{array}$$(43) )–(44(44) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle g_{incl}(\mathit{\eta })=\frac{g(\mathit{\eta })}{\mathcal{A}(S(G_n,\mathit{\eta }))}\text{and}{g}_{cont}(\mathit{\eta })=g(\mathit{\eta }).}\hfill \end{array}\end{array}$$(44) ). To overcome these two difficulties, we proceed in two steps:

Step 1: In order to determine the final state $u(·,T)$ in $\mathrm{\Omega }$ of the main problem (1(1) $$\begin{array}{c}\hfill L[u](x,t)=F(x,t)\text{in}\mathrm{\Omega }\times (0,T),\end{array}$$(1) )–(2(2) $$\begin{array}{c}\hfill L[u](x,t):={\mathit{\partial }}_{t}u(x,t)-\mathrm{d}iv(D\mathrm{\nabla }u(x,t))+V·\mathrm{\nabla }u(x,t)+Ru(x,t),\end{array}$$(2) ) and (8(8) $$\begin{array}{c}\hfill \begin{array}{c}u(·,0)=0\text{in}\mathrm{\Omega }\hfill \\ u=0\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ D\mathrm{\nabla }u·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\times (0,T)\hfill \end{array}\end{array}$$(8) )–(9(9) $$\begin{array}{c}\hfill {\displaystyle F(x,t)=\sum _{n=1}^N{\mathit{\lambda }}_n(t){\mathit{\chi }}_{{\mathit{\omega }}_n}(x)\text{in}\mathrm{\Omega }\times (0,T),}\end{array}$$(9) ), we employ the change of variables: $U(x,t)=e^{\frac{1}{2}\mathit{\psi }(x)}u(x,t)$ in $\mathrm{\Omega }\times (0,T)$. Then, since ${\mathit{\lambda }}_{n=1,\cdots ,N}$ satisfy (11(11) $$\begin{array}{c}\hfill {\int }_0^T{\mathit{\lambda }}_n(t)e^{Rt}\mathrm{d}t\ne 0\text{and}\exists T^0\in (0,T)\text{such that}{\mathit{\lambda }}_n=0\text{in}(T^0,T),\forall n=1,\cdots ,N.\end{array}$$(11) ) it follows that U solves for all $T^{\ast }\in (T^0,T)$(46) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathit{\partial }}_{t}U-\mathrm{d}iv(D\mathrm{\nabla }U)+\mathit{\rho }U=0\text{in}\mathrm{\Omega }\times (T^{\ast },T)\hfill \\ U(·,T^{\ast })\in L^2(\mathrm{\Omega })\text{in}\mathrm{\Omega }\hfill \\ U=0\text{on}{\mathrm{\Gamma }}_{in}\times (T^{\ast },T)\hfill \\ {\displaystyle (D\mathrm{\nabla }U+\frac{1}{2}UV)·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\times (T^{\ast },T)}\hfill \end{array}\right.\end{array}$$(46)

where $\mathit{\rho }=R+\frac{1}{4}{V}^{\top }{D}^{-1}V$. Moreover, in view of the condition $(C_3)$ in (13(13) $$\begin{array}{c}\hfill \begin{array}{c}(C_1){\mathrm{\Gamma }}_i\cap {\mathrm{\Gamma }}_j=\mathrm{\varnothing },\forall i\ne j\in \{0,\cdots ,N_{max}+1\}.\hfill \\ (C_2)|{\mathrm{\Gamma }}_i\cap {\mathrm{\Gamma }}_{L_l}|=|{\mathrm{\Gamma }}_i\cap {\mathrm{\Gamma }}_{L_u}|=1,\forall i=1,\cdots ,N_{max}.\hfill \\ (C_3)\overline{\mathrm{\Omega }}={\cup }_{i=1}^{N_{max}+1}{\overline{\mathrm{\Omega }}}_i\text{where:}{\mathrm{\Omega }}_{N_{max}+1}\subset (\mathrm{\Omega }\backslash {\cup }_{i=1}^N{\overline{\mathit{\omega }}}_n),\hfill \end{array}\end{array}$$(13) ), U solves in ${\mathrm{\Omega }}_{N_{max}+1}\times (0,T)$ a system similar to (46(46) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathit{\partial }}_{t}U-\mathrm{d}iv(D\mathrm{\nabla }U)+\mathit{\rho }U=0\text{in}\mathrm{\Omega }\times (T^{\ast },T)\hfill \\ U(·,T^{\ast })\in L^2(\mathrm{\Omega })\text{in}\mathrm{\Omega }\hfill \\ U=0\text{on}{\mathrm{\Gamma }}_{in}\times (T^{\ast },T)\hfill \\ {\displaystyle (D\mathrm{\nabla }U+\frac{1}{2}UV)·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\times (T^{\ast },T)}\hfill \end{array}\right.\end{array}$$(46) ) where the initial condition becomes $U(·,0)=0$ in ${\mathrm{\Omega }}_{N_{max}+1}$ and the first boundary condition is replaced by $U=e^{\frac{1}{2}\mathit{\psi }}u$ on ${\mathrm{\Gamma }}_{N_{max}}\times (0,T)$. Thus, given records of the state u on ${\mathrm{\Gamma }}_{N_{max}}\times (0,T)$ we employ a numerical method to compute u in ${\mathrm{\Omega }}_{N_{max}+1}\times (0,T)$. Then, we consider the problem of determining the final state $u(·,T)$ in $\mathrm{\Omega }$ of the problem (1(1) $$\begin{array}{c}\hfill L[u](x,t)=F(x,t)\text{in}\mathrm{\Omega }\times (0,T),\end{array}$$(1) )–(2(2) $$\begin{array}{c}\hfill L[u](x,t):={\mathit{\partial }}_{t}u(x,t)-\mathrm{d}iv(D\mathrm{\nabla }u(x,t))+V·\mathrm{\nabla }u(x,t)+Ru(x,t),\end{array}$$(2) ) and (8(8) $$\begin{array}{c}\hfill \begin{array}{c}u(·,0)=0\text{in}\mathrm{\Omega }\hfill \\ u=0\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ D\mathrm{\nabla }u·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\times (0,T)\hfill \end{array}\end{array}$$(8) )–(9(9) $$\begin{array}{c}\hfill {\displaystyle F(x,t)=\sum _{n=1}^N{\mathit{\lambda }}_n(t){\mathit{\chi }}_{{\mathit{\omega }}_n}(x)\text{in}\mathrm{\Omega }\times (0,T),}\end{array}$$(9) ) from the computed data u in ${\mathrm{\Omega }}_{N_{max}+1}\times (T^{\ast },T)$, see [28]. Hence, we prove as in [6] the following result:

Proposition 4.3:

Let u be the solution of the problem (1(1) $$\begin{array}{c}\hfill L[u](x,t)=F(x,t)\text{in}\mathrm{\Omega }\times (0,T),\end{array}$$(1) )–(2(2) $$\begin{array}{c}\hfill L[u](x,t):={\mathit{\partial }}_{t}u(x,t)-\mathrm{d}iv(D\mathrm{\nabla }u(x,t))+V·\mathrm{\nabla }u(x,t)+Ru(x,t),\end{array}$$(2) ) and (8(8) $$\begin{array}{c}\hfill \begin{array}{c}u(·,0)=0\text{in}\mathrm{\Omega }\hfill \\ u=0\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ D\mathrm{\nabla }u·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\times (0,T)\hfill \end{array}\end{array}$$(8) )–(9(9) $$\begin{array}{c}\hfill {\displaystyle F(x,t)=\sum _{n=1}^N{\mathit{\lambda }}_n(t){\mathit{\chi }}_{{\mathit{\omega }}_n}(x)\text{in}\mathrm{\Omega }\times (0,T),}\end{array}$$(9) ), $U=e^{\frac{1}{2}\mathit{\psi }}u$ in $\mathrm{\Omega }\times (0,T)$ and ${\mathrm{\Omega }}_{N_{max}+1}\subset \mathrm{\Omega }$ as introduced in (13(13) $$\begin{array}{c}\hfill \begin{array}{c}(C_1){\mathrm{\Gamma }}_i\cap {\mathrm{\Gamma }}_j=\mathrm{\varnothing },\forall i\ne j\in \{0,\cdots ,N_{max}+1\}.\hfill \\ (C_2)|{\mathrm{\Gamma }}_i\cap {\mathrm{\Gamma }}_{L_l}|=|{\mathrm{\Gamma }}_i\cap {\mathrm{\Gamma }}_{L_u}|=1,\forall i=1,\cdots ,N_{max}.\hfill \\ (C_3)\overline{\mathrm{\Omega }}={\cup }_{i=1}^{N_{max}+1}{\overline{\mathrm{\Omega }}}_i\text{where:}{\mathrm{\Omega }}_{N_{max}+1}\subset (\mathrm{\Omega }\backslash {\cup }_{i=1}^N{\overline{\mathit{\omega }}}_n),\hfill \end{array}\end{array}$$(13) ). Provided the assertion (11(11) $$\begin{array}{c}\hfill {\int }_0^T{\mathit{\lambda }}_n(t)e^{Rt}\mathrm{d}t\ne 0\text{and}\exists T^0\in (0,T)\text{such that}{\mathit{\lambda }}_n=0\text{in}(T^0,T),\forall n=1,\cdots ,N.\end{array}$$(11) ) holds true, the data u in ${\mathrm{\Omega }}_{N_{max}+1}\times (T^{\ast },T)$ where $T^{\ast }\in (T^0,T)$ determines in a unique manner the final state $u(·,T)$ in $\mathrm{\Omega }$ and we have(47) $$\begin{array}{c}\hfill {\displaystyle {\Vert U(·,T)\Vert }_{L^2(\mathrm{\Omega })}\le C{\Vert U\Vert }_{L^2({\mathrm{\Omega }}_{N_{max}+1}\times (T^{\ast },T))},}\end{array}$$(47)

where C is a Carleman constant [29] that does not depend on $U(·,T^{\ast })$.

ProofSee the Appendix 1.

To determine the final state $u(·,T)$ in $\mathrm{\Omega }$ using the computed data u in ${\mathrm{\Omega }}_{N_{max}+1}\times (T^{\ast },T)$, we denote by ${(e_k)}_{k\ge 0}$ the normalized eigenfunctions of the following problem:(48) $$\begin{array}{c}\hfill \left\{\begin{array}{c}-\mathrm{d}iv(D\mathrm{\nabla }e)+\mathit{\rho }e=\mathit{\mu }e\text{in}\mathrm{\Omega }\hfill \\ e=0\text{on}{\mathrm{\Gamma }}_{in}\hfill \\ (D\mathrm{\nabla }e+\frac{1}{2}eV)·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\hfill \end{array}\right.\end{array}$$(48)

that form a complete orthonormal family of $L^2(\mathrm{\Omega })$, see [30]. Then, the solution of the problem (46(46) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathit{\partial }}_{t}U-\mathrm{d}iv(D\mathrm{\nabla }U)+\mathit{\rho }U=0\text{in}\mathrm{\Omega }\times (T^{\ast },T)\hfill \\ U(·,T^{\ast })\in L^2(\mathrm{\Omega })\text{in}\mathrm{\Omega }\hfill \\ U=0\text{on}{\mathrm{\Gamma }}_{in}\times (T^{\ast },T)\hfill \\ {\displaystyle (D\mathrm{\nabla }U+\frac{1}{2}UV)·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\times (T^{\ast },T)}\hfill \end{array}\right.\end{array}$$(46) ) is expressed as follows:(49) $$\begin{array}{c}\hfill U(x,t)=\sum _{k\ge 0}{⟨U(·,T),e_k⟩}_{L^2(\mathrm{\Omega })}{e}^{{\mathit{\mu }}_k(T-t)}{e}_k(x)\text{in}\mathrm{\Omega }\times (T^{\ast },T)\end{array}$$(49)

where ${\mathit{\mu }}_k$ is the eigenvalue associated to $e_k$ and ${⟨.,.⟩}_{L^2(\mathrm{\Omega })}$ denotes the inner product in $L^2(\mathrm{\Omega })$. Therefore, by truncating the series in (49(49) $$\begin{array}{c}\hfill U(x,t)=\sum _{k\ge 0}{⟨U(·,T),e_k⟩}_{L^2(\mathrm{\Omega })}{e}^{{\mathit{\mu }}_k(T-t)}{e}_k(x)\text{in}\mathrm{\Omega }\times (T^{\ast },T)\end{array}$$(49) ) using a sufficiently large number K of terms, we determine the coefficients $y_k:={⟨U(·,T),e_k⟩}_{L^2(\mathrm{\Omega })}$ for $k=0,\cdots ,K$ by solving the following least squares problem:(50) $$\begin{array}{c}\hfill {\displaystyle \underset{y_0,\cdots ,y_K}{min}\frac{1}{2}\Vert \sum _{k=0}^K{y}_k{e}^{{\mathit{\mu }}_k(T-t)}{e}_k-U{\Vert }_{L^2({\mathrm{\Omega }}_{N_{max}+1}\times (T^{\ast },T))}^2.}\end{array}$$(50)

Afterwards, we deduce the approximation of the final state $u(·,T)$ in $\mathrm{\Omega }$ associated to the main problem (1(1) $$\begin{array}{c}\hfill L[u](x,t)=F(x,t)\text{in}\mathrm{\Omega }\times (0,T),\end{array}$$(1) )–(2(2) $$\begin{array}{c}\hfill L[u](x,t):={\mathit{\partial }}_{t}u(x,t)-\mathrm{d}iv(D\mathrm{\nabla }u(x,t))+V·\mathrm{\nabla }u(x,t)+Ru(x,t),\end{array}$$(2) ) and (8(8) $$\begin{array}{c}\hfill \begin{array}{c}u(·,0)=0\text{in}\mathrm{\Omega }\hfill \\ u=0\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ D\mathrm{\nabla }u·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\times (0,T)\hfill \end{array}\end{array}$$(8) )–(9(9) $$\begin{array}{c}\hfill {\displaystyle F(x,t)=\sum _{n=1}^N{\mathit{\lambda }}_n(t){\mathit{\chi }}_{{\mathit{\omega }}_n}(x)\text{in}\mathrm{\Omega }\times (0,T),}\end{array}$$(9) ):(51) $$\begin{array}{c}\hfill u(x,T)\approx e^{-\frac{1}{2}\mathit{\psi }(x)}\sum _{k=0}^K{y}_k{e}_k(x),x\in \mathrm{\Omega }.\end{array}$$(51) Step 2: As far as the not given term $(Vu-D\mathrm{\nabla }u)·\mathit{\nu }$ involved in (43(43) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\overline{\mathit{\lambda }}}_n=\frac{g(\mathit{\eta })}{\mathcal{A}({\mathit{\omega }}_n\cap S(G_n,\mathit{\eta }))},\forall \mathit{\eta }\in (0,{\mathit{\eta }}^i],}\hfill \\ {\displaystyle \text{where:}g(\mathit{\eta })=e^{RT}{\int }_{S(G_n,\mathit{\eta })}u(x,T)\mathrm{d}x+{\int }_{\mathit{\partial }S\times (0,T)}{e}^{Rt}(Vu-D\mathrm{\nabla }u)·\mathit{\nu }\mathrm{d}x\mathrm{d}t.}\hfill \end{array}\end{array}$$(43) )–(44(44) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle g_{incl}(\mathit{\eta })=\frac{g(\mathit{\eta })}{\mathcal{A}(S(G_n,\mathit{\eta }))}\text{and}{g}_{cont}(\mathit{\eta })=g(\mathit{\eta }).}\hfill \end{array}\end{array}$$(44) ) is concerned, in practice we proceed as follows: (1) For the function $g_{cont}$, since the aim is to determine ${\mathit{\eta }}_{out}\in (0,{\mathit{\eta }}^i)$ from which this function becomes equal to its final constant value it follows that the curve of $g_{cont}$ is more interesting on its second part where $\mathit{\eta }\in ({\mathit{\eta }}_{out},{\mathit{\eta }}^i]$ that corresponds to ${\mathit{\omega }}_n\subset S(G_n,\mathit{\eta })\subseteq {\mathrm{\Omega }}_i$. Thus, for $g_{cont}$ we consider that $(Vu-D\mathrm{\nabla }u)·\mathit{\nu }$ on $\mathit{\partial }S\times (0,T)$ is approximated by its value given by the measurements taken on $\mathit{\partial }{\mathrm{\Omega }}_i\times (0,T)$. (2) For the function $g_{incl}$, the aim is to determine until which side length ${\mathit{\eta }}_{in}\in (0,{\mathit{\eta }}^i)$ this function keeps its initial constant value and thus, the curve of $g_{incl}$ is rather more valuable on its first part where $\mathit{\eta }\in (0,{\mathit{\eta }}_{in}]$ that corresponds to $S(G_n,\mathit{\eta })\subseteq {\mathit{\omega }}_n$. Moreover, within the source spatial support ${\overline{\mathit{\omega }}}_n$ one could assume there is enough of loaded material that in turn affects the state u to be saturated and thus, it doesn’t vary in space within ${\mathit{\omega }}_n$. Hence, for the function $g_{incl}$ we omit the integral on $\mathit{\partial }S\times (0,T)$ of $(Vu-D\mathrm{\nabla }u)·\mathit{\nu }$.

4.3. Identification of the unknown source intensity function ${\mathit{\lambda }}_n$

In view of the previous subsection and as far as the detected source ${\mathit{\lambda }}_n{\mathit{\chi }}_{{\mathit{\omega }}_n}$ occurring in ${\mathrm{\Omega }}_i\subset \mathrm{\Omega }$ is concerned, we consider now to be known the biggest side length ${\mathit{\eta }}_{in}$ as well as the smallest side length ${\mathit{\eta }}_{out}$ defining the two squares centred at the already localized geometric centre $G_n$ of the unknown source spatial support ${\overline{\mathit{\omega }}}_n$ that yield: $S(G_n,{\mathit{\eta }}_{in})\subseteq {\mathit{\omega }}_n\subseteq S(G_n,{\mathit{\eta }}_{out})$. Then, to identify the unknown source intensity function ${\mathit{\lambda }}_n$ we set the subdomain $\mathit{\omega }$ involved in the problem (23(23) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathit{\partial }}_{t}v-\mathrm{d}iv(D\mathrm{\nabla }v)-V·\mathrm{\nabla }v+Rv=0\text{in}\mathrm{\Omega }\times (0,T)\hfill \\ v(·,0)=0\text{in}\mathrm{\Omega }\hfill \\ v={\mathit{\zeta }}_{in}\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ (D\mathrm{\nabla }v+vV)·\mathit{\nu }=0\text{on}{\mathrm{\Gamma }}_L\times (0,T)\hfill \\ (D\mathrm{\nabla }v+vV)·\mathit{\nu }={\mathit{\zeta }}_{out}\text{on}{\mathrm{\Gamma }}_{out}\times (0,T)\hfill \end{array}\right.\end{array}$$(23) )–(24(24) $$\begin{array}{c}\hfill {\displaystyle \text{such that}{\int }_{\mathit{\omega }}v(x,·)\mathrm{d}x\ne 0\text{a.e. in}(0,T)}\end{array}$$(24) ) to the middle square centred at $G_n$, i.e.(52) $$\begin{array}{c}\hfill \mathit{\omega }=S(G_n,{\mathit{\eta }}_{mid}),\text{where}{\mathit{\eta }}_{mid}=({\mathit{\eta }}_{in}+{\mathit{\eta }}_{out})/2\end{array}$$(52)

and determine from Remark 2.4 two boundary controls ${\mathit{\zeta }}_{in}$ and ${\mathit{\zeta }}_{out}$ that drive the solution v of the problem (23(23) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathit{\partial }}_{t}v-\mathrm{d}iv(D\mathrm{\nabla }v)-V·\mathrm{\nabla }v+Rv=0\text{in}\mathrm{\Omega }\times (0,T)\hfill \\ v(·,0)=0\text{in}\mathrm{\Omega }\hfill \\ v={\mathit{\zeta }}_{in}\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ (D\mathrm{\nabla }v+vV)·\mathit{\nu }=0\text{on}{\mathrm{\Gamma }}_L\times (0,T)\hfill \\ (D\mathrm{\nabla }v+vV)·\mathit{\nu }={\mathit{\zeta }}_{out}\text{on}{\mathrm{\Gamma }}_{out}\times (0,T)\hfill \end{array}\right.\end{array}$$(23) ) to satisfy the assertion (24(24) $$\begin{array}{c}\hfill {\displaystyle \text{such that}{\int }_{\mathit{\omega }}v(x,·)\mathrm{d}x\ne 0\text{a.e. in}(0,T)}\end{array}$$(24) ) for $\mathit{\omega }$ as in (52(52) $$\begin{array}{c}\hfill \mathit{\omega }=S(G_n,{\mathit{\eta }}_{mid}),\text{where}{\mathit{\eta }}_{mid}=({\mathit{\eta }}_{in}+{\mathit{\eta }}_{out})/2\end{array}$$(52) ). Afterwards, we replace in the second equation of (35(35) $$\begin{array}{cc}\hfill {\mathrm{\Psi }}_i(G_n)& =\left(\begin{array}{c}{\displaystyle \frac{P_{e^{\mathit{\psi }}}^i}{P_1^i}}\\ {\displaystyle \frac{P_{{\mathit{\psi }}^{\perp }}^i}{P_1^i}}\end{array}\right)\text{and}\hfill \\ \hfill & {\displaystyle {\int }_0^{\mathit{\tau }}{\mathit{\lambda }}_n(t)({\int }_{{\mathit{\omega }}_n}v(x,\mathit{\tau }-t)\mathrm{d}x)\mathrm{d}t=Q^i(\mathit{\tau }),\forall \mathit{\tau }\in (0,T),}\hfill \end{array}$$(35) ) ${\mathit{\omega }}_n$ by $S(G_n,{\mathit{\eta }}_{mid})$ and focus on identifying an approximation of the source intensity function ${\mathit{\lambda }}_n$ by solving the following deconvolution problem:(53) $$\begin{array}{c}\hfill {\displaystyle {\int }_0^{\mathit{\tau }}{\mathit{\lambda }}_n(t)\left({\int }_{S(G_n,{\mathit{\eta }}_{mid})}v(x,\mathit{\tau }-t)\mathrm{d}x\right)\mathrm{d}t=Q^i(\mathit{\tau }),\forall \mathit{\tau }\in (0,T),}\end{array}$$(53)

where $Q^i$ is the function in (34(34) $$\begin{array}{cc}\hfill Q^i(\mathit{\tau })& {\displaystyle ={\int }_{({\mathrm{\Gamma }}_{i-1}\cup {\mathrm{\Gamma }}_i)\times (0,\mathit{\tau })}(u(x,t)[D\mathrm{\nabla }v(x,\mathit{\tau }-t)+v(x,\mathit{\tau }-t)V]}\hfill \\ \hfill & -v(x,\mathit{\tau }-t)D\mathrm{\nabla }u(x,t))·\mathit{\nu }\mathrm{d}x\mathrm{d}t,\hfill \end{array}$$(34) ) defined from v the solution of the problem (23(23) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathit{\partial }}_{t}v-\mathrm{d}iv(D\mathrm{\nabla }v)-V·\mathrm{\nabla }v+Rv=0\text{in}\mathrm{\Omega }\times (0,T)\hfill \\ v(·,0)=0\text{in}\mathrm{\Omega }\hfill \\ v={\mathit{\zeta }}_{in}\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ (D\mathrm{\nabla }v+vV)·\mathit{\nu }=0\text{on}{\mathrm{\Gamma }}_L\times (0,T)\hfill \\ (D\mathrm{\nabla }v+vV)·\mathit{\nu }={\mathit{\zeta }}_{out}\text{on}{\mathrm{\Gamma }}_{out}\times (0,T)\hfill \end{array}\right.\end{array}$$(23) )–(24(24) $$\begin{array}{c}\hfill {\displaystyle \text{such that}{\int }_{\mathit{\omega }}v(x,·)\mathrm{d}x\ne 0\text{a.e. in}(0,T)}\end{array}$$(24) ) with $\mathit{\omega }=S(G_n,{\mathit{\eta }}_{mid})$. To this end, given a desired number of time steps $\mathcal{M}$, we employ the regularly distributed discrete times $t_m=m\mathrm{\Delta }t$ for $m=0,\cdots ,\mathcal{M}$, where $\mathrm{\Delta }t=T/\mathcal{M}$. Then, using the trapezoidal rule we get(54) $$\begin{array}{cc}& {\displaystyle {\int }_0^{t_{m+1}}{\mathit{\lambda }}_n(t)\left({\int }_{S(G_n,{\mathit{\eta }}_{mid})}v(x,t_{m+1}-t)\mathrm{d}x\right)\mathrm{d}t}\hfill \\ \hfill & {\displaystyle =\sum _{k=0}^m{\int }_{t_k}^{t_{k+1}}{\mathit{\lambda }}_n(t)\left({\int }_{S(G_n,{\mathit{\eta }}_{mid})}v(x,t_{m+1}-t)\mathrm{d}x\right)\mathrm{d}t}\hfill \\ \hfill & {\displaystyle \approx \frac{\mathrm{\Delta }t}{2}\sum _{k=0}^m\left({\mathit{\lambda }}_n(t_k){\int }_{S(G_n,{\mathit{\eta }}_{mid})}v(x,t_{m+1-k})\mathrm{d}x+{\mathit{\lambda }}_n(t_{k+1}){\int }_{S(G_n,{\mathit{\eta }}_{mid})}v(x,t_{m-k})\mathrm{d}x\right)}\hfill \\ \hfill & {\displaystyle =\mathrm{\Delta }t\sum _{k=1}^m{\mathit{\lambda }}_n(t_k){\int }_{S(G_n,{\mathit{\eta }}_{mid})}v(x,t_{m+1-k})\mathrm{d}x,}\hfill \end{array}$$(54) where according to (23(23) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathit{\partial }}_{t}v-\mathrm{d}iv(D\mathrm{\nabla }v)-V·\mathrm{\nabla }v+Rv=0\text{in}\mathrm{\Omega }\times (0,T)\hfill \\ v(·,0)=0\text{in}\mathrm{\Omega }\hfill \\ v={\mathit{\zeta }}_{in}\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ (D\mathrm{\nabla }v+vV)·\mathit{\nu }=0\text{on}{\mathrm{\Gamma }}_L\times (0,T)\hfill \\ (D\mathrm{\nabla }v+vV)·\mathit{\nu }={\mathit{\zeta }}_{out}\text{on}{\mathrm{\Gamma }}_{out}\times (0,T)\hfill \end{array}\right.\end{array}$$(23) ), we used $v(·,0)=0$ in $\mathrm{\Omega }$ and ${\mathit{\lambda }}_n(0)=0$. Thus, using the notation ${\mathit{\lambda }}_n^k\approx {\mathit{\lambda }}_n(t_k)$ and in view of (54(54) $$\begin{array}{cc}& {\displaystyle {\int }_0^{t_{m+1}}{\mathit{\lambda }}_n(t)\left({\int }_{S(G_n,{\mathit{\eta }}_{mid})}v(x,t_{m+1}-t)\mathrm{d}x\right)\mathrm{d}t}\hfill \\ \hfill & {\displaystyle =\sum _{k=0}^m{\int }_{t_k}^{t_{k+1}}{\mathit{\lambda }}_n(t)\left({\int }_{S(G_n,{\mathit{\eta }}_{mid})}v(x,t_{m+1}-t)\mathrm{d}x\right)\mathrm{d}t}\hfill \\ \hfill & {\displaystyle \approx \frac{\mathrm{\Delta }t}{2}\sum _{k=0}^m\left({\mathit{\lambda }}_n(t_k){\int }_{S(G_n,{\mathit{\eta }}_{mid})}v(x,t_{m+1-k})\mathrm{d}x+{\mathit{\lambda }}_n(t_{k+1}){\int }_{S(G_n,{\mathit{\eta }}_{mid})}v(x,t_{m-k})\mathrm{d}x\right)}\hfill \\ \hfill & {\displaystyle =\mathrm{\Delta }t\sum _{k=1}^m{\mathit{\lambda }}_n(t_k){\int }_{S(G_n,{\mathit{\eta }}_{mid})}v(x,t_{m+1-k})\mathrm{d}x,}\hfill \end{array}$$(54) ), we obtain a discrete version of the deconvolution problem defined from (53(53) $$\begin{array}{c}\hfill {\displaystyle {\int }_0^{\mathit{\tau }}{\mathit{\lambda }}_n(t)\left({\int }_{S(G_n,{\mathit{\eta }}_{mid})}v(x,\mathit{\tau }-t)\mathrm{d}x\right)\mathrm{d}t=Q^i(\mathit{\tau }),\forall \mathit{\tau }\in (0,T),}\end{array}$$(53) ) that leads to the following recursive formula:(55) $$\begin{array}{cc}\hfill {\mathit{\lambda }}_n^m& {\displaystyle =\frac{1}{{\displaystyle {\int }_{S(G_n,{\mathit{\eta }}_{mid})}v(x,t_1)\mathrm{d}x}}\left(\frac{Q^i(t_{m+1})}{\mathrm{\Delta }t}-\sum _{k=1}^{m-1}{\mathit{\lambda }}_n^k{\int }_{S(G_n,{\mathit{\eta }}_{mid})}v(x,t_{m+1-k})\mathrm{d}x\right),}\hfill \\ \hfill & \forall m\ge 1.\hfill \end{array}$$(55)

In other words, by denoting ${\mathrm{\Lambda }}_n=({\mathit{\lambda }}_n^1,\cdots ,{\mathit{\lambda }}_n^{\mathcal{M}}{)}^{\top }$ and ${\mathbf{Q}}^{\mathbf{i}}=(Q^i(t_2),\cdots ,Q^i(t_{\mathcal{M}}),$$Q^i(t_{\mathcal{M}}){)}^{\top }$, it follows from (53(53) $$\begin{array}{c}\hfill {\displaystyle {\int }_0^{\mathit{\tau }}{\mathit{\lambda }}_n(t)\left({\int }_{S(G_n,{\mathit{\eta }}_{mid})}v(x,\mathit{\tau }-t)\mathrm{d}x\right)\mathrm{d}t=Q^i(\mathit{\tau }),\forall \mathit{\tau }\in (0,T),}\end{array}$$(53) )–(54(54) $$\begin{array}{cc}& {\displaystyle {\int }_0^{t_{m+1}}{\mathit{\lambda }}_n(t)\left({\int }_{S(G_n,{\mathit{\eta }}_{mid})}v(x,t_{m+1}-t)\mathrm{d}x\right)\mathrm{d}t}\hfill \\ \hfill & {\displaystyle =\sum _{k=0}^m{\int }_{t_k}^{t_{k+1}}{\mathit{\lambda }}_n(t)\left({\int }_{S(G_n,{\mathit{\eta }}_{mid})}v(x,t_{m+1}-t)\mathrm{d}x\right)\mathrm{d}t}\hfill \\ \hfill & {\displaystyle \approx \frac{\mathrm{\Delta }t}{2}\sum _{k=0}^m\left({\mathit{\lambda }}_n(t_k){\int }_{S(G_n,{\mathit{\eta }}_{mid})}v(x,t_{m+1-k})\mathrm{d}x+{\mathit{\lambda }}_n(t_{k+1}){\int }_{S(G_n,{\mathit{\eta }}_{mid})}v(x,t_{m-k})\mathrm{d}x\right)}\hfill \\ \hfill & {\displaystyle =\mathrm{\Delta }t\sum _{k=1}^m{\mathit{\lambda }}_n(t_k){\int }_{S(G_n,{\mathit{\eta }}_{mid})}v(x,t_{m+1-k})\mathrm{d}x,}\hfill \end{array}$$(54) ) that the identification of the intensity function ${\mathit{\lambda }}_n$ defining the detected source occurring in ${\mathrm{\Omega }}_i\subset \mathrm{\Omega }$ is transformed into solving the linear system(56) $$\begin{array}{c}\hfill A{\mathrm{\Lambda }}_n=\frac{1}{\mathrm{\Delta }t}{\mathbf{Q}}^{\mathbf{i}},\end{array}$$(56)

where A is the $\mathcal{M}\times \mathcal{M}$ lower triangular matrix defined for $m=1,\cdots ,\mathcal{M}$ by(57) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle A_{mk}={\int }_{S(G_n,{\mathit{\eta }}_{mid})}v(x,t_{m+1-k})\mathrm{d}x,\text{for}k=1,\cdots ,m}\hfill \\ A_{mk}=0,\text{for}k=m+1,\cdots ,\mathcal{M}.\hfill \end{array}\right.\end{array}$$(57)

In practice, due to measurement inaccuracies, the vector ${\mathbf{Q}}^{\mathbf{i}}$ could be contaminated by some errors. In addition, the matrix A could be ill-conditioned. Therefore, the identification of ${\mathrm{\Lambda }}_n$ using the recursive formula in (55(55) $$\begin{array}{cc}\hfill {\mathit{\lambda }}_n^m& {\displaystyle =\frac{1}{{\displaystyle {\int }_{S(G_n,{\mathit{\eta }}_{mid})}v(x,t_1)\mathrm{d}x}}\left(\frac{Q^i(t_{m+1})}{\mathrm{\Delta }t}-\sum _{k=1}^{m-1}{\mathit{\lambda }}_n^k{\int }_{S(G_n,{\mathit{\eta }}_{mid})}v(x,t_{m+1-k})\mathrm{d}x\right),}\hfill \\ \hfill & \forall m\ge 1.\hfill \end{array}$$(55) ) which corresponds to the straightforward solution of the linear system (56(56) $$\begin{array}{c}\hfill A{\mathrm{\Lambda }}_n=\frac{1}{\mathrm{\Delta }t}{\mathbf{Q}}^{\mathbf{i}},\end{array}$$(56) )–(57(57) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle A_{mk}={\int }_{S(G_n,{\mathit{\eta }}_{mid})}v(x,t_{m+1-k})\mathrm{d}x,\text{for}k=1,\cdots ,m}\hfill \\ A_{mk}=0,\text{for}k=m+1,\cdots ,\mathcal{M}.\hfill \end{array}\right.\end{array}$$(57) ) could not yield a stable approximation of the unknown source intensity function ${\mathit{\lambda }}_n$. To overcome this difficulty, one could employ, for example, the Tikhonov regularization method that replaces the linear system (56(56) $$\begin{array}{c}\hfill A{\mathrm{\Lambda }}_n=\frac{1}{\mathrm{\Delta }t}{\mathbf{Q}}^{\mathbf{i}},\end{array}$$(56) )–(57(57) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle A_{mk}={\int }_{S(G_n,{\mathit{\eta }}_{mid})}v(x,t_{m+1-k})\mathrm{d}x,\text{for}k=1,\cdots ,m}\hfill \\ A_{mk}=0,\text{for}k=m+1,\cdots ,\mathcal{M}.\hfill \end{array}\right.\end{array}$$(57) ) by a penalized least-squares problem under the form:(58) $$\begin{array}{c}\hfill {\displaystyle \underset{{\mathrm{\Lambda }}_n\in {\mathbb{R}}^{\mathcal{M}}}{min}\frac{1}{2}\Vert A{\mathrm{\Lambda }}_n-\frac{1}{\mathrm{\Delta }t}{\mathbf{Q}}^{\mathbf{i}}{\Vert }_2^2+\frac{r}{2}\Vert {\mathrm{\Lambda }}_n{\Vert }_2^2,}\end{array}$$(58)

where ${\Vert .\Vert }_2$ denotes the Euclidean vector norm and $r>0$ is the regularization parameter. For other kinds of regularization and the computation of r see [31] and references therein.

We end this section by summarizing in the following algorithm the different steps defining the non-iterative detection–identification method developed in the present study to determine from the observation operator M[F] introduced in (15(15) $$\begin{array}{c}\hfill M[F]:=\left\{D\mathrm{\nabla }u·\mathit{\nu }\text{on}\sum _{in};{\Vert V\Vert }_{2}u\text{on}\sum _L;(u,D\mathrm{\nabla }u·\mathit{\nu })\text{on}\sum _{i=1,\cdots ,N_{max}}\right\},\end{array}$$(15) ) the unknown elements defining in (9(9) $$\begin{array}{c}\hfill {\displaystyle F(x,t)=\sum _{n=1}^N{\mathit{\lambda }}_n(t){\mathit{\chi }}_{{\mathit{\omega }}_n}(x)\text{in}\mathrm{\Omega }\times (0,T),}\end{array}$$(9) ) the multiple sources occurring in the inverse problem (1(1) $$\begin{array}{c}\hfill L[u](x,t)=F(x,t)\text{in}\mathrm{\Omega }\times (0,T),\end{array}$$(1) )–(2(2) $$\begin{array}{c}\hfill L[u](x,t):={\mathit{\partial }}_{t}u(x,t)-\mathrm{d}iv(D\mathrm{\nabla }u(x,t))+V·\mathrm{\nabla }u(x,t)+Ru(x,t),\end{array}$$(2) ) and (8(8) $$\begin{array}{c}\hfill \begin{array}{c}u(·,0)=0\text{in}\mathrm{\Omega }\hfill \\ u=0\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ D\mathrm{\nabla }u·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\times (0,T)\hfill \end{array}\end{array}$$(8) ):

Algorithm. Proceed as follows:

     $\mathbf{1}.$ Solve the forward problem satisfied by u in ${\mathrm{\Omega }}_{N_{max}+1}\times (0,T)$.

     $\mathbf{2}.$ Compute ${(e_k)}_{k=1,\cdots ,K}$ and ${({\mathit{\mu }}_k)}_{k=1,\cdots ,K}$ of the eigenvalue problem (48(48) $$\begin{array}{c}\hfill \left\{\begin{array}{c}-\mathrm{d}iv(D\mathrm{\nabla }e)+\mathit{\rho }e=\mathit{\mu }e\text{in}\mathrm{\Omega }\hfill \\ e=0\text{on}{\mathrm{\Gamma }}_{in}\hfill \\ (D\mathrm{\nabla }e+\frac{1}{2}eV)·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\hfill \end{array}\right.\end{array}$$(48) ).

     $\mathbf{3}.$ Solve the least squares problem (50(50) $$\begin{array}{c}\hfill {\displaystyle \underset{y_0,\cdots ,y_K}{min}\frac{1}{2}\Vert \sum _{k=0}^K{y}_k{e}^{{\mathit{\mu }}_k(T-t)}{e}_k-U{\Vert }_{L^2({\mathrm{\Omega }}_{N_{max}+1}\times (T^{\ast },T))}^2.}\end{array}$$(50) ) and determine $u(·,T)$ in $\mathrm{\Omega }$ from (51(51) $$\begin{array}{c}\hfill u(x,T)\approx e^{-\frac{1}{2}\mathit{\psi }(x)}\sum _{k=0}^K{y}_k{e}_k(x),x\in \mathrm{\Omega }.\end{array}$$(51) ).

     $\mathbf{4}.$ For $i=1$ to $N_{max}$ do

           $\bullet$ Compute the coefficient $P_1^i$ defined in (32(32) $$\begin{array}{cc}\hfill P_1^i& {\displaystyle =e^{RT}{\int }_{{\mathrm{\Omega }}_i}u(x,T)\mathrm{d}x+{\int }_{({\mathrm{\Gamma }}_{i-1}\cup {\mathrm{\Gamma }}_i)\times (0,T)}{e}^{Rt}(uV-D\mathrm{\nabla }u)·\mathit{\nu }\mathrm{d}x\mathrm{d}t}\hfill \\ \hfill & {\displaystyle +{\int }_{{\mathrm{\Gamma }}_L^i\times (0,T)}{e}^{Rt}uV·\mathit{\nu }\mathrm{d}x\mathrm{d}t,}\hfill \\ \hfill P_{e^{\mathit{\psi }}}^i& {\displaystyle =e^{RT}{\int }_{{\mathrm{\Omega }}_i}{e}^{\mathit{\psi }(x)}u(x,T)\mathrm{d}x-{\int }_{({\mathrm{\Gamma }}_{i-1}\cup {\mathrm{\Gamma }}_i)\times (0,T)}{e}^{\mathit{\psi }+Rt}D\mathrm{\nabla }u·\mathit{\nu }\mathrm{d}x\mathrm{d}t,}\hfill \\ \hfill P_{{\mathit{\psi }}^{\perp }}^i& {\displaystyle =e^{RT}{\int }_{{\mathrm{\Omega }}_i}{\mathit{\psi }}^{\perp }(x)u(x,T)\mathrm{d}x}\hfill \\ \hfill & {\displaystyle +{\int }_{({\mathrm{\Gamma }}_{i-1}\cup {\mathrm{\Gamma }}_i)\times (0,T)}{e}^{Rt}(u[{\mathit{\psi }}^{\perp }V-D{V}^{\perp }]-{\mathit{\psi }}^{\perp }D\mathrm{\nabla }u)·\mathit{\nu }\mathrm{d}x\mathrm{d}t}\hfill \\ \hfill & {\displaystyle +{\int }_{{\mathrm{\Gamma }}_L^i\times (0,T)}{e}^{Rt}u[{\mathit{\psi }}^{\perp }V-D{V}^{\perp }]·\mathit{\nu }\mathrm{d}x\mathrm{d}t.}\hfill \end{array}$$(32) ).

           $\bullet$ If $|P_1^i|/T\le \mathit{\epsilon }$ then, there is no source in ${\mathrm{\Omega }}_i$.

           $\bullet$ Else, there is an unknown source ${\mathit{\lambda }}_n{\mathit{\chi }}_{{\mathit{\omega }}_n}$ occurring in ${\mathrm{\Omega }}_i$.

               $▶$ Determine from (33(33) $$\begin{array}{c}\hfill {\displaystyle e^{-RT}{P}_1^i\le e^{-R{T}^0}{P}_1^i\le \mathcal{A}({\mathit{\omega }}_n){\int }_0^T{\mathit{\lambda }}_n(t)\mathrm{d}t\le P_1^i.}\end{array}$$(33) ) the total amount: ${\displaystyle \mathcal{A}({\mathit{\omega }}_n){\int }_0^T{\mathit{\lambda }}_n(t)\mathrm{d}t}$ loaded in ${\mathrm{\Omega }}_i$.

               $▶$ Compute the two coefficients $P_{e^{\mathit{\psi }}}^i$ and $P_{{\mathit{\psi }}^{\perp }}^i$ from (32(32) $$\begin{array}{cc}\hfill P_1^i& {\displaystyle =e^{RT}{\int }_{{\mathrm{\Omega }}_i}u(x,T)\mathrm{d}x+{\int }_{({\mathrm{\Gamma }}_{i-1}\cup {\mathrm{\Gamma }}_i)\times (0,T)}{e}^{Rt}(uV-D\mathrm{\nabla }u)·\mathit{\nu }\mathrm{d}x\mathrm{d}t}\hfill \\ \hfill & {\displaystyle +{\int }_{{\mathrm{\Gamma }}_L^i\times (0,T)}{e}^{Rt}uV·\mathit{\nu }\mathrm{d}x\mathrm{d}t,}\hfill \\ \hfill P_{e^{\mathit{\psi }}}^i& {\displaystyle =e^{RT}{\int }_{{\mathrm{\Omega }}_i}{e}^{\mathit{\psi }(x)}u(x,T)\mathrm{d}x-{\int }_{({\mathrm{\Gamma }}_{i-1}\cup {\mathrm{\Gamma }}_i)\times (0,T)}{e}^{\mathit{\psi }+Rt}D\mathrm{\nabla }u·\mathit{\nu }\mathrm{d}x\mathrm{d}t,}\hfill \\ \hfill P_{{\mathit{\psi }}^{\perp }}^i& {\displaystyle =e^{RT}{\int }_{{\mathrm{\Omega }}_i}{\mathit{\psi }}^{\perp }(x)u(x,T)\mathrm{d}x}\hfill \\ \hfill & {\displaystyle +{\int }_{({\mathrm{\Gamma }}_{i-1}\cup {\mathrm{\Gamma }}_i)\times (0,T)}{e}^{Rt}(u[{\mathit{\psi }}^{\perp }V-D{V}^{\perp }]-{\mathit{\psi }}^{\perp }D\mathrm{\nabla }u)·\mathit{\nu }\mathrm{d}x\mathrm{d}t}\hfill \\ \hfill & {\displaystyle +{\int }_{{\mathrm{\Gamma }}_L^i\times (0,T)}{e}^{Rt}u[{\mathit{\psi }}^{\perp }V-D{V}^{\perp }]·\mathit{\nu }\mathrm{d}x\mathrm{d}t.}\hfill \end{array}$$(32) ).

               $▶$ Localize the geometric centre $G_n$ of the unknown source spatial support ${\overline{\mathit{\omega }}}_n$

                   from (42(42) $$\begin{array}{c}\hfill (P_1)\left\{\begin{array}{c}{\displaystyle x_1^{G_n}=-\frac{V_1}{V{D}^{-1}V}\mathrm{l}n\left({\displaystyle \frac{P_{e^{\mathit{\psi }}}^i}{P_1^i}}\right)-\frac{\mathit{\beta }}{V{D}^{-1}V}\frac{P_{{\mathit{\psi }}^{\perp }}^i}{P_1^i},}\hfill \\ {\displaystyle x_2^{G_n}=-\frac{V_2}{V{D}^{-1}V}\mathrm{l}n\left({\displaystyle \frac{P_{e^{\mathit{\psi }}}^i}{P_1^i}}\right)+\frac{\mathit{\alpha }}{V{D}^{-1}V}\frac{P_{{\mathit{\psi }}^{\perp }}^i}{P_1^i}.}\hfill \end{array}\right.\end{array}$$(42) ) and deduce, as in (43(43) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\overline{\mathit{\lambda }}}_n=\frac{g(\mathit{\eta })}{\mathcal{A}({\mathit{\omega }}_n\cap S(G_n,\mathit{\eta }))},\forall \mathit{\eta }\in (0,{\mathit{\eta }}^i],}\hfill \\ {\displaystyle \text{where:}g(\mathit{\eta })=e^{RT}{\int }_{S(G_n,\mathit{\eta })}u(x,T)\mathrm{d}x+{\int }_{\mathit{\partial }S\times (0,T)}{e}^{Rt}(Vu-D\mathrm{\nabla }u)·\mathit{\nu }\mathrm{d}x\mathrm{d}t.}\hfill \end{array}\end{array}$$(43) )–(45(45) $$\begin{array}{c}\hfill \begin{array}{c}(P_4):\mathcal{A}({\mathit{\omega }}_n)=g_{cont}(\mathit{\eta })/{\overline{\mathit{\lambda }}}_n\text{for}\mathit{\eta }\in [{\mathit{\eta }}_{out},{\mathit{\eta }}^i],\hfill \\ \text{where}{\overline{\mathit{\lambda }}}_n=g_{incl}(\mathit{\eta })\text{for}\mathit{\eta }\in (0,{\mathit{\eta }}_{in}].\hfill \end{array}\end{array}$$(45) ), the elements: ${\mathit{\eta }}_{in},{\mathit{\eta }}_{out},{\overline{\mathit{\lambda }}}_n$ and $\mathcal{A}({\mathit{\omega }}_n)$.

               $▶$ Identify the source intensity function ${\mathit{\lambda }}_n$ by computing ${\mathrm{\Lambda }}_n$ from (55(55) $$\begin{array}{cc}\hfill {\mathit{\lambda }}_n^m& {\displaystyle =\frac{1}{{\displaystyle {\int }_{S(G_n,{\mathit{\eta }}_{mid})}v(x,t_1)\mathrm{d}x}}\left(\frac{Q^i(t_{m+1})}{\mathrm{\Delta }t}-\sum _{k=1}^{m-1}{\mathit{\lambda }}_n^k{\int }_{S(G_n,{\mathit{\eta }}_{mid})}v(x,t_{m+1-k})\mathrm{d}x\right),}\hfill \\ \hfill & \forall m\ge 1.\hfill \end{array}$$(55) ) or (58(58) $$\begin{array}{c}\hfill {\displaystyle \underset{{\mathrm{\Lambda }}_n\in {\mathbb{R}}^{\mathcal{M}}}{min}\frac{1}{2}\Vert A{\mathrm{\Lambda }}_n-\frac{1}{\mathrm{\Delta }t}{\mathbf{Q}}^{\mathbf{i}}{\Vert }_2^2+\frac{r}{2}\Vert {\mathrm{\Lambda }}_n{\Vert }_2^2,}\end{array}$$(58) ).

5. Numerical experiments

We carry out numerical experiments in the case of a monitored domain $\mathrm{\Omega }$ defined by:$$\mathrm{\Omega }:=\{x=(x_1,x_2)\text{such that}0<x_1<L\text{and}0<x_2<\ell \}=(0,L)\times (0,\ell ),$$

where the associated inflow ${\mathrm{\Gamma }}_{in}$, lateral ${\mathrm{\Gamma }}_L$ and outflow ${\mathrm{\Gamma }}_{out}$ boundaries are given by(59) $$\begin{array}{c}\hfill \begin{array}{c}{\mathrm{\Gamma }}_{in}:=\{x=(x_1,x_2)\text{such that}{x}_1=0\text{and}0\le x_2\le \ell \},\hfill \\ {\mathrm{\Gamma }}_{out}:=\{x=(x_1,x_2)\text{such that}{x}_1=L\text{and}0\le x_2\le \ell \},\hfill \\ {\mathrm{\Gamma }}_L:=\{x=(x_1,x_2)\text{such that}{x}_2=0\text{and}0\le x_1\le L\}\hfill \\ \cup \{x=(x_1,x_2)\text{such that}{x}_2=\ell \text{and}0\le x_1\le L\},\hfill \end{array}\end{array}$$(59)

for $L=1000m$ and $\ell =100m$. Then, we set $N_{max}=4$ and define the interfaces ${\mathrm{\Gamma }}_{i=1,\cdots ,N_{max}}$ for recording the state and its flux crossing each source suspected section ${\mathrm{\Omega }}_i\subset \mathrm{\Omega }$ as follows:(60) $$\begin{array}{cc}\hfill {\mathrm{\Gamma }}_i& :=\{x=(x_1,x_2)\text{such that}{x}_1=i\times 200\text{and}0\le x_2\le \ell \},\hfill \\ \hfill & \text{for}i=1,\cdots ,N_{max}.\hfill \end{array}$$(60)

That implies: ${\mathrm{\Omega }}_i=((i-1)\times 200,i\times 200)\times (0,\ell )$ for $i=1,\cdots ,N_{max}+1$. We consider a uniform flow crossing the monitored domain $\mathrm{\Omega }$ defined by a mean velocity vector V perpendicular to the inflow boundary ${\mathrm{\Gamma }}_{in}$, i.e. $V=(V_1,0{)}^{\top }$ and thus, a dispersion tensor reduced to the diagonal matrix $D=\mathrm{d}iag(D_1,D_2)$, see [32,33]. To generate the measurements (15(15) $$\begin{array}{c}\hfill M[F]:=\left\{D\mathrm{\nabla }u·\mathit{\nu }\text{on}\sum _{in};{\Vert V\Vert }_{2}u\text{on}\sum _L;(u,D\mathrm{\nabla }u·\mathit{\nu })\text{on}\sum _{i=1,\cdots ,N_{max}}\right\},\end{array}$$(15) ) defining the observation operator M[F], we solve the forward problem (1(1) $$\begin{array}{c}\hfill L[u](x,t)=F(x,t)\text{in}\mathrm{\Omega }\times (0,T),\end{array}$$(1) )–(2(2) $$\begin{array}{c}\hfill L[u](x,t):={\mathit{\partial }}_{t}u(x,t)-\mathrm{d}iv(D\mathrm{\nabla }u(x,t))+V·\mathrm{\nabla }u(x,t)+Ru(x,t),\end{array}$$(2) ) and (8(8) $$\begin{array}{c}\hfill \begin{array}{c}u(·,0)=0\text{in}\mathrm{\Omega }\hfill \\ u=0\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ D\mathrm{\nabla }u·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\times (0,T)\hfill \end{array}\end{array}$$(8) ) where F is as introduced in (9(9) $$\begin{array}{c}\hfill {\displaystyle F(x,t)=\sum _{n=1}^N{\mathit{\lambda }}_n(t){\mathit{\chi }}_{{\mathit{\omega }}_n}(x)\text{in}\mathrm{\Omega }\times (0,T),}\end{array}$$(9) )–(11(11) $$\begin{array}{c}\hfill {\int }_0^T{\mathit{\lambda }}_n(t)e^{Rt}\mathrm{d}t\ne 0\text{and}\exists T^0\in (0,T)\text{such that}{\mathit{\lambda }}_n=0\text{in}(T^0,T),\forall n=1,\cdots ,N.\end{array}$$(11) ) for $N=3$ time-dependent sources spatially supported at ${\overline{\mathit{\omega }}}_{n=1,2,3}$ and loading the intensity functions defined in $(0,T^0)$ by(61) $$\begin{array}{cc}\hfill {\mathit{\lambda }}_1(t)& {\displaystyle =\frac{4}{{T^0}^2}t(T^0-t),{\mathit{\lambda }}_2(t)={\mathit{\chi }}_{(\frac{T^0}{5},T^0)}(t)\text{and}}\hfill \\ \hfill {\mathit{\lambda }}_3(t)& {\displaystyle =\frac{T^0-t}{T^0}(e^{3-t/T^0}-e^{3-2t/T^0}),}\hfill \end{array}$$(61)

whereas ${\mathit{\lambda }}_{n=1,2,3}(t)=0$ for all $t\ge T^0$. Thus, the source intensity functions are such that(62) $$\begin{array}{cc}\hfill {\displaystyle {\int }_0^T{\mathit{\lambda }}_1(t)\mathrm{d}t}& {\displaystyle =\frac{2T^0}{3},{\int }_0^T{\mathit{\lambda }}_2(t)\mathrm{d}t=\frac{4T^0}{5}\text{and}}\hfill \\ \hfill {\displaystyle {\int }_0^T{\mathit{\lambda }}_3(t)\mathrm{d}t}& {\displaystyle =T^0(e^2-\frac{e^1+e^3}{4}).}\hfill \end{array}$$(62)

As far as the source spatial supports are concerned and in view of $(C_3)$ in (13(13) $$\begin{array}{c}\hfill \begin{array}{c}(C_1){\mathrm{\Gamma }}_i\cap {\mathrm{\Gamma }}_j=\mathrm{\varnothing },\forall i\ne j\in \{0,\cdots ,N_{max}+1\}.\hfill \\ (C_2)|{\mathrm{\Gamma }}_i\cap {\mathrm{\Gamma }}_{L_l}|=|{\mathrm{\Gamma }}_i\cap {\mathrm{\Gamma }}_{L_u}|=1,\forall i=1,\cdots ,N_{max}.\hfill \\ (C_3)\overline{\mathrm{\Omega }}={\cup }_{i=1}^{N_{max}+1}{\overline{\mathrm{\Omega }}}_i\text{where:}{\mathrm{\Omega }}_{N_{max}+1}\subset (\mathrm{\Omega }\backslash {\cup }_{i=1}^N{\overline{\mathit{\omega }}}_n),\hfill \end{array}\end{array}$$(13) ), we use(63) $$\begin{array}{cc}& \bullet {\mathit{\omega }}_1=R(G_1;{\mathit{\eta }}_1=10,{\mathit{\eta }}_2=8):\text{Rectangle centred at}{G}_1=(x_1^{G_1},x_2^{G_1})\hfill \\ \hfill & \text{of sides length}{\mathit{\eta }}_1,{\mathit{\eta }}_2.\hfill \\ \hfill & \bullet {\mathit{\omega }}_2=T(G_2;ABC):\text{Triangle of vertices}A=(a-\mathit{\delta }a,b),B=(a+\mathit{\delta }a,b)\text{and}\hfill \\ \hfill & C=(a,b+\mathit{\delta }b)\text{centred at}{G}_2=(x_1^{G_2}=a,x_2^{G_2}=b+\mathit{\delta }b/3),\text{where}\hfill \\ \hfill & \mathit{\delta }a=10,\mathit{\delta }b=18.\hfill \\ \hfill & \bullet {\mathit{\omega }}_3=S(G_3;\mathit{\eta }=4):\text{Square centred at}{G}_3=(x_1^{G_3},x_2^{G_3})\text{of side length}\mathit{\eta }.\hfill \end{array}$$(63)

In order to illustrate our numerical experiments, we represent all introduced elements regarding the monitored domain $\mathrm{\Omega }$ in the following graphic:

We apply the detection–identification method developed in the previous section by following the steps of Algorithm. Therefore, we start in view of $(C_3)$ in (13(13) $$\begin{array}{c}\hfill \begin{array}{c}(C_1){\mathrm{\Gamma }}_i\cap {\mathrm{\Gamma }}_j=\mathrm{\varnothing },\forall i\ne j\in \{0,\cdots ,N_{max}+1\}.\hfill \\ (C_2)|{\mathrm{\Gamma }}_i\cap {\mathrm{\Gamma }}_{L_l}|=|{\mathrm{\Gamma }}_i\cap {\mathrm{\Gamma }}_{L_u}|=1,\forall i=1,\cdots ,N_{max}.\hfill \\ (C_3)\overline{\mathrm{\Omega }}={\cup }_{i=1}^{N_{max}+1}{\overline{\mathrm{\Omega }}}_i\text{where:}{\mathrm{\Omega }}_{N_{max}+1}\subset (\mathrm{\Omega }\backslash {\cup }_{i=1}^N{\overline{\mathit{\omega }}}_n),\hfill \end{array}\end{array}$$(13) ) by solving numerically the forward problem satisfied by the state u in ${\mathrm{\Omega }}_{N_{max}+1}\times (0,T)$. Afterwards, using the computed data u in ${\mathrm{\Omega }}_{N_{max}+1}\times (0,T)$, we solve the least squares problem (50(50) $$\begin{array}{c}\hfill {\displaystyle \underset{y_0,\cdots ,y_K}{min}\frac{1}{2}\Vert \sum _{k=0}^K{y}_k{e}^{{\mathit{\mu }}_k(T-t)}{e}_k-U{\Vert }_{L^2({\mathrm{\Omega }}_{N_{max}+1}\times (T^{\ast },T))}^2.}\end{array}$$(50) ) to determine the final state $u(·,T)$ in $\mathrm{\Omega }$. To this end, we compute the normalized eigenfunctions ${(e_{nm})}_{n,m\ge 0}$ of the problem (48(48) $$\begin{array}{c}\hfill \left\{\begin{array}{c}-\mathrm{d}iv(D\mathrm{\nabla }e)+\mathit{\rho }e=\mathit{\mu }e\text{in}\mathrm{\Omega }\hfill \\ e=0\text{on}{\mathrm{\Gamma }}_{in}\hfill \\ (D\mathrm{\nabla }e+\frac{1}{2}eV)·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\hfill \end{array}\right.\end{array}$$(48) ) for a mean velocity vector $V=(V_1,0{)}^{\top }$ and a dispersion tensor $D=\mathrm{d}iag(D_1,D_2)$ with $\mathit{\rho }=R+V_1^2/(4D_1)$. We find

Figure 1. Functions $g_{incl}$(a) and $g_{cont}$(b) corresponding to ${\mathit{\omega }}_1$ defined by $G_1$ in Table 3.

(64) $$\begin{array}{c}\hfill {\displaystyle e_{nm}(x_1,x_2)=c_{nm}sin({\mathit{\alpha }}_n{x}_1)cos(\frac{m\mathit{\pi }}{\ell }{x}_2),\forall n,m\ge 0,}\end{array}$$(64)

where for all $n\ge 0$, the coefficient ${\mathit{\alpha }}_n$ is determined from solving the following equation:(65) $$\begin{array}{c}\hfill {\displaystyle \mathrm{t}an({\mathit{\alpha }}_{n}L)+\frac{2D_1}{V_{1}L}{\mathit{\alpha }}_{n}L=0,\text{in}((2n+1)\mathit{\pi }/2,(2n+3)\mathit{\pi }/2)}\end{array}$$(65)

and the normalizing coefficient $c_{nm}$ is defined by(66) $$\begin{array}{c}\hfill c_{nm}=\left\{\begin{array}{c}{\displaystyle \frac{\sqrt{2}}{\sqrt{\ell L}{\mathit{\beta }}_n}\text{if}m=0}\hfill \\ {\displaystyle \frac{2}{\sqrt{\ell L}{\mathit{\beta }}_n}\text{if}m\ne 0}\hfill \end{array}\right.\text{where}{\mathit{\beta }}_n=\sqrt{{\displaystyle 1-\frac{sin(2{\mathit{\alpha }}_{n}L)}{2{\mathit{\alpha }}_{n}L}}}.\end{array}$$(66)

Figure 2. Functions $g_{incl}$(a) and $g_{cont}$(b) corresponding to ${\mathit{\omega }}_2$ defined by $G_2$ in Table 3.

Furthermore, the eigenvalue ${\mathit{\mu }}_{nm}$ associated to the eigenfunction $e_{nm}$ is given by ${\mathit{\mu }}_{nm}=\mathit{\rho }+D_1{\mathit{\alpha }}_n^2+D_2(m\mathit{\pi }/\ell {)}^2$. To expand the state u solution of the problem (1(1) $$\begin{array}{c}\hfill L[u](x,t)=F(x,t)\text{in}\mathrm{\Omega }\times (0,T),\end{array}$$(1) )–(2(2) $$\begin{array}{c}\hfill L[u](x,t):={\mathit{\partial }}_{t}u(x,t)-\mathrm{d}iv(D\mathrm{\nabla }u(x,t))+V·\mathrm{\nabla }u(x,t)+Ru(x,t),\end{array}$$(2) ) and (8(8) $$\begin{array}{c}\hfill \begin{array}{c}u(·,0)=0\text{in}\mathrm{\Omega }\hfill \\ u=0\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ D\mathrm{\nabla }u·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\times (0,T)\hfill \end{array}\end{array}$$(8) )–(9(9) $$\begin{array}{c}\hfill {\displaystyle F(x,t)=\sum _{n=1}^N{\mathit{\lambda }}_n(t){\mathit{\chi }}_{{\mathit{\omega }}_n}(x)\text{in}\mathrm{\Omega }\times (0,T),}\end{array}$$(9) ) in the orthonormal family ${\{e_{nm}\}}_{n,m\ge 0}$, we use the earlier introduced change of variables $U(x;t)=e^{\mathit{\psi }(x)/2}u(x;t)$ for all $x=(x_1,x_2)\in (0,L)\times (0,\ell )$ and $t\in (0,T)$. It follows that the variable U solves the following system:(67) $$\begin{array}{c}\hfill \begin{array}{c}{\mathit{\partial }}_{t}U-D_1{\mathit{\partial }}_{x_1{x}_1}^{2}U-D_2{\mathit{\partial }}_{x_2{x}_2}^{2}U+\mathit{\rho }U\hfill \\ {\displaystyle =e^{\mathit{\psi }(x)/2}{\sum }_{k=1}^3{\mathit{\lambda }}_k(t){\mathit{\chi }}_{{\mathit{\omega }}_k}(x)\text{in}(0,L)\times (0,\ell )\times (0,T),}\hfill \\ U(x_1,x_2;0)=0\text{in}(0,L)\times (0,\ell ),\hfill \\ U(0,x_2;t)=0\text{on}(0,\ell )\times (0,T),\hfill \\ D_2{\mathit{\partial }}_{x_2}U(x_1,0;t)=D_2{\mathit{\partial }}_{x_2}U(x_1,\ell ,t)=0\text{on}(0,L)\times (0,T),\hfill \\ {\displaystyle D_1{\mathit{\partial }}_{x_1}U(L,x_2;t)+\frac{V_1}{2}U(L,x_2;t)=0\text{on}(0,\ell )\times (0,T),}\hfill \end{array}\end{array}$$(67)

where $\mathit{\psi }(x)=-V_1{x}_1/D_1$. From setting $U(x,t)={\sum }_{n,m\ge 0}{a}_{nm}(t)e_{nm}(x)$ for all $x=(x_1,x_2)\in (0,L)\times (0,\ell )$ and $t\in (0,T)$ it follows that the coefficient $a_{nm}$ solves(68) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle a_{nm}^{\prime }(t)+{\mathit{\mu }}_{nm}{a}_{nm}(t)={\sum }_{k=1}^3{\mathit{\lambda }}_k(t){\int }_{{\mathit{\omega }}_k}{e}^{\mathit{\psi }(x)/2}{e}_{nm}(x)\mathrm{d}x\text{in}(0,T),}\hfill \\ a_{nm}(0)=0\hfill \end{array}\right.\end{array}$$(68)

for all $n,m\ge 0$. Therefore, by solving (68(68) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle a_{nm}^{\prime }(t)+{\mathit{\mu }}_{nm}{a}_{nm}(t)={\sum }_{k=1}^3{\mathit{\lambda }}_k(t){\int }_{{\mathit{\omega }}_k}{e}^{\mathit{\psi }(x)/2}{e}_{nm}(x)\mathrm{d}x\text{in}(0,T),}\hfill \\ a_{nm}(0)=0\hfill \end{array}\right.\end{array}$$(68) ) and using $u=e^{-\mathit{\psi }(x)/2}U$ we obtain for all $x=(x_1,x_2)\in (0,L)\times (0,\ell )$ and $t\in (0,T)$,(69) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle u(x;t)=e^{\frac{V_1}{2D_1}{x}_1}{\sum }_{n,m\ge 0}{a}_{nm}(t)e_{nm}(x),}\hfill \\ {\displaystyle \text{where}{a}_{nm}(t)={\sum }_{k=1}^3{\int }_0^t{\mathit{\lambda }}_k(\mathit{\eta })e^{-{\mathit{\mu }}_{nm}(t-\mathit{\eta })}d\mathit{\eta }{\int }_{{\mathit{\omega }}_k}{e}^{-\frac{V_1}{2D_1}{x}_1}{e}_{nm}(x)\mathrm{d}x.}\hfill \end{array}\end{array}$$(69)

Then, we truncate the double series defining the state u in (69(69) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle u(x;t)=e^{\frac{V_1}{2D_1}{x}_1}{\sum }_{n,m\ge 0}{a}_{nm}(t)e_{nm}(x),}\hfill \\ {\displaystyle \text{where}{a}_{nm}(t)={\sum }_{k=1}^3{\int }_0^t{\mathit{\lambda }}_k(\mathit{\eta })e^{-{\mathit{\mu }}_{nm}(t-\mathit{\eta })}d\mathit{\eta }{\int }_{{\mathit{\omega }}_k}{e}^{-\frac{V_1}{2D_1}{x}_1}{e}_{nm}(x)\mathrm{d}x.}\hfill \end{array}\end{array}$$(69) ) by considering the first $N\times M$ terms and generate the simulated observations defining the operator M[F] introduced in (15(15) $$\begin{array}{c}\hfill M[F]:=\left\{D\mathrm{\nabla }u·\mathit{\nu }\text{on}\sum _{in};{\Vert V\Vert }_{2}u\text{on}\sum _L;(u,D\mathrm{\nabla }u·\mathit{\nu })\text{on}\sum _{i=1,\cdots ,N_{max}}\right\},\end{array}$$(15) ) from using the three time-dependent intensity functions ${\mathit{\lambda }}_{k=1,2,3}$ introduced in (61(61) $$\begin{array}{cc}\hfill {\mathit{\lambda }}_1(t)& {\displaystyle =\frac{4}{{T^0}^2}t(T^0-t),{\mathit{\lambda }}_2(t)={\mathit{\chi }}_{(\frac{T^0}{5},T^0)}(t)\text{and}}\hfill \\ \hfill {\mathit{\lambda }}_3(t)& {\displaystyle =\frac{T^0-t}{T^0}(e^{3-t/T^0}-e^{3-2t/T^0}),}\hfill \end{array}$$(61) ) and their associated source spatial supports ${\overline{\mathit{\omega }}}_{k=1,2,3}$ given in (63(63) $$\begin{array}{cc}& \bullet {\mathit{\omega }}_1=R(G_1;{\mathit{\eta }}_1=10,{\mathit{\eta }}_2=8):\text{Rectangle centred at}{G}_1=(x_1^{G_1},x_2^{G_1})\hfill \\ \hfill & \text{of sides length}{\mathit{\eta }}_1,{\mathit{\eta }}_2.\hfill \\ \hfill & \bullet {\mathit{\omega }}_2=T(G_2;ABC):\text{Triangle of vertices}A=(a-\mathit{\delta }a,b),B=(a+\mathit{\delta }a,b)\text{and}\hfill \\ \hfill & C=(a,b+\mathit{\delta }b)\text{centred at}{G}_2=(x_1^{G_2}=a,x_2^{G_2}=b+\mathit{\delta }b/3),\text{where}\hfill \\ \hfill & \mathit{\delta }a=10,\mathit{\delta }b=18.\hfill \\ \hfill & \bullet {\mathit{\omega }}_3=S(G_3;\mathit{\eta }=4):\text{Square centred at}{G}_3=(x_1^{G_3},x_2^{G_3})\text{of side length}\mathit{\eta }.\hfill \end{array}$$(63) ). We carry out numerical experiments using a final monitoring time $T=14400s$ (4 hours), a time active limit in (11(11) $$\begin{array}{c}\hfill {\int }_0^T{\mathit{\lambda }}_n(t)e^{Rt}\mathrm{d}t\ne 0\text{and}\exists T^0\in (0,T)\text{such that}{\mathit{\lambda }}_n=0\text{in}(T^0,T),\forall n=1,\cdots ,N.\end{array}$$(11) ), $T^0=3T/4$ and the flow coefficients $D_1=29m^2{s}^{-1}$, $D_2=5m^2{s}^{-1}$, $V_1=0.10m{s}^{-1}$, $R={10}^{-5}{s}^{-1}$. For simplicity, we set $T^{\ast }=T^0$ and identify the required final state $u(·,T)$ in $\mathrm{\Omega }$ by solving using the conjugate gradient method the least squares problem (50(50) $$\begin{array}{c}\hfill {\displaystyle \underset{y_0,\cdots ,y_K}{min}\frac{1}{2}\Vert \sum _{k=0}^K{y}_k{e}^{{\mathit{\mu }}_k(T-t)}{e}_k-U{\Vert }_{L^2({\mathrm{\Omega }}_{N_{max}+1}\times (T^{\ast },T))}^2.}\end{array}$$(50) )–(51(51) $$\begin{array}{c}\hfill u(x,T)\approx e^{-\frac{1}{2}\mathit{\psi }(x)}\sum _{k=0}^K{y}_k{e}_k(x),x\in \mathrm{\Omega }.\end{array}$$(51) ).

We start by presenting some numerical experiments on the established active source detection procedure: We generate simulated measures M[F] using three different sources loading the intensity functions ${\mathit{\lambda }}_{n=1,2,3}$ introduced in (61(61) $$\begin{array}{cc}\hfill {\mathit{\lambda }}_1(t)& {\displaystyle =\frac{4}{{T^0}^2}t(T^0-t),{\mathit{\lambda }}_2(t)={\mathit{\chi }}_{(\frac{T^0}{5},T^0)}(t)\text{and}}\hfill \\ \hfill {\mathit{\lambda }}_3(t)& {\displaystyle =\frac{T^0-t}{T^0}(e^{3-t/T^0}-e^{3-2t/T^0}),}\hfill \end{array}$$(61) ) and by varying, in view of (14(14) $$\begin{array}{cc}& \forall i\in \{1,\cdots ,N_{max}\},\text{there exists}\underline{atmost}\text{one element}n\in \{1,\cdots ,N\}\hfill \\ \hfill & \text{such that}{\mathit{\omega }}_n\subset {\mathrm{\Omega }}_i.\hfill \end{array}$$(14) ), the locations of the geometric centres $G_{n=1,2,3}$ defining their spatial supports ${\overline{\mathit{\omega }}}_{n=1,2,3}$ in (63(63) $$\begin{array}{cc}& \bullet {\mathit{\omega }}_1=R(G_1;{\mathit{\eta }}_1=10,{\mathit{\eta }}_2=8):\text{Rectangle centred at}{G}_1=(x_1^{G_1},x_2^{G_1})\hfill \\ \hfill & \text{of sides length}{\mathit{\eta }}_1,{\mathit{\eta }}_2.\hfill \\ \hfill & \bullet {\mathit{\omega }}_2=T(G_2;ABC):\text{Triangle of vertices}A=(a-\mathit{\delta }a,b),B=(a+\mathit{\delta }a,b)\text{and}\hfill \\ \hfill & C=(a,b+\mathit{\delta }b)\text{centred at}{G}_2=(x_1^{G_2}=a,x_2^{G_2}=b+\mathit{\delta }b/3),\text{where}\hfill \\ \hfill & \mathit{\delta }a=10,\mathit{\delta }b=18.\hfill \\ \hfill & \bullet {\mathit{\omega }}_3=S(G_3;\mathit{\eta }=4):\text{Square centred at}{G}_3=(x_1^{G_3},x_2^{G_3})\text{of side length}\mathit{\eta }.\hfill \end{array}$$(63) ). For each used locations of the geometric centres $G_{n=1,2,3}$ to generate new simulated measures, we present in a same table the Source Detection coefficient, as in Algorithm, $P_1^i/T$ computed at each suspected source section ${\mathrm{\Omega }}_i$ for $i=1,\cdots ,N_{max}=4$, as well as the identified geometric centre $G_n$, determined from (42(42) $$\begin{array}{c}\hfill (P_1)\left\{\begin{array}{c}{\displaystyle x_1^{G_n}=-\frac{V_1}{V{D}^{-1}V}\mathrm{l}n\left({\displaystyle \frac{P_{e^{\mathit{\psi }}}^i}{P_1^i}}\right)-\frac{\mathit{\beta }}{V{D}^{-1}V}\frac{P_{{\mathit{\psi }}^{\perp }}^i}{P_1^i},}\hfill \\ {\displaystyle x_2^{G_n}=-\frac{V_2}{V{D}^{-1}V}\mathrm{l}n\left({\displaystyle \frac{P_{e^{\mathit{\psi }}}^i}{P_1^i}}\right)+\frac{\mathit{\alpha }}{V{D}^{-1}V}\frac{P_{{\mathit{\psi }}^{\perp }}^i}{P_1^i}.}\hfill \end{array}\right.\end{array}$$(42) ), defining the spatial support of the detected source occurring in ${\mathrm{\Omega }}_i$. We indicate in the caption of each table the locations of the geometric centres $G_{n=1,2,3}$ in (63(63) $$\begin{array}{cc}& \bullet {\mathit{\omega }}_1=R(G_1;{\mathit{\eta }}_1=10,{\mathit{\eta }}_2=8):\text{Rectangle centred at}{G}_1=(x_1^{G_1},x_2^{G_1})\hfill \\ \hfill & \text{of sides length}{\mathit{\eta }}_1,{\mathit{\eta }}_2.\hfill \\ \hfill & \bullet {\mathit{\omega }}_2=T(G_2;ABC):\text{Triangle of vertices}A=(a-\mathit{\delta }a,b),B=(a+\mathit{\delta }a,b)\text{and}\hfill \\ \hfill & C=(a,b+\mathit{\delta }b)\text{centred at}{G}_2=(x_1^{G_2}=a,x_2^{G_2}=b+\mathit{\delta }b/3),\text{where}\hfill \\ \hfill & \mathit{\delta }a=10,\mathit{\delta }b=18.\hfill \\ \hfill & \bullet {\mathit{\omega }}_3=S(G_3;\mathit{\eta }=4):\text{Square centred at}{G}_3=(x_1^{G_3},x_2^{G_3})\text{of side length}\mathit{\eta }.\hfill \end{array}$$(63) ) used to generate the simulated measures M[F]. We carried out numerical results using different truncation values of $N=M$ and observed that the accuracy on the computed $P_1^i$ as well as on the localized geometric centres $G_{n=1,\cdots ,3}$ is improved as $N=M$ increase. The results presented in the following tables are obtained with $N=M=200$.

Table 1. Source detection: simulation using $G_1=(97,70);G_2=(273,7);G_3=(514,96)$.

${\mathrm{\Omega }}_i=((i-1)\times 200,i\times 200)\times (0,\ell )$	${\mathrm{\Omega }}_1$	${\mathrm{\Omega }}_2$	${\mathrm{\Omega }}_3$	${\mathrm{\Omega }}_4$
Detection coefficient: $P_1^i/T$	42.22	115.23	21.35	-0.05
Identified geometric centre $G_n$	(96.88, 69.99)	(272.90, 6.97)	(513.89, 95.99)	No source

Table 2. Source detection: simulation using $G_1=(43,6);G_2=(327,86);G_3=(716,3)$.

${\mathrm{\Omega }}_i=((i-1)\times 200,i\times 200)\times (0,\ell )$	${\mathrm{\Omega }}_1$	${\mathrm{\Omega }}_2$	${\mathrm{\Omega }}_3$	${\mathrm{\Omega }}_4$
Detection coefficient: $P_1^i/T$	42.19	115.25	-0.03	21.35
Identified geometric centre $G_n$	(42.99, 5.99)	(326.95, 86.01)	No source	(715.87, 2.99)

Table 3. Source detection: simulation using $G_1=(160,84);G_2=(415,20);G_3=(695,40)$.

${\mathrm{\Omega }}_i=((i-1)\times 200,i\times 200)\times (0,\ell )$	${\mathrm{\Omega }}_1$	${\mathrm{\Omega }}_2$	${\mathrm{\Omega }}_3$	${\mathrm{\Omega }}_4$
Detection coefficient: $P_1^i/T$	42.25	0.036	115.18	21.26
Identified geometric centre $G_n$	(159.99, 83.99)	No source	(414.95, 20.01)	(694.95, 39.99)

Table 4. Source detection: simulation using $G_1=(304,61);G_2=(496,7);G_3=(623,97)$.

${\mathrm{\Omega }}_i=((i-1)\times 200,i\times 200)\times (0,\ell )$	${\mathrm{\Omega }}_1$	${\mathrm{\Omega }}_2$	${\mathrm{\Omega }}_3$	${\mathrm{\Omega }}_4$
Detection coefficient: $P_1^i/T$	$-7.0E-5$	42.22	115.20	21.30
Identified geometric centre $G_n$	No source	(303.96, 60.98)	(495.91, 6.95)	(622.97, 96.98)

Figure 3. Functions $g_{incl}$(a) and $g_{cont}$(b) corresponding to ${\mathit{\omega }}_3$ defined by $G_3$ in Table 3.

The analysis of the numerical results presented in Tables 1–4 shows that the established active source detection procedure defined by computing the detection coefficient $P_1^i/T$ from (31(31) $$\begin{array}{c}\hfill {\overline{\mathit{\lambda }}}_n\mathcal{A}({\mathit{\omega }}_n)=P_1^i,{\overline{\mathit{\lambda }}}_n{\int }_{{\mathit{\omega }}_n}{e}^{\mathit{\psi }(x)}\mathrm{d}x=P_{e^{\mathit{\psi }}}^i\text{and}{\overline{\mathit{\lambda }}}_n{\int }_{{\mathit{\omega }}_n}{\mathit{\psi }}^{\perp }(x)\mathrm{d}x=P_{{\mathit{\psi }}^{\perp }}^i,\end{array}$$(31) )–(32(32) $$\begin{array}{cc}\hfill P_1^i& {\displaystyle =e^{RT}{\int }_{{\mathrm{\Omega }}_i}u(x,T)\mathrm{d}x+{\int }_{({\mathrm{\Gamma }}_{i-1}\cup {\mathrm{\Gamma }}_i)\times (0,T)}{e}^{Rt}(uV-D\mathrm{\nabla }u)·\mathit{\nu }\mathrm{d}x\mathrm{d}t}\hfill \\ \hfill & {\displaystyle +{\int }_{{\mathrm{\Gamma }}_L^i\times (0,T)}{e}^{Rt}uV·\mathit{\nu }\mathrm{d}x\mathrm{d}t,}\hfill \\ \hfill P_{e^{\mathit{\psi }}}^i& {\displaystyle =e^{RT}{\int }_{{\mathrm{\Omega }}_i}{e}^{\mathit{\psi }(x)}u(x,T)\mathrm{d}x-{\int }_{({\mathrm{\Gamma }}_{i-1}\cup {\mathrm{\Gamma }}_i)\times (0,T)}{e}^{\mathit{\psi }+Rt}D\mathrm{\nabla }u·\mathit{\nu }\mathrm{d}x\mathrm{d}t,}\hfill \\ \hfill P_{{\mathit{\psi }}^{\perp }}^i& {\displaystyle =e^{RT}{\int }_{{\mathrm{\Omega }}_i}{\mathit{\psi }}^{\perp }(x)u(x,T)\mathrm{d}x}\hfill \\ \hfill & {\displaystyle +{\int }_{({\mathrm{\Gamma }}_{i-1}\cup {\mathrm{\Gamma }}_i)\times (0,T)}{e}^{Rt}(u[{\mathit{\psi }}^{\perp }V-D{V}^{\perp }]-{\mathit{\psi }}^{\perp }D\mathrm{\nabla }u)·\mathit{\nu }\mathrm{d}x\mathrm{d}t}\hfill \\ \hfill & {\displaystyle +{\int }_{{\mathrm{\Gamma }}_L^i\times (0,T)}{e}^{Rt}u[{\mathit{\psi }}^{\perp }V-D{V}^{\perp }]·\mathit{\nu }\mathrm{d}x\mathrm{d}t.}\hfill \end{array}$$(32) ) for each source suspected section ${\mathrm{\Omega }}_{i=1,\cdots ,N_{max}}$ of the monitored domain $\mathrm{\Omega }$ enables to distinguish clearly a section ${\mathrm{\Omega }}_i$ where there is an occurring source from another where there is no active source. In addition, once an active source ${\mathit{\lambda }}_n{\mathit{\chi }}_{{\mathit{\omega }}_n}$ is detected to be occurring in ${\mathrm{\Omega }}_i\subset \mathrm{\Omega }$ and as far as property $(P_1)$ in (42(42) $$\begin{array}{c}\hfill (P_1)\left\{\begin{array}{c}{\displaystyle x_1^{G_n}=-\frac{V_1}{V{D}^{-1}V}\mathrm{l}n\left({\displaystyle \frac{P_{e^{\mathit{\psi }}}^i}{P_1^i}}\right)-\frac{\mathit{\beta }}{V{D}^{-1}V}\frac{P_{{\mathit{\psi }}^{\perp }}^i}{P_1^i},}\hfill \\ {\displaystyle x_2^{G_n}=-\frac{V_2}{V{D}^{-1}V}\mathrm{l}n\left({\displaystyle \frac{P_{e^{\mathit{\psi }}}^i}{P_1^i}}\right)+\frac{\mathit{\alpha }}{V{D}^{-1}V}\frac{P_{{\mathit{\psi }}^{\perp }}^i}{P_1^i}.}\hfill \end{array}\right.\end{array}$$(42) ) is concerned, the numerical results in Tables 1–4 show that the localization of the geometric centre $G_n$ defining the unknown spatial support ${\overline{\mathit{\omega }}}_n$ of the detected source is accurate.

Besides, to verify the upper and lower bounds obtained in (33(33) $$\begin{array}{c}\hfill {\displaystyle e^{-RT}{P}_1^i\le e^{-R{T}^0}{P}_1^i\le \mathcal{A}({\mathit{\omega }}_n){\int }_0^T{\mathit{\lambda }}_n(t)\mathrm{d}t\le P_1^i.}\end{array}$$(33) ) framing the total amount discharged by each detected source ${\mathit{\lambda }}_n{\mathit{\chi }}_{{\mathit{\omega }}_n}$ occurring in ${\mathrm{\Omega }}_i$, we use (62(62) $$\begin{array}{cc}\hfill {\displaystyle {\int }_0^T{\mathit{\lambda }}_1(t)\mathrm{d}t}& {\displaystyle =\frac{2T^0}{3},{\int }_0^T{\mathit{\lambda }}_2(t)\mathrm{d}t=\frac{4T^0}{5}\text{and}}\hfill \\ \hfill {\displaystyle {\int }_0^T{\mathit{\lambda }}_3(t)\mathrm{d}t}& {\displaystyle =T^0(e^2-\frac{e^1+e^3}{4}).}\hfill \end{array}$$(62) )–(63(63) $$\begin{array}{cc}& \bullet {\mathit{\omega }}_1=R(G_1;{\mathit{\eta }}_1=10,{\mathit{\eta }}_2=8):\text{Rectangle centred at}{G}_1=(x_1^{G_1},x_2^{G_1})\hfill \\ \hfill & \text{of sides length}{\mathit{\eta }}_1,{\mathit{\eta }}_2.\hfill \\ \hfill & \bullet {\mathit{\omega }}_2=T(G_2;ABC):\text{Triangle of vertices}A=(a-\mathit{\delta }a,b),B=(a+\mathit{\delta }a,b)\text{and}\hfill \\ \hfill & C=(a,b+\mathit{\delta }b)\text{centred at}{G}_2=(x_1^{G_2}=a,x_2^{G_2}=b+\mathit{\delta }b/3),\text{where}\hfill \\ \hfill & \mathit{\delta }a=10,\mathit{\delta }b=18.\hfill \\ \hfill & \bullet {\mathit{\omega }}_3=S(G_3;\mathit{\eta }=4):\text{Square centred at}{G}_3=(x_1^{G_3},x_2^{G_3})\text{of side length}\mathit{\eta }.\hfill \end{array}$$(63) ) to compute analytically the total amount loaded in ${\mathrm{\Omega }}_i$ by the involved source and determine from the computed coefficient $P_1^i$: the lower bound $e^{-RT}{P}_1^i$ and the upper bound $P_1^i$ obtained in (33(33) $$\begin{array}{c}\hfill {\displaystyle e^{-RT}{P}_1^i\le e^{-R{T}^0}{P}_1^i\le \mathcal{A}({\mathit{\omega }}_n){\int }_0^T{\mathit{\lambda }}_n(t)\mathrm{d}t\le P_1^i.}\end{array}$$(33) ). We carry out this verification, for example, on the results presented in Table 4:(70) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle e^{-RT}{P}_1^2=36.55T\le \mathcal{A}({\mathit{\omega }}_1){\int }_0^T{\mathit{\lambda }}_1(t)\mathrm{d}t=40T\le P_1^2=42.22T,}\hfill \\ {\displaystyle e^{-RT}{P}_1^3=99.75T\le \mathcal{A}({\mathit{\omega }}_2){\int }_0^T{\mathit{\lambda }}_2(t)\mathrm{d}t=108T\le P_1^3=115.20T,}\hfill \\ {\displaystyle e^{-RT}{P}_1^4=18.44T\le \mathcal{A}({\mathit{\omega }}_3){\int }_0^T{\mathit{\lambda }}_3(t)\mathrm{d}t=20.25T\le P_1^4=21.30T.}\hfill \end{array}\right.\end{array}$$(70)

From (70(70) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle e^{-RT}{P}_1^2=36.55T\le \mathcal{A}({\mathit{\omega }}_1){\int }_0^T{\mathit{\lambda }}_1(t)\mathrm{d}t=40T\le P_1^2=42.22T,}\hfill \\ {\displaystyle e^{-RT}{P}_1^3=99.75T\le \mathcal{A}({\mathit{\omega }}_2){\int }_0^T{\mathit{\lambda }}_2(t)\mathrm{d}t=108T\le P_1^3=115.20T,}\hfill \\ {\displaystyle e^{-RT}{P}_1^4=18.44T\le \mathcal{A}({\mathit{\omega }}_3){\int }_0^T{\mathit{\lambda }}_3(t)\mathrm{d}t=20.25T\le P_1^4=21.30T.}\hfill \end{array}\right.\end{array}$$(70) ), we observe that the lower and upper bounds established in (33(33) $$\begin{array}{c}\hfill {\displaystyle e^{-RT}{P}_1^i\le e^{-R{T}^0}{P}_1^i\le \mathcal{A}({\mathit{\omega }}_n){\int }_0^T{\mathit{\lambda }}_n(t)\mathrm{d}t\le P_1^i.}\end{array}$$(33) ) framing the total amount discharged in ${\mathrm{\Omega }}_i$ by the detected source are effective. Moreover, the upper bound $P_1^i$ is nearer to the exact value of the total amount discharged in ${\mathrm{\Omega }}_i$. Actually, from the first equation in (31(31) $$\begin{array}{c}\hfill {\overline{\mathit{\lambda }}}_n\mathcal{A}({\mathit{\omega }}_n)=P_1^i,{\overline{\mathit{\lambda }}}_n{\int }_{{\mathit{\omega }}_n}{e}^{\mathit{\psi }(x)}\mathrm{d}x=P_{e^{\mathit{\psi }}}^i\text{and}{\overline{\mathit{\lambda }}}_n{\int }_{{\mathit{\omega }}_n}{\mathit{\psi }}^{\perp }(x)\mathrm{d}x=P_{{\mathit{\psi }}^{\perp }}^i,\end{array}$$(31) ) and since ${\overline{\mathit{\lambda }}}_n={\int }_0^T{e}^{Rt}{\mathit{\lambda }}_n(t)\mathrm{d}t$ it follows that the coefficient $P_1^i$ yields for all R sufficiently small an approximation of the total amount discharged in ${\mathrm{\Omega }}_i$ by the occurring source ${\mathit{\lambda }}_n{\mathit{\chi }}_{{\mathit{\omega }}_n}$.

The second part of our numerical experiments concerns the properties $(P_2)$ and $(P_3)$. More specifically, once an active source is detected to be occurring in a suspected region ${\mathrm{\Omega }}_i\subset \mathrm{\Omega }$ and the geometric centre $G_n$ of its unknown spatial support ${\overline{\mathit{\omega }}}_n\subset {\mathrm{\Omega }}_i$ is already localized using $(P_1)$, we aim to determine the biggest side length ${\mathit{\eta }}_{in}$ and the smallest side length ${\mathit{\eta }}_{out}$ that yield $S(G_n,{\mathit{\eta }}_{in})\subseteq {\mathit{\omega }}_n\subseteq S(G_n,{\mathit{\eta }}_{out})$, where $S(G_n,\mathit{\eta })$ is the square of side length $\mathit{\eta }$ centred at the same localized geometric centre $G_n$ of ${\mathit{\omega }}_n$. Moreover, as already established in (43(43) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\overline{\mathit{\lambda }}}_n=\frac{g(\mathit{\eta })}{\mathcal{A}({\mathit{\omega }}_n\cap S(G_n,\mathit{\eta }))},\forall \mathit{\eta }\in (0,{\mathit{\eta }}^i],}\hfill \\ {\displaystyle \text{where:}g(\mathit{\eta })=e^{RT}{\int }_{S(G_n,\mathit{\eta })}u(x,T)\mathrm{d}x+{\int }_{\mathit{\partial }S\times (0,T)}{e}^{Rt}(Vu-D\mathrm{\nabla }u)·\mathit{\nu }\mathrm{d}x\mathrm{d}t.}\hfill \end{array}\end{array}$$(43) )–(45(45) $$\begin{array}{c}\hfill \begin{array}{c}(P_4):\mathcal{A}({\mathit{\omega }}_n)=g_{cont}(\mathit{\eta })/{\overline{\mathit{\lambda }}}_n\text{for}\mathit{\eta }\in [{\mathit{\eta }}_{out},{\mathit{\eta }}^i],\hfill \\ \text{where}{\overline{\mathit{\lambda }}}_n=g_{incl}(\mathit{\eta })\text{for}\mathit{\eta }\in (0,{\mathit{\eta }}_{in}].\hfill \end{array}\end{array}$$(45) ), the determination of ${\mathit{\eta }}_{in}$ and ${\mathit{\eta }}_{out}$ can be achieved from analysing the curves of the two functions $g_{incl}$ and $g_{cont}$ in (43(43) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\overline{\mathit{\lambda }}}_n=\frac{g(\mathit{\eta })}{\mathcal{A}({\mathit{\omega }}_n\cap S(G_n,\mathit{\eta }))},\forall \mathit{\eta }\in (0,{\mathit{\eta }}^i],}\hfill \\ {\displaystyle \text{where:}g(\mathit{\eta })=e^{RT}{\int }_{S(G_n,\mathit{\eta })}u(x,T)\mathrm{d}x+{\int }_{\mathit{\partial }S\times (0,T)}{e}^{Rt}(Vu-D\mathrm{\nabla }u)·\mathit{\nu }\mathrm{d}x\mathrm{d}t.}\hfill \end{array}\end{array}$$(43) )–(44(44) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle g_{incl}(\mathit{\eta })=\frac{g(\mathit{\eta })}{\mathcal{A}(S(G_n,\mathit{\eta }))}\text{and}{g}_{cont}(\mathit{\eta })=g(\mathit{\eta }).}\hfill \end{array}\end{array}$$(44) ) defined from the measures in M[F] taken on $\mathit{\partial }{\mathrm{\Omega }}_i\times (0,T)$. To this end, we use for example the results presented in Table 3 and draw for each detected source occurring in ${\mathrm{\Omega }}_i$ the curves of the two corresponding functions $g_{incl}$ and $g_{cont}$ defined in (43(43) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\overline{\mathit{\lambda }}}_n=\frac{g(\mathit{\eta })}{\mathcal{A}({\mathit{\omega }}_n\cap S(G_n,\mathit{\eta }))},\forall \mathit{\eta }\in (0,{\mathit{\eta }}^i],}\hfill \\ {\displaystyle \text{where:}g(\mathit{\eta })=e^{RT}{\int }_{S(G_n,\mathit{\eta })}u(x,T)\mathrm{d}x+{\int }_{\mathit{\partial }S\times (0,T)}{e}^{Rt}(Vu-D\mathrm{\nabla }u)·\mathit{\nu }\mathrm{d}x\mathrm{d}t.}\hfill \end{array}\end{array}$$(43) )–(44(44) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle g_{incl}(\mathit{\eta })=\frac{g(\mathit{\eta })}{\mathcal{A}(S(G_n,\mathit{\eta }))}\text{and}{g}_{cont}(\mathit{\eta })=g(\mathit{\eta }).}\hfill \end{array}\end{array}$$(44) ) and approximated later on in Step 2. Then, in a separated graphic we represent the sought source spatial support ${\overline{\mathit{\omega }}}_n$ in the red colour and draw $S(G_n,{\mathit{\eta }}_{in})$, $S(G_n,{\mathit{\eta }}_{out})$, where ${\mathit{\eta }}_{in}$ and ${\mathit{\eta }}_{out}$ are deduced from the two curves of $g_{incl}$ and $g_{cont}$ given just above. We start by presenting the obtained results concerning the source spatial support ${\overline{\mathit{\omega }}}_1$ defined in (63(63) $$\begin{array}{cc}& \bullet {\mathit{\omega }}_1=R(G_1;{\mathit{\eta }}_1=10,{\mathit{\eta }}_2=8):\text{Rectangle centred at}{G}_1=(x_1^{G_1},x_2^{G_1})\hfill \\ \hfill & \text{of sides length}{\mathit{\eta }}_1,{\mathit{\eta }}_2.\hfill \\ \hfill & \bullet {\mathit{\omega }}_2=T(G_2;ABC):\text{Triangle of vertices}A=(a-\mathit{\delta }a,b),B=(a+\mathit{\delta }a,b)\text{and}\hfill \\ \hfill & C=(a,b+\mathit{\delta }b)\text{centred at}{G}_2=(x_1^{G_2}=a,x_2^{G_2}=b+\mathit{\delta }b/3),\text{where}\hfill \\ \hfill & \mathit{\delta }a=10,\mathit{\delta }b=18.\hfill \\ \hfill & \bullet {\mathit{\omega }}_3=S(G_3;\mathit{\eta }=4):\text{Square centred at}{G}_3=(x_1^{G_3},x_2^{G_3})\text{of side length}\mathit{\eta }.\hfill \end{array}$$(63) ) i.e. ${\mathit{\omega }}_1$ is the rectangle centred at $G_1=(160,84)$ and of sides lenth ${\mathit{\eta }}_1=10$ following the $x_1$-axis and ${\mathit{\eta }}_2=8$ following the $x_2$-axis. For this first occurring source, we give in two graphics the curves of $g_{incl}$ and $g_{cont}$ drew for different values of $N=M$.

Figure 4. Identification of ${\mathit{\lambda }}_1$: (a) Noise $3\%$; Error 0.18, (b) Noise $10\%$; Error 0.20.

Figure 5. Identification of ${\mathit{\lambda }}_2$: (a) Noise $3\%$; Error 0.45, (b) Noise $10\%$; Error 0.48.

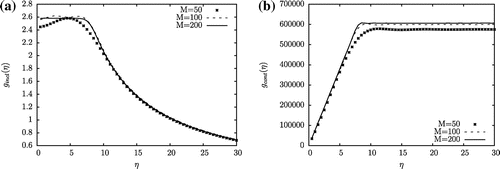
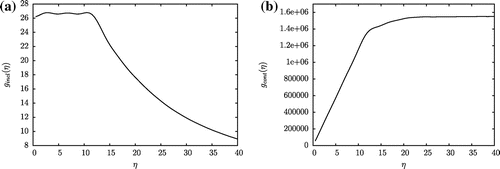
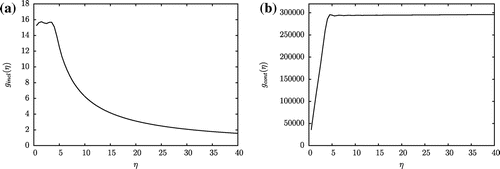
The numerical results presented in Figures 2 and 3 were obtained for $N=M=100$. The analysis of the experiments in Figures 1–3 shows that the two functions $g_{incl}$ and $g_{cont}$ defined in (43(43) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\overline{\mathit{\lambda }}}_n=\frac{g(\mathit{\eta })}{\mathcal{A}({\mathit{\omega }}_n\cap S(G_n,\mathit{\eta }))},\forall \mathit{\eta }\in (0,{\mathit{\eta }}^i],}\hfill \\ {\displaystyle \text{where:}g(\mathit{\eta })=e^{RT}{\int }_{S(G_n,\mathit{\eta })}u(x,T)\mathrm{d}x+{\int }_{\mathit{\partial }S\times (0,T)}{e}^{Rt}(Vu-D\mathrm{\nabla }u)·\mathit{\nu }\mathrm{d}x\mathrm{d}t.}\hfill \end{array}\end{array}$$(43) )–(44(44) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle g_{incl}(\mathit{\eta })=\frac{g(\mathit{\eta })}{\mathcal{A}(S(G_n,\mathit{\eta }))}\text{and}{g}_{cont}(\mathit{\eta })=g(\mathit{\eta }).}\hfill \end{array}\end{array}$$(44) ) and approximated later on in Step 2 lead to determine effective approximations of the biggest side length ${\mathit{\eta }}_{in}$ and the smallest side length ${\mathit{\eta }}_{out}$ that yield $S(G_n,{\mathit{\eta }}_{in})\subseteq {\mathit{\omega }}_n\subseteq S(G_n,{\mathit{\eta }}_{out})$. Moreover, the approximation considered in Step 2 for the function $g_{incl}$ leads to determine ${\mathit{\eta }}_{in}$ whereas $g_{incl}({\mathit{\eta }}_{in})$ doesn’t correspond to the value of the associated ${\overline{\mathit{\lambda }}}_n$ as in (43(43) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\overline{\mathit{\lambda }}}_n=\frac{g(\mathit{\eta })}{\mathcal{A}({\mathit{\omega }}_n\cap S(G_n,\mathit{\eta }))},\forall \mathit{\eta }\in (0,{\mathit{\eta }}^i],}\hfill \\ {\displaystyle \text{where:}g(\mathit{\eta })=e^{RT}{\int }_{S(G_n,\mathit{\eta })}u(x,T)\mathrm{d}x+{\int }_{\mathit{\partial }S\times (0,T)}{e}^{Rt}(Vu-D\mathrm{\nabla }u)·\mathit{\nu }\mathrm{d}x\mathrm{d}t.}\hfill \end{array}\end{array}$$(43) )–(44(44) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle g_{incl}(\mathit{\eta })=\frac{g(\mathit{\eta })}{\mathcal{A}(S(G_n,\mathit{\eta }))}\text{and}{g}_{cont}(\mathit{\eta })=g(\mathit{\eta }).}\hfill \end{array}\end{array}$$(44) ) due to the omitted term. However, the approximation given in Step 2 for the function $g_{cont}$ is such that $g_{cont}({\mathit{\eta }}_{out})\approx {\overline{\mathit{\lambda }}}_n\mathcal{A}({\mathit{\omega }}_n)$. This last remark can be verified from comparing the final constant value reached by $g_{cont}$ as discussed in (43(43) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\overline{\mathit{\lambda }}}_n=\frac{g(\mathit{\eta })}{\mathcal{A}({\mathit{\omega }}_n\cap S(G_n,\mathit{\eta }))},\forall \mathit{\eta }\in (0,{\mathit{\eta }}^i],}\hfill \\ {\displaystyle \text{where:}g(\mathit{\eta })=e^{RT}{\int }_{S(G_n,\mathit{\eta })}u(x,T)\mathrm{d}x+{\int }_{\mathit{\partial }S\times (0,T)}{e}^{Rt}(Vu-D\mathrm{\nabla }u)·\mathit{\nu }\mathrm{d}x\mathrm{d}t.}\hfill \end{array}\end{array}$$(43) )–(44(44) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle g_{incl}(\mathit{\eta })=\frac{g(\mathit{\eta })}{\mathcal{A}(S(G_n,\mathit{\eta }))}\text{and}{g}_{cont}(\mathit{\eta })=g(\mathit{\eta }).}\hfill \end{array}\end{array}$$(44) ) with the value given in Table 3 of the coefficient $P_1^i$ computed from (31(31) $$\begin{array}{c}\hfill {\overline{\mathit{\lambda }}}_n\mathcal{A}({\mathit{\omega }}_n)=P_1^i,{\overline{\mathit{\lambda }}}_n{\int }_{{\mathit{\omega }}_n}{e}^{\mathit{\psi }(x)}\mathrm{d}x=P_{e^{\mathit{\psi }}}^i\text{and}{\overline{\mathit{\lambda }}}_n{\int }_{{\mathit{\omega }}_n}{\mathit{\psi }}^{\perp }(x)\mathrm{d}x=P_{{\mathit{\psi }}^{\perp }}^i,\end{array}$$(31) ).

Once ${\mathit{\eta }}_{in}$ and ${\mathit{\eta }}_{out}$ are determined, we set $\mathcal{A}({\mathit{\omega }}_n)\approx \mathcal{A}(S(G_n,{\mathit{\eta }}_{mid}))={\mathit{\eta }}_{mid}^2$, and deduce from (31(31) $$\begin{array}{c}\hfill {\overline{\mathit{\lambda }}}_n\mathcal{A}({\mathit{\omega }}_n)=P_1^i,{\overline{\mathit{\lambda }}}_n{\int }_{{\mathit{\omega }}_n}{e}^{\mathit{\psi }(x)}\mathrm{d}x=P_{e^{\mathit{\psi }}}^i\text{and}{\overline{\mathit{\lambda }}}_n{\int }_{{\mathit{\omega }}_n}{\mathit{\psi }}^{\perp }(x)\mathrm{d}x=P_{{\mathit{\psi }}^{\perp }}^i,\end{array}$$(31) ) the following approximation: ${\overline{\mathit{\lambda }}}_n\approx P_1^i/\mathcal{A}(S(G_n,{\mathit{\eta }}_{mid}))$.

The last part of our numerical experiments is devoted to the identification of the time-dependent intensity functions loaded by the different detected sources occurring in $\mathrm{\Omega }$. To this end, since we have already determined for each detected unknown source ${\mathit{\lambda }}_n{\mathit{\chi }}_{{\mathit{\omega }}_n}$ occurring in ${\mathrm{\Omega }}_i\subset \mathrm{\Omega }$ where $i\in \{1,\cdots ,N_{max}\}$ the geometric centre $G_n$ of its spatial support ${\overline{\mathit{\omega }}}_n$ as well as the biggest side length ${\mathit{\eta }}_{in}$ and the smallest side length ${\mathit{\eta }}_{out}$ that yield $S(G_n,{\mathit{\eta }}_{in})\subseteq {\mathit{\omega }}_n\subseteq S(G_n,{\mathit{\eta }}_{out})$ then, we use, as in (52(52) $$\begin{array}{c}\hfill \mathit{\omega }=S(G_n,{\mathit{\eta }}_{mid}),\text{where}{\mathit{\eta }}_{mid}=({\mathit{\eta }}_{in}+{\mathit{\eta }}_{out})/2\end{array}$$(52) ), the following approximation: ${\mathit{\omega }}_n\approx S(G_n,{\mathit{\eta }}_{mid})$.

Therefore, to identify the historic of the intensity function ${\mathit{\lambda }}_n$ defining the unknown source detected in ${\mathrm{\Omega }}_i$ where $i\in \{1,\cdots ,N_{max}\}$ we consider, as discussed in Remark 2.4, the two problems (23(23) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathit{\partial }}_{t}v-\mathrm{d}iv(D\mathrm{\nabla }v)-V·\mathrm{\nabla }v+Rv=0\text{in}\mathrm{\Omega }\times (0,T)\hfill \\ v(·,0)=0\text{in}\mathrm{\Omega }\hfill \\ v={\mathit{\zeta }}_{in}\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ (D\mathrm{\nabla }v+vV)·\mathit{\nu }=0\text{on}{\mathrm{\Gamma }}_L\times (0,T)\hfill \\ (D\mathrm{\nabla }v+vV)·\mathit{\nu }={\mathit{\zeta }}_{out}\text{on}{\mathrm{\Gamma }}_{out}\times (0,T)\hfill \end{array}\right.\end{array}$$(23) )–(25(25) $$\begin{array}{c}\hfill \left\{\begin{array}{c}-{\mathit{\partial }}_t\mathit{\xi }-\mathrm{d}iv(D\mathrm{\nabla }\mathit{\xi })+V·\mathrm{\nabla }\mathit{\xi }+R\mathit{\xi }={\mathit{\chi }}_{\mathit{\omega }}(x)\text{in}\mathrm{\Omega }\times (0,T)\hfill \\ \mathit{\xi }(·,T)=0\text{in}\mathrm{\Omega }\hfill \\ \mathit{\xi }=0\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ D\mathrm{\nabla }\mathit{\xi }·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\times (0,T)\hfill \end{array}\right.\end{array}$$(25) ) in ${\mathrm{\Omega }}_i\times (0,T)$ where we set $\mathit{\omega }=S(G_n,{\mathit{\eta }}_{mid})$. Moreover, to solve numerically the two systems (23(23) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathit{\partial }}_{t}v-\mathrm{d}iv(D\mathrm{\nabla }v)-V·\mathrm{\nabla }v+Rv=0\text{in}\mathrm{\Omega }\times (0,T)\hfill \\ v(·,0)=0\text{in}\mathrm{\Omega }\hfill \\ v={\mathit{\zeta }}_{in}\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ (D\mathrm{\nabla }v+vV)·\mathit{\nu }=0\text{on}{\mathrm{\Gamma }}_L\times (0,T)\hfill \\ (D\mathrm{\nabla }v+vV)·\mathit{\nu }={\mathit{\zeta }}_{out}\text{on}{\mathrm{\Gamma }}_{out}\times (0,T)\hfill \end{array}\right.\end{array}$$(23) )–(25(25) $$\begin{array}{c}\hfill \left\{\begin{array}{c}-{\mathit{\partial }}_t\mathit{\xi }-\mathrm{d}iv(D\mathrm{\nabla }\mathit{\xi })+V·\mathrm{\nabla }\mathit{\xi }+R\mathit{\xi }={\mathit{\chi }}_{\mathit{\omega }}(x)\text{in}\mathrm{\Omega }\times (0,T)\hfill \\ \mathit{\xi }(·,T)=0\text{in}\mathrm{\Omega }\hfill \\ \mathit{\xi }=0\text{on}{\mathrm{\Gamma }}_{in}\times (0,T)\hfill \\ D\mathrm{\nabla }\mathit{\xi }·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\times (0,T)\hfill \end{array}\right.\end{array}$$(25) ) in ${\mathrm{\Omega }}_i\times (0,T)$ we use a discretization employing the following uniform mesh sizes: $\mathrm{\Delta }{x}_1=200/N_1$, $\mathrm{\Delta }{x}_2=\ell /N_2$ with a time-step $\mathrm{\Delta }t=T/\mathcal{M}$ and use a 5-points finite differences Crank-Nicholson scheme for $N_1=40$, $N_2=25$ and $\mathcal{M}=240$. Then, we determine the loaded time-dependent intensity function ${\mathit{\lambda }}_n$ from the recursive formula obtained in (55(55) $$\begin{array}{cc}\hfill {\mathit{\lambda }}_n^m& {\displaystyle =\frac{1}{{\displaystyle {\int }_{S(G_n,{\mathit{\eta }}_{mid})}v(x,t_1)\mathrm{d}x}}\left(\frac{Q^i(t_{m+1})}{\mathrm{\Delta }t}-\sum _{k=1}^{m-1}{\mathit{\lambda }}_n^k{\int }_{S(G_n,{\mathit{\eta }}_{mid})}v(x,t_{m+1-k})\mathrm{d}x\right),}\hfill \\ \hfill & \forall m\ge 1.\hfill \end{array}$$(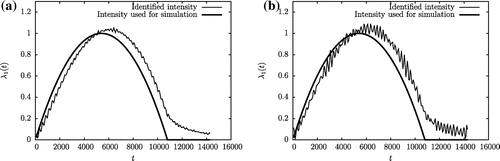55) ). In the sequel, we introduce a Gaussian noise on the simulated measures and present in the same graphic for each detected source in Table 3 its intensity function identified from (55(55) $$\begin{array}{cc}\hfill {\mathit{\lambda }}_n^m& {\displaystyle =\frac{1}{{\displaystyle {\int }_{S(G_n,{\mathit{\eta }}_{mid})}v(x,t_1)\mathrm{d}x}}\left(\frac{Q^i(t_{m+1})}{\mathrm{\Delta }t}-\sum _{k=1}^{m-1}{\mathit{\lambda }}_n^k{\int }_{S(G_n,{\mathit{\eta }}_{mid})}v(x,t_{m+1-k})\mathrm{d}x\right),}\hfill \\ \hfill & \forall m\ge 1.\hfill \end{array}$$(55) ) and the associated intensity function in (61(61) $$\begin{array}{cc}\hfill {\mathit{\lambda }}_1(t)& {\displaystyle =\frac{4}{{T^0}^2}t(T^0-t),{\mathit{\lambda }}_2(t)={\mathit{\chi }}_{(\frac{T^0}{5},T^0)}(t)\text{and}}\hfill \\ \hfill {\mathit{\lambda }}_3(t)& {\displaystyle =\frac{T^0-t}{T^0}(e^{3-t/T^0}-e^{3-2t/T^0}),}\hfill \end{array}$$(61) ) used for simulation. We indicate for each identified source intensity function the percent of the introduced Gaussian noise as well as the associated $L^2$ relative error i.e. $\Vert {\mathit{\lambda }}_n^{identified}-{\mathit{\lambda }}_n^{simulation}{\Vert }_{L^2(0,T)}/{\Vert {\mathit{\lambda }}_n^{simulation}\Vert }_{L^2(0,T)}$.

Figure 6. Identification of ${\mathit{\lambda }}_3$: (a) Noise $3\%$; Error 0.29, (b) Noise $10\%$; Error 0.32.

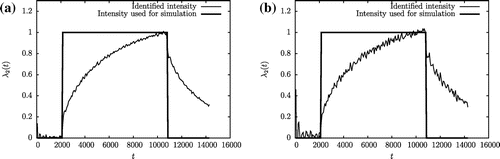
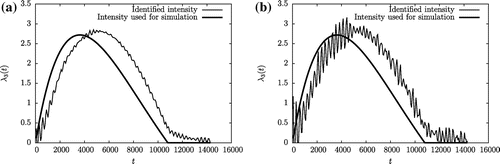
The numerical results presented in Figures 4–6 show that the recurssive formula established in (55(55) $$\begin{array}{cc}\hfill {\mathit{\lambda }}_n^m& {\displaystyle =\frac{1}{{\displaystyle {\int }_{S(G_n,{\mathit{\eta }}_{mid})}v(x,t_1)\mathrm{d}x}}\left(\frac{Q^i(t_{m+1})}{\mathrm{\Delta }t}-\sum _{k=1}^{m-1}{\mathit{\lambda }}_n^k{\int }_{S(G_n,{\mathit{\eta }}_{mid})}v(x,t_{m+1-k})\mathrm{d}x\right),}\hfill \\ \hfill & \forall m\ge 1.\hfill \end{array}$$(55) ) enables to identify the time-dependent intensity functions ${\mathit{\lambda }}_{n=1,\cdots ,N}$. Moreover, although the identified source intensity functions seem to be somewhat shifted/delayed with respect to the corresponding intensity functions used for simulation, which in our opinion is due to the time needed by the loaded material to reach sensors on $\mathit{\partial }{\mathrm{\Omega }}_i$, the identified results are accurate and stable with respect to the introduction of a noise on the used simulated measures. We believe that the significant error on the identified second source intensity function ${\mathit{\lambda }}_2$ in Figure 5 is mainly due to the error already committed from replacing ${\mathit{\omega }}_2$ by $S(G_2,{\mathit{\eta }}_{mid})$ while computing the coefficients $A_{mk}$ and $Q^i(t_m)$ in (55(55) $$\begin{array}{cc}\hfill {\mathit{\lambda }}_n^m& {\displaystyle =\frac{1}{{\displaystyle {\int }_{S(G_n,{\mathit{\eta }}_{mid})}v(x,t_1)\mathrm{d}x}}\left(\frac{Q^i(t_{m+1})}{\mathrm{\Delta }t}-\sum _{k=1}^{m-1}{\mathit{\lambda }}_n^k{\int }_{S(G_n,{\mathit{\eta }}_{mid})}v(x,t_{m+1-k})\mathrm{d}x\right),}\hfill \\ \hfill & \forall m\ge 1.\hfill \end{array}$$(55) )–(58(58) $$\begin{array}{c}\hfill {\displaystyle \underset{{\mathrm{\Lambda }}_n\in {\mathbb{R}}^{\mathcal{M}}}{min}\frac{1}{2}\Vert A{\mathrm{\Lambda }}_n-\frac{1}{\mathrm{\Delta }t}{\mathbf{Q}}^{\mathbf{i}}{\Vert }_2^2+\frac{r}{2}\Vert {\mathrm{\Lambda }}_n{\Vert }_2^2,}\end{array}$$(58) ).

6. Conclusion and outlook

We studied the non-linear inverse source problem of identifying multiple unknown time-dependent sources compactly supported in a two-dimensional monitored domain subject to an evolution advection–dispersion-reaction equation. From assuming the involved unknown sources could occur only one by one in some suspected sections within the monitored domain that are separated by interfaces available for recording the state and its flux crossing each intersection, we proved that those records yield uniqueness of the unknown elements defining all occurring sources. We developed a detection–identification method that goes throughout the monitored domain to detect in each suspected section whether there exists or not an occurring source. Once a source is detected, the developed method determines lower and upper bounds of the total amount discharged by the occurring source and localizes the geometric centre of its unknown spatial support. Then, given two desired reference geometries for example, squares/discs centred at the already localized geometric centre, the method determines also the biggest domain defined by a first reference geometry included in the sought source spatial support as well as the smallest domain defined by a second reference geometry containing this unknown support and identifies its time-dependent intensity function. Some numerical experiments on a variant of the surface water BOD pollution model were carried out. The obtained numerical results show that the developed detection–identification method is accurate and relatively stable with respect to the introduction of Gaussian noise in the measurements.

An outlook for the results established in the present study is their extension towards at least the following three directions: (1) Numerically: To apply the developed detection–identification method using other reference geometries and real life measurements taken on a flow crossing a monitored domain $\mathrm{\Omega }$ of an arbitrary geometric shape. (2) Theoretically: To treat the three-dimensional case which requires the introduction of a third dispersion-current function ${\mathit{\psi }}^{\perp \perp }$ added to $\mathit{\psi }$ and ${\mathit{\psi }}^{\perp }$ in (4(4) $$\begin{array}{c}\hfill D\mathrm{\nabla }\mathit{\psi }+V=0\text{and}\mathrm{\nabla }{\mathit{\psi }}^{\perp }+V^{\perp }=0.\end{array}$$(4) ). (3) Applicability: Since using a simple change of variables we transform the operator L in (2(2) $$\begin{array}{c}\hfill L[u](x,t):={\mathit{\partial }}_{t}u(x,t)-\mathrm{d}iv(D\mathrm{\nabla }u(x,t))+V·\mathrm{\nabla }u(x,t)+Ru(x,t),\end{array}$$(2) ) into a dispersion-reaction equation it follows that the developed method could cover a wider spectrum of applications.

Notes

No potential conflict of interest was reported by the author.

Appendix 1

Here, we establish the proof of Proposition 4.3:

ProofIn view of [34], we consider the null controllability problem of determining a distributed control $\mathit{\gamma }\in L^2({\mathrm{\Omega }}_{N_{max}+1}\times (T^{\ast },T))$ where ${\mathrm{\Omega }}_{N_{max}+1}\subset \mathrm{\Omega }$ and $0<T^{\ast }<T$ that to a given initial state ${\mathit{\phi }}_0\in L^2(\mathrm{\Omega })$ drives the solution $\mathit{\phi }$ of the following system:(A1) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathit{\partial }}_t\mathit{\phi }-\mathrm{d}iv(D\mathrm{\nabla }\mathit{\phi })+\mathit{\rho }\mathit{\phi }=\mathit{\gamma }(x,t){\mathit{\chi }}_{{\mathrm{\Omega }}_{N_{max}+1}}(x)\text{in}\mathrm{\Omega }\times (T^{\ast },T)\hfill \\ \mathit{\phi }(·,T^{\ast })={\mathit{\phi }}_0\text{in}\mathrm{\Omega }\hfill \\ \mathit{\phi }=0\text{on}{\mathrm{\Gamma }}_{in}\times (T^{\ast },T)\hfill \\ {\displaystyle (D\mathrm{\nabla }\mathit{\phi }+\frac{1}{2}\mathit{\phi }V)·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\times (T^{\ast },T)}\hfill \end{array}\right.\end{array}$$(A1) (A2) $$\begin{array}{c}\hfill \text{to the final state:}\mathit{\phi }(·,T)=0\text{in}\mathrm{\Omega }.\end{array}$$(A2)

Multiplying the first equation in (A1(A1) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathit{\partial }}_t\mathit{\phi }-\mathrm{d}iv(D\mathrm{\nabla }\mathit{\phi })+\mathit{\rho }\mathit{\phi }=\mathit{\gamma }(x,t){\mathit{\chi }}_{{\mathrm{\Omega }}_{N_{max}+1}}(x)\text{in}\mathrm{\Omega }\times (T^{\ast },T)\hfill \\ \mathit{\phi }(·,T^{\ast })={\mathit{\phi }}_0\text{in}\mathrm{\Omega }\hfill \\ \mathit{\phi }=0\text{on}{\mathrm{\Gamma }}_{in}\times (T^{\ast },T)\hfill \\ {\displaystyle (D\mathrm{\nabla }\mathit{\phi }+\frac{1}{2}\mathit{\phi }V)·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\times (T^{\ast },T)}\hfill \end{array}\right.\end{array}$$(A1) ) by $\mathit{\xi }$ the solution of the adjoint problem that to a given ${\mathit{\xi }}_0\in L^2(\mathrm{\Omega })$ associates(A3) $$\begin{array}{c}\hfill \left\{\begin{array}{c}-{\mathit{\partial }}_t\mathit{\xi }-\mathrm{d}iv(D\mathrm{\nabla }\mathit{\xi })+\mathit{\rho }\mathit{\xi }=0\text{in}\mathrm{\Omega }\times (T^{\ast },T)\hfill \\ \mathit{\xi }(·,T)={\mathit{\xi }}_0\text{in}\mathrm{\Omega }\hfill \\ \mathit{\xi }=0\text{on}{\mathrm{\Gamma }}_{in}\times (T^{\ast },T)\hfill \\ {\displaystyle (D\mathrm{\nabla }\mathit{\xi }+\frac{1}{2}\mathit{\xi }V)·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\times (T^{\ast },T)}\hfill \end{array}\right.\end{array}$$(A3)

and integrating by parts over $\mathrm{\Omega }\times (T^{\ast },T)$ using Green’s formula gives(A4) $$\begin{array}{c}\hfill {\displaystyle {\int }_{{\mathrm{\Omega }}_{N_{max}+1}\times (T^{\ast },T)}\mathit{\xi }\mathit{\gamma }\mathrm{d}x\mathrm{d}t={\int }_{\mathrm{\Omega }}[\mathit{\phi }(x,t)\mathit{\xi }(x,t){]}_{T^{\ast }}^T\mathrm{d}x,\forall {\mathit{\xi }}_0\in L^2(\mathrm{\Omega }).}\end{array}$$(A4)

Therefore, a distributed control $\mathit{\gamma }\in L^2({\mathrm{\Omega }}_{N_{max}+1}\times (T^{\ast },T))$ solves the null controllability problem introduced in (A1(A1) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathit{\partial }}_t\mathit{\phi }-\mathrm{d}iv(D\mathrm{\nabla }\mathit{\phi })+\mathit{\rho }\mathit{\phi }=\mathit{\gamma }(x,t){\mathit{\chi }}_{{\mathrm{\Omega }}_{N_{max}+1}}(x)\text{in}\mathrm{\Omega }\times (T^{\ast },T)\hfill \\ \mathit{\phi }(·,T^{\ast })={\mathit{\phi }}_0\text{in}\mathrm{\Omega }\hfill \\ \mathit{\phi }=0\text{on}{\mathrm{\Gamma }}_{in}\times (T^{\ast },T)\hfill \\ {\displaystyle (D\mathrm{\nabla }\mathit{\phi }+\frac{1}{2}\mathit{\phi }V)·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\times (T^{\ast },T)}\hfill \end{array}\right.\end{array}$$(A1) )–(A2(A2) $$\begin{array}{c}\hfill \text{to the final state:}\mathit{\phi }(·,T)=0\text{in}\mathrm{\Omega }.\end{array}$$(A2) ) if and only if it yields(A5) $$\begin{array}{c}\hfill {\displaystyle {\int }_{{\mathrm{\Omega }}_{N_{max}+1}\times (T^{\ast },T)}\mathit{\xi }\mathit{\gamma }\mathrm{d}x\mathrm{d}t=-{\int }_{\mathrm{\Omega }}\mathit{\phi }(x,T^{\ast })\mathit{\xi }(x,T^{\ast })\mathrm{d}x,\forall {\mathit{\xi }}_0\in L^2(\mathrm{\Omega }).}\end{array}$$(A5)

The necessary condition in (A5(A5) $$\begin{array}{c}\hfill {\displaystyle {\int }_{{\mathrm{\Omega }}_{N_{max}+1}\times (T^{\ast },T)}\mathit{\xi }\mathit{\gamma }\mathrm{d}x\mathrm{d}t=-{\int }_{\mathrm{\Omega }}\mathit{\phi }(x,T^{\ast })\mathit{\xi }(x,T^{\ast })\mathrm{d}x,\forall {\mathit{\xi }}_0\in L^2(\mathrm{\Omega }).}\end{array}$$(A5) ) is implied by (A4(A4) $$\begin{array}{c}\hfill {\displaystyle {\int }_{{\mathrm{\Omega }}_{N_{max}+1}\times (T^{\ast },T)}\mathit{\xi }\mathit{\gamma }\mathrm{d}x\mathrm{d}t={\int }_{\mathrm{\Omega }}[\mathit{\phi }(x,t)\mathit{\xi }(x,t){]}_{T^{\ast }}^T\mathrm{d}x,\forall {\mathit{\xi }}_0\in L^2(\mathrm{\Omega }).}\end{array}$$(A4) ) whereas the sufficient condition is obtained from observing that if the solution $\mathit{\phi }$ of (A1(A1) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathit{\partial }}_t\mathit{\phi }-\mathrm{d}iv(D\mathrm{\nabla }\mathit{\phi })+\mathit{\rho }\mathit{\phi }=\mathit{\gamma }(x,t){\mathit{\chi }}_{{\mathrm{\Omega }}_{N_{max}+1}}(x)\text{in}\mathrm{\Omega }\times (T^{\ast },T)\hfill \\ \mathit{\phi }(·,T^{\ast })={\mathit{\phi }}_0\text{in}\mathrm{\Omega }\hfill \\ \mathit{\phi }=0\text{on}{\mathrm{\Gamma }}_{in}\times (T^{\ast },T)\hfill \\ {\displaystyle (D\mathrm{\nabla }\mathit{\phi }+\frac{1}{2}\mathit{\phi }V)·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\times (T^{\ast },T)}\hfill \end{array}\right.\end{array}$$(A1) ) with a given $\mathit{\gamma }\in L^2({\mathrm{\Omega }}_{N_{max}+1}\times (T^{\ast },T))$ satisfies (A5(A5) $$\begin{array}{c}\hfill {\displaystyle {\int }_{{\mathrm{\Omega }}_{N_{max}+1}\times (T^{\ast },T)}\mathit{\xi }\mathit{\gamma }\mathrm{d}x\mathrm{d}t=-{\int }_{\mathrm{\Omega }}\mathit{\phi }(x,T^{\ast })\mathit{\xi }(x,T^{\ast })\mathrm{d}x,\forall {\mathit{\xi }}_0\in L^2(\mathrm{\Omega }).}\end{array}$$(A5) ) then, from (A4(A4) $$\begin{array}{c}\hfill {\displaystyle {\int }_{{\mathrm{\Omega }}_{N_{max}+1}\times (T^{\ast },T)}\mathit{\xi }\mathit{\gamma }\mathrm{d}x\mathrm{d}t={\int }_{\mathrm{\Omega }}[\mathit{\phi }(x,t)\mathit{\xi }(x,t){]}_{T^{\ast }}^T\mathrm{d}x,\forall {\mathit{\xi }}_0\in L^2(\mathrm{\Omega }).}\end{array}$$(A4) ) we get ${\int }_{\mathrm{\Omega }}\mathit{\phi }(·,T){\mathit{\xi }}_0\mathrm{d}x=0$ for all ${\mathit{\xi }}_0\in L^2(\mathrm{\Omega })$. That leads to $\mathit{\phi }(·,T)=0$ in $\mathrm{\Omega }$ and thus, $\mathit{\gamma }$ solves the null controllability problem (A1(A1) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathit{\partial }}_t\mathit{\phi }-\mathrm{d}iv(D\mathrm{\nabla }\mathit{\phi })+\mathit{\rho }\mathit{\phi }=\mathit{\gamma }(x,t){\mathit{\chi }}_{{\mathrm{\Omega }}_{N_{max}+1}}(x)\text{in}\mathrm{\Omega }\times (T^{\ast },T)\hfill \\ \mathit{\phi }(·,T^{\ast })={\mathit{\phi }}_0\text{in}\mathrm{\Omega }\hfill \\ \mathit{\phi }=0\text{on}{\mathrm{\Gamma }}_{in}\times (T^{\ast },T)\hfill \\ {\displaystyle (D\mathrm{\nabla }\mathit{\phi }+\frac{1}{2}\mathit{\phi }V)·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\times (T^{\ast },T)}\hfill \end{array}\right.\end{array}$$(A1) )–(A2(A2) $$\begin{array}{c}\hfill \text{to the final state:}\mathit{\phi }(·,T)=0\text{in}\mathrm{\Omega }.\end{array}$$(A2) ).

Besides, let $\widehat{\mathit{\xi }}$ be the solution of the adjoint problem introduced in (A3(A3) $$\begin{array}{c}\hfill \left\{\begin{array}{c}-{\mathit{\partial }}_t\mathit{\xi }-\mathrm{d}iv(D\mathrm{\nabla }\mathit{\xi })+\mathit{\rho }\mathit{\xi }=0\text{in}\mathrm{\Omega }\times (T^{\ast },T)\hfill \\ \mathit{\xi }(·,T)={\mathit{\xi }}_0\text{in}\mathrm{\Omega }\hfill \\ \mathit{\xi }=0\text{on}{\mathrm{\Gamma }}_{in}\times (T^{\ast },T)\hfill \\ {\displaystyle (D\mathrm{\nabla }\mathit{\xi }+\frac{1}{2}\mathit{\xi }V)·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\times (T^{\ast },T)}\hfill \end{array}\right.\end{array}$$(A3) ) using the initial data $\widehat{\mathit{\xi }}(·,T)={\widehat{\mathit{\xi }}}_0$ that yields the minimizer of the functional $J:L^2(\mathrm{\Omega })⟶IR$ which to a given ${\mathit{\xi }}_0$ associates (for the coercivity and the strict convexity of J see [30,35]):(A6) $$\begin{array}{c}\hfill {\displaystyle J({\mathit{\xi }}_0)=\frac{1}{2}{\Vert \mathit{\xi }\Vert }_{L^2({\mathrm{\Omega }}_{N_{max}+1}\times (T^{\ast },T))}^2+{\int }_{\mathrm{\Omega }}\mathit{\phi }(x,T^{\ast })\mathit{\xi }(x,T^{\ast })\mathrm{d}x.}\end{array}$$(A6)

Then, $\mathrm{\nabla }J({\widehat{\mathit{\xi }}}_0){\mathit{\xi }}_0={\int }_{{\mathrm{\Omega }}_{N_{max}+1}\times (T^{\ast },T)}\widehat{\mathit{\xi }}\mathit{\xi }\mathrm{d}x\mathrm{d}t+{\int }_{\mathrm{\Omega }}\mathit{\phi }(x,T^{\ast })\mathit{\xi }(x,T^{\ast })\mathrm{d}x=0$ for all ${\mathit{\xi }}_0\in L^2(\mathrm{\Omega })$ and thus, in view of (A5(A5) $$\begin{array}{c}\hfill {\displaystyle {\int }_{{\mathrm{\Omega }}_{N_{max}+1}\times (T^{\ast },T)}\mathit{\xi }\mathit{\gamma }\mathrm{d}x\mathrm{d}t=-{\int }_{\mathrm{\Omega }}\mathit{\phi }(x,T^{\ast })\mathit{\xi }(x,T^{\ast })\mathrm{d}x,\forall {\mathit{\xi }}_0\in L^2(\mathrm{\Omega }).}\end{array}$$(A5) ), the so-called Hilbert Uniqueness Method (HUM) distributed control defined by: $\mathit{\gamma }=\widehat{\mathit{\xi }}$ in ${\mathrm{\Omega }}_{N_{max}+1}\times (T^{\ast },T)$ solves the null controllability problem (A1(A1) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathit{\partial }}_t\mathit{\phi }-\mathrm{d}iv(D\mathrm{\nabla }\mathit{\phi })+\mathit{\rho }\mathit{\phi }=\mathit{\gamma }(x,t){\mathit{\chi }}_{{\mathrm{\Omega }}_{N_{max}+1}}(x)\text{in}\mathrm{\Omega }\times (T^{\ast },T)\hfill \\ \mathit{\phi }(·,T^{\ast })={\mathit{\phi }}_0\text{in}\mathrm{\Omega }\hfill \\ \mathit{\phi }=0\text{on}{\mathrm{\Gamma }}_{in}\times (T^{\ast },T)\hfill \\ {\displaystyle (D\mathrm{\nabla }\mathit{\phi }+\frac{1}{2}\mathit{\phi }V)·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\times (T^{\ast },T)}\hfill \end{array}\right.\end{array}$$(A1) )–(A2(A2) $$\begin{array}{c}\hfill \text{to the final state:}\mathit{\phi }(·,T)=0\text{in}\mathrm{\Omega }.\end{array}$$(A2) ). Furthermore, by setting ${\mathit{\xi }}_0={\widehat{\mathit{\xi }}}_0$ in (A5(A5) $$\begin{array}{c}\hfill {\displaystyle {\int }_{{\mathrm{\Omega }}_{N_{max}+1}\times (T^{\ast },T)}\mathit{\xi }\mathit{\gamma }\mathrm{d}x\mathrm{d}t=-{\int }_{\mathrm{\Omega }}\mathit{\phi }(x,T^{\ast })\mathit{\xi }(x,T^{\ast })\mathrm{d}x,\forall {\mathit{\xi }}_0\in L^2(\mathrm{\Omega }).}\end{array}$$(A5) ), the HUM distributed control fulfills(A7) $$\begin{array}{c}\hfill {\Vert \mathit{\gamma }\Vert }_{L^2({\mathrm{\Omega }}_{N_{max}+1}\times (T^{\ast },T))}\le C{\Vert \mathit{\phi }(·,T^{\ast })\Vert }_{L^2(\mathrm{\Omega })},\end{array}$$(A7)

where C is a Carleman constant [29]. Let $\widehat{\mathit{\phi }}(x,t)=\mathit{\phi }(x,T+T^{\ast }-t)$ in $\mathrm{\Omega }\times (T^{\ast },T)$, where $\mathit{\phi }$ is the solution of the null controllability problem (A1(A1) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathit{\partial }}_t\mathit{\phi }-\mathrm{d}iv(D\mathrm{\nabla }\mathit{\phi })+\mathit{\rho }\mathit{\phi }=\mathit{\gamma }(x,t){\mathit{\chi }}_{{\mathrm{\Omega }}_{N_{max}+1}}(x)\text{in}\mathrm{\Omega }\times (T^{\ast },T)\hfill \\ \mathit{\phi }(·,T^{\ast })={\mathit{\phi }}_0\text{in}\mathrm{\Omega }\hfill \\ \mathit{\phi }=0\text{on}{\mathrm{\Gamma }}_{in}\times (T^{\ast },T)\hfill \\ {\displaystyle (D\mathrm{\nabla }\mathit{\phi }+\frac{1}{2}\mathit{\phi }V)·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\times (T^{\ast },T)}\hfill \end{array}\right.\end{array}$$(A1) )–(A2(A2) $$\begin{array}{c}\hfill \text{to the final state:}\mathit{\phi }(·,T)=0\text{in}\mathrm{\Omega }.\end{array}$$(A2) ) involving the HUM distributed control $\mathit{\gamma }=\widehat{\mathit{\xi }}$ in ${\mathrm{\Omega }}_{N_{max}+1}\times (T^{\ast },T)$. Then, from multiplying the first equation in (46(46) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathit{\partial }}_{t}U-\mathrm{d}iv(D\mathrm{\nabla }U)+\mathit{\rho }U=0\text{in}\mathrm{\Omega }\times (T^{\ast },T)\hfill \\ U(·,T^{\ast })\in L^2(\mathrm{\Omega })\text{in}\mathrm{\Omega }\hfill \\ U=0\text{on}{\mathrm{\Gamma }}_{in}\times (T^{\ast },T)\hfill \\ {\displaystyle (D\mathrm{\nabla }U+\frac{1}{2}UV)·\mathit{\nu }=0\text{on}({\mathrm{\Gamma }}_L\cup {\mathrm{\Gamma }}_{out})\times (T^{\ast },T)}\hfill \end{array}\right.\end{array}$$(46) ) by $\widehat{\mathit{\phi }}$ and integrating by parts over $\mathrm{\Omega }\times (T^{\ast },T)$ using Green’s formula we find(A8) $$\begin{array}{c}\hfill {\displaystyle {\int }_{\mathrm{\Omega }}U(x,T)\mathit{\phi }(x,T^{\ast })\mathrm{d}x=-{\int }_{{\mathrm{\Omega }}_{N_{max}+1}\times (T^{\ast },T)}U(x,t)\mathit{\gamma }(x,T^{\ast }+T-t)\mathrm{d}x\mathrm{d}t.}\end{array}$$(A8)

Moreover, using $\mathit{\phi }(·,T^{\ast })=U(·,T)$ in $\mathrm{\Omega }$ and according to (A7(A7) $$\begin{array}{c}\hfill {\Vert \mathit{\gamma }\Vert }_{L^2({\mathrm{\Omega }}_{N_{max}+1}\times (T^{\ast },T))}\le C{\Vert \mathit{\phi }(·,T^{\ast })\Vert }_{L^2(\mathrm{\Omega })},\end{array}$$(A7) )–(A8(A8) $$\begin{array}{c}\hfill {\displaystyle {\int }_{\mathrm{\Omega }}U(x,T)\mathit{\phi }(x,T^{\ast })\mathrm{d}x=-{\int }_{{\mathrm{\Omega }}_{N_{max}+1}\times (T^{\ast },T)}U(x,t)\mathit{\gamma }(x,T^{\ast }+T-t)\mathrm{d}x\mathrm{d}t.}\end{array}$$(A8) ) we get (47(47) $$\begin{array}{c}\hfill {\displaystyle {\Vert U(·,T)\Vert }_{L^2(\mathrm{\Omega })}\le C{\Vert U\Vert }_{L^2({\mathrm{\Omega }}_{N_{max}+1}\times (T^{\ast },T))},}\end{array}$$(47) ).