Robin–Dirichlet algorithms for the Cauchy problem for the Helmholtz equation

Abstract

The Cauchy problem for the Helmholtz equation is considered. It was demonstrated in a previous paper by the authors that the alternating algorithm suggested by V.A. Kozlov and V.G. Maz’ya does not converge for large wavenumbers k in the Helmholtz equation. Here, we present some simple modifications of the algorithm which may restore the convergence. They consist of the replacement of the Neumann–Dirichlet iterations by the Robin–Dirichlet ones which repairs the convergence for $k^2$ less than the first Dirichlet–Laplacian eigenvalue. In order to treat large wavenumbers, we present an algorithm based on iterative solution of Robin–Dirichlet boundary value problems in a sufficiently narrow border strip. Numerical implementations obtained using the finite difference method are presented. The numerical results illustrate that the algorithms suggested in this paper, produce convergent iterative sequences.

Keywords:

• Helmholtz equation
• Cauchy problem
• alternating iterative method
• inverse problem
• ill-posed problem

AMS Subject Classifications:

• 35J05
• 35R25
• 35R30

1. Introduction

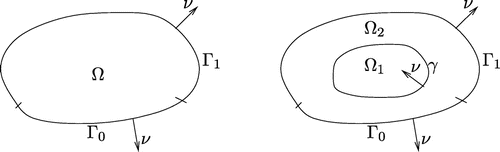
Let $\mathrm{\Omega }$ be a bounded domain in ${\mathbf{R}}^d$ with a Lipschitz boundary $\mathrm{\Gamma }$ and let $\mathit{\nu }$ be the exterior unit normal to $\mathrm{\Gamma }$. Let $\mathrm{\Gamma }$ also be divided into two disjoint parts ${\mathrm{\Gamma }}_0$ and ${\mathrm{\Gamma }}_1$ such that ${\overline{\mathrm{\Gamma }}}_0\cap {\overline{\mathrm{\Gamma }}}_1$ is Lipschitz; see illustration in Figure 1 on the left. We consider the Cauchy problem of finding a real-valued solution u to the problem(1) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \end{array}\right.\end{array}$$(1)

where $k>0$ is the wavenumber, ${\mathit{\partial }}_{\mathit{\nu }}$ denote the outward normal derivative and f and g are specified Cauchy data. This problem plays an important role in the study of problems related to acoustic and electromagnetic wave propagation, for example, the determination of a radiation field surrounding a source of radiation [1], the detection of the source of acoustical noise [2], the detection of surface vibrations from interior acoustical pressure [3], etc.

This problem is ill-posed in the sense of Hadamard. The classical numerical methods are thus inappropriate for solving the problem. Different regularization methods such as the potential function method [4], the modified Tikhonov regularization method [5,6], the truncation method [7], the method of approximate solutions [1], the wavelet moment method [8], the method of fundamental solutions [9], the conjugate gradient methods with the boundary element method [10,11], an alternating algorithm [12,13] and the accelerated alternating method [14] have been considered for solving the Cauchy problem for the Helmholtz equation.

Figure 1. Description of the domain considered here and the description of the domain with the interior boundary.

If $k=0$ then one can apply the alternating algorithm suggested in [15,16] which consists of iterative solution of the Neumann–Dirichlet problems. It has been shown in [13, Section 1.3] that this alternating procedure does not always converge for large values of $k^2$ in the Helmholtz equation. We therefore proposed in [13] a modification of the alternating algorithm that we used to solve problem (1(1) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \end{array}\right.\end{array}$$(1) ), based on an introduction of an auxiliary boundary and a positive parameter, which are chosen to guarantee positivity of a certain quadratic form associated with the Helmholtz operator, our auxiliary boundary and parameter. It was proved in [13] that the modified algorithm is convergent but the convergence of this modified algorithm is slow. However, since the quadratic form associated with the problem is positive, we can introduce a scalar product that gives us a natural framework that can be used to implement more sophisticated regularization methods. This was done in [14,17] where we showed that the conjugate gradient method can be used for solving the Cauchy problem for the Helmholtz equation efficiently. Since the conjugate gradient iterations have regularizing effect, see [18], we could also solve the problem with noisy data.

In [13,14] it became clear that the main reason of the improved convergence is played by the replacement of the Neumann–Dirichlet iterations by the Robin–Dirichlet ones. In this paper, we present some simple modifications of the algorithm which may restore the convergence of the alternative algorithm from [15,16]. They consist of the replacement of the Neumann–Dirichlet iterations by the Robin–Dirichlet ones on ${\mathrm{\Gamma }}_0$ or ${\mathrm{\Gamma }}_1$ or on both ${\mathrm{\Gamma }}_0$ and ${\mathrm{\Gamma }}_1$ which repairs the convergence for $k^2$ less than the first Dirichlet–Laplacian eigenvalue. In order to treat large wavenumbers, we present an algorithm based on iterative solution of Robin–Dirichlet boundary value problems in a sufficiently narrow border strip.

An important advantage of the proposed algorithms is that they can be readily applied to more general problems. First, we can treat more general second-order elliptic equations in divergence form with variable coefficients, i.e.$$\mathrm{\nabla }·(A(x)\mathrm{\nabla }u(x))+k(x)u(x)=0,\text{in}\mathrm{\Omega },$$

and$$u=f,\mathit{\nu }·(A(x)\mathrm{\nabla }u(x))=\mathit{\psi },\text{on}{\mathrm{\Gamma }}_0,$$

where A is a bounded matrix function with variable coefficients and k is a bounded measurable function. Secondly, we can reconstruct elastic oscillations, with a fixed frequency, in non-homogeneous and non-isotropic media by boundary measurements, i.e.$$\sum _{j=1}^3\frac{\mathit{\partial }}{\mathit{\partial }{x}_j}{\mathit{\sigma }}_{ij}(u)+\mathit{\rho }(x)k^2{u}_i=0,\text{in}\mathrm{\Omega },i=1,2,3,$$

and$$u=\mathit{\varphi },\mathit{\nu }·\mathit{\sigma }=\mathrm{\Psi },\text{on}{\mathrm{\Gamma }}_0,$$

where $\mathit{\sigma }$ is the stress tensor,$${\mathit{\sigma }}_{ij}=\frac{1}{2}\sum _{k,\ell =1}^3{A}_{ij}^{k\ell }(x)\left(\frac{\mathit{\partial }{u}_k}{\mathit{\partial }{x}_{\ell }}+\frac{\mathit{\partial }{u}_{\ell }}{\mathit{\partial }{x}_k}\right),$$$A_{ij}^{k\ell }$ and $\mathit{\rho }$ are space dependent functions, and $u=(u_1,u_2,u_3)$ is the displacement vector.

2. Description of the algorithms

In this section, we describe several iterative methods for solving the problem (1(1) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \end{array}\right.\end{array}$$(1) ). The methods are based on solving two well-posed boundary value problems for the original Helmholtz equation. In each iteration, we fix one of the known Cauchy data and choose the other one in an appropriate way so that the resulting boundary value problem is well posed. We also discuss the choice of the interior boundary $\mathit{\gamma }$ and the positive constant $\mathit{\mu }$ which ensures the validity of inequality (6(6) $$\begin{array}{c}\hfill {\int }_{{\mathrm{\Omega }}_2}\left({|\mathrm{\nabla }u|}^2-k^2{u}^2\right)\mathrm{d}x+\mathit{\mu }{\int }_{\mathit{\gamma }}{u}^2\mathrm{d}S>0,\end{array}$$(6) ) in Section 2.2. For solving problem with mixed boundary conditions involved in each iterative method described below, we refer to [19–22] and to [23] with superconvergence.

Before proceeding we recall the following definition:

Definition 2.1:

A function $u\in H^1(\mathrm{\Omega })$ is called a weak solution to the Helmholtz equation in $\mathrm{\Omega }$ if$$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}\mathrm{\nabla }u·\mathrm{\nabla }v\mathrm{d}x-k^2{\int }_{\mathrm{\Omega }}uv\mathrm{d}x=0\end{array}$$

for all $v\in H^1(\mathrm{\Omega })$ such that $v=0$ on $\mathrm{\Gamma }$.

2.1. The Robin–Dirichlet algorithm

In the first iterative algorithm, we alternate the Robin–Dirichlet boundary conditions on ${\mathrm{\Gamma }}_1$. The Dirichlet–Neumann boundary conditions are also alternated on ${\mathrm{\Gamma }}_0$. In order to formulate the methods, let us first assume that one can choose a positive constant $\mathit{\mu }$ so that(2) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}\left({|\mathrm{\nabla }u|}^2-k^2{u}^2\right)\mathrm{d}x+\mathit{\mu }{\int }_{{\mathrm{\Gamma }}_1}{u}^2\mathrm{d}S>0,\end{array}$$(2)

for all $u\in H^1(\mathrm{\Omega })\backslash \{0\}$.

As it was shown in [13, Lemma 2.1], the inequality (2(2) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}\left({|\mathrm{\nabla }u|}^2-k^2{u}^2\right)\mathrm{d}x+\mathit{\mu }{\int }_{{\mathrm{\Gamma }}_1}{u}^2\mathrm{d}S>0,\end{array}$$(2) ) is valid for sufficiently large $\mathit{\mu }$ if and only if the first integral in (2(2) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}\left({|\mathrm{\nabla }u|}^2-k^2{u}^2\right)\mathrm{d}x+\mathit{\mu }{\int }_{{\mathrm{\Gamma }}_1}{u}^2\mathrm{d}S>0,\end{array}$$(2) ) is positive on non-zero functions from $H^1(\mathrm{\Omega })$ vanishing on ${\mathrm{\Gamma }}_1$. We note that the correct formulation of [13, Theorem 2.2] may be found in [24]. Consider now the following boundary value problems:(3) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u+\mathit{\mu }u=\mathit{\eta }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \end{array}\right.\end{array}$$(3)

and(4) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ u=\mathit{\varphi }\hfill & \text{on}{\mathrm{\Gamma }}_1.\hfill \end{array}\right.\end{array}$$(4)

Here, $f\in H^{1/2}({\mathrm{\Gamma }}_0)$ and $g\in H^{-1/2}({\mathrm{\Gamma }}_0)$ are the data in (1(1) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \end{array}\right.\end{array}$$(1) ). For $\mathit{\eta }\in H^{-1/2}({\mathrm{\Gamma }}_1)$ and $\mathit{\varphi }\in H^{1/2}({\mathrm{\Gamma }}_1)$, problems (3(3) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u+\mathit{\mu }u=\mathit{\eta }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \end{array}\right.\end{array}$$(3) ) and (4(4) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ u=\mathit{\varphi }\hfill & \text{on}{\mathrm{\Gamma }}_1.\hfill \end{array}\right.\end{array}$$(4) ) are well posed and their weak solutions are defined below. Let us mention that in the following, $H^{-1/2}({\mathrm{\Gamma }}_0)$ and $H^{-1/2}({\mathrm{\Gamma }}_1)$ denote the dual spaces to $H^{1/2}({\mathrm{\Gamma }}_0)$ and $H^{1/2}({\mathrm{\Gamma }}_1)$, respectively.

Definition 2.2:

Let $f\in H^{1/2}({\mathrm{\Gamma }}_0)$ and $\mathit{\eta }\in H^{-1/2}({\mathrm{\Gamma }}_1)$. We call $u\in H^1(\mathrm{\Omega })$ a weak solution to problem (3(3) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u+\mathit{\mu }u=\mathit{\eta }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \end{array}\right.\end{array}$$(3) ) if u satisfies$${\int }_{\mathrm{\Omega }}(\mathrm{\nabla }u·\mathrm{\nabla }v-k^{2}uv)\mathrm{d}x+\mathit{\mu }{\int }_{{\mathrm{\Gamma }}_1}uv\mathrm{d}S={\int }_{{\mathrm{\Gamma }}_1}\mathit{\eta }v\mathrm{d}S$$

for every function $v\in H^1(\mathrm{\Omega })$ such that $v=0$ on ${\mathrm{\Gamma }}_0$ and $u=f$ on ${\mathrm{\Gamma }}_0$.

In a similar way, we give the definition of a weak solution to (4(4) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ u=\mathit{\varphi }\hfill & \text{on}{\mathrm{\Gamma }}_1.\hfill \end{array}\right.\end{array}$$(4) ).

Definition 2.3:

Let $g\in H^{-1/2}({\mathrm{\Gamma }}_0)$ and $\mathit{\varphi }\in H^{1/2}({\mathrm{\Gamma }}_1)$. We call $u\in H^1(\mathrm{\Omega })$ a weak solution to problem (4(4) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ u=\mathit{\varphi }\hfill & \text{on}{\mathrm{\Gamma }}_1.\hfill \end{array}\right.\end{array}$$(4) ) if it satisfies$${\int }_{\mathrm{\Omega }}(\mathrm{\nabla }u·\mathrm{\nabla }v-k^{2}uv)\mathrm{d}x={\int }_{{\mathrm{\Gamma }}_0}gv\mathrm{d}S$$

for every function $v\in H^1(\mathrm{\Omega })$ such that $v=0$ on ${\mathrm{\Gamma }}_1$ and $u=\mathit{\varphi }$ on ${\mathrm{\Gamma }}_1$.

The algorithm for solving (1(1) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \end{array}\right.\end{array}$$(1) ) is then described as follows:

(1)	The first approximation $u_0$ is obtained by solving (3(3) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u+\mathit{\mu }u=\mathit{\eta }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \end{array}\right.\end{array}$$(3) ), where $\mathit{\eta }$ is an arbitrary initial approximation of the Robin condition on ${\mathrm{\Gamma }}_1$.
(2)	Having constructed $u_{2n}$, we find $u_{2n+1}$ by solving (4(4) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ u=\mathit{\varphi }\hfill & \text{on}{\mathrm{\Gamma }}_1.\hfill \end{array}\right.\end{array}$$(4) ) with $\mathit{\varphi }=u_{2n}$ on ${\mathrm{\Gamma }}_1$.
(3)	We then obtain $u_{2n+2}$ by solving (3(3) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u+\mathit{\mu }u=\mathit{\eta }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \end{array}\right.\end{array}$$(3) ) with $\mathit{\eta }={\mathit{\partial }}_{\mathit{\nu }}{u}_{2n+1}+\mathit{\mu }{u}_{2n+1}$ on ${\mathrm{\Gamma }}_1$.

We now state the theorem about the convergence of this algorithm which can be proved in the same manner as in [13, Theorem 3.1].

Theorem 2.4:

Suppose that $\mathit{\mu }$ is a positive constant chosen so that the positivity of the quadratic form (2(2) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}\left({|\mathrm{\nabla }u|}^2-k^2{u}^2\right)\mathrm{d}x+\mathit{\mu }{\int }_{{\mathrm{\Gamma }}_1}{u}^2\mathrm{d}S>0,\end{array}$$(2) ) is fulfilled. Let $f\in H^{1/2}({\mathrm{\Gamma }}_0)$ and $g\in H^{-1/2}({\mathrm{\Gamma }}_0)$, and let $u\in H^1(\mathrm{\Omega })$ be the solution to problem (1(1) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \end{array}\right.\end{array}$$(1) ). Then, for every $\mathit{\eta }\in H^{-1/2}({\mathrm{\Gamma }}_1)$, the sequence ${(u_n)}_{n=0}^{\infty }$, obtained using the algorithm described above, converges to u in $H^1(\mathrm{\Omega })$.

One can also consider the following two alternatives for the algorithm presented above:

(I)

Assume that there exists a positive constant $\mathit{\sigma }$ so that (5a) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}(|\mathrm{\nabla }{u}^2|-k^2{u}^2)\mathrm{d}x+\mathit{\sigma }{\int }_{{\mathrm{\Gamma }}_0}{u}^2\mathrm{d}S>0\end{array}$$(5a) for all $u\in H^1(\mathrm{\Omega })\backslash \{0\}$. From [13, Lemma 2.1] it follows that the validity of the last condition for sufficiently large $\mathit{\sigma }$ is equivalent to positivity of the first integral in (5a(5a) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}(|\mathrm{\nabla }{u}^2|-k^2{u}^2)\mathrm{d}x+\mathit{\sigma }{\int }_{{\mathrm{\Gamma }}_0}{u}^2\mathrm{d}S>0\end{array}$$(5a) ) on functions from $H^1(\mathrm{\Omega })$ vanishing on ${\mathrm{\Gamma }}_0$. One can describe, in the same way as above, an alternating algorithm through the following auxiliary problems: $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u+\mathit{\sigma }u=g+\mathit{\sigma }f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ u=\mathit{\varphi }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \end{array}\right.\end{array}$$ and $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=\mathit{\eta }\hfill & \text{on}{\mathrm{\Gamma }}_1.\hfill \end{array}\right.\end{array}$$

(II)

Another alternative algorithm requires the existence of two positive constants $\mathit{\sigma }$ and $\mathit{\mu }$ such that (5b) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}(|\mathrm{\nabla }{u}^2|-k^2{u}^2)\mathrm{d}x+\mathit{\sigma }{\int }_{{\mathrm{\Gamma }}_0}{u}^2\mathrm{d}S+\mathit{\mu }{\int }_{{\mathrm{\Gamma }}_1}{u}^2\mathrm{d}S>0\end{array}$$(5b) for all $u\in H^1(\mathrm{\Omega })\backslash \{0\}$. Again by [13, Lemma 2.1] the validity of this condition for sufficiently large $\mathit{\sigma }$ and $\mathit{\mu }$ is equivalent to positivity of the first integral in (5b(5b) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}(|\mathrm{\nabla }{u}^2|-k^2{u}^2)\mathrm{d}x+\mathit{\sigma }{\int }_{{\mathrm{\Gamma }}_0}{u}^2\mathrm{d}S+\mathit{\mu }{\int }_{{\mathrm{\Gamma }}_1}{u}^2\mathrm{d}S>0\end{array}$$(5b) ) on functions from $H^1(\mathrm{\Omega })$ vanishing on $\mathit{\gamma }$. In that case, the algorithm considered in this section, can similarly be described through boundary value problems: $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u+\mathit{\sigma }u=g+\mathit{\sigma }f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ u=\mathit{\varphi }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \end{array}\right.\end{array}$$ and $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u+\mathit{\mu }u=\mathit{\eta }\hfill & \text{on}{\mathrm{\Gamma }}_1.\hfill \end{array}\right.\end{array}$$

Similar to Theorem 2.4, one can prove the convergence of the above algorithms (I) and (II) in $H^1(\mathrm{\Omega })$ provided condition (5a(5a) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}(|\mathrm{\nabla }{u}^2|-k^2{u}^2)\mathrm{d}x+\mathit{\sigma }{\int }_{{\mathrm{\Gamma }}_0}{u}^2\mathrm{d}S>0\end{array}$$(5a) ) (or (5b(5b) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}(|\mathrm{\nabla }{u}^2|-k^2{u}^2)\mathrm{d}x+\mathit{\sigma }{\int }_{{\mathrm{\Gamma }}_0}{u}^2\mathrm{d}S+\mathit{\mu }{\int }_{{\mathrm{\Gamma }}_1}{u}^2\mathrm{d}S>0\end{array}$$(5b) ) in the case (II)) is fulfilled.

2.2. The Robin–Dirichlet algorithm with interior boundary

The algorithm proposed in the previous section may also diverge for large values of $k^2$ in the Helmholtz equation. We shall therefore consider a variation of this method. The new method consists of introducing an artificial interior boundary $\mathit{\gamma }$ inside $\mathrm{\Omega }$ and a positive constant $\mathit{\mu }$. We now solve the Helmholtz equation in a narrow border strip between $\mathit{\gamma }$ and $\mathrm{\Gamma }$ with the Dirichlet–Neumann boundary conditions on ${\mathrm{\Gamma }}_0$ and ${\mathrm{\Gamma }}_1$ and the Robin–Dirichlet boundary conditions on $\mathit{\gamma }$.

Assume that ${\mathrm{\Omega }}_1$ is a subdomain of $\mathrm{\Omega }$ with a Lipschitz boundary $\mathit{\gamma }$. Define ${\mathrm{\Omega }}_2=\mathrm{\Omega }\backslash \overline{{\mathrm{\Omega }}_1}$; see Figure 1 on the right. Assume also that $\mathit{\mu }$ is a positive constant chosen so that(6) $$\begin{array}{c}\hfill {\int }_{{\mathrm{\Omega }}_2}\left({|\mathrm{\nabla }u|}^2-k^2{u}^2\right)\mathrm{d}x+\mathit{\mu }{\int }_{\mathit{\gamma }}{u}^2\mathrm{d}S>0,\end{array}$$(6)

for all $u\in H^1({\mathrm{\Omega }}_2)$, $u\ne 0$. Again, using [13, Lemma 2.1] one can show that the validity of (2(2) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}\left({|\mathrm{\nabla }u|}^2-k^2{u}^2\right)\mathrm{d}x+\mathit{\mu }{\int }_{{\mathrm{\Gamma }}_1}{u}^2\mathrm{d}S>0,\end{array}$$(2) ), for large $\mathit{\mu }$, is equivalent to positivity of the first integral in (2(2) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}\left({|\mathrm{\nabla }u|}^2-k^2{u}^2\right)\mathrm{d}x+\mathit{\mu }{\int }_{{\mathrm{\Gamma }}_1}{u}^2\mathrm{d}S>0,\end{array}$$(2) ) for non-zero $u\in H^1({\mathrm{\Omega }}_2)$ vanishing on $\mathit{\gamma }$. The new alternating procedure involves the following boundary value problems:(7) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}{\mathrm{\Omega }}_2,\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=\mathit{\eta }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u+\mathit{\mu }u=\mathit{\xi }\hfill & \text{on}\mathit{\gamma },\hfill \end{array}\right.\end{array}$$(7)

and(8) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}{\mathrm{\Omega }}_2,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ u=\mathit{\varphi }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \\ u=\mathit{\psi }\hfill & \text{on}\mathit{\gamma }.\hfill \end{array}\right.\end{array}$$(8)

The algorithm thus consists of solving in an alternating way two well-posed boundary value problems (7(7) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}{\mathrm{\Omega }}_2,\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=\mathit{\eta }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u+\mathit{\mu }u=\mathit{\xi }\hfill & \text{on}\mathit{\gamma },\hfill \end{array}\right.\end{array}$$(7) ) and (8(8) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}{\mathrm{\Omega }}_2,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ u=\mathit{\varphi }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \\ u=\mathit{\psi }\hfill & \text{on}\mathit{\gamma }.\hfill \end{array}\right.\end{array}$$(8) ). We define their weak solutions.

Definition 2.5:

Let $f\in H^{1/2}({\mathrm{\Gamma }}_0)$, $\mathit{\eta }\in H^{-1/2}({\mathrm{\Gamma }}_1)$ and $\mathit{\xi }\in H^{-1/2}(\mathit{\gamma })$. We call a function $u\in H^1({\mathrm{\Omega }}_2)$ a weak solution to problem (7(7) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}{\mathrm{\Omega }}_2,\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=\mathit{\eta }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u+\mathit{\mu }u=\mathit{\xi }\hfill & \text{on}\mathit{\gamma },\hfill \end{array}\right.\end{array}$$(7) ) if it satisfies$${\int }_{{\mathrm{\Omega }}_2}(\mathrm{\nabla }u·\mathrm{\nabla }v-k^{2}uv)\mathrm{d}x+\mathit{\mu }{\int }_{\mathit{\gamma }}uv\mathrm{d}S={\int }_{{\mathrm{\Gamma }}_1}\mathit{\eta }v\mathrm{d}S+{\int }_{\mathit{\gamma }}\mathit{\xi }v\mathrm{d}S$$

for every function $v\in H^1({\mathrm{\Omega }}_2)$ such that $v=0$ on ${\mathrm{\Gamma }}_0$ and $u=f$ on ${\mathrm{\Gamma }}_0$.

In a similar way, we define a weak solution to (8(8) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}{\mathrm{\Omega }}_2,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ u=\mathit{\varphi }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \\ u=\mathit{\psi }\hfill & \text{on}\mathit{\gamma }.\hfill \end{array}\right.\end{array}$$(8) ).

Definition 2.6:

Let $g\in H^{-1/2}({\mathrm{\Gamma }}_0)$, $\mathit{\varphi }\in H^{1/2}({\mathrm{\Gamma }}_1)$ and $\mathit{\psi }\in H^{1/2}(\mathit{\gamma })$. We call a function $u\in H^1({\mathrm{\Omega }}_2)$ a weak solution to problem (8(8) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}{\mathrm{\Omega }}_2,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ u=\mathit{\varphi }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \\ u=\mathit{\psi }\hfill & \text{on}\mathit{\gamma }.\hfill \end{array}\right.\end{array}$$(8) ) if it satisfies$${\int }_{{\mathrm{\Omega }}_2}(\mathrm{\nabla }u·\mathrm{\nabla }v-k^{2}uv)\mathrm{d}x={\int }_{{\mathrm{\Gamma }}_0}gv\mathrm{d}S$$

for every function $v\in H^1({\mathrm{\Omega }}_2)$ such that $v=0$ on ${\mathrm{\Gamma }}_1$ and on $\mathit{\gamma }$, $u=\mathit{\varphi }$ on ${\mathrm{\Gamma }}_1$ and $u=\mathit{\psi }$ on $\mathit{\gamma }$.

The algorithm for solving (1(1) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \end{array}\right.\end{array}$$(1) ) is described as follows:

(1)	The first approximation $u_0$ is obtained by solving (7(7) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}{\mathrm{\Omega }}_2,\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=\mathit{\eta }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u+\mathit{\mu }u=\mathit{\xi }\hfill & \text{on}\mathit{\gamma },\hfill \end{array}\right.\end{array}$$(7) ), where $\mathit{\eta }$ is an arbitrary approximation of the Neumann boundary condition on ${\mathrm{\Gamma }}_1$ and $\mathit{\xi }$ is an arbitrary initial approximation of the Robin condition on $\mathit{\gamma }$.
(2)	Having constructed $u_{2n}$, we find $u_{2n+1}$ by solving (8(8) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}{\mathrm{\Omega }}_2,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ u=\mathit{\varphi }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \\ u=\mathit{\psi }\hfill & \text{on}\mathit{\gamma }.\hfill \end{array}\right.\end{array}$$(8) ) with $\mathit{\varphi }=u_{2n}$ on ${\mathrm{\Gamma }}_1$ and $\mathit{\psi }=u_{2n}$ on $\mathit{\gamma }$.
(3)	We then obtain $u_{2n+2}$ by solving the problem (7(7) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}{\mathrm{\Omega }}_2,\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=\mathit{\eta }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u+\mathit{\mu }u=\mathit{\xi }\hfill & \text{on}\mathit{\gamma },\hfill \end{array}\right.\end{array}$$(7) ) with $\mathit{\eta }={\mathit{\partial }}_{\mathit{\nu }}{u}_{2n+1}$ on ${\mathrm{\Gamma }}_1$ and $\mathit{\xi }={\mathit{\partial }}_{\mathit{\nu }}{u}_{2n+1}+\mathit{\mu }{u}_{2n+1}$ on $\mathit{\gamma }$.

Theorem 2.7:

Suppose that assumptions on the choice of the interior boundary and the constant $\mathit{\mu }$ in Section 2.3 are fulfilled and the positivity condition (6(6) $$\begin{array}{c}\hfill {\int }_{{\mathrm{\Omega }}_2}\left({|\mathrm{\nabla }u|}^2-k^2{u}^2\right)\mathrm{d}x+\mathit{\mu }{\int }_{\mathit{\gamma }}{u}^2\mathrm{d}S>0,\end{array}$$(6) ) holds. Let $f\in H^{1/2}({\mathrm{\Gamma }}_0)$ and $g\in H^{-1/2}({\mathrm{\Gamma }}_0)$, and let $u\in H^1(\mathrm{\Omega })$ be the solution to problem (1(1) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \end{array}\right.\end{array}$$(1) ). Then, for every $\mathit{\eta }\in H^{-1/2}({\mathrm{\Gamma }}_1)$ and every $\mathit{\xi }\in H^{-1/2}(\mathit{\gamma })$, the sequence ${(u_n)}_{n=0}^{\infty }$, obtained using the alternating algorithm described in Section 2.2, converges to u in $H^1(\mathrm{\Omega })$.

The proof of this theorem can be carried out in a similar way as in [13, Section 3].

2.3. Sufficient condition for $a_{\mathit{\mu }}$ to be positive definite

In this section, we discuss the choice of the interior boundary $\mathit{\gamma }$ and the positive constant $\mathit{\mu }$ which ensures the validity of (6(6) $$\begin{array}{c}\hfill {\int }_{{\mathrm{\Omega }}_2}\left({|\mathrm{\nabla }u|}^2-k^2{u}^2\right)\mathrm{d}x+\mathit{\mu }{\int }_{\mathit{\gamma }}{u}^2\mathrm{d}S>0,\end{array}$$(6) ). We consider the two-dimensional case.

Let $l(\mathrm{\Gamma })$ denote the length of the boundary $\mathrm{\Gamma }$. Assume that the curve $\mathrm{\Gamma }$ is parametrized in terms of the arc length s with $0\le s\le l(\mathrm{\Gamma })$ and introduce the parametrization $r(s)=(x(s),y(s))$, counterclockwise. In that case, the unit tangent and the unit normal are given by $T(s)=(\dot{x}(s),\dot{y}(s))$ and $N(s)=(-\dot{y}(s),\dot{x}(s))$, respectively. At any point t; $0\le t\le h$, inside $\mathrm{\Omega }$, we thus have the following parametrization:$$\begin{array}{c}\hfill (x(t),y(t))=(x(s),y(s))+t(-\dot{y}(s),\dot{x}(s)).\end{array}$$

Let us define(9) $$\begin{array}{c}\hfill a_{\mathit{\mu }}(u,u)={\int }_{\mathrm{\Omega }}{(|\mathrm{\nabla }u|}^2-k^2{u}^2)\mathrm{d}x+\mathit{\mu }{\int }_{\mathit{\gamma }}{u}^2\mathrm{d}S\end{array}$$(9)

Using the parametrization described above, we can rewrite (9(9) $$\begin{array}{c}\hfill a_{\mathit{\mu }}(u,u)={\int }_{\mathrm{\Omega }}{(|\mathrm{\nabla }u|}^2-k^2{u}^2)\mathrm{d}x+\mathit{\mu }{\int }_{\mathit{\gamma }}{u}^2\mathrm{d}S\end{array}$$(9) ) as(10) $$\begin{array}{cc}\hfill a_{\mathit{\mu }}(u,u)& ={\int }_0^{l(\mathrm{\Gamma })}{\int }_0^h(u_t^2+\frac{1}{{(1-\mathit{\rho }(s)t)}^2}{u}_s^2-k^2{u}^2)(1-\mathit{\rho }(s)t)\mathrm{d}t\mathrm{d}s\hfill \\ \hfill & +\mathit{\mu }{\int }_0^{l(\mathrm{\Gamma })}{u}^2(h)(1-\mathit{\rho }(s)h)\mathrm{d}s\hfill \\ \hfill & \ge \hfill & \hfill {\int }_0^{l(\mathrm{\Gamma })}\left({\int }_0^h(u_t^2-k^2{u}^2)(1-\mathit{\rho }(s)t)\mathrm{d}t+\mathit{\mu }{u}^2(h)(1-\mathit{\rho }(s)h)\right)\mathrm{d}s\end{array}$$(10)

where $\mathit{\rho }(s)=\ddot{y}\dot{x}-\ddot{x}\dot{y}$ is the curvature of $\mathrm{\Gamma }$ at the point r(s). In order for relation (6(6) $$\begin{array}{c}\hfill {\int }_{{\mathrm{\Omega }}_2}\left({|\mathrm{\nabla }u|}^2-k^2{u}^2\right)\mathrm{d}x+\mathit{\mu }{\int }_{\mathit{\gamma }}{u}^2\mathrm{d}S>0,\end{array}$$(6) ) to hold, we shall determine h and $\mathit{\mu }$ so that $a_{\mathit{\mu }}(u,u)>0$. From (10(10) $$\begin{array}{cc}\hfill a_{\mathit{\mu }}(u,u)& ={\int }_0^{l(\mathrm{\Gamma })}{\int }_0^h(u_t^2+\frac{1}{{(1-\mathit{\rho }(s)t)}^2}{u}_s^2-k^2{u}^2)(1-\mathit{\rho }(s)t)\mathrm{d}t\mathrm{d}s\hfill \\ \hfill & +\mathit{\mu }{\int }_0^{l(\mathrm{\Gamma })}{u}^2(h)(1-\mathit{\rho }(s)h)\mathrm{d}s\hfill \\ \hfill & \ge \hfill & \hfill {\int }_0^{l(\mathrm{\Gamma })}\left({\int }_0^h(u_t^2-k^2{u}^2)(1-\mathit{\rho }(s)t)\mathrm{d}t+\mathit{\mu }{u}^2(h)(1-\mathit{\rho }(s)h)\right)\mathrm{d}s\end{array}$$(10) ), it is sufficient to determine h and $\mathit{\mu }$ so that(11) $$\begin{array}{c}\hfill {\int }_0^h(u_t^2-k^2{u}^2)(1-\mathit{\rho }(s)t)\mathrm{d}t+\mathit{\mu }{u}^2(h)(1-\mathit{\rho }(s)h)t>0\end{array}$$(11)

holds for all non-zero $u\in H^1(0,h)$. Then (11(11) $$\begin{array}{c}\hfill {\int }_0^h(u_t^2-k^2{u}^2)(1-\mathit{\rho }(s)t)\mathrm{d}t+\mathit{\mu }{u}^2(h)(1-\mathit{\rho }(s)h)t>0\end{array}$$(11) ) follows from$$\begin{array}{c}\hfill {\int }_0^h\left(u_t^2-k^2\frac{1-{\mathit{\rho }}_{-}}{1-\mathit{\rho }+}{u}^2\right)\mathrm{d}t+\mathit{\mu }{u}^2(h)>0\end{array}$$

where$$\begin{array}{c}\hfill {\mathit{\rho }}_{-}=\underset{\begin{array}{c}0\le t\le h\\ 0\le s\le l(\mathrm{\Gamma })\end{array}}{min}\mathit{\rho }(s)t\text{and}{\mathit{\rho }}_{+}=\underset{\begin{array}{c}0\le t\le h\\ 0\le s\le l(\mathrm{\Gamma })\end{array}}{max}\mathit{\rho }(s)t.\end{array}$$

We assume that h is sufficiently small. Consider the spectral problem(12) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}-u^{″}(t)=\mathrm{\Lambda }u(t)\hfill & \text{for}t\in (0,h),\hfill \\ u^{\prime }(0)=0,\hfill \\ u^{\prime }(h)+\mathit{\mu }u(h)=0.\hfill \end{array}\right.\end{array}$$(12)

Consider the case when $0<\mathit{\mu }<\infty$ and put ${\mathit{\beta }}^2=\mathrm{\Lambda }$. Solving problem (12(12) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}-u^{″}(t)=\mathrm{\Lambda }u(t)\hfill & \text{for}t\in (0,h),\hfill \\ u^{\prime }(0)=0,\hfill \\ u^{\prime }(h)+\mathit{\mu }u(h)=0.\hfill \end{array}\right.\end{array}$$(12) ), we find that(13) $$\begin{array}{c}\hfill \mathit{\beta }tan(\mathit{\beta }h)=\mathit{\mu }.\end{array}$$(13)

Therefore the first positive root of (13(13) $$\begin{array}{c}\hfill \mathit{\beta }tan(\mathit{\beta }h)=\mathit{\mu }.\end{array}$$(13) ) lies in the interval(14) $$\begin{array}{c}\hfill 0<k^2<{\mathit{\beta }}^2<{(\mathit{\pi }/2h)}^2.\end{array}$$(14)

We see that the positivity condition holds and conclude that the value of h must be so that (12(12) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}-u^{″}(t)=\mathrm{\Lambda }u(t)\hfill & \text{for}t\in (0,h),\hfill \\ u^{\prime }(0)=0,\hfill \\ u^{\prime }(h)+\mathit{\mu }u(h)=0.\hfill \end{array}\right.\end{array}$$(12) ) is satisfied. Denote by ${\mathrm{\Lambda }}_1$ the least eigenvalue. Then if$$\begin{array}{c}\hfill {\mathrm{\Lambda }}_1>k^2\frac{1-{\mathit{\rho }}_{-}}{1-\mathit{\rho }+}\end{array}$$

the inequality (11(11) $$\begin{array}{c}\hfill {\int }_0^h(u_t^2-k^2{u}^2)(1-\mathit{\rho }(s)t)\mathrm{d}t+\mathit{\mu }{u}^2(h)(1-\mathit{\rho }(s)h)t>0\end{array}$$(11) ) is satisfied.

3. Numerical experiments

In this section, we present some numerical results that illustrate the algorithms developed in Section 2. We only investigate the case of exact data. For our tests, we start by finding the value of the wavenumber $k^2$ in the Helmholtz equation for which the iterative procedure studied in [15] does not converge. This algorithm is described as the algorithm in Section 2.1 where the Robin boundary condition in problem (3(3) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u+\mathit{\mu }u=\mathit{\eta }\hfill & \text{on}{\mathrm{\Gamma }}_1,\hfill \end{array}\right.\end{array}$$(3) ) is replaced by the Neumann boundary condition instead. We then apply the iterative methods presented in Sections 2.1 and 2.2.

For the numerical implementation of these methods, we solve problem (1(1) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \end{array}\right.\end{array}$$(1) ) in a circular domain $\mathrm{\Omega }=\{(r,\mathit{\theta }):0\le r<R_1\text{and}0\le \mathit{\theta }<2\mathit{\pi }\}$, where $R_1$ is the radius of the circle. The boundaries ${\mathrm{\Gamma }}_0$ and ${\mathrm{\Gamma }}_1$ are given by$$\begin{array}{c}\hfill {\mathrm{\Gamma }}_0=\{(R_1,\mathit{\theta }):0\le \mathit{\theta }<{\mathit{\theta }}_1\}\text{and}{\mathrm{\Gamma }}_1=\{(R_1,\mathit{\theta }):{\mathit{\theta }}_1\le \mathit{\theta }<2\mathit{\pi }\},\end{array}$$

respectively. We should mention here that various choices of ${\mathit{\theta }}_1$ have been considered in order to investigate the ill-posedness of the Cauchy problem with respect to the lengths of the known and unknown parts of the boundary ${\mathrm{\Gamma }}_0$ and ${\mathrm{\Gamma }}_1$, respectively. The interior boundary described in Section 2.2 is given by $\mathit{\gamma }=\{(R_0,\mathit{\theta }):0\le \mathit{\theta }<2\mathit{\pi }\}$, where $R_0$ is the radius for the inner circle.

The auxiliary problems involved in the description of each method are solved by a finite difference method. For all the boundary value problems, we discretize the Helmholtz equation(15) $$\begin{array}{c}\hfill \frac{{\mathit{\partial }}^{2}u}{{\mathit{\partial }}^{2}r}+\frac{1}{r}\frac{\mathit{\partial }u}{\mathit{\partial }r}+\frac{1}{r^2}\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{\mathit{\theta }}^2}+k^{2}u=0,0<r<R,0<\mathit{\theta }<2\mathit{\pi }\end{array}$$(15)

together with the periodicity condition(16) $$\begin{array}{c}\hfill u(r,0)=u(r,2\mathit{\pi }),0<r<R_1,\end{array}$$(16)

to ensure the continuity at the end points. Depending on the algorithm, we also need to discretize the boundary conditions for the inner and outer circles corresponding to $r=R_0$ and $r=R_1$, respectively. These boundary conditions are the Dirichlet boundary condition:(17) $$\begin{array}{c}\hfill u(r,\mathit{\theta })=f(\mathit{\theta }),0\le \mathit{\theta }<2\mathit{\pi },\end{array}$$(17)

the Neumann boundary condition:(18) $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }r}(r,\mathit{\theta })=g(\mathit{\theta }),0\le \mathit{\theta }<2\mathit{\pi },\end{array}$$(18)

and the Robin boundary condition:(19) $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }r}(r,\mathit{\theta })+\mathit{\mu }u(r,\mathit{\theta })=\mathit{\eta }(\mathit{\theta }),0\le \mathit{\theta }<2\mathit{\pi }.\end{array}$$(19)

3.1. Finite difference approximation

We discretize the problem in polar coordinates. We consider the grid points as $(r_i,{\mathit{\theta }}_j)$, where $i=0,\cdots ,M$ and $j=0,\cdots ,N$. The grid size in the r and $\mathit{\theta }$ coordinates will be given by $\mathrm{\Delta }r=R_1/M$ and $\mathrm{\Delta }\mathit{\theta }=2\mathit{\pi }/N$, respectively. Let $u_{i,j}$ denote the discrete approximation to $u(r_i,{\mathit{\theta }}_j)$. We approximate the first- and second-order derivatives of the function u with respect to r by the centred differences$$\begin{array}{c}\hfill {\mathit{\partial }}_{r}u=(u_{i+1,j}-u_{i-1,j}){(2\mathrm{\Delta }r)}^{-1}\text{and}{\mathit{\partial }}_r^{2}u=(u_{i+1,j}-2u_{i,j}+u_{i-1,j}){(\mathrm{\Delta }{r}^2)}^{-1}\end{array}$$

respectively. Similarly, the second-order derivative of the function u with respect to $\mathit{\theta }$ can be defined. As a result, the finite difference approximation of the Helmholtz equation (15(15) $$\begin{array}{c}\hfill \frac{{\mathit{\partial }}^{2}u}{{\mathit{\partial }}^{2}r}+\frac{1}{r}\frac{\mathit{\partial }u}{\mathit{\partial }r}+\frac{1}{r^2}\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{\mathit{\theta }}^2}+k^{2}u=0,0<r<R,0<\mathit{\theta }<2\mathit{\pi }\end{array}$$(15) ) at each interior grid point corresponding to (i, j), $i=1,\cdots ,M-1$ and $j=1,\cdots N-1$ thus simplifies to$$\begin{array}{c}\hfill -a_i{u}_{i,j}+b_i{u}_{i-1,j}+c_i{u}_{i+1,j}+d_i{u}_{i,j-1}+d_i{u}_{i,j+1}=0.\end{array}$$

where$$\begin{array}{cc}\hfill a_i& =\frac{2}{\mathrm{\Delta }{r}^2}+\frac{2}{r_i^2\mathrm{\Delta }{\mathit{\theta }}^2}-k^2,b_i=\frac{1}{\mathrm{\Delta }{r}^2}-\frac{1}{2r_i\mathrm{\Delta }r},\hfill \\ \hfill c_i& =\frac{1}{\mathrm{\Delta }{r}^2}+\frac{1}{2r_i\mathrm{\Delta }r}\text{and}{d}_i=\frac{1}{r_i^2\mathrm{\Delta }{\mathit{\theta }}^2}.\hfill \end{array}$$

The periodicity condition (16(16) $$\begin{array}{c}\hfill u(r,0)=u(r,2\mathit{\pi }),0<r<R_1,\end{array}$$(16) ) gives$$\begin{array}{c}\hfill u_{i,N}=u_{i,0},i=1,\cdots ,M-1.\end{array}$$

Since there is only one point at the origin denoted by $u_0=u_{0,j}$, $j=0,\cdots N$, the discretization at that point is given by:$$\begin{array}{c}\hfill (1-k^2\mathrm{\Delta }{r}^2)u_0=\frac{1}{N}\sum _{j=0}^N{u}_{1j}.\end{array}$$

For the Dirichlet boundary conditions (17(17) $$\begin{array}{c}\hfill u(r,\mathit{\theta })=f(\mathit{\theta }),0\le \mathit{\theta }<2\mathit{\pi },\end{array}$$(17) ), we get the discretization of the form$$\begin{array}{c}\hfill u_{i,j}=f_j,i=i_0\text{or}i=M,\text{and}j=1,\cdots ,N,\end{array}$$

where $i_0$ corresponds to the index for $r=R_0$. The discretizations of the Neumann boundary condition (18(18) $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }r}(r,\mathit{\theta })=g(\mathit{\theta }),0\le \mathit{\theta }<2\mathit{\pi },\end{array}$$(18) ) obtained using the forward difference on $r=R_0$ and backward difference on $r=R_1$ are given by$$\begin{array}{c}\hfill (3u_{i,j}-4u_{i+1,j}+u_{i+2,j}){(2\mathrm{\Delta }r)}^{-1}=g_j,i=i_0\text{and}j=1,\cdots ,N\end{array}$$

and$$\begin{array}{c}\hfill (3u_{i,j}-4u_{i-1,j}+u_{i-2,j}){(2\mathrm{\Delta }r)}^{-1}=g_j,i=M\text{and}j=1,\cdots ,N,\end{array}$$

respectively. This particular choice means that we approximate the Neumann boundary condition with accuracy $\mathcal{O}(\mathrm{\Delta }{r}^2)$. The discretization of the Robin boundary conditions is obtained as a combination of the Neumann and Dirichlet discretizations.

Since for each of the iterative methods considered here, we only solve two boundary value problems, the discretization of each method leads to two different types of linear systems $A_{i}u=b_i$, $i=1,2$, where each $A_i$ is a large sparse matrix of size $MN\times MN$, and each $b_i$ is a vector that contains the boundary data values. Each system of equations is solved using the LU factorization. The advantage of these methods is that since the matrix $A_i$, $i=1,2$ does not depend on the boundary data, we can save the matrix $A_i$, $i=1,2$ and its sparse LU factorization between iterations. This significantly improves the computational speed.

3.2. The test problem

For the numerical computations, we choose the radius of the circle $R_1=0.2$ and the computational grid $N=300$ and $M=80$, in the $\mathit{\theta }$- and r-coordinates, respectively. The exact solution $u_e(x,y)$ is computed numerically by solving the Helmholtz equation with the Dirichlet boundary condition on $r=R_1$ given by$$\begin{array}{c}\hfill f(x,y)=sin(x+1)cosh(\sqrt{1-k^2}(y+2));\end{array}$$

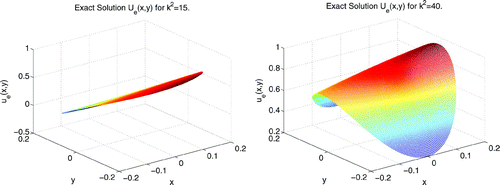
where $x=R_{1}cos(\mathit{\theta })$ and $y=R_{1}sin(\mathit{\theta })$. The exact Neumann boundary data g(x, y) is evaluated numerically from the exact solution $u_e(x,y)$. We observe that as $k^2$ increases the shape of the function f(x, y) above changes as well as the exact solution (see Figure 2) so that the problem becomes difficult to solve. It is therefore difficult to compare the quality of the computed solutions. But we can investigate the convergence or divergence of the algorithms presented in Sections 2.1 and 2.2 with respect to the wavenumber $k^2$.

Figure 2. Exact numerical solution $u_e(x,y)$ obtained by solving the direct problem with the Dirichlet boundary conditions f(x, y) with different wavenumbers $k^2$. On the left, $k^2=15$ and on the right $k^2=40$.

In order to start the iterative algorithms, we also need to choose initial approximations described in each method. For this, we solve the direct problem for the Helmholtz equation with Dirichlet boundary condition $f_0$ on $r=R_1$. The function $f_0$ is selected by interpolation of the function f using a cubic spline. This function is created so that $f=f_0$ on ${\mathrm{\Gamma }}_0$ but with different values on ${\mathrm{\Gamma }}_1$. The reason to do this is to avoid the discontinuity in the function $f_0$ at the end points of the boundary ${\mathrm{\Gamma }}_0$ and ${\mathrm{\Gamma }}_1$ that may lead to the Gibbs phenomena. The solution to this direct problem is thus the initial approximation $u_0$ from which we evaluate initial approximations required by any of the algorithms. It should be noted here that with the choice of $f_0=0$ so that $u_0=0$, all the methods considered here produce an iterative sequence that converges to the exact solution. The initial guess $f_0$ chosen here is not far from the exact solution on ${\mathrm{\Gamma }}_1$.

Figure 3. Results from the original algorithm when $k^2=14$. In the left the convergence history is presented when $\mathit{\epsilon }=0\%$. The exact and numerical solutions are presented in the right where the vertical dotted line separates the known and unknown part of the boundary. Here the solid line (–), the dash starred line (–$\star$–), the dashed triangulated line (–$△$–), the dash squared line (–$\square$–) and the dashed circular line (–$\circ$–) correspond the the noise level $\mathit{\epsilon }=0\%$, $\mathit{\epsilon }=1\%$, $\mathit{\epsilon }=3\%$ and $\mathit{\epsilon }=5\%$, respectively.

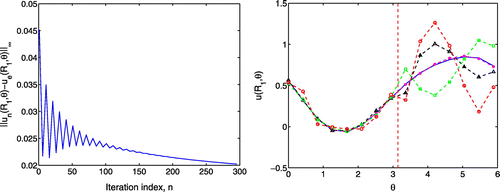
Figure 4. The value of the wavenumber $k^2=15$. We alternate the Dirichlet–Neumann conditions on ${\mathrm{\Gamma }}_0$ and the Robin–Dirichlet conditions on ${\mathrm{\Gamma }}_1$ with $\mathit{\mu }=6.5$. The values of the exact and numerical Dirichlet boundary data are presented on the right and the convergence history is shown on the left. The vertical dotted line separates the known and unknown part of the boundary. For both figures, the solid line (–), the dash starred line (–$\star$–), the dashed triangulated line (–$△$–), the dash squared line (–$\square$–) and the dashed circular line (–$\circ$–) correspond the the noise level $\mathit{\epsilon }=0\%$, $\mathit{\epsilon }=1\%$, $\mathit{\epsilon }=3\%$ and $\mathit{\epsilon }=5\%$, respectively.

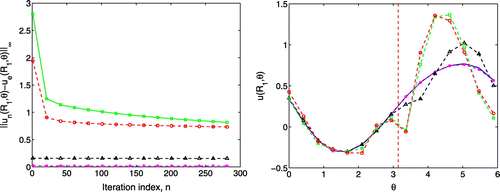
Figure 5. Divergence histories. On the left, the algorithm for which the Neumann–Dirichlet boundary conditions are alternated on ${\mathrm{\Gamma }}_0$ and on ${\mathrm{\Gamma }}_1$ diverges for $k^2=15$. On the right, the Dirichlet–Neumann boundary conditions are alternated on ${\mathrm{\Gamma }}_0$ and the Robin–Dirichlet boundary conditions on ${\mathrm{\Gamma }}_1$. The iterative sequence diverges for $k^2=40$.

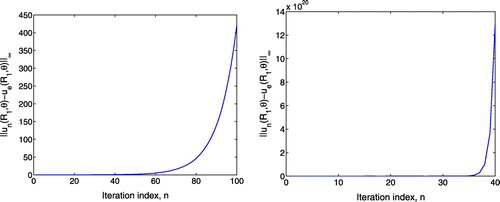
Figure 6. The value of the wavenumber $k^2=15$. We alternate the Robin–Dirichlet conditions on ${\mathrm{\Gamma }}_0$ with $\mathit{\sigma }=2.5$ and the Dirichlet–Neumann conditions on ${\mathrm{\Gamma }}_1$. The values of the exact and numerical Dirichlet boundary data are presented on the right and the convergence history is shown on the left. The vertical dotted line separates the known and unknown part of the boundary. The exact and numerical solutions are presented in the right where the vertical dotted line separates the known and unknown part of the boundary. Here the solid line (–), the dash starred line (–$\star$–), the dashed triangulated line (–$△$–), the dash squared line (–$\square$–) and the dashed circular line (–$\circ$–) correspond the the noise level $\mathit{\epsilon }=0\%$, $\mathit{\epsilon }=1\%$, $\mathit{\epsilon }=3\%$ and $\mathit{\epsilon }=5\%$, respectively.

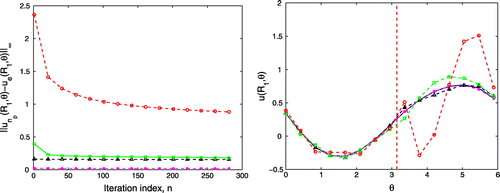
Figure 7. The value of the wavenumber $k^2=15$. We alternate the Robin–Dirichlet conditions on ${\mathrm{\Gamma }}_0$ and on ${\mathrm{\Gamma }}_1$ with parameters $\mathit{\sigma }=1$ and $\mathit{\mu }=1$. The values of the exact and numerical Dirichlet boundary data are presented on the right and the convergence history is shown on the left. The vertical dotted line separates the known and unknown part of the boundary. The exact and numerical solutions are presented in the right where the vertical dotted line separates the known and unknown part of the boundary. The solid line (–), the dash starred line (–$\star$–), the dashed triangulated line (–$△$–), the dash squared line (–$\square$–) and the dashed circular line (–$\circ$–) correspond the the noise level $\mathit{\epsilon }=0\%$, $\mathit{\epsilon }=1\%$, $\mathit{\epsilon }=3\%$ and $\mathit{\epsilon }=5\%$, respectively.

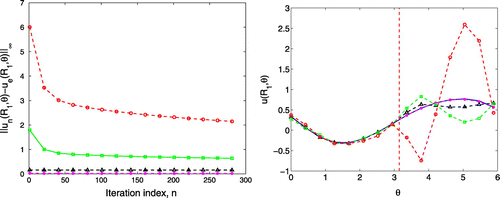
Figure 8. In this figure the value of the wavenumber $k^2=15$. We solve the problem in a narrow strip for $k^2=15$ and the constant $\mathit{\mu }=15$ in the Robin boundary condition. The values of the exact and numerical solutions are presented on the right and the convergence history is shown on the left. The vertical dotted line separates the known and unknown part of the boundary. The exact and numerical solutions are presented in the right where the vertical dotted line separates the known and unknown part of the boundary. Here the solid line (–), the dash starred line (–$\star$–), the dashed triangulated line (–$△$–), the dash squared line (–$\square$–) and the dashed circular line (–$\circ$–) correspond the noise level $\mathit{\epsilon }=0\%$, $\mathit{\epsilon }=1\%$, $\mathit{\epsilon }=3\%$ and $\mathit{\epsilon }=5\%$, respectively.

For our numerical tests, we only present the numerical reconstruction of u on ${\mathrm{\Gamma }}_1$ since the reconstruction of ${\mathit{\partial }}_{r}u$ on ${\mathrm{\Gamma }}_1$ is more ill-conditioned. This instability may due to the fact that the numerical differentiation in itself is ill-posed; see [18].

3.3. Results and discussion

In the following, we investigate the convergence of the methods presented in Sections 2 with respect to the wavenumber $k^2$. We consider the case of exact Cauchy data as well as noisy data. The noisy data are obtained by adding a normally distributed random noise of variance $\mathit{\epsilon }$ on the data f (x, y) and g(x, y), respectively. We only describe the numerical results obtained when ${\mathit{\theta }}_1=\mathit{\pi }$.

In order to apply our algorithms, we first find the value of the wavenumber $k^2$ for which the alternating algorithm in [15] does not converge. We observe that this method produces a convergent numerical solution when $k^2<15$; see Figure 3 and diverges for $k^2\ge 15$; see Figure 5 on the left. We have noticed that as $k^2$ increases, the error $\Vert u_n(r,\mathit{\theta })-u_e{(r,\mathit{\theta })\Vert }_{\infty }$ oscillates at the beginning of iterations before it becomes stable and decreases slowly; see Figure 3 on the left. We only present the results for exact data, i.e. $\mathit{\epsilon }=0\%$. But similar behaviour is observed for noisy data. Therefore, we apply the algorithms described in Sections 2.1 and 2.2 for $k^2\ge 15$. The results for all the four algorithms are summarized in Table 1.

Table 1. This table presents the convergence and/or divergence of the algorithms presented in this paper with respect to the wavenumber and the choice of the parameters $\mathit{\mu }$ and/or $\mathit{\sigma }$ in the Robin boundary conditions involved for a given method.

$k^2$	Original	Robin on ${\mathrm{\Gamma }}_1$	Robin on ${\mathrm{\Gamma }}_0$	Robin on ${\mathrm{\Gamma }}_1$ and ${\mathrm{\Gamma }}_0$	Strip
14	converges	converges	converges	converges	converges
		$\mathit{\mu }=6$	$\mathit{\sigma }=2.5$	$\mathit{\mu }=1$, $\mathit{\sigma }=1$	$\mathit{\mu }=12$
15	diverges	converges	converges	converges	converges
		$\mathit{\mu }=6.5$	$\mathit{\sigma }=4.5$	$\mathit{\mu }=5$, $\mathit{\sigma }=5$	$\mathit{\mu }=15$
30	diverges	converges	converges	converges	converges
		$\mathit{\mu }=30$	$\mathit{\sigma }=20$	$\mathit{\mu }=10$, $\mathit{\sigma }=10$	$\mathit{\mu }=80$
36	diverges	diverges	diverges	converges	converges
				$\mathit{\mu }=15$, $\mathit{\sigma }=15$	$\mathit{\mu }=100$
50	diverges	diverges	diverges	diverges	converges
					$\mathit{\mu }=200$

We now apply the algorithms developed in Section 2.1 for $k^2=15$. The numerical results are presented in Figures 4–7, respectively. These results depend on appropriate choices of the parameters $\mathit{\mu }$ and/or $\mathit{\sigma }$ in the Robin boundary conditions involved in each method as presented in Table 1. We observe that replacing the Neumann boundary conditions by the Robin boundary conditions, we improve the convergence of the method for the wavenumber for which the first algorithm fails. We also observe that as $k^2$ increases, the constant $\mathit{\mu }$ and/or $\mathit{\sigma }$ in the Robin boundary conditions increases also. For $k^2>30$, the error $\Vert u_n(r,\mathit{\theta })-u_e{(r,\mathit{\theta })\Vert }_{\infty }$ is unstable at the first iterations. The algorithm becomes increasingly unstable as $k^2$ increases and diverges for $k^2=40$, see Figure 5 on the right.

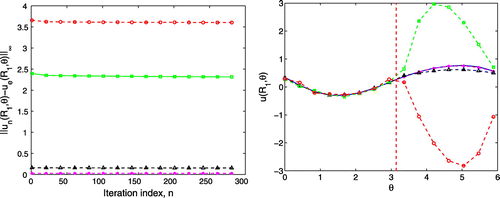
Figure 9. In this figure, we solve the problem in a narrow strip for $k^2=50$ and the constant $\mathit{\mu }=200$ in the Robin boundary condition. The values of the exact (- - -) and numerical (—) solutions are presented on the right and the convergence history is shown on the left. The vertical dotted line separates the known and unknown part of the boundary.

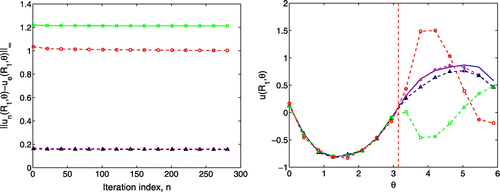
We finally investigate the algorithm presented in Section 2.2 as it is shown in Figures 8, 9 and Table 1. Compared to the previous methods, this method is accurate as the wavenumber $k^2$ increases. From the results in Table 1, we also observe that the constant $\mathit{\mu }$ in the Robin boundary condition also increases very much as the wavenumber increases.

For all the results presented here, we observe that as the noise level increases, the reconstruction of the numerical solutions becomes difficult. It is thus important to study the regularization effect in the future.

4. Conclusions

It was proved in [13] that the alternating algorithm suggested by V.A. Kozlov and V.G. Maz’ya in [15] does not converge for large values of the wave number in the Helmholtz equation. In this paper, we have considered iterative methods based on replacing Neumann–Dirichlet iterations by the Robin–Dirichlet ones. We observed that the algorithms presented in Section 2.1 may be used to improve the convergence of the algorithms in [15] for solving the Cauchy problem for the Helmholtz equation. As we expected, these algorithms fail to produce a convergent sequence for some large values of the wavenumber $k^2$. It becomes thus important to consider the algorithm in Section 2.2 based on solving the Cauchy problem for the Helmholtz equation in a narrow strip. The results reported above show that with this new method, the Cauchy problem for the Helmholtz equation is solved for large values in the wavenumber $k^2$.

It should be noted here that accurate results were obtained for the case of exact Cauchy data. Thus, we have demonstrated that the proposed methods are all related to positive quadratic forms. This means that we get a scalar product that is natural for the problem. By reformulating the Cauchy problem (1(1) $$\begin{array}{c}\hfill \left\{\begin{array}{cc}\mathrm{\Delta }u+k^{2}u=0\hfill & \text{in}\mathrm{\Omega },\hfill \\ u=f\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \\ {\mathit{\partial }}_{\mathit{\nu }}u=g\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \end{array}\right.\end{array}$$(1) ) as a linear operator equation, we thus have a natural setting with a scalar product that allows us to compute the adjoint operator by solving a similar boundary value problem. This can be used to implement faster methods, see [14,17], based on the conjugate gradient algorithm. For the same geometry, one can also compare the algorithm in Section 2.2 with our previous algorithm developed in [13].

In our future work, we will investigate the stability of these methods and improve our results in the case of inexact Cauchy data. We will also work to add regularization to the iterative methods. Also we remark that in our iterative methods we need to solve well-posed boundary value for the Helmholtz equation. If an application involves a complicated domain the finite element method may be more suitable to use. This is also something we intend to demonstrate in future papers.

Additional information

Funding

The work of Lydie Mpinganzima was supported by the Swedish International Development Cooperation Agency (Sida) and the University of Rwanda (UR) [Sida Contribution No: 51160027–02, 51160059–02].

Notes

No potential conflict of interest was reported by the authors.