Direct collocation method for identifying the initial conditions in the inverse wave problem using radial basis functions

ABSTRACT

A direct collocation method associated with explicit time integration using radial basis functions is proposed for identifying the initial conditions in the inverse problem of wave propagation. Optimum weights for the boundary conditions and additional condition are derived based on Lagrange’s multiplier method to achieve the prime convergence. Tikhonov regularization is introduced to improve the stability for the ill-posed system resulting from the noise, and the L-curve criterion is employed to select the optimum regularization parameter. No iteration scheme is required during the direct collocation computation which promotes the accuracy and stability for the solutions, while Galerkin-based methods demand the iteration procedure to deal with the inverse problems. High accuracy and good stability of the solution at very high noise level make this method a superior scheme for solving inverse problems.

KEYWORDS:

• Direct collocation method
• radial basis functions
• initial conditions
• inverse wave problem
• ill-posed system

Ams SUBJECT CLASSIFICATIONS:

• 65N21
• 65N35
• 35L20

1. Introduction

Inverse problem of wave propagation is currently of flourishing interest in many areas of applications, such as signal processing, remote sensing, nondestructive evaluation, biomedical and electromagnetic imaging, seismology, geophysics, oceanography and elsewhere. Problems of this type are characterized by a forward relation with loss of some information which results in calculating the backward relation so difficult. The solution does not continuously depend on the measurement data because of the unavoidable error in the observations. This makes inverse wave propagation an ill-posed problem that requires special treatments.

The identification of parameters corresponding to the heterogeneous materials attracted much attention in the past decades and different methods were proposed for solving such problems. Conventionally, finite difference method [1,2] and Galerkin method [3–5] were popular methods for the discretization of inverse problems to recover coefficients. In general, the ill-posed inverse problem is transformed into an optimization problem and iteration methods are utilized to achieve the optimum solution. Karr et al. [6] constructed the framework to solve the inverse problem of identifying the parameter via genetic algorithm in which the iteration might introduce the instability, and not only the initial guesses but also the characteristics of the space were vital to the solution accuracy. Without noise in the observed data, a well-posed coefficient inverse wave problem can be studied instead of an ill-posed problem [7]. For the noisy data in the measurement, regularization methods can be adopted to handle the resulting ill-conditioned matrix for optimization. To improve the optimization methods with local convergences, some globally convergent numerical algorithms [8], such as Quasi-Reversibility Method [9] and genetic method [6] were introduced for the inverse problems. Moreover, Erdem [10] presented a polynomial regression scheme with perturbation method to reconstruct the diffusion coefficient in a linear partial parabolic equation. Ramm and Sjostrand [11] investigated the inverse problem of finding unknown coefficients using asymptotic expansion and ray transforms. By employing the transformation method and radial basis functions approximations, Dehghan and Tatari [12] determined the control parameter in a one-dimensional (1d) parabolic equation. However, the transform formulation is only applicable to this parameter identification problem. Furthermore, Blazek et al. [13] provided a theoretical foundation for the parameter identification in wave propagation, and Bamberger et al. [14] explored the stability conditions for the 1d inverse wave problem of identifying the coefficient for the seismic profiles.

Source term identification is another type of typical inverse problems [15]. Iteration method is a natural choice for the optimization originated from the inverse problems [16,17]. However, sometimes after many iterations, the accuracy is still not high enough. Transformation method [18,19] is also a classical method for source term identification in the inverse problems, while the frame formulation merely works for the specified equations. By converting the problem into an inverse heat problem of finding source term, a numerical differentiation method associated with finite element method and Tikhonov regularization was introduced to approximate a single variable function from its noise data [18]. Although this method is highly feasible and stable with respect to data noise, the accuracy is undesirable. Recently, Wang et al. [20] developed a non-iterative reconstruction method to determine a source term in the Helmholtz equation using Fourier series expansion. Wang et al. [21] proposed a mesh-free scheme based on strong form collocation associated with radial basis functions and explicit time integration to solve ill-posed inverse wave problems of identifying the material parameter and source term. Even handling with very high noise in the input data, this method can achieve stable and highly accurate solutions.

Some other efforts were made on the determination of the boundary information [22,23]. By introducing the classical variational iteration method, Li [24] solved the two-dimensional (2d) inverse heat conduction problem and restored its boundary conditions. Without noise, this method is of high efficiency and accuracy since it can produce globally smooth approximation solution. However, the solution depends on the initial approximation and choosing appropriate initial approximation should be very careful. Wang et al. [25] investigated a 1d inverse heat conduction problem to determine the boundary. Even though a smooth technique is used to smoothen the measurement data, instability is also obvious and the error is quite serious in some cases. Therefore, a stable numerical method consisting of Tikhonov regularization was presented to solve an inverse wave problem of identifying the boundary condition, which revealed that solutions obtained by Tikhonov regularization were more accurate than those obtained by the singular value decomposition (SVD) regularization with noisy data, and the solutions were stable with respect to small perturbations in the input data [26]. Stability can also be improved using the future time in the problem to identify the boundary [27]. Besides, Hon and Wei [28] developed a fundamental solution method to identify the boundary in the inverse heat conduction problem in which seeking the fundamental solution was not an easy task. Cheng and Cabral [29] proposed the radial basis function collocation method to directly solve the Cauchy problem with missing boundary conditions. Without iterations, this method can also obtain accurate solutions with good stability.

Although a variety of contributions were accomplished on the inverse wave problems, few activities have been found to identify the initial conditions in the boundary value problems. Through considering ordinary differential equations, Ahmed et al. [30] proposed an instrumental variable method to recover the transient initial conditions. Liu and Uhlmann [31] tried to find the sound speed and the initial source in thermoacoustic tomography and photoacoustic tomography. Clason and Klibanov [32] determined the unknown initial conditions in a wave equation using the method of quasi-reversibility. In the past decades, radial basis collocation method (RBCM) became popular because of its easy implementation and high accuracy [33–43]. This method also showed very good performances in solving direct wave propagation problems [44–47]. Therefore, we introduce the strong form collocation method associated with radial basis functions for the initial conditions identification in the inverse wave problem. No iteration scheme needs to be adopted in the collocation computation which avoids the instability in this process. Tikhonov regularization is employed to improve the resulting matrix in the solution. Even with very high noise, stable and convergent solutions can be obtained.

2. Radial basis functions

Generally, a radial basis function (RBF) interpolant for a function $u\left(\mathbf{x}\right)$ can be expressed as(1) $$u\left(\mathbf{x}\right)\approx \tilde{u}\left(\mathbf{x}\right)=\sum _{I=1}^N\phi \left(\mathbf{x}-{\mathbf{x}}_I\right)d_I$$(1)

where $\tilde{u}\left(\mathbf{x}\right)$ is the approximation of $u\left(\mathbf{x}\right)$, N is the number of source points, $\phi$ is the RBF and the node ${\mathbf{x}}_I=(\begin{array}{ccc}{x}_I\hfill & y_I\hfill & z_I\hfill \end{array})$ is called centre and $d_I$ is the expansion coefficient. The commonly used RBFs are listed as follows [35]:

Inverse Multiquadric:(2) $$\phi \left(r\right)={\left(r^2+{\vartheta }^2\right)}^{-\frac{1}{2}}$$(2)

Linear Multiquadric:

(3) $$\phi \left(r\right)={\left(r^2+{\vartheta }^2\right)}^{\frac{1}{2}}$$(3)

Gaussian:(4) $$\phi \left(r\right)=exp(-\frac{r^2}{{\vartheta }^2})$$(4)

where $r=∥\mathbf{x}-{\mathbf{x}}_I∥$ is the radial distance from the centre and $\vartheta$ is the shape parameter. If the approximation functions are in the native space of the basis functions, it has been proved that RBF interpolation converges at exponential rates with respect to the node distance $h:={\text{sup}}_{\mathbf{x}\in \mathrm{\Omega }}\underset{I=1,\cdots ,N}{\text{min}}∥\mathbf{x}-{\mathbf{x}}_I∥$ for all the data sites ${\mathbf{x}}_I$, which takes the form(5) $${∥u-u^h∥}_{L_{\infty }(\mathrm{\Omega })}\le C{\varpi }^{\vartheta /h}{∥u∥}_{\ell }$$(5)

where C is a constant, $\varpi \in \left(0,1\right)$ is a real number and ${∥u∥}_{\ell }$ is the norm induced in [48].

3. Collocation method with explicit time integration for the identification of initial conditions in the wave problems

3.1. Wave problem statement and discretization

A general problem of wave propagation can be stated as(6) $$\ddot{\mathbf{u}}\left(\mathbf{x},t\right)=\alpha \left(\mathbf{x}\right)\mathbf{Lu}\left(\mathbf{x},t\right)+\mathbf{f}\left(\mathbf{x},t\right),\mathbf{x}\in \mathrm{\Omega },t\in \left[0,T\right]$$(6)

the boundary conditions are(7) $${\mathbf{B}}^h\mathbf{u}\left(\mathbf{x},t\right)=\mathbf{h}\left(\mathbf{x},t\right),\mathbf{x}\in {\mathrm{\Gamma }}_h,t\in \left[0,T\right]$$(7) (8) $${\mathbf{B}}^g\mathbf{u}\left(\mathbf{x},t\right)=\mathbf{g}\left(\mathbf{x},t\right),\mathbf{x}\in {\mathrm{\Gamma }}_g,t\in \left[0,T\right]$$(8)

and the additional condition observed from the measurement data within the domain can be expressed as(9) $$\mathbf{Au}\left(\mathbf{x},t\right)=\mathbf{b}\left(\mathbf{x},t\right),\mathbf{x}\in \mathrm{\Pi },t\in \left[0,T\right]$$(9)

For the inverse problem of identifying the initial displacement in wave propagation, the initial conditions are shown as(10) $$\mathbf{u}\left(\mathbf{x},0\right)={\mathbf{u}}_0\left(\mathbf{x}\right)=\xi \left(\mathbf{x}\right),\mathbf{x}\in \overline{\mathrm{\Omega }}$$(10) (11) $$\dot{\mathbf{u}}\left(\mathbf{x},0\right)={\mathbf{c}}_0\left(\mathbf{x}\right),\mathbf{x}\in \overline{\mathrm{\Omega }}$$(11)

where $\xi \left(\mathbf{x}\right)$ is an unknown function needs recognition and ${\mathbf{c}}_0\left(\mathbf{x}\right)$ is a known function. For the inverse problem of identifying the initial velocity, the initial conditions signify(12) $$\mathbf{u}\left(\mathbf{x},0\right)={\mathbf{u}}_0\left(\mathbf{x}\right),\mathbf{x}\in \overline{\mathrm{\Omega }}$$(12) (13) $$\dot{\mathbf{u}}\left(\mathbf{x},0\right)={\mathbf{c}}_0\left(\mathbf{x}\right)=\zeta \left(\mathbf{x}\right),\mathbf{x}\in \overline{\mathrm{\Omega }}$$(13)

Herein, ${\mathbf{u}}_0\left(\mathbf{x}\right)$ is a known function and $\zeta \left(\mathbf{x}\right)$ is the function for identification. In the equations above, $\mathrm{\Omega }$ is an open problem domain, ${\mathrm{\Gamma }}_h$ and ${\mathrm{\Gamma }}_g$ are the Neumann boundary and Dirichlet boundary, respectively, where $\mathrm{\Omega }\cup {\mathrm{\Gamma }}_h\cup {\mathrm{\Gamma }}_g=\overline{\mathrm{\Omega }};\mathrm{\Pi }\in \overline{\mathrm{\Omega }}$ is a subdomain of known condition, and T is the time interval for evaluation; $\mathbf{L},{\mathbf{B}}^h,{\mathbf{B}}^g,\mathbf{A}$ are the spatial differential operators in $\mathrm{\Omega }$, on ${\mathrm{\Gamma }}_h,{\mathrm{\Gamma }}_g$ and in $\mathrm{\Pi }$ in turn. In wave problem, $L={\mathrm{\nabla }}^2$ and $\alpha$ is the positive parameters. In addition, $\mathbf{u}$ is the displacement vector, $\mathbf{f}$ is the source term, $\mathbf{h}$ is the traction vector associated with Neumann boundary condition and $\mathbf{g}$ is the displacement vector associated with Dirichlet boundary condition. ${\mathbf{u}}_0$ and ${\mathbf{c}}_0$ are the initial displacement vector and initial velocity vector, respectively. $\mathbf{b}$ is the known vector of measurement data. $\xi \left(\mathbf{x}\right)$ and $\zeta \left(\mathbf{x}\right)$ are the unknown functions for identification.

Introducing the central difference method to discretize the time domain of equations (6(6) $$\ddot{\mathbf{u}}\left(\mathbf{x},t\right)=\alpha \left(\mathbf{x}\right)\mathbf{Lu}\left(\mathbf{x},t\right)+\mathbf{f}\left(\mathbf{x},t\right),\mathbf{x}\in \mathrm{\Omega },t\in \left[0,T\right]$$(6) )–(9(9) $$\mathbf{Au}\left(\mathbf{x},t\right)=\mathbf{b}\left(\mathbf{x},t\right),\mathbf{x}\in \mathrm{\Pi },t\in \left[0,T\right]$$(9) ) at n time step counter gives(14) $${\mathbf{u}}_{n+1}(\mathbf{x})-2{\mathbf{u}}_n(\mathbf{x})+{\mathbf{u}}_{n-1}(\mathbf{x})=\mathrm{\Delta }{t}^2\alpha {\mathbf{Lu}}_n\left(\mathbf{x}\right)+\mathrm{\Delta }{t}^2{\mathbf{f}}_n\left(\mathbf{x}\right),\mathbf{x}\in \mathrm{\Omega }$$(14) (15) $${\mathbf{B}}^h{\mathbf{u}}_{n+1}\left(\mathbf{x}\right)={\mathbf{h}}_{n+1}\left(\mathbf{x}\right),\mathbf{x}\in {\mathrm{\Gamma }}_h$$(15) (16) $${\mathbf{B}}^g{\mathbf{u}}_{n+1}\left(\mathbf{x}\right)={\mathbf{g}}_{n+1}\left(\mathbf{x}\right),\mathbf{x}\in {\mathrm{\Gamma }}_g$$(16) (17) $${\mathbf{Au}}_{n+1}\left(\mathbf{x}\right)={\mathbf{b}}_{n+1}\left(\mathbf{x}\right),\mathbf{x}\in \mathrm{\Pi }$$(17)

in which ${\mathbf{u}}_n\left(\mathbf{x}\right)=\mathbf{u}\left(\mathbf{x},t_n\right)$.

The problem unknown $\mathbf{u}$ is approximated by the RBF approximation $\tilde{\mathbf{u}}$ discretized by N source points which is expressed as following (18) $$\mathbf{u}\left(\mathbf{x},t\right)\approx \tilde{\mathbf{u}}\left(\mathbf{x},t\right)=\mathrm{\Phi }\left(\mathbf{x}\right)\mathbf{d}\left(t\right)$$(18)

and(19) $${\mathbf{u}}_n\left(\mathbf{x}\right)\approx {\tilde{\mathbf{u}}}_n\left(\mathbf{x}\right)=\mathrm{\Phi }\left(\mathbf{x}\right){\mathbf{d}}_n$$(19) (20) $$\mathbf{u}\left(\mathbf{x},0\right)={\mathbf{u}}_0\left(\mathbf{x}\right)\approx {\tilde{\mathbf{u}}}_0\left(\mathbf{x}\right)=\mathrm{\Phi }\left(\mathbf{x}\right){\mathbf{d}}_0$$(20) (21) $$\dot{\mathbf{u}}\left(\mathbf{x},0\right)={\mathbf{c}}_0\left(\mathbf{x}\right)=\mathrm{\Phi }\left(\mathbf{x}\right){\dot{\mathbf{d}}}_0$$(21)

in which(22) $$\begin{array}{c}\mathrm{\Phi }=\left(\begin{array}{cccc}{\mathrm{\Phi }}_1\hfill & {\mathrm{\Phi }}_2\hfill & \cdots \hfill & {\mathrm{\Phi }}_N\hfill \end{array}\right),{\mathrm{\Phi }}_I={\phi }_I\mathbf{I},\hfill \\ \mathbf{d}={\left(\begin{array}{cccc}{\left({\mathbf{d}}^1\right)}^T\hfill & {\left({\mathbf{d}}^2\right)}^T\hfill & \cdots \hfill & {\left({\mathbf{d}}^N\right)}^T\hfill \end{array}\right)}^T,{\left({\mathbf{d}}^I\right)}^T=\left(\begin{array}{ccc}{d}^{1I}\hfill & d^{2I}\hfill & d^{3I}\hfill \end{array}\right)\hfill \end{array}$$(22)

and $\mathbf{I}$ is the identity matrix. Define the sets of collocation points as(23) $$\begin{array}{c}\mathbf{P}=\left\{{\mathbf{p}}_1,{\mathbf{p}}_2,\cdots ,{\mathbf{p}}_{N_p}\right\}\subseteq \mathrm{\Omega },\mathbf{Q}=\left\{{\mathbf{q}}_1,{\mathbf{q}}_2,\cdots ,{\mathbf{q}}_{N_q}\right\}\subseteq {\mathrm{\Gamma }}_h,\hfill \\ \mathbf{R}=\left\{{\mathbf{r}}_1,{\mathbf{r}}_2,\cdots ,{\mathbf{r}}_{N_r}\right\}\subseteq {\mathrm{\Gamma }}_g,\mathbf{O}=\left\{{\mathbf{o}}_1,{\mathbf{o}}_2,\cdots ,{\mathbf{o}}_{N_o}\right\}\subseteq \mathrm{\Pi }\hfill \end{array}$$(23)

in which N _p is the number of collocation points in Ω, N _q is the number of collocation points on Γ _h , N _r is the number of collocation points on Γ _g , N _o is the number of collocation points in the subdomain Π and N _c = N _p + N _q + N _r + N _o is the number of total collocation points for solution.

3.2. Identification of initial displacement condition

In this identification problem, the initial velocity c ₀ is known and we try to find the solution of the initial displacement u ₀ from the given governing equation, boundary conditions and additional condition. The forward difference provides(24) $${\mathbf{u}}_1={\mathbf{c}}_0\mathrm{\Delta }t+{\mathbf{u}}_0$$(24)

and(25) $${\mathbf{d}}_1={\dot{\mathbf{d}}}_0\mathrm{\Delta }t+{\mathbf{d}}_0$$(25)

where ${\dot{\mathbf{d}}}_0$ is known which can be obtained from Equation (21(21) $$\dot{\mathbf{u}}\left(\mathbf{x},0\right)={\mathbf{c}}_0\left(\mathbf{x}\right)=\mathrm{\Phi }\left(\mathbf{x}\right){\dot{\mathbf{d}}}_0$$(21) ) of known ${\mathbf{c}}_0\left(\mathbf{x}\right)$. Substituting (19(19) $${\mathbf{u}}_n\left(\mathbf{x}\right)\approx {\tilde{\mathbf{u}}}_n\left(\mathbf{x}\right)=\mathrm{\Phi }\left(\mathbf{x}\right){\mathbf{d}}_n$$(19) ), (20(20) $$\mathbf{u}\left(\mathbf{x},0\right)={\mathbf{u}}_0\left(\mathbf{x}\right)\approx {\tilde{\mathbf{u}}}_0\left(\mathbf{x}\right)=\mathrm{\Phi }\left(\mathbf{x}\right){\mathbf{d}}_0$$(20) ) and (25(25) $${\mathbf{d}}_1={\dot{\mathbf{d}}}_0\mathrm{\Delta }t+{\mathbf{d}}_0$$(25) ) into (14(14) $${\mathbf{u}}_{n+1}(\mathbf{x})-2{\mathbf{u}}_n(\mathbf{x})+{\mathbf{u}}_{n-1}(\mathbf{x})=\mathrm{\Delta }{t}^2\alpha {\mathbf{Lu}}_n\left(\mathbf{x}\right)+\mathrm{\Delta }{t}^2{\mathbf{f}}_n\left(\mathbf{x}\right),\mathbf{x}\in \mathrm{\Omega }$$(14) )–(17(17) $${\mathbf{Au}}_{n+1}\left(\mathbf{x}\right)={\mathbf{b}}_{n+1}\left(\mathbf{x}\right),\mathbf{x}\in \mathrm{\Pi }$$(17) ) yields(26) $${\mathrm{\Phi }\mathbf{d}}_2-\left(\mathrm{\Phi }+\mathrm{\Delta }{t}^2\alpha \mathbf{L}\mathrm{\Phi }\right){\mathbf{d}}_0=\left(2\mathrm{\Delta }t\mathrm{\Phi }+\mathrm{\Delta }{t}^3\alpha \mathbf{L}\mathrm{\Phi }\right){\dot{\mathbf{d}}}_0+\mathrm{\Delta }{t}^2{\mathbf{f}}_1$$(26) (27) $${\mathbf{B}}^h\mathrm{\Phi }\left(\mathbf{x}\right){\mathbf{d}}_2={\mathbf{h}}_2\left(\mathbf{x}\right),{\mathbf{B}}^h\mathrm{\Phi }\left(\mathbf{x}\right){\mathbf{d}}_0={\mathbf{h}}_0\left(\mathbf{x}\right),\mathbf{x}\in {\mathrm{\Gamma }}_h$$(27) (28) $${\mathbf{B}}^g\mathrm{\Phi }\left(\mathbf{x}\right){\mathbf{d}}_2={\mathbf{g}}_2\left(\mathbf{x}\right),{\mathbf{B}}^g\mathrm{\Phi }\left(\mathbf{x}\right){\mathbf{d}}_0={\mathbf{g}}_0\left(\mathbf{x}\right),\mathbf{x}\in {\mathrm{\Gamma }}_g$$(28) (29) $$\mathbf{A}\mathrm{\Phi }\left(\mathbf{x}\right){\mathbf{d}}_2={\mathbf{b}}_2\left(\mathbf{x}\right),\mathbf{A}\mathrm{\Phi }\left(\mathbf{x}\right){\mathbf{d}}_0={\mathbf{b}}_0\left(\mathbf{x}\right),\mathbf{x}\in \mathrm{\Pi }$$(29)

We can rewrite Equation (26(26) $${\mathrm{\Phi }\mathbf{d}}_2-\left(\mathrm{\Phi }+\mathrm{\Delta }{t}^2\alpha \mathbf{L}\mathrm{\Phi }\right){\mathbf{d}}_0=\left(2\mathrm{\Delta }t\mathrm{\Phi }+\mathrm{\Delta }{t}^3\alpha \mathbf{L}\mathrm{\Phi }\right){\dot{\mathbf{d}}}_0+\mathrm{\Delta }{t}^2{\mathbf{f}}_1$$(26) ) of the conjoined unknowns as(30) $$\left[\begin{array}{cc}\mathrm{\Phi }\hfill & -\left(\mathrm{\Phi }+\mathrm{\Delta }{t}^2\alpha \mathbf{L}\mathrm{\Phi }\right)\hfill \end{array}\right]\left[\begin{array}{c}{\mathbf{d}}_2\\ {\mathbf{d}}_0\end{array}\right]=\left(2\mathrm{\Delta }t\mathrm{\Phi }+\mathrm{\Delta }{t}^3\alpha \mathbf{L}\mathrm{\Phi }\right){\dot{\mathbf{d}}}_0+\mathrm{\Delta }{t}^2{\mathbf{f}}_1$$(30)

Define(31) $$\mathbf{D}=\left[\begin{array}{c}{\mathbf{d}}_2\\ {\mathbf{d}}_0\end{array}\right]$$(31)

The discretized equations (26(26) $${\mathrm{\Phi }\mathbf{d}}_2-\left(\mathrm{\Phi }+\mathrm{\Delta }{t}^2\alpha \mathbf{L}\mathrm{\Phi }\right){\mathbf{d}}_0=\left(2\mathrm{\Delta }t\mathrm{\Phi }+\mathrm{\Delta }{t}^3\alpha \mathbf{L}\mathrm{\Phi }\right){\dot{\mathbf{d}}}_0+\mathrm{\Delta }{t}^2{\mathbf{f}}_1$$(26) )–(29(29) $$\mathbf{A}\mathrm{\Phi }\left(\mathbf{x}\right){\mathbf{d}}_2={\mathbf{b}}_2\left(\mathbf{x}\right),\mathbf{A}\mathrm{\Phi }\left(\mathbf{x}\right){\mathbf{d}}_0={\mathbf{b}}_0\left(\mathbf{x}\right),\mathbf{x}\in \mathrm{\Pi }$$(29) ) are enforced to be satisfied on the collocation points denoted in Equation (23(23) $$\begin{array}{c}\mathbf{P}=\left\{{\mathbf{p}}_1,{\mathbf{p}}_2,\cdots ,{\mathbf{p}}_{N_p}\right\}\subseteq \mathrm{\Omega },\mathbf{Q}=\left\{{\mathbf{q}}_1,{\mathbf{q}}_2,\cdots ,{\mathbf{q}}_{N_q}\right\}\subseteq {\mathrm{\Gamma }}_h,\hfill \\ \mathbf{R}=\left\{{\mathbf{r}}_1,{\mathbf{r}}_2,\cdots ,{\mathbf{r}}_{N_r}\right\}\subseteq {\mathrm{\Gamma }}_g,\mathbf{O}=\left\{{\mathbf{o}}_1,{\mathbf{o}}_2,\cdots ,{\mathbf{o}}_{N_o}\right\}\subseteq \mathrm{\Pi }\hfill \end{array}$$(23) ) to solve the two unknowns jointly and those equations can be summarized as(32) $$\mathbf{KD}=\mathbf{F}$$(32)

where(33) $$\mathbf{K}=\left[\begin{array}{c}{\mathbf{K}}_1\\ {\mathbf{K}}_2\\ {\mathbf{K}}_3\\ {\mathbf{K}}_4\end{array}\right];\mathbf{F}=\left[\begin{array}{c}{\mathbf{F}}_1\\ {\mathbf{F}}_2\\ {\mathbf{F}}_3\\ {\mathbf{F}}_4\end{array}\right]$$(33)

in which(34) $$\begin{array}{c}{\mathbf{K}}_1=\left[\begin{array}{cc}\mathrm{\Phi }\hfill & -\left(\mathrm{\Phi }+\mathrm{\Delta }{t}^2\alpha \mathbf{L}\mathrm{\Phi }\right)\hfill \end{array}\right],\hfill \\ {\mathbf{F}}_1=\left(2\mathrm{\Delta }t\mathrm{\Phi }+\mathrm{\Delta }{t}^3\alpha \mathbf{L}\mathrm{\Phi }\right){\dot{\mathbf{d}}}_0+\mathrm{\Delta }{t}^2{\mathbf{f}}_1,\hfill \\ \mathrm{\Phi }=\left[\begin{array}{c}\mathrm{\Phi }\left({\mathbf{p}}_1\right)\\ \mathrm{\Phi }\left({\mathbf{p}}_2\right)\\ ⋮\\ \mathrm{\Phi }\left({\mathbf{p}}_{N_p}\right)\end{array}\right],{\mathbf{f}}_1=\left[\begin{array}{c}\mathbf{f}\left({\mathbf{p}}_1,t_1\right)\\ \mathbf{f}\left({\mathbf{p}}_2,t_1\right)\\ ⋮\\ \mathbf{f}\left({\mathbf{p}}_{N_p},t_1\right)\end{array}\right]\hfill \end{array}$$(34) (35) $${\mathbf{K}}_2=\left[\begin{array}{cc}{\mathbf{B}}^h\mathrm{\Phi }\hfill & \mathbf{0}\hfill \\ \mathbf{0}\hfill & {\mathbf{B}}^h\mathrm{\Phi }\hfill \end{array}\right],{\mathbf{B}}^h\mathrm{\Phi }=\left[\begin{array}{c}{\mathbf{B}}^h\mathrm{\Phi }\left({\mathbf{q}}_1\right)\\ {\mathbf{B}}^h\mathrm{\Phi }\left({\mathbf{q}}_2\right)\\ ⋮\\ {\mathbf{B}}^h\mathrm{\Phi }\left({\mathbf{q}}_{N_q}\right)\end{array}\right],{\mathbf{F}}_2=\left[\begin{array}{c}{\mathbf{F}}_{21}\\ {\mathbf{F}}_{22}\end{array}\right],{\mathbf{F}}_{21}=\left[\begin{array}{c}\mathbf{h}\left({\mathbf{q}}_1,t_2\right)\\ \mathbf{h}\left({\mathbf{q}}_2,t_2\right)\\ ⋮\\ \mathbf{h}\left({\mathbf{q}}_{N_q},t_2\right)\end{array}\right],{\mathbf{F}}_{22}=\left[\begin{array}{c}\mathbf{h}\left({\mathbf{q}}_1,t_0\right)\\ \mathbf{h}\left({\mathbf{q}}_2,t_0\right)\\ ⋮\\ \mathbf{h}\left({\mathbf{q}}_{N_q},t_0\right)\end{array}\right]$$(35) (36) $${\mathbf{K}}_3=\left[\begin{array}{cc}{\mathbf{B}}^g\mathrm{\Phi }\hfill & \mathbf{0}\hfill \\ \mathbf{0}\hfill & {\mathbf{B}}^g\mathrm{\Phi }\hfill \end{array}\right],{\mathbf{B}}^g\mathrm{\Phi }=\left[\begin{array}{c}{\mathbf{B}}^g\mathrm{\Phi }\left({\mathbf{r}}_1\right)\\ {\mathbf{B}}^g\mathrm{\Phi }\left({\mathbf{r}}_2\right)\\ ⋮\\ {\mathbf{B}}^g\mathrm{\Phi }\left({\mathbf{r}}_{N_r}\right)\end{array}\right],{\mathbf{F}}_3=\left[\begin{array}{c}{\mathbf{F}}_{31}\\ {\mathbf{F}}_{32}\end{array}\right],{\mathbf{F}}_{31}=\left[\begin{array}{c}\mathbf{g}\left({\mathbf{r}}_1,t_2\right)\\ \mathbf{g}\left({\mathbf{r}}_2,t_2\right)\\ ⋮\\ \mathbf{g}\left({\mathbf{r}}_{N_r},t_2\right)\end{array}\right],{\mathbf{F}}_{32}=\left[\begin{array}{c}\mathbf{g}\left({\mathbf{r}}_1,t_0\right)\\ \mathbf{g}\left({\mathbf{r}}_2,t_0\right)\\ ⋮\\ \mathbf{g}\left({\mathbf{r}}_{N_r},t_0\right)\end{array}\right]$$(36) (37) $${\mathbf{K}}_4=\left[\begin{array}{cc}\mathbf{A}\mathrm{\Phi }\hfill & \mathbf{0}\hfill \\ \mathbf{0}\hfill & \mathbf{A}\mathrm{\Phi }\hfill \end{array}\right],\mathbf{A}\mathrm{\Phi }=\left[\begin{array}{c}\mathbf{A}\mathrm{\Phi }\left({\mathbf{o}}_1\right)\\ \mathbf{A}\mathrm{\Phi }\left({\mathbf{o}}_2\right)\\ ⋮\\ \mathbf{A}\mathrm{\Phi }\left({\mathbf{o}}_{N_o}\right)\end{array}\right],{\mathbf{F}}_4=\left[\begin{array}{c}{\mathbf{F}}_{41}\\ {\mathbf{F}}_{42}\end{array}\right],{\mathbf{F}}_{41}=\left[\begin{array}{c}\mathbf{b}\left({\mathbf{o}}_1,t_2\right)\\ \mathbf{b}\left({\mathbf{o}}_2,t_2\right)\\ ⋮\\ \mathbf{b}\left({\mathbf{o}}_{N_o},t_2\right)\end{array}\right],{\mathbf{F}}_{42}=\left[\begin{array}{c}\mathbf{b}\left({\mathbf{o}}_1,t_0\right)\\ \mathbf{b}\left({\mathbf{o}}_2,t_0\right)\\ ⋮\\ \mathbf{b}\left({\mathbf{o}}_{N_o},t_0\right)\end{array}\right]$$(37)

3.3. Identification of initial velocity condition

To identify the initial velocity condition c ₀ in the inverse problem of wave propagation, we define the RBF approximation of ${\mathbf{c}}_0$ as ${\tilde{\mathbf{c}}}_0$ which is stated as(38) $${\mathbf{c}}_0\left(\mathbf{x}\right)\approx {\tilde{\mathbf{c}}}_0\left(\mathbf{x}\right)=\mathrm{\Phi }\left(\mathbf{x}\right){\dot{\mathbf{d}}}_0$$(38)

where ${\dot{\mathbf{d}}}_0$ is the unknown for evaluation. Introducing (38(38) $${\mathbf{c}}_0\left(\mathbf{x}\right)\approx {\tilde{\mathbf{c}}}_0\left(\mathbf{x}\right)=\mathrm{\Phi }\left(\mathbf{x}\right){\dot{\mathbf{d}}}_0$$(38) ) into (24(24) $${\mathbf{u}}_1={\mathbf{c}}_0\mathrm{\Delta }t+{\mathbf{u}}_0$$(24) ) gives(39) $${\mathbf{u}}_1={\mathrm{\Phi }\dot{\mathbf{d}}}_0\mathrm{\Delta }t+{\mathbf{u}}_0$$(39)

Substituting (19(19) $${\mathbf{u}}_n\left(\mathbf{x}\right)\approx {\tilde{\mathbf{u}}}_n\left(\mathbf{x}\right)=\mathrm{\Phi }\left(\mathbf{x}\right){\mathbf{d}}_n$$(19) ) into (14(14) $${\mathbf{u}}_{n+1}(\mathbf{x})-2{\mathbf{u}}_n(\mathbf{x})+{\mathbf{u}}_{n-1}(\mathbf{x})=\mathrm{\Delta }{t}^2\alpha {\mathbf{Lu}}_n\left(\mathbf{x}\right)+\mathrm{\Delta }{t}^2{\mathbf{f}}_n\left(\mathbf{x}\right),\mathbf{x}\in \mathrm{\Omega }$$(14) )–(17(17) $${\mathbf{Au}}_{n+1}\left(\mathbf{x}\right)={\mathbf{b}}_{n+1}\left(\mathbf{x}\right),\mathbf{x}\in \mathrm{\Pi }$$(17) ) and invoking (39(39) $${\mathbf{u}}_1={\mathrm{\Phi }\dot{\mathbf{d}}}_0\mathrm{\Delta }t+{\mathbf{u}}_0$$(39) ) render(40) $${\mathrm{\Phi }\mathbf{d}}_2-\left(2\mathrm{\Phi }\mathrm{\Delta }t+\mathrm{\Delta }{t}^3\alpha \mathbf{L}\mathrm{\Phi }\right){\dot{\mathbf{d}}}_0=\mathrm{\Delta }{t}^2\alpha {\mathbf{L}\mathrm{\Phi }\mathbf{d}}_0+{\mathbf{u}}_0+\mathrm{\Delta }{t}^2{\mathbf{f}}_1$$(40) (41) $${\mathbf{B}}^h\mathrm{\Phi }\left(\mathbf{x}\right){\mathbf{d}}_2={\mathbf{h}}_2\left(\mathbf{x}\right),{\mathbf{B}}^h\mathrm{\Phi }\left(\mathbf{x}\right){\dot{\mathbf{d}}}_0=\frac{{\mathbf{h}}_1\left(\mathbf{x}\right)-{\mathbf{h}}_0\left(\mathbf{x}\right)}{\mathrm{\Delta }t},\mathbf{x}\in {\mathrm{\Gamma }}_h$$(41) (42) $${\mathbf{B}}^g\mathrm{\Phi }\left(\mathbf{x}\right){\mathbf{d}}_2={\mathbf{g}}_2\left(\mathbf{x}\right),{\mathbf{B}}^g\mathrm{\Phi }\left(\mathbf{x}\right){\dot{\mathbf{d}}}_0=\frac{{\mathbf{g}}_1\left(\mathbf{x}\right)-{\mathbf{g}}_0\left(\mathbf{x}\right)}{\mathrm{\Delta }t},\mathbf{x}\in {\mathrm{\Gamma }}_g$$(42) (43) $$\mathbf{A}\mathrm{\Phi }\left(\mathbf{x}\right){\mathbf{d}}_2={\mathbf{b}}_2\left(\mathbf{x}\right),\mathbf{A}\mathrm{\Phi }\left(\mathbf{x}\right){\dot{\mathbf{d}}}_0=\frac{{\mathbf{b}}_1\left(\mathbf{x}\right)-{\mathbf{b}}_0\left(\mathbf{x}\right)}{\mathrm{\Delta }t},\mathbf{x}\in \mathrm{\Pi }$$(43)

in which Equation (40(40) $${\mathrm{\Phi }\mathbf{d}}_2-\left(2\mathrm{\Phi }\mathrm{\Delta }t+\mathrm{\Delta }{t}^3\alpha \mathbf{L}\mathrm{\Phi }\right){\dot{\mathbf{d}}}_0=\mathrm{\Delta }{t}^2\alpha {\mathbf{L}\mathrm{\Phi }\mathbf{d}}_0+{\mathbf{u}}_0+\mathrm{\Delta }{t}^2{\mathbf{f}}_1$$(40) ) of the conjoined unknowns can be reformulated as(44) $$\left[\begin{array}{cc}\mathrm{\Phi }\hfill & -\left(2\mathrm{\Phi }\mathrm{\Delta }t+\mathrm{\Delta }{t}^3\alpha \mathbf{L}\mathrm{\Phi }\right)\hfill \end{array}\right]\left[\begin{array}{c}{\mathbf{d}}_2\\ {\dot{\mathbf{d}}}_0\end{array}\right]=\mathrm{\Delta }{t}^2\alpha {\mathbf{L}\mathrm{\Phi }\mathbf{d}}_0+{\mathbf{u}}_0+\mathrm{\Delta }{t}^2{\mathbf{f}}_1$$(44)

Denote

(45) $$\tilde{\mathbf{D}}=\left[\begin{array}{c}{\mathbf{d}}_2\\ {\dot{\mathbf{d}}}_0\end{array}\right]$$(45)

To solve the two unknowns in (45(45) $$\tilde{\mathbf{D}}=\left[\begin{array}{c}{\mathbf{d}}_2\\ {\dot{\mathbf{d}}}_0\end{array}\right]$$(45) ) jointly, we summarize the governing equation (44(44) $$\left[\begin{array}{cc}\mathrm{\Phi }\hfill & -\left(2\mathrm{\Phi }\mathrm{\Delta }t+\mathrm{\Delta }{t}^3\alpha \mathbf{L}\mathrm{\Phi }\right)\hfill \end{array}\right]\left[\begin{array}{c}{\mathbf{d}}_2\\ {\dot{\mathbf{d}}}_0\end{array}\right]=\mathrm{\Delta }{t}^2\alpha {\mathbf{L}\mathrm{\Phi }\mathbf{d}}_0+{\mathbf{u}}_0+\mathrm{\Delta }{t}^2{\mathbf{f}}_1$$(44) ) and boundary equations (41(41) $${\mathbf{B}}^h\mathrm{\Phi }\left(\mathbf{x}\right){\mathbf{d}}_2={\mathbf{h}}_2\left(\mathbf{x}\right),{\mathbf{B}}^h\mathrm{\Phi }\left(\mathbf{x}\right){\dot{\mathbf{d}}}_0=\frac{{\mathbf{h}}_1\left(\mathbf{x}\right)-{\mathbf{h}}_0\left(\mathbf{x}\right)}{\mathrm{\Delta }t},\mathbf{x}\in {\mathrm{\Gamma }}_h$$(41) )–(42(42) $${\mathbf{B}}^g\mathrm{\Phi }\left(\mathbf{x}\right){\mathbf{d}}_2={\mathbf{g}}_2\left(\mathbf{x}\right),{\mathbf{B}}^g\mathrm{\Phi }\left(\mathbf{x}\right){\dot{\mathbf{d}}}_0=\frac{{\mathbf{g}}_1\left(\mathbf{x}\right)-{\mathbf{g}}_0\left(\mathbf{x}\right)}{\mathrm{\Delta }t},\mathbf{x}\in {\mathrm{\Gamma }}_g$$(42) ) as well as the equation of the additional condition (43(43) $$\mathbf{A}\mathrm{\Phi }\left(\mathbf{x}\right){\mathbf{d}}_2={\mathbf{b}}_2\left(\mathbf{x}\right),\mathbf{A}\mathrm{\Phi }\left(\mathbf{x}\right){\dot{\mathbf{d}}}_0=\frac{{\mathbf{b}}_1\left(\mathbf{x}\right)-{\mathbf{b}}_0\left(\mathbf{x}\right)}{\mathrm{\Delta }t},\mathbf{x}\in \mathrm{\Pi }$$(43) ) as(46) $$\tilde{\mathbf{K}}\tilde{\mathbf{D}}=\tilde{\mathbf{F}}$$(46)

where(47) $$\tilde{\mathbf{K}}=\left[\begin{array}{c}{\tilde{\mathbf{K}}}_1\\ {\tilde{\mathbf{K}}}_2\\ {\tilde{\mathbf{K}}}_3\\ {\tilde{\mathbf{K}}}_4\end{array}\right];\tilde{\mathbf{F}}=\left[\begin{array}{c}{\tilde{\mathbf{F}}}_1\\ {\tilde{\mathbf{F}}}_2\\ {\tilde{\mathbf{F}}}_3\\ {\tilde{\mathbf{F}}}_4\end{array}\right]$$(47)

and(48) $$\begin{array}{c}{\tilde{\mathbf{K}}}_1=\left[\begin{array}{cc}\mathrm{\Phi }\hfill & -\left(2\mathrm{\Phi }\mathrm{\Delta }t+\mathrm{\Delta }{t}^3\alpha \mathbf{L}\mathrm{\Phi }\right)\hfill \end{array}\right],\hfill \\ {\tilde{\mathbf{F}}}_1=\mathrm{\Delta }{t}^2\alpha {\mathbf{L}\mathrm{\Phi }\mathbf{d}}_0+{\mathbf{u}}_0+\mathrm{\Delta }{t}^2{\mathbf{f}}_1,\hfill \\ \mathrm{\Phi }=\left[\begin{array}{c}\mathrm{\Phi }\left({\mathbf{p}}_1\right)\\ \mathrm{\Phi }\left({\mathbf{p}}_2\right)\\ ⋮\\ \mathrm{\Phi }\left({\mathbf{p}}_{N_p}\right)\end{array}\right],{\mathbf{f}}_1=\left[\begin{array}{c}\mathbf{f}\left({\mathbf{p}}_1,t_1\right)\\ \mathbf{f}\left({\mathbf{p}}_2,t_1\right)\\ ⋮\\ \mathbf{f}\left({\mathbf{p}}_{N_p},t_1\right)\end{array}\right]\hfill \end{array}$$(48) (49) $$\begin{array}{c}{\tilde{\mathbf{K}}}_2=\left[\begin{array}{cc}{\mathbf{B}}^h\mathrm{\Phi }\hfill & \mathbf{0}\hfill \\ \mathbf{0}\hfill & {\mathbf{B}}^h\mathrm{\Phi }\hfill \end{array}\right],{\mathbf{B}}^h\mathrm{\Phi }=\left[\begin{array}{c}{\mathbf{B}}^h\mathrm{\Phi }\left({\mathbf{q}}_1\right)\\ {\mathbf{B}}^h\mathrm{\Phi }\left({\mathbf{q}}_2\right)\\ ⋮\\ {\mathbf{B}}^h\mathrm{\Phi }\left({\mathbf{q}}_{N_q}\right)\end{array}\right],\hfill \\ {\tilde{\mathbf{F}}}_2=\left[\begin{array}{c}{\tilde{\mathbf{F}}}_{21}\\ {\tilde{\mathbf{F}}}_{22}\end{array}\right],{\tilde{\mathbf{F}}}_{21}=\left[\begin{array}{c}\mathbf{h}\left({\mathbf{q}}_1,t_2\right)\\ \mathbf{h}\left({\mathbf{q}}_2,t_2\right)\\ ⋮\\ \mathbf{h}\left({\mathbf{q}}_{N_q},t_2\right)\end{array}\right],{\tilde{\mathbf{F}}}_{22}=\frac{1}{\mathrm{\Delta }t}\left[\begin{array}{c}\mathbf{h}\left({\mathbf{q}}_1,t_1\right)-\mathbf{h}\left({\mathbf{q}}_1,t_0\right)\\ \mathbf{h}\left({\mathbf{q}}_2,t_1\right)-\mathbf{h}\left({\mathbf{q}}_2,t_0\right)\\ ⋮\\ \mathbf{h}\left({\mathbf{q}}_{N_q},t_1\right)-\mathbf{h}\left({\mathbf{q}}_{N_q},t_0\right)\end{array}\right]\hfill \end{array}$$(49) (50) $$\begin{array}{c}{\tilde{\mathbf{K}}}_3=\left[\begin{array}{cc}{\mathbf{B}}^g\mathrm{\Phi }\hfill & \mathbf{0}\hfill \\ \mathbf{0}\hfill & {\mathbf{B}}^g\mathrm{\Phi }\hfill \end{array}\right],{\mathbf{B}}^g\mathrm{\Phi }=\left[\begin{array}{c}{\mathbf{B}}^g\mathrm{\Phi }\left({\mathbf{r}}_1\right)\\ {\mathbf{B}}^g\mathrm{\Phi }\left({\mathbf{r}}_2\right)\\ ⋮\\ {\mathbf{B}}^g\mathrm{\Phi }\left({\mathbf{r}}_{N_r}\right)\end{array}\right],\hfill \\ {\tilde{\mathbf{F}}}_3=\left[\begin{array}{c}{\tilde{\mathbf{F}}}_{31}\\ {\tilde{\mathbf{F}}}_{32}\end{array}\right],{\tilde{\mathbf{F}}}_{31}=\left[\begin{array}{c}\mathbf{g}\left({\mathbf{r}}_1,t_2\right)\\ \mathbf{g}\left({\mathbf{r}}_2,t_2\right)\\ ⋮\\ \mathbf{g}\left({\mathbf{r}}_{N_r},t_2\right)\end{array}\right],{\tilde{\mathbf{F}}}_{32}=\frac{1}{\mathrm{\Delta }t}\left[\begin{array}{c}\mathbf{g}\left({\mathbf{r}}_1,t_1\right)-\mathbf{g}\left({\mathbf{r}}_1,t_0\right)\\ \mathbf{g}\left({\mathbf{r}}_2,t_1\right)-\mathbf{g}\left({\mathbf{r}}_2,t_0\right)\\ ⋮\\ \mathbf{g}\left({\mathbf{r}}_{N_r},t_1\right)-\mathbf{g}\left({\mathbf{r}}_{N_r},t_0\right)\end{array}\right]\hfill \end{array}$$(50) (51) $$\begin{array}{c}{\tilde{\mathbf{K}}}_4=\left[\begin{array}{cc}\mathbf{A}\mathrm{\Phi }\hfill & \mathbf{0}\hfill \\ \mathbf{0}\hfill & \mathbf{A}\mathrm{\Phi }\hfill \end{array}\right],\mathbf{A}\mathrm{\Phi }=\left[\begin{array}{c}\mathbf{A}\mathrm{\Phi }\left({\mathbf{o}}_1\right)\\ \mathbf{A}\mathrm{\Phi }\left({\mathbf{o}}_2\right)\\ ⋮\\ \mathbf{A}\mathrm{\Phi }\left({\mathbf{o}}_{N_o}\right)\end{array}\right],\hfill \\ {\tilde{\mathbf{F}}}_4=\left[\begin{array}{c}{\tilde{\mathbf{F}}}_{41}\\ {\tilde{\mathbf{F}}}_{42}\end{array}\right],{\tilde{\mathbf{F}}}_{41}=\left[\begin{array}{c}\mathbf{b}\left({\mathbf{o}}_1,t_2\right)\\ \mathbf{b}\left({\mathbf{o}}_2,t_2\right)\\ ⋮\\ \mathbf{b}\left({\mathbf{o}}_{N_o},t_2\right)\end{array}\right],{\tilde{\mathbf{F}}}_{42}=\frac{1}{\mathrm{\Delta }t}\left[\begin{array}{c}\mathbf{b}\left({\mathbf{o}}_1,t_1\right)-\mathbf{b}\left({\mathbf{o}}_1,t_0\right)\\ \mathbf{b}\left({\mathbf{o}}_2,t_1\right)-\mathbf{b}\left({\mathbf{o}}_2,t_0\right)\\ ⋮\\ \mathbf{b}\left({\mathbf{o}}_{N_o},t_1\right)-\mathbf{b}\left({\mathbf{o}}_{N_o},t_0\right)\end{array}\right]\hfill \end{array}$$(51)

4. Convergence study for the optimum solution

4.1. Inverse wave problem of identifying the initial displacement

The solution for strong form collocation of governing equation (26(26) $${\mathrm{\Phi }\mathbf{d}}_2-\left(\mathrm{\Phi }+\mathrm{\Delta }{t}^2\alpha \mathbf{L}\mathrm{\Phi }\right){\mathbf{d}}_0=\left(2\mathrm{\Delta }t\mathrm{\Phi }+\mathrm{\Delta }{t}^3\alpha \mathbf{L}\mathrm{\Phi }\right){\dot{\mathbf{d}}}_0+\mathrm{\Delta }{t}^2{\mathbf{f}}_1$$(26) ) and boundary conditions (27(27) $${\mathbf{B}}^h\mathrm{\Phi }\left(\mathbf{x}\right){\mathbf{d}}_2={\mathbf{h}}_2\left(\mathbf{x}\right),{\mathbf{B}}^h\mathrm{\Phi }\left(\mathbf{x}\right){\mathbf{d}}_0={\mathbf{h}}_0\left(\mathbf{x}\right),\mathbf{x}\in {\mathrm{\Gamma }}_h$$(27) )–(28(28) $${\mathbf{B}}^g\mathrm{\Phi }\left(\mathbf{x}\right){\mathbf{d}}_2={\mathbf{g}}_2\left(\mathbf{x}\right),{\mathbf{B}}^g\mathrm{\Phi }\left(\mathbf{x}\right){\mathbf{d}}_0={\mathbf{g}}_0\left(\mathbf{x}\right),\mathbf{x}\in {\mathrm{\Gamma }}_g$$(28) ) as well as the measured condition (29(29) $$\mathbf{A}\mathrm{\Phi }\left(\mathbf{x}\right){\mathbf{d}}_2={\mathbf{b}}_2\left(\mathbf{x}\right),\mathbf{A}\mathrm{\Phi }\left(\mathbf{x}\right){\mathbf{d}}_0={\mathbf{b}}_0\left(\mathbf{x}\right),\mathbf{x}\in \mathrm{\Pi }$$(29) ) is equivalent to minimizing the least-squares functional with quadratures of the corresponding equations. Therefore, we try to look for the functional of this initial displacement identification inverse problem. Define the function and its approximation of the conjoined unknowns ${\mathbf{u}}_2$ and the initial displacement ${\mathbf{u}}_0$ for solution as(52) $$\underset{-}{\mathbf{u}}=\left[\begin{array}{c}{\mathbf{u}}_2\\ {\mathbf{u}}_0\end{array}\right],\mathbf{v}=\left[\begin{array}{c}{\tilde{\mathbf{u}}}_2\\ {\tilde{\mathbf{u}}}_0\end{array}\right]$$(52)

We consider the following least-squares functional(53) $$\begin{array}{cc}E(\mathbf{v})\hfill & =\frac{1}{2}{\int }_{\mathrm{\Omega }}{\left(\overline{\mathbf{L}}\mathbf{v}-\overline{\mathbf{f}}\right)}^T\left(\overline{\mathbf{L}}\mathbf{v}-\overline{\mathbf{f}}\right)\text{d}\mathrm{\Omega }+\frac{1}{2}{\int }_{{\mathrm{\Gamma }}_h}{\left({\mathbf{B}}^h\mathbf{v}-\mathbf{h}\right)}^T\left({\mathbf{B}}^h\mathbf{v}-\mathbf{h}\right)\text{d}\mathrm{\Gamma }\hfill \\ \hfill & +\frac{1}{2}{\int }_{{\mathrm{\Gamma }}_g}{\left({\mathbf{B}}^g\mathbf{v}-\mathbf{g}\right)}^T\left({\mathbf{B}}^g\mathbf{v}-\mathbf{g}\right)\text{d}\mathrm{\Gamma }+\frac{1}{2}{\int }_{\mathrm{\Pi }}{\left(\mathbf{Av}-\mathbf{b}\right)}^T\left(\mathbf{Av}-\mathbf{b}\right)\text{d}\mathrm{\Omega }\hfill \end{array}$$(53)

where(54) $$\begin{array}{c}\overline{\mathbf{L}}\mathbf{v}={\tilde{\mathbf{u}}}_2(\mathbf{x})-{\tilde{\mathbf{u}}}_0(\mathbf{x})-\mathrm{\Delta }{t}^2\alpha {\mathbf{L}\tilde{\mathbf{u}}}_0(\mathbf{x}),\hfill \\ \overline{\mathbf{f}}=2\mathrm{\Delta }t{\dot{\mathbf{u}}}_0+\mathrm{\Delta }{t}^3\alpha {\mathbf{L}\dot{\mathbf{u}}}_0+\mathrm{\Delta }{t}^2{\mathbf{f}}_1\hfill \end{array}$$(54)

In Equation (54(54) $$\begin{array}{c}\overline{\mathbf{L}}\mathbf{v}={\tilde{\mathbf{u}}}_2(\mathbf{x})-{\tilde{\mathbf{u}}}_0(\mathbf{x})-\mathrm{\Delta }{t}^2\alpha {\mathbf{L}\tilde{\mathbf{u}}}_0(\mathbf{x}),\hfill \\ \overline{\mathbf{f}}=2\mathrm{\Delta }t{\dot{\mathbf{u}}}_0+\mathrm{\Delta }{t}^3\alpha {\mathbf{L}\dot{\mathbf{u}}}_0+\mathrm{\Delta }{t}^2{\mathbf{f}}_1\hfill \end{array}$$(54) ), ${\tilde{\mathbf{u}}}_2$ and ${\tilde{\mathbf{u}}}_0$ are unknown, and ${\dot{\mathbf{u}}}_0$ is known. Define a norm(55) $${∥\mathbf{v}∥}_H^2={∥\overline{\mathbf{L}}\mathbf{v}∥}_{0,\mathrm{\Omega }}^2+{∥{\mathbf{B}}^h\mathbf{v}∥}_{0,{\mathrm{\Gamma }}_h}^2+{∥{\mathbf{B}}^g\mathbf{v}∥}_{0,{\mathrm{\Gamma }}_g}^2+{∥\mathbf{Av}∥}_{0,\mathrm{\Pi }}^2$$(55)

Seek an optimal solution $\widehat{\mathbf{v}}$ satisfying(56) $$E\left(\widehat{\mathbf{v}}\right)=\underset{\mathbf{v}\in U}{inf}E\left(\mathbf{v}\right)$$(56)

where $U={\cup }_{i=1}^{\gamma }{V}_i$ is denoted as the admissible space spanned by the radial basis functions in which $V_i=\text{span}\left\{{\phi }_I\right\}\left(I=1,2,\cdots ,N\right)$ and γ is the dimension of the space. The following estimate can be attained by invoking Lax–Milgram lemma [49](57) $$\begin{array}{c}\Vert \underset{-}{\mathbf{u}}-\widehat{\mathbf{v}}{\Vert }_H\le C\underset{\mathbf{v}\in U}{inf}{\Vert \underset{-}{\mathbf{u}}-\mathbf{v}\Vert }_H\hfill \\ \le C_1{\Vert \overline{\mathbf{L}}\mathbf{v}-\overline{\mathbf{f}}\Vert }_{0,\mathrm{\Omega }}+C_2\Vert {\mathbf{B}}^h\mathbf{v}-\mathbf{h}{\Vert }_{0,{\mathrm{\Gamma }}_h}+C_3\Vert {\mathbf{B}}^g\mathbf{v}-\mathbf{g}{\Vert }_{0,{\mathrm{\Gamma }}_g}+C_4{\Vert \mathbf{Av}-\mathbf{b}\Vert }_{0,\mathrm{\Pi }}\hfill \end{array}$$(57)

The errors in least-squares method are unbalanced in the domain, on the boundaries, and for the additional condition in the subdomain. Accordingly, a weighted least-squares functional should be introduced as(58) $$\begin{array}{cc}{E}_{\xi }(\mathbf{v})\hfill & =\frac{1}{2}{\int }_{\mathrm{\Omega }}{\left(\overline{\mathbf{L}}\mathbf{v}-\overline{\mathbf{f}}\right)}^T\left(\overline{\mathbf{L}}\mathbf{v}-\overline{\mathbf{f}}\right)\text{d}\mathrm{\Omega }+\frac{{\left({\xi }_h\right)}^2}{2}{\int }_{{\mathrm{\Gamma }}_h}{\left({\mathbf{B}}^h\mathbf{v}-\mathbf{h}\right)}^T\left({\mathbf{B}}^h\mathbf{v}-\mathbf{h}\right)\text{d}\mathrm{\Gamma }\hfill \\ \hfill & +\frac{{\left({\xi }_g\right)}^2}{2}{\int }_{{\mathrm{\Gamma }}_g}{\left({\mathbf{B}}^g\mathbf{v}-\mathbf{g}\right)}^T\left({\mathbf{B}}^g\mathbf{v}-\mathbf{g}\right)\text{d}\mathrm{\Gamma }+\frac{{\left({\xi }_o\right)}^2}{2}{\int }_{\mathrm{\Pi }}{\left(\mathbf{Av}-\mathbf{b}\right)}^T\left(\mathbf{Av}-\mathbf{b}\right)\text{d}\mathrm{\Omega }\hfill \end{array}$$(58)

where ξ _h and ξ _g are the weights associated with Neumann boundary Γ _h and Dirichlet boundary Γ _g , respectively, and ξ _o is the weight associated with the measured condition in the subdomain Π. Therefore, a modified norm should be considered(59) $${\Vert \mathbf{v}\Vert }_B^2={\Vert \overline{\mathbf{L}}\mathbf{v}\Vert }_{0,\mathrm{\Omega }}^2+{\left({\xi }_h\right)}^2\Vert {\mathbf{B}}^h\mathbf{v}{\Vert }_{0,{\mathrm{\Gamma }}_h}^2+{\left({\xi }_g\right)}^2\Vert {\mathbf{B}}^g\mathbf{v}{\Vert }_{0,{\mathrm{\Gamma }}_g}^2+{\left({\xi }_o\right)}^2{\Vert \mathbf{Av}\Vert }_{0,\mathrm{\Pi }}^2$$(59)

In the numerical solutions, we need to seek an optimal solution $\widehat{\mathbf{v}}$ satisfying(60) $${\overline{E}}_{\xi }\left(\widehat{\mathbf{v}},{\xi }_h,{\xi }_g,{\xi }_o\right)=\underset{\mathbf{v}\in U}{inf}{\overline{E}}_{\xi }\left(\mathbf{v},{\xi }_h,{\xi }_g,{\xi }_o\right)$$(60)

where ${\overline{E}}_{\xi }\left(\mathbf{v}\right)$ is the discrete form of functional $E_{\xi }\left(\mathbf{v}\right)$. The corresponding error estimate is(61) $$\begin{array}{c}{∥\underset{-}{\mathbf{u}}-\widehat{\mathbf{v}}∥}_B\le C\underset{\mathbf{v}\in U}{inf}{∥\underset{-}{\mathbf{u}}-\mathbf{v}∥}_B\hfill \\ \le {\overline{C}}_1{∥\overline{\mathbf{L}}\mathbf{v}-\overline{\mathbf{f}}∥}_{0,\mathrm{\Omega }}+{\overline{C}}_2{\xi }_h{∥{\mathbf{B}}^h\mathbf{v}-\mathbf{h}∥}_{0,{\mathrm{\Gamma }}_h}+{\overline{C}}_3{\xi }_g{∥{\mathbf{B}}^g\mathbf{v}-\mathbf{g}∥}_{0,{\mathrm{\Gamma }}_g}+{\overline{C}}_4{\xi }_o{∥\mathbf{Av}-\mathbf{b}∥}_{0,\mathrm{\Pi }}\hfill \\ \le \overline{C}\left({∥\overline{\mathbf{L}}\mathbf{v}-\overline{\mathbf{f}}∥}_{0,\mathrm{\Omega }}+{\xi }_h{∥{\mathbf{B}}^h\mathbf{v}-\mathbf{h}∥}_{0,{\mathrm{\Gamma }}_h}+{\xi }_g{∥{\mathbf{B}}^g\mathbf{v}-\mathbf{g}∥}_{0,{\mathrm{\Gamma }}_g}+{\xi }_o{∥\mathbf{Av}-\mathbf{b}∥}_{0,\mathrm{\Pi }}\right)\hfill \end{array}$$(61)

Since there exists exponential convergence in the domain (including the subdomain of measured condition) and on the boundaries using RBCM in each time step, we have(62) $${∥\underset{-}{\mathbf{u}}-\widehat{\mathbf{v}}∥}_B\le \mathrm{O}\left({\varpi }^{\vartheta /h}\right)$$(62)

The discretized form of functional (58(58) $$\begin{array}{cc}{E}_{\xi }(\mathbf{v})\hfill & =\frac{1}{2}{\int }_{\mathrm{\Omega }}{\left(\overline{\mathbf{L}}\mathbf{v}-\overline{\mathbf{f}}\right)}^T\left(\overline{\mathbf{L}}\mathbf{v}-\overline{\mathbf{f}}\right)\text{d}\mathrm{\Omega }+\frac{{\left({\xi }_h\right)}^2}{2}{\int }_{{\mathrm{\Gamma }}_h}{\left({\mathbf{B}}^h\mathbf{v}-\mathbf{h}\right)}^T\left({\mathbf{B}}^h\mathbf{v}-\mathbf{h}\right)\text{d}\mathrm{\Gamma }\hfill \\ \hfill & +\frac{{\left({\xi }_g\right)}^2}{2}{\int }_{{\mathrm{\Gamma }}_g}{\left({\mathbf{B}}^g\mathbf{v}-\mathbf{g}\right)}^T\left({\mathbf{B}}^g\mathbf{v}-\mathbf{g}\right)\text{d}\mathrm{\Gamma }+\frac{{\left({\xi }_o\right)}^2}{2}{\int }_{\mathrm{\Pi }}{\left(\mathbf{Av}-\mathbf{b}\right)}^T\left(\mathbf{Av}-\mathbf{b}\right)\text{d}\mathrm{\Omega }\hfill \end{array}$$(58) ) can be expressed as(63) $$\begin{array}{cc}{\overline{E}}_{\xi }\hfill & =\frac{1}{2}\sum _{i=1}^{N_p}{\left(\overline{\mathbf{L}}\mathrm{\Phi }\left(\mathbf{p}\right)\mathbf{D}-\overline{\mathbf{f}}\right)}^T\left(\overline{\mathbf{L}}\mathrm{\Phi }\left(\mathbf{p}\right)\mathbf{D}-\overline{\mathbf{f}}\right)+\frac{{\left({\xi }_h\right)}^2}{2}\sum _{i=1}^{N_q}{\left({\mathbf{B}}^h\mathrm{\Phi }\left(\mathbf{q}\right)\mathbf{D}-\mathbf{h}\right)}^T\left({\mathbf{B}}^h\mathrm{\Phi }\left(\mathbf{q}\right)\mathbf{D}-\mathbf{h}\right)\hfill \\ \hfill & +\frac{{\left({\xi }_g\right)}^2}{2}\sum _{i=1}^{N_r}{\left({\mathbf{B}}^g\mathrm{\Phi }\left(\mathbf{r}\right)\mathbf{D}-\mathbf{g}\right)}^T\left({\mathbf{B}}^g\mathrm{\Phi }\left(\mathbf{r}\right)\mathbf{D}-\mathbf{g}\right)+\frac{{\left({\xi }_o\right)}^2}{2}\sum _{i=1}^{N_o}{\left(\mathbf{A}\mathrm{\Phi }\left(\mathbf{o}\right)\mathbf{D}-\mathbf{b}\right)}^T\left(\mathbf{A}\mathrm{\Phi }\left(\mathbf{o}\right)\mathbf{D}-\mathbf{b}\right)\hfill \end{array}$$(63)

Based on method of Lagrange’s multiplier, minimizing ${\overline{E}}_{\xi }$ requires(64) $$\frac{\partial {\overline{E}}_{\xi }}{\partial D^J}=0$$(64)

and seeking the optimum weights ξ _h , ξ _g and ξ _o demands (65) $$\frac{\partial {\overline{E}}_{\xi }}{\partial {\xi }_h}=0,\frac{\partial {\overline{E}}_{\xi }}{\partial {\xi }_g}=0,\frac{\partial {\overline{E}}_{\xi }}{\partial {\xi }_o}=0$$(65)

Combining (64(64) $$\frac{\partial {\overline{E}}_{\xi }}{\partial D^J}=0$$(64) ) and (65(65) $$\frac{\partial {\overline{E}}_{\xi }}{\partial {\xi }_h}=0,\frac{\partial {\overline{E}}_{\xi }}{\partial {\xi }_g}=0,\frac{\partial {\overline{E}}_{\xi }}{\partial {\xi }_o}=0$$(65) ) renders(66) $$\left[\begin{array}{c}\frac{\partial {\overline{E}}_{\xi }}{\partial D^J}\\ \frac{\partial {\overline{E}}_{\xi }}{\partial {\xi }_h}\\ \frac{\partial {\overline{E}}_{\xi }}{\partial {\xi }_g}\\ \frac{\partial {\overline{E}}_{\xi }}{\partial {\xi }_o}\end{array}\right]:=\eta \left(\stackrel{⌢}{\mathbf{D}}\right)=\mathbf{0}$$(66)

where the unknown $\stackrel{⌢}{\mathbf{D}}$ is defined as(67) $$\stackrel{⌢}{\mathbf{D}}={\left[\begin{array}{ccccccccccc}{\mathbf{d}}_2^1\hfill & {\mathbf{d}}_2^2\hfill & \cdots \hfill & {\mathbf{d}}_2^N\hfill & {\mathbf{d}}_0^1\hfill & {\mathbf{d}}_0^2\hfill & \cdots \hfill & {\mathbf{d}}_0^N\hfill & {\xi }_h\hfill & {\xi }_g\hfill & {\xi }_o\hfill \end{array}\right]}^T$$(67)

Since Equation (66(66) $$\left[\begin{array}{c}\frac{\partial {\overline{E}}_{\xi }}{\partial D^J}\\ \frac{\partial {\overline{E}}_{\xi }}{\partial {\xi }_h}\\ \frac{\partial {\overline{E}}_{\xi }}{\partial {\xi }_g}\\ \frac{\partial {\overline{E}}_{\xi }}{\partial {\xi }_o}\end{array}\right]:=\eta \left(\stackrel{⌢}{\mathbf{D}}\right)=\mathbf{0}$$(66) ) is a non-linear function, Newton’s iteration method is utilized for the solution. At m iteration step, we have(68) $${\stackrel{⌢}{\mathbf{D}}}^{(m+1)}={\stackrel{⌢}{\mathbf{D}}}^{(m)}-{\left({\eta }^{\prime }{\left({\mathbf{d}}_2^i,{\mathbf{d}}_0^i,{\xi }_h,{\xi }_g,{\xi }_o\right)}^{(m)}\right)}^{-1}\eta {\left({\mathbf{d}}_2^i,{\mathbf{d}}_0^i,{\xi }_h,{\xi }_g,{\xi }_o\right)}^{(m)},i=1,2,\cdots ,N$$(68)

where(69) $$\eta {\left({\mathbf{d}}_2^i,{\mathbf{d}}_0^i,{\xi }_h,{\xi }_g,{\xi }_o\right)}^{(m)}=\left[\begin{array}{c}{\eta }_1\\ {\eta }_2\\ {\eta }_3\\ {\eta }_4\end{array}\right],{\eta }^{\prime }{\left({\mathbf{d}}_2^i,{\mathbf{d}}_0^i,{\xi }_h,{\xi }_g,{\xi }_o\right)}^{(m)}=\left[\begin{array}{cccc}{{\eta }^{\prime }}_{11}\hfill & {{\eta }^{\prime }}_{12}\hfill & {{\eta }^{\prime }}_{13}\hfill & {{\eta }^{\prime }}_{14}\hfill \\ \hfill & {{\eta }^{\prime }}_{22}\hfill & {{\eta }^{\prime }}_{23}\hfill & {{\eta }^{\prime }}_{24}\hfill \\ \hfill & \hfill & {{\eta }^{\prime }}_{33}\hfill & {{\eta }^{\prime }}_{34}\hfill \\ \mathit{sym}\hfill & \hfill & \hfill & {{\eta }^{\prime }}_{44}\hfill \end{array}\right]$$(69)

and(70) $$\begin{array}{c}{\eta }_1={\left(\overline{\mathbf{L}}\mathrm{\Phi }\right)}^T\left(\overline{\mathbf{L}}\mathrm{\Phi }\mathbf{D}-\overline{\mathbf{f}}\right)+{\xi }_h^2{\left({\mathbf{B}}^h\mathrm{\Phi }\right)}^T\left({\mathbf{B}}^h\mathrm{\Phi }\mathbf{D}-\mathbf{h}\right)+{\xi }_g^2{\left({\mathbf{B}}^g\mathrm{\Phi }\right)}^T\left({\mathbf{B}}^g\mathrm{\Phi }\mathbf{D}-\mathbf{g}\right)+{\xi }_o^2{\left(\mathbf{A}\mathrm{\Phi }\right)}^T\left(\mathbf{A}\mathrm{\Phi }\mathbf{D}-\mathbf{b}\right)\hfill \\ {\eta }_2={\xi }_h\sum _{j=1}^{N_q}{\left({\mathbf{B}}^h\mathrm{\Phi }\mathbf{D}-\mathbf{h}\right)}^2,{\eta }_3={\xi }_g\sum _{j=1}^{N_r}{\left({\mathbf{B}}^g\mathrm{\Phi }\mathbf{D}-\mathbf{g}\right)}^2,{\eta }_4={\xi }_o\sum _{j=1}^{N_o}{\left(\mathbf{A}\mathrm{\Phi }\mathbf{D}-\mathbf{b}\right)}^2\hfill \end{array}$$(70) (71) $$\begin{array}{c}{{\eta }^{\prime }}_{11}={\left(\overline{\mathbf{L}}\mathrm{\Phi }\right)}^T\overline{\mathbf{L}}\mathrm{\Phi }+{\xi }_h^2{\left({\mathbf{B}}^h\mathrm{\Phi }\right)}^T{\mathbf{B}}^h\mathrm{\Phi }+{\xi }_g^2{\left({\mathbf{B}}^g\mathrm{\Phi }\right)}^T{\mathbf{B}}^g\mathrm{\Phi }+{\xi }_o^2{\left(\mathbf{A}\mathrm{\Phi }\right)}^T\mathbf{A}\mathrm{\Phi }\hfill \\ {{\eta }^{\prime }}_{12}=2{\xi }_h{\left({\mathbf{B}}^h\mathrm{\Phi }\right)}^T\left({\mathbf{B}}^h\mathrm{\Phi }\mathbf{D}-\mathbf{h}\right),{{\eta }^{\prime }}_{13}=2{\xi }_g{\left({\mathbf{B}}^g\mathrm{\Phi }\right)}^T\left({\mathbf{B}}^g\mathrm{\Phi }\mathbf{D}-\mathbf{g}\right),{{\eta }^{\prime }}_{14}=2{\xi }_o{\left(\mathbf{A}\mathrm{\Phi }\right)}^T\left(\mathbf{A}\mathrm{\Phi }\mathbf{D}-\mathbf{b}\right),\hfill \\ {{\eta }^{\prime }}_{22}=\sum _{j=1}^{N_q}{\left({\mathbf{B}}^h\mathrm{\Phi }\mathbf{D}-\mathbf{h}\right)}^2,{{\eta }^{\prime }}_{23}=\mathbf{0},{{\eta }^{\prime }}_{24}=\mathbf{0},\hfill \\ {{\eta }^{\prime }}_{33}=\sum _{j=1}^{N_r}{\left({\mathbf{B}}^g\mathrm{\Phi }\mathbf{D}-\mathbf{g}\right)}^2,{{\eta }^{\prime }}_{34}=\mathbf{0},{{\eta }^{\prime }}_{44}=\sum _{j=1}^{N_o}{\left(\mathbf{A}\mathrm{\Phi }\mathbf{D}-\mathbf{b}\right)}^2.\hfill \end{array}$$(71)

For the same kind identification problem of the same material parameters, the optimum weights for the boundary conditions and additional condition in different examples are quite close. Therefore, this calculation process using iteration procedure in (68(68) $${\stackrel{⌢}{\mathbf{D}}}^{(m+1)}={\stackrel{⌢}{\mathbf{D}}}^{(m)}-{\left({\eta }^{\prime }{\left({\mathbf{d}}_2^i,{\mathbf{d}}_0^i,{\xi }_h,{\xi }_g,{\xi }_o\right)}^{(m)}\right)}^{-1}\eta {\left({\mathbf{d}}_2^i,{\mathbf{d}}_0^i,{\xi }_h,{\xi }_g,{\xi }_o\right)}^{(m)},i=1,2,\cdots ,N$$(68) ) should only be carried out once. Other examples of this class can just follow the same weights for simulations. Consequently, introducing the optimum weights obtained from (66(66) $$\left[\begin{array}{c}\frac{\partial {\overline{E}}_{\xi }}{\partial D^J}\\ \frac{\partial {\overline{E}}_{\xi }}{\partial {\xi }_h}\\ \frac{\partial {\overline{E}}_{\xi }}{\partial {\xi }_g}\\ \frac{\partial {\overline{E}}_{\xi }}{\partial {\xi }_o}\end{array}\right]:=\eta \left(\stackrel{⌢}{\mathbf{D}}\right)=\mathbf{0}$$(66) ) into the discrete equation (32(32) $$\mathbf{KD}=\mathbf{F}$$(32) ) yields the following weighted discrete equation(72) $$\left[\begin{array}{c}{\mathbf{K}}_1\\ {\xi }_h{\mathbf{K}}_2\\ {\xi }_g{\mathbf{K}}_3\\ {\xi }_o{\mathbf{K}}_4\end{array}\right]\mathbf{D}=\left[\begin{array}{c}{\mathbf{F}}_1\\ {\xi }_h{\mathbf{F}}_2\\ {\xi }_g{\mathbf{F}}_3\\ {\xi }_o{\mathbf{F}}_4\end{array}\right]$$(72)

4.2. Inverse wave problem of identifying the initial velocity

Define the function and the approximation of the conjoined unknowns ${\mathbf{u}}_2$ and the initial velocity ${\dot{\mathbf{u}}}_0$ for solution as(73) $$\underset{\sim }{\mathbf{u}}=\left[\begin{array}{c}{\mathbf{u}}_2\\ {\dot{\mathbf{u}}}_0\end{array}\right],\mathbf{w}=\left[\begin{array}{c}{\tilde{\mathbf{u}}}_2\\ {\dot{\tilde{\mathbf{u}}}}_0\end{array}\right]$$(73)

The governing equation (40(40) $${\mathrm{\Phi }\mathbf{d}}_2-\left(2\mathrm{\Phi }\mathrm{\Delta }t+\mathrm{\Delta }{t}^3\alpha \mathbf{L}\mathrm{\Phi }\right){\dot{\mathbf{d}}}_0=\mathrm{\Delta }{t}^2\alpha {\mathbf{L}\mathrm{\Phi }\mathbf{d}}_0+{\mathbf{u}}_0+\mathrm{\Delta }{t}^2{\mathbf{f}}_1$$(40) ), boundary conditions (41(41) $${\mathbf{B}}^h\mathrm{\Phi }\left(\mathbf{x}\right){\mathbf{d}}_2={\mathbf{h}}_2\left(\mathbf{x}\right),{\mathbf{B}}^h\mathrm{\Phi }\left(\mathbf{x}\right){\dot{\mathbf{d}}}_0=\frac{{\mathbf{h}}_1\left(\mathbf{x}\right)-{\mathbf{h}}_0\left(\mathbf{x}\right)}{\mathrm{\Delta }t},\mathbf{x}\in {\mathrm{\Gamma }}_h$$(41) )–(42(42) $${\mathbf{B}}^g\mathrm{\Phi }\left(\mathbf{x}\right){\mathbf{d}}_2={\mathbf{g}}_2\left(\mathbf{x}\right),{\mathbf{B}}^g\mathrm{\Phi }\left(\mathbf{x}\right){\dot{\mathbf{d}}}_0=\frac{{\mathbf{g}}_1\left(\mathbf{x}\right)-{\mathbf{g}}_0\left(\mathbf{x}\right)}{\mathrm{\Delta }t},\mathbf{x}\in {\mathrm{\Gamma }}_g$$(42) ) and measured condition (43(43) $$\mathbf{A}\mathrm{\Phi }\left(\mathbf{x}\right){\mathbf{d}}_2={\mathbf{b}}_2\left(\mathbf{x}\right),\mathbf{A}\mathrm{\Phi }\left(\mathbf{x}\right){\dot{\mathbf{d}}}_0=\frac{{\mathbf{b}}_1\left(\mathbf{x}\right)-{\mathbf{b}}_0\left(\mathbf{x}\right)}{\mathrm{\Delta }t},\mathbf{x}\in \mathrm{\Pi }$$(43) ) can be obtained identically by considering the following least-squares functional(74) $$\begin{array}{cc}E(\mathbf{w})\hfill & =\frac{1}{2}{\int }_{\mathrm{\Omega }}{\left(\tilde{\mathbf{L}}\mathbf{w}-\tilde{\mathbf{f}}\right)}^T\left(\tilde{\mathbf{L}}\mathbf{w}-\tilde{\mathbf{f}}\right)\text{d}\mathrm{\Omega }+\frac{1}{2}{\int }_{{\mathrm{\Gamma }}_h}{\left({\mathbf{B}}^h\mathbf{w}-\mathbf{h}\right)}^T\left({\mathbf{B}}^h\mathbf{w}-\mathbf{h}\right)\text{d}\mathrm{\Gamma }\hfill \\ \hfill & +\frac{1}{2}{\int }_{{\mathrm{\Gamma }}_g}{\left({\mathbf{B}}^g\mathbf{w}-\mathbf{g}\right)}^T\left({\mathbf{B}}^g\mathbf{w}-\mathbf{g}\right)\text{d}\mathrm{\Gamma }+\frac{1}{2}{\int }_{\mathrm{\Pi }}{\left(\mathbf{Aw}-\mathbf{b}\right)}^T\left(\mathbf{Aw}-\mathbf{b}\right)\text{d}\mathrm{\Omega }\hfill \end{array}$$(74)

in which(75) $$\begin{array}{c}\tilde{\mathbf{L}}\mathbf{w}={\tilde{\mathbf{u}}}_2(\mathbf{x})-2\mathrm{\Delta }t{\dot{\tilde{\mathbf{u}}}}_0(\mathbf{x})-\mathrm{\Delta }{t}^3\alpha {\mathbf{L}\dot{\tilde{\mathbf{u}}}}_0(\mathbf{x}),\hfill \\ \tilde{\mathbf{f}}=\mathrm{\Delta }{t}^2\alpha {\mathbf{Lu}}_0+{\mathbf{u}}_0+\mathrm{\Delta }{t}^2{\mathbf{f}}_1\hfill \end{array}$$(75)

To balance the errors in different types of collocation equations, a weighted least squares functional of (74(74) $$\begin{array}{cc}E(\mathbf{w})\hfill & =\frac{1}{2}{\int }_{\mathrm{\Omega }}{\left(\tilde{\mathbf{L}}\mathbf{w}-\tilde{\mathbf{f}}\right)}^T\left(\tilde{\mathbf{L}}\mathbf{w}-\tilde{\mathbf{f}}\right)\text{d}\mathrm{\Omega }+\frac{1}{2}{\int }_{{\mathrm{\Gamma }}_h}{\left({\mathbf{B}}^h\mathbf{w}-\mathbf{h}\right)}^T\left({\mathbf{B}}^h\mathbf{w}-\mathbf{h}\right)\text{d}\mathrm{\Gamma }\hfill \\ \hfill & +\frac{1}{2}{\int }_{{\mathrm{\Gamma }}_g}{\left({\mathbf{B}}^g\mathbf{w}-\mathbf{g}\right)}^T\left({\mathbf{B}}^g\mathbf{w}-\mathbf{g}\right)\text{d}\mathrm{\Gamma }+\frac{1}{2}{\int }_{\mathrm{\Pi }}{\left(\mathbf{Aw}-\mathbf{b}\right)}^T\left(\mathbf{Aw}-\mathbf{b}\right)\text{d}\mathrm{\Omega }\hfill \end{array}$$(74) ) is proposed as(76) $$\begin{array}{cc}{E}_{\zeta }(\mathbf{w})\hfill & =\frac{1}{2}{\int }_{\mathrm{\Omega }}{\left(\tilde{\mathbf{L}}\mathbf{w}-\tilde{\mathbf{f}}\right)}^T\left(\tilde{\mathbf{L}}\mathbf{w}-\tilde{\mathbf{f}}\right)\text{d}\mathrm{\Omega }+\frac{{\left({\zeta }_h\right)}^2}{2}{\int }_{{\mathrm{\Gamma }}_h}{\left({\mathbf{B}}^h\mathbf{w}-\mathbf{h}\right)}^T\left({\mathbf{B}}^h\mathbf{w}-\mathbf{h}\right)\text{d}\mathrm{\Gamma }\hfill \\ \hfill & +\frac{{\left({\zeta }_g\right)}^2}{2}{\int }_{{\mathrm{\Gamma }}_g}{\left({\mathbf{B}}^g\mathbf{w}-\mathbf{g}\right)}^T\left({\mathbf{B}}^g\mathbf{w}-\mathbf{g}\right)\text{d}\mathrm{\Gamma }+\frac{{\left({\zeta }_o\right)}^2}{2}{\int }_{\mathrm{\Pi }}{\left(\mathbf{Aw}-\mathbf{b}\right)}^T\left(\mathbf{Aw}-\mathbf{b}\right)\text{d}\mathrm{\Omega }\hfill \end{array}$$(76)

Accordingly, consider a modified norm(77) $${∥\mathbf{w}∥}_B^2={∥\tilde{\mathbf{L}}\mathbf{w}∥}_{0,\mathrm{\Omega }}^2+{\left({\zeta }_h\right)}^2{∥{\mathbf{B}}^h\mathbf{w}∥}_{0,{\mathrm{\Gamma }}_h}^2+{\left({\zeta }_g\right)}^2{∥{\mathbf{B}}^g\mathbf{w}∥}_{0,{\mathrm{\Gamma }}_g}^2+{\left({\zeta }_o\right)}^2{∥\mathbf{Aw}∥}_{0,\mathrm{\Pi }}^2$$(77)

Seeking an optimal solution $\widehat{\mathbf{w}}$ meets the condition(78) $${\overline{E}}_{\zeta }\left(\widehat{\mathbf{w}},{\zeta }_h,{\zeta }_g,{\zeta }_o\right)=\underset{\mathbf{w}\in U}{inf}{\overline{E}}_{\zeta }\left(\mathbf{w},{\zeta }_h,{\zeta }_g,{\zeta }_o\right)$$(78)

where ${\overline{E}}_{\zeta }\left(\mathbf{w}\right)$ is the discrete functional form of $E_{\zeta }\left(\mathbf{w}\right)$. The corresponding error estimate is(79) $$\begin{array}{cc}{∥\underset{\sim }{\mathbf{u}}-\widehat{\mathbf{w}}∥}_B\hfill & \le C\underset{\mathbf{w}\in U}{inf}{∥\underset{\sim }{\mathbf{u}}-\mathbf{w}∥}_B\hfill \\ \hfill & \le {\tilde{C}}_1{∥\tilde{\mathbf{L}}\mathbf{w}-\tilde{\mathbf{f}}∥}_{0,\mathrm{\Omega }}+{\tilde{C}}_2{\zeta }_h{∥{\mathbf{B}}^h\mathbf{w}-\mathbf{h}∥}_{0,{\mathrm{\Gamma }}_h}+{\tilde{C}}_3{\zeta }_g{∥{\mathbf{B}}^g\mathbf{w}-\mathbf{g}∥}_{0,{\mathrm{\Gamma }}_g}+{\tilde{C}}_4{\zeta }_o{∥\mathbf{Aw}-\mathbf{b}∥}_{0,\mathrm{\Pi }}\hfill \\ \hfill & \le \tilde{C}\left({∥\tilde{\mathbf{L}}\mathbf{w}-\tilde{\mathbf{f}}∥}_{0,\mathrm{\Omega }}+{\zeta }_h{∥{\mathbf{B}}^h\mathbf{w}-\mathbf{h}∥}_{0,{\mathrm{\Gamma }}_h}+{\zeta }_g{∥{\mathbf{B}}^g\mathbf{w}-\mathbf{g}∥}_{0,{\mathrm{\Gamma }}_g}+{\zeta }_o{∥\mathbf{Aw}-\mathbf{b}∥}_{0,\mathrm{\Pi }}\right)\hfill \end{array}$$(79)

Since there exists exponential convergence in the domain and on the boundaries in each time step, we have(80) $${∥\underset{\sim }{\mathbf{u}}-\widehat{\mathbf{w}}∥}_B\le \mathrm{O}\left({\varpi }^{\vartheta /h}\right)$$(80)

The discretized form of (76(76) $$\begin{array}{cc}{E}_{\zeta }(\mathbf{w})\hfill & =\frac{1}{2}{\int }_{\mathrm{\Omega }}{\left(\tilde{\mathbf{L}}\mathbf{w}-\tilde{\mathbf{f}}\right)}^T\left(\tilde{\mathbf{L}}\mathbf{w}-\tilde{\mathbf{f}}\right)\text{d}\mathrm{\Omega }+\frac{{\left({\zeta }_h\right)}^2}{2}{\int }_{{\mathrm{\Gamma }}_h}{\left({\mathbf{B}}^h\mathbf{w}-\mathbf{h}\right)}^T\left({\mathbf{B}}^h\mathbf{w}-\mathbf{h}\right)\text{d}\mathrm{\Gamma }\hfill \\ \hfill & +\frac{{\left({\zeta }_g\right)}^2}{2}{\int }_{{\mathrm{\Gamma }}_g}{\left({\mathbf{B}}^g\mathbf{w}-\mathbf{g}\right)}^T\left({\mathbf{B}}^g\mathbf{w}-\mathbf{g}\right)\text{d}\mathrm{\Gamma }+\frac{{\left({\zeta }_o\right)}^2}{2}{\int }_{\mathrm{\Pi }}{\left(\mathbf{Aw}-\mathbf{b}\right)}^T\left(\mathbf{Aw}-\mathbf{b}\right)\text{d}\mathrm{\Omega }\hfill \end{array}$$(76) ) is(81) $$\begin{array}{cc}{\overline{E}}_{\zeta }\hfill & =\frac{1}{2}\sum _{i=1}^{N_p}{\left(\tilde{\mathbf{L}}\mathrm{\Phi }\left(\mathbf{p}\right)\tilde{\mathbf{D}}-\tilde{\mathbf{f}}\right)}^T\left(\tilde{\mathbf{L}}\mathrm{\Phi }\left(\mathbf{p}\right)\tilde{\mathbf{D}}-\tilde{\mathbf{f}}\right)+\frac{{\left({\zeta }_h\right)}^2}{2}\sum _{i=1}^{N_q}{\left({\mathbf{B}}^h\mathrm{\Phi }\left(\mathbf{q}\right)\tilde{\mathbf{D}}-\mathbf{h}\right)}^T\left({\mathbf{B}}^h\mathrm{\Phi }\left(\mathbf{q}\right)\tilde{\mathbf{D}}-\mathbf{h}\right)\hfill \\ \hfill & +\frac{{\left({\zeta }_g\right)}^2}{2}\sum _{i=1}^{N_r}{\left({\mathbf{B}}^g\mathrm{\Phi }\left(\mathbf{r}\right)\tilde{\mathbf{D}}-\mathbf{g}\right)}^T\left({\mathbf{B}}^g\mathrm{\Phi }\left(\mathbf{r}\right)\tilde{\mathbf{D}}-\mathbf{g}\right)+\frac{{\left({\zeta }_o\right)}^2}{2}\sum _{i=1}^{N_o}{\left(\mathbf{A}\mathrm{\Phi }\left(\mathbf{o}\right)\tilde{\mathbf{D}}-\mathbf{b}\right)}^T\left(\mathbf{A}\mathrm{\Phi }\left(\mathbf{o}\right)\tilde{\mathbf{D}}-\mathbf{b}\right)\hfill \end{array}$$(81)

Following the same procedure from (64(64) $$\frac{\partial {\overline{E}}_{\xi }}{\partial D^J}=0$$(64) )–(66(66) $$\left[\begin{array}{c}\frac{\partial {\overline{E}}_{\xi }}{\partial D^J}\\ \frac{\partial {\overline{E}}_{\xi }}{\partial {\xi }_h}\\ \frac{\partial {\overline{E}}_{\xi }}{\partial {\xi }_g}\\ \frac{\partial {\overline{E}}_{\xi }}{\partial {\xi }_o}\end{array}\right]:=\eta \left(\stackrel{⌢}{\mathbf{D}}\right)=\mathbf{0}$$(66) ), we have(82) $$\rho \left(\stackrel{⌣}{\mathbf{D}}\right)=\mathbf{0}$$(82)

where

(83) $$\stackrel{⌣}{\mathbf{D}}={\left[\begin{array}{ccccccccccc}{\mathbf{d}}_2^1\hfill & {\mathbf{d}}_2^2\hfill & \cdots \hfill & {\mathbf{d}}_2^N\hfill & {\dot{\mathbf{d}}}_0^1\hfill & {\dot{\mathbf{d}}}_0^2\hfill & \cdots \hfill & {\dot{\mathbf{d}}}_0^N\hfill & {\zeta }_h\hfill & {\zeta }_g\hfill & {\zeta }_o\hfill \end{array}\right]}^T$$(83)

The iteration process can be repeated as

(84) $${\stackrel{⌣}{\mathbf{D}}}^{(m+1)}={\stackrel{⌣}{\mathbf{D}}}^{(m)}-{\left({\rho }^{\prime }{\left({\mathbf{d}}_2^i,{\dot{\mathbf{d}}}_0^i,{\zeta }_h,{\zeta }_g,{\zeta }_o\right)}^{(m)}\right)}^{-1}\rho {\left({\mathbf{d}}_2^i,{\dot{\mathbf{d}}}_0^i,{\zeta }_h,{\zeta }_g,{\zeta }_o\right)}^{(m)},i=1,2,\cdots ,N$$(84)

where

(85) $$\rho {\left({\mathbf{d}}_2^i,{\dot{\mathbf{d}}}_0^i,{\zeta }_h,{\zeta }_g,{\zeta }_o\right)}^{(m)}=\left[\begin{array}{c}{\rho }_1\\ {\rho }_2\\ {\rho }_3\\ {\rho }_4\end{array}\right],{\rho }^{\prime }{\left({\mathbf{d}}_2^i,{\dot{\mathbf{d}}}_0^i,{\zeta }_h,{\zeta }_g,{\zeta }_o\right)}^{(m)}=\left[\begin{array}{cccc}{{\rho }^{\prime }}_{11}\hfill & {{\rho }^{\prime }}_{12}\hfill & {{\rho }^{\prime }}_{13}\hfill & {{\rho }^{\prime }}_{14}\hfill \\ \hfill & {{\rho }^{\prime }}_{22}\hfill & {{\rho }^{\prime }}_{23}\hfill & {{\rho }^{\prime }}_{24}\hfill \\ \hfill & \hfill & {{\rho }^{\prime }}_{33}\hfill & {{\rho }^{\prime }}_{34}\hfill \\ \mathit{sym}\hfill & \hfill & \hfill & {{\rho }^{\prime }}_{44}\hfill \end{array}\right]$$(85) (86) $$\begin{array}{c}{\rho }_1={\left(\tilde{\mathbf{L}}\mathrm{\Phi }\right)}^T\left(\tilde{\mathbf{L}}\mathrm{\Phi }\tilde{\mathbf{D}}-\tilde{\mathbf{f}}\right)+{\zeta }_h^2{\left({\mathbf{B}}^h\mathrm{\Phi }\right)}^T\left({\mathbf{B}}^h\mathrm{\Phi }\tilde{\mathbf{D}}-\mathbf{h}\right)+{\zeta }_g^2{\left({\mathbf{B}}^g\mathrm{\Phi }\right)}^T\left({\mathbf{B}}^g\mathrm{\Phi }\tilde{\mathbf{D}}-\mathbf{g}\right)+{\zeta }_o^2{\left(\mathbf{A}\mathrm{\Phi }\right)}^T\left(\mathbf{A}\mathrm{\Phi }\tilde{\mathbf{D}}-\mathbf{b}\right)\hfill \\ {\rho }_2={\zeta }_h\sum _{j=1}^{N_q}{\left({\mathbf{B}}^h\mathrm{\Phi }\tilde{\mathbf{D}}-\mathbf{h}\right)}^2,{\rho }_3={\zeta }_g\sum _{j=1}^{N_r}{\left({\mathbf{B}}^g\mathrm{\Phi }\tilde{\mathbf{D}}-\mathbf{g}\right)}^2,{\rho }_4={\zeta }_o\sum _{j=1}^{N_o}{\left(\mathbf{A}\mathrm{\Phi }\tilde{\mathbf{D}}-\mathbf{b}\right)}^2\hfill \end{array}$$(86) (87) $$\begin{array}{c}{{\rho }^{\prime }}_{11}={\left(\tilde{\mathbf{L}}\mathrm{\Phi }\right)}^T\tilde{\mathbf{L}}\mathrm{\Phi }+{\zeta }_h^2{\left({\mathbf{B}}^h\mathrm{\Phi }\right)}^T{\mathbf{B}}^h\mathrm{\Phi }+{\zeta }_g^2{\left({\mathbf{B}}^g\mathrm{\Phi }\right)}^T{\mathbf{B}}^g\mathrm{\Phi }+{\zeta }_o^2{\left(\mathbf{A}\mathrm{\Phi }\right)}^T\mathbf{A}\mathrm{\Phi }\hfill \\ {{\rho }^{\prime }}_{12}=2{\zeta }_h{\left({\mathbf{B}}^h\mathrm{\Phi }\right)}^T\left({\mathbf{B}}^h\mathrm{\Phi }\tilde{\mathbf{D}}-\mathbf{h}\right),{{\rho }^{\prime }}_{13}=2{\zeta }_g{\left({\mathbf{B}}^g\mathrm{\Phi }\right)}^T\left({\mathbf{B}}^g\mathrm{\Phi }\tilde{\mathbf{D}}-\mathbf{g}\right),{{\rho }^{\prime }}_{14}=2{\zeta }_o{\left(\mathbf{A}\mathrm{\Phi }\right)}^T\left(\mathbf{A}\mathrm{\Phi }\tilde{\mathbf{D}}-\mathbf{b}\right),\hfill \\ {{\rho }^{\prime }}_{22}=\sum _{j=1}^{N_q}{\left({\mathbf{B}}^h\mathrm{\Phi }\tilde{\mathbf{D}}-\mathbf{h}\right)}^2,{{\rho }^{\prime }}_{23}=\mathbf{0},{{\rho }^{\prime }}_{24}=\mathbf{0},\hfill \\ {{\rho }^{\prime }}_{33}=\sum _{j=1}^{N_r}{\left({\mathbf{B}}^g\mathrm{\Phi }\tilde{\mathbf{D}}-\mathbf{g}\right)}^2,{{\rho }^{\prime }}_{34}=\mathbf{0},{{\rho }^{\prime }}_{44}=\sum _{j=1}^{N_o}{\left(\mathbf{A}\mathrm{\Phi }\tilde{\mathbf{D}}-\mathbf{b}\right)}^2.\hfill \end{array}$$(87)

Introducing the weights obtained from (82(82) $$\rho \left(\stackrel{⌣}{\mathbf{D}}\right)=\mathbf{0}$$(82) ) into the discrete equation (32(32) $$\mathbf{KD}=\mathbf{F}$$(32) ) renders the weighted form as below(88) $$\left[\begin{array}{c}{\tilde{\mathbf{K}}}_1\\ {\zeta }_h{\tilde{\mathbf{K}}}_2\\ {\zeta }_g{\tilde{\mathbf{K}}}_3\\ {\zeta }_o{\tilde{\mathbf{K}}}_4\end{array}\right]\tilde{\mathbf{D}}=\left[\begin{array}{c}{\tilde{\mathbf{F}}}_1\\ {\zeta }_h{\tilde{\mathbf{F}}}_2\\ {\zeta }_g{\tilde{\mathbf{F}}}_3\\ {\zeta }_o{\tilde{\mathbf{F}}}_4\end{array}\right]$$(88)

5. Tikhonov regularization

Generally, there are some noises in the input data which lead to the ill-conditioned resulting matrix. Tikhonov regularization is introduced to deal with the noisy data before solving the Equations in (32(32) $$\mathbf{KD}=\mathbf{F}$$(32) ) and (46(46) $$\tilde{\mathbf{K}}\tilde{\mathbf{D}}=\tilde{\mathbf{F}}$$(46) ). The collocation of noise input data can be discretized as a general form(89) $$\beta \mathbf{d}=\mathbf{H}$$(89)

Here, $\mathbf{\beta }$ is a N _R × N (N _R ≥ N) matrix in which N _R denotes the number of known noise data. In Tikhonov regularization method [50], we try to minimize the functional as follows(90) $$E=min\left\{{∥\beta \mathbf{d}-\mathbf{H}∥}_2^2+\lambda {∥\mathbf{d}∥}_2^2\right\}$$(90)

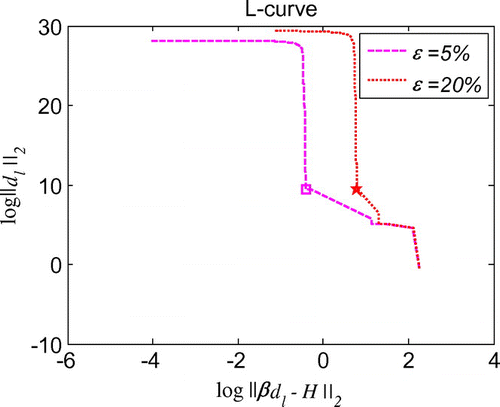
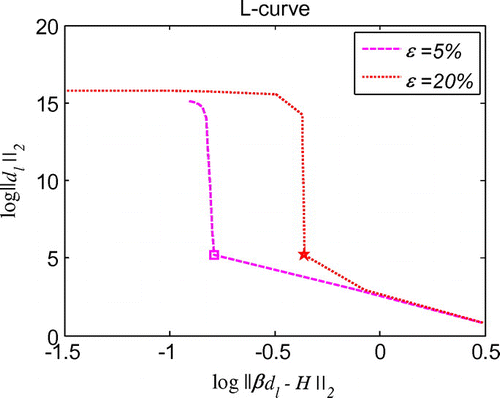
where $\lambda$ is a positive constant called regularization parameter which depends on the problem and the input noisy data. There are many methods proposed for selecting the regularization parameter in which the L-curve criterion is reported to be an efficient one [51]. L-curve criterion presents a parametric log–log plot of the residual and solution norms which can be expressed as(91) $$\left\{log{∥{\beta \mathbf{d}}_l-\mathbf{H}∥}_2,log{∥{\mathbf{d}}_l∥}_2\right\},l=1,2,\cdots ,\iota \left(\iota \le N\right)$$(91)

The optimal regularization parameter is corresponding to the location of maximum curvature [52]. For the case of noisy data in the measured condition, replace ${\mathbf{F}}_4$ in (37(37) $${\mathbf{K}}_4=\left[\begin{array}{cc}\mathbf{A}\mathrm{\Phi }\hfill & \mathbf{0}\hfill \\ \mathbf{0}\hfill & \mathbf{A}\mathrm{\Phi }\hfill \end{array}\right],\mathbf{A}\mathrm{\Phi }=\left[\begin{array}{c}\mathbf{A}\mathrm{\Phi }\left({\mathbf{o}}_1\right)\\ \mathbf{A}\mathrm{\Phi }\left({\mathbf{o}}_2\right)\\ ⋮\\ \mathbf{A}\mathrm{\Phi }\left({\mathbf{o}}_{N_o}\right)\end{array}\right],{\mathbf{F}}_4=\left[\begin{array}{c}{\mathbf{F}}_{41}\\ {\mathbf{F}}_{42}\end{array}\right],{\mathbf{F}}_{41}=\left[\begin{array}{c}\mathbf{b}\left({\mathbf{o}}_1,t_2\right)\\ \mathbf{b}\left({\mathbf{o}}_2,t_2\right)\\ ⋮\\ \mathbf{b}\left({\mathbf{o}}_{N_o},t_2\right)\end{array}\right],{\mathbf{F}}_{42}=\left[\begin{array}{c}\mathbf{b}\left({\mathbf{o}}_1,t_0\right)\\ \mathbf{b}\left({\mathbf{o}}_2,t_0\right)\\ ⋮\\ \mathbf{b}\left({\mathbf{o}}_{N_o},t_0\right)\end{array}\right]$$(37) ) or ${\tilde{\mathbf{F}}}_4$ in (51(51) $$\begin{array}{c}{\tilde{\mathbf{K}}}_4=\left[\begin{array}{cc}\mathbf{A}\mathrm{\Phi }\hfill & \mathbf{0}\hfill \\ \mathbf{0}\hfill & \mathbf{A}\mathrm{\Phi }\hfill \end{array}\right],\mathbf{A}\mathrm{\Phi }=\left[\begin{array}{c}\mathbf{A}\mathrm{\Phi }\left({\mathbf{o}}_1\right)\\ \mathbf{A}\mathrm{\Phi }\left({\mathbf{o}}_2\right)\\ ⋮\\ \mathbf{A}\mathrm{\Phi }\left({\mathbf{o}}_{N_o}\right)\end{array}\right],\hfill \\ {\tilde{\mathbf{F}}}_4=\left[\begin{array}{c}{\tilde{\mathbf{F}}}_{41}\\ {\tilde{\mathbf{F}}}_{42}\end{array}\right],{\tilde{\mathbf{F}}}_{41}=\left[\begin{array}{c}\mathbf{b}\left({\mathbf{o}}_1,t_2\right)\\ \mathbf{b}\left({\mathbf{o}}_2,t_2\right)\\ ⋮\\ \mathbf{b}\left({\mathbf{o}}_{N_o},t_2\right)\end{array}\right],{\tilde{\mathbf{F}}}_{42}=\frac{1}{\mathrm{\Delta }t}\left[\begin{array}{c}\mathbf{b}\left({\mathbf{o}}_1,t_1\right)-\mathbf{b}\left({\mathbf{o}}_1,t_0\right)\\ \mathbf{b}\left({\mathbf{o}}_2,t_1\right)-\mathbf{b}\left({\mathbf{o}}_2,t_0\right)\\ ⋮\\ \mathbf{b}\left({\mathbf{o}}_{N_o},t_1\right)-\mathbf{b}\left({\mathbf{o}}_{N_o},t_0\right)\end{array}\right]\hfill \end{array}$$(51) ) by $\overline{\mathbf{H}}={\beta \mathbf{d}}_p$ where ${\mathbf{d}}_p$ is the optimum solution obtained from (91(91) $$\left\{log{∥{\beta \mathbf{d}}_l-\mathbf{H}∥}_2,log{∥{\mathbf{d}}_l∥}_2\right\},l=1,2,\cdots ,\iota \left(\iota \le N\right)$$(91) ). For the case of noisy data in the boundary condition, replace ${\mathbf{F}}_2,{\mathbf{F}}_3$ in (35(35) $${\mathbf{K}}_2=\left[\begin{array}{cc}{\mathbf{B}}^h\mathrm{\Phi }\hfill & \mathbf{0}\hfill \\ \mathbf{0}\hfill & {\mathbf{B}}^h\mathrm{\Phi }\hfill \end{array}\right],{\mathbf{B}}^h\mathrm{\Phi }=\left[\begin{array}{c}{\mathbf{B}}^h\mathrm{\Phi }\left({\mathbf{q}}_1\right)\\ {\mathbf{B}}^h\mathrm{\Phi }\left({\mathbf{q}}_2\right)\\ ⋮\\ {\mathbf{B}}^h\mathrm{\Phi }\left({\mathbf{q}}_{N_q}\right)\end{array}\right],{\mathbf{F}}_2=\left[\begin{array}{c}{\mathbf{F}}_{21}\\ {\mathbf{F}}_{22}\end{array}\right],{\mathbf{F}}_{21}=\left[\begin{array}{c}\mathbf{h}\left({\mathbf{q}}_1,t_2\right)\\ \mathbf{h}\left({\mathbf{q}}_2,t_2\right)\\ ⋮\\ \mathbf{h}\left({\mathbf{q}}_{N_q},t_2\right)\end{array}\right],{\mathbf{F}}_{22}=\left[\begin{array}{c}\mathbf{h}\left({\mathbf{q}}_1,t_0\right)\\ \mathbf{h}\left({\mathbf{q}}_2,t_0\right)\\ ⋮\\ \mathbf{h}\left({\mathbf{q}}_{N_q},t_0\right)\end{array}\right]$$(35) )–(36(36) $${\mathbf{K}}_3=\left[\begin{array}{cc}{\mathbf{B}}^g\mathrm{\Phi }\hfill & \mathbf{0}\hfill \\ \mathbf{0}\hfill & {\mathbf{B}}^g\mathrm{\Phi }\hfill \end{array}\right],{\mathbf{B}}^g\mathrm{\Phi }=\left[\begin{array}{c}{\mathbf{B}}^g\mathrm{\Phi }\left({\mathbf{r}}_1\right)\\ {\mathbf{B}}^g\mathrm{\Phi }\left({\mathbf{r}}_2\right)\\ ⋮\\ {\mathbf{B}}^g\mathrm{\Phi }\left({\mathbf{r}}_{N_r}\right)\end{array}\right],{\mathbf{F}}_3=\left[\begin{array}{c}{\mathbf{F}}_{31}\\ {\mathbf{F}}_{32}\end{array}\right],{\mathbf{F}}_{31}=\left[\begin{array}{c}\mathbf{g}\left({\mathbf{r}}_1,t_2\right)\\ \mathbf{g}\left({\mathbf{r}}_2,t_2\right)\\ ⋮\\ \mathbf{g}\left({\mathbf{r}}_{N_r},t_2\right)\end{array}\right],{\mathbf{F}}_{32}=\left[\begin{array}{c}\mathbf{g}\left({\mathbf{r}}_1,t_0\right)\\ \mathbf{g}\left({\mathbf{r}}_2,t_0\right)\\ ⋮\\ \mathbf{g}\left({\mathbf{r}}_{N_r},t_0\right)\end{array}\right]$$(36) ) or ${\tilde{\mathbf{F}}}_2,{\tilde{\mathbf{F}}}_3$ in (49(49) $$\begin{array}{c}{\tilde{\mathbf{K}}}_2=\left[\begin{array}{cc}{\mathbf{B}}^h\mathrm{\Phi }\hfill & \mathbf{0}\hfill \\ \mathbf{0}\hfill & {\mathbf{B}}^h\mathrm{\Phi }\hfill \end{array}\right],{\mathbf{B}}^h\mathrm{\Phi }=\left[\begin{array}{c}{\mathbf{B}}^h\mathrm{\Phi }\left({\mathbf{q}}_1\right)\\ {\mathbf{B}}^h\mathrm{\Phi }\left({\mathbf{q}}_2\right)\\ ⋮\\ {\mathbf{B}}^h\mathrm{\Phi }\left({\mathbf{q}}_{N_q}\right)\end{array}\right],\hfill \\ {\tilde{\mathbf{F}}}_2=\left[\begin{array}{c}{\tilde{\mathbf{F}}}_{21}\\ {\tilde{\mathbf{F}}}_{22}\end{array}\right],{\tilde{\mathbf{F}}}_{21}=\left[\begin{array}{c}\mathbf{h}\left({\mathbf{q}}_1,t_2\right)\\ \mathbf{h}\left({\mathbf{q}}_2,t_2\right)\\ ⋮\\ \mathbf{h}\left({\mathbf{q}}_{N_q},t_2\right)\end{array}\right],{\tilde{\mathbf{F}}}_{22}=\frac{1}{\mathrm{\Delta }t}\left[\begin{array}{c}\mathbf{h}\left({\mathbf{q}}_1,t_1\right)-\mathbf{h}\left({\mathbf{q}}_1,t_0\right)\\ \mathbf{h}\left({\mathbf{q}}_2,t_1\right)-\mathbf{h}\left({\mathbf{q}}_2,t_0\right)\\ ⋮\\ \mathbf{h}\left({\mathbf{q}}_{N_q},t_1\right)-\mathbf{h}\left({\mathbf{q}}_{N_q},t_0\right)\end{array}\right]\hfill \end{array}$$(49) )–(50(50) $$\begin{array}{c}{\tilde{\mathbf{K}}}_3=\left[\begin{array}{cc}{\mathbf{B}}^g\mathrm{\Phi }\hfill & \mathbf{0}\hfill \\ \mathbf{0}\hfill & {\mathbf{B}}^g\mathrm{\Phi }\hfill \end{array}\right],{\mathbf{B}}^g\mathrm{\Phi }=\left[\begin{array}{c}{\mathbf{B}}^g\mathrm{\Phi }\left({\mathbf{r}}_1\right)\\ {\mathbf{B}}^g\mathrm{\Phi }\left({\mathbf{r}}_2\right)\\ ⋮\\ {\mathbf{B}}^g\mathrm{\Phi }\left({\mathbf{r}}_{N_r}\right)\end{array}\right],\hfill \\ {\tilde{\mathbf{F}}}_3=\left[\begin{array}{c}{\tilde{\mathbf{F}}}_{31}\\ {\tilde{\mathbf{F}}}_{32}\end{array}\right],{\tilde{\mathbf{F}}}_{31}=\left[\begin{array}{c}\mathbf{g}\left({\mathbf{r}}_1,t_2\right)\\ \mathbf{g}\left({\mathbf{r}}_2,t_2\right)\\ ⋮\\ \mathbf{g}\left({\mathbf{r}}_{N_r},t_2\right)\end{array}\right],{\tilde{\mathbf{F}}}_{32}=\frac{1}{\mathrm{\Delta }t}\left[\begin{array}{c}\mathbf{g}\left({\mathbf{r}}_1,t_1\right)-\mathbf{g}\left({\mathbf{r}}_1,t_0\right)\\ \mathbf{g}\left({\mathbf{r}}_2,t_1\right)-\mathbf{g}\left({\mathbf{r}}_2,t_0\right)\\ ⋮\\ \mathbf{g}\left({\mathbf{r}}_{N_r},t_1\right)-\mathbf{g}\left({\mathbf{r}}_{N_r},t_0\right)\end{array}\right]\hfill \end{array}$$(50) ) by $\overline{\mathbf{H}}$, and for the case of noisy data in the initial condition, replace ${\mathbf{u}}_0$ in (20(20) $$\mathbf{u}\left(\mathbf{x},0\right)={\mathbf{u}}_0\left(\mathbf{x}\right)\approx {\tilde{\mathbf{u}}}_0\left(\mathbf{x}\right)=\mathrm{\Phi }\left(\mathbf{x}\right){\mathbf{d}}_0$$(20) ) or ${\mathbf{c}}_0$ in (21(21) $$\dot{\mathbf{u}}\left(\mathbf{x},0\right)={\mathbf{c}}_0\left(\mathbf{x}\right)=\mathrm{\Phi }\left(\mathbf{x}\right){\dot{\mathbf{d}}}_0$$(21) ) by the solution after regularization before solving the Equations in (32(32) $$\mathbf{KD}=\mathbf{F}$$(32) ) and (46(46) $$\tilde{\mathbf{K}}\tilde{\mathbf{D}}=\tilde{\mathbf{F}}$$(46) ).

6. Numerical examples

6.1. Initial displacement identification in 1d inverse wave problem

Firstly, consider a 1d initial displacement identification inverse wave problem to evaluate the performance of the propose algorithm. In the following solutions of all the numerical examples, we take inverse Multiquadric as the shape function. The governing equation of a 1d wave propagation is expressed as(92) $$\ddot{u}=\frac{1}{4+2x}{u}^{″}+e^{-t}(2+x^2)-\frac{e^{-t}}{2+x},x\in \left(0,1\right),t\in \left(0,1\right)$$(92)

with boundary conditions(93) $${\left.u\right|}_{x=0}=2e^{-t},{\left.u\right|}_{x=1}=3e^{-t}$$(93)

and known initial velocity condition(94) $${\left.\dot{u}\right|}_{t=0}=-(2+x^2)$$(94)

An additional condition observed from the measurement is given as(95) $${\left.u(x,t)\right|}_{x=0.5}=\frac{9}{4}{e}^{-t}$$(95)

The analytical solution for the inner domain and the initial displacement condition that needs determination are(96) $$u(x,t)=(2+x^2)e^{-t},{\left.u\right|}_{t=0}=2+x^2$$(96)

The noises involved in the different conditions are shown as(97) $${\left.u^{\epsilon }\left(i\right)\right|}_{x=0.5}={\left.u\right|}_{x=0.5}\left(1+\sigma (i)\epsilon \right)=\frac{9}{4}{e}^{-t}\left(1+\sigma (i)\epsilon \right)$$(97) (98) $${\left.u^{\epsilon }\left(i\right)\right|}_{x=0}={\left.u\right|}_{x=0}\left(1+\sigma (i)\epsilon \right)=2e^{-t}\left(1+\sigma (i)\epsilon \right)$$(98) (99) $${\left.u^{\epsilon }\left(i\right)\right|}_{x=1}={\left.u\right|}_{x=1}\left(1+\sigma (i)\epsilon \right)=3e^{-t}\left(1+\sigma (i)\epsilon \right)$$(99) (100) $${\left.{\dot{u}}^{\epsilon }\left(i\right)\right|}_{t=0}={\left.\dot{u}\right|}_{t=0}\left(1+\sigma (i)\epsilon \right)=-(2+x^2)\left(1+\sigma (i)\epsilon \right)$$(100)

where $u^{\epsilon }\left(i\right)$ and ${\dot{u}}^{\epsilon }\left(i\right)$ are the displacement and velocity in regard to the noise level ɛ and i random number, $\sigma (i)\in \left[-1,1\right]$ is the random number of normal distribution. $error\left(u_0\right)$ presented in the figures denotes the error of u ₀, i.e. $error\left(u_0\right)=u_0-{\tilde{u}}_0$. N = 13 source points and N _c = 25 + 3 collocation points are utilized for this solution. $N_R=100$ random numbers from normal distribution are introduced in the input noise data. The optimum weights for the solution ξ _g ≈ 10² and ξ _o ≈ 1 can be obtained from (66(66) $$\left[\begin{array}{c}\frac{\partial {\overline{E}}_{\xi }}{\partial D^J}\\ \frac{\partial {\overline{E}}_{\xi }}{\partial {\xi }_h}\\ \frac{\partial {\overline{E}}_{\xi }}{\partial {\xi }_g}\\ \frac{\partial {\overline{E}}_{\xi }}{\partial {\xi }_o}\end{array}\right]:=\eta \left(\stackrel{⌢}{\mathbf{D}}\right)=\mathbf{0}$$(66) ).

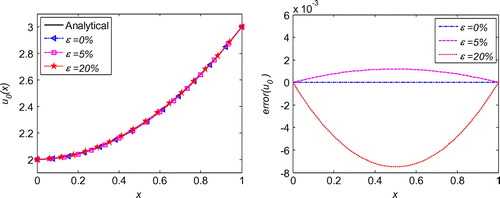
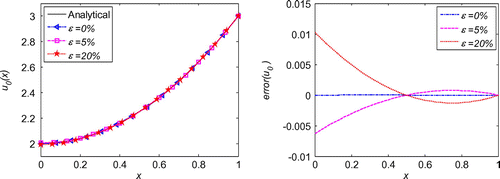
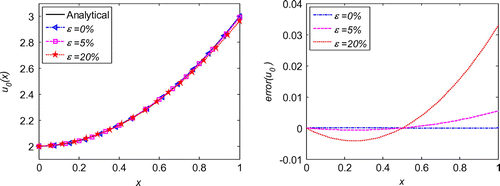
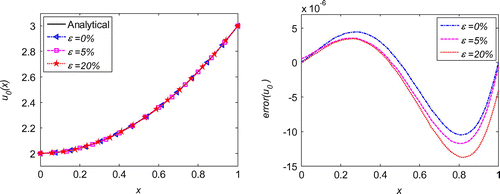
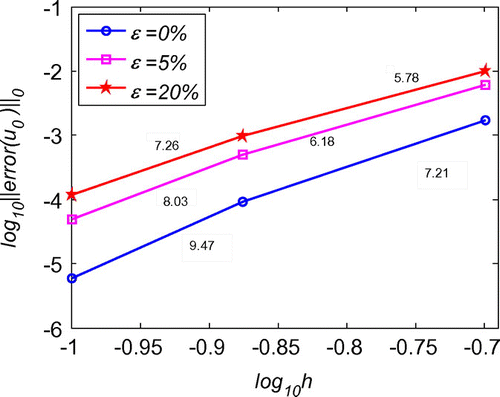
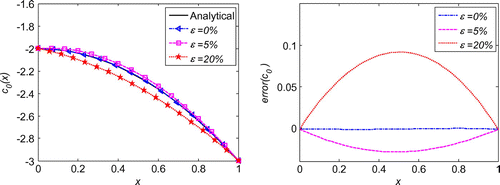
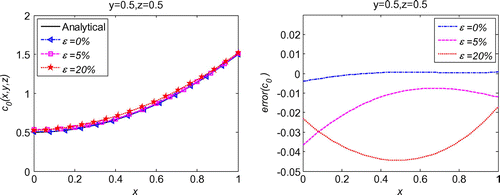
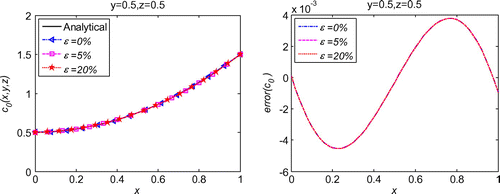
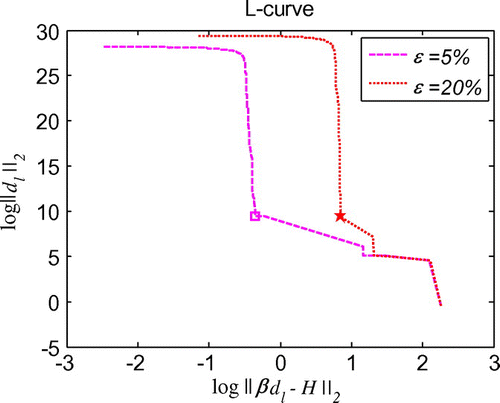
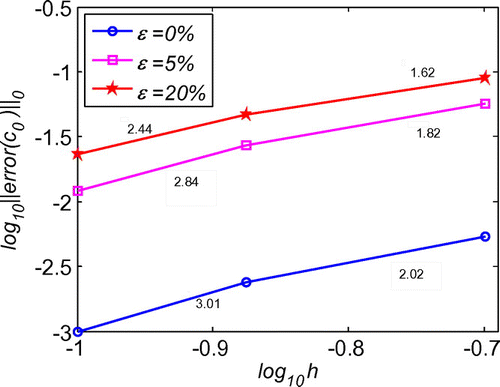
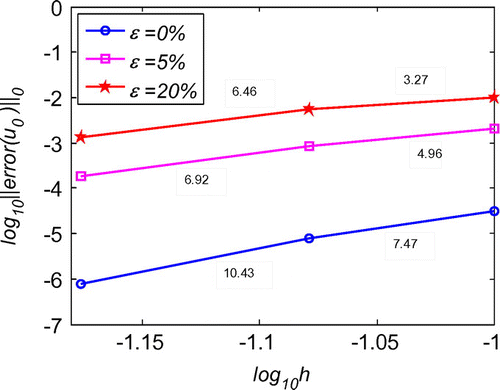
We first evaluate the necessity of the regularization in the inverse problems. As schematized in Figure 1, after regularization, the solution is much smoother than that without regularization. Moreover, the error throughout the whole problem domain after regularization is also reduced by the regularization calculation. With quite sparse mesh, we can obtain very good accuracy and stability of the initial displacement solutions for the noises in the measured condition, boundary conditions or initial condition, as shown Figures 2–5. Diagrams of L-curve predict the optimum regularization parameter for each case presented in Figures 6–9. Even though the noise level is quite high as ε = 20%, the accuracy is satisfying and the solutions are quite stable. This outmatches many other numerical methods with big error when involving measurement data with high noise level. When the noise level is decreasing, the error is diminishing. This ensures the convergence of the proposed algorithm. Figure 10 presents that this algorithm also converges at exponential rates in the initial displacement identification inverse problem as in the direct problems.

Figure 1. Comparison of solutions using regularization and not using regularization in 1d initial displacement identification problem with noise ${\left.u\right|}_{x=0.5}$.

Figure 2. Solution of 1d initial displacement identification problem with noise on ${\left.u\right|}_{x=0.5}$.

Figure 3. Solution of 1d initial displacement identification problem with noise on ${\left.u\right|}_{x=0}$.

Figure 4. Solution of 1d initial displacement identification problem with noise on ${\left.u\right|}_{x=1}$.

Figure 5. Solution of 1d initial displacement identification problem with noise on ${\left.\dot{u}\right|}_{t=0}$.

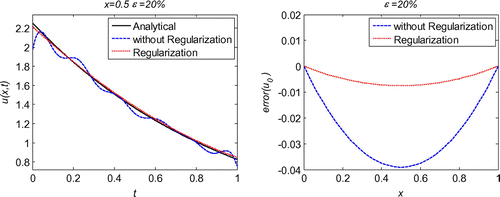
Figure 6. L-curve for the regularization parameter in 1d initial displacement identification problem with noise on ${\left.u\right|}_{x=0.5}$.

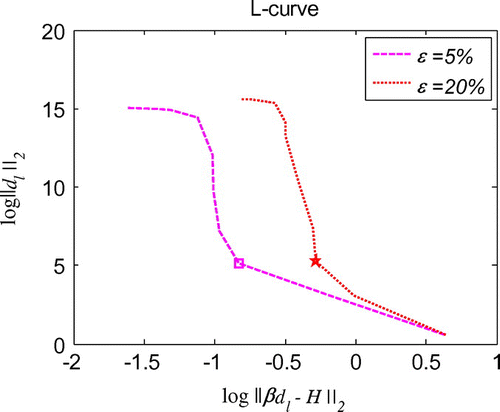
Figure 7. L-curve for the regularization parameter in 1d initial displacement identification problem with noise on ${\left.u\right|}_{x=0}$.

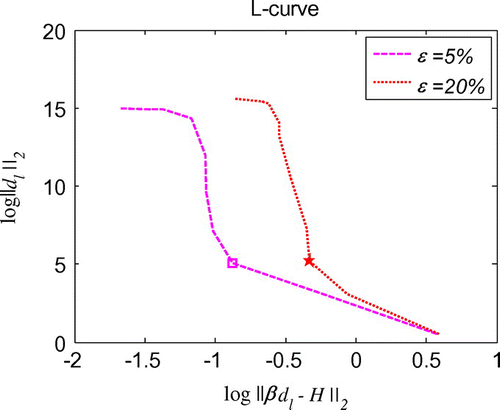
Figure 8. L-curve for the regularization parameter in 1d initial displacement identification problem with noise on ${\left.u\right|}_{x=1}$.

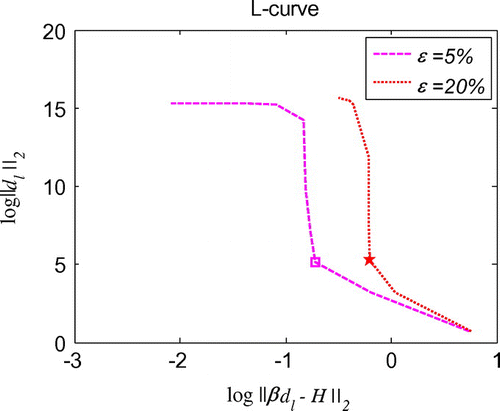
Figure 9. L-curve for the regularization parameter in 1d initial displacement identification problem with noise on ${\left.\dot{u}\right|}_{t=0}$.

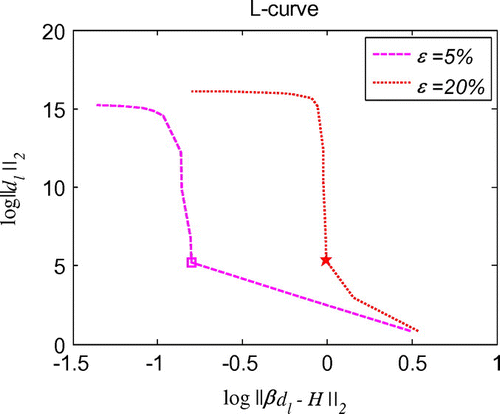
Figure 10. Convergence of RBCM for the 1d initial displacement identification problem with noise on ${\left.u\right|}_{x=0.5}$.

Comparatively, for a parameter identification problem presented in [2], without noise in the overspecified data, the maximum relative error is 3.5% for the solution. For a source identification problem [17], with 6% noise level in the Neumann boundary condition, after using some smooth techniques for the data, obvious error can be observed in the numerical solutions, and the maximum relative error goes to 40% after 60 iterations. For another source term identification problem [18], with 10% noise level, the maximum relative error detected in the domain and on the boundary is 9%. Even adding more known conditions on the boundary, the maximum relative error is still 2%. For the boundary identification problem [1], with 1% noise level, the relative error for identifying the boundary is almost 1.2%. Moreover, instability can be observed in some numerical simulations [17,26]. However, in the solutions of this paper, with noise level 20% in 1d inverse problem, the maximum relative error is approximately to be 1%. The high accuracy and good stability make the proposed algorithm a great method for identifying the initial conditions which cannot be matched by many other numerical methods.

6.2. Initial displacement identification in 3d inverse wave problem

A three-dimensional (3d) wave propagation equation takes the form

(101) $$\ddot{u}={(x+y+z)}^2\mathrm{\Delta }u+\left[e^t(2+4t+x^2+y^2+z^2+t^2)-6e^t{(x+y+z)}^2\right]$$(101)

with boundary conditions(102) $$\begin{array}{c}{u|}_{x=0}=(y^2+z^2+t^2)e^t{,u|}_{x=1}=(1+y^2+z^2+t^2)e^t\hfill \\ {u|}_{y=0}=(x^2+z^2+t^2)e^t{,u|}_{y=1}=(1+x^2+z^2+t^2)e^t\hfill \\ {u|}_{z=0}=(x^2+y^2+t^2)e^t{,u|}_{z=1}=(1+x^2+y^2+t^2)e^t\hfill \end{array}$$(102)

initial velocity condition(103) $${\left.\dot{u}\right|}_{t=0}=x^2+y^2+z^2$$(103)

and the additional condition obtained from the measurement data(104) $${\left.u\right|}_{z=0.5}=(\frac{1}{4}+x^2+y^2+t^2)e^t$$(104)

The analytical solution and the initial displacement condition for identification are(105) $$u=(x^2+y^2+z^2+t^2)e^t,{\left.u\right|}_{t=0}=x^2+y^2+z^2$$(105)

Some noises are introduced into the measured condition, boundary conditions and initial velocity condition to evaluate the accuracy and stability as follows(106) $${\left.u^{\epsilon }\left(i\right)\right|}_{z=0.5}={\left.u\right|}_{z=0.5}\left(1+\sigma (i)\epsilon \right)=(\frac{1}{4}+x^2+y^2+t^2)e^t\left(1+\sigma (i)\epsilon \right)$$(106) (107) $${\left.u^{\epsilon }\left(i\right)\right|}_{z=0}{=u|}_{z=0}\left(1+\sigma (i)\epsilon \right)=(x^2+y^2+t^2)e^t\left(1+\sigma (i)\epsilon \right)$$(107) (108) $${\left.u^{\epsilon }\left(i\right)\right|}_{z=1}{=u|}_{z=1}\left(1+\sigma (i)\epsilon \right)=(1+x^2+y^2+t^2)e^t\left(1+\sigma (i)\epsilon \right)$$(108) (109) $${\left.{\dot{u}}^{\epsilon }\left(i\right)\right|}_{t=0}={\left.\dot{u}\right|}_{t=0}\left(1+\sigma (i)\epsilon \right)=\left(x^2+y^2+z^2\right)\left(1+\sigma (i)\epsilon \right)$$(109)

Using 3d RBFs, the discretization and formulation of RBCM for 3d inverse problem are the same as those for 1d problem. N = 7 × 7 × 7 source points, N _c = 9 × 9 × 9 + 7 × 11 × 11 collocation points and N _R = 500 random numbers from normal distribution are utilized for the discretization and solution. The optimum weights obtained from (66(66) $$\left[\begin{array}{c}\frac{\partial {\overline{E}}_{\xi }}{\partial D^J}\\ \frac{\partial {\overline{E}}_{\xi }}{\partial {\xi }_h}\\ \frac{\partial {\overline{E}}_{\xi }}{\partial {\xi }_g}\\ \frac{\partial {\overline{E}}_{\xi }}{\partial {\xi }_o}\end{array}\right]:=\eta \left(\stackrel{⌢}{\mathbf{D}}\right)=\mathbf{0}$$(66) ) are ξ _g ≈ 10⁴ for the Dirichlet boundary and ξ _o ≈ 1 for the known condition. As presented in Figures 11–14, for the initial displacement identification of 3d inverse wave problem, we can also attain stable and highly accurate solutions as in the 1d inverse problem. Regularization can obviously improve the solutions with noise in the known condition, boundary conditions or initial condition, and the corresponding optimum regularization parameters are selected from Figures 15–18. For the case of noise ε = 20% in the known condition and boundary conditions, the maximum relative error for the solution is less than $0.15\%$. 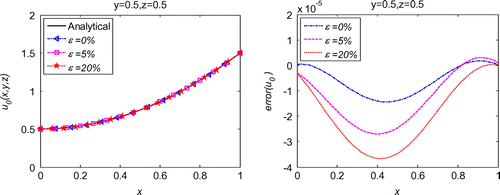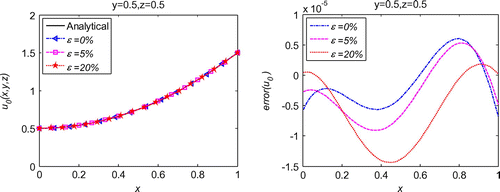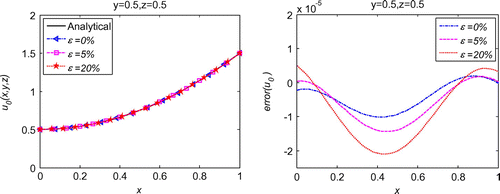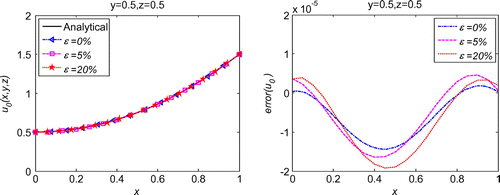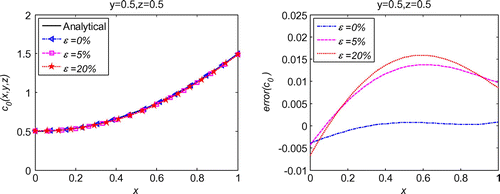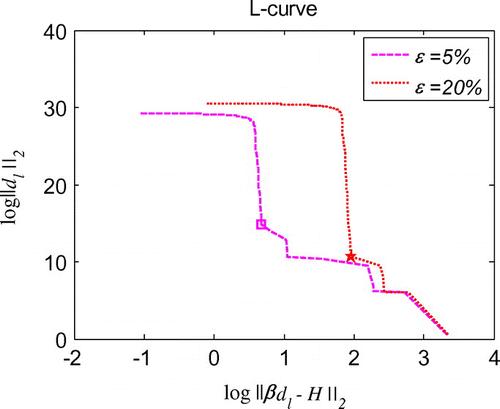If the noises are involved in the initial velocity with noise level ε = 20%, the maximum relative error is no more than $2\%$, which is also much less than the error introduced in the known data. Decreasing noise level leads to reduced error confirms the convergence and good stability of the proposed method. Convergence study presented in Figure 19 indicates that RBCM has exponential convergence not only in 1d inverse problems, but also in 3d inverse problems. The numerical simulations prove that the proposed method also works very well for 3d inverse wave problems.

Figure 11. Solution of 3d initial displacement identification problem with noise on ${\left.u\right|}_{z=0.5}$.

Figure 12. Solution of 3d initial displacement identification problem with noise on ${\left.u\right|}_{z=0}$.

Figure 13. Solution of 3d initial displacement identification problem with noise on ${\left.u\right|}_{z=1}$.

Figure 14. Solution of 3d initial displacement identification problem with noise on ${\left.\dot{u}\right|}_{t=0}$.

Figure 15. L-curve for the regularization parameter in 3d initial displacement identification problem with noise on ${\left.u\right|}_{z=0.5}$.

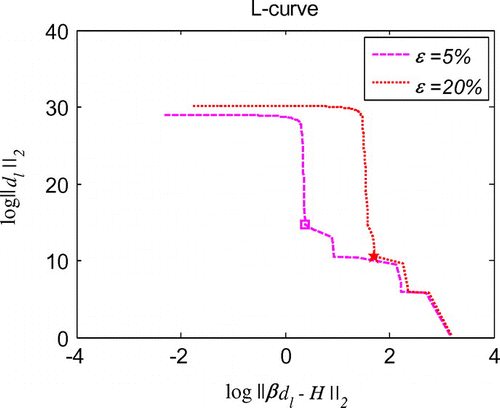
Figure 16. L-curve for the regularization parameter in 3d initial displacement identification problem with noise on ${\left.u\right|}_{z=0}$.

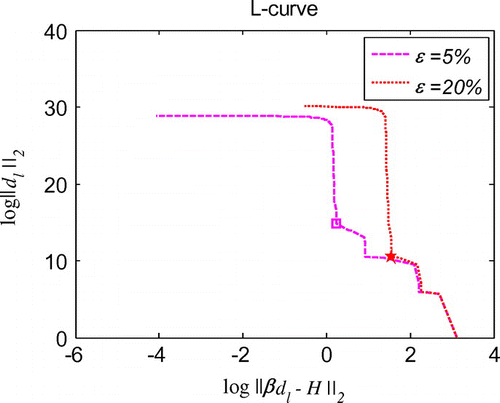
Figure 17. L-curve for the regularization parameter in 3d initial displacement identification problem with noise on ${\left.u\right|}_{z=1}$.

Figure 18. L-curve for the regularization parameter in 3d initial displacement identification problem with noise on ${\left.\dot{u}\right|}_{t=0}$.

Figure 19. Convergence of RBCM for the 3d initial displacement identification problem with noise on ${\left.u\right|}_{z=0.5}$.

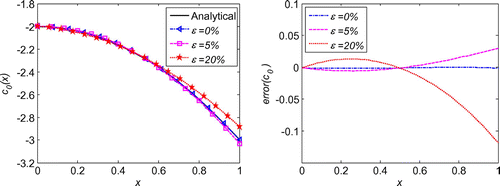
6.3. Initial velocity identification in 1d inverse wave problem

In this numerical simulation, the same governing Equation in (92(92) $$\ddot{u}=\frac{1}{4+2x}{u}^{″}+e^{-t}(2+x^2)-\frac{e^{-t}}{2+x},x\in \left(0,1\right),t\in \left(0,1\right)$$(92) ) and boundary conditions (93(93) $${\left.u\right|}_{x=0}=2e^{-t},{\left.u\right|}_{x=1}=3e^{-t}$$(93) ) as well as the additional condition (95(95) $${\left.u(x,t)\right|}_{x=0.5}=\frac{9}{4}{e}^{-t}$$(95) ) with known initial displacement $u\left(x,0\right)$ are utilized to identify the unknown initial velocity $\dot{u}\left(x,0\right)$ in 1d inverse wave problem. 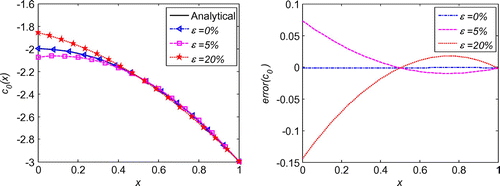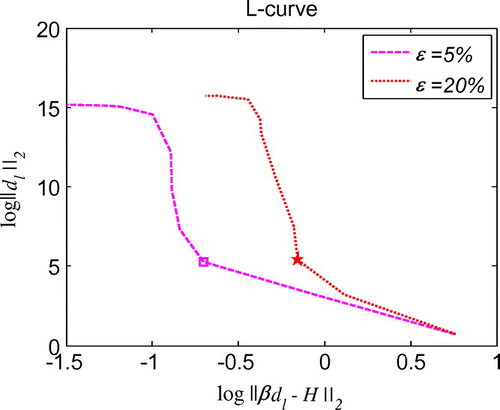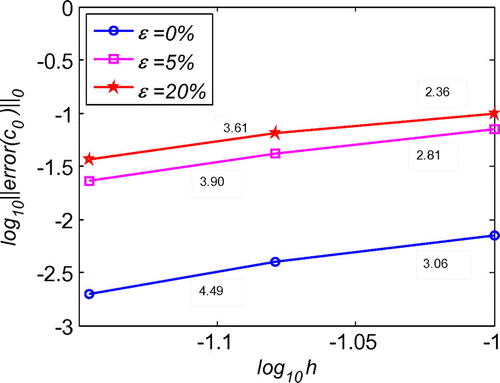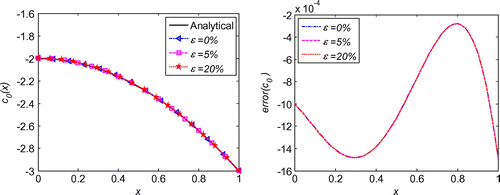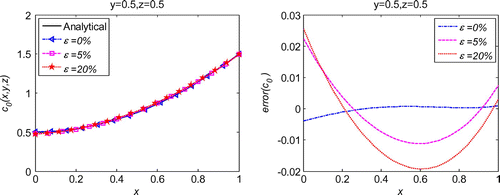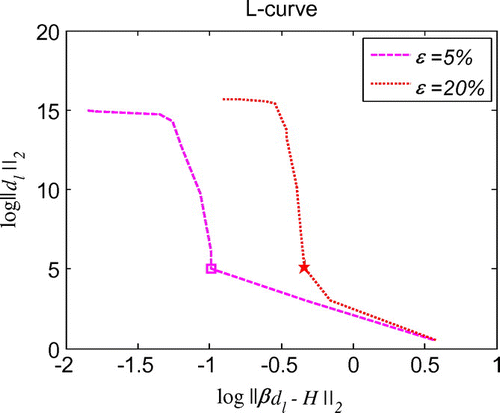N = 13 source points and 100 random numbers are used, and the optimum weights are ${\varsigma }_g\approx {10}^2,{\varsigma }_o\approx 1$ which are the same as in the initial displacement identification inverse problem described in section 6.1. As shown in Figure 20, regularization is also proved to be essential for the good stability and high accuracy of the solutions. For the cases of noise in the additional condition and boundary conditions, the maximum relative error is less than 7.5% with noise level $\epsilon =20\%$, as shown in Figures 21–23. The corresponding regularization parameters can be detected in the L-curve diagrams in Figures 24–26. Once again, exponential convergence can be obtained in the initial velocity identification problem which is displayed in Figure 27. For the case of noise in the initial displacement condition, the maximum relative error is less than 0.08% and the solutions look independent of the noise level, which is depicted in Figure 28. This is because in Equation (40(40) $${\mathrm{\Phi }\mathbf{d}}_2-\left(2\mathrm{\Phi }\mathrm{\Delta }t+\mathrm{\Delta }{t}^3\alpha \mathbf{L}\mathrm{\Phi }\right){\dot{\mathbf{d}}}_0=\mathrm{\Delta }{t}^2\alpha {\mathbf{L}\mathrm{\Phi }\mathbf{d}}_0+{\mathbf{u}}_0+\mathrm{\Delta }{t}^2{\mathbf{f}}_1$$(40) ) ${\mathbf{u}}_0$ is quite small compared to $\left(\mathrm{\Delta }{t}^2\alpha {\mathbf{L}\mathrm{\Phi }\mathbf{d}}_0+\mathrm{\Delta }{t}^2{\mathbf{f}}_1\right)$ and the variation in ${\mathbf{u}}_0$ does not have obvious influence on the solutions. Its optimum regularization parameter can be found in Figure 29.

Figure 20. Comparison of solutions using regularization and not using regularization for the 1d initial velocity identification problem with noise ${\left.u\right|}_{x=0.5}$.

Figure 21. Solution of 1d initial velocity identification problem with noise on ${\left.u\right|}_{x=0.5}$.

Figure 22. Solution of 1d initial velocity identification problem with noise on ${\left.u\right|}_{x=0}$.

Figure 23. Solution of 1d initial velocity identification problem with noise on ${\left.u\right|}_{x=1}$.

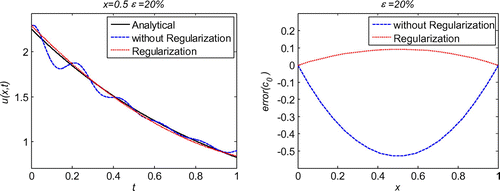
Figure 24. L-curve for the regularization parameter in 1d initial velocity identification problem with noise on ${\left.u\right|}_{x=0.5}$.

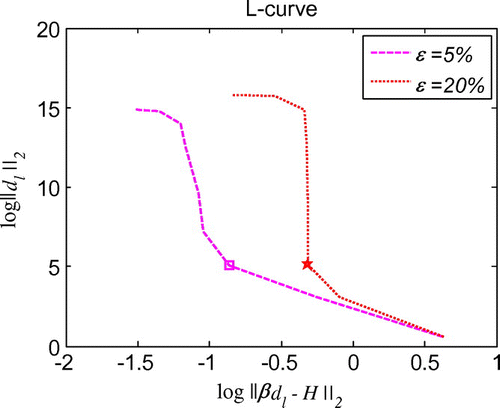
Figure 25. L-curve for the regularization parameter in 1d initial velocity identification problem with noise on ${\left.u\right|}_{x=0}$.

Figure 26. L-curve for the regularization parameter in 1d initial velocity identification problem with noise on ${\left.u\right|}_{x=1}$.

Figure 27. Convergence of RBCM for the 1d initial velocity identification problem with noise on ${\left.u\right|}_{x=0.5}$.

Figure 28. Solution of 1d initial velocity identification problem with noise on ${\left.u\right|}_{t=0}$.

Figure 29. L-curve for the regularization parameter in 1d initial velocity identification problem with noise on ${\left.u\right|}_{t=0}$.

6.4. Initial velocity identification in 3d inverse wave problem

The same Equations in (101(101) $$\ddot{u}={(x+y+z)}^2\mathrm{\Delta }u+\left[e^t(2+4t+x^2+y^2+z^2+t^2)-6e^t{(x+y+z)}^2\right]$$(101) ), (102(102) $$\begin{array}{c}{u|}_{x=0}=(y^2+z^2+t^2)e^t{,u|}_{x=1}=(1+y^2+z^2+t^2)e^t\hfill \\ {u|}_{y=0}=(x^2+z^2+t^2)e^t{,u|}_{y=1}=(1+x^2+z^2+t^2)e^t\hfill \\ {u|}_{z=0}=(x^2+y^2+t^2)e^t{,u|}_{z=1}=(1+x^2+y^2+t^2)e^t\hfill \end{array}$$(102) ) and (104(104) $${\left.u\right|}_{z=0.5}=(\frac{1}{4}+x^2+y^2+t^2)e^t$$(104) ) with known initial displacement $u\left(x,0\right)$ described in (105(105) $$u=(x^2+y^2+z^2+t^2)e^t,{\left.u\right|}_{t=0}=x^2+y^2+z^2$$(105) ) are utilized to identify the unknown initial velocity $\dot{u}\left(x,0\right)$ whose analytical solution is presented in (103(103) $${\left.\dot{u}\right|}_{t=0}=x^2+y^2+z^2$$(103) ). We also use N = 7 × 7 × 7 source points and 500 random numbers as well as weights on the Dirichlet boundary ς _g ≈ 10⁴ and known condition ς _o ≈ 1 for this initial velocity identification problem in 3d wave propagation. As displayed in Figures 30–33, high accurate solutions with good stability can be achieved once again, and when the noises are reduced, the solutions are convergent. When 20% high noise level is brought in 3d inverse problem for identifying initial velocity, the relative errors are no more than 5%. The explanation for Figure 33 is the same as that for Figure 28. The corresponding regularization parameters are shown in the L-curve diagrams of Figures 34–37. For the 3d initial velocity identification problem, there also exists the exponential convergence using RBCM as shown in Figure 38. All the solutions are stable and convergent which demonstrate that the proposed method is an excellent candidate for solving ill-posed initial conditions identification inverse problems.

Figure 30. Solution of 3d initial velocity identification problem with noise on ${\left.u\right|}_{z=0.5}$.

Figure 31. Solution of 3d initial velocity identification problem with noise on ${\left.u\right|}_{z=0}$.

Figure 32. Solution of 3d initial velocity identification problem with noise on ${\left.u\right|}_{z=1}$.

Figure 33. Solution of 3d initial velocity identification problem with noise on ${\left.u\right|}_{t=0}$.

Figure 34. L-curve for the regularization parameter in 3d initial velocity identification problem with noise on ${\left.u\right|}_{z=0.5}$.

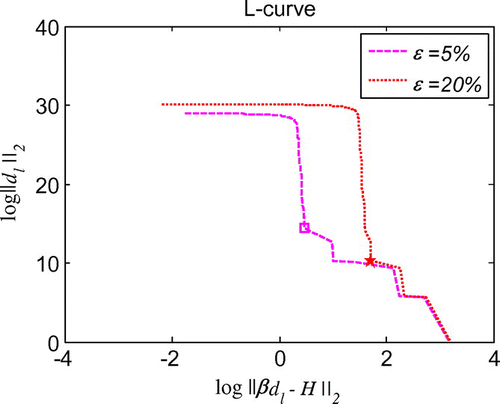
Figure 35. L-curve for the regularization parameter in 3d initial velocity identification problem with noise on ${\left.u\right|}_{z=0}$.

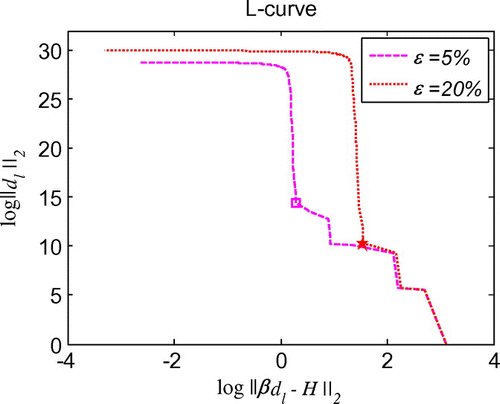
Figure 36. L-curve for the regularization parameter in 3d initial velocity identification problem with noise on ${\left.u\right|}_{z=1}$.

Figure 37. L-curve for the regularization parameter in 3d initial velocity identification problem with noise on ${\left.u\right|}_{t=0}$.

Figure 38. Convergence of RBCM for the 3d initial velocity identification problem with noise on ${\left.u\right|}_{z=0.5}$.

7. Conclusions

A direct collocation method using radial basis functions and explicit time integration is presented to identify the initial conditions in the inverse problems of wave propagation, which can solve two unknowns at the same time without any iteration. Optimum weights for imposing the boundary conditions and known condition are formulated to achieve the prime convergence. Tikhonov regularization is utilized to treat the ill-posed problem for improving the stability. High accurate and stable solutions can be obtained and reduced noise level introduces less error in the solution states the convergence of the proposed algorithm. When 20% high noise level is involved in the measurement data, for the initial displacement identification problem, the maximum relative error is less than 2%, and for the initial velocity identification problem, the maximum relative error is no more than 7.5%. The performance of the proposed method surpasses many numerical methods for the inverse problems by much higher accuracy and better stability.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was supported by National Natural Science Foundation of China [project number 11572229], [project number 11472193]; Shanghai Chenguang Plan [project number 14CG18]; Fundamental Research Funds for the Central Universities [project number 22120180063].