Nonlinear Tikhonov regularization in Hilbert scales with balancing principle tuning parameter in statistical inverse problems

ABSTRACT

In this article, we study the balancing principle for Tikhonov regularization in Hilbert scales for deterministic and statistical nonlinear inverse problems. While the rates of convergence in deterministic setting is order optimal, they prove to be order optimal up to a logarithmic term in the stochastic framework. The two-step approach allows us to consider a data-driven algorithm in a general error model for which an exponential behaviour of the tail of the estimator chosen in the first step is valid. Finally, we compute the overall rate of convergence for a Hammerstein operator equation and for a parameter identification problem. Moreover, we illustrate these rates for the last application after we study some large sample properties of the local polynomial estimator in a general stochastic framework.

KEYWORDS:

• Statistical inverse problem
• nonlinear Tikhonov regularization
• Hilbert scales
• balancing principle

AMS SUBJECT CLASSIFICATIONS:

• Primary: 65J20
• Secondary: 47N20

1. Introduction

Solving inverse problems in a deterministic setting involves reconstructing a mathematical object in an ill-posed operator equation (see e.g. [1]). The original article [2] considers the stochastic extension of inverse problems to (Gaussian) random fields and formalize it as a statistical estimation question by discretization with the help of sample functions. Loosely speaking, statistical inverse problems are inverse problems with random noise. Moreover, classical statistical problems like convolution or error-in-variables models could be rewritten as linear statistical inverse problems [3].

In this paper, we consider the problem of estimating an unknown, not directly observable quantity $a^{†}$ from the noisy values of an element $u^{†}$ related to $a^{†}$ by the operator equation(1) $$\begin{array}{c}\hfill F(a^{†})=u^{†},\end{array}$$(1)

where $F:D(F)\subseteq \mathcal{X}\to \mathcal{Y}$ is a nonlinear, injective operator between two Hilbert spaces $\mathcal{X}$ and $\mathcal{Y}$. We assume that the equation is ill-posed, in the sense that $F^{-1}$ is not continuous. First, we have at our disposal the data Y perturbed by deterministic noise such that(2) $$\begin{array}{c}\hfill Y=u^{†}+\delta \xi \end{array}$$(2)

where $\xi \in \mathcal{Y}$, $\Vert \xi \Vert \le 1$ is the normalized deterministic error and $\delta$ is the deterministic noise level. The results obtained in the framework (2(2) $$\begin{array}{c}\hfill Y=u^{†}+\delta \xi \end{array}$$(2) ) are further utilized in the stochastic process setting that is generalized here to the abstract noise model(3) $$\begin{array}{c}\hfill Y=u^{†}+\sigma ϵ\end{array}$$(3)

where $ϵ$ is a normalized Hilbert space process, $\sigma$ is the corresponding stochastic noise levels, and the relation (3(3) $$\begin{array}{c}\hfill Y=u^{†}+\sigma ϵ\end{array}$$(3) ) is understood in the weak sense. Our general noise model is inspired by [4] and its relation to several common used statistical models was investigated in [3]. A classical example is the inverse nonparametric regression problem, where the data are indirectly related to the functional mean by an operator equation in contrast to the direct regression where we observe noisy values of this function.

A first method for solving nonlinear inverse problems in the statistical setting, inspired by Tikhonov regularization and named Method of Regularization, was studied by O’Sullivan, Lukas and Wahba (see [5–7]). The straightforward generalization of this method to the infinite-dimensional noise model is $$\begin{array}{c}\hfill \overline{a}:={\mathit{argmin}}_{a\in D(F)}\left({\Vert F(a)-Y\Vert }_{\mathcal{Y}}^2+\alpha {\Vert a-a_0\Vert }_{\mathcal{X}}^2\right).\end{array}$$

where $a_0$ is an initial guess for $a^{†}$. However, in the important case when $ϵ$ is white noise ${\Vert F(a)-Y\Vert }_{\mathcal{Y}}$ is infinite with probability 1 for all $a\in D(F)$, so $\overline{a}$ is not well-defined.

Since our aim is to focus on data-driven methods, we will like to include statistical models that go beyond the additive setting and for whom the direct statistical problem (like the direct nonparametric regression problem) is already studied and better understood. Hence, we choose a two-step estimator as suggested and studied in [8] that gives us the flexibility to embed progress made in the direct stochastic setting into statistical nonlinear inverse problems. In the deterministic case, a pre-smoothing step allows to overcome the oversmoothing effect of the Tikhonov and Landweber regularization method (see [9]). Data estimation in this framework could be achieved by Tikhonov regularization, regularization of the embedding operator or by wavelet shrinkage (see [10]). In the first step, a possibly biased estimator $\widehat{u}$ of $u^{†}$ is determined from the data Y such that the error estimate(4) $$\begin{array}{c}\hfill \sqrt{\mathbf{E}\left(\Vert \widehat{u}-u^{†}{\Vert }_{\mathcal{Y}}^2\right)}\le \beta .\end{array}$$(4)

holds true and the rate of convergence $\beta$ that depends on the stochastic noise $\sigma$ is known. This is a nonparametric regression problem which has been studied intensively in the statistical literature if $ϵ$ is a Gaussian white noise process and the smoothness conditions are ellipsoids in the Sobolev spaces $H^b$ on the domain (0, 1) (see [11] and references therein). In this case, the optimal rates of convergence (4(4) $$\begin{array}{c}\hfill \sqrt{\mathbf{E}\left(\Vert \widehat{u}-u^{†}{\Vert }_{\mathcal{Y}}^2\right)}\le \beta .\end{array}$$(4) ) for adaptive and non-adaptive estimators are $\beta \sim {\sigma }^{\frac{b}{2b+1}}$. Moreover, this rate will also hold for non-Gaussian white noise if the error probability distribution is regular in classical sense since in this case the distribution-free nonparametric regression problem is asymptotically equivalent to a homoskedastic Gaussian shift white noise model (see [12,13]). $\beta$ will play the role of thenoise level in the next step. In the second step, the estimator $\widehat{a}$ is constructed as the solution of the Tikhonov minimization problem (5) $$\begin{array}{c}\hfill \widehat{a}:={\mathit{argmin}}_{a\in D(F)}\left(\Vert F(a)-\widehat{u}{\Vert }_{\mathcal{Y}}^2+\alpha {\Vert a-a_0\Vert }_{\mathcal{X}}^2\right).\end{array}$$(5)

Therefore, this method allows the discretization of the problem (3(3) $$\begin{array}{c}\hfill Y=u^{†}+\sigma ϵ\end{array}$$(3) ) for a large variety of designs and the unknown noise level is de facto estimated in the first step. On the other hand, this step can make the computation cumbersome and it is superfluous for designs for which methods and convergence analysis are already available (like for Poisson noise in [14]). Moreover, the rates of convergence depend on the nature of the noise through the tail behaviour of the stochastic method chosen in the first step, making necessary to specify conditions on the error probability distribution to concretize this result for different settings. It follows from [8] that the method is consistent in the sense that for any choice of minimizing elements $\widehat{a}\in D(F)$ we have(6) $$\begin{array}{c}\hfill \mathbf{E}\left(\Vert \widehat{a}-a^{†}{\Vert }_{\mathcal{X}}^2\right)\to 0\end{array}$$(6)

if $\alpha \to 0$ and ${\beta }^2/\alpha \to 0$. Moreover, in [15] rates of convergence for a large set of smoothness classes expressed with the help of Hilbert scales were computed and optimality of this method was proved for linear operators. Regularization in Hilbert scales was studied for the first time by Natterer [16] for linear and by Neubauer [17] for nonlinear deterministic inverse problems. Linear statistical inverse problems have been studied in a Hilbert scale framework in [4,18–22]. In [15] rates of convergence were obtained for nonlinear statistical inverse problems in Hilbert scale for a-priori choice of the regularization parameter $\alpha$. A-priori choice of the regularization parameter yields order-optimal rates of convergence but requires the knowledge of the noise levels $\delta$ and $\sigma$, and of the smoothness of the solution q. We focus in this paper on an adaptive tuning parameter rule, the balancing principle, which was proposed by Lepskii for the choice of the regularization parameter for a regression problem in [23]. His principle of bounding the best possible accuracy by a function which is non-increasing with respect to $\alpha$-values was used by Mathé and Pereverzev to obtain order-optimal estimators in variable Hilbert scales (see [24]). Afterwards this principle was applied by different authors for deterministic linear and nonlinear inverse problems [24–26].

Our aim is to study rates of convergence of the two-step method with balancing principle choice of the regularization parameter in a general noise model for a large class of smoothnesses expressed with the help of Hilbert scales. This extends the method in [15] to a fully data-driven algorithm in both steps for a general class of additive noise models, including some non-Gaussian white noise processes, as specified before. To this aim, we introduce in the following section Hilbert scales ${\mathcal{X}}_s$ and their corresponding norms ${\Vert ·\Vert }_s,s\in \mathbf{R}$, and prove rates of convergence of the error for the Lepskii estimator in nonlinear deterministic inverse problems. In addition to the common assumptions on the operator F as in [15], a smallness condition on the noise level $\delta$ is necessary as it is usual the case for Lepskii tuning methods. The deterministic rates of convergence allow us to get rates of convergence of $\mathbf{E}\left(\Vert \widehat{a}-a^{†}{\Vert }_0^2\right)$ with respect to $\beta$ that are order optimal up to a log-factor for nonlinear statistical inverse problems under a supplementary condition on the tail behaviour of the estimator $\widehat{u}$ in Section 2.2. The overall rate of convergence for the two-step method depends on the nature of the noise through the asymptotic behaviour of the tail and the mean square error of the estimator chosen in the first step. We will illustrate the overall capacity of the two-step approach to reach order optimal (up to a logarithmic term) rates of convergence in the Section 3 of our article, containing the numerical simulation for the reconstruction of a reaction coefficient from Gaussian noisy data in the setting of an inverse nonparametric regression. The asymptotic equivalence between this discrete model and that of the Gaussian white noise (3(3) $$\begin{array}{c}\hfill Y=u^{†}+\sigma ϵ\end{array}$$(3) ) is discussed for example in [11] as well as the relation between the variance in the continuous setting and the sample size n: $\sigma \sim \frac{1}{\sqrt{n}}$. We also present new results regarding this behaviour for the local polynomial estimator in the case of errors with Gaussian or log-concave probability distribution, that are useful to illustrate the numerical performance of our algorithm in the last section. Due to the great flexibility of the two-step method, methodological progress in the study of the local polynomial estimator in a large class of statistical models like binary response model, inhomogeneous exponential and Poisson models by adaptive weights smoothing could provide the necessary tools to deal with non-Gaussian settings (see [27]). The study of the overall optimal rates of convergence for these cases is subject of further research.

Two different applications are considered in this paper: one statistical inverse problem defined by the Hammerstein operator, for which we also define the corresponding Hilbert scale and the problem of the reconstruction of a reaction coefficient already studied in [15]. We compute the overall rate of convergence for these two examples that turns out to be optimal up to a log-factor, and graphically compare the numerical and theoretical rates of convergence for the second application in the last section.

2. Balancing principle for nonlinear inverse problems in Hilbert scales

The overall rate of convergence of the two-step method for the balancing choice of the regularization parameter depends on the stochastic model and can be computed by considering first the deterministic setting and afterwards extending it to the statistical framework. In the following, we focus on the rates of convergence for the Lepskii choice of the regularization parameter for nonlinear inverse problems in Hilbert scales separately in a deterministic and in a stochastic framework. The order optimal rates of convergence proved in the deterministic setting and the properties of the nonparametric estimator in the pre-smoothing step lead to optimal up to a logarithm term rates of convergence in the Gaussian stochastic case.

2.1. Rates of convergence for balancing principle in deterministic setting

We consider in this section a deterministic framework, meaning that we assume the noise model (2(2) $$\begin{array}{c}\hfill Y=u^{†}+\delta \xi \end{array}$$(2) ). To characterize the smoothness of the solution $a^{†}$, a Hilbert scale is defined in the following with the help of a densely defined, unbounded, self-adjoint, strictly-positive operator L in the Hilbert space $\mathcal{X}$. We consider the set $\mathbb{M}$ of the elements x for which all powers of L are defined$$\mathbb{M}={\cap }_{k=0}^{\infty }D(L^k)$$ $\mathbb{M}$ is dense in $\mathcal{X}$ and, by spectral theorem, $L^s$ is well-defined for all $s\in \mathbf{R}$. For $x,y\in \mathbb{M}$ and $s\in \mathbf{R}$, let$$\begin{array}{cc}\hfill {〈x,y〉}_s& :=〈L^{s}x,L^{s}y〉,\hfill \\ \hfill {\Vert x\Vert }_s& =\Vert L^{s}x\Vert .\hfill \end{array}$$

Then the Hilbert space ${\mathcal{X}}_s$ is defined as the completion of $\mathbb{M}$ with respect to the norm ${\Vert ·\Vert }_s$ and ${({\mathcal{X}}_s)}_{s\in \mathbf{R}}$ is called the Hilbert scale induced by L. A comprehensive introduction in Hilbert scales can be found in [1,28]. In our proofs we are going to use repeatedly the interpolation inequality(7) $$\begin{array}{c}\hfill {\Vert x\Vert }_r\le {\Vert x\Vert }_t^{\frac{s-r}{s-t}}{\Vert x\Vert }_s^{\frac{r-t}{s-t}},x\in {\mathcal{X}}_s\end{array}$$(7)

which holds for any $t<r<s$. We define our estimator $a_{\alpha }^{\delta }$ as (8) $$\begin{array}{c}\hfill a_{\alpha }^{\delta }:={\mathit{argmin}}_{a\in D(F)\cap \left(a_0+{\mathcal{X}}_s\right)}\left({\Vert F(a)-Y\Vert }_{\mathcal{Y}}^2+\alpha {\Vert a-a_0\Vert }_s^2\right)\end{array}$$(8)

where $s\ge 0$ and $a_0\in D(F)$ is an initial guess. We obtain rates of convergence for the deterministic error $\Vert a_{\alpha }^{\delta }-a^{†}{\Vert }_0$ if the following assumptions on the operator F hold:

Assumptions 2.1:

(A)	(assumptions on F) If $F(a)=F(a^{†})$ for some $a\in D(F)\cap \left(a_0+{\mathcal{X}}_s\right)$, then $a=a^{†}$. Moreover, D(F) is convex, $F:D(F)\cap \left(a_0+{\mathcal{X}}_s\right)\to \mathcal{Y}$ is weakly sequentially closed, and $F:D(F)\subset \mathcal{X}\to \mathcal{Y}$ has a Fréchet derivative $F^{\prime }:D(F)\to L(\mathcal{X},\mathcal{Y})$.
(B)	(smoothing properties of $F^{\prime }$) There exist constants $p\in [0,s]$ and $\lambda ,\mathrm{\Lambda }>0$ such that for all $h\in \mathcal{X}$ (9) $$\begin{array}{c}\hfill {\lambda \Vert h\Vert }_{-p}\le \Vert F^{\prime }(a^{†}){h\Vert }_{\mathcal{Y}}\le \mathrm{\Lambda }{\Vert h\Vert }_{-p}.\end{array}$$(9)
(C)	(Lipschitz continuity of $F^{\prime }$ and boundedness condition on D(F)) There exists a constant $C_L>0$ such that (10) $$\begin{array}{c}\hfill \Vert F^{\prime }(a)-F^{\prime }(a^{†}){\Vert }_{\mathcal{Y}\leftarrow {\mathcal{X}}_{-p}}\le C_L{\Vert a-a^{†}\Vert }_0\le \frac{{\lambda }^2}{2\mathrm{\Lambda }}\end{array}$$(10) for all $a\in {\mathbf{B}}_{\rho }(a^{†})\cap \left(a_0+{\mathcal{X}}_s\right)$ for some $\rho >0$ such that ${\mathbf{B}}_{\rho }\subset D(F)$.

We define the estimator $a_{\alpha }$ corresponding to the exact data $u^{†}$ by (11) $$\begin{array}{c}\hfill a_{\alpha }:={\mathit{argmin}}_{a\in D(F)\cap \left(a_0+{\mathcal{X}}_s\right)}\left(\Vert F(a)-u^{†}{\Vert }_{\mathcal{Y}}^2+\alpha {\Vert a-a_0\Vert }_s^2\right).\end{array}$$(11)

We treat the noise free error $\Vert a_{\alpha }-a^{†}{\Vert }_0$ and the data noise error $\Vert a_{\alpha }^{\delta }-a_{\alpha }{\Vert }_0$ separately as it is common for this adaptive methods (see e.g. [29]).

Theorem 2.2:

If the Assumptions 2.1 hold true and if $a^{†}\in D(F)$ fulfills(12) $$\begin{array}{c}\hfill a^{†}-a_0\in {\mathcal{X}}_q\text{for some}q\in [s,2s+p]\end{array}$$(12)

then the estimation$$\begin{array}{c}\hfill \Vert a_{\alpha }-a^{†}{\Vert }_0\le K{\alpha }^{\frac{q}{2(p+s)}}\end{array}$$

holds true, where $c=\Vert a^{†}-a_0{\Vert }_q$ and K is a constant dependending on $s,p,q,\lambda ,\mathrm{\Lambda },c$.

For a better readability of this paper, the proof can be found in the Appendix 1. The interval $[s,2s+p]$ for the smoothness degree is due to the technical condition (7(7) $$\begin{array}{c}\hfill {\Vert x\Vert }_r\le {\Vert x\Vert }_t^{\frac{s-r}{s-t}}{\Vert x\Vert }_s^{\frac{r-t}{s-t}},x\in {\mathcal{X}}_s\end{array}$$(7) ) and can be interpreted as a saturation limit (see e.g. [17]). The exponent of $\alpha$ in the bound on the noise free error is similar to those computed for linear inverse problems, but the constant depends on the $q-$norm of $a^{†}-a_0$. It was not the aim of this research, to overcome this restriction, but it might be an interesting topic to study.

Theorem 2.3:

Under the assumptions of Theorem 2.2 we have that(13) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill \Vert a_{\alpha }^{\delta }-a_{\alpha }{\Vert }_0^2\le & k_1{\alpha }^{\frac{q}{p+s}}+\left(k_1+k_2\right){\delta }^2{\alpha }^{-\frac{p}{s+p}}\hfill \end{array}\end{array}$$(13)

where $k_1\ge K$ and $k_2$ are constants dependending on $s,p,q,\lambda ,\mathrm{\Lambda },c$, respectively $s,p,\lambda ,\mathrm{\Lambda }$.

The proof of this Theorem can also be found in Appendix 1. This is based, together with the proof of the previous theorem, on the computation of bounds for the noise-free and data noise term in ${\Vert ·\Vert }_s$ and ${\Vert ·\Vert }_{-p}$ norms, and the interpolation inequality (7(7) $$\begin{array}{c}\hfill {\Vert x\Vert }_r\le {\Vert x\Vert }_t^{\frac{s-r}{s-t}}{\Vert x\Vert }_s^{\frac{r-t}{s-t}},x\in {\mathcal{X}}_s\end{array}$$(7) ). The classical results for the linear inverse problems yield a decreasing function in $\alpha$ as upper-bound for the data noise error term. Due to the non-linearity, the product $\Vert a_{\alpha }^{\delta }-a_{\alpha }{\Vert }_{-p}{\Vert a_{\alpha }-a^{†}\Vert }_{-p}^2$ appears in the upper bound and because of the adaptivity, we can control it only through expressions containing the term ${\alpha }^{\frac{q}{p+s}}$. The constants can be explicitely computed i.e.(14) $$\begin{array}{c}\hfill k_2=12{\left(\frac{{\mathrm{\Lambda }}^2}{{\lambda }^2}+\frac{1}{4}\right)}^{1+\frac{s}{s+p}}{\mathrm{\Lambda }}^{-\frac{2s}{s+p}}\end{array}$$(14)

but for the sake of simplicity we renounced to formally calculate them in the proof. Finally, we get a sum between an increasing and a decreasing function in the tuning parameter, and we define an adaptive choice of the regularization parameter based on this. To ensure consistency of the method, a smallness conditions on $\sigma$ and c needs to be fulfilled, as we will see below. First, we present a direct consequence of the previous results.

Corollary 2.4:

Under the assumptions and notations of Theorems 2.2 and 2.3, it holds(15) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill \Vert a_{\alpha }^{\delta }-a^{†}{\Vert }_0^2\le & 4k_1{\alpha }^{\frac{q}{p+s}}+2\left(k_1+k_2\right){\delta }^2{\alpha }^{-\frac{p}{s+p}}\hfill \end{array}\end{array}$$(15)

where $k_1$ and $k_2$ are the constants from Theorem 2.3.

The choice of the regularization parameter ${\alpha }^{†}\sim {\delta }^{\frac{2(p+s)}{p+q}}$ gives the order optimal rate of convergence$$\begin{array}{c}\hfill \Vert a_{{\alpha }^{†}}^{\delta }-a^{†}{\Vert }_0^2\le 2C^{\ast }{\delta }^{\frac{2q}{p+q}}\end{array}$$

with $C^{\ast }$ which depends on $a^{†}$, p, s, q, $\lambda$, $\mathrm{\Lambda }$ and c.

Proof The first inequality follows immediately from Theorems 2.2 and 2.3 and allows us to estimate the tuning parameter $\alpha$, by balancing between the upper bounds of the approximation and noise-free errors. For $\alpha ={\alpha }^{†}\sim {\delta }^{\frac{2(p+s)}{p+q}}$ we get$$\begin{array}{c}\hfill \Vert a_{\alpha }^{\delta }-a^{†}{\Vert }_0^2\le 2C^{\ast }{({\delta }^{\frac{2(p+s)}{p+q}})}^{\frac{q}{p+q}}=2C^{\ast }{\delta }^{\frac{2q}{p+q}}.\end{array}$$

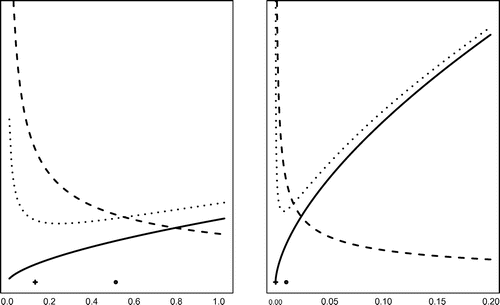
Figure 1. Upper bounds for the nonlinear data noise error (dotted line), Lepskii rule $\mathrm{\Phi }$ (dashed line), linear data noise error (full line) for error level ${\delta }^2=0.5$ (left, diamond) and 0.01 (right, diamond), and the corresponding minimum points for $\mathrm{\Psi }$ (circle).

We discuss now an adaptive choice of the regularization parameter based on the balancing principle and on the previous bounds computed in Theorems 2.2 and 2.3. We follow here the approach from [24,25,30]. Hence, we estimate the value of the regularization parameter $\alpha$ that approximates the minimizer of the total error $\Vert a_{\alpha }^{\delta }-a_{†}{\Vert }_0^2$ by the minimizer of the bounding sum resulting from the aforesaid theorems. This optimum is computed from a finite set of possible parameters$$\begin{array}{c}\hfill M=\left\{{\alpha }_1,{\alpha }_j={\alpha }_1{(l^2)}^{j-1},j=2,\cdots ,m,\text{with}m=min\left\{k:{\alpha }_k\ge 1\right\}\right\}\end{array}$$

where $l>1$, ${\alpha }_1$ is usually equal to ${\delta }^2$, and we denote $a_{{\alpha }_j}^{\delta }=a_j$. We define the non-increasing function $\mathrm{\Psi }:\{1,2,\cdots ,m\}\to {\mathbf{R}}^{+}$,$$\mathrm{\Psi }(j)=6k_2{\delta }^2{\alpha }_j^{-\frac{p}{s+p}}$$

and the function $\mathrm{\Phi }:\{1,2,\cdots ,m\}\to {\mathbf{R}}^{+}$,$$\mathrm{\Phi }(j)=4k_1{\alpha }_j^{\frac{q}{p+s}}+2k_1{\delta }^2{\alpha }_j^{-\frac{p}{s+p}}$$

with the constants $k_1$ and $k_2$ as in Theorem 2.3. It can be easily checked that $\mathrm{\Phi }$ is non-decreasing on the set M if ${\alpha }_1>\frac{1}{2}{\delta }^2$ since the minimum point of the real-valued expression $4k_1{\alpha }^{\frac{q}{p+s}}+2k_1{\delta }^2{\alpha }^{-\frac{p}{s+p}}$ is smaller than $\frac{1}{2}{\delta }^2$ in our setting.

If the inequality(16) $$\begin{array}{cc}\hfill \mathrm{\Phi }(1)& \le \mathrm{\Psi }(1)\hfill \end{array}$$(16)

holds, then we can formulate a rule to choose the tuning parameter $\alpha$ and define an order-optimal estimator independent from smoothness q. Condition (16(16) $$\begin{array}{cc}\hfill \mathrm{\Phi }(1)& \le \mathrm{\Psi }(1)\hfill \end{array}$$(16) ) assures the existence of at least one intersection point between the curves defined by $\mathrm{\Phi }$ and $\mathrm{\Psi }$ and is similar to the one usual used in the framework of the linear inverse problems, as the Figure 1 also illustrates. It implies as well that our results will be valid only for $q-$distances c and noise levels small enough such that the right hand side term of (16(16) $$\begin{array}{cc}\hfill \mathrm{\Phi }(1)& \le \mathrm{\Psi }(1)\hfill \end{array}$$(16) ) bounds an algebraic expression involving these two values. An explicit example of this relationship is given in Section 4.2.

Therefore, we determine the regularization parameter in the set M for which the following inequality holds$$\begin{array}{cc}\hfill i_{\ast }=& max\left\{i:{\alpha }_i\in M,k_1\left(2{\alpha }_i^{\frac{q+p}{p+s}}+{\delta }^2\right)\le 3k_2{\delta }^2\right\}\hfill \end{array}$$

and ${\alpha }_{\ast }={\alpha }_{i_{\ast }}$. The computation of ${\alpha }_{\ast }$ and $a_{\ast }=a_{{\alpha }_{i_{\ast }}}$ is unfeasible, since q is unknown, therefore we approximate them by$$\begin{array}{c}\hfill i_{+}=max\left\{i:\Vert a_i-a_j{\Vert }_0^2\le 32k_2{\delta }^2{\alpha }_j^{-\frac{p}{s+p}},j=1,2,\cdots ,i\right\}\end{array}$$

where $a_i=a_{{\alpha }_i}$, ${\alpha }_{+}={\alpha }_{i_{+}}$ and $a_{+}=a_{{\alpha }_{+}}$(see [29] for details). Moreover, a simplified version of Lepskii criterion was also presented in the aforementioned article, which had the origins in the quasi-optimality choice of the regularization parameter proposed by Tikhonov and Glasko. In this case, we choose the estimator $a_{\diamond }=a_{{\alpha }_{i_{\diamond }}}$ corresponding to the regularization parameter ${\alpha }_{\diamond }={\alpha }_{i_{\diamond }}$ with the index$$\begin{array}{c}\hfill i_{\diamond }=max\left\{i:\Vert a_j-a_{j-1}{\Vert }_0^2\le 32k_2{\delta }^2{\alpha }_{j-1}^{-\frac{p}{s+p}},j=1,2,\cdots ,i\right\}.\end{array}$$

If condition (16(16) $$\begin{array}{cc}\hfill \mathrm{\Phi }(1)& \le \mathrm{\Psi }(1)\hfill \end{array}$$(16) ) holds, all three sets defined above are different from the empty set and, for $k_1\le k_2$, not equal to M.

Theorem 2.5:

If the assumptions of Theorem 2.2 and the inequality (16(16) $$\begin{array}{cc}\hfill \mathrm{\Phi }(1)& \le \mathrm{\Psi }(1)\hfill \end{array}$$(16) ) hold true, we have that$$\begin{array}{c}\hfill i_{\ast }\le i_{+}\le i_{\diamond }\end{array}$$

and we get order optimal rates of convergence both for $a_{+}$ and $a_{\diamond }$ i.e.$$\begin{array}{cc}\hfill \Vert a_{+}-a^{†}{\Vert }_0& \le c^{+}{\alpha }^{\frac{q}{p+q}}\hfill \\ \hfill \Vert a_{\diamond }-a^{†}{\Vert }_0& \le c^{\diamond }{\alpha }^{\frac{q}{p+q}}\hfill \end{array}$$

for constants $c^{+}$ and $c^{\diamond }$ which depends on $a^{†},p,s,\gamma ,\mathrm{\Gamma }$ and c.

Proof The inequalities in Theorem 2.5 follow from the order relation between the sets involved in the definition of the three tuning rules. $a_{\ast }$ fulfills$$\begin{array}{cc}\hfill \Vert a_{\ast }-a_j{\Vert }_0^2\le & 2\left(\Vert a_{\ast }-a^{†}{\Vert }_0^2+{\Vert a_j-a^{†}\Vert }_0^2\right)\hfill \\ \hfill \le & 32k_2{\delta }^2{\alpha }_j^{-\frac{p}{s+p}}\hfill \end{array}$$

for any $j\le i_{\ast }$ since ${\alpha }_{\ast }^{-\frac{p}{s+p}}\ge {\alpha }_j^{-\frac{p}{s+p}}$, and it is obvious that$$\Vert a_j-a_{j-1}{\Vert }_0^2\le 32k_2{\delta }^2{\alpha }_{j-1}^{-\frac{p}{s+p}}$$

for $j\le i_{+}$ (see [29]). Since the proof of the second part of the theorem is similar for both rates of convergence, we just show the second result in the following paragraph. From the previous inequality $i_{\diamond }$ it holds that $i_{\ast }\le i_{\diamond }$ and we can write$$\begin{array}{cc}\hfill \Vert a_{\diamond }-a^{†}{\Vert }_0& \le \Vert a_{\ast }-a^{†}{\Vert }_0+\sum _{j=i_{\ast }+1}^{i_{\diamond }}{\Vert a_{{\alpha }_j-1}-a_j\Vert }_0\hfill \\ \hfill & \le \Vert a_{\ast }-a^{†}{\Vert }_0+4\sqrt{2k_2}\delta \sum _{j=0}^{i_{\diamond }-i_{\ast }-1}\frac{1}{{\alpha }_{\ast }^{\frac{p}{2(s+p)}}{l}^{\frac{\mathit{pj}}{s+p}}}\hfill \end{array}$$

Moreover, the definition of ${\alpha }_{\ast }$ allows us to obtain order optimal rates of convergence (see e.g. [15,16] and references therein for a discussion about optimal rates for Tikhonov regularization in Hilbert scales.)$$\begin{array}{cc}\hfill \Vert a_{\diamond }-a^{†}{\Vert }_0\le & 4\sqrt{2k_2}\frac{\delta }{{\alpha }_{\ast }^{\frac{p}{2(s+p)}}}\frac{1-\frac{1}{l^{\frac{(i_{\diamond }-i_{+})p}{s+p}}}}{1-\frac{1}{l^{\frac{p}{s+p}}}}+4\sqrt{2k_2}\delta {\alpha }_{\ast }^{\frac{-p}{2(s+p)}}\hfill \\ \hfill \le & c^{\diamond }{\delta }^{\frac{q}{p+q}}.\hfill \end{array}$$

Remark 1:

The last condition (16(16) $$\begin{array}{cc}\hfill \mathrm{\Phi }(1)& \le \mathrm{\Psi }(1)\hfill \end{array}$$(16) ) implies that our results will be valid only for a set of noise levels depending on the $q-$norm c. Generally, the feasibility of the estimator depends on the initial guess, and this problem can be solved for example by considering different a-priori values and applying the algorithm for each of them.

2.2. Rates of convergence for balancing principle in stochastic setting

In this section we consider the stochastic noise model (3(3) $$\begin{array}{c}\hfill Y=u^{†}+\sigma ϵ\end{array}$$(3) ) and apply the two-step method for this statistical inverse problems. Hence, we choose first an estimator $\widehat{u}$ as data and its known rate of convergence (4(4) $$\begin{array}{c}\hfill \sqrt{\mathbf{E}\left(\Vert \widehat{u}-u^{†}{\Vert }_{\mathcal{Y}}^2\right)}\le \beta .\end{array}$$(4) ) as noise level. We define the estimators ${\widehat{a}}_{\alpha }$ as (17) $$\begin{array}{c}\hfill {\widehat{a}}_{\alpha }:={\mathit{argmin}}_{a\in D(F)\cap \left(a_0+{\mathcal{X}}_s\right)}\left(\Vert F(a)-\widehat{u}{\Vert }_{\mathcal{Y}}^2+\alpha {\Vert a-a_0\Vert }_s^2\right)\end{array}$$(17)

where $s\ge 0$ and $a_0\in \mathcal{X}$ is an initial guess. In the following, the balancing principle is going to be applied in a similar way as in the previous section and rates of convergence are going to be proven. These results are obtained under the supplementary condition for the tail of the probability distribution of the estimator $\widehat{u}$ (18) $$\begin{array}{c}\hfill \mathbf{P}\left\{\omega :\Vert \widehat{u}-\mathbf{E}\left(\widehat{u}\right){\Vert }_{\mathcal{Y}}^2\ge \tau \mathbf{E}\left(\Vert \widehat{u}-\mathbf{E}\left(\widehat{u}\right){\Vert }_{\mathcal{Y}}^2\right)\right\}\le l_{1}exp(-l_2{\tau }^{\eta })\end{array}$$(18)

for any $\tau$ greater than 1 such that ${\left(\frac{\tau -1}{l_2}\right)}^{\eta }>l_3$, where $l_1$, $l_2$ and $l_3$ are positive universal constants and $0<\eta \le 1$. We choose the set of regularization parameters as$$\begin{array}{c}\hfill M:=\left\{{\alpha }_j={\beta }^2{(l^2)}^{j-1},j=2,\cdots ,min\left\{k:{\alpha }_k\ge 1\right\}\right\}\end{array}$$

with $l>1$ and the estimator ${\widehat{a}}_{+}={\widehat{a}}_{{\alpha }_{i_{s+}}}$ with$$\begin{array}{cc}\hfill i_{s+}=& max\{i:\Vert {\widehat{a}}_i-{\widehat{a}}_j{\Vert }_0\le 4\sqrt{2·k_2\left(1+{(l_{2}ln\frac{1}{\beta })}^{\frac{1}{\eta }}\right)}\beta {\alpha }_j^{\frac{-p}{2(s+p)}},\hfill \\ \hfill & j=1,2,\cdots ,i\}.\hfill \end{array}$$

The rates of convergence for this estimator can be computed using similar techniques as in [31,32].

Theorem 2.6:

If the assumptions of Theorem 2.2 and the conditions (16(16) $$\begin{array}{cc}\hfill \mathrm{\Phi }(1)& \le \mathrm{\Psi }(1)\hfill \end{array}$$(16) ) and (18(18) $$\begin{array}{c}\hfill \mathbf{P}\left\{\omega :\Vert \widehat{u}-\mathbf{E}\left(\widehat{u}\right){\Vert }_{\mathcal{Y}}^2\ge \tau \mathbf{E}\left(\Vert \widehat{u}-\mathbf{E}\left(\widehat{u}\right){\Vert }_{\mathcal{Y}}^2\right)\right\}\le l_{1}exp(-l_2{\tau }^{\eta })\end{array}$$(18) ) are fulfilled then, for all $\beta \le exp(-l_3\frac{p+q}{2q})$, we have the following error bound for ${\widehat{a}}_{+}$ $$\begin{array}{c}\hfill \mathbf{E}\left(\Vert {\widehat{a}}_{+}-a^{†}{\Vert }_0^2\right)\le K_{+}{\beta }^{\frac{2q}{p+q}}{\left(ln\frac{1}{\beta }\right)}^{\frac{1}{\eta }\frac{q}{p+q}}\end{array}$$

where $K_{+}$ is a constant which depends on $c^{+}$, $l_1$, $l_2$ and $C_L$.

Proof For $\tau$ fulfilling the conditions of the Theorem 2.6 we denote(19) $$\begin{array}{c}\hfill {\mathrm{\Omega }}_{\tau }=\left\{\Vert \widehat{u}-u^{†}{\Vert }_{\mathcal{Y}}^2\ge \tau \mathbf{E}\left(\Vert \widehat{u}-u^{†}{\Vert }_{\mathcal{Y}}^2\right)\right\}\end{array}$$(19)

as the set of extreme values of the $\mathcal{Y}-$error of the estimator $\widehat{u}$. Due to the bias-variance decomposition$$\begin{array}{c}\hfill \mathbf{E}\left(\Vert \widehat{u}-u^{†}{\Vert }_{\mathcal{Y}}^2\right)=\mathbf{E}\left(\Vert \widehat{u}-\mathbf{E}(\widehat{u}){\Vert }_{\mathcal{Y}}^2\right)+{\Vert \mathbf{E}(\widehat{u})-u^{†}\Vert }_{\mathcal{Y}}^2\end{array}$$

we can rewrite the inequality (19(19) $$\begin{array}{c}\hfill {\mathrm{\Omega }}_{\tau }=\left\{\Vert \widehat{u}-u^{†}{\Vert }_{\mathcal{Y}}^2\ge \tau \mathbf{E}\left(\Vert \widehat{u}-u^{†}{\Vert }_{\mathcal{Y}}^2\right)\right\}\end{array}$$(19) ) as$$\begin{array}{cc}& \Vert \widehat{u}-\mathbf{E}\left(\widehat{u}\right){\Vert }_{\mathcal{Y}}^2+2{〈\widehat{u}-\mathbf{E}\left(\widehat{u}\right),\mathbf{E}\left(\widehat{u}\right)-u^{†}〉}_{\mathcal{Y}}+{\Vert \mathbf{E}\left(\widehat{u}\right)-u^{†}\Vert }_{\mathcal{Y}}^2\hfill \\ \hfill & \ge \tau \mathbf{E}\left(\Vert \widehat{u}-\mathbf{E}\left(\widehat{u}\right){\Vert }_{\mathcal{Y}}^2\right)+\tau {\Vert \mathbf{E}\left(\widehat{u}\right)-u^{†}\Vert }_{\mathcal{Y}}^2.\hfill \end{array}$$

From Cauchy-Schwarz inequality, the set inclusion holds$$\begin{array}{cc}\hfill {\mathrm{\Omega }}_{\tau }& \subseteq \{\Vert \widehat{u}-\mathbf{E}\left(\widehat{u}\right){\Vert }_{\mathcal{Y}}^2+\frac{1}{\tau -1}\Vert \widehat{u}-\mathbf{E}\left(\widehat{u}\right){\Vert }_{\mathcal{Y}}^2+(\tau -1){\Vert \mathbf{E}\left(\widehat{u}\right)-u^{†}\Vert }_{\mathcal{Y}}^2\hfill \\ \hfill & +\Vert \mathbf{E}\left(\widehat{u}\right)-u^{†}{\Vert }_{\mathcal{Y}}^2\ge \tau \mathbf{E}\left(\Vert \widehat{u}-\mathbf{E}\left(\widehat{u}\right){\Vert }_{\mathcal{Y}}^2\right)+\tau {\Vert \mathbf{E}\left(\widehat{u}\right)-u^{†}\Vert }_{\mathcal{Y}}^2\}\hfill \\ \hfill \end{array}$$

leading to$${\mathrm{\Omega }}_{\tau }\subseteq \left\{\Vert \widehat{u}-\mathbf{E}\left(\widehat{u}\right){\Vert }_{\mathcal{Y}}^2\ge (\tau -1)\mathbf{E}\left(\Vert \widehat{u}-\mathbf{E}\left(\widehat{u}\right){\Vert }_{\mathcal{Y}}^2\right)\right\}.$$

From (18(18) $$\begin{array}{c}\hfill \mathbf{P}\left\{\omega :\Vert \widehat{u}-\mathbf{E}\left(\widehat{u}\right){\Vert }_{\mathcal{Y}}^2\ge \tau \mathbf{E}\left(\Vert \widehat{u}-\mathbf{E}\left(\widehat{u}\right){\Vert }_{\mathcal{Y}}^2\right)\right\}\le l_{1}exp(-l_2{\tau }^{\eta })\end{array}$$(18) ) we get(20) $$\begin{array}{c}\hfill \mathbf{P}({\mathrm{\Omega }}_{\tau })\le l_{1}exp\left(-\frac{{(\tau -1)}^{\eta }}{l_2}\right)\end{array}$$(20)

for all $\tau \ge 1$ such that ${\left(\frac{\tau -1}{l_2}\right)}^{\eta }>l_3$. With the help of conditional expectation we can write$$\begin{array}{cc}\hfill \mathbf{E}\left(\Vert {\widehat{a}}_{+}-a^{†}{\Vert }_0^2\right)& =\mathbf{P}({\mathrm{\Omega }}_{\tau })\mathbf{E}\left(\Vert {\widehat{a}}_{+}-a^{†}{\Vert }_0^2|{\mathrm{\Omega }}_{\tau }\right)+\mathbf{P}(\mathbf{C}{\mathrm{\Omega }}_{\tau })\mathbf{E}\left(\Vert {\widehat{a}}_{+}-a^{†}{\Vert }_0^2|\mathbf{C}{\mathrm{\Omega }}_{\tau }\right)\hfill \end{array}$$

where $\mathbf{C}{\mathrm{\Omega }}_{\tau }=\mathrm{\Omega }\backslash {\mathrm{\Omega }}_{\tau }$ is the complementary set of ${\mathrm{\Omega }}_{\tau }$ in $\mathrm{\Omega }$. We apply the deterministic convergence result for Lepskii choice of the regularization parameter (see Theorem 2.5) on the set $\mathbf{C}{\mathrm{\Omega }}_{\tau }$ for $\tau =1+{\left(l_2\frac{2q}{p+q}ln\frac{1}{\beta }\right)}^{\frac{1}{\eta }}$ and use the exponential inequality (20(20) $$\begin{array}{c}\hfill \mathbf{P}({\mathrm{\Omega }}_{\tau })\le l_{1}exp\left(-\frac{{(\tau -1)}^{\eta }}{l_2}\right)\end{array}$$(20) ) to bound $\mathbf{P}({\mathrm{\Omega }}_{\tau })$ for noise levels $\beta \le exp(-l_3\frac{p+q}{2q})$ . This yields$$\begin{array}{cc}\hfill \mathbf{E}\left(\Vert {\widehat{a}}_{+}-a^{†}{\Vert }_0^2\right)& \le l_{1}exp\left(-\frac{{(\tau -1)}^{\eta }}{l_2}\right)\frac{{\lambda }^2}{2\mathrm{\Lambda }{C}_L}+\left(1-\mathbf{P}({\mathrm{\Omega }}_{\tau })\right)c^{+}{(\tau {\beta }^2)}^{\frac{q}{p+q}}\hfill \\ \hfill & \le l_1\frac{{\lambda }^2}{2\mathrm{\Lambda }{C}_L}exp\left(-\frac{2q}{p+q}ln\frac{1}{\beta }\right)+c^{+}{\left[{\beta }^2\left(1+{\left(l_2\frac{2q}{p+q}ln\frac{1}{\beta }\right)}^{\frac{1}{\eta }}\right)\right]}^{\frac{q}{p+q}}\hfill \\ \hfill & \le l_1\frac{{\lambda }^2}{2\mathrm{\Lambda }{C}_L}{\beta }^{\frac{2q}{p+q}}+c^{+}{\beta }^{\frac{2q}{p+q}}\left(1+{\left(l_2\frac{2q}{p+q}ln\frac{1}{\beta }\right)}^{\frac{q}{\eta (p+q)}}\right)\hfill \\ \hfill & \le K_{+}{\beta }^{\frac{2q}{p+q}}{\left(ln\frac{1}{\beta }\right)}^{\frac{q}{\eta (p+q)}}.\hfill \end{array}$$

Remark 2:

Like in the deterministic setting, we can choose a simplified version for the choice of the regularization parameter that reduces the computational cost. We select the estimator ${\widehat{a}}_{\diamond }={\widehat{a}}_{{\alpha }_{i_{\diamond }}}$ with$$\begin{array}{c}\hfill \begin{array}{cc}\hfill i_{\diamond }=& max\left\{i=1,2,\cdots m:\Vert {\widehat{a}}_i-{\widehat{a}}_{i-1}{\Vert }_0\le 4\sqrt{2k_2\left(1+{(l_{2}ln\frac{1}{\beta })}^{\frac{1}{\eta }}\right)}\beta {\alpha }_{i-1}^{\frac{-p}{2(s+p)}}\right\}\hfill \end{array}\end{array}$$

In the same way as in the Theorem 2.6 we can prove that the rate of convergence is equal to(21) $$\begin{array}{c}\hfill \mathbf{E}(\Vert {\widehat{a}}_{\diamond }-a^{†}{\Vert }_0^2)\le K_{\diamond }{\beta }^{\frac{2q}{p+q}}{\left(ln\frac{1}{\beta }\right)}^{\frac{1}{\eta }\frac{q}{p+q}}.\end{array}$$(21)

3. Applications

3.1. Hammerstein operator

In the last section, we compute the overall rate of convergence of the two-step method for an inverse problem originating in a non-linear integral equation and inspired by [33]. We consider here the Hammerstein operator(22) $$\begin{array}{cc}& F:H^1\to L^2\hfill \\ \hfill & a\mapsto {\int }_0^{\bullet }\mathrm{\Phi }(a(t))\mathrm{d}t\hfill \end{array}$$(22)

where $\mathrm{\Phi }$ is a function in the space of Hölder continuous functions $C^{2,1}\left(\mathbf{R}\right)$ with bounded second derivative(23) $$\begin{array}{c}\hfill \Vert {\mathrm{\Phi }}^{″}{(t)\Vert }_{C^{0,1}}\le K\end{array}$$(23)

for all $t\in \mathbf{R}$, and $H^1$ denotes the Sobolev space of index 1 of functions on the interval [0, 1]. Our inverse problem is to determine a from the knowledge of F(a). Similar conditions as in Assumptions 2.1 were used in [34] to study the Landweber iterative method in Hilbert scales. The following properties of the operator F and its Fréchet derivative are going to be useful for choosing an appropriate Hilbert scale. The detailed proofs of the following theoretical results can be found in [35].

Lemma 3.1:

F is a continuous, compact, weakly closed and Fréchet differentiable operator with the Fréchet derivative(24) $$\begin{array}{c}\hfill (F^{\prime }(a)h)(t)={\int }_0^t{\mathrm{\Phi }}^{\prime }(a(s))h(s)\mathrm{d}s\end{array}$$(24)

The adjoint of the Fréchet derivative is given by(25) $$\begin{array}{c}\hfill F^{\prime }{(a)}^{\ast }g=B^{-1}\left({\mathrm{\Phi }}^{\prime }(a(·)){\int }_{\bullet }^{1}g(s)\mathrm{d}s\right).\end{array}$$(25)

Here $B:\left\{v\in H^2:v^{\prime }(0)=v^{\prime }(1)=0\right\}\to L^2$ is defined by $Bv:=-v^{″}+v$.

We assume from now on that(26) $$\begin{array}{c}\hfill {\mathrm{\Phi }}^{\prime }(s)>0,\text{for all}s\in \mathbf{R}.\end{array}$$(26)

In this case, the operator F is injective and we determine the set $R(F^{\prime }{(a^{†})}^{\ast })$ in order to choose a Hilbert scale which fulfills Assumptions 2.1. Let the linear integral operator $A:L^2\to L^2$ be defined as $(Af)(x)={\int }_0^{x}f(t)\mathrm{d}t$. $F^{\prime }{(a^{†})}^{\ast }$ is the composition of three operators: $A^{\ast }$, the multiplication operator $M_{{\mathrm{\Phi }}^{\prime }\circ a^{†}}:L^2\to L^2,M_{{\mathrm{\Phi }}^{\prime }\circ a^{†}}(h)=({\mathrm{\Phi }}^{\prime }\circ a^{†})h$ and $B^{-1}$. The operator $A^{\ast }:L^2\to L^2,A^{\ast }(g)(s)={\int }_s^{1}g(t)\mathrm{d}t$ has the range$$\begin{array}{c}\hfill R(A^{\ast })=\left\{u\in H^1:u(1)=0\right\}\end{array}$$

and$$\begin{array}{c}\hfill M({\mathrm{\Phi }}^{\prime }\circ a^{†})(R(A^{\ast }))=\left\{u\in H^1:u(1)=0\right\}\end{array}$$

as ${\mathrm{\Phi }}^{\prime }\circ a^{†}$ is in $H^1$. Note that due to (26(26) $$\begin{array}{c}\hfill {\mathrm{\Phi }}^{\prime }(s)>0,\text{for all}s\in \mathbf{R}.\end{array}$$(26) ) there exists $\gamma >1$ such that$$\begin{array}{c}\hfill \frac{1}{\gamma }\le {\mathrm{\Phi }}^{\prime }(a^{†}(s))\le \gamma \end{array}$$

for all $s\in [0,1]$ since $\Vert a^{†}{\Vert }_{\infty }<\infty$. Since the restriction$$\begin{array}{c}\hfill \tilde{B}{:=B|}_{D(B)\cap H^3}:\left\{v\in H^3:v^{\prime }(0)=v^{\prime }(1)=0\right\}\to H^1\end{array}$$

is an isomorphism by elliptic regularity results and since $(Bv)(1)=0$ is equivalent to $v^{″}(1)=v(1)$ we finally get$$\begin{array}{c}\hfill R(F^{\prime }{(a^{†})}^{\ast })=R(B^{-1}\circ M_{{\mathrm{\Phi }}^{\prime }\circ a^{†}}\circ A^{\ast })=\left\{v\in H^3:v^{\prime }(0)=v^{\prime }(1)=0,v(1)=v^{″}(1)\right\}.\end{array}$$

As the operators $A^{\ast },M({\mathrm{\Phi }}^{\prime }\circ a^{†})$ and $B^{-1}$ are injective, we have that $F^{\prime }{(a^{†})}^{\ast }$ is bijective between $L^2$ and $R(F^{\prime }{(a^{†})}^{\ast })$ and $\Vert F^{\prime }{(a^{†})}^{\ast }{w\Vert }_{H^3}\sim {\Vert w\Vert }_{L^2}$ for all $w\in L^2$.

We would like to have a Hilbert scale ${\left\{{\mathcal{X}}_s\right\}}_{s\in \mathbf{R}}$ with the following properties: it holds (27a) $$\begin{array}{c}\hfill {\mathcal{X}}_0=H^1\end{array}$$(27a) (or higher regularity of ${\mathcal{X}}_0$) to be able to show Assumptions 2.1, and we need$R(F^{\prime }{(a^{†})}^{\ast })$

to be a member of the Hilbert scale, e.g.(27b) $$\begin{array}{cc}\hfill {\mathcal{X}}_2& =\left\{w\in H^3:w^{\prime }(0)=w^{\prime }(1)=0,w(1)=w^{″}(1)\right\}\hfill \\ \hfill {〈w,v〉}_{{\mathcal{X}}_2}& ={〈\tilde{B}w,\tilde{B}v〉}_{H^1}={\int }_0^1{w}^{(3)}{v}^{(3)}+3w^{″}{v}^{″}+3w^{\prime }{v}^{\prime }+wv\mathrm{d}x.\hfill \end{array}$$(27b) Unfortunately, the restriction $\tilde{B}:R(F^{\prime }{(a^{†})}^{\ast })\to H^1$ is not self-adjoint and we need to consider the operator defined underneath as the generator of the Hilbert scale below.

Proposition 3.2:

The operator$$\begin{array}{cc}\hfill L:D(L)& =\left\{w\in H^5:w^{\prime }(0)=w^{\prime }(1)=w^{(3)}(0)=0,w(1)=w^{″}(1)\right\}\to H^1\hfill \\ \hfill & Lw:=w-2w^{″}+w^{(4)}.\hfill \end{array}$$

is self-adjoint in $H^1$, and(27c) $$\begin{array}{c}\hfill D(L^{\frac{1}{2}})=R(F^{\prime }{(a^{†})}^{\ast }).\end{array}$$(27c)

It follows thereof that the Hilbert scale $\left\{{\mathcal{X}}_s\right\}$ generated by the operator $L^{\frac{1}{4}}$ has the desired properties (27a(27a) $$\begin{array}{c}\hfill {\mathcal{X}}_0=H^1\end{array}$$(27a) ), (27b(27b) $$\begin{array}{cc}\hfill {\mathcal{X}}_2& =\left\{w\in H^3:w^{\prime }(0)=w^{\prime }(1)=0,w(1)=w^{″}(1)\right\}\hfill \\ \hfill {〈w,v〉}_{{\mathcal{X}}_2}& ={〈\tilde{B}w,\tilde{B}v〉}_{H^1}={\int }_0^1{w}^{(3)}{v}^{(3)}+3w^{″}{v}^{″}+3w^{\prime }{v}^{\prime }+wv\mathrm{d}x.\hfill \end{array}$$(27b) ) and (27c(27c) $$\begin{array}{c}\hfill D(L^{\frac{1}{2}})=R(F^{\prime }{(a^{†})}^{\ast }).\end{array}$$(27c) ).

Theorem 3.3:

For the Hilbert scale $\left\{{\mathcal{X}}_s\right\}$ defined before and under the supplementary conditions (23(23) $$\begin{array}{c}\hfill \Vert {\mathrm{\Phi }}^{″}{(t)\Vert }_{C^{0,1}}\le K\end{array}$$(23) ) and (26(26) $$\begin{array}{c}\hfill {\mathrm{\Phi }}^{\prime }(s)>0,\text{for all}s\in \mathbf{R}.\end{array}$$(26) ), Assumption 2.1(B) is fulfilled with $p=2$. Moreover, Assumptions 2.1(C) is also satisfied under the same conditions if the diameter of $D(F)\cap (a_0+{\mathcal{X}}_s)$ in ${\mathcal{X}}_0$-norm is smaller than a $\rho >0$.

Proof Assumptions 2.1(C) is equivalent to(28) $$\begin{array}{c}\hfill \Vert {\left(F^{\prime }(a)-F^{\prime }(a^{†})\right)}^{\ast }{\Vert }_{\mathcal{Y}\to {\mathcal{X}}_2}\le C_L{\Vert a-a^{†}\Vert }_0\le \frac{{\lambda }^2}{2\mathrm{\Lambda }}\end{array}$$(28)

for all $a\in {\mathbf{B}}_{\rho }(a^{†})\cap \left(a_0+{\mathcal{X}}_s\right)$ for some $\rho >0$ such that ${\mathbf{B}}_{\rho }\subset D(F)$. It follows, by (25(25) $$\begin{array}{c}\hfill F^{\prime }{(a)}^{\ast }g=B^{-1}\left({\mathrm{\Phi }}^{\prime }(a(·)){\int }_{\bullet }^{1}g(s)\mathrm{d}s\right).\end{array}$$(25) ) that$$\begin{array}{cc}\hfill \Vert (F^{\prime }{(a^{†})}^{\ast }-F^{\prime }{(a)}^{\ast }){h\Vert }_{{\mathcal{X}}_2}& =\Vert ({\mathrm{\Phi }}^{\prime }(a^{†}(·))-{\mathrm{\Phi }}^{\prime }(a(·))){\int }_{·}^1{h(s)\mathrm{d}s\Vert }_0\hfill \\ \hfill & \le \Vert ({\mathrm{\Phi }}^{\prime }\circ a^{†})-({\mathrm{\Phi }}^{\prime }\circ a){\Vert }_{H^1}{\Vert {\int }_{·}^{1}h(s)\mathrm{d}s\Vert }_{H^1}\hfill \\ \hfill & \le K(2+\Vert a^{†}{\Vert }_0)\Vert a^{†}{-a\Vert }_0{\Vert h\Vert }_{L^2}.\hfill \end{array}$$

The last inequality holds because$$\begin{array}{cc}\hfill \Vert ({\mathrm{\Phi }}^{\prime }\circ a^{†})-({\mathrm{\Phi }}^{\prime }\circ a){\Vert }_{H^1}& =\Vert {\mathrm{\Phi }}^{\prime }\circ a^{†}-{\mathrm{\Phi }}^{\prime }{\circ a\Vert }_{L^2}+{\Vert ({\mathrm{\Phi }}^{″}\circ a^{†}){(a^{†})}^{\prime }-({\mathrm{\Phi }}^{″}\circ a)a^{\prime }\Vert }_{L^2}\hfill \\ \hfill & \le K\Vert a^{†}-a{\Vert }_{L^2}+\Vert ({\mathrm{\Phi }}^{″}\circ a)({(a^{†})}^{\prime }-a^{\prime })\hfill \\ \hfill & +{(a^{†})}^{\prime }({\mathrm{\Phi }}^{″}\circ a^{†}-{\mathrm{\Phi }}^{″}\circ a){)\Vert }_{L^2}\hfill \\ \hfill & \le K\Vert a^{†}{-a\Vert }_{L^2}+K{\Vert {(a^{†})}^{\prime }-a^{\prime }\Vert }_{L^2}\hfill \\ \hfill & +\Vert {\mathrm{\Phi }}^{″}\circ a^{†}-{\mathrm{\Phi }}^{″}{\circ a\Vert }_{\infty }{\Vert {(a^{†})}^{\prime }\Vert }_{L^2}\hfill \\ \hfill & \le 2K\Vert a^{†}{-a\Vert }_{H^1}+\Vert {\mathrm{\Phi }}^{″}{\Vert }_{C^{0,1}}\Vert a^{†}{-a\Vert }_{\infty }{\Vert a^{†}\Vert }_{H^1}\hfill \\ \hfill & \le 2K\Vert a^{†}{-a\Vert }_{H^1}+\Vert {\mathrm{\Phi }}^{″}{\Vert }_{C^{0,1}}\Vert a^{†}{\Vert }_{H^1}\Vert a^{†}{-a\Vert }_{H^1}{\Vert a^{†}\Vert }_{H^1}\hfill \\ \hfill & \le K(2+\Vert a^{†}{\Vert }_0)\Vert a^{†}{-a\Vert }_{H^1}.\hfill \end{array}$$

Hence, the diameter $\rho$ should be smaller than $\frac{{\lambda }^2}{4\mathrm{\Lambda }K(2+\Vert a^{†}{\Vert }_0)}$.

Proposition 3.4:

If $a^{†}\in H^{q+1}$ and $\mathrm{\Phi }\in C^{\lceil q\rceil +1,1}$, where $\lceil q\rceil$ is the biggest integer smaller than q, then $u^{†}\in H^{q+2}$.

Proof Since the composition between $\mathrm{\Phi }$ and $a^{†}$ belongs to $H^{q+1}$ (see [36]), it follows immediately that $u^{†}\in H^{q+2}$, for $q\ge 2$.

Now, the overall rate of convergence can be computed.

Corollary 3.5:

In the case of the stochastic noise model (3(3) $$\begin{array}{c}\hfill Y=u^{†}+\sigma ϵ\end{array}$$(3) ), assuming $ϵ$ white noise with Gaussian or regular non-Gaussian probability distribution, if the conditions of Theorem 3.3 hold true and if $s\ge 2$, $q\in [s,2s+2]$, $a^{†}-a_0\in {\mathcal{X}}_q$, and $a^{†}\in H^{q+1}$, then $u^{†}$ can be estimated such that the rate of convergence (4(4) $$\begin{array}{c}\hfill \sqrt{\mathbf{E}\left(\Vert \widehat{u}-u^{†}{\Vert }_{\mathcal{Y}}^2\right)}\le \beta .\end{array}$$(4) ) holds true with $\beta \sim {\sigma }^{\frac{q+2}{q+2+1/2}}$. If the white noise has Gaussian distribution and the condition (16(16) $$\begin{array}{cc}\hfill \mathrm{\Phi }(1)& \le \mathrm{\Psi }(1)\hfill \end{array}$$(16) ) holds, then we get the rates of convergence$$\begin{array}{cc}\hfill \sqrt{\mathbf{E}\Vert \widehat{a}-a^{†}{\Vert }_0^2}& =\mathcal{O}\left({\sigma }^{\frac{q}{q+2+1/2}}{\left(log\frac{1}{\sigma }\right)}^{\frac{3q}{2(q+2)}}\right)\hfill \end{array}$$

while for regular concave log-probability distributions we obtain$$\begin{array}{cc}\hfill \sqrt{\mathbf{E}\Vert \widehat{a}-a^{†}{\Vert }_0^2}& =\mathcal{O}\left({\sigma }^{\frac{q}{q+2+1/2}}{\left(log\frac{1}{\sigma }\right)}^{\frac{2q}{q+2}}\right).\hfill \end{array}$$

Proof The first statement follows from Proposition 3.4, from asymptotic equivalence in Le Cam’s sense between nonparametric regression with regular error distribution i.e. presenting a locally asymptotic stochastic expansion (for exact definition of the regularity conditions see [12]) and the white noise with drift, and from the theory of nonparametric regression (see [11]). The smoothness of $u^{†}$ is Sobolev of order $q+2$ , and rates of convergence on Sobolev balls were computed for nonparametric regression problems in the last reference and they correspond to the statement from the Corollary 3.5. The second statement is a consequence of the rates of convergence computed in [37], Theorem 2.6 and Lemma 4.3.

3.2. Reconstruction of a reaction coefficient

To illustrate the convergence behaviour of our method, we consider in this section a parameter identification problem as a nonlinear operator equation and compute over-all rates of convergence for the Lepskii estimator based on theoretical properties already proved in [15]. Furthermore, we compare its numerical and theoretical rates of convergence for different smoothness conditions with the help of Monte-Carlo simulations.

3.2.1. Theoretical rates of convergence

The direct problem is modeled by the differential equation$$\begin{array}{c}\hfill \left\{\begin{array}{cc}-\mathrm{\Delta }u(x)+a(x)u(x)\hfill & =f(x),x\in \mathrm{\Omega }\hfill \\ {u|}_{\partial \mathrm{\Omega }}\hfill & =g\hfill \end{array}\right.\end{array}$$

where f and g are infinitely smooth, and the domain $\mathrm{\Omega }$ is chosen to be (0, 1) for simplicity. For a given bound $\gamma >0$ we introduce the set(29) $$\begin{array}{c}\hfill D(F)=\}a\in L^2((0,1)):0\le a(t)\le \gamma ,\forall t\in [0,1]\{\end{array}$$(29)

and we formulate the inverse problem of identifying the parameter $a\in D(F)$ knowing $u_a=u_a(x)$ as an operator equation with the help of parameter-to-solution operator(30) $$\begin{array}{c}\hfill F:D(F)\to L^2\left((0,1)\right),F(a):=u_a.\end{array}$$(30)

The Hilbert scale ${\left({\mathcal{X}}_s\right)}_{s\in \mathbf{R}}$ will be generated by the square root $B^{\frac{1}{2}}$ of the positive, self-adjoint operator B defined by$$\begin{array}{c}\hfill B:H_0^1\left((0,1)\right)\cap H^2\left((0,1)\right)\to L^2\left((0,1)\right),Bv:=-\mathrm{\Delta }v+v.\end{array}$$

We notice that the elements of this Hilbert scale with integer index are subsets of Sobolev spaces with Dirichlet boundary conditions on the even derivatives$$\begin{array}{cc}\hfill {\mathcal{X}}_1& =H_0^1((0,1)),{\mathcal{X}}_2=H_2((0,1))\cap H_0^1((0,1)),\hfill \\ \hfill {\mathcal{X}}_3& =\{v\in H_3((0,1)):v,\mathrm{\Delta }v\in H_0^1((0,1))\}.\hfill \end{array}$$

In [15] it was proven that the operator F together with this choice of Hilbert scale fulfills the Assumptions 2.1 for $p=2$ and $s=2$ when the condition(31) $$\begin{array}{c}\hfill c_u=\underset{x\in (0,1)}{inf}{u}^{†}\left(x\right)>0\end{array}$$(31)

and the smallness condition on the D(F) hold, and that the regularity of the parameter $a^{†}\in H^q((0,1))$ with $q>1/2$ determines the smoothness of the exact data $u^{†}\in H^{q+2}((0,1))$. Hence, we can get an over-all convergence rate results in this case, also.

Corollary 3.6:

In the case of the stochastic noise model (3(3) $$\begin{array}{c}\hfill Y=u^{†}+\sigma ϵ\end{array}$$(3) ), assuming $ϵ$ white noise with Gaussian or regular non-Gaussian probability distribution, for the Hilbert scale defined above $\left({\mathcal{X}}_s\right)$ and under the supplementary condition (32(32) $$\begin{array}{c}\hfill Y_i=u^{†}(X_i)+{ϵ}_i,i=1,\cdots ,n\end{array}$$(32) ) and if $s\ge 2$, $q\in [s,2s+2]$, $a^{†}-a_0\in {\mathcal{X}}_q$, and $a^{†}\in H^q((0,1))$, then $u^{†}$ can be estimated such that the rate of convergence (4(4) $$\begin{array}{c}\hfill \sqrt{\mathbf{E}\left(\Vert \widehat{u}-u^{†}{\Vert }_{\mathcal{Y}}^2\right)}\le \beta .\end{array}$$(4) ) holds true with $\beta \sim {\sigma }^{\frac{q+1}{q+1+1/2}}$. If the white noise has Gaussian distribution and the conditions (16(16) $$\begin{array}{cc}\hfill \mathrm{\Phi }(1)& \le \mathrm{\Psi }(1)\hfill \end{array}$$(16) ) holds, then we get the rates of convergence$$\begin{array}{cc}\hfill \sqrt{\mathbf{E}\Vert \widehat{a}-a^{†}{\Vert }_0^2}& =\mathcal{O}\left({\sigma }^{\frac{q}{q+2+1/2}}{\left(log\frac{1}{\sigma }\right)}^{\frac{3q}{2(q+2)}}\right)\hfill \end{array}$$

while for regular concave log-probability distributions we obtain$$\begin{array}{cc}\hfill \sqrt{\mathbf{E}\Vert \widehat{a}-a^{†}{\Vert }_0^2}& =\mathcal{O}\left({\sigma }^{\frac{q}{q+2+1/2}}{\left(log\frac{1}{\sigma }\right)}^{\frac{2q}{q+2}}\right).\hfill \end{array}$$

4. Numerical simulations

In this final section we present the employment of the balancing principle and the influence of the smoothness of the parameter $a^{†}$ on the rate of convergence of $\widehat{u}$ in the two-step method for the reconstruction of a reaction coefficient by numerical simulations. First, we choose the local polynomial estimator as the pre-smoothing method and review some of its properties in the framework of a discretized version of the problem (3(3) $$\begin{array}{c}\hfill Y=u^{†}+\sigma ϵ\end{array}$$(3) ). A new result about the tail behaviour (18(18) $$\begin{array}{c}\hfill \mathbf{P}\left\{\omega :\Vert \widehat{u}-\mathbf{E}\left(\widehat{u}\right){\Vert }_{\mathcal{Y}}^2\ge \tau \mathbf{E}\left(\Vert \widehat{u}-\mathbf{E}\left(\widehat{u}\right){\Vert }_{\mathcal{Y}}^2\right)\right\}\le l_{1}exp(-l_2{\tau }^{\eta })\end{array}$$(18) ) of the local polynomial estimator in a general, non-Gaussian noise model (see [38] for a review of the literature on this subject) is also proved. Moreover, the values of $\lambda$ and $\mathrm{\Lambda }$ for parameter-to-solution operator (31(31) $$\begin{array}{c}\hfill c_u=\underset{x\in (0,1)}{inf}{u}^{†}\left(x\right)>0\end{array}$$(31) ), and the empirical overall rate of convergence for the two-step method are computed, and the rates are illustrated in our graphics for different smoothnesses of $a^{†}$.

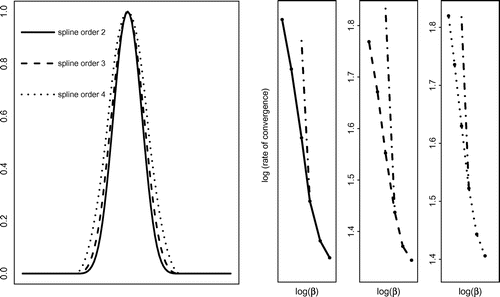
Figure 2. Exact parameter $a^{†}$ (full line - $q=2.5$, dashed line - $q=3.5$, dotted line - $q=4.5$), and its corresponding empirical and theoretical (dashed - dotted) rate of convergence on a log-log scale

4.1. Tail behaviour of local polynomial estimator

In the first step, we consider the nonparametric regression problem of estimating $u^{†}$ from the data ${\left(Y_i,X_i\right)}_{i=1,\cdots ,n}$ such that(32) $$\begin{array}{c}\hfill Y_i=u^{†}(X_i)+{ϵ}_i,i=1,\cdots ,n\end{array}$$(32)

where ${\left({ϵ}_i\right)}_{i=1,\cdots ,n}$ are independent, centred random variables with $\mathsf{v}ar({ϵ}_i)\le v\le \infty$ and $X_i\in \left(0,1\right),i=1,\cdots ,n$ is a deterministic design. In the case of Gaussian nonparametric regression, when ${\left\{ϵ\right\}}_{i=1,\cdots ,n}$ are independent, identically normal distributed N(0, 1), this is the discretized version of the Gaussian white noise model in (3(3) $$\begin{array}{c}\hfill Y=u^{†}+\sigma ϵ\end{array}$$(3) ) with $ϵ$ the standard Wiener process on [0,1] and the stochastic noise level $\sigma =\frac{1}{\sqrt{n}}$ (see e.g. [11]).

As usual in this setting, we assume that $u^{†}$ belongs to the Hölder class $\mathrm{\Sigma }(l,M)$ on $\left(0,1\right)$ i.e. it is a $\lfloor l\rfloor$ times differentiable function whose derivative ${\left(u^{†}\right)}^{\lfloor l\rfloor }$ satisfies$$\begin{array}{c}\hfill \left|{\left(u^{†}\right)}^{\lfloor l\rfloor }(x)-{\left(u^{†}\right)}^{\lfloor l\rfloor }(x^{\prime })\right|\le M{\left|x-x^{\prime }\right|}^{l-\lfloor l\rfloor },\forall x,x^{\prime }\in \left(0,1\right)\end{array}$$

where $\lfloor l\rfloor$ is the integer part of $l>0$. For the case that the co-domain $\mathcal{Y}$ of the operator F is the Sobolev space $W^{\lfloor l\rfloor +1,2}$, the compact embedding of the Hilbert space $W^{\lfloor l\rfloor +1,2}$ into the Hölder space $\mathrm{\Sigma }(l,M)$ follows from the Morrey’s inequality (as in [39]).

The regression function $u^{†}$ can be locally approximated by$$\begin{array}{c}\hfill u^{†}(x+f)\simeq \sum _{k=0}^{\lfloor l\rfloor }\frac{{\left(u^{†}\right)}^{\left(k\right)}(x)}{k!}{f}^k\end{array}$$

for $f>0$ small enough. The vector $\theta (x)={\left\{{\left(u^{†}\right)}^{\left(k\right)}(x)f^k\right\}}_{k=0,\cdots ,\lfloor l\rfloor }$ can be estimated by means of the local polynomial estimator of order $d=\lfloor l\rfloor$.

Definition 4.1:

The local polynomial estimator of order d of $\theta (x)$ is defined by (33) $$\begin{array}{c}\hfill {\widehat{\theta }}_{\mathit{nh}}(x)={\mathit{argmin}}_{\theta \int {\mathbf{R}}^{d+1}}\left\{\frac{1}{\mathit{nh}}\sum _{i=1}^n{\left[Y_i-{\theta }^{T}V\left(\frac{X_i-x}{h}\right)\right]}^{2}K\left(\frac{X_i-x}{h}\right)\right\}\end{array}$$(33)

where $V(u)=\left(1,u,\frac{u^2}{2!},\cdots ,\frac{u^d}{d!}\right)$, $K:\mathbf{R}\to \mathbf{R}$ is a kernel i.e. an integrable function satisfying $\int K(u)du=1$ , $h>0$ is the bandwidth and $d\ge 0$ is an integer. The local polynomial estimator of order d of $u^{†}(x)$ is the first element of the vector ${\widehat{\theta }}_{\mathit{nh}}(x)$ and is denoted by ${\widehat{u}}_{\mathit{nh}}(x)=V^t(0){\widehat{\theta }}_{\mathit{nh}}(x)$.

The existence and uniqueness of the optimization problem (34(34) $$\begin{array}{cc}\hfill {\widehat{\theta }}_{\mathit{nh}}(x)& =\frac{1}{\mathit{nh}}\sum _{i=1}^n{Y}_i{B}_{\mathit{hx}}^{-1}V\left(\frac{X_i-x}{h}\right)K\left(\frac{X_i-x}{h}\right)\hfill \\ \hfill {\widehat{u}}_{\mathit{nh}}(x)& =\frac{1}{\mathit{nh}}\sum _{i=1}^n{Y}_i{V}^t(0)B_{\mathit{hx}}^{-1}V\left(\frac{X_i-x}{h}\right)K\left(\frac{X_i-x}{h}\right).\hfill \end{array}$$(34) ) was proven in [11] under the following hypothesis which will assume to hold from now on.

Assumptions 4.2:

(A)	There exists an $n_0\in \mathbf{N}$ such that the eigenvalues of the Hessian matrix of the objective function in the optimization problem (34(34) $$\begin{array}{cc}\hfill {\widehat{\theta }}_{\mathit{nh}}(x)& =\frac{1}{\mathit{nh}}\sum _{i=1}^n{Y}_i{B}_{\mathit{hx}}^{-1}V\left(\frac{X_i-x}{h}\right)K\left(\frac{X_i-x}{h}\right)\hfill \\ \hfill {\widehat{u}}_{\mathit{nh}}(x)& =\frac{1}{\mathit{nh}}\sum _{i=1}^n{Y}_i{V}^t(0)B_{\mathit{hx}}^{-1}V\left(\frac{X_i-x}{h}\right)K\left(\frac{X_i-x}{h}\right).\hfill \end{array}$$(34) ) $$\begin{array}{cc}\hfill B_{\mathit{hx}}& ={\left\{B_{\mathit{hx}}^{\mathit{pq}}(\theta )\right\}}_{p,q=1,\cdots ,d+1}\hfill \\ \hfill & ={\left\{\frac{\partial }{\partial {\theta }_p}\frac{\partial }{\partial {\theta }_q}\left\{\frac{1}{\mathit{nh}}\sum _{i=1}^n{\left[Y_i-{\theta }^{T}V\left(\frac{X_i-x}{h}\right)\right]}^{2}K\left(\frac{X_i-x}{h}\right)\right\}\right\}}_{p,q=0,\cdots ,d}\hfill \\ \hfill & =\frac{2}{\mathit{nh}}\sum _{i=1}^{n}V\left(\frac{X_i-x}{h}\right)V^T\left(\frac{X_i-x}{h}\right)K\left(\frac{X_i-x}{h}\right)\hfill \end{array}$$ are bounded from below uniformly in x by a ${\lambda }_0>0$ for any $n\ge n_0$.
(B)	The frequency of the points ${\left\{X_i\right\}}_{i=1,\cdots ,n}$ in any interval $\left(a,b\right)\subset \left(0,1\right)$ is uniformly bounded with respect to n by $a_{0}max\left(b-a,\frac{1}{n}\right)$ for a positive constant $a_0$.
(C)	K is bounded by a constant $K_{\mathit{max}}$ on $\mathbf{R}$ and has compact support $supp(K)\subseteq [-1,1]$.

Consequently, the local polynomial estimator of order d of $\theta (x)$ as well as of $u^{†}(x)$ exist and are given by(34) $$\begin{array}{cc}\hfill {\widehat{\theta }}_{\mathit{nh}}(x)& =\frac{1}{\mathit{nh}}\sum _{i=1}^n{Y}_i{B}_{\mathit{hx}}^{-1}V\left(\frac{X_i-x}{h}\right)K\left(\frac{X_i-x}{h}\right)\hfill \\ \hfill {\widehat{u}}_{\mathit{nh}}(x)& =\frac{1}{\mathit{nh}}\sum _{i=1}^n{Y}_i{V}^t(0)B_{\mathit{hx}}^{-1}V\left(\frac{X_i-x}{h}\right)K\left(\frac{X_i-x}{h}\right).\hfill \end{array}$$(34)

We focus in the following on the tail behaviour of the local polynomial estimator for a fixed bandwidth h under different noise conditions.

Lemma 4.3:

Let us assume that the vector of errors $ϵ={\left\{{ϵ}_i\right\}}_{i=1,\cdots ,n}$ has a log-concave, continuous distribution on ${\mathbf{R}}^n$ i.e. the logarithm of this probability density is concave on the set where its logarithm is defined. If the Assumptions 4.2 hold, we have$$\begin{array}{c}\hfill \mathbf{P}\left\{\Vert {\widehat{u}}_{\mathit{nh}}-\mathbf{E}\left({\widehat{u}}_{\mathit{nh}}\right){\Vert }_{L^2(0,1)}^2\ge t\mathbf{E}{\Vert {\widehat{u}}_{\mathit{nh}}-\mathbf{E}\left({\widehat{u}}_{\mathit{nh}}\right)\Vert }_{L^2(0,1)}^2\right\}\le e·\mathbf{e}xp\left\{-\frac{\sqrt{t}}{\frac{C_{1}e}{2}}\right\}\end{array}$$

where $C_1$ is an universal constant, $h>0$ and $t\ge e^2{C}_1^2$.

Moreover, if the errors ${\left\{{ϵ}_i\right\}}_{i=1,\cdots ,n}$ are independent, centred Gaussian random variables, then it holds$$\begin{array}{c}\hfill \mathbf{P}\left\{\Vert {\widehat{u}}_{\mathit{nh}}-\mathbf{E}\left({\widehat{u}}_{\mathit{nh}}\right){\Vert }_{L^2(0,1)}^2\ge t\mathbf{E}{\Vert {\widehat{u}}_{\mathit{nh}}-\mathbf{E}\left({\widehat{u}}_{\mathit{nh}}\right)\Vert }_{L^2(0,1)}^2\right\}\le \mathbf{e}xp\left\{-C_2·t\right\}\end{array}$$

where $C_2$ is an universal constant.

Proof From (35(35) $$\begin{array}{c}\hfill \mathbf{P}\left\{f(ϵ)\ge t\mathbf{E}\left(f(ϵ)\right)\right\}\le {\left(\frac{\frac{C_{1}q}{2}}{\sqrt{t}}\right)}^q\end{array}$$(35) ) we can write$$\begin{array}{cc}& \Vert {\widehat{u}}_{\mathit{nh}}-\mathbf{E}\left({\widehat{u}}_{\mathit{nh}}\right){\Vert }_{L^2(0,1)}^2={\int }_0^1{\left(\frac{1}{\mathit{nh}}\sum _{i=1}^n{ϵ}_i{V}^t(0)B_{\mathit{hx}}^{-1}V\left(\frac{X_i-x}{h}\right)K\left(\frac{X_i-x}{h}\right)\right)}^2\mathrm{d}x\hfill \\ \hfill & =\frac{1}{{(nh)}^2}\sum _{i,j=1}^n{ϵ}_i{ϵ}_j{\int }_0^1{V}^t(0)B_{\mathit{hx}}^{-1}V\left(\frac{X_i-x}{h}\right)K\left(\frac{X_i-x}{h}\right)V^t(0)B_{\mathit{hx}}^{-1}V\left(\frac{X_j-x}{h}\right)\hfill \\ \hfill & ·K\left(\frac{X_j-x}{h}\right)\mathrm{d}x.\hfill \end{array}$$

This is a positive polynomial of order two with symmetric coefficients in the random variables ${ϵ}_i,i=1,\cdots ,n$. In this case, results regarding the higher moments are already available (see Theorem 7 in [40]). For the sake of completeness we reproduce this result in Appendix 1 (see Lemma 1) and use it to bound the moments of the polynomial$$\begin{array}{cc}& f(ϵ)=\frac{1}{{(nh)}^2}\sum _{i,j=1}^n{ϵ}_i{ϵ}_j{\int }_0^1{V}^t(0)B_{\mathit{hx}}^{-1}V\left(\frac{X_i-x}{h}\right)K\left(\frac{X_i-x}{h}\right)V^t(0)B_{\mathit{hx}}^{-1}V\left(\frac{X_j-x}{h}\right)\hfill \\ \hfill & ·K\left(\frac{X_j-x}{h}\right)\mathrm{d}x\hfill \end{array}$$

as$$\begin{array}{c}\hfill \mathbf{E}\left(f{(ϵ)}^{\frac{q}{2}}\right)\le {\left(C_1\frac{q}{2}\right)}^q{\left(\mathbf{E}f(ϵ)\right)}^{\frac{q}{2}}\end{array}$$

where $d=r=2$, $q\ge 2$ and $C_1$ is an universal constant. From the Markov inequality we get(35) $$\begin{array}{c}\hfill \mathbf{P}\left\{f(ϵ)\ge t\mathbf{E}\left(f(ϵ)\right)\right\}\le {\left(\frac{\frac{C_{1}q}{2}}{\sqrt{t}}\right)}^q\end{array}$$(35)

Let us choose now the integer $q^{\ast }$ such that $\frac{2\sqrt{t}}{e{C}_1}-1\le q^{\ast }\le \frac{2\sqrt{t}}{e{C}_1}$. For values of t such that $q^{\ast }\ge 2$ we can apply the previous inequality and obtain$$\begin{array}{c}\hfill \mathbf{P}\left\{f(ϵ)\ge t\mathbf{E}\left(f(ϵ)\right)\right\}\le {\left(\frac{\frac{C_1{q}^{\ast }}{2}}{\sqrt{t}}\right)}^{q^{\ast }}\le exp\left(-q^{\ast }\right)\le e·exp\left(-\frac{\sqrt{t}}{C_1\frac{e}{2}}\right).\end{array}$$

The second inequality in Lemma 4.3, leading to Chernoff bound like estimates, is a direct consequence of hypercontractivity inequalities for Gaussian Hilbert spaces (see Theorem 6.7 in [41]).

Remark 3:

The log-concave probability distributions include normal, exponential, logistic, chi-square, chi and Laplace. A survey of these can be found in [42]. The stochastic error is assumed to be a zero mean stochastic process with bounded covariance operator. Therefore, considering a general class of distributions larger than the Gaussian fit into the general setting of our problem. Due to Lemma 4.3, the overall rate of convergence of the two-step method will depend of the class of probability distributions to which the discretized noise term belongs to.

Remark 4:

Results about asymptotically optimality of local polynomial estimator with the regularization parameter chosen by cross-validation were proved in [43,44]. Details about practical implementation of this method could be found in [45].

Remark 5:

An adaptive local polynomial estimator based on a particular implementation of Lepskii scheme and its convergence properties for local and global risks for a wide range of characterizations of smoothness and accuracy measures are presented in [37]. The rates of convergence depend on the smoothness in the scale of Sobolev spaces of the exact data $u^{†}$, the degree of the polynomial and the index of the Lebesgue norm of the global risk, and are optimal or optimal up to a logarithmic term, as expected from [46,47].

Remark 6:

A data-driven approach leading to adaptive estimation of both polynomial order and the bandwidth with the help of cross-validation can be found in [48]. This method is uniformly consistent for a large class of functions $u^{†}$ and reaches the optimal rate for the case of correctly specified parametric model i.e. when $u^{†}$ is a polynomial whose order does not depend on sample size. Nevertheless, an order optimal approach aiming to adaptively tailor the degree and the tuning parameter of the local polynomial estimator is still an open problem.

4.2. Rate of convergence of the Tikhonov estimator for the balancing principle

In the following we compute and illustrate the empirical rate of convergence of the Tikhonov estimator for the balancing principle in the stochastic setting with the local polynomial estimator as pre-smoothing method. Since theoretical and numerical results imply that the Lepskii constant $k_2$ depend on the chosen application, we present a result concerning the computation of this constant for the inverse problem defined in (31(31) $$\begin{array}{c}\hfill c_u=\underset{x\in (0,1)}{inf}{u}^{†}\left(x\right)>0\end{array}$$(31) ). To this aim, the values of $\mathrm{\Lambda }$ and $\lambda$ are given in the following lemma under general conditions for the direct operator.

Lemma 4.4:

If the assumptions from Corollary 3.6 are fulfilled and the supplementary conditions(36) $$\begin{array}{c}\hfill \left\{\begin{array}{c}f\ge 0,\hfill \\ g>0,\hfill \\ f-a^{†}·g\ge 0\hfill \end{array}\right.\end{array}$$(36)

hold, then we have$$\begin{array}{cc}\hfill \lambda & =\frac{1}{\mathrm{m}ax(1,\gamma )}\underset{\partial \mathrm{\Omega }}{inf}g\hfill \\ \hfill \mathrm{\Lambda }& =\frac{\sqrt{1+3·{\gamma }^2·{\left(1+\frac{D}{\pi }\right)}^2}}{1+{\left(\frac{D}{\pi }\right)}^2}·\left(\frac{1}{2}{D}^2·\underset{\mathrm{\Omega }}{sup}f+\underset{\partial \mathrm{\Omega }}{sup}g\right)·D\hfill \\ \hfill \end{array}$$

where D is the length of the interval $\mathrm{\Omega }$.

Proof The Fréchet derivative of the operator defined in (31(31) $$\begin{array}{c}\hfill c_u=\underset{x\in (0,1)}{inf}{u}^{†}\left(x\right)>0\end{array}$$(31) ) is$$F^{\prime }(a)h=T{(a)}^{-1}(-h·u_a),T(a):H^2(\mathrm{\Omega })\cap H_0^1(\mathrm{\Omega })\to L^2(\mathrm{\Omega })$$

where $T(a)=u_a$ (see [1]).The following bounds follow from the Gelfand triple structure of the Hilbert scale and the Banach algebra property of the Hilbert space $H^2(\mathrm{\Omega })$ (see [15] and references within):$$\begin{array}{c}\hfill \frac{1}{\mathrm{m}ax(1,\gamma )}\frac{1}{\Vert \frac{1}{u_a}{\Vert }_{\infty }}{\Vert h\Vert }_{-2}\le \Vert F^{\prime }{(a)h\Vert }_0\le \frac{\sqrt{1+3·{\gamma }^2·k^2}}{C}·\Vert u_a{\Vert }_{{\mathcal{X}}_0}{\Vert h\Vert }_{-2}\end{array}$$

where k and C are Sobolev constants corresponding to embedding of $H_0^1(\mathrm{\Omega })$, respectively $H^2(\mathrm{\Omega })\cap H_0^1(\mathrm{\Omega })$ into $L^2(\mathrm{\Omega })$. From [49,50] it follows that these constants take the values $k=1+\frac{D}{\pi }$ and $C=1+{\left(\frac{D}{\pi }\right)}^2$.

Under the supplementary conditions (3.6), classical methods in partial differential equations lead to following bounds on the solution of the direct problem$$\begin{array}{cc}\hfill \underset{\partial \mathrm{\Omega }}{inf}g\le u_a(x)& \le -V(x)·\underset{\mathrm{\Omega }}{sup}f+\underset{\partial \mathrm{\Omega }}{sup}g\hfill \\ \hfill \underset{\partial \mathrm{\Omega }}{inf}g\le u_a(x)& \le \frac{1}{2}{D}^2·\underset{\mathrm{\Omega }}{sup}f+\underset{\partial \mathrm{\Omega }}{sup}g\hfill \\ \hfill \end{array}$$

where $V(x)=\frac{1}{2}\left(|x-x_0{|}^2-D^2\right),x\in \mathrm{\Omega }$ for an $x_0\in \mathrm{\Omega }$ (see e.g. Exercise 4 in [51]). Since$$\begin{array}{c}\hfill \frac{1}{\mathrm{m}ax(1,\gamma )}\frac{1}{\Vert \frac{1}{u_a}{\Vert }_{\infty }}=\underset{\mathrm{\Omega }}{inf}{u}_q=\underset{\partial \mathrm{\Omega }}{inf}g\end{array}$$

and$$\begin{array}{c}\hfill \Vert u_a{\Vert }_{{\mathcal{X}}_0}\le D·\left(\frac{1}{2}{D}^2·\underset{\mathrm{\Omega }}{sup}f+\underset{\partial \mathrm{\Omega }}{sup}g\right)\end{array}$$

we get $\lambda$ and $\mathrm{\Lambda }$ from Lemma 3.6.

Remark 7:

The computation of the Lepskii constant is also feasible for smooth domains $\mathrm{\Omega }$ in ${\mathbf{R}}^n$, $n>1$. For example, results about the value of the Poincaré constant for convex domains in ${\mathbf{R}}^n$, $n>1$ are available in [52].

In our numerical simulations, the unknown parameter $a^{†}$ is chosen as a B-spline of order 2, 3 or 4 which corresponds to smoothness up to $H^{2.5}$, $H^{3.5}$ respectively $H^{4.5}$, and its upper bound $\gamma$ is equal to 1. The use of different larger values of $\gamma$ does not change the asymptotic rates of convergence, hence the method is robust with respect to $\gamma$. The exact data $u^{†}$ has smoothness up to $H^{4.5}$, $H^{5.5}$ respectively $H^{6.5}$ corresponding to the chosen B-splines. From Sobolev embedding theorem, this implies a Hölder condition of order up to 4, 5 and 6.

The Gaussian white noise was discretized such that we obtain an inverse regression problem with equidistant deterministic design $X_1,\dots X_n\in (0,1)$ and normally distributed errors with variance ${\sigma }^2=0.01$. Since the discrete regression design is asymptotically equivalent to the Guassian white noise model (3(3) $$\begin{array}{c}\hfill Y=u^{†}+\sigma ϵ\end{array}$$(3) ) (see e.g. [11]), we consider the increasing sample sizes n 1000 , 2512 , 6310 , 15849 , 39811 , 100000 instead of letting the noise level going to 0 in the theoretical noise model, and 100 simulations for each sample size.

Remark 8:

Theorem 2.6 holds for noise levels that fulfill the inequality (16(16) $$\begin{array}{cc}\hfill \mathrm{\Phi }(1)& \le \mathrm{\Psi }(1)\hfill \end{array}$$(16) ). In our numerical example, we can explicitly formulate the relation between the noise level $\beta$ and the $q-$norm of the difference between the initial guess and exact solution c. From Lemma 4.4, we get the values $\lambda =1$ and $\mathrm{\Lambda }=3.4$ since $\gamma =1$, $D=1$, ${sup}_{\mathrm{\Omega }}f=1$ and ${sup}_{\partial \mathrm{\Omega }}g=1$ for a choice of the exact data $u^{†}(x)=1+x·(1-x)$. The values of the constants $k_1$ and $k_2$ can be accordingly derived as$$\begin{array}{cc}\hfill k_1& =54·2^{\frac{q}{4}}{c}^2+597.42·2^{\frac{3(q+2)}{16}}{c}^{1.5}+195.98·2^{\frac{q}{2}}c+136.199·2^{\frac{q}{2}}\sqrt{c}\hfill \\ \hfill k_2& =143.24\hfill \end{array}$$

and, for a choice of the initial value for the regularization parameter ${\alpha }_1={\beta }^2$, (16(16) $$\begin{array}{cc}\hfill \mathrm{\Phi }(1)& \le \mathrm{\Psi }(1)\hfill \end{array}$$(16) ) becomes$$\begin{array}{c}\hfill k_1·\left(2{\beta }^{\frac{2(q-s)}{p+2}}+1\right)\le 3·k_2\end{array}$$

For $q=2.5$ we have$$\begin{array}{c}\hfill \left(83.28·c^2+941.53·c^{1.5}+490.948·c+151.77·\sqrt{c}\right)\left(2{\beta }^{\frac{1}{4}}+1\right)\le 429.73\end{array}$$

and the sufficient conditions for this inequality to hold are $c^{\frac{1}{2}}\left(1+2{\beta }^{\frac{1}{4}}\right)\le 0.26$ and $c\le 1$. Hence, for a noise level of 0.01, our initial guess should be as close in the $q-$norm to the exact solution as 0.16 to ensure that condition (16(16) $$\begin{array}{cc}\hfill \mathrm{\Phi }(1)& \le \mathrm{\Psi }(1)\hfill \end{array}$$(16) ) holds. Moreover, the quality of the reconstruction is very sensitive to the choice of the a-priori guess.

To illustrate the rates of convergence for the two-step method with Lepskii choice of the regularization parameter, we used in the first step of the algorithm a local polynomial estimator with Gaussian kernel for the direct regression problem as stated in (33(33) $$\begin{array}{c}\hfill {\widehat{\theta }}_{\mathit{nh}}(x)={\mathit{argmin}}_{\theta \int {\mathbf{R}}^{d+1}}\left\{\frac{1}{\mathit{nh}}\sum _{i=1}^n{\left[Y_i-{\theta }^{T}V\left(\frac{X_i-x}{h}\right)\right]}^{2}K\left(\frac{X_i-x}{h}\right)\right\}\end{array}$$(33) ) and an a-priori chosen bandwidth. We chose quadratic local polynomial estimator, since the linear estimator shows larger bias in regions with higher curvatures , and we varied the values of the bandwidth by using a constant $c_h$ chosen from the grid between 0.1 and 1 with step size 0.1 as factor to the a-priori value $n^{-\frac{1}{5}}$. The empirical values of the rates of convergence $\widehat{\beta }$ were computed by leave-1-out cross-validation and used in the second step of the method. An exhaustive introduction to the application of the local polynomial estimator and its challenges can be found in [45]. The tail behaviour for this estimator fulfills the condition in Theorem 2.6 as a consequence of Lemma 4.3. For a polynomial of degree 2, it follows from Theorem 5.10 and Remark 5.13 in [41] that $l_2=\frac{1}{e}$ and $\eta =1$.

In the second step, we applied the balancing principle to choose the regularization parameter as studied in Theorem 2.6. The Lepskii factor $k_{\ast }$ was chosen from a grid of values between 0.1 and 0.05, by minimizing the empirical mean square error, and the Lepskii constant is computed as $k_{\ast }·\sqrt{1+{\left(l_{2}log\frac{1}{\widehat{\beta }}\right)}^{\frac{1}{\eta }}}\widehat{\beta }$. An overview of the constants used for simulations and computation is given in the Table 1.

We present in Figure 2 the convergence rates for the chosen smoothness of the exact solution, considering the sample sizes 1000 , 2512 , 6310 , 15849 , 39811 , 100000. The logarithm of the empirical estimation of the expected squared error $\sqrt{\mathbf{E}(\Vert {\widehat{a}}_{+}-a^{†}{\Vert }_0^2)}$ of $\widehat{a}$ is plotted over the logarithm of the empirical values of the rates of convergence of the local polynomial estimator for the three choices of $a^{†}$ shown in Figure 2. The empirical rates of convergence are plotted in full, dashed and dotted lines according to the three different smoothness conditions, while the theoretical ones corresponding to a line with slope $\frac{q}{2+q}$ are illustrated in the dashed-dotted lines. Starting with a sample size $n=15849$, the linear trend dominates, approaching asymptotically the theoretical linear slopes.

Table 1. Overview of the constants.

No.	Parameter	Definition	Value
1	q	Sobolev smoothness of $a^{†}$	2.5, 3.5, 4.5
2	$\gamma$	Upper bound on $a^{†}$	1
3	s	Smoothness of the penalization term in Tikhonov functional	2
4	p	Degree of ill-posedness	2
5	$q+2$	Sobolev smoothness of the exact data $u^{†}$	4.5, 5.5, 6.5
6	$q+1.5$	Hölder smoothness of the exact data $u^{†}$	4,5,6
7	$\beta$	Theoretical order optimal rate for local pol. est.	$n^{-\frac{4}{9}},n^{-\frac{5}{11}},n^{-\frac{6}{13}}$
8	$c_h$	Factor for bandwidth	[0.1, 1]
9	$l_2$	Factor in the tail behaviour of the loc.pol.est.	$\frac{1}{e}$
10	$\eta$	Exponent of the tail behaviour of the loc.pol.est.	1
11	$k_{\ast }$	Factor in the Lepskii rule	[0.05, 0.1]
12	n	Sample size	1000,2512,6310,15849,39811,10000
13	D	Length of the interval	1
14	g	Boundary conditions	1
15	$\lambda$	Lipschitz constant	1
16	$\mathrm{\Lambda }$	Lipschitz constant	4

Acknowledgements

The author would like to thank the Isaac Newton Institute for Mathematical Sciences for support and hospitality during the programme ‘Variational methods and effective algorithms for imaging and vision’ when work on this paper was also undertaken.

Additional information

Funding

This work was supported by the Research Training Group 1023: Identification in Mathematical Models that was founded in 2004 at the Faculty of Mathematics at the University of Göttingen and was supported by the DFG (Deutsche Forschungsgemeinschaft) and by the Isaac Newton Institute for Mathematical Sciences (EPSRC [grant number EP/K032208/1], [grant number EP/R014604/]).

Notes

No potential conflict of interest was reported by the author.

Appendix 1

Proof of the Theorem 2.2:

As $a_{\alpha }$ is a solution of the minimization problem for the Tikhonov functional, the following inequality holds$$\begin{array}{cc}\hfill \Vert F(a_{\alpha })-u^{†}{\Vert }_{\mathcal{Y}}^2+\alpha {\Vert a_{\alpha }-a_0\Vert }_s^2& \le \Vert F(a^{†})-u^{†}{\Vert }_{\mathcal{Y}}^2+\alpha {\Vert a^{†}-a_0\Vert }_s^2\hfill \\ \hfill & =\alpha \Vert a^{†}-a_0{\Vert }_s^2.\hfill \end{array}$$

It follows that$$\begin{array}{cc}\hfill \Vert F(a_{\alpha })-u^{†}{\Vert }_{\mathcal{Y}}^2+\alpha {\Vert a_{\alpha }-a^{†}\Vert }_s^2& \le \alpha (\Vert a^{†}-a_0{\Vert }_s^2+\Vert a_{\alpha }-a^{†}{\Vert }_s^2-\Vert a_{\alpha }-a_0{\Vert }_s^2)\hfill \\ \hfill & =2\alpha {〈a^{†}-a_0,a^{†}-a_{\alpha }〉}_s.\hfill \end{array}$$

From Assumption 2.1 C it follows that$$\begin{array}{c}\hfill F(a_{\alpha })=F(a^{†})+F^{\prime }(a^{†})(a_{\alpha }-a^{†})+r_{\alpha },\text{with}\Vert r_{\alpha }{\Vert }_{\mathcal{Y}}\le \frac{{\lambda }^2}{4\mathrm{\Lambda }}{\Vert a_{\alpha }-a^{†}\Vert }_{-p}.\end{array}$$

Replacing the difference $F(a_{\alpha })-F(a^{†})$ in the previous inequality we obtain(37) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill \Vert F^{\prime }(a^{†})(a_{\alpha }-a^{†}){\Vert }_{\mathcal{Y}}^2+{\Vert r_{\alpha }\Vert }_{\mathcal{Y}}^2& +2〈F^{\prime }(a^{†})(a_{\alpha }-a^{†}),r_{\alpha }〉+\alpha {\Vert a_{\alpha }-a^{†}\Vert }_s^2\hfill \\ \hfill & \le 2\alpha {〈a^{†}-a_0,a^{†}-a_{\alpha }〉}_s.\hfill \end{array}\end{array}$$(37)

Using now Assumption 2.1 B we get that$$\begin{array}{c}\hfill {\lambda }^2\Vert a_{\alpha }-a^{†}{\Vert }_{-p}^2+\alpha \Vert a_{\alpha }-a^{†}{\Vert }_s^2\le 2\mathrm{\Lambda }\frac{{\lambda }^2}{4\mathrm{\Lambda }}{\Vert a_{\alpha }-a^{†}\Vert }_{-p}^2+2\alpha {〈a^{†}-a_0,a^{†}-a_{\alpha }〉}_s.\end{array}$$

Since we assumed that $a^{†}-a_0\in {\mathcal{X}}_q$ we have that$$\begin{array}{c}\hfill \frac{{\lambda }^2}{2}\Vert a_{\alpha }-a^{†}{\Vert }_{-p}^2+\alpha \Vert a_{\alpha }-a^{†}{\Vert }_s^2\le 2c\alpha {\Vert a_{\alpha }-a^{†}\Vert }_{2s-q}\end{array}$$

where $c=\Vert a^{†}-a_0{\Vert }_q$. We apply the interpolation inequality (7(7) $$\begin{array}{c}\hfill {\Vert x\Vert }_r\le {\Vert x\Vert }_t^{\frac{s-r}{s-t}}{\Vert x\Vert }_s^{\frac{r-t}{s-t}},x\in {\mathcal{X}}_s\end{array}$$(7) ) for $-p\le 2s-q\le s$ and obtain(A1) $$\begin{array}{c}\hfill \frac{{\lambda }^2}{2}\Vert a_{\alpha }-a^{†}{\Vert }_{-p}^2+\alpha \Vert a_{\alpha }-a^{†}{\Vert }_s^2\le 2c\alpha \Vert a_{\alpha }-a^{†}{\Vert }_{-p}^{\frac{-s+q}{s+p}}{\Vert a_{\alpha }-a^{†}\Vert }_s^{\frac{2s-q+p}{s+p}}.\end{array}$$(A1)

Then it holds$$\begin{array}{c}\hfill \Vert a_{\alpha }-a^{†}{\Vert }_{-p}^2\le \frac{4c}{{\lambda }^2}\alpha \Vert a_{\alpha }-a^{†}{\Vert }_{-p}^{\frac{-s+q}{s+p}}{\Vert a_{\alpha }-a^{†}\Vert }_s^{\frac{2s-q+p}{s+p}}\end{array}$$

and we can write$$\begin{array}{c}\hfill \Vert a_{\alpha }-a^{†}{\Vert }_{-p}^2\le {\left(\frac{4c}{{\lambda }^2}\right)}^{\frac{2(s+p)}{3s+2p-q}}{\alpha }^{\frac{2(s+p)}{3s+2p-q}}{\Vert a_{\alpha }-a^{†}\Vert }_s^{\frac{2(2s-q+p)}{3s+2p-q}}.\end{array}$$

From (A2(A2) $$\begin{array}{cc}\hfill \Vert a_{\alpha }-a^{†}{\Vert }_{-p}^2& \le {\left(\frac{4c}{{\lambda }^2}\alpha \right)}^{\frac{2(s+p)}{3s+2p-q}}{2}^{\frac{q+2p+s}{s+p}\frac{2s-q+p}{3s+2p-q}}{c}^{2\frac{2s-q+p}{3s+2p-q}}{\left(\frac{\alpha }{{\lambda }^2}\right)}^{\frac{-s+q}{s+p}\frac{2s+p-q}{3s+2p-q}}\hfill \\ \hfill & \le 2^{\frac{2s+3p+q}{s+p}}{c}^2{\left(\frac{\alpha }{{\lambda }^2}\right)}^{\frac{p+q}{s+p}}.\hfill \end{array}$$(A2) ) we have that$$\begin{array}{cc}\hfill \Vert a_{\alpha }-a^{†}{\Vert }_s^2& \le 2c\Vert a_{\alpha }-a^{†}{\Vert }_s^{\frac{2s-q+p}{s+p}}{\left(\frac{4c}{{\lambda }^2}\right)}^{\frac{q-s}{3s+2p-q}}{\alpha }^{\frac{-s+q}{3s+2p-q}}{\Vert a_{\alpha }-a^{†}\Vert }_s^{\frac{(-s+q)(2s-q+p)}{(s+p)(3s+2p-q)}}\hfill \\ \hfill & =2^{\frac{q+2p+s}{3s+2p-q}}{c}^{\frac{2(s+p)}{3s+2p-q}}{\left(\frac{\alpha }{{\lambda }^2}\right)}^{\frac{-s+q}{3s+2p-q}}{\Vert a_{\alpha }-a^{†}\Vert }_s^{\frac{2(2s-q+p)}{3s+2p-q}}\hfill \end{array}$$

and it follows$$\begin{array}{cc}\hfill \Vert a_{\alpha }-a^{†}{\Vert }_s^2& \le 2^{\frac{q+2p+s}{s+p}}{c}^2{\left(\frac{\alpha }{{\lambda }^2}\right)}^{\frac{-s+q}{s+p}}\hfill \end{array}$$

and(A2) $$\begin{array}{cc}\hfill \Vert a_{\alpha }-a^{†}{\Vert }_{-p}^2& \le {\left(\frac{4c}{{\lambda }^2}\alpha \right)}^{\frac{2(s+p)}{3s+2p-q}}{2}^{\frac{q+2p+s}{s+p}\frac{2s-q+p}{3s+2p-q}}{c}^{2\frac{2s-q+p}{3s+2p-q}}{\left(\frac{\alpha }{{\lambda }^2}\right)}^{\frac{-s+q}{s+p}\frac{2s+p-q}{3s+2p-q}}\hfill \\ \hfill & \le 2^{\frac{2s+3p+q}{s+p}}{c}^2{\left(\frac{\alpha }{{\lambda }^2}\right)}^{\frac{p+q}{s+p}}.\hfill \end{array}$$(A2)

Using the interpolation inequality (7(7) $$\begin{array}{c}\hfill {\Vert x\Vert }_r\le {\Vert x\Vert }_t^{\frac{s-r}{s-t}}{\Vert x\Vert }_s^{\frac{r-t}{s-t}},x\in {\mathcal{X}}_s\end{array}$$(7) ) the desired rate of convergence is obtained$$\begin{array}{cc}\hfill \Vert a_{\alpha }-a^{†}{\Vert }_0& \le \Vert a_{\alpha }-a^{†}{\Vert }_{-p}^{\frac{s}{p+s}}{\Vert a_{\alpha }-a^{†}\Vert }_s^{\frac{p}{s+p}}\hfill \\ \hfill & \le 2^{1+\frac{q}{2(s+p)}}c{\left(\frac{\alpha }{{\lambda }^2}\right)}^{\frac{1}{2}\frac{q}{p+s}}\hfill \\ \hfill & \le K·{\alpha }^{\frac{1}{2}\frac{q}{p+s}}\hfill \end{array}$$

with K a constant that depends on $s,p,q,\lambda ,c$. $\square$

Proof of the Theorem 2.3:

Let $a_{\alpha }^{\delta }$ be a solution of the optimization problem (8(8) $$\begin{array}{c}\hfill a_{\alpha }^{\delta }:={\mathit{argmin}}_{a\in D(F)\cap \left(a_0+{\mathcal{X}}_s\right)}\left({\Vert F(a)-Y\Vert }_{\mathcal{Y}}^2+\alpha {\Vert a-a_0\Vert }_s^2\right)\end{array}$$(8) ) and let us consider the Lagrange-Euler equation for the optimization problem (8(8) $$\begin{array}{c}\hfill a_{\alpha }^{\delta }:={\mathit{argmin}}_{a\in D(F)\cap \left(a_0+{\mathcal{X}}_s\right)}\left({\Vert F(a)-Y\Vert }_{\mathcal{Y}}^2+\alpha {\Vert a-a_0\Vert }_s^2\right)\end{array}$$(8) ). From classical results for calculus of variations we know that the first variation of the Tikhonov functional $J_{\alpha }$ defined as the right hand side in (8(8) $$\begin{array}{c}\hfill a_{\alpha }^{\delta }:={\mathit{argmin}}_{a\in D(F)\cap \left(a_0+{\mathcal{X}}_s\right)}\left({\Vert F(a)-Y\Vert }_{\mathcal{Y}}^2+\alpha {\Vert a-a_0\Vert }_s^2\right)\end{array}$$(8) ), is null for every direction $h\in X_s$ and, since we have Fréchet differentiability in $a_{\alpha }^{\delta }$ it follows that ${J_{\alpha }}^{\prime }(a_{\alpha }^{\delta })h=0$ for all $h\in {\mathcal{X}}_s$. This means$$\begin{array}{c}\hfill {〈F(a_{\alpha }^{\delta })-Y,F^{\prime }(a_{\alpha }^{\delta })h〉}_{\mathcal{Y}}+\alpha {〈a_{\alpha }^{\delta }-a_0,h〉}_s=0,h\in {\mathcal{X}}_s.\end{array}$$

Due to the same arguments, since $a_{\alpha }$ is the solution of the minimization problem (11(11) $$\begin{array}{c}\hfill a_{\alpha }:={\mathit{argmin}}_{a\in D(F)\cap \left(a_0+{\mathcal{X}}_s\right)}\left(\Vert F(a)-u^{†}{\Vert }_{\mathcal{Y}}^2+\alpha {\Vert a-a_0\Vert }_s^2\right).\end{array}$$(11) ) and from the Lagrange-Euler equation it follows$$\begin{array}{c}\hfill {〈F(a_{\alpha })-u^{†},F^{\prime }(a_{\alpha })h〉}_{\mathcal{Y}}+\alpha {〈a_{\alpha }-a_0,h〉}_s=0,h\in {\mathcal{X}}_s.\end{array}$$

As $a_{\alpha }^{\delta }-a_0,a_{\alpha }-a_0\in {\mathcal{X}}_s$ we have that $a_{\alpha }^{\delta }-a_{\alpha }\in {\mathcal{X}}_s$ and we can choose the direction $h=a_{\alpha }^{\delta }-a_{\alpha }$ in both equalities. It follows that$$\begin{array}{c}\hfill {〈F(a_{\alpha }^{\delta })-Y,F^{\prime }(a_{\alpha }^{\delta })(a_{\alpha }^{\delta }-a_{\alpha })〉}_{\mathcal{Y}}+\alpha {〈a_{\alpha }^{\delta }-a_0,a_{\alpha }^{\delta }-a_{\alpha }〉}_s=0,\end{array}$$ $$\begin{array}{c}\hfill {〈F(a_{\alpha })-u^{†},F^{\prime }(a_{\alpha })(a_{\alpha }^{\delta }-a_{\alpha })〉}_{\mathcal{Y}}+\alpha {〈a_{\alpha }-a_0,a_{\alpha }^{\delta }-a_{\alpha }〉}_s=0.\end{array}$$

Taking the difference between these two relations we obtain(A3) $$\begin{array}{c}\hfill \begin{array}{cc}& {〈F(a_{\alpha }^{\delta })-Y,F^{\prime }(a_{\alpha }^{\delta })(a_{\alpha }^{\delta }-a_{\alpha })〉}_{\mathcal{Y}}-{〈F(a_{\alpha })-u^{†},F^{\prime }(a_{\alpha })(a_{\alpha }^{\delta }-a_{\alpha })〉}_{\mathcal{Y}}\hfill \\ \hfill & +\alpha {〈a_{\alpha }^{\delta }-a_{\alpha },a_{\alpha }^{\delta }-a_{\alpha }〉}_s=0.\hfill \end{array}\end{array}$$(A3)

From Assumption 2.1 we can write the Taylor polynomial as$$\begin{array}{c}\hfill F(a_{\alpha })=F(a^{†})+F^{\prime }(a^{†})(a_{\alpha }-a^{†})+{\int }_0^1\left\{F^{\prime }(a^{†}+t(a_{\alpha }-a^{†}))-F^{\prime }(a^{†})\right\}(a_{\alpha }-a^{†})\mathrm{d}t\\ \hfill F(a_{\alpha }^{\delta })=F(a^{†})+F^{\prime }(a^{†})(a_{\alpha }^{\delta }-a^{†})+{\int }_0^1\left\{F^{\prime }(a^{†}+t(a_{\alpha }^{\delta }-a^{†}))-F^{\prime }(a^{†})\right\}(a_{\alpha }^{\delta }-a^{†})\mathrm{d}t\end{array}$$

and we get$$\begin{array}{cc}\hfill F(a_{\alpha }^{\delta })-F(a_{\alpha })& =F^{\prime }(a^{†})(a_{\alpha }^{\delta }-a_{\alpha })\hfill \\ \hfill & -{\int }_0^1\left\{F^{\prime }(a^{†}+t(a_{\alpha }-a^{†}))-F^{\prime }(a^{†})\right\}(a_{\alpha }-a^{†})\mathrm{d}t\hfill \\ \hfill & +{\int }_0^1\left\{F^{\prime }(a^{†}+t(a_{\alpha }^{\delta }-a^{†}))-F^{\prime }(a^{†})\right\}(a_{\alpha }^{\delta }-a_{\alpha })\mathrm{d}t\hfill \\ \hfill & +{\int }_0^1\left\{F^{\prime }(a^{†}+t(a_{\alpha }^{\delta }-a^{†}))-F^{\prime }(a^{†})\right\}(a_{\alpha }-a^{†})\mathrm{d}t.\hfill \end{array}$$

We denote the three integrals as $I_1,I_2$ respectively $I_3$ and, from Assumption 2.1, we can bound their norms by$$\begin{array}{cc}\hfill \Vert I_1\Vert & \le {\int }_0^1\Vert F^{\prime }(a^{†}+t(a_{\alpha }-a^{†}))-F^{\prime }(a^{†}){\Vert }_{\mathcal{Y}\leftarrow {\mathcal{X}}_{-p}}{\Vert a_{\alpha }-a^{†}\Vert }_{-p}\mathrm{d}t\hfill \\ \hfill & \le {\int }_0^1{C}_{L}t\Vert a_{\alpha }-a^{†}{\Vert }_0\Vert a_{\alpha }-a^{†}{\Vert }_{-p}\mathrm{d}t=\frac{C_L}{2}\Vert a_{\alpha }-a^{†}{\Vert }_0{\Vert a_{\alpha }-a^{†}\Vert }_{-p}\hfill \\ \hfill & \le \frac{{\lambda }^2}{4\mathrm{\Lambda }}{\Vert a_{\alpha }-a^{†}\Vert }_{-p}\hfill \\ \hfill \Vert I_2\Vert & \le {\int }_0^1\Vert F^{\prime }(a^{†}+t(a_{\alpha }^{\delta }-a^{†}))-F^{\prime }(a^{†}){\Vert }_{\mathcal{Y}\leftarrow {\mathcal{X}}_{-p}}{\Vert a_{\alpha }^{\delta }-a_{\alpha }\Vert }_{-p}\mathrm{d}t\hfill \\ \hfill & \le {\int }_0^1{C}_{L}t\Vert a_{\alpha }^{\delta }-a^{†}{\Vert }_0\Vert a_{\alpha }^{\delta }-a_{\alpha }{\Vert }_{-p}\mathrm{d}t\le \frac{C_L}{2}\Vert a_{\alpha }^{\delta }-a^{†}{\Vert }_0{\Vert a_{\alpha }^{\delta }-a_{\alpha }\Vert }_{-p}\hfill \\ \hfill & \le \frac{{\lambda }^2}{4\mathrm{\Lambda }}{\Vert a_{\alpha }^{\delta }-a_{\alpha }\Vert }_{-p}\hfill \\ \hfill \Vert I_3\Vert & \le {\int }_0^1\Vert F^{\prime }(a^{†}+t(a_{\alpha }^{\delta }-a^{†}))-F^{\prime }(a^{†}){\Vert }_{Y\leftarrow {\mathcal{X}}_{-p}}{\Vert a_{\alpha }-a^{†}\Vert }_{-p}\mathrm{d}t\hfill \\ \hfill \Vert I_3\Vert & \le {\int }_0^1{C}_{L}t\Vert a_{\alpha }^{\delta }-a^{†}{\Vert }_0\Vert a_{\alpha }-a^{†}{\Vert }_{-p}\mathrm{d}t\le \frac{C_L}{2}\Vert a_{\alpha }^{\delta }-a^{†}{\Vert }_0{\Vert a_{\alpha }-a^{†}\Vert }_{-p}\hfill \\ \hfill & \le \frac{{\lambda }^2}{4\mathrm{\Lambda }}{\Vert a_{\alpha }-a^{†}\Vert }_{-p}.\hfill \end{array}$$ We write now the relation (A4(A4) $$\begin{array}{cc}\hfill {\lambda }^2\Vert a_{\alpha }^{\delta }-a_{\alpha }{\Vert }_{-p}^2+\alpha {\Vert a_{\alpha }^{\delta }-a_{\alpha }\Vert }_s^2& \le \left(\frac{{\lambda }^2}{2}+\frac{{\lambda }^4}{16{\mathrm{\Lambda }}^2}\right){\Vert a_{\alpha }^{\delta }-a_{\alpha }\Vert }_{-p}^2\hfill \\ \hfill & +\left({\lambda }^2+\frac{{\lambda }^4}{8{\mathrm{\Lambda }}^2}\right)\Vert a_{\alpha }-a^{†}{\Vert }_{-p}{\Vert a_{\alpha }^{\delta }-a_{\alpha }\Vert }_{-p}\hfill \\ \hfill & +\left(\mathrm{\Lambda }+\frac{{\lambda }^2}{4\mathrm{\Lambda }}\right)\delta {\Vert a_{\alpha }^{\delta }-a_{\alpha }\Vert }_{-p}\hfill \end{array}$$(A4) ) as$$\begin{array}{cc}& {〈F(a_{\alpha }^{\delta })-F(a_{\alpha })+F(a_{\alpha })-u^{†}+u^{†}-Y,(F^{\prime }(a_{\alpha }^{\delta })-F^{\prime }(a^{†}))(a_{\alpha }^{\delta }-a_{\alpha })〉}_{\mathcal{Y}}\hfill \\ \hfill & -{〈F(a_{\alpha })-u^{†},(F^{\prime }(a_{\alpha })-F^{\prime }(a^{†}))(a_{\alpha }^{\delta }-a_{\alpha })〉}_{\mathcal{Y}}\hfill \\ \hfill & +{〈F(a_{\alpha }^{\delta })-F(a_{\alpha })-Y+u^{†},F^{\prime }(a^{†})(a_{\alpha }^{\delta }-a_{\alpha })〉}_{\mathcal{Y}}+\alpha {\Vert a_{\alpha }^{\delta }-a_{\alpha }\Vert }_s^2=0.\hfill \end{array}$$

Using the Taylor formula we get$$\begin{array}{cc}& 〈F^{\prime }(a^{†})(a_{\alpha }^{\delta }-a_{\alpha })-I_1+I_2+I_3+F^{\prime }(a^{†})(a_{\alpha }-a^{†})+I_1+u^{†}-Y,\hfill \\ \hfill & {(F^{\prime }(a_{\alpha }^{\delta })-F^{\prime }(a^{†}))(a_{\alpha }^{\delta }-a_{\alpha })〉}_{\mathcal{Y}}+\alpha {\Vert a_{\alpha }^{\delta }-a_{\alpha }\Vert }_s^2\hfill \\ \hfill & -{〈F^{\prime }(a^{†})(a_{\alpha }-a^{†})+I_1,(F^{\prime }(a_{\alpha })-F^{\prime }(a^{†}))(a_{\alpha }^{\delta }-a_{\alpha })〉}_{\mathcal{Y}}\hfill \\ \hfill & +{〈F^{\prime }(a^{†})(a_{\alpha }^{\delta }-a_{\alpha })-I_1+I_2+I_3+u^{†}-Y,F^{\prime }(a^{†})(a_{\alpha }^{\delta }-a_{\alpha })〉}_{\mathcal{Y}}=0.\hfill \end{array}$$

It follows$$\begin{array}{cc}& \alpha \Vert a_{\alpha }^{\delta }-a_{\alpha }{\Vert }_s^2+{\Vert F^{\prime }(a^{†})(a_{\alpha }^{\delta }-a_{\alpha })\Vert }_{\mathcal{Y}}^2\hfill \\ \hfill & ={〈F^{\prime }(a^{†})(a_{\alpha }-a^{†})+I_1,(F^{\prime }(a_{\alpha })-F^{\prime }(a^{†}))(a_{\alpha }^{\delta }-a_{\alpha })〉}_{\mathcal{Y}}\hfill \\ \hfill & -{〈-I_1+I_2+I_3+u^{†}-Y,F^{\prime }(a^{†})(a_{\alpha }^{\delta }-a_{\alpha })〉}_{\mathcal{Y}}\hfill \\ \hfill & -〈F^{\prime }(a^{†})(a_{\alpha }^{\delta }-a_{\alpha })+I_2+I_3+F^{\prime }(a^{†})(a_{\alpha }-a^{†})+u^{†}-Y,\hfill \\ \hfill & {(F^{\prime }(a_{\alpha }^{\delta })-F^{\prime }(a^{†}))(a_{\alpha }^{\delta }-a_{\alpha })〉}_{\mathcal{Y}}.\hfill \end{array}$$

From Cauchy-Schwarz inequality, Assumptions 2.1 and the norm estimates for $I_1$, $I_2$ and $I_3$ we have$$\begin{array}{cc}& {\lambda }^2\Vert a_{\alpha }^{\delta }-a_{\alpha }{\Vert }_{-p}^2+\alpha {\Vert a_{\alpha }^{\delta }-a_{\alpha }\Vert }_s^2\hfill \\ \hfill & \le \left(\mathrm{\Lambda }\Vert a_{\alpha }-a^{†}{\Vert }_{-p}+\frac{{\lambda }^2}{4\mathrm{\Lambda }}{\Vert a_{\alpha }-a^{†}\Vert }_{-p}\right)\frac{{\lambda }^2}{4\mathrm{\Lambda }}{\Vert a_{\alpha }^{\delta }-a_{\alpha }\Vert }_{-p}\hfill \\ \hfill & +\mathrm{\Lambda }\Vert a_{\alpha }^{\delta }-a_{\alpha }{\Vert }_{-p}\left(\frac{{\lambda }^2}{4\mathrm{\Lambda }}\Vert a_{\alpha }-a^{†}{\Vert }_{-p}+\frac{{\lambda }^2}{4\mathrm{\Lambda }}{\Vert a_{\alpha }^{\delta }-a_{\alpha }\Vert }_{-p}\right.\hfill \\ \hfill & \left.+\frac{{\lambda }^2}{4\mathrm{\Lambda }}{\Vert a_{\alpha }-a^{†}\Vert }_{-p}+\delta \right)+\left(\delta +\mathrm{\Lambda }\Vert a_{\alpha }^{\delta }-a_{\alpha }{\Vert }_{-p}+\frac{{\lambda }^2}{4\mathrm{\Lambda }}{\Vert a_{\alpha }^{\delta }-a_{\alpha }\Vert }_{-p}\right.\hfill \\ \hfill & \left.+\mathrm{\Lambda }\Vert a_{\alpha }-a^{†}{\Vert }_{-p}+\frac{{\lambda }^2}{4\mathrm{\Lambda }}{\Vert a_{\alpha }-a^{†}\Vert }_{-p}\right)\frac{{\lambda }^2}{4\mathrm{\Lambda }}{\Vert a_{\alpha }^{\delta }-a_{\alpha }\Vert }_{-p}.\hfill \end{array}$$

We can rewrite this inequality as(A4) $$\begin{array}{cc}\hfill {\lambda }^2\Vert a_{\alpha }^{\delta }-a_{\alpha }{\Vert }_{-p}^2+\alpha {\Vert a_{\alpha }^{\delta }-a_{\alpha }\Vert }_s^2& \le \left(\frac{{\lambda }^2}{2}+\frac{{\lambda }^4}{16{\mathrm{\Lambda }}^2}\right){\Vert a_{\alpha }^{\delta }-a_{\alpha }\Vert }_{-p}^2\hfill \\ \hfill & +\left({\lambda }^2+\frac{{\lambda }^4}{8{\mathrm{\Lambda }}^2}\right)\Vert a_{\alpha }-a^{†}{\Vert }_{-p}{\Vert a_{\alpha }^{\delta }-a_{\alpha }\Vert }_{-p}\hfill \\ \hfill & +\left(\mathrm{\Lambda }+\frac{{\lambda }^2}{4\mathrm{\Lambda }}\right)\delta {\Vert a_{\alpha }^{\delta }-a_{\alpha }\Vert }_{-p}\hfill \end{array}$$(A4)

As $\lambda \le \mathrm{\Lambda }$ we have $\frac{{\lambda }^4}{16{\mathrm{\Lambda }}^2}\le \frac{{\lambda }^2}{16}$ and it holds$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \frac{7{\lambda }^2}{16}\Vert a_{\alpha }^{\delta }-a_{\alpha }{\Vert }_{-p}^2+\alpha {\Vert a_{\alpha }^{\delta }-a_{\alpha }\Vert }_s^2\le & \left({\lambda }^2+\frac{{\lambda }^4}{8{\mathrm{\Lambda }}^2}\right)\Vert a_{\alpha }-a^{†}{\Vert }_{-p}{\Vert a_{\alpha }^{\delta }-a_{\alpha }\Vert }_{-p}\hfill \\ \hfill & +\left(\mathrm{\Lambda }+\frac{{\lambda }^2}{4\mathrm{\Lambda }}\right)\delta {\Vert a_{\alpha }^{\delta }-a_{\alpha }\Vert }_{-p}\hfill \end{array}\end{array}$$

To simplify the notation, we introduce a positive constant $k_{\ast }\in \mathbf{R}$ that will vary from line to line in the following paragraphs. We have that$$\begin{array}{cc}\hfill \Vert a_{\alpha }^{\delta }-a_{\alpha }{\Vert }_{-p}^2& \le \frac{16}{7}\left(1+\frac{{\lambda }^2}{8{\mathrm{\Lambda }}^2}\right)\Vert a_{\alpha }-a^{†}{\Vert }_{-p}\Vert a_{\alpha }^{\delta }-a_{\alpha }{\Vert }_{-p}+\frac{16}{7}\left(\frac{\mathrm{\Lambda }}{{\lambda }^2}+\frac{1}{4\mathrm{\Lambda }}\right)\delta {\Vert a_{\alpha }^{\delta }-a_{\alpha }\Vert }_{-p}\hfill \\ \hfill & \le k_{\ast }\left(\Vert a_{\alpha }-a^{†}{\Vert }_{-p}\Vert a_{\alpha }^{\delta }-a_{\alpha }{\Vert }_{-p}+\left(\frac{\mathrm{\Lambda }}{{\lambda }^2}+\frac{1}{4\mathrm{\Lambda }}\right)\delta {\Vert a_{\alpha }^{\delta }-a_{\alpha }\Vert }_{-p}\right)\hfill \end{array}$$

and this implies(A5) $$\begin{array}{cc}\hfill \Vert a_{\alpha }^{\delta }-a_{\alpha }{\Vert }_{-p}& \le k_{\ast }\left(\Vert a_{\alpha }-a^{†}{\Vert }_{-p}+\left(\frac{\mathrm{\Lambda }}{{\lambda }^2}+\frac{1}{4\mathrm{\Lambda }}\right)\delta \right)\hfill \\ \hfill & \le k_{\ast }\left(c{\left(\frac{2\alpha }{{\lambda }^2}\right)}^{\frac{p+q}{2(s+p)}}+\left(\frac{\mathrm{\Lambda }}{{\lambda }^2}+\frac{1}{4\mathrm{\Lambda }}\right)\delta \right)\hfill \end{array}$$(A5)

since we computed the rates of convergence for the $-p-$norm of the approximation error $\Vert a_{\alpha }-a^{†}{\Vert }_{-p}^2$ in (A3(A3) $$\begin{array}{c}\hfill \begin{array}{cc}& {〈F(a_{\alpha }^{\delta })-Y,F^{\prime }(a_{\alpha }^{\delta })(a_{\alpha }^{\delta }-a_{\alpha })〉}_{\mathcal{Y}}-{〈F(a_{\alpha })-u^{†},F^{\prime }(a_{\alpha })(a_{\alpha }^{\delta }-a_{\alpha })〉}_{\mathcal{Y}}\hfill \\ \hfill & +\alpha {〈a_{\alpha }^{\delta }-a_{\alpha },a_{\alpha }^{\delta }-a_{\alpha }〉}_s=0.\hfill \end{array}\end{array}$$(A3) ). Using (A3(A3) $$\begin{array}{c}\hfill \begin{array}{cc}& {〈F(a_{\alpha }^{\delta })-Y,F^{\prime }(a_{\alpha }^{\delta })(a_{\alpha }^{\delta }-a_{\alpha })〉}_{\mathcal{Y}}-{〈F(a_{\alpha })-u^{†},F^{\prime }(a_{\alpha })(a_{\alpha }^{\delta }-a_{\alpha })〉}_{\mathcal{Y}}\hfill \\ \hfill & +\alpha {〈a_{\alpha }^{\delta }-a_{\alpha },a_{\alpha }^{\delta }-a_{\alpha }〉}_s=0.\hfill \end{array}\end{array}$$(A3) ) and (A6(A6) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill \Vert a_{\alpha }^{\delta }-a_{\alpha }{\Vert }_0^2\le & k_1{\alpha }^{\frac{q}{p+s}}+\left(k_1+k_2\right){\delta }^2{\alpha }^{-\frac{p}{s+p}}\hfill \end{array}\end{array}$$(A6) ) in (A5(A5) $$\begin{array}{cc}\hfill \Vert a_{\alpha }^{\delta }-a_{\alpha }{\Vert }_{-p}& \le k_{\ast }\left(\Vert a_{\alpha }-a^{†}{\Vert }_{-p}+\left(\frac{\mathrm{\Lambda }}{{\lambda }^2}+\frac{1}{4\mathrm{\Lambda }}\right)\delta \right)\hfill \\ \hfill & \le k_{\ast }\left(c{\left(\frac{2\alpha }{{\lambda }^2}\right)}^{\frac{p+q}{2(s+p)}}+\left(\frac{\mathrm{\Lambda }}{{\lambda }^2}+\frac{1}{4\mathrm{\Lambda }}\right)\delta \right)\hfill \end{array}$$(A5) ) we notice that$$\begin{array}{cc}\hfill \Vert a_{\alpha }^{\delta }-a_{\alpha }{\Vert }_s^2& \le \frac{1}{\alpha }{\Vert a_{\alpha }^{\delta }-a_{\alpha }\Vert }_{-p}\left(\frac{9}{8}{\lambda }^2{\Vert a_{\alpha }-a^{†}\Vert }_{-p}+\frac{5}{4}\mathrm{\Lambda }\delta \right)\hfill \\ \hfill & \le \frac{1}{\alpha }{k}_{\ast }\left(c{\left(\frac{2\alpha }{{\lambda }^2}\right)}^{\frac{p+q}{2(s+p)}}+\left(\frac{\mathrm{\Lambda }}{{\lambda }^2}+\frac{1}{4\mathrm{\Lambda }}\right)\delta \right)\left(\frac{9}{4}{\lambda }^{2}c{\left(\frac{2\alpha }{{\lambda }^2}\right)}^{\frac{p+q}{2(s+p)}}+\frac{5}{4}\mathrm{\Lambda }\delta \right)\hfill \\ \hfill & \le k_{\ast }\left(c^2{\left(\frac{2\alpha }{{\lambda }^2}\right)}^{\frac{q-s}{p+s}}+c\mathrm{\Lambda }\delta {\left(\frac{2}{{\lambda }^2}\right)}^{\frac{p+q}{2(p+s)}}{\alpha }^{\frac{-2s-p+q}{2(p+s)}}+\left(\frac{{\mathrm{\Lambda }}^2}{{\lambda }^2}+\frac{1}{4}\right)\frac{{\delta }^2}{\alpha }\right)\hfill \end{array}$$

From (A6(A6) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill \Vert a_{\alpha }^{\delta }-a_{\alpha }{\Vert }_0^2\le & k_1{\alpha }^{\frac{q}{p+s}}+\left(k_1+k_2\right){\delta }^2{\alpha }^{-\frac{p}{s+p}}\hfill \end{array}\end{array}$$(A6) ) it holds$$\begin{array}{cc}\hfill \Vert a_{\alpha }^{\delta }-a_{\alpha }{\Vert }_{-p}^2& \le k_{\ast }\left(c^2{\left(\frac{2\alpha }{{\lambda }^2}\right)}^{\frac{p+q}{s+p}}+{\left(\frac{\mathrm{\Lambda }}{{\lambda }^2}+\frac{1}{4\mathrm{\Lambda }}\right)}^2{\delta }^2\right)\hfill \\ \hfill & \le k_{\ast }\left(c^2{\left(\frac{2\alpha }{{\lambda }^2}\right)}^{\frac{p+q}{s+p}}+{\left(\frac{\mathrm{\Lambda }}{{\lambda }^2}+\frac{1}{4\mathrm{\Lambda }}\right)}^2{\delta }^2\right)\hfill \end{array}$$

We apply now the interpolation inequality (7(7) $$\begin{array}{c}\hfill {\Vert x\Vert }_r\le {\Vert x\Vert }_t^{\frac{s-r}{s-t}}{\Vert x\Vert }_s^{\frac{r-t}{s-t}},x\in {\mathcal{X}}_s\end{array}$$(7) ) to obtain$$\begin{array}{cc}\hfill \Vert a_{\alpha }^{\delta }-a_{\alpha }{\Vert }_0^2\le & \Vert a_{\alpha }^{\delta }-a_{\alpha }{\Vert }_{-p}^{\frac{2s}{p+s}}{\Vert a_{\alpha }^{\delta }-a_{\alpha }\Vert }_s^{\frac{2p}{p+s}}\hfill \end{array}$$

Since ${(x+y)}^r\le x^r+y^r$ for all x, y positive and $0\le r\le 1$, we get the following inequality$$\begin{array}{cc}& \Vert a_{\alpha }^{\delta }-a_{\alpha }{\Vert }_0^2\le k_{\ast }\left(c^{\frac{2s}{s+p}}{\left(\frac{2\alpha }{{\lambda }^2}\right)}^{\frac{s(p+q)}{{(s+p)}^2}}+{\left(\frac{\mathrm{\Lambda }}{{\lambda }^2}+\frac{1}{4\mathrm{\Lambda }}\right)}^{\frac{2s}{s+p}}{\delta }^{\frac{2s}{s+p}}\right)·\hfill \\ \hfill & k_{\ast }\left({\left(\frac{2\alpha }{{\lambda }^2}\right)}^{\frac{p(q-s)}{{(p+s)}^2}}+{\mathrm{\Lambda }}^{\frac{p}{s+p}}{\left(\frac{2}{{\lambda }^2}\right)}^{\frac{p(p+q)}{2{(p+s)}^2}}{\alpha }^{\frac{p(-2s-p+q)}{2{(p+s)}^2}}{\delta }^{\frac{p}{s+p}}+{\left(\frac{{\mathrm{\Lambda }}^2}{{\lambda }^2}+\frac{1}{4}\right)}^{\frac{p}{s+p}}{\left(\frac{{\delta }^2}{\alpha }\right)}^{\frac{p}{s+p}}\right)\hfill \\ \hfill \end{array}$$

meaning that$$\begin{array}{cc}& \Vert a_{\alpha }^{\delta }-a_{\alpha }{\Vert }_0^2\le k_{\ast }\left(c^2{\left(\frac{2\alpha }{{\lambda }^2}\right)}^{\frac{q}{p+s}}+{\alpha }^{\frac{2sq+pq-p^2}{2{(s+p)}^2}}{\left(\frac{2}{{\lambda }^2}\right)}^{\frac{(p+q)(2s+p)}{2{(s+p)}^2}}{\delta }^{\frac{p}{s+p}}\right.\hfill \\ \hfill & +{\left(\frac{{\mathrm{\Lambda }}^2}{{\lambda }^2}+\frac{1}{4}\right)}^{1+\frac{s}{s+p}}{\mathrm{\Lambda }}^{-\frac{2s}{s+p}}{\alpha }^{-\frac{p}{s+p}}{\delta }^2\hfill \\ \hfill & +{\left(\frac{\mathrm{\Lambda }}{{\lambda }^2}+\frac{1}{4\mathrm{\Lambda }}\right)}^{\frac{2s}{s+p}}{c}^{\frac{2p}{s+p}}{\left(\frac{2\alpha }{{\lambda }^2}\right)}^{\frac{p(q-s)}{{(s+p)}^2}}{\delta }^{\frac{2s}{s+p}}\hfill \\ \hfill & +c^{\frac{p}{s+p}}{\mathrm{\Lambda }}^{\frac{p}{s+p}}{\left(\frac{\mathrm{\Lambda }}{{\lambda }^2}+\frac{1}{4\mathrm{\Lambda }}\right)}^{\frac{2s}{s+p}}{\left(\frac{2}{{\lambda }^2}\right)}^{\frac{p(p+q)}{2{(s+p)}^2}}{\alpha }^{\frac{p(-2s-p+q)}{2{(s+p)}^2}}{\delta }^{1+\frac{s}{s+p}}\hfill \\ \hfill & \left.+c^{\frac{2s}{s+p}}{\left(\frac{{\mathrm{\Lambda }}^2}{{\lambda }^2}+\frac{1}{4}\right)}^{\frac{p}{s+p}}{\left(\frac{2}{{\lambda }^2}\right)}^{\frac{s(p+q)}{{(s+p)}^2}}{\alpha }^{\frac{qs-p^2}{{(s+p)}^2}}{\delta }^{\frac{2p}{s+p}}\right)\hfill \\ \hfill \end{array}$$

where we used the inequalities $\frac{p}{s+p}\le 0.5$ and $\frac{s}{s+p}\le 1$ to bound the numerical constants. We now apply four times the Young inequality$$\begin{array}{c}\hfill ab\le \frac{a^k}{k}+\frac{b^l}{l},\end{array}$$

which holds for all $a,b>0$, $1<k,l<\infty$ and $\frac{1}{k}+\frac{1}{l}=1$ with $a^k={\delta }^2{\alpha }^{\frac{-p}{s+p}}$. For the second term we take $b={\alpha }^{\frac{2qs+pq}{2{(s+p)}^2}}$, $k=\frac{2(s+p)}{p}$ and $l=\frac{2(s+p)}{2s+p}$, for the fourth $b={\alpha }^{\frac{\mathit{pq}}{{(s+p)}^2}}$, $l=\frac{s+p}{p}$ and $k=\frac{s+p}{s}$, for the fifth $b={\alpha }^{\frac{\mathit{pq}}{2{(s+p)}^2}}$, $k=\frac{2(s+p)}{2s+p}$ and $l=\frac{2(s+p)}{p}$, for the sixth term $b={\alpha }^{\frac{\mathit{pq}}{{(s+p)}^2}}$, $k=\frac{s+p}{s}$ and $l=\frac{s+p}{p}$. This yields(A6) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill \Vert a_{\alpha }^{\delta }-a_{\alpha }{\Vert }_0^2\le & k_1{\alpha }^{\frac{q}{p+s}}+\left(k_1+k_2\right){\delta }^2{\alpha }^{-\frac{p}{s+p}}\hfill \end{array}\end{array}$$(A6)

where and $k_2=12{\left(\frac{{\mathrm{\Lambda }}^2}{{\lambda }^2}+\frac{1}{4}\right)}^{1+\frac{s}{s+p}}{\mathrm{\Lambda }}^{-\frac{2s}{s+p}}$ can be easily computed from the second term and from an upper bound for $k_{\ast }$, and $k_1$ is a constant that depends on $s,p,q,\lambda ,\mathrm{\Lambda },c$ such that $k_1\ge K$. $\square$

For the sake of completeness, we state now the following result from [40] that was applied in our article in the proof of Lemma 4.3.

Lemma A.1:

Let $p:{\mathbf{R}}^n\to \mathbf{R}$ be a polynomial of degree at most d. Suppose $0<r\le q<\infty$ and $\mu$ is a log-concave probability measure on ${\mathbf{R}}^n$. Then there is an absolute constant C such that$$\begin{array}{c}\hfill {\left({\int \Vert p(x)\Vert }^{\frac{p}{q}}\mathrm{d}\mu (x)\right)}^{\frac{1}{q}}\le C\frac{max(q,1)}{max(r,1)}{\left({\int \Vert p(x)\Vert }^{\frac{r}{d}}\mathrm{d}\mu (x)\right)}^{\frac{1}{r}}.\end{array}$$