Collocation method based on shifted Chebyshev and radial basis functions with symmetric variable shape parameter for solving the parabolic inverse problem

ABSTRACT

This work introduces a new numerical solution to the inverse parabolic problem with source control parameter that has important applications in large fields of applied science. We expand the approximate solution of the inverse problem in terms of shifted Chebyshev polynomials in time and radial basis functions with symmetric variable shape parameter in space, with unknown coefficients. Unknown coefficient matrix determined using the collocation technique. Sample results show that the proposed method is very accurate. Moreover, the proposed method is compared with two other methods, fourth-order compact difference scheme and method of lines. Finally, we examine the stability of our method for the case where there is additive noise in input data.

KEYWORDS:

• Inverse parabolic problem
• radial basis function
• variable shape parameter
• shifted Chebyshev polynomial
• stability

AMS SUBJECT CLASSIFICATIONS:

• 65M32
• 65N21
• 65N99
• 94A11
• 65D20

1. Introduction

This paper concerns an application of the radial basis functions (RBFs) with variable shape parameter (VSP) and basis functions of Chebyshev polynomials in order to find the solution of a parabolic inverse problem with source control parameter. Comparing with partial differential equations with standard boundary conditions, on which several works have been done, the numerical approximation of parabolic partial differential equations with overspecified data have been much less interesting for researchers to work on it.

Recently, many phenomena in physics and engineering such as heat conduction processes, population dynamics, nuclear reactor dynamics, thermoelasticity, control theory and vibration problems [1–9] have been described as a parabolic inverse problem with source control parameter. Determination of this parameter from the overspecified data is a technique that is used to identify the unknown properties, such as conductivity medium, by measuring data only on its boundary or a specified location in the domain. These properties usually cannot be measured directly and have to be determined by the observable data with measured errors. In general, these problems are ill-posed and any small error in measurement can lead to large error in the solution of the problem.

Here we study the inverse problem consisting in finding a source control parameter p(t) as following:(1.1) $$\begin{array}{c}\hfill u_t=u_{\mathit{xx}}+p(t)u+\phi (x,t),0\le x\le 1,0<t\le T,\end{array}$$(1.1)

subject to the initial and boundary conditions:(1.2) $$\begin{array}{c}\hfill u(x,0)=f(x),0\le x\le 1,\end{array}$$(1.2) (1.3) $$\begin{array}{c}\hfill u(0,t)=g_0(t),0<t\le T,\end{array}$$(1.3) (1.4) $$\begin{array}{c}\hfill u(1,t)=g_1(t),0<t\le T,\end{array}$$(1.4)

with the overspecification at a point in the spatial domain(1.5) $$\begin{array}{c}\hfill u(x_0,t)=H(t),0<t\le T,\end{array}$$(1.5)

where $T>0$ is constant and $\phi ,f,g_0,g_1$ and H are known functions. Equation (1.1(1.1) $$\begin{array}{c}\hfill u_t=u_{\mathit{xx}}+p(t)u+\phi (x,t),0\le x\le 1,0<t\le T,\end{array}$$(1.1) ) can be used to describe a heat transfer process with a source parameter p(t). Equation (1.5(1.5) $$\begin{array}{c}\hfill u(x_0,t)=H(t),0<t\le T,\end{array}$$(1.5) ) represents the temperature at a given point $x_0$ in a spatial domain at time t and u is the temperature distribution. Thus, the purpose of solving the inverse problem (1.1(1.1) $$\begin{array}{c}\hfill u_t=u_{\mathit{xx}}+p(t)u+\phi (x,t),0\le x\le 1,0<t\le T,\end{array}$$(1.1) )–(1.5(1.5) $$\begin{array}{c}\hfill u(x_0,t)=H(t),0<t\le T,\end{array}$$(1.5) ) is to identify the source parameter that will produce at any time t, a desired temperature at a given point $x_0$ in a spatial domain. In the direct problem, parameter p(t) is a known function whereas in the inverse problem, it is unknown and the problem is to find u(x, t) and p(t) simultaneously. Theoretical topics for this problem are studied in [10–12]. In [1–3], Dehghan considered several traditional explicite and implicite finite difference methods (FDM).Their convergence were of second order and forth order, to solve this problem. Dehghan and Tatari in [13] have found the solution of this problem with Gaussian Radial basis functions and have compared it with well-known finite difference methods and have concluded that this technique is more accurate. In [14], Lyu Yang et al. have designed a stable algorithm based on the optimal control framework, Cheng [5] used the approximation of moving least square (MLS) to find the solution of this inverse problem and compared it with other numerical methods such as FDM, finite element method (FEM) and boundary element method (BEM). Other techniques for this problem are provided in [6–9], Mohebbi and Abbasi [4] in 2014 have used a high-order scheme for determining unknown control parameter and unknown solution of parabolic inverse problem. They have replaced the space derivation with a fourth-order compact finite difference approximation and have showed that the convergence of this scheme order is $O({\tau }^2+h^4)$ where h denotes the step size of spatial variable, and $\tau$ denotes the step size of time variable.

Nowadays, a new class of numerical methods, which approximate various kinds of partial differential equations, are developed based on a set of scattered nodes without a need for an additional mesh. These methods are called meshfree methods. Some meshfree methods include the diffuse element method [15], the element free Galerkin method [16] and the meshless local petro-Galerkin method [17].

Traditional methods such as FDM and FEM are most well-known methods that rely on a mesh. Working with techniques that need to mesh has its own problems, for example, having conditional stability on explicit FDMs, requiring a large amount of CPU time in implicit FDMs and decreasing accuracy for non-smooth and irregular geometries. Although the FEM is flexible in geometry, it is hard to achieve high-order accuracy and moreover, mesh generation becomes increasingly difficult when the number of space dimensions increases.

The method that not only devoid of above techniques defects and disadvantages, but also has some features like high-order accuracy, computational efficiency, flexibility with respect to geometry and easiness in implementation. These features properties of an almost ideal numerical method for solving partial differential equations is RBF method. The main advantage of this method is the meshless property since fitting the appropriate mesh on the domain of the problem is very time-consuming. The RBFs were introduced by Hardy [18] and became popular in multivariate interpolation, in addition, RBF method for the solution of differential equations was introduced by Kansa [19,20] in 1990.

The RBF method is widely applied to approximate scattered data. The use of this method for solving partial differential equations is based on the collocation scheme. As shown by Kansa, using this RBFs to solve PDEs possesses the following advantages: first of all, it is a truly mesh-free method and is independent of spatial dimension in the sense that the convergence order is $O(h^{d+1})$ where h is the density of the collocation points and d is the spatial dimension. Second, in the context of scattered data interpolation, it is known that some RBFs have spectral convergence. In other words, as the spatial step of the problem increases, the convergence order also increases, and hence, much fewer scattered collocation points will be needed to maintain the same accuracy as compared with conventional FDM, FEM and finite volume method (FVM). This shows the advantage of the RBFs for solving multi-dimensional problems.

RBFs are a class of functions where the Euclidean distance of a centre point from a variable field point is used as the independent variable. This distance is denoted by $r=\Vert \mathit{x}-{\mathit{x}}_j{\Vert }_2$ where $\mathit{x}$ and ${\mathit{x}}_j$ are variable field point and centre point, respectively. Therefore, Radial basis function depends on this distance i.e. ${\varphi }^{\ast }=\varphi (\Vert \mathit{x}-{\mathit{x}}_j{\Vert }_2)$. This property concludes that the radial basis function $\varphi$ is radially symmetric about ${\mathit{x}}_j$. Since the method only needs pairwise distances between points, it is easy to use in higher dimensions. The meshless property of the RBFs method even allows us to solve problems with non-regular and very complicated geometry. Some well-known RBFs are listed in Table 1.

Table 1. Some well-known functions that generate RBFs.

$\text{Name of radial basis function}$		$\text{Abbreviations}$		$\text{Definition}$
Multiquadric		$\text{MQ}$		$\varphi (r)=\sqrt{c^2+r^2}$
Inverse Multiquadric		$\text{IMQ}$		$\varphi (r)={\displaystyle \frac{1}{\sqrt{c^2+r^2}}}$
Inverse Quadric		$\text{IQ}$		$\varphi (r)={\displaystyle \frac{1}{c^2+r^2}}$
Gaussian		$\text{GA}$		$\varphi (r)=exp(-c^2{r}^2)$
Thin Plate Spline		$\text{TPS}$		$\varphi (r)=r^{2}log(r)$

RBFs are classified into two classes: infinitely smooth and piecewise smooth. Infinitely smooth RBFs are infinitely differentiable and involve a shape parameter. Multiquadric, inverse multiquadric and Gaussian are examples of this class. Piecewise smooth RBFs are not infinitely differentiable and do not involve a shape parameter such as thin plate spline. Compared with the former class, the latter has less accuracy. As it is mentioned above and seen in Table 1, most available RBFs contain a free parameter called shape parameter that plays an important role for the accuracy of the method. Determining good shape parameter is still an outstanding research topic. Although research done by many scientists to develop algorithms for selecting the values of shape parameter which produce the most accurate interpolation, the optimal choice of shape parameter is still an open problem. The simplest strategy is to perform a series of interpolation experiments with varying shape parameter and then to pick the best one. Hardy [18] suggested using constant shape parameter (CSP) $c=0.815d$, where $d=\frac{1}{N}{\sum }_{j=1}^N{d}_j$ and $d_j$ is the distance from ${\mathit{x}}_j$ to its nearest neighbour and N denotes the number of centre points. $c=1.25\frac{D}{\sqrt{N}}$ was used by Franke [21], where D is the diameter of the smallest circle containing all centre points and N is the same as above. In [22], Foley presented a new strategy to find a good value for shape parameter based on his observation, which this value was similar for MQ and IMQ.

Rippa [23] proposed the LOOCV (Leave-One-Out Cross-Validation) algorithm for selecting a value of shape parameter. Later, Fasshauer in [24] offered the extension of LOOCV algorithm.

A shape parameter that scales inversely with a data centre’s separation distance is suggested by Flyer in [25]. A lot of works have been done to optimize constant shape parameter up to now which some of the latest works are [26] that its authors found a good shape parameter with generic algorithm. In [27], Iurlaro et al present a novel algorithm based on the principle of the minimum of the total potential energy to gain an optimal shape parameter.

Although working with constant shape parameter is simple, in papers [19,28–30], it is shown that accuracy of RBF methods with variable shape parameter has an advantage over a constant shape parameter strategy. In this regard, Kansa [19] suggested three formulas, exponentially varying shape parameter (ESP), increasing linear varying shape parameter (ILSP) and decreasing linear varying shape parameter (DLSP) to compute different shape parameters corresponding to each centre point.

In 2009, Sarra and Sturgill [31] have introduced a random VSP strategy as(1.6) $$\begin{array}{c}\hfill c_j=c_{\mathit{min}}+(c_{max}-c_{\mathit{min}})\times rand(1,N),j=1,2,\dots ,N,\end{array}$$(1.6)

where $c_{min}$ and $c_{max}$ are the minimum and maximum of $c_j$’s, respectively, and $c_j$ is the jth shape parameter corresponding to the jth centre point ${\mathit{x}}_j$ and rand(1, N) is a function that produces N uniformly distributed pseudo-random number on [0, 1] interval. Xiang et al. [32] have used a trigonometric VSP for generalized MQ-RBF with following formula(1.7) $$\begin{array}{c}\hfill c_j=c_{min}+(c_{max}-c_{min})sin(j),j=1,2,\dots ,N.\end{array}$$(1.7)

In [33], Golbabaie and Rabiei have changed the argument of $sin$ function because it produces non-positive shape parameters and also in the same paper they have suggested a hybrid shape parameter strategy with combination of Kansa’s formula. In [34], Ranjbar has used a new formula to compute VSP which is called symmetric variable shape parameter (SVSP).

The main purpose of this paper is to solve the inverse parabolic problem with source control parameter using GA-RBFs with SVSP and shifted Chebyshev basis functions (SCH-BF).

This work is organized as follows: In Section 2, we will give an outline of the radial basis functions. In Section 3, variable shape parameter will be discussed. In Section 5, we will present an implementation of SVSP strategy to the governing problem. Finally, some numerical samples and their comparison with other methods will be shown in Section 6.

2. Radial basis functions and Chebyshev polynomials

A radial basis function is a function of the distance of the point to the origin. That is, $\varphi$ is an RBF if $\varphi (x)=\varphi (\Vert \mathit{x}{\Vert }_2)$, so $\varphi$ acts on $\mathit{x}=(x_1,x_2,\dots ,x_d)$, a vector in ${\mathbb{R}}^d$ where d is the dimension of the problem, but only through the norm.

To approximate a function u(x) with the RBF method, we can use the idea of constructing the interpolant $\mathcal{P}(x)$ by a linear combination of translates of a single radial function on a set of scattered centres ${\mathit{x}}_1,{\mathit{x}}_2,\dots ,{\mathit{x}}_N$ in ${\mathbb{R}}^d$ i.e.(2.1) $$\begin{array}{c}\hfill u(\mathit{x})\approx \mathcal{P}(\mathit{x})=\sum _{j=1}^N{\lambda }_j\varphi (\Vert \mathit{x}-{\mathit{x}}_j{\Vert }_2,c),\end{array}$$(2.1)

where c is the shape parameter and the coefficients ${\{{\lambda }_j\}}_{j=1}^N$ are unknowns which will be determined by enforcing the interpolation conditions(2.2) $$\begin{array}{c}\hfill \mathcal{P}({\mathit{x}}_{\mathit{i}})=u({\mathit{x}}_{\mathit{i}}),i=1,2,\dots ,N.\end{array}$$(2.2)

Enforcing above conditions at N centres results in an $N\times N$ linear system. In matrix form, the values of the unknown coefficients ${\lambda }_j$ can be obtained from solving the following linear system(2.3) $$\begin{array}{c}\hfill A\mathrm{\Lambda }=\mathbf{u},\end{array}$$(2.3)

where ${\mathrm{\Lambda }}^T=[{\lambda }_1,{\lambda }_2,\dots ,{\lambda }_N]$, ${\mathbf{u}}^T=[u({\mathit{x}}_1),u({\mathit{x}}_2),\dots ,u({\mathit{x}}_N)]$ and the matrix A is called the interpolation matrix or the system matrix with the entries(2.4) $$\begin{array}{c}\hfill a_{\mathit{ij}}=\varphi (\Vert {\mathit{x}}_i-{\mathit{x}}_j{\Vert }_2),i,j=1,2,\dots ,N.\end{array}$$(2.4)

From [35,36], it is concluded that system (2.3(2.3) $$\begin{array}{c}\hfill A\mathrm{\Lambda }=\mathbf{u},\end{array}$$(2.3) ) with distinct centres for GA, IMQ, IQ and MQ is solvable because matrix A in (2.3(2.3) $$\begin{array}{c}\hfill A\mathrm{\Lambda }=\mathbf{u},\end{array}$$(2.3) ) is nonsingular; however, it is usually very ill-conditioned. This means that the condition number is very large. Condition number is used to quantify the sensitivity to perturbation of linear system and to estimate the accuracy of a computed solution, the matrix condition number is(2.5) $$\begin{array}{c}\hfill \kappa (A)=\Vert A{\Vert }_s\Vert A^{-1}{\Vert }_s,s=1,2,\infty .\end{array}$$(2.5)

Note that if $\Vert ·\Vert =\Vert ·{\Vert }_2$, then $\Vert A\Vert ={\sigma }_{max}$ and $\Vert A^{-1}\Vert =1/{\sigma }_{min}$. Thus $\kappa (A)={\sigma }_{max}/{\sigma }_{min}$ in the 2-norm where ${\sigma }_{max}$ and ${\sigma }_{min}$ are maximum and minimum of singular values of matrix A, respectively. The condition number of matrix and accuracy of interpolation depend on two factors, shape parameter and node distribution which shape parameter has a greater impact on condition number and accuracy. The RBF method is more accurate for the smaller values of constant shape parameter where the system matrix is ill-conditioned.

For interpolation of scattered data by RBFs, Schaback [37] proved uncertainly relation which states that the error and the condition number cannot both be kept small.

The well-known Chebyshev polynomials of the second kind are defined on the interval $[-1,1]$ and can be defined with the following recurrence formulae:(2.6) $$\begin{array}{c}\hfill {\psi }_0(z)=1,{\psi }_1(z)=2z,{\psi }_n(z)=2z{\psi }_{n-1}(z)-{\psi }_{n-2}(z).\end{array}$$(2.6)

For analytical and numerical works, it is often convenient to use the half interval [0, 1] instead of the full interval $[-1,1]$. For this purpose, the shifted Chebyshev polynomials are defined by applying the change of variable(2.7) $$\begin{array}{c}\hfill z=2t-1,0<t\le 1.\end{array}$$(2.7)

The shifted Chebyshev polynomials are obtained as(2.8) $$\begin{array}{c}\hfill {\psi }_0^{\ast }(t)=1,{\psi }_1^{\ast }(t)={\psi }_1(2t-1),{\psi }_n^{\ast }(t)={\psi }_n(2t-1).\end{array}$$(2.8)

3. Variable shape parameter strategy

Choosing a suitable value for shape parameter is an important argument when RBFs are used for interpolation or for the numerical solution of PDE’s.

Generally, two strategies are available for choosing shape parameter. The first one is CSP that takes same value for shape parameters corresponding to each centre. This strategy is used by many scientists and mathematicians due to its simple analysis. The second one is VSP that uses different values of the shape parameter at different centre points and is more difficult to analyse. As mentioned previously, the VSP strategy brings several advantages versus the CSP strategy. For example, Kansa [19] has shown that VSP can improve the accuracy of the RBF interpolation. In addition, VSP leads to the distinction of the interpolation matrix columns which can usually decrease its condition number. As mentioned before, there is a contradiction between the accuracy and condition number, known as ‘uncertainly principle’, VSP is used to balance the accuracy and stability.

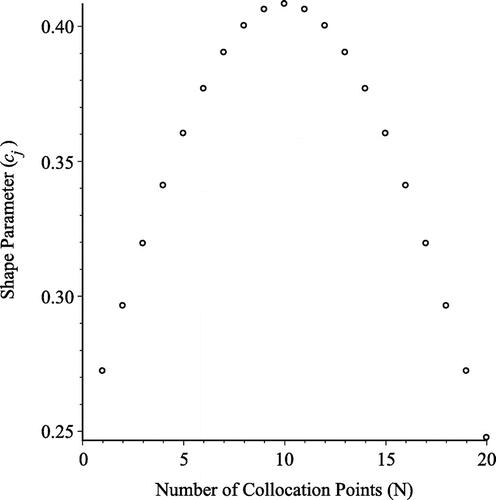
In this paper, we use SVSP, as follows(3.1) $$\begin{array}{c}\hfill c_j=c^{\ast }exp\left(-\frac{1}{2}{\left(\frac{j-\mu }{\sigma }\right)}^2\right),\end{array}$$(3.1)

where $c^{\ast }$ is an arbitrary shape parameter, $c^{\ast }\in [c_{min},c_{max}]$, and $\mu =0.5N$, $\sigma =0.5N$ where N is the total number of centres. Note that, the shape parameter values $c_j$ are controlled around $c^{\ast }$ by $\mu$ and $\sigma$. The graph of SVSP is plotted in Figure 1.

Figure 1. Plot of SVSP with $N=21$ and $c^{\ast }=1/\sqrt{6}$.

4. Statement of the problem

In this section, the Gaussian radial basis functions and basis functions of shifted Chebyshev polynomials of the second kind are used to solve the problem (1.1(1.1) $$\begin{array}{c}\hfill u_t=u_{\mathit{xx}}+p(t)u+\phi (x,t),0\le x\le 1,0<t\le T,\end{array}$$(1.1) )–(1.5(1.5) $$\begin{array}{c}\hfill u(x_0,t)=H(t),0<t\le T,\end{array}$$(1.5) ). First, we make the following transformations;(4.1) $$\begin{array}{cc}\hfill r(t)& =exp\left(-{\int }_0^{t}p(s)\mathrm{d}s\right),\hfill \end{array}$$(4.1) (4.2) $$\begin{array}{cc}\hfill w(x,t)& =r(t)u(x,t),\hfill \end{array}$$(4.2)

which transforms equations (1.1(1.1) $$\begin{array}{c}\hfill u_t=u_{\mathit{xx}}+p(t)u+\phi (x,t),0\le x\le 1,0<t\le T,\end{array}$$(1.1) )–(1.5(1.5) $$\begin{array}{c}\hfill u(x_0,t)=H(t),0<t\le T,\end{array}$$(1.5) ) into another direct parabolic problem, and then we apply GA-RBFs and CH-BF on the resulting equation. Using above transformations, equations (1.1(1.1) $$\begin{array}{c}\hfill u_t=u_{\mathit{xx}}+p(t)u+\phi (x,t),0\le x\le 1,0<t\le T,\end{array}$$(1.1) )–(1.5(1.5) $$\begin{array}{c}\hfill u(x_0,t)=H(t),0<t\le T,\end{array}$$(1.5) ) can be transformed into the following forms(4.3) $$\begin{array}{c}\hfill w_t=w_{\mathit{xx}}+r(t)\phi (x,t)0\le x\le 1,0<t\le T,\end{array}$$(4.3)

with the initial condition(4.4) $$\begin{array}{c}\hfill w(x,0)=f(x)0\le x\le 1,\end{array}$$(4.4)

and boundary conditions(4.5) $$\begin{array}{cc}\hfill w(0,t)& =r(t)g_0(t)0<t\le T,\hfill \end{array}$$(4.5) (4.6) $$\begin{array}{cc}\hfill w(1,t)& =r(t)g_1(t)0<t\le T,\hfill \end{array}$$(4.6)

and if $H(t)\ne 0$ the r(t) can be obtained from (4.2(4.2) $$\begin{array}{cc}\hfill w(x,t)& =r(t)u(x,t),\hfill \end{array}$$(4.2) ) in the following form(4.7) $$\begin{array}{c}\hfill r(t)={\displaystyle \frac{w(x_0,t)}{H(t)}}.\end{array}$$(4.7)

Now we use the GA-RBFs for discretization of space variable and the SCH-BFs for discretization of time variable. Let $x_1,x_M$ and ${\mathrm{\Omega }}_1=\{x_i|0<x_i<1,i=2,3,\dots ,M-1\}$ be a set of scattered nodes on [0, 1] and $t_1=0$ and ${\mathrm{\Omega }}_2=\{t_j|0<t_j\le 1,j=2,3,\dots ,N\}$ be a set of scattered nodes on [0, T]. Then the solution of the problem (4.3(4.3) $$\begin{array}{c}\hfill w_t=w_{\mathit{xx}}+r(t)\phi (x,t)0\le x\le 1,0<t\le T,\end{array}$$(4.3) )–(4.7(4.7) $$\begin{array}{c}\hfill r(t)={\displaystyle \frac{w(x_0,t)}{H(t)}}.\end{array}$$(4.7) ) is considered as follows(4.8) $$\begin{array}{c}\hfill \tilde{w}(x,t)\simeq \sum _{i=1}^M\sum _{j=1}^N{\lambda }_{\mathit{ij}}{\varphi }_i(x){\psi }_j^{\ast }(t)={\mathrm{\Phi }}_M^T(x)\mathrm{\Lambda }{\mathrm{\Psi }}_N^{\ast }(t),\end{array}$$(4.8)

where ${\varphi }_i(x)$ is the GA-RBF with SVSP $c_i$ i.e. ${\varphi }_i(x)=exp(-c_i^2{(x-x_i)}^2)$ and ${\psi }_j^{\ast }(t)$ is the SCH-BF of degree $j-1$ and ${\mathrm{\Phi }}_M(x)={[{\varphi }_1(x),{\varphi }_2(x),\dots ,{\varphi }_M(x)]}^T$, ${\mathrm{\Psi }}_N^{\ast }(t)={[{\psi }_1^{\ast }(t),{\psi }_2^{\ast }(t),\dots ,{\psi }_N^{\ast }(t)]}^T$ where upper index T refers to the vector transpose and finally,$$\begin{array}{c}\hfill \mathrm{\Lambda }=\left[\begin{array}{cccc}{\lambda }_{11}& {\lambda }_{12}& \cdots & {\lambda }_{1N}\\ {\lambda }_{21}& {\lambda }_{22}& \cdots & {\lambda }_{2N}\\ ⋮& ⋮& \ddots & ⋮\\ {\lambda }_{M1}& {\lambda }_{M2}& \cdots & {\lambda }_{\mathit{MN}}\end{array}\right],\end{array}$$

is an $M\times N$ unknown coefficients matrix that should be determined.

According to (4.8(4.8) $$\begin{array}{c}\hfill \tilde{w}(x,t)\simeq \sum _{i=1}^M\sum _{j=1}^N{\lambda }_{\mathit{ij}}{\varphi }_i(x){\psi }_j^{\ast }(t)={\mathrm{\Phi }}_M^T(x)\mathrm{\Lambda }{\mathrm{\Psi }}_N^{\ast }(t),\end{array}$$(4.8) ), we have(4.9) $$\begin{array}{c}\hfill {\tilde{w}}_t={\mathrm{\Phi }}_M^T(x)\mathrm{\Lambda }\left({\displaystyle \frac{\partial }{\partial t}}{\mathrm{\Psi }}_N^{\ast }(t)\right),\end{array}$$(4.9)

and(4.10) $$\begin{array}{c}\hfill {\tilde{w}}_{\mathit{xx}}=\left({\displaystyle \frac{{\partial }^2}{\partial x^2}}{\mathrm{\Phi }}_M^T(x)\right)\mathrm{\Lambda }{\mathrm{\Psi }}_N^{\ast }(t).\end{array}$$(4.10)

Now (4.3(4.3) $$\begin{array}{c}\hfill w_t=w_{\mathit{xx}}+r(t)\phi (x,t)0\le x\le 1,0<t\le T,\end{array}$$(4.3) )–(4.7(4.7) $$\begin{array}{c}\hfill r(t)={\displaystyle \frac{w(x_0,t)}{H(t)}}.\end{array}$$(4.7) ) are approximated using (4.8(4.8) $$\begin{array}{c}\hfill \tilde{w}(x,t)\simeq \sum _{i=1}^M\sum _{j=1}^N{\lambda }_{\mathit{ij}}{\varphi }_i(x){\psi }_j^{\ast }(t)={\mathrm{\Phi }}_M^T(x)\mathrm{\Lambda }{\mathrm{\Psi }}_N^{\ast }(t),\end{array}$$(4.8) )–(4.10(4.10) $$\begin{array}{c}\hfill {\tilde{w}}_{\mathit{xx}}=\left({\displaystyle \frac{{\partial }^2}{\partial x^2}}{\mathrm{\Phi }}_M^T(x)\right)\mathrm{\Lambda }{\mathrm{\Psi }}_N^{\ast }(t).\end{array}$$(4.10) ) as follows(4.11) $$\begin{array}{c}\hfill {\mathrm{\Phi }}_M^T(x)\mathrm{\Lambda }\left({\displaystyle \frac{\partial }{\partial t}}{\mathrm{\Psi }}_N^{\ast }(t)\right)-\left({\displaystyle \frac{{\partial }^2}{\partial x^2}}{\mathrm{\Phi }}_M^T(x)\right)\mathrm{\Lambda }{\mathrm{\Psi }}_N^{\ast }(t)-{\displaystyle \frac{{\mathrm{\Phi }}_M^T(x_0)\mathrm{\Lambda }{\mathrm{\Psi }}_N^{\ast }(t)}{H(t)}}\phi (x,t)=0,\end{array}$$(4.11) (4.12) $$\begin{array}{cc}\hfill {\mathrm{\Phi }}_M^T(x)\mathrm{\Lambda }{\mathrm{\Psi }}_N^{\ast }(0)& =f(x),\hfill \end{array}$$(4.12) (4.13) $$\begin{array}{cc}\hfill {\mathrm{\Phi }}_M^T(0)\mathrm{\Lambda }{\mathrm{\Psi }}_N^{\ast }(t)& ={\displaystyle \frac{{\mathrm{\Phi }}_M^T(x_0)\mathrm{\Lambda }{\mathrm{\Psi }}_N^{\ast }(t)}{H(t)}}{g}_0(t),\hfill \end{array}$$(4.13) (4.14) $$\begin{array}{cc}\hfill {\mathrm{\Phi }}_M^T(1)\mathrm{\Lambda }{\mathrm{\Psi }}_N^{\ast }(t)& ={\displaystyle \frac{{\mathrm{\Phi }}_M^T(x_0)\mathrm{\Lambda }{\mathrm{\Psi }}_N^{\ast }(t)}{H(t)}}{g}_1(t).\hfill \end{array}$$(4.14)

The collocation technique is then used for determining the unknown coefficient matrix $\mathrm{\Lambda }$. One can collocate (4.11(4.11) $$\begin{array}{c}\hfill {\mathrm{\Phi }}_M^T(x)\mathrm{\Lambda }\left({\displaystyle \frac{\partial }{\partial t}}{\mathrm{\Psi }}_N^{\ast }(t)\right)-\left({\displaystyle \frac{{\partial }^2}{\partial x^2}}{\mathrm{\Phi }}_M^T(x)\right)\mathrm{\Lambda }{\mathrm{\Psi }}_N^{\ast }(t)-{\displaystyle \frac{{\mathrm{\Phi }}_M^T(x_0)\mathrm{\Lambda }{\mathrm{\Psi }}_N^{\ast }(t)}{H(t)}}\phi (x,t)=0,\end{array}$$(4.11) ) at $(M-2)\times (N-1)$ collocation points ${\mathrm{\Gamma }}_1=\{(x_i,t_j)|x_i\in {\mathrm{\Omega }}_1,t_j\in {\mathrm{\Omega }}_2\}$, to get(4.15) $$\begin{array}{c}\hfill {\mathrm{\Phi }}_M^T(x_i)\mathrm{\Lambda }\left({\displaystyle \frac{\partial }{\partial t}}{\mathrm{\Psi }}_N^{\ast }(t_j)\right)-\left({\displaystyle \frac{{\partial }^2}{\partial x^2}}{\mathrm{\Phi }}_M^T(x_i)\right)\mathrm{\Lambda }{\mathrm{\Psi }}_N^{\ast }(t_j)-{\displaystyle \frac{{\mathrm{\Phi }}_M^T(x_0)\mathrm{\Lambda }{\mathrm{\Psi }}_N^{\ast }(t_j)}{H(t_j)}}\phi (x_i,t_j)=0.\end{array}$$(4.15)

Further, with collocating (4.12(4.12) $$\begin{array}{cc}\hfill {\mathrm{\Phi }}_M^T(x)\mathrm{\Lambda }{\mathrm{\Psi }}_N^{\ast }(0)& =f(x),\hfill \end{array}$$(4.12) ) at M points $x_i\in {\mathrm{\Omega }}_1\cup \{x_1,x_M\}$, we have(4.16) $$\begin{array}{c}\hfill {\mathrm{\Phi }}_M^T(x_i)\mathrm{\Lambda }{\mathrm{\Psi }}_N^{\ast }(0)=f(x_i).\end{array}$$(4.16)

Further collocation of (4.13(4.13) $$\begin{array}{cc}\hfill {\mathrm{\Phi }}_M^T(0)\mathrm{\Lambda }{\mathrm{\Psi }}_N^{\ast }(t)& ={\displaystyle \frac{{\mathrm{\Phi }}_M^T(x_0)\mathrm{\Lambda }{\mathrm{\Psi }}_N^{\ast }(t)}{H(t)}}{g}_0(t),\hfill \end{array}$$(4.13) ) and (4.14(4.14) $$\begin{array}{cc}\hfill {\mathrm{\Phi }}_M^T(1)\mathrm{\Lambda }{\mathrm{\Psi }}_N^{\ast }(t)& ={\displaystyle \frac{{\mathrm{\Phi }}_M^T(x_0)\mathrm{\Lambda }{\mathrm{\Psi }}_N^{\ast }(t)}{H(t)}}{g}_1(t).\hfill \end{array}$$(4.14) ) at $N-1$ points $t_j\in {\mathrm{\Omega }}_2$, we have(4.17) $$\begin{array}{cc}\hfill {\mathrm{\Phi }}_M^T(0)\mathrm{\Lambda }{\mathrm{\Psi }}_N^{\ast }(t_j)& ={\displaystyle \frac{{\mathrm{\Phi }}_M^T(x_0)\mathrm{\Lambda }{\mathrm{\Psi }}_N^{\ast }(t_j)}{H(t_j)}}{g}_0(t_j),\hfill \end{array}$$(4.17) (4.18) $$\begin{array}{cc}\hfill {\mathrm{\Phi }}_M^T(1)\mathrm{\Lambda }{\mathrm{\Psi }}_N^{\ast }(t_j)& ={\displaystyle \frac{{\mathrm{\Phi }}_M^T(x_0)\mathrm{\Lambda }{\mathrm{\Psi }}_N^{\ast }(t_j)}{H(t_j)}}{g}_1(t_j).\hfill \end{array}$$(4.18)

Equations (4.15(4.15) $$\begin{array}{c}\hfill {\mathrm{\Phi }}_M^T(x_i)\mathrm{\Lambda }\left({\displaystyle \frac{\partial }{\partial t}}{\mathrm{\Psi }}_N^{\ast }(t_j)\right)-\left({\displaystyle \frac{{\partial }^2}{\partial x^2}}{\mathrm{\Phi }}_M^T(x_i)\right)\mathrm{\Lambda }{\mathrm{\Psi }}_N^{\ast }(t_j)-{\displaystyle \frac{{\mathrm{\Phi }}_M^T(x_0)\mathrm{\Lambda }{\mathrm{\Psi }}_N^{\ast }(t_j)}{H(t_j)}}\phi (x_i,t_j)=0.\end{array}$$(4.15) )–(4.18(4.18) $$\begin{array}{cc}\hfill {\mathrm{\Phi }}_M^T(1)\mathrm{\Lambda }{\mathrm{\Psi }}_N^{\ast }(t_j)& ={\displaystyle \frac{{\mathrm{\Phi }}_M^T(x_0)\mathrm{\Lambda }{\mathrm{\Psi }}_N^{\ast }(t_j)}{H(t_j)}}{g}_1(t_j).\hfill \end{array}$$(4.18) ) give an $M\times N$ system of linear algebraic equations with the $M\times N$ unknown coefficient ${\lambda }_{\mathit{ij}}$. We get the unknown matrix $\mathrm{\Lambda }$ after solving this linear system. As soon as this unknown matrix is determined, the unknown function $\tilde{w}(x,t)$ can be found.

According to (4.7(4.7) $$\begin{array}{c}\hfill r(t)={\displaystyle \frac{w(x_0,t)}{H(t)}}.\end{array}$$(4.7) ), an approximation of r(t) is obtained as follow(4.19) $$\begin{array}{c}\hfill \tilde{r}(t)={\displaystyle \frac{\tilde{w}(x_0,t)}{H(t)}},\end{array}$$(4.19)

and therefore, the main problem (1.1(1.1) $$\begin{array}{c}\hfill u_t=u_{\mathit{xx}}+p(t)u+\phi (x,t),0\le x\le 1,0<t\le T,\end{array}$$(1.1) )-(1.5(1.5) $$\begin{array}{c}\hfill u(x_0,t)=H(t),0<t\le T,\end{array}$$(1.5) ) has the following approximate solution(4.20) $$\begin{array}{c}\hfill \tilde{u}(x,t)={\displaystyle \frac{\tilde{w}(x,t)}{\tilde{r}(t)}},\end{array}$$(4.20)

and finally the approximate value of source parameter p(t) is(4.21) $$\begin{array}{c}\hfill \tilde{p}(t)=-{\displaystyle \frac{{\tilde{r}}^{\prime }(t)}{\tilde{r}(t)}}.\end{array}$$(4.21)

5. Numerical examples

In this section, we present two numerical examples to test the accuracy and efficiency of our proposed method. For both examples, the exact solutions are available. We performed all the symbolic and numerical computations using Maple 16 with $\eta =40$, where $\eta$ is the number of floating point arithmetic. The following error norms(5.1) $$\begin{array}{cc}\hfill E_{\infty }^u& =\underset{1\le i\le M}{max}\left\{\underset{1\le j\le N}{max}|u(x_i,t_j)-\tilde{u}(x_i,t_j)|\right\},\hfill \\ \hfill E_{\infty }^p& =\underset{1\le j\le N}{max}|p(t_j)-\tilde{p}(t_j)|,\hfill \\ \hfill E_2^u& =\sqrt{\sum _{i=1}^M\sum _{j=1}^N{|u(x_i,t_j)-\tilde{u}(x_i,t_j)|}^2},\hfill \\ \hfill E_2^p& =\sqrt{\sum _{j=1}^N{|p(t_j)-\tilde{p}(t_j)|}^2},\hfill \\ \hfill RMS(u)& =\sqrt{\frac{1}{\mathit{MN}}\sum _{i=1}^M\sum _{j=1}^N{|u(x_i,t_j)-\tilde{u}(x_i,t_j)|}^2},\hfill \\ \hfill RMS(p)& =\sqrt{\frac{1}{N}\sum _{j=1}^N{|p(t_j)-\tilde{p}(t_j)|}^2},\hfill \end{array}$$(5.1)

are computed to show the accuracy of the proposed method and are used to compare them with other methods [4,38].

In all the numerical examples, we have used the Gaussian radial basis function. The reason behind this is that the Gaussian radial basis function interpolation has been shown to exhibit spectral convergence. The numerical rate of convergence (ROC) with respect to the number of collocation points is often calculated by the following formula(5.2) $$\begin{array}{c}\hfill ROC=log\left({\displaystyle \frac{E_{j+1}}{E_j}}\right)/log\left({\displaystyle \frac{{\mathcal{N}}_j}{{\mathcal{N}}_{j+1}}}\right),\end{array}$$(5.2)

where $E_j$ is $E_{\infty }^u$, $E_2^u$ or RMS(u) error norms correspond to the number of collocation points ${\mathcal{N}}_j$ where ${\mathcal{N}}_j=M_j\times N_j$.

In practical application, inherent errors in measurement data are unavoidable. Since small perturbation in initial data may produce a large amount of perturbation in the solution, we produce the noise in H(t) using noisy data given as follow(5.3) $$\begin{array}{c}\hfill H_{ϵ}(t)=H(t)+ϵsin(\delta t),\end{array}$$(5.3)

where $ϵ$ shows the noise level and $\delta$ displays noise frequency of the measurement data. We compare the $E_{\infty }^u$ and $E_{\infty }^p$ for three levels of $ϵ$ with various $\delta$ for both examples to illustrate the effect of noisy input data on solutions $\tilde{u}(x,t)$ and $\tilde{p}(t)$.

5.1. Example 1

This example considers the inverse problem given by (1.1(1.1) $$\begin{array}{c}\hfill u_t=u_{\mathit{xx}}+p(t)u+\phi (x,t),0\le x\le 1,0<t\le T,\end{array}$$(1.1) )–(1.5(1.5) $$\begin{array}{c}\hfill u(x_0,t)=H(t),0<t\le T,\end{array}$$(1.5) ) with(5.4) $$\begin{array}{cc}& f(x)=cos(\pi x)+sin(\pi x),\hfill \\ \hfill & g_0(t)=exp(-t^2),\hfill \\ \hfill & g_1(t)=-exp(-t^2),\hfill \\ \hfill & \phi (x,t)=({\pi }^2-{(t+1)}^2)exp(-t^2)(cos(\pi x)+sin(\pi x)),\hfill \\ \hfill & H(t)=\sqrt{2}exp(-t^2),\hfill \end{array}$$(5.4)

and $x_0=0.25$. The exact solution for this problem is(5.5) $$\begin{array}{c}\hfill u(x,t)=exp(-t^2)(cos(\pi x)+sin(\pi x)),\end{array}$$(5.5)

and(5.6) $$\begin{array}{c}\hfill p(t)=1+t^2.\end{array}$$(5.6)

We use the method proposed in Section 4 and compute the absolute error $|u(x,t)-\tilde{u}(x,t)|$ with $t=1$ for different values of M and N, which are stated in Table 2, with both CSP $(c=1/\sqrt{6})$ and SVSP $(c^{\ast }=1/\sqrt{6})$ strategies. 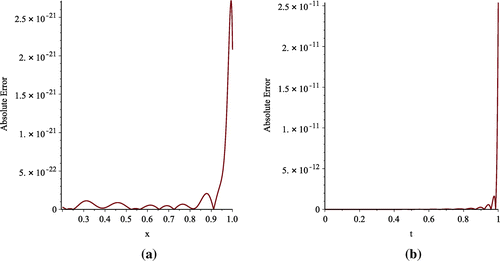Besides we compare the results with the obtained results using the method of lines [38] with $\mathrm{\Delta }x=0.02$ and $\mathrm{\Delta }t=6.6667e-005$, and the fourth-order compact difference scheme described in [4] with $\mathrm{\Delta }x=0.025$ and $\mathrm{\Delta }t=0.01$ in the same table. The values of absolute error for p(t) obtained by the present method and other methods [4,38] with the same data, used for Table 2, are compared in Table 3. Moreover, In Figure 2, the absolute error functions $|u(x,t)-\tilde{u}(x,t)|$ and $|p(t)-\tilde{p}(t)|$ are plotted using GA-RBFs and SCH-BFs with $M=21$ and $N=19$.

Table 2. Absolute errors between the exact and approximating solution u(x, 1) at $x=0,0.1,0.2,\dots ,1.0$ and comparison with other methods for Example 1.

x	Method of	fourth-order compact	Present method with CSP			Present method with SVSP
	lines [38]	difference scheme [4]	$M=17,N=14$	$M=21,N=19$		$M=17,N=14$	$M=21,N=19$
0	$-$	$-$	$6.04\times {10}^{-14}$	$4.86\times {10}^{-10}$		$5.80\times {10}^{-16}$	$1.99\times {10}^{-21}$
0.1	$1.92\times {10}^{-7}$	$1.33\times {10}^{-15}$	$4.73\times {10}^{-14}$	$5.89\times {10}^{-10}$		$6.11\times {10}^{-17}$	$7.32\times {10}^{-23}$
0.2	$5.78\times {10}^{-8}$	$3.33\times {10}^{-16}$	$2.14\times {10}^{-14}$	$6.43\times {10}^{-10}$		$1.13\times {10}^{-16}$	$3.01\times {10}^{-23}$
0.3	$5.08\times {10}^{-8}$	$2.11\times {10}^{-15}$	$4.37\times {10}^{-14}$	$6.43\times {10}^{-10}$		$4.55\times {10}^{-18}$	$1.05\times {10}^{-22}$
0.4	$1.30\times {10}^{-7}$	$1.78\times {10}^{-15}$	$2.88\times {10}^{-14}$	$5.89\times {10}^{-10}$		$1.10\times {10}^{-17}$	$2.22\times {10}^{-23}$
0.5	$1.82\times {10}^{-7}$	$1.11\times {10}^{-16}$	$1.05\times {10}^{-15}$	$4.86\times {10}^{-10}$		$6.37\times {10}^{-19}$	$4.19\times {10}^{-23}$
0.6	$2.09\times {10}^{-7}$	$8.88\times {10}^{-16}$	$9.87\times {10}^{-15}$	$3.45\times {10}^{-10}$		$3.15\times {10}^{-18}$	$4.96\times {10}^{-23}$
0.7	$2.18\times {10}^{-7}$	$1.05\times {10}^{-15}$	$4.38\times {10}^{-14}$	$1.78\times {10}^{-10}$		$2.35\times {10}^{-18}$	$4.56\times {10}^{-23}$
0.8	$2.17\times {10}^{-7}$	$1.25\times {10}^{-16}$	$9.06\times {10}^{-14}$	$3.84\times {10}^{-12}$		$1.16\times {10}^{-16}$	$2.35\times {10}^{-23}$
0.9	$2.15\times {10}^{-7}$	$3.61\times {10}^{-16}$	$8.35\times {10}^{-14}$	$1.63\times {10}^{-10}$		$7.46\times {10}^{-17}$	$1.12\times {10}^{-22}$
1	$-$	$-$	$2.60\times {10}^{-14}$	$3.04\times {10}^{-10}$		$6.63\times {10}^{-16}$	$2.08\times {10}^{-21}$

Table 3. Absolute errors between the exact and approximating solution p(t) at $t=0.1,0.2,\dots ,1.0$ and comparison with other methods for Example 1.

t	Method of	fourth-order compact	Present method with CSP			Present method with SVSP
	lines [38]	difference scheme [4]	$M=17,N=14$	$M=21,N=19$		$M=17,N=14$	$M=21,N=19$
0.1	$6.37\times {10}^{-5}$	$4.17\times {10}^{-6}$	$1.20\times {10}^{-11}$	$1.13\times {10}^{-10}$		$1.20\times {10}^{-11}$	$3.18\times {10}^{-15}$
0.2	$5.70\times {10}^{-5}$	$4.17\times {10}^{-6}$	$5.40\times {10}^{-12}$	$1.86\times {10}^{-12}$		$5.42\times {10}^{-12}$	$1.52\times {10}^{-15}$
0.3	$3.37\times {10}^{-4}$	$4.17\times {10}^{-6}$	$6.68\times {10}^{-12}$	$6.04\times {10}^{-14}$		$6.69\times {10}^{-12}$	$6.43\times {10}^{-15}$
0.4	$1.65\times {10}^{-4}$	$4.17\times {10}^{-6}$	$3.23\times {10}^{-11}$	$5.01\times {10}^{-14}$		$3.23\times {10}^{-11}$	$5.99\times {10}^{-15}$
0.5	$4.06\times {10}^{-4}$	$4.17\times {10}^{-6}$	$8.70\times {10}^{-11}$	$2.69\times {10}^{-15}$		$8.70\times {10}^{-11}$	$1.31\times {10}^{-23}$
0.6	$3.94\times {10}^{-5}$	$4.17\times {10}^{-6}$	$1.90\times {10}^{-10}$	$4.41\times {10}^{-14}$		$1.90\times {10}^{-10}$	$1.56\times {10}^{-14}$
0.7	$4.63\times {10}^{-4}$	$4.17\times {10}^{-6}$	$4.02\times {10}^{-10}$	$1.06\times {10}^{-12}$		$4.02\times {10}^{-10}$	$4.53\times {10}^{-14}$
0.8	$4.78\times {10}^{-4}$	$4.17\times {10}^{-6}$	$1.09\times {10}^{-9}$	$1.58\times {10}^{-11}$		$1.09\times {10}^{-9}$	$3.23\times {10}^{-14}$
0.9	$2.18\times {10}^{-3}$	$4.17\times {10}^{-6}$	$3.79\times {10}^{-9}$	$1.04\times {10}^{-9}$		$3.79\times {10}^{-9}$	$2.72\times {10}^{-13}$
1	$2.25\times {10}^{-4}$	$4.17\times {10}^{-6}$	$2.21\times {10}^{-7}$	$3.63\times {10}^{-8}$		$2.21\times {10}^{-7}$	$2.54\times {10}^{-11}$

As it can be observed, the proposed method leads to satisfactory results and has a good accuracy compared to those presented in [4,38]. From Tables 2 and 3, one can easily see that the SVSP strategy is more efficient than CSP one. Note that the inefficiency in the CSP strategy comes from due to increment in the number of nodes. In contrast, the SVSP strategy yields better results in the same position.

Figure 2. Absolute Error in approximating u(x, 1) (Graph a) and p(t) (Graph b) with $M=21$ and $N=19$ with SVSP for Example 1.

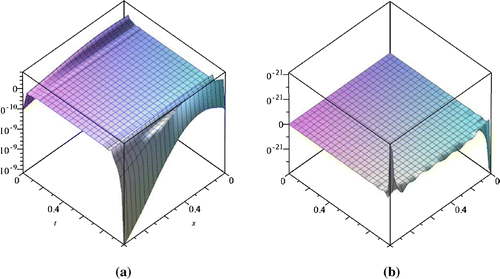
The $E_{\infty },E_2$ and RMS errors of u(x, t) and p(t) and condition number of system matrix for this example are listed in Table 4 to compare CSP and SVSP strategies. The error function $u(x,t)-\tilde{u}(x,t)$ is plotted in Figure 3. The advantage of SVSP approach with regards to CSP one is also observed in Table 4, especially when the number of nodes tends to increase.

Table 4. The $E_{\infty }$, $E_2$ and RMS errors for u and p for Example 1 with $c=1/\sqrt{6}$ and $c^{\ast }=1/\sqrt{6}$.

		$\text{Present method with CSP}$			$\text{Present method with SVSP}$
$\text{Error}$		$M=17,N=14$	$M=21,N=19$		$M=17,N=14$	$M=21,N=19$
$E_{\infty }^u$		$1.19\times {10}^{-13}$	$8.05\times {10}^{-10}$		$9.76\times {10}^{-16}$	$1.94\times {10}^{-21}$
$E_{\infty }^p$		$1.71\times {10}^{-7}$	$3.43\times {10}^{-8}$		$1.71\times {10}^{-7}$	$1.98\times {10}^{-11}$
$E_2^u$		$1.48\times {10}^{-6}$	$1.35\times {10}^{-4}$		$6.45\times {10}^{-8}$	$9.98\times {10}^{-11}$
$E_2^p$		$4.13\times {10}^{-4}$	$2.71\times {10}^{-4}$		$4.13\times {10}^{-4}$	$4.45\times {10}^{-6}$
RMS(u)		$9.62\times {10}^{-8}$	$6.74\times {10}^{-6}$		$4.18\times {10}^{-9}$	$4.99\times {10}^{-12}$
RMS(p)		$1.11\times {10}^{-4}$	$6.22\times {10}^{-5}$		$1.10\times {10}^{-4}$	$1.02\times {10}^{-6}$
$\text{Cond}$		$1.34\times {10}^{14}$	$6.75\times {10}^{14}$		$2.80\times {10}^{13}$	$1.28\times {10}^{14}$

Figure 3. Plot of error function $u-\tilde{u}$ with $M=21$ and $N=19$ using CSP with $c=1/\sqrt{6}$ (Graph a) and SVSP with $c^{\ast }=1/\sqrt{6}$ (Graph b) for Example 1.

Also we present the resulting error in approximate solution $\tilde{u}(x,t)$ and $\tilde{p}(t)$ in Tables 5 and 6, respectively, with $M=21$ and $N=19$ for various values of noise level $ϵ={10}^{-3},{10}^{-4}$ and ${10}^{-5}$ with three different noise frequencies $\delta =10,20$ and 30 for both CSP and SVSP strategies.

Table 5. Error for approximate u(x, t) with noisy input data for Example 1.

		$E_{\infty }^u\text{with CSP}$				$E_{\infty }^u\text{with SVSP}$
$\delta$		$ϵ={10}^{-3}$	$ϵ={10}^{-4}$	$ϵ={10}^{-5}$		$ϵ={10}^{-3}$	$ϵ={10}^{-4}$	$ϵ={10}^{-5}$
10		$4.91\times {10}^{-3}$	$2.85\times {10}^{-3}$	$2.01\times {10}^{-3}$		$3.91\times {10}^{-3}$	$3.90\times {10}^{-4}$	$3.90\times {10}^{-5}$
20		$3.63\times {10}^{-2}$	$2.27\times {10}^{-3}$	$2.20\times {10}^{-4}$		$7.43\times {10}^{-3}$	$7.34\times {10}^{-4}$	$7.34\times {10}^{-5}$
30		$6.44\times {10}^{-2}$	$2.62\times {10}^{-2}$	$2.42\times {10}^{-4}$		$1.17\times {10}^{-2}$	$1.18\times {10}^{-3}$	$1.18\times {10}^{-4}$

Table 6. Error for approximate p(t) with noisy input data for Example 1.

		$E_{\infty }^p\text{with CSP}$				$E_{\infty }^p\text{with SVSP}$
$\delta$		$ϵ={10}^{-3}$	$ϵ={10}^{-4}$	$ϵ={10}^{-5}$		$ϵ={10}^{-3}$	$ϵ={10}^{-4}$	$ϵ={10}^{-5}$
10		$1.50\times {10}^{-1}$	$9.03\times {10}^{-2}$	$7.39\times {10}^{-2}$		$1.86\times {10}^{-1}$	$1.86\times {10}^{-2}$	$1.86\times {10}^{-3}$
20		1.93	$9.87\times {10}^{-1}$	$4.32\times {10}^{-3}$		$2.53\times {10}^{-1}$	$2.56\times {10}^{-2}$	$2.56\times {10}^{-3}$
30		$1.24\times {10}^{-1}$	$1.30\times {10}^{-1}$	$1.45\times {10}^{-2}$		$1.98\times {10}^{-1}$	$1.97\times {10}^{-2}$	$1.96\times {10}^{-3}$

Looking at the results of Tables 5 and 6, we find that the proposed method with SVSP produces acceptable results and is stable with respect to the noise in the input data H(t). One of the remarkable things in Tables 5 and 6 is that in same noise frequencies and with changing noise level, the error due to noise varies by special discipline in SVSP strategy meaning the mantissa of errors in each row are very close together, while in CSP strategy, there is no discipline. In Table 7, the rate of convergence is presented for this example.

Table 7. Error norms and rate of convergence for various numbers of collocation points with $\eta =40$ for Example 1.

	Rate of convergence with CSP					Rate of convergence with SVSP
M, N	$E_{\infty }^u$	$ROC(E_{\infty }^u)$	$E_2^u$	$ROC(E_2^u)$		$E_{\infty }^u$	$ROC(E_{\infty }^u)$	$E_2^u$	$ROC(E_2^u)$
2, 2	3.31	$-$	1.95	$-$		1.90	$-$	2.31	$-$
4, 4	0.85	0.98	1.19	0.36		0.56	0.88	1.01	0.60
8, 8	$8.33\times {10}^{-4}$	5.00	$4.60\times {10}^{-2}$	2.35		$1.77\times {10}^{-4}$	5.80	$2.53\times {10}^{-2}$	2.66
16, 16	$9.52\times {10}^{-15}$	18.17	$5.62\times {10}^{-7}$	8.16		$1.39\times {10}^{-14}$	16.80	$2.11\times {10}^{-7}$	8.44
21, 19	$1.40\times {10}^{-9}$	$-26.81$	$2.44\times {10}^{-4}$	$-13.69$		$1.94\times {10}^{-21}$	35.57	$9.98\times {10}^{-11}$	17.25

The results obtained in Table 7 show that the convergence rate of the CSP strategy is encountered with the drawback that it gets worse by increasing the number of collocation points. It seems to be due to the machine error. The problem is visible as a negative convergence rate in the last row of table, while the SVSP approach has no such limitation. This is another advantage of the SVSP strategy.

5.2. Example 2

Consider the problem (1.1(1.1) $$\begin{array}{c}\hfill u_t=u_{\mathit{xx}}+p(t)u+\phi (x,t),0\le x\le 1,0<t\le T,\end{array}$$(1.1) )–(1.5(1.5) $$\begin{array}{c}\hfill u(x_0,t)=H(t),0<t\le T,\end{array}$$(1.5) ) with $T=1$ and the following initial, boundary and other additional conditions(5.7) $$\begin{array}{cc}& f(x)=-\frac{1}{2}sinxexp(-x^2),\hfill \end{array}$$(5.7) (5.8) $$\begin{array}{cc}& g_0(t)=0,\hfill \end{array}$$(5.8) (5.9) $$\begin{array}{cc}& g_1(t)=-\frac{1}{2}sin(1)exp(-t^3-t^2-1),\hfill \end{array}$$(5.9) (5.10) $$\begin{array}{cc}& \phi (x,t)=exp\left(-t^3-t^2-x^2\right)\left(tsinx-2sinx-2xcosx+2x^{2}sinx\right),\hfill \end{array}$$(5.10) (5.11) $$\begin{array}{cc}& H(t)=-\frac{1}{2}sin\left(\frac{1}{2}\right)exp\left(-t^3-t^2-\frac{1}{4}\right),\hfill \end{array}$$(5.11)

and $x_0=0.5$. The exact solution for this problem is(5.12) $$\begin{array}{c}\hfill u(x,t)=-\frac{1}{2}sinxexp(-t^3-t^2-x^2),\end{array}$$(5.12)

and(5.13) $$\begin{array}{c}\hfill p(t)=-3t^2-1.\end{array}$$(5.13)

In Tables 8 and 9, we compare the numerical results of the proposed method with obtained results of methods in [38] and [4] when $\mathrm{\Delta }x=0.02$ and $\mathrm{\Delta }t=0.001$. The absolute error functions $|u(x,t)-\tilde{u}(x,t)|$ and $|p(t)-\tilde{p}(t)|$ are plotted using GA-RBsF and SCH-BFs with $M=21$ and $N=19$ in Figure 4.

Table 8. Absolute errors between the exact and approximating solution u(x, 1) at $x=0,0.1,0.2,\dots ,1.0$ and comparison with other methods for Example 2.

x	Method of	fourth-order compact	Present method with CSP			Present method with SVSP
	lines [38]	difference scheme [4]	$M=17,N=14$	$M=21,N=19$		$M=17,N=14$	$M=21,N=19$
0	$-$	$-$	$2.00\times {10}^{-12}$	$2.00\times {10}^{-7}$		$5.08\times {10}^{-14}$	$3.36\times {10}^{-18}$
0.1	$5.76\times {10}^{-9}$	$2.88\times {10}^{-10}$	$4.19\times {10}^{-12}$	$2.97\times {10}^{-7}$		$4.25\times {10}^{-15}$	$3.33\times {10}^{-19}$
0.2	$4.86\times {10}^{-9}$	$4.79\times {10}^{-10}$	$1.11\times {10}^{-12}$	$3.84\times {10}^{-7}$		$6.19\times {10}^{-15}$	$6.64\times {10}^{-20}$
0.3	$3.58\times {10}^{-9}$	$5.01\times {10}^{-10}$	$1.21\times {10}^{-12}$	$4.53\times {10}^{-7}$		$1.07\times {10}^{-16}$	$1.56\times {10}^{-19}$
0.4	$1.91\times {10}^{-9}$	$3.30\times {10}^{-10}$	$6.53\times {10}^{-13}$	$5.09\times {10}^{-7}$		$3.38\times {10}^{-16}$	$3.83\times {10}^{-20}$
0.5	0	0	$1.28\times {10}^{-12}$	$5.44\times {10}^{-7}$		$8.54\times {10}^{-28}$	$5.60\times {10}^{-20}$
0.6	$1.95\times {10}^{-9}$	$4.01\times {10}^{-10}$	$7.49\times {10}^{-14}$	$5.60\times {10}^{-7}$		$5.52\times {10}^{-16}$	$1.12\times {10}^{-19}$
0.7	$3.65\times {10}^{-9}$	$7.44\times {10}^{-10}$	$5.74\times {10}^{-13}$	$5.60\times {10}^{-7}$		$6.38\times {10}^{-17}$	$7.65\times {10}^{-20}$
0.8	$4.84\times {10}^{-9}$	$8.81\times {10}^{-10}$	$1.26\times {10}^{-12}$	$5.41\times {10}^{-7}$		$6.12\times {10}^{-15}$	$3.33\times {10}^{-20}$
0.9	$5.30\times {10}^{-9}$	$6.70\times {10}^{-10}$	$2.43\times {10}^{-13}$	$5.12\times {10}^{-7}$		$3.25\times {10}^{-15}$	$2.29\times {10}^{-19}$
1	$-$	$-$	$6.88\times {10}^{-13}$	$4.69\times {10}^{-7}$		$4.55\times {10}^{-14}$	$2.61\times {10}^{-18}$

Table 9. Absolute errors between the exact and approximating solution p(t) at $t=0.1,0.2,\dots ,1.0$ and comparison with other methods for Example 2.

t	Method of	fourth-order compact	Present method with CSP			Present method with SVSP
	lines [38]	difference scheme [4]	$M=17,N=14$	$M=21,N=19$		$M=17,N=14$	$M=21,N=19$
0.1	$1.60\times {10}^{-3}$	$7.36\times {10}^{-7}$	$6.83\times {10}^{-10}$	$4.35\times {10}^{-5}$		$2.08\times {10}^{-11}$	$3.93\times {10}^{-17}$
0.2	$2.32\times {10}^{-6}$	$7.24\times {10}^{-7}$	$1.09\times {10}^{-10}$	$3.31\times {10}^{-6}$		$2.20\times {10}^{-11}$	$1.34\times {10}^{-17}$
0.3	$8.39\times {10}^{-5}$	$6.65\times {10}^{-7}$	$3.93\times {10}^{-11}$	$7.62\times {10}^{-8}$		$2.29\times {10}^{-11}$	$3.61\times {10}^{-17}$
0.4	$2.35\times {10}^{-4}$	$6.73\times {10}^{-7}$	$2.84\times {10}^{-11}$	$1.31\times {10}^{-10}$		$2.86\times {10}^{-11}$	$2.29\times {10}^{-17}$
0.5	$3.42\times {10}^{-3}$	$6.73\times {10}^{-7}$	$3.60\times {10}^{-11}$	$2.36\times {10}^{-10}$		$3.61\times {10}^{-11}$	$5.99\times {10}^{-19}$
0.6	$2.21\times {10}^{-3}$	$6.63\times {10}^{-7}$	$4.64\times {10}^{-11}$	$9.63\times {10}^{-10}$		$4.37\times {10}^{-11}$	$2.20\times {10}^{-17}$
0.7	$1.08\times {10}^{-3}$	$6.68\times {10}^{-7}$	$5.86\times {10}^{-11}$	$1.10\times {10}^{-7}$		$5.54\times {10}^{-11}$	$3.71\times {10}^{-17}$
0.8	$3.07\times {10}^{-4}$	$6.89\times {10}^{-7}$	$1.94\times {10}^{-10}$	$3.57\times {10}^{-6}$		$9.34\times {10}^{-11}$	$2.50\times {10}^{-17}$
0.9	$5.63\times {10}^{-4}$	$7.26\times {10}^{-7}$	$4.64\times {10}^{-10}$	$4.40\times {10}^{-5}$		$2.05\times {10}^{-10}$	$3.78\times {10}^{-17}$
1	$-$	$-$	$6.76\times {10}^{-9}$	$1.85\times {10}^{-4}$		$7.62\times {10}^{-9}$	$8.90\times {10}^{-17}$

The depicted results in Tables 8 and 9 demonstrate the ability of proposed method for solving this test problem. In this example again, one can easily see that the SVSP strategy is more efficient than the CSP one. The inefficiency in the CSP strategy when increasing the number of points is visible in Tables 8 and 9. We observe that in the case of SVSP strategy the accuracy grows as the number of nodes is incremented.

Figure 4. Absolute Error in approximating u(x, 1) (Graph a) and p(t) (Graph b) with $M=21$ and $N=19$ with SVSP for Example 2.

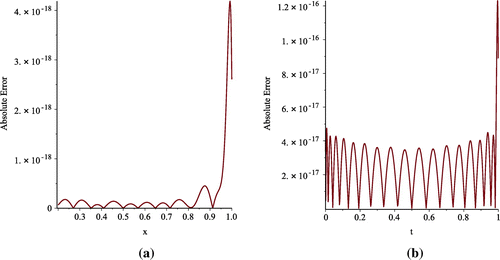
Table 10 shows the results of computing the $E_2,E_{\infty }$ and RMS errors of approximate u(x, t) and p(t) and condition number of system matrix for example 2 with CSP ($c=1/\sqrt{6}$) and SVSP ($c^{\ast }=1/\sqrt{6}$) strategies. In this table, similar to the results of Table 4, we can observe that SVSP strategy with regard to CSP one is more efficient, especially when the number of nodes tends to increase. 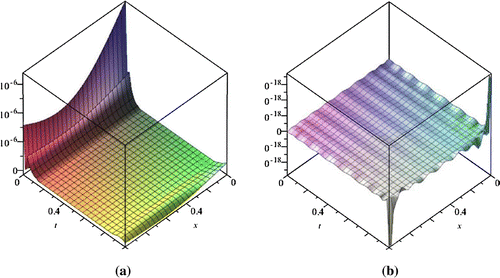The error function $u(x,t)-\tilde{u}(x,t)$ for this example is plotted in Figure 5.

Table 10. The $E_{\infty }$, $E_2$ and RMS errors for u and p for Example 2 with $c=1/\sqrt{6}$ and $c^{\ast }=1/\sqrt{6}$.

		$\text{Present method with CSP}$			$\text{Present method with SVSP}$
$\text{Error}$		$M=17,N=14$	$M=21,N=19$		$M=17,N=14$	$M=21,N=19$
$E_{\infty }^u$		$2.71\times {10}^{-11}$	$1.47\times {10}^{-6}$		$5.92\times {10}^{-14}$	$4.12\times {10}^{-18}$
$E_{\infty }^p$		$4.81\times {10}^{-9}$	$1.84\times {10}^{-4}$		$5.97\times {10}^{-9}$	$1.13\times {10}^{-16}$
$E_2^u$		$3.65\times {10}^{-5}$	$9.67\times {10}^{-3}$		$6.61\times {10}^{-7}$	$5.32\times {10}^{-9}$
$E_2^p$		$1.16\times {10}^{-4}$	$3.36\times {10}^{-2}$		$7.73\times {10}^{-5}$	$1.23\times {10}^{-8}$
RMS(u)		$2.37\times {10}^{-6}$	$4.84\times {10}^{-4}$		$4.28\times {10}^{-8}$	$2.66\times {10}^{-10}$
RMS(p)		$3.09\times {10}^{-5}$	$7.71\times {10}^{-3}$		$2.07\times {10}^{-5}$	$2.82\times {10}^{-9}$
$\text{Cond}$		$2.47\times {10}^{13}$	$1.70\times {10}^{15}$		$1.96\times {10}^{13}$	$5.23\times {10}^{14}$

Figure 5. Plot of error function $u-\tilde{u}$ with $M=21$ and $N=19$ using CSP with $c=1/\sqrt{6}$ (Graph a) and VSP with $c^{\ast }=1/\sqrt{6}$ (Graph b) for Example 2.

Tables 11 and 12 present the error for approximate u(x, t) and p(t), respectively, with $M=21$ and $N=19$ and noisy data H(t) with different noise levels and various noise frequencies for example 2. Moreover, this example as the previous example shows that the results in the proposed method with SVSP is more stable compared with the same method with CSP. In Tables 11 and 12, we can observe a special discipline in the mantissa of errors in SVSP approach when we fix noise frequencies and change noise level. The rate of convergence is presented in Table 13.

Table 11. Error for approximate u(x, t) with noisy input data for Example 2.

		$E_{\infty }^u\text{with CSP}$				$E_{\infty }^u\text{with SVSP}$
$\delta$		$ϵ={10}^{-3}$	$ϵ={10}^{-4}$	$ϵ={10}^{-5}$		$ϵ={10}^{-3}$	$ϵ={10}^{-4}$	$ϵ={10}^{-5}$
10		$1.03\times {10}^{-2}$	$1.10\times {10}^{-3}$	$2.02\times {10}^{-3}$		$9.80\times {10}^{-4}$	$9.80\times {10}^{-5}$	$9.80\times {10}^{-6}$
20		$1.22\times {10}^{-2}$	$1.56\times {10}^{-3}$	$1.88\times {10}^{-4}$		$1.01\times {10}^{-3}$	$1.01\times {10}^{-4}$	$1.01\times {10}^{-5}$
30		$7.12\times {10}^{-3}$	$3.26\times {10}^{-3}$	$1.48\times {10}^{-3}$		$1.84\times {10}^{-3}$	$1.73\times {10}^{-4}$	$1.72\times {10}^{-5}$

Table 12. Error for approximate p(t) with noisy input data for Example 2.

		$E_{\infty }^p\text{with CSP}$				$E_{\infty }^p\text{with SVSP}$
$\delta$		$ϵ={10}^{-3}$	$ϵ={10}^{-4}$	$ϵ={10}^{-5}$		$ϵ={10}^{-3}$	$ϵ={10}^{-4}$	$ϵ={10}^{-5}$
10		$8.94\times {10}^{-1}$	$1.83\times {10}^{-1}$	$2.04\times {10}^{-1}$		$5.36\times {10}^{-1}$	$5.46\times {10}^{-2}$	$5.46\times {10}^{-3}$
20		2.22	$3.69\times {10}^{-1}$	$3.83\times {10}^{-2}$		$8.20\times {10}^{-1}$	$8.08\times {10}^{-2}$	$8.08\times {10}^{-3}$
30		1.67	$1.64\times {10}^{-1}$	$1.94\times {10}^{-1}$		$9.61\times {10}^{-1}$	$9.75\times {10}^{-2}$	$9.76\times {10}^{-3}$

Table 13. Error norms and rate of convergence for various numbers of collocation points with $\eta =40$ for Example 2.

	Rate of convergence with CSP					Rate of convergence with SVSP
M, N	$E_{\infty }^u$	$ROC(E_{\infty }^u)$	$E_2^u$	$ROC(E_2^u)$		$E_{\infty }^u$	$ROC(E_{\infty }^u)$	$E_2^u$	$ROC(E_2^u)$
2, 2	0.44	$-$	0.88	$-$		0.28	$-$	0.72	$-$
4, 4	$6.81\times {10}^{-3}$	3.01	0.17	1.19		$7.08\times {10}^{-3}$	2.65	0.17	1.04
8, 8	$9.33\times {10}^{-6}$	4.76	$6.97\times {10}^{-3}$	2.30		$6.19\times {10}^{-6}$	5.08	$5.48\times {10}^{-3}$	2.48
16, 16	$1.04\times {10}^{-12}$	11.55	$5.17\times {10}^{-6}$	5.20		$4.66\times {10}^{-13}$	11.83	$1.92\times {10}^{-6}$	5.74
21, 19	$1.99\times {10}^{-6}$	$-32.59$	$7.92\times {10}^{-3}$	$-16.53$		$4.12\times {10}^{-18}$	26.22	$5.32\times {10}^{-9}$	13.27

The results presented in Table 13 show that in this example, like the previous one, the negative convergence rate problem in CSP approach is produced in the last row of the above table. It can be seen that the SVSP approach shows a better performance in view of convergence.

6. Conclusion

In this paper, we have solved an inverse parabolic problem with source control parameter using two kinds of basis functions. The proposed approach is based on the Chebyshev-RBF collocation method. We have used Gaussian radial basis functions with SVSP for the space variable and shifted Chebyshev basis functions for the time variable. Using nonuniform collocation points, a linear system has been achieved and solving this linear system has yielded the problem solutions. Then, two examples have been presented to check the proposed method. The results show efficiency and high accuracy of the method compared with those which have been reported in the literature. We have shown that if Gaussian radial basis function methods are applied with SVSP strategies for space variable, the error decreases quickly as the number of nodes increases. The influence of input data perturbation on output solutions has been investigated for both examples and interesting results have been obtained. In the same noise frequencies and by changing noise level, the error which is occurred by noise, varies by special discipline in SVSP strategy, while there is no discipline in the CSP strategy. Finding the reasons of this discipline’s creation can be a useful investigation. Finally, numerical rate of convergence analysis of the numerical approximation has also been obtained. It is observed that by comparing between the obtained ROC values of the $E_{\infty }^u$ and $E_2^u$ error norms by the SVSP and CSP method, SVSP results are considered acceptable.

Additional information

Funding

The authors fully appreciate financial support from Azarbaijan Shahid Madani University.

Notes

The authors have no conflict of interest.