Born approximation for the magnetic Schrödinger operator

ABSTRACT

We prove the existence of scattering solutions for multidimensional magnetic Schrödinger equation such that the scattered field belongs to the weighted Lebesgue space $L_{-\delta }^2({\mathbb{R}}^n)$ $(n\ge 2)$ with some $\delta >\frac{1}{2}$. As a consequence of this we provide the mathematical foundation of the direct Born approximation for the magnetic Schrödinger operator. Connection to the inverse Born approximation is discussed with numerical examples illustrating the applicability of the method.

KEYWORDS:

• Magnetic Schrödinger operator
• scattering
• Born approximation
• inverse problems
• numerical solution

AMS SUBJECT CLASSIFICATIONS:

• 35P25
• 35R30

1. Introduction

We develop a time harmonic scattering theory for the magnetic Schrödinger operator, analogous to the well-known theory for the Schrödinger operator. For this purpose we consider a Lippmann–Schwinger equation and prove that it is a Fredholm equation on the weighted Lebesgue space $L_{\delta }^2$. We then establish the asymptotic behaviour of the scattering operator and its Born, or linear, approximation and an explicit formula for the first nonlinear term in the Born series.

The direct Born approximation is known as the most applicable approximate method in the numerous practical problems. It is also known that the inverse scattering Born approximation is well-defined and perfectly works (as a mathematical tool) in the case of linear and nonlinear Schrödinger operators and for all types of scattering data: full scattering, backscattering, fixed angle scattering and fixed energy scattering. For some scattering data, it is possible to get the uniqueness and reconstruction procedure while for some data we are able to reconstruct singularities and jumps of unknowns even when there is no uniqueness. We mention here the results of Päivärinta and Somersalo [1], Nachman [2,3], Sun and Uhlmann [4], Isakov and Sylvester [5], Päivärinta, Serov and Somersalo [6], Päivärinta and Serov [7–9], Ola, Päivärinta and Serov [10], Ruiz [11], Ruiz and Vargas [12], Päivärinta and Serov [13], Reyes [14], Serov [15], Serov and Harju [16,17], Serov and Sandhu [18], Lechleiter [19], Reyes and Ruiz [20]. The main point of all these results is the precise calculation of the first (quadratic) nonlinear term in the Born series.

For the magnetic Schrödinger operator, the direct scattering problem (i.e. existence of the scattering solutions) as well as the inverse scattering Born approximation are much less familiar. We are only aware of [21–23]. Indeed, in [21] the authors assumed that magnetic and electric potentials with derivatives up to orders 4 and 5, respectively, decay exponentially. They were able to prove that the scattering amplitude at fixed energy determine uniquely the electric potential. In [22] the authors relaxed these assumptions to one derivative of magnetic potential and just electric potential decaying exponentially while proving the same main result. The inverse backscattering problem for magnetic Schrödinger was considered in [23] in the two-dimensional case under the assumptions that the magnetic potential, its gradient and electric potential have some polynomial decay at infinity.

In this work we continue to study the inverse backscattering problem in the multidimensional case. The big interest to this problem is connected to the fact that the knowledge of the scattering amplitude with backscattering data allows us to obtain essential information about the unknowns. The main goal of the present work is to justify the direct and inverse Born approximation for the magnetic Schrödinger operator. What is more, we will give the first (to the best of our knowledge) numerical examples illustrating this in two dimensions using backscattering data.

We consider the magnetic Schrödinger operator$$\begin{array}{c}\hfill H=-{(\mathrm{\nabla }+\mathrm{i}\overrightarrow{W}(x))}^2+V(x),x\in {\mathbb{R}}^n,\end{array}$$

in dimensions $n\ge 2$ where the coefficients $\overrightarrow{W}(x)$ and V(x) are assumed to be real-valued. We assume generally that(1) $$\begin{array}{c}\hfill \overrightarrow{W}\in W_{p,\sigma }^1({\mathbb{R}}^n),V\in L_{\sigma }^p({\mathbb{R}}^n),\end{array}$$(1)

where(2) $$\begin{array}{c}\hfill \sigma >max\left(1;n\left(1-\frac{2}{p}\right)\right),p>n.\end{array}$$(2)

Here $L_{\sigma }^p({\mathbb{R}}^n)$ denotes usual weighted Lebesgue space defined by finiteness of the norm$${\Vert f\Vert }_{L_{\sigma }^p({\mathbb{R}}^n)}:={\left({\int }_{{\mathbb{R}}^n}{(1+|x|)}^{p\sigma }{|f(x)|}^p\mathrm{d}x\right)}^{1/p}.$$

The Sobolev space $W_{p,\sigma }^1({\mathbb{R}}^n)$ is understood so that f belongs to $W_{p,\sigma }^1({\mathbb{R}}^n)$ if and only if f and $\mathrm{\nabla }f$ belong to $L_{\sigma }^p({\mathbb{R}}^n)$. It is the same (up to equivalent norms) that ${(1+|x|}^2{)}^{\sigma /2}f\in W_p^1({\mathbb{R}}^n)$. For the case $p=2$ instead of the symbol $W_{2,\sigma }^1({\mathbb{R}}^n)$ we use the symbol $H_{\sigma }^1({\mathbb{R}}^n)$.

It is known, see [24], that under these conditions for the coefficients of the magnetic Schrödinger operator the following Gårding’s inequality holds:$${(Hu,u)}_{L^2({\mathbb{R}}^n)}\ge {\nu \Vert \mathrm{\nabla }u\Vert }_{L^2({\mathbb{R}}^n)}^2-C{\Vert u\Vert }_{L^2({\mathbb{R}}^n)}^2,$$

where $0<\nu <1$ and $C>0$. This inequality allows us to define symmetric operator H by the method of quadratic forms. Then H has a self-adjoint Friedrichs extension with the domain (in general)$$D(H)=\{f\in W_2^1({\mathbb{R}}^n):Hf\in L^2({\mathbb{R}}^n)\}.$$

In our particular case it is possible to prove that actually(3) $$\begin{array}{c}\hfill D(H)=W_2^2({\mathbb{R}}^n),\end{array}$$(3)

see Appendix 1.

In the scattering theory the main role are played by the special solutions (scattering solutions) of the equation$$Hu(x)=k^{2}u(x)$$

which are of the form$$u(x)=u_0(x)+u_{\mathrm{s}c}(x),$$

where $u_0(x)={\mathrm{e}}^{\mathrm{i}k(x,\theta )}$ is incident plane wave with direction $\theta \in {\mathbb{S}}^{n-1}$ and the scattered wave $u_{\mathrm{s}c}(x)$ satisfies the Sommerfeld radiation condition at the infinity, i.e.$$\begin{array}{c}\hfill \underset{r\to +\infty }{lim}{r}^{\frac{n-1}{2}}\left(\frac{\partial u_{\mathrm{s}c}(x)}{\partial r}-\mathrm{i}k{u}_{\mathrm{s}c}(x)\right)=0,r=|x|.\end{array}$$

In this case the total field u satisfies the so-called Lippmann–Schwinger equation(4) $$\begin{array}{c}\hfill u(x)=u_0(x)+{\int }_{{\mathbb{R}}^n}{G}_k^{+}(|x-y|)\left(2\mathrm{i}\mathrm{\nabla }(\overrightarrow{W}(y)u(y))-q(y)u(y)\right)\mathrm{d}y,\end{array}$$(4)

where $q:=\mathrm{i}\mathrm{\nabla }\overrightarrow{W}+{|\overrightarrow{W}|}^2+V$ and $G_k^{+}$ is the kernel of integral operator ${(-\mathrm{\Delta }-k^2-\mathrm{i}0)}^{-1}$. Since $\overrightarrow{W}\in W_p^1({\mathbb{R}}^n)\subset L^{\infty }({\mathbb{R}}^n),p>n$ then$$q\in L_{\sigma }^p({\mathbb{R}}^n)$$

with the same p and $\sigma$ as in (2(2) $$\begin{array}{c}\hfill \sigma >max\left(1;n\left(1-\frac{2}{p}\right)\right),p>n.\end{array}$$(2) )

In Section 2, we show that, for every incident wave $u_0(x)$, there exists a unique scattering solution to the equation $Hu=k^{2}u$ such that the scattered field $u_{\mathrm{s}c}$ belongs to the weighted Lebesgue space $L_{-\delta }^2({\mathbb{R}}^n)$ with some $\delta >\frac{1}{2}$. We do this by showing that the Lippmann–Schwinger integral Equation (4(4) $$\begin{array}{c}\hfill u(x)=u_0(x)+{\int }_{{\mathbb{R}}^n}{G}_k^{+}(|x-y|)\left(2\mathrm{i}\mathrm{\nabla }(\overrightarrow{W}(y)u(y))-q(y)u(y)\right)\mathrm{d}y,\end{array}$$(4) ) is Fredholm on this Hilbert space.

In Section 3, (in order to define the scattering amplitude) we prove the asymptotic$$u_{\mathrm{s}c}\asymp c\frac{{\mathrm{e}}^{\mathrm{i}kr}}{r^{\frac{n-1}{2}}}A(k,{\theta }^{\prime },\theta )$$

as $r=|x|\to \infty$, where ${\theta }^{\prime }=\frac{x}{|x|}$. The function $A(k,{\theta }^{\prime },\theta )$ here is the scattering amplitude, the kernel of the relative scattering operator (also called the far field operator), which summarizes all the data that can be obtained from scattering experiments.

The dependence of the scattering operator on the potentials V and $\overrightarrow{W}$ is not linear. The Born, or single scattering approximation, provides insight into the full non-linear problem, and is often a good enough approximation to provide meaningful results in many applied inverse problems. In Section 3, we compute the Born approximation of the scattering operator for the magnetic Schrödinger operator. Even more, we go one step further and compute the second term in the Born series. In Section 4, we discuss connection to inverse Born approximation and give numerical examples of it in Section 5.

2. Existence of the scattering solutions

Using the representation $u=u_0+u_{\mathrm{s}c}$ we rewrite the integral Equation (4(4) $$\begin{array}{c}\hfill u(x)=u_0(x)+{\int }_{{\mathbb{R}}^n}{G}_k^{+}(|x-y|)\left(2\mathrm{i}\mathrm{\nabla }(\overrightarrow{W}(y)u(y))-q(y)u(y)\right)\mathrm{d}y,\end{array}$$(4) ) only for scattered field $u_{\mathrm{s}c}$ as(5) $$\begin{array}{c}\hfill u_{\mathrm{s}c}(x)={\tilde{u}}_0(x)+{\int }_{{\mathbb{R}}^n}{G}_k^{+}(|x-y|)\left(2\mathrm{i}\mathrm{\nabla }(\overrightarrow{W}(y)u_{\mathrm{s}c}(y))-q(y)u_{\mathrm{s}c}(y)\right)\mathrm{d}y,\end{array}$$(5)

where ${\tilde{u}}_0$ is equal to$$\begin{array}{c}\hfill {\tilde{u}}_0(x)={\int }_{{\mathbb{R}}^n}{G}_k^{+}(|x-y|)\left(2\mathrm{i}\mathrm{\nabla }(\overrightarrow{W}(y)u_0(y))-q(y)u_0(y)\right)\mathrm{d}y.\end{array}$$

We use the following results of Agmon [25, Remark 2, Appendix A]: for any $g\in H_{-\delta }^2({\mathbb{R}}^n)$ it is true that$$\frac{1}{|k|}{\Vert g\Vert }_{H_{-\delta }^2({\mathbb{R}}^n)}+{\Vert g\Vert }_{H_{-\delta }^1({\mathbb{R}}^n)}+{|k|\Vert g\Vert }_{L_{-\delta }^2({\mathbb{R}}^n)}\le c\Vert (\mathrm{\Delta }+k^2){g\Vert }_{L_{\delta }^2({\mathbb{R}}^n)},|k|\ge 1,$$

where $\delta >\frac{1}{2}$ and $H_{-\delta }^s({\mathbb{R}}^n),s=0,1,2,$ denotes the weighted Sobolev spaces. As a consequence we have uniformly in $|k|\ge 1$ the crucial estimates(6) $$\begin{array}{cc}\hfill \Vert {(-\mathrm{\Delta }-k^2-\mathrm{i}0)}^{-1}{f\Vert }_{L_{-\delta }^2({\mathbb{R}}^n)}& \le \frac{\beta }{|k|}{\Vert f\Vert }_{L_{\delta }^2({\mathbb{R}}^n)},\hfill \\ \hfill \Vert {(-\mathrm{\Delta }-k^2-\mathrm{i}0)}^{-1}{f\Vert }_{H_{-\delta }^1({\mathbb{R}}^n)}& \le {\beta \Vert f\Vert }_{L_{\delta }^2({\mathbb{R}}^n)}.\hfill \end{array}$$(6)

The constant $\beta$ will be used below precisely.

The operator ${(-\mathrm{\Delta }-k^2-\mathrm{i}0)}^{-1}$ is the integral operator of convolution type. Then using duality we can conclude that uniformly in $|k|\ge 1$ it maps continuously $H_{\delta }^{-1}({\mathbb{R}}^n)$ to $L_{-\delta }^2({\mathbb{R}}^n)$ with the same norm estimate $\beta$ as above, i.e.(7) $$\begin{array}{c}\hfill \Vert {(-\mathrm{\Delta }-k^2-\mathrm{i}0)}^{-1}{f\Vert }_{L_{-\delta }^2({\mathbb{R}}^n)}\le \beta {\Vert f\Vert }_{H_{\delta }^{-1}({\mathbb{R}}^n)},\end{array}$$(7)

where $H_{\delta }^{-1}({\mathbb{R}}^n)$ denotes the dual of the Sobolev space $H_{-\delta }^1({\mathbb{R}}^n)$.

We rewrite (5(5) $$\begin{array}{c}\hfill u_{\mathrm{s}c}(x)={\tilde{u}}_0(x)+{\int }_{{\mathbb{R}}^n}{G}_k^{+}(|x-y|)\left(2\mathrm{i}\mathrm{\nabla }(\overrightarrow{W}(y)u_{\mathrm{s}c}(y))-q(y)u_{\mathrm{s}c}(y)\right)\mathrm{d}y,\end{array}$$(5) ) as the operator equation$$u_{\mathrm{s}c}={\tilde{u}}_0+L_k(u_{\mathrm{s}c}),{\tilde{u}}_0=L_k(u_0),$$

where the integral operator $L_k$ is defined as(8) $$\begin{array}{c}\hfill L_{k}f(x):={\int }_{{\mathbb{R}}^n}{G}_k^{+}(|x-y|)\left(2\mathrm{i}\mathrm{\nabla }(\overrightarrow{W}(y)f(y))-q(y)f(y)\right)\mathrm{d}y.\end{array}$$(8)

The mapping properties and asymptotic expansion of the operator $L_k$ are studied in the following lemmas which have also independent interest.

Lemma 2.1:

Let us assume that conditions (1(1) $$\begin{array}{c}\hfill \overrightarrow{W}\in W_{p,\sigma }^1({\mathbb{R}}^n),V\in L_{\sigma }^p({\mathbb{R}}^n),\end{array}$$(1) ) and (2(2) $$\begin{array}{c}\hfill \sigma >max\left(1;n\left(1-\frac{2}{p}\right)\right),p>n.\end{array}$$(2) ) are fulfilled. Then ${\tilde{u}}_0\in L_{-\sigma /2}^2({\mathbb{R}}^n)$ and the integral operator $L_k$ maps $L_{-\sigma /2}^2({\mathbb{R}}^n)$ into itself, where $\sigma$ is the same as in (2(2) $$\begin{array}{c}\hfill \sigma >max\left(1;n\left(1-\frac{2}{p}\right)\right),p>n.\end{array}$$(2) ). Moreover, uniformly in $|k|\ge 1$ the following estimates hold(9) $$\begin{array}{c}\hfill \Vert {\tilde{u}}_0{\Vert }_{L_{-\sigma /2}^2({\mathbb{R}}^n)}\le \beta \left(2\Vert \overrightarrow{W}{\Vert }_{L_{\sigma /2}^2({\mathbb{R}}^n)}+{\Vert q\Vert }_{L_{\sigma /2}^2({\mathbb{R}}^n)}\right)\end{array}$$(9)

and(10) $$\begin{array}{c}\hfill \Vert L_k{f\Vert }_{L_{-\sigma /2}^2({\mathbb{R}}^n)}\le \beta \left(2\Vert \overrightarrow{W}{\Vert }_{L_{\sigma }^{\infty }({\mathbb{R}}^n)}+C_p{\Vert q\Vert }_{L_{\sigma }^p({\mathbb{R}}^n)}\right){\Vert f\Vert }_{L_{-\sigma /2}^2({\mathbb{R}}^n)},\end{array}$$(10)

where the constant $C_p$ is equal to$$C_p={\left(\frac{1}{{(2\sqrt{\pi })}^n}\frac{\mathrm{\Gamma }(\frac{p-n}{2})}{\mathrm{\Gamma }(\frac{p}{2})}\right)}^{\frac{1}{p}}.$$

Proof Conditions (2(2) $$\begin{array}{c}\hfill \sigma >max\left(1;n\left(1-\frac{2}{p}\right)\right),p>n.\end{array}$$(2) ) for p and $\sigma$ imply that $\frac{\sigma }{2}>\frac{1}{2}$ and$$L_{\sigma }^p({\mathbb{R}}^n)\subset L_{\sigma /2}^2({\mathbb{R}}^n).$$

It is therefore true that under the conditions (1(1) $$\begin{array}{c}\hfill \overrightarrow{W}\in W_{p,\sigma }^1({\mathbb{R}}^n),V\in L_{\sigma }^p({\mathbb{R}}^n),\end{array}$$(1) ) and (2(2) $$\begin{array}{c}\hfill \sigma >max\left(1;n\left(1-\frac{2}{p}\right)\right),p>n.\end{array}$$(2) ) the functions V, $\overrightarrow{W}$, $\mathrm{\nabla }\overrightarrow{W}$ and $|\overrightarrow{W}{|}^2$ belong to $L_{\sigma /2}^2({\mathbb{R}}^n)$. Since $u_0$ is bounded then using Agmon’s result (6(6) $$\begin{array}{cc}\hfill \Vert {(-\mathrm{\Delta }-k^2-\mathrm{i}0)}^{-1}{f\Vert }_{L_{-\delta }^2({\mathbb{R}}^n)}& \le \frac{\beta }{|k|}{\Vert f\Vert }_{L_{\delta }^2({\mathbb{R}}^n)},\hfill \\ \hfill \Vert {(-\mathrm{\Delta }-k^2-\mathrm{i}0)}^{-1}{f\Vert }_{H_{-\delta }^1({\mathbb{R}}^n)}& \le {\beta \Vert f\Vert }_{L_{\delta }^2({\mathbb{R}}^n)}.\hfill \end{array}$$(6) ) we obtain$$\Vert {\tilde{u}}_0{\Vert }_{L_{-\sigma /2}^2({\mathbb{R}}^n)}\le \frac{\beta }{|k|}\left(2|k|\Vert \overrightarrow{W}{\Vert }_{L_{\sigma /2}^2({\mathbb{R}}^n)}+{\Vert q\Vert }_{L_{\sigma /2}^2({\mathbb{R}}^n)}\right).$$

Hence, the estimate (9(9) $$\begin{array}{c}\hfill \Vert {\tilde{u}}_0{\Vert }_{L_{-\sigma /2}^2({\mathbb{R}}^n)}\le \beta \left(2\Vert \overrightarrow{W}{\Vert }_{L_{\sigma /2}^2({\mathbb{R}}^n)}+{\Vert q\Vert }_{L_{\sigma /2}^2({\mathbb{R}}^n)}\right)\end{array}$$(9) ) is proved. Next, applying (7(7) $$\begin{array}{c}\hfill \Vert {(-\mathrm{\Delta }-k^2-\mathrm{i}0)}^{-1}{f\Vert }_{L_{-\delta }^2({\mathbb{R}}^n)}\le \beta {\Vert f\Vert }_{H_{\delta }^{-1}({\mathbb{R}}^n)},\end{array}$$(7) ) we obtain for any $f\in L_{-\sigma /2}^2({\mathbb{R}}^n)$ that$$\begin{array}{cc}\hfill \Vert L_k{f\Vert }_{L_{-\sigma /2}^2({\mathbb{R}}^n)}& \le \beta \left(2\Vert \mathrm{\nabla }(\overrightarrow{W}f){\Vert }_{H_{\sigma /2}^{-1}({\mathbb{R}}^n)}+{\Vert qf\Vert }_{H_{\sigma /2}^{-1}({\mathbb{R}}^n)}\right)\hfill \\ \hfill & \le \beta \left(2\Vert \overrightarrow{W}{f\Vert }_{L_{\sigma /2}^2({\mathbb{R}}^n)}+{\Vert qf\Vert }_{H_{\sigma /2}^{-1}({\mathbb{R}}^n)}\right)\hfill \\ \hfill & \le \beta \left(2\Vert \overrightarrow{W}{\Vert }_{L_{\sigma }^{\infty }({\mathbb{R}}^n)}{\Vert f\Vert }_{L_{-\sigma /2}^2({\mathbb{R}}^n)}+{\Vert qf\Vert }_{H_{\sigma /2}^{-1}({\mathbb{R}}^n)}\right)\hfill \end{array}$$

since the conditions (1(1) $$\begin{array}{c}\hfill \overrightarrow{W}\in W_{p,\sigma }^1({\mathbb{R}}^n),V\in L_{\sigma }^p({\mathbb{R}}^n),\end{array}$$(1) ) and (2(2) $$\begin{array}{c}\hfill \sigma >max\left(1;n\left(1-\frac{2}{p}\right)\right),p>n.\end{array}$$(2) ) guarantee that $\overrightarrow{W}$ belongs to $L_{\sigma }^{\infty }({\mathbb{R}}^n)$. In order to estimate the second term ${\Vert qf\Vert }_{H_{\sigma /2}^{-1}({\mathbb{R}}^n)}$ we proceed as follows. First, we rewrite and estimate this norm (using Hölder’s and Hausdorff-Young inequalities) as$$\begin{array}{cc}\hfill {\Vert qf\Vert }_{H_{\sigma /2}^{-1}({\mathbb{R}}^n)}& =\Vert \tilde{q}\tilde{f}{\Vert }_{H^{-1}({\mathbb{R}}^n)}=\Vert F(\tilde{q}\tilde{f}){\Vert }_{L_{-1}^2({\mathbb{R}}^n)}\le C_0{\Vert F(\tilde{q}\tilde{f})\Vert }_{L^{\frac{2p}{p-2}}({\mathbb{R}}^n)}\hfill \\ \hfill & \le C_0{(2\pi )}^{-n/p}\Vert \tilde{q}\tilde{f}{\Vert }_{L^{\frac{2p}{p+2}}({\mathbb{R}}^n)}\le C_0{(2\pi )}^{-n/p}\Vert \tilde{q}{\Vert }_{L^p({\mathbb{R}}^n)}{\Vert \tilde{f}\Vert }_{L^2({\mathbb{R}}^n)},p>n,\hfill \end{array}$$

where F is the Fourier transform, $\tilde{q}(x)={(1+|x|}^2{)}^{\sigma /2}q(x)$, $\tilde{f}(x)={(1+|x|}^2{)}^{-\sigma /4}f(x)$ and the constant $C_0$ is equal to$$C_0={\left({\int }_{{\mathbb{R}}^n}\frac{1}{{(1+|x|}^2{)}^{p/2}}\mathrm{d}x\right)}^{1/p}={\left(\frac{{\sqrt{\pi }}^n}{\mathrm{\Gamma }(\frac{n}{2})}{\int }_0^{\infty }{r}^{\frac{n-2}{2}}{(1+r)}^{-p/2}\mathrm{d}r\right)}^{1/p}.$$

Combining this constant $C_0$ with the latter inequality we obtain the value for the constant $C_p$ from lemma and the inequality (10(10) $$\begin{array}{c}\hfill \Vert L_k{f\Vert }_{L_{-\sigma /2}^2({\mathbb{R}}^n)}\le \beta \left(2\Vert \overrightarrow{W}{\Vert }_{L_{\sigma }^{\infty }({\mathbb{R}}^n)}+C_p{\Vert q\Vert }_{L_{\sigma }^p({\mathbb{R}}^n)}\right){\Vert f\Vert }_{L_{-\sigma /2}^2({\mathbb{R}}^n)},\end{array}$$(10) ). Thus, lemma is proved.

Corollary 2.1:

The integral operator $L_k$ for fixed $k>0$ maps $L^{\infty }({\mathbb{R}}^n)$ into itself with the norm estimate depending on the norms $\Vert \overrightarrow{W}{\Vert }_{L_{\sigma }^p({\mathbb{R}}^n)}$ and ${\Vert q\Vert }_{L_{\sigma }^p({\mathbb{R}}^n)}$.

Lemma 2.2:

Under the same assumptions as in Lemma 2.1, for any fixed $k>0$ and for any $f\in C_0^{\infty }({\mathbb{R}}^n)$ the following asymptotical representation holds:(11) $$\begin{array}{cc}\hfill L_{k}f(x)& =C\frac{{\mathrm{e}}^{\mathrm{i}k|x|}{k}^{\frac{n-3}{2}}}{{|x|}^{\frac{n-1}{2}}}{\int }_{{\mathbb{R}}^n}{\mathrm{e}}^{-\mathrm{i}k({\theta }^{\prime },y)}\left(2k{\theta }^{\prime }\overrightarrow{W}(y)f(y)+q(y)f(y)\right)\mathrm{d}y\hfill \\ \hfill & +O\left(\frac{1}{{|x|}^{\frac{n+1}{2}}}\right),|x|\to \infty ,\hfill \end{array}$$(11)

where ${\theta }^{\prime }=\frac{x}{|x|}$ and constant $C>0$ depends only on n.

Proof Since $f\in C_0^{\infty }({\mathbb{R}}^n)$ then integration by parts in (8(8) $$\begin{array}{c}\hfill L_{k}f(x):={\int }_{{\mathbb{R}}^n}{G}_k^{+}(|x-y|)\left(2\mathrm{i}\mathrm{\nabla }(\overrightarrow{W}(y)f(y))-q(y)f(y)\right)\mathrm{d}y.\end{array}$$(8) ) leads to$$L_{k}f(x)=-2\mathrm{i}{\int }_{{\mathbb{R}}^n}{\mathrm{\nabla }}_y{G}_k^{+}(|x-y|)\overrightarrow{W}(y)f(y)\mathrm{d}y-{\int }_{{\mathbb{R}}^n}{G}_k^{+}(|x-y|)q(y)f(y)\mathrm{d}y.$$

In view of this version of (8(8) $$\begin{array}{c}\hfill L_{k}f(x):={\int }_{{\mathbb{R}}^n}{G}_k^{+}(|x-y|)\left(2\mathrm{i}\mathrm{\nabla }(\overrightarrow{W}(y)f(y))-q(y)f(y)\right)\mathrm{d}y.\end{array}$$(8) ) one must study the behaviour for $|x|\to \infty$ of the functions $G_k^{+}$ and $\mathrm{\nabla }{G}_k^{+}$, i.e.$$\frac{\mathrm{i}}{4}{\left(\frac{k}{2\pi |x-y|}\right)}^{\frac{n-2}{2}}{H}_{\frac{n-2}{2}}^{(1)}(k|x-y|),k\frac{x-y}{|x-y|}\frac{\mathrm{i}}{4}{\left(\frac{k}{2\pi |x-y|}\right)}^{\frac{n-2}{2}}{H}_{\frac{n}{2}}^{(1)}(k|x-y|),$$

respectively, where $H_{\nu }^{(1)}$ denotes the Hankel function of first kind and of order $\nu$. Since $k>0$ is fixed and y is bounded then $k|x-y|\to \infty$ as $|x|\to \infty$. Thus, we may use the behaviour of the Hankel functions $H_{\nu }^{(1)}$ for large argument (see, e.g. [26]), i.e.$$H_{\frac{n-2}{2}}^{(1)}(z)=c_n\frac{{\mathrm{e}}^{\mathrm{i}z}}{\sqrt{z}}+O\left(\frac{1}{z^{3/2}}\right),H_{\frac{n}{2}}^{(1)}(z)=-\mathrm{i}{c}_n\frac{{\mathrm{e}}^{\mathrm{i}z}}{\sqrt{z}}+O\left(\frac{1}{z^{3/2}}\right),$$

where $z\to +\infty$ and the constant $c_n$ (which is the same for both asymptotic) is equal to (see, e.g. [26])$$c_n=\sqrt{\frac{2}{\pi }}{\mathrm{e}}^{-\mathrm{i}\frac{\pi }{4}(n-1)},n=2,3,\dots$$

Hence, we obtain$$G_k^{+}(|x-y|)=\frac{\mathrm{i}{c}_n}{4{(2\pi )}^{\frac{n-2}{2}}}\frac{{\mathrm{e}}^{\mathrm{i}k|x-y|}{k}^{\frac{n-3}{2}}}{{|x-y|}^{\frac{n-1}{2}}}+O\left(\frac{1}{{|x|}^{\frac{n+1}{2}}}\right),|x|\to +\infty$$

and (using $\frac{x-y}{|x-y|}=\frac{x}{|x|}+O(\frac{1}{|x|})$) we have also$${\mathrm{\nabla }}_y{G}_k^{+}(|x-y|)=\frac{c_n}{4{(2\pi )}^{\frac{n-2}{2}}}{\theta }^{\prime }k\frac{{\mathrm{e}}^{\mathrm{i}k|x-y|}{k}^{\frac{n-3}{2}}}{{|x-y|}^{\frac{n-1}{2}}}+O\left(\frac{1}{{|x|}^{\frac{n+1}{2}}}\right),|x|\to +\infty$$

with ${\theta }^{\prime }=\frac{x}{|x|}$. In addition to these asymptotics, for bounded y and $|x|\to +\infty$ we have$${|x-y|}^{-\frac{n-1}{2}}={|x|}^{-\frac{n-1}{2}}+{O(|x|}^{-\frac{n+1}{2}}),{\mathrm{e}}^{\mathrm{i}k|x-y|}={\mathrm{e}}^{\mathrm{i}k|x|}{\mathrm{e}}^{-\mathrm{i}({\theta }^{\prime },y)}+{O(|x|}^{-1}),$$

and therefore$$L_{k}f(x)={\tilde{c}}_n\frac{{\mathrm{e}}^{\mathrm{i}k|x|}{k}^{\frac{n-3}{2}}}{{|x|}^{\frac{n-1}{2}}}{\int }_{{\mathbb{R}}^n}{\mathrm{e}}^{-\mathrm{i}k({\theta }^{\prime },y)}\left(2k{\theta }^{\prime }\overrightarrow{W}(y)f(y)+q(y)f(y)\right)\mathrm{d}y+O\left(\frac{1}{{|x|}^{\frac{n+1}{2}}}\right),$$

where ${\tilde{c}}_n=-\frac{\mathrm{i}{c}_n}{4{(2\pi )}^{\frac{n-2}{2}}}$. Thus, lemma is proved.

These lemmas allow us to achieve the main goal of this section in the form of the first main result of this work. Let us denote by $\alpha$ and $\gamma$ the following norms:(12) $$\begin{array}{c}\hfill \alpha :=2\Vert \overrightarrow{W}{\Vert }_{L_{\sigma }^{\infty }({\mathbb{R}}^n)}+C_p{\Vert q\Vert }_{L_{\sigma }^p({\mathbb{R}}^n)},\gamma :=2\Vert \overrightarrow{W}{\Vert }_{L_{\sigma /2}^2({\mathbb{R}}^n)}+{\Vert q\Vert }_{L_{\sigma /2}^2({\mathbb{R}}^n)}.\end{array}$$(12)

Theorem 2.1:

Assume that the conditions (1(1) $$\begin{array}{c}\hfill \overrightarrow{W}\in W_{p,\sigma }^1({\mathbb{R}}^n),V\in L_{\sigma }^p({\mathbb{R}}^n),\end{array}$$(1) ) and (2(2) $$\begin{array}{c}\hfill \sigma >max\left(1;n\left(1-\frac{2}{p}\right)\right),p>n.\end{array}$$(2) ) for the coefficients of H are satisfied and assume that $\alpha \beta <1$. Then for any $|k|\ge 1$ the integral Equation (5(5) $$\begin{array}{c}\hfill u_{\mathrm{s}c}(x)={\tilde{u}}_0(x)+{\int }_{{\mathbb{R}}^n}{G}_k^{+}(|x-y|)\left(2\mathrm{i}\mathrm{\nabla }(\overrightarrow{W}(y)u_{\mathrm{s}c}(y))-q(y)u_{\mathrm{s}c}(y)\right)\mathrm{d}y,\end{array}$$(5) ) has a unique solution $u_{\mathrm{s}c}$ from the space $L_{-\sigma /2}^2({\mathbb{R}}^n)$. Moreover, uniformly in $|k|\ge 1$ the following estimate holds(13) $$\begin{array}{c}\hfill \Vert u_{\mathrm{s}c}{\Vert }_{L_{-\sigma /2}^2({\mathbb{R}}^n)}\le \frac{\beta \gamma }{1-\beta \alpha }.\end{array}$$(13)

Proof Lemma 2.1 and the conditions of this theorem say that the integral operator $L_k$ maps in $L_{-\sigma /2}^2({\mathbb{R}}^n)$ with the norm estimate(14) $$\begin{array}{c}\hfill \Vert L_k{\Vert }_{L_{-\sigma /2}^2({\mathbb{R}}^n)\to L_{-\sigma /2}^2({\mathbb{R}}^n)}\le \beta \alpha <1.\end{array}$$(14)

In particular,$$\begin{array}{c}\hfill \Vert L_k{\Vert }_{H_{-\sigma /2}^{1/2}({\mathbb{R}}^n)\to L_{-\sigma /2}^2({\mathbb{R}}^n)}\le \beta \alpha .\end{array}$$

Since ${\tilde{u}}_0$ also belongs to $L_{-\sigma /2}^2({\mathbb{R}}^n)$ (see Lemma 2.1) with the norm estimate $\beta \gamma$ then the integral equation has a unique solution $u_{\mathrm{s}c}$ that can be obtained by the iterations as$$u_{\mathrm{s}c}={(I-L_k)}^{-1}({\tilde{u}}_0)=\sum _{j=0}^{\infty }{L}_k^j({\tilde{u}}_0).$$

The norm estimate follows now from Lemma 2.1 and the latter representation. It proves the theorem.

Corollary 2.2:

Under the conditions of Theorem 2.1, $u_{\mathrm{s}c}(x,k,\theta )$ belongs to $L^{\infty }({\mathbb{R}}^n)$ in x for any fixed $k>0$ and uniformly in $\theta \in {\mathbb{S}}^{n-1}$.

3. Scattering amplitude and direct backscattering Born approximation

In this section, we will consider the direct backscattering Born approximation for the magnetic Schrödinger operator H with conditions (1(1) $$\begin{array}{c}\hfill \overrightarrow{W}\in W_{p,\sigma }^1({\mathbb{R}}^n),V\in L_{\sigma }^p({\mathbb{R}}^n),\end{array}$$(1) )–(2(2) $$\begin{array}{c}\hfill \sigma >max\left(1;n\left(1-\frac{2}{p}\right)\right),p>n.\end{array}$$(2) ) but with $\sigma >n-n/p$ there. The motivation for this problem is connected to the fact that the knowledge of the scattering amplitude with the backscattering data gives essential information about the unknown functions V and $\overrightarrow{W}$.

Theorem 2.1, Lemma 2.2 (see representation (11(11) $$\begin{array}{cc}\hfill L_{k}f(x)& =C\frac{{\mathrm{e}}^{\mathrm{i}k|x|}{k}^{\frac{n-3}{2}}}{{|x|}^{\frac{n-1}{2}}}{\int }_{{\mathbb{R}}^n}{\mathrm{e}}^{-\mathrm{i}k({\theta }^{\prime },y)}\left(2k{\theta }^{\prime }\overrightarrow{W}(y)f(y)+q(y)f(y)\right)\mathrm{d}y\hfill \\ \hfill & +O\left(\frac{1}{{|x|}^{\frac{n+1}{2}}}\right),|x|\to \infty ,\hfill \end{array}$$(11) )) and Corollary 2.1 yield the following asymptotical representation (we may integrate by parts in (5(5) $$\begin{array}{c}\hfill u_{\mathrm{s}c}(x)={\tilde{u}}_0(x)+{\int }_{{\mathbb{R}}^n}{G}_k^{+}(|x-y|)\left(2\mathrm{i}\mathrm{\nabla }(\overrightarrow{W}(y)u_{\mathrm{s}c}(y))-q(y)u_{\mathrm{s}c}(y)\right)\mathrm{d}y,\end{array}$$(5) ) with these new conditions (1(1) $$\begin{array}{c}\hfill \overrightarrow{W}\in W_{p,\sigma }^1({\mathbb{R}}^n),V\in L_{\sigma }^p({\mathbb{R}}^n),\end{array}$$(1) )–(2(2) $$\begin{array}{c}\hfill \sigma >max\left(1;n\left(1-\frac{2}{p}\right)\right),p>n.\end{array}$$(2) ) for the coefficients of H since u is bounded for fixed $k>0$) for the scattering solutions $u(x,k,\theta )$ with fixed $k>0$ as $|x|\to +\infty$:(15) $$\begin{array}{c}\hfill u(x,k,\theta )={\mathrm{e}}^{\mathrm{i}k(x,\theta )}+C\frac{{\mathrm{e}}^{\mathrm{i}k|x|}{k}^{\frac{n-3}{2}}}{{|x|}^{\frac{n-1}{2}}}A(k,{\theta }^{\prime },\theta )+o\left(\frac{1}{{|x|}^{\frac{n-1}{2}}}\right),\end{array}$$(15)

where the function A is called the scattering amplitude and defined by(16) $$\begin{array}{c}\hfill A(k,{\theta }^{\prime },\theta )={\int }_{{\mathbb{R}}^n}{\mathrm{e}}^{-\mathrm{i}k({\theta }^{\prime },y)}\left(2k{\theta }^{\prime }\overrightarrow{W}(y)u(y)+q(y)u(y)\right)\mathrm{d}y.\end{array}$$(16)

Here (as above) $q=\mathrm{i}\mathrm{\nabla }\overrightarrow{W}+{|\overrightarrow{W}|}^2+V$, the constant $C>0$ depends only on n and the latter equality is understood in the sense of tempered distributions.

Substituting $u=u_0+u_{\mathrm{s}c}$ into (16(16) $$\begin{array}{c}\hfill A(k,{\theta }^{\prime },\theta )={\int }_{{\mathbb{R}}^n}{\mathrm{e}}^{-\mathrm{i}k({\theta }^{\prime },y)}\left(2k{\theta }^{\prime }\overrightarrow{W}(y)u(y)+q(y)u(y)\right)\mathrm{d}y.\end{array}$$(16) ) gives that(17) $$\begin{array}{cc}\hfill A(k,{\theta }^{\prime },\theta )& ={\int }_{{\mathbb{R}}^n}{\mathrm{e}}^{-\mathrm{i}k({\theta }^{\prime },y)}\left(2k{\theta }^{\prime }\overrightarrow{W}(y)u_0(y)+q(y)u_0(y)\right)\mathrm{d}y\hfill \\ \hfill & +{\int }_{{\mathbb{R}}^n}{\mathrm{e}}^{-\mathrm{i}k({\theta }^{\prime },y)}\left(2k{\theta }^{\prime }\overrightarrow{W}(y)u_{\mathrm{s}c}(y)+q(y)u_{\mathrm{s}c}(y)\right)\mathrm{d}y\hfill \\ \hfill & =:A_{\mathrm{B}}(k,{\theta }^{\prime },\theta )+R(k,{\theta }^{\prime },\theta ).\hfill \end{array}$$(17)

The function $A_{\mathrm{B}}$ is called the direct Born approximation. It can be easily checked that $A_{\mathrm{B}}$ is actually equal to(18) $$\begin{array}{cc}\hfill A_{\mathrm{B}}(k,{\theta }^{\prime },\theta )& =2k{\theta }^{\prime }F(\overrightarrow{W})(k(\theta -{\theta }^{\prime }))+F(q)(k(\theta -{\theta }^{\prime }))\hfill \\ \hfill & =k(\theta +{\theta }^{\prime })F(\overrightarrow{W})(k(\theta -{\theta }^{\prime }))+F(|\overrightarrow{W}{|}^2+V)(k(\theta -{\theta }^{\prime })),\hfill \end{array}$$(18)

where F denotes the $n-$dimensional Fourier transform$$F(f)(\xi )={\int }_{{\mathbb{R}}^n}f(x){\mathrm{e}}^{\mathrm{i}(x,\xi )}\mathrm{d}x.$$

Next we establish a connection between the direct Born approximation and the coefficients of the magnetic Schrödinger operator. In the future, this might give insight into the inverse scattering problem with full scattering data.

Proposition 3.1:

Let $\xi \ne 0$ be an arbitrary vector from ${\mathbb{R}}^n$ and let ${\widehat{\xi }}_{\perp }$ be the unit vector that is orthogonal to $\xi$. Let also $k>0$ be such that ${\xi }^2\le 4k^2$. Let us choose $\theta$ and ${\theta }^{\prime }$ as follows:$$\theta =\frac{\xi }{2k}+\frac{{\widehat{\xi }}_{\perp }}{2k}\sqrt{4k^2-{\xi }^2},{\theta }^{\prime }=-\frac{\xi }{2k}+\frac{{\widehat{\xi }}_{\perp }}{2k}\sqrt{4k^2-{\xi }^2}.$$

Then $\theta ,{\theta }^{\prime }\in {\mathbb{S}}^{n-1}$, $\xi =k(\theta -{\theta }^{\prime })$, and(19) $$\begin{array}{cc}\hfill F(|\overrightarrow{W}{|}^2+V)(\xi )& =\frac{1}{2}\left(A_{\mathrm{B}}(k,{\theta }^{\prime },\theta )+A_{\mathrm{B}}(k,-\theta ,-{\theta }^{\prime })\right)\hfill \\ \hfill \sqrt{4k^2-{\xi }^2}{({\widehat{\xi }}_{\perp },F(\overrightarrow{W})(\xi ))}_{{\mathbb{R}}^n}& =\frac{1}{2}\left(A_{\mathrm{B}}(k,{\theta }^{\prime },\theta )-A_{\mathrm{B}}(k,-\theta ,-{\theta }^{\prime })\right).\hfill \end{array}$$(19)

Proof Follows straightforwardly from (18(18) $$\begin{array}{cc}\hfill A_{\mathrm{B}}(k,{\theta }^{\prime },\theta )& =2k{\theta }^{\prime }F(\overrightarrow{W})(k(\theta -{\theta }^{\prime }))+F(q)(k(\theta -{\theta }^{\prime }))\hfill \\ \hfill & =k(\theta +{\theta }^{\prime })F(\overrightarrow{W})(k(\theta -{\theta }^{\prime }))+F(|\overrightarrow{W}{|}^2+V)(k(\theta -{\theta }^{\prime })),\hfill \end{array}$$(18) ).

Our next main interest (with respect to inverse problems) concerns to the particular case ${\theta }^{\prime }=-\theta$. This case leads to the so-called direct backscattering Born approximation, i.e.(20) $$\begin{array}{c}\hfill A_{\mathrm{B}}^{\mathrm{b}}(k,-\theta ,\theta )=F(|\overrightarrow{W}{|}^2+V)(2k\theta ).\end{array}$$(20)

Formulae (17(17) $$\begin{array}{cc}\hfill A(k,{\theta }^{\prime },\theta )& ={\int }_{{\mathbb{R}}^n}{\mathrm{e}}^{-\mathrm{i}k({\theta }^{\prime },y)}\left(2k{\theta }^{\prime }\overrightarrow{W}(y)u_0(y)+q(y)u_0(y)\right)\mathrm{d}y\hfill \\ \hfill & +{\int }_{{\mathbb{R}}^n}{\mathrm{e}}^{-\mathrm{i}k({\theta }^{\prime },y)}\left(2k{\theta }^{\prime }\overrightarrow{W}(y)u_{\mathrm{s}c}(y)+q(y)u_{\mathrm{s}c}(y)\right)\mathrm{d}y\hfill \\ \hfill & =:A_{\mathrm{B}}(k,{\theta }^{\prime },\theta )+R(k,{\theta }^{\prime },\theta ).\hfill \end{array}$$(17) )–(20(20) $$\begin{array}{c}\hfill A_{\mathrm{B}}^{\mathrm{b}}(k,-\theta ,\theta )=F(|\overrightarrow{W}{|}^2+V)(2k\theta ).\end{array}$$(20) ) show that in the frame of the backscattering Born approximation$$A(k,-\theta ,\theta )\approx F(|\overrightarrow{W}{|}^2+V)(2k\theta ).$$

But we want to write precisely more terms in the Born series. This is presented in the following theorems which constitute the second main result of this work.

Theorem 3.1:

The backscattering amplitude $A(k,-\theta ,\theta )$ admits the following representation(21) $$\begin{array}{c}\hfill A(k,-\theta ,\theta )=F(|\overrightarrow{W}{|}^2+V)(2k\theta )+2k\theta h_1(k\theta )+h_0(k\theta ),\end{array}$$(21)

where the functions $h_1(\eta ),h_0(\eta )$ both belong to $L^{\infty }({\mathbb{R}}^n)$ with the norm estimates(22) $$\begin{array}{c}\hfill \Vert h_1{\Vert }_{L^{\infty }({\mathbb{R}}^n)},{\Vert h_0\Vert }_{L^{\infty }({\mathbb{R}}^n)}\le \frac{\beta {\gamma }^2}{1-\beta \alpha }.\end{array}$$(22)

Proof The formula (17(17) $$\begin{array}{cc}\hfill A(k,{\theta }^{\prime },\theta )& ={\int }_{{\mathbb{R}}^n}{\mathrm{e}}^{-\mathrm{i}k({\theta }^{\prime },y)}\left(2k{\theta }^{\prime }\overrightarrow{W}(y)u_0(y)+q(y)u_0(y)\right)\mathrm{d}y\hfill \\ \hfill & +{\int }_{{\mathbb{R}}^n}{\mathrm{e}}^{-\mathrm{i}k({\theta }^{\prime },y)}\left(2k{\theta }^{\prime }\overrightarrow{W}(y)u_{\mathrm{s}c}(y)+q(y)u_{\mathrm{s}c}(y)\right)\mathrm{d}y\hfill \\ \hfill & =:A_{\mathrm{B}}(k,{\theta }^{\prime },\theta )+R(k,{\theta }^{\prime },\theta ).\hfill \end{array}$$(17) ) shows that$$R(k,-\theta ,\theta )=-2k\theta {\int }_{{\mathbb{R}}^n}{\mathrm{e}}^{\mathrm{i}k(\theta ,y)}\overrightarrow{W}(y)u_{\mathrm{s}c}(y,k,\theta )\mathrm{d}y+{\int }_{{\mathbb{R}}^n}{\mathrm{e}}^{\mathrm{i}k(\theta ,y)}q(y)u_{\mathrm{s}c}(y,k,\theta )\mathrm{d}y.$$

Since$$u_{\mathrm{s}c}(x,k,\theta )=\sum _{j=1}^{\infty }{L}_k^j(u_0),u_0(x,k,\theta )={\mathrm{e}}^{\mathrm{i}k(\theta ,x)}$$

then the representation (21(21) $$\begin{array}{c}\hfill A(k,-\theta ,\theta )=F(|\overrightarrow{W}{|}^2+V)(2k\theta )+2k\theta h_1(k\theta )+h_0(k\theta ),\end{array}$$(21) ) follows from the latter formulas. The estimates (22(22) $$\begin{array}{c}\hfill \Vert h_1{\Vert }_{L^{\infty }({\mathbb{R}}^n)},{\Vert h_0\Vert }_{L^{\infty }({\mathbb{R}}^n)}\le \frac{\beta {\gamma }^2}{1-\beta \alpha }.\end{array}$$(22) ) can be easily obtained from (10(10) $$\begin{array}{c}\hfill \Vert L_k{f\Vert }_{L_{-\sigma /2}^2({\mathbb{R}}^n)}\le \beta \left(2\Vert \overrightarrow{W}{\Vert }_{L_{\sigma }^{\infty }({\mathbb{R}}^n)}+C_p{\Vert q\Vert }_{L_{\sigma }^p({\mathbb{R}}^n)}\right){\Vert f\Vert }_{L_{-\sigma /2}^2({\mathbb{R}}^n)},\end{array}$$(10) ) and (13(13) $$\begin{array}{c}\hfill \Vert u_{\mathrm{s}c}{\Vert }_{L_{-\sigma /2}^2({\mathbb{R}}^n)}\le \frac{\beta \gamma }{1-\beta \alpha }.\end{array}$$(13) ) by using the Hölder’s inequality since $\overrightarrow{W},q$ belong to $L_{\sigma /2}^2({\mathbb{R}}^n)$ and $u_{\mathit{sc}}$ belongs to $L_{-\sigma /2}^2({\mathbb{R}}^n)$. Thus, theorem is proved.

Concerning the latter terms in the Born series (21(21) $$\begin{array}{c}\hfill A(k,-\theta ,\theta )=F(|\overrightarrow{W}{|}^2+V)(2k\theta )+2k\theta h_1(k\theta )+h_0(k\theta ),\end{array}$$(21) ) we have the following result.

Theorem 3.2:

The sum of the functions $2k\theta h_1$ and $h_0$ admits the following representation:(23) $$\begin{array}{cc}\hfill 2k\theta h_1(k\theta )+h_0(k\theta )& =-\frac{1}{{(2\pi )}^n}{\int }_{{\mathbb{R}}^n}\frac{F(\overline{q})(k\theta +\eta )F(q)(k\theta -\eta )}{{\eta }^2-k^2-\mathrm{i}0}\mathrm{d}\eta \hfill \\ \hfill & +\frac{4k}{{(2\pi )}^n}{\int }_{{\mathbb{R}}^n}\frac{\theta F(\overrightarrow{W})(k\theta +\eta )\eta F(\overrightarrow{W})(k\theta -\eta )}{{\eta }^2-k^2-\mathrm{i}0}\mathrm{d}\eta +h_{\mathrm{r}est}(k\theta ),\hfill \end{array}$$(23)

where $\overline{q}$ denotes the complex conjugate of q, and where the function $h_{\mathrm{r}est}$ has the following estimate for $|k|\ge 1$ (24) $$\begin{array}{c}\hfill \Vert h_{\mathrm{r}est}{\Vert }_{L^{\infty }({\mathbb{R}}^n)}\le 3\frac{{\beta }^2\alpha {\gamma }^2}{1-\beta \alpha }.\end{array}$$(24)

Proof The formulas (17(17) $$\begin{array}{cc}\hfill A(k,{\theta }^{\prime },\theta )& ={\int }_{{\mathbb{R}}^n}{\mathrm{e}}^{-\mathrm{i}k({\theta }^{\prime },y)}\left(2k{\theta }^{\prime }\overrightarrow{W}(y)u_0(y)+q(y)u_0(y)\right)\mathrm{d}y\hfill \\ \hfill & +{\int }_{{\mathbb{R}}^n}{\mathrm{e}}^{-\mathrm{i}k({\theta }^{\prime },y)}\left(2k{\theta }^{\prime }\overrightarrow{W}(y)u_{\mathrm{s}c}(y)+q(y)u_{\mathrm{s}c}(y)\right)\mathrm{d}y\hfill \\ \hfill & =:A_{\mathrm{B}}(k,{\theta }^{\prime },\theta )+R(k,{\theta }^{\prime },\theta ).\hfill \end{array}$$(17) ) and (21(21) $$\begin{array}{c}\hfill A(k,-\theta ,\theta )=F(|\overrightarrow{W}{|}^2+V)(2k\theta )+2k\theta h_1(k\theta )+h_0(k\theta ),\end{array}$$(21) ) imply that the $R(k,-\theta ,\theta )=2k\theta h_1+h_0=R_1+R_2$, where$$\begin{array}{cc}\hfill R_1& =-2k\theta {\int }_{{\mathbb{R}}^n}{\mathrm{e}}^{\mathrm{i}k(\theta ,y)}\overrightarrow{W}(y)L_k{u}_0(y,k,\theta )\mathrm{d}y+{\int }_{{\mathbb{R}}^n}{\mathrm{e}}^{\mathrm{i}k(\theta ,y)}q(y)L_k{u}_0(y,k,\theta )\mathrm{d}y,\hfill \\ \hfill R_2& =-2k\theta {\int }_{{\mathbb{R}}^n}{\mathrm{e}}^{\mathrm{i}k(\theta ,y)}\overrightarrow{W}(y)\sum _{j=1}^{\infty }{L}_k^j\widetilde{u_0}(y,k,\theta )\mathrm{d}y+{\int }_{{\mathbb{R}}^n}{\mathrm{e}}^{\mathrm{i}k(\theta ,y)}q(y)\sum _{j=1}^{\infty }{L}_k^j\widetilde{u_0}(y,k,\theta )\mathrm{d}y\hfill \end{array}$$

with $L_k{u}_0$ equal to (see (8(8) $$\begin{array}{c}\hfill L_{k}f(x):={\int }_{{\mathbb{R}}^n}{G}_k^{+}(|x-y|)\left(2\mathrm{i}\mathrm{\nabla }(\overrightarrow{W}(y)f(y))-q(y)f(y)\right)\mathrm{d}y.\end{array}$$(8) ))$$L_k{u}_0(y,k,\theta )=-2k\theta {\int }_{{\mathbb{R}}^n}{\mathrm{e}}^{\mathrm{i}k(\theta ,z)}\overrightarrow{W}(z)G_k^{+}(|y-z|)\mathrm{d}z-{\int }_{{\mathbb{R}}^n}{\mathrm{e}}^{\mathrm{i}k(\theta ,z)}\overline{q}(z)G_k^{+}(|y-z|)\mathrm{d}z.$$

Using integration by parts, $R_2$ can be written as$$\begin{array}{cc}\hfill R_2& =\mathrm{i}{\int }_{{\mathbb{R}}^n}{\mathrm{e}}^{\mathrm{i}k(\theta ,y)}\mathrm{\nabla }·\overrightarrow{W}(y)\sum _{j=1}^{\infty }{L}_k^j\widetilde{u_0}(y,k,\theta )\mathrm{d}y\hfill \\ \hfill & +2\mathrm{i}{\int }_{{\mathbb{R}}^n}{\mathrm{e}}^{\mathrm{i}k(\theta ,y)}\overrightarrow{W}(y)·\mathrm{\nabla }\left(\sum _{j=1}^{\infty }{L}_k^j\widetilde{u_0}(y,k,\theta )\right)\mathrm{d}y\hfill \\ \hfill & -{\int }_{{\mathbb{R}}^n}{\mathrm{e}}^{\mathrm{i}k(\theta ,y)}(|\overrightarrow{W}{|}^2+V)(y)\sum _{j=1}^{\infty }{L}_k^j\widetilde{u_0}(y,k,\theta )\mathrm{d}y.\hfill \end{array}$$

Then we can easily obtain the representation(25) $$\begin{array}{cc}\hfill R_1& =4k^2{\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}{\mathrm{e}}^{\mathrm{i}k(\theta ,y+z)}{G}_k^{+}(|y-z|)\theta \overrightarrow{W}(y)\theta \overrightarrow{W}(z)\mathrm{d}y\mathrm{d}z\hfill \\ \hfill & +2k{\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}{\mathrm{e}}^{\mathrm{i}k(\theta ,y+z)}{G}_k^{+}(|y-z|)\theta \overrightarrow{W}(y)(\overline{q}(z)-q(z))\mathrm{d}y\mathrm{d}z\hfill \\ \hfill & -{\int }_{{\mathbb{R}}^n}{\int }_{{\mathbb{R}}^n}{\mathrm{e}}^{\mathrm{i}k(\theta ,y+z)}{G}_k^{+}(|y-z|)q(y)\overline{q}(z)\mathrm{d}y\mathrm{d}z=:I_1+I_2+I_3\hfill \end{array}$$(25)

in the sense of tempered distributions. Let us consider$$\begin{array}{cc}\hfill I_1& =4k^2{\int }_{{\mathbb{R}}^n}\theta \overrightarrow{W}(z){\mathrm{e}}^{\mathrm{i}k(\theta ,2z)}{\int }_{{\mathbb{R}}^n}{\mathrm{e}}^{\mathrm{i}k(\theta ,u)}{G}_k^{+}(|u|)\theta \overrightarrow{W}(u+z)\mathrm{d}u\mathrm{d}z.\hfill \end{array}$$

The integral with respect to u can be written as the Fourier transform of a product. Using $F(\varphi ·\psi )={(2\pi )}^{-n}F(\varphi )\ast F(\psi )$ this Fourier transform becomes the convolution$${(2\pi )}^{-n}F(G_k^{+}(|u|))\ast F(\theta \overrightarrow{W}(u+z))(k\theta ).$$

Using $F(G_k^{+})(s)=\frac{1}{s^2-k^2-\mathrm{i}0}$ the latter expression can be written as$${(2\pi )}^{-n}{\int }_{{\mathbb{R}}^n}\frac{F(\theta \overrightarrow{W}(u+z))(\eta )}{{(k\theta -\eta )}^2-k^2-\mathrm{i}0}\mathrm{d}\eta ={(2\pi )}^{-n}{\int }_{{\mathbb{R}}^n}{\mathrm{e}}^{-\mathrm{i}(z,\eta )}\frac{\theta F(\overrightarrow{W})(\eta )}{{\eta }^2-2k(\theta ,\eta )-\mathrm{i}0}\mathrm{d}\eta$$

after elementary simplifications. This allows us to compute $I_1$ as$$\begin{array}{cc}\hfill I_1& =\frac{4k^2}{{(2\pi )}^n}{\int }_{{\mathbb{R}}^n}\frac{\theta F(\overrightarrow{W})(\eta )}{{\eta }^2-2k(\theta ,\eta )-\mathrm{i}0}{\int }_{{\mathbb{R}}^n}\theta \overrightarrow{W}(z){\mathrm{e}}^{\mathrm{i}(2k\theta -\eta ,z)}\mathrm{d}z\mathrm{d}\eta \hfill \\ \hfill & =\frac{4k^2}{{(2\pi )}^n}{\int }_{{\mathbb{R}}^n}\frac{\theta F(\overrightarrow{W})(\eta )\theta F(\overrightarrow{W})(2k\theta -\eta )}{{\eta }^2-2k(\theta ,\eta )-\mathrm{i}0}\mathrm{d}\eta \hfill \\ \hfill & =\frac{4k^2}{{(2\pi )}^n}{\int }_{{\mathbb{R}}^n}\frac{\theta F(\overrightarrow{W})(k\theta +\eta )\theta F(\overrightarrow{W})(k\theta -\eta )}{{\eta }^2-k^2-\mathrm{i}0}\mathrm{d}\eta .\hfill \end{array}$$

Proceeding similarly for $I_2$ and $I_3$ yields(26) $$\begin{array}{cc}\hfill I_2& =-\frac{4\mathrm{i}k}{{(2\pi )}^n}{\int }_{{\mathbb{R}}^n}\frac{\theta F(\overrightarrow{W})(k\theta +\eta )F(\mathrm{\nabla }\overrightarrow{W})(k\theta -\eta )}{{\eta }^2-k^2-\mathrm{i}0}\mathrm{d}\eta ,\hfill \\ \hfill I_3& =-\frac{1}{{(2\pi )}^n}{\int }_{{\mathbb{R}}^n}\frac{F(\overline{q})(k\theta +\eta )F(q)(k\theta -\eta )}{{\eta }^2-k^2-\mathrm{i}0}\mathrm{d}\eta .\hfill \end{array}$$(26)

Since $I_2$ is actually equal to$$\begin{array}{cc}\hfill I_2& =-\frac{4\mathrm{i}k}{{(2\pi )}^n}{\int }_{{\mathbb{R}}^n}\frac{\theta F(\overrightarrow{W})(k\theta +\eta )(-\mathrm{i}k\theta +\mathrm{i}\eta )F(\overrightarrow{W})(k\theta -\eta )}{{\eta }^2-k^2-\mathrm{i}0}\mathrm{d}\eta \hfill \\ \hfill & =-I_1+\frac{4k}{{(2\pi )}^n}{\int }_{{\mathbb{R}}^n}\frac{\theta F(\overrightarrow{W})(k\theta +\eta )\eta F(\overrightarrow{W})(k\theta -\eta )}{{\eta }^2-k^2-\mathrm{i}0}\mathrm{d}\eta \hfill \end{array}$$

then the main part in the representation (23(23) $$\begin{array}{cc}\hfill 2k\theta h_1(k\theta )+h_0(k\theta )& =-\frac{1}{{(2\pi )}^n}{\int }_{{\mathbb{R}}^n}\frac{F(\overline{q})(k\theta +\eta )F(q)(k\theta -\eta )}{{\eta }^2-k^2-\mathrm{i}0}\mathrm{d}\eta \hfill \\ \hfill & +\frac{4k}{{(2\pi )}^n}{\int }_{{\mathbb{R}}^n}\frac{\theta F(\overrightarrow{W})(k\theta +\eta )\eta F(\overrightarrow{W})(k\theta -\eta )}{{\eta }^2-k^2-\mathrm{i}0}\mathrm{d}\eta +h_{\mathrm{r}est}(k\theta ),\hfill \end{array}$$(23) ) is proved. It remains now to estimate $h_{\mathrm{r}est}$ (or $R_2$). Indeed (see, (12(12) $$\begin{array}{c}\hfill \alpha :=2\Vert \overrightarrow{W}{\Vert }_{L_{\sigma }^{\infty }({\mathbb{R}}^n)}+C_p{\Vert q\Vert }_{L_{\sigma }^p({\mathbb{R}}^n)},\gamma :=2\Vert \overrightarrow{W}{\Vert }_{L_{\sigma /2}^2({\mathbb{R}}^n)}+{\Vert q\Vert }_{L_{\sigma /2}^2({\mathbb{R}}^n)}.\end{array}$$(12) )–(14(14) $$\begin{array}{c}\hfill \Vert L_k{\Vert }_{L_{-\sigma /2}^2({\mathbb{R}}^n)\to L_{-\sigma /2}^2({\mathbb{R}}^n)}\le \beta \alpha <1.\end{array}$$(14) )),$$\begin{array}{cc}\hfill |R_2|& \le {\int }_{{\mathbb{R}}^n}|\mathrm{\nabla }·\overrightarrow{W}(y)|\left|\sum _{j=1}^{\infty }{L}_k^j\widetilde{u_0}(y,k,\theta )\right|\mathrm{d}y+2{\int }_{{\mathbb{R}}^n}|\overrightarrow{W}(y)|\left|\mathrm{\nabla }\sum _{j=1}^{\infty }{L}_k^j\widetilde{u_0}(y,k,\theta )\right|\mathrm{d}y\hfill \\ \hfill & +{\int }_{{\mathbb{R}}^n}(|\overrightarrow{W}{|}^2+|V|)(y)\left|\sum _{j=1}^{\infty }{L}_k^j\widetilde{u_0}(y,k,\theta )\right|\mathrm{d}y\hfill \\ \hfill & \le {\Vert q\Vert }_{L_{\sigma /2}^2({\mathbb{R}}^n)}\Vert \sum _{j=1}^{\infty }{L}_k^j\widetilde{u_0}{\Vert }_{L_{-\sigma /2}^2({\mathbb{R}}^n)}+2\Vert \overrightarrow{W}{\Vert }_{H_{\sigma /2}^1({\mathbb{R}}^n)}{\Vert \mathrm{\nabla }\sum _{j=1}^{\infty }{L}_k^j\widetilde{u_0}\Vert }_{H_{-\sigma /2}^{-1}({\mathbb{R}}^n)}\hfill \\ \hfill & \le \left({\Vert q\Vert }_{L_{\sigma /2}^2({\mathbb{R}}^n)}+2{\Vert \overrightarrow{W}\Vert }_{H_{\sigma /2}^1({\mathbb{R}}^n)}\right)\frac{{\beta }^2\alpha \gamma }{1-\beta \alpha }\le 3\frac{{\beta }^2\alpha {\gamma }^2}{1-\beta \alpha }.\hfill \end{array}$$

The latter inequality together with (24(24) $$\begin{array}{c}\hfill \Vert h_{\mathrm{r}est}{\Vert }_{L^{\infty }({\mathbb{R}}^n)}\le 3\frac{{\beta }^2\alpha {\gamma }^2}{1-\beta \alpha }.\end{array}$$(24) )–(26(26) $$\begin{array}{cc}\hfill I_2& =-\frac{4\mathrm{i}k}{{(2\pi )}^n}{\int }_{{\mathbb{R}}^n}\frac{\theta F(\overrightarrow{W})(k\theta +\eta )F(\mathrm{\nabla }\overrightarrow{W})(k\theta -\eta )}{{\eta }^2-k^2-\mathrm{i}0}\mathrm{d}\eta ,\hfill \\ \hfill I_3& =-\frac{1}{{(2\pi )}^n}{\int }_{{\mathbb{R}}^n}\frac{F(\overline{q})(k\theta +\eta )F(q)(k\theta -\eta )}{{\eta }^2-k^2-\mathrm{i}0}\mathrm{d}\eta .\hfill \end{array}$$(26) ) show that Theorem 3.2 is completely proved.

Summarizing our considerations (see (20(20) $$\begin{array}{c}\hfill A_{\mathrm{B}}^{\mathrm{b}}(k,-\theta ,\theta )=F(|\overrightarrow{W}{|}^2+V)(2k\theta ).\end{array}$$(20) )–(26(26) $$\begin{array}{cc}\hfill I_2& =-\frac{4\mathrm{i}k}{{(2\pi )}^n}{\int }_{{\mathbb{R}}^n}\frac{\theta F(\overrightarrow{W})(k\theta +\eta )F(\mathrm{\nabla }\overrightarrow{W})(k\theta -\eta )}{{\eta }^2-k^2-\mathrm{i}0}\mathrm{d}\eta ,\hfill \\ \hfill I_3& =-\frac{1}{{(2\pi )}^n}{\int }_{{\mathbb{R}}^n}\frac{F(\overline{q})(k\theta +\eta )F(q)(k\theta -\eta )}{{\eta }^2-k^2-\mathrm{i}0}\mathrm{d}\eta .\hfill \end{array}$$(26) )) we may conclude that neglecting $h_{\mathrm{r}}est$ the following direct backscattering Born approximation for the magnetic Schrödinger operator holds(27) $$\begin{array}{cc}\hfill A(k,-\theta ,\theta )& \approx \tilde{A}(k,-\theta ,\theta ):=F(|\overrightarrow{W}{|}^2+V)(2k\theta )\hfill \\ \hfill & -\frac{1}{{(2\pi )}^n}{\int }_{{\mathbb{R}}^n}\frac{F(\overline{q})(k\theta +\eta )F(q)(k\theta -\eta )}{{\eta }^2-k^2-\mathrm{i}0}\mathrm{d}\eta \hfill \\ \hfill & +\frac{4k}{{(2\pi )}^n}{\int }_{{\mathbb{R}}^n}\frac{\theta F(\overrightarrow{W})(k\theta +\eta )\eta F(\overrightarrow{W})(k\theta -\eta )}{{\eta }^2-k^2-\mathrm{i}0}\mathrm{d}\eta ,\hfill \end{array}$$(27) (28) $$\begin{array}{cc}\hfill u^{\mathrm{b}}(x,k,\theta )& ={\mathrm{e}}^{\mathrm{i}k(x,\theta )}+C\frac{{\mathrm{e}}^{\mathrm{i}k|x|}{k}^{\frac{n-3}{2}}}{{|x|}^{\frac{n-1}{2}}}\tilde{A}(k,-\theta ,\theta ).\hfill \end{array}$$(28)

These formulas give very good approximation for the backscattering amplitude A and for the scattering solutions u uniformly in $\theta \in {\mathbb{S}}^{n-1}$. It is important that for this approximation we need to have only the magnetic potential $\overrightarrow{W}$ and electric potential V, but we do not need to have the exact solution $u(x,k,\theta )$ of the differential equation $Hu(x)=k^{2}u(x).$

4. Inverse Born approximation

The direct approximation (28(28) $$\begin{array}{cc}\hfill u^{\mathrm{b}}(x,k,\theta )& ={\mathrm{e}}^{\mathrm{i}k(x,\theta )}+C\frac{{\mathrm{e}}^{\mathrm{i}k|x|}{k}^{\frac{n-3}{2}}}{{|x|}^{\frac{n-1}{2}}}\tilde{A}(k,-\theta ,\theta ).\hfill \end{array}$$(28) ) can be used for the inverse backscattering Born approximation as well. Theorems 3.1 and 3.2 give us the key to define the inverse backscattering Born approximation as(29) $$\begin{array}{c}\hfill q_{\mathrm{B}}^{\mathrm{b}}(x):=\frac{1}{{(2\pi )}^n}{\int }_0^{\infty }{k}^{n-1}\mathrm{d}k{\int }_{S^{n-1}}{\mathrm{e}}^{-\mathrm{i}k(\theta ,x)}A\left(\frac{k}{2},-\theta ,\theta \right)\mathrm{d}\theta .\end{array}$$(29)

Due to this definition and formula (20(20) $$\begin{array}{c}\hfill A_{\mathrm{B}}^{\mathrm{b}}(k,-\theta ,\theta )=F(|\overrightarrow{W}{|}^2+V)(2k\theta ).\end{array}$$(20) ) (see also (28(28) $$\begin{array}{cc}\hfill u^{\mathrm{b}}(x,k,\theta )& ={\mathrm{e}}^{\mathrm{i}k(x,\theta )}+C\frac{{\mathrm{e}}^{\mathrm{i}k|x|}{k}^{\frac{n-3}{2}}}{{|x|}^{\frac{n-1}{2}}}\tilde{A}(k,-\theta ,\theta ).\hfill \end{array}$$(28) )) we conclude that$$\begin{array}{c}\hfill q_{\mathrm{B}}^{\mathrm{b}}(x)=(|\overrightarrow{W}{|}^2+V)(x)+q_{\mathrm{q}uad}(x)+q_{\mathrm{r}est}(x),\end{array}$$

where the quadratic form $q_{\mathrm{q}uad}$ can easily be calculated precisely from (27(27) $$\begin{array}{cc}\hfill A(k,-\theta ,\theta )& \approx \tilde{A}(k,-\theta ,\theta ):=F(|\overrightarrow{W}{|}^2+V)(2k\theta )\hfill \\ \hfill & -\frac{1}{{(2\pi )}^n}{\int }_{{\mathbb{R}}^n}\frac{F(\overline{q})(k\theta +\eta )F(q)(k\theta -\eta )}{{\eta }^2-k^2-\mathrm{i}0}\mathrm{d}\eta \hfill \\ \hfill & +\frac{4k}{{(2\pi )}^n}{\int }_{{\mathbb{R}}^n}\frac{\theta F(\overrightarrow{W})(k\theta +\eta )\eta F(\overrightarrow{W})(k\theta -\eta )}{{\eta }^2-k^2-\mathrm{i}0}\mathrm{d}\eta ,\hfill \end{array}$$(27) ) as(30) $$\begin{array}{cc}\hfill q_{\mathrm{q}uad}(x)& =-\frac{1}{{(2\pi )}^n}{F}_{\xi \to x}^{-1}\left({\int }_{{\mathbb{R}}^n}\frac{F(\overline{q})(\xi -\eta )F(q)(\eta )}{{\eta }^2-(\xi ,\eta )-\mathrm{i}0}\mathrm{d}\eta \right)\hfill \\ \hfill & +\frac{1}{{(2\pi )}^n}{F}_{\xi \to x}^{-1}\left({\int }_{{\mathbb{R}}^n}\frac{\xi F(\overrightarrow{W})(\eta )(2\eta -\xi )F(\overrightarrow{W})(\xi -\eta )}{{\eta }^2-(\xi ,\eta )-\mathrm{i}0}\mathrm{d}\eta \right).\hfill \end{array}$$(30)

This equality must be understood in the sense of tempered distributions. The precise form (30(30) $$\begin{array}{cc}\hfill q_{\mathrm{q}uad}(x)& =-\frac{1}{{(2\pi )}^n}{F}_{\xi \to x}^{-1}\left({\int }_{{\mathbb{R}}^n}\frac{F(\overline{q})(\xi -\eta )F(q)(\eta )}{{\eta }^2-(\xi ,\eta )-\mathrm{i}0}\mathrm{d}\eta \right)\hfill \\ \hfill & +\frac{1}{{(2\pi )}^n}{F}_{\xi \to x}^{-1}\left({\int }_{{\mathbb{R}}^n}\frac{\xi F(\overrightarrow{W})(\eta )(2\eta -\xi )F(\overrightarrow{W})(\xi -\eta )}{{\eta }^2-(\xi ,\eta )-\mathrm{i}0}\mathrm{d}\eta \right).\hfill \end{array}$$(30) ) of the quadratic term $q_{\mathrm{q}uad}$ allows us to estimate its smoothness in the two dimensional case. Indeed, we have the following result from [23, Theorem 2.2].

Proposition 4.1:

[$n=2$] Let us assume that conditions (1(1) $$\begin{array}{c}\hfill \overrightarrow{W}\in W_{p,\sigma }^1({\mathbb{R}}^n),V\in L_{\sigma }^p({\mathbb{R}}^n),\end{array}$$(1) ) and (2(2) $$\begin{array}{c}\hfill \sigma >max\left(1;n\left(1-\frac{2}{p}\right)\right),p>n.\end{array}$$(2) ) are fulfilled. Let us also assume that $F(q),F(\overrightarrow{W})\in L^s({\mathbb{R}}^2)$ for some $1<s<2$. Then $q_{\mathrm{q}}uad$ belongs to the space

(1)	$H^t({\mathbb{R}}^2),t<4/s-2$ for $4/3<s<2$;
(2)	$H^1({\mathbb{R}}^2)$ for $s=4/3$;
(3)	$C({\mathbb{R}}^2)\cap L^{\infty }({\mathbb{R}}^2)$ for $1<s<4/3$.

The latter proposition means that the term $q_{\mathrm{q}}uad$ is smoother than the original potential V (note that $\overrightarrow{W}$ is continuous and bounded). It means that we can recover the main singularities of V (such as jumps over smooth curves) using the inverse Born backscattering approximation.

Remark 4.1:

If we assume that $V\in H^{\alpha }({\mathbb{R}}^n)$ and $\overrightarrow{W}\in H^{\alpha +1}({\mathbb{R}}^n)$ with compact supports and with$$\frac{n-1}{2}<\alpha <\frac{n}{2},n=2,3$$

then $q_{\mathrm{q}}uad\in C({\mathbb{R}}^n)\cap L^{\infty }({\mathbb{R}}^n)$. This further simplifies the recovery of singularities of V. More precisely, using the inverse Born backscattering approximation we can reconstruct all jumps and singularities of V.

5. Numerical examples

In this section we study numerically in two dimensions how well $q_{\mathrm{B}}^{\mathrm{b}}$ approximates $|\overrightarrow{W}{|}^2+V$. To this end, we employ the following scheme proposed in [27,28]. For given $V,\overrightarrow{W}$ we compute an approximation to the scattered field $u_{\mathrm{s}}c$ as$$u_{\mathrm{s}}c(x)\approx \sum _{j=1}^J{u}_j,u_j=L_k{u}_{j-1},$$(see the proof of Theorem 3.1) by performing numerical integration over the supports of $\overrightarrow{W},V$, see [27,28] for details.

Then (synthetic) backscattering data is obtained from the approximation$$A(k,-\theta ,\theta )\approx \frac{4\sqrt{\pi kR}}{-1-\mathrm{i}}{\mathrm{e}}^{-\mathrm{i}kR}{u}_{\mathrm{s}c}(-R\theta ,k,\theta )$$

after putting $x=R{\theta }^{\prime }=-R\theta$ in (15(15) $$\begin{array}{c}\hfill u(x,k,\theta )={\mathrm{e}}^{\mathrm{i}k(x,\theta )}+C\frac{{\mathrm{e}}^{\mathrm{i}k|x|}{k}^{\frac{n-3}{2}}}{{|x|}^{\frac{n-1}{2}}}A(k,{\theta }^{\prime },\theta )+o\left(\frac{1}{{|x|}^{\frac{n-1}{2}}}\right),\end{array}$$(15) ). We use $J=2,R={10}^5$ in our examples and we add 1% of Gaussian noise to scattering data.

In order to compute $q_{\mathrm{B}}^{\mathrm{b}}$ we invert (29(29) $$\begin{array}{c}\hfill q_{\mathrm{B}}^{\mathrm{b}}(x):=\frac{1}{{(2\pi )}^n}{\int }_0^{\infty }{k}^{n-1}\mathrm{d}k{\int }_{S^{n-1}}{\mathrm{e}}^{-\mathrm{i}k(\theta ,x)}A\left(\frac{k}{2},-\theta ,\theta \right)\mathrm{d}\theta .\end{array}$$(29) ) to read(31) $$\begin{array}{c}\hfill {\int }_{{\mathbb{R}}^2}{\mathrm{e}}^{\mathrm{i}k(x,\theta )}{q}_{\mathrm{B}}^{\mathrm{b}}(x)\mathrm{d}x=A(k/2,-\theta ,\theta ).\end{array}$$(31)

We represent $q_{\mathrm{B}}^{\mathrm{b}}$ in the discrete form$$q_{\mathrm{B}}^{\mathrm{b}}(x)=\sum _{j=1}^N{f}_j{\chi }_{r_j}(x),$$

where $r_j$ is a subdivision of unit cube, our area of interest, and ${\chi }_{\mathrm{\Omega }}$ is the characteristic function of $\mathrm{\Omega }\subset {\mathbb{R}}^2$. If we substitute this representation into (31(31) $$\begin{array}{c}\hfill {\int }_{{\mathbb{R}}^2}{\mathrm{e}}^{\mathrm{i}k(x,\theta )}{q}_{\mathrm{B}}^{\mathrm{b}}(x)\mathrm{d}x=A(k/2,-\theta ,\theta ).\end{array}$$(31) ) and evaluate it at several points $k,\theta$ we obtain a linear system $Ef=g$ for the solution of unknown coefficients $f={(f_j)}_{j=1}^N$.

We use $N={80}^2$, 12 values for k and 40 values for $\theta$ uniformly from the unit circle. Hence our linear system is of size $480\times 6400$. The regularized solution of our underdetermined and ill-conditioned linear system is obtained by truncated singular value decomposition (TSVD) as follows. If $E=US{V}^{\ast }$ with $S=\mathrm{d}iag(s_1,\dots ,s_n)$ is the singular value decomposition of E then we compute$$f=VL{U}^{\ast }g,$$

where $L=\mathrm{d}iag(1/s_1,\dots ,1/s_r,0,\dots ,0)$ and $s_r$ is the last singular value exceeding a prescribed tolerance $s_{\mathrm{t}ol}=0.02$.

Figure 1. Potential combination $|\overrightarrow{W}{|}^2+V$ (left) and TSVD reconstruction (right), Example 1.

Figure 2. Potential combination $|\overrightarrow{W}{|}^2+V$ (left) and TSVD reconstruction (right), Example 2.

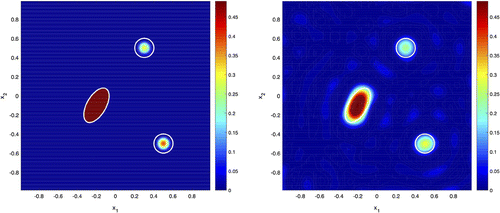
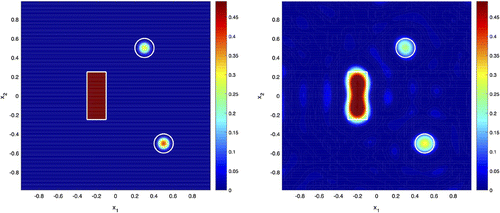
Next we describe our sample scatterers. Since $\overrightarrow{W}$ is actually bounded and continuous we concentrate our attention to recovering jumps of V. We put $V(x)=0.5{\chi }_{\mathrm{\Omega }}(x)$, where the domain $\mathrm{\Omega }$ is an ellipse in Example 1 and a rectangle in Example 2, see Figures 1 and 2. For $\overrightarrow{W}=(W_1,W_2)$ we use the (infinitely smooth) bump function$$W_j(x)=w_{j}exp(1){\chi }_{|x-c_j{|}^2<r_j^2}(x)exp(r_j^2/(|x-c_j{|}^2-r_j^2)),j=1,2$$

supported in the ball of radius $r_j$ centered at $c_j$ with scaled height $w_j$. The following table summarizes the parameters of magnetic potentials for both examples.

Table

j	$w_j$	$c_j$	$r_j$
1	$\sqrt{0.4}$	(0.3, 0.5)	0.2
2	$\sqrt{0.3}$	$(0.5,-0.5)$	0.2

In Figures 1 and 2, the left panel shows the unknown combination $|\overrightarrow{W}{|}^2+V$. The right panel shows the reconstruction of $q_{\mathrm{B}}^{\mathrm{b}}$. In both figures white line indicates the true geometry of the support of the scatterers. We see that the inverse Born approximation is able to locate quite accurately the shape and location of these supports from noisy data, even in the case of non-smooth support of V.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was supported by the Academy of Finland; Luonnontieteiden ja Tekniikan Tutkimuksen Toimikunta [application number 250215, Finnish Programme for Centres of Excellence in Research 2012–2017].

Appendix 1

Proof of (3(3) $$\begin{array}{c}\hfill D(H)=W_2^2({\mathbb{R}}^n),\end{array}$$(3) )

We rewrite first the magnetic Schrödinger operator in the form$$H=-\mathrm{\Delta }-2\mathrm{i}\overrightarrow{W}·\mathrm{\nabla }+\overline{q},$$

where $q=\mathrm{i}\mathrm{\nabla }\overrightarrow{W}+{|\overrightarrow{W}|}^2+V$. If now $f\in W_2^2({\mathbb{R}}^n)$ then for inclusion $W_2^2({\mathbb{R}}^n)\subset D(H)$ it is enough to show that $\overrightarrow{W}·\mathrm{\nabla }f$ and $\overline{q}f$ belong to $L^2({\mathbb{R}}^n)$, since obviously $\mathrm{\Delta }f\in L^2({\mathbb{R}}^n)$. We have $\overrightarrow{W}\in W_{p,\sigma }^1({\mathbb{R}}^n)\subset W_p^1({\mathbb{R}}^n)\subset L^{\infty }({\mathbb{R}}^n)$ for $\sigma >0$ and $p>n$. This fact implies that $\overrightarrow{W}·\mathrm{\nabla }f\in L^2({\mathbb{R}}^n)$ and $\overline{q}\in L^p({\mathbb{R}}^n)$. Further, since $W_2^2({\mathbb{R}}^n)\subset L^{\infty }({\mathbb{R}}^n)$ for $n=2,3$ then$$\begin{array}{cc}\hfill {\int }_{{\mathbb{R}}^n}|\overline{q}{|}^2{|f|}^2\mathrm{d}x& ={\int }_{|\overline{q}|<1}|\overline{q}{|}^2{|f|}^2\mathrm{d}x+{\int }_{|\overline{q}|>1}|\overline{q}{|}^2{|f|}^2\mathrm{d}x\hfill \\ \hfill & \le {\Vert f\Vert }_{L^2({\mathbb{R}}^n)}^2+{\Vert f\Vert }_{L^{\infty }({\mathbb{R}}^n)}^2{\Vert \overline{q}\Vert }_{L^p({\mathbb{R}}^n)}^p<\infty \hfill \end{array}$$

for $p>n$. If $n\ge 5$ then using the imbedding $W_2^2({\mathbb{R}}^n)\subset L^{\frac{2n}{n-4}}({\mathbb{R}}^n)$ we obtain analogously that$$\begin{array}{cc}\hfill {\int }_{{\mathbb{R}}^n}|\overline{q}{|}^2{|f|}^2\mathrm{d}x& \le {\Vert f\Vert }_{L^2({\mathbb{R}}^n)}^2+{\Vert f\Vert }_{L^{2n/(n-4)}({\mathbb{R}}^n)}^2{\Vert \overline{q}\Vert }_{L^p({\mathbb{R}}^n)}^{4p/n}<\infty ,p>n.\hfill \end{array}$$

The same result is valid for $n=4$ due to the imbedding $W_2^2({\mathbb{R}}^4)\subset L^s({\mathbb{R}}^4)$ for any $s<\infty$. Thus$$W_2^2({\mathbb{R}}^n)\subset D(H),n\ge 2.$$

For the opposite inclusion we need to show that if $g=Hf$ belongs to $L^2({\mathbb{R}}^n)$ with $f\in W_2^1({\mathbb{R}}^n)$ then actually $f\in W_2^2({\mathbb{R}}^n)$. To this end, we use the identity$$f={(-\mathrm{\Delta }+I)}^{-1}(g+2\mathrm{i}\overrightarrow{W}·\mathrm{\nabla }f-\overline{q}f+f).$$

Using now the imbedding $W_2^1({\mathbb{R}}^n)\subset L^{\frac{2n}{n-2}}({\mathbb{R}}^n)$ for $n\ge 3$ and $W_2^1({\mathbb{R}}^2)\subset L^s({\mathbb{R}}^2)$ for any $s<\infty$ we may easily obtain that$$g+2\mathrm{i}\overrightarrow{W}·\mathrm{\nabla }f-\overline{q}f+f\in L^2({\mathbb{R}}^n),n\ge 2.$$

Thus, $f\in W_2^2({\mathbb{R}}^n)$ since$${(-\mathrm{\Delta }+I)}^{-1}:L^2({\mathbb{R}}^n)\to W_2^2({\mathbb{R}}^n),n\ge 2.$$

This proves the needed opposite imbedding.