New approach to identify the initial condition in degenerate hyperbolic equation

ABSTRACT

This paper deals with the determination of an initial condition in degenerate hyperbolic equation from final observations. With the aim of reducing the execution time, this inverse problem is solved using an approach based on double regularization: a Tikhonov’s regularization and regularization in equation by viscose-elasticity. So, we obtain a sequence of weak solutions of degenerate linear viscose-elastic problems. Firstly, we prove the existence and uniqueness of each term of this sequence. Secondly, we prove the convergence of this sequence to the weak solution of the initial problem. Also we present some numerical experiments to show the performance of this approach.

KEYWORDS:

• Data assimilation
• adjoint method
• regularization
• wave equation
• inverse problem
• degenerate equations
• optimization

AMS SUBJECT CLASSIFICATIONS:

• 15A29
• 47A52
• 93C20
• 35L05
• 35L80

1. Introduction and main results

The inverse problems of finding unknown coefficients of a PDE from the partial knowledge of the system in a limited time interval are of interest in many applications: cosmology [1], medicine [2], in data assimilation [3], it is used for the numerical weather forecast, ocean circulation, environmental prediction, geophysics [4], remote sensing [5] and many other areas.

Recently such type of problems received much attention, in particular, in degenerate parabolic and hyperbolic equations. Indeed, many problems coming from physics (models of Kolmogorov type in [6], boundary layer models in [7], . . . ), economics (Black-Merton-Scholes equations in [8]) and biology (Fleming-Viot models in [9] and Wright-Fisher models in [10]) are described by degenerate parabolic or hyperbolic equations [11]. This work is the continuity of [12] and [13], in which we identify the initial condition and we study numerically the null controllability of degenerate/singular parabolic problem. In this paper, we are interested in the estimation of the initial state of the degenerate hyperbolic problem (1.1(1.1) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )=f,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.1) ) below, thanks to a final observations ${\psi }^{\mathit{obs}}$. The resolution of this inverse problem using only the Tikhonov’s regularization takes a considerable time of execution, to reduce it, we propose a new approach based on double regularization: the Tikhonov’s regularization and regularization in equation by viscose-elasticity.

Consider the degenerate hyperbolic equation(1.1) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )=f,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.1)

where, $\mathrm{\Omega }=]0,1[$, $f\in L^2(\mathrm{\Omega }\times ]0,T[)$, and $\alpha \in ]0,1[$.

Let ${(t_j)}_{j\in \left\{0,1,2\dots M+1\right\}}$ a discritization of [0, T] with $t_j=j\mathrm{\Delta }t$, $\mathrm{\Delta }t$ is the step in time, and $T=(M+1)\mathrm{\Delta }t$.

We suppose that the observation ${\psi }^{\mathit{obs}}$ of $\psi$ is known in some points in vicinity of T:

$\exists N\in \left\{0,1,2\dots M+1\right\}$ such that ${\psi }^{\mathit{obs}}$ is known in $t_j$, with $j\in I=\left\{N,N+1,\dots M+1\right\}$.

The problem can be stated as follows:(1.2) $$\begin{array}{c}\hfill \begin{array}{c}\text{find}{u}^{\ast }=({\psi }_0,v_0)\in A_{\mathit{ad}}\text{such that}\\ \\ E(u^{\ast })=\underset{u\in A_{\mathit{ad}}}{min}E(u),\end{array}\end{array}$$(1.2)

where the cost function E is defined as follows(1.3) $$\begin{array}{c}\hfill E(u)={\displaystyle \frac{1}{2}}\sum _{j\in I}{∥\psi (t_j)-{\psi }_j^{\mathit{obs}}∥}_{L^2(\mathrm{\Omega })}^2.\end{array}$$(1.3)

Subject to $\psi$ being the weak solution of the hyperbolic problem (1.1(1.1) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )=f,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.1) ), with initial state u. The space $A_{\mathit{ad}}$ is the set of admissible initial states (will be defined later).

To solve this inverse problem, we propose an approach based on double regularization. The first is a regularization by viscose-elasticity, this gives the following degenerate linear viscose-elastic problem(1.4) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )-\lambda {\partial }_{\mathit{xxt}}\psi =f,\lambda >0,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.4)

The second, is Tikhonov’s regularization. Since the problem (1.2(1.2) $$\begin{array}{c}\hfill \begin{array}{c}\text{find}{u}^{\ast }=({\psi }_0,v_0)\in A_{\mathit{ad}}\text{such that}\\ \\ E(u^{\ast })=\underset{u\in A_{\mathit{ad}}}{min}E(u),\end{array}\end{array}$$(1.2) ) is ill-posed in the sense of Hadamard, some regularization technique is needed in order to guarantee numerical stability of the computational procedure even with noisy input data. The problem thus consists in minimizing a functional of the form(1.5) $$\begin{array}{c}\hfill J(u)={\displaystyle \frac{1}{2}}\sum _{t_j\in I}{∥\psi (t_j)-{\psi }^{\mathit{obs}}(t_j)∥}_{L^2(\mathrm{\Omega })}^2+\frac{\epsilon }{2}{∥u-\overline{u}∥}_{L^2(\mathrm{\Omega })\times L^2(\mathrm{\Omega })}^2,\end{array}$$(1.5)

subject to $\psi$ is the weak solution of the problem (1.4(1.4) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )-\lambda {\partial }_{\mathit{xxt}}\psi =f,\lambda >0,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.4) ) with initial state u.

Here, the last term in (1.5(1.5) $$\begin{array}{c}\hfill J(u)={\displaystyle \frac{1}{2}}\sum _{t_j\in I}{∥\psi (t_j)-{\psi }^{\mathit{obs}}(t_j)∥}_{L^2(\mathrm{\Omega })}^2+\frac{\epsilon }{2}{∥u-\overline{u}∥}_{L^2(\mathrm{\Omega })\times L^2(\mathrm{\Omega })}^2,\end{array}$$(1.5) ) stands for the so$-$called Tikhonov-type regularization ([14,15]), $\epsilon$ being a small regularizing coefficient that provides extra convexity to the functional J. $\overline{u}$ an a priori (information) knowledge of the exact initial condition of the problem (1.1(1.1) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )=f,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.1) ).

Firstly, we present a new theorem which gives the existence and uniqueness of the weak solutions of the problems (1.4(1.4) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )-\lambda {\partial }_{\mathit{xxt}}\psi =f,\lambda >0,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.4) ), for each $\lambda >0$. Secondly, we prove that: when $\lambda ⟶0$, the sequence ${({\psi }_{\lambda })}_{\lambda >0}$ of weak solutions of the problem (1.4(1.4) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )-\lambda {\partial }_{\mathit{xxt}}\psi =f,\lambda >0,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.4) ) converges to the weak solution of the problem (1.1(1.1) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )=f,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.1) ). Thirdly, with the aim of showing that the minimization problem and the direct problem are well-posed, we prove that the solution’s behaviour changes continuously with the initial conditions, for this we prove the continuity of the function $\phi :({\psi }_0,v_0)⟶\psi$, where $\psi$ is the weak solution of (1.4(1.4) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )-\lambda {\partial }_{\mathit{xxt}}\psi =f,\lambda >0,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.4) ) with initial state $({\psi }_0,v_0)$. Finally, we prove the differentiability of the functional J, which gives the existence of the gradient of J, that is computed using the adjoint state method. Also we present some numerical experiments to show the performance of this approach.

We now specify some notations. Let us introduce the functional spaces (see [16–18])$$\begin{array}{cc}\hfill H_{\alpha ,0}^1& =\}u\in H_{\alpha }^1\mid u(0)=u(1)=0\{,\hfill \\ \hfill H_{\alpha }^1& =\}u\in L^2(\mathrm{\Omega })\cap H_{\mathit{Loc}}^1(]0,1])\mid x^{\frac{\alpha }{2}}{u}_x\in L^2(\mathrm{\Omega })\{,\hfill \end{array}$$

with the inner product$$\begin{array}{c}\hfill {⟨u,v⟩}_{H_{\alpha }^1}={\int }_{\mathrm{\Omega }}(uv+x^{\alpha }{u}_x{v}_x)\mathrm{d}x.\end{array}$$

The weak formulation of the problem (1.4(1.4) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )-\lambda {\partial }_{\mathit{xxt}}\psi =f,\lambda >0,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.4) ) is:(1.6) $$\begin{array}{c}\hfill {\int }_{\mathrm{\Omega }}{\partial }_{\mathit{tt}}\psi v\mathrm{d}x+{\int }_{\mathrm{\Omega }}{x}^{\alpha }{\partial }_x\psi {\partial }_{x}v\mathrm{d}x+{\int }_{\mathrm{\Omega }}\lambda {\partial }_{\mathit{xt}}\psi {\partial }_{x}v\mathrm{d}x={\int }_{\mathrm{\Omega }}fv\mathrm{d}x,\forall v\in H_0^1(\mathrm{\Omega }).\end{array}$$(1.6)

Let(1.7) $$\begin{array}{c}\hfill A_{\mathit{ad}}=\}(u,v)\in H_{\alpha }^1(\mathrm{\Omega })\times L^2{(\mathrm{\Omega });\Vert u\Vert }_{H_{\alpha }^1(\mathrm{\Omega })}⩽{rand\Vert v\Vert }_{L^2(\mathrm{\Omega })}⩽r\{,\text{where}r\in {\mathbb{R}}_{+}^{\ast }.\end{array}$$(1.7)

We have the following results

Theorem 1.1:

[19]]For any $f\in L^1(0,T,L^2(\mathrm{\Omega }))$ and $({\psi }_0,v_0)\in H_{\alpha }^1(\mathrm{\Omega })\times L^2(\mathrm{\Omega }),$ there exists a unique weak solution which solves the problem (1.1(1.1) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )=f,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.1) ) such that$$\begin{array}{c}\hfill \psi \in C\left(\left[0,T\right];H_{\alpha }^1(\mathrm{\Omega })\right)\cap C^1\left(\left[0,T\right];L^2(\mathrm{\Omega })\right).\end{array}$$

Moreover, there exists a constant $C=C(T,\alpha )$ such that for any solution of (1.1(1.1) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )=f,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.1) )(1.8) $$\begin{array}{c}\hfill \begin{array}{c}{∥\psi ∥}_{L^{\infty }(0,T;L^2(\mathrm{\Omega }))}+{∥{\partial }_t\psi ∥}_{L^{\infty }(0,T;L^2(\mathrm{\Omega }))}+{∥x^{\alpha }{({\partial }_x\psi )}^2∥}_{L^{\infty }(0,T;L^1(\mathrm{\Omega }))}\hfill \\ \hfill \\ ⩽C\left({∥{\psi }_0∥}_{H_{\alpha }^1(\mathrm{\Omega })}+{∥f∥}_{L^1(0,T;L^2(\mathrm{\Omega }))}+{∥v_0∥}_{L^2(\mathrm{\Omega })}\right).\square \hfill \end{array}\end{array}$$(1.8)

Theorem 1.2:

Let $\mathrm{\Omega }$ a bounded regular open of $\mathbb{R}$. We assume that $v_0\in L^2(\mathrm{\Omega })$ and ${\psi }_0\in H_{\alpha }^1(\mathrm{\Omega })$ then the problem (1.4(1.4) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )-\lambda {\partial }_{\mathit{xxt}}\psi =f,\lambda >0,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.4) ) has a unique weak solution such that(1.9) $$\begin{array}{c}\hfill \psi \in L^2\left(0,T;H_{\alpha }^1(\mathrm{\Omega })\right)\cap L^{\infty }\left(0,T;L^2(\mathrm{\Omega })\right),{\partial }_t\psi \in L^2(0,T;L^2(\mathrm{\Omega })),\end{array}$$(1.9)

and we have the estimate(1.10) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle \underset{t\in [0,T]}{sup}\Vert \psi (t){\Vert }_{L^2(\mathrm{\Omega })}^2+\Vert {\partial }_t\psi {\Vert }_{L^2(0,T;L^2(\mathrm{\Omega }))}^2+\Vert \sqrt{x^{\alpha }}{\partial }_x\psi {\Vert }_{L^2(0,T;L^2(\mathrm{\Omega }))}^2}\\ +\Vert \sqrt{\lambda }{\partial }_{\mathit{xt}}\psi {\Vert }_{L^2(0,T;L^2(\mathrm{\Omega }))}^2\\ ⩽C\left(\Vert {\psi }_0{\Vert }_{H_{\alpha }^1(\mathrm{\Omega })}^2+\Vert v_0{\Vert }_{L^2(\mathrm{\Omega })}^2+\Vert f{\Vert }_{L^2(0,T;L^2(\mathrm{\Omega })}^2\right).\end{array}\end{array}$$(1.10)

The constant C depending on $\mathrm{\Omega }$, and T.

Theorem 1.3:

When $\lambda ⟶0$, the sequence of the weak solutions of the problem (1.4(1.4) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )-\lambda {\partial }_{\mathit{xxt}}\psi =f,\lambda >0,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.4) ) converges to the weak solution of the problem (1.1(1.1) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )=f,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.1) ).

Theorem 1.4:

Under the assumptions of Theorem 1.2, the functional J is continuous on $A_{\mathit{ad}}$.

Theorem 1.5:

Under the assumptions of Theorem 1.2, the functional J is G-derivable on $A_{\mathit{ad}}$.

2. Proof

Proof of Theorem 1.2:

For any positive integer n, consider the nondegenerate wave equation(2.1) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\partial }_{\mathit{tt}}{\psi }^n-{\partial }_x(\left(x^{\alpha }+\frac{1}{n}\right){\partial }_x{\psi }^n)-\lambda {\partial }_{\mathit{xxt}}{\psi }^n=f(x,t),}\\ {\psi }^n(0,t)={\psi }^n(1,t)=0,\forall t\in \left[0;T\right],\\ {\psi }^n(x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega },\\ {\partial }_t{\psi }^n(x,0)=v_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(2.1)

By the classical theory of wave equations, the system (2.1(2.1) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\partial }_{\mathit{tt}}{\psi }^n-{\partial }_x(\left(x^{\alpha }+\frac{1}{n}\right){\partial }_x{\psi }^n)-\lambda {\partial }_{\mathit{xxt}}{\psi }^n=f(x,t),}\\ {\psi }^n(0,t)={\psi }^n(1,t)=0,\forall t\in \left[0;T\right],\\ {\psi }^n(x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega },\\ {\partial }_t{\psi }^n(x,0)=v_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(2.1) ) admits a unique classical solution ${\psi }^n$. Multiplying both sides of the first equation of (2.1(2.1) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\partial }_{\mathit{tt}}{\psi }^n-{\partial }_x(\left(x^{\alpha }+\frac{1}{n}\right){\partial }_x{\psi }^n)-\lambda {\partial }_{\mathit{xxt}}{\psi }^n=f(x,t),}\\ {\psi }^n(0,t)={\psi }^n(1,t)=0,\forall t\in \left[0;T\right],\\ {\psi }^n(x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega },\\ {\partial }_t{\psi }^n(x,0)=v_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(2.1) ) by ${\partial }_t{\psi }^n$ and integrating it in $\mathrm{\Omega }$, we have that(2.2) $$\begin{array}{c}\hfill {\displaystyle {\int }_{\mathrm{\Omega }}{\partial }_{\mathit{tt}}{\psi }^n{\partial }_t{\psi }^n\mathrm{d}x+{\int }_{\mathrm{\Omega }}\left(x^{\alpha }+\frac{1}{n}\right){\partial }_x{\psi }^n{\partial }_{\mathit{xt}}{\psi }^n\mathrm{d}x+\lambda {\int }_{\mathrm{\Omega }}{({\partial }_{\mathit{xt}}{\psi }^n)}^2\mathrm{d}x={\int }_{\mathrm{\Omega }}f{\partial }_t{\psi }^n\mathrm{d}x.}\end{array}$$(2.2) $\mathrm{\Omega }$ is independent of t, and by green’s formula, we arrive at(2.3) $$\begin{array}{c}\hfill {\displaystyle \frac{1}{2}\frac{\mathrm{d}}{\mathrm{d}t}{\int }_{\mathrm{\Omega }}{({\partial }_t{\psi }^n)}^2\mathrm{d}x+\frac{1}{2}\frac{\mathrm{d}}{\mathrm{d}t}{\int }_{\mathrm{\Omega }}\left(x^{\alpha }+\frac{1}{n}\right){({\partial }_x{\psi }^n)}^2\mathrm{d}x+\lambda {\int }_{\mathrm{\Omega }}{({\partial }_{\mathit{xt}}{\psi }^n)}^2\mathrm{d}x⩽{\int }_{\mathrm{\Omega }}f{\partial }_t{\psi }^n\mathrm{d}x.}\end{array}$$(2.3)

Integrating between 0 and t, with $t\in [0,T]$, gives(2.4) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle \Vert {\partial }_t{\psi }^n(t){\Vert }_{L^2(\mathrm{\Omega })}^2+\Vert \sqrt{\left(x^{\alpha }+\frac{1}{n}\right)}{\partial }_x{\psi }^n(t){\Vert }_{L^2(\mathrm{\Omega })}^2}\\ \\ {\displaystyle ⩽\left[\Vert {\partial }_t{\psi }^n(0){\Vert }_{L^2(\mathrm{\Omega })}^2+\Vert \sqrt{\left(x^{\alpha }+\frac{1}{n}\right)}{\partial }_x{\psi }_0{\Vert }_{L^2(\mathrm{\Omega })}^2\right]}\\ +\Vert f{\Vert }_{L^2(0,T;L^2(\mathrm{\Omega }))}^2+{\int }_0^t\Vert {\partial }_t{\psi }^n(s){\Vert }_{L^2(\mathrm{\Omega })}^2\mathrm{d}s.\end{array}\end{array}$$(2.4)

We have $x^{\alpha }⩽1\forall x\in ]0,1[$, and ${\displaystyle \frac{1}{n}<1}$, then(2.5) $$\begin{array}{c}\hfill \sqrt{x^{\alpha }+\frac{1}{n}}⩽\sqrt{2}\forall x\in \mathrm{\Omega }.\end{array}$$(2.5)

We pose(2.6) $$\begin{array}{c}\hfill {\displaystyle C_1=\left[\Vert v_0{\Vert }_{L^2(\mathrm{\Omega })}^2+2\Vert {\psi }_0{\Vert }_{H^1(\mathrm{\Omega })}^2\right]+\Vert f{\Vert }_{L^2(0,T;L^2(\mathrm{\Omega }))}^2.}\end{array}$$(2.6)

Therefore(2.7) $$\begin{array}{c}\hfill {\displaystyle \Vert {\partial }_t{\psi }^n(t){\Vert }_{L^2(\mathrm{\Omega })}^2+\Vert \sqrt{\left(x^{\alpha }+\frac{1}{n}\right)}{\partial }_x{\psi }^n(t){\Vert }_{L^2(\mathrm{\Omega })}^2⩽C_1+{\int }_0^t\Vert {\partial }_t{\psi }^n(s){\Vert }_{L^2(\mathrm{\Omega })}^2\mathrm{d}s.}\end{array}$$(2.7)

We have(2.8) $$\begin{array}{c}\hfill {\psi }^n(x,t)={\int }_0^t{\partial }_t{\psi }^n(x,s)\mathrm{d}s+{\psi }^n(x,0),\end{array}$$(2.8)

then(2.9) $$\begin{array}{c}\hfill {\left({\psi }^n(x,t)\right)}^2={\left({\int }_0^t{\partial }_t{\psi }^n(x,s)\mathrm{d}s\right)}^2+{\left({\psi }^n(x,0)\right)}^2+2{\psi }^n(x,0){\int }_0^t{\partial }_t{\psi }^n(x,s)\mathrm{d}s.\end{array}$$(2.9)

By Hölder inequality, we arrive at(2.10) $$\begin{array}{c}\hfill {\displaystyle {\int }_0^t\mid {\partial }_t{\psi }^n(x,s)\mid \mathrm{d}s⩽\sqrt{t}{\left({\int }_0^t{\left({\partial }_t{\psi }^n(x,s)\right)}^2\mathrm{d}s\right)}^{\frac{1}{2}},}\end{array}$$(2.10)

then(2.11) $$\begin{array}{c}\hfill {\displaystyle {\left({\int }_0^t{\partial }_t{\psi }^n(x,s)\mathrm{d}s\right)}^2⩽T\left({\int }_0^t{\left({\partial }_t{\psi }^n(x,s)\right)}^2\mathrm{d}s\right).}\end{array}$$(2.11)

In addition we have $2ab⩽a^2+b^2$ from where(2.12) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle 2{\psi }^n(x,0){\int }_0^t{\partial }_t{\psi }^n(x,s)\mathrm{d}s⩽{\left({\psi }^n(x,0)\right)}^2+{\left({\int }_0^t{\partial }_t{\psi }^n(x,s)\mathrm{d}s\right)}^2}\hfill \\ \hfill \\ {\displaystyle ⩽{\left({\psi }^n(x,0)\right)}^2+T\left({\int }_0^t{\left({\partial }_t{\psi }^n(x,s)\right)}^2\mathrm{d}s\right).}\hfill \end{array}\end{array}$$(2.12)

From (2.9(2.9) $$\begin{array}{c}\hfill {\left({\psi }^n(x,t)\right)}^2={\left({\int }_0^t{\partial }_t{\psi }^n(x,s)\mathrm{d}s\right)}^2+{\left({\psi }^n(x,0)\right)}^2+2{\psi }^n(x,0){\int }_0^t{\partial }_t{\psi }^n(x,s)\mathrm{d}s.\end{array}$$(2.9) ), (2.11(2.11) $$\begin{array}{c}\hfill {\displaystyle {\left({\int }_0^t{\partial }_t{\psi }^n(x,s)\mathrm{d}s\right)}^2⩽T\left({\int }_0^t{\left({\partial }_t{\psi }^n(x,s)\right)}^2\mathrm{d}s\right).}\end{array}$$(2.11) ) and (2.12(2.12) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle 2{\psi }^n(x,0){\int }_0^t{\partial }_t{\psi }^n(x,s)\mathrm{d}s⩽{\left({\psi }^n(x,0)\right)}^2+{\left({\int }_0^t{\partial }_t{\psi }^n(x,s)\mathrm{d}s\right)}^2}\hfill \\ \hfill \\ {\displaystyle ⩽{\left({\psi }^n(x,0)\right)}^2+T\left({\int }_0^t{\left({\partial }_t{\psi }^n(x,s)\right)}^2\mathrm{d}s\right).}\hfill \end{array}\end{array}$$(2.12) ), we arrive at(2.13) $$\begin{array}{c}\hfill {\displaystyle \Vert {\psi }^n(t){\Vert }_{L^2(\mathrm{\Omega })}^2⩽2\Vert {\psi }_0{\Vert }_{L^2(\mathrm{\Omega })}^2+2T{\int }_0^t\Vert {\partial }_t{\psi }^n(s){\Vert }_{L^2(\mathrm{\Omega })}^2\mathrm{d}s.}\end{array}$$(2.13)

Let(2.14) $$\begin{array}{c}\hfill C_2=C_1+2\Vert {\psi }_0{\Vert }_{L^2(\mathrm{\Omega })}^2\text{and}M=2T+1,\end{array}$$(2.14)

and(2.15) $$\begin{array}{c}\hfill {\displaystyle y(t)=\Vert {\psi }^n(x,t){\Vert }_{L^2(\mathrm{\Omega })}^2+\Vert {\partial }_t{\psi }^n(t){\Vert }_{L^2(\mathrm{\Omega })}^2+\Vert \sqrt{\left(x^{\alpha }+\frac{1}{n}\right)}{\partial }_x{\psi }^n(t){\Vert }_{L^2(\mathrm{\Omega })}^2.}\end{array}$$(2.15)

From (2.7(2.7) $$\begin{array}{c}\hfill {\displaystyle \Vert {\partial }_t{\psi }^n(t){\Vert }_{L^2(\mathrm{\Omega })}^2+\Vert \sqrt{\left(x^{\alpha }+\frac{1}{n}\right)}{\partial }_x{\psi }^n(t){\Vert }_{L^2(\mathrm{\Omega })}^2⩽C_1+{\int }_0^t\Vert {\partial }_t{\psi }^n(s){\Vert }_{L^2(\mathrm{\Omega })}^2\mathrm{d}s.}\end{array}$$(2.7) ) and (2.13(2.13) $$\begin{array}{c}\hfill {\displaystyle \Vert {\psi }^n(t){\Vert }_{L^2(\mathrm{\Omega })}^2⩽2\Vert {\psi }_0{\Vert }_{L^2(\mathrm{\Omega })}^2+2T{\int }_0^t\Vert {\partial }_t{\psi }^n(s){\Vert }_{L^2(\mathrm{\Omega })}^2\mathrm{d}s.}\end{array}$$(2.13) ), we arrive at(2.16) $$\begin{array}{c}\hfill {\displaystyle y(t)⩽C_2+M{\int }_0^{t}y(s)\mathrm{d}s.}\end{array}$$(2.16)

Gronwall’s Lemma gives(2.17) $$\begin{array}{c}\hfill {\displaystyle y(t)⩽C_{2}exp(MT)\forall t\in [0,T].}\end{array}$$(2.17)

Let $M_1=C_{2}exp(MT)$, which gives(2.18) $$\begin{array}{c}\hfill {\displaystyle \Vert {\psi }^n(x,t){\Vert }_{L^2(\mathrm{\Omega })}^2+\Vert {\partial }_t{\psi }^n(t){\Vert }_{L^2(\mathrm{\Omega })}^2+\Vert \sqrt{\left(x^{\alpha }+\frac{1}{n}\right)}{\partial }_x{\psi }^n(t){\Vert }_{L^2(\mathrm{\Omega })}^2⩽M_1,\forall t\in [0,T].}\end{array}$$(2.18)

Hence,(2.19) $$\begin{array}{c}\hfill {\displaystyle \Vert \sqrt{x^{\alpha }}{\partial }_x{\psi }^n(t){\Vert }_{L^2(\mathrm{\Omega })}^2⩽M_1,\forall t\in [0,T],}\end{array}$$(2.19)

and there exist a subsequence $\{{\psi }^{n_j}\}$ of $\{{\psi }^n\}$ and a function $\psi \in L^{\infty }(0,T;L^2(\mathrm{\Omega }))\cap L^2\left(0,T;H_{\alpha }^1(\mathrm{\Omega })\right)$ satisfying ${\partial }_t\psi \in L^{\infty }(0,T;L^2(\mathrm{\Omega }))$, such that as $n_j\to \infty$ (2.20) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\psi }^{n_j}\rightharpoonup \psi \text{weakly in}{L}^{\infty }(0,T;L^2(\mathrm{\Omega })),}\\ \\ {\displaystyle {\psi }^{n_j}\rightharpoonup \psi \text{weakly in}{L}^2(0,T;H_{\alpha }^1(\mathrm{\Omega })),}\\ \\ {\displaystyle {\partial }_t{\psi }^{n_j}\rightharpoonup {\partial }_t\psi \text{weakly in}{L}^2(0,T;L^2(\mathrm{\Omega })),}\\ \\ {\displaystyle \sqrt{(x^{\alpha }+\frac{1}{{}^{n_j}})}{\partial }_x{\psi }^{n_j}\rightharpoonup \sqrt{x^{\alpha }}{\partial }_x\psi \text{weakly in}{L}^2(0,T;L^2(\mathrm{\Omega })).}\end{array}\end{array}$$(2.20)

Since $\{{\psi }^{n_j}\}$ is the solution of system (2.1(2.1) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\partial }_{\mathit{tt}}{\psi }^n-{\partial }_x(\left(x^{\alpha }+\frac{1}{n}\right){\partial }_x{\psi }^n)-\lambda {\partial }_{\mathit{xxt}}{\psi }^n=f(x,t),}\\ {\psi }^n(0,t)={\psi }^n(1,t)=0,\forall t\in \left[0;T\right],\\ {\psi }^n(x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega },\\ {\partial }_t{\psi }^n(x,0)=v_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(2.1) ), we have that ${\psi }^{n_j}(x,0)={\psi }_0$ and ${\partial }_t{\psi }^{n_j}(x,0)=v_0$.

Return to Equation (2.3(2.3) $$\begin{array}{c}\hfill {\displaystyle \frac{1}{2}\frac{\mathrm{d}}{\mathrm{d}t}{\int }_{\mathrm{\Omega }}{({\partial }_t{\psi }^n)}^2\mathrm{d}x+\frac{1}{2}\frac{\mathrm{d}}{\mathrm{d}t}{\int }_{\mathrm{\Omega }}\left(x^{\alpha }+\frac{1}{n}\right){({\partial }_x{\psi }^n)}^2\mathrm{d}x+\lambda {\int }_{\mathrm{\Omega }}{({\partial }_{\mathit{xt}}{\psi }^n)}^2\mathrm{d}x⩽{\int }_{\mathrm{\Omega }}f{\partial }_t{\psi }^n\mathrm{d}x.}\end{array}$$(2.3) ), by integrating between 0 and T, we obtain(2.21) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle \frac{1}{2}{\int }_{\mathrm{\Omega }}{({\partial }_t{\psi }^{n_j})}^2(T)\mathrm{d}x-\frac{1}{2}{\int }_{\mathrm{\Omega }}{({\partial }_t{\psi }^{n_j})}^2(0)\mathrm{d}x+\frac{1}{2}{\int }_{\mathrm{\Omega }}\left(x^{\alpha }+\frac{1}{n_j}\right){({\partial }_x{\psi }^{n_j})}^2(T)\mathrm{d}x}\\ \\ {\displaystyle -\frac{1}{2}{\int }_{\mathrm{\Omega }}\left(x^{\alpha }+\frac{1}{n_j}\right){({\partial }_x{\psi }^{n_j})}^2(0)\mathrm{d}x+\lambda {\int }_0^T{\int }_{\mathrm{\Omega }}{({\partial }_{\mathit{xt}}{\psi }^{n_j})}^2\mathrm{d}x\mathrm{d}t}\\ \\ {\displaystyle ⩽{\int }_0^T{\int }_{\mathrm{\Omega }}f{\partial }_t{\psi }^{n_j}\mathrm{d}x\mathrm{d}t.}\end{array}\end{array}$$(2.21)

From where(2.22) $$\begin{array}{cc}\hfill {\displaystyle \lambda {\int }_0^T{\int }_{\mathrm{\Omega }}{({\partial }_{\mathit{xt}}{\psi }^{n_j})}^2⩽}& {\int }_0^T{\int }_{\mathrm{\Omega }}|f{\partial }_t{\psi }^{n_j}|\hfill \\ \hfill & +\frac{1}{2}\left[{\int }_{\mathrm{\Omega }}{({\partial }_t{\psi }^{n_j})}^2(t=0)+{\int }_{\mathrm{\Omega }}\left(x^{\alpha }+\frac{1}{n_j}\right){({\partial }_x{\psi }^{n_j})}^2(t=0)\right].\hfill \end{array}$$(2.22)

From (2.18(2.18) $$\begin{array}{c}\hfill {\displaystyle \Vert {\psi }^n(x,t){\Vert }_{L^2(\mathrm{\Omega })}^2+\Vert {\partial }_t{\psi }^n(t){\Vert }_{L^2(\mathrm{\Omega })}^2+\Vert \sqrt{\left(x^{\alpha }+\frac{1}{n}\right)}{\partial }_x{\psi }^n(t){\Vert }_{L^2(\mathrm{\Omega })}^2⩽M_1,\forall t\in [0,T].}\end{array}$$(2.18) ), we obtain(2.23) $$\begin{array}{c}\hfill {\displaystyle \Vert \sqrt{\lambda }{\partial }_{\mathit{xt}}{\psi }^{n_j}{\Vert }_{L^2(0,T,L^2(\mathrm{\Omega }))}^2⩽\frac{1}{2}\Vert f{\Vert }_{L^2(0,T,L^2(\mathrm{\Omega }))}^2+\frac{1}{2}\Vert {\partial }_t{\psi }^{n_j}{\Vert }_{L^2(0,T,L^2(\mathrm{\Omega }))}^2+\frac{1}{2}{M}_1.}\end{array}$$(2.23)

and(2.24) $$\begin{array}{c}\hfill {\displaystyle \Vert {\partial }_t{\psi }^{n_j}{\Vert }_{L^2(0,T,L^2(\mathrm{\Omega }))}^2⩽T{M}_1.}\end{array}$$(2.24)

Then(2.25) $$\begin{array}{c}\hfill {\displaystyle \Vert \sqrt{\lambda }{\partial }_{\mathit{xt}}{\psi }^{n_j}{\Vert }_{L^2(0,T,L^2(\mathrm{\Omega }))}^2⩽\frac{1}{2}\Vert f{\Vert }_{L^2(0,T,L^2(\mathrm{\Omega }))}^2+\left(\frac{1}{2}+\frac{T}{2}\right)M_1.}\end{array}$$(2.25)

Consequently,(2.26) $$\begin{array}{c}\hfill \sqrt{\lambda }{\partial }_{\mathit{xt}}{\psi }^{n_j}\rightharpoonup \sqrt{\lambda }{\partial }_{\mathit{xt}}\psi \text{weakly in}{L}^2(0,T;L^2(\mathrm{\Omega })).\end{array}$$(2.26)

The weak formulation of (2.1(2.1) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\partial }_{\mathit{tt}}{\psi }^n-{\partial }_x(\left(x^{\alpha }+\frac{1}{n}\right){\partial }_x{\psi }^n)-\lambda {\partial }_{\mathit{xxt}}{\psi }^n=f(x,t),}\\ {\psi }^n(0,t)={\psi }^n(1,t)=0,\forall t\in \left[0;T\right],\\ {\psi }^n(x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega },\\ {\partial }_t{\psi }^n(x,0)=v_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(2.1) ) is(2.27) $$\begin{array}{c}\hfill {\displaystyle {\int }_{\mathrm{\Omega }}{\partial }_{\mathit{tt}}{\psi }^{n}v\mathrm{d}x+{\int }_{\mathrm{\Omega }}\left(x^{\alpha }+\frac{1}{n}\right){\partial }_x{\psi }^n{\partial }_{x}v\mathrm{d}x+\lambda {\int }_{\mathrm{\Omega }}{\partial }_{\mathit{xt}}{\psi }^n{\partial }_{x}v\mathrm{d}x={\int }_{\mathrm{\Omega }}fv\mathrm{d}x\forall v\in H_0^1(\mathrm{\Omega }).}\end{array}$$(2.27)

If we take $v\in H_0^1(\mathrm{\Omega })$ as $\Vert v{\Vert }_{H_0^1(\mathrm{\Omega })}⩽1$, we obtain(2.28) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle <{\partial }_{\mathit{tt}}{\psi }^{n_j},v{>}_{L^2(\mathrm{\Omega })}⩽\sqrt{2}\Vert \sqrt{x^{\alpha }+\frac{1}{n}}{\partial }_x{\psi }^{n_j}{\Vert }_{L^2(\mathrm{\Omega })}\Vert v{\Vert }_{H_0^1(\mathrm{\Omega })}}\hfill \\ \hfill \\ +\lambda \Vert {\partial }_{\mathit{xt}}{\psi }^{n_j}{\Vert }_{L^2(\mathrm{\Omega })}\Vert v{\Vert }_{H_0^1(\mathrm{\Omega })}+\Vert f{\Vert }_{L^2(\mathrm{\Omega })}\Vert v{\Vert }_{H_0^1(\mathrm{\Omega })}\hfill \end{array}\end{array}$$(2.28) (2.29) $$\begin{array}{c}\hfill \Vert {\partial }_{\mathit{tt}}{\psi }^{n_j}{\Vert }_{H^{-1}(\mathrm{\Omega })}⩽\sqrt{2}\Vert \sqrt{x^{\alpha }+\frac{1}{n}}{\partial }_x{\psi }^{n_j}{\Vert }_{L^2(\mathrm{\Omega })}+\lambda \Vert {\partial }_{\mathit{xt}}{\psi }^{n_j}{\Vert }_{L^2(\mathrm{\Omega })}+\Vert f{\Vert }_{L^2(\mathrm{\Omega })}.\end{array}$$(2.29)

From (2.18(2.18) $$\begin{array}{c}\hfill {\displaystyle \Vert {\psi }^n(x,t){\Vert }_{L^2(\mathrm{\Omega })}^2+\Vert {\partial }_t{\psi }^n(t){\Vert }_{L^2(\mathrm{\Omega })}^2+\Vert \sqrt{\left(x^{\alpha }+\frac{1}{n}\right)}{\partial }_x{\psi }^n(t){\Vert }_{L^2(\mathrm{\Omega })}^2⩽M_1,\forall t\in [0,T].}\end{array}$$(2.18) ) and (2.25(2.25) $$\begin{array}{c}\hfill {\displaystyle \Vert \sqrt{\lambda }{\partial }_{\mathit{xt}}{\psi }^{n_j}{\Vert }_{L^2(0,T,L^2(\mathrm{\Omega }))}^2⩽\frac{1}{2}\Vert f{\Vert }_{L^2(0,T,L^2(\mathrm{\Omega }))}^2+\left(\frac{1}{2}+\frac{T}{2}\right)M_1.}\end{array}$$(2.25) ), we obtain(2.30) $$\begin{array}{c}\hfill \Vert {\partial }_{\mathit{tt}}{\psi }^{n_j}{\Vert }_{L^2\left(0,T;H^{-1}(\mathrm{\Omega })\right)}<\infty .\end{array}$$(2.30)

Hence,(2.31) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\partial }_{\mathit{tt}}{\psi }^{n_j}\text{is bounded in}{L}^2(0,T,H^{-1}(\mathrm{\Omega })).}\hfill \end{array}\end{array}$$(2.31)

We conclude that(2.32) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\psi }^{n_j}\rightharpoonup \psi \text{weakly in}{L}^{\infty }(0,T;L^2(\mathrm{\Omega })),}\\ \\ {\displaystyle {\psi }^{n_j}\rightharpoonup \psi \text{weakly in}{L}^2(0,T;H_{\alpha }^1(\mathrm{\Omega })),}\\ \\ {\displaystyle {\partial }_t{\psi }^{n_j}\rightharpoonup {\partial }_t\psi \text{weakly in}{L}^2(0,T;L^2(\mathrm{\Omega })),}\\ \\ \sqrt{\lambda }{\partial }_{\mathit{xt}}{\psi }^{n_j}\rightharpoonup \sqrt{\lambda }{\partial }_{\mathit{xt}}\psi \text{weakly in}{L}^2(0,T;L^2(\mathrm{\Omega })),\\ \\ {\displaystyle \sqrt{(x^{\alpha }+\frac{1}{{}^{n_j}})}{\partial }_x{\psi }^{n_j}\rightharpoonup \sqrt{x^{\alpha }}{\partial }_x\psi \text{weakly in}{L}^2(0,T;L^2(\mathrm{\Omega })),}\\ \\ {\partial }_{\mathit{tt}}{\psi }^{n_j}\rightharpoonup {\partial }_{\mathit{tt}}\psi \text{weakly in}{L}^2(0,T;H^{-1}(\mathrm{\Omega })).\end{array}\end{array}$$(2.32)

We find upon passing to weak limits that(2.33) $$\begin{array}{c}\hfill {\displaystyle {\int }_{\mathrm{\Omega }}{\partial }_{\mathit{tt}}\psi v+{\int }_{\mathrm{\Omega }}{x}^{\alpha }{\partial }_x\psi {\partial }_{x}v+\lambda {\int }_{\mathrm{\Omega }}{\partial }_{\mathit{xt}}\psi {\partial }_{x}v\mathrm{d}x={\int }_{\mathrm{\Omega }}fv,\forall v\in H_0^1(\mathrm{\Omega }),a.e.t\in ]0,T[.}\end{array}$$(2.33)

We obtain that $\psi$ is the weak solution of(2.34) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )-\lambda {\partial }_{\mathit{xxt}}\psi =f(x,t),\\ \psi (0,t)=\psi (1,t)=0,\forall t\in \left[0;T\right],\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega },\\ {\partial }_t\psi (x,0)=v_0(x)\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(2.34)

Next, we prove the existence of weak solutions of (1.4(1.4) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )-\lambda {\partial }_{\mathit{xxt}}\psi =f,\lambda >0,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.4) ) for any $({\psi }_0,v_0)\in H_{\alpha }^1(\mathrm{\Omega })\times L^2(\mathrm{\Omega })$ and $f\in L^2(0;T;L^2(\mathrm{\Omega }))$. Let $\left\{{\psi }_0^m\right\}$, $\left\{v_0^m\right\}$ and $\left\{f^m\right\}$ be Cauchy sequences of smooth functions, respectively, such that as $m⟶\infty$,

${\psi }_0^m⟶{\psi }_0$ in $H_{\alpha }^1(\mathrm{\Omega })$, $v_0^m⟶v_0$ in $L^2(\mathrm{\Omega })$ and $f^m⟶f$ in $L^2(0,T;L^2(\mathrm{\Omega }))$.

Denote by ${\psi }^m$ the solution of (1.4(1.4) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )-\lambda {\partial }_{\mathit{xxt}}\psi =f,\lambda >0,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.4) ) associated to $({\psi }_0^m,v_0^m)$ and $f^m$, and ${\psi }^n$ the solution of (1.4(1.4) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )-\lambda {\partial }_{\mathit{xxt}}\psi =f,\lambda >0,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.4) ) associated to $({\psi }_0^n,v_0^n)$ and $f^n$.

We have the following variational problem(2.35) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\int }_{\mathrm{\Omega }}{\partial }_{\mathit{tt}}({\psi }^n-{\psi }^m)v\mathrm{d}x+{\int }_{\mathrm{\Omega }}{x}^{\alpha }{\partial }_x({\psi }^n-{\psi }^m){\partial }_{x}v\mathrm{d}x+{\int }_{\mathrm{\Omega }}\lambda {\partial }_{\mathit{xt}}({\psi }^n-{\psi }^m){\partial }_{x}v\mathrm{d}x}\\ ={\int }_{\mathrm{\Omega }}(f^n-f^m)v\mathrm{d}x,\forall v\in H_0^1(\mathrm{\Omega }),\\ ({\psi }^n-{\psi }^m)(x,t)=0,\forall x\in \partial \mathrm{\Omega },\forall t\in ]0;T[,\\ ({\psi }^n-{\psi }^m)(x,0)=({\psi }_0^n-{\psi }_0^m),\forall x\in \mathrm{\Omega },\\ {\partial }_t({\psi }^n-{\psi }^m)(x,0)=(v_0^n-v_0^m),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(2.35)

Similarly at Equations (2.18(2.18) $$\begin{array}{c}\hfill {\displaystyle \Vert {\psi }^n(x,t){\Vert }_{L^2(\mathrm{\Omega })}^2+\Vert {\partial }_t{\psi }^n(t){\Vert }_{L^2(\mathrm{\Omega })}^2+\Vert \sqrt{\left(x^{\alpha }+\frac{1}{n}\right)}{\partial }_x{\psi }^n(t){\Vert }_{L^2(\mathrm{\Omega })}^2⩽M_1,\forall t\in [0,T].}\end{array}$$(2.18) ) and (2.19(2.19) $$\begin{array}{c}\hfill {\displaystyle \Vert \sqrt{x^{\alpha }}{\partial }_x{\psi }^n(t){\Vert }_{L^2(\mathrm{\Omega })}^2⩽M_1,\forall t\in [0,T],}\end{array}$$(2.19) ), let $M=2T+1,$ and$$\begin{array}{c}\hfill M_1=4exp(MT)\left[\Vert v_0^n-v_0^m{\Vert }_{L^2(\mathrm{\Omega })}^2+\Vert {\psi }_0^n-{\psi }_0^m{\Vert }_{H^1(\mathrm{\Omega })}^2+\Vert f^n-f^m{\Vert }_{L^2(0,T;L^2(\mathrm{\Omega }))}^2\right].\end{array}$$

We obtain(2.36) $$\begin{array}{c}\hfill \Vert {\partial }_t{\psi }^n-{\partial }_t{\psi }^m){\Vert }_{L^2(0,T;L^2(\mathrm{\Omega }))}^2⩽M_1,\end{array}$$(2.36)

and(2.37) $$\begin{array}{c}\hfill \Vert {\psi }^n-{\psi }^m{\Vert }_{L^{\infty }(0,T;L^2(\mathrm{\Omega }))}^2⩽M_1,\end{array}$$(2.37)

and(2.38) $$\begin{array}{c}\hfill \Vert {\psi }^n-{\psi }^m{\Vert }_{L^2(0,T;H_{\alpha }^1(\mathrm{\Omega }))}^2⩽M_1.\end{array}$$(2.38)

Therefore, there exists $\psi \in L^2(0,T;H_{\alpha }^1(\mathrm{\Omega }))\cap L^{\infty }(0,T;L^2(\mathrm{\Omega }))$ and ${\partial }_t\psi \in L^2(0,T;L^2(\mathrm{\Omega }))$, such that as $m⟶\infty$ (2.39) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\psi }^m⟶\psi \text{in}{L}^{\infty }(0,T;L^2(\mathrm{\Omega }))\text{, and}{\partial }_t{\psi }^m⟶{\partial }_t\psi \text{in}{L}^2(0,T;L^2(\mathrm{\Omega })),}\\ \\ \text{and}{\psi }^m⟶\psi \text{in}{L}^2(0,T;H_{\alpha }^1(\mathrm{\Omega })).\end{array}\end{array}$$(2.39)

Now, we prove that the weak solution of problem (1.4(1.4) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )-\lambda {\partial }_{\mathit{xxt}}\psi =f,\lambda >0,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.4) ) is unique.

Let ${\psi }_1$ and ${\psi }_2$ two weak solutions of the problem (1.4(1.4) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )-\lambda {\partial }_{\mathit{xxt}}\psi =f,\lambda >0,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.4) ).

Let $D\psi ={\psi }_1-{\psi }_2$, consequently $D\psi$ verifies(2.40) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\int }_{\mathrm{\Omega }}{\partial }_{\mathit{tt}}D\psi v\mathrm{d}x+{\int }_{\mathrm{\Omega }}{x}^{\alpha }{\partial }_{x}D\psi {\partial }_{x}v\mathrm{d}x+{\int }_{\mathrm{\Omega }}\lambda {\partial }_{\mathit{xt}}D\psi {\partial }_{x}v\mathrm{d}x=0,\forall v\in H_0^1(\mathrm{\Omega })}\\ D\psi (x,t)=0,\forall x\in \partial \mathrm{\Omega }\text{,}\forall t\in ]0;T[\\ D\psi (x,0)=0,\forall x\in \mathrm{\Omega }\\ {\partial }_{t}D\psi (x,0)=0,\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(2.40)

By same way to obtain Equation (2.18(2.18) $$\begin{array}{c}\hfill {\displaystyle \Vert {\psi }^n(x,t){\Vert }_{L^2(\mathrm{\Omega })}^2+\Vert {\partial }_t{\psi }^n(t){\Vert }_{L^2(\mathrm{\Omega })}^2+\Vert \sqrt{\left(x^{\alpha }+\frac{1}{n}\right)}{\partial }_x{\psi }^n(t){\Vert }_{L^2(\mathrm{\Omega })}^2⩽M_1,\forall t\in [0,T].}\end{array}$$(2.18) ), we get(2.41) $$\begin{array}{c}\hfill \Vert D\psi {\Vert }_{L^2(0,T;H_{\alpha }^1(\mathrm{\Omega }))}^2=0.\end{array}$$(2.41)

From where$$\begin{array}{c}\hfill {\psi }_1={\psi }_2,a.e.t\in [0,T].\end{array}$$

Proof of Theorem 1.3:

Let the problem(2.42) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}{\psi }^{\lambda }-{\partial }_x(x^{\alpha }{\partial }_x{\psi }^{\lambda })-\lambda {\partial }_{\mathit{xxt}}{\psi }^{\lambda }=f(x,t),\\ {\psi }^{\lambda }(0,t)={\psi }^{\lambda }(1,t)=0,\forall t\in \left[0;T\right],\\ {\psi }^{\lambda }(x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega },\\ {\partial }_t{\psi }^{\lambda }(x,0)=v_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(2.42)

Multiplying both sides of the first equation of (2.42(2.42) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}{\psi }^{\lambda }-{\partial }_x(x^{\alpha }{\partial }_x{\psi }^{\lambda })-\lambda {\partial }_{\mathit{xxt}}{\psi }^{\lambda }=f(x,t),\\ {\psi }^{\lambda }(0,t)={\psi }^{\lambda }(1,t)=0,\forall t\in \left[0;T\right],\\ {\psi }^{\lambda }(x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega },\\ {\partial }_t{\psi }^{\lambda }(x,0)=v_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(2.42) ) by ${\partial }_t{\psi }^{\lambda }$ and integrating it in $\mathrm{\Omega }$, we have that(2.43) $$\begin{array}{c}\hfill {\displaystyle {\int }_{\mathrm{\Omega }}{\partial }_{\mathit{tt}}{\psi }^{\lambda }{\partial }_t{\psi }^{\lambda }\mathrm{d}x+{\int }_{\mathrm{\Omega }}{x}^{\alpha }{\partial }_x{\psi }^{\lambda }{\partial }_{\mathit{xt}}{\psi }^{\lambda }\mathrm{d}x+\lambda {\int }_{\mathrm{\Omega }}{({\partial }_{\mathit{xt}}{\psi }^{\lambda })}^2\mathrm{d}x={\int }_{\mathrm{\Omega }}f{\partial }_t{\psi }^{\lambda }\mathrm{d}x.}\end{array}$$(2.43) $\mathrm{\Omega }$ is independent of t, and by green’s formula, we arrive at(2.44) $$\begin{array}{c}\hfill {\displaystyle \frac{1}{2}\frac{\mathrm{d}}{\mathrm{d}t}{\int }_{\mathrm{\Omega }}{({\partial }_t{\psi }^{\lambda })}^2\mathrm{d}x+\frac{1}{2}\frac{\mathrm{d}}{\mathrm{d}t}{\int }_{\mathrm{\Omega }}{x}^{\alpha }{({\partial }_x{\psi }^{\lambda })}^2\mathrm{d}x+\lambda {\int }_{\mathrm{\Omega }}{({\partial }_{\mathit{xt}}{\psi }^{\lambda })}^2\mathrm{d}x⩽{\int }_{\mathrm{\Omega }}f{\partial }_t{\psi }^{\lambda }\mathrm{d}x,}\end{array}$$(2.44)

Integrating between 0 and t, with $t\in [0,T]$, gives(2.45) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle \Vert {\partial }_t{\psi }^{\lambda }(t){\Vert }_{L^2(\mathrm{\Omega })}^2+\Vert \sqrt{x^{\alpha }}{\partial }_x{\psi }^{\lambda }(t){\Vert }_{L^2(\mathrm{\Omega })}^2}\\ \\ {\displaystyle ⩽\left[\Vert v_0{\Vert }_{L^2(\mathrm{\Omega })}^2+\Vert {\psi }_0{\Vert }_{H_{\alpha }^1(\mathrm{\Omega })}^2\right]+\Vert f{\Vert }_{L^2(0,T;L^2(\mathrm{\Omega }))}^2+{\int }_0^t\Vert {\partial }_t{\psi }^{\lambda }(s){\Vert }_{L^2(\mathrm{\Omega })}^2\mathrm{d}s.}\end{array}\end{array}$$(2.45)

We pose(2.46) $$\begin{array}{c}\hfill {\displaystyle C_1=\left[\Vert v_0{\Vert }_{L^2(\mathrm{\Omega })}^2+\Vert {\psi }_0{\Vert }_{H_{\alpha }^1(\mathrm{\Omega })}^2\right]+\Vert f{\Vert }_{L^2(0,T;L^2(\mathrm{\Omega }))}^2.}\end{array}$$(2.46)

Therefore we have(2.47) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle \Vert {\partial }_t{\psi }^{\lambda }(t){\Vert }_{L^2(\mathrm{\Omega })}^2+\Vert \sqrt{x^{\alpha }}{\partial }_x{\psi }^{\lambda }(t){\Vert }_{L^2(\mathrm{\Omega })}^2⩽C_1+{\int }_0^t\Vert {\partial }_t{\psi }^{\lambda }(s){\Vert }_{L^2(\mathrm{\Omega })}^2\mathrm{d}s.}\hfill \end{array}\end{array}$$(2.47)

We have(2.48) $$\begin{array}{c}\hfill {\psi }^{\lambda }(x,t)={\int }_0^t{\partial }_t{\psi }^{\lambda }(x,s)\mathrm{d}s+{\psi }^{\lambda }(x,0),\end{array}$$(2.48)

By the same way as that used to obtain (2.8(2.8) $$\begin{array}{c}\hfill {\psi }^n(x,t)={\int }_0^t{\partial }_t{\psi }^n(x,s)\mathrm{d}s+{\psi }^n(x,0),\end{array}$$(2.8) )–(2.13(2.13) $$\begin{array}{c}\hfill {\displaystyle \Vert {\psi }^n(t){\Vert }_{L^2(\mathrm{\Omega })}^2⩽2\Vert {\psi }_0{\Vert }_{L^2(\mathrm{\Omega })}^2+2T{\int }_0^t\Vert {\partial }_t{\psi }^n(s){\Vert }_{L^2(\mathrm{\Omega })}^2\mathrm{d}s.}\end{array}$$(2.13) ), we arrive at(2.49) $$\begin{array}{c}\hfill {\displaystyle \Vert {\psi }^{\lambda }(t){\Vert }_{L^2(\mathrm{\Omega })}^2⩽2\Vert {\psi }_0{\Vert }_{L^2(\mathrm{\Omega })}^2+2T{\int }_0^t\Vert {\partial }_t{\psi }^{\lambda }(s){\Vert }_{L^2(\mathrm{\Omega })}^2\mathrm{d}s.}\end{array}$$(2.49)

Let $C_2=C_1+2\Vert {\psi }_0{\Vert }_{L^2(\mathrm{\Omega })}^2\text{and}M=1+2T$, and(2.50) $$\begin{array}{c}\hfill {\displaystyle y(t)=\Vert {\psi }^{\lambda }(x,t){\Vert }_{L^2(\mathrm{\Omega })}^2+\Vert {\partial }_t{\psi }^{\lambda }(t){\Vert }_{L^2(\mathrm{\Omega })}^2+\Vert \sqrt{x^{\alpha }}{\partial }_x{\psi }^{\lambda }(t){\Vert }_{L^2(\mathrm{\Omega })}^2.}\end{array}$$(2.50)

From (2.47(2.47) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle \Vert {\partial }_t{\psi }^{\lambda }(t){\Vert }_{L^2(\mathrm{\Omega })}^2+\Vert \sqrt{x^{\alpha }}{\partial }_x{\psi }^{\lambda }(t){\Vert }_{L^2(\mathrm{\Omega })}^2⩽C_1+{\int }_0^t\Vert {\partial }_t{\psi }^{\lambda }(s){\Vert }_{L^2(\mathrm{\Omega })}^2\mathrm{d}s.}\hfill \end{array}\end{array}$$(2.47) ) and (2.49(2.49) $$\begin{array}{c}\hfill {\displaystyle \Vert {\psi }^{\lambda }(t){\Vert }_{L^2(\mathrm{\Omega })}^2⩽2\Vert {\psi }_0{\Vert }_{L^2(\mathrm{\Omega })}^2+2T{\int }_0^t\Vert {\partial }_t{\psi }^{\lambda }(s){\Vert }_{L^2(\mathrm{\Omega })}^2\mathrm{d}s.}\end{array}$$(2.49) ), we arrive at(2.51) $$\begin{array}{c}\hfill {\displaystyle y(t)⩽C_2+M{\int }_0^{t}y(s)\mathrm{d}s.}\end{array}$$(2.51)

Gronwall’s Lemma gives(2.52) $$\begin{array}{c}\hfill {\displaystyle y(t)⩽C_{2}exp(MT)\forall t\in [0,T].}\end{array}$$(2.52)

Let $M_1=C_{2}exp(MT)$, which gives(2.53) $$\begin{array}{c}\hfill {\displaystyle \Vert {\psi }^{\lambda }(x,t){\Vert }_{L^2(\mathrm{\Omega })}^2+\Vert {\partial }_t{\psi }^{\lambda }(t){\Vert }_{L^2(\mathrm{\Omega })}^2+\Vert \sqrt{x^{\alpha }}{\partial }_x{\psi }^{\lambda }(t){\Vert }_{L^2(\mathrm{\Omega })}^2⩽M_1,\forall t\in [0,T].}\end{array}$$(2.53)

Hence,(2.54) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_t{\psi }^{\lambda }\text{is bounded in}{L}^{\infty }(0,T,L^2(\mathrm{\Omega })),\hfill \end{array}\end{array}$$(2.54)

and(2.55) $$\begin{array}{c}\hfill \begin{array}{c}{\psi }^{\lambda }\text{is bounded in}{L}^{\infty }(0,T,L^2(\mathrm{\Omega })),\hfill \end{array}\end{array}$$(2.55)

and(2.56) $$\begin{array}{c}\hfill \begin{array}{c}{\psi }^{\lambda }\text{is bounded in}{L}^2(0,T,H_{\alpha }^1(\mathrm{\Omega })).\hfill \end{array}\end{array}$$(2.56)

Return to Equation (2.44(2.44) $$\begin{array}{c}\hfill {\displaystyle \frac{1}{2}\frac{\mathrm{d}}{\mathrm{d}t}{\int }_{\mathrm{\Omega }}{({\partial }_t{\psi }^{\lambda })}^2\mathrm{d}x+\frac{1}{2}\frac{\mathrm{d}}{\mathrm{d}t}{\int }_{\mathrm{\Omega }}{x}^{\alpha }{({\partial }_x{\psi }^{\lambda })}^2\mathrm{d}x+\lambda {\int }_{\mathrm{\Omega }}{({\partial }_{\mathit{xt}}{\psi }^{\lambda })}^2\mathrm{d}x⩽{\int }_{\mathrm{\Omega }}f{\partial }_t{\psi }^{\lambda }\mathrm{d}x,}\end{array}$$(2.44) ), by integrating between 0 and T we obtain(2.57) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle \frac{1}{2}{\int }_{\mathrm{\Omega }}{({\partial }_t{\psi }^{\lambda })}^2(T)+\frac{1}{2}{\int }_{\mathrm{\Omega }}{x}^{\alpha }{({\partial }_x{\psi }^{\lambda })}^2(T)\mathrm{d}x+\lambda {\int }_0^T{\int }_{\mathrm{\Omega }}{({\partial }_{\mathit{xt}}{\psi }^{\lambda })}^2}\\ \\ {\displaystyle ⩽{\int }_0^T{\int }_{\mathrm{\Omega }}f{\partial }_t{\psi }^{\lambda }+\frac{1}{2}{\int }_{\mathrm{\Omega }}{({\partial }_t{\psi }^{\lambda })}^2(0)+\frac{1}{2}{\int }_{\mathrm{\Omega }}{x}^{\alpha }{({\partial }_x{\psi }^{\lambda })}^2(0)\mathrm{d}x.}\end{array}\end{array}$$(2.57)

From where(2.58) $$\begin{array}{c}\hfill {\displaystyle \lambda {\int }_0^T{\int }_{\mathrm{\Omega }}{({\partial }_{\mathit{xt}}{\psi }^{\lambda })}^2⩽{\int }_0^T{\int }_{\mathrm{\Omega }}|f{\partial }_t{\psi }^{\lambda }|+\frac{1}{2}{\int }_{\mathrm{\Omega }}{({\partial }_t{\psi }^{\lambda })}^2(0)+\frac{1}{2}{\int }_{\mathrm{\Omega }}{x}^{\alpha }{({\partial }_x{\psi }^{\lambda })}^2(0)\mathrm{d}x.}\end{array}$$(2.58)

Since $\lambda <<1$ then(2.59) $$\begin{array}{c}\hfill {\displaystyle {\int }_0^T{\int }_{\mathrm{\Omega }}{(\lambda {\partial }_{\mathit{xt}}{\psi }^{\lambda })}^2⩽{\int }_0^T{\int }_{\mathrm{\Omega }}\lambda {({\partial }_{\mathit{xt}}{\psi }^{\lambda })}^2.}\end{array}$$(2.59)

From where(2.60) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle \Vert \lambda {\partial }_{\mathit{xt}}{\psi }^{\lambda }{\Vert }_{L^2(0,T,L^2(\mathrm{\Omega }))}^2⩽\frac{1}{2}\Vert f{\Vert }_{L^2(0,T,L^2(\mathrm{\Omega }))}^2}\\ +\frac{1}{2}\left[\Vert {\partial }_t{\psi }^{\lambda }(t){\Vert }_{L^2(0,T,L^2(\mathrm{\Omega }))}^2+\Vert {\partial }_t{\psi }^{\lambda }(0){\Vert }_{L^2(\mathrm{\Omega })}^2+\Vert \sqrt{x^{\alpha }}{\partial }_x{\psi }^{\lambda }(0){\Vert }_{L^2(\mathrm{\Omega })}^2\right].\end{array}\end{array}$$(2.60)

From Equation (2.53(2.53) $$\begin{array}{c}\hfill {\displaystyle \Vert {\psi }^{\lambda }(x,t){\Vert }_{L^2(\mathrm{\Omega })}^2+\Vert {\partial }_t{\psi }^{\lambda }(t){\Vert }_{L^2(\mathrm{\Omega })}^2+\Vert \sqrt{x^{\alpha }}{\partial }_x{\psi }^{\lambda }(t){\Vert }_{L^2(\mathrm{\Omega })}^2⩽M_1,\forall t\in [0,T].}\end{array}$$(2.53) )(2.61) $$\begin{array}{c}\hfill {\displaystyle \Vert \lambda {\partial }_{\mathit{xt}}{\psi }^{\lambda }{\Vert }_{L^2(0,T,L^2(\mathrm{\Omega }))}^2⩽\frac{1}{2}\Vert f{\Vert }_{L^2(0,T,L^2(\mathrm{\Omega }))}^2+\frac{1}{2}\left(M_{1}T+2M1\right).}\end{array}$$(2.61)

Consequently,(2.62) $$\begin{array}{c}\hfill {\displaystyle \lambda {\partial }_{\mathit{tx}}{\psi }^{\lambda }\text{is bounded in}{L}^2(0,T,L^2(\mathrm{\Omega })).}\end{array}$$(2.62)

The weak formulation of (2.42(2.42) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}{\psi }^{\lambda }-{\partial }_x(x^{\alpha }{\partial }_x{\psi }^{\lambda })-\lambda {\partial }_{\mathit{xxt}}{\psi }^{\lambda }=f(x,t),\\ {\psi }^{\lambda }(0,t)={\psi }^{\lambda }(1,t)=0,\forall t\in \left[0;T\right],\\ {\psi }^{\lambda }(x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega },\\ {\partial }_t{\psi }^{\lambda }(x,0)=v_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(2.42) ) is(2.63) $$\begin{array}{c}\hfill {\displaystyle {\int }_{\mathrm{\Omega }}{\partial }_{\mathit{tt}}{\psi }^{\lambda }v\mathrm{d}x+{\int }_{\mathrm{\Omega }}{x}^{\alpha }{\partial }_x{\psi }^{\lambda }{\partial }_{x}v\mathrm{d}x+\lambda {\int }_{\mathrm{\Omega }}{\partial }_{\mathit{xt}}{\psi }^{\lambda }{\partial }_{x}v\mathrm{d}x={\int }_{\mathrm{\Omega }}fv\mathrm{d}x,\forall v\in H_0^1(\mathrm{\Omega }).}\end{array}$$(2.63)

We take $v\in H_0^1(\mathrm{\Omega })$ as $\Vert v{\Vert }_{H_0^1(\mathrm{\Omega })}⩽1$, we obtain(2.64) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle <{\partial }_{\mathit{tt}}{\psi }^{\lambda },v{>}_{L^2(\mathrm{\Omega })}⩽\Vert x^{\alpha }{\partial }_x{\psi }^{\lambda }{\Vert }_{L^2(\mathrm{\Omega })}\Vert v{\Vert }_{H_0^1(\mathrm{\Omega })}}\hfill \\ \hfill \\ +\Vert \lambda {\partial }_{\mathit{xt}}{\psi }^{\lambda }{\Vert }_{L^2(\mathrm{\Omega })}\Vert v{\Vert }_{H_0^1(\mathrm{\Omega })}+\Vert f{\Vert }_{L^2(\mathrm{\Omega })}\Vert v{\Vert }_{H_0^1(\mathrm{\Omega })}.\hfill \end{array}\end{array}$$(2.64)

Since $x^{\alpha }⩽\sqrt{x^{\alpha }}$ $\forall x\in \mathrm{\Omega }$, then(2.65) $$\begin{array}{c}\hfill \Vert {\partial }_{\mathit{tt}}{\psi }^{\lambda }{\Vert }_{H^{-1}(\mathrm{\Omega })}⩽\Vert \sqrt{x^{\alpha }}{\partial }_x{\psi }^{\lambda }{\Vert }_{L^2(\mathrm{\Omega })}+\Vert \lambda {\partial }_{\mathit{xt}}{\psi }^{\lambda }{\Vert }_{L^2(\mathrm{\Omega })}+\Vert f{\Vert }_{L^2(\mathrm{\Omega })}.\end{array}$$(2.65)

From Equations (2.53(2.53) $$\begin{array}{c}\hfill {\displaystyle \Vert {\psi }^{\lambda }(x,t){\Vert }_{L^2(\mathrm{\Omega })}^2+\Vert {\partial }_t{\psi }^{\lambda }(t){\Vert }_{L^2(\mathrm{\Omega })}^2+\Vert \sqrt{x^{\alpha }}{\partial }_x{\psi }^{\lambda }(t){\Vert }_{L^2(\mathrm{\Omega })}^2⩽M_1,\forall t\in [0,T].}\end{array}$$(2.53) ) and (2.61(2.61) $$\begin{array}{c}\hfill {\displaystyle \Vert \lambda {\partial }_{\mathit{xt}}{\psi }^{\lambda }{\Vert }_{L^2(0,T,L^2(\mathrm{\Omega }))}^2⩽\frac{1}{2}\Vert f{\Vert }_{L^2(0,T,L^2(\mathrm{\Omega }))}^2+\frac{1}{2}\left(M_{1}T+2M1\right).}\end{array}$$(2.61) ), we have(2.66) $$\begin{array}{c}\hfill \Vert {\partial }_{\mathit{tt}}{\psi }^{\lambda }{\Vert }_{L^2\left(0,T;H^{-1}(\mathrm{\Omega })\right)}<\infty .\end{array}$$(2.66)

Hence,(2.67) $$\begin{array}{c}\hfill \begin{array}{c}{\psi }^{\lambda }\rightharpoonup \psi \text{weakly in}{L}^{\infty }(0,T;L^2(\mathrm{\Omega })),\\ \\ {\psi }^{\lambda }\rightharpoonup \psi \text{weakly in}{L}^2(0,T;H_{\alpha }^1(\mathrm{\Omega })),\\ \\ {\partial }_t{\psi }^{\lambda }\rightharpoonup {\partial }_t\psi \text{weakly in}{L}^2(0,T;L^2(\mathrm{\Omega })),\\ \\ {\partial }_{\mathit{tt}}{\psi }^{\lambda }\rightharpoonup {\partial }_{\mathit{tt}}\psi \text{weakly in}{L}^2(0,T;H^{-1}(\mathrm{\Omega })),\\ \\ \lambda {\partial }_{\mathit{xt}}{\psi }^{\lambda }\rightharpoonup 0\text{weakly in}{L}^2(0,T;L^2(\mathrm{\Omega })).\end{array}\end{array}$$(2.67)

We find upon passing to weak limits that(2.68) $$\begin{array}{c}\hfill {\displaystyle {\int }_{\mathrm{\Omega }}{\partial }_{\mathit{tt}}\psi v+{\int }_{\mathrm{\Omega }}{x}^{\alpha }{\partial }_x\psi {\partial }_{x}v={\int }_{\mathrm{\Omega }}fv,\forall v\in H_0^1(\mathrm{\Omega }).}\end{array}$$(2.68)

Hence, $\psi$ is the weak solution of the problem (1.1(1.1) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )=f,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.1) ).

Proof of Theorem 1.4:

The continuity of the functional J is deduced from the continuity of the function$$\begin{array}{c}\hfill \phi :({\psi }_0,v_0)⟶\psi .\end{array}$$

We have the following lemma$\square$

Lemma 2.1:

Let $\psi$ the weak solution of (1.4(1.4) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )-\lambda {\partial }_{\mathit{xxt}}\psi =f,\lambda >0,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.4) ) with initial state $({\psi }_0,v_0)$. The function(2.69) $$\begin{array}{c}\hfill \begin{array}{c}\phi :H_{\alpha }^1(\mathrm{\Omega })\times L^2(\mathrm{\Omega })⟶L^2\left(0,T;H_{\alpha }^1(\mathrm{\Omega })\right)\cap L^{\infty }\left(0,T;L^2(\mathrm{\Omega })\right)\hfill \\ ({\psi }_0,v_0)⟼\psi \hfill \end{array}\end{array}$$(2.69)

is continuous.

Proof of Lemma 2.1:

Let $(\delta {\psi }_0,\delta v_0)\in H_{\alpha }^1(\mathrm{\Omega })\times L^2(\mathrm{\Omega })$ a small variation such that $({\psi }_0+\delta {\psi }_0,v_0+\delta v_0)\in A_{\mathit{ad}}.$

Consider $\delta \psi ={\psi }^{\delta }-\psi$, with $\psi$ is the weak solution of (1.4(1.4) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )-\lambda {\partial }_{\mathit{xxt}}\psi =f,\lambda >0,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.4) ) with initial state (${\psi }_0$, $v_0$) and ${\psi }^{\delta }$ is the weak solution of (1.4(1.4) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )-\lambda {\partial }_{\mathit{xxt}}\psi =f,\lambda >0,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.4) ) with initial state $({\psi }_0+\delta {\psi }_0,v_0+\delta v_0).$ Consequently, $\delta \psi$ is the solution of the following variational problem(2.70) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\int }_{\mathrm{\Omega }}{\partial }_{\mathit{tt}}\delta \psi v\mathrm{d}x+{\int }_{\mathrm{\Omega }}{x}^{\alpha }{\partial }_x\delta \psi {\partial }_{x}v\mathrm{d}x+{\int }_{\mathrm{\Omega }}\lambda {\partial }_{\mathit{xt}}\delta \psi {\partial }_{x}v\mathrm{d}x=0,\forall v\in H_0^1(\mathrm{\Omega }),}\\ \delta \psi (t,x)=0,\forall t\in \left]0;T\right[\text{,}\forall x\in \partial \mathrm{\Omega },\\ \delta \psi (t=0)=\delta {\psi }_0(x),\forall x\in \mathrm{\Omega },\\ {\partial }_t\delta \psi (t=0)=\delta v_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(2.70)

Hence, $\delta \psi$ is weak solution of (1.4(1.4) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )-\lambda {\partial }_{\mathit{xxt}}\psi =f,\lambda >0,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.4) ) with $f=0$. We apply the estimate in Theorem 1.2, we obtain(2.71) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle \underset{t\in [0,T]}{sup}\Vert \delta \psi (t){\Vert }_{L^2(\mathrm{\Omega })}^2+\Vert {\partial }_t\delta \psi {\Vert }_{L^2(0,T;L^2(\mathrm{\Omega }))}^2}\\ +\Vert \sqrt{x^{\alpha }}{\partial }_x\delta \psi {\Vert }_{L^2(0,T;L^2(\mathrm{\Omega }))}^2+\Vert \sqrt{\lambda }{\partial }_{\mathit{xt}}\delta \psi {\Vert }_{L^2(0,T;L^2(\mathrm{\Omega }))}^2\\ \\ ⩽C\left(\Vert \delta {\psi }_0{\Vert }_{H_{\alpha }^1(\mathrm{\Omega })}^2+\Vert \delta v_0{\Vert }_{L^2(\mathrm{\Omega })}^2\right).\end{array}\end{array}$$(2.71)

From where,(2.72) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle \Vert \delta \psi {\Vert }_{L^{\infty }\left(0,T;L^2(\mathrm{\Omega })\right)}^2⩽C\left(\Vert \delta {\psi }_0{\Vert }_{H_{\alpha }^1(\mathrm{\Omega })}^2+\Vert \delta v_0{\Vert }_{L^2(\mathrm{\Omega })}^2\right),}\end{array}\end{array}$$(2.72)

and(2.73) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle \Vert \delta \psi {\Vert }_{L^2\left(0,T;H_{\alpha }^1(\mathrm{\Omega })\right)}^2⩽C\left(\Vert \delta {\psi }_0{\Vert }_{H_{\alpha }^1(\mathrm{\Omega })}^2+\Vert \delta v_0{\Vert }_{L^2(\mathrm{\Omega })}^2\right).}\end{array}\end{array}$$(2.73)

Which implies the continuity of the function(2.74) $$\begin{array}{c}\hfill \begin{array}{c}\phi :H_{\alpha }^1(\mathrm{\Omega })\times L^2(\mathrm{\Omega })⟶L^2\left(0,T;H_{\alpha }^1(\mathrm{\Omega })\right)\cap L^{\infty }\left(0,T;L^2(\mathrm{\Omega })\right)\hfill \\ ({\psi }_0,v_0)⟼\psi .\hfill \end{array}\end{array}$$(2.74)

Hence, the cost function J is continuous on $A_{\mathit{ad}}$.$\square$

Proof of Theorem 1.5:

The differentiability of the functional J is deduced from the differentiability of the function$$\begin{array}{c}\hfill \phi :({\psi }_0,v_0)⟶\psi ,\end{array}$$

where $\psi$ is the weak solution of the problem (1.4(1.4) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )-\lambda {\partial }_{\mathit{xxt}}\psi =f,\lambda >0,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.4) ) with initial condition $({\psi }_0,v_0)$. We have the following result$\square$

Lemma 2.2:

Let $\psi$ the weak solution of (1.4(1.4) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )-\lambda {\partial }_{\mathit{xxt}}\psi =f,\lambda >0,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.4) ) with initial state $({\psi }_0,v_0)$. The function(2.75) $$\begin{array}{c}\hfill \begin{array}{c}\phi :H_{\alpha }^1(\mathrm{\Omega })\times L^2(\mathrm{\Omega })⟶L^2\left(0,T;H_{\alpha }^1(\mathrm{\Omega })\right)\cap L^{\infty }\left(0,T;L^2(\mathrm{\Omega })\right)\hfill \\ ({\psi }_0,v_0)⟼\psi \hfill \end{array}\end{array}$$(2.75)

is G-derivable.

Proof of Lemma 2.2:

Let $b=({\psi }_0,v_0)\in A_{\mathit{ad}}$ and $\delta b=(\delta {\psi }_0,\delta v_0)$ a small variation such that $b+\delta b\in A_{\mathit{ad}}$, we define the function(2.76) $$\begin{array}{c}\hfill {\phi }^{\prime }(b):\delta b\in A_{\mathit{ad}}⟶\delta \psi ,\end{array}$$(2.76)

where $\delta \psi$ is the solution of the following variational problem(2.77) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\int }_{\mathrm{\Omega }}{\partial }_{\mathit{tt}}\delta \psi v\mathrm{d}x+{\int }_{\mathrm{\Omega }}{x}^{\alpha }{\partial }_x\delta \psi {\partial }_{x}v\mathrm{d}x+{\int }_{\mathrm{\Omega }}\lambda {\partial }_{\mathit{xt}}\delta \psi {\partial }_{x}v\mathrm{d}x=0,\forall v\in H_0^1(\mathrm{\Omega }),}\\ \delta \psi (0,t)=\delta \psi (1,t)=0,\forall t\in ]0;T[,\\ \delta \psi (x,0)=\delta {\psi }_0,\forall x\in \mathrm{\Omega },\\ {\partial }_t\delta \psi (x,0)=\delta v_0,\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(2.77)

We pose(2.78) $$\begin{array}{c}\hfill \varphi (b)=\phi (b+\delta b)-\phi (b)-{\phi }^{\prime }(b)\delta b.\end{array}$$(2.78)

We want to show that(2.79) $$\begin{array}{c}\hfill \varphi (b)=o(\delta b).\end{array}$$(2.79)

We easily verify that the function $\varphi$ is solution of following variational problem(2.80) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\int }_{\mathrm{\Omega }}{\partial }_{\mathit{tt}}\varphi v\mathrm{d}x+{\int }_{\mathrm{\Omega }}{x}^{\alpha }{\partial }_x\varphi {\partial }_{x}v\mathrm{d}x+{\int }_{\mathrm{\Omega }}\lambda {\partial }_{\mathit{xt}}\varphi {\partial }_{x}v\mathrm{d}x=0,\forall v\in H_0^1(\mathrm{\Omega }),}\\ \varphi (0,t)=\varphi (1,t)=0,\forall t\in ]0;T[,\\ \varphi (x,0)=\delta {\psi }_0-\delta {\psi }_0^2-\delta v_0^2,\forall x\in \mathrm{\Omega },\\ {\partial }_t\varphi (x,0)=\delta v_0,\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(2.80)

By the same way as that used in the proof of continuity, we deduce(2.81) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle \Vert \varphi {\Vert }_{L^{\infty }\left(0,T;L^2(\mathrm{\Omega })\right)}^2⩽C\left({∥\delta {\psi }_0-\delta {\psi }_0^2-\delta v_0^2∥}_{H_{\alpha }^1(\mathrm{\Omega })}^2+{∥\delta v_0∥}_{L^2(\mathrm{\Omega })}^2\right),}\hfill \end{array}\end{array}$$(2.81)

and(2.82) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle \Vert \varphi {\Vert }_{L^2\left(0,T;H_{\alpha }^1(\mathrm{\Omega })\right)}^2⩽C\left({∥\delta {\psi }_0-\delta {\psi }_0^2-\delta v_0^2∥}_{H_{\alpha }^1(\mathrm{\Omega })}^2+{∥\delta v_0∥}_{L^2(\mathrm{\Omega })}^2\right).}\hfill \end{array}\end{array}$$(2.82)

Hence, The function $\phi :({\psi }_0,v_0)⟶\psi$ is G-derivable, and we deduce that J is G-derivable on $A_{\mathit{ad}}$. $\square$

Now, we compute the gradient of J using the adjoint state method.

3. Adjoint state method

We define the Gâteaux derivative of $\psi$ at $k=({\psi }_0,v_0)$ in the direction $h=(h_1,h_2)\in L^2(\mathrm{\Omega })$, by(3.1) $$\begin{array}{c}\hfill \widehat{\psi }=\underset{s\to 0}{lim}{\displaystyle \frac{\psi (k+sh)-\psi (k)}{s}},\end{array}$$(3.1) $\psi (k+sh)$ is the solution of (1.4(1.4) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )-\lambda {\partial }_{\mathit{xxt}}\psi =f,\lambda >0,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.4) ) with initial state $k+sh,$ and $\psi (k)$ is the solution of (1.4(1.4) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )-\lambda {\partial }_{\mathit{xxt}}\psi =f,\lambda >0,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.4) ) with initial state k.

We compute the Gâteaux (directional) derivative of (1.4(1.4) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )-\lambda {\partial }_{\mathit{xxt}}\psi =f,\lambda >0,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.4) ) at k in some direction $h\in L^2(\mathrm{\Omega }),$ and we get the so-called tangent linear model(3.2) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_t^2\widehat{\psi }-{\partial }_x(x^{\alpha }{\partial }_x\widehat{\psi })-{\partial }_x(\lambda {\partial }_{\mathit{xt}}\widehat{\psi })=0,\\ \widehat{\psi }(0,t)=\widehat{\psi }(1,t)=0,\forall t\in \left[0;T\right],\\ \widehat{\psi }(x,0)=h_1,\forall x\in \left[0;1\right],\\ {\partial }_t\widehat{\psi }(x,0)=h_2,\forall x\in \left[0;1\right].\end{array}\end{array}$$(3.2)

We introduce the adjoint variable P, and we integrate(3.3) $$\begin{array}{c}\hfill {\int }_0^1{\int }_0^T{\partial }_{\mathit{tt}}\widehat{\psi }P-{\int }_0^1{\int }_0^T{\partial }_x(x^{\alpha }{\partial }_x\widehat{\psi }(x))P-{\int }_0^1{\int }_0^T{\partial }_x(\lambda {\partial }_{\mathit{xt}}\widehat{\psi })P=0.\end{array}$$(3.3)

We have(3.4) $$\begin{array}{c}\hfill {\int }_0^T{\int }_0^1{\partial }_x(\lambda {\partial }_{\mathit{xt}}\widehat{\psi })P={\int }_0^T{\left[\lambda {\partial }_{\mathit{xt}}\widehat{\psi }P\right]}_0^1-{\int }_0^T{\int }_0^1\lambda {\partial }_{\mathit{xt}}\widehat{\psi }{\partial }_{x}P.\end{array}$$(3.4)

We pose $P(x=0)=P(x=1)=0$, then we obtain(3.5) $$\begin{array}{c}\hfill {\int }_0^T{\int }_0^1{\partial }_x(\lambda {\partial }_{\mathit{xt}}\widehat{\psi })P=-{\int }_0^T{\left[\lambda {\partial }_t\widehat{\psi }{\partial }_{x}P\right]}_0^1+{\int }_0^T{\int }_0^1\lambda {\partial }_t\widehat{\psi }{\partial }_x^{2}P.\end{array}$$(3.5)

Since $\widehat{\psi }(0,t)=\widehat{\psi }(1,t)=0$ $\forall t\in ]0,T[$, then ${\partial }_t\widehat{\psi }(0,t)={\partial }_t\widehat{\psi }(1,t)=0$ $\forall t\in ]0,T[$.

From where(3.6) $$\begin{array}{c}\hfill {\int }_0^T{\int }_0^1{\partial }_x(\lambda {\partial }_{\mathit{xt}}\widehat{\psi })P={\int }_0^1{\left[\lambda \widehat{\psi }{\partial }_x^{2}P\right]}_0^T-{\int }_0^T{\int }_0^1\lambda \widehat{\psi }{\partial }_x{\partial }_{\mathit{xt}}P.\end{array}$$(3.6)

Since $\forall x\in \mathrm{\Omega }$ $P(x,t=T)=0$, then ${\partial }_{x}P(x,T)=0$ and ${\partial }_x^{2}P(x,T)=0$. In addition, we have $\widehat{\psi }(x,0)=h_1$ $\forall x\in \mathrm{\Omega }$. which gives(3.7) $$\begin{array}{c}\hfill {\int }_0^T{\int }_0^1{\partial }_x(\lambda {\partial }_{\mathit{xt}}\widehat{\psi })P=-{\int }_0^1\lambda h_1{\partial }_x^{2}P(t=0)-{\int }_0^T{\int }_0^1\lambda \widehat{\psi }{\partial }_x{\partial }_{\mathit{xt}}P.\end{array}$$(3.7)

Based on the calculations done in the previous paragraph, we have(3.8) $$\begin{array}{c}\hfill {\int }_0^1{\int }_0^T{\partial }_{\mathit{tt}}\widehat{\psi }P-{\int }_0^1{\int }_0^T{\partial }_x(x^{\alpha }{\partial }_x\widehat{\psi }(x))P={〈h_1,-{\partial }_{t}P(t=0)〉}_{L^2(\mathrm{\Omega })}+{〈h_2,P(0)〉}_{L^2(\mathrm{\Omega })}.\end{array}$$(3.8)

This gives(3.9) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\int }_0^T{〈{\partial }_{\mathit{tt}}P-{\partial }_x(x^{\alpha }{\partial }_{x}P)+\lambda {\partial }_x{\partial }_{\mathit{xt}}P,\widehat{\psi }〉}_{L^2(\mathrm{\Omega })}={〈h_1,-{\partial }_{t}P(t=0)-\lambda {\partial }_x^{2}P(t=0)〉}_{L^2(\mathrm{\Omega })}}\\ +{〈h_2,P(0)〉}_{L^2(\mathrm{\Omega })}\\ P(x=0)=P(x=1)=0\text{,}P(T)=0,{\partial }_{t}P(T)=0.\end{array}\end{array}$$(3.9)

The discretization in time of (3.9(3.9) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\int }_0^T{〈{\partial }_{\mathit{tt}}P-{\partial }_x(x^{\alpha }{\partial }_{x}P)+\lambda {\partial }_x{\partial }_{\mathit{xt}}P,\widehat{\psi }〉}_{L^2(\mathrm{\Omega })}={〈h_1,-{\partial }_{t}P(t=0)-\lambda {\partial }_x^{2}P(t=0)〉}_{L^2(\mathrm{\Omega })}}\\ +{〈h_2,P(0)〉}_{L^2(\mathrm{\Omega })}\\ P(x=0)=P(x=1)=0\text{,}P(T)=0,{\partial }_{t}P(T)=0.\end{array}\end{array}$$(3.9) ), using the Rectangular integration method, gives(3.10) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\sum }_{j=0}^{M+1}{〈\widehat{\psi }(t_j),{\partial }_{\mathit{tt}}P(t_j)-{\partial }_x(x^{\alpha }{\partial }_{x}P(t_j))+\lambda {\partial }_x{\partial }_{\mathit{xt}}P(t_j)〉}_{L^2(\mathrm{\Omega })}\mathrm{\Delta }t}\\ ={〈h_1,-{\partial }_{t}P(t=0)-\lambda {\partial }_x^{2}P(t=0)〉}_{L^2(\mathrm{\Omega })}+{〈h_2,P(0)〉}_{L^2(\mathrm{\Omega })},\\ P(x=0)=P(x=1)=0\text{,}P(T)=0,{\partial }_{t}P(T)=0.\end{array}\end{array}$$(3.10)

We pose $\overline{u}=(\overline{{\psi }_0},\overline{v_0})$, the Gâteaux derivative of the cost function$$\begin{array}{c}\hfill {\displaystyle J({\psi }_0,v_0)={\displaystyle \frac{\epsilon }{2}}\left({∥({\psi }_0-\overline{{\psi }_0}∥}_{L^2(\mathrm{\Omega })}^2+{∥v_0-\overline{v_0})∥}_{L^2(\mathrm{\Omega })}^2\right)+{\displaystyle \frac{1}{2}}\sum _{j\in I}{∥\psi (t_j)-{\psi }^{\mathit{obs}}(t_j)∥}_{L^2(\mathrm{\Omega })}^2}\end{array}$$

at $k=({\psi }_0,v_0)$ in the direction $h=(h_1,h_2)\in L^2(\mathrm{\Omega })$ is given by$$\begin{array}{c}\hfill {\displaystyle \widehat{J}(h)=\underset{s\to 0}{lim}{\displaystyle \frac{J(k+sh)-J(k)}{s}}.}\end{array}$$

After some compute, we arrive at(3.11) $$\begin{array}{c}\hfill \widehat{J}(h)={〈\epsilon \left({\psi }_0-\overline{{\psi }_0}\right),h_1〉}_{L^2(\mathrm{\Omega })}+{〈\epsilon \left(v_0-\overline{v_0}\right),h_2〉}_{L^2(\mathrm{\Omega })}+\sum _{j\in I}{〈\psi (t_j)-{\psi }^{\mathit{obs}}(t_j),\widehat{\psi }〉}_{L^2(\mathrm{\Omega })}\mathrm{d}t.\end{array}$$(3.11)

The adjoint problem is(3.12) $$\begin{array}{c}\hfill \begin{array}{c}\begin{array}{c}{\displaystyle {\partial }_{\mathit{tt}}P(t_j)-{\partial }_x(x^{\alpha }{\partial }_{x}P(t_j))+{\partial }_x(\lambda {\partial }_{\mathit{xt}}P(t_j))=\frac{1}{\mathrm{\Delta }t}(\psi (t_j)-{\psi }^{\mathit{obs}}(t_j)),\forall j\in I,}\\ {\displaystyle {\partial }_{\mathit{tt}}P(t_j)-{\partial }_x(x^{\alpha }{\partial }_{x}P(t_j))+{\partial }_x(\lambda {\partial }_{\mathit{xt}}P(t_j))=0,\forall j\notin I,}\end{array}\\ P(x=0)=P(x=1)=0,\\ P(T)=0,{\partial }_{t}P(T)=0.\end{array}\end{array}$$(3.12)

The problem (3.12(3.12) $$\begin{array}{c}\hfill \begin{array}{c}\begin{array}{c}{\displaystyle {\partial }_{\mathit{tt}}P(t_j)-{\partial }_x(x^{\alpha }{\partial }_{x}P(t_j))+{\partial }_x(\lambda {\partial }_{\mathit{xt}}P(t_j))=\frac{1}{\mathrm{\Delta }t}(\psi (t_j)-{\psi }^{\mathit{obs}}(t_j)),\forall j\in I,}\\ {\displaystyle {\partial }_{\mathit{tt}}P(t_j)-{\partial }_x(x^{\alpha }{\partial }_{x}P(t_j))+{\partial }_x(\lambda {\partial }_{\mathit{xt}}P(t_j))=0,\forall j\notin I,}\end{array}\\ P(x=0)=P(x=1)=0,\\ P(T)=0,{\partial }_{t}P(T)=0.\end{array}\end{array}$$(3.12) ) is retrograde, we make the change of variable $t⟷T-t$, the gradient of J becomes(3.13) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle \frac{\partial J}{\partial {\psi }_0}}={\partial }_{t}P(T)+\epsilon \left({\psi }_0-\overline{{\psi }_0}\right)-\lambda {\partial }_x^{2}P(T),\\ \\ {\displaystyle \frac{\partial J}{\partial v_0}}=P(T)+\epsilon \left(v_0-\overline{v_0}\right).\end{array}\end{array}$$(3.13)

To calculate a gradient of J, we solve two problems: direct problem (1.4(1.4) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )-\lambda {\partial }_{\mathit{xxt}}\psi =f,\lambda >0,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.4) ), and the adjoint problem (3.12(3.12) $$\begin{array}{c}\hfill \begin{array}{c}\begin{array}{c}{\displaystyle {\partial }_{\mathit{tt}}P(t_j)-{\partial }_x(x^{\alpha }{\partial }_{x}P(t_j))+{\partial }_x(\lambda {\partial }_{\mathit{xt}}P(t_j))=\frac{1}{\mathrm{\Delta }t}(\psi (t_j)-{\psi }^{\mathit{obs}}(t_j)),\forall j\in I,}\\ {\displaystyle {\partial }_{\mathit{tt}}P(t_j)-{\partial }_x(x^{\alpha }{\partial }_{x}P(t_j))+{\partial }_x(\lambda {\partial }_{\mathit{xt}}P(t_j))=0,\forall j\notin I,}\end{array}\\ P(x=0)=P(x=1)=0,\\ P(T)=0,{\partial }_{t}P(T)=0.\end{array}\end{array}$$(3.12) ) with the change of variable $t⟷T-t$.

4. Discretization of problem

Step 1. Full discretization

Discrete approximations of these problems need to be made for numerical implementation. To resolve the direct problem and the adjoint problem, we use the Method $\theta$-schema in time. This method is unconditionally stable for $1>\theta \ge {\displaystyle \frac{1}{2}}.$

Let h the step in space and $\mathrm{\Delta }t$ the step in time.

Let $x_i=ih$ with $i\in \left\{0,1,2\dots N+1\right\},$

$t_j=j\mathrm{\Delta }t$ with $j\in \left\{0,1,2\dots M+1\right\},$

$f_i^j=f(x_i,t_j).$

Let ${\psi }_i^j=\psi (x_i,t_j)$, $a(x)=x^{\alpha }$, $b(x_i)=a(x_i)$ and(4.1) $$\begin{array}{c}\hfill \varphi (x_i,t_j)={\varphi }_i^j=b(x_i){\displaystyle \frac{\partial }{\partial x}}\psi (x_i,t_j).\end{array}$$(4.1)

We have(4.2) $$\begin{array}{c}\hfill {\displaystyle \frac{{\partial }^2\psi }{\partial t^2}}(x_i,t_j)\simeq {\displaystyle \frac{{\psi }_i^{j+1}-2{\psi }_i^j+{\psi }_i^{j-1}}{\mathrm{\Delta }{t}^2}}\end{array}$$(4.2) (4.3) $$\begin{array}{c}\hfill {\displaystyle \frac{\partial }{\partial x}}(b{\displaystyle \frac{\partial }{\partial x}}{\psi }^j)(x_i)\simeq {\displaystyle \frac{\left(1-\theta \right)}{h}}({\varphi }_{i+1}^j-{\varphi }_i^j)+{\displaystyle \frac{\theta }{2h}}({\varphi }_{i+1}^{j+1}-{\varphi }_i^{j+1})+{\displaystyle \frac{\theta }{2h}}({\varphi }_{i+1}^{j-1}-{\varphi }_i^{j-1})\end{array}$$(4.3)

with back affine approximation of $\psi$ in $x_i$ we get(4.4) $$\begin{array}{c}\hfill \psi (x_i-h,t_j)\simeq \psi (x_i,t_j)-h{\displaystyle \frac{\partial }{\partial x}}\psi (x_i,t_j)\end{array}$$(4.4) (4.5) $$\begin{array}{c}\hfill {\displaystyle \frac{\partial }{\partial x}}\psi (x_i,t_j)\simeq {\displaystyle \frac{\psi (x_i,t_j)-\psi (x_{i-1},t_j)}{h}},\end{array}$$(4.5)

this gives(4.6) $$\begin{array}{c}\hfill {\displaystyle \frac{\partial {\psi }^j}{\partial x}}(x_i)\simeq {\displaystyle \frac{1}{h}}({\psi }_i^j-{\psi }_{i-1}^j),\end{array}$$(4.6)

the same, with back affine approximation of $\psi$ in $x_{i+1}$ we get(4.7) $$\begin{array}{c}\hfill {\displaystyle \frac{\partial {\psi }^j}{\partial x}}(x_{i+1})\simeq {\displaystyle \frac{1}{h}}({\psi }_{i+1}^j-{\psi }_i^j).\end{array}$$(4.7)

From where(4.8) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle \frac{1}{h}}({\varphi }_{i+1}^j-{\varphi }_i^j)\simeq {\displaystyle \frac{b(x_{i+1})}{h}}\left[{\displaystyle \frac{1}{h}}({\psi }_{i+1}^j-{\psi }_i^j)\right]-{\displaystyle \frac{b(x_i)}{h}}\left[{\displaystyle \frac{1}{h}}({\psi }_i^j-{\psi }_{i-1}^j)\right]\hfill \\ \hfill \\ \simeq {\displaystyle \frac{b(x_{i+1})}{h}}\left[{\displaystyle \frac{1}{h}}({\psi }_{i+1}^j-{\psi }_i^j)\right]+{\displaystyle \frac{b(x_i)}{h}}\left[{\displaystyle \frac{1}{h}}({\psi }_{i+1}^j-{\psi }_i^j)\right]\hfill \\ \hfill \\ \hfill \\ -{\displaystyle \frac{b(x_i)}{h}}\left[{\displaystyle \frac{1}{h}}({\psi }_{i+1}^j-{\psi }_i^j)\right]-{\displaystyle \frac{b(x_i)}{h}}\left[{\displaystyle \frac{1}{h}}({\psi }_i^j-{\psi }_{i-1}^j)\right]\hfill \end{array}\end{array}$$(4.8) (4.9) $$\begin{array}{c}\hfill {\displaystyle \frac{1}{h}}({\varphi }_{i+1}^j-{\varphi }_i^j)\simeq {\displaystyle \frac{b(x_{i+1})-b(x_i)}{h}}\left[{\displaystyle \frac{1}{h}}({\psi }_{i+1}^j-{\psi }_i^j)\right]+b(x_i){\displaystyle \frac{{\psi }_{i+1}^j-2{\psi }_i^j+{\psi }_{i-1}^j}{h^2}}.\end{array}$$(4.9)

Let(4.10) $$\begin{array}{c}\hfill da(x_i)={\displaystyle \frac{b(x_{i+1})-b(x_i)}{h}},\end{array}$$(4.10)

and We have$$\begin{array}{c}\hfill \lambda {\partial }_t{\partial }_{\mathit{xx}}\psi \simeq \frac{\lambda }{\mathrm{\Delta }t{h}^2}\left[{\psi }_{i+1}^{j+1}-2{\psi }_i^{j+1}+{\psi }_{i-1}^{j+1}-\left({\psi }_{i+1}^j-2{\psi }_i^j+{\psi }_{i-1}^j\right)\right].\end{array}$$

Hence, ${\partial }_{\mathit{tt}}\psi -A\psi =f$ is approximated by(4.11) $$\begin{array}{c}\hfill \begin{array}{c}{g}_1(x_i){\psi }_{i-1}^{j+1}+g_2(x_i){\psi }_i^{j+1}+g_3(x_i){\psi }_{i+1}^{j+1}\\ \\ =k_1(x_i){\psi }_{i-1}^j+k_2(x_i){\psi }_i^j+k_3(x_i){\psi }_{i+1}^j+h_1(x_i){\psi }_{i-1}^{j-1}\\ \\ +h_2(x_i){\psi }_i^{j-1}+h_3(x_i){\psi }_{i+1}^{j-1}+\mathrm{\Delta }{t}^2[\left(1-\theta \right)f_i^j+{\displaystyle \frac{\theta }{2}}(f_i^{j+1}+f_i^{j-1})]\end{array}\end{array}$$(4.11)

where(4.12) $$\begin{array}{c}\hfill g_1(x_i)=-{\displaystyle \frac{\theta \mathrm{\Delta }{t}^2}{2h^2}}b(x_i)-\frac{\lambda }{\mathrm{\Delta }t{h}^2}\end{array}$$(4.12) (4.13) $$\begin{array}{c}\hfill g_2(x)=1+{\displaystyle \frac{\theta \mathrm{\Delta }{t}^2}{h^2}}b(x_i)+da(x_i){\displaystyle \frac{\theta \mathrm{\Delta }{t}^2}{2h}}+2\frac{\lambda }{\mathrm{\Delta }t{h}^2},\end{array}$$(4.13) (4.14) $$\begin{array}{c}\hfill g_3(x)=-\left({\displaystyle \frac{\theta \mathrm{\Delta }{t}^2}{2h^2}}b(x_i)+da(x_i){\displaystyle \frac{\theta \mathrm{\Delta }{t}^2}{2h}}\right)-\frac{\lambda }{\mathrm{\Delta }t{h}^2},\end{array}$$(4.14) (4.15) $$\begin{array}{c}\hfill k_1(x_i)={\displaystyle \frac{\left(1-\theta \right)\mathrm{\Delta }{t}^2}{h^2}}b(x_i)-\frac{\lambda }{\mathrm{\Delta }t{h}^2},\end{array}$$(4.15) (4.16) $$\begin{array}{c}\hfill k_2(x_i)=2-{\displaystyle \frac{\left(1-\theta \right)\mathrm{\Delta }{t}^2}{h}}da(x_i)-{\displaystyle \frac{2\left(1-\theta \right)\mathrm{\Delta }{t}^2}{h^2}}b(x_i)+2\frac{\lambda }{\mathrm{\Delta }t{h}^2},\end{array}$$(4.16) (4.17) $$\begin{array}{c}\hfill k_3(x_i)={\displaystyle \frac{\left(1-\theta \right)\mathrm{\Delta }{t}^2}{h}}da(x_i)+{\displaystyle \frac{\left(1-\theta \right)\mathrm{\Delta }{t}^2}{h^2}}b(x_i)-\frac{\lambda }{\mathrm{\Delta }t{h}^2},\end{array}$$(4.17) (4.18) $$\begin{array}{c}\hfill h_1(x_i)={\displaystyle \frac{\theta \mathrm{\Delta }{t}^2}{2h^2}}b(x_i),\end{array}$$(4.18) (4.19) $$\begin{array}{c}\hfill h_2(x)=-\left(1+{\displaystyle \frac{\theta \mathrm{\Delta }{t}^2}{h^2}}b(x_i)+da(x_i){\displaystyle \frac{\theta \mathrm{\Delta }{t}^2}{2h}}\right),\end{array}$$(4.19) (4.20) $$\begin{array}{c}\hfill h_3(x)={\displaystyle \frac{\theta \mathrm{\Delta }{t}^2}{2h^2}}b(x_i)+da(x_i){\displaystyle \frac{\theta \mathrm{\Delta }{t}^2}{2h}}.\end{array}$$(4.20)

We have(4.21) $$\begin{array}{c}\hfill \begin{array}{c}{g}_1(x_i){\psi }_{i-1}^{j+1}+g_2(x_i){\psi }_i^{j+1}+g_3(x_i){\psi }_{i+1}^{j+1}\\ \\ =k_1(x_i){\psi }_{i-1}^j+k_2(x_i){\psi }_i^j+k_3(x_i){\psi }_{i+1}^j+h_1(x_i){\psi }_{i-1}^{j-1}\\ \\ +h_2(x_i){\psi }_i^{j-1}+h_3(x_i){\psi }_{i+1}^{j-1}+\mathrm{\Delta }{t}^2[\left(1-\theta \right)f_i^j+{\displaystyle \frac{\theta }{2}}(f_i^{j+1}+f_i^{j-1})],\end{array}\end{array}$$(4.21)

with ${\psi }^j={\left({\psi }_i^j\right)}_{i\in \left\{1,2,..N\right\}}$ we have(4.22) $$\begin{array}{c}\hfill \begin{array}{c}K{\psi }^{j+1}=B{\psi }^j+C{\psi }^{j-1}+V^j\text{avec}j\in \left\{1,2,..M\right\}\\ {\psi }^0={\left({\psi }_0(ih)\right)}_{i\in \left\{1,2,..N\right\}}\\ {\psi }^1={\left({\psi }_1(ih)\right)}_{i\in \left\{1,2,..N\right\}}.\end{array}\end{array}$$(4.22)

where(4.23) $$\begin{array}{c}\hfill {\psi }_1(ih)\simeq {\psi }_0(ih)+\mathrm{\Delta }t{v}_0+{\displaystyle \frac{\mathrm{\Delta }{t}^2}{2}}{\partial }_{\mathit{tt}}\psi (ih,t=0)\end{array}$$(4.23) (4.24) $$\begin{array}{cc}\hfill {\psi }_1(ih)\simeq & {\psi }_0(ih)+\mathrm{\Delta }t{v}_0(ih)+{\displaystyle \frac{\mathrm{\Delta }{t}^2}{2}}\left[\left({\partial }_x\left((a+\gamma ){\partial }_x\psi \right)\right)(ih,t=0)+f(ih,t=0)\right]\hfill \\ \hfill & +\lambda \frac{\mathrm{\Delta }{t}^2}{2}{\partial }_t\mathrm{\Delta }\psi (ih,t=0).\hfill \end{array}$$(4.24)

We have $\mathrm{\Delta }({\partial }_t\psi )(ih,t=0)=\mathrm{\Delta }{v}_0(ih)$, from where$$\begin{array}{c}\hfill \begin{array}{c}{\psi }_1(ih)\simeq {\psi }_0(ih)+\mathrm{\Delta }t{v}_0(ih)+{\displaystyle \frac{\mathrm{\Delta }{t}^2}{2}}\left[\left({\partial }_x\left((a){\partial }_x\psi \right)\right)(ih,t=0)+f(ih,t=0)\right]\\ \\ {\displaystyle +\frac{\lambda \mathrm{\Delta }{t}^2\left[v_0((i+1)h)-2v_0(ih)+v_0((i-1)h)\right]}{2h^2},}\end{array}\end{array}$$

and$$\begin{array}{c}\hfill K=\left[\begin{array}{cccccc}{g}_2(x_1)& g_3(x_1)& 0& & & 0\\ g_1(x_2)& g_2(x_2)& g_3(x_2)& 0& & \\ 0& g_1(x_3)& g_2(x_3)& g_3(x_3)& 0& & \\ & 0& g_1(x_4)& g_2(x_4)& g_3(x_4)& 0& \\ & 0& .& .& .& 0& \\ & & .& .& .& .& 0\\ & & 0& g_1(x_{N-1})& g_2(x_{N-1})& g_3(x_{N-1})\\ 0& & & 0& g_1(x_N)& g_2(x_N)\end{array}\right]\end{array}$$ $$\begin{array}{c}\hfill B=\left[\begin{array}{cccccc}{k}_2(x_1)& k_3(x_1)& 0& & & 0\\ k_1(x_2)& k_2(x_2)& k_3(x_2)& 0& & \\ 0& k_1(x_3)& k_2(x_3)& k_3(x_3)& 0& & \\ & 0& k_1(x_4)& k_2(x_4)& k_3(x_4)& 0& \\ & 0& .& .& .& 0& \\ & & .& .& .& .& 0\\ & & 0& k_1(x_{N-1})& k_2(x_{N-1})& k_3(x_{N-1})\\ 0& & & 0& k_1(x_N)& k_2(x_N)\end{array}\right]\end{array}$$ $$\begin{array}{c}\hfill C=\left[\begin{array}{cccccc}{h}_2(x_1)& h_3(x_1)& 0& & & 0\\ h_1(x_2)& h_2(x_2)& h_3(x_2)& 0& & \\ 0& h_1(x_3)& h_2(x_3)& h_3(x_3)& 0& & \\ & 0& h_1(x_4)& h_2(x_4)& h_3(x_4)& 0& \\ & 0& .& .& .& 0& \\ & & .& .& .& .& 0\\ & & 0& h_1(x_{N-1})& h_2(x_{N-1})& h_3(x_{N-1})\\ 0& & & 0& h_1(x_N)& h_2(x_N)\end{array}\right]\end{array}$$ $$\begin{array}{c}\hfill V^j=\left[\begin{array}{c}\mathrm{\Delta }{t}^2[\left(1-\theta \right)f_1^j+{\displaystyle \frac{\theta }{2}}(f_1^{j+1}+f_1^{j-1})]\\ \mathrm{\Delta }{t}^2[\left(1-\theta \right)f_2^j+{\displaystyle \frac{\theta }{2}}(f_2^{j+1}+f_2^{j-1})]\\ .\\ .\\ .\\ .\\ \mathrm{\Delta }{t}^2[\left(1-\theta \right)f_{N-1}^j+{\displaystyle \frac{\theta }{2}}(f_{N-1}^{j+1}+f_{N-1}^{j-1})]\\ \mathrm{\Delta }{t}^2[\left(1-\theta \right)f_N^j+{\displaystyle \frac{\theta }{2}}(f_N^{j+1}+f_N^{j-1})]\\ \end{array}\right]\end{array}$$ Step 2. Discretization of the functional(4.25) $$\begin{array}{c}\hfill {\displaystyle J(u)={\displaystyle \frac{\epsilon }{2}}\left({\int }_0^1{({\psi }_0-\overline{{\psi }_0})}^2\mathrm{d}x+{\int }_0^1{(v_0-\overline{v_0})}^2\mathrm{d}x\right)+{\displaystyle \frac{1}{2}}\sum _{j\in I}{∥\psi (t_j)-{\psi }^{\mathit{obs}}(t_j)∥}_{L^2(\mathrm{\Omega })}^2.}\end{array}$$(4.25)

We recall that the method of Thomas Simpson to calculate an integral is$$\begin{array}{c}\hfill {\displaystyle {\int }_a^{b}f(x)\mathrm{d}x\simeq \frac{h}{2}\left[f(x_0)+2\sum _{i=1}^{\frac{N+1}{2}-1}f(x_{2i})+4\sum _{i=1}^{\frac{N+1}{2}}f(x_{2i+1})+f(x_{N+1})\right],}\end{array}$$

with $x_0=a$, $x_{N+1}=b$, $x_i=a+ih$, $i\in \left\{1..N+1\right\}$.

Let the functions(4.26) $$\begin{array}{c}\hfill W(x)={({\psi }_0-\overline{{\psi }_0})}^2(x)\forall x\in \mathrm{\Omega },\end{array}$$(4.26) (4.27) $$\begin{array}{c}\hfill S(x)={(v_0-\overline{v_0})}^2(x)\forall x\in \mathrm{\Omega },\end{array}$$(4.27)

and(4.28) $$\begin{array}{c}\hfill \phi (x,t)={(\psi -{\psi }^{\mathit{obs}})}^2(x,t)\forall t\in I,x\in \mathrm{\Omega }.\end{array}$$(4.28)

We have$$\begin{array}{c}\hfill {\displaystyle {\int }_0^{1}W(x)\mathrm{d}x\simeq \frac{h}{2}\left[W(0)+2\sum _{i=1}^{\frac{N+1}{2}-1}W(x_{2i})+4\sum _{i=1}^{\frac{N+1}{2}}W(x_{2i+1})+W(1)\right],}\end{array}$$

and$$\begin{array}{c}\hfill {\displaystyle {\int }_0^{1}S(x)\mathrm{d}x\simeq \frac{h}{2}\left[S(0)+2\sum _{i=1}^{\frac{N+1}{2}-1}S(x_{2i})+4\sum _{i=1}^{\frac{N+1}{2}}S(x_{2i+1})+S(1)\right].}\end{array}$$

Let$$\begin{array}{c}\hfill {\displaystyle \varnothing (t)={\int }_0^1\phi (x,t)\mathrm{d}x.}\end{array}$$

This gives$$\begin{array}{c}\hfill {\displaystyle \varnothing (t)\simeq \frac{h}{2}\left[\phi (0,t)+2\sum _{i=1}^{\frac{N+1}{2}-1}\phi (x_{2i},t)+4\sum _{i=1}^{\frac{N+1}{2}}\phi (x_{2i+1},t)+\phi (1,t)\right].}\end{array}$$

From where$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle {\displaystyle \frac{1}{2}}{\sum }_{j\in I}{∥\psi (t_j)-{\psi }^{\mathit{obs}}(t_j)∥}_{L^2(\mathrm{\Omega })}^2\simeq {\displaystyle \frac{1}{2}}{\sum }_{j\in I}\varnothing (t_j).}\hfill \end{array}\end{array}$$

Therefore(4.29) $$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle J(u)\simeq \frac{\epsilon h}{4}\left[W(0)+2{\sum }_{i=1}^{\frac{N+1}{2}-1}W(x_{2i})+4{\sum }_{i=1}^{\frac{N+1}{2}}W(x_{2i+1})+W(1)\right]}\hfill \\ \hfill \\ {\displaystyle +\frac{\epsilon h}{4}\left[S(0)+2{\sum }_{i=1}^{\frac{N+1}{2}-1}S(x_{2i})+4{\sum }_{i=1}^{\frac{N+1}{2}}S(x_{2i+1})+S(1)\right]}\hfill \\ \hfill \\ {\displaystyle +{\displaystyle \frac{1}{2}}{\sum }_{t_j\in I}\varnothing (t_j).}\hfill \end{array}\end{array}$$(4.29)

The main steps for descent method at each iteration are:

• Calculate ${\psi }^k$ solution of (1.4(1.4) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )-\lambda {\partial }_{\mathit{xxt}}\psi =f,\lambda >0,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.4) ) with initial condition $({\psi }_0,v_0)$,

• Calculate $P^k$ solution of adjoint problem,

• Calculate the descent direction $d_k=-\mathrm{\nabla }j({\psi }_0,v_0)$,

• Find ${\displaystyle t_k=\underset{t>0}{\mathit{argmin}}}$ $j(({\psi }_0,v_0)+t{d}_k)$,

• Update the variable $({\psi }_0,v_0)=({\psi }_0,v_0)+t_k{d}_k$.

The algorithm ends when ${\displaystyle \mid j({\psi }_0,v_0)\mid <\mu }$, where $\mu$ is a given precision.

The value $t_k$ is chosen by the inaccurate linear search by Rule Armijo-Goldstein as following:

• let ${\alpha }_i,\beta \in [0,1[$ and $\alpha >0$ (for example $\alpha ={\displaystyle \frac{1}{2}}$ and $\beta =0.9$)

• if $j({({\psi }_0,v_0)}^k+{\alpha }_i{d}_k)⩽j({({\psi }_0,v_0)}^k)+\beta {\alpha }_i{d}_k^T{d}_k$

• $t_k={\alpha }_i$ and stop

• if not, ${\alpha }_i=\alpha {\alpha }_i$.

5. Numerical experiments

In this section, we do three tests:

In the first test, we show numerically that : when $\lambda ⟶0$, the sequence ${({\psi }_{\lambda })}_{\lambda >0}$ of weak solutions of the problem (1.4(1.4) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )-\lambda {\partial }_{\mathit{xxt}}\psi =f,\lambda >0,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.4) ) converges to the weak solution of the problem (1.1(1.1) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )=f,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.1) ). And we make a comparison between the proposed method and method based only on regularization Tikhonov.

In the second test, we study the impact of the percent of final knowledge (${\psi }^{\mathit{obs}}$) on the construction of the initial state.

In the third test, we study the noise resistance of the proposed method.

Remark: It is known in the literature that $\epsilon$ is very difficult to determine([20,21]). In order to choose $\epsilon$, we make each test for different values of $\epsilon$, and we choose the value of $\epsilon$ which gives the best result.

We did all the tests on Pc with the following configurations: Intel Core i3 CPU 2.27GHz; $RAM=4GB(2.93\text{usable}).$ We take step in space ${\displaystyle h=\frac{1}{60}}$ and step in time ${\displaystyle \mathrm{\Delta }t=\frac{1}{60}}$.

5.1. Convergence of the sequence ${({\psi }_{\lambda })}_{\lambda >0}$, when $\lambda ⟶0$

$$\begin{array}{c}\hfill {\displaystyle Let{\psi }_0^{\mathit{exact}}=\frac{x(1-x)}{T}and{v}_0^{\mathit{exact}}=-\frac{x(1-x)}{T^2},}\end{array}$$ $({\psi }_0^{\mathit{exact}},v_0^{\mathit{exact}})$ the true state, and is the state to estimate.

In figures below, the true initial state is drawn red, and rebuilt initial state of the problem (1.4(1.4) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )-\lambda {\partial }_{\mathit{xxt}}\psi =f,\lambda >0,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.4) ) in blue.

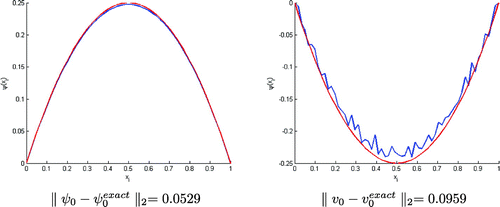
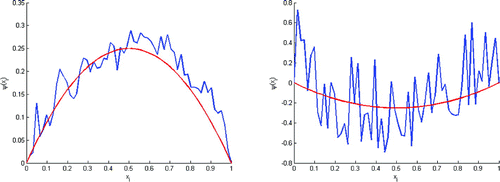
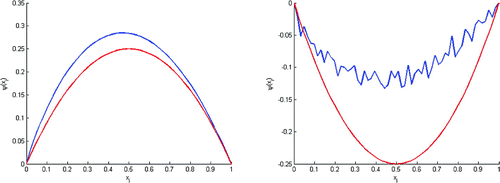
Figure 1. Test with $\lambda ={10}^{-2}$. The value of $\lambda$ is not enough small, this figure shows that we can’t rebuild the solution.

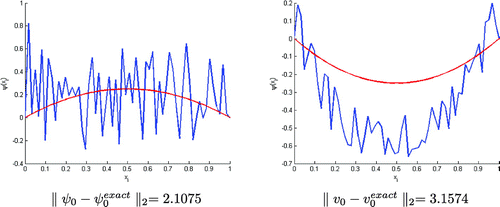
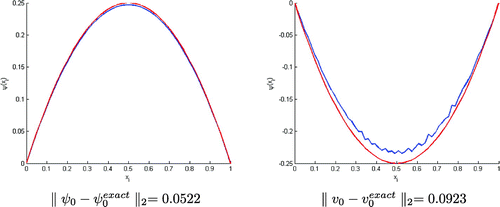
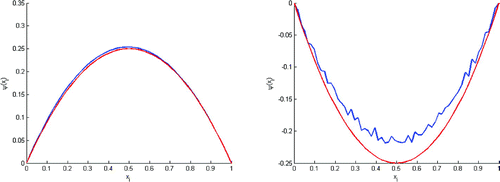
Figure 2. Test with $\lambda ={10}^{-4}$. The value of $\lambda$ is not enough small, we can’t rebuild the true state. But the reconstructed initial condition starts to get near to the true state..

Figure 3. Test with $\lambda ={10}^{-6}$. The reconstructed initial condition is near to the true state.

Figure 4. Test with $\lambda ={10}^{-8}$. This figure shows that we can rebuild the solution.

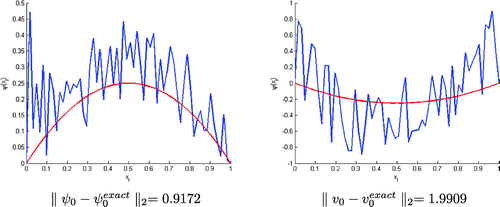
Table 1. Minimum value of J as function of $\lambda$. To get a better value of J, we must choose the value of $\lambda$ small enough.

Value of $\lambda$	Minimum value of J	execution time
${10}^{-04}$	$1.171651.{10}^{-01}$	2 min
${10}^{-06}$	$8.791377.{10}^{-05}$	16 h
${10}^{-08}$	$8.784509.{10}^{-05}$	30 h

Table 1 shows the values of J obtained for different lambda value’s. These tests show numerically that when $\lambda ⟶0$, the sequence ${({\psi }_{\lambda })}_{\lambda >0}$ of weak solutions of the problem (1.4(1.4) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )-\lambda {\partial }_{\mathit{xxt}}\psi =f,\lambda >0,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.4) ) converges to the weak solution of the problem (1.1(1.1) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )=f,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.1) ) (Figures 1–4). The rebuilt initial state begins to approach the true initial state as soon as $\lambda$ be lower than ${10}^{-6}$ (Figures 3 and 4).

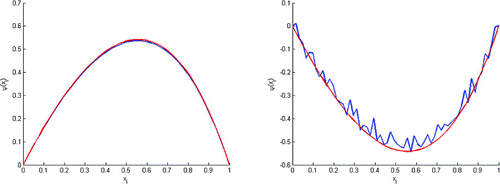
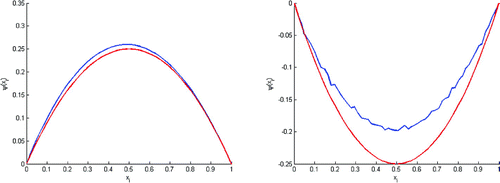
To validate this result, we did another test with $\lambda ={10}^{-6}$, to construct the initial state $({\psi }_0^{\mathit{exact}},v_0^{\mathit{exact}})$ with ${\displaystyle {\psi }_0^{\mathit{exact}}=x(e-e^x)}$ and ${\displaystyle v_0^{\mathit{exact}}=e-e^x-x{e}^x}$, we obtain the result follows

Figure 5. This figure shows that we can rebuild ${\psi }_0$ (left) and $v_0$ (right).

This test (Figure 5) shows that we can rebuild the initial state $({\psi }_0^{\mathit{exact}},v_0^{\mathit{exact}})$ with $\lambda ={10}^{-6}$. As the first test, we found that we can rebuild the initial state with $\lambda ⩽{10}^{-6}$. And when $\lambda ⟶0$, the sequence ${({\psi }_{\lambda })}_{\lambda >0}$ of weak solutions of the problem (1.4(1.4) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )-\lambda {\partial }_{\mathit{xxt}}\psi =f,\lambda >0,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.4) ) converges to the weak solution of the problem (1.1(1.1) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )=f,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.1) ).

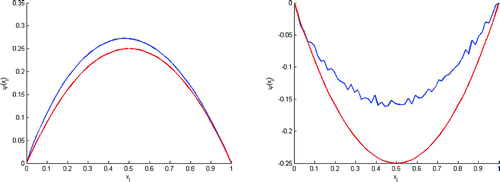
In order to compare the proposed method based in double regularization with the Tikonov’s method, we did another test based only on tikhonov’s regularization, to reconstruct the initial state $({\psi }_0^{\mathit{exact}},v_0^{\mathit{exact}})$, with ${\displaystyle {\psi }_0^{\mathit{exact}}=\frac{x(1-x)}{T}and{v}_0^{\mathit{exact}}=-\frac{x(1-x)}{T^2}.}$ The algorithm has found the solution with the minimum value of J equal to $8.78.{10}^{-05}$ in 72 h 54 min. Compared with the results in Table 1, we have a $50\%$ of time gain with the double regularization method. This shows the effectiveness of this method to reduce the execution time to find the initial condition of the problem (1.1(1.1) $$\begin{array}{c}\hfill \begin{array}{c}{\partial }_{\mathit{tt}}\psi -{\partial }_x(x^{\alpha }{\partial }_x\psi )=f,(x,t)\in \mathrm{\Omega }\times ]0,T[,\\ \psi (0,t)=\psi (1,t)=0,\forall t\in ]0,T[,\\ {\partial }_t\psi (x,0)=v_0(x),\forall x\in \mathrm{\Omega },\\ \psi (x,0)={\psi }_0(x),\forall x\in \mathrm{\Omega }.\end{array}\end{array}$$(1.1) ).

5.2. The impact of the percent of final knowledge ${\psi }^{\mathit{obs}}$ on the construction of the initial state

In these tests, we study the necessary percent of final knowledge of ${\psi }^{\mathit{obs}}$ to estimate the initial state. In all tests we take $\lambda ={10}^{-8}$.

Figure 6. Test with $100\%$ of final knowledge of ${\psi }^{\mathit{obs}}$. This figure shows that we can rebuild ${\psi }_0$ (left) and $v_0$ (right).

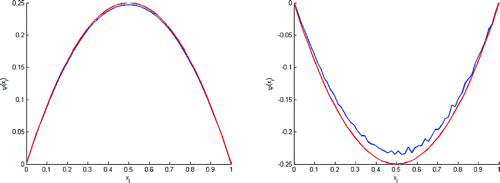
Figure 7. Test with $50\%$ of final knowledge of ${\psi }^{\mathit{obs}}$. This figure shows that we can rebuild ${\psi }_0$ (left) and $v_0$ (right).

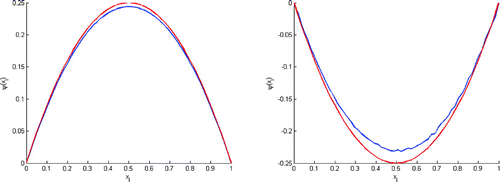
Figure 8. Test with $40\%$ of final knowledge of ${\psi }^{\mathit{obs}}$. This figure shows that we can rebuild ${\psi }_0$ (left) and $v_0$ (right).

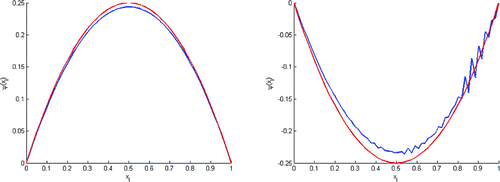
Figure 9. Test with $30\%$ of final knowledge of ${\psi }^{\mathit{obs}}$. This figure shows that we can rebuild ${\psi }_0$ (left), but we can’t rebuild $v_0$ (right).

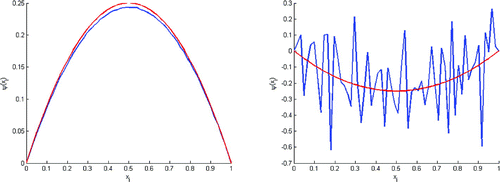
Figure 10. Test with $20\%$ of final knowledge of ${\psi }^{\mathit{obs}}$. This figure shows that we can rebuild ${\psi }_0$ (left), but we can’t rebuild $v_0$ (right).

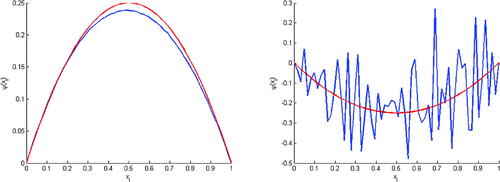
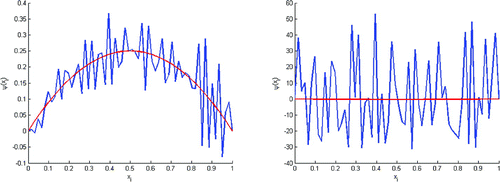
These tests show that we can rebuild ${\psi }_0$ with $20\%$ of final knowledge of ${\psi }^{\mathit{obs}}$ (Figures 6–10), but we lose $v_0$ as soon as the percent of final knowledge be lower than $40\%$ (Figures 9 and 10). Remark, The figure 11 shows that we can’t rebuild the initial state in the case where $\epsilon =0$ (Test without double regulation).

Figure 11. Test without regularization. This figure shows that we can’t rebuild ${\psi }_0$ (left) and $v_0$ (right).

Figure 12. Test with $err=5\%\Vert ({\psi }_0^{\mathit{exact}},v_0^{\mathit{exact}}){\Vert }_2$. This figure shows that we can rebuild ${\psi }_0$ (left), and $v_0$ is nearly $v_0^{\mathit{exact}}$, $\Vert v_0-v_0^{\mathit{exact}}{\Vert }_2=0.1344$ (right).

Figure 13. Test with $err=10\%\Vert ({\psi }_0^{\mathit{exact}},v_0^{\mathit{exact}}){\Vert }_2$. This figure shows that we can rebuild ${\psi }_0$ (left), and $v_0$ begins to move away from $v_0^{\mathit{exact}}$, $\Vert v_0-v_0^{\mathit{exact}}{\Vert }_2=0.1938$ (right).

Figure 14. Test with $err=\Vert ({\psi }_0^{\mathit{exact}},v_0^{\mathit{exact}}){\Vert }_2$. This figure shows that we can’t rebuild ${\psi }_0$ (left), and $v_0$ is far from $v_0^{\mathit{exact}}$ (right).

Figure 15. Test with $er{r}^{\mathit{obs}}=5\%\Vert {\psi }^{\mathit{exact}}{\Vert }_2$ . This figure shows that we can rebuild ${\psi }_0$ (left) and $v_0$ (right).

Figure 16. Test with $er{r}^{\mathit{obs}}=10\%\Vert {\psi }^{\mathit{exact}}{\Vert }_2$ . This figure shows that we can rebuild ${\psi }_0$ (left) and $v_0$ begins to move away from $v_0^{\mathit{exact}}$ (right).

Figure 17. Test with $er{r}^{\mathit{obs}}=20\%\Vert {\psi }^{\mathit{exact}}{\Vert }_2$ . This figure shows that we can rebuild ${\psi }_0$ (left) and $v_0$ is far from $v_0^{\mathit{exact}}$ (right).

Figure 18. Test with $er{r}^{\mathit{obs}}=30\%\Vert {\psi }^{\mathit{exact}}{\Vert }_2$ . This figure shows that ${\psi }_0$ begins to move away from ${\psi }_0^{\mathit{exact}}$ (left) and $v_0$ is far from $v_0^{\mathit{exact}}$ (right).

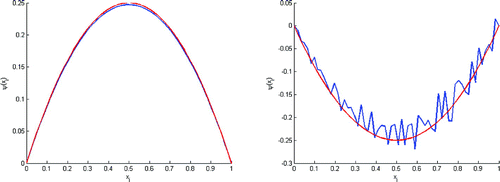
5.3. The noise resistance of the proposed method

The data $\overline{u}=(\overline{{\psi }_0},\overline{v_0})$ and ${\psi }^{\mathit{obs}}$ are assumed to be corrupted by measurement errors, which we will refer to as noise. In particular, we suppose that $\overline{u}=u^{\mathit{exact}}+e$ and ${\psi }^{\mathit{obs}}={\psi }^{\mathit{exact}}+e^{\mathit{obs}}$. Let $err=\Vert e{\Vert }_2$ and $er{r}^{\mathit{obs}}=\Vert e^{\mathit{obs}}{\Vert }_2$. We consider that we have $50\%$ of knowledge in final observation, we take $\lambda ={10}^{-8}$. And we did two tests:

In the first, we suppose $er{r}^{\mathit{obs}}=0$, and we study the impact of err on the construction of the initial state. In the second test, we suppose $err=0$, and we study the impact of $er{r}^{\mathit{obs}}$ on the construction of the initial state.

5.3.1. Impact of err on the construction of the initial state

These tests (Figures 12–14) show that the proposed algorithm is uniformly stable to noise. And we can conclude that the tolerable percentage of err to rebuild the initial state is $err=5\%\Vert ({\psi }_0^{\mathit{exact}},v_0^{\mathit{exact}}){\Vert }_2$.

5.3.2. Impact of $er{r}^{\mathit{obs}}$ on the construction of the initial state

These tests (Figures 15–18) show that the proposed algorithm is uniformly stable to noise. And we can rebuild ${\psi }_0$ with $er{r}^{\mathit{obs}}⩽20\%$ (Figures 15–17), but we lose $v_0$ as soon as $er{r}^{\mathit{obs}}$ be superior than $5\%$ (Figures 16–18).

6. Conclusion

We have presented in this paper a new method based on double regularization applied to the determination of an initial state of hyperbolic degenerated problem from final observations. So, we have obtained a sequence of weak solutions of degenerate linear viscose-elastic problems. Firstly, we have proved the existence and uniqueness of each term of this sequence, and that this sequence converges to the weak solution of the initial problem. Secondly, we have proved that the solution’s behaviour changes continuously with the initial conditions. Also, in the numerical part, we have studied the noise resistance of the proposed method, and we have shown that this method proves effective to reduce the execution time.

Disclosure statement

No potential conflict of interest was reported by the authors.