Reconstruction of impact load on structures with limited measurements using dynamic hybrid adaptive differential search algorithm

Abstract

In this paper, we present an approach for reconstruction of an impact load time history on structures by formulating the associated inverse analysis as a constraint optimization problem by minimizing the error between measured data and predicted data obtained from the forward analysis. The identification process is carried out by solving the formulated constraint optimization problem associated with the inverse analysis of impact load reconstruction. A newly developed hybrid adaptive differential search with dynamic interaction is employed for solving the complex constrained nonlinear multimodal optimization problem. The proposed variant of the differential search technique employs small multiple populations which perform the search independently and exchange the information with the dynamic neighbourhood. The adaptive features and local search ability features are built into the algorithm in order to improve the convergence characteristics of the technique. The constraint optimization formulations can considerably improve the robustness of the inverse problem associated with reconstruction of the impact load. Numerical simulation studies presented to demonstrate the effectiveness of the proposed approach indicate that it can precisely identify the spatial location of the impact load on the structure as well as the impact load time history even in the presence of measurement noise.

KEYWORDS:

• Structural health monitoring
• impact load
• constrained optimization
• dynamic hybrid adaptive differential search algorithm
• principal component analysis
• Nelder-Mead algorithm
• optimal sensor placement

1. Introduction

Engineering structures and particularly civil engineering structures are often subjected to impacts. It is essential to identify the impact load in order to investigate the dynamic characteristics of the structure or to assess the performance of the parametric design. It is also required to identify the impact load on the structure to identify the vulnerable locations of the structure for possible damage and strengthen it accordingly and thus improve the overall integrity of the structure. It is useful to understand the characteristics of the loading profile, such as impact location and it's time history as impact force is the main cause for material fatigue of many structures especially the lightweight structures.

Identification of impact load involves two aspects, i.e. identification of force history as well as identification of the spatial location of force acting on the structure. Most of the identification techniques in the field of impact load identification rely on deconvolution of the dynamic equation of motion and are based on the assumption that the structure is linear. Several approaches based on this inverse formulation have been developed for impact load identification both in time domain [1–11] as well as frequency domain [12–17]. However, direct deconvolution is a well-known ill-conditioned problem and its results are strongly influenced by the quality of the experimental data, accuracy of the mathematical model and robustness of the employed algorithm. Attempts have also been made to use artificial neural networks (ANN) for identification of impact forces [18–20]. However, ANN requires exhaustive collection of impact data sets for training, which may not be feasible for practical use.

However, the most efficient and effective methods reported so far to identify the spatial location of impact and its force history are based on optimization theory. Mathematically speaking, determination of the external loads of a structure based on the sensor signals is a nonlinear inverse optimization problem and also multi-modal especially for complex structures. Several attempts have been made to solve the underlying optimization problem using different classical gradient-based numerical optimization algorithms [21–28]. In these formulations, the efficiency of the optimization algorithms is an important factor for real-time application of the method. For complex structures, the inverse optimization formulation associated impact load identification can typically be a multi-modal problem. The traditional optimization methods use Gradient functions or other additional differential information, which are difficult and time-consuming to calculate or even cannot be obtained depending on the model chosen. Hence, meta-heuristic algorithms are recently being preferred for this class of problems involving impact load identification. However, the performance of these approaches depends rather heavily on the robustness and computation efficiency of the meta-heuristic algorithm employed to use them for real-time problems. GA has so far been popularly used for solving impact load identification problems [20,29] and quite recently particle swarm optimization algorithm (PSO) is used by Ahmari and Yang [30]. Although most of the methods mentioned earlier yield a good estimate of excitation force and system parameters, when the complete time history response of the structure is available, they perform rather poorly, when response measurements are not available at all locations.

Since measurement noise in the response time history measurements is inevitable and also complete measurements of the response are difficult to realize, it is desirable to develop identification algorithms which are least sensitive to limited instrumentation and also measurement noise. Further, the complexity of the optimization involved with the inverse problem associated impact force excitation is high, multi-modal and nonlinear, we need to carefully choose the appropriate meta-heuristic algorithm for this class of problems.

The No-Free Lunch theorem proposed by Wolpert and Macready [31], clearly highlights the most important limitation of global optimization algorithms i.e. one single algorithm cannot cater efficiently to all class of problems. In other words, if we improve an algorithm for one class of problem, it is likely to perform more poorly for other problems. This means that when we propose a new or improved global optimization algorithm [32], it should be targeted towards a particular application or set of applications rather than tested against a fixed set of problems. Keeping this in view we present a vastly improved version of differential search algorithm originally proposed by Civivioglu [33] which can work effectively for the inverse problem associated with the simultaneous reconstruction of impact force and its spatial location using the noise polluted measured time history responses with limited instrumentation.

Differential search is a much recent one among the algorithms proposed based on swarm intelligence and reported to be effective in dealing with multimodal optimization problems. Apart from this, unlike many meta-heuristic algorithms, the differential search has only a few parameters to adjust for optimal performance. Further, it is reported that the differential search converges faster than several other recent swarm intelligence algorithms [34]. However, there are still some shortcomings in the classical differential search algorithm. This algorithm is built with extremely good diversification mechanism. However, intensification mechanism is rather weak. This lack of effective exploitative mechanism may lead to slow convergence in some complex optimization problems at later stages. Hence in this paper, we present a vastly improved meta-heuristic algorithm by augmenting with the following features.

1. Adaptivity

2. Powerful neighbourhood search algorithm and

3. Dynamic exchange of information with multiple superorganisms.

The proposed features enhance the intensification mechanism of the algorithm and thereby strike a good balance between intensification and diversification. This will result in faster convergence and also provide a globally optimal solution. We use the resulting dynamic hybrid adaptive differential search algorithm (DHADSA) for simultaneous reconstruction of impact force and structural parameters as well as the spatial location of the impact load on the structure.

The impact force reconstruction has been carried out assuming that the structure continues to behave linearly even under impact loading. It is also assumed that there is no damage or failure of any part of the structure due to the applied impact load so that the acceleration response is linearly dependent on the impact loading. It is preferred to use acceleration time history data as it is most commonly measured data in the majority of structural health monitoring schemes. Further, it is also reported by Uhl [35] that acceleration data will give a more accurate and stable solution for the force identification problems when compared to displacement and velocity data.

We use only limited measurements in our formulations, to simulate the practical situations. The effect of limited measurements and also the effect of measurement noise on the accuracy of the proposed formulation is explored. Numerical simulation studies presented later in this paper clearly indicate that the proposed algorithm is very effective in solving complex optimization algorithms associated with the class of identification problems dealt with in this paper.

2. Impact load reconstruction

The impact load reconstruction problem is formulated as a constrained optimization problem, thus, the complex inverse identification problem which is non-unique and unstable is transformed into a forward problem. Even though several earlier attempts have been made to formulate the inverse problems as an optimization problem, for the first time we are formulating the problem as a constrained optimization problem in order to improve the robustness of the resulting multi-modal problem especially when limited measurements are available.

The impact load is represented by a set of 3 parameters. This parameterization allows the impact identification problem, especially the reconstruction of impact force history, to be more simple and tractable, since identifying several unknown parameters is much easier than directly reconstructing the values of impact force at the many discrete time points in the time domain [22]. Then, combining with a forward model, which characterizes the dynamic response of the structure subject to a known impact force, the unknown parameters depicting impact force history can be identified by minimizing the difference between the computed analytical responses and the actually measured responses. In the proposed identification strategy, a problem arising from the identification process is that the resulting optimization problem is nonlinear and multimodal especially for complex structures. Gradient functions or other additional differential information, which is required by traditional optimization approaches, may be difficult and time-consuming to calculate or even cannot be obtained depending on the model chosen, thus, the metaheuristic algorithm is employed in this impact load identification strategy.

The impact force time histories can be approximated using a series of a smooth base trigonometric function, $\sin \left(\delta \right(i\left)\right)$. Thus the impact force f(t) can be written as (1) $f\left(t\right)=f\left({\alpha }_i\right(t\left)\right)=\sum _{i=1}^{N_f}{\alpha }_i\left(t\right)\sin \left(\delta \right(i\left)\right),t\in \left[0,T\right],$(1) where, the number of base functions, $N_f$ the coefficients ${\alpha }_i\left(t\right)$ and angle $\delta \left(i\right)$ of each base function, constitute the unknown parameters to be identified. A study conducted by Hu et al. [22] shows that this parameterizing approach can approximate the impact force history very well; however, the disadvantage is that it may need too many numbers of base functions to obtain converged results, leading to a large search space and slow convergence rate. A simple but effective impact force representation method with a few unknown parameters is proposed in this study. Observing the experimentally measured impact load, researchers have shown that a general impact force history can be represented as a half-sine pulse shape [27,36].

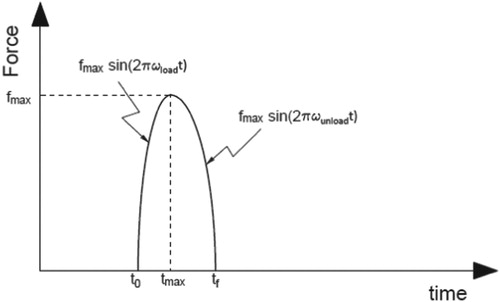
In this study, the impact force history is approximately considered as a combination of two $1/4$ cycle-sine pulses, while the loading frequency and unloading frequency are different, as illustrated in Figure 1. Therefore, three parameters are used to depict such a general impact load, namely the magnitude of the impact force, $f_{\max }$, the loading frequency ${\omega }_{\mathrm{load}}$ and the unloading frequency ${\omega }_{\mathrm{unload}}$ of the impact force. For simplicity, only impact perpendicular to the structure is considered, and the material is assumed to be linear without any damage during impact. After the unknown parameters to be identified are defined, the impact load identification is formulated as a constrained optimization problem to be solved. In this study, for demonstrating the effectiveness of the proposed algorithm, the acceleration response of the structure under impact is taken as the measurement. The difference between the theoretical acceleration response of the forward model and the measured acceleration response is used as the objective function to be minimized during the optimization process with a constraint on the subspace angle. The objective function is given as: (2) $\text{Err}(f_{\max },{\omega }_{\mathrm{load}},{\omega }_{\mathrm{unload}})=\sum _{i=1}^{N_p}\left(\sum _{n=1}^{N_s}{\left({\ddot{x}}_{im}\right(n)-{\ddot{x}}_{ic}(f_{\max },{\omega }_{\mathrm{load}},{\omega }_{\mathrm{unload}},n\left)\right)}^2\right).$(2) In Equation (2), N_s is the number of discrete sampling points in the time domain, and N_p is the number of sensors used for recording responses for identification. ${\ddot{x}}_{im}$ represents the measured acceleration response and ${\ddot{x}}_{ic}$ represents the theoretical acceleration response.

Figure 1. General impact load.

It may be noted that the objective function defined in equation (2) can only be used to reconstruct the impact load time history. However, we do need the location of the impact force also to complete the identification process. In order to accomplish this, we include two additional parameters $(x_{\mathrm{impact}},y_{\mathrm{impact}})$ (i.e. Cartesian points to define the spatial location of the impact load) in the objective function defined in equation (2). Thus, the impact load is modelled using a set of 5 parameters. It enables fine-tuning the impact location in the space domain and identifying the parameters portraying the impact force history in time domain simultaneously within a single algorithm. Thus, the modified objective function is given by: (3) $\begin{array}{rl}& \text{Err}(x_{\mathrm{impact}},y_{\mathrm{impact}},f_{\max },{\omega }_{\mathrm{load}},{\omega }_{\mathrm{unload}})\\ & =\sum _{i=1}^{N_p}\left(\sum _{n=1}^{N_S}{\left({\ddot{x}}_{im}\right(n)-{\ddot{x}}_{ic}(x_{\mathrm{impact}},y_{\mathrm{impact}},f_{\max },{\omega }_{\mathrm{load}},{\omega }_{\mathrm{unload}},n\left)\right)}^2\right).\end{array}$(3)

2.1. Subspace angle as a constraint

Since we use limited measurements, the proposed complex optimization problem associated with the inverse problem of estimation of impact load can lead to multimodal solutions. In order to converge to the true/unique solution, we propose to apply constraints to the optimization problem defined earlier and solve as a constraint optimization algorithm in order to improve the robustness and also faster convergence to the true solution. The principal angle between the measured and estimated subspaces is considered as a constraint in the proposed formulations.

One way to compare hyperplane is to use the concept of angles between the two subspaces. This concept allows quantifying the spatial coherence between two time-history blocks of an oscillating system. Let $A\in {\mathrm{\Re }}^{n_{s}Xp}$ and $B\in {\mathrm{\Re }}^{n_{s}Xp}$ each with linearly independent columns. The principal angles between two subspaces are a generalization of an angle between two vectors, and their number is equal to the dimension of the smallest subspace. An algorithm for the computation of principal angles proposed by Bjorck and Golub [37] using QR factorization and singular value decomposition can be used for this purpose. First, a QR factorization allows computing the orthonormal bases of A and B. (4) $\begin{array}{rl}& A=Q_A{R}_A{Q}_A\in {\mathrm{\Re }}^{n_{s}Xp}\\ & B=Q_B{R}_B{Q}_B\in {\mathrm{\Re }}^{n_{s}Xp},\end{array}$(4) Thus, the singular values of $Q_A^T{Q}_B^T$ define the q cosines of the principal angles ${\theta }_i$ between A and B. (5) $\text{SVD}\left(Q_A^T{Q}_B^T\right)\to \text{Diag(cos(}{\theta }_i\left)\right)i=1,2,\dots q.$(5) The largest angle allows quantifying how the subspaces A and B are globally different.

This principal angle is considered as a constraint in the proposed optimization algorithm associated with impact force estimation. The subspace angle between the measured acceleration time history responses and the estimated (rather computed) acceleration responses are compared by computing the principal angles. This principal angle between these two subspaces should be constrained to be zero in the proposed optimization algorithm in order to match the dynamic state of the true and estimated system with impact load. Hence the optimization problem on hand can be defined as minimization of the objective function defined in Equation (3) with the constraint related to subspace angle as zero.

3. Differential search algorithm (DSA)

The input force identification problem is usually solved by using inverse computational algorithms [38]. However, recently this class of inverse problems are being popularly solved using meta-heuristic algorithms by formulating the associated inverse problem as an optimization problem [39]. In the present work, we follow a similar procedure. The present inverse optimization problem requires the measured time history responses from the structure of interest in order to reconstruct the impact force time history and also its spatial location. Field measurements obtained will obviously be corrupted by noise. Hence, the optimization algorithm employed should exhibit less sensitivity to measurement noise. However, we present a more efficient meta-heuristic algorithm for solving this class of problems. Further, the optimization problem associated with damage quantification is extremely complex, multi-modal and nonlinear, hence there is a need to carefully select the suitable meta-heuristic algorithm for this kind of problems. Further, to incorporate in the SHM scheme, apart from finding the globally optimal solution, the algorithm should also have the capability of faster convergence.

Several meta-heuristic algorithms are reported in the literature and the majority of them are applied to solve inverse problems. However, the majority of meta-heuristic algorithms have several parameters to adjust so that the convergence characteristics can be improved by balancing the diversification and intensification process. In this paper, we use a vastly improved version of differential search algorithm originally proposed by Civivioglu [33]. Differential search is a much recent one among the algorithms proposed based on swarm intelligence and reported to be effective in dealing with multimodal optimization problems. Apart from this, unlike many meta-heuristic algorithms, the differential search has few parameters to adjust for optimal performance. Further, it is reported that the differential search converges faster than several other recent swarm intelligence algorithms [34]. However, there are still some shortcomings in the classical differential search algorithm. This algorithm is built with extremely good diversification mechanism. However, intensification mechanism is rather weak. This lack of effective exploitative mechanism may lead to slow convergence in some complex optimization problems at later stages. Hence in this paper, we present a vastly improved meta-heuristic algorithm by augmenting with adaptive features, augmenting with a powerful neighbourhood search algorithm and also with a dynamic exchange of information. The proposed features enhance the intensification mechanism of the algorithm and thereby strike a good balance between intensification and diversification. This will result in faster convergence and also provide a globally optimal solution.

It is proposed to improve the intensification mechanism in the basic differential search algorithm by augmenting with a neighbourhood search algorithm. It is known very well that in general, meta-heuristic algorithms cannot outperform the specialized neighbourhood search algorithms. Nevertheless, the neighbourhood search methods face initialization problem in most of the cases. Precisely, the local optimizer performs based on the function of the initial solution. Therefore, combining a meta-heuristic algorithm with an efficient neighbourhood search algorithm is expected to provide a much better solution for the reason that the good initial solutions for the neighbourhood search algorithm are provided by the meta-heuristic algorithms for further exploration. In the present work, we use the resulting dynamic hybrid adaptive differential search algorithm (DHADSA) to quantify the extent of damage present in the structure. First, the basic DSA will be presented followed by the improvements made in the proposed algorithm.

3.1. Basic differential search algorithm (DSA)

Similar to any other optimization algorithm based on stochastic search, DSA, made up of random solutions of the respective problem, corresponds to an artificial-super organism migrating to the global optimum solution of the problem. This algorithm is developed by drawing inspiration from the seasonal migration of living organisms in search of ideal sources for food. Since the quality and quantity of food will obviously vary from season to season, due to the periodical climatic changes, this migration takes place throughout the year and move from poor region to suitable and efficient habitat where capacity and diversity of natural sources are high. A large number of migrating living organisms constitute the superorganism. The differential search algorithm simulates the Brownian-like random-walk movement to describe the search mechanism during migration.

In differential search algorithm, the artificial superorganism (consists of a population of generated random solutions) migrates to the global minimum. During this migration process, the randomly selected positions (places) will be explored for their suitability for temporary settlement. If a suitable temporary stopover position is found during the migration by the members of the artificial-superorganism (i.e. artificial-organisms) that made such discovery immediately migrates to the new position and continue their migration process from this newly discovered position.

The migration process of the superorganism will continue from the current position. The basic steps involved in differential search algorithms are:

In DSA, each of the artificial organism represents a possible solution $V_i=(v_{i1},v_{i2},v_{i3},\dots ,v_{iD})$ (i = 1, N) where N signifies the number of artificial organisms in the superorganism and D depends on the number of design variables to define the specific optimization problem on hand. Initially, all the solutions (artificial organisms) are generated randomly. Accordingly, the initial position of each artificial organism can be defined by using the upper and lower limits of each design variable of the optimization problem on hand (6) $v_{ij}=\text{Lowe}{\text{r}}_j+\text{rand}\ast \text{(Uppe}{\text{r}}_j-\text{Lowe}{\text{r}}_j\text{)},$(6) where Upper_j and Lower_j are the user-defined upper and lower bounds of the jth design variable.

The search mechanism for finding the stopover sites at the areas in between the artificial-organisms follows the Brownian-like random walk model. In order to discover the new stopover site, the individuals are chosen randomly (artificial organisms) move towards the targets of the donor. The order of the number of the elements in the set is randomly changed each time through random shuffling. The positional change (i.e. stopover position) of the artificial organisms is controlled by a value ‘scale’. Accordingly, we can compute the stopover vectors (St) for each artificial organism as (7) $S{t}_{ik}=V_{ik}\text{ + scale}\cdot (V_{dk}-V_{ik}\text{),}$(7) where d is the donor, $d\in [1,2,\dots N]$ are randomly chosen integers obtained using the $\text{random\_shuffling}$ function and $d\ne i$. It must be mentioned here that the value of scale is produced by a gamma random number generator (i.e. randg) controlled by a uniform distribution random number generator (i.e. rand) in the range of 0 and 1.

The stopover site is controlled to remain in determined search space range. In DSA, the stopover site found by the search process is evaluated and if the newly discovered stopover site of an artificial organism has better quality than the current sources of that artificial-organism, it goes to that stopover site. The stopover position(site) can be calculated by the artificial organisms of the superorganism and can be determined as (8) $\tilde{S}{t}_{ij}^g=\left\{\begin{array}{l}S{t}_{ij}^g\text{if }R(i,j)=0;\\ v_{ij}^g\text{if }R(i,j)=1;\end{array}\right.,$(8) where j = [1,2, … D]; R(i, j) is an integer number either 0 or 1. ${\tilde{S}t}_{\mathrm{ij}}^g$ is the trial vector of the ith particle in the jth dimension at the gth generation. While the artificial organisms of a superorganism change site, that respective superorganism continues its movement towards the global optimum. The new population (i.e. g = g + 1) is chosen between the stopover site population and the artificial-organism population using the following selection process. (9) $V_i^{g+1}=\left\{\begin{array}{l}\tilde{S}{t}_i^g,\text{if }f\left(\tilde{S}{t}_i^G\right)\le f\left(V_i^G\right);\\ V_i^g,\text{if }f\left(\tilde{S}{t}_i^G\right)>f\left(V_i^G\right);\end{array}\right..$(9) It should be mentioned here that the differential search algorithm may simultaneously use more than one individual unlike other stochastic algorithms like differential evolution (DE) or Artificial Bee Colony (ABC) algorithm. Similarly, DSA has no inclination to correctly move towards the best possible solution to the problem which is in contrast to the behaviour of DE, ABC or particle swarm optimization (PSO) algorithm. In view of this, DSA is more adaptive towards finding multi-modal solutions

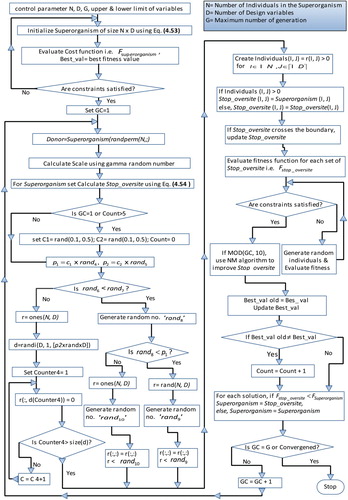
3.2. Adaptive DSA

The differential search algorithm is reported to have a better capability in terms of exploring search spaces when compared to other population-based meta-heuristic algorithms especially while dealing with multi-modal optimization problems. However, there are still some limitations in the classical DS algorithm. Even though the DSA is built with better exploration capabilities, it is rather weak in the exploitation of the solution. In view of this, the convergence rate is rather slow in some instances. Major attributes of any successful meta-heuristic algorithms are strong exploitation and exploration capabilities and striking a good balance between them in order to accelerate the convergence rate and at the same time preventing the algorithm from premature convergence. Hence the majority of the efforts in algorithmic research are devoted to enhancing the exploitation capability while simultaneously building up good exploration capability in order to accelerate convergence rate and avoid premature convergence. In the initial stages, of execution, the algorithm should exhibit high diversification capability in order to explore the search space vigorously and at the later stages i.e. near convergence, the intensification capability should be high with low or marginal diversification for faster convergence to the optimal solution.

The control parameters play an important role in all the meta-heuristic algorithms to improve the convergence rate and also preventing premature convergence. One of the major advantages of DSA is that we need to set only two control parameters i.e. p1 and p2 in the DSA algorithm, unlike many popular meta-heuristic algorithms. Earlier investigations on these control parameters indicate that they depend on the complexity and also particularity of the problem on hand. In the majority of the cases, these two parameters P1 and P2 are set to (0.3*rand) to obtain good results. However, in the present work, we propose to adjust the values of these two control parameters dynamically during the search process based on the feedback on the improvements in the fitness values (rather convergence rate). These adaptive feature built into the proposed algorithm certainly enhances the convergence rate of the solution, by ensuring a good balance between exploitation and exploration.

3.3. Hybrid adaptive differential search algorithm (HADSA)

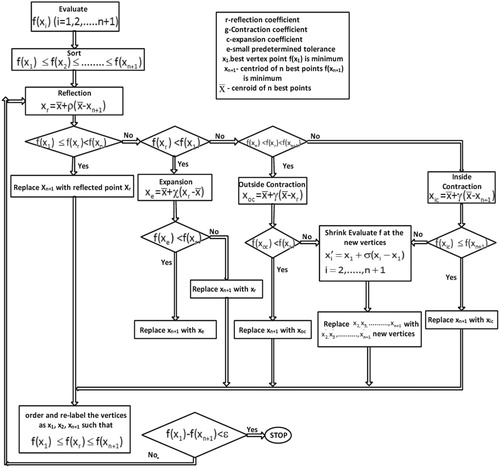
The exploitation capability of the classical differential search algorithm is rather weak and it requires strengthening. Keeping this in view, we propose to augment the adaptive differential search algorithm with a local search algorithm in order to substantially enhance the exploitation capabilities. It should be mentioned here that the meta-heuristic algorithms including the present differential search cannot compete with a promising local search algorithm in obtaining an optimal solution without converging to local optima. However, the major limitation of the local search algorithms lies in the selection of the good initial point in the search space i.e. initialization problem. Hence the performance of these local search algorithm is always a function of the initial solution to which it is applied. We can exploit the exemplary capabilities of these local search algorithms by feeding good potential initial points identified using meta-heuristic algorithms to exploit the search space and provide improved solutions. The resulting hybrid algorithms (i.e.. meta-heuristic algorithm combining with local search algorithm) will obviously exhibit superior convergence capabilities. Keeping this in view the proposed adaptive DSA is combined with a popular non-gradient based local search algorithm called Nelder-Mead (NM) algorithm [40] shown in Figure 2. The flowchart of the resulting hybrid adaptive differential search algorithm given in Figure 3 details the computational procedure associated with it.

Figure 2. Nelder-Mead algorithm.

Figure 3. The hybrid adaptive differential search algorithm (HADSA).

Hybridizing with a local search algorithm will enhance drastically the exploration capabilities [41]. However, it may take away the balance between exploitation and exploration and thereby effects the performance of the algorithm and its efficiencies. More focus on the exploitation due to the augmentation of local search requires the exploration to be limited to only a part of the search space. This may result in an increased probability of getting trapped in local optima. Keeping this in view, the convergence characteristics of the HADSA are further improved by formulating a new version of the differential search algorithm with dynamically changing subpopulations. The details of the proposed hybrid adaptive differential search algorithm with dynamically changing subpopulations are presented in the next section.

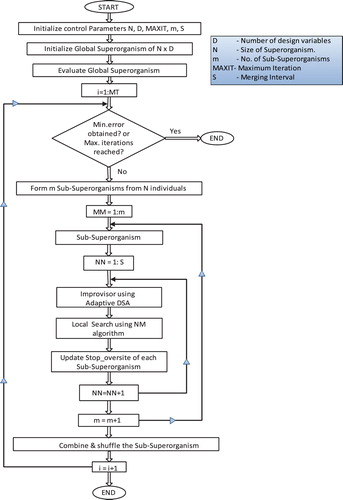
3.4. Hybrid adaptive differential search with multi superorganisms

The classical differential search algorithm basically works with a single superorganism. There is sufficient evidence in the literature to indicate that meta-heuristic algorithms with models comprising of multiple small populations perform better than a single population model [35]. Island models developed for evolutionary computing techniques is also another example of successful implementation of multi-population models which are generally found superior to their single population counterparts [42]. Inspired by these facts, we propose a new differential search algorithm with multiple superorganisms, each with a small number of organisms in order to maintain faster convergence while maintaining larger diversity during the search. Since the organisms in each sub-superorganism dynamically migrate to other sub-superorganism, the proposed algorithm is termed as a differential search algorithm with dynamic superorganisms. In the proposed algorithm, the randomly generated artificial organisms at the initial stage are grouped into small sized sub-superorganism, with each consisting of an equal smaller number of artificial organisms. Each sub-superorganism uses its own artificial organisms to migrate to new stopover sites using the search process associated with the hybrid adaptive differential search explained in the earlier section using their own best historical information. Since the number of artificial organisms is small in number, the solution is likely to converge to a local optimum. In order to avoid this premature convergence, the information needs to be exchanged across sub-superorganisms. It is also mandatory to maintain higher diversity in the sub-superorganisms while exchanging information. To ensure this, a neighbourhood structure for the artificial organisms in each sub-superorganism, which changes dynamically, is proposed through a shuffling schedule. Accordingly, the population is shuffled after ‘m’ generations, defined by the user, and the process of migration to the next stopover site is continued in the pursuit of reaching the optimal solution. Exchange of information of each sub-superorganism during the previous regrouping period ‘m’ takes place after every ‘m’ trials. The search process in each artificial superorganism is carried out using the proposed hybrid adaptive differential search algorithm shown in Figure 3. However, we use different control parameters at the start in each sub-superorganism which may change adaptively during the search process. The parallel search involved in the proposed multi sub-superorganism model with a dynamic exchange of information across sub superorganisms accelerates the search process towards an optimal solution. It should be mentioned here that the exploration capabilities are significantly enhanced in the proposed algorithm through parallel search and dynamic exchange of information among the sub superorganisms. The exploitation capabilities are also significantly enhanced by augmenting with an effective local search algorithm like a Nelder-Mead algorithm. The complete details related to the computational procedure associated with the proposed hybrid adaptive differential search with multiple sub-organisms is presented in the flowchart shown in Figure 4.

Figure 4. Dynamic hybrid adaptive differential search algorithm (DHADSA).

4. Limited measurements

Practically, due to cost and accessibility issues, the number of sensors placed on the structures will be rather limited. It is usually recommended to place the sensors at a limited number of optimal locations in order to capture the important structural responses with minimum cost for structural health monitoring applications. Majority of these current sensor placement methods are based on the mode shapes of the pretext finite element model (FEM). These methods basically aim at optimizing sensor locations for extracting the desired number of modes and other important issues like structural damping, dynamic forces acting on the structure and their spatial locations are not accounted for. Hence, here we employ a sensor placement technique based on the principal component analysis. This technique is a generalization of the Effective Independence approach [43]. Effective independence approach for sensor placement is based on a relatively small set of target modes within the range of interested frequency. However, for an impact load of small duration ($\mu$-sec range), the exciting frequency is broad banded. At high frequencies, the wavelengths are small. In order to capture all the higher order modes, we need to employ high fidelity finite element models and result in a large number of densely packed modes in the structure. In order to overcome the difficulty associated with effective independence approach based on mode shapes, we use frequency response functions (FRF) to arrive at optimal sensor locations. This gives generality to the optimal sensor placement algorithm, which can be applied to any range of frequencies or loading conditions. Analytical frequency response can be calculated employing finite element models for any specified frequency bands, damping, and input locations. The analytical frequency response data matrix, $H=\left[h\left({\omega }_1\right)h\left({\omega }_2\right)h\left({\omega }_3\right)\dots h\left({\omega }_f\right)\right]$ obtained from finite element analysis of the structure with the known locations of input excitation can be decomposed (using singular value decomposition) into principal directions and singular values, which can be directly related to the system's energy. Using principal directions, we can account for the effects of input location and damping. Since the principal directions are always orthogonal, they are more robust to modelling errors and experimental noise. Hence they are the more suitable basis for describing the structural response.

Principal component analysis (PCA) is a multivariate technique that linearly transforms an original set of variables into a substantially smaller set of uncorrelated variables that represents most of the information in the original set of variables. From the dynamic time history response, the principal components can be obtained by applying the Singular Value Decomposition (SVD) on FRF data. Using the SVD, a packet of sensor data X (N × n matrix of data, n FRF points with N different spatial locations) can be decomposed as (10) $X=U\sum V^T,$(10) where U indicates the principal components (PCs) of size N X N and V indicates the principal coordinate history of size n ×  n respectively which contains the normalized response of the principal directions. The diagonal matrix $\mathrm{\Sigma }$ is termed as the singular matrix in which the elements are arranged in the decreasing order of energy present in each mode. In order to characterize the system, we use only a first few singular values based on energy criteria corresponding to 99% of total energy [44].

The basic aim of the PCA-based effective independence (PEfi) technique is to place sensors at dynamically sensitive locations on the structure in order to capture the important information contained in the dynamic response. Since the active principal directions are chosen based on the energy criteria, the important dynamic information lies in these principal directions. Hence by choosing the active principal components instead of mode shapes, we can optimally choose the dynamically sensitive spatial locations on the structure. Accordingly, we can define the Fisher information matrix with principal components as (11) $Q_c=U_c^{T}W{U}_c,$(11) where U_c are the active principal components and W is the inverse of the noise covariance matrix usually termed as a weighting matrix. The weighting matrix, W is generally chosen as the identity matrix. In order to obtain the best state estimate, the information matrix will be maximized in an appropriate norm. This, in turn, minimizes the error covariance matrix. We prefer to use the determinant of the Fisher information matrix as a norm for maximization in the present work as it results in maximizing the signal strength. In the proposed PCA based optimal sensor placement technique (PEfI), the sensor positions are truncated following the same procedure of EfI. The contribution of each candidate sensor node is examined and sensor position that has a lower determinant of the information matrix is truncated in an iterative fashion. The PEfi value corresponding to the ith sensor is given by (12) $\text{PEf}{\text{i}}_i={\psi }_i{Q}^{-1}{\psi }_i^T,$(12) where PEfi_i, represents the fractional reduction of the information matrix determinant if the ith sensor is removed from the candidate set. The sensor corresponding to lowest PEfi value is removed after sorting the possible candidate sensor locations based on PEfi. Similar to Efi, we can remove the less significant sensors using sequential iterative process until the remaining active candidate sensors meet the target number specified.

5. Numerical studies

Numerical simulation studies have been carried out to identify a single impact load using the proposed dynamic hybrid adaptive differential search algorithm. For this purpose, two numerical examples are considered: simply supported beam girder, and simply supported plate. A sinusoidal impact load of 40 µsec duration is considered in the present numerical simulations. Acceleration time history data obtained from limited measurements are used for reconstructing the impact load time history.

The robustness of the structural damage diagnostic techniques to the effect of measurement noise is one of the important issues in real situations of SHM. Therefore, to investigate the effect of measurement noise on the robustness of the proposed approach, the computed time history measurements are contaminated with white Gaussian noise with zero mean statistics. A Gaussian random component is added to the noise-free acceleration time-history response to obtain the noisy sequences as follows: (13a) ${\ddot{x}}_m=\ddot{x}+{\xi }_p{N}_{\mathrm{noise}}\sigma \left(\ddot{x}\right),$(13a) where ${\xi }_p$ is the level of noise in percentage, $N_{\mathrm{noise}}$ is the standard normal distribution, $\sigma \left(\ddot{x}\right)$ is the standard deviation of the measured (computed) time-history response, uncorrupted with noise. In the present numerical studies, the random noise levels are varied in 3%, 5% and 8%. Moreover, the noisy sequences affecting different nodes are uncorrelated, in this way severe experimental conditions are simulated.

We have also employed the following strategies during the optimization process in order to improve the convergence characteristics as well as the robustness of the proposed variants of the meta-heuristic algorithm.

We start the optimization algorithm initially as an unconstrained optimization problem and after few iterations, when the design variables settle down, we employ the constraint related to the principal angle between the subspaces of measured and estimated responses. The imposition of the constraint after initial few iterations will reduce the computational cost overheads and also helps the otherwise multimodal optimization problem converging towards the true solution under uncertainties associated with measurement noise, limited measurements and also modelling errors.

As mentioned earlier, we have used a wider search space by setting the upper and lower limits of the design variables (i.e. element stiffness coefficients) as 0.1 and 2.0. However, these upper limits and lower limits of the design variables are changed dynamically making use of the feedback from the previous iterations, during the execution of the optimization algorithm. This dynamic reduction of search space during the execution of optimization algorithm is not new in the context for meta-heuristic algorithms and it is reported to be very effective in improving the accuracy of the converged solution, robustness and also substantially improves the computational performance [45]. Hence it is proposed to adopt the similar concept of dynamic resetting the search space. Initially, the proposed variants of the DS algorithms are executed with initially present wider search space for the design variables. After the initially chosen random design variables are settled down, i.e. after few iterations say after every fifteen iterations, the search space is reset based on the feedback from the solutions obtained from the previous fifteen iterations. The upper and lower limits are chosen by considering the weighted mean of the converged design variables during the past fifteen iterations and also the weighted variance. The new upper lower limits are now set by considering the upper limit of each design variable as ‘weighted mean value of the design variable + five times the weighted variance of the design variable’. Similarly, the lower limit of the design variable is set as ‘weighted mean value of the design variable – five times the weighted variance of the design variable’. The weighting function to arrive at the weighted mean and variance is taken as the ratio of fitness of each converged solution to the best fitness. This resetting of the upper and lower limits of the search space is carried out dynamically all through the optimization process using the proposed variants of the DS algorithm

5.1. Numerical study 1: identification of impact load on a simply supported plate from noisy measurement data

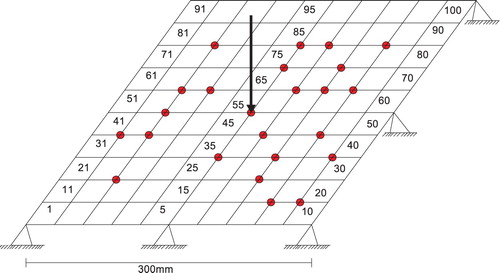
A 300 × 300 mm laminated composite plate is considered as the first numerical example and it is shown in Figure 5. The stacking sequence of the carbon-epoxy laminate composite plate is [45₂/−45₄/45₂]_S. The plate is idealized using 4-noded Mindlin plate elements and a finite element mesh of 10 × 10 is employed. Even though the number of possible sensor locations is 81, we have considered only 24 sensor measurements. The locations are dictated by the proposed PEfi algorithm presented in the earlier sections. These sensor locations are clearly marked in Figure 5. The material properties of the lamina are shown in Table 1. The first four natural frequencies of the model are 4.4671, 10.5764, 18.4353, and 20.8317 Hz, respectively.

Figure 5. Simply supported plate with a midpoint loading.

Table 1. Properties of Lamina [22].

Youngs modulus,	Youngs modulus,	Shear modulus,	Poisson's ratio	Mass density
E1	E2	G12	ν	ρ
142 GPa	10.8 GPa	5.49 GPa	0.30	1600 kg/m^3

The impact load is assumed to be acting at the midpoint of the plate as shown in Figure 5. The spatial location of the impact load and its time history is identified using the proposed differential search algorithm. The objective function defined in Equation (3) is used for impact load reconstruction. The design variables are the spatial location of the impact load, the maximum amplitude of the impact load, loading and unloading frequencies of the load. The upper and lower limits are appropriately defined for each design variable. The total number of organisms is considered as 24 for all the differential search variants employed to solve the numerical examples considered in this paper. The solution is assumed to have converged if there is no improvement in the solution for the last 5 iterations.

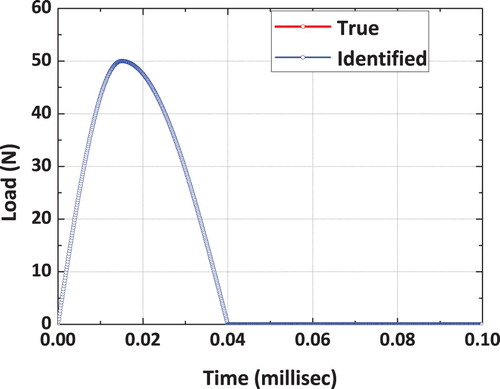
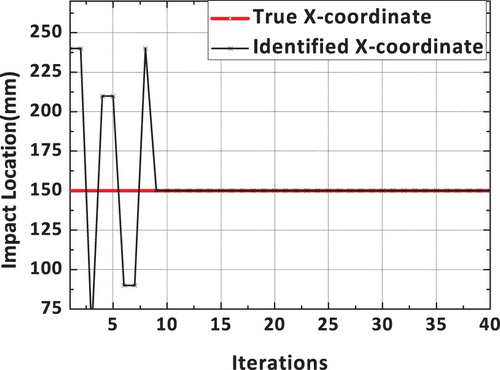
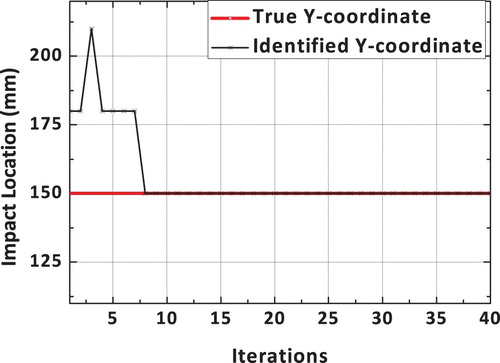
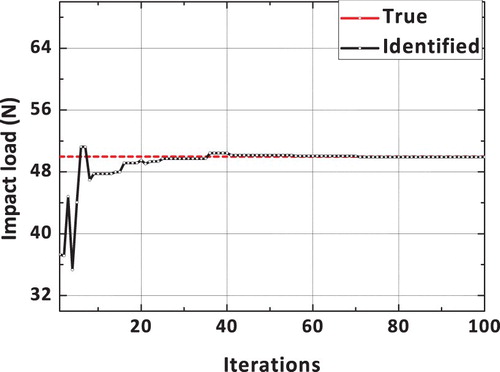
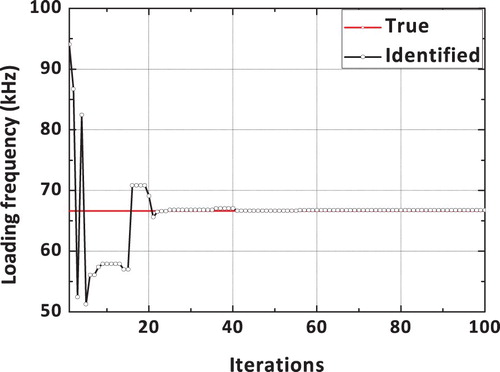
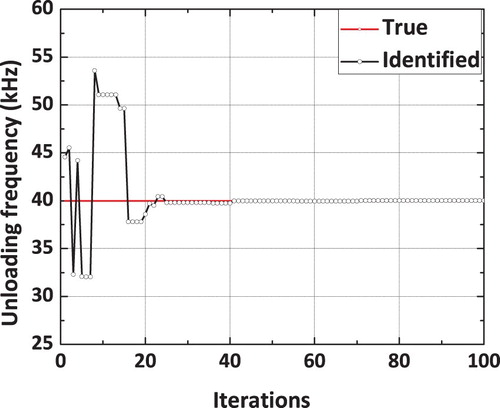
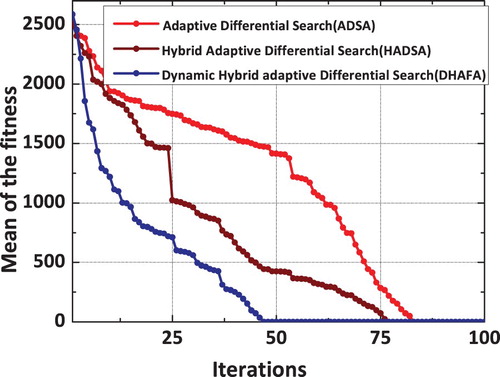
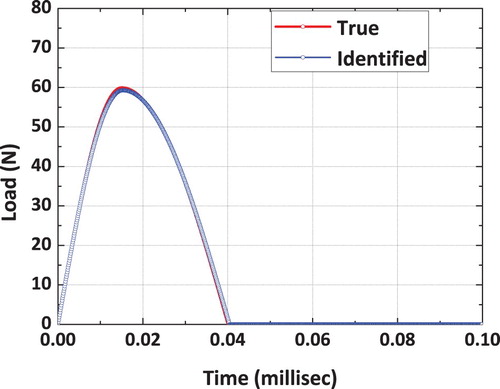
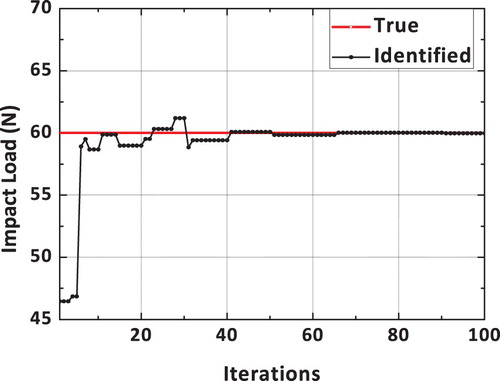
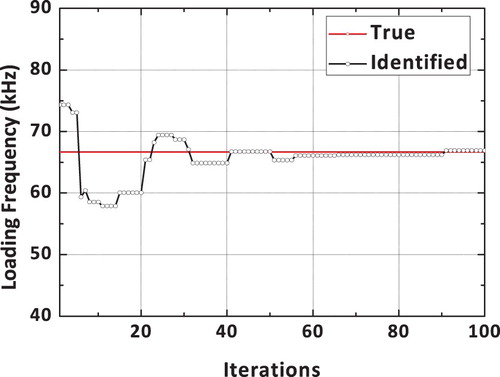
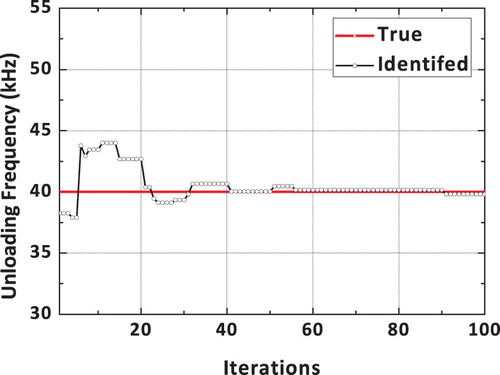
The true and identified impact loading, obtained using a dynamic hybrid adaptive differential search algorithm, is shown in Figure 6. It can be observed that the reconstructed load using the proposed DHADS algorithm is found to be comparing very well with the true impact load time history. The spatial location of the impact load is exactly identified by the proposed DHADS algorithm. The convergence plots corresponding to x and y spatial coordinates is shown in Figures 7 and 8 respectively. It can be observed from the convergence plots that the correct spatial location is identified in only 8 iterations. Hence, the convergence is quite rapid. Figure 9 shows the convergence plot of the loading amplitude using the proposed dynamic hybrid adaptive differential search algorithm (DHADSA). It can be observed that the reconstructed impact load using the proposed constrained optimization formulations is comparing very well with the true load. Similarly, the convergence of the loading and unloading frequencies using the proposed DHADSA are shown in Figures 10 and 11 respectively. The convergence characteristics of various DSA implementations using the mean fitness value as the parameter is shown in Figure 12. The converge plot shown in Figure 12 reflects the superior convergence characteristics, of the proposed dynamic hybrid adaptive differential search algorithm.

Figure 6. Identified and True Impact loading on a simply supported plate using DHADSA.

Figure 7. X-coordinate convergence plot for simply supported plate.

Figure 8. Y-coordinate convergence plot for simply supported plate.

Figure 9. Loading amplitude convergence plot for simply supported plate-DHADS algorithm.

Figure 10. Loading frequency convergence plot for simply supported plate-DHADS algorithm.

Figure 11. Unloading frequency convergence plot for simply supported plate-DHADS algorithm.

Figure 12. Convergence studies of various DSA implementations.

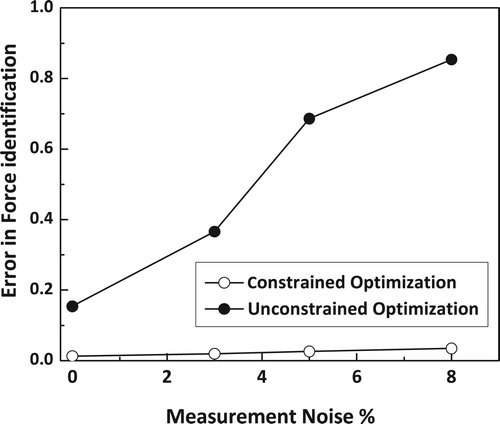
In order to test the proposed impact load reconstruction algorithm with varying levels of measurement noise, we have considered three test cases by corrupting the measured acceleration time history data with 3%, 5%, and 8% respectively. Similarly, we have also investigated the convergence characteristics of the proposed formulation of the inverse problem as a constrained optimization problem by comparing with the unconstrained optimization. As mentioned earlier, we have considered only limited sensors with their spatial locations shown in Figure 5. The details of these investigations in the form of percentage error in the reconstruction of impact load time history are presented in Figure 13. The percentage error in the identification of impact force time history is calculated, as we already know the true simulated dynamic force and it is defined as (13) $\text{error}=\frac{||f_{\mathrm{id}}-f_{\mathrm{real}}||}{||f_{\mathrm{real}}||}\times 100\mathrm{\%},$(13) where $f_{\mathrm{id}}$ and $f_{\mathrm{real}}$ respectively are the identified and real impact load time histories.

Figure 13. Percentage error in the reconstruction of impact load on a simply supported composite plate using DHADS algorithm.

The DHADS algorithm is a stochastic optimization algorithm and so there is no assurance that the final solutions arrived in every execution is the same. In view of this, the concept of practical reliability (PR) is used to assure the consistency of the proposed meta-heuristic algorithms. Practical reliability is defined as the percentage of converged solutions obtained using the DHADS stochastic algorithm with the exact stiffness and damping coefficients. However, a variation of 0.01 in the values of the exact solutions obtained is ignored. The evaluation of the practical reliability is performed by executing the stochastic algorithm for 30 different instances and by calculating the ratio of the maximum number of converged solutions that satisfy the above requirement to the number of independent executions of the algorithm. The practical reliability obtained for this example for the conventional differential search, hybrid adaptive differential search and proposed DHADSA are found to be 0.88, 0.96, 0.99 respectively. Similarly, the practical reliability is reduced to 0.78, 0.80, 0.84 and 0.85 respectively for the conventional differential search, hybrid adaptive differential search (HADS) and proposed DHADS algorithms when the problem is solved as an unconstrained optimization problem with limited sensors.

In order to measure the efficiency of the proposed algorithm, another measure which is the normalized price (NP) of each run [38,39], is used in the present numerical experiments. The definition of price is formulated as the total number of function evaluations per complete execution of the proposed algorithm. The ratio of the mean price of the 30 executions of the proposed meta-heuristic algorithms to the practical reliability is defined as the normalized price. The normalized price is worked out to be 6220, 3946, 2870 and 1688 for solving the constrained optimization problem using classical DS, adaptive DS, hybrid adaptive DS and the proposed DHADSA respectively. It clearly reflects the superior computational performance of the proposed algorithm.

It can be concluded from the studies presented in Figure 13 that the consistency coupled with faster convergence makes the proposed DHADS algorithm highly suitable for complex optimization problems associated with structural system identification or damage quantification. The constrained optimization formulations are more robust especially while solving the inverse problems with limited measurements and it is also found to be highly immune to the measurement noise

5.2. Numerical study 2: identification of impact load on a simply supported beam girder from noisy measurement data

A simply-supported concrete beam girder, shown in Figure 14, is taken as the second numerical example. The girder has a span of length 10 m and cross-section 0.3 × 0.8 m. The modulus of elasticity and mass density are 34,500 N/mm² and 2400 kg/m³ respectively. The beam is idealized using 20 beam elements for the present investigations. The first five natural frequencies of the system are 13.761, 55.043, 123.851, 189.863, and 220.196 Hz. The number of sensors for acceleration measurements is considered as 7 and the optimal nodal locations obtained using the proposed PEfi algorithm are 7, 8, 9, 10, 11, 12, 13.

Figure 14. Simply supported beam girder of span 10 m.

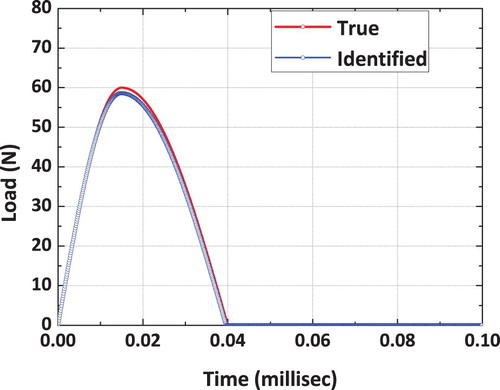
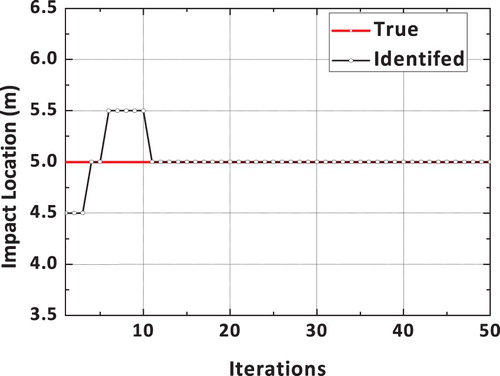
The impact load is assumed to be acting at the midpoint of the beam. The spatial location of the impact load is identified using the proposed dynamic hybrid adaptive differential search algorithm. The reconstructed impact load time history is shown in Figure 15 and it is compared with the true impact load. It can be observed from the plots shown in Figure 15 that the reconstructed impact load is comparing very well with the true impact load. The convergence plot corresponding to the spatial location of the impact load using the proposed DS algorithm is shown in Figure 16. It can be observed from the convergence plot that the correct spatial location is identified in only 11 iterations.

Figure 15. True and identified impact loading on simply supported beam.

Figure 16. Convergence plot related to the spatial location of the impact load-simply supported beam.

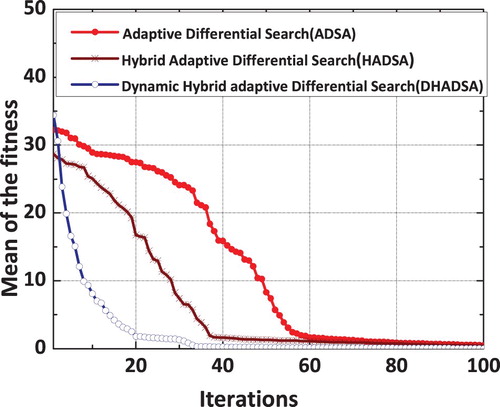
The convergence plot of the loading amplitude using the proposed dynamic hybrid adaptive differential search (DHADS) algorithm is shown in Figure 17. It can be observed that the converged value of the amplitude of the reconstructed impact load is comparing very well with the true load. Similarly, the convergence of the loading and unloading frequencies using the proposed DHADS algorithm are shown in Figures 18 and 19 respectively. The convergence characteristics of various DSA implementations using the mean fitness value as the parameter is shown in Figure 20. The converge plot shown in Figure 20 clearly reflects the superior convergence characteristics of the proposed dynamic hybrid adaptive differential search algorithm. The number of function evaluations for convergence is found to be 6096, 2880, 2024 and 1264 respectively for classical DS, adaptive DS, hybrid adaptive DS and the proposed DHADSA. It can easily be concluded that the proposed vastly improved DS algorithm reduced the computational burden by approximately 1/5 when compared to its classical counterpart.

Figure 17. Convergence plot of impact load amplitude – simply supported beam.

Figure 18. Loading frequency convergence plot for simply supported beam.

Figure 19. Unloading frequency convergence plot for simply supported beam.

Figure 20. Convergence characteristics of the various differential search implementations- Simply supported beam.

In order to investigate the effectiveness of the inverse problem associated with reconstruction of impact load using the proposed constrained optimization formulations, and also the influence of noise populated measurements, numerical simulations have been carried out to reconstruct the impact load time history using noise-corrupted acceleration time history measurements at limited optimal spatial locations. Studies with measurement noise of 3%, 5%, and 8% are presented in Figure 21. Similar studies have been carried out using the proposed DHADS algorithm using unconstrained optimization. The results are presented in Figure 21.

Figure 21. Percentage error in the reconstruction of impact load on simply supported beam using DHADS algorithm.

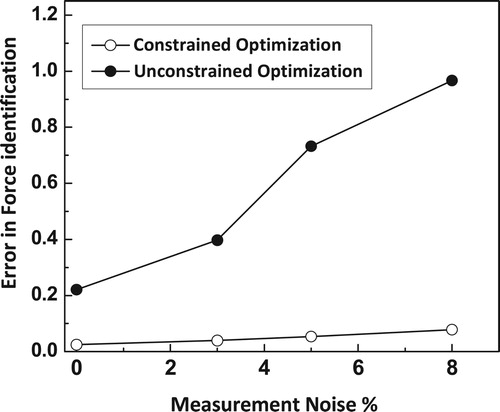
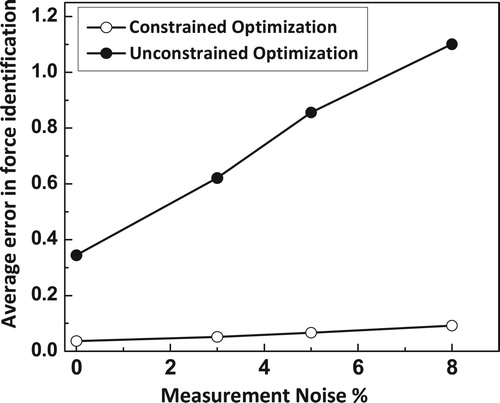
It can be concluded from studies presented in the section that the proposed impact load reconstruction algorithm based on constrained optimization formulations can be effective in generating a pretty accurate reconstruction of the load even with limited measurements. The proposed DHADS algorithm found to be faster in convergence and also pretty accurate as reflected in the results presented in Figures 15–20. Further, it is evident from Figure 21 that proposed constrained optimization formulation to solve the inverse problem associated with reconstruction of impact load can provide a good reconstruction of the load even with measurement noise of 8% and with limited sensor data. The unconstrained optimization is found to be less accurate with limited noise corrupted time history measurements.

5.3. Numerical study 3: reconstruction of multiple impact loads on a simply supported beam girder with noisy measurements

It is sometimes possible that there will be multiple impact loads acting simultaneously on the structure. In order to test the effectiveness of the proposed impact force reconstruction algorithm, to identify the spatial location and also the multiple impact loads on the structure, we have considered three impact loads acting on the simply supported beam shown in Figure 14. A sinusoidal impact load of 40µsec duration is considered and it is acting simultaneously at the mid-span, one-quarter span (i.e. 1/3rd span) and two-quarter span (2/3rd span) of the beam. While the amplitude of all the impact loads acting at the midspan, quarter span and three-quarter span are considered as 60 N, 40 N and 40 N respectively, the loading and unloading frequencies for all the three impact loads are considered as 68 kHz and 40 kHz respectively.

The noise corrupted acceleration time history responses obtained from the numerical model are used for reconstructing the impact load time history of the three impact loads. The spatial locations of the impact load and also the reconstructed impact loads are obtained using the proposed dynamic hybrid adaptive differential search (DHADS) algorithm. Since three impact loads and its spatial locations need to be identified, the proposed algorithm takes more number of iterations to converge, when compared to the single impact load problem considered earlier. Precisely, we could obtain the convergence in 160 iterations. It is observed that the three spatial locations are exactly identified by the proposed algorithm even with noisy measurements. Since we have three impact loads acting simultaneously on the structure, the errors in the reconstruction of the impact load are presented in the form of average error of the three impact loads for varying measurement noise levels. Studies with measurement noise of 3%, 5%, and 8% are presented in Figure 22. Similar studies have been carried out using the proposed DHADS algorithm using unconstrained optimization. The results are presented in Figure 22. It can be observed from the plots shown in Figure 22, that the proposed algorithm can handle multiple impact loads also effectively with minimal error in the reconstruction even with noisy measurements. The constrained optimization formulation is found to be more effective than the unconstrained optimization formulations.

Figure 22. Percentage average error in the reconstruction of the three impact loads on a simply supported beam using the proposed DHADS algorithm.

5.4. Numerical study 4: simultaneous identification of system and impact force on a simply supported beam with measurement noise

Until now all the investigations presented in this paper are based on the assumption that the system is known a priori and only impact loading needs to be determined. In the subsequent investigations, it is assumed that both the system as well as impact loading is unknown and are to be estimated simultaneously. The same simply supported beam girder shown in Figure 14, and solved earlier for only impact load identification is used here for simultaneous identification of system as well as the reconstruction of the impact load. Since the system parameters are unknown, the impact force identification cannot be carried out using the objective function given in Equation (3). It requires modification.

For system identification problem, system parameters to be estimated include stiffness, mass and damping properties of the structure. In this paper, the system parameters are identified by minimizing the error between the analytical response obtained from the forward model and the measured acceleration time history, using the newly proposed dynamic hybrid adaptive differential search algorithm. It is reasonable to assume that the mass of the system is known and it is invariant with time. The parameters left to be identified are stiffness coefficients ${\alpha }_i$ of each element, I, and the damping parameters a₁ and a₂ as given in the following equation (14) $K=\underset{i=1}{\overset{\mathrm{Nel}}{\mathrm{A}}}{\alpha }_i{k}_i\text{,}C=a_{1}K+a_{2}M,$(14) where $\text{{A}}$ is the assembly operator.$\alpha =\left\{{\alpha }_1,{\alpha }_2,{\alpha }_3,\dots {\alpha }_{\mathrm{Nel}}\right\}\in {\mathrm{\Re }}^{\mathrm{nel}}$ are the element stiffness coefficients. Hence, these $\alpha =\left\{{\alpha }_1,{\alpha }_2,{\alpha }_3,\dots {\alpha }_{\mathrm{Nel}}\right\}\in {\mathrm{\Re }}^{\mathrm{nel}}$ are taken as the design variables of the optimization algorithm. The objective of any identification procedure is to find the best estimates of the structural parameters defined using $\alpha =\left\{{\alpha }_1,{\alpha }_2,{\alpha }_3,\dots {\alpha }_{Nel}\right\}\in {\mathrm{\Re }}^{\mathrm{nel}}$ and to minimize the error between the measured acceleration response and the predicted (or computed) response using a set of parameters $\alpha$ over the entire time history.

In addition, to the three force parameters, element stiffness parameters (α) and Rayleigh damping coefficients (ξ = {a₁, a₂}) are also taken as unknown in this optimization problem. The modified objective function is constructed as follows: (15) $\begin{array}{rl}& \text{Err}(x_{\mathrm{impact}},y_{\mathrm{impact}},f_{max},{\omega }_{\mathrm{load}},{\omega }_{\mathrm{unload}},\alpha ,\xi )\\ & =\sum _{i=1}^{N_p}\left(\sum _{n=1}^{N_s}{\left({\ddot{x}}_{im}\right(n)-{\ddot{x}}_{ic}(x_{\mathrm{impact}},y_{\mathrm{impact}},f_{max},{\omega }_{\mathrm{load}},{\omega }_{\mathrm{unload}},\alpha ,\xi \left)\right)}^2\right).\end{array}$(15)

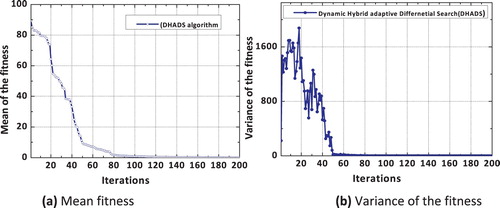
The proposed dynamic adaptive hybrid differential search algorithm (DHADS) is employed for solving the problem of simultaneous identification of system parameters and reconstruction of the impact load. To simulate experimental measurements, the white Gaussian noise of 8% is added to the acceleration time history data. The identified element stiffness coefficients of the system are compared with the original system parameters and the details are furnished in Table 2. It can be verified from the results furnished in Table 2 that there is a good agreement in the results evaluated and the actual parameters. The reconstructed and true impact loading plots are presented in Figure 23. It can be verified from Figure 23 that the reconstructed load is comparing well with the true load. The convergence characteristics of the algorithm are also investigated using the mean fitness as well as the variance in the fitness values in each iteration and the corresponding convergence plots are shown in Figure 24.

Figure 23. Identified and True Impact loading on the unknown system.

Figure 24. Convergence characteristics of the proposed DHADS algorithm.

Table 2. True and converged stiffness parameters of the simply supported beam using DHADS algorithm with constrained optimization formulations.

Element no.	1	2	3	4	5	6	7	8	9	10
True stiffness parameter	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00
Estimated stiffness parameter	1.0152	0.9638	0.9946	1.0273	0.9794	1.0167	0.9944	0.9946	0.9989	1.0442
Element no.	11	12	13	14	15	16	17	18	19	20
True stiffness parameter	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00
Estimated stiffness parameter	0.9869	1.0331	0.9927	1.0312	0.9941	0.9965	0.9889	0.9901	0.9994	0.9976

The identification of the parameters is performed with the assumption that the mass matrix is exact. Nevertheless, in many instances, the precise values of the mass of each element are difficult to obtain. In view of this practical reason, we assume that the element mass is not known precisely and only known in the form of a normal distribution. Two case studies, where the mass matrix is assumed as known precisely and also the element mass as a normally distributed variable is considered for the investigation. The uncertainty in the values of the element mass is simulated by considering them as normally distributed which are centred on the correct value with a 7% standard deviation of the corrected value.

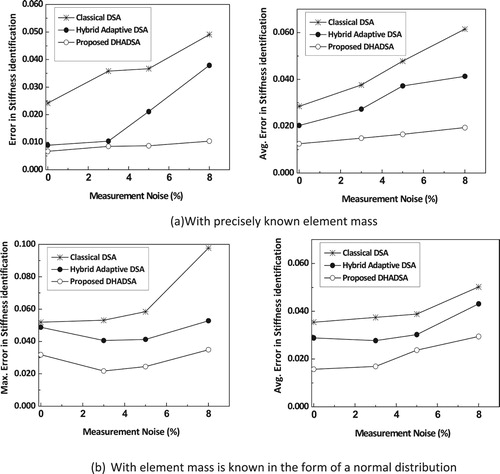
To demonstrate the efficiency of the proposed algorithm to identify the stiffness parameter when the mass values follow the normal distribution, the acceleration data is generated. Using this generated data, the stiffness parameters are obtained for all the elements. The maximum, average errors in the identification of stiffness reduction factors of all elements in the beam with measurement noise of 3%, 5%, and 8% are shown in Figure 25. Since the true parameters are already known, the error in parametric identification is calculated as (16) ${\epsilon }_i=\left|\frac{{\tilde{\alpha }}_i-{\alpha }_i}{{\alpha }_i}\right|\left(i=1,2,\dots \text{Nel}\right),$(16) where ${\tilde{\alpha }}_i$ and ${\alpha }_i$ are the estimated and true values of the ith element stiffness coefficient respectively.

Figure 25. Error in the identification of stiffness parameters of the simply supported beam and with varied noise values using the variants of differential search implementations using constrained optimization formulations.

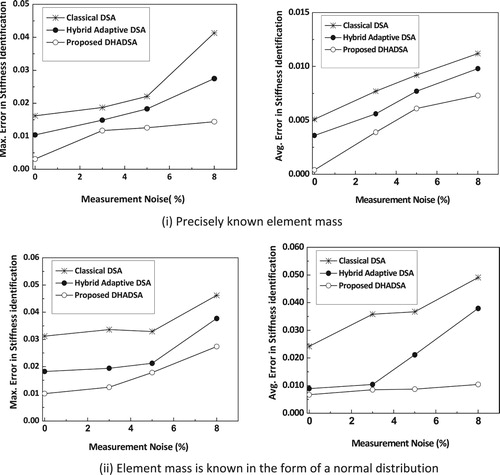
From the results presented in Figure 25, it can be observed that the errors in the identification of element stiffness coefficients with imprecise values of element masses (i.e. assumed to be known as normal distribution) are marginally higher than those of the precisely known masses. These errors are due to the imprecise knowledge of the element mass. Nevertheless, such small error magnitudes indicate that the uncertainties associated with the mass of the structure have less influence on the identification of the stiffness reduction factors.

In order to test and verify the effectiveness of the proposed constrained optimization model for identification of system parameters, we have carried out investigations using all the proposed variants of DS algorithms without considering the constraint (i.e. treating it as unconstrained optimization problem). The error in identification using precise values of elemental mass and with imprecise values of elemental mass with measurement noise of 3%, 5%, and 8% is shown in Figure 26. It can be observed from the results given in Figure 26 that errors in the estimation of system parameters are consistently higher with the unconstrained optimization problem. Further, the errors in the estimation of system parameters with imprecise values of elemental mass (i.e. mass assumed in the form of normal distribution) are found to be much higher. Similarly, the errors in the reconstruction of impact load and system parameters with constrained and unconstrained optimization models using varied implementations of the differential search are shown in Figure 26.

Figure 26. Error in the identification of stiffness parameters of the simply supported beam and with varied noise values using the variants of differential search implementations using unconstrained optimization formulations.

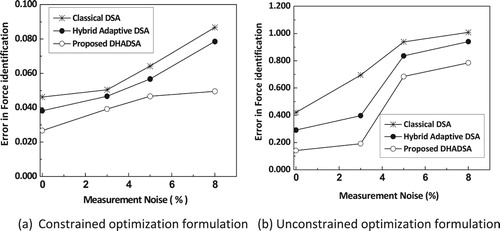
Similar observations can be made from the results presented in Figure 27 where the error in the reconstruction of impact load with constrained and unconstrained optimization formulations is presented for measurement noise of 3%, 5%, and 8%. Apart from this, the number of function evaluations are consistently increased while using the unconstrained optimization by about 28%. Hence it can be concluded from this investigation that using the subspace angle as a constraint in the proposed formulation increases the computational efficiency as well as the accuracy in the estimation of the system parameters as well as the reconstruction of the impact load.

Figure 27. Error in the reconstruction of impact load on simply supported beam using with varied noise values using the variants of differential search implementations with simultaneous identification of system parameters using limited instrumentation using constrained and unconstrained optimization formulations.

6. Conclusion

In this paper, an approach for impact load identification on structures is proposed by formulating the associated inverse problem as a constrained optimization problem in order to handle multi-modal solutions due to limited measurements. This new identification approach formulated as a constraint optimization problem has the capability to identify the impact location and reconstruct the impact load history simultaneously. This method is applied to impact load identification of beam girder and plate problems. Efforts have also been made in this paper for the simultaneous identification of system parameters as well as the impact force acting on the system along with its spatial location. A newly proposed dynamic hybrid adaptive differential search algorithm (DHADSA) is employed to solve the resulting constrained optimization problem. In order to improve the convergence characteristics, the basic differential search algorithm (DSA) is built with adaptive features in order to improve the diversification mechanism. Similarly, a gradient-free local search algorithm called the Nelder-Mead algorithm is also integrated with the proposed DSA in order to improve the intensification mechanism. The algorithm is further improved with dynamic sub superorganisms and is termed as dynamic hybrid adaptive DSA (DHADSA). This newly proposed version of DSA (DHADSA) maintains a very good balance between intensification and diversification and it is clearly reflected by superior convergence characteristics exhibited over the adaptive DSA and hybrid adaptive DSA. In order to improve the convergence characteristics, features like shrinking search space is also introduced. The conclusions drawn based on the numerical investigations carried out in this paper are as follows

1. The impact force identification algorithm presented in this paper provides a very accurate reconstruction of the impact force and also its spatial location even with limited measurements and noise corrupted signals.

2. The constrained optimization formulations attempted here for the first time found to be effective to solve the multi-modal problem associated with simultaneous identification of system parameters, impact force and its spatial location. Numerical simulation studies presented in this paper clearly reflects that the constrained optimization formulations are effective to improve the computational efficiency as well as convergence characteristics especially while dealing with noise corrupted time history responses from a limited number of sensors.

3. The DHADSA proposed in this paper for solving the complex constrained optimization problem associated with system and impact force identification converges much faster than hybrid adaptive DSA and the adaptive DSA. DHADSA is found to be effective while dealing with modelling errors, noise-corrupted measured time history responses.

4. Numerical simulation studies carried out using multiple impact loads clearly indicate that the proposed DHADSA can precisely reconstruct multiple impact loads acting at different spatial locations.

5. Unlike several popular meta-heuristic algorithms like differential evolution (DE), particle swarm optimization (PSO), ABC (Artificial Bee Colony)algorithm etc., the DHADS algorithm has no inclination to correctly go towards the best possible solution of the problem. For this reason, it has a successful search strategy for the solution of multimodal functions. Apart from this, DHADS algorithm may simultaneously use more than one individual, unlike DE and ABC algorithms. Further, the proposed DHADS algorithm is built with a higher degree of exploration capability through multi superorganisms concept and a higher degree of exploitation through neighbourhood search algorithm. These enhanced exploration and exploitation features with perfect balance contribute effectively for faster convergence of multi-modal problems without getting trapped in local optima. Another major advantage of the proposed DHADS algorithm lies in its simple algorithmic structure, which helps in easy implementation and also allows easy application for different practical engineering problems.

Acknowledgement

This paper is being published with the permission of Director, CSIR-Structural Engineering Research Centre, Taramani, Chennai.

Disclosure statement

No potential conflict of interest was reported by the authors.