The monotonicity method for the inverse crack scattering problem

Abstract

The monotonicity method for the inverse acoustic scattering problem is to understand the inclusion relation between an unknown object and artificial one by comparing the far field operator with the artificial operator. This paper introduces the development of this method to the inverse crack scattering problem. Our aim is to give the following two indicators: One (Theorem 1.1) is to determine whether an artificial small arc is contained in the unknown arc. The other one (Theorem 1.2) is whether an artificial large domain contains the unknown one. Finally, numerical examples based on Theorem 1.1 are given.

Keywords:

• Inverse scattering
• monotonicity method
• crack detection
• far field operator
• Helmholz equation

2010 AMS Subject Classification:

• 35R30

1. Introduction

Let $\mathrm{\Gamma }\subset {\mathbb{R}}^2$ be a smooth non-intersecting open arc, and we assume that Γ can be extended to an arbitrary smooth, simply connected, closed curve $\mathrm{\partial }\mathrm{\Omega }$ enclosing a bounded domain Ω in ${\mathbb{R}}^2$. Let k>0 be the wave number, and let $\theta \in {\mathbb{S}}^1$ be incident direction, where ${\mathbb{S}}^1=\{x\in {\mathbb{R}}^2:|x|=1\}$ denotes the unit sphere in ${\mathbb{R}}^2$. We consider the following direct scattering problem: For $\theta \in {\mathbb{S}}^1$ determine $u^s$ such that (1) $\begin{array}{rl}& \mathrm{\Delta }{u}^s+k^2{u}^s=0\mathrm{in}{\mathbb{R}}^2\setminus \mathrm{\Gamma },\end{array}$(1) (2) $\begin{array}{rl}& u^s=-{\mathrm{e}}^{ik\theta \cdot x}\mathrm{on}\mathrm{\Gamma }\end{array}$(2) (3) $\begin{array}{rl}& \underset{r\to \mathrm{\infty }}{lim}\sqrt{r}(\frac{\mathrm{\partial }{u}^s}{\mathrm{\partial }r}-ik{u}^s)=0,\end{array}$(3) where $r=|x|$, and (3(3) $\begin{array}{rl}& \underset{r\to \mathrm{\infty }}{lim}\sqrt{r}(\frac{\mathrm{\partial }{u}^s}{\mathrm{\partial }r}-ik{u}^s)=0,\end{array}$(3) ) is the Sommerfeld radiation condition. Precisely, this problem is understood in the variational form, that is, determine $u^s\in H_{loc}^1({\mathbb{R}}^2\setminus \overline{\mathrm{\Gamma }})$ satisfying $u^s{|}_{\mathrm{\Gamma }}=-{\mathrm{e}}^{ik\theta \cdot x}$, the Sommerfeld radiation condition (3(3) $\begin{array}{rl}& \underset{r\to \mathrm{\infty }}{lim}\sqrt{r}(\frac{\mathrm{\partial }{u}^s}{\mathrm{\partial }r}-ik{u}^s)=0,\end{array}$(3) ), and (4) ${\int }_{{\mathbb{R}}^2\setminus \mathrm{\Gamma }}[\mathrm{\nabla }{u}^s\cdot \mathrm{\nabla }\overline{\phi }-k^2{u}^s\overline{\phi }]\mathrm{d}x=0,$(4) for all $\phi \in H^1({\mathbb{R}}^2\setminus \overline{\mathrm{\Gamma }})$, $\phi {|}_{\mathrm{\Gamma }}=0$, with compact support. Here, $H_{loc}^1({\mathbb{R}}^2\setminus \overline{\mathrm{\Gamma }})=\{u:{\mathbb{R}}^2\setminus \overline{\mathrm{\Gamma }}\to \mathbb{C}:u{|}_{B\setminus \overline{\mathrm{\Gamma }}}\in H^1(B\setminus \overline{\mathrm{\Gamma }})\mathrm{for}\mathrm{all}\mathrm{open}\mathrm{balls}B\mathrm{including}\mathrm{\Gamma }\}$ denotes the local Sobolev space of one order.

It is well known that there exists a unique solution $u^s$ and it has the following asymptotic behaviour (see, e.g.[1]): (5) $u^s(x)=\frac{{\mathrm{e}}^{ikr}}{\sqrt{r}}\{u^{\mathrm{\infty }}(\hat{x},\theta )+O(1/r)\},r\to \mathrm{\infty },\hat{x}:=\frac{x}{|x|}.$(5) The function $u^{\mathrm{\infty }}$ is called the far field pattern of $u^s$. With the far field pattern $u^{\mathrm{\infty }}$, we define the far field operator $F:L^2({\mathbb{S}}^1)\to L^2({\mathbb{S}}^1)$ by (6) $Fg(\hat{x}):={\int }_{{\mathbb{S}}^1}{u}^{\mathrm{\infty }}(\hat{x},\theta )g(\theta )\mathrm{d}s(\theta ),\hat{x}\in {\mathbb{S}}^1.$(6) The inverse scattering problem we consider in this paper is to reconstruct the unknown arc Γ from the far field pattern $u^{\mathrm{\infty }}(\hat{x},\theta )$ for all $\hat{x}\in {\mathbb{S}}^1$, all $\hat{x}\in {\mathbb{S}}^1$ with one k>0. In other words, given the far field operator F, reconstruct Γ.

In order to solve such an inverse problem, we use the idea of the monotonicity method. The feature of this method is to understand the inclusion relation of an unknown object and artificial one by comparing the data operator with some operator corresponding to an artificial object. For electrical impedance tomography (EIT) we refer to [2], for the inverse boundary value problem for the Helmholtz equation we refer to [3 5], and for the inverse medium scattering problem we refer to [6,7].

Our aim in this paper is to provide the following two theorems.

Theorem 1.1

Let $\sigma \subset {\mathbb{R}}^2$ be a smooth non-intersecting open arc. Then, (7) $\sigma \subset \mathrm{\Gamma }⟺H_{\sigma }^{\ast }{H}_{\sigma }{\le }_{\mathrm{fin}}-\mathrm{Re}F,$(7) where the Herglotz operator $H_{\sigma }:L^2({\mathbb{S}}^1)\to L^2(\sigma )$ is given by (8) $H_{\sigma }g(x):={\int }_{{\mathbb{S}}^1}{\mathrm{e}}^{ik\theta \cdot x}g(\theta )\mathrm{d}s(\theta ),x\in \sigma ,$(8) and the inequality on the right-hand side in (7(7) $\sigma \subset \mathrm{\Gamma }⟺H_{\sigma }^{\ast }{H}_{\sigma }{\le }_{\mathrm{fin}}-\mathrm{Re}F,$(7) ) denotes that $-\mathrm{Re}F-H_{\sigma }^{\ast }{H}_{\sigma }$ has only finitely many negative eigenvalues, and the real part of an operator A is self-adjoint operators given by $\mathrm{Re}(A):=1/2(A+A^{\ast })$.

Theorem 1.2

Let $B\subset {\mathbb{R}}^2$ be a bounded open set. Then, (9) $\mathrm{\Gamma }\subset B⟺-\mathrm{Re}F{\le }_{\mathrm{fin}}{\tilde{H}}_{\mathrm{\partial }B}^{\ast }{\tilde{H}}_{\mathrm{\partial }B},$(9) where ${\tilde{H}}_{\mathrm{\partial }B}:L^2({\mathbb{S}}^1)\to H^{1/2}(\mathrm{\partial }B)$ is given by (10) ${\tilde{H}}_{\mathrm{\partial }B}g(x):={\int }_{{\mathbb{S}}^1}{\mathrm{e}}^{ik\theta \cdot x}g(\theta )\mathrm{d}s(\theta ),x\in \mathrm{\partial }B.$(10)

Theorem 1.1 determines whether an artificial open arc σ is contained in Γ or not. While, Theorem 1.2 determines an artificial domain B contains Γ. In two theorems we can understand Γ from the inside and outside.

This paper is organized as follows. In Section 2, we give a rigorous definition of the above inequality. Furthermore, we recall the properties of the far field operator and technical lemmas which are useful to prove main results. In Sections 3 and 4, we prove Theorems 1.1 and 1.2, respectively. In Section 5, we give numerical examples based on Theorem 1.1.

2. Preliminary

First, we give a rigorous definition of the inequality in Theorems 1.1 and 1.2.

Definition 2.1

Let $A,B:X\to X$ be self-adjoint compact linear operators on a Hilbert space X. We write (11) $A{\le }_{\mathrm{fin}}B,$(11) if B−A has only finitely many negative eigenvalues.

The following lemma was shown in Corollary 3.3 of [4].

Lemma 2.2

Let $A,B:X\to X$ be self-adjoint compact linear operators on a Hilbert space X with an inner product $⟨\cdot ,\cdot ⟩$. Then, the following statements are equivalent:

1. $A{\le }_{\mathrm{fin}}B$

2. There exists a finite dimensional subspace V in X such that (12) $⟨(B-A)v,v⟩\ge 0,$(12) for all $v\in V^{\mathrm{\perp }}$.

Secondly, we define several operators in order to mention properties of the far field operator F. The data-to-pattern operator $G:H^{1/2}(\mathrm{\Gamma })\to L^2({\mathbb{S}}^1)$ is defined by (13) $Gf:=v^{\mathrm{\infty }},$(13) where $v^{\mathrm{\infty }}$ is the far field pattern of a radiating solution v (that is, v satisfies the Sommerfeld radiation condition) such that (14) $\begin{array}{rl}\mathrm{\Delta }v+k^{2}v& =0\mathrm{in}{\mathbb{R}}^2\setminus \mathrm{\Gamma },\end{array}$(14) (15) $\begin{array}{rl}v& =f\mathrm{on}\mathrm{\Gamma }.\end{array}$(15) The following lemma was given by the same argument in Lemma 1.13 of [8].

Lemma 2.3

The data-to-pattern operator G is compact and injective.

We define the single layer boundary operator $S:{\tilde{H}}^{-1/2}(\mathrm{\Gamma })\to H^{1/2}(\mathrm{\Gamma })$ by (16) $S\phi (x):={\int }_{\mathrm{\Gamma }}\phi (y)\mathrm{\Phi }(x,y)\mathrm{d}s(y),x\in \mathrm{\Gamma },$(16) where $\mathrm{\Phi }(x,y)$ denotes the fundamental solution to Helmholtz equation in ${\mathbb{R}}^2$, i.e. (17) $\mathrm{\Phi }(x,y):=\frac{i}{4}{H}_0^{(1)}(k|x-y|),x\ne y.$(17) Here, we denote by (18) $\begin{array}{rl}{H}^{1/2}(\mathrm{\Gamma })& :=\{u{|}_{\mathrm{\Gamma }}:u\in H^{1/2}(\mathrm{\partial }\mathrm{\Omega })\},\end{array}$(18) (19) $\begin{array}{rl}{\tilde{H}}^{1/2}(\mathrm{\Gamma })& :=\{u\in H^{1/2}(\mathrm{\partial }\mathrm{\Omega }):\mathrm{supp}(u)\subset \overline{\mathrm{\Gamma }}\},\end{array}$(19) and $H^{-1/2}(\mathrm{\Gamma })$ and ${\tilde{H}}^{-1/2}(\mathrm{\Gamma })$ the dual spaces of ${\tilde{H}}^{1/2}(\mathrm{\Gamma })$ and $H^{1/2}(\mathrm{\Gamma })$, respectively. Then, we have the following inclusion relation: (20) ${\tilde{H}}^{1/2}(\mathrm{\Gamma })\subset H^{1/2}(\mathrm{\Gamma })\subset L^2(\mathrm{\Gamma })\subset {\tilde{H}}^{-1/2}(\mathrm{\Gamma })\subset H^{-1/2}(\mathrm{\Gamma }).$(20) For these details, we refer to [9]. The following two Lemmas was shown in Section 3 of [10].

Lemma 2.4

1. S is an isomorphism from ${\tilde{H}}^{-1/2}(\mathrm{\Gamma })$ onto $H^{1/2}(\mathrm{\Gamma })$.

2. Let $S_i$ be the boundary integral operator (16(16) $S\phi (x):={\int }_{\mathrm{\Gamma }}\phi (y)\mathrm{\Phi }(x,y)\mathrm{d}s(y),x\in \mathrm{\Gamma },$(16) ) corresponding to the wave number k = i. The operator $S_i$ is self-adjoint and coercive, i.e, there exists $c_0>0$ such that (21) $⟨\phi ,S_i\phi ⟩\ge c_0{\Vert \phi \Vert }_{{\tilde{H}}^{-1/2}(\mathrm{\Gamma })}^{2}forall\phi \in {\tilde{H}}^{-1/2}(\mathrm{\Gamma }),$(21) where $⟨\cdot ,\cdot ⟩$ denotes the duality pairing in $⟨{\tilde{H}}^{-1/2}(\mathrm{\Gamma }),H^{1/2}(\mathrm{\Gamma })⟩$.

3. $S-S_i$ is compact.

4. There exists a self-adjoint and positive square root $S_i^{1/2}:L^2(\mathrm{\Gamma })\to L^2(\mathrm{\Gamma })$ of $S_i$ which can be extended such that $S_i^{1/2}:{\tilde{H}}^{-1/2}(\mathrm{\Gamma })\to L^2(\mathrm{\Gamma })$ is an isomorphism and $S_i^{1/2\ast }{S}_i^{1/2}=S_i.$

Lemma 2.5

The far field operator F has the following factorization: (22) $F=-G{S}^{\ast }{G}^{\ast }.$(22) where $G^{\ast }:L^2({\mathbb{S}}^1)\to {\tilde{H}}^{-1/2}(\mathrm{\Gamma })$ and $S^{\ast }:{\tilde{H}}^{-1/2}(\mathrm{\Gamma })\to H^{1/2}(\mathrm{\Gamma })$ are the adjoints of G and S, respectively.

Thirdly, we recall the following technical lemmas which will be useful to prove Theorems 1.1 and 1.2. We refer to Lemma 4.6 and 4.7 in [4].

Lemma 2.6

Let X, Y, and Z be Hilbert spaces, and let $A:X\to Y$ and $B:X\to Z$ be bounded linear operators. Then, (23) $\mathrm{\exists }C>0:{\Vert Ax\Vert }^2\le C{\Vert Bx\Vert }^{2}forallx\in X⟺\mathrm{Ran}(A^{\ast })\subseteq \mathrm{Ran}(B^{\ast }).$(23)

Lemma 2.7

Let X, Y, $V\subset Z$ be subspaces of a vector space Z. If (24) $X\cap Y=\{0\},andX\subseteq Y+V,$(24) then $\dim (X)\le \dim (V)$.

3. Proof of Theorem 1.1

In Section 3, we will show Theorem 1.1. Let $\sigma \subset \mathrm{\Gamma }$. We denote by $R:L^2(\mathrm{\Gamma })\to L^2(\sigma )$ the restriction operator, $J:H^{1/2}(\mathrm{\Gamma })\to L^2(\mathrm{\Gamma })$ the compact embedding, and $H:L^2({\mathbb{S}}^1)\to L^2(\mathrm{\Gamma })$, $\hat{H}:L^2({\mathbb{S}}^1)\to H^{1/2}(\mathrm{\Gamma })$ the Herglotz operators, respectively. Since $e^{-ik\hat{x}\cdot y}$ is a far field pattern of $\mathrm{\Phi }(x,y)$, we have by definitions of G and S (25) $GS\phi (\hat{x})={\int }_{\mathrm{\Gamma }}{e}^{-ik\hat{x}\cdot y}\phi (y)\mathrm{d}s(y).$(25) The right-hand side is identical with ${\hat{H}}^{\ast }\phi (\hat{x})$ (see the proof of Lemma 3.4 in [10]). Then, we have ${\hat{H}}^{\ast }=GS$. By this equality we have (26) $\begin{array}{rl}{H}_{\sigma }& =RH\\ & =RJ\hat{H}\\ & =RJ{S}^{\ast }{G}^{\ast }.\end{array}$(26) Using (26(26) $\begin{array}{rl}{H}_{\sigma }& =RH\\ & =RJ\hat{H}\\ & =RJ{S}^{\ast }{G}^{\ast }.\end{array}$(26) ) and Lemmas 2.4 and 2.5, $-\mathrm{Re}F-H_{\sigma }^{\ast }{H}_{\sigma }$ has the following factorization: (27) $\begin{array}{rl}-\mathrm{Re}F-H_{\sigma }^{\ast }{H}_{\sigma }& =G[\mathrm{Re}S-S{J}^{\ast }{R}^{\ast }RJ{S}^{\ast }]G^{\ast }\\ & =G[S_i+\mathrm{Re}(S-S_i)-S{J}^{\ast }{R}^{\ast }RJ{S}^{\ast }]G^{\ast }\\ & =[G{W}^{\ast }]W^{\ast -1}[S_i+\mathrm{Re}(S-S_i)-S{J}^{\ast }{R}^{\ast }RJ{S}^{\ast }]W^{-1}[G{W}^{\ast }{]}^{\ast }\\ & =[G{W}^{\ast }][I_{L^2(\mathrm{\Gamma })}+K][G{W}^{\ast }{]}^{\ast },\end{array}$(27) where $W:=S_i^{1/2}:{\tilde{H}}^{-1/2}(\mathrm{\Gamma })\to L^2(\mathrm{\Gamma })$ is an extension of the square root of $S_i^{1/2}$, $K:=W^{\ast -1}[\mathrm{Re}(S-S_i)-S{J}^{\ast }{R}^{\ast }RJ{S}^{\ast }]W^{-1}:L^2(\mathrm{\Gamma })\to L^2(\mathrm{\Gamma })$ is self-adjoint compact, and $I_{L^2(\mathrm{\Gamma })}$ is the identity operator on $L^2(\mathrm{\Gamma })$. Let V be the sum of eigenspaces of K associated to eigenvalues less than $-1/2$. Then, V is a finite dimensional and (28) $⟨(I_{L^2(\mathrm{\Gamma })}+K)v,v⟩\ge 0,$(28) for all $v\in V^{\mathrm{\perp }}$. Since for $g\in L^2({\mathbb{S}}^1)$ (29) $[G{W}^{\ast }{]}^{\ast }g\in V^{\mathrm{\perp }}⟺g\in [(G{W}^{\ast })V{]}^{\mathrm{\perp }},$(29) and $\dim [(G{W}^{\ast })V]\le \dim (V)<\mathrm{\infty }$, we have by (28(28) $⟨(I_{L^2(\mathrm{\Gamma })}+K)v,v⟩\ge 0,$(28) ) and Lemma 2.2 that $H_{\sigma }^{\ast }{H}_{\sigma }{\le }_{\mathrm{fin}}-\mathrm{Re}F$.

Let now $\sigma \not\subset \mathrm{\Gamma }$ and assume on the contrary $H_{\sigma }^{\ast }{H}_{\sigma }{\le }_{\mathrm{fin}}-\mathrm{Re}F$, that is, by Lemma 2.2 there exists a finite dimensional subspace V in $L^2({\mathbb{S}}^1)$ such that (30) $⟨(-\mathrm{Re}F-H_{\sigma }^{\ast }{H}_{\sigma })v,v⟩\ge 0,$(30) for all $v\in V^{\mathrm{\perp }}$. Since $\sigma \not\subset \mathrm{\Gamma }$, we can take a small open arc ${\sigma }_0\subset \sigma$ such that ${\sigma }_0\cap \mathrm{\Gamma }=\mathrm{\varnothing }$, which implies that for all $v\in V^{\mathrm{\perp }}$ (31) $\begin{array}{rl}{\Vert H_{{\sigma }_0}v\Vert }_{L^2({\sigma }_0)}^2& \le {\Vert H_{\sigma }v\Vert }_{L^2(\sigma )}^2\\ & \le ⟨(-\mathrm{Re}F)v,v{⟩}_{L^2({\mathbb{S}}^1)}\\ & =⟨(\mathrm{Re}{S}^{\ast })G^{\ast }v,G^{\ast }v⟩\\ & \le \Vert \mathrm{Re}{S}^{\ast }\Vert {\Vert G^{\ast }v\Vert }^2.\end{array}$(31) Before showing a contradiction with (31(31) $\begin{array}{rl}{\Vert H_{{\sigma }_0}v\Vert }_{L^2({\sigma }_0)}^2& \le {\Vert H_{\sigma }v\Vert }_{L^2(\sigma )}^2\\ & \le ⟨(-\mathrm{Re}F)v,v{⟩}_{L^2({\mathbb{S}}^1)}\\ & =⟨(\mathrm{Re}{S}^{\ast })G^{\ast }v,G^{\ast }v⟩\\ & \le \Vert \mathrm{Re}{S}^{\ast }\Vert {\Vert G^{\ast }v\Vert }^2.\end{array}$(31) ), we will show the following lemma.

Lemma 3.1

1. $\dim (\mathrm{Ran}(H_{{\sigma }_0}^{\ast }))=\mathrm{\infty }$

2. $\mathrm{Ran}(G)\cap \mathrm{Ran}(H_{{\sigma }_0}^{\ast })=\{0\}$.

Proof of Lemma 3.1.

1. By the same argument in (26(26) $\begin{array}{rl}{H}_{\sigma }& =RH\\ & =RJ\hat{H}\\ & =RJ{S}^{\ast }{G}^{\ast }.\end{array}$(26) ) we have (32) $H_{{\sigma }_0}=J_{{\sigma }_0}{\hat{H}}_{{\sigma }_0}=J_{{\sigma }_0}{S}_{{\sigma }_0}^{\ast }{G}_{{\sigma }_0}^{\ast },$(32) where $G_{{\sigma }_0}:H^{1/2}({\sigma }_0)\to L^2({\mathbb{S}}^1)$, $S_{{\sigma }_0}:{\tilde{H}}^{-1/2}({\sigma }_0)\to H^{1/2}({\sigma }_0)$, and $J_{{\sigma }_0}:H^{1/2}({\sigma }_0)\to L^2({\sigma }_0)$ are the data-to-pattern operator, the single layer boundary operator, and the compact embedding, respectively, corresponding to ${\sigma }_0$. Since $H_{{\sigma }_0}^{\ast }=G_{{\sigma }_0}{S}_{{\sigma }_0}{J}_{{\sigma }_0}^{\ast }$, $\mathrm{Ran}(J_{{\sigma }_0}^{\ast })$ is dense, and $G_{{\sigma }_0}{S}_{{\sigma }_0}$ is injective (see Lemma 2.3 and (a) of Lemma 2.4.), we have $\dim (\mathrm{Ran}(H_{{\sigma }_0}^{\ast }))=\dim (\mathrm{Ran}(J_{{\sigma }_0}^{\ast }))=\mathrm{\infty }$.

2. By (32(32) $H_{{\sigma }_0}=J_{{\sigma }_0}{\hat{H}}_{{\sigma }_0}=J_{{\sigma }_0}{S}_{{\sigma }_0}^{\ast }{G}_{{\sigma }_0}^{\ast },$(32) ), we have $\mathrm{Ran}(H_{{\sigma }_0}^{\ast })\subset \mathrm{Ran}(G_{{\sigma }_0})$. Let $h\in \mathrm{Ran}(G)\cap \mathrm{Ran}(G_{{\sigma }_0})$, i.e. $h=v_{\mathrm{\Gamma }}^{\mathrm{\infty }}=v_{{\sigma }_0}^{\mathrm{\infty }}$ where $v_{\mathrm{\Gamma }}^{\mathrm{\infty }}$ and $v_{{\sigma }_0}^{\mathrm{\infty }}$ are far field patterns of the scattered field $v_{\mathrm{\Gamma }}$ and $v_{{\sigma }_0}$ associated to scatterers Γ and ${\sigma }_0$, respectively. Then by Rellich lemma and unique continuation we have $v_{\mathrm{\Gamma }}=v_{{\sigma }_0}\mathrm{in}{\mathbb{R}}^2\setminus (\mathrm{\Gamma }\cup {\sigma }_0)$. Hence, we can define $v\in H_{loc}^1({\mathbb{R}}^2)$ by (33) $v:=\{\begin{array}{ll}{v}_{\mathrm{\Gamma }}=v_{{\sigma }_0}& \text{in}{\mathbb{R}}^2\setminus (\mathrm{\Gamma }\cup {\sigma }_0)\\ v_{\mathrm{\Gamma }}& \text{on}{\sigma }_0\\ v_{{\sigma }_0}& \text{on}\mathrm{\Gamma }\end{array}$(33) and v is a radiating solution to (34) $\mathrm{\Delta }v+k^{2}v=0\mathrm{in}{\mathbb{R}}^2.$(34) Thus $v=0\mathrm{in}{\mathbb{R}}^2$, which implies that h = 0.

By the above lemma we have $\mathrm{\infty }=\dim (\mathrm{Ran}(H_{{\sigma }_0}^{\ast }))\nleqq \dim V<\mathrm{\infty }$ and $\mathrm{Ran}(H_{{\sigma }_0}^{\ast })\cap \mathrm{Ran}(G)=\{0\}$. By a contraposition of Lemma 2.7, we have (35) $\mathrm{Ran}(H_{{\sigma }_0}^{\ast })⊈\mathrm{Ran}(G)+V=\mathrm{Ran}(G,P_V),$(35) where $P_V:L^2({\mathbb{S}}^1)\to L^2({\mathbb{S}}^1)$ is the orthognal projection on V. Lemma 2.6 implies that for any C>0 there exists a $v_c$ such that (36) ${\Vert H_{{\sigma }_0}{v}_c\Vert }^2>C^2{\Vert \left(\begin{array}{c}{G}^{\ast }\\ P_V\end{array}\right)v_c\Vert }^2=C^2({\Vert G^{\ast }{v}_c\Vert }^2+{\Vert P_V{v}_c\Vert }^2).$(36) Hence, there exists a sequence $(v_m{)}_{m\in \mathbb{N}}\subset L^2({\mathbb{S}}^1)$ such that $\Vert H_{{\sigma }_0}{v}_m\Vert \to \mathrm{\infty }$ and $\Vert G^{\ast }{v}_m{\Vert }^2+\Vert P_V{v}_m\Vert \to 0$ as $m\to \mathrm{\infty }$. Setting ${\tilde{v}}_m:=v_m-P_V{v}_m\in V^{\mathrm{\perp }}$ we have as $m\to \mathrm{\infty }$, (37) $\begin{array}{rl}\Vert H_{{\sigma }_0}{\tilde{v}}_m\Vert & \ge \Vert H_{{\sigma }_0}{v}_m\Vert -\Vert H_{{\sigma }_0}\Vert \Vert P_V{v}_m\Vert \to \mathrm{\infty },\end{array}$(37) (38) $\begin{array}{rl}\Vert G^{\ast }{\tilde{v}}_m\Vert & \le \Vert G^{\ast }{v}_m\Vert +\Vert G^{\ast }\Vert \Vert P_V{v}_m\Vert \to 0.\end{array}$(38) This contradicts (31(31) $\begin{array}{rl}{\Vert H_{{\sigma }_0}v\Vert }_{L^2({\sigma }_0)}^2& \le {\Vert H_{\sigma }v\Vert }_{L^2(\sigma )}^2\\ & \le ⟨(-\mathrm{Re}F)v,v{⟩}_{L^2({\mathbb{S}}^1)}\\ & =⟨(\mathrm{Re}{S}^{\ast })G^{\ast }v,G^{\ast }v⟩\\ & \le \Vert \mathrm{Re}{S}^{\ast }\Vert {\Vert G^{\ast }v\Vert }^2.\end{array}$(31) ). Therefore, we have $H_{\sigma }^{\ast }{H}_{\sigma }{\nleqq }_{\mathrm{fin}}-\mathrm{Re}F$. Theorem 1.1 has been shown.

4. Proof of Theorem 1.2

In Section 4, we will show Theorem 1.2. Let $\mathrm{\Gamma }\subset B$. We denote by $G_{\mathrm{\partial }B}:H^{1/2}(\mathrm{\partial }B)\to L^2({\mathbb{S}}^1)$ and $S_{\mathrm{\partial }B}:H^{-1/2}(\mathrm{\partial }B)\to H^{1/2}(\mathrm{\partial }B)$ are the data-to-pattern operator and the single layer boundary operator, respectively corresponding to closed curve $\mathrm{\partial }B$. They have the same properties like Lemmas 2.3 and 2.4 and we have ${\tilde{H}}_{\mathrm{\partial }B}^{\ast }=G_{\mathrm{\partial }B}{S}_{\mathrm{\partial }B}$. (See, e.g. Lemma 1.14, Theorem 1.15 in [8].) We define $T:H^{1/2}(\mathrm{\Gamma })\to H^{1/2}(\mathrm{\partial }B)$ by (39) $Tf:=v{|}_{\mathrm{\partial }B},$(39) where v is a radiating solution such that (40) $\begin{array}{rl}\mathrm{\Delta }v+k^{2}v& =0\mathrm{in}{\mathbb{R}}^2\setminus \mathrm{\Gamma },\end{array}$(40) (41) $\begin{array}{rl}v& =f\mathrm{on}\mathrm{\Gamma }.\end{array}$(41) T is compact since its mapping is from $H^{1/2}(\mathrm{\Gamma })$ to $C^{\mathrm{\infty }}(\mathrm{\partial }B)$. Furthermore, by the definition of T we have that $G=G_{\mathrm{\partial }B}T$. Thus, we have (42) $\begin{array}{rl}{\tilde{H}}_{\mathrm{\partial }B}^{\ast }{\tilde{H}}_{\mathrm{\partial }B}+\mathrm{Re}F& =G_{\mathrm{\partial }B}{S}_{\mathrm{\partial }B}{S}_{\mathrm{\partial }B}^{\ast }{G}_{\mathrm{\partial }B}^{\ast }+G_{\mathrm{\partial }B}[-T\mathrm{Re}(S)T^{\ast }]G_{\mathrm{\partial }B}^{\ast }\\ & =G_{\mathrm{\partial }B}[S_{\mathrm{\partial }B,i}{S}_{\mathrm{\partial }B,i}^{\ast }+K]G_{\mathrm{\partial }B}^{\ast }\\ & =[G_{\mathrm{\partial }B}{W}^{\ast }][W^{\ast -1}{S}_{\mathrm{\partial }B,i}{S}_{\mathrm{\partial }B,i}^{\ast }{W}^{-1}+K^{\prime }][G_{\mathrm{\partial }B}{W}^{\ast }{]}^{\ast },\end{array}$(42) where K and $K^{\prime }$ are some self-adjoint compact operators, and $W:=S_{\mathrm{\partial }B,i}^{1/2}:H^{-1/2}(\mathrm{\partial }B)\to L^2(\mathrm{\partial }B)$ is an extension of the square root of $S_{\mathrm{\partial }B,i}$ where $S_{\mathrm{\partial }B,i}:{\tilde{H}}^{-1/2}(\mathrm{\partial }B)\to H^{1/2}(\mathrm{\partial }B)$ is the single layer boundary operator corresponding to $\mathrm{\partial }B$ and the wave number k = i. Let V be the sum of eigenspaces of $K^{\prime }$ associated to eigenvalues less than $-\frac{1}{2}\Vert (S_{\mathrm{\partial }B,i}^{\ast }{W}^{-1}{)}^{-1}{\Vert }^{-2}$. Then V is a finite dimensional, and for all $g\in [(G_{\mathrm{\partial }B}{W}^{\ast })V{]}^{\mathrm{\perp }}$ we have (43) $\begin{array}{rl}⟨({\tilde{H}}_{\mathrm{\partial }B}^{\ast }{\tilde{H}}_{\mathrm{\partial }B}+\mathrm{Re}F)g,g⟩& ={\Vert (S_{\mathrm{\partial }B,i}^{\ast }{W}^{-1})[G_{\mathrm{\partial }B}{W}^{\ast }{]}^{\ast }g\Vert }_{H^{1/2}(\mathrm{\partial }B)}^2\\ & +⟨K^{\prime }[G_{\mathrm{\partial }B}{W}^{\ast }{]}^{\ast }g,[G_{\mathrm{\partial }B}{W}^{\ast }{]}^{\ast }g{⟩}_{L^2(\mathrm{\partial }B)}\\ & \ge {\Vert (S_{\mathrm{\partial }B,i}^{\ast }{W}^{-1}{)}^{-1}\Vert }^{-2}{\Vert [G_{\mathrm{\partial }B}{W}^{\ast }{]}^{\ast }g\Vert }^2\\ & -\frac{1}{2}{\Vert (S_{\mathrm{\partial }B,i}^{\ast }{W}^{-1}{)}^{-1}\Vert }^{-2}{\Vert [G_{\mathrm{\partial }B}{W}^{\ast }{]}^{\ast }g\Vert }^2\\ & \ge 0.\end{array}$(43) Therefore, $-\mathrm{Re}F{\le }_{\mathrm{fin}}{\tilde{H}}_{\mathrm{\partial }B}^{\ast }{\tilde{H}}_{\mathrm{\partial }B}$.

Let now $\mathrm{\Gamma }\not\subset B$ and assume on the contrary $-\mathrm{Re}F{\le }_{\mathrm{fin}}{\tilde{H}}_{\mathrm{\partial }B}^{\ast }{\tilde{H}}_{\mathrm{\partial }B}$, i.e. by Lemma 2.2 there exists a finite dimensional subspace V in $L^2({\mathbb{S}}^1)$ such that (44) $⟨({\tilde{H}}_{\mathrm{\partial }B}^{\ast }{\tilde{H}}_{\mathrm{\partial }B}+\mathrm{Re}F)v,v⟩\ge 0,$(44) for all $v\in V^{\mathrm{\perp }}$. Since $\mathrm{\Gamma }\not\subset B$, we can take a small open arc ${\mathrm{\Gamma }}_0\subset \mathrm{\Gamma }$ such that ${\mathrm{\Gamma }}_0\cap B=\mathrm{\varnothing }$. We define $L:H^{1/2}({\mathrm{\Gamma }}_0)\to H^{1/2}(\mathrm{\Gamma })$ by (45) $Lf:=v{|}_{\mathrm{\Gamma }},$(45) where v is a radiating solution such that (46) $\begin{array}{rl}\mathrm{\Delta }v+k^{2}v& =0\mathrm{in}{\mathbb{R}}^2\setminus {\mathrm{\Gamma }}_0,\end{array}$(46) (47) $\begin{array}{rl}v& =f\mathrm{on}{\mathrm{\Gamma }}_0.\end{array}$(47) By the definition of L, we have $G_{{\mathrm{\Gamma }}_0}=GL$ where $G_{{\mathrm{\Gamma }}_0}:H^{1/2}({\mathrm{\Gamma }}_0)\to L^2({\mathbb{S}}^1)$ is the data-to-pattern operator corresponding to ${\mathrm{\Gamma }}_0$. We denote by $S_{{\mathrm{\Gamma }}_0}:{\tilde{H}}^{-1/2}({\mathrm{\Gamma }}_0)\to H^{1/2}({\mathrm{\Gamma }}_0)$ the single layer boundary operator corresponding to ${\mathrm{\Gamma }}_0$, and $H_{{\mathrm{\Gamma }}_0}:L^2({\mathbb{S}}^1)\to L^2({\mathrm{\Gamma }}_0)$, ${\hat{H}}_{{\mathrm{\Gamma }}_0}:L^2({\mathbb{S}}^1)\to H^{1/2}({\mathrm{\Gamma }}_0)$ the Herglotz operators corresponding to ${\mathrm{\Gamma }}_0$, respectively. By the same argument in (25(25) $GS\phi (\hat{x})={\int }_{\mathrm{\Gamma }}{e}^{-ik\hat{x}\cdot y}\phi (y)\mathrm{d}s(y).$(25) ) we have ${\hat{H}}_{{\mathrm{\Gamma }}_0}=S_{{\mathrm{\Gamma }}_0}^{\ast }{G}_{{\mathrm{\Gamma }}_0}^{\ast }$. Then, we have (48) $\begin{array}{rl}{\Vert H_{{\mathrm{\Gamma }}_0}x\Vert }_{L^2({\mathrm{\Gamma }}_0)}^2& \le {\Vert {\hat{H}}_{{\mathrm{\Gamma }}_0}x\Vert }_{H^{1/2}({\mathrm{\Gamma }}_0)}^2\\ & \le {\Vert S_{{\mathrm{\Gamma }}_0}^{\ast }\Vert }^2{\Vert G_{{\mathrm{\Gamma }}_0}^{\ast }x\Vert }^2\\ & \le {\Vert S_{{\mathrm{\Gamma }}_0}^{\ast }\Vert }^2{\Vert L^{\ast }\Vert }^2{\Vert G^{\ast }x\Vert }^2,\end{array}$(48) for $x\in L^2({\mathbb{S}}^1)$. Since $\mathrm{Re}S$ is of the form $\mathrm{Re}S=S_i+\mathrm{Re}(S-S_i)$, by the similar argument in (27(27) $\begin{array}{rl}-\mathrm{Re}F-H_{\sigma }^{\ast }{H}_{\sigma }& =G[\mathrm{Re}S-S{J}^{\ast }{R}^{\ast }RJ{S}^{\ast }]G^{\ast }\\ & =G[S_i+\mathrm{Re}(S-S_i)-S{J}^{\ast }{R}^{\ast }RJ{S}^{\ast }]G^{\ast }\\ & =[G{W}^{\ast }]W^{\ast -1}[S_i+\mathrm{Re}(S-S_i)-S{J}^{\ast }{R}^{\ast }RJ{S}^{\ast }]W^{-1}[G{W}^{\ast }{]}^{\ast }\\ & =[G{W}^{\ast }][I_{L^2(\mathrm{\Gamma })}+K][G{W}^{\ast }{]}^{\ast },\end{array}$(27) )–(28(28) $⟨(I_{L^2(\mathrm{\Gamma })}+K)v,v⟩\ge 0,$(28) ) and (42(42) $\begin{array}{rl}{\tilde{H}}_{\mathrm{\partial }B}^{\ast }{\tilde{H}}_{\mathrm{\partial }B}+\mathrm{Re}F& =G_{\mathrm{\partial }B}{S}_{\mathrm{\partial }B}{S}_{\mathrm{\partial }B}^{\ast }{G}_{\mathrm{\partial }B}^{\ast }+G_{\mathrm{\partial }B}[-T\mathrm{Re}(S)T^{\ast }]G_{\mathrm{\partial }B}^{\ast }\\ & =G_{\mathrm{\partial }B}[S_{\mathrm{\partial }B,i}{S}_{\mathrm{\partial }B,i}^{\ast }+K]G_{\mathrm{\partial }B}^{\ast }\\ & =[G_{\mathrm{\partial }B}{W}^{\ast }][W^{\ast -1}{S}_{\mathrm{\partial }B,i}{S}_{\mathrm{\partial }B,i}^{\ast }{W}^{-1}+K^{\prime }][G_{\mathrm{\partial }B}{W}^{\ast }{]}^{\ast },\end{array}$(42) )–(43(43) $\begin{array}{rl}⟨({\tilde{H}}_{\mathrm{\partial }B}^{\ast }{\tilde{H}}_{\mathrm{\partial }B}+\mathrm{Re}F)g,g⟩& ={\Vert (S_{\mathrm{\partial }B,i}^{\ast }{W}^{-1})[G_{\mathrm{\partial }B}{W}^{\ast }{]}^{\ast }g\Vert }_{H^{1/2}(\mathrm{\partial }B)}^2\\ & +⟨K^{\prime }[G_{\mathrm{\partial }B}{W}^{\ast }{]}^{\ast }g,[G_{\mathrm{\partial }B}{W}^{\ast }{]}^{\ast }g{⟩}_{L^2(\mathrm{\partial }B)}\\ & \ge {\Vert (S_{\mathrm{\partial }B,i}^{\ast }{W}^{-1}{)}^{-1}\Vert }^{-2}{\Vert [G_{\mathrm{\partial }B}{W}^{\ast }{]}^{\ast }g\Vert }^2\\ & -\frac{1}{2}{\Vert (S_{\mathrm{\partial }B,i}^{\ast }{W}^{-1}{)}^{-1}\Vert }^{-2}{\Vert [G_{\mathrm{\partial }B}{W}^{\ast }{]}^{\ast }g\Vert }^2\\ & \ge 0.\end{array}$(43) ), there exists a finite dimensional subspace W in $L^2({\mathbb{S}}^1)$ such that for $x\in W^{\mathrm{\perp }}$ (49) ${\Vert G^{\ast }x\Vert }^2\le C⟨(\mathrm{Re}S)G^{\ast }x,G^{\ast }x⟩=C⟨(-\mathrm{Re}F)x,x⟩.$(49) Collecting (48(48) $\begin{array}{rl}{\Vert H_{{\mathrm{\Gamma }}_0}x\Vert }_{L^2({\mathrm{\Gamma }}_0)}^2& \le {\Vert {\hat{H}}_{{\mathrm{\Gamma }}_0}x\Vert }_{H^{1/2}({\mathrm{\Gamma }}_0)}^2\\ & \le {\Vert S_{{\mathrm{\Gamma }}_0}^{\ast }\Vert }^2{\Vert G_{{\mathrm{\Gamma }}_0}^{\ast }x\Vert }^2\\ & \le {\Vert S_{{\mathrm{\Gamma }}_0}^{\ast }\Vert }^2{\Vert L^{\ast }\Vert }^2{\Vert G^{\ast }x\Vert }^2,\end{array}$(48) ), (49(49) ${\Vert G^{\ast }x\Vert }^2\le C⟨(\mathrm{Re}S)G^{\ast }x,G^{\ast }x⟩=C⟨(-\mathrm{Re}F)x,x⟩.$(49) ), and ${\tilde{H}}_{\mathrm{\partial }B}^{\ast }=G_{\mathrm{\partial }B}{S}_{\mathrm{\partial }B}$, we have (50) $\begin{array}{rl}{\Vert H_{{\mathrm{\Gamma }}_0}x\Vert }^2& \le C⟨(-\mathrm{Re}F)x,x⟩\le C{\Vert {\tilde{H}}_{\mathrm{\partial }B}x\Vert }^2\\ & \le C{\Vert S_{\mathrm{\partial }B}^{\ast }\Vert }^2{\Vert G_{\mathrm{\partial }B}^{\ast }x\Vert }_{H^{-1/2}(\mathrm{\partial }B)}^2.\end{array}$(50) for $x\in (V\cup W{)}^{\mathrm{\perp }}$.

Lemma 4.1

1. $\dim (\mathrm{Ran}(H_{{\mathrm{\Gamma }}_0}^{\ast }))=\mathrm{\infty }$

2. $\mathrm{Ran}(G_{\mathrm{\partial }B})\cap \mathrm{Ran}(H_{{\mathrm{\Gamma }}_0}^{\ast })=\{0\}$.

Proof of Lemma 4.1.

1. is given by the same argument in Lemma 3.1.

2. Since (32(32) $H_{{\sigma }_0}=J_{{\sigma }_0}{\hat{H}}_{{\sigma }_0}=J_{{\sigma }_0}{S}_{{\sigma }_0}^{\ast }{G}_{{\sigma }_0}^{\ast },$(32) ) replacing ${\sigma }_0$ by ${\mathrm{\Gamma }}_0$ holds, by taking a conjugation in (32(32) $H_{{\sigma }_0}=J_{{\sigma }_0}{\hat{H}}_{{\sigma }_0}=J_{{\sigma }_0}{S}_{{\sigma }_0}^{\ast }{G}_{{\sigma }_0}^{\ast },$(32) ) we have $\mathrm{Ran}(H_{{\mathrm{\Gamma }}_0}^{\ast })\subset \mathrm{Ran}(G_{{\mathrm{\Gamma }}_0})$. Let $h\in \mathrm{Ran}(G_{\mathrm{\partial }B})\cap \mathrm{Ran}(G_{{\mathrm{\Gamma }}_0})$, i.e. $h=v_B^{\mathrm{\infty }}=v_{{\mathrm{\Gamma }}_0}^{\mathrm{\infty }}$ where $v_B^{\mathrm{\infty }}$ and $v_{{\mathrm{\Gamma }}_0}^{\mathrm{\infty }}$ are far field patterns of the scattered field $v_B$ and $v_{{\mathrm{\Gamma }}_0}$ associated to scatterers B and ${\mathrm{\Gamma }}_0$, respectively. Then by Rellich lemma and unique continuation we have $v_B=v_{{\mathrm{\Gamma }}_0}\mathrm{in}{\mathbb{R}}^2\setminus (B\cup {\mathrm{\Gamma }}_0)$. Hence, we can define $v\in H_{loc}^1({\mathbb{R}}^2)$ by (51) $v:=\{\begin{array}{ll}{v}_B=v_{{\mathrm{\Gamma }}_0}& \text{in}{\mathbb{R}}^2\setminus (B\cup {\mathrm{\Gamma }}_0)\\ v_{{\mathrm{\Gamma }}_0}& \text{on}B\\ v_B& \text{on}{\mathrm{\Gamma }}_0\end{array}$(51) and v is a radiating solution to (52) $\mathrm{\Delta }v+k^{2}v=0\mathrm{in}{\mathbb{R}}^2.$(52) Thus $v=0\mathrm{in}{\mathbb{R}}^2$, which implies that h = 0.

By the above lemma we have $\mathrm{\infty }=\dim (\mathrm{Ran}(H_{{\mathrm{\Gamma }}_0}^{\ast }))\nleqq \dim (V\cup W)<\mathrm{\infty }$ and $\mathrm{Ran}(H_{{\mathrm{\Gamma }}_0}^{\ast })\cap \mathrm{Ran}(G_{\mathrm{\partial }B})=\{0\}$. By a contraposition of Lemma 2.7, we have (53) $\mathrm{Ran}(H_{{\mathrm{\Gamma }}_0}^{\ast })⊈\mathrm{Ran}(G_{\mathrm{\partial }B})+(V\cup W)=\mathrm{Ran}(G_{\mathrm{\partial }B},P_{V\cup W}),$(53) where $P_{V\cup W}:L^2({\mathbb{S}}^1)\to L^2({\mathbb{S}}^1)$ is the orthognal projection on $V\cup W$. Lemma 2.6 implies that for any C>0 there exists a $x_c$ such that (54) ${\Vert H_{{\mathrm{\Gamma }}_0}{x}_c\Vert }^2>C^2{\Vert \left(\begin{array}{c}{G}_{\mathrm{\partial }B}^{\ast }\\ P_{V\cup W}\end{array}\right)x_c\Vert }^2=C^2({\Vert G_{\mathrm{\partial }B}^{\ast }{x}_c\Vert }^2+{\Vert P_{V\cup W}{x}_c\Vert }^2).$(54) Hence, there exists a sequence $(x_m{)}_{m\in \mathbb{N}}\subset L^2({\mathbb{S}}^1)$ such that $\Vert H_{{\mathrm{\Gamma }}_0}{x}_m\Vert \to \mathrm{\infty }$ and $\Vert G_{\mathrm{\partial }B}^{\ast }{x}_m{\Vert }^2+\Vert P_{V\cup W}{x}_m\Vert \to 0$ as $m\to \mathrm{\infty }$. Setting ${\tilde{x}}_m:=x_m-P_{V\cup W}{x}_m\in (V\cup W{)}^{\mathrm{\perp }}$ we have as $m\to \mathrm{\infty }$, (55) $\begin{array}{rl}\Vert H_{{\mathrm{\Gamma }}_0}{\tilde{x}}_m\Vert & \ge \Vert H_{{\mathrm{\Gamma }}_0}{x}_m\Vert -\Vert H_{{\mathrm{\Gamma }}_0}\Vert \Vert P_{V\cup W}{x}_m\Vert \to \mathrm{\infty },\end{array}$(55) (56) $\begin{array}{rl}\Vert G_{\mathrm{\partial }B}^{\ast }{\tilde{x}}_m\Vert & \le \Vert G_{\mathrm{\partial }B}^{\ast }{x}_m\Vert +\Vert G_{\mathrm{\partial }B}^{\ast }\Vert \Vert P_{V\cup W}{x}_m\Vert \to 0.\end{array}$(56) This contradicts (50(50) $\begin{array}{rl}{\Vert H_{{\mathrm{\Gamma }}_0}x\Vert }^2& \le C⟨(-\mathrm{Re}F)x,x⟩\le C{\Vert {\tilde{H}}_{\mathrm{\partial }B}x\Vert }^2\\ & \le C{\Vert S_{\mathrm{\partial }B}^{\ast }\Vert }^2{\Vert G_{\mathrm{\partial }B}^{\ast }x\Vert }_{H^{-1/2}(\mathrm{\partial }B)}^2.\end{array}$(50) ). Therefore, we have $-\mathrm{Re}F{\nleqq }_{\mathrm{fin}}{\tilde{H}}_{\mathrm{\partial }B}^{\ast }{\tilde{H}}_{\mathrm{\partial }B}$. Theorem 1.2 has been shown.

5. Numerical examples

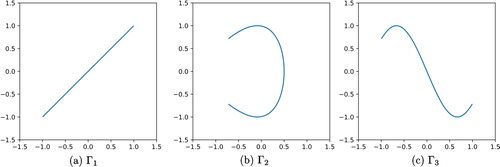
In Section 5, we discuss the numerical examples based on Theorem 1.1. The following three open arcs ${\mathrm{\Gamma }}_j$ (j = 1, 2, 3) are considered. (see Figure 1)

Figure 1. The original open arc.

1. ${\mathrm{\Gamma }}_1=\{(s,s)|-1\le s\le 1\}$

2. ${\mathrm{\Gamma }}_2=\{(2\sin (\frac{\pi }{8}+(1+s)\frac{3\pi }{8})-\frac{2}{3},\sin (\frac{\pi }{4}+(1+s)\frac{3\pi }{4})|-1\le s\le 1\}$

3. ${\mathrm{\Gamma }}_3=\{(s,\sin (\frac{\pi }{4}+(1+s)\frac{3\pi }{4})|-1\le s\le 1\}$

Based on Theorem 1.1, the indicator function in our examples is given by (57) $I(\sigma ):=\mathrm{\#}\{\mathrm{negative}\mathrm{eigenvalues}\mathrm{of}-\mathrm{Re}F-H_{\sigma }^{\ast }{H}_{\sigma }\}.$(57) The idea to reconstruct ${\mathrm{\Gamma }}_j$ is to plot the value of $I(\sigma )$ for many of small σ in the sampling region. Then, we expect from Theorem 1.1 that the value of the function $I(\sigma )$ is low if σ is close to ${\mathrm{\Gamma }}_j$.

Here, σ is chosen in two ways; One is the vertical line segment ${\sigma }_{i,j}^{\mathrm{ver}}:=z_{i,j}+\{0\}\times [-\frac{R}{2M},\frac{R}{2M}]$ where $z_{i,j}:=(\frac{Ri}{M},\frac{Rj}{M})$ ($i,j=-M,-M+1,\dots ,M$) denote the centre of ${\sigma }_{i,j}^{\mathrm{ver}}$, and $\frac{R}{M}$ is the length of ${\sigma }_{i,j}^{\mathrm{ver}}$, and R>0 is length of sampling square region $[-R,R{]}^2$, and $M\in \mathbb{N}$ is large to take a small segment. The other is horizontal one ${\sigma }_{i,j}^{\mathrm{hor}}:=z_{i,j}+[-\frac{R}{2M},\frac{R}{2M}]\times \{0\}$.

The far field operator F is approximated by the matrix (58) $F\approx \frac{2\pi }{N}(u^{\mathrm{\infty }}({\hat{x}}_l,{\theta }_m){)}_{1\le l,m\le N}\in {\mathbb{C}}^{N\times N},$(58) where ${\hat{x}}_l=(\cos (\frac{2\pi l}{N}),\sin (\frac{2\pi l}{N}))$ and ${\theta }_m=(\cos (\frac{2\pi m}{N}),\sin (\frac{2\pi m}{N}))$. The far field pattern $u^{\mathrm{\infty }}$ of the problem (1(1) $\begin{array}{rl}& \mathrm{\Delta }{u}^s+k^2{u}^s=0\mathrm{in}{\mathbb{R}}^2\setminus \mathrm{\Gamma },\end{array}$(1) )–(3(3) $\begin{array}{rl}& \underset{r\to \mathrm{\infty }}{lim}\sqrt{r}(\frac{\mathrm{\partial }{u}^s}{\mathrm{\partial }r}-ik{u}^s)=0,\end{array}$(3) ) is computed by the Nyström method in [11]. The operator $H_{\sigma }^{\ast }{H}_{\sigma }$ is approximated by (59) $H_{\sigma }^{\ast }{H}_{\sigma }\approx \frac{2\pi }{N}({\int }_{\sigma }{e}^{iky\cdot ({\theta }_m-{\hat{x}}_l)}dy{)}_{1\le l,m\le N}\in {\mathbb{C}}^{N\times N}.$(59) When σ is given by the vertical and horizontal line segment, we can compute the integrals (60) $\begin{array}{rl}{\int }_{{\sigma }_{i,j}^{\mathrm{ver}}}{e}^{iky\cdot ({\theta }_m-{\hat{x}}_l)}dy& =\frac{R}{M}{e}^{ik({\theta }_m-{\hat{x}}_l)\cdot z_{i,j}}\mathrm{sinc}(\frac{kR}{2M\pi }(\sin \left(\frac{2\pi m}{N}\right)-\sin \left(\frac{2\pi l}{N}\right))),\end{array}$(60) (61) $\begin{array}{rl}{\int }_{{\sigma }_{i,j}^{\mathrm{hor}}}{e}^{iky\cdot ({\theta }_m-{\hat{x}}_l)}dy& =\frac{R}{M}{e}^{ik({\theta }_m-{\hat{x}}_l)\cdot z_{i,j}}\mathrm{sinc}(\frac{kR}{2M\pi }(\cos \left(\frac{2\pi m}{N}\right)-\cos \left(\frac{2\pi l}{N}\right))).\end{array}$(61)

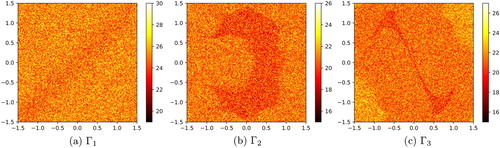
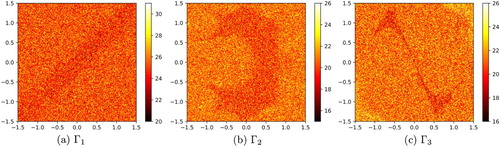
In our examples we fix R = 1.5, M = 100, N = 60, and wavenumber k = 1. Figure 2 is given by plotting the values of the vertical indicator function (62) $I_{\mathrm{ver}}(z_{i,j}):=I({\sigma }_{i,j}^{\mathrm{ver}}),$(62) for each $i,j=-100,99,\dots ,100$. Figure 3 is given by plotting the values of the horizontal indicator function (63) $I_{\mathrm{hor}}(z_{i,j}):=I({\sigma }_{i,j}^{\mathrm{hor}}),$(63) for each $i,j=-100,-99,\dots ,100$. We obverse that ${\mathrm{\Gamma }}_j$ seems to be reconstructed independently of the direction of linear segment.

Figure 2. Reconstruction by the vertical indicator function $I_{\mathrm{ver}}$.

Figure 3. Reconstruction by the horizontal indicator function $I_{\mathrm{hor}}$.

Acknowledgments

Authors thank to Professor Bastian von Harrach, who gave us helpful comments in our study.

Disclosure statement

No potential conflict of interest was reported by the author(s).

ORCID

Takashi Furuya http://orcid.org/0000-0001-6132-6846