A backward problem for distributed order diffusion equation: uniqueness and numerical solution

Abstract

In this paper we consider the identification of the initial condition for a distributed order diffusion equation. We first prove the unique existence and the regularity properties of the strong solution on the bounded temporal-spacial domain based on the eigenfunction expansions. The ill-posedness of the backward problem is interpreted by the compactness of the observation operator. Next the Laplace transformation technique and analytic continuation method are adopted to prove the uniqueness of the backward problem. Then for stabilizing the ill-posed problem, the backward problem is formulated as a Tikhonov type optimization problems, and the conjugate gradient method is adopted to solve the optimization problem with the help of the variational adjoint technique. Finally four numerical examples are given to show the efficiency and stability of the proposed method.

Keywords:

• Backward problem
• distributed order
• Laplace transformation
• uniqueness
• conjugate gradient method

2000 MR Subject Classifications:

• 65M06
• 65M12
• 65M32

1. Introduction

Research during the past several decades on the anomalous diffusion equation, especially about the time fractional diffusion equation with a single-term temporal derivative, has been widely carried out by large numbers researchers due to the extensive application in describing the dynamics of physical processes involving anomalous diffusion mechanism. For example, fractional diffusion has been successfully used to modelling diffusion process in media with fractal geometry [1], highly heterogeneous aquifer [2] and underground water pollution problem [3]. Accompanying by the numerous application of the fractional order diffusion equation, many researchers have developed different numerical methods to approximate the solution of the time-fractional diffusion equation. We refer the interested reader to [4–6] for the finite element methods, [7–10] for the finite difference methods, [11,12] for the spectral methods, etc.

In order to archive more accuracy description for some complex anomalous diffusion process with fractional order equations, many researchers detect that whose orders of the fractional derivatives may change in time and/or spatial coordinates. This yields the time-fractional diffusion equations of distributed order. The distributed order fractional derivative was firstly introduced by Caputo [13], which is an integral of fractional derivatives with respect to the order on a finite interval. There are some mathematical researches to the initial-boundary value problems of the distributed order diffusion equation. The existence and the uniqueness of the solution to distributed order initial-boundary value problem was derived by the variables separation method and the maximum principle, respectively, in [14]. Kochubei [15] investigated the existence and the asymptotics of the solutions to the Cauchy problems for both the partial and the ordinary fractional differential equations with distributed order derivatives. Li et al. [16] established the existence, uniqueness and analyticity of the solution to a distributed order time-fractional diffusion equation by adopting the Laplace transform and the eigenfunctions expansion method. In [17], existence, uniqueness and regularity of the solution to the distributed order time-fractional diffusion model were given. Li et al. [18] investigated some important asymptotic behaviour of solutions to initial-boundary-value problems for distributed order time fractional diffusion equations initial-boundary value problem in multi-dimensional domains.

Meanwhile, the numerical solution methods to the distributed order diffusion equation have been extensively studied, such as finite element methods [19–22], reproducing kernel method [23], spectral methods [24], and finite difference methods, see, for example, [25–30]. The idea of numerical approximation of the above mentioned numerical methods for distributed order diffusion equation is that the distributed order diffusion equation is reasonably approximated as the multi-term fractional differential equation. Essentially, the multi-term fractional differential equation is the particular case of the distributed order diffusion equation, in which the weight function is taken in form of a finite linear combination of the Dirac δ-functions with the positive weight coefficient. Henceforth, the numerical methods for the multi-term fractional differential equations are valuable to the approximation methods for the distributed order diffusion equation. Considering the numerical approximation method for the multi-term fractional diffusion equation, we refer the interested readers to [31–34].

Corresponding to the research of the direct problem of the diffusion equation with the distributed order, the inverse problems of the distributed order diffusion equation are attracting considerable attention of many researchers. Li et al. [35] investigated the uniqueness of determining the weight function in the distributed order time derivative by a Harnack type inequality of the solution in the frequency domain with one point observation. Applying the Stone-Weierstrass and M$\ddot{u}$ntz-S$\acute{z}$asz theorems, [17] considered the uniqueness of identifying the weight function in 1-D time-fractional diffusion equation of distributed order under an important representation theorem by one point observation data or the flux at one point. Li et al. [16] proved the uniqueness of recovering the weight function of distributed order time derivative by Laplace transformation with one point observation data. Zhang and Liu [36] considered a time-dependent inverse source problem from a nonlocal integral observation.

In this paper, we consider the following one-dimensional distributed order initial boundary value problem (1) ${\mathbb{D}}_t^{(\mu )}u={\mathrm{\partial }}_x(a(x){\mathrm{\partial }}_{x}u(x,t))-c(x)u(x,t)+f(x,t),x\in (0,l),t>0,$(1) with homogeneous Neumann boundary condition (2) $\frac{\mathrm{\partial }u}{\mathrm{\partial }x}{|}_{x=0}=\frac{\mathrm{\partial }u}{\mathrm{\partial }x}{|}_{x=l}=0,t>0,$(2) and initial condition (3) $u(x,0)=\phi (x),x\in [0,l],$(3) where $a(x)\in C^1[0,l],c(x)\in C[0,l],a(x)\ge a_0>0,c(x)\ge 0,\mathrm{\forall }x\in [0,l]$. ${\mathbb{D}}_t^{(\mu )}u$ is the distributed order fractional derivative defined by (4(4) ${\mathbb{D}}_t^{(\mu )}F(t)={\int }_0^1{\mathrm{\partial }}_t^{\alpha }F(t)\mu (\alpha )\mathrm{d}\alpha ,t>0,$(4) ). (4) ${\mathbb{D}}_t^{(\mu )}F(t)={\int }_0^1{\mathrm{\partial }}_t^{\alpha }F(t)\mu (\alpha )\mathrm{d}\alpha ,t>0,$(4) where μ is a non-negative and continuous weighted function, and ${\mathrm{\partial }}_t^{\alpha }$ is the left Caputo derivative of order α defined as follows ${\mathrm{\partial }}_t^{\alpha }F(t)=\{\begin{array}{ll}F(t),& \alpha =0,\\ {\displaystyle \frac{1}{\mathrm{\Gamma }(1-\alpha )}}{\int }_0^t{\displaystyle \frac{F^{\prime }(\tau )}{(t-\tau {)}^{\alpha }}}\mathrm{d}\tau ,& 0<\alpha <1,\\ F^{\prime }(t),& \alpha =1.\end{array}$ Here we consider the restructure problem of the initial function $\phi (x)$ by the measurement $g^{\delta }(t)$ at the left end point, which is the noise-contaminated data for the exact value $g(t)=u[\phi ](0,t)$: (5) $\Vert g^{\delta }(\cdot )-g(\cdot ){\Vert }_{L^2(0,T)}\le \delta ,$(5) where δ is some known error level. For backward problem of the time fractional diffusion equation, we refer the interested readers to references [37–39].

As the initial-boundary value problem (1(1) ${\mathbb{D}}_t^{(\mu )}u={\mathrm{\partial }}_x(a(x){\mathrm{\partial }}_{x}u(x,t))-c(x)u(x,t)+f(x,t),x\in (0,l),t>0,$(1) )–(3(3) $u(x,0)=\phi (x),x\in [0,l],$(3) ) is a linear problem, the principle of superposition holds. Without loss of generality, we assume the governing equation (1(1) ${\mathbb{D}}_t^{(\mu )}u={\mathrm{\partial }}_x(a(x){\mathrm{\partial }}_{x}u(x,t))-c(x)u(x,t)+f(x,t),x\in (0,l),t>0,$(1) ) is homogeneous, i.e. $f(x,t)=0$. Next, we organize the rest of the paper as follows. In Section 2, regularizing properties of the solution to the direct problem and ill-posedness analysis to the inverse problem are presented. The uniqueness of identifying the initial condition is given in Section 3. The backward problem is transformed into a regularization optimization problem of Tikhonov-type, and the conjugate gradient algorithm is proposed to solve the regularization problem in Section 4. Finally several numerical examples are investigated in Section 5.

2. Regularity of solution for the direct problem and ill-posedness analysis for the backward problem

By $a(x)\ge a_0>0,c(x)\ge 0,\mathrm{\forall }x\in [0,l]$, we know that the differentiation operator $-L(u)=-{\mathrm{\partial }}_x(a(x){\mathrm{\partial }}_{x}u)+c(x)u$ is a symmetric uniformly elliptic operator. Hence the spectrum of operator $-L$ only includes the counting eigenvalues. Let $\{{\lambda }_k,{\varphi }_k(x)\},k=1,\dots ,$ be the eigensystem of $-L$. For convenience of derivation, we take ${\varphi }_k$ satisfying ${\varphi }_k(0)=1$ and set ${\varrho }_k=\Vert {\varphi }_k(x){\Vert }_{L^2(\mathrm{\Omega })}^{-2},k=1,\dots$. From [40], we see that ${\varrho }_k=c_0+o(1)$.

We know that the sequence $\{{\varphi }_k(x){\}}_{k=0}^{\mathrm{\infty }}$ forms an orthogonal basis in $L^2(0,l)$. We define a fractional power $(-L{)}^{\gamma }$ of $-L$ as follow $D((-L{)}^{\gamma })=\{\psi :\sum _{k=1}^{\mathrm{\infty }}{\lambda }_k^{2\gamma }{\varrho }_k|<\psi ,{\varphi }_k>{|}^2<\mathrm{\infty }\},$ where the symbol $<\cdot ,\cdot >$ represents the inner products in $L^2(0,l)$. $D((-L{)}^{\gamma })$ becomes a Hilbert space equipped with the following norm: $\Vert \psi {\Vert }_{D((-L{)}^{\gamma })}={\{\sum _{k=1}^{\mathrm{\infty }}{\lambda }_k^{2\gamma }{\varrho }_k|<\psi ,{\varphi }_k>{|}^2\}}^{1/2}.$ We have $D((-L{)}^{\gamma })\subset L^2(0,l)$ for $\gamma \ge 0$.

2.1. Regularity of solution for the direct problem

Before establishing the regularity estimation of the solution to the direct problem, we first define a strong solution to problem (1(1) ${\mathbb{D}}_t^{(\mu )}u={\mathrm{\partial }}_x(a(x){\mathrm{\partial }}_{x}u(x,t))-c(x)u(x,t)+f(x,t),x\in (0,l),t>0,$(1) )–(3(3) $u(x,0)=\phi (x),x\in [0,l],$(3) ) as follows.

Definition 2.1

We say that u is a strong solution to the initial-boundary value problem (1(1) ${\mathbb{D}}_t^{(\mu )}u={\mathrm{\partial }}_x(a(x){\mathrm{\partial }}_{x}u(x,t))-c(x)u(x,t)+f(x,t),x\in (0,l),t>0,$(1) )–(3(3) $u(x,0)=\phi (x),x\in [0,l],$(3) ) with f = 0 if (1) hold in $L^2(0,l)$ and $u(x,t)\in H^2(0,l)$ for almost all $t\in (0,T)$, and $u(x,t)\in C([0,T];L^2(0,l))$, and (2(2) $\frac{\mathrm{\partial }u}{\mathrm{\partial }x}{|}_{x=0}=\frac{\mathrm{\partial }u}{\mathrm{\partial }x}{|}_{x=l}=0,t>0,$(2) ) holds for all $t\in [0,T]$, $\underset{t\to 0}{lim}\Vert u(\cdot ,t)-\phi \Vert =0$.

In order to prove the existence of a unique strong solution to the direct problem (1(1) ${\mathbb{D}}_t^{(\mu )}u={\mathrm{\partial }}_x(a(x){\mathrm{\partial }}_{x}u(x,t))-c(x)u(x,t)+f(x,t),x\in (0,l),t>0,$(1) )–(3(3) $u(x,0)=\phi (x),x\in [0,l],$(3) ), we first consider the properties of the following ordinary distributed fractional order differentiation equation. (6) $\begin{array}{ll}& {\mathbb{D}}_t^{(\mu )}v(t)=-\lambda v(t),\lambda >0,t>0,\\ & v(0)=1.\end{array}$(6) Applying Laplace transform to (6(6) $\begin{array}{ll}& {\mathbb{D}}_t^{(\mu )}v(t)=-\lambda v(t),\lambda >0,t>0,\\ & v(0)=1.\end{array}$(6) ), we get ${\hat{v}}_{\lambda }(s){\int }_0^1{s}^{\alpha }\mu (\alpha )\mathrm{d}\alpha +\lambda {\hat{v}}_{\lambda }(s)={\int }_0^1{s}^{\alpha -1}\mu (\alpha )\mathrm{d}\alpha ,\mathfrak{R}s>M,$ where ${\hat{v}}_{\lambda }(s)$ is the phase function of the Laplace transformation for v. Solving the above algebraic equation, we have ${\hat{v}}_{\lambda }(s)=\frac{w(s)}{sw(s)+\lambda },\mathfrak{R}s>M,$ where auxiliary function $w(s)$ is defined as follows $w(s)={\int }_0^1{s}^{\alpha -1}\mu (\alpha )\mathrm{d}\alpha ={\int }_0^1{\mathrm{e}}^{(\alpha -1)\log s}\mu (\alpha )\mathrm{d}\alpha .$ By cutting along the negative part of the real axis, we can extend the function $w(s)$ to an analytic function by taking the principal value of the logarithmic function on the complex plane with the cut. Meanwhile, it is easy to know that the function $\hat{v}(s)$ has no singularities on the main sheet of the Riemann surface for the logarithmic function. As matter of fact, for $s=r{\mathrm{e}}^{i\rho },\rho \in (-\pi ,\pi )$, the imaginary part of $sw(s)$, i.e. $\mathfrak{I}(sw(s))={\int }_0^1{r}^{\alpha }\mu (\alpha )\sin (\alpha \rho )\mathrm{d}\alpha$ is equal to zero only if $\rho =\arg s=0$. If $\rho =0$ and $\lambda >0$, we have $sw(s)+\lambda ={\int }_0^1{r}^{\alpha }\mu (\alpha )\mathrm{d}\alpha +\lambda >0$. Therefore, ${\hat{v}}_{\lambda }(s)$ is an analytic function on the main sheet of the Riemann surface of the complex plane cut along the negative part of the real axis. Next, we go to analyse the regularity of the solution to problem (1(1) ${\mathbb{D}}_t^{(\mu )}u={\mathrm{\partial }}_x(a(x){\mathrm{\partial }}_{x}u(x,t))-c(x)u(x,t)+f(x,t),x\in (0,l),t>0,$(1) )–(3(3) $u(x,0)=\phi (x),x\in [0,l],$(3) ). Based on the idea of reference [18], we firstly define a useful contour $\gamma (ϵ,\theta )$ including three parts on the complex plane as follows

1. arg $s=-\theta$, $s\ge ϵ$,

2. $-\theta \le$ arg s $\le \theta$, $|s|=ϵ$,

3. arg $s=\theta$, $s\ge ϵ$,

where $\theta \in (\pi /2,\pi ).$ For the completeness, we introduce the Lemmas 2.1 and  2.2 which are proved in reference [15] and in reference [18], respectively.

Lemma 2.1

[15]

If $\lambda >0$ and $\mu (1)\ne 0,$ the solution $v_{\lambda }(t)$ to (6(6) $\begin{array}{ll}& {\mathbb{D}}_t^{(\mu )}v(t)=-\lambda v(t),\lambda >0,t>0,\\ & v(0)=1.\end{array}$(6) ) is continuous at the origin t, completely monotone and belongs to $C^{\mathrm{\infty }}(0,\mathrm{\infty })$.

Lemma 2.2

[18]

If $\mu (\alpha )\in C[0,1]$ is a non-negative function satisfying $\mu (0)>0,$ we have $|w(s)|\le \Vert \mu {\Vert }_{C[0,1]}\frac{|s|-1}{|s|\log |s|},s\in \gamma (ϵ,\theta )$ and $|sw(s)+\lambda |\ge \{\begin{array}{ll}{\displaystyle \frac{\lambda }{2}},& |s|\le {\displaystyle \frac{\lambda }{2\Vert \mu {\Vert }_{C[0,1]}}},\\ C,& |s|\ge {\displaystyle \frac{\lambda }{2\Vert \mu {\Vert }_{C[0,1]}}},\end{array}$ where $\lambda \ge c_0=2\Vert \mu {\Vert }_{C[0,1]}$ and C>0 is a constant independent of λ and s.

With the help of the above lemma, we go to estimate the solution to problem (6(6) $\begin{array}{ll}& {\mathbb{D}}_t^{(\mu )}v(t)=-\lambda v(t),\lambda >0,t>0,\\ & v(0)=1.\end{array}$(6) ).

Theorem 2.1

If $\lambda \ge c_0>0$ and $\mu (0)\mu (1)\ne 0,$ there exists a unique solution $v(t)$ to (6(6) $\begin{array}{ll}& {\mathbb{D}}_t^{(\mu )}v(t)=-\lambda v(t),\lambda >0,t>0,\\ & v(0)=1.\end{array}$(6) ), satisfying $|v(t)|\le (C/(\lambda t{)}^{\overline{\theta }}),\mathrm{\forall }\overline{\theta }\in (0,1],t\in (0,T]$.

Proof.

By Fourier–Mellin formula (see e.g. [41]), we obtain $v_{\lambda }(t)={\displaystyle \frac{1}{2\pi i}}{\int }_{M-i\mathrm{\infty }}^{M+i\mathrm{\infty }}{\hat{v}}_{\lambda }(s){\mathrm{e}}^{st}\mathrm{d}s.$ Applying the residue theorem, for t>0 we know that the inverse Laplace transform of ${\hat{v}}_{\lambda }(s)$ can be reformulated as the following integral along the contour $v_{\lambda }(t)={\displaystyle \frac{1}{2\pi i}}{\int }_{\gamma (ϵ,\theta )}{\hat{v}}_{\lambda }(s){\mathrm{e}}^{st}\mathrm{d}s={\displaystyle \frac{1}{2\pi i}}{\int }_{\gamma (ϵ,\theta )}{\displaystyle \frac{w(s)}{sw(s)+\lambda }}{\mathrm{e}}^{st}\mathrm{d}s.$ If $\lambda \ge c_0=2\Vert \mu {\Vert }_{C[0,1]}$, by the additivity of integration, we have (7) $\begin{array}{rl}|v_{\lambda }(t)|& \le \left|{\displaystyle \frac{1}{2\pi i}}{\int }_{\gamma (\theta ,ϵ)\cap \{|s|=ϵ\}}{\displaystyle \frac{w(s)}{sw(s)+\lambda }}{\mathrm{e}}^{st}\mathrm{d}s\right|+\left|{\displaystyle \frac{1}{2\pi i}}{\int }_{\gamma (\theta ,ϵ)\cap \{ϵ<|s|\le \frac{\lambda }{c_0}\}}{\displaystyle \frac{w(s)}{sw(s)+\lambda }}{\mathrm{e}}^{st}\mathrm{d}s\right|\\ & +\left|{\displaystyle \frac{1}{2\pi i}}{\int }_{\gamma (\theta ,ϵ)\cap \{|s|>\frac{\lambda }{c_0}\}}{\displaystyle \frac{w(s)}{sw(s)+\lambda }}{\mathrm{e}}^{st}\mathrm{d}s\right|:=\sum _{j=1}^3|J_j(t)|.\end{array}$(7) Writing the complex variable s as $s=ϵ{\mathrm{e}}^{-i\rho }$, by Lemma 2.2 and $\lambda \ge c_0$, we have (8) $\begin{array}{rl}|J_1(t)|& \le \frac{1}{2\pi }{\int }_{\gamma (\theta ,ϵ)\cap \{|s|=ϵ\}}\left|\frac{w(s)}{sw(s)+\lambda }{\mathrm{e}}^{st}\right||\mathrm{d}s|\\ & \le \frac{1}{2\pi }{\int }_{\gamma (\theta ,ϵ)\cap \{|s|=ϵ\}}\left|\frac{w(s)}{sw(s)+\lambda }{\mathrm{e}}^{st}\mathrm{d}s\right|\le \overline{C}{\int }_{-\theta }^{\theta }\frac{\frac{1}{-ϵ\log ϵ}}{\lambda }{\mathrm{e}}^{ϵt\cos (\rho )}ϵ\mathrm{d}\rho \\ & \le C\frac{1}{-\lambda \log ϵ}{\int }_{-\theta }^{\theta }{\mathrm{e}}^{ϵt\cos (\rho )}\mathrm{d}\rho \le \frac{2C\theta }{\lambda }{\mathrm{e}}^{ϵt}\le \frac{2C\theta }{\lambda }{\mathrm{e}}^{ϵT}\\ & \le \frac{\overline{C}{\mathrm{e}}^{ϵT}(\lambda t{)}^{\overline{\theta }}}{(\lambda t{)}^{\overline{\theta }}\lambda }\le \frac{\overline{C}{\mathrm{e}}^{ϵT}{T}^{\overline{\theta }}}{(\lambda t{)}^{\overline{\theta }}{\lambda }^{1-\overline{\theta }}}\le \frac{\overline{C}{\mathrm{e}}^{ϵT}{T}^{\overline{\theta }}}{(\lambda t{)}^{\overline{\theta }}{c}_0^{1-\overline{\theta }}}\le \frac{C}{(\lambda t{)}^{\overline{\theta }}},t\in (0,T].\end{array}$(8) Similarly, by the additivity of integration, we have $|J_2(t)|\le \frac{\overline{C}}{\lambda }{\int }_{ϵ}^{{\mathrm{e}}^{-1}}\frac{r-1}{r\log r}{\mathrm{e}}^{rt\cos \theta }\mathrm{d}\mathrm{r}+\frac{\overline{C}}{\lambda }{\int }_{{\mathrm{e}}^{-1}}^{\frac{\lambda }{c_0}}\frac{r-1}{r\log r}{\mathrm{e}}^{rt\cos \theta }\mathrm{d}\mathrm{r}:=K_1(t)+K_2(t).$ If $ϵ\ll 1$, we have $\log (|\log (ϵ)|)<|\log (ϵ)|\le 1/ϵ$. By direct derivation, we get $\begin{array}{rl}|K_1(t)|& \le \frac{\overline{C}}{\lambda }{\int }_{ϵ}^{{\mathrm{e}}^{-1}}\frac{1}{r|\log r|}\mathrm{d}\mathrm{r}=\frac{\overline{C}}{\lambda }(\log (|\log ϵ|)-\log (|\log {\mathrm{e}}^{-1}|))\\ & \le \frac{\overline{C}}{\lambda }|\log ϵ|\le \frac{\overline{C}}{\lambda ϵ}.\end{array}$ Let ${ϵ}_0$ be a sufficiently small positive constant. We set $ϵ=({ϵ}_{0}t{)}^{\overline{\theta }}$, $t\in (0,T]$. Therefore, we have $|K_1(t)|\le \frac{C}{\lambda t^{\overline{\theta }}}.$ Obviously, we have $((r-1)r\log r)\le C$ if $r>{\mathrm{e}}^{-1}$ and ${\mathrm{e}}^{-r}\le r^{-\overline{\theta }}$ if $r\ge 0$ and $\overline{\theta }\in (0,1]$, which yields the following inequalities $|K_2(t)|\le \frac{\overline{C}}{\lambda }{\int }_{{\mathrm{e}}^{-1}}^{\frac{\lambda }{c_0}}\frac{r-1}{r\log r}{\mathrm{e}}^{rt\cos \theta }\mathrm{d}\mathrm{r}\le \frac{C}{t^{\overline{\theta }}{\lambda }^{\overline{\theta }}}.$ Collecting the above two inequalities, we obtain (9) $J_2(t)\le \frac{C}{(t\lambda {)}^{\overline{\theta }}},t\in (0,T].$(9) Next, we consider the last integral $J_3(t)$. (10) $\begin{array}{rl}|J_3(t)|& =|\frac{1}{2\pi i}{\int }_{\gamma (\theta ,ϵ)\cap \{|s|>\frac{\lambda }{c_0}\}}\frac{w(s)}{sw(s)+\lambda }\mathrm{d}\mathrm{s}|\\ & \le \overline{C}{\int }_{\frac{\lambda }{c_0}}^{\mathrm{\infty }}\frac{\frac{r-1}{r\log r}}{\sqrt{({\int }_0^1{r}^{\alpha }\mu (\alpha )\cos (\theta \alpha )\mathrm{d}\alpha +\lambda {)}^2+{({\int }_0^1{r}^{\alpha }\mu (\alpha )\sin (\theta \alpha )\mathrm{d}\alpha )}^2}}{\mathrm{e}}^{rt\cos (\theta )}\mathrm{d}\mathrm{r}\end{array}$(10) As μ is a non-negative and continuous weighted function on $[0,1]$ and meets $\mu (1)\ne 0$, there exists a constant ${\delta }_0\in (0,1)$ such that $\mu (\alpha )>0,\mathrm{\forall }\alpha \in [{\delta }_0,1]$. Then for any $s\in \gamma (ϵ,\theta )$, we have $\mathfrak{I}(sw(s))={\int }_0^1{r}^{\alpha }\mu (\alpha )\sin (\alpha \rho )\mathrm{d}\alpha \ge {\int }_{{\delta }_0}^1{r}^{\alpha }\mu (\alpha )\sin (\alpha \rho )\mathrm{d}\alpha \ge C\frac{r-r^{{\delta }_0}}{\log r}.$ For $r\ge (\lambda /c_0)\ge 1$, we have $\frac{r-1}{r\log r}\le \frac{C}{\log r}\mathrm{and}\frac{r-r^{{\delta }_0}}{\log r}>\frac{Cr}{\log r}.$ By (10(10) $\begin{array}{rl}|J_3(t)|& =|\frac{1}{2\pi i}{\int }_{\gamma (\theta ,ϵ)\cap \{|s|>\frac{\lambda }{c_0}\}}\frac{w(s)}{sw(s)+\lambda }\mathrm{d}\mathrm{s}|\\ & \le \overline{C}{\int }_{\frac{\lambda }{c_0}}^{\mathrm{\infty }}\frac{\frac{r-1}{r\log r}}{\sqrt{({\int }_0^1{r}^{\alpha }\mu (\alpha )\cos (\theta \alpha )\mathrm{d}\alpha +\lambda {)}^2+{({\int }_0^1{r}^{\alpha }\mu (\alpha )\sin (\theta \alpha )\mathrm{d}\alpha )}^2}}{\mathrm{e}}^{rt\cos (\theta )}\mathrm{d}\mathrm{r}\end{array}$(10) ), we have (11) $\begin{array}{rl}|J_3(t)|& \le \overline{C}{\int }_{\frac{\lambda }{c_0}}^{\mathrm{\infty }}\frac{1}{\sqrt{(\log r{\int }_0^1{r}^{\alpha }\mu (\alpha )\cos (\theta \alpha )\mathrm{d}\alpha +\log r\lambda {)}^2+r^2}}{\mathrm{e}}^{rt\cos (\theta )}\mathrm{d}\mathrm{r}\\ & \le \frac{\overline{C}}{(\cos (\theta ){)}^{\overline{\theta }}}{\int }_{\frac{\lambda }{c_0}}^{\mathrm{\infty }}\frac{1}{r}(rt{)}^{-\overline{\theta }}\mathrm{d}\mathrm{r}\le \frac{\overline{C}}{(\cos (\theta ){)}^{\overline{\theta }}}{t}^{-\overline{\theta }}{\int }_{\frac{\lambda }{c_0}}^{\mathrm{\infty }}{r}^{-\overline{\theta }-1}\mathrm{d}\mathrm{r}\le \frac{C}{(\lambda t{)}^{\overline{\theta }}},t\in (0,T].\end{array}$(11) From (8(8) $\begin{array}{rl}|J_1(t)|& \le \frac{1}{2\pi }{\int }_{\gamma (\theta ,ϵ)\cap \{|s|=ϵ\}}\left|\frac{w(s)}{sw(s)+\lambda }{\mathrm{e}}^{st}\right||\mathrm{d}s|\\ & \le \frac{1}{2\pi }{\int }_{\gamma (\theta ,ϵ)\cap \{|s|=ϵ\}}\left|\frac{w(s)}{sw(s)+\lambda }{\mathrm{e}}^{st}\mathrm{d}s\right|\le \overline{C}{\int }_{-\theta }^{\theta }\frac{\frac{1}{-ϵ\log ϵ}}{\lambda }{\mathrm{e}}^{ϵt\cos (\rho )}ϵ\mathrm{d}\rho \\ & \le C\frac{1}{-\lambda \log ϵ}{\int }_{-\theta }^{\theta }{\mathrm{e}}^{ϵt\cos (\rho )}\mathrm{d}\rho \le \frac{2C\theta }{\lambda }{\mathrm{e}}^{ϵt}\le \frac{2C\theta }{\lambda }{\mathrm{e}}^{ϵT}\\ & \le \frac{\overline{C}{\mathrm{e}}^{ϵT}(\lambda t{)}^{\overline{\theta }}}{(\lambda t{)}^{\overline{\theta }}\lambda }\le \frac{\overline{C}{\mathrm{e}}^{ϵT}{T}^{\overline{\theta }}}{(\lambda t{)}^{\overline{\theta }}{\lambda }^{1-\overline{\theta }}}\le \frac{\overline{C}{\mathrm{e}}^{ϵT}{T}^{\overline{\theta }}}{(\lambda t{)}^{\overline{\theta }}{c}_0^{1-\overline{\theta }}}\le \frac{C}{(\lambda t{)}^{\overline{\theta }}},t\in (0,T].\end{array}$(8) ), (9(9) $J_2(t)\le \frac{C}{(t\lambda {)}^{\overline{\theta }}},t\in (0,T].$(9) ) and (11(11) $\begin{array}{rl}|J_3(t)|& \le \overline{C}{\int }_{\frac{\lambda }{c_0}}^{\mathrm{\infty }}\frac{1}{\sqrt{(\log r{\int }_0^1{r}^{\alpha }\mu (\alpha )\cos (\theta \alpha )\mathrm{d}\alpha +\log r\lambda {)}^2+r^2}}{\mathrm{e}}^{rt\cos (\theta )}\mathrm{d}\mathrm{r}\\ & \le \frac{\overline{C}}{(\cos (\theta ){)}^{\overline{\theta }}}{\int }_{\frac{\lambda }{c_0}}^{\mathrm{\infty }}\frac{1}{r}(rt{)}^{-\overline{\theta }}\mathrm{d}\mathrm{r}\le \frac{\overline{C}}{(\cos (\theta ){)}^{\overline{\theta }}}{t}^{-\overline{\theta }}{\int }_{\frac{\lambda }{c_0}}^{\mathrm{\infty }}{r}^{-\overline{\theta }-1}\mathrm{d}\mathrm{r}\le \frac{C}{(\lambda t{)}^{\overline{\theta }}},t\in (0,T].\end{array}$(11) ), we have $|v(t)|\le \frac{C}{(\lambda t{)}^{\overline{\theta }}},\mathrm{\forall }\overline{\theta }\in (0,1],t\in (0,T]\mathrm{if}\lambda \ge c_0=2\Vert \mu {\Vert }_{C[0,1]}.$ Next, we consider the case of ${\lambda }_0<\lambda \le c_0=2\Vert \mu {\Vert }_{C[0,1]}$. Obviously, there exists a constant $r_1>1$ and $C_0>0$ that meets the condition $|sw(s)+\lambda |>C_0>0$ for any $s\in \gamma (\theta ,ϵ)$ such that $|s|\le r_1$. Similarly, by the additivity of integration, we have (12) $\begin{array}{rl}|v_{\lambda }(t)|& \le \left|\frac{1}{2\pi i}{\int }_{\gamma (\theta ,ϵ)\cap \{|s|=ϵ\}}\frac{w(s)}{sw(s)+\lambda }{\mathrm{e}}^{st}\mathrm{d}s\right|+\left|\frac{1}{2\pi i}{\int }_{\gamma (\theta ,ϵ)\cap \{ϵ<|s|\le r_1\}}\frac{w(s)}{sw(s)+\lambda }{\mathrm{e}}^{st}\mathrm{d}s\right|\\ & +\left|\frac{1}{2\pi i}{\int }_{\gamma (\theta ,ϵ)\cap \{|s|>r_1\}}\frac{w(s)}{sw(s)+\lambda }{\mathrm{e}}^{st}\mathrm{d}s\right|:=\sum _{j=1}^3{\overline{J}}_j(t).\end{array}$(12) By Lemma 2.2, we get (13) $\begin{array}{rl}|{\overline{J}}_1(t)|& \le \frac{1}{2\pi }{\int }_{\gamma (\theta ,ϵ)\cap \{|s|=ϵ\}}\left|\frac{w(s)}{sw(s)+\lambda }{\mathrm{e}}^{st}\mathrm{d}s\right|\le \frac{1}{2\pi C_0}{\int }_{-\theta }^{\theta }\Vert \mu {\Vert }_{C[0,1]}\frac{ϵ-1}{ϵ\log ϵ}{\mathrm{e}}^{ϵt\cos (\rho )}ϵ\mathrm{d}\rho \\ & \le \frac{c_0}{4\pi C_0}{\int }_{-\theta }^{\theta }\frac{1}{-\log ϵ}{\mathrm{e}}^{ϵt\cos (\rho )}\mathrm{d}\rho \le \frac{c_0}{4\pi C_0}{\int }_{-\theta }^{\theta }{\mathrm{e}}^{ϵt\cos (\rho )}\mathrm{d}\rho \\ & \le \frac{c_0}{4\pi C_0}{\int }_{-\theta }^{\theta }{\mathrm{e}}^{ϵt}\mathrm{d}\rho \le \frac{c_0\theta }{2\pi C_0}{\mathrm{e}}^{ϵt}\\ & \le \frac{c_0\theta T^{\overline{\theta }}}{2\pi C_0{t}^{\overline{\theta }}}{\mathrm{e}}^{ϵT}\le \frac{C_T}{t^{\overline{\theta }}},t\in (0,T].\end{array}$(13) Obviously, we have $|{\overline{J}}_2(t)|\le \overline{C}({\int }_{ϵ}^{{\mathrm{e}}^{-1}}\frac{r-1}{r\log r}{\mathrm{e}}^{rt\cos \theta }\mathrm{d}\mathrm{r}+{\int }_{{\mathrm{e}}^{-1}}^{r_1}\frac{r-1}{r\log r}{\mathrm{e}}^{rt\cos \theta }\mathrm{d}\mathrm{r}).$ Let $ϵ=({ϵ}_{0}t{)}^{\overline{\theta }}$, by direct estimation, we have $\begin{array}{rl}\overline{C}{\int }_{ϵ}^{{\mathrm{e}}^{-1}}\frac{r-1}{r\log r}{\mathrm{e}}^{rt\cos \theta }\mathrm{d}\mathrm{r}& \le -\overline{C}{\int }_{ϵ}^{{\mathrm{e}}^{-1}}\frac{1}{\log r}{\mathrm{e}}^{rt\cos \theta }\mathrm{d}\log \mathrm{r}\le \overline{C}\log |\log ϵ|\le \overline{C}|\log ϵ|\\ & \le \frac{\overline{C}}{ϵ}\le \frac{\overline{C}}{({ϵ}_{0}t{)}^{\overline{\theta }}}\le \frac{C}{t^{\overline{\theta }}}.{\int }_{{\mathrm{e}}^{-1}}^{r_1}\frac{r-1}{r\log r}{\mathrm{e}}^{rt\cos \theta }\mathrm{d}\mathrm{r}\le \overline{C}{\int }_{{\mathrm{e}}^{-1}}^{r_1}{\mathrm{e}}^{rt\cos \theta }\mathrm{d}\mathrm{r}\\ & \le \overline{C}{\int }_{{\mathrm{e}}^{-1}}^{r_1}|rt\cos \theta {|}^{-\overline{\theta }}\mathrm{d}\mathrm{r}\le \frac{C}{t^{\overline{\theta }}}.\end{array}$ So, we obtain (14) $|{\overline{J}}_2(t)|\le C\frac{1}{t^{\overline{\theta }}}.$(14) Since $r\ge r_1>1$, we have (15) $\begin{array}{rl}& \frac{r-1}{r\log r}\le \frac{C}{\log r},\frac{r-r^{{\delta }_0}}{\log r}>\frac{Cr}{\log r}and{\mathrm{e}}^{rt\cos (\theta )}\le |\cos (\theta )rt{|}^{-\overline{\theta }}.\\ & |{\overline{J}}_3(t)|\le \overline{C}{\int }_{r_1}^{\mathrm{\infty }}\frac{\frac{r-1}{r\log r}{\mathrm{e}}^{rt\cos \theta }}{\sqrt{({\int }_0^1{r}^{\alpha }\mu (\alpha )\cos (\theta \alpha )\mathrm{d}\alpha +{\lambda }_n{)}^2+(\frac{r-r^{{\delta }_0}}{\log r}{)}^2}}\mathrm{d}r\\ & \phantom{|{\overline{J}}_3(t)|}\le \overline{C}{\int }_{r_1}^{\mathrm{\infty }}\frac{{\mathrm{e}}^{rt\cos \theta }}{r}\mathrm{d}r\le \frac{C}{t^{\overline{\theta }}}.\end{array}$(15) By $0<{\lambda }_0<\lambda \le c_0$ and (13(13) $\begin{array}{rl}|{\overline{J}}_1(t)|& \le \frac{1}{2\pi }{\int }_{\gamma (\theta ,ϵ)\cap \{|s|=ϵ\}}\left|\frac{w(s)}{sw(s)+\lambda }{\mathrm{e}}^{st}\mathrm{d}s\right|\le \frac{1}{2\pi C_0}{\int }_{-\theta }^{\theta }\Vert \mu {\Vert }_{C[0,1]}\frac{ϵ-1}{ϵ\log ϵ}{\mathrm{e}}^{ϵt\cos (\rho )}ϵ\mathrm{d}\rho \\ & \le \frac{c_0}{4\pi C_0}{\int }_{-\theta }^{\theta }\frac{1}{-\log ϵ}{\mathrm{e}}^{ϵt\cos (\rho )}\mathrm{d}\rho \le \frac{c_0}{4\pi C_0}{\int }_{-\theta }^{\theta }{\mathrm{e}}^{ϵt\cos (\rho )}\mathrm{d}\rho \\ & \le \frac{c_0}{4\pi C_0}{\int }_{-\theta }^{\theta }{\mathrm{e}}^{ϵt}\mathrm{d}\rho \le \frac{c_0\theta }{2\pi C_0}{\mathrm{e}}^{ϵt}\\ & \le \frac{c_0\theta T^{\overline{\theta }}}{2\pi C_0{t}^{\overline{\theta }}}{\mathrm{e}}^{ϵT}\le \frac{C_T}{t^{\overline{\theta }}},t\in (0,T].\end{array}$(13) ), (14(14) $|{\overline{J}}_2(t)|\le C\frac{1}{t^{\overline{\theta }}}.$(14) ) and (15(15) $\begin{array}{rl}& \frac{r-1}{r\log r}\le \frac{C}{\log r},\frac{r-r^{{\delta }_0}}{\log r}>\frac{Cr}{\log r}and{\mathrm{e}}^{rt\cos (\theta )}\le |\cos (\theta )rt{|}^{-\overline{\theta }}.\\ & |{\overline{J}}_3(t)|\le \overline{C}{\int }_{r_1}^{\mathrm{\infty }}\frac{\frac{r-1}{r\log r}{\mathrm{e}}^{rt\cos \theta }}{\sqrt{({\int }_0^1{r}^{\alpha }\mu (\alpha )\cos (\theta \alpha )\mathrm{d}\alpha +{\lambda }_n{)}^2+(\frac{r-r^{{\delta }_0}}{\log r}{)}^2}}\mathrm{d}r\\ & \phantom{|{\overline{J}}_3(t)|}\le \overline{C}{\int }_{r_1}^{\mathrm{\infty }}\frac{{\mathrm{e}}^{rt\cos \theta }}{r}\mathrm{d}r\le \frac{C}{t^{\overline{\theta }}}.\end{array}$(15) ), we have (16) $v_{\lambda }(t)\le \frac{C}{(\lambda t{)}^{\overline{\theta }}},\mathrm{\forall }\overline{\theta }\in (0,1],t\in (0,T].$(16) This finishes the proof of theorem.

Theorem 2.2

If $\phi (x)\in L^2(0,l),$ then there exists a unique strong solution to (1(1) ${\mathbb{D}}_t^{(\mu )}u={\mathrm{\partial }}_x(a(x){\mathrm{\partial }}_{x}u(x,t))-c(x)u(x,t)+f(x,t),x\in (0,l),t>0,$(1) )–(3(3) $u(x,0)=\phi (x),x\in [0,l],$(3) ) and the solution $u(x,t)$ can be represented as follows (17) $u(x,t)=\sum _{k=1}^{\mathrm{\infty }}{\phi }_k{\varrho }_k{u}_{{\lambda }_k}(t){\varphi }_k(x),x\in [0,l],t\in [0,T],$(17) where ${\phi }_k$ is the Fourier coefficient of $\phi (x)$, i.e. ${\phi }_k=<\phi ,{\varphi }_k(x)>,$ and $u_{{\lambda }_k}(t)=\frac{1}{2\pi i}{\int }_{\gamma (\theta ,ϵ)}\frac{w(s)}{sw(s)+{\lambda }_k},k=1,\dots ,\mathrm{\infty }.$ Moreover, we have the following estimates $\begin{array}{rl}\Vert u{\Vert }_{C([0,T];L^2(0,l))}& \le \Vert \phi {\Vert }_{L^2(0,l)},\\ \Vert u{\Vert }_{L^2(0,T;D((-L{)}^{\gamma }))}& \le C\Vert \phi {\Vert }_{L^2(0,l)},0<\gamma <\frac{1}{2},\\ \Vert {\mathbb{D}}_t^{(\mu )}u(\cdot ,t){\Vert }_{L^2(0,l)}+\Vert u(\cdot ,t){\Vert }_{H^2(0,l)}& \le \frac{C}{t}\Vert \phi {\Vert }_{L^2(0,l)},\mathrm{\forall }t\in (0,T].\end{array}$

Proof.

Applying the separation of variables, we can derive a solution of series form to the direct problem (1(1) ${\mathbb{D}}_t^{(\mu )}u={\mathrm{\partial }}_x(a(x){\mathrm{\partial }}_{x}u(x,t))-c(x)u(x,t)+f(x,t),x\in (0,l),t>0,$(1) )–(3(3) $u(x,0)=\phi (x),x\in [0,l],$(3) ) as (17(17) $u(x,t)=\sum _{k=1}^{\mathrm{\infty }}{\phi }_k{\varrho }_k{u}_{{\lambda }_k}(t){\varphi }_k(x),x\in [0,l],t\in [0,T],$(17) )(see (3.1) in [18]). We will verify that (17(17) $u(x,t)=\sum _{k=1}^{\mathrm{\infty }}{\phi }_k{\varrho }_k{u}_{{\lambda }_k}(t){\varphi }_k(x),x\in [0,l],t\in [0,T],$(17) ) certainly means a strong solution to (1(1) ${\mathbb{D}}_t^{(\mu )}u={\mathrm{\partial }}_x(a(x){\mathrm{\partial }}_{x}u(x,t))-c(x)u(x,t)+f(x,t),x\in (0,l),t>0,$(1) )–(3(3) $u(x,0)=\phi (x),x\in [0,l],$(3) ). From the Lemma 2.1, we know that $u_{{\lambda }_k}(t)$ is completely monotone. So we have $u_{{\lambda }_k}(t)\in C[0,T]$ and $|u_{{\lambda }_k}(t)|\le 1.$ We first have $\Vert u(x,t){\Vert }_{C(0,T;L^2(0,l))}\le {\left|{(\sum _{k=1}^{\mathrm{\infty }}{\varrho }_k{\phi }_k^2{u}_{{\lambda }_k}^2(t))}^{1/2}\right|}_{C[0,T]}\le {\left(\sum _{k=1}^{\mathrm{\infty }}{\varrho }_k{\phi }_k^2\right)}^{1/2}=\Vert \phi {\Vert }_{L^2(0,l)}.$ Moreover by Theorem 2.1, i.e. $u_{{\lambda }_k}(t)\le \frac{C}{({\lambda }_{k}t{)}^{\overline{\theta }}},\mathrm{\forall }\overline{\theta }\in (0,1],t\in (0,T].$ If we take $\overline{\theta }=\gamma ,\gamma \in (0,\frac{1}{2})$, we have $\begin{array}{rl}\Vert u{\Vert }_{L^2(0,T;D((-L{)}^{\gamma }))}& \le {({\int }_0^T\sum _{k=1}^{\mathrm{\infty }}{\lambda }_k^{2\gamma }{\varrho }_k{\phi }_k^2{u}_{{\lambda }_k}^2(t)\mathrm{d}t)}^{1/2}\\ & \le {\left({\int }_0^T\sum _{k=1}^{\mathrm{\infty }}{\lambda }_k^{2\gamma }{\left({\displaystyle \frac{C}{({\lambda }_{k}t{)}^{\gamma }}}\right)}^2{\varrho }_k{\phi }_k^2\mathrm{d}t\right)}^{1/2}\\ & \le C{\left(\sum _{k=1}^{\mathrm{\infty }}{\varrho }_k{\phi }_k^2{\int }_0^T{\displaystyle \frac{1}{t^{2\gamma }}}\right)}^{1/2}\le C{\left(\sum _{k=1}^{\mathrm{\infty }}{\varrho }_k{\phi }_k^2{\displaystyle \frac{1}{1-2\gamma }}{T}^{1-2\gamma }\right)}^{1/2}\\ & \le C_T\Vert \phi {\Vert }_{L^2(0,l)}.\end{array}$ Similarly, by Theorem 2.1, we obtain $\begin{array}{rl}\Vert u(\cdot ,t){\Vert }_{H^2(0,l)}& \le C\Vert Lu(x,t){\Vert }_{L^2(0,l)}={\Vert \sum _{k=1}^{\mathrm{\infty }}{\phi }_k{u}_{{\lambda }_k}(t){\lambda }_k{\varrho }_k{\varphi }_k(\cdot )\Vert }_{L^2(0,l)}\\ & \le C{\left(\sum _{k=1}^{\mathrm{\infty }}{\varrho }_k{\left(\frac{{\phi }_k}{{\lambda }_{k}t}\right)}^2{\lambda }_k^2\right)}^{1/2}\le \frac{C}{t}\Vert \phi {\Vert }_{L^2(0,l)},\mathrm{\forall }t\in (0,T],\end{array}$ and $\begin{array}{rl}\Vert {\mathbb{D}}_t^{(\mu )}u(\cdot ,t){\Vert }_{L^2(0,l)}& =\Vert \sum _{k=1}^{\mathrm{\infty }}{\lambda }_k{\varrho }_k{\phi }_k{u}_{{\lambda }_k}(t){\varphi }_k(\cdot ){\Vert }_{L^2(0,l)}\\ & \le C{\left(\sum _{k=1}^{\mathrm{\infty }}{\varrho }_k{\left(\frac{{\phi }_k}{{\lambda }_{k}t}\right)}^2{\lambda }_k^2\right)}^{1/2}\le \frac{C}{t}\Vert \phi {\Vert }_{L^2(0,l)},\mathrm{\forall }t\in (0,T].\end{array}$ Hence, we get $\Vert {\mathbb{D}}_t^{(\mu )}u(\cdot ,t){\Vert }_{L^2(0,l)}+\Vert u(\cdot ,t){\Vert }_{H^2(0,l)}\le \frac{C}{t}\Vert \phi {\Vert }_{L^2(0,l)}.$ Obviously, we have $\underset{t\to 0}{lim}\Vert u(\cdot ,t)-\phi (\cdot ){\Vert }_{L^2(0,l)}={\Vert \sum _{k=1}^{\mathrm{\infty }}{\varrho }_k{\phi }_k{\varphi }_k(\cdot )-\phi (\cdot )\Vert }_{L^2(0,l)}=0.$ The uniqueness of strong solution lies in the uniqueness of the ordinary fractional differential equation (6(6) $\begin{array}{ll}& {\mathbb{D}}_t^{(\mu )}v(t)=-\lambda v(t),\lambda >0,t>0,\\ & v(0)=1.\end{array}$(6) )(see Lemma 2.2 in [17], for example). The proof of the theorem is completed.

2.2. Ill-posedness analysis for the backward problem

We defining a linear operator $K_{\mu }:$ $L^2(0,l)\mapsto L^2(0,T)$ as follows: (18) $K_{\mu }\phi (x)=\sum _{k=1}^{\mathrm{\infty }}{\varrho }_k{\phi }_k{u}_{{\lambda }_k}(t),t\in (0,T),0<\alpha <1.$(18)

Theorem 2.3

The observation operator $K_{\mu }:\phi (x)\in L^2(0,l)\mapsto g(t)\in L^2(0,T)$ is compact.

Proof.

We will prove the compactness of the observation operator $K_{\mu }$. Defining the finite dimensional operators $K_{\mu ,N}$ as follows: (19) $K_{\mu ,N}\phi (x)=\sum _{k=1}^N{\varrho }_k{\phi }_k{u}_{{\lambda }_k}(t),t\in (0,T),0<\alpha <1,$(19) Set $\overline{\theta }\in (\frac{1}{4},\frac{1}{2})$, from (18(18) $K_{\mu }\phi (x)=\sum _{k=1}^{\mathrm{\infty }}{\varrho }_k{\phi }_k{u}_{{\lambda }_k}(t),t\in (0,T),0<\alpha <1.$(18) ), (19(19) $K_{\mu ,N}\phi (x)=\sum _{k=1}^N{\varrho }_k{\phi }_k{u}_{{\lambda }_k}(t),t\in (0,T),0<\alpha <1,$(19) ) and Theorem 2.1, we obtain $\begin{array}{rl}\Vert K_{\mu }\phi (x)-K_{\mu ,N}\phi (x){\Vert }_{L^2(0,T)}& ={\Vert \sum _{k=N+1}^{\mathrm{\infty }}{\varrho }_k{\phi }_k{u}_{{\lambda }_k}(t)\Vert }_{L^2(0,T)}\\ & \le {\Vert \sum _{k=N+1}^{\mathrm{\infty }}\frac{C}{({\lambda }_{k}t{)}^{\overline{\theta }}}{\varrho }_k|{\phi }_k|\Vert }_{L^2(0,T)}\\ & \le C\sqrt{\sum _{k=N+1}^{\mathrm{\infty }}\frac{1}{{\lambda }_k^{2\overline{\theta }}}}\sqrt{\sum _{k=N+1}^{\mathrm{\infty }}{\phi }_k^2}{\left({\int }_0^T{t}^{-2\overline{\theta }}\mathrm{d}\mathrm{t}\right)}^{1/2}\\ & \le C_T\sqrt{\sum _{k=N+1}^{\mathrm{\infty }}\frac{1}{{\lambda }_k^{2\overline{\theta }}}}\Vert \phi (\cdot ){\Vert }_{L^2(0,l)}.\end{array}$ By ${\lambda }_k\sim k^2$, obviously, $\Vert K_{\mu ,N}-K_{\mu }{\Vert }_{L^2(0,T;L^2(0,l))}\to 0$ in the sense of operator norm in $L^2(0,T;L^2(0,l))$ as $N\to \mathrm{\infty }$. Therefore, $K_{\mu }$ is a compact operator.

From the Theorem 2.3, we know that identifying initial condition $\phi (x)$ in $L^2(0,l)$ from the observation data $g(t)$ in $L^2(0,T)$ is ill-posed. Some regularization strategies should be considered. We will adopt the Tikhonov regularization method to deal with the backward problem in Section 4.

3. Uniqueness

In order to explore the unique theorem of the backward problem, first we need to prove the following lemma.

Lemma 3.1

Assume $\phi (x)\in D((-L{)}^{\gamma /2}),$ $\gamma \ge 0,$ there exist a unique strong solution $u(x,t)$ to direct problem (1(1) ${\mathbb{D}}_t^{(\mu )}u={\mathrm{\partial }}_x(a(x){\mathrm{\partial }}_{x}u(x,t))-c(x)u(x,t)+f(x,t),x\in (0,l),t>0,$(1) )–(3(3) $u(x,0)=\phi (x),x\in [0,l],$(3) ). Moreover, we have the following estimate $\Vert u{\Vert }_{L^2(0,T;H^{\gamma +1-ϵ}(0,l))}\le C\Vert \phi {\Vert }_{D((-L{)}^{\frac{\gamma }{2}})},\mathrm{\forall }ϵ\in (0,1),$ if $\gamma >1$, $\Vert u{\Vert }_{C[0,T;C[0,l]]}\le C\Vert \phi {\Vert }_{D((-L{)}^{\gamma /2})}.$

Proof.

From the Theorem 2.2, the unique strong solution is given by (17(17) $u(x,t)=\sum _{k=1}^{\mathrm{\infty }}{\phi }_k{\varrho }_k{u}_{{\lambda }_k}(t){\varphi }_k(x),x\in [0,l],t\in [0,T],$(17) ). We have $\begin{array}{rl}\Vert u{\Vert }_{L^2(0,T;D((-L{)}^{((\gamma +1-ϵ)/2)}))}& ={\Vert \sum _{k=1}^{\mathrm{\infty }}{\phi }_k{\varrho }_k{u}_{{\lambda }_k}(t){\varphi }_k(\cdot )\Vert }_{L^2(0,T;D((-L{)}^{((\gamma +1-ϵ)/2)}))},\\ & \le {({\int }_0^T\sum _{k=1}^{\mathrm{\infty }}{\lambda }_k^{\gamma +1-ϵ}{\phi }_k^2{\varrho }_k{u}_{{\lambda }_k}^2(t)\mathrm{d}\mathrm{t})}^{1/2},\\ & \le {\left({\int }_0^T\sum _{k=1}^{\mathrm{\infty }}{\lambda }_k^{\gamma +1-ϵ}{\phi }_k^2{\varrho }_k\frac{c^2}{({\lambda }_{k}t{)}^{1-ϵ}}\mathrm{d}\mathrm{t}\right)}^{1/2},\\ & \le C{\left(\sum _{k=1}^{\mathrm{\infty }}{\lambda }_k^{\gamma }{\phi }_k^2{\varrho }_k\right)}^{1/2}\le C\Vert \phi {\Vert }_{D((-L{)}^{(}\gamma /2))},\mathrm{\forall }ϵ\in (0,1).\end{array}$ As $D((-L)((\gamma +1-ϵ)/2))\subset H^{\gamma +1-ϵ}(0,l)$, we obtain $\Vert u{\Vert }_{L^2(0,T;H^{\gamma +1-ϵ}(0,l))}\le C\Vert \phi {\Vert }_{D((-L)(\gamma /2))}$. By the Sobolev embedding theorem, we get $\Vert {\varphi }_k{\Vert }_{C[0,l]}\le \tilde{C}{\lambda }_k^{\frac{1}{4}+ϵ}\Vert {\varphi }_k{\Vert }_{L^2[0,l]},\mathrm{\forall }ϵ>0.$ Note that $\Vert {\varphi }_k{\Vert }_{L^2[0,l]}=O(1/\sqrt{c_0})$. If $\gamma >1$, take ε satisfying $0<ϵ\le ((\gamma -1)/2),$ from Theorem 2.1 we have $\begin{array}{rl}\underset{x\in [0,l]}{max}|u(x,t)|& =\underset{x\in [0,l]}{max}|\sum _{k=1}^{\mathrm{\infty }}{\phi }_k{\varrho }_k{u}_{{\lambda }_k}(t){\varphi }_k(x)|,0<\alpha <1,\\ & \le \tilde{C}\sum _{k=1}^{\mathrm{\infty }}|{\phi }_k|{\varrho }_k|u_{{\lambda }_k}(t)|{\lambda }_k^{1/4+ϵ},0<\alpha <1,\\ & \le \tilde{C}\sum _{k=1}^{\mathrm{\infty }}{\varrho }_k{\lambda }_k^{\gamma /2}|{\phi }_k|{\lambda }_k^{1/4+ϵ-(\gamma /2)},0<\alpha <1,\\ & \le \tilde{C}\Vert \phi {\Vert }_{D((-L{)}^{\gamma }/2)}\sqrt{\sum _{k=1}^{\mathrm{\infty }}{\lambda }_k^{1/2-\gamma +2ϵ}},0<\alpha <1,\\ & \le C\Vert \phi {\Vert }_{D((-L{)}^{\frac{\gamma }{2}})},\mathrm{\forall }t\ge 0,0<\alpha <1.\end{array}$ From the above inequality, we have $\Vert u{\Vert }_{C[0,T;C[0,l]]}={\Vert \sum _{k=1}^{\mathrm{\infty }}{\phi }_k{\varrho }_k{u}_{{\lambda }_k}(t){\varphi }_k(\cdot )\Vert }_{C[0,T;C[0,l]]}\le C\Vert \phi {\Vert }_{D((-L{)}^{(\gamma /2)})},\gamma >1.$ The proof of the lemma is finished.

Theorem 3.1

Assume $\phi (x)\in D((-L{)}^{(}\gamma /2)),\gamma >1,$ the initial function $\phi (x)$ can be identified uniquely by the observation data at left end point, i.e. $g(t)=u(0,t),$ $t\in [0,T]$.

Proof.

From Lemma 3.1, the observation data $g(t)\in C[0,T]$ is meaningful if $\phi (x)\in D((-L{)}^{\frac{\gamma }{2}}),$ $\gamma >1$. By contradiction, we assume there exist two different functions, denoting by ${\phi }_i(x)$ i = 1, 2. The solutions about ${\phi }_1(x)$ and ${\phi }_2(x)$, respectively, are expressed as follows $u_i(x,t)=\sum _{k=1}^{\mathrm{\infty }}{\varrho }_k{\phi }_{i,k}{u}_{{\lambda }_k}(t){\varphi }_k(x),x\in (0,l),t\in [0,T],i=1,2,$ where ${\phi }_{i,k}=<{\phi }_i(x),{\varphi }_k(x)>$, $i=1,2,k=1,\dots ,\mathrm{\infty }.$ By Lemma 3.1, the two series $\sum _{k=1}^{\mathrm{\infty }}{\varrho }_k{\phi }_{1,k}{u}_{{\lambda }_k}(t)$ and $\sum _{k=1}^{\mathrm{\infty }}{\varrho }_k{\phi }_{2,k}{u}_{{\lambda }_k}(t)$ are uniformly convergent on interval $[0,T]$. Applying analytic continuation technique, we know that the above two series are uniform convergence on $[0,\mathrm{\infty })$. By Lemma 3.1, one have $|{\mathrm{e}}^{-tRez}\sum _{k=1}^{\mathrm{\infty }}{\phi }_{i,k}{u}_{{\lambda }_k}(t){\varrho }_k|\le {\mathrm{e}}^{-tRez}\Vert {\phi }_i{\Vert }_{D((-L{)}^{(}\gamma /2))},t>0,i=1,2.$ As ${\mathrm{e}}^{-tRez}$ is integral in $t\in (0,\mathrm{\infty })$ for fixed z such that $Rez>0$. Taking Laplace transform with respect to the time variable t on the both sides of equation $u_1(0,t)=u_2(0,t)$, by the Lebesgue dominated convergence theorem, we have (20) $\sum _{k=1}^{\mathrm{\infty }}{\phi }_{1,k}{\varrho }_k\frac{w(s)}{sw(s)+{\lambda }_k}=\sum _{k=1}^{\mathrm{\infty }}{\phi }_{2,k}{\varrho }_k\frac{w(s)}{sw(s)+{\lambda }_k},Res>0.$(20) Therefore, (20(20) $\sum _{k=1}^{\mathrm{\infty }}{\phi }_{1,k}{\varrho }_k\frac{w(s)}{sw(s)+{\lambda }_k}=\sum _{k=1}^{\mathrm{\infty }}{\phi }_{2,k}{\varrho }_k\frac{w(s)}{sw(s)+{\lambda }_k},Res>0.$(20) ) yields $\sum _{k=1}^{\mathrm{\infty }}{\phi }_{1,k}{\varrho }_k\frac{1}{sw(s)+{\lambda }_k}=\sum _{k=1}^{\mathrm{\infty }}{\phi }_{2,k}{\varrho }_k\frac{1}{sw(s)+{\lambda }_k},Res>0.$ That is (21) $\sum _{k=1}^{\mathrm{\infty }}{\phi }_{1,k}{\varrho }_k\frac{1}{\eta +{\lambda }_k}=\sum _{k=1}^{\mathrm{\infty }}{\phi }_{2,k}{\varrho }_k\frac{1}{\eta +{\lambda }_k},Re\eta >0.$(21) We know that $\sum _{k=1}^{\mathrm{\infty }}{\varrho }_k{\phi }_{i,k}(1/(\eta +{\lambda }_k))$ is internally closed uniform convergence in $\eta \in \mathbb{C}/\{-{\lambda }_k{\}}_{k=1}^{\mathrm{\infty }}$. So, applying the Weierstrass theorem, we can analytically continue $\sum _{k=1}^{\mathrm{\infty }}{\varrho }_k{\phi }_{i,k}(1/(\eta +{\lambda }_k))$ in η and (21(21) $\sum _{k=1}^{\mathrm{\infty }}{\phi }_{1,k}{\varrho }_k\frac{1}{\eta +{\lambda }_k}=\sum _{k=1}^{\mathrm{\infty }}{\phi }_{2,k}{\varrho }_k\frac{1}{\eta +{\lambda }_k},Re\eta >0.$(21) ) holds for $\eta \in \mathbb{C}/\{-{\lambda }_k{\}}_{k=1}^{\mathrm{\infty }}$. We take a small disk which only includes $-{\lambda }_1$ and does not include others. Integrating (21(21) $\sum _{k=1}^{\mathrm{\infty }}{\phi }_{1,k}{\varrho }_k\frac{1}{\eta +{\lambda }_k}=\sum _{k=1}^{\mathrm{\infty }}{\phi }_{2,k}{\varrho }_k\frac{1}{\eta +{\lambda }_k},Re\eta >0.$(21) ) in the disk, we get $2\pi {\varrho }_1{\phi }_{1,1}=2\pi {\varrho }_1{\phi }_{2,1}$, which means ${\phi }_{1,1}={\phi }_{2,1}$ as ${\varrho }_1\ne 0$. Repeating this procedure, we have ${\phi }_{1,k}={\phi }_{2,k},k=1,2,\dots .$ Therefore, we obtain ${\phi }_1(x)={\phi }_2(x),x\in [0,l].$ The proof of the theorem is completed.

4. Variational optimization and the conjugate gradient method

From the above ill-posedness analysis, we know the backward problem is ill-posed. In order to obtain the stable numerical solution of the backward problem, we adopt the classic Tikhonov regularization method to deal with this problem. Define a Tikhonov regularization functional as follows (22) $J_{\beta }(\phi )=\frac{1}{2}\Vert K_{\mu }(\phi )-g^{\delta }{\Vert }_{L^2(0,T)}+\frac{\beta }{2}\Vert \phi {\Vert }_{L^2(0,l)},$(22) where β is a regularization parameter. Therefore, the backward problem is transformed into the following variational optimization problem $\underset{\phi \in L^2(0,l)}{min}{J}_{\beta }(\phi ).$ From the theory of the classic Tikhonov regularization, we see that the minimizer ${\phi }^{\beta ,\delta }(x)$ exists uniquely and converges to the exact initial function $\phi (x)$ if a suitable regularization parameter β is chosen, see Theorems 5.1–5.2 in [42]. In this paper, we adopt the conjugate gradient method (CGM) to seek the minimizer of functional (22(22) $J_{\beta }(\phi )=\frac{1}{2}\Vert K_{\mu }(\phi )-g^{\delta }{\Vert }_{L^2(0,T)}+\frac{\beta }{2}\Vert \phi {\Vert }_{L^2(0,l)},$(22) ). As we know, the key step of using the conjugate gradient method is to find the gradient of the functional (22(22) $J_{\beta }(\phi )=\frac{1}{2}\Vert K_{\mu }(\phi )-g^{\delta }{\Vert }_{L^2(0,T)}+\frac{\beta }{2}\Vert \phi {\Vert }_{L^2(0,l)},$(22) ). Here we compute the functional gradient by the means of the variational adjoint technique.

In the following, we derive formally the gradient of the regularization functional with the help of variational adjoint method. Let $\delta \phi (x)$ be a small perturbation of initial function $\phi (x)$, then the small change $w=u[\phi +\delta \phi ](x,t)-u[\phi ](x,t)$ of the solution to the forward problem (1(1) ${\mathbb{D}}_t^{(\mu )}u={\mathrm{\partial }}_x(a(x){\mathrm{\partial }}_{x}u(x,t))-c(x)u(x,t)+f(x,t),x\in (0,l),t>0,$(1) )–(3(3) $u(x,0)=\phi (x),x\in [0,l],$(3) ) satisfies (23) $\begin{array}{rl}& {\mathbb{D}}_t^{(\mu )}w(x,t)=(Lw)(x,t),x\in (0,l),t>0,0<\alpha \le 1,\\ & \frac{\mathrm{\partial }w}{\mathrm{\partial }x}(0,t)=0,\frac{\mathrm{\partial }w}{\mathrm{\partial }x}(l,t)=0,t\ge 0,\\ & w(x,0)=\delta \phi (x),x\in [0,l].\end{array}$(23) For obtaining the gradient of the optimization functional (22(22) $J_{\beta }(\phi )=\frac{1}{2}\Vert K_{\mu }(\phi )-g^{\delta }{\Vert }_{L^2(0,T)}+\frac{\beta }{2}\Vert \phi {\Vert }_{L^2(0,l)},$(22) ), we firstly calculate the first order variation of functional (22(22) $J_{\beta }(\phi )=\frac{1}{2}\Vert K_{\mu }(\phi )-g^{\delta }{\Vert }_{L^2(0,T)}+\frac{\beta }{2}\Vert \phi {\Vert }_{L^2(0,l)},$(22) ). From (22(22) $J_{\beta }(\phi )=\frac{1}{2}\Vert K_{\mu }(\phi )-g^{\delta }{\Vert }_{L^2(0,T)}+\frac{\beta }{2}\Vert \phi {\Vert }_{L^2(0,l)},$(22) ), we have (24) $\begin{array}{rl}\delta J_{\beta }(\phi )& =J_{\beta }(\phi +\delta \phi )-J_{\beta }(\phi )\\ & =\frac{1}{2}\Vert K_{\mu }(\phi +\delta \phi )-g^{\delta }{\Vert }_{L^2(0,T)}+\frac{\beta }{2}\Vert \phi +\delta \phi {\Vert }_{L^2(0,l)}\\ & -\frac{1}{2}\Vert K_{\mu }(\phi )-g^{\delta }{\Vert }_{L^2(0,T)}-\frac{\beta }{2}\Vert \phi {\Vert }_{L^2(0,l)},\\ & ={\int }_0^T(u[\phi ](0,t)-g^{\delta }(t))w(0,t)\mathrm{d}t+\beta {\int }_0^l\phi (x)\delta \phi (x)\mathrm{d}x\\ & +o(\Vert w(0,\cdot ){\Vert }_{L^2(0,T)}+\Vert \delta \phi {\Vert }_{L^2(0,l)}).\end{array}$(24) Let $v(x,t)$ be a smooth function, multiplying both side of governing equation in (23(23) $\begin{array}{rl}& {\mathbb{D}}_t^{(\mu )}w(x,t)=(Lw)(x,t),x\in (0,l),t>0,0<\alpha \le 1,\\ & \frac{\mathrm{\partial }w}{\mathrm{\partial }x}(0,t)=0,\frac{\mathrm{\partial }w}{\mathrm{\partial }x}(l,t)=0,t\ge 0,\\ & w(x,0)=\delta \phi (x),x\in [0,l].\end{array}$(23) ) by $v(x,t)$ and integrating with respect to the temporal-spatial variables on $Q=[0,T]\times [0,l]$, we have $\begin{array}{rl}0& ={\int }_0^l{\int }_0^T({\mathbb{D}}_t^{(\mu )}w(x,t)-L(w)(x,t))v(x,t)\mathrm{d}t\mathrm{d}x\\ & ={\int }_0^l{\int }_0^T{\int }_0^1\mu (\alpha )v(x,t){\int }_0^t\frac{1}{\mathrm{\Gamma }(1-\alpha )}(t-\tau {)}^{-\alpha }\frac{\mathrm{\partial }w(x,\tau )}{\mathrm{\partial }\tau }\mathrm{d}\tau \mathrm{d}\alpha \mathrm{d}t\mathrm{d}x\\ & -{\int }_0^l{\int }_0^{T}L(w)(x,t)v(x,t)\mathrm{d}t\mathrm{d}x.\end{array}$ After interchanging the integral variables of t and τ two times and integrating by parts, we have (25) $\begin{array}{rl}& {\int }_0^l\mathrm{d}x{\int }_0^1\mu (\alpha )\mathrm{d}\alpha {\int }_0^T\frac{\mathrm{\partial }w(x,\tau )}{\mathrm{\partial }\tau }(\frac{1}{\mathrm{\Gamma }(2-\alpha )}v(x,T)(T-\tau {)}^{1-\alpha })\mathrm{d}\tau \\ & +{\int }_0^l\mathrm{d}x{\int }_0^1\mu (\alpha )\mathrm{d}\alpha {\int }_0^T{\mathrm{\partial }}_{t}v(x,t)\mathrm{d}t\frac{1}{\mathrm{\Gamma }(2-\alpha )}w(x,0)t^{1-\alpha }\\ & -{\int }_0^l\mathrm{d}x{\int }_0^{T}w(x,\tau )\mathrm{d}\tau {\int }_{\tau }^T{\int }_0^1\mu (\alpha )\mathrm{d}\alpha \frac{1}{\mathrm{\Gamma }(1-\alpha )}{\mathrm{\partial }}_{t}v(x,t)(t-\tau {)}^{-\alpha }\mathrm{d}t\\ & -{\int }_0^T((-wa(x)\frac{\mathrm{\partial }v}{\mathrm{\partial }x}){|}_0^l+{\int }_0^{l}L(v)(x,\tau )w(x,\tau )\mathrm{d}x)\mathrm{d}\tau =0.\end{array}$(25) Combing (24(24) $\begin{array}{rl}\delta J_{\beta }(\phi )& =J_{\beta }(\phi +\delta \phi )-J_{\beta }(\phi )\\ & =\frac{1}{2}\Vert K_{\mu }(\phi +\delta \phi )-g^{\delta }{\Vert }_{L^2(0,T)}+\frac{\beta }{2}\Vert \phi +\delta \phi {\Vert }_{L^2(0,l)}\\ & -\frac{1}{2}\Vert K_{\mu }(\phi )-g^{\delta }{\Vert }_{L^2(0,T)}-\frac{\beta }{2}\Vert \phi {\Vert }_{L^2(0,l)},\\ & ={\int }_0^T(u[\phi ](0,t)-g^{\delta }(t))w(0,t)\mathrm{d}t+\beta {\int }_0^l\phi (x)\delta \phi (x)\mathrm{d}x\\ & +o(\Vert w(0,\cdot ){\Vert }_{L^2(0,T)}+\Vert \delta \phi {\Vert }_{L^2(0,l)}).\end{array}$(24) ) with (25(25) $\begin{array}{rl}& {\int }_0^l\mathrm{d}x{\int }_0^1\mu (\alpha )\mathrm{d}\alpha {\int }_0^T\frac{\mathrm{\partial }w(x,\tau )}{\mathrm{\partial }\tau }(\frac{1}{\mathrm{\Gamma }(2-\alpha )}v(x,T)(T-\tau {)}^{1-\alpha })\mathrm{d}\tau \\ & +{\int }_0^l\mathrm{d}x{\int }_0^1\mu (\alpha )\mathrm{d}\alpha {\int }_0^T{\mathrm{\partial }}_{t}v(x,t)\mathrm{d}t\frac{1}{\mathrm{\Gamma }(2-\alpha )}w(x,0)t^{1-\alpha }\\ & -{\int }_0^l\mathrm{d}x{\int }_0^{T}w(x,\tau )\mathrm{d}\tau {\int }_{\tau }^T{\int }_0^1\mu (\alpha )\mathrm{d}\alpha \frac{1}{\mathrm{\Gamma }(1-\alpha )}{\mathrm{\partial }}_{t}v(x,t)(t-\tau {)}^{-\alpha }\mathrm{d}t\\ & -{\int }_0^T((-wa(x)\frac{\mathrm{\partial }v}{\mathrm{\partial }x}){|}_0^l+{\int }_0^{l}L(v)(x,\tau )w(x,\tau )\mathrm{d}x)\mathrm{d}\tau =0.\end{array}$(25) ), we define the adjoint problem as follows (26) $\begin{array}{rl}& {\mathbb{D}}_{T_{-}}^{(\mu )}v(x,t)=L(v)(x,t),x\in (0,l),t>0,0<\alpha \le 1,\\ & \frac{\mathrm{\partial }v(0,t)}{\mathrm{\partial }x}=\frac{1}{a(0)}(u[\phi ](0,t)-g^{\delta }(t)),\frac{\mathrm{\partial }v(l,t)}{\mathrm{\partial }x}=0,t>0,\\ & v(x,T)=0,x\in [0,l],\end{array}$(26) where ${\mathbb{D}}_{T_{-}}^{(\mu )}y(t)$ is the Caputo fractional right derivative defined by ${\mathbb{D}}_{T_{-}}^{(\mu )}y(t)=-{\int }_0^1\mu (\alpha )\mathrm{d}\alpha \frac{1}{\mathrm{\Gamma }(1-\alpha )}{\int }_t^T\frac{y^{\mathrm{\prime }}(s)}{(s-t{)}^{\alpha }}\mathrm{d}s,0<\alpha <1.$ From the equality (25(25) $\begin{array}{rl}& {\int }_0^l\mathrm{d}x{\int }_0^1\mu (\alpha )\mathrm{d}\alpha {\int }_0^T\frac{\mathrm{\partial }w(x,\tau )}{\mathrm{\partial }\tau }(\frac{1}{\mathrm{\Gamma }(2-\alpha )}v(x,T)(T-\tau {)}^{1-\alpha })\mathrm{d}\tau \\ & +{\int }_0^l\mathrm{d}x{\int }_0^1\mu (\alpha )\mathrm{d}\alpha {\int }_0^T{\mathrm{\partial }}_{t}v(x,t)\mathrm{d}t\frac{1}{\mathrm{\Gamma }(2-\alpha )}w(x,0)t^{1-\alpha }\\ & -{\int }_0^l\mathrm{d}x{\int }_0^{T}w(x,\tau )\mathrm{d}\tau {\int }_{\tau }^T{\int }_0^1\mu (\alpha )\mathrm{d}\alpha \frac{1}{\mathrm{\Gamma }(1-\alpha )}{\mathrm{\partial }}_{t}v(x,t)(t-\tau {)}^{-\alpha }\mathrm{d}t\\ & -{\int }_0^T((-wa(x)\frac{\mathrm{\partial }v}{\mathrm{\partial }x}){|}_0^l+{\int }_0^{l}L(v)(x,\tau )w(x,\tau )\mathrm{d}x)\mathrm{d}\tau =0.\end{array}$(25) ) and adjoint problem (26(26) $\begin{array}{rl}& {\mathbb{D}}_{T_{-}}^{(\mu )}v(x,t)=L(v)(x,t),x\in (0,l),t>0,0<\alpha \le 1,\\ & \frac{\mathrm{\partial }v(0,t)}{\mathrm{\partial }x}=\frac{1}{a(0)}(u[\phi ](0,t)-g^{\delta }(t)),\frac{\mathrm{\partial }v(l,t)}{\mathrm{\partial }x}=0,t>0,\\ & v(x,T)=0,x\in [0,l],\end{array}$(26) ), we have (27) $\begin{array}{rl}& {\int }_0^{l}w(x,0)\mathrm{d}x{\int }_0^1\mu (\alpha )\mathrm{d}\alpha {\int }_0^T\frac{1}{\mathrm{\Gamma }(2-\alpha )}{t}^{1-\alpha }{\mathrm{\partial }}_{t}v(x,t)\mathrm{d}t\\ & -{\int }_0^{T}w(0,t)(u[\phi ](0,t)-g^{\delta }(t))\mathrm{d}t=0.\end{array}$(27) By (24(24) $\begin{array}{rl}\delta J_{\beta }(\phi )& =J_{\beta }(\phi +\delta \phi )-J_{\beta }(\phi )\\ & =\frac{1}{2}\Vert K_{\mu }(\phi +\delta \phi )-g^{\delta }{\Vert }_{L^2(0,T)}+\frac{\beta }{2}\Vert \phi +\delta \phi {\Vert }_{L^2(0,l)}\\ & -\frac{1}{2}\Vert K_{\mu }(\phi )-g^{\delta }{\Vert }_{L^2(0,T)}-\frac{\beta }{2}\Vert \phi {\Vert }_{L^2(0,l)},\\ & ={\int }_0^T(u[\phi ](0,t)-g^{\delta }(t))w(0,t)\mathrm{d}t+\beta {\int }_0^l\phi (x)\delta \phi (x)\mathrm{d}x\\ & +o(\Vert w(0,\cdot ){\Vert }_{L^2(0,T)}+\Vert \delta \phi {\Vert }_{L^2(0,l)}).\end{array}$(24) ) and (27(27) $\begin{array}{rl}& {\int }_0^{l}w(x,0)\mathrm{d}x{\int }_0^1\mu (\alpha )\mathrm{d}\alpha {\int }_0^T\frac{1}{\mathrm{\Gamma }(2-\alpha )}{t}^{1-\alpha }{\mathrm{\partial }}_{t}v(x,t)\mathrm{d}t\\ & -{\int }_0^{T}w(0,t)(u[\phi ](0,t)-g^{\delta }(t))\mathrm{d}t=0.\end{array}$(27) ), we obtain (28) $J_{\beta }^{\prime }(\phi )={\int }_0^1\mu (\alpha )\mathrm{d}\alpha {\int }_0^T\frac{1}{\mathrm{\Gamma }(2-\alpha )}{t}^{1-\alpha }{\mathrm{\partial }}_{t}v(x,t)\mathrm{d}t+\beta \phi ,0<\alpha \le 1.$(28) Assume that ${\phi }_k(x)$ is the k-th approximate solution of $\phi (x)$. Set (29) ${\phi }_{k+1}={\phi }_k+{\vartheta }_k{d}_k,k=0,1,\dots ,$(29) where $d_k$ is a descent direction and ${\vartheta }_k$ is the step size in the k-th iteration. The descent direction of the CGM is updated by using the following iteration formula (30) $d_k=-J_{\beta }^{\prime }({\phi }_k)+{\varsigma }_k{d}_{k-1},$(30) where ${\varsigma }_k$ is conjugate coefficient updated by (31) ${\varsigma }_k=\frac{{\int }_0^T(J_{\beta }^{\prime }({\phi }_k){)}^2\mathrm{d}\mathrm{t}}{{\int }_0^T(J_{\beta }^{\prime }({\phi }_{k-1}){)}^2\mathrm{d}\mathrm{t}},{\varsigma }_0=0.$(31) The optimal descent step size ${\vartheta }_k$ in the k-th iteration can be obtained by minimizing the problem (32(32) $J_{\beta }({\phi }_k+{\vartheta }_k{d}_k)=\frac{1}{2}\Vert K_{\mu }({\phi }_k)+{\vartheta }_k{K}_{\mu }(d_k)-g^{\delta }{\Vert }_{L^2(0,T)}+\frac{\beta }{2}\Vert {\phi }_k+{\vartheta }_k{d}_k{\Vert }_{L^2(0,l)}.$(32) ). From (22(22) $J_{\beta }(\phi )=\frac{1}{2}\Vert K_{\mu }(\phi )-g^{\delta }{\Vert }_{L^2(0,T)}+\frac{\beta }{2}\Vert \phi {\Vert }_{L^2(0,l)},$(22) ), we have (32) $J_{\beta }({\phi }_k+{\vartheta }_k{d}_k)=\frac{1}{2}\Vert K_{\mu }({\phi }_k)+{\vartheta }_k{K}_{\mu }(d_k)-g^{\delta }{\Vert }_{L^2(0,T)}+\frac{\beta }{2}\Vert {\phi }_k+{\vartheta }_k{d}_k{\Vert }_{L^2(0,l)}.$(32) Take $\begin{array}{rl}\frac{\mathrm{d}{J}_{\beta }({\phi }_k+{\vartheta }_k{d}_k)}{\mathrm{d}{\vartheta }_k}& ={\int }_0^T(K_{\mu }({\phi }_k)+{\vartheta }_k{K}_{\mu }(d_k)-g^{\delta })K_{\mu }(d_k)\mathrm{d}t\\ & +\beta {\int }_0^l({\phi }_k+{\vartheta }_k{d}_k)d_k\mathrm{d}x=0,\end{array}$ we obtain the k-th iteration optimal step size as follows (33) ${\vartheta }_k=-\frac{{\int }_0^T(K_{\mu }({\phi }_k)-g^{\delta })K_{\mu }(d_k)\mathrm{d}t+\beta {\int }_0^l{\phi }_k{d}_k\mathrm{d}x}{{\int }_0^T(K_{\mu }(d_k){)}^2\mathrm{d}t+\beta {\int }_0^l{d}_k^2\mathrm{d}x}.$(33) For the fixed regularization parameter β, we take the CGM to solve the optimization problem (22(22) $J_{\beta }(\phi )=\frac{1}{2}\Vert K_{\mu }(\phi )-g^{\delta }{\Vert }_{L^2(0,T)}+\frac{\beta }{2}\Vert \phi {\Vert }_{L^2(0,l)},$(22) ) by adopting the well-known Morozovs discrepancy principle as the stopping condition, i.e. we choose $k=k_{\beta }$ satisfying the following inequality: (34) ${\mathrm{e}}_{k_{\beta }}^{\beta }\le \tau \delta \le {\mathrm{e}}_{k_{\beta }-1}^{\beta },$(34) where $\tau \ge 1$ is a positive constant, ${\mathrm{e}}_k^{\beta }=\Vert K_{\mu }({\phi }_k(\beta ))-g^{\delta }{\Vert }_{L^2(0,T)}$. So, we obtain the CGM to solve the optimization problem with the fixed regularization parameter β as follows

In the numerical implementations, we apply quasi-optimality criterion [43] to choose β, i.e. we give a decreasing regularization parameter sequence of $\{{\beta }_{\iota }\},{\beta }_{\iota }={\beta }_0{r}^{\iota },0<r<1,\iota =0,1,2,\dots ,M_{\iota }$, ${\beta }_0$ is a positive constant, and choose ${\beta }_{\overline{\iota }}$ as the minimizer of $\Vert \phi ({\beta }_{\iota })-\phi ({\beta }_{\iota -1}){\Vert }_{L^2(0,l)}$. Therefore, we formulate the inversion algorithm based on the CGM as follows

5. Numerical examples

In this section, we present several numerical examples to illustrate the effectiveness of the conjugate gradient algorithm. Without loss of generality, we take ${\beta }_0={10}^{-3},r=0.5$, $(0,l)=(0,1)$ and T = 1 for all the numerical simulations. To obtain the (noisy) observation data $g^{\delta }(t)$, we first give the true initial function ${\phi }^{\star }(x)$ and solve the direct problem (1(1) ${\mathbb{D}}_t^{(\mu )}u={\mathrm{\partial }}_x(a(x){\mathrm{\partial }}_{x}u(x,t))-c(x)u(x,t)+f(x,t),x\in (0,l),t>0,$(1) )–(3(3) $u(x,0)=\phi (x),x\in [0,l],$(3) ) by finite difference method proposed in [29], then add pointwise noise by $g^{\delta }(t_i)=K_{\alpha }({\phi }^{\star })(t_i)(1+\delta \xi )$, where $t_i$ is the discretization time nodal point, δ is the noise level and ξ is a uniform random variable in $[-1,1]$.

Example 5.1

Let $\mu (\alpha )=\mathrm{\Gamma }(2-\alpha )$, $a(x)=1$, $c(x)=0$, $f(x,t)=((t-1)/\log t)\cos (\pi x)+{\pi }^2(1+t)\cos (\pi x)$. We take $\phi (x)=\cos (\pi x)$ as the exact initial condition, and the direct problem (1(1) ${\mathbb{D}}_t^{(\mu )}u={\mathrm{\partial }}_x(a(x){\mathrm{\partial }}_{x}u(x,t))-c(x)u(x,t)+f(x,t),x\in (0,l),t>0,$(1) )–(3(3) $u(x,0)=\phi (x),x\in [0,l],$(3) ) has exact solution $u(x,t)=(1+t)\cos (\pi x)$.

Example 5.2

Let $\mu (\alpha )=\mathrm{\Gamma }(4-\alpha )$, $a(x)=1$, $c(x)=0$, $f(x,t)=0$. We take $\phi (x)=\{\begin{array}{ll}0,& x\in [0,1/10)\cup (9/10,1],\\ {\displaystyle \frac{5}{2}}(x-1/10),& x\in [1/10,1/2),\\ {\displaystyle \frac{5}{2}}(9/10-x),& x\in [1/2,9/10].\end{array}$ as the exact initial function, and the direct problem (1(1) ${\mathbb{D}}_t^{(\mu )}u={\mathrm{\partial }}_x(a(x){\mathrm{\partial }}_{x}u(x,t))-c(x)u(x,t)+f(x,t),x\in (0,l),t>0,$(1) )–(3(3) $u(x,0)=\phi (x),x\in [0,l],$(3) ) has no exact solution.

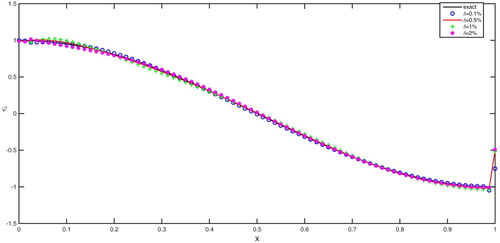
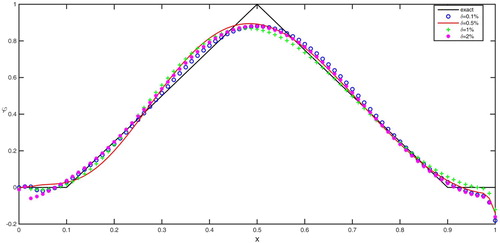
Numerical results for Examples 5.1 and 5.2 are showed in Figures 1, 2 and Table 1 with relative noise level $0.1\mathrm{\%}$, $0.5\mathrm{\%}$, $1\mathrm{\%}$ and $2\mathrm{\%}$, respectively. From the Table 1, we see the inversion solution becomes much closer to the exact solution when the relative error level becomes much smaller.

Figure 1. inversion solution for Example 5.1.

Figure 2. inversion solution for Example 5.2.

Table 1. Inversion results for the four numerical examples with different relative errors.

Example	δ	$\overline{\iota }$	$\frac{\Vert {\phi }_k({\beta }_{\overline{\iota }})-{\phi }^{\star }{\Vert }_{L^2(0,l)}}{\Vert {\phi }^{\star }{\Vert }_{L^2(0,l)}}$
Example 5.1	0.1%	5	3.27%
	0.5%	4	3.83%
	1%	4	4.62%
	2%	3	5.11%
Example 5.2	0.1%	5	5.45%
	0.5%	4	5.69%
	1%	4	7.35%
	2%	4	7.73%
Example 5.3	0.1%	5	6.39%
	0.5%	4	7.22%
	1%	4	7.92%
	2%	3	9.13%
Example 5.4	0.1%	5	3.70%
	0.5%	5	3.90%
	1%	4	5.67%
	2%	4	6.28%

Example 5.3

Let $\mu (\alpha )=\mathrm{\Gamma }(5-\alpha )$, $a(x)=1$, $c(x)=1$, $f(x,t)=((24/\log t)(t^4-t^3)+1+t^4)(1+100x^2(1-x{)}^2)-200(1+t^4)(1-6x+6x^2)$. We take $\phi (x)=1+100x^2(1-x{)}^2$ as the exact initial condition. The exact solution to the direct problem (1(1) ${\mathbb{D}}_t^{(\mu )}u={\mathrm{\partial }}_x(a(x){\mathrm{\partial }}_{x}u(x,t))-c(x)u(x,t)+f(x,t),x\in (0,l),t>0,$(1) )–(3(3) $u(x,0)=\phi (x),x\in [0,l],$(3) ) can be given explicitly as $u(x,t)=(1+t^4)(1+100x^2(1-x{)}^2)$.

Example 5.4

Let $\mu (\alpha )=1+\alpha$, $a(x)=1$, $c(x)=0$, $f(x,t)=0$. The exact initial function is taken as $\phi (x)=\cos (2\pi x)$, and the exact solution to the direct problem (1(1) ${\mathbb{D}}_t^{(\mu )}u={\mathrm{\partial }}_x(a(x){\mathrm{\partial }}_{x}u(x,t))-c(x)u(x,t)+f(x,t),x\in (0,l),t>0,$(1) )–(3(3) $u(x,0)=\phi (x),x\in [0,l],$(3) ) is unknown.

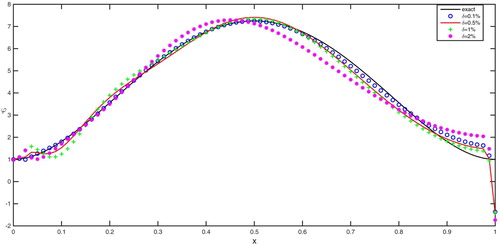
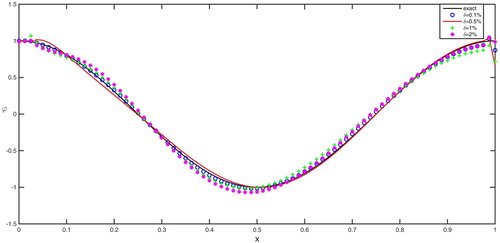
The reconstructions for Examples 5.3 and 5.4 are exhibited in Figures 3, 4 and Table 1. The relative noise levels for Examples  5.3, 5.4 are also chosen as $\delta =0.1\mathrm{\%},0.5\mathrm{\%},1\mathrm{\%},2\mathrm{\%}$, respectively. From Table 1, we find the inversion results become worse as noise level δ becomes larger, which shows the inversion algorithm is stable. The CPU time for above every numerical inversion problems is around 110 seconds with the computer configuration as follows, System: Microsoft Windows; CPU: inter(R) core(TM) i7-4500U @ 2.40 GHz; RAM:8.00 GB.

Figure 3. inversion solution for Example 5.3.

Figure 4. inversion solution for Example 5.4.

6. Conclusions

In this paper, we consider the identification problem of initial function for one-dimensional distributed order diffusion equation. The unique existence and the regularity properties of the strong solution are established by the eigenfunction expansions. Based on the uniform convergence of the observation operator, we interpret the ill-posedness of the backward problem. The uniqueness of the backward problem is proven by Laplace transformation technique and analytic continuation method. Several numerical examples show that the inversion algorithm based on the conjugate gradient method is effective and stable.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This work is supported by National Natural Science Foundation of China [11661004, 11861007, 11961002], Foundation of Academic and Technical Leaders Program for Major Subjects in Jiangxi Province [20172BCB22019].