Recovery of a degenerate space-dependent heat capacity

Abstract

We are concerned with the reconstruction of the heat capacity coefficient of a one-dimensional heat equation from a sequence of observations of solutions at a single fixed point. This new direct method reconstructs the principal eigenfunction by extracting its Fourier coefficients from the observations of the solution. The algorithm presented here is an alternative to Krein's inverse spectral theory, minimization and iterative procedures. Error estimates and numerical experiments are presented.

Keywords:

• Inverse problem
• parameter identification
• Krein string

2010 Mathematics Subject Classifications:

• 35R30
• 65M32

1. Introduction

We are concerned with the reconstruction of the heat capacity coefficient $\rho \in L^2(0,1)$ appearing in the one-dimensional heat equation (1) $\{\begin{array}{l}{u}_t(x,t)={\displaystyle \frac{1}{\rho (x)}}{u}_{xx}(x,t)0<x<1,t>0\\ u_x(0,t)-hu(0,t)=0t>0\\ u_x(1,t)+Hu(1,t)=0t>0\\ u(x,0)=f(x)x\in (0,1)\end{array}$(1) from observations of a sequence of temperatures taken at an arbitrary single point, i.e. $u(b,t)$ where b is a fixed but arbitrary point in $[0,1]$. Here the real values h and H in the boundary conditions describe the constant heat transfer occurring at the endpoints, and $f\in C(0,1)$ is the initial condition.

We recall that in [1] the idea was to extract the complete spectral data $\{{\lambda }_n,{\alpha }_n{\}}_{n\ge 1}$ of the operator ${\rho }^{-1}(x){\mathrm{\partial }}_{xx}$, from the observation of a single solution on the boundary, i.e. $u(0,t)$ and $u(1,t)$ based on Krein's inverse spectral theory of the string [8,10]. The main difficulty of applying Krein's theory is its requirement of having the full and complete spectral data, which is impossible to extract in practice.

This note implements numerically the new method introduced in [4], which applies to multidimensional partial differential equations, and presents an alternative to methods such as the Gelfand–Levitan or Krein inverse spectral theories, optimal control, minimization methods, Newton's and fixed points methods, see [2,6,7,9,11,12]. It is based on a simple idea of computing the Fourier coefficients of the first eigenfunction which allows for a simple approximating scheme of ρ. However, because ρ is unknown, the Fourier coefficients of the principal eigenfunction are not available as in [4,5], and so the analysis needs to be modified which is the purpose of this note. The main result can be stated as follows:

Theorem 1.1

Let $\{{\psi }_j{\}}_{j\in {\mathbb{N}}^{\star }}$ be a basis of $L^2(0,1)$ that we take for the initial condition $u(x,0)={\psi }_j(x)$ for $x\in (0,1),j\in {\mathbb{N}}^{\star }$ and let $b\in (0,1)$. If $h+H+hH\ne 0,$ then we can reconstruct $0\le \rho \in L^2(0,1)$ from the map ${\psi }_j\mapsto \{u(b,k){\}}_{k\in {\mathbb{N}}^{\star }}$. In the Neumann case, i.e. h = H = 0, then we also need the mean value of ${\int }_0^1\rho (x)\mathrm{d}x.$

We now briefly describe the content of the paper. Notations are in Section 2, and in Section 3, the idea on how to reconstruct ρ by computing the first eigenvalue ${\lambda }_1$ and ${\phi }_1(x)\rho (x)$ from the observation of the solution at one point is given. By solving an auxiliary boundary problem we then find ${\varphi }_1$ and deduce the sought coefficient ρ. The Dirichlet and the Neumann cases are examined respectively in Section 4 and Section 5. Convergence is proved in Section 6 while the algorithm is exposed in Section 7. Numerical examples are provided in the last section.

2. Preliminaries

By the Fourier method, the solution of Equation (1(1) $\{\begin{array}{l}{u}_t(x,t)={\displaystyle \frac{1}{\rho (x)}}{u}_{xx}(x,t)0<x<1,t>0\\ u_x(0,t)-hu(0,t)=0t>0\\ u_x(1,t)+Hu(1,t)=0t>0\\ u(x,0)=f(x)x\in (0,1)\end{array}$(1) ) can be written as (2) $u(x,t)=\sum _{n\ge 1}{c}_n\left(f\right)e^{-{\lambda }_{n}t}{\phi }_n\left(x\right),$(2) where the Fourier coefficients are given by (3) $c_n\left(f\right)={\int }_0^{1}f(x){\phi }_n\left(x\right)\rho \left(x\right)\mathrm{d}x,n\in {\mathbb{N}}^{\star }$(3) and ${\phi }_n$ are eigenfunctions of the Sturm–Liouville operator A defined by (4) $\{\begin{array}{l}A{\phi }_n\left(x\right)={\displaystyle \frac{-1}{\rho (x)}}{\phi }_n^{\mathrm{\prime }\mathrm{\prime }}(x)={\lambda }_n{\phi }_n(x),0<x<1,\\ {\phi }_n^{\mathrm{\prime }}\left(0\right)-h{\phi }_n\left(0\right)=0\mathrm{and}{\phi }_n^{\mathrm{\prime }}\left(1\right)+H{\phi }_n\left(1\right)=0,\end{array}$(4) where $0\le \rho (x)\in L^2(0,1)$, and $h,H\in \mathbb{R}.$ It is also known that A, defined by (4(4) $\{\begin{array}{l}A{\phi }_n\left(x\right)={\displaystyle \frac{-1}{\rho (x)}}{\phi }_n^{\mathrm{\prime }\mathrm{\prime }}(x)={\lambda }_n{\phi }_n(x),0<x<1,\\ {\phi }_n^{\mathrm{\prime }}\left(0\right)-h{\phi }_n\left(0\right)=0\mathrm{and}{\phi }_n^{\mathrm{\prime }}\left(1\right)+H{\phi }_n\left(1\right)=0,\end{array}$(4) ), is a self-adjoint operator acting in the Hilbert space $L_{\rho }^2(0,1)=\left\{f\text{ measurable: }{\Vert f\Vert }_{\rho }^2={\int }_0^1|f(x){|}^2\rho (x)\mathrm{d}x<\mathrm{\infty }\right\}$and its spectrum is discrete and simple. Since $-{\phi }_n^{\mathrm{\prime }\mathrm{\prime }}(x)={\lambda }_n\rho (x){\phi }_n(x)$ and $\rho \in L^2(0,1),$ then ${\phi }_n\in H^2(0,1),$ and $\{{\phi }_n{\}}_{n\ge 1}$ forms an orthonormal basis of $L_{\rho }^2(0,1)$ normalized by $\Vert {\phi }_n{\Vert }_{\rho }=1.$

In the fifties, Krein used the inverse spectral theory of the string operator which is generated by the differential operator $\frac{d}{dM(x)}\frac{d^{+}}{\mathrm{d}{x}^{+}},$where $dM$is a Stieljtes measure defined by a nondecreasing function M, which represents the mass of a string, and $\frac{d^{+}}{\mathrm{d}{x}^{+}}$ is the right derivative at x, see [8,10] for the spectral theory of the string. When $M(x)$ is an absolutely continuous function, the string operator reduces to (4(4) $\{\begin{array}{l}A{\phi }_n\left(x\right)={\displaystyle \frac{-1}{\rho (x)}}{\phi }_n^{\mathrm{\prime }\mathrm{\prime }}(x)={\lambda }_n{\phi }_n(x),0<x<1,\\ {\phi }_n^{\mathrm{\prime }}\left(0\right)-h{\phi }_n\left(0\right)=0\mathrm{and}{\phi }_n^{\mathrm{\prime }}\left(1\right)+H{\phi }_n\left(1\right)=0,\end{array}$(4) ) and $Af=g\in L_{\rho }^2(0,1)$ is understood as $f(x)=ax+b+{\int }_0^x(x-\eta )g(\eta )\rho (\eta )\mathrm{d}\eta ,$and thus, when ρ vanishes on a subinterval, the solution f is a linear function.

We assume that $f\in C(0,1)$ so the Fourier coefficients $c_n(f)$in (3(3) $c_n\left(f\right)={\int }_0^{1}f(x){\phi }_n\left(x\right)\rho \left(x\right)\mathrm{d}x,n\in {\mathbb{N}}^{\star }$(3) ) are well defined although the weight $\rho \in L^2(0,1)$ is yet unknown. We still have $\{c_n(f){\}}_{n\ge 1}\in {\ell }^2$ and $f\left(x\right)=\sum _{n=1}^{\mathrm{\infty }}{c}_n\left(f\right){\phi }_n\left(x\right)\mathrm{holds}\mathrm{in}{L}_{\rho }^2(0,1).$

Remark 2.1

The sum in Equation (2(2) $u(x,t)=\sum _{n\ge 1}{c}_n\left(f\right)e^{-{\lambda }_{n}t}{\phi }_n\left(x\right),$(2) ) provides a representation of the solution only, although all its terms are unknown. The objective is to use the observation $u(b,t)$ to extract the Fourier coefficients $c_n$ and ${\lambda }_n$, whenever they are present, as the ${\phi }_n(b)$ can vanish. Obviously, if a coefficient is not present in the sum then it cannot be extracted.

3. Reconstructing ρ

In principle, to reconstruct ρ it is enough to reconstruct the first eigenfunction ${\phi }_1$, since ρ is a solution of the algebraic equation (5) $-{\phi }_1^{\mathrm{\prime }\mathrm{\prime }}\left(x\right)={\lambda }_1\rho \left(x\right){\phi }_1\left(x\right),x\in (0,1).$(5) To do so we only need the first eigenvalue ${\lambda }_1\ne 0,$ as we already have ${\phi }_1(x)\ne 0$ for all $x\in (0,1).$ To reconstruct ${\phi }_1,$ we could use a basis of  $L^2(0,1),$ say $\{{\psi }_k{\}}_{k\ge 1}$, to write (6) ${\phi }_1\left(x\right)=\sum _{k\ge 1}({\int }_0^1{\phi }_1(\xi ){\psi }_k(\xi )\mathrm{d}\xi ){\psi }_k(x)$(6) with the hope that we can read the coefficients ${\int }_0^1{\phi }_1(x){\psi }_k(x)\mathrm{d}x$ from the solution $u(b,t),$ as done in [4]. Unfortunately, the observation $u(b,t),$ in (2(2) $u(x,t)=\sum _{n\ge 1}{c}_n\left(f\right)e^{-{\lambda }_{n}t}{\phi }_n\left(x\right),$(2) ) contains a different coefficient of the exponential, namely, (7) $({\int }_0^1{\phi }_1(x){\psi }_k(x)\rho (x)\mathrm{d}x){\phi }_1\left(b\right)$(7) with initial condition $f={\psi }_k.$ In other words, even if we could extract the whole sequence ${\left\{({\int }_0^1{\phi }_1(\xi ){\psi }_k(\xi )\rho (\xi )d\xi ){\phi }_1\left(b\right)\right\}}_{k\ge 1},$from (2(2) $u(x,t)=\sum _{n\ge 1}{c}_n\left(f\right)e^{-{\lambda }_{n}t}{\phi }_n\left(x\right),$(2) ), we still cannot reconstruct ${\phi }_1$ by (6(6) ${\phi }_1\left(x\right)=\sum _{k\ge 1}({\int }_0^1{\phi }_1(\xi ){\psi }_k(\xi )\mathrm{d}\xi ){\psi }_k(x)$(6) ), but (8) $\begin{array}{rl}{\phi }_1(x)\rho (x){\phi }_1\left(b\right)& =\sum _{k\ge 1}({\int }_0^1{\phi }_1(\xi ){\psi }_k(\xi )\rho (\xi )d\xi ){\phi }_1\left(b\right){\psi }_k\left(x\right)\\ & =\sum _{k\ge 1}{c}_1\left({\psi }_k\right){\phi }_1\left(b\right){\psi }_k\left(x\right)\mathrm{in}{L}^2(0,1)\end{array}$(8) where we used the notation (3(3) $c_n\left(f\right)={\int }_0^{1}f(x){\phi }_n\left(x\right)\rho \left(x\right)\mathrm{d}x,n\in {\mathbb{N}}^{\star }$(3) ). To proceed further we now show how to extract the coefficients (7(7) $({\int }_0^1{\phi }_1(x){\psi }_k(x)\rho (x)\mathrm{d}x){\phi }_1\left(b\right)$(7) ) from (2(2) $u(x,t)=\sum _{n\ge 1}{c}_n\left(f\right)e^{-{\lambda }_{n}t}{\phi }_n\left(x\right),$(2) ).

3.1. Extracting $c_1({\psi }_k){\phi }_1(b)$ from observations

To capture $c_1({\psi }_k){\phi }_1(b)$ from (2(2) $u(x,t)=\sum _{n\ge 1}{c}_n\left(f\right)e^{-{\lambda }_{n}t}{\phi }_n\left(x\right),$(2) ), it is enough to use the method of limits, [3], on the sequence of observations or data given by $\{u(b,j){\}}_{j\in {\mathbb{N}}^{\star }}$ for a fixed $b\in (0,1).$ Assume that ${\psi }_1$ does not change sign, say ${\psi }_1(x)>0$ and since ${\lambda }_1<{\lambda }_2<\cdots <{\lambda }_n<\cdots ,$ the sequence $\{u(b,j){\}}_{j\in {\mathbb{N}}^{\star }}$ generated by $f={\psi }_1$ is nontrivial and has the asymptotic for large j, (9) $\begin{array}{rl}u(b,j)& =e^{-{\lambda }_{1}j}\{c_1\left({\psi }_1\right){\phi }_1\left(b\right)+\sum _{n\ge 2}{c}_n\left({\psi }_1\right)e^{-({\lambda }_n-{\lambda }_1)j}{\phi }_n\left(b\right)\}\\ & =c_1\left({\psi }_1\right){\phi }_1\left(b\right)e^{-{\lambda }_{1}j}+O\left(e^{-({\lambda }_2-{\lambda }_1)j}\right),\end{array}$(9) which yields (10) $\underset{j\to \mathrm{\infty }}{lim}\frac{u(b,j+1)}{u(b,j)}=e^{-{\lambda }_1}.$(10) Although the limit is easy to set up, its existence hinges on the facts that ${\phi }_1(b)\ne 0,$ as the first eigenfunction does not vanish inside, and also on $c_1({\psi }_1)={\int }_0^1{\phi }_1(x){\psi }_1(x)\rho (x)\mathrm{d}x\ne 0,$ as the functions do not change sign. The limit can then be used to find the sought Fourier coefficients $c_1({\psi }_k){\phi }_1(b)$ (11) $\underset{j\to \mathrm{\infty }}{lim}{e}^{{\lambda }_{1}j}u(b,j)=c_1\left({\psi }_k\right){\phi }_1\left(b\right)={\int }_0^1{\phi }_1(x){\phi }_1(b){\psi }_k(x)\rho (x)\mathrm{d}x.$(11) From (11(11) $\underset{j\to \mathrm{\infty }}{lim}{e}^{{\lambda }_{1}j}u(b,j)=c_1\left({\psi }_k\right){\phi }_1\left(b\right)={\int }_0^1{\phi }_1(x){\phi }_1(b){\psi }_k(x)\rho (x)\mathrm{d}x.$(11) ), and (8(8) $\begin{array}{rl}{\phi }_1(x)\rho (x){\phi }_1\left(b\right)& =\sum _{k\ge 1}({\int }_0^1{\phi }_1(\xi ){\psi }_k(\xi )\rho (\xi )d\xi ){\phi }_1\left(b\right){\psi }_k\left(x\right)\\ & =\sum _{k\ge 1}{c}_1\left({\psi }_k\right){\phi }_1\left(b\right){\psi }_k\left(x\right)\mathrm{in}{L}^2(0,1)\end{array}$(8) ) we have (12) ${\phi }_1(x){\phi }_1(b)\rho (x)=\sum _{k\ge 1}{c}_1\left({\psi }_k\right){\phi }_1(b){\psi }_k(x)\mathrm{in}{L}^2(0,1).$(12) Since we have reconstructed ${\phi }_1(x){\phi }_1(b)\rho (x),$ we only need ${\phi }_1(x){\phi }_1(b)$ to deduce ρ. To this end, since we already have ${\lambda }_1$ and ${\phi }_1(x){\phi }_1(b)\rho (x),$ it means we have the right-hand side of a rescaled (5(5) $-{\phi }_1^{\mathrm{\prime }\mathrm{\prime }}\left(x\right)={\lambda }_1\rho \left(x\right){\phi }_1\left(x\right),x\in (0,1).$(5) ), i.e. (13) ${\phi }_1^{\mathrm{\prime }\mathrm{\prime }}\left(x\right){\phi }_1(b)=-{\lambda }_1{\phi }_1(x){\phi }_1(b)\rho (x)\in L^2(0,1),$(13) where ${\phi }_1(x){\phi }_1(b)\in H^2(0,1),$ which is easily obtained by the Green's function of the boundary value problem (14) $\{\begin{array}{l}{y}^{\mathrm{\prime }\mathrm{\prime }}\left(x\right)=f(x)0<x<1,\\ y^{\mathrm{\prime }}\left(0\right)-hy\left(0\right)=0\mathrm{and}{y}^{\mathrm{\prime }}\left(1\right)+Hy\left(1\right)=0.\end{array}$(14) The existence and uniqueness is given by the following lemma.

Lemma 3.1

If $H+h+hH\ne 0$ then ${\lambda }_1\ne 0$and the solution to the boundary value problem  (13(13) ${\phi }_1^{\mathrm{\prime }\mathrm{\prime }}\left(x\right){\phi }_1(b)=-{\lambda }_1{\phi }_1(x){\phi }_1(b)\rho (x)\in L^2(0,1),$(13) ) exists and is given explicitly by $y(x)=G(f)(x):={\int }_0^{1}G(x,t)f(t)\mathrm{d}t$ with $G(x,t)$ defined by  (15(15) $G(x,t)=\{\begin{array}{c}{\displaystyle \frac{1}{\omega }}(1+H(1-x))(1+ht)\mathrm{for}0<t<x,\\ {\displaystyle \frac{1}{\omega }}(1+H(1-t))(1+hx)\mathrm{for}x<t<1,\end{array}$(15) ). Furthermore, the map $f\mapsto y$ is a bounded operator from $L^2(0,1)\to C(0,1).$

Proof.

If ${\lambda }_1=0,$ then ${\phi }_1^{\mathrm{\prime }\mathrm{\prime }}(x)=0$from (5(5) $-{\phi }_1^{\mathrm{\prime }\mathrm{\prime }}\left(x\right)={\lambda }_1\rho \left(x\right){\phi }_1\left(x\right),x\in (0,1).$(5) ) and so ${\phi }_1(x)=ax+b.$ Using the boundary conditions, at $x=0,1,$ yield the system $\{\begin{array}{r}a-hb=0\\ (1+H)a+Hb=0\end{array}$which gives a nontrivial solution, i.e. $a^2+b^2\ne 0,$ if and only if its determinant, which is the Wronskian $\omega =H+h+Hh=0.$The same condition also implies that (14(14) $\{\begin{array}{l}{y}^{\mathrm{\prime }\mathrm{\prime }}\left(x\right)=f(x)0<x<1,\\ y^{\mathrm{\prime }}\left(0\right)-hy\left(0\right)=0\mathrm{and}{y}^{\mathrm{\prime }}\left(1\right)+Hy\left(1\right)=0.\end{array}$(14) ) has a unique solution, which we can obtain using the Green's function (15) $G(x,t)=\{\begin{array}{c}{\displaystyle \frac{1}{\omega }}(1+H(1-x))(1+ht)\mathrm{for}0<t<x,\\ {\displaystyle \frac{1}{\omega }}(1+H(1-t))(1+hx)\mathrm{for}x<t<1,\end{array}$(15) where $\omega \ne 0$. From $|G(f)(x)|\le \Vert G(x,.)\Vert \Vert f\Vert$ and the fact that the Green function is continuous, we deduce that (16) $\underset{0\le x\le 1}{sup}|G(f)(x)|\le M\Vert f(x)\Vert$(16) with $M=\underset{0\le x\le 1}{sup}\Vert G(x,.)\Vert .$

Once we have reconstructed ${\lambda }_1{\phi }_1(x){\phi }_1(b)\rho (x),$ we can solve (13(13) ${\phi }_1^{\mathrm{\prime }\mathrm{\prime }}\left(x\right){\phi }_1(b)=-{\lambda }_1{\phi }_1(x){\phi }_1(b)\rho (x)\in L^2(0,1),$(13) ) to obtain (17) $\begin{array}{rl}{\phi }_1(x){\phi }_1(b)& =G(-{\lambda }_1{\phi }_1(x){\phi }_1(b)\rho (x))\\ & =-{\lambda }_1\frac{(1+H-xH)}{H+h+hH}{\int }_0^x(1+ht){\phi }_1(t){\phi }_1(b)\rho (t)\mathrm{d}t\\ & -{\lambda }_1\frac{(1+hx)}{H+h+hH}{\int }_x^1(1+H-tH){\phi }_1(t){\phi }_1(b)\rho (t)\mathrm{d}t.\end{array}$(17) Combining (12(12) ${\phi }_1(x){\phi }_1(b)\rho (x)=\sum _{k\ge 1}{c}_1\left({\psi }_k\right){\phi }_1(b){\psi }_k(x)\mathrm{in}{L}^2(0,1).$(12) ) and (17(17) $\begin{array}{rl}{\phi }_1(x){\phi }_1(b)& =G(-{\lambda }_1{\phi }_1(x){\phi }_1(b)\rho (x))\\ & =-{\lambda }_1\frac{(1+H-xH)}{H+h+hH}{\int }_0^x(1+ht){\phi }_1(t){\phi }_1(b)\rho (t)\mathrm{d}t\\ & -{\lambda }_1\frac{(1+hx)}{H+h+hH}{\int }_x^1(1+H-tH){\phi }_1(t){\phi }_1(b)\rho (t)\mathrm{d}t.\end{array}$(17) ) yield (18) $\rho (x)=\frac{{\phi }_1(x){\phi }_1(b)\rho (x)}{{\phi }_1(x){\phi }_1(b)}=\frac{S(x)}{G\left(S\right)(x)},$(18) where (19) $S(x)={\phi }_1(x){\phi }_1(b)\rho (x)=\sum _{k\ge 1}{c}_1\left({\psi }_k\right){\phi }_1(b){\psi }_k(x).$(19) Recall that the denominator is non zero since ${\phi }_1(x)\ne 0$ for all $x\in (0,1)$. Thus, we have proved the main result of the paper stated previously in Theorem 1.1.

Remark 3.2

The condition $H+h+hH\ne 0$ excludes two cases, namely the Dirichlet and the Neumann cases which will be treated separately below. Note that their Green's function is easier to compute.

4. The Dirichlet case

With few modifications, we can also treat the Dirichlet case which corresponds to the limiting case $h=H=\mathrm{\infty },$ in (1(1) $\{\begin{array}{l}{u}_t(x,t)={\displaystyle \frac{1}{\rho (x)}}{u}_{xx}(x,t)0<x<1,t>0\\ u_x(0,t)-hu(0,t)=0t>0\\ u_x(1,t)+Hu(1,t)=0t>0\\ u(x,0)=f(x)x\in (0,1)\end{array}$(1) ) i.e. (20) $\{\begin{array}{l}{u}_t(x,t)={\displaystyle \frac{1}{\rho (x)}}{u}_{xx}(x,t),0<x<1,t>0,\\ u(0,t)=0\mathrm{and}u(1,t)=0,t>0\\ u(x,0)=f(x),x\in (0,1),\end{array}$(20) whose solution is given by (21) $u(x,t)=\sum _{n\ge 1}{d}_n\left(f\right){\varphi }_n\left(x\right)e^{-{\mu }_{n}t},$(21) where ${\varphi }_n$ are the eigenfunctions, (22) $\{\begin{array}{l}-{\varphi }_n^{\mathrm{\prime }\mathrm{\prime }}\left(x\right)={\mu }_n\rho (x){\varphi }_n\left(x\right)x\in (0,1),\\ {\varphi }_n(0)={\varphi }_n(1)=0.\end{array}$(22) It is readily seen that ${\mu }_1\ne 0,$ otherwise ${\varphi }_1(x)=0,$ and clearly all eigenvalues are positive $0<{\mu }_1<\cdots <{\mu }_n<\cdots$ . The Fourier coefficients are given by $d_n\left(f\right)={\int }_0^{1}f(x){\varphi }_n\left(x\right)\rho (x)\mathrm{d}x.$Next, we use the basis $\{\sin (\pi nx){\}}_{n\ge 1},$ to extract ${\mu }_1$ and the coefficients $d_1(\sin \left(n\pi x\right)){\varphi }_1\left(b\right)={\int }_0^1\sin \left(n\pi x\right){\varphi }_1\left(x\right){\varphi }_1\left(b\right)\rho (x)\mathrm{d}x,\mathrm{for}n\in \mathbb{N}$from the observation $u(b,t)$, from (21(21) $u(x,t)=\sum _{n\ge 1}{d}_n\left(f\right){\varphi }_n\left(x\right)e^{-{\mu }_{n}t},$(21) ) by the method of limits. Using the sequence $\{d_1(\sin (n\pi x)){\}}_{n\ge 1}$ we reconstruct (23) ${\varphi }_1\left(x\right){\varphi }_1\left(b\right)\rho (x)=\sum _{n\ge 1}2d_1(\sin \left(n\pi x\right)){\varphi }_1\left(b\right)\sin \left(n\pi x\right)\mathrm{in}{L}^2(0,1).$(23) One of the advantages of the Dirichlet problem is the simplicity of its Green's function. From (22(22) $\{\begin{array}{l}-{\varphi }_n^{\mathrm{\prime }\mathrm{\prime }}\left(x\right)={\mu }_n\rho (x){\varphi }_n\left(x\right)x\in (0,1),\\ {\varphi }_n(0)={\varphi }_n(1)=0.\end{array}$(22) ) we have (24) $-{\varphi }_1^{\mathrm{\prime }\mathrm{\prime }}\left(x\right){\varphi }_1\left(b\right)={\mu }_1{\varphi }_1\left(x\right){\varphi }_1\left(b\right)\rho (x).$(24) From (24(24) $-{\varphi }_1^{\mathrm{\prime }\mathrm{\prime }}\left(x\right){\varphi }_1\left(b\right)={\mu }_1{\varphi }_1\left(x\right){\varphi }_1\left(b\right)\rho (x).$(24) ) and (23(23) ${\varphi }_1\left(x\right){\varphi }_1\left(b\right)\rho (x)=\sum _{n\ge 1}2d_1(\sin \left(n\pi x\right)){\varphi }_1\left(b\right)\sin \left(n\pi x\right)\mathrm{in}{L}^2(0,1).$(23) ) it follows that (25) ${\varphi }_1\left(x\right){\varphi }_1\left(b\right)=2{\mu }_1\sum _{n\ge 1}{d}_1(\sin \left(n\pi x\right)){\varphi }_1\left(b\right)\frac{\sin \left(n\pi x\right)}{n^2{\pi }^2}.$(25) In order words, we deduce from (25(25) ${\varphi }_1\left(x\right){\varphi }_1\left(b\right)=2{\mu }_1\sum _{n\ge 1}{d}_1(\sin \left(n\pi x\right)){\varphi }_1\left(b\right)\frac{\sin \left(n\pi x\right)}{n^2{\pi }^2}.$(25) ) (26) $\rho \left(x\right)=\frac{\sum _{n\ge 1}{d}_1(\sin \left(n\pi x\right)){\varphi }_1\left(b\right)\sin \left(n\pi x\right)}{{\mu }_1\sum _{n\ge 1}{d}_1(\sin \left(n\pi x\right)){\varphi }_1\left(b\right){\displaystyle \frac{\sin \left(n\pi x\right)}{n^2{\pi }^2}}}.$(26) Thus after obtaining ${\mu }_1$ and ${\varphi }_1(x)\rho (x),$ we can reconstruct $\rho \in L^2(0,1)$ by (26(26) $\rho \left(x\right)=\frac{\sum _{n\ge 1}{d}_1(\sin \left(n\pi x\right)){\varphi }_1\left(b\right)\sin \left(n\pi x\right)}{{\mu }_1\sum _{n\ge 1}{d}_1(\sin \left(n\pi x\right)){\varphi }_1\left(b\right){\displaystyle \frac{\sin \left(n\pi x\right)}{n^2{\pi }^2}}}.$(26) ). Thus we have proved the following theorem

Theorem 4.1

In the Dirichlet case we can reconstruct $\rho \in L^2(0,1)$ by  (26(26) $\rho \left(x\right)=\frac{\sum _{n\ge 1}{d}_1(\sin \left(n\pi x\right)){\varphi }_1\left(b\right)\sin \left(n\pi x\right)}{{\mu }_1\sum _{n\ge 1}{d}_1(\sin \left(n\pi x\right)){\varphi }_1\left(b\right){\displaystyle \frac{\sin \left(n\pi x\right)}{n^2{\pi }^2}}}.$(26) ) from the map $\sin (n\pi x)\mapsto \{u(b,k){\}}_{k\in {\mathbb{N}}^{\star }}$ for any fixed $b\in (0,1),$ where u is a solution of  (20(20) $\{\begin{array}{l}{u}_t(x,t)={\displaystyle \frac{1}{\rho (x)}}{u}_{xx}(x,t),0<x<1,t>0,\\ u(0,t)=0\mathrm{and}u(1,t)=0,t>0\\ u(x,0)=f(x),x\in (0,1),\end{array}$(20) ).

Remark 4.2

Although ${\varphi }_1(b)\ne 0,$ we still cannot simplify (26(26) $\rho \left(x\right)=\frac{\sum _{n\ge 1}{d}_1(\sin \left(n\pi x\right)){\varphi }_1\left(b\right)\sin \left(n\pi x\right)}{{\mu }_1\sum _{n\ge 1}{d}_1(\sin \left(n\pi x\right)){\varphi }_1\left(b\right){\displaystyle \frac{\sin \left(n\pi x\right)}{n^2{\pi }^2}}}.$(26) ) because it is unknown.

We now work out the Neumann boundary condition which is very different because 0 is an eigenvalue.

5. The Neumann case

Neumann boundary conditions means we have $h=H=0,$ in (1(1) $\{\begin{array}{l}{u}_t(x,t)={\displaystyle \frac{1}{\rho (x)}}{u}_{xx}(x,t)0<x<1,t>0\\ u_x(0,t)-hu(0,t)=0t>0\\ u_x(1,t)+Hu(1,t)=0t>0\\ u(x,0)=f(x)x\in (0,1)\end{array}$(1) ) i.e. (27) $\{\begin{array}{l}{u}_t(x,t)={\displaystyle \frac{1}{\rho (x)}}{u}_{xx}(x,t),0<x<1,t>0,\\ u_x(0,t)=0\mathrm{and}{u}_x(1,t)=0,t>0,\\ u(x,0)=f(x)x\in (0,1),\end{array}$(27) whose solution is given by (28) $u(b,t)=h_0\left(f\right){\chi }_0\left(b\right)+\sum _{n\ge 1}{h}_n\left(f\right){\chi }_n\left(b\right)e^{-{\xi }_{n}t}.$(28) Here ${\chi }_n$ are the normalized eigenfunctions in $L_{\rho }^2(0,1)$ with $\Vert {\chi }_n{\Vert }_{\rho }=1,$ and are solutions of (29) $\{\begin{array}{l}-{\chi }_n^{\mathrm{\prime }\mathrm{\prime }}\left(x\right)={\xi }_n\rho (x){\chi }_n\left(x\right)0<x<1,n=0,1,2,\dots ,\\ {\chi }_n^{\mathrm{\prime }}\left(0\right)={\chi }_n^{\mathrm{\prime }}\left(1\right)=0\end{array}$(29) with eigenvalues (30) $0={\xi }_0<{\xi }_1<{\xi }_2<\cdots <{\xi }_n<\mathrm{and}{\chi }_0(x)={({\int }_0^1\rho (x)\mathrm{d}x)}^{-1/2}.$(30) The Fourier coefficients in (28(28) $u(b,t)=h_0\left(f\right){\chi }_0\left(b\right)+\sum _{n\ge 1}{h}_n\left(f\right){\chi }_n\left(b\right)e^{-{\xi }_{n}t}.$(28) ) are given by $h_n\left(f\right)={\int }_0^{1}f(x){\chi }_n\left(x\right)\rho (x)\mathrm{d}x\mathrm{for}n=0,1,2,\dots .$It follows from (28(28) $u(b,t)=h_0\left(f\right){\chi }_0\left(b\right)+\sum _{n\ge 1}{h}_n\left(f\right){\chi }_n\left(b\right)e^{-{\xi }_{n}t}.$(28) ) that $u(b,t)\to h_0\left(f\right){\chi }_0\left(b\right)\mathrm{as}t\to \mathrm{\infty }.$Note we are not looking for the first eigenvalue, as it is already known to be zero. Next, we use the basis $\{\cos (nx\pi ){\}}_{n\ge 0},$ as initial conditions to extract the first coefficients in (28(28) $u(b,t)=h_0\left(f\right){\chi }_0\left(b\right)+\sum _{n\ge 1}{h}_n\left(f\right){\chi }_n\left(b\right)e^{-{\xi }_{n}t}.$(28) ), and use (30(30) $0={\xi }_0<{\xi }_1<{\xi }_2<\cdots <{\xi }_n<\mathrm{and}{\chi }_0(x)={({\int }_0^1\rho (x)\mathrm{d}x)}^{-1/2}.$(30) ) (31) $\begin{array}{rl}{h}_0(\cos \left(nx\pi \right)){\chi }_0\left(b\right)& ={\int }_0^1\cos \left(nx\pi \right)\rho (x){\chi }_0\left(b\right)\mathrm{d}x{\chi }_0\left(b\right)\\ & ={({\int }_0^1\rho (x)\mathrm{d}x)}^{-1}{\int }_0^1\cos \left(nx\pi \right)\rho (x)\mathrm{d}x\mathrm{for}n=0,1,2,\dots \end{array}$(31) Next observe that for $n=0,$ (31(31) $\begin{array}{rl}{h}_0(\cos \left(nx\pi \right)){\chi }_0\left(b\right)& ={\int }_0^1\cos \left(nx\pi \right)\rho (x){\chi }_0\left(b\right)\mathrm{d}x{\chi }_0\left(b\right)\\ & ={({\int }_0^1\rho (x)\mathrm{d}x)}^{-1}{\int }_0^1\cos \left(nx\pi \right)\rho (x)\mathrm{d}x\mathrm{for}n=0,1,2,\dots \end{array}$(31) ) reduces to $h_0\left(1\right)=1$and the Fourier cosine coefficient of ρin terms of the observation (32) ${\int }_0^1\cos \left(nx\pi \right)\rho (x)\mathrm{d}x=h_0(\cos \left(nx\pi \right)){\chi }_0\left(b\right){\int }_0^1\rho (x)\mathrm{d}x.$(32) Recall that the Fourier cosine series of ρ in $L^2(0,1)$ is $\begin{array}{rl}\rho (x)& ={\int }_0^1\rho (x)\mathrm{d}x+2\sum _{n\ge 1}{\int }_0^1\cos \left(n\pi x\right)\rho (x)\mathrm{d}x\cos (n\pi x)\\ & ={\int }_0^1\rho (x)\mathrm{d}x[1+2\sum _{n\ge 1}{h}_0(\cos \left(nx\pi \right)){\chi }_0\left(b\right)\cos (n\pi x)]\mathrm{in}{L}^2(0,1).\end{array}$Thus we need the value ${\int }_0^1\rho (x)\mathrm{d}x$in order to reconstruct ρ.

Theorem 5.1

In the Neumann case we can reconstruct ρ provided we know ${\int }_0^1\rho (x)\mathrm{d}x$ and the map $\cos (n\pi x)\mapsto \{u(b,k){\}}_{k\in \mathbb{N}}$ for $b\in [0,1].$

Remark 5.2

If we could extract the second eigenvalue, ${\xi }_1\ne 0,$ then we can recover ρ by a similar formula to (26(26) $\rho \left(x\right)=\frac{\sum _{n\ge 1}{d}_1(\sin \left(n\pi x\right)){\varphi }_1\left(b\right)\sin \left(n\pi x\right)}{{\mu }_1\sum _{n\ge 1}{d}_1(\sin \left(n\pi x\right)){\varphi }_1\left(b\right){\displaystyle \frac{\sin \left(n\pi x\right)}{n^2{\pi }^2}}}.$(26) ) and we would not need the value ${\int }_0^1\rho (x)\mathrm{d}x.$

6. Convergence

In practice, we can only use a finite sum to approximate $S(x)={\phi }_1(x){\phi }_1(b)\rho (x)=\sum _{k\ge 1}{c}_1\left({\psi }_k\right){\phi }_1(b){\psi }_k(x)$given in (19(19) $S(x)={\phi }_1(x){\phi }_1(b)\rho (x)=\sum _{k\ge 1}{c}_1\left({\psi }_k\right){\phi }_1(b){\psi }_k(x).$(19) ). Using the notation of section 3, let us denote the approximation of ρ by (33) ${\rho }_N(x)=\frac{S_N(x)}{G\left(S_N\right)(x)}\mathrm{where}{S}_N(x)=\sum _{k=1}^{k=N}{c}_1\left({\psi }_k\right){\phi }_1(b){\psi }_k(x).$(33) If $S_N(x)={\phi }_1(x){\phi }_1(b)\rho (x)+{\epsilon }_N(x)$then $\begin{array}{rl}\rho (x)-{\rho }_N(x)& =\frac{G(S_N(x))S(x)-G(S(x))S_N(x)}{G\left(S_N\right)(x)G\left(S\right)(x)}\\ & =\frac{S(x)G({\epsilon }_N(x))-G(S(x)){\epsilon }_N(x)}{G\left(S\right)(x)G\left(S\right)(x)+G\left(S\right)(x)G\left({\epsilon }_N\right)(x)}.\end{array}$Note that as ${\epsilon }_N\to 0$ in $L^2(0,1),$ it follows that $sup|G({\epsilon }_N)(x)|\to 0$as $N\to \mathrm{\infty }.$ Recall that we have $G(S)(x)={\phi }_1(x){\phi }_1(b)>0$ for 0<x<1 and thus for any interval $(a,b)$ such that 0<a<b<1 we have $\underset{a<x<b}{inf}|G\left(S\right)(x)G\left(S\right)(x)+G\left(S\right)(x)G\left({\epsilon }_N\right)(x)|=\delta (a,b,N)>0\mathrm{for}N\mathrm{largeenough}.$Then, it follows $\begin{array}{rl}\sqrt{{\int }_a^b{|\rho (x)-{\rho }_N(x)|}^2\mathrm{d}x}& \le \frac{1}{\delta (a,b,N)}(\Vert S\Vert \underset{0\le x\le 1}{sup}\left|G({\epsilon }_N(x))\right|+\underset{0\le x\le 1}{sup}\left|G(S(x))\right|\Vert {\epsilon }_N\Vert )\\ & \le \frac{1}{\delta (a,b,N)}(\Vert S\Vert M\Vert {\epsilon }_N\Vert +M\Vert S\Vert \Vert {\epsilon }_N\Vert )\\ & \le \frac{2M}{\delta (a,b,N)}\Vert S\Vert \Vert {\epsilon }_N\Vert ,\end{array}$where M is defined in (16(16) $\underset{0\le x\le 1}{sup}|G(f)(x)|\le M\Vert f(x)\Vert$(16) ). Therefore we have proved the following theorem.

Theorem 6.1

${\rho }_N$ defined by (33(33) ${\rho }_N(x)=\frac{S_N(x)}{G\left(S_N\right)(x)}\mathrm{where}{S}_N(x)=\sum _{k=1}^{k=N}{c}_1\left({\psi }_k\right){\phi }_1(b){\psi }_k(x).$(33) ) converges to ρ on any subinterval of $(0,1)$, i.e. ${\rho }_N\to \rho$ in $L^2(a,b)$ for any $(a,b)\subset (0,1).$

7. Algorithm

The whole reconstruction procedure is based on the infinite limits (10(10) $\underset{j\to \mathrm{\infty }}{lim}\frac{u(b,j+1)}{u(b,j)}=e^{-{\lambda }_1}.$(10) ) and (11(11) $\underset{j\to \mathrm{\infty }}{lim}{e}^{{\lambda }_{1}j}u(b,j)=c_1\left({\psi }_k\right){\phi }_1\left(b\right)={\int }_0^1{\phi }_1(x){\phi }_1(b){\psi }_k(x)\rho (x)\mathrm{d}x.$(11) ). Since we cannot take them in practice, we shall use the tolerance, ε say, to find a stopping time numerically. Thus from the limit in (10(10) $\underset{j\to \mathrm{\infty }}{lim}\frac{u(b,j+1)}{u(b,j)}=e^{-{\lambda }_1}.$(10) ) we have (34) $\begin{array}{rl}& \text{for any }\epsilon >0,\\ & \text{there exists }{T}_0,\text{ such that for }T>T_0\text{ we have }|\frac{u(b,T+1)}{u(b,T)}-e^{-{\lambda }_1}|<\epsilon ,\end{array}$(34) where $T_0$ is determined numerically. We also use the same idea to compute the Fourier coefficients $c_1({\psi }_k){\phi }_1(b)$ from the limits in (11(11) $\underset{j\to \mathrm{\infty }}{lim}{e}^{{\lambda }_{1}j}u(b,j)=c_1\left({\psi }_k\right){\phi }_1\left(b\right)={\int }_0^1{\phi }_1(x){\phi }_1(b){\psi }_k(x)\rho (x)\mathrm{d}x.$(11) ). As we shall see in the examples, due to the rapid decay of the exponentials, in general, $T_0\le 3.$ We now work out few numerical examples to illustrate the method.

8. Numerical examples

For the sake of simplicity, we shall use Dirichlet and Neumann boundary conditions where the initial condition $f(x)$ is chosen from the basis $\{\sin (kx\pi ){\}}_{k\in {\mathbb{N}}^{\ast }}$ for the former and $\{\cos (kx\pi ){\}}_{k\in \mathbb{N}}$ for the latter. The observations of the solution are taken at either $b=1/2$ or $b=1/4$ and generated by solving (1(1) $\{\begin{array}{l}{u}_t(x,t)={\displaystyle \frac{1}{\rho (x)}}{u}_{xx}(x,t)0<x<1,t>0\\ u_x(0,t)-hu(0,t)=0t>0\\ u_x(1,t)+Hu(1,t)=0t>0\\ u(x,0)=f(x)x\in (0,1)\end{array}$(1) ) using the Crank–Nicholson method up to T. 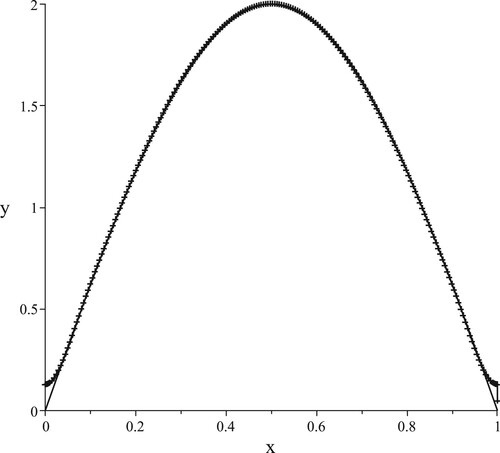We recall that it follows from (10(10) $\underset{j\to \mathrm{\infty }}{lim}\frac{u(b,j+1)}{u(b,j)}=e^{-{\lambda }_1}.$(10) ) that the sequence of ratios ${\displaystyle r(k)=\frac{u(1/2,(k+1)/100)}{u(1/2,k/100)}\mathrm{yields}\underset{k\to \mathrm{\infty }}{lim}r(k)=e^{-{\lambda }_1/100}.}$Example 1. Consider $\{\begin{array}{l}{u}_t(x,t)={\displaystyle \frac{1}{2\sin (\pi x)}}{u}_{xx}(x,t)x\in (0,1),t\in (0,T)\\ u(0,t)=0,u(1,t)=0t\in (0,T)\\ u(x,0)=\sin (kx\pi )x\in (0,1),k\in {\mathbb{N}}^{\ast }\end{array}$

Figure 1. $2\sin (\pi x)$ –  and ${\rho }_{20}$ +++.

Figure 2. $(2x-1{)}^2$ – and ${\rho }_{20}$ +++

To find the stopping time $T_0$, we observe the sequence $u(1/2,k/100)$ for $k\ge 1$ and

k,  r(k)

35, 0.9437854846474063

36, 0.9437854846439294

37, 0.9437854846420766

38, 0.9437854846410607

39, 0.9437854846405333

40, 0.9437854846402476

41, 0.9437854846400894

42, 0.9437854846400063

Thus, tolerance $\epsilon ={10}^{-12}$ is achieved at time $39/100,\underset{\_}{0.943785484640}5333$ which means that $T_0\ge 40\times 1/100=0.4$. This yields ${\lambda }_1:=5.7856379507$ from $\exp (-{\lambda }_1/100)=0.943785484640$. Next we obtain the sequence of Fourier coefficients by evaluating $u(1/2,0.4)\exp (-{\lambda }_1\ast 0.4):$

0.1794, 7.333 e−16, −0.0390, −3.667e−17, −0.4194e−2, −2.649e−17, −0.1497e−2, 1.111 e−16, −6.936e−4, −4.778e−16, −3.768e−4, −1.235e−16, −2.272e−4, −5.787e−16, −1.474e−4, 4.971 e−16, −1.011e−4, −4.776e−16, −7.232e−5, 9.872 e−16.

Using (26(26) $\rho \left(x\right)=\frac{\sum _{n\ge 1}{d}_1(\sin \left(n\pi x\right)){\varphi }_1\left(b\right)\sin \left(n\pi x\right)}{{\mu }_1\sum _{n\ge 1}{d}_1(\sin \left(n\pi x\right)){\varphi }_1\left(b\right){\displaystyle \frac{\sin \left(n\pi x\right)}{n^2{\pi }^2}}}.$(26) ) we get

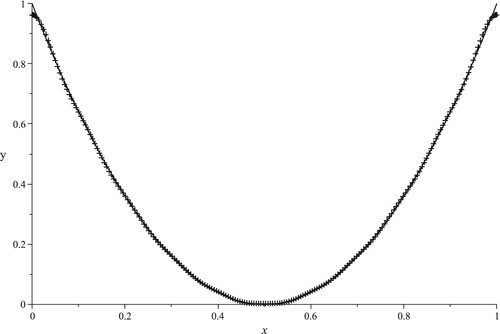
Example 2: We now treat the Neumann case $\{\begin{array}{l}{u}_t(x,t)={\displaystyle \frac{1}{(2x-1{)}^2}}{u}_{xx}(x,t)0<x<1,t>0\\ u_x(0,t)=0,u_x(1,t)=0t>0\\ u(x,0)=\cos (kx\pi )x\in (0,1)k\in \mathbb{N}\end{array}$$\rho (x)=(2x-1{)}^2$ and so the extra data is ${\int }_0^1\rho (x)\mathrm{d}x=\frac{1}{3}.$ We also know that the first eigenvalue is ${\xi }_0=0$ and we shall observe the $u(1/4,T_0)$. To find $T_0$ use the ratios k,  r(k)

284, 0.99996174

285, 0.99998622

286, 0.99998188

287, 1.00001679

288, 1.00000472

289, 1.00033535

290, 0.99944850

291, 1.00031139

292, 1.00000228 we conclude that $T_0$ =3 for $\epsilon ={10}^{-3}.$ The sequence of Fourier coefficients is seq(c[k],k= 0.20):

1.0000, 3.7746 e−13 , 0.6079, −1.1207e−11, 0.1519, 5.1966 e−11, 0.0674, −1.4377e−10, 0.0379,3.1113 e−10 , 0.0242, −5.8620e−10, 0.0168, 1.0112 e−9, 0.0124, −1.6288e−9, 0.00956, 2.4390 e−9 , 0.0076, −3.2949e−9, 0.0063.

9. Conclusion

We have shown that tools from signal processing can help extract spectral data to reconstruct an unknown weight of a parabolic equation. It also shows that good imaging and non-destructive testing in industry can be achieved with few measurements done with one accurate sensor.

Acknowledgements

The authors sincerely thank the referees for their valuable comments and insight. Both authors also thank KFUPM for its support.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This work is supported by KFUPM [grant number SB191035].