The representation of coupling interactions in the Material Properties Open Database (MPOD)

ABSTRACT

The Material Properties Open Database (MPOD, http://mpod.cimav.edu.mx) is a functional element of the web-based open databases system linked with crystallography. MPOD delivers single-crystal tensor properties in several representations, ranging from numerical matrices to 3D printing. Longitudinal moduli surfaces can be displayed in computers as well as in smart cell phones. Properties are stored as ‘.mpod’ files. IUCr formatting standards (CIF) are followed. The original published paper containing the data is cited. Structural and experimental information is also registered and linked. ‘Coupling properties’, say piezo-effects and magnetoelectricity, represent interactions linking different subsystems in a material. Currently, piezoelectricity occupies a significant fraction of cases in MPOD. The implications of crystal symmetry in piezoelectricity are systematically taken into account. Matrices’ elements and longitudinal moduli surfaces are checked for consistency with the Neumann principle. The inclusion of magnetoelectric axial tensors introduces exciting features into MPOD.

KEYWORDS:

• Crystal properties
• open database
• anisotropy
• Neumann principle

Introduction

The physical properties of crystalline materials are necessary in many fields, from education to engineering. The properties most commonly considered in traditional studies (Young’s modulus, dielectric constant …) correspond to experiments in which both the stimulus and the sample’s response are associated with a given subsystem in the material (elasticity, electricity …). We denote these interactions and properties as ‘principal’. Today's technology is decidedly dependent on ‘coupling properties’ (piezoelectricity, magnetostriction, magnetoelectricity …) in which a stimulus in one subsystem generates a response in another one. The most complete, though not intuitive, manner of presenting physical properties is by means of the tensor representation. The classical reference in this field is the Landolt–Börnstein collection [1]. The Materials Project [2,3], UC-Berkeley, represents a highly interesting effort in the direction of calculating theoretically and disclosing the physical properties of materials. Kaminsky’s programmes and data concerning crystalline morphology and properties are also of interest [4]. In this universe, the contribution of the Material Properties Open Database (MPOD) is to openly offer a collection of properties values based on published experimental data. MPOD was initiated by Chateigner in 2010 and developed in collaboration with Pepponi and Grazulis [5]. In the recent years, with contributions from the Crystallography Group at CIMAV (Centro de Investigación en Materiales Avanzados), MPOD is being expanded. Some directions in which MPOD has grown comprise the inclusion of new electromagnetic properties and the delivery of graphic representations of properties [6]. This article describes the current MPOD tasks. Some focus is put on coupling properties, their representation by different means and the interesting effect of crystal symmetry on materials properties. The organisation of the paper is as follows. First, a brief description of the treatment given to crystal properties in MPOD is given. Second, a representative scan of MPOD cases is presented. Finally, a sampling of the tensor and group theoretical tools behind MPOD is divulged.

Data treatment in MPOD

The open database MPOD describes the physical properties of single crystals. The information provided is based on experimentally measured tensor magnitudes. In all cases, reference to the original source is included. Following standard treatments [7,8,9] physical properties are defined, in linear approximation, by means of constitutive equations (1).(1) $Y=K\cdot X$(1)

Tensor X (rank m) represents the action (cause) on the sample, Y (rank n) is the materials response (effect) and K (m+n) is the linking property. Principal and coupling properties scan several tensor ranks. To decrease the dimensionality of writing tensors of rank equal to or greater than 2, the so-called matrix or compact notation is frequently used. 3 × 3 symmetric matrices (say the stress tensor) are represented as 6 × 1 hypervectors. Piezoelectric and elastic tensors are written, respectively, as 3 × 6 and 6 × 6 matrices. The constitutive equation for the piezoelectric charge coefficients tensor d is written as follows.(2) $P=d\cdot T$(2) (3) $\left[\begin{array}{c}{P}_1\\ P_2\\ P_3\end{array}\right]=\left[\begin{array}{ccc}{d}_{11}& d_{12}& d_{13}\\ d_{21}& d_{22}& d_{23}\\ d_{31}& d_{32}& d_{33}\end{array}\begin{array}{ccc}{d}_{14}& d_{15}& d_{16}\\ d_{24}& d_{25}& d_{26}\\ d_{34}& d_{35}& d_{36}\end{array}\right]\cdot \left[\begin{array}{c}\begin{array}{c}{T}_1\\ T_2\end{array}\\ \begin{array}{c}{T}_3\\ T_4\\ T_5\end{array}\\ T_6\end{array}\right]$(3) P is the electric polarisation and T is the mechanical stress.

The characterisation of material’s symmetry is essential for properties investigation. MPOD is consistent with theoretically derived ‘selection rules’ for the structure of principal and coupling properties tensors [10,11]. In MPOD, the introduction of new data is performed through a programme that builds the properties matrices, depending on the rank of the considered tensor and according to symmetry. Besides the atomic distribution symmetry, magnetic symmetry may also be taken into account. The polar or axial nature of the property, as well as magnitudes’ behaviour under time inversion, is part of the symmetry analysis. This issue is discussed in Fuentes-Cobas et al. [12,13].

The MPOD data files are written in the International Union of Crystallography ‘CIF’ format. The contents of these files include a link to the original source, the applicable symmetry point group, the measurement technique and conditions and the properties matrices. The user can search files by chemical composition, by phase name or by property. The default output consists of the properties matrices. Commands are available for plotting the properties in the so-called longitudinal surface representation. The output screen contains the commands for generating ‘STL’ files for 3D prints.

We illustrate the conversion from tensor to surface representation through the example of piezoelectricity. The longitudinal piezoelectric surface d(h) represents the following. Consider a tensile stress in an arbitrary direction, which we denote $O{x}_1^{\mathrm{\prime }}$. In tensor notation, we name this stress $T_{11}^{\mathrm{\prime }}$. (In compact notation it would be $T_1^{\mathrm{\prime }}$). In a general case, the piezoelectric polarisation that will appear on the crystal will not be parallel to $O{x}_1^{\mathrm{\prime }}$. It will show several Cartesian components. We focus on $P_1^{\mathrm{\prime }}$, the projection of the polarisation along $O{x}_1^{\mathrm{\prime }}$. We write(4) $P_1^{\mathrm{\prime }}=d_{111}^{\mathrm{\prime }}{T}_{11}^{\mathrm{\prime }}$(4) $d_{111}^{\mathrm{\prime }}$describes the longitudinal piezoelectric effect. The surface of $d_{111}^{\mathrm{\prime }}$ is constructed by varying $O{x}_1^{\mathrm{\prime }}$through all directions in space and plotting for each orientation a point at a distance from the origin proportional to $d_{111}^{\mathrm{\prime }}$. The calculation of $d_{111}^{\mathrm{\prime }}$ starting from the knowledge of the tensor $d_{ijk}$ is done by means of Equation (5)(5) $d\left(\phi ,\beta \right)=d_{111}^{\mathrm{\prime }}={\sum }_{i,j,k}{a}_{1i}{a}_{1j}{a}_{1k}{d}_{ijk}$(5) The coefficients $a_{1i}$ and analogous are the direction cosines of the direction $O{x}_1^{\mathrm{\prime }}$ relative to Cartesian axes $O{x}_i^{}$ (i, j, k = 1, 2, 3).

MPOD contains the equations for plotting the longitudinal surfaces associated with tensor ranks from 2 to 4, polar and axial. Matrices are read in compact notation (two indices) and orientations in space h = (φ, β) are characterised by polar (φ) and azimuthal (β) angles.

The representation of the tensor properties as longitudinal surfaces is useful for the visualisation and the spatial analysis of the properties. An important advantage of this type of representation is that it facilitates the comparative analysis between the structural and the property’s symmetries. As a general regularity the following Neumann principle is valid: ‘The symmetry of the effect is at least equal to the symmetry of the cause’. In crystal physics the Neumann principle may be stated as follows: The symmetry group of any macroscopic property must contain the crystal structure point group as a subgroup.

MPOD case studies

Principal interactions in BaTiO₃

BaTiO₃ is registered in the Database as file ‘1000304.mpod’. The link to the original source leads to the classical report by Berlincourt and Jaffe [14]. The structure point group is 4 mm.

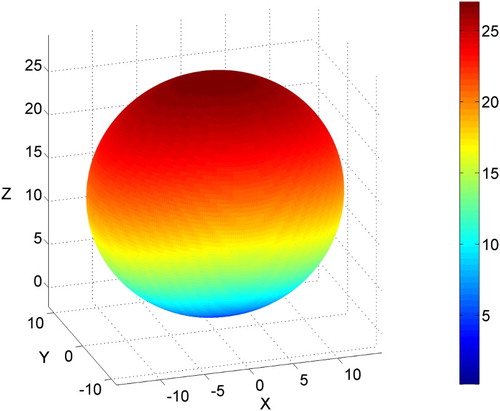
Dielectric constant ε_r

Equation (6) gives the ε_r tensor and Figure 1 represents the ε_r(h) surface(6) ${\epsilon }_r=\left[\begin{array}{ccc}2920& 0& 0\\ 0& 2920& 0\\ 0& 0& 168\end{array}\right]$(6)

Figure 1. BaTiO₃ longitudinal dielectric constant surface. Dielectric constant is a polar second rank tensor. The ε_r(h) surface wraps the coordinates’ origin. The equatorial plane (z = 0) is a symmetry mirror for the dielectric constant. The property point group is ∞/mmm ⊇ 4 mm.

Elasticity

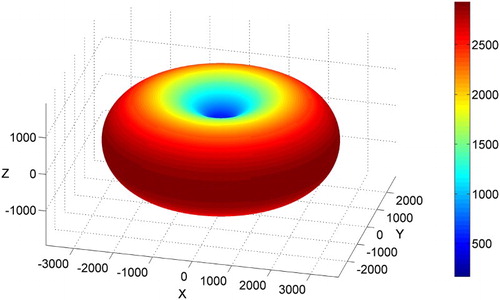
Equation (7) represents the BaTiO₃ elastic compliance tensor (at constant electric field) s^E. Figure 2(a) shows the longitudinal compliance surface s^E(h). Figure 2(b) represents the Young modulus surface E(h) = 1/s^E(h).(7) $s^{\mathrm{E}}=\left[\begin{array}{cc}\begin{array}{ccc}8.05& -2.35& -5.24\\ -2.35& 8.05& -5.24\\ -5.24& -5.24& 15.7\end{array}& \begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\\ \begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}& \begin{array}{ccc}18.4& 0& 0\\ 0& 18.4& 0\\ 0& 0& 8.84\end{array}\end{array}\right]{10}^{-12}\text{P}{\text{a}}^{-1}$(7)

Figure 2. BaTiO₃ (a) elastic compliance and (b) Young modulus. Elasticity is described by polar fourth rank tensors. The s^E(h) and E(h) surfaces wrap the origin. The equatorial plane is a mirror. The property point group is 4/mmm ⊇ 4 mm.

Piezoelectricity in BaTiO3 and quartz

BaTiO₃

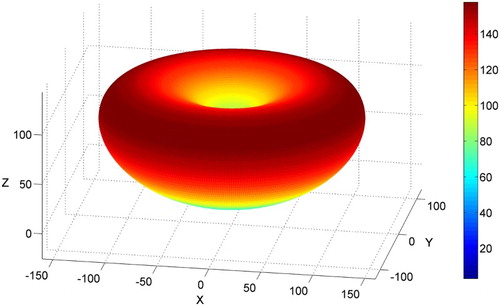
Equation (8) represents the d tensor for BaTiO₃. Figure 3 shows the longitudinal piezoelectric surface d(h).(8) $d=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ -34.5& -34.5& 85.6\end{array}\begin{array}{ccc}0& 392& 0\\ 392& 0& 0\\ 0& 0& 0\end{array}\right]\text{pC}\cdot {\text{N}}^{-1}$(8)

Figure 3. Piezoelectric charge constant d(h) surface for BaTiO₃. Piezoelectricity is represented by polar third rank tensors. The d(h) surface grazes but cannot wrap the origin. The z = 0 plane is not a mirror. Property point group is ∞ mm ⊇ 4 mm.

Quartz (1000055.mpod)

Piezoelectric tensor e for quartz, Equation (9), is taken from Ogi et al. [15]. Tensor e is a useful alternative to d in textured polycrystals’ effective properties calculations [16]. Structure point group is 32. Figure 4 shows the piezoelectric longitudinal surface.(9) $e=\left[\begin{array}{ccc}0.151& -0.151& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\begin{array}{ccc}-0.061& 0& 0\\ 0& 0.061& -0.302\\ 0& 0& 0\end{array}\right]\text{C}\cdot {\text{m}}^{-2}$(9)

Figure 4. Longitudinal piezoelectric surface e(h) for α-quartz. The three characteristic ‘almonds’ graze the origin. The equatorial plane is a mirror. Property point group: −6 m2 ⊇ 32.

Magnetoelectricity

The constitutive equation for magnetoelectricity is P = α·H. Magnetic field intensity H is an axial vector, P is polar and the magnetoelectric tensor α is axial, second rank.

LiCoPO₄ (1000360.mpod)

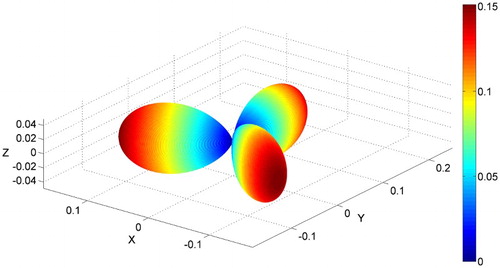
The atomic distribution space group for LiCoPO₄, at 4.2 K, is Pnma (point group mmm). The magnetic symmetry point group, taking into account the atomic magnetic dipoles orientations is mmm’ [17]. Equation (10), from Rivera and Schmid [18], represents the magnetoelectric tensor. The magnetoelectric longitudinal surface α(h) is shown as Figure 5.(10) $\alpha =\left[\begin{array}{ccc}0& 18.4& 0\\ 30.6& 0& 0\\ 0& 0& 0\end{array}\right]\text{ps}\cdot {\text{m}}^{-1}$(10)

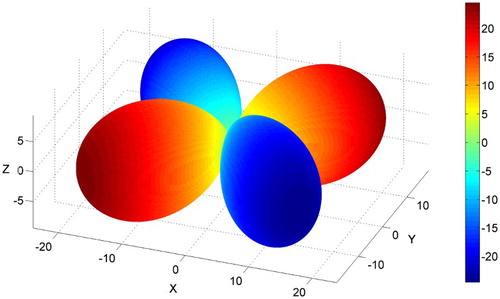
Figure 5. Longitudinal magnetoelectric coefficient α(h). LiCoPO₄ single crystal at 4.2 K. The mmm’ magnetic symmetry associated with the axial nature of magnetoelectric coefficients leads to interesting observations: vertical mirror planes (xz) and (yz) convert positive to negative. Horizontal antimirror (xy) plane preserves sign.

3D printing of properties surfaces

The MPOD graphic interface includes the command to generate 3D print files, in STL format. Figure 6 shows photos of representative 3D impressions.

Figure 6. MPOD 3D printing of longitudinal properties. (a) Quartz piezoelectricity; (b) LiCoPO₄ magnetoelectricity. Positive and negative values are observable.

The maths behind MPOD

The diversity of geometries observed in the presented figures corresponds to the equally diverse collection of matrices representing physical properties. The physical law underlying this diversity is the aforementioned Neumann principle. The starting point for a property’s symmetry analysis is to identify the mathematical nature of the ‘cause’ (X) and ‘effect’ (Y) magnitudes involved in the definitions of the considered ‘property’ K (Equation (1)). Any element of a matrix representing a property, say piezoelectric d₂₄ = 392 pC N⁻¹ in Equations (3) and (8), expresses the effect of an elementary component of the stress [T₄ (matrix) = T₂₃ (tensor) = T_yz] on one of the elementary components of the polarisation [P₂ = P_y].

Let us analyse the relation X → Y from the point of view of Neumann's principle, using group theory tools.

An irreducible representation (irrep) of a point group contains its characters and bases. The bases represent coordinates or components of polar vectors (x, y, z), components of axial vectors (R_x, R_y, R_z), tensor components, hypervectors (t₁, … t₆) or coordinate products. These bases, under the symmetry operations of the group, are transformed according to the characters of the irreps table. An irrep characterises the way each operation of a point group acts on the elementary components of vectors and tensors.

Table 1 shows the irreps of the mm2 point group. This group represents the symmetry of the water molecule and also of some of the so-called ‘Aurivillius ceramics’ (an important family of ferro-piezoelectrics). For example, in the mm2 group, the ‘x’ basis is transformed following the B₁ irrep.

Table 1. Irreducible representations for mm2 point group.

					Representation bases
C2v	E	C2(z)	σ^xz	σ^yz	Polar and axial vector components	Hypervector components
A1	1	1	1	1	z	t1; t2; t3
A2	1	1	−1	−1	Rz	t6
B1	1	−1	1	−1	x, Ry	t5
B2	1	−1	−1	1	y, Rx	t4

According to the Neumann principle, all properties must satisfy, at least, the symmetry of the structural point group. A property describes the action-response relationship. If a property is symmetrical about a certain rotation, the components of the response to a given action must be transformed in the same way as the components of the action are transformed. Formally, the components of the vectors and/or tensors of action and response must share the same irrep.

We illustrate the related methodology by analysing a case of interest.

Pyro- and Piezoelectricity in Aurivillius phases

Let us analyse pyro- and piezoelectricity in materials with mm2 symmetry.

We start considering the so-called fully symmetric irrep A₁. In this irrep, the characters of all the symmetry operations are +1. The z component of any vector remains invariant under all the transformations of this group. Scalars, like temperature, are also invariant under all the operations. The coincidence of z and scalars in A₁ implies that mm2 objects (say, the water molecule) exhibit a spontaneous electric dipole moment, this moment points along the z axis and may depend on the scalar temperature.

Consider now the elements linked with A₁ in the hypervector components column. The stress components T₁, T₂ and T₃ are represented there. The coincidence of these tensor components in the same irrep as P₃ (z) implies that there can exist a linear cause–effect relationship. In other words, the coefficients d₃₁, d₃₂ y d₃₃ may be different from zero.

Following a similar reasoning it is found that d₁₅ and d₂₄ may also be non-zero. In this way, it is deduced that the piezoelectric matrix for the mm2 point group has the form given in Equation (11).(11) $d=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ d_{31}& d_{32}& d_{33}\end{array}\begin{array}{ccc}0& d_{15}& 0\\ d_{24}& 0& 0\\ 0& 0& 0\end{array}\right]$(11)

The particular case of the Aurivillius compound Bi₂WO₆ has been measured by Takeda et al. [19]. His results are reproduced in Equation (12).(12) $d=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ -17& -4.4& 27\end{array}\begin{array}{ccc}0& 46& 0\\ 24& 0& 0\\ 0& 0& 0\end{array}\right]\text{pC}\cdot N^{-1}$(12)

Figure 7 shows the piezoelectric surface of Bi₂WO₆.

Figure 7. Longitudinal piezoelectric coefficient d(h). Bi₂WO₆ single crystal at room temperature. Structure and property point group: mm2.

Conclusions

Crystal thermo–electro–magneto–elastic couplings exhibit a wide spectrum of anisotropic responses, linked with structural and magnetic symmetry, polar and axial nature of magnitudes and tensor ranks.

MPOD (http://mpod.cimav.edu.mx) is an open database that delivers measured materials properties in matrix, surface and 3D printing descriptions.

Properties’ data in MPOD are computer processed, based on tensor analysis and group theory criteria.

Disclosure statement

No potential conflict of interest was reported by the authors.

ORCID

Luis E. Fuentes-Cobas http://orcid.org/0000-0001-6063-3967

Daniel Chateigner http://orcid.org/0000-0001-7792-8702

María E. Fuentes-Montero http://orcid.org/0000-0002-3388-8224

Additional information

Funding

Support from Consejo Nacional de Ciencia y Tecnología – CONACYT, Project 257912 “Representación y pronóstico de las propiedades físicas de los materiales mono- y policristalinos”, is recognised. This project has received funding from the European Union's Horizon 2020 research and innovation program under grant agreement No. 689868, SOLSA project.