A machine learning approach to investigating the effects of mathematics dispositions on mathematical literacy

ABSTRACT

Mathematics competency is fast becoming an essential requirement in ever greater parts of day-to-day work and life. Thus, creating strategies for improving mathematics learning in students is a major goal of education research. However, doing so requires an ability to look at many aspects of mathematics learning, such as demographics and psychological dispositions, in an integrated way as part of the same system. Large-scale assessments such as the Programme for International Student Assessment (PISA) provide an accessible and large volume of coherent data, and this gives researchers the opportunity to employ data-driven approaches to gain an overview of the system. For these reasons, we have used machine learning to explore the relationships between psychological dispositions and mathematical literacy in Australian 15-year-olds using the PISA 2012 data set. Our results from this strongly data-driven approach re-affirm the primacy of mathematics self-efficacy and highlight novel complex interactions between mathematics self-efficacy, mathematics anxiety and socio-economic status. In this paper, we demonstrate how education researchers can usefully employ data-driven modelling techniques to find complex non-linear relationships and novel interactions in a multidimensional data set.

KEYWORDS:

• Machine learning
• data analysis
• PISA
• mathematics education
• dispositions
• demographics
• gradient boosting
• psychology

Introduction

Mathematics achievement has been shown to be influenced by a range of features, from knowledge, skills and working memory, to psychological dispositions and demographics. Thus, any development of a new intervention or a change to education policy would usefully take into account that this is a complex system with hard-to-predict wider effects. For example, there is strong evidence that affecting a student’s dispositions can directly influence their learning, with many theoretical frameworks co-existing in this space (Gottfried 1985; Dweck 2008; Ferla, Valcke, and Cai 2009; Maloney and Beilock 2012; Richardson, Abraham, and Bond 2012). However, including all of these features into a single, coherent framework has not seen much success. The existence of, and easy access to large-scale assessments in modern education research provides the opportunity to use modern data mining techniques to explore multidimensional problems like these using a data-driven approach.

In this paper, we demonstrate how we can build and interpret machine learning (ML) models to interrogate an education research question. We have used ML to explore the relationships between psychological dispositions, demographics and mathematical literacy in an Australian context using the PISA 2012 data set. We have trained two different models to demonstrate how we can get different kinds of insights based on different representations of the data. In the following sections we give a brief overview of the PISA 2012 survey, followed by a description of each of the dispositions and demographics that we are including in our models. This paper is aimed at education researchers who may not necessarily be familiar with computer science or ML, and so we provide an introduction to ML and the boosted regression trees (BRT) algorithm, together with an explanation of how they can provide new perspectives on problems such as the one presented here.

PISA 2012

The Programme for International Student Assessment (PISA) is an international survey conducted by the OECD with 15-year-old students that measures academic performance and records a range of personal and demographic background information. We analysed the Australian subset of the PISA 2012 data to investigate the relationships between students’ psychological dispositions, demographics and mathematical literacy. The data set is publicly available from the Australian Council for Educational Research (ACER; http://www.acer.edu.au/ozpisa/the-australian-pisa-data-files).

Through careful sampling, the data set has good coverage of all Australian jurisdictions and contains data on more than 14,000 students. We have chosen to follow ACER’s choice of psychological dispositions from their Australian Report on the PISA 2012 assessment (Thomson, De Bortoli, and Buckley 2013).

Dispositions

To be good at mathematics, a student needs to develop an understanding of concepts, become fluent at procedures, be able to reason, and have the ability to strategize these components. These facets are all rightly recognized in various national curricula (ACARA 2014; Education 2014). However, the successful learning of mathematics depends on more than the acquisition of knowledge and skills; it depends on the development of positive dispositions towards mathematics. By dispositions, we refer to the attitudes and beliefs that a student has in relation to learning mathematics.

Mathematics self-efficacy and self-concept

There is a wealth of psychology studies that have found self-efficacy and the closely related self-concept to be the strongest correlates among the dispositions of academic achievement and participation, both generally and specific to mathematics (Marks, McMillan, and Hillman 2001; Schulz 2005; Richardson, Abraham, and Bond 2012). Although they are both related to self-evaluation, self-efficacy and self-concept are distinct constructs (Ferla, Valcke, and Cai 2009). Self-efficacy is the task- or situation-specific belief that an individual has that they can succeed (Bandura 1997); an example from PISA 2012 is, ‘How confident do you feel about calculating how many square metres of tiles you need to cover a floor?’ In contrast, self-concept is an individual’s own judgement of their achievements, abilities or skills (Stankov, Morony, and Lee 2014); for example, ‘Do you agree with the statement: I learn mathematics quickly?’

Mathematics anxiety

Mathematics anxiety has been shown to be a strong negative influence on participation and lifelong learning of mathematics (Goetz et al. 2013). It can be defined as ‘feelings of fear, apprehension, or dread that many people experience when they are in situations that require solving math problems’ (Maloney, Sattizahn, and Beilock 2014); an example from PISA 2012 is, ‘I get very nervous doing maths problems.’ It has been widely studied in its relationship with gender. However, there is little consensus in the field, with reports variously finding girls or boys being more affected, or no gender effect at all (for a review, see Devine et al. 2012; Maloney and Beilock 2012).

Motivation

Psychological studies have suggested that motivation is, by and large, beneficial to learning and engagement in mathematics (see Newcombe et al. 2009). The PISA 2012 assessment surveyed both intrinsic motivation (referred to as ‘mathematics interest’) and extrinsic motivation (termed ‘instrumental motivation’). Intrinsic motivation is the drive that an individual has to do an activity simply because they enjoy or are interested in doing it (OECD 2013). Theoretical and experimental studies have tended to agree that intrinsic motivation is positively related to mathematics achievement (Ryan and Deci 2000; Viljaranta et al. 2009; Murayama et al. 2013). In contrast, extrinsic motivation is a goal-oriented drive; for example, it could describe a student’s belief that studying mathematics will help them in their future employment (Ryan and Deci 2000). The relationship between extrinsic motivation and achievement is ambiguous, with some studies showing weak positive correlations, while others have even indicated weak negative relationships (Sansone and Harackiewicz 2000; Watt et al. 2012).

Perceived control, subjective norms and attributions of failure

PISA 2012 surveyed students’ perceived control in mathematics classes and in school in general. Perceived control is the sense that an individual has of being able to influence the events and situations that they face. It has been shown to be a negative predictor of anxiety (Pekrun 2006; Ahmed et al. 2013) and a positive predictor of academic success (Stupnisky et al. 2012).

The relationships between subjective norms and attributions of failure to performance in mathematics have been shown to be complex, with neither of them having a simple positive or negative effect. A student’s subjective norms reflect the degree of importance that their family and friends place on studying, using and doing mathematics (Thomson, De Bortoli, and Buckley 2013). Attributions of failure describes the degree to which students attribute failures in mathematics to themselves or to external sources. ACER’s own report into the PISA 2012 survey suggested a weak negative correlation between attributions of failure and mathematical literacy (Thomson, De Bortoli, and Buckley 2013).

Demographics

Beyond knowledge, skills and dispositions, demographic factors can also have a strong effect on student academic achievement, and in this study, we aim to investigate the effects of dispositions and demographics in the context of each other. The PISA 2012 Australian assessment recorded a number of demographics for each student, and following the Australian Report on the PISA 2012 assessment (Thomson, De Bortoli, and Buckley 2013) we have chosen to analyse economic, social and cultural status (ESCS), gender, indigenous status and Australian state/territory.

ESCS

ESCS has been shown to be one of the strongest and most robust predictors of academic achievement (Barr 2015). It has been shown to be positively correlated with numeracy, both at the level of the student and the level of the school (Sirin 2005). In PISA 2012, ESCS was derived from a linear combination of three indices: home possessions, highest parental occupation and highest parental education (OECD 2014).

Gender

Two meta-analyses published in 2010 both found little evidence of a difference in overall mathematics achievement between male and female students (Else-Quest, Hyde, and Linn 2010; Lindberg et al. 2010). The study by Lindberg et al. (2010) analysed 242 peer-reviewed studies published between 1990 and 2007 covering all ages from elementary school to college, and found that overall girls have similar performance to boys. However, for complex problem-solving they suspected a small gender difference favouring male students in high school. Else-Quest and colleagues focussed on the Trends in International Mathematics and Science Study (TIMSS) 2003 and PISA 2003. In their analyses of these international data sets, they reported no difference between the genders in mathematics performance (as measured by TIMSS), but a slight difference in favour of boys in PISA’s measure of mathematical literacy.

Indigenous status

On average, students with indigenous status in Australia are among the most disadvantaged in terms of educational outcomes, both compared to non-indigenous Australians and to other indigenous populations around the world (Australian Bureau of Statistics 2011; Yeung, Craven, and Ali 2013). Compared to non-indigenous students, Australian indigenous students are more likely to be in the lowest ESCS quartile (Australian Bureau of Statistics 2011). These students report low academic self-concept (Yeung, Craven, and Ali 2013).

States

Australia’s federal system includes six states and two territories (hereafter simply referred to as states), to which the primary responsibility of school education is devolved (Santiago et al. 2011). The state and federal governments share priorities and agree initiatives on a national level via consultative arrangements such as the Council of Australian Governments (COAG) and the Ministerial Council on Education, Early Childhood Development and Youth Affairs (Education Council) (Santiago et al. 2011). Assessments have shown that there are differences in mathematics performance between states, with the Australian Capital Territory having better than average and the Northern Territory having lower than average performance (Thomson and Fleming 2004; Thomson et al. 2012).

Introduction to ML

We are using data from the Australian subset of PISA 2012 investigate how demographics and psychological dispositions are related to student mathematical literacy. Modern ML techniques were designed to work well with data sets such as these with large numbers of variables that have complex interactions with each other (Hastie, Tibshirani, and Friedman 2009).

Fundamentally, ML is a process for using computers to optimize models based on data. ML algorithms are used widely in the information technology industry for tasks such as automated decision-making (Aberdeen, Pacovsky, and Slater 2010), image recognition (Taigman et al. 2014), and product recommendation (Zhou et al. 2008), with companies such as Google, Facebook and Netflix being heavily reliant on sophisticated ML tools to operate their businesses. Broadly speaking, ML models can be divided into two main categories: supervised, where we have a defined output variable that we are trying to predict; and unsupervised, where the model is designed to find patterns in the data with no defined output variable (Hastie, Tibshirani, and Friedman 2009). The investigation in this paper is a supervised problem, since we have a target variable (mathematical literacy) that we can try to predict.

The main difference between ML model building and statistical or mechanistic model building comes down to how data and theory are used, with ML being generally more data-driven. At one extreme, a statistical or mechanistic model can be built based solely on a set of theoretical interactions between variables, then tuned to match the available data. At the other extreme, a ML model can be built in an entirely data-driven fashion, with the learning algorithm deciding on how to use each variable and how to combine variables together in order to produce the most accurate possible model. In practice, however, these extremes are rarely the best model building approaches, and a blend of theory- and data-driven strategies is recommended. In ML, this would mean including steps to select, exclude, transform, split-up or combine input variables based on prior knowledge or theory. For education research, this gives us the opportunity to utilize expertise without having to rely solely upon it.

This difference in focus has the pay-off that, in general, ML models are more accurate but less easy to interpret than their statistical and mechanistic counterparts. ML models are not ‘black boxes’, though, and it is reasonable to assume that a ML model with high accuracy will have learnt to use and combine the input variables in a manner similar to the real-life system. It is this property of ML models that allows data-driven hypothesis generation.

Model optimization

Supervised ML models are optimized (or ‘trained’) by a process that intelligently searches for the set of parameters that gives the lowest training error for that model’s level of complexity. Here, training error is some measure of the difference between the predicted and the actual output values from the set of data used for training (for regression problems this is often mean-squared error (MSE) or mean absolute error), and the complexity describes the structure of a model and its ability to fit complex data (e.g. a linear regression model which includes two-way interactions is more complex than a purely additive model).

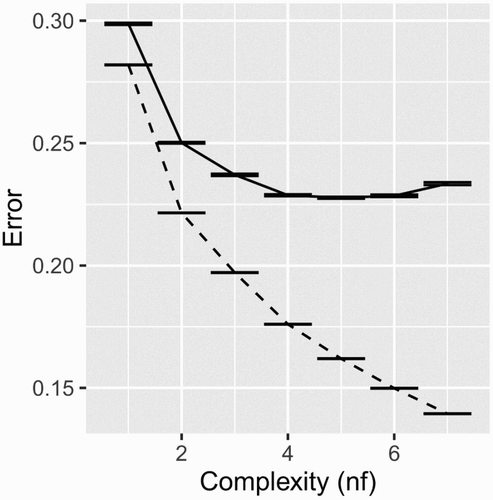
The minimum training prediction error for a model is defined by its complexity, and the complexity is controlled by the choice of structural components called ‘hyperparameters’ (e.g. the order of interactions [two-way, three-way, etc.] is a hyperparameter in a linear regression model). As the complexity of a model increases, this training error decreases as the model becomes more and more able to fit outlying data points. Eventually, the complexity will increase to a level where the model can fit any training data set perfectly. However, these models are unlikely to perform well on new test data (i.e. data unseen by the model during training). Figure 1 shows how the estimated prediction error (solid line) and training error (dashed line) both decrease as complexity increases, but only up to a point. Beyond this, training error continues to decrease, but test error increases. Once this happens, the model is too complex and ends up fitting the random noise in the data, that is, it is overfitting. By finding the level of complexity that minimizes estimated test error, we will be able to train a model that generalizes well. The most commonly used method for tuning the complexity of a model currently in ML is K-fold cross-validation (CV) (Friedman, Hastie, and Tibshirani 2001). The CV process is detailed in Figure 2.

Figure 1. Cross-validation for tuning the missing data imputation model. As the complexity of the model (number of hidden features; nf) increases, it becomes more and more able to fit outliers in the training data, and the training error (dashed line) decreases continually. The test error (solid line) was estimated using fivefold cross-validation, and is minimized when nf = 5. Above this, the test error rises as the model is overfitting. Error bars equal one standard error of the mean of the error-estimates from the five CV folds.

Figure 2. An illustrative example of the cross-validation (CV) process.

Boosted regression trees

BRT is one of the most popular and powerful algorithms for supervised learning (Friedman 2001; Elith, Leathwick, and Hastie 2008; Hamner 2015). The base unit of a BRT is the classification and regression decision tree (CART). This is a straightforward and intuitive algorithm for sorting data into categories or levels based on some variable of interest (i.e. the output variable).

A CART is essentially a set of yes/no rules arranged in a tree-style hierarchy (Breiman 2001). For example, imagine we are interested in how high a group of students can jump (Figure 3). Say we have recorded their ages, heights and a selection of other variables. The CART learning algorithm will find the variable that best splits up the data set based on the jumping heights (i.e. it tries to put all the high jumps on one side and all the low jumps on the other). In this (fictional) example, the rule that results in the best split is, ‘Is age > 12?’ So all those aged 13 and over will follow the rules on the right side of the tree, and the rest will follow the rules on the left. The next split on the right side is, ‘Is height > 125 cm?’ This splitting continues until all of the students are partitioned into groups based on how high they can jump. The CART that was built from these data can now be used to predict how high a new student should be able to jump, by querying ‘Is age > 12’, ‘Is height > 125 cm’, etc.

Figure 3. Basic format of a classification and regression decision tree (CART). The training data set (left) has four instances (Amy, Belinda, Courtney, Dee), two input variables (Age, Height) and an output variable (Jump). The CART algorithm iteratively splits the data set using the input variable that best purifies the output variable. In this case, “Age > 12” is the best first split. Amy and Belinda do not meet this criterion, so are filtered to the left. They are then separated again by Age. On the other side, Courtney and Dee are separated by Height. With the data fully partitioned, the terminal nodes (“leaves”) are assigned values according to the output variable. The CART can now be used to predict Jump for a new instance (Xanthe). The CART filters Xanthe along the YES branch for “Age > 12”, then along the NO branch for “Height > 155”, which results in a prediction of Jump = 40 cm.

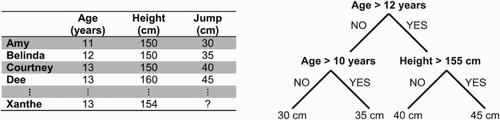
By querying different variables along a branch, the CART model is able to naturally find interactions (in this case an interaction between height and age), while querying the same variable multiple times in the tree allows the model to fit non-linear relationships between inputs and the output.

In terms of predictive accuracy, BRTs are a huge improvement over individual CARTs (Friedman 2001). CARTs are very powerful as they do not rely on there being linear relationships between the inputs and the output, interactions between variables can be found by the model, and they are able to easily accept numerical, ordinal or categorical data as inputs. However, individual CARTs are sensitive to noisy data, and are susceptible to overfitting.

The BRT methodology overcomes these shortcomings by using ensembles of shallow CARTs. In an ordinary (deep) CART, the data are fully purified using as many splits as necessary, but the structure (and thus the predictions) of the CART can change markedly depending on the amount of noise in the data. A shallow CART restricts the number of allowed splits, so the data will only ever be partially purified, but the structure of the tree is much more robust. A BRT is a collection of hundreds or thousands of CARTs that only partially purify the data. In doing so, the model becomes very robust to noise in the data, while still being able to fit complex relationships.

The BRT model is further improved by the use of boosting (Friedman 2001). This is a methodology whereby the ensemble of trees is built sequentially, with each tree learning from the mistakes of the previous. That is, a BRT will train its first shallow CART and then calculate the prediction error for each item. It then re-weights the data so that the most poorly predicted items receive the highest weighting. The BRT then trains a second shallow CART on the weighted data and then re-weights the data again. This process is continued until the BRT ensemble’s training error is minimized. The strength of the re-weighting is determined by a hyperparameter called the ‘learning rate’, that is, with a high learning rate, the data are heavily re-weighted after each iteration, thus the BRT is ‘learning’ quickly.

As discussed above, the complexity of a ML model needs to be tuned to avoid overfitting. For BRTs, the common hyperparameters to tune are the depth of the CARTs, the learning rate and the number of trees in the ensemble (Friedman, Hastie, and Tibshirani 2001).

The BRT algorithm builds models in a piecewise manner that is well suited for finding interactions and modelling complex, multidimensional relationships. This places them firmly among the most powerful of the supervised learning models, and makes them ideal for interrogating interdisciplinary questions like those we address in this paper.

Methods

We built two BRT models (Models 1 and 2) to analyse the PISA 2012 data at two different levels of detail. The two levels of detail are (1) the raw response level and (2) the aggregated response level.

The PISA 2012 data

In this study, we have analysed Australian student questionnaire and mathematics literacy data from the PISA 2012 assessment, published by the OECD. The data set contains responses from a sample of 14,481 15-year-old students from 775 schools across all Australian states. Smaller states and indigenous students were oversampled for statistical reliability. The PISA 2012 assessment includes a weighting for each student to account for these sampling biases, which we have included in our modelling.

The PISA 2012 assessment focussed on the domain of mathematical literacy, that is, the ability to apply mathematical knowledge and skills to real-life situations. It is defined by the OECD as

an individual’s capacity to identify and understand the role that mathematics plays in the world, to make well-founded judgements and to use and engage with mathematics in ways that meet the needs of that individual’s life as a constructive, concerned and reflective citizen. (, Hillman, and De Bortoli 2013)

From the published PISA 2012 data, we used the plausible value (PV) scores in mathematics as the measure of a student’s mathematical literacy. The PV scores are imputed values that are estimates of each student’s mathematical literacy given their performance in the subset of the assessment that they were set. PISA’s imputation process estimates a range of plausible mathematical literacy scores for each student. PISA provides a random sample of five PV scores per student. The mathematical literacy scale is scored from 0 to 1000. The OECD splits this range into six proficiency levels, starting at the lowest proficiency of Level 1 between 358 and 420 points, through to the highest proficiency of Level 6 at above 669 points (OECD 2013).

The Australian student survey items captured demographic information, including; gender, indigenous status, geographic location (urban, provincial or rural), state and items to calculate ESCS. The PISA 2012 ESCS score is a standardized linear combination of the index of home possessions, the scale of highest parental occupation, and the scale of highest parental education (OECD 2013).

We investigated the same disposition measures that were analysed in Chapter 7 of the ACER Australian Report on the PISA 2012 assessment (Thomson, De Bortoli, and Buckley 2013), namely: mathematics self-efficacy; mathematics self-concept; mathematics anxiety; instrumental motivation in mathematics; interest in mathematics; subjective norms surrounding mathematics; perceived failure in mathematics; perceived control in mathematics and perceived control in school. Each measure was surveyed using 4–8 statements with 4-point Likert-type responses of, ‘strongly agree’, ‘agree’, ‘disagree’ and ‘strongly disagree’; these were used as inputs for Model 1. From these Likert responses, PISA produced aggregated indices (z scores) for each disposition (see Thomson, De Bortoli, and Buckley 2013, 312); these were used as inputs for Model 2.

Techniques

All analyses were performed using the R statistical language (R Core Team 2014). Data analysis scripts can be found in the Supplemental Material.

Model tuning and validation

K-folds CV was used to estimate the prediction errors of the models; for a detailed explanation of the CV procedure, see (Hastie, Tibshirani, and Friedman 2009). All instances of CV in this paper are fivefold CV; five is a commonly used number of folds and gives a good trade-off between speed and bias (Hastie, Tibshirani, and Friedman 2009). CV was performed using the mlr package in R (Bischl et al. 2016).

The hyperparameters tuned in this paper are: the learning rate of a model; the maximum depth of decision trees in an ensemble; and the depth of the hidden feature matrices in low-rank matrix factorization (see below; missing data).

For the purposes of this study, we were mostly interested in the feature importance and feature interaction outputs. Thus, we used as much data as possible for training with only a small random sample of 400 rows held out to illustrate the model’s predictive accuracy on unseen data.

Missing data

Roughly one-third of Australian students who participated in PISA 2012 were given the full set of disposition questions. The remaining students were given a subset of the disposition items. For the purposes of this study, we decided to keep only those students who had been given the whole set, and so did not need to impute responses for entire dispositions. If we had kept all 14,481 rows, there would have been a strong possibility of the models being compromised by the large blocks of missing-not-at-random data. This left us with 4700 instances for Model 1 and 4528 for Model 2.

Within this kept group, there were a number of values missing due to being skipped by students, or by students giving invalid responses. We imputed these values using an ML technique called low-rank matrix factorization (Koren, Bell, and Volinsky 2009), following the general formula: minimize (Y– U^T V)², where Y is the m × n matrix (objects × features) of responses with missing values that we wish to impute, U is an a × m matrix and V is an a × n matrix. U and V are matrices of hidden features that are randomly initialized and then optimized such that the product of U^T and V most closely matches Y. The optimum depth, a, of U and V was determined using fivefold CV. From this we were also able to estimate the imputation error.

Boosted regression trees

Two BRT models were trained. This allowed us to model the dispositions at two different levels of detail: at the individual item response level; and at the aggregated index level. In doing so, the different models were expected to give us complementary insights into the low-level and high-level disposition effects and interactions.

Both models had a single set of PV for mathematics literacy as their output variable. Using a single PV should not be problematic because all the PVs are drawn at random from a posterior probability distribution, so there should not be a systematic bias associated with picking one PV over another PV.

Both models had the five demographics listed above as input variables. Model 1 was trained on the raw disposition item responses whereas Model 2 was trained on the indices of disposition. Two different implementations of BRT were used in this study: Model 1 was trained using the xgboost package in R (Chen, He, and Benesty 2016); and Model 2 was trained using the gbm package in R (Ridgeway 2015). Learning rate and tree-depth hyperparameters were tuned using fivefold CV using the mlr package in R (Bischl et al. 2016). To rank each variable by its total importance (i.e. including all interaction effects), we calculated their relative influences. Relative influence is a measure of the information gain associated with each variable in a BRT model. All relative influences are reported to the nearest percent.

Interaction analysis

The R package, dismo, was used to calculate two-way interaction strengths from Model 2 (Hijmans et al. 2016). Briefly, interaction strength between variables a and b was calculated by first calculating the predicted output values (i.e. mathematical literacy score) where a and b are allowed to vary while all other variables are held constant, then calculating the output values of a purely additive linear model of a and b (i.e. f(x) = β₁ .a + β₂ .b), and finally reporting the mean-squared difference between the two models. A resulting score of zero would indicate that the variables did not have any interaction, and the larger the number, the stronger the interaction.

Results

Missing data imputation for disposition responses

The CV error was minimized with five hidden features (Figure 1). The estimated prediction MSE is 0.23 item response points, which compares favourably with imputing by the mean value for each column (MSE = 0.66). This means that on average, the difference between the predicted value and the actual value is roughly half a response point on the Likert item response scale.

Model 1

The CV prediction error was minimized with a maximum tree depth of 5 and a learning rate (eta) of 0.005 (Figure 4(A)). The mean absolute CV prediction error was approximately 51 mathematical literacy score points. In Figure 5(A), we can see that the error in the hold-out set is fairly consistent across the range of scores and there is a fairly good correlation (R² = 0.51). Analysing the spread of the errors in the hold-out set showed that 50% of the predictions were within 49 points, 90% were within 112 points and 99% were within 167 points.

Figure 4. Cross-validation for tuning Models 1 and 2. BRT Models 1 and 2 were both tuned across a grid of maximum tree depth and learning rate using fivefold CV. Five different tree depths (1, 2, 5, 10, 20) and three different learning rates (0.005, 0.01, 0.02) were tested. The error metric was the mean absolute error. Model 1’s CV error was minimized at a tree depth of 5 and a learning rate of 0.005 (A). Model 2's CV error was minimized at a tree depth of 10 and a learning rate of 0.005 (B).

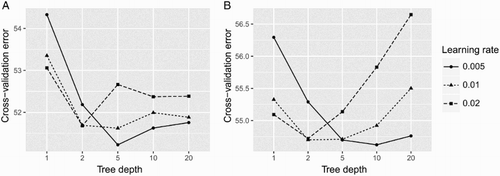
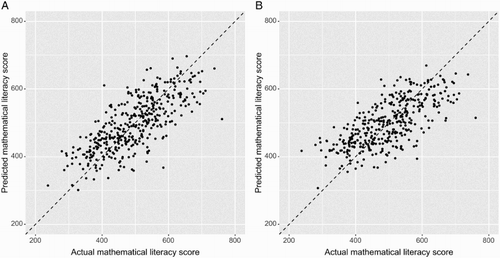
Figure 5. Scatter plots to illustrate prediction accuracy of Models 1 and 2. A small hold-out set (400 instances) was retained to test the models on unseen data. The actual mathematical literacy scores for the hold-out set were plotted against the predicted scores for Model 1 (A) and Model 2 (B). This allows us to perform a visual inspection of the goodness-of-fit. Both models have a similar magnitude of error across the range of mathematical literacy scores.

The most influential input variable was the self-efficacy item, ST37Q05 (‘How confident do you feel about having to do the following mathematics task: Solving an equation like 3x + 5 = 17’), which accounted for 22% of the relative influence (Figure 6). The second most influential input variable was the demographic, ESCS, which accounted for 11% of the relative influence. Of the top 10 most influential features, four were self-efficacy items and three were demographic identifiers. Self-efficacy was the greatest overall contributor to the model with a sum total influence 41%.

Figure 6. Relative influence of disposition response items and demographics in Model 1. The input variables are ordered by the amount of relative influence they have on Model 1’s predictions. The most influential item was ST37Q05 (“How confident are you about solving an equation like 3x + 5 = 17?”) with ∼22% of the relative influence. The fully worded items are listed in Appendix A.

Partial dependency plots allow for more detailed analyses of each variable’s contribution to the model (Figure 7). The first facet of Figure 5 shows the partial dependency plot for the most influential item, ST37Q05. It shows that, if all the other variables are held constant at their mean values (or mode values for categorical variables), responding ‘1’ (‘highly confident’) to this item would result in an above average mathematical literacy score of 509, but a response of ‘2’, ‘3’ or ‘4’ would result in below average mathematical literacy scores (475, 463 and 460, respectively).

Figure 7. Partial dependency plots for the 10 most influential inputs to Model 1. Variables are shown in order of relative influence, read row by row from left to right. Four of the top 10 variables were mathematics self-efficacy items (dark grey labels) and three were demographics (white labels). On the disposition item response scale, “1” is “highly confident” or “strongly agree”, and “4” is “highly unconfident” or “strongly disagree”. Each of the self-efficacy items has a positive relationship between confidence and mathematical literacy score. The other three dispositions had a negative relationship between agreement and mathematical literacy (ST43Q06 “I do badly in mathematics whether or not I study for my exams”; ST42Q02 “I am just not good at maths”; ST91Q06 “I do poorly at school whether or not I study”). The fully worded items are listed in Appendix A.

The second facet shows the partial dependency for ESCS. The overall trend shows that, all other variables being constant, being below the median ESCS (i.e. 0) results in a below average mathematical literacy score, whereas being above the median ESCS results in an above average score. However, as seen in the plot, this relationship is non-linear and fairly complex. In the region just below the median ESCS, the predicted score drops sharply to 442, and is lower than the predicted score for ESCS scores in the lowest quartile (the score for the lowest ESCS is predicted to be 481).

Interactions

There were no strong interactions between the input variables.

Model 2

The second model used the disposition indices from the PISA 2012 data set to look at interactions between dispositions and demographics. These indices were calculated from the students’ responses to the disposition questionnaire and were standardized. The CV prediction error was minimized with an ensemble size of 1500, a maximum tree depth of 10 and a learning rate of 0.005 (Figure 4(B)). The mean absolute CV prediction error was 54 mathematical literacy score points, which was marginally worse than model 1. The correlation between predictions and actual scores in the hold-out set was also lower (R² = 0.45). Analysing the spread of the errors in the hold-out set showed that both models have a comparable distribution of errors; 50% of the predictions were within 49 points, 90% were within 114 points and 99% were within 176 points (see Figure 5(B)).

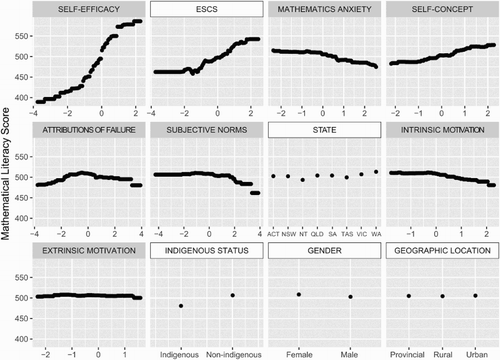
The most influential variable was mathematics self-efficacy, which accounted for 52% of the relative influence. The next highest was ESCS, which accounted for 14%, then came mathematics anxiety and self-concept at 6% each. The partial dependency plots (Figure 8) show that mathematics self-efficacy has a positive relationship with mathematics literacy across its range, with a range of nearly 200 mathematics literacy points. ESCS and mathematics self-concept also have a positive relationship with mathematics literacy, whereas mathematics anxiety and intrinsic motivation have a negative relationship.

Figure 8. Partial dependency plots for the inputs to Model 2. Variables are shown in order of relative influence, read row by row from left to right. Mathematics self-efficacy is the most influential variable (52% relative influence). Relative influences (rounded to the nearest percent) for the other inputs were: ESCS 14%; mathematics anxiety 6%; mathematics self-concept 6%; attributions to failure in mathematics 5%; subjective norms in mathematics 5%; state 4%; intrinsic mathematics motivation 4%; extrinsic mathematics motivation 2%; indigenous status 1%; gender 1%; geographic location 0%.

Interactions

The two strongest interactions were between mathematics anxiety and mathematics self-efficacy (interaction strength = 69,225), and between mathematics anxiety and mathematics self-concept (interaction strength = 64,308; Figure 9(A,B)). Figure 9(A) suggests that mathematics anxiety would have very little effect on the mathematical literacy score of students who report very low self-efficacy, whereas there would be a noticeable detrimental effect in students who report very high self-efficacy. At the same time, the model suggests that the most anxious students gain less of a positive effect from high self-efficacy than the least anxious students. The interaction between mathematics anxiety and mathematics self-concept is similar, where self-concept would have little effect on the most anxious students, but would have a large effect on the least anxious.

Figure 9. Two-way interaction plots for Model 2. The 2-dimensional partial dependency plots and the measures of interaction strength for Model 2 were produced using the “dismo” package in R. The shapes of the plots give an indication of the nature of the interactions. The interaction between mathematics self-efficacy and mathematics anxiety was the strongest (A). At the top end of the self-efficacy scale, there is a strong negative relationship between mathematics anxiety and mathematics literacy. This relationship is not present at the bottom end of the self-efficacy scale. There is a similar relationship between mathematics self-concept and mathematics anxiety (B). We were also able to observe interactions between dispositions and demographics; the interactions of mathematics self-efficacy and anxiety with ESCS are shown in C & D (note the axis labels have been flipped between these two plots; this was done for readability purposes). Intrinsic motivation had an unexpected negative effect on mathematics literacy where mathematics anxiety was high (E). There was little interaction between mathematics anxiety and gender (F).

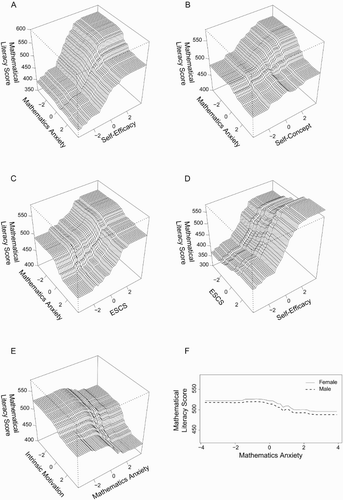
The two strongest interactions between a disposition and a demographic were between mathematics self-efficacy and ESCS (interaction strength = 36,998), and mathematics anxiety and ESCS (interaction strength = 14,348; Figure 9(C,D)). Mathematics anxiety is generally detrimental to mathematical literacy score in this model. However, its effect in this model is much more pronounced in low ESCS students than in high ESCS students (∼50 point maximum difference vs. a ∼25 point maximum difference; Figure 9(C)). Similarly, mathematics self-efficacy has a greater positive effect on mathematical literacy score in high ESCS students than in low ESCS students (Figure 9(D)).

The model identified an interaction between mathematics anxiety and intrinsic motivation in which mathematics anxiety elicited a stronger negative effect on mathematical literacy when intrinsic motivation was high, and intrinsic motivation had a negative effect when anxiety was high (Figure 9(E)). Given the reports in the literature on the interaction between mathematics anxiety and gender, we were surprised to find that the strength of this interaction was relatively very small (interaction strength = 1748) and there was no clear interaction effect on the plot (Figure 9(F)).

Discussion

In this paper, we explored the educational impact of psychological dispositions and demographics. We have used ML to produce two BRT models that has allowed us to investigate how a set of dispositions and demographics may act in concert to influence mathematics literacy. Our data set was the Australian subset of the PISA 2012 survey, which was a carefully designed, well-collected survey with high-quality structured data, making it ideal for the BRT approach.

Two models

Model 1 had the more extensive input variable set, having all 50 raw disposition item responses along with the 5 demographic variables being used to predict mathematical literacy. Given that there were so many disposition items in the inputs, it was notable that the predictions were dominated by a single mathematics self-efficacy question (ST37Q05: ‘How confident are you about solving an equation like 3x + 5 = 17?’). This one question accounted for around one-fifth of the relative influence and had more than three times the influence of the next disposition item. Overall, self-efficacy was by far the most influential disposition.

Model 1 allows us to make inferences about the role of individual items. For example, the shape of the partial dependence plot for the question ‘How confident are you about solving an equation like 3x + 5 = 17?’ (item ST37Q05) shows the predicted drop in mathematical literacy score from a response of ‘1’ to ‘2’ is greater than that from ‘2’ to ‘4’. This suggests that there may be a meaningful difference between students who rate themselves as ‘highly confident’ as opposed to merely ‘confident’ in being able to do simple linear algebra.

In Model 2, mathematics self-efficacy was identified as the most influential input variable, accounting for over half of the relative influence, which is well in line with the literature (OECD 2013). Mathematics anxiety and self-concept were ranked as the next highest dispositions. The most influential demographic, and the second most influential variable overall in both models, was ESCS, which is again consistent with the literature (Sirin 2005; Perry and McConney 2010).

Comparing the partial dependence plots of the models shows that both models used the demographic inputs in a very similar manner. In both models: ESCS has an overall strong positive effect; gender has very little influence; indigenous status is a negative predictor of mathematical literacy; geographic location has little influence, but living in a rural area has a slight negative effect; and state has little influence, except for living in the Northern Territory, which is a negative predictor.

Automatically finding interactions between variables is one of the strengths of CART-based models. In Model 1 we did not find any strong interactions, whereas in Model 2 we were able to identify several strong two-way interactions (e.g. mathematics anxiety × mathematics self-efficacy, and ESCS × mathematics self-efficacy). This difference is caused in part by the different maximum tree depths of the two models; that is, the maximum tree depth of Model 2 was 10 while Model 1 was only 5. From Figure 4, we can see that Model 1 would have been less accurate if richer interactions were allowed (i.e. if the maximum tree depth were allowed to be deeper). These tree depths were selected using a data-driven process (CV), and so revealed that the most accurate version of Model 1 did not require complex interactions.

This form of modelling allows us to find non-linear and piecewise relationships between inputs and outputs, as well as complex interactions between the inputs; these details are not easily found using other modelling methods such as linear regression. The models agree with the existing literature in that they show a positive relationship between mathematics self-efficacy and ESCS (e.g. Artlet et al. 2003), and also a negative relationship between mathematics self-efficacy and mathematics anxiety (Dowker, Sarkar, and Looi 2016). Furthermore, Model 2 suggests that these variables have strong interactions with each other when used to predict mathematical literacy. While it is possible to identify interaction effects with procedures like ANOVA or linear regression, the BRT models can go further to reveal how the degree of interaction changes across the ranges of the variables. For example, in Model 2 the negative effect of mathematics anxiety is amplified at the lower end of the ESCS scale, and the positive effect of mathematics self-efficacy is amplified at the higher end of ESCS. This type of subtle, fine-grained detail may be very useful for planning further experiments, designing interventions, and even interpreting existing data.

Intrinsic motivation has variously been reported as either a positive or uninformative variable with regard to mathematics performance. ACER’s report on the PISA 2012 data found that intrinsic motivation was not needed in their models of disposition and mathematical literacy (Thomson 2014). Similarly, our analyses showed that intrinsic motivation has only a small relative influence. However, this appears to be masking an interesting effect. A correlation of intrinsic motivation with mathematics literacy shows a positive relationship between them (Thomson, De Bortoli, and Buckley 2013). But, the partial dependency plots show that when intrinsic motivation is considered together with a range of dispositions and demographics, it may in fact have a negative effect. This discrepancy indicates that there should be interaction effects. The interaction of intrinsic motivation with mathematics anxiety is of comparable magnitude to the interaction between mathematics anxiety and ESCS, and suggests that mathematics anxiety disproportionately negatively affects students with a high level of intrinsic motivation. Conversely, according to this model, students who have low intrinsic motivation would be unaffected by having low or high anxiety because they have no interest in mathematics.

Model evaluation, or, Australia’s next top model

ML models can be judged by a number of metrics. For our models we have chosen to use fivefold CV to estimate the mean absolute prediction error, and we have used visual inspection of truth vs. response scatter plots to see if the error is roughly even across the range of outputs and if the model is able to fit values at the tails of the distribution. Interpreting metrics such as the mean absolute error requires domain-specific expertise as there are no standard p-value-like evaluation cut-offs. In other words, we need to use our knowledge of the mathematical literacy scale and our prior knowledge of the relationship between the inputs and output to decide whether or not Model 2’s MAE of 54 mathematical literacy points is ‘good enough’.

The mathematical literacy scale is scored from 0 to 1000, within which the OECD defines 6 proficiency levels to describe student ability. Level 1 starts at 358 points, and the width of each level is between 61 and 62 points. From this, we can see that our mean prediction error is well within the size of a single proficiency band. Our prior expectation was that, while dispositions and demographics should have some explanatory power, they would be highly unlikely to be able to map perfectly onto mathematical literacy. Other inputs such as the students’ mathematics knowledge, their working memory, and their past exam scores would be strong candidates for improving the accuracy of the models. Furthermore, the output variable used here is itself an imputed value, which is an added source of noise. Thus, even with the expectation that we would be far from able to train a perfect model, we have been able to produce a model that can accurately predict a student’s proficiency level in mathematical literacy.

We can gain further confidence in our model by comparing the relative influences, the partial dependencies and the interactions with other published studies. Both of our models identified mathematics self-efficacy as the most influential disposition for predicting mathematical literacy. This aligns well with the broad consensus in the literature (McConney and Perry 2010; OECD 2013; Thomson 2014), and according to the ACER PISA 2012 report on Australia, the difference in mathematical literacy between students in the highest and lowest ESCS quartile was, on average, equivalent to around two and a half years’ worth of schooling (Thomson, De Bortoli, and Buckley 2013). Of the demographics, ESCS was identified as the most influential. This is also broadly agreed on in the literature (Perry and McConney 2010; OECD 2013). There has been much debate as to whether or not mathematics anxiety interacts with gender; depending on the study, it can more strongly affect girls, boys, or have no strong interaction (see Devine et al. 2012). We did not attempt to impose any interactions on our models, preferring to use a more strongly data-driven approach, and found no strong evidence of an interaction.

Although we have analysed a broad selection of dispositions and demographics, our choice of input variables is not exhaustive, and there is scope for extending the models to include extra variables. A strength of this type of modelling is that they can be easily incorporate new variables. It is important to note that it remains the decision of the domain expert to decide which features to select. For example, another researcher may wish to include school type and detailed ages of the students, where another may wish to examine data from other countries in the OECD.

Our analyses can also provide us with testable data-driven hypotheses that can be further pursued. The models suggested that intrinsic motivation may influence mathematics literacy in a very context-dependent manner. Previous studies have found it to either positively influence mathematics performance or to be non-influential (Gottfried 1985; Spinath et al. 2006; Thomson 2014; Garon-Carrier et al. 2016). From our models, we can hypothesize that intrinsic motivation may actually have an overall (weak) negative effect that is amplified in students with high mathematics anxiety. We have also seen that there may be a combinatorial effect that may be investigated, where mathematics anxiety disproportionately negatively affects low ESCS students while mathematics self-efficacy disproportionally positively affects high ESCS students (Perry and McConney 2010).

Implications

An important aspect of modern research is the relative ease with which data can be generated, collected, shared and analysed. Where there is a high density of good quality data, the ground is ready for us to use data-driven techniques, not only to make predictions, but also to gain new insights and to generate new hypotheses.

As already discussed, ML techniques are well suited for these challenges as they were designed to work with high-dimensional data and complex systems. The ability here to identify variable influences and interactions in a holistic manner is incredibly powerful. Models built in this way will be useful for designing future experiments and for helping policy makers to make the most of existing data sets because they can direct researchers and decision-makers to some of the implications of existing and future results (e.g. our model predicts that an intervention to improve mathematics self-efficacy to improve mathematical literacy may not result in the same gains being achieved across all demographic sub-groups).

It may be tempting for some to represent analyses such as ours as a ‘truth’ rather than an indication of the importance of multiple dimensions within the data. When a particular, narrow analysis of data is used to push a singular interpretation over-reaching claims can sometimes result in the form of ‘the data says teachers should do this in their classrooms’. Of course, data will never be able to effectively dictate teachers’ practice. Even data specifically related to teacher practices, when analysed and interpreted into evidence, will have utility limited to the particular set of circumstances in which the data were collected. Space must be created for the findings to be processed through the professional judgement of educators and education leaders in order to develop an appropriate response in practice or policy.

ML … is it for me?

ML works best where there is a large amount of high-quality data. These terms are deliberately ambiguous, as the amount of data and the required level of accuracy of the data collection are strongly dependent on the goals of the modelling exercise. However, as a rule of thumb, we suggest the following starting points:

• For a problem with a relatively simple mapping from inputs to outputs (e.g. the example used in Figure 3), a data set on the order of tens to hundreds of rows with a handful of variables would normally suffice;

• For more complex problems, such as the one we have presented, more rows are needed, normally in the range of hundreds to thousands to tens of thousands, with between ten and one hundred input variables;

• For more complex problems where you need high predictive accuracy, you could easily need to increase the number of rows and variables again by an order of magnitude or more.

Note that these guidelines are not intended to be prescriptive; they are merely to give readers unfamiliar with ML a rough idea of the amount of data they may require.

In the case we have presented, the quantity and quality of the data was fit for our purposes, as determined by the degree of accuracy achieved by each model. It is not generally possible to tell whether or not a data set is big enough until you have attempted to build a model and evaluated its accuracy. In practice, the more data that you can generate/collect, the better the models will be. Large-scale assessments are an obvious choice of data set in this regard, but these techniques can equally be applied to smaller-scale primary research data.

There are some points about supervised ML that any new user needs to be aware of. Having good quality data is the central requirement for ML. Poor quality input data will lead to your models being difficult to train, systematically biased, or just plain wrong. If you plan on using one of these models for prediction purposes, be aware that they should not be used to extrapolate too far beyond the range of the training data; if you present them with new data with values far outside the training data, there is no guarantee that the model will perform well.

From a practical perspective, there is a danger of becoming over-reliant on these models and using their predictions outside the realm they were intended for. For example, an education authority may use the maths achievement predictions from our models to stream students into different classes. However, since these predictions would be based on their dispositions and demographics rather than their measured ability, doing so would risk entrenching societal barriers to mathematics achievement.

A BRT model cannot tell us about the causal nature of the relationships between variables, only that certain relationships occur in the context of the modelled system. However, if the model was developed well, then these relationships will be principled and data-driven, and may be used as the basis for developing new hypotheses for investigating a complex system. Thus, building these models may help you to validate existing theories and show you effects and interactions that you would not have otherwise suspected.

Conclusion

We have demonstrated an analysis of multidimensional data exploring the relationships between psychological dispositions, demographics and mathematical literacy using the PISA 2012 data set. The ML approach used here is conceptually different to other modelling approaches in that it is very strongly data-driven and the interpretation relies on the application of domain-specific knowledge, yet the model outputs are highly intuitive. There are many techniques being actively developed in the field of ML, and we have built models using implementations of one type of algorithm (BRT). ML is a fast-moving field, and as such, ML algorithms should not be treated simply as tools, but as part of a discipline that can advance and adapt together with the research questions being asked.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was supported by the Australian Research Council-SRI: Science of Learning Research Centre (project number SR120300015).

Appendix A: List of questions

Intrinsic motivation

Thinking about your views on mathematics: to what extent do you agree with the following statements?

ST29Q01: I enjoy reading about mathematics.

ST29Q03: I look forward to my mathematics lessons.

ST29Q04: I do mathematics because I enjoy it.

ST29Q06: I am interested in the things I learn in mathematics.

Extrinsic motivation

Thinking about your views on mathematics: to what extent do you agree with the following statements?

ST29Q02: Making an effort in maths is worth it because it will help me in later work.

ST29Q05: Learning maths is worthwhile because it will improve my career prospects.

ST29Q07: Mathematics is important because I need it for later study.

ST29Q08: I will learn many things in maths that will help me get a job.

Self-concept

Thinking about studying mathematics: to what extent do you agree with the following statements?

ST42Q02: I am just not good at maths.

ST42Q04: I get good grades in maths.

ST42Q06: I learn mathematics quickly.

ST42Q07: I have always believed that maths is one of my best subjects.

ST42Q09: In my maths class I understand even the most difficult work.

Self-efficacy

How confident do you feel about having to do the following mathematics tasks?

ST37Q01: Using a train timetable to work out how long it would take to get from one place to another.

ST37Q02: Calculating how much cheaper a TV would be after a 30% discount.

ST37Q03: Calculating how many square metres of tiles you need to cover a floor.

ST37Q04: Understanding graphs presented in the newspapers.

ST37Q05: Solving an equation like 3x + 5 = 17.

ST37Q06: Finding the actual distance between two places on a map with a 1:10,000 scale.

ST37Q07: Solving an equation 2(x + 3) = (x + 3) (x − 3).

ST37Q08: Calculating the petrol consumption rate of a car.

Mathematics anxiety

Thinking about studying mathematics: to what extent do you agree with the following statements?

ST42Q01: I often worry it will be difficult for me in maths classes.

ST42Q03: I get very tense when I have to do maths homework.

ST42Q05: I get very nervous doing maths problems.

ST42Q08: I feel helpless when doing maths problems.

ST42Q10: I worry that I will get poor grades in maths.

Perceived control in school

Thinking about your school: to what extent do you agree with the following statements?

ST91Q01: If I put in enough effort I can succeed at school.

ST91Q02: It is my choice whether or not I do well in school.

ST91Q03: Family demands, etc. prevent me from putting time into my school work.

ST91Q04: I would try harder with different teachers.

ST91Q05: If I wanted to I could perform well at school.

ST91Q06: I do poorly at school whether or not I study.

Perceived control in mathematics

Suppose that you are a student in the following situation:

Each week, your mathematics teacher gives a short quiz. Recently you have done badly on these quizzes. Today you are trying to figure out why.

How likely are you to have these thoughts or feelings in this situation?

ST44Q01: I’m not very good at solving maths problems.

ST44Q03: My teacher did not explain the concepts well this week.

ST44Q04: This week I made bad guesses on the quiz.

ST44Q05: Sometimes the course material is too hard.

ST44Q07: The teacher did not get students interested in the material.

ST44Q08: Sometimes I am just unlucky.

Subjective norms

Thinking about how people important to you view mathematics: how strongly do you agree with the following statements?

ST35Q01: Most of my friends do well in maths.

ST35Q02: Most of my friends work hard at maths.

ST35Q03: My friends enjoy taking maths tests.

ST35Q04: My parents believe it is important for me to study maths.

ST35Q05: My parents believe that maths is important for my career.

ST35Q06: My parents like maths.

Attributions of failure in mathematics

Thinking about your mathematics lessons: to what extent do you agree with the following statements?

ST43Q01: If I put in enough effort I can succeed at mathematics.

ST43Q02: Whether or not I do well in maths is up to me.

ST43Q03: Family demands or other problems prevent me from putting a lot of time into my mathematics work.

ST43Q04: If I had different teachers, I would try harder in mathematics.

ST43Q05: If I wanted, I could do well in mathematics.

ST43Q06: I do badly in mathematics whether or not I study for my exams.