On the existence of shadow prices for optimal investment with random endowment

Abstract

In this paper, we consider a numéraire-based utility maximization problem under constant proportional transaction costs and random endowment. Assuming that the agent cannot short sell assets and is endowed with a strictly positive contingent claim, a primal optimizer of this utility maximization problem exists. Moreover, we observe that the original market with transaction costs can be replaced by a frictionless shadow market that yields the same optimality. On the other hand, we present an example to show that in some case when these constraints are relaxed, the existence of shadow prices is still warranted.

Keywords:

• Utility maximization
• random endowment
• transaction costs
• no-short-selling constraint
• shadow prices

1. Introduction

Recently, the problem of utility maximization in the market under proportional transaction costs has received many authors’ attention. In such a market, the investor is assumed to buy securities at an ask price which is higher than the bid one that he/she receives when selling. The presence of proportional transaction costs enables the consideration of the portfolio optimization with models beyond semimartingales in an arbitrage-free way, which is economically meaningful (cf. [27,28]).

The portfolio optimization problem under proportional transaction costs on the Merton model with the logarithm utility dates back to Magill and Constantinides [42] and Constantinides [8]. In their heuristic works, they concluded that the optimal way is to keep the current holdings in all assets in a no-trade region and to trade merely at the boundaries of such region. Later on, this problem has been studied extensively by many authors, among them, Taksar et al. [47] first introduced the tools of singular stochastic control in the context of maximization of the growth rate of wealth. Davis and Norman [16] provided a rigorous formulation of the problem in [8,42] and computed the location of the boundaries by solving a free boundary problem for the nonlinear partial differential equation. Afterwards, Shreve and Soner [46] extended the results of [16] by introducing viscosity solutions. We also refer to Dumas and Luciano [20] for the maximization problem of the asymptotic power growth rate, in which an explicit solution is constructed in a tractable case. Apart from the stochastic control approach, this utility maximization problem has also been studied with more general models by the convex duality approach. Initiated by Cvitanić and Karatzas [9], the idea of constructing an auxiliary dual problem is widely applied to various cases (e.g. [3,5,12,15,17,31]).

It is observed that even small transaction costs could dramatically influence the optimal choice of the investor in utility maximization (cf. [40]). Therefore, a natural question that arises is whether impacts of transaction costs on both the optimal strategy and the maximal utility can be reproduced in a frictionless market; mathematically speaking, for a given utility maximization problem, we wonder whether there exists a semimartingale process lying between the bid and ask price, called shadow price, such that trading in a frictionless way for this price process leads to the same optimality under transaction costs. The answer to this question is affirmative in finite probability spaces according to Kallsen and Muhle-Karbe [34]. However, for more general settings, this question is elusive.

With geometric Brownian motion models, Kallsen and Muhle-Karbe [33] considered an infinite-horizon optimal investment and consumption problem with logarithmic utility by employing tools from stochastic control and constructed explicitly a shadow price by solving a free boundary problem. In the same framework, this idea was afterward generalized in [7,29] for power utility to derive a shadow price. By the same token, Gerhold et al. [22,23] constructed shadow prices for logarithmic and long-run power utility functions when the time horizon becomes finite.

While considering a similar problem by the convex duality method, the authors of [9] showed that if the solution of a suitable dual problem could be attained by a so-called consistent price system (CPS) which is a (local) martingale, then the optimal solution could be characterized by solving a hedging problem in the ‘shadow’ market associated with this CPS. This ‘folklore’ has been clarified and sharpened very recently by Czichowsky et al. in two aspects: first, it is observed in [12] that the result of Cvitanić and Karatzas holds true even in the framework of general càdlàg stock-price processes S with only natural regularity conditions on utility functions; secondly, a sufficient (but not necessary) condition for ensuring the local martingale property of the optimal dual processes is found in [15], that is, S is continuous and satisfies no unbounded profit with bounded risk (NUPBR). Subsequently, this condition is replaced by a weaker condition of (TWC) of ‘two way crossing’ in [11]. It is worth mentioning that the notion of shadow price is generalized to a sandwiched form in [12], which is adapted to the market driven by a stock-price process with càdlàg paths. This idea is afterward adopted by Bayraktar and Yu [1] in order to study a similar problem but with random endowment: they constructed shadow prices in the sandwiched sense as [12], whenever the duality result holds and a sufficient condition on the dual optimizer is assumed. When the utility function is defined on the whole real line, Czichowsky and Schachermayer [14] proved that the dual optimizer defines a shadow price as long as the primal optimizer is attainable. In particular, this can be ensured if S is an exponential fractional Brownian motion. In addition, we refer to [39] for the generalization of the results in [14] with random endowment.

Instead of studying the dual optimizer, Loewenstein [41] constructed shadow markets directly from the derivatives of dynamic primal value functions under no-short-selling constraints. This argument is based on the existence of the constrained primal solution, which was a hypothesis assumed by [41] but has been affirmed by Benedetti et al. [2] when they applied Loewenstein’s approach to a similar problem with Kabanov’s multi-currency model.

In this paper, we consider on the one hand a numéraire-based utility maximization problem with constant proportional transaction costs and random endowment under no-short-selling constraint. In contrast to [1], our method is to study straight away the primal problem without the formulation of the dual problem. First, we are inspired by [43, Section 3.3] and prove the existence of constrained primal solutions. Second, under the assumption that the agent is endowed with a strictly positive random endowment rather than a deterministic initial wealth, we follow the lines of [2,41] to construct a shadow price directly from the primal solution. Comparing with [1], our result aims to prove the existence of a classical shadow price process instead of the sandwiched one and moreover the regularity conditions assumed in [1] on the random endowment is removed. On the other hand, we discuss the existence of shadow prices when the constraints are violated and the random endowment is allowed to be negative. We provide an example in the Black–Scholes framework with a constructive random endowment. In this example, shadow prices exist and can be explicitly defined.

This paper is organized as follows. In Section 2, we introduce notations and formulate the utility maximization problem under proportional transaction costs with random endowment. Section 3 presents our main result, i.e. the existence of shadow prices under the no-short-selling constraint. Next, we provide in Section 4 an example which falls out of the framework studied in Section 3, however shadow prices can be explicitly defined.

2. Formulation of the problem

In this section, we shall briefly introduce the basic setting of the utility maximization problem in markets with random endowment and transaction costs, as well as the definition of the shadow price in the classical sense. The reader, who has more interests in the details of these topics, is referred to [2,10,15,33,34].

We consider a numéraire-based model: the financial market consists of two assets, one bond and one stock, where the price of the bond B is constant and normalized to . We denote by the price process of the stock, which is based on a filtered probability space satisfying the usual hypotheses of right continuity and saturatedness, where is assumed to be trivial. Here, T is a finite time horizon. In the sequel, we denote by and by . Throughout the paper we make the following assumptions:

Assumption 2.1:

The price process is adapted to , with càdlàg and strictly positive paths. Additionally, and .

Similarly to [15], we introduce constant proportional transaction costs for the trading of the stock, which models the width of the bid-ask spread. The agent has to pay a higher ask price to buy stock shares but only receives a lower bid price when selling them.

As the counterpart of martingale measures in the frictionless case, CPSs play a very important role in the framework with transaction costs (compare, e.g. [32,45]). In the present paper, to establish the utility maximization problem, we adopt an extended notion – -supermartingale-CPSs, similarly defined as in [2].

Definition 2.2:

Fix and the price process satisfying Assumption 2.1. A -supermartingale-CPS is a couple of two strictly positive processes consisting of two supermartingales and , such that(2.1)

for all .

The set of all -supermartingale-CPSs is denoted by .

We introduce now the following assumption on the existence of a supermartingale-CPS:

Assumption 2.3:

For some , we have that .

Remark 2.4:

We remark that this condition corresponds to the ‘NUPBR’ with the no-short-selling constraint on portfolios in the frictionless theory, see [35].

Remark 2.5:

Instead of all , we only need that the condition above holds for some , similar to Lemma 3.1 in [45]. This condition is sufficient to show the convex compactness and the -boundedness of the set of admissible terminal wealth.

In this market under transaction costs, the following definition of self-financing trading strategies is commonly adopted, e.g. in [44,45].

Definition 2.6:

Fix . A self-financing trading strategy under transaction costs is a predictable -valued finite variation process such that

for all , where and denote the Jordan-Hahn decomposition of .

The processes and describe the amount of bond and the number of stock shares held at time .

Assume that as well as being able to trade on the financial market, the agent is endowed with a strictly positive random endowment at the terminal time T, which is described by an -measurable random variable.

Assumption 2.7:

The endowment is a strictly positive and finite-valued random variable, which can be decomposed into a deterministic part and a random part, i.e. , where and , a.s. We assume that x is the initial wealth of the agent and is endowed at time T.

Remark 2.8:

In the financial market, can be explained as a positive contingent claim, e.g. an option contract.

In this paper, we shall consider a utility maximization problem similar to the one in Benedetti et al. [2], where the agent is facing the no-short-selling constraint, which forces him to keep both the amount of bond and the number of stock shares positive. In other words, with the initial wealth x, the agent is only allowed to trade with the admissible strategies defined as follows:

Definition 2.9:

Under transaction costs , a self-financing strategy with and is called admissible, if for each we have that

We denote by the collection of all such strategies. Moreover, we define

We suppose that the agent’s preferences over terminal wealth are modelled by a utility function , which is strictly increasing, strictly concave, continuously differentiable. Furthermore, the function U satisfies the Inada conditions, i.e.

and the following condition of reasonable asymptotic elasticity (RAE).

Assumption 2.10:

The utility function U satisfies the RAE, i.e.

Denote the convex conjugate function of U defined by

which is strictly decreasing, strictly convex and continuously differentiable and satisfies

For financial interpretation and more results about the previous assumption, we refer to [37,38].

Without loss of generality, we may assume to simplify the analysis and we define whenever .

Then, the problem for the agent is to maximize expected utility at terminal time T from his bond account derived from trading and the random endowment, i.e.(2.2)

For , define . By the definition, is a strictly positive semimartingale taking values in . Then, we can construct a frictionless market consisting of one bond with zero interest rate and an underlying asset, whose price process is . Similarly to the previous setting under transaction costs, we adopt the following notion of self-financing trading strategies.

Definition 2.11:

In the frictionless market associated with , an -valued predictable process starting from (x, 0) is a self-financing trading strategy, if is -integrable and

Here, and describe the amount of bond and the number of stock shares held at time .

We shall formulate a utility maximization problem for the frictionless model with . In accordance with (2.2(2.2) ), we always assume that neither asset can be shorted, so that the maximization problem is established over all admissible strategies defined as follows.

Definition 2.12:

Let , for some . A self-financing strategy is admissible in the market driven by , if we have

for all .

We denote by the collection of all such admissible trading strategies starting from (x, 0). Moreover, we define

Lemma 2.13:

The payoff of a trading strategy in the market S with transaction costs can be dominated by some outcomes from trading in the potentially more favourable frictionless markets driven by , . Namely, fix and let be arbitrary, then there exists a such that(2.3)

for all .

Proof For any , since is a -self-financing trading strategy, we have that

We remark that we adopt throughout this paper the notion of stochastic integrals in [13, Section 7]. Then, define a self-financing trading strategy in the frictionless market associated with by

which satisfies (2.3(2.3) ).

Obviously, , for any . Therefore, letting

it follows that

which means each frictionless market with affords better, at least not worse, investment opportunity than the market with transaction costs. An interesting question is whether there exists a least favourable , such that the gap is closed, i.e. the inequality becomes equality. If so, the corresponding price process is called shadow price. Below is the definition of the shadow price similar to [2, Definition 3.9].

Definition 2.14:

Fix the initial value x and the terminal random endowment . We assume that short selling of either asset is not allowed. Then, the process associated with some is called a shadow price process, if

3. Solvability of the problem and existence of shadow prices

In this section, we shall present our main result, that is, the solvability of (2.2(2.2) ) and the existence of shadow prices.

3.1. Main theorems

The existence of shadow prices for the utility maximization problem with neither the no-short-selling constraint nor random endowment has been studied in [10,12,15,34] by duality methods. By contrast, we shall solve (2.2(2.2) ) directly by following the line of [2].

First of all, we display a superreplication theorem as an analogue of [2, Lemma 4.1]:

Lemma 3.1:

For any , the process is a positive supermartingale, for any .

Proof As is of finite variation and is a supermartingale, we obtain that

The first integral defines a supermartingale due to the positivity of and . The second integral defines a decreasing process by the fact that is -self-financing and that takes values in . Therefore, the process is a positive supermartingale.

Remark 3.2:

Comparing with [45, Theorem 1.4], we require less on the underlying asset price S for the superreplication theorem, since we are working with a smaller set of trading strategies.

Furthermore, we have some properties of the convex sets and as follows.

Lemma 3.3:

Under Assumption 2.1 and 2.3, the total variation and remain bounded in , when runs through .

Proof Write and as the canonical differences of increasing processes. Then, we could define a strategy by

and prove by Lemma 3.1 that for ,

Inspired by the proof of [6, Lemma 3.2], we construct a probability measure by defining

where . Then, we have

The remainder of the proof is identical with the one of [45, Lemma 3.1].

Then, we state the following lemma without proof and refer the reader to [45, Theorem 3.4].

Lemma 3.4:

Under Assumptions 2.1 and 2.3, the set is convex closed and bounded in .

In what follows, we shall establish the existence and uniqueness result for the primal solution of (2.2(2.2) ). In the frictionless case, a similar result without random endowment has been proved in [43] (compare also [2,26]). The author of [43] applied a technical lemma ([43, Lemma 3.16]) to conduct a proof by contradiction and show that the limit of a maximizing sequence indeed solves the utility maximization problem. We find that the assumption in [43, Lemma 3.16] is not essentially needed for proceeding the argument. Thus, we reorganize a lemma in Appendix 1 and for the sake of completeness, we also give the proof of the following theorem.

Theorem 3.5:

Let Assumptions 2.1, 2.3, 2.7 and 2.10 hold. Assume moreover that

Then, the utility maximization problem (2.2(2.2) ) admits a unique solution

Proof The uniqueness is trivial due to the strict concavity of U. Thus, we only have to show the existence.

(i)	Since , we could find a maximizing sequence for (2.2(2.2) ), i.e. By passing to a sequence of convex combinations , still denoted by , and applying Lemma 3.4 as well as the Komlós-type theorem (e.g. [18, Lemma A1.1a]), we may suppose that converges a.s. to .
(ii)	We claim that is integrable and thus exists. Without loss of generality we assume that . For any , . It is easy to verify that u is still a concave function in x and thus implies . We suppose for the sake of contradiction that is not integrable, then which is contradiction.
(iii)	We now prove that is the primal optimizer. If not, there exists an such that For each n, denote and denote . Fixing , there exists an , such that for each , (3.1) Since , by [37, Lemma 6.3], there exists some , such that , for all . Note that for each and any , Thus, for any , we can choose sufficiently large with and find such that for any , Due to the integrability of , for properly chosen , holds for any . From Lemma A.1, we fix such that (3.2) Then, Furthermore, due to the positivity of , and , we have and Therefore, we can deduce from (3.1(3.1) ) and (3.2(3.2) ) that Letting , we have which is a contradiction to the maximality of .

Now we turn to consider the frictionless market associated with , for . Similarly to Lemma 3.1, we have the supermartingale property of for The subsequent lemma has been reviewed in [2, Lemma 4.1]. However, for the convenience of the reader, we prove it in the numéraire-based case.

Lemma 3.6:

Fix . The process is a positive supermartingale, for any

Proof Note that by the frictionless self-financing condition. Using Itô’s formula and [24, Proposition A.1], we obtain that

It follows from the frictionless self-financing condition again and [30, I.4.36] that

therefore, . By [30, I.4.37, Definition I.4.45], we obtain

which is a positive local supermartingale and hence a supermartingale.

Then, it is easy to deduce that for each and ,(3.3)

Therefore, to prove the existence of shadow prices, it suffices to have the following lemma, whose proof is postponed to the next subsection.

Lemma 3.7:

Let Assumptions 2.1, 2.3, 2.7 and 2.10 hold. There exists a , such that

(i)	;
(ii)

Theorem 3.8:

The -supermartingale-CPS satisfying Lemma 3.7 (i)–(ii) defines a shadow price .

Proof Consider the frictionless market associated with . By Lemma 3.7, we have

where the last inequality follows from (3.3(3.3) ). The inequality above implies , which proves that is a shadow price for the problem (2.2(2.2) ).

Remark 3.9:

By the strict concavity of U, is the unique solution in for the frictionless problem . Moreover, the trading strategy , that attains the maximum in the market with transaction costs, does the same in the frictionless one associated with the shadow price . Therefore, the optimal trading strategy for S under transaction costs satisfies

for all .

Remark 3.10:

In our case, shadow prices are determined not only by the random endowment but also by its decomposition (see Assumption 2.7). The decomposition of the random endowment together with the no-short-selling constraint can be explained as the agent’s trading rule created by his/her controller. Precisely, if the random endowment that the agent will eventually receive is decomposed into by his/her controller, then it means that the agent is allowed to spend at most x in the bond market for trading the stock. Thus, the different ways of decomposition mean the different limits of short selling in bond, which lead to different maximal utilities and also shadow prices.

3.2. Proof of Lemma 3.7

In this subsection, we shall prove Lemma 3.7 by following [2, p. 814–816]. Thus, we only give the sketch in order to show how it develops in the numéraire-based context and how a positive random endowment works.

The proof is divided in several stages.

Firstly, similar to [2, Lemma 4.4], we have the following dynamic programming principle (see also [21, Theorem 1.17]), which could be proved in a direct way with the numéraire-based model.

Proposition 3.11:

Define

where is the set of all admissible -self-financing trading strategies, which agree with in [0, s].

Then, the process is a martingale i.e.

for all optimal trading strategies attaining .

Proof Without loss of generality, it suffices to verify the following claim(3.4)

for all .

To obtain a contradiction, we suppose that (3.4(3.4) ) is not true, i.e. there exists a and a set with defined as(3.5)

Then define

We have

which is in contradiction to the maximality of . Thus, by the definition of and (3.4(3.4) ), we obtain

Finally, the tower property of conditional expectations yields the desired result.

The next step goes in the exact same way as in [2], i.e. we should first construct a pair , then verify a shadow price can be defined by . The additional positive in the dynamic will not alter the following results.

Proposition 3.12:

The following processes are well defined:(3.6)

for , and(3.7)

Furthermore, define(3.8)

Then, the process is a càdlàg supermartingale and moreover, for all , we have(3.9)

Consequently, is a -supermartingale-CPS.

Proof Firstly, is well-defined, since the right-hand side of (3.6(3.6) ) is monotone due to the concavity of U and the definition of . Furthermore, the set

is directed upwards, thus there exists a sequence of

such that

Then, by proceeding a similar procedure as in the proof of [2, Proposition 4.5], we can verify the supermartingale property of , which is not necessarily càdlàg. Recalling that is finitely valued and concave on , we have that

takes finite values for . Consequently, by [36, Proposition 1.3.14(iii)], (3.8(3.8) ) is a well-defined càdlàg supermartingale. In particular, .

On the other hand, the proof of (3.9(3.9) ) goes in the same way as (57) in [41]. We complete the proof.

Proof of Lemma 3.7:

It remains to proof (2) in Lemma 3.7. Since , we have(3.10)

It remains to show the reversed inequality. For , we note that . By the concavity of u, we obtain

Therefore, it follows from the strict concavity and the continuous differentiability of U that(3.11)

Letting , monotone convergence yields(3.12)

We complete the proof by comparing (3.10(3.10) ) and (3.12(3.12) ).

Remark 3.13:

We have seen here that the nonnegativity of the random endowment is important. This ensures the strict positivity of , for , such that in (3.11(3.11) ) is well defined.

Remark 3.14:

We study in this paper the numéraire-based two-asset model just for the sake of simplicity, however, the argument could adapt to the multi-currency setting as in [2] with no essential changes. Notice that both the present paper and [2] concern a univariate utility function.

4. Example: when the random endowment becomes negative

We have discussed the existence of shadow price processes for the utility maximization problem with positive random endowment under the no-short-selling constraint of each asset. Actually, the positivity constraint on the random endowment is a sufficient condition. However, when the random endowment becomes negative, the existence of shadow prices is not clear if we keep our setting. This will be an interesting problem for our future research. We need to mention here that with a different definition of admissibility for portfolios, the existence of sandwiched shadow price is proved in [1], in which the random endowment could be negative.

In this section, we provide a nontrivial and heuristic example showing that even when the random endowment becomes negative, there may exist a shadow price for the utility maximization problem in the market under transaction costs. In particular, we discuss maximal trading strategies in the context with transaction costs. Notice that the random endowment constructed in our example is associated with such a maximal trading strategy.

We consider the Black–Scholes model with finite time horizon. Assume that the market consists of a saving account with zero interest rate and a stock with price dynamics

where is a Brownian motion on a filtered probability space .

Now fix a level of transaction costs . We assume that an agent is endowed with the initial capital at time 0 and the random endowment at terminal time T, where is an -measurable (0, 1)-valued uniformly distributed random variable which is independent of . Then, we have the following proposition.

Proposition 4.1:

The buy-hold-sell strategy(4.1)

solves the utility maximization problem (2.2(2.2) ).

Before proceeding the proof of this proposition, we first introduce the notion of maximal trading strategy in this market with transaction costs. Notice that a similar notion in frictionless markets is created by Delbaen and Schachermayer [18] for considering a superreplication problem.

Definition 4.2:

An element is called maximal, if for satisfying , a.s., we have , a.s. A trading strategy is called maximal in , if it is associated with , where is a maximal element in .

Remark 4.3:

The existence of a maximal element in could be deduced by transfinite induction, provided that is bounded in and closed w.r.t. the convergence in probability (cf. Schachermayer [45]).

Indeed, the trading strategy defined by (4.1(4.1) ) is maximal in .

Proposition 4.4:

The random variable is a maximal element in . Therefore, the trading strategy defined by (4.1(4.1) ) is maximal in .

Before proving the proposition above, we first give the proof of Proposition 4.1 with the help of the maximality of (4.1(4.1) ).

Proof of Proposition 4.1:

Consider an element such that . From the maximality of , we have . Therefore, there exists , such that

Note that and is independent of . Then,

which implies . Consequently, .

On the other hand, by the definition of , we have

Thus, . The proof is completed.

Remark 4.5:

Even without the no-short-selling constraint, is still the unique strategy on [0, T / 2] solving the problem (2.2(2.2) ). Indeed, we shall prove in the next subsection that is a maximal trading strategy in a larger space introduced in [12,15] (still denoted by ).

Next, we shall construct a shadow price in the following corollary. It is evident that the shadow price is not unique in our case.

Corollary 4.6:

Define

Then, the process is a shadow price of the utility maximization problem (2.2(2.2) ).

Proof It follows from the definition of that .

Obviously, the wealth process associated with the buy-hold-sell strategy under is itself. Thus, we can find an equivalent martingale measure , under which this wealth process is a uniformly integrable martingale. By [19, Corollary 4.6], is a maximal element in , where

Similarly to the proof of Proposition 4.1, one can see that solves the utility maximization problem in the frictionless market , and

which implies that is the desired shadow price.

Figure 1. Case 1.

We now prove that (4.1(4.1) ) defines a maximal trading strategy in , i.e. Proposition 4.4. Here, could be the set of admissible trading strategies defined in [12] without the no-short-selling constraint.

Proof of Proposition 4.4:

Let be another trading strategy in . Since the stock-price process S is continuous and the predictable trading strategies are pathwisely of finite variation, we could only consider those with right-continuous paths (cf. [15]). In addition, we assume that the agent buys no more stocks after the time T / 2.

In what follows, we shall discuss trading strategies in two cases and furthermore, we shall prove that the following statement cannot hold(4.2)

and thus is a maximal trading strategy in .

Case I. Suppose that there exists a and a set with such that for , , , -a.s. (i.e. the holding in stock never excesses ). Our aim is to construct a set with , such that for , .

For , define . Then, by choosing sufficiently small, we can find an -measurable set defined by

such that . It is obvious that and for , . Furthermore, we define

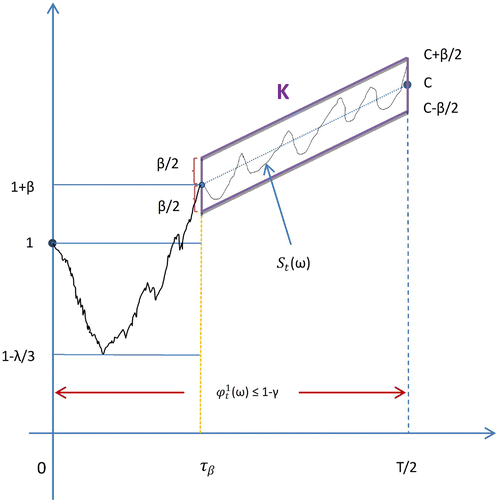
From , we have . We now construct a corridor K of stock price on the time interval with the width (see Figure 1). The centre point of the corridor at is while at T / 2 is a sufficiently large number C. Obviously, the stock-price process S has conditional full support (see, e.g. [28]), which implies the set

has a strictly positive measure, i.e. . For , the most advisable trading strategy is to buy stock shares at the lowest price, which should be at least , and hold them until T / 2. Therefore,

On the other hand,

By properly choosing , we could ensure that .

Case II. Suppose that Case I cannot happen, then for almost every , the following stopping time takes values in [0, T / 2]:

For any stopping times and taking values in [0, T / 2], , we have:(4.3)

In the sequel, we shall consider two situations, i.e.

(i)	For almost every ,
(ii)	There exists an -measurable set D, with , for ,

Assume that (i) holds, then we observe that for almost every ,(4.4)

Indeed, if , then

if , then , and thus from the self-financing constraint,

Consider a frictionless market in which the agent trades for , where the agent gains better than trading in the market with transaction costs. Then, we can deduce

Since and is a maximal trading strategy when trading for , we can prove (4.4(4.4) ).

Now we calculate . From (4.3(4.3) ), we obtain(4.5)

It is obvious that trading for , is uniformly bounded from below, and thus admissible. Comparing (4.5(4.5) ) with

we can conclude from the maximality of that (4.2(4.2) ) cannot happen.

On the other hand, if (ii) holds, then by similar reasoning, we have for ,(4.6)

Again, is uniformly bounded from below when trading for , and thus admissible. Comparing with , we can conclude that either for almost every ,

or there exists a subset , , such that for ,

In particular, we exclude (4.2(4.2) ) by recalling (4.6(4.6) ).

Acknowledgements

This work is partially done during the visit of L. Gu and J. Yang hosted by Prof. N. Touzi at CMAP, École Polytechnique, which is very much appreciated. The authors are grateful to Prof. W. Schachermayer for his suggestions on the Appendix and to the anonymous reviewers for their kind comments.

Additional information

Funding

This work was supported by the Austrian Science Fund (FWF) [grant number P25815]; the European Research Council under ERC Advanced [grant number 321111].

Notes

No potential conflict of interest was reported by the authors.

Appendix 1

In the appendix, we prove the technical lemma, which was used to prove our main result in Section 3.

Lemma A.1:

Suppose is a sequence in , , almost surely. Moreover, is finite and is integrable. We denote . In particular, if , we note . Then, we have for any ,(A1)

Proof We suppose, contrary to our claim (A1(A1) ), there exists , such that(A2)

which implies the boundedness of . Suppose , then we have

Thus,(A3)

From (A3(A3) ) and (A2(A2) ), we can conclude that , which contradicts to the assumption. Therefore, . In this case, we have(A4)

where the equality is deduced from the convergence of and the boundedness of . Obviously, (A4(A4) ) is a contradiction.

Remark A.2:

A generalized version of this lemma also holds, which is similar to [43, Lemma 3.16] (ii) (see Gu [25] for the detailed proof). Precisely, if we assume the same as the above lemma, then for any and , there exists a subsequence and a sequence of disjoint sets , such that for each , on , and