Multi-dimensional sequential testing and detection

Abstract

We study extensions to higher dimensions of the classical Bayesian sequential testing and detection problems for Brownian motion. In the main result, we show that, for a large class of problem formulations, the cost function is unilaterally concave. This concavity result is then used to deduce structural properties for the continuation and stopping regions in specific examples.

Keywords:

• Sequential analysis
• optimal stopping
• Bayesian quickest detection problem

1. Introduction

In the classical paper [19], two sequential problems of determining an unknown drift of a one-dimensional Wiener process were studied: (i) the sequential testing problem of determining a constant drift as quickly as possible, and (ii) the problem of quickest detection where one seeks to determine a change-point as quickly as possible. In the current article, we study multi-dimensional analogues of these problems.

To describe these problems, let $Y=(Y^1,\dots ,Y^n)$ be an n-dimensional continuous-time Markov chain with state-space $\{0,1{\}}^n$, and with a transition rate matrix $Q=\left(\begin{array}{cc}-{\lambda }_i& {\lambda }_i\\ 0& 0\end{array}\right)$ for the ith component. Here, ${\lambda }_i\ge 0$, $i=1,\dots ,n$ are given constants, and we assume a random starting point $Y_0$ such that $\mathbb{P}(Y_0^i=1)={\pi }_i$ and $\mathbb{P}(Y_0^i=0)=1-{\pi }_i$ for ${\pi }_i\in [0,1]$. Moreover, let $X=(X^1,\dots ,X^n)$ be a stochastic process given by $X_t^i={\mu }_i{\int }_0^t{Y}_s^i\mathrm{d}s+W_t^i,$ where ${\mu }_i\ne 0$ and $W=(W^1,\dots ,W^n)$ is an n-dimensional standard Brownian motion. Furthermore, we assume that $Y^1,\dots ,Y^n,W^1,\dots ,W^n$ are independent.

In [19], the problem of sequential testing between two hypotheses and the problem of quickest detection of a drift change in the one-dimensional setting (n = 1) are solved (according to [19], the solution of the hypotheses testing problem was already obtained in [14] and proved optimal in the subclass consisting of so-called regular solutions; we have unfortunately been unable to locate the article [14]). For constants $a,b,c\in (0,\mathrm{\infty })$, in the sequential testing problem one assumes $\lambda :={\lambda }_1=0$ and seeks a strategy $(\tau ,d)$ to minimize (1) $a\mathbb{P}(d=0,Y_0^1=1)+b\mathbb{P}(d=1,Y_0^1=0)+c\mathbb{E}[\tau ]$(1) over ${\mathcal{F}}^X$-stopping times τ and ${\mathcal{F}}_{\tau }^X$-measurable decisions $d\in \{0,1\}$. In the quickest detection problem one assumes $\lambda >0$, and one seeks τ to minimize (2) $b\mathbb{P}(Y_{\tau }^1=0)+c\mathbb{E}\left[{\int }_0^{\tau }{Y}_t^1\mathrm{d}t\right],$(2) where the infimum is taken over ${\mathcal{F}}^X$-stopping times τ. Both these problems can be reduced to optimal stopping problems of the form (3) $\underset{\tau }{inf}\mathbb{E}[g({\mathrm{\Pi }}_{\tau })+{\int }_0^{\tau }h({\mathrm{\Pi }}_s)\mathrm{d}s]$(3) written in terms of the conditional probability process ${\mathrm{\Pi }}_t:=\mathbb{E}[Y_t^1|{\mathcal{F}}_t],$ where g and h are certain penalty function (for the sequential testing problem, $g(\pi )=a\pi \wedge b(1-\pi )$ and $h(\pi )=c$, whereas in the detection problem, $g(\pi )=b(1-\pi )$ and $h(\pi )=c\pi$). In [19], problems (1(1) $a\mathbb{P}(d=0,Y_0^1=1)+b\mathbb{P}(d=1,Y_0^1=0)+c\mathbb{E}[\tau ]$(1) ) and (2(2) $b\mathbb{P}(Y_{\tau }^1=0)+c\mathbb{E}\left[{\int }_0^{\tau }{Y}_t^1\mathrm{d}t\right],$(2) ) are studied separately using a ‘guess and verify’ approach involving an associated free-boundary problem for the cost function.

The two examples above are the generic formulations in the one-dimensional case, and there is rich literature on various extensions. For example, testing and detection problems for a Poisson process with unknown intensity have been studied in [16,17], and a multi-source variant has been studied in [3]. The references [5,6] treat some aspects of testing and detection problems with general distributions of the random drift; since the penalties for a wrong decision in [5,6] are binary, the sufficient statistic is one-dimensional, but time-inhomogeneous, Markov process. Formulations allowing for non-binary penalties appear in [2,15,20], in which the natural sufficient statistic is two-dimensional and the analysis thus becomes more involved.

In the literature cited above, the observation process is one-dimensional; the existing literature on multi-dimensional versions is sparser. In [8], a three-dimensional Brownian motion is observed for which exactly one coordinate has non-zero drift, and the problem of determining this coordinate as quickly as possible is studied. In the set-up of [8], the three random drifts are heavily dependent; in fact, if one drift is non-zero, then the remaining two drifts have to be zero. In [1], a less constrained set-up is used, in which two Poisson processes change intensity at two independent exponential times, and the problem of detecting the minimum of these two times is considered.

In the current article, we use a similar unconstrained set-up as in [1] to study sequential testing and detection problems for a multi-dimensional Wiener process. The variety of possible versions of such testing and detection problems is very rich; indeed, in some applications it would be natural to seek to determine all drifts as accurately as possible, whereas it would be more natural in other applications to determine only one of all possible drifts. Similarly, in the quickest detection problem, some applications would suggest to look for the smallest change-point (as in [1]), whereas one in other applications would try to detect the last change-point; further variants are listed below. In the formulations we suggest, coordinates are modelled independently, and the only interdependence is via the choice of a single stopping time at which the decision is made. Thus, the underlying theme of the problems under consideration is that the cost of monitoring does not scale linearly with the number of processes to observe.

Rather than studying all different formulations on a case by case basis, the multitude of multi-dimensional formulations motivates a unified treatment of the corresponding stopping problems. It turns out that a large class of such problems can be written in the form (3(3) $\underset{\tau }{inf}\mathbb{E}[g({\mathrm{\Pi }}_{\tau })+{\int }_0^{\tau }h({\mathrm{\Pi }}_s)\mathrm{d}s]$(3) ) (or rather, a multi-dimensional version of (3(3) $\underset{\tau }{inf}\mathbb{E}[g({\mathrm{\Pi }}_{\tau })+{\int }_0^{\tau }h({\mathrm{\Pi }}_s)\mathrm{d}s]$(3) )), with g and h both unilaterally concave (concave in each variable separately). A key insight of the current article is that unilateral concavity of the cost function is a generic property for a unified study of structural properties in higher dimensions. In fact, we show that that unilateral concavity of the penalty functions is preserved in the sense that also the corresponding cost function is unilaterally concave (Theorem 3.6). Since many multi-dimensional penalty functions are unilaterally piecewise affine, the concavity property provides valuable information about the structure of the corresponding continuation and stopping regions.

There is related literature on the preservation of spatial concavity/convexity (and consequences for volatility misspecification) for martingale diffusions within the mathematical finance literature, see, for example, [9,11] for one-dimensional results. In higher dimensions, preservation of concavity is a rather rare property, compare [7,10]. With this in mind, we point out that preservation of unilateral concavity is a weaker property; however, it is of less financial importance, and has therefore been less studied in the financial literature. Also note that for the multi-dimensional version of (3(3) $\underset{\tau }{inf}\mathbb{E}[g({\mathrm{\Pi }}_{\tau })+{\int }_0^{\tau }h({\mathrm{\Pi }}_s)\mathrm{d}s]$(3) ), the natural choices of g and h are typically not concave, but only unilaterally concave. We also remark that the authors of [1] use a three-dimensional embedding of a detection problem in order to obtain concavity of the value function; for unilateral concavity, however, one may remain in the two-dimensional set-up of the problem.

The paper is organized as follows. In Section 2, we specify the multi-dimensional versions of the sequential testing and quickest detection problems, and we provide a list of natural examples. In Section 3, we provide a unilateral concavity result for the multi-dimensional problem, and in Sections 4 and 5, we use unilateral concavity to derive structural properties of continuation regions for specific examples.

2. The multi-dimensional set-up

Recall that we continuously observe an n-dimensional process X given by $\mathrm{d}{X}_t^i={\mu }_i{Y}_t^i\mathrm{d}t+\mathrm{d}{W}_t^i,$ where the drift is modelled using a continuous-time Markov chain $Y^i$ with state-space $\{0,1\}$ and transition rate matrix $Q^i=\left(\begin{array}{cc}-{\lambda }_i& {\lambda }_i\\ 0& 0\end{array}\right).$ Moreover, the initial condition satisfies $\mathbb{P}(Y_0^i=1)={\pi }_i\in [0,1]$. In parallel to the one-dimensional case, we introduce the multi-dimensional posterior probability process $\mathrm{\Pi }=({\mathrm{\Pi }}^1,\dots {\mathrm{\Pi }}^n)$ by ${\mathrm{\Pi }}_t^i:=\mathbb{E}[Y_t^i|{\mathcal{F}}_t^X].$ By our independence assumption we note that ${\mathrm{\Pi }}_t^i=\mathbb{E}[Y_t^i|{\mathcal{F}}_t^{X^i}]$, and, in particular, that the coordinates of Π are independent.

It is well-known from filtering theory (cf. [13]) that the process Π is given explicitly by ${\mathrm{\Pi }}_t^i=\frac{j_i(t,\{X_s,0\le s\le t\})}{1+j_i(t,\{X_s,0\le s\le t\})},$ where $\begin{array}{rl}{j}_i(t,\{X_s,0\le s\le t\})& =\exp \{{\mu }_i{X}_t^i-(\frac{{\mu }_i^2}{2}-{\lambda }_i)t\}\\ & \times (\frac{{\pi }_i}{1-{\pi }_i}+{\lambda }_i{\int }_0^t\exp \{-{\mu }_i{X}_s^i+(\frac{{\mu }_i^2}{2}-{\lambda }_i)s\}\mathrm{d}s).\end{array}$ Moreover, it satisfies (4) $\mathrm{d}{\mathrm{\Pi }}_t^i={\lambda }_i(1-{\mathrm{\Pi }}_t^i)\mathrm{d}t+{\mu }_i{\mathrm{\Pi }}_t^i(1-{\mathrm{\Pi }}_t^i)\mathrm{d}{\overline{W}}_t^i$(4) for $i=1,\dots ,n$, where the innovation process $\overline{W}=({\overline{W}}^1,\dots ,{\overline{W}}^n)$ defined by ${\overline{W}}_t^i=X_t^i-{\mu }_i{\int }_0^t{\mathrm{\Pi }}_s^i\mathrm{d}s$ is an n-dimensional Brownian motion with independent coordinates. Consequently, Π is an n-dimensional time-homogeneous Markov process with independent coordinates; allowing for an arbitrary starting point $\pi \in [0,1{]}^n$, we define a cost function $V:[0,1{]}^n\to [0,\mathrm{\infty })$ by (5) $V(\pi )=\underset{\tau }{inf}{\mathbb{E}}_{\pi }[g({\mathrm{\Pi }}_{\tau })+{\int }_0^{\tau }h({\mathrm{\Pi }}_s)\mathrm{d}s],$(5) where g and h are given continuous functions. We also introduce the continuation region $\mathcal{C}:=\{\pi \in [0,1{]}^n:V(\pi )<g(\pi )\}$ and its complement, the stopping region $\mathcal{D}=[0,1{]}^n\setminus \mathcal{C}$, and we recall from optimal stopping theory that the stopping time ${\tau }^{\ast }=inf\{t\ge 0:{\mathrm{\Pi }}_t\in \mathcal{D}\}$ is optimal in (5(5) $V(\pi )=\underset{\tau }{inf}{\mathbb{E}}_{\pi }[g({\mathrm{\Pi }}_{\tau })+{\int }_0^{\tau }h({\mathrm{\Pi }}_s)\mathrm{d}s],$(5) ).

In the next subsections, we list a few natural formulations of multi-dimensional sequential testing problems and multi-dimensional detection problems. All these examples can be written as stopping problems of the form (5(5) $V(\pi )=\underset{\tau }{inf}{\mathbb{E}}_{\pi }[g({\mathrm{\Pi }}_{\tau })+{\int }_0^{\tau }h({\mathrm{\Pi }}_s)\mathrm{d}s],$(5) ).

2.1. Sequential testing formulations

Assume that ${\lambda }_i=0$, $i=1,\dots ,n$ and that the penalization in time is linear, i.e. of the type $c\mathbb{E}[\tau ]$ for some constant c>0. All formulations below can then be written on the form (5(5) $V(\pi )=\underset{\tau }{inf}{\mathbb{E}}_{\pi }[g({\mathrm{\Pi }}_{\tau })+{\int }_0^{\tau }h({\mathrm{\Pi }}_s)\mathrm{d}s],$(5) ) with h = c but with different penalty functions g. For simplicity, we consider symmetric penalization (corresponding to a = b = 1 in (1(1) $a\mathbb{P}(d=0,Y_0^1=1)+b\mathbb{P}(d=1,Y_0^1=0)+c\mathbb{E}[\tau ]$(1) )); generalizations to set-ups with non-symmetric weights are straightforward.

(ST1)	Consider the problem $\underset{\tau ,d}{inf}\{\sum _{i=1}^n\mathbb{P}(d_i\ne Y_0^i)+c\mathbb{E}[\tau ]\},$ where the infimum is taken over ${\mathcal{F}}^X$-stopping times τ and decisions $d\in \{0,1{\}}^n$ such that d is ${\mathcal{F}}_{\tau }^X$-measurable, i.e. the tester is penalized equally for every faulty decision. This problem can be written on the form (5(5) $V(\pi )=\underset{\tau }{inf}{\mathbb{E}}_{\pi }[g({\mathrm{\Pi }}_{\tau })+{\int }_0^{\tau }h({\mathrm{\Pi }}_s)\mathrm{d}s],$(5) ) with $g(\pi )=\sum _{i=1}^n{\pi }_i\wedge (1-{\pi }_i).$
(ST2)	Consider the problem $\underset{\tau ,d,\tilde{d}}{inf}\{\mathbb{P}(d\ne Y_0^{\tilde{d}})+c\mathbb{E}[\tau ]\},$ where the infimum is taken over ${\mathcal{F}}^X$-stopping times τ and decisions $d\in \{0,1\}$ and $\tilde{d}\in \{1,\dots ,n\}$ that are ${\mathcal{F}}_{\tau }^X$-measurable. Thus the tester seeks to determine as quickly as possible a drift for only one of the processes. For this problem, the penalty function is given by $g(\pi )=\underset{i=1}{\overset{n}{\bigwedge }}({\pi }_i\wedge (1-{\pi }_i)).$
(ST3)	Let for simplicity n = 2 (generalizations are straightforward), let ${\mu }_1={\mu }_2=:\mu$ and let $\gamma \in [0,1]$ be a given constant. Consider the problem $\underset{{\tau }_1,{\tau }_2,d_1,d_2}{inf}\{\mathbb{P}(d_1\ne Y_0^1)+\mathbb{P}(d_2\ne Y_0^2)+c\mathbb{E}[{\tau }_1\wedge {\tau }_2+(1-\gamma )({\tau }_1\vee {\tau }_2-{\tau }_1\wedge {\tau }_2)]\},$ where the infimum is taken over stopping times ${\tau }_1$, ${\tau }_2$ and decisions $d_1,d_2\in \{0,1\}$ such that $d_i$ is ${\mathcal{F}}_{{\tau }_i}^X$-measurable. Here, γ is a cost reduction parameter that describes how the cost (per unit of time) of observing two processes relates to the cost of observing only one process. Using the strong Markov property, this multiple stopping problem reduces to a problem of type (5(5) $V(\pi )=\underset{\tau }{inf}{\mathbb{E}}_{\pi }[g({\mathrm{\Pi }}_{\tau })+{\int }_0^{\tau }h({\mathrm{\Pi }}_s)\mathrm{d}s],$(5) ) with penalty $g({\pi }_1,{\pi }_2)=\underset{i=1}{\overset{2}{\bigwedge }}({\pi }_i\wedge (1-{\pi }_i)+u^{\mu ,c(1-\gamma )}({\pi }_{3-i})),$ where $u^{\mu ,c(1-\gamma )}$ is the value function of the one-dimensional sequential testing problem with cost $c(1-\gamma )$ per unit of time, see (6(6) $u(\pi ):=u^{\mu ,c}(\pi ):=\underset{\tau }{inf}{\mathbb{E}}_{\pi }[{\mathrm{\Pi }}_{\tau }\wedge (1-{\mathrm{\Pi }}_{\tau })+c\tau ].$(6) ) below.

2.2. Quickest detection formulations

Now assume that ${\lambda }_i>0$ for all i, and let c>0 be a constant. In all of the formulations below, the infimum is taken over ${\mathcal{F}}^X$-stopping times.

(QD1)	Consider the problem $\underset{\tau }{inf}\{\mathbb{P}(\underset{1\le i\le n}{max}{Y}_{\tau }^i=0)+c\mathbb{E}\left[{\int }_0^{\tau }\underset{1\le i\le n}{max}{Y}_t^i\mathrm{d}t\right]\}.$ Here, one seeks to determine the first change-point (this problem formulation was treated in [1] for a detection problem involving two Poisson processes); the problem can be written on the form (5(5) $V(\pi )=\underset{\tau }{inf}{\mathbb{E}}_{\pi }[g({\mathrm{\Pi }}_{\tau })+{\int }_0^{\tau }h({\mathrm{\Pi }}_s)\mathrm{d}s],$(5) ) with $g(\pi )={\mathrm{\Pi }}_{i=1}^n(1-{\pi }_i)$ and $h(\pi )=c(1-{\mathrm{\Pi }}_{i=1}^n(1-{\pi }_i)).$
(QD2)	A problem of determining the last change-point is obtained by instead considering $\underset{\tau }{inf}\{\mathbb{P}(\underset{1\le i\le n}{min}{Y}_{\tau }^i=0)+c\mathbb{E}\left[{\int }_0^{\tau }\underset{1\le i\le n}{min}{Y}_t^i\mathrm{d}t\right]\}.$ Again, this problem can be written on the form (5(5) $V(\pi )=\underset{\tau }{inf}{\mathbb{E}}_{\pi }[g({\mathrm{\Pi }}_{\tau })+{\int }_0^{\tau }h({\mathrm{\Pi }}_s)\mathrm{d}s],$(5) ); the corresponding functions g and h are given by $g(\pi )=1-{\mathrm{\Pi }}_{i=1}^n{\pi }_i$ and $h(\pi )=c{\mathrm{\Pi }}_{i=1}^n{\pi }_i,$ respectively.
(QD3)	Assume that a tester wants to detect one coordinate for which the change-point has happened. One possible formulation of this is $\underset{\tau ,\tilde{d}}{inf}\{\mathbb{P}(Y_{\tau }^{\tilde{d}}=0)+c\mathbb{E}\left[{\int }_0^{\tau }\sum _{i=1}^n{Y}_t^i\mathrm{d}t\right]\},$ where the infimum is taken also over ${\mathcal{F}}_{\tau }^X$-measurable decisions $\tilde{d}\in \{1,\dots ,n\}$. The problem can be written on the form (5(5) $V(\pi )=\underset{\tau }{inf}{\mathbb{E}}_{\pi }[g({\mathrm{\Pi }}_{\tau })+{\int }_0^{\tau }h({\mathrm{\Pi }}_s)\mathrm{d}s],$(5) ) where the corresponding functions g and h are given by $g(\pi )=\underset{i=1}{\overset{n}{\bigwedge }}(1-{\pi }_i)$ and $h(\pi )=c\sum _{i=1}^n{\pi }_i.$

2.3. The one-dimensional case

To introduce notation, we end this section with a short review of the one-dimensional problems.

2.3.1. Sequential testing

In the case n = 1 and $\lambda =0$, let (6) $u(\pi ):=u^{\mu ,c}(\pi ):=\underset{\tau }{inf}{\mathbb{E}}_{\pi }[{\mathrm{\Pi }}_{\tau }\wedge (1-{\mathrm{\Pi }}_{\tau })+c\tau ].$(6) The notation $u^{\mu ,c}$ is used when we want to emphasize the dependence on the drift μ and the cost of observation parameter c, and we refer to this one-dimensional testing problem as $ST(\mu ,c)$. We then know that $u:[0,1]\to [0,1]$ is concave with $u(\pi )\le \pi \wedge (1-\pi )$. Moreover, $\mathcal{C}:=\{\pi \in [0,1]:u(\pi )<\pi \wedge (1-\pi )\}=(A^{\ast },1-A^{\ast })$ for some $A^{\ast }\in (0,1/2)$; further details on u and $A^{\ast }$ can be found in [18].

2.3.2. Quickest detection

Assuming that n = 1 and $\lambda >0$, let $u(\pi ):=u^{\mu ,\lambda ,c}({\pi }_{)}:=\underset{\tau }{inf}{\mathbb{E}}_{\pi }[1-{\mathrm{\Pi }}_{\tau }+c{\int }_0^{\tau }{\mathrm{\Pi }}_t\mathrm{d}t],$ where the notation $u^{\mu ,\lambda ,c}$ is used when we want to emphasize the dependence on the parameters μ, λ and c, and we refer to this one-dimensional detection problem as $QD(\mu ,\lambda ,c)$. The function $u:[0,1]\to [0,1]$ is then concave and non-increasing. Moreover, $\mathcal{C}:=\{\pi \in [0,1]:u(\pi )<1-\pi \}=[0,B^{\ast })$ for some $B^{\ast }\in (0,1)$; again, further details on u and $B^{\ast }$ can be found in [18].

3. Properties of the cost function

In this section, we derive Lipschitz continuity and the unilateral concavity for the multi-dimensional stopping problem (5(5) $V(\pi )=\underset{\tau }{inf}{\mathbb{E}}_{\pi }[g({\mathrm{\Pi }}_{\tau })+{\int }_0^{\tau }h({\mathrm{\Pi }}_s)\mathrm{d}s],$(5) ). Throughout the remainder of this article, we make the following assumption.

Assumption 3.1

We assume that

• the functions $g,h:[0,1{]}^n\to [0,\mathrm{\infty })$ are Lipschitz continuous;

• the functions $g(\pi )$ and $h(\pi )$ are concave in each variable ${\pi }_i$ separately;

• if ${\lambda }_i=0$ for some $i=1,\dots ,n$, then h is constant.

Remark 3.2

Note that all examples (ST1)–(ST3) and (QD1)–(QD3) are covered by Assumption 3.1. Also note that the assumption of unilateral concavity is strictly weaker than (joint) concavity. In fact, g and h are not concave in (QD1)–(QD2).

3.1. Continuity

Theorem 3.3

The cost function $V:[0,1{]}^n\to [0,\mathrm{\infty })$ is Lipschitz continuous.

Proof.

It suffices to check that V is Lipschitz in each variable ${\pi }_i$ separately. To do that, let i = 1 and denote by ${\mathrm{\Pi }}_t$ the solution of (4(4) $\mathrm{d}{\mathrm{\Pi }}_t^i={\lambda }_i(1-{\mathrm{\Pi }}_t^i)\mathrm{d}t+{\mu }_i{\mathrm{\Pi }}_t^i(1-{\mathrm{\Pi }}_t^i)\mathrm{d}{\overline{W}}_t^i$(4) ) with initial condition ${\mathrm{\Pi }}_t=\pi \in [0,1{]}^n$, and denote by ${\tilde{\mathrm{\Pi }}}_t$ the solution with initial condition $\tilde{\pi }=({\tilde{\pi }}_1,\dots ,{\tilde{\pi }}_n)$, where ${\pi }_j={\tilde{\pi }}_j$, $j=2,\dots ,n$ and ${\pi }_1<{\tilde{\pi }}_1$. By a comparison result for one-dimensional stochastic differential equations, ${\mathrm{\Pi }}_t^1\le {\tilde{\mathrm{\Pi }}}_t^1$ for all $t\ge 0$. Moreover, $\mathrm{d}({\tilde{\mathrm{\Pi }}}_t^1-{\mathrm{\Pi }}_t^1)=-{\lambda }_1({\tilde{\mathrm{\Pi }}}_t^1-{\mathrm{\Pi }}_t^1)\mathrm{d}t+\mathrm{d}{M}_t$ where M is a continuous martingale, so ${\tilde{\mathrm{\Pi }}}_t^1-{\mathrm{\Pi }}_t^1$ is a bounded supermartingale. Consequently, by optional sampling, $0\le \mathbb{E}[{\tilde{\mathrm{\Pi }}}_{\tau }^1-{\mathrm{\Pi }}_{\tau }^1]\le {\tilde{\pi }}_1-{\pi }_1$ for any stopping time τ. Thus $|\mathbb{E}[g({\tilde{\mathrm{\Pi }}}_{\tau })-g({\mathrm{\Pi }}_{\tau })]|\le C\mathbb{E}[|{\tilde{\mathrm{\Pi }}}_{\tau }-{\mathrm{\Pi }}_{\tau }|]\le C|{\tilde{\pi }}_1-{\pi }_1|$ where C is a Lipschitz constant of g. This shows that if h is constant, then V is Lipschitz in its first argument, and thus it is Lipschitz also in π.

Furthermore, if ${\lambda }_1>0$, then $\mathbb{E}[{\tilde{\mathrm{\Pi }}}_t^1-{\mathrm{\Pi }}_t^1]={\tilde{\pi }}_1-{\pi }_1-{\lambda }_1{\int }_0^t\mathbb{E}[{\tilde{\mathrm{\Pi }}}_s^1-{\mathrm{\Pi }}_s^1]\mathrm{d}s,$ so $\mathbb{E}[{\tilde{\mathrm{\Pi }}}_t^1-{\mathrm{\Pi }}_t^1]=({\tilde{\pi }}_1-{\pi }_1){\mathrm{e}}^{-{\lambda }_{1}t}.$ Consequently, $\mathbb{E}[{\int }_0^{\tau }|h({\tilde{\mathrm{\Pi }}}_t)-h({\mathrm{\Pi }}_t)|\mathrm{d}t]\le D{\int }_0^{\mathrm{\infty }}\mathbb{E}[|{\tilde{\mathrm{\Pi }}}_t-{\mathrm{\Pi }}_t|]\mathrm{d}t=\frac{D}{{\lambda }_1}({\tilde{\pi }}_1-{\pi }_1),$ where D is a Lipschitz constant of h. It follows that $|\mathbb{E}[g({\tilde{\mathrm{\Pi }}}_{\tau })+{\int }_0^{\tau }h({\tilde{\mathrm{\Pi }}}_t)\mathrm{d}t]-\mathbb{E}[g({\mathrm{\Pi }}_{\tau })+{\int }_0^{\tau }h({\mathrm{\Pi }}_t)\mathrm{d}t]|\le (C+\frac{D}{{\lambda }_1})({\tilde{\pi }}_1-{\pi }_1)$ for any stopping time τ. Therefore, $V({\pi }_1,\dots ,{\pi }_n)$ is Lipschitz in its first argument. Consequently, if ${\lambda }_i>0$ for all $i=1,\dots ,n$, then V is Lipschitz also in π.

Remark 3.4

It follows from the proof above that if ${\lambda }_i=0$ for $i=1,\dots ,n$, g is Lipschitz 1 in each variable separately and h is constant, then also V is Lipschitz 1 in each variable separately.

3.2. Unilateral concavity

Next, we study the unilateral concavity of the value function. Our proof is an adaption of an argument for concavity in [15] to the present setting. Due to the presence of a multi-dimensional observation process X, we only obtain the unilateral concavity (as opposed to joint concavity obtained in [15]). The line of proof is essentially one-dimensional, and independence of the coordinates of the Π-process is used.

Let $\tilde{\mathbb{P}}$ be a new measure defined so that ${\frac{\mathrm{d}\tilde{\mathbb{P}}}{\mathrm{d}\mathbb{P}}|}_{{\mathcal{F}}_t^X}=\exp \{-\frac{1}{2}\sum _{i=1}^n{\mu }_i^2{\int }_0^t({\mathrm{\Pi }}_s^i{)}^2\mathrm{d}s-\sum _{i=1}^n{\int }_0^t{\mu }_i{\mathrm{\Pi }}_s^i\mathrm{d}{\overline{W}}_s^i\},$ and denote by $\tilde{\mathbb{E}}$ the corresponding expectation operator. By the Girsanov theorem, $X_t$ is an n-dimensional $\tilde{\mathbb{P}}$-Brownian motion. Define the probability likelihood process $\mathrm{\Phi }=({\mathrm{\Phi }}^1,\dots ,{\mathrm{\Phi }}^n)$ by ${\mathrm{\Phi }}_t^i=\frac{{\mathrm{\Pi }}_t^i}{1-{\mathrm{\Pi }}_t^i}$ and observe that ${\mathrm{\Phi }}_0^i=\frac{{\pi }_i}{1-{\pi }_i}=:{\varphi }_i$. Also note that an application of Ito's formula yields (7) $\mathrm{d}{\mathrm{\Phi }}_t^i={\lambda }_i(1+{\mathrm{\Phi }}_t^i)\mathrm{d}t+{\mu }_i{\mathrm{\Phi }}_t^i\mathrm{d}{X}_t^i.$(7) In the following result, we establish that the Radon–Nikodym derivative can be expressed in terms of the process Φ (this was noted in [12] in a one-dimensional setting).

Proposition 3.5

We have $\frac{V(\pi )}{{\displaystyle \prod _{i=1}^n(1-{\pi }_i)}}=\underset{\tau }{inf}\tilde{\mathbb{E}}[{\mathrm{e}}^{-\lambda \tau }\left({\displaystyle \prod _{i=1}^n(1+{\mathrm{\Phi }}_{\tau }^i)}\right)g({\mathrm{\Pi }}_{\tau })+{\int }_0^{\tau }{\mathrm{e}}^{-\lambda t}\left({\displaystyle \prod _{i=1}^n(1+{\mathrm{\Phi }}_t^i)}\right)h({\mathrm{\Pi }}_t)\mathrm{d}t],$ where $\lambda =\sum _{i=1}^n{\lambda }_i$.

Proof.

Define a process $Y_t$ by $Y_t={\mathrm{e}}^{-\lambda t}\prod _{i=1}^n\frac{1-{\pi }_i}{1-{\mathrm{\Pi }}_t^i}={\mathrm{e}}^{-\lambda t}\prod _{i=1}^n(1+{\mathrm{\Phi }}_t^i)(1-{\pi }_i)$ and observe that $Y_0=1$. Using Ito's formula and (4(4) $\mathrm{d}{\mathrm{\Pi }}_t^i={\lambda }_i(1-{\mathrm{\Pi }}_t^i)\mathrm{d}t+{\mu }_i{\mathrm{\Pi }}_t^i(1-{\mathrm{\Pi }}_t^i)\mathrm{d}{\overline{W}}_t^i$(4) ), we find that $\begin{array}{rl}\mathrm{d}{Y}_t& =-\lambda Y_t\mathrm{d}t+Y_t\sum _{i=1}^n\frac{1}{1-{\mathrm{\Pi }}_t^i}\mathrm{d}{\mathrm{\Pi }}_t^i+Y_t\sum _{i=1}^n\frac{1}{(1-{\mathrm{\Pi }}_t^i{)}^2}(\mathrm{d}{\mathrm{\Pi }}_t^i{)}^2\\ & =-\lambda Y_t\mathrm{d}t+Y_t\sum _{i=1}^n({\lambda }_i\mathrm{d}t+{\mu }_i{\mathrm{\Pi }}_t^i\mathrm{d}{\overline{W}}_t^i)+Y_t\sum _{i=1}^n{\mu }_i^2({\mathrm{\Pi }}_t^i{)}^2\mathrm{d}t\\ & =Y_t\sum _{i=1}^n{\mu }_i{\mathrm{\Pi }}_t^i\mathrm{d}{X}_t^i.\end{array}$ Since ${\frac{\mathrm{d}\mathbb{P}}{\mathrm{d}\tilde{\mathbb{P}}}|}_{{\mathcal{F}}_t^X}=\exp \{-\frac{1}{2}\sum _{i=1}^n{\mu }_i^2{\int }_0^t({\mathrm{\Pi }}_s^i{)}^2\mathrm{d}s-\sum _{i=1}^n{\int }_0^t{\mu }_i{\mathrm{\Pi }}_s^i\mathrm{d}{X}_s^i\},$ it follows that ${\frac{\mathrm{d}\mathbb{P}}{\mathrm{d}\tilde{\mathbb{P}}}|}_{{\mathcal{F}}_t^X}=Y_t,$ so we can rewrite the value function as $\begin{array}{rl}\frac{V(\pi )}{{\displaystyle \prod _{i=1}^n(1-{\pi }_i)}}& =\frac{1}{{\displaystyle \prod _{i=1}^n(1-{\pi }_i)}}\underset{\tau }{inf}{\mathbb{E}}_{\pi }[g({\mathrm{\Pi }}_{\tau })+{\int }_0^{\tau }h({\mathrm{\Pi }}_t)\mathrm{d}t]\\ & =\frac{1}{{\displaystyle \prod _{i=1}^n(1-{\pi }_i)}}\underset{\tau }{inf}{\tilde{\mathbb{E}}}_{\pi }\left[Y_{\tau }(g({\mathrm{\Pi }}_{\tau })+{\int }_0^{\tau }h({\mathrm{\Pi }}_t)\mathrm{d}t)\right]\\ & =\underset{\tau }{inf}{\tilde{\mathbb{E}}}_{\pi }\left[{\mathrm{e}}^{-\lambda \tau }{\displaystyle \prod _{i=1}^n(1+{\mathrm{\Phi }}_{\tau }^i)g({\mathrm{\Pi }}_{\tau })+{\mathrm{e}}^{-\lambda \tau }{\displaystyle \prod _{i=1}^n(1+{\mathrm{\Phi }}_{\tau }^i){\int }_0^{\tau }h({\mathrm{\Pi }}_t)\mathrm{d}t}}\right]\\ & =\underset{\tau }{inf}{\tilde{\mathbb{E}}}_{\pi }\left[{\mathrm{e}}^{-\lambda \tau }{\displaystyle \prod _{i=1}^n(1+{\mathrm{\Phi }}_{\tau }^i)g({\mathrm{\Pi }}_{\tau })+{\int }_0^{\tau }{\mathrm{e}}^{-\lambda t}{\displaystyle \prod _{i=1}^n(1+{\mathrm{\Phi }}_t^i)h({\mathrm{\Pi }}_t)\mathrm{d}t}}\right],\end{array}$ which completes the proof.

Theorem 3.6

The function ${\pi }_i\mapsto V(\pi )$ is concave in each variable separately (i.e. ${\pi }_i\mapsto V(\pi )$ is concave for each $i=1,\dots ,n$).

Proof.

It suffices to check that ${\pi }_1\mapsto V(\pi )$ is concave. To do that, first note that since (7(7) $\mathrm{d}{\mathrm{\Phi }}_t^i={\lambda }_i(1+{\mathrm{\Phi }}_t^i)\mathrm{d}t+{\mu }_i{\mathrm{\Phi }}_t^i\mathrm{d}{X}_t^i.$(7) ) is a linear equation, it can be solved explicitly as (8) ${\mathrm{\Phi }}_t^i={\mathrm{e}}^{({\lambda }_i-\frac{{\mu }_i^2}{2})t+{\mu }_i{X}_t^i}({\varphi }_i+{\lambda }_i{\int }_0^t{\mathrm{e}}^{-({\lambda }_i-\frac{{\mu }_i^2}{2})s-{\mu }_i{X}_s^i}\mathrm{d}s).$(8) Thus ${\mathrm{\Phi }}_t^i$ is affine in ${\varphi }_i$ and independent of ${\varphi }_j$, $j\ne i$. Moreover, denoting $Z_t={\mathrm{e}}^{({\lambda }_1-\frac{{\mu }_1^2}{2})t+{\mu }_1{X}_t^1},$ we have that $\frac{\mathrm{\partial }{\mathrm{\Phi }}_t^1}{\mathrm{\partial }{\pi }_1}=\frac{Z_t}{(1-{\pi }_1{)}^2}$ and $\frac{{\mathrm{\partial }}^2{\mathrm{\Phi }}_t^1}{\mathrm{\partial }{\pi }_1^2}=\frac{2Z_t}{(1-{\pi }_1{)}^3}$ so that (9) $2\frac{\mathrm{\partial }{\mathrm{\Phi }}_t^1}{\mathrm{\partial }{\pi }_1}=(1-\pi )\frac{{\mathrm{\partial }}^2{\mathrm{\Phi }}_t^1}{\mathrm{\partial }{\pi }_1^2}.$(9) Fix an ${\mathcal{F}}^X$-stopping time τ; we next claim that (10) $G(\pi ,\omega ):=(1-{\pi }_1)(1+{\mathrm{\Phi }}_{\tau }^1)g({\mathrm{\Pi }}_{\tau })$(10) is concave in ${\pi }_1$. To see this, assume that g is $C^2$ (the general case follows by approximation). Then $\begin{array}{rl}{G}_{{\pi }_1{\pi }_1}& =-2\frac{\mathrm{\partial }}{{\mathrm{\partial }}_{{\pi }_1}}((1+{\mathrm{\Phi }}_{\tau }^1)g({\mathrm{\Pi }}_{\tau }))+(1-{\pi }_1)\frac{\mathrm{\partial }}{{\mathrm{\partial }}_{{\pi }_1{\pi }_1}}((1+{\mathrm{\Phi }}_{\tau }^1)g({\mathrm{\Pi }}_{\tau }))\\ & =-2\frac{\mathrm{\partial }{\mathrm{\Phi }}_{\tau }^1}{\mathrm{\partial }{\pi }_1}(g+\frac{g_{{\pi }_1}}{1+{\mathrm{\Phi }}_{\tau }^1})\\ & +(1-{\pi }_1)(\frac{{\mathrm{\partial }}^2{\mathrm{\Phi }}_{\tau }^1}{\mathrm{\partial }{\pi }_1^2}(g+\frac{g_{{\pi }_1}}{1+{\mathrm{\Phi }}_{\tau }^1})+{\left(\frac{\mathrm{\partial }{\mathrm{\Phi }}_{\tau }^1}{\mathrm{\partial }{\pi }_1}\right)}^2\frac{g_{{\pi }_1{\pi }_1}}{(1+{\mathrm{\Phi }}_{\tau }^1{)}^3})\\ & ={\left(\frac{1-{\mathrm{\Pi }}_{\tau }^1}{1-{\pi }_1}\right)}^3{Z}_{\tau }^2{g}_{{\pi }_1{\pi }_1}\end{array}$ by (9(9) $2\frac{\mathrm{\partial }{\mathrm{\Phi }}_t^1}{\mathrm{\partial }{\pi }_1}=(1-\pi )\frac{{\mathrm{\partial }}^2{\mathrm{\Phi }}_t^1}{\mathrm{\partial }{\pi }_1^2}.$(9) ), so G in (10(10) $G(\pi ,\omega ):=(1-{\pi }_1)(1+{\mathrm{\Phi }}_{\tau }^1)g({\mathrm{\Pi }}_{\tau })$(10) ) is concave in ${\pi }_1$. Taking expectation we have that ${\pi }_1\mapsto \prod _{i=1}^n(1-{\pi }_i)\tilde{\mathbb{E}}\left[({\mathrm{e}}^{-\lambda \tau }\prod _{i=1}^n(1+{\mathrm{\Phi }}_{\tau }^i)g({\mathrm{\Pi }}_{\tau }))\right]$ is concave in ${\pi }_1$. By similar arguments, ${\pi }_1\mapsto {\int }_0^{\tau }{\mathrm{e}}^{-\lambda t}(\prod _{i=1}^n(1+{\mathrm{\Phi }}_t^i))h({\mathrm{\Pi }}_t^i)\mathrm{d}t$ is concave, so $\prod _{i=1}^n(1-{\pi }_i)\tilde{\mathbb{E}}[({\mathrm{e}}^{-\lambda \tau }\prod _{i=1}^n(1+{\mathrm{\Phi }}_{\tau }^i)g({\mathrm{\Pi }}_{\tau }))+{\int }_0^{\tau }{\mathrm{e}}^{-\lambda t}(\prod _{i=1}^n(1+{\mathrm{\Phi }}_t^i))h({\mathrm{\Pi }}_t^i)\mathrm{d}t]$ is concave in ${\pi }_1$ for each stopping time τ. Taking infimum over stopping times τ, it follows that ${\pi }_1\mapsto V(\pi )$ concave, which completes the proof.

Remark 3.7

Consider the setting of (ST2) with n = 2, where $g(\pi )={\pi }_1\wedge (1-{\pi }_1)\wedge {\pi }_2\wedge (1-{\pi }_2)$. If a finite time horizon T is imposed, then the time derivative of the cost function $V(t,\pi )$ for t close to T along the line segment $\{({\pi }_1,{\pi }_2):{\pi }_1={\pi }_2\in [0,1/2)\}$ is proportional to ${\pi }_1^2(1-{\pi }_1{)}^2$, which is not convex. This indicates that $V(\pi ,t)$ is non-concave along ${\pi }_1={\pi }_2$ for t close to T. Thus joint concavity is not to expect (even when g and h are concave).

4. Sequential testing problems

In this section, we use the general results of Section 3 to provide structural results for the multi-dimensional sequential testing problems (ST1)–(ST3). For the sake of graphical illustrations, we present the results for the case n = 2; the higher-dimensional version works similarly, and our results easily carry over to that case.

Remark 4.1

In the structural studies of (ST1)–(ST3) and (QD1)–(QD3) below, we focus on what conclusions can be drawn from our main result on unilateral concavity. Refined studies would aim at further properties of the stopping boundaries that we find. For example, a lower bound on the continuation region is provided by the set $\{\mathcal{L}g+h<0\}$, where $\mathcal{L}$ is the infinitesimal generator of Π, methods to prove that wedges of g are automatically contained in the continuation region can be obtained, and studies of continuity of stopping boundaries can be performed along the lines of [4].

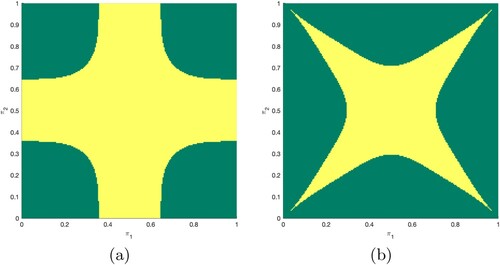
4.1. (ST1)

In this section, we provide further details for the problem (ST1) of determining all (i.e. both) drifts. Thus we consider the stopping problem $V(\pi )=\underset{\tau }{inf}{\mathbb{E}}_{\pi }[g({\mathrm{\Pi }}_{\tau })+c\tau ],$ where $g(\pi )={\pi }_1\wedge (1-{\pi }_1)+{\pi }_2\wedge (1-{\pi }_2)$. Denote by $R_1=[0,1/2]\times [0,1/2]$ so that $g={\pi }_1+{\pi }_2$ on $R_1$. Let $(A_i^{\ast },1-A_i^{\ast })$ be the continuation region for the one-dimensional problem $ST({\mu }_i,c)$, i = 1, 2.

Proposition 4.2

There exists a non-increasing upper semi-continuous function $b:[0,A_1^{\ast }]\to [0,A_2^{\ast }]$ such that $\mathcal{D}\cap R_1=\{\pi \in R_1:{\pi }_1\le A_1^{\ast },{\pi }_2\le b({\pi }_1)\}.$

Proof.

First note that $V({\pi }_1,0)=u^{{\mu }_1,c}({\pi }_1)$, so $({\pi }_1,0)\in \mathcal{C}$ precisely if ${\pi }_1\in (A_1^{\ast },1-A_1^{\ast })$. Since $V$ is Lipschitz continuous with parameter 1 in each direction by Remark 3.4, and since g has slope 1 in the ${\pi }_2$-direction for ${\pi }_2\le 1/2$, it follows that $\mathcal{D}\cap R_1=\{\pi \in R_1:{\pi }_1\le A_1^{\ast },{\pi }_2\le b({\pi }_1)\}$ for some $b:[0,A_1^{\ast }]\to [0,1/2]$. By a similar argument, starting from $(0,{\pi }_2)$ instead, it follows that $b\le A_2^{\ast }$ and that b is non-increasing. Finally, the continuity of V implies that $\mathcal{C}$ is open, and b is thus upper semi-continuous.

By symmetry, the part of the continuation region within each square $R_2:=[1/2,1]\times [0,1/2]$, $R_3:=[1/2,1]\times [1/2,1]$ and $R_4:=[0,1/2]\times [0,1/2]$ can be described similarly as in Proposition 4.2. For a graphical illustration, see Figure 1(a); all pictures have been produced using a standard finite difference scheme and an approximation of the value function using a finite, but large, fixed horizon.

Figure 1. Continuation regions (light) in (ST1) on the left and in (ST2) on the right. The parameters are ${\mu }_1={\mu }_2=1$ and c = 0.2.

4.2. (ST2)

Next, we provide further details for the problem (ST2) in the case n = 2. Thus we consider the stopping problem $V(\pi )=\underset{\tau }{inf}{\mathbb{E}}_{\pi }[g({\mathrm{\Pi }}_{\tau })+c\tau ],$ where $g(\pi )={\pi }_1\wedge (1-{\pi }_1)\wedge {\pi }_2\wedge (1-{\pi }_2)$. Consider the triangular region $T:=\{{\pi }_2\le {\pi }_1\wedge (1-{\pi }_1)\}$, and note that $g={\pi }_2$ in this region.

Proposition 4.3

There exists an upper semi-continuous function $b:[0,1]\to [0,1]$ with $b({\pi }_1)\le {\pi }_1\wedge (1-{\pi }_1)$ such that $\mathcal{D}\cap T=\{\pi \in T:{\pi }_2\le b({\pi }_1)\}.$ Furthermore, b is non-decreasing on $[0,1/2]$ and satisfies $b({\pi }_1)=b(1-{\pi }_1)$.

Proof.

Since $V({\pi }_1,0)=0=g({\pi }_1,0)$, we clearly have that $({\pi }_1,0)$ is in the stopping region. Now, since V is Lipschitz(1) in each direction by Remark 3.4, and since g has slope 1 in the ${\pi }_2$-direction, the existence of b follows.

The monotonicity property is a consequence of symmetry and concavity: if $({\pi }_1,{\pi }_2)\in T\cap \mathcal{D}$ then also $(1-{\pi }_1,{\pi }_2)\in T\cap \mathcal{D}$, so unilateral concavity yields that the whole line segment $\{(p,{\pi }_2);{\pi }_1\le p\le 1-{\pi }_1\}$ belongs to the stopping region. Finally, the asserted upper semi-continuity of b follows from the continuity of V.

Let $(A_i^{\ast },1-A_i^{\ast })$ be the continuation region of $ST({\mu }_i,c)$, i = 1, 2.

Proposition 4.4

The rectangle $R:=(A_1^{\ast },1-A_1^{\ast })\times (A_2^{\ast },1-A_2^{\ast })$ is contained in the continuation region.

Proof.

Take $\pi \in R$, and let $i\in \{1,2\}$ be such that $g(\pi )={\pi }_i\wedge (1-{\pi }_i)$. Define ${\tau }_i:=inf\{t\ge 0:{\mathrm{\Pi }}_t^i\notin (A_i^{\ast },1-A_i^{\ast })\}$ to be the optimal stopping time in the one-dimensional problem of determining $Y^i$. Then $\begin{array}{rl}V(\pi )& \le {\mathbb{E}}_{\pi }[g({\mathrm{\Pi }}_{{\tau }_i})+c{\tau }_i]\le {\mathbb{E}}_{\pi }[{\mathrm{\Pi }}_{{\tau }_i}^i\wedge (1-{\mathrm{\Pi }}_{{\tau }_i}^i)+c{\tau }_i]\\ & =u^{{\mu }_i,c}({\pi }_i)<{\pi }_i\wedge (1-{\pi }_i)=g(\pi ),\end{array}$ which shows that $\pi \in \mathcal{C}$.

For a graphical illustration of the continuation region in (ST2), see Figure 1(b).

4.3. (ST3)

We now study the sequential testing problem (ST3) with cost reduction given by $\gamma \in (0,1)$ (we exclude the cases $\gamma \in \{0,1\}$ since they correspond to (ST1) and (ST2), respectively). The value function of this problem is $V(\pi )=\underset{\tau }{inf}{\mathbb{E}}_{\pi }[g({\mathrm{\Pi }}_{\tau }^1,{\mathrm{\Pi }}_{\tau }^2)+c\tau ],$ where $g({\pi }_1,{\pi }_2):=({\pi }_1\wedge (1-{\pi }_1)+u({\pi }_2))\wedge (u({\pi }_1)+{\pi }_2\wedge (1-{\pi }_2))$ and $u=u^{\mu ,c(1-\gamma )}$ is the value function of the one-dimensional problem $ST(\mu ,c(1-\gamma ))$. Since u is concave and Lipschitz(1), the value function V is also concave and Lipschitz(1) in each variable. Denote by $T:=\{\pi \in [0,1{]}^2:0\le {\pi }_2\le {\pi }_1\wedge (1-{\pi }_1)\}$, and note that $g({\pi }_1,{\pi }_2)=u({\pi }_1)+{\pi }_2$ on T.

Proposition 4.5

There exists an upper semi-continuous function $b:[0,1]\to [0,1/2]$ with $b({\pi }_1)\le {\pi }_1\wedge (1-{\pi }_1)$ such that $\mathcal{D}\cap T=\{\pi \in T:{\pi }_2\le b({\pi }_1)\}$. Moreover, $b({\pi }_1)=b(1-{\pi }_1)$.

Proof.

We first claim that $[0,1]\times \{0\}\subseteq \mathcal{D}$. To see this, note that $g({\pi }_1,0)=u({\pi }_1)$ and that $u({\mathrm{\Pi }}_t^1)+ct$ is a submartingale. It follows that $V({\pi }_1,0)=u({\pi }_1)$.

Next, the fact that g is affine in ${\pi }_2$ on T together with the unilateral concavity of V give the existence of b. The upper semi-continuity of b follows from continuity of V, and the symmetry of b follows from the symmetric set-up.

For a graphical illustration of Proposition 4.5, see Figure 2.

Figure 2. Continuation regions (light) in (ST3) for different values of the cost reduction parameter γ. The parameters are ${\mu }_1={\mu }_2=1$ and c = 0.2; the cost reduction parameter is $\gamma =0.2$, $\gamma =0.5$ and $\gamma =0.8$, respectively.

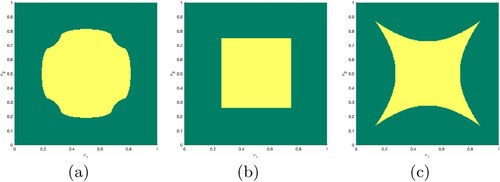
Remark 4.6

A few estimates on the stopping/continuation regions in (ST3) are readily obtained. Let $(A^{\mu ,c},1-A^{\mu ,c})$ be the continuation region in $ST(\mu ,c)$.

If $\frac{1}{2}\le \gamma <1$, then $u^{\mu ,(1-\gamma )c}({\pi }_1)+u^{\mu ,(1-\gamma )c}({\pi }_2)\le V\le g.$ Consequently, the continuation region is contained in the square $(A^{\mu ,(1-\gamma )c},1-A^{\mu ,(1-\gamma )c}{)}^2$.

If $0<\gamma \le \frac{1}{2}$, then $u^{\mu ,c/2}({\pi }_1)+u^{\mu ,c/2}({\pi }_2)\le V\le u^{\mu ,(1-\gamma )c}({\pi }_1)+u^{\mu ,(1-\gamma )c}({\pi }_2).$ Thus $(A^{\mu ,(1-\gamma )c},1-A^{\mu ,(1-\gamma )c}{)}^2\subseteq \mathcal{C}\subseteq \{\pi :{\pi }_1\mathrm{or}{\pi }_2\in (A^{\mu ,c/2},1-A^{\mu ,c/2})\}.$ In particular, if $\gamma =1/2$, then $V(\pi )=u^{\mu ,c/2}({\pi }_1)+u^{\mu ,c/2}({\pi }_2)$ and $\mathcal{C}=(A^{\mu ,c/2},1-A^{\mu ,c/2}{)}^2$.

5. Quickest detection problems

In this section, we provide structural results for the multi-dimensional quickest detection problems (QD1)–(QD3). For the sake of graphical illustrations, we present the results for n = 2.

5.1. (QD1)

Consider the stopping problem $V(\pi )=\underset{\tau }{inf}{\mathbb{E}}_{\pi }[g({\mathrm{\Pi }}_{\tau })+{\int }_0^{\tau }h({\mathrm{\Pi }}_s)\mathrm{d}s],$ where $g(\pi )=(1-{\pi }_1)(1-{\pi }_2)$ and $h(\pi )=c(1-(1-{\pi }_1)(1-{\pi }_2))$.

Proposition 5.1

There exists a non-increasing lower semi-continuous function $b:[0,1]\to [0,1]$ such that (11) $\mathcal{C}=\{\pi \in [0,1{]}^2:{\pi }_2<b({\pi }_1)\}.$(11)

Proof.

We first note that boundary points $({\pi }_1,1)$ and $(1,{\pi }_2)$ are stopping points since V = g = 0 at such points. Consequently, by unilateral concavity it follows that if a point $({\pi }_1,{\pi }_2)\in \mathcal{C}$, then also $[0,{\pi }_1]\times [0,{\pi }_2]\subseteq \mathcal{C}$. The existence of a non-increasing function $b:[0,1]\to [0,1]$ such that (11(11) $\mathcal{C}=\{\pi \in [0,1{]}^2:{\pi }_2<b({\pi }_1)\}.$(11) ) holds thus follows; the lower semi-continuity of b is a direct consequence of the continuity of V.

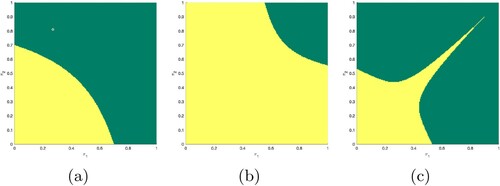
For a graphical illustration, see Figure 3(a).

Figure 3. Continuation regions (yellow) in (QD1) on the left, (QD2) in the middle and in (QD3) on the right. The parameters are ${\mu }_1={\mu }_2=1$ and c = 1.

5.2. (QD2)

We now study the stopping problem (5(5) $V(\pi )=\underset{\tau }{inf}{\mathbb{E}}_{\pi }[g({\mathrm{\Pi }}_{\tau })+{\int }_0^{\tau }h({\mathrm{\Pi }}_s)\mathrm{d}s],$(5) ) with $g(\pi )=1-{\pi }_1{\pi }_2$ and $h(\pi )=c{\pi }_1{\pi }_2$. Let $[0,B_i^{\ast })$ be the continuation region for the one dimensional problem $QD({\mu }_i,{\lambda }_i,c)$, i = 1, 2.

Proposition 5.2

There exists a non-increasing lower semi-continuous function $b:[B_1^{\ast },1]\to [B_2^{\ast },1]$ such that $\mathcal{C}=\{\pi \in [0,1{]}^2:{\pi }_2<b({\pi }_1)\}\cup [0,B_1^{\ast })\times [0,1].$

Proof.

We first note that the line segment $[B_1^{\ast },1]\times \{1\}$ belongs to the stopping region and that g is affine in the ${\pi }_2$-direction. Consequently, concavity yields the existence of a function $b:[B_1^{\ast },1]\to [0,1]$ so that $\mathcal{C}\cap \{{\pi }_1\ge B_1^{\ast }\}=\{{\pi }_1\ge B_1^{\ast },{\pi }_2<b({\pi }_1\}$.

We now claim that $\{{\pi }_2<B_2^{\ast }\}\subseteq \mathcal{C}$. To see this, let $H({\pi }_1,{\pi }_2):={\pi }_1{u}_2({\pi }_2)+1-{\pi }_1$ where $u_2:=u^{{\mu }_2,{\lambda }_2,c}$ is the value function in $QD({\mu }_2,{\lambda }_2,c)$. Then H = g if ${\pi }_2\ge B_2^{\ast }$, and $\mathcal{L}H+c{\pi }_1{\pi }_2=-(1-u_2({\pi }_2)){\lambda }_1(1-{\pi }_1)\le 0$ on $[0,1]\times [0,B_2^{\ast })$, where the inequality is strict provided ${\pi }_1<1$. Now consider the stopping time ${\tau }_2:=inf\{t\ge 0:{\mathrm{\Pi }}_t^2\ge B_2^{\ast }\}$ which is optimal in $QD({\mu }_2,{\lambda }_2,c)$. Then $\begin{array}{rl}V({\pi }_1,{\pi }_2)& \le {\mathbb{E}}_{\pi }[g({\mathrm{\Pi }}_{{\tau }_2}^1,{\mathrm{\Pi }}_{{\tau }_2}^2)+c{\int }_0^{{\tau }_2}{\mathrm{\Pi }}_t^1{\mathrm{\Pi }}_t^2\mathrm{d}t]\\ & =\mathbb{E}[H({\mathrm{\Pi }}_{{\tau }_2}^1,{\mathrm{\Pi }}_{{\tau }_2}^2)+c{\int }_0^{{\tau }_2}{\mathrm{\Pi }}_t^1{\mathrm{\Pi }}_t^2\mathrm{d}t]\le H({\pi }_1,{\pi }_2)\end{array}$ by supermartingality. Moreover, if ${\pi }_2<B_2^{\ast }$ and ${\pi }_1<1$, then the second inequality is strict. Thus, if ${\pi }_2<B_2^{\ast }$ then $V({\pi }_1,{\pi }_2)\le H({\pi }_1,{\pi }_2)\le 1-{\pi }_1{\pi }_2=g({\pi }_1,{\pi }_2),$ where the first inequality is strict if ${\pi }_1<1$, and the second inequality is strict if ${\pi }_1>0$. Consequently, $\{{\pi }_2<B_2^{\ast }\}\subseteq \mathcal{C}$.

Using $\{{\pi }_2<B_2^{\ast }\}\subseteq \mathcal{C}$, it follows that $b\ge B_2^{\ast }$; interchanging ${\pi }_1$ and ${\pi }_2$ shows that $\{{\pi }_1<B_1^{\ast }\}\subseteq \mathcal{C}$ and that b is non-increasing. Finally, the continuity of V implies lower semi-continuity of b.

The continuation region in (QD2) is illustrated in Figure 3(b).

5.3. (QD3)

Now assume that $g(\pi )=1-{\pi }_1\vee {\pi }_2$ and $h(\pi )=c({\pi }_1+{\pi }_2)$. By symmetry, it suffices to describe the structure of the continuation region in $T:=\{\pi \in [0,1{]}^2:{\pi }_1\le {\pi }_2\}$.

Proposition 5.3

There exists a function $b:[0,1]\to [0,1]$ with $b({\pi }_1)\ge {\pi }_1$ such that (12) $\mathcal{C}\cap T=\{\pi \in T:{\pi }_2<b({\pi }_1)\}.$(12) Moreover, b is lower semi-continuous and first non-increasing and then non-decreasing.

Proof.

We first note that $g({\pi }_1,1)=0$, so $[0,1]\times \{1\}\subseteq \mathcal{D}$, and that g is affine in ${\pi }_2$ on T; concavity thus implies the existence of b such that (12(12) $\mathcal{C}\cap T=\{\pi \in T:{\pi }_2<b({\pi }_1)\}.$(12) ) holds. Moreover, g is affine also in ${\pi }_1$ on T, so horizontal sections of the stopping region inside T are intervals. Consequently, the function b is first non-increasing and then non-decreasing. Lower semi-continuity follows from the continuity of V.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This work was supported by Vetenskapsrådet [grant number 2019-03525].