Geometrically nonlinear nonlocal strain gradient vibration of FG shear deformable curved nanobeams

Abstract

This article focuses on studying the nonlinear vibration of functionally graded (FG) curved nanobeams resting on the Pasternak-Winkler elastic foundation based on the nonlocal strain gradient theory along with the first-order shear deformation beam theory (FSDBT) considering von-Kármán hypothesis. The Hamilton principle is applied to extract three nonlinear motion equations and the Galerkin method (GM) is utilized to spatially reduce the differential equations. The analytical approach based on the two-step perturbation method (TSPM) was employed to deal with nonlinear governing equations. To verify the outcomes of the present article, the natural frequencies and frequency ratios are validated with those reported in the literature. Subsequently, the results presented in this paper are of a significant point to describe the nonlinear vibration of FG curved nanobeams in conjunction with different parameters.

KEYWORDS:

• Nonlinear vibration
• curved nanobeam
• functionally graded materials
• nonlocal strain gradient theory
• shear deformable beam theory
• two-step perturbation technique

1. Introduction

On the basis of experimental observations, the mechanics of small scales structures are size-dependent and the classical continuum theory (CT) cannot be effectively used for such cases due to the lack of parameters to address the size effects. Hence, to consider the size-dependency, different generalized continuum theories have been developed [1–5]. Namely, based on nonlocal elasticity theory (NLT), the stress at a reference point is a function of the strain through all points of the body considering softening effect [1,6–11]. Following the strain gradient theory (SGT), the higher-order derivatives of the strains are included within the mathematical formulation which leads to the hardening effect in structural behavior [2,3,12,13]. By the combination of these two ideas, the NLSGT [5] involves the NLT and SGT simultaneously to capture both softening and hardening effects. Taking the advantages of NLSG into consideration, plenty of research works have been conducted on the size-dependent structural analysis of small-scale objects via the NLSGT [14–18]. For instance, the fundamental formulations for linear analysis of nanobeams and plates under the NLSGT can be found in [15,19] and [18], respectively. The applications of NLSGT in generalized thermoelasticity of nanobeams [20,21], thermomechanical vibrations of nanobeams [22,23], and torsional vibrations of nanorods with non-circular cross-sections [24,25] have been recently demonstrated in the literature. Besides, a limited number of studies considered the importance of the geometrical nonlinear terms in the structural behavior within the NLSGT [26,27]. Related to this work, Li et al. [28] investigated the nonlocal strain gradient nonlinear vibration of FG porous beams with geometric imperfection under the Euler–Bernoulli beam model and the von Kármán type nonlinearity. The electromechanical instability analysis of nanobeams under the nonlocal and strain gradient models was reported in [29].

The basic properties of FG materials are a mixture of ceramics and metals to improve the overall structural performance in which their properties gradually change in a specific direction. Generally, the metals have high fracture toughness and the ceramics have excellent performance in heat and corrosive resistance, therefore, this combination can lead to excellent materials. Consequently, the applications of FG structures in several industries such as aerospace, marine, and automotive have been extensively broadened over the past two decades. On the other hand, the recent progress in manufacturing technologies has facilitated the applications of small-scale structures like micro and nanosensors. Therefore, the NLSG structural analysis of FG structures has been widely investigated in the open literature [26–31].

As one of the most efficient analytical approaches to deal with the nonlinear governing equations of bending, vibration, and postbuckling problems, the two-step perturbation method (TSPM) was first proposed by Shen [32]. The applications of this technique in nonlinear strain gradient problems have been demonstrated in a limited number of studies. Gao et al. [33] analyzed the nonlinear vibration of FG straight beams by the NLSGT using the TSPM. Babaei and Eslami [34] also applied the TSPM to analyze the vibration and snap-through buckling of FG porous cylindrical panels under thermal loadings.

On the other hand, the thermomechanical analysis of micro/nano-scale curved beams using the NLSGT has received considerable attention among research communities. Ebrahimi and Barati [35,36] performed a study on the linear vibration and instability of FG curved nanobeams using the NLSGT and analytical approach. The Euler–Bernoulli and higher-order refined beam theories were respectively employed for vibration and buckling analyses. Linear static and dynamic analysis, as well as the instability of viscoelastic FG curved nanobeams, were reported by Allam and Radwan [37] employing the strain gradient higher-order refined curved nanobeam theory. In addition, the strain gradient mechanical analyses of FG porous curved nanobeams have been recently investigated [38,39]. Although some studies have beam performed on the nonlinear mechanical analysis of small-scale curved beams under the NLT [40,41], the literature is still limited for NLSGT. Therefore, motivated by the reviewed literature, this article deals with the size-dependent nonlinear vibration of FG curved nanobeams resting on an elastic medium on the basis of NLSGT. In this pathway, the nonlinear equations of motion are first derived following the FSDBT along with von-Kármán geometric nonlinearity. Afterward, the analytical methodology is applied to solve the nonlinear differential equations where GM is first exerted to convert the governing equations into a time-domain considering different edge constraints, and then, the TSPM is implemented to treat the nonlinearity in the governing equations. To validate the proposed model, the natural frequencies and frequency ratios are verified with published results. As an achievement, the impacts of length scale, nonlocal, geometrical parameters, FG material index, and foundation components on the nonlinear vibration of FG curved nanobeams are discussed in detail.

2. Kinematic equation

2.1. Nonlocal strain gradient model

The nonlocal strain gradient theory presents an efficient framework to capture the size-effect in small-scale structures by employing the advantages of NLT and SGT. According to this theory [5], by introducing ${\sigma }_{ij}$ and ${\sigma }_{ij}^{(1)}$ as the classical and higher-order stresses, the total stress of the body can be presented as (1) $\begin{array}{r}{t}_{ij}={\sigma }_{ij}+\mathrm{\nabla }{\sigma }_{ijk}^{(1)},\end{array}$(1) with the following definition (2) $\begin{array}{r}\begin{array}{c}{\sigma }_{ij}=\underset{V}{\int }{a}_0(x^{\mathrm{\prime }},x,e_{0}a)C_{ijmn}{\epsilon }_{mn}^{{}^{\mathrm{\prime }}}d{V}^{\mathrm{\prime }},\\ {\sigma }_{ijk}^{(1)}={\eta }^2\underset{V}{\int }{a}_1(x^{\mathrm{\prime }},x,e_{1}a)C_{ijmn}{\epsilon }_{mn,k}^{{}^{\mathrm{\prime }}}d{V}^{\mathrm{\prime }}\end{array}\end{array}$(2) in which $C_{ijmn}$ stands for the components of material stiffness tensor, ${\epsilon }_{kl}^{{}^{\mathrm{\prime }}},$ ${\epsilon }_{kl,m}^{{}^{\mathrm{\prime }}}$ are the components of strain and strain gradient tensors, and $a_0(x^{\mathrm{\prime }},x,e_{0}a),$ and $a_1(x^{\mathrm{\prime }},x,e_{1}a)$ are the related nonlocal kernel functions. In addition, $e_0$ and $e_1$ denote the nonlocal material constant, $a$ is an internal characteristic length, and $\eta$ presents the material length scale. Taking this point into account that the two nonlocal kernel functions satisfy the condition given by Eringen [1] and assuming $\mu =e_{0}tia=e_{1}a$, the constitutive equation of the starin gradient theory is given as follows [5] (3) $\begin{array}{r}[1-{\mu }^2{\mathrm{\nabla }}^2]t_{ij}=(1-{\eta }^2{\mathrm{\nabla }}^2)C_{ijmn}{\epsilon }_{mn},\end{array}$(3) where ${\mathrm{\nabla }}^2$ is the Laplacian operator. It should be noted that $\mu$ is the nonlocal parameter presented to capture the impacts of the nonlocal elastic stress field and $\eta$ is the material length scale introduced to take the significance of the strain gradient stress field into consideration. Generally, Equation (3) can be reduced to the case of NLT if $\eta =0$, SGT if $\mu =0$, and the classic theory if $\mu =\eta =0$.

2.2. Functionally graded curved nanobeam

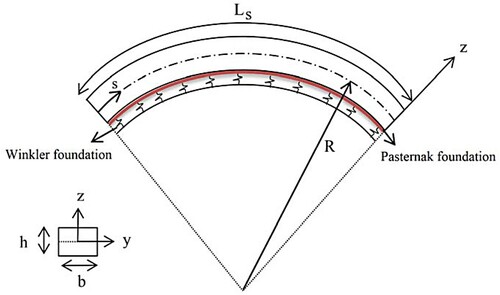
The FG curved nanobeam of length $L_s$, radius $R$ and thickness $h$ is considered. The coordinate system of ($s,z$) with $s$ along the length of the curved beam and $z$ in the thickness direction is considered to present the mathematical formulation. Following the FSDBT, the displacement components can be expressed as (4) $\begin{array}{r}{u}_1(s,z,t)=u(s,t)+(z-z_0)\psi (s,t),u_2=0,u_3(s,z,t)=w(s,t),\end{array}$(4) where $w(s,t)$ and $u(s,t)$ are the lateral and axial displacements, and $\psi (s,t)$ is the cross-section rotation. $t$ stands for the time domain. Furthermore, $z_0$ is the constant coefficient related to the distance from the mid-surface which can be remarked as (5) $\begin{array}{r}{z}_0=\frac{{\displaystyle {\int }_{-h/2}^{h/2}zE(z)\text{d}z}}{{\displaystyle {\int }_{-h/2}^{h/2}E(z)\text{d}z}}\end{array}$(5) where $E(z)$ stands for Young’s modulus of the FG material. In order to define the material distribution through the thickness of the FG beam, various distribution functions such as power-law, exponential-law and sigmoid-law gradation have been introduced and applied in the open literature [42]. However, it is shown that the differences in the results for different distribution patterns are small [43]. Therefore, the well-known power-law distribution function is employed in this study, and the non-homogeneous properties of Young’s modulus and the mass density are given by (6) $\begin{array}{r}\begin{array}{c}E(z)=E_m+(E_c-E_m){\left({\displaystyle \frac{1}{2}}+{\displaystyle \frac{z}{h}}\right)}^n,\\ \rho (z)={\rho }_m+({\rho }_c-{\rho }_m){\left({\displaystyle \frac{1}{2}}+{\displaystyle \frac{z}{h}}\right)}^n,\end{array}\end{array}$(6) with $n$ as the gradient index which defines the material composition of the FG structure. Note that the subscripts$c$ and $m$ express the properties of ceramic and metal constituents.

2.3. Governing equations

Herein, by using the displacement field and the von-Kármán nonlinear kinematic relations, the strain components are (7) $\begin{array}{r}\begin{array}{c}{\epsilon }_{11}={\displaystyle \frac{\mathrm{\partial }u}{\mathrm{\partial }s}}-{\displaystyle \frac{w}{R}}+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{\mathrm{\partial }w}{\mathrm{\partial }s}}\right)}^2+(z-z_0){\displaystyle \frac{\mathrm{\partial }\psi }{\mathrm{\partial }s}},\\ {\gamma }_{13}=\left({\displaystyle \frac{\mathrm{\partial }w}{\mathrm{\partial }s}}+\psi \right),\end{array}\end{array}$(7) where ${\epsilon }_{11}$ and ${\gamma }_{13}$ signify the axial and shear strain components respectively. Following the NLSGT and Equation (2), the generalized constitutive equations of the FG curved nanobeam are expressed as (8) $\begin{array}{rl}\left[1-{\mu }^2\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{s}^2}\right]t_{11}& =\frac{E(z)}{1-{\nu }^2}\left(1-{\eta }^2\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{s}^2}\right){\epsilon }_{11},\end{array}$(8) (9) $\begin{array}{rl}\left[1-{\mu }^2\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{s}^2}\right]t_{13}& =\frac{E(z)}{2(1+\nu )}\left(1-{\eta }^2\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{s}^2}\right){\gamma }_{13}.\end{array}$(9) Besides, the force and moment resultants $N_{11}$, $P_{11}$, $Q_{13}$ are defined as below (10) $\begin{array}{r}(N_{11},P_{11},Q_{13})=\underset{\frac{-h}{2}}{\overset{\frac{h}{2}}{\int }}(t_{11},(z-z_0)t_{11},t_{13})\text{d}z.\end{array}$(10) By setting Equation (7) into Equations (8) and (9) then into Equation (10), one can respectively write (11) $\begin{array}{rl}\left[1-{\mu }^2\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{s}^2}\right]N_{11}& =\left(1-{\eta }^2\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{s}^2}\right)C_1{\epsilon }_{11}^0,\end{array}$(11) (12) $\begin{array}{rl}\left[1-{\mu }^2\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{s}^2}\right]M_{11}& =\left(1-{\eta }^2\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{s}^2}\right)C_2{\epsilon }_{11}^1,\end{array}$(12) (13) $\begin{array}{rl}\left[1-{\mu }^2\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{s}^2}\right]Q_{13}& =\left(1-{\eta }^2\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{s}^2}\right)C_3{\gamma }_{13},\end{array}$(13)

with (14) $\begin{array}{r}{\epsilon }_{11}^0=\frac{\mathrm{\partial }u}{\mathrm{\partial }s}-\frac{w}{R}+\frac{1}{2}{\left(\frac{\mathrm{\partial }w}{\mathrm{\partial }s}\right)}^2,{\epsilon }_{11}^1=\frac{\mathrm{\partial }\psi }{\mathrm{\partial }s}.\end{array}$(14) where the constant coefficients $C_i=(i=1,2,3)$ are (15) $\begin{array}{r}(C_1,C_2)=\frac{1}{1-{\nu }^2}\underset{\frac{-h}{2}}{\overset{\frac{h}{2}}{\int }}E(z)(1,{(z-z_0)}^2)dz,C_3=\underset{\frac{-h}{2}}{\overset{\frac{h}{2}}{\int }}\frac{E(z)}{2(1+\nu )}dz.\end{array}$(15) Now, by introducing $\mathrm{\Pi },{\mathrm{\Pi }}_e,W$, and $T$ respectively as the strain energy, potential energy of the elastic medium, work done by the applied loads, and kinetic energy, the equations of motion is obtained by Hamilton’s principle expressed as (16) $\begin{array}{r}\underset{t_0}{\overset{t_1}{\int }}(\delta \mathrm{\Pi }+\delta {\mathrm{\Pi }}_e-\delta \text{W}-\delta \text{T})dt=0.\end{array}$(16) The first variation of strain energy is (17) $\begin{array}{r}\mathrm{\partial }\mathrm{\Pi }={\int }_V(t_{11}\delta {\epsilon }_{11}+t_{13}\delta {\gamma }_{12})\text{d}V.\end{array}$(17) By considering ${\overline{K}}_1$ and ${\overline{K}}_2$ as the Winkler and Pasternak coefficients of the medium, corresponding first variation of the potential energy can be defined as (18) $\begin{array}{r}\mathrm{\partial }{\mathrm{\Pi }}_e=\underset{0}{\overset{L_s}{\int }}\left[{\overline{K}}_{1}w\delta w+{\overline{K}}_2\frac{\mathrm{\partial }w}{\mathrm{\partial }s}\delta \left(\frac{\mathrm{\partial }w}{\mathrm{\partial }s}\right)\right]\text{d}s,\end{array}$(18) The first variation of the work done by the transverse load ($F$) is also given as (19) $\begin{array}{r}\mathrm{\partial }\text{W}=\underset{0}{\overset{L_s}{\int }}F\delta wds,\end{array}$(19) In addition, the kinetic energy is (20) $\begin{array}{r}\begin{array}{c}\mathrm{\partial }T=\underset{V}{\int }\rho (z)\left[{\displaystyle \frac{\mathrm{\partial }{u}_1}{\mathrm{\partial }t}}\delta \left({\displaystyle \frac{\mathrm{\partial }{u}_1}{\mathrm{\partial }t}}\right)+{\displaystyle \frac{\mathrm{\partial }{u}_3}{\mathrm{\partial }t}}\delta \left({\displaystyle \frac{\mathrm{\partial }{u}_3}{\mathrm{\partial }t}}\right)\right]\\ \text{d}V=\underset{0}{\overset{L_s}{\int }}\left(I_a{\displaystyle \frac{\mathrm{\partial }w}{\mathrm{\partial }t}}\delta \left({\displaystyle \frac{\mathrm{\partial }w}{\mathrm{\partial }t}}\right)+\left(I_b{\displaystyle \frac{\mathrm{\partial }\psi }{\mathrm{\partial }t}}\right)\delta \left({\displaystyle \frac{\mathrm{\partial }\psi }{\mathrm{\partial }t}}\right)\right)\text{d}s\end{array}\end{array}$(20) in which the axial inertia is ignored and the coefficients $I_a,I_b$ are (21) $\begin{array}{r}(I_a,I_b)=\underset{\frac{-h}{2}}{\overset{\frac{h}{2}}{\int }}\rho (z)(1,{(z-z_0)}^2)dz,\end{array}$(21) By setting Equations (17)–(20) into Hamilton’s principle and following the conventional procedure, the equations of motion are obtained as (22) $\begin{array}{rl}& \mathrm{\partial }u:\frac{\mathrm{\partial }{N}_{11}}{\mathrm{\partial }s}=0,\end{array}$(22) (23) $\begin{array}{rl}& \mathrm{\partial }\psi :I_b\frac{{\mathrm{\partial }}^2\psi }{\mathrm{\partial }{t}^2}-\frac{\mathrm{\partial }{M}_{11}}{\mathrm{\partial }s}+Q_{12}=0,\end{array}$(23) (24) $\begin{array}{rl}& \mathrm{\partial }w:I_a\frac{{\mathrm{\partial }}^{2}w}{\mathrm{\partial }{t}^2}-\frac{\mathrm{\partial }}{\mathrm{\partial }s}\left(N_{11}\frac{\mathrm{\partial }w}{\mathrm{\partial }s}\right)-\frac{\mathrm{\partial }{Q}_{13}}{\mathrm{\partial }s}-\frac{N_{11}}{R}+{\overline{K}}_{1}w-{\overline{K}}_2\frac{{\mathrm{\partial }}^{2}w}{\mathrm{\partial }{s}^2}=F.\end{array}$(24) The boundary conditions (BCs) for clamped–clamped and simply supported edges are:

Clamped–Clamped (CC): (25) $\begin{array}{r}\text{at}s=0,L_s:u=w=\psi =\frac{\mathrm{\partial }u}{\mathrm{\partial }s}=\frac{\mathrm{\partial }w}{\mathrm{\partial }s}=\frac{\mathrm{\partial }\psi }{\mathrm{\partial }s}=0\end{array}$(25) Simply supported- Simply supported (SS): (26) $\begin{array}{r}\text{at}s=0,L_s:u=w=M_{11}=\frac{\mathrm{\partial }u}{\mathrm{\partial }s}=Q_{13}^{(1)}=M_{11}^{(1)}=0\end{array}$(26) Taking the first equation of motion into consideration, the second derivative of $N_{11}$ is zero and Equation (11) can be rewritten as below (27) $\begin{array}{r}{N}_{11}=\left(1-{\eta }^2\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{s}^2}\right)C_1\left[\frac{\mathrm{\partial }u}{\mathrm{\partial }s}-\frac{w}{R}+\frac{1}{2}{\left(\frac{\mathrm{\partial }w}{\mathrm{\partial }s}\right)}^2\right].\end{array}$(27) By substituting Equation (27) into (22) and integrating over the axial coordinate ($s$) along with the classical and nonclassical BC for axially immovable edges of the beam (i.e. $u(0)=u(L_s)=\frac{{\mathrm{\partial }}^{2}u(0)}{\mathrm{\partial }{s}^2}=\frac{{\mathrm{\partial }}^{2}u(L_s)}{\mathrm{\partial }{s}^2}=0$), the axial force are obtained as [27] (28) $\begin{array}{r}{N}_{11}=\frac{1}{L_s}\underset{0}{\overset{L_s}{\int }}\left(1-{\eta }^2\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{s}^2}\right)\left[\frac{C_1}{2}{\left(\frac{\mathrm{\partial }w}{\mathrm{\partial }s}\right)}^2-C_1\frac{w}{R}\right]\text{d}s.\end{array}$(28) By setting Equations (11)–(13), into Equations (23) and (24), the governing nonlinear differential equations of the FG curved nanobeam under the NLSGT is obtained as follows (29) $\begin{array}{rl}& \mathrm{\partial }\psi :\left(1-{\eta }^2\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{s}^2}\right)\left[C_2\frac{{\mathrm{\partial }}^2\psi }{\mathrm{\partial }{s}^2}-C_3\left(\frac{\mathrm{\partial }w}{\mathrm{\partial }s}+\psi \right)\right]-\left(1-{\mu }^2\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{s}^2}\right)\left(I_b\frac{{\mathrm{\partial }}^2\psi }{\mathrm{\partial }{t}^2}\right)=0,\end{array}$(29) (30) $\begin{array}{rl}& \begin{array}{l}\mathrm{\partial }W:\left(1-{\eta }^2{\displaystyle \frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{s}^2}}\right)\left[-C_3\left({\displaystyle \frac{{\mathrm{\partial }}^{2}w}{\mathrm{\partial }{s}^2}}+{\displaystyle \frac{\mathrm{\partial }\psi }{\mathrm{\partial }s}}\right)\right]\\ +\left(1-{\mu }^2{\displaystyle \frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{s}^2}}\right)\left(I_a{\displaystyle \frac{{\mathrm{\partial }}^{2}w}{\mathrm{\partial }{t}^2}}-N_{11}\left({\displaystyle \frac{{\mathrm{\partial }}^{2}w}{\mathrm{\partial }{s}^2}}+{\displaystyle \frac{1}{R}}\right)+{\overline{K}}_{1}w-{\overline{K}}_2{\displaystyle \frac{{\mathrm{\partial }}^{2}w}{\mathrm{\partial }{s}^2}}\right)=F.\end{array}\end{array}$(30) At this time, the following dimensionless parameters are applied (31) $\begin{array}{r}\begin{array}{l}x={\displaystyle \frac{\pi s}{L_s}},\mathrm{\Psi }={\displaystyle \frac{\psi }{\pi }},Y={\displaystyle \frac{w}{L_s}},\overline{\mu }={\displaystyle \frac{\pi \mu }{L_s}},\overline{\eta }={\displaystyle \frac{\pi \eta }{L_s}},K_1={\overline{K}}_1{\displaystyle \frac{{L_s}^4}{{\pi }^{4}D}},K_2={\overline{K}}_2{\displaystyle \frac{{L_s}^2}{{\pi }^{2}D}},\\ \chi ={\displaystyle \frac{L_s}{R{\pi }^2}},{\lambda }^F={\displaystyle \frac{F{L_s}^3}{D{\pi }^4}},a_2={\displaystyle \frac{1}{D}}{C}_2,(a_1,a_3)={\displaystyle \frac{{L_s}^2}{D{\pi }^2}}(C_1,C_3),b_0={\displaystyle \frac{E_m{I}_a{L_s}^2}{{\rho }_{m}D{\pi }^2}},\\ b_1={\displaystyle \frac{E_m}{{\rho }_{m}D}}{I}_b,T={\displaystyle \frac{\pi t}{L_s}}\sqrt{{\displaystyle \frac{E_m}{{\rho }_m}}},{\omega }_L={\overline{\omega }}_L{\displaystyle \frac{L_s}{\pi }}\sqrt{{\displaystyle \frac{{\rho }_m}{E_m}}},\end{array}\end{array}$(31) with $D={\int }_{\frac{-h}{2}}^{\frac{h}{2}}E(z)z^2\text{d}z$ to acquire the nondimensional equations of the FG curved nanobeam as below (32) $\begin{array}{rl}& \begin{array}{l}\delta Y:\left(1-{\overline{\eta }}^2{\displaystyle \frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}}\right)\left[-a_3\left({\displaystyle \frac{{\mathrm{\partial }}^{2}Y}{\mathrm{\partial }{x}^2}}+{\displaystyle \frac{\mathrm{\partial }\mathrm{\Psi }}{\mathrm{\partial }x}}\right)\right]-\left(1-{\overline{\mu }}^2{\displaystyle \frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}}\right)\\ \left[\pi a_1\underset{0}{\overset{\pi }{\int }}\left(1-{\overline{\eta }}^2{\displaystyle \frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}}\right)\left({\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{\mathrm{\partial }Y}{\mathrm{\partial }x}}\right)}^2-\chi Y\right)\text{d}x\right]\\ \left({\displaystyle \frac{{\mathrm{\partial }}^{2}Y}{\mathrm{\partial }{x}^2}}+\chi \right)+\left(1-{\overline{\mu }}^2{\displaystyle \frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}}\right)\left[b_0{\displaystyle \frac{{\mathrm{\partial }}^{2}Y}{\mathrm{\partial }{T}^2}}+K_{1}Y-K_2{\displaystyle \frac{{\mathrm{\partial }}^{2}Y}{\mathrm{\partial }{x}^2}}\right]={\lambda }^F,\end{array}\end{array}$(32) (33) $\begin{array}{rl}& \delta \mathrm{\Psi }:\left(1-{\overline{\eta }}^2\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}\right)\left[a_2\frac{{\mathrm{\partial }}^2\mathrm{\Psi }}{\mathrm{\partial }{x}^2}-a_3\left(\frac{\mathrm{\partial }Y}{\mathrm{\partial }x}+\mathrm{\Psi }\right)\right]-\left(1-{\overline{\mu }}^2\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}\right)\left[-b_1\frac{{\mathrm{\partial }}^2\mathrm{\Psi }}{\mathrm{\partial }{T}^2}\right]=0.\end{array}$(33)

3. Solution methodology

The two-step perturbation method is one of the most efficient analytical approaches in solving the nonlinear governing equations of bending, vibration, and postbuckling problems, and its accuracy in solving nonlinear differential equations has been shown in the open literature. Based on the TSPM [34], the closed-form solution of the problem can be obtained with the help of the following series of solutions (34) $\begin{array}{r}Y=\sum _{i=1}^3{Y}_i{\epsilon }^i,\mathrm{\Psi }=\sum _{i=1}^3{\psi }_i{\epsilon }^i,{\lambda }^F=\sum _{i=1}^3{\lambda }_i{\epsilon }^i.\end{array}$(34) The effects of the number of terms in Equation (34) on the accuracy and convergence of the results were investigated in previous studies [34]. Therefore, the first three terms are considered here. By setting Equation (34) in Equations (32) and (33) the following sets of partial differential equations are derived via collecting the terms of perturbation parameters;

The first-order perturbation equations are (35) $\begin{array}{rl}& \begin{array}{l}O({\epsilon }^1):\left(1-{\overline{\eta }}^2{\displaystyle \frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}}\right)\left[-a_3\left({\displaystyle \frac{{\mathrm{\partial }}^2{Y}_1}{\mathrm{\partial }{x}^2}}+{\displaystyle \frac{\mathrm{\partial }{\mathrm{\Psi }}_1}{\mathrm{\partial }x}}\right)\right]+\left(1-{\overline{\mu }}^2{\displaystyle \frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}}\right)\\ \left[K_1{Y}_1-K_2{\displaystyle \frac{{\mathrm{\partial }}^2{Y}_1}{\mathrm{\partial }{x}^2}}+{\chi }^2\pi a_1\underset{0}{\overset{\pi }{\int }}\left(1-{\overline{\eta }}^2{\displaystyle \frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}}\right)Y_{1}dx\right]={\lambda }_1,\end{array}\end{array}$(35) (36) $\begin{array}{rl}& \left(1-{\overline{\eta }}^2\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}\right)\left[a_2\frac{{\mathrm{\partial }}^2{\mathrm{\Psi }}_1}{\mathrm{\partial }{x}^2}-a_3\left(\frac{\mathrm{\partial }{Y}_1}{\mathrm{\partial }x}+{\mathrm{\Psi }}_1\right)\right]=0.\end{array}$(36) The second-order perturbation equations are (37) $\begin{array}{rl}O({\epsilon }^2)& =\left(1-{\overline{\eta }}^2\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}\right)\left[-a_3\left(\frac{{\mathrm{\partial }}^2{Y}_2}{\mathrm{\partial }{x}^2}+\frac{\mathrm{\partial }{\mathrm{\Psi }}_2}{\mathrm{\partial }x}\right)\right]+\left(1-{\overline{\mu }}^2\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}\right)\\ & \times \left[\chi \pi a_1\underset{0}{\overset{\pi }{\int }}\left(1-{\overline{\eta }}^2\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}\right)Y_{1}dx\right]\\ & \frac{{\mathrm{\partial }}^2{Y}_1}{\mathrm{\partial }{x}^2}+\left(1-{\overline{\mu }}^2\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}\right)[K_1{Y}_2-K_2\frac{{\mathrm{\partial }}^2{Y}_2}{\mathrm{\partial }{x}^2}+\chi \pi a_1\underset{0}{\overset{\pi }{\int }}\left(1-{\overline{\eta }}^2\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}\right)\\ & \times \left(\frac{1}{2}{\left(\frac{\mathrm{\partial }{Y}_1}{\mathrm{\partial }x}\right)}^2-\chi Y_2\right)dx]={\lambda }_2,\end{array}$(37) (38) $\begin{array}{rl}& \left(1-{\overline{\eta }}^2\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}\right)\left[a_2\frac{{\mathrm{\partial }}^2{\mathrm{\Psi }}_2}{\mathrm{\partial }{x}^2}-a_3\left(\frac{\mathrm{\partial }{Y}_2}{\mathrm{\partial }x}+{\mathrm{\Psi }}_2\right)\right]=0.\end{array}$(38) Lastly, the third-order perturbation equations are (39) $\begin{array}{rl}& \begin{array}{l}O({\epsilon }^3):\left(1-{\overline{\eta }}^2{\displaystyle \frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}}\right)\left[-a_3\left({\displaystyle \frac{{\mathrm{\partial }}^2{Y}_3}{\mathrm{\partial }{x}^2}}+{\displaystyle \frac{\mathrm{\partial }{\mathrm{\Psi }}_3}{\mathrm{\partial }x}}\right)\right]-\left(1-{\overline{\mu }}^2{\displaystyle \frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}}\right)\\ \left[\chi \pi a_1\underset{0}{\overset{\pi }{\int }}\left(1-{\overline{\eta }}^2{\displaystyle \frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}}\right)\left({\displaystyle \frac{\mathrm{\partial }{Y}_1}{\mathrm{\partial }x}}+{\displaystyle \frac{\mathrm{\partial }{Y}_2}{\mathrm{\partial }x}}-\chi Y_3\right)\text{d}x\right]-\left(1-{\overline{\mu }}^2{\displaystyle \frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}}\right)\\ \left[\pi a_1\underset{0}{\overset{\pi }{\int }}\left(1-{\overline{\eta }}^2{\displaystyle \frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}}\right)\left({\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{\mathrm{\partial }{Y}_1}{\mathrm{\partial }x}}\right)}^2-\chi Y_2\right)\text{d}x\right]{\displaystyle \frac{{\mathrm{\partial }}^2{Y}_1}{\mathrm{\partial }{x}^2}}+\left(1-{\overline{\mu }}^2{\displaystyle \frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}}\right)\\ \left[K_1{Y}_2-K_2{\displaystyle \frac{{\mathrm{\partial }}^2{Y}_2}{\mathrm{\partial }{x}^2}}+\left[\chi \pi a_1\underset{0}{\overset{\pi }{\int }}\left(1-{\overline{\eta }}^2{\displaystyle \frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}}\right)\left({\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{\mathrm{\partial }{Y}_1}{\mathrm{\partial }x}}\right)}^2-\chi Y_2\right)\text{d}x\right]{\displaystyle \frac{{\mathrm{\partial }}^2{Y}_2}{\mathrm{\partial }{x}^2}}\right]\\ -{\epsilon }^2\left(1-{\overline{\mu }}^2{\displaystyle \frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}}\right)b_0{\displaystyle \frac{{\mathrm{\partial }}^2{Y}_1}{\mathrm{\partial }{T}^2}}={\lambda }_3,\end{array}\end{array}$(39) (40) $\begin{array}{rl}& \left(1-{\overline{\eta }}^2\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}\right)\left[a_2\frac{{\mathrm{\partial }}^2{\mathrm{\Psi }}_3}{\mathrm{\partial }{x}^2}-a_3\left(\frac{\mathrm{\partial }{Y}_3}{\mathrm{\partial }x}+{\mathrm{\Psi }}_3\right)\right]-{\epsilon }^2\left(1-{\overline{\mu }}^2\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}\right)b_1\frac{{\mathrm{\partial }}^2{\mathrm{\Psi }}_1}{\mathrm{\partial }{T}^2}=0.\end{array}$(40) Next, clamped–clamped BCs of Equation (25) can be addressed with the following solutions for the first-order perturbation: (41) $\begin{array}{r}{Y}_1(x,T)=A_x(T)[1-\cos (2mx)],{\mathrm{\Psi }}_1(x,T)=B_x(T)\sin (2mx)\end{array}$(41) By substituting Equation (41) into Equations (35) and (36) one can write (42) $\begin{array}{rl}& \begin{array}{l}O({\epsilon }^1):\\ [(-4m^2{a}_3(1+4{\overline{\eta }}^2{m}^2)-(K_1+4m^2{K}_2)(1+4{\overline{\mu }}^2{m}^2))A_x(T)-2m{a}_3(1+4{\overline{\eta }}^2{m}^2)B_x(T)]\\ \cos (2mx)+(a_1{\pi }^2{\chi }^2+K_1)A_x(T)={\lambda }_1,\end{array}\end{array}$(42) (43) $\begin{array}{rl}& -2(1+4{\overline{\eta }}^2{m}^2)\left(m{a}_3{A}_x(T)+\frac{1}{2}(4m^2{a}_2+a_3)B_x(T)\right)=0.\end{array}$(43) from Equation (43) one can arrive at (44) $\begin{array}{r}{B}_x(T)=-\frac{2m{a}_3}{(4m^2{a}_2+a_3)}{A}_x(T).\end{array}$(44) Subsequently, the following solution is acquired via setting Equation (44) into Equation (42) (45) $\begin{array}{r}\begin{array}{l}{\lambda }_1\\ =\left(\left[-16m^4(1+4{\overline{\eta }}^2{m}^2)\left(a_3\frac{a_2}{4m^2{a}_2+a_3}\right)\right]-[(1+4{\overline{\mu }}^2{m}^2)(K_1+4m^2{K}_2)]\right)\\ \cos (2mx)A_x(T)+({\pi }^2{a}_1{\chi }^2+K_1)A_x(T).\end{array}\end{array}$(45) The solutions of the second-order perturbation are given by (46) $\begin{array}{r}{Y}_2(x,T)=A_{2x}(T)[1-\cos (4mx)],{\mathrm{\Psi }}_2(x,T)=B_{2x}(T)\sin (4mx).\end{array}$(46) By setting Equations (41) and (46) into Equations (37) and (38) one can find (47) $\begin{array}{rl}& O({\epsilon }^2)\\ & =((-16m^2{a}_3(1+16{\overline{\eta }}^2{m}^2)-(K_1+16m^2{K}_2)(1+16{\overline{\mu }}^2{m}^2))A_{2x}(T)\\ & -4m{a}_3(1+16{\overline{\eta }}^2{m}^2)B_{2x}(T))\\ & \cos (4mx)+(4a_1{\pi }^2{m}^2\chi (1+4{\overline{\mu }}^2{m}^2))\cos (2mx)A_x(T{)}^2+(A_1{\pi }^2{\chi }^2+K_1)\\ & A_{2x}(T)-(a_1{\pi }^2\chi m^2)A_x(T{)}^2={\lambda }_2,\end{array}$(47) (48) $\begin{array}{rl}& [-(4m{a}_3{A}_{2x}(T)+(16m^2{a}_2+a_3)B_{2x}(T))(1+16{\overline{\eta }}^2{m}^2)]\sin (4mx)=0.\end{array}$(48) From Equations (47) and (48), it can be written (49) $\begin{array}{r}{A}_{2x}(T)=0,B_{2x}(T)=0,{\lambda }_2=[4m^2{\pi }^2\chi a_1\cos (2mx)-(a_1{\pi }^2\chi m^2)]A_x(T{)}^2.\end{array}$(49) In a similar way, the solutions of the third-order perturbation equations can be expressed as (50) $\begin{array}{r}{Y}_3(x,T)=A_{3x}(T)[1-\cos (6mx)],{\mathrm{\Psi }}_3(x,T)=B_{3x}(T)\sin (2mx).\end{array}$(50) By setting Equations (41), (46), and (50) into Equations (39) and (40), one can reach (51) $\begin{array}{rl}& \begin{array}{l}O({\epsilon }^3)=[-36m^2{a}_3(1+36{\overline{\eta }}^2{m}^2)-(K_1+36m^2{K}_2)(1+36{\overline{\mu }}^2{m}^2)]\\ A_{3x}(T)\cos (6mx)+((1+4{\overline{\mu }}^2{m}^2)b_0\cos (2mx)+b_0)\\ {\displaystyle \frac{{\mathrm{\partial }}^2{A}_x(T)}{\mathrm{\partial }{T}^2}}+(4a_1{\pi }^2{m}^4\chi (1+4{\overline{\mu }}^2{m}^2)A_x{(T)}^3+2m(1+4{\overline{\eta }}^2{m}^2)a_3{B}_{3x}(T))\\ \cos (2mx)+(a_1{\pi }^2{\chi }^2+K_1)A_{3x}(T)={\lambda }_3,\end{array}\end{array}$(51) (52) $\begin{array}{rl}& \begin{array}{l}[-6m{a}_3(1+36{\overline{\eta }}^2{m}^2)]A_{3x}(T)\cos (6mx)\\ -{\displaystyle \frac{\left[-(2m{a}_3{b}_1)(1+4{\overline{\mu }}^2{m}^2){\displaystyle \frac{{\mathrm{\partial }}^2{A}_x(T)}{\mathrm{\partial }{T}^2}}+4(1+4{\overline{\eta }}^2{m}^2){(4m^2{a}_2+a_3)}^2\right]}{4m^2{a}_2+a_3}}\sin (2mx)=0.\end{array}\end{array}$(52) Moreover, Equation (52) yields to (53) $\begin{array}{r}{A}_{3x}(T)=0,B_{3x}(T)=\frac{2m(1+4{\overline{\mu }}^2{m}^2)}{(1+4{\overline{\eta }}^2{m}^2)(4m^2{a}_2+a_3)}\left(b_1\frac{a_3}{4m^2{a}_2+a_3}\right)\frac{{\mathrm{\partial }}^2{A}_x(T)}{\mathrm{\partial }{T}^2}.\end{array}$(53) By setting Equation (53) into (51), the following expression is obtained (54) $\begin{array}{r}\begin{array}{l}{\lambda }_3=\left[\left(4m^2(1+4{\overline{\mu }}^2{m}^2)\left(-{\displaystyle \frac{b_1{a_3}^2}{{(4m^2{a}_2+a_3)}^2}}-{\displaystyle \frac{b_0}{4m^2}}\right)\right)\cos (2mx)+b_0\right]\\ {\displaystyle \frac{{\mathrm{\partial }}^2{A}_x(T)}{\mathrm{\partial }{T}^2}}-4m^4{\pi }^2{a}_1(1+4{\overline{\mu }}^2{m}^2)A_x(T{)}^3\cos (2mx).\end{array}\end{array}$(54) Thereupon, approximate functions for vibration of the FG curved nanobeams is acquired as follows (55) $\begin{array}{rl}Y(x,T,\epsilon )& =\epsilon A_x(T)[1-\cos (2mx)]+O({\epsilon }^4),\end{array}$(55) (56) $\begin{array}{rl}\mathrm{\Psi }(x,T,\epsilon )& =[\epsilon B_x(T)+{\epsilon }^3{B}_{3x}(T)]\sin (2mx)+O({\epsilon }^4),\end{array}$(56) (57) $\begin{array}{rl}{\lambda }^F(x,T,\epsilon )& ={\lambda }_1\epsilon +{\lambda }_2{\epsilon }^2+{\lambda }_3{\epsilon }^3+O({\epsilon }^4).\end{array}$(57)

Finally, by substituting Equations (45), (49), and (54) into Equation (57), the asymptotic solution is expressed as follow (58) $\begin{array}{r}{\lambda }^F=d_0\frac{{\mathrm{\partial }}^2(\epsilon A_x(T))}{\mathrm{\partial }{T}^2}+d_1(\epsilon A_x(T))+d_2(\epsilon A_x(T){)}^2+d_3(\epsilon A_x(T){)}^3+O({\epsilon }^4)+\dots \end{array}$(58) in which for the clamped–clamped BC one has (59) $\begin{array}{rl}{d}_0& =\frac{\pi }{2}\left[b_0(3+4{\overline{\mu }}^2{m}^2)+4m^2{b}_1\frac{{a_3}^2}{{(4m^2{a}_2+a_3)}^2}(1+4{\overline{\mu }}^2{m}^2)\right],\end{array}$(59) (60) $\begin{array}{rl}{d}_1& =\frac{\pi }{2}[2{\pi }^2{\chi }^2{a}_1+K_1(3+4{\overline{\mu }}^2{m}^2)+4m^2{K}_2(1+4{\overline{\mu }}^2{m}^2)\\ & +16m^4(1+4{\overline{\eta }}^2{m}^2)\left(\frac{(a_2{a}_3)}{(4m^2{a}_2+a_3)}\right)],\end{array}$(60) (61) $\begin{array}{rl}{d}_2& =-m^2{\pi }^3\chi a_1(3+8{\overline{\mu }}^2{m}^2),\end{array}$(61) (62) $\begin{array}{rl}{d}_3& =2m^4{\pi }^3{a}_1(1+4{\overline{\mu }}^2{m}^2).\end{array}$(62) Furthermore, by following the same procedure with appropriate shape functions for both simply supported edges, the following coefficients are obtained (63) $\begin{array}{rl}{d}_0& =\frac{\pi }{2}(1+{\overline{\mu }}^2{m}^2)\left[b_0+m^2{b}_1\frac{{a_3}^2}{{(m^2{a}_2+a_3)}^2}\right],\end{array}$(63) (64) $\begin{array}{rl}{d}_1& =\frac{\pi }{2m^2}\left[\left(8{\chi }^2{a}_1+m^6\frac{a_2{a}_3}{(m^2{a}_2+a_3)}\right)(1+{\overline{\eta }}^2{m}^2)+m^2(m^2{K}_2+K_1)(1+{\overline{\mu }}^2{m}^2)\right],\end{array}$(64) (65) $\begin{array}{rl}{d}_2& =-{\pi }^2\chi a_1\left[\frac{3}{2}m+{\overline{\mu }}^2{\overline{\eta }}^2{m}^5+({\overline{\mu }}^2+{\overline{\eta }}^2)m^3\right],\end{array}$(65) (66) $\begin{array}{rl}{d}_3& =\frac{1}{8}{m}^4{\pi }^3{a}_1(1+{\overline{\mu }}^2{m}^2),\end{array}$(66) To obtain the free vibration response, one needs to set ${\lambda }^F=0$ which results in: (67) $\begin{array}{r}{d}_0\frac{{\mathrm{\partial }}^2(\epsilon A_x(T))}{\mathrm{\partial }{T}^2}+d_1(\epsilon A_x(T))+d_2(\epsilon A_x(T){)}^2+d_3(\epsilon A_x(T){)}^3=0.\end{array}$(67) Explicit solutions of the third-order Duffing-type Equation (67) are obtained as (68) $\begin{array}{r}{\omega }_L=\sqrt{\frac{d_1}{d_0}},{\omega }_{NL}={\omega }_L\sqrt{1+\frac{9d_1{d}_3-10{d_2}^2}{12d_1^2}{\sigma }^2},\end{array}$(68) where $\sigma =\frac{w_{max}}{L_s}$, and ${\omega }_L$, ${\omega }_{NL}$ are the nondimensional linear and nonlinear frequencies, respectively.

4. Results and discussion

The mathematical formulations and the closed-form analytical response for nonlinear vibration analysis of FG curved beam (demonstrated in Figure 1) under the NLSGT were presented. The numerical examples are presented in this section for FG materials made of the SUS304 ($E_m=207.79\text{GPa}$, ${\rho }_m=8166\text{kg}/{\text{m}}^3$, ${\nu }_m=0.3$) and Si3N4 ($E_c=322.27\text{GPa}$, ${\rho }_c=2370\text{kg}/{\text{m}}^3$, ${\nu }_c=0.3$) respectively as the metal and ceramic phases. It should be noted that the several factors such as material, boundary supports, and external loadings affect the value of the nonlocal parameter. experimental or comparative studies with molecular models can be used to determine the nonlocal parameter. The value of the length scale parameter also depends on the microstructures of the material. The main objective of this research is to study the effects of geometric nonlinear terms on the vibration analysis of the FG curved nanobeam following the NLSGT. Therefore, the non-dimensional nonlocal and length scale parameter are utilized to capture the size-effect.

Figure 1. The schematic view of the curved beam with related geometric parameters.

First, the accuracy of the proposed model and the solution methodology is checked via a comparative study. In this regard, the linear nondimensional frequencies ($\mathrm{\Omega }={\overline{\omega }}_L(L_s/h)\sqrt{{\rho }_m/E_m}$) of the FG curved nanobeam are compared in Table 1 based on NLSGT with the published results in Ref. [34]. The close agreement of the results shows the accuracy of the model. In what follows, a wide range of parametric results is demonstrated. The reported nondimensional frequencies are based on the relation given in Equation (31) for ${\omega }_L$.

Table 1. Comparisons of the linear nondimensional natural frequencies ($\mathrm{\Omega }={\overline{\omega }}_L(L_s/h)\sqrt{{\rho }_m/E_m}$) for FG curved nanobeam considering simply supported edges ($L_s/h=25,L_s/R=0.2,n=1,K_1=0,K_2=0$).

		$\mu /L_s$
$\eta /L_s$		$0$	0.05	$0.1$	$0.15$	$0.2$	$0.25$
0	Ref. [34]	7.8246	7.7299	7.4649	7.0781	6.6254	6.1536
	Present study	7.8247	7.7299	7.4649	7.0781	6.6254	6.1536
0.05	Ref. [34]	7.9206	7.8246	7.5565	7.1649	6.7066	6.2291
	Present study	7.9206	7.8247	7.5565	7.1649	6.7066	6.2291
0.1	Ref. [34]	8.2017	8.1023	7.8246	7.4192	6.9446	6.4501
	Present study	8.2017	8.1024	7.8247	7.4192	6.9446	6.4501
0.15	Ref. [34]	8.6499	8.5451	8.2523	7.8246	7.3242	6.8026
	Present study	8.6499	8.5452	8.2523	7.8247	7.3242	6.8026
0.2	Ref. [34]	9.2410	9.1290	8.8162	8.3593	7.8246	7.2675
	Present study	9.2410	9.1291	8.8162	8.3593	7.8247	7.2675

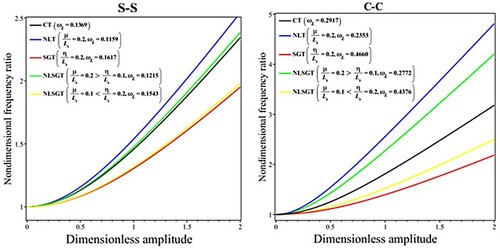
In Figure 2, the fundamental frequency ratios versus dimensionless amplitude are presented for the CT, NLT, SGT and NLSGT with the CC and SS BCs. It is observed that the NLT has a higher nondimenional frequency ratio than other continuum theories, but the SGT has the lowest ratio. The higher discrepancies can be also found for fully clamped edges than simply supported ones.

Figure 2. Comparison of the results of the CT, NLT, SGT, and NLSGT for nondimensional fundamental frequency ratio (${\omega }_{NL}/{\omega }_L$) versus dimensionless amplitude ($W_{max}/h$) $\left(K_1=0,K_2=0,n=1,\frac{L_s}{h}=10,\frac{L_s}{R}=0.1\right)$.

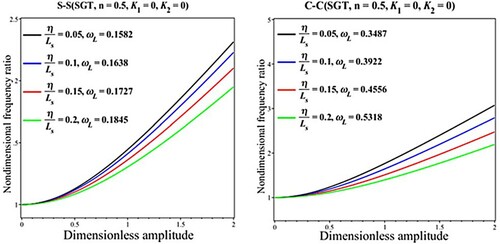
In Figures 3 and 4, the nondimensional frequency ratios against dimensionless amplitude are plotted on the basis of NLT and SGT to highlight the importance of the nonlocal and length scale parameters. Both clamped and simply supported edges are considered. As expected, the increases in nonlocal and length scale parameters respectively result in lower and higher values of the frequencies. One can also find that the fundamental frequency ratio increases when the larger values of the nonlocal parameter are considered. This is due to the fact that the structure with higher values of the nonlocal parameter is more flexible with a smaller linear natural frequency and so that the larger fundamental frequency ratio is obtained. Also, the reduction effects of the length parameter on the frequency ratios are observed. Indeed, by the increase of the length-scale parameter, the model predicts a stiffer structure and gives a larger linear frequency which results in the lower frequency ratio.

Figure 3. Impact of the nonlocal parameter on the results for the nondimensional frequency ratio (${\omega }_{NL}/{\omega }_L$) versus dimensionless amplitude ($W_{max}/h$) based on the NLT $\left(\frac{L_s}{h}=10,\frac{L_s}{R}=0.1\right)$.

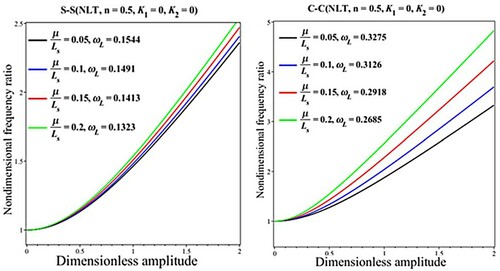
Figure 4. Impact of the length scale parameter on the results for the nondimensional frequency ratio (${\omega }_{NL}/{\omega }_L$) versus dimensionless amplitude ($W_{max}/h$) based on the SGT $\left(\frac{L_s}{h}=10,\frac{L_s}{R}=0.1\right)$.

In Table 2, the variations of the nondimensional linear frequency and nondimensional frequency ratio for different initial amplitudes are discussed in detail considering various size effects. Besides, more details are provided in Figures 5 and 6 where the effects of dimensionless amplitude are demonstrated by plotting nondimensional frequency ratio against nonlocal strain gradient parameters. Comparing the results for different BCs reveals the more importance of the geometrical nonlinearity for clamped edges than the simply supported ones. In addition, different trends are observed for Figures 5 and 6 which show different nonlinear vibrational behavior.

Figure 5. Impact of dimensionless amplitude on the results for the nondimensional frequency ratio (${\omega }_{NL}/{\omega }_L$) versus length scale parameter $\left(\frac{L_s}{h}=10,\frac{L_s}{R}=0.1\right)$.

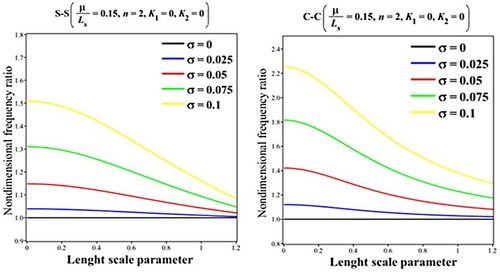
Figure 6. Impact of dimensionless amplitude on the results for the nondimensional frequency ratio (${\omega }_{NL}/{\omega }_L$) versus nonlocal parameter $\left(\frac{L_s}{h}=10,\frac{L_s}{R}=0.1\right)$.

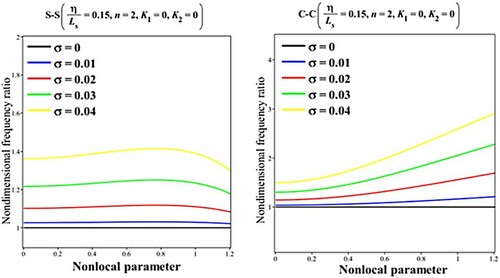
Table 2. The variations of the nondimensional linear frequency (${\omega }_L$) and nondimensional frequency ratio (${\omega }_r={\omega }_{NL}/{\omega }_L$) for different initial amplitudes ($h=1\text{nm},L_s/h=10,L_s/R=0.2$, $K_1=100,K_2=10,n=0.5$).

				$\sigma$
BC	$\mu /L_s$	$\eta /L_s$	${\omega }_L$	$0.02$	$0.04$	$0.06$	$0.08$	$0.1$
	0	0	0.25669	1.00400	1.01594	1.03552	1.06233	1.09583
		0.04	0.25775	1.00380	1.01514	1.03376	1.05928	1.09122
		0.08	0.26088	1.00322	1.01282	1.02864	1.05037	1.07768
S-S	0.05	0	0.25508	1.00410	1.01632	1.03637	1.06380	1.09807
		0.04	0.25611	1.00390	1.01551	1.03457	1.06068	1.09333
		0.08	0.25919	1.00329	1.01313	1.02930	1.05153	1.07944
	0.1	0	0.25062	1.00438	1.01741	1.03878	1.06797	1.10437
		0.04	0.25160	1.00416	1.01654	1.03684	1.06462	1.09930
		0.08	0.25452	1.00351	1.01397	1.03117	1.05478	1.08439
	0	0	0.40536	1.02723	1.10493	1.22351	1.37242	1.54289
		0.04	0.41454	1.02644	1.10197	1.21748	1.36284	1.52958
		0.08	0.44095	1.02426	1.09382	1.20084	1.33634	1.49259
C-C	0.05	0	0.40185	1.02925	1.11242	1.23868	1.39639	1.57615
		0.04	0.41082	1.02842	1.10933	1.23244	1.38654	1.56251
		0.08	0.43662	1.02613	1.10083	1.21516	1.35917	1.52446
	0.1	0	0.39244	1.03469	1.13241	1.27879	1.45926	1.66275
		0.04	0.40081	1.03378	1.12910	1.27219	1.44896	1.64862
		0.08	0.42494	1.03127	1.11985	1.25366	1.41996	1.60872

The impacts of the FG gradient index ($n$) on the linear nondimensional frequency and the frequency ratio are investigated in Table 3 and Figure 7 based on the NLSGT. The edges with both clamped and simply supported constraints are considered. It is seen that by increasing $n$, the nondimensional frequency and frequency ratio decreases relatively. Indeed, the structure with a larger material index has a lower stiffness which leads to smaller frequencies. Besides, similar trends can be seen for both BCs.

Figure 7. Impact of the power-law index on the results for the nondimensional frequency ratio (${\omega }_{NL}/{\omega }_L$) versus dimensionless amplitude ($W_{max}/h$) under the NLSGT $\left(\frac{L_s}{h}=20\right)$.

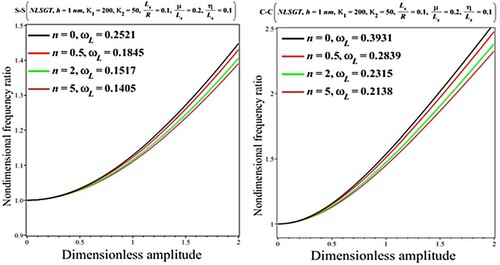
Table 3. The variations of the nondimensional linear frequency (${\omega }_L$) and nondimensional frequency ratio (${\omega }_r={\omega }_{NL}/{\omega }_L$) for different material gradient indices ($h=1\text{nm},L_s/h=15,L_s/R=0.1,\sigma =0.13,K_1=150,K_2=20$).

			$n$
BC	$\mu /L_s$	$\eta /L_s$		$0$	$0.5$	$1$	$2$	$5$
	0	0	${\omega }_L$	0.2715	0.1953	0.1744	0.1587	0.1460
			${\omega }_r$	1.6897	1.6671	1.6502	1.6289	1.6045
		0.03	${\omega }_L$	0.2721	0.1957	0.1747	0.1590	0.1462
			${\omega }_r$	1.6841	1.6622	1.6457	1.6248	1.6008
		0.13	${\omega }_L$	0.2807	0.2013	0.1795	0.1631	0.1498
			${\omega }_r$	1.6029	1.5904	1.5795	1.5648	1.5469
S-S	0.06	0	${\omega }_L$	0.2693	0.1939	0.1732	0.1576	0.1450
			${\omega }_r$	1.7025	1.6787	1.6610	1.6389	1.6137
		0.03	${\omega }_L$	0.2699	0.1942	0.1735	0.1579	0.1452
			${\omega }_r$	1.6969	1.6738	1.6565	1.6348	1.6100
		0.13	${\omega }_L$	0.2782	0.1996	0.1781	0.1619	0.1488
			${\omega }_r$	1.6145	1.6011	1.5897	1.5743	1.5558
	0.1	0	${\omega }_L$	0.2667	0.1922	0.1717	0.1564	0.1439
			${\omega }_r$	1.7176	1.6922	1.6737	1.6506	1.6243
		0.03	${\omega }_L$	0.2672	0.1926	0.1720	0.1566	0.1441
			${\omega }_r$	1.7118	1.6872	1.6691	1.6465	1.6206
		0.13	${\omega }_L$	0.2752	0.1977	0.1764	0.1605	0.1475
			${\omega }_r$	1.6280	1.6136	1.6016	1.5854	1.5661
	0	0	${\omega }_L$	0.4230	0.2962	0.2618	0.2362	0.2150
			${\omega }_r$	2.5725	2.5388	2.5013	2.4505	2.3978
		0.03	${\omega }_L$	0.4292	0.3003	0.2653	0.2394	0.2178
			${\omega }_r$	2.5451	2.5132	2.4766	2.4267	2.3751
		0.13	${\omega }_L$	0.5138	0.3568	0.3142	0.2827	0.2564
			${\omega }_r$	2.2314	2.2161	2.1892	2.1499	2.1102
C-C	0.06	0	${\omega }_L$	0.4191	0.2942	0.2602	0.2350	0.2141
			${\omega }_r$	2.7080	2.6675	2.6256	2.5697	2.5117
		0.03	${\omega }_L$	0.4250	0.2981	0.2636	0.2380	0.2168
			${\omega }_r$	2.6799	2.6413	2.6004	2.5456	2.4886
		0.13	${\omega }_L$	0.5059	0.3519	0.3102	0.2792	0.2535
			${\omega }_r$	2.3541	2.3344	2.3041	2.2606	2.2165
	0.1	0	${\omega }_L$	0.4147	0.2919	0.2585	0.2337	0.2132
			${\omega }_r$	2.8538	2.8050	2.7582	2.6968	2.6327
		0.03	${\omega }_L$	0.4203	0.2956	0.2617	0.2365	0.2157
			${\omega }_r$	2.8252	2.7786	2.7328	2.6725	2.6096
		0.13	${\omega }_L$	0.4971	0.3465	0.3057	0.2754	0.2503
			${\omega }_r$	2.4894	2.4642	2.4299	2.3817	2.3325

Presented in Table 4 and Figure 8 are the effects of the length-to-radius ratio on the nondimensional frequency and frequency ratio for CC and SS edges. It is found that the nondimensional linear frequency and frequency ratio lessen by increasing $L_R$. A comparison of the results for boundary conditions demonstrates that there are more discrepancies in the results of simply supported nanobeam than the clamped one.

Figure 8. Impact of the length-to-radius ratio on the results for the nondimensional fundamental frequency ratio (${\omega }_{NL}/{\omega }_L$) versus dimensionless amplitude ($W_{max}/h$) based on the NLSGT $\left(\frac{L_s}{h}=15\right)$.

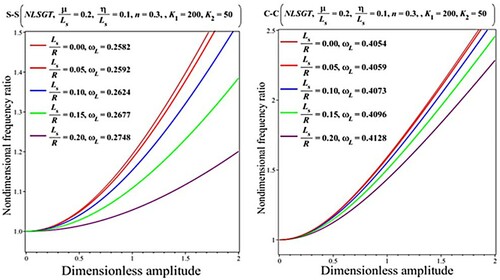
Table 4. Impact of length-to-radius ratio on the nondimensional linear frequency (${\omega }_L$) and nondimensional frequency ratio (${\omega }_r={\omega }_{NL}/{\omega }_L$) for the FG curved nanobeam $(h=1\text{nm},L_s/h=15,\sigma =0.1,n=1.1,K_1=200,K_2=20)$.

				$L_s/R=L_R$
B.C	$\mu /L_s$	$\eta /L_s$		$0.00$	$0.03$	$0.05$	$0.10$	$0.15$
	0	0	${\omega }_L$	0.1729	0.1733	0.1741	0.1777	0.1837
			${\omega }_r$	1.5142	1.5010	1.4780	1.3751	1.2208
		0.08	${\omega }_L$	0.1742	0.1747	0.1755	0.1794	0.1856
			${\omega }_r$	1.5076	1.4937	1.4694	1.3613	1.1998
		0.16	${\omega }_L$	0.1782	0.1788	0.1797	0.1841	0.1913
			${\omega }_r$	1.4887	1.4728	1.4449	1.3214	1.1384
S-S	0.1	0	${\omega }_L$	0.1709	0.1713	0.1721	0.1754	0.1809
			${\omega }_r$	1.5239	1.5111	1.4886	1.3879	1.2352
		0.08	${\omega }_L$	0.1722	0.1726	0.1734	0.1769	0.1827
			${\omega }_r$	1.5176	1.5041	1.4803	1.3740	1.2133
		0.16	${\omega }_L$	0.1758	0.1763	0.1772	0.1813	0.1879
			${\omega }_r$	1.4997	1.4840	1.4564	1.3334	1.1487
	0.15	0	${\omega }_L$	0.1689	0.1693	0.1699	0.1730	0.1780
			${\omega }_r$	1.5343	1.5218	1.5000	1.4016	1.2507
		0.08	${\omega }_L$	0.1700	0.1704	0.1711	0.1744	0.1796
			${\omega }_r$	1.5284	1.5152	1.4920	1.3876	1.2279
		0.16	${\omega }_L$	0.1734	0.1739	0.1747	0.1784	0.1844
			${\omega }_r$	1.5115	1.4960	1.4687	1.3463	1.1599
C-C	0	0	${\omega }_L$	0.2537	0.2540	0.2544	0.2565	0.2599
			${\omega }_r$	2.0487	2.0395	2.0232	1.9478	1.8254
		0.08	${\omega }_L$	0.2721	0.2723	0.2727	0.2747	0.2779
			${\omega }_r$	1.9442	1.9369	1.9239	1.8637	1.7660
		0.16	${\omega }_L$	0.3210	0.3212	0.3215	0.3232	0.3259
			${\omega }_r$	1.7314	1.7271	1.7196	1.6846	1.6275
	0.1	0	${\omega }_L$	0.2516	0.2518	0.2522	0.2541	0.2571
			${\omega }_r$	2.2366	2.2260	2.2072	2.1197	1.9762
		0.08	${\omega }_L$	0.2680	0.2682	0.2686	0.2703	0.2732
			${\omega }_r$	2.1278	2.1191	2.1037	2.0322	1.9150
		0.16	${\omega }_L$	0.3121	0.3123	0.3126	0.3141	0.3166
			${\omega }_r$	1.8976	1.8923	1.8829	1.8393	1.7677
	0.15	0	${\omega }_L$	0.2496	0.2498	0.2501	0.2517	0.2544
			${\omega }_r$	2.4091	2.3970	2.3757	2.2758	2.1102
		0.08	${\omega }_L$	0.2641	0.2642	0.2646	0.2661	0.2686
			${\omega }_r$	2.3003	2.2902	2.2723	2.1888	2.0506
		0.16	${\omega }_L$	0.3034	0.3035	0.3038	0.3052	0.3074
			${\omega }_r$	2.0617	2.0553	2.0438	1.9904	1.9020

In Table 5, the impacts of the length-to-thickness ratio on the nondimensional nonlinear frequency of the FG curved nanobeams are studied for different nonlocal and length scale parameters. Besides, Figures 9 and 10 highlight the numerical results for the frequency ratio versus dimensionless amplitude considering various length-to-thickness ratios under the NLSGT effect. It can be inferred that the nondimensional linear and nonlinear frequencies as well as the frequency ratio of the FG curved nanobeam decrease when the $L_h$ increases. In addition, the less influence of the thickness ratio on the frequency ratio can be seen for the clamped BC.

Figure 9. Impact of the length-to-thickness ratio on the results for the nondimensional fundamental frequency ratio (${\omega }_{NL}/{\omega }_L$) versus dimensionless amplitude ($W_{max}/h$) based on the NLSGT with $\mu >\eta$ $(K_1=200,K_2=50,n=0.9,L_s/R=0.1)$.

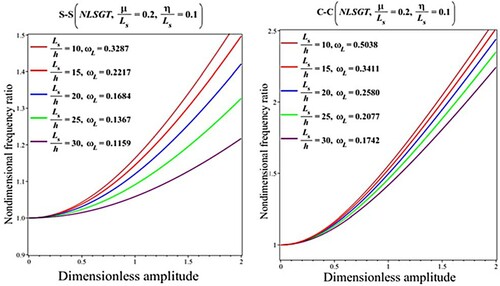
Figure 10. Impact of the length-to-thickness ratio on the results for the nondimensional fundamental frequency ratio (${\omega }_{NL}/{\omega }_L$) versus dimensionless amplitude ($W_{max}/h$) based on the NLSGT with $\eta >\mu$ $(K_1=200,K_2=50,n=0.9,L_s/R=0.1)$.

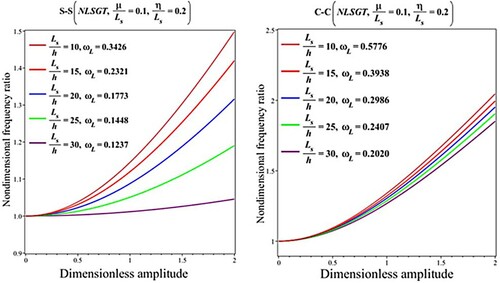
Table 5. Impact of length-to-thickness ratio on the nondimensional frequency for the FG curved nanobeam ($L_s/R=0.2,\sigma =0.02,n=1.5,K_1=150,K_2=5$).

				$L_s/h=L_h$
BC	$\mu /L_s$	$\eta /L_s$		$10$	$15$	$20$	$30$
S-S	0	0	${\omega }_{NL}$	0.2114	0.1511	0.1205	0.0882
		0.05	${\omega }_{NL}$	0.2126	0.1520	0.1213	0.0889
		0.1	${\omega }_{NL}$	0.2160	0.1548	0.1237	0.0912
	0.04	0	${\omega }_{NL}$	0.2106	0.1504	0.1198	0.0874
		0.05	${\omega }_{NL}$	0.2118	0.1514	0.1206	0.0882
		0.1	${\omega }_{NL}$	0.2152	0.1541	0.1230	0.0904
	0.08	0	${\omega }_{NL}$	0.2085	0.1486	0.1180	0.0854
		0.05	${\omega }_{NL}$	0.2096	0.1495	0.1188	0.0860
		0.1	${\omega }_{NL}$	0.2129	0.1521	0.1211	0.0881
C-C	0	0	${\omega }_{NL}$	0.3299	0.2336	0.1809	0.1149
		0.05	${\omega }_{NL}$	0.3409	0.2413	0.1872	0.1210
		0.1	${\omega }_{NL}$	0.3716	0.2627	0.2044	0.1367
	0.04	0	${\omega }_{NL}$	0.3282	0.2324	0.1796	0.1123
		0.05	${\omega }_{NL}$	0.3390	0.2400	0.1859	0.1186
		0.1	${\omega }_{NL}$	0.3693	0.2611	0.2030	0.1346
	0.08	0	${\omega }_{NL}$	0.3234	0.2288	0.1757	0.1041
		0.05	${\omega }_{NL}$	0.3337	0.2361	0.1820	0.1110
		0.1	${\omega }_{NL}$	0.3628	0.2566	0.1989	0.1282

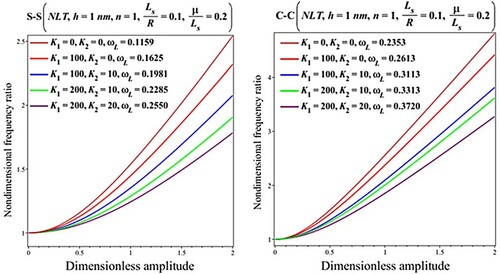
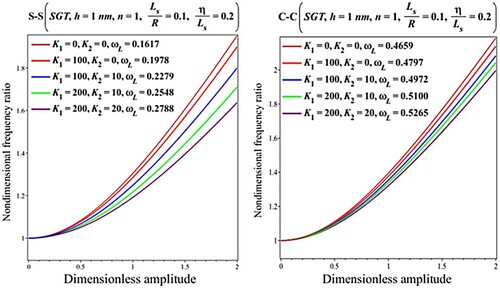
The effects of the coefficients of the elastic medium on the nonlinear vibration behavior of G curved nanobeams following the NLSGT, NLT, and SGT are studied in Figures 11–14 where the results are provided for nondimensional frequency ratio versus dimensionless amplitude including the linear frequencies. As a general finding, it can be seen that the existence of the elastic medium results in a more stable curved beam and enhances the linear frequencies. However, the lower frequency ratios are observed for higher values of elastic medium coefficients. For the assumed geometrical and material factors, the results also reveal that the natural frequencies of the curve nanobeam with simply supported edges are more sensitive to the elastic medium than the clamped one.

Figure 11. Impact of the elastic medium on the results for the nondimensional fundamental frequency ratio (${\omega }_{NL}/{\omega }_L$) versus dimensionless amplitude ($W_{max}/h$) based on the NLSGT $\left(\frac{L_s}{h}=10\right)$.

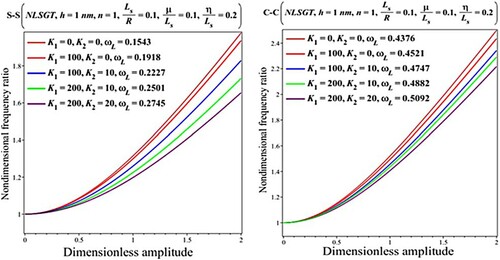
Figure 12. Impact of the elastic medium on the results for the nondimensional fundamental frequency ratio (${\omega }_{NL}/{\omega }_L$) versus dimensionless amplitude ($W_{max}/h$) based on the NLSGT $\left(\frac{L_s}{h}=10\right)$.

Figure 13. Impact of the elastic medium on the results for the nondimensional fundamental frequency ratio (${\omega }_{NL}/{\omega }_L$) versus dimensionless amplitude ($W_{max}/h$) based on the NLT $\left(\frac{L_s}{h}=10\right)$.

Figure 14. Impact of the elastic medium on the results for the nondimensional fundamental frequency ratio (${\omega }_{NL}/{\omega }_L$) versus dimensionless amplitude ($W_{max}/h$) based on the SGT $\left(\frac{L_s}{h}=10\right)$.

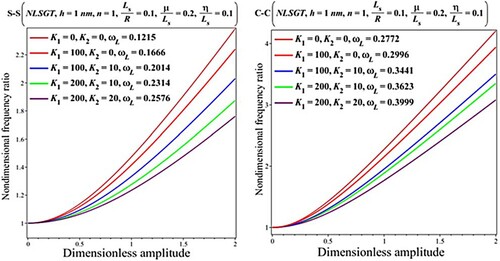
5. Conclusion

The size-dependent nonlinear vibration of FG curved nanobeams resting on the elastic medium was analytically investigated in this study NLSGT. The kinematic relations were under the FSDBT with von Kármán geometrically nonlinear assumptions. The analytical solution by the TSPM and Galerkin technique was developed. The results were verified via matching the nondimensional linear frequency with the published results. The main findings of the study can be summarized as follow:

• Studying the impacts of size-dependency on the nonlinear vibration of FG curved nanobeams revealed that the larger values of nonlocal and length scale parameters respectively lead to a higher and lower nonlinear frequency ratio while there is a reverse effect on the linear frequencies.

• It was found that the larger values of the gradient index of the FG materials make the structure more flexible and result in lower linear nondimensional frequencies and nonlinear frequency ratios.

• Results indicated that by the increase of the thickness and radius ratios, the linear nondimensional frequency decreases and increases, respectively. Increasing both geometrical ratios had a decreasing influence on the nonlinear frequency ratio.

• It was observed that for the fully clamped curved nanobeam, the variations of the thickness and radius ratios have a less important influence on the nonlinear frequency ratios rather than the simply supported one.

• It was found that increasing the coefficients of the elastic medium has an incremental influence on the linear frequency as well as a decreasing influence on the nonlinear frequency ratio.

Disclosure statement

No potential conflict of interest was reported by the author(s).