Axiomatic scale theory

Abstract

Scales are a fundamental concept of musical practice around the world. They commonly exhibit symmetry properties that are formally studied using cyclic groups in the field of mathematical scale theory. This paper proposes an axiomatic framework for mathematical scale theory, embeds previous research, and presents the theory of maximally even scales and well-formed scales in a uniform and compact manner. All theorems and lemmata are completely proven in a modern and consistent notation. In particular, new simplified proofs of existing theorems such as the equivalence of non-degenerate well-formedness and Myhill's property are presented. This model of musical scales explicitly formalizes and utilizes the cyclic order relation of pitch classes.

Keywords:

• scales
• mathematical scale theory
• axiomatic modeling
• cyclic ordered sets
• generalized interval systems
• maximally even sets
• well-formed scales

2010 Mathematics Subject Classification:

• 08C10
• 06F99

1. Introduction

The concept of a musical scale as a collection of pitch classes is universal throughout the world (Savage et al. 2015), even though these scales exhibit great variety and differences. While the notion of the octave and octave equivalence are found universal, differences involve the amount of the “tone material” within the octave, the scale's interval patterns, and the tuning systems. On the other hand, commonalities include the amount of tones in a scale often ranging between five and seven1, intervals between adjacent scale tones being between one and three semitones in size, and asymmetric scales being more common than symmetric ones (Patel 2008).

Mathematical scale theory studies the inner symmetry structures of a scale, or, respectively, a single chord, key, or rhythm. It originally emerged from the study of European and North-American classical and popular music (Clough and Myerson 1985; Carey and Clampitt 1989; Clough and Douthett 1991; Tymoczko 2008) and was generalized to study rhythmical structures (Wooldridge 1992) and musical chords inside scales (Douthett 2008). In particular, classical diatonic scale theory studies and generalizes the properties of major scales such as the C major scale consisting of the pitch classes C, D, E, F, G, A, and B. Two important outcomes of mathematical scale theory are the discovery of general scale properties that can be found in keys as well as in chords and rhythms and the development of a concise vocabulary of music theoretical concepts.

This paper addresses the research communities of mathematical music theory, computational musicology, and music cognition. Its main contribution is to reformulate mathematical scale theory within an algebraic framework based on the concept of cyclic order, presenting the theory in a compact manner and at a more abstract level than in previous work. We describe core results and proofs of the field in a modern mathematical language, revealing cross-relations between previously unrelated proofs. The second most important contribution is the self-contained presentation of the arguments used in the proofs of this paper. Music research is inherently interdisciplinary. We therefore give detailed descriptions of the arguments used in the proofs to open up scale theory to a broad audience of music researchers with sufficient mathematical background. We believe that it is crucial to facilitate interdisciplinary research on music wherever possible.

Cross-cultural commonalities of scales have been argued to arise from psychological constraints. The typical number of scale tones relates to the amount of distinct pitches that a human can reliably keep track of (Miller 1956; Clough, Douthett, and Ramanathan 1993). The prevalence of moderately small intervals between consecutive scale degrees may result from constraints that large intervals are more difficult to sing and too small intervals are hard to distinguish by the human ear (Burns and Ward 1978). The most remarkable commonality is the asymmetry that enables the creation of complex tonal structures by making the positions in the scale easy to perceive and to remember (Balzano 1980; Trehub, Schellenberg, and Kamenetsky 1999). It has been found from a mathematical perspective, however, that there is only one – up to isomorphism unique – “maximally asymmetric” scale for each tone material and given scale size (Clough and Douthett 1991). More sophisticated concepts and quantifications of asymmetry are therefore necessary to account for subtle characteristics of scales. Both the diminished-seventh chord and the octatonic scale (also known as the second Messiaen mode or the half-step/whole step diminished scale (Levine 1995) can for example be considered symmetric. Closer inspection reveals, however, that the former is totally symmetric – that is every tone has the same relations to all other tones – while the latter is not.

This paper argues that the transpositional symmetry of a scale can be formalized using automorphism groups that model different degrees of symmetry. Central results from previous research are the formulation of scale properties such as maximal evenness (Clough and Douthett 1991), well-formedness (Carey and Clampitt 1989), and Myhill's property (Clough and Myerson 1985) and theorems about the relations between those properties to distinguish between different kinds of transpositionally non-symmetric scales. A taxonomy of scale properties can be found in Clough, Engebretsen, and Kochavi (1999), a formal concept lattice is presented in Noll (2015), and an overview of different scale definitions used in the literature can be found in Harasim, Schmidt, and Rohrmeier (2016).

More generally, both pitch-class collections and rhythms are cyclic structures, the former in the pitch class dimension and the latter with respect to bars in western music or talas in Indian music. In this analogy, a rhythmic pattern is a sequence of note onsets drawn from a metrical grid just as a western scale is a sequence of pitch classes drawn from a chromatic universe (Pressing 1983; Wooldridge 1992). Because of the similar formal nature of chords, keys, and rhythms, this paper therefore uses the word scale to refer to any of these concepts. In particular, chords such as triads can be understood as a collection of pitch classes chosen from a diatonic scale analogous to that a western scale is a collection of pitch classes chosen from the chromatic scale. The framework proposed here therefore particularly includes the description of the building blocks of sequential structures of music (Conklin and Witten 1995; Cohn 1996, 1997; Tymoczko 2006; Rohrmeier 2011; Harasim, Rohrmeier, and O'Donnell 2018; Sears et al. 2018; Moss et al. 2019).

2. Scales as cyclic embeddings

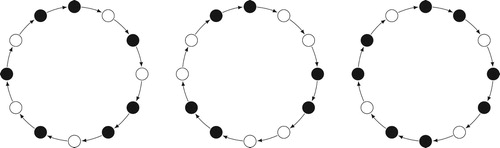
All scales in the enharmonically identified chromatic universe using western 12-tone equal temperament can be visualized by a vertex-colored directed circle of length 12 where vertices contained in the scale are colored black and all remaining vertices are colored white. A scale is called symmetric if this graph has a non-trivial automorphism group. Figure 1 shows three scales. The first one is a diatonic scale. It contains seven tones and is not symmetric. The second scale is a hexatonic scale. It is a symmetric scale containing six tones that is isomorphic to its complement. The third scale of Figure 1 is an octatonic scale. It distributes its eight scale tones as evenly as possible in the chromatic scale.

Figure 1. A diatonic, a hexatonic, and an octatonic scale in the 12-tone equal tempered chromatic universe. The tones of the scale are represented by black vertices. The diatonic scale does not have proper (non-trivial) rotational symmetries whereas the the hexatonic and the octatonic scale have three and four proper rotational symmetries, respectively. In contrast to the hexatonic scale, the octatonic scale and the diatonic scale are maximally even. That is their tones are as evenly distributed around the chromatic circle as possible. The hexatonic scale is not maximally even since the whole-tone scale (a circle of alternating black and white vertices) is more even. For a formal definition of maximal evenness see Section 6.

Musical scales are equipped with a cyclic order relation. For example, the pitch class (pc) D is not generally higher than the pc C, since the pitch of D can be realized in a lower octave than the pitch of C. If the pc cycle is, however, cut at any pc, it defines a linear order with respect to the cut point as the lowest pitch. If the pc cycle is for example cut at B, then the result inherits a linear order in which C is lower than D. If the cycle is in contrast cut at C♯, then D is lower than C in the implied linear order. Although previous research has described formal properties of musical scales and proposed mathematical proofs of their relations, to the best of our knowledge so far no study has explicitly modeled this cyclic order relation nor given an axiomatic description of musical scales. Mathematical scale theorists have, however, probably always thought about cyclic orderings of, for example, the chromatic scale, but never used this relational concept explicitly, see for example Carey (1998), Noll (2007), and Tymoczko (2008). Cyclic ordering is a standard concept of modern algebra formally defined as follows (Huntington 1916; Megiddo 1976; Galil and Megiddo 1977).

Definition 2.1

A partially cyclic ordered set consists of a set S and a ternary relation $[\cdot ,\cdot ,\cdot ]\subseteq S^3$ such that

• $[s,t,u]⟹s\ne t\mathrm{a}\mathrm{n}\mathrm{d}s\ne u\mathrm{a}\mathrm{n}\mathrm{d}t\ne u$ (strictness)

• $[s,t,u]⟹[t,u,s]$ (cyclicality),

• $[s,t,u]\mathrm{a}\mathrm{n}\mathrm{d}[s,u,w]⟹[s,t,w]$ (transitivity), and

• $[s,t,u]⟹\mathrm{\neg }[s,u,t]$ (antisymmetry)

for $s,t,u,w\in S$. It is called (totally) cyclic ordered if additionally it is total. That is, either $[s,t,u]$ or $[s,u,t]$ for distinct $s,t,u\in S$.

Note that the statement $[s,t,u]$ implies that s, t, and u are mutually different. Cyclic order relations are therefore most naturally compared to strict total order relations. For any set S and ternary relation $[\cdot ,\cdot ,\cdot ]\subseteq S^3$, the statement that $(S,[\cdot ,\cdot ,\cdot \left]\right)$ is cyclic ordered is equivalent to the statement that for all $s\in S$, the binary relation ${<}_s$ defined by $t{<}_{s}u:⟺[s,t,u]$ is a strict total order relation on S. For distinct $s,t,u\in S$, the intuition behind $[s,t,u]$ is that t lies on the path from s to u.

Definition 2.2

Let S and T be cyclic ordered sets. A cyclic morphism is a mapping $f:S\to T$ that reflects the cyclic order. This is $\left[f\right(s_1),f(s_2),f(s_3\left)\right]⟹[s_1,s_2,s_3]$ for all $s_1,s_2,s_3\in S$. It is a cyclic embedding if additionally it is injective and preserves the cyclic order, $[s_1,s_2,s_3]⟹\left[f\right(s_1),f(s_2),f(s_3\left)\right]$ for $s_1,s_2,s_3\in S$. A cyclic isomorphism is a surjective cyclic embedding.

Definition 2.3

A scale is defined as a cyclic embedding $\sigma :D\to C$ of a finite cyclic ordered set D of diatonic tones into a finite cyclic ordered set C of chromatic tones. The cardinalities of the domain and codomain of σ are called diatonic size and chromatic size, respectively. They are denoted by d and c.

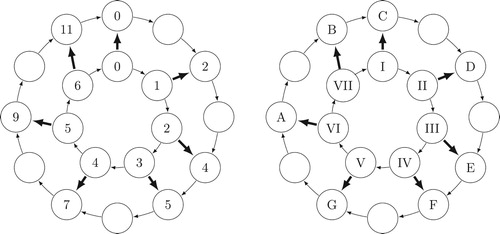
Figure 2 illustrates the definitions using the example of the C major scale. The sets of diatonic and chromatic tones D and C are modeled by ${\mathbb{Z}}_7$ and ${\mathbb{Z}}_{12}$, the rings of integers modulo 7 and 12. Throughout the whole paper, we use the symbol ${\mathbb{Z}}_n$ for any positive natural number n to denote the set $0,1,2,\dots ,n-1$ of non-negative numbers less than n together with ${+}_n:{\mathbb{Z}}_n^2\to {\mathbb{Z}}_n,s{+}_{n}t:=s+t\mathrm{m}\mathrm{o}\mathrm{d}n,$ the addition modulo n. We particularly use ${+}_n$ instead of just + in situations where we want to stress calculations modulo n. We also use the subscript n to denote other operations modulo n, such as ${-}_n:{\mathbb{Z}}_n^2\to {\mathbb{Z}}_n,s{-}_{n}t:=s-t\mathrm{m}\mathrm{o}\mathrm{d}n$. We identify the pitch class of C with 0. Then the diatonic scale is $\sigma :{\mathbb{Z}}_7\to {\mathbb{Z}}_{12},0\mapsto 0,1\mapsto 2,2\mapsto 4,3\mapsto 5,4\mapsto 7,5\mapsto 9,6\mapsto 11,$ visualized in Figure 2. The diatonic and chromatic sizes of, for example, the interval between the tone D, identified with 1 mod 7 and 2 mod 12, and the tone A, identified with 5 mod 7 and 9 mod 12, are $5{-}_{7}1=4$ and $\sigma \left(5\right){-}_{12}\sigma \left(1\right)=9{-}_{12}2=7$, respectively.

Figure 2. The C major scale as a cyclic embedding. The left circle shows the scale as a embedding from ${\mathbb{Z}}_7$ into ${\mathbb{Z}}_{12}$. Since it it is possible to draw this picture without crossing arrows, the mapping preserves the cyclic order. The right circle shows the same scale with renamed elements in the domain and codomain according to music theory conventions. The scale tones (the vertices of the inner circle) are named using roman numerals and the chromatic tones are named using the latin letters from A to G where $\text{C}=0_{{\mathbb{Z}}_{12}}$.

A characteristic feature of a scale is the possibility to calculate the size of musical intervals between tones (paths along the circle in clockwise direction) in two different ways (Clough and Myerson 1985, 1986). In the circle visualization of Figure 1, the specific or chromatic size of an interval between two (black) scale tones is one plus the number of white and black vertices strictly in between them in clockwise direction. The generic or diatonic size of an interval between two scale tones is one plus the number of only black tones strictly in between them in clockwise direction.

3. Cyclic ordered sets, generalized interval systems, and regular group actions

This section provides the preliminary definitions and notation of generalized interval systems and regular group actions as subclasses of them are in 1-to-1 relation to finite cyclic ordered sets. Technical proofs and lemmata are presented in the appendix in detail. The core result of this section is Theorem 3.5. It shows how the algebraic concepts,

• finite generalized interval systems with cyclic interval group,

• regular group actions of a finite cyclic group, and

• finite cyclic ordered sets,

are three different viewpoints of a pitch class system. Generalized interval systems formalize how intervals between tones are calculated. Regular cyclic group actions model the concept of musical transposition. A transposition of a tone t up by an interval i is denoted by $t◃i$ (read as “t transposed by i”). Note that other authors also use the notation $T_i\left(t\right)$ (Lewin 1987; Clough and Douthett 1991; Tymoczko 2008). Cyclic orderings show how to formalize the intuition that, for example, the pitch class of F is higher than the pitch class of E and lower than the pitch class of G. Because of the cyclic nature of the pitch class system, a binary order relation cannot be used here to model that intuition.

Definition 3.1

A generalized interval system (GIS) is a triple $(S,\delta ,I)$ where S is a set of tones, $(I,+)$ is a group of (generalized) intervals, and $\delta :S\times S\to I$ maps pairs of tones to intervals such that the restriction $\delta (s,\cdot ):S\to I$ is bijective and $\delta (s,t)+\delta (t,u)=\delta (s,u)$ for all $s,t,u\in S$.

We use the definition by Lewin (1987) here with the notation by Neumaier and Wille (1990) who referred to GISs as tone systems. The group $(I,+)$ does in general not need to be commutative. In this paper, however, only cyclic interval groups are considered that are commutative. Note that the equations $\delta (s,s)=0$ and $\delta (s,t)=-\delta (t,s)$ follow directly from the definition for all $s,t\in S$.

Definition 3.2

A (right) group action $◃:S\times I\to S$ is a mapping that satisfies

• $s◃0_I=s$ (identity) and

• $(s◃i)◃j=s◃(i+j)$ (compatibility)

for $s\in S$ and $i,j\in I$ where S is a set and $(I,+)$ is a (in general not necessarily commutative) group. We jump back and forth between prefix and infix notation as needed. In the case of $I={\mathbb{Z}}_n$ for some $n\in \mathbb{N}$, the second argument of $◃$ is always understood modulo n. A group action is called regular (also known as simply transitive) if the restriction $◃(S,\cdot ):I\to S$ on the second argument is bijective.

Lemma 3.3

(Lewin 1987)

Generalized interval systems $(S,\delta ,I)$ and regular group actions $◃:S\times I\to S$ are in 1-to-1 relation by $\delta (s,t)=i⟺s◃i=t$ for $s,t\in S$ and $i\in I$.

Proof.

See Appendix A.1.

A cyclic ordering on a set S can be used to define respective open, semi-open, and closed intervals $(s,u):=t\mid [s,t,u]$, $(s,u]:=\left(\right(s,u)\cup u)minuss$, and $[s,u]:=(s,u)\cup s,u$. The semi-open intervals can be used to define a generalized interval system on a cyclic ordered set. The (musical) interval mapping then returns the cardinality of the respective semi-open (mathematical) interval, $\delta :S\times S\to {\mathbb{Z}}_{\mathrm{\#}S},\delta (s,u):=\mathrm{\#}(s,u]$. The following results show that the so defined δ is indeed an interval mapping of the generalized interval system $(S,\delta ,{\mathbb{Z}}_{\mathrm{\#}S})$.

Lemma 3.4

Let $(S,[\cdot ,\cdot ,\cdot \left]\right)$ be a cyclic ordered set. Then $(S,\delta ,{\mathbb{Z}}_{\mathrm{\#}S})$ with $\delta :S\times S\to {\mathbb{Z}}_{\mathrm{\#}S},\delta (s,t)=\mathrm{\#}(s,t]$ is a generalized interval system.

Proof.

See Appendix A.4.

Theorem 3.5

Finite cyclic ordered sets $(S,[\cdot ,\cdot ,\cdot \left]\right),$ generalized interval systems $(S,\delta ,{\mathbb{Z}}_n),$ and regular group actions $◃:S\times {\mathbb{Z}}_n\to S$ are in one-to-one relation by $[s,t,u]⟺0<\delta (s,t)<\delta (s,u),\delta (s,t)=\mathrm{\#}(s,t],\mathrm{a}\mathrm{n}\mathrm{d}s◃i=t⟺\delta (s,t)=i$ for $s,t,u\in S$ and $i\in {\mathbb{Z}}_n$ where $n:=\mathrm{\#}S$ is the cardinality of S and ${\mathbb{Z}}_n$ denotes the additive cyclic group of cardinality n.

Proof.

See Appendix A.5.

Note that in particular, $s◃\delta (s,t)=t$ and $\delta (s,s◃i)=i$ for all $s,t\in S$ and $i\in {\mathbb{Z}}_n$. To illustrate the theorem, we characterize the canonical cyclic order on ${\mathbb{Z}}_n$. Let n be a positive natural number. The additive group ${\mathbb{Z}}_n$ acts on itself via the action $s◃i=s{+}_{n}i$ for $s,i\in {\mathbb{Z}}_n$. The respective interval mapping is thus defined by $\delta (s,t)=t{-}_{n}s$ for $s,t\in {\mathbb{Z}}_n$. Following theorem 3.5, the corresponding cyclic order is then characterized by $[s,t,u]⟺0<\delta (s,t)<\delta (s,u)⟺0<t{-}_{n}s<u{-}_{n}s$ for $s,t,u\in S$.

The fundamental correspondences between finite cyclic ordered sets, finite cyclic generalized interval systems and finite regular cyclic group actions described in Theorem 3.5 are used throughout the whole paper. All cyclic ordered sets are thus assumed to be finite. The following corollaries show the interactions between these structures.

Corollary 3.6

The interval mapping is invariant under musical transposition. That is $\delta (s◃i,t◃i)=\delta (s,t)$ for all tones s, t and all intervals i.

Proof.

See Appendix A.6

Lemma 3.7

Let S and T be cyclic ordered sets with $\mathrm{\#}S\ge 3$. For a mapping $f:S\to T,$ the following are equivalent:

1. f preserves the cyclic order,

2. f is an injective cyclic morphism, and

3. f is a cyclic embedding.

Proof.

(i)⇒(ii) Let f preserve the cyclic order, and $s,t,u\in S$. Then $\mathrm{\neg }[s,t,u]⟹[s,u,t]⟹\left[f\right(s),f(u),f(t\left)\right]⟹\mathrm{\neg }\left[f\right(s),f(t),f(u\left)\right]$ and $s\ne t⟹\mathrm{\exists }r\in S:[r,s,t]⟹\mathrm{\exists }r\in S:\left[f\right(r),f(s),f(t\left)\right]⟹f\left(s\right)\ne f\left(t\right).$ Therefore, f is an injective cyclic morphism.

(ii)⇒(iii) Let f be an injective cyclic morphisms. Then f is a cyclic embedding since $\mathrm{\neg }\left[f\right(s),f(t),f(u\left)\right]⟹\left[f\right(s),f(u),f(t\left)\right]⟹[s,u,t]⟹\mathrm{\neg }[s,t,u]$ for all $s,t,u\in S$.

(iii)⇒(i) All cyclic embeddings preserve the cyclic order by definition.

Corollary 3.8

A mapping with equally sized domain and codomain is a cyclic isomorphism if and only if the interval mapping is invariant under it.

Proof.

Let S and T be finite cyclic ordered sets and let $f:S\to T$ be a cyclic isomorphism. Then $\delta (s,t)=\mathrm{\#}(s,t]=\mathrm{\#}\left(f\right(s),f(t\left)\right]=\delta \left(f\right(s),f(t\left)\right)$ for all $s,t\in S$.

Conversely, let $f:S\to T$ be a mapping such that $\delta (s,t)=\delta \left(f\right(s),f(t\left)\right)$ for all $s,t\in S$. Then $\begin{array}{rl}[s,t,u]& ⟹0<\delta (s,t)<\delta (s,u)\\ & ⟹0<\delta \left(f\right(s),f(t\left)\right)<\delta \left(f\right(s),f(u\left)\right)\\ & ⟹\left[f\right(s),f(t),f(u\left)\right]\end{array}$ for all $s,t,u\in S$. Therefore, f is a cyclic embedding by Lemma 3.7. It is an isomorphism, because its domain and codomain are of equal cardinality.

Corollary 3.9

Musical transposition $◃(\cdot ,i):S\to S$ is a cyclic automorphism for all $i\in {\mathbb{Z}}_d$.

Proof.

The interval mapping is invariant under musical transposition by Corollary 3.6. Musical transposition is thus a cyclic automorphism by Corollary 3.8.

Corollary 3.10

The mapping $\delta (s_0,\cdot ):S\to {\mathbb{Z}}_n$ is a cyclic isomorphism between the cyclic ordered set S and the cyclic ordered interval group ${\mathbb{Z}}_n$ for all $s_0\in S$.

Proof.

For all $s_0,s,t\in S$, $\delta \left(\delta \right(s_0,s),\delta (s_0,t\left)\right)=\delta (s_0,t){-}_n\delta (s_0,s)=\delta (s_0,t){+}_n\delta (s,s_0)=\delta (s,t).$ Therefore, $\delta (s_0,\cdot ):S\to {\mathbb{Z}}_n$ is a cyclic isomorphism by Corollary 3.8.

Corollary 3.11

The automorphism group of a finite cyclic ordered set S with $\mathrm{\#}S=n$ is isomorphic to ${\mathbb{Z}}_n$.

Proof.

Fix some $s_0\in S$. We show that $\mathrm{\Phi }:({\mathbb{Z}}_n,{+}_n)\to \mathrm{A}\mathrm{u}\mathrm{t}\left(S\right),\mathrm{\Phi }\left(i\right)=(s\mapsto s◃i)$ is a group isomorphism. It is a group homomorphism since $\left(\mathrm{\Phi }\right(i{+}_{n}j\left)\right)\left(s\right)=s◃i{+}_{n}j=(s◃j)◃i=\left(\mathrm{\Phi }\right(i)\circ \mathrm{\Phi }(j\left)\right)\left(s\right)$ for all $i,j\in {\mathbb{Z}}_n$ and $s\in S$. It is injective since $\mathrm{\Phi }\left(i\right)=\mathrm{\Phi }\left(j\right)⟹\mathrm{\forall }s\in S:s◃i=s◃j⟹\mathrm{\forall }s\in S:s◃i{-}_{n}j=s⟹i=j$ for all $i,j\in {\mathbb{Z}}_n$. For showing the surjectivity of Φ, let $f\in \mathrm{A}\mathrm{u}\mathrm{t}\left(S\right)$ be an automorphism of S, fix any $s_0\in S$, and set $i:=\delta (s_0,f(s_0\left)\right)$. We show that $\mathrm{\Phi }\left(i\right)=f$. For all $s\in S$, $i=\delta (s_0,f(s_0\left)\right)=\delta (s_0,s){+}_n\delta (s,f(s_0\left)\right)=\delta \left(f\right(s_0),f(s\left)\right){+}_n\delta (s,f(s_0\left)\right)=\delta (s,f(s\left)\right).$ Therefore, $\left(\mathrm{\Phi }\right(i\left)\right)\left(s\right)=s◃i=s◃\delta (s,f(s\left)\right)=f\left(s\right)$ for all $s\in S$.

4. Scale morphisms

Definition 4.1

A scale morphism $(\phi ,\psi ):\sigma \to {\sigma }^{\prime }$ from a scale $\sigma :D\to C$ to a scale ${\sigma }^{\prime }:D^{\prime }\to C^{\prime }$ is a pair of cyclic morphisms $\phi :D\to D^{\prime }$ and $\psi :C\to C^{\prime }$ such that the following diagram commutes.

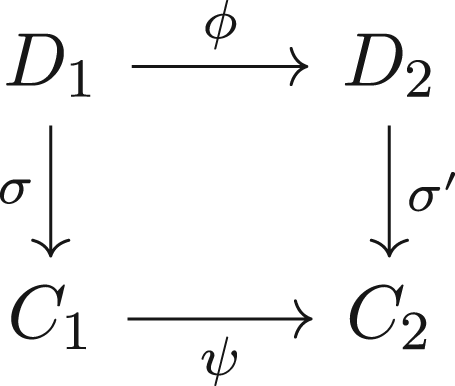
That is ${\sigma }^{\prime }\circ \phi =\psi \circ \sigma$. A scale morphism $(\phi ,\psi )$ is called a scale isomorphism if both φ and ψ are cyclic isomorphisms. A scale is called transpositionally symmetric if its automorphism group is not trivial.

 The concept of a transpositionally symmetric scale corresponds nicely to the musical notion. Consider for example the diatonic, hexatonic, and octatonic scales defined in Figure 1. The cyclic automorphism group of the C major scale is trivial whereas the cyclic automorphism groups of hexatonic and octatonic scales are isomorphic to ${\mathbb{Z}}_3$ and ${\mathbb{Z}}_4$, respectively.

Since the automorphism group of a cyclic ordered set is isomorphic to the additive cyclic group of its cardinality (see Corollary 3.11), two scales $\sigma ,{\sigma }^{\prime }:D\to C$ that share their diatonic and chromatic tones are isomorphic if and only if there exist $i\in {\mathbb{Z}}_d$ and $j\in {\mathbb{Z}}_c$ such that ${\sigma }^{\prime }(s◃i)=\sigma \left(s\right)◃j$ for all $s\in D$. We denote the fact that σ and ${\sigma }^{\prime }$ are isomorphic by $\sigma \cong {\sigma }^{\prime }$. In sum, we have $\sigma \cong {\sigma }^{\prime }⟺\mathrm{\exists }i\in {\mathbb{Z}}_d,\mathrm{\exists }j\in {\mathbb{Z}}_c\mathrm{\forall }s\in D:{\sigma }^{\prime }(s◃i)=\sigma \left(s\right)◃j.$

Theorem 4.2

For every scale $\sigma :D\to C,$ there exists an isomorphic scale ${\sigma }^{\prime }:{\mathbb{Z}}_d\to {\mathbb{Z}}_c$.

Proof.

Fix any $s_0\in D$. By Corollary 3.10, the mapping $\delta (s_0,\cdot ):D\to {\mathbb{Z}}_d$ and the mapping $\delta \left(\sigma \right(s_0),\cdot ):C\to {\mathbb{Z}}_c$ are cyclic isomorphisms. Thus, ${\sigma }^{\prime }:=\delta \left(\sigma \right(s_0),\cdot )\circ \sigma \circ \left(\delta \right(s_0,\cdot ){)}^{-1}$ is a scale from ${\mathbb{Z}}_d$ to ${\mathbb{Z}}_c$ such that the following diagram commutes.

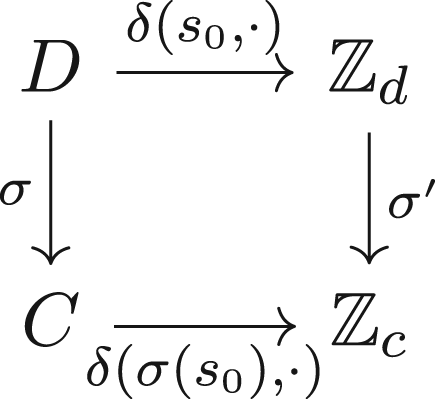
Therefore, $\left(\delta \right(s_0,\cdot ),\delta (\sigma \left(s_0\right),\cdot \left)\right):\sigma \to {\sigma }^{\prime }$ is a scale isomorphism.

The next theorem shows how our scale definition sharpens the formalization of scales used by theorists such as Clough and Douthett (1991) in their article “Maximally even sets.”. In the following quoted definition, the set $D_{c,d}$ corresponds to a scale $\sigma :{\mathbb{Z}}_d\to {\mathbb{Z}}_c$.

Definition 4.3

To indicate a subset of d pcs selected from the chromatic universe of c pcs we write $D_{c,d}=D_0,D_1,D_2,\dots ,D_{d-1}$. Thus $D_0,D_1,D_2,\dots ,D_{d-1}$ is a subset of $0,1,2,\dots ,c-1$. We generally assume $D_0<D_1<\cdots <D_{d-1}$. We say that d is the diatonic cardinality of $D_{c,d}$. We write $D(c,d)$ to represent the set of all sets.

Theorem 4.4

For each subset $S\subseteq T$ of a cyclic ordered set T, there exists exactly one cyclic ordering of S such that the identity ${\mathrm{i}\mathrm{d}}_{S,T}:S\to T,s\mapsto s$ is a scale.

Proof.

The cyclic ordering $[\cdot ,\cdot ,\cdot {]}_S$ of S is uniquely determined by the cyclic ordering $[\cdot ,\cdot ,\cdot {]}_T$ of T, since $[s_1,s_2,s_3{]}_S⟺[{\mathrm{i}\mathrm{d}}_{S,T}\left(s_1\right),{\mathrm{i}\mathrm{d}}_{S,T}\left(s_2\right),{\mathrm{i}\mathrm{d}}_{S,T}\left(s_3\right){]}_T⟺[s_1,s_2,s_3{]}_T$ must hold for all $s_1,s_2,s_3\in S$ if ${\mathrm{i}\mathrm{d}}_{S,T}$ is a scale.

5. Maximal evenness, Myhill's property, well-formedness, and the fundamental theorem of diatonic scale theory

This section presents the established scale properties maximal evenness, Myhill's property, and well-formedness, and shows their fundamental connection. Maximal evenness and Myhill's property presuppose the concept of the spectrum of a scale that maps the diatonic scale intervals to the set of their possible chromatic realizations. In a major scale for example, $\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\left(2\right)=3,4$ (any third is either a minor third spanning three semitones or a major third spanning four semitones) and $\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\left(4\right)=6,7$ (any fifth is either a diminished fifth spanning six semitones or a perfect fifth spanning seven semitones). The notion of a spectrum of an interval was introduced by Clough and Myerson (1985) as follows:

Definition 5.1

The spectrum of a scale $\sigma :D\to C$ is defined by $\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}:{\mathbb{Z}}_d\to 2^{{\mathbb{Z}}_c},i\mapsto \left\{\delta \right(\sigma \left(s\right),\sigma (s◃i))\mid s\in D\}.$

The following lemma is helpful for arguments that include the spectrum mapping. It shows that in all scales, the sum of all specific intervals of any generic size $i\in {\mathbb{Z}}_d$ equals the product of i and the scale's chromatic size.

Lemma 5.2

(Clough and Myerson 1985)

For all scales $\sigma :D\to C$ and diatonic intervals $i\in {\mathbb{Z}}_d,$ $\sum _{s\in D}\delta \left(\sigma \right(s),\sigma (s◃i\left)\right)=ci.$

Proof.

For all diatonic intervals $i\in {\mathbb{Z}}_d$, $\sum _{s\in D}\delta \left(\sigma \right(s),\sigma (s◃i\left)\right)=\sum _{s\in D}\sum _{j=0}^{i-1}\delta \left(\sigma \right(s◃j),\sigma (s◃j+1\left)\right)=\sum _{j=0}^{i-1}\sum _{t\in D}\delta \left(\sigma \right(t),\sigma (t◃1\left)\right)=\sum _{j=0}^{i-1}c$ since $D\to D$, $s\mapsto s◃j$ is bijective for all $j\in {\mathbb{Z}}_d$ by Lemma 3.9.

A maximally even scale can intuitively be understood as a scale whose tones are as evenly distributed as possible in the underlying scale, for example in the chromatic scale. While six tones can be totally evenly distributed in the chromatic scale, seven tones cannot. The result of distributing seven tones in the chromatic scale as evenly as possible gives the diatonic scale. Asymmetric maximally even scales were first studied by Clough and Myerson (1985). The general notion of maximally evenness was in introduced by Clough and Douthett (1991).

Definition 5.3

(Clough and Douthett 1991)

A scale is maximally even if the spectrum of any generic interval consists either of a single integer or two consecutive integers. It is totally even if additionally $gcd(c,d)=d$ where $gcd(c,d)$ denotes the greatest common divisor of c and d.

Definition 5.4

A scale is non-degenerate maximally even if it is maximally even and $gcd(c,d)=1$

For example, the diatonic, hexatonic, and octatonic scale shown in Figure 1 are respectively non-degenerate maximally even, not maximally even, and degenerate maximally even. The whole-tone scale ${\mathbb{Z}}_6\to {\mathbb{Z}}_{12},s\mapsto 2s$ is an example of a totally even scale. More recently, Quinn (2004) and Amiot (2007) presented an equivalent more intuitive definition of maximal evenness using the magnitude of Fourier coefficients. For a third alternative but equivalent definition using interacting weighting functions see Douthett and Krantz (2007).

We choose the term non-degenerate maximally even in analogy to non-degenerate well-formed proposed by Carey and Clampitt (1989), since both describe scales which satisfy $gcd(c,d)=1$. Note that under this definition, degenerate maximally even scales (like the octatonic scale) are “not as degenerate” as degenerate well-formed scales (like the whole-tone scale). Alternatively, degenerate and non-degenerate maximally even scales could be called transpositional symmetric and transpositional asymmetric maximally even scales, respectively. Since non-degenerate maximally even scales are the scales which were studied by Clough and Myerson (1985), Harasim, Noll, and Rohrmeier (2019) also call them Clough–Myerson scales.

Non-degenerate maximal evenness is a strong condition and Myhill's property can be seen as a generalization of it as the next lemma shows.

Definition 5.5

(Clough and Myerson 1985)

A scale has Myhill's property if the spectrum of any non-zero diatonic interval consists of exactly two distinct numbers.

Lemma 5.6

(Clough and Myerson 1985)

All non-degenerate maximally even scales have Myhill's property.

Proof.

The lemma is shown by contradiction. Assume there is a diatonic interval i and a chromatic interval a such that $\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\left(i\right)=\left\{a\right\}$ is a singleton set. Then $\frac{d}{i}=\frac{c}{a}$ and thus $c\cdot i=d\cdot a$. Since $gcd(c,d)=1$, d therefore must divide i which contradicts 0<i<d.

The concepts of generated scales and well-formed scales are additional means to characterize scales. They are – intuitively speaking – complementary or orthogonal to the spectrum mapping. The C major scale $0,2,4,5,7,9,11\subseteq {\mathbb{Z}}_{12}$ is for example generated by the chromatic interval of seven semitones beginning by F (pitch class 5), $0,7,14,21,28,35,42\equiv 5,0,7,2,9,4,11=0,2,4,5,7,9,11\mathrm{mod}12.$ It is also well-formed since there is a diatonic interval class (diatonic interval class 4 in this example) that corresponds to the 7 semitones such that the generation process can also be formulated in the diatonic domain of the scale, $3,7,11,15,19,23,27\equiv 3,0,4,1,5,2,6\mathrm{mod}7.$

Definition 5.7

(Carey and Clampitt 1989)

A scale $\sigma :D\to C$ is generated if there exists a $s\in D$ and a specific interval $g\in {\mathbb{Z}}_c$ such that $\sigma \left(D\right)=\sigma \left(s\right)◃kg|k\in {\mathbb{Z}}_d$. The interval g is then called a generating interval for σ. A scale is well-formed if additionally there is a $q\in {\mathbb{Z}}_d$ such that $\sigma (s◃kq)=\sigma \left(s\right)◃kg$ for all $k\in {\mathbb{Z}}_d$. A well-formed scale is called non-degenerate if $gcd(c,d)=1$.

Note that for a well-formed scale σ, q is invertible in ${\mathbb{Z}}_d$ since $\sigma \left(D\right)=\sigma (s◃kq)|k\in {\mathbb{Z}}_d$ implies $kq|k\in {\mathbb{Z}}_d={\mathbb{Z}}_d$.

The next theorem is what we call the fundamental theorem of diatonic scale theory. It connects the properties maximal evenness, well-formedness, and Myhill's property and will further be used for proving their characterizations in the next sections. The theorem was first stated and proven by Clough and Myerson (1985), although they did not yet use the terms maximally even and well-formed. For the example of the C major scale, we have c = 12, d = 7, s = 5 (pitch class of F), q = 4, and g = 7 as described above.

Theorem 5.8

(Clough and Myerson 1985)

Non-degenerate maximally even scales are non-degenerate well-formed. In particular, all non-degenerate maximally even scales with equal diatonic and chromatic sizes are isomorphic.

Proof.

Let σ be a non-degenerate maximally even scale. We show the existence of $q\in {\mathbb{Z}}_d$ and $g\in {\mathbb{Z}}_c$ such that $\sigma (s◃kq)=\sigma \left(s\right)◃kg$ for all $k\in {\mathbb{Z}}_d$. For all $q\in {\mathbb{Z}}_d$ there is a $g\in {\mathbb{Z}}_c$ such that $\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\left(q\right)=g,g-1$, because σ fulfills Myhill's property (Lemma 5.6). Let $\lambda :=dg-cq$. Then $(d-\lambda )g+\lambda (g-1)=qc=\sum _{s\in D}\delta \left(\sigma \right(s),\sigma (s◃q\left)\right)$ by Lemma 5.2. Since $\delta \left(\sigma \right(s),\sigma (s◃q\left)\right)\in \mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\left(q\right)=g,g-1$ for all $s\in D,$ $\mathrm{\#}s\in D|\delta \left(\sigma \right(s),\sigma (s◃q\left)\right)=a=\left\{\begin{array}{ll}\lambda ,& \mathrm{i}\mathrm{f}a=g-1\\ d-\lambda ,& \mathrm{i}\mathrm{f}a=g.\end{array}\right.$ The quantity λ is thus the number of how often the generic interval q is realized as specific interval g−1. By setting $\lambda :=1$, a g that generates σ and its corresponding diatonic size q can be obtained from the definition of λ. q is given by $\lambda \equiv -cq\mathrm{mod}d$ since $gcd(c,d)=1$ and g is given by $g=\frac{cq+\lambda }{d}$.

In particular, all non-degenerate scales with diatonic size d and chromatic size c are generated by the same interval g as calculated here and are thus isomorphic.

6. Maximal evenness and the J-function

This section shows the 1-to-1 relation between maximally even scales and the so called J-functions, introduced by Clough and Douthett (1991). This correspondence is particularly useful to show that for all diatonic and chromatic cardinalities d and c there is up to isomorphism exactly one maximally even scale. For natural numbers c, d, and m with 0<d<c and $0\le m<c$, the J-function $J_{c,d}^m$ is defined by $J_{c,d}^m:{\mathbb{Z}}_d\to {\mathbb{Z}}_c,k\mapsto ⌊\frac{kc+m}{d}⌋$ where $\lfloor \cdot \rfloor$ denotes the floor function. The number m is called the mode index of the scale. In this definition, k iterates over the diatonic tones of the scale and $J_{c,d}^m$ assigns k to the “nearest” chromatic tone that it finds, where the mode index m shifts the pattern. For example, the C major scale is the J-function $J_{12,7}^5$.

The first theorem in this section shows that all J-functions are scales. The rest of the section then shows that a scale is maximally even if and only if it is isomorphic to a J-function, formulating the argumentation by Clough and Douthett (1991) in our axiomatic framework.

Lemma 6.1

As a function $\mathbb{Z}\to \mathbb{Z},$ every J-function preserves the strict order of $\mathbb{Z}$. In particular, all J-functions are injective.

Proof.

Let $c,d,m,i,j\in \mathbb{N}$ such that $0\le i<j<d<c$ and $0\le m<c$. Then there is a positive natural number k such that i + k = j. Therefore, $\frac{ic+m}{d}+\left[\frac{kc}{d}\right]+⌊\frac{kc}{d}⌋=\frac{jc+m}{d}$ which implies $\underset{\ge ⌊\frac{ic+m}{d}⌋}{\underbrace{⌊\frac{ic+m}{d}+\left[\frac{kc}{d}\right]⌋}}+\underset{>0}{\underbrace{⌊\frac{kc}{d}⌋}}=⌊\frac{jc+m}{d}⌋,$ where $\left[x\right]$ denotes the fractional part and $\lfloor x\rfloor$ denotes the integer part of x. Thus, $J_{c,d}^m\left(i\right)<J_{c,d}^m\left(j\right)$.

Theorem 6.2

Every J-function is a scale.

Proof.

Let $c,d,m\in \mathbb{N}$ and $i,j,k\in {\mathbb{Z}}_d$ such that 0<d<c, $0\le m<c$, and $[i,j,k]$. We use the abbreviation $J:=J_{c,d}^m$ and show $\left[J\right(i),J(j),J(k\left)\right]$. Then J is a scale by Lemma 3.7. Without loss of generality, let $0\le i<j<k$. Then $J\left(i\right)<J\left(j\right)$ and $J\left(j\right)<J\left(k\right)$ by the previous lemma. Therefore, $0<J\left(j\right){-}_{c}J\left(i\right)<J\left(k\right){-}_{c}J\left(i\right)$ which is $\left[J\right(i),J(j),J(k\left)\right]$.

Lemma 6.3

For each maximally even scale σ and all divisors e of its diatonic and chromatic sizes, $\sigma (s◃\frac{d}{e})=\sigma \left(s\right)◃\frac{c}{e}$ for all $s\in D$.

Proof.

We show $\sigma (s◃\frac{d}{e})=\sigma \left(s\right)◃\frac{c}{e}$ for $s\in D$ by contradiction. Assume there is an $s\in D$ such that $\delta \left(\sigma \right(s),\sigma (s◃\frac{d}{e}\left)\right)<\frac{c}{e}$ (the case $\delta \left(\sigma \right(s),\sigma (s◃\frac{d}{e}\left)\right)>\frac{c}{e}$ is analogous). Since $\sum _{s\in D}\delta \left(\sigma \right(s),\sigma (s◃\frac{d}{e})=c\frac{d}{e}=d\frac{c}{e}$ by Lemma 5.2, there is then an $s^{\prime }\in D$ such that $\delta \left(\sigma \right(s^{\prime }),\sigma (s^{\prime }◃\frac{d}{e}\left)\right)>\frac{c}{e}$, contradicting the maximal evenness of σ.

Lemma 6.4

Let $\sigma :{\mathbb{Z}}_d\to {\mathbb{Z}}_c$ be a maximally even scale and $e\in \mathbb{N}$ a divisor of its diatonic and chromatic sizes d and c. Then the restriction $\sigma {|}_{{\mathbb{Z}}_{\frac{d}{e}}}^{{\mathbb{Z}}_{\frac{c}{e}}}:{\mathbb{Z}}_{\frac{d}{e}}\to {\mathbb{Z}}_{\frac{c}{e}},k\mapsto \sigma \left(k\right)$ is a maximally even scale.

Proof.

Lemma 6.3 implies $s\equiv t\mathrm{mod}\frac{d}{e}⟹\sigma \left(s\right)\equiv \sigma \left(t\right)\mathrm{mod}\frac{c}{e}$ for all $s,t\in {\mathbb{Z}}_d$ since $\begin{array}{rl}s\equiv t\mathrm{mod}\frac{d}{e}& ⟹\mathrm{\exists }m\in \mathbb{Z}:s=t+m\frac{d}{e}\\ & ⟹\mathrm{\exists }m\in \mathbb{Z}:\sigma \left(s\right)=\sigma (t+m\frac{d}{e})\equiv \sigma \left(t\right)+m\frac{c}{e}\mathrm{mod}c\\ & ⟹\sigma \left(s\right)\equiv \sigma \left(t\right)\mathrm{mod}\frac{c}{e}.\end{array}$ Denote $\sigma {|}_{{\mathbb{Z}}_{\frac{d}{e}}}^{{\mathbb{Z}}_{\frac{c}{e}}}$ by ${\sigma }^{\prime }$. Then $\begin{array}{rl}{\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}}_{{\sigma }^{\prime }}\left(i\right)& =\delta \left({\sigma }^{\prime }\right(s),{\sigma }^{\prime }(s◃i\left)\right)|s\in {\mathbb{Z}}_{\frac{d}{e}}\\ & =\delta \left(\sigma \right(s),\sigma (s{+}_{\frac{d}{e}}i\left)\right)|s\in {\mathbb{Z}}_{\frac{d}{e}}\\ & =\delta \left(\sigma \right(s\mathrm{m}\mathrm{o}\mathrm{d}\frac{d}{e}),\sigma (s{+}_{d}i\mathrm{m}\mathrm{o}\mathrm{d}\frac{d}{e}\left)\right)|s\in {\mathbb{Z}}_d\\ & \equiv \delta \left(\sigma \right(s),\sigma (s◃i\left)\right)|s\in {\mathbb{Z}}_d\\ & ={\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}}_{\sigma }\left(i\right)\end{array}$ modulo $\frac{c}{e}$ for all $i\in {\mathbb{Z}}_{\frac{d}{e}}$. Therefore, $\sigma {|}_{{\mathbb{Z}}_{\frac{d}{e}}}^{{\mathbb{Z}}_{\frac{c}{e}}}$ is maximally even if σ is maximally even.

The previous lemmas imply that every maximally even scale consists of $e:=gcd(c,d)$ copies of the smaller maximally even scale $\sigma {|}_{{\mathbb{Z}}_{\frac{d}{e}}}^{{\mathbb{Z}}_{\frac{c}{e}}}$. For non-degenerate maximally even scales such as the C major scale $J_{12,7}^5$, this is trivial. For the octatonic scale $J_{12,8}^0$ (induced by $0,1,3,4,6,7,9,10\subseteq {\mathbb{Z}}_{12}$; see Figure 1, right) which has transpositional symmetries, e = 4 and $\sigma {|}_{{\mathbb{Z}}_{\frac{d}{e}}}^{{\mathbb{Z}}_{\frac{c}{e}}}=\sigma {|}_{{\mathbb{Z}}_2}^{{\mathbb{Z}}_3}=J_{3,2}^0$. This octatonic scale therefore consists of 4 copies of the scale $J_{3,2}^0$ which is induced by $0,1\subseteq {\mathbb{Z}}_3$.

Theorem 6.5

(Clough and Douthett 1991)

A scale is maximally even if and only if it is isomorphic to a J-function.

Proof.

All J-functions are maximally even since $\begin{array}{rl}\delta \left(J_{c,d}^m\right(i),J_{c,d}^m(i+j\left)\right)& \equiv J_{c,d}^m(i+j)-J_{c,d}^m\left(i\right)\\ & =⌊\frac{(i+j)c+m}{d}⌋-⌊\frac{ic+m}{d}⌋\\ & =⌊⌊\frac{ic+m}{d}⌋+\left[\frac{ic+m}{d}\right]+\frac{jc}{d}⌋-⌊\frac{ic+m}{d}⌋\\ & =⌊\left[\frac{ic+m}{d}\right]+\frac{jc}{d}⌋\\ & \in \left\{⌊\frac{jc}{d}⌋,⌊\frac{jc}{d}⌋+1\right\}\end{array}$ modulo c for all $c,d\in \mathbb{N}$ with 0<d<c, $i,j\in {\mathbb{Z}}_d$, and $m\in {\mathbb{Z}}_c$.

We now show that all maximally even scales that share the same diatonic and chromatic sizes are isomorphic. It then follows that every maximally even scale is isomorphic to a J-function since every J-function is maximally even.

Let σ be a maximally even scale and $e:=gcd(c,d)$. By Lemma 6.4, $\sigma {|}_{{\mathbb{Z}}_{\frac{d}{e}}}^{{\mathbb{Z}}_{\frac{c}{e}}}$ is maximally even and thus unique up to isomorphism according to its diatonic and chromatic sizes by Theorem 5.8. Therefore σ is also unique up to isomorphism according to its diatonic and chromatic sizes, since Lemma 6.3 implies that σ consists of e copies of $\sigma {|}_{{\mathbb{Z}}_{\frac{d}{e}}}^{{\mathbb{Z}}_{\frac{c}{e}}}$.

To sum up, this section showed how maximally even scales can be understood. On the one hand, there is up to isomorphism one unique maximally even scale for each diatonic and chromatic size and this scale is given in closed form by a J-function. On the other hand, there are two distinguished kinds of maximally even scales: non-degenerate (without proper transpositional symmetries) and degenerate (with proper transpositional symmetries) where each degenerate maximally even scale can be obtained from a non-degenerate maximally even scale by copying it multiple times.

7. The equivalence of Myhill's property and non-degenerate well-formedness

Lemma 7.1

A scale that has Myhill's property fulfills $gcd(c,d)=1$.

Proof.

Assume $gcd(c,d)=:e\ne 1$. Then $\sum _{s\in D}\delta \left(\sigma \right(s),\sigma (s◃\frac{d}{e}\left)\right)=c\frac{d}{e}=d\frac{c}{e}$ by Lemma 5.2. Therefore, Myhill's property implies the existence of a positive natural number $n<\frac{c}{e}$ and a partition $D_1\cup D_2=D$ of D into two not empty disjunct sets such that $\delta \left(\sigma \right(s),\sigma (s◃\frac{d}{e}\left)\right)\equiv \frac{c}{e}-n\mathrm{mod}c$ for all $s\in D_1$ and $\delta \left(\sigma \right(s),\sigma (s◃\frac{d}{e}\left)\right)\equiv \frac{c}{e}+n\mathrm{mod}c$ for all $s\in D_2$. Thus, either $\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\left(2\frac{d}{e}\right)\equiv \left\{2\frac{c}{e}\right\}\mathrm{mod}c$ in case $D_1$ and $D_2$ alternate, or $\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\left(2\frac{d}{e}\right)\equiv \left\{2\right(\frac{c}{e}-n),2\frac{c}{e},2(\frac{c}{e}+n\left)\right\}\mathrm{mod}c$ otherwise, contradicting Myhill's property.

Definition 7.2

A scale that has Myhill's property is reduced if $\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\left(1\right)=\{1,2\}$.

Lemma 7.3

Reduced scales that have Myhill's property are non-degenerate maximally even.

Proof.

Let $\sigma :D\to C$ be a reduced scale that has Myhill's property. Then $\mathrm{\#}\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\left(i\right)=2$ for all $i\in {\mathbb{Z}}_d$ and $\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\left(1\right)=1,2$. We show that the spectra of all non-zero intervals consist of consecutive integers. Let $i\in {\mathbb{Z}}_d$. Then $\begin{array}{rl}\delta \left(\sigma \right(s),\sigma (s◃i\left)\right)-\delta \left(\sigma \right(s◃1),\sigma (s◃i+1\left)\right)& \equiv \delta \left(\sigma \right(s),\sigma (s◃1\left)\right)+\delta \left(\sigma \right(s◃1),\sigma (s◃i\left)\right)\\ & -\delta \left(\sigma \right(s◃1),\sigma (s◃i\left)\right)\\ & -\delta \left(\sigma \right(s◃i),\sigma (s◃i+1\left)\right)\\ & \equiv \underset{\in 1,2}{\underbrace{\delta \left(\sigma \right(s),\sigma (s◃1\left)\right)}}-\underset{\in 1,2}{\underbrace{\delta \left(\sigma \right(s◃i),\sigma (s◃i+1\left)\right)}}\end{array}$ modulo c. Therefore, $\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\left(i\right)$ consists of consecutive integers.

We prove the equivalence of Myhill's property and non-degenerate well-formedness using the concept of interval words of scales. The connection between interval words and well-formed scales was first described by Clampitt, Domìnguez, and Noll (2007) and Domínguez, Clampitt, and Noll (2009). Further studies on this topic include for example Castrillon Lopez and Domìnguez Romero (2016) and a recent special issue of the Journal of Mathematics and Music (Brlek, Chemillier, and Reutenauer 2018).

Definition 7.4

Let $\sigma :D\to C$ be a scale with $\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\left(1\right)=a_1,\dots ,a_n$ where $a_1<\cdots <a_n$. An interval word of σ is a word w such that $w_k=i:⟺\delta \left(\sigma \right(s◃k),\sigma (s◃k+1\left)\right)=a_i$ for all $k\in {\mathbb{Z}}_d$ and some $s\in D$ where $w_k$ denotes the kth letter of the word w. Two scales $\sigma :D\to C$ and ${\sigma }^{\prime }:D\to C^{\prime }$ are equivalent under the interval word relation, denoted by $\sigma \approx {\sigma }^{\prime }$, if they have a common interval word.

Note that the letters of interval words are the indices of the intervals in the totally ordered set $\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\left(1\right)$. Interval words therefore do not contain information about the concrete sizes of the intervals, but only information about the ordering of the interval sizes. Consider for example the pentatonic scale σ induced by $0,3,5,7,10\subseteq {\mathbb{Z}}_{12}$. The interval words of this scale are the cyclic permutations of 21121, because $\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\left(1\right)=2,3$. The scale ${\sigma }^{\prime }$, induced by $0,3,4,7,10\subseteq {\mathbb{Z}}_{11}$, has the same class of interval words as σ. Therefore, $\sigma \approx {\sigma }^{\prime }$. Since σ is maximally even but ${\sigma }^{\prime }$ is not, this example shows that maximal evenness is not invariant under the interval word relation.

Lemma 7.5

Myhill's property and well-formedness are invariant under the interval word relation.

Proof.

Let $\sigma :D\to C$ and ${\sigma }^{\prime }:D\to C^{\prime }$ be equivalent scales and let $a_1,\dots ,a_n$ and $b_1,\dots ,b_n$ be natural numbers such that for all $k\in {\mathbb{Z}}_d$ there is an $i_k$ with $\delta \left(\sigma \right(s◃k),\sigma (s◃k+1\left)\right)=a_{i_k}⟺\delta \left({\sigma }^{\prime }\right(s◃k),{\sigma }^{\prime }(s◃k+1\left)\right)=b_{i_k}.$ For all $s,t\in D$, there then exist non-negative ${\lambda }_1,\dots ,{\lambda }_n\in \mathbb{N}$ such that $\delta \left(\sigma \right(s),\sigma (t\left)\right)=\sum _i{\lambda }_i{a}_i⟺\delta \left({\sigma }^{\prime }\right(s),{\sigma }^{\prime }(t\left)\right)=\sum _i{\lambda }_i{b}_i.$ In particular, $\mathrm{\#}{\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}}_{\sigma }\left(i\right)=\mathrm{\#}{\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}}_{{\sigma }^{\prime }}\left(i\right)$ for all $i\in {\mathbb{Z}}_d$ which implies that σ has Myhill's property if and only if ${\sigma }^{\prime }$ has.

Furthermore if σ is well-formed, then there exist $s\in D$, $q\in {\mathbb{Z}}_d$, and ${\hat{\lambda }}_1,\dots ,{\hat{\lambda }}_n\in \mathbb{N}$ such that for all $k\in 0,\dots ,d-2$ $\delta \left(\sigma \right(s◃kq),\sigma (s◃(k+1)q\left)\right)=\sum _i{\hat{\lambda }}_i{a}_i.$ Therefore, $\delta \left({\sigma }^{\prime }\right(s◃kq),{\sigma }^{\prime }(s◃(k+1)q\left)\right)=\sum _i{\hat{\lambda }}_i{b}_i$ for all $k\in 0,\dots ,d-2$ and ${\sigma }^{\prime }$ is thus well-formed.

Theorem 7.6

(Carey and Clampitt 1996)

A scale has Myhill's Property if and only if it is non-degenerate well-formed.

Proof.

($⟸$) We first show that non-degenerate well-formed scales have Myhill's property. For this, let $\sigma :D\to C$ be a well-formed scale with $gcd(c,d)=1$. Then there exist $s\in D$, $q\in {\mathbb{Z}}_d$, and $g\in {\mathbb{Z}}_c$ such that $\sigma (s◃kq)=\sigma \left(s\right)◃kg$ for all $k\in {\mathbb{Z}}_d$. Thus, $\delta \left(\sigma \right(s◃kq),\sigma (s◃(k+1)q\left)\right)=g$ for all $k\in 0,\dots ,d-2$ and $\delta \left(\sigma \right(s◃(d-1)q),\sigma (s\left)\right)\equiv -\delta \left(\sigma \right(s),\sigma (s◃(d-1)q\left)\right)\equiv -(d-1)g=g-dg$ modulo c. In the following, we calculate $\delta \left(\sigma \right(t),\sigma (t◃i\left)\right)$ for arbitrary $t\in D$ and $i\in {\mathbb{Z}}_d$ to show $\mathrm{\#}\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\left(i\right)=2$. Let $j:=\delta (s,t)$. Since $gcd(q,d)=1$, there exist unique $k,l\in {\mathbb{Z}}_d$ such that $i\equiv kq$ and $j\equiv lq$ modulo d. Therefore, $\delta \left(\sigma \right(t),\sigma (t◃i\left)\right)=\delta \left(\sigma \right(s◃j),\sigma (s◃i+j\left)\right)=\delta \left(\sigma \right(s◃lq),\sigma (s◃(k+l)q\left)\right)$ If $k+l\le d-1$, then $\delta \left(\sigma \right(s◃lq),\sigma (s◃(k+l)q\left)\right)=\delta \left(\sigma \right(s)◃lg,\sigma (s)◃(k+l\left)g\right)\equiv kg$ modulo c. If otherwise $k+l\ge d$, then $\begin{array}{rl}\delta \left(\sigma \right(s◃lq),\sigma (s◃(k+l)q\left)\right)& =\delta \left(\sigma \right(s)◃lg,\sigma (s)◃(k+l-1)g+(g-dg\left)\right)\\ & \equiv (k-1)g+g-dg\\ & \equiv kg-dg\end{array}$ modulo c and $dg\not\equiv 0$ modulo c, because $gcd(c,d)=1$.

($⟹$) We now show that a scale which has Myhill's property is non-degenerate well-formed. Let $\sigma :D\to C$ be a scale with $\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\left(1\right)=\{a_1,a_2\}$ that has Myhill's property. We construct a reduced scale ϱ with $\varrho \approx \sigma$ by $\varrho \left(0\right)=\sigma \left(0\right)\mathrm{a}\mathrm{n}\mathrm{d}\varrho (k◃1)=\left\{\begin{array}{ll}\varrho \left(k\right)◃1,& \mathrm{i}\mathrm{f}\delta \left(\sigma \right(k),\sigma (k◃1\left)\right)=a_1\\ \varrho \left(k\right)◃2,& \mathrm{i}\mathrm{f}\delta \left(\sigma \right(k),\sigma (k◃1\left)\right)=a_2\end{array}\right.$ for $k\in {\mathbb{Z}}_d$. Since $\varrho \approx \sigma$ and ϱ is reduced, $\begin{array}{rl}\sigma \mathrm{h}\mathrm{a}\mathrm{s}\mathrm{M}\mathrm{y}\mathrm{h}\mathrm{i}\mathrm{l}{\mathrm{l}}^{\prime }\mathrm{s}\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{t}\mathrm{y}& ⟹\varrho \mathrm{h}\mathrm{a}\mathrm{s}\mathrm{M}\mathrm{y}\mathrm{h}\mathrm{i}\mathrm{l}{\mathrm{l}}^{\prime }\mathrm{s}\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{t}\mathrm{y}\\ & ⟹\varrho \mathrm{i}\mathrm{s}\text{non-degenerate maximally even}\\ & ⟹\varrho \mathrm{i}\mathrm{s}\text{well-formed}\\ & ⟹\sigma \mathrm{i}\mathrm{s}\text{well-formed}.\end{array}$ by Lemma 7.5, Lemma 7.3, Theorem 5.8, and again Lemma 7.5, respectively. $gcd(c,d)=1$ follows additionally from σ having Myhill's property by Lemma 7.1.

The first part of the proof of Theorem 7.6 $(⟸)$ is elementary and in a similar way already presented by Carey and Clampitt (1989). The second part $(⟹)$ was first proven by Carey and Clampitt (1996), also in an elementary way. In contrast, our new proof of this established theorem connects it closer 1) to the theory of maximally even sets by factoring out Theorem 5.8 and 2) to combinatory word theory by utilizing the fact that well-formedness and Myhill's property only depend on the interval word of a scale.

To sum up, this section characterized the different kinds of well-formed scales. The first kind, degenerate well-formed scales, are scales that are generated by a generator that is not coprime to the chromatic size of the scale. All these scales are subscales of a totally even scale. The second kind are maximally even scales that do not have transpositional symmetries. The third and last kind are scales that are pumped-up versions of scales of the second kind. They also have Myhill's property, but are not maximally even.

8. Summary and conclusion

This paper proposes an axiomatic algebraic framework to model musical scales. It utilizes cyclic order relations to define scales as embeddings of cyclic ordered sets and to express their properties and relations. This is the first paper that brings together the core results and arguments of diatonic scale theory into a uniform system to study symmetry properties of scales. We did not state new propositions but reformulated fundamental theorems and proofs in a modern mathematical language. This improves existing frameworks by providing a firmer foundation for future research. We particularly hope that it also will help to establish new connections to related fields such as music cognition and computational musicology.

Additionally, we provided a new more sophisticated proof for the equivalence of Myhill's property and non-degenerate well-formedness. In particular, we showed that the fundamental theorem of diatonic scale theory (Theorem 5.8) can be used to prove both, the characterization of maximally even scales through the J-function and the characterization of non-degenerate well-formedness by Myhill's property.

There are two main directions on which future work can proceed from this paper. The first one is to incorporate other scale properties into the unified framework and to study mathematically the commonalities and differences of the symmetry properties of scales and rhythms from different cultures. The second direction is to use the presented scale-theoretic basis to study voice-leading induced geometries as proposed by Harasim, Schmidt, and Rohrmeier (2016).

Acknowledgments

The authors would like to thank Thomas Fiore, Fabian C. Moss, Christoph Finkensiep, the editors Jason Yust and Emmanuel Amiot, and the anonymous reviewer for their constructive and helpful comments on previous versions of this paper.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (GA Nr 760081) as well as the Zukunftskonzept at TU Dresden funded by the Exzellenzinitiative of the Deutsche Forschungsgemeinschaft. We thank Claude Latour for supporting this research through the Latour Chair in Digital Musicology.

Notes

1 with the notable exceptions of scales used in Jazz and extended tonality of western music of the nineteenth century.

Appendix 1.

Proofs of Section 3

Proposition A.1

(Lewin 1987)

Generalized interval systems $(S,\delta ,I)$ and regular group actions $◃:S\times I\to S$ are in 1-to-1 relation by $\delta (s,t)=i⟺s◃i=t$ for $s,t\in S$ and $i\in I$.

Proof.

Let fist $(S,\delta ,I)$ be a generalized interval system. Then $◃$, defined by $s◃i=t:⟺\delta (s,t)=i$ for $s,t\in S$ and $i\in I$ is a regular group action. It is a group action since 1) $\delta (s,s)=0$ implies $s◃0=s$ and 2) $\begin{array}{rl}(s◃i)◃j& =(s◃\delta (s,t\left)\right)◃\delta (t,u)\\ & =t◃\delta (t,u)\\ & =u\\ & =s◃\delta (s,u)\\ & =s◃\left(\delta \right(s,t)+\delta (t,u\left)\right)\\ & =s◃(i+j)\end{array}$ for $s,t,u\in S$ with $\delta (s,t)=i$ and $\delta (t,u)=j$. The regularity of $◃$ follows from the bijectivity of δ in the second argument. Let in converse be $◃:S\times I\to S$ a regular group action. Then δ, defined by $\delta (s,t)=i:⟺s◃i=t$ for $s,t\in S$ and $i\in I$ is the interval mapping of the generalized interval system $(S,\delta ,I)$ since $\delta (s,t)+\delta (t,u)=\delta (s,u)$ for $s,t,u\in S$ follows from $s◃\left(\delta \right(s,t)+\delta (t,u\left)\right)=(s◃\delta (s,t\left)\right)◃\delta (t,u)=t◃\delta (t,u)=u=s◃\delta (s,u)$ with the injectivity of $◃(s,\cdot )$. The bijectivity of δ in the second argument follows from the regularity of $◃$. It is moreover obvious that the presented constructions which translate between generalized interval systems and regular group actions are inverse to each other.

Lemma A.2

Let $(S,[\cdot ,\cdot ,\cdot \left]\right)$ be a cyclic ordered set. Then for all $s,u\in S$ with $s\ne u,\overline{(s,u]}=(u,s],$ where $\overline{(s,u]}$ denotes the complement $\overline{(s,u]}:=Sminus(s,u]$.

Proof.

For all $s,t,u\in S$ with $s\ne u$, $\begin{array}{rl}t\in \overline{(s,u]}& ⟹\mathrm{n}\mathrm{o}\mathrm{t}\left(\right([s,t,u]\mathrm{o}\mathrm{r}t=u)\mathrm{a}\mathrm{n}\mathrm{d}t\ne s)\\ & ⟹\left(\right([s,u,t]\mathrm{a}\mathrm{n}\mathrm{d}t\ne u)\mathrm{o}\mathrm{r}t=s)\\ & ⟹\left(\right[s,u,t]\mathrm{o}\mathrm{r}t=s)\mathrm{a}\mathrm{n}\mathrm{d}(t\ne u\mathrm{o}\mathrm{r}t=s)\\ & ⟹\left(\right[u,t,s]\mathrm{o}\mathrm{r}t=s)\mathrm{a}\mathrm{n}\mathrm{d}t\ne u\\ & ⟹t\in (u,s].\end{array}$ Therefore, $\overline{(s,u]}\subseteq (u,s]$ and thus also $(u,s]=\overline{\overline{(u,s]}}\subseteq \overline{(s,u]}$.

Lemma A.3

Let $(S,[\cdot ,\cdot ,\cdot \left]\right)$ be a cyclic ordered set. Then for all distinct $s,t,u\in S,$ the following are equivalent.

1. $[s,t,u]$

2. $(s,t]\cup (t,u]=(s,u],(t,u]\cup (u,s]=(t,s],\mathrm{a}\mathrm{n}\mathrm{d}(u,s]\cup (s,t]=(u,t]$

3. $(s,t]\cap (t,u]=(t,u]\cap (u,s]=(u,s]\cap (s,t]=\mathrm{\varnothing }$

4. $(s,u]\cup (u,t]=(u,t]\cup (t,s]=(t,s]\cup (s,u]=S$

5. $(s,u]\cap (u,t]=(s,t],(u,t]\cap (t,s]=(u,s],\mathrm{a}\mathrm{n}\mathrm{d}(t,s]\cap (s,u]=(t,u]$

Proof.

We show the equivalences in two cycles, proving $\left(i\right)⟹\left(ii\right)⟹\left(v\right)$, and $\mathrm{\neg }\left(i\right)⟹\mathrm{\neg }\left(v\right)$, and $\left(i\right)⟹\left(iii\right)⟹\left(iv\right)$, and $\mathrm{\neg }\left(i\right)⟹\mathrm{\neg }\left(iv\right)$. In any step, we prove only one of the three equalities. The other two ones follow always analogously.

$\left(i\right)⟹\left(ii\right)$. We show $(s,t]\cup (t,u]\subseteq (s,u]$ and $(s,t]\cup (t,u]\supseteq (s,u]$. Let $v\in (s,t]\cup (t,u]$. Then either $[s,v,t]$ or v = t or $[t,v,u]$ or v = u. Therefore, $[s,v,u]$ or v = u, since $[s,t,u]$. Thus, $v\in (s,u]$. Let in converse be $v\in (s,u]$. If v = u then $v\in (t,u]$. Otherwise either $[s,v,t]$, implying $v\in (s,t]$, or $[s,t,v]$. The latter and $[u,s,v]$ imply $[u,t,v]$ and thus $v\in (t,u]$. In any case, $v\in (s,t]\cup (t,u]$.

$\left(ii\right)⟹\left(v\right)$. We show $(s,u]\cap (u,t]=(s,t]$. Since $(t,u]\cup (u,s]=(t,s]$, $(s,u]\cap (u,t]=\overline{(t,u]\cup (u,s]}=\overline{(t,s]}=(s,t]$ by Lemma A.2.

$\mathrm{\neg }\left(i\right)⟹\mathrm{\neg }\left(v\right)$. Since $[s,u,t]$, $(s,u]\cap (u,t]=\mathrm{\varnothing }\ne (s,t]$ by the argumentation of $\left(i\right)⟹\left(iii\right)$.

$\left(i\right)⟹\left(iii\right)$ Let $v\in (s,t]\cap (t,u]$. Then $[s,v,t]$ or v = t, and $[t,v,u]$ or v = u. Therefore, $\left(\right[s,v,t\left]\mathrm{a}\mathrm{n}\mathrm{d}\right[t,v,u\left]\right)\mathrm{o}\mathrm{r}[s,v,t]\mathrm{a}\mathrm{n}\mathrm{d}v=u\left)\mathrm{o}\mathrm{r}\right(v=t\mathrm{a}\mathrm{n}\mathrm{d}[t,v,u]\left)\mathrm{o}\mathrm{r}\right(v=t\mathrm{a}\mathrm{n}\mathrm{d}v=u).$ Hence, $[t,s,u]\mathrm{o}\mathrm{r}[s,u,t]\mathrm{o}\mathrm{r}[t,t,u]\mathrm{o}\mathrm{r}t=u$ which contradicts $[s,t,u]$. There thus does not exist a $v\in (s,t]\cap (t,u]$, implying $(s,t]\cap (t,u]=\mathrm{\varnothing }$.

$\left(iii\right)⟹\left(iv\right)$. We show $(s,u]\cup (u,t]=S$. Since $(t,u]\cap (u,s]=\mathrm{\varnothing }$, $(s,u]\cup (u,t]=\overline{(t,u]\cap (u,s]}=\overline{\mathrm{\varnothing }}=S$ by Lemma A.2.

$\mathrm{\neg }\left(i\right)⟹\mathrm{\neg }\left(iv\right)$. Since $[s,u,t]$, $(s,u]\cup (u,t]=(s,t]\ne S$ by the argumentation of $\left(i\right)⟹\left(ii\right)$.

Proposition A.4

Let $(S,[\cdot ,\cdot ,\cdot \left]\right)$ be a cyclic ordered set. Then $(S,\delta ,{\mathbb{Z}}_{\mathrm{\#}S})$ with $\delta :S\times S\to {\mathbb{Z}}_{\mathrm{\#}S},\delta (s,t)=\mathrm{\#}(s,t]$ is a generalized interval system.

Proof.

Denote the cardinality of S by n. We first show $\delta (s,t)+\delta (t,u)\equiv \delta (s,u)$ mod n for any pairwise distinct $s,t,u\in S$ considering two cases. If s, t, and u are not pairwise distinct, one of $\delta (s,t)$, $\delta (t,u)$, and $\delta (s,u)$ is zero and the equality holds trivially.

Case 1: $(s,t]\cap (t,u]=\mathrm{\varnothing }$. Then $[s,t,u]$ by Lemma A.3. Therefore, $\delta (s,t)+\delta (t,u)=\mathrm{\#}(s,t]+\mathrm{\#}(t,u]=\mathrm{\#}\left(\right(s,t]\cup (t,u\left]\right)=\mathrm{\#}(s,u]=\delta (s,u).$ Case 2: $(s,t]\cap (t,u]\ne \mathrm{\varnothing }$. Then $[s,u,t]$ by Lemma A.3. Therefore, $\begin{array}{rl}\delta (s,t)+\delta (t,u)& =\mathrm{\#}(s,t]+\mathrm{\#}(t,u]\\ & =\mathrm{\#}\left(\right(s,t]\cup (t,u\left]\right)-\mathrm{\#}\left(\right(s,t]\cap (t,u\left]\right)\\ & =S+\mathrm{\#}(s,u]\\ & \equiv \mathrm{\#}(s,u]\\ & =\delta (s,u)\end{array}$ mod n by Lemma A.3.

We show now by induction over ${\mathbb{Z}}_n$ that $\delta (s,\cdot ):S\to {\mathbb{Z}}_n$ is bijective for any $s\in S$. The base case follows from $\delta (s,s)=\mathrm{\#}(s,s]=0$. For the inductive step, let $u\in S$ be the unique element of S with $\delta (s,u)=i$. A $t\in S$ with $\delta (s,t)=i+1$ can be found using the following procedure. At first, choose randomly some $t\in S$ that is distinct from u. If $\mathrm{\neg }[u,v,t]$ holds for all $v\in S$, then $\delta (s,t)\equiv \delta (s,u)+\delta (u,t)=i+\mathrm{\#}(u,t]=i+1$ mod n. If otherwise there is a $v\in S$ with $[u,v,t]$, then set t: = v and iterate. The algorithm terminates since S is finite. For showing the uniqueness of the found t, assume there are distinct $t_1,t_2\in S$ with $\delta (u,t_1)=1=\delta (u,t_2)$. Then $(u,t_1]=t_1$ and $(u,t_2]=t_2$. Since either $[u,t_1,t_2]$ or $[u,t_2,t_1]$, either $t_1\in (u,t_2]$ or $t_2\in (u,t_1]$, implying $t_1=t_2$ which contradicts the assumption.

Theorem A.5

Finite cyclic ordered sets $(S,[\cdot ,\cdot ,\cdot \left]\right),$ finite generalized interval systems $(S,\delta ,{\mathbb{Z}}_n),$ and regular group actions $◃:S\times {\mathbb{Z}}_n\to S$ are in one-to-one relation by $[s,t,u]⟺0<\delta (s,t)<\delta (s,u),\delta (s,t)=\mathrm{\#}(s,t],\mathrm{a}\mathrm{n}\mathrm{d}s◃i=t⟺\delta (s,t)=i$ for $s,t,u\in S$ and $i\in {\mathbb{Z}}_n$ where $n:=\mathrm{\#}S$ is the cardinality of S and ${\mathbb{Z}}_n$ denotes the additive cyclic group of cardinality n.

Proof.

The one-to-one relation between generalized interval systems and regular group actions is shown in Theorem 3.3. Theorem 3.4 shows further that $(S,\delta ,{\mathbb{Z}}_{\mathrm{\#}S})$ with $\delta :S\times S\to {\mathbb{Z}}_{\mathrm{\#}S},\delta (s,t)=\mathrm{\#}(s,t]$ is a generalized interval system. We first here show that for all generalized interval systems $(S,\delta ,{\mathbb{Z}}_{\mathrm{\#}S})$, the relation $[s,t,u]:⟺\delta (s,t)<\delta (s,u)$ is a cyclic ordering on S.

Since < is a strict total order on $\mathbb{N}$, the binary relation ${\le }_s$ defined by $t{\le }_{s}u:⟺\delta (s,t)<\delta (s,u)$ is a strict total order on S. Hence, $[\cdot ,\cdot ,\cdot ]$ is a cyclic order. For the cyclicality, let $s,t,u\in S$ with $[s,t,u]$ and $n=\mathrm{\#}S$. Then, $\delta (s,t)<\delta (s,u)$ and therefore $\begin{array}{rl}\delta (t,u)& =\delta (t,s){+}_n\delta (s,u)\\ & =\delta (s,u){-}_n\delta (s,t)\\ & =\delta (s,u)-\delta (s,t)\\ & <n-\delta (s,t)\\ & ={-}_n\delta (s,t)\\ & =\delta (t,s),\end{array}$ where ${+}_n$ and ${-}_n$ denote the addition and subtraction modulo n, and + and − denote the usual addition and subtraction of integers. Thus, $\delta (t,u)<\delta (t,s)$ which is $[t,u,s]$ by definition, proving the cyclicality.

We now show that the presented constructions that translate cyclic ordered sets into generalized interval systems and vice versa are inverse. Let $(S,[\cdot ,\cdot ,\cdot \left]\right)$ be a cyclic ordered set and $\delta (s,u):=\mathrm{\#}[s,u)$. We show that $[s,t,u]⟺\delta (s,t)<\delta (s,u)(⟺:[s,t,u{]}^{\prime })$. (⇒) Let $s,t,u\in S$ be pairwise distinct elements with $[s,t,u]$. For all $v\in S$ with $[s,v,t]$, $[s,v,u]$ by transitivity. Therefore, $(s,t)\subseteq (s,u)$ implying $\mathrm{\#}[s,t)<\mathrm{\#}[s,u)$ which is $[s,t,u{]}^{\prime }$ by definition.

(⇐) Let $s,t,u\in S$ be pairwise distinct elements with $[s,t,u{]}^{\prime }$. Since $[\cdot ,\cdot ,\cdot ]$ is anitsymmetric, either $[s,t,u]$ or $[s,u,t]$ must hold. Assume that $[s,u,t]$. Then, we have $[s,u,t{]}^{\prime }$ analogously to the if part, contradicting $[s,t,u{]}^{\prime }$ and the cyclicality of $[\cdot ,\cdot ,\cdot {]}^{\prime }$. Therefore, $[s,t,u]$.

Let now $(S,\delta ,{\mathbb{Z}}_{\mathrm{\#}S})$ be a generalized interval system. We show that $\delta (s,u)=\mathrm{\#}[s,u):=\{t\in S\mid \delta (s,t)<\delta (s,u\left)\right\}$ for $s,u\in S$. Since $\delta (s,\delta (s,\cdot {)}^{-1}\left(i\right))=i$ for any $i\in {\mathbb{Z}}_{\mathrm{\#}S}$, $\delta (s,\cdot {)}^{-1}(\{0,1,\dots ,\delta (s,u)-1\})=\{t\in S\mid \delta (s,t)<\delta (s,u)\}.$ Together with the bijectivity of $\delta (s,\cdot {)}^{-1}$, this implies $\delta (s,u)=\mathrm{\#}[s,u)$.

Corollary A.6

The interval mapping is invariant under musical transposition.

Proof.

Let S be cyclic ordered and $n=\mathrm{\#}S<\mathrm{\infty }$, $s,t\in S$, and $i\in {\mathbb{Z}}_n$. Then $\begin{array}{rl}t◃i& =s◃\delta (s,t◃i)\\ & =s◃\delta (s,t){+}_n\delta (t,t◃i)\\ & =s◃\delta (s,t){+}_{n}i\\ & =(s◃i)◃\delta (s,t).\end{array}$ Therefore, $\delta (s◃i,t◃i)=\delta (s,t)$.