Why topology?

Abstract

Music theorists have modeled voice leadings as paths through higher-dimensional configuration spaces. This paper uses topological techniques to construct two-dimensional diagrams capturing these spaces’ most important features. The goal is to enrich set theory’s contrapuntal power by simplifying the description of its geometry. Along the way, I connect homotopy theory to “transformational theory,” show how set-class space generalizes the neo-Riemannian transformations, extend the Tonnetz to arbitrary chords, and develop a simple contrapuntal “alphabet” for describing voice leadings. I mention several compositional applications and analyze short excerpts from Gesualdo, Mozart, Wagner, Stravinsky, Schoenberg, Schnittke, and Mahanthappa.

Keywords:

• Topology
• voice leading
• geometrical music theory
• neo-Riemannian theory
• contextual inversion

Geometrical music theory models n-voice chords as points in a generalized donut, a twisted, mirrored, higher-dimensional orbifold that is difficult to visualize and understand. Some theorists have simply recorded how music moves through these spaces, relying on the reader’s visual intuition to convert geometrical paths into analytically useful observations. Others have described parts of the geometry, typically graphing single-step voice leading among the nearly even chords in some particular scale (Douthett and Steinbach 1998; Tymoczko 2011, §3.11). This restriction has been justified on the grounds that maximally even sonorities are optimal from various points of view (e.g. combining harmonic consistency with stepwise voice leading). But we do not have to look hard to find successful music departing from optimality: more than fifty years ago Herbert Simon criticized the tendency to overemphasize the superlative, coining the term “satisficing” to refer to the pursuit of the merely good-enough (Simon 1956). Hence the need for voice-leading models applying to arbitrary chords and scales – including those that might not be theoretically ideal.

This paper will use topology for this purpose, proposing simple models of the voice-leading relations among arbitrary chords and set classes. The paper’s main innovation is to associate structural features of existing geometrical spaces (such as “loops” and “boundaries”) with familiar voice-leading transformations (such as “transpositions along the chord,” “voice exchanges,” and “generalized neo-Riemannian transformations”). This leads to two-dimensional representations of voice leading that are structure-neutral, applying to any chord in any scale and hence freeing us from the constraints of near-evenness and single-step voice leading. These representations simultaneously describe the topology of the higher-dimensional voice-leading spaces and the algebraic structure of the voice leadings connecting chords, with transformational theory providing a tool for exploring the geometry of contrapuntal possibility. This in turn will lead me to distinguish two different sorts of musical transformation, global symmetries that show us how to fold up musical space and the contrapuntal possibilities that describe how we can move around the resulting geometry.

My argument is long and detailed, so it may help to keep the following picture in mind. Musical symmetries create configuration spaces whose features correspond to different kinds of voice leading; attending to some subset of voice-leading possibilities leads to simplified models containing only the relevant geometrical features. To understand the geometry it is therefore useful to understand voice-leading transformations and vice versa. The (bijective) voice leadings from a chord to any of its transpositions can be decomposed into a sequence of simpler voice leadings VTR, where V is a (possibly complicated) voice exchange, T is a transposition along the scale moving every note in the same direction by the same number of steps, and R is a “residual” to be described momentarily.¹ These voice leadings can be associated with elements in what is called the “fundamental group” of voice-leading space, recording the various kinds of loops to be found in the n-dimensional mirrored donut modeling n-note chords; intuitively the voice crossings V correspond to the mirrored boundaries of chord space while the transpositions T are associated with its circular dimension. The voice exchanges and transpositional voice leadings generate normal subgroups which can be safely ignored (abstracted-away-from or “quotiented out”). Deemphasizing voice exchanges is broadly familiar from Schenkerian analysis and characteristic of the two-dimensional annular spaces in §2 below; it corresponds to disregarding the singular, mirrored boundaries of chord space.² Deemphasizing transposition is familiar from set theory and embodied in the two-dimensional polygonal diagrams of §3–4; it corresponds to disregarding the circular dimension of chord space. In transpositional set-class space, the “residual” voice leadings are “transpositions along the chord” to be discussed below. In inversional set-class space, the residual voice leadings generalize the familiar transformations of neo-Riemannian theory. Topology thus connects diverse music-theoretical fields from Schenkerian analysis to set theory to neo-Riemannian theory.

One practical benefit of these ideas is to clarify the music-theoretical notion of inversion. As we will see in §§2–3, the residual transpositions along the chord are forms of registral inversion, described by terms like “root position,” “first inversion,” and “second inversion.” But where traditional theory is concerned only with a chord’s lowest note, constructing inversions by successively moving bass to soprano, the geometrical approach preserves chordal spacing as measured in chordal steps; this is useful in contexts where spacing is musically significant. The residual transformations of inversional set-class space (§4) extend this idea to what set theorists call pitch- or pitch-class inversion, an operation that turns musical space upside-down; these generalizations of the familiar neo-Riemannian transformations again preserve spacing as measured in chordal steps. As we will see, the residual transformations operate similarly on both notes and voices: a “transposition along the chord” sends note x in voice y to note x + c in voice y + d, while a generalized neo-Riemannian inversion sends note x in voice y to note c–x in voice d–y (assuming voices labeled in pitch-class order). It is this double action that allows for efficient voice leading, with the operation on voices negating or nearly negating the operation on pitch classes.

Since my goal is to introduce a general framework to a broad musical audience, I try to write in a way that is comprehensible to nonmathematicians, presuming only a basic understanding of voice-leading geometry. For the same reason, I do not offer lemmas, theorems, and proofs, trusting that mathematically inclined readers can either find these in the existing literature or supply them themselves. (I do, however, offer mathematical details in the appendix.) Each section summarizes the central concepts before diving into the technical weeds. I have also created five websites allowing users to explore these ideas in a hands-on way; I strongly encourage readers to use these interactive resources as they work through the paper, for beyond understanding general principles, music theorists need a good intuitive sense for how to make their way around the spaces they study.³

1. Mysteries of the Tonnetz

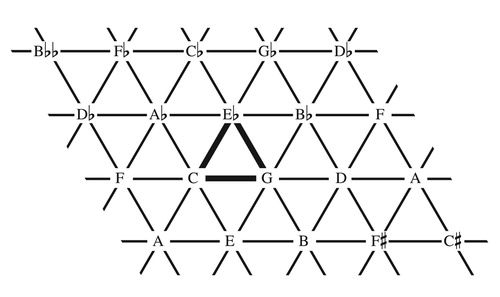
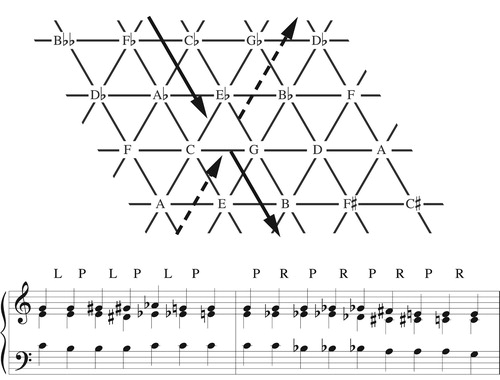
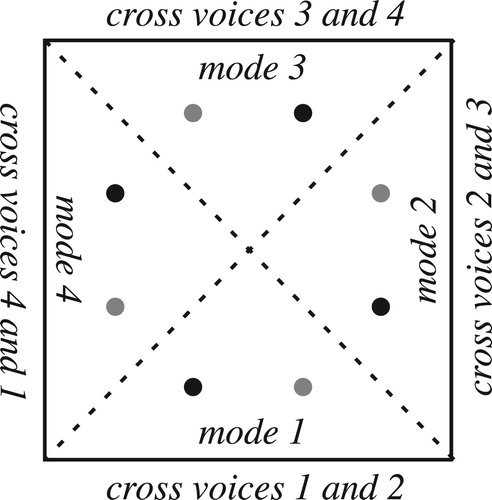
For centuries people have been drawing pictures of musical possibilities. One of the oldest, the Tonnetz, originates with the eighteenth-century mathematician Leonhard Euler, who used the figure to show how major and minor chords were composed of consonant intervals. With perfect fifths on the horizontal axis and major thirds on the northwest diagonal, major and minor triads can be represented by equilateral triangles (Figure 1).⁴ Two chords share a vertex when they have one common tone and a side when they have two. Mathematically, the figure is a torus because its left edge is identified with its right and its bottom edge is identified with its top: on Figure 1, the left side D♭–F–A is duplicated as F–A–C♯ on the right, and the bottom A–E–B–F♯–C♯ is respelled on the top as B♭♭–F♭–C♭–G♭–D♭. Thus as we move off one edge we reappear on the opposite side, much like an old-fashioned video game.

Figure 1. The Tonnetz.

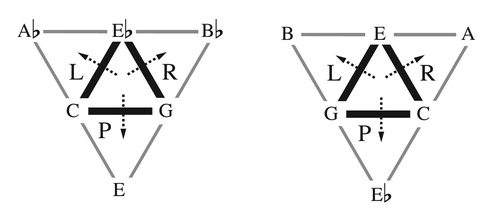
More than two centuries later, Richard Cohn (1996) noticed that the Tonnetz could be repurposed to represent voice leading among major and minor triads.⁵ He used “triangle flips” to model progressions with two common tones and one stepwise melodic voice, with the triangle’s three vertices representing three musical voices. These flips, illustrated in Figure 2, evoke relations central to Hugo Riemann’s music theory: the parallel relationship between triads sharing a perfect fifth; the relative relationship between triads sharing a major third; and the leading-tone-exchange between triads sharing a minor third. Reinterpreted as voice-leading transformations, or things you can do to a chord, these triangle-flips combine to generate a wide range of contrapuntal possibilities, providing a useful tool for modeling complex chromatic passages. The result is an intriguing connection between eighteenth-century mathematics, nineteenth-century theory, and twentieth-century analysis.

Figure 2. L, P, and R triangle flips for minor triads (left) and major triads (right). Each flip fixes an edge whose vertices represent common tones; the third voice moves by one or two semitones.

The reinterpreted Tonnetz, however, is more subtle than it seems. The two paths in Figure 3 look similar, both moving along one of the figure’s “alleys” to return to their starting point by a series of triangle flips. Yet when we compare the resulting music we find that the southeast path returns every voice to its initial position while the northeast path moves each voice down to the next chord tone: G down to E, E down to C, and C down to G. The cumulative effect of the southeast path is trivial, equivalent to doing nothing at all, whereas the cumulative effect of the northeast path is a nontrivial “transposition along the chord.” This difference is suggestive in light of the mathematical discipline known as homotopy theory, where trivial loops are precisely those that can be smoothly contracted to a point. Perhaps only one of the Tonnetz’s axes surrounds a genuine hole in the space of contrapuntal possibilities.

Figure 3. The solid path represents the LP cycle (LPLPLP) and returns each note to its starting point; the dashed path represents the PR cycle (PRPRPRPR) and moves each voice downward along the C major chord.

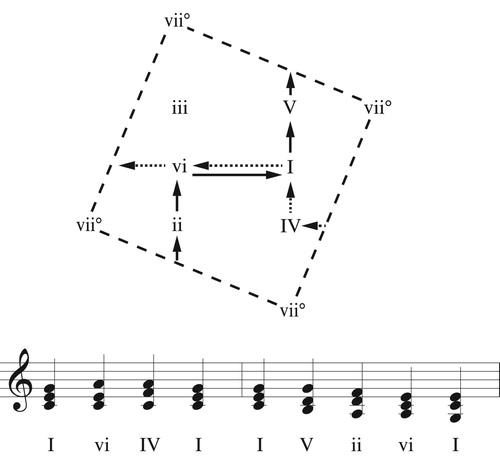
This phenomenon is surprisingly general. Figure 4 shows F. G. Vial’s eighteenth-century model of key relations, made popular by Gottfried Weber. Here points represent keys with modulations along the SW/NE diagonal moving by fifth and modulations along the SE/NW diagonal alternating between “parallel” and “relative” keys. These can be formalized as applying separate voice leadings to a tonic triad and a superordinate scale as described in chapter 4 of Tymoczko (2011).⁶ The figure shows two similar-seeming paths that loop around different axes. As before, one leaves each note of the scale where it began while the other shifts each scale degree up by step. However, the location of the trivial loops has shifted: on the triadic Tonnetz a series of LP moves forms a trivial loop (Figure 3), while on Vial’s figure it has a nontrivial effect on the scale.⁷ Thus even though the figures are visually similar, they represent distinct spaces of contrapuntal possibility. Figure 5 identifies a similar issue in Fred Lerdahl’s map of the diatonic triads.⁸ From a superficial perspective these graphs have the topology of a two-dimensional torus, but when we treat them as voice-leading spaces we find hints of something else.

Figure 4. Two paths on the chart of the regions, again with different effects.

Figure 5. Lerdahl’s toroidal model of diatonic triads, along with two paths in the space.

Cohn’s reinterpreted Tonnetz was a significant music-theoretical achievement, a quantitative and geometrical model of the voice leadings connecting major and minor triads. But its structure remains poorly understood: while theorists long ago noticed the difference between “trivial” and “nontrivial” paths on the Tonnetz, they have struggled to provide a principled explanation for the difference; nor is it obvious how triangle flips relate to the more general phenomenon of efficient voice leading, nor how to extend the Tonnetz to larger collections.⁹ We will answer these questions over the course of the following pages.

2. Topological models of chord space

How can we understand the circular topology that so often appears in our voice-leading models? This section will answer that question by describing two-dimensional annular spaces that are topological in a double sense: first, in being neutral with respect to chord structure, and second in associating voice leadings with homotopy classes of paths.¹⁰ These annular structures are most useful when we ignore voice exchanges to focus on “strongly crossing-free” voice leadings, but we will see that they can be extended beyond this limitation.

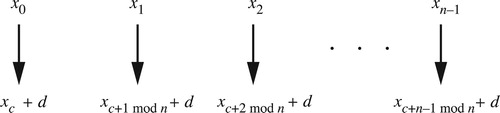
I begin by reviewing some basic definitions. A path in pitch-class space is an ordered pair (p, r) whose first element is a pitch class and whose second element is a real number representing how the note moves, measured in scale steps, with positive numbers corresponding to ascending musical motion and negative numbers descending. In this formalism pitch classes are subject to octave equivalence, but musical motions are not: I distinguish ascents by x, x + o, x + 2o, etc., as well as descents by o–x, o–x–o, o–x–2o, etc. (with o the size of the octave and 0 ≤ x < o). These represent musical actions like “start at any C and move up by 4 semitones,” “start at any C and move up by 16 semitones,” and “start at any C and move down by 8 semitones,” all of which are aurally distinct, even though they all move C to E.

A voice leading is a multiset of paths in pitch-class space, representing a specific way of moving the notes of one chord to those of another: “C stays fixed, E moves up by one semitone, G moves up by two semitones.” (A transpositional voice-leading schema is an equivalence class of voice leadings related by transposition: “the root of the major triad stays fixed, the third moves up by semitone, the fifth moves up by two semitones.”¹¹) A voice leading is strongly crossing free if its voices never cross no matter how they are arranged in register. The space of n-note chords is a singular quotient space, the orbifold ${\mathbb{T}}^n$/S_n. We form it by taking the n-dimensional torus, whose axes are all circular, and gluing together those points whose coordinates are equivalent under reordering. The result is a twisted higher-dimensional mirrored donut: a space with one circular dimension, whose coordinate is the sum of its chords’ pitch classes, with the remaining dimensions forming a simplex or higher-dimensional triangle; the space is bounded by mirror singularities representing chords with duplicate pitch classes. Paths in these spaces can be associated with voice leadings. A fundamental idea of voice-leading geometry is, first, to associate these paths with the glissandi they naturally represent, and second, to associate these glissandi with the discrete voice leadings to which they are formally equivalent. This is not because actual music involves actual glissandi, but rather because the two different kinds of object have the same mathematical structure. (Indeed, this link between the discrete and the continuous is characteristic of homotopy theory, and voice leadings as I define them are isomorphic to homotopy classes of paths in these configuration spaces.) Readers unfamiliar with these ideas can review the appendix or see Tymoczko (2011) for a thorough introduction.

Geometrical music theory describes higher-dimensional spaces containing all possible voice leadings among all possible n-note chords. The models in this section use two dimensions to depict some of the voice leadings among some n-note chords. The basic idea is to place a collection of n-note chords, useful for some particular analytical or theoretical purpose, in an annulus or punctured disk, with angular position given by the sum of the chord’s pitch classes modulo the octave. As in the full geometrical spaces, points represent chords and continuous paths represent voice leadings between their endpoints. The circular dimension of the annulus corresponds to the circular dimension of the higher-dimensional spaces, with the remaining n–1 dimensions compressed into a line segment.¹² The boundaries of the annulus, like those of higher-dimensional chord space, represent voice exchanges, and I will avoid placing chords there. Chords’ radial positions are otherwise completely free, and indeed not fundamental to the model – though in my experience it is useful to place distinct chords at different spatial locations; after all, part of the point of geometrical modeling is to provide intuitive pictures of musical phenomena. What is surprising is that relatively little analytical power is lost by these simplifications.

Figure 6 draws the annular spaces for the standard chromatic and diatonic scales, in the latter case treating diatonic steps as having size 1. I arrange pitch-class sums so that clockwise motion is descending; this is because descending musical motion and clockwise geometrical motion are both defaults. When I am modeling a collection of transpositionally related chords, I will sometimes place them along a spiral representing transposition as in Figure 19 below, but this is merely to facilitate intuition: all relevant calculations can be performed without the spiral. These models are not consistent if we try to combine chords of different cardinalities, for reasons discussed in Callender, Quinn, and Tymoczko (2008) and Genuys (2019).¹³

Figure 6. Annular models of chromatic and diatonic space. Angular position corresponds to pitch-class sum.

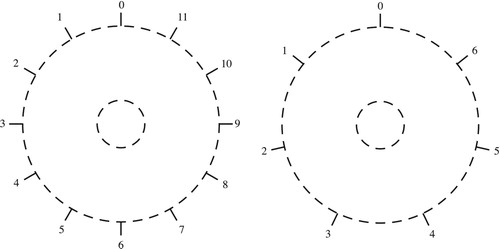
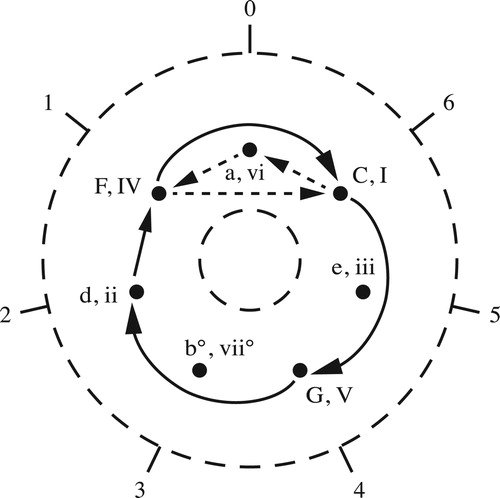
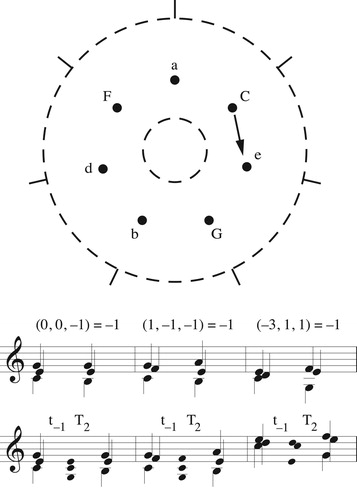
Voice leadings that touch the boundaries (either of annular space or the higher-dimensional spaces they represent) are those with voice exchanges, or voice crossings in pitch-class space; in this section, we will mostly ignore them to focus on bijective strongly crossing-free voice leadings, or those that preserve a chord’s registral ordering no matter how its notes are deployed in pitch space.¹⁴ (Again, this deemphasizing of voice exchanges is reminiscent of Schenkerian thinking.) These are represented by paths, not touching any boundary, whose angular component is determined by the sum of the real numbers in the voice leading’s paths (Figure 7). Since there is at most one bijective strongly crossing-free voice leading for every real number, every sequence of voice leadings that forms a complete circle, not enclosing the center of the annulus, composes to form a “trivial” voice leading leaving every voice exactly where it began; by contrast, a complete circle enclosing the center represents a strongly crossing-free voice leading from a chord to itself involving one octave of total motion (Figure 8). These motions are sometimes known as “transpositions along the chord,” moving each voice along the chord as if it was a very small scale; they can be conceived as the higher-dimensional analogues of octave shifts. I will notate them with a lowercase t (see the appendix for a list of notational conventions). The (bijective) strongly crossing-free voice leadings from a chord to itself X→X are transpositions along the chord t_i; those connecting distinct transpositions combine transpositions along the chord t_i with transpositions along the scale T_j. The voice leadings t_n and T_o are equivalent both musically and topologically, moving every voice by octave and making n loops through chord space.

Figure 7. Trajectories in the annular spaces are determined by the sum of the real numbers in a voice leading’s pitch-class paths.

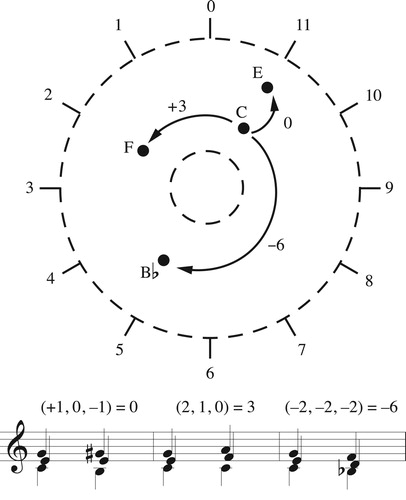
Figure 8. Loops such as A and B, which do not enclose the center of the space, return each voice to its starting point, as in the passages in (b). Loops such as C, which do enclose the center of the space, represent “transpositions along the chord” in which each note moves up or down by one chordal step (c). The top staff of (c) shows the voice leadings while the bottom staff shows that they each involve an octave of total motion in all voices.

For chords unrelated by transposition we can use a little algebra. Let o be the size of the octave and let X and Y be a pair of chords whose pitch classes sum to ΣX and ΣY; then for every number s = ΣY–ΣX + io, with integer i, there is exactly one strongly crossing-free voice leading X→Y whose paths’ real numbers sum to s. We can derive these by composing an arbitrary strongly crossing-free voice leading X→Y with the set of transpositions-along-the-chord Y→Y (Figure 9). (Musically we can identify the resulting voice leadings by placing both X and Y in “close position” so that they span less than an octave; moving the bottom note of one chord to the top, or top to bottom, while continuing to map notes in registral order, changes the total sum of the real numbers in the voice leading’s paths by one octave.) Here, the integer i determines how many times the voice leading Y→Y circles the center of the annulus (positive corresponding to ascending musical motion and counter-clockwise geometrical motion, negative descending and clockwise). This number can be taken to represent an element in the annulus’s fundamental group, a topological object parameterizing the different voice leadings from Y to Y, and hence from X to Y.

Figure 9. The voice leadings between two separate chords X and Y can be written as a fixed voice leading X→Y composed with some number of loops Y→Y. In the annular space, the numbers represent sum of the real components in voice leadings X (which takes f^ø7 to E⁷) and t_i (which are the transpositions up and down i steps along the chord E–G♯–B–D).

We are now in a position to understand the phenomena in the previous section. Figure 10 uses annular space to model the two sequences in Figure 3: the first involves no cumulative angular motion and does not contain the annulus’s center; the second makes a complete clockwise circle and moves each voice by one step along the chord.¹⁵ Figures 11 and 12 repeat the demonstration for the “chart of the regions” and Lerdahl’s diatonic torus respectively.¹⁶ These graphs show that the annular topology can appear in our theoretical models even if we do not explicitly put it there. It captures a general and ineluctable feature of the space in which contrapuntal motion takes place.

Figure 10. The paths in Figure 3 in annular space.

Figure 11. The paths in Figure 4 in annular space. Here I represent minor keys with harmonic-minor scales.

Figure 12. The paths in Figure 5 in annular space.

Since the structure of the annular spaces is independent of the particular intervallic constitution of chord and scale, Figure 13 can be taken to represent the strongly crossing-free voice leadings connecting the transpositions of any three-note chord in any seven-note scale. To see this, let us place some form of our chord at the location marked C. It follows that the point marked B, 3/7 of the way clockwise around the circle, must represent its transposition down by scale step. (This is because the voice leading that lowers each note by scale step has paths whose real numbers sum to –3, and hence is represented by a clockwise path moving 3/7 of the way around the circle.) Continuing in this way, we see that diatonic trichords are evenly spaced around the circle, each a third below its nearest clockwise neighbor. It also follows that there is a transpositional voice-leading schema generating all the clockwise voice leadings on the figure; this is the motion that links one chord to its nearest clockwise neighbor, and whose retrograde links chords to their nearest counterclockwise neighbors. This basic voice leading always combines one-step transposition downward along the chord with two-step transposition upward along the scale – the former requiring seven total descending steps of motion and the latter six ascending steps, combining for one descending step in total.¹⁷ We can obtain any path on the figure by repeatedly applying this schema or its retrograde.

Figure 13. Three diatonic voice leadings that can be represented by the same graph. Lowercase t represents transposition along the chord; uppercase T represents transposition along the diatonic scale.

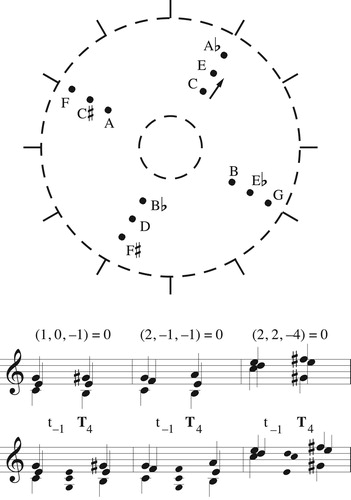
Contrast this with the graph of any three-note chord in any twelve-note scale (Figure 14). Here we have three chords occupying the same angular position – from which it follows that there will be a transpositional voice-leading schema that, having been applied three times, returns each voice to its original position. Once again, this is true regardless of the structure of the chord and scale. This voice leading simultaneously transposes the chord by one third of an octave (e.g. up four semitones) while moving the voices along the chord by one third of an octave in the opposite direction (e.g. down a chordal step). (Since it involves two countervailing motions by one third of an octave, I call it a diagonal action.¹⁸) One of these involves an octave of ascending motion while the other involves an octave of descending motion, canceling out to produce a purely radial path. Once again this contrapuntal logic is independent of the chord’s intervallic structure.

Figure 14. Three chromatic voice leadings that can be represented by the same graph. Lowercase t represents transposition along the chord while boldface T represents transposition along the chromatic scale.

The annular representations suggest a number of compositional applications. First, as mentioned in the introduction, it gives us a notion of registral inversion general enough to be useful to twenty-first century musicians. Students are taught to construct inversions by moving the bottom note of a chord to the top, a procedure that works in the conventionalized language of classical tonality – where harmonies are always familiar, bass and melody are paramount, and the precise configuration of inner voices is often secondary. In modern contexts, when we are operating with a much wider range of chords and spacing may be important, the procedure breaks down (Figure 15). The loops in annular space suggest an alternative strategy of transposing along the chord, preserving its registral spacing as measured in chordal steps. I have found this to be a useful technique for dealing with complex harmonies: when combined with scalar transposition, it generates a wealth of broadly similar sonorities from a single chord (Figure 16). Indeed, transposition along the chord and transposition along the scale are the two operations preserving transpositional set class and spacing as measured in chordal steps.

Figure 15. Two strategies of registral inversion. (a) Placing the bottom note of a chord at the top. (b–c) Moving each voice by one chordal step, preserving the chord’s registral spacing when measured in steps along the chord.

Figure 16. Generating a sequence of complex harmonies by combining motion along the chord with motion along the scale. The top system moves by one step along the initial chord. The bottom system transposes these harmonies chromatically to produce a progression of sonorities with the same spacing as measured in chordal steps.

Annular space also allows us to transport musical procedures between musical domains: for instance, given a sequence of n-voice voice leadings linking the transpositions of some n-note chord in an o-note scale, we can construct a structural analogue for any other n-note chord in any other o-note scale, simply by moving the geometrical patterns from one annular space to another. Sometimes we can transport procedures between dissimilar domains – for instance, constructing broadly analogous passages that iterate two chords’ respective “basic voice leadings.” This in turn allows us to construct hierarchical passages that use similar contrapuntal techniques on multiple musical levels (Figure 17). Finally, if we take the repeated application of a transpositional voice-leading schema to represent a “generalized circle of fifths,” we can use this structure to generate analogues of the melodic and harmonic minor collections, thus adapting traditional voice-leading relationships to arbitrary musical domains (Figure 18).¹⁹ Understanding the compositional and perceptual significance of these ideas is a matter for future work; here I simply mention some potential compositional directions.

Figure 17. A hierarchical passage in which chords and scales each take short counterclockwise motions in their respective annular spaces. Here, r, t, f, s, and n stand for root, third, fifth, seventh, and ninth.

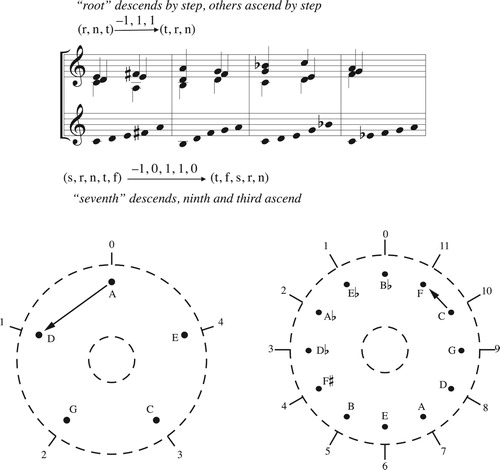
Figure 18. (top) Annular space for the diatonic hexachord. (bottom) Scrambling the voice leadings in any repeating voice-leading pattern produces analogues to the melodic minor collection. Here, the boldfaced chords represent a generalized “circle of fifths” that moves radially in annular space; by rearranging every pair of these voice leadings we obtain alternate pathways, generating hexatonic scales. See Tymoczko (2011, §3.11) for more.

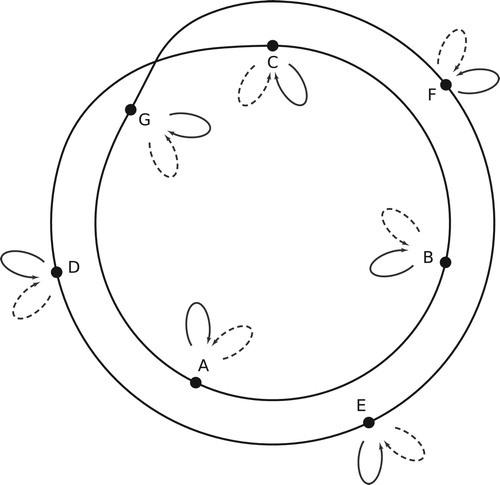
Analytically these tools show us how different genres make use of similar techniques. In a forthcoming book, I argue that there are many contexts in which we can find short clockwise motions in the annular spaces, ranging from rock harmony to Renaissance counterpoint to classical modulation. (In this work I sometimes represent voice crossings by attaching loops as shown in Figure 19, using the spiral to indicate transposition; the result can be used to model all the two-voice voice leadings among the transpositions of any dyad in any seven-note scale.) Here geometrical music theory approaches the generality of Lewin’s transformational theory, providing tools that apply to any chord and scale. What makes this possible is the realization that we do not need to represent voice-leading spaces in all their higher-dimensional glory; instead, we can use simpler and more abstract representations containing only the harmonies we happen to be interested in. My own experience is that this simplification greatly boosts analytical intuition, clarifying relationships that are much harder to see in the more complete geometry of chord space.

Figure 19. Annular space for dyads in a seven-note scale, with the loops representing two basic voice exchanges. For the diatonic third, these move notes by two and five contrary-motion steps respectively.

3. Topological models of transpositional set-class space

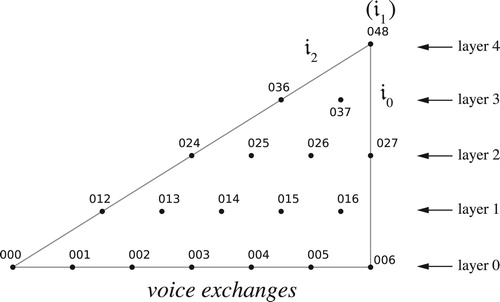
Musical geometry’s core claim is that n-note chords live in the higher-dimensional analogue of a donut, with one dimension circular and the remaining n–1 dimensions forming a mirrored simplex. The annular spaces prioritize the circular dimension, using a single line segment to represent the rest. Another family of models prioritizes the simplicial dimensions, ignoring the circular dimension altogether. These are the three varieties of set-class space, the permutation region, transpositional set-class space, and inversional set-class space. Set theory and the annular spaces thus arise from complementary processes of abstraction, one deemphasizing voice exchanges, the other transposition.

In “Generalized Voice-Leading Spaces,” Clifton Callender, Ian Quinn, and I described these n-note set-class spaces as (n − 1)-dimensional simplexes, or generalized tetrahedra, with some of their points acting like mirrors or being glued together. (This description is mathematically awkward as the identifications form spaces that are no longer meaningfully “simplicial,” but it has the advantage of providing a way to picture them.) Once again we associated voice leadings with the paths arising when each note makes a smooth glissando from its starting point to its destination.²⁰ In lower dimension these spaces can simply be drawn, allowing theorists to directly observe the relevant musical trajectories. In higher dimension the graphical strategy is unavailable, yet Callender, Quinn, and I provided no useful alternative. For this reason it would be fair to say that our work stopped prematurely, couching our description of set-class space in terms that were too complex to be musically useful.²¹

In transpositional set-class space, points represent equivalence classes of chords related by transposition. Paths represent equivalence classes of individually T-related voice leadings – that is, voice leadings equivalent under the independent transposition of their chords (Figure 20). Since these are the set-class analogues of voice leadings, I will refer to them as “voice leadings between set classes” or just “voice leadings” when the context is clear. The group of n-voice voice leadings from a transpositional set class to itself can be decomposed into two familiar subgroups: the voice exchanges, generated by the n pairwise swaps of adjacent notes, with voices moving by the same distance in opposite directions, and the previous section’s transpositions along the chord.²² As before, the voice leadings between set classes X and Y can be represented by joining a default voice leading X→Y (usually taken to be a small perturbation, if one exists) to the complete collection of voice leadings Y→Y, the fundamental group of set-class space. Thus we use the voice leadings from a set class to itself to understand the entire space.²³

Figure 20. Individually T-related voice leadings, representing the same voice leading in transpositional set-class space. The chords in the top voice leading are transposed by different amounts to produce the bottom voice leading. Nevertheless, both begin with major chords, moving root by c, the third by c + 1, and fifth by c + 2. A single path in set-class space represents all such voice leadings, starting at any major chord and for every value of c.

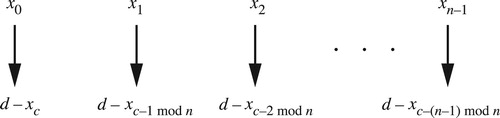
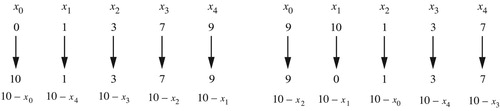
For an n-note chord or set class there are n fundamental transpositions-along-the-chord which I will label t_i, with the subscript corresponding to the number of steps. (I use an uppercase T for traditional transposition along the scale.) These compose additively for both chords and set classes, so that the result of following t_i with t_j is t_i+j. However, addition works differently in the two cases: with n-note chords, the n-fold application of t₁ moves each voice up by octave, which is not the same as t₀; in set-class space, the n-fold application of t₁ is exactly equal to t₀ since we factor out transposition (Figure 21).²⁴ Transposition along the chord thus determines an action of the cyclic group C_n in set-class space but not in chord space. (Somewhat surprisingly, this is the only difference between the two spaces’ fundamental groups.) Thus subscripts in set-class space should always be understood modulo n: t_–1 and t₄ are equivalent for pentachords. An interesting property of the transformations t_iT_j, which combine transposition along both chord and scale, is that they apply addition to both pitch classes and voice labels (Figure 22).

Figure 21. In trichordal set-class space, three ascending steps-along-the-chord are equal to the identity.

Figure 22. Let (x₀, x₁, … , x_n–1) be a chord in non-descending pitch-class order spanning less than an octave. The combination of transposition along the chord and transposition along the scale moves the pitch class x_i to the pitch class x_i+c mod n + d, with addition acting on both pitch classes and voice labels. Voices move along paths ||x_i+c–x_i||₊ + d, where ||x_i+c–x_i||₊ is the ascending c-step scalar interval from x_i to x_i+c, which is x_i+c–x_i if i + c ≥ i and x_i+c–x_i + o otherwise. In set-class space we ignore d, while in the annular spaces we do not.

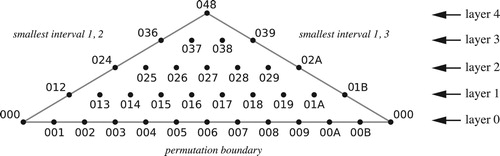
An n-voice voice leading traces a path through an n-dimensional simplex with various identifications and mirror singularities. Because of these, the path might seem to disappear off one boundary to reappear on its identified boundary, or bounce off a singular point that acts like a mirror. The central claim of this section is that there is a principled association between boundaries and voice-leading transformations: in every transpositional set-class space, one boundary, the “permutation boundary,” represents a voice exchange, swapping the set class’s closest notes, while the remaining boundaries represent the nontrivial transpositions-along-the-chord. Geometrically, the permutation boundary acts like a mirror while the transpositional facets are identified pairwise, with the t_x and t_–x facets glued together. (In even dimension half of the t_n/2 facet is glued to the other half.) The claim that the boundaries are “associated with” a particular transformation has two meanings. First, that the transformation describes the structural changes occurring when any glissando encounters that boundary – for example, changes in the ordering of its voices by pitch-class, or the location of its smallest interval. Second, and somewhat more intuitively, that any path that starts at the interior of the simplex, moves to that boundary, and returns to its starting point (either reflecting off a mirror singularity or disappearing off the boundary to reappear on an identified face), articulates the associated transformation.

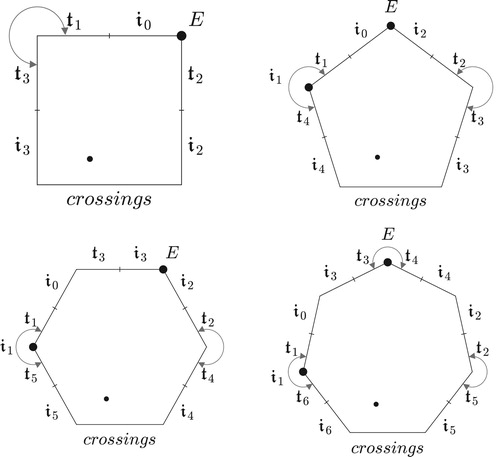
This leads to a graphical strategy in which we replace higher-dimensional “simplexes” with two-dimensional polygons (Figure 23), labeling each edge with its associated transformation – which is to say, the element of the fundamental group associated with loops passing only through that facet of set-class space. In higher-dimensional voice-leading space, each path can be associated with a unique voice leading between set classes; in the polygonal models, paths instead correspond to a broad class of topologically equivalent voice leadings (Figure 24). What is surprising is that there is only a small loss of analytical power resulting from this reduction to two dimensions. In large part this is because the boundaries are the spaces’ most relevant features, musically and topologically.

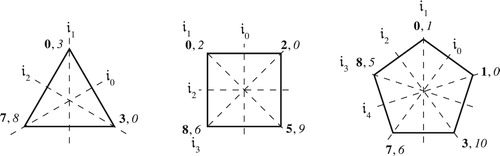
Figure 23. Polygons representing set-class spaces for three, four, five, and six notes. Dark dots represent a chord’s normal form, light dots its inversion; arrows represent sides that are glued together. E is the completely even chord dividing the octave into n pieces.

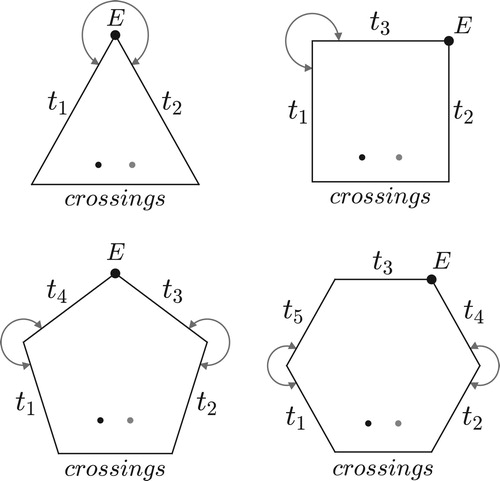
Figure 24. Pentachordal transpositional set-class space, with a path representing one-step transposition-along-the-chord. If we choose the dark point to represent the standard pentatonic scale, then this path will correspond to all of the voice leadings on the top system; if the point represents the dominant ninth chord, then the path corresponds to those on the bottom.

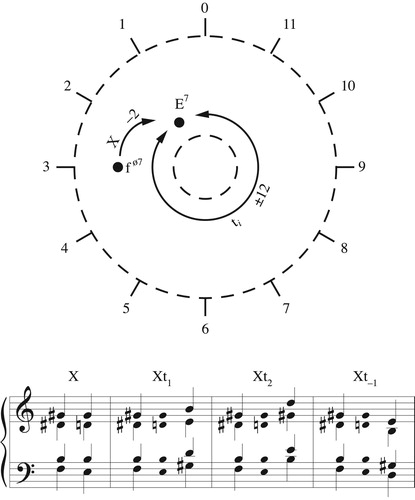
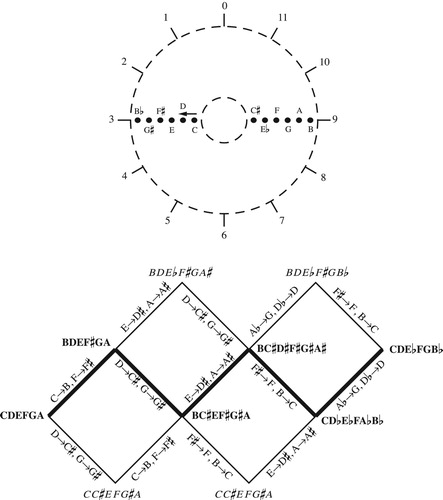
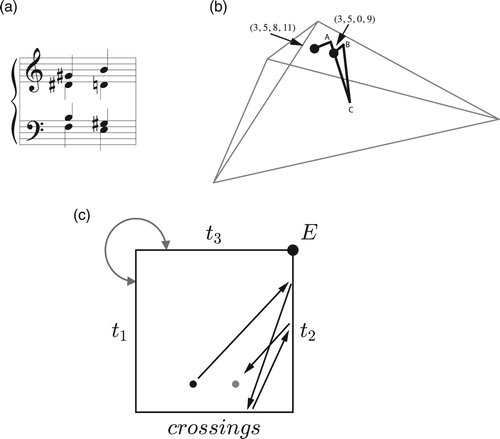
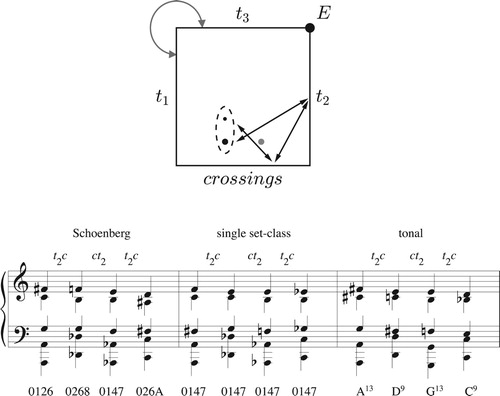
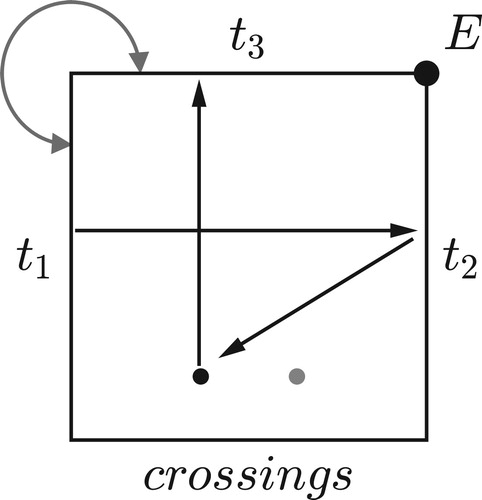
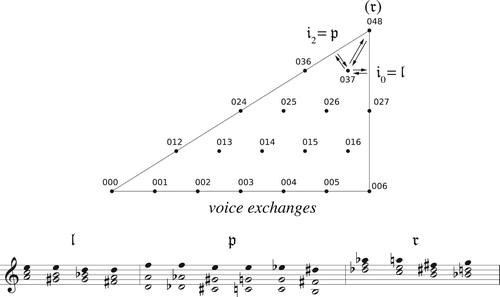
Before diving into the details, it will be useful to consider a specific example. Figure 25 presents the opening progression of Wagner’s Tristan. Callender, Quinn, and I associated this progression with a generalized line segment in our tetrahedral model of four-note set classes; in that model, this path originates at the point representing the half-diminished seventh, moves to the boundary at A where it disappears, reappearing at B to move down to C, “bounces off” the bottom edge to return to A, disappears again to reappear at B, and moves finally to the point representing the dominant-seventh chord. (This path, like most of the others in this paper, was determined computationally, with each voice gliding smoothly from its initial pitch to its destination over the same span of time.) To a musician this path is relatively uninformative. More useful is the knowledge that it first touches the t₂ boundary, then the voice-crossings boundary, and finally t₂ again. Figure 25c diagrams the path in polygonal space. We can think of the pattern of boundary interactions, t₂ct₂, either as recording the changing structure of the chord as the voices glide smoothly from start to finish, or more abstractly as transformations applied to the initial chord. I will consider each interpretation in turn.

Figure 25. (a) The opening voice leading of Tristan, (b) the path it takes through tetrachordal transpositional set-class space, and (c) its appearance in the polygonal representation.

First, the geometrically faithful approach. Figure 26 shows some of the harmonies that result from a smooth glissando taking the first chord to the second. For simplicity I transpose the destination chord from E to F, since we are in set-class space where absolute transpositional level does not matter. In geometrical music theory, a chord’s “normal form” is determined by the position of its smallest interval, as we will discuss shortly. We start with (3, 5, 8, 11), a half-diminished set class whose smallest interval lies between its first two notes; over the course of the voice leading, the G♯ glides up four semitones while the B glides down two. This path intersects with the t₂ boundary at the moment where the chord has two distinct “smallest intervals” (both of size 2), appearing between the first and final pairs in (3, 5, 8.66, 10.66); after interacting with this boundary, the sole smallest interval lies between the third and fourth notes. We can understand the t₂ label as representing the shifting position of the set class’s smallest interval, from the first two voices up two chordal steps to the final two. The interaction with the voice-crossing boundary occurs when these two closest voices sound the same pitch class at (3, 5, 10, 10); after this point the third voice has moved above the fourth. (Here the voice-crossing boundary is associated with the fact that we need a different permutation to put the voices in ascending pitch-class order.) The second t₂ interaction occurs when the third voice is two semitones above the fourth, at (3, 5, 11.33, 9.33), with the chord again having two “smallest intervals” when ordered by pitch class. After that point, the smallest interval lies exclusively between the first two notes, as at the beginning. (Hence t₂ once again moves the smallest interval by two chordal steps.) From this point of view, the transformations record the general changes of the chord’s structure – both its ordering in pitch class and the location of its smallest interval – that result when we represent the voice leading (3, 5, 8, 11)→(3, 5, 9, 12) as a glissando, sliding root to root, seventh to seventh, third to fifth, and fifth to third.²⁵

Figure 26. The opening voice leading of Tristan with the second chord transposed up by semitone, and each voice making a smooth glissando from start to finish. The glissando touches the t₂ boundary when the moving voices are two semitones apart and the crossing boundary when they sound the same pitch class.

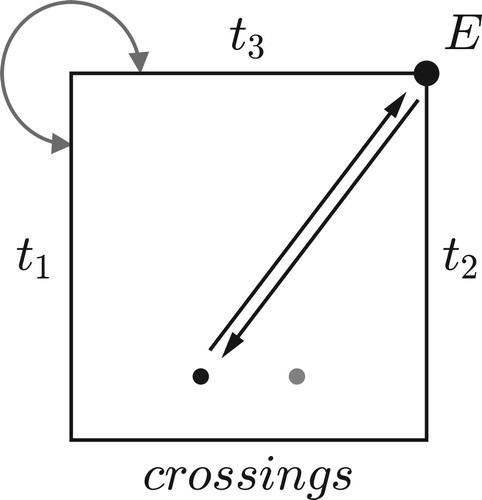
Alternatively, and more intuitively, we can interpret the geometrical pattern of boundary interactions as a sequence of abstract transformations combining to produce the total voice leading. Figure 27 represents the transformational labels as voice leadings from the Tristan chord to itself, with the geometrical path now returning to the initial Tristan chord (the dark dot) after every boundary interaction, ending with a short path from the Tristan chord to its inversion. The path in Figure 27b is topologically equivalent to that in Figure 25c and represents the same total voice leading. We start with a t₂ that moves each voice up by two chordal steps, so that the seventh lies between soprano and tenor; these voices then cross by reflecting off the permutation boundary (which always exchanges the chord’s closest notes along the shortest possible path); the music then reflects again off the t₂ boundary to return the seventh to the bass/alto pair before coming to rest at a different set class, here the inversion of our starting chord.²⁶ Once again we use the voice leadings X→X to understand the space, analyzing the Tristan voice leading as a series of voice leadings from the half-diminished chord to itself, coupled with a single “default” voice leading X→Y.²⁷ The geometrical path – which was determined by a computer – thus gives us an analysis of the Tristan voice leading into a sequence of transformational “moves,” here interpreted as voice leadings from the Tristan chord to itself (with one final move connecting the normal-form Tristan chord to the normal-form dominant-seventh).²⁸ We have, in other words, identified a connection between the geometrical and the algebraic, represented respectively by boundary interactions and contrapuntal transformations.

Figure 27. A transformational interpretation of the opening of Tristan, in which the boundary interactions are treated as voice leadings from the Tristan chord to itself. Here r, t, f, s stand for root, third, fifth, and seventh.

None of this is surprising: once we associate glissandi with voice leadings and construct the configuration space of set classes, then everything follows from the definition of the fundamental group. What is interesting, rather, is that familiar mathematics leads to simple, novel, and practical analytical tools. The next paragraphs will explain this connection in detail, describing the structure of transpositional set-class space, linking geometrical boundaries and contrapuntal transformations, and justifying the two-dimensional polygonal models. The main goal here is to show how paths through set-class space can be associated with sequences of transformations. Less mathematical readers may want to skip ahead to the conclusion of this section, circling back to the technical discussion as desired. (The polygonal models can be used even by those who do not follow the technical minutiae, treating them as convenient graphical representations of reasonably familiar voice-leading moves.) Mathematical readers may want to consult the appendix before proceeding.

A more detailed understanding begins with the notion of geometrical normal form as defined in Callender, Quinn, and Tymoczko (2008).²⁹ An n-tuple (x₀, x₁, … , x_n–1) is in geometrical normal form if it meets the following criteria:

• NF1. Its first element is 0;³⁰

• NF2. It is in ascending order, with the final element less than or equal to the octave o;

• NF3. Its smallest interval lies between its first two notes (including the “wraparound” interval o–x_n–1 among the chord’s intervals).

These equations determine a region of ordinary Euclidean space that can help us understand the more complicated geometry of set classes; the region represents set classes as n-tuples of real numbers in the range 0 ≤ x ≤ o, with 0 and o the same pitch class an octave apart.³¹ The first important departure from traditional set theory is that we allow multisets or chords with multiple copies of the same pitch class. The second is that geometrical normal form is non-unique: a single set class can have multiple normal-form orderings, for example (0, 1, 2) and (0, 1, 11) in twelve-tone equal temperament. Where traditional theory mandates a process of tie-breaking to select one ordering as the unique normal-form representative, the geometrical alternative instead accepts that some set classes have multiple normal forms. We will see that this redundancy is actually a virtue of the geometrical approach.

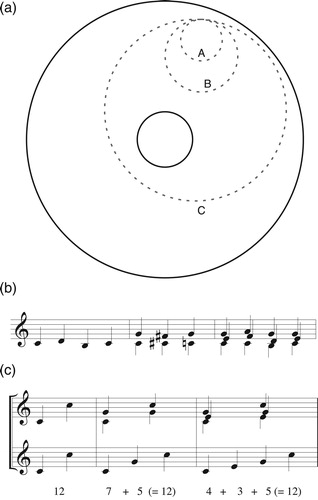
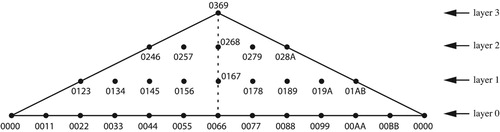
Before considering set-class space in all its complexity, it is worth thinking about the simpler space that results from NF1–2. By elementary arithmetic, these define an (n − 1)-dimensional simplex consisting of all n-tuples meeting the criteria, a Euclidean fundamental domain for a more complicated orbifold I call the permutation region.³² Its vertices are the n combinations of 0 and o containing at least one 0 and sorted in ascending order; these each have a single nonzero interval of size o, occurring in a different order position³³ $\left(0,0,\dots 0\right),\left(0,\dots 0,\mathit{o}\right),\left(0,\dots 0,\mathit{o},\mathit{o}\right),\dots ,\left(0,\mathit{o},\dots ,\mathit{o}\right).$ This simplex is the cross section of chord space, containing a separate point for each of the n modes of a given set class; thus the major chord is represented by (0, 4, 7), (0, 3, 8), and (0, 5, 9), all of which satisfy NF1–2.³⁴ Here we have a particularly clear example of the complementary relationship between the annular and set-class spaces, the former compressing the cross section into a single line segment, the latter ignoring the circular dimension in favor of the cross section itself. We can represent the cross section symbolically as an n-sided polygon whose sides exchange one pair of voices (Figure 28); together, the total collection of paths, starting and ending at the same point and reflecting off some series of boundaries, represents the subgroup of voice exchanges.³⁵ The space can be divided into n equivalent parts containing exactly one mode of each transpositional set class; each of these equivalent parts contains orderings whose smallest interval is in the same order position. (In analytical contexts we therefore have to make an arbitrary choice about which configuration of notes in a score represents “mode 1.”) Despite its redundancy, this cross section usefully represents the various combinations of voice exchanges and transpositions-along-the-chord: for instance, analysts might prefer Figure 29 to the earlier depiction of the same progression in Figure 25c, as it eliminates all but one boundary interaction.³⁶ Here we see a trade-off between abstraction and analytical clarity, with the more abstract set-class spaces representing familiar transformations in counterintuitive ways. We will return to this issue below.

Figure 28. The permutation region represents the cross section of annular space; its n boundaries represent the n exchanges of pairwise voices. Each of its n regions contains a different mode of each set class.

Figure 29. The first voice leading of Tristan plotted in the permutation region.

To pass from the cross section to transpositional set-class space, we use NF3, which requires that the smallest interval be in the first position. This replaces the vertex (0, o, … , o), whose largest interval is between its first two notes, with the perfectly even chord E dividing the octave into n precisely equal parts (Figure 30). A great deal of theoretical effort has gone into describing the internal structure of the resulting space, but there is an important sense in which this project is uninteresting: the interior of the simplex simply gives us the various ways to divide a single quantity o into n parts, with the stipulation that the first be no larger than any of the others.³⁷ (This banality of set-class space is what allows us to represent the higher-dimensional simplex with a two-dimensional polygon.) There is nothing specifically musical about this structure, which could just as well represent groups of people of size o choosing among n mutually exclusive alternatives – say, the workers at an office splitting up to see movies at a multiplex. (This familiar geometry arises in music because a set class’s n intervals divide the octave o.) It is at the boundaries where we find the characteristically musical phenomena, “gluings” arising from octave and permutational equivalence.

Figure 30. The vertices of transpositional set-class space for dimensions two through six.

Closer examination shows that the fundamental domain has the structure of a cone parameterized by the size of the set class’s smallest interval (Callender, Quinn, and Tymoczko 2008). For example, the different layers of Figure 31 are essentially similar in structure, line segments whose endpoints are modes of the same set class. (These will therefore be glued together so that each layer forms a circle.) These layers are related by a set-theoretic analogue of the multiplicative (or M) transform that moves each chord linearly toward the perfectly even chord E, expanding intervals smaller than o/n while shrinking larger intervals, so that set classes get more and more even as we ascend toward the cone point.³⁸ We can use this conical structure by fixing the size of the smallest interval, drawing only one layer of some higher-dimensional space – as in Figure 32, which shows the semitonal layer of four-note set-class space.³⁹ Every four-note set class, other than the diminished-seventh E, is related by our multiplicative transform to exactly one point in this layer; consequently we can use it as a two-dimensional representation of four-voice voice leadings – quotienting out by our geometrical “M transform.” As we will see, an analogous process gives rise to three-dimensional representations of five-note set classes, a four-dimensional space that is otherwise difficult to visualize.

Figure 31. Transpositional set-class space has the structure of a cone.

Figure 32. The semitonal layer of tetrachordal set-class space.

Set classes in the interior of the space have no note-duplications and a unique smallest interval. One boundary, the permutational facet, contains set classes with more than one copy of some pitch class, with normal form (0, 0, x₂, … , x_n–1). This is the base of the cone.⁴⁰ The remaining boundaries contain set classes with two or more instances of their smallest interval.⁴¹ Since all have one smallest interval in the first position (by NF3), they can be labeled by the position of their second smallest interval: one facet will contain chords whose second smallest interval is in the second position, another whose second smallest interval is in the third position, and so on. In Figures 31 and 32, the rightmost boundary contains chords whose second smallest interval is found in the “wraparound” position between its final note and the octave above its initial note.

These duplications determine how the simplex’s facets are to be identified. Suppose any set class is in geometrical normal form and has its smallest intervals in the first two positions; then its one-step transposition-along-the-chord is also in geometrical normal form. For example, the one-step transposition of (0, x, 2x, y, z), with x the smallest interval, is (0, x, y–x, z–x, o–x), which is again in normal form.⁴² The 1, 2 and 1, 5 facets must therefore be identified or “glued together,” as they contain exactly the same set classes; the same is true for the 1, 3 and 1, 4 facets. Thus we see that n − 1 of transpositional set-class space’s boundaries are identified pairwise, with the t_x and t_−x facets glued together. In even dimension, half of the facet representing n/2-step scalar transposition is identified with the other half, with chords like (0, 1, 5, 6) reappearing on the same face as (0, 1, 7, 8). This can be seen in Figure 33, where equivalent set classes are symmetrically arranged around the central vertical line containing transpositionally symmetrical chords.

Figure 33. The 1, 3 face of tetrachordal transpositional set-class space. The central line is transpositionally symmetrical; each chord on the right side has a partner on the left.

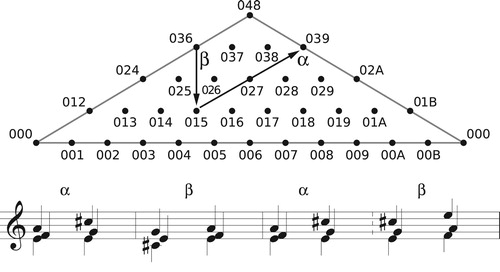
If a facet has its smallest intervals in the 1, x + 1 position, then its set classes will be kept in normal form by t_x, the voice leading that moves all notes up by x steps along the chord. A little thought will show that each facet acts like the inverse of this transposition, t_–x, in the following sense: a path that starts in the interior of the space and moves toward that boundary will reappear on its paired facet; if it then returns to its starting point, it will articulate the scalar transposition that preserves the normal ordering of the second, paired facet (Figure 34). This follows from the fact that line segments in the simplex represent voice leadings preserving normal ordering; to attach a pair of these, as in Figure 34, we need to transpose the second voice leading along the chord so that it matches the first; the relevant transposition will necessarily be the one that keeps its chords in normal order.⁴³ (We can imagine the transposition occurs as we move off one boundary to reappear on the other.) Thus we can label each facet t_−x with x the transposition-along-the-chord that keeps its chords in normal order. A single loop will represent both ascending and descending x­-step transposition-along-the-chord, with the musical direction-of-transposition corresponding to the geometrical direction-along-the-path. It follows that the strategy in Callender, Quinn, and Tymoczko (2008), of plotting voice leadings in the simplicial fundamental domain, determines a series of voice-leading transformations corresponding to the boundaries lying along the voice leading’s path.

Figure 34. Two paths in trichord space, along with instances of the voice leadings they represent. We need to transpose β by one step upward along the chord to attach it to the endpoint of α.

We have now completed our derivation of the polygonal graphs. Readers should be able to understand why the polygons in Figure 23 have one edge representing the voice exchanges (the base of the cone, containing chords with pitch-class duplications), and n − 1 edges representing the scalar transpositions, identified as appropriate. Motion within the polygon represents a voice leading from one normal form to another, changing the relative size of a chord’s intervals while keeping the smallest interval in the first position. It should also be clear why a pattern of geometrical boundary-interactions (as in Figure 25b–c above) can be translated into a pattern of transformations (as in Figure 27), for the crossing of a transpositional boundary represents a shift in the position of the set class’s smallest interval; this is topologically equivalent to a transposition along the chord, coupled with a voice leading which remains within the interior of set-class space, preserving the normal ordering.

The main benefit of set-class space is to reduce a multitude of voice-leading possibilities to a much smaller number of basic templates. For an n-note chord in a o-note scale, there are no distinct combinations of transposition-along-the-chord and transposition-along-the-scale (counting t_x and t_x+n as the same, since they differ only by an octave in each voice). By factoring out the transpositions-along-the-scale we reduce these to just n basic possibilities. If we want to consider distinct chord types we simply adjoin a single default voice leading X→Y to the total collection Y→Y. In Tymoczko (2011) I have used this simplification for a variety of analytical and theoretical purposes, including (a) analyzing chromatic pieces that systematically explore the various voice-leading routes from one chord to another; (b) calculating the most efficient bijective voice leading from one chord to another; and (c) describing sequential passages with varying intervals of transposition. In the interest of space, I will not review these applications here.

A second use for transpositional set-class space, and for the polygonal models in particular, is in exploring voice exchanges. Since this raises interesting questions about the relative merits of the permutation region and transpositional set-class space, I will defer further discussion to §5.

A third use for these spaces is in modeling passages where chords are nearly but not exactly transpositionally related. Figure 35 shows the opening of the fifth song of Schoenberg’s Book of the Hanging Gardens (Op. 15). Since each sonority belongs to a different set class, it might seem beyond the reach of conventional set theory; yet its three voice leadings each involve the exact same type of path in set-class space, interacting with both the permutation and t₂ boundaries. Figure 35 shows that we can conceive its four sonorities as small perturbations of a single abstract structure – or better, as points in a region containing broadly similar set classes, each no more than two semitones away from 0147. (The graph encloses this region in an oval.⁴⁴) The figure also shows a late-romantic descending-fifth sequence of extended dominants involving the very same pattern of boundary interactions.⁴⁵ Schoenberg’s progression lies somewhere between these two models, at once distorting a tonal predecessor while pointing toward the more rigid structures of his later music. Without geometry we might be tempted to devalue such intuitions as “broadly similar harmonies” or “distortions of a familiar tonal schema” – notions that can seem defectively vague when compared to more precise music-theoretical language. But I would argue that such flexibility is fundamental to early atonality, requiring something like the analytical perspective we are exploring here.⁴⁶ One might say that geometry gives us a harmonic analogue to the theory of contour, defining flexible vertical structures analogous to contour theory’s flexible melodic categories (Callender, Quinn, and Tymoczko 2008). And while this analysis could in principle use the complete tetrahedral set-class space, the two-dimensional representation is considerably more intuitive.

Figure 35. A single diagram in tetrachordal transpositional set-class space that can represent a four-chord progression from Schoenberg, a similar progression using just a single set class, or a descending-fifth series of extended dominants. In the first and third cases we conceive of our musical object as a region of set class space (the dotted oval); in the second, this region shrinks to a point, as in traditional set theory.

Three final points about the contrast between geometry and topology. In earlier work, I associated voice leadings with “generalized line segments,” the specific paths that arise when each voice glides smoothly from its starting point to its destination. This can sometimes produce counterintuitive results: for example, the generalized line segment associated with the one-step ascending scalar transposition (0, 1, 4, 6)→(1, 4, 6, 12) interacts with two boundaries, decomposing t₁ as t₃t₂ (Figure 36). This because there is a point along the glissando where the smallest interval briefly lies between the second and third voices before moving to the “wraparound” position. In analytical contexts, we are typically more interested in the fact that a voice leading is an instance of t₁, not that linear interpolation happens to generate a somewhat counterintuitive path through set-class space for one set class but not another. Thus this paper associates voice leadings not with the specific paths resulting from linear interpolation but rather homotopy classes of paths all producing the same voice leading between their endpoints. Here topological abstraction may be preferable to geometrical particularity.

Figure 36. Linear interpolation (0, 1, 4, 6)→(1, 4, 6, 12) produces a generalized line segment that interacts with the t₃ and t₂ boundaries.

This same strategy is needed for voice leadings that pass through the highly singular tip of the set-class cone where the boundaries shrink to a single point. In the polygonal representations, as in the more complicated “simplicial” representations of Callender, Quinn, and Tymoczko (2008), voice leadings appear to “bounce off” this point to return to the interior of the space. However the musical meaning of these paths depends on the structure of the chord.⁴⁷ Thus the path in Figure 37 represents t₁ when we start with (0, 1, 3, 7), t₂ when we start with (0, 1, 3, 9), and t₃ when we start with (0, 1, 6, 8).⁴⁸ Intuitively, this is because the tip of conical set-class space can act as any of the transpositions-along-the-chord – that is any of the boundaries that shrink to this single point. Once again this is a reason to associate voice leadings with homotopy classes rather than specific paths: if a voice leading is associated with a particular path that passes through the tip of the set-class cone, then we cannot determine the contrapuntal transformation from its geometrical representation; if we instead associate voice-leading transformations with homotopy classes, then we can always find an unambiguous path representing a voice leading.

Figure 37. The effect of this path cannot be described topologically as it depends on the intervallic structure of the chord.

Finally, the polygonal models cannot faithfully model the intersections of the boundaries of the higher-dimensional spaces. This is because every pair of simplicial facets intersects, while only the adjacent sides of a polygon do. (For clarity, I arrange the polygonal graphs so the identified facets t_x and t_–x are adjacent.) Once again, this means that our polygonal diagrams cannot perspicuously model those specific paths that move through these highly singular boundary intersections; instead, we must represent them with topologically equivalent paths touching the relevant boundaries one at a time. As with voice leadings passing through the cone’s tip, the algebraic language in §5 provides a useful alternative here.

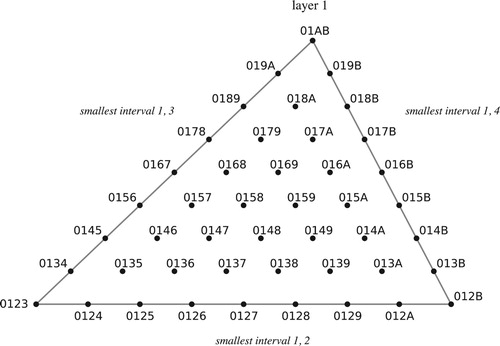
4. Topological models of inversional set-class space

We now repeat the argument for inversional set-class space. Points here represent equivalence classes of tuples related by transposition, inversion, and permutation. Paths represent equivalence classes of individually T-or-I-related voice leadings – that is, voice leadings equivalent under the independent transposition of their chords, possibly combined with the inversion of the entire voice leading (Figure 38). As before, the resulting space is a conical orbifold which can be described, loosely, as an (n − 1)-dimensional simplex with various singularities and identifications. The base of the simplex contains sets with note duplications and represents voice exchanges; the remaining boundaries now represent a host of dualistic transformations including transpositional equivalence classes of bijective strongly crossing-free voice leadings between a chord and its inversion. These are simultaneously the dualistic or inversional analogues of the transpositions-along-the-chord and also generalizations of the basic transformations of Cohn’s neo-Riemannian theory. Understanding these transformations is the main obstacle to comprehending inversional set-class space.

Figure 38. All of these voice leadings are represented by the same path in inversional set-class space. That path represents voice leadings that either start with a major triad, moving root by c and third and fifth by c + 1 semitones, or start with a minor triad, moving root and third by c–1 semitones and fifth by c semitones.

Music theorists use the term “inversion” in a confusing variety of ways, even when we bracket the notion of registral inversion (“root position,” “first inversion,” etc.) to focus on inversion in pitch or pitch-class space. Theorists initially defined inversion as a global symmetry that turns musical space upside down, sending note x in voice A to its inversional partner c − x, once again in voice A; the parameter c, sometimes called the index number, was initially conceived as a fixed constant not depending on the structure of the chord. Later theorists defined contextual inversions in which the index number varies with the notes it is applied to; inversion in this sense is less a symmetry of musical space than a localized musical move, something you can do to a chord, as David Lewin put it. For instance, following Fiore and Satyendra (2005) we could define a contextual inversion that transforms an ordered pitch set (x₀, x₁, … , x_n−1) into (x₀ + x₁ − x₀, x₀ + x₁ − x₁, … , x₀ + x₁ − x_n−1). Here the index number c = x₀ + x₁ is “contextual” because it depends on the input ordering. (For exactly this reason, contextual inversion is not a global symmetry of musical space.) If we interpret order positions as voices then this contextual inversion again has the property of mapping note x in voice A to c − x in voice A. Alternatively, we can apply contextual inversions to unordered chords by focusing on a smaller collection of sonorities and defining the inversions in structural terms – for instance, “the inversion that preserves the perfect fifth of a major or minor triad.” Here again, the most straightforward interpretation is of an inversion operating individually on pitches or pitch classes, with the fixed point determined by the collection itself.

Generalized neo-Riemannian transformations, or bijective and strongly crossing-free voice leadings from a set class to its inversion, are neither traditional nor contextual inversions. Instead, they are transformations with the interesting property of acting analogously on pitch classes and voices, sending note x in voice A to note c − x in voice d − A, where d − A is a separate inversion applying to voice labels (Figure 39). In this respect they are similar to the previous section’s transpositions-along-the-chord, which apply addition to both pitch classes and order numbers (c.f. the earlier Figure 22). This simultaneous action on both pitch classes and voice numbers is the crucial feature of Cohn’s version of neo-Riemannian theory, encoded in the intuitive operation of a “triangle flip” (§1).⁴⁹ There is a close connection between this double action and voice-leading efficiency, as the operation on voices is capable of counteracting or undoing the operation on pitches. This is the conceptual link between Cohnian triangle-flips and the phenomenon of “voice leading parsimony” (Tymoczko 2008).

Figure 39. Let (x₀, x₁, … , x_n–1) be a chord in non-descending pitch-class order spanning less than an octave. A strongly crossing-free voice leading from a chord to its inversion moves the pitch class x_i to the pitch class d–x_{c–i mod n}, with subtraction acting on both pitch classes and voice labels. Voices move along paths d–x_c–x_i + ||x_c–x_{c–i mod n}||_+, with ||x||₊ defined as in Figure 22 .

These generalized neo-Riemannian voice leadings will always preserve the distance between at least one pair of voices. When we are dealing with specific chords, we can define these transformations by choosing any two notes to be common tones: typically, there is a unique bijective and strongly crossing-free voice leading connecting the chord to its inversion and fixing those notes.⁵⁰ When we apply this voice leading to a specific registral configuration, we hold the chosen pitches constant, preserving the chord’s spacing when measured in chordal steps – exactly as with the generalized “registral inversions” of Figure 15 (Figure 40). I have found this to be a fruitful compositional technique, for where traditional music theory tells us only how to invert chords in pitch- or pitch-class space, the neo-Riemannian approach generates a package of voicings that are broadly similar insofar as they share the same abstract spacing (Figure 41). By combining these neo-Riemannian voice leadings with transposition along the scale, we obtain all the strongly crossing-free voice leadings between the transpositions and inversions of a set class; in other words, exactly the voice leadings represented by the annular spaces of §2. Readers are encouraged to hone their intuitions by making use of the websites I have constructed.⁵¹

Figure 40. A recipe for constructing a generalized neo-Riemannian transformation.

Figure 41. Combining neo-Riemannian voice leadings with chromatic transposition to generate a wealth of related sonorities from a single starting point. The inversional labels 𝔦_i will be explained shortly.

In set-class space, we need to consider equivalence classes containing all the voice leadings individually T-or-I-related to these. For want of a better term, I will call them “neo-Riemannian voice leadings in set-class space” or just “neo-Riemannian voice leadings” when the context is clear. We can label them relative to a chord’s normal ordering: define 𝔦_0, as applied to normally-ordered S as the strongly crossing-free voice leading preserving the set class’s smallest interval, sending its first note to the inversion of its second, its second to the inversion of its first, and so on (i.e. Figure 39 with c = 1 and d unspecified since we are in set-class space).⁵² We define 𝔦_i, as applied to normally ordered S, as t_i𝔦₀, combining 𝔦₀ with i-step transposition along the chord.⁵³ Since we are operating in inversional set-class space, we define these operations dualistically, so that 𝔦_a(I(S)) is equal to I(𝔦_a(S)), with I representing traditional inversion (the global symmetry); this stipulation, that 𝔣(I(S)) be equivalent to I(𝔣(S)) for some transformation 𝔣, is the defining feature of “dualism” as I use the term. (I will use a fraktur font for dualistic transformations.) Since the inversion of an ascending a-step transposition-along-a-chord is a descending a-step transposition-along-its-inversion, this means that 𝔦_a(I(S)) is t_–a𝔦₀; it also implies that 𝔦_a is an involution, with 𝔦_a𝔦_a equal to the identity.⁵⁴ It follows that 𝔦₀, 𝔦₁, 𝔦₂, … map the first note x₀ of the normally ordered S to the inversion of its second, first, last, … , and third notes; thus each note x_i in the normal ordering is sent to I(x_1–a–i), the pitch-class inversion of note x_1–a–i. For inversions, things work backwards: when applied to I(S), 𝔦_a maps the first note x₀ of its transpositional normal ordering to the inversion of its second, third, fourth, … , last and first notes, sending note x_i in the transpositional normal ordering to I(x_1+a–i) (Figure 42). Under these definitions the neo-Riemannian L, R, and P voice leadings are instances of 𝔦₀, 𝔦₁, and 𝔦₂ respectively, whose set-class-space analogues we can write as 𝔩, 𝔯, and 𝔭.⁵⁵

Figure 42. The operation ${\mathfrak{i}}_1$ applied to a normal-form chord (left), where it moves x₀ to x₀, and its inversion (right), where it moves x₀ to x₂. Each voice leading is the other’s inverse. Subscripts are relative to each chord’s transpositional normal form.

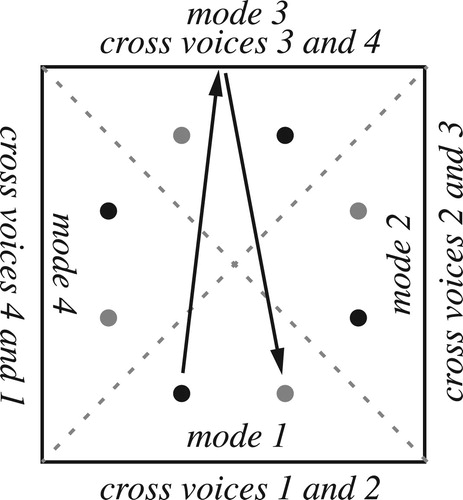
Where the n transpositions-along-the-chord combine like the cyclic group C_n, the 2n neo-Riemannian set-class voice leadings combine like the dihedral group D_2n, with an even number of inversions producing the “dualistic” transposition-along-the-chord 𝔱_x, ascending for the normal form and descending for its inversion. (Algebraically, 𝔦_x𝔦_y is equal to 𝔱_x–y while 𝔦_x𝔦_y𝔦_z is equal to 𝔦_x–y+z, or 𝔱_x–y𝔦_z.) These somewhat counterintuitive relationships can be understood with the symmetries of a regular polygon: cut an n-sided polygon out of paper and label the vertices on one side with an n-note chord’s notes in clockwise ascending order; on the other side of the paper, label the vertices with the inversion’s notes in ascending clockwise order, with the two chords’ smallest intervals sharing an edge. Voices correspond to the vertices’ spatial position and neo-Riemannian set-class voice leadings to outline-preserving flips. Figure 43 demonstrates using boldface and italics for the two sets of labels. Two distinct flips form a rotation, sending the two sets of labels in the same spatial direction but opposite musical directions. (Transpositional set-class space contains only these rotations, recognizing no similarity between the chords on opposite sides of the polygon.) In odd dimension every flip preserves an edge while in even dimension only the even-numbered inversions preserve edges; odd-numbered inversions instead preserve two vertices and the distances between two pairs of notes that are adjacent-but-for-one-note. These flips are the larger-cardinality, set-class generalizations of Cohn’s “triangle flip” operation.⁵⁶

Figure 43. Polygonal models of the neo-Riemannian set-class voice leadings for the major/minor triad (left), the half-diminished/dominant seventh (center), and the 01378 pentachord in Figure 41 (right). Bold labels are on the front of the polygon, italics on the reverse side. The neo-Riemannian set-class voice leadings are flips around different axes; two such flips form a rotation that transposes the two sides in opposite directions along the chord.

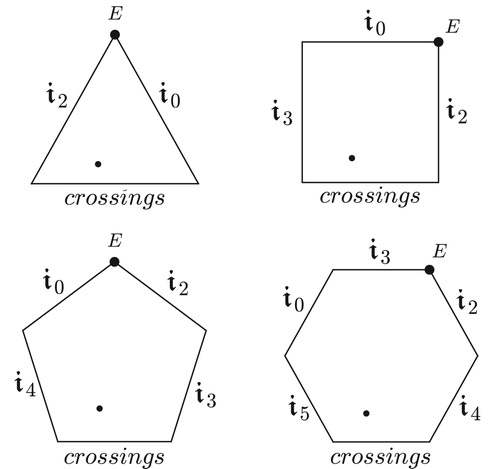
We will associate these dualistic transformations with the “boundaries” of inversional set-class space, leading to models like those in Figure 44. Here every inversion other than 𝔦₁ is associated with a unique facet of the space. A geometrical path through the space thus analyzes a voice leading into a series of neo-Riemannian set-class voice leadings just as a geometrical path through transpositional set-class space analyzes the voice leading into a series of transpositions-along-the-chord (plus voice exchanges, in both cases). Hence the neo-Riemannian set-class voice leadings are the voice leadings that remain when we quotient out by transpositions, inversions, and voice exchanges, much as transpositions-along-the-chord are the voice leadings that remain when we quotient out by transposition and voice exchanges (described as R in the introduction).⁵⁷

Figure 44. Schematic models of inversional set-class space, for trichords, tetrachords, pentachords, and hexachords. These graphs involve slight simplifications that will be described shortly.

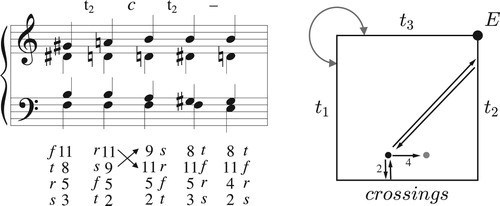
Musically the generalized neo-Riemannian voice leadings are important because they preserve the distance between two voices. Such voice leadings often appear when composers move those voices in parallel, the remainder shifting so as to create strongly crossing-free voice leadings among inversionally related sonorities. Each of the passages in Figure 45 is of this form, repeatedly applying the same voice leading in set-class space.⁵⁸ Geometrically, this means that they each repeatedly move along a single line segment. (Collectively, the passages are related in a more general sense, making similar use of the space’s different boundaries.) From a traditional standpoint, we can think of these voice leadings as repeatedly combining a familiar neo-Riemannian operation (either L, P, or R) with additional transpositions. Geometrically the 𝔦₀ and 𝔦₂ voice leadings are represented by paths that reflect off nearby edges before returning to their starting point. For triads, the 𝔦₁ voice leading bounces off the completely-even augmented triad E, but this is not true for other trichords: when a trichord’s second-largest interval is not a major third, then 𝔦₁ is represented by paths such as 𝔦₂𝔦₀𝔦₂ or 𝔦₀𝔦₂𝔦₀ (𝔭𝔩𝔭 or 𝔩𝔭𝔩), which reflect three times off the two inversional faces.

Figure 45. Passages in which two voices descend in parallel while the third alternates between prime and inverted forms: Mozart, C major piano sonata K. 309, I, mm. 73–76, featuring the $\mathfrak{l}$ voice leading; the Benedictus from Schnittke’s Requiem, featuring $\mathfrak{p}$; and the opening of Gesualdo’s Moro Lasso, featuring $\mathfrak{r}$.

These sorts of voice leadings can also be found in nontriadic contexts. Figure 46 shows three passages from Stravinsky’s Rite of Spring that connect 016 triads with neo-Riemannian set-class voice leadings; here we see Stravinsky using two of the three possibilities, preserving the semitone in the first and third examples and the perfect fourth in the second. (Note that here 𝔦₁, or neo-Riemannian 𝔯, is represented by 𝔦₀𝔦₂𝔦₀.) Figure 47 shows a passage that juxtaposes sonorities that are approximately related by inversion, as in Figure 35 above. (The examples in this paragraph were developed in collaboration with Jon Russell, whose remarkable Ph.D. dissertation [Russell 2018] reveals a wealth of intricate voice-leading structure in The Rite of Spring; the musical portion of Figure 47 is entirely his.) Figure 48 shows a four-voice version of the technique, moving back and forth along a single path in set-class space and preserving the distance between two pairs of voices since the chord’s size is even. (Here we shift from a three-voice geometrical picture to a four-voice topological representation.) Unlike the earlier examples, Stravinsky does not simply alternate between inversionally related forms; instead, he moves the top voices in parallel thirds along the C diatonic collection, allowing the quality of the resulting third to determine the set form. Since the lower voices are chromatic transpositions of the upper, the passage’s four melodies move along three different diatonic scales.⁵⁹ What results is an unusual combination of set-theoretical and contrapuntal thinking, with the former reflected by the music’s harmonic consistency (its use of inversionally related set classes) and the latter its traditional focus on efficient voice leading. The simplicity of the graphical analysis aptly reflects the devastating clarity of Stravinsky’s musical thinking.

Figure 46. Three passages in The Rite of Spring that connect 016 trichords using generalized neo-Riemannian voice leadings: (top left) R114, m. 2 (solid line); (top right) R15, m. 1 (dotted line); (bottom) R64, mm. 5–6 (brass part only, solid line).

Figure 47. Measures 4–6 present fifteen successive 𝔦₂ voice leadings relating 015 and 025 set classes.

Figure 48. A passage from the Rite of Spring involving inversionally related four-note chords; the interval between alto and tenor is always eight semitones; between soprano and bass is fifteen semitones. The entire passage is a repeating series of 𝔦₂ voice leadings.

It should be emphasized that inversional set-class space encodes the dualistic view that ascending transposition along a normal-form chord is equivalent to descending transposition along its inversion, a perspective that is not always analytically appropriate. To the extent that musicians think nondualistically (for instance, grouping together ascending transpositions-along-the-chord regardless of a set class’s internal structure), the most natural framework is transpositional set-class space, perhaps augmented by the postulate that inversionally related chords are to be considered similar. Fundamentally, the issue is that the (mostly atonal) composers who tend to categorize chords inversionally are least likely to be concerned with efficient voice leading, while the (mostly tonal) composers who are concerned with efficient voice leading are least likely to categorize chords inversionally. This is a significant limitation. Thus while I am convinced that inversional set-class space can be a useful tool for thinking about progressions between inversionally or nearly-inversionally related chords (as in the preceding examples), I am much less confident about its ability to relate transpositions.

Now for the mathematical details. The inversional spaces are defined by an additional constraint on normal-form ordering:

NF4. The second interval in the ordering is less than or equal to the wraparound interval: for a set class (0, x₁, x₂, … , x_n–1), we require x₂ – x₁ ≤ o−x_n−1, with o the size of the octave.

In transpositional set-class space, the major and minor triads are different set classes with normal forms (0, 3, 8) and (0, 3, 7) respectively; in inversional set-class space they belong to the same equivalence class, with NF4 selecting (0, 3, 7) as the sole normal form.

Geometrically, this replaces one of the vertices of transpositional set-class space, (0, 0, o, … , o), with a new vertex (0, 0, o/2, o/2, … , o/2), creating a new simplex half as large as in the transpositional case. The facet representing t_–1 is unaffected, since its chords have their smallest intervals in their first two positions and hence satisfy NF4.⁶⁰ Meanwhile the t₁ facet disappears entirely by virtue of containing points whose minimal interval is in the first and wraparound positions; its replacement contains orderings whose second and wraparound intervals are equal.⁶¹ The remaining facets are subspaces of facets of transpositional space; this is because the original transpositional facets contained both (0, 0, … , 0) and (0, 0, o, o, … , o), and the new vertex (0, 0, o/2, o/2, … , o/2) bisects the line connecting them. These relations are spelled out in Figure 49.

Figure 49. A comparison of the vertices and facets for transpositional and inversional set-class space. Here “opposite facet” means the facet that does not contain the vertex in question.

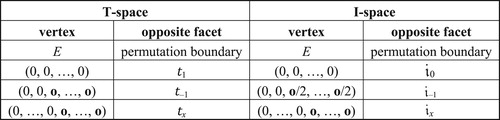
The interior of the simplex is again banal, recording the divisions of a fixed quantity o into n parts, now subject to the requirements that the first is no larger than any other, and that the second is no larger than the last.⁶² This is again a cone whose layers are parameterized by the chord’s smallest interval (Figures 50–52). Its base contains set classes with pitch-class duplications, representing voice exchanges as in transpositional space. The remaining boundaries contain pairs of inversionally related set classes as well as inversionally symmetrical chords, with each nonpermutational facet containing pairs of set classes related under one particular neo-Riemannian set-class inversion that can serve as its label. For example, if a pair of normal-form n-tuples are related by 𝔦_–1 then their first and second intervals are minimal, which means they lie on the facet that is a subset of the 𝔱_–1 fact of transpositional set-class space; the same is true for 𝔦_–2 and the 𝔱_–2 facet of transpositional set-class space, etc. (Figure 53). Pairs of set classes on these facets are related by the relevant neo-Riemannian set-class inversion; line segments from the interior of the simplex can reflect off these facets, returning to their starting point and articulating the relevant inversion. Points on the interior of the simplex cannot be inversionally symmetrical.⁶³ This explains why we can represent inversional set-class space with the polygons of Figure 44.

Figure 50. Trichordal inversional set-class space as a cone.

Figure 51. Three layers of tetrachordal inversional set-class space, with smallest interval 0, 1, and 2.

Figure 52. Two layers of pentachordal inversional set-class space, with smallest interval 1 and 2.

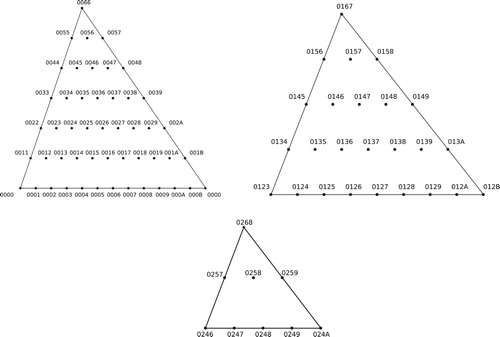
Figure 53. If two normal-form orderings are related by 𝔦_–1, then their first and second intervals (a and b) must be the same size, and no larger than any other interval. For 𝔦_–2 this is true of the first and third intervals (a and c).

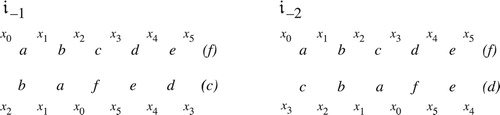
There is however an important complication not arising in the transpositional case: higher-dimensional set-class spaces contain features representing not just the inversions but every other element of the crossing-free voice leading group as well – which is to say, all of the dualistic transpositions-along-the-chord and the “missing” inversion 𝔦₁. This can already be seen in tetrachordal space, which contains linear subspaces acting as 𝔱₁, 𝔱₂, and 𝔱₃ (Figure 54). The phenomenon is more dramatic in pentachordal space, with the 𝔦₂/𝔱₂ and 𝔦₃/𝔱₃ facets containing substantial transpositional regions (Figure 55). Here still, however, the 𝔦₄/𝔱₄ and 𝔦₀/𝔱₁ facets are almost exclusively taken up with inversionally related pairs, with only a single line segment representing transposition (Figure 56).⁶⁴ In higher dimension such facets acquire larger transpositional regions; these spaces also add 𝔦₁, which in lower dimension is represented only by E (Figure 57). Figure 58 thus provides a more accurate picture of inversional set-class space, with each edge representing both a neo-Riemannian set-class inversion and a transposition-along-the chord. – subsuming transpositions-along-the-chord while also adding inversions. (Note that the paired transposition and inversion share the same subscript except in the case of 𝔱₁/𝔦₀.) Linear interpolation can produce a variety of different boundary interactions all equivalent to the same basic transformation (Figure 59).

Figure 54. Four-note inversional set-class space contains subspaces representing 𝔱₁ and 𝔱₂; the former consists of a pair of glued-together line segments, and the latter a mirror-like line segment of 𝔱₂-symmetrical chords. There can no subspace representing 𝔦₁-invariant set classes, for such chords would have step-interval sequence abcd by hypothesis equal to dcba, which by NF1–4 implies a = b = c = d. The voice leading in the first example, when represented by linear interpolation, passes through the identified line segment; this is the origin of the square root.

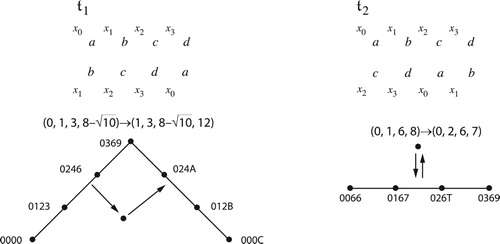
Figure 55. The semitonal layer of the 𝔦₂ and 𝔦₃ facets of pentachordal space. The shaded triangles are glued together as in transpositional space, representing 𝔱_±2. The lighter areas contain pairs of inversionally related chords, with the dotted line inversionally symmetrical. Every chord on the 𝔦₃ facet either has an inversional partner on its facet or a transpositional partner on the 𝔦₂ facet: if its normal-form step-interval sequence is abcde, then its 𝔱₂ and 𝔦₃ orderings are cdeab and cbaed respectively; if d ≤ b, the t₂ ordering is normal and on the 𝔦₂ facet; if b ≤ d, the 𝔦₃ ordering is normal and on the 𝔦₃ facet. If b = d, then both situations obtain. See the appendix for a more general argument.

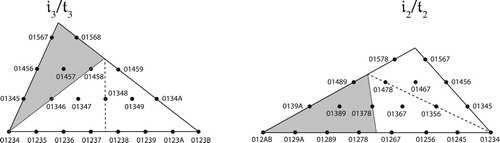
Figure 56. The semitonal layer of the 𝔦₄/𝔱₄ and 𝔦₀/𝔱₁ facets of pentachordal inversional set-class space. Each facet is divided into in inversionally related halves. However, their bottom edges are glued together and can represent transposition: thus a 𝔱_–1 voice leading can move from the interior of the space to the bottom edge of the 𝔦₄ boundary, reappear on the bottom edge of 𝔦₀ facet, and return to its starting point, just like the transpositional case.

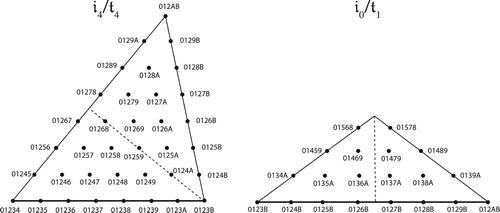
Figure 57. Subspaces invariant under 𝔦₁. (a) In pentachordal space, this is a line containing interval cycles. The voice leading on the figure moves from the interior of the space, reflects off the line and returns to itself, acting as 𝔦₁. (b) In heptachordal inversional set-class space, there is a two-dimensional subspace of chords symmetrical under i₁, containing sets of the form (0, a, 2a, 2a + b, 12 − 2a − b, 12 − 2a, 12 − a), with a ≤ b, and a ≤ 12 − 4a − 2b.

Figure 58. A more accurate picture of inversional set-class space for n = 4, 5, 6, 7.

Figure 59. The dotted line is the path traced out by the two-step ascending transposition-along-the-chord (0, 1, 3, 5, 7)→(3, 5, 7, 12, 13); the solid line represents the two-step ascending transposition-along-the-chord (0, 1, 3, 5, 9)→(3, 5, 9, 12, 13). Here linear interpolation produces different patterns of boundary interactions.

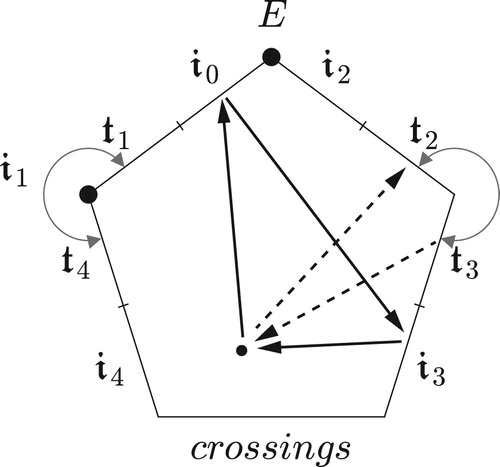
5. Transformation, symmetry, and analytical utility

Geometrical music theory initially used linear interpolation to associate voice leadings with “generalized line segments,” relying on visual intuition to convert these paths into analytical observations. This paper instead models voice leadings with homotopy classes of paths, leading to greatly simplified representations. We can go farther by replacing the geometry with an “alphabet” of voice-leading transformations: n pairwise voice-exchanges, n transpositions along the chord, and n neo-Riemannian voice leadings. A path in set-class space spells out a word in this alphabet, the algebraic correlate of a difficult-to-visualize geometrical object. In contexts where we care about specific chords rather than set classes, we can add letters controlling the absolute transpositional level of the destination chord.⁶⁵ It is also possible to devise letters that double or eliminate notes in the initial chord, or link unrelated sonorities by a “default” voice leading, or represent the simultaneous crossing of multiple voices.⁶⁶

Specific transformations can be defined by their action on a set class’s normal form, dualistically if we impose NF4 and nondualistically if not.⁶⁷ For instance, the top line of Figure 60 defines a voice exchange that swaps the second and third notes in the normal ordering: if we do not use inversion to categorize chords, then the dominant seventh’s normal form is (0, 2, 6, 9) and the relevant voice exchange is (0, 2, 6, 9)→(0, 6, 2, 9); if we do, then the dominant seventh’s normal form is (0, 2, 5, 8) and we have to invert the voice leading (0, 2, 5, 8)→(0, 5, 2, 8) to obtain the dominant-seventh equivalent (2, 0, 9, 6)→(2, –3, 12, 6) or (0, 2, 6, 9)→(–3, 2, 6, 12) upon reordering.⁶⁸ (As the example shows, we can represent the dualistic voice leadings using the same visual pattern of arrows if we write the dominant seventh in descending pitch-class order.) In inversional space the dualistic transformations are more or less forced upon us; but in the other spaces, or when we are using purely algebraic language, we are free to choose.⁶⁹

Figure 60. Dualistic and non-dualistic versions of the basic voice-leading transformations. On the left, the transformation expressed with the inversionally normal half-diminished seventh; in the middle, a non-dualistic equivalent; on the right, the dualistic form. The transformations can be expressed by their effect on a normally ordered collection: c₃ exchanges the second and third notes of the normal ordering, t₁ moves each note up by one step along the normal ordering, and i₁ is the crossing-free voice leading between the chord and its inversion that sends the smallest interval down by one order position when the first chord is normally ordered.

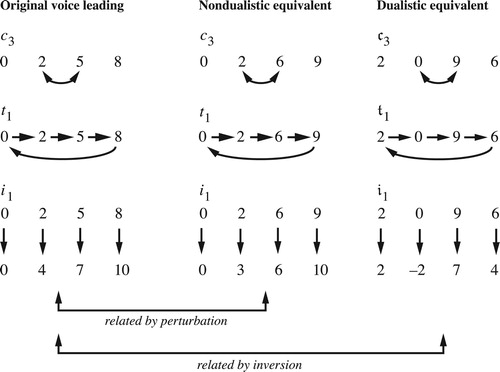
Figure 61 presents four voice leadings from the prelude to Wagner’s Tristan, each moving a half-diminished seventh to its inversion, the dominant seventh. The four voice leadings can be labeled 𝔱₂𝔠₀𝔦₂, 𝔱₃𝔠₀𝔦₂, 𝔱₀𝔠₀𝔦₂, and the retrograde of 𝔱₁𝔠₀𝔦₂.⁷⁰ I have written them this way to clarify their structural similarity, indicating that they are all equivalent up to an initial transposition that rotates the destination chord’s mode; structurally, each moves the root of the half-diminished seventh to a different note of the dominant seventh, crossing the two voices that sound the dominant seventh’s third and fifth. (The fourth voice leading, meanwhile, crosses the Tristan chord’s third and fifth.⁷¹) Our labels provide a structure-neutral description that can be applied to any four-note chord. This is possible because the alphabet mirrors the topological structure of the various musico-geometrical spaces, its elements generating their fundamental groups.⁷²

Figure 61. Four voice leadings from the Tristan prelude along with their descriptions in the alphabet.

In analytical contexts, the permutation region typically provides the clearest view (§3, Figures 28 and 29), with its n boundaries corresponding to the alphabet’s n pairwise voice exchanges, its n transpositions the “transpositions along the chord” and the remaining n points the neo-Riemannian set-class inversions (Figure 62). Figure 63 uses the permutation region to plot the four Tristan voice leadings, with the dark dots representing the four modes of the half-diminished seventh and the lighter dots the dominant seventh.⁷³ The four voice leadings start at the same point but arrive at different modes of the dominant seventh, collectively exhausting the four possible destinations.⁷⁴ Furthermore, the first three reflect off the boundary opposite the final dominant seventh, which is the visual representation of the crossing of the dominant’s third and fifth. The last voice leading proceeds from its starting point to the opposite boundary and then to its destination chord; it is visually clear that this would be like the others were the direction reversed and light dots exchanged with dark dots – which is to say that it is the retrograde inversion of the “missing” fourth path.⁷⁵ (Since the dualistic transformations include the inversional relationship by definition, this geometrical observation is equivalent to the algebraic point in the previous paragraph.) Visual representation thus clarifies the voice leadings’ structural logic, allowing us to ask questions like “what would the fourth voice leading look like if it more closely paralleled the other three?” (Answer: it would be the retrograde inversion of the one Wagner actually uses.) Indeed, it was the visual resemblance that first alerted me to the presence of the algebraic relationship.⁷⁶

Figure 62. The twelve elements of the basic tetrachordal alphabet in the permutation region. On the left, the inversionally normal half-diminished seventh. In the middle, the non-dualistic versions of these transformations as applied to the dominant seventh. On the right, the dualistic equivalents, reflecting the left figure along its vertical center.

Figure 63. The four Tristan voice leadings plotted in the tetrachordal permutation region. The first three touch a crossing boundary and arrive at the opposite dominant-seventh. The last is the retrograde inversion of such a path.

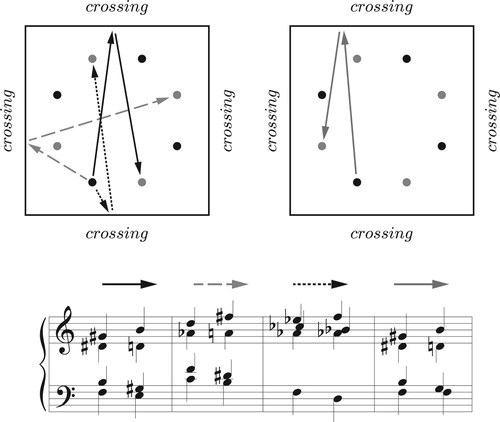
Such connections are considerably more obscure in the inversional set-class space of Figure 64. The first two voice leadings end similarly, reflecting off the permutation boundary, 𝔦₀, and 𝔦₂; since 𝔦₀𝔦₂ is 𝔱₂, the combination can be understood to cross the voices that have the dominant seventh’s third and fifth. (Each begins by touching a different inversional boundary that, in combination with 𝔦₀𝔦₂, produces a different mode of the dominant seventh.) However, the third voice leading is not obviously similar to the first two, reflecting solely off the crossing and 𝔦₂ boundaries; instead of three separate inversions, it contains only one. Nor is the retrograde-inversion relationship to the fourth voice leading nearly so obvious: where the first two have the structure 𝔦_x𝔠𝔦₀𝔦₂ (with 𝔠 representing the crossing), the latter is 𝔦₂𝔠𝔦_x𝔦₀. The issue here is that as we move to more abstract geometries, standard musical operations are represented in more and more complex ways, with an ever-increasing distance between geometrical representation and familiar musical categories.⁷⁷ Thus c_x in the permutation region (with n copies of each set class) becomes t_xc₀t_–x in transpositional set-class space (with just two copies of each set class), and 𝔦₀𝔦_–x𝔠𝔦_–x𝔦₀ in inversional space (with each set class represented just once). For this reason, the permutation region may be the most analytically useful model, with the more abstract spaces better-suited to abstract theoretical questions.

Figure 64. The four Tristan voice leadings in inversional set-class space. The paths are much less comprehensible than in the preceding figure.

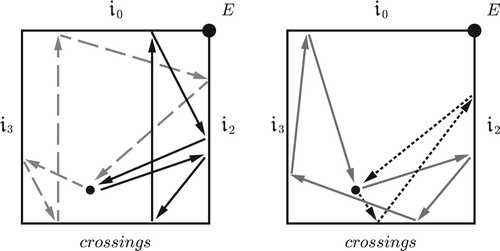
I have argued that the main benefit of the more abstract set-class spaces is to clarify the connection between efficient voice leading and symmetry (Tymoczko 2006, 2011). Indeed, the three letters in our alphabet, c_x, t_x, and i_x correspond to the three basic symmetries (or near-symmetries) a chord can have. Geometrically this is a matter of being close to singular points in set-class space.⁷⁸ The more abstract set-class spaces directly manifest these possibilities in the structure of their boundaries. Permutational near-symmetry (or symmetry under c_x) obtains when the set class’s notes are close together, which is to say that it is near the permutational boundary. Inversional near symmetry or symmetry under i_x, occurs when a chord is near the inversionally symmetrical points dispersed along the i_x boundaries.

Transpositional near-symmetry (or near-symmetry under t_x) comes in two forms. Transpositional symmetry due to evenness exploits the conical structure of set-class spaces; nearly even set classes are near the tip of the cone so that all of the transpositions-along-the-chord are small.⁷⁹ The other sort of transpositional symmetry exploits some subgroup of the possible transpositions-along-the-chord, represented geometrically by boundaries that are identified with themselves so as to form mirror singularities; thus it is closely analogous to inversional and permutational symmetry, which similarly exploit mirror singularities. For example, an uneven tetrachord can be symmetrical under t₂ by virtue of being close to Figure 33’s singular central line; by contrast, uneven tetrachords cannot be nearly symmetrical under t₁ or t₃ since these boundaries are identified, and hence lack mirror singularities of the appropriate sort. We can find transpositional mirror singularities on all and only those boundaries t_x where x divides the size of the chord and is not equal to 1 or –1 (Figure 65).⁸⁰

Figure 65. The semitonal layer of the intersection of the t₂ and t₄ boundaries in hexachordal set-class space, containing set classes that remain in normal form under both t₂ and t_–2 and whose smallest interval appears in the first, third, and fifth positions of the normal ordering. Each set class appears three times and is mapped onto its equivalents by 120° rotation. The central point, meanwhile, is symmetrical under t₂, and hence acts like a mirror in the higher dimensional orbifold. Nearby chords like (0, 0.1, 4, 4.2, 8, 8.3) can be nearly symmetrical under t₂ even though they are close to the base of the cone.

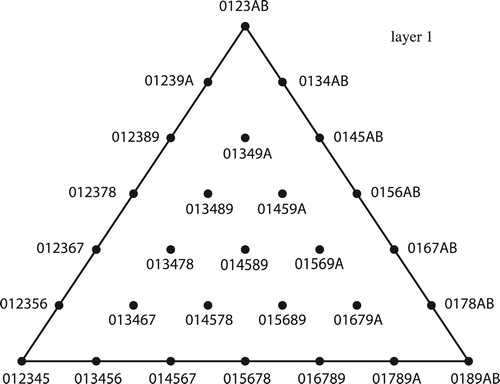
Thus we have a hierarchy of increasingly abstract models, ranging from geometrically faithful representations to abstract polygonal diagrams (annular if we focus on chords, polygonal if we focus on set classes) to the completely algebraic letters of our voice-leading alphabet. These are all more or less equivalent, providing different ways to think about the same fundamental relationships. Moreover, within the category of polygonal diagrams there is an important choice between the permutation region, which is more analytically useful, and the more abstract transpositional and inversional set-class spaces, which clarify general theoretical relationships. At the very end of this process, we can represent a vast set of contrapuntal possibilities using an extremely parsimonious alphabet; indeed, the appendix explains that the bijective voice leadings between the transpositions of any n-note chord can be expressed as the repeated application of just three transformations, a single crossing, a single transposition along the scale, and a single transposition along the chord.

6. Conclusion

Though this paper uses mathematical language, musicians in many different genres manage to internalize transformations like “shift a collection by step as if it were a scale,” “swap two of a collection’s notes,” or “invert a chord so as to preserve its spacing in chordal steps.” Figure 66, from Mark Levine’s Jazz Piano Book, shows his catalogue of the five inversions of Bill Evans’s “So What” chord. Levine moves each note by step along the notes of the chord, the pentatonic scale C–D–F–G–A, looping counterclockwise through annular space precisely as in Figure 15. Figure 67 shows the opening of Rudresh Mahanthappa’s “The Decider,” articulating a series of inversionally related 025 and 035 sonorities, much like Figures 45–48. For all its theoretical abstraction, the topological approach is eminently practical, its fundamental transformations both compositionally fruitful and musically ubiquitous.

Figure 66. Mark Levine’s illustration of the five inversions of the “So What” chord. Each voice ascends by step along the pentatonic scale D–F–G–A–C.

Figure 67. Rudresh Mahanthappa’s 2006 composition “The Decider” is based on the 025 set class, moving the perfect fourth in parallel, the middle voice alternately a major second below the top voice and a major second above the bottom. This is very similar to Figures 45 and 46 above.

Theorists, however, may find that the shift from geometry to topology requires some conceptual reorientation. When I first started thinking about musical geometry, I wrongly dismissed the neo-Riemannian operations as unnatural (Figure 68). I now realize that a deeper understanding of musical geometry requires us to distinguish two classes of transformation: those representing global symmetries, which allow us to “glue together” regions of musical space, and the contrapuntal possibilities that remain once we have used these symmetries to create a geometry, known to musicians as voice leadings and to topologists as the fundamental group. The global symmetries are the input to the process of musical modeling, while the contrapuntal possibilities are the output of the process, something we learn from the resulting geometry. The difference between them – the difference between traditional transposition and the transpositions-along-the-chord, or between traditional inversion and the neo-Riemannian voice leadings – is a measure of what we can hope to gain from the geometrical approach.

Figure 68. In the annular spaces, traditional transposition and inversion are geometrically straightforward, corresponding to rotation and reflection (here around the solid line). By contrast, dualistic transpositions-along-the-chord move inversions in opposite directions and hence do not correspond to standard geometrical symmetries.

Philosophically, the global symmetries are something you can do to a passage of music while the contrapuntal possibilities are, as David Lewin put it, something you can do inside a piece of music (Lewin 1987, 159). The shift between these two perspectives was extremely gradual, and in Lewin’s work global symmetries are not always distinguished from contrapuntal moves. Schoenberg’s 1941 lecture “Composition with Twelve Tones” explicitly connects transposition and inversion to the symmetries of musical space, conceiving them as transformations that can be applied to extended passages such as twelve-tone rows (Schoenberg 1975; these symmetries in turn inspired the five “OPTIC” symmetries in Callender, Quinn, and Tymoczko 2008). The neo-Riemannian transformations, reinterpreted as voice leadings by Cohn, are instead localized moves that can be made inside a particular musical game, and in this sense they are more limited than the global symmetries. But they are no less important, being a crucial first step toward understanding the spaces formed by those global symmetries. This paper has generalized Cohn’s voice leadings to arbitrary chords inside arbitrary scales. An even more basic step is the passage from the octave shifts that create pitch-class space to the fundamental group’s associated “paths in pitch-class space” – represented geometrically by loops in the pitch-class circle.⁸¹ In higher dimension, these paths become the “transpositions along the chord,” creating the annular topology that can be found in countless discrete voice-leading graphs (e.g. Figure 1; Douthett and Steinbach 1998 or §3.11 of Tymoczko 2011). Thus theorists built a piecemeal understanding of the various routes through contrapuntal space, whose totality we can now comprehend as the fundamental group.

It can be challenging to distinguish an orbifold’s fundamental group from its symmetry group, as there is a mathematical theorem telling us they are isomorphic (Hughes 2015). This means we are guaranteed to find similar structures serving subtly different musical functions. For musicians the connection between the two kinds of transformation is clearest in the case of voice crossings, which manifestly embody the permutation symmetry giving rise to the space itself while also being familiar as voice leadings.⁸² By contrast, transpositions-along-the-chord are not at all salient among the global symmetries of chord space even while playing a crucial role in the fundamental group.⁸³ With inversion the situation is more complex, as the term is used to describe a range of conceptually distinct phenomena, including reflection around a fixed pitch or pitch class (typically a global symmetry), generalized neo-Riemannian voice leadings (paths in voice-leading space, or elements of the fundamental group), and “contextual inversions” having something of the character of each.⁸⁴ The result can be confusing, with theorists rightly intuiting that there should be “inversion-like” voice leadings even while being unsure how to define them in mathematically or musically fruitful ways.⁸⁵ It can be genuinely surprising to find the dihedral group appearing not in its familiar guise as the group of transpositions and inversions (global symmetries), nor in its slightly less familiar guise as the group of Wechsels and Schritts (contextual inversions and dualistic transpositions), but as a collection of voice leadings linking a set class to itself (the crossing-free subgroup of the fundamental group of set-class space). Here the n-note chord is closely analogous to the o-note scale that contains it.

Ironically, by distinguishing global symmetries from the fundamental group, we can start to bridge the divide between the geometrical and transformational approaches to music theory, a divide that is as much philosophical as technical. My own interest in musical geometry reflects a realist methodology, a pursuit of musical constraints that transcend the explicit decisions of any individual composer. By contrast, transformational theory has often been associated with a more relativist philosophy, treating “transformations” as postulates and not attempting to justify them on psychological or other grounds. (These two perspectives can be loosely associated with tonality and atonality, the one language grounded in acoustics, convention, and perhaps biology, the other aspiring to surpass those limits.) This in turn leads to numerous technical divergences, with transformational theory modeling intervals as abstract symmetry groups rather than more concrete geometrical objects such as paths or elements of a tangent space (Tymoczko 2009). Because of this philosophical difference, I was initially slow to realize that a transformational approach to voice leading was closely related to homotopy theory – a lapse which in turn led me to overlook the important fact that boundaries of the simplicial set-class models can be identified with specific voice-leading transformations. The current paper reflects my dawning realization that transformational theory could play a crucial simplifying role entirely compatible with a robust realism: we can employ topology without suggesting that all chords are equal, or that any transformation is as good as any other, but simply because we have encountered geometrical structures too complicated to intuit directly.

Acknowledgment

Thanks to Giovanni Albini, Emmanuel Amiot, Julian Hook, Frank Lehman, Jason Yust, and especially Jacob Shulman for helpful suggestions and corrections.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Notes

1 “Bijective” voice leadings between non-transpositionally related chords can involve doublings but those must be fixed in advance. Nonbijective voice leadings, in which doubling is more flexible, are more complex but can be treated using the tools introduced here; exploring this is a topic for future work. The term “scale” includes the limiting case of continuous and unquantized pitch space. See the appendix for more.

2 Here I am referring to the general Schenkerian idea that voice exchanges decorate a simpler uncrossed background (e.g. Brown 2005, 78).

3 See http://dmitri.mycpanel.princeton.edu/cs.html and /multichord.html for the annular spaces of §2, /sc.html for the set-class polygons of §§3–4, /sc.html and /nr.html for the voice-leading alphabet in §5, and /nr.html and /tonnetz.html for generalized neo-Riemannian theory (§4). These programs, along with explanatory videos, can also be found at madmusicalscience.com.

4 For histories of the Tonnetz see Cohn (1997, 2011b). The specific version I have used, with tilted rather than rectangular axes, originates with Otakar Hostinský.

5 Here Cohn drew on the work of David Lewin (1987, 175ff) and Brian Hyer (1989), both of whom understood neo-Riemannian transformations as contextual inversions applying to entire chords. See §4 for more.

6 On Vial’s map the L transform applies L to the tonic triad while adding or subtracting one of the scale’s sharps; P leaves the tonic triad unchanged but adds or subtracts three of the scale’s sharps; and R applies R to the tonic triad while leaving the scale unchanged.

7 See Cohn (2011b) for a perspective that emphasizes the similarity between the traditional Tonnetz and Vial’s figure.

8 Lerdahl (2001, 2020) does not use this space to model voice leading, but rather an abstract harmonic distance that serves as one input to a complex algorithm whose ultimate output is a “tension value,” one of the primary empirical quantities in his theory. My point is that if we were to use the “diatonic torus” to model voice leading, we would find the same issue once again.

9 See Siciliano (2002, 134), for comments on trivial and non-trivial loops.

10 Two loops are homotopic, or belong to the same homotopy class, if one can be smoothly deformed into the other. In the musical context this means that the voice leading corresponding to a path depends not on its specific geometry but on its general topological features.

11 See the appendix for a more formal definition.

12 A simplex is the higher-dimensional analogue of a triangle or tetrahedron, an n-dimensional figure bounded by n+1 points all connected by edges. Topologically we can think of it as a closed ball. See Callender, Quinn, and Tymoczko 2008; Tymoczko 2011.

13 Intuitively, the issue is that transposition by o/n preserves a chord’s radial position, preventing us from embodying transpositional symmetry when we try to combine chords of different sizes

14 See the appendix or Tymoczko (2011) for technical details. While we can think of the two boundaries of the annulus as representing voice exchanges or voice crossings, there is no principled way to associate them with particular voice exchanges.

15 In Tymoczko (2010, 2011), I criticized the Tonnetz on the grounds that its distances do not fully match voice-leading distances; Cohn (2011a) answered by adding augmented triads to the Tonnetz. Here I raise a further issue that applies even to this modified Tonnetz, namely that it does not perspicuously reflect the underlying annular topology of the voice leadings it purports to model.

16 Readers can verify these graphs using the multichord.html website described in footnote 5.

17 Hook (2008) first considered basic voice leadings (called the “signature transformation”) in the specific case of the familiar 7-in-12 diatonic scale; Hook (2011) later generalized this idea to arbitrary seven-note collections.

18 Mathematically, we have the cyclic group acting simultaneously as a transposition-along-the-scale and a transposition-along-the-chord (cf. Figure 22 below).

19 When the initial schema is the basic voice leading for a maximally even chord, we can describe the intervallic structure of the generalized minor scales.

20 To be more accurate, this earlier work associated voice leadings with “generalized line segments,” the paths arising when each note glides linearly from its starting point to its destination, beginning and ending at the same time. This was to avoid defining the fundamental group at singular basepoints. See the appendix for more.

21 Again, identifications and singularities mean that these spaces can be topologically quite complex: for example, four-note transpositional set-class space is a cone over the real projective plane with singular base and tip (Callender, Quinn, and Tymoczko 2008).

22 See the appendix and Tymoczko and Sivakumar (2018).

23 My approach here is broadly reminiscent of Roeder (1984, 1987).

24 For an n-note chord in an o-note scale, transposition by n chordal steps is equivalent to transposition by o scale steps, and this is reflected by the topological equivalence of the associated paths.

25 See the appendix for an explanation of the notation.

26 In set-class space, any crossing of other pairs of voices requires a transposition along the chord that moves the chord’s smallest interval so that it lies between the appropriate voices.

27 For convenience, I have chosen this final voice leading to be the unique crossing-free voice leading from Tristan to dominant seventh that preserves a chord’s normal ordering, though we could in principle choose any voice leading between the two set classes. We could also apply the transformations t₂ct₂ to the dominant seventh instead.

28 Readers can use the sc.html website to determine these paths.

29 Thanks to Noam Elkies for helping Callender, Quinn, and myself understand musical geometry, and in particular the definition of geometrical normal form.

30 NF1 provides the most useful set-class labels, at the cost of complicating the calculation of voice-leading distances; a less intuitive but geometrically more accurate alternative is to require that the set classes sum to a particular value, in which case we typically need negative numbers.

31 We will see that these octave-related pitches are needed to determine which boundaries are to be identified.

32 In this context, a fundamental domain is a region of ordinary Euclidean space whose interior contains exactly one point for each point in the “interior” of the orbifold; it can be transformed into the orbifold by characterizing the singularities and indentified boundary points.

33 The chord (0, 0, … , 0) has this interval in the “wraparound” position between its final note and the octave above its initial note.

34 This simplex is closely related to what is called the standard simplex whose vertices are (1, 0, … , 0), (0, 1, 0, … , 0), … , (0,  … , 0, 1). The entries in the standard simplex can be understood as the set-class’s step intervals expressed as fractions of an octave (Regener 1974), whereas points in our simplex represent pitch classes (Tymoczko 2011, Appendix B); these differ only by a linear transformation. The standard simplex appears throughout applied mathematics, representing (for instance) the possible results of an n-candidate election.

35 When voices cross, they also exchange their numbers: if voice 1 initially sounds C and voice 2 D, then voice 1 ends up sounding D and acquiring the label “voice 2” while voice 2 sounds C and acquires the label “voice 1.” This relabeling ensures that the edge-labels remain accurate.

36 In set-class space, there is only one voice-crossing boundary and it exchanges the closest pair of notes. Thus the musical function of the t₂ transformations is merely to cross the correct pair of voices. Mathematically, the pattern of boundary interactions analyzes the voice-crossing subgroup into combinations of transpositions-along-the-chord and a single crossing. The permutation region gives a more perspicuous representation of voice exchanges.

37 See Roeder (1984, 1987), Cohn (2003), Callender (2004), Straus (2007) and Callender, Quinn, and Tymoczko (2008). The connection to the standard simplex is clearer when we switch from the note-based representation of set classes (e.g. 0, 4, 7 for the major triad) to Regener’s step-interval representation (e.g. 4, 3, 5 for the major triad).

38 This process is mathematically equivalent to the standard M transform when we use coordinates where the perfectly even chord is at the origin. In this coordinate system (1, 0, –1) is (C♯, E, G), (2, 0, –2) is (D, E, F♯), and (3, 0, –3) is (D♯, E, F), with the new coordinates related by the M transform and lying on the line segment from (C, C, C) to (C, E, G♯).

39 The fundamental domain for each layer of n-note set-class space is similar to that of the (n − 1)-note permutation region described above. This is because the distance between the first two notes is fixed, leaving n – 1 voices to divide up the remaining portion of the octave.

40 The term “facet” refers to the (n – 1)-dimensional boundary of an n-dimensional simplex; for a triangle it is an edge, for a tetrahedron a face, and so on.

41 The presence of duplicate “smallest intervals” on the boundaries follows from NF3: the boundary is the place where one voice can no longer be raised (or lowered) and this is because doing so would form an interval smaller than the first with the next-highest (or next-lowest) note. This can also be seen by considering the vertices of each facet: the perfectly even set class contains the same interval at each order position, while the remaining vertices contain a unison at all but one order position; a set consisting of the perfectly even set class and n − 2 of the remaining vertices will collectively have their smallest intervals at two common order positions. Linear interpolation will preserve this property.

42 For a concrete example, transposing (0, 1, 2, 5, 7) by one step along the chord gives us another normal-form ordering, (1, 2, 5, 7, 12), or (0, 1, 4, 6, 11) when we start on 0. Here the one-semitone intervals lie in the first and “wraparound” positions (11, 12 with 12 being the octave transposition of the initial 0).

43 The initial voice leading, moving from the starting point to the departure boundary, by definition ends with the chord in normal order.

44 Note that we cannot determine chord similarity by comparing normal orderings: sometimes, two set classes’ normal forms can be relatively far apart, even while other modes of the chords are quite close. For instance, the normal form (0, 0.9, 6, 7, 8, 9) is farther from the normal form (0, 0.9, 2, 3, 6, 7) than it is from the non-normal (0, 1, 6, 6.9, 8, 9). My strategy can be adapted to such cases by choosing a region of space containing a transpositional boundary.

45 See Stuckenschmidt (1965). This pattern can be considered a subset of a more complex five-voice structure has two voices sounding a fifth, two sounding a tritone, and an additional voice moving in contrary motion to sound chord roots.

46 See Haimo (1996) and Callender, Quinn, and Tymoczko (2008) for a similar claim.

47 Classifying these problematic paths is a topic for future work, requiring a more sophisticated approach to the singularities.

48 Moving linearly toward E increases the size of any intervals smaller than o/n while decreasing the size of any larger intervals. After having moved through E, intervals continue to grow and shrink at the same rate, the largest interval in the initial chord becoming the smallest interval in the resultant. Exploring this continuous multiplicative transform is a matter for a future paper.

49 Readers can verify that the three Cohnian triangle flips on the Tonnetz send note x in voice A to note c – x in voice d – A.

50 Exceptions can occur when the chosen notes are o/x scale steps and n/x chordal steps apart, in which case we can specify the inversions using the notation described momentarily.

51 The nr.html website allows readers to explore the combination of neo-Riemannian voice leadings and transpositions, the tonnetz.html website represents neo-Reimannian inversions as polygon flips, the multichord.html website represents them in annular space, and the sc.html website displays neo-Riemannian voice leadings in set-class space.

52 This definition is ambiguous for chords with multiple normal-form orderings; to label the contextual inversions in that case we need to arbitrarily choose an ordering. I will ignore this complication in what follows.

53 This strategy is similar to Fiore and Satyendra (2005), only using a chord’s normal ordering rather than an arbitrary ordering.

54 That 𝔦₀ is an involution, and that it commutes with the nondualistic transpositions-along-the-chord t_a, both follow from direct inspection; this proves that 𝔦_a𝔦_a, or t_a𝔦₀t_–a𝔦₀, is the identity.

55 The triad’s geometrical normal form is 037. L is 𝔦₀ or (0, 3, 7)→(0, 3, 8), moving 0 to I₃(3), R is 𝔦₁ or (0, 3, 7)→(10, 3, 7), moving 0 to I₁₀(0), and P is 𝔦₂ or (0, 3, 7)→(0, 4, 7), moving 0 to I₇(7).

56 Cohn’s “triangle flips” associate voices with vertices and pitch classes with spatial positions. This approach is hard to generalize, first, because only the three-note Tonnetz tiles the plane, and second, because only in the three-note case is the number of edges equal to the number of pairs of notes. The polygonal models in this paper instead associate spatial positions with voices and vertices with pitch classes. The tonnetz.html website in footnote 5 realizes a general chordal Tonnetz. See also Tymoczko (2012).

57 Around 2002, Callender and I puzzled over the relation between neo-Riemannian theory, his trichordal set-class space (Callender 2004), and my own scalar and interscalar interval matrices (Tymoczko 2008). This paper’s answer is that the latter (in particular, the interscalar interval matrices relating inversionally related chords) depict the crossing-free subgroup of the homotopy group of Callender’s trichordal set-class space, which in turn lifts to the Cohnian Tonnetz.

58 These sorts of passages answer a delicate question in neo-Riemannian theory, namely “when should we assert the presence of a genuinely dualistic transformation like L, P, and R, rather than simply an efficient voice leading between inversionally related chords?” A composerly focus on the fixed pair of voices can give us reason to favor the dualistic reading.

59 Furthermore, the passage’s underlying voice leading (0, 1, 4, 4)→(0, 0, 3, 4) takes advantage of the inversional symmetry of a two-note set class, as described in Tymoczko (2011, §2.9) (and particularly Figure 2.9.5).

60 This is the facet that neither includes the new vertex nor the vertex it replaced.

61 The t₁ facet does not contain (0, 0, … , 0); the remaining vertices of set-class space have their second and wraparound intervals equal.

62 Now the office workers are going to n events in different locations, and the smallest car is going to see movie i₀ while the car going to see i₁ is smaller than the car going to see i_–1.

63 This follows from the fact that they have a unique smallest interval and thus could be symmetrical only under 𝔦₀ (by the definition of 𝔦₀). But any set class symmetrical under that inversion has its second interval equal to its wraparound interval and hence lies on the 𝔦₀ facet of the simplex.

64 The 𝔱_–1 voice leading (0, 0.5, 2, 3, 9.5)→(0, 2.5, 3, 4.5, 5.5) is an example of the type of voice leading mentioned in the caption to Figure 56. It moves from the interior of the space to the 𝔦₄ boundary at (0, 7/6, 14/6, 21/6, 49/6), corresponding to (0, 1, 2, 3, 7.97) on the semitonal layer, reappears on the 𝔦₀ facet at (0, 7/6, 14/6, 42/6, 65/6), or (0, 1, 2, 6.97, 11) on the semitonal layer, and returns to its starting point.

65 For instance, let W be any ordered sequence of voice exchanges, transpositions along the chord, and neo-Riemannian voice leadings (c, t, and i as defined below); we can define WS_x as the form of the voice leading whose paths sum to x. For a given starting chord, this is unique.

66 Here again we touch on ideas similar to those in Roeder (1984).

67 See the appendix. For chords with multiple normal-form orderings we must arbitrarily choose one.

68 The pairwise voice exchanges exchange two voices pitch classes without crossing any other voices. In the two-note case we need to distinguish c₀, which crosses the closest notes by the smallest possible paths, as in (C4, E4)→(E4, C4), from c₁, which crosses the same voices by a longer path, as in (C4, E4)→(E3, C5). For the tritone the distinction between these two voice leadings evaporates as they are the same size.

69 Readers can use the sc.html website to explore the alphabet.

70 The retrogrades of 𝔠_x and 𝔦_y are 𝔠_x and 𝔦_y respectively; the retrograde of 𝔱_x is 𝔱_−x since reversing an ascending x-step transposition-along-the-chord produces a descending transposition by x steps. Thus the retrograde of 𝔱₁𝔠₀𝔦₂ is 𝔦₂𝔠₀𝔱₃ rather than 𝔦₂𝔠₀𝔱₁.

71 The inversion of (F, A♭, B, E♭)→(F, B, G, D) around F is (F, D, B, G)→(F, B, E♭, A♭) whose reordered retrograde is (F, A♭, B, E♭)→(F, G, D, B), which is analogous to the other voice leadings in crossing the dominant seventh’s third and fifth.

72 The fundamental group of the permutation region is the group of voice exchanges; for transpositional or inversional set-class space it is the semidirect product of the voice exchanges with either the cyclic group C_n or the dihedral group D_n. In chord space the transpositions along the chord are instead represented by ℤ.

73 Again, readers can use sc.html website to calculate these paths.

74 Meyer (1989, 283) argues that the Tristan prelude marks the beginning of the decline of the notion of inversional equivalence, but this point seems inconsistent with Wagner’s prominent use of inverted Tristan chords, for example in measure 10.

75 It is the “missing” voice leading insofar as it maps the root of the half-diminished seventh to the seventh of the dominant seventh, whereas the others map root to root, root to third, and root to fifth (ignoring the crossing).

76 In A Geometry of Music (Tymoczko 2011) I proposed that we could best understand Tristan if we chose to disregard voice exchanges; the polygonal models allows us to see that the crossings have an interesting structure as well.

77 The Cohnian Tonnetz represents transpositions-along-the-chord as the product of neo-Riemannian inversions, a similarly counterintuitive factoring. In some ways the Tonnetz is a chord-based structure reflecting features of inversional set-class space.

78 A symmetrical chord is invariant under some word W, a combination of c_x, t_y, and i_z, and therefore under the subgroup of voice leadings generated by W; chords near this symmetrical chord can be connected by efficient voice leading to their W­-forms.

79 Here it can be useful to imagine the cone’s layers as an (n − 1)-sided polygon whose edges represent the non-trivial transpositions along the chord, containing all those set classes whose smallest interval is of a certain size. As the smallest interval increases, this polygon shrinks to a single point. The permutational boundary does not appear in this representation because it is the cone’s bottom layer.

80 These points can be thought of as recreating features of lower-dimensional set-class space within the more complicated spaces representing larger collections.

81 To form pitch-class space we glue together octave-related points, forming the circular quotient space ℝ/ℤ. The elements of the circle’s homotopy group, ℤ, can in turn be interpreted as paths (or voice leadings) moving by some integral number of octaves in pitch class space. When I first started writing about these paths I encountered numerous theorists who claimed they were mathematically ill-defined.

82 Even here, however, the resemblance can be misleading, as permutation in ℝⁿ is not a voice exchange as I define it, sending (x, y) to (y, x) regardless of content. My c₀ transform instead sends (C4, E5) to (E4, C5), which is not a permutation of pitches; it is also distinct from the c₁ voice exchange, which sends (C4, E5) to (E3, C6).

83 Two-note chord space is ℝ²/(S₂ ⋉ ℤ²⁾, with the two factors representing permutation (S₂) and octave equivalence (ℤ²). The transpositions along the chord do not appear among these global symmetries as their effect depends on the ordering of the dyad: for (C4, E4) it is the first note that moves up by four semitones, while for (E4, C4) it is the second.

84 There is significant disagreement in the literature about whether neo-Riemannian transformations are contextual inversions, in part because of the way they evolved over time. Earlier work such as Lewin (1987) and Hyer (1989) tends to define neo-Riemannian transformations as contextual inversions, while later work, following Cohn (1996), tends not to. However, some later writers, such as Straus (2011), adopt the former definition while some early writers, like Morris (1998), adopt the latter.

85 Straus (2003) defines “inversion-like” voice leadings mapping note x in voice A into note c – x in voice A; geometrically these correspond to somewhat unnatural transformations such as 𝔠₀𝔠₂𝔠₀𝔦₂ for trichords and 𝔠₀𝔠₃𝔠₀𝔠₂𝔠₃𝔠₀𝔦 for tetrachords; musically, they are uncommon insofar as they involve a large number of crossings in pitch-class space. Though it is not obvious, Cohn’s neo-Riemannian voice leadings are arguably the more natural “inversion-like” voice leadings, being the homotopy group’s manifestation of inversional symmetry.

86 In Tymoczko (2006) I used traditional pitch-class intervals rather than paths in pitch-class space as I was afraid to abandon music-theoretical orthodoxy.

87 Every voice leading is a bijective voice leading between the two multisets X and Y as just defined. A nonbijective voice leading is one in which the chords’ doublings are not fixed in advance, e.g. (C, C, E, G)→(A, C, F, F), which is a bijective voice leading from (C, C, E, G) to (F, F, A, C) but a nonbijective voice leading from (C, E, G) to (F, A, C).

88 While this formal definition is new to this paper, the underlying strategy is implicit in many of my previous analyses, where I often write, e.g. (F, C)→(A, A)→(C, F) to indicate that one voice moves F–A–C while the other moves C–A–F (for an example see Tymoczko 2016, 269).

89 In set-class space we do sometimes need the additional structure provided by orbifold homotopy theory to account for the highly singular perfectly even chord (§3).

90 For example t_–1 is t_n–1T_–o while T₁ is t_nT_1–o.

Mathematical Appendix

Unless otherwise noted all definitions can be found in Tymoczko (2011), Callender, Quinn, and Tymoczko (2008), and Tymoczko (2006).⁸⁶

The basic setting is the continuous circular pitch-class space whose points are ordered by log-frequency modulo the octave. A scale is a collection of o distinct pitch classes defining a piecewise linear metric with the distance between adjacent notes equal to one (“the scale step”); we use this metric to label pitch classes with integers, choosing an arbitrary element as pitch class 0 and proceeding in the ascending direction. In principle, pitch classes need not lie within the scale, though in most musical applications they will. A one-note scale gives the limiting case of an undivided pitch-class space. Every scale defines a notion of addition and hence rotation (musical “transposition”) and reflection (musical “inversion”). Typically I choose the octave to have either size 12, with 0 = C, 1 = C♯, etc., or size 7, with 0 = C, 1 = D, etc.

As described in the paper, a path in pitch class space is an ordered pair (p, r) whose first element is a pitch class and whose second element is a real number representing how the note moves, as measured in scale steps. Neither p nor r need be integers. Paths in pitch-class space can be associated with points in the tangent space of the pitch-class circle; each path connecting a pitch class to itself can be identified with a unique element of the circle’s fundamental group. A path (p₁, r₁) is connected to (p₂, r₂) if it ends where the second begins, p₂ = (p₁ + r₁) mod o. A voice leading is a multiset of paths in pitch-class space; it links two chords, or multisets of notes, X = {p_i} and Y = {(p_i+ r_i) mod o}.⁸⁷ The notation (x₀, x₁, … , x_n–1)→(y₀, y₁, … , y_n–1) refers to the voice leading {(x_i, y_i–x_i)}. I sometimes use real numbers or pitches to notate pitch-class voice leadings, e.g. writing (0, 4)→(–8, 12) or (C4, E4)→(E3, C5) to indicate the voice leading in which pitch class C (in any octave) moves down by eight semitones while E (in any octave) moves up by eight semitones. When I use octave-free names, as in (C, E, G)→(C, F A), the assumption is that each voice moves to its destination along the shortest possible path. Voice leadings can be transposed and inverted in the obvious way: transposition rotates a voice leading’s pitch classes while leaving its real numbers unchanged; inversion inverts the pitch classes while multiplying the real numbers by –1. Two voice leadings represent the same transpositional voice-leading schema if they are related by transposition. A concatenation of two voice leadings v₁ and v₂ is a bijection between their paths such that each path in v₁ is connected to its partner in v₂.

It is often useful to add the real components of a collection of paths. A voice exchange is a bijective voice leading from a chord to itself whose paths’ real numbers sum to zero. A transpositional voice leading by x scale steps is a voice leading whose real numbers are all equal to x. A voice leading is strongly crossing-free if its voices never cross no matter how they are arranged in register. Strongly crossing-free voice leadings preserve a chord’s spacing as measured in chordal steps. A voice leading that is not strongly crossing free has voice crossings in pitch-class space. Define path extension as the operation of adding the same constant to each of the real numbers in each of a voice leading’s paths: two voice leadings are related by individual transposition if they are related by a combination of transposition and path extension; they are related by individual inversion if they are related by a combination of inversion and path extension. Voice leadings in transpositional set-class space are equivalence classes of voice leadings related by individual transposition; voice leadings in inversional set-class space are equivalence classes of voice leadings related by individual transposition or individual inversion.

Let (x₀, x₁, … , x_n–1) be a multiset of pitch classes in normal order as defined by either NF1–3 or NF1–4. The one-step ascending transposition along the chord t₁ is $\left(x_0,x_1,\dots ,{x_n}_{\text{--}1}\right)\to \left(x_1,x_2,\dots ,x_0+\mathit{o}\right)$ The one-step descending transposition along the chord is its retrograde, with n-step transpositions generated by iterating these single-step operations. The pairwise voice exchanges c_i cross only adjacent voices: $\begin{array}{rl}& \left(\dots ,x_i,{x_i}_{+1},\dots \right)\to \left(\dots ,{x_i}_{+1},x_i,\dots \right),i<n-1\\ & \left(x_0,\dots ,{x_n}_{-1}\right)\to \left({x_n}_{-1}-\mathit{o},\dots ,x_0+\mathit{o}\right),i=n-1\end{array}$ The neo-Riemannian inversion i₀ is $\left(x_0,x_1,\dots ,{x_n}_{-1}\right)\to (-x_1,-x_0,\mathit{o}-{x_n}_{-1},\mathit{o}-{x_n}_{-2},\dots ,\mathit{o}-x_2)$ with the remaining neo-Riemannian inversions i_i defined by t_ii₀ and sending note x₀ to the inversion of x_1–i. (When working with chords rather than sets, it is typical to define more specific transformations that combine these neo-Riemannian inversions with an additional transposition.) If normal forms are defined using NF1–3 only, then we have non-dualistic transformations notated with lowercase: t_i, c_i, and i_i, to which we can add T_i for transpositions along the scale (transpositional voice leadings as defined above). For “dualistic” transformations defined with NF1–4, I use the same labels in fraktur font: 𝔱_i, 𝔠_i, and 𝔦_i, with uppercase 𝔗_i for transpositions along the scale (a notation not appearing in this paper).

Every n-note chord corresponds to a unique point in the orbifold ${\mathbb{T}}^n$/S_n, with the symmetric group S_n permuting the n circular coordinates. This “symmetric product space” can be described as the twisted product of a simplex and a circle, with its circular dimension coordinatized by the sum of the chord’s pitch classes modulo o. (Equations defining a fundamental domain are given below.) The space’s boundaries are singular and contain chords with note duplications. For a non-singular chord X (i.e. one in the interior of the space with n distinct pitch classes) there is an isomorphism between the group of bijective voice leadings X→X (combining by the concatenation of connected paths) and the orbifold fundamental group with basepoint X (Hughes 2015). This is true even though voice leadings are discrete objects while the fundamental group represents collections of continuous paths; in general, continuous glissandi provide an intuitive model of the discrete objects, helping us understand what voice leading corresponds to a given path and vice versa.

For a singular chord S (i.e. one with pitch-class duplications), there are multiple ways to concatenate the voice leadings S→S. The orbifold fundamental group at basepoint s, described in Hughes (2015), includes musically unobservable operations that recreate the same fundamental group found at the non-singular basepoints. In musical contexts this is problematic for reasons that are best explained by example. Suppose you were to put your fingers on C4 and F4; there are four basic voice leadings that collectively generate all the voice leadings to any other C, F pair: two voice exchanges, c₀ or (C4, F4)→(F4, C4) and c₁ or (C4, F4)→(F3, C5), moving voices in contrary motion by 5 and 7 semitones respectively, and two one-step transpositions along the chord, t₁ or (C4, F4)→(F4, C5) and its retrograde t_–1 or (C5, F4)→(F4, C4). If on the other hand you place your fingers on A3 and A4, then the small voice exchange c₀ is no longer distinguishable from the identity, while each of the remaining transformations can be applied in two different ways: for c₁ you have both (A3, A4)→(A4, A3) and (A3, A4)→(A2, A5), for t₁ you have (A3, A4)→(A4, A4) and (A3, A4)→(A3, A5), and for t_–1 you have the retrogrades of the t₁ voice leadings.

From the musician’s standpoint this is a significant difference; in the one case there are four possibilities while in the other there are six. The orbifold fundamental group identifies the two situations by postulating an unobservable permutation c₀ (A3, A4)→(A3, A4) that is distinct from the identity (A3, A4)→(A3, A4). The analytical problem with this strategy is illustrated by Figure A1, which presents a succession of voice leadings from the multiset {A, A} to itself. Underneath the music I show that each voice leading is systematically ambiguous depending on whether we choose to include the unobservable permutation c₀ or not. (When voices change octaves there is the additional freedom to put the voice crossing before or after the transposition, which for a nonsingular chord generates distinct voice leadings.) The result is a proliferation of indistinguishable analyses, all arising from the imposition of the same group structure at singular and nonsingular basepoints.

Figure A1. A passage of music containing voice leadings from the singular (A, A) to itself. This passage defines a unique melodic design, but can be described in multiple ways using elements from the orbifold fundamental group.

Hughes has suggested that this redundancy is the price we have to pay to model voice exchanges. But my own work uses an alternative strategy that seems to me more musical, namely specifying how voice leadings are to be concatenated. This can be accomplished by modeling an n-voice, m-chord passage as a contrapuntal design, or multiset of m-tuples whose elements form a sequence of paths in pitch-class space, each connected to its successor, with each m-tuple representing a distinct melodic line.⁸⁸ As with voice leadings themselves, these lines are specified only by their sequence of pitch-class paths, rather than by instrument, register, etc. In the case of non-singular chords, a contrapuntal design is just a sequence of concatenated voice leadings; when singularities are involved, the contrapuntal design adds structure by stipulating how the concatenation is to occur.

The top of Figure A1 shows the unique contrapuntal design corresponding to the passage, determined by the voices as expressed by musical notation. In general, two sequences of orbifold fundamental-group elements map to the same contrapuntal design if and only if they define the same sequence of paths-in-pitch-class-space in each voice, precisely as in the non-singular case. For this reason there is no increased music-analytical power resulting from the additional structure in the orbifold fundamental group, over and above what can be expressed using contrapuntal designs: contrapuntal designs collect musically indistinguishable group-theoretical descriptions into analytically relevant categories. In this sense, the theory of voice leading extracts the musically relevant portion of orbifold homotopy theory.⁸⁹ Since these complications are largely tangential to this paper, as well as to the practical concerns of music making, I will ignore them in what follows, assuming non-singular chords for the sake of expositional simplicity.

The orbifold fundamental group for an n-note chord X is ℤ ⋉ (S_n ⋉ ℤ^n–1) with ℤ the subgroup of strongly crossing-free voice leadings and S_n ⋉ ℤ^n–1 the subgroup of voice exchanges (Tymoczko and Sivakumar 2018). The voice exchanges are bijective voice leadings from a chord to itself whose paths have real components summing to 0; these combine a permutation S_n with a set of octave displacements ℤ^n–1, with the superscript n–1 because one displacement is determined by the sum-0 condition (Hughes 2015). Voice exchanges are generated by the pairwise voice exchanges c_i defined above. The crossing-free subgroup ℤ acts by repeated transposition-along-the-chord t_i and contains the transpositional voice leadings nℤ as a normal subgroup. The quotient ℤ/nℤ is the cyclic group of transpositions-along-the-chord in set-class space and one of the primary objects discussed in this paper; it is the crossing-free subgroup of the fundamental group of transpositional set-class space. (In all the set-class spaces, the subgroup of voice exchanges is S_n ⋉ ℤ^n–1, just as in chord space.) This cyclic group is in turn the rotational subgroup of the dihedral group corresponding to the generalized neo-Riemannian voice leadings, the crossing-free subgroup of the fundamental group of inversional set-class space, generated by combining the voice leading 𝔦₀ with the dualistic transpositions along the chord 𝔱_i.

Thus each of the main categories of voice leading is associated with a different group: the scalar transpositions with the cyclic group, the neo-Riemannian set-class inversions with the dihedral group, and the voice exchanges with the symmetric group (augmented by octave shifts summing to zero). The bijective voice leadings between the transpositions of any n-note chord in any o-note scale, regardless of cardinality, can in fact be generated by repeated application of just three transformations, a single voice-exchange c₀, the one-step ascending transposition along the chord t₁, and the one step descending transposition along the scale T_–1. This is because t₁ and T_–1 combine to form all the combinations of transposition along the chord and transpositions along the scale, and because t_ict_–i produces the pairwise voice exchanges.⁹⁰ For transpositional set-class space we need only c₀ and t₁, while for inversional space we need 𝔠₀, 𝔱₁, and 𝔦₀.

A fundamental domain for ${\mathbb{T}}^n$/S_n, can be obtained by conjoining NF2 in the paper with $\text{NF}{1}^{\mathrm{\prime }}.0\le \mathrm{\Sigma }{x}_i\le \mathit{o}$ In the orbifold, the sum-0 facet is identified with the sum-o facet; the circular dimension’s coordinate is given by Σx_i mod o. Since the space’s only singularities are on the boundary, its interior is a manifold. The previous paragraph’s crossing-free subgroup ℤ is isomorphic to the fundamental group of this interior. This isomorphism has a natural musical interpretation: two continuous paths in the interior are homotopic if they represent glissandi whose net effect is to move every pitch class by the same number of semitones, and they can be identified with the unique voice leading whose paths move those same pitch classes by those same amounts. That is, every homotopic glissando moves pitch class p_i by r_i semitones in total, with {(p_i, r_i)} the associated voice leading. This isomorphism motivates the annular spaces in §2. The construction can be straightforwardly extended to include voice leadings between distinct (non-singular) chord types and voice leadings passing through the orbifold’s singularities (that is, voice leadings with voice crossings in pitch-class space), though these last are difficult to represent visually.

A fundamental domain for the permutation region in §3 can be obtained by combining NF2 with the constraint Σx_i = k for some constant k. For transpositional set-class space, or ${\mathbb{T}}^n$^–1/S_n, we add NF3. A detailed description of these spaces (including their conical structure, which plays a significant role in this paper) is given in Callender, Quinn, and Tymoczko (2008). The main argument of §3 connects all but one of the “boundaries” of transpositional set-class space to the nontrivial transpositions-along-the-chord (here, ℤ/nℤ). The argument proceeds by describing the facets of the simplicial fundamental domain for set-class space, showing that these facets are identified in the appropriate way, and explaining why paths in the quotient space are associated with glissandi having the appropriate effect. This is another application of the basic postulate of voice-leading geometry, linking voice leadings to equivalence classes of glissandi, only now in a space that ignores transpositions. The reasoning is straightforward in large part because of the choice of fundamental domain; with a different choice the connection between boundaries, homotopy classes, and voice leadings would be much less clear.

The argument in §4 largely parallels that of §3 but with the addition of NF4, augmenting the group ℤ/nℤ with the neo-Riemannian set-class voice leading 𝔦₀, acting as described in the text. Once again, the paper associates the boundaries of the simplicial fundamental domain with transformations. The reasoning is more involved than in the transpositional case because a single boundary of the fundamental domain can represent both a transposition along the chord and a neo-Riemannian inversion. This is shown, in the lower-dimensional cases, by direct construction. To see that the phenomenon occurs in higher dimensions, consider a normal-form point X with step intervals (s₀, s₁, … , s_i, s_i+1, … , s_n–1), with s₁ ≤ s_n–1 by NF4. Let s₀ = s_i so that X is on the 1, i + 1 facet of inversional set-class space. Now consider the i-step transposition-along-the-chord 𝔱_i(X) = (s_i, s_i+1, … , s_n–1, s₀, s₁, … , s_i–1). If s_i+1 ≤ s_i–1 then this ordering is normal and we have a pair of transpositionally related boundary points X, 𝔱_i(X). Alternatively, if s_i+1 ≥ s_i–1 then 𝔦_–i(X) = (s_i, s_i–1, … , s₁, s₀, … , s_i+1) is normal and on the 1, i + 1 facet, giving us a pair of inversionally related boundary points X, 𝔦_–i(X).

None of these ideas are complicated by the standards of contemporary mathematics, nor are any of the relevant proofs challenging: mostly it is a matter of choosing musically and mathematically appropriate definitions and understanding familiar geometry, particularly that of quotient spaces and the standard simplex. The interest, in my view, lies in the many musical consequences that flow from this simple mathematical picture, leading to new technological tools both literal and metaphorical. To my mind this reflects music theory’s status as an applied discipline: where mathematicians are more likely to be interested in generality and proof, music theorists need a detailed and intuitive understanding of the specific spaces arising in musical contexts.