Evolutionary computation to search Mandelbrot sets for aesthetic images

Abstract

We describe an evolutionary algorithm for searching Mandelbrot sets for aesthetic images. Artistic intent is enforced through the design of fitness functions that drive the evolutionary search. Our fitness function employs a mask that specifies a desired iterative behaviour at sample points within the image. The mask used to define a specific instance of the fitness function can be derived from an existing image of the Mandelbrot set. Because of this the artist need not be skilled in programming or familiar with the arithmetic of complex numbers. Once a mask has been chosen, our method uses an evolutionary algorithm to perform a three-parameter search of a specified Mandelbrot set. This paper applies our techniques to the quadratic and cubic Mandelbrot sets.

Keywords:

• Fractals
• Evolutionary algorithm
• Evolved art
• Mandelbrot set

AMS Subject Classification: 2000 Mathematics Subject Classifications: :

• 28A80
• 37F45

1. Introduction

A fractal is a mathematical or geometric object whose topological dimension is not a whole number 1. Fractals were used in art long before the notion of fractal dimension was formalized. In 1 Mandelbrot includes a 17th century painting, taken from a series of 36 views of Mount Fuji, depicting a great wave threatening an open boat. The wave is an approximation to a self-similar fractal. This example of a fractal in art appears well before the 1868 birth of Felix Hausdorff, who first quantified the notion of fractal dimension.

Sometimes fractals are presented as an art form in themselves 2–6; other times they are incorporated as elements of a piece of visual art 7–9. Fractals have been used to add natural-looking objects in scenes 1, 10, 11. Fractals can be used as a way of making the beauty of maths apparent to an audience whose last contact with maths was in the context of a less-than-enjoyed class 12, 13; several efforts in this direction can be found at 14.

1.1. Mandelbrot sets

For any complex-valued function f(z) there is a corresponding Mandelbrot set M _f that is computed in the following fashion. Given a complex number z there is an associated sequence of points z, f(z) + z, f(f(z) + z) + z, f(f(f(z) + z) + z), … called the Mandelbrot sequence for the point. The points in M _f are those points for which this sequence fails to diverge to infinity. Mandelbrot sets are described in detail in 1. Two pictures of the Mandelbrot set are shown in figure 1, and a picture of the set is shown in figure 2. is called the quadratic Mandelbrot set, and is referred to as the cubic Mandelbrot set. The Mandelbrot set referred to as ‘the Mandelbrot set' in the literature is the quadratic Mandelbrot set.

Figure 1. The quadratic Mandelbrot set together with nearby regions of the complex plane (left) and an enlargement of its upper-right flank (right).

Figure 2. A view of the cubic Mandelbrot set and the surrounding areas of the complex plane.

An excellent exploration of the properties of the quadratic Mandelbrot set appears in the works of R. L. Devaney. In 15 Devaney demonstrates a connection between the Fibonacci sequence and the Mandelbrot set. In the right-hand image in figure 1 three of the regions of the set are labelled with the numbers 3, 5, and 8. These labels are near features of the set which consist of discs with branching structures coming out of them. These features are called bulbs and the branching structures are called antennas. For any two bulbs there is a largest bulb between them. The branching factor of the antenna of the intermediate bulb is the sum of the branching factors of the other two bulbs 15. This means that sequences of bulbs exist with branching factors that are the members of integer sequences obeying the same recursion as the Fibonacci numbers, F _n  = F _{n −1} + F _{n −2}. This, in turn, demonstrates that new structures, in the form of antennas with arbitrarily large branching factors, appear at all levels of magnification. In 16 it is demonstrated that careful examination of the antennas associated with a bulb predict the dynamic behaviour of points in the complex plane under the iteration that generates the quadratic Mandelbrot set.

1.2. Evolutionary algorithms

Evolutionary algorithms 17 are algorithms inspired by the process of biological evolution. An evolutionary algorithm operates on a population of structures — tentative solutions to the problem of interest — in the following manner. A selection process picks solutions, with a bias toward higher quality, to reproduce. These selected solutions are copied. The copies may then be mixed in some fashion with a binary variation or crossover operator. The copies, or the structures resulting from their mixture, are then modified by a unary variation or mutation operator. The resulting new structures are evaluated and then are either discarded or used to replace members of the existing population. The fundamental loop of an evolutionary algorithm is as follows.

Initialize a random population

Repeat

 Evaluate population member quality

 Variations of better structures replace worse structures

Until(results satisfactory)

Report results

In order to implement an evolutionary algorithm a number of steps are required. First a representation for the problem being solved is required. This is the data structure in which members of the population are stored. A fitness function which measures or approximates the quality of solutions must be selected. The variation operators (crossover and mutation operators) must be selected. There may be one or several of each of these and they may always either be applied, or applied with some probability. A population size and a model of evolution must be selected. The population size is the number of members in the population the algorithm operates on. The model of evolution specifies exactly how the fitness function is used to select members of the population for reproduction and replacement. Examples of different possible models of evolution are given in 17. Finally a stopping criterion must be selected. This might simply be a fixed number of iterations of the algorithm, or it might be a minimal acceptable fitness value such that the algorithm terminates when it is reached.

This paper is not the first to offer techniques for evolving fractals. However, our method falls within a difficult category that is distinguished by not including a human as part of the image fitness evaluation process. Designing a fitness function that can judge whether or not a fractal is aesthetically pleasing is not a well-defined problem. Because of this the most common fractal evolution method is human in the loop, or interactive, evolution where a human's aesthetic evaluation is used in lieu of a fitness function. Our first attempt to use the non-interactive evolution technique presented here appears in 5. An early paper that generates both plant-like images and textures with an interactive form of evolution is 18. Examples of human-in-the-loop evolution include systems that use genetic programming 19 and systems which select parameters of (generalized) Mandelbrot sets to generate biomorphs 20. Fractals that are located by evolutionary real-parameter optimization to match pictures of faces appear in 21. Iterated function system fractals, explained in detail in 22, are the target of evolution in 23 and were used to perform fractal rendering of DNA sequences in 24. A hybrid representation using both finite state machines and iterated function systems was evolved to render fractals from different types of DNA. In 25 this fractal rendering technique was used to visually distinguish introns and exons in Zea Mays (corn). The same system was used in 26 to distinguish the genomes of the HIV1 virus and of two bacteria Methanococcus jannaschii and Helicobacter pylori.

A number of efforts to evolve art in which human input was limited purely to algorithm design have been made. A first step in quantifying the qualities that make a good image appears in 27. Another such attempt at quantification appears in 28. The digital clockwork muse 29 is an example of a system with artificial agents possessing an aesthetic sense based on both features extracted by image processing and the novelty of an image. The issue of artificial (or computational) creativity is also examined at length in 30. A software tool that uses evolutionary computation together with an internal image database is described in 31. A careful study of some quantitative aspects of the aesthetics of fractals appears in 32. This paper concludes that fractals with dimensions in the range 1.3–1.5 are more likely to be selected as aesthetically pleasing. Artificial ant techniques are used to produce art in a number of studies, both using human-in-the-loop techniques 33 and later automatically 34, 35. In 36 art is automatically produced by a swarm of painting robots; this technique is later employed using virtual robots in 37.

The remainder of this paper is structured as follows. Section 2 defines our new type of fitness function. Section 3 gives our experimental design. Section 4 gives the results of our evolutionary searches in the form of thumbnails of the views discovered by the evolutionary algorithm. Finally, section 5 suggests alternative fitness functions as well as ways to apply these techniques to other kinds of fractals.

2. Genetic representation and fitness function design

We now define the genetic representation, which we call a view, used by the evolutionary algorithm in this paper.

Definition 2.1:

A view is a square in the complex plane given by three real parameters (x, y, r). The square has upper left corner x + yi and side length r. A view that has a non-empty intersection with the Mandelbrot set is called a view of the Mandelbrot set.

The evolutionary algorithm will optimize the fitness function relative to the value of these parameters. The fitness functions used in this paper are based on the number of terms of the Mandelbrot sequence before the first appearance of a number with modulus in excess of 2.

Definition 2.2:

Given a Mandelbrot set M _f , and a point z in the complex plane, the divergence value of z is the number of terms appearing in its Mandelbrot sequence prior to the first term with a modulus of at least two.

We first remark that for z in M _f the divergence value is infinite (these points fail to diverge to infinity) otherwise it is a non-negative integer. Next we observe that if a complex number has a modulus in excess of 2 its divergence value is zero. The cut-off modulus of 2 is not an appropriate choice for all Mandelbrot sets, but is appropriate for and , because having a complex number with a modulus of at least 2 in the Mandelbrot sequence of a point for either of these Mandelbrot sets is indicative of divergence to infinity 1. We will use the divergence values of a finite set of points to define our fitness functions.

The fitness functions used in this paper all sample the Mandelbrot sequence on a grid of points arranged within the view. This grid is square, equally spaced, and anchored at the corners of the view. In order to specify a fitness function, a desired divergence value at each grid point, called a mask, is given. The fitness of a view is the sum, over the points in the grid, of the square of the difference of the divergence values in the view with those given by the mask. This fitness value is minimized by the evolutionary algorithm; in effect searching for the best possible match to the divergence values in the mask. The hand of the artist enters the process in the design of the mask.

Two types of experiment are performed. In the first the masks are designed with values specified by a mathematical function. In the second the masks are induced from views of the Mandelbrot set selected by the artist. For the designed masks the grids are 11 × 11, and for the induced masks grid sizes of 11 × 11, 21 × 21, and 31 × 31 are tested. Each point in the grid requires an evaluation of a divergence value and so has a non-trivial computational cost. The grid size value of 11 × 11 was selected experimentally in 5 as providing an acceptable trade-off between having reasonable computation time and getting results that looked different (in the opinion of the authors) for different masks. Various values were used for the induced masks in order to make a similar estimate for an effective grid size for induced masks.

Two designed masks were used and their values are given by equations (1) and (2). The constants u and v in the equations used to specify masks in this paper are real numbers taking on 11 equally spaced values in the range −1 ≤ u, v ≤ 1. The values of the functions are rounded to the nearest integer before use. A mask can be specified by filling in desired integer values in an array the same size as the grid. Equation (1) is a unimodal function centred in the middle of the mask; equation (2) is a constant function. The integral values for the first mask are given in table 1.

Table 1. Desired divergence values for the first mask, the mask derived from equation (1)

34	40	47	53	58	60	58	53	47	40	34
40	49	60	70	78	82	78	70	59	49	40
47	60	75	93	109	115	109	93	75	60	47
53	70	93	122	150	162	150	122	93	70	53
58	78	109	150	193	200	193	150	109	78	58
60	82	115	162	200	200	200	162	115	82	60
58	78	109	150	193	200	193	150	109	78	58
53	70	93	122	150	162	150	122	93	70	53
47	59	75	93	109	115	109	93	75	59	47
40	49	60	70	78	82	78	70	59	49	40
34	40	47	53	58	60	58	53	47	40	34

Since points in the complex plane can take on arbitrarily large divergence values, a finite cutoff value M _max is needed to serve as a surrogate for infinite divergence values. In this paper the cutoff 200 was chosen because, at the levels of magnification permitted by the bounds we set on r, points that yield a divergence value of 200 or more are always within one pixel in the final rendered image of points that actually lie within the Mandelbrot set. Therefore whenever values of 200 are used within the mask, in effect we are requesting that points at that position in the mask be either in the Mandelbrot set or, at worst, pixel-adjacent to a point in the Mandelbrot set.

The rationale behind these masks is that the first yields views that share a clear visual feature, while the second yields views with widely varying visual characteristics. The first mask was applied to both the quadratic and cubic Mandelbrot sets, while the second was applied only to the quadratic set. There are a vast number of other possible masks; the lack of anything other than simple intuition guiding the search for desirable masks in 5 led to the idea of using induced masks.

In order to create an induced mask, the artist selects a view V of the Mandelbrot set. The two views used to create induced masks in this paper are shown in figure 3. The mask is induced by placing the sample grid on the view and computing the divergence values at each grid point. These divergence values form a mask such that the view V has a ‘perfect fitness’ of 0. Our hypothesis is that induced masks will evolve views that are similar in some fashion to the view used to induce the mask. If the view V is aesthetically pleasing, then at least one optimum of the fitness function using the induced map, the view V itself, is also. If our hypothesis is correct, then at least some of the other optima of the fitness function will also be aesthetically pleasing. It is not a priori obvious that the fitness function is multi-modal, but in all of our independent runs using the same mask, the evolutionary algorithm never located the same view twice. This we take to be strong evidence that the fitness function is highly multi-modal.

Figure 3. A spiral view and a starburst view selected from the quadratic Mandelbrot set. These views are used to generate induced masks.

2.1. The colouring algorithm

The colour for a pixel in our renderings of Mandelbrot sets is based on the divergence value of a sample point within the area of the complex plane covered by the pixel. An RGB-representation for colour is used, requiring a red, green, and blue value in the range 0 ≤ r, g, b ≤ 255 to specify a colour. A point with divergence value i less than the maximum value 200 is assigned a colour with the following red (R), green (G), and blue (B) colour values:

The A _* values control how fast each of the three colour values cycle, while the B _* values control the phase of their cycles. The palette is thus cyclic and continuously varying as a function of the parameter i. The smoothness of colour transitions is controlled by the A _* parameters with smaller values yielding smaller differences between the colours assigned to divergence values i and i + 1. The phase control afforded by the three B _* parameters permits substantial control over which colours appear at particular divergence values. The palette used for all the figures in this paper (with the exception of figure 9) uses the values A _R  = 0.019, A _G  = 0.015, A _B  = 0.011, which yield smooth colour transitions. The phase shift control values were set to B _R  = B _G  = B _B  = 0.8, so that the first colour, for i = 0, is a shade of grey and when the cosine waves that control each colour are in phase, then the colour is some shade of grey. Since the parameters A _* controlling speed differ, the hue changes with i.

Views that have different values of the parameter r have different levels of magnification. The majority of pixels visible in views at different levels of magnification have distinct sets of common divergence values and so draw the majority of their colours from a different part of the palette. Points in the Mandelbrot set are assigned the 200th value in the palette, a light green, because the maximum divergence value permitted is 200. The background shade of different images varies from grey through various shades of blue, because of the position of the divergence value for the pixels comprising the backgrounds in the pallete.

3. Experimental design

A collection of 20 evolutionary runs with distinct random initial populations (independent populations) was performed for each of the two designed masks. Four sets of 19 runs with independent populations were performed for the induced masks. Two different views were used to induce the masks (details are given below). Three different grid sizes, 11 × 11, 21 × 21, and 31 × 31, were tested in the runs that used the first induced mask. This testing indicated that the variation in the appearance of evolved images from the supplied image decreased as the mask density was increased. The goal of evolution using induced masks is to approximate the appearance of the image supplied by the artist and so only a 31 × 31 grid was used for evolutionary runs using the second induced mask. The missing run for the induced masks, 19 instead of 20, is intended to leave a space in the upper left hand corner of the 4 × 5 array of thumbnails to display the original view used to induce the mask.

Initial populations are generated by placing (x, y) uniformly at random in the square region with corners (−2, −1.5) and (1, 1.5) which includes both of the Mandelbrot sets and . The value of r is initialized in the range 0.0001 ≤ r ≤ 0.01 using a distribution whose natural log is uniformly distributed. In each run evolution is conducted for 100 000 mating events (see below) with the most fit view saved at the end of the run.

The model of evolution used for mating events is steady-state single tournament selection of size seven. In this model of evolution seven views are selected, and the two most fit are copied over the two least fit. The copies are crossed by always exchanging the y-values of the copies and exchanging the r-values 50% of the time. After crossover the new structures are mutated. There are two steps in mutation. The first consists of adding a displacement in the plane to (x, y) in a direction selected uniformly at random and with magnitude given by a normal random variable with mean zero and standard deviation of 0.002. In the small range of values for r used in this paper this constant standard deviation was acceptable. If the range of r values were increased, then this parameter would require a mutation operator whose standard deviation was conditioned on the current value of r. After the corner of the view has been displaced in this fashion, the side length r is multiplied by e ^{ln(1.1)N(0,1)} where N(0,1) is a standard normal random variable. The effect of this is to multiply r by a value near 1. These mutation operators were chosen to permit incremental exploration of the view space with as little mutational bias as possible; separate mutation of the x and y co-ordinates, for example, would have biased search along the co-ordinate axes. The multiplicative mutation operator used for r makes small adjustments whose scale does not depend on the current value of the side length.

Induced masks were produced from the two views shown in figure 3. The left view in figure 3, called the spiral, has upper left corner −0.7689 − 0.1082i and side length 0.0012. The right view, called the starburst, has upper left corner −0.0788 − 0.8292i and side length 0.001. Recall that, in order to produce a mask from a view, the associated grid is placed on the view, and then the divergence values at the grid points within the view are used as the mask values.

4. Results and discussion

Depictions of the 20 best-of-run views for the mask designed from equation (1) are shown in figure 4. Those for the mask designed from equation (2) appear in figure 5. Views generated in experiments testing grid size for masks induced from the spiral view are shown in figure 6, and views generated using the mask induced from the starburst view are shown in figure 7.

Figure 4. The 20 best-of-run views of the quadratic Mandelbrot set (upper) and the cubic Mandelbrot set (lower) found using a fitness function incorporating the first designed mask.

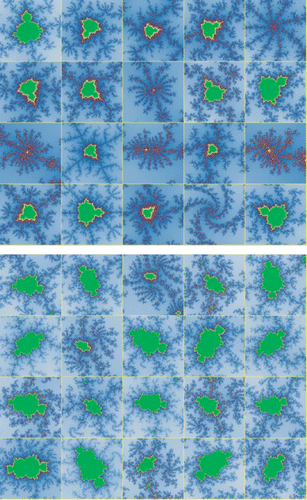
Figure 5. The 20 best-of-run views of the quadratic Mandelbrot set found using a fitness function incorporating the second designed mask. See insert for colour version of this figure.

Figure 6. The 19 best-of-run views of the quadratic Mandelbrot set using a fitness function derived from the spiral view. The spiral is displayed as the first image. The upper set of images uses a 21 × 21 grid while the lower uses 31 × 31.

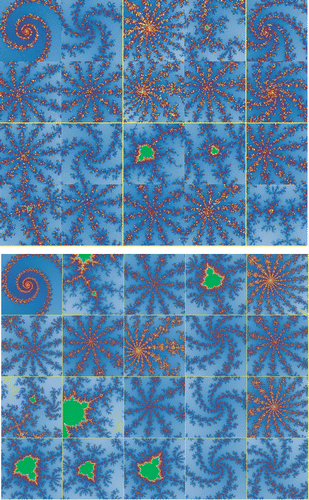
Figure 7. The 19 best-of-run views of the quadratic Mandelbrot set found using a fitness function derived from the starburst image. The starburst itself is displayed as the first image in the set. These images use a 31 × 31 sample grid.

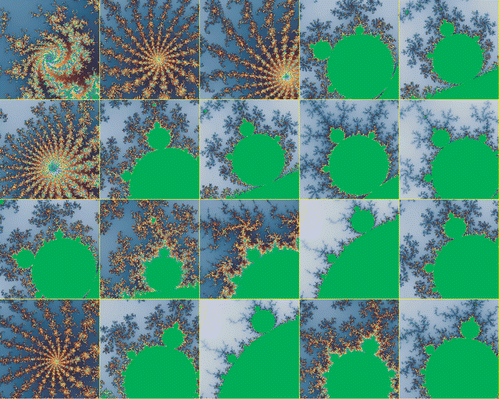
Figure 8. Squares in inverted grey scale above show the locations of views found by the evolutionary algorithm using the first mask on the quadratic Mandelbrot set. The squares shown above are substantially larger than the actual views; all views are smaller than single pixels at this scale.

Figure 9. A view located with an alternate fitness function that failed to find a diversity of visual characteristics.

Examination of figures 4, 5, 6, and 7 makes it clear that changing the mask results in a substantial change in the selection of views located. A minibrot is a smaller copy of a Mandelbrot set located somewhere within the Mandelbrot set. The mask designed from equation (1) proved highly effective at locating minibrots with 14 of 20 views containing a minibrot for the quadratic Mandelbrot set and 20 of 20 views containing a minibrot for the cubic Mandelbrot set. This outcome reflects the fact that a minibrot in the centre of a view yields good agreement with the central 200 values in the mask.

The outcome for the mask designed from equation (2) was startling. This mask, initially intended as a type of control, located a collection of views that encompassed more distinct visual characteristics than any of the others. The mask exerts little control over the visual characteristics of views located (examine figure 5), but the substantial majority of the views shows complex structure. In retrospect this is not too surprising, because points with a divergence value of 150, the value of all grid points in the second mask, are in the highly active regions of the Mandelbrot set but are also fairly far from the maximum divergence value permitted, 200.

As stated previously independent runs always yielded different views. Moreover, the visual characteristics of these views were almost always strikingly different from one another. While the masks permit some control over the type of view located, they do not strongly limit the variety. Suggestions for improving the degree of control are given in section 5. The large number of different views located by the evolutionary algorithm is worth additional discussion. Typically local optima–places in the fitness search space that are good compared to other nearby configurations but not globally best–are the bane of optimization techniques. Many published papers in the area of optimization are, in essence, about techniques for breaking out of local optima and thus improving the chance of finding a global optimum. When trying to locate interesting views of the Mandelbrot set, there is little reason to think that the local optima are inferior to global optima in an aesthetic sense. The fitness function guides the search and permits the artist to exert some control over the type of views located. It does not give an absolute numerical value for aesthetic quality.

For the evolutionary runs performed with induced masks there is a global optimum, the view used to induce the mask. This means that finding good local optima is preferred to finding this global optimum. It seems unlikely that there are additional global optima, and certainly none were located in any of the experiments performed. The phenomenon of local optima being acceptable, or even desirable, outcomes of the optimization of a function that is at best a surrogate for aesthetic judgment may be common in attempts to produce art by algorithmic means.

The runs using induced masks did not function exactly as we had hoped. All four sets of runs using induced masks took place over the quadratic Mandelbrot set. The clean spiral used in the first set of experiments was not reproduced by the evolutionary algorithm. Figure 6 shows the thumbnail views associated with the experiments using 21 × 21 and 31 × 31 grids to induce the mask. The 11 × 11 experiments had only three of 19 runs finding a spiral (image not shown). Increasing the number of sample points in the grid increased the number of spirals, and in particular increased the degree to which the spirals found spiralled outward from the centre of the image. Of the two sets of runs shown in figure 6, neither seems clearly superior. The finer grid (with more points) finds more minibrots, a feature not appearing in the view used to induce the mask, but it also locates more spirals that spiral outward from the centre of the image.

The experiment using the starburst mask located four other starburst-like views and 15 that contained a large number of points within the quadratic Mandelbrot set. This suggests that the fact that the 31 × 31 grid for the starburst contains a lot of values not too far from the 200 divergence value cutoff for membership in the approximate Mandelbrot set makes big chunks of the Mandelbrot set a good approximate solution to the search problem posed by the induced mask. Increasing the limit on the divergence value or imposing a penalty for points within the Mandelbrot set might improve performance.

An issue in any evolutionary computation problem is the nature of its fitness landscape. In each of the sets of runs performed, different views were located by each independent run. This was ascertained by comparing the co-ordinates of the upper left corners of the views. This suggests that the fitness landscapes for the fitness functions defined here are quite rough. Figure 8 shows the locations, not to scale, of the views located with the mask defined by equation (1) on the quadratic Mandelbrot set. The views show preferences for certain parts of the Mandelbrot set, clustering to some degree.

The fitness functions used in this paper were not the first tried. There are two regions in a Mandelbrot set that are clearly worth avoiding: views purely in the interior of the set and views well outside of it. Both these regions are boring, having little or no variation in divergence value or shape. The first fitness function tried maximized the sum of divergence values strictly less than the maximum divergence value on the sample grid. Points achieving the maximum divergence value were assigned a score of zero and so contributed nothing to the value being maximized. This function attempts to place the sample points in locations with the largest possible divergence value below the limit, while avoiding placing them on points in or immediately adjacent to the Mandelbrot set at the resolution of sampling. The views located with this fitness function are striking but quite similar to one another. An example of one of these views is shown in figure 9. The view depicted in figure 9 is far denser than any of the views located using the designed-mask-based or induced-mask-based fitness functions.

5. Conclusions and future work

This section makes suggestions for other directions for evolutionary search for aesthetic fractals. The simplest and most obvious direction for future work is to use other masks than the ones used here. This includes trying different functions for defining designed masks and also different views to create induced masks. Further experiments are needed to better understand the influence of the number of points in the sampling grid on the views located by evolution.

5.1. Alternate methods of computing fitness

The mask-based fitness function used in this paper is only one of many possible related methods of evaluating the fitness of a view of a Mandelbrot set. We suggest two alternative types of mask. Masks with indifference would incorporate a special value that indicates indifference to the value at particular mask points. One simple encoding would be to permit negative values within the mask and then not include the values from those grid points into the mask's fitness calculation. This is a simple modification of the current square mask to permit subsets of the mask to be active in fitness evaluation.

Another possibility, an unstructured mask, would not be defined in terms of a grid of sample points, but instead use a sequence of points determined by triples of the form (ΔX, ΔY, Value) where (ΔX, ΔY) represent a displacement from the upper left corner of the mask's view and v is the target divergence value at that point. This sort of unstructured mask would permit a broader variety of evolutionary searches of the Mandelbrot set.

5.2. Restriction of the search space

This paper studied random initial populations of views within a bounding box containing an entire Mandelbrot set. Choosing instead a small box containing part of the boundary of the Mandelbrot set would both enrich the search space and limit the type of views that could be located. The Mandelbrot set varies spatially across the set, and nearby views often have a similar appearance. This permits the exploitation of the substantial knowledge of the Mandelbrot set already in the literature to be introduced into the evolutionary search process.

5.3. Consideration of Julia sets

The cubic, quartic, quintic, and higher-order Mandelbrot sets, those based on the function f(z) = z ⁿ , have visual characters different from, but reminiscent of, the quadratic Mandelbrot set. The Mandelbrot sets based on transcendental functions such as sine and cosine are radically different. All of these can be used as targets for the evolutionary algorithm presented in this paper with a minimum of effort. The Julia set is a type of fractal closely related to Mandelbrot sets. Rather than adding the point z under consideration back in at each iteration when checking for set membership, a fixed complex constant w is added. The equations used to define a Julia set associated with a complex function f is based on the sequence:

Julia sets are more repetitive at smaller scales than the Mandelbrot set, and so searching for values of w that yield interesting overall appearances of a Julia set is a more natural target for an evolutionary algorithm than searching for views that depict only a portion of a Julia set. This, in turn, suggests that unstructured masks would be a better choice than grid-based masks for Julia-set search. It is worth noting that the Mandelbrot set indexes the Julia set in the following sense. The appearance of the Mandelbrot set near the value w is strongly predictive of the overall appearance of the Julia set 1. With such a ready visual index, the value of an evolutionary algorithm to search for aesthetically pleasing Julia sets is doubtful; views (x, y, r) located by the evolutionary algorithm presented in this paper could be rendered as Julia sets with parameter w = x + yi, removing the need for a specialized Julia set search algorithm.

Quite by accident we were led to consider the following generalization. Let w ₁ and w ₂ be complex constants. Then the series:

defines a new type of fractal, a two-parameter Julia set. If w ₁ = w ₂, then the result is a standard Julia set. When w ₁ and w ₂ are distinct, the resulting fractals exhibit properties, such as disconnected regions with positive area, that Julia sets are known not to exhibit 1. While a form of 4-dimensional Mandelbrot set does index these Julia sets, it does not admit the same sort of convenient visual index that the (two-dimensional) Mandelbrot set does for standard Julia sets.

Although it is possible to visualize slices and sections of certain four-dimensional objects 1, this topic is beyond the scope of this paper. However, it does suggest that a four (real) parameter evolutionary algorithm might be valuable for locating such generalized Julia sets. The generalization given is for two constants; there is an obvious generalization to any number of constants w ₁, w ₂, … , w _k which yields ever more challenging targets for evolutionary search.

In conclusion, this paper demonstrates that an evolutionary algorithm can search Mandelbrot sets for complex and potentially aesthetically pleasing views. The hand of the artist can influence the search by specifying a mask, either numerically or by supplying an existing view from which to induce a mask. Many other applications of the techniques given in this paper are possible and some of a large number of variations of the technique have been outlined in this section.

Acknowledgments

The authors would like to thank the University of Guelph Department of Mathematics and Statistics for its support of this research.