Geometry in the walnut grove: an applied mathematical approach to art

Abstract

A land art project exploring the landscape and geometry of a beautiful grove of walnut trees gives a setting to consider a perceptualist framework for creativity, bringing in mathematical abstraction as a tool to document and reflect on a first intuitive experience of place. We visit mathematics as metaphor, projective geometry and Andy Goldsworthy on the way to the art project and a discussion of the application of the ideas to teaching.

Keywords:

• Perceptualism
• geometry
• projective geometry
• land art
• Mathematics education

1. An enchanted wood

Lord Kelvin gave us this delightful insight into mathematical arrogance:

I often say that when you can measure what you are speaking about, and express it in numbers, you know something about it; but when you cannot measure it, when you cannot express it in numbers, your knowledge is of a meagre and unsatisfactory kind. [23]

Nabokov gives a different perspective:

There is no science without fancy, and no art without fact. [1]

With the addition of the arts to the STEM subjects to make STEAM, there is a lot of current activity working on introducing ‘fancy’ to science [37]. What about the other direction, using science and fact to help develop and refine art and design? Perhaps taking a prompt from Lord Kelvin, we can see what mathematics and geometry can bring to an artistic process; applying the power of knowing with number, shape and form to help develop the expectations and personal experience of design. This is our experience of exploring that idea.

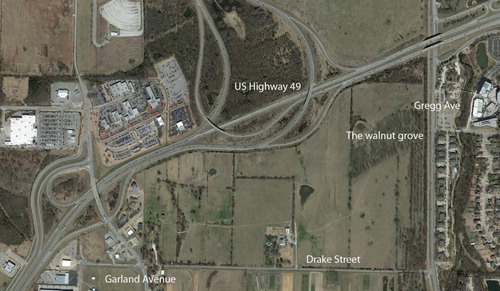
Let us begin again by grounding everything in the site chosen for our project. It is situated two and half miles north of the University of Arkansas in Fayetteville; a Walnut grove planted almost a century ago by the late Professor Noah Fields Drake Ph.D. (1864–1945) a former student of Civil Engineering and Professor of Geology at the university (Figure 2). Professor Drake's vision was the planting of around 300 walnut trees at his farm, sourced from across the United States and grafted onto local root stock, in order to provide a testing ground for edible, soft-shelled Black Walnuts. Though an engineer and geologist by training (he worked in this capacity in the US and overseas most notably in Tientsin, China, for the US Geological Survey) and a teacher by vocation (at the University of Pei Yang, Stanford University and, until his retirement, the University of Arkansas), Dr. Drake's experiments in the culture of walnuts attracted a great deal of national attention. He was Arkansas' sole member of the Northern Nut Growers Association, in which he also served as vice president. Further to his interests in geology, engineering, mining and agriculture, Dr. Drake was also active in local civic affairs and real-estate development. His unexpected passing in 1945, from a heart attack ‘removed one of the oldest and most widely known residents of Northwest Arkansas’ [14]. Dr. Noah Drake was born and raised within 20 miles of Fayetteville, and it is fitting that his name was bequeathed to both a small airfield and a road within the city. Furthermore, his walnut plantation stands to this day as a celebration of agricultural craft and diversity: an evocative human story that has left a magical mark on the landscape (Figure 3).

In the summer of 2015, the authors were commissioned by the current land owners, the Pendergraft family, to create a temporary art piece that would celebrate the walnut plantation and its history, a place where the two Pendergraft girls played as children, knowing the grove only as the ‘enchanted wood’. Before we go further read again about the site, and look at the pictures, what strikes you? How might one create artful design in this place, a place already of great character and beauty? (Figure 4).

Figure 1. Domes in the walnut grove, photograph by Tim Hursley.

Figure 2. Professor Noah Fields Drake Ph.D. [29] and his hand-drawn plan for his experimental walnut grove at Drake Farm, Fayetteville [11].

Figure 3. View of the grove and its surroundings on Google Earth.

Figure 4. Views of the walnut grove or ‘enchanted wood’.

2. Shaking hands with the landscape

In grappling with this rich, complex site loaded with significance, meaning and memory, our approach could be broadly described as perceptualist, with an intention of facing the challenge respectfully and judiciously; specifically the avoidance of being overwhelmed by the mosaic of potential themes and narratives. The perceptualist view of aesthetics, summarized for example by landscape architecture academic Simon Bell [2] rests on the notion that one's initial appreciation of a place is not dependent on a priori knowledge of a site's history, ecology or other objectively manifest truths (an integrationalist view), but rather is based solely on how the place is freely perceived through the senses. Bell speaks to the advocacy of this approach in the philosophical writings of German aesthetic theorists; that a place or scene can be appreciated for its own sake through the senses, but only when the observer is unencumbered by self-conscious interest or concern for the nature of that appreciation. This provides a way for an authentic personal experience that avoids too great an emphasis on practical concerns, Arthur Schopenhauer's ‘absence of will’, where even the question of the objective validity of the experience is not considered to be a central issue, what Immanuel Kant terms ‘free beauty’.

This approach has been operationalized by French landscape architect and academic Christophe Girot as the acts of ‘landing and grounding’, arrival at a place and the formation of intuitive impressions, followed by discovery and understanding through study, immersion, orientation and rootedness [15]. Historically, creative pieces that resonate with and are drawn from the instinct and the intuition have equal value to works that excel in their exactitude and technique. In other words, the richness of the process and the resonance of the product rest on both rational and instinctive values. For example, during the golden period of the Hudson River School of landscape painting, the dominant mode struck a balance between spatial exactitude (rational) and poetic expression (instinctive) through drawing and painting; and these works translate on an emotional level with the general public to this day  [42].

To achieve this, the formation of intuitive impressions is not passive, but documented and reflective. A powerful vehicle for documentation and reflection is on site drawing, which, as noted by Crowe and Laseau [9], has the potential to investigate an evocative spirit of place, capturing a personal experience of space, character and feeling.

The vehicle for documentation and reflection might not be drawing, for example, in Thomas Riedelsheimer's 2001 documentary Rivers and Tides, Andy Goldsworthy Working with Time [36], the sculptor's method, which tends towards the perceptualist approach described, is introduced, in Goldsworthy's own words, ‘as shaking hands with the landscape’. That is, free of any previous understanding of the natural or cultural processes at work, the artist responds to the patterns and perceptions he experiences that are then made visible in his sculptural pieces, entirely built out of the quirks and beauty of the place itself. The exploration of these sensory inputs can lead to wondering about the nature of the site, how it came to be, and the processes that form its patterns. This curiosity leads quite naturally into the exploration of the complexity of the site, from history to ecology and hydrology and through stories of other experiences. Yet the initial personal experience places these discoveries in a meaningful context and a deeply personal narrative, and their relative sensory impact gives these phenomena a kind of hierarchy, that moves one beyond a simple fire-hose of information.

To be more succinct, our process develops an understanding of site by first allowing a free personal experience, documenting and reflecting on that before a deep exploration of the ideas uncovered, driven by intellectual curiosity. What can mathematics bring to such a process?

3. Mathematics as metaphor

In our version of ‘shaking hands with the landscape’, mathematics and geometry provide a key and, we believe, natural toolkit. They act as an additional abstract ‘sense’, helping to understand and experience place. The natural rigour of mathematical thinking provides a counter to the danger of perceptualism not moving beyond a pleasant and romantic whimsy.

This fits into the process alongside drawing or sculpture, questioning and refining what is instinctively felt. Subsequently (again like drawing and sculpture), mathematical ideas can clarify and communicate these feelings to others through creative action and response in the product. It should be noted that just like a drawing can be purely representational as well as capturing emotional content, this is not just the scientific mathematics most readily associated with the discipline. Instead the formal abstraction of mathematics can play a role in further investigation. By abstracting certain aspects of a space, it can be simplified in a variety of different ways, and these simple models can then be investigated to find interesting properties of the experience of place, that might not be obvious when considering the full, somewhat cluttered mélange of sights, sounds, movement and so on. In turn, these properties can be brought back into the full place through a conceptual intervention, with the potential to create new forms, expressions and experiences. This is close to well-established ideas in the design and art professions; for example (design), metaphor and other tropes can be used to establish appropriate forms in landscape architecture or in Goldworthy's case land art, where the site's preexisting character or sensory qualities are one of the inspirations to be considered [34].

This process of moving from a complex world into a simpler abstraction, studying what happens, and then returning that understanding to the world is at the heart of mathematical applications and science. In most cases, for perceptualism the concepts will not be a full mathematical model, instead fitting neatly into the notion of a (mathematical) metaphor, a distinction described by Yuri Manin:

In order to understand how mathematics is applied to understanding of the real world it is convenient to subdivide it into the following three modes of functioning: model, theory, metaphor. A mathematical model describes a certain range of phenomena qualitatively or quantitatively…A (mathematical) metaphor, when it aspires to be a cognitive tool, postulates that some complex range of phenomena might be compared to a mathematical construction. [27]

Our approach can, therefore, be thought of as an applied counterpart to the more pure spirit of constructivist or concrete art described particularly clearly by Max Bill in his The Mathematical Approach in Contemporary Art [3], i.e. it is in service to design rather than to art. In the latter, the mathematical thinking is used as a means to explore pure form without direct reference to the world, whereas we wish to apply the mathematics to the design-thinking process, with the perceptualism playing the role of science in more traditional applied mathematics. Despite this difference, the first sentence of Bill's work does a lot to sum up what we are not trying to achieve:

By a mathematical approach to art it is hardly necessary to say I do not mean any fanciful ideas for turning out art by some ingenious system of ready reckoning with the aid of mathematical formulas.

Later, he answers directly the concern of introducing any mathematics into an artistic context, his conclusion echoing Nabokov's ‘no art without fact’:

It is objected that art has nothing to do with mathematics; that mathematics, besides being by its very nature as dry as dust and as unemotional, is a branch of speculative thought and as such in direct antithesis to those emotive values inherent in aesthetics; and finally that anything approaching ratiocination is repugnant, indeed positively injurious to art, which is purely a matter of feeling. Yet art plainly calls for both feeling and reasoning.

This is especially true in the applied plastic arts of architecture and more especially in the craft of landscape architecture, where reason balances and enriches the artistic impulse in service to the not insignificant and insensitive receptors of change, land and communities.

In our current world, mathematical abstraction has an additional strength; it is no longer only the province of the human mind, but can also be created within computers. This provides another channel for investigation and experience; another path to return from the abstract. This strength grows further with the ability of computers to drive robots and actions in the physical world. Parametric models provide the ability to create and play with spaces of artworks, conjecture about potential ideas and test. The computer manufacturing process gives the ability to go cleanly from idea and abstraction to manufactured objects.

It should be noted here that we do not think that this approach is completely novel or unique, and we do not wish to be exhaustive in related threads, through history. We should, however, mention the related themes present in the work of the College of ‘Pataphysics, whose work grew from the absurdity of symbolist Alfred Jarry who gave one competing definition:

‘Pataphysics will be, above all, the science of the particular, despite the common opinion that the only science is that of the general. ‘Pataphysics will examine the laws governing exceptions, and will explain the universe supplementary to this one. [21]

Of particular relevance is the literary work of the College's mid-20th Century off-shoot, the OuLiPo [30]; a collection of authors and mathematicians who explored formal rules and constraints as an approach to creating literature. For example, George Perec's masterpiece Life: A User's Manual [33] draws its structure from a Knight's tour of the chess board, with each chapter written according to rules defined by Greco-Roman squares of numbers, and Raymond Queneau's Cent mille milliards de poémes [35], which offers more sonnets than the rest of the human race combined, as each line can be picked freely from the 10 sonnets given for a grand total of 100,000,000,000,000 distinct poems. These works and many others explicitly use mathematical ideas to explore story telling and push creativity, which are certainly an applied mathematics of art, but something distinct from our approach.

A work more similar, perhaps, but certainly on a grander scale (looking at the whole of human history rather than a single, physical place) is Manuel de Landa's 1000 years of non-linear history [10], which explores a philosophy of human history through ideas of dynamical systems, such as phase shifts and bifurcations. Although we would claim this work applies mathematics, his description makes the link to science, stating in the introduction: ‘…we must now allow physics to infiltrate human history ’. Nevertheless, what is again clear is the potential utility of mathematically describable actions and abstractions, as a way of offering a new lens with which to re-frame or re-conceptualize something with an apparent, comprehensible order, be it chronological or topographical.

Now before we tell you about what we actually experienced and how it became an act of design, take another look at the description and images of the site, and imagine how it would inspire to sketch and draw; to abstract and re-apply; to land and to ground.

4. Our landing and grounding

At the start of the project, following the process we described above we simply went to spend time in the grove. We immersed ourselves in the place working with the sights, sounds, memories and abstractions that were experienced. During a variety of visits to the site, alone and together, over the period of about a week, we created a series of gestural and abstract drawings and diagrams as an internal exploration and record of those experiences Figure 5, 6, 7.

By necessity the drawings were loose, open-ended and imprecise, the principal media was paper wet with dew, smudged by mud, lump charcoal and cheap, disposable writing pens. The drawings, as artefacts in and of themselves, had little value or preciousness, but as records of experience were spontaneous, raw and free, and therefore incredibly evocative and rich with embodied memory. As suggested by Nicholas G. Carr, author of The Shallows: What the Internet Is Doing to Our Brains [5], and Pulitzer Prize finalist, hand drawing can allow one to access tacit knowledge, experience and emotion as well as consolidate the memory of what is being experienced by the artist.

From these experiences of landing and grounding, and the documentation of our impressions through drawing, we settled on what we felt were the essential features of the site. First, the beautiful grid laid out in Drake's drawings, and second the perceptual changes of solid versus void, light and shadow that occurred as you changed position and direction in the grove. Both of these concepts provide opportunities for geometric interpretation, with the twin goals of being lead to interesting ideas, and finding fresh insight with which to return to the site through design tropes. We will now follow one of those mathematical rabbit holes in detail and explore the projective geometry of lattices.

5. The projective geometry of lattices

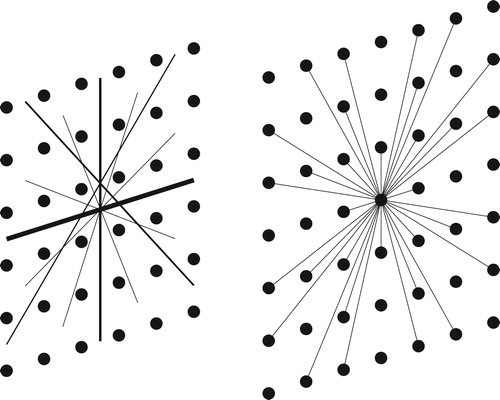
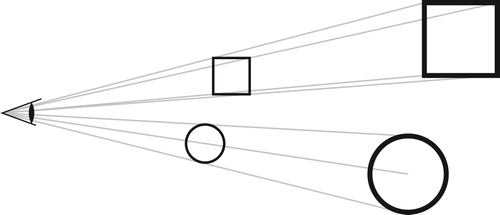
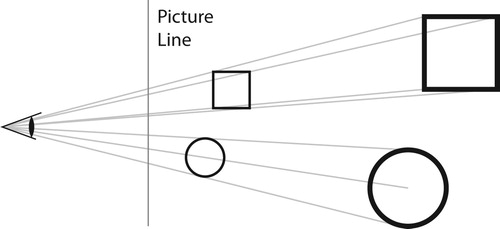
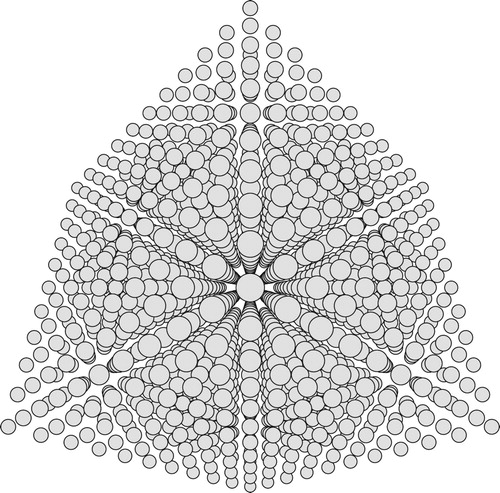
Imagine you are a creature in two dimensions and that your eye is a point. As you look out from the point, you see things that lie along each straight line through your eye. In Figure 8 for example, the two squares and the two circles will both be perceived in the same way by the eye. This gives a simple way to model our perception of the world, as things move away they appear smaller. The geometry of this situation (projective geometry [8]) was first explored by artists with the study of perspective, placing a 3D image onto a plane. In the 2D world, this corresponds to pulling the image onto a picture line some distance from the eye (Figure 9).

Figure 5. Perceptual sketches of the grove.

Figure 6. Diagrams of the grove.

Figure 7. More perceptual sketches of the grove.

Figure 8. Objects in a projective view.

The image on the line will imitate the full 2D image. This framework works very well to explore our perception of viewing a grid of trees as at least to some height they are roughly cylinders. We can ignore the effects of distance in height and just consider the distance on the plane (Figure 10). This corresponds to two point perspective in art  [24].

Figure 9. Linking a projective view to perspective and a picture line.

Figure 10. A grid in perspective.

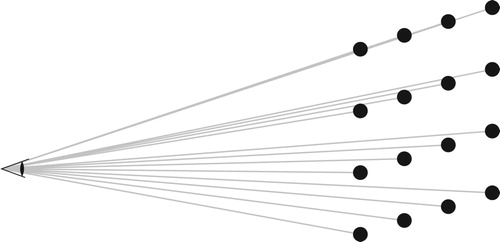
In this view, the regular structure of the grid changes depending on the angle of view. At the top of the view, where the viewing angle lines up with a line in the grid, there is a big gap between perceived points, whereas at the lower down the points are more spread out. Exploring further, we can see that this will happen not just in the main lines of points but in many other directions where the points seem to line up (Figure 11).

Figure 11. Rotating viewpoint of a grid.

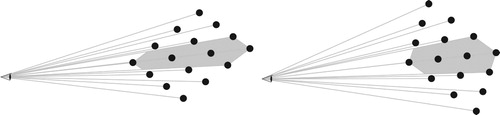
When we look down a line of points, only the first is seen. On the other hand because of the nature of the grid, on either side of the line of points there will be a small gap with no points. As this distance is fixed it will get smaller with distance, but will also reveal a view deep into the structure along two ‘tunnels’ at either side of the main line (shown in grey in Figure 12).

Figure 12. The tunnels visible in a perspective grid.

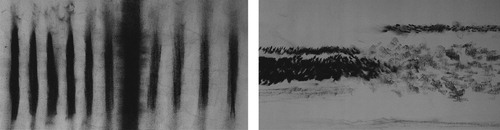
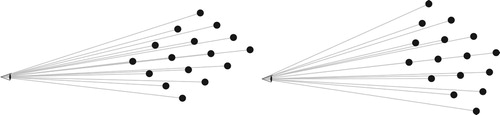
This top down view is informative about the whole image, but as we are talking about the ways in which our eyes actually process information it can be a lot more instructive to construct the image as perceived (viewed along a diagonal in Figure 13).

Figure 13. Grid in perspective without height.

That is slightly unclear, our eyes are tuned to a 3D perspective rather than just this line version. So we can also add the length of the pieces shrinking with distance (Figure 14).

Figure 14. Grid in perspective with height.

We now get a view that might be familiar from driving next to an orchard. This gives a sense of a view of a grid of columns within projective geometry. We can go up another dimension and consider a 3D grid of spheres and the same thing will happen but now with gaps between sheets of 2D grids, as well as the tunnels. If you were to look at a cube of ping pong balls suspended in a room looking down the diagonal of the cube you would see Figure 15.

Figure 15. 3D perspective grid.

Figure 16. Design sketches.

Figure 17. Simulation of the domes made in Rhino and Grasshopper.

Figure 18. Rendering of the domes.

Figure 19. Map of the trees with domes.

Figure 20. Cutting the domes by a CNC machine.

Figure 21. Construction of the domes.

6. Design and construction

We continued to sketch as we honed in on moving from ideas and appreciation of a site to an actual design. We discussed and tested possibilities around the drawing board, on site and at materials suppliers. Sketches were passed around from one team member to another, scribbling, diagraming and imagining without preciousness or proprietary, allowing the design to develop organically over a matter of weeks (Figure 16).

The final design iteration that was selected for development was of an object field comprised of ‘domes’ around the base of a selection of trees. The domes were designed to be slice forms, a collection of parallel planar cuts through a geometric form. The parallel planes or ‘fins’ give a very strong sense of the shape from certain directions, but open up when looked at along the parallel direction. In order to explore and prototype these designs we made a parametric 3D model in Rhino and Grasshopper (Figure 17). This reveals the other strength of an abstract method, one can create large spaces of possible solutions that can be explored visually and perceptually. The parametric system we created generated a dome for every tree in the grove, all facing towards a central tree (Figure 18).

At the point the slice form disappears, you can therefore look up to see a line of trees disappearing into the distance. Using the artwork simulator we had built, we chose nine trees to receive a dome, the number dictated simply by construction budget. Our final dome shapes were ellipsoids of different dimensions, conceived as buried in the ground to varying degrees. They were designed to elongate as they got closer to the aforementioned central tree and also get larger. As the materials provided a hard limit of 8 feet on the length of any dome, the ellipsoids also sank into the ground as they moved closer to the gravity of the central tree, seemingly pulled down and toward its roots (Figure 19).

The parametric models from Grasshopper were designed to also create the cut paths for a CNC router using Edmund's CAMel software. Our set-up meant that any changes to the design would immediately change the cut file, so no post-processing was needed from the design into the manufacturing. Again this is a strength of an abstract method, it can be connected to machines like 3D printers, laser cutters and CNC mills that translate ideas into physical forms. This proved very useful, as we were able to create and build a full prototype dome to pilot the idea, and this lead to several refinements of our design. Knowing that we could make changes without having to redo all of the later work was a great relief (Figure 20).

At this stage we had a tested design, and all that remained was to actually build nine, rather large domes. This took place at the ‘Drake Street Earth Day’ event on the 22nd of April 2016, sponsored by the Pendergraft family and the Fay Jones School of Architecture and Design at the University of Arkansas. Together with a group of students and others from the community, we built the finished piece (Figure 21).

To document the project, we were very fortunate to commission renowned architectural photographer Tim Hursley with the support of the Fay Jones School of Architecture and Design. His beautiful photographs include the image with lighting with which we started this paper and in Figure 22.

Figure 22. Photos of the grove and domes by Tim Hursley.

7. Teaching and learning

It should be clear from the previous sections that this piece and, more importantly, our general approach is transferable, and has great value to inspire pedagogy across disciplines and in many different forms. In fact, at the time of writing EH and CS are leading a cross-disciplinary group of students, investigating and re-imagining a courtyard Space at the University of Arkansas, supported by the University's Honors College. The work was the subject of a regional radio program which begins by stating the clear importance of mathematical thinking in this process, balanced against the more obvious utility of the techniques of landscape architecture  [22]. The rich and relatively quickly accumulated sense of place experienced by the students was due to a method of drawing, and recognizing similarity and difference through counting and pattern recognition. We accept that the willingness to engage with the process and, less importantly, the elegance of the products (mathematical system or drawing) are biased by the students’ a priori experience, competence and familiarity with disciplinary technique and sensibility. However, this is not a hurdle to the viability of the methods outlined here. In fact, given that perceptualism deals with place which, in turn is a complex amalgam of spatial reality and internal moods, memories and associations, struggles in drawing or conceiving mathematical relationships, gives rise to an enriched rather than a weakened process. Put simply, the further the students are from their comfort zone, with careful nurturing and encouragement, their struggles amplify the need for careful observation and mindfulness; a nuanced sense of spatial relationships and self-awareness.

Before we turn our attention to teaching the creative application of mathematics, we offer a precis of what this approach might mean for landscape architecture, that returns us to a point we make earlier in the paper, that reason balances and enriches the artistic impulse. The key word here is balance. Since the mid-twentieth century, a profession which had, previously, embraced a kinship with similarly hybrid factual and fanciful (to paraphrase Nabokov) endeavours such as landscape painting and theatre-set design, began to clamber towards a more prosaic position entirely predicated on an integrationalist approach, defined and discussed below.

Integrationalism, the antithesis of preceptualism, posits that it is only through objective, scientific knowledge, that one can appreciate the world around you or, indeed, make informed and rational decisions for action to change that world. This approach reached its operational apotheosis with the 1969 publication of landscape architect Ian McHarg's Design with Nature [28]. The book lays reasonable claim to be the template on which Geological Information Systems (GIS) are based: a careful and ordered geo-located layering of information drawn from the social, and especially, physical earth sciences, from which fully rational and robust decisions of land planning, design and management can be inferred. As discussed by Farr [13] and Orr [31], this approach is, however, free of consideration of nuanced reflections on human experience and ecological literacy; a modernist credo of (land) form following (land) function writ large across whole landscapes that has been incredibly pernicious to other forms of site understanding and interpretation. Ironically, near contemporaries of McHarg, Aldo Leopold [26] and Rachel Carson [6], both advocated that land-ethics and stewardship be underpinned by a sense of romance, wonder and curiosity. Yet, as suggested by landscape architect and academic, James Corner in 1991 [7]:

It is not unfair to say that contemporary theory and practice [of landscape architecture] have all but lost their metaphysical and mythopoetic dimensions, promoting a landscape architecture of primarily prosaic and technical construction.

Contemporary mathematics education has been struggling with its own version of this dilemma sometimes in messy ways, as a period of US math education policy described as the math wars [39], would suggest. The central problem is described by Jo Boaler in Mathematical Mindsets [4]:

–if you ask most students what they think their role is in math classrooms, they will tell you it is to get questions right. Students rarely think that they are in math classrooms to appreciate the beauty of mathematics.

There are a couple of interconnected points of concern here: mathematics as prosaic product and mathematical education as a classroom-bound process. Of course neither needs to be the case. Just as landscape architecture needs to break-free of treating land as simply a repository of objective data to be analysed and coolly applied to a spatial or environmental problem, so mathematics must embrace its potential for facilitating externalized beauty, and for embodying beauty in its very process. The first of these is, arguably, easier to grasp. Through our work, and some of the historic citations gathered here, we have demonstrated mathematics’ ability to dovetail with the arts to enrich the artistic product through abstraction and understanding. Of course, the use of geometry to elucidate the architectural imagination, in particular, has a rich tradition whether through the use of perspective in the renaissance [20] or the formal diagram in the understanding of typology [43]. But what of the beauty of the process of mathematics itself? This question is addressed headlong by mathematics education researcher Nathalie Sinclair [40] yet she points out, the beauty can be hard to find:

most contributors to discussions on aesthetics in mathematics…are eminent mathematicians who talk about beauty, elegance and purity, which only very few people seem to be able to – or want to – appreciate.

Sinclair challenges this view as the only way to interpret mathematical aesthetics and also connects the importance of aesthetic to cognitive growth. In her conclusion, she returns to this idea, however, pointing out that a view of mathematics as an art can sound appealing, but actually reduces accessibility as the beauty is only there to those who perceive it. Similarly Paul Ernest identified in 1989 the importance of the personal knowledge beliefs and attitudes of mathematics teachers in their teaching  [12].

There is a growing collection of approaches taking on this challenge, trying to make the beauty of mathematics more approachable and make the beliefs and thinking of mathematicians part of the educational experience. As examples, Tracy Zager writing in Becoming the math teacher you wish you'd had [44] says

my goal is to close the gap between math as it is taught and math as it is.

Furthermore, Zager structures her book around the habits of mathematicians. Malke Rosenfeld takes on the embodied approach discussed by Sinclair in Math on the Move [38], and Seymour Papert's seminal work Mindstorms [32] originally published in 1980 began a tradition of mathematics using computer making (originally using a robot called a ‘turtle’) that is very active today. All these approaches lead to an address of the emotional needs of students in a mathematics classroom, a key part of motivating them towards the subject, as studied for example by Markku Hannula [17,18] and linked to teacher experience and practical advice for the classroom by Illana Horn [19]. Such work has even been identified as having significant potential to connect to those historically disenfranchised from mathematics [16,25].

The approach outlined in this paper adds to the literature in several ways. First of all, it provides further recount of mathematics within an artistic setting, providing genuine problems for mathematical investigation and solution. It also aims to ally for students and teachers, the more difficult aesthetic of mathematical process within a more accessible artistic or craft-based one. There could be none of the latter without the former. Second, we provide evidence of mathematics having to step outside of the classroom, mathematicians, and mathematics students collaborating and creating in the landscape. As suggested by Umbach and Wawrzynski [41], education is particularly resonant with students when it is enriched with field work, is reliant on self-directed creativity and collaborative exercises, and when it engages higher order cognitive activities such as synthesizing and organizing ideas, information or experiences into new, more complex interpretations and relationships. Finally, this paper introduces a complimentary link between two disciplines looking to engage with poetics as well as the prosaic in a replicable, creative method: the action of abstraction that facilitates the desirous poetics of place is enriched by inarguable geometry. Just as perceptualism places the human back into the landscape, our work provides insight into how to place the human at the heart of mathematics.

What Lord Kelvin might make of this hybrid approach is open to conjecture.

8. Coda

Figure 23.

Figure 23. The piece aged gracefully into the landscape that inspired it.

Acknowledgments

This work was made possible through the support of Ro Di Brezzo, Vice Provost for Faculty Development and Enhancement, and the Office of the Provost and Vice Chancellor for Academic Affairs at the University of Arkansas through the award of a Collaborative Research Grant. The follow-up course was made possible by the vision and leadership of Dean Lynda Coon, at the University of Arkansas Honors College. We would also like to extend our warmest thanks to Neal and Gina Pendergraft for their enthusiasm, hospitality and generosity as land owners and sponsors of the work and the Drake Street Earth Day event. Thanks also to Deans Peter MacKeith and Ethel Goodstein at the Fay Jones School of Architecture and Design for their logistical support and encouragement of the Earth Day event, and to the Department of Mathematics for their generous support of additional funding. We'd also like to acknowledge Gavin Smith of Ecological Design Group and Justin Tucker at the Fay Jones School of Architecture and Design for their help in rallying the Earth Day teams; the wonderful Earth Day volunteers; and Rachel Smith Loerts and the late, and much-missed, Tim LaTourette in the School woodshop for their patience and assistance.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was supported from University of Arkansas through the award of a Collaborative Research Grant.