A comic page for the first isomorphism theorem

Abstract

Given a homomorphism between algebras, there exists an isomorphism between the quotient of the domain by its kernel and the subalgebra in the codomain given by its image. This theorem, commonly known as the first isomorphism theorem, is a fundamental algebraic result. Different problems have been identified in its instruction, mainly related to the abstraction inherent to its content and to the lack of conceptual models to improve its understanding. In response to this situation, in this paper, we present an illustration that explores the narrative and graphical resources of comics with the aim of describing the set-theoretic elements that are involved in the proof of this theorem.

GRAPHICAL ABSTRACT

Keywords:

• Algebra
• comic
• communication
• illustration
• isomorphism
• quotients
• substructures

Mathematics Subject Classifications (2020):

• 03E02
• 97C70
• 97I20

1. Introduction

The concepts of subobject and quotient object, as well as the concept of homomorphism between algebraic structures, have been fundamental for the development of abstract algebra (Dummit & Foote, 2004). The first isomorphism theorem describes the relationship between these three concepts. It states that, given a homomorphism between algebras of the same signature, the quotient algebra of the domain with respect to the kernel of the homomorphism is isomorphic to the subalgebra of the codomain given by the image. We owe these theorems and their current presentation in some of the best-known algebras, as e.g. groups or rings, to the mathematician Emmy Noether (McLarty, 2006), who recognized the importance and usefulness of these results and helped to disseminate and raise awareness of them.

This theorem, in its different presentations, is part of the algebraic curriculum of many scientific university degrees. However, some problems have been identified in its instruction (Brown et al., 1997; Ioannou & Iannone, 2011). To a greater extent, these problems are caused by the abstraction of the subject itself, but also by the lack of models where students can verify their intuitions and review the elements that are involved in the proof of the first isomorphism theorem.

As a possible strategy to overcome these obstacles, it has been proposed to familiarize the students with the set-theoretic elements that occur in the proof of this theorem (Larsen & Lockwood, 2013; Mena-Lorca & Marcela Parraguez, 2016), particularly in the factoring result that underlies its proof. This proposition states that every mapping between sets can be represented as the composition of three mappings: a surjective one, given by the projection of the domain to the quotient; a bijective one, from the quotient to the image, and, finally, an injective one, given by the inclusion of the image in the codomain.

In order to improve the understanding of this proposition, we find in the literature some examples of conceptual diagrams that capture key aspects in the proof of this factorization result (Bradley, 2016; Carter, 2009; Dummit & Foote, 2004; Maddox, 2008; Sankappanavar & Burris, 1981; Santilli, 2020). These diagrams, according to Rapp (2005), must have the ultimate goal of providing a mental model, able to portray the objects of study and their relationships, conceptualizing the principal ideas, clarifying the main arguments and communicating the results with the aim of opening up further reflection and discussion.

In this paper, we provide an illustration representing the set-theoretic elements that occur in the proof of the first isomorphism theorem. In our case, we have explored the resources and techniques offered by comics as a medium for representing information. In particular, we take advantage of the comic's capacity to configure panoptic representations, where the main elements for the narration coexist. We also consider the possibility of translinear readings and the re-evaluation of content for the self discovery of the result (Bartual, 2020; Bordes, 2017; García López, 2016, may; Groensteen, 1999). In doing so, we are incorporating some of the considerations that have been made in recent decades in comic studies, with the exploration of the narrative possibilities of the medium, the incorporation of diagrammatic solutions (García López, 2016, may; Sousanis, 2015) and their ability to provide useful contextual models for the transmission of information (Cohn, 2013, 2020b).

In this way, we want to highlight the comic as a tool for configuring mental models in which one can test the comprehension of the elements involved in the proof of mathematical results.

To achieve this goal, we have counted on people who knew their languages. This project is the result of the collaboration of two mathematicians and an illustrator, who have been able to synthesize the beauty of their respective worlds in the proposal here presented. For us, this project builds bridges for understanding. Indeed, Poincaré never ceased to repeat that a scientist is ultimately a translator and his own essays were attempts to translate the mathematical and physical advances of his time into comprehensible language (González Fernández, 2012, p. 17).

We provide a brief summary of the content of the subsequent sections of this article. The reader will find a more detailed explanation at the beginning of each section.

In Section 2 we present the mathematical background of our work. We begin with a brief review of the historical development leading to the proof of the first isomorphism theorem and we introduce, for the reader's convenience, the version of this result in the context of universal algebra. This section will also help us to fix notation, introducing the most important definitions and recalling how they are involved in the proof of the theorem. This will allow us to keep our exposure self-contained. Afterwards we review the studies that have described the difficulties experienced by undergraduate students in understanding this result, mainly in the context of abstract group theory, and the different strategies that have been proposed to improve its comprehension. We end the section with the introduction and discussion of some diagrammatic solutions that we have found in the literature, designed with the aim of improving the understanding of the first isomorphism theorem.

In Section 3 we review the benefits of using visual thinking in scientific communication and we will focus on the ability of comics to configure mental models that are capable of representing both the objects of interest and their interactions. We also present a brief introduction to the theoretical foundations of comics as a narrative medium, focussing specifically on the description of the mechanisms involved in the representation, organization and transmission of information.

In Section 4 we present an illustration that, using specific elements and mechanisms of comics, aims to introduce the set-theoretic elements involved in the proof of the first isomorphism theorem. We also describe the process that we have followed for its realization. We identify the benefits and drawbacks of this approach and discuss its usefulness in shaping valuable mental models that support a narrative reconstruction of the result. We also present possible future applications that could implement the strategies that we have identified in this project.

In Section 5 we present the conclusions of this work and a summary of the experiences and lessons that we have learned from it.

In what follows we use standard concepts and constructions from classical universal algebra (Bergman, 2015; Sankappanavar & Burris, 1981) and set theory (Bourbaki, 2006). Notwithstanding, regarding set theory, we have adopted the following conventions. We will denote the set of all the natural numbers by $\mathbb{N}$ and, every $n\in \mathbb{N}$ will be identified with the set $n=\{0,\dots ,n-1\}$. If Φ is an equivalence relation on a set A and $x\in A$, we denote by $[x{]}_{\mathrm{\Phi }}$ the class of x with respect to Φ, that is, $[x{]}_{\mathrm{\Phi }}=\{a\in A\mid (x,a)\in \mathrm{\Phi }\}$, the set of all the elements in A that are related with x in Φ. We denote by $\mathrm{F}\mathrm{n}\mathrm{c}(A,B)$ to the set of all functions from A to B. We recall that a function (also called a family) from A to B is a subset F of $A\times B$ satisfying the functional condition, that is, for every $x\in A$, there exists a unique $y\in B$ such that $(x,y)\in F$. A function F from A to B will be sometimes denoted by $(F_x{)}_{x\in A}$. We denote by $\mathrm{H}\mathrm{o}\mathrm{m}(A,B)$ (and, sometimes, also by $B^A$) to the set of all mappings from A to B. We recall that a mapping from A to B is an ordered tuple $f=(A,F,B)$, also denoted by $f:A⟶B$, in which F is a function from A to B. Therefore, $\mathrm{H}\mathrm{o}\mathrm{m}(A,B)=\left\{A\right\}\times \mathrm{F}\mathrm{n}\mathrm{c}(A,B)\times \left\{B\right\}$. More specific assumptions, conditions and conventions will be included and explained in subsequent sections.

Materials and methods: The illustration accompanying this work has been sketched in pencil and coloured in digital format. The work has been presented at the International Mathematics Day 2021. It is available under a Creative Commons licence.

2. The first isomorphism theorem

In this section, we introduce the mathematical content of this article. We present a brief historical summary in order to contextualize the first isomorphism theorem. Afterwards we present the version of this result in the context of universal algebra. This will help us to clarify the notation and to recall the elements involved in its proof. Following this we expose the problems that have been described in teaching this result and the strategies that have been identified to enhance its understanding. We also include some examples of diagrams that we have found in the literature that are intended to give a visual aid for the understanding of the first isomorphism theorem. We conclude by describing and commenting on these diagrams.

2.1. Quotients and substructures

The history of modern algebra has its origins in the solution of algebraic equations and the study of their solutions (Stillwell, 2010). Many of the initial concepts and results are based on the study of the roots of polynomials or the factorization of integers.

The concept of group brings together a wide range of mathematical structures for which there is a notion of combination. The first fundamental theorem, now known as Lagrange's theorem, is prior to the formalization of the theory and we owe it, in its current presentation, to Jordan (Stillwell, 2010). To achieve this result one requires the notion of subgroup. We say that a subset H of a group G is a subgroup if H is also a group under the same operation of composition in G. Lagrange's theorem refers to the number of elements of a subgroup H, what we call its order and we denote by $\left|H\right|$. The theorem states that if H is a subgroup of a finite group G, then $\left|H\right|$ divides $\left|G\right|$. Its proof depends on the notion of cosets of H. For a subgroup H of a finite group G, the left coset of H with respect to $g\in G$ is the set $gH=\{gh\mid h\in H\}$. That is, gH is the set that results from multiplying each member of H on the left by g. These cosets can also be considered on the right. The main properties of these cosets can be summarized below:

1. Every left coset gH has $\left|H\right|$ elements.

2. If two left cosets $g_{1}H$ and $g_{2}H$ are different, then they are disjoint.

It follows from these two properties that G can be split into disjoint sets, each of size $\left|H\right|$, so that $\left|H\right|$ divides $\left|G\right|$.

Familiarity with this partition also contributed to questioning whether this new quotient set was equipped with group structure. For this to be meaningful, it is required that the multiplication not depend on the class representative, that is, that $g_1{g}_{2}H=g_1^{\prime }{g}_2^{\prime }H$ whenever $g_{1}H=g_1^{\prime }H$ and $g_{2}H=g_2^{\prime }H$. This is always the case when gH = Hg, for every $g\in G$, or, in other words, when H is a normal subgroup of G. Only in this case, the set of all cosets of G with respect to H is equipped with group structure, with the operation defined over representatives. Thus, if $g_{1}H$ and $g_{2}H$ are two cosets, the result of the product of $g_{1}H$ by $g_{2}H$ is defined as the left coset $\left(g_1{g}_2\right)H$. The quotient set equipped with such a structure is called the quotient group and is denoted by G/H.

It is worth noting that the concept was present on many occasions before the explicit definition of a group. Galois, for example, was the first to make use of the concept of a group and the normality of a subgroup. However, we also owe to Jordan the birth of the notion of the quotient group in the context of permutation group theory (Nicholson, 1993). The idea of calculating modulo a normal subgroup allowed Jordan to understand the importance of the quotient group, in analogy to Gauss's work on arithmetic congruences over the integers.

The refinement of the reasoning and methods in group theory of the late 19th century helped to shape a favourable environment for the adoption of the modern conception of the theory, based on the idea of structure and the identification of abstract properties that allowed reasoning about groups and their relationships, independently of their representation (Gray, 2018). The development of the concept of the quotient group is therefore closely related to the process of abstraction that gave rise to the modern conception of group theory.

Other authors recognized the value of these techniques, particularly the usefulness of the concept of equivalence, which was recognized and used by Dedekind, Cantor and Frege, among others (Asghari, 2019). In this period it began to be understood that the principle of abstraction, i.e. the formation of the quotient set of a set by an equivalence relation on it, was a new way of defining mathematical objects. This led to a change in the very conception of equivalence: from an organizational method to a creative tool (Asghari, 2019).

Dedekind glimpsed the creative capacity of the equivalence relation in group theory but his writings remained unpublished until after his death in 1916. During his lifetime he mentioned this work to Frobenius in a letter in 1895 (Nicholson, 1993). Dedekind explored the concept of homomorphism in a section entitled ‘Äquivalenz von Gruppen’. In this work, he formed a homomorphic image by matching each element of a group G with elements of another group M. Under certain conditions, which we now recognize as the conditions defining a homomorphism of groups, this correspondence allowed him to identify a homomorphic image of G in M. Moreover, the elements of G that corresponded to the identity in M formed a subgroup H of G that turned out to be normal. He expressed G in terms of H and its cosets and claimed that a composition of cosets can be defined. Furthermore, he observed that there was a correspondence between the cosets and the elements of M in the image of G, so that each coset corresponded to an element in M and each element in the image corresponded to a coset. Dedekind gave no name to either the concept of homomorphism or the concept of quotient group (Nicholson, 1993).

Dedekind was the last student of Gauss and devoted an important part of his life to disseminating and contributing to the ideas of his mentor. To Dedekind we also owe a modern approach to the algebraic concept of ring, which emerged from attempts to find integer solutions to equations (Gray, 2018). Many of these concepts were implicit in earlier works by Abel and Galois in the theory of equations, but became explicit when Dedekind introduced finite degree number fields as a distinguished structure in algebraic number theory. He was also able to concretize the results of unique factorization and primality conditions in rings by using ideals. This concept paved the way for working with factorizations in a ring of abstract integers modulo the content of an ideal.

Ring theory, in its modern version, is mainly the result of the work of the mathematician Emmy Noether, who, in particular, was one of the editors of the collected works of Dedekind. Noether completely reformulated the theory of ideals by generalizing Dedekind's earlier work. There is a simple way of measuring Noether's achievements in abstract algebra: by picking up any advanced textbook on the subject, ‘mathematicians simply do ring theory her way’ (Gray, 2018, p. 294).

In her approach to algebra, Noether abandoned concerns with operations on elements and went on to describe algebraic structures in terms of distinguished subsets (normal subgroups in a group or ideals in a ring, for example) and homomorphisms. Noether's idea was truly profound, for she was able to relate these highlighted subsets to the notion of homomorphism and used this correspondence to prove the isomorphism theorems. Noether used these results as an essential part of her algebraic development (McLarty, 2006).

Noether originally presented these theorems for the algebraic theory of modules in her 1927 paper ‘Abstrakter Aufbau der Idealtheorie in algebraischen Zahl- und Funktionenkörpern’ (Noether, 1927). Noether was explicit in pointing out that there were different algebraic structures and that each of them had its own isomorphism theorems. She was able to give the corresponding version of this result for at least groups, abelian groups, groups with a domain of operators, rings, commutative rings and rings with operators.¹ This methodology was a breakthrough for the structuralist conception of mathematics and made Noether a decisive figure in 20th century mathematics.

The subsequent study of other algebraic structures is more difficult to relate to the case of groups or rings, largely because of the need to replace the relevant substructures studied by Noether with the notion of congruence. A congruence relation is an equivalence relation on an algebra that is compatible with the operations². This means that operations performed on equivalent elements will result in equivalent elements. This is the property which allows the definition of an algebraic structure in the quotient.

The definition of congruence depends on the algebraic structure and the operations under consideration. The typical example is the congruence relation modulo n defined on $\mathbb{Z}$, introduced by Gauss. This relationship is compatible with the operations of addition and multiplication defined on the integers. Thus, if a, b, c, d are elements in $\mathbb{Z}$ satisfying $a\equiv c\left(\mathrm{mod}n\right)$ and $b\equiv d\left(\mathrm{mod}n\right)$, then it holds that $a+b\equiv c+d\left(\mathrm{mod}n\right)$ and $ab\equiv cd\left(\mathrm{mod}n\right)$. This means we can define a ring structure in the quotient set $\mathbb{Z}/n\mathbb{Z}$, the integer ring modulo n, based on the operations of addition and multiplication in $\mathbb{Z}$.

The concept of congruence captures the relevant substructures that Noether studied. Thus, in the particular case of groups, a congruence defined on a group is completely determined by the class of 1 which, in turn, forms a normal subgroup. Moreover, every congruence corresponds bijectively to some normal subgroup. Therefore, instead of referring to congruences over groups, the theory is usually presented in terms of normal subgroups. A similar situation allows one to characterize the congruences over rings in relation to the class of 0, which corresponds, precisely, to the ideals. Unfortunately, this situation cannot be extended to other algebras. In this regard, let us consider the words of Howie on semigroup theory:

In a group a congruence is determined if we know a single congruence class, in particular, if we know the normal subgroup which is the class containing the identity. Similarly, in a ring a congruence is determined if we know the ideal which is the congruence class containing the zero. In semigroups there is no such fortunate occurrence, and we are therefore faced with the necessity of studying congruences as such. More than anything else, it is this necessity that gives semigroup theory its characteristic flavour. (Howie, 1976, p. V)

Moreover, in contrast to the case of groups, two classes for a congruence do not necessarily have the same cardinal. This fact can be seen immediately in the following example. Consider the algebraic structure of ordered lattice on the set $\{a,b,c\}$ with the total order a<b<c and the congruence associated with the partition $\left\{\right\{a\},\{b,c\left\}\right\}$. It is easy to see that this equivalence relation is compatible with the operations of infimum and supremum but, for this congruence, not all the classes have the same cardinal.

All the knowledge acquired in this process has converged in recent decades in the theory of universal algebra (Bergman, 2015; Sankappanavar & Burris, 1981). This theory was conceived with the aim of configuring a corpus of concepts and propositions common to all algebras, which emphasizes its central ideas. In this theory, we still find the first isomorphism theorem as a fundamental result to explain the relationship between homomorphisms, quotients and substructures. We devote the following subsection to introduce the concepts that are needed for the proof of this result in the general setting of universal algebra.

2.2. The mathematical development

In this subsection, we introduce the definitions and propositions needed to obtain the proof of the first isomorphism theorem on algebras for a given signature. We have decided to include this section for the sake of completeness, with the main purpose of fixing notation and recalling the proof of this theorem. In doing so, we have followed the presentation of Sankappanavar and Burris (1981, Chapter II § 6).

We now introduce the notions of algebraic signature and algebra for a given algebraic signature.

Definition 2.1

An algebraic signature is a pair $\mathbf{\Sigma }=(\mathrm{\Sigma },\mathrm{a}\mathrm{r})$ where Σ is a set of operation symbols and $\mathrm{a}\mathrm{r}$, the arity, is a mapping from Σ to $\mathbb{N}$. If $\sigma \in \mathrm{\Sigma }$ and $\mathrm{a}\mathrm{r}\left(\sigma \right)=n$, we will say that σ is an n-ary operation symbol and, for every $n\in \mathbb{N}$, we will denote by ${\mathrm{\Sigma }}_n$ the set of all n-ary operation symbols in Σ. Specifically, if n = 0, n = 1 or n = 2 we will say that these are nullary, unary or binary operations, respectively.

Definition 2.2

A Σ-algebra is a pair $\mathbf{A}=(A,F)$, where A is a set and F is a mapping from Σ to $\bigcup _{\sigma \in \mathrm{\Sigma }}\mathrm{H}\mathrm{o}\mathrm{m}(A^{\mathrm{a}\mathrm{r}\left(\sigma \right)},A)$ such that, for every $\sigma \in \mathrm{\Sigma }$, $F\left(\sigma \right)\in \mathrm{H}\mathrm{o}\mathrm{m}(A^{\mathrm{a}\mathrm{r}\left(\sigma \right)},A)$. We will say that $F\left(\sigma \right)$ is the interpretation of σ as a $\mathrm{a}\mathrm{r}\left(\sigma \right)$-ary operation. We will introduce, for simplicity, ${\sigma }^{\mathbf{A}}$ to denote $F\left(\sigma \right)$. Moreover, for a nullary operation we have that $1=A^0$, so we will denote by ${\sigma }^{\mathbf{A}}$ the value of $F\left(\sigma \right):1⟶A$ on the unique element of 1.

We now present the notion of homomorphism between algebras for the same signature and the related concept of isomorphic algebras.

Definition 2.3

Let $\mathbf{A}$ and $\mathbf{B}$ be two Σ-algebras. A Σ-homomorphism from $\mathbf{A}$ to $\mathbf{B}$, denoted by $f:\mathbf{A}⟶\mathbf{B}$, is a mapping $f:A⟶B$ such that, for every $n\in \mathbb{N}$, every operation symbol $\sigma \in {\mathrm{\Sigma }}_n$ and every family $(a_i{)}_{i\in n}\in A^n$, the following equality holds $f\left({\sigma }^{\mathbf{A}}\left({\left(a_i\right)}_{i\in n}\right)\right)={\sigma }^{\mathbf{B}}\left({\left(f\left(a_i\right)\right)}_{i\in n}\right).$We will say that $\mathbf{A}$ is isomorphic to $\mathbf{B}$ if there exists a bijective Σ-homomorphism from $\mathbf{A}$ to $\mathbf{B}$. We will denote this fact by $\mathbf{A}\cong \mathbf{B}$.

We now introduce the notion of closed set and the associated concept of subalgebra. As a consequence we have the existence of an injective homomorphism, given by the inclusion mapping, from any subalgebra to the algebra containing it.

Definition 2.4

Let $\mathbf{A}$ be a Σ-algebra and $\sigma \in {\mathrm{\Sigma }}_n$ an n-ary operation symbol. We will say that $X\subseteq A$ is closed under σ if, for every $(x_i{)}_{i\in n}\in X^n$, we have that ${\sigma }^{\mathbf{A}}\left(\right(x_i{)}_{i\in n})\in X$. We will say that X is closed in $\mathbf{A}$ if, for every operation symbol $\sigma \in \mathrm{\Sigma }$, X is closed under σ.

If X is closed in $\mathbf{A}$ we can consider a Σ-algebra structure on it, denoted by $\mathbf{X}$, where, for every n-ary operation symbol $\sigma \in {\mathrm{\Sigma }}_n$ and every family of elements $(x_i{)}_{i\in n}\in X^n$, we define the interpretation of the operation σ as ${\sigma }^{\mathbf{X}}\left({\left(x_i\right)}_{i\in n}\right)={\sigma }^{\mathbf{A}}\left({\left(x_i\right)}_{i\in n}\right).$The definition of closed subset allows one to conclude that all these operations are well defined and that $\mathbf{X}$ is a Σ-algebra, which will be called subalgebra of $\mathbf{A}$ in X.

Proposition 2.5

Let $\mathbf{A}$ be a Σ-algebra and $\mathbf{X}$ a subalgebra of $\mathbf{A}$. Then the inclusion mapping, from X to A, that assigns to every $x\in X$ the element $x\in A$, is an injective Σ-homomorphism ${\mathrm{i}\mathrm{n}}^X:\mathbf{X}⟶\mathbf{A}$.

We introduce the notion of congruence and the associated concept of quotient algebra. As a consequence we have the existence of a surjective homomorphism from an algebra to its quotient algebra given by the projection of an element to its class.

Definition 2.6

Let $\mathbf{A}$ be a Σ-algebra and Φ an equivalence relation on A. We will say that Φ is a congruence on $\mathbf{A}$ if, for every $n\in \mathbb{N}$, every operation $\sigma \in {\mathrm{\Sigma }}_n$ and every pair of families $(a_i{)}_{i\in n},(a_i^{\prime }{)}_{i\in n}\in A^n$ satisfying that, for every $i\in n$, $(a_i,a_i^{\prime })\in \mathrm{\Phi }$, the following holds. $({\sigma }^{\mathbf{A}}\left({\left(a_i\right)}_{i\in n}\right),{\sigma }^{\mathbf{A}}\left({\left(a_i^{\prime }\right)}_{i\in n}\right))\in \mathrm{\Phi }$If Φ is a congruence on $\mathbf{A}$ we can endow the quotient set $A/\mathrm{\Phi }$ with a structure of Σ-algebra, denoted by $\mathbf{A}/\mathrm{\Phi }$, where, for every n-ary operation symbol $\sigma \in {\mathrm{\Sigma }}_n$ and every family of classes $\left(\right[a_i{]}_{\mathrm{\Phi }}{)}_{i\in n}\in (A/\mathrm{\Phi }{)}^n$, the interpretation of the operation σ is given by ${\sigma }^{\mathbf{A}/\mathrm{\Phi }}\left({\left(\right[a_i{]}_{\mathrm{\Phi }})}_{i\in n}\right)={\left[{\sigma }^{\mathbf{A}}\left({\left(a_i\right)}_{i\in n}\right)\right]}_{\mathrm{\Phi }}.$The definition of a congruence allows one to conclude that all these operations are well-defined and that $\mathbf{A}/\mathrm{\Phi }$ is a Σ-algebra, which we will call the quotient algebra of $\mathbf{A}$ by Φ.

Proposition 2.7

Let $\mathbf{A}$ be a Σ-algebra and Φ a congruence on $\mathbf{A}$. Then the projection mapping with respect to Φ, from A to $A/\mathrm{\Phi }$, that assigns to every element $a\in A$ its class $[a{]}_{\mathrm{\Phi }}\in A/\mathrm{\Phi }$, is a surjective Σ-homomorphism ${\mathrm{p}\mathrm{r}}^{\mathrm{\Phi }}:\mathbf{A}⟶\mathbf{A}/\mathrm{\Phi }$.

We now introduce the notions of kernel and image of a homomorphism between algebras and show that these concepts are, respectively, a congruence in the domain and a closed set in the codomain.

Definition 2.8

Let $f:\mathbf{A}⟶\mathbf{B}$ be a Σ-homomorphism between Σ-algebras. We define the kernel of f to be the relation on A given by $\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)=\left\{\right(a,a^{\prime })\in A\times A\mid f(a)=f(a^{\prime }\left)\right\}.$We define the image of f as the subset of B given by $\mathrm{I}\mathrm{m}\left(f\right)=\left\{f\right(a)\in B\mid a\in A\}.$

Proposition 2.9

Let $f:\mathbf{A}⟶\mathbf{B}$ be a Σ-homomorphism between Σ-algebras. Then $\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)$ is a congruence on $\mathbf{A}$ and $\mathrm{I}\mathrm{m}\left(f\right)$ is a closed subset in $\mathbf{B}$.

Proof.

Let us firstly consider the kernel. Let σ be an n-ary operation symbol in ${\mathrm{\Sigma }}_n$ and let $(a_i{)}_{i\in n}$, $(a_i^{\prime }{)}_{i\in n}$ be two families of elements in $A^n$ satisfying that, for every $i\in n$, $(a_i,a_i^{\prime })\in \mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)$. From the definition of kernel we have that, for every $i\in n$, $f\left(a_i\right)=f\left(a_i^{\prime }\right)$. Therefore, from the definition of Σ-homomorphism, we conclude that $f\left({\sigma }^{\mathbf{A}}\left({\left(a_i\right)}_{i\in n}\right)\right)={\sigma }^{\mathbf{B}}\left({\left(f\left(a_i\right)\right)}_{i\in n}\right)={\sigma }^{\mathbf{B}}\left({\left(f\left(a_i^{\prime }\right)\right)}_{i\in n}\right)=f\left({\sigma }^{\mathbf{A}}\left({\left(a_i^{\prime }\right)}_{i\in n}\right)\right).$From this equality, it follows that $\left({\sigma }^{\mathbf{A}}\right(\left(a_i{)}_{i\in n}\right),{\sigma }^{\mathbf{A}}\left(\right(a_i^{\prime }{)}_{i\in n}\left)\right)\in \mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)$. Thus, $\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)$ is a congruence on $\mathbf{A}$.

Let us now consider the image. Let σ be an n-ary operation symbol in ${\mathrm{\Sigma }}_n$ and let $\left(f\right(a_i){)}_{i\in n}$ be a family of elements in $\mathrm{I}\mathrm{m}(f{)}^n$. Then, following the definition of Σ-homomorphism, we have that ${\sigma }^{\mathbf{B}}\left({\left(f\left(a_i\right)\right)}_{i\in n}\right)=f\left({\sigma }^{\mathbf{A}}\left({\left(a_i\right)}_{i\in n}\right)\right).$Since ${\sigma }^{\mathbf{A}}\left(\right(a_i{)}_{i\in n})\in \mathrm{A}$, we have that ${\sigma }^{\mathbf{B}}\left(\right(f\left(a_i\right){)}_{i\in n})\in \mathrm{I}\mathrm{m}(f)$. Thus, $\mathrm{I}\mathrm{m}\left(f\right)$ is closed in $\mathbf{B}$.

Following Proposition 2.9, given a homomorphism between algebras we can consider algebraic structures both in the quotient of the domain by its kernel and in its image set in the codomain.

Remark 2.10

Given a homomorphism between algebras $f:\mathbf{A}⟶\mathbf{B}$, we denote by $\mathbf{A}/\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)$ the algebraic structure in $A/\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)$ and we denote by $\mathbf{I}\mathbf{m}\left(f\right)$ the algebraic structure in $\mathrm{I}\mathrm{m}\left(f\right)$, according to Definitions 2.6 and  2.4, respectively.

We now present the central result of this summary, known as the first isomorphism theorem. It states that, for any homomorphism between algebras, the associated algebras given by the quotient of the domain by its kernel and its image in the codomain are isomorphic algebras.

Theorem 2.11

First isomorphism theorem

Let $f:\mathbf{A}⟶\mathbf{B}$ be a Σ-homomorphism between Σ-algebras, then $\mathbf{A}/\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)\cong \mathbf{I}\mathbf{m}\left(f\right)$.

Proof.

Consider the mapping $f^{\mathrm{b}}$ given by $\begin{array}{rccl}{f}^{\mathrm{b}}:& A/\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)& ⟶& \mathrm{I}\mathrm{m}\left(f\right)\\ & [a{]}_{\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)}& ⟼& f\left(a\right)\end{array}.$Let us note that $f^{\mathrm{b}}$ is well-defined because, if $(a,a^{\prime })$ is a pair in $\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)$, then $f\left(a\right)=f\left(a^{\prime }\right)$. That is, its definition does not depend on the representative of the class under consideration. Moreover, for every $a\in A$, $f\left(a\right)$ is an element in $\mathrm{I}\mathrm{m}\left(f\right)$. If $a,a^{\prime }$ are two elements in A with $f\left(a\right)=f\left(a^{\prime }\right)$, then $(a,a^{\prime })\in \mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)$. From this it follows that $f^{\mathrm{b}}$ is an injective mapping. Furthermore, according to its definition, all the elements of $\mathrm{I}\mathrm{m}\left(f\right)$ have the form $f\left(a\right)$ for some $a\in A$. Therefore, $f^{\mathrm{b}}\left(\right[a{]}_{\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)})=f(a)$ and we conclude that $f^{\mathrm{b}}$ is a surjective mapping.

All that remains is to verify that $f^{\mathrm{b}}$ is a Σ-homomorphism. Let σ be an n-ary operation symbol in ${\mathrm{\Sigma }}_n$ and $\left(\right[a_i{]}_{\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)}{)}_{i\in n}$ a family of elements in $(\mathrm{A}/\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right){)}^n$, then the following sequence of equalities holds

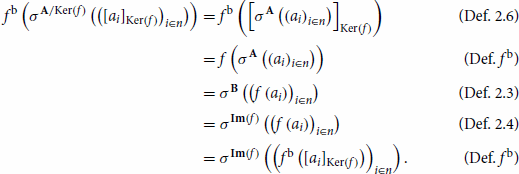
Consequently, $f^{\mathrm{b}}:\mathbf{A}/\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)⟶\mathbf{I}\mathbf{m}\left(f\right)$ is a bijective Σ-homomorphism. We conclude that the Σ-algebras $\mathbf{A}/\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)$ and $\mathbf{I}\mathbf{m}\left(f\right)$ are isomorphic.

Since the mapping considered in the proof of Theorem 2.11 will be mentioned later, we introduce the following definition.

Definition 2.12

Let $f:\mathbf{A}⟶\mathbf{B}$ be a Σ-homomorphism. We define the bijectivization of f, denoted by $f^{\mathrm{b}}$, to be the Σ-isomorphism from $\mathbf{A}/\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)$ to $\mathbf{I}\mathbf{m}\left(f\right)$ introduced in the proof of Theorem 2.11.

2.3. Understanding the first isomorphism theorem

Abstract algebra presents a serious educational problem. Introductory university courses in the subject pose a great difficulty for students, both in the treatment of content and in the development of attitudes towards abstract mathematics that go beyond learning ‘imitative behaviour patterns’ (Dubinsky et al., 1994, p. 268). In such courses, students must assimilate abstract concepts, work with important mathematical principles and learn to construct proofs. There is a need in mathematics education for developing effective pedagogical strategies to improve students' predisposition towards mathematical abstraction.

Although Theorem 2.11 is present in most mathematics degree curricula, specifically presented for known algebras such as groups or rings, many problems have been identified in teaching this result. For the specific case of groups, according to the study carried out in Brown et al. (1997), most students do not understand the notion of quotient and its algebraic structure. In Ioannou and Iannone (2011), the authors specifically emphasize students' need for visualization methods for cosets and the quotient set.

In the study carried out in Dubinsky et al. (1994), on the teaching of abstract group theory to secondary school teachers, it is recalled that, when faced with a strange situation, the individual ‘will attempt to reequilibrate by assimilating the situation to existing schemas available to her or him, or, if necessary, use reflective abstraction to reconstruct those schemas at a higher level of sophistication’. The education system is therefore required to provide the student with useful mental schemas for the understanding of the concepts he or she will be working on. This study also argues that it is necessary to look for alternatives to linear and cumulative teaching and that it would be advisable to revisit previous concepts and examples each time a new piece of information is incorporated, thus shaping an increasingly refined and detailed model.

The study published in Mena-Lorca and Marcela Parraguez (2016), conducted on undergraduate students, suggests to familiarize the student with the set-theoretic aspects of the first isomorphism theorem –regarding sets and applications, and based on the more intuitive concepts of equivalence relations and partitions– as a useful technique for improving the understanding of this result. The notion of partition is also found in Larsen and Lockwood (2013) as a key point for the initial understanding of the quotient structure.

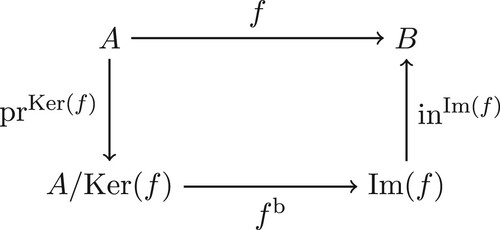
In fact, in the previous section we can observe that the algebraic structure only intervened in the proof of Theorem 2.11 during the verification of the homomorphism condition for the bijectivization of the initial homomorphism. Aside from the algebraic content, what remains is a result between sets and mappings, which we can state as a corollary below. The proof is virtually the same, without any reference to algebraic structures.

Corollary 2.13

Let $f:A⟶B$ be a mapping between sets. Then the sets $A/\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)$ and $\mathrm{I}\mathrm{m}\left(f\right)$ are bijective.

In fact, it can be said further; every mapping between sets factors canonically as a composition of three mappings, these being surjective, bijective and injective, respectively.

Corollary 2.14

Let $f:A⟶B$ be a mapping between sets. Then there is a unique bijective mapping $f^{\mathrm{b}}$, the bijectivization of f, from $A/\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)$ to $\mathrm{I}\mathrm{m}\left(f\right)$, which makes the diagram in Figure 1 commute.

Figure 1. Canonical factorization of a mapping.

This is the canonical factorization of a mapping through the co-image and the image. In the study presented in Mena-Lorca and Marcela Parraguez (2016) it is claimed that students' familiarity with this factorization allows them to intuitively reconstruct Theorem 2.11 for groups and helps them to take the qualitative leap of considering an algebraic structure in the quotient. These authors argue that, from a cognitive point of view, it is more natural to construct partitions and then examine the possibility of introducing a compatible algebraic structure. They conclude that students who were able to reason about these set-theoretic concepts ‘worked faster, had a clearer view of the result and seemed more confident’.

The study (Mena-Lorca & Marcela Parraguez, 2016) also presents conceptual representations, made by students, of the elements involved in the proof of Theorem 2.11. Aids like these, in the form of more elaborated diagrams, can also be found in the literature. Without the intention of making an exhaustive review, we have included some examples of these representations to give the reader an idea of the available solutions. They can be seen in Figures 2–7.

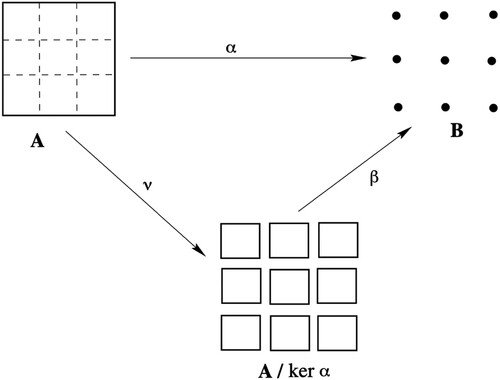
Figure 2. R. Maddox. A Transition to Abstract Mathematics: Learning Mathematical Thinking and Writing (Maddox, 2008, Figure 8.3, p. 285).

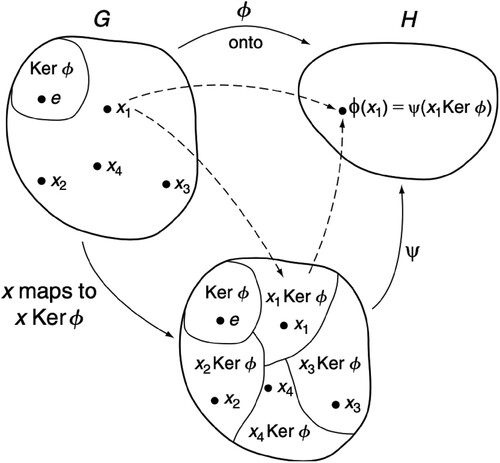
Figure 3. H. P. Sankappanavar and S. Burris. A course in universal algebra (Sankappanavar & Burris, 1981, Figure 12, p. 50).

It is worth noting the peculiarity that these diagrams only represent surjective mappings. This follows from the fact that the image set associated to a homomorphism is closed and we can always consider its corestriction. This situation can be easily transferred to the corestriction of a mapping to its image set to obtain a surjective mapping. However, this option masks the difference between the image set and the codomain. Moreover, we rarely introduce an arbitrary mapping in this form. If this option is chosen, we understand that this is done for the sake of simplification. Most of them follow the scheme depicted in Figure 1 for the surjective case, where $\mathrm{I}\mathrm{m}\left(f\right)=B$, although the Figures 4 and 6 only represent the bijectivised mapping $f^{\mathrm{b}}:A/\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)⟶\mathrm{I}\mathrm{m}\left(f\right)$.

Figure 4. D. S. Dummit and R. M. Foote. Abstract Algebra (Dummit & Foote, 2004, Figure 3, p. 78).

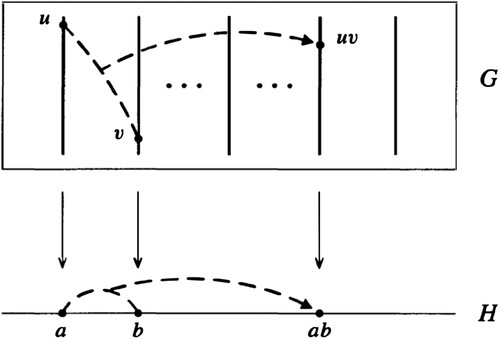
Figure 5. T. D. Bradley. The First Isomorphism Theorem, Intuitively. Math3ma.com (Bradley, 2016).

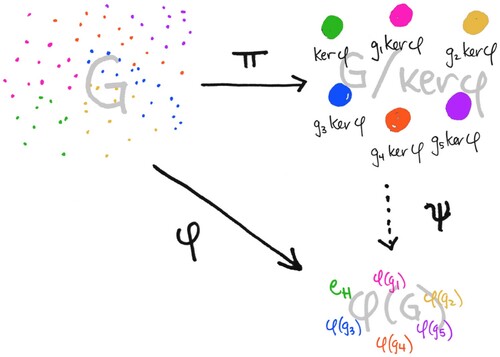
Figure 6. C. Santilli. Diagram of the fundamental theorem on homomorphism (Santilli, 2020).

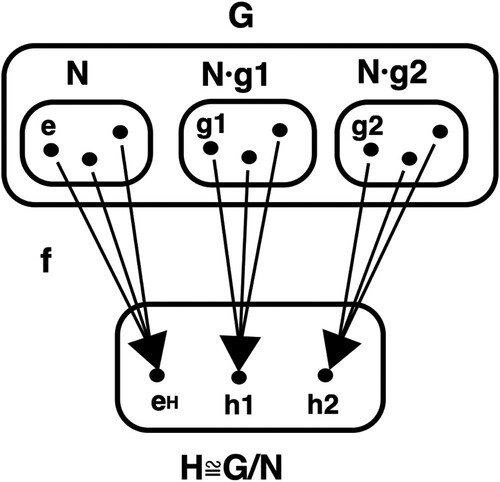
Figure 7. N. Carter. Visual Group Theory (Carter, 2009, Figure 8.14, p. 169).

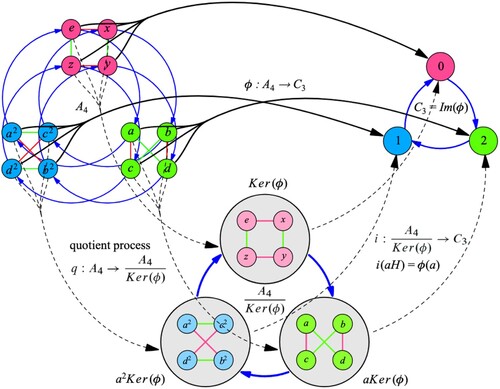
There are particular solutions that deserve further comment. The concept of partition appears in all proposals although the representations differ. On the one hand, we find an action of disassembling in Figures 2–4 whereas, on the other hand, in Figures 6 and 7 this action is performed by surrounding the elements. In Figure 5, the partition is achieved by assimilating the elements of the initial set into an element of the quotient, in this case the class, differentiated by size. The characteristic shared by the elements and their class is the colour. Figure 7 uses the same solution.

Figure 3 emphasizes the difference between the subsets of the original set (in dotted lines) and their conception as classes, i.e.elements of the quotient (separated and in solid lines). This example is the only one depicting an abstract algebra, not necessarily a group, but, nevertheless, represents the classes as squares of the same size and shape. Figure 4 highlights the representation of the classes as fibres splitting the original set according to the associated elements in the image.

In the diagrams of Figures 2, 4, 6, and 7, the value of each element is also represented. In Figure 2 we can differentiate between the mappings on sets (in solid lines) and the concrete values of these mappings on distinguished elements (in dotted lines). This solution is also found in Figure 7, but for every possible element. The diagram of Figure 6 mixes the value of the original mapping with the value of the bijectivised mapping, whereas in the diagram in Figure 7 we find a grouping of the arrows, possibly to allow a better reading, but we understand that also to reinforce the groupings that give rise to the first isomorphism theorem.

It should be noted that the diagrams in Figures 4 and 7 are the only ones that aim to represent algebraic structure. In Figure 4 we have a representation of the result of a binary operation that is replicated both in the quotient and in the image. The result obtained in the image, supposedly on elements, is replicated in the quotient on representatives of the respective classes. The proposal presented in Figure 7 goes one step further by attempting to reproduce the transformation of the associated Cayley diagram in a concrete example. The author considers the example of the alternating group $A_4$, containing 12 elements, and its quotient with respect to the Klein 4-group to obtain a quotient group of order 3, isomorphic to the cyclic group $C_3$.

As we can see, the representation of a quotient set is a delicate problem. There are at least three different interpretations about what is intended to be represented: quotients as partitions of the original set, the partitions in turn as elements with an entity of its own, and the resolution of the process that the elements of the original set undergo until they are diluted within the classes. All these intentions are valid and coexist in tension in each of the solutions here collected.

3. The iconic language of comics

In this section, we present a brief review of the benefits of using visual thinking and graphic storytelling for science communication. We explore the theoretical foundations that explain the capacity of comics to transmit information and shape situational models. To this end, we present an introduction to comic studies and the basic explanation of its mechanisms, clarifying the functionality of the panels and the medium's own resources for structuring the narration. We conclude with a review of new formats that bring comics closer to diagrammatic representation.

3.1. Visual thinking in science communication

We are currently witnessing a growing search for forms of scientific communication capable of competing with other actors in the saturated media space. Science communication experts argue for the need to develop more interactive and conscious methods (Mancosu et al., 2006; Pauwels, 2006). There is a need to further develop understanding of the ways of communicating and conveying scientific ideas, not only to engage the public, but also for the researcher to make visible what cannot be captured in explicit words (Jonsson & Grafström, 2021).

Art is becoming a privileged medium for this task. Art-based research has been developed as a method for creating, presenting and interpreting science. Making scientific concepts visible is especially valuable because the process itself generates new ideas and thoughts (Trumbo, 1999).

According to Rapp (2005), visualization methods must have the ultimate goal of providing an internalized mental model that organizes knowledge structures with respect to the spatial, temporal or causal relationships of a concept. They must also serve to solve problems and generate inferences in a wide variety of situations. The work on each of these aspects is directly relevant to education in scientific fields. The processes involved in constructing meaning from language, evaluating logical premises and understanding conceptual systems are fundamental. These approaches emphasize the usefulness of the knowledge, how it is applied and the ability to assess the accuracy of the information that is presented (Silva, 2009). According to O'Sullivan and Kozinets, the value of art-based communication methods ‘lies in their ability to render “visible” implicit meanings by encouraging audiences to seek for extra-ordinary viewpoints’ (O'Sullivan & Kozinets, 2020, p. 572).

Rapp (2005) identifies three factors that positively influence the experience of learning and the shaping of mental models. First of all, there has to be cognitive engagement, i.e. active attention to stimuli, as well as a predisposition for generating connections between stimuli and prior knowledge representations. Another factor to take into account is interactivity, i.e. the possibility to manipulate the characteristics of what is being studied, to change the pace or to personalize the representations. The last factor is multimedia learning, with different representations of the same concept, e.g. in combination of text and images. At this point, the author recommends that the representations should be pre-designed and that they should complement each other, to avoid interferences and confusion.

Rapp pays special attention to visualization as a procedure to achieve the configuration of a mental model. Visualizations give cohesion to concept maps and explanations of processes. In particular, visual thinking is closely related to the mathematical activity. Visual images and diagrams serve to illustrate cases of a definition, describe a mathematical situation or the steps of a reasoning. They can suggest a proposition or an idea. Visualizations have a facilitating role, but they are also a source of discovery, justification or even proof. As Giaquinto states, visual thinking has ‘epistemological utility’ (Giaquinto, 2011, p. 12).

The aim of a visualization is to describe the connection of elements by means of metaphors, forms, properties or relationships. In a diagram, relationships are simultaneously displayed rather than sequentially stated. Moreover, spatial relations between parts of the diagram indicate relations between the things represented by the parts (Giaquinto, 2011, p. 245). Visualization also provides experience with the concepts represented and helps to shape narratives to explain the models. They are therefore tools for creating more interesting and enjoyable learning environments that facilitate association and enable effective and descriptive learning (Özpinar et al., 2017).

However, Rapp points out, a visualization on its own does not necessarily have to show immediately all these benefits and calls for design and reflection on what is represented, paying attention to factors such as the elements being shown, their colours or their distribution. Educationally relevant material will be that which can display information effectively, directing the reader to construct a correct and potentially useful mental model.

Comics have the ability to bring together many of these qualities. Comics can help to depict ideas, clarify the main arguments and communicate science with the intention of opening new insights and debates in the researcher and the reader (Jonsson & Grafström, 2021). As Farinella says, the comic not only manages to break the information into more digestible units, but it also helps to reassemble it into meaningful compositions that affect the understanding of the message. Moreover, the comics lend themselves to non-linear explanations, encouraging the reader to constantly re-evaluate previous panels in the light of each new piece of information. Similarly, science requires readers ‘to make connections between multiple scales and domains of knowledge, not necessarily arranged in a hierarchical, linear order’ (Farinella, 2018, p. 6).

As Cohn puts it,

Comprehenders access semantic information about objects and events in images. A narrative grammar assigns images categorical roles and groups them into hierarchic constituents so that semantic information can be organized sequentially and construct a coherent situation model. While the narrative grammar eventually fades from memory, a situation model shifts from working memory to episodic long-term memory as the meaning of a visual narrative is retained into the future. In online processing, both semantics and narrative use forward-and backward-looking mechanisms in an iterative cycle of prediction and updating in the ongoing processing of sequential images. (Cohn, 2020b, p. 377)

Comics have emerged as an increasingly popular form of science education and communication with the potential to make subjects more accessible and engaging. They are not only an effective method of communication closely related to diagrams (García López, 2016, may; Giaquinto, 2011), but also one that remains largely unexplored. As Sousanis says, perhaps we have found in comics a way ‘to capture and convey our thoughts in all their tangled complexity’ (Sousanis, 2015, p. 67).

3.2. An approach to comic studies

In recent decades comics have become an active object of study because of their intrinsic qualities. This explosion in the study of its foundations has led to the publication of critical works focussing on the analysis of its resources and structure, as well as its semiotic, pedagogical, sociological and informative components (Bartual, 2010, 2020; Bordes, 2017; Cohn, 2013, 2020a; Groensteen, 1999; McCloud, 1993; Sousanis, 2015).

It is worth noting that the approaches to the description of comics and their mechanisms have required a profound vision, internal to the industry, which emphasized the mechanisms involved in graphic storytelling and which made it possible to explain the resources inherent to this language (Bordes, 2017, p. 22). These insights, however, have highlighted the impossibility of defining the medium itself. In the words of Groensteen,

So great is the diversity of what has been claimed as comics, or what is claimed today under diverse latitudes, that it has become almost impossible to retain any definitive criteria that is universally held to be true. (Groensteen, 1999, p. 20)

Among the most commonly used criteria, we encounter the definition given by McCloud: ‘juxtaposed pictorial and other images in deliberate sequence, intended to convey information and or to produce an aesthetic response in the viewer’ (McCloud, 1993, p. 9). Although these characteristics are constantly being challenged in experimental or abstract comics that are attempting to capture atmospheres, sensations or rhythms (Bordes, 2017, pp. 25–28).

According to Groensteen, the foundational principle for the study of the medium is centred on what he calls the solidarité iconique, that is, interdependent images which are participating in a series and present the double characteristic of being both separate and linked plastically and semantically by the fact that they coexist in praesentia (Groensteen, 1999, p. 23). Groensteen is aware that this meaning allows for the consideration of alien forms that have occurred in other contexts and historical moments such as stelae, frescoes, Mayan codices, tapestries, via crucis, story boards, etc.

Over the last few decades, it has become clear how much ground remains to be explored, both within the boundaries of what is accepted to be comics, and in the use of comics in other fields (Bordes, 2017; McCloud, 2000; Sousanis, 2015). Although it may seem an inconvenience, Bordes says that this ‘opens up a space for reflection on the medium³’ (Bordes, 2017, p. 29).

3.3. The mechanisms of comics

In the theoretical study of comics, there is also no consensus when it comes to defining a fundamental semantic unit. There are different positions that advocate for either the panel, the sequence or the page as basic semantic units (Carrier, 2000; Groensteen, 1999; McCloud, 1993).

According to Groensteen, these narrative panels have little in common with cinematic framing or painting, neither temporally nor spatially. As opposed to the constant succession of shots in the same frame in the cinema or the totality represented in a painting, what the comic reader experiences is just the opposite, ‘the feeling of being confronted with a multitude of narrative iterations’, which accumulate until they give rise to the whole story.

With respect to comics, this disposition finds itself constantly embattled, and in a certain measure neutralized, by the properties that we have seen in the panels. The network that they form is certainly an oriented network, since it is crossed by the instance of the story, but it also exists in a dechronologized mode, that of the collection, of the panoptical spread and of coexistence, considering the possibility of translinear relations and plurivectoral courses. (Groensteen, 1999, p. 123)

Groensteen has coined the term arthrology to denote this system of meaning specific to comics, characterized by the panels and their articulations and interrelationships. Thus, the panels will always be in relation to shape, proportion and area with the page and the multi-frame that they configure. Once established, the panel has a specific relationship with each of the frames that surround it (Bordes, 2017, p. 35). Moreover, if the composition of the page defines the spatio-topical characteristics, the decomposition into fragments would, in Groensteen's opinion, provide a temporal coordinate (Groensteen, 1999, p. 36).

According to Groensteen (1999, p. 40), the frame of the panel, in its configuration in the multi-frame, will have up to six different functions; closure, separative, rhythmic, structural, expressive and readerly⁴.

For Groensteen, the intericonic space is not the place of a virtual image but of an ideal articulation. It will be the reader's job to fill in the gaps and move the story forward. According to Bartual (2020, p. 48), this action can be assimilated to the basic notion of gestalt. Furthermore, Bartual establishes that this articulation appeals to four different forms of closure in the reader; spatial, causal, temporal or metaphorical. These closures are the articulations that make it possible to read the succession of panels and put them in context with the surrounding content.

Nevertheless, the most important feature is that the sequence of images contains a narration laid out for reading. According to Bordes,

Any surface that is taken up by the language of the comic becomes a message likely to be read⁵. (Bordes, 2017, p. 50)

When preparing a page, the comic author must decide, in Groensteen's words, not only on the distribution of spaces and the occupation of places, but also on the sense of reading, i.e. the narrative precipitation. According to Cohn (2013) the comic page is articulated on several layers. We find a first graphic structure, of lines and shapes, which assembles a scheme that conveys meanings. Each of these schemes needs to be supported by a navigational structure, which indicates the direction of the sequence and how to progress through it. To create meaning, these sequential schemes rely on conceptual structures, which imbue adjacent panels with meaning, and various morphological visual tools specific to the medium, such as moving lines or text bubbles. All of this occurs around a consistent spatial structure, which will bring together geometric information with ‘our abstract conceptual knowledge’. Finally, colour and other graphic mechanisms will allow the author to incorporate the expressive nuances she or he deems necessary.

While the majority of comics follow a linear articulation around logically or symbolically related sequences, in recent years we can find authors who try to overcome these ideas by planning a page with an architectonic or diagrammatic conception (Bartual, 2020; Bordes, 2017; García López, 2016, may), where linearity, temporality or a preconceived sense of reading is altered.

These modifications on the usual reading direction have traditionally used resources such as arrows or numbers to indicate the alteration in case a wrong arrangement could lead to an unwanted ambiguity in the reading flow direction (Bordes, 2017, p. 53). In recent decades, however, there has been carried out some experimentation with the concept of narrative multilinearity and other format possibilities such as written comics, poster pages, narrative pathways or band comics (García Sánchez, 2000). These proposals are based on linked successions of images with a high degree of iconic abstraction that allow the creation of complex narratives by accumulation. As they are assimilated with legible signs, they do not require frames, as long as they are placed in an orderly manner (Bordes, 2017, p. 54).

In the specific case of the poster page, in similarity with the diagram, the reading lines will be drawing pathways. What Bartual (2010) calls ‘diegetic routes’. That is, paths with their own narrative content that are articulated from the journey of some characters that appear repeatedly and, occasionally, cross paths. Bartual incorporates the notion of vectors in order to propose alternatives to the conventional reading sequence. Among the possible options, we encounter pages with free, crossed or parallel vectors, configuring multiple alternatives to the reading direction or the temporal or spatial configuration of the page. This also imposes a rather more theatrical than cinematic conception of the page, which is reflected in the size and iteration of the characters at different times, as well as in the configuration of the background as a stage. This is what Lew Andrews has called continuous narration (Andrews, 1998, p. 120).

It is interesting to know these insights about the comic because they bring its task closer to diagrammatic representation, a resource that has traditionally been useful in mathematics.

4. A proposal in comic format

In this section, we present and analyse a proposal for a graphic-narrative representation describing the set-theoretic elements occurring in the proof of Theorem 2.11. To do so, we follow the pedagogical strategies described in Section 2, in accordance with the different mechanisms of the comic medium, analyzed in Section 3.

4.1. The proposal

To set up our synthesis we start from the diagram depicted in Figure 1, where we can find the sets and the applications that are involved in the proof of this result. The strength of the proposition lies in the commutativity of the diagram. That is, for the elements in the domain, taking its image for the mapping under consideration results in the same element that is obtained by taking the alternative path, composed by the other three mappings. The mappings that constitute the alternative path are not arbitrary and depend on the original mapping.

We have, first of all, the projection to the kernel, assigning to every element all the other elements having the same image according to the original mapping. For the representation of the quotient, we will use the correspondence between equivalence relations and partitions. In doing so, we will split the original set into classes. Secondly, we have the bijectivization of the original mapping, which assigns to each class the image of any of its representatives. At this point, we consider it important to highlight what is a mapping with a quotient set for its domain, where the assignment is established for the entire class although we use a representative element of the class for its definition. Thirdly, we have the inclusion of the image as a subset of the codomain. In this case, we think it is important to differentiate between the image set and the codomain.

With all the previous conditions, we have decided to represent a mapping that is neither injective nor surjective. In this way, we will have classes with more than one element and we will be able to differentiate the image set from the codomain. This will also highlight the differences between the original mapping and its bijectivization.

For the representation of the diagram, we have considered that it was important to pay attention to the narrative aspects that will allow the articulation of a story capable of capturing all the previous details. Firstly, as opposed to representing mappings as abstract assignments, we have decided to represent mappings as transforming processes. In this way, we promote the emergence of a narrative by contrasting an element with its transformation. This option requires a representation that does not lose the essence of the transformed element, otherwise the assignment will become more abstract. In our case, we have decided to use the representation of objects and groupings of objects. This also makes it possible to represent the partition in the quotient.

In our proposal, we have decided to use a practical example. We have taken a vegetable field as the domain for our mapping and we have set the act of harvesting as the transformation process. This solution makes the organization and categorization in boxes natural. The contrast occurs between vegetables in the field and harvested vegetables. For further differentiation we will represent vegetables of different types and quantities. We will also represent the initial set without any sort of organization, thus highlighting the difference with the quotient set, which will become structured. To differentiate the image set from the codomain, we will represent empty boxes referring to vegetables that do not appear in the field and cannot be harvested.

Following Corollary 2.14, the act of harvesting vegetables is equivalent to the acts of arranging the vegetables into piles according to their destination, transporting the piles to the corresponding boxes and, finally, transporting the boxes full of vegetables to its destination. In summary, a possible account of the reasoning underlying the proof of the first isomorphism theorem.

As the development of this approach requires a character who carries out the action, we will take advantage of this circumstance by representing the mathematician Emmy Noether, author of the original result. This will add a layer of information that we think is important because it establishes a dialogue about the origin of the result and one of its main protagonists. This is hardly possible with a decontextualized proposition.

For the representation of this proposal, we have worked with the illustrator and comic book author Núria Tamarit, who represented this story-diagram and put her experience and technique at the service of the planned narrative. Although we came from different backgrounds –mathematics and illustration– we were at the same time both determined to develop an understanding of each other's perspectives and interpretations, and to discuss together what we could see and contrast it with our backgrounds and experience. The result is the poster depicted in Figure 8.

Figure 8. Poster for the International Day of Mathematics 2021 – Mathematics for a Better World. Cosme and Tamarit (2021). Licensed under CC BY-SA.

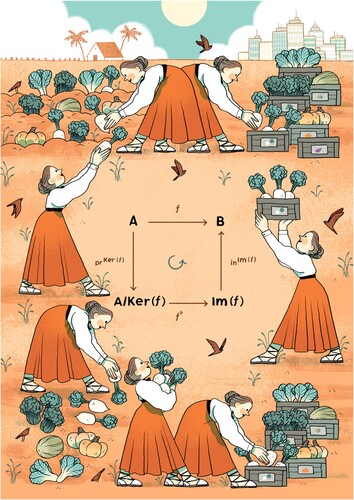
This poster was presented for the International Day of Mathematics (IDM), a celebration organized by the International Mathematical Union that takes place every 14th of March. For the 2021 edition, the organizers proposed a challenge entitled ‘Mathematics for a Better World’, with the aim of exploring mathematics as a universal language. The organization asked participants to use images combined with numbers, formulas or geometric figures to express mathematical ideas, without words, so that other people could understand them even if they did not share the same language.

Our proposal was selected and displayed on the IDM website. The text accompanying the image is reproduced below.

The poster depicts a factorization. At the top we find a mapping f, from A to B, represented by the work of picking vegetables from the field and depositing them in the warehouse. It decomposes into three mappings, a surjective one (left), the projection from A to $A/\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)$, given by the partition of the vegetables according to their storage place; a bijective one (bottom), from $A/\mathrm{K}\mathrm{e}\mathrm{r}\left(f\right)$ to $\mathrm{I}\mathrm{m}\left(f\right)$, given by the deposit of the piles in the corresponding boxes; and an injective one (right), the inclusion from $\mathrm{I}\mathrm{m}\left(f\right)$ to B, given by the movement of the boxes to its destination. The farmer is the mathematician Emmy Noether, author of this theorem and a fundamental figure of modern day algebra.

This poster, licensed under Creative Commons BY-SA, is available for download and derivative use.

4.2. Round trips between the abstract and the concrete

At first glance, the page in Figure 8 conveys a sense of instantaneousness. Everything that is important is represented without the need for a linear development. The images call to be understood and analyzed. We are presented with a layout that begins to organize the information and which requires a sense of reading to assist our comprehension.

In order to discover the reading direction, we are assisted by different elements. The female character, Emmy Noether, indicates with her face the direction of the action. This is also indicated by the direction in which her arms are pointing. In a smaller size and centred we find the representation of the diagram in Figure 1. The arrows correspond to the directions in which the main character moves, thus establishing a metaphorical closure, by proximity, between the arrows and the action. In addition, in the centre, we find the curved arrow which is used to indicate commutativity in mathematical diagrams and which, in this case, also indicates the reading sense. The association between the arrows and the characters also contributes to discovering a diagonal association, between the sets and the collections of items. This effect is enhanced by the colour of the composition, with a predominance of orange for the actions and a predominance of green for the objects.

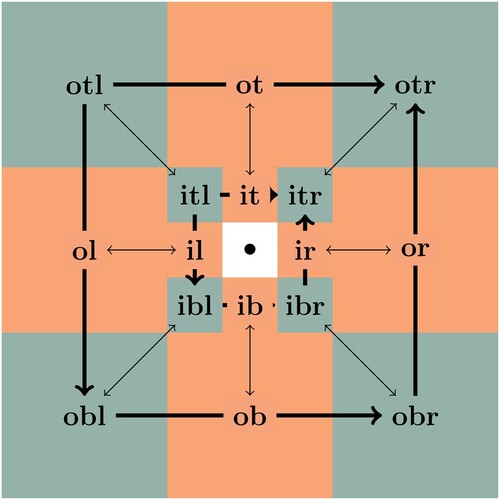
In the poster we distinguish three dimensionalities stemming from the centre; from inside (i) to outside (o); from left (l) to right (r); and from top (t) to bottom (b). These dimensionalities are depicted in Figure 9. The inner dimension represents the diagrammatic realization of the mathematical idea. Here we find a diagram with sets and mappings. This figure is not intended to have a narrative content but does add an additional layer for the reader who is mathematically literate and can identify the notation. On the other hand, in the outer dimension, we find a concrete instance of the mathematical idea. We also have a temporal dimension, which results from the iteration of the character, that helps to set up a sequential explanation.

Figure 9. Spatial diagram: Inside (i) to outside (o); left (l) to right (r); and top (t) to bottom (b).

Once the main elements have been identified, the reading begins. Vegetables appear repeatedly, but in different configurations. It is easy to see that the heroine intends to organize the vegetables and it will be our task to find out how she does it. In all the scenes we notice that the main character holds different objects in her hands, but all of them are related to the same vegetable in different presentations. Each scene is a completed action and the heroine represents the process that she has followed to arrive at each configuration.

When we try to differentiate the scenes, we notice two dispositions; one prior disposition, on the left side of the page, associated with a natural state, and another posterior disposition, on the right side of the page, associated with a processed state. This effect is supported by the elements in the background, on the left a country house, on the right a large city. From this point on, harvesting appears as the main action. We note that the boxes contain labels with sketches of the vegetables, so the action of the character is to collect them and group them in their respective boxes.

In this representation we can distinguish the process that each element follows. The process that explains the alternative path is understood by contrasting the arbitrary arrangement that appears in the field with the ordered arrangement of the vegetables by type in the quotient, with the intention of grouping them according to their destination. This is where the tension that we discussed at the end of Section 2 appears. It arises from treating the partition in each class as an element in the quotient. On entering the quotient the elements enter differentiated, but on leaving the quotient we find that the block is the new object of interest. This change appears represented in the hands of the main character.

The main idea is represented in the space below, where it can be noticed that there are the same number of piles on the left as there are boxes on the right. This fact appeals to the bijection that is established between these two sets. The bijectivised mapping is described in terms of the initial mapping; where the single vegetable would go, now goes the bundle of vegetables, which has been previously organized. The action on the right simply brings the filled box to its final state. One can tell the difference between the image set and the codomain by an empty box. This box has not been filled as the vegetables it should contain are not in the field, so we do not need it for harvesting.

The full reading occurs when one understands that the result of the actions, one way or the other, is identical. To reach this conclusion, the reader will have had to update her or his understanding with each new discovery, gradually forming an idea of the event being depicted and shaping a narrative richer in detail with each successive reading. In this way, we break away from a linear presentation and let the reader experience the details that accumulate until they configure the whole story.

4.3. Challenging the proposal

We cannot pretend that, just because we have drawn the application of this result in a particular case, the theorem is understood to its full extent. The actual usefulness of this material remains to be evaluated. There are many factors involved in reading, and especially in understanding, this page which need to be investigated and which we propose as a natural continuation of this project.

However, we can expect that anyone who views the page will realize that this work is intended to convey information and tell a story. This is an objective that is rarely achieved by a decontextualized diagram.

What has been obtained is an example that can aid to concretize ideas, a toy model for discussion with students. This model can also introduce details gradually. Students may start with an incomplete understanding of the concept, with errors and gaps, but they can improve understanding of the theorem by trying to make sense of the image and the underlying properties. As Miller puts it

For most people, visual memory is more powerful than linear memory of steps in a proof. Moreover, the various relationships embedded on a good diagram represent real mathematics awaiting recognition and verbalization. So as a device to help students learn and remember mathematics, proofs without words are often more accurate than (mis-remembered) proofs with words. (Miller, 2012, p. 23)

We consider equally important the representation of Emmy Noether as the protagonist of her own discovery. This can help to contextualize the authorship of the theorem and to highlight one of her most important contributions.

The proposal breaks new ground. Without going any further, the second and third isomorphism theorems are results that arise as a direct consequence of the application of the first isomorphism theorem. Interested readers can find them in Sankappanavar and Burris (1981). It would be interesting to contrast the other two theorems with our proposal and see how we can reuse some of the solutions that we have found in this project for similar representations.

The process to obtain this comic page has been very interesting and has allowed a reflection on what is represented and how it is represented. The comic format certainly has interesting qualities to assist in shaping useful models for communicating scientific ideas and for developing narrative solutions for its reconstruction.

5. Discussion

The first isomorphism theorem is an important algebraic result that relates the notions of homomorphism, quotients and substructures. We owe this result in its present form for some important structures, such as groups or rings, to the mathematician Emmy Noether. The teaching of this theorem to undergraduate students faces some problems, mainly related to the abstraction of the result and the lack of models on which students can contrast their intuitions. Some strategies have been identified to handle these problems, mainly based on familiarizing the students with the set-theoretic elements occurring in this result and reinforcing the understanding of the factorization that underlies the theorem.

In the literature, we find different examples of diagrams depicting this theorem. The objective of any diagram is to present information by relating the elements that comprise it in the most refined way. To understand a diagram is to understand the relationships that are configured therein, be they spatial, temporal or metaphorical.

The act of narrating with images is present in all areas of our daily lives. Visual storytelling has become a primary source of information. Comics have been used as a resource with the potential for shaping mental models in order to aid the understanding of scientific ideas. In the educational process we cannot leave these techniques aside, even more so when the reflection on the medium begins to bring comics closer to communicative processes that explore diagrammatic representation as a fundamental part of its language, as often happens in mathematics.

In this paper, we have presented an illustration that uses the mechanisms of the comic, particularly the concept of diegetic routes on a poster page, to synthesize in a concrete example the set-theoretic elements involved in the proof of the first isomorphism theorem, without reference to any kind of algebraic structure. Our aim is to reinforce the intuition about the result underlying this theorem, namely that every mapping between sets factors as a product of three other mappings, which are surjective, bijective and injective, respectively.

The work has allowed us to explore the representation of the theorem and to find graphic-narrative solutions for the reconstruction of the result. We are, therefore, looking for pedagogical strategies to explain the first isomorphism theorem. Along the way we will be focussing on an important lesson; mathematics, like any other human activity, is fundamentally articulated with narrative processes. Exploring comics as a medium to represent these processes opens up a bridge for understanding.

Acknowledgments

The authors wish to express their appreciation to the reviewers and to Henry Segerman, editor of the Journal of Mathematics and the Arts, for their careful reading of the manuscript and very helpful comments.

We would like to thank our dear friend Juan Climent Vidal for his advice and for the mathematical (and non-mathematical) lessons that he has taught us. Special thanks to Asunción de Montesa for her categorical knowledge. Finally, our sincere thanks to Cristina Cosme Llópez for the linguistic corrections. Any remaining typos in the text are our fault.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

The first author was supported by the Ministerio de Ciencia, Innovación y Universidades, the Agencia Estatal de Investigación, Spain, and FEDER, European Union [grant number PGC2018-095140-B-I00].

Notes

1 All of them examples of categories in the modern sense.

2 The formal definition of a Σ-algebra congruence is presented in Definition 2.6.

3 Esto abre el campo a la reflexión sobre el medio.

4 Clôture, separatrice, rhytmique, structurante, expressive, lecturale'.

5 Aquella superfície que sea ocupada por el lenguaje del cómic se convierte en un mensaje susceptible de ser leído.