Monsters in the hollow: counting Naiki braid patterns using de Bruijn's Monster theorem

ABSTRACT

The Japanese braids known as Naiki, which are distinguished by their hollow interior, have a simple structure shared by many other fiber arts and crafts. The way in which this structure forms a cylindrical braid imposes a particular set of symmetries on the final product. This paper uses enumerative combinatorics, including de Bruijn's Monster Theorem, to count the number of two-color Naiki braids under equivalence by this natural set of symmetries.

GRAPHICAL ABSTRACT

KEYWORDS:

• Braiding
• Japanese crafts
• fiber arts
• weaving
• counting
• patterns
• enumerative combinatorics
• generating functions
• Monster theorem
• symmetry

1. Introduction

Kumihimo, the Japanese word for braid, is used in Western countries to describe a collection of styles of Japanese braiding, usually using relatively simple looms to braid between 4 and 36 strands or bunches of fiber. This paper focuses on Naiki, a traditional braid usually made with 16 strands which has a hollow interior which can either be filled with a core or squeezed flat. Some examples are shown in Figure 1.

Figure 1. Examples of Naiki braids. Braiding and photography by Rosalie Neilson.

Three red and yellow Naiki braids, each shown next to a U.S. penny for size comparison.

The same braid with 8 strands is known as Edo Yatsu; Edo from the former name for Tokyo and Yatsu meaning eight (Combs, 2016, p. 15). It seems likely that Edo Yatsu is older than Naiki, but probably not as old as some other kumihimo braids. The earliest Japanese braids seem to have been made using a fingerloop braiding technique (Tada, 1999, pp. 10–11), which does not lend itself well to cylindrical braids. Most cylindrical braids seem to have developed after the invention of the marudai, a traditional stand, which probably occurred during the Muromachi period (1333–1573 CE) (Tada, 1999, p. 14). It seems likely Edo Yatsu was also developed during this period, as the city of Edo was founded in the 12th century CE and served as an important fortified city starting in the 15th century CE. Early in this period, kumihimo braids were used for tying together pieces of the traditional samurai armor. By the end of the period, they were being used in fashion and decoration by ordinary people as well as aristocrats and samurai (Cassan, 2022; Tada, 1999, pp. 14–15).

Neither the origin of Naiki nor the meaning of its name is clear; according to Rebecca Combs (Combs, 2016, p. 73), it is probably named after the Naikidai, a braiding machine from the Edo period (1603–1868 CE) in Japan. In this machine, 16 weighted threads are hung around a cylinder. Sliding a wooden handle back and forth moves a set of wooden pieces with metal hooks. These hooks grab selected threads and lift them over other threads. (Pictures and a video can be found at Cassan, 2022.) It is not known how the Naikidai got its name. Instructions for making the braid on a marudai may be found in Tada (1999, p. 87); we will be focusing on the final result.

The structure of Naiki is a simple over-and-under interlacement, as shown in Figure 2(a). This structure also appears in several other contexts. It is listed in the Ashley Book of Knots (1944, p. 498) as #3021 ‘Round Sinnet’. It is the same structure as that of plain weave, with the bias oriented along the axis of the braid. It is also the same as the structure produced by the maypole dance known as Grand Chain (Tian, 2019). The numbering in the figure corresponds to the numbering of the strands as they are placed around the disk, as shown in the row of numbers above the braid. Odd-numbered threads become oriented in the lower right to upper left direction within the braid, like a ‘backslash’ or the diagonal stroke of the letter S. Even-numbered threads become oriented in the lower left to upper right direction, like a ‘forward slash’ or the diagonal stroke of the letter Z. We will follow terminology often used by spinners and weavers and call the first direction S and the second direction Z. The long red and yellow stripes in Figure 1, for instance, are in the Z direction.

Figure 2. (a) The structure of Naiki. Strands going off one side are assumed to wrap around to the other. (b) An abstracted version of the structure, with a fundamental region marked.

A grid of blue and yellow interlaced strands, labeled with numbers, and a grid of blue and yellow diamonds, labeled with numbers, with an 8x8 red diamond superimposed on it.

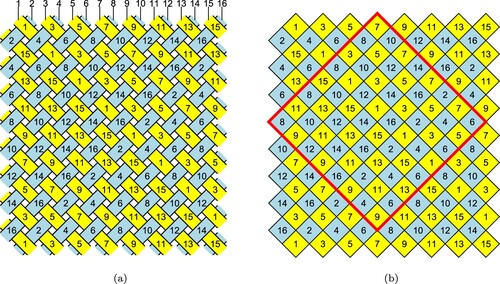
In Figure 2(b), we abstract the structure into a grid. Each square of the grid in the figure corresponds to a crossing of an odd-numbered thread with an even-numbered thread, with the odd and even threads visible in alternate squares.

This paper will focus on the situation with 16 strands, each having one of two colors. We will refer to the ‘spots’ of the pattern as being the grid squares showing the color used in fewer strands. The number of spots will be counted in the 8-by-8 fundamental region shown in Figure 2(b), and will (in the 16-strand case) be four times the corresponding number of strands. For example, Figure 3(c-d) on page 13 each have 16 spots, which are blue. If there are equal numbers of strands of each color, such as in Figure 3(a-b), we will refer to 32 spots without identifying which color they correspond to.

Figure 3. (a) A stripe pattern in the S direction. (b) A stripe pattern in the Z direction. (c) Regularly spaced spots in the S direction. (d) Regularly spaced spots in the Z direction.

Four grids of blue and yellow interlaced strands, labeled with numbers 1 through 16.

In 2011, Rosalie Neilson published The Twenty-Four Interlacements of Edo Yatsu Gumi (Neilson, 2011). This book gave a complete inventory of the Edo Yatsu braids with 8 strands, each of one of two colors, up to equivalence of color pattern under rotations and translations. That work was done by exhaustive search; the goal of this paper is to do a similar inventory of 16-strand Naiki patterns, but guided by theorems in enumerative combinatorics. Similar work was done by the author for the Kongō Gumi kumihimo technique (Holden, 2022).

2. The group of permutations

In the author's previous work on Kongō Gumi kumihimo (Holden, 2022), the group of permutations of threads that left the pattern invariant was just the dihedral group. In the case of Naiki braids, the group is more complicated due to the independence of the two sets of threads and the lack of inherent chirality in the braid.

The group of symmetries of a Naiki braid, like that of the Kongō Gumi braid, is a three-dimensional line group, which can be thought of as a wallpaper group wrapped around a cylinder. We will consider the braid to be divided into grid squares as above. Recall that the grid squares alternate between threads with an S-orientation and threads with a Z-orientation in a checkerboard pattern. A priori, we need to decide whether or not we will consider two braids to be equivalent if their color patterns are equivalent, even if the thread orientations are not equivalent under the same symmetry. However, we will show that with a single exception, this distinction does not occur.

A symmetry of Naiki either keeps all or swaps all of the thread orientations. Suppose a symmetry fixes the color pattern of a braid but swaps the thread orientation. Without loss of generality, we can assume thread 1 has color A and crosses over threads 2, 6, 10, 14, as in Figure 2(b). If another pattern has the same colors but opposite thread orientation, then threads 2, 6, 10, 14 must have color A. Similarly, thread 3 crosses over threads 4, 8, 12, 16 in the first pattern, so those threads must have the same color in the second pattern, and likewise with thread 2 crossing over threads 3, 7, 11, 15 and thread 4 crossing over threads 1, 5, 9, 13.

Now there are four possibilities. If all four batches of threads are the same color, then every symmetry fixes the pattern. If the even threads are one color and the odd threads are another color, we get a checked pattern (as shown in Figure 2(a)). Every symmetry fixes this pattern up to a color reversal, regardless of how one considers the thread orientations. If the even threads and the odd threads both alternate colors, then we get stripes, as in Figure 3(a-b). Every symmetry fixes these patterns up to a color reversal and/or glide plane reflection.

Finally, there is the interesting case, where three of the four batches of threads are the same color and the fourth is different. In this case, we get a regularly spaced grid of spots, all of which have the same thread orientation. This thread orientation could be in either direction, as shown in Figure 3(c-d), so this is the only case where two patterns are equivalent under color symmetry but not thread orientation symmetry. It will prove to be convenient to consider only symmetries that preserve thread orientation, and therefore to count these two patterns as distinct but equivalent under a glide plane reflection. (Note that the same proof shows that if any symmetries reverse the chirality of a pattern, the set of such symmetries is exactly the set of symmetries that swap the even and odd sets of threads.)

If every strand is the same color, the symmetries that preserve thread orientation are now generated by the 8 rotations around the axis, the 8 distinct translations along the axis, a ${180}^{\circ }$ rotation around a line perpendicular to the axis, and a glide plane reflection, parallel to the axis. (This symmetry group is P$\overline{4}$2c in Hermann-Mauguin crystallographic notation (Radaelli, 2011, Secs. 8.1 and 10.2).)

Let's consider what each of these symmetries does to the set of threads. The rotations rotate the braid by a multiple of two threads around its axis, so that even-numbered threads stay even-numbered and odd-numbered threads stay odd-numbered, as shown in Figure 4(a). These rotations are generated by the permutation $(1,3,5,7,9,11,13,15)(2,4,6,8,10,12,14,16)$. A minimal translation followed by a rotation by 2 threads, as shown in Figure 4(b), gives a helical transformation which has the effect of leaving the odd threads unchanged and permuting the even threads $(2,6,10,14)(4,8,12,16)$. 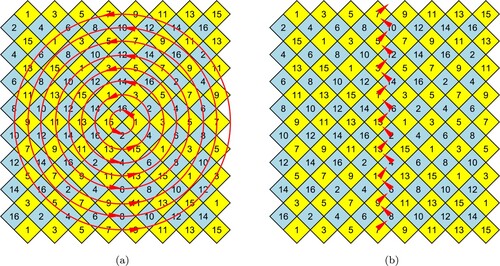The rotation perpendicular to the axis, shown in Figure 5(a), reverses the order of both sets of threads, thus giving the permutation $(1,15)(3,13)(5,11)(7,9)(2,16)(4,14)(6,12)(8,10)$. Lastly, the glide plane reflection swaps the even and odd threads and also translates, as shown in Figure 5(b), with permutation $(1,14,3,12,5,10,7,8,9,6,11,4,13,2,15,16)$. These permutations generate a permutation group on 16 symbols with 128 elements.

Figure 4. (a) A rotation of the braid around its axis. (b) A helical transformation of the braid fixing the odd-numbered threads.

A grid of blue and yellow diamonds, labeled with numbers 1 through 16, with short red left-pointing arrows superimposed, and a grid of blue and yellow diamonds, labeled with numbers 1 through 16, with short red left-and-down arrows superimposed.

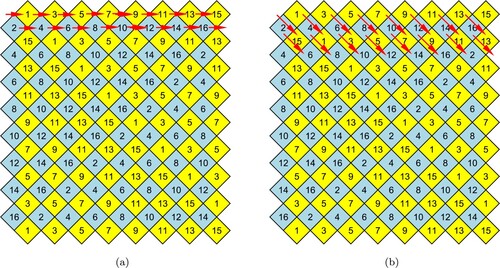
Figure 5. (a) A rotation of the braid around a line perpendicular to its axis. (b) A glide plane reflection of the braid.

A grid of blue and yellow diamonds, labeled with numbers 1 through 16, with concentric half-circle arrows superimposed, and a grid of blue and yellow diamonds, labeled with numbers 1 through 16, with short red arrows zigzagging upwards superimposed.

3. Cycle indices

Our aim is now to count Naiki patterns up to the equivalences above and also up to changing the colors. The theorems that we will use come from the same ideas as the Orbit-Counting Theorem¹ and the Redfield-Pólya Enumeration Theorem. (See Brualdi, 2009, Chap. 14 for an elementary introduction to these theorems, which are often taught towards the end of undergraduate combinatorics courses.) These theorems work by relating the number of objects fixed by certain symmetries to the number of symmetries fixing certain objects. This latter information can be kept track of using a multivariable generating function called the cycle index (Brualdi, 2009, Sec. 14.3).

Definition 3.1

If G is a permutation group on m symbols, then the cycle index of G is the generating function $P(x_1,\dots ,x_m)=\frac{1}{\left|G\right|}\sum _{g\in G}\prod _{k=1}^m{x}_k^{j_k\left(g\right)}$where $j_k\left(g\right)$ is the number of cycles of g with length k.

For example, the cycle index of $G=\left\{\right(1\left)\right(2),(12\left)\right\}$ is $\frac{1}{2}(x_1^2+x_2)$, signifying two cycles of length 1 and one cycle of length 2. More examples can be found in Supplement 1 of Holden (2022). General formulas for the cycle indices of many types of permutation groups are known, and also some formulas for combining indices for smaller groups into indices for larger ones. For the symmetry groups we will consider in this paper, however, brute force seems to be the best method. Built-in commands for this calculation are provided in many computer algebra systems; Maple was used for the particular calculations in this paper.

4. A version of de Bruijn's Theorem

We will start by using the version of de Bruijn's Theorem from Holden (2022) to count the number of Naiki patterns with a given number of threads of each color, up to the equivalences above and also up to changing the colors. We introduce the following notation: let ${\eta }_s$ be the power series expansion in x of $e^{s(z_{s}x+z_{2s}{x}^2+\dots )}=1+s{z}_{s}x+(\frac{1}{2}{s}^2{z}_s^2+s{z}_{2s})x^2+\dots$with $x^{\ell }$ replaced by $w_{\ell }^s$ for each ℓ: ${\eta }_s=1+s{z}_s{w}_1^s+(\frac{1}{2}{s}^2{z}_s^2+s{z}_{2s})w_2^s+\dots$The monomial $w_{\ell }^s$ will be used to track when s threads have color ℓ.

Then the theorem can be stated as:

Theorem

de Bruijn, 1959, Special case of Thm. 1

If an object has m locations which can each be colored with one of q different colors, and a group G of symmetries with cycle index $P_m(x_1,\dots ,x_m)$, then the number of non-equivalent ways to color the object with the first color in $m_1$ locations, the second color in $m_2$ locations, and so on, is the coefficient of $w_1^{m_1}{w}_2^{m_2}\dots$ in $P_m(\frac{\mathrm{\partial }}{\mathrm{\partial }{z}_1},\dots ,\frac{\mathrm{\partial }}{\mathrm{\partial }{z}_m})S_q({\eta }_1,\dots {\eta }_q)$where $S_q(x_1,\dots ,x_q)$ is the cycle index of all ways to permute q colors, the whole expression evaluated at $z_1=z_2=\cdots =z_m=0$.

Let G be the group of symmetries described above. Maple commands were used to compute the elements from the generators and then the cycle index from the elements. This gave us the cycle index of G: $\begin{array}{rl}{P}_{16}(x_1,\dots ,x_{16})& =\frac{1}{128}{x}_1^{16}+\frac{1}{64}{x}_1^8{x}_2^4+\frac{1}{32}{x}_1^8{x}_4^2+\frac{1}{8}{x}_1^4{x}_2^6+\frac{17}{128}{x}_2^8+\frac{1}{32}{x}_2^4{x}_4^2+\frac{1}{32}{x}_4^4\\ & +\frac{1}{8}{x}_8^2+\frac{1}{2}{x}_{16}.\end{array}$With q = 2 colors, the cycle index $S_q$ is $S_2(x_1,x_2)=\frac{1}{2}(x_1^2+x_2)$as described in Section 3. Then $\begin{array}{rl}& P_{16}(\frac{\mathrm{\partial }}{\mathrm{\partial }{z}_1},\dots ,\frac{\mathrm{\partial }}{\mathrm{\partial }{z}_{16}})S_2({\eta }_1,{\eta }_2)\\ & =\frac{1}{128}\frac{{\mathrm{\partial }}^{16}{S}_2}{\mathrm{\partial }{z_1}^{16}}+\frac{1}{64}\frac{{\mathrm{\partial }}^{12}{S}_2}{\mathrm{\partial }{z_2}^4\mathrm{\partial }{z_1}^8}+\frac{1}{32}\frac{{\mathrm{\partial }}^{10}{S}_2}{\mathrm{\partial }{z_4}^2\mathrm{\partial }{z_1}^8}+\frac{1}{8}\frac{{\mathrm{\partial }}^{10}{S}_2}{\mathrm{\partial }{z_2}^6\mathrm{\partial }{z_1}^4}+\frac{17}{128}\frac{{\mathrm{\partial }}^8{S}_2}{\mathrm{\partial }{z_2}^8}\\ & +\frac{1}{32}\frac{{\mathrm{\partial }}^6{S}_2}{\mathrm{\partial }{z_4}^2\mathrm{\partial }{z_2}^4}+\frac{1}{32}\frac{{\mathrm{\partial }}^4{S}_2}{\mathrm{\partial }{z_4}^4}+\frac{1}{8}\frac{{\mathrm{\partial }}^2{S}_2}{\mathrm{\partial }{z_8}^2}+\frac{1}{2}\frac{\mathrm{\partial }{S}_2}{\mathrm{\partial }{z}_{16}},\end{array}$which evaluated at $z_1=z_2=\cdots =z_{16}=0$ gives $\begin{array}{rl}& w_0{w}_{16}+w_1{w}_{15}+5w_2{w}_{14}+11w_3{w}_{13}+30w_4{w}_{12}+52w_5{w}_{11}\\ & +95w_6{w}_{10}+120w_7{w}_9+91w_8^2.\end{array}$Thus there are a total of 406 patterns using one or two colors, with colors distributed as in Table 1. Of these, 404 have mirror images that are not otherwise equivalent.

Table 1. Inventory of patterns given by de Bruijn's Theorem.

Spots:	0	4	8	12	16	20	24	28	32	Total
Patterns:	1	1	5	11	30	52	95	120	91	406

5. The Monster Theorem

At this point it seems logical to further break down the classification according to how many even-numbered threads were of each color and how many odd-numbered threads had each color. Suppose we have a permutation group H acting on a set of colors. For each color ℓ we arbitrarily choose an index $r_{\ell }$ subject to the constraint that $r_{\ell }=r_{{\ell }^{\prime }}$ if there is an h in H such that h takes ℓ to ${\ell }^{\prime }$. (In our application, H will be the full symmetry group, and thus all of the $r_{\ell }$ will be equal.) Similarly to Theorem 4.1, we let ${\eta }_{s,i,j,\ell }$ be the power series expansion in x of $e^{s(z_{s}x+z_{2s}{x}^2+\dots )}=1+s{z}_{s}x+(\frac{1}{2}{s}^2{z}_s^2+s{z}_{2s})x^2+\dots$with $x^t$ replaced by $w_{i,r_{\ell },t}^s$ for each t: ${\eta }_{s,i,j,\ell }=1+s{z}_s{w}_{i,r_{\ell },1}^s+(\frac{1}{2}{s}^2{z}_s^2+s{z}_{2s})w_{i,r_{\ell },2}^s+\dots$The variable $w_{i,r_{\ell },t}$ will be used to track when t threads with parity i have color ℓ.

Looking for further generalizations of de Bruijn's Theorem, we then find:

Theorem 5.1

de Bruijn's Monster Theorem de Bruijn, 1971, Thm. 8.2, somewhat simplified

Suppose an object has m locations partitioned into k sets $D_1,\dots ,D_k$, and each location can each be colored with one of q different colors, with two colorings being considered equivalent if they are related by a permutation h in a group H acting on q symbols, and the locations have a group G of symmetries such that g takes $D_i$ to itself for all i. Let $D_{i,g}^{\left(j\right)}$, $j=1,\dots ,J$, be the orbits of the action of g restricted to $D_i$, and let $R_h^{\left(\ell \right)}$, $\ell =1,\dots ,L$, be the orbits of the action of h on the colors. Then the number of non-equivalent ways to color the object with the first color in $m_{1,i}$ locations of $D_i$, the second color in $m_{2,i}$ locations of $D_i$, and so on, is the coefficient of $w_{1,r_1,m_{1,1}}\cdots w_{k,r_1,m_{1,k}}{w}_{1,r_2,m_{2,1}}\cdots w_{k,r_2,m_{2,k}}\cdots w_{1,r_q,m_{q,1}}\cdots w_{k,r_q,m_{q,k}},$in ${\left|G\right|}^{-1}{\left|H\right|}^{-1}\sum _{g\in G}\sum _{h\in H}\prod _{i=1}^k\left(\prod _{j=1}^J\frac{\mathrm{\partial }}{\mathrm{\partial }{z}_{\left|D_{i,g}^{\left(j\right)}\right|}}\right)\left(\prod _{\ell =1}^L{\eta }_{\left|R_h^{\left(\ell \right)}\right|,i,j,\ell }\right),$the whole expression evaluated at $z_1=z_2=\cdots =z_m=0$.

(In an abuse of notation, we are using ℓ in the theorem to represent both a color and an orbit of colors. Since two colors in the same orbit must have the same $r_{\ell }$, this should be harmless.)

Applying the theorem with m = 16, k = 2, q = 2, G as above, $D_1=\{1,3,5,7,9,11,13,15\}$, $D_2=\{2,4,6,8,10,12,14,16\}$, and H being all permutations of 2 colors (and suppressing the values of $r_{\ell }$ which are all equal to 1), we get the generating polynomial $\begin{array}{rl}& 2w_{1,0}{w}_{1,8}{w}_{2,0}{w}_{2,8}+2w_{1,0}{w}_{1,8}{w}_{2,1}{w}_{2,7}+8w_{1,0}{w}_{1,8}{w}_{2,2}{w}_{2,6}+10w_{1,0}{w}_{1,8}{w}_{2,3}{w}_{2,5}\\ & +8w_{1,0}{w}_{1,8}{w}_{2,4}^2+2w_{1,1}{w}_{1,7}{w}_{2,0}{w}_{2,8}+4w_{1,1}{w}_{1,7}{w}_{2,1}{w}_{2,7}+12w_{1,1}{w}_{1,7}{w}_{2,2}{w}_{2,6}\\ & +20w_{1,1}{w}_{1,7}{w}_{2,3}{w}_{2,5}+13w_{1,1}{w}_{1,7}{w}_{2,4}^2+8w_{1,2}{w}_{1,6}{w}_{2,0}{w}_{2,8}+12w_{1,2}{w}_{1,6}{w}_{2,1}{w}_{2,7}\\ & +48w_{1,2}{w}_{1,6}{w}_{2,2}{w}_{2,6}+68w_{1,2}{w}_{1,6}{w}_{2,3}{w}_{2,5}+52w_{1,2}{w}_{1,6}{w}_{2,4}^2+10w_{1,3}{w}_{1,5}{w}_{2,0}{w}_{2,8}\\ & +20w_{1,3}{w}_{1,5}{w}_{2,1}{w}_{2,7}+68w_{1,3}{w}_{1,5}{w}_{2,2}{w}_{2,6}+116w_{1,3}{w}_{1,5}{w}_{2,3}{w}_{2,5}+79w_{1,3}{w}_{1,5}{w}_{2,4}^2\\ & +8w_{1,4}^2{w}_{2,0}{w}_{2,8}+13w_{1,4}^2{w}_{2,1}{w}_{2,7}+52w_{1,4}^2{w}_{2,2}{w}_{2,6}+79w_{1,4}^2{w}_{2,3}{w}_{2,5}+96w_{1,4}^2{w}_{2,4}^2.\end{array}$For ease of reference, we represent this in tabular fashion as Table 2.

Table 2. Generating polynomial coefficients of $w_{1,a}{w}_{1,8-a}{w}_{2,b}{w}_{2,8-b}$.

This is obviously a very powerful theorem. It does have a few limitations for our purposes, however. First, note that we would like $D_1$ to be the odd threads and $D_2$ to be the even threads, but the theorem does not cover the permutations that swap these sets of threads. We have determined that these symmetries only preserve the single pattern with 0 spots and the single pattern with 32 spots, so we will treat these as special cases, colored in red in Table 2. In the cases corresponding to $w_{1,a}{w}_{1,8-a}{w}_{2,a}{w}_{2,8-a}$ for a = 1, 2, 3, 4, swapping even with odd threads gives the same or opposite color distributions. Therefore, by failing to account for that swap we are double-counting those patterns. We take that into account by dividing by 2 the coefficients shown in blue in Table 2. In every other case, swapping even with odd threads merely shows that the coefficient of $w_{1,a}{w}_{1,8-a}{w}_{2,b}{w}_{2,8-b}$ must be equal to that of $w_{1,b}{w}_{1,8-b}{w}_{2,a}{w}_{2,8-a}$, which can be confirmed in Table 2. The two coefficients represent the same equivalence class in these cases.

The other limitation comes from the fact that colors in the same orbit of H must have the same variables in the generating function. Let X be the set of patterns with a odd threads of color A, b odd threads of color B, c even threads of color A, and d even threads of color B. Let Y be the set with a odd threads of color A, b odd threads of color B, d even threads of color A, and c even threads of color B. Then both X and Y will correspond to the monomial $w_{1,1,a}{w}_{1,1,b}{w}_{2,1,c}{w}_{2,1,d}$, so it will not be possible to separate the patterns in X from the patterns in Y. (Indeed, it is difficult to see how any generating function could make this distinction while allowing colors to be exchanged.)

Again, a close look at the particular situation will rescue us. If a = b or c = d, then the two sets of patterns above coincide up to exchange of colors. The coefficient of $w_{1,1,a}{w}_{1,1,b}{w}_{2,1,c}{w}_{2,1,d}$, adjusted as above if a = b = c = d, will give us the correct count. If $a\ne b$ and $c\ne d$, it is not possible for a member of one set of patterns to be equivalent to a member of the other. Also, there is an equivalence-respecting bijection between the sets induced by exchanging the colors of either the even or odd threads, but not both. (Since exchanging colors on both thread parities gives a pattern equivalent to the original, it does not matter which side we exchange.) Therefore the coefficient of $w_{1,1,a}{w}_{1,1,b}{w}_{2,1,c}{w}_{2,1,d}$ represents the sum of two different but equal-sized equivalence classes of patterns, one with a>b and c<d and the other with a>b and c>d. These are the coefficients that are unboxed in Table 2. Arbitrarily choosing representatives such that there are at least as many spots from the odd threads as from the even, we arrive at Table 3, which uses the same color-coding as Table 2.

Table 3. Inventory of patterns given by the Monster Theorem.

With the help of a computer, we can generate diagrams for the complete set of patterns corresponding to each element of the table. These diagrams are available on GitHub (Holden, 2023), along with some notes on how they were systematically generated.

6. Future work

As previously noted, the traditional Edo Yatsu braid has the same structure as Naiki, but with 8 strands. Naiki braid kits with 20 strands are available on the Internet (Huntoon, 2023). The author is not aware of other numbers of strands documented in the context of kumihimo, but Ashley (1944, p. 498) notes that the structure will work with any even number. With n strands, the symmetries that preserve thread orientation are generated by the n/2 rotations around the axis, the n/2 distinct translations along the axis, a ${180}^{\circ }$ rotation around a line perpendicular to the axis, and a glide plane reflection, parallel to the axis. (This symmetry group is P$\overline{\left(n/2\right)}$2c in Hermann-Mauguin crystallographic notation.)

As a check on the work, the analyses of Sections 4 and 5 were done with 8 strands as well as 16. These analyses should go through without difficulty for any even number of strands, simply with longer computations. (As far as the author knows, there are no closed form formulas for the generating function coefficients needed, so a general analysis is probably not possible.)

We could also consider more than 2 colors. The author has not been able to find any historical examples, but Tada (1999) gives modern examples of and patterns for braids with three and with five colors. With more than two colors, the analysis of Section 4 should again go through without difficulty, using longer computations. The Monster Theorem of course also still applies, but the separation described in Section 5 of different color patterns with the same monomial will be more complicated. In any given case this seems doable, but it is not clear whether there is a general algorithm. De Bruijn's own examples for the Monster Theorem contain instances where the ‘colors’ refer to patterns in sets of locations rather than a single color in a single location, but it is not clear how to apply that here.

Since the structure of Naiki is the same as that of plain weave, it seems reasonable to ask if we can classify plain weave patterns using the same techniques. The symmetries that produce equivalent patterns are not the same, however, since the fabric is not usually oriented on the bias and there may be no distinguished axis. In particular, it is not clear how to deal with the symmetry that rotates the fabric ${90}^{\circ }$. Like the glide plane reflection, this rotation swaps the odd and even threads. However, there are many more possible patterns fixed by the rotation that would need to be dealt with as special cases. Possibly there is a further extension of the Monster Theorem that can deal with the situation where elements of G are allowed to permute the $D_i$ as well as preserving them.

Acknowledgments

The author would like to thank Rosalie Neilson for introducing him to the Naiki technique and suggesting the project. Thanks also to the editors and to the anonymous reviewers for many helpful suggestions.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Notes

1 Traditionally called Burnside's Lemma but not due to Burnside, see Neumann (1979) for more.