Dynamic reduction with applications to mathematical biology and other areas

Abstract

In a difference or differential equation one is usually interested in finding solutions having certain properties, either intrinsic properties (e.g. bounded, periodic, almost periodic) or extrinsic properties (e.g. stable, asymptotically stable, globally asymptotically stable). In certain instances it may happen that the dependence of these equations on the state variable is such that one may (1) alter that dependency by replacing part of the state variable by a function from a class having some of the above properties and (2) solve the ‘reduced’ equation for a solution having the remaining properties and lying in the same class. This then sets up a mapping 𝒯 of the class into itself, thus reducing the original problem to one of finding a fixed point of the mapping. The procedure is applied to obtain a globally asymptotically stable periodic solution for a system of difference equations modeling the interaction of wild and genetically altered mosquitoes in an environment yielding periodic parameters. It is also shown that certain coupled periodic systems of difference equations may be completely decoupled so that the mapping 𝒯 is established by solving a set of scalar equations. Periodic difference equations of extended Ricker type and also rational difference equations with a finite number of delays are also considered by reducing them to equations without delays but with a larger period. Conditions are given guaranteeing the existence and global asymptotic stability of periodic solutions.

Keywords:

• Dynamic reduction
• Periodic difference equation
• Global stability
• Discrete delay equations
• Ricker map

1. Introduction

Dynamic reduction is a problem-dependent algorithm or procedure which allows one to find a solution to a problem having specified properties by reducing the problem to a sequence of simpler ones, each having a solution with the desired properties. To illustrate the technique, consider the problem of finding a p-periodic solution of the p-periodic difference equation

We will show in certain applications that the dependence of f _n (x) on x can be decomposed into a convenient form

such that for each in a certain class of p-periodic sequences 𝒫 _p , the ‘reduced’ equation

has a unique p-periodic solution . One then has an induced mapping

Clearly, a fixed point of the map (4) is equivalent to a p-periodic solution of (1). Throughout the presentation the function ‘g’ will be used solely to indicate the grouping of the state variables on which the reduction is performed. In certain cases, with proper choice of the function ‘g’, the image under the map 𝒯 will have all the desired stability properties.

Linearization of a difference or differential equation is a form of dynamic reduction: about a solution ,

or about a periodic solution φ(t),

In the following sections we consider some applications of the technique to various problems. The first involves a model describing the interaction between wild and genetically altered mosquitoes in a periodically varying environment. Under certain conditions we find a globally attracting periodic state yielding a solution to a coupled system of two equations of Ricatti/Ricker type. In subsequent sections we apply dynamic reduction to other systems including systems of Ricker equations with delays and rational difference equations with delays. In certain instances large systems may be completely decoupled, thus reducing their solution to an application of known results.

1.1 Stability

Throughout this work, we mean and . While the theorem to follow is quite general, we will restrict ourselves to the setting most common in problems in mathematical biology where the state variable x lies in or . By global asymptotic stability (GAS) of a periodic orbit we shall mean that v globally attracts all solutions starting in and is locally exponentially asymptotically stable.

That GAS of a periodic solution of (1) (or equivalently (2)) does not immediately follow from the GAS of the same solution of (3) is seen from the following simple example. Consider an autonomous Ricker equation

If we let g(x)=x then every v∈(0, 2) is a GAS fixed point of (3) on , but not of (2). However, with a smallness condition on g′, e.g. , the fixed point and is a GAS solution of (2) with respect to .

In order to quantify this smallness condition let be a fixed point of 𝒯 and hence a periodic point of (1), which we write, taking into account (2), as

Notation: For and a p-periodic vector valued sequence of functions with we define . For a fixed periodic with , and with define . For F= F(x, g(ξ)), we will use ∂₂ F and ∂ _g F interchangeably to mean differentiation with respect to the second argument.

We now state a theorem which will be used to establish GAS in the applications to follow.

Theorem 1.1

Assume there are convex compact such that (where the subscripts are interpreted mod p and is convex and compact) and assume every initial point is ultimately mapped by (1) into one of the K _n . Assume F _n and g _n are C ¹ functions. Define 𝒫 _p to be that subset of p-periodic sequences such that

Then, if is sufficiently small,

• (i) the mapping is a contraction and thus there is a unique fixed point 𝒯 (v*) = v* and

• (ii) v* is a GAS periodic point of (1).

Remark 1.1

Item (ii) does not immediately follow from (i). A further reduction on the size of may be required.

Proof

For let us denote by y(v) the image of v under , i.e. . Then expressing the periodicity of y(v), one has

Letting D _v denote differentiation,

Thus, from (7),

Repeating this for subsequent expressions under (7), one obtains

where all subscripts are interpreted ‘mod p’. The Δ^(k) all share the same characteristic polynomial [1, p. 320] and hence the same spectrum σ(*). From the assumed exponential asymptotic stability of y(v) as a periodic point of (3), one has

Thus has a bounded inverse and from (10),

Next we define a norm in 𝒫 _p to be

Then it follows from (11) that for δ∈(0, 1) and sufficiently small,

and from the mean value estimate,

for any pair . Thus,

and 𝒯 is a contraction.

It remains to prove that the unique fixed point v* of 𝒯 is GAS as a solution of (2). We first prove v* is asymptotically stable. The matrix of the equation of first variation of (2) at v* is

By the same argument given above we see that the spectrum of is independent of n and lies inside the unit circle in the complex plane.

We finally show v* is globally attracting. Let be the basin of attraction of v*. Since ℬ is open, from (12) with w=v*, it follows that for δ sufficiently small the entire image under 𝒯 of 𝒫 _p lies in . Thus for each there exists a such that the solution x _n of (13) with x ₀=v ₀ lies in ℬ for n=T(v) and by continuity, some open neighborhood of is carried into ℬ in the same number of iterations: symbolically,

Let be a finite sub-cover of 𝒫 _p and define . Thus every initial point is mapped by (3) into ℬ upon τ iterations, and the same will remain true for (2) provided is sufficiently small. A sufficient (but not necessary) condition to accomplish this would be to assume small.    ▪

Remark 1.2

• (a) The estimate (12) is the very raison d’ê tre for the reduction method. The spectrum σ of the product of F _x (x, y)'s along a periodic sequence does not, in general, lie inside the unit circle in the complex plane. What the reduction method accomplishes is that for each fixed t∈(0, 1) the solution of (3) with v=u _t ‘runs’ over to the GAS periodic orbit y(v) of that system and it is there that .

• (b) In certain cases, notably rational difference equations (section 3.3), it is possible it achieve the smallness condition on without making small, c.f. (50).

The next lemma is needed in the sections to follow.

Lemma 1.2

2 The periodic Ricker equation,

with has a globally asymptotically stable p-periodic solution {x _n *}. Moreover,

i.e. neither attenuation nor resonance prevails.

2. Genetically altered mosquitos

This model was first introduced in the time independent or autonomous case by Jia Li 3 and later considered in 4 5 by the authors where the technique of ‘ratio dynamics’ was introduced. In an attempt to describe more accurately a periodically varying environment we consider the following p-periodic system where x and y represent, respectively, the populations of wild (W) and genetically altered (GA) mosquitos

where the initial conditions x ₀, y ₀ and all the coefficients are positive and thus x _n and y _n remain positive for all . We assume all the coefficients to be periodic of period p in the integer variable n. The expressions

are the growth functions, i.e. the per-capita rate of offspring production and are derived (following 3) as follows. Let N _n =x _n +y _n represent the total population at generation n and c(N _n ) be the total number of encounters or matings per individual, per unit of time. Concentrating first on the x equation governing the wild (W) mosquitoes,

the number of matings that are with W or GA mosquitoes at generation n is or , respectively. Let A _{1, n} and B _{1, n} be the number of W offspring that a W produces through a mating with a W and a GA at generation n. Similarly, let A _{2, n} and B _{2, n} be the number of GA offspring that a GA produces through a mating with a W and a GA, respectively, at generation n. Then the total number of W offspring produced by a single W at generation n is just

For large populations it is reasonable to assume that the function c(N _n ) reaches a constant saturation level, c(N _n )=c ₀. Defining and we obtain (14).

The expressions

are the survival probabilities. The d _{i, n} are the ambient mortality rates while the k _{i, n} are the rates of density dependent mortality and characterize the instantaneous carrying capacity at generation n.

We first eliminate the ‘’ terms by absorbing them into the coefficients a _i , b _i (, and ) to obtain

Remark 2.1

We assume that each species is self-sustaining in the sense that if (15)–(16) evolves with the parameters all fixed at any then each species, in the complete absence of the other, can grow to a non-extinction state. This imposes the conditions a _{1, n} >1 and .

Our interest is in establishing the existence of a periodic state which globally attracts all initial states (x, y) with x>0 and y>0.

In the case of equal rates of density-dependent mortality we obtain a globally asymptotically stable periodic solution (section 2.1). When these rates are not the same, ratio dynamics fails. In section 2.2 we apply dynamic reduction to obtain a new set of equations to which ratio dynamics will apply to give the desired periodic solution and hence the mapping (4).

Ratio dynamics ultimately leads to the study of the scalar p-periodic Ricker equation

to which Lemma 1.2 applies.

2.1 Ratio dynamics, k _{1, n} =k _{2, n} , n=1, 2, …, p

We first describe the case of equal rates of density-dependent mortality, k _{1, n} and k _{2, n} . This case, while quite artificial in practice, is nevertheless quite useful in solving the more general problem.

In (15) we form the ratio to obtain

We then have the following lemma:

Lemma 2.1

For each fixed n assume a _{1, n} /a _{2, n} <1 and b _{1, n} /b _{2, n} >1. Then (18) has a globally asymptotically stable periodic solution .

Proof

For each n the right-hand side of (18) is a concave mapping from that intersects the diagonal. The rest follows from 6.    ▪

Remark 2.2

Referring to equations (15)–(16), and recalling that x represents Wild type while y represents GA, the conditions a _{2, *}>a _{1, *} imply that the likelihood of a GA producing a GA when mating with a Wild, is greater than the likelihood of a Wild producing a Wild when mating with a Wild. Similarly, the conditions b _{1, *}>b _{2, *} imply that the likelihood of a Wild producing a Wild when mating with a GA, is greater than the likelihood of a GA producing a GA when mating with a GA. The conditions preclude an attracting fixed point of (15)–(16) on one of the axes, i.e. the case in which one of the species reaches extinction. See 3 for a discussion of these extinction cases in the autonomous, or time-independent case.

Substituting into the second equation in (15) we obtain

Using the substitution u _n =K(n)y _n in (19) we get, in the same form as in (17), the following Ricker equation

Thus, we have the following theorem:

Theorem 2.2

Assume . Then (21) has a globally asymptotically stable (with respect to ) p-periodic solution and hence (15)–(16), with , has a globally asymptotically stable (with respect to the open first quadrant) solution

Remark 2.3

The condition in Theorem 2.2 is a sufficient condition only and it precludes period doubling bifurcations from occurring (see 3 where these bifurcations were studied in the autonomous case). The condition is, however, not necessary, as pointed out in 7 where periodic coefficients were treated and some results, largely numerical, were obtained for periods 2 and 3 where some of the σ _n are allowed to exceed 2, provided their average remains less than 2.

Remark 2.4

In 6 the following was shown: let two concave maps have fixed points x _f and x _g with x _f <x _g . Then and . This is useful in estimating the ‘spread’ of the invariant set of lines in the (x, y) plane determined by the periodic solution given by Lemma 2.1. More precisely, if P _n is the fixed point of the n ^th map in (18), then the slopes of the invariant lines are 1/ζ _n and lie in the open interval , where S _n =1/P _n . Note that P _n is simply the solution of .

2.2 Dynamic reduction leads to ratio dynamics, the case k _{1, n} ≠k _{2, n} for some n

The whole point of dynamic reduction is to reduce a given problem to one for which a known solution technique is readily available. In order to reduce this case to the one treated in section 2.1, we rewrite (15) as

which has the form (2). Our aim is to define a region as

and a subset

such that for each sequence , the ‘reduced’ system,

with initial conditions x ₀>0 and y ₀>0, has a globally asymptotically stable (with respect to the open first quadrant), and hence unique, periodic solution . Thus the mapping (4) will be established. If v* is a fixed point of 𝒯, i.e. a solution of

then it remains to show that v* is GAS as a solution of the original system (22)–(23).

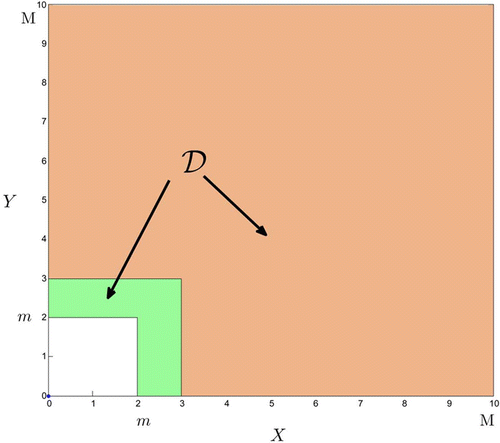
Note that while a fixed point of the mapping 𝒯 in (4) is a p-periodic solution of (22)–(23) and therefore (15)–(16), the converse is not true since (15)–(16) has p-periodic points on the two intervals of the boundary of 𝒟 where x=0 or y=0. It turns out that the mapping 𝒯 will send sequences lying on those portions of the boundary to sequences with values in that part of 𝒟 lying on the interior of the first quadrant.

Hence, we are interested first in defining the region 𝒟 in (25) that is mapped into itself by the right-hand side of (26)–(27) with some mild restrictions on g. Then we explore conditions guaranteeing that the ratio system

formed from (26)–(27) by setting z=x/y has a globally asymptotically stable (with respect to ) solution. This will establish a positively invariant set of lines in the (x, y) plane which attract every solution starting in the open first quadrant. Finally, the stability of the solution of the system corresponding to (19) will be established.

We first consider the following scalar mapping containing a parameter λ,

and the associated family of mappings (simple multiplication by φ),

Note in particular that when a, b>1.

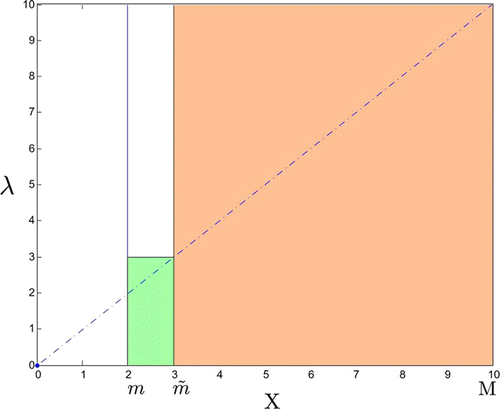
Lemma 2.3

Assume a, b>1 and let M be such that Then for there exist small positive numbers, m and [mtilde] depending on M, with m<[mtilde]<M such that each member of the family (32) satisfies

• (a) For and one has

• (b) For and one has

Proof

For x and λ small, may be approximated by , and thus

since the above expression is a convex combination of a and b. Thus there exists a small [mtilde]>0 such that (b) holds. Next observe that

again using convexity on the first ‘max’. Then choose such that

so that (a) follows.    ▪

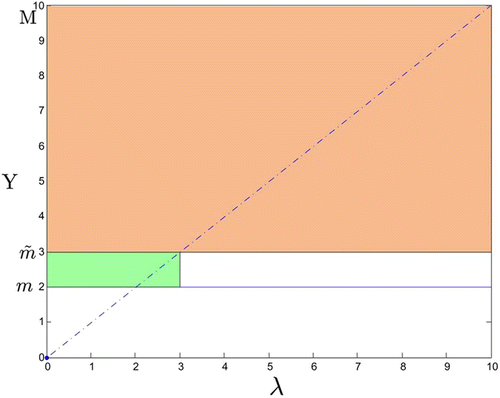
Figure 1 is an interpretation of Lemma 2.3. Part (a) implies that for (x, λ) in the large rectangle, each member f of the family ℱ maps x to the interval [m, M] while part (b) implies that for (x, λ) in the small rectangle f moves x to the right, but not past M. Thus, in either case the interval [m, M] is invariant under application of .

Figure 1. Parameter region for which m≤x≤M is invariant.

Now fix n, and consider the mapping (26)–(27). The first component (26) has the form considered in Lemma 2.3. But x and y occur symmetrically in (26)–(27), so that Lemma 2.3 applies to the family

which includes the second component (26), see figure 2. Finally we consider the mapping (26)–(27), with sufficiently small so that g satisfies the condition (with n suppressed),

If then one of the variables must lie in the interval [m, M] so that Lemma 2.3 implies the image under the right side of (26)–(27) lies in 𝒟, the two shaded regions in figure 3. But more can be inferred from Lemma 2.3 which we state as:

Corollary 2.4

Let condition (33) hold and m, and M be defined as in Lemma 2.3. If 𝒟 is the region

then 𝒟 and its convex hull co𝒟 are each invariant under the mapping

Figure 2.  Parameter region for which m≤y≤M is invariant.

Figure 3.  Region 𝒟 in x, y-plane left invariant.

Proof

From Lemma 2.3(b) it follows that any that satisfies y≥m−x is mapped to a point (x ₁, y ₁) with and .    ▪

Thus we have the following theorem:

Theorem 2.5

• (a) In the reduced system (26)–(27) assume and define

  Assume sufficiently small so that when x≤M and y≤M, one has
  Then there exists an m, 0<m<M, such that the region
  and its convex hull co𝒟 are invariant under the mapping (26) – (27), i.e. if then and x _n y _n >0 for all .

• (b) Further, if for each is sufficiently small so that and , then the ratio equation (29) has a globally asymptotically stable (with respect to p-periodic solution

• (c)Assume σ(n) defined in (2.8) and computed from (21) satisfies . Then the reduced system (28)–(29)) has a globally asymptotically stable (with respect to the open first quadrant) p-periodic solution . If, for each is sufficiently small, then is a GAS solution of the original system (22)–(23).

Proof

• (a) This follows immediately from Corollary 2.4 since each map in the sequence satisfies the conditions of Lemma 2.3.

• (b)Toward ultimately defining the mapping

  let be chosen and consider (26)–(27). Letting z _n =x _n /y _n we obtain the ‘ratio’ equation:
  From the hypotheses, for each is concave and the graph of η=h _n (z) crosses the ‘diagonal’, η=z in the (z, η) plane. The proof of part (b) follows from the results of section 2.1.

• (c) Theorem 2.2 tells us that the reduced equation (26)–(27) has a globally asymptotically stable solution v* thus giving us the mapping 𝒯. It is clearly continuous and carries points in 𝒫 _p having values on the axes in co𝒟 (see figure 3) to points in 𝒫 _p having no values on the axes in co𝒟. Clearly a fixed point (periodic sequence in ℝ²) has no values lying on either axis.

  To see that 𝒯 is a contraction and its unique fixed point v* is GAS as a solution of the original system, we will verify the smallness condition of Theorem 1.1. Noting that F _n is the right-hand side of (22)–(23), and defining , we have

  From Lemma 2.3, . The rest follows from by letting be sufficiently small for each n.    ▪

Remark 2.5

We saw earlier in Remark 2.1, the assumption that each species is self sustaining imposed the condition . In Remark 2.2 the assumptions a _{1, n} /a _{2, n} <1, b _1,n /b_2,n >1 were interpreted biologically and were seen to preclude extinction states. From these it follows that . The condition is a sufficient condition that precludes period doubling, Remark 2.3.

3. Other applications

The possible applications of dynamic reduction are limited only by the user's imagination. The key point is that the reduced equation should have a solution having all the properties desired of the solution of the original problem. As we saw in the mosquito model, some of these properties (periodicity) are built into the class 𝒫 _p on which 𝒯 acts while other properties (global asymptotic stability) are obtained by carefully defining the map. Here we state a few applications with just enough details to establish the mapping on a subset of periodic sequences such that each point in the range of 𝒯 is a globally asymptotically stable solution of the reduced system. As noted earlier, a fixed point yields a solution of the original problem. We also calculate the derivatives needed to verify the smallness conditions of the stability theorem, Theorem 1.1.

The first two examples are systems of Ricker equations with coupling and delays. Although Ricker's equation arose in the modeling of problems in Biology, the authors have no specific application in mind. The aim is to illustrate the use of dynamic reduction.

3.1 Systems may be decoupled

Consider

where g _{*, n} is periodic in n of period p and whenever , where

and where the constants are chosen as follows. With 0<c<2, the maximum of xexp(c−x) on ℝ⁺ is . Thus we take M=e. Using this value for x and c=0 gives a lower bound m on how close to the origin a point can be mapped:

Using these values the region 𝒟 is invariant under the action of (38). Here g is periodic in n and we seek a globally asymptotically stable periodic solution. To this end define such that

Then for , the globally asymptotically stable solution v* of

To obtain the contraction property and global asymptotic stability as a solution of (38) one then must restrict the size of in order to verify smallness condition of Theorem 1.1 where

3.2 Periodic systems with delays

These can be handled similarly, e.g. consider

where multiplication and exponentiation on the right side are done element-wise. In this case, with the same m as in (39), we define the region 𝒟 and as

where λ is determined as follows. If p is the minimal period of the system (41) then where μ is the unique positive integer such that

The mapping, , is then established by finding the solution v* of the reduced system

where again we assume .

Remark 3.1

Even though a fixed point of 𝒯 yields a λ-periodic solution of (46), λ need not be the minimal period of that solution.

To verify 𝒯 is a contraction and that the unique fixed point v* is a GAS solution of (41) one then must restrict the size of in order to satisfy the conditions of Theorem 1.1. For each n, is the diagonal d×d matrix

and letting D _j represent differentiation with respect to the jth argument, the term in is interpreted to mean the d×k+1 matrix

3.3 Rational difference equations

The following equation has been the subject of much attention 8,

where all coefficients are assumed non-negative (other conditions to follow). Adding periodicity gives

Separating out the delayed terms, one has

Consider, for the reduced equation

For each n we assume β_{0, n} >0, B _{0, n} >0. Then

Our aim is to give additional conditions that guarantee that each φ _n is concave so that . Since the values of each φ _i are acted on by φ _i+1, we may restrict the upper boundary of the domain of φ _i+1 to be M _i and thus define the region 𝒟 and the subset of λ-periodic sequences, to be

where λ is chosen as in (43).

There is some latitude in the choice of m. In order to render (47) concave for each n we require

Then by the result 6, the λ-periodic equation

has a globally asymptotically stable periodic solution v* thus establishing the mapping

As noted in Remark 3.1, a fixed point of 𝒯 yields a λ-periodic solution of (46) but λ need not be the minimal period of that solution.

To verify 𝒯 is a contraction and that the unique fixed point v* is a GAS solution of (46) one then must satisfy the smallness conditions of Theorem 1.1. To that end, one needs to evaluate the derivatives ∂ _g F and ∂ _x g (a d×k matrix) that are given by

where D _j is differentiation with respect to the jth variable.

Remark 3.2

If at least one of the α _n in (46) is positive we may actually choose m=0 since the identically zero solution is then impossible and therefore the zero sequence is not in the range of 𝒯. Even in this case, however, it might be advantageous to use a larger m in order to satisfy the smallness condition on . This would be the case if g ₂ was not identically zero. No general statement seems possible.

4. Conclusions

Dynamic reduction is a procedure for solving a difference equation by replacing certain ‘excess’ state variables by a function lying in a class having some of the desired properties of the sought after solution. Done properly, the resulting or reduced equation will have a solution having the remaining properties and lying in the same class. This sets up a mapping 𝒯 of the class into itself, a fixed point of which solves the original problem. The technique is illustrated by applying it to various problems.

In the application to the periodic model for wild (W) and genetically altered (GA) mosquitos, it is shown (see Remark 2.2) that if the growth parameters satisfy certain inequalities then neither species goes extinct and in fact their population ratios are attracted to a periodically varying state and thus the dynamics of the model takes place on a periodic set of lines in the plane of x, the W population and y, the GA population. When restricted to these lines, further conditions (shown to preclude period doubling by Jia Li 3 in the autonomous case) guarantee the existence of a periodic state to which all initial non-zero populations are attracted. In Remark 2.4 it is noted that the population ratios asymptotically lie between certain easily calculated bounds: solutions ξ of scalar equations of the form aξ=b.

It is also shown that certain coupled periodic systems of difference equations may be completely decoupled so that the mapping 𝒯 is established by solving a set of scalar equations. Periodic difference equations of extended Ricker type and also rational difference equations with a finite number of delays are also treated by reducing them to equations without delays but with a larger period.

Acknowledgements

Supported by University of Southern California, Letters Arts and Sciences Faculty Development Grant. The authors thank Cymra Haskell for several helpful discussions and the referees for several constructive suggestions.