Effect of pathogen-resistant vectors on the transmission dynamics of a vector-borne disease

Abstract

A model is introduced for the transmission dynamics of a vector-borne disease with two vector strains, one wild and one pathogen-resistant; resistance comes at the cost of reduced reproductive fitness. The model, which assumes that vector reproduction can lead to the transmission or loss of resistance (reversion), is analyzed in a particular case with specified forms for the birth and force of infection functions. The vector component can have, in the absence of disease, a coexistence equilibrium where both strains survive. In the case where reversion is possible, this coexistence equilibrium is globally asymptotically stable when it exists. This equilibrium is still present in the full vector–host system, leading to a reduction of the associated reproduction number, thereby making elimination of the disease more feasible. When reversion is not possible, there can exist an additional equilibrium with only resistant vectors.

Keywords:

• Vector–host disease
• Pair formation
• Multiple disease-free equilibria

1. Introduction

Since the pioneering work of Ross in the late 19th and early 20th centuries 1 2, the classical approach for controlling vector-borne diseases involves the eradication or strict population control of the vectors. In the case of malaria, for instance, sanitization, drainage of mosquito breeding grounds and the use of insecticides have long proved effective in reducing the number of human cases. However, the total eradication of the vector population is not always feasible, nor is it always desirable to put it in effect in practice. There is increasing resistance to insecticides in vectors 3 and insecticides may be harmful to other species. Furthermore, there are issues concerning the reduction of biodiversity (vectors are part of the food chain) and uncertainties about alternatives (if a given type of vector disappears, pathogens might evolve to utilize other species).

Because the elimination of vectors is difficult in practice (and may not be ecologically desirable), other control methods must be used simultaneously to effectively control the spread of the disease. For many vector-borne infections, no long-term immunization methods are available for the hosts and other options, such as prophylactic measures preventing contacts between vectors and hosts, are often employed. If a vector has several host species that are affected by the pathogen, then the efficacy of prophylactic measures is greatly diminished. Also, prophylactic measures require permanent compliance from the hosts.

Another approach to the fight against vector-borne diseases is based on using the natural resistance (or refractoriness) of the vectors to the pathogens. In the case of malaria, among the about 430 known species in the genus Anopheles, the mosquito vector, only a limited number (30–40) are vectors of Plasmodium, the parasite causing the disease. This parasite has a complicated life cycle within the mosquito. The normal cycle of the parasite is as follows (see, e.g. [4, figure 1]). During a blood meal on an infected host, the female mosquito ingests gametocytes, which then become successively gametes and zygotes. After about 24 h, ookinetes invade the gut, and differentiate into oocysts. The oocysts rupture after about 2 weeks, giving sporozoites, which then invade the salivary gland and can subsequently infect another host. In resistant vectors, encapsulation is detected: Plasmodium ookinetes are coated with a melanin-like substance, after traversing the gut wall 5. This substance consists of lamellocytes, which are large flat cells that are part of the primitive immune system of insects. These cells form a capsule around the ookinetes, isolating, immobilizing and ultimately, killing them 6. Encapsulation thus inhibits transmission of Plasmodium to humans or other hosts. Elucidating the origins of this resistance has long been an active research topic. A promising avenue of research has been opened by progress in genetic engineering 7, as vectors can be genetically altered to express resistance to Plasmodium (see, for instance, 4 8 9). For this purpose, mosquitoes are genetically transformed with transposable elements, resulting in a reduced ability to transmit the disease, but with a fitness cost. The reduced fitness of transgenic mosquitoes prevents the efficient spread of their genes in the wild vector population. Hence, understanding the conditions required for the spread of pathogen-resistance in the vector population is an important issue.

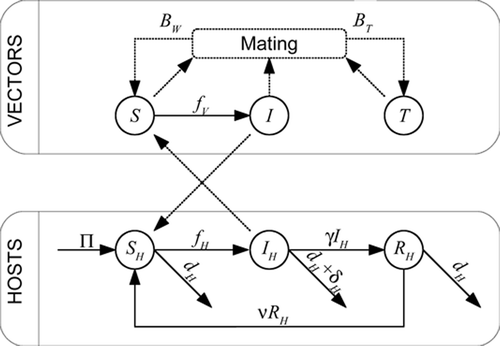
Figure 1. Flow diagram of the model. The upper box describes flows within the vector states, the lower box represents flows within the host states. The flows between boxes are the cross infection effects. The logistic-type dynamics of the vectors is not represented.

Mathematical models for vector-borne diseases have been studied for a long time; see, e.g. 10–12 and the references therein. Models coupling genetic aspects to epidemiology are considered, e.g. in 13. Finally, pathogen-resistance, its transmission and impact on disease prevalence has been studied in 14 15. In line with the latter works, the model presented here has two main objectives:

• (i) to study the propagation of resistance in a population of wild vectors that interbreed with an introduced type that is resistant to a given pathogen; and

• (ii) to study the epidemiological consequences of the presence of pathogen-resistant vectors on the transmission dynamics of a vector-borne disease.

As resistance traits exhibit complex modes of inheritance, only a phenomenological description of resistance transmission during reproduction is given. The present model is formulated using ordinary differential equations, allowing a rigorous mathematical analysis to be conducted.

2. Modeling

2.1 Hypotheses

The population of vectors under consideration is divided into two types: a wild (natural) type, denoted by W, and a type that is resistant to the pathogen, denoted by T. The working hypotheses of the model are as follows.

• H1 Resistant vectors are completely immune to the pathogen.

• H2 _a  A proportion p ₁ of the offspring resulting from the interbreeding of wild and resistant vectors are resistant to the pathogen.

• H2 _b  A proportion p ₂ of the offspring resulting from inbreeding within the resistant type are resistant to the pathogen.

• H3 In the absence of disease, wild vectors are better fitted for competition than resistant vectors.

• H4 Wild vectors are ill-fitted for competition when they carry the disease.

These hypotheses are now discussed in the context of malaria, where a significant amount of work has been carried out; they are however general enough to be applicable to any vector-borne diseases in which a mechanism of resistance of vectors can exist (for instance, dengue and yellow fevers).

H1 is a simplifying hypothesis motivated by experimental observations. In 5, for example, the resistance of various strains of Anopheles gambiae is quantified, by counting the number of encapsulated ookinetes present in the guts of lines of resistant mosquitoes and mosquitoes susceptible to the pathogen. It is observed that in the resistant strain, almost all ookinetes are encapsulated, as opposed to none for the susceptible strain.

In the case of malaria, one mechanism used to induce and propagate resistance is through transposable elements. The latter can be considered as mobile DNA sequences that are able to colonize the genome of their host by inserting new copies of themselves in it (transposition). Existence of non-Mendelian mechanisms such as the regulation of the rate of transposition, deletion (loss of copies) and genetic recombinations allow to consider loss of resistance and non-systematic resistance transmission 16, accounted for in the model by H2 _b and H2 _a , respectively.

Note that H2 makes a phenomenological description of the propagation of resistance to the offspring; the precise mechanisms that lead to inheritance of the resistant phenotype are not explicitly modeled. Also, when considered in conjunction with H1, hypothesis H2 can be interpreted as follows: a vector is resistant if its load in resistance-causing genetic material is sufficient. A vector that does not have enough of this material is considered susceptible.

Hypothesis H3 also stems from biological observations. Insertions of new copies of transposable elements can damage the genome if, for instance, insertion takes place into a coding sequence. For example, in the case of Aedes aegypi (a mosquito transmitting yellow fever), 17 finds a severe reduction in the net reproductive rate, with the control strain exhibiting a net reproductive rate 42–72% higher than that of the three transgenic strains it studies. These effects on fitness are confirmed by many other studies; see, e.g. 18–22.

Finally, H4 is a modeling hypothesis. Although there is still some debate about the precise effect on vectors 23, and a great deal of variability depending on the parasite and vector strains 24, some studies document reduced fertility of Plasmodium-infected mosquitoes (fertility being one component of fitness). Plasmodium yoelii nigeriensis is shown in 25 to reduce overall fertility of Anopheles stephensi by between approximately 40 and 50%. In 26, the mean egg production is found to be significantly lower for Anopheles gambiae infected with Plasmodium falciparum than for uninfected ones. In 27, it is shown that when competing (without interbreeding), resistant mosquitoes win the competition in the presence of Plasmodium, and wild mosquitoes win the competition in the absence of Plasmodium. Reduced fitness of infected vectors is also observed for other pathogen–vector pairs; see, e.g. 28.

2.2 Vector demography

Wild vectors can have two epidemiological states, susceptible (denoted by S) or infected (denoted by I), whereas resistant vectors are denoted by T. By H1, resistant vectors are totally immune to the pathogen. The simplifying assumption of a constant sex ratio is made.

In the following sections,

represent susceptible wild, infected wild and resistant vectors. From now on, depending on the context, X and Y, and also S, I and T, will refer either to the state of a vector, or to the abundance of vectors of that state.

2.2.1 Birth and transmission of resistance

Associated with the numbers of vectors of each state, there are birth functions b _i (X, Y). These functions describe the formation pairs and the resulting rate of birth. Assuming symmetry of the birth functions, i.e. , there are six different types of pairings, hence six birth functions b _i , i=1, …, 6; see table 1.

Table 1. Reproduction hypotheses: types of pairings, birth functions and mating outcomes.

Pairing		Birth function	Mating outcome
			Proportion	Class
S	S	b 1(S)	1	S
I	I	b 2(I)	1	S
T	T	b 3(T)	p 2	T
			1−p 2	S
S	I	b 4(S, I)	1	S
S	T	b 5(S, T)	p 1	T
			1−p 1	S
I	T	b 6(I, T)	p 1	T
			1−p 1	S

The progeny belong to the different states. Since it is assumed that there is no vertical transmission, newborns can either be susceptible (wild) or resistant. Depending on the type of parents, a certain fraction of the newborns are resistant, and the remaining fraction are susceptible wild. For simplicity, transmission of resistance is assumed independent of disease status, for the wild-type vectors. This gives the mating outcomes in table 1, which account for H2 _a and H2 _b .

At this point, the functional forms of the b _i 's are not specified. However, it is assumed that they are of the same nature for all types of pairings, and that they satisfy the so-called pair-formation properties 29–31, as detailed below.

The birth functions and type of offspring are put together in the type-specific birth functions B _W (S, I, T) and B _T (S, I, T) for wild and resistant vectors, given, respectively, by

Since the functions B _W and B _T are linear combinations of functions that satisfy the pair-formation hypotheses, they also satisfy pair-formation hypotheses. From 29–31, for a given vector type X∈{W, T},

• PF1 ,

• PF2  for all u, v, w≥0,

• PF3  for all ,

• PF4 .

Consequently, the total birth function also satisfies properties PF1–. Additionally, it is assumed that B(S, I, T) satisfies the following hypothesis,

• PF5 There exist such that for all V=S+I+T,

2.2.2 Vector dynamics

Motivated by a logistic formulation where the population has a linear net growth rate and is subject to a quadratic competition term, the vector dynamics in the absence of new infections is governed by the following system:

where V=S+I+T is the total vector population.

For a given vector type X∈{W, T}, the net growth represents the difference between the net birth rate B _X and the net natural per-capita death rate d _X . Since there is no vertical transmission of the disease, all the birth into the wild type occurs in S with type-specific rate B _W .

The parameters and κ _T represent the rates of competition-induced mortality for susceptible wild, infective wild and resistant vectors, respectively. Note that the κ _X 's should in fact be κ _XY 's, rates of mortality of state X when competing with state Y. However, for simplicity, it is assumed that competition affects a given state at the same rate, regardless of the state of its competitor. Evidence of the effect of crowding is given, for example, by 32 and references therein.

Finally, infected vectors suffer additional disease-induced death at a per-capita rate δ _W (see, e.g. 22 33 in the case of malaria).

This system is not logistic in a strict sense, but in the proof of Theorem 2.1, it is shown that the total vector population is almost logistic.

2.2.3 Considerations on fitness

To account for hypothesis H3, it is assumed that resistance comes at the cost of reduced fitness. Furthermore, infection reduces fitness (H4). The precise definition of fitness in assumptions H3 and H4 is difficult to give. It is supposed, as in 9 14 22, that being fit describes a set of attributes that makes the vector better suited for survival.

Reproductive fitness is taken into account by ranking the associated fecundities, with the most fecund vectors being the susceptible wild, followed by the resistant, and the least fecund being the infected wild vectors. For each mating pair, it is assumed that fecundity is always determined by the less fit of the pair. As a consequence, for given appropriate (X, Y), the functions b _i (X, Y)'s can be ordered as follows for positive population values

where {b ₃, b ₄, b ₅} indicates that it is not possible a priori to order b ₃, b ₄ and b ₅, and that this will come as a modeling hypothesis or an experimental observation. For example, b ₁≥b ₄ means that for all S and I.

Similar to the birth functions, the rates of competition-induced mortality are partially ordered to account for vector fitness. Susceptible wild vectors are better fitted than both infectious wild and resistant, but the latter two cannot be ordered a priori, so

Finally, the natural death rate, d _T , for resistant vectors includes the cost of resistance ().

2.3 Host demography

The demography for hosts is supposed to follow a simple SIRS model. The hosts are susceptible (S _H ), infective (I _H ) or recovered (R _H ). Birth occurs into the state S _H at the constant rate Π, and death at the per-capita rate d _H in all states. Upon infection, susceptible individuals proceed to the infective state, where they are subject to disease-induced death with per-capita rate δ _H . The sojourn time in the infective state is exponentially distributed with mean 1/γ, giving the per-capita rate γ of moving from the I _H to the R _H state. In the R _H state, individuals are immune to infection. The duration of the immune period is exponentially distributed with mean 1/ν.

Note that this is a crude simplification of the dynamics of most vector-borne diseases. In the case of malaria, for example, a realistic model 11 categorizes humans into eight different epidemiological states. However, SIRS models capture some of the essential mechanisms in the transmission of a disease without the burden of additional parameters and nonlinearities. Furthermore, the analysis here can be extended in a straightforward way to models with a latent state (such as those in 11).

2.4 Force of infection

Assume that the rate of infection of a susceptible host by an infected vector is f _H , and the rate of infection of a susceptible vector by an infected host is f _V . These functions aggregate two different processes: vector bites, which represent the contacts, and transmission of the disease. The force of infection f _H depends directly on S _H and I, while f _V depends directly on S and I _H . In accordance with H1, there is no direct dependence on T. Both f _V and f _H can, however, depend indirectly on T, through dependence on the total vector population V. They might also depend on the total host population H.

In its most general formulation, the model uses generic forms for f _H and f _V , assuming that the following hypotheses are satisfied:

• (i) f _V and f _H are C ¹;

• (ii) f _V ≥0 and f _H ≥0;

• (iii) 

  • (a) f _V =0 if either S=0 or I _H =0;

  • (b) f _H =0 if either S _H =0 or I=0.

2.5 The model

The model, taking into account the above hypotheses, is given below (see figure 1 for a schematic diagram and table 2 for a description of parameters and variables).

where V=S+I+T. This model is considered with nonnegative initial conditions such that V(0)>0 and the initial total host population .

Table 2. Model variables and parameters, and assumptions on parameter values. Note that all parameters are assumed positive unless otherwise stated in the text

Variables
S	susceptible wild vectors
I	infected wild vectors
T	resistant vectors
S H	susceptible hosts
I H	infected hosts
R H	recovered hosts
Composite variables
W=S+I	total population of wild vectors
V=S+I+T	total vector population
	total host population
Parameters
p 1	proportion of T in offspring of W–T matings
p 2	proportion of T in offspring of T–T matings
b i	birth functions (i=1, …, 6)
α i	birth rates (i=1, …, 6) — special case
κ X	competition rates ()
d W	natural death rate of wild vector
d T	natural death rate of resistant vector
δ W	disease-specific mortality rate of infected vectors
f V	force of infection of vectors by hosts
f H	force of infection of hosts by vectors
ν	rate of loss of infection-acquired immunity in hosts
δ H	disease-specific mortality rate of hosts
γ	recovery rate of infected hosts
Composite parameters
b and defined by (2)
Fitness-related assumptions on parameters
d T ≥d W

3. Some general properties of the system

Define composite parameters b, , , r, , , , K and as in table 2.

Theorem 3.1

The total vector population V(t) is such that, for all t≥0,

The total host population H(t) converges, and is such that

Finally, solutions of (4) are nonnegative and bounded.

Proof

First, it is clear that the positive orthant is invariant under the flow of (4). As a consequence, V(t)>0 and H(t)>0, for all t≥0, for positive V(0) and H(0). The total vector population V in system (4) satisfies

Since d _W ≤d _T by hypothesis, there holds that

and from PF5, it follows that

Our assumptions imply that . Then, the inequalities above are equivalent to

Integrating this equation gives (5).

Now summing the equations for hosts gives

Integrating (9),

where and . Since H(t) is nonnegative, there holds that . The integrand in Φ is nonnegative, and thus Φ(t) is a nondecreasing function of t. As Φ is bounded above by Ψ, which has a finite limit, Φ must therefore converge. It follows that . As a consequence, the total host population H(t) converges. From (9), it follows that , and integrating,

Taking the limits in the above inequality gives (6). Finally, the boundedness of (4) is established by combining the results obtained for V and H.    ▪

Thus the vector component of system (4) is almost logistic, in the sense that, from (8), the evolution of the total vector population is bounded by two logistic equations. From now on, it is assumed that the maximal intrinsic growth rate . This is a natural assumption, since it implies that wild vectors are present in the absence of disease or competition.

The next result about reproduction numbers for system (4) is obtained using the method of 34. The present model is one case where this method must be applied carefully.

Theorem 3.2

Consider a disease-free equilibrium of (4) taking the form

where S¯ and T¯ satisfy the relations

Define the reproduction number at Ē as

Assume that conditions (A1)–(A5) in Appendix A are satisfied. If , then the disease-free equilibrium (10) is a locally asymptotically stable equilibrium; if , then Ē is unstable.

Proof

In the absence of disease, the vector population is V=S+T and

Further, at the disease-free equilibrium, the following relations must hold

giving the condition in equation (11) when (1) is used. Also, if there is no disease, then the equations for the host population and the vector population decouple. The disease-free equilibrium for the host is given by

and thus a disease-free equilibrium of (4) takes the form (10). Using the next generation matrix method of 34, noting that the infective states are I and I _H , write

From this, it follows that

and the reproduction number with resistant vectors ℛ is given by the spectral radius of the matrix

evaluated at a disease-free equilibrium. The result follows from Theorem 2 in 34, provided that conditions (A1)–(A5) of that theorem hold.

Note that Theorem 3.2 does not address uniqueness of the disease-free equilibrium. In fact, the disease-free equilibrium is not in general, unique, as exemplified in the special case of sections 4 and 5. In the case of multiple disease-free equilibria, ℛ should be defined for each equilibrium at which Theorem 2.2 can be applied. Further analysis is then required to determine parameter regions where the disease might go extinct or persist in the population.

Also note that caution should be used when applying Theorem 3.2. Condition (A5) states that the system without disease must have its spectrum to the left of the imaginary axis. In section 5, it is shown that this is not always true; refer to the discussions following Theorems 5.1, 5.2 and 5.3 for details.

4. Special case—vectors only and no disease

In order to investigate the first objective of the paper (potential coexistence of the two vector types, wild and resistant), system (3) is considered using a specific functional form for the birth functions.

In this special case, it is assumed that birth obeys the following law. First, for vectors of the same state ,

where α _i is the birth rate associated to each type of pair (corresponding to b _i , i=1, 2, 3, in table 1). To describe the birth of offspring of vectors of different states , define for small η>0, a ball of radius η about the origin. Then,

where α _i is the birth rate associated to each type of pair (corresponding to b _i , i=4, 5, 6 in table 1). The function ϵ is only used to resolve the problem of b _i not being defined at the origin in the case of breeding between different states. It is assumed to satisfy

• (i) .

• (ii) ,

• (iii) ,

• (iv)  is nonincreasing in X and Y for positive X and Y,

• (v)  and its partial derivatives are zero on the boundary of .

Note that (14) only satisfies PF3 outside , so in practice, it is assumed that whenever (X, Y)≠(0, 0). Outside of , the pair-formation function (14) satisfies the pair-formation hypotheses PF1–, while (13) satisfies them everywhere. Using (13) and (14),

for variables outside of , which we assume from now on unless otherwise specified. Let and . From the ordering of birth functions (see section 2.2.3), and . Then, noting that

it follows that

On the other hand,

and thus PF5 is also satisfied.

4.1 Coexistence of vectors

The first question concerns the possibility for both vector types (wild and resistant) to coexist, in the absence of disease. System (4) with only noninfectious vectors reduces to

Two boundary equilibria are readily found,

with Ē ₀ obtained by using the function (14) with . It is worth recalling that it is assumed that , which translates here to , so that the S component of Ē _W is always positive. This value of S represents the equilibrium in the absence of other factors. It is chosen as a measure of the fitness of the wild population in the absence of disease, and is denoted 𝔽 _S . A similar quantity 𝔽 _T can be defined for the resistant population, taking into account the proportion of (T, T) pairings with T offspring. Thus, the fitness for the susceptible wild and resistant populations, in the absence of disease and interbreeding, are

respectively. Because of the assumptions made in section 2.2.3, there always holds that

Note, also, that while , 𝔽 _T can be negative. The definition of fitness given by (16) is not exactly the one that would be given by using, for example, the methods in 35 36, since (16) has a unit of vector population size. Proceeding this way, however, allows for a compact formulation of most results while retaining closeness to the classic notion of reproductive fitness.

The existence of an additional equilibrium point and the stability of the various equilibria are determined by the following theorem.

Theorem 4.1

The extinction equilibrium Ē ₀ is always unstable. Additionally, suppose that p ₂<1. Then:

• (a) If , then system (15) has a coexistence equilibrium point Ē _C , which is globally asymptotically stable; the equilibrium with only wild vectors, Ē _W , is unstable.

• (b) If , then system (15) has no coexistence equilibrium point, and the equilibrium with only wild vectors, Ē _W , is globally asymptotically stable.

Interpretation

𝔽 _S is a characteristic of the wild species in the absence of disease. measures the relative fitnesses of wild and resistant vectors in the absence of disease and interbreeding. If the fitness advantage of wild vectors relative to resistant vectors decreases past a threshold, then the resistant vectors become established in the population. This threshold, , is the contribution to resistance from interbreeding.

Proof

Conditions for the existence of the coexistence equilibrium Ē _C are established in Appendix B.

At Ē ₀=(0, 0), i.e. in , the Jacobian matrix Df takes the form

and has eigenvalues and . It follows that Ē ₀ is always unstable. At an arbitrary point , the Jacobian matrix is given by Df=[j _ik ], where

At Ē _W , the eigenvalues

are found. Thus, denoting LAS a locally asymptotically stable equilibrium,

Table

	Sign λ1	Sign λ2
	−	−	LAS
	−	−	LAS
	−	+	Unstable

Case (b) in the Theorem corresponds to the first and second lines in this table.

When Ē _C exists, that is, if , Ē _W is unstable. Using the Dulac function on the vector field f, the divergence of the Jacobian takes the form

which is always negative in the positive quadrant, and thus there are no periodic orbits, homoclinic orbits or heteroclinic cycles for system (15). Since solutions of (15) are bounded (Theorem 3.1), it follows that Ē _C , when it exists, is globally asymptotically stable in the interior of .

When Ē _C does not exist, then Ē _W is locally asymptotically stable and using the same argument, is globally asymptotically stable.    ▪

Figure 2 shows nullclines of (15). Using notations as in Appendix B, the nullcline of (15a) is the curve Γ _S =0, represented by a dashed line. The nullcline of (15b) consists of the curve Γ _T =0 (the parabolic arc joining both axes, shown as a continuous line), together with the S-axis. The coexistence equilibrium Ē _C , when it exists, lies at the intersection of the curves Γ _S =0 and Γ _T =0 (top left figure). In the case of the figure on the bottom, a transcritical bifurcation has taken place at the point where Γ _S =0 and Γ _T =0 coincide on the S-axis. As the curve Γ _S =0 moves to the right (this is achieved here by increasing α₁), the equilibrium Ē _C at the intersection of Γ _S =0 and Γ _T =0 exchanges stability with Ē _W (and becomes irrelevant biologically).

Figure 2. Left column: nullclines of (15a) (Γ _S =0, dashed lines) and (15b) (Γ _T =0, continuous line), in the case p ₂<1, as in section 4.1. Right column: a few corresponding sample solutions. First row: case 1 in Theorem 4.1, where 𝔽 _S −𝔽 _T <(p ₁α₅/κ _T ) (both Ē _W and the coexistence equilibrium Ē _C exist, Ē _C is globally asymptotically stable). Second row: case 2 in Theorem 4.1, where 𝔽 _S −𝔽 _T ≥(p ₁α₅/κ _T ) (only Ē _W exists, and is globally asymptotically stable).

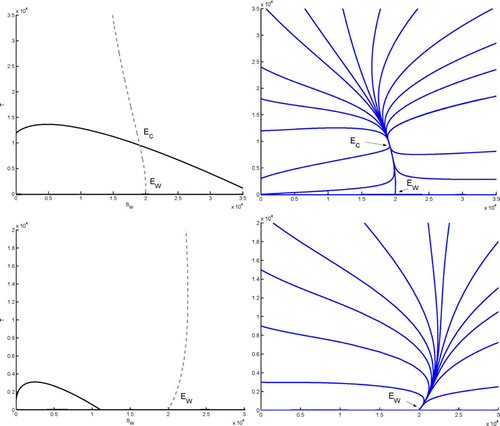
Note that Theorem 4.1 implies that at Ē _C , when it exists, both eigenvalues of have negative real parts, which is used in Theorem 4.2.

4.2 Another equilibrium can exist when there is no loss of resistance

Suppose now that p ₂=1, i.e. there is no loss of resistance in the offspring of two resistant parents. Additionally to Ē ₀, Ē _W and, when it exists, Ē _C , the additional equilibrium is found

which is biologically meaningful when . Note that here, , since p ₂=1. The situation that prevails in this case is summarized in the following theorem.

Theorem 4.2

Ē ₀ is unstable. Suppose that p ₂=1. Then the existence and stability of the equilibria Ē _W , Ē _C and Ē _T are summarized in the following table.

Table

		Ē W	Ē C	Ē T
		GAS	DNE	DNE
		Unstable	GAS	DNE
		GAS	DNE	Unstable
		Unstable	GAS	Unstable
		Unstable	DNE	GAS
(DNE: Does Not Exist, GAS: Globally Asymptotically Stable).

Interpretation

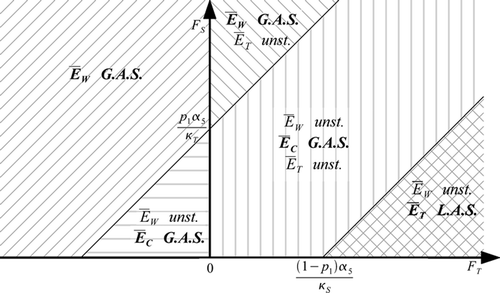
Here, the mating of T vectors always leads to T offspring. This hypothesis can be interpreted as an absence of reversion, i.e. resistance cannot be lost. In this case, if the fitness of resistant vectors is positive, another situation with only resistant vectors becomes possible. When the fitness of resistant vectors relative to the fitness of wild-type vectors is very large, then the outcome of competition is the presence of only resistant vectors. For lower values of the fitness of resistant vectors, the situation is very similar to that of the case with reversion (Theorem 4.1). See figure 3.

Figure 3. Regions of existence and stability of the various equilibria, in the absence of disease, in the wild and resistant fitness plane, as given by Theorem 4.2 (p ₂=1).

Proof

The instability of Ē ₀ is proved as before. It is possible here to compute explicitly the value of the coexistence equilibrium. Using Maple, and after some manipulations, it is found that at Ē _C ,

and

In the proof of the existence part of Theorem 4.1 (Appendix B), the following modifications must be made to take into account that p ₂=1. The vertical asymptote of Γ _S =0 now becomes the T-axis, and the cubic Γ _S =0 becomes reducible, the union of a simple conic section and the T-axis. Thus the T-axis is a nullcline for (15b), and there can exist another equilibrium, Ē _T , if Γ _T =0 intersects the T-axis for T>0. This gives the conditions for the existence of Ē _T . At Ē _T , the jacobian matrix takes the form

and so the stability of Ē _T is determined by the sign of . The global stability of the equilibria then follows by using the same Dulac function as in the proof of Theorem 4.1, the boundedness of solutions given by Theorem 3.1, and the existence, in each of these cases, of a unique locally stable equilibrium point.    ▪

The regions in the -plane that are deduced from Theorem 4.2 are illustrated in figure 3.

4.3 The competitive exclusion principle holds in the absence of interbreeding

From Theorem 4.1, both wild and resistant vector strains can coexist in the absence of disease. This is quite different from the standard context of competition models, where the competitive exclusion principle usually holds. This principle states that the species that is most adapted to survival when resources are low, survives the competition, and all others become extinct. Intuitively, the coexistence must stem here from interbreeding.

To ascertain this, consider now system (15) without interbreeding of vectors (α₅=0) or reversion (p ₂=1),

The following result holds, which shows that in this case, the competitive exclusion principle holds, with wild vectors always winning the competition.

Theorem 4.3

System (15) with α₅=0 and p ₂=1, i.e. system (17), has three equilibria, Ē ₀, Ē _W and Ē _T , with Ē ₀ and Ē _T unstable, and Ē _W globally asymptotically stable.

Proof

The same three equilibria Ē ₀ and Ē _W (section 4.1), and Ē _T (section 4.2), are found. At the origin, eigenvalues are

and thus the origin is always unstable. At Ē _W , eigenvalues are

whereas at Ē _T , they are

It follows that, depending on the sign of , one of the equilibria Ē _W or Ē _T is locally asymptotically stable, and the other is unstable. If , then wild vectors are better fitted for competition and they dominate resistant vectors. If , then the situation is reversed. Because of the assumptions on fitness (see section 4.1), it holds that ; so Ē _W is locally asymptotically stable and Ē _T is unstable. Here, the Dulac function gives the divergence for all , and since solutions are bounded by Theorem 3.1, Ē _W is globally asymptotically stable.    ▪

Note that this conclusion is very similar to that drawn in 27. Indeed, suppose a reversed fitness situation, as would be the case in the presence of disease. Then the resistant vectors become established, driving the wild ones extinct.

5. Special case—disease dynamics in the full system

To address the second objective of the paper, namely, to assess the effect of resistance on the transmission dynamics, the full six-dimensional system (4) is now considered.

5.1 Force of infection

Let be the rate at which bites are received by a single host per unit time. Let c ₂ be the per-capita biting rate of vectors (on a host); for simplicity, assume that, within the population of interest, c ₂ is a constant. This is a justified assumption; for mosquitoes, for example, the female has a certain number of blood meals over its lifetime.

For the number of bites to be conserved (that is, the total number of vector bites all hosts get equals the total number of bites made by all vectors), the following relation must hold:

The force of infection in vectors is given by

where β is the probability of transmission of the pathogen. Similarly, the force of infection in hosts is given by

since from (18). This formulation is consistent with that in 37.

5.2 The model

With the assumptions on the birth and force of infection functions, system (4) takes the form

where B _W and B _T are given from (1) by

and

5.3 Analysis—case of no intervention

In order to assess the effect of resistant vectors, the behavior of the system in the absence of resistant vectors, i.e. when T≡ 0, is first studied. This describes the disease dynamics in its natural setting, without any outside intervention. From PF4, setting T=0 in (19c) implies that T remains identically zero in (19). Recall that in the absence of disease, the vector and host subsystems decouple. In this case, there are two equilibria for the vector component, one with S=0, Ē ₀, and another with , Ē _W . To each of these two-vector equilibria corresponds the unique disease-free equilibrium for the host component, S _H =Π/d _H . As a consequence, in the vector–host system, there are two equilibria [Etilde]₀ and [Etilde] _W without disease. Proceeding as in the proof of Theorem 3.2, the following theorem can be established, which gives the basic reproduction number in the absence of resistant vectors.

Theorem 5.1

For system (19) without resistant vectors (T≡ 0), there are two disease-free equilibria. The equilibrium

is always unstable. Now, let

If , then the equilibrium

is locally asymptotically stable, whereas it is unstable if .

Proof

At the equilibrium [Etilde]₀, the Jacobian matrix has the eigenvalues , , −d _H , , −(d _H +ν) and , giving the instability of [Etilde]₀. The expression of (20) and the stability of [Etilde] _W is a direct application of Theorem 3.2 with T≡ 0.    ▪

Remark that it is not possible to use Theorem 3.2 at [Etilde]₀, since [Etilde]₀ is always unstable even in the system without disease, implying that assumption (A5) in Theorem 3.2 does not hold.

5.4 Analysis—full system

The disease-free equilibria of the full system (19) are the equilibria found for the simplified system (15) with only vectors studied in section 4, together with the equilibrium without disease for the hosts component.

Thus, the equilibria [Etilde]₀ and [Etilde] _W (as given in Theorem 5.1) are the equilibria with no vectors and only the wild vectors present, respectively. Also, when they exist,

is the equilibrium where only the resistant vectors survive, and

is the coexistence equilibrium, where both wild and resistant vectors are present, with the vector components of [Stilde] and [Ttilde] obtained as in Theorem 4.1. At the coexistence equilibrium [Etilde] _C , when it exists, define the reproduction number with resistant vectors,

using Theorem 3.2.

Theorem 5.2

[Etilde]₀ is always unstable. Additionally, if p ₂<1, then:

• (a)  If , then both [Etilde] _W and [Etilde] _C exist, with [Etilde] _W always unstable. If , then [Etilde] _C is locally asymptotically stable; if , then [Etilde] _C is unstable.

• (b)  If , then [Etilde] _C does not exist. If , [Etilde] _W is locally asymptotically stable, whereas it is unstable if .

Interpretation

This is similar to the situation with no disease and only vectors. The effect of resistant vectors on the disease dynamics is shown in particular in Case (a), where there is coexistence of both types. The disease cannot go extinct without intervention, since [Etilde] _W , the equilibrium for the disease in its natural setting, is unstable, but could potentially be brought to extinction if . Note that the results obtained are only local, implying a possibility of control of the disease, not a certain outcome.

Proof

The instability of [Etilde]₀ is established in Theorem 4.1. The conditions for existence of [Etilde] _W and [Etilde] _C are the same as in Theorem 4.1.

• Case (a). The stability of [Etilde] _C follows from Theorem 3.2. At [Etilde] _W , there is an unstable manifold of dimension at least equal to 1, corresponding to the unstable manifold of dimension 1 of Ē _W found in the case in the proof of Theorem 4.1. This implies that [Etilde] _W is unstable.

• Case (b). The stability of [Etilde] _W is considered in Theorem 5.1.    ▪

Note that in Case (a), the system without disease, which decouples into independent components for vectors and hosts, has its vector component governed by Case (a) in Theorem 4.1: when Ē _C exists, Ē _W is unstable. This implies that in this case, in the absence of disease [Etilde] _W is always unstable, so condition (A5) of Theorem 3.2 is not fulfilled at [Etilde] _W , and as defined by Theorem 3.2 plays no role in determining the stability of [Etilde] _W .

Theorem 5.3

[Etilde]₀ is unstable. Suppose that p ₂=1. Firstly, if , then the existence and stability of the equilibria [Etilde] _W , [Etilde] _C and [Etilde] _T is summarized in the following table:

Table

		DNE	DNE
	Unst.		DNE

Secondly, if , then the existence and stability of the equilibria [Etilde] _W , [Etilde] _C and [Etilde] _T is summarized in the following table:

Table

		DNE	DNE
	Unst.		Unst.
	Unst.	DNE	LAS
(DNE: Does Not Exist, LAS: Locally Asymptotically Stable, Unst.: Unstable).

Interpretation

In the case where there is no reversion, resistant vectors can only invade the population if their fitness advantage over the wild vectors is sufficiently large. Note that the fitness advantage required for resistant vectors to have the possibility of invading the vector population in this case, is the same as the one required in the absence of disease (as given by Theorem 4.2).

Proof

Remark that is the condition for existence of Ē _T in Theorem 4.2, and as a consequence, of [Etilde] _T . Suppose now that [Etilde] _T exists. At [Etilde] _T , the Jacobian matrix takes the form

with J ₁₁ given by

and

Clearly, J ₂₂ has all its eigenvalues negative, and it follows that the stability of [Etilde] _T depends solely on J ₁₁. Then can be computed by developing along the third column, giving eigenvalues

and . The latter two are negative if [Etilde] _T exists, and the local asymptotic stability of [Etilde] _T is thus determined by the sign of the first one.

It is interesting to note that Theorem 3.2 cannot be applied to [Etilde] _T . Indeed, ordering the variables as , it follows that when evaluated at [Etilde] _T , the block in the jacobian matrix corresponding to the variables S, T is

with J ₁₁ as in the proof above. It follows that condition (A5) of Theorem 3.2 is not satisfied when [Etilde] _T is unstable. Note also that the same remark holds for at [Etilde] _W and at [Etilde] _C when their corresponding vector components are unstable in Theorem 4.2.

The last result concerns the relationship between the basic reproduction numbers in the natural setting and with resistant vectors. As remarked earlier, these two numbers cannot be defined simultaneously in the context of Theorem 3.2. It is, however, possible to compare the expressions obtained when both equilibria exist simultaneously, without considerations on stability.

Theorem 5.4

At the coexistence equilibrium [Etilde] _C , when it exists, there holds that

where is defined in the absence of resistant vectors (T=0) by (20), and is defined with resistant vectors by (21).

Interpretation

If conditions are such that the resistant vectors can coexist with the wild vectors, then the potential for effective control of the disease is better than in the natural case.

Proof

Suppose that [Etilde] _C exists. The expression for is then obtained using Theorem 3.2. Also, there holds that . Indeed, using the notations of Appendix B, . This implies that, using the expression for Γ _S =0,

and so

Now, comparing and , there holds that

Using , it follows that

which is always satisfied.    ▪

6. Discussion

In this paper, an ordinary differential equations model for the spread of pathogen resistance in the vectors of a vector-borne disease is formulated. Two vector types are considered: wild and resistant. A phenomenological description of pathogen-resistance inheritance is incorporated: the two types interbreed, and a given proportion of the offspring of resistant vectors are resistant. It is also assumed that resistance comes at the cost of a reduced fitness, which is modeled by supposing that resistant vectors have lower reproduction rates and higher rates of natural and competition-induced mortalities. It is proved that:

• (i) The spread of pathogen resistance in the vector population is possible in the absence of disease. This is established by analyzing the vector only system in the absence of disease (Theorems 4.1 and 4.2).

• (ii) Pathogen resistence of the vectors leads to a reduction of the reproduction number, thereby making control of the disease potentially more feasible (Theorem 5.4).

These conclusions are not altogether unexpected, and are in line with the numerical results of 14, which are obtained using a discrete generation genetic model. By using a continuous time description rather than a discrete time one, the model avoids some of the complicated behavior that is inherent to discrete time models (for example, two models in 38 are shown to exhibit chaotic behavior). Also, an interesting conclusion of the model is that resistance can become established in the vector population, even when there is the possibility of reversion, if the fitness disadvantage of resistance is balanced by the ability of resistance to be propagated by interbreeding. The measures of fitness of vectors used are easy to parametrize, as they involve the birth and death rates, as well as the competition coefficients, which can be deduced from the equilibrium values of wild and resistant vectors in the absence of disease.

Mathematically, the model also has interesting features. The existence of up to four disease-free equilibria is quite unusual. This is due to the multiple nonlinearities that are present even in the absence of disease. To circumvent the difficulties inherent to these nonlinearities, it was necessary to use ideas from projective geometry to show the existence and uniqueness of the co- existence equilibrium. Another interesting characteristic is the fact that, contrary to many models, it is here not always possible to use the result of 34 to estimate the basic reproduction number and its influence on the local asymptotic stability of disease-free equilibria. It appears that, at a given point in parameter space, Theorem 3.2 can only be used at one of the disease-free equilibria, namely, the one that is globally stable. Whether this is a feature of the present model, or a more general characteristic of the method of 34, raises interesting mathematical questions.

This paper is a preliminary work. The modeling of resistance and its inheritance should be made more realistic. Also, the model is complicated and some of the more challenging mathematical aspects have not been tackled. The existence of endemic equilibria in the full, six-dimensional case, is a hard problem, and is left untouched here. Also, it is not certain that in the cases and , the disease indeed goes extinct (Theorem 5.2 is a local result). Numerical simulations seem to indicate that such is the case, but so far this fact is not proved.

Acknowledgements

We are greatly indebted to Claudio Struchiner for introducing us to the subject of Transposable Elements, and for comments on earlier versions of the manuscript. We acknowledge expert help for the proof of the existence part of Theorem 4.1 from Bernard Gibert, and discussions with P. van den Driessche and James Watmough about the next generation technique. Four anonymous referees of two different versions of this paper provided helpful comments. The work of JA, AB and SP is supported in part by NSERC. JA and AB are also supported in part by MITACS.

Appendix A: Hypotheses for the van den Driessche and Watmough method

To compute reproduction numbers for a general epidemic model x′=f(x), with , 34 suppose that it is written in the form

with , and where the m≤n variables considered are those corresponding to infective states; for example, I and I _H in system (4). Let

be the set of all disease-free states. States x _i for i>m are the uninfected compartments; for example, S, T, S _H , R _H in system (4). The following assumptions are made:

• (A1) If x≥0 then for i=1, …, n.

• (A2) If x _i =0, then . In particular, if , then for i=1, …, m.

• (A3)  for i>m.

• (A4) At a disease-free equilibrium, for i=1, …, m.

• (A5) If is set to zero, then all eigenvalues of the Jacobian matrix Df(x ₀) have negative real parts at a DFE .

Appendix B: Proof of the existence part of Theorem 4.1

Proof

To find nontrivial equilibria, suppose that (15) is at equilibrium and multiply both equations by S+T. This gives equations for the nullclines for (15a),

and for (15b), the union of the plane curves T=0 and

where

and

The nontrivial equilibria of (15) are found at the intersections of the plane curves defined by (B1) and (B2), and at the intersections of (B1) and T=0. Since the curve defined by (B1) is a cubic and that the curve defined by (B2) is a conic section, it follows from Bézout's theorem that there are six points of intersection (real or complex, and including multiplicities) 39. Since and , where R ₁ and R ₂ are first-, and second-degree polynomials, respectively, Γ _T =0 and Γ _S =0 have a common double point at infinity (on the second bisectrix), and the origin is also a common double point. So there remain two intersection points, real or complex, to account for. These two points cannot lie on the T-axis, and therefore they also belong to the conic section , where

To find the two remaining points of intersection of Γ _T =0 and Γ _S =0, Θ=0 can be used. The remainder of the proof is as follows:

• first, show that Θ=0 consists of two lines,

  • if , they have no intersection with the positive quadrant (no coexistence equilibrium -no CEP-),

  • if , one of them intersects the positive quadrant (undetermined),

• to lift this indetermination, turn to Γ _T =0 and show that

  • either Γ _T =0 does not intersect the first quadrant (no CEP),

  • or Γ _T =0 intersects the first quadrant with two positive intercepts (CEP),

  • or Γ _T =0 is a parabolic arc containing the origin (undetermined),

• in the latter case, the line of Θ=0 through the first quadrant is shown to intersect Γ _S =0 (CEP).

Define, using (16), 𝔽 _S the S-intercept of Γ _S =0, the S-intercept of Γ _T =0, and 𝔽 _T , the T-intercept of Γ _T =0. Study of Θ Dividing Θ by gives

This conic section degenerates into two lines. The following cases are theoretically possible [40, pp. 205–206]: a pair of imaginary lines with a common real point, a pair of intersecting lines, or a double line. But here, only the real cases occur. Indeed, suppose that the conic section consists of two lines L ₁ and L ₂ intersecting at the origin and taking the form

Identifying with the terms in , it follows that

and

Writing this as a ₁+a ₂=A and a ₁ a ₂=B, a ₁ and a ₂ are found as roots of the polynomial X ²−AX+B. The discriminant of this polynomial is , and therefore a ₁ and a ₂ are real valued. The exact values of a ₁ and a ₂ are not needed to study Θ=0, just their signs. There are two cases.

If , then a ₁ a ₂>0, implying that the lines L ₁ and L ₂ have slopes with the same sign, which is the same as the sign of a ₁+a ₂. Rewriting the terms in a ₁+a ₂ gives

It was seen earlier that , and so . It follows that a ₁+a ₂<0 when ; so both L ₁ and L ₂ have negative slopes, and Θ=0 has no intersection with Γ _T =0 in the positive quadrant. This gives the condition in part 2 of the theorem.

If }, it follows that a ₁ a ₂<0, implying that L ₁ and L ₂ have slopes with opposite signs. In the rest of the proof, assume, without loss of generality, that L ₁ is the line that intersects the first quadrant.

Study of Γ _T The origin belongs to the curve Γ _T =0. An algebraic calculation shows that, provided , (B2) is a parabola in the coordinate system rotated of an angle 3π/4. Also, there always holds that , so that the parabola always opens towards the fourth quadrant of the (S, T)-plane. There are three cases.

If both intercepts are negative, there is no intersection of the conic section with the positive quadrant and thus there are no positive equilibria (and the boundary equilibrium Ē _T is not feasible). This gives the condition () in the part 2 of the theorem.

If both intercepts are positive, the intersection of the conic section defined by Γ _T =0 with the positive quadrant of the (S, T)-plane consists in a concave down parabolic arc between both intercepts. There is one point of intersection between Γ _T =0 and L ₁ in the positive quadrant.

If only is positive, then the intersection of Γ _T =0 with the positive quadrant consists in the concave down parabolic arc joining to the origin, and so the intersection with L ₁ is undetermined (there might not be an intersection, if the slope of Γ _T =0 at the origin were less than the slope of L ₁).

Study of Γ _S Use the cubic Γ _S =0; letting T→∞ in Γ _S =0 gives that is a vertical asymptote of Γ _S , and it follows that Θ=0 intersects Γ _S =0 in the positive quadrant. The first assertion in the theorem is proved, completing the proof of the existence part of Theorem 4.1.   ▪