SIS epidemic attractors in periodic environments

Abstract

The demographic dynamics are known to drive the disease dynamics in constant environments. In periodic environments, we prove that the demographic dynamics do not always drive the disease dynamics. We exhibit a chaotic attractor in an SIS epidemic model, where the demograhic dynamics are asymptotically cyclic. Periodically forced SIS epidemic models are known to exhibit multiple attractors. We prove that the basins of attraction of these coexisting attractors have infinitely many components.

Keywords:

• Basin of attraction
• Compact attractor
• Multiple attractors
• Periodic dynamical system

1. Introduction

The role of periodic environments in determining the long-term dynamics of populations has become an area of intensive study in both ecological and epidemiological research 1–27. In a recent paper, Franke and Yakubu studied the impact of seasonal factors on a discrete-time SIS (susceptible–infected–susceptible) epidemic model 13. For the periodically forced SIS model, Franke and Yakubu, computed the epidemic threshold parameter, ℛ₀, and used it to prove that if then the disease goes extinct whereas if then the disease is endemic and may even be cyclic. In addition, Franke and Yakubu, used simulations to show that in periodic environments, it is possible for the infective population to be on a chaotic attractor while the demographic dynamics is non-chaotic 13. For certain parameter values, the SIS model of Franke and Yakubu, a periodically forced hierarchical model, has multiple attractors when . What is the nature and structure of the basins of attraction of these coexisting attractors?

In this paper, we focus on deriving verifiable conditions that guarantee the existence of cyclic or chaotic attractors in periodically forced hierarchical models. When the periodically forced SIS model exhibits multiple compact attractors, we prove that at least one of the basins of attraction of the coexisting attractors has infinitely many components. That is, it is almost impossible to accurately specify all the initial conditions that lead to each of the coexisting attractors. This ‘uncertainty’ phenomenon is known to occur in deterministic models that exhibit sensitive dependence on initial conditions 28–34.

The paper is organized as follows. In section 2, we introduce the periodically forced SIS model of Franke and Yakubu. We review, in section 3, the results of Franke and Selgrade on ‘time-dependent’ versus ‘time-independent’ dynamical systems. In section 4, we use a general non-autonomous hierarchical model to derive conditions for the existence of cyclic or chaotic attractors. The periodically forced SIS model of Franke and Yakubu fits into our hierarchical framework. Illustrative examples of cyclic and chaotic dynamics in SIS models are provided in section 5. In these examples, the SIS epidemic model is under asymptotically cyclic demographic dynamics and infections are modeled as Poisson processes 13, 28–30, 35, 36. Section 6 is on the basins of attraction of multiple (coexisting) compact attractors. Illustrative examples of cyclic attractors with basins that have infinitely many components are demonstrated in section 7, and concluding remarks are presented in section 8.

2. SIS epidemic model in periodic environments

In this section, we introduce the main model, the periodically forced SIS epidemic model of Franke and Yakubu 13. To do this, we first assume that the dynamics of the total population size in generation t, denoted by N(t), are governed by the p-periodic demographic equation

where ∃ such that

In equation (1), models the birth or recruitment process and γ∈(0, 1) is the constant ‘probability’ of surviving per generation. Franke and Yakubu studied Model (1) with the periodic constant recruitment function

and with the periodic Beverton–Holt recruitment function

where the carrying capacity k _t is p-periodic, k _t+p =k _t for all 3–13, 24, 27–34, 37, 38. Franke and Yakubu proved that, the periodically forced recruitment functions generate globally attracting cycles in Model (1) 12, 13. For reference, we summarize their results in the following two theorems.

Theorem 1

[12,13] Model (1) with has a globally attracting positive s-periodic cycle that starts at

where s divides p.

Theorem 2

[12 13] Model (1) with and μ>1 has a globally attracting positive s-cycle, where s divides p.

By these two results, the total population is asymptotically periodic (bounded) and lives on a cyclic attractor, denoted by , when the recruitment function is either a periodic constant or the Beverton–Holt model.

Next, we build a simple SIS epidemic process on ‘top’ of the periodic demographic equation, equation (1). As in 13, 28–30, we let S(t) denote the population of susceptibles; I(t) denote the population of the infected, assumed infectious; denote the total population size at generation t, N _∞ denote the demographic steady state or attracting population and the initial point on a globally attracting cycle, when they exist. We assume that individuals survive with constant probability γ each generation, and infected individuals recover with constant probability (1−σ).

Let be a monotone convex probability function with and for all We assume that the susceptible individuals become infected with nonlinear probability per generation, where the transmission constant α>0. When infections are modeled as Poisson processes, then 13, 28–30, 35, 36.

Our assumptions and notation lead to the following SIS epidemic model in p-periodic environments:

where and N(t)>0. When the environment is constant, and Model (2) reduces to the model of Castillo-Chavez and Yakubu 28–30. The total population in generation t+1, the sum of the two equations of Model (2), is the demographic equation (equation (1)).

Using the substitution , the I-equation in Model (2) becomes

Let

When F _N has a unique positive fixed point and critical point, we denote them by I _N and C _N , respectively.

and the set of iterates of the nonautonomous map F _N(t) is the set of density sequences generated by the infective equation.

Franke and Yakubu, used the map F _N to study disease dynamics in the periodic SIS epidemic model, Model (2). In particular, they obtained the basic reproduction number,

for the model. Franke and Yakubu proved that implies disease extinction, whereas implies disease persistence. In addition, they obtained that it is possible for the uniformly persistent epidemic to live on a globally attracting cycle and even a chaotic attractor. To study the nature of these attractors and their basins of attraction, we need the following auxiliary result of Franke and Yakubu on the properties of F _N 13.

Lemma 3

satisfies the following conditions.

• (a)  and

• (b) F _N (I) is concave down on [0, N].

• (c)  on [0, N].

• (d) If then F _N has a unique positive fixed point I _N in [0, N].

• (e) Let Then . That is, Ψ _N is a topological conjugacy between F ₁ and F _N .

• (f) If N ₀<N ₁ and , then where is the positive fixed point of in [0, N _i ].

• (g) If C ₁ exists, then C _N =NC ₁.

• (h) If N ₀<N ₁, then for all I∈(0, N ₀].

3. Review of time-periodic dynamical systems

Our periodically forced SIS epidemic model is a time-periodic dynamical system. To study the attractors generated by the model when , we use a very general time-independent discrete-time dynamical system to motivate definitions of attractors for a time-periodic dynamical system. In 9, Franke and Selgrade showed that the classical definitions from time-independent discrete dynamical systems theory applied to autonomous systems lead to important new concepts for the corresponding time-periodic dynamical system.

As in 9, let (X, d) be a metric space (usually an open subset of ℝ ⁿ ). A discrete \ dynamical system is a finite sequence of maps where for . Extend this sequence to a periodic infinite sequence by defining for i≥p. The trajectory {x(t)} of a point x∈X is given by the t-fold composition of these p maps. That is,

Let

For the metric on 𝒳, let

where

For and a point , define the autonomous map

by

To simplify notation, the first component of ordered pairs in 𝒳 will always be taken mod p. 𝒳 is the fibered cylinder for X and ℱ is the cylinder map (see figure 1).

𝒳 consists of p copies of X referred to as fibers (see figure 1). Open sets in 𝒳 are open sets in each copy of X. For each

denotes the ith fiber. Furthermore, for every convergent sequence {i _n , y _n } in 𝒳, there is an M>0 such that if m, n>M then i _m =i _n . Consequently, all the points past M are in the same fiber.

Figure 1. The fibered cylinder 𝒳 and the cylinder map ℱ corresponding to the dynamical system {F ₀, F ₁, …, F _p−1}.

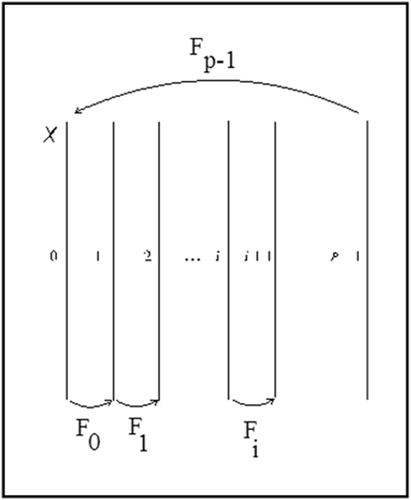
ℱ is an autonomous dynamical system on 𝒳, and the standard definitions for an invariant set, attractor and ω -limits apply. In 9, Franke and Selgrade introduced similar concepts for time-periodic dynamical systems.

As in 9, define the projection by

𝒳 is a finite number of copies of X, and the projection map is an open mapping.

Definition

A set is invariant under the time-periodic dynamical system if there is a set with and 9.

Trapping regions play an important role in understanding the long-term dynamics of many systems.

Definition

A set U⊂X is a trapping region for the time-periodic dynamical system if there is an open set with compact closure so that and 9. 𝒰 is called a corresponding trapping region to U.

a nonempty compact invariant set, is an attractor for ℱ whenever 𝒰 is a trapping region. We capture this in the following precise definition.

Definition

A set is an attractor for the time-periodic dynamical system if it has a trapping region U, with corresponding trapping region , such that where 17.

By these definitions, an attractor Γ in 𝒳 produces an attractor Λ in X for the time-periodic dynamical system.

4. Compact attractors

To study the nature and structure of compact attractors in our SIS epidemic model, we assume that the p-periodic demographic equation (equation (1)) has a globally attracting positive cycle . Recall that, when the recruitment function is either periodically constant or periodic Beverton–Holt, the demographic equation is asymptotically cyclic (Theorems 1 and 2). If in addition Franke and Yakubu showed that it is possible for the uniformly persistent epidemic to live on a cyclic or chaotic attractor.

To understand compact attractors for our epidemic process, we consider the following general hierarchical system.

where and are smooth functions,

and

is a dynamical system on V.

In our SIS epidemic model, let

Then V is a connected set and for each

is a connected set. By letting

and

it is easy to see that the (N, I) system (our epidemic model),

is an example of Model (3).

Assume throughout this section that is a globally attracting p-periodic orbit for the p-periodic dynamical system g(t,_), where each x _i is unique. Let

Then

Let

H is a one-dimensional map formed by the composition of the h(x _i , y) maps.

Next, we obtain that the p-periodic dynamical system, G, has an attractor whenever the one dimensional map H has one, and vice versa.

Theorem 4

The p-periodic dynamical system on V has a compact attractor if and only if has a compact attractor.

Proof

Let A be a compact attractor for the p-periodic dynamical system on V and be the globally attracting p-periodic orbit for the g(t,_) p-periodic dynamical system. Then, in the fiber cylinder there is a compact attractor ˜A which projects onto A. Let U be a compact trapping neighborhood of ˜A whose image under the fiber map 𝒢 is in its interior. 𝒢 ^p maps the 0th fiber into itself. In the x variable, this mapping has x ₀ as a globally attracting fixed point. The projection of the part of U in the 0th fiber onto the first coordinate produces a compact neighborhood U _x of x ₀. Since x ₀ is a globally attracting fixed point,

Now the dynamics of the x variable under 𝒢 is determined by g(t, x). Thus, the projection of onto the first coordinate is Hence, the part of ˜A in the 0th fiber can be viewed as a subset of Let

Since ˜A is invariant under 𝒢 and is invariant under 𝒢 ^p , B is invariant under H. Also, the projection of onto the second coordinate, U _B , gives a compact neighborhood of B such that H maps U _B into its interior and

Thus, B is a compact attractor for H and A=

The other direction of this proof is easier. If B is a compact attractor for H with U _B a compact neighborhood which is mapped into its interior and , then let A=

To get ˜A, think of each of the pieces in the union as coming from different fibers in the fiber cylinder. Since is a globally attracting cycle, there is a compact neighborhood of x ₀ such that is contained in the interior of and

Let , which can be thought of as being in the 0th fiber. W ₀ is a compact neighborhood of and is in the interior of W ₀. By continuity, there is a (possible) smaller compact neighborhood of x ₀ such that is in the interior of W ₀ and . contains but it may not be a neighborhood of it. The continuity of 𝒢 allows us to find a compact neighborhood W ₁ of with the property that is in the interior of W ₀. Proceeding in a similar way we construct compact neighborhoods W _i \ of each , which can be thought of as being in the fiber, such that W _i contains and is in the interior of W ₀. is the desired attracting neighborhood of Thus, A is a compact attractor for the p-periodic dynamical system G(t, x, y) on V.   ▪

The above proof gives a relationship between the structure of attractors for G and H. We capture this relationship in the following two corollaries.

Corollary 5

If the p-periodic dynamical system on V has a compact attractor A, then has a compact attractor B and A=

Corollary 6

If has a compact attractor B, then the p-periodic dynamical system on V has A=

as a compact attractor.

The cardinality of attractor A is p times the cardinality of attractor B. Hence, by Theorem 4 the following result is immediate.

Corollary 7

The one parameter family of p-periodic dynamical systems

on V undergoes period-doubling bifurcation route to chaos if and only if

undergoes period-doubling bifurcation route to chaos.

Chaotic attractors have-positive Lyapunov exponents 39. Next, we obtain that the attractor for the p-periodic dynamical system, G, is chaotic whenever that of the one-dimensional map H is chaotic, and vice versa.

Theorem 8

If has a compact attractor B with a positive Lyapunov exponent then G has a compact attractor A with a positive Lyapunov exponent.

Proof

By Corollary 6, the compact attractor B for H corresponds to a compact attractor A for G. Under G iterations, the first coordinate has a globally attracting periodic orbit. Hence, the first coordinate cannot produce a positive Lyapunov exponent. Under G iterations, the second coordinate on A corresponds exactly to that of H on B. Thus, if has a compact attractor B with a positive Lyapunov exponent then G has a compact attractor with a positive Lyapunov exponent.   ▪

5. Illustrative examples: cyclic and chaotic attractors

In this section, we use a specific example to illustrate the predicted cyclic and chaotic attractors in our SIS epidemic model by Corollary 6 and Theorem 7, where the demographic dynamics is cyclic and non-chaotic. In this example, we consider our epidemic model with periodic constant recruitment function, where infections are modeled as Poisson processes.

Example 9

Consider Model (4) with 2-periodic constant recruitment function

and

where

With our choice of parameters, the 2-periodic demographic equation has a globally attracting 2-cycle (Theorem 1). Figure 2 shows period-doubling bifurcation route to chaos in the infective population (H dynamics) as the transmission constant α is varied between 0 and 400. By Corollary 6, the corresponding SIS epidemic model undergoes period doubling bifurcation route to chaos, where the demographic dynamics is non-chaotic.

Figure 2. Period-doubling bifurcation route to chaos in the infective population. On the horizontal axis, 0≤α≤400 and on the vertical axis, 0≤I≤160.

Figure 3 shows an attracting 24-cycle in the infective population (H dynamics). For this choice of parameters, Corollary 7 and Sharkovskii's Theorem guarantee a chaotic attractor (Li–Yorke type 39) in the corresponding epidemic model.

Figure 3. A period-24 cycle in the infective population. On the horizontal axis, 300≤α≤400 and on the vertical axis, 120≤I≤160.

By Corollary 7 and Theorem 8, the general pattern illustrated in figures 2 and 3 are not restricted to our choice of the periodic constant recruitment function, but also follows when the periodic Beverton–Holt and Ricker models are used 2, 12, 13, 24, 27–34, 40.

6. Multiple attractors

Franke and Yakubu showed that Model (2) is capable of exhibiting multiple (coexisting) compact attractors when the critical point of F ₁, C ₁, is less than the fixed point of F ₁ (). In this section, we study the structure of the basins of attraction of these coexisting attractors.

Throughout this section,

where

and

Furthermore, we assume throughout the section that g(t, x) is a positive, increasing homeomorphism for each t with a globally attracting positive period-p point, denoted by . Recall that when the recruitment function f(t, x) is either a periodic constant or the Beverton–Holt model, then g(t, x) is a positive, increasing homeomorphism with a globally attracting positive periodic orbit (Theorems 1 and 2).

Next, we obtain a closed interval on which our composition map,

is increasing.

Theorem 10

If C ₁ is less than the positive fixed point of F ₁ and is an orbit of the p-periodic dynamical system

then

has a maximum point smaller than its smallest positive fixed point and is increasing on . Moreover, is a continuous function.

Proof

Since is an orbit of the p-periodic dynamical system

and the domain of is [0, x ₀]. For each x _j , is topologically conjugate to F ₁ (Lemma 3). So is less than the positive fixed point of on , on and . Furthermore, on and . Thus,

and

The ray satisfies the conditions of the theorem for the case of one function . For an induction proof we assume that the composition map is increasing on some interval , there are no positive fixed points on this interval, and is a maximum point for on its domain [0, x ₀]. There are two cases to consider depending on whether

or

In the first case, is an increasing homeomorphism with on . Hence,

on is increasing on this interval and takes on its maximum value at Let . Note that this construction is continuous on some neighborhood of x ₀. When

maps a unique point onto (Intermediate Value Theorem). is the maximum point for . Hence, is a maximum point for . Since is increasing on and is increasing on , is increasing on . Similarly, on this interval. Thus,

has a maximum point smaller than its smallest positive fixed point. To get the continuity of in this case, first consider when . Then by continuity of the dynamical system, there is a neighborhood U of x ₀ such that if y ₀∈U then

Since g(t, x) is a homeomorphism for each t, our dynamical system preserves vertical lines and no two vertical lines go to the same vertical line. Thus,

is a homeomorphism on . Thus, the inverse image of the ray intersected with a small neighborhood of is a continuous function of x. The remaining case is when . In this case,

For y close to x ₀, can come in either of the two ways. First it can be on the ray I=xC ₁=C _x , which keeps you close to the point or it comes from the inverse of the homeomorphism

which also must keep you close to by continuity. Thus, in either case we obtain the continuity of at x ₀.This completes the induction proof.   ▪

In Corollary 11 and Lemma 12, we obtain regions on which the composition map

is a homeomorphism.

Corollary 11

If C ₁ is less than the positive fixed point of F ₁, then

is a homeomorphism on .

The proof of Corollary 11 is contained in that of Theorem 10.

Lemma 12

If C ₁ is less than the positive fixed point of F ₁, then there is an L>0 such that

is a homeomorphism on and .

Proof

From the proof of Theorem 10, so moves the origin to a point of the positive x-axis. Since this axis is invariant,

is also on the positive x− axis. Continuity gives an L>0 such that for each is below the ray of critical points I=C _x when }. Thus, for , for 0 <x≤L. Consequently, the only critical points of on and is the critical ray I=C _x . G(0, x, I) has the critical points and the following G(i, x, I) are homeomorphisms on the image. On each fixed vertical line in this set, G(0, x, I) increases to the critical point and then decreases. Hence, is a homeomorphism on and as well as on and    ▪

Next, we establish that in our epidemic model, Model (4), the point is not in the basin of attraction of any set of coexisting attractors.

Lemma 13

If Model (4) has multiple disjoint compact attractors and C ₁ is less than the positive fixed point of F ₁, then the point is not in the basin of attraction of these multiple attractors.

Proof

{0} is a repelling fixed point of . By Theorem 10, any neighborhood of {0} eventually gets mapped onto the entire range. Hence, every neighborhood of {0} contains points of all basins of attraction. Thus cannot be in any basin of attraction of Model (4).   ▪

In 11, Franke and Yakubu obtained that periodically forced models can exhibit multiple (coexisting) attractors via cusp bifurcations, where the corresponding unforced models exhibit no multiple attractors. When our SIS epidemic model has coexisting attractors, then at least one of the basins of these attractors has infinitely many components. That is, the basins of attraction are in the cylinder space and a component of the basins is a subset of one of the fibers. We capture this in the following result.

Theorem 14

If Model\/ (4) has multiple disjoint compact attractors and C ₁ is less than the positive fixed point of F ₁, then at least one of the basins of attraction has infinitely many components.

Proof

We will show that the 0th fiber contains infinitely many components. By Corollary 5, to each attractor A _i of Model (4) there is a corresponding attractor B _i of the composition map

So has multiple disjoint attractors whenever Model (4) has multiple disjoint attractors. By Lemma 13, {0} is not in any of the B _i basins of attraction. Let U _B be the basin of attraction for an attractor B and be a connected component of U _B that contains a point of B. Then is a relatively open set in [0, N ₀] and whenever By Theorem 10, there is an interval, on which is a homeomorphism onto the range. Thus, there is a connected, relatively open subset of which is mapped onto

and hence is in the basin of attraction for B _i . Note that when . Since is an increasing homeomorphism with from onto the range, there is a sequence of connected, relatively open subsets of which are mapped onto and hence are in the basin of attraction for B _i . Since {0} is repelling, this sequence of sets must limit on {0}. Similarly there is a sequence of connected, relatively open subsets of which are mapped onto and hence are in the basin of attraction for B _j . This sequence must also limit on {0}. Furthermore the union of the sets are disjoint from the union of the sets. Hence the basins of attraction for each B _j has an infinite number of components. Let U _A be the basin of attraction for an attractor A and be the connected component of U _A that contains . Here we are viewing the V ₀ as being a vertical line segment in the 0th fiber of the cylinder space with first coordinate . Then is a relatively open set in the 0th fiber of the cylinder space and whenever By Corollary 11,

is a homeomorphism on the set in the 0th fiber of the cylinder space given by with range equal to the entire range of in the 0th fiber of the cylinder space. Thus, there is a connected relatively open subset of W which is mapped onto a connected component of

which contains a point of A. Hence is in the basin of attraction for A _i and contains an open neighborhood of some point with first coordinate . Note that when There is a sequence of connected relatively open subsets of W which are mapped onto and hence are in the basin of attraction for A _i . Similarly there is a sequence of connected relatively open subsets of W which are mapped onto and hence are in the basin of attraction for A _j . Note that

when . The intersection of V ₀ with and each has an infinite number of components as we saw in the first paragraph of this proof. The question is to determine if enough of these components can connect by going to the left or right to have only a finite numbers for components for one of the basins of attraction. We first show that this cannot happen by going to the left. Since contains an open neighborhood of some point with first coordinate , it\ contains a horizontal line segment H _i containing this point as its midpoint. The inverse image of H _i under restricted to W, is the graph of a continuous function, since vertical line segments are sent to vertical line segments. Since each g(t, x) is a homeomorphism with a globally attracting periodic point, the horizontal expanse of is larger than that of H _i . The maximum of is smaller than that of H _i \ because

on . If \ is not a subset of the of the image of

restricted to W, replace it with the component of intersected with this image that contains a point of V ₀. The horizontal expanse of this (possibly smaller) is larger than that of H _i .\ Note that . By repeating this process successively, we produce a sequence of connected sets which are the graphs of continuous functions. The domains of these functions continue to grow and the maximum height continues to shrink. On the left, compactness gives that the maximum height goes to 0. By Lemma 12 there is an L>0 such that

is a homeomorphism on and . Since the maximum of the to the left of goes to 0, there is a k such that this maximum is less than the second coordinate of

Thus, if k is large enough the left endpoint of is on the image of the graph of under

and it intersects the image of the diagonal at a point in the image of and . Thus, the inverse image of contains a connected curve starting on the diagonal and containing Since this same construction can be done starting with attractor A _j , the basins of attraction for each A _i intersected with have an infinite number of components. Thus, we do not get a finite number of components by going to the left. A different outcome is possible by going to the right. Assume that the inverse image of , and \ contain curves connecting points on the diagonal to points with first component and that the curve corresponding to is between the other two curves. Also assume that the curves coming form and are in the same component of the basin of attraction of A _i . Since open connected subsets of locally path connected spaces are path connected, there is a path that must go to the right that connects these two curves. This gives us a path from the diagonal back to the diagonal that surrounds the third curve. Thus, the basin of attraction of A _j has a component that is surrounded by this curve. For the basin of attraction of A _i to have only a finite number of components, this must happen an infinite number of times. Hence, if A _i has finitely many components then A _j must have an infinite number of components.   ▪

7. Illustrative examples: multiple attractors

Here, we use a specific example to demonstrate coexisting attractors with basins of attraction having infinitely many components. As in Example 9, we consider Model (4) with periodic constant recruitment function, where infections are modeled as Poisson processes.

Example 15

Consider Model (4) with 4 - constant recruitment function

and

where

With our choice of parameters, the 4-periodic demographic equation has a globally attracting 4-cycle (Theorem 1). Figure 4 shows that Example 15 has two coexisting 4-cycle attractors (multiple attractors) at

and

Figure 4. Two coexisting 4-cycle attractors. On the horizaontal axis, 0≤N≤175, and on the vertical axis, 0≤I≤75.

Figures 5–7 show the basins of attraction of the two coexisting 4-cycle attractors in Example 15 (or figure 4), where the red and blue regions are, respectively, the basins of attraction of the 4-cycle attractors R and B.

Figure 5. Basins of the two coexisting 4-cycle attractors in Example 15, where the red and blue regions are, respectively, the basins of attraction of attractors R and B. On the horizaontal axis, 0≤N≤100, and on the vertical axis, 0≤I≤100.

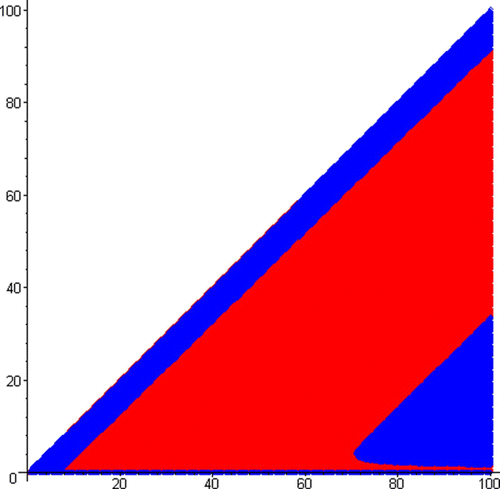
Figure 6. Zoom of figure 5 around the origin by a factor of 1000, where the red and blue regions are, respectively, the basins of attraction of attractors R and B. On the horizaontal axis, 0≤N≤0.1, and on the vertical axis, 0≤I≤0.1.

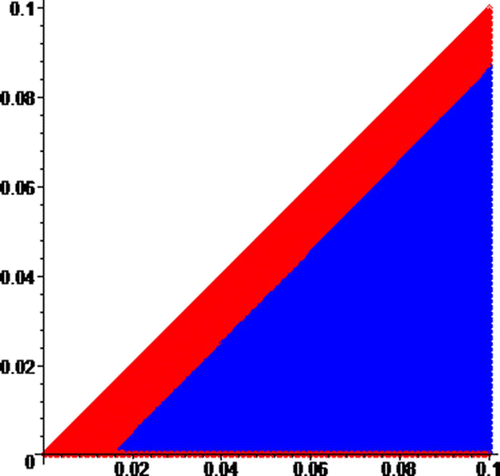
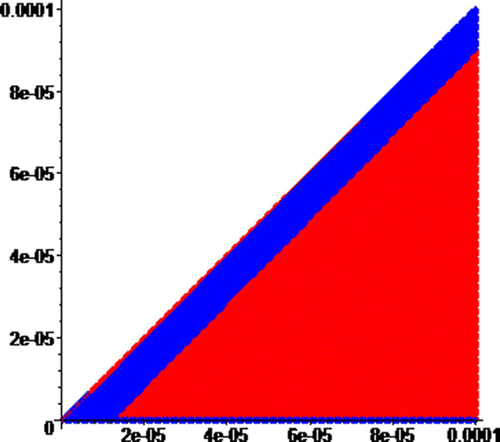
To demonstrate that the basins of the attractors have infinitely many components, we zoom into the origin of figure 5 by a factor 1000 to obtain figure 6. Similarly, we obtain figure 7 by zooming into the origin of figure 6 by a factor of 1000. As predicted by Theorem 14, our sequence of zooms produces pictures with the colors switching back and forth. The edge of the diagonal changes color back and forth as you zoom into the origin.

Figure 7. Zoom of figure 6 around the origin by a factor of 1000, where the red and blue regions are, respectively, the basins of attraction of attractors R and B. On the horizaontal axis, 0≤N≤0.0001, and on the vertical axis, 0≤I≤0.0001.

Figure 8, a zoom of figure 5 away from the origin, shows that the blue basin of attraction has an end; making the red basin a connected set.

Figure 8. Blue basin ends and red basin is connected. On the horizaontal axis, 2000≤N≤2600, and on the vertical axis, 2000≤I≤2600.

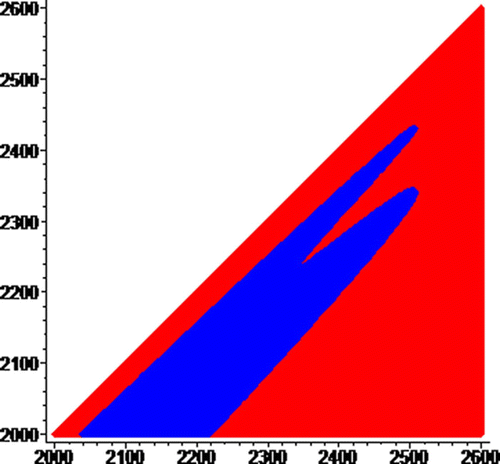
As illustrated by Theorem 14, the general pattern illustrated in figures 5–8 are not restricted to our choice of the periodic constant recruitment function, but also follows when the periodic Beverton–Holt model is used, and certainly hold for any increasing homeomorphism with a globally attracting positive periodic orbit.

8. Conclusion

The periodically forced SIS model of Franke and Yakubu has illustrated several important principles, both concerning the role of periodic environments, and the complexity of the interaction between infectives and susceptibles in discrete-time models 2, 12–14, 25, 26, 41–43.

Castillo-Chavez and Yakubu obtained that in constant environments the demographic equation drives the disease dynamics 28–30. That is, when the demographic dynamics are cyclic and non-chaotic, then the disease dynamics are cycle and non-chaotic. Similarly, when the demographic dynamics are chaotic, then the disease dynamics are chaotic. In the current paper, we prove that in periodic environments it is possible for the infective population to be on a chaotic attractor while the demographic dynamics are cyclic and nonchaotic. That is, in periodic environments, the demographic dynamics do not drive the disease dynamics 13.

In constant environments, simple SIS models do not exhibit multiple attractors 1, 2, 12, 13, 28–30, 35, 36, 39. However, in periodic environments the corresponding simple models can have multiple attractors with basins of attraction having infinitely many components. In this situation, it is impossible to make accurate predictions of the final outcome of all initial population sizes despite the fact that and the disease is endemic 13. This extreme dependence of the long-term behavior on initial population sizes may have serious implications on the persistence and control of infectious diseases.