Asymptotic behaviour of the non-autonomous competing two-species Lotka–Volterra models with impulsive effect

Abstract

In this paper, the nonautonomous competing two-species Lotka–Volterra models with impulsive effect are considered, where all the parameters are time-dependent and asymptotically approach the corresponding periodic functions. Under some conditions, it is shown that the semi-trivial positive solutions of the models asymptotically approach the semi-trivial positive periodic solutions of the corresponding periodic system. It is also shown that the positive solution of the models asymptotically approach the positive periodic solution of the corresponding periodic system.

Keywords:

• competing system
• impulsive effect
• asymptotically approach
• positive periodic solution
• topological degree

AMS subject classification :

• 34C05
• 92D25

1. Introduction

One of the most famous models for dynamics of population is the Lotka–Volterra competition system in mathematical ecology; the following equations are studied in 12,

where b _i (t) and are continuous and bounded above and below by positive constants on the half-infinite interval , and b _i (t), a _ij (t) are asymptotic to periodic functions , respectively. This is motivated by many temporal variations in the environment of a species. The temporal variations are naturally assumed to be cyclic or periodic or asymptotic to periodic, such as seasonal (or daily) effects of food availability, weather conditions, temperature, mating habits, contact with predators, and other resource or physical environmental quantities. However, the ecological system is often affected by the environmental changes and other human activities; we need to consider the use of impulsive differential equations. Impulsive differential equations provide a natural description of such systems. Equations of this kind are found in almost every domain of applied sciences. Numerous examples were given in Bainov‘s and his collaborators books 3 9. Some impulsive equations have recently been introduced in population dynamics, such as 1 2 4 5 7 8 10 11,13–17.

In this paper, we consider the following system with impulsive effect

assume that the conditions of b _i (t) and are the same as (1.1). are constants and there exists an integer q>0 such that . Because of biological meanings, a natural constraint is for all k ∈ Z ₊, .

With the above model (1.2), we can take into account the possible exterior effects under which the population densities change very rapidly. For instance, the model (1.2) can describe the two competing fish species that are exploited seasonally by human activities, that is, we can take impulsive harvesting strategies. In this case, h _1k <0 and h _2k <0 denote impulse harvesting efforts of the species x and the species y, respectively. Then, we will have the question: how should we control the harvesting efforts to make both fish species coexist? The model (1.2) can also describe the dynamics of normal and tumour cells in a periodically (or asymptotic to periodically) changing environment under the effects of the impulsive chemotherapy, therefore, in this case, we are interested in the existence and stability of tumour-free periodic solution and how the impulsive treatment affects the interaction of tumour and normal cells.

In this paper, we investigate that which relates between the dynamics of the semi-trivial periodic solution of (1.2) and its corresponding semi-trivial periodic solution of the corresponding system. Meanwhile, we give the existence and global stability of the positive periodic solution of the corresponding system, and study the relationship between the dynamics of the positive periodic solution of (1.2) and its corresponding positive periodic solution of the corresponding system.

The dynamics of the semi-trivial positive solutions

We begin with some definitions.

Definition 2.1

Let . φ is said asymptotic to ψ, in notation if .

Definition 2.2

Let . Then, (x, y) is said to be asymptotic to in notation if and .

It is easy to verify that ‘∼’ is an equivalence relation on Banach space. In the following, we shall use notations: , where g(t) is a T-periodic function, , . In the next section, we prove the following theorem.

Theorem 2.1

For i, j=1, 2, let b _i (t) and a _ij (t) be continuous and bounded above and below by positive constants on the half-infinite interval and b _i (t), a _ij (t) are asymptotic to periodic functions respectively. If, in addition, (or ) holds, then for the semi-trivial positive solution (x(t), 0) (or (0, y(t))) of (1.2), we have (or ), where (or ) is the semi-trivial positive periodic solution of

The proof of is similar to so we only need to prove holds. To prove Theorem 2.1, we need a series of lemmas.

Lemma 2.1

Both the open first quadrant and the first closed quadrant in the x, y−plane are invariant with respect to (1.2).

Proof

Since the assertion of the Lemma immediately follows for all and the proof is complete.   ▪

Let us consider the following two systems:

and

where are continuous and bounded above and below by positive constants on the half-infinite interval [0,+∞).

Lemma 2.2

Suppose that (u ₁(t), 0) and (v ₁(t), 0) are solutions of (2.2) and (2.3), respectively, satisfying . If, for all there exist inequalities then for all .

Proof

Since , the inequality will hold for t − t ₀ sufficiently small and positive. If does not hold for all t > t ₀, there exists a t ₁>t ₀, such that holds for t ₀<t < t ₁ and . Suppose that holds and is not the impulsive point, as by Lemma 2.1. Now, as on (t ₀, t ₁) and , we must have . On the other hand, from (2.2) and (2.3), we have this is a contradiction, suppose that t ₁ is the impulsive point and t ₁=τ _k , similar to the above argument, we can also get contradiction. This contradiction shows that is impossible. This shows that for all . The proof is complete.   ▪

Assume that and . Then, for any , there exists a such that

for all . We construct the following two systems:

and

From Lemma 2.2 and inequalities (2.4), we have the following lemma.

Lemma 2.3

Suppose that and are solutions of (2.5) and (2.6), respectively, satisfying . Then for all where (x(t), 0) is the solution of (1.2) satisfying

Proof

Inequality (2.4) leads to , for all , which implies that compared with (1.2), we have (2.5) and (2.6) satisfy the conditions described in Lemma 2.2, respectively. Therefore, from Lemma 2.2, the result holds immediately. The proof is complete.   ▪

If are continuous, positive T-periodic functions, we wish that there exist semi-trivial positive T-periodic solutions of (2.1), (2.5), (2.6), respectively. In fact, we have the following lemma that assure the existences of periodic solutions.

As an application of the results obtained in 10, we have the following lemma.

Lemma 2.4

Under conditions of Theorem 2.1, there exist the semi-trivial positive T -periodic solutions of (2.1), (2.5), (2.6), respectively.

Lemma 2.5

Suppose that and are the positive T -periodic solutions described in Lemma 2.4. If we denote them by and respectively, then for η>0, there exists a ρ>0 such that and (the η-neighborhood of Γ) for all in notations and .

Remark

Because of the continuity and dependence of solutions of impulsive differential equations with respect to initial conditions and parameters, it follows that and for η>0, there exists a ρ>0, such that and for . The method to establish the two inequalities is similar, so to prove Lemma 2.5, we only need to show that, for η>0, there exists a , such that

Proof of Lemma 2.5

Suppose (2.7) does not hold. Then This is because is continuous and T-periodic function, there exists a such that Without loss of generality, we can assume that , namely that In fact, if we denote , then is also the unique T-periodic solution of (2.5) and From , there exist , such that . But is a bounded set. Because the Euclid space R ² is complete, there exist , without loss of generality we can assume , such that . Let (u(t), 0) denote the solution of (2.1) having the initial value (u(0), 0). Continuous dependence on initial conditions and parameters for (2.5) leads to is T-periodic; so is (u(t), 0). But under the conditions of Theorem 2.1, there exists a unique semi-trivial positive T-periodic solution of (2.1). Consequently, as a consequence of which, we have This is a contradiction. Therefore, (2.7) holds. From Remark 2.1, the proof of Lemma 2.5 is complete.   ▪

Proof of Theorem 2.1

Let (x(t), 0) be a ‘fixed’ positive semi-trivial solution of (1.2). After constructing systems (2.5) and (2.6), from Lemma 2.5, for η>0, there exists a such that for Pick any . Since , there exists a t ₂>0 such that for all t ≥ t ₂. Let and be the solutions of (2.5) and (2.6), respectively, satisfying . From Lemmas 2.2 and 2.3, we have

From Lemmas 2.4 and 2.5, we have

So (2.8) and (2.9) lead to and the proof is complete.   ▪

3. Existence and global stability of the positive periodic solution of (2.1)

By using the continuation theorem of coincidence degree theory, the existence of a periodic solution is established. In this section, we shall study the existence of strictly positive (component-wise) periodic solution of system (2.1). First, we shall make some preparations.

Let J ⊂ R. Denote by PC(J, R) the set of functions which are continuous for , are continuous from the left for t ∈ J and have discontinuities of the first kind at the points τ _k ∈J. Denote by PC′(J, R) the set of functions with a derivative . We deal with the Banach spaces of T-periodic functions Let X and Z be real Banach spaces, L: be a linear mapping, and N: be a continuous mapping. The mapping L will be called a Fredholm mapping of index zero if and Im L is closed in Z. If L is a Fredholm mapping of index zero there exist continuous projectors P: and Q: , such that . It follows that is invertible. We denote the inverse of that map by K _P . If Ω is an open bounded subset of X, the mapping N will be called L-compact on if is bounded and K _P (I − Q)N: is compact. Since ImQ is isomorphic to Ker L, there exist isomorphisms .

In the proof of our existence below, we will use the following Lemmas.

Definition 3.1

The set F is said to be quasi-equicontinuous in [0, T] if for any there exists a δ>0, such that and then .

Lemma 3.1

(Compactness criterion) The set is relatively compact if and only if: (1) F is bounded, that is, for each x∈F and some M>0; (2) F is quasi-equicontinuous in J.

Proof

Necessity. Without loss of generality, we suppose that the first kind discontinuous points on [0, T] are . Since F is relatively compact, we have F is totally bounded, then it is bounded. In the following, we prove that F is quasi-equicontinuous in [0, T]. According to the definition of totally bounded, we suppose that is a net of F, then for arbitrary x ∈ F, there exists a such that . We redefine functions on as follows:

Then and X are continuous on . Therefore, X _i is uniformly continuous on . Then, there exists a δ _p >0, such that we have when and . For arbitrary X, there exists an i such that

Let , then we have when . Hence, F is quasi-equicontinuous in J.   ▪

Sufficiency. PC _T is a Banach space, we only need to prove F is totally bounded. For arbitrary , from the definition of quasi-equicontinuous, we can choose a δ>0, such that when and , we have

Since is a compact set, then it is totally bounded. For every , there exists a finite δ net: , such that composes a finite δ net of [0, T]. For convenience, we assume that compose a finite δ net of [0, T]. From (3.1), we have for arbitrary t∈[0, T], there exists t _i such that

Denote . For arbitrary , we have , that is, [Ftilde] is a bounded set in R ⁿ . So, [Ftilde] is totally bounded. Then, for , [Ftilde] has a finite net on R ⁿ : . In the following, we will prove is a ϵ net of F on PC _T . In fact, for arbitrary x ∈ F, we have . Then for , we have

Thus, for arbitrary 1≤i ≤ n, we have . For arbitrary t∈[0, T], there exists a t _i , such that and . From (3.2), (3.3), it follows that

Then, . Thus, F is totally bounded. The proof is complete.

For convenience, we first introduce Mawhin's continuation theorem 6 as follows.

Lemma 3.2

(Continuation theorem) Let L be a Fredholm mapping of index zero and let N be L -compact on . Suppose (a) for each β∈(0, 1), every solution x of Lx=β Nx is such that x . (b) QNx≠0 for each and . Then the equation Lx=Nx has at least one solution lying in .

Theorem 3.1

Assume that the conditions for are the same as Theorem 2.1. If, in addition and hold, where . Then system (2.1) has at least one positive T -periodic solution.

Proof

Making the change of variable , then (2.1) is reformulated as

Let and ,

and let with

obviously,

and .   ▪

Since Im L is closed in Z, L is a Fredholm mapping of index zero. It is easy to show that P and Q are continuous projectors such that , , where P and Q are defined by

and

Furthermore, the generalized inverse (to L) is given by

Thus,

Clearly, QN and K _P (I − Q)N are continuous. Using Lemma 3.1 and Arzela–Ascoli theorem, it is not difficult to show that is compact for any open bounded set . The isomorphism J of Im Q onto Ker L may be defined by

Now, for using the continuation theorem, we need to find an open bounded set Ω, corresponding to the operator equation , we have

We prove the existence of M>0 such that every T-periodic solution of system (3.5) satisfies .

Let be a T-periodic solution of system (3.5). By integrating (3.5) on the interval [0, T], we can obtain

From Equations (3.5) and (3.6), we have

Noting , so there exist , such that by (3.6), we obtain , hence hence

Noting , so there exist such that From (3.5) and (3.7), we have

By (3.7), we have

from (3.6) we can obtain so

From (3.8) and (3.10), we obtain Again by (3.7), we have

so Clearly, B ₁, B ₂ are independent of β. Let B be a ball of R ² centered at the origin of radius greater than M and This satisfies condition (a) of Lemma 3.2.

Now, we prove condition (b) of Lemma 3.2.

When is a constant vector in R ² and , then

We consider the following system

If X is a solution of system (3.12) for , we have . Therefore, QNX≠0. Define ,

where μ∈[0, 1] is a parameter, is a constant vector in R ² and .

In the following, we prove that when . If the conclusion is not true, i.e., constant vector satisfies , then

By the above arguments, we have , which contradicts the fact that the constant vector satisfies .

In view of the conditions of Theorem 3.1, then the system of algebraic equations

has a unique solution (u*, v*). Therefore By now, we have proved that Ω verifies all the requirements in Lemma 3.2. Hence, system (2.1) has at least one T-periodic solution in , which implies that the result of Theorem 3.1 is true and the proof is complete.

Theorem 3.2

Under the conditions of Theorem 3.1, and where α is a positive constant, then there is a positive T -periodic solution of (2.1) which is globally asymptotically stable.

Proof

Assume that is a solution of (2.1) with positive initial value x(0)>0 and y(0)>0. Since the solution of (2.1) keeps non-negative, we can let where is a strictly positive T-periodic solution of (2.1), its existence is guaranteed by Theorem 3.1. Therefore,

We consider Lyapunov function Calculating the upper right derivative of L(t) along solutions of (3.14), we have

Hence, L(t) is monotone decreasing for [0,+∞). Thus, Since U(t) is the positive T-periodic solution, there exist , such that . Therefore, ln u(t) and ln v(t) is bounded. Noting Thus, are also bounded. We can suppose that there exists a constant M ₀>0, such that Then, where , so We can calculate We say L*=0. If L*>0, then for . Therefore , for If , then L(t)<0, this leads to contradiction. Noting we have . The proof is complete.   ▪

Global asymptotical stability of T-periodic solution must lead to the unique T-periodic solution.

The relation of solutions between (1.2) and (2.1)

The positive solution of (1.2) and the solution of (2.1) have the following relation.

Theorem 4.1

Assume that the conditions for are the same as Theorem 2.1, if, in addition hold, where α is a positive constant, then for any positive solution (x(t), y(t)) of (1.2), we have where is the unique positive T -periodic solution of (2.1).

To prove Theorem 4.1, we need a series of lemmas.

Lemma 4.1

Suppose that and are solutions of (2.2) and (2.3), respectively, satisfying . If, for all there exist inequalities and then, and for all .

Lemma 4.2

Suppose that and are solutions of (2.5) and (2.6), respectively, satisfying and Then for all where (x(t), y(t)) is the solution of (1.2)satisfying and .

Lemma 4.3

Under the conditions of Theorem 4.1, there exist positive T -periodic solutions and of (2.1), (2.5) and (2.6), respectively, which are all globally asymptotically stable.

Lemma 4.4

Suppose that are the positive T -periodic solutions described in Lemma 4.3, if we denote them by and respectively, then for all η>0, there exists a ρ′>0 such that and (the η-neighborhood of Γ) for all in notations and .

The proof of Lemmas 4.1, 4.2, 4.4 is similar to Lemmas 2.2, 2.3, 2.5, respectively.

Proof of Theorem 4.1

Let (x(t), y(t)) be a ‘fixed’ positive solution of (1.2). After constructing systems (2.5) and (2.6), from Lemma 4.4, for η>0, there exists a such that and for . Pick any . Since , there exists a t ₂′>0 such that for all t ≥ t ₂′. Let and be the solutions of (2.5) and (2.6), respectively, satisfying and From Lemmas 4.1 and 4.2, we have

for all t > t ₂′. From Lemmas 4.3 and 4.4, we have

so (4.1) and (4.2) lead to and the proof is complete.   ▪

Conclusion

In this paper, we have investigated the dynamic behaviours of a non-autonomous competing two-species Lotka–Volterra model with impulsive effect, where all the parameters are asymptotically approach-periodic functions. From Theorems 2.1 and 2.2, we can see that the semi-trivial positive solutions of (1.2) asymptotically approach the corresponding semi-trivial periodic solutions of (2.2), if the conditions are met. It has been proved that there exists a unique periodic solution of (2.1) using topological degree and constructing Lyapunov function. Liu and Chen 10 investigated the corresponding periodic system, that is, system (2.1). They obtained the local stability of trivial and semi-trivial periodic solutions, and proved the existence of the positive periodic solution which arises near semi-trivial periodic solution by standard bifurcation theorem. However, in this paper, we study the existence of the positive periodic solution of the corresponding periodic system using the topological degree method, and proved its global stability by constructing Lyapunov function. Finally, we found that any positive solutions of (1.2) approach asymptotically the unique strictly positive solution of the corresponding periodic system (2.1).

As mentioned in the introduction, we consider model (5.1) which can be described by two competing species which released seasonally.

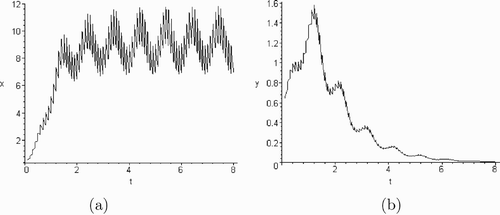
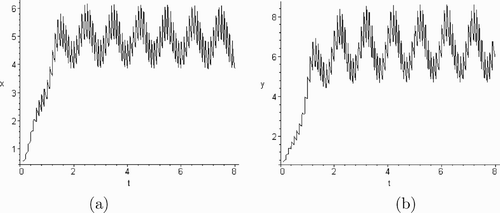
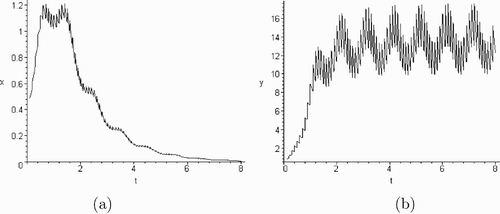
Let b ₁=0.2, b ₂=0.3, and choose p ₁ and p ₂ as control variables. If we choose p ₁=0.2, p ₂=0.35 (or p ₁=0.3, p ₂=0.1), then the conditions of Theorems 2.1 (or 2.2) are satisfied, and from Figure 1 (or Figure 2) we may observe that x (or y) species extinct, y (or x) asymptotic to the semi-trivial periodic solutions of (5.1). If the release p ₁ and p ₂ are both large, then the two species can coexist, asymptotic to the periodic solution of (5.1) (Figure 3).

Figure 1. Time-series of system (5.1) with x eradication: b ₁=0.2, b ₂=0.3, p ₁=0.1, p ₂=0.35, T=0.1.

Figure 2. Time-series of system (5.1) with y eradication: b ₁=0.2, b ₂=0.3, p ₁=0.3, p ₂=0.1, T=0.1.

Figure 3. Time-series of system (5.1) with positive periodic solution: b ₁=0.2, b ₂=0.3, p ₁=0.25, p ₂=0.27, T=0.1.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Nos 10771104 and 10471117), the Henan Innovation Project for University Prominent Research Talents (No. 2005KYCX017) and the Scientific Research Foundation for the Returned Overseas Chinese Scholars, State Education Ministry.