Persistence in a discrete-time stage-structured fungal disease model

Abstract

A discrete-time susceptible and infected (SI) epidemic model, with less than 100% vertical disease transmission, for the spread of a fungal disease in a structured amphibian host population, is analysed. Criteria for persistence of the population as well as the disease are established. Stability results for host extinction and for the disease-free equilibrium are presented. Bifurcation theory is used to establish existence of an endemic equilibrium.

Keywords:

• structured populations
• SI epidemic model
• persistence
• vertical transmission
• bifurcation

AMS Clasification :

• 39A11
• 92D30

1. Introduction

Amphibian populations have been declining worldwide for decades 11 15 17 due to habitat loss and disease. According to Skerratt 11, the relatively recent global emergence of the fungal disease chytridiomycosis has resulted in ‘the most spectacular loss of vertebrate biodiversity due to disease in recorded history’. Individual frogs contract this disease either when their skin comes into contact with water that contains spores from infected animals, or by direct contact with any infected animal. After infection, the fungus invades the surface layers of the frog skin, causing damage to the keratin layer.

A family of discrete-time models that incorporate the life-stage structure of an amphibian population, which may include larva (L), juvenile (J) and adult (A) stages, afflicted with a fungal disease were formulated by Emmert and Allen 6. The most general models were of LJA-SI and LJA-susceptible, infected and recovered (SIR) type, meaning that they included all three stages and were of SI or SIR epidemic type. A notable feature of the models was the assumption of 100% efficient vertical transmission of disease from infected adults to their larval offspring. The authors also considered several sub-models characterized by simpler population stage structure (JA or even simply A). Their mathematical results establish persistence and extinction of the population, not of the disease, but persistence is established in a somewhat narrow sense – the existence of a disease-free equilibrium. Numerous numerical simulations and bifurcation diagrams show that quite complicated dynamic behaviour is possible in the models, especially, with the Ricker recruitment nonlinearity and large intrinsic birth rates.

Emmert and Allen extended their models to seasonal models 7, by considering the birth functions, as well as the survival probabilities within stages, and transition probabilities from one stage to another to be periodic functions. In the same paper, they also analyse some stochastic versions of the models (discrete-Markov chains branching processes). Using the ‘next generation matrix approach’, Allen and van den Driessche 1 obtained explicit formulae for the basic reproductive ratio for the adult model with infection included.

Motivated by 6, the authors in 10 applied theoretical ideas from persistence theory to the model of Allen and Emmert to establish that: (1) the disease cannot lead to the extinction of the amphibian population (persistence of the host) and (2) the disease can become endemic in the population (persistence of the disease) under suitable conditions. Persistence here is used in the stronger, dynamical sense of persistence theory 14 18. Along with the natural condition for persistence of the disease, namely, that the disease-free state is unstable to invasion of the disease, we were forced to assume that the disease-free dynamics was convergent. More precisely, we assumed that in the absence of the disease, the population settled into a globally attracting fixed point. While we could give sufficient conditions for global convergence, and although simulations suggested it occurred for a much larger parameter set, nonetheless, it is a quite restrictive hypothesis, as simulations in 6 clearly show.

The paper of Thieme et al. 16 examines the question of whether a disease can drive a host population to extinction or not. They proposed a traditional ordinary differential equation model with mass action incidence but with general disease-free host dynamics that may include an Allee effect. Among many interesting outcomes, one is host eradication due to the disease. In recent models of chytridiomycosis, Briggs et al. 3 and Mitchell et al. 9 also show through numerical simulations that the extinction of the amphibian host can occur. Mitchell et al. use a deterministic model, in which extinction is interpreted in the sense of total population decreasing below a given threshold. In 3 extinction may occur due to the stochastic nature of the model.

The present paper builds on our earlier work 10. As noted above, the Emmert–Allen model assumes 100% efficient vertical transmission of the disease from infected host to their offspring. An unusual consequence of this assumption for the LJA-SI model is that, in addition to the usual disease-free invariant set, there exists a dynamical regime (invariant set) in which the host population consists entirely of infected individuals. It seems unlikely that this state could be an attractor for realistic parameter regions and therefore it probably can be ignored on biological grounds since a viable ‘disease-free’ host population is a prerequisite for the emergence of disease. However, this feature certainly complicated the mathematics. Moreover, from a biological point of view, the hypothesis of completely faithful vertical transmission seems unlikely and from the mathematical point of view it leads to a structurally unstable system. For, if the model is modified by assuming that a (very small) proportion of offspring of infected adults is born susceptible, then the ‘all-infectives dynamical regime’ disappears. For this reason, we are motivated to modify the Emmert–Allen model as just described, and to reconsider our analysis in 10. Furthermore, motivated by issues of mathematical tractability, we restrict attention here to the JA-SI model, dropping consideration of the larval stage.

Our earlier results 10 continue to hold for the modified model and we can sharpen some of these. We establish that the disease cannot drive the host to extinction, as we did in 10, and we provide sufficient conditions for the disease to persist in the population which are completely similar to those in 10, requiring the restrictive hypothesis of a globally attracting steady state for the disease-free subsystem. We hope to relax this assumption in future work. However, we can obtain somewhat better sufficient conditions for this global convergence to hold due to the lower dimensionality of the disease-free system in the absence of a larval stage. Finally, we employ an extension of the Rabinowitz global bifurcation theorem to establish the existence of an endemic disease steady state for all values of the disease transmission rate exceeding the critical value at which the disease-free state loses stability. The illuminating application of the Rabinowitz bifurcation theorem to a broad class of models in population dynamics has been championed by Cushing 4 5. We dedicate this paper to him on the occasion of his 65th birthday.

In the next section, we state our results without proofs. Unless otherwise specified, proofs can be found in Section 4.

2. The SI juvenile and adult model

The Emmert–Allen model 6 considers Juvenile J, and Adult A stages of the host population, labelled with subscripts S, I indicating their status as susceptible or recovered. F denotes density of fungus in the environment. We consider here the case when we have less than 100% vertical transmission. In addition, all parameters in the model are assumed to be positive, except for and (see below), which are assumed to be non-negative (we allow them to be zero). The JA-SI model is

where . The function is strictly decreasing, and has the property that is bounded. A common choice is (Ricker) or (Beverton–Holt). Following 7, we give below a brief explanation of parameters used in the model, where K=S, I (see 7 for more details on this):

•	p JK , p AK are the probabilities of survival within a stage;
•	p F is the probability that fungi survive in the environment without a live host;
•	q LK , q JK are the probabilities of transition among stages, but remaining in the same class (susceptible or infected) – for examples is the probability that a juvenile becomes an adult, but remains susceptible;
•	b K φ(T) is the number of eggs/adults that survive to larval stage;
•	b F is the birth of fungal zoospores from growth on dead larvae, juveniles or adults;
•	are the disease transmission rates.

The probability of becoming infected in stage N:(N=J, A), that is, , increases with increasing values of infection in the population and environment, infection represented by the weighted sum of the infected stages and fungus:

The following inequalities among parameters are assumed:

Let

Also, we denote by x, in short. In our next result, we analyse the boundedness of (1), as well as the existence of boundary fixed points.

Proposition 2.1

The following hold:

a.	If c AK >0, K=S, I then (1) has a global attractor of bounded sets. In particular, there exists a bounded set that attracts all orbits.
b.	and the are positively invariant sets for (1).
c.	There exists a unique non-trivial boundary fixed point E S of (1) if and only if Δ S >1. When it exists, , with

Parts (b) and (c) are trivial to check, and for a proof of (a) see an analogous result in [10, Proposition 2.1].

represents no disease states, and the F-axis represents no host states.

Notice that 0 is always a fixed point of (1).

2.1. Disease-free dynamics

When infection is not present, the model takes the form

where . By Proposition 2.1 it is clear that is the unique non-zero fixed point of (5).

Parameter Δ _S distinguishes between extinction and survival of the host.

Theorem 2.2

The following hold:

a.	If Δ S <1 then 0 is a globally asymptotically stable fixed point.
b.	If Δ S >1 then there exists such that

The proof of this theorem is similar to that of one of [10, Theorem 3.3], and we will omit it here. Part (a) can also be found in 6.

In the following theorem we give sufficient conditions for global stability of E _S .

Theorem 2.3

Assume that Δ _S >1, and is asymptotically stable. Let . In any of the following two cases, attracts all solutions starting in

a.	\ and
b.	\ and\ .

Conditions in Theorem 2.3 hold, for example, for the set of parameters given in the first column of Table 1 except for b _S =16, where , but we can extend the range of these parameters to nearby values (see 13). Although, numerical simulations suggest that the conclusion of Theorem 2.3 holds for a much larger set of parameters than required by our hypotheses. However, simulations in 7 suggest that the dynamics exhibit a period-doubling cascade as parameter b _S is increased.

Table 1. Parameters used in the numerical simulations.

Susceptible	Infected	Contact	Fungus
		w J =0.4	p F =0.5
		w A =0.4	v J =1
		w F =0.4	v A =1
			b F =10
b S =18	b I =9
	f=0.9

2.2. Main results

We begin by determining the stability of the boundary fixed points of (1). Then we establish sufficient conditions for persistence of the host and of the disease, and finally we analyse the bifurcation of a positive, endemic equilibrium from E _S .

The Jacobian of (1) at 0 is

Clearly, its spectral radius, , equals , where

We mention that our next three results (i.e., Lemma 2.4 and Theorems 2.5 and 2.6) are similar, respectively, to those given in 10, Lemma 3.1, Theorems 4.3 and 4.4; thus we encourage the reader to find the analogous proofs in the above mentioned reference.

The relationship between Δ _K (see (3)) and , is given in the following Lemma.

Lemma 2.4

, with equality if and only if Δ _K =1.

One can view the Δ _K s as basic reproductive numbers (see 1).

The matrix

closely related to is useful for global stability of .

The 5×5 Jacobian matrix J(E _S ) evaluated at E _S decomposes as

where C determines the stability of E _S as a fixed point of the disease-free system and

pertains to the ability of the disease to invade the disease-free state. We denote T evaluated at E _S by T¯ _S , and the 3×2 zero matrix by O.

Below we give a result with regard to the stability of the boundary fixed points.

Theorem 2.5

The following hold:

a.	0 is asymptotically stable if , and unstable if either Δ S >1 or Δ I >1. If r(B)<1 then 0 is globally asymptotically stable.
b.	If E S is asymptotically stable in and , then E S is asymptotically stable in .

Now we give sufficient conditions for persistence of the host and for persistence of both the host and the disease.

Theorem 2.6

Persistence and positive fixed points for (1):

I.	If Δ S >1 then there exists an such that
II.	If one of the following holds: a. and E S is asymptotically stable in and attracts all initial data in ; b. Δ S <1 and Δ I >1; then there exists an such that and (1) has a fixed point in .

Under the hypotheses of Theorem 2.6(II) there exists a positive ‘endemic fixed point’, which may or may not be stable. The first two hypotheses in (IIa) are natural, E _S should exist and be unstable, but the last hypothesis (‘E _S is asymptotically stable in and attracts all initial data in ’) is too strong; hypotheses in (IIb) are biologically implausible as is expected.

An alternative approach to obtain a positive fixed point is to use the bifurcation theory, but then we must select a ‘bifurcation parameter’. If we fix disease-free parameters () then E _S is fixed and we may vary disease-associated parameters (, , , , b _I , f, w _K , v _K , β _K ; K=J, A). The matrix is monotone increasing in all these parameters, so by the Perron–Frobenius theory, its principal eigenvalue is monotone increasing in these parameters. Roughly speaking, stability of E _S is reduced by the increase of any of these. We select the disease transmission rates for special attention in our next result, but this choice is somewhat arbitrary. Other natural choices include the vertical transmission efficiency f, disease-related reduction in maximal reproduction rate b _I =b _S −μ, disease-related increase in adult death , disease-related decrease in juvenile maturation , or infection weighting factors w _K , v _K .

Theorem 2.7

Let and assume that E _S is a non-degenerate fixed point of the disease-free system and that . Then is continuous and strictly increasing on [0, ∞) with r(0)<1 and . There exists a unique β₀>0 such that , E _S is unstable for and for each such β there exists at least one positive fixed point in .

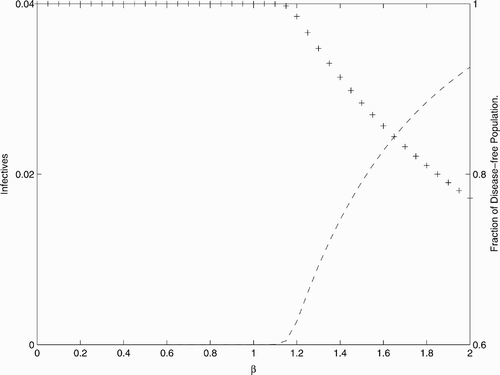
As our calculations indicate, for the values of parameters given in Table 1 (, not given in the table, are all equal to 0.1), the bifurcation for the positive fixed point occurs at a value of β in the interval (1.16, 1.17) (see also Figure 1). By increasing the value of β (in a certain neighbourhood of the bifurcation value), the positive fixed point increases in the I components and decreases in the S components, as it can be observed from Figure 2. Our last result shows that the population decreases at a fixed point from E _S level to the endemic fixed point.

Proposition 2.8

Assume that

If is a fixed point, then , where T _x is T evaluated at x, and T¯ _S is T evaluated at E _S . If, in addition,

then .

Figure 1. Bifurcation of a positive fixed point from the disease-free state.

Figure 2. Four orbits with the same initial condition, converging to the disease-free fixed point (β=1 and 1.1) and to a positive fixed point (β=1.2 and 1.3).

3. Discussion

As noted in the introduction, the Emmert–Allen model 6 assumes 100% efficient vertical transmission of the disease from the infected host to their offspring. Because this seems unlikely to be satisfied, we have introduced a vertical transmission efficiency parameter f∈[0, 1) in the JA-SI model of 6. When f=1 we recover the original model, while for f<1 the fraction 1−f of offspring of infected host begin life disease-free and susceptible.

Our previous work 11 provides sufficient conditions for persistence of the host and for persistence of the disease for both the LJA-SI and LJA-SIR models formulated by Emmert and Allen 6. These same results carry over to the JA-SI model, modified to include the vertical transmission efficiency parameter, considered here. Specifically, the disease cannot drive the host population to extinction (Theorem 2.6 (I)) and when the disease can invade the disease-free fixed point then the disease persists, provided the disease-free state attracts all non-trivial initial data for the disease-free system (Theorem 2.6 (IIa)).

By neglecting the larval stage of the full model, which we did here, we were able to obtain somewhat better sufficient conditions for this global convergence to hold in Theorem 2.3 than in the corresponding result in 10. Strictly speaking, the results are not comparable but here we were not forced to assume either that vanishes or that the system is monotone 12.

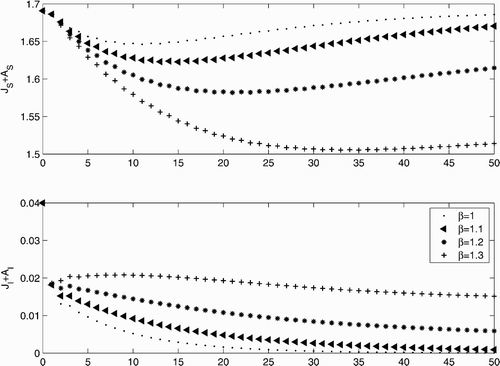
Our result guaranteeing persistence of the disease also implies the existence of a positive fixed point – the endemic equilibrium. An alternative approach to showing the existence of this equilibrium is to use bifurcation theory, which avoids any assumptions on the disease-free dynamics. We used an extension of the Rabinowitz global bifurcation theorem to establish the existence of an endemic disease steady state for all values of the disease transmission rate exceeding the critical value at which the disease-free state loses stability. Furthermore, we showed analytically and numerically that the host population at the endemic fixed point is less than the host population at the disease-free fixed point. Our numerical calculations show that this reduction can be substantial. The large reduction in host population due to the disease would leave the host vulnerable to extinction in a model that includes demographic stochasticity.

4. Proofs

We first introduce some notation that will be used throughout this section. We denote by A ^T the transpose of matrix A, and by O _mn the m×n zero matrix. As it is clear from the context, we will omit the subscripts, and simply write O for O _mn . We call the matrix

• positive, and write A>O if and A≠O;

• strictly positive, and write A≫O if

• non-negative, and write A≥O if .

We define the partial-order relation on the set of non-negative matrices as follows: . Assume analogous definitions for ‘<’ and ‘≪’. Also, we assume the same notation for vectors in ℝ ^m .

For a differentiable function , we denote the derivative of f at x by .

We denote sequences that arise from the iteration of the difference equation in a model, by using superscripts (i.e., , etc.). Other sequences used have subscripts. The components of a vector are denoted by .

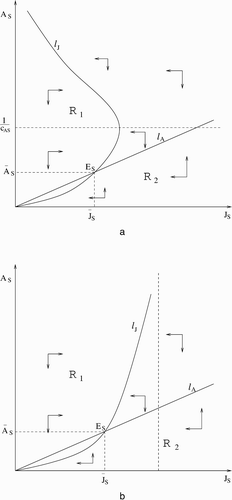
Proof of Theorem 2.3

Let and denote the right-hand side of (5) by . Abusing notation, denote also by E _S .

(a) Let . Note that g is strictly increasing on ℝ₊; hence exists and it is strictly increasing. The curves

represent the J _S and A _S nullclines, respectively. Δ _S >1 implies , and the hypothesis is equivalent to . For the points on l _J , we have that when A _S =0, , and when , . The map is increasing for and decreasing when . Hence J _S =h(A _S ) is increasing for , and decreasing for . So there exists a unique point on l _J with the largest J _S coordinate, and that point is . Next, we want to determine the way the points are mapped, depending on their position relative to the nullclines l _J and l _A . If is ‘above’ l _A , i.e. then . Similarly, if is ‘below’ l _A then . On the other hand, if is such that then . Similarly, if is such that then we have that . From the discussion above we conclude that the dynamics of the model look as indicated in Figure 3(a), where ℛ₁ is the region bounded by l _A , the line A _S =Ā _S and , and ℛ₂ is the region bounded by l _A , the line J _S =J¯ _S and (the boundary lines are considered part of the regions).

We now make the following assertion, which is trivial to check:

Next, we claim that

This is obvious for and (i.e., x ⁰ is situated right of the nullcline l _J ). So assume . We have that . Thus, considering A _S fixed, is decreasing in J _S for J _S <J _S * and increasing in J _S for . So, no matter what J _S * is, the maximum value of is attained either when or when . But , since . On the other hand,

and we know that the last inequality above holds by hypothesis. Thus, we proved claim (ii). Now, we show that

Based on (i), it suffices to show that with (i.e., (J _S , A _S ) is situated ‘left’ of l _J ), we have . So let be such a point. By the same arguments as above, the maximum value of is attained either when or when . But , since . On the other hand, . The map is increasing on [0, 1], and since , we have that . So, we need . But this is equivalent to , which holds by hypothesis, and so claim (iii) is proved.

Now, based on (iii), we show that

Suppose that is false. Then there exists an such that . We can write (5) as , where

Then, since E _S is asymptotically stable, there exists U, a neighbourhood of E _S such that . From this it follows, using the fact that φ is strictly decreasing, that there exists an such that

where

Now, E _S being a fixed point of (5), we have that ; hence 1 is an eigenvalue of A ₀ (we denote by A ₀ the matrix from which we remove ϵ). But since A ₀ is strictly positive (hence irreducible) and , from the Perron–Frobenius theory, we have that r(A ₀)=1. Also, implies , hence . Then, using (v) we obtain , and since , we have that , a contradiction. So (iv) holds. Our last claim is

Again, we will argue by contradiction; suppose (vi) does not hold. So let such that . Then from (iii) we have that . Thus we have three possibilities:

I.	such that . Then is decreasing, and hence convergent. Then, from the A S equation in (5), we have that is convergent and by the continuity of Q the limit of must be a fixed point of Q, hence . So , a contradiction (because ).
II.	such that . In this case is a decreasing sequence, and we can argue similarly (as in (I)) to arrive at a contradiction.
III.	x n ‘oscillates’ in between ℛ1 and ℛ2; x n belongs to each and for infinitely many n’s. Then . Let and let such that . So by assumption, . Then, notice that (i) and (ii) imply . Moreover, from (i) we have that there exists an such that and . But being invariant, , and we have a contradiction.

So (vi) holds. Now let . From Theorem 2.2 we know that . Then using (vi) we have that there exists a . Then (iv) implies , hence . Using the asymptotic stability of E _S , we conclude that .

• (b) The J _S and A _S nullclines are

  and l _A the same as in (9). It is trivial to check that u′(J _S )>0 for , hence u is strictly increasing. Also, as (see Figure 3(b)), where ℛ₁ and ℛ₂ have the same definitions as in (a). The rest of the proof is completely analogous to the proof of (a).

  ▪

Figure 3. Dynamics of the disease-free model with (a) Ricker and (b) Beverton-Holt nonlinearities.

Proof of Theorem 2.7

We may express (1) as where the 5×5 matrix A depends on both x and the parameter β. We want to explore the solution set of , especially, near so we set . Define . Then is continuous. Let , and note that S contains the ‘trivial branch’ . Also note that can be written as , where , which is obviously differentiable.

We begin by establishing that a local bifurcation from the trivial branch can occur. We write the Jacobian matrix as

where U is a 2×2 matrix for which one is not an eigenvalue, and is given in (8). By the Implicit function theorem, a bifurcation can occur from 𝒯 at only if this matrix is singular. Since one is not an eigenvalue of U, this can only happen when one is an eigenvalue of .

As has all positive entries and is strictly increasing in β, its spectral radius is continuous and strictly increasing, by the Perron–Frobenius theory (see 2). r(β) lies between the column sums of (see 2), and so as . r(0) is the spectral radius of

which is the maximum of p _F and the spectral radius of the upper-right 2×2 block. The spectral radius of this block is greater (less) than one if and only if is greater (less) than one. But since we have . Hence r(0)<1. Therefore, there exists a unique value of such that .

The nullspace of , , equals , where and v _I is an eigenvector of corresponding to the eigenvalue one. Hence . , where , and such that is an eigenvector of . In order to show that a bifurcation occurs at β₀ from the trivial branch 𝒯, it follows by the Crandall–Rabinowitz theorem that we must show (see e.g. [8, Theorem I.5.1]). Calculation gives

where

Consequently, . We conclude from the Crandall–Rabinowitz theorem that there is a local bifurcation of a non-trivial branch of solutions of at of the form

for any |s|<δ, for some δ>0. We assume that δ is so small that satisfies for s>0 and for s<0. The Crandall–Rabinowitz theorem also implies that the intersection of a small neighbourhood of with S yields only points of the trivial branch and points of the branch given by (12).

Therefore, in a neighbourhood of there are precisely two branches of fixed points of G, the trivial branch and corresponding to .

Now, we apply the extension of the Rabinowitz global bifurcation theorem in Kielhöfer; see [8, Theorem II.5.9] for more details. Denote by the branch of solutions (12) corresponding to s≥0, and let denote the branch of solutions (12) corresponding to s≤0. Let C denote the component of containing ; Obviously, . Following 8, let C ⁺ denote the maximal component containing in and C ⁻ denote the maximal component containing in . Then but C ⁺=C ⁻ is not excluded. According to [8, Theorem II.5.9], C ⁺ (and C ⁻) satisfies one of the alternatives: C ⁺ is unbounded (i), or it contains some where (ii), or it contains a pair of points where (iii).

Let , and note that it is open in S; then . We claim that is the only limit point of P not belonging to P. Let be a limit point of P and let . First note that cannot hold since it is an isolated fixed point by Theorem 2.6(I). In fact, the same argument that establishes Theorem 2.6(I) implies that the persistence is robust, meaning that the same epsilon may be used for all parameters β in a neighbourhood of a given one (see 14). Therefore, no sequence with and , such that exists. More generally, if then either or , since these are the only boundary equilibria. We have already shown that the latter cannot occur. We now show that if then . Indeed, the definition of as a limit point of P implies that there exists a sequence satisfying and , and where and . Then

Some subsequence of converges to a unit vector satisfying . Since (or else , see (11)) and , the Perron–Frobenius theorem implies that r(β)=1 and therefore , Hence cannot be a limit point of P unless . Finally, suppose that is a limit point of P. We may assume that since we have already shown that x cannot be a boundary point of ℝ⁵ regardless of the value of β≥0. If this were the case, then

and

Denote the above matrix multiplying x _S by . As , the matrix multiplying x _I , call it , has spectral radius equal to one (from the Perron–Frobenius theory). Let . By hypothesis, we have , or . By Lemma 2.4 (see [10, Proof of Lemma 3.1]) it follows that , with equality if and only if . Thus . Now by Cramer's Rule we obtain that , a contradiction to .

The above arguments establish the claim that is the only limit point of P not belonging to P, so . Therefore and can have at most the point in common, but this point is missing from C ⁺. So, we may express the connected set C ⁺ as the disjoint union of two subsets: ; each subset is closed in C ⁺. One of these sets is empty since C ⁺ is connected, and clearly it is . Thus C ₊⊂P and, consequently, alternatives (ii) and (iii) cannot hold. We conclude that C ⁺ is unbounded. But the existence of a compact attracting set that is independent of β for the dynamics (see Proposition 2.1) implies that is bounded. It follows that is unbounded, and because it is connected and contains β₀, our final assertion is proved.   ▪

Proof of Proposition 2.8

Let be a fixed point and J=J _S +J _I and A=A _S +A _I . Then

Using the hypotheses, we find that satisfies

By Perron–Frobenius theory the spectral radius of the matrix must be greater than or equal to one or, equivalently,

It follows that and therefore . The final assertion follows from the definition of T.   ▪

Acknowledgements

Financial support was provided by a National Science Foundation Grant, DMS 0414270. The authors would like to acknowledge the useful comments of the reviewers.