The relationship between endophyte transition and plant species coexistence

Abstract

The survival possibilities of terrestrial plant species are determined by their competitive abilities. One factor that affects competitive ability is the community of microorganisms that lives in association with the plants. Microorganisms affect the competitive dominance among plants by means of their metabolites. In this paper, we study the multiple plant species coexistence mediated by interactions with endophytes (fungi). The population dynamics are described by a revised lottery competition model for multiple plant species, each of which is divided into two classes: plants with endophytes (denoted EP) and plants without endophytes (NEP). The model includes the transition of seeds from EP to NEP. We show multiple species of plants cannot coexist in a steady state if this transition is density independent, but can coexist in a steady state if this transition is an increasing function of population density.

Keywords:

• species coexistence
• endophyte
• co-occurrence
• lottery model

2000 Mathematical Subject Classification Codes :

• 39A11
• 92D25
• 92D40

1. Introduction

There are many species in the world and to find out the mechanism that promotes species coexistence is a central problem of ecology 1 14. Species coexistence is determined by the order of competitive abilities among species, and multiple species can coexist if there is some trade-off among these abilities. Ecologists have emphasized that physical heterogeneity is important, because it determines competitive hierarchies 11. However, biotic interactions can also be factors. It is known that some microorganisms, for example Neotyphodium endophytes and mycorrhizal fungi, can change plants physiologically and thereby their competitive abilities 9 12. Using a simple mathematical model, Umbanhowar and McCann 12 considered the coexistence of plant species in interaction with mycorrhizal fungi that affect their nutrient uptake rates. In their model, there are four state variables: two plant species, microorganisms and nutrients. They discuss the coexistence possibility for multiple species of plants as a function of nutrition utilization.

In this paper, we do not consider the nutrient, but we consider the case where fungi directly have an effect on production and mortality of the plants. We focus on the endophyte fungi. Endophyte fungi live intimately associated with terrestrial plants, because fungi are weak against dryness and high temperature if there is no refuge 5 9 10 13. So, there are merits for fungi to avoid dryness and high temperature by living with plants. Furthermore, fungi affect both the production ability and the survival rate of plants and give some useful traits for plant species, for example, the ability to fight against dryness or insects 5. In fact, one of the endophyte metabolites is toxin for the herbivores (i.e. insects, grazing animals). Consequently, both plant species and microorganisms have merits to live together. Clay and Schardl 4 suggested that the modified interaction among plant species mediated with the endophytes affects the web structure of the ecosystem. Clay and Schardl 4 classified the life cycle of endophyte species into three types. Type I: the fungi are heterothallic and require transmission of conidia (spermatia) between mating types for successful reproduction. Further the transmission of fungi to the plants is horizontal. Type II: mixed with Type I and Type III. Type III: the fungi are hermaphrodite, do clonal reproduction and seed mediated transmission. The transmission type is vertical. In this research, we focus on Type III. For Type III endophyte, the invasion of the endophyte into the seeds happens in the ovary and not all seeds produced by EP plants are EP seeds. Gyllenberg et al. 7 presented a mathematical model which includes this effect. The model has been used to analyse conditions for both infected and uninfected plants to co-occur. Furthermore, Lwata and Takeuchi 8 proposed a mathematical model based on the lottery model 2 3 and considered the co-occurrence of infected and uninfected plants. However, these two papers consider only one species that is divided into infected and uninfected classes.

This paper considers the transition process from infected class to uninfected class, and investigates the possibility for multiple species coexistence by the analysis of a revised lottery competition model. Here we use the term ‘transition’ for the seeds changing class from plants with endophyte (EP) to plants without endophyte (NEP) and ‘transmission’ or ‘invasion’ for endophyte from plant to plant (plant to seeds). To study how endophytes affect plant species coexistence is important for all species, because plant species is a producer in the ecological community 6. Since the transition process has not been clarified yet in biology, our mathematical model will be helpful for the observation of plants (or grass) diversity mediated with endophytes.

This paper is constructed as follows. First, we propose the model based on the revised lottery model for n species, each of which is divided into two classes, one is EP and the other is NEP. Next, we consider two possibilities of transition process. One is density-independent transition and the other is density-dependent transition. Finally, we discuss the relationship between the transition process and plant species coexistence.

2. Population dynamics of plant species

The lottery model 3 is used to investigate the population dynamics of the n plant species, each composed of EP and NEP. In the model, P _{i, t} denotes the fraction of sites occupied by individuals of NEP i and denotes the fraction of sites occupied by individuals of EP i. , denote the mortality rate of NEP and EP, respectively. So, the fraction of sites occupied by surviving plant species from time t to t+1 is given by or . In a lottery type competition model, the vacant sites will be created by the dead plant individuals. The fraction of vacant sites can be denoted by

Furthermore, β _i >0, denote the per capita production rates for NEP and EP, respectively. Therefore, the seed amount of each species i is , . We will consider the transition process from EP to NEP, of which transition fraction per unit seed number of EP is given as θ _i . θ _i have not been clarified yet in biology, so there are many possibilities. The simplest type of θ _i is density independent, . For the other possibility, the transition fraction depends on the density of seeds. Here the transition fraction is assumed to be higher for abundant seeds. In such a situation, θ _i may have the following characteristics, , and for all i>0. Seeds of EP and NEP invading the vacant space S are proportional to the ratio of the seed amounts of EP or those of NEP to all seeds, that is

for NEP and

for EP. Therefore, we obtain the following population dynamics described by difference equations for i=1, …, n.

We consider the above system on with initial state .

We can easily prove that set Ω is forward invariant. Denote the solution to Equations (1) and (2) as .

Proposition 1

, if holds.

Proof

The summation of Equations (1) and (2) for all j>0 gives . By , must be satisfied. Furthermore, if . The statement of the proposition holds by the inductive method. This completes the proof.   ▪

This proposition ensures that the fraction of sites occupied by EP and NEP is always positive and no vacant space exists. Furthermore, this system can be reduced to the original lottery model 3, if holds for all i. So multiple species cannot coexist at an equilibrium point if for ∀ i.

3. Multiple species coexistence

In this section, we investigate the possibility of the multiple species coexistence by considering the asymptotic behaviour of population dynamics. We consider the possibility of multiple species coexistence steady state, , where , for all i > 0. From Equation (1), it is trivial that the zero equilibrium of NEP species i (P _i =0) implies the corresponding zero value of EP () by the definition of R _i . On the other hand, does not imply P _i =0 in general from Equation (2) and the definition of . Hence, it is possible to have an equilibrium in which all species are present but all have only type NEP. This equilibrium gives one for the original lottery model and does not exist in general for n≥2. Also, there may exist an equilibrium point with P _j >0 (∀ j) and (for some i) in which all species are present and some have only type NEP. Note that this is impossible in general from Equation (1). Hence, in this paper, we consider only E ₊ in which all species are present and each has the co-occurrence of EP and NEP seeds.

3.1. Density-independent transition

Let us consider the simplest case where the transition fraction takes a density-independent value for each species i, where . One species case with EP and NEP was studied by Iwata and Takeuchi 8 and it was shown that EP and NEP can survive in general. We use the term ‘co-occurrence of EP and NEP’ meaning that both EP and NEP can survive in one species. They proved that co-occurrence of EP and NEP is possible, if the following condition holds:

Here 1/δ (1/δ ^e ) is a mean time of NEP (respectively EP) life span. So, () represents the expected number of seeds produced by NEP (respectively produced by EP and remained to be EP) during their life span. The co-occurrence of EP and NEP holds if EP has an advantage for the production ability. However, multiple species cannot coexist at E ₊ in general.

Proposition 2

Multiple species cannot coexist in general at a positive equilibrium point for density-independent transition case.

Proof

From Equation (2) at E ₊, we have the following equation for any i≠j:

which is not satisfied in general.   ▪

3.2. Density-dependent transition

Let us consider the case where θ _i depends on seeds amount . For simplicity, we assume that

without loss of generality where . Δ _ij indicates the ratio for EP species j to EP i of the expected number of seeds in life. From (H0), we have , which implies that EP 1 produces the smallest expected number of seeds, EP 2 is the next and EP n produces the most.

Furthermore, we assume for all i:

• for all ,

• for all .

From Appendix 1, we can obtain the following proposition.

Proposition 3

There exists at least one coexistence equilibrium point E ₊ if the following conditions hold:

where and is an inverse function of θ _i .

Since by (H0) and the definition of θ _i , (H1) implies that for , which means biologically that the transition fraction from EP 1 to NEP 1 is lower than one for any other species j. In other words, many seeds of EP species 1 remain endophyte free. This is reasonable since EP 1 has the least expected number of the seeds by (H0). (H2) implies that the expected number of seeds produced by EP i and remained to be EP (i.e. ) is larger than the number of NEP i (i.e. ) for all i>0. That is, EP is more advantageous than NEP with respect to the production ability. This corresponds to Equation (3) for one species case.

Let us consider the stability of E ₊. First we give some notations.

denotes the net productive rate for NEP i where there is no transition from EP to NEP. Here .

denotes the net productive rate for EP i without transition. Further,

is the increasing rate of supply for the seeds from EP to NEP by the transition. According to Appendix 2, we can summarize the stability conditions for E ₊ as follows.

Proposition 4

The E ₊ is locally asymptotically stable if the following conditions hold:

(H4) represents the order among NEPs with respect to net productive ability. Remember that from (H0) the ability of the production of seeds by EP i increases as i increases. For the stability, (H4) requires that net productive ability for NEP i decreases as i increases. (H5) can be interpreted as the order of the strength of density dependence effect on the transition. implies that the increasing rate for the supply from EP to NEP should be larger than the net production rate for EP. Note that always holds when is large. This means that the coexistence is possible when the transition fraction from EP to NEP becomes larger with the increase in the density of EP.

On the other hand, (H6) is rewritten as

This condition is satisfied if the coefficient of in the left-hand side of the above is less than 1, since . That is, the above is true if G _j −B _j >−1, ∀ j>0. Note that G _j represents the net production rate for NEP without the transition of seeds from EP. On the other hand, B _j denotes the increasing rate of supply for the seeds without endophyte from EP to NEP. Hence (H6) is satisfied when the net production of NEP is larger than the increasing rate of supply from EP in the sense G _j >B _j −1.

3.3. Numerical examples

Previous section gives the sufficient conditions for the existence and stability of the coexistence point E ₊. In this section, these results are checked by using some numerical examples for two species, n=2. Now for simplicity, we define several types of equilibrium points :

where [Pcirc] _i >0, P¯ _i >0 and for i=1, 2.

We assume that the transition functions are given by

First, we check the assumptions in Propositions 3 and 4 are not empty. In Figure 1(a), region A gives the set where E ₊ exists (i.e. (H1)–(H3) hold). Region B in Figure 1(b) shows the region where stable E ₊ exists (i.e. (H1)–(H6) hold). Of course, region B is included in A. Numerical simulations of Equations (1) and (2) with the parameters belonging to region A but not to region B show that E ₊ is stable. This suggests that E ₊ is always stable if it exists.

Figure 1. The δ₂−β₂ parameter plane for two species with the density-dependent transition from EP to NEP for i=1, 2. (a) Region A denotes the region where (H1)–(H3) hold (the existence region of E ₊). (b) Region B denotes the region where (H1)–(H6) hold (the stability region of E ₊). The parameters are , δ₂∈[0, 1] and β₂∈[0, 4].

Second, we show an example (Figure 2) of temporally change of the solution with the parameter values in region B in Figure 1. We can check that the solution tends to . Note that the transition functions also temporally change as time evolves. Figure 3 gives time evolution of θ _i for seven initial conditions. We can see all (θ₁, θ₂) tend to a single point . This is reasonable since E ₊ is stable. In Figure 3 three regions , and E ₂ denote the parameter regions where any solution for density-independent transition case with and β₂=0.3 tends to the single species co-occurrence state or or single NEP E ₂, respectively. It is interesting to note that the transition function evolves to the point which is located at the boundary between and .

Figure 2. This diagram shows the time evolution of the species. The values of E ₊ are , , , . The parameters are the same as Figure 1 except for δ₂=0.6, β₂=0.3 which belong to region B in Figure 1. The initial conditions are P ₁(0)=0.345, P ₂(0)=0.345, , .

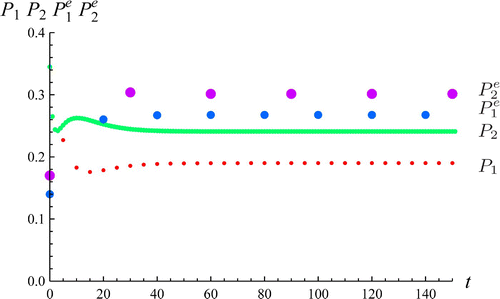
Figure 3. The θ₁−θ₂ parameter plane for two species with the density-independent transition from EP to NEP. The parameters are the same as Figure 1 except for δ₂=0.6, β₂=0.3 and θ _i ∈[0, 1] for i=1, 2. The plane is divided into three regions , and E ₂ and any solution for density-independent transition case with θ _i (i=1, 2) in each region tends to the single species co-occurrence state or or single NEP E ₂, respectively. The dot in this figure shows time evolution of the point of the solutions for density-dependent transition case for seven initial conditions. Every (θ₁, θ₂) tends to , which is a point at the boundary of and .

4. Discussions

We have investigated the possibility of coexistence of multiple plants species by considering their population dynamics mediated by endophytes, where we incorporate a transition process from infected seeds EP to uninfected seeds NEP.

For the density-independent transition case, Proposition 2 shows that multiple species cannot coexist (Figure 3). This is because of the overdetermined number of equations (Equation (4)) that must be satisfied for different species at a coexistence equilibrium. We refer to these equations as interspecific balances. These balances cannot all be satisfied in general. Note that they can be satisfied for density-dependent transition case, however. NEP seeds are always present if EP seeds are present, since EP seeds can ultimately produce both types of seeds. Therefore, the co-occurrence of both types of seeds in a species requires that EP seeds have an advantage over NEP seeds in the sense that 8, which is called as an intraspecific imbalance. These two facts suggest that the coexistence for multiple plant species requires both intraspecific imbalance and interspecific balances. A density-independent transition promotes only the intraspecific imbalance within a single plant species (with or without endophytes).

In the density-dependent transition case, from Propositions 3 and 4, we know that multiple plant species can coexist if the transition fraction θ _i from EP to NEP depends on the density of EP seeds. The coexistence conditions under the density-dependent transition are as follows:

• The expected number of the seeds produced by EP and remained to be EP is larger than the number of NEP (H2).

• The density dependence effect is intermediate (in the sense that and G _i −B _i >−1 for all i>0).

The first condition is common to both cases when the transition process is density independent or density dependent. This condition is required for the intraspecific imbalance within a plant species, that is, for the co-occurrence of both EP and NEP seed types within a plant species. The second condition characterizes those density-dependent transition processes that promote multiple species coexistence. In the density-independent case, species cannot coexist under any circumstances. In the density-dependent transition case, however, there is a possibility of coexistence if the density-dependence effect is intermediate.

Acknowledgements

This research was financially supported by the Sasakawa Scientific Research Grant from The Japan Science Society. Moreover the authors thank to the Takuya Kubo, Takenori Takada, Takami Satomura and Masayuki Yamashita for their comments on endophytes. The authors thank the anonymous reviewers for the comments on the manuscript, which helped revise our original manuscript.

Appendix 1.  The existence of interior equilibrium point

Here we prove Proposition 3.

Proof

Let (H1)–(H3) hold. At the coexistence equilibrium point, the following equations hold:

First we consider the feasibility of . For simplicity, we assume and j>1. From the second equation in Equation (A1), we can easily yield the following equation:

From assumption (H1), must hold. Secondly, we consider the feasibility of for all k>0, which can yield the following from Equation (A1):

Here (H2) guarantees for all k>0. Finally, we prove the feasibility of . Equations (A2) and (A3) yield the following equation for :

where is an inverse function of θ _i , and .

As shown above, and for i≠1, j>0 if . So Q (1)>1 is clear. Q(0)<1 is satisfied if (H3) holds. The continuity of completes the proof.   ▪

Appendix 2.  Jacobian systems of Equations (1) and (2) and proof of Proposition 4

We denote the right-hand term of Equations (1) and (2) as F _i , , respectively. The elements of Jacobian are as follows:

where Δ ^ik is Kronecker delta (Δ ^ik =1 for i=k, Δ ^ik =0 for i ≠k). We obtain the following characteristic equation C(λ):

Proof

[Proof of Proposition 4] From Equation (A7), C(G _m ) and satisfy:

By the definition of , G _i and assumption of (H5), equations (A8) and (A9) yield the following relationships:

Note that for all i>0 at E ₊ and . Hence the absolute values of 2n−1 roots of characteristic Equation (A7) are lower than one.

where . Furthermore, the absolute value of the remaining root of characteristic Equation (A7) is less than one if C(−1)>0 holds (that is, assumption (H6) holds).   ▪