Malaria model with periodic mosquito birth and death rates

Abstract

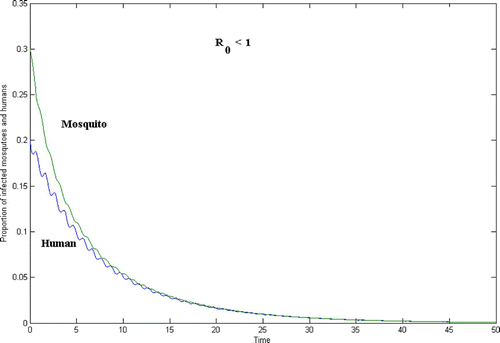
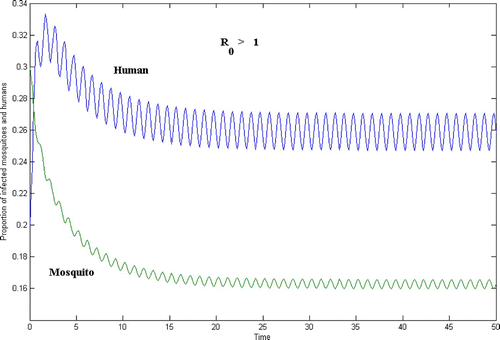
In this paper, we introduce a model of malaria, a disease that involves a complex life cycle of parasites, requiring both human and mosquito hosts. The novelty of the model is the introduction of periodic coefficients into the system of one-dimensional equations, which account for the seasonal variations (wet and dry seasons) in the mosquito birth and death rates. We define a basic reproduction number R ₀ that depends on the periodic coefficients and prove that if R ₀<1 then the disease becomes extinct, whereas if R ₀>1 then the disease is endemic and may even be periodic.

Keywords:

• asymptotic stability
• basic reproduction number
• periodic birth and death rates

1. Introduction

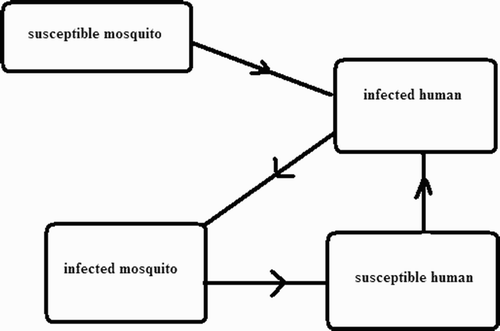
Malaria is a disease caused by a parasite called plasmodium sporozoite. Humans become infected by bites from infected mosquitoes, and mosquitoes become infected by biting infected humans. Animals can also get infected by malaria but they do not spread it to humans or to other animals 2–6,8 9 11,14–23,25 27. The human–mosquito interaction is described in Figure 1.

Figure 1. Susceptible mosquitoes bite infected humans and become infected; infected mosquitoes bite susceptible humans and these humans then become infected.

In this paper, we study the effect of seasonal variations (wet and dry seasons) on the spread of malaria. Since the mosquito population varies periodically, we introduce a seasonal variation into the birth rate of the mosquito population and into the death rates of mosquito and human. In the literature, the malaria disease is generally modelled as SIRS (susceptible, infected, recovered, susceptible) disease for the humans and SIS (susceptible, infected, susceptible) disease for the vectors, i.e. for the mosquitoes. Some studies also include the incubation period 11. Further malaria model developments have appeared in the work of Bailey 2, Bekessey et al. 3, Dietz 7 8, Macdonald 18, McKenzie and Bossert 20, and Struchiner et al. 25. The most general deterministic model of malaria, which includes both human and mosquito interactions, is due to Gideon and Shu 11. Their model is described by a system of one-dimensional equations (ODEs) with constant coefficients. In spite of all the work on malaria models, little has been done with regard to seasonal variations 5. However, there are several papers in the literature which discuss the role of seasonal variations in other disease models 14 17 26. For example, Greenhalgh and Moneim 13 studied an SIRS epidemic model with a general seasonal variation in the contact rate; their model is motivated by diseases such as measles, chickenpox, mumps, and rubella.

2. Experimental motivation and main results

Our mathematical model of malaria is based on previously published extensions of the classical Macdonald–Ross model 18 23. In our model, the total human population (N _h) is split into susceptibles (S _h), infectives (I _h) and recovered (R _h) while the total mosquito population (N _m) is split into susceptibles (S _m) and infectives (I _m). The non-autonomous model has time-dependent periodic coefficients which account for the seasonal variations (wet and dry seasons) in the birth rate of the mosquito population, and the death rates of both mosquito and human populations.

Our model is given by the following system of ODEs:

where the parameters are defined in Table 1.

Table 1. Parameters for the malaria model.

	constant, infectivity of humans
	constant, infectivity of mosquitoes
b m	constant, man-biting rate of mosquitoes
	constant, human per capita birth rate
αh	constant, human recovery rate
βh	constant, rate of loss of immunity
	periodic mosquito per capita birth rate
μm(t)	periodic mosquito per capita death rate
μh(t)	periodic human per capita death rate

To analyse the model, we introduce the following variables:

Then, and , so that and . In the new variables, the malaria model becomes

where and . After normalization of the initial data, we obtain

and

The variables of the model are defined in Table 2.

Table 2. Variables for the rescaled malaria model.

s h	proportion of susceptible individuals (humans)
i h	proportion of infected individuals
r h	proportion of recovered individuals
s m	proportion of susceptible mosquitoes
i m	proportion of infected mosquitoes

By definition, the variables in Table 2 should satisfy the equations and this is indeed proved in Lemma 3.2.

All the parameters in Table 1 are positive constants except the T-periodic functions , μ_m(t) and μ_h(t). The parameter β_h relates to the period of time during which the recovered humans are immune, and it represents the rate of loss of immunity. The parameter represents birth rate; children of infected and of recovered individuals are born as susceptible individuals, and thus there is a loss of the infected and recovered populations at rate . On the other hand, it is assumed that birth rate does not increase or reduce the relative proportions of susceptibles. Newborn mosquitoes of the infected population are assumed to be susceptible and thus new births decrease i _m at a rate and increase s _m at the same rate . We assume that birth rate of susceptible mosquitoes does not increase or reduce their relative proportion. Worldwide, there are about 300–500 million annual cases of malaria with 1–3 million deaths 5. For example, in Mali more than 50,000 people die from malaria annually. A large percentage of these malaria deaths occur during the wet season. To capture this in our model, we assume that the mosquito and human death rates (and thus their longevity), μ_m(t) and μ_h(t), may vary periodically with time. Furthermore, the birth rate of mosquitoes, , is also periodic. Our model does not include a latent period for bitten humans or mosquitoes; including these classes of populations would introduce a time delay into the system. To make the ratio of mosquito to human populations periodic, we assume throughout the paper that

Then, is T-periodic (see Lemma 3.4).

The function varies with the season. It is a periodic function which takes larger values during the wet season and smaller values during the dry season. In this paper, we focus on the following question: Under what assumptions on the model coefficients is the malaria disease endemic?

In the case where , μ_m(t) and μ_h(t) are constant functions, the answer can be given in terms of the so-called basic reproduction number R ₀: When R ₀<1 the disease goes extinct, whereas when R ₀>1 the disease persists 1 2 7 18.

The novelty of the present paper is that it provides an answer to the above question when , μ_m(t) and μ_h(t) are non-constant, namely when , μ_m(t) and μ_h(t) are T-periodic. We shall compute the basic reproduction number as

assuming, of course, that for all t. We shall prove by rigorous mathematical analysis that if R ₀<1 then the disease goes extinct in both human and mosquito populations, as illustrated in Figure 2, whereas if R ₀>1 then the disease remains endemic in both populations and could even be periodic as illustrated in Figure 3. In both Figures 2 and 3, we have taken

Figure 2. Human and mosquito population for the case R ₀<1.

Figure 3. Human and mosquito population for the case R ₀>1.

In Figure 2, γ=0.9, whereas in Figure 3, γ=2.5. In both figures, the initial population size is

and the time t in the horizontal axis is measured in years.

In Figures 2 and 3, the time t=50 on the horizontal axis corresponds to 50 years. Since and are periodic of period 1, each period corresponds to one season.

The ideas involved in our analysis could be applied to other systems of ODEs with periodic coefficients. Examples of previous work on disease models with periodic coefficients include Bacaër and Guernaoui 1, Chitnis et al. 5, Franke and Yakubu 10, Grassly and Fraser 12, Greenhalgh and Moneim 13, Hoshen and Morse 14, Ma and Ma 17, Smith 24, Wang and Zhao 26, and Wyse et al. 27.

According to the 2006 UNICEF report, malaria is one of the most life-threatening tropical diseases for which no successful vaccine has been developed. Sulphadoxine-pyrimethamine (SP) is an effective drug for a person infected with the malaria disease. In a 2002 experimental study of the effectiveness of SP as a temporary vaccine, Coulibaly et al. 6 considered two groups of people at a site in Bandiagara (Mali), a region of endemic malaria. The first group was administered SP at the beginning of the wet season, and the second group was not given the drug. The two groups were monitored during the entire wet season for the first malaria disease episode. Coulibaly et al. observed that in the first four weeks much fewer first episodes occurred in the first group. However, this was slowly reversed between the fourth week and eighth week. The experimental data of Coulibaly et al. over the entire wet season in Mali (May–August) showed no significant advantage to the group that received SP. We believe that our mathematical malaria model framework could be used to explore possible SP administration protocols that would optimize its effectiveness as malaria vaccine.

The paper is organized as follows: preliminary technical results on our model are given in Section 3. In Section 4, the basic reproduction number R ₀ is introduced and is used to determine the global extinction of the infective population when R ₀<1. Sections 5 and 6 deal with the persistence of the disease and with existence of a periodic solution when R ₀>1.

3. Preliminary results

In this section, we establish the invariance of the first quadrant, the plane

and the line

Lemma 3.1

Let A(t) and B(t) be n×n matrices of bounded measurable functions on [0, ∞). If , B(t)≥0 for 0<t<t ₀ and r(0)>0, or r(0)=0 but B(0)>0, then r(t)>0 for all 0<t<t ₀.

Indeed, this follows from the integrated form of the differential equation

Lemma 3.2

The following identities hold:

Proof

Adding Equations (2)–(4), we obtain

and recalling Equation (7), the assertion (13) follows. Similarly, we obtain the assertion (14).   ▪

Lemma 3.3

The following inequalities hold:

Furthermore, if i _h(0)>0 then these inequalities are strict inequalities.

Proof

Consider first the case where i _h(0)>0. Let {0<t<t ₀} be any interval such that i _h(t)>0 for 0<t<t ₀. By Equations (4)–(6) we have,

so that, by Lemma 3.1, r _h(t)>0, i _m(t)>0 and s _m(t)>0 for 0<t≤t ₀.

Next, equations by (2) and (13),

so that also s _h(t)>0 for 0<t≤t ₀.

We next show that i _h(t) remains positive for all t>0. Proceeding by contradiction we suppose that i _h(t)>0 for 0≤t<t ₀ and . Then . On the other hand, by Equation (3),

which is a contradiction. This completes the proof of the lemma in the case i _h(0)>0. It remains to consider the case i _h(0)=0. In this case so that either s _h(0)>0 or r _h(0)>0. Suppose s _h(0)>0 and denote by , , , , , the solution of Equations (2)–(6) with , , , , , where . By what we have already proved, all the components of the δ -solution remain strictly positive for all t>0. Taking , the lemma follows. The case where r _h(0)>0 is treated in the same manner.   ▪

Lemma 3.4

Proof

From model (1), and . Hence, whenever N _m(0)>0. Similarly, N _h(t)>0 whenever N _h(0)>0. Let . Then, . Hence,

and, by Equation (10),

  ▪

4. Global stability of disease-free equilibrium

In this section, we define a basic reproduction number R ₀ and prove that, independent of the initial population size, if R ₀<1 then the disease will die out.

In view of Lemma 3.2, it suffices to consider the sub-system of Equations (2)–(6) for s _h, i _h and i _m which we conveniently write in the form

The following matrix will play a fundamental role in the sequel:

The point

is the disease-free equilibrium point of Equations (15)–(17).

R ₀ is defined by Equation (11). Note that the average infectious period of a single person is , since (when i _m=0) . Also, the average infectious period of a single mosquito (when i _h=0) is . Hence, R ₀ may be viewed as the average value of the expected number of secondary infection cases produced by a single infected individual entering the population at the DFE. R ₀ is called the basic reproduction number.

We note that if R ₀<1 then the two eigenvalues of the matrix A have negative real parts, whereas if R ₀>1 then one eigenvalue is positive and the other is negative.

Theorem 4.1

If R ₀<1 then the disease-free equilibrium point, DFE=(1, 0, 0), is globally asymptotically stable.

Proof

Since and , using Lemma 3.4 we have that and .

Let be the solution of

with , δ>0. By integration we obtain, for any integer n≥0 and t=nT+t ₀ (),

where A is the matrix defined in Equation (18).

Since R ₀<1, the eigenvalues of A have negative real parts and the same is true for A+δ I provided δ is small enough. Hence,

We claim that

Indeed, otherwise there exists a first point t=t ₀>0 such that either or . Suppose that the first case occurs. Then

On the other hand, since for t<t ₀ and , we obtain , which is a contradiction. The case can be handled in the same way. Letting in Equation (20) and using Equation (19), we conclude that

It remains to show that . By Equation (15),

where as , by Equation (21). Using the relation (12), we deduce that as .   ▪

5. Endemic malaria

Here, we use a series of auxiliary results to prove that R ₀>1 implies the persistence of malaria disease in the periodic environment.

Theorem 5.1

If R ₀>1 then there exist numbers δ₀>0 and δ₁>0 such that for any initial values there is a time such that and for all .

We first establish several lemmas.

Lemma 5.2

Let a and b be any positive numbers.

1. If

   and then for all T ₀<t<ξ, where

2.  If

   and then for all T ₁<t<ξ, where

The proof follows from the integrated form of the differential inequalities (22) and (23).

Lemma 5.3

Let η₀ be any positive number such that

and set

If for 0<t<ξ where then

Proof

By Equation (4), and . Applying Lemma 5.2(i) with , the assertion follows.   ▪

If , and x ₁≥y ₁, x ₂≥y ₂, then we write X≥Y.

Lemma 5.4

Let η₀ and η₁ be any small positive numbers, and assume that

where T ₀(η₀) is defined by Equation (24) and . Then, for any positive integer n such that there holds

where and K is a positive constant.

Proof

By Equations (13), (16) and (17) we have

where

By Equation (25) and Lemma 5.3,

and

where . Let

with , and .

Claim.  For t>T ₀,

Indeed, otherwise there is a first point T ₁ such that the claim holds for all t<T ₁ but either

Consider case (i). Then

From Equations (27) and (29), at t=T ₁

a contradiction to Equation (30).

Similarly, we derive a contradiction in case (ii). This completes the proof of the claim.

Taking , we conclude that the claim holds even when . Set

Then by the representation formula for Y in the proof of Theorem 4.1,

where

Combining this with the inequalities

and

the proof of the lemma is complete.   ▪

Lemmas 5.2 and 5.3 did not use the assumption R ₀>1. But from now on we shall use this assumption. We shall also always choose η₀ and η₁ sufficiently small so that one eigenvalue of the matrix in Equation (26) is positive and bounded from below by a positive constant. Setting

the inequality (26) implies the following result.

Corollary 5.5

Under the assumptions of Lemma 5.4, if η₀ and η₁ are sufficiently small, then

where c ₁ and μ are positive constants, independent of η₀ and η₁.

Lemma 5.6

For any sufficiently small positive η₀, set

where . If ξ>T ₁ and for 0<t<ξ, then for T ₁ ≤ t ≤ ξ.

Proof

Since , we have from Equation (17)

By Lemma 5.2(ii) with z ₀=0, , we conclude that

if .   ▪

Lemma 5.7

For any sufficiently small η₁>0, set

If ξ>T ₂ and for 0<t<ξ, then for T ₂<t<ξ.

Proof

From Equation (15), we have

Applying Lemma 5.2(ii) with z ₀=0, , we conclude that

if T¯<t<ξ, where . Substituting this estimate into Equation (16) and using the assumption that in Equation (17), we obtain

for T¯<t<ξ. We now use Lemma 5.2(ii) again with initial value z(T¯)=0 and to conclude that if T ₂<t<ξ.   ▪

For future reference we state the following fact which follows immediately from the differential equations for i _h and i _m.

Lemma 5.8

There exists a positive number B such that, for any

and

Lemma 5.9

Let η₀ and η₁ be sufficiently small positive numbers and set

where μ and c ₁ are as in Equation (33). Then there exists a time such that either

Proof

Suppose, to the contrary, that

By Corollary 5.5 and Lemma 5.8, we obtain

and the right-hand side is larger than if

Hence, there must be a time t ₁ in the interval (0, t¯ ₁) for which at least one of the inequalities in Equation (36) is reversed.   ▪

We shall now use Lemmas 5.2–5.4 Lemmas 5.6–5.9 and Corollary 5.5 to prove Theorem 5.1.

Proof of Theorem 5.1

Consider first the case where, in Lemma 5.9, . Then, by Lemma 5.8,

and, by Lemma 5.6,

if , where T ₁ is as in Lemma 5.6. Hence, there exists a time t ₂ such that

and

Consider next the case where in Lemma 5.9. Then

and, by Lemma 5.7,

where and T ₂ is as in Lemma 5.7. We may increase T¯ or ¯T¯ to make them equal. Then, in both the cases which may occur in Equation (35),

and

for some where [ctilde] depends on the coefficients of the differential system, but not on η₀ and η₁.

We now repeat the above process starting at time t=t ₁+t ₂. We note, however, that whereas in Equation (34) if , in the present case the time is uniformly bounded by a constant which depends on η₀ and η₁ but not on i ⁻(0). Indeed this is a consequence of the estimates (37)–(40). We conclude that either or where t ₃∈ . Thus, as before, there exists a time t ₄ such that and , . Proceeding in this way step by step, we obtain a monotone increasing sequence of points t _k such that , , , , , and , where depends on η₀ and η₁, but ĉ is independent of η₀ and η₁. Using Lemma 5.8 to estimate i _h(t), i _m(t) in the intervals t _k <t<t _k+1, the proof of Theorem 5.1 is complete.   ▪

6. Endemic malaria on periodic solution

In this section, we prove that if R ₀>1 then there exists at least one periodic solution of the system (2)–(6). The proof is based on Theorem 5.1 and on the following fixed point theorem of Horn.

Theorem 6.1

(Horn's fixed point theorem 13) Let be non-empty convex sets in a Banach space X such that X ₀ and X ₂ are compact and X ₁ is open relative to X ₂. Let W be a continuous mapping such that, for some positive integer m, for and for , where . Then W has a fixed point in X ₀.

Theorem 6.2

If R ₀>1, then there exists at least one T - periodic solution of the system (12)–(14). That is, R ₀>1 implies the persistence of the infective human and mosquito populations on a periodic solution.

Proof

The proof uses the same argument as Greenhalgh and Moneim 13. We write a variable point in R ⁵ in the form and we write z≥0 if all the component of z are nonnegative. We introduce the convex sets

where δ₀ and δ₁ are as in Theorem 5.1. Given any in R ⁵, let z(t) denote the solution of Equations (2)–(6) with initial data z ₀, and set W=z(T). Clearly, W maps continuously, and by Lemmas 3.2 and 3.3, for j=1, 2, 3, …. By Theorem 5.1, if then . Furthermore, X ₁ is open relative to X ₂. Hence, we can apply Horn's fixed point theorem to conclude that W has a fixed point, which is clearly a T-periodic solution of Equations (2)– (6).   ▪

Acknowledgements

We thank the referees for useful comments and suggestions that improved our manuscript. This work was partially written when the first author was visiting the Mathematical Biosciences Institute (MBI) at Ohio State University; he wishes to thank the MBI for its hospitality. He also wishes to thank Drs. Winston Anderson, Frances Mather and Ousmane Koita for their support throughout this study. This work was partially supported by the National Sciences Foundation upon grant No. 0112050. Abdul-Aziz Yakubu was partially supported by Howard University MHIRT Program 2006 and NIH Award No. 9T37MD001582-09.