Dynamics of discrete-time larch budmoth population models

Abstract

The larch budmoth (LBM) population in the Swiss Alps is well known for its periodic outbreaks and regular oscillations over several centuries. The ecological mechanisms that drive these oscillations, however, have not been unambiguously identified, although a number of hypotheses have been proposed. In this article, we investigate several LBM resulting from these different ecological hypotheses. We first study a leaf quality-moth population model and then two moth–parasitoid models. Existence and stability of equilibria are investigated and sufficient conditions for which populations can persist are derived. We then provide conclusions based on our analysis.

Keywords:

• larch budmoth
• leaf quality
• asymptotic stability
• period-doubling bifurcation
• uniform persistence

1. Introduction

Outbreaking forest insects provide fascinating examples of complex population dynamics. The population of larch budmoth (LBM), Zeiraphera diniana, in the Swiss Alps is well known for its periodic outbreaks and regular oscillations 2. As in most outbreaking forest insects, identifying causal mechanisms for LBM outbreaks has proven difficult. It is becoming clear, however, that exogenous factors cannot generate consistent periodic cycles and that density-dependent effects from biotic interactions are the most likely mechanisms 5.

A number of biotic mechanisms have been proposed. There is a lack of empirical support for maternal effects, and although viral infections were observed to cause substantial mortality during two intensively studied LBM outbreaks, subsequent outbreaks collapsed without being accompanied by an increase in viral mortality 2. Two non-mutually exclusive hypotheses for the cause of LBM cycles are currently en vogue: (1) plant quality effects and (2) parasitoid–host interactions. Plant quality and parasitism both have the necessary interaction effects to induce cycles 12. For example, it usually takes several years for the leaf quality to recover after a serious LBM outbreak, and field and laboratory studies show that poor plant quality has a strong effect on LBM survival and reproduction 2, the consequence of which could result in regular cycles. As for parasitoid effects, previous analyses for direct density-dependent effects suggested that parasitoids had little role in creating population cycles because parasitism rates at peaks in LBM population size were relatively low 2. However, as Turchin et al. 12 pointed out, population cycles are the result of second-order lags in density-dependent effects, and thus rejection of the parasitoid hypothesis was inappropriate.

The goal of the present study is to provide mathematical analysis on the models proposed by Turchin et al. 12. We first investigate a leaf quality-LBM model and then two LBM-parasitoid models. Because LBM has an annual life cycle with non-overlapping generations, the models are systems of difference equations. We investigate the existence of simple stationary solutions of the systems and their stabilities. Bifurcation analysis for each of the models will also be performed. Criterion for population persistence will be derived. We will compare and contrast these analytical results. In the following section, we study a leaf quality-LBM model. Section 3 investigates parasitoid-LBM models. The final section provides some biological conclusions.

2. A plant quality-LBM model

Let N _t denote the LBM density at time t, t=0, 1, …, where the moth population density is measured in terms of the number of third instar larvae per kilogram of larch branches. Since third instar larvae have approximately the same dimensions, the density is proportional to the biomass. On the other hand, population densities are usually used in host–parasitoid interactions. For these reasons, the LBM density is used in the leaf quality LBM model instead of biomass.

The leaf quality (e.g., raw fibre and protein content) at time t is denoted by Q _t . Good leaf quality means low fibre and high protein content. The needle length is a good index of plant quality since it is well correlated with raw fibre and protein content of needles 7 10. Moreover, data collected in 4 also indicated that needle length has a strong effect on larval survival and pupal biomass, where pupal biomass is closely related to adult fecundity. Therefore, the index of plant quality Q is measured in terms of average needle length L from field studies using a linear conversion

where the average minimum and maximum needle lengths of larch trees observed in the data collected are 15 and 30 mm, respectively 12. As a consequence, Q _t is dimensionless and lies between 0 and 1.

The dynamics of leaf quality in the absence of the moth population is modelled by a simple linear recursive equation , where 1−α is the recovery rate of plant quality. The plant quality decays to 0 at a rate α if the plant cannot renew itself. It is also assumed that the effect of leaf quality is on budmoth's intrinsic growth rate but not on its carrying capacity, and the effect of plant quality on budmoth is modelled by a simple expression with saturation , where δ>0 is the half-saturation constant for the plant quality. The uptake of the moth population upon the plant is modelled using a Michaelis–Menton form , where γ>0 is the half-saturation constant for the moth population uptake.

Under the above biological consideration, the interaction between plant quality and LBM population can be described by the following system of two first-order non-linear difference equations:

where parameters are positive and 0<α<1. Notice that since

when the density-dependent mechanism is not incorporated, we see that the per capita growth rate of the moth population is an increasing function of leaf quality Q. Parameter β is the intraspecific competition coefficient for the moth population, which denotes how intensively individuals compete for space and other resources within the moth population, and parameter λ is the intrinsic growth rate of the moth population. The population will either grow to infinity or decay to zero exponentially depending on whether λ is greater than or less than one if there is no density-dependent effect incorporated into the interaction.

We first rescale the system by letting and . Then system (1) can be rewritten as

Observe that x _t =0 for t≥1 if either x ₀=0 or Q ₀=0. In this case, . Also x _t >0 and Q _t >0 for t≥1 if x ₀>0 and Q ₀>0. Since for t≥0, we have

Also for t≥0 implies

We conclude that solutions of system (2) remain non-negative and are bounded, and therefore model (1) is biologically sound.

Lemma 2.1

Solutions of system (2) remain non-negative for t>0 and are bounded.

System (2) has a trivial stationary solution E ₀=(0, 1) for all parameter values where LBM population is extinct. The Jacobian matrix of system (2) evaluated at E ₀ has the form

Hence E ₀ is locally asymptotically stable if and unstable if . It can be easily shown that E ₀ is globally asymptotically stable if .

Theorem 2.2

If then equilibrium E ₀=(0, 1) is globally asymptotically stable for system (2).

Proof

We claim that if . This is clear if λ<1. If λ=1, then x _t+1<x _t for t≥0 implies . If ◯>0, then from the first equation of (2) we would have a contradiction, namely

by Lemma 2.1. Hence ◯=0. Suppose now . It follows from (3) that for any ϵ>0, we can find t ₀>0 such that for t≥t ₀. We choose ϵ>0 so that

Therefore,

and thus . This shows that if . Hence, for any ϵ>0, there exists t ₁>0 such that for t≥t ₁. Consequently,

implies

Letting , we have by (3). Since E ₀ is locally asymptotically stable, E ₀ is globally asymptotically stable.   ▪

Since 1 is the maximum plant quality which the larch trees can maintain, can be interpreted as the maximal growth rate of the moth population. The moth population can attain this maximal growth rate only when the tree quality is at its optimal condition. Consequently, the moth population becomes extinct if this maximal growth rate is less than 1.

Suppose now . Then E ₀ is unstable with stable manifold lying on the non-negative Q-axis. The x, Q-components of a coexisting equilibrium where both populations can persist must satisfy

and

Note that Equation (4) has a positive solution if and only if , where the positive solution is unique. Consequently, system (2) has a unique interior steady state if and only if , where x¯>0 satisfies Equation (4) and . Moreover, we see from Equation (4) that x¯ is an increasing function of both m and λ. However, x¯ is independent of α. On the other hand, since Q¯ is a decreasing function of x¯, Q¯ is a decreasing function of λ, but it is also independent of α.

The Jacobian matrix of system (2) evaluated at Ē has the form

with and

Applying the Jury conditions 1, we see that Ē is locally asymptotically stable if . Using , we obtain

Moreover, is equivalent to

The second inequality is always true since 0<α<1. Therefore, Ē is locally asymptotically stable if the first inequality holds, which results in

At those parameter values for which (5) becomes an equality, one of the eigenvalues of J¯ is of −1 while the other eigenvalue has modulus less than 1. We conclude that a period-doubling bifurcation may occur at those parameter values that equate inequality (5).

We next prove that both populations can persist if . System (2) is said to be uniformly persistent if there exists a constant A>0 such that and for all solutions (x _t , Q _t ) of system (2) with x ₀>0 and Q ₀>0. We shall apply the techniques introduced by Hofbauer and So 8.

Theorem 2.3

Let . Then system (2) has a unique interior steady state and system (2) is uniformly persistent. Moreover, Ē is locally asymptotically stable if (5) holds.

Proof

By the above discussion, we only need to prove the uniform persistence of system (2). Let . Then is forward invariant for system (2) and (2) has a global attractor X. It is clear that the only invariant set in Y is {E ₀}. We proceed to verify that {E ₀} is isolated in X and the stable set of E ₀ is contained in Y.

Since , there exists ϵ>0 such that

If {E ₀} is not isolated in X, then there exists a maximal invariant set M in with , where denotes the open ball centred at E ₀ of radius ϵ. Let . Note that and there exists Q _*, such that . Let . It follows that

and we obtain a contradiction since M is invariant. This shows that {E ₀} is isolated in X. To verify that the stable set of E ₀ lies in Y, by contradiction, suppose there exists (x ₀, Q ₀) with x ₀>0, Q ₀>0 such that . Then by a similar argument as above, we see that

for all except finitely many t, where

Hence , and we obtain another contradiction. Therefore, the stable set of E ₀ lies in Y and system (2) is uniformly persistent by [8, Theorem 4.1].   ▪

In order to study the system further, we numerically simulate system (2). We choose δ=2, m=15, α=0.5, and use λ as a bifurcation parameter. The choice of using λ as the bifurcation parameter is motivated by the fact that fecundity of female adult LBM can vary significantly depending on environment factors such as temperature, moisture, etc.

When λ is less than 3=δ+1, the moth population crashes as demonstrated analytically in Theorem 2.2. When λ is between 3 and 10, then simulations revealed that there is only steady-state dynamics. All solutions randomly chosen converge to the coexisting equilibrium. The bifurcation diagrams presented here start with λ=10 and end with λ=60. It is clear that a period-doubling bifurcation occurs when λ is somewhere between 22 and 25 and the moth population density of the coexisting steady state in Figure 1(a) increases as we increase λ before hitting the first bifurcation value. The opposite situation is observed for the plant quality in Figure 1(b).

Figure 1. Bifurcation diagrams for system (2) with λ as the bifurcation parameter. Other parameter values are δ=2, m=15, and α=0.5. The vertical axis represents moth population density (a) and leaf quality (b).

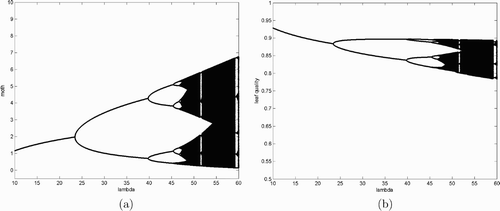
These numerical results confirm our earlier analysis. It can be seen that the system clearly has a positive period two solution when λ is just beyond 25, right after the period-doubling bifurcation. Figure 1(a) and (b) are the bifurcation diagrams of system (2) for the moth population density and plant quality, respectively. We see from these diagrams that period-doubling bifurcations occur continuously and the system eventually becomes chaotic when λ is further increased. Notice that similar dynamical behaviour of system (2) is observed when we change parameter values of δ, α, and m. In particular, bifurcation diagrams similar to those of Figure 1 for the budmoth population and leaf quality are obtained when we vary parameter values of δ, α, and m.

3. Moth–parasitoid models

It is well known that parasitoids play an important role in population dynamics of forest insects 11. For this reason, LBM parasitoids were intensively studied from the beginning of the systematic research on LBM oscillations. There are two main groups of parasitoids that are important in affecting LBM population, eulophid species, and ichneumonids. Eulophids attack primarily the third instar of LBM, while the ichneumonid attack mainly the fifth instar. In this section, we present and investigate two models proposed by Turchin et al. 12.

3.1. A simple moth–parasitoid model

Similar to the previous section, we let N _t be the LBM population density at time t. The parasitoid population density at time t is denoted by P _t , which is the number of adult parasitoids per kilogram of larch branches. Following that of Beddington et al. 3, the first model is based on the Nicholson–Bailey model 9 with parasitoid interference functional response, aP/(1+awP), as suggested by the preliminary data analysis on the moth–parasitoid interaction, where a is the parasitoid searching rate and w is the parasitoid wasted time. The model is given below:

where parameters , b, and a are positive. Parameter b is the number of surviving parasitoid produced by each parasitized moth, and parameters λ, β have the same biological meanings as in the leaf quality-LBM model (1) presented in the previous section. Note that (6) is the model proposed by Beddington et al. 3 when w=0. It is assumed in 12 that 0<w≤1.

To simplify the system, we define new state variables , y _t =aP _t , and let c=ab/β. Then system (6) becomes

Observe that each of the non-negative coordinate axes is forward invariant for system (7). Moreover, system (7) reduces to the classical Ricker equation

when the parasitoid population is absent. It is also clear that solutions of system (7) satisfy

for t≥2. Therefore, model (6) is also biologically reasonable.

Lemma 3.1

Solutions of system (7) remain non-negative for t>0 and are bounded.

Since system (7) is a predator–prey model, steady state E ₀=(0, 0) always exists where both populations are extinct. The Jacobian matrix of system (7) evaluated at E ₀ has a simple form . It follows that E ₀ is locally asymptotically stable if λ<1 and unstable if λ>1. Since and for t≥0, it can be easily shown that E ₀ is globally asymptotically stable if λ<1. The proof of the following theorem is omitted.

Theorem 3.2

Steady state E ₀=(0, 0) is globally asymptotically stable for system (7) in if λ<1.

Observe that λ is the inherent net growth rate of the moth population. It is the growth rate of the population when population size is very small before intraspecific competition making any effect. The population cannot survive if the inherent growth rate λ is less than 1. If λ>1, then E ₀ is unstable with stable manifold lying on the non-negative y-axis and there exists another boundary steady state where only the budmoth population can survive. The linearization of system (7) with respect to E ₁ yields the Jacobian matrix Therefore, E ₁ is locally asymptotically stable if

and

Note that inequality (10) is also the sufficient condition for local stability of lnλ as the positive steady state for the corresponding Ricker equation (8). Equilibrium lnλ is globally asymptotically stable in (0, ∞) for Equation (8) if (10) holds, it is unstable if inequality (10) is reversed, and a period-doubling bifurcation occurs when 1.

It can be shown that E ₁ is globally asymptotically stable for system (7) whenever it is locally asymptotically stable.

Theorem 3.3

Let λ>1. Then system (7) has two boundary equilibria E ₀=(0, 0) and , where E ₀ is unstable and E ₁ is globally asymptotically stable in if inequalities (10) and (11) hold.

Proof

We only need to prove global attractiveness of E ₁ in when Equations (10) and (11) are satisfied. Let (x _t , y _t ) be an arbitrary solution of system (7) with x ₀>0. Since lnλ is globally asymptotically stable for Equation (8) in (0, ∞) by Equation (10) and holds for t>0, . Therefore, for any ϵ>0, we can find t ₀>0 such that for t≥t ₀. Since , we can choose ϵ>0 such that . It follows from the second equation of (7) that for t≥t ₀. This shows that , and as a result we have . Consequently, E ₁ is globally attracting in and the proof is complete.   ▪

Since each parasitized LBM can reproduce c number of parasitoids, clnλ can be interpreted as the reproductive number of the parasitoid when the moth population is stabilized at the lnλ level. The parasitoid population cannot invade the moth population if this reproductive number is less than one.

We proceed to discuss the existence of coexisting equilibria. Let (x, y) be an interior steady state of system (7). Then

and

Letting z=y/(1+wy), Equation (13) becomes

Observe that y>0 if and only if 0<z<1/w, and if and only if . We conclude that Equation (7) has a coexisting steady state if and only if Equation (14) has a solution z* such that

with and . Consequently, we will look for a solution z* of Equation (14) that satisfies inequality (15).

Let and for . Then g(0)=0, , and g is increasing and concave up on (0, 1/w). Also , , for , and has a unique solution in , i.e., h(x) is a one-humped function on . Using these, it can be shown that system (7) has a unique interior steady state when .

Theorem 3.4

Let λ>1. Then system (7) has a unique interior equilibrium if and only if . Moreover, system (7) is uniformly persistent if and .

Proof

Suppose . We claim that Equation (14) has no solutions satisfying (15). For simplicity, we let . Since cr<1, it is clear that for 0<x<1/w. Moreover, holds for 0<x<r. Therefore, for and Equation (14) has no solutions satisfying (15). Consequently, system (7) has no interior steady state if .

Suppose now . It can be easily shown that Equation (14) has a unique solution satisfying (15). Indeed, by our assumption of cr>1, we see that y=h(x) lies above y=g(x) for x>0 and x small. Assume r≤1/w. The case when r>1/w can be argued similarly. Notice h(r)=0 and g(r)>0 imply that h(x)=g(x) has at least one solution in (0, r). If there were more than one solution in (0, r), let 0<x ₁<x ₂<r be the first two solutions. Then we must have and . Since , we obtain by the above two inequalities and arrive at a contradiction because h is concave down on (0, r). Therefore, (14) has a unique solution satisfying (15) and we conclude that system (7) has a unique interior equilibrium if and only if .

To prove the uniform persistence of system (7), observe that since , Equation (8) has only simple dynamics, namely the positive steady state lnλ is globally asymptotically stable in (0, ∞). The proof is similar to the proof of Theorem 2.3. We shall apply Theorem 4.1 of 8. Let Y be the set of non-negative x- and y-axes. It is clear that system (7) has a global attractor X and the only invariant subset in Y is {E ₀, E ₁}. We need to verify that {E _i } is isolated in X and the stable set of E _i lies in Y for i=0, 1. It is straightforward to show that {E ₀} is isolated in X using λ>1. Indeed, if {E ₀} is not isolated in X, then for any ϵ>0 we can find a maximal invariant set M ₀ in such that {E ₀} is a proper subset of M ₀. Since λ>1, we can choose ϵ>0 such that and let . Then and there exists y _s , , such that . Let . It follows that which contradicts the choice of x ₀. Similarly, if {E ₁} is not isolated in X, then for any ϵ>0 given we can find a maximal invariant subset M ₁ in with . Notice . We choose ϵ so that and . Notice there exists x _u , , such that . Let . Then which is impossible.

It remains to verify that the stable set of E _i lies in Y. Suppose there exist x ₀>0 and y ₀>0 such that . Then for any ϵ>0 there exists t ₀>0 such that and for t≥t ₀ We choose ϵ>0 such that . It follows that x _t+1>x _t for t≥t ₀, and we would have , which is impossible. The proof for the stable set of E ₁ lying in Y is similar. Therefore, system (7) is uniformly persistent by Theorem 4.1 of 8.   ▪

Notice in the above theorem we only showed that both populations can persist when and . It is suspected that populations can coexist even when lnλ is greater than 2 but not too large. We use a numerical example to demonstrate that the parasitoid population may become extinct when lnλ is large. The parameter values used in these simulations are c=10, w=1, and λ ranges from 30 to 60. It can be seen from Figure 2(b) that the parasitoid population crashes when λ is just less than 55. This is somewhat biologically unexpected. One would expect that the large inherent net reproductive rate of the moth population will enhance the growth of parasitoid since it relies on the moth population for its own reproduction. Figure 2(a) is the corresponding bifurcation diagram for the moth population. From this we see that the LBM population survives, whereas the parasitoid population goes extinct when λ is large. This unexpected phenomenon is probably due to the frequent fluctuation of the LBM, which drives the parasitoid to extinction.

Figure 2. Bifurcation diagrams for system (7) using λ as the bifurcation parameter with c=10 and w=1. (a) budmoth population; (b) parasitoid population.

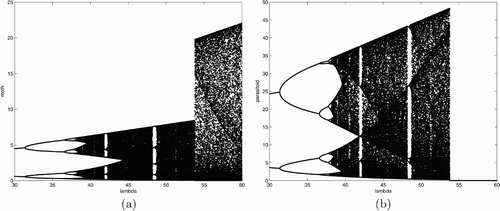
Suppose now so that E ₁ is unstable and system (7) has a unique coexisting equilibrium . Note from (12) we have , i.e., the LBM population density in the coexisting steady state is always less than the LBM population density of the non-trivial boundary steady state for which the parasitoid population is extinct. The stability of E* can be determined by the corresponding Jacobian matrix

It can be easily verified that for all w>0. Indeed, is equivalent to

and

if and only if

which is clearly valid for all w>0. Hence, always holds for all 0<w≤1. Therefore, a +1 bifurcation is impossible to occur when E* loses its stability. Furthermore, a direct computation shows that is equivalent to

where

and

if and only if

We conclude that if w≥1/2, i.e., a Hopf bifurcation cannot occur if w≥1/2. As a consequence, only a period-doubling bifurcation is possible when E* loses its stability if w≥1/2.

Recall that in Figure 2 we use w=1 for the simulations. Although we are only able to prove analytically that only a period-doubling bifurcation can occur when E* loses its stability for w≥1/2, bifurcation analysis seems to suggest that this is the case for all 0<w≤1. Moreover, it is showed that a +1 bifurcation cannot occur for all 0<w≤1 when E* loses its stability. Although the figures are not presented here, similar bifurcation diagrams as those in Figure 2 are obtained if we vary parameters w and c.

3.2. A moth–parasitoid model with host self-regulation

In this subsection we investigate a moth–parasitoid model that is also based on the Nicholson–Bailey model. Similar to system (6), N _t and P _t are denoted as the LBM and parasitoid densities at time t, respectively. In addition to the parasitoid mutual interference incorporated in system (6), the model also takes into account of the host self-regulation and saturation. The probability of an individual host being parasitized per unit time is now given by , where h>0 is the handling time of the parasitoid and parameters a and w have the same biological meanings as in the previous model (6). The new model takes the following form:

To simplify the system, we let , and s=ah/β, then system (16) becomes

It is clear that solutions of system (17) also satisfy inequalities (9), remain non-negative, and are bounded.

Lemma 3.5

Solutions of system (17) remain non-negative and are bounded.

Similar to the previous moth–parasitoid model (7), system (17) always has the trivial steady state E ₀=(0, 0) where both populations are extinct. Notice E ₀ is locally asymptotically stable if λ<1, and it can be easily shown that it is globally asymptotically stable whenever λ<1. Therefore, global extinction of the two populations occurs when the inherent net growth rate, λ, of the moth population is less than one. The proof of the following theorem is straightforward and is omitted.

Lemma 3.6

Steady state E ₀=(0, 0) is globally asymptotically stable for system (17) if λ<1.

Assume λ>1. Then E ₀ is a saddle point, with the stable manifold lying on the non-negative $y$-axis, and there exists another boundary steady state where only the LBM population can persist. The Jacobian matrix of (17) evaluated at E ₁ has the form

It follows that E ₁ is locally asymptotically stable if Equation (10) holds and

Since system (17) also reduces to the scalar Ricker Equation (8) when the parasitoid population is absent, it can be shown that E ₁ is globally asymptotically stable whenever it is locally asymptotically stable. The proof of the following lemma is similar to Theorem 3.3 and is therefore omitted.

Lemma 3.7

Let λ>1. Then system (17) has another steady state and E ₁ is globally asymptotically stable in if and .

Let (x, y) denote an interior steady state of system (17) and set . Then

and z must satisfy

It follows that system (17) has an interior steady state if (19) has a solution z* satisfying

where and . Let as defined in Section 3.1 and for . We first consider the case when . Recall that h is a one-hump function with and . A simple calculation yields

and

Since for all . Let . Then , for 0<x<1/w, and . Thus is monotonically increasing and concave up on (0, 1/w) with . Similar to the proof of Theorem 3.4, it can be shown that when , Equation (19) has a solution satisfying inequality (20) if and only if , i.e., when , system (17) has a unique interior steady state if and only if .

We next consider the case when . Set d(x)=0, we have

If , then x _± are not real numbers and so that and moreover for . Therefore, system (17) has an interior steady state if and only if (18) is reversed. If , then [gtilde] is a linear increasing function and the same conclusion can be arrived at. If , then x _± are positive real numbers. However, it can be verified that and so that has at most one solution and [gtilde] is concave down in . It is then clear that lies above y=h(x) on when Equation (18) holds and the two curves intersect only once if (18) is reversed. Therefore, we have the following result, where the persistence of the two populations can be proved similarly as in Theorem 3.4.

Theorem 3.8

Let λ>1. Then system (17) has a unique interior steady state if and only if Moreover, system (17) is uniformly persistent if and

We now use simulations to study system (17). Fix w=1, c=10 as in Figure 2, and s=0.5, and let λ be a bifurcation parameter with values ranging from 10 to 60. Since

it follows from our analysis that system (17) has a unique interior state when λ=10. Although we do not investigate its local stability analytically as we did for system (7), bifurcation diagrams reveal that the unique interior steady state is globally asymptotically stable in the interior of the positive cone when λ is less than 16.5; See Figure 3(a) for moth population densities and Figure 3(b) for parasitoid densities. From these diagrams, it appears that the interior steady state also loses its stability via a period-doubling bifurcation and the parasitoid population also goes extinct when λ is large. Similar bifurcation diagrams are obtained when we change parameter values of w, c, and s.

Figure 3. This figure provides bifurcation diagrams for system (17) when w=1, c=10, and s=0.5, (a) and (b) moth and parasitoid population densities, respectively.

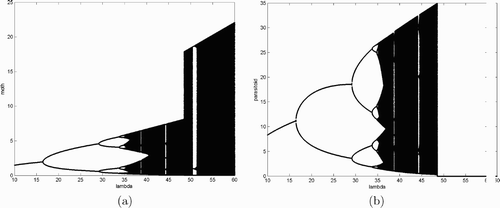
4. Conclusions

In this article, we studied one LBM-leaf quality model and two LBM-parasitoid models, proposed by Turchin et al. 12. From the mathematical analysis and bifurcation diagrams presented in Sections 2 and 3, it seems to suggest that the dynamics of leaf quality LBM and LBM parasitoid systems are topologically conjugate 6 to each other under some restrictions on the parameter values. In other words, although the systems are derived from very different biological phenomena and assumptions, their dynamics seem to be topologically equivalent to each other. Therefore, it is very difficult to arrive at conclusions based on mathematical analysis performed on these models as whether leaf quality or parasitoid is the main factor that is responsible for the LBM population cycling. However, each of these models does confirm our biological intuition. Namely, there exist population thresholds in terms of model parameters above which populations can persist and below which populations go extinct. Furthermore, the statistical study provided by Turchin et al. 12 does suggest that the parasitism is probably the more important factor for LBM cycling.

Acknowledgements

The authors thank the referees for their suggestions.

Additional information

Notes on contributors

Sophia R.-J. Jang

†Present address: Department of Mathematics and Statistics, Texas Tech University, Lubbock, TX USA